自动控制原理MATLAB仿真实验报告.
北工大自控matlab实验报告

自动控制原理实验报告一、试验设计构造一个二阶闭环系统,使得该系统的%30≥p M对于任意二阶系统,其闭环传递函数为2222)(G nn nc s s s ωξωω++=,其中ξ为二阶系统的阻尼比,n ω为二阶系统的无阻尼振荡频率,该系统的超调量为πξξ21--=e M p 。
若要%30≥p M ,则0.36≤ξ。
取0.3=ξ,又n ω任意,所以取20=n ω,则要求设计的闭环传递函数为40012400)(2++=s s s G c 。
二、实验内容及步骤1.以MATLAB 命令行的方式,进行系统仿真,确定系统时域性能指标 num=[400]; den=[1 12 400]; step(num,den)由图可知,该系统的超调量为%30%37>=p M ,满足要求,上升时间为0985.0=r t ,峰值时间为164.0=p t ,调节时间为0.472=s t 。
2.通过改变系统的开环放大倍数K (分增大和减小两种情况)和系统的阻尼比系数(分增大和减小两种情况),进行系统仿真分析,确定新的性能指标,并与原构造系统的进行比较,根据响应曲线分析并说明出现的现象 (1)增大开环放大倍数num=[500]; den=[1 12 500]; step(num,den)由图可知,该系统的超调量为%30%42>=p M ,上升时间为0858.0=r t ,峰值时间146.0=p t ,调节时间0.48=s t 。
(2)减小开环放大倍数 num=[300]; den=[1 12 300]; step(num,den)由图可知,该系统的超调量为%30%31>=p M ,上升时间为119.0=r t ,峰值时间为0.1921=p t ,调节时间为0.455=s t 。
(3)增大阻尼比 num=[400];den=[1 12.4 400]; step(num,den)由图可知,该系统的超调量为%30%36>=p M ,上升时间为0995.0=r t ,峰值时间为0.163=p t ,调节时间为0.486=s t 。
自控MATLAB实验一

《自动控制原理》课程实验报告实验名称初步认识MATLAB和系统仿真专业班级过程自动化03班学号2011500169姓名鲁雅洁指导教师李离学院名称电气信息学院2013 年10 月22 日实验一初步认识MATLAB和控制系统仿真一、实验目的(1)了解并掌握MATLAB仿真软件的使用方法;(2)掌握控制系统数学模型的多种描述方法及其仿真实现和互相转换; (3)熟悉控制系统仿真常用的MATLAB函数。
二、实验设备(1)硬件:个人计算机;(2)软件:MATLAB仿真软件(版本6.5或以上)。
三、实验内容和步骤1.质量—弹簧—阻尼器系统的零输入响应修改并运行程序lab1_1.m以求取下列情形的零输入响应曲线并存盘:Lab1_1_1.m程序:y0=0.15;wn=sqrt(2);zeta=1/(2*sqrt(2));t=[0:0.1:10];c=(y0/sqrt(1-zeta^2));y=c*exp(-zeta*wn*t).*sin(wn*sqrt(1-zeta^2)*t+acos(zeta));bu=c*exp(-zeta*wn*t);bl=-bu;plot(t,y,t,bu,'k--',t,bl,'k--'),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(1)零输入响应曲线Lab1_1_2.m程序:y0=0.15;wn=sqrt(2);zeta=1;t=[0:0.1:10];y=y0*(exp(-wn*t)+wn*t.*exp(-wn*t));plot(t,y),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(2)零输入响应曲线Lab1_1_3.m程序:y0=0.15;wn=sqrt(2);zeta=sqrt(2);t=[0:0.1:10];s1=-wn*(zeta+sqrt(zeta^2-1));s2=-wn*(zeta-sqrt(zeta^2-1));k1=(1-zeta/sqrt(zeta^2-1))/2;k2=(1+zeta/sqrt(zeta^2-1))/2;y=y0*(k1*exp(s1*t)+k2*exp(s2*t));plot(t,y),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(3)零输入响应曲线2.系统传递函数的MATLAB实现及零极点分布(1)多项式的表示及求值:系数按降幂顺序构成行向量;求值函数polyval;(2)多项式的根:由函数roots求得;函数poly(roots())的功能;(3)多项式的积:由函数conv实现;(4)系统传递函数:由函数tf实现;(5)传递函数的零极点表示:函数pole,zero和pzmap的运用。
(最新版)自动控制原理MATLAB仿真实验报告

实验一 MATLAB及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、预习要点1、系统的典型响应有哪些?2、如何判断系统稳定性?3、系统的动态性能指标有哪些?三、实验方法(一)四种典型响应1、阶跃响应:阶跃响应常用格式:1、;其中可以为连续系统,也可为离散系统。
2、;表示时间范围0---Tn。
3、;表示时间范围向量T指定。
4、;可详细了解某段时间的输入、输出情况。
2、脉冲响应:脉冲函数在数学上的精确定义:其拉氏变换为:所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式:①;②③(二)分析系统稳定性有以下三种方法:1、利用pzmap绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 运行结果: p =-1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
自动控制原理 matlab实验报告

自动控制原理实验(二)一、实验名称:基于MATLAB的控制系统频域及根轨迹分析二、实验目的:(1)、了解频率特性的测试原理及方法;(2)、理解如何用MATLAB对根轨迹和频率特性进行仿真和分析;(3)、掌握控制系统的根轨迹和频率特性两大分析和设计方法。
三、实验要求:(1)、观察给定传递函数的根轨迹图和频率特性曲线;(2)、分析同一传递函数形式,当K值不同时,系统闭环极点和单位阶跃响应的变化情况;(3)、K值的大小对系统的稳定性和稳态误差的影响;(4)、分析增加系统开环零点或极点对系统的根轨迹和性能的影响。
四、实验内容及步骤(1)、实验指导书:实验四(1)、“rlocus”命令来计算及绘制根轨迹。
会出根轨迹后,可以交互地使用“rlocfind”命令来确定点击鼠标所选择的根轨迹上任意点所对应的K值,K值所对应的所有闭环极点值也可以使用形如“[K, PCL] = rlocfind(G1)”命令来显示。
(2)、波特图:bode(G1, omga)另外,bode图还可以通过下列指令得出相位和裕角:[mag,phase,w] = bode(sys)(3)、奈奎斯特图:nuquist(G, omega)(2)课本:例4-1、4-2、4-7五实验报告要求(1)、实验指导书:实验四思考题请绘制下述传递函数的bode图和nyquist图。
1. 根据实验所测数据分别作出相应的幅频和相频特性曲线;2. 将思考题的解题过程(含源程序)写在实验报告中。
幅频特性曲线相频特性曲线Gs = zpk([10], [-5; -16; 9], 200)subplot(1, 2, 1)bode(Gs)gridsubplot(1, 2, 2)nyquist(Gs)grid(2)课本:例4-1、4-2、4-7图像结果:程序:Gs = zpk([-1], [0; -2; -3],1) rlocus(Gs)图像结果:程序:Gs = zpk([-2], [-1-j; -1+j],1) rlocus(Gs)程序:K=[0.5 1 2]for i=1:1:3num=[1,1,0,0]; den=[1,1,K(i)]; sys=tf(num,den); rlocus(sys); hold ongrid onend图像结果:目标:改变增益K和转折频率依次调节源程序:k1=[4.44,10,20];num=[1,2];den=conv([1,1],[1,2,4]);%一阶转折频率 1/T(wn1=2,wn2=1)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 num1=[1,1];den1=conv([1,2],[1,2,4]);%一阶转折频率 1/T(wn1=1,wn2=2)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 t=[0:0.1:7]; %for i=1:3g0=tf(k1(i)*num,den);g=feedback(g0,1);[y,x]=step(g,t);c(:,i)=y;g1=tf(k1(i)*num1,den1);g(1)=feedback(g1,1);[y1,x]=step(g(1),t);c1(:,i)=y1;endplot(t,c(:,1),'-',t,c(:,2),'-',t,c(:,3),'-',t,c1(:,1),'-',t,c1(:,2), '-',t,c1(:,3),'-');gridxlabel('Time/sec'),ylabel('out')结果分析:在本题中(1)改变k值:k值越大,超调量越大,调节时间越长,峰值时间越短,稳态误差越小(2)改变转折频率:超调量,调节时间,峰值时间,稳态误差同样有相应的变化。
自动控制原理MATLAB实验报告
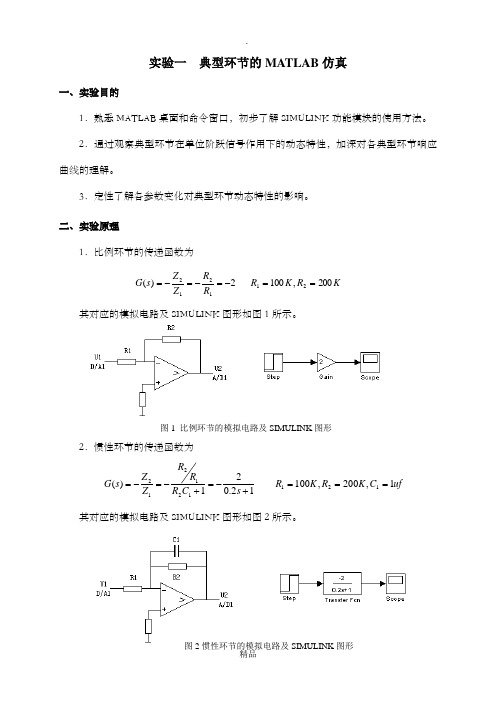
实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为 K R K R R R Z ZsG 200,1002)(211212==-=-=-=其对应的模拟电路及SIMULINK 图形如图1所示。
2.惯性环节的传递函数为uf C K R K R s C R R R Z Z s G 1,200,10012.021)(121121212===+-=+-=-=其对应的模拟电路及SIMULINK 图形如图2所示。
图1 比例环节的模拟电路及SIMULINK 图形3.积分环节(I)的传递函数为uf C K R s s CR Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图3所示。
4.微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图4所示。
5.比例+微分环节(PD )的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<===其对应的模拟电路及SIMULINK 图形如图5所示。
图3 积分环节的模拟电路及及SIMULINK 图形图4 微分环节的模拟电路及及SIMULINK 图形6.比例+积分环节(PI )的传递函数为 )11(1)(11212sR s C R Z Z s G +-=+-=-= uf C K R R 10,100121=== 其对应的模拟电路及SIMULINK 图形如图6所示。
自动控制原理MATLAB仿真实验报告

实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性; 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为:)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ; ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =(二) 分析系统稳定性 有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果: p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
自动控制原理MATLAB仿真实验报告

实验一MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、预习要点1、系统的典型响应有哪些?2、如何判断系统稳定性?3、系统的动态性能指标有哪些?三、实验方法(一)四种典型响应1、阶跃响应:阶跃响应常用格式:1 、step ( sys ) ;其中 sys 可以为连续系统,也可为离散系统。
2 、step ( sys ,Tn ) ;表示时间范围0---Tn 。
3 、step ( sys ,T ) ;表示时间范围向量T 指定。
4 、Y step ( sys , T ) ;可详细了解某段时间的输入、输出情况。
2、脉冲响应:f (x)dx 1脉冲函数在数学上的精确定义:f ( x) 0, t 0f ( s) 1其拉氏变换为:Y ( s) G (s) f (s) G ( s)所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式:①impulse ( sys ) ;impulse ( sys , Tn );②impulse ( sys , T );③Y impulse ( sys ,T )(二)分析系统稳定性有以下三种方法:1、利用 pzmap绘制连续系统的零极点图;2、利用 tf2zp 求出系统零极点;3、利用 roots 求分母多项式的根来确定系统的极点(三)系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容(一) 稳定性1.系统传函为4 3 23s 2s 5s 4s 6G s ,试判断其稳定性5 4 3 2s 3s 4 s 2s 7s 22.用 Matlab 求出2s 2 s 2G 的极点。
( s)4 3 2s 7 s 3s 5 s 2%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果:p =-1.7680 + 1.2673i-1.7680 - 1.2673i0.4176 + 1.1130i0.4176 - 1.1130i-0.2991Pole-Zero Map 1.510.5sixAyranigamI-0.5-1-1.5-2 -1.5 -1 -0.5 0 0.5Real Axis图 1-1 零极点分布图由计算结果可知,该系统的 2 个极点具有正实部,故系统不稳定。
自动控制原理MATLAB仿真实验一(控制系统地时域分析报告)
实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的 学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、实验容(一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性num1=[0 3 2 5 4 6];den1=[1 3 4 2 7 2];sys1=tf(num1,den1);figure(1);hold on[gm,pm,wcp,wcg]=margin(sys1);margin(sys1);title('对数频率特性图');xlabel('频率rad/sec');ylabel('Gain dB');2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
a=[0 0 1 2 2];b=[1 7 3 5 2];[z,p,k]=tf2zpk(a,b) ;(二)阶跃响应1. 二阶系统()102102++=s s s G1)键入程序,观察并记录单位阶跃响应曲线num1=[10];den1=[1 2 10];step(num1,den1);grid on ;2)计算系统的闭环根、阻尼比、无阻尼振荡频率,并记录 wn=sqrt(10);%自然振荡频率zunibi=2/wn;%阻尼比syms s ;S=solve(s^2+2*s+10);%求闭环根3)修改参数,分别实现1=ζ和2=ζ的响应曲线,并记录 n0=10;d0=[1 2 10]; step(n0,d0);%原响应曲线hold on ;n1=10;d1=[1 6.32 10];step(n1,d1);n2=10;d2=[1 12.64 10];step(n2,d2);4)修改参数,分别写出程序实现0121w w n =和022w w n =的响应曲线,并记录 n0=10;d0=[1 2 10];step(n0,d0);%原响应曲线hold on ;n1=2.5;d1=[1 1 2.5];step(n1,d1);n2=40;d2=[1 4 40];step(n2,d2);2. 作出以下系统的阶跃响应,并分析结果 (1)()10210221+++=s s s s G (2)()102105.0222++++=s s s s s G (3)()1025.0222+++=s s s s s G (4)()10222++=s s ss Gn0=[2 10];d0=[1 2 10];step(n0,d0);hold on ;n1=[1 0.5 10];d1=[1 2 10];step(n1,d1);hold on ;n2=[1 0.5 0];d2=[1 2 10];step(n2,d2);hold on ;n3=[1 0];d3=[1 2 10]; step(n3,d3);3. 25425)()(2++=s s s R s C 求该系统单位阶跃响应曲线,并在所得图形上加网格线和标题 num0=[25];den0=[1 4 25]; step(num0,den0); grid on ;xlabel('X'); ylabel('Y ');title('单位阶跃曲线');(三)系统动态特性分析 用Matlab 求二阶系统12012120)(2++=s s s G 和01.0002.001.0)(2++=s s s G 的峰值时间p t ,上升时间r t ,调整时间s t ,超调量%σ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理实验报告学院电子信息与电气工程学院实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性; 二、预习要点1、 系统的典型响应有哪些?2、 如何判断系统稳定性?3、 系统的动态性能指标有哪些? 三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为:)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ; ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =(二) 分析系统稳定性 有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果: p =-1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
%求取极点num=[1 2 2];den=[1 7 3 5 2];p=roots(den)运行结果: p =-6.6553 0.0327 + 0.8555i 0.0327 - 0.8555i -0.4100故253722)(2342++++++=s s s s s s s G 的极点s1=-6.6553 , s2=0.0327 + 0.8555i ,s3= 0.0327 - 0.8555i , s4=-0.41(二)阶跃响应1. 二阶系统()102102++=s s s G1)键入程序,观察并记录单位阶跃响应曲线2)计算系统的闭环根、阻尼比、无阻尼振荡频率,并记录 3)记录实际测取的峰值大小、峰值时间及过渡过程时间,并填表:由图1-3及其相关理论知识可填下表:3//πωπ==d p t =1.0472实际值 理论值 峰值C max 1.35 1.3509 峰值时间t p 1.091.0472 过渡时间t s%5±3.5 %2±4.54)修改参数,分别实现1=ζ和2=ζ的响应曲线,并记录5)修改参数,分别写出程序实现0121w w n =和022w w n =的响应曲线,并记录%单位阶跃响应曲线num=[10];den=[1 2 10];step(num,den);title('Step Response of G(s)=10/(s^2+2s+10)');4.52%(00.9)3.55%n s nt ζωζζω⎧∆=⎪⎪=<<⎨⎪∆=⎪⎩01234560.20.40.60.811.21.4Step Response of G(s)=10/(s 2+2s+10)Time (sec)A m p l i t u d e图1-2 二阶系统()102102++=s s s G 单位阶跃响应曲线%计算系统的闭环根、阻尼比、无阻尼振荡频率 num=[10];den=[1 2 10];G=tf(num,den); [wn,z,p]=damp(G)运行结果: wn =3.1623 3.1623 z =0.3162 0.3162 p =-1.0000 + 3.0000i -1.0000 - 3.0000i由上面的计算结果得系统的闭环根s= -1±3i ,阻尼比=ς3162.0、无阻尼振荡频率1623.3=n ω实验二 MATLAB 及仿真实验(控制系统的根轨迹分析)一 实验目的1.利用计算机完成控制系统的根轨迹作图 2.了解控制系统根轨迹图的一般规律 3.利用根轨迹图进行系统分析 二 预习要点1. 预习什么是系统根轨迹?2. 闭环系统根轨迹绘制规则。
三 实验方法(一) 方法:当系统中的开环增益k 从0到变化时,闭环特征方程的根在复平面上的一组曲线为根轨迹。
设系统的开环传函为:)()()(0s Q s N ks G =,则系统的闭环特征方程为:0)()(1)(10=+=+s Q s N ks G 根轨迹即是描述上面方程的根,随k 变化在复平面的分布。
(二) MATLAB 画根轨迹的函数常用格式:利用Matlab 绘制控制系统的根轨迹主要用pzmap ,rlocus ,rlocfind ,sgrid 函数。
1、零极点图绘制❑ [p,z]=pzmap(a,b,c,d):返回状态空间描述系统的极点矢量和零点矢量,而不在屏幕上绘制出零极点图。
❑ [p,z]=pzmap(num,den):返回传递函数描述系统的极点矢量和零点矢量,而不在屏幕上绘制出零极点图。
❑ pzmap(a,b,c,d)或pzmap(num,den):不带输出参数项,则直接在s 复平面上绘制出系统对应的零极点位置,极点用×表示,零点用o 表示。
❑ pzmap(p,z):根据系统已知的零极点列向量或行向量直接在s 复平面上绘制出对应的零极点位置,极点用×表示,零点用o 表示。
2、根轨迹图绘制❑ rlocus(a,b,c,d)或者rlocus(num,den):根据SISO 开环系统的状态空间描述模型和传递函数模型,直接在屏幕上绘制出系统的根轨迹图。
开环增益的值从零到无穷大变化。
❑ rlocus(a,b,c,d,k)或rlocus(num,den,k): 通过指定开环增益k 的变化范围来绘制系统的根轨迹图。
❑ r=rlocus(num,den,k) 或者[r,k]=rlocus(num,den) :不在屏幕上直接绘出系统的根轨迹图,而根据开环增益变化矢量k ,返回闭环系统特征方程1+k*num(s)/den(s)=0的根r ,它有length(k)行,length(den)-1列,每行对应某个k 值时的所有闭环极点。
或者同时返回k 与r 。
❑ 若给出传递函数描述系统的分子项num 为负,则利用rlocus 函数绘制的是系统的零度根轨迹。
(正反馈系统或非最小相位系统) 3、rlocfind()函数❑ [k,p]=rlocfind(a,b,c,d)或者[k,p]=rlocfind(num,den) 它要求在屏幕上先已经绘制好有关的根轨迹图。
然后,此命令将产生一个光标以用来选择希望的闭环极点。
命令执行结果:k 为对应选择点处根轨迹开环增益;p 为此点处的系统闭环特征根。
❑ 不带输出参数项[k,p]时,同样可以执行,只是此时只将k 的值返回到缺省变量ans中。
4、sgrid()函数❑ sgrid :在现存的屏幕根轨迹或零极点图上绘制出自然振荡频率wn 、阻尼比矢量z对应的格线。
❑ sgrid(‘new’):是先清屏,再画格线。
❑ sgrid(z,wn):则绘制由用户指定的阻尼比矢量z 、自然振荡频率wn 的格线。
四 实验内容 1.()()()21++=s s s k s G g 要求:二、 记录根轨迹的起点、终点与根轨迹的条数; 三、 确定根轨迹的分离点与相应的根轨迹增益; 四、 确定临界稳定时的根轨迹增益gL k %Matlab 计算程序z=[];p=[0 -1 -2];k=1;G=zpk(z,p,k);figure(1);pzmap(G) figure(2);rlocus(G)title('实验2.1所作曲线');(a )由图2-2知,起点分别为0,-1,-2,终点为无穷远处,共三条根轨迹. (b) 结合图2-3和图2-5得分离点d=-0.4226,相应的根轨迹增益k=-0.3849. (c) 结合图2-3和图2-4得临界稳定时的根轨迹增益gL k =6.01P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.20-1-0.8-0.6-0.4-0.200.20.40.60.81System: G P ole : -2Damping: 1Overshoot (%): 0Frequency (rad/sec): 2System: G P ole : -1Damping: 1Overshoot (%): 0Frequency (rad/sec): 1System: G P ole : 0Damping: -1Overshoot (%): 0Frequency (rad/sec): 0图2-1 零、极点分布图-7-6-5-4-3-2-1012-5-4-3-2-1012345实验2.1所作曲线Real AxisI m a g i n a r y A x i s图2-2 根轨迹图-7-6-5-4-3-2-112-5-4-3-2-1012345System: G Gain: 0.384P ole: -0.442Damping: 1Overshoot (%): 0Frequency (rad/sec): 0.442System: G Gain: 6.25P ole: 0.0128 + 1.44i Damping: -0.00893Overshoot (%): 103Frequency (rad/sec): 1.44System: G Gain: 6.03P ole: 0.00303 - 1.42i Damping: -0.00214Overshoot (%): 101Frequency (rad/sec): 1.42实验2.1所作曲线Real AxisI m a g i n a r y A x i s图2-3 根轨迹图(2)%求临界稳定时的根轨迹增益Kgl z=[];p=[0 -1 -2];k=1;G=zpk(z,p,k); rlocus(G)title('实验2.1 临界稳定时的根轨迹增益Kgl'); [k,p]=rlocfind(G)运行结果:Select a point in the graphics windowselected_point =0.0059 + 1.4130i k =6.0139 p =-3.0013 0.0006 + 1.4155i 0.0006 - 1.4155i-7-6-5-4-3-2-1012-5-4-3-2-1012345实验2.1 临界稳定时的根轨迹增益KglReal AxisI m a g i n a r y A x i s图2-4 根轨迹图(3)实验三 MATLAB及仿真实验(控制系统的频域分析)一实验目的1. 利用计算机作出开环系统的波特图2. 观察记录控制系统的开环频率特性3. 控制系统的开环频率特性分析二预习要点1.预习Bode图和Nyquist图的画法;2.映射定理的内容;3.Nyquist稳定性判据内容。
