2016年江苏高考数学试题(Word版-)
2016年江苏省高考数学试卷

2016年江苏省高考数学试卷一、填空题(共14小题,每小题5分,满分70分)1.(5分)(2016•江苏)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B=.2.(5分)(2016•江苏)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是.3.(5分)(2016•江苏)在平面直角坐标系xOy中,双曲线﹣=1的焦距是.4.(5分)(2016•江苏)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是.5.(5分)(2016•江苏)函数y=的定义域是.6.(5分)(2016•江苏)如图是一个算法的流程图,则输出的a的值是.7.(5分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.8.(5分)(2016•江苏)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是.9.(5分)(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.10.(5分)(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.11.(5分)(2016•江苏)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是.12.(5分)(2016•江苏)已知实数x,y满足,则x2+y2的取值范围是.13.(5分)(2016•江苏)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是.14.(5分)(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.二、解答题(共6小题,满分90分)15.(14分)(2016•江苏)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.16.(14分)(2016•江苏)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.17.(14分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?18.(16分)(2016•江苏)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.19.(16分)(2016•江苏)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.20.(16分)(2016•江苏)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)(2016•江苏)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC 的中点,求证:∠EDC=∠ABD.B.【选修4—2:矩阵与变换】22.(10分)(2016•江苏)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.C.【选修4—4:坐标系与参数方程】23.(2016•江苏)在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.24.(2016•江苏)设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.附加题【必做题】25.(10分)(2016•江苏)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px(p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.26.(10分)(2016•江苏)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.2016年江苏省高考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(5分)(2016•江苏)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B={﹣1,2}.解:∵集合A={﹣1,2,3,6},B={x|﹣2<x<3},∴A∩B={﹣1,2},故答案为:{﹣1,2}2.(5分)(2016•江苏)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是5.解:z=(1+2i)(3﹣i)=5+5i,则z的实部是5,故答案为:5.3.(5分)(2016•江苏)在平面直角坐标系xOy中,双曲线﹣=1的焦距是2.解:双曲线﹣=1中,a=,b=,∴c==,∴双曲线﹣=1的焦距是2.故答案为:2.4.(5分)(2016•江苏)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是0.1.解:∵数据4.7,4.8,5.1,5.4,5.5的平均数为:=(4.7+4.8+5.1+5.4+5.5)=5.1,∴该组数据的方差:S2=[(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1.故答案为:0.1.5.(5分)(2016•江苏)函数y=的定义域是[﹣3,1].解:由3﹣2x﹣x2≥0得:x2+2x﹣3≤0,解得:x∈[﹣3,1],故答案为:[﹣3,1]6.(5分)(2016•江苏)如图是一个算法的流程图,则输出的a的值是9.解:当a=1,b=9时,不满足a>b,故a=5,b=7,当a=5,b=7时,不满足a>b,故a=9,b=5当a=9,b=5时,满足a>b,故输出的a值为9,故答案为:97.(5分)(2016•江苏)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.解:将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,基本事件总数为n=6×6=36,出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,出现向上的点数之和不小于10包含的基本事件有:(4,6),(6,4),(5,5),(5,6),(6,5),(6,6),共6个,∴出现向上的点数之和小于10的概率:p=1﹣=.故答案为:.8.(5分)(2016•江苏)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是20.解:∵{a n}是等差数列,S n是其前n项和,a1+a22=﹣3,S5=10,∴,解得a1=﹣4,d=3,∴a9=﹣4+8×3=20.故答案为:20.9.(5分)(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是7.解:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:由图可知,共7个交点.故答案为:7.10.(5分)(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),由∠BFC=90°,可得k BF•k CF=﹣1,即有•=﹣1,化简为b2=3a2﹣4c2,由b2=a2﹣c2,即有3c2=2a2,由e=,可得e2==,可得e=,故答案为:.11.(5分)(2016•江苏)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是﹣.解:f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,∴f(﹣)=f(﹣)=﹣+a,f()=f()=|﹣|=,∴a=,∴f(5a)=f(3)=f(﹣1)=﹣1+=﹣,故答案为:﹣12.(5分)(2016•江苏)已知实数x,y满足,则x2+y2的取值范围是[,13].解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点距离的平方,由图象知A到原点的距离最大,点O到直线BC:2x+y﹣2=0的距离最小,由得,即A(2,3),此时z=22+32=4+9=13,点O到直线BC:2x+y﹣2=0的距离d==,则z=d2=()2=,故z的取值范围是[,13],故答案为:[,13].13.(5分)(2016•江苏)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是.解:∵D是BC的中点,E,F是AD上的两个三等分点,∴=+,=﹣+,=+3,=﹣+3,∴•=2﹣2=﹣1,•=92﹣2=4,∴2=,2=,又∵=+2,=﹣+2,∴•=42﹣2=,故答案为:14.(5分)(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是8.解:由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,可得sinBcosC+cosBsinC=2sinBsinC,①由三角形ABC为锐角三角形,则cosB>0,cosC>0,在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,又tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣②,则tanAtanBtanC=﹣•tanBtanC,由tanB+tanC=2tanBtanC可得tanAtanBtanC=﹣,令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,由②式得1﹣tanBtanC<0,解得t>1,tanAtanBtanC=﹣=﹣,=()2﹣,由t>1得,﹣≤<0,因此tanAtanBtanC的最小值为8,当且仅当t=2时取到等号,此时tanB+tanC=4,tanBtanC=2,解得tanB=2+,tanC=2﹣,tanA=4,(或tanB,tanC互换),此时A,B,C均为锐角.二、解答题(共6小题,满分90分)15.(14分)(2016•江苏)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.解:(1)∵△ABC中,cosB=,∴sinB=,∵,∴AB==5;(2)cosA=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣.∵A为三角形的内角,∴sinA=,∴cos(A﹣)=cosA+sinA=.16.(14分)(2016•江苏)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.解:(1)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∴DE∥AC,∵ABC﹣A1B1C1为棱柱,∴AC∥A1C1,∴DE∥A1C1,∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,∴DE∥A1C1F;(2)∵ABC﹣A1B1C1为直棱柱,∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,又∵A1C1⊥A1B1,且AA1∩A1B1=A1,AA1、A1B1⊂平面AA1B1B,∴A1C1⊥平面AA1B1B,∵DE∥A1C1,∴DE⊥平面AA1B1B,又∵A1F⊂平面AA1B1B,∴DE⊥A1F,又∵A1F⊥B1D,DE∩B1D=D,且DE、B1D⊂平面B1DE,∴A1F⊥平面B1DE,又∵A1F⊂平面A1C1F,∴平面B1DE⊥平面A1C1F.17.(14分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?解:(1)∵PO1=2m,正四棱柱的高O1O是正四棱锥的高PO1的4倍.∴O1O=8m,∴仓库的容积V=×62×2+62×8=312m3,(2)若正四棱锥的侧棱长为6m,设PO1=xm,则O1O=4xm,A1O1=m,A1B1=m,则仓库的容积V=×(•)2•x+(•)2•4x=x3+312x,(0<x<6),∴V′=﹣26x2+312,(0<x<6),当0<x<2时,V′>0,V(x)单调递增;当2<x<6时,V′<0,V(x)单调递减;故当x=2时,V(x)取最大值;即当PO1=2m时,仓库的容积最大.18.(16分)(2016•江苏)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.解:(1)∵N在直线x=6上,∴设N(6,n),∵圆N与x轴相切,∴圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,又圆N与圆M外切,圆M:x2+y2﹣12x﹣14y+60=0,即圆M:((x﹣6)2+(x﹣7)2=25,∴|7﹣n|=|n|+5,解得n=1,∴圆N的标准方程为(x﹣6)2+(y﹣1)2=1.(2)由题意得OA=2,k OA=2,设l:y=2x+b,则圆心M到直线l的距离:d==,则|BC|=2=2,BC=2,即2=2,解得b=5或b=﹣15,∴直线l的方程为:y=2x+5或y=2x﹣15.(3)=,即,即||=||,||=,又||≤10,即≤10,解得t∈[2﹣2,2+2],对于任意t∈[2﹣2,2+2],欲使,此时,||≤10,只需要作直线TA的平行线,使圆心到直线的距离为,必然与圆交于P、Q两点,此时||=||,即,因此实数t的取值范围为t∈[2﹣2,2+2],.19.(16分)(2016•江苏)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.解:函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①方程f(x)=2;即:=2,可得x=0.②不等式f(2x)≥mf(x)﹣6恒成立,即≥m()﹣6恒成立.令t=,t≥2.不等式化为:t2﹣mt+4≥0在t≥2时,恒成立.可得:△≤0或即:m2﹣16≤0或m≤4,∴m∈(﹣∞,4].实数m的最大值为:4.(2)g(x)=f(x)﹣2=a x+b x﹣2,g′(x)=a x lna+b x lnb=a x[+],0<a<1,b>1可得,令h(x)=+,则h(x)是递增函数,而,lna<0,lnb>0,因此,x0=时,h(x0)=0,因此x∈(﹣∞,x0)时,h(x)<0,a x lnb>0,则g′(x)<0.x∈(x0,+∞)时,h(x)>0,a x lnb>0,则g′(x)>0,则g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此g(x)的最小值为:g(x0).①若g(x0)<0,x<log a2时,a x>=2,b x>0,则g(x)>0,因此x1<log a2,且x1<x0时,g(x1)>0,因此g(x)在(x1,x0)有零点,则g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,函数g(x)=f(x)﹣2有且只有1个零点,g(x)的最小值为g(x0),可得g(x0)=0,由g(0)=a0+b0﹣2=0,因此x0=0,因此=0,﹣=1,即lna+lnb=0,ln(ab)=0,则ab=1.可得ab=1.20.(16分)(2016•江苏)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.解:(1)当T={2,4}时,S T=a2+a4=a2+9a2=30,因此a2=3,从而a1==1,故a n=3n﹣1,(2)S T≤a1+a2+…a k=1+3+32+…+3k﹣1=<3k=a k+1,(3)设A=∁C(C∩D),B=∁D(C∩D),则A∩B=∅,分析可得S C=S A+S C∩D,S D=S B+S C∩D,则S C+S C∩D﹣2S D=S A﹣2S B,因此原命题的等价于证明S C≥2S B,由条件S C≥S D,可得S A≥S B,①、若B=∅,则S B=0,故S A≥2S B,②、若B≠∅,由S A≥S B可得A≠∅,设A中最大元素为l,B中最大元素为m,若m≥l+1,则其与S A<a i+1≤a m≤S B相矛盾,因为A∩B=∅,所以l≠m,则l≥m+1,S B≤a1+a2+…a m=1+3+32+…+3m﹣1=<=,即S A≥2S B,综上所述,S A≥2S B,故S C+S C∩D≥2S D.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)(2016•江苏)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC 的中点,求证:∠EDC=∠ABD.解:由BD⊥AC可得∠BDC=90°,因为E为BC的中点,所以DE=CE=BC,则:∠EDC=∠C,由∠BDC=90°,可得∠C+∠DBC=90°,由∠ABC=90°,可得∠ABD+∠DBC=90°,因此∠ABD=∠C,而∠EDC=∠C,所以,∠EDC=∠ABD.B.【选修4—2:矩阵与变换】22.(10分)(2016•江苏)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.解:∵B﹣1=,∴B=(B﹣1)﹣1==,又A=,∴AB==.C.【选修4—4:坐标系与参数方程】23.(2016•江苏)在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.解:由,由②得,代入①并整理得,.由,得,两式平方相加得.联立,解得或.∴|AB|=.24.(2016•江苏)设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.证明:由a>0,|x﹣1|<,|y﹣2|<,可得|2x+y﹣4|=|2(x﹣1)+(y﹣2)|≤2|x﹣1|+|y﹣2|<+=a,则|2x+y﹣4|<a成立.附加题【必做题】25.(10分)(2016•江苏)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px(p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.解:(1)∵l:x﹣y﹣2=0,∴l与x轴的交点坐标(2,0),即抛物线的焦点坐标(2,0).∴,∴抛物线C:y2=8x.(2)证明:①设点P(x1,y1),Q(x2,y2),则:,即:,k PQ==,又∵P,Q关于直线l对称,∴k PQ=﹣1,即y1+y2=﹣2p,∴,又PQ的中点在直线l上,∴==2﹣p,∴线段PQ的中点坐标为(2﹣p,﹣p);②因为Q中点坐标(2﹣p,﹣p).∴,即∴,即关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,∴△>0,(2p)2﹣4(4p2﹣4p)>0,∴p∈.26.(10分)(2016•江苏)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.解:(1)7=﹣4×=7×20﹣4×35=0.证明:(2)对任意m∈N*,①当n=m时,左边=(m+1)=m+1,右边=(m+1)=m+1,等式成立.②假设n=k(k≥m)时命题成立,即(m+1)C+(m+2)C+(m+3)C+…+k+(k+1)=(m+1),当n=k+1时,左边=(m+1)+(m+2)+(m+3)++(k+1)+(k+2)=,右边=∵=(m+1)[﹣]=(m+1)×[k+3﹣(k﹣m+1)]=(k+2)=(k+2),∴=(m+1),∴左边=右边,∴n=k+1时,命题也成立,∴m,n∈N*,n≥m,(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.。
2016年高考江苏卷数学试题(含答案)

绝密★启用前2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,均为非选择题(第1题~第20题,共20题)。
本卷满分为160分,考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。
4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5.如需作图,需用2B铅笔绘、写清楚,线条、符号等须加黑、加粗。
参考公式:棱柱的体积V sh=,其中S是棱柱的底面积,h是高.棱锥的体积V=13Sh,其中S是累赘的底面积,h是高。
一、填空题:本大题共14小题,每小题5分,共计70分。
请把答案填写在答题卡相应位置.......上.。
1.已知集合A=|-1,2,3,6|,B={x|-2<x<3},则A⋂B= ▲。
2.复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是▲。
3.在平面直角坐标系xOy中,双曲线27x-27y=1,其中i为虚数单位,则z的实部是▲。
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则改组数据的方差是▲。
5.函数y=的定义域是▲。
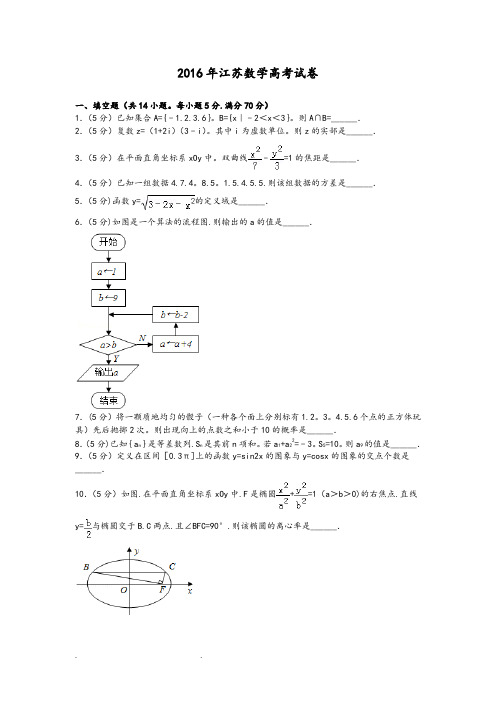
6.右图是一个算法的流程图,则输出的a的值是▲。
7.讲一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 ▲8.已知{a m }是等差数列,S m 是其前n 项的和,a 1+a 22=-3,S 5=10,则a 9的值是 ▲9.定于在区间[0,3π]上的函数y=sin2x 的图像与y=cosx 的图像的交点个数是 ▲10.如图,在平面直角坐标系xOy 中,F 是椭圆2222=1(0)x y a b a b+>>的右焦点,直线2b y =与椭圆相较于B,C 两点,∠BFC=90°,则该椭圆的离心率是 ▲11.设22x y + ()f x 是定义在R 上且周期为2的函数,在区间[1,1)-上,,10()5,012x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中a R ∈,若59()()22f f -=,则(5)f a的值是 ▲12.已知实数x,y 满足240,220,330,x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩则22x y +的取值范围是的取值范围 ▲13. 如图,在△ABC 中,D 是BC 的中点,E ,F ,是AD 上的两个三等分点,·4BACA = ,·1BF CF =- ,则·BE CE 的值是 ▲14.在锐角三角形ABC 中,若SINA=2sinBsinC ,则tanAtanBtanC 的最小值是 ▲二、解答题:本大题共6小题,共计90分。
2016年江苏高考数学试题(解析版)

2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1. 已知集合{}1,2,3,6A =-,{}|23B x x =-<<,则A B = . 【答案】{}1,2-;【解析】由交集的定义可得{}1,2A B =- .2. 复数()()12i 3i z =+-,其中i 为虚数单位,则z 的实部是 . 【答案】5;【解析】由复数乘法可得55i z =+,则则z 的实部是5.3. 在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是 .【答案】【解析】c ==,因此焦距为2c =4. 已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 . 【答案】0.1; 【解析】 5.1x =,()22222210.40.300.30.40.15s =++++=. 5.函数y =的定义域是 . 【答案】[]3,1-;【解析】2320x x --≥,解得31x -≤≤,因此定义域为[]3,1-. 6. 如图是一个算法的流程图,则输出a 的值是 .【答案】9;【解析】,a b 的变化如下表:则输出时9a =.7. 将一个质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点为正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 . 【答案】56; 【解析】将先后两次点数记为(),x y ,则共有6636⨯=个等可能基本事件,其中点数之和大于等于10有()()()()()()4,6,5,5,5,6,6,4,6,5,6,6六种,则点数之和小于10共有30种,概率为305366=. 8. 已知{}n a 是等差数列,n S 是其前n 项和.若2123a a +=-,510S =,则9a 的值是 . 【答案】20;【解析】设公差为d ,则由题意可得()2113a a d ++=-,151010a d +=,解得14a =-,3d =,则948320a =-+⨯=.9. 定义在区间[]0,3π上的函数sin 2y x =的图象与cos y x =的图象的交点个数是. 【答案】7;【解析】画出函数图象草图,共7个交点.10. 如图,在平面直角坐标系xOy 中,F 是椭圆()222210x y a b a b +=>>的右焦点,直线2by =与椭圆交于,B C两点,且90BFC ∠=︒,则该椭圆的离心率是 .FC BOyx【解析】由题意得(),0F c ,直线2by =与椭圆方程联立可得2b B ⎛⎫ ⎪ ⎪⎝⎭,2b C ⎫⎪⎪⎭, 由90BFC ∠=︒可得0BF CF ⋅=,2b BF c ⎛⎫=+- ⎪ ⎪⎝⎭,2b CF c ⎛⎫=-- ⎪ ⎪⎝⎭ , 则22231044c a b -+=,由222b a c =-可得223142c a =,则c e a ===. 11. 设()f x 是定义在R 上且周期为2的函数,在区间[)1,1-上(),10,2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中a ∈R ,若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,则()5f a 的值是 . 【答案】25-;【解析】由题意得511222f f a ⎛⎫⎛⎫-=-=-+ ⎪ ⎪⎝⎭⎝⎭,91211225210f f ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭, 由5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭可得11210a -+=,则35a =,则()()()325311155f a f f a ==-=-+=-+=-. 12. 已知实数,x y 满足240,220,330,x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩ 则22x y +的取值范围是 .【答案】4,135⎡⎤⎢⎥⎣⎦;【解析】在平面直角坐标系中画出可行域如下xyB A –1–2–3–41234–1–2–3–4123422x y+为可行域内的点到原点距离的平方.可以看出图中A点距离原点最近,此时距离为原点A到直线220x y+-=的距离,d,则()22min45x y+=,图中B点距离原点最远,B点为240x y-+=与330x y--=交点,则()2,3B,则()22max13x y+=.13.如图,在ABC△中,D是BC的中点,,E F是AD上两个三等分点,4BA CA⋅=,1BF CF⋅=-,则BE CE⋅的值是.【答案】78;【解析】令DF a=,DB b=,则DC b=-,2DE a=,3DA a=,则3BA a b=-,3CA a b=+,2BE a b=-,2CE a b=+,BF a b=-,CF a b=+,则229BA CA a b⋅=-,22BF CF a b⋅=-,224BE CE a b⋅=-,由4BA CA⋅=,1BF CF⋅=-可得2294a b-=,221a b-=-,因此22513,88a b==,因此22451374888BE CE a b⨯⋅=-=-=.14.在锐角三角形ABC中,sin2sin sinA B C=,则tan tan tanA B C的最小值是.【答案】8;【解析】由()()sin sinπsin sin cos cos sinA ABC B C B C=-=+=+,sin2sin sinA B C=,可得sin cos cos sin2sin sinB C B C B C+=(*),由三角形ABC为锐角三角形,则cos0,cos0B C>>,在(*)式两侧同时除以cos cosB C可得tan tan2tan tanB C B C+=,又()()tan tantan tanπtan1tan tanB CA AB CB C+=--=-+=--(#),则tan tantan tan tan tan tan1tan tanB CA B C B CB C+=-⨯-,由tan tan2tan tanB C B C+=可得()22tan tantan tan tan1tan tanB CA B CB C=--,令tan tanB C t=,由,,A B C为锐角可得tan0,tan0,tan0A B C>>>,由(#)得1tan tan0B C-<,解得1t>FED CBA2222tan tan tan 111t A B C t t t=-=---, 221111124t t t ⎛⎫-=-- ⎪⎝⎭,由1t >则211104t t >-≥-,因此tan tan tan A B C 最小值为8, 当且仅当2t =时取到等号,此时tan tan 4B C +=,tan tan 2B C =,解得tan 2tan 2tan 4B C A ===(或tan ,tan B C 互换),此时,,A B C 均为锐角.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤. 15. (本小题满分14分)在ABC △中,6AC =,4cos 5B =,π4C =. ⑴ 求AB 的长; ⑵ 求πcos 6A ⎛⎫- ⎪⎝⎭的值.【答案】⑴. 【解析】⑴ 4cos 5B =,B 为三角形的内角 3sin 5B ∴= sinC sin AB ACB=635=,即:AB = ⑵ ()cos cos sin sin cos cos A C B B C B C =-+=-cos A ∴=又A 为三角形的内角sin A ∴=π1cos sin 62A A A ⎛⎫∴-=+= ⎪⎝⎭16. (本小题满分14分)如图,在直三棱柱111ABC A B C -中,,D E 分别为,AB BC 的中点,点F 在侧棱1B B 上, 且11B D A F ⊥,1111A C A B ⊥. 求证:⑴ 直线//DE 平面11A C F ;⑵ 平面1B DE ⊥平面11A C F .【答案】见解析;【解析】⑴ ,D E 为中点,DE ∴为ABC ∆的中位线//DE AC ∴又111ABC A B C - 为棱柱,11//AC A C ∴11//DE A C ∴,又11A C ⊂ 平面11A C F ,且11DE A C F ⊄ //DE ∴平面11A C F ;⑵ 111ABC A B C - 为直棱柱,1AA ∴⊥平面111A B C111AA A C ∴⊥,又1111A C A B ⊥且1111AA A B A = ,111,AA A B ⊂平面11AA B B 11A C ∴⊥平面11AA B B ,又11//DE A C ,DE ∴⊥平面11AA B B 又1A F ⊂ 平面11AA B B ,1DE A F ∴⊥又11A F B D ⊥ ,1DE B D D = ,且1,DE B D ⊂平面1B DE 1A F ∴⊥平面1B DE ,又111A F A C F ⊂ ∴平面1B DE ⊥平面11A C F .17. (本小题满分14分)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥1111P A B C D -,下部分的形状是正四棱柱1111ABCD A B C D -(如图所示),并要求正四棱柱的高1O O 是正四棱锥的高1PO 的4倍. ⑴ 若6m AB =,12m PO =,则仓库的容积是多少;⑵ 若正四棱锥的侧棱长为6m ,当1PO 为多少时,仓库的容积最大?【答案】⑴3312m;⑵m ; 【解析】⑴ 12m PO =,则18m OO =,FEDC BAC 1B 1A 11A1111231116224m 33P A B C D ABCD V S PO -⋅=⨯⨯==,111123168288m ABCD A B C D ABCD V S OO -⋅=⨯==,111111113312m =P A B C D ABCD A B C D V V V --+=,故仓库的容积为3312m ;⑵ 设1m PO x =,仓库的容积为()V x则14m OO x =,11m A O =,11m A B =,()111123331111272224m 3333P A B C D ABCD V S PO x x x x x -⋅=⨯⨯=-=-=,1111233142888m ABCD A B C D ABCD V S OO x x x-⋅=⨯=-=,()()111111113332262428883120633=P A B C D ABCD A B C D V x V V x x x x x x x --+=-+-=-+<<, ()()22'263122612V x x x =-+=--()06x <<,当(x ∈时,()'0V x >,()V x 单调递增,当()x ∈时,()'0V x <,()V x 单调递减,因此,当x =时,()V x 取到最大值,即1m PO =时,仓库的容积最大.18. (本小题满分14分)如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :221214600x y x y +--+= 及其上一点()2,4A .⑴ 设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; ⑵ 设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;⑶ 设点(),0T t 满足:存在圆M 上的两点P 和Q ,使得TA TP TQ +=,求实数t 的取值范围.【答案】⑴()()22611x y -+-=⑵25y x =+或215y x =-⑶2⎡-+⎣【解析】⑴ 因为N 在直线6x =上,设()6,N n ,因为与x 轴相切,则圆N 为()()2226x y n n -+-=,0n >又圆N 与圆M 外切,圆M :()()226725x x -+-=,则75n n -=+,解得1n =,即圆N 的标准方程为()()22611x y -+-=;⑵ 由题意得OA =,2OA k = 设:2l y x b =+,则圆心M 到直线l 的距离d则BC ==BC =,即=,解得5b =或15b =-,即l :25y x =+或215y x =-;⑶ TA TP TQ += ,即TA TQ TP PQ =-=,即TA PQ = ,,又10PQ≤,10,解得2t ⎡∈-+⎣,对于任意2t ⎡∈-+⎣,欲使TA PQ =,此时10TA ≤,只需要作直线TA必然与圆交于P Q 、两点,此时TA PQ = ,即TA PQ =,因此对于任意2t ⎡∈-+⎣,均满足题意,综上2t ⎡∈-+⎣.19. (本小题满分14分)已知函数()()0,0,1,1x x f x a b a b a b =+>>≠≠. ⑴ 设2a =,12b =. ① 求方程()2f x =的根;② 若对于任意x ∈R ,不等式()()26f x mf x -≥恒成立,求实数m 的最大值; ⑵ 若01a <<,1b >,函数()()2g x f x =-有且只有1个零点,求ab 的值. 【答案】⑴ ①0x =;②4;⑵1;【解析】⑴ ① ()122xxf x ⎛⎫=+ ⎪⎝⎭,由()2f x =可得1222x x +=,则()222210x x -⨯+=,即()2210x -=,则21x =,0x =;② 由题意得221122622x x x x m ⎛⎫++- ⎪⎝⎭≥恒成立,令122x xt =+,则由20x >可得2t =≥, 此时226t mt --≥恒成立,即244t m t t t +=+≤恒成立 ∵2t ≥时44t t +=≥,当且仅当2t =时等号成立,因此实数m 的最大值为4.()()22xxg x f x a b =-=+-,()ln 'ln ln ln ln x xxxa b g x a a b b a b b a ⎡⎤⎛⎫=+=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,由01a <<,1b >可得1b a >,令()ln ln xb ah x a b⎛⎫=+ ⎪⎝⎭,则()h x 递增,而ln 0,ln 0a b <>,因此0ln log ln b a a x b ⎛⎫=- ⎪⎝⎭时()00h x =,因此()0,x x ∈-∞时,()0h x <,ln 0x a b >,则()'0g x <;()0,x x ∈+∞时,()0h x >,ln 0x a b >,则()'0g x >;则()g x 在()0,x -∞递减,()0,x +∞递增,因此()g x 最小值为()0g x , ① 若()00g x <,log 2a x <时,log 22a x a a >=,0x b >,则()0g x >; x >log b 2时,0x a >,log 22b x b b >=,则()0g x >;因此1log 2a x <且10x x <时,()10g x >,因此()g x 在()10,x x 有零点, 2log 2b x >且20x x >时,()20g x >,因此()g x 在()02,x x 有零点, 则()g x 至少有两个零点,与条件矛盾;② 若()00g x ≥,由函数()g x 有且只有1个零点,()g x 最小值为()0g x , 可得()00g x =, 由()00020g a b =+-=, 因此00x =,因此ln log 0ln b aa b ⎛⎫-= ⎪⎝⎭,即ln 1ln a b -=,即ln ln 0a b +=, 因此()ln 0ab =,则1ab =.20. (本小题满分14分)记{}1,2,,100U = .对数列{}n a (*n ∈N )和U 的子集T ,若T =∅,定义0T S =;若{}12,,,k T t t t = ,定义12k T t t t S a a a =+++ .例如:{}1,3,66T =时,1366T S a a a =++. 现设{}n a (*n ∈N )是公比为3的等比数列,且当{}2,4T =时,30T S =. ⑴ 求数列{}n a 的通项公式;⑵ 对任意正整数k (1100k ≤≤),若{}1,2,,T k ⊆ ,求证:1T k S a +<; ⑶ 设C U ⊆,D U ⊆,C D S S ≥,求证:2C C D D S S S + ≥. 【答案】⑴13n n a -=;⑵⑶详见解析;【解析】⑴ 当{}2,4T =时,2422930T S a a a a =+=+=,因此23a =,从而2113a a ==,13n n a -=; ⑵ 2112131133332k k k T k k S a a a a -+-++=++++=<= ≤;⑶ 设()C A C D = ð,()D B C D = ð,则A B =∅ ,C A C D S S S =+ ,D B C D S S S =+ ,22C C D D A B S S S S S +-=- ,因此原题就等价于证明2A B S S ≥.由条件C D S S ≥可知A B S S ≥.① 若B =∅,则0B S =,所以2A B S S ≥.② 若B ≠∅,由A B S S ≥可知A ≠∅,设A 中最大元素为l ,B 中最大元素为m , 若1m l +≥,则由第⑵小题,1A l m B S a a S +<≤≤,矛盾. 因为A B =∅ ,所以l m ≠,所以1l m +≥, 211123113332222m m m l A B m a a S S a a a -+-+++=++++=< ≤≤≤,即2A B S S >.综上所述,2A B S S ≥,因此2C C D D S S S + ≥.数学Ⅱ(附加题)21. [选做题]本题包括A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,在ABC △中,90ABC ∠=︒,BD AC ⊥,D 为垂足,E 是BC 中点. 求证:EDC ABD ∠=∠.【答案】详见解析;【解析】由BD AC ⊥可得90BDC ∠=︒,由E 是BC 中点可得12DE CE BC ==, 则EDC C ∠=∠,EDCBA由90BDC ∠=︒可得90C DBC ∠+∠=︒, 由90ABC ∠=︒可得90ABD DBC ∠+∠=︒, 因此ABD C ∠=∠,又EDC C ∠=∠可得EDC ABD ∠=∠.B .[选修4-2:矩阵与变换](本小题满分10分)已知矩阵1202⎡⎤=⎢⎥-⎣⎦A ,矩阵B 的逆矩阵111202-⎡⎤-⎢⎥=⎢⎥⎣⎦B ,求矩阵AB . 【答案】51401⎡⎤⎢⎥⎢⎥-⎣⎦;【解析】()11112124221010222--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦B B ,因此151121*********⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦AB .C .[选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,已知直线l的参数方程为()11,2,x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数,椭圆C 的参数方程为()cos ,2sin ,x y θθθ=⎧⎨=⎩为参数,设直线l 与椭圆C 相交于,A B 两点,求线段AB 的长. 【答案】167; 【解析】直线l0y --=,椭圆C 方程化为普通方程为2214y x +=,联立得22014y y x --=⎨+=⎪⎩,解得10x y =⎧⎨=⎩或17x y ⎧=-⎪⎪⎨⎪=⎪⎩,因此167AB ==.D .[选修4-5:不等式选讲](本小题满分10分)设0a >,13a x -<,23ay -<,求证:24x y a +-<.【答案】详见解析; 【解析】由13a x -<可得2223a x -<, 22422233a ax y x y a +--+-<+=≤.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤. 22. (本小题满分10分)如图,在平面直角坐标系xOy 中,已知直线:20l x y --=,抛物线()2:20C y px p =>. ⑴ 若直线l 过抛物线C 的焦点,求抛物线C 的方程; ⑵ 已知抛物线C 上存在关于直线l 对称的相异两点P 和Q . ①求证:线段PQ 上的中点坐标为()2,p p --; ②求p 的取值范围.Cl yxO 【答案】⑴28y x =;⑵①见解析;②40,3⎛⎫⎪⎝⎭【解析】⑴ :20l x y --= ,∴l 与x 轴的交点坐标为()2,0即抛物线的焦点为()2,0,22p∴= 28y x ∴=;⑵ ① 设点()11,P x y ,()22,Q x y则:21122222y px y px ⎧=⎪⎨=⎪⎩,即21122222y x py x p⎧=⎪⎪⎨⎪=⎪⎩,12221212222PQ y y p k y y y y p p -==+- 又,P Q 关于直线l 对称,1PQ k ∴=- 即122y y p +=-,122y y p +∴=- 又PQ 中点一定在直线l 上 12122222x x y y p ++∴=+=- ∴线段PQ 上的中点坐标为()2,p p --;② 中点坐标为()2,p p --122212122422y y p y y x x p p +=-⎧⎪∴+⎨+==-⎪⎩即1222212284y y p y y p p +=-⎧⎨+=-⎩ 12212244y y py y p p+=-⎧∴⎨=-⎩,即关于222440y py p p ++-=有两个不等根 0∴∆>,()()2224440p p p -->,40,3p ⎛⎫∴∈ ⎪⎝⎭.23. (本小题满分10分)⑴ 求34677C 4C -的值;⑵ 设*,m n ∈N ,n m ≥,求证:()()()()()212121C 2C 3C C 1C 1C m m m m m m m m m n n n m m m n n m +++-++++++++++=+ .【答案】⑴0;⑵详见解析;【解析】⑴ 34677C 4C 7204350-=⨯-⨯=;⑵ 对任意的*m ∈N ,① 当n m =时,左边()1C 1m m m m =+=+,右边()221C 1m m m m ++=+=+,等式成立,② 假设()n k k m =≥时命题成立,即()()()()()212121C 2C 3C C 1C 1C m m m m m m m m m k k k m m m k k m +++-++++++++++=+ ,当1n k =+时,左边=()()()()()12111C 2C 3C C 1C 2C m m m m m m m m m k k k m m m k k k ++-++++++++++++ ()()2211C 2C m m k k m k +++=+++,右边()231C m k m ++=+, 而()()22321C 1C m m k k m m +++++-+,()()()()()()()()()()()()()()()()13!2!12!1!2!!2!1312!1!1!2!1!2C m k k k m m k m m k m k m k k m m k m k k m k m k +⎡⎤++=+-⎢⎥+-++-⎢⎥⎣⎦+=+⨯+--+⎡⎤⎣⎦+-++=+-+=+ 因此()()()222131C 2C 1C m m m k k k m k m ++++++++=+,因此左边=右边,因此1n k =+时命题也成立,综合①②可得命题对任意n m ≥均成立.另解:因为()()111C 1C m m k k k m +++=+,所以左边()()()1111211C 1C 1C m m m m m n m m m ++++++=++++++ ()()1111211C C C m m m m m n m ++++++=++++ 又由111C C C k k k n n n ---=+,知2212112111112111221121C C C C C C C C C C C C m m m m m m m m m m m m n n n n n n m m n m m n ++++++++++++++++++++++=+=++==+++=+++ , 所以,左边=右边.。
2016年江苏省高考数学试卷(含详细答案解析)

2016年江苏省高考数学试卷一、填空题(共14小题,每小题5分,满分70分)1.(5分)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B=.2.(5分)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是.3.(5分)在平面直角坐标系xOy中,双曲线﹣=1的焦距是.4.(5分)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是.5.(5分)函数y=的定义域是.6.(5分)如图是一个算法的流程图,则输出的a的值是.7.(5分)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.8.(5分)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是.9.(5分)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.10.(5分)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.11.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f (x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是.12.(5分)已知实数x,y满足,则x2+y2的取值范围是.13.(5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是.14.(5分)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.二、解答题(共6小题,满分90分)15.(14分)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.17.(14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?18.(16分)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.19.(16分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.20.(16分)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC的中点,求证:∠EDC=∠ABD.B.【选修4—2:矩阵与变换】22.(10分)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.C.【选修4—4:坐标系与参数方程】23.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.24.设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.附加题【必做题】25.(10分)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px(p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.26.(10分)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.2016年江苏省高考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(5分)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B={﹣1,2} .【分析】根据已知中集合A={﹣1,2,3,6},B={x|﹣2<x<3},结合集合交集的定义可得答案.【解答】解:∵集合A={﹣1,2,3,6},B={x|﹣2<x<3},∴A∩B={﹣1,2},故答案为:{﹣1,2}【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题.2.(5分)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是5.【分析】利用复数的运算法则即可得出.【解答】解:z=(1+2i)(3﹣i)=5+5i,则z的实部是5,故答案为:5.【点评】本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题.3.(5分)在平面直角坐标系xOy中,双曲线﹣=1的焦距是2.【分析】确定双曲线的几何量,即可求出双曲线﹣=1的焦距.【解答】解:双曲线﹣=1中,a=,b=,∴c==,∴双曲线﹣=1的焦距是2.故答案为:2.【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础.4.(5分)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是0.1.【分析】先求出数据4.7,4.8,5.1,5.4,5.5的平均数,由此能求出该组数据的方差.【解答】解:∵数据4.7,4.8,5.1,5.4,5.5的平均数为:=(4.7+4.8+5.1+5.4+5.5)=5.1,∴该组数据的方差:S2=[(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1.故答案为:0.1.【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运用.5.(5分)函数y=的定义域是[﹣3,1] .【分析】根据被开方数不小于0,构造不等式,解得答案.【解答】解:由3﹣2x﹣x2≥0得:x2+2x﹣3≤0,解得:x∈[﹣3,1],故答案为:[﹣3,1]【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题.6.(5分)如图是一个算法的流程图,则输出的a的值是9.【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量a的值,模拟程序的运行过程,可得答案.【解答】解:当a=1,b=9时,不满足a>b,故a=5,b=7,当a=5,b=7时,不满足a>b,故a=9,b=5当a=9,b=5时,满足a>b,故输出的a值为9,故答案为:9【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.7.(5分)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.【分析】出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,由此利用对立事件概率计算公式能求出出现向上的点数之和小于10的概率.【解答】解:将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,基本事件总数为n=6×6=36,出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,出现向上的点数之和不小于10包含的基本事件有:(4,6),(6,4),(5,5),(5,6),(6,5),(6,6),共6个,∴出现向上的点数之和小于10的概率:p=1﹣=.故答案为:.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.8.(5分)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是20.【分析】利用等差数列的通项公式和前n项和公式列出方程组,求出首项和公差,由此能求出a9的值.【解答】解:∵{a n}是等差数列,S n是其前n项和,a1+a22=﹣3,S5=10,∴,解得a1=﹣4,d=3,∴a9=﹣4+8×3=20.故答案为:20.【点评】本题考查等差数列的第9项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.9.(5分)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是7.【分析】法1:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象即可得到答案;法2:由sin2x=cosx,即cosx(2sinx﹣1)=0,可得cosx=0或sinx=,结合题意,解之即可.【解答】解:法1:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:由图可知,共7个交点.法2:依题意,sin2x=cosx,即cosx(2sinx﹣1)=0,故cosx=0或sinx=,因为x∈[0,3π],故x=,,,,,,,共7个,故答案为:7.【点评】本题考查正弦函数与余弦函数的图象,作出函数y=sin2x与y=cosx在区间[0,3π]上的图象是关键,属于中档题.10.(5分)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.【分析】设右焦点F(c,0),将y=代入椭圆方程求得B,C的坐标,运用两直线垂直的条件:斜率之积为﹣1,结合离心率公式,计算即可得到所求值.方法二、运用向量的数量积的性质,向量垂直的条件:数量积为0,结合离心率公式计算即可得到所求.【解答】解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),由∠BFC=90°,可得k BF•k CF=﹣1,即有•=﹣1,化简为b2=3a2﹣4c2,由b2=a2﹣c2,即有3c2=2a2,由e=,可得e2==,可得e=,另解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),=(﹣a﹣c,),=(a﹣c,),•=0,则c2﹣a2十b2=0,因为b2=a2﹣c2,代入得3c2=2a2,由e=,可得e2==,可得e=.故答案为:.【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为﹣1,考查化简整理的运算能力,属于中档题.11.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f (x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是﹣.【分析】根据已知中函数的周期性,结合f(﹣)=f(),可得a值,进而得到f(5a)的值.【解答】解:f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,∴f(﹣)=f(﹣)=﹣+a,f()=f()=|﹣|=,∴a=,∴f(5a)=f(3)=f(﹣1)=﹣1+=﹣,故答案为:﹣【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出a 值,是解答的关键.12.(5分)已知实数x,y满足,则x2+y2的取值范围是[,13] .【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合两点间的距离公式以及点到直线的距离公式进行求解即可.【解答】解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点距离的平方,由图象知A到原点的距离最大,点O到直线BC:2x+y﹣2=0的距离最小,由得,即A(2,3),此时z=22+32=4+9=13,点O到直线BC:2x+y﹣2=0的距离d==,则z=d2=()2=,故z的取值范围是[,13],故答案为:[,13].【点评】本题主要考查线性规划的应用,涉及距离的计算,利用数形结合是解决本题的关键.13.(5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是.【分析】由已知可得=+,=﹣+,=+3,=﹣+3,=+2,=﹣+2,结合已知求出2=,2=,可得答案.【解答】解:∵D是BC的中点,E,F是AD上的两个三等分点,∴=+,=﹣+,=+3,=﹣+3,∴•=2﹣2=﹣1,•=92﹣2=4,∴2=,2=,又∵=+2,=﹣+2,∴•=42﹣2=,故答案为:【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档.14.(5分)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是8.【分析】结合三角形关系和式子sinA=2sinBsinC可推出sinBcosC+cosBsinC=2sinBsinC,进而得到tanB+tanC=2tanBtanC,结合函数特性可求得最小值.【解答】解:由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,可得sinBcosC+cosBsinC=2sinBsinC,①由三角形ABC为锐角三角形,则cosB>0,cosC>0,在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,又tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣②,则tanAtanBtanC=﹣•tanBtanC,由tanB+tanC=2tanBtanC可得tanAtanBtanC=﹣,令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,由②式得1﹣tanBtanC<0,解得t>1,tanAtanBtanC=﹣=﹣,=()2﹣,由t>1得,﹣≤<0,因此tanAtanBtanC的最小值为8,另解:由已知条件sinA=2sinBsinc,sin(B十C)=2sinBsinC,sinBcosC十cosBsinC=2sinBcosC,两边同除以cosBcosC,tanB十tanC=2tanBtanC,∵﹣tanA=tan(B十C)=,∴tanAtanBtanC=tanA十tanB十tanC,∴tanAtanBtanC=tanA十2tanBtanC≥2,令tanAtanBtanC=x>0,即x≥2,即x≥8,或x≤0(舍去),所以x的最小值为8.当且仅当t=2时取到等号,此时tanB+tanC=4,tanBtanC=2,解得tanB=2+,tanC=2﹣,tanA=4,(或tanB,tanC互换),此时A,B,C 均为锐角.【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性.二、解答题(共6小题,满分90分)15.(14分)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.【分析】(1)利用正弦定理,即可求AB的长;(2)求出cosA、sinA,利用两角差的余弦公式求cos(A﹣)的值.【解答】解:(1)∵△ABC中,cosB=,B∈(0,π),∴sinB=,∵,∴AB==5;(2)cosA═﹣cos(π﹣A)=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣.∵A为三角形的内角,∴sinA=,∴cos(A﹣)=cosA+sinA=.【点评】本题考查正弦定理,考查两角和差的余弦公式,考查学生的计算能力,属于基础题.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.【分析】(1)通过证明DE∥AC,进而DE∥A1C1,据此可得直线DE∥平面A1C1F1;(2)通过证明A1F⊥DE结合题目已知条件A1F⊥B1D,进而可得平面B1DE⊥平面A1C1F.【解答】解:(1)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∴DE∥AC,∵ABC﹣A1B1C1为棱柱,∴AC∥A1C1,∴DE∥A1C1,∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,∴DE∥A1C1F;(2)在ABC﹣A1B1C1的直棱柱中,∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,又∵A1C1⊥A1B1,且AA1∩A1B1=A1,AA1、A1B1⊂平面AA1B1B,∴A1C1⊥平面AA1B1B,∵DE∥A1C1,∴DE⊥平面AA1B1B,又∵A1F⊂平面AA1B1B,∴DE⊥A1F,又∵A1F⊥B1D,DE∩B1D=D,且DE、B1D⊂平面B1DE,∴A1F⊥平面B1DE,又∵A1F⊂平面A1C1F,∴平面B1DE⊥平面A1C1F.【点评】本题考查直线与平面平行的证明,以及平面与平面相互垂直的证明,把握常用方法最关键,难度不大.17.(14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?【分析】(1)由正四棱柱的高O1O是正四棱锥的高PO1的4倍,可得PO1=2m时,O1O=8m,进而可得仓库的容积;(2)设PO1=xm,则O1O=4xm,A1O1=m,A1B1=•m,代入体积公式,求出容积的表达式,利用导数法,可得最大值.【解答】解:(1)∵PO1=2m,正四棱柱的高O1O是正四棱锥的高PO1的4倍.∴O1O=8m,答:仓库的容积V=×62×2+62×8=312m3,(2)若正四棱锥的侧棱长为6m,设PO1=xm,则O1O=4xm,A1O1=m,A1B1=•m,则仓库的容积V=×(•)2•x+(•)2•4x=x3+312x,(0<x<6),∴V′=﹣26x2+312,(0<x<6),当0<x<2时,V′>0,V(x)单调递增;当2<x<6时,V′<0,V(x)单调递减;故当x=2时,V(x)取最大值;答:当PO1=2m时,仓库的容积最大.【点评】本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档.18.(16分)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.【分析】(1)设N(6,n),则圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,从而得到|7﹣n|=|n|+5,由此能求出圆N的标准方程.(2)由题意得OA=2,k OA=2,设l:y=2x+b,则圆心M到直线l的距离:d=,由此能求出直线l的方程.(3)=,即||=,又||≤10,得t∈[2﹣2,2+2],对于任意t∈[2﹣2,2+2],欲使,只需要作直线TA的平行线,使圆心到直线的距离为,由此能求出实数t的取值范围.【解答】解:(1)∵N在直线x=6上,∴设N(6,n),∵圆N与x轴相切,∴圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,又圆N与圆M外切,圆M:x2+y2﹣12x﹣14y+60=0,即圆M:(x﹣6)2+(x﹣7)2=25,∴|7﹣n|=|n|+5,解得n=1,∴圆N的标准方程为(x﹣6)2+(y﹣1)2=1.(2)由题意得OA=2,k OA=2,设l:y=2x+b,则圆心M到直线l的距离:d==,则|BC|=2=2,BC=2,即2=2,解得b=5或b=﹣15,∴直线l的方程为:y=2x+5或y=2x﹣15.(3)设P(x1,y1),Q(x2,y2),∵A(2,4),T(t,0),,∴,①∵点Q在圆M上,∴(x2﹣6)2+(y2﹣7)2=25,②将①代入②,得(x1﹣t﹣4)2+(y1﹣3)2=25,∴点P(x1,y1)即在圆M上,又在圆[x﹣(t+4)]2+(y﹣3)2=25上,从而圆(x﹣6)2+(y﹣7)2=25与圆[x﹣(t+4)]2+(y﹣3)2=25有公共点,∴5﹣5≤≤5+5.解得2﹣2≤t,∴实数t的取值范围是[2﹣2,2+2].【点评】本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.19.(16分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.【分析】(1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函数的最值,转化求解即可.(2)求出g(x)=f(x)﹣2=a x+b x﹣2,求出函数的导数,构造函数h(x)=+,求出g(x)的最小值为:g(x0).①若g(x0)<0,g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,利用函数g(x)=f(x)﹣2有且只有1个零点,推出g(x0)=0,然后求解ab=1.【解答】解:函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①方程f(x)=2;即:=2,y=2x在R上单调,可得x=0.②不等式f(2x)≥mf(x)﹣6恒成立,即≥m()﹣6恒成立.令t=,t≥2.不等式化为:t2﹣mt+4≥0在t≥2时,恒成立.可得:△≤0或即:m2﹣16≤0或m≤4,∴m∈(﹣∞,4].实数m的最大值为:4.(2)g(x)=f(x)﹣2=a x+b x﹣2,g′(x)=a x lna+b x lnb=a x[+]lnb,0<a<1,b>1可得,令h(x)=+,则h(x)是递增函数,而,lna<0,lnb>0,因此,x0=时,h(x0)=0,因此x∈(﹣∞,x0)时,h(x)<0,a x lnb>0,则g′(x)<0.x∈(x0,+∞)时,h(x)>0,a x lnb>0,则g′(x)>0,则g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此g(x)的最小值为:g(x0).①若g(x0)<0,x<log a2时,a x>=2,b x>0,则g(x)>0,因此x1<log a2,且x1<x0时,g(x1)>0,因此g(x)在(x1,x0)有零点,则g(x)至少有两个零点,与条件矛盾.②若g(x0)≥0,函数g(x)=f(x)﹣2有且只有1个零点,g(x)的最小值为g(x0),可得g(x0)=0,由g(0)=a0+b0﹣2=0,因此x0=0,因此=0,﹣=1,即lna+lnb=0,ln(ab)=0,则ab=1.可得ab=1.【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒成立的应用,考查分析问题解决问题的能力.20.(16分)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.【分析】(1)根据题意,由S T的定义,分析可得S T=a2+a4=a2+9a2=30,计算可得a2=3,进而可得a1的值,由等比数列通项公式即可得答案;(2)根据题意,由S T的定义,分析可得S T≤a1+a2+…a k=1+3+32+…+3k﹣1,由等比数列的前n项和公式计算可得证明;(3)设A=∁C(C∩D),B=∁D(C∩D),则A∩B=∅,进而分析可以将原命题转化为证明S C≥2S B,分2种情况进行讨论:①、若B=∅,②、若B≠∅,可以证明得到S A≥2S B,即可得证明.【解答】解:(1)等比数列{a n}中是公比为3的等比数列,则a4=3a3=9a2,当T={2,4}时,S T=a2+a4=a2+9a2=30,因此a2=3,从而a1==1,故a n=3n﹣1,(2)S T≤a1+a2+…a k=1+3+32+…+3k﹣1=<3k=a k+1,(3)设A=∁C(C∩D),B=∁D(C∩D),则A∩B=∅,分析可得S C=S A+S C∩D,S D=S B+S C∩D,则S C+S C∩D﹣2S D=S A﹣2S B,因此原命题的等价于证明S A≥2S B,由条件S C≥S D,可得S A≥S B,①、若B=∅,则S B=0,故S A≥2S B,②、若B≠∅,由S A≥S B可得A≠∅,设A中最大元素为l,B中最大元素为m,若m≥l+1,则其与S A<a1+1≤a m≤S B相矛盾,因为A∩B=∅,所以l≠m,则l≥m+1,S B≤a1+a2+…a m=1+3+32+…+3m﹣1=≤=,即S A≥2S B,综上所述,S A≥2S B,故S C+S C∩D≥2S D.【点评】本题考查数列的应用,涉及新定义的内容,解题的关键是正确理解题目中对于新定义的描述.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC的中点,求证:∠EDC=∠ABD.【分析】依题意,知∠BDC=90°,∠EDC=∠C,利用∠C+∠DBC=∠ABD+∠DBC=90°,可得∠ABD=∠C,从而可证得结论.【解答】解:在△ABC中,由BD⊥AC可得∠BDC=90°,因为E为BC的中点,所以DE=CE=BC,则:∠EDC=∠C,由∠BDC=90°,可得∠C+∠DBC=90°,由∠ABC=90°,可得∠ABD+∠DBC=90°,因此∠ABD=∠C,而∠EDC=∠C,所以,∠EDC=∠ABD.【点评】本题考查三角形的性质应用,利用∠C+∠DBC=∠ABD+∠DBC=90°,证得∠ABD=∠C是关键,属于中档题.B.【选修4—2:矩阵与变换】22.(10分)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.【分析】依题意,利用矩阵变换求得B=(B﹣1)﹣1==,再利用矩阵乘法的性质可求得答案.【解答】解:∵B﹣1=,∴B=(B﹣1)﹣1==,又A=,∴AB==.【点评】本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题.C.【选修4—4:坐标系与参数方程】23.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.【分析】分别化直线与椭圆的参数方程为普通方程,然后联立方程组,求出直线与椭圆的交点坐标,代入两点间的距离公式求得答案.【解答】解:由,由②得,代入①并整理得,.由,得,两式平方相加得.联立,解得或.∴|AB|=.【点评】本题考查直线与椭圆的参数方程,考查了参数方程化普通方程,考查直线与椭圆位置关系的应用,是基础题.24.设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.【分析】运用绝对值不等式的性质:|a+b|≤|a|+|b|,结合不等式的基本性质,即可得证.【解答】证明:由a>0,|x﹣1|<,|y﹣2|<,根据绝对值不等式的性质,可得|2x+y﹣4|=|2(x﹣1)+(y﹣2)|≤2|x﹣1|+|y﹣2|<+=a,则|2x+y﹣4|<a成立.【点评】本题考查绝对值不等式的证明,注意运用绝对值不等式的性质,以及不等式的简单性质,考查运算能力,属于基础题.附加题【必做题】25.(10分)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px(p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.【分析】(1)求出抛物线的焦点坐标,然后求解抛物线方程.(2):①设点P(x1,y1),Q(x2,y2),通过抛物线方程,求解k PQ,通过P,Q 关于直线l对称,点的k PQ=﹣1,推出,PQ的中点在直线l上,推出=2﹣p,即可证明线段PQ的中点坐标为(2﹣p,﹣p);②利用线段PQ中点坐标(2﹣p,﹣p).推出,得到关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出p的范围.【解答】解:(1)∵l:x﹣y﹣2=0,∴l与x轴的交点坐标(2,0),即抛物线的焦点坐标(2,0).∴,∴抛物线C:y2=8x.(2)证明:①设点P(x1,y1),Q(x2,y2),则:,即:,k PQ==,又∵P,Q关于直线l对称,∴k PQ=﹣1,即y1+y2=﹣2p,∴,又PQ的中点在直线l上,∴==2﹣p,∴线段PQ的中点坐标为(2﹣p,﹣p);②因为Q中点坐标(2﹣p,﹣p).∴,即∴,即关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,∴△>0,(2p)2﹣4(4p2﹣4p)>0,∴p∈.【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力.26.(10分)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【分析】(1)由已知直接利用组合公式能求出7的值.(2)对任意m∈N*,当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【解答】解:(1)7=﹣4×=7×20﹣4×35=0.证明:(2)对任意m∈N*,①当n=m时,左边=(m+1)=m+1,右边=(m+1)=m+1,等式成立.②假设n=k(k≥m)时命题成立,即(m+1)C+(m+2)C+(m+3)C+…+k+(k+1)=(m+1),当n=k+1时,左边=(m+1)+(m+2)+(m+3)++(k+1)+(k+2)=,右边=∵=(m+1)[﹣]=(m+1)×[k+3﹣(k﹣m+1)]=(k+2)=(k+2),∴=(m+1),∴左边=右边,∴n=k+1时,命题也成立,∴m,n∈N*,n≥m,(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【点评】本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和数学归纳法的合理运用.。
2016年江苏省高考数学试题含答案(Word版)

2016年江苏省高考数学试题含答案(Word版)2016年江苏卷数学Ⅰ非选择题注意事项:1.本试卷共20道填空题,满分160分,考试时间120分钟。
考试结束后,请将试卷和答题卡一并交回。
2.请务必在试卷和答题卡上填写自己的姓名和准考证号,核对监考员粘贴的条形码信息。
3.作答必须用0.5毫米黑色墨水的签字笔在答题卡上指定位置作答,其他位置作答无效。
4.如需作图,须用2B铅笔绘制,线条、符号等需加黑、加粗。
一、填空题:1.已知集合A={-1,2,3,6},B={x|-2<x<3},则AB=________。
2.复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是________。
3.在平面直角坐标系xOy中,双曲线(x^2)/(9)-(y^2)/(4)=1的焦距是________。
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是________。
5.函数y=3-2x-x^2的定义域是________。
6.如图是一个算法的流程图,则输出的a的值是________。
7.将一颗质地均匀的骰子先后抛掷2次,则出现向上的点数之和小于10的概率是________。
8.已知{an}是等差数列,Sn是其前n项和。
若a1+a2/2=-3,S5=10,则a9的值是________。
9.定义在区间[0,3π]上的函数y=sin^2x的图象与y=cosx的图象的交点个数是________。
10.如图,F是椭圆(x^2)/(a^2)+(y^2)/(b^2)=1(a>b>0)的右焦点,在平面直角坐标系xOy中,直线y=-x/2与椭圆交于B,FB的斜率是________。
参考公式:样本数据x1,x2,…,xn的方差s^2=(∑(xi-x)^2)/n,其中x=(∑xi)/n。
棱柱的体积公式:V=Sh,其中S是棱柱的底面积,h为高。
棱锥的体积公式:V=(1/3)Sh,其中S是棱锥的底面积,h为高。
2016年高考真题——数学(江苏卷) Word版含解析

【说明】: 【参考版答案】非官方版正式答案,有可能存在少量错误,仅供参考使用。
2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式: 样本数据12,,,n x x x 的方差()2211n i i s x x n ==-∑,其中11ni i x x n ==∑.棱柱的体积V Sh =,其中S 是棱柱的底面积,h 是高.棱锥的体积13V Sh =,其中S 是棱锥的底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1. 已知集合{}1,2,3,6A =-,{}|23B x x =-<<,则A B = .【答案】{}1,2-;【解析】由交集的定义可得{}1,2AB =-.2. 复数()()12i 3i z =+-,其中i 为虚数单位,则z 的实部是 . 【答案】5;【解析】由复数乘法可得55i z =+,则则z 的实部是5.3. 在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是 .【答案】【解析】c,因此焦距为2c =.4. 已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是 . 【答案】0.1; 【解析】 5.1x =,()22222210.40.300.30.40.15s =++++=. 5.函数y 的定义域是 . 【答案】[]3,1-;【解析】2320x x --≥,解得31x -≤≤,因此定义域为[]3,1-.6. 如图是一个算法的流程图,则输出a 的值是 .【答案】9;【解析】,a b 的变化如下表:则输出时9a =.7. 将一个质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点为正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是 . 【答案】56; 【解析】将先后两次点数记为(),x y ,则共有6636⨯=个等可能基本事件,其中点数之和大于等于10有()()()()()()4,6,5,5,5,6,6,4,6,5,6,6六种,则点数之和小于10共有30种,概率为305366=. 8. 已知{}n a 是等差数列,n S 是其前n 项和.若2123a a +=-,510S =,则9a 的值是 . 【答案】20;【解析】设公差为d ,则由题意可得()2113a a d ++=-,151010a d +=,解得14a =-,3d =,则948320a =-+⨯=.9. 定义在区间[]0,3π上的函数s i n 2y x =的图象与c o s y x =的图象的交点个数是 . 【答案】7;【解析】画出函数图象草图,共7个交点.10. 如图,在平面直角坐标系xOy 中,F 是椭圆()222210x y a b a b +=>>的右焦点,直线2b y =与椭圆交于,B C 两点,且90BFC ∠=︒,则该椭圆的离心率是.【解析】由题意得(),0F c ,直线2by =与椭圆方程联立可得2b B ⎛⎫ ⎪ ⎪⎝⎭,2b C ⎫⎪⎪⎝⎭, 由90BFC ∠=︒可得0BF CF ⋅=,2b BFc ⎛⎫=+- ⎪ ⎪⎝⎭,2b CF c ⎛⎫=- ⎪ ⎪⎝⎭, 则22231044c a b -+=,由222b a c =-可得223142c a =,则c e a ==.11. 设()f x 是定义在R 上且周期为2的函数,在区间[)1,1-上(),10,2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中a ∈R ,若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,则()5f a 的值是 .【答案】25-;【解析】由题意得511222f f a ⎛⎫⎛⎫-=-=-+ ⎪ ⎪⎝⎭⎝⎭,91211225210f f ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭, 由5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭可得11210a -+=,则35a =,则()()()325311155f a f f a ==-=-+=-+=-. 12. 已知实数,x y 满足240,220,330,x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩ 则22x y +的取值范围是 .【答案】4,135⎡⎤⎢⎥⎣⎦;【解析】在平面直角坐标系中画出可行域如下22x y +为可行域内的点到原点距离的平方.可以看出图中A 点距离原点最近,此时距离为原点A 到直线220x y +-=的距离, d ==()22min45x y +=, 图中B 点距离原点最远,B 点为240x y -+=与330x y --=交点,则()2,3B , 则()22max13x y +=.13. 如图,在ABC △中,D 是BC 的中点,,E F 是AD 上两个三等分点,4BA CA ⋅=,1BF CF ⋅=-,则BE CE ⋅的值是 .B【答案】78; 【解析】令DF a =,DB b =,则DC b =-,2DE a =,3DA a =,则3BA a b =-,3CA a b =+,2BE a b =-,2CE a b =+,BF a b =-,CF a b =+, 则229BA CA a b ⋅=-,22BF CF a b ⋅=-,224BE CE a b ⋅=-,由4BA CA ⋅=,1BF CF ⋅=-可得2294a b -=,221a b -=-,因此22513,88a b ==,因此22451374888BE CE a b ⨯⋅=-=-=. 14. 在锐角三角形ABC 中,sin 2sin sin A B C =,则t a n t a n t a n AB C 的最小值是 .【答案】8;【解析】由()()sin sin πsin sin cos cos sin A A B C B C B C =-=+=+,sin 2sin sin A B C =,可得sin cos cos sin 2sin sin B C B C B C +=(*), 由三角形ABC 为锐角三角形,则cos 0,cos 0B C >>,在(*)式两侧同时除以cos cos B C 可得tan tan 2tan tan B C B C +=, 又()()tan tan tan tan πtan 1tan tan B CA ABC B C+=--=-+=--(#),则tan tan tan tan tan tan tan 1tan tan B CA B C B C B C+=-⨯-,由tan tan 2tan tan B C B C +=可得()22tan tan tan tan tan 1tan tan B C A B C B C=--,令tan tan B C t =,由,,A B C 为锐角可得tan 0,tan 0,tan 0A B C >>>, 由(#)得1tan tan 0B C -<,解得1t > 2222tan tan tan 111t A B C t t t=-=---,221111124t t t ⎛⎫-=-- ⎪⎝⎭,由1t >则211104t t >-≥-,因此tan tan tan A B C 最小值为8, 当且仅当2t =时取到等号,此时tan tan 4B C +=,tan tan 2B C =,解得tan 224B C A ===(或tan ,tan B C 互换),此时,,A B C 均为锐角.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤. 15. (本小题满分14分)在ABC △中,6AC =,4cos 5B =,π4C =. ⑴ 求AB 的长; ⑵ 求πcos 6A ⎛⎫- ⎪⎝⎭的值.【答案】⑴. 【解析】⑴ 4cos 5B =,B 为三角形的内角 3sin 5B ∴=sinC sin AB ACB =635=,即:AB = ⑵ ()cos cos sin sin cos cos A C B B C B C =-+=-cos A ∴= 又A 为三角形的内角sin A ∴=π1cos sin 62A A A ⎛⎫∴-=+= ⎪⎝⎭.16. (本小题满分14分)如图,在直三棱柱111ABC A B C -中,,D E 分别为,AB BC 的中点,点F 在侧棱1B B 上, 且11B D A F ⊥,1111AC A B ⊥. 求证:⑴ 直线//DE 平面11AC F ;⑵ 平面1B DE ⊥平面11AC F .【答案】见解析;【解析】⑴ ,D E 为中点,DE ∴为ABC ∆的中位线//DE AC ∴又111ABC A B C -为棱柱,11//AC AC ∴11//DE AC ∴,又11AC ⊂平面11AC F ,且11DE AC F ⊄FEC BAC 1B 1A 1//DE ∴平面11AC F ;⑵111ABC A B C -为直棱柱,1AA ∴⊥平面111A B C 111AA AC ∴⊥,又1111AC A B ⊥且1111AA A B A =,111,AA A B ⊂平面11AA B B11AC ∴⊥平面11AA B B ,又11//DE AC ,DE ∴⊥平面11AA B B 又1A F ⊂平面11AA B B ,1DE A F ∴⊥ 又11A F B D ⊥,1DEB D D =,且1,DE B D ⊂平面1B DE 1A F ∴⊥平面1B DE ,又111A F AC F ⊂∴平面1B DE ⊥平面11AC F .17. (本小题满分14分)现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥1111P A B C D -,下部分的形状是正四棱柱1111ABCD A B C D -(如图所示),并要求正四棱柱的高1O O 是正四棱锥的高1PO 的4倍.⑴ 若6m AB =,12m PO =,则仓库的容积是多少;⑵ 若正四棱锥的侧棱长为6m ,当1PO 为多少时,仓库的容积最大?【答案】⑴3312m;⑵m ; 【解析】⑴ 12m PO =,则18m OO =,1111231116224m 33P A B C D ABCD V S PO -⋅=⨯⨯==,111123168288m ABCD A B C D ABCD V S OO -⋅=⨯==, 111111113312m =P A B C D ABCD A B C D V V V --+=, 故仓库的容积为3312m ;⑵ 设1m PO x =,仓库的容积为()V x则14m OO x =,11AO,11m A B =,()111123331111272224m 3333P A B C D ABCD V S PO x x x x x -⋅=⨯⨯=-=-=,1A1111233142888m ABCD A B C D ABCD V S OO x x x -⋅=⨯=-=,()()111111113332262428883120633=P A B C D ABCD A B C D V x V V x x x x x x x --+=-+-=-+<<,()()22'263122612V x x x =-+=--()06x <<,当(0,x ∈时,()'0V x >,()V x 单调递增,当()x ∈时,()'0V x <,()V x 单调递减,因此,当x =()V x 取到最大值,即1PO =时,仓库的容积最大.18. (本小题满分14分)如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :221214600x y x y +--+= 及其上一点()2,4A .⑴ 设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; ⑵ 设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;⑶ 设点(),0T t 满足:存在圆M 上的两点P 和Q ,使得TA TP TQ +=,求实数t 的取值范围.【答案】⑴()()22611x y -+-=⑵25y x =+或215y x =-⑶2⎡-+⎣【解析】⑴ 因为N 在直线6x =上,设()6,N n ,因为与x 轴相切,则圆N 为()()2226x y n n -+-=,0n >又圆N 与圆M 外切,圆M :()()226725x x -+-=,则75n n -=+,解得1n =,即圆N 的标准方程为()()22611x y -+-=; ⑵ 由题意得OA =2OA k = 设:2l y x b =+,则圆心M 到直线l 的距离d ==则BC =BC =,即=解得5b =或15b =-,即l :25y x =+或215y x =-; ⑶ TA TP TQ +=,即TA TQ TP PQ =-=,即TA PQ =,(TA t =又10PQ ≤,10,解得2t ⎡∈-+⎣,对于任意2t ⎡∈-+⎣,欲使TA PQ =,此时10TA ≤,只需要作直线TA 2TA必然与圆交于P Q 、两点,此时TA PQ =,即TA PQ =,因此对于任意2t ⎡∈-+⎣,均满足题意,综上2t ⎡∈-+⎣.19. (本小题满分14分)已知函数()()0,0,1,1x x f x a b a b a b =+>>≠≠. ⑴ 设2a =,12b =. ① 求方程()2f x =的根;② 若对于任意x ∈R ,不等式()()26f x mf x -≥恒成立,求实数m 的最大值; ⑵ 若01a <<,1b >,函数()()2g x f x =-有且只有1个零点,求ab 的值. 【答案】⑴ ①0x =;②4;⑵1;【解析】⑴ ① ()122xxf x ⎛⎫=+ ⎪⎝⎭,由()2f x =可得1222x x +=,则()222210x x -⨯+=,即()2210x -=,则21x =,0x =;② 由题意得221122622x x x x m ⎛⎫++- ⎪⎝⎭≥恒成立,令122x xt =+,则由20x>可得2t =≥, 此时226t mt --≥恒成立,即244t m t t t +=+≤恒成立∵2t ≥时44t t +≥,当且仅当2t =时等号成立,因此实数m 的最大值为4.()()22xxg x f x a b =-=+-,()ln 'ln ln ln ln x x x xa b g x a a b b a b b a ⎡⎤⎛⎫=+=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,由01a <<,1b >可得1b a >,令()ln ln xb ah x a b ⎛⎫=+ ⎪⎝⎭,则()h x 递增,而ln 0,ln 0a b <>,因此0ln log ln b aa xb ⎛⎫=- ⎪⎝⎭时()00h x =,因此()0,x x ∈-∞时,()0h x <,ln 0x a b >,则()'0g x <; ()0,x x ∈+∞时,()0h x >,ln 0x a b >,则()'0g x >;则()g x 在()0,x -∞递减,()0,x +∞递增,因此()g x 最小值为()0g x , ① 若()00g x <,log 2a x <时,log 22a x a a >=,0x b >,则()0g x >; x >log b 2时,0x a >,log 22b x b b >=,则()0g x >;因此1log 2a x <且10x x <时,()10g x >,因此()g x 在()10,x x 有零点, 2l o g 2bx >且20x x >时,()20g x >,因此()g x 在()02,x x 有零点, 则()g x 至少有两个零点,与条件矛盾;② 若()00g x ≥,由函数()g x 有且只有1个零点,()g x 最小值为()0g x , 可得()00g x =, 由()00020g a b =+-=, 因此00x =,因此ln log 0ln b a a b ⎛⎫-= ⎪⎝⎭,即ln 1ln a b -=,即ln ln 0a b +=, 因此()ln 0ab =,则1ab =.20. (本小题满分14分) 记{}1,2,,100U =.对数列{}n a (*n ∈N )和U 的子集T ,若T =∅,定义0T S =;若{}12,,,k T t t t =,定义12k T t t t S a a a =+++.例如:{}1,3,66T =时,1366T S a a a =++.现设{}n a (*n ∈N )是公比为3的等比数列,且当{}2,4T =时,30T S =. ⑴ 求数列{}n a 的通项公式;⑵ 对任意正整数k (1100k ≤≤),若{}1,2,,T k ⊆,求证:1T k S a +<; ⑶ 设C U ⊆,D U ⊆,C D S S ≥,求证:2C CDD S S S +≥.【答案】⑴13n n a -=;⑵⑶详见解析;【解析】⑴ 当{}2,4T =时,2422930T S a a a a =+=+=,因此23a =,从而2113a a ==,13n n a -=;⑵ 2112131133332k k k T k k S a a a a -+-++=++++=<=≤;⑶ 设()C A CD =ð,()D B C D =ð,则A B =∅,C A CDS S S =+,D B CDS S S =+,22C CDD A B S S S S S +-=-,因此原题就等价于证明2A B S S ≥.由条件C D S S ≥可知A B S S ≥.① 若B =∅,则0B S =,所以2A B S S ≥.② 若B ≠∅,由A B S S ≥可知A ≠∅,设A 中最大元素为l ,B 中最大元素为m , 若1m l +≥,则由第⑵小题,1A l m B S a a S +<≤≤,矛盾. 因为A B =∅,所以l m ≠,所以1l m +≥, 211123113332222m m m lA B m a a S S a a a -+-+++=++++=<≤≤≤,即2A B S S >.综上所述,2A B S S ≥,因此2C CDD S S S +≥.数学Ⅱ(附加题)21. [选做题]本题包括A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,在ABC △中,90ABC ∠=︒,BD AC ⊥,D 为垂足,E 是BC 中点. 求证:EDC ABD ∠=∠.【答案】详见解析;【解析】由BD AC ⊥可得90BDC ∠=︒,由E 是BC 中点可得12DE CE BC ==, 则EDC C ∠=∠,由90BDC ∠=︒可得90C DBC ∠+∠=︒, 由90ABC ∠=︒可得90ABD DBC ∠+∠=︒, 因此ABD C ∠=∠,又EDC C ∠=∠可得EDC ABD ∠=∠.B .[选修4-2:矩阵与变换](本小题满分10分)ECBA已知矩阵1202⎡⎤=⎢⎥-⎣⎦A ,矩阵B 的逆矩阵111202-⎡⎤-⎢⎥=⎢⎥⎣⎦B ,求矩阵AB . 【答案】51401⎡⎤⎢⎥⎢⎥-⎣⎦;【解析】()11112124221010222--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦B B ,因此151121*********⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦AB .C .[选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,已知直线l的参数方程为()11,2,x t t y ⎧=+⎪⎪⎨⎪⎪⎩为参数,椭圆C 的参数方程为()cos ,2sin ,x y θθθ=⎧⎨=⎩为参数,设直线l 与椭圆C 相交于,A B 两点,求线段AB 的长.【答案】167; 【解析】直线l0y -,椭圆C 方程化为普通方程为2214y x +=,联立得22014y y x --=⎨+=⎪⎩,解得10x y =⎧⎨=⎩或17x y ⎧=-⎪⎪⎨⎪=⎪⎩,因此167AB .D .[选修4-5:不等式选讲](本小题满分10分)设0a >,13a x -<,23ay -<,求证:24x y a +-<.【答案】详见解析; 【解析】由13a x -<可得2223a x -<, 22422233a ax y x y a +--+-<+=≤.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤. 22. (本小题满分10分)如图,在平面直角坐标系xOy 中,已知直线:20l x y --=,抛物线()2:20C y px p =>. ⑴ 若直线l 过抛物线C 的焦点,求抛物线C 的方程; ⑵ 已知抛物线C 上存在关于直线l 对称的相异两点P 和Q . ①求证:线段PQ 上的中点坐标为()2,p p --; ②求p 的取值范围.【答案】⑴28y x =;⑵①见解析;②40,3⎛⎫⎪⎝⎭【解析】⑴ :20l x y --=,∴l 与x 轴的交点坐标为()2,0即抛物线的焦点为()2,0,22p∴= 28y x ∴=;⑵ ① 设点()11,P x y ,()22,Q x y则:21122222y px y px ⎧=⎪⎨=⎪⎩,即21122222y x p y x p⎧=⎪⎪⎨⎪=⎪⎩,12221212222PQ y y p k y y y y p p -==+- 又,P Q 关于直线l 对称,1PQ k ∴=- 即122y y p +=-,122y y p +∴=- 又PQ 中点一定在直线l 上12122222x x y y p ++∴=+=- ∴线段PQ 上的中点坐标为()2,p p --;②中点坐标为()2,p p --122212122422y y p y y x x p p +=-⎧⎪∴+⎨+==-⎪⎩即1222212284y y p y y p p +=-⎧⎨+=-⎩ 12212244y y py y p p+=-⎧∴⎨=-⎩,即关于222440y py p p ++-=有两个不等根 0∴∆>,()()2224440p p p -->,40,3p ⎛⎫∴∈ ⎪⎝⎭.23. (本小题满分10分)⑴ 求34677C 4C -的值;⑵ 设*,m n ∈N ,n m ≥,求证:()()()()()212121C 2C 3C C 1C 1C m m m m m m m m m n n n m m m n n m +++-++++++++++=+.【答案】⑴0;⑵详见解析;【解析】⑴ 34677C 4C 7204350-=⨯-⨯=;⑵ 对任意的*m ∈N ,① 当n m =时,左边()1C 1m m m m =+=+,右边()221C 1m m m m ++=+=+,等式成立,② 假设()n k k m =≥时命题成立,即()()()()()212121C 2C 3C C 1C 1C m m m m m m m m m k k k m m m k k m +++-++++++++++=+,当1n k =+时, 左边=()()()()()12111C 2C 3C C 1C 2C m m mm m mm m m k k k m m m k k k ++-++++++++++++()()2211C 2C m m k k m k +++=+++,右边()231C m k m ++=+, 而()()22321C 1C m m k k m m +++++-+,()()()()()()()()()()()()()()()()13!2!12!1!2!!2!1312!1!1!2!1!2C m k k k m m k m m k m k m k k m m k m k k m k m k +⎡⎤++=+-⎢⎥+-++-⎢⎥⎣⎦+=+⨯+--+⎡⎤⎣⎦+-++=+-+=+ 因此()()()222131C 2C 1C m m m k k k m k m ++++++++=+,因此左边=右边,因此1n k =+时命题也成立,综合①②可得命题对任意n m ≥均成立.另解:因为()()111C 1C m m k k k m +++=+,所以 左边()()()1111211C 1C 1C m m m m m n m m m ++++++=++++++()()1111211C C C m m m m m n m ++++++=++++又由111C C C k k k n n n ---=+,知2212112111112111221121C C C C C C C C C C C C m m m m m m m m m m m m n n n n n n m m n m m n ++++++++++++++++++++++=+=++==+++=+++,所以,左边=右边.。
2016年江苏数学高考试卷含答案和解析
2016年江苏数学高考试卷一、填空题(共14小题。
每小题5分.满分70分)1.(5分)已知集合A={﹣1.2.3.6}。
B={x|﹣2<x<3}。
则A∩B=______.2.(5分)复数z=(1+2i)(3﹣i)。
其中i为虚数单位。
则z的实部是______.3.(5分)在平面直角坐标系xOy中。
双曲线﹣=1的焦距是______.4.(5分)已知一组数据4.7.4。
8.5。
1.5.4.5.5.则该组数据的方差是______.5.(5分)函数y=的定义域是______.6.(5分)如图是一个算法的流程图.则输出的a的值是______.7.(5分)将一颗质地均匀的骰子(一种各个面上分别标有1.2。
3。
4.5.6个点的正方体玩具)先后抛掷2次。
则出现向上的点数之和小于10的概率是______.8.(5分)已知{a n}是等差数列.S n是其前n项和。
若a1+a22=﹣3。
S5=10。
则a9的值是______.9.(5分)定义在区间[0.3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是______.10.(5分)如图.在平面直角坐标系xOy中.F是椭圆+=1(a>b>0)的右焦点.直线y=与椭圆交于B.C两点.且∠BFC=90°.则该椭圆的离心率是______.11.(5分)设f(x)是定义在R上且周期为2的函数.在区间[﹣1.1)上。
f(x)=.其中a∈R。
若f(﹣)=f().则f(5a)的值是______.12.(5分)已知实数x。
y满足.则x2+y2的取值范围是______.13.(5分)如图.在△ABC中.D是BC的中点.E.F是AD上的两个三等分点。
•=4。
•=﹣1。
则•的值是______.14.(5分)在锐角三角形ABC中。
若sinA=2sinBsinC。
则tanAtanBtanC的最小值是______.二、解答题(共6小题。
满分90分)15.(14分)在△ABC中.AC=6.cosB=.C=.(1)求AB的长;(2)求cos(A﹣)的值.16.(14分)如图。
【真题】2016年江苏省高考数学试题(含附加题+答案)

绝密★启用前2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:棱锥的体积13V Sh =,其中S 为底面积,h 为高.一、填空题:本大题共14个小题,每小题5分,共70分.请把答案写在答题卡相应位置上。
1.已知集合{1,2,3,6},{|23},A B x x =-=-<<则=A B ▲.2.复数(12i)(3i),z =+-其中i 为虚数单位,则z 的实部是▲.3.在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是▲.4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是▲.5.函数y =232x x --的定义域是▲.6.如图是一个算法的流程图,则输出的a 的值是▲.7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是▲.8.已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是▲.9.定义在区间[0,3π]上的函数y =sin2x 的图象与y =cos x 的图象的交点个数是▲.10.如图,在平面直角坐标系xOy 中,F 是椭圆22221()x y a b a b +=>>0的右焦点,直线2by =与椭圆交于B ,注意事项考生在答题前请认真阅读本注意事项及各题答题要求:1.本试卷共4页,均为非选择题(第1题~第20题,共20题)。
本卷满分为160分。
考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、考试证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.作答试题必须用0.5毫米黑色墨水的签字笔在答题卡的指定位置作答,在其它位置作答一律无效。
5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
(2021年整理)2016江苏高考数学卷word版(理)及参考答案

(完整)2016江苏高考数学卷word版(理)及参考答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)2016江苏高考数学卷word版(理)及参考答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)2016江苏高考数学卷word版(理)及参考答案的全部内容。
绝密★启用前2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据n x x x ,,,21⋅⋅⋅的方差∑=-=ni i x x n s 122)(1其中∑==ni ixnx 11圆柱的体积公式:V 圆柱=Sh ,其中S 是圆柱的底面积,h 为高 棱锥的体积13V Sh =,其中S 为底面积,h 为高.一、填空题:本大题共14个小题,每小题5分,共70分.请把答案写在答题卡相应位置上。
1。
已知集合{1,2,3,6},{|23},A B x x =-=-<<则=⋂B A ▲ . 2.复数(12i)(3i),z =+-其中i 为虚数单位,则z 的实部是。
▲ .3。
在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是 ▲ .4。
已知一组数据4。
7,4.8,5.1,5。
4,5.5,则该组数据的方差是 ▲ . 5。
函数y 232x x --的定义域是 ▲ .6.如图是一个算法的流程图,则输出的a 的值是 ▲ .7.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求:1.本试卷共4页,均为非选择题(第1题~第20题,共20题).本卷满分为160分。
2016年江苏数学高考试卷含答案和解析

2016年江苏数学高考试卷一、填空题(共14小题,每小题5分,满分70分)1.(5分)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B=______.2.(5分)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是______.3.(5分)在平面直角坐标系xOy中,双曲线﹣=1的焦距是______.4.(5分)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是______.5.(5分)函数y=的定义域是______.6.(5分)如图是一个算法的流程图,则输出的a的值是______.7.(5分)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是______.8.(5分)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是______.9.(5分)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是______.10.(5分)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是______.11.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是______.12.(5分)已知实数x,y满足,则x2+y2的取值范围是______.13.(5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是______.14.(5分)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是______.二、解答题(共6小题,满分90分)15.(14分)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.17.(14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?18.(16分)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.19.(16分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.20.(16分)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC的中点,求证:∠EDC=∠ABD.B.【选修4—2:矩阵与变换】22.(10分)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.C.【选修4—4:坐标系与参数方程】23.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.24.设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.附加题【必做题】25.(10分)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px (p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.26.(10分)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.2016年江苏数学参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(5分)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B={﹣1,2} .【分析】根据已知中集合A={﹣1,2,3,6},B={x|﹣2<x<3},结合集合交集的定义可得答案.【解答】解:∵集合A={﹣1,2,3,6},B={x|﹣2<x<3},∴A∩B={﹣1,2},故答案为:{﹣1,2}【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题.2.(5分)复数z=(1+2i)(3﹣i),其中i为虚数单位,则z的实部是5.【分析】利用复数的运算法则即可得出.【解答】解:z=(1+2i)(3﹣i)=5+5i,则z的实部是5,故答案为:5.【点评】本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题.3.(5分)在平面直角坐标系xOy中,双曲线﹣=1的焦距是2.【分析】确定双曲线的几何量,即可求出双曲线﹣=1的焦距.【解答】解:双曲线﹣=1中,a=,b=,∴c==,∴双曲线﹣=1的焦距是2.故答案为:2.【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础.4.(5分)已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是0.1.【分析】先求出数据4.7,4.8,5.1,5.4,5.5的平均数,由此能求出该组数据的方差.【解答】解:∵数据4.7,4.8,5.1,5.4,5.5的平均数为:=(4.7+4.8+5.1+5.4+5.5)=5.1,∴该组数据的方差:S2=[(4.7﹣5.1)2+(4.8﹣5.1)2+(5.1﹣5.1)2+(5.4﹣5.1)2+(5.5﹣5.1)2]=0.1.故答案为:0.1.【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运用.5.(5分)函数y=的定义域是[﹣3,1] .【分析】根据被开方数不小于0,构造不等式,解得答案.【解答】解:由3﹣2x﹣x2≥0得:x2+2x﹣3≤0,解得:x∈[﹣3,1],故答案为:[﹣3,1]【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题.6.(5分)如图是一个算法的流程图,则输出的a的值是9.【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量a的值,模拟程序的运行过程,可得答案.【解答】解:当a=1,b=9时,不满足a>b,故a=5,b=7,当a=5,b=7时,不满足a>b,故a=9,b=5当a=9,b=5时,满足a>b,故输出的a值为9,故答案为:9【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.7.(5分)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.【分析】出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,由此利用对立事件概率计算公式能求出出现向上的点数之和小于10的概率.【解答】解:将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,基本事件总数为n=6×6=36,出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,出现向上的点数之和不小于10包含的基本事件有:(4,6),(6,4),(5,5),(5,6),(6,5),(6,6),共6个,∴出现向上的点数之和小于10的概率:p=1﹣=.故答案为:.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.8.(5分)已知{a n}是等差数列,S n是其前n项和,若a1+a22=﹣3,S5=10,则a9的值是20.【分析】利用等差数列的通项公式和前n项和公式列出方程组,求出首项和公差,由此能求出a9的值.【解答】解:∵{a n}是等差数列,S n是其前n项和,a1+a22=﹣3,S5=10,∴,解得a1=﹣4,d=3,∴a9=﹣4+8×3=20.故答案为:20.【点评】本题考查等差数列的第9项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.9.(5分)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是7.【分析】画出函数y=sin2x与y=cosx在区间[0,3π]上的图象即可得到答案.【解答】解:画出函数y=sin2x与y=cosx在区间[0,3π]上的图象如下:由图可知,共7个交点.故答案为:7.【点评】本题考查正弦函数与余弦函数的图象,作出函数y=sin2x与y=cosx在区间[0,3π]上的图象是关键,属于中档题.10.(5分)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.【分析】设右焦点F(c,0),将y=代入椭圆方程求得B,C的坐标,运用两直线垂直的条件:斜率之积为﹣1,结合离心率公式,计算即可得到所求值.【解答】解:设右焦点F(c,0),将y=代入椭圆方程可得x=±a=±a,可得B(﹣a,),C(a,),由∠BFC=90°,可得k BF•k CF=﹣1,即有•=﹣1,化简为b2=3a2﹣4c2,由b2=a2﹣c2,即有3c2=2a2,由e=,可得e2==,可得e=,故答案为:.【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为﹣1,考查化简整理的运算能力,属于中档题.11.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是﹣.【分析】根据已知中函数的周期性,结合f(﹣)=f(),可得a值,进而得到f(5a)的值.【解答】解:f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,∴f(﹣)=f(﹣)=﹣+a,f()=f()=|﹣|=,∴a=,∴f(5a)=f(3)=f(﹣1)=﹣1+=﹣,故答案为:﹣【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出a值,是解答的关键.12.(5分)已知实数x,y满足,则x2+y2的取值范围是[,13].【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合两点间的距离公式以及点到直线的距离公式进行求解即可.【解答】解:作出不等式组对应的平面区域,设z=x2+y2,则z的几何意义是区域内的点到原点距离的平方,由图象知A到原点的距离最大,点O到直线BC:2x+y﹣2=0的距离最小,由得,即A(2,3),此时z=22+32=4+9=13,点O到直线BC:2x+y﹣2=0的距离d==,则z=d2=()2=,故z的取值范围是[,13],故答案为:[,13].【点评】本题主要考查线性规划的应用,涉及距离的计算,利用数形结合是解决本题的关键.13.(5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=4,•=﹣1,则•的值是.【分析】由已知可得=+,=﹣+,=+3,=﹣+3,=+2,=﹣+2,结合已知求出2=,2=,可得答案.【解答】解:∵D是BC的中点,E,F是AD上的两个三等分点,∴=+,=﹣+,=+3,=﹣+3,∴•=2﹣2=﹣1,•=92﹣2=4,∴2=,2=,又∵=+2,=﹣+2,∴•=42﹣2=,故答案为:【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档.14.(5分)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是8.【分析】结合三角形关系和式子sinA=2sinBsinC可推出sinBcosC+cosBsinC=2sinBsinC,进而得到tanB+tanC=2tanBtanC,结合函数特性可求得最小值.【解答】解:由sinA=sin(π﹣A)=sin(B+C)=sinBcosC+cosBsinC,sinA=2sinBsinC,可得sinBcosC+cosBsinC=2sinBsinC,①由三角形ABC为锐角三角形,则cosB>0,cosC>0,在①式两侧同时除以cosBcosC可得tanB+tanC=2tanBtanC,又tanA=﹣tan(π﹣A)=﹣tan(B+C)=﹣②,则tanAtanBtanC=﹣•tanBtanC,由tanB+tanC=2tanBtanC可得tanAtanBtanC=﹣,令tanBtanC=t,由A,B,C为锐角可得tanA>0,tanB>0,tanC>0,由②式得1﹣tanBtanC<0,解得t>1,tanAtanBtanC=﹣=﹣,=()2﹣,由t>1得,﹣≤<0,因此tanAtanBtanC的最小值为8,当且仅当t=2时取到等号,此时tanB+tanC=4,tanBtanC=2,解得tanB=2+,tanC=2﹣,tanA=4,(或tanB,tanC互换),此时A,B,C均为锐角.【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性.二、解答题(共6小题,满分90分)15.(14分)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.【分析】(1)利用正弦定理,即可求AB的长;(2)求出cosA、sinA,利用两角差的余弦公式求cos(A﹣)的值.【解答】解:(1)∵△ABC中,cosB=,∴sinB=,∵,∴AB==5;(2)cosA=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣.∵A为三角形的内角,∴sinA=,∴cos(A﹣)=cosA+sinA=.【点评】本题考查正弦定理,考查两角和差的余弦公式,考查学生的计算能力,属于基础题.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.【分析】(1)通过证明DE∥AC,进而DE∥A1C1,据此可得直线DE∥平面A1C1F1;(2)通过证明A1F⊥DE结合题目已知条件A1F⊥B1D,进而可得平面B1DE⊥平面A1C1F.【解答】解:(1)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∴DE∥AC,∵ABC﹣A1B1C1为棱柱,∴AC∥A1C1,∴DE∥A1C1,∵A1C1⊂平面A1C1F,且DE⊄平面A1C1F,∴DE∥A1C1F;(2)∵ABC﹣A1B1C1为直棱柱,∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,又∵A1C1⊥A1B1,且AA1∩A1B1=A1,AA1、A1B1⊂平面AA1B1B,∴A1C1⊥平面AA1B1B,∵DE∥A1C1,∴DE⊥平面AA1B1B,又∵A1F⊂平面AA1B1B,∴DE⊥A1F,又∵A1F⊥B1D,DE∩B1D=D,且DE、B1D⊂平面B1DE,∴A1F⊥平面B1DE,又∵A1F⊂平面A1C1F,∴平面B1DE⊥平面A1C1F.【点评】本题考查直线与平面平行的证明,以及平面与平面相互垂直的证明,把握常用方法最关键,难度不大.17.(14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?【分析】(1)由正四棱柱的高O1O是正四棱锥的高PO1的4倍,可得PO1=2m时,O1O=8m,进而可得仓库的容积;(2)设PO1=xm,则O1O=4xm,A1O1=m,A1B1=•m,代入体积公式,求出容积的表达式,利用导数法,可得最大值.【解答】解:(1)∵PO1=2m,正四棱柱的高O1O是正四棱锥的高PO1的4倍.∴O1O=8m,∴仓库的容积V=×62×2+62×8=312m3,(2)若正四棱锥的侧棱长为6m,设PO1=xm,则O1O=4xm,A1O1=m,A1B1=•m,则仓库的容积V=×(•)2•x+(•)2•4x=x3+312x,(0<x<6),∴V′=﹣26x2+312,(0<x<6),当0<x<2时,V′>0,V(x)单调递增;当2<x<6时,V′<0,V(x)单调递减;故当x=2时,V(x)取最大值;即当PO1=2m时,仓库的容积最大.【点评】本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档.18.(16分)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.【分析】(1)设N(6,n),则圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,从而得到|7﹣n|=|n|+5,由此能求出圆N的标准方程.(2)由题意得OA=2,k OA=2,设l:y=2x+b,则圆心M到直线l的距离:d=,由此能求出直线l的方程.(3)=,即||=,又||≤10,得t∈[2﹣2,2+2],对于任意t∈[2﹣2,2+2],欲使,只需要作直线TA的平行线,使圆心到直线的距离为,由此能求出实数t的取值范围.【解答】解:(1)∵N在直线x=6上,∴设N(6,n),∵圆N与x轴相切,∴圆N为:(x﹣6)2+(y﹣n)2=n2,n>0,又圆N与圆M外切,圆M:x2+y2﹣12x﹣14y+60=0,即圆M:((x﹣6)2+(x﹣7)2=25,∴|7﹣n|=|n|+5,解得n=1,∴圆N的标准方程为(x﹣6)2+(y﹣1)2=1.(2)由题意得OA=2,k OA=2,设l:y=2x+b,则圆心M到直线l的距离:d==,则|BC|=2=2,BC=2,即2=2,解得b=5或b=﹣15,∴直线l的方程为:y=2x+5或y=2x﹣15.(3)=,即,即||=||,||=,又||≤10,即≤10,解得t∈[2﹣2,2+2],对于任意t∈[2﹣2,2+2],欲使,此时,||≤10,只需要作直线TA的平行线,使圆心到直线的距离为,必然与圆交于P、Q两点,此时||=||,即,因此实数t的取值范围为t∈[2﹣2,2+2],.【点评】本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.19.(16分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.【分析】(1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函数的最值,转化求解即可.(2)求出g(x)=f(x)﹣2=a x+b x﹣2,求出函数的导数,构造函数h(x)=+,求出g(x)的最小值为:g(x0).同理①若g(x0)<0,g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,利用函数g(x)=f(x)﹣2有且只有1个零点,推出g(x0)=0,然后求解ab=1.【解答】解:函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①方程f(x)=2;即:=2,可得x=0.②不等式f(2x)≥mf(x)﹣6恒成立,即≥m()﹣6恒成立.令t=,t≥2.不等式化为:t2﹣mt+4≥0在t≥2时,恒成立.可得:△≤0或即:m2﹣16≤0或m≤4,∴m∈(﹣∞,4].实数m的最大值为:4.(2)g(x)=f(x)﹣2=a x+b x﹣2,g′(x)=a x lna+b x lnb=a x[+]lnb,0<a<1,b>1可得,令h(x)=+,则h(x)是递增函数,而,lna<0,lnb>0,因此,x0=时,h(x0)=0,因此x∈(﹣∞,x0)时,h(x)<0,a x lnb>0,则g′(x)<0.x∈(x0,+∞)时,h(x)>0,a x lnb>0,则g′(x)>0,则g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此g(x)的最小值为:g(x0).①若g(x0)<0,x<log a2时,a x>=2,b x>0,则g(x)>0,因此x1<log a2,且x1<x0时,g(x1)>0,因此g(x)在(x1,x0)有零点,则g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,函数g(x)=f(x)﹣2有且只有1个零点,g(x)的最小值为g(x0),可得g(x0)=0,由g(0)=a0+b0﹣2=0,因此x0=0,因此=0,﹣=1,即lna+lnb=0,ln(ab)=0,则ab=1.可得ab=1.【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒成立的应用,考查分析问题解决问题的能力.20.(16分)记U={1,2,…,100},对数列{a n}(n∈N*)和U的子集T,若T=∅,定义S T=0;若T={t1,t2,…,t k},定义S T=++…+.例如:T={1,3,66}时,S T=a1+a3+a66.现设{a n}(n∈N*)是公比为3的等比数列,且当T={2,4}时,S T=30.(1)求数列{a n}的通项公式;(2)对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:S T<a k+1;(3)设C⊆U,D⊆U,S C≥S D,求证:S C+S C∩D≥2S D.【分析】(1)根据题意,由S T的定义,分析可得S T=a2+a4=a2+9a2=30,计算可得a2=3,进而可得a1的值,由等比数列通项公式即可得答案;(2)根据题意,由S T的定义,分析可得S T≤a1+a2+…a k=1+3+32+…+3k﹣1,由等比数列的前n项和公式计算可得证明;(3)设A=∁C(C∩D),B=∁D(C∩D),则A∩B=∅,进而分析可以将原命题转化为证明S C ≥2S B,分2种情况进行讨论:①、若B=∅,②、若B≠∅,可以证明得到S A≥2S B,即可得证明.【解答】解:(1)当T={2,4}时,S T=a2+a4=a2+9a2=30,因此a2=3,从而a1==1,故a n=3n﹣1,(2)S T≤a1+a2+…a k=1+3+32+…+3k﹣1=<3k=a k+1,(3)设A=∁C(C∩D),B=∁D(C∩D),则A∩B=∅,分析可得S C=S A+S C∩D,S D=S B+S C∩D,则S C+S C∩D﹣2S D=S A﹣2S B,因此原命题的等价于证明S C≥2S B,由条件S C≥S D,可得S A≥S B,①、若B=∅,则S B=0,故S A≥2S B,②、若B≠∅,由S A≥S B可得A≠∅,设A中最大元素为l,B中最大元素为m,若m≥l+1,则其与S A<a i+1≤a m≤S B相矛盾,因为A∩B=∅,所以l≠m,则l≥m+1,S B≤a1+a2+…a m=1+3+32+…+3m﹣1=≤=,即S A≥2S B,综上所述,S A≥2S B,故S C+S C∩D≥2S D.【点评】本题考查数列的应用,涉及新定义的内容,解题的关键是正确理解题目中对于新定义的描述.附加题【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.【选修4—1几何证明选讲】21.(10分)如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E为BC的中点,求证:∠EDC=∠ABD.【分析】依题意,知∠BDC=90°,∠EDC=∠C,利用∠C+∠DBC=∠ABD+∠DBC=90°,可得∠ABD=∠C,从而可证得结论.【解答】解:由BD⊥AC可得∠BDC=90°,因为E为BC的中点,所以DE=CE=BC,则:∠EDC=∠C,由∠BDC=90°,可得∠C+∠DBC=90°,由∠ABC=90°,可得∠ABD+∠DBC=90°,因此∠ABD=∠C,而∠EDC=∠C,所以,∠EDC=∠ABD.【点评】本题考查三角形的性质应用,利用∠C+∠DBC=∠ABD+∠DBC=90°,证得∠ABD=∠C是关键,属于中档题.B.【选修4—2:矩阵与变换】22.(10分)已知矩阵A=,矩阵B的逆矩阵B﹣1=,求矩阵AB.【分析】依题意,利用矩阵变换求得B=(B﹣1)﹣1==,再利用矩阵乘法的性质可求得答案.【解答】解:∵B﹣1=,∴B=(B﹣1)﹣1==,又A=,∴AB==.【点评】本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题.C.【选修4—4:坐标系与参数方程】23.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),椭圆C的参数方程为(θ为参数),设直线l与椭圆C相交于A,B两点,求线段AB的长.【分析】分别化直线与椭圆的参数方程为普通方程,然后联立方程组,求出直线与椭圆的交点坐标,代入两点间的距离公式求得答案.【解答】解:由,由②得,代入①并整理得,.由,得,两式平方相加得.联立,解得或.∴|AB|=.【点评】本题考查直线与椭圆的参数方程,考查了参数方程化普通方程,考查直线与椭圆位置关系的应用,是基础题.24.设a>0,|x﹣1|<,|y﹣2|<,求证:|2x+y﹣4|<a.【分析】运用绝对值不等式的性质:|a+b|≤|a|+|b|,结合不等式的基本性质,即可得证.【解答】证明:由a>0,|x﹣1|<,|y﹣2|<,可得|2x+y﹣4|=|2(x﹣1)+(y﹣2)|≤2|x﹣1|+|y﹣2|<+=a,则|2x+y﹣4|<a成立.【点评】本题考查绝对值不等式的证明,注意运用绝对值不等式的性质,以及不等式的简单性质,考查运算能力,属于基础题.附加题【必做题】25.(10分)如图,在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px (p>0).(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.①求证:线段PQ的中点坐标为(2﹣p,﹣p);②求p的取值范围.【分析】(1)求出抛物线的焦点坐标,然后求解抛物线方程.(2):①设点P(x1,y1),Q(x2,y2),通过抛物线方程,求解k PQ,通过P,Q关于直线l对称,点的k PQ=﹣1,推出,PQ的中点在直线l上,推出=2﹣p,即可证明线段PQ的中点坐标为(2﹣p,﹣p);②利用线段PQ中点坐标(2﹣p,﹣p).推出,得到关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,列出不等式即可求出p的范围.【解答】解:(1)∵l:x﹣y﹣2=0,∴l与x轴的交点坐标(2,0),即抛物线的焦点坐标(2,0).∴,∴抛物线C:y2=8x.(2)证明:①设点P(x1,y1),Q(x2,y2),则:,即:,k PQ==,又∵P,Q关于直线l对称,∴k PQ=﹣1,即y1+y2=﹣2p,∴,又PQ的中点在直线l上,∴==2﹣p,∴线段PQ的中点坐标为(2﹣p,﹣p);②因为Q中点坐标(2﹣p,﹣p).∴,即∴,即关于y2+2py+4p2﹣4p=0,有两个不相等的实数根,∴△>0,(2p)2﹣4(4p2﹣4p)>0,∴p∈.【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力.26.(10分)(1)求7C﹣4C的值;(2)设m,n∈N*,n≥m,求证:(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【分析】(1)由已知直接利用组合公式能求出7的值.(2)对任意m∈N*,当n=m时,验证等式成立;再假设n=k(k≥m)时命题成立,推导出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【解答】解:(1)7=﹣4×=7×20﹣4×35=0.证明:(2)对任意m∈N*,①当n=m时,左边=(m+1)=m+1,右边=(m+1)=m+1,等式成立.②假设n=k(k≥m)时命题成立,即(m+1)C+(m+2)C+(m+3)C+…+k+(k+1)=(m+1),当n=k+1时,左边=(m+1)+(m+2)+(m+3)++(k+1)+(k+2)=,右边=∵=(m+1)[﹣]=(m+1)×[k+3﹣(k﹣m+1)]=(k+2)=(k+2),∴=(m+1),∴左边=右边,∴n=k+1时,命题也成立,∴m,n∈N*,n≥m,(m+1)C+(m+2)C+(m+3)C+…+nC+(n+1)C=(m+1)C.【点评】本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和数学归纳法的合理运用.2016数学21。
2016年高考江苏数学试题及答案(word解析版)

2016年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式: 样本数据12,,,n x x x 的方差()2211ni i s x xn ==-∑,其中11ni i x x n ==∑.棱柱的体积V Sh =,其中S 是棱柱的底面积,h 是高.棱锥的体积13V Sh =,其中S 是棱锥的底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共计70分. 请把答案填写在答题卡相应位置上......... (1)【2016年江苏,1,5分】已知集合{}1,2,3,6A =-,{}|23B x x =-<<,则A B =_______.【答案】{}1,2-【解析】由交集的定义可得{}1,2AB =-.【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题.(2)【2016年江苏,2,5分】复数()()12i 3i z =+-,其中i 为虚数单位,则z 的实部是_______. 【答案】5【解析】由复数乘法可得55i z =+,则则z 的实部是5.【点评】本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题.(3)【2016年江苏,3,5分】在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是_______.【答案】210【解析】2210c a b =+=,因此焦距为2210c =.【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础 (4)【2016年江苏,4,5分】已知一组数据4。
7,4。
8,5。
1,5.4,5。
5,则该组数据的方差是_______. 【答案】0.1【解析】 5.1x =,()22222210.40.300.30.40.15s =++++=.【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运用. (5)【2016年江苏,5,5分】函数232y x x =--的定义域是_______. 【答案】[]3,1-【解析】2320x x --≥,解得31x -≤≤,因此定义域为[]3,1-.【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题. (6)【2016年江苏,6,5分】如图是一个算法的流程图,则输出a 的值是________. 【答案】9【解析】,a b 的变化如下表:a 1 5 9b 9 7 5 则输出时9a =.【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答. (7)【2016年江苏,7,5分】将一个质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点为正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是________.【答案】56【解析】将先后两次点数记为(),x y ,则共有6636⨯=个等可能基本事件,其中点数之和大于等于10有()()()()()()4,6,5,5,5,6,6,4,6,5,6,6六种,则点数之和小于10共有30种,概率为305366=.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.(8)【2016年江苏,8,5分】已知{}n a 是等差数列,n S 是其前n 项和.若2123a a +=-,510S =,则9a 的值是_______. 【答案】20【解析】设公差为d ,则由题意可得()2113a a d ++=-,151010a d +=,解得14a =-,3d =,则948320a =-+⨯=. 【点评】本题考查等差数列的第9项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.(9)【2016年江苏,9,5分】定义在区间[]0,3π上的函数sin 2y x =的图象与cos y x =的图象的交点个数是________.【答案】7【解析】画出函数图象草图,共7个交点.【点评】本题考查正弦函数与余弦函数的图象,作出函数sin 2y x =与cos y x =在区间[]0,3π上的图象是关键,属于中档题.(10)【2016年江苏,10,5分】如图,在平面直角坐标系xOy 中,F 是椭圆()222210x y a b a b +=>>的右焦点,直线2by =与椭圆交于,B C 两点,且90BFC ∠=︒,则该椭圆的离心率是________【解析】由题意得(),0F c ,直线2by =与椭圆方程联立可得2b B ⎛⎫ ⎪ ⎪⎝⎭,2b C ⎫⎪⎪⎝⎭,由90BFC ∠=︒可得 0BF CF ⋅=,2b BF c ⎛⎫=+- ⎪ ⎪⎝⎭,2b CF c ⎛⎫=- ⎪ ⎪⎝⎭,则22231044c a b -+=,由222b a c =-可得 223142c a =,则c e a ==. 【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为﹣1,考查化简整理的运算能力,属于中档题.(11)【2016年江苏,11,5分】设()f x 是定义在R 上且周期为2的函数,在区间[)1,1-上(),10,2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中a ∈R ,若5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,则()5f a 的值是________.【答案】25-【解析】由题意得511222f f a ⎛⎫⎛⎫-=-=-+ ⎪ ⎪⎝⎭⎝⎭,91211225210f f ⎛⎫⎛⎫==-= ⎪ ⎪⎝⎭⎝⎭,由5922f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭可得11210a -+=,则35a =,则()()()325311155f a f f a ==-=-+=-+=-.【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出a 值,是解答的关键.(12)【2016年江苏,12,5分】已知实数,x y 满足240,220,330,x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩ 则22x y +的取值范围是________.【答案】4,135⎡⎤⎢⎥⎣⎦【解析】在平面直角坐标系中画出可行域如下:22x y +为可行域内的点到原点距离的平方.可以看出图中A 点距离原点最近,此时距离为原点A 到直线220x y +-=的距离,d ==,则()22min 45x y +=,图中B 点距离原点最远,B 点为240x y -+=与330x y --=交点,则()2,3B ,则()22max13x y +=.【点评】本题主要考查线性规划的应用,涉及距离的计算,利用数形结合是解决本题的关键. (13)【2016年江苏,13,5分】如图,在ABC △中,D 是BC 的中点,,E F 是AD 上两个三等分点,4BA CA ⋅=,1BF CF ⋅=-,则BE CE ⋅的值是________.【答案】78【解析】令DF a =,DB b =,则DC b =-,2DE a =,3DA a =,则3BA a b =-,3CA a b =+,2BE a b =-,2CE a b =+,BF a b =-,CF a b =+,则229BA CA a b ⋅=-,22BF CF a b ⋅=-, 224BE CE a b ⋅=-,由4BA CA ⋅=,1BF CF ⋅=-可得2294a b -=,221a b -=-,因此22513,88a b ==,因此22451374888BE CE a b ⨯⋅=-=-=.【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档. (14)【2016年江苏,14,5分】在锐角三角形ABC 中,sin 2sin sin A B C =,则tan tan tan A B C 的最小值是_______. 【答案】8【解析】由()()sin sin πsin sin cos cos sin A A B C B C B C =-=+=+,sin 2sin sin A B C =,可得sin cos cos sin 2sin sin B C B C B C +=(*),由三角形ABC 为锐角三角形,则cos 0,cos 0B C >>, 在(*)式两侧同时除以cos cos B C 可得tan tan 2tan tan B C B C +=,又()()tan tan tan tan πtan 1tan tan B CA ABC B C+=--=-+=--(#),则tan tan tan tan tan tan tan 1tan tan B CA B C B C B C+=-⨯-,由tan tan 2tan tan B C B C +=可得()22tan tan tan tan tan 1tan tan B C A B C B C=--,令tan tan B C t =,由,,A B C 为锐角可得tan 0,tan 0,tan 0A B C >>>, 由(#)得1tan tan 0B C -<,解得1t >,2222tan tan tan 111t A B C t t t =-=---,221111124t t t ⎛⎫-=-- ⎪⎝⎭,由1t >则211104t t >-≥-,因此tan tan tan A B C 最小值为8, 当且仅当2t =时取到等号,此时tan tan 4B C +=,tan tan 2B C =,解得tan 2tan 2tan 4B C A ===(或tan ,tan B C 互换),此时,,A B C 均为锐角.【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性. 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出必要的文字说明、证明过程或演算步骤.(15)【2016年江苏,15,14分】在ABC △中,6AC =,4cos 5B =,π4C =.(1)求AB 的长;(2)求πcos 6A ⎛⎫- ⎪⎝⎭的值. 解:(1)4cos 5B =,B 为三角形的内角,3sin 5B ∴=,sinC sin AB ACB =,635=,即:AB = (2)()cos cos sin sin cos cos A C B B C B C =-+=-,cos A ∴=又A 为三角形的内角,sin A ∴=,π1cos sin 62A A A ⎛⎫∴-+ ⎪⎝⎭【点评】本题考查正弦定理,考查两角和差的余弦公式,考查学生的计算能力,属于中档题.(16)【2016年江苏,16,14分】如图,在直三棱柱111ABC A B C -中,,D E 分别为,AB BC 的中点,点F 在侧棱1B B 上,且11B D A F ⊥,1111AC A B ⊥.求证: (1)直线//DE 平面11A C F ; (2)平面1B DE ⊥平面11A C F .解:(1),D E 为中点,DE ∴为ABC ∆的中位线,//DE AC ∴,又111ABC A B C -为棱柱,11//AC AC ∴11//DE AC ∴,又11AC ⊂平面11A C F ,且11DE AC F ⊄,//DE ∴平面11A C F .(2)111ABC A B C -为直棱柱,1AA ∴⊥平面111A B C ,111AA AC ∴⊥,又1111AC A B ⊥,且1111AA A B A =,111,AA A B ⊂平面11AA B B ,11AC ∴⊥平面11AA B B ,又11//DE AC ,DE ∴⊥平面11AA B B , 又1A F ⊂平面11AA B B ,1DE A F ∴⊥,又11A F B D ⊥,1DEB D D =,且1,DE B D ⊂平面1B DE ,1A F ∴⊥平面1B DE ,又111A F AC F ⊂,∴平面1B DE ⊥平面11A C F .【点评】本题考查直线与平面平行的证明,以及平面与平面相互垂直的证明,把握常用方法最关键,难答不大. (17)【2016年江苏,17,14分】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥1111P A B C D -,下部分的形状是正四棱柱1111ABCD A B C D -(如图所示),并要求正四棱柱 的高1O O 是正四棱锥的高1PO 的4倍.(1)若6m AB =,12m PO =,则仓库的容积是多少;(2)若正四棱锥的侧棱长为6m ,当1PO 为多少时,仓库的容积最大?解:(1)12m PO =,则18m OO =,1111231116224m 33P A B C D ABCD V S PO -⋅=⨯⨯==, 111123168288m ABCD A B C D ABCD V S OO -⋅=⨯==,111111113312m =P A B C D ABCD A B C D V V V --+=,故仓库的容积为3312m . (2)设1m PO x =,仓库的容积为()V x ,则14m OO x =,11m A O =,11m A B =,()111123331111272224m 3333P A B C D ABCD V S PO x x x x x -⋅=⨯⨯=-=-=,1111233142888m ABCD A B C D ABCD V S OO x x x-⋅=⨯=-=,()()111111113332262428883120633=P A B C D ABCD A B C D V x V V x x x x x x x --+=-+-=-+<<,()()22'263122612V x x x =-+=--()06x <<,当(x ∈时,()'0V x >,()V x 单调递增,当()x ∈时,()'0V x <,()V x 单调递减,因此,当x =时,()V x 取到最大值,即1m PO =时,仓库的容积最大.【点评】本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档. (18)【2016年江苏,18,16分】如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :221214600x y x y +--+=及其上一点()2,4A .(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; (2)设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;(3)设点(),0T t 满足:存在圆M 上的两点P 和Q ,使得TA TP TQ +=,求实数t 的取值范围.解:(1)因为N 在直线6x =上,设()6,N n ,因为与x 轴相切,则圆N 为()()2226x y n n -+-=,0n >,又圆N 与圆M 外切,圆M :()()226725x x -+-=,则75n n -=+,解得1n =,即圆N 的标准方程为()()22611x y -+-=.(2)由题意得OA =2OA k = 设:2l y x b =+,则圆心M 到直线l的距离d =,则BC ==BC ==1A FEDCBAC 1B 1A 1解得5b =或15b =-,即l :25y x =+或215y x =-. (3)TA TP TQ +=,即TA TQ TP PQ =-=,即TA PQ =,(TA t =10PQ ≤,10,解得2t⎡∈-+⎣,对于任意2t ⎡∈-+⎣,欲使TA PQ =,此时10TA ≤,只需要作直线TA 的平行线,2TA 必然与圆交于P Q 、两点,此时TA PQ=,即TA PQ =,因此对于任意2t ⎡∈-+⎣,均满足题意,综上2t ⎡∈-+⎣.【点评】本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.(19)【2016年江苏,19,16分】已知函数()()0,0,1,1x x f x a b a b a b =+>>≠≠. (1)设2a =,12b =. ①求方程()2f x =的根;②若对于任意x ∈R ,不等式()()26f x mf x -≥恒成立,求实数m 的最大值;(2)若01a <<,1b >,函数()()2g x f x =-有且只有1个零点,求ab 的值. 解:(1)①()122xxf x ⎛⎫=+ ⎪⎝⎭,由()2f x =可得1222x x +=,则()222210x x -⨯+=,即()2210x -=,则21x =,0x =.②由题意得221122622x x x x m ⎛⎫++- ⎪⎝⎭≥恒成立,令122xx t =+,则由20x >可得2t =≥,此时226t mt --≥恒成立,即244t mt t t+=+≤恒成立∵2t ≥时44t t +=≥,当且仅当2t =时 等号成立,因此实数m 的最大值为4.(2)()()22x x g x f x a b =-=+-,()ln 'ln ln ln ln x x x xa b g x a a b b a b b a ⎡⎤⎛⎫=+=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,由01a <<,1b >可得1b a >,令()ln ln xb a h x a b ⎛⎫=+ ⎪⎝⎭,则()h x 递增,而ln 0,ln 0a b <>,因此0ln log ln b a a x b ⎛⎫=- ⎪⎝⎭时()00h x =, 因此()0,x x ∈-∞时,()0h x <,ln 0x a b >,则()'0g x <;()0,x x ∈+∞时,()0h x >,ln 0x a b >, 则()'0g x >;则()g x 在()0,x -∞递减,()0,x +∞递增,因此()g x 最小值为()0g x ,① 若()00g x <,log 2a x <时,log 22a x a a >=,0x b >,则()0g x >;x >log b 2时,0x a >,log 22b x b b >=, 则()0g x >;因此1log 2a x <且10x x <时,()10g x >,因此()g x 在()10,x x 有零点, 2log 2b x >且20x x >时,()20g x >,因此()g x 在()02,x x 有零点, 则()g x 至少有两个零点,与条件矛盾;② 若()00g x ≥,由函数()g x 有且只有1个零点,()g x 最小值为()0g x ,可得()00g x =,由()00020g a b =+-=,因此00x =,因此ln log 0ln b a a b ⎛⎫-= ⎪⎝⎭,即ln 1ln a b -=,即ln ln 0a b +=, 因此()ln 0ab =,则1ab =.【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒成立的应用,考查分析问题解决问题的能力.(20)【2016年江苏,20,16分】记{}1,2,,100U =.对数列{}n a (*n ∈N )和U 的子集T ,若T =∅,定义0T S =;若{}12,,,k T t t t =,定义12k T t t t S a a a =+++.例如:{}1,3,66T =时,1366T S a a a =++.现设{}n a (*n ∈N )是公比为3的等比数列,且当{}2,4T =时,30T S =. (1)求数列{}n a 的通项公式;(2)对任意正整数k (1100k ≤≤),若{}1,2,,T k ⊆,求证:1T k S a +<;(3)设C U ⊆,D U ⊆,C D S S ≥,求证:2C CDD S S S +≥.解:(1)当{}2,4T =时,2422930T S a a a a =+=+=,因此23a =,从而2113a a ==,13n n a -=. (2)2112131133332k k kT k k S a a a a -+-++=++++=<=≤(3)设()C A C D =,()D B C D =,A B =∅,C A C D S S S =+,D B CDS S S =+, 22C CDD A B S S S S S +-=-,因此原题就等价于证明2A B S S ≥.由条件C D S S ≥可知A B S S ≥. ① 若B =∅,则0B S =,所以2A B S S ≥.② 若B ≠∅,由A B S S ≥可知A ≠∅,设A 中最大元素为l ,B 中最大元素为m ,若1m l +≥,则由第⑵小题,1A l m B S a a S +<≤≤,矛盾.因为A B =∅,所以l m ≠,所以1l m +≥,211123113332222m m m lA B m a a S S a a a -+-+++=++++=<≤≤≤,即2A B S S >.综上所述,2A B S S ≥,因此2C C D D S S S +≥.【点评】本题考查数列的应用,涉及新定义的内容,解题的关键是正确理解题目中对于新定义的描述.数学Ⅱ【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题......,并在相应的答题区域内作答............,若多做,则按作答 的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (21—A)【2016年江苏,21—A ,10分】(选修4-1:几何证明选讲)如图,在ABC △中,90ABC ∠=︒,BD AC ⊥,D 为垂足,E 是BC 中点,求证:EDC ABD ∠=∠.解:由BD AC ⊥可得90BDC ∠=︒,由E 是BC 中点可得12DE CE BC ==,则EDC C ∠=∠, 由90BDC ∠=︒可得90C DBC ∠+∠=︒,由90ABC ∠=︒可得90ABD DBC ∠+∠=︒,因此ABD C ∠=∠, 又EDC C ∠=∠可得EDC ABD ∠=∠.【点评】本题考查三角形的性质应用,利用∠C+∠DBC=∠ABD+∠DBC=90°,证得∠ABD=∠C 是关键,属于中档题.(21—B )【2016年江苏,21—B ,10分】(选修4—2:矩阵与变换)已知矩阵1202⎡⎤=⎢⎥-⎣⎦A ,矩阵B 的逆矩阵111202-⎡⎤-⎢⎥=⎢⎥⎣⎦B ,求矩阵AB .解:()11112124221010222--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦B B ,因此151121*********⎡⎤⎡⎤⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦AB . 【点评】本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题. (21—C )【2016年江苏,21—C,10分】(选修4-4:坐标系与参数方程)在平面直角坐标系xOy 中,已知直线l 的参数方程为()11,2,x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数,椭圆C 的参数方程为()cos ,2sin ,x y θθθ=⎧⎨=⎩为参数,设直线l 与椭圆C 相交于,A B 两点,求线段AB 的长.ED CB A解:直线l0y -,椭圆C 方程化为普通方程为2214y x +=,联立得22014y y x --=⎨+=⎪⎩,解得10x y =⎧⎨=⎩或17x y ⎧=-⎪⎪⎨⎪=⎪⎩因此167AB ==. 【点评】本题考查直线与椭圆的参数方程,考查了参数方程化普通方程,考查直线与椭圆位置关系的应用,是基础题.(21—D )【2016年江苏,21-D 】(本小题满分10分)(选修4—4:不等式选讲)设0a >,13a x -<,23ay -<,求证:24x y a +-<.解:由13a x -<可得2223a x -<,22422233a a x y x y a +--+-<+=≤. 【点评】本题考查绝对值不等式的证明,注意运用绝对值不等式的性质,以及不等式的简单性质,考查运算能力,属于基础题.【必做题】第22、23题,每小题10分,计20分.请把答案写在答题卡的指定区域内............ (22)【2016年江苏,22,10分】如图,在平面直角坐标系xOy 中,已知直线:20l x y --=,抛物线()2:20C y px p =>.(1)若直线l 过抛物线C 的焦点,求抛物线C 的方程;(2)已知抛物线C 上存在关于直线l 对称的相异两点P 和Q .①求证:线段PQ 上的中点坐标为()2,p p --; ②求p 的取值范围.解:(1):20l x y --=,∴l 与x 轴的交点坐标为()2,0,即抛物线的焦点为()2,0,22p∴=,28y x ∴=. (2)① 设点()11,P x y ,()22,Q x y ,则:21122222y px y px ⎧=⎪⎨=⎪⎩,即21122222y x p y x p⎧=⎪⎪⎨⎪=⎪⎩,12221212222PQ y y p k y y y y p p -==+-, 又,P Q 关于直线l 对称,1PQ k ∴=-,即122y y p +=-,122y y p +∴=-,又PQ 中点一定在直线l 上,12122222x x y y p ++∴=+=-,∴线段PQ 上的中点坐标为()2,p p --;② 中点坐标为()2,p p --,122212122422y y p y y x x p p +=-⎧⎪∴+⎨+==-⎪⎩即1222212284y y p y y p p +=-⎧⎨+=-⎩,12212244y y p y y p p +=-⎧∴⎨=-⎩, 即关于222440y py p p ++-=有两个不等根,0∴∆>,()()2224440p p p -->,40,3p ⎛⎫∴∈ ⎪⎝⎭.【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力. (23)【2016年江苏,23,10分】(1)求34677C 4C -的值;(2)设*,m n ∈N ,n m ≥,求证:()()()()()212121C 2C 3C C 1C 1C m m m m m m m m m n n n m m m n n m +++-++++++++++=+.解:(1)34677C 4C 7204350-=⨯-⨯=.(2)对任意的*m ∈N ,① 当n m =时,左边()1C 1m m m m =+=+,右边()221C 1m m m m ++=+=+,等式成立,② 假设()n k k m =≥时命题成立,即()()()()()212121C 2C 3C C 1C 1C m m mm m m m m m k k k m m m k k m +++-++++++++++=+,当1n k =+时,左边=()()()()()12111C 2C 3C C 1C 2C m m mm m mm m m k k k m m m k k k ++-++++++++++++()()2211C2Cm m k k m k +++=+++,右边()231C m k m ++=+,而()()()()()()()()()22323!2!1C 1C 12!1!2!!m m k k k k m m m m k m m k m ++++⎡⎤+++-+=+-⎢⎥+-++-⎢⎥⎣⎦()()()()()()()()()12!1!13122C 2!1!!1!mk k k m k k m k k m k m m k m +++=+⨯+--+=+=+⎡⎤⎣⎦+-+-+ 因此()()()222131C 2C 1C m m m k k k m k m ++++++++=+,因此左边=右边,因此1n k =+时命题也成立,综合①②可得命题对任意n m ≥均成立.另解:因为()()111C 1C m m k k k m +++=+,所以左边()()()1111211C 1C 1C m m m m m n m m m ++++++=++++++()()1111211C C C m m m m m n m ++++++=++++又由111C CCkk k n n n ---=+,知2212112111112111221121C C C C C C C C C C C C m m m m m m m m m m m m n n n n n n m m n m m n ++++++++++++++++++++++=+=++==+++=+++,所以,左边=右边.【点评】本题考查组合数的计算与证明,是中档题,解题时要认真审题,注意组合数公式和数学归纳法的合理运用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年江苏高考数学试题(Word 版-)
2016年江苏数学高考试题
数学Ⅰ试题
一、填空题:本大题共14个小题,每小题5分,共70分
1.已知集合{1,2,3,6},{|23},A B x x =-=-<<则=A B ________________.
2.复数(12i)(3i),z =+-其中i 为虚数单位,则z 的实部是________________.
3.在平面直角坐标系xOy 中,双曲线22
173x y -=的焦距是
________________.
4.已知一组数据4.7,4.8,
5.1,5.4,5.5,则该组数据的方差是________________.
5.函数y 2
32x x --________
10.如图,在平面直角坐标系xOy 中,F 是椭圆2222
1()x y a b a b +=>>0的右焦点,直线2b y =与椭圆交于B ,C 两点,且90BFC ∠= ,则该椭圆的离心率是________
11.设f (x )是定义在R 上且周期为2的函数,在区间[ −1,1)上,,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -=,则f (5a )的值是________
12. 已知实数x ,y 满足240220
330x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩,则x 2+y 2的取值范围
是________
13.如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,4BC CA ⋅=,1BF CF ⋅=-,则BE CE ⋅的值是________
14.在锐角三角形ABC 中,若sin A =2sin B sin C ,则tan
A tan
B tan
C 的最小值是________
二、解答题 (本大题共6小题,共90分)
15.(本小题满分14分)
在ABC △中,AC =6,4πcos .54
B C , (1)求AB 的长; (2)求πcos(6A )的值.
16.(本小题满分14分)
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且11
AC A B
⊥.
⊥,1111
B D A F
求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
17.(本小题满分14分)
现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥1111P A B C D -,下部分的形状是正四棱柱1111ABCD A B C D -(如图所示),并要求正四棱柱的高1PO 的四倍. (1)若16,PO 2,AB m m ==则仓库的容积是多少?
(2)若正四棱柱的侧棱长为6m ,则当1
PO 为多少时,仓库的容积最大?
18. (本小题满分16分)
如图,在平面直角坐标系中,已知以M 为圆心的圆M ﹕22
1214600x y x y +--+=及其上一点A(2,4)
(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线x =6上,求圆N 的标准方程;
(2)设平行于OA 的直线l 与圆M 相交于B 、C 两点,
且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得,
+=,求实数t的取值范围。
TA TP TQ
19. (本小题满分16分)
已知函数()(0,0,1,1)
x x
=+>>≠≠.
f x a b a b a b
.
(1)设a=2,b=1
2
①求方程()
f x=2的根;
②若对任意x R∈,不等式(2)f()6
≥-恒成立,求实数m的
f x m x
最大值;
(2)若01,1a b <<>,函数()()2g x f x =-有且只有1个零点,求ab 的值。
20.(本小题满分16分)
记{}1,2,100U =…,
.对数列{}()*n a n N ∈和U 的子集T ,若T =∅,定义0T S =;若{}12,,k T t t t =…,,定义12+k T t t t S a a a =++….例如:{}=1,3,66T 时,1366+T S a a a =+.现设{}()*n a n N ∈是公比为3的等比数列,且当{}=2,4T 时,=30T S .
(1)求数列{}n a 的通项公式;
(2)对任意正整数()1100k k ≤≤,若{}1,2,k T ⊆…,
,求证:1T k S a +<; (3)设,,C D C U D U S S ⊆⊆≥,求证:2C C D D
S S S +≥.
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.【选修4—1几何证明选讲】(本小题满分10分)
如图,在△ABC中,∠ABC=90°,BD⊥AC,D为垂足,E是BC的中点,求证:∠EDC=∠ABD.
B.【选修4—2:矩阵与变换】(本小题满分10分) 已知矩阵12,02A ⎡⎤=⎢⎥-⎣⎦矩阵B 的逆矩阵111=202B -⎡⎤-⎢⎥⎢⎥⎣⎦,求矩阵AB.
C.【选修4—4:坐标系与参数方程】(本小题满分10分) 在平面直角坐标系xOy 中,已知直线l 的参数方程为
1123x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),椭圆C 的参数方程为cos ,2sin x y θθ=⎧⎨=⎩(θ为参
数).设直线l 与椭圆C 相交于A ,B 两点,求线段AB 的长.
D.设a >0,∣x -1∣<3a ,∣y -2∣<3
a ,求证:∣2x +y -4∣<a.
【必做题】第22题、第23题,每题10分,共计20分. 请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.
22. (本小题满分10分)
如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).
(1)若直线l过抛物线C的焦点,求抛物线C的方程;(2)已知抛物线C上存在关于直线l对称的相异两点P 和Q.
①求证:线段PQ的中点坐标为(2-p,-p);
②求p的取值范围.
23.(本小题满分10分) (1)求34
67–47C C 的值;
(2)设m ,n N*,n≥m , 求证:(m +1)C m m +(m +2)+1C m
m +(
m +3)+2C m m +…+n –1C m n +(n +1)C m n =(m +1)+2
+2C m n .。
