2013广东高考数学试题(文科A卷)
2013年广东高考文科数学A卷试题及答案(word)版

绝密★启用前试卷类型:A2013年普通高等学校招生全国统一考试(广东卷)数学(文科)本试卷共4页,21小题,满分150分.考试用时120分钟注意事项: 1.答卷前,考生务必用黑色笔迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上。
用2B 铅笔讲试卷类型(A )填涂在答题卡相应的位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁,考试结束后,将试题与答题卡一并交回。
参考公式:锥体的体积公式为1=3V Sh ,其中S 为锥体的底面积,h 为锥体的高。
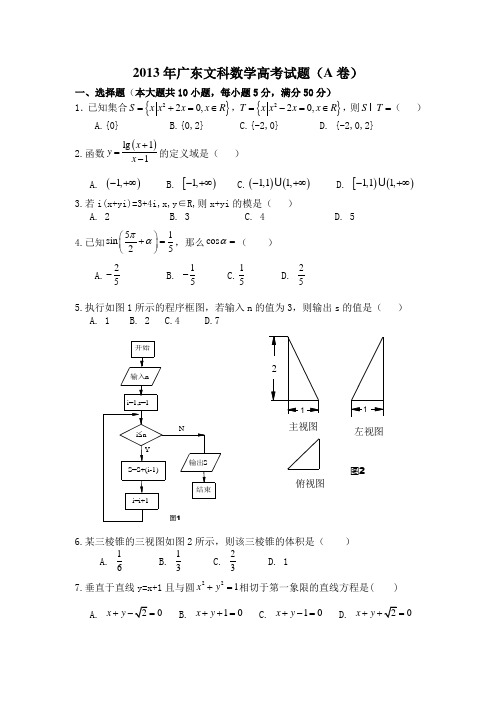
一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}- 2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 A .2 B .3 C .4 D .5 4.已知51sin()25πα+=,那么cos α=图 2俯视图侧视图A .25-B .15-C .15D .255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是 A .1 B .2 C .4 D .76.某三棱锥的三视图如图2所示,则该三棱锥的体积是 A .16 B .13 C .23D .1 7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是A .0x y +=B .10x y ++=C .10x y +-=D .0x y += 8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥ 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 10.设a 是已知的平面向量且≠0a ,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使=+a b c ;②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ;④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ; 上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是 A .1B .2C .3D .4二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 12.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = .13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.(二)选做题(14、15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 . 15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB =3BC =,BE AC ⊥,垂足为E ,则ED = .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:图 3图 4(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率. 18.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中BC =. (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ;(3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列.(1) 证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. 20.(本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈. (1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M .2013年广东高考文科数学A 卷参考答案二、填空题11. 15 12.12 13.5 14. 1cos sin x y θθ=+⎧⎨=⎩ (θ为参数) 15. 2三、解答题16. 解:(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.17. 解:1)苹果的重量在[90,95)的频率为20=0.450; (2)重量在[80,85)的有54=15+15⋅个; (3)设这4个苹果中[80,85)分段的为1,[)95,100分段的为2、3、4,从中任取两个,可能的情况有: (1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[80,85)和[)95,100中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==. 18. 解:(1)在等边三角形ABC 中,AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中也成立, //DE BC ∴ ,DE ⊄平面BCF ,BC ⊂平面BCF ,//DE ∴平面BCF ;(2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,2BC =,222BC BF CF CF BF ∴=+∴⊥② BF CF F CF ABF ⋂=∴⊥平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.11111113232333F DEG E DFGV V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅= ⎝⎭19. 解:(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+ ∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =,由(1)可知,212145=4,1a a a =-∴=21312a a -=-=∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-. (3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 20. 解:(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的, ∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-= 0020x y --=()222200000021=221AF BF y y x y y y ∴⋅=-++-+++220019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为9221. 解:()'2321fx x kx =-+(1)当1k =时()'2321,41280fx x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,其开口向上,对称轴3kx =,且过()01,(i )当(241240k k k ∆=-=+-≤,即0k ≤<时,()'0f x ≥,()f x 在[],k k -上单调递增,从而当x k =时,()f x 取得最小值()m f k k == ,当x k =-时,()f x 取得最大值()3332M f k k k k k k =-=---=--.(ii )当(241240k k k ∆=-=+>,即k <()'23210f x x kx =-+=解得:12x x ==,注意到210k x x <<<,(注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) ()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+>()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=-->所以 3max ()()2f x f k k k =-=--, min ()()f x f k k ==薄雾浓云愁永昼, 瑞脑消金兽。
2013年高考文科数学广东卷-答案

2013年普通高等学校招生全国统一考试(广东卷)数学(文科)答案解析一、选择题 1.【答案】A【解析】由题意知{0,2}S =-,{0,2}T =,故{0}S T =I ,故选A . 【提示】先求一元二次方程的根,再用列举法求交集元素. 【考点】集合的交集运算. 2.【答案】C【解析】由题意知1010x x +>⎧⎨-≠⎩,解得1x >-且1x ≠,所以定义域为(1,1)(1,)-+∞U 【提示】从函数有意义的角度分析求解定义域,再由各个集合的交集得出定义域. 【考点】函数的定义域和集合的交集运算. 3.【答案】D【解析】因为i(i)34i x y +=+,所以i 34i x y -=+,根据两个复数相等的条件得:3y -=即3y =-,4x =,所以x yi +43i =-,i x y +的模5=;【提示】通过等式两边增添、通分等手段化简求出复数的代数形式,进而求出复数的模.【解析】由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形,高为2,所以该三棱锥的体积111112323V ==g ggg; 【提示】由三视图还原出直观图,根据“长对正、高对齐、宽相等”寻找出三棱锥的相关数据,代入棱锥的体积公式进行计算.【考点】平面图形的三视图的和棱锥的体积. 7.【答案】A【解析】设所求直线为l ,因为l 垂直直线1y x =+,故l 的斜率为1-,设直线l 的方程为y x b =-+,化为一般式为0x y b +-=;因为l 与圆相切221x y +=相切,所以圆心(0,0)到直线l 的距离1==,所以b =0b >,故b ,所以l 的方程为0x y +=;【提示】给定所求直线与已知直线垂直和已知圆相切的位置关系,利用待定系数法求出直线方程,再利用数形结合法对所求参数值进行取舍.【考点】直线与圆的位置关系,直线的方程. 8.【答案】B【解析】若α与β相交,且l 平行于交线,则也符合A ,显然A 错;若l l αβ⊥,∥,则αβ⊥,故C 错;l αβα⊥,∥,若l 平行交线,则l β∥,故D 错;【提示】由线面平行或垂直的某些给定条件来判断相关线面的位置关系. 【考点】空间中直线、平面之间的位置关系.9.【答案】由线面平行或垂直的某些给定条件来判断相关线面的位置关系.【解析】由焦点可知(1,0F )可知椭圆焦点在x 轴上,由题意知1c =,12ca =,所以2a b ===,故椭圆标准方程为22143x y +=;【提示】给定椭圆的离心率和焦点,求出各参数从而确定其标准方程. 【考点】椭圆的标准方程和椭圆的几何性质. 10.【答案】C【解析】对于①,若向量a ,b 确定,因为a b -是确定的,故总存在向量c ,满足c a b =-,即a b c =+,故正确.对于②,因为c 和b 不共线,由平面向量基本定理可知,总存在唯一的一对实数λ,μ,满足a b c λμ=+,故正确;对于③,如果a b c λμ=+,则以||a ,||b λ,||c μ为三边长可以构成一个三角形,如果单位向量b 和正数μ确定,则一定存在单位向量c 和实数λ,使a b c λμ=+,故正确;对于④,如果给定的正数λ和μ不能满足“以||a ,||b λ,||c μ为三边长可以构成一个三角形”,这时单位向量b 和c 就不存在,故错误.因此选C【提示】给定某些向量,利用平行四边形或三角形法则及平面向量基本定理来进行判断. 【考点】平面向量基本定理. 二、填空题 11.【答案】15【解析】由题意知11a =,22a =-,34a =,48a =-,所以;1234a a a a +++124815=+++=;【解析】因为2ln y ax x =-,所以12y ax x'=-,因为曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,所以1210x y a ='=-=,所以12a =; 【提示】给定曲线上某点切线在坐标轴上的位置关系,利用该点导数的几何意义求解原方程,从而求出待定系数.【考点】曲线的切线与导数的联系,导数的几何意义. 13.【答案】5【解析】作出可行域可得直角梯形的四个顶点分别为(1,1)-,(1,2)-,(1,1),(1,4)代入可知z 的最大值为145z =+=;【提示】画出线性约束条件表示的平面区域,用图解法求最值. 【考点】线性规划问题的最值求解. 14.【答案】cos 1sin x y αα=+⎧⎨=⎩,(α为参数)【解析】因为曲线C 的极坐标方程为2cos ρθ=;所以2cos 2cos 1cos2x ρθθθ===+①,sin 2sin cos sin 2y ρθθθθ===②;①可变形得:cos21x θ=-③,②可变形得:sin 2y θ=;由22sin 2cos 21θθ+=得:22(1)1x y -+=;【解析】因为在矩形ABCD 中,AB =,3BC =,BE AC ⊥,所以30BCA ∠=︒,所以cos30CE CB =︒=g CDE △中,因为60ECD ∠=︒,由余弦定理得: 2222021212cos60224DE CE CD CE CD =+-=+-=⎝⎭g g g ,所以CD ;(2)因为3cos 5θ=,3π,2π2θ⎛⎫∈ ⎪⎝⎭,所以4sin 5θ=-; ππππππcos cos sin sin 6612333f θθθθθ⎛⎫⎛⎫⎛⎫⎫-=--=-=+ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎭314525⨯-=⎭;(2)若采用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,则重量在[80,85)的个数541515=⨯=+; (3)设在[80,85)中抽取的一个苹果为x ,在[95,100)中抽取的三个苹果分别为a b c ,,,从抽出的4个苹果中,任取2个共有(,)x a ,(,)x b ,(,)x c ,(,)a b ,(,)a c ,(,)b c 66种情况,其中符合“重量在[80,85)和[95,100)中各有一个”的情况共有(,)x a ,(,)x b ,(,)x c 种;设“抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个”为事件A ,则事件A 的概率31()62P A ==; 【提示】由频数分布表找出相应范围内的频数,由分层抽样确定在某范围内的个体数目,用列举法求解古典图5中,因为DG BF ∥,//GE FC ,所以平面DGE ∥平面BCF ,所以DE BCF ∥平面; (2)证明:在图4中,因为因为ABC 是等边三角形,且F 是BC 的中点,所以AF BC ⊥;在图5中,因为在BFC △中,12BF FC BC ===,,所以222BF FC BC +=,BF CF ⊥,又因为AF CF ⊥,所以CF ABF ⊥平面(3)因为AF CF AF BF ⊥⊥,,所以AF ⊥平面BCF ,又因为平面DGE ∥平面BCF ,所以AF ⊥平面DGE ;所以11111113323233F DEG DGE V S FG DG GE FG -====g g g g g g g g g △; 【提示】通过折叠问题来分析折叠前后变化的元素和不变化的元素,从而得出线面平行或垂直关系以及三(2)当2n ≥时,2211444(41)4(1)1n n n n n a S S a n a n -+⎡⎤=-=------⎣⎦2214n n a a +=--, 所以221(2)n n a a +=+,因为{}n a 各项均为正数,所以12n n a a +=+;因为2a ,5a ,14a 构成等比数列,所以22145a a a =g ,即2222(24)(6)a a a +=+,解得23a =,因为2a =,所以11a =,212a a =+,符合12n n a a +=+,所以12n n a a +=+对1n =也符合,所以数列{}n a 是一个以11a =为首项,2d =为公差的等差数列,1(1)221n a n n =+-=-g; (3)因为111111(21)(21)22121n n a a n n n n +⎛⎫==- ⎪+--+⎝⎭, 所以1223111111111111121323522121n n a a a a a a n n +⎛⎫⎛⎫⎛⎫+++=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭L 111111111112133521212121212n n n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅-=-=< ⎪ ⎪-+++⎝⎭⎝⎭; 所以对一切正整数n ,有1223111112n n a a a a a a ++++<L . 【提示】把等式、不等式、等差数列和等比数列等知识结合在一起来考查,考查了递推公式、等比中项、等差数列的概念和通项公式,会用列项相消法求数列的前n 项和,放缩法证明不等式的知识. 【考点】等差数列、等比数列的定义及应用,函数与方程的思想以及不等式的证明.所以2d=,又因为0c>,所以解得1c=,抛物线的焦点坐标为(0,1),所以抛物线C的方程为24x y=;(2)因为抛物线的方程为24x y=,即214y x=,所以12y x'=,设过00(,)P x y点的切线l'与抛物线的切点坐标为21,4m m⎛⎫⎪⎝⎭,所以直线l'的斜率210412y mk mx m-==-,解得10m x=+或20m x=;不妨设A点坐标为2111,4m m⎛⎫⎪⎝⎭,B点坐标为2221,4m m⎛⎫⎪⎝⎭,==>,所以12m m≠;221112441201211()42ABm mk m m xm m-==+=-;所以直线AB的方程为210111()42y m x x m-=-,代入整理得:12y x=;(3)A点坐标为2111,4m m⎛⎫⎪⎝⎭,B点坐标为2221,4m m⎛⎫⎪⎝⎭,F点坐标为(0,1),因为0020x y--=;所以10m x x=+=+200m x x==,1202m mx+=,12048m mx=-;因此=||AF BFg22222222121212121212 11111111()1()[()2]1 44164164m m m m m m m m m m m m⎛⎫⎛⎫=++=+++=++-+⎪⎪⎝⎭⎝⎭22220000001139(48)[(2)2(48)]1269216422x x x x x x⎛⎫=-+--+=-+=-+⎪⎝⎭,所以当32x=时,||||AF BFg取最小值92;【提示】由点到直线的距离公式建立关于c的方程,从而确定c并写出抛物线的标准方程;设出点坐标并求出切线方程从而得到所求直线方程;利用抛物线的定义转化为点到准线的距离,建立关于y的目标函数,从而确定函数的最小值.【考点】点到直线的距离公式,直线的点斜式方程,抛物线的定义和标准方程,导数的几何意义,直线与抛物线的交点,二次函数的最值以及待定系数法的应用.①当0∆≤时,即0k <时,()0f x '≥,()f x 在R 上单调递增,此时无最小值和最大值;②当0∆>时,即k <时,令()0f x '=,解得x =或x =()0f x '>,解得x <或x ;令()0f x '<,解得x <0k <=<-23kk >=>作()f x 的最值表如下:【提示】由抛物线与直线方程的位置关系来求解方程,通过导数来求函数及函数的单调区间;对于导数中含有未知数,需要讨论判别式∆的符号,然后比较区间端点的函数值与极值的大小从而确定最值. 【考点】导数的计算和导数在研究函数中的应用,利用导数来求函数的单调区间和最值.。
2013年广东高考文科数学试卷(含参考答案)

2012年普通高等学校招生全国统一考试(广东卷)A数学(文科)本试卷共4页,21题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔盒涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:球的体积34=3V R π,其中R 为球的半径.锥体的体积公式为1=3V Sh ,其中S 为锥体的底面积,h 为锥体的高。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合22S=|x|x +20,|,|x|x -20,|x x R T x x R =∈==∈,则S T ⋂=A. |0|B. |02|,C. |2,0|-D. |2,0,2|- 2.函数lg(1)1x y x +=-的定义域是 A.(1,)-+∞ B.[1,)-+∞ C.(1,1)(1,)-+∞ D. [)1,1(1,)-+∞ 3.若()34,,,i x yi i x y R +=+∈则复数x yi +的模是 A.2 B.3 C.4) D.54.已知51sin()25πα+=,那么cos α= 2.5A - 1.5B - 1.5C 2.5D5.执行如图1所示的程序框图,若输入n 的值为3,则输入s 的值是.1A .2B .3C .7D6.某三棱锥的三视图如图2所示,则该三棱锥的体积是1.6A 1.3B 2.3C .1A 7.垂直于直线1y x =+且于圆 的直线方程是.0A x y += .10B x y ++= .10C x y +-= .0D x y +=8.设l 为直线,,αβ是两个不同的平面.下列命题中正确的是.,,A l l αβαβ 若则 .,,B l l αβαβ⊥⊥ 若则.,,C l l αβαβ⊥ 若则 .,,D l l αβαβ⊥⊥ 若则9.已知中心在原点的椭圆C 的右焦点为F (1,0),离心率等于12,则C 的方程是 22.134x y A += 22.14x B =22.142x y C += 22.143x y D +=10.设α是已知的平面向量且0α≠.关于向量α的分解,有如下四个命题: ①给定向量b,总存在向量c ,使a b c =+;②给定向量b 和c,总存在实数λ和μ,使a b c λμ=+; ③给定向量b 和正数,总存在单位向量c,使a b c λμ=+.④给定正数λ和μ,总存在单位向量b 和单位向量c,使a b c λμ=+. 上述命题中的向量b,c 和a 在同一平面内且两两不共线,则真命题的个数是 A.1 B.2 C.3 D.4二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
2013广东高考数学文科试题及解析

2013年普通高等学校招生全国统一考试(广东卷)数学(文科)乐享玲珑,为中国数学增光添彩!免费玲珑3D 画板,全开放的几何教学软件,功能强大,好用实用一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T = A .{0} B .{0,2} C .{2,0}- D .{2,0,2}- 2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞ 3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 A .2 B .3 C .4 D .5 4.已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是图 1A .1B .2C .4D .7 6.某三棱锥的三视图如图2所示,则该三棱锥的体积是图 2俯视图侧视图正视图A .16 B .13 C .23D .1 7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是 A .0x y += B .10x y ++=C .10x y +-=D .0x y +=8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥ 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 10.设 a 是已知的平面向量且≠0 a ,关于向量a 的分解,有如下四个命题:①给定向量 b ,总存在向量 c ,使=+a b c ;②给定向量 b 和 c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量 b 和正数μ,总存在单位向量 c 和实数λ,使λμ=+a b c ;④给定正数λ和μ,总存在单位向量 b 和单位向量 c ,使λμ=+a b c ;上述命题中的向量 b , c 和a 在同一平面内且两两不共线,则真命题的个数是A .1B .2C .3D .4二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 12.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = .13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.(二)选做题(14、15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 . 15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB =3BC =,BE AC ⊥,垂足为E ,则ED = . 图 3三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中2BC =. (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -. 图 419.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1) 证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++< .已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈.(1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M ,()'2321f x x kx =-+参考答案一、选择题 1.A 由题意知{}0,2S=-,{}0,2T =,故{}0S T = ;2.C 由题意知1010x x +>⎧⎨-≠⎩,解得1x >-且1x ≠,所以定义域为()()1,11,-+∞ ;3.D 因为()34ix yi i +=+,所以34xi y i -=+,根据两个复数相等的条件得:3y -=即3y =-,4x =,所以x yi +43i =-,x yi +的模5==;4.C 51sin sin()cos ()cos()cos 22225ππππααααα⎛⎫⎡⎤+=+=-+=-==⎪⎢⎥⎝⎭⎣⎦;5.C ;1i =时,1(11)1s =+-=;2i =时,1(21)2s =+-=;3i =时,2(31)4s =+-=; 6.B 由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形,高为2, 所以该三棱锥的体积111112323V =⋅⋅⋅⋅=; 7.A 设所求直线为l ,因为l 垂直直线1y x =+,故l 的斜率为1-,设直线l 的方程为y x b =-+,化为一般式为0x y b +-=;因为l 与圆相切221x y +=相切,所以圆心(0,0)到直线l 的距离1==,所以b =为相切与第一象限,所以0b >,故b =l 的方程为0x y +=;8.B 若α与β相交,且l 平行于交线,则也符合A ,显然A 错;若,//l l αβ⊥,则αβ⊥,故C 错;,l αβα⊥//,若l 平行交线,则//l β,故D 错;9.D 由焦点可知()1,0F可知椭圆焦点在x 轴上,由题意知11,2c c a ==,所以2,a b ===准方程为22143x y += 10.B ①②容易判断是对的,③给定单位向量b 和正数μ,可知b λ 的方向确定,c μ的模确定,如图,若c AB μ< ,则等式不能成立;④给定正数λ和μ,则b λ 和c μ的模确定,若b c a λμ+< ,则等式不成立。
2013年高考真题文科数学(广东卷)解析版含答案

2013年普通高等学校招生全国统一考试(广东卷)数学(文科A 卷)解析从今以后,不再是大学特学综合科,而是大学特学数学科了!让别的科扼杀学生的能 力吧,数学出基础题就好一一感恩广东今年数学出题老师一一湛江 -农垦-小徐注 (QQ:808068)本试卷共4页,21小题,满分150分.考试用时120分钟.1锥体的体积公式: V 1 Sh .其中S 表示锥体的底面积,h 表示锥体的高.3一、选择题:本大题共 10小题,每小题5分,满分50分,在每小题给出的四个选项中, 只有一项是符合题目要求的.1.设集合 S {x|x 2 2x 0,x R} , T {x|x 2 2x 0,x R},则 S TA . {0}B- {0, 2}C. { 2,0} D . { 2,0, 2} 【解析】:先解两个一元二次方程,再取交集,选A , 5分到手,妙!2 .函数f (x) lg( x ——9的定义域是x 1A . ( 1,) B . [ 1, ) C. ( 1,1) (1, )D . [ 1,1) (1,【解析】: 对数真数大于零, 分母不等于零,目测C !3 .若 i(x yi) 3 4i ,x, y R ,则复数xyi 的模是A . 2B . 3C. 4D . 54,y模为5,选D.4 .已知sin(2)—, 那么cos21C 1A .B. C. -555【解析】考 查 三角5 S "(2)sin(2 +—) si n —2 2cos1—,选 C.55.执行如图1所示的程序框图,若输入n的值为3,则输出s的值是A. 1B. 2C. 4D. 7【解析】选C•本题只需细心按程序框图运行一下即可.正视图侧视图俯视图6.某三棱锥的三视图如图 2所示,则该三棱锥的体积是【解析】由三视图判断底面为等腰直角三角形,三棱锥的高为 选B.排除B 、C ;相切于第一象限排除 D ,选A •直接法可设所求的直线方程为:①给定向量b ,总存在向量c ,使a b c ; ②给定向量b 和c ,总存在实数 和,使a b③给定单位向量 b 和正数 ,总存在单位向量 c 和实数④给定正数和,总存在单位向量b 和单位向量c ,使a b c ;1 A .61 B.3C. 23D. 12=3,7 .垂直于直线.. 2 2y x 1且与圆x y 1相切于第一象限的直线方程是A . x yB .C . x yD .【解析】本题考查直线与圆的位置关系,直接由选项判断很快,圆心到直线的距离等于再利用圆心到直线的距离等于r 1,求得k 2 .&设I 为直线, 是两个不同的平面,下列命题中正确的是 A .若 I//, I //,则 // B .若I ,I ,则 //C .若 I , I //,则 //D .若,I// ,则【解析】基础题,在脑海里把线面可能性一想,就知道选9.已知中心在原点的椭圆C 的右焦点为2 2x y .A.————22x yB .— 1 4 3C .D .【解析】基础题,c1,a 2,b3,选 D.10.设a 是已知的平面向量且’a ;0,关.于向量 a 的分解, 有如下四个命,使a b上述命题中的向量b, c和a在同一平面内且两两不共线,则真命题的个数是D. 4A. 1B. 2C. 3【解析】本题是选择题中的压轴题, 主要考查平面向量的基本定理和向量加法的三角形法则 利用向量加法的三角形法则,易的①是对的; 利用平面向量的基本定理,易的②是对的;以 a 的终点作长度为 的圆,这个圆必须和向量 b 有交点,这个不一定能满足,③是错的; 利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须a ,所以④是假命题•综上,本题选B •平面向量的基本定理考前还强调过,不懂学生做得如何•【品味选择题】 文科选择题答案:ACDCC BABD 选择题3322再次出现!今年的选择题很基 础,希望以后高考年年出基础题!二、填空题:本大题共 5小题•考生作答4小题•每小题5分,满分20分. (一)必做题(11〜13题)11 •设数列{a n }是首项为1,公比为 2的等比数列, 【解析】这题相当于直接给出答案了 15212.若曲线y ax In x 在点(1,a )处的切线平行于标系,则曲线C 的参数方程为【解析】本题考了备考弱点x 1 cos1,易的则曲线 C 的参数方程为(为参数)则 a 1 |a 21 a s |a 41x 轴,【解析】本题考查切线方程、方程的思想.依题意y2ax1 ',y x 1 2a 1 x13.已知变量x, y 满足约束条件 x 1,则 z 1最大值是【解析】画出可行域如图,最优解为1,4,故填5(二)选做题(14、15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题) 已知曲线C 的极坐标方程为2cos .以极点为原点,极轴为x 轴的正半轴建立直角坐.讲参数方程的时候,参数的意义要理解清楚•先化成直角坐标方程X 1 2 y 2y sin15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB 3, BC 3, BE AC,垂足为E,则ED⑵用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在【解析】本题对数值要敏感,由AB 3, BC 3,可知 BAC 60从而AE 计,CAD 30,【品味填空题】 选做题还是难了点,比理科还难些•三、解答题:本大题共 6小题,满分80分•解答须写出文字说明、证明过程和演算步骤. 16. (本小题满分12分)已知函数 f(x) 2 cos x 一 , x R . 12(1)求f 的值;333⑵若cos -,——,2 ,求f 526 【解析】(1) fcos - —v 2 cos -13 3 12441 Vcos3 3,2sin2cos5 25f=2 cos2 cos cossin sin —1644 45【解析】这个题实在是太简单,两角差的余弦公式不要记错了17. (本小题满分13分)从一批苹果中,随机抽取 50个,其重量(单位:克)的频数分布表如下:分组(重量) [80,85)[85,90)[90,95)[95,100)频数(个)5102015(1)根据频数分布表计算苹果的重量在 [90,95)的频率;DEAE 2 AD 2 2AE AD cos3021 2图3[80,85)的有几个?⑶ 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.20【解析】(1)苹果的重量在 90,95的频率为20 =0 4 ;505(2) ------------------------- 重量在80,85的有4 =1个;5+15(3)设这4个苹果中80,85分段的为1, 95,100分段的为2、3、4,从中任取两个,可 能的情况有:(1,2)( 1,3)( 1 ,4)( 2, 3)(2,4)( 3, 4)共 6 种;设任取 2 个,重量在 80,85 和 95,1003 1 中各有1个的事件为A ,贝U 事件A 包含有(1, 2)( 1 , 3)( 1, 4)共3种,所以p (A ) 3 '.6 2【解析】这个基础题,我只强调:注意格式!18. (本小题满分13分)如图4,在边长为1的等边三角形 ABC中,D,E 分别是AB, AC 边上的点,AD AE , F是BC 的中点,AF 与DE 交于点G ,将 ABF 沿AF 折起,得到如图A BCF ,其中 BC(1)证明:DE //平面BCF ;⑵证明:CF 平面ABF ;⑶当AD —时,求三棱锥F3 DEG 的体积V【解析】(1)在等边三角形ABC 中, AD AEADAE,在折叠后的三棱A BCF 中DB EC 1 1也成立, DE / /BC ., DE 平面 BCF ,5所示的三棱锥G图5BC 平面BCF , DE // 平面BCF ;(2)在等边三角形ABC中,F是BC的中点,所以AF BC①,BF CF 1.2在三棱锥A BCF中,BC BC2BF2CF2CF BF ②(2)两问是已知S n 求a n , a n 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(易错点在分成n 1,n 2来做后,不会求印,没有证明q 也满足通项公式. 20.(本小题满分14分) 已知抛物线C 的顶点为原点,其焦点 F 0,c c 0到直线I : X y 2 o 的距离为3 2.设P 为直线I 上的点,过点P 作抛物线C 的两条切线PA,PB ,其中代B 为切点. 2(1)求抛物线C 的方程;(2)当点P X o ,y °为直线l 上的定点时,求直线 AB 的方程;⑶ 当点P 在直线I 上移动时,求|AF | |BF |的最小值.抛物线C 的方程为X 2 4y ; (2)设点 A(X 1, y 1),B(X 2,y 2),C 在点A 处的切线PA 的方程为y 力 ;(x X 1),11 1 12 2n 121 2n 1 2n 1【解析】(1)依题意d-&2,解得c 1 (负根舍去)2由X 24y ,即卩 y - x 2,得 y4【解析】本题考查很常规, 2)问,作出第(3)问•本题P(x o , y o ),•••抛物线X 1—X 21 2y12X1.?X * . •••点P(x o , y o )在切线I 1 上,• y oX 1刁《y 「同理,y°qx。
2013年高考数学广东卷(文科)试题+详细解析+试卷分析

图 21俯视图侧视图正视图212013广东文普宁二中 杜林生 整理发布,仅供参考1. 2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞ 3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是A .2B .3C .4D .54.已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是A .1B .2C .4D .76.某三棱锥的三视图如图2所示,则该三棱锥的体积是 A .16 B .13 C .23D .1 7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是A .20x y +-=B .10x y ++=C .10x y +-=D .20x y ++= 8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 10.设 a 是已知的平面向量且≠0 a ,关于向量 a 的分解,有如下命题,这四个命题中的向量 b , c 和 a 在同一平面内且两两不共线,则真命题的个数是:①给定向量 b ,总存在向量 c ,使=+a b c ;②给定向量 b 和 c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量 b 和正数μ,总存在单位向量 c 和实数λ,使λμ=+a b c ;④给定正数λ和μ,总存在单位向量 b 和单位向量 c ,使λμ=+a b c ;图 1是否结束输出s i=i +1i ≤ ni=1, s=1输入n 开始s=s+(i -1)A .1B .2C .3D .411.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 12.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = .13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 .15.(几何证明选讲选做题)如图3,在矩形ABCD 中,3,AB =3BC =,BE AC ⊥,垂足为E ,则ED = .16.(12分)()2cos ,12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值;(2) 若33cos ,,252πθθπ⎛⎫=∈⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.17.(12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:分组(重量) [80,85) [85,90) [90,95) [95,100) 频数(个)5 10 20 15(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.图 3ECBDA图 4G E FAB C D 图 5D GBF CAE18.(14分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中22BC =.(1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ;(3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.19.(14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈ 且2514,,a a a 构成等比数列. (1) 证明:2145a a =+;(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++< .20.(14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为322. 设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值. 21.(14分)设函数x kx x x f +-=23)( ()R k ∈. (1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M .2013广东文参考答案1A 2C 3D 4C 5C 6B 7A 8B 9D 10C6B 解:由三视图判断底面为等腰直角三角形,三棱锥的高为2,则111=112=323V ⋅⋅⋅⋅ 7A 解:圆心到直线的距离等于1r =,排除B 、C ;相切于第一象限排除D ,选A.直接法可设所求的直线方程为:()0y x k k =-+>,再利用圆心到直线的距离等于1r =,求得2k =.10B 解:考查平面向量的基本定理和向量加法的三角形法则.利用向量加法的三角形法则,易的①是对的;利用平面向量的基本定理,易的②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量λb 有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须=+λμλμ+≥b c a ,所以④是假命题.11. 1512. 12考查切线方程、方程的思想.依题意 ''1112,210,2x y ax y a a x ==-=-=∴=13. 5 画出可行域如图,最优解为()1,414解:1cos ()sin 为参数θθθ=+⎧⎨=⎩x y ,本题考了备考弱点.讲参数方程的时候,参数的意义要理解清楚.先化成直角坐标方程()2211x y -+=,再化成参数方程15解:212 由3,AB =3BC =,可知60BAC ∠= ,从而3,302AE CAD =∠= ,22212cos302DE AE AD AE AD =+-⋅⋅= . 16解:(1)2cos 2cos 133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,24sin 1cos 5θθ=--=-,1=2cos 2cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎛⎫∴--=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【注意】两角差的余弦公式不要记错了. 17解:(1)苹果的重量在[)95,90的频率为20=0.450; (2)重量在[)85,80的有54=15+15⋅个; (3)设这4个苹果中[)85,80分段的为1,[)100,95分段的为2、3、4,从中任取两个,可能的情况有: (1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[)85,80和[)100,95中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==.【注意】注意格式!18解:(1)在等边三角形ABC 中,AD AE =AD AEDB EC ∴=,在折叠后的三棱锥A BCF -中也成立, //DE BC ∴ ,DE ⊄ 平面BCF ,BC ⊂平面BCF , //DE ∴平面BCF ; (2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,22BC =,222BC BF CF CF BF ∴=+∴⊥②BF CF F CF ABF ⋂=∴⊥ 平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.11111131332323323324F DEG E DFG V V DG FG GF --⎛⎫∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎪ ⎪⎝⎭【品题】考查了平行线分线段成比例这个平面几何的内容.19解:(1)当1n =时,22122145,45a a a a =-=+,21045n a a a >∴=+(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =, 由(1)可知,212145=4,1a a a =-∴=21312a a -=-= ∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-. (3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+ 11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 【品题】本题考查很常规,第(1)(2)两问是已知n S 求n a ,{}n a 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(2)问,作出第(3)问.本题易错点在分成1n =,2n ≥来做后,不会求1a ,没有证明1a 也满足通项公式.20解:(1)依题意023222c d --==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =; (2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x xy y -=-,即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= .∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的,∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+,所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-= 0020x y --=()22220000021=221AF BF y y x y y y ∴⋅=-++-+++2200019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭ ∴当012y =-时,AF BF ⋅取得最小值为9221解:()'2321fx x kx =-+(1)当1k =时()'2321,41280f x x x =-+∆=-=-< ()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,其开口向上,对称轴3kx =,且过()01,(i )当()()24124330k k k ∆=-=+-≤,即30k -≤<时,()'0f x ≥,()f x 在[],k k -上单调递增, 从而当x k =时,()f x 取得最小值()m f k k == ,当x k =-时,()f x 取得最大值()3332M f k k k k k k =-=---=--.(ii )当()()24124330k k k ∆=-=+->,即3k <-时,令()'23210fx xkx =-+=解得:221233,33k k k k x x +---==,注意到210k x x <<<,(注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) -kk 3k x =()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+>()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=-->所以 3max ()()2f x f k k k =-=--,min ()()f x f k k ==【品题】常规解法完成后,结合图像感知x k = 时最小,x k =-时最大,只需证()()()f k f x f k ≤≤-即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.2013年广东高考数学试卷遵循《2013年普通高等学校招生全国统一考试(广东卷)数学大纲》的规定:贯彻了有利于中学数学教学与有利于高校选拔人才相结合的原则,贯彻了“总体保持稳定,深化能力立意,积极改革创新”的指导思想.试卷立足现行高中教材,在注重对基础知识和基本方法全面考查的同时,又突出了对数学思想、数学核心能力的综合考查.试卷具有以下鲜明特点:1.题型稳定,保持风格2013年高考数学试卷和2012年高考数学试卷犹如双胞胎,其考查的知识内容、题型和整体难易程度与2012年基本一致, 打破了试题难度大小年的规律。
2013年高考广东卷文科数学试题及答案

设函数 .
(1)当 时,求函数 的单调区间;
(2)当 时,求函数 在 上的最小值 和最大值 .
【解析】:
(1)当 时
, 在 上单调递增.
(2)当 时, ,其开口向上,对称轴 ,且过
(i)当 ,即 时, , 在 上单调递增,
从而当 时, 取得最小值 ,
当 时, 取得最大值 .
7.垂直于直线 且与圆 相切于第Ⅰ象限的直线方程是
A. B.
C. D.
【解析】直接法可设所求的直线方程为: ,再利用圆心到直线的距离等于 ,求得 .选A.
8.设 为直线, 是两个不同的平面,下列命题中正确的是
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
【解析】借助长方体判断,可知B正确..
分组(重量)
频数(个)
5
10
20
15
(1)根据频数分布表计算苹果的重量在 的频率;
(2)用分层抽样的方法从重量在 和 的苹果中共抽取4个,其中重量在 的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在 和 中各有1个的概率.
【解析】(1)苹果的重量在 的频率为 ;
(2)重量在 的有 个;
【解析】:考查三角函数诱导公式, ,选C.
5.执行如图1所示的程序框图,若输入 的值为3,则输出 的值是
A.1 B.2 C.4 D.7
【解析】根据程序框图,s=1+0+1+2=4.选C.
6.某三棱锥的三视图如图2所示,则该三棱锥的体积是
A. B. C. D.
【解析】由三视图判断底面为等腰直角三角形,三棱锥的高为2,则 ,选B.
(ii)当 ,即 时,令
2013年高考真题-文科数学(广东卷A)含答案

图 2俯视图侧视图正视图2013年普通高等学校招生全国统一考试(广东卷)数学(文科A 卷)解析本试卷共4页,21小题,满分150分.考试用时120分钟. 锥体的体积公式:13V Sh =.其中S 表示锥体的底面积,h 表示锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}- 【解析】:先解两个一元二次方程,再取交集,选A ,5分到手,妙! 2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞【解析】:对数真数大于零,分母不等于零,目测C ! 3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 A .2 B .3 C .4 D .5【解析】:复数的运算、复数相等,目测4,3x y ==-,模为5,选D . 4.已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .25【解析】:考查三角函数诱导公式,51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭,选C. 5.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是 A .1 B .2 C .4 D .7 【解析】选C.本题只需细心按程序框图运行一下即可. 6.某三棱锥的三视图如图2所示,则该三棱锥的体积是 A .16 B .13 C .23D .1 【解析】由三视图判断底面为等腰直角三角形,三棱锥的高为2,则11=112=323V ⋅⋅⋅⋅,选B. 7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是图 1A .20x y +-=B .10x y ++=C .10x y +-=D .20x y ++=【解析】本题考查直线与圆的位置关系,直接由选项判断很快,圆心到直线的距离等于1r =,排除B 、C ;相切于第一象限排除D ,选A.直接法可设所求的直线方程为:()0y x k k =-+>,再利用圆心到直线的距离等于1r =,求得2k =.8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥ 【解析】基础题,在脑海里把线面可能性一想,就知道选B 了. 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 【解析】基础题,1,2,3c a b ===,选D.10.设a 是已知的平面向量且≠0a ,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使=+a b c ;②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ;ks5u③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ; 上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是 A .1B .2C .3D .4【解析】本题是选择题中的压轴题,主要考查平面向量的基本定理和向量加法的三角形法则. 利用向量加法的三角形法则,易的①是对的;利用平面向量的基本定理,易的②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量λb 有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须=+λμλμ+≥b c a ,所以④是假命题.综上,本题选B.平面向量的基本定理考前还强调过,不懂学生做得如何.二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 【解析】这题相当于直接给出答案了1512.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = . 【解析】本题考查切线方程、方程的思想.依题意''1112,210,2x y ax y a a x ==-=-=∴= 13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.【解析】画出可行域如图,最优解为()1,4,故填 5 ; (二)选做题(14、15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 .【解析】本题考了备考弱点.讲参数方程的时候,参数的意义要理解清楚.先化成直角坐标方程()2211x y -+=,易的则曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩ (θ为参数)15.(几何证明选讲选做题)如图3,在矩形ABCD 中,3,AB =3BC =,BE AC ⊥,垂足为E ,则ED = . 【解析】本题对数值要敏感,由3,AB =3BC =,可知60BAC ∠= 从而3,302AE CAD =∠=, 22212cos302DE AE AD AE AD =+-⋅⋅=. 【品味填空题】选做题还是难了点,比理科还难些.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()2cos ,12f x x x R π⎛⎫=-∈ ⎪⎝⎭.图 3ECBDA(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【解析】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ=-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.【解析】这个题实在是太简单,两角差的余弦公式不要记错了.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率. 【解析】(1)苹果的重量在[)95,90的频率为20=0.450; (2)重量在[)85,80的有54=15+15⋅个; (3)设这4个苹果中[)85,80分段的为1,[)100,95分段的为2、3、4,从中任取两个,可能的情况有: (1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[)85,80和[)100,95中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==. 【解析】这个基础题,我只强调:注意格式!图 418.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中2BC =. (1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ;ks5u (3) 当23AD =时,求三棱锥F DEG -的体积F V -【解析】(1)在等边三角形ABC 中,AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ ,DE ⊄平面BCF ,BC ⊂平面BCF ,//DE ∴平面BCF ;(2)在等边三角形ABC 中,F是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,BC =222BC BF CF CF BF ∴=+∴⊥② BF CF F CF ABF ⋂=∴⊥平面;(3)由(1)可知//GE CF ,结合(2)可得GEDFG ⊥平面.11111113232333F DEG E DFG V V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅= ⎝⎭【解析】这个题是入门级的题,除了立体几何的内容,还考查了平行线分线段成比例这个平面几何的内容.19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1) 证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. 【解析】(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=-- ()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+ ∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =, 由(1)可知,212145=4,1a a a =-∴=21312a a -=-=∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-. (3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 【解析】本题考查很常规,第(1)(2)两问是已知n S 求n a ,{}n a 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(2)问,作出第(3)问.本题易错点在分成1n =,2n ≥来做后,不会求1a ,没有证明1a 也满足通项公式.20.(本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为2.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程;(3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.【解析】(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ks5u ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的, ∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-= 0020x y --=()222200000021=221AF BF y y x y y y ∴⋅=-++-+++220019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为92【解析】2013广州模直接命中了这一题,广一模20题解法2正是本科第(2)问的解法,并且广一模大题结构和高考完全一致.21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈. (1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M . 【解析】:()'2321fx x kx =-+(1)当1k =时()'2321,41280fx x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,其开口向上,对称轴3kx =,且过()01,(i)当(241240k k k ∆=-=≤,即0k ≤<时,()'0f x ≥,()f x 在[],k k -上单调递增,从而当x k =时,()f x 取得最小值()m f k k == , 当x k =-时,()f x 取得最大值()3332M f k k k k k k =-=---=--.(ii)当(241240k k k ∆=-=>,即k <()'23210f x x kx =-+=解得:1233k k x x +==,注意到210k x x <<<,(注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) ()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+>()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=--> 所以 3max ()()2f x f k k k =-=--,min ()()f x f k k ==ks5u【解析】:看着容易,做着难!常规解法完成后,发现不用分类讨论,奇思妙解也出现了:结合图像感知x k = 时最小,x k =-时最大,只需证()()()f k f x f k ≤≤-即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.。
2013年广东省高考数学试卷(文科)

2013年广东省高考数学试卷(文科)一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合S={x|x2+2x=0,x∈R},T={x|x2﹣2x=0,x∈R},则S∩T=()A.{0}B.{0,2}C.{﹣2,0}D.{﹣2,0,2}2.(5分)函数f(x)=的定义域为()A.(﹣1,+∞)B.[﹣1,+∞)C.(﹣1,1)∪(1,+∞) D.[﹣1,1)∪(1,+∞)3.(5分)若i(x+yi)=3+4i,x,y∈R,则复数x+yi的模是()A.2 B.3 C.4 D.54.(5分)已知sin(+α)=,cosα=()A.B.C.D.5.(5分)执行如图所示的程序框图,若输入n的值为3,则输出s的值是()A.1 B.2 C.4 D.76.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积是()A.B.C.D.17.(5分)垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是()A.B.x+y+1=0 C.x+y﹣1=0 D.8.(5分)设l为直线,α,β是两个不同的平面,下列命题中正确的是()A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥β9.(5分)已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于,则C 的方程是()A.B.C.D.10.(5分)设是已知的平面向量且,关于向量的分解,有如下四个命题:①给定向量,总存在向量,使;②给定向量和,总存在实数λ和μ,使;③给定单位向量和正数μ,总存在单位向量和实数λ,使;④给定正数λ和μ,总存在单位向量和单位向量,使;上述命题中的向量,和在同一平面内且两两不共线,则真命题的个数是()A.1 B.2 C.3 D.4二、填空题:本大题共3小题.每小题5分,满分15分.(一)必做题(11~13题)11.(5分)设数列{a n}是首项为1,公比为﹣2的等比数列,则a1+|a2|+a3+|a4|=.12.(5分)若曲线y=ax2﹣lnx在点(1,a)处的切线平行于x轴,则a=.13.(5分)已知变量x,y满足约束条件,则z=x+y的最大值是.选做题(14、15题,考生只能从中选做一题)14.(5分)(坐标系与参数方程选做题)已知曲线C的极坐标方程为ρ=2cosθ.以极点为原点,极轴为x轴的正半轴建立直角坐标系,则曲线C的参数方程为.15.(几何证明选讲选做题)如图,在矩形ABCD中,,BC=3,BE⊥AC,垂足为E,则ED=.四、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(12分)已知函数.(1)求的值;(2)若,求.17.(13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1)根据频数分布表计算苹果的重量在[90,95)的频率;(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.18.(13分)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF,其中BC=.(1)证明:DE∥平面BCF;(2)证明:CF⊥平面ABF;.(3)当AD=时,求三棱锥F﹣DEG的体积V F﹣DEG19.(14分)设各项均为正数的数列{a n}的前n项和为S n,满足4S n=a n+12﹣4n﹣1,n∈N*,且a2,a5,a14构成等比数列.(1)证明:a 2=;(2)求数列{a n}的通项公式;(3)证明:对一切正整数n,有.20.(14分)已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x ﹣y﹣2=0的距离为,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.(1)求抛物线C的方程;(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;(3)当点P在直线l上移动时,求|AF|•|BF|的最小值.21.(14分)设函数f(x)=x3﹣kx2+x(k∈R).(1)当k=1时,求函数f(x)的单调区间;(2)当k<0时,求函数f(x)在[k,﹣k]上的最小值m和最大值M.2013年广东省高考数学试卷(文科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合S={x|x2+2x=0,x∈R},T={x|x2﹣2x=0,x∈R},则S∩T=()A.{0}B.{0,2}C.{﹣2,0}D.{﹣2,0,2}【分析】根据题意,分析可得,S、T分别表示二次方程的解集,化简S、T,进而求其交集可得答案.【解答】解:分析可得,S为方程x2+2x=0的解集,则S={x|x2+2x=0}={0,﹣2},T为方程x2﹣2x=0的解集,则T={x|x2﹣2x=0}={0,2},故集合S∩T={0},故选:A.【点评】本题考查集合的交集运算,首先分析集合的元素,可得集合的意义,再求集合的交集.2.(5分)函数f(x)=的定义域为()A.(﹣1,+∞)B.[﹣1,+∞)C.(﹣1,1)∪(1,+∞) D.[﹣1,1)∪(1,+∞)【分析】依题意可知要使函数有意义需要x+1>0且x﹣1≠0,进而可求得x的范围.【解答】解:要使函数有意义需,解得x>﹣1且x≠1.∴函数的定义域是(﹣1,1)∪(1,+∞).故选:C.【点评】本题主要考查对数函数的定义域及其求法,熟练解不等式组是基础,属于基础题.3.(5分)若i(x+yi)=3+4i,x,y∈R,则复数x+yi的模是()A.2 B.3 C.4 D.5【分析】利用复数的运算法则把i(x+yi)可化为3+4i,利用复数相等即可得出x=4,y=﹣3.再利用模的计算公式可得|x+yi|=|4﹣3i|==5.【解答】解:∵i(x+yi)=xi﹣y=3+4i,x,y∈R,∴x=4,﹣y=3,即x=4,y=﹣3.∴|x+yi|=|4﹣3i|==5.故选:D.【点评】熟练掌握复数的运算法则和模的计算公式是解题的关键.4.(5分)已知sin(+α)=,cosα=()A.B.C.D.【分析】已知等式中的角变形后,利用诱导公式化简,即可求出cosα的值.【解答】解:sin(+α)=sin(2π++α)=sin(+α)=cosα=.故选:C.【点评】此题考查了诱导公式的作用,熟练掌握诱导公式是解本题的关键.5.(5分)执行如图所示的程序框图,若输入n的值为3,则输出s的值是()A.1 B.2 C.4 D.7【分析】由已知中的程序框图及已知中输入3,可得:进入循环的条件为i≤3,即i=1,2,3.模拟程序的运行结果,即可得到输出的S值.【解答】解:当i=1时,S=1+1﹣1=1;当i=2时,S=1+2﹣1=2;当i=3时,S=2+3﹣1=4;当i=4时,退出循环,输出S=4;故选:C.【点评】本题考查的知识点是程序框图,在写程序的运行结果时,我们常使用模拟循环的变法,但程序的循环体中变量比较多时,要用表格法对数据进行管理.6.(5分)某三棱锥的三视图如图所示,则该三棱锥的体积是()A.B.C.D.1【分析】由三视图可知:该几何体是一个三棱锥,其中PA⊥底面ABC,PA=2,AB⊥BC,AB=BC=1.据此即可得到体积.【解答】解:由三视图可知:该几何体是一个三棱锥,其中PA⊥底面ABC,PA=2,AB⊥BC,AB=BC=1.∴.因此V===.故选:B.【点评】由三视图正确恢复原几何体是解题的关键.7.(5分)垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是()A.B.x+y+1=0 C.x+y﹣1=0 D.【分析】设所求的直线为l,根据直线l垂直于y=x+1,设l方程为y=﹣x+b,即x+y+b=0.根据直线l与圆x2+y2=1相切,得圆心0到直线l的距离等于1,由点到直线的距离公式建立关于b的方程,解之可得b=±,最后根据切点在第一象限即可得到满足题意直线的方程.【解答】解:设所求的直线为l,∵直线l垂直于直线y=x+1,可得直线l的斜率为k=﹣1∴设直线l方程为y=﹣x+b,即x+y﹣b=0∵直线l与圆x2+y2=1相切,∴圆心到直线的距离d=,解之得b=±当b=﹣时,可得切点坐标(﹣,﹣),切点在第三象限;当b=时,可得切点坐标(,),切点在第一象限;∵直线l与圆x2+y2=1的切点在第一象限,∴b=﹣不符合题意,可得b=,直线方程为x+y﹣=0故选:A.【点评】本题给出直线l垂直于已知直线且与单位圆相切于第一象限,求直线l 的方程.着重考查了直线的方程、直线与直线位置关系和直线与圆的位置关系等知识,属于基础题.8.(5分)设l为直线,α,β是两个不同的平面,下列命题中正确的是()A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥β【分析】根据线面平行的几何特征及面面平行的判定方法,可判断A;根据面面平行的判定方法及线面垂直的几何特征,可判断B;根据线面平行的性质定理,线面垂直及面面垂直的判定定理,可判断C;根据面面垂直及线面平行的几何特征,可判断D.【解答】解:若l∥α,l∥β,则平面α,β可能相交,此时交线与l平行,故A 错误;若l⊥α,l⊥β,根据垂直于同一直线的两个平面平行,可得B正确;若l⊥α,l∥β,则存在直线m⊂β,使l∥m,则m⊥α,故此时α⊥β,故C错误;若α⊥β,l∥α,则l与β可能相交,可能平行,也可能线在面内,故D错误;故选:B.【点评】本题考查的知识点是空间中直线与直线的位置关系,直线与平面的位置关系及平面与平面之间的位置关系,熟练掌握空间线面关系的几何特征及判定方法是解答的关键.9.(5分)已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于,则C 的方程是()A.B.C.D.【分析】由已知可知椭圆的焦点在x轴上,由焦点坐标得到c,再由离心率求出a,由b2=a2﹣c2求出b2,则椭圆的方程可求.【解答】解:由题意设椭圆的方程为.因为椭圆C的右焦点为F(1,0),所以c=1,又离心率等于,即,所以a=2,则b2=a2﹣c2=3.所以椭圆的方程为.故选:D.【点评】本题考查了椭圆的标准方程,考查了椭圆的简单性质,属中档题.10.(5分)设是已知的平面向量且,关于向量的分解,有如下四个命题:①给定向量,总存在向量,使;②给定向量和,总存在实数λ和μ,使;③给定单位向量和正数μ,总存在单位向量和实数λ,使;④给定正数λ和μ,总存在单位向量和单位向量,使;上述命题中的向量,和在同一平面内且两两不共线,则真命题的个数是()A.1 B.2 C.3 D.4【分析】选项①由向量加减的几何意义可得;选项②③均可由平面向量基本定理判断其正确性;选项④λ和μ为正数,这就使得向量不一定能用两个单位向量的组合表示出来.【解答】解:选项①,给定向量和,只需求得其向量差即为所求的向量,故总存在向量,使,故①正确;选项②,当向量,和在同一平面内且两两不共线时,向量,可作基底,由平面向量基本定理可知结论成立,故可知②正确;选项③,取=(4,4),μ=2,=(1,0),无论λ取何值,向量λ都平行于x轴,而向量μ的模恒等于2,要使成立,根据平行四边形法则,向量μ的纵坐标一定为4,故找不到这样的单位向量使等式成立,故③错误;选项④,因为λ和μ为正数,所以和代表与原向量同向的且有固定长度的向量,这就使得向量不一定能用两个单位向量的组合表示出来,故不一定能使成立,故④错误.故选:B.【点评】本题考查命题真假的判断与应用,涉及平面向量基本定理及其意义,属基础题.二、填空题:本大题共3小题.每小题5分,满分15分.(一)必做题(11~13题)11.(5分)设数列{a n}是首项为1,公比为﹣2的等比数列,则a1+|a2|+a3+|a4|= 15.【分析】根据条件求得等比数列的通项公式,从而求得a1+|a2|+a3+|a4|的值.【解答】解:∵数列{a n}是首项为1,公比为﹣2的等比数列,∴a n=a1•q n﹣1=(﹣2)n﹣1,∴a1=1,a2=﹣2,a3=4,a4=﹣8,∴则a1+|a2|+a3+|a4|=1+2+4+8=15,故答案为15.【点评】本题主要考查等比数列的定义、通项公式,属于基础题.12.(5分)若曲线y=ax2﹣lnx在点(1,a)处的切线平行于x轴,则a=.【分析】先求出函数的导数,再由题意知在1处的导数值为0,列出方程求出k 的值.【解答】解:由题意得,∵在点(1,a)处的切线平行于x轴,∴2a﹣1=0,得a=,故答案为:.【点评】本题考查了函数导数的几何意义应用,难度不大.13.(5分)已知变量x,y满足约束条件,则z=x+y的最大值是5.【分析】先画出线性约束条件表示的可行域,再将目标函数赋予几何意义,最后利用数形结合即可得目标函数的最值.【解答】解:画出可行域如图阴影部分,由得A(1,4)目标函数z=x+y可看做斜率为﹣1的动直线,其纵截距越大z越大,=1+4=5.由图数形结合可得当动直线过点A(1,4)时,z最大故答案为:5.【点评】本题主要考查了线性规划,以及二元一次不等式组表示平面区域的知识,数形结合的思想方法,属于基础题.选做题(14、15题,考生只能从中选做一题)14.(5分)(坐标系与参数方程选做题)已知曲线C的极坐标方程为ρ=2cosθ.以极点为原点,极轴为x轴的正半轴建立直角坐标系,则曲线C的参数方程为(θ为参数).【分析】首先把曲线的极坐标方程化为直角坐标方程,然后化直角坐标方程为参数方程.【解答】解:由曲线C的极坐标方程为ρ=2cosθ,得ρ2=2ρcosθ,即x2+y2﹣2x=0.化圆的方程为标准式,得(x﹣1)2+y2=1.令,得.所以曲线C的参数方程为.故答案为.【点评】本题考查了圆的参数方程,考查了极坐标与直角坐标的互化,解答此题的关键是熟记互化公式,是中档题.15.(几何证明选讲选做题)如图,在矩形ABCD中,,BC=3,BE⊥AC,垂足为E,则ED=.【分析】由矩形ABCD,得到三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,进而得到AB为AC的一半,利用直角三角形中直角边等于斜边的一半得到∠ACB=30°,且利用射影定理求出EC的长,在三角形ECD中,利用余弦定理即可求出ED的长.【解答】解:∵矩形ABCD,∴∠ABC=90°,∴在Rt△ABC中,AB=,BC=3,根据勾股定理得:AC=2,∴AB=AC,即∠ACB=30°,EC==,∴∠ECD=60°,在△ECD中,CD=AB=,EC=,根据余弦定理得:ED2=EC2+CD2﹣2EC•CDcos∠ECD=+3﹣=,则ED=.故答案为:【点评】此题考查了余弦定理,勾股定理,直角三角形的性质,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.四、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(12分)已知函数.(1)求的值;(2)若,求.【分析】(1)把x=直接代入函数解析式求解.(2)先由同角三角函数的基本关系求出sinθ的值,然后将x=θ﹣代入函数解析式,并利用两角和与差公式求得结果.【解答】解:(1)(2)∵,,∴.【点评】本题主要考查了特殊角的三角函数值的求解,考查了和差角公式的运用,属于知识的简单综合.17.(13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1)根据频数分布表计算苹果的重量在[90,95)的频率;(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.【分析】(1)用苹果的重量在[90,95)的频数除以样本容量,即为所求.(2)根据重量在[80,85)的频数所占的比例,求得重量在[80,85)的苹果的个数.(3)用列举法求出所有的基本事件的个数,再求出满足条件的事件的个数,即可得到所求事件的概率.【解答】解:(1)苹果的重量在[90,95)的频率为.(2)重量在[80,85)的有个.(3)设这4个苹果中,重量在[80,85)段的有1个,编号为1.重量在[95,100)段的有3个,编号分别为2、3、4,从中任取两个,可能的情况有:(1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种.设任取2个,重量在[80,85)和[95,100)中各有1个的事件为A,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以.【点评】本题考查古典概型问题,用列举法计算可以列举出基本事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想.本题还考查分层抽样的定义和方法,利用了总体中各层的个体数之比等于样本中对应各层的样本数之比,属于基础题.18.(13分)如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF,其中BC=.(1)证明:DE∥平面BCF;(2)证明:CF⊥平面ABF;.(3)当AD=时,求三棱锥F﹣DEG的体积V F﹣DEG【分析】(1)在等边三角形ABC中,由AD=AE,可得,在折叠后的三棱锥A﹣BCF中也成立,故有DE∥BC,再根据直线和平面平行的判定定理证得DE ∥平面BCF.(2)由条件证得AF⊥CF ①,且.在三棱锥A﹣BCF中,由,可得BC2=BF2+CF2,从而CF⊥BF②,结合①②,证得CF⊥平面ABF.(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.再由,运算求得结果.【解答】解:(1)在等边三角形ABC中,AD=AE,∴,在折叠后的三棱锥A﹣BCF中也成立,∴DE∥BC.又∵DE⊄平面BCF,BC⊂平面BCF,∴DE∥平面BCF.(2)在等边三角形ABC中,F是BC的中点,所以AF⊥BC,即AF⊥CF ①,且.∵在三棱锥A﹣BCF中,,∴BC2=BF2+CF2,∴CF⊥BF②.又∵BF∩AF=F,∴CF⊥平面ABF.(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.∴=.【点评】本题主要考查直线和平面平行的判定定理、直线和平面垂直的判定的定理的应用,用等体积法求三棱锥的体积,属于中档题.19.(14分)设各项均为正数的数列{a n}的前n项和为S n,满足4S n=a n+12﹣4n﹣1,n∈N*,且a2,a5,a14构成等比数列.(1)证明:a 2=;(2)求数列{a n}的通项公式;(3)证明:对一切正整数n,有.【分析】(1)对于,令n=1即可证明;(2)利用,且,(n≥2),两式相减即可求出通项公式.(3)由(2)可得=.利用“裂项求和”即可证明.【解答】解:(1)当n=1时,,∵(2)当n≥2时,满足,且,∴,∴,∵a n>0,∴a n=a n+2,+1∴当n≥2时,{a n}是公差d=2的等差数列.∵a2,a5,a14构成等比数列,∴,,解得a2=3,由(1)可知,,∴a1=1∵a2﹣a1=3﹣1=2,∴{a n}是首项a1=1,公差d=2的等差数列.∴数列{a n}的通项公式a n=2n﹣1.(3)由(2)可得式=.∴【点评】熟练掌握等差数列与等比数列的通项公式、“裂项求和”、通项与前n项和的关系a n=S n﹣S n﹣1(n≥2)是解题的关键.20.(14分)已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x ﹣y﹣2=0的距离为,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.(1)求抛物线C的方程;(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;(3)当点P在直线l上移动时,求|AF|•|BF|的最小值.【分析】(1)利用焦点到直线l:x﹣y﹣2=0的距离建立关于变量c的方程,即可解得c,从而得出抛物线C的方程;(2)先设,,由(1)得到抛物线C的方程求导数,得到切线PA,PB的斜率,最后利用直线AB的斜率的不同表示形式,即可得出直线AB的方程;(3)根据抛物线的定义,有,,从而表示出|AF|•|BF|,再由(2)得x1+x2=2x0,x1x2=4y0,x0=y0+2,将它表示成关于y0的二次函数的形式,从而即可求出|AF|•|BF|的最小值.【解答】解:(1)焦点F(0,c)(c>0)到直线l:x﹣y﹣2=0的距离,解得c=1,所以抛物线C的方程为x2=4y.(2)设,,由(1)得抛物线C的方程为,,所以切线PA,PB的斜率分别为,,所以PA:①PB:②联立①②可得点P的坐标为,即,,又因为切线PA的斜率为,整理得,直线AB的斜率,所以直线AB的方程为,整理得,即,因为点P(x0,y0)为直线l:x﹣y﹣2=0上的点,所以x0﹣y0﹣2=0,即y0=x0﹣2,所以直线AB的方程为x0x﹣2y﹣2y0=0.(3)根据抛物线的定义,有,,所以=,由(2)得x1+x2=2x0,x1x2=4y0,x0=y0+2,所以=.所以当时,|AF|•|BF|的最小值为.【点评】本题以抛物线为载体,考查抛物线的标准方程,考查利用导数研究曲线的切线方程,考查计算能力,有一定的综合性.21.(14分)设函数f(x)=x3﹣kx2+x(k∈R).(1)当k=1时,求函数f(x)的单调区间;(2)当k<0时,求函数f(x)在[k,﹣k]上的最小值m和最大值M.【分析】(1)当k=1时,求出f′(x)=3x2﹣2x+1,判断△即可得到单调区间;(2)解法一:当k<0时,f′(x)=3x2﹣2kx+1,其开口向上,对称轴,且过(0,1).分△≤0和△>0即可得出其单调性,进而得到其最值.解法二:利用“作差法”比较:当k<0时,对∀x∈[k,﹣k],f(x)﹣f(k)及f (x)﹣f(﹣k).【解答】解:f′(x)=3x2﹣2kx+1(1)当k=1时f′(x)=3x2﹣2x+1,∵△=4﹣12=﹣8<0,∴f′(x)>0,f(x)在R上单调递增.(2)当k<0时,f′(x)=3x2﹣2kx+1,其开口向上,对称轴,且过(0,1)(i)当,即时,f′(x)≥0,f(x)在[k,﹣k]上单调递增,从而当x=k时,f(x)取得最小值m=f(k)=k,当x=﹣k时,f(x)取得最大值M=f(﹣k)=﹣k3﹣k3﹣k=﹣2k3﹣k.(ii)当,即时,令f′(x)=3x2﹣2kx+1=0解得:,注意到k<x2<x1<0,∴m=min{f(k),f(x1)},M=max{f(﹣k),f(x2)},∵,∴f(x)的最小值m=f(k)=k,∵,∴f(x)的最大值M=f(﹣k)=﹣2k3﹣k.综上所述,当k<0时,f(x)的最小值m=f(k)=k,最大值M=f(﹣k)=﹣2k3﹣k解法2:(2)当k<0时,对∀x∈[k,﹣k],都有f(x)﹣f(k)=x3﹣kx2+x﹣k3+k3﹣k=(x2+1)(x﹣k)≥0,故f(x)≥f(k).f(x)﹣f(﹣k)=x3﹣kx2+x+k3+k3+k=(x+k)(x2﹣2kx+2k2+1)=(x+k)[(x﹣k)2+k2+1]≤0,故f(x)≤f(﹣k),而f(k)=k<0,f(﹣k)=﹣2k3﹣k>0.所以,f(x)min=f(k)=k.【点评】熟练掌握利用导数研究函数的单调性、二次函数的单调性、分类讨论思想方法、作差法比较两个数的大小等是解题的关键.第21页(共21页)。
2013广东高考数学(文科)试题及详解

图 2俯视图侧视图正视图2013广东高考数学(文科)试题及详解一、选择题:本大题共10小题,每小题5分,满分50分,1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =AA .{0}B .{0,2}C .{2,0}-D .{2,0,2}- 2.函数lg(1)()1x f x x +=-的定义域是C A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是D A .2 B .3 C .4 D .54.已知51sin()25πα+=,那么cos α=C A .25- B .15- C .15 D .255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是CA .1B .2C .4D .76.某三棱锥的三视图如图2所示,则该三棱锥的体积是B A .16 B .13 C .23D .1 7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是AA .0x y +=B .10x y ++=C .10x y +-= D .0x y += 解:圆心到直线的距离等于1r =,排除B 、C ;相切于第一象限排除D ,选A. 8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是B A .若//l α,//l β,则//αβ B .若l α⊥,l β⊥,则//αβ C .若l α⊥,//l β,则//αβ D .若αβ⊥,//l α,则l β⊥ 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是D A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 10.设a 是已知的平面向量且≠0a ,关于向量a 的分解,有如下四个命题:①给定向量b ,总存在向量c ,使=+a b c ; ②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ; ③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ; 上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是 A .1B .2C .3D .4图 1【解析】本题是选择题中的压轴题,主要考查平面向量的基本定理和向量加法的三角形法则.利用向量加法的三角形法则,易的①是对的;利用平面向量的基本定理,易的②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量λb 有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须=+λμλμ+≥b c a ,所以④是假命题.综上,本题选B.平面向量的基本定理考前还强调过,不懂学生做得如何.二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. 11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 12.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = .13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 .【解析】本题考了备考弱点.讲参数方程的时候,参数的意义要理解清楚.先化成直角坐标方程()2211x y -+=,易的则曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩ (θ为参数)15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB =3BC =,BE AC ⊥,垂足为E ,则ED = .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数(),12f x x x Rπ⎛⎫=-∈ ⎪⎝⎭. (1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.图 318.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中BC(1) 证明:DE //平面BCF ;(2) 证明:CF ⊥平面ABF ;(3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -. 【解析】(1)在等边三角形ABC 中,AD AE = AD AE DB EC∴=,在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ ,DE ⊄平面BCF , BC ⊂平面BCF ,//DE ∴平面BCF ;(2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A B C -2222BC BF CF CF BF ∴=+∴⊥② B F C F F C FA B ⋂=∴⊥平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.11111113232333F DEG E DFGV V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅= ⎝⎭【解析】这个题是入门级的题,除了立体几何的内容,还考查了平行线分线段成比例这个平面几何的内容.19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1) 证明:2a =(2) 求数列{}n a 的通项公式;(3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. 【解析】(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+ ∴当2n ≥时,{}n a 是公差2d =的等差数列. 2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =,由(1)可知,212145=4,1a a a =-∴= 21312a a -=-=∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-. (3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 【解析】本题考查很常规,第(1)(2)两问是已知n S 求n a ,{}n a 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(2)问,作出第(3)问.本题易错点在分成1n =,2n ≥来做后,不会求1a ,没有证明1a 也满足通项公式.20.(本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程; (2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.【解析】(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =; (2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理,20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002.∵经过1122(,),(,)A x y B x y 两点的直线是唯一的,∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-=0020x y --= ()22220000021=221AF BF y y x y y y ∴⋅=-++-+++2200019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为92【解析】2013广州模直接命中了这一题,广一模20题解法2正是本科第(2)问的解法,并且广一模大题结构和高考完全一致. 紫霞仙子:我的意中人是个盖世英雄,有一天他会踩着七色云彩来娶我,我只猜中了前头,可是我却猜不中这结局……形容这次高考,妙极!21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈.(1) 当1=k 时,求函数)(x f 的单调区间; (2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M . 【解析】:()'2321fx x kx =-+ (1)当1k =时()'2321,41280f x x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321f x x kx =-+,其开口向上,对称轴3kx = ,且过()01,(i)当(241240k k k ∆=-=≤,即0k <时,()'0f x ≥,()f x 在[],k k -上单调递增,从而当x k =时,()f x 取得最小值()m f k k == ,当x k =-时,()f x 取得最大()3332M f k k k k k k =-=---=--.(ii )当(24124330kkk∆=-=>,即k <时,令()'23210f x x kx =-+=解得:12x x ==,注意到210k x x <<<, (注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) ()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+> ()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=-->所以 3max ()()2f x f k k k =-=--,min ()()f x f k k ==【解析】:看着容易,做着难!常规解法完成后,发现不用分类讨论,奇思妙解也出现了:结合图像感知x k = 时最小,x k =-时最大,只需证()()()f k f x f k ≤≤-即可,避免分类讨论.本题第二问关键在求最大值,需要因式.。
2013年普通高等学校招生全国统一考试(广东卷)数学文科试题含答案(纯word版)

2013年普通高等学校招生全国统一考试(广东卷)数学(文科)本试卷共4页,21小题,满分150分.考试用时120分钟注意事项:1. 答卷前,考生务必用黑色笔迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上。
用2B铅笔讲试卷类型(A)填涂在答题卡相应的位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁,考试结束后,将试题与答题卡一并交回。
参考公式:球的体积,其中R为球的半径.锥体的体积公式为,其中S为锥体的底面积,h为锥体的高。
一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的1、设集合,,则=()A.{0} B.{0,2} C.{-2,0} D.{-2,0,Array 2}2、函数的定义域是()A.(-1,+∞) B.,+∞)C. D.3、若,x,R,则复数的模是()A.2 B.3 C.4 D.54、已知,则()A. B. C. D.5、执行如图1所示的程序框图,若输入的值为3,则输出s的值为A.1 B.2 C.4 D.76、某三棱锥的三视图如图2所示,则该棱锥的体积是()A. B. C. D. 17、垂直于直线且与圆相切于第Ⅰ象限的直线方程是()A. B.C. D.8、设l是直线,,是两个不同的平面,下列命题中正确的是()A .若l ∥,l ∥,则∥ B.若,,则∥ C.若,l ∥,则∥ D.若,l ∥,则9、已知中心在原点的椭圆C 的右焦点为,离心率等于,则C 的方程是( ) A . B. C. D.10、设是已知的平面向量,且。
2013年高考文科数学广东卷有答案

数学试卷 第1页(共14页) 数学试卷 第2页(共14页)绝密★启用前2013年普通高等学校招生全国统一考试(广东卷)数学(文科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液,不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x =+=∈R ,2{|20,}T x x x x =-=∈R ,则ST =( ) A .{0}B .{0,2}C .{2,0}-D .{2,0,2}-2.函数lg(1)()1x f x x +=-的定义域是( ) A .(1,)-+∞B .[1,)-+∞C .(1,1)(1,)-+∞D .[1,1)(1,)-+∞3.若i(+i)=3+4i x y ,,x y ∈R ,则复数+i x y 的模是( )A .2B .3C .4D .5 4.已知5π1sin()25α+=,那么cos α=( ) A .25-B .15-C .15D .255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是( ) A .1 B .2C .4D .76.某三棱锥的三视图如图2所示,则该三棱锥的体积是( ) A .16B .13C .23D .17.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是( )A.0x y +- B .10x y ++= C .10x y +-=D.0x y +=8.设l 为直线,α,β是两个不同的平面,下列命题中正确的是( )A .若l α∥,l β∥,则αβ∥B .若l α⊥,l β⊥,则αβ∥C .若l α⊥,l β∥,则αβ∥D .若αβ⊥,l α∥,则l β⊥9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于12,则C 的方程是 ( )姓名________________ 准考证号_____________------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------------数学试卷 第3页(共14页) 数学试卷 第4页(共14页)A .22134x y +=B.2214x = C .22142x y +=D .22143x y += 10.设a 是已知的平面向量且0≠a ,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使=+a b c ;②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ;上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是 ( ) A .1B .2C .3D .4二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11-13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= . 12.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = .13.已知变量x ,y 满足约束条件30111,x y x y -+⎧⎪-⎨⎪⎩≥,≤≤,≥则z x y =+的最大值是 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 . 15.(几何证明选讲选做题)如图3,在矩形ABCD 中,AB =,3BC =,BE AC ⊥,垂足为E ,则ED = .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数π())12f x x =-,x ∈R . (Ⅰ)求π()3f 的值;(Ⅱ)若3cos 5θ=,3π(,2π)2θ∈,求π()6f θ-. 17.(本小题满分13分)(Ⅰ)根据频数分布表计算苹果的重量在[90,95)的频率;(Ⅱ)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个;(Ⅲ)在(Ⅱ)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.18.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF △沿AF 折起,得到如图5所示的三棱锥A B C F -,其中BC =(Ⅰ)证明:DE ∥平面BCF ; (Ⅱ)证明:CF ⊥平面ABF ;(Ⅲ)当23AD =时,求三棱锥F DEG -的体积F DEG V -.19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441n n S a n +=--,*n ∈N ,且2a,5a ,14a 构成等比数列.(Ⅰ)证明:2a = (Ⅱ)求数列{}n a 的通项公式;(Ⅲ)证明:对一切正整数n ,有1223111112n n a a a a a a ++++<.20.(本小题满分14分)数学试卷 第5页(共14页) 数学试卷 第6页(共14页)已知抛物线C 的顶点为原点,其焦点(0,)(0)F c c >到直线l :20x y --=的距离为2.设P 为直线l 上的点,过P 点作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点.(Ⅰ)求抛物线C 的方程;(Ⅱ)当点00(,)P x y 为直线l 上的定点时,求直线AB 的方程;(Ⅲ)当点P 在直线l 上移动时,求||||AF BF 的最小值.21.(本小题满分14分)设函数32()()f x x kx x k =-+∈R . (Ⅰ)当1k =时,求函数()f x 的单调区间;(Ⅱ)当k <0时,求函数()f x 在[,]k k -上的最小值m 和最大值M .数学试卷 第7页(共14页)数学试卷 第8页(共14页)2013年普通高等学校招生全国统一考试(广东卷)数学(文科)答案解析一、选择题 1.【答案】A【解析】由题意知{0,2}S =-,{0,2}T =,故{0}ST =,故选A .【提示】先求一元二次方程的根,再用列举法求交集元素. 【考点】集合的交集运算. 2.【答案】C【解析】由题意知1010x x +>⎧⎨-≠⎩,解得1x >-且1x ≠,所以定义域为(1,1)(1,)-+∞【提示】从函数有意义的角度分析求解定义域,再由各个集合的交集得出定义域. 【考点】函数的定义域和集合的交集运算. 3.【答案】D【解析】因为i(i)34i x y +=+,所以i 34i x y-=+,根据两个复数相等的条件得:3y -=即3y =-,4x =,所以x yi +43i =-,i x y +的模5=;6.【答案】B【解析】由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形,高为2, 所以该三棱锥的体积111112323V ==;【提示】由三视图还原出直观图,根据“长对正、高对齐、宽相等”寻找出三棱锥的相关数据,代入棱锥的体积公式进行计算. 【考点】平面图形的三视图的和棱锥的体积.7.【答案】A【解析】设所求直线为l ,因为l 垂直直线1y x =+,故l 的斜率为1-,设直线l 的方程为y x b =-+,化为一般式为0x y b +-=;因为l 与圆相切221x y +=相切,所以圆心(0,0)到直线l 的距离1=,所以b =0b >,【解析】若α与β相交,且l 平行于交线,则也符合A ,显然A 错;若l l αβ⊥,∥,则αβ⊥,故C 错;l αβα⊥,∥,若l 平行交线,则l β∥,故D 错;【提示】由线面平行或垂直的某些给定条件来判断相关线面的位置关系. 【考点】空间中直线、平面之间的位置关系.9.【答案】由线面平行或垂直的某些给定条件来判断相关线面的位置关系. 【解析】由焦点可知(1,0F )可知椭圆焦点在x 轴上,由题意知1c =,12c a =,所以2a b ===,22143x y +=; 【提示】给定椭圆的离心率和焦点,求出各参数从而确定其标准方程. 【考点】椭圆的标准方程和椭圆的几何性质. 10.【答案】C【解析】对于①,若向量a ,b 确定,因为a b -是确定的,故总存在向量c ,满足c a b =-,数学试卷 第9页(共14页) 数学试卷 第10页(共14页)即a b c =+,故正确.对于②,因为c 和b 不共线,由平面向量基本定理可知,总存在唯一的一对实数λ,μ,满足a b c λμ=+,故正确;对于③,如果a b c λμ=+,则以||a ,||b λ,||c μ为三边长可以构成一个三角形,如果单位向量b 和正数μ确定,则一定存在单位向量c 和实数λ,使a b c λμ=+,故正确;对于④,如果给定的正数和不能满足“以||a ,||b λ,||c μ为三边长可以构成一个三角形”,这时单位向量b 和c 就不存在,故错误.因此选C【提示】给定某些向量,利用平行四边形或三角形法则及平面向量基本定理来进行判断. 【考点】平面向量基本定理. 二、填空题 11.【答案】15【解析】由题意知11a =,22a =-,34a =,48a =-,所以;1234a a a a +++【解析】因为2ln y ax x =-,所以2y ax x'=-,因为曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,所以1210x y a ='=-=,所以12a =;【提示】给定曲线上某点切线在坐标轴上的位置关系,利用该点导数的几何意义求解原方程,从而求出待定系数.【考点】曲线的切线与导数的联系,导数的几何意义. 13.【答案】5【解析】作出可行域可得直角梯形的四个顶点分别为(1,1)-,(1,2)-,(1,1),(1,4)代入可知z 的最大值为145z =+=;【提示】画出线性约束条件表示的平面区域,用图解法求最值. 【考点】线性规划问题的最值求解.14.【答案】,(为参数)【解析】因为曲线C 的极坐标方程为2cos ρθ=;所以2cos 2cos 1cos2x ρθθθ===+①,sin 2sin cos sin 2y ρθθθθ===②; ①可变形得:cos21x θ=-③,②可变形得:sin 2y θ=;由2222(1)1x y -+=【解析】因为在矩形ABCD 中,AB =3BC =,BE AC ⊥,所以30BCA ∠=︒,所以cos30CE CB =︒=CDE △中,因为60ECD ∠=︒,由余弦定理得: 2222021212cos60224DE CE CD CE CD =+-=+-=⎝⎭,所以CD =; ππππππcos cos sin sin 6612333f θθθθθ⎛⎫⎛⎫⎛⎫⎫-=--=-=+ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎭314525210⨯-⨯=⎭; 【提示】给定余弦函数表达式,利用同角三角函数的基本关系式、两角差的余弦公式等λμcos 1sin x y αα=+⎧⎨=⎩α数学试卷 第11页(共14页) 数学试卷 第12页(共14页)(2)若采用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,则重量在[80,85)的个数541515=⨯=+; (3)设在[80,85)中抽取的一个苹果为x ,在[95,100)中抽取的三个苹果分别为a b c ,,,从抽出的4个苹果中,任取2个共有(,)x a ,(,)x b ,(,)x c ,(,)a b,(,)a c ,(,)b c 6种情况,其中符合“重量在[80,85)和[95,100)中各有一个”的情况共有(,)x a ,(,)x b ,(,)x c种;设“抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个”为事件A ,则事件A 的概率31()P A ==;(2)证明:在图4中,因为因为ABC 是等边三角形,且F 是BC 的中点,所以AF BC ⊥;在图5中,因为在BFC △中,122BF FC BC ===,,所以222BF FC BC +=,BF CF ⊥,又因为AF CF ⊥,所以CF ABF ⊥平面(3)因为AF CF AF BF ⊥⊥,,所以AF ⊥平面BCF ,又因为平面DGE ∥平面BCF ,所以AF ⊥平面DGE;所以11111113333232336324F D EGDGE V S FG DG GE FG -====△; 【提示】通过折叠问题来分析折叠前后变化的元素和不变化的元素,从而得出线面平行或垂直关系以及三棱锥的体积.【考点】线面平行、线面垂直和面面平行的判定与性质,平面图形的折叠问题和三棱锥(2)当2n ≥时,2211444(41)4(1)1n n n n n a S S a n a n -+⎡⎤=-=------⎣⎦2214n n a a +=--, 所以221(2)n n a a +=+,因为{}n a 各项均为正数,所以12n n a a +=+; 因为2a ,5a ,14a 构成等比数列,所以22145a a a =,即2222(24)(6)a aa +=+,解得23a =,因为2a =,所以11a =,212a a =+,符合12n n a a +=+,所以12n n a a +=+对1n =也符合,所以数列{}n a 是一个以11a =为首项,2d =为公差的等差数列,1(1)221n a n n =+-=-;(3)因为111111(21)(21)22121n n a a n n n n +⎛⎫==- ⎪+--+⎝⎭, 所以1223111111111111121323522121n n a a a a a a n n +⎛⎫⎛⎫⎛⎫+++=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭111111111112133521212121212n n n nn ⎛⎫⎛⎫=-+-+⋅⋅⋅-=-=< ⎪ ⎪-+++⎝⎭⎝⎭; 所以对一切正整数n ,有11112a a a a a a +++<.以抛物线C 的方程为24x y =; (2)因为抛物线的方程为24x y =,即214y x =,所以12y x '=,设过00(,)P x y 点的切线l '与抛物线的切点坐标为21,4m m ⎛⎫ ⎪⎝⎭,所以直线l '的斜率2104012y m k m x m -==-,解得10m x =或20m x =;不妨设A 点坐标为2111,4m m ⎛⎫ ⎪⎝⎭,B 点数学试卷 第13页(共14页) 数学试卷 第14页(共14页)坐标为2221,4m m ⎛⎫ ⎪⎝⎭0,所以12m m ≠;221112441201211()42AB m m k m m x m m -==+=-; 所以直线AB 的方程为210111()42y m x x m -=-,代入整理得:012y x =;(3)A 点坐标为2111,4m m ⎛⎫ ⎪⎝⎭,B 点坐标为2221,4m m ⎛⎫ ⎪⎝⎭,F 点坐标为(0,1),因为0020x y --=;所以100m x x =,200m x x ==1202m m x +=, 12048m m x =-;因此=22222222221122121111|||11114444AF BF m m m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-+-=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2222222212121212121211111111()1()[()2]44164164m m m m m m m m m m m m ⎛⎫⎛⎫=++=+++=++-+ ⎪⎪⎝⎭⎝⎭22220000001139(48)[(2)2(48)]1269216422x x x x x x ⎛⎫=-+--+=-+=-+ ⎪⎝⎭, 所以当03x =时,||||AF BF 取最小值9;①当0∆≤时,即0k ≤<时,()0f x '≥,()f x 在R 上单调递增,此时无最小值和最大值;②当0∆>时,即k <()0f x '=,解得x ==或。
2013年全国高考(文科)数学试卷(广东卷)【已整理】

2013年广东高考数学试题(文科)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合{ EMBED Equation.KSEE3 \* MERGEFORMAT |} , 02|{2R x x x x S ∈=+=,,则( ) A . B . C . D .2、函数的定义域是( )A .B .C .D .3、若,、,则复数的模是( )A .2B .3C .4D .54、已知,那么( )A .B .C .D .5、执行如图所示的程序框图,若输入的值为3,则输入的值是( )A .1B .2C .3D .76、某三棱锥的三视图如图所示,则该三棱锥的体积是( )A .B .C .D .17、垂直于直线且与圆相切于第一象限的直线方程是( )A .B .C .D .8、设为直线,、是两个不同的平面,下列命题中正确的是()A.若,,则B.若,,则C.若,,则D.若,,则9、已知中心在原点的椭圆的右焦点为,离心率等于,则的方程是()A.B.C.D.10、设是已知的平面向量,且.关于向量的分解,有如下四个命题:①给定向量,总存在向量,使;②给定向量和,总存在实数和,使;③给定向量和正数,总存在单位向量,使;④给定正数和,总存在单位向量和单位向量,使.上述命题中的向量,和在同一平面内且两两不共线,则真命题的个数是()A.1 B.2 C.3 D.4二、填空题:本大题共5个小题,考生作答4个小题,每小题5分,满分20分.(一)必做题(11~13题)11、设数列是首项为1,公比为的等比数列,则________.12、若曲线在点处的切线平行于轴,则________.13、已知变量、满足约束条件,则的最大值是________.(二)选做题(14~15题,考生只能从中选做一题)14、(坐标系与参数方程选做题)已知曲线的极坐标方程,以极点为原点,极轴为轴的正半轴建立直角坐标系,则曲线的参数方程为________.15、(几何证明选讲选做题)如图3,在矩形中,,,,垂足为,则________.三、解答题:本大题共6个小题,满分80分.解答题写出文字说明、证明过程和演算步骤.16、(本小题满分12分)已知函数,.(1)求的值;(2)若,,求.17、(本小题满分12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1)根据频数分布表计算苹果的重量在的频率;(2)用分层抽样的方法从重量在和的苹果中共抽取4个,其中重量在的有几个?(3)在(2)中抽出的4个苹果中,任取2个,求重量在和中各有1个的概率.18、(本小题满分14分)如图4,在边长为1的等边中,、分别是、上的点,,是的中点,与交于点,将沿折起,得到如图5所示的三棱锥,其中.(1)证明:平面;(2)证明:平面;(3)当时,求棱锥的体积.19、(本小题满分14分)设各项均为正数的数列的前项和为,满足,,且、、构成等比数列.(1)证明:;(2)求数列的通项公式;(3)证明:对一切正整数,有.20、(本小题满分14分)已知抛物线的顶点为原点,其焦点()到直线的距离为.设为直线上的点,过点做抛物线的两条切线、,其中、为切点.(1)求抛物线的方程;(2)当点为直线上的定点时,求直线的方程;(3)当点在直线上移动时,求的最小值.21、(本小题满分14分)设函数().(1)当时,求函数的单调区间;(2)当时,求函数在上的最小值和最大值.。
2013年普通高等学校招生全国统一考试(广东卷)数学(文科A卷)解析

图 2俯视图侧视图正视图2013年普通高等学校招生全国统一考试(广东卷)数学(文科A 卷)解析本试卷共4页,21小题,满分150分.考试用时120分钟. 锥体的体积公式:13V Sh =.其中S 表示锥体的底面积,h 表示锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =A .{0}B .{0,2}C .{2,0}-D .{2,0,2}- 【解析】:先解两个一元二次方程,再取交集,选A ,5分到手,妙! 2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞【解析】:对数真数大于零,分母不等于零,目测C ! 3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 A .2 B .3 C .4 D .5【解析】:复数的运算、复数相等,目测4,3x y ==-,模为5,选D . 4.已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .25【解析】:考查三角函数诱导公式,51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭,选C. 5.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是 A .1 B .2 C .4 D .7 【解析】选C.本题只需细心按程序框图运行一下即可. 6.某三棱锥的三视图如图2所示,则该三棱锥的体积是 A .16 B .13 C .23D .1 【解析】由三视图判断底面为等腰直角三角形,三棱锥的高为2,则111=112=323V ⋅⋅⋅⋅,选B.7.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是图 1A .0x y +=B .10x y ++=C .10x y +-=D .0x y +=【解析】本题考查直线与圆的位置关系,直接由选项判断很快,圆心到直线的距离等于1r =,排除B 、C ;相切于第一象限排除D ,选A.直接法可设所求的直线方程为:()0y x k k =-+>,再利用圆心到直线的距离等于1r =,求得k =8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥ 【解析】基础题,在脑海里把线面可能性一想,就知道选B 了. 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x 【解析】基础题,1,2,3c a b ===,选D.10.设a 是已知的平面向量且≠0a ,关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使=+a b c ;②给定向量b 和c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使λμ=+a b c ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使λμ=+a b c ; 上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是 A .1B .2C .3D .4【解析】本题是选择题中的压轴题,主要考查平面向量的基本定理和向量加法的三角形法则.利用向量加法的三角形法则,易的①是对的;利用平面向量的基本定理,易的②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量λb 有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须=+λμλμ+≥b c a ,所以④是假命题.综上,本题选B.平面向量的基本定理考前还强调过,不懂学生做得如何.【品味选择题】文科选择题答案:ACDCC BABDB.选择题3322再次出现!今年的选择题很基础,希望以后高考年年出基础题!二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 【解析】这题相当于直接给出答案了1512.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = . 【解析】本题考查切线方程、方程的思想.依题意''1112,210,2x y ax y a a x ==-=-=∴= 13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.【解析】画出可行域如图,最优解为()1,4,故填 5 ; (二)选做题(14、15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 .【解析】本题考了备考弱点.讲参数方程的时候,参数的意义要理解清楚.先化成直角坐标方程()2211x y -+=,易的则曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩(θ为参数)15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB =3BC =,BE AC ⊥,垂足为E ,则ED = . 【解析】本题对数值要敏感,由AB =3BC =,可知60BAC ∠=从而30AE CAD =∠=,212DE ==. 【品味填空题】选做题还是难了点,比理科还难些.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)图 3已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值;(2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【解析】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.【解析】这个题实在是太简单,两角差的余弦公式不要记错了.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率. 【解析】(1)苹果的重量在[)95,90的频率为20=0.450; (2)重量在[)85,80的有54=15+15⋅个; (3)设这4个苹果中[)85,80分段的为1,[)100,95分段的为2、3、4,从中任取两个,可能的情况有: (1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[)85,80和[)100,95中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==. 【解析】这个基础题,我只强调:注意格式!18.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图52BC =.(1) 证明:DE //平面BCF ; (2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -. 【解析】(1)在等边三角形ABC 中,AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ ,DE ⊄平面BCF ,BC ⊂平面BCF ,//DE ∴平面BCF ;(2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,2BC =,222BC BF CF CF BF ∴=+∴⊥② BF CF F CF ABF ⋂=∴⊥平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.111111132323323324F DEG E DFGV V DG FG GF --⎛⎫∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎪ ⎪⎝⎭【解析】这个题是入门级的题,除了立体几何的内容,还考查了平行线分线段成比例这个平面几何的内容. 19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1)证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. 【解析】(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =,由(1)可知,212145=4,1a a a =-∴=21312a a -=-=∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-.(3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 【解析】本题考查很常规,第(1)(2)两问是已知n S 求n a ,{}n a 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(2)问,作出第(3)问.本题易错点在分成1n =,2n ≥来做后,不会求1a ,没有证明1a 也满足通项公式.20.(本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为32.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,AB 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.【解析】(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-,即2111212x y x x y -+=. ∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的, ∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-= 0020x y --=()222200000021=221AF BF y y x y y y ∴⋅=-++-+++2200019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为92【解析】2013广州模直接命中了这一题,广一模20题解法2正是本科第(2)问的解法,并且广一模大题结构和高考完全一致. 紫霞仙子:我的意中人是个盖世英雄,有一天他会踩着七色云彩来娶我,我只猜中了前头,可是我却猜不中这结局……形容这次高考,妙极!21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈.(1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M . 【解析】:()'2321fx x kx =-+(1)当1k =时()'2321,41280fx x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,其开口向上,对称轴3kx =,且过()01,(i)当(241240k k k ∆=-=≤,即0k <时,()'0f x ≥,()f x 在[],k k -上单调递增,从而当x k =时,()f x 取得最小值()m f k k == , 当x k =-时,()f x 取得最大值()3332M f k k k k k k =-=---=--.(ii)当(241240k k k ∆=-=+>,即k <()'23210f x x kx =-+=解得:221233k k k k x x +---==注意到210k x x <<<,(注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) ()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+>()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=-->所以 3max ()()2f x f k k k =-=--,min ()()f x f k k ==【解析】:看着容易,做着难!常规解法完成后,发现不用分类讨论,奇思妙解也出现了:结合图像感知x k = 时最小,x k =-时最大,只需证()()()f k f x f k ≤≤-即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.。
2013广东高考文科数学试卷扫描版及答案

2013年广东高考文科数学A 卷参考答案一、选择题 题号 1 2345678910选项ACDCCBABDB二、填空题11. 15 12. 12 13.5 14. 1cos sin x y θθ=+⎧⎨=⎩ (θ为参数) 15.212三、解答题16. 解:(1)2cos 2cos 133124f ππππ⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,24sin 1cos 5θθ=--=-,1=2cos 2cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎛⎫∴--=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.17. 解:1)苹果的重量在[90,95)的频率为20=0.450; (2)重量在[80,85)的有54=15+15⋅个; (3)设这4个苹果中[80,85)分段的为1,[)95,100分段的为2、3、4,从中任取两个,可能的情况有:(1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[80,85)和[)95,100中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==. 18. 解:(1)在等边三角形ABC 中,AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中也成立, //DE BC ∴ ,又DE ⊄ 平面BCF ,BC ⊂平面BCF , //DE ∴平面BCF ;(2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,22BC =,222BC BF CF CF BF ∴=+∴⊥②BF CF F CF ABF ⋂=∴⊥ 平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.11111131332323323324F DEG E DFGV V DG FG GF --⎛⎫∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎪ ⎪⎝⎭19. 解:(1)当1n =时,22122145,45a a a a =-=+,21045n a a a >∴=+(2)当2n ≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=-- ()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =,由(1)可知,212145=4,1a a a =-∴=21312a a -=-=*)(21N n a a n n ∈=-∴+∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-. (3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+ 11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 20. 解:(1)依题意023222c d --==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-,-kk3k x =抛物线C 在点B 处的切线PB 的方程为)(2222x x x y y -=-, ∵21141x y =, ∴P A :112y x x y -= .同理PB :222y x x y -= ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的, ∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+,∴()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=,其两根为21,y y 2212001202,y y x y y y y ∴+=-= 0020x y --=()222200000021=221AF BF y y x y y y ∴⋅=-++-+++220019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为9221. 解:函数)(x f 的定义域为R ,且()'2321f x x kx =-+(1)当1k =时()'2321,41280fx x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,此为开口向上,对称轴3kx =,且过()01,的二次函数。
2013年高考真题——数学文科(广东卷)word解析版

图 2俯视图侧视图正视图2013年普通高等学校招生全国统一考试(广东卷)数学(文科A 卷)解析本试卷共4页,21小题,满分150分.考试用时120分钟. 锥体的体积公式:13V Sh =.其中S 表示锥体的底面积,h 表示锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T = A .{0} B .{0,2} C .{2,0}- D .{2,0,2}- 【解析】:先解两个一元二次方程,再取交集,选A ,5分到手,妙! 2.函数lg(1)()1x f x x +=-的定义域是 A .(1,)-+∞ B .[1,)-+∞ C .(1,1)(1,)-+∞ D .[1,1)(1,)-+∞ 【解析】:对数真数大于零,分母不等于零,目测C ! 3.若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是 A .2 B .3 C .4 D .5【解析】:复数的运算、复数相等,目测4,3x y ==-,模为5,选D . 4.已知51sin()25πα+=,那么cos α= A .25- B .15- C .15 D .25【解析】:考查三角函数诱导公式,51sin()sin(2+)sin cos 2225πππαπααα⎛⎫+=+=+== ⎪⎝⎭,选C. 5.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是 A .1 B .2 C .4 D .7 【解析】选C.本题只需细心按程序框图运行一下即可. 6.某三棱锥的三视图如图2所示,则该三棱锥的体积是 A .16 B .13 C .23D .1 【解析】由三视图判断底面为等腰直角三角形,三棱锥的高为2,则111=112=323V ⋅⋅⋅⋅,选B.图 17.垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是A .0x y +=B .10x y ++=C .10x y +-=D .0x y +=【解析】本题考查直线与圆的位置关系,直接由选项判断很快,圆心到直线的距离等于1r =,排除B 、C ;相切于第一象限排除D ,选A.直接法可设所求的直线方程为:()0y x k k =-+>,再利用圆心到直线的距离等于1r =,求得k =8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥ 【解析】基础题,在脑海里把线面可能性一想,就知道选B 了. 9.已知中心在原点的椭圆C 的右焦点为(1,0)F ,离心率等于21,则C 的方程是 A .14322=+y x B .13422=+y x C .12422=+y x D .13422=+y x【解析】基础题,1,2,c a b ==,选D.10.设 a 是已知的平面向量且≠0 a ,关于向量a 的分解,有如下四个命题:①给定向量 b ,总存在向量 c ,使=+a b c ;②给定向量 b 和 c ,总存在实数λ和μ,使λμ=+a b c ;③给定单位向量 b 和正数μ,总存在单位向量 c 和实数λ,使λμ=+a b c ;④给定正数λ和μ,总存在单位向量 b 和单位向量 c ,使λμ=+a b c ;上述命题中的向量 b , c 和a 在同一平面内且两两不共线,则真命题的个数是A .1B .2C .3D .4【解析】本题是选择题中的压轴题,主要考查平面向量的基本定理和向量加法的三角形法则.利用向量加法的三角形法则,易的①是对的;利用平面向量的基本定理,易的②是对的;以a 的终点作长度为μ的圆,这个圆必须和向量λb 有交点,这个不一定能满足,③是错的;利用向量加法的三角形法则,结合三角形两边的和大于第三边,即必须=+λμλμ+≥b c a ,所以④是假命题.综上,本题选B.平面向量的基本定理考前还强调过,不懂学生做得如何.【品味选择题】文科选择题答案:ACDCC BABDB.选择题3322再次出现!今年的选择题很基础,希望以后高考年年出基础题!二、填空题:本大题共5小题.考生作答4小题.每小题5分,满分20分. (一)必做题(11~13题)11.设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= 【解析】这题相当于直接给出答案了1512.若曲线2ln y ax x =-在点(1,)a 处的切线平行于x 轴,则a = . 【解析】本题考查切线方程、方程的思想.依题意''1112,210,2x y ax y a a x ==-=-=∴= 13.已知变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤≤-≥+-11103y x y x ,则z x y =+的最大值是.【解析】画出可行域如图,最优解为()1,4,故填 5 ; (二)选做题(14、15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=.以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为 .【解析】本题考了备考弱点.讲参数方程的时候,参数的意义要理解清楚.先化成直角坐标方程()2211x y -+=,易的则曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩(θ为参数) 15.(几何证明选讲选做题)如图3,在矩形ABCD中,AB =3BC =,BE AC ⊥,垂足为E ,则ED = . 【解析】本题对数值要敏感,由AB =3BC =,可知60BAC ∠=从而30AE CAD =∠= ,2DE ==. 【品味填空题】选做题还是难了点,比理科还难些.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)图 3已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值;(2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫-⎪⎝⎭.【解析】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-,1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.【解析】这个题实在是太简单,两角差的余弦公式不要记错了.17.(本小题满分13分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[90,95)的频率;(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个? (3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率. 【解析】(1)苹果的重量在[)95,90的频率为20=0.450; (2)重量在[)85,80的有54=15+15⋅个; (3)设这4个苹果中[)85,80分段的为1,[)100,95分段的为2、3、4,从中任取两个,可能的情况有: (1,2)(1,3)(1,4)(2,3)(2,4)(3,4)共6种;设任取2个,重量在[)85,80和[)100,95中各有1个的事件为A ,则事件A 包含有(1,2)(1,3)(1,4)共3种,所以31(A)62P ==. 【解析】这个基础题,我只强调:注意格式!18.(本小题满分13分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5BC =(1) 证明:DE //平面BCF ;(2) 证明:CF ⊥平面ABF ; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -. 【解析】(1)在等边三角形ABC 中,AD AE =AD AEDB EC∴=,在折叠后的三棱锥A BCF -中 也成立,//DE BC ∴ ,DE ⊄ 平面BCF ,BC ⊂平面BCF ,//DE ∴平面BCF ;(2)在等边三角形ABC 中,F 是BC 的中点,所以AF BC ⊥①,12BF CF ==. 在三棱锥A BCF -中,2BC =,222BC BF CF CF BF ∴=+∴⊥②BF CF F CF ABF ⋂=∴⊥ 平面;(3)由(1)可知//GE CF ,结合(2)可得GE DFG ⊥平面.11111113232333F DEG E DFGV V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅= ⎝⎭【解析】这个题是入门级的题,除了立体几何的内容,还考查了平行线分线段成比例这个平面几何的内容. 19.(本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441,,n n S a n n N *+=--∈且2514,,a a a 构成等比数列. (1)证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++< . 【解析】(1)当1n =时,22122145,45a a a a =-=+,20n a a >∴=(2)当2n≥时,()214411n n S a n -=---,22114444n n n n n a S S a a -+=-=--()2221442n n n n a a a a +=++=+,102n n n a a a +>∴=+∴当2n ≥时,{}n a 是公差2d =的等差数列.2514,,a a a 构成等比数列,25214a a a ∴=⋅,()()2222824a a a +=⋅+,解得23a =,由(1)可知,212145=4,1a a a =-∴=21312a a -=-= ∴ {}n a 是首项11a =,公差2d =的等差数列.∴数列{}n a 的通项公式为21n a n =-.(3)()()1223111111111335572121n n a a a a a a n n ++++=++++⋅⋅⋅-+ 11111111123355721211111.2212n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+-+-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎡⎤=⋅-<⎢⎥+⎣⎦ 【解析】本题考查很常规,第(1)(2)两问是已知n S 求n a ,{}n a 是等差数列,第(3)问只需裂项求和即可,估计不少学生猜出通项公式,跳过第(2)问,作出第(3)问.本题易错点在分成1n =,2n ≥来做后,不会求1a ,没有证明1a 也满足通项公式.20.(本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点. (1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (3) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.【解析】(1)依题意2d ==,解得1c =(负根舍去) ∴抛物线C 的方程为24x y =;(2)设点11(,)A x y ,22(,)B x y ,),(00y x P ,由24x y =,即214y x ,=得y '=12x . ∴抛物线C 在点A 处的切线PA 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=.∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点1122(,),(,)A x y B x y 的坐标都满足方程 y x xy -=002. ∵经过1122(,),(,)A x y B x y 两点的直线是唯一的, ∴直线AB 的方程为y x xy -=002,即00220x x y y --=; (3)由抛物线的定义可知121,1AF y BF y =+=+, 所以()()121212111AF BF y y y y y y ⋅=++=+++联立2004220x y x x y y ⎧=⎨--=⎩,消去x 得()22200020y y x y y +-+=, 2212001202,y y x y y y y ∴+=-= 0020x y --=()222200000021=221AF BF y y x y y y ∴⋅=-++-+++220019=22+5=2+22y y y ⎛⎫++ ⎪⎝⎭∴当012y =-时,AF BF ⋅取得最小值为92【解析】2013广州模直接命中了这一题,广一模20题解法2正是本科第(2)问的解法,并且广一模大题结构和高考完全一致. 紫霞仙子:我的意中人是个盖世英雄,有一天他会踩着七色云彩来娶我,我只猜中了前头,可是我却猜不中这结局……形容这次高考,妙极!21.(本小题满分14分)设函数x kx x x f +-=23)( ()R k ∈.(1) 当1=k 时,求函数)(x f 的单调区间;(2) 当0<k 时,求函数)(x f 在[]k k -,上的最小值m 和最大值M . 【解析】:()'2321fx x kx =-+(1)当1k =时()'2321,41280fx x x =-+∆=-=-<()'0f x ∴>,()f x 在R 上单调递增.(2)当0k <时,()'2321fx x kx =-+,其开口向上,对称轴3kx =,且过()01,(i)当(241240k k k ∆=-=+≤,即0k <时,()'0f x ≥,()f x 在[],k k -上单调递增,从而当x k =时,()f x 取得最小值()m f k k == , 当x k =-时,()f x 取得最大值()3332M f k k k k k k =-=---=--.(ii)当(241240k k k ∆=-=+>,即k <()'23210f x x kx =-+=解得:12x x ==注意到210k x x <<<,(注:可用韦达定理判断1213x x ⋅=,1223kx x k +=>,从而210k x x <<<;或者由对称结合图像判断) ()(){}()(){}12min ,,max ,m f k f x M f k f x ∴==-()()()()32211111110f x f k x kx x k x k x -=-+-=-+>()f x ∴的最小值()m f k k ==,()()()()()232322222222=[1]0f x f k x kx x k k k k x k x k k --=-+---⋅-+-++<()f x ∴的最大值()32M f k k k =-=--综上所述,当0k <时,()f x 的最小值()m f k k ==,最大值()32M f k k k =-=--解法2(2)当0k <时,对[],x k k ∀∈-,都有32332()()(1)()0f x f k x kx x k k k x x k -=-+-+-=+-≥,故()()f x f k ≥32332222()()()(221)()[()1]0f x f k x kx x k k k x k x kx k x k x k k --=-++++=+-++=+-++≤故()()f x f k ≤-,而 ()0f k k =<,3()20f k k k -=-->所以 3max ()()2f x f k k k =-=--,min ()()f x f k k ==【解析】:看着容易,做着难!常规解法完成后,发现不用分类讨论,奇思妙解也出现了:结合图像感知x k =时最小,x k =-时最大,只需证()()()f k f x f k ≤≤-即可,避免分类讨论.本题第二问关键在求最大值,需要因式分解比较深的功力,这也正符合了2012年高考年报的“对中学教学的要求——重视高一教学与初中课堂衔接课”.。
2013年广东文科数学高考试题及答案
2013年广东文科数学高考试题(A 卷)一、选择题(本大题共10小题,每小题5分,满分50分)1.已知集合{}220,S x x x x R =+=∈,{}220,T x x x x R =-=∈,则S T =( )A.{0}B.{0,2}C.{-2,0}D. {-2,0,2} 2.函数()lg 11x y x +=-的定义域是( ) A. ()1,-+∞ B. [)1,-+∞ C.()()1,11,-+∞ D. [)()1,11,-+∞3.若i(x+yi)=3+4i,x,y ∈R,则x+yi 的模是( )A. 2B. 3C. 4D. 54.已知51sin 25πα⎛⎫+= ⎪⎝⎭,那么cos α=( ) A.25- B. 15- C.15 D. 255.执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是( ) A. 1 B. 2 C.4 D.76.某三棱锥的三视图如图2所示,则该三棱锥的体积是( )A. 16B. 13C. 23D. 17.垂直于直线y=x+1且与圆221x y +=相切于第一象限的直线方程是( )A. 0x y +=B. 10x y ++=C. 10x y +-=D. 0x y +图2俯视图左视图主视图8.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( )A. 若//,//l l αβ,则//αβ,则//αβB. 若,l l αβ⊥⊥,则//αβC. 若,//l l αβ⊥,则//αβD. 若,//l αβα⊥,则l β⊥9.已知中心在原点的椭圆C 的右焦点为F(1,0),离心率等于12,则C 的方程是( )A.22134x y +=B. 2214x += C. 22142x y += D. 22143x y += 10.设a 是已知的平面向量且a ≠0。
关于向量a 的分解,有如下四个命题: ①给定向量b ,总存在向量c ,使a =b +c ; ②给定向量b 和c ,总存在实数λ和μ,使a =λb +μc ;③给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使a =λb +μc ; ④给定正数λ和μ,总存在单位向量b 和单位向量c ,使a =λb +μc 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年普通高等学校招生全国统一考试(广东卷)A
数学(文科)
本试卷共4页,21题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室
号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相
应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡对应题目选项的答案信息点
涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指
定区域相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;
不准使用铅笔盒涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:球的体积34=3
V R π,其中R 为球的半径. 锥体的体积公式为1=3
V Sh ,其中S 为锥体的底面积,h 为锥体的高。
一选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合22S=|x|x +20,|,|x|x -20,|x x R T x x R =∈==∈,则S T ⋂=
A. |0|
B. |02|,
C. |2,0|-
D. |2,0,2|-
2.函数lg(1)1
x y x +=-的定义域是 A.(1,)-+∞ B.[1,)-+∞ C.(1,1)(1,)-+∞ D. [)1,1(1,)-+∞
3.若()34,,,i x yi i x y R +=+∈则复数x yi +的模是
A.2
B.3
C.4)
D.5
4.已知51sin()25
πα+=,那么cos α= 2.5A - 1.5B - 1.5C 2.5
D
5.执行如图1所示的程序框图,若输入n 的值为3,则输入s 的值是
.1A .2B .3C .7D
6.某三棱锥的三视图如图2所示,则该三棱锥的体积是
1
.6A 1.3B 2
.3C .1A
7.垂直于直线1y x =+且于圆 的直线方程是
.20A x y += .10B x y ++= .10C x y +-= .20D x y ++=
8.设l 为直线,,αβ是两个不同的平面.下列命题中正确的是
.,,A l l αβαβ若则 .,,B l l αβαβ⊥⊥若则
.,,C l l αβαβ⊥若则 .,,D l l αβαβ⊥⊥若则
9.已知中心在原点的椭圆C 的右焦点为F (1,0),离心率等于1
2,则C 的方程是
22
.134x y A +=
22.14x B +=
22.142x y C += 22
.143
x y D +=
10.设α是已知的平面向量且0α≠.关于向量α的分解,有如下四个命题:
①给定向量b,总存在向量c ,使a b c =+;
②给定向量b 和c,总存在实数λ和μ,使a b c λμ=+;
③给定向量b 和正数,总存在单位向量c,使a b c λμ=+.
④给定正数λ和μ,总存在单位向量b 和单位向量c,使a b c λμ=+.
上述命题中的向量b,c 和a 在同一平面内且两两不共线,则真命题的个数是
A.1
B.2
C.3
D.4
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
(一)必做题(11~13题)
11.设数列{n a }是首项为1,公比为2-的等比数列,则1234||||a a a a +++=________。
12.若曲线2
ln y ax x =-在点(1,a )处的切线平行于x 轴,则a =________。
13.已知变量x ,y 满足约束条件30111x y x y -+≥⎧⎪-≤≤⎨⎪≥⎩
则z x y =+的最大值是________。
(二)选做题(14-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)已知曲线C 的极坐标方程=2cos ρθ,以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为________。
15.(几何证明选讲选做题)如图3,在矩形ABCD
中,AB =3BC =,BE AC ⊥,垂足为E ,则ED =________。
三、解答题:本大题共6小题,满分30分,解答题写出文字说明、证明过程和演算步骤。
16、(本小题满分12分)
已知函数())12f x x π
=-,x R ∈
(1) 求()3
f π
的值; (2) 3cos 5θ=,3(,2)2πθπ∈,求()6
f πθ-。
17、(本小题满分12分)
(1) 根据频数分布表计算苹果的重量在[90,95)的频率;
(2) 用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量
在[80,85)的有几个?
(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)
和[95,100)中各有1
的概率。
18.(本小题满分14分)
如图4,在边长为1的等边三角形ABC 中,D,E 分别是AB,AC 上的点,AD AE = ,F 是BC 的中点,AF 与DE 交于G ,将ABF 沿AF 折起,得到如图5所示的三棱锥A-BCF,其中2
BC =
(1) 证明:DE BCF 平面;
(2) 证明:CF ABF ⊥平面;
(3) 当23
AD =时,求:棱锥F DEG -的体积F DEG V -。
19.(本小题满分14分)
设各项均为正数的数列n {}a 的前n 项和为n s ,满足2n 14s 41n a n +=--,n N +∈,且2a ,
4a ,2a ,6a 构成等比数列。
(1) 证明:2145a a =+
(2) 求数列n a 的通项公式;
(3) 证明:对一切正整数n ,有
1223111112n n a a a a a a +++⋅⋅⋅+< 20.(本小题满分14分)
已知抛物线C 的顶点为原点,其焦点(0,)(0)F c c >到直线:20l x y --=的距离为322,设P 为直线l 上的点,过点P 做抛物线C 的两条切线PA,PB 其中A,B 为切点。
(1) 求抛物线C 的方程;
(2) 当点00(,)p x y 为直线l 上的定点时,求直线AB 的方程;
(3) 当点P 在直线l 上移动时,求||||AF BP 的最小值。
21.(本小题满分14分)
设函数32()()f x x kx x k R =-+∈
(1) 当1k =时,求函数()f x 的单调区间;
(2) 当0k <时,求函数()f x 在{1,}k 上最小值m 和最大值M.
数学(文科)试卷A 第4页(共4页)。
