第四章狭义相对论基础习题
狭义相对论习题和答案

作业6狭义相对论基础研究:惯性系中得物理规律;惯性系间物理规律得变换。
揭示:时间、空间与运动得关系.知识点一:爱因斯坦相对性原理与光速不变K 相对性原理:物理规律对所有惯性系都就是一样得,不存在任何一个特殊(如“绝对静止”)惯性系。
2s 光速不变原理:任何惯性系中,光在真空中得速率都相等。
(A )1(基础训练1)、宇宙飞船相对于地面以速度v 作匀速直线飞行,某一时刻飞船头部得宇航员 向飞船尾部发出一个光讯号,经过K 飞船上得钟)时间后,被尾部得接收器收到,则由此可知飞船得固 有长度为(c 表示真空中光速)(A) c ・t (B) V/ (C) (D)【解答】飞船得固有长度为飞船上得宇航员测得得长度,即为°知识点二:洛伦兹变换由牛顿得绝对时空观=> 伽利略变换,由爱因斯坦相对论时空观=> 洛仑兹变换。
(1) 在相对论中,时、空密切联系在一起(在X 得式子中含有t,t 式中含X)。
(2) 当u « c 时,洛仑兹变换=> 伽利略变换。
(3) 若UAC , P 式等将无意义1(自测与提髙5)、地而上得观察者测得两艘宇宙飞船相对于地而以速度v = 0. 90c 逆向飞行.其中一 艘飞船测得另一艘飞船速度得大小【解答】知识点三:时间膨胀(1) 固有时间:相对事件发生地静止得参照系中所观测得时间。
(2) 运动时间:相对事件发生地运动得参照系中所观测得时间。
(B )1 (基础训练2)、在某地发生两件事,静止位于该地得甲测得时间间隔为4 s,若相对于甲作匀速直线 运动得乙测得时间间隔为5 s,则乙相对于甲得运动速度就是(c 表示真空中光速)(A) (4/5) c. (B) (3/5) c ・ (C) (2/5) c ・ (D) ("5)c.【解答】飞行•当两飞船即将相遇时飞船在自己得天窗处相隔2s 发射两颗信号弹•在飞船得观测者测得两颗信 号弹相隔得时间间隔为多少?° 【解答】以地而为K 系,飞船A 为/T 系,以正东为x 轴正向侧飞船B 相对于飞船A 得相对速度-0.6c-0.8c0.8c 1一一^(一0・6。
狭义相对论基础

北理珠09-10(2)大学物理B 第四章 狭义相对论基础(自测题) 第1页洛伦兹坐标变换x '=;y y '=;z z '=;2v t x t -'=一、判断题1. 狭义相对论的相对性原理是伽利略相对性原理的推广。
………………………………[ ]2. 物理定律在一切惯性参考系中都具有相同的数学表达式。
……………………………[ ]3. 伽利略变换是对高速运动和低速运动都成立的变换。
…………………………………[ ]4. 在一惯性系中同时发生的两个事件,在另一相对它运动的惯性系中,并不一定同时发生。
…………………………………………………………………………………………[ ]5. K '系相对K 系运动,在K '中测量相对K 系静止的尺的长度,测量时必须同时测量尺的两端。
…………………………………………………………………………………………[ ]6. 信息与能量的传播速度不可以超过光速。
………………………………………………[ ]7. 人的眼睛可以直接观测到“动尺缩短”效应。
…………………………………………[ ]二、填空题8. 狭义相对论的两条基本原理是:1、 ;2、 。
9. 静止的细菌能存活4分钟,若它以速率0.6c 运动,存活的时间为 。
10. 静止时边长为a 的正立方体,当它以速率v 沿与它的一个边平行的方向相对于S 系运动时,在S 系中测得它的体积等于 。
11. 静止质量为0m ,以速率为v 运动,其相对论的动量为 ;能量为 ;动能为 。
三、计算题12. 在惯性系K 中观测到两事件同时发生,空间距离相隔1m ,惯性系K '沿两事件连线的方向相对于K 运动,在K '系中观测到两事件之间的距离为3m ,求K '系相对于K 的速度和在其中测得两事件之间的时间间隔。
13. 在S 系中观察到在同一地点发生两个事件,第二事件发生在第一事件之后2s 。
狭义相对论基础习题.doc

狭义相对论基础习题班级_________ 姓名 ___________学号____________ 成绩______一、选择题1、(1)所有惯性系对物理规律都是等价的。
(2)在任何惯性系中,真空中光的速度与光的频率、光源的运动状态无关。
(3)在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
上述哪些说法是正确的?[](A)只有(1)、(2)是正确的;(B)只有(1)、(3)是正确的;(C)只有(2)、(3)是正确的;(D)三种说法都是正确的。
2、宇宙飞船相对于地面以速度v作匀速直线飞行,某一时刻飞船头部的宇航员向飞船尾部发出一光信号,经过AZ (飞船上的时钟)时间后,被尾部的接收器接收到,则由此可知飞船的固有长度为[13、一火箭的固有长度为厶,相对地面作匀速直线运动的速度为片,火箭上有一人从火箭后端向火箭前端的靶子发射一颗子弹,该子弹相对于火箭的速度为卩2,在火箭上测得子弹从射出到击中靶的时间间隔是【】(A)L/(V| + v2) (B) L/V2 (C) L/{y} -v2)4、(1)对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系中同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生?关于上述两个问题的正确答案是【】(A) (1)同时,(2)不同时。
(B) (1)不同时,(2)同时。
(C) (1)同时,(2)同时。
(D) (1)不同时,(2)不同时。
5、一宇航员要到离地球5光年的星球上去旅行。
如果宇航员希望把这路程缩短为3光年,则他所乘火箭相对于地球的速度为【1(A)v = c/2 (B) v = 3c/5 (C) v = 4c/5 (D) v = 9c/106、在狭义相对论中,下列说法哪些正确?【】(1) 一切运动物体相对于观察者的速度都不能大于真空中的光速。
(2)质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的。
大学物理第4章 狭义相对论时空观习题解答改

习 题4-1 一辆高速车以0.8c 的速率运动。
地上有一系列的同步钟,当经过地面上的一台钟时,驾驶员注意到它的指针在0=t ,她即刻把自己的钟拨到0'=t 。
行驶了一段距离后,她自己的钟指到6 us 时,驾驶员瞧地面上另一台钟。
问这个钟的读数就是多少? 【解】s)(10)/8.0(16/12220μ=-μ=-∆=∆c c s cu t t所以地面上第二个钟的读数为)(10's t t t μ=∆+=4-2 在某惯性参考系S 中,两事件发生在同一地点而时间间隔为4 s,另一惯性参考系S′ 以速度c u 6.0=相对于S 系运动,问在S′ 系中测得的两个事件的时间间隔与空间间隔各就是多少?【解】已知原时(s)4=∆t ,则测时(s)56.014/1'222=-=-∆=∆s cu t t由洛伦兹坐标变换22/1'c u ut x x --=,得:)(100.9/1/1/1'''8222220221012m c u t u c u ut x c u ut x x x x ⨯=-∆=-----=-=∆4-3 S 系中测得两个事件的时空坐标就是x 1=6×104 m,y 1=z 1=0,t 1=2×10-4 s 与x 2=12×104 m,y 2=z 2=0,t 2=1×10-4 s 。
如果S′ 系测得这两个事件同时发生,则S′ 系相对于S 系的速度u 就是多少?S′ 系测得这两个事件的空间间隔就是多少? 【解】(m)1064⨯=∆x ,0=∆=∆z y ,(s)1014-⨯-=∆t ,0'=∆t0)('2=∆-∆γ=∆cxu t t 2cxu t ∆=∆⇒ (m/s)105.182⨯-=∆∆=⇒x t c u (m )102.5)('4⨯=∆-∆γ=∆t u x x4-4 一列车与山底隧道静止时等长。
4-3 狭义相对论的时空观
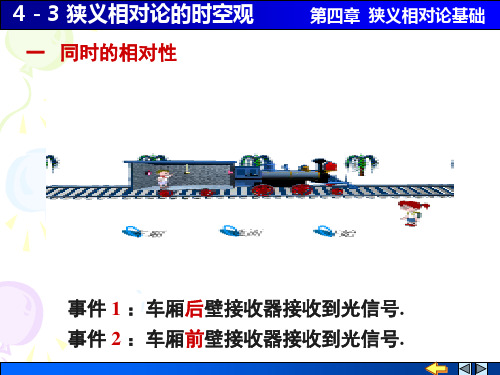
6
2
12 x' x 9 3
6
S 系 ( 地面参考系 ) S' 系 (车厢参考系 )
事件 1 (x1, y1, z1,t1) (x'1 , y'1 , z'1 ,t'1 )
事件 2 (x2 , y2 , z2 ,t2 ) (x'2 , y'2 , z'2 ,t'2 )
同时 不同地
t' t'2 t'1 0
当 v c时 l l0 .
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
例2 设想有一光子火箭, 相对于地球以速率
v 0.95c 飞行,若以火箭为参考系测得火箭长度为
15 m,问以地球为参考系,此火箭有多长?
y y'
l0 15m
o o'
s'
v x' s
x
火箭参照系 地面参照系
解 :固有长度
S系(宇航员)观察,船身通过观测站的时间间隔为
t
x v
l0 v
3.75107 s
是否是原时?
S系(观测站): x1 x2 x
同一地点!
t t 1 (v)2 c
( t 为原时)
t t 1 ( v)2 2.25107 s c
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
方法三:洛仑兹变换
固有长度:物体相对静止时所测得的长度 .(最长)
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
注意
长度缩短纯粹是一种相对论效应,与物体内部结 构无关 . 长度测量值与被测物体相对于观测者的运动有关, 相对静止时最长 .
狭义相对论基础习题解答

狭义相对论基础习题解答一 选择题1.判断下面几种说法是否正确 ( ) (1) 所有惯性系对物理定律都是等价的。
(2) 在真空中,光速与光的频率和光源的运动无关。
(3) 在任何惯性系中,光在真空中沿任何方向传播的速度都相同。
A. 只有 (1) (2) 正确B. 只有 (1) (3) 正确C. 只有 (2) (3) 正确D. 三种说法都正确解:答案选D 。
2. (1)对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系中发生于同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生?关于上述两个问题的正确答案是:( )A. (1) 同时, (2) 不同时B. (1) 不同时, (2) 同时C. (1) 同时, (2) 同时D. (1)不同时, (2) 不同时 解:答案选A 。
3.在狭义相对论中,下列说法中哪些是正确的?( )(1) 一切运动物体相对于观察者的速度都不能大于真空中的光速.(2) 质量、长度、时间的测量结果都随物体与观察者的相对运动状态而改变 (3) 在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.(4) 惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些。
A. (1),(3),(4)B.(1),(2),(4)C.(1),(2),(3)D.(2),(3),(4) 解:同时是相对的。
答案选B 。
4. 一宇宙飞船相对地球以0.8c 的速度飞行,一光脉冲从船尾传到船头。
飞船上的观察者测得飞船长为90m ,地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为 ( )A. 90mB. 54mC. 270mD. 150m 解:x ′=90m, u =0.8c ,8790/(310)310s t -'∆=⨯=⨯2()/1(/)270m x x u t u c ''∆=∆+∆-=。
狭义相对论基础习题课
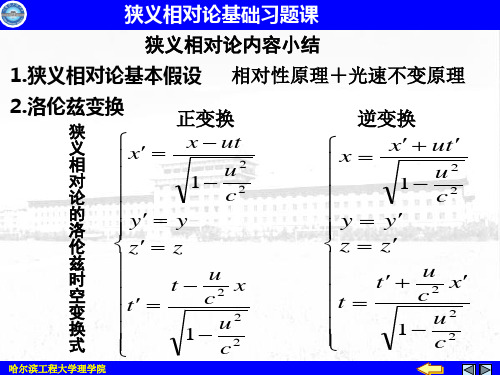
电子的动能为:Ek E E0 4.488 MeV 电子的动量为:
p (E E )
2
2 1/ 2 0
/ c 2.66 10
2
21
kg m/s
E E ) 电子的速率为: v c( 2 E
哈尔滨工程大学理学院
2 0 1/ 2
0.995 c
狭义相对论基础习题课 6. 若给一电子为0. 5MeV的能量,并让该电子在垂直 于某均匀磁场的方向上运动,其运动轨迹是半径为 2.0cm的圆。求:该磁场的磁感应强度的大小。 解:由题意有
哈尔滨工程大学理学院
狭义相对论基础习题课 4.相对论动力学
m m0 / 1 v / c 2 2 P mv m0 v / 1 v / c dv dm F dP / dt m v dt dt 2 2 E mc E0 m0 c
2 2
E K E E0 E mc 2 E E P c
1 u 2 / c2
t2 t1
t2 t1 1 u / c
2 2
相对论中同地的相对性: x2 x1
( x2 x1 ) u (t2 t1) 1 u / c
2 2
u (t 2 t1 ) ( x2 x1 ) 2 c 相对论中同时的相对性: t 2 t1 2 2 1 u / c
2
y y0
V xyz V0
z z0
v 1 2 c
2
相应体积为:
哈尔滨工程大学理学院
狭义相对论基础习题课
观察者A测得立方体的质量:
m
m0 v 1 2 c
2
故相应密度为:
v m0 / 1 2 m0 c m /V 2 2 v v V0 (1 2 ) V0 1 2 c c
狭义相对论习题、答案与解法(2010.11.22)

狭义相对论习题、答案与解答一. 选择题 1. 有下列几种说法:(1) 真空中,光速与光的频率、光源的运动、观察者的运动无关; (2) 在所有惯性系中光在真空中沿任何方向的传播速率都相同; (3) 所有惯性系对物理基本规律都是等价的。
请在以下选择中选出正确的答案(C )A 、 只有(1)、(2)正确;B 、 只有(1)、(3)正确;C 、 只有(2)、(3)正确;D 、 3种说法都不正确。
2.(1)对某观察者来说,发生在某惯性系同一地点、同一时刻两个事件,对于相对该惯性系做匀速直线运动的其他惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系不同地点、同一时刻的两个事件,它们在其他惯性系中是否同时发生?(A )A 、(1)同时,(2)不同时;B 、(1)不同时,(2)同时;C 、(1)同时,(2)同时;D 、(1)不同时,(2)不同时。
参考答案:(1) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=∆=∆-∆-∆='∆001222x t c v x c v t t 0='∆t(2) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≠'∆='∆-''∆+'∆=∆001222x t c v x cv t t 2221c v x c v t -'∆=∆3.K 系中沿x 轴方向相距3m 远的两处同时发生两事件,在K '系中上述两事件相距5m 远,则两惯性系间的相对速度为(A ) A 、c )54( ; B 、c )53(; C 、c )52(; D 、c )51(。
参考答案:221cv vt x x --=' 221cv t v x x -∆-∆='∆ c c x x c v 54531122=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛'∆∆-=4.两个惯性系K 和K ',沿x x '轴方向作相对运动,相对速度为v ,设在K '系中某点先后发生两个事件,用固定于该系的钟测出两事件的时间间隔为0t ∆,而用固定在K 系的钟测出这两个事件的时间间隔为t ∆。
狭义相对论总结+试题

t
=3c
V = 3/5c
s vt
4、观察者甲以(4/5)c的速度(c为真空中光速)相对 于静止的参考者乙运动,若甲携带一长度为L、截面 积为S,质量为m的棒,且这根棒被安放在运动方向 上. 则 m/(LS) (1)甲测得此棒的密度为 ; (2)乙测得此棒的密度为 。
m l s
m ls
8、相对论中物体的质量M与能量有一定的对应关系 Mc2 ,这个关系是:E= ;静止质量为MO 的粒子,以速度V运动,其动能是:EK = M0c2/(1-v2/c2)1/2 –M0c2 ;当物体运动速度 V=0.8c(c为真空中光速)时, M:M0 = 5/3 。
9、将一静止质量为MO的电子从静止加速到0.8c( c 为真空中光速)的速度, 则加速器对电子作功是 (2/3)M0c2 .
四、狭义相对论动力学基础
1、质速关系
m
m0 v 1 2 c
2
2
2、质能关系
E mc
E0 m0 c
2
3、相对论静止能量
4 、动能
2
E k mc m0 c
2
5、相对论能量与动量关系
E
p c m0 c
2 2
2 4
6、 相对论的加速度和经典力学 中的加速度大小和方向都不同
dP F dt
狭义相对论
一、狭义相对论的两个基本假设:
1、相对性原理:
2、光速不变原理: 测量技术: 测量物体位置必须用本地尺, 测量事件发生时间必须用本地钟。
二、相对论时空观
1、同时的相对性: 1)同地同时是绝对的。 2)异地同时是相对的。 2、时序的相对性 1)有因果关系的时序是绝对的。 2)无因果关系的时序是相对的。 3、尺缩效应 1)原长和运动长度
狭义相对论基础练习题及答案

狭义相对论基础练习题一、填空1、一速度为U的宇宙飞船沿X轴的正方向飞行,飞船头尾各有一个脉冲光源在工作,处于船尾的观察者测得船头光源发出的光脉冲的传播速度大小为________________________;处于船头的观察者测得船尾光源发出的光脉冲的传播速度大小为________________________。
2、一门宽为a,今有一固有长度为L0(L>a)的水平细杆,在门外贴近门的平面内沿其长度方向匀速运动。
若站在门外的观察者认为此杆的两端可同时被拉进此门,则该杆相对于门的运动速率u至少为________________________。
3、在地球上进行的一场足球赛持续的时间为90秒,在以速率为0.8cυ=飞行的飞船上观测,这场球赛的持续时间为_______________________。
4、狭义相对论的两条基本原理中,相对性原理说的是_________________________________________;光速不变原理说的是_________________________________________。
5、当粒子的动能等于它静止能量时,它的运动速度为_______________________;当粒子的动量等于非相对论动量的2倍时,它的运动速度为______________________。
6、观察者甲以4c/5的速度(c为真空中光速)相对于静止的观察者乙运动,若甲携带一长度为L,截面积为S,质量为m的棒,这根棒安放在运动方向上,则甲携带测得此棒的密度为_____________________;乙测得此棒的密度为_______________。
7、一米尺静止在'K系,且与'X轴的夹角为30,'K系相对于K系的X轴的正向的运动速度为0.8c,则K系中测得的米尺的长度为L=___________;他与X轴的夹角为θ=___________。
8、某加速器将电子加速到能量E=2×106eV时,该电子的动能Ek=_______________________eV。
狭义相对论习题、答案与解法(2010.11.22)

狭义相对论习题、答案与解答一. 选择题 1. 有下列几种说法:(1) 真空中,光速与光的频率、光源的运动、观察者的运动无关; (2) 在所有惯性系中光在真空中沿任何方向的传播速率都相同; (3) 所有惯性系对物理基本规律都是等价的。
请在以下选择中选出正确的答案(C )A 、 只有(1)、(2)正确;B 、 只有(1)、(3)正确;C 、 只有(2)、(3)正确;D 、 3种说法都不正确。
2.(1)对某观察者来说,发生在某惯性系同一地点、同一时刻两个事件,对于相对该惯性系做匀速直线运动的其他惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系不同地点、同一时刻的两个事件,它们在其他惯性系中是否同时发生?(A )A 、(1)同时,(2)不同时;B 、(1)不同时,(2)同时;C 、(1)同时,(2)同时;D 、(1)不同时,(2)不同时。
参考答案:(1) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=∆=∆-∆-∆='∆001222x t c v x c v t t 0='∆t(2) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≠'∆='∆-''∆+'∆=∆001222x t c v x cv t t 2221c v x c v t -'∆=∆3.K 系中沿x 轴方向相距3m 远的两处同时发生两事件,在K '系中上述两事件相距5m 远,则两惯性系间的相对速度为(A ) A 、c )54( ; B 、c )53(; C 、c )52(; D 、c )51(。
参考答案:221cv vt x x --=' 221cv t v x x -∆-∆='∆ c c x x c v 54531122=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛'∆∆-=4.两个惯性系K 和K ',沿x x '轴方向作相对运动,相对速度为v ,设在K '系中某点先后发生两个事件,用固定于该系的钟测出两事件的时间间隔为0t ∆,而用固定在K 系的钟测出这两个事件的时间间隔为t ∆。
第四章 狭义相对论习题以及答案

第4章狭义相对论习题及答案一 选择题1.下列几中说法:(1) 所有惯性系对物理基本规律都是等价的。
(2) 在真空中,光的速度与光的频率、光源的运动状态无关。
(3) 在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
其中哪些说法是正确的?(A) 只有(1)、(2)是正确的。
(B) 只有(1)、(3)是正确的。
(C) 只有(2)、(3)是正确的。
(D) 三种说法都是正确的。
2.边长为a 的正方形薄板静止于惯性系K 的XOY 平面内,且两边分别与X ,Y 轴平行。
今有惯系K ′以0.8c(c 为真空中的光速)的速度相对于K 系沿X 轴作匀速直线运动,则从K ′系测得薄板的面积为(A)a ². (B)0.6a ² (C)0.8a ² (D)a ²/0.63.在某地发生两件事,静止位于该地的甲测得时间间隔为4s ,若相对于甲作匀速直线运动的乙测得时间间隔为5s ,测乙相对于甲的运动速度是(C 表示真空中光速)(A )(4/5)C (B )(3/5)C (C )(1/5)C (D )(2/5)C4.α粒子在加速器中被加速,其质量为静止质量的3倍时,动能为静止能量的(A)2倍 (B)3倍 (C)4倍 (D)5倍5.把一个静止质量为m 0的粒子,由静止加速到v=0.6c(c 为真空中光速)需作的功等于(A)0.18m 0c2 (B)0.25m 0c 2 (C)0.36m 0c 2 (D)1.25m 0c 2二 填空题1.狭义相对论的两条基本原理中,相对性原理说的是 __;光速不变原理说的是__________________________________.2.已知惯性系S ′相对于惯性系S 系以0.5c 的匀速度沿X轴的负方向运动,若从S ′系的坐标原点O′沿X轴正方向发出一光波,则S 系中测得此光波的波速为_____ ____.3.π+介子是不稳定的粒子,在它自己的参照系中测得平均寿命是2.6×10-8s ,如果它相对实验以0.8c (c 为真空中光速)的速度运动,那么实验坐标系中测得π+介子的寿命是____s.4.一门宽为 a.今有一固有长度为l 0(l 0>a)的水平细杆,在门外贴近门的平面内沿其长度方向匀速运动。
《大学物理》课后解答题 第四章狭义相对论基础

第四章 狭义相对论基础一、思考讨论题1、根据相对论问答下列问题: (1)在一个惯性系中同时、同地点发生的两事件,在另一惯性系中是否也是同时同地点发生? (2)在一个惯性系中同地点、不同时发生的两事件,可否在另一惯性系中为同时、同地点发生?(3)在一惯性系中的不同地点发生的两事件,应满足什么条件才可找另一惯性系,使它们成为同地点发生的事件?(4)在一惯性系中的不同时刻发生的两事件,应满足什么条件才可找到另一惯性系,使它们成为同时的事件?答:依据洛仑兹时空坐标变换)(ut x x -='γ )(2c ux t t -='γ (其中2211c u -=γ)得 )(t u x x ∆-∆='∆γ )(2c x u t t ∆-∆='∆γ(其中12x x x -=∆,'-'='∆12x x x ,12t t t -=∆,'-'='∆12t t t ) 所以有 (1)是。
(2)不能。
(3)若0≠∆x ,而欲0='∆x 应有0=∆-∆t u xxu c t∆∴=<∆ (4)若0≠∆t 而欲0='∆t ,应有02=∆-∆x u t2x c c t u∆∴=>∆ 2、一个光源沿相反方向放出两个光子(以光速c 运动),问两光子的相对速度的大小是多少?答:由相对论速度变换式易算得,相对速度大小仍为c 。
3、一发射台向东西两侧距离均为L 0的两个接收站发射光讯号,今有一飞机自西向东匀速飞行,在飞机上观察,两个接收站是否同时接到讯号?哪个先接到?如飞机在水平内向其它方向运动,又如何?解:以地面为S 系,飞机为S '系,设飞机相对于地面的速度为u 。
西、东两接收站接到光信号的时刻分别为:系中)(和系)(和S t t S t t '''2121S显然 021=∆⇒=t t t 0111222022222212<---=-∆-=-∆-∆='-'cu c L u cu c x u cu c x u t t t'<'∴12t t 即东边的接收台先接到。
狭义相对论训练题

狭义相对论训练题1、+π介子的平均固有寿命是s 8105.2-⨯=τ,今有以c 73.0运行的+π介子脉冲,其平均寿命是多少?在其平均寿命内,+π介质行进的距离是多少?若不考虑相对论效应时,+π介子运行的距离为多大?若以c 99.0运行,又将如何?2、μ子在相对自身静止的惯性参考系中的平均寿命s 100.260-⨯≈τ.宇宙射线与大气在高空某处发生核反应产生一批μ子,以v = 0.99c 的速度(c 为真空中的光速)向下运动并衰变.根据放射性衰变定律,相对给定惯性参考系,若t = 0时刻的粒子数为N (0), t 时刻剩余的粒子数为N (t ),则有()()τt N t N -=e 0,式中τ为相对该惯性系粒子的平均寿命.若能到达地面的μ子数为原来的5%,试估算μ子产生处相对于地面的高度h .不考虑重力和地磁场对μ子运动的影响。
3、设在S ′系中静止立方体的体积为L 03,立方体各边与坐标轴平行,试求在相对于S ′系以速度v 沿S ′系中坐标轴运动的S 系中测得立方体的体积为多少?4、一个电子以0.99c 的速率运动。
设电子的静止质量为9.1×10-31kg ,问:⑴、 电子的总能量是多少?⑵、 电子的经典力学的动能与相对论动能之比是多大?5、两个电子以0.8c 的速率相向运动,它们的相对速度是多少?6、在相对于实验室静止的平面直角坐标系S 中,有一个光子,沿x 轴正方向射向一个静止于坐标原点O 的电子。
在y 轴方向探测到一个散射光子。
已知电子的静止质量为m 0,光速为c ,入射光子的能量与散射光子的能量之差等于电子静止能量的101。
⑴、 试求电子运动速度的大小v ;电子运动的方向与轴的夹角θ;电子运动到离原点距离为L 0(作为已知量)的A 点所经历的时间Δt ;⑵、 在电子以⑴中的速度v 开始运动时,一观察者相对于坐标系S 也以速度v 沿S 中电子运动的方向运动(即相对于电子静止),试求测出的OA 的长度。
第四章 狭义相对论基础 南京大学出版社 习题解答

第4章 狭义相对论基础习题解答4-1 在惯性系K 中,相距∆x=5⨯106m 的两地两事件时间间隔∆t=10-2s ;在相对K 系沿x 轴正向匀速运动的K'系测得这两事件却是同时发生的,求 K'系中发生这两事件的地点间距∆x '. 解 设K'系相对于K 系的速度大小为u,4-2 在惯性系K 中,有两个事件同时发生在x 轴上相距31.010m ⨯处,从惯性系K ′观测到这两个事件相距32.010m ⨯,试问从K ′测到此两事件的时间间隔是多少?解 根据洛仑兹变换,有2 u x t x t ∆∆-''∆=∆依题设条件,31.010x =⨯Δ m ,0s t ∆=,32.010x '=⨯Δ m ,解得u ==6 57710s u xt .-∆-'∆=-⨯ 负号表示在K '系中观测,'22()x x 处的事件先发生。
4-3 在正负电子对撞机中,电子和正电子以0.9c υ=的速率相向运动,两者的相对速率是多少?解 取地球为K 系,电子为K '系,并沿x 轴负方向运动,正电子为研究对象,根据洛仑兹速度变换公式,有21x x x u 'uc υυυ-=-209(09)099409(09)1.c .c .c .c .c c --==--4-4 一光源在K ′系的原点'O 发出一光线,其传播方向在''y x 平面内且与'x 轴夹角为'θ。
试求在K 系中测得的此光线的传播方向,并证明在K 系中此光线的速度仍是c 。
解 已知'cos x c υθ'=,'sin yc υθ'=。
根据洛仑兹速度变换,有Δt '=Δt-ΔΔ2t uc x=()226410m t x c x ∆∆-'∆===⨯2''1x x x u u cυυυ+=+cos cos 1c u u c θθ'+='+,21y x c υ=+1c +在K 系中与x 轴的夹角为arctany x υθυ=而光的速度为c υ==4-5 固有长度为50m 的飞船,以3910m/s u =⨯的速率相对于地面匀速飞行,地面上观察者测量飞船的长度是多少? 解 已知 3050m,910m/s l u ==⨯地面上观察者测量飞船的长度是运动长度50l l ==()25150131049.99999998(m)2-⎛⎫≈⨯-⨯⨯= ⎪⎝⎭可见低速时运动长度和固有长度的差别是难以测出的。
第04章(狭义相对论)习题答案

1 1 - ( u / c ) 2
(SI) ]
解:由题意,车厢上的观察者测得的这两个痕迹之间的距离为固有长度 L 0 ,而地面上 的观察者测看来,这两个痕迹是随车厢一起运动的,测得长度会发生相对论长度收缩,则
L 0 =
1 1 u 2 c 2
4-5 在惯性系 S 中,有两事件发生于同一地点,且第二事件比第一事件晚发生Dt =2s;而 在另一惯性系 S'中,观测第二事件比第一事件晚发生Dt¢=3s.那么在 S'系中发生两事件 8 的地点之间的距离是多少?[6.72×10 m] 解: 设两惯性系的相对运动速度为 u , 由题意, S 系中测得的两事件的时间间隔 Dt = 2 s 为固有时间,根据相对论时间膨胀效应, S ¢ 系测得的时间间隔
¢= Dt
Dt 1 u c 2
2
即: 3 =
2 1 u c 2
2
解得: u =
5 c 3
则 S ¢ 系中发生的这两事件的地点之间的距离 L 为:
L = u Dt =
5 8 c ´ 3 » 6.71´ 10 m 3
4-6
一体积为 V0,质量为 m0 的立方体沿其一棱的方向相对于观察者 A 以速度 v 运动.观
t 0
1 u 2 c 2
则 5 =
4 1 u 2 c 2
解得: u =
3 c 5
4-2
-6 m 子是一种基本粒子,在相对于 m 子静止的坐标系中测得其寿命为 t 0 =2×10 s.如
果 m 子相对于地球的速度为v = 0.988c (c 为真空中光速),则在地球坐标系中测出的 m 子的 寿命是多长?[1.29×10 5 s] 解:由题意, m 子的固有寿命为 t 0 = 2 ´10 s ,根据相对论时间膨胀效应,对于地面 参考系运动的 m 子的寿命为: t=
狭义相对论练习册答案

狭义相对论练习册答案狭义相对论是爱因斯坦于1905年提出的理论,它主要研究在不同惯性参考系中物理定律的不变性。
以下是一些狭义相对论的练习题及其答案。
练习一:时间膨胀假设一个宇航员以接近光速的速度(例如0.9c)旅行了10光年。
根据狭义相对论,宇航员经历的时间与地面观察者测量的时间有何不同?答案:根据狭义相对论的时间膨胀公式:\[ \Delta t' = \frac{\Delta t}{\gamma} \]其中,\( \Delta t \) 是地面观察者测量的时间,\( \Delta t' \) 是宇航员经历的时间,\( \gamma = \frac{1}{\sqrt{1-v^2/c^2}} \) 是洛伦兹因子。
对于0.9c的速度,\( \gamma \) 大约为2.294。
因此,宇航员经历的时间是:\[ \Delta t' = \frac{10}{2.294} \approx 4.36 \text{ 光年} \]练习二:长度收缩一个物体在静止参考系中的长度是10米。
当它以0.9c的速度相对于观察者运动时,观察者会测量到的长度是多少?答案:长度收缩公式为:\[ L = L_0 \sqrt{1-v^2/c^2} \]其中,\( L \) 是运动参考系中的长度,\( L_0 \) 是静止参考系中的长度。
代入数值:\[ L = 10 \times \sqrt{1-(0.9)^2} \approx 4.5 \text{ 米} \]练习三:质能等价一个质量为1千克的物体,当它以接近光速的速度运动时,它的相对论质量是多少?答案:相对论质量公式为:\[ m = m_0 / \sqrt{1-v^2/c^2} \]其中,\( m \) 是相对论质量,\( m_0 \) 是静止质量。
对于0.9c的速度,\( \gamma \) 大约为2.294。
因此,相对论质量是:\[ m = 1 / \sqrt{1-(0.9)^2} \approx 2.294 \text{ 千克} \]练习四:速度相加两个物体A和B,A相对于地面以0.6c的速度运动,B相对于A以0.8c的速度运动。
2016第四章狭义相对论

论 过渡到经典力学.经典力学是相对论力学的一种特
例或近似.
3
§4.1 伽利略变换 经典力学的时空观
普
通
物 狭义相对论和广义相对论
理
教 程
狭义相对论是关于高速情况下的时空观理论;
广义相对论是关于引力和时空结构的理论.
狭义相对论适用于一切惯性参考系,而广义
第 四
相对论适用于一切参考系.
章
相对论和时空观
伽利略坐标变换
当u c 变换无意义 速度有极限
12
普
通
物
理 教
作业: 普通物理教程(上):
程
习题4 P97
第 四
三、计算题
章
狭
2 、3 、6
义
相
对
论
13
普 §4.3 狭义相对论的时空观
通 物
理 4.3.1 同时性的相对性
教
程 在牛顿力学中,时间是绝对的。如两事
件在S系中被同时观察到,那么在S′中也是
普 通 物 理 教 程
第四章 狭义相对论
北京建筑工程学院 理学院 应用物理系
1
第四章 狭义相对论
普
通
物
理
教 程
§4.1
伽利略变换
经典力学的时空观
§4.2 狭义相对论的基本原理 洛伦兹变换
第
四 §4.3 狭义相对论的时空观
章
狭 §4.4 狭义相对论动力学基础
义 相 对 论
2
§4.1 伽利略变换 经典力学的时空观
15
普 §4.3 狭义相对论的时空观
通
物 理
设 S系中x1、x2两处发生两事件,时间
教 程
间隔为Δt t2 t1 .问 S′系中这两事件
狭义相对论基础练习题及答案

狭义相对论基础练习题一、填空1、一速度为U的宇宙飞船沿X轴的正方向飞行,飞船头尾各有一个脉冲光源在工作,处于船尾的观察者测得船头光源发出的光脉冲的传播速度大小为________________________;处于船头的观察者测得船尾光源发出的光脉冲的传播速度大小为________________________。
2、一门宽为a,今有一固有长度为L0(L>a)的水平细杆,在门外贴近门的平面内沿其长度方向匀速运动。
若站在门外的观察者认为此杆的两端可同时被拉进此门,则该杆相对于门的运动速率u至少为________________________。
3、在地球上进行的一场足球赛持续的时间为90秒,在以速率为0.8cυ=飞行的飞船上观测,这场球赛的持续时间为_______________________。
4、狭义相对论的两条基本原理中,相对性原理说的是_________________________________________;光速不变原理说的是_________________________________________。
5、当粒子的动能等于它静止能量时,它的运动速度为_______________________;当粒子的动量等于非相对论动量的2倍时,它的运动速度为______________________。
6、观察者甲以4c/5的速度(c为真空中光速)相对于静止的观察者乙运动,若甲携带一长度为L,截面积为S,质量为m的棒,这根棒安放在运动方向上,则甲携带测得此棒的密度为_____________________;乙测得此棒的密度为_______________。
7、一米尺静止在'K系,且与'X轴的夹角为30,'K系相对于K系的X轴的正向的运动速度为0.8c,则K系中测得的米尺的长度为L=___________;他与X轴的夹角为θ=___________。
8、某加速器将电子加速到能量E=2×106eV时,该电子的动能Ek=_______________________eV。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019秋学期大学物理(2)例题习题
程守洙 编《普通物理学》上下册(第七版) 高教出版
第四章 狭义相对论基础
【一】 思考题:
P.152/ 2(洛伦兹变换); 3(除光子外的质点的运动速度)。
P.159/ 5(相对论长度收缩与参考系)。
P.166/ 2(相对论动量等); 3(相对论能量与动量,质量与能量,静质量与静能量)。
【二】 例题:
P.151/ 1(洛伦兹空间时间坐标变换);P.164/ 3 (核反应中质量与能)。
【三】 习题:
一、选择题
1. 关于同时性的以下结论中,正确的是( )
A .在一惯性系中同时发生的两事件,在另一惯性系一定不同时发生。
B .在一惯性系不同地点同时发生的两个事件,在另一惯性系一定同时发生。
C. 在一惯性系同一地点同时发生的两个事件,在另一惯性系一定同时发生。
D. 在一惯性系不同地点不同时发生的两个事件,在另一惯性系一定不同时。
2. 某宇航员以0.8c (c 为真空中光速)的速度离开地球,若地球上测得他发出的两个信号的时间间隔为10 s ,则宇航员测出的相应的时间间隔为( )
A. 5 s ;
B.10/3 s ;
C. 6 s ;
D.10 s 。
3. 一电子的 运动速度v = 0.99c ,电子的静止能量为0.51MeV ,它的动能是( )
A. 3.5 MeV ;
B. 4.0 MeV ;
C. 3.1MeV ;
D. 2.5MeV 。
[1MeV=106×1.6×10-19 J; 电子质量m 0 = 9.11×10-31kg; =1v c ;
1 ]
4. 质子被加速后,其动能为静止能量的4倍,其质量m 为静止质量m 0的( )
A .5倍; B. 6倍; C. 4倍; D. 8倍。
二、填空题
1. 静止时边长为50 cm 的立方体,当它沿着与它的一个棱边平行的方向相对于地面以匀速度
2.4×10 ms 运动时,在地面测得它的体积是 。
2. 牛郎星相距地球16光年,宇宙飞船若以的匀速度飞行,将用4年的
时间(宇宙飞船上的钟指示的时间)抵达牛郎星。
3. 一个门的宽度为a,一固有长度为L0(L0 > a)的水平细杆,在门外与门贴近
的平面内沿杆长度方向匀速运动。
若站在门外的观察者认为此杆的两端可同时被拉进此门,则该杆相对于门的运动速率u至少应为。
4. 两个静止质量均为m0的粒子,以大小相等、方向相反的速度u相撞后合成一个复合粒子,则该复合粒子的动量为,静止质量M0 = 。
[建议参考教材P.165例4]
三、计算题
1. 在惯性系S中,沿x轴相距1 km的两事件发生在同一时刻,而在以恒定速度
沿x轴运动的另一惯性系S’中,测得此两件事沿x’轴相距2 km,试问在S’中测得两事件的时间差是多少?
2. 一惯性系中同一地点发生的两个事件时间相隔为4 s,若在另一惯性系中测得
此两事件时间间隔为6 s,计算两个事件的空间间隔。
3. 一粒子的静止质量为m ,其固有寿命为实验室测量到其寿命的1/n ,计算此
粒子的动能。
