江西省2015年高考全省理科前50名学生数学各题小分得分情况

合集下载

江西省2015年高三九校联合考试理数

2015年江西省南城一中南康中学高安中学高三联合考试彭泽一中泰和中学樟树中学数学试卷（理科）命题：高安中学、泰和中学、分宜中学注意事项：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分.考试时间为120分钟.2、本试卷分试题卷和答题卷，第Ⅰ卷（选择题）的答案应填在答题卷卷首相应的空格内，做在第Ⅰ卷的无效.一．选择题（12×5分=60分）1. 已知集合A ＝{x ||x |≤2，x ∈Z}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪1x ＋1>0，x ∈R ，则A ∩B ＝( ) A ．(－1,2] B ．[0,2] C ．{－1,0,1,2} D ．{0,1,2} 2．若复数i z )54(sin )53(cos -+-=θθ是纯虚数，则tan 4πθ⎛⎫-⎪⎝⎭的值为（） A.-7B.17-C.7D.7-或17-3．下列四个命题111:(0,),23xxp x ⎛⎫⎛⎫∃∈+∞< ⎪ ⎪⎝⎭⎝⎭；21123:(0,1),log log p x x x ∃∈>3121:(0,),log 2xp x x ⎛⎫∀∈+∞> ⎪⎝⎭；41311:(0,),log 32xp x x ⎛⎫∀∈< ⎪⎝⎭其中的真命题是（） A.1p ，3p B.1p ,4pC.2p ,4pD.2p ,3p4.如右图，程序框图箭头a 指向①时，输出s= 箭头指向②时,输出s=A.7; 7!B.6; 6!C.7; 7D.6; 65．等比数列{}n a 中，12a =，8a =4，函数()128()()()f x x x a x a x a =---，则=')0(f （）A ．62 B ．92 C ．122 D ．1526．已知某几何体的三视图如图所示，则该几何体的体积为( )A.163 B.803C.643D.4337．将6名报名参加运动会的同学分别安排到跳绳、接力，投篮三项比赛中（假设这些比赛都不设人数上限），每人只参加一项，则共有x 种不同的方案，若每项比赛至少要安排一人时，则共有y 种不同的方案，其中x y +的值为（） A ．1269 B ．1206 C ．1719 D ．7568. 设x 、y 满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤--≥+-0004402y x y x y x ，若目标函数)0,0(>>+=b a by ax z 的最大值为8，）.A. 2B. 2C. 6D. 169、已知P 是ABC ∆所在平面内一点，4530PB PC PA ++=，现将一粒红豆随机撒在ABC ∆内，PBC ∆）ABC D10．S －ABC O 为球O 的直径，OA ⊥,SC OB ⊥，OAB ∆为等边三角形，三棱锥S －ABC O 的表面积为（） A. πB. 4πC. 12πD. 18π11．已知椭圆12222=+by a x )0(>>b a 上一点A 关于原点的对称点为点B ，F 为其右焦点，若BF AF ⊥，设α=∠ABF ，且⎥⎦⎤⎢⎣⎡∈4,6ππα，则该椭圆离心率e 的取值范围为（）A.]13,22[-B.)1,22[C.]23,22[D.]36,33[12.已知R 上的不间断函数()g x 满足：①当0x >时，0)(>'x g 恒成立；②对任意的x R ∈都有()()g x g x =-。

2015临川一中高考成绩

2015临川一中高考成绩篇一：临川一中2011---2015年录取清华北大人数统计表临川一中2011—2015年高考录取清华北大情况篇二：江西省2015年高考全省理科前50名学生数学各题小分得分情况江西省2015年高考全省理科前50名学生数学各题小分得分情况篇三：江西省临川一中2015届高三压轴卷江西省临川一中2015届高三压轴卷高三2013-05-31 19:44江西省临川一中2015届高三压轴卷语文第Ⅰ卷（共36分）一、（15分，每小题3分）1．下列词语中加点字的读音无误的一项是（）A．果屑（xiāo）从（cóng）容精湛（zhàn）恪（ka）守信用B．作（zuò）弊熨（yù）帖哺（bǔ）育横征暴敛（liǎn）C．抨（pēng）击翩跹（xiān）占卜（pǔ）揠（yà）苗助长D．炮（pào）制骁（xiāo）勇剽（piāo）窃心有余悸（jì）1．B（A果屑，xia；C占卜，bǔ；D炮制，páo）2．下列各组词语中没有错别字的一项是（）A．编纂兰天蔚然成风诙谐幽默B．瞭望重叠杳无音信颗粒归仓C．赝品痉孪心劳力拙知书达礼D．弦律蛰伏人参鹿茸舐犊情深2．B（A“兰天”改为“蓝天”；C“痉孪”改为“痉挛”，“知书达礼”改为“知书达理”；D“弦律”改为“旋律”）3．依次填入下列各句横线处词语，最恰当的一组是（）①基于丰田NBC平台打造而来的新威驰是一款针对亚洲用户而做的小车，采用了丰田的8A和5A技术，空间并不很。

②该公司拥有先进的生产设备和的技术工艺。

③南京楼市成交量继续，显现调整中的“疲态”。

A．宽绰精湛下滑B．宽泛精致下落C．宽泛精湛下落D．宽绰精致下滑3．A（宽绰：空间宽阔，不狭窄。

宽泛：涉及的面宽。

精湛：精深。

精致：精巧细致，细密。

下滑：向下滑落。

下落：掉下）4．下列句子中标点符号使用正确的一项是（）A．除了上述睡前应避免吃的食物外，也须注意：忌睡前用脑：如果有在晚上工作和学习的习惯，要先做比较费脑筋的事，后做比较轻松的事。

2015年全国高考数学试卷理科含答案

2０15年普通高等学校招生全国统一考试理科数学一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。

（1)设复数Z 满足＝则＝－Z ZZ,i 11+ （Ａ)1 (Ｂ) (C ） (D)2 (2）=-010sin 160cos 10cos 20sin （A ）23－(B)23 (Ｃ)21－ (D ） 21 (3）设命题为则P n N n P n⌝>∈∃,2,:2(A ）nn N n 2,2>∈∀ (Ｂ)nn N n 2,2≤∈∃ (C ）nn N n 2,2≤∈∀ (D ）n n N n 2,2＝∈∃（４)投篮测试中,每人投3次，至少2次命中才能通过测试，已知某同学每次投篮命中的概率为０。

6,且各次投篮是否命中相互独立,则该同学通过测试的概率为（A ）0。

6４８ (B ）0.４32 (C ）0。

36 (D)０．３12(5)已知),(00y x M 是双曲线C:1222=-y x 上的一点,的是双曲线C F F 21,两个焦点，若021<⋅MF MF ，则的取值范围是（A ）)33,33(-(Ｂ))63,63(- (C))322,322(- (D ）)332,332(-（6）《九章算术》是我国古代极为丰富的数学名著，书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问：积及米几何？”,其意为：“在屋内角处堆放米(如图,米堆是一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为５尺,问米堆的的体积和米堆放的米各为多少?”已知一斛米的体积约为1.６２立方尺，圆周率约为3，估算出米堆的米约为 (A)１４斛（B)22斛 (Ｃ）36斛（Ｄ）66斛 (７）设D 为所在平面内一点ABC ∆,CD BC 3=，则(A ）AC AB AD 3431+-= （B)AC AB AD 3431－= (C)AC AB AD 3134+= (D)AC AB AD 3134－=(8）函数)cos()(ϕω+=x x f 的部分图像如图所示，则)(x f 的单调减区间为(Ａ)Z k k k ∈+-,43,41）（ππ (Ｂ）Z k k k ∈+-,432,412）（ππ （C ）Z k k k ∈+-,43,41）（（D ）Z k k k ∈+-,432,412）（(９)执行右边的程序框图，如果输入的t=0.01，则输出的n= (A)5 (B)６ (C)７（D)８（１0）52）（y x x ++的展开式中,25y x 的系数为 (Ａ）10 （Ｂ）２0 (C ）30(D)６0(11)圆柱被一平面截去一部分后与半球(半径为r ）组成一个几何休,该几何体的正视图和俯视图如图所示，若该几何体的表面积为１6＋20π,则ｒ=（A)1 （B)2 (C ）4 （D ）8(12）设函数ｆ（x)=e x(2x-1）—a ｘ＋a,其中ａ1,若存在唯一的整数x ０,使得f （x 0)0，则a 的取值范围是（）（A)［— —，1)（B ）［—，）(C)［,)（Ｄ) ［,1)二、填空题:本大题共4小题,每小题5分。

江西省2015年高考全省理科50名

考生号准考证号姓名b姓名身份证后4位地市名称中学名称语文成绩15360111150213211101528夏子哲夏子哲4337南昌市江西师大附中137 15361002155511200207123汪川汪川2017抚州市明达培训中心125 15360111150277211104916俞晨露俞晨露5322南昌市江西师大附中130 15360681150013268102709席照炜席照炜6818鹰潭市贵溪市第一中学118 15360983151179298310203廖帆廖帆4614宜春市高安中学133 15360403153681240304227程晨程晨1219九江市九江一中112 15360735150001273501226许星宇许星宇0018赣州市石城中学119 15360826150574282602621王敏虎王敏虎0613吉安市泰和中学117 15361002153830200205124尧旻昊尧旻昊0016抚州市临川一中118 15360824151604282400317曾启程曾启程0018吉安市新干中学117 15360983151214298303828卢晗怡卢晗怡2429宜春市高安中学124 15360403153718240306301曾子扬曾子扬0019九江市九江一中118 15360111150270211103322罗欣月罗欣月0029南昌市江西师大附中121 15360203150710220301524陈付恺陈付恺301X景德镇市景德镇一中118 15360403153686240304409高子杰高子杰4971九江市九江一中116 15360403153689240300930胡昊哲胡昊哲1814九江市九江一中113 15360121152609212100620徐瑞翔徐瑞翔0041南昌市莲塘一中122 15360111150249211101608涂钰藩涂钰藩0518南昌市江西师大附中117 15360203150709220302602邓若琪邓若琪4021景德镇市景德镇一中131 15360121152536212104609高亦博高亦博0012南昌市莲塘一中115 15360203150717220302026付奕楚付奕楚3549景德镇市景德镇一中114 15360121152548212105604罗来威罗来威6117南昌市莲塘一中118 15360111150192211101511余翰良余翰良1011南昌市江西师大附中117 15361002155616200219426汪瑜汪瑜002X抚州市明达培训中心121 15360111150744211105511肖剑肖剑0035南昌市江西师大附中109 15360111150731211103503夏照越夏照越0014南昌市江西师大附中116 15360111150722211106722何欣蔚何欣蔚0513南昌市江西师大附中114 15360111150794211101120傅怀颖傅怀颖0529南昌市江西师大附中129 15360502150015259100221彭宇翀彭宇翀1614新余市新余市第四中学125 15360111150246211103826王勃竣王勃竣2811南昌市江西师大附中109 15360502150001259102106敖明皓敖明皓1311新余市新余市第四中学115 15360481150145248104109柯彦楚柯彦楚0021九江市瑞昌一中118 15360111150769211101711石少宏石少宏6316南昌市江西师大附中123 15360428153626242801108黄杰黄杰1012九江市都昌二中121 15360923150001292303918古闻宇古闻宇0813宜春市上高二中120 15360981151726298105405熊凌峰熊凌峰281X宜春市丰城中学118 15360111150718211106501吴啸隽吴啸隽8054南昌市江西师大附中106 15361029150001202901522乐依俊乐依俊0339抚州市东乡一中121 15361002155523200210404付逸麟付逸麟3510抚州市明达培训中心118 15360782150020278202325刘堂兴刘堂兴1110赣州市南康中学112 15361002153954200209918黄强黄强0012抚州市临川一中116 15360121152539212101801黄龙黄龙0015南昌市莲塘一中116 15360111150271211106403曾霄曾霄6049南昌市江西师大附中110 15361002153956200209411徐雄斌徐雄斌0318抚州市临川一中108 15360802151067280203221过靖过靖1050吉安市白鹭洲中学118 15360121152558212107627王立新王立新6435南昌市莲塘一中121 15360902150659290204213张莫凡张莫凡0217宜春市宜春中学112 15360802150047280202109伍仕骏伍仕骏0031吉安市吉安一中117 15360702152105270209320沈运恒沈运恒0015赣州市赣州中学120 15360313150622231302509汤林汤林2016萍乡市湘东中学111数学成绩外语成绩综合成绩技术成绩人武成绩优惠加分违纪情况本科总分本科总分排名14014629200007151 14915028600007102 14414228300006993 14914528100506984 14714427400006985 14914428600506966 14914527600506947 14913829000006948 14414428700006939 149140286000069210 146146275000069111 143140290000069112 150147272000069013 150139283000069014 148137289000069015 141142289005069016 140144284000069017 149144279000068918 149145263000068819 145144284000068820 145142287000068821 144144282000068822 144147279000068723 142146278000068724 150140287000068625 149145276000068626 149145278000068627 138146273000068628 150144266000068529 149143279005068530 145146279000068531 144137286000068532 142140275005068533 140140284000068534 132143290000068535 150139277000068436 149143286000068437 143138281000068338 141141283000068339 141141289000068340 150138278000068241 149145272000068242 148147277000068243 148143283000068244 143142279000068245 143140278000068246 137138295000068247 149136279000068148 148132281000068149 146141282000068050专科总分专科总分排名423763442473604169595417930542473604101145641889734041343940612769406127694169595401144914188973407124294011449140114491406127694101145642571124041343940114491406127694081209840911772399152824101145640812098413105364198671406127694061276939915282410114564011449139516831407124293981566840214138400149223941721640413439410114564051310239915282403137964041343938720259402141384001492239815668。

【恒心】【揭秘】2015年高考江西省(新课标Ⅰ卷)全省理科前50名英语各题小分得分情况

2
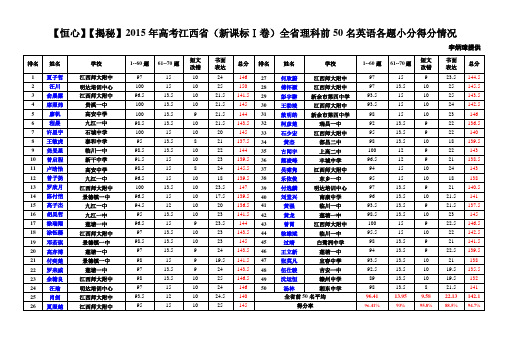
汪川
明达培训中心
100
15
10
25
150
28
傅怀颖
江西师大附中
97
13.5
10
25
145.5
3
俞晨露
江西师大附中
96.5
13.5
10
21.5
141.5
29
彭宇翀
新余市第四中学
93.5
15
10
25
143.5
4
席照炜
贵溪一中
100
13.5
10
21.5
145
30
王勃竣
江西师大附中
93.5
15
10
24
142.5
97
15
10
24
146
50
汤林
湘东中学
98
13.5
8
21.5
141
25
肖剑
江西师大附中
93.5
12
10
24.5
140
全省前50名平均
96.41
13.95
9.58
22.13
142.1
26
夏照越
江西师大附中
95
15
10
25
145
得分率
96.41℅
93℅
95.8℅
88.5℅
94.7℅
景德镇一中
98
15
9
19.5
141பைடு நூலகம்5
47
张莫凡
宜春中学
93.5
13.5
10
21
138
22
罗来威
莲塘一中
97

高考数学2015江西十校联考数学(理)试题和答案

江西省重点中学盟校2015届第一次联考数学（理）试卷第Ⅰ卷（选择题共60分）一、选择题(本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1、已知集合101x M xx +⎧⎫=≥⎨⎬-⎩⎭，则R M =C （）.A {}11x x -<< .B {}11x x -<≤ .C {}11x x x <-≥或 .D {}11x x x ≤-≥或2、已知11abi i=-+，其中,a b 是实数，i 是虚数单位，则||a bi -=（） .A 3 .B 2 .C 5 .D 3、函数3y x =的图象在原点处的切线方程为（）.A y x = .B 0x = .C 0y = .D 不存在4、函数2lg(2)y x x a =-+的值域不可能是（）.A (,0]-∞ .B [0,)+∞ .C [1,)+∞ .D R5、实数,x y 满足10(2)(26)0x y x y x y -+≥⎧⎨--+≤⎩，若2t y x ≤+恒成立，则t 的取值范围是（）.A 13t ≤ .B 5t ≤- .C 13t ≤- .D 5t ≤ 6、如图是某算法的程序框图，则程序运行后输出的T 是( ).A 1 .B 2 .C 3 .D 47、已知12F F 、分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点，过点2F 与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ，若点M 在以线段12F F 为直径的圆外，则双曲线离心率的取值范围是( ).A .B )+∞ .C 2) .D (2,)+∞8、已知()3sin 2cos 2f x x a x =+，其中a 为常数.()f x 的图象关于直线6x =π对称，则()f x 在以下区间上是单调函数的是( ).A 31[,]56--ππ .B 71[,]123--ππ .C 11[,]63-ππ .D 1[0,]2π9、一个几何体的三视图如图所示,该几何体外接球的表面积为（）.A 9π .B 283π .C 8π .D 7π10、已知焦点在x 轴上的椭圆方程为222141x y a a +=-，2正视图随着a 的增大该椭圆的形状（）.A 越接近于圆 .B 越扁.C 先接近于圆后越扁 .D 先越扁后接近于圆11、坐标平面上的点集S 满足2442{(,)|log (2)2sin 2cos [,]}84S x y x x y y y =-+=+∈,-ππ，将点集S 中的所有点向x 轴作投影，所得投影线段的长度为（）.A 1 .B2.C.D 212.已知函数1ln 1)(-+=x x x f ,*)()(N k xkx g ∈=，若对任意的1c >,存在实数b a ,满足0a b <<c <，使得)()()(b g a f c f ==，则k 的最大值为( ).A 2 .B 3 .C 4 .D 5第Ⅱ卷 (非选择题)二、填空题(本题共4小题，每小题5分，共20分.将答案填入答题纸相应位置) 13、在ABC 中，3,2,30a b A ===，则cos B = .14.已知()f x 是定义在R 上周期为4的奇函数，当(0,2]x ∈时，2()2log xf x x =+，则(2015)f = .15、从左至右依次站着甲、乙、丙3个人，从中随机抽取2个人进行位置调换，则经过两次这样的调换后，甲在乙左边的概率是 . 16、如图所示，在O 中，AB 与CD 是夹角为60°的两条直径，,E F 分别是O 与直径CD 上的动点，若0OE BF OA OC λ⋅+⋅=，则λ的取值范围是________．三、解答题（共6小题，共70分；要求写出必要的文字说明，解题过程和演算步骤） 17、(本小题满分12分)某校随机调查了80位学生，以研究学生中爱好羽毛球运动与性别的关系，得到下面的数据表：（1）将此样本的频率估计为总体的概率，随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为X ，求X 的分布列和期望值；（2）根据表中数据，能否有充分证据判定爱好羽毛球运动与性别有关联？若有，有多大把握？附：2()()()()()n ad bc a b c d a c b d χ-=++++18、(本小题满分12分)ABCDO EF已知数列{}n a 为等差数列，首项11a =，公差0d ≠.若123,,,,,n b b b b a a a a 成等比数列，且11b =，22b =，35b =.(1)求数列{}n b 的通项公式n b ；(2)设3(21)n n c log b =-，求和12233445212221n n n n n T c c c c c c c c c c c c -+=-+-+⋅⋅⋅+-.19、(本小题满分12分)在三棱柱111ABC A B C -中，侧面11ABB A 为矩形，2AB =，1AA =D 是1AA 的中点，BD 与1AB 交于点O ，且CO ⊥平面11ABB A . (1)证明：1BC AB ⊥；(2)若OC OA =，求直线CD 与平面ABC 所成角的正弦值.20、(本小题满分12分)已知抛物线2:2(0)C x py p =>的焦点为F ，过F 的直线l 交抛物线C 于点,A B ，当直线l 的倾斜角是45时，AB 的中垂线交y 轴于点(0,5)Q . （1）求p 的值；（2）以AB 为直径的圆交x 轴于点,M N ，记劣弧MN 的长度为S ，当直线l 绕F 旋转时，求SAB的最大值.21、(本小题满分12分)已知函数()ln ln ,(),()au x x x x v x x a w x x=-=-=,（1）若()()u x v x ≥恒成立，满足条件的实数a 组成的集合为B ，试判断集合A 与B 的关系，并说明理由；（2）记()()[()()][()]2w x G x u x w x v x =--，是否存在m N *∈，使得对任意的实数(,)a m ∈+∞，函数()G x 有且仅有两个零点？若存在，求出满足条件的最小正整数m ；若不存在，说明理由.（以下数据供参考：1)0.8814e ≈≈ ）请考生在第22、23、24题中任选一题做答，如果多做，则按所做第一题记分.在答题卡选答相交于点E . （1）求BD 长；（2）当CE ⊥OD 时，求证：AO AD =.BA CD1A1B1OAEODCB（2）过点M 平行于直线l 的直线与曲线C 交于,A B 两点，若83MA MB ⋅=，求点M 轨迹的直角坐标方程.24、（本小题满分10分）选修4－5:不等式选讲. 已知函数()223,()12f x x a x g x x =-++=-+. (1)解不等式()5g x <；(2)若对任意1x R ∈，都有2x R ∈，使得12()()f x g x =成立，求实数a 的取值范围.江西省重点中学盟校2015届第一次联考数学（理）试卷答案一、CDCAB CDBBA DB12、分析：易知()()g()f c g b c =>,即lnc 1c c kc c+>-lnc 1c c k c +∴<-,1c >. 令ln ()1c c cp c c +=-,1c >, 则()()()()2211ln 1ln 2ln ()11c c c c c c c p c c c ++-----'==--令()2ln 1q c c c c =-->，,1'()10q c c=->, ()q c 递增,()(1)1q c q ∴>=-.又()31ln30q =-<,()42ln 40q =->, ,∴存在()03,4c ∈,使得0()0q c =，即002ln c c -=当()01,c c ∈时,()0q c <,()p c 递减，当()0,c c ∈+∞时,()0q c >,()p c 递增.000min 00ln ()()1c c c p c p c c +==- 002ln c c -=代入得000000min 000ln (2)()11c c c c c c p c c c c ++-===-- 03k c k ∴<≤易知10a e<<，当3k =时可证明()()()f a g b g a =< max 3k ∴=. 二、13．3 14.-2 15. 2316. [- 16、解：设圆的半径为r ，以O 为原点，OB 为x 轴建立直角坐标系，则1(,0),(,)22B rC r r -设(cos ,sin )E r r αα，(,)(11)2OF OC r r μ=μ=-≤μ≤ 212OA OC r λ⋅=- 2[(1)c o s s i n]2OE BF r μ⋅=-αα (2)cos sin ∴λ=μ-αα )3λ[∴λ∈-三、17、解：(1)任一学生爱好羽毛球的概率为38，故X ～3(3,)8B ………………2分 0335125(0)()8512P XC ===12335225(1)()88512P X C === 22335135(2)()88512P X C ===333327(3)()8512P X C === X 的分布列为39388EX =⨯=…………8分（2）2280(20201030)800.3556 2.70630503050225χ⨯-⨯==≈<⨯⨯⨯……………………10分故没有充分证据判定爱好羽毛球运动与性别有关联. ……………………12分 18、解：(1)222152(1)1(14)12142=0a a a d d d d d d d =⋅⇒+=⨯+++=+⇒=或（舍去）1211, 3.3b b a a a q ===∴=……………………3分11(1)22113n n b n n a b b -=+-⨯=-=⨯ , 1312n n b -+∴=……………………6分(2)3(21)n n c log b =-1n =- ……………………7分213435657221()()()()n nn nT c c c c c c c c c c c c -+=-+-+-+⋅⋅⋅+- 2422()n c c c =-++⋅⋅⋅+22[135(21)]2n n =-+++⋅⋅⋅+-=-……………………12分19、解：(1)由题意tan 2AD ABD AB ∠==，11tan AB AB B BB ∠==，又0ABD <∠，12AB B π∠<，1ABD AB B ∴∠=∠，1112AB B BAB ABD BAB π∴∠+∠=∠+∠=，2AOB π∠=，1AB BD ∴⊥.又11CO ABB A ⊥平面，1AB CO ∴⊥，BD 与CO 交于点O ，1AB CBD ∴⊥平面，又BC CBD ⊂平面，1AB BC ∴⊥.…6分(2)如图，分别以1,,OD OB OC 所在直线为,,x y z 轴，以O 为坐标原点，建立如图所示的空间直角坐标系O xyz -，则(0,(A B，C D ,262323236(,,0),(0,,),(,0,333333AB AC CD =-==-，设平面ABC 的法向量为(,,)n x yz =，则0n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩，即00x y y x ⎧+=⎪⎪+=，令1y =，则1z =-，2x=，所以(1)2n =-. 设直线CD 与平面ABC 所成角为α，则1)sincos ,||||CD nCD n CD n α⋅-⋅===⋅0((1)++-⨯-==，所以直线CD 与平面ABC 所成角的正弦值为5.……………………12分 20、解：（1）(0,)2p F 当l 的倾斜角为45时，l 的方程为2p y x =+ 设1122(,),(,)A x y B x y 222p y x x py ⎧=+⎪⎨⎪=⎩得2220x px p --=1212122,3x x p y y x x p p +=+=++= 得AB 中点为3(,)2D p p …………3分 AB 中垂线为3()2y p x p -=-- 0x =代入得552y p == 2p ∴=……6分（2）设l 的方程为1y kx =+，代入24x y =得2440x kx --=212122()444AB y y k x x k =++=++=+ AB 中点为2(2,21)D k k +令2MDN ∠=α 122S AB AB =α⋅=α⋅ S AB∴=α…………8分 D 到x 轴的距离221DE k =+222211cos 1122222DE k k k AB +α===-++…………10分当20k =时cos α取最小值12α的最大值为3π 故S AB的最大值为3π.……………………12分 21.解：(1)()1()()ln ln ().()ln ,1,u x v x a x x x x m x m x x x x'≥⇒≥-+==-∈+∞. 易知1()ln m x x x'=-在(1,)+∞上递减，()(1)1m x m ''∴<=…………6分存在0(1,)x ∈+∞，使得0()0m x '=，函数()m x 在()01,x x ∈递增，在()0+x x ∈∞，递减0()a m x ≥. 由0()0m x '=得001ln x x =0000000111()11m x x x x x x x =-⋅+=+-> 1a ∴> B A ⊆……………………6分(2)()()()()ln ln ,()(),(1,)22a w x af x u x w x x x xg x v x x a x x x=-=--=-=--∈+∞令. ①21()ln 10,(1,)af x x x x x '=+-+>∈+∞，由于(),1,(1)0,a m a f a ∈+∞⇒>=-< ,()x f x →+∞→+∞，由零点存在性定理可知：()1,,a ∀∈+∞函数()f x 在定义域内有且仅有一个零点……………………8分②2()10,(1,)2a g x x x'=+>∈+∞，3(1)10,2ag =-<,()x g x →+∞→+∞，同理可知()1,,a ∀∈+∞函数()g x 在定义域内有且仅有一个零点……………………9分③假设存在0x 使得()()000f x g x ==，2000000ln ln 2a x x x x a x a x⎧=-⎪⎨-=⎪⎩消a 得002002ln 021x x x x -=-- 令22()ln 21x h x x x x =--- 222142()0(21)x h x x x x +'=+>-- ()h x ∴递增44132(2)ln 2ln 01)0.88140553h h e =-=<=->()01x ∴∈此时200001181,21125422x a x x x ⎛⎫==++-∈ ⎪⎛⎫⎝⎭++ ⎪⎝⎭所以满足条件的最小整数2m =……………………12分22、解：（1）∵OC =OD ，∴∠OCD =∠ODC ，∴∠OAC =∠ODB ．∵∠BOD =∠A ，∴△OBD ∽△AOC ． ∴ACODOC BD =， ∵OC =OD =6，AC =4，∴466=BD ，∴BD=9．……………………5分（2）证明：∵OC =OE ，CE ⊥OD ．∴∠COD =∠BOD =∠A ．∴∠AOD =180º–∠A –∠ODC=180º–∠COD –∠OCD=∠ADO ． ∴AD =AO ……………………10分23、解：（1）直线:l y x = 曲线22:12x C y +=……………………4分（2）设点()00,M x y 及过点M的直线为0102:2x x l y y ⎧=+⎪⎪⎨⎪=+⎪⎩由直线1l 与曲线C 相交可得：222000032202t x y +++-= 220022883332x y MA MB +-⋅=⇒=，即：220026x y += 2226x y +=表示一椭圆……………………8分取y x m =+代入2212x y +=得：2234220x mx m ++-= 由0∆≥得m ≤≤故点M 的轨迹是椭圆2226x y +=夹在平行直线y x =±10分24.解(1)由125x -+<得5125x -<-+<713x ∴-<-< 得不等式的解为24x -<<……………………5分(2)因为任意1x R ∈，都有2x R ∈，使得12()()f x g x =成立，所以{|()}{|()}y y f x y y g x =⊆=，又()223|(2)(23)||3|f x x a x x a x a =-++≥--+=+，()|1|22g x x =-+≥，所以|3|2a +≥，解得1a ≥-或5a ≤-，所以实数a 的取值范围为1a ≥-或5a ≤-.……………………10分。

2015年江西省八所重点中学高考一模数学试卷(理科)【解析版】

C．[﹣5，﹣ ）
11．（5 分）正三角形 ABC 的边长为 2，将它沿高 AD 翻折，使点 B 与点 C 间的距离为 A．7π ，此时四面体 ABCD 外接球表面积为（ B．19π C． π ） D． π
12．（5 分）已知在平面直角坐标系中，点 P 是直线 l：x＝﹣ 上一动点，定点 F （，0），点 Q 为 PF 的中点，动点 M 满足 • ＝0， • ＝λ （λ∈R）．过）
2015 年江西省八所重点中学高考数学一模试卷（理科）
一、选择题（共 12 小题，每小题 5 分，满分 60 分） 1．（5 分）已知集合 A＝{x|x2﹣x﹣2≤0}， B＝{x|y＝ln （1﹣x） }，则 A∩B＝（ A．（1，2） 2．（5 分）如果 z＝ A．0 B．（1，2] C．[﹣1，1）） D．1 |＝| |” （） D．（﹣1，1））
第 2 页（共 21 页）
15．（5 分）如图，圆 O 与 x 轴的正半轴的交点为 A，点 C、B 在圆 O 上，且点 C 位于第一象限，点 B 的坐标为（ ﹣sin cos ﹣ 的值为， ﹣ ．）， ∠AOC＝α，若|BC|＝1，则 cos2
16．（5 分）用 g（n）表示自然数 n 的所有因数中最大的那个奇数；例如：9 的因数有 1，3，9，g（9）＝9，10 的因数有 1，2，5，10，g（10）＝5，那么 g（1）+g（2）+g（3）+…+g（22015﹣1）＝三、解答题（共 5 小题，满分 60 分） 17．（12 分）已知 f（x）＝2sin x，集合 M＝{x||f（x）|＝2，x＞0}，把 M 中的．
元素从小到大依次排成一列，得到数列{an}，n∈N*．（1）求数列{an}的通项公式；（2）记 bn＝，设数列{bn}的前 n 项和为 Tn，求证 Tn＜．

2015八校联考江西省八所重点中学2015届高三4月联考数学(理)试题 Word版含答案

江西省八所重点中学2015届高三联考数学（理科）试卷九江一中张思意宜春一中舒红艳一、选择题(本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)．1. 已知集合{-=2x x A }02≤-x ，{==y x B })1ln(x -，则=⋂B A （）A ．)21(， B ．]21(， C ．)11[，- D ．)11(，- 2. 如果iaiz +-=11为纯虚数，则实数a 等于（） A.0 B. -1或1 C. -1 D. 13. 在△ABC 中, AB AC BA BC ⋅=⋅“” 是 AC BC =“”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 4.数列{n a }的前n 项和)(322+∈-=N n n n S n ，若p-q=5,则q p a a -= （）A. 10B. 15C. -5D.20 5.对任意非零实数a 、b ,若a b ⊗的运算原理如图所示，则12)31(4log -⊗的值为（）A.31 B.1 C.34D.2 6.在某次联考数学测试中，学生成绩ξ服从正态分布()()2100,,0σσ>，若ξ在()80,120内的概率为0.8，则落在()0,80内的概率为（）A. 0.05B. 0.1C. 0.15D.0.27.函数()sin (0,0)f x A x A ωω=>>的部分图象如图所示，则`)1(f +)2(f +)3(f ++)2015(f 的值为（）8.若)1(x +8822107)21(x a x a x a a x ++++=- ，则721a a a +++ 的值是（） A ．-2 B.-3 C.125 D.-1319.已知圆1C ：0222=++y cx x ，圆2C ：0222=+-y cx x ，椭圆C ：22221x y a b+=，若圆12,C C都在椭圆内，则椭圆离心率的范围是（） A. )1,21[ B.]21,0(C. )1,22[D. 22,0( 10.定义在R 上的函数)(x f 对任意1x 、)(212x x x ≠都有0)()(2121<--x x x f x f ，且函数(1)y f x =-的图象关于(1,0)成中心对称，若s ，t 满足不等式22(2)(2)f s s f t t -≤--．则当14s ≤≤时，ts st +-2的取值范围是（） A ．21,3[-- B ．]21,3[-- C ．)21,5[-- D ．]21,5[--11.正三角形ABC 的边长为2，将它沿高AD翻折，使点B 与点C ABCD 外接球表面积为（）A ．π7B ．π19C ．π767 D ．π1961912.在平面直角坐标系中，点P 是直线21:-=x l 上一动点，定点1,02F ⎛⎫⎪⎝⎭,点Q 为PF 的中点，动点M 满足0=⋅,λ=)(R ∈λ,过点M 作圆2)3(22=+-y x 的切线，切点分别为T S ,,则⋅的最小值是（） A ．53 B ． 935 C ．310 D ．31-二、填空题（本题共4个小题，每小题5分，共20分） 13.计算：⎰-333)cos (dx x x = .14.已知点(,)(0,4)(2,0)P x y A B -到和的距离相等，则24x y+的最小值为 .15.如图，圆O 与x 轴的正半轴的交点为A ，点C 、B 在圆O 上，且点C 位于第一象限，点B 的坐标为（135,1312-），A O C α∠=．若1BC =2sin cos 2222ααα--的值为 .16.用)(n g 表示自然数n 的所有因数中最大的那个奇数，例如:9的因数有1,3,9,(9)9g =，10的因数有1,2,5,10,(10)5g =,那么)12()3()2()1(2015-++++g g g g = .三、解答题(本题共6小题，共70分，解答题应写出文字说明、证明过程和演算步骤．) 17.（本小题12分）已知x x f 2sin2)(π=，集合M =(){}2,0x f x x =>，把M 中的元素从小到大依次排成一列，得到数列{}n a ，*∈N n .（1）求数列{}n a 的通项公式；（2）记211+=n n a b ，设数列{}n b 的前n 项和为n T ，求证41<n T .18. (本题12分)如图，四棱锥P ABCD -中，底面ABCD 是直角梯形，90DAB ∠=，//AD BC ，AD ⊥侧面PAB ，△PAB 是等边三角形，2D A A B ==，12BC AD =，E 是线段AB 的中点．（1）求证：PE CD ⊥；（2）求PC 与平面PDE 所成角的正弦值．19. (本题12分)已知集合{1,2,3,4}A =，函数()f x 的定义域、值域都是A ，且对于任意i A ∈，i i f ≠)(. 设4321,,,a a a a 是4,3,2,1的任意一个排列，定义数表12341234()()()()a a a a f a f a f a f a ⎛⎫⎪⎝⎭，若两个数表的对应位置上至少有一个数不同，就说这是两张不同的数表.（1）求满足条件的不同的数表的张数;(2)若i a i =(4,3,2,1=i )，从所有数表中任意抽取一张，记ξ为表中)(i f a i >的个数，求ξ的分布列及期望.20．(本题12分)已知椭圆C:12222=+by a x （0>>b a ）的离心率e =21，且过点M （1，23）（1）求椭圆C 的方程；（2）椭圆C 长轴两端点分别为A 、B,点P 为椭圆上异于A 、B 的动点，定直线4=x 与直线PA 、PB分别交于M 、N 两点，又E(7，0)，过 E 、M 、N 三点的圆是否过x 轴上不同于点E 的定点？若经过，求出定点坐标；若不经过，请说明理由.21. (本题12分)已知x ax x x f 2sin)(2π++= )1,0(∈x（1）若)(x f 在定义域内单调递增，求a 的取值范围;（2）当a =-2时，记)(x f 得极小值为)(0x f 。

【恒心】【揭秘】2015年高考江西省(新课标Ⅰ卷)全省理科前50名数学各题小分得分情况

【恒心】【揭秘】2015年高考江西省（新课标Ⅰ卷）全省理科前50名数学各题小分得分情况
李炳璋提供
省排名
姓名
学校
1--12题
13--16题
17题
18题
19题
20题
21题
22--24题
总分
60分
20分
12分
12分
12分
12分
12分
10分
150分
1
夏子哲
江西师大附中
55
15
11.5
12
12
12
12
10
139.5
12
8.5
12
12
6
9
139.5
18
涂钰藩
江西师大附中
60
20
12
11.5
12
12
11
10
148.5
19
邓若琪
景德镇一中
60
20
12
11.5
12
12
11.5
10
149
20
高亦博
莲塘一中
60
15
12
12
12
12
11.5
10
144.5
21
付奕楚
景德镇一中
60
20
12
12
12
12
7
10
145
22
罗来威
莲塘一中
27
何欣蔚
江西师大附中
60
20
12
12
12
12
11
10
149
28
傅怀颖
江西师大附中
55

2015届南昌市高三“二模”测试数学（理科）参考答案及评分标准

2015届南昌市高三“二模”测试数学（理科）参考答案及评分标准—高三数学(理科)答案第1页—2015 年高三测试卷数学(理科)参考答案及评分标准一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目二、填空题：本大题共4小题，每小题5分．13．214．13π 15．13 16．2212x y -= 三、解答题：解答应写出文字说明，证明过程或演算步骤．17．解：（Ⅰ）由点,C B 的坐标可以得到34AOC π∠=，23AOB π∠=，…………………2分所以cos cos()COB AOC AOB ∠=∠+∠1()222=--=；……6分（Ⅱ）因为c 23AOB π∠=，所以3C π=，所以2sin sin a b A B ===，………8分所以22sin 2sin()3a b A A π+=+-2sin()6A π=+，2(0)3A π<<，……………………11分所以当3A π=时，a b +最大，最大值是12分18．解：（Ⅰ）该校运动会开幕日共有13种选择，其中运动会期间至少两天空气质量优良的选择有：1日，2日，3日，5日，9日，10日，12日，所以运动会期间至少两天空气质量优良的概率是2713P =．…………………………………6分（Ⅱ）随机变量ξ所有可能取值有：0,1,2,3；………………………………………………7分(0)P ξ==113，(1)P ξ==613，(2)P ξ==613，(3)P ξ==113，……………………9分所以随机变量ξ的分布列是：随机变量ξ的数学期望是1661012313131313E ξ=?+?+?+?=2113．……………………12分……………………10分—高三数学(理科)答案第2页—19．（Ⅰ）证明：在梯形ABCD 中，因为2AD DC CB ===，4AB =，4212cos 22CBA -∠==，所以60,ABC ∠=?由余弦定理求得AC =90ACB ∠=?即BC⊥又因为平面AEFC ⊥平面ABCD ，所以BC ⊥平面所以BC AG⊥，………………………………………3分在矩形AEFC 中，tan 1AE AGE EG ∠==，4AGE π∴∠=tan 1CF CGF GF ∠==，4CGF π∠=，所以2CGF AGE π∠+∠=，即AG CG ⊥，所以AG ⊥平面BCG ；……………………………………………………………………………6分（Ⅱ）FC AC ⊥，平面AEFC ⊥平面ABCD ，所以FC ⊥平面ABCD ，以点C 为原点，,,CA CB CF 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则)(0,0,0),(0,2,0),1,0)C A B D-,G ，…………………………8分平面BCG 的法向量(3,0,GA =，设平面GCD 的法向量(,,)n x y z =，则00n CG n CD ??==??，从而00x z y +=??-=，令1x =则(1,3,1)n =-，…………………………………………………………………………10分所以cos ,n GA <>==11分而二面角D —GCB 为钝角，故所求二面角的余弦值为．………………………………………………………………12分20．解：（Ⅰ）当l 垂直于OD 时||AB 最小，因为||2OD ==，所以2r ==，…………………………………2分因为圆1C 222:(0)x y r r +=>的一条直径是椭圆2C 的长轴，所以2a =，又点D 在椭圆22222:1(0)x y C a b a b +=>>上，所以291414b b +=?=，—高三数学(理科)答案第3页—所以圆1C 的方程为224x y +=，椭圆2C 的方程为22143x y +=；………………………5分（Ⅱ）椭圆2C 的右焦点F 的坐标是(1,0)，当直线m 垂直于x轴时，||PQ = ||4MN =，四边形PMQN的面积S =当直线m 垂直于y 轴时，||4PQ =，||3MN =，四边形PMQN 的面积6S =，…………6分当直线m 不垂直于坐标轴时，设n 的方程为(1)y k x =-(0)k ≠，此时直线m 的方程为1(1)y x k=--，圆心O 到直线m的距离为：d =，所以||PQ ==8分将直线n 的方程代入椭圆2C 的方程得到：()22224384120k x k x k +-+-=，||MN =所以：四边形PMQN 的面积1||||2S PQ MN =?===∈，综上：四边形PMQN的面积的取值范围是．…………………………………………12分21．解：（Ⅰ）21221'()22x ax f x x a x x-+=+-=(0)x >，记2()221g x x ax =-+………1分（一）当0a ≤时，因为0x >，所以()10g x >>，函数()f x 在(0,)+∞上单调递增；……2分（二）当0a <≤时，因为24(2)0a =-≤△，所以()0g x ≥，函数()f x 在(0,)+∞上单调递增；…………………………………………………………………………………………………3分（三）当a >0()0x g x >??>?，解得x ∈，所以函数()f x在区间(,)2a a +上单调递减，在区间)+∞上单调递增．…………………………5分（Ⅱ）由（1）知道当(1a ∈时，函数()f x 在区间(0,1]上单调递增，所以(0,1]x ∈时，函数()f x 的最大值是(1)22f a =-，对任意的(1a ∈，都存在0(0,1]x ∈使得不等式20()ln ()f x a m a a +>-成立，等价于对任意的(1a ∈，不等式222ln ()a a m a a -+>-都成立，……………………………………6分即对任意的(1a ∈，不等式2ln (2)20a ma m a +-++>都成立，—高三数学(理科)答案第4页—记2()ln (2)2h a a ma m a =+-++，则(1)0h =，1(21)(1)'()2(2)a ma h a ma m a a --=+-+=，因为(1a ∈，所以210a a->，当1m ≥时，对任意(1a ∈，10ma ->，所以'()0h a >，即()h a在区间上单调递增，()(1)0h a h >=成立；…………………………………………………………………………9分当1m <时，存在0(1a ∈使得当0(1,)a a ∈时，10ma -<，'()0h a <，()h a 单调递减，从而()(1)0h a h <=，所以(1a ∈时，()0h a >不能恒成立．综上：实数m 的取值范围是[1,)+∞．……………………………………………………………12分 22．解：AF 是圆的切线，且18,15AF BC ==，∴由切割线定理得到2218(15)12AF FB FC FB FB FB =??=?+?=，…………………3分,AB AD ABD ADB =∴∠=∠，则,//FAB ABD AF BD ∠=∠∴，…………………………………………………………………6分又//AD FC ，∴四边形ADBF 为平行四边形．12,,18AD FB ACF ADB F AC AF ==∠=∠=∠∴==，//,18AE ADAD FC AE BC∴=-，解得8AE =。

2015届江西省八校联考数学(理)答案

江西省八所重点中学2015届高三联考数学（理科）试卷参考答案13 . 0 14. 13516 . 3142015-17.解：（1）Θ2)(=x f ∴22πππ+=k x 12+=k x Z k ∈ ……（3分）又Θ0>x ∴12-=n a n )(*∈N n ……（6分）（2）Θ211+=n n a b 2)12(1+=n )(*∈N n ……（7分） 2)12(1+=n b n 14412++=n n n n 4412+<)111(41+-=n n ……（10分）∴<+⋅⋅⋅+=n n b b T 13121211(41-+-=)111+-⋅⋅⋅+n n 41)1(4141<+-=n ∴41<n T得证 ……（12分） 18.解：（1）证明：因为AD ⊥侧面PAB ，PE ⊂平面PAB ，所以AD PE ⊥．…………2分又因为△PAB 是等边三角形，E 是线段AB 的中点，所以PE AB ⊥．因为AD AB A =I ，所以PE ⊥平面ABCD ．……4分而CD ⊂平面ABCD ，所以PE CD ⊥．………5分（2）以E 为原点，建立如图所示的空间直角坐标系E xyz -．则(0,0,0)E ，(1,1,0)C -，(2,1,0)D ，P ．(2,1,0)ED =u u u r ，EP =u u u r ，(1,1,PC =-u u u r．设(,,)x y z =n 为平面PDE 的法向量．由0,0.ED EP ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n 即20,0.x y +=⎧⎪= 令1x =，可得(1,2,0)=-n ．……9分设PC 与平面PDE 所成的角为θ．||3sin cos ,5||||PC PC PC θ⋅=<>==u u u ru u u r u u u r n n n ．所以PC 与平面PDE 所成角的正弦值为35． ……12分 19.解：（1）944A =216 ……5分（2） p(ξ=1) =91, p(ξ=2) =97p(ξ=3) =91……9分因此，ξ的分布列如下：∴E ξ =2 ……12分20．解：（1）13422=+y x ………5分 (2)设PA,PB的斜率分别为21,k k ,),(00y x p ，则4321-=k k ………7分则PA:)2(1+=x k y ，则)6,4(1k MPB: )2(2-=x k y ,则)2,4(2k N 又11236k k k EM -=-=，322k k EN -=1-=EN EM k k ………10分设圆过定点F(m,o),则1424621-=--mk m k ，则m=1或m=7(舍)故过点E 、M 、N 三点的圆是以MN 为直径的圆过点F （1,0）………12分解：21.解：（1）x a x x f 2cos22)(ππ++=' )1,0(∈x依题意0)(≥'x f 恒成立，a x x -≥+2cos22ππ令=)(x g x x 2cos22ππ+)1,0(∈xx x g 2sin42)(2ππ-=' Θ)(x g '在)1,0(∈x 单调递减，且0)0(>'g ，0)1(<'g ∴)(x g '在区间)1,0(∈x 上存在唯一零点0x ………3分∴)(x g 在),0(ξ上单调递增，在)1,(ξ上单调递减。