专训四种常见确定函数解析式的方法
求函数解析式常用的方法

求函数解析式常用的方法:
1)待定系数法
根据已知条件设出一个含有待定系数的代数式或函数式或方程,然后利用恒等式的性质,或将已知条件带入,建立起方程组,通过方程组而求出待定系数的值,或者消除这些待定系数,找出原来已知系数间存在的关系,这种方法叫做待定系数法。
2)换元法
换元法就是通过引入一个或几个新的变量来替换原来的某些量的解题方法,它的基本功能是化难为易、换繁为简,以快速实现从未知向已知的转换,从而达到顺利解题的目的,常见的换元法是多种多样的,诸如局部换元、整体换元、三角换元、分母换元、平均换元等等,它的应用极为广泛。
3)配凑法
根据具体解析式凑出复合变量的形式,从而求出解析式。
1)消元法
此法的实质是解函数方程
5)赋值法
此类解法的依据是:如果一个函数关系式中的变量对某个范围内的一切值都成立,则对该范围内的某些特殊值必成立,结合题设条件的结构特点,由特殊到一般寻找普遍规律。
【二次函数强化练习】(五)求解析式的四种常见类型【部编 人教 湘教 苏教通用版】
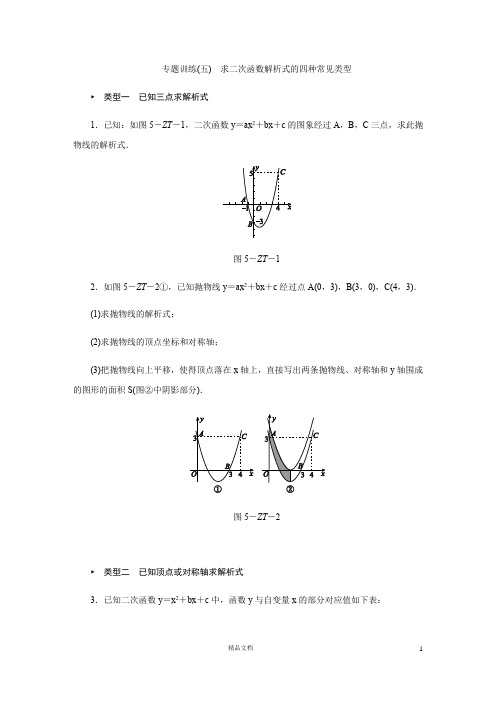
专题训练(五)求二次函数解析式的四种常见类型►类型一已知三点求解析式1.已知:如图5-ZT-1,二次函数y=ax2+bx+c的图象经过A,B,C三点,求此抛物线的解析式.图5-ZT-12.如图5-ZT-2①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).(1)求抛物线的解析式;(2)求抛物线的顶点坐标和对称轴;(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).图5-ZT-2►类型二已知顶点或对称轴求解析式3.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:则该二次函数的解析式为____________________.4.在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0),求该二次函数的解析式.5.已知抛物线经过点A(1,0),B(0,3),且对称轴是直线x=2,求该抛物线的解析式.6.如图5-ZT-3,已知抛物线的顶点为A(1,4),与y轴交于点B(0,3),与x轴交于C,D两点,点P是x轴上的一个动点.(1)求此抛物线的解析式;(2)当PA+PB的值最小时,求点P的坐标.图5-ZT-3►类型三已知抛物线与x轴的交点求解析式7.抛物线与x轴交于点(-1,0)和(3,0),与y轴交于点(0,-3),则此抛物线的解析式为()A.y=x2+2x+3B.y=x2-2x-3C.y=x2-2x+3D.y=x2+2x-3图5-ZT-48.如图5-ZT-4,已知抛物线过A,B,C三点,点A的坐标为(-1,0),点B的坐标为(3,0),且3AB=4OC,则此抛物线的解析式为__________________.9.已知抛物线的顶点坐标为(1,9),它与x轴有两个交点(交点的横坐标均为整数),两交点间的距离为6,求此抛物线的解析式.►类型四根据图形平移求解析式10.2017·义乌矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数解析式为y=x2,再次平移这张透明纸,使这个点与点C重合,则此时抛物线的函数解析式变为() A.y=x2+8x+14B.y=x2-8x+14C.y=x2+4x+3D.y=x2-4x+311.2017·天津已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B的左侧),顶点为M.平移该抛物线,使点M平移后的对应点M′落在x轴上,点B平移后的对应点B′落在y轴上,则平移后的抛物线的解析式为()A.y=x2+2x+1B.y=x2+2x-1C.y=x2-2x+1D.y=x2-2x-112.把抛物线y=x2先向左平移1个单位长度,再向下平移4个单位长度,得到如图5-ZT-5所示的二次函数的图象.(1)求此二次函数的解析式;(2)在平移后的抛物线上存在一点M,使△ABM的面积为20,请直接写出点M的坐标.图5-ZT-513.2018·苏州如图5-ZT-6,已知抛物线y=x2-4与x轴交于点A,B(点A位于点B 的左侧),C为顶点.直线y=x+m经过点A,与y轴交于点D.(1)求线段AD的长;(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数解析式.图5-ZT-6详解详析1.解:把(-1,0),(0,-3),(4,5)代入y =ax 2+bx +c ,得⎩⎪⎨⎪⎧a -b +c =0,c =-3,16a +4b +c =5,解得⎩⎪⎨⎪⎧a =1,b =-2,c =-3.所以此抛物线的解析式为y =x 2-2x -3.2.解:(1)把(0,3),(3,0),(4,3)代入y =ax 2+bx +c ,得 ⎩⎪⎨⎪⎧c =3,9a +3b +c =0,16a +4b +c =3,解得⎩⎪⎨⎪⎧a =1,b =-4,c =3. 所以抛物线的解析式为y =x 2-4x +3. (2)因为y =x 2-4x +3=(x -2)2-1,所以抛物线的顶点坐标为(2,-1),对称轴是直线x =2. (3)阴影部分的面积为2. 3.[答案]y =x 2-4x +5[解析]从表格中的数据可以看出,当x =1和x =3时,函数值y =2,可见,抛物线的顶点坐标为(2,1),故可设二次函数解析式为y =a (x -2)2+1,再由二次函数图象过点(1,2),得2=a (1-2)2+1,解得a =1,故二次函数的解析式为y =(x -2)2+1,即y =x 2-4x +5.4.解:∵二次函数图象的顶点为A (1,-4),∴设该二次函数的解析式为y =a (x -1)2-4.将(3,0)代入解析式,得a =1, 故y =(x -1)2-4,即该二次函数的解析式为y =x 2-2x -3. 5.解:∵抛物线的对称轴是直线x =2且经过点A (1,0), ∴由抛物线的对称性可知,抛物线还经过点(3,0). 设抛物线的解析式为y =a (x -1)(x -3).把(0,3)代入解析式,得3=3a ,∴a =1,∴y =(x -1)(x -3), 即该抛物线的解析式为y =x 2-4x +3. 6.解:(1)∵抛物线的顶点坐标为(1,4), ∴设此抛物线的解析式为y =a (x -1)2+4. ∵抛物线过点B (0,3),∴3=a (0-1)2+4,解得a =-1,∴y =-(x -1)2+4,即此抛物线的解析式为y =-x 2+2x +3.(2)作点B 关于x 轴的对称点E (0,-3),连接AE 交x 轴于点P ,此时P A +PB 的值最小.设直线AE 的解析式为y =kx +b ,则⎩⎪⎨⎪⎧k +b =4,b =-3,解得⎩⎪⎨⎪⎧k =7,b =-3,∴直线AE 的解析式为y =7x -3.当y =0时,x =37,∴当P A +PB 的值最小时,点P 的坐标为(37,0).7.B [解析]由抛物线与x 轴交于点(-1,0)和(3,0),设此抛物线的解析式为y =a (x +1)(x -3).又因为抛物线与y 轴交于点(0,-3),把x =0,y =-3代入y =a (x +1)(x -3),得-3=a (0+1)(0-3),即-3a =-3,解得a =1,故此抛物线的解析式为y =(x +1)(x -3)=x 2-2x -3.故选B.8.[答案]y =-x 2+2x +39.解:由抛物线的对称性可知抛物线与x 轴的两个交点分别为(-2,0)和(4,0), 所以设其解析式为y =a (x +2)(x -4). 将(1,9)代入解析式,得9=a (1+2)(1-4), 解得a =-1,所以y =-(x +2)(x -4),即此抛物线的解析式为y=-x2+2x+8.10.A[解析]因为矩形ABCD的两条对称轴为坐标轴,所以矩形ABCD关于坐标原点对称.因为A,C是矩形对角线上的两个点,所以点A,C关于原点对称,所以点C的坐标为(-2,-1),所以抛物线向左平移了4个单位长度,向下平移了2个单位长度,所以平移后抛物线的函数解析式为y=(x+4)2-2=x2+8x+14.故选A.11.A[解析]令y=0可得x2-4x+3=0,解得x1=1,x2=3,可得A(1,0),B(3,0),根据抛物线顶点坐标公式可得M(2,-1),由点M平移后的对应点M′落在x轴上,点B平移后的对应点B′落在y轴上,可知抛物线向左平移了3个单位长度,向上平移了1个单位长度,根据抛物线平移规律,可知平移后的抛物线的解析式为y=(x+1)2=x2+2x+1,故选A.12.解:(1)此二次函数的解析式为y=(x+1)2-4,即y=x2+2x-3.(2)∵当y=0时,x2+2x-3=0,解得x1=-3,x2=1,∴A(1,0),B(-3,0),∴AB=4.设点M的坐标为(m,n).∵△ABM的面积为20,∴12AB·|n|=20,解得n=±10.当n=10时,m2+2m-3=10,解得m=-1+14或m=-1-14,∴点M的坐标为(-1+14,10)或(-1-14,10);当n=-10时,m2+2m-3=-10,此方程无解.故点M的坐标为(-1+14,10)或(-1-14,10).13.解:(1)由x2-4=0解得x1=2,x2=-2.∵点A位于点B的左侧,∴A(-2,0).∵直线y=x+m经过点A,∴-2+m=0,m=2.∴D(0,2).∴AD=OA2+OD2=2 2.(2)∵直线CC′平行于直线AD,并且经过点C(0,-4),∴直线CC′的函数解析式为y=x-4.∵新抛物线的顶点C′在直线y=x-4上,∴设顶点C′的坐标为(n,n-4),∴新抛物线对应的函数解析式为y=(x-n)2+n-4.∵新抛物线经过点D(0,2),∴n2+n-4=2.解得n1=-3,n2=2.∴新抛物线对应的函数解析式为y=(x+3)2-7或y=(x-2)2-2,即y=x2+6x+2或y=x2-4x+2.。
求函数f(x)解析式常用的方法

求函数)(x f 解析式常用的方法济宁一中高一数学组 贾广素(邮编272000)电话:130****4397根据实际问题求解函数的表达式,是利用函数知识解决实际问题的基础。
因此,有必要掌握函数解析式的求法,下面就介绍几种求解函数解析式的常用方法:一、直接法直接法就是从题设(已知)条件出发,执因索果,进行演绎推导,从而得出函数解式的方法。
例1、 已知432)(2++=x x x f ,求函数)1(+x f 的解析式。
解:由于432)(2++=x x x f ,∴)1(+x f =4)1(3)1(22++++x x =9722++x x。
例2、 已知)(x f 是奇函数,且当0>x 时)1()(x x x f -=,求当0<x 时)(x f 的解析式。
解: 当0>x 时)1()(x x x f -=,∴当x<0时,-x>0,从而)1())(1)(()(x x x x x f +-=---=-又 )(x f 是奇函数,)()(x f x f -=-;)1()(x x x f +=∴。
注:直接法是一种正向的思维,解决问题时要善于将稍复杂的问题进行分解,各个击破,它不需要特殊的技巧。
二、待定系数法用一些字母作为待定系数,然后根据条件列出含有待定系数的方程式或方程组,解出这些待定系数,从而求出函数解析式的方法称为待定系数法。
例3、已知)(x f 是一次函数,并且满足172)1(2)1(3+=--+x x f x f ,求函数)(x f 的解析式。
解:设)0()(≠+=a b ax x f ,则)1(2)1(3--+x f x f =ba axb a ax 222333-+-++=b a ax ++5,又 172)1(2)1(3+=--+x x f x f ,比较系数得⎩⎨⎧=+=1752a b a 解得7,2==b a ,所以所求函数的解析为72)(+=x x f 。
例4、已知二次函数)(x f y =的最大值等于13,且,5)1()3(=-=f f 求函数)(x f 的解析式。
函数解析式常见的求解方法

函数解析式常见的求解方法函数的解析式是指用数学表达式来表示函数的关系式,它是研究函数性质和求解函数值的基本工具。
常见的求解函数解析式的方法有以下几种:1.数学归纳法:对于一些特定的函数关系,在给定一些初始条件的情况下,通过递推关系式或递推公式,可以用数学归纳法来求解函数的解析式。
举个例子,求解斐波那契数列的解析式,我们知道当n=1时,F(1)=1;n=2时,F(2)=1;而当n>2时,斐波那契数列的数值等于它前两项的值之和,即F(n)=F(n-1)+F(n-2)。
根据这个递推关系式,可以通过数学归纳法求解得到斐波那契数列的解析式。
2.函数关系的图像法:通过观察函数关系图像的特点,可以得到函数的解析式。
举个例子,我们知道一次函数的图像是一条直线,它的解析式通常表示为y=ax+b,其中a和b是常数,a表示斜率,b表示截距。
因此,通过观察一次函数的图像的斜率和截距,可以得到函数的解析式。
3.函数关系的特殊情况法:对于一些特殊的函数关系,可以通过特定的方法求解函数的解析式。
举个例子,对于二次函数y=ax^2+bx+c,如果已知函数的图像经过三个点(x1, y1)、(x2, y2)和(x3, y3),可以通过代数的方法求解得到函数的解析式。
4.函数关系的逆运算法:对于一些函数关系,如果已知逆运算的解析式,可以通过求解逆运算的解析式来得到函数的解析式。
举个例子,对于指数函数y=a^x,如果已知函数的解析式为y=a^x,可以通过求解对数函数y=log_a(y),其中log_a表示以a为底的对数,来得到函数的解析式。
5.差值法和插值法:对于一些离散函数关系,可以通过差值和插值的方法来求解函数的解析式。
差值法是指通过已知的离散数据点,通过构造等差差分的方式,来求解函数的解析式。
插值法是指通过已知的离散数据点,通过构造合适的插值函数,并通过插值误差的原则,来求解函数的解析式。
综上所述,函数解析式的求解方法有数学归纳法、函数关系的图像法、函数关系的特殊情况法、函数关系的逆运算法、差值法和插值法等多种方法。
求函数解析式的几种方法

求函数解析式的几种方法函数解析式是表示一个函数关系的代数表达式,可以用来描述函数的定义域、值域、图像等特征。
在数学领域,有多种方法来推导函数的解析式,下面将介绍几种常见的方法。
一、直接法直接法是最常见和最基础的方法,可以根据函数的定义以及给定的条件,通过逐步推导得到函数的解析式。
例如,要求解函数y=f(x)的解析式,可以根据问题给出的条件进行如下推导:1.将函数的定义形式转化为解析式的形式。
例如,如果函数给出了一些点的坐标,可以通过观察得到点的横坐标和纵坐标之间的关系,从而得到函数的解析式。
2.确定函数的定义域和值域。
函数的定义域是自变量x可以取的值的集合,值域是函数所有可能的输出值的集合。
根据问题给出的条件,可以确定函数的定义域和值域。
3.根据函数的定义和给定的条件,逐步推导出函数的解析式。
例如,可以根据函数的一些性质或特点,通过观察和分析来确定函数的解析式。
二、利用已知函数逐步构建利用已知函数逐步构建函数的方法是一种常见的推导函数解析式的方法。
如果在问题中给出了一些已知的函数,可以利用这些函数作为基础来构建新的函数。
根据函数的性质和基本运算,通过运用函数的组合、反函数、平移、缩放等操作,逐步构建出所需的函数解析式。
例如,已知两个函数f(x)和g(x)的解析式,要求构建新函数h(x)的解析式,可以通过以下步骤进行:1.利用已知函数f(x)和g(x)进行基本运算,如加、减、乘、除等,得到中间函数u(x)。
2.对中间函数u(x)进行平移、缩放等操作,得到最终要求的函数h(x)。
三、利用函数的性质和特点函数具有一些普遍的性质和特点,如奇偶性、周期性、对称性等,可以根据这些性质和特点来推导函数的解析式。
例如,已知函数f(x)是偶函数,可以根据偶函数的性质得到f(-x)=f(x),然后通过观察和分析,逐步推导出函数的解析式。
四、利用已知点的坐标如果在问题中给出了函数的一些点的坐标,可以通过观察这些坐标点之间的关系,从而推导出函数的解析式。
求函数解析式的六种常用方法精编版

求函数解析式的六种常用方法精编版函数解析式是描述函数数学规律的公式或表达式。
在数学中,常用的方法有很多,但以下列举的六种方法是最常见且常用的。
一、直接给出公式或表达式最简单直接的方法是通过给出函数解析式来描述函数的规律。
例如,对于一元二次方程 y = ax^2 + bx + c,其中a、b、c为常数,就是一种直接给出函数解析式的方法。
这种方法适用于已知函数规律的情况,可以方便地求函数的值和图像。
二、通过函数图像导出函数解析式对于一些函数,可以通过观察函数的图像来导出其解析式。
例如,对于二次函数y = ax^2 + bx + c,如果已知函数的图像,并能确定顶点坐标和开口方向,那么就可以根据函数图像反推函数解析式。
这种方法适用于已知函数图像的情况,可以通过观察图像特点来确定函数解析式。
三、通过给定函数值求解析式有时候,我们已知函数在一些特定点的函数值,可以通过这些函数值来求解析式。
例如,已知一元一次函数的两个点的函数值,可以通过求解线性方程组来确定函数解析式。
这种方法适用于已知一些特定点的函数值,可以通过点与点之间的关系来求解析式。
四、通过已知函数性质求解析式有时候,我们已知函数满足一些特定的性质,可以通过这些性质来求解析式。
例如,对于一元一次函数y = kx + b,如果已知函数过点(1, 2)和(3, 4),可以利用点斜式或两点式来求解析式。
这种方法适用于已知函数的性质和特点,可以通过这些性质和特点来求解析式。
五、通过已知导数求解析式对于函数的解析式,如果已知其导数的解析式,可以通过积分来求解析式。
例如,对于函数y=2x^2+3x+1,如果已知其导数为y'=4x+3,可以通过积分来求得原始函数的解析式。
这种方法适用于已知函数的导数解析式,可以通过反向求导来求解析式。
六、通过泰勒级数展开求解析式对于一些特殊的函数,如三角函数、指数函数和对数函数等,可以通过泰勒级数展开来求解析式。
泰勒级数展开是利用函数的导数来逼近函数的方法,通过取泰勒级数展开的前几项,就可以得到函数的近似解析式。
函数解析式的求法

函数解析式的求法1.待定系数法例1.求一次函数y=f(x)解析式,使f(f(x))=4x+3.解:设f(x)=ax+b(a≠0).∴f(f(x))==af(x)+b=a(ax+b)+b=a^2x+ab+b∴a^2x+ab+b=4x+3∴a^2=4,ab+b=3解得a=2,b=1或a=-2,b=-3.∴f(x)=2x+1或f(x)=-2x-3.总结:当已知函数类型时,求函数解析式,常用待定系数法。
其基本步骤:设出函数的一般式,代入已知条件通过解方程(组)确定未知系数。
2.换元法换元法就是引进一个或几个新的变量来替换原来的某些量的解题方法,它的目的是化繁为简、化难为易,以快速的实现从未知向已知的转换,从而达到顺利解题的目的。
常见换元法是多种多样的,如局部换元、整体换元、分母换元、平均换元等,应用极为广泛。
例2.已知f(1-√x)=x.求f(x).解:设1-√x=t,则x=(1-t)^2∵x≥0,∴t≤1,∴f(t)=(1-t)^2(t≤1)∴f(x)=(1-x)^2(x≤1)(函数变量的无关性)总结:(1)利用换元法解题时,要注意在换元时易引起定义域的变化,所以最后的结果要注意所求函数的定义域。
(2)函数变量的无关性,变量无论是用x还是用t表示,都无关紧要,函数依然成立。
3.配凑法例3.已知f(3x+1)=9x^2-6x+5,求f(x).解:∵f(3x+1)=9x^2-6x+5=(3x+1)^2-12x+4=(3x+1)^2-4(3x+1)+8∴f(x)=x^2-4x+8总结:当已知函数表达式比较简单时,可直接应用配凑法,即根据具体的解析式凑出复合变量的形式,从而求出函数解析式。
4.消元法(又叫解方程组法)例4.已知函数f(x)满足条件:f(x)+2f(1/x)=x,求f(x).分析:用1/x代替条件方程中的x得:f(1/x)+2f(x)=1/x.把它与原条件式联立。
用消元法消去f(1/x),即得f(x)的解析式。
必修1求函数解析式的常用方法

必修1求函数解析式的常用方法在数学中,函数解析式是表示函数关系的一种方法,能够通过输入一个自变量的值来计算对应的函数值。
在求函数解析式时,有几种常用的方法可以帮助我们推导出函数解析式,包括代数法、求导法、极限法和积分法等。
一、代数法(方程法)代数法是一种常用的求函数解析式的方法,通过建立方程组来解决问题。
具体步骤如下:1.确定未知数:观察函数关系,确定未知数的个数和性质。
2.建立方程:将已知条件和未知数之间的关系转化为方程。
3.求解方程组:利用代数运算的方法求解方程组。
4.验证:将求得的解带入原方程进行验证,确保解的正确性。
例如,已知函数f(x)满足f(x)-f(x-1)=x,我们可以采用代数法求函数解析式。
解:设f(x) = ax + b,将f(x)的表达式带入已知条件f(x) - f(x - 1) = x中,得到:ax + b - a(x - 1) - b = x整理得:ax + b - ax + a - b = x去掉相同项后得:a=1再将a=1代入f(x),得到f(x)=x+b。
因此,函数f(x)的解析式是f(x)=x+b,其中b是常数。
二、求导法求导法是一种通过对函数求导来求解函数解析式的方法。
该方法主要适用于求解一阶线性微分方程。
1.已知已知函数的导数表达式;2.将导数表达式带入微分方程,得到关于未知函数的微分方程;3.求解微分方程,得到未知函数;4.对求得的未知函数进行验证。
例如,已知函数f'(x)=2x+1,我们可以采用求导法求函数解析式。
解:对已知函数f'(x) = 2x + 1进行积分,得到f(x) = ∫(2x + 1)dx = x^2 + x + C其中C为常数。
因此,函数f(x)的解析式是f(x)=x^2+x+C。
三、极限法极限法是一种通过取极限的方法来求解函数解析式的方法。
该方法主要适用于求解极限关系存在的函数。
1.观察函数的极限特征;2.利用极限性质推导函数解析式;3.对推导的解析式进行验证。
函数解析式的求解方法

函数解析式的求解方法一、通过观察函数的性质和特点推导出函数的解析式。
这种方法适用于一些常见函数,比如多项式函数、指数函数、对数函数等。
对于这些函数,我们可以通过观察函数的图像、性质和特点来推导出函数的解析式。
例如,对于二次多项式函数 y = ax^2 + bx + c,可以通过观察函数的性质来求解函数的解析式。
二次多项式函数的图像是一个抛物线,而且它的对称轴是直线 x = -b/2a。
根据这些性质,我们可以得到函数的一般形式为 y = a(x - p)(x - q),其中 p 和 q 是抛物线的两个零点。
二、通过已知点求解函数的解析式。
当我们知道函数过一些特定点时,可以通过这些点来求解函数的解析式。
通常我们需要至少知道函数过两个不同的点来确定函数的解析式。
例如,已知函数过点 (1, 2) 和 (3, 4),我们可以设函数的解析式为 y = ax + b,并将这两个点的坐标代入方程求解 a 和 b 的值。
代入第一个点可以得到 2 = a(1) + b,代入第二个点可以得到 4 = a(3) + b。
求解这个方程组可以得到 a = 1 和 b = 1,因此函数的解析式为 y = x+ 1三、通过函数的导数求解函数的解析式。
对于一些函数,我们可以通过求解函数的导数来确定函数的解析式。
这种方法通常适用于一些特殊的函数,比如三角函数、指数函数等。
例如,对于函数 y = e^x,我们可以通过求解函数的导数来确定函数的解析式。
函数的导数是 dy/dx = e^x,所以函数的解析式就是 y = e^x。
四、通过求解函数的积分来确定函数的解析式。
对于一些函数,我们可以通过求解函数的积分来确定函数的解析式。
这种方法通常适用于一些特殊的函数,比如多项式函数、三角函数等。
例如,对于函数 y = x^2,我们可以通过求解函数的积分来确定函数的解析式。
函数的积分是∫y dx = ∫x^2 dx = x^3/3 + C,其中 C 是一个常数。
函数解析式的几种基本方法及例题

求函数解析式的几种基本方法及例题:1、凑配法:已知复合函数[()]f g x 的表达式,求()f x 的解析式,[()]f g x 的表达式容易配成()g x 的运算形式时,常用配凑法。
但要注意所求函数()f x 的定义域不是原复合函数的定义域,而是()g x 的值域。
此法较适合简单题目。
例1、(1)已知f(x+1)=x 2+2x,求f(x)及f(x-2).(2) 已知221)1(x x x x f +=+ )0(>x ,求 ()f x 的解析式 解:(1)f(x+1)=(x+1)2-1,∴f (x )=x 2-1.f(x-2)=(x-2)2-1=x 2-4x+3.(2) 2)1()1(2-+=+x x x x f , 21≥+xx2)(2-=∴x x f )2(≥x2、换元法:已知复合函数[()]f g x 的表达式时,还可以用换元法求()f x 的解析式。
与配凑法一样,要注意所换元的定义域的变化。
例2 (1) 已知x x x f 2)1(+=+,求)1(+x f(2)如果).(,,)(x f x xx x f 时,求则当1011≠-= 解:(1)令1+=x t ,则1≥t ,2)1(-=t xx x x f 2)1(+=+∴,1)1(2)1()(22-=-+-=t t t t f1)(2-=∴x x f )1(≥xx x x x f 21)1()1(22+=-+=+∴ )0(≥x(2)设.)(,,,111111111-=∴-=-===x x f t tt f t x t x t )(代入已知得则 3、待定系数法:当已知函数的模式求解析式时适合此法。
应用此法解题时往往需要解恒等式。
例3、已知f(x)是二次函数,且满足f(x+1)+f(x-1)=2x 2-4x,求f(x). 解:设f(x)=ax 2+bx+c(a ≠0),∴f(x+1)+f(x-1)=a(x+1)2+b(x+1)+c +a(x-1)2+b(x-1)+c=2ax 2+2bx+2a+2c=2x 2-4x,则应有.)(1212102242222--=∴⎪⎩⎪⎨⎧-=-==∴⎪⎩⎪⎨⎧=+-==x x x f c b a c a b a四、构造方程组法:若已知的函数关系较为抽象简约,则可以对变量进行置换,设法构造方程组,通过解方程组求得函数解析式。
求函数解析式的四种常用方法(1)

3.设 y=f(x)是二次函数,方程 f(x)=0 有两个相等实根,
且 f′(x)=2x+2,求 f(x)的解析式.
解:设 f(x)=ax2+bx+c(a≠0), 则 f′(x)=2ax+b=2x+2, ∴a=1,b=2,f(x)=x2+2x+c. 又∵方程 f(x)=0 有两个相等实根, ∴Δ=4-4c=0,c=1,故 f(x)=x2+2x+1.
求函数解析式的四种常用方法
(3)换元法:已知复合函数 f(g(x))的解析式, 可用换元法,此时要注意新元的取值范围;
求函数解析式的四种常用方法
(4)解方程组法:已知关于 f(x)与 f1x或 f(- x)的表达式,可根据已知条件再构造出另 外一个等式组成方程组,通过解方程求出 f(x).
求函数解析式的四种常用方法
求函数解析式的四种常用方法
(1) 配凑法:由已知条件 f(g(x))=F(x), 可将 F(x)改写成关于 g(x)的表达式, 然后以 x 替代 g(x),便得 f(x)的表达式;
变式 题
换元法 拼凑法
求函数解析式的四种常用方法
(2)待定系数法:若已知函数的类型 (如一次函数、二次函数)可用待定系数法;
(4).已知f(1-cosx)=sin2x,求f(x)
(5).二次函数f(x)满足f(x+2)=f(2-x),且f(x)=0 的两实根平方和为10,图象过点(0,3),求f(x) 的解析式。
(6):已知:方程:x2+ax+a+1=0的两根满足一 个条件:一根大于k,一根小于k(k是实数),求a 的取值范围。
(4)定义在(-1,1)内的ቤተ መጻሕፍቲ ባይዱ数 f(x)满足 2f(x)-f(-x)=lg(x+1), 求函数 f(x)的解析式.
函数解析式求解方法总结

函数解析式求解方法总结对于一次函数(0,,y kx b k k b =+≠为常数)解析式的确定,说明了就是通过一定的方法确定k ,b 的值,最常用的方法就是两点待定解析式法。
一. 定义型:一次函数(0,,y kx b k k b =+≠为常数)中,首先k ≠0,其次x 的次数为1,b 值可取任意实数(当说明是正比例函数时b=0)。
例如:1.若函数()2212m y m x m -=+++是一次函数,求该一次函数的解析式。
2.若函数()32y m x m =++-是正比例函数,求其解析式。
二. 两点确定法:两点确定一条直线,因此我们可以通过将两点坐标带入一次函数标准式(0y kx b k =+≠)中,得到关于k,b 的二元一次方程组,通过解方程组得到k,b 的值,从而得到一次函数解析式。
1. 直接告诉两点坐标:例如:一次函数图像经过点(-1,2)和(3,-5),求该函数解析式。
2. 间接告诉两点:➢ 告诉一点坐标,然后间接告诉你它与x 轴交点的坐标:例如:某一次函数图像与直线y=x+6在x 轴上交于同一点,且过(1,4)点,求其解析式。
➢ 告诉一点坐标,然后间接告诉你它与y 轴交点的坐标:例如:某一次函数图像与直线y= - 3x+2在y 轴上交于同一点,且过点(2,-3),求其解析式。
➢ 告诉一点坐标,在说它与其他直线交于一点P:例如:已知一次函数的图像过点A (2,-2),且与正比例函数的图像交于点B (-1,4),求此一次函数和正比例函数的解析式。
➢ 图像型:在图中读出两点坐标,带入(0,,y kx b k k b =+≠为常数)求k,b例如:已知某个一次函数的图像如图所示,求该一次函数解析式。
三. 一点确定1. 告诉b ,让你确定k例如:已知y=kx+3的图像过点(2,-1),求其解析式 。
2. 告诉k ,让你确定b两条直线L 1:11y k x b =+,L 2:22y k x b =+的位置关系(1)两直线平行⇔21k k =且21b b ≠ (2)两直线相交⇔21k k ≠(3)两直线重合⇔21k k =且21b b = (4)两直线垂直⇔121-=k k例如:已知一次函数图像过点(1,-1)且与直线2x+y=5平行,求其解析式。
求函数解析式的方法

求函数解析式的方法要求函数解析式的方法,首先需要了解什么是函数解析式。
函数解析式是指表示函数数学关系的表达式,通常使用字母表示自变量和因变量,并使用数学符号和运算表示函数关系。
函数解析式在数学中起到非常重要的作用,它可以描述和表示函数的特性、性质和变化规律,并且可以用来求函数的值、图像和导数等。
下面给出几种常见的求函数解析式的方法。
一、通过观察和总结法观察函数的数列、图像和表格等信息,总结函数的特点和性质,然后利用已知的数学知识和方法进行推导和求解。
这种方法一般适用于简单函数和常见函数。
例如,对于一次函数y = kx + b,我们可以通过给定的两个点的坐标,利用直线的斜率公式和截距公式求解k和b。
二、通过已知函数的基本性质和运算规则对于已知的函数,如果知道其基本性质和运算规则,可以利用这些规则和性质进行组合和计算,得到新的函数解析式。
例如,对于两个已知函数f(x)和g(x),我们可以通过函数的加减乘除运算规则,将两个函数相加、相减、相乘或相除得到新的函数解析式。
三、通过已知函数的导数和微分对于已知的函数,如果知道其导数和微分,可以通过求导和微分的运算法则来推导新的函数的解析式。
导数和微分可以描述函数的变化率和曲线的斜率,因此对于一些需要描述变化规律和趋势的函数,求导和微分方法非常有效。
例如,对于二次函数y = ax^2 + bx + c,我们可以通过求导得到它的导函数y' = 2ax + b。
四、通过已知函数的级数展开对于已知函数,如果知道其级数展开式,可以通过级数展开来求解函数的解析式。
级数展开可以将函数表示为无穷级数的形式,适用于解析式不容易求得的情况。
例如,对于指数函数e^x,我们可以通过级数展开得到级数表示式e^x=1+x+x^2/2!+x^3/3!+...。
五、通过已知函数的积分对于已知函数,如果知道其积分,可以通过积分和反函数的关系来求解函数的解析式。
积分可以描述函数的累积变化和曲线下方的面积,因此对于需要求函数原函数和面积的情况,积分方法非常有效。
求函数解析式的方法和例题

求函数解析式的方法和例题在数学学习中,我们经常会遇到需要求解函数解析式的问题。
函数解析式是描述函数规律的数学式子,它可以帮助我们更好地理解函数的性质和行为。
那么,如何求函数解析式呢?接下来,我将介绍一些常见的方法和例题,希望能帮助大家更好地掌握这一内容。
一、常见的求函数解析式的方法。
1. 根据函数图像求解析式,当已知函数的图像时,我们可以通过观察图像的性质来推导函数解析式。
例如,对于一元一次函数y=kx+b,我们可以根据函数的斜率k和截距b来确定函数解析式。
同样地,对于二次函数、指数函数、对数函数等,也可以通过观察图像的特点来求解析式。
2. 根据函数性质求解析式,有些函数具有特定的性质,我们可以利用这些性质来求解析式。
例如,对于奇偶函数、周期函数、对数函数等,我们可以根据其性质来确定函数解析式。
3. 根据已知条件求解析式,有时候,我们会遇到一些特定的条件,例如函数的零点、极值点、导数等,我们可以利用这些已知条件来求解析式。
通过建立方程组,我们可以求解未知的函数解析式。
二、求函数解析式的例题。
1. 已知一元一次函数的图像经过点(2,3),斜率为4,求函数解析式。
解,根据一元一次函数的一般形式y=kx+b,我们可以利用已知的斜率和点的坐标来求解析式。
首先,斜率为4,即k=4;其次,函数经过点(2,3),代入x=2,y=3,得到3=4×2+b,解得b=-5。
因此,函数解析式为y=4x-5。
2. 已知函数f(x)满足f(1)=2,f'(x)=3x^2,求函数f(x)的解析式。
解,根据已知条件f(1)=2,我们可以利用这一条件来求解析式。
由导数的定义可知,f'(x)=3x^2,对f(x)进行积分得到f(x)=x^3+C,其中C为积分常数。
代入f(1)=2,得到2=1+C,解得C=1。
因此,函数f(x)的解析式为f(x)=x^3+1。
通过以上例题,我们可以看到,求解函数解析式的关键在于利用已知条件和函数的性质来建立方程,进而求得未知的函数解析式。
求函数解析式的常用四法

求函数解析式的常用四法一、方程组法型型和此法主要适用(x) )()()()()(c tx bf x af x c x t bf x af =+=+。
。
即函数的解析式为得:替换为解析:把。
联立方程组,即可解出替换为分析:把的解析式。
,求满足函数例3)(3)(-)(2)-()(2)(,)(,)()(2)()(.1x x f x x f x x f x f x x f x f x x x f x x x f x x f x f x f ==⇒⎩⎨⎧=-=----=--。
即函数的解析式为得:替换为解析:把。
联立方程组,即可解出替换为分析:把的解析式。
,求满足函数例)2(31)()2(31)(1)(2)1()1(2)(,1)(,1)()1(2)()(.2x x x f x x x f x x f x f x x f x f x x x f xx x f x xf x f x f +--=+--=⇒⎪⎪⎩⎪⎪⎨⎧-=--=----=--点评:方程组法求函数解析式关键是根据所给表达式列出方程组。
)()()()()()()()()()(x f x t c x bf x t af x c x t bf x af x t x x c x t bf x af 即可解出,即替换为型需把⎪⎪⎩⎪⎪⎨⎧=+=+=+,).()()()()()()((x) )()(x f tx c x bf tx af x c tx bf x af tx x c tx bf x af 即可解出,即替换为型需把⎩⎨⎧=+=+=+二、构造法的解析式。
,求函数例)(1)1(.32x f x x x f -= 分析:构造法求函数解析式,主要是要抓住给出的表达式的特征。
此题要把x 1看着一个整体,把所给表达式中的x 都改成x 1的形式。
且函数的解析式为解析:01,1)(1)1(11)1(222≠±≠-=∴-=-=x x x x x f x xx x x f点评: 解析式。
求函数解析式常用的方法

求函数解析式常用的方法函数解析式是指用数学表达式来表示一个函数的关系式。
常用的方法有以下几种:一、常数法:当函数表达式中只包含常数时,可以直接表示为一个确定的常数。
例如,函数f(x)=5表示f(x)始终等于5,不管x的取值如何。
二、线性函数法:线性函数是指函数的表达式中只包含一次项(通常是x)和常数项的函数。
常用的线性函数有一次函数、斜率截距式和两点式。
一次函数的函数表达式为f(x) = ax + b,其中a和b为常数。
通过给定的一对坐标点,可以利用斜率公式或两点式公式求解得到函数解析式。
三、二次函数法:二次函数是指函数的表达式中包含二次项(x的平方)的函数。
函数解析式为f(x) = ax^2 + bx + c,其中a、b和c为常数。
常用的求解方法有配方法和因式分解法。
配方法是通过将二次项与其他项配对,使得被配对的两项的和或差为一个完全平方。
通过这种方法可以将二次函数转化为完全平方的形式从而求解。
因式分解法是将二次函数进行因式分解,通过找出两个一次函数的乘积形式来求解。
通过因式分解可以得到二次函数的解析式。
四、指数函数法:指数函数是指函数的表达式中包含指数项的函数。
函数解析式为f(x)=a^x,其中a为底数,x为指数。
指数函数的图像表现为指数的增长或衰减。
五、对数函数法:对数函数是指函数的表达式中包含对数项的函数。
函数解析式为f(x) = loga(x),其中a为底数,x为真数。
对数函数的性质使得复杂的乘除运算可以转化为简单的加减运算。
六、三角函数法:三角函数是指函数的表达式中包含三角函数项的函数。
常用的三角函数有正弦函数、余弦函数和正切函数等。
函数解析式可以表示为一个周期性的曲线。
通过这些常用的方法,我们可以求解各种函数的解析式,根据函数的特点和已知条件选择适当的方法进行求解。
需要注意的是,在求解函数解析式时,需要满足函数的定义域和值域的限制,以确保函数的合法性和准确性。
人教八年级数学下册专训1.四种常见确定函数解析式的方法.docx

初中数学试卷桑水出品专训1.四种常见确定函数解析式的方法名师点金:确定一次函数解析式的常用方法:一是直接利用定义确定k和b的值;二是利用待定系数法选取关于x,y的两对对应值代入解析式建立关于k,b的方程组,从而求出k和b;三是根据实际问题中变量间的数量关系列解析式;四是根据函数图象确定解析式.根据函数定义确定解析式1.已知函数y=(k+5)xk2-24是关于x的正比例函数,则解析式为________.2.当m为何值时,函数y=(m-3)xm2-8+3m是关于x的一次函数?并求其函数解析式.3.已知y=(a-1)x2-a2+b-3.(1)当a,b取何值时,y是x的一次函数?(2)当a,b取何值时,y是x的正比例函数?用待定系数法确定解析式4.若y-2与x+2成正比,且x=0时,y=6,求y关于x的函数解析式.5.一个一次函数的图象平行于直线y=-2x,且过点A(-4,2),求这个函数的解析式.根据实际问题中变量间的数量关系列解析式6.“黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子的价格打8折.(1)根据题意,填写下表:购买种子数量/kg 1.5 2 3.5 4 …付款金额/元7.5 16 …(2)设购买种子数量为x kg,付款金额为y元,求y关于x的函数解析式;(3)若小张一次购买该种子花费了30元,求他购买种子的数量.根据函数图象确定解析式7.如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.(1)求直线AB对应的函数解析式;(2)点P在直线AB上,是否存在点P使得三角形AOP的面积为1,如果存在,求出所有满足条件的点P的坐标.(第7题)专训2.一次函数常见的四类易错题忽视函数定义中的隐含条件而致错1.已知关于x的函数y=(m+3)x|m+2|是正比例函数,求m的值.2.已知关于x的函数y=kx-2k+3-x+5是一次函数,求k的值.忽视分类或分类不全而致错3.已知一次函数y =kx +4的图象与两坐标轴围成的三角形的面积为16,求这个一次函数的解析式.4.一次函数y =kx +b ,当-3≤x ≤1时,对应的函数值的取值范围为1≤y ≤9,求k +b 的值.5.在平面直角坐标系中,点P(2,a)到x 轴的距离为4,且点P 在直线y =-x +m 上,求m 的值.忽视自变量的取值范围而致错6.(中考·齐齐哈尔)若等腰三角形的周长是80 cm ,则能反映这个等腰三角形的腰长y(cm )与底边长x(cm )的函数关系的图象是( )7.若函数y =⎩⎨⎧x 2+6(x ≤3),5x (x>3),则当y =20时,自变量x 的值是( )A .±14B .4C .±14或4D .4或-148.现有450本图书供给学生阅读,每人9本,求余下的图书数y(本)与学生人数x(人)之间的函数解析式,并求自变量x 的取值范围.忽视一次函数的性质而致错9.若正比例函数y =(2-m)x 的函数值y 随x 的增大而减小,则m 的取值范围是( ) A .m<0 B .m>0 C .m<2 D .m>210.下列各图中,表示一次函数y =mx +n 与正比例函数y =mnx(m ,n 是常数,且mn ≠0)的大致图象的是( )11.若一次函数y =kx +b 的图象不经过第三象限,则k ,b 的取值范围分别为k________0,b________0.答案专训1 1.y =10x2.解:由题意得⎩⎨⎧m 2-8=1,m -3≠0,所以m =-3.所以函数解析式为y =-6x -9.3.解:(1)由题意得⎩⎨⎧2-a 2=1,a -1≠0,所以a =-1.所以当a =-1,b 取任意数时,y 是x 的一次函数.(2)由题意得⎩⎨⎧2-a 2=1,a -1≠0,b -3=0,所以a =-1,b =3.所以当a =-1,b =3时,y 是x 的正比例函数. 4.解:设y -2=k(x +2). 因为当x =0时,y =6.所以6-2=k(0+2),解得k =2.将k =2代入y -2=k(x +2)中,得y =2x +6. 所以y 关于x 的函数解析式为y =2x +6.5.解:设这个函数的解析式为y =kx +b ,由函数图象平行于直线y =-2x 得k =-2,由于图象经过点A(-4,2). 所以2=-2×(-4)+b ,解得b =-6. 所以这个函数的解析式为y =-2x -6. 6.解:(1)10;18(2)根据题意,知当0≤x ≤2时,种子的价格为5元/kg ,所以y =5x ; 当x >2时,其中有2 kg 的种子按5元/kg 付款, 其余的(x -2)kg 种子按4元/kg (即8折)付款. 所以y =5×2+4(x -2)=4x +2.所以y 关于x 的函数解析式为y =⎩⎨⎧5x ,0≤x ≤2,4x +2,x >2.(3)因为30>10,所以他一次购买种子的数量超过2 kg . 令30=4x +2,解得x =7. 答:他购买种子的数量是7 kg .7.解:(1)根据题意得A(0,2),B(4,0),设直线AB 对应的函数解析式为y =kx +b ,把A(0,2),B(4,0)的坐标分别代入y =kx +b 得b =2,0=4×k +2,解得k =-12,∴直线AB 对应的函数解析式为y =-12x +2.(2)存在点P 使得三角形AOP 的面积为1.设点P 的横坐标为a ,根据题意得S △AOP =12OA·|a|=|a|=1,解得a =1或a =-1,则点P 的坐标为(1,1.5)或(-1,2.5).专训21.解:若关于x 的函数y =(m +3)x |m +2|是正比例函数, 需满足m +3≠0且|m +2|=1,解得m =-1.2.解:若关于x 的函数y =kx -2k +3-x +5是一次函数,则有以下三种情况: ①-2k +3=1,解得k =1,当k =1时,函数y =kx -2k +3-x +5可化简为y =5,不是一次函数. ②x -2k +3的系数为0,即k =0,则原函数化简为y =-x +5,是一次函数, 所以k =0.③-2k +3=0,解得k =32,原函数化简为y =-x +132,是一次函数, 所以k =32.综上可知,k 的值为0或32.3.解:设函数y=kx+4的图象与x轴、y轴的交点分别为A,B,坐标原点为O.当x=0时,y=4,所以点B的坐标为(0,4).所以OB=4.因为S△AOB=12OA·OB=16,所以OA=8.所以点A的坐标为(8,0)或(-8,0).把(8,0)代入y=kx+4,得0=8k+4,解得k=-1 2.把(-8,0)代入y=kx+4,得0=-8k+4,解得k=1 2.所以这个一次函数的解析式为y=-12x+4或y=12x+4.4.解:①若k>0,则y随x的增大而增大,则当x=1时y=9,即k+b=9.②若k<0,则y随x的增大而减小,则当x=1时y=1,即k+b=1.综上可知,k+b的值为9或1.5.解:因为点P到x轴的距离为4,所以|a|=4,所以a=±4,当a=4时,P(2,4);此时4=-2+m,m=6;当a=-4时,同理可得m=-2.综上可知,m的值为-2或6.6.D7.D8.解:余下的图书数y(本)与学生人数x(人)之间的函数解析式为y=450-9x,自变量x 的取值范围是0≤x≤50,且x为整数.9.D10.A11.<;≥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“把”字句:_______________________ ______ ______ ______ ______ ______ ______ ______ “被”字句:_______________________ ______ ______ ______ ______ ______ ______ ______
21、怠惰是贫穷的制造厂。 22、先知三日,富贵十年。 23、自信是向成功迈出的第一步。——爱因斯 坦 24、一个人除非自己有信心,否则不能 带给别 人信心 ;已经 信服的 人,方 能使人 信服。 ——麦 修·阿诺 德 25、凡是挣扎过来的人都是真金不怕火 炼的; 任何幻 灭都不 能动摇 他们的 信仰: 因为他 们一开 始就知 道信仰 之路和 幸福之 路全然 不同, 而他们 是不能 选选择 的,只 有往这 条路走 ,别的 都是死 路。这 样的自 信不是 一朝一 夕所能 养成的 。你绝 不能以 此期待 那些十 五岁左 右的孩 子。在 得到这 个信念 之之前 ,先得 受尽悲 痛,流 尽眼泪 。可是 这样是 好的, 应该要 这样… …——罗 曼·罗 兰 26、一个人在科学探索的道路上,走过 弯路, 犯过错 误,并 不是坏 事,更 不是什 么耻辱 ,要在 实践中 勇于承 认和改 正错误 。——爱因斯 坦88我 们的理 想应该 是高尚 的。我 们不能 登上顶 峰,但 可以爬 上半山 腰,这 总比待 在平地 上要好 得多。 如果我 们的内 心为爱 的光辉 所照亮 ,我们 面前前 又有理 想,那 么就不 会有战 胜不了 的困难 。——普列姆 昌德 27、旁观者的姓名永远爬不到比赛的计 分板上 。
1、世上没有绝望的处境,只有对处境 绝望的 人。 2、挑水如同武术,武术如同做人。循序 渐进, 逐步实 现目标 ,才能 避免许 多无谓 的挫折 。
3、别想一下造出大海,必须先由小河川 开始。 4、自信是所有成功人士必备的素质之一 ,要想 成功, 首先必 须建立 起自信 心,而 你若想 在自己 内心建 立信心 ,即应 像洒扫 街道一 般,首 先将相 当于街 道上最 阴湿黑 暗之角 落的自 卑感清 除干净 ,然后 再种植 信心, 并加以 巩固。 信心建 立之后 ,新的 机会才 会随之 而来。
5、一个人在科学探索的道路上,走过弯 路,犯 过错误 ,并不 是坏事 ,更不 是什么 耻辱, 要在实 践中勇 于承认 和改正 错误。 ——爱 因斯坦 6、瓜是长大在营养肥料里的最甜,天才 是长在 恶性土 壤中的 最好。 ——培 根 7、发光并非太阳的专利,你也可以发光 。
8、人们常用“心有余而力不足”来为自 己不愿 努力而 开脱, 其实, 世上无 难事, 只怕有 心人, 积极的 思想几 乎能够 战胜世 间的一 切障碍 。 9、如果你希望成功,当以恒心为良友, 以经验 为参谋 ,以当 心为兄 弟,以 希望为 哨兵。 ——爱 迪生
九、要点梳理(课文回放)。
作者用细腻的笔触、传神的语言介绍了 《蒙娜 丽莎》 画像, 具体介 绍了___ ______ _,___ ______ _,特 别详细 描写了 蒙娜丽 莎的___ ______ _和___ ______ _,以 及她___ ______ _、___ ______ _和___ ______ _;最 后用精 炼而饱 含激情 的语言 告诉大 家,蒙 娜丽莎 给人带 来了心 灵的震 撼,留 下了永 不磨灭 的印象 。 综合能力日日新
10、涓滴之水终可磨损大石,不是由于 它力量 大,而 是由于 昼夜不 舍的滴 坠。只 有勤奋 不懈的 努力才 能够获 得那些 技巧, 因此, 我们可 以确切 地说: 说:不 积跬步 ,无以 致千里 。——贝多芬 11、一定要做最适合自己的事情,不要 迎合别 人的口 味而去 做一件 不属于 自我的 “难事 ”。一 旦“发 现自我 ”,就 要尽力 而为, 但要全 面了解 自己和 周围的 环境, 知道适 可而止 。 12、要有自信,然后全力以赴--假如具有 这种观 念,任 何事情 十之八 九都能 成功。 ——威 尔逊 13、莫找借口失败,只找理由成功。 14、一个有坚强心志的人,财产可以被 人掠夺 ,勇气 却不会 被人剥 夺的。 ——雨 果 15、积极的人在每一次忧患中都看到一 个机会 ,而消 极的人 则在每 个机会 都看到 某种忧 患。 16、不是境况造就人,而是人造就境况 。
17、在人生的竞赛场上,没有确立明确 目标的 人,是 不容易 得到成 功的。 许多人 并不乏 信心、 能力、 智力, 只是没 有确立 目标或 没有选 准目标 ,所以 没有走 上成功 的途径 。这道 理很简 单,正 如一位 百发百 中的神 射击手 ,如果 他漫无 目标地 乱射, 也不能 在比赛 中获胜 。 18、生活就像海洋,只有意志坚强的人 ,才能 到达彼 岸。——马克 思
习题课 阶段方法技巧训练(一)
专训1 四种常见确定函数 解析式的方法
确定一次函数解析式的常用方法:一是直接利用 定义确定k和b的值;二是利用待定系数法选取关于x, y的两对对应值代入解析式建立关于k,b的方程组,从 而求出k和b;三是根据实际问题中变量间的数量关系 列解析式;四是根据函数图象确定解析式.
解:(2)根据题意,知当0≤x≤2时,种子的价格为5元/kg,
所以y=5x;
当x>2时,其中有2 kg的种子按5元/kg付款,
其余的(x-2)kg种子按4元/kg(即8折)付款.
所以y=5×2+4(x-2)=4x+2.
所以y关于x的函数解析式为y=
5x,0 x 2, 4x 2, x 2.
(3)因为30>10,所以他一次购买种子的数量超过2 kg.
十、理解感悟。
(一)
蒙娜丽莎那微抿的双唇,微挑( )的嘴角,好像有话要跟你说。在 那极富 个性的 嘴角和 眼神里 ,悄然 流露出 恬静、 淡雅的 微笑。 那微笑 ,有时 让人觉 得舒畅 温柔, 有时让 人觉得 略含哀 伤,有 时让人 觉得十 分亲切 ,有时 又让人 觉得有 几分矜 ( )持。蒙娜丽莎那“神秘的微笑”是 那样耐 人寻味 ,难以 捉摸。 达·芬奇 凭着他 的天才 想象为 和他那 神奇的 画笔, 使蒙娜 丽莎转 瞬即逝 的面部 表情, 成了永 恒的美 的象征 。
b 3 0,
所以当a=-1,b=3时,y是x的正比例函数.
方法 2 用待定系数法确定解析式
4.若y-2与x+2成正比,且x=0时,y=6,求y关于 x的函数解析式.
解:设y-2=k(x+2). 因为当x=0时,y=6. 所以6-2=k(0+2),解得k=2. 将k=2代入y-2=k(x+2)中,得y=2x+6. 所以y关于x的函数解析式为y=2x+6.
4.四周一片( ),听不到一点声响。 5.越是在紧张时刻,越要保持头脑的( )。
八、句子工厂。
1.世界上有多少人能亲睹她的风采呢? (陈述 句)
_________________________________ ______ ______ ______ ______ ______ ______ ______ 2.达·芬奇的“蒙娜丽莎”是全人类文 化宝库 中一颗 璀璨的 明珠。 (缩写 句子) ___________________________________ ______ ______ ______ ______ ______ ______ ____ 3.我在她面前只停留了短短的几分钟。 她已经 成了我 灵魂的 一部分 。(用 关联词 连成一 句话) __________________________________ ______ ______ ______ ______ ______ ______ _____
19、别因为落入了一把牛毛就把一锅奶 油泼掉 ,别因 为犯了 一点错 误就把 一生的 事业扔 掉。——蒙古 20、许多人之所以在生活中一事无成, 最根本 原因在 于他们 不知道 自己到 底要做 什么。 在生活 和工作 中,明 确自己 的目标 和方向 是非常 必要的 。只有 在知道 你的目 标是什 么、你 到底想 做什么 之后, 你才能 够达到 自己的 目的, 你的梦 想才会 变成现 实。
5.一个一次函数的图象平行于直线y=-2x,且过点 A(-4,2),求这个函数的解析式.
解:设这个函数的解析式为y=kx+b,由函数图象平 行于直线y=-2x得k=-2, 由于图象经过点A(-4,2). 所以2=-2×(-4)+b,解得b=-6. 所以这个函数的解析式为y=-2x-6.
方法 3 根据实际问题中变量间的数量关系列解析式
3.已知y=(a-1)x 2-a2+b-3. (1)当a,b取何值时,y是x的一次函数? (2)当a,b取何值时,y是x的正比例函数?
解:(1)由题意得
2
a2
பைடு நூலகம்
1,
所以a=-1.
a 1 0,
所以当a=-1,b取任意数时,y是x的一次函数.
2 a2 1, (2)由题意得 a 1 0, 所以a=-1,b=3.
6.“黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg 以上的种子,超过2 kg部分的种子的价格打8折. (1)根据题意,填写下表:
购买种子数量/kg 1.5
2
3.5
4…
付款金额/元
7.5
10
16
18
…
(2)设购买种子数量为x kg,付款金额为y元,求y关于 x的函数解析式;
(3)若小张一次购买该种子花费了30元,求他购买种子 的数量.
方法 1 根据函数定义确定解析式
1.已知函数y=(k+5)x k2-24是关于x的正比例函数, 则解析式为____y_=__1_0_x___.
2.当m为何值时,函数y=(m-3)x m2-8+3m是关于 x的一次函数?并求其函数解析式.
解:由题意得
m2
