(完整word版)PISA数学试题
pisa数学试题及答案b卷

pisa数学试题及答案b卷PISA数学试题及答案B卷一、选择题1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米答案:C3. 如果一个数的平方是36,那么这个数是多少?A. 6B. ±6C. 9D. ±9答案:B二、填空题4. 一个数的立方是-27,这个数是______。
答案:-35. 如果一个直角三角形的两条直角边分别是3和4,那么斜边的长度是______。
答案:5三、简答题6. 一个班级有40名学生,其中20名学生是男生,20名学生是女生。
如果随机选择一名学生,那么选择男生的概率是多少?答案:选择男生的概率是50%,因为男生和女生的数量相等。
7. 一个长方体的长、宽、高分别是6米、4米和3米,计算这个长方体的体积。
答案:长方体的体积是72立方米(6米× 4米× 3米)。
四、计算题8. 计算下列表达式的值:(3x - 2) / (x^2 + 5x + 6),当x = 4时。
答案:当x = 4时,表达式的值为1。
9. 一个公司在第一年的销售额是100万元,如果每年的增长率是10%,那么第三年的销售额是多少?答案:第三年的销售额是121万元(100万元× (1 + 10%)^2)。
五、解答题10. 一个农场有鸡和兔子共30只,它们的腿总共有74条。
问农场里各有多少只鸡和兔子?答案:设鸡的数量为x,兔子的数量为y。
根据题目,我们有两个方程:x + y = 30(总数量)2x + 4y = 74(总腿数)解这个方程组,我们得到x = 13(鸡的数量),y = 17(兔子的数量)。
六、证明题11. 证明勾股定理:在一个直角三角形中,斜边的平方等于两直角边的平方和。
答案:设直角三角形的两直角边分别为a和b,斜边为c。
根据勾股定理,我们有:c^2 = a^2 + b^2证明略。
八年级pisa数学试题及答案

八年级pisa数学试题及答案八年级PISA数学试题及答案1. 题目:一个班级有40名学生,其中30%的学生喜欢数学,20%的学生喜欢科学,剩下的学生既不喜欢数学也不喜欢科学。
问喜欢数学的学生人数是多少?答案:首先计算喜欢数学的学生人数。
40名学生中有30%喜欢数学,即 \(40 \times 0.30 = 12\) 名学生喜欢数学。
2. 题目:一个正方形的边长是10厘米,求它的周长。
答案:正方形的周长等于边长乘以4。
所以,周长 \(10 \times 4 = 40\) 厘米。
3. 题目:如果一个数的平方是36,那么这个数是多少?答案:一个数的平方是36,意味着这个数是36的平方根。
因此,这个数可以是6或-6,因为 \(6^2 = 36\) 且 \((-6)^2 = 36\)。
4. 题目:一个长方形的长是15厘米,宽是10厘米,求它的面积。
答案:长方形的面积等于长乘以宽。
所以,面积 \(15 \times 10 = 150\) 平方厘米。
5. 题目:一个班级有50名学生,其中25名学生参加了数学竞赛,20名学生参加了科学竞赛,有5名学生同时参加了数学和科学竞赛。
问至少参加了一个竞赛的学生人数是多少?答案:首先计算只参加数学竞赛的学生人数:\(25 - 5 = 20\) 名。
只参加科学竞赛的学生人数:\(20 - 5 = 15\) 名。
然后加上同时参加两个竞赛的学生人数:\(20 + 15 + 5 = 40\) 名学生至少参加了一个竞赛。
6. 题目:一个数的3倍是45,求这个数。
答案:要找到这个数,将45除以3。
所以,这个数是 \(45 \div 3 = 15\)。
7. 题目:一个三角形的底是8厘米,高是5厘米,求它的面积。
答案:三角形的面积等于底乘以高的一半。
所以,面积 \(8\times 5 \div 2 = 20\) 平方厘米。
8. 题目:一个数的5倍减去3等于22,求这个数。
答案:设这个数为 \(x\),则 \(5x - 3 = 22\)。
pisa数学试题及答案初中

pisa数学试题及答案初中一、选择题1. 下列哪个选项是正确的数学表达式?A. 2 + 3 = 5B. 2 × 3 = 6C. 2 ÷ 3 = 0.6D. 2 - 3 = -1答案:B2. 一个圆的直径是10厘米,那么它的半径是多少?A. 5厘米B. 10厘米C. 20厘米D. 15厘米答案:A3. 如果一个数的平方是36,那么这个数是多少?A. 6B. -6C. 6或-6D. 36答案:C二、填空题4. 一个长方形的长是8厘米,宽是5厘米,它的面积是______平方厘米。
答案:405. 一个数的3倍加上4等于20,这个数是______。
答案:4三、解答题6. 一个班级有40名学生,其中女生占60%,男生占40%。
如果班级中增加了5名女生,那么男生和女生的比例将如何变化?答案:班级原有女生人数为40 × 60% = 24人,男生人数为40 × 40% = 16人。
增加5名女生后,女生人数变为24 + 5 = 29人,男生人数仍为16人。
新的比例为男生:女生 = 16 : 29。
7. 一个数列的前三项是2, 4, 8,每一项都是前一项的2倍。
求这个数列的第10项。
答案:数列的第10项可以通过连续乘以2来得到。
第10项为2 ×2^9 = 2 × 512 = 1024。
四、证明题8. 证明:对于任意正整数n,n^2 - 1总是一个奇数。
答案:设n为任意正整数,n可以表示为2k或2k+1,其中k为整数。
若n=2k,则n^2 = (2k)^2 = 4k^2,n^2 - 1 = 4k^2 - 1 = 4(k^2 -1/4) + 3,因为k^2 - 1/4是整数,所以n^2 - 1是奇数。
若n=2k+1,则n^2 = (2k+1)^2 = 4k^2 + 4k + 1,n^2 - 1 = 4k^2 + 4k =4k(k+1),因为k和k+1中至少有一个是偶数,所以4k(k+1)是偶数,因此n^2 - 1是奇数。
Pisa数学试题
PISA数学试题PISA(国际学生能力评估项目的缩写,试题注重于应用与情景化),权重在10℅左右。
例1 玛雅住在距离学校2千米的地方,马丁住的地方离学校有5千米,他们彼此的家距离有多远?例2 学校食堂出售两种厚度一样但大小不同的面饼,小饼直径30cm,售价30分;大饼直径40cm,售价40分.你更愿意买饼,原因是 . (2005杭州)例3 一只海豹即使在睡觉的时候也要呼吸。
马丁对海豹观察了一个小时。
开始时,海豹跳入海底睡觉。
8分钟后,慢慢浮出水面开始呼吸。
3分钟后,他又回到海底,整个过程从开始到结束都非常有规律。
一小时后,海豹在( ):A.海底B.上浮的过程中C.呼吸D.下沉的过程中。
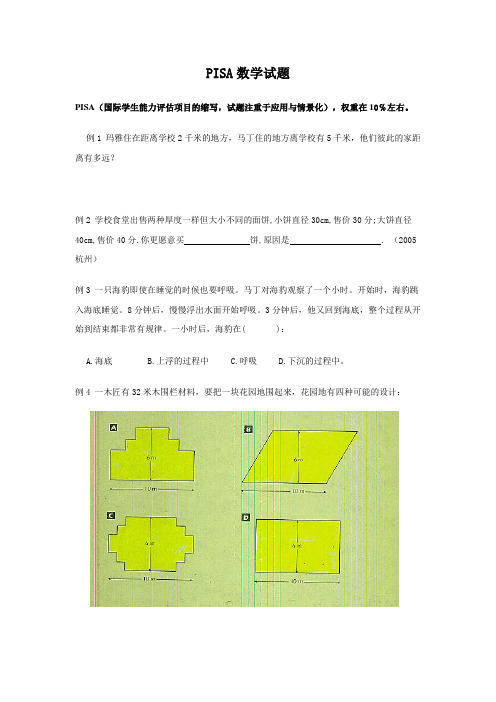
例4 一木匠有32米木围栏材料,要把一块花园地围起来,花园地有四种可能的设计:答案:依次为能、不能、能、能。
点评:显然方案D可以用32米围栏围起来,而方案A、C设计的地块周长也是32米,因此也可以围起来,只有方案B设计地块的周长超过32米,不能围起来。
这里灵活使用图形的数学知识和技能。
例5.如图一个楼梯有14级,总高度为252厘米,求每级楼梯的高度。
[答案:18厘米]例6.下图是一个男人走路时的脚印。
步长表示两个相连脚步后跟间的距离。
对于男人,公式n/p=140 表示n 和p 之间的关系,其中p 表示步长,n表示男人每分钟走的步数。
黑格每分钟走70步,求黑格的步长。
[答案:黑格的步长为0.5米。
]例7 .爱列克是一个滑板迷。
他到滑板商店查询滑板的价格。
在商店中你可以买一个滑板成品,或者买一块底版、一组轮子(包括4个轮子)、一组轴(2件)和一套金属配件,自己来装配一个滑板。
价格如下表所列:爱列克购买部件自己组装,其最低价格和最高价格各几何?答案:最低价为80Zed,最高价为137Zed。
PISA数学题

这部分涵盖的数学知识包括空间现象、几何现象和两者的关系。
考查的内容包括分析图形组成部分,找出异同点,找出以不同形式、不用角度呈现的图形,并了解对象的性质和他们相对的位置关系。
例题1 木匠一个木匠想用一条32米长的木条来围着花园。
以下哪个花圃的涉及可以用32米长的木条造出来?答案:ACD 题目类型:多项选择题内容:空间和形状过程:联系能力群情境:教育情境难度:687分这道多选题属于教育情境,因为它是一个准真实问题,经常能在数学课堂上碰到。
它是一道非常规问题,属于联系能力群,学生必须具备能力认识A、C、D的周长相等才能解决问题,因此,需要学生解读形象信息并看到存在的形似和差异。
在四个图形中,32米要围成平行四边形显然长度不够,矩形的答案非常明显。
关键考察学生运用洞察力、论证技巧和几何知识解答出A、C两个图形的周长与矩形的周长是相等的。
本题属于6级水平。
这部分涵盖的数学内容,包括变化的数学表现形式和变量间的函数关系及从属关系。
考查学生对于不同的表征方式相互转换的能力,因为表征转换常常是处理情境和任务的关键。
例题2 成长下图是1998年,荷兰男女青年的平均身高:问:1)自1980年以来,20岁女性的平均身高增加了2.3cm,达到了170.6cm。
1980年20岁女性的平均身高是多少?答案:168.3cm 题目类型:简答题内容:变化和关系过程:再现能力群情境:科学情境难度:477分科学经常使用图标表征,这道题把身高变化和年龄联系起来,把问题情境转化成数学背景,考查的是基本算法之一:减法。
属于再现能力群:所要求的思维和推理能力涉及问题最基本的形式。
对于论证能力的考查也是如此:学生只需照着标准的数量计算过程就行。
这道题的冗余信息是“图”本身,学生不需看图即可做出答案。
总之,这道题目时要求学生从单个来源提取相关信息,使用单一的表征形式,并进行减法运算,属于2级能力水平。
问:2)解释图中如何显示女孩12岁后平均身高增长趋缓。
数学PISA试题

1、妈妈给小明一个大盒子,里面装着6个纸盒子,每个纸盒又装着4个小盒子,小明一共有多少个盒子?2、玛雅和罗斯的家在一条直线上。
玛雅住在距离学校2千米的地方,罗斯住的地方离学校有5千米,他们彼此的家距离有多远?3、史前期的算题考古学家在西班牙发现了一处史前期壁画,上面除了绘着一些人形和野兽的图形外,还绘着一些莫明其妙的算题,这些算题也是阿拉伯数字,但考古学家们看了半天,怎么也弄不明白这些算题。
后来他们恍然大悟,原来这些算题中的数字与我们现在的数字并不是一回事,但是绝对符合四则运算的法则。
同学们,请你们仔细看看这些算式,想一想算式中的数字各等于现在的什么数字,然后把它翻译出来。
5+6+7=5×6×75+5=66÷5=67×5=7根据: 6÷5=6 , 7×5=7可知: 5代表现在的1根据: 5+5=6可知: 6代表现在的2根据: 5+6+7=5×6×7可知: 7代表现在的34、巧手摆花坛学校门口修了一个正方形花坛,花坛竣工时,大队部在花坛旁挂出一块小黑板,上面写着:“各中队少先队员:花坛修好了,同学们都希望管理这个花坛。
哪个中队的少先队员能做出下面两道题,就请那个中队的少先队员负责管理这个花坛。
①要在这个花坛的四周摆上16盆麦冬,要求每边都是7盆,应该怎样摆?②还要在这个花坛四周摆上24盆串红,要求每边也是7盆,应该怎样摆?“同学们,你会摆吗?请你画图试试看。
5、韩信点兵韩信是我国汉代著名的大将,曾经统率过千军万马,他对手下士兵的数目了如指掌。
他统计士兵数目有个独特的方法,后人称为“韩信点兵”。
他的方法是这样的,部队集合齐后,他让士兵1、2、3--1、2、3、4、5--1、2、3、4、5、6、7地报三次数,然后把每次的余数再报告给他,他便知道部队的实际人数和缺席人数。
他的这种计算方法历史上还称为“鬼谷算”,“隔墙算”,“剪管术”,外国人则叫“中国剩余定理”。
初中数学pisa测试题及答案

初中数学pisa测试题及答案一、选择题1. 下列哪个选项是正确的?A. 2的平方根是2B. 圆的周长等于直径乘以πC. 直角三角形的内角和是180度D. 所有偶数都是质数答案:B2. 如果一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 无法确定答案:A3. 下列哪个等式是正确的?A. 3x + 2 = 5x - 4B. 2x - 3 = 2x + 3C. 4x = 8D. 5x + 3 = 5x - 3答案:C二、填空题4. 一个数的绝对值是5,这个数可能是______或______。
答案:5或-55. 如果一个三角形的两边长分别为3cm和4cm,且这两边的夹角为90度,那么这个三角形的周长是_______cm。
答案:8三、解答题6. 一个长方形的长是宽的两倍,如果宽增加2cm,长减少2cm,长方形的面积减少了32平方厘米。
求原长方形的长和宽。
答案:设原长方形的宽为x cm,则长为2x cm。
根据题意,有方程:x(2x) - (x+2)(2x-2) = 32。
解得x=8,所以原长方形的长为16cm,宽为8cm。
7. 一个工厂生产了100个零件,其中有10个是次品。
如果随机抽取一个零件,抽到次品的概率是多少?答案:抽到次品的概率为10/100,即1/10。
四、应用题8. 一个农场有鸡和兔子共50只,腿的总数是140条。
问农场里有多少只鸡和多少只兔子?答案:设鸡有x只,兔子有y只。
根据题意,有方程组:x + y = 50 和 2x + 4y = 140。
解得x=35,y=15。
所以农场里有35只鸡和15只兔子。
(完整版)PISA数学试题(最新整理)

PISA试题(B)卷共25题考试时间100分钟学校-----------班级----------性别--------出生--------年------月1. 地衣全球性暖化会造成一部分冰川融化的结果。
约在冰川消失的十二年后,微小的植物—地衣,会开始在岩石间生长。
地衣生长的形式有如圆圈一般,圆圈的直径与地衣的年龄之间关系约可用下列公式来表示:,其中,d 表示圆圈直径(每毫米),t 表示冰川消失后的年数。
问题1:利用公式,算出冰川消失后16年的地衣直径。
写出你的计算方法。
问题2:安安测量出某地区地衣的直径为35毫米。
请问在这地区的冰川是多少年前消失?写出你的计算方法。
2. 苹果农夫将苹果树种在正方形的果园。
为了保护苹果树不怕风吹,他在苹果树的周围种针叶树。
在下图里,你可以看到农夫所种植苹果树的列数(n),和苹果树数量及针叶树数量的规律:问题1:完成下表的空格n 苹果树数针叶树数1 1 82 4345问题2:你可以用以下的2个公式来计算上面提到的苹果树数量及针叶树数量的规律:苹果树的数量= n2 针叶树的数量= 8n n代表苹果树的列数当n为某一个数值时,苹果树数量会等于针叶树数量。
找出n值,并写出你的计算方法。
问题3:若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,那一种树会增加得比较快?是苹果树的数量或是针叶树的数量?解释你的想法。
3. 骰子问题1:在这张相片中你可以看见六个骰子,分别被标记(a)到(f)。
所有骰子都有个规则:每两个相对的面之点数和都是七。
写下照片中盒子里的每个骰子底部的点数为何。
4. 成长青少年长得更高了下图显示1998年荷兰的年轻男性和女性的平均身高:问题1:自1980年以来20岁女性的平均身高增加了 2.3 公分,变成170.6 公分。
则1980年20岁女性的平均身高是多少?答:......................公分问题2:根据这张图,平均而言,哪一段时期的女孩身高会比同年龄的男孩高?问题3:依据上图说明为何女孩12岁以后身高的增加率会减小。
pisa八年级数学试题及答案

pisa八年级数学试题及答案PISA八年级数学试题及答案1. 题目:如果一个矩形的长是宽的三倍,且周长为40厘米,求矩形的面积。
答案:设矩形的宽为x厘米,则长为3x厘米。
根据周长公式,2(x + 3x) = 40,解得x = 5厘米。
因此,矩形的长为15厘米,宽为5厘米。
矩形的面积为长乘以宽,即15厘米× 5厘米 = 75平方厘米。
2. 题目:计算以下表达式的值:(3x^2 - 2x + 1) - (x^2 + 4x - 3)。
答案:首先去括号,得到3x^2 - 2x + 1 - x^2 - 4x + 3。
然后合并同类项,得到2x^2 - 6x + 4。
3. 题目:一个圆的半径是5厘米,求这个圆的周长。
答案:圆的周长公式为C = 2πr,其中r为半径。
将半径r = 5厘米代入公式,得到周长C = 2 × π × 5厘米≈ 31.4厘米。
4. 题目:一个数的25%加上这个数的50%等于30。
求这个数。
答案:设这个数为x,则0.25x + 0.5x = 30。
合并同类项,得到0.75x = 30。
解得x = 30 ÷ 0.75 = 40。
5. 题目:一个班级有40名学生,其中20%的学生喜欢数学,30%的学生喜欢英语,剩下的学生既不喜欢数学也不喜欢英语。
求既不喜欢数学也不喜欢英语的学生人数。
答案:首先计算喜欢数学的学生人数,40 × 20% = 8人。
接着计算喜欢英语的学生人数,40 × 30% = 12人。
既喜欢数学又喜欢英语的学生人数为8 + 12 - 40 = 0人(因为题目中提到剩下的学生既不喜欢数学也不喜欢英语,所以不存在既喜欢数学又喜欢英语的学生)。
因此,既不喜欢数学也不喜欢英语的学生人数为40 - 8 - 12 = 20人。
结束语:通过以上试题及答案的分析,我们可以看出PISA八年级数学试题涵盖了几何、代数和概率等多个数学领域,旨在评估学生的数学知识和解决问题的能力。
PISA数学精彩试题

PISA数学精彩试题PISA试题(B)卷共25题考试时间100分钟学校-----------班级----------性别--------出生--------年------月1. 地衣全球性暖化会造成一部分冰川融化的结果。
约在冰川消失的十二年后,微小的植物—地衣,会开始在岩石间生长。
地衣生长的形式有如圆圈一般,圆圈的直径与地衣的年龄之间关系约可用下列公式来表示:,其中,d 表示圆圈直径(每毫米),t 表示冰川消失后的年数。
问题1:利用公式,算出冰川消失后16年的地衣直径。
写出你的计算方法。
问题2:安安测量出某地区地衣的直径为35毫米。
请问在这地区的冰川是多少年前消失?写出你的计算方法。
2. 苹果农夫将苹果树种在正方形的果园。
为了保护苹果树不怕风吹,他在苹果树的周围种针叶树。
在下图里,你可以看到农夫所种植苹果树的列数(n),和苹果树数量及针叶树数量的规律:问题1:完成下表的空格n 苹果树数针叶树数1 1 82 4345问题2:你可以用以下的2个公式来计算上面提到的苹果树数量及针叶树数量的规律:苹果树的数量 = n2 针叶树的数量 = 8n n代表苹果树的列数当n为某一个数值时,苹果树数量会等于针叶树数量。
找出n值,并写出你的计算方法。
问题3:若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,那一种树会增加得比较快?是苹果树的数量或是针叶树的数量?解释你的想法。
3. 骰子问题1:在这张相片中你可以看见六个骰子,分别被标记(a)到(f)。
所有骰子都有个规则:每两个相对的面之点数和都是七。
写下照片中盒子里的每个骰子底部的点数为何。
4. 成长青少年长得更高了下图显示1998年荷兰的年轻男性和女性的平均身高:问题1:自1980年以来20岁女性的平均身高增加了2.3 公分,变成170.6 公分。
则1980年20岁女性的平均身高是多少?答: ......................公分问题2:根据这张图,平均而言,哪一段时期的女孩身高会比同年龄的男孩高?问题3:依据上图说明为何女孩12岁以后身高的增加率会减小。
PISA数学试题选

学校 ------- 班级 ------- 性别 ----- 出生 ----- 年……月1.地衣全球性暖化会造成-部分冰川融化的结果。
约在冰川消失的十二年后,微小的植物 一地衣,会开始在岩石间生长。
地衣生长的形式有如圆圈-•般,圆圈的直径与地衣 的年龄Z 间关系约可用下列公式来表示:,其中,d 表示圆圈直径(每亳米),r 表 示冰川消失后的年数。
问题1:利用公式,算出冰川消失后16年的地衣直径。
写出你的计算方法。
问题2:安安测量出某地区地衣的直径为35亳米。
请问在这地区的冰川是多少年 前消失?写出你的计算方法。
2.苹果农夫将苹果树种在正方形的果园。
为了保护苹果树不怕风吹,他在苹果树的周圉种 针叶树。
在下图里,你可以看到农夫所种植苹果树的列数(n),和苹果树数量及针问题1:完成下表的空格n苹果树数针叶树数 1 1 8 2 43 4 5问题2:你可以用以下的2个公式来计算上面提到的苹果树数量及针叶树数量的规 律:苹果树的数量二朋针叶树的数量=8nn 代表苹果树的列数当门为某一个数 值时,苹果树数量会等于针叶树数量。
找出门值,并写出你的计算方法。
PISA 试题(B)卷共25 考试时间100分钟n 二 1 n = 2 n =3 X X X X X X X XXXX X • X X • • X x • X X XX X XX • • X X •X X X X XX X •XXXX X X X X X X X X X X X X • • Xx • ■■• XX XX ■• Xx •■■• XXXX • • X X •■• XX X X XXXX •■■• XX X X X X X XX X叶树数量的规律:X = conife 「tree • = apple treen =4问题3:若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,那-•种树会增加得比较快?是苹果树的数量或是针叶树的数量?解释你的想法。
小学数学pisa试题及答案

小学数学pisa试题及答案一、整数1. 下面哪个数是负数?()A. 8B. -5C. 3D. 0答案:B2. 请写出一个正数和一个负数的例子。
答案:正数:7负数:-33. 下面哪个数是零?()A. -2B. 5C. 0D. 1答案:C二、小数1. 把1.5和6/4比较大小。
答案:1.5 = 1.56/4 = 1.5两者相等。
2. 请把0.8写成最简形式的分数。
答案:0.8 = 4/53. 将下列数按从小到大的顺序排列:0.6,1/2,0.75,2/3。
答案:1/2,0.6,2/3,0.75三、几何1. 下图中哪个是正方形?┌───┐ ┌───┐│ │ │ ││ │ │ │└───┘ └───┘答案:右边的图形是正方形。
2. 如果一个直角三角形的两条直角边分别是3 cm和4 cm,求斜边的长度。
答案:斜边的长度为5 cm。
3. 下图中哪个是圆?┌─────┐ ┌─────┐┌┘ │ ┌│ ┘┐└┐ │ │ ┌┘└─────┘ └─────┘答案:左边的图形是圆。
四、代数1. 如果a = 5,b = 2,求a - b的值。
答案:a - b = 5 - 2 = 32. 如果x = 3,y = 2,求2xy的值。
答案:2xy = 2 * 3 * 2 = 123. 如果m = 4,n = 3,求m² - n²的值。
答案:m² - n² = 4² - 3² = 16 - 9 = 7五、数据分析1. 下面是小明的数学成绩:85,78,92,80,88。
请计算他的平均成绩。
答案:平均成绩 = (85 + 78 + 92 + 80 + 88) ÷ 5 = 424 ÷ 5 = 84.82. 小华每天跑步的距离(单位:公里)是:3,4,2,3,5。
请计算他每天跑步的平均距离。
答案:平均距离 = (3 + 4 + 2 + 3 + 5) ÷ 5 = 17 ÷ 5 = 3.43. 请用折线图表示小明一周的每天体温变化情况。
初一数学披萨试题及答案

初一数学披萨试题及答案一、选择题(每题3分,共30分)1. 一个披萨饼的半径为10厘米,那么它的面积是多少平方厘米?A. 100πB. 314C. 200πD. 628答案:C2. 如果一个披萨饼被切成8等份,每份的面积占整个披萨饼面积的几分之几?A. 1/8B. 1/4C. 1/2D. 1/16答案:A3. 一个披萨饼的直径是20厘米,那么它的周长是多少厘米?A. 20πB. 40πC. 31.4D. 62.8答案:D4. 如果一个披萨饼的半径增加了10%,那么它的面积增加了多少百分比?A. 10%B. 21%C. 33.1%D. 44.1%答案:C5. 一个披萨饼的直径是30厘米,那么它的面积是多少平方厘米?A. 706.5B. 706.86C. 706.9D. 707答案:B6. 如果一个披萨饼被切成12等份,每份的面积占整个披萨饼面积的几分之几?A. 1/12B. 1/6C. 1/4D. 1/3答案:A7. 一个披萨饼的周长是62.8厘米,那么它的直径是多少厘米?B. 20C. 30D. 40答案:B8. 如果一个披萨饼的直径减少了20%,那么它的面积减少了百分之几?A. 20%B. 36%C. 44%D. 64%答案:B9. 一个披萨饼的半径是15厘米,那么它的周长是多少厘米?A. 94.2B. 47.1D. 90答案:A10. 如果一个披萨饼被切成16等份,每份的面积占整个披萨饼面积的几分之几?A. 1/16B. 1/8C. 1/4D. 1/2答案:A二、填空题(每题4分,共40分)11. 一个披萨饼的直径是25厘米,那么它的面积是______平方厘米。
答案:1962.5π12. 如果一个披萨饼被切成6等份,每份的面积占整个披萨饼面积的______。
答案:1/613. 一个披萨饼的周长是31.4厘米,那么它的半径是______厘米。
答案:514. 如果一个披萨饼的半径增加了20%,那么它的面积增加了______百分比。
PISA数学试题

8 数树叶针
5 4 3 4 2 1 1 n 数树果苹 格空的表下成完�1 题问
�律规的量数树叶 针及量数树果苹和�)n( 数列的树果苹植种所夫农到看以可你�里图下在 。树叶针 种围周的树果苹在他�吹风怕不树果苹护保了为。园果的形方正在种树果苹将夫农 果苹 .2
。法方算计的你出写 �失消前 年少多是川冰的区地这在问请 。米毫 53 为径直的衣地区地某出量测安安 �2 题问 。法方算计的你出写。径直衣地的年 61 后失消川冰出算�式公用利 �1 题问 。数年的后失消川冰示 表 t �)米毫每(径直圈圆示表 d �中其 � �示表来式公列下用可约系关间之龄年的 衣地与径直的圈圆�般一圈圆如有式形的长生衣地 。长生间石岩在始开会�衣地— 物植的小微�后年二十的失消川冰在约。果结的化融川冰分部一成造会化暖性球全 衣地 .1 月------年--------生出--------别性----------级班-----------校学 钟分 001 间时试考题 52 共 卷)B(题试 ASIP
。错交互相暗和亮的号灯 。律规的光亮塔灯个某到看以可你图下 。律规的己自它有塔灯座每。亮光出发式方的律规定固以塔灯 。道航的们他到找船助帮以可间夜在塔灯 �候时的岸靠要只船当。塔的灯有端顶座一是塔灯 塔灯�91
)sdez万百�位单( 图配分品物销外 dnaldeZ 年 0002 额总销外度年 dnaldeZ 年 0002-年 6991 。sdez为称名币货的家国个这�息信的品物销外家国个这dnaldeZ明说图下
口出销外 .11
8
否 / 是 。的矮最是仍克俊 否 / 是 。变改有没度高均平的生学以所 否 / 是 。高身的同相有生学个两 否 / 是 。生女是个一另�生男是生学个一 否 / 是 。生女是都生学位两 论推个这得获可否是 论推 否或是 出圈�论推个一每对针 �论推种何列下得获以可息讯些这从 。变改 有没都高身均平的生女和生男�是的讶惊人令。均平的高身算计新重并�高身了量 测也们他。了课上来都们他天隔但�席缺生学位两有课上天那 。分公031是高身的 他�的矮最是克俊。分公081是高身的她�的高最是蕾晓。分公051为高身均平生女 �分公061为高身均平生男。高身了量测都生学有所�上课学数的天一某 �1 题问 高身生学 .51 �架书个几做以可匠木问请 �丝螺个 015 和夹长个 02 �夹短个 002 �板木 短个 33 �板木长个 62 有匠木在现 。丝螺个 41 和夹长个 2 �夹短个 21 �板木短个 6 �板木长个 4 �料材下以要需架书个一作制匠木 � 1 题问 架书 .41 以可定一 E 能可有常非 D 能可的%05 约大 C 能可太不 B 能可不 A �何为性能可 的品奖到得书小问请 。次一戏游个这了玩书小。品奖到得能就珠弹的色黑到抽当
pisa数学试题及答案

pisa数学试题及答案PISA数学试题及答案一、选择题1. 下列哪个选项表示了数学中的“奇数”?A. 能被2整除的数B. 不能被2整除的数C. 能被3整除的数D. 能被4整除的数答案:B2. 如果一个圆的半径是5厘米,那么它的直径是多少厘米?A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案:A3. 一个班级有40名学生,其中30名学生参加了数学竞赛。
参加数学竞赛的学生占班级总人数的百分比是多少?A. 75%B. 80%C. 85%D. 90%答案:A二、填空题4. 一个数的平方根是4,那么这个数是________。
答案:165. 如果一个直角三角形的两条直角边分别为3和4,那么它的斜边长度是________。
答案:56. 一个数的立方是27,这个数是________。
答案:3三、简答题7. 解释什么是“勾股定理”并给出一个例子。
答案:勾股定理是指在一个直角三角形中,斜边的平方等于两条直角边的平方和。
例如,如果一个直角三角形的两条直角边分别是3和4,那么斜边的长度是√(3² + 4²) = √(9 + 16) = √25 = 5。
8. 描述如何计算一个数的百分比增长。
答案:要计算一个数的百分比增长,首先确定增长量,即新值减去旧值。
然后,将增长量除以旧值,最后将结果乘以100得到百分比。
公式为:百分比增长 = ((新值 - 旧值) / 旧值) * 100%。
四、解答题9. 一个农场主有一块长方形的土地,长是100米,宽是50米。
如果农场主决定将土地的长增加20米,那么新的土地面积是多少?答案:首先,计算原始土地面积:100米 * 50米 = 5000平方米。
然后,增加长度:100米 + 20米 = 120米。
新的土地面积是:120米* 50米 = 6000平方米。
10. 一个班级有50名学生,其中25名男生和25名女生。
如果班级平均分是85分,那么班级总分是多少?答案:班级总分 = 学生人数 * 平均分 = 50 * 85 = 4250分。
PISA数学试题(DOC)

PISA试题(B)卷共25题考试时间100分钟学校-----------班级----------性别--------出生--------年------月1. 地衣全球性暖化会造成一部分冰川融化的结果。
约在冰川消失的十二年后,微小的植物—地衣,会开始在岩石间生长。
地衣生长的形式有如圆圈一般,圆圈的直径与地衣的年龄之间关系约可用下列公式来表示:,其中,d 表示圆圈直径(每毫米),t 表示冰川消失后的年数。
问题1:利用公式,算出冰川消失后16年的地衣直径。
写出你的计算方法。
问题2:安安测量出某地区地衣的直径为35毫米。
请问在这地区的冰川是多少年前消失?写出你的计算方法。
2. 苹果农夫将苹果树种在正方形的果园。
为了保护苹果树不怕风吹,他在苹果树的周围种针叶树。
在下图里,你可以看到农夫所种植苹果树的列数(n),和苹果树数量及针叶树数量的规律:问题1:完成下表的空格n 苹果树数针叶树数1 1 82 4345问题2:你可以用以下的2个公式来计算上面提到的苹果树数量及针叶树数量的规律:苹果树的数量= n2 针叶树的数量= 8n n代表苹果树的列数当n为某一个数值时,苹果树数量会等于针叶树数量。
找出n值,并写出你的计算方法。
问题3:若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,那一种树会增加得比较快?是苹果树的数量或是针叶树的数量?解释你的想法。
3. 骰子问题1:在这张相片中你可以看见六个骰子,分别被标记(a)到(f)。
所有骰子都有个规则:每两个相对的面之点数和都是七。
写下照片中盒子里的每个骰子底部的点数为何。
4. 成长青少年长得更高了下图显示1998年荷兰的年轻男性和女性的平均身高:问题1:自1980年以来20岁女性的平均身高增加了2.3 公分,变成170.6 公分。
则1980年20岁女性的平均身高是多少?答:......................公分问题2:根据这张图,平均而言,哪一段时期的女孩身高会比同年龄的男孩高?问题3:依据上图说明为何女孩12岁以后身高的增加率会减小。
PISA测试数学试题

PISA测试数学试题题目一:USB随身碟USB随身碟是一种体积小、携带方便的计算机储存装置。
冠达有一个容量为1GB(1000MB)的USB随身碟,存有音乐和照片。
他的USB随身碟目前的储存状态为:音乐(650MB),照片(198MB),可用空间(152MB)。
问题1:冠达想要把350MB的照片集转存到他的USB随身碟中,但USB随身碟没有足够的可用空间。
他不想删除USB随身碟里的任何照片,但他可以删除USB随身碟中某两张音乐专辑。
冠达的USB随身碟中存有下列不同大小的8张音乐专辑。
专辑1:100MB专辑2:75MB专辑3:80MB专辑4:55MB专辑5:60MB专辑6:80MB专辑7:75MB专辑8:125MB如果最多只删除两个音乐专辑,冠达的USB随身碟是否就有足够的空间可以储存新的照片集?请圈选「是」或「否」,并列出计算过程来支持你的答案。
题旨:题目描述:比较并计算数值以满足给定的条件内容领域:数量情境脉络:个人的数学历程:诠释满分答案:是,明确地表示或暗示,并列举任何一个例子,当中的2张专辑所使用的空间为198MB或更多。
他需要删除198MB(350-152),因此他需要删掉任意两张加起来空间大于198MB的音乐专辑,例如专辑1和8。
是。
他可以删除专辑7和8,这样得到的可用空间有152+75+125=352MB。
题目二:冰淇淋店下图为雯雯冰淇淋店的平面图,她正在装修店铺。
服务区的周围是柜台。
问题1:雯雯想沿着柜台的外缘加装新的边饰,她一共需要多长的边饰?写出你的计算过程。
题旨:题目描述:利用勾股定理或使用正确的测量方法,找出直角三角形的斜边并进行比例尺的转换内容领域:空间与形状情境脉络:职业的数学历程:应用满分答案:介于4.5到4.55之间的答案(以公尺或米为单位,有、无写单位皆可。
)部分分数:答案中有部分的计算步骤是正确的(如使用勾股定理或使用比例尺),但有错误,如比例尺不正确或计算错误。
pisa小学数学测试题目及答案

pisa小学数学测试题目及答案一、选择题(每题2分,共10分)1. 下列哪个数字是偶数?A. 3B. 5C. 8D. 7答案:C2. 一个长方形的长是10厘米,宽是4厘米,它的周长是多少厘米?A. 28B. 14C. 20D. 40答案:A3. 一个数加上8等于20,这个数是多少?A. 12B. 16C. 8D. 18答案:A4. 一个班级有30名学生,其中2/3是男生,那么女生有多少人?A. 10B. 15C. 20D. 55. 下列哪个分数是最接近1/2的?A. 1/3B. 2/5C. 3/7D. 4/9答案:B二、填空题(每题3分,共15分)6. 一个数乘以5等于25,这个数是______。
答案:57. 一个数的3倍是27,这个数是______。
答案:98. 一个数加上它的一半等于10,这个数是______。
答案:6.67(保留两位小数)9. 一个数的1/4加上这个数的1/2等于2,这个数是______。
答案:410. 一个数减去它的1/3等于4,这个数是______。
答案:6三、解答题(每题5分,共20分)11. 一个班级有40名学生,其中男生和女生的数量相等。
如果班级中增加了5名男生,那么男生和女生的比例是多少?答案:班级原有男生20名,女生20名。
增加5名男生后,男生变为25名,女生仍为20名。
因此,男生和女生的比例为25:20,简化后为12. 一个长方形的长是宽的两倍,如果宽增加3厘米,长不变,新的长方形的面积比原来的面积大多少平方厘米?答案:设原来的宽为x厘米,则长为2x厘米。
原来的面积为x*2x=2x^2平方厘米。
宽增加3厘米后,新的宽为x+3厘米,新的面积为(x+3)*(2x)=2x^2+6x平方厘米。
新的面积比原来的面积大的平方厘米数为(2x^2+6x)-2x^2=6x。
由于题目没有给出具体的宽值,所以无法计算具体的数值。
13. 一个数的1/3加上这个数的1/4等于9,求这个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PISA试题(B)卷共25题考试时间100分钟学校-----------班级----------性别--------出生--------年------月1. 地衣全球性暖化会造成一部分冰川融化的结果。
约在冰川消失的十二年后,微小的植物—地衣,会开始在岩石间生长。
地衣生长的形式有如圆圈一般,圆圈的直径与地衣的年龄之间关系约可用下列公式来表示:,其中,d 表示圆圈直径(每毫米),t 表示冰川消失后的年数。
问题1:利用公式,算出冰川消失后16年的地衣直径。
写出你的计算方法。
问题2:安安测量出某地区地衣的直径为35毫米。
请问在这地区的冰川是多少年前消失?写出你的计算方法。
2. 苹果农夫将苹果树种在正方形的果园。
为了保护苹果树不怕风吹,他在苹果树的周围种针叶树。
在下图里,你可以看到农夫所种植苹果树的列数(n),和苹果树数量及针叶树数量的规律:问题1:完成下表的空格n 苹果树数针叶树数1 1 82 4345问题2:你可以用以下的2个公式来计算上面提到的苹果树数量及针叶树数量的规律:苹果树的数量= n2 针叶树的数量= 8n n代表苹果树的列数当n为某一个数值时,苹果树数量会等于针叶树数量。
找出n值,并写出你的计算方法。
问题3:若农夫想要种更多列,做一个更大的果园,当农夫将果园扩大时,那一种树会增加得比较快?是苹果树的数量或是针叶树的数量?解释你的想法。
3. 骰子问题1:在这张相片中你可以看见六个骰子,分别被标记(a)到(f)。
所有骰子都有个规则:每两个相对的面之点数和都是七。
写下照片中盒子里的每个骰子底部的点数为何。
4. 成长青少年长得更高了下图显示1998年荷兰的年轻男性和女性的平均身高:问题1:自1980年以来20岁女性的平均身高增加了2.3 公分,变成170.6 公分。
则1980年20岁女性的平均身高是多少?答:......................公分问题2:根据这张图,平均而言,哪一段时期的女孩身高会比同年龄的男孩高?问题3:依据上图说明为何女孩12岁以后身高的增加率会减小。
5. 形狀問題1:上面哪個圖形的面積最大?請寫出你的理由。
問題2:寫出一個估算圖C面積的方法。
問題3:寫出一個估算圖C周長的方法。
6. 三角形问题1:圈选出符合下面叙述的三角形:三角形PQR是一个直角三角形,且R为直角。
RQ线段比线段PR短。
M为线段PQ的中点,且N为线段QR的中点。
S是三角形内部的一个点。
线段MN比线段MS长。
7. 木匠问题1:木匠有32公尺的木材,想要在花圃周围做边界。
他考虑将花圃设计成以下的造型。
上面花圃的设计是否可以用长度32公尺的木板来围成,在下表中的每一种设计圈出是或否。
花圃的设计是否能用长度32公尺的木板围成A设计是/ 否B设计是/ 否C设计是/ 否D设计是/ 否8. 阳台问题1:尼尼想要在新房子的长方形阳台铺磁砖。
这个阳台的长为5.25公尺,宽为3.00公尺。
每1平方公尺牠需要81块磁砖。
请计算尼尼铺完整个阳台需要多少磁砖。
9. 积木苏珊想要利用下图的小立方体来做出积木模型:苏珊有许多像上面这样的小立方体,小立方体图A她利用胶水将许多的小立方体黏起来成为积木模型。
首先,苏珊拿了8个小立方体做出图A的积木模型。
图B 图C问题1:苏珊需要拿多少个小立方体才能做出图B的积木模型?答:........................个。
问题2:苏珊需要拿多少个小立方体才能做成图C的积木模型?答:.........................个。
问题3:苏珊想到可以用比实际还要少的小立方体来作出图C的积木模型。
她想用胶水黏出一个看起来像图C,但是内部是中空的积木模型。
问苏珊需要多少个小立方体来做出这个看起来像图C,但是内部却是中空的积木模型。
答:............................个。
问题4:现在,苏珊想要做出一个6个小立方体长、5个小立方体宽、4个小立方体高的积木模型。
假如她想要用最少的小立方体,并在内部留出可能最大的空心空间。
苏珊需要最少几个小立方体?答:.........................个。
11. 外销出口下图说明Zedland这个国家外销物品的信息,这个国家的货币名称为zeds。
1996年-2000年Zedland年度外销总额2000年Zedland外销物品分配图(单位:百万zeds)问题1:1998年Zedland的外销总额有多少?(单位:百万zeds)答:...............问题2:2000年Zedland的果汁外销总额(单位:百万zeds)?A 1.8 百万zeds。
B 2.3 百万zeds。
C 2.4 百万zeds。
D 3.4 百万zeds。
E 3.8 百万zeds。
12. 彩色糖果问题1:系德的妈妈让他在无法看到袋子里糖果的情形下从袋子里抽出一颗糖果。
下图是袋子里各种颜色糖果的数量。
问题1:系德的妈妈让他在无法看到袋子里糖果的情形下从袋子里抽出一颗糖果。
下图是袋子里各种颜色糖果的数量。
02468红色橘色黄色绿色蓝色粉色紫色褐色系德抽到红色糖果的机率为何?A 10%B 20%C 25%D 50%13. 春天园游会问题1:春天园游会有一个摊位的游戏,是先旋转一个转盘的指针。
如果指针箭头停在奇数的位置,玩的人就可以从袋子抽出一个弹珠。
转盘和袋子里的弹珠如下图所示。
当抽到黑色的弹珠就能得到奖品。
小书玩了这个游戏一次。
请问小书得到奖品的可能性为何?A 不可能B 不太可能C 大约50%的可能D 非常有可能E 一定可以14. 书架问题1:木匠制作一个书架需要以下材料:4个长木板,6个短木板,12个短夹,2个长夹和14个螺丝。
现在木匠有26个长木板,33个短木板,200个短夹,20个长夹和510个螺丝,请问木匠可以做几个书架?15. 学生身高问题1:某一天的数学课上,所有学生都测量了身高。
男生平均身高为160公分,女生平均身高为150公分。
晓蕾是最高的-她的身高是180公分。
俊克是最矮的-他的身高是130公分。
那天上课有两位学生缺席,但隔天他们都来上课了。
他们也测量了身高,并重新计算身高的平均。
令人惊讶的是,男生和女生的平均身高都没有改变。
从这些讯息可以获得下列何种推论?针对每一个推论,圈出是或否推论是否可获得这个推论两位学生都是女生。
是/ 否一个学生是男生,另一个是是/ 否女生。
两个学生有相同的身高。
是/ 否是/ 否所以学生的平均高度没有改变。
俊克仍是最矮的。
是/ 否16. 地震问题:有一个节目报导关于地震和其发生频率,同时也讨论地震的可预测性。
一个地质学家提到:「未来的20年内,在Zed这个城市发生地震的机会是三分之二」以下哪一个叙述最能够反映出这个地质学家的意思?A 因为,所以在Zed这个城市从现在经过13~14年将会发生一次地震。
B 因为大于,所以我们可以确定在未来20年内将会发生一次地震。
C 未来20年内,在Zed这个城市发生地震比没有发生地震的可能性大。
D 我们不能判断未来会发生什么事,因为没有人可以确定何时会有地震发生。
17. 测验分数问题1:下图是两组学生参加科学测验的结果,这两组学生分别称为A组和B组。
A组的平均分数是62.0分,B组的平均分数是64.5分。
当学生得分为50分或以上时他们便通过这个测验。
由上图,老师认为B组学生比A组学生的表现较佳。
但A组学生不同意老师的看法。
他们詴着说服老师B组并不一定比较好。
依据上图,写出一个A组学生可能使用的数学论点。
18.滑板奕涵是一位狂热的滑板迷。
他到一家名为SKATERS的商店去确认几种价格。
在这家店你可以买到一个组装好的滑板。
或者,你也可以买一块板子,4个为一组的轮子,2个为一组轮架和一套金属零件,来组装你自己专属的滑板。
商店里的产品价格如下表。
产品价格(zeds)组装好的滑板82或84板子40,60或654个为一组的轮子14或362个为一组的轮架16一套金属零件(轴承,橡胶垫,螺丝和螺丝钉) 10或20问题1:奕涵想组装他自己的滑板。
在这家店自己组装滑板的最低价格及最高价格分别是多少?(a) 最低价格:zeds。
(b) 最高价格:zeds问题2:店里提供三种不同的板子,两组不同的轮子和两套不同的金属零件。
但只有一组轮架可以选择。
奕涵可以组装几种不同的滑板?A 6B 8C 10D 12问题3:奕涵有120 zeds,他想用这些钱买最贵的滑板。
奕涵在以下4个部件分别可以负担多少钱?在下表中写出你的答案。
部件总价(zeds)板子轮子轮架金属零件19.灯塔灯塔是一座顶端有灯的塔。
当船只要靠岸的时候,灯塔在夜间可以帮助船找到他们的航道。
灯塔以固定规律的方式发出光亮。
每座灯塔有它自己的规律。
下图你可以看到某个灯塔亮光的规律。
灯号的亮和暗相互交错。
时间(秒)这是一个固定的规律。
一段时间后规律会再次重复。
在开始重复之前的一个完整规律循环所用的时间,称之为周期。
当你找出一个规律的周期,便很容易延伸上图来找出下一个、或者数分钟、甚至数小时后灯塔的亮、暗情形。
问题1:下列哪一个是这个灯塔亮、暗的周期?A 2秒B 3秒C 5秒D 12秒问题2:在这一分钟内这座灯塔有几秒是亮的?A 4B 12C 20D 24问题3:在下图中画出一个灯塔的规律,这个灯塔每一分钟发出亮光30秒,亮光规律的周期为六秒钟。
时间(秒)10. 汇率来自新加坡的美玲准备前往南非当交换学生3个月。
她需要将新加坡币(SGD)兑换为南非币(ZAR)。
问题1:美玲发现两国间的货币汇率为:1 SGD = 4.2 ZAR 依此汇率中,美玲将3000元的新加坡币兑换为南非币。
美玲可兑换成多少元的南非币?答:.........................问题2:3个月后回到新加坡时,美玲身上还有3900元的南非币,她想要换回新加坡币,此时两国间的汇率为:1 SGD = 4.0 ZAR 美玲可换得多少新加坡币?答:.............................。
问题3:在这3个月间,汇率从每1元新加坡币兑换4.2元南非币,变成为4.0元南非币。
此时以这个汇率换回新加坡币,对美玲而言是否有利?请写出你的理由。
20.旋转建筑物在现代建筑风格中,建筑物通常会有不规则的形状。
下图呈现一个「旋转建筑物」的计算机模型和一楼的楼面设计。
下图指针的指向是建筑物的方向。
建筑物的一楼包含了主要的入口和商店。
在一楼之上还有另外20层的公寓。
每一楼层的平面设计图都与一楼的平面设计相似。
但每一层之间的方向都有一些差异。
圆柱部分则是电梯和各层楼的阳台。
问题1:以公尺为单位,估算建筑物的总高度,并解释你如何得到答案。
问题2:「侧面1」是从哪一个方位画出来的?A 从北方。
B 从西方。
C 从东方。
D 从南方。
问题3:「侧面2」是从那一个方位画出来的?A 从西北方。
