哈尔滨工业大学机械课程机器人技术课程大作业

合集下载

机器人大作业

IRB1600型机器人的运动学分析及仿真目录1.引言................................................................................................................ - 2 -1.1 ABB公司简介.................................................................................... - 3 -1.2ABB发展历史 .................................................................................... - 4 -2. IRB1600 ........................................................................................................ - 5 -2.1 IRB1600的资料................................................................................. - 6 -2.2建立基于D-H方法的连杆坐标系 ................................................... - 8 -2.3建立六自由度点焊机器人的运动学方程....................................... - 10 -3. 虚拟样机的建立........................................................................................ - 12 -3.1 导入.................................................................................................. - 12 -3.2 添加约束副...................................................................................... - 13 -3.3 基于ADAMS的机器人运动学仿真 ............................................. - 14 -4. 结语............................................................................................................ - 18 -5. 参考资料.................................................................................................... - 19 -1.引言通过这学期对《机器人技术基础》这门课的学习，我对工业机器人有了一定的了解。

哈工大机器人大作业

一、运动学正解程序及结果1、程序：syms x1x2x3x4x5x6d1d2d4a2a3x d aRx=[1 0 0 0;0 cos(x) -sin(x) 0;0 sin(x) cos(x) 0;0 0 0 1];Rz=[cos(x) -sin(x) 0 0;sin(x) cos(x) 0 0;0 0 1 0;0 0 0 1];Tx=[1 0 0 a;0 1 0 0;0 0 1 0;0 0 0 1];Tz=[1 0 0 0;0 1 0 0;0 0 1 d;0 0 0 1];t=pi/180;y1=90;y2=-90;y3=-90;T01=subs(Rz,x,x1)*subs(Tz,d,d1)*subs(Rx,x,y1*t);T12=subs(Rz,x,x2)*subs(Tz,d,d2)*subs(Tx,a,a2);T23=subs(Rz,x,x3)*subs(Tx,a,a3)*subs(Rx,x,y3*t);T34=subs(Rz,x,x4)*subs(Tz,d,d4)*subs(Rx,x,y4*t);T45=subs(Rz,x,x5)*subs(Rx,x,90);T=T01*T12*T23*T34*T45;t=subs(T,{y1,y3,y4,y5},[pi/2,-pi/2,-pi/2,pi/2]);t= simplify(t);nx=t(1,1);ny=t(2,1);nz=t(3,1);ox=t(1,2);oy=t(2,2);oz=t(3,2);ax=t(1,3);ay=t(2,3);az=t(3,3);px=t(1,4);py=t(2,4);pz=t(3,4);结果：Nx=sin(x2 + x3)*cos(x1)*sin(x5) - cos(x5)*sin(x1)*sin(x4)+cos(x1)*cos(x2)*cos(x3)*cos(x4)*cos(x5) - cos(x1)*cos(x4)*cos(x5)*sin(x2)*sin(x3)Ny=cos(x1)*cos(x5)*sin(x4) + sin(x2 + x3)*sin(x1)*sin(x5)+cos(x2)*cos(x3)*cos(x4)*cos(x5)*sin(x1) - cos(x4)*cos(x5)*sin(x1)*sin(x2)*sin(x3)Nz=sin(x2 + x3)*cos(x4)*cos(x5) - cos(x2 + x3)*sin(x5)Ox=sin(x4)*(cos(x1)*sin(x2)*sin(x3) - cos(x1)*cos(x2)*cos(x3)) - cos(x4)*sin(x1)Oy=cos(x1)*cos(x4) - sin(x4)*(cos(x2)*cos(x3)*sin(x1) - sin(x1)*sin(x2)*sin(x3))Oz=-sin(x2 + x3)*sin(x4)Ax=cos(x1)*cos(x2)*cos(x3)*cos(x4)*sin(x5) - sin(x2 + x3)*cos(x1)*cos(x5) - sin(x1)*sin(x4)*sin(x5) - cos(x1)*cos(x4)*sin(x2)*sin(x3)*sin(x5)Ay=cos(x1)*sin(x4)*sin(x5) - sin(x2 + x3)*cos(x5)*sin(x1) + cos(x2)*cos(x3)*cos(x4)*sin(x1)*sin(x5) - cos(x4)*sin(x1)*sin(x2)*sin(x3)*sin(x5)Az=cos(x2 + x3)*cos(x5) + sin(x2 + x3)*cos(x4)*sin(x5)Px=d2*sin(x1) - d4*(cos(x1)*cos(x2)*sin(x3) + cos(x1)*cos(x3)*sin(x2)) + a2*cos(x1)*cos(x2) + a3*cos(x1)*cos(x2)*cos(x3) - a3*cos(x1)*sin(x2)*sin(x3)Py=a2*cos(x2)*sin(x1) - d2*cos(x1) - d4*(cos(x2)*sin(x1)*sin(x3) + cos(x3)*sin(x1)*sin(x2)) + a3*cos(x2)*cos(x3)*sin(x1) - a3*sin(x1)*sin(x2)*sin(x3)Pz=d1 + d4*cos(x2 + x3) + a3*sin(x2 + x3) + a2*sin(x2)二、绘制工作空间（一）正解1、程序syms x1x2x3x4x5x6d1d2d4a2a3x d aRx=[1 0 0 0;0 cos(x) -sin(x) 0;0 sin(x) cos(x) 0;0 0 0 1];Rz=[cos(x) -sin(x) 0 0;sin(x) cos(x) 0 0;0 0 1 0;0 0 0 1];Tx=[1 0 0 a;0 1 0 0;0 0 1 0;0 0 0 1];Tz=[1 0 0 0;0 1 0 0;0 0 1 d;0 0 0 1];t=pi/180;T01=subs(Rz,x,x1)*subs(Tz,d,d1)*subs(Rx,x,90*t);T12=subs(Rz,x,x2)*subs(Tz,d,d2)*subs(Tx,a,a2);T23=subs(Rz,x,x3)*subs(Tx,a,a3)*subs(Rx,x,-90*t);T34=subs(Rz,x,x4)*subs(Tz,d,d4)*subs(Rx,x,-90*t);T45=subs(Rz,x,x5)*subs(Rx,x,90);T=T01*T12*T23*T34*T45;Px=T(1,4);Py=T(2,4);Pz=T(3,4);k=1;for th1=-160*t:10*t:160*tfor th2=-225*t:10*t:45*tfor th3=-45*t:10*t:225*tpx(k)=subs(Px,{x1,x2,x3,a2,a3,d1,d2,d4},[th1,th2,th3,431.8,20.32, 0,149.09,433.07]);py(k)=subs(Py,{x1,x2,x3,a2,a3,d1,d2,d4},[th1,th2,th3,431.8,20.32, 0,149.09,433.07]);pz(k)=subs(Pz,{x1,x2,x3,a2,a3,d1,d2,d4},[th1,th2,th3,431.8,20.32, 0,149.09,433.07]);k=k+1;endendendplot3(px,py,pz,'.');grid on2、结果俯视图3、总结：1).从图形看出，PUMA工作空间是一个中间为圆柱空心的椭球区域。

哈工大机械原理大作业-连杆

哈工大机械原理大作业-连杆本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.MarchHarbin Institute of Technology机械原理大作业一课程名称：机械原理设计题目：连杆运动分析院系：机电工程学院班级：设计者：学号：指导教师：陈明设计时间：2013年6月25日1、运动分析题目在图1-10中所示的干草压缩机中，已知LAB=150mm,LBC=600mm,LCE=120mm,LCD=500mm,LEF=600mm,XD=400mm,YD=500mm,YF=600mm,曲柄1作等速转动，其转速n1=50r/min。

求在一个运动循环中活塞5的位移、速度和加速度的变化曲线。

图1-102、机构的结构分析（1）基本杆组的划分①AB即杆件1为原动件②DECB即杆件2、3为RRR型II级杆组，其中CE为同一构件上点。

③ EF 和滑块即4、5为RRP 型II 级杆组（2）、建立以点A 为原点的固定平面直角系3、确定已知参数和求解流程(1)原动件1（I 级杆组RR ）如图所示，已知原动件1的转角 πϕ2~01=原动件杆1的角速度 s rad /236.51=ω原动件1的角加速度01=α运动副A 的位置坐标0,0==A A y x运动副A 的速度0,0==yA xA v v运动副A 的加速度0,0==yA xA a a原动件杆I 的长度mm l 1501=可求出B 的位置B 的速度B 的加速度(2)构件2、3（II 级杆组RRR ）D 的位置500400==D D y xD 的速度 0==yD xD v vD 的加速度00==yD xD a a杆长mm l l CD j 500==，mm l l BC i 600== 由关系j j D i i B C l x l x x ϕϕcos cos +=+= j j D i i B C l y l y y ϕϕsin sin +=+= 其中)(20sin cos B D i i i x x l A C B A -==-+ ϕϕ)(2B D i y y l B -=222j BD i l l l C -+=222)()(B D B D BD y y X x l -+-= 可解得C A C B A B i +-++=222arctan 2ϕDC DC j x x y y --=arctan ϕ由上面两个式子可以得到两杆的角速度1)()(G y y s x x c w B D j B D j i i -+-==•ϕ132G s G c Gij i i +==ϕα其中i j j i s c s c G -=1，i i i l c ϕcos =，i i i l s ϕsin =，j j j l c ϕcos =，j j j l s ϕsin =可得E 的位置iB E iB E y y x x ϕϕsin 480cos 480+=+=E 的速度 i i yB E yE i i xB E xE v yv v xv ωϕωϕcos 480sin 480+==-==E 的加速度i i i i xB E xE a xa αϕωϕsin 480cos 4802--== i i i i yB E yE a ya ϕαϕωcos 480sin 4802+-== （3)、构件4、5杆组（II 级杆组RRP ）在建立的坐标系中取一参考点K600,0==K K y x 则速度0,0==yK xK v v加速度0,0==yK xK a a杆长mm l EF 600=,设F 位移为s 由s x l x x K i EF E F +=+='cos ϕK i EF E F y l y y =+='sin ϕ由上面两个式子可以得到600600arcsin arcsin'E EF E k i y l y y -=-=ϕ 所以：F 点位移 )600600arcsin(cos 600E E F y x x s -+== 速度F F xv = 加速度F F xa =四、编程计算并输出结果（VB编程）主程序：Private Sub Command1_Click()Dim s5(3600) As DoubleDim v5(3600) As DoubleDim a5(3600) As Double Dim pi As DoubleDim pa As Doublepi = 3.1415926pa = pi / 180Dim i As LongDim f1(3600) As Double Dim RR1 As RRDim RR2 As RRDim RRR1 As RRRDim RRP1 As RRPSet RR1 = New RRSet RR2 = New RRSet RRR1 = New RRRSet RRP1 = New RRPFor i = 0 To 3600 Step 1 f1(i) = i * pa / 10RR1.delt = 0RR1.f = f1(i)RR1.w = 5.24RR1.e = 0RR1.L = 150RR1.xA = 0RR1.yA = 0RR1.vxA = 0RR1.vyA = 0RR1.axA = 0RR1.ayA = 0RR1.calRRR1.Li = 600RRR1.Lj = 500RRR1.xB = RR1.xBRRR1.yB = RR1.yBRRR1.vxB = RR1.vxBRRR1.vyB = RR1.vyBRRR1.axB = RR1.axBRRR1.ayB = RR1.ayBRRR1.xD = 400RRR1.yD = 500RRR1.vxD = 0RRR1.vyD = 0RRR1.axD = 0RRR1.ayD = 0RRR1.M = 1RRR1.calRRRRR2.delt = 0RR2.f = RRR1.fi RR2.w = RRR1.wi RR2.e = RRR1.ei RR2.L = 480RR2.xA = RR1.xB RR2.yA = RR1.yB RR2.vxA = RR1.vxB RR2.vyA = RR1.vyB RR2.axA = RR1.axB RR2.ayA = RR1.ayB RR2.calRRP1.Li = 600RRP1.Lj = 0RRP1.fj = piRRP1.wj = 0RRP1.ej = 0RRP1.xB = RR2.xB RRP1.yB = RR2.yB RRP1.vxB = RR2.vxB RRP1.vyB = RR2.vyB RRP1.axB = RR2.axB RRP1.ayB = RR2.ayB RRP1.xK = 0RRP1.yK = 600RRP1.vxK = 0RRP1.vyK = 0RRP1.axK = 0RRP1.ayK = 0RRP1.M = 1RRP1.cals5(i) = RRP1.ssv5(i) = RRP1.vssa5(i) = RRP1.assNext iPicture1.Scale (-30, 700)-(360, 580)Picture1.Line (0, 0)-(360, 0) 'XPicture1.Line (0, 580)-(0, 700) 'YFor i = 0 To 360 Step 10 'X轴坐标Picture1.DrawStyle = 2Picture1.Line (i, 700)-(i, 580)Picture1.CurrentX = i - 10: Picture1.CurrentY = 0 Picture1.Print iNext iFor i = 580 To 700 Step 10 'Y轴坐标Picture1.DrawStyle = 2Picture1.Line (0, i)-(360, i)Picture1.CurrentX = -10: Picture1.CurrentY = iPicture1.Print iNext iFor i = 0 To 3600 Step 1Picture1.PSet (i / 10, s5(i))Next iEnd SubRR:Public L As DoublePublic f As DoublePublic delt As DoublePublic w As DoublePublic e As DoublePublic xA As DoublePublic yA As DoublePublic vxA As DoublePublic vyA As DoublePublic axA As DoublePublic vxB As DoublePublic vyB As DoublePublic axB As DoublePublic ayB As DoublePublic Sub cal()xB = xA + L * Cos(f + delt)yB = yA + L * Sin(f + delt)vxB = vxA - w * L * Sin(f + delt)vyB = vyA + w * L * Cos(f + delt)axB = axA - w ^ 2 * L * Cos(f + delt) - e * L * Sin(f + delt) ayB = ayA - w ^ 2 * L * Sin(f + delt) + e * L * Cos(f + delt) End SubRRR:Public Li As DoublePublic Lj As DoublePublic fi As DoublePublic fj As DoublePublic wi As DoublePublic wj As DoublePublic ei As DoublePublic ej As DoublePublic xB As DoublePublic yB As DoublePublic vxB As DoublePublic vyB As DoublePublic axB As DoublePublic ayB As DoublePublic xC As DoublePublic yC As DoublePublic vxC As DoublePublic vyC As DoublePublic axC As DoublePublic ayC As DoublePublic xD As DoublePublic yD As DoublePublic vxD As DoublePublic vyD As DoublePublic M As DoublePublic Sub calRRR()Dim fDB As DoubleDim Ci As DoubleDim Cj As DoubleDim Si As DoubleDim Sj As DoubleDim G1 As DoubleDim G2 As DoubleDim G3 As DoubleDim LBD As DoubleDim JCBD As DoubleDim val As Doublepi = 3.1415926LBD = Sqr((xB - xD) ^ 2 + (yD - yB) ^ 2)If LBD < Li + Lj And LBD > Abs(Li - Lj) Thenval = (Li ^ 2 + LBD ^ 2 - Lj ^ 2) / (2 * Li * LBD) JCBD = Atn(-val / Sqr(-val * val + 1)) + 2 * Atn(1) End IfRRP:Public Li As DoublePublic Lj As DoublePublic fi As DoublePublic fj As DoublePublic wi As DoublePublic wj As DoublePublic ei As DoublePublic ej As DoublePublic xB As DoublePublic yB As DoublePublic vxB As DoublePublic vyB As DoublePublic axB As DoublePublic ayB As DoublePublic xK As DoublePublic vyK As DoublePublic axK As DoublePublic ayK As DoublePublic xC As DoublePublic yC As DoublePublic vxC As DoublePublic vyC As DoublePublic axC As DoublePublic ayC As DoublePublic xD As DoublePublic yD As DoublePublic vxD As DoublePublic vyD As DoublePublic axD As DoublePublic ayD As DoublePublic M As SinglePublic ss As DoublePublic vss As DoublePublic ass As DoublePublic Sub cal()Dim A0 As DoubleDim Q1 As DoubleDim Q2 As DoubleDim Q3 As DoubleDim Q4 As DoubleDim Q5 As DoubleDim val As DoubleDim pi As Doublepi = 3.14159216A0 = Lj + ((yK - yB) * Cos(fj) - (xK - xB) * Sin(fj)) val = A0 / Lifi = M * Atn(val / Sqr(-val * val + 1)) + fjxC = xB + Li * Cos(fi)yC = yB + Li * Sin(fi)ss = (xC - xK) * Cos(fj) + (yC - yK) * Sin(fj)xD = xK + ss * Cos(fj)yD = yK + ss * Sin(fj)Q1 = vxK - vxB - wj * (ss * Sin(fj) + Lj * Cos(fj))Q2 = vyK - vyB + wj * (ss * Cos(fj) - Lj * Sin(fj))Q3 = Li * Sin(fi) * Sin(fj) + Li * Cos(fi) * Cos(fj)wi = (-Q1 * Sin(fj) + Q2 * Cos(fj)) / Q3vss = -(Q1 * Li * Cos(fi) + Q2 * Li * Sin(fi)) / Q3vxC = vxB - wi * Li * Sin(fi)vyC = vyB + wi * Li * Cos(fi)vxD = vxK + vss * Cos(fj) - ss * wj * Sin(fj)vyD = vyK + vss * Sin(fj) + ss * wj * Cos(fj)Q4 = axK - axB + wi ^ 2 * Li * Cos(fi) - ej * (ss * Sin(fj) + Lj * Cos(fj)) - wj ^ 2 * (ss * Cos(fj) - Lj * Sin(fj)) - 2 * vss * wj * Sin(fj)Q5 = ayK - ayB + wi ^ 2 * Li * Sin(fi) + ej * (ss * Cos(fj) - Lj * Sin(fj)) - wj ^ 2 * (ss * Sin(fj) + Lj * Cos(fj)) + 2 * vss * wj * Cos(fj)ei = (-Q4 * Sin(fj) + Q5 * Cos(fj)) / Q3ass = (-Q4 * Li * Cos(fi) - Q5 * Li * Sin(fi)) / Q3axC = axB - ei * Li * Sin(fi) - wi ^ 2 * Li * Cos(fi)ayC = ayB + ei * Li * Cos(fi) - wi ^ 2 * Li * Sin(fi)axD = axK + ass * Cos(fj) - ss * ej * Sin(fj) - ss * wj ^ 2 * Cos(fj) - 2 * vss * wj * Sin(fj)ayD = ayK + ass * Sin(fj) + ss * ej * Cos(fj) - ss * wj ^ 2 * Sin(fj) + 2 * vss * wj * Cos(fj)End Sub五、计算结果数据如图：位移曲线：速度曲线：加速度曲线：六、计算结果分析主动件转角为0时,滑块的位移为628mm,随着转角的匀速增加,滑块位移先上升,速度为负快速下降,加速度为负且开始值较小并逐渐下降,到达最低点-2200左右,此时速度为0, 然后位移开始继续下降,速度继续下降,然后到达最小值-100左右,此时加速度为0,又开始上升(向左运动),速度正向增大,在后面一段时期速度继续增大,加速度也正向增大,然后速度下降,加速度下降.滑块分别在4.2s,11.4s速度达到正向最大，1.7s,7.7s速度达到负向最大，0.8s,2.7s,5.8s,9.6s加速度达到极值，滑块就是这样周期性的左右运动。

哈工大机械原理大作业

H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业一课程名称：机械原理设计题目：连杆机构运动分析院系：机电学院班级： 1208105分析者：殷琪学号：指导教师：丁刚设计时间：哈尔滨工业大学设计说明书1 、题目如图所示机构，一只机构各构件的尺寸为AB=100mm，BC=4.28AB，CE=4.86AB，BE=8.4AB，CD=2.14AB，AD=4.55AB，AF=7AB，DF=3.32AB，∠BCE=139?。

构件1的角速度为ω1=10rad/s，试求构件2上点E的轨迹及构件5的角位移、角速度和角加速度，并对计算结果进行分析。

2、机构结构分析该机构由6个构件组成，4和5之间通过移动副连接，其他各构件之间通过转动副连接，主动件为杆1，杆2、3、4、5为从动件，2和3组成Ⅱ级RRR基本杆组，4和5组成Ⅱ级RPR 基本杆组。

如图建立坐标系3、各基本杆组的运动分析数学模型1) 位置分析2) 速度和加速度分析将上式对时间t 求导，可得速度方程：将上式对时间t 求导，可得加速度方程:RRR Ⅱ级杆组的运动分析如下图所示当已知RRR 杆组中两杆长L BC 、L CD 和两外副B 、D 的位置和运动时，求内副C的位置、两杆的角位置、角运动以及E 点的运动。

1) 位置方程由移项消去j ϕ后可求得i ϕ：式中，可求得j ϕ：E 点坐标方程：其中2) 速度方程两杆角速度方程为式中，点E 速度方程为3) 加速度方程两杆角加速度为式中，点E 加速度方程为RPR Ⅱ级杆组的运动分析（1）位移方程（2）速度方程其中（3）加速度方程4、计算编程利用MATLAB 软件进行编程，程序如下:% 点B 和AB 杆运动状态分析>>r=pi/180;w 1=10;e 1=0;l 1=100;Xa=0;Ya=0;Vax=0;Vay=0;aax=0;aay=0;f1=0:1: 360;% B 点位置Xb=Xa+l1*cos(r*f1);Yb=Ya+l1*sin(r*f1);% B点速度Vbx=Vax-w1*l1*sin(r*f1);Vby=Vay+w1*l1*cos(r*f1);% B点加速度abx=aax-l1*w1.^2.*cos(r*f1);aby=aay-l1*w1.^2.*sin(r*f1);% RRR2级杆组运动分析% 输入D点参数l2=428;l3=214;Xd=455;Yd=0;Vdx=0;Vdy=0;adx=0;ady=0;% 计算E点、2杆、3杆运动参数lbe=840;lce=486;a0=2*l2*(Xd-Xb);b0=2*l2*(Yd-Yb);c0=l2^2+(Xb-Xd).^2+(Yb-Yd).^2-l3^2;f2=2*atan((b0+sqrt(a0.^2+b0.^2-c0.^2))./(a0+c0)); % C点位置Xc=Xb+l2*cos(f2);Yc=Yb+l2*sin(f2);% 2杆、3杆运动参数计算dX=Xc-Xd;dY=Yc-Yd;for n=1:length(dX)if dX(n)>0&dY(n)>=0f3(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f3(n)=pi/2;elseif dX(n)<0&dY(n)>=0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f3(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f3(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f3(n)=2*pi+atan(dY(n)/dX(n));endendC2=l2*cos(f2);C3=l3*cos(f3);S2=l2*sin(f2);S3=l3*sin(f3);G1=C2.*S3-C3.*S2;w2=(C3.*(Vdx-Vbx)+S3.*(Vdy-Vby))./G1;w3=(C2.*(Vdx-Vbx)+S2.*(Vdy-Vby))./G1;G2=adx-abx+(w2.^2).*C2-(w3.^2).*C3;G3=ady-aby+(w2.^2).*S2-(w3.^2).*S3;e2=(G2.*C3+G3.*S3)./G1;% E点位置w=acos((l2^2+lbe^2-lce^2)/(2*l2*lbe));Xe=Xb+lbe*cos(f2-w);Ye=Yb+lbe*sin(f2-w);Vex=Vbx-lbe*w2.*sin(f2-w);Vey=Vby+lbe*w2.*cos(f2-w);aex=abx-lbe*(e2.*sin(f2-w)+w2.^2.*cos(f2-w));aey=aby+lbe*(e2.*cos(f2-w)-w2.^2.*sin(f2-w));% 计算杆5运动参数Xf=646.2912088;Yf=-268.9008617;l5=sqrt((Xe-Xf).^2+(Ye-Yf).^2);dX=Xe-Xf;dY=Ye-Yf;for n=1:length(dX)if dX(n)>0&dY(n)>=0f5(n)=atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)>0f5(n)=pi/2;elseif dX(n)<0&dY(n)>=0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)<0&dY(n)<0f5(n)=pi+atan(dY(n)/dX(n));elseif dX(n)==0&dY(n)<0f5(n)=1.5*pi;elseif dX(n)>0&dY(n)<0f5(n)=2*pi+atan(dY(n)/dX(n));endendw5=(-Vex.*sin(f5)+Vey.*cos(f5))./l5;a5=(-aex.*sin(f5)+aey.*cos(f5))./l5;% 画出各参数曲线figure(1);plot(Xe,Ye,'k');xlabel('Xe/\mm');ylabel('Ye/mm');grid on;title('E点位置');figure(2);plot(f1,f5,'k');xlabel('f/\circ');ylabel('f5/\circ');grid on;title('5杆角位移');figure(3);plot(f1,w5,'k');xlabel('f/\circ');ylabel('w5/rad/s');grid on;title('5杆角速度');figure(4);plot(f1,a5,'k');xlabel('f/\circ');ylabel('a5/rad/s2');gridon;title('5杆角加速度');Warning: Unable to interpret TeX string "Xe/\mm"5、计算结果图一：E点的运动轨迹图二：5杆角位移图三：5杆角速度图四：5杆角加速度6、计算结果分析由E点位置图像可看出，构件4做周期往复运动，由图二、三、四可看出，构件5的角位移、角速度、角加速度均成周期性变化。

哈工大机械原理大作业

H a r b i n I n s t i t u t e o f T e c h n o l o g y大作业设计说明书课程名称：机械原理设计题目：凸轮机构院系：机电学院班级：姓名：学号：指导教师：丁刚设计时间：2014.5.29哈尔滨工业大学1.设计题目第31题：升程/mm 升程运动角/。

升程运动规律升程许用压力角/。

回程运动角/。

回程运动规律回程许用压力角/。

远休止角/。

近休止角/。

150 90 等加等减速40 80 余弦加速度70 40 1502.运动方程式及运动线图由题目要求凸轮逆时针旋转（1）确定凸轮机构推杆升程、回程运动方程，并绘制推杆位移、速度、加速度线图。

升程第一段：（0 <φ< pi /4）φ0=pi/2;s1 = 73*φ^2;v1=146*w*φ;a1 = 146*w^2;升程第二段：（pi/4 <φ< pi /2）s2 =90-73*(pi/2-φ)^2;v2=146*w*( pi/2-φ);a2 =-146*w.^2;远休止程：（pi/2 <φ< 10*pi/9)s3 = 90;v3 = 0;a3 = 0;回程：(10*pi/9)< φ< ( 14*pi/9)s4 =45*(1+cos(9/4*(φ-10*pi/9)));v4 =-101.25*w*sin(9/4*(φ-10*pi/9)) ;a4 =-227.8*w^2* cos(9/4*(φ-10*pi/9)); 近休止程：(14*pi/9)< φ < ( 2*pi);s5 =0;v5 =0;a5 =0;1.由上述公式通过编程得到位移、速度、加速度曲线如下：（编程见附录）.基圆半径为r0 = (50^2+100^2)0.5=112mm，偏距e = 50mm。

3.凸轮实际轮廓，理论轮廓，基圆，偏距圆绘制4.整体图像附录1.求位移、速度、加速度的程序（matlab）w = input('请输入W=');x = 0:(pi/1000):(pi/4);s1 = 73*x.^2;v1=146*w*x;a1 = 146*w.^2;y = (pi/4):(pi/1000):(pi/2);s2 =90-73*(pi/2-y).^2;v2=146*w*( pi/2-y);a2 =-146*w.^2;z = (pi/2 ):(pi/1000):(10*pi/9);s3 = 90;v3 = 0;a3 = 0;c = (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));v4 =-101.25*w*sin(9/4*( c-10*pi/9)) ;a4 =-227.8*w.^2* cos(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0; v5 =0; a5 =0;subplot (2,2,1)plot(x,s1,'b',y,s2,'b',z,s3,'b',c,s4,'b', d,s5,'b');xlabel('转角/rad')ylabel('位移/(mm/s)')title('位移与转角曲线')grid onsubplot (2,2,2)plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g', d,v5,'g')ds4 =45*9/4*sin(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0;ds5 =0;plot(ds1,s1,'b',ds2,s2,'b',ds3,s3,'b',ds4,s4,'b',ds5,s5,'b'); xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s曲线')grid onhold onx3=-150:0.001:0;y3 = 0.577*x3;plot (x3,y3,'r');hold onx1=-150:0.001:150;for i=1:1:250;k1=(s1(i+1)-s1(i))/ (ds1(i+1)-ds1(i));if(k1>=-1.733 && k1<=-1.731)y1=k1*(x1-ds1(i))+s1(i);plot (x1,y1,'r');end3.确定滚子半径（1）先求凸轮理论轮廓曲线，程序如下：Clc；clear;w = input('请输入w=');s0 = 100;s = 90;e = 50; x = 0:(pi/100):(pi/4);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (pi/4):(pi/100):(pi/2);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi/2 ):(pi/100):(10*pi/9);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (10*pi/9):(pi/1000):( 14*pi/9);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);d=(14*pi/9):(pi/1000):( 2*pi);x5 = (s + s0)*cos(d)-e*sin(d);y5 = (s0 + s)*sin(d) - e*cos(d);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b',x5,y5,'b');xlabel('x/mm')ylabel('y/mm')title('理论轮廓曲线')grid on（2）理论轮廓线最小曲率半径编程代码：由下程序结果可知pmin =81.6667这里滚子半径为 r r < pmin-ΔΔ=3~5mm；取r r=10mm;clear;clc;v=[];syms x1 x2 x3 x4 x5s0 = 100;e = 50;s1 = 73*x1.^2;t1 = (s1 + s0)*cos(x1)-e*sin(x1);y1 = (s0 + s1)*sin(x1) - e*cos(x1);tx1=diff(t1,x1);txx1=diff(t1,x1,2);yx1=diff(y1,x1);yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(pi/4);k1=subs(abs((tx1*yxx1-txx1*yx1)/(tx1^2+yx1^2)^1.5),{x1},{xx1}); v=[v,1/k1];ends2 =90-73*(pi/2-x2).^2;t2 = (s2 + s0)*cos(x2)-e*sin(x2);y2 = (s0 + s2)*sin(x2) - e*cos(x2);tx2=diff(t2,x2);txx2=diff(t2,x2,2);yx2=diff(y2,x2);yxx2=diff(y2,x2,2);for xx2=(pi/4):(pi/100):(pi/2);k2=subs(abs((tx2*yxx2-txx2*yx2)/(tx2^2+yx2^2)^1.5),{x2},{xx2});k4=subs(abs((tx4*yxx4-txx4*yx4)/(tx4^2+yx4^2)^1.5),{x4},{xx4}); v=[v,1/k4];ends5 =0;t5 = (s5 + s0)*cos(x5)-e*sin(x5);y5 = (s0 + s5)*sin(x5) - e*cos(x5);tx5=diff(t5,x5);txx5=diff(t5,x5,2);yx5=diff(y5,x5);yxx5=diff(y5,x5,2);for xx5=(10*pi/9):(pi/100):( 4*pi/3);k5=subs(abs((tx5*yxx5-txx5*yx5)/(tx5^2+yx5^2)^1.5),{x5},{xx5}); v=[v,1/k5];endpmin=min(v)4.绘制凸轮轮廓曲线clear ;clc;syms x y z c dw= input('请输入w=');n3 = diff(x3);m3 = diff(y3);xt3= subs(x3 + (r*m3)./sqrt(m3.^2+n3.^2),z,zz);yt3 = subs(y3 - (r*n3)./sqrt(m3.^2+n3.^2),z,zz);cc= (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = (s0 +s4).*sin(c) - e*cos(c);n4 = diff(x4);m4 = diff(y4);xt4= subs(x4 + (r*m4)./sqrt(m4.^2+n4.^2),c,cc);yt4 =subs( y4 - (r*n4)./sqrt(m4.^2+n4.^2),c,cc);dd=(14*pi/9):(pi/1000):( 2*pi);s5 =0;x5 = (s5 + s0).*cos(d)-e*sin(d);y5 = (s0 +s5).*sin(d) - e*cos(d);n5 = diff(x5);m5 = diff(y5);xt5= subs(x5 + (r*m5)./sqrt(m5.^2+n5.^2),d,dd);yt5 =subs( y5 - (r*n5)./sqrt(m5.^2+n5.^2),d,dd);plot(xt1,yt1,'b',xt2,yt2,'b',xt3,yt3,'b',xt4,yt4,'b',xt5,yt5,'b')for i=1:3601if yy(1,i)<=y0/2s(1,i)=2*h*(yy(i)./y0).^2;v(1,i)=4*h*w*yy(i)./(y0.^2);a(1,i)=4*h*w.^2./(y0.^2);elseif yy(1,i)>y0/2 && yy(1,i)<y0s(1,i)=h-2*h./y0.^2.*(y0-yy(i)).^2;v(1,i)=4*h*w*(y0-yy(i))./(y0.^2);a(1,i)=-4*h*w.^2./(y0.^2);elseif yy(1,i)>=y0 && yy(1,i)<y0+yss(1,i)=h;v(1,i)=0;a(1,i)=0;elseif yy(1,i)>=y0+ys && yy(1,i)<y0+ys+y01s(1,i)=h/2*(1+cos(pi/y01*(yy(1,i)-y0-ys)));v(1,i)=-pi*h*w/2/y01*sin(pi/y01*(yy(1,i)-y0-ys));a(1,i)=-pi^2*h*w^2/2/y01^2*cos(pi/y01*(yy(1,i)-y0-ys)); elseif yy(1,i)>=y0+ys+y01 && yy(1,i)<=360s(1,i)=0;v(1,i)=0;a(1,i)=0;subplot(2,3,5) ;plot(x,y,'r',xt,yt,eex,eey,'g',r0x,r0y,'k')%画图title('实际理论轮廓线')axis equal%使坐标轴比例相等grid on%画网格线。

哈工大机械原理大作业3

Harbin Institute of Technology机械原理大作业三课程名称：设计题目：院系：班级：设计者：学号：指导教师：设计时间：哈尔滨工业大学大作业3 齿轮传动设计 1、设计题目1.1机构运动简图1.2机械传动系统原始参数2、传动比的分配计算由已知条件，电动机转速n=1450r/min ，输出转速n 1=27 r/min ，n 2=31 r/min ，n 3=37 r/min ，带传动最大传动比max p i =2.5,滑移齿轮传动最大传动比=4，定轴齿轮传动最大传动比=4。

可求得：传动系统的总传动比为:11n ni == 1450/27=53.70322n ni == 1450/31=46.774 33n ni == 1450/37=39.189 传动系统的总传动比分别由带传动、滑移齿轮传动和定轴齿轮传动三部分实现。

设带传的传送比为其最大传送比5.2max =p i ，滑移齿轮的传动比为321,,v v v i i i ，定轴齿轮传动的传动比为f i ，则总传动比由于1i > 2i > 3i ，故取1max 4v v i i ==则定轴齿轮传动部分的传动比为1max max5.37f p v i i i i ==滑移齿轮传动的传动比22max3.49v f p i i i i ==33m a x2.92v f p i i i i ==定轴齿轮传动由3对齿轮传动组成，每对齿轮的传动比为：1.754d i ==≤3、齿轮齿数的确定滑移齿轮齿数3=v i 65622.9521z z == 2=v i 8766 3.4719z z ==1=v i 10967 3.9417z z ==齿轮7，齿轮8：719z = 866z =781()852a m z z =+=齿轮9，齿轮10：917z =1067z =此时已知条件为'a =85mm ，910211()842()ni i a m z z X X ==+=-∑mm ''arccos(cos )21.78a aαα==总变位系数：'910()0.552tan z z x inv inv ααα∑+=-=根据x ∑值和1093.94 3.0z uz ==>，按选择变位系数线图左部斜线⑤分配变位系数，得90.45x =齿轮5，齿轮6：5=21z662z =此时已知'a =85mm ，561()832a m z z =+= ''arccos(cos )23.42a a αα==100.10x =总变位系数：'65() 1.082tan z z x inv inv ααα∑+=-=根据x ∑值和652.953z u z ==>，按选择变位系数线图左部斜线④分配变位系数，得 50.5x =60.58x =定轴圆柱齿轮齿数=d i 1214111326 1.5317z z z z ===齿轮11，齿轮12：角度变位正传动。

哈工大机械原理大作业直动从动件盘形凸轮机构满分完美版哈尔滨工业大学

y(i)=(s0+s(i))*cosd(Phi(i))-e*sind(Phi(i));
end
%曲率半径
dx=diff(x);
dx(36001)=0;
dy=diff(y);
dy(36001)=0;
dydx=dy./dx;
ddy=diff(dydx);
ddy(36001)=0;
ddy=ddy./dx;
~7~
xlabel('凸轮转角φ/°');
ylabel('从动件加速度 a/(mm/s^2)');
title('加速度');
subplot(2,3,4);
plot(dsdPhi,s);
axis equal
axis([-30 50 -50 30]);
hold on
plot(x1,f1,'r');
hold on
axis equal
hold on
plot(x,y,'k')
legend('理论廓线',-1);
hold on
%轮廓图
%实际廓线
%理论廓线
~8~
哈尔滨工业大学
直动从动件盘型凸轮机构设计说明书
plot(x0,y0,':')
hold on
%基圆
plot(xe,ye,'k:')
%偏距圆
legend('实际廓线','理论廓线','基圆','偏距圆',-1);
subplot(2,3,1);
plot(Phi,s);
grid on
axis([0 360 0 27]);

哈工大PUMA机器人大作业

2017 年秋季学期研究生课程考核（读书报告、研究报告）考核科目:机器人技术:机电学院学生所在院（系）学生所在学科:机械电子学生姓名:王学号:17S学生类别:学硕考察结果:阅卷人:PUMA 机器人正逆运动学推导及运动空间解算图1 PUMA 机器人模型任务:1.建立坐标系；2.给出D-H参数表；3.推导正、逆运动学；4.编程得工作空间。

一、建立坐标系根据PUMA 机器人运动自由度，在各关节处建立坐标系如图2所示。

图2 PUMA 机器人坐标系建立图其中0O ∑与1O ∑原点交于一点, 4O ∑与5O ∑原点交于一点。

二、 D-H 参数表D-H 参数表可根据坐标系设定而得出，见表1。

1) i θ为绕1i Z -轴，从1i X -到i X 的角度； 2) i a 为绕i X 轴，从1i Z -到i Z 的角度； 3) i l 为沿i X 轴，从1i Z -与i X 交点到i O 的距离； 4) i d 为沿1i Z -轴，从1i Z -与i X 到1i O -的距离。

表1 PUMA 机器人杆件参数表三、正运动学推导由坐标系及各杆件参数可得到6个连杆变换矩阵。

111101cos 0sin 0sin 0cos 001000001T θθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦ 22222222122cos sin 0cos sin cos 0sin 0010001a a T d θθθθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3333333323cos 0sin cos sin 0cos sin 01000001a a T θθθθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦ 4444344cos 0sin 0sin 0cos 00100001T d θθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦555545cos 0sin 0sin 0cos 001000001T θθθθ⎡⎤⎢⎥-⎢⎥=-⎢⎥⎢⎥⎣⎦ 6666566cos sin 00sin cos 000010001T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据各连杆变换矩阵相乘，可以得到PUMA 机械手变换矩阵，其矩阵为关节变量的函数。

机器人课程考核大作业

《机器人技术基础》课程考核大作业一、进行课程学习考核（大作业形式）的目的：工业机器人系统设计是专业选修课的一个理论与实践相结合的教学环节，是机械类基础课程的延伸，可以巩固和加强机械类基础课程学习和工程应用知识的拓展，可以为毕业设计和就业工作打下良好基础，其目的是：1、通过资料查询与整理，联系生产实际，运用所学过的知识，使学生得到对课题的论证与分析、问题解决对策、自主学习、团队合作等能力的培养。

2、利用机械类的前序课知识，学会并掌握工业机器人系统设计的特点及方法，学会并掌握工业机器人系统设计中“总体方案设计”、“参数设计”、“组成机构原理与分析”、“机械结构装置设计”、“控制系统设计”等方面的一般方法和技术要求。

3、加强机械设计中基本技能的训练，如：设计计算能力，运用有关设计资料、设计手册、标准、规范及经验数据的能力，以及机械、电气系统的综合运用能力。

二、同学可以选择的课题领域：（01）玻璃、陶瓷加工业用的工业机器人（02）化学工业中应用的工业机器人（03）建筑行业应用的工业机器人（04）塑料工业中应用的工业机器人（如：装配、搬运）（05）用于包装工业的工业机器人（06）电气和电子工业中应用的工业机器人：工件搬运和存放的工业机器人（07）医疗行业应用的工业机器人（如：医疗、残疾、家庭）（08）用于金属生产和加工的工业机器人（铸造机器人）（09）用于木加工业的工业机器人：木加工行业装配和搬运的工业机器人（10）用于食品供应和加工的工业机器人：食品工业中的装配和搬运的工业机器人（11）承担复杂机具搬运任务的工业机器人（12）搬运和托盘堆码应用的工业机器人（13）普通机械制造领域的装配和搬运作业的工业机器人（14）用于机床上下料件的工业机器人（15）用于粘接和密封的工业机器人（16）锻冶场所装卸的工业机器人（17）金属生产和加工业的装配和搬运的工业机器人（18）用于压铸和注模成型机装卸的工业机器人（19）用于车辆制造的焊接工业机器人（20）用于车辆制造的装配工业机器人（21）用于仓储、材料管理和控制及后勤的工业机器人：一般工厂自动化装配和搬运系统三、设计内容与要求：1．介绍所选工业机器人系统的组成及各部分的关系，理解其机、电组成系统的要求（包括：需求分析、功能分析与分解、功能求解与集成、设计方案的形成、方案的评价等），掌握工业机器人系统方案设计的主要进程以及各阶段的主要工作内容，初步领会工业机器人系统的设计方案及一般程序。

机器人技术大作业

机器⼈技术⼤作业机器⼈技术⼤作业-标准化⽂件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《机器⼈技术》⼤作业（2015年秋季学期）题⽬⼯业机器⼈概述姓名学号班级专业机械设计制造及其⾃动化报告提交⽇期2015年12⽉5⽇哈尔滨⼯业⼤学内容及要求1.以某种机器⼈(如搬运、焊接、喷漆、装配等⼯业机器⼈；服务机器⼈；仿⽣鱼、蛇等仿⽣机器⼈；军⽤及其它机器⼈等)为例，撰写⼀篇⼤作业，题⽬⾃拟，以下内容仅作参考：1) 机器⼈的机械结构设计(包括各部分名称、功能、传动等)；2) 机器⼈的运动学及动⼒学分析；3) 机器⼈的控制及轨迹规划；4) 驱动及伺服系统设计；5) 电⽓控制电路图及部分控制⼦程序。

2.题⽬⾃拟，拒绝雷同和抄袭；3.参考⽂献不少于7篇，其中⾄少有2篇外⽂⽂献；4.报告统⼀⽤该模板撰写，字数不少于5000字，上限不限；5.正⽂为⼩四号宋体，1.25倍⾏距；图表规范，标注为五号宋体；6.⽤A4纸单⾯打印；左侧装订，1枚钉；7.提交打印稿及03版word电⼦⽂档，由班长收齐。

8.此页不得删除。

评语：教师签名：成绩（20分）：年⽉⽇⼯业机器⼈概述机器⼈学是当今世界极为活跃的研究领域之⼀，它涉及计算机科学、机械学、电⼦学、⾃动控制、⼈⼯智能等多种学科。

随着计算机、⼈⼯智能和光机电⼀体化技术的迅速发展，机器⼈已经成为⼈类的好帮⼿。

在航空航天，深海探测中，往往使⽤机器⼈代替⼈类去完成复杂的极限⼯作任务。

⼯业机器⼈是⼀个多功能、多⾃由度的机械和电⽓⼀体化的⾃动机械设备和系统，它可以在制造过程中完成各种任务。

它结合制造主机或⽣产线，可以形成⼀个单⼀的或多台机器⾃动化系统，在⽆⼈参与下，实现搬运、焊接、装配和喷涂等多种⽣产作业。

⽬前，⼯业机器⼈技术飞速发展，在⽣产中的应⽤⽇益⼴泛，已成为现代制造业重要的⽣产⾼度⾃动化设备。

⼀、⼯业机器⼈特性⾃20世纪60年代美国第⼀代机器⼈的开始，⼯业机器⼈的发展和应⽤迅速发展起来，⼯业机器⼈的最重要的特性概括如下。

哈工大机械设计大作业轴系设计5.1.2

Harbin Institute of Technology大作业设计说明书课程名称：机械设计设计题目：轴系部件设计设计时间：2017.12哈尔滨工业大学设计任务原始数据如下：有冲击，室内工作，机器成批生产一．选择轴的材料、热处理方式因传递功率不大，并对质量及结构尺寸无特殊要求，故选用45号钢，调制处理。

二.按扭转强度估算轴径由大作业四P=3.84KW ，n =480r/min ，对于转轴，扭转强度初算轴径，查参考文献[1]表10.2得C =106~118，考虑轴端弯矩比转矩小，故取 C =106，则mm n P c d 2.2148084.310633min =⨯== 其中P ——轴的传递功率 n ——轴的转速C ——由许用扭转剪应力确定的系数由于考虑到轴的最小直径处要安装大带轮或小齿轮有键槽存在，故将其扩大为1.05倍，得mm d 26.222.2105.11=⨯≥，按标准GB2822-81的R10圆整后取d=25mm 。

三．设计轴的结构3.1确定机体和轴的结构形式箱体内无传动件，不需经常拆卸，箱体采用整体式。

由轴的功能可知，该轴应具有带轮、齿轮的安装段，两个轴承的安装段以及两个轴承对外的密封段，共7段尺寸。

由于没有轴向力的存在，且载荷、转速较低，故选用深沟球轴承。

由于传递功率小，转速不高，发热小，故轴承采用两端固定式。

由于轴转速较低，且两轴承间无传动件，所以采用脂润滑、毛毡圈密封。

确定轴的草图如图1所示：图1 确定轴的草图3.1．阶梯轴各部分直径的确定1) 轴段1和7轴段1和轴段7分别安放大带轮和小齿轮，所以其长度由带轮和齿轮轮毂长度确定，而直径由初算的最小直径得到。

所以，mm d d 2571==。

2) 轴段2和6轴段2和轴段6的确定应考虑齿轮、带轮的轴向固定和密封圈的尺寸。

由参考文献[3]图10.9计算得到轴肩高度mm h d d d )30~5.28(21162=⨯+==由参考文献[3]表14.4取毡圈油封直径mm d 29=，取轴径mm d d 3062==。

哈工大机械原理大作业2-29

设计说明书1 设计题目如图所示直动从动件盘形凸轮机构，其原始参数见表2-1。

从表2-1中选择一组凸轮机构的原始参数，据此设计该凸轮机构。

2、推杆升程、回程运动方程及位移、速度、加速度线图2.1凸轮运动分析推程运动方程; 01cos 2h s πϕ⎡⎤⎛⎫=-⎢⎥ ⎪Φ⎝⎭⎣⎦100sin 2h v πωπϕ⎛⎫=⎪ΦΦ⎝⎭221200cos 2h a πωπϕ⎛⎫= ⎪ΦΦ⎝⎭回程运动方程：()'1s s hϕ-Φ+Φ⎡⎤=-⎢⎥Φ⎣⎦1'hvω=-Φa=2.2求位移、速度、加速度线图MATLAB源程序pi=3.1415926;c=pi/180;h=140;f0=120;fs=45;f01=90;fs1=105;%升程阶段f=0:1:360;for n=0:f0s(n+1)=h/2*(1-cos(pi/f0*f(n+1)));v(n+1)=pi*h/(2*f0*c)*sin(pi/f0*f(n+1));a(n+1)=pi^2*h/(2*f0^2*c^2)*cos(pi/f0*f(n+1));end%远休止阶段for n=f0:f0+fss(n+1)=140;v(n+1)=0;a(n+1)=0;end%回程阶段for n=f0+fs:f0+fs+f01s(n+1)=h*(1-(f(n+1)-(f0+fs))/f01);v(n+1)=-h/(f01*c);a(n+1)=0;end;%近休止阶段for n=f0+fs+f01:360;s(n+1)=0;v(n+1)=0;a(n+1)=0;endfigure(1);plot(f,s,'r');xlabel('\phi/\circ');ylabel('s/mm');grid on;title('推杆位移线图')figure(2);plot(f,v,'r');xlabel('\phi/\circ');ylabel('v/\ommiga');grid on;title('推杆速度线图') figure(3);plot(f,a,'r');xlabel('\phi/\circ');ylabel('a/\ommiga');grid on;title('推杆加速度线图')2.3位移、速度、加速度线图3 凸轮机构的dssdϕ-线图，确定基圆半径和偏心距3.1理论分析机构压力角α应按下式计算：以d s/dφ为横坐标，以s(φ)为纵坐标，可作出d s/dφ-s(φ)曲线如图4-16所示，再作斜直线D t d t 与升程的[d s/dφ-s(φ)]曲线相切并使与纵坐标夹角为升程[α]，则D t d t线的右下方为选择凸轮轴心的许用区。

黑龙江哈尔滨工业大学机械课程机器人技术课程大作业

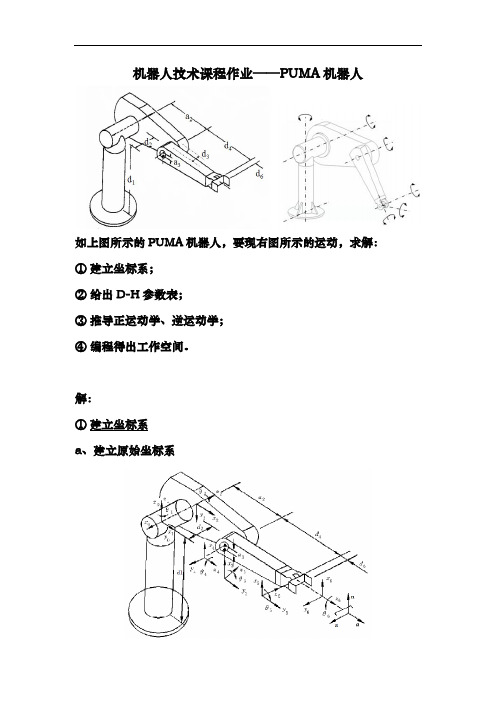
机器人技术课程作业——PUMA机器人如上图所示的PUMA机器人，要现右图所示的运动，求解：①建立坐标系；②给出D-H参数表；③推导正运动学、逆运动学；④编程得出工作空间。

解：①建立坐标系a、建立原始坐标系b 、坐标系简化② 给出D-H 参数表a 、PUMA 机器人的杆件参数1d 0.6604m =，2d 0.14909m =，4d 0.43307m =，6d 0.05625m = 2a 0.4318m =，3a 0.02032m =b 、D-H 参数表关节i i θ i α i L i d运动围 1 90 0 0 0-160o ~160o2 0 -90 02d 0.14909m = -225o ~45o3-902a 0.4318m =-45o ~225o4 0 -90 3a 0.02032m = 4d 0.43307m =-110 o~170 o 590-100 o~100 o③ 推导正运动学、逆运动学 a 、正运动学推导由式111111111100001ii i i i i i i i i i ii i i i i i i c s a s c c c s d s T s s c s c d c θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦可得： 111101000000100001c s s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦222122200001000001c s d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦33233230000010001c s a s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦44343444000100001c s a d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦ 554555000010000001c s T s c -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦ 665666000010000001c s T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦由00123456123456T T T T T T T =，得机械手变换矩阵：601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦23654164123651654164123654164123651654164123654642365()()()x y z n c c c c c s s c s c s c c c s s s c s n c c c c s s s s s c s s c c s c s c c n s c c c s s c c s =--++=----=--- 23654164123651654164123654164123651645164123654642365()()()x y z o c s c c c c s c s s s c s c s s c c s o c s c c s c s s s s s s s s c c c c c o s s c c s s c c s =-++-+=-+++-=++2354123515412354123515412352354x y z a c s c c s c c s s s a c s c s s c s s s c a c c s s c =---=--+=-+3231221423121323122142312142332322x y z p a c c a c c d s c d s p a c s a c s d s s d c p d c a s a s =+--=+-+=---b 、逆运动学推导 1)．求1θ用逆变换011T -左乘方程00123456123456T T T T T T T =两边：10123451623456T T T T T T T -=11111600000010000101xx x x yy y y zz z z c s n o a p s c n o a p T n o a p ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦得112x y s p c p d -+=三角代换 cos x p ρφ=，sin y p ρφ=式中，ρ=tan 2(,)x y a p p φ=得到1θ的解12a tan 2(,)a tan 2(,y x p p d θ=-2)．求3θ矩阵方程两端的元素（1，4）和（2，4）分别对应相等113232242342332322x y z c p s p a c a c d s p d c a s a s +=+-⎧⎨-=++⎩ 平方和为：4333d s a c k += 其中 2222222242322x y z p p p d d a a k a ++----=解得：334a tan 2(,)a tan 2(,a d k θ=- 3)．求θ在矩阵方程00123456123456T T T T T T T =两边左乘逆变换013T -。

哈工大——机器人技术作业

机器人技术作业（轨迹规划）姓名：学号：专业：机械工程定义下列变量：t ：归一化时间变量，[0,1]t ∈τ：实际时间，单位为秒i τ：第i 段轨迹终点的实际时间1i i t ττ-=-：通过第i 段轨迹所需的实际时间在每段轨迹中关节变量的多项式用归一化时间表示为：432111413121110321223222120432133433323130()()()()h t a t a t a t a t a h t a t a t a t a h t a t a t a t a t a =++++=+++=++++第1段（第2段）（第3段）这些关节轨迹分段多项式所应满足的边界条件： 1、初始点位置：00θθ=（t ） 2、初始速度的幅值：0ν（通常为0） 3、初始加速度的幅值：0a （通常为0） 4、提升点位置：11()t θθ=5、 1t 时刻位置的连续性：11()()t t θθ-+=6、 1t 时刻速度的连续性：11()()t t νν-+=7、 1t 时刻加速度的连续性：11()()a t a t -+=8、下落点位置：22()t θθ=9、2t 时刻位置的连续性：22()()t t θθ-+= 10、 2t 时刻速度的连续性：22()()t t νν-+= 11、 2t 时刻加速度的连续性：22()()a t a t -+= 12、终止点位置：()f f t θθ= 13、终止速度的幅值：(0)f ν通常为 14、终止加速度的幅值：a (0)f 通常为下面求取各段轨迹的系数对于第一段轨迹：43211141312111032114131211111121141312112211()432()()1262()()h t a t a t a t a t a a t a t a t a h t t t t a t a t a h t a t t t ν=+++++++==++==由第一个边界条件（初始点位置：00θθ=（t ））可知：100a θ=由第二个边界条件（初始速度的幅值：0ν（通常为0））可知： 1101a t ν=由第三个边界条件（初始加速度的幅值：0a （通常为0））可知： 201122a t a = 由第六个边界条件（1t 时刻速度的连续性：11()()t t νν-+=）以及上述结果可知：2141301011111143(1)(1)a a a t t h t t ννν∆+++===由第七个边界条件（1t 时刻加速度的连续性：11()()a t a t -+=）以及上述结果可知：21413011112211126(1)(1)a a a t h a a t t ∆++=== 对于第二段轨迹：32122322212021232221222212322222222()32()()62()()h t a t a t a t a a t a t a h t t t t a t a ht a t t t ν=+++++==+== 由第四个边界条件（下落点位置：11()t θθ=）可知：201(0)a θ=由第六个边界条件（1t 时刻速度的连续性：11()()t t νν-+=）可知：2112a t ν=由第七个边界条件（1t 时刻加速度的连续性：11()()a t a t -+=）可知：212222a t a = 由第十个边界条件（2t 时刻速度的连续性：22()()t t νν-+=）可知： 23222122232222232(1)62(1)a a a t a a a t ν++=+=对于第三段轨迹：432133433323130()h t a t a t a t a t a =++++将上式中以1t t =-代替t ，可以将归一化时间t 由[0,1][1,0]t t ∈∈-移至则：43213343332313032133433323133321334333232233()()432()()1262()h t a t a t a t a t a h t a t a t a t a t t t h t a t a t a a t t t ν=+++++++==++== 由第十二个边界条件（终止点位置：()f f t θθ=）可知：30f a θ=由第十三个边界条件（终止速度的幅值：(0)f ν通常为）可知：313f a t ν=由第十四个边界条件（终止加速度的幅值：a (0)f 通常为）可知：23322f a t a =另外由中间点处的速度和加速度连续的边界条件可以得到下面4个方程：2130101211421111213012214222221112343333232221322223433323222223223406212043320126620f f f a a t t a a t t t t t a a t a a t t t t a a a t t a a a t t t t a a a t a a t t t νν-++++=-+++=-+-+++=-+-++=由各相连轨迹段间关节角之差可以得到一下三个方程：20111011141301221222322212333323334333(1)(0)2(1)(0)(0)(1)2f a t h h a a t h h a a a a t h h a a t δθθνδθθδθθν=-=-=+++=-=-=++=-=--=-+-+由上述七个等式可以得到轨迹多项式的七个系数，用矩阵改写方程如下：y Cx =其中：2230110*********,,,,,,22Tf f f f f a t a t y t a t a a t a t δννδνδν⎡⎤=------++-⎢⎥⎢⎥⎣⎦[]13142122233334,,,,,,TX a a a a a a a =1122221122223322222233110000034100006122000000111001233400266120000011t t t t t t C t t t t t t t t t ⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎣⎦因而有：1X C Y -=对于第三段轨迹，把归一化时间t 由[]1,0-重新变回[]0,1可以解出最终结果。

2021年哈工大继续教育机械工程专业课作业第2部分参考

2021年哈工大继续教育机械工程专业课作业第2部分参考2021年哈工大继续教育机械工程专业课作业第2部分参考,有利于学生进一步分析和更好的完成作业。

仅做参考,特此提示。

2021年黑龙江省专业技术人员继续教育知识更新培训机械工程专业作业参考4-5题说明：中、高级职称学员“专业课作业”为论述题1-5题；同时提交3000字左右“学习心得”一篇。

论述题4.试述轮式移动机器人的位置控制精度远不如操作臂型机器人定位精度，为实现大范围内灵活移动和较高操作定位精度，试给出采用轮式移动机器人与操作臂型机器人联合创新设计的方案及完成作业控制策略。

机器人如何知道自己所在的位置？移动机器人一边移动一边知道自己所处的位置是非常重要的而且也是必须的。

移动机器人是用计算机控制来工作的。

计算机对所有的信息进行数字处理，移动机器人的位置和姿态是用数字表示的。

即在地面上建立二维坐标系，将移动机器人坐标位置与方向用数值表示即可以了。

机器人的移动环境地图可以描述在同一坐标系中，从当前的位置姿态来看立即就能明白移动机器人在地图上位于何处。

测程法：是移动机器人推定当前所处位置和姿态常用的方法，是对车体速度积分的方法。

车体的速度是根据车轮单位时间转过的角度求得的。

因此，由单位时间内车轮转角的积分就可以计算出移动机器人当前所的位置和姿态。

这些物理量当然能够有传感器测得。

上述有关移动机器人位置和姿态推算的测和法是最基本的方法。

可是，当机器人车轮一旦产生滑移，如上所述方法中积分挖法就会产生误差。

行走距离越远产生的误差就越大。

车轮的回转角、角速度的测量方法独立二轮驱动型移动机器人的行进方向速度V和回转角速度ω可用公式计算出来。

因此为用测程法计算行进方向速度V和回去转角速度ω，测量回转轴转角的传感器除上述提到的光电编码器外，还有测速电机、电位计等等。

轮式移动机器人的控制方法：由与位移成比例的操纵机构操纵的直线行走；与位移、位移的时间微分成比例操纵方法的直线行走；独立二轮驱动型移动机器人的直线行走。

哈工大机械设计大作业

哈工大机械设计大作业哈尔滨工业大学机械设计大作业：汽车零部件设计引言：本次机械设计大作业的题目是汽车零部件的设计，本文将详细介绍该零部件的设计需求、设计方案、设计计算以及制造工艺等相关内容。

一、设计需求：该汽车零部件是一种在车辆发动机舱内起到隔热保温作用的零部件，其要求具备以下特点：1.具备良好的隔热保温性能，能够有效降低发动机舱内的温度。

2.具备良好的耐高温性能，能够在高温环境下长时间稳定工作。

3.具备较高的强度和刚度，能够承受汽车运行时的振动和冲击力。

二、设计方案：为了满足上述设计需求，我们选择使用陶瓷材料作为该零部件的材料，该材料具备良好的隔热性能和耐高温性能，并且具备较高的强度和刚度。

三、设计计算：1.隔热性能计算：根据该零部件的尺寸和所使用的陶瓷材料的导热系数，计算出其热传导率，进而计算出其隔热性能。

2.强度计算：根据该零部件所承受的力和所使用的陶瓷材料的弹性模量，计算出其应力和变形情况，进行强度计算。

3.刚度计算：根据该零部件所承受的力和所使用的陶瓷材料的弹性模量，计算出其刚度，并与设计要求进行对比。

四、制造工艺：1.材料选取：根据设计方案选择合适的陶瓷材料，并进行材料实验验证其性能。

2.模具设计：根据零部件的几何形状设计合适的模具，并制造出模具。

3.注塑成型：使用模具对陶瓷材料进行注塑成型，并在合适的温度和压力条件下进行成型工艺。

4.烧结处理：对注塑成型后的零部件进行烧结处理，使其形状固定并获得良好的耐高温性能。

5.精加工：对烧结后的零部件进行精加工，如修磨、打磨等工艺，以达到设计要求的尺寸和表面质量。

五、结论：通过对该汽车零部件的设计需求、设计方案、设计计算以及制造工艺的详细论述，我们可以得出结论：1.该零部件的设计方案合理，能够满足设计需求。

2.该零部件所选用的陶瓷材料具备良好的隔热保温性能和耐高温性能。

3.该零部件的制造工艺合理，能够实现零部件的精确加工。

综上所述，本次机械设计大作业详细介绍了汽车零部件的设计需求、设计方案、设计计算以及制造工艺等内容，并得出了相应的结论。

机械动力学大作业哈尔滨工业大学

大作业：如下图所示，两端简支梁（自己也可设定其他支承形式，如悬臂梁等），梁的截面尺寸及材料属性如下。

横截面积A = 1.006 x 10-2 m2截面惯性矩I = 1.774 x 10-4 m 4梁的高度 h = 0.3063 m 弹性模量E = 207x109 Nm -2密度 ρ= 7860 kg/m 3 泊松比可设定为0.25，响应计算时阻尼自己设定（小于0.05即可），要求完成如下分析计算： 1. 梁的固有频率理论值（1000Hz 以内）2. 利用有限元方法，分别用梁单元及板单元计算其固有频率及振型，同时分析不同单元数对计算结果的影响（如单元数为2、5、10、20、50、100等）；3. 在有限元软件中利用模态叠加法进行响应计算（取前10阶模态）：激振力为正弦形式，作用点与幅值自己设定，频率5-250Hz 范围内，步长5Hz 。

4. 计算至少3个频响函数。

撰写报告时要注意：报告要有理论说明，步骤要尽量详细。

计算结果用图表形式表示。

1 梁的固有频率理论值（1000Hz 以内）解：由参考文献可知，假设等截面简支梁长度为l ，抗弯刚度为EI ，密度为ρ，横截面积为A ，r表示第r 阶振型，则可以得到简支梁的自由振动的固有频率为：r w =由Matlab 计算梁的前十阶固有频率如下图所示：计算程序为：function NatFre = Natural_frequency_10 ( A , h , Rou , L , E , I ) clc; %其中，A=横截面积，h=梁高度，Rou=材料密度，L为梁长度clear; % E=材料的弹性模量，I=截面惯性矩NatFre = randn(1,10,'double');for r = 1 : 10NatFre[r] = r*r*pi*pi*sqrt( E*I /(A*h*Rou*L^3) );NatFre = NatFre / (2*pi) ;end2 利用有限元方法，分别用梁单元及板单元计算其固有频率及振型，同时分析不同单元数对计算结果的影响（如单元数为2、5、10、20、50、100等）；(1)梁单元模型a 单元数为2 时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.840 1 1 12 56.601 1 2 23 141.47 1 3 34 143.93 1 4 45 255.98 1 5 5第1阶模态振型（单元数为2）：第2阶模态振型（单元数为2）：第3阶模态振型（单元数为2）：第4阶模态振型（单元数为2）：第5阶模态振型（单元数为2）：b 单元数为5 时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.791 1 1 12 51.083 1 2 23 115.06 1 3 34 140.88 1 4 45 206.14 1 5 5第1阶模态振型（单元数为5）：第2阶模态振型（单元数为5）：第3阶模态振型（单元数为5）：第5阶模态振型（单元数为5）：c 单元数为10时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.789 1 1 12 51.004 1 2 23 114.22 1 3 34 140.45 1 4 45 201.85 1 5 5第2阶模态振型（单元数为10）：第3阶模态振型（单元数为10）：第5阶模态振型（单元数为10）：d 单元数为20时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.789 1 1 12 50.999 1 2 23 114.16 1 3 34 140.34 1 4 45 201.54 1 5 5第2阶模态振型（单元数为20）：第3阶模态振型（单元数为20）：第5阶模态振型（单元数为20）：e 单元数为50时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.789 1 1 12 50.999 1 2 23 114.16 1 3 34 140.31 1 4 45 201.51 1 5 5第2阶模态振型（单元数为50）：第3阶模态振型（单元数为50）：第5阶模态振型（单元数为50）：f 单元数为100时的固有频率：SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 12.789 1 1 12 50.999 1 2 23 114.16 1 3 34 140.31 1 4 45 201.51 1 5 5第2阶模态振型（单元数为100）：第3阶模态振型（单元数为100）：第5阶模态振型（单元数为100）：由以上可以看出，当选定为梁单元时，选择的划分网格的单元数越多，所得到的固有频率与理论值越精确。