导数中的任意性与存在性问题探究
求解任意性问题与存在性问题

3. 不同函数,相等关系 求值域
(1)x A, f (x) g(x) y f (x) g(x)有零点 (2)x1 A,x2 B, f (x1) g(x2)成立
{ f (x) | x A} {g(x) | x B}
(3)x1 A,x2 B, f (x1) g(x2)成立 { f (x) | x A} {g(x) | x B}
(1)若对 x [3,,3都] 有 f (x) 成g(立x),求 范围;k (2)若对 x [3,都3] 有 f (x) 成g(立x),求 范围;k
1.不同函数,相同变量 构造函数求最值
(1)x A, f (x) g(x)成立 [ f (x) g(x)]max 0 [g(x) f (x)]min 0
f (x1)max g(x2 )min
(2)x1 A,x2 B, f (x1) g(x2 )成立 f (x1)min g(x2 )min
(3)x1 A, x2 B, f (x1) g(x2 )成立 f (x1)min g(x2 )max
(4)x1 A, x2 B, f (x1) g(x2 )成立
f (x1)max g(x2 )max
活动探究
1.已知两个函数 f (x) 8x2 16x k, x [3,3]
g(x) 2x3 5x2 4x, x [3,3], k R
(1)若对 x [3,,3都] 有 f (x) g成(立x) ,求 范围k; (2)若对 x [3,都3] 有 f (x) 成g(立x),求 范围;k
(2)x A, f (x) g(x)成立 [ f (x) g(x)]min 0 [g(x) f (x)]max 0
高中数学例谈和导数有关的“任意”与“存在”问题

例谈和导数有关的“任意”与“存在”问题考点一单一任意与存在问题(1)∀x ,使得f (x )>g (x ),只需h (x )min =[f (x )-g (x )]min >0.如图①.(2)∃x ,使得f (x )>g (x ),只需h (x )max =[f (x )-g (x )]max >0.如图②.[典例]设函数f (x )=ln(1+x ),g (x )=af ′(x ),其中f ′(x )是f (x )的导函数.(1)若对于任意x ≥0,总有f (x )≥g (x ),求实数a 的取值范围;(2)若存在x ≥0,使得f (x )≥g (x ),求实数a 的取值范围.[解析](1)设h (x )=f (x )-g (x )=ln(1+x )-a 1+x(x ≥0),则h ′(x )=11+x +a (1+x )2=x +1+a (1+x )2.当a ≥-1时,h ′(x )≥0,h (x )在[0,+∞)上单调递增,∴h (x )≥h (0)=-a ,则-a ≥0,a ≤0,∴a ∈[-1,0].当a <-1时,ln(1+x )≥0,-a 1+x>0,所以h (x )≥0恒成立.综上可知,实数a 的取值范围为[-∞,0].(2)由(1)可知,当a ≥-1时,存在x ≥0,使得f (x )≥g (x ),当a <-1时,f (x )≥g (x )恒成立.综上可知,实数a 的取值范围为(-∞,+∞).[关键点拨](1)这是较为常见的一类恒成立问题,运用数形结合的思想可知,当x 0≥0时,总有f (x 0)≥g (x 0),即f (x 0)-g (x 0)≥0(注意不是f (x )min ≥g (x )max ),可以转化为当x ≥0时,h (x )=f (x )-g (x )≥0恒成立问题.(2)存在x ≥0,使得f (x )≥g (x ),即至少有一个x 0≥0,满足f (x 0)-g (x 0)不是负数,可以转化为当x ≥0时,h (x )=f (x )-g (x )的函数值至少有一个是非负数.考点二双任意与存在相等问题“若∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2)”与“∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2)”的辨析(1)∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2)等价于函数f (x )在D 1上的值域A 与g (x )在D 2上的值域B 的交集不是空集,即A ∩B ≠∅,如图③.其等价转化的目标是两个函数有相等的函数值.(2)∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2)等价于函数f (x )在D 1上的值域A 是g (x )在D 2上的值域B 的子集,即A ⊆B ,如图④.其等价转化的目标是函数y =f (x )的值域都在函数y =g (x )的值域之中.说明:图③,图④中的条形图表示函数在相应定义域上的值域在y 轴上的投影.[典例]已知函数f (x )=x 2-23ax 3,a >0,x ∈R ,g (x )=1x 2(1-x ).(1)若∃x 1∈(-∞,-1],∃x 2f (x 1)=g (x 2),求实数a 的取值范围;(2)当a =32时,求证:对任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)=g (x 2).[解析](1)∵f (x )=x 2-23ax 3,∴f ′(x )=2x -2ax 2=2x (1-ax ).令f ′(x )=0,得x =0或x =1a.∵a >0,∴1a >0,∴当x ∈(-∞,0)时,f ′(x )<0,∴f (x )在(-∞,-1]上单调递减,f (x )≥f (-1)=1+2a 3,故f (x )在(-∞,-1]上的值域为1+2a 3,+∵g (x )=1x 2(1-x ),∴g ′(x )=3x 2-2x x 4(1-x )2=3x -2x 3(1-x )2.当x <-12时,g ′(x )>0,∴g (x )∞g (x )<=83,故g (x )∞∞若∃x 1∈(-∞,-1],∃x 2∞f (x 1)=g (x 2),则1+2a 3<83,解得0<a <52,故实数a(2)证明:当a=32时,f(x)=x2-x3,∴f′(x)=2x-3x2=3当x>2时,f′(x)<0,∴f(x)在(2,+∞)上单调递减,且f(2)=-4,∴f(x)在(2,+∞)上的值域为(-∞,-4).则g(x)=1x2(1-x)=1f(x)(1,+∞)上单调递增,∴g(x)=1x2(1-x)在(1,+∞)上的值域为(-∞,0).∵(-∞,-4) (-∞,0),∴对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)=g(x2).[关键点拨]本题第(1)问等价转化的基本思想是:两个函数有相等的函数值,即它们的值域有公共部分;第(2)问等价转化的基本思想是:函数f(x)的任意一个函数值都与函数g(x)的某一函数值相等,即f(x)的值域都在g(x)的值域中.考点三双任意与双存在不等问题f(x),g(x)是闭区间D上的连续函数,“∀x1,x2∈D,使得f(x1)>g(x2)”与“∃x1,x2∈D,使得f(x1)>g(x2)”的辨析(1)f(x),g(x)是在闭区间D上的连续函数且∀x1,x2∈D,使得f(x1)>g(x2),等价于f(x)min>g(x)max.其等价转化的目标是函数y=f(x)的任意一个函数值均大于函数y=g(x)的任意一个函数值.如图⑤.(2)存在x1,x2∈D,使得f(x1)>g(x2),等价于f(x)max>g(x)min.其等价转化的目标是函数y=f(x)的某一个函数值大于函数y=g(x)的某些函数值.如图⑥.[典例]已知f(x)=x+a2x(a>0),g(x)=x+ln x.(1)若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,求实数a的取值范围;(2)若存在x1,x2∈[1,e],使得f(x1)<g(x2),求实数a的取值范围.[解析](1)对任意的x 1,x 2∈[1,e],都有f (x 1)≥g (x 2)成立,等价于x ∈[1,e]时,f (x )min ≥g (x )max .当x ∈[1,e]时,g ′(x )=1+1x>0,所以g (x )在[1,e]上单调递增,所以g (x )max =g (e)=e +1.只需证f (x )≥e +1,即x +a 2x≥e +1⇔a 2≥(e +1)x -x 2在[1,e]上恒成立即可.令h (x )=(e +1)x -x 2,当x ∈[1,e]时,h (x )=(e +1)x -x 2的最大值为.所以a 2,即a ≥e +12(舍去负值).故实数a 的取值范围是e +12,+(2)存在x 1,x 2∈[1,e],使得f (x 1)<g (x 2),等价于x ∈[1,e]时,f (x )min <g (x )max .当x ∈[1,e]时,g ′(x )=1+1x>0,所以g (x )在[1,e]上单调递增,所以g (x )max =g (e)=e +1.又f ′(x )=1-a 2x2,令f ′(x )=0,得x =a ,故f (x )=x +a 2x(a >0)在(0,a )上单调递减,在(a ,+∞)上单调递增.当0<a <1时,f (x )在[1,e]上单调递增,f (x )min =f (1)=1+a 2<e +1,符合题意;当1≤a ≤e 时,f (x )在[1,a ]上单调递减,在[a ,e]上单调递增,f (x )min =f (a )=2a ,此时,2a <e +1,解得1≤a <e +12;当a >e 时,f (x )在[1,e]上单调递减,f (x )min =f (e)=e +a 2e ,此时,e +a 2e <e +1,即a <e ,与a >e 矛盾,不符合题意.综上可知,实数a [关键点拨](1)本题第(1)问从数的角度看,问题的本质就是f (x )min ≥g (x )max .从形的角度看,问题的本质就是函数f (x )图象的最低点不低于g (x )图象的最高点.(2)本题第(2)问从数的角度看,问题的本质就是f (x )min <g (x )max .从形的角度看,问题的本质就是函数f (x )图象的最低点低于g (x )图象的最高点.考点四存在与任意嵌套不等问题(1)∀x 1∈D 1,∃x 2∈D 2,使f (x 1)>g (x 2),等价于函数f (x )在D 1上的最小值大于g (x )在D 2上的最小值,即f (x )min >g (x )min (这里假设f (x )min ,g (x )min 存在).其等价转化的目标是函数y =f (x )的任意一个函数值大于函数y =g (x )的某一个函数值.如图⑦.(2)∀x 1∈D 1,∃x 2∈D 2,使f (x 1)<g (x 2),等价于函数f (x )在D 1上的最大值小于g (x )在D 2上的最大值,即f (x )max <g (x )max .其等价转化的目标是函数y =f (x )的任意一个函数值小于函数y =g (x )的某一个函数值.如图⑧.[典例]已知函数f (x )=ln x -14x +34x-1,g (x )=x 2-2bx +4,若对任意的x 1∈(0,2),总存在x 2∈[1,2],使f (x 1)≥g (x 2),求实数b 的取值范围.[解析]依题意知f (x )在(0,2)上的最小值不小于g (x )在[1,2]上的最小值,即f (x )min ≥g (x )min .因为f ′(x )=1x -14-34x 2=-(x -1)(x -3)4x 2,则当0<x <1时,f ′(x )<0,f (x )单调递减;当1<x <2时,f ′(x )>0,f (x )单调递增,所以当x ∈(0,2)时,f (x )min =f (1)=-12.又g (x )=x 2-2bx +4,①当b <1时,可求得g (x )min =g (1)=5-2b .由5-2b ≤-12,解得b ≥114,这与b <1矛盾,不符合题意;②当1≤b ≤2时,可求得g (x )min =g (b )=4-b 2.由4-b 2≤-12,得b 2≥92,这与1≤b ≤2矛盾,不符合题意;③当b >2时,可求得g (x )min =g (2)=8-4b .由8-4b ≤-12,得b ≥178.综合①②③得,实数b 的取值范围是178,+[关键点拨]“对任意x 1∈(0,2),总存在x 2∈[1,2],使f (x 1)≥g (x 2)”等价于“f (x )在(0,2)上的最小值大于或等于g (x )在[1,2]上的最小值”.。
(完整版)函数导数任意存在”-型问题归纳总结,推荐文档

战略思想三: x R ,都有" f (x1) f (x) f (x2 )" f (x1), f (x2 ) 分别是 f (x) 的最小值和最大值, | x1 x2 | min 是同时出现最大值和最小值的最短区间.
y x1
x2 x
例 3.
已知函数
f
(x) 2sin( x 2
) ,若对 5
" f ( x1 x2 ) f (x1) f (x2 ) "恒成立的函数的个数是( )
2
2
A.0 B.1 C.2 D.3
解:本题实质就是考察函数的凸凹性,即满足条件" f ( x1 x2 ) f (x1) f (x2 ) "的函数,应是凸函
2
2
数的性质,画草图即知 y log2 2x 符合题意;
即 f (x) 在[1,1]上为增函数.
∵ f (1) 1,∴ x [1,1] ,恒有 f (x) 1; ∴要使 f (x) t2 2at 1 对所有 x [1,1] , a [1,1] 恒成立,
即要 t2 2at 1 1恒成立,故 t2 2at 0 恒成立,
令 g(a) 2at t2 ,只须 g(1) 0 且 g(1) 0 ,
x R ,都有"
f
(x1)
f (x)
f
(x2 )" 成立,则
| x1 x2 | 的最小值为____.
解 ∵对任意 x∈R,不等式 f (x1) f (x) f (x2 ) 恒成立,
∴ f (x1), f (x2 ) 分别是 f (x) 的最小值和最大值.
对于函数 y sin x ,取得最大值和最小值的两点之间最小距离是 π,即半个周期.
解得 t 2 或 t 0 或 t 2 .
高中数学导数题中的“任意”与“存在”

导数题中的“任意”与“存在”常见这样一类导数问题:对区间内任意自变量,不等式成立,求参数取值范围;或在区间内存在一个自变量,不等式成立,求参数取值范围等等.由于这类问题本身的抽象性及隐蔽性,同学们在解决这类问题时,感到束手无策.为使这类问题解决有章可循,有法可依,本文拟对常见的该类问题进行分类并说明其求解策略,以供参考.例 已知两个函数2()728f x x x c =--,32()2440g x x x x =+-. (1)若对任意的[2,3]x ?,都有()2f x >成立,求实数c 的取值范围; (2)若对任意的[2,3]x ?,都有()()f x g x >成立,求实数c 的取值范围; (3)若对任意的1[2,3]x ?,2[3,3]x ?,都有12()()f x g x >成立,求实数c 的取值范围;(4)若存在0[2,3]x ?,使0()2f x >成立,求实数c 的取值范围; (5)若存在0[2,3]x ?,使00()()f x g x >成立,求实数c 的取值范围;(6)若存在1[2,3]x ?,2[3,3]x ?,使12()()f x g x >成立,求实数c 的取值范围; (7)若存在1[2,3]x ?,2[3,3]x ?,使12()()f x g x =成立,求实数c 的取值范围; (8)若对任意的1[2,3]x ?,总存在2[3,3]x ?,使12()()f x g x >成立,求实数c 的取值范围;(9)若对任意的1[2,3]x ?,总存在2[3,3]x ?,使12()()f x g x =成立,求实数c 的取值范围;(10)若对任意的1[2,3]x ?,总存在2[3,3]x ?,使12()()f x g x <成立,求实数c 的取值范围.为解决上述问题方便,我们先求()f x 在[2,3]-上的最大值和最小值,()g x 在[3,3]-上的最大值和最小值.2()728f x x x c =--,对称轴2x =,当[2,3]x ?时,()f x 在区间(1,2)-上递减,在区间(2,3)上递增.max ()(2)84f x f c =-=-,min ()(2)28f x f c ==--. 32()2440g x x x x =+-,22()68402(3420)2(310)(2)g x x x x x x x ¢=+-=+-=+-,令()0g x ¢=,解得103x =-或2x =, 当[3,3]x ?时,()g x 在区间(3,2)-上递减,在区间(2,3)上递增.(3)102g -=,(3)30g =-,max ()102g x =,min ()(2)48g x g ==-.上述问题可分为下面三类:一、对区间内任意自变量,不等式成立型 (1)~(3)属于此类型.(1)解:min ()2f x >,282c -->,30c <-.评注:若对任意[,]x a b Î,不等式()f x m >(或()f x m >)恒成立,则需要函数在该区间上的最小值大于m (或最大值小于m ).(2)解:设32()()()2312h x f x g x x x x c =-=-++-,2()66126(2)(1)h x x x x x ¢=-++=--+.()h x 在区间(2,1)--,(2,3)上递减,在区间(1,2)-上递增. (1)7h c -=--,(3)9h c =-,min ()7h x c =--. min ()0h x >,7c <-.评注:对任意的[,]x a b Î,都有()()f x g x >成立,是不同函数对同一变量下的恒成立问题,如图1,()y f x =的图象恒在()y g x =的图象上方,设()()()h x f x g x =-,则可转化为求()h x 的最小值大于0即可.本题易错误认为min max ()()f x g x >.若函数(),()f x g x 在区间[,]a b 上恒为正值,此类问题也可以设()()()f x h xg x =,让()h x 的最小值大于1即可.图1(3)解:min max ()()f x g x >,28102c -->,130c <-.评注:本题12,x x 是两个无关的变量1()f x 和2()g x 的取得互不影响,所以只需使()f x 的最小值大于()g x 的最大值.我们用图2表示()f x 在[2,3]-上的值域,用图2表示()g x 在[3,3]-上的值域. 固定图2,使图3竖直上下移动,只有如图4所示时才能符合题意.f (x )maxg (x )ma f (x )ming (x )mig (x )max g (x )ming (x )minf (x )ming (x )max f (x )max图2 图3 图4 二、区间内存在自变量,使不等式(等式)成立型 (4)~(7)属于此类型.(4)解:max ()2f x >,842c ->,82c <.评注:存在0[,]x a b Î,使0()f x m > (或0()f x m <)成立, 只需函数()f x 在区间[,]a b 上的最大值max ()f x m >(或min ()f x m <).本题易错误认为min ()f x m >.(5)解:设()()()h x f x g x =-,存在0[2,3]x ?,使0()0h x >,转化为(4)类型,只需max ()0h x >.(2)4h c -=-,(2)20h c =-,max ()20h x c =-.200c ->,20c <.评注:存在0[,]x a b Î,使00()()f x g x >(或00()()f x g x <)成立,此类问题强调的是不同函数在同一变量下的函数值大小的问题,应设()()()h x f x g x =-,可转化为让函数()h x 的最大值大于O (或()h x 的最小值小于O )即可.本题容易与恒成立问题混淆,从而错误的去让函数()h x 的最小值大于0. 若函数(),()f x g x 在区间[,]a b 上恒为正值,此类问题也可以设()()()f x h xg x =. (6)解:max min ()()f x g x >,8448c ->-,132c <.评注:存在1[,]x a b Î,2[,]x c d Î,使12()()f x g x >成立,满足max min ()()f x g x >,如图5.g (x )minf (x )ming (x )max f (x )max图5(7)解:max min min max.()(),()()f x g x f x g x ì³ïïíï£ïî8448,28102.c c ì-?ïïíï--?ïî130132c -#. 评注:若存在1[,]x a b Î,2[,]x cd Î,使12()()f x g x =成立,要求()f x 的值域和()g x 的值域交集不为空,即max min ()()f x g x ³,如图6,且min max ()()f x g x £,如图7.f (x )maxg (x )max f (x )ming (x )minf (x )maxg (x )max f (x )ming (x )min图6 图7 三、任意、存在同时出现,使不等式(等式)成立型 (8)~(9)属于此类型.(8)解:min min ()()f x g x >,2848c -->-,20c <评注:对任意的1[,]x a b Î,总存在2[,]x c d Î,使12()()f x g x >成立,就是说1x 取区间[,]a b 上的任意一个值,总存在2[,]x c d Î,使得21()()g x f x <,就要求min min ()()f x g x >,如图8.g (x )minf (x )ming (x )maxf (x )max图8(9)解:max max min min.()(),()()g x f x g x f x ì³ïïíï£ïî10284,4828.c c ì?ïïíï-?-ïî1820c -#.评注:对任意的1[,]x a b Î,总存在2[,]x c d Î,使12()()f x g x =成立,就是说1x 取区间[,]a b 上的任意一个值,总存在2[,]x c d Î,使得21()()g x f x =,就要求函数()g x 的值域包含函数()f x 的值城,如图9.f (x )max f (x )ming (x )maxg (x )min图9(10)解:max max ()()f x g x <,84102c -<,18c >-.评注:对任意的1[,]x a b Î,总存在2[,]x c d Î,使12()()f x g x <成立,就是说1x 取区间[,]a b 上的任意一个值,总存在2[,]x c d Î,使得21()()g x f x >,就要求max max ()()f x g x <,如图10.g(x)max f(x)maxg(x)min f(x)min图10。
函数导数任意存在”-型问题归纳总结

令 g(x)x 2 2x x ln xx [1,e] , 又 g (x)(x 1)(x 2 2ln x)(x ln x)2函数导数任意性和存在性问题探究导学语函数导数问题是高考试题中占比重最大的题型,前期所学利用导数解决函数图像切线、函数单调性、 函数极值最值等问题的方法, 仅可称之为解决这类问题的“战术” ,若要更有效地彻底解决此类问题还必须研究“战略,”因为此类问题是函数导数结合全称命题和特称命题形成的综合性题目 .常用战略思想如下:题型分类解析一.单一函数单一“任意”型f(x)上限战略思想一: “ x A , a ( )f ( x)恒成立”等价于“当x A 时, a ( ) f (x)max ;”f(x)下限“ x A , a ( ) f (x) 恒成立”等价于“当x A 时, a ( )f ( x) min ”.例 1 :已知二次函数 f (x) ax 2 x ,若 x [0,1] 时,恒有 | f (x)| 1,求实数 a 的取值范围 解: | f (x)| 1 ,∴ 1 ax 2 x 1;即 1 x ax 2 1 x ; 当 x 0 时,不等式显然成立,∴ a ∈R.21 1 1 1 当 0 x 1 时,由 1 x ax 21 x 得:2 a 2 , x x x x11 又∵(2 )max2 ,∴a 2, 2 a 0 ,xx综上得 a 的范围是 a [ 2,0] . .单一函数单一“存在”型x A ,使得 a ( ) f ( x)成立”等价于“当x A 时, a ( )f ( x) max取值范围解析:f (x) (a 2)x a(x ln x) x 2 2x . ∵x [1,e] ,∴ln x 1 x 且等号不能同时取,所以 ln x x ,即 x ln x 0 , x 2 2x因而 a x [1,e] ,x ln x ,而(x 12 1x )min 0,∴a 0.xx战略思想x A ,使得 a ( ) f (x) 成立”等价于“当x A 时,a ( ) f(x)min ”;f ( x)上限f ( x)下限例 2. 已知函数 f (x) aln x x 2(a R ),若存在 x [1,e] ,使得f (x) (a 2)x 成立,求实数 a 的当x [1, e]时,x 1 0,ln x 1,x 2 2ln x 0,从而g (x) 0 (仅当x=1 时取等号),所以g(x)在[1, e]上为增函数,故g(x) 的最小值为g(1) 1,所以 a 的取值范围是[ 1, ) .三.单一函数双“任意”型战略思想三:x R,都有" f(x1) f (x) f(x2)" f(x1), f (x2) 分别是f (x) 的最小值和最大值,|x1 x2 | min 是同时出现最大值和最小值的最短区间.例 3. 已知函数f (x) 2sin( x ) ,若对x R,都有" f (x1) f (x) f (x2)" 成立,则| x1 x2 |25的最小值为 __ .解∵对任意x∈R ,不等式f (x1) f (x) f (x2) 恒成立,∴f (x1), f (x2)分别是f (x) 的最小值和最大值对于函数y sin x ,取得最大值和最小值的两点之间最小距离是π,即半个周期x又函数f (x) 2sin( 2 5 )的周期为4,∴| x1 x2 |的最小值为 2.战略思想四:x1,x2 A, " f (x1 x2)f (x1) f (x2)"成立22f (x) 在 A 上是上凸函数 f ''(x) 02例 4. 在y 2x,y log2 2x,y x ,y cosx 这四个函数中,当0 x1 x2 1时,使" f (x1 x2)f(x1) f ( x2 )"恒成立的函数的个数是( )22A.0B.1C.2D.3解:本题实质就是考察函数的凸凹性,即满足条件" f(x1 x2)f (x1) f (x2)" 的函数,应是凸函22数的性质,画草图即知y log2 2x 符合题意;战略思想五:x1,x2 A,"f (x1) f (x2)0"成立f(x)在 A 上是增函数x1 x2例 5 已知函数f (x) 定义域为[ 1,1],f (1) 1,若m,n [ 1,1],m n 0时,都有f(m) f(n) 0" ,若f(x) t2 2at 1对所有x [ 1,1],a [ 1,1]恒成立,求实数t取值范围. mn解:任取1 x1 x2 1,则f (x1) f (x2) f (x1) f (x2) (x1 x2),x1 x2由已知 f (x1) f (x2) 0,又x1 x2 0,∴f (x1) f (x2) 0,x1 x2即f (x) 在[ 1,1]上为增函数.∵f (1) 1,∴x [ 1,1],恒有f (x) 1;2∴要使f (x) t2 2at 1对所有x [ 1,1],a [ 1,1]恒成立,即要t2 2at 1 1恒成立,故t2 2at 0 恒成立,2令g(a) 2at t2,只须g( 1) 0且g(1) 0,解得t 2或t 0或t 2.战略思想六:x1,x2 A,| f (x1) f (x2)| t ( t为常数)成立t= f (x)max f (x)min4 3 1例 6. 已知函数f (x) x4 2x3,则对任意t1,t2 [ ,2](t1 t2)都有| f(t1) f (t2)| 恒2成立,当且仅当t1 = __ ,t2 = ___ 时取等号.解:因为| f (x1) f (x2)| |[ f ( x)] max [ f ( x)] min |恒成立,4 3 1由f(x) x4 2x3,x [ ,2] ,23 27 1 5易求得[ f (x)]max f (3) 27,[ f (x)]min f ( 1) 5,2 16 2 16∴| f (x1) f (x2)| 2.战略思想七:x1,x2 A,| f (x1) f (x2)| t |x1 x2 ||f(x1) f(x2)| t | f '(x)| t(t 0)例7. 已知函数y f (x)满足:(1)定义域为[ 1,1] ;(2)方程f (x) 0 至少有两个实根1和1;(3)过f (x) 图像上任意两点的直线的斜率绝对值不大于 1.(1)证明:| f(0) | 1;(2)证明:对任意x1,x2 [ 1,1],都有| f (x1) f (x2)| 1.证明(1) 略;(2)由条件(2)知f( 1) f (1) 0,不妨设 1 x 1 x 2 1,由(3)知| f (x 1) f (x 2)| |x 1 x 2 | x 2 x 1, 又∵| f(x 1) f(x 2)| |f(x 1)| | f(x 2)| | f(x 1) f( 1)| |f(x 2) f(1)|x 1 1 1 x 2 2 (x 2 x 1) 2 | f(x 1) f(x 2)|;∴|f(x 1) f(x 2)| 133 例 8. 已知函数 f(x)x 3 ax b ,对于 x 1,x 2(0, )(x 1 x 2 )时总有 | f (x 1) f (x 2)| |x 1 x 2 |成3立,求实数 a 的范围 .3 ' 2解 由 f (x) x 3 ax b ,得 f '(x) 3x 2 a ,评注 由导数的几何意义知道,函数 y f (x)图像上任意两点 P(x 1,y 1),Q(x 2,y 2) 连线的斜率k y2 y1 (x 1 x 2 )的取值范围,就是曲线上任一点切线的斜率(如果有的话 )的范围,利用这个结论,可x 2 x1以解决形如 |f(x 1) f(x 2)| m|x 1 x 2||或| f(x 1) f(x 2)| m|x 1 x 2 | (m >0)型的不等式恒成立问题四.双函数“任意”+“存在”型: x 1A,x 2 B ,使得 f (x 1) g (x 2)成立 f (x)min g(x)min ;x 1 A, x 2B ,使得 f (x 1)g(x 2)成立f (x)maxg(x)max .总有 f (x 1) g( x 2 )成立,求实数 m 的取值范围 .解析:题意等价于 f(x)在(0,1)上的最大值大于或等于 g ( x)在[1,2] 上的最大值 2 2x 2 5x 2 1 f (x) 2 ,由 f '(x) 0得, x 或 x 2,x211 当 x (0, ) 时, f (x) 0,当 x ( ,1)时 f (x) 0 , 221 所以在( 0,1)上, f ( x)max f (1) 3 5ln2 .2当 x (0, 33)时,a f (x) 1 a ,∵| f(x 1) f(x 2)| |x 1 x 2 |,∴| f(x 1) f(x 2) | 1x 1 x 2a1 1a11a0战略思想八: 例 9 .已知函数2 f (x) 2xx 25ln x , g(x) xmx 4 ,若存在 x 1 (0,1) ,对任意 x 2 [1,2] ,又g(x)在[1,2]上的最大值为 max{g(1),g(2)} ,所以有所以实数 m 的取值范围是 m 8 5ln 2.战略思想九: “ x 1 A , x 2 B ,使得 f (x 1) g(x 2)成立”“f (x) 的值域包含于.g( x ) 的值域”.例 10.设函数 f (x)1x 3 1 x 2 5x 4.333(1)求 f (x) 的单调区间.32(2)设 a ≥1,函数 g(x) x 3 3a 2x 2a .若对于任意 x 1 [0,1] ,总存在 x 0 [0,1] ,使得 f (x 1) g( x 0 )成立,求 a 的取值范围.' 22 5 ' 2 2 5 5解析:( 1 ) f '(x) x 2x ,令 f '(x)≥0,即 x 2 x ≤ 0 ,解得: ≤ x ≤1,3 3 3 3 355f(x) 的单增区间为 [ ,1] ;单调减区间为 ( , ]和[1, ) .33(2)由(1)可知当 x [0,1]时, f ( x)单调递增, ∴当 x [0,1]时, f(x) [f (0), f (1)] , 即 f(x) [ 4, 3] ;又g '(x) 3x 2 3a 2,且 a ≥1,∴当x [0,1]时, g '( x) ≤ 0 , g( x)单调递减, ∴当 x [0,1] 时, g(x) [ g (1),g (0)] ,即 g(x) [ 3a 2 2a 1, 2a] , 又对于任意 x 1 [0,1] ,总存在 x 0 [0,1] ,使得 f (x 1) g(x 0)成立 [ 4, 3] [ 3a 2 2a 1, 2a] ,1a例 11 .已知函数 f(x) ln x ax 1(a R) ; x1(1) 当 a 时,讨论 f (x) 的单调性;222)设 g(x) x 2 2bx 4 ,1当 a 时,若对 x 1 (0, 2) , x 2 [1,2] ,使 f(x 1) g(x 2) ,求实数4f(21) g(1) f(21) g(2)3 5ln 2 5 m 3 5ln 2 8 2mm 8 5ln 21m (11 5ln 2)2m 8 5ln 2 ,f(x)上限f(x)下限即3a 2 2a 1 ≤ 3 ≤ 2a4,解得:≤a ≤3g(x)上限b 的取值范围;解:(1)(解答过程略去,只给出结论)当 a ≤0 时,函数 f(x)在( 0,1 )上单调递减,在( 1,+∞)上单调递增;1 当 a= 时,函数 f(x) 在( 0, +∞)上单调递减;2 11当 0<a< 时,函数 f (x) 在(0,1 )上单调递减,在 (1, 1)上单调递增,在 2'21, ) 上单调递减; a2 )函数的定义域为( 0 , +∞),f (x )=1-a+ a21xxax 2 x 1 aa= 1 时,由 f4x )=0 可得 x 1=1,x 2=3.因为a= 1∈(0, 1 ),x 2=3 (0,2),结合( 1)可知 42函数 f(x)在( 0,1 )上单调递减,在( 1,2 )上单调递增, 所以f(x) 在( 0,2 )上的最小值为 f(1)= - 12由于 对 x 1∈(0,2), x 2∈[1,2], 使 f(x 1) ≥g(x 2) ”等价于 “g(x)在[1,2]上的最小值不大于 f(x) 在( 0,2)上的最小值 f(1)= 1”2”※)又 g(x)=(x -b)2+4-b 2, x ∈[1,2], 所以当 b<1 时,因为 [g(x)] min =g(1)=5 - 2b>0, 此时与(※)矛盾; 当 b ∈[1,2]时, 因为 [g(x)] min =4 -b 2≥0,同样与(※)矛盾; 当 b ∈(2,+∞)时,因为 [g(x)] min =g(2)=8 -4b.1 17 解不等式 8- 4b ≤- ,可得b ≥ .2817 综上, b 的取值范围是[ ,+ ∞).8五.双函数“任意”+“任意”型战略思想十: x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立 f (x)min g(x)max例 12. 已 知 函 数 f(x) 1x 3 x 2 3x 4,g(x)3 3 29x c,若对任x 1,x 2 [ 2,2] ,都有 f (x 1) g(x 2),求 c 的范围 .解:因为对任意的 x 1,x 2 [ 2,2] ,都有 f(x 1) g(x 2)成立,∴[ f ( x)] max [g(x)]min ,∵f '(x) x2 2x 3,令f '(x) 0得x 3,x 1x>3 或x<-1;f '(x) 0得1 x 3;∴f(x)在[ 2, 1]为增函数,在[ 1,2]为减函数.18 c∵f( 1) 3, f (2) 6,∴[ f (x)]max 3,.∴3 ,∴c 24.22 3 2例13.已知两个函数f(x) 8x2 16x k,g(x) 2x3 5x2 4x,x [ 3,3], k R;(1) 若对x [ 3,3] ,都有f (x) g(x)成立,求实数k 的取值范围;(2) 若x [ 3,3] ,使得f (x) g(x) 成立,求实数k的取值范围;(3) 若对x1,x2 [ 3,3] ,都有f (x1) g(x2)成立,求实数k的取值范围;解:(1)设h(x) g(x) f (x) 2x3 3x2 12x k ,(1)中的问题可转化为:x [ 3,3] 时,h(x) 0 恒成立,即[ h( x)] min 0.'2h'(x) 6x2 6x 12 6(x 2)(x 1);当x 变化时,h(x),h'(x) 的变化情况列表如下:因为h( 1) k 7, h(2) k 20 ,所以,由上表可知[ h( x)] min k 45,故k-45 ≥0,得k≥45,即k∈[45,+ ∞).小结:①对于闭区间I,不等式f(x)<k 对x∈I 时恒成立[f(x)] max <k, x ∈I;不等式f(x)>k 对x∈I 时恒成立[f(x)] min>k, x ∈I.②此题常见的错误解法:由[f(x)] max ≤[g(x)] min 解出k 的取值范围.这种解法的错误在于条件“ [f(x)] max ≤[g(x)] min”只是原题的充分不必要条件,不是充要条件,即不等价.( 2)根据题意可知, ( 2)中的问题等价于h(x)= g(x) -f(x) ≥0 在x ∈[-3,3]时有解,故[h(x)] max≥0.由( 1)可知[h(x)] max = k+7 ,因此k+7 ≥0,即k∈[7,+ ∞).(3)根据题意可知, (3)中的问题等价于 [f(x)] max ≤[g(x)] min ,x ∈[-3,3].由二次函数的图像和性质可得 , x ∈[-3,3]时, [f(x)] max =120 -k. 仿照( 1),利用导数的方法可求得 x ∈[-3,3]时, [g(x)] min =-21. 由 120 - k ≥-21 得 k ≥141,即 k ∈[141,+ ∞). 说明:这里的 x 1,x 2 是两个互不影响的独立变量从上面三个问题的解答过程可以看出 ,对于一个不等式一定要看清是对“ x ”恒成立,还是“ x ”使之成还是两个独立的变量 ,然后再根据不同的情况采取不同的等价条件 ,千万不要稀里糊涂的去猜六.双函数“存在”+“存在”型战略思想十一: x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立f (x)min g(x)max ;x 1 A, x 2 B ,使得 f(x 1) g(x 2)成立f(x)max g(x)min .x 3 2例 14.已知函数 f (x) ln x 1, g(x) x 2 2bx 4.若存在 x 1 (0,2) , x 2 1,2 ,使4 4xf (x 1) g(x 2) ,求实数 b 取值范围1 f (x)在(0,1)上单调递增,在 (1,2)上单调递减,f(x)min f (1) .2依题意有 f ( x) min g(x)max ,所以 g(x)max12.又g(x) (x b)2 b 2 4,g(1) 1 从而g(2) 212,解得b 187.战略思想十二: “ x 1 A, x 2 B ,使得 f (x 1) g(x 2) 成立”等价于f (x) 的值域与 g(x) 的值域相交非空”3 219 1例 15 .已知函数 f(x) x 3 (1 a)x 2 a(a 2)x(a R) , g(x) x .是否存在实数 a ,存63在 x 11,1 , x 2 0,2 ,使得 f '(x 1) 2ax 1 g(x 2)成立?若存在,求出 a 的取值范围;若不存在,说明理由立,同时还要看清不等式两边是同一个变量, 解析: f (x) 1 1 32x 4 4x 2(x 1)(x 3)4x 219 1 1解析:在0,2 上g x x 是增函数,故对于x 0,2 ,g x ,66 3 32设h x f x 2ax 3x22x a a 2 ,当x 1,1 时,h(x) [-a2 2a 13,-a2 2a 5].3要存在x1 [ 1,1] ,x2 [0,2] 使得h x1 g x2 成立,只要[-a2 2a 13,-a2 2a 5] [ 13,6]33考虑反面,[-a2 2a 31,-a2 2a 5] [ 13,6]1 2 2 1 57 57则5 a 2a 或6< -a 2a 1,解得a 1 或a 1 ,3 3 3 357 57从而所求为1 a 1 .33。
函数与导数中任意性和存在性问题探究
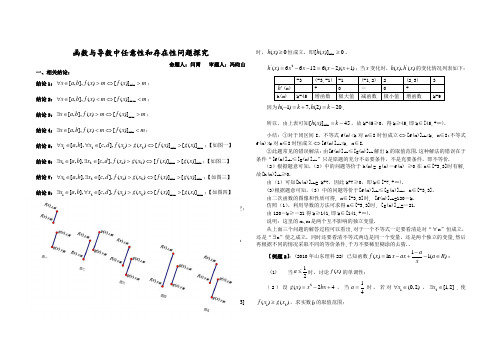
函数与导数中任意性和存在性问题探究命题人:闫霄 审题人:冯昀山 一、相关结论:结论1:min [,],()[()]x a b f x m f x m ∀∈>⇔>; 结论2:max [,],()[()]x a b f x m f x m ∀∈<⇔<; 结论3:max [,],()[()]x a b f x m f x m ∃∈>⇔>; 结论4:min [,],()[()]x a b f x m f x m ∃∈<⇔<;结论5:1212min max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∀∈>⇔>;【如图一】 结论6:1212max min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∃∈>⇔>;【如图二】 结论7:1212min min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∃∈>⇔>;【如图三】 结论8:1212max max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∀∈>⇔>;【如图四】 结论9:1212[,],[,],()()()x a b x c d f x g x f x ∃∈∃∈=⇔的值域和()g x 的值域交集不为空; 结论10:1212[,],[,],()()()x a b x c d f x g x f x ∀∈∃∈=⇔的值域是()g x 的值域的子集 【例题1】:已知两个函数232()816,()254,[3,3],f x x x k g x x x x x k R =+-=++∈-∈;(1) 若对[3,3]x ∀∈-,都有()()f x g x ≤成立,求实数k 的取值范围; (2) 若[3,3]x ∃∈-,使得()()f x g x ≤成立,求实数k 的取值范围; (3) 若对12,[3,3]x x ∀∈-,都有12()()f x g x ≤成立,求实数k 的取值范围;解:(1)设32()()()2312h x g x f x x x x k =-=--+,(1)中的问题可转化为:[3,3]x ∈-时,()0h x ≥恒成立,即min [()]0h x ≥。
导数大题放招---任意与存在性问题

2020-导数大题放招---任意与存在性问题(1) 任意x∈[a ,b],使得f(x)≥g(x)成立,等价于f (x )-g (x )≥0等价于{f (x )-g (x )}min ≥0(2) 对任意x 1∈[a ,b],x 2∈[c ,d]都有f (x 1)≥g (x 2),等价于f (x )min ≥g (x )max ,进而转化为函数的最值问题;(3) 存在x 1∈[a ,b],x 2∈[c ,d],使得f (x 1)≥g (x 2),等价于f (x )max ≥g (x )min ,进而转化为函数的最值问题.(4) 任意x 1∈[a ,b],存在x 2∈[c ,d],使得f(x 1)≥g(x 2)成立,等价于f (x )min ≥g (x )min ,进而转化为函数的最值问题;(5) 任意x 1∈[a ,b],存在x 2∈[c ,d],使得f(x 1)≤g(x 2)成立,等价于f (x )max ≤g (x )max ,进而转化为函数的最值问题;(6) (6) 若对任意x 1∈[a ,b],,存在x 2x 2∈[c ,d],使得f(x 1)=g(x 2)等价于f (x )值域g (x )值域拿到一个难题,不要去想这道题难不难,我能不能做完整,只要想我会做多少,也可以不理会题目有没有看懂,只要做我能读懂的部分,重视审题 1、f(x)=lnx -41x+x43-1,g(x)=x 2-2bx+4,任意x 1∈(0,2),存在x 2∈[1,2] ,,使得f(x 1)≥g(x 2)成立,求b 范围分析 :任意x 1∈(0,2),存在x 2∈[1,2] ,,使得f(x 1)≥g(x 2)等价于任意一个f(x)≥某一个g(x) 等价于f(x)最小值≥g(x)最小值2.设f (x )=x 3﹣x 2﹣3.(Ⅰ)求f (x )的单调区间;(Ⅱ)若函数y=f (x )﹣m 在[﹣1,2]上有三个零点,求实数m 的范围;(Ⅲ)设g (x )=x a +xlnx ,如果对任意的x 1,x 2∈[21,2],都有f (x 1)≤g (x 2)成立,求实数a 范围.3.已知函数f (x )=lnx+ax (a ∈R ).(1)求f (x )的单调区间;(2)设g (x )=x 2﹣4x+2,若对任意x 1∈(0,+∞),均存在x 2∈[0,1],使得f (x 1)<g (x 2),求a 的取值范围.4.设f (x )=xa+xlnx ,g (x )=x 3﹣x 2﹣3.(1)当a=2时,求y=f (x )在x=1处的切线的斜率;(2)如果存在x 1,x 2∈[0,2],使得g (x 1)﹣g (x 2)≥M 成立,求满足上述条件的最大整数M .5.设f (x )=(x 2+ax+b )e 3﹣x(x ∈R )的一个极值点是x=3.(Ⅰ)求a 与b 的关系式(用a 表示b ,并求f (x )的单调区间;(Ⅱ)设a >0,g (x )=(a 2+425)e x若存在ε1,ε2∈[0,4]使得f (ε1)﹣g (ε2)<1成立,求a 取值范围.。
任意性与存在性问题探究

函数中任意性和存在性问题探究高考中全称命题和存在性命题与导数的结合是近年高考的一大亮点,下面结合高考试题对此类问题进行归纳探究 一、相关结论:结论1:1212min max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∀∈>⇔>;【如图一】 结论2:1212max min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∃∈>⇔>;【如图二】 结论3:1212min min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∃∈>⇔>;【如图三】 结论4:1212max max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∀∈>⇔>;【如图四】 结论5:1212[,],[,],()()()x a b x c d f x g x f x ∃∈∃∈=⇔的值域和()g x 的值域交集不为空;【如图五】【例题1】:已知两个函数232()816,()254,[3,3],f x x x k g x x x x x k R =+-=++∈-∈;(1) 若对[3,3]x ∀∈-,都有()()f x g x ≤成立,求实数k 的取值范围; (2) 若[3,3]x ∃∈-,使得()()f x g x ≤成立,求实数k 的取值范围; (3) 若对12,[3,3]x x ∀∈-,都有12()()f x g x ≤成立,求实数k 的取值范围;解:(1)设32()()()2312h x g x f x x x x k =-=--+,(1)中的问题可转化为:[3,3]x ∈-时,()0h x ≥恒成立,即min [()]0h x ≥。
'2()66126(2)(1)h x x x x x =--=-+;当x 变化时,'(),()h x h x 的变化情况列表如下:x -3(-3,-1) -1 (-1,2) 2 (2,3) 3 h '(x)+ 0 - 0 + h(x)k-45增函数极大值减函数极小值增函数k-9。
导数中的任意性与存在性问题探究

导数中的任意性与存在性问题探究函数中任意性和存在性问题探究高考中全称命题和存在性命题与导数的结合是近年高考的一大亮点,下面结合高考试题对此类问题进行归纳探究一、相关结论:结论1:∀x 1∈[a , b ],∀x 2∈[c , d ],f (x 1) >g (x 2) ⇔[f (x )]min >[g (x )]max ;【如图一】结论2:∃x 1∈[a , b ],∃x 2∈[c , d ],f (x 1) >g (x 2) ⇔[f (x )]max >[g (x )]min ;【如图二】结论3:∀x 1∈[a , b ],∃x 2∈[c ,d ],f (x 1) >g (x 2) ⇔[f (x )]min >[g (x )]min ;【如图三】结论4:∃x 1∈[a , b ],∀x 2∈[c , d ],f (x 1) >g (x 2) ⇔[f (x )]max >[g (x )]max ;【如图四】结论5:∃x 1∈[a , b ],∃x 2∈[c , d ],f (x 1) =g (x 2) ⇔f (x ) 的值域和g(x ) 的值域交集不为空;【如图五】例题1:已知两个函数f (x ) =8x 2+16x -k , g (x ) =2x 3+5x 2+4x , x ∈[-3,3],k ∈R ;(1) 若对∀x ∈[-3,3], 都有f (x ) ≤g (x ) 成立,求实数k 的取值范围; (2)若∃x ∈[-3,3], 使得f (x ) ≤g (x ) 成立,求实数k 的取值范围; (3) 若对∀x 1, x 2∈[-3,3], 都有f (x 1) ≤g (x 2) 成立,求实数k 的取值范围;解:(1)设h (x ) =g (x ) -f (x ) =2x 3-3x 2-12x +k (, 1)中的问题可转化为:x ∈[-3,3]时,h (x ) ≥0恒成立,即[h (x )]min ≥0。
导数题中“任意、存在”型的归纳辨析

导数题中“任意、存在”型的归纳辨析导数题是高考题中的常客,而且大都以压轴题的面目出现,所以拿下导数题是迈入高分段的标志。
导数题虽年年有,但却悄然之中发生着些改变。
这其中,尤以关于“任意”、“存在”的内容最为明显。
“任意”、“存在”可以说是导数题最为明显的特色,从早期单一型,发展到现今的混合型。
下面对此作一归纳。
一.单一函数单一“任意”型例1.已知函数()ln()f x x x a =-+的最小值为0,其中0a >。
(1)求a 的值;(2)若对任意的[0,)x ∈+∞,有2()f x kx ≤成立,求实数k 的最小值。
解析:(1)1()x a f x x a+-'=+,()f x ∴在(,1)a a --单调递减,在(1,)a -+∞单调递增,所min ()f x (1)01f a a =-=⇒=。
(2)设2()ln()g x kx x x a =-++,则问题等价于()0g x ≥对[0,)x ∈+∞恒成立,即min ()0g x ≥。
因为当0k ≤时,x →+∞时,()f x →-∞,所以0k >。
由22(21)()1kx k x g x x +-'=+,若2104k k-->,则当21(0,)4k x k -∈-时,()0g x '<,()g x 单调递减,()(0)0g x g <=,矛盾。
从而2104k k--≤,解得12k ≥。
即实数k 的最小值是12。
点评:“任意”的意思是不管x 取给定集合中的哪一个值,得到的函数值都要满足给定的不等式,它有两种形式:“对任意的x A ∈,()()a f x >≥恒成立”等价于“当x A ∈时,max ()()a f x >≥”;“对任意的x A ∈,()()a f x <≤恒成立”等价于“当x A ∈时,min ()()a f x <≤”。
二.单一函数单一“存在”型例 2. 已知函数2()ln f x a x x =+(a R ∈),若存在[1,]x e ∈,使得()(2)f x a x ≤+成立,求实数a 的取值范围。
导数的任意性及存在性问题

恒成立问题及存在性问题知识方法总结:恒成立问题及存在性问题重要结论:(1)对于任意的1[,]∈x a b ,总存在2[,]∈x m n ,使得121max 2max ()()()()≤⇔≤f x g x f x g x ;(2)对于任意的1[,]∈x a b ,总存在2[,]∈x m n ,使得121min 2min ()()()()≥⇔≥f x g x f x g x ;(3)若存在1[,]∈x a b ,对任意的2[,]∈x m n ,使得121min 2min ()()()()≤⇔≤f x g x f x g x ;(4)若存在1[,]∈x a b ,对任意的2[,]∈x m n ,使得121max 2max ()()()()≥⇔≥f x g x f x g x ;(5)对于任意的1[,]∈x a b , 2[,]∈x m n ,使得121max 2min ()()()()≤⇔≤f x g x f x g x ;(6)对于任意的1[,]∈x a b , 2[,]∈x m n ,使得121min 2max ()()()()≥⇔≥f x g x f x g x ;(7)若存在1[,]∈x a b ,总存在2[,]∈x m n ,使得121min 2max ()()()()≤⇔≤f x g x f x g x ;(8)若存在1[,]∈x a b ,总存在2[,]∈x m n ,使得121max 2min ()()()()≥⇔≥f x g x f x g x ;1. [2014·湖北卷] 已知函数f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=12(|x -a 2|+|x -2a 2|-3a 2).若∀x ∈R , f (x -1)≤ f (x ),则实数a 的取值范围为( )A.⎣⎡⎦⎤-16,16B.⎣⎡⎦⎤-66,66C.⎣⎡⎦⎤-13,13D.⎣⎡⎦⎤-33,332. [2014·四川卷] 以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数φ(x )组成的集合:对于函数φ(x ),存在一个正数M ,使得函数φ(x )的值域包含于区间[-M ,M ].例如,当φ1(x )=x 3,φ2(x )=sin x 时,φ1(x )∈A ,φ2(x )∈B .现有如下命题:①设函数f (x )的定义域为D ,则“f (x )∈A ”的充要条件是“∀b ∈R ,∃a ∈D ,f (a )=b ”;②函数f (x )∈B 的充要条件是f (x )有最大值和最小值;③若函数f (x ),g (x )的定义域相同,且f (x )∈A ,g (x )∈B ,则f (x )+g (x )∉B ;④若函数f (x )=a ln(x +2)+x x 2+1(x >-2,a ∈R )有最大值,则f (x )∈B .其中的真命题有 .(写出所有真命题的序号)3. (2013年高考四川卷(理))设函数()f x =a R ∈,e 为自然对数的底数).若曲线sin y x =上存在00(,)x y 使得00(())f f y y =,则a 的取值范围是( )(A)[1,]e (B)1[,-11]e -, (C)[1,1]e + (D)1[-1,1]e e -+4. 已知函数].1,0[,274)(2∈--=x x x x f (Ⅰ)求)(x f 的单调区间和值域;(Ⅱ)设1≥a ,函数32()32,[0,1].g x x a x a x =--∈若对于任意1[0,1]x ∈,总存在0[0,1]x ∈,使得)()(10x f x g =成立,求a 的取值范围.5、 已知函数21()(1)ln 2f x ax a x x =-++ , 27()28g x x bx =-+. (Ⅰ)当0a =时,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)当1a <时,求函数()f x 的单调区间; (Ⅲ)当14a =时,函数()f x 在(0,2]上的最大值为M ,若存在[1,2]x ∈,使得()g x M ≥成立,求实数b 的取值范围.6、已知函数2()4ln(1)f x ax x =--,a ∈R . (Ⅰ)当1a =时,求()f x 的单调区间;(Ⅱ)已知点(1,1)P 和函数()f x 图象上动点(,())M m f m ,对任意[2,e 1]m ∈+,直线PM 倾斜角都是钝角,求a 的取值范围.7、 [2014·福建卷] 已知函数f (x )=e x -ax (a 为常数)的图像与y 轴交于点A ,曲线y =f (x )在点A 处的切线斜率为-1.(1)求a 的值及函数f (x )的极值; (2)证明:当x >0时,x 2<e x ;(3)证明:对任意给定的正数c ,总存在x 0,使得当x ∈(x 0,+∞)时,恒有x 2<c e x .8.已知函数()ln f x x a x =-,1(), (R).a g x a x+=-∈ (Ⅰ)若1a =,求函数()f x 的极值; (Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间; (Ⅲ)若在[]1,e (e 2.718...=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.9.已知函数1()ln 1a f x x ax x -=-+-()a R ∈. (Ⅰ)当12a ≤时,讨论()f x 的单调性; (Ⅱ)设2()2 4.g x x bx =-+当14a =时,若对任意1(0,2)x ∈,存在[]21,2x ∈,使12()()f x g x ≥,求实数b 取值范围.。
高中数学函数中任意性与存在性的综合问题探讨

高中数学函数中任意性与存在性的综合问题探讨本课题经由高中一届学生的函数知识学习实际情况结合本人教学经验,结合新课程标准,综合分析相关原由,给出部分建设性教学建议,以便和广大教育工作者进行交流和参考。
标签:高中数学;新课程标准;任意性;存在性;教学一、选题理由学生对形如这类成立,求某个参数的取值范围。
学生基本上知道这是最值的比较,但是到底哪个是取最大值,哪个是取最小值来作比较,并不是特别清楚,可以说是模糊的,所以将这个课题选出来和大家一起探讨。
二、具体举例典例、已知函数,,如果对任意的,均存在,使得成立,求的取值范围.分析:这类问题是高中数学中《函数与导数》这一章节中的一类常见的问题,其考察的基本内容为用导数知识来求函数的最值问题,进而得到相应的参数的范围,而学生对于如下的两个被分解题目都能够进行求解分解一:已知函数,如果对任意的,恒成立,求的取值范围.分解二:已知函数,均存在,使得成立,求的取值范围.分解一为一个恒成立问题,分解二为一个存在性问题,所以单独求解这两个问题是比较简单的,而本例是一个将这两种情形糅合在一起的函数综合题,但是按照相应的思路拆分来看,问题就会迎刃而解了。
解析:先令,则原命题等价于已知函数如果对任意的,恒成立,这样就明显的转化为成立,其中.接下来就来处理,这样原命题就进一步可以理解为,已知函数,如果存在,使得成立.所以整个命题就为,其中,由二次函数在区间上的最值的相关知识易知因为,所以化简为当时,,所以在上,,在上,当时,在上,,在上,,在上,当时,在上,当时,在上,在上,在上,所以,综上所述,就有当时,函数在区间上为单调递增函数,故,解得此时的范围为当时,函数在上位单调递增函数,在上位单调递减函数,故,由于,所以所以,则在时恒成立此时的范围为综上所述,本题所求的的取值范围为点评:函数与导数这部分知识中间的恒成立问题和存在性问题是一类常见问题,对两者的综合考察也是一个常规考点,在此例子中将这样一个综合性问题进行分开分析,这样就变成了连个独立恒成立問题和存在性问题,进而就可以用熟悉的知识来进行求解了。
高中数学任意性与存在性问题探究

高中数学任意性与存在性问题探究函数中任意性和存在性问题探究近年的高考中,全称命题和存在性命题与导数的结合成为了一大亮点。
本文将结合高考试题对此类问题进行归纳探究。
一、相关结论:结论1:对于任意的x1∈[a,b]和x2∈[c,d],若f(x1)>g(x2),则有[f(x)]min>[g(x)]max;【如图一】结论2:存在x1∈[a,b]和x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]max>[g(x)]XXX;【如图二】结论3:对于任意的x1∈[a,b]和存在x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]min>[g(x)]XXX;【如图三】结论4:存在x1∈[a,b]和任意的x2∈[c,d],使得f(x1)>g(x2),则有[f(x)]max>[g(x)]max;【如图四】结论5:存在x1∈[a,b]和x2∈[c,d],使得f(x1)=g(x2),则f(x)的值域和g(x)的值域交集不为空;【如图五】例题1】:已知两个函数f(x)=8x+16x-k,g(x)=2x+5x+4x,x∈[-3,3],k∈R;1) 若对于任意的x∈[-3,3],都有f(x)≤g(x),求实数k的取值范围;2) 若存在x∈[-3,3],使得f(x)≤g(x),求实数k的取值范围;3) 若对于任意的x1,x2∈[-3,3],都有f(x1)≤g(x2),求实数k的取值范围;解:1)设h(x)=g(x)-f(x)=2x-3x-12x+k,问题可转化为:对于x∈[-3,3],h(x)≥常数成立,即[h(x)]XXX≥常数。
由结论1可知,当f(x1)>g(x2)时,[f(x)]min>[g(x)]max,即h(x)的最小值出现在f(x)和g(x)的交点处。
因此,我们可以求出h(x)的导数h'(x)并列出变化情况表格,得到[h(x)]min=k-45.因此,k≥45,即k∈[45,+∞)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数中任意性和存在性问题探究高考中全称命题和存在性命题与导数的结合是近年高考的一大亮点,下面结合高考试题对此类问题进行归纳探究 一、相关结论:结论1:1212min max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∀∈>⇔>;【如图一】 结论2:1212max min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∃∈>⇔>;【如图二】 结论3:1212min min [,],[,],()()[()][()]x a b x c d f x g x f x g x ∀∈∃∈>⇔>;【如图三】 结论4:1212max max [,],[,],()()[()][()]x a b x c d f x g x f x g x ∃∈∀∈>⇔>;【如图四】 结论5:1212[,],[,],()()()x a b x c d f x g x f x ∃∈∃∈=⇔的值域和()g x 的值域交集不为空;【如图五】例题1:已知两个函数232()816,()254,[3,3],f x x x k g x x x x x k R =+-=++∈-∈;(1) 若对[3,3]x ∀∈-,都有()()f x g x ≤成立,求实数k 的取值范围; (2) 若[3,3]x ∃∈-,使得()()f x g x ≤成立,求实数k 的取值范围; (3) 若对12,[3,3]x x ∀∈-,都有12()()f x g x ≤成立,求实数k 的取值范围;解:(1)设32()()()2312h x g x f x x x x k =-=--+,(1)中的问题可转化为:[3,3]x ∈-时,()0h x ≥恒成立,即min [()]0h x ≥。
'2()66126(2)(1)h x x x x x =--=-+;当x 变化时,'(),()h x h x 的变化情况列表如下:x-3(-3,-1) -1 (-1,2) 2 (2,3) 3 h '(x )+ 0 - 0 + h(x)k-45增函数极大值减函数极小值增函数k-9因为(1)7,(2)20h k h k -=+=-,所以,由上表可知min [()]45h x k =-,故k-45≥0,得k ≥45,即k ∈[45,+∞).小结:①对于闭区间I ,不等式f(x)<k 对x ∈I 时恒成立⇔[f(x)]max <k, x ∈I;不等式f(x)>k 对x ∈I 时恒成立⇔[f(x)]min >k, x ∈I.②此题常见的错误解法:由[f(x)]max ≤[g(x)]min 解出k 的取值范围.这种解法的错误在于条件“[f(x)]max ≤[g(x)]min ”只是原题的充分不必要条件,不是充要条件,即不等价. (2)根据题意可知,(2)中的问题等价于h(x)= g(x)-f(x) ≥0在x ∈[-3,3]时有解,故[h(x)]max ≥0.由(1)可知[h(x)]max = k+7,因此k+7≥0,即k ∈[-7,+∞). (3)根据题意可知,(3)中的问题等价于[f(x)]max ≤[g(x)]min ,x ∈[-3,3]. 由二次函数的图像和性质可得, x ∈[-3,3]时, [f(x)]max =120-k. 仿照(1),利用导数的方法可求得x ∈[-3,3]时, [g(x)]min =-21. 由120-k ≥-21得k ≥141,即k ∈[141,+∞). 说明:这里的x 1,x 2是两个互不影响的独立变量.从上面三个问题的解答过程可以看出,对于一个不等式一定要看清是对“∀x ”恒成立,还是“∃x ”使之成立,同时还要看清不等式两边是同一个变量,还是两个独立的变量,然后再根据不同的情况采取不同的等价条件,千万不要稀里糊涂的去猜.. 例题2:(2010年山东理科22) 已知函数1()ln 1()af x x ax a R x-=-+-∈; (1) 当12a ≤时,讨论()f x 的单调性; (2)设2()24g x x bx =-+,当14a =时,若对1(0,2)x ∀∈,2[1,2]x ∃∈,使12()()f x g x ≥,求实数b 的取值范围;解:(1)(解答过程略去,只给出结论)当a ≤0时,函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;当a=21时,函数f(x)在(0,+∞)上单调递减; 当0<a<21时,函数()f x 在(0,1)上单调递减,在1(1,1)a-上单调递增,在(1(1,)a -+∞上单调递减;(2)函数的定义域为(0,+∞),f '(x )=x 1-a+21xa -=-221x a x ax -+-,a=41时,由f '(x )=0可得x 1=1,x 2=3. 因为a=41∈(0,21),x 2=3∉(0,2),结合(1)可知函数f(x)在(0,1)上单调递减,在(1,2)上单调递增,所以f(x) 在(0,2)上的最小值为f(1)= -21.由于“对∀x 1∈(0,2),∃x 2∈[1,2],使f(x 1) ≥g(x 2)”等价于“g(x)在[1,2]上的最小值不大于f(x) 在(0,2)上的最小值f(1)= -21”. (※)又g(x)=(x -b)2+4-b 2, x ∈[1,2],所以① 当b<1时,因为[g(x)]min =g(1)=5-2b>0,此时与(※)矛盾;② 当b ∈[1,2]时, 因为[g(x)]min =4-b 2≥0,同样与(※)矛盾; ③ 当b ∈(2,+∞)时,因为[g(x)]min =g(2)=8-4b. 解不等式8-4b ≤-21,可得b ≥817.综上,b 的取值范围是[817,+∞). 二、相关类型题: 〈一〉、"()"a f x ≥型;形如"()","()"a f x a f x ≥≤型不等式,是恒成立问题中最基本的类型,它的理论基础是“()a f x ≥在x D ∀∈上恒成立,则max ()();a f x x D ≥∈()a f x ≤在x ∈D 上恒成立,则min ()();a f x x D ≤∈”.许多复杂的恒成立问题最终都可归结到这一类型.例1 :已知二次函数2()f x ax x =+,若∀[0,1]x ∈时,恒有|()|1f x ≤,求实数a 的取值范围. 解:|()|1f x ≤,∴211ax x -≤+≤;即211x ax x --≤≤-;当0x =时,不等式显然成立, ∴a ∈R. 当01x <≤时,由211x ax x --≤≤-得:221111a x x x x --≤≤-,而min 211()0x x-=∴0a ≤. 又∵max 211()2x x--=-,∴2,20a a ≥-∴-≤≤, 综上得a 的范围是[2,0]a ∈-。
〈二〉、12"()()()"f x f x f x ≤≤型 例2 已知函数()2sin()25x f x ππ=+,若对∀x R ∈,都有12"()()()"f x f x f x ≤≤成立,则12||x x -的最小值为____.解 ∵对任意x ∈R ,不等式12()()()f x f x f x ≤≤恒成立, ∴12(),()f x f x 分别是()f x 的最小值和最大值.对于函数sin y x =,取得最大值和最小值的两点之间最小距离是π,即半个周期.又函数()2sin()25x f x ππ=+的周期为4,∴12||x x -的最小值为2. 〈三〉、.1212()()"()"22x x f x f x f ++>型 例3: (2005湖北)在222,log 2,,cos y x y x y x y x ====这四个函数中,当1201x x <<<时,使1212()()"()"22x x f x f x f ++>恒成立的函数的个数是( ) A.0 B.1 C.2 D.3解:本题实质就是考察函数的凸凹性,即满足条件1212()()"()"22x x f x f x f ++>的函数,应是凸函数的性质,画草图即知2log 2y x =符合题意;选C 〈四〉、.1212()()"0"f x f x x x ->-型例 4 已知函数()f x 定义域为[1,1]-,(1)1f =,若,[1,1]m n ∈-,0m n +≠时,都有()()"0"f m f n m n->-,若2()21f x t at ≤-+对所有[1,1]x ∈-,[1,1]a ∈-恒成立,求实数t 取值范围.解:任取1211x x -≤<≤,则12121212()()()()()f x f x f x f x x x x x --=--,由已知1212()()0f x f x x x ->-,又120x x -<,∴12()()0f x f x -<f ,即()f x 在[1,1]-上为增函数.∵(1)1f =,∴[1,1]x ∈-,恒有()1f x ≤;∴要使2()21f x t at ≤-+对所有[1,1]x ∈-,[1,1]a ∈-恒成立,即要2211t at -+≥恒成立,故220t at -≥恒成立,令2()2g a at t =-+,只须(1)0g -≥且(1)0g ≥, 解得2t ≤-或0t =或2t ≥。
评注: 形如不等式1212()()"0"f x f x x x ->-或1212()()"0"f x f x x x -<-恒成立,实际上是函数的单调性的另一种表现形式,在解题时要注意此种类型不等式所蕴涵的重要信息. 〈五〉、."()()"f x g x <型: 例5: 已知1()lg(1)2f x x =+,()lg(2)g x x t =+,若当[0,1]x ∈时,()()f x g x ≤)恒成立,求实数t 的取值范围.解:()()f x g x ≤在[0,1]x ∈恒成立,即20x t -≤在[0,1]x ∈恒成立2x t ⇔-在[0,1]上的最大值小于或等于零.令()2F x x t =-,'()F x =,∵[0,1]x ∈∴'()0F x <,即()F x 在[0,1]上单调递减,F(0)是最大值. ∴()(0)10f x F t ≤=-≤,即1t ≥。
