坐标系与参数方程(解析版)
2020年高考数学(文)二轮专项复习专题13 坐标系与参数方程含答案

专题13 坐标系与参数方程【知识要点】1.极坐标系的概念,极坐标系中点的表示.在平面内取一个定点O ,O 点出发的一条射线Ox ,一个长度单位及计算角度的正方向(通常取逆时针方向),合称为一个极坐标系.O 称为极点,Ox 称为极轴.设M 是平面内任意一点,极点O 与点M 的距离|OM |叫做点M 的极径,记作ρ ;以极轴Ox 为始边,射线OM 为终边的角xOM 叫做点M 的极角,记作θ ,有序数对(ρ ,θ )叫做点M 的极坐标.一般情况下,约定ρ ≥0.2.极坐标系与直角坐标系的互化.直角坐标化极坐标:x =ρ cos θ ,y =ρ sin θ ; 极坐标化直角坐标:, 3.参数方程的概念设在平面上取定一个直角坐标系xOy ,把坐标x ,y 表示为第三个变量t 的函数……①,如果对于t 的每一个值(a ≤t ≤b ),①式所确定的点M (x ,y )都在一条曲线上;而这条曲线上任意一点M (x ,y ),都可由t 的某个值通过①式得到,则称①式为该曲线的参数方程,其中t 称为参数.4.参数方程与普通方程的互化把参数方程化为普通方程,需要根据其结构特征,选取适当的消参方法.常见的消参方法有:代入消元法;加减消参法;平方和(差)消参法;乘法消参法等.把曲线C 的普通方程F (x ,y )=0化为参数方程的关键:一是适当选取参数;二是确保互化前后方程的等价性.要注意方程中的参数的变化范围. 5.直线、圆、椭圆的参数方程.(1)经过一定点P 0(x 0,y 0),倾斜角为α 的直线l 的参数方程为(t 为参数);(2)直线参数方程的一般形式为(t 为参数);222y x +=ρ).0(tan =/=x xyθ⎩⎨⎧==)()(t g y t f x b t a ≤≤⎩⎨⎧+=+=ααsin ,cos 00t y y t x x ⎩⎨⎧+=+=bt y y at x x 00,(3)圆的参数方程为(θ 为参数);(4)椭圆的参数方程为(θ 为参数).【复习要求】1.理解坐标系的作用.2.能在极坐标系中用极坐标表示点的位置,理解在极坐标系和平面直角坐标系中表示点的位置的区别,能进行极坐标和直角坐标的互化.3.了解参数方程.4.能选择适当的参数写出直线、圆和圆锥曲线的参数方程,并会简单的应用. 【例题分析】例1 (1)判断点是否在曲线上. (2)点P 的直角坐标为,则点P 的极坐标为______.(限定0<θ ≤2π)(3)点P 的极坐标为,则点P 的直角坐标为______.解:(1)因为,所以点是在曲线上. (2)根据ρ 2=x 2+y 2,, 得ρ =2,,又点P 在第四象限,,所以,所以点P 的极坐标为 (3)根据x =ρ cos θ ,y =ρ sin θ ,得, 所以点P 的直角坐标为 例2 (1)圆ρ =2(cos θ +sin θ )的半径为______.⎩⎨⎧+=+=θθsin ,cos 00r y y r x x )0(12222>>=+b a b y a x ⎩⎨⎧==θθsin ,cos b y a x )35π,23(-2cos θρ=)3,1(-)4π,3(-2365πcos2cos-==θ)35π,23(-2cos θρ=)0(tan =/=x xy θ3tan -=θ2π23π≤<θ35π=θ).3π5,2(223,223-==y x ).223,223(-(2)直线与圆ρ =2sin θ 交与A ,B 两点,则|AB |=______. 解:(1)由ρ =2(cos θ +sin θ ),得ρ 2=2ρ (cos θ +sin θ ), 所以,x 2+y 2=2x +2y ,即(x -1)2+(y -1)2=2, 所以圆ρ =2(cos θ +sin θ )的半径为. (2)将直线与圆ρ =2sin θ 化为直角坐标方程,得 由得,即, 由ρ =2sin θ ,变形为ρ 2=2ρ sin θ ,得x 2+y 2=2y ,即x 2+(y -1)2=1, 因为圆的半径为1,圆心到直线的距离为, 所以评述:(1)应熟练运用直角坐标与极坐标互化的方法解决有关极坐标的问题;(2)由直角坐标化极坐标时要注意点位于哪一个象限才能确定θ 的大小,如例1(2),否则,极坐标不唯一; (3)例2也可以用极坐标有关知识直接解决.这需要知道一些直线与圆的极坐标方程的知识.如: ①过极点,倾斜角为α 的直线:θ =α (ρ ∈R )或写成θ =α 及θ =α +π. ②过A (a ,α)垂直于极轴的直线:ρ cos θ =a cos α . ③以极点O 为圆心,a 为半径的圆(a >0):ρ =a .④若O (0,0),A (2a ,0),以OA 为直径的圆:ρ =2a cos θ . ⑤若O (0,0),A (2a ,),以OA 为直径的圆:ρ =2a sin θ . 对于例2(2),可以利用结论①⑤,作出直线与圆,通过解三角形的方法求|AB |,当然也可以用极坐标方程直接解ρ ,根据ρ 的几何意义求|AB |.例3 圆O 1和圆O 2的极坐标方程分别为ρ =4cos θ ,ρ =-4sin θ . (1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程; (2)求经过圆O 1和圆O 2交点的直线的直角坐标方程.)(3πR ∈=ρθ2)(3πR ∈=ρθ3π=θxy=3πtan x y 3=21311=+=d .3)21(12||2=-=AB 2π解:(1)由ρ =4cos θ 得ρ 2=4ρ cos θ ,根据x =ρ cos θ ,y =ρ sin θ ,所以x 2+y 2=4x . 即x 2+y 2-4x =0为圆O 1的直角坐标方程,同理x 2+y 2+4y =0为圆O 2的直角坐标方程.(2)由解得 即圆O 1和圆O 2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y =-x .例4(1)曲线的参数方程是(t 为参数,t ≠0),它的普通方程是________. (2)在平面直角坐标系xOy 中,直线l 的参数方程为 (参数t ∈R ),圆C 的参数方程为(参数θ ∈[0,2π]),则圆C 的圆心坐标为______,圆心到直线l 的距离为______. 解:(1)由得,带入y =1-t 2,得 注意到,所以已知参数的普通方程为 (2)直线l 的普通方程为x +y -6=0,圆C 的普通方程为x 2+(y -2)2=4, 所以圆心坐标为(0,2),圆心到直线l 的距离评述:(1)应熟练运用将参数方程化为普通方程的方法解决有关参数方程的问题;(2)在将参数方程化为普通方程的过程中应注意消参带来的范围变化问题.如例4(1),若参数方程为(t 为参数,t >0),则其普通方程为 例5 求椭圆的内接矩形的最大面积.解:设内接矩形在第一象限内的顶点为P (a cos θ ,b sin θ ),P 点在两轴上的投影分别为A 、B ,则有S 内接矩形=4S 矩形OAPB =4·a cos θ ·b sin θ =2ab sin2θ . 因为,所以2θ ∈(0,π),S 内接矩形的最大值为2ab . ⎪⎩⎪⎨⎧=++=-+,04,042222y y x x y x ⎩⎨⎧==;0,011y x ⎩⎨⎧-==.2,222y x ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=21,11t y t x ⎩⎨⎧-=+=t y t x 3,3⎩⎨⎧+==2sin 2,cos 2θθy x t x 11-=x t -=11,)1()2()11(122--=--=x x x x y 111=/-=t x ⋅--=2)1()2(x x x y .222|620|=-+=d ⎪⎪⎩⎪⎪⎨⎧-=-=21,11t y t x ).1()1()2(2<--=x x x x y 12222=+by a x )2π,0(∈θ评述:圆锥曲线参数方程主要应用于利用参数方程设圆锥曲线上的点,从而讨论最值等有关问题.椭圆的参数方程为 (θ 为参数).抛物线y 2=2px (p >0)的参数方程为.例6 圆M 的参数方程为x 2+y 2-4Rx cos α -4Ry sin α +3R 2=0(R >0). (1)求该圆的圆心坐标以及圆M 的半径;(2)当R 固定,α 变化时,求圆心M 的轨迹,并证明此时不论α 取什么值,所有的圆M 都外切于一个定圆. 解:(1)依题意得圆M 的方程为(x -2R cos α )2+(y -2R sin α )2=R 2, 故圆心的坐标为M (2R cos α ,2R sin α ),半径为R .(2)当α 变化时,圆心M 的轨迹方程为 (α 为参数),两式平方相加得x 2+y 2=4R 2,所以圆心M 的轨迹是圆心在原点,半径为2R 的圆.由于所以所有的圆M 都和定圆x 2+y 2=R 2外切,和定圆x 2+y 2=9R 2内切.例7 过P (5,-3),倾斜角为α ,且的直线交圆x 2+y 2=25于P 1、P 2两点.(1)求|PP 1|·|PP 2|的值;(2)求弦P 1P 2的中点M 的坐标.解:(1)由已知得所以已知直线的参数方程为…………………①(t 为参数)代入圆的方程化简,得…………………② ②的两个解t 1、t 2就是P 1、P 2对应的参数,由参数的几何意义及韦达定理知)0,0(12222>>=+b a b y a x ⎩⎨⎧==θθtan sec b y a x ⎩⎨⎧==pty ptx 222⎩⎨⎧==,sin 2,cos 2ααR y R x ,32)sin 2()cos 2(22R R R R R -==+αα,2)sin 2()cos 2(22R R R R R +==+αα53cos -=α53cos -=α,54sin =α⎪⎪⎩⎪⎪⎨⎧+-=-=,543,535t y t x .095542=+-t t|PP 1|·|PP 2|=|t 1|·|t 2|=9.(2)设M (x ,y )为P 1P 2的中点,则点M 对应的参数,代入参数方程, 得 所以 评述:根据直线的参数方程的标准式中t 的几何意义,有如下常用结论: ①直线与圆锥曲线相交,交点对应的参数分别为t 1,t 2,则弦长l =|t 1-t 2|; ②定点M 0是弦M 1M 2的中点t 1+t 2=0;③设弦M 1M 2的中点为M ,则点M 对应的参数值,(由此可求得|M 2M |及中点坐标). 习题13一、选择题 1.极坐标的直角坐标为 (A)(1,)(B)(-,-1)(C)(-1,-)(D)(-1,)2.椭圆(θ 为参数)的焦距等于( )(A) (B)2 (C) (D)3.已知某条曲线的参数方程为(0≤t ≤5),则该曲线是( )(A)线段 (B)圆弧 (C)双曲线的一支 (D)射线4.若是极坐标系中的一点,则四点中与P 重合的点有( )(A)1个(B)2个(C)3个(D)4个527221=+=t t t ,2533,2544==y x M PP PP ,9||||21=⋅).2533,2544(⇒221t t t M +=)34π(2,3333⎩⎨⎧==θθsin 5,cos 2y x 212129292⎪⎩⎪⎨⎧-=+=1,2322t y t x )3π,2(--P 、、、)3π5,2()3π8,2()3π2,2(-M R Q )3π5π2,2(-k N )(Z ∈k5.在极坐标系中,若等边△ABC 的两个顶点是,那么顶点C 的坐标可能是( ) (A) (B) (C)(D)(3,π)二、选择题6.过极点,倾斜角是的直线的极坐标方程为____________. 7.点M 的直角坐标(3,-3)化为极坐标是____________. 8.直线(t 为参数)过定点____________.9.曲线(t 为参数)与y 轴的交点坐标是____________.10.参数方程(θ 为参数)表示的曲线的普通方程是____________.三、解答题11.求过点,并且和极轴垂直的直线的极坐标方程.12.在椭圆上求一点,使点M 到直线的距离最小,并求出最小距离.13.设圆C 是以C (4,0)为圆心,半径等于4的圆.(1)求圆C 的极坐标方程;(2)从极点O 作圆C 的弦ON ,求ON 的中点M 的轨迹方程.)4π5,2()4π,2(B A 、)4π3,4()43π,32()π,32(6π⎩⎨⎧+-=+=t y at x 41,3⎩⎨⎧=+-=t y t x ,12⎩⎨⎧+==θθθcos sin ,2sin y x )4π,3(14922=+y x 021032=-+y x14.已知点M (2,1)和双曲线,求以M 为中点的双曲线右支的弦AB 所在直线l 的方程.专题13 坐标系与参数方程参考答案习题13一、选择题1.C 2.B 3.A 4.C 5.B 二、填空题 6.; 7.; 8.(3,-1); 9.(0,1),(0,-1); 三、解答题 11. 12.解:由题设知椭圆参数方程为(θ 为参数).设M 的坐标(3cos θ ,2sin θ )由点到直线距离 即d 的最小值为,此时.所以M 的坐标为13.解:(1)设P (ρ ,θ )为圆C 上任意一点,圆C 交极轴于另一点A .由已知|OA |=8,在Rt △ABC 中,|OP |=|OA |cos θ ,即ρ =8cos θ ,这就是圆C 的方程.1222=-y x )(6πR ∈=ρθ)47π,23(⋅=223cos θρ⎩⎨⎧==θθsin 2,cos 3y x ,13|210)4πsin(26|13|210sin 6cos 6|-+=-+=θθθd 261344π=θ).2,223((2)连结CM ,因为M 是ON 的中点,所以CM ⊥ON ,故M 在以OC 为直径的圆上. 由r =|OC |=4,得动点M 的轨迹方程是ρ =4cos θ .14.解:设AB 的方程为(t 为参数),代入双曲线方程,得(2cos 2α -sin 2α )t 2+(8cos α -2sin α )t +5=0,由于M 为AB 的中点,则t 1+t 2=0,则tan α =4,从而AB 的方程为:4x -y -7=0.⎩⎨⎧+=+=ααsin 1,cos 2t y t x。
2020年高考数学(理)二轮专题学与练 20 坐标系与参数方程(考点解读)(解析版)

专题20 坐标系与参数方程1.考查参数方程与普通方程、极坐标方程与直角坐标方程的互化.2.考查利用曲线的参数方程、极坐标方程计算某些量或讨论某些量之间的关系.知识点一、直角坐标与极坐标的互化如图,把直角坐标系的原点作为极点,x 轴正半轴作为极轴,且在两坐标系中取相同的长度单位.设M是平面内的任意一点,它的直角坐标、极坐标分别为(x ,y )和(ρ,θ),则⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,⎩⎪⎨⎪⎧ρ2=x 2+y 2,tan θ=y x x ≠0.【特别提醒】在曲线方程进行互化时,一定要注意变量的范围,要注意转化的等价性. 知识点二、直线、圆的极坐标方程 (1)直线的极坐标方程若直线过点M (ρ0,θ0),且极轴到此直线的角为α,则它的方程为:ρsin(θ-α)=ρ0sin(θ0-α). 几个特殊位置直线的极坐标方程 ①直线过极点:θ=α;②直线过点M (a ,0)且垂直于极轴:ρcos θ=a ; ③直线过点M ⎝⎛⎭⎫b ,π2且平行于极轴:ρsin θ=b . (2)几个特殊位置圆的极坐标方程 ①圆心位于极点,半径为r :ρ=r ;②圆心位于M (r ,0),半径为r :ρ=2r cos θ;③圆心位于M ⎝⎛⎭⎫r ,π2,半径为r :ρ=2r sin θ. 【特别提醒】当圆心不在直角坐标系的坐标轴上时,要建立圆的极坐标方程,通常把极点放置在圆心处,极轴与x 轴同向,然后运用极坐标与直角坐标的变换公式.知识点三、参数方程 (1)直线的参数方程过定点M (x 0,y 0),倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数).(2)圆、椭圆的参数方程①圆心在点M (x 0,y 0),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =x 0+r cos θ,y =y 0+r sin θ(θ为参数,0≤θ≤2π).②椭圆x 2a 2+y 2b 2=1的参数方程为⎩⎪⎨⎪⎧x =a cos θ,y =b sin θ(θ为参数).【特别提醒】在参数方程和普通方程的互化中,必须使x ,y 的取值范围保持一致.高频考点一 坐标系与极坐标例1.【2019年高考全国Ⅲ卷理数】如图,在极坐标系Ox 中,(2,0)A ,)4B π,)4C 3π,(2,)D π,弧AB ,BC ,CD 所在圆的圆心分别是(1,0),(1,)2π,(1,)π,曲线1M 是弧AB ,曲线2M 是弧BC ,曲线3M 是弧CD .(1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.【答案】(1)1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭. (2)π3,6⎛⎫ ⎪⎝⎭或π3,3⎛⎫ ⎪⎝⎭或2π3,3⎛⎫ ⎪⎝⎭或5π3,6⎛⎫ ⎪⎝⎭.【解析】(1)由题设可得,弧,,AB BC CD 所在圆的极坐标方程分别为2cos ρθ=,2sin ρθ=,2cos ρθ=-.所以1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤ ⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭. (2)设(,)P ρθ,由题设及(1)知若π04θ≤≤,则2cos 3θ=,解得π6θ=; 若π3π44θ≤≤,则2sin 3θ=,解得π3θ=或2π3θ=; 若3ππ4θ≤≤,则2cos 3θ-=,解得5π6θ=. 综上,P 的极坐标为π3,6⎛⎫ ⎪⎝⎭或π3,3⎛⎫ ⎪⎝⎭或2π3,3⎛⎫ ⎪⎝⎭或5π3,6⎛⎫⎪⎝⎭.【变式探究】在极坐标系中,直线4cos()106ρθπ-+=与圆2sin ρθ=的公共点的个数为___________.【答案】2【解析】直线为23210x y ++= ,圆为22(1)1x y +-= ,因为314d =< ,所以有两个交点 【变式探究】在极坐标系中,直线cos 3sin 10ρθρθ--=与圆2cos ρθ=交于A ,B 两点,则||AB =______.【答案】2【解析】直线310x y -=过圆22(1)1x y -+=的圆心,因此 2.AB =【变式探究】在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( ) A .θ=0(ρ∈R )和ρcos θ=2B .θ=π2(ρ∈R )和ρcos θ=2C .θ=π2(ρ∈R )和ρcos θ=1D .θ=0(ρ∈R )和ρcos θ=1【解析】由ρ=2cos θ得x 2+y 2-2x =0. ∴(x -1)2+y 2=1,圆的两条垂直于x 轴的切线方程为x =0和x =2. 故极坐标方程为θ=π2(ρ∈R )和ρcos θ=2,故选B.【答案】B高频考点二 参数方程例2.【2019年高考全国Ⅰ卷理数】在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为.(1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.【答案】(1)221(1)4y x x +=≠-;l的直角坐标方程为2110x ++=;(2)7.【解析】(1)因为221111t t --<≤+,且()22222222141211y t t x t t ⎛⎫-⎛⎫+=+= ⎪ ⎪+⎝⎭⎝⎭+,所以C 的直角坐标方程为221(1)4y x x +=≠-.l的直角坐标方程为2110x ++=. (2)由(1)可设C 的参数方程为cos ,2sin x y αα=⎧⎨=⎩(α为参数,ππα-<<).C 上的点到lπ4cos 11α⎛⎫-+ ⎪=.2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩,2cos sin 110ρθθ+=当2π3α=-时,π4cos 113α⎛⎫-+ ⎪⎝⎭取得最小值7,故C 上的点到l 距离的最小值为7.【变式探究】在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t t y =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C 的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.【答案】5【解析】直线l 的普通方程为280x y -+=. 因为点P 在曲线C上,设()22,P s ,从而点P 到直线l 的的距离224s d +==,当s =min d =. 因此当点P 的坐标为()4,4时,曲线C上点P 到直线l 的距离取到最小值5. 【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为cos 1sin x a ty a t=⎧⎨=+⎩(t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ.(I)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(II)直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a . 【答案】(I)圆,222sin 10a ρρθ-+-=(II)1【解析】解:(Ⅰ)消去参数t 得到1C 的普通方程222)1(a y x =-+.1C 是以)1,0(为圆心,a 为半径的圆.将θρθρsin ,cos ==y x 代入1C 的普通方程中,得到1C 的极坐标方程为01sin 222=-+-a θρρ.(Ⅰ)曲线21,C C 的公共点的极坐标满足方程组⎩⎨⎧==-+-,cos 4,01sin 222θρθρρa 若0≠ρ,由方程组得01cos sin 8cos 1622=-+-a θθθ,由已知2tan =θ,可得0cos sin 8cos162=-θθθ,从而012=-a ,解得1-=a (舍去),1=a .1=a 时,极点也为21,C C 的公共点,在3C 上.所以1=a .【变式探究】已知直线l 的参数方程为1,1x t y t =-+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2cos 2θ=4⎝⎛⎭⎫ρ>0,3π4<θ<5π4,则直线l 与曲线C 的交点的极坐标为________.【解析】直线l 的直角坐标方程为y =x +2,由ρ2cos 2θ=4得ρ2(cos 2θ-sin 2θ)=4,直角坐标方程为x 2-y 2=4,把y =x +2代入双曲线方程解得x =-2,因此交点为(-2,0),其极坐标为(2,π).【答案】(2,π)【变式探究】若以直角坐标系的原点为极点,x 轴的非负半轴为极轴建立极坐标系,则线段y =1-x (0≤x ≤1)的极坐标方程为( )A .ρ=1cos θ+sin θ,0≤θ≤π2B .ρ=1cos θ+sin θ,0≤θ≤π4C .ρ=cos θ+sin θ,0≤θ≤π2D .ρ=cos θ+sin θ,0≤θ≤π4【解析】∵cos ,sin ,x y ρθρθ=⎧⎨=⎩∴y =1-x 化为极坐标方程为ρcos θ+ρsin θ=1,即ρ=1cos θ+sin θ.∵0≤x ≤1,∴线段在第一象限内(含端点),∴0≤θ≤π2.故选A.【答案】A1.【2019年高考北京卷理数】已知直线l 的参数方程为13,24x t y t=+=+⎧⎨⎩(t 为参数),则点(1,0)到直线l 的距离是( )A .15B .25C .45D .65【答案】D【解析】由题意,可将直线l 化为普通方程:1234x y --=,即()()41320x y ---=,即4320x y -+=,所以点(1,0)到直线l的距离65d ==,故选D . 2.【2019年高考全国Ⅰ卷理数】在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为.(1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.【答案】(1)221(1)4y x x +=≠-;l的直角坐标方程为2110x ++=;(2)7.【解析】(1)因为221111t t --<≤+,且()22222222141211y t t x t t ⎛⎫-⎛⎫+=+= ⎪ ⎪+⎝⎭⎝⎭+,所以C 的直角坐标方程为221(1)4y x x +=≠-.l的直角坐标方程为2110x ++=.(2)由(1)可设C 的参数方程为cos ,2sin x y αα=⎧⎨=⎩(α为参数,ππα-<<).C 上的点到lπ4cos 11α⎛⎫-+ ⎪=.2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩,2cos sin 110ρθθ++=当2π3α=-时,π4cos 113α⎛⎫-+ ⎪⎝⎭取得最小值7,故C 上的点到l 距离的最小值为7.3.【2019年高考全国Ⅱ卷理数】在极坐标系中,O 为极点,点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上,直线l 过点(4,0)A 且与OM 垂直,垂足为P .(1)当0=3θπ时,求0ρ及l 的极坐标方程; (2)当M 在C 上运动且P 在线段OM 上时,求P 点轨迹的极坐标方程.【答案】(1)0ρ=l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭; (2)4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.【解析】(1)因为()00,M ρθ在C 上,当03θπ=时,04sin 3ρπ== 由已知得||||cos23OP OA π==. 设(,)Q ρθ为l 上除P 的任意一点.在Rt OPQ △中,cos ||23OP ρθπ⎛⎫-== ⎪⎝⎭, 经检验,点(2,)3P π在曲线cos 23ρθπ⎛⎫-= ⎪⎝⎭上. 所以,l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭. (2)设(,)P ρθ,在Rt OAP △中,||||cos 4cos ,OP OA θθ== 即 4cos ρθ=. 因为P 在线段OM 上,且AP OM ⊥,故θ的取值范围是,42ππ⎡⎤⎢⎥⎣⎦.所以,P 点轨迹的极坐标方程为4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.4.【2019年高考全国Ⅲ卷理数】如图,在极坐标系Ox 中,(2,0)A ,)4B π,)4C 3π,(2,)D π,弧AB ,BC ,CD 所在圆的圆心分别是(1,0),(1,)2π,(1,)π,曲线1M 是弧AB ,曲线2M 是弧BC ,曲线3M 是弧CD .(1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.【答案】(1)1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤ ⎪⎝⎭.(2)π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.【解析】(1)由题设可得,弧,,AB BC CD 所在圆的极坐标方程分别为2cos ρθ=,2sin ρθ=,2cos ρθ=-.所以1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤ ⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭. (2)设(,)P ρθ,由题设及(1)知若π04θ≤≤,则2cos θ=,解得π6θ=;若π3π44θ≤≤,则2sin θ=π3θ=或2π3θ=;若3ππ4θ≤≤,则2cos θ-=5π6θ=.综上,P 的极坐标为π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.5.【2019年高考江苏卷数学】在极坐标系中,已知两点3,,42A B ππ⎛⎫⎫ ⎪⎪⎝⎭⎭,直线l 的方程为sin 34ρθπ⎛⎫+= ⎪⎝⎭.(1)求A ,B 两点间的距离;(2)求点B 到直线l 的距离. 【答案】(1)5;(2)2.【解析】(1)设极点为O .在△OAB 中,A (3,4π),B (2,2π), 由余弦定理,得AB =223(2)232cos()524ππ+-⨯⨯⨯-=. (2)因为直线l 的方程为sin()34ρθπ+=, 则直线l 过点(32,)2π,倾斜角为34π. 又(2,)2B π,所以点B 到直线l 的距离为3(322)sin()242ππ-⨯-=. 1. (2018年全国I 卷理数)在直角坐标系中,曲线的方程为.以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求的直角坐标方程;(2)若与有且仅有三个公共点,求的方程. 【答案】 (1). (2)的方程为.【解析】 (1)由,得的直角坐标方程为 .(2)由(1)知是圆心为,半径为的圆. 由题设知,是过点且关于轴对称的两条射线.记轴右边的射线为,轴左边的射线为.由于在圆的外面,故与有且仅有三个公共点等价于与只有一个公共点且与有两个公共点,或与只有一个公共点且与有两个公共点.当与只有一个公共点时,到所在直线的距离为,所以,故或.经检验,当时,与没有公共点;当时,与只有一个公共点,与有两个公共点.当与只有一个公共点时,到所在直线的距离为,所以,故或.经检验,当时,与没有公共点;当时,与没有公共点.综上,所求的方程为.2. (2018年全国Ⅰ卷理数)在直角坐标系中,曲线的参数方程为(为参数),直线的参数方程为(为参数).(1)求和的直角坐标方程;(2)若曲线截直线所得线段的中点坐标为,求的斜率.【答案】(1)当时,的直角坐标方程为,当时,的直角坐标方程为.(2)【解析】(1)曲线的直角坐标方程为.当时,的直角坐标方程为,当时,的直角坐标方程为.(2)将的参数方程代入的直角坐标方程,整理得关于的方程.①因为曲线截直线所得线段的中点在内,所以①有两个解,设为,,则.又由①得,故,于是直线的斜率.3. (2018年全国Ⅰ卷理数)在平面直角坐标系中,的参数方程为(为参数),过点且倾斜角为的直线与交于两点.(1)求的取值范围;(2)求中点的轨迹的参数方程.【答案】(1)(2)为参数,【解析】(1)的直角坐标方程为.当时,与交于两点.当时,记,则的方程为.与交于两点当且仅当,解得或,即或.综上,的取值范围是.(2)的参数方程为为参数,.设,,对应的参数分别为,,,则,且,满足.于是,.又点的坐标满足所以点的轨迹的参数方程是 为参数, .4. (2018年江苏卷)在极坐标系中,直线l 的方程为,曲线C 的方程为,求直线l 被曲线C 截得的弦长.【答案】直线l 被曲线C 截得的弦长为 【解析】因为曲线C 的极坐标方程为,所以曲线C 的圆心为(2,0),直径为4的圆. 因为直线l 的极坐标方程为,则直线l 过A (4,0),倾斜角为, 所以A 为直线l 与圆C 的一个交点. 设另一个交点为B ,则∠OAB =.连结OB ,因为OA 为直径,从而∠OBA =, 所以.因此,直线l 被曲线C 截得的弦长为. 1.【2017天津,理11】在极坐标系中,直线4cos()106ρθπ-+=与圆2sin ρθ=的公共点的个数为___________.【答案】2【解析】直线为23210x y ++= ,圆为22(1)1x y +-= ,因为314d =< ,所以有两个交点 2. 【2017北京,理11】在极坐标系中,点A 在圆22cos 4sin 40ρρθρθ--+=上,点P 的坐标为(1,0),则|AP |的最小值为___________.【答案】1【解析】将圆的极坐标方程化为普通方程为222440x y x y +--+= ,整理为()()22121x y -+-= ,圆心()1,2C ,点P 是圆外一点,所以AP 的最小值就是211AC r -=-=.3. 【2017课标1,理22】在直角坐标系xOy 中,曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩(θ为参数),直线l的参数方程为4,1,x a t t y t =+⎧⎨=-⎩(为参数). (1)若a =−1,求C 与l 的交点坐标;(2)若C 上的点到la. 【答案】(1)C 与l 的交点坐标为()3,0, 2124,2525⎛⎫-⎪⎝⎭;(2)8a =或16a =-. 【解析】(1)曲线C 的普通方程为2219x y +=. 当1a =-时,直线l 的普通方程为430x y +-=.由22430{ 19x y x y +-=+=解得3{ 0x y ==或2125{ 2425x y =-=. 从而C 与l 的交点坐标为()3,0, 2124,2525⎛⎫-⎪⎝⎭. (2)直线l 的普通方程为440x y a +--=,故C 上的点()3cos ,sin θθ到l 的距离为d =当4a ≥-时, d=8a =; 当4a <-时, d=16a =-.综上, 8a =或16a =-.【2017·江苏】[选修4-4:坐标系与参数方程](本小题满分10分)在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t ty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.【答案】5【解析】直线l 的普通方程为280x y -+=. 因为点P 在曲线C上,设()22,P s ,从而点P 到直线l 的的距离224s d +==,当s =min d =. 因此当点P 的坐标为()4,4时,曲线C上点P 到直线l 的距离取到最小值5. 1.【2016年高考北京理数】在极坐标系中,直线cos sin 10ρθθ-=与圆2cos ρθ=交于A ,B 两点,则||AB =______.【答案】2【解析】直线10x -=过圆22(1)1x y -+=的圆心,因此 2.AB = 2.【2016高考新课标1卷】(本小题满分10分)选修4—4:坐标系与参数方程 在直角坐标系x O y 中,曲线C 1的参数方程为cos 1sin x a ty a t =⎧⎨=+⎩(t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ. (I)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(II)直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a . 【答案】(I)圆,222sin 10a ρρθ-+-=(II)1【解析】解:(Ⅰ)消去参数t 得到1C 的普通方程222)1(a y x =-+.1C 是以)1,0(为圆心,a 为半径的圆.将θρθρsin ,cos ==y x 代入1C 的普通方程中,得到1C 的极坐标方程为01sin 222=-+-a θρρ.(Ⅰ)曲线21,C C 的公共点的极坐标满足方程组⎩⎨⎧==-+-,cos 4,01sin 222θρθρρa 若0≠ρ,由方程组得01cos sin 8cos 1622=-+-a θθθ,由已知2tan =θ,可得0cos sin 8cos162=-θθθ,从而012=-a ,解得1-=a (舍去),1=a .1=a 时,极点也为21,C C 的公共点,在3C 上.所以1=a .3.【2016高考新课标2理数】选修4—4:坐标系与参数方程 在直角坐标系xOy 中,圆C 的方程为22(6)25x y ++=.(Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(Ⅰ)直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩(t 为参数), l 与C 交于,A B 两点,||AB =,求l 的斜率.【答案】(Ⅰ)212cos 110ρρθ++=;(Ⅰ)3±. 【解析】(I)由cos ,sin x y ρθρθ==可得C 的极坐标方程212cos 110.ρρθ++= (II)在(I)中建立的极坐标系中,直线l 的极坐标方程为()R θαρ=∈ 由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得212cos 110.ρρα++=于是121212cos ,11,ρραρρ+=-=22121212||||()4144cos 44,AB ρρρρρρα=-=+-=-由||10AB =得2315cos,tan 8αα==±, 所以l 的斜率为153或153-. 4. 【2016高考新课标3理数】(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的参数方程为3()sin x y ααα⎧=⎪⎨=⎪⎩为参数,以坐标原点为极点,以x 轴的正半轴为极轴,,建立极坐标系,曲线2C 的极坐标方程为sin()224ρθπ+=(I)写出1C 的普通方程和2C 的直角坐标方程;(II)设点P 在1C 上,点Q 在2C 上,求PQ 的最小值及此时P 的直角坐标.【答案】(Ⅰ)1C 的普通方程为2213x y +=,2C 的直角坐标方程为40x y +-=;(Ⅰ)31(,)22. 【解析】(Ⅰ)1C 的普通方程为2213x y +=,2C 的直角坐标方程为40x y +-=. (Ⅰ)由题意,可设点P 的直角坐标为3,sin )αα,因为2C 是直线,所以||PQ 的最小值即为P 到2C 的距离()d α的最小值,|3cos sin 4|()2sin()2|32d ααπαα+-==+-.当且仅当2()6k k Z παπ=+∈时,()d α取得最小值,2,此时P 的直角坐标为31(,)22.。
高考数学-坐标系与参数方程(含22年真题讲解)

高考数学-坐标系与参数方程 (含22年真题讲解)1.【2022年全国甲卷】在直角坐标系xOy 中,曲线C 1的参数方程为{x =2+t 6y =√t(t 为参数),曲线C 2的参数方程为{x =−2+s 6y =−√s(s 为参数).(1)写出C 1的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 3的极坐标方程为2cosθ−sinθ=0,求C 3与C 1交点的直角坐标,及C 3与C 2交点的直角坐标. 【答案】(1)y 2=6x −2(y ≥0);(2)C 3,C 1的交点坐标为(12,1),(1,2),C 3,C 2的交点坐标为(−12,−1),(−1,−2).【解析】 【分析】(1)消去t ,即可得到C 1的普通方程;(2)将曲线C 2,C 3的方程化成普通方程,联立求解即解出. (1) 因为x =2+t 6,y =√t ,所以x =2+y 26,即C 1的普通方程为y 2=6x −2(y ≥0).(2) 因为x =−2+s 6,y =−√s ,所以6x =−2−y 2,即C 2的普通方程为y 2=−6x −2(y ≤0),由2cosθ−sinθ=0⇒2ρcosθ−ρsinθ=0,即C 3的普通方程为2x −y =0. 联立{y 2=6x −2(y ≥0)2x −y =0 ,解得:{x =12y =1 或{x =1y =2 ,即交点坐标为(12,1),(1,2);联立{y 2=−6x −2(y ≤0)2x −y =0 ,解得:{x =−12y =−1 或{x =−1y =−2 ,即交点坐标为(−12,−1),(−1,−2). 2.【2022年全国乙卷】在直角坐标系xOy 中,曲线C 的参数方程为{x =√3cos2t y =2sint ,(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知直线l 的极坐标方程为ρsin (θ+π3)+m =0. (1)写出l 的直角坐标方程;(2)若l 与C 有公共点,求m 的取值范围. 【答案】(1)√3x +y +2m =0 (2)−1912≤m ≤52 【解析】 【分析】(1)根据极坐标与直角坐标的互化公式处理即可;(2)联立l 与C 的方程,采用换元法处理,根据新设a 的取值范围求解m 的范围即可. (1)因为l :ρsin (θ+π3)+m =0,所以12ρ⋅sinθ+√32ρ⋅cosθ+m =0,又因为ρ⋅sinθ=y,ρ⋅cosθ=x ,所以化简为12y +√32x +m =0,整理得l 的直角坐标方程:√3x +y +2m =0 (2)联立l 与C 的方程,即将x =√3cos2t ,y =2sint 代入 √3x +y +2m =0中,可得3cos2t +2sint +2m =0, 所以3(1−2sin 2t)+2sint +2m =0, 化简为−6sin 2t +2sint +3+2m =0,要使l 与C 有公共点,则2m =6sin 2t −2sint −3有解,令sint =a ,则a ∈[−1,1],令f(a)=6a 2−2a −3,(−1≤a ≤1), 对称轴为a =16,开口向上,所以f(a)max =f(−1)=6+2−3=5, f(a)min =f(16)=16−26−3=−196,所以−196≤2m ≤5m 的取值范围为−1912≤m ≤52.1.(2022·宁夏·吴忠中学三模(文))在平面直角坐标系xOy 中,曲线1C 的参数方程为244x t y t ⎧=-⎨=⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2cos ρθ=.(1)求曲线1C 与2C 的直角坐标方程;(2)已知直线l 的极坐标方程为πR 02θαρα⎛⎫ ⎪=∈⎝<<⎭,,直线l 与曲线1C ,2C 分别交于M ,N (均异于点O )两点,若4OMON=,求α. 【答案】(1)曲线1C 的直角坐标方程为24y x =-,曲线2C 的直角坐标方程为2220x y x +-=, (2)π4α=【解析】 【分析】(1)1C 的参数方程消参可求出1C 的直角坐标方程;2C 的极坐标方程同乘ρ,把cos x ρθ=,222x y ρ=+代入2C 的极坐标方程可求出2C 的直角坐标方程.(2)设M 、N 两点的极坐标分别为()1,ρα、()2,ρα,用极径的几何意义表示出4OMON=,即124ρρ=,解方程即可求出α. (1)解:1C 的参数方程为244x t y t ⎧=-⎨=⎩(t 为参数),把2216y t =代入24x t =-中可得,24y x =-,所以曲线1C 的直角坐标方程为24y x =-,2C 的极坐标方程为2cos ρθ=,即22cos ρρθ=,所以曲线2C 的直角坐标方程为2220x y x +-=,综上所述:曲线1C 的直角坐标方程为24y x =-,曲线2C 的直角坐标方程为2220x y x +-=, (2)由(1)知,1C 的极坐标方程为2sin 4cos ρθθ=-, 设M 、N 两点的极坐标分别为()1,ρα、()2,ρα,则21sin 4cos ραα=-,22cos ρα=,由题意知02πα<<可得sin 0α≠,因为4OMON=,所以124ρρ=,所以24cos 42cos sin ααα-=⨯,故21sin 2α=,所以sin 2α=或sin 2α=(舍) 所以π4α=.2.(2022·四川·宜宾市叙州区第一中学校模拟预测(理))在平面直角坐标系xOy 中,曲线1C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩(θ为参数),曲线2C 的参数方程为2221x t t y t ⎧=-⎨=-⎩(t 为参数).已知曲线2C 与x ,y 正半轴分别相交于,A B 两点.(1)写出曲线1C 的极坐标方程,并求出,A B 两点的直角坐标;(2)若过原点O 且与直线AB 垂直的直线l 与曲线1C 交于P 点,与直线AB 交于Q 点,求线段PQ 的长度.【答案】(1)2cos ρθ=,A 点为()3,0,B 点为()0,3(2)2【解析】 【分析】(1)普通方程()2211x y -+=,即可得2cos ρθ=(2)求出直线AB 的方程为3y x =-+,然后求出直线l 的方程,然后可求出PQ 的长度 (1)曲线1C 的普通方程()2211x y -+=,极坐标方程()()22cos 1sin 1ρθρθ-+=,∴2cos ρθ=.在曲线2C 上,当0x =时,0=t 或2t =,此时3y =或1y =-(舍),所以B 点为()0,3. 当0y =时,1t =-或1t =,此时3x =或1x =-(舍),所以A 点为()3,0. (2)直线AB 的方程为3y x =-+,极坐标方程为sin cos 3ρθρθ=-+, ∴()sin cos 3ρθθ+=,过原点O 且与直线AB 垂直的直线l 的极坐标方程为4πθ=.4πθ=与2cos ρθ=联立,得1ρ 4πθ=与()sin cos 3ρθθ+=联立,得2ρ=∴21PQ ρρ=-=. 3.(2022·江西·南昌市八一中学三模(理))在直角坐标系xOy 中,直线l的参数方程为11x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为4sin 6πρθ⎛⎫=-+ ⎪⎝⎭.(1)求C 和l 的直角坐标方程;(2)设点Q的直角坐标为(,P 为C 上的动点,求PQ 中点R 的轨迹的极坐标方程. 【答案】(1)直线l 的普通方程为2x y +=,曲线C 的普通方程为()(2214x y ++=;(2)21ρ= 【解析】 【分析】(1)消去参数t ,即可得到直线l 的普通方程,再由两角和的正弦公式及222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪=+⎩,将曲线C 的极坐标方程化为直角坐标方程;(2)设(),R x y ,即可表示P 点坐标,再根据点P 在曲线C 上,代入C 的方程,即可得到点R 的轨迹方程,再将直角坐标方程化为极坐标方程即可;(1)解:因为直线l的参数方程为11x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数), 所以直线l 的普通方程为2x y +=,因为曲线C 的极坐标方程为4sin 6πρθ⎛⎫=-+ ⎪⎝⎭,即4sin cos cos sin 66ππρθθ⎛⎫=-+ ⎪⎝⎭,即2cos ρθθ=--,所以2sin 2cos ρθρθ=--,又222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪=+⎩,所以222x y x +=--,即()(2214x y +++=,即曲线C 的普通方程为()(2214x y ++=;(2)解:设(),R x y,则(21,2P x y -,因为点P 在曲线C 上,所以()(2221124x y -++=,即221x y +=,所以PQ 中点R 的轨迹方程为221x y +=,即21ρ=4.(2022·黑龙江·哈尔滨三中模拟预测(理))在平面直角坐标系xOy 中,已知直线l 的参数方程为21x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为()2cos θsin θρ=+. (1)求直线l 的普通方程和曲线C 的直角坐标方程; (2)设点()2,1P ,直线l 与曲线C 的交点为A ,B ,求PA PBPB PA+的值. 【答案】(1)10x y --=,22220x y x y +--= (2)4 【解析】 【分析】(1)直接消去参数,将直线l 的方程化为普通方程,利用互化公式将曲线C 的极坐标方程转化为直角坐标方程(2)将直线的参数方程代入曲线C的普通方程,得到210t -=,得到12121t t t t +==- ,化简()222121212122112122PA PBt t t t t t t t PB PA t t t t t t +-++=+==,代入韦达定理,即可得到答案 (1)直线l的参数方程为21x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数), 消去参数t 可得l 的普通方程为10x y --=.曲线C 的极坐标方程为2(cos θsin θ)ρ=+,即22(cos θsin θ)ρρ=+,根据222cos θsin θx y x y ρρρ=⎧⎪=⎨⎪=+⎩,可得2222x y x y +=+.∴曲线C 的直角坐标方程为22220x y x y +--= (2)在直线l的参数方程21x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数)中,设点A ,B 对应的参数分别为1t ,2t , 将直线l的参数方程221x y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),代入22220x y x y +--=,得210t +-=,∴12t t +=121t t =-.∴()2221212121221121224PA PBt t t t t t t t PB PA t t t t t t +-++=+=== 5.(2022·安徽淮南·二模(文))在平面直角坐标系xOy 中,曲线C 的参数方程为2cos 22sin x y αα=⎧⎨=+⎩(其中α为参数,02πα≤<),以原点O 为极点,x 轴非负半轴为极轴,取相同的单位长度建立极坐标系,直线1l 的极坐标方程为(R)3πθρ=∈.(1)求曲线C 的极坐标方程与直线1l 的直角坐标方程;(2)设直线1l 与曲线C 交于点O ,A ,直线2l 与曲线C 交于点O ,B ,求AOB 面积的最大值. 【答案】(1)4sin ρθ=,y(2)【解析】【分析】(1)依据参数方程与普通方程的互化和极坐标方程与直角坐标方程的互化即可解决; (2)先求得AOB 面积的表达式,再对其求最大值即可. (1)曲线C 的直角坐标方程为22(2)4x y +-=,展开得2240x y y +-=, 则曲线C 的极坐标方程为4sin ρθ=. 直线1l的直角坐标方程为y (2)由(1)可知π||4sin3OA == 设直线2l 的极坐标方程为(R)θβρ=∈,根据条件知要使AOB 面积取最大值,则ππ3β<<,则||4sin OB β=,于是1ππsin sin 233OAB S OA OB βββ⎛⎫⎛⎫=⨯⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭2π6sin cos cos 2)3sin 226ββββββ⎛⎫=-=--=+ ⎪⎝⎭,所以当π3π262β+=即2π3β=时,AOB的面积取最大值,最大值为6.(2022·内蒙古呼和浩特·二模(理))在直角坐标系xOy 中,曲线C的参数方程为))cos sin cos sin 2x y ϕϕϕϕ⎧=+⎪⎨=-⎪⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,两坐标系取相同单位长度,直线l 的极坐标方程为2cos 3sin 100ρθρθ+-=. (1)求曲线C 的普通方程和直线l 的直角坐标方程; (2)求曲线C 上的点到直线l 距离的最小值. 【答案】(1)2214x y +=,23100x y +-=;【解析】 【分析】(1)消去曲线C 的参数方程中的参数即可得解,利用极坐标与直角坐标互化得直线l 的直角坐标方程作答.(2)设出曲线C 上任意一点的坐标,利用点到直线距离公式及辅助角公式求解作答. (1)由))cos sin cos sin x y ϕϕϕϕ⎧=+⎪⎨=-⎪⎩(ϕ为参数),消去参数得2214x y +=, 所以曲线C 的普通方程为2214x y +=,把cos sin x y ρθρθ=⎧⎨=⎩代入直线l 的极坐标方程2cos 3sin 100ρθρθ+-=得:23100x y +-=,所以直线l 的直角坐标方程为23100x y +-=. (2)由(1)知,曲线C 的参数方程为2cos sin x y αα=⎧⎨=⎩(α为参数),设()2cos ,sin P αα为曲线C 上一点,P 到直线l 的距离为d ,则105sin d αϕ-+===ϕ由4tan 3ϕ=确定,因此,当()sin 1αϕ+=时,d所以曲线C 上的点到直线l 7.(2022·甘肃·武威第六中学模拟预测(文))在直角坐标系xOy 中,曲线C 的参数方程为11x t ty t t ⎧=+⎪⎪⎨⎪=-⎪⎩(t 为参数),以坐标原点极点,以x 轴正半轴为极轴建立极坐标系,直线l 的极坐sin cos 0θρθ-.(1)求曲线C 的普通方程和直线l 的直角坐标方程: (2)若直线与曲线C 交于A ,B 两点,点P 的坐标为(0,1),求11||||PA PB +的值. 【答案】(1)224x y -=,0x+= (2)5【解析】【分析】(1)消去参数t 可得曲线C 的方程,利用公式法转化得到直线l 的直角坐标方程; (2)利用直线l 的参数方程中t 的几何意义求解. (1)∴11x t ty t t ⎧=+⎪⎪⎨⎪=-⎪⎩(t 为参数),∴22222222112112x t t t t y t t t t ⎧⎛⎫=+=++⎪ ⎪⎪⎝⎭⎨⎛⎫⎪=-=+- ⎪⎪⎝⎭⎩,所以224x y -=, 所以曲线C 的方程为224x y -=又∴cos x ρθ=,sin y ρθ=,0x - 所以直线l的直角坐标方程为0x =; (2)∴()0,1P 在直线l 上,∴直线l的参数方程为112x y t⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数)设A ,B 对应的参数分别为1t 与2t将直线l 的参数方程代入到224x y -=得22100t t --=. ∴2Δ(2)41(10)440=--⨯⨯-=>, ∴122t t +=,12100t t ⋅=-<, ∴1||PA t =,2||PB t =∴1212121111||||-+=+====t tPA PB t t t t,所以11||||+=PA PB 8.(2022·全国·赣州市第三中学模拟预测(理))在平面直角坐标系xOy 中,曲线1C 满足参数方程2241421t x t y t ⎧=⎪⎪+⎨⎪=-⎪+⎩(t 为参数且11t -≤≤).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,点P 为曲线1C 上一动点,且极坐标为(),ρθ. (1)求曲线1C 的直角坐标方程; (2)求()cos 3sin ρθθ+的取值范围.【答案】(1)y =()2204y x y +=≥(2)⎡-⎣ 【解析】 【分析】(1)消去参数t 可得普通方程,由11t -≤≤,得到0y ≥,即可求出曲线1C 的直角坐标方程; (2)先判断出2ρ=利用三角函数出()cos 3sin ρθθ+的范围. (1)由2241421t x t y t ⎧=⎪⎪+⎨⎪=-⎪+⎩消去t 可得:224x y +=. 由于11t -≤≤,则212t +≤,即0y ≥.因此曲线1C的直角坐标方程为y ()2204y x y +=≥(2)曲线1C 为上半圆,点P 在1C 上,因此2ρ=,0,θπ⎡⎤∈⎣⎦ 由三角函数的性质知,在[]0,π上,1cos 3sin θθ-≤+≤因此()cos 3sin 2,ρθθ⎡+∈-⎣9.(2022·黑龙江·哈尔滨三中三模(理))在平面直角坐标系xOy 中,已知直线l 的参数方程为22x y t ⎧=⎪⎨=-⎪⎩(t 为参数).以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为22cos 4sin 10ρρθρθ---=. (1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点A 、B ,若点P 的坐标为()2,2,求1PA PB-.【答案】(1)()()22126x y -+-=;【解析】 【分析】(1)将222x y ρ=+、cos x ρθ=、sin y ρθ=代入圆C 的极坐标方程即可求其直角坐标方程; (2)将直线l 的参数方程化为标准形式,代入圆C 的直角坐标方程得到关于参数t 的二次方程,根据韦达定理和直线参数方程参数的几何意义即可求出1PA PB-.(1)∴22cos 4sin 10ρρθρθ---=,∴222410x y x y +---=, 即()()22126x y -+-=; (2)直线l参数方程的标准形式为2122x y t ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数), 代入圆C直角坐标方程整理得250t -=, 设方程的两根为1t 、2t ,则A 、B 对应参数1t 、2t ,则121250t t t t ⋅=-<⎧⎪⎨+⎪⎩,∴1PA PB-121211t t t t ==+-10.(2022·河南·模拟预测(理))在平面直角坐标系xOy 中,曲线1C 的参数方程为222x m y m⎧=⎨=⎩(m 为参数),直线l 的参数方程为12x tcos y tsin αα⎧=+⎪⎨⎪=⎩,(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2cos ρθ=,直线l 与1C 交于点P ,Q ,与2C 交于点S ,T ,与x 轴交于点R .(1)写出曲线1C 的普通方程和曲线2C 的直角坐标方程; (2)若()4PR QR SR TR -=-,求直线l 的倾斜角. 【答案】(1)22y x =,()2211x y -+= (2)2π或4π或34π【解析】 【分析】(1)消参求得曲线1C 的普通方程为22y x =.由2cos ρθ=同乘ρ得到2C 的直角坐标方程. (2)l 过定点1,02R ⎛⎫ ⎪⎝⎭.将直线l 的参数方程代入21:2C y x =,整理得22sin 2cos 10t t αα--=,利用参数的几何含义化简求解. (1)曲线1C 的普通方程为22y x =.由2cos ρθ=得22cos ρρθ=.所以2C 的直角坐标方程为222x y x +=,即()2211x y -+=.(2)不妨设0απ<<,则sin 0α>.易知1,02R ⎛⎫ ⎪⎝⎭是l 过的定点.将直线l 的参数方程代入21:2C y x =,整理得22sin 2cos 10t t αα--=,设P ,Q 对应的参数分别为P t ,Q t ,则22cos sin P Q PR QR t t αα-=+=.将直线l 的参数方程代入()222:11C x y -+=,得23cos 04t t α--=, 设S ,T 对应的参数分别为S t ,T t ,则cos S T SR TR t t α-=+=.由()4PR QR SR TR -=-得22cos 4cos sin ααα=,得cos 0α=或sin α=l 的倾斜角为2π或4π或34π. 11.(2022·河南洛阳·三模(理))在直角坐标系xOy 中,直线1l的参数方程为12x ty kt⎧=⎪⎨=⎪⎩(t 为参数),直线2l的参数方程为x m m y k ⎧=⎪⎨=-⎪⎩(m 为参数),设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线1C .(1)求曲线1C 的普通方程;(2)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,设曲线2C 的极坐标方程为2cos ρθ=,射线OM :()04πθρ=≥与1C ,2C 分别交于A ,B 两点,求线段AB 的长.【答案】(1)22163x y +=,()0y ≠(2)2【解析】 【分析】(1)消去参数得到直线1l 、2l 的普通方程,联立两方程消去k ,即可得到P 的轨迹; (2)首先将1C 的方程化为极坐标方程,再将()04πθρ=≥代入两极坐标方程即可求出OA ,OB ,即可得解;(1)解:因为直线1l的参数方程为12x ty kt⎧⎪⎨=⎪⎩(t 为参数), 消去参数t 得直线1l的普通方程为(12y k x =①, 直线2l的参数方程为x m m y k ⎧=⎪⎨=-⎪⎩(m 为参数), 消去参数m 得直线2l的普通方程为(1y x k=-②, 设(),P x y ,由①②联立得((121y k x y x k ⎧=⎪⎪⎨⎪=-⎪⎩,消去k 得()22162y x =--即曲线1C 的普通方程为22163x y +=,()0y ≠;(2)解:设1OA ρ=,2OB ρ=,由cos sin x y ρθρθ=⎧⎨=⎩得曲线1C 的极坐标方程为2261sin ρθ=+(02θπ<<,θπ≠),代入()04πθρ=≥得12OA ρ==,将()04πθρ=≥代入2cos ρθ=得2OB ρ==所以2AB OA OB =-= 即线段AB的长度为212.(2022·安徽省芜湖市教育局模拟预测(理))在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 3sin x y ββ=+⎧⎨=⎩(β为参数),将曲线1C 经过伸缩变换13x xy y =⎧''⎪⎨=⎪⎩得到曲线2C .以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线2C 的极坐标方程;(2)已知射线():0l θαρ=≥与曲线2C 交于A 、B 两点,若3OB OA =,求tan α的值. 【答案】(1)24cos 30ρρθ-+= (2)0 【解析】 【分析】(1)求出曲线2C 的参数方程,化为普通方程,再利用极坐标方程与直角坐标方程之间的转换关系可得出曲线2C 的极坐标方程;(2)设()1,A ρα、()2,B ρα,则1ρ、2ρ为方程24cos 30ρρα-+=的两根,由已知可得213ρρ=,结合韦达定理可求得cos α的值,利用同角三角函数的基本关系可求得tan α的值. (1)解:由题可得2C 的参数方程为2cos sin x y ββ=+⎧⎨=⎩(β为参数),则2C 的直角方程为()2221x y -+=,即22430x y x +-+=, 因为cos x ρθ=,sin y ρθ=,所以24cos 30ρρθ-+=,所以曲线2C 的极坐标方程为24cos 30ρρθ-+=. (2)解:设()1,A ρα、()2,B ρα,则1ρ、2ρ为方程24cos 30ρρα-+=的两根, 2Δ16cos 120α=->,则124cos ρρα+=①,123ρρ=②, 因为3OB OA =,所以213ρρ=③,由①②③解得cos 1α=,则sin 0α=,tan 0α∴=,此时16120∆=->,合乎题意. 故tan 0α=.13.(2022·贵州遵义·三模(文))在极点为O 的极坐标系中,经过点π2,6M ⎛⎫⎪⎝⎭的直线l 与极轴所成角为α,且与极轴的交点为N . (1)当π2α=时,求l 的极坐标方程; (2)当ππ,43α⎡⎤∈⎢⎥⎣⎦时,求MON △面积的取值范围.【答案】(1)cos ρθ=(2)⋃⎣⎦⎣⎦【解析】 【分析】(1)先求得l 的直角坐标方程,再转化为极坐标方程.(2)对直线l 的倾斜角进行分类讨论,结合三角形的面积公式求得MON △面积的取值范围. (1)点π2,6M ⎛⎫ ⎪⎝⎭,则π2cos 6π2sin 16x y ⎧=⨯=⎪⎪⎨⎪=⨯=⎪⎩,所以M点的直角坐标为),当π2α=时,直线l的直角坐标方程为x =转化为极坐标方程为cos ρθ=.(2)在极坐标系下:经过点π2,6M ⎛⎫⎪⎝⎭的直线l 与极轴所成角为α,在直角坐标系下:经过点)M的直线l 的倾斜角为α或πα-.即直线l 的倾斜角是α或πα-. 当直线l 的倾斜角为α时,直线l 的方程为(1tan y x α-=,令0y =得1tan N x α-=ππ,43α⎡⎤∈⎢⎥⎣⎦,tan α⎡∈⎣,111,1,,tan tan tan N x ααα⎤⎡∈-∈-=-⎥⎢⎣⎦⎣⎦⎦,所以1π111sin 2262tan 2MONSOM ON α⎛=⨯⨯⨯=⨯⨯-+⨯ ⎝11tan 2α⎛=-⨯∈ ⎝⎣⎦.当直线l 的倾斜角为πα-时,直线l 的方程为()((1tan πtan y x x αα-=-=-,令0y =得1tan N x α=11,1tan tan N x αα⎤⎤∈=⎥⎥⎣⎦⎣⎦,所以1π111sin 2262tan 2MONSOM ON α⎛=⨯⨯⨯=⨯⨯⨯ ⎝11tan 2α⎛=⨯∈ ⎝⎣⎦.综上所述,MON △面积的取值范围是⋃⎣⎦⎣⎦. 14.(2022·江西·上饶市第一中学二模(文))在平面直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线1C 的普通方程为:22(2)4x y -+=,曲线2C 的参数方程是2cos x y θθ=⎧⎪⎨=⎪⎩(θ为参数),点2,2P π⎛⎫⎪⎝⎭.(1)求曲线1C 和2C 的极坐标方程; (2)设射线(0)3πθρ=>分别与曲线1C 和2C 相交于A ,B 两点,求PAB △的面积.【答案】(1)4cos ρθ=,22123sin ρθ=+(2)1 【解析】 【分析】(1)由公式法求极坐标方程(2)联立方程后分别求出A ,B 坐标,及P 到直线AB 距离后求面积 (1)曲线1C 的直角坐标方程为:2240x y x +-=, 将cos ,sin x y ρθρθ==代入上式并化简, 得曲线1C 的极坐标方程为:4cos ρθ=. 曲线2C 的普通方程是:22143x y +=, 将cos ,sin x y ρθρθ==代入上式并化简, 得曲线2C 的极坐标方程为:22123sin ρθ=+.(2)设12,,,33A B ππρρ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则1||4cos23OA πρ===,22221216||53sin 3OB ρπ===+,所以||OB =,所以||||||2AB OA OB =-=-. 又(0,2)P到直线:AB y =的距离为:1d ==所以12112PABS⎛=⨯⨯= ⎝⎭ 15.(2022·全国·模拟预测(文))在直角坐标系xOy 中,曲线C的参数方程为x y θθ⎧=⎪⎨=⎪⎩(θ为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos sin 4ρθθ=. (1)求C 和l 的直角坐标方程;(2)若点M ,N 分别为曲线C 和直线l 上的动点,求MN 的最小值.【答案】(1)22163x y +=,40x -=2- 【解析】 【分析】(1)利用22cos sin 1θθ+=消去参数θ,可得曲线C 的普通方程,利用极坐标与直角坐标的互化公式可求出直线l 的直角坐标方程, (2)设曲线C上任意一点)Mθθ到直线l 的距离为d ,然后利用点到直线的距离公式表示出d ,再根据三角函数的性质可求出其最小值 (1)由曲线C的参数方程为x y θθ⎧=⎪⎨=⎪⎩(θ为参数)可知2222cos sin 1θθ+=+=,故曲线C 的直角坐标方程为22163x y +=.由直线l的极坐标方程为cos sin 4ρθθ=,结合cos x ρθ=,sin y ρθ=可知l的直角坐标方程为40x -=. (2)MN 的最小值即为曲线C 上任意一点到直线l 距离的最小值.设曲线C上任意一点)Mθθ到直线l 的距离为d ,则2cos 24d πθ⎛⎫==+≥ ⎪⎝⎭,故MN 2..。
坐标系与参数方程高考常考题型及解析

析
联 立方
( , 厂 1 ) _
.
导 一
,
当“ < 0时 , / ’ ( ) 在 ( 0 , 一 ) 上 单 调递 增 , 在
又p ≥o , 故所 求距 离 为
变 式 ( 2 O 1 3年 北 京 理 )在 极 坐 标 系 巾, 点
( 一 ÷, +。 。 ) 上单 调递 ) >0 , 在 问 ( ~ , +一 ) 上,
人 — , 得 p s i n 一 C O S 0 , 即p c o s ! 一 s i n 一0 . 所 以 曲 线 的 极 标 方 程 为 p c o s 一s i n c 7 = = 0 .
是等 价转 化 , 抓住 这点 , 才 能“ 以不变 应万 变” .
彝 釜 袭
即 可.
蒜荔 量 蓑
c 作 者 单 位 : : ; : 妻 主 幸 : { 分 校 ,
吖 救 1 o
直 线方程. 然 后 求 直 角 坐 标 系下 的 点 到 直 线 的 距 离
考常 考题 型及 解析
◇ 山 东 杜 兆 洲
又 g ( 2 ) 一 号 , g ‘ 1 ) 一 3 。 故 2 n < 号 一 , “ < 号 .
所 以实 数 “的取 值范 同是 ( …一 , 7 - ) .
随 着 高 考 改 革 的不 但 深 入 , 考 试 内容 也 不 断 改
( 2 , ) 到 直线 p s i n 一2的距 离等 = F . 标 为
值, . , ’ ( 一 ) 一一1 +I n ( — L) =一l —I n ( 一“ ) , 所 以
析
在极坐 标 系
J ' r ) 化 为直触
2 > 一l —l n ( ~n ) , 解得 “ < 一÷ .
专题14坐标系与参数方程-2020年高考数学(理)二轮专项习题练(解析版)

直线 = ,则 tan = 3 ,化为直角坐标方程为 3
3x - y = 0 ,圆心 (0, 4) 到直线
的距离为 | - 4 | = 2 ,所以圆上的点到直线距离的最大值为
6.
4
7 . (2018 全国卷Ⅰ ) [ 选修 4–4 :坐标系与参数方程 ]( 10 分)
在直角坐标系 xOy 中,曲线 C1 的方程为 y k|x| 2 .以坐标原点为极点, x 轴正半轴为极轴建立极坐 标系,曲线 C2 的极坐标方程为 2 2 cos 3 0 .
即 |1 a | 1 ,∴ a 1 2 或 1 2 又 a 0 ,∴ a 1 2 . 2
2 .在极坐标系中,点 A 在圆 2 2 cos 4 sin 4 0 上,点 P 的坐标为 (1,0) ),则 | AP | 的最小
值为 __________._
1 【解析】圆的普通方程为 x2 y2 2x 4 y 4 0 ,即 ( x 1)2 ( y 2)2 1 .
|AB|=2 r =2 .
5 .已知直线 l 的极坐标方程为 2 sin(
)
2 ,点 Α的极坐标为
2
7 2,
) ,则点 Α到直线 l 的距
4
4
离为
.
5 2 【解析】由 2 sin( -)=2ຫໍສະໝຸດ 2 ?2 (sin2
4
2
cos ) = 2 ,所以 y - x = 1 ,
故直线 l 的直角坐标方程为
x - y +1= 0 ,而点 A(2
在平面直角坐标系 xOy 中, e O 的参数方程为
x
cos
,(
为参数),过点 (0,
y sin
2) 且倾斜角为
的直线 l 与 e O 交于 A , B 两点.
2020高考文数选修4-4坐标系与参数方程

第1讲 选修4-4坐标系与参数方程解答题1.(2019河北石家庄模拟)在平面直角坐标系中,直线l 的参数方程是{x =t,y =2t (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为ρ2+2ρsin θ-3=0.(1)求直线l 的极坐标方程;(2)若直线l 与曲线C 相交于A,B 两点,求|AB|.解析 (1)由{x =t,y =2t 消去t 得y=2x,把{x =ρcosθ,y =ρsinθ代入y=2x,得ρsin θ=2ρcos θ, ∴直线l 的极坐标方程为sin θ=2cos θ.(2)∵ρ2=x 2+y 2,y=ρsin θ,∴曲线C 的方程可化为x 2+y 2+2y-3=0,即x 2+(y+1)2=4,则曲线C 是以(0,-1)为圆心,2为半径的圆.又圆C 的圆心C(0,-1)到直线l 的距离d=√55,∴|AB|=22=2√955. 2.(2019江西南昌一模)在平面直角坐标系xOy 中,曲线C 的参数方程为{x =2cosφ,y =√3sinφ(φ为参数).以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线l 的极坐标方程为ρsin θ-kρcos θ+k=0(k ∈R).(1)请写出曲线C 的普通方程与直线l 的一个参数方程;(2)若直线l 与曲线C 交于A,B 两点,且点M(1,0)为线段AB 上的一个三等分点,求|AB|. 解析 (1)由已知得,曲线C 的普通方程为x 24+y 23=1.易知直线l 的直角坐标方程为y=k(x-1),则其一个参数方程为{x =1+tcosα,y =tsinα(t 为参数). (2)联立(1)中直线l 的参数方程与曲线C 的普通方程,并化简得(3+sin 2α)t 2+6tcos α-9=0, 设点A,B 对应的参数分别为t 1,t 2,∴{t 1+t 2=-6cosα3+sin 2α,t 1·t 2=-93+sin 2α<0.① 不妨设t 1>0,t 2<0,t 1=-2t 2,代入①中得cos 2α=49, sin 2α=59,所以|AB|=|t 1-t 2|=√(t 1+t 2)2-4t 1t 2=123+sin 2α=278.3.(2019广西桂林联考)在平面直角坐标系xOy 中,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的参数方程为{x =tcosα,y =y 0+tsinα(t 为参数,α为l 的倾斜角),曲线E 的极坐标方程为ρ=4sin θ,射线θ=β,θ=β+π6,θ=β-π6与曲线E 分别交于不同于极点的A,B,C 三点.(1)求证:|OB|+|OC|=√3|OA|;(2)当β=π3时,直线l 过B,C 两点,求y 0与α的值.解析 (1)证明:依题意知,|OA|=4sin β,|OB|=4sin (β+π6),|OC|=4sin (β-π6),则|OB|+|OC|=4sin (β+π6)+4sin (β-π6)=4√3sin β=√3|OA|.(2)当β=π3时,点B 的极坐标为(4sin π2,π2)=(4,π2),点C 的极坐标为(4sin π6,π6)=(2,π6),故B,C 化为直角坐标为B(0,4),C(√3,1),因为直线l 过B,C 两点,所以直线l 的普通方程为y=-√3x+4,所以y 0=4,α=2π3.4.(2019广西南宁模拟)已知曲线C 1的参数方程为{x =cosθ,y =1+sinθ(θ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=4sin (θ+π3),直线l 的直角坐标方程为y=√33x.(1)求曲线C 1和直线l 的极坐标方程;(2)已知直线l 分别与曲线C 1、曲线C 2的图象相交于异于极点的A,B 两点,若A,B 的极径分别为ρ1,ρ2,求|ρ1-ρ2|的值.解析 (1)由曲线C 1的参数方程{x =cosθ,y =1+sinθ(θ为参数),得C 1的普通方程为x 2+(y-1)2=1,则曲线C 1的极坐标方程为ρ=2sin θ.易知直线l 过原点,且倾斜角为π6,所以直线l 的极坐标方程为θ=π6(ρ∈R).(2)将θ=π6代入C 1的极坐标方程得ρ1=1,将θ=π6代入C 2的极坐标方程得ρ2=4,所以|ρ1-ρ2|=3.5.(2019广东广州联考)已知曲线C 的参数方程为{x =2+√5cosα,y =1+√5sinα(α为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程;(2)设l 1:θ=π6,l 2:θ=π3,若l 1,l 2与曲线C 相交于异于原点的A,B 两点,求△AOB 的面积. 解析 (1)∵曲线C 的参数方程为{x =2+√5cosα,y =1+√5sinα(α为参数),∴曲线C 的普通方程为(x-2)2+(y-1)2=5.将{x =ρcosθ,y =ρsinθ代入并化简得ρ=4cos θ+2sin θ, ∴曲线C 的极坐标方程为ρ=4cos θ+2sin θ. (2)由{θ=π6,ρ=4cosθ+2sinθ,得|OA|=2√3+1. 同理|OB|=2+√3,又∠AOB=π6,∴S △AOB =12|OA|·|OB|sin ∠AOB=8+5√34, ∴△AOB 的面积为8+5√34. 6.(2019江西南昌模拟)在平面直角坐标系xOy 中,曲线C 1的参数方程为{x =-3+t,y =-1-t(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆C 2的极坐标方程为ρ=4√2sin (3π4-θ).(1)求C 1的普通方程和C 2的直角坐标方程;(2)过曲线C 2上任意一点P 作与C 1夹角为π4的直线,交C 1于点A,求|PA|的最大值与最小值.解析 (1)由{x =-3+t,y =-1-t得C 1的普通方程为x+y+4=0, 由ρ=4√2sin (3π4-θ),得ρ=4cos θ+4sin θ,∴ρ2=4ρcos θ+4ρsin θ,x 2+y 2=4x+4y,即(x-2)2+(y-2)2=8,∴C 2的直角坐标方程为(x-2)2+(y-2)2=8.(2)在曲线C 2上任意取一点P(2+2√2cos θ,2+2√2sin θ),则P 到C 1的距离d=√2(cosθ+sinθ)|√2=|8+4sin(θ+π4)|√2, |PA|=√22=|8+4sin (θ+π4)|,∴当sin (θ+π4)=1时,|PA|取最大值,为12;当sin (θ+π4)=-1时,|PA|取最小值,为4.7.(2019山东淄博模拟)在平面直角坐标系xOy 中,直线l 的方程是x=4.曲线C 的参数方程是{x =1+√2cosφ,y =1+√2sinφ(φ为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求直线l 和曲线C 的极坐标方程;(2)若射线θ=α(ρ≥0,0<α<π4)与曲线C 交于O,A 两点,与直线l 交于点B,求|OA||OB|的取值范围. 解析 (1)由ρcos θ=x 及直线l 的方程为x=4,得直线l 的极坐标方程为ρcos θ=4. 又曲线C 的参数方程是{x =1+√2cosφ,y =1+√2sinφ(φ为参数), 消去参数φ得曲线C 的普通方程为(x-1)2+(y-1)2=2,即x 2+y 2-2x-2y=0,将x 2+y 2=ρ2,x=ρcos θ,y=ρsin θ代入上式得ρ2=2ρcos θ+2ρsin θ,所以曲线C 的极坐标方程为ρ=2cos θ+2sin θ.(2)设A(ρ1,α),B(ρ2,α),则ρ1=2cos α+2sin α,ρ2=4cosα, 所以|OA||OB|=ρ1ρ2=(2cosα+2sinα)cosα4= cos 2α+sinαcosα2 =14(sin 2α+cos 2α)+14=√24sin (2α+π4)+14,因为0<α<π4,所以π4<2α+π4<3π4,所以√22<sin (2α+π4)≤1,故12<√24sin (2α+π4)+14≤1+√24, 所以|OA||OB|的取值范围是(12,1+√24]. 8.(2019河南郑州测试)在平角直角坐标系xOy 中,直线l 的参数方程为{x =tcosα,y =1+tsinα(t 为参数,α∈[0,π)).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.设曲线C 的极坐标方程为ρcos 2θ=4sin θ.(1)设M(x,y)为曲线C 上任意一点,求x+y 的取值范围;(2)若直线l 与曲线C 交于不同的两点A,B,求|AB|的最小值.解析 (1)将曲线C 的极坐标方程ρcos 2θ=4sin θ化为直角坐标方程,得x 2=4y.∵M(x,y)为曲线C 上任意一点,∴x+y=x+14x 2=14(x+2)2-1≥-1,∴x+y 的取值范围是[-1,+∞).(2)将{x =tcosα,y =1+tsinα代入x 2=4y,得t 2cos 2α-4tsin α-4=0.∴Δ=16sin 2α+16cos 2α=16>0,设方程t 2cos 2α-4tsin α-4=0的两个根分别为t 1,t 2,则t 1+t 2=4sinαcos 2α,t 1t 2=-4cos 2α,∴|AB|=|t 1-t 2|=√(t 1+t 2)2-4t 1t 2=4cos 2α≥4,当且仅当α=0时,取等号.故当α=0时,|AB|取得最小值4.。
2023年高考数学真题分训练 极坐标系与参数方程(含答案含解析)

专题34 极坐标系与参数方程2⎩2 2考点 116 平面直角坐标系中的伸缩变换 考点 117 极坐标和直角坐标的互化⎧x = t + 1,⎪x = 4cos 2θ, 1.(2023 全国Ⅱ文理 21)已知曲线C 1 , C 2 的参数方程分别为C 1 : ⎨ (θ为参数),C : ⎪ t ( t 为 ⎩ y = 4sin 2θ⎪ y = t - 1参数).(1) 将C 1 , C 2 的参数方程化为一般方程;⎪ t(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系.设C 1 , C 2 的交点为 P ,求圆心在极轴上,且经过极点和 P 的圆的极坐标方程.(解析)(1)由cos 2 θ+ sin 2 θ= 1得C 1 的一般方程为: x + y = 4 ,⎧x = t + 1 ⎧x 2= t 2 + 1 + 2 ⎪ t ⎪ t 2 C 2 2由⎨ 1 得: ⎨1 ,两式作差可得2 的一般方程为: x - y = 4 . ⎪ y = t - ⎪ y 2 = t 2 + - 2 ⎪ t ⎪ t 2⎧x = 5 ⎧x + y = 4 ⎪ (2)由 得: 2 ,即 P ⎛ 5 , 3 ⎫. ⎨x 2 - y 2= 4 ⎨ ⎪ y = 3 ⎩ 2 ⎪ ⎝ ⎭⎛ 5 ⎫2⎛3 ⎫217设所求圆圆心的直角坐标为(a , 0),其中 a > 0 ,则 a - ⎪ + 0 - ⎪ = a 2 ,解得:a = ,⎝2 ⎭⎝2 ⎭10∴ 17 ∴⎛ 17 ⎫2⎛ 17 ⎫222 2 17 所求圆的半径 r = , 10 所求圆的直角坐标方程为: x - 10 ⎪ + y = 10 ⎪ ,即 x + y = x ,5 ∴所求圆的极坐标方程为ρ= 17cos θ.5⎝ ⎭ ⎝ ⎭103⎩⎪x = 2 - t - t 2, 2.(2023 全国Ⅲ文理 22)在直角坐标系 xOy 中,曲线C 的参数方程为⎪ y = 2 - 3t + t 2( t 为参数且t ≠ 1),C与坐标轴交于 A , B 两点.(1) 求 AB ;(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,求直线 AB 的极坐标方程.(解析)(1)令 x = 0 ,则t 2 + t - 2 = 0 ,解得t = -2 或t =1(舍),则 y = 2 + 6 + 4 = 12 ,即 A (0,12) . 令 y = 0 ,则t 2 - 3t + 2 = 0 ,解得t = 2 或t =1(舍),则 x = 2 - 2 - 4 = -4 ,即 B (-4, 0) .∴ AB == 4 .(2)由(1)可知 k AB =12 - 00 - (-4)= 3 ,则直线 AB 的方程为 y = 3(x + 4) ,即3x - y +12 = 0 .由 x = ρcos θ, y = ρsin θ可得,直线 AB 的极坐标方程为3ρcos θ- ρsin θ+12 = 0 .3.(2023 江苏 22)在极坐标系中,已知点 A (ρ, π) 在直线l : ρcos θ= 2 上,点 B (ρ , π) 在圆C : ρ= 4 sin θ上1 32 6(其中ρ≥ 0 , 0 ≤θ< 2π).(1)求ρ1 , ρ2 的值(2)求出直线l 与圆C 的公共点的极坐标.(解析)(1) Q ρ cos π = 2∴ρ = 4; Q ρ = 4 s inπ2 .131 26 ∴ρ2 = (2) Q ρcos θ= 2, ρ= 4 sin θ∴ 4 sin θcos θ= 2,∴sin 2θ= 1 Q θ∈0, 2π)∴θ= π, 5π,4 4当θ= π时ρ= 2 4;当θ= 5π 时ρ= -2 4 < 0 (舍);即所求交点坐标为当π (2 2, ) . 4 4.(2023 全国 II 文理 22)在极坐标系中,O 为极点,点 M (ρ0 ,θ0 )(ρ0 > 0)在曲线C : ρ= 4 s in θ上,直线 l 过点 A (4, 0) 且与OM 垂直,垂足为 P . (1)当θ = π时,求ρ 及 l 的极坐标方程;3(2)当 M 在 C 上运动且 P 在线段 OM 上时,求 P 点轨迹的极坐标方程.(解析)(1)因为 M (ρ,θ ) 在C 上,当θ = π 时,ρ = 4 s in π= 2 .0 0 0 3 03由已知得| OP |=| OA | cos π= 2 .322333⎢⎥⎢⎥设Q (ρ,θ) 为l 上除P 的任意一点.在Rt △OPQ 中ρcos⎛θ-π ⎫=| OP |= 2 , 3 ⎪ ⎝ ⎭π ⎛ π ⎫经检验,点P (2, ) 在曲线ρcos θ- ⎪ = 2 上. ⎝ ⎭所以,l 的极坐标方程为ρcos ⎛θ- π ⎫= 2 .3 ⎪ ⎝ ⎭(2)设 P (ρ,θ) ,在Rt △OAP 中, | OP |=| OA | cos θ= 4 cos θ,即 ρ= 4 cos θ..因为P 在线段OM 上,且 AP ⊥ OM ,故θ的取值范围是⎡π , π⎤. ⎣ 4 2 ⎦所以,P 点轨迹的极坐标方程为ρ= 4 cos θ,θ∈ ⎡π , π⎤ .⎣4 2 ⎦5.(2023 全国 III 文理 22)如图,在极坐标系 Ox 中, A (2, 0) , B ( 2, π) ,C ( 2, 3π) , D (2, π) ,弧 AB ,4 4 A , A 所在圆的圆心分别是(1, 0) ,π, (1, π) ,曲线 M 是弧 A ,曲线 M 是弧 A ,曲线 M 是BC CD(1, ) 21 AB2 BC3 弧C D .(1) 分别写出 M 1 , M 2 , M 3 的极坐标方程;(2) 曲线 M 由 M 1 , M 2 , M 3 构成,假设点 P 在 M 上,且| OP |= ,求P 的极坐标.(解析)(1)由题设可得,弧 AB , B C ,C D 所在圆的极坐标方程分别为ρ= 2 cos θ,ρ= 2 s in θ,ρ= -2 cos θ,所以 M 的极坐标方程为ρ= 2 cos θ⎛0 θ π ⎫ , M 的极坐标方程为 1 4⎪ 2⎝⎭ρ= 2 sin θ⎛ π θ3π ⎫ , M 的极坐标方程为ρ= -2 cos θ⎛ 3πθ π ⎫ . 4 4 ⎪ 34 ⎪ ⎝ ⎭ ⎝ ⎭(2)设 P (ρ,θ) ,由题设及(1)知3332⎩⎩⎩⎩⎩θ假设0 θπ,则 2 cos θ=,解得θ=π;4 6假设 π θ 3π ,则 2 sin θ= ,解得θ= π 或θ= 2π ; 4 4 3 3 假设 3π θ π ,则-2 cos θ= ,解得θ= 5π .4 ⎛ 综上,P 的极坐标为3, π ⎫ 或⎛3, π ⎫ 或⎛63,2π ⎫ 或⎛3, 5π ⎫ .6⎪ 3⎪ 3 ⎪ 6 ⎪ ⎝⎭ ⎝⎭ ⎝⎭ ⎝ ⎭考点 118 参数方程与一般方程的互化6.(2023 上海 14)已知直线方程3x + 4 y +1 = 0 的一个参数方程可以是()⎧x = 1+ 3t A . ⎨ y = -1+ 4t ⎧x = 1- 4tB . ⎨y = -1- 3t⎧x = 1- 3tC . ⎨y = -1+ 4t ⎧x = 1+ 4t D . ⎨y = -1- 3t(答案)D(解析)A .参数方程可化简为 4x - 3y - 7 = 0 ,故 A 不正确;B .参数方程可化简为3x - 4 y - 7 = 0 ,故B 不正确;C .参数方程可化简为 4x + 3y -1 = 0 ,故 C 不正确;D .参数方程可化简为3x + 4 y +1 = 0 , 故 D 正确.应选 D .7.(2023 全国Ⅲ)选修 4—4:坐标系与参数方程](10 分)在平面直角坐标系 xOy 中, A O 的参数方程为⎧x = cos θ(θ为参数),过点(0, -2) 且倾斜角为α的直线l 与A O 交于 A , B 两点.(1) 求α的取值范围;(2) 求 AB 中点 P 的轨迹的参数方程.⎨ y = sin ,(解析)(1) A O 的直角坐标方程为 x 2 + y 2 = 1. 当α= π时, l 与A O 交于两点.2当α≠ π时,记 tan α= k ,则l 的方程为 y = kx -.l 与A O 交于两点当且仅当< 1 ,解得 k < -1 或2α∈π ππ 3πk > 1,即( , ) 或α∈ ( , ) .4 2 2 4α π 3π 综上,的取值范围是( , ) . 4 4222222⎨(2) l 的参数方程为⎪x = t cos α, (t 为参数, π < α< 3π) . ⎨⎩ y = - + t sin α 4 4 设 A , B , P 对应的参数分别为 t , t , t ,则t =t A + t B,且t , t 满足t 2 - 2 2t sin α+ 1 = 0 .ABPP2A B于是t A + t B= 2 2 sin α, t P =2 sin α.又点 P 的坐标(x , y ) 满足 ⎪x = t P cos α,y = - + t sin α.⎧ ⎪x =2sin 2α, 2 ⎩P π 3π 所以点 P 的轨迹的参数方程是⎨ ⎪ y = - 2 - 2 cos 2α (α为参数, < α< ) . 4 4 ⎪ 2 2考点 119 极坐标方程与参数方程的综合应用8.(2023 北京文理)在极坐标系中,直线ρcos θ+ ρsin θ= a (a > 0) 与圆ρ=2 cos θ相切,则 a =.(答案)1+ (解析)利用 x = ρcos θ, y = ρsin θ,可得直线的方程为 x + y - a = 0 ,圆的方程为(x -1)2 + y 2 = 1 ,所以圆心(1, 0) ,半径 r = 1,由于直线与圆相切,故圆心到直线的距离等于半径,即|1- a |= 1 ,∴ a = 1+ 或1- ,又 a > 0 ,∴ a = 1+ .9.(2023 北京文理)在极坐标系中,点 A 在圆ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 上,点 P 的坐标为(1, 0) ),则| AP | 的最小值为.(答案)1(解析)圆的一般方程为 x 2 + y 2 - 2x - 4y + 4 = 0 ,即(x -1)2 + ( y - 2)2 = 1 .设圆心为C (1, 2) ,所以| AP |min =| PC | -r = 2 -1 = 1 .10.(2023 天津文理)在极坐标系中,直线4ρcos(θ- π) +1 = 0 与圆ρ= 2 s in θ的公共点的个数为.6(答案)2(解析)直线的一般方程为 2 3x + 2 y +1 = 0 ,圆的一般方程为 x 2 + ( y -1)2= 1 ,因为圆心到直 3线的距离 d = < 1 4,所以有两个交点.11.(2023 北京文理)在极坐标系中,直线ρcos θ- | AB |= .3ρsin θ-1 = 0 与圆ρ= 2 cos θ交于 A , B 两点,则(答案)2(解析)将ρcos θ-3ρsin θ-1 = 0 化为直角坐标方程为 x - 3y -1 = 0 ,将ρ=2cos θ化为直角坐标方程为(x -1)2+ y 2= 1 ,圆心坐标为(1,0),半径 r=1,又(1,0)在直线 x - 3y -1 = 0 上,所以|AB|=2r=2.222234y x ⎩⎩⎩)⎩12.(2023 广东文理)已知直线l 的极坐标方程为 2ρsin(θ- π= 47πA (2 2,) ,则点 Α 到直线l 的距离为 .42 ,点 Α 的极坐标为(答案)(解析)由 2ρsin(θ- 2π ) = 得2ρ´ 4 2 7π(sin θ- cos θ) = ,所以 y - x = 1, 故直线l 的直角坐标方程为 x - y +1 = 0 ,而点 A (2 2, ) 对应的直角坐标为4 A (2,-2) ,所以点 A (2,-2) 到直线l : x - y +1 = 0 的距离为| 2 + 2 +1| = 5 2. 213.(2023 安徽文理)在极坐标系中,圆ρ= 8sin θ上的点到直线θ=是.π(ρ∈ R ) 距离的最大值 3(答案)6(解析)圆ρ= 8sin θ即ρ2= 8ρsin θ,化为直角坐标方程为 x 2+ ( y - 4)2= 16 ,π直线θ=,则tan θ=,化为直角坐标方程为 3x - y = 0 ,圆心(0, 4) 到直线3的距离为| -4 |= 2 ,所以圆上的点到直线距离的最大值为 6.14.(2023 全国Ⅰ文理 21)⎧x = cos k t ,在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ y = sin k t(t 为参数) .以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线C 2 的极坐标方程为 4ρcos θ-16ρsin θ+ 3 = 0 .(1) 当 k = 1时, C 1 是什么曲线?(2) 当 k = 4 时,求C 1 与C 2 的公共点的直角坐标.(解析)(1)当 k = 1时,曲线C 的参数方程为⎧x = cos t ,( t 为参数),两式平方相加得 x 2 + y 2 = 1 ,1⎨y = sin t∴曲线C 1 表示以坐标原点为圆心,半径为 1 的圆.⎧x = cos 4 t ,(2)当 k = 4 时,曲线C 1 的参数方程为⎨ y = sin 4t ( t 为参数),∴ x ≥ 0, y ≥ 0 ,曲线C 1 的参数方程化为⎧ x = cos 2 t ⎨ y = sin 2t(t 为参数),两式相加得曲线C 1 方程为 + = 1,得 = 1 - ,平方得 5 22x yx 77⎩2y = x - 2 + 1, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 ,曲线C 2 的极坐标方程为4ρcos θ-16ρsin θ+ 3 = 0 ,曲线C 2 直角坐标方程为4x -16 y + 3 = 0 ,联立C , C 方程⎪ y = x - 2 +1 , ,整理得12 x - 32 + 13 = 0 ,解得 x = 1 或 = 13(舍去),1 2⎨ ⎩4x -16 y + 3 = 02 6 ∴ x = 1 , y = 1 ,∴C ,C 1 1 公共点的直角坐标为( , ) .4 4 1 24 4⎧ 1- t 2 ⎪x =1+ t 215.(2023 全国 1 文理 22)在直角坐标系 xOy 中,曲线 C 的参数方程为⎨ ⎪ y = ⎩ 4t 1+ t 2(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线 l 的极坐标方程为 2ρcos θ+ 3ρsin θ+11 = 0 .(1) 求 C 和 l 的直角坐标方程;(2) 求 C 上的点到 l 距离的最小值.1- t 2⎛ y ⎫2⎛ 1- t 2 ⎫24t 2 (解析)(1)因为-1 < ≤ 1 ,且 x 2 + ⎪ = ⎪ + = 1,所以C 的直角坐标方程为2y 2 1+ t 2⎝ 2 ⎭ ⎝1 + t 2 ⎭ (1+ t 2 )2x += 1(x ≠ -1) .4l 的直角坐标方程为 2x + 3y +11 = 0 .⎧x = cos α, (2)由(1)可设C 的参数方程为 (α为参数, -π <α< π ).⎨y = 2sin α4 cos ⎛α- π ⎫ +113 ⎪ C 上的点到l 的距离为 = ⎝ ⎭.当α= - 2π 时, 4 c os ⎛α- π ⎫+11 取得最小值7,故C 上的点到l 距离的最小值为 . 3 3 ⎪ ⎝ ⎭16.(2023 全国Ⅰ文理) 在直角坐标系 xOy 中,曲线C 1 的方程为 y = k |x | + 2 .以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2+ 2ρcos θ- 3 = 0 . (1) 求C 2 的直角坐标方程;x x x | 2 c os α+ 2 3 sin α+11|7⎨y = 4 s in θ,⎩(2) 假设C 1 与C 2 有且仅有三个公共点,求C 1 的方程.(解析)(1)由 x = ρcos θ, y = ρsin θ得C 2 的直角坐标方程为(x +1)2 + y 2 = 4 .(2)由(1)知C 2 是圆心为 A (-1, 0) ,半径为 2 的圆.由题设知,C 1 是过点 B (0, 2) 且关于 y 轴对称的两条射线.记 y 轴右边的射线为l 1 ,y 轴左边的射线为l 2 .由于 B 在圆C 2 的外面,故C 1 与C 2 有且仅有三个公共点等价于l 1 与C 2 只有一个公共点且l 2 与C 2 有两个公共点,或l 2 与C 2 只有一个公共点且l 1 与C 2 有两个公共点.当l 与C 只有一个公共点时, A 到l 所在直线的距离为 2 ,所以| -k + 2 |= 2 ,故 k = - 4 或 k = 0 .1213经检验,当k = 0 时, l 与C 没有公共点;当 k = - 4时, l 与C 只有一个公共点, l 与C 有两个公共点.1231 2 2 2| k + 2 | 当l 与C 只有一个公共点时, A 到l 所在直线的距离为2 ,所以= 2 ,故 k = 0 或 k = 4 .2 2 23经检验,当k = 0 时, l 与C 没有公共点;当 k = 4时, l 与C 没有公共点.1 2 32 2综上,所求C 的方程为 y = - 4| x | +2 .1317.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,曲线C 的参数方程为⎧x = 2 cos θ,( θ 为参数),直线l 的参数⎩⎧x = 1+ t cos α 方程为⎨ y = 2 + t sin α ( t 为参数).(1) 求C 和l 的直角坐标方程;(2) 假设曲线C 截直线l 所得线段的中点坐标为(1, 2) ,求l 的斜率.x 2 + y 2 =(解析)(1)曲线C 的直角坐标方程为 1. 4 16当cos α≠ 0 时, l 的直角坐标方程为 y = tan α⋅ x + 2 - tan α; 当cos α= 0 时, l 的直角坐标方程为 x = 1 .(2)将l 的参数方程代入C 的直角坐标方程,整理得关于t 的方程(1+ 3cos 2 α)t 2 + 4(2 cos α+ sin α)t - 8 = 0 .①3317⎩⎨ y = 1- ty 因为曲线C 截直线l 所得线段的中点(1, 2) 在C 内,所以①有两个解,设为t 1 , t 2 ,则t 1 + t 2 = 0 .4(2 cos α+ sin α)又由①得t 1 + t 2 = -1+ 3cos 2α,故 2 cos α+ sin α= 0 ,于是直线l 的斜率 k = tan α= -2 .18.(2023 江苏)在极坐标系中,直线l 的方程为ρsin( π-θ) = 2 ,曲线C 的方程为ρ= 4 cos θ,求直线l 被曲6 线C 截得的弦长.(解析)因为曲线C 的极坐标方程为ρ=4 cos θ,所以曲线C 的圆心为(2, 0) ,直径为 4 的圆.因为直线l 的极坐标方程为ρsin( π -θ) = 2 ,则直线l 过 A (4, 0) ,倾斜角为 π,所以 A 为直线l 与圆C 的一6 6 个交点.设另一个交点为 B ,则∠OAB= π ,连结 OB ,因为 OA 为直径,从而∠OBA= π ,所以 AB = 4 c os π= 2 .6 因此,直线l 被曲线C 截得的弦长为 2 .2 6⎧x = 3cos θ19.(2023 全国Ⅰ文理)在直角坐标系 xOy 中,曲线C 的参数方程为⎨ y = sin θ ,(θ为参数),直线l 的参数方程为⎧x = a + 4t( t 为参数).⎩ (1) 假设 a = -1,求C 与l 的交点坐标;(2) 假设C 上的点到l 距离的最大值为 ,求 a .(解析)(1)曲线C 的一般方程为 x 2 + 29= 1.当a = -1时,直线l 的一般方程为 x + 4 y - 3 = 0 .⎧x + 4 y - 3 = 0⎧x = - 21 ⎪ ⎧x = 3 ⎪25 21 24由⎨ x 2 2解得⎨ y = 0 或⎨ ,从而C 与l 的交点坐标为(3, 0) , (- 24 , ) . ⎩ 9+ y = 1 ⎩⎪ y = ⎩ 25 25 25171717171733342⎩(2)直线l 的一般方程为 x + 4 y - a - 4 = 0 ,故C 上的点(3cos θ, sin θ) 到l 的距离为| 3cos θ+ 4 sin θ- a - 4 |d =.当a ≥-4 时, d 的最大值为a + 9.由题设得a + 9= ,所以a = 8 ;当a < -4 时, d 的最大值为 -a + 1 .由题设得 -a + 1= ,所以 a = -16 . 综上, a = 8 或 a = -16 .20.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系,曲线C 1 的极坐标方程为ρcos θ= 4 .(1) M 为曲线C 1 上的动点,点 P 在线段OM 上,且满足| OM | ⋅ | OP |= 16 ,求点 P 的轨迹C 2 的直角坐标方程;π(2) 设点 A 的极坐标为(2, 3) ,点 B 在曲线C 2 上,求∆OAB 面积的最大值. (解析)(1)设 P 的极坐标为(ρ,θ) (ρ> 0) , M 的极坐标为(ρ1 ,θ) (ρ1 > 0) .由椭圆知| OP |= ρ, | OM |= ρ1 =cos θ.由| OM | ⋅ | OP |= 16 得C 2 的极坐标方程ρ= 4 cos θ(ρ> 0) , 因此C 的直角坐标方程为(x - 2)2 + y 2= 4(x ≠ 0) .(2)设点 B 的极坐标为(ρB ,α) (ρB > 0) .由题设知| OA |= 2 , ρB = 4cos α,于是∆OAB 面积1 π π 3S = 2 | OA | ⋅ρB ⋅sin ∠AOB = 4cos α| sin(α- 3 ) | = 2 | sin(2α- 3 ) - | ≤ 2 + . 2 当α= - π时, S 取得最大值 2 + ,所以∆OAB 面积的最大值为 2 + .1221.(2023 全国Ⅲ文理)在直角坐标系 xOy 中,直线l 的参数方程为⎧x = 2 + t( t 为参数),直线l 的参数方⎧x = -2 + m⎪1 ⎨ y = kt 2程为⎨ ⎩ y = m k( m 为参数).设l 1 与l 2 的交点为 P ,当 k 变化时, P 的轨迹为曲线C .(1) 写出C 的一般方程;17175224 5⎨t⎩(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l3 :ρ(cosθ+ sinθ) -交点,求M 的极径.= 0 ,M 为l3与C 的(解析)(1)消去参数t 得l 的一般方程l : y =k (x -2),消去参数m 得l 的一般方程l : y =1 (x+2).11⎧y =k (x-2)22k⎪设P(x, y) ,由题设得⎨⎩y=1 (x+2)k,消去k 得x2-y2=4 (y ≠0),所以C 的一般方程为x2-y2=4 (y ≠0).⎪ρ2(cos2θ-sin2θ)=4(2)C的极坐标方程为ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π),联立⎨得⎩ρ(cosθ+sinθ)-2=0cosθ- sinθ=2 (cosθ+sinθ),故tanθ=-1,从而cos2θ=9,sin2θ=1,代入ρ2(cos2θ-sin2θ)=4得3ρ2=5,所以交点M的极径为.10 10⎧x =-8 +t22.(2023 江苏)在平面坐标系中xOy 中,已知直线l 的参考方程为⎪y = ( t 为参数),曲线C 的参数方⎧x=2s2⎪2程为⎨⎩y=22s( s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.(解析)直线l 的一般方程为x - 2 y + 8 = 0 .因为点P 在曲线C 上,设P(2s2 , 2 2s) ,从而点P 到直线l 的的距离4 5d == ,当s =时,dmin=5.因此当点P 的坐标为(4, 4) 时,曲线C 上点P 到直线l 的距离取到最小值.5⎧x =a cos t23.(2023 全国I 文理)在直角坐标系xOy 中,曲线C1 的参数方程为⎨y = 1+a sin t(t 为参数,a>0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C2 :ρ= 4 cosθ.(I)说明C1 是哪种曲线,并将C1 的方程化为极坐标方程;(II)直线C3 的极坐标方程为θ=a0 ,其中a0 满足tan a0 =2 ,假设曲线C1 与C2 的公共点都在C3上,求a.22(s -2)2 +4510 10 ⎫2152⎩1123⎩⎨⎩=⎧x = a cos t (解析)(1) ⎨ y = 1 + a sin t( t 均为参数),∴x 2 + ( y - 1)2= a 2 ①∴ C 为以(0 ,1) 为圆心, a 为半径的圆.方程为 x 2 + y 2 - 2 y +1 - a 2 = 0 .∵ x 2 + y 2 = ρ2 ,y = ρsin θ,∴ ρ2- 2ρsin θ+ 1 - a 2 = 0 ,即为C 的极坐标方程.(2) C :ρ= 4cos θ,两边同乘ρ得ρ2 = 4ρcos θ ρ2= x 2 + y 2 ,ρcos θ= x ,∴ x 2 + y 2 = 4x ,即( x - 2)2+ y 2 = 4 ②C 3 :化为一般方程为 y = 2x ,由题意: C 1 和C 2 的公共方程所在直线即为C 3 ,①—②得: 4x - 2 y + 1 - a 2 = 0 ,即为C ,∴1 - a 2 = 0 ,∴ a = 1 .24.(2023 全国 II 文理)在直角坐标系 xOy 中,圆 C 的方程为( x + 6)2+ y 2 = 25 .(I) 以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求 C 的极坐标方程;⎧x = t cos α(II)直线 l 的参数方程是⎨ y = t sin α(t 为参数),l 与 C 交于 A 、B 两点, AB = ,求 l 的斜率.⎧ρ2 = x 2 + y 2 (解析)(Ⅰ)整理圆的方程得 x 2 + y 2 + 12 + 11 = 0 ,由⎪ρcos θ= x ⎪ρsin θ= y 可知圆C 的极坐标方程为ρ2 + 12ρcos θ+ 11 = 0 .(Ⅱ)记直线的斜率为 k ,则直线的方程为 kx - y = 0 ,由垂径定理及点到直线距离公式知:= 36k 2 290 ,整理得 k 2 = 5 ,则 k = ± . 1 + k 4 3 3⎪x =3 cos α25.(2023 全国 III 文理)在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ ⎩ y = sin α(α为参数),以坐标原点为极点,以 x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为ρsin(θ+ π) = 2.24(Ⅰ)写出C 1 的一般方程和C 2 的直角坐标方程;(Ⅱ)设点 P 在C 1 上,点 Q 在C 2 上,求| PQ |的最小值及此时 P 的直角坐标.x 2 2(解析)(Ⅰ) C 1 的一般方程为 3+ y = 1, C 2 的直角坐标方程为 x + y - 4 = 0 .(Ⅱ)由题意,可设点 P 的直角坐标为( 3 cos α, sin α) ,因为C 2 是直线,所以| PQ | 的最小值,即为 P 到C 2| 3 cos α+sin α- 4 |2222⎨⎩⎪=1⎩的距离d (α) 的最小值, d (α) ==π2 | sin(α+ π ) - 2 | .3 3 1当且仅当α= 2k π+(k ∈ Z ) 时, d (α) 取得最小值,最小值为 6,此时 P 的直角坐标为( , ) . 2 2 ⎧x = 1 + 1t , 26.(2023 江苏)在平面直角坐标系 xOy 中,已知直线l 的参数方程为⎪ ⎪ y = ⎩ 2 3 t , 2(t 为参数) ,椭圆C 的参数⎧x = cos θ,方程为⎨ y = 2sin θ, (θ为参数) ,设直线l 与椭圆C 相交于 A , B 两点,求线段 AB 的长.⎧x = 1+ 1t(解析)椭圆C 的一般方程为 x 2 + y 4 = 1,将直线l 的参数方程⎨ ⎪ y = ⎩2 3 t2 ,代入 x 2 + y 4 = 1,得(1+ 1 t )2 + 3 t )22 = 1,即7t 2 +16t = 0 ,解得t = 0 , t = - 16 ,所以 AB =| t - t | 16 .2 4 1 2 71 2727.(2023 全国Ⅰ文理)在直角坐标系 xOy 中,直线C : x = -2 ,圆C :(x -1)2 + ( y - 2)2= 1 ,以坐标原12点为极点, x 轴的正半轴为极轴建立极坐标系.(Ⅰ)求C 1 , C 2 的极坐标方程;(Ⅱ)假设直线C 3 的极坐标方程为θ=(ρ∈ R ) ,设C 2 与C 3 的交点为 M , N ,求∆C 2MN 的面积.4(解析)(Ⅰ)因为 x = ρcos θ, y = ρsin θ,∴ C 的极坐标方程为ρcos θ= -2 , C 的极坐标方程为ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 .12(Ⅱ)将θ= π代入ρ2- 2ρcos θ- 4ρsin θ+ 4 = 0 ,得ρ2- 3 2ρ+ 4 = 0 ,解得ρ = 2, ρ = , 4|MN|= ρ - ρ = ,因为C 的半径为 1,则A C MN 的面积 ⨯ 122 ⨯1⨯sin 45o = 1 . 1 2 22 2 2 ⎧x = t cos α,28.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,曲线C 1 : ⎨ y = t sin α, ( t 为参数,t ≠0)其中0 ≤α<π,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2 : ρ= 2 sin θ, C 3 : ρ= 2 3 cos θ. (Ⅰ)求C 2 与C 3 交点的直角坐标;(Ⅱ)假设C 1 与C 2 相交于点 A , C 1 与C 3 相交于点 B ,求| AB | 的最大值.222(π3623)( x -1+ y +1= )()⎨(解析)(Ⅰ)曲线C 的直角坐标方程为 x 2 + y 2 - 2 y = 0 ,曲线C 的直角坐标方程为 x 2 + y 2- 2 3x = 0 .联⎪x 2+ y 2- 2 y = 0,⎧x = 0, ⎧ 3 ⎪x = 2 , 立⎨x 2 + y 2 - 2 3x = 0,解得⎨ y = 0, 或⎨ 3 ⎪ ⎩ ⎪ y = ,⎩ 23所以C 2 与C 1 交点的直角坐标为(0, 0) 和( , ) .2 2(Ⅱ)曲线C 1 的极坐标方程为θ= α(ρ∈ R , ρ≠ 0) ,其中0 ≤α<π. 因此 A 得到极坐标为(2 sin α,α) , B 的极坐标为(2 3 cos α,α) . π5π所以 AB = 2 sin α- 2 3 cos α = 4 s in(α-) ,当α= 时, AB 取得最大值,最大值为 4 . 3 629.(2023 江苏) 已知圆 C 的极坐标方程为ρ2+ 2 2ρsin(θ- π- 4 = 0 ,求圆 C 的半径.4(解析) 以极坐标系的极点为平面直角坐标系的原点O ,以极轴为 x 轴的正半轴,建立直角坐标系 xoy .圆C 的极坐标方程为ρ2 + 2⎛ 2 sin θ- 2cos ⎫4 = 0 ,化简,得ρ2 + 2ρsin θ- 2ρcos θ- 4 = 0 . ρ 22 θ⎪⎪ - ⎝ ⎭则圆C 的直角坐标方程为 x 2 + y 2 - 2x + 2 y - 4 = 0 ,即2 2,所以圆C 的半径为 . ⎧x = 3 + 1 t 30.(2023 陕西文理)在直角坐标系 xOy 中,直线l 的参数方程为⎪2⎪ y = 3 t ⎩ 2 轴正半轴为极轴建立极坐标系,⊙ C 的极坐标方程为ρ= 2 3 sin θ. (Ⅰ)写出⊙ C 的直角坐标方程;( t 为参数).以原点为极点, x(Ⅱ) P 为直线l 上一动点,当 P 到圆心C 的距离最小时,求 P 的直角坐标.(解析)(Ⅰ) 由ρ= 2 3 sin θ, 得ρ2= 2 3ρsin θ,从而有 x 2+y 2= 2 3y , 所以x 2+ (y -3 )2= 3 .(Ⅱ)设P (3 += ,故当t =0 时,| PC |取最小值,此时 P 点的直角坐标为(3, 0) .21t,3t), 又C(0, 3) ,则| PC |=3222 3 ⎪55⎨y = 2 - 2t⎩⎩31.(2023 全国Ⅰ文理)已知曲线C : x 4 + y 29 = 1,直线l : ⎧x = 2 + t ( t 为参数). ⎩(Ⅰ)写出曲线C 的参数方程,直线l 的一般方程;(Ⅱ)过曲线C 上任一点 P 作与l 夹角为30o的直线,交l 于点 A ,求| PA |的最大值与最小值.⎧x = 2 cos θ.(解析)〔I 〕曲线C 的参数方程为⎨ y = 3sin θ. (θ为参数).直线l 的一般方程为2x + y - 6 = 0. ……5 分(Ⅱ)曲线C 上任意一点P(2cos θ.3sin θ)到l 的距离为d =4 cos θ+ 3sin θ- 6 .则 PA =d = sin 30︒ 5sin(θ+α) - 6 , 其中α为锐角,且tan α= 4 . 3当sin (θ+α)=-1时,PA 取得最大值,最大值为22 5 .5当sin(θ+α) = 1时,PA 取得最小值,最小值为2 5 .532.(2023 全国Ⅱ文理)在直角坐标系 xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆 C 的极坐标方程为ρ= 2 cos θ,θ∈ ⎡0,π⎤ .(Ⅰ)求 C 的参数方程;⎣⎢ 2 ⎥⎦(Ⅱ)设点 D 在 C 上,C 在 D 处的切线与直线l : y = 3x + 2 垂直,依据(Ⅰ)中你得到的参数方程,确定 D 的坐标.(解析)(I)C 的一般方程为(x -1)0 ≤ t ≤ x ).2 + y 2⎧x = 1+ cos t , = 1(0 ≤ y ≤ 1) ,可得 C 的参数方程为⎨ y = sin t ,(t 为参数,(Ⅱ)设 D (1+ cos t , sin t ) .由(I)知 C 是以 G(1,0)为圆心,1 为半径的上半圆. π因为 C 在点D 处的切线与 t 垂直,所以直线 GD 与 t 的斜率相同, tan t = 3, t =.32 5523⎩⎩⎩1⎩⎩ππ 3故D 的直角坐标为(1+ cos , s in ) ,即( , ) .3 3 2 233.(2023 全国Ⅰ文理)已知曲线C 的参数方程为⎧x = 4 + 5 cos t( t 为参数),以坐标原点为极点,x 轴的正1 ⎨y = 5 + 5sin t半轴为极轴建立极坐标系,曲线C2 的极坐标方程为ρ= 2 s inθ.(Ⅰ)把C1 的参数方程化为极坐标方程;(Ⅱ)求C1 与C2 交点的极坐标( ρ≥0 ,0 ≤θ≤2π).⎧x = 4 + 5 c os t2 2(解析)将⎨y = 5 + 5sin t消去参数t ,化为一般方程(x - 4) + ( y -5) = 25 ,即C1 :x 2 +y2⎧x =ρcosθ-8x -10 y+16 = 0 ,将⎨y =ρsinθ代入x 2 +y2- 8x -10 y + 16 = 0 得,ρ2 - 8ρcosθ-10ρsinθ+16 = 0 ,∴C 的极坐标方程为ρ2 - 8ρcosθ-10ρsinθ+16 = 0 .⎪x2+y2-8x-10y+16=0(Ⅱ) C 的一般方程为x2 +y2 - 2 y = 0 ,由⎨⎧x =1解得⎨⎧x = 0或⎨,2∴C1 与C2 的交点的极坐标分别为(⎩x2+y2-2y=0π),(2, ) .4 2⎩y =1 ⎩y = 2 34.(2023 全国Ⅱ文理)已知动点P ,Q 都在曲线C与β= 2α( 0 <α< 2π) M 为PQ 的中点.⎧x = 2 c os β:⎨y = 2 s in β(β为参数)上,对应参数分别为β=α(Ⅰ)求M的轨迹的参数方程(Ⅱ)将M 到坐标原点的距离d 表示为α的函数,并推断M 的轨迹是否过坐标原点.(解析)(Ⅰ)由题意有P(2c osα,2sinα),Q(2c os2α,2sin2α),因此M(cosα+cos2α,sinα+sin2α),⎧x = cosα+ cos 2α,M 的轨迹的参数方程为⎨y = sinα+ sin 2α, (0 <α< 2π).(Ⅱ)M 点到坐标原点的距离d ==0 <α< 2π),当α=π时,d = 0 ,故M 的轨迹过坐标原点.2,π3⎩100⎩135.(2023 全国文理)已知曲线C 的参数方程是⎧x = 2 cos ϕϕ为参数),以坐标原点为极点, x 轴的正半轴1⎨y = 3sin ϕ(为极轴建立极坐标系,曲线C 2 的极坐标方程是ρ= 2 .正方形 ABCD 的顶点都在C 2 上,且 A 、 B 、C 、πD 依逆时针次序排列,点 A 的极坐标为(2, ) . 3(Ⅰ)求点 A 、 B 、C 、 D 的直角坐标;(Ⅱ)设 P 为C 上任意一点,求| PA |2 + | PB |2 + | PC |2 + | PD |2 的取值范围.π5π 4π 11π(解析)(1)点 A , B , C , D 的极坐标为(2, ), (2, ), (2, ), (2, ) ,3 6 3 6点 A , B , C , D 的直角坐标为(1, 3),(-⎧x 0 = 2cos ϕ3,1), (-1, - 3),( 3, -1) .(2)设 P (x 0 , y 0 ) ;则⎨ y = 3sin (ϕ为参数) , ⎩ 0ϕt = PA 2+ PB 2+ PC 2+ PD 2= 4x 2 + 4 y 2 +16 = 32 + 20 sin 2ϕ∈32, 52.⎧x = 2 c os α 36.(2011 全国文理)在直角坐标系 xOy 中,曲线C 1 的参数方程为⎨ y = 2 + 2 s in(α为参数),M 是C 上 α的动点, P 点满足OP = 2OM , P 点的轨迹为曲线C 2(Ⅰ)求C 2 的方程(Ⅱ)在以 O 为极点,x 轴的正半轴为极轴的极坐标系中,射线θ= π与C 的异于极点的交点为 A ,与C 的异于极点的交点为 B ,求 AB .31 2(解析)(I)设 P (x , y ) ,则由条件知 M( x , y).由于 M 点在C 上,⎧ x = 2 cos α ⎪ 2 2 2⎧ x = 4 cos α 1⎧ x = 4 cos α 所以⎨ y ,即⎨y = 4 + 4 s in ,从而C 2 的参数方程为⎨y = 4 + 4 s in (α为参数), ⎪ = 2 + 2 s in α ⎩ α ⎩ α⎩ 2(Ⅱ)曲线C 1 的极坐标方程为ρ= 4sin θ,曲线C 2 的极坐标方程为ρ= 8sin θ.射线θ= π与C 的交点 A 的极径为ρ = 4sin π,射线θ= π与C 的交点 B 的极径为ρ = 8sin π.3 1 1 3 32 23所以| AB |=| ρ2 - ρ1 |= 2 .。
2022版高考数学(文理通用新课标)一轮复习教师用书:选修4-4 坐标系与参数方程 Word版含解析

选修4-4⎪⎪⎪坐标系与参数方程 第一节 坐 标 系突破点(一) 平面直角坐标系下图形的伸缩变换基础联通 抓主干学问的“源”与“流”设点P (x ,y )是平面直角坐标系中的任意一点,在变换φ:⎩⎪⎨⎪⎧x ′=λ·x (λ>0),y ′=μ·y (μ>0)的作用下,点P (x ,y )对应到点P ′(x ′,y ′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.考点贯穿 抓高考命题的“形”与“神”平面直角坐标系下图形的伸缩变换典例] 求椭圆x 24+y 2=1,经过伸缩变换⎩⎪⎨⎪⎧x ′=12x ,y ′=y 后的曲线方程.解] 由⎩⎪⎨⎪⎧x ′=12x ,y ′=y得到⎩⎪⎨⎪⎧x =2x ′,y =y ′.①将①代入x 24+y 2=1,得4x ′24+y ′2=1,即x ′2+y ′2=1.因此椭圆x 24+y 2=1经伸缩变换后得到的曲线方程是x 2+y 2=1.方法技巧]应用伸缩变换公式时的两个留意点(1)曲线的伸缩变换是通过曲线上任意一点的坐标的伸缩变换实现的,解题时肯定要区分变换前的点P 的坐标(x ,y )与变换后的点P ′的坐标(X ,Y ),再利用伸缩变换公式⎩⎪⎨⎪⎧X =ax (a >0),Y =by (b >0)建立联系.(2)已知变换后的曲线方程f (x ,y )=0,一般都要改写为方程f (X ,Y )=0,再利用换元法确定伸缩变换公式.力量练通 抓应用体验的“得”与“失”1.在同一平面直角坐标系中,已知伸缩变换φ:⎩⎪⎨⎪⎧x ′=3x ,2y ′=y .求点A ⎝⎛⎭⎫13,-2经过φ变换所得的点A ′的坐标.解:设A ′(x ′,y ′),由伸缩变换φ:⎩⎪⎨⎪⎧x ′=3x ,2y ′=y ,得到⎩⎪⎨⎪⎧x ′=3x ,y ′=12y ,由于点A 的坐标为⎝⎛⎭⎫13,-2, 于是x ′=3×13=1,y ′=12×(-2)=-1,所以A ′(1,-1)为所求.2.求直线l :y =6x 经过φ:⎩⎪⎨⎪⎧x ′=3x ,2y ′=y 变换后所得到的直线l ′的方程.解:设直线l ′上任意一点P ′(x ′,y ′), 由题意,将⎩⎪⎨⎪⎧x =13x ′,y =2y ′代入y =6x 得2y ′=6×⎝⎛⎭⎫13x ′, 所以y ′=x ′,即直线l ′的方程为y =x . 3.求双曲线C :x 2-y 264=1经过φ:⎩⎪⎨⎪⎧x ′=3x ,2y ′=y 变换后所得曲线C ′的焦点坐标. 解:设曲线C ′上任意一点P ′(x ′,y ′), 由题意,将⎩⎪⎨⎪⎧x =13x ′,y =2y ′代入x 2-y 264=1得x ′29-4y ′264=1,化简得x ′29-y ′216=1,本节主要包括2个学问点: 1.平面直角坐标系下图形的伸缩变换; 2.极坐标系.即x 29-y 216=1为曲线C ′的方程,可见经变换后的曲线仍是双曲线, 则所求焦点坐标为F 1(-5,0),F 2(5,0).4.将圆x 2+y 2=1变换为椭圆x 29+y 24=1的一个伸缩变换公式为φ:⎩⎪⎨⎪⎧X =ax (a >0),Y =by (b >0),求a ,b 的值.解:由⎩⎪⎨⎪⎧X =ax ,Y =by知⎩⎨⎧x =1a X ,y =1b Y ,代入x 2+y 2=1中得X 2a 2+Y 2b2=1,所以a 2=9,b 2=4,即a =3,b =2.突破点(二) 极坐标系基础联通 抓主干学问的“源”与“流” 1.极坐标系的概念 (1)极坐标系如图所示,在平面内取一个定点O ,点O 叫做极点,自极点O 引一条射线Ox ,Ox 叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.(2)极坐标一般地,没有特殊说明时,我们认为ρ≥0,θ可取任意实数. (3)点与极坐标的关系一般地,极坐标(ρ,θ)与(ρ,θ+2k π)(k ∈Z)表示同一个点,特殊地,极点O 的坐标为(0,θ)(θ∈R),和直角坐标不同,平面内一个点的极坐标有很多种表示.假如规定ρ>0,0≤θ<2π,那么除极点外,平面内的点可用唯一的极坐标(ρ,θ) 表示;同时,极坐标(ρ,θ)表示的点也是唯一确定的.2.极坐标与直角坐标的互化点M直角坐标(x ,y )极坐标(ρ,θ)互化公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ ⎩⎪⎨⎪⎧ρ2=x 2+y 2,tan θ=y x (x ≠0)考点贯穿 抓高考命题的“形”与“神”极坐标与直角坐标的互化1.极坐标方程化为直角坐标方程的步骤第一步推断极坐标的极点与直角坐标系的原点是否重合,且极轴与x 轴正半轴是否重合,若上述两个都重合,则极坐标方程与直角坐标方程可以互化其次步通过极坐标方程的两边同乘ρ或同时平方构造ρcos θ,ρsin θ,ρ2的形式,肯定要留意变形过程中方程要保持同解,不要消灭增解或漏解第三步 依据极坐标方程与直角坐标方程的互化公式⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ及ρ2=x 2+y 2将极坐标方程转化为直角坐标方程2.直角坐标方程化为极坐标方程或直角坐标系中的点的坐标化为极坐标(1)直角坐标方程化为极坐标方程较为简洁,只需将直角坐标方程中的x ,y 分别用ρcos θ,ρsin θ代替即可得到相应极坐标方程.(2)求直角坐标系中的点(x ,y )对应的极坐标的一般步骤:第一步,依据直角坐标系中两点间的距离公式计算该点与坐标原点的距离,即计算ρ;其次步,依据角θ的正切值tan θ=yx (x ≠0)求出角θ(若正切值不存在,则该点在y 轴上),问题即解.例1] 在极坐标系下,已知圆O :ρ=cos θ+sin θ和直线l :ρsin ⎝⎛⎭⎫θ-π4=22. (1)求圆O 和直线l 的直角坐标方程;(2)当θ∈(0,π)时,求直线l 与圆O 公共点的一个极坐标. 解] (1)圆O :ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ,圆O 的直角坐标方程为:x 2+y 2=x +y ,即x 2+y 2-x -y =0,直线l :ρsin ⎝⎛⎭⎫θ-π4=22,即ρsin θ-ρcos θ=1,则直线l 的直角坐标方程为:y -x =1,即x -y +1=0.(2)由⎩⎪⎨⎪⎧ x 2+y 2-x -y =0,x -y +1=0得⎩⎪⎨⎪⎧x =0,y =1,则直线l 与圆O 公共点的一个极坐标为⎝⎛⎭⎫1,π2. 方法技巧]1.应用互化公式的三个前提条件 (1)取直角坐标系的原点为极点. (2)以x 轴的正半轴为极轴. (3)两种坐标系规定相同的长度单位. 2.直角坐标化为极坐标时的两个留意点(1)依据终边相同的角的意义,角θ的表示方法具有周期性,故点M 的极坐标(ρ,θ)的形式不唯一,即一个点的极坐标有无穷多个.当限定ρ≥0,θ∈0,2π)时,除极点外,点M 的极坐标是唯一的.(2)当把点的直角坐标化为极坐标时,求极角θ应留意推断点M 所在的象限(即角θ的终边的位置),以便正确地求出角θ(θ∈0,2π))的值.极坐标方程的应用例2] (2021·福州五校联考)已知曲线C 的极坐标方程为ρ2-22ρcos ⎝⎛⎭⎫θ+π4-2=0.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系xOy .(1)若直线l 过原点,且被曲线C 截得的弦长最小,求直线l 的直角坐标方程; (2)若M 是曲线C 上的动点,且点M 的直角坐标为(x ,y ),求x +y 的最大值. 解] (1)ρ2-22ρcos ⎝⎛⎭⎫θ+π4-2=0,即ρ2-2ρcos θ+2ρsin θ-2=0, 将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ代入得曲线C 的直角坐标方程为(x -1)2+(y +1)2=4, 圆心C (1,-1),若直线l 被曲线C 截得的弦长最小,则直线l 与OC 垂直, 即k l ·k OC =-1,k OC =-1,因而k l =1,故直线l 的直角坐标方程为y =x .(2)由于M 是曲线C 上的动点,因而利用圆的参数方程可设⎩⎪⎨⎪⎧x =1+2cos φ,y =-1+2sin φ(φ为参数),则x +y =2sinφ+2cos φ=22sin ⎝⎛⎭⎫φ+π4,当sin ⎝⎛⎭⎫φ+π4=1时,x +y 取得最大值2 2.易错提示]用极坐标系解决问题时要留意题目中的几何关系,假如几何关系不简洁通过极坐标表示时,可以先化为直角坐标方程,将不生疏的问题转化为生疏的问题加以解决.力量练通 抓应用体验的“得”与“失”1.考点一、二]已知直线l 的极坐标方程为2ρsin ⎝⎛⎭⎫θ+π4=2,点A 的极坐标为A ⎝⎛⎭⎫22,7π4,求点A 到直线l 的距离.解:由2ρsin ⎝⎛⎭⎫θ+π4=2, 得2ρ⎝⎛⎭⎫22sin θ+22cos θ=2,由坐标变换公式,得直线l 的直角坐标方程为y +x =1,即x +y -1=0. 由点A 的极坐标为⎝⎛⎭⎫22,7π4得点A 的直角坐标为(2,-2),所以点A 到直线l 的距离d =|2-2-1|2=22.2.考点一]已知圆C 的极坐标方程为ρ2+22ρsin θ-π4-4=0,求圆C 的半径.解:以极坐标系的极点为平面直角坐标系的原点O ,以极轴为x 轴的正半轴,建立直角坐标系xOy . 圆C 的极坐标方程为ρ2+22ρ⎝⎛⎭⎫22sin θ-22cos θ-4=0,化简,得ρ2+2ρsin θ-2ρcos θ-4=0.由坐标变换公式,得圆C 的直角坐标方程为x 2+y 2-2x +2y -4=0, 即(x -1)2+(y +1)2=6, 所以圆C 的半径为 6.3.考点二]在极坐标系中,直线ρ(sin θ-cos θ)=a 与曲线ρ=2cos θ-4sin θ相交于A ,B 两点,若|AB |=23,求实数a 的值.解:直线的极坐标方程化为直角坐标方程为x -y +a =0,曲线的极坐标方程化为直角坐标方程为(x -1)2+(y +2)2=5,所以圆心C 的坐标为(1,-2),半径r =5,所以圆心C 到直线的距离为|1+2+a |2=r 2-⎝⎛⎭⎫|AB |22=2,解得a =-5或a =-1.故实数a 的值为-5或-1.4.考点一、二](2021·洛阳统考)已知圆O 1和圆O 2的极坐标方程分别为ρ=2,ρ2-22ρcos ⎝⎛⎭⎫θ-π4=2. (1)将圆O 1和圆O 2的极坐标方程化为直角坐标方程; (2)求经过两圆交点的直线的极坐标方程.解:(1)由ρ=2知ρ2=4,由坐标变换公式,得x 2+y 2=4. 由于ρ2-22ρcos ⎝⎛⎭⎫θ-π4=2, 所以ρ2-22ρ⎝⎛⎭⎫cos θcos π4+sin θsin π4=2. 由坐标变换公式, 得x 2+y 2-2x -2y -2=0.(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x +y =1.化为极坐标方程为ρcos θ+ρsin θ=1,即ρsin ⎝⎛⎭⎫θ+π4=22. 全国卷5年真题集中演练——明规律]1.(2022·全国乙卷)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =a cos t ,y =1+a sin t (t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ.(1)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(2)直线C 3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C 1与C 2的公共点都在C 3上,求a . 解:(1)消去参数t 得到C 1的一般方程为x 2+(y -1)2=a 2, 则C 1是以(0,1)为圆心,a 为半径的圆.将x =ρcos θ,y =ρsin θ代入C 1的一般方程中,得到C 1的极坐标方程为ρ2-2ρsin θ+1-a 2=0. (2)曲线C 1,C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2-2ρsin θ+1-a 2=0,ρ=4cos θ. 若ρ≠0,由方程组得16cos 2θ-8sin θcos θ+1-a 2=0,由已知tan θ=2,可得16cos 2θ-8sin θcos θ=0, 从而1-a 2=0,解得a =-1(舍去)或a =1.当a =1时,极点也为C 1,C 2的公共点,且在C 3上. 所以a =1.2.(2021·新课标全国卷Ⅰ)在直角坐标系xOy 中,直线C 1:x =-2,圆C 2:(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.(1)求C 1,C 2的极坐标方程;(2)若直线C 3的极坐标方程为θ=π4(ρ∈R),设C 2与C 3的交点为M ,N ,求△C 2MN 的面积.解:(1)由于x =ρcos θ,y =ρsin θ, 所以C 1的极坐标方程为ρcos θ=-2, C 2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0. (2)将θ=π4代入ρ2-2ρcos θ-4ρsin θ+4=0,得ρ2-32ρ+4=0, 解得ρ1=22,ρ2= 2. 故ρ1-ρ2=2,即|MN |= 2. 由于C 2的半径为1, 所以△C 2MN 的面积为12.课时达标检测] 基础送分题——高考就考那几点,练通就能把分捡1.在极坐标系中,已知圆C 经过点P ⎝⎛⎭⎫2,π4,圆心为直线ρsin ⎝⎛⎭⎫θ-π3=-32与极轴的交点,求圆C 的极坐标方程.解:在ρsin ⎝⎛⎭⎫θ-π3=-32中,令θ=0,得ρ=1,所以圆C 的圆心坐标为(1,0). 由于圆C 经过点P ⎝⎛⎭⎫2,π4, 所以圆C 的半径PC = (2)2+12-2×1×2cos π4=1,于是圆C 过极点,所以圆C 的极坐标方程为ρ=2cos θ.2.设M ,N 分别是曲线ρ+2sin θ=0和ρsin ⎝⎛⎭⎫θ+π4=22上的动点,求M ,N 的最小距离. 解:由于M ,N 分别是曲线ρ+2sin θ=0和ρsin ⎝⎛⎭⎫θ+π4=22上的动点,即M ,N 分别是圆x 2+y 2+2y =0和直线x +y -1=0上的动点,要求M ,N 两点间的最小距离,即在直线x +y -1=0上找一点到圆x 2+y 2+2y =0的距离最小,即圆心(0,-1)到直线x +y -1=0的距离减去半径,故最小值为|0-1-1|2-1=2-1.3.在极坐标系中,求直线ρ(3cos θ-sin θ)=2与圆ρ=4sin θ的交点的极坐标. 解:ρ(3cos θ-sin θ)=2化为直角坐标方程为3x -y =2,即y =3x -2. ρ=4sin θ可化为x 2+y 2=4y , 把y =3x -2代入x 2+y 2=4y ,得4x 2-83x +12=0,即x 2-23x +3=0, 所以x =3,y =1.所以直线与圆的交点坐标为(3,1),化为极坐标为⎝⎛⎭⎫2,π6. 4.(2021·山西质检)在极坐标系中,曲线C 的方程为ρ2=31+2sin 2θ,点R ⎝⎛⎭⎫22,π4. (1)以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系,把曲线C 的极坐标方程化为直角坐标方程,R 点的极坐标化为直角坐标;(2)设P 为曲线C 上一动点,以PR 为对角线的矩形PQRS 的一边垂直于极轴,求矩形PQRS 周长的最小值,及此时P 点的直角坐标.解:(1)曲线C :ρ2=31+2sin 2θ,即ρ2+2ρ2sin 2θ=3,从而ρ2cos 2θ3+ρ2sin 2θ=1. ∵x =ρcos θ,y =ρsin θ,∴曲线C 的直角坐标方程为x 23+y 2=1,点R 的直角坐标为R (2,2). (2)设P (3cos θ,sin θ),依据题意可得|PQ |=2-3cos θ,|QR |=2-sin θ, ∴|PQ |+|QR |=4-2sin ⎝⎛⎭⎫θ+π3, 当θ=π6时,|PQ |+|QR |取最小值2,∴矩形PQRS 周长的最小值为4, 此时点P 的直角坐标为⎝⎛⎭⎫32,12.5.(2021·南京模拟)已知直线l :ρsin ⎝⎛⎭⎫θ-π4=4和圆C :ρ=2k cos ⎝⎛⎭⎫θ+π4(k ≠0),若直线l 上的点到圆C 上的点的最小距离等于2.求实数k 的值并求圆心C 的直角坐标.解:圆C 的极坐标方程可化为ρ=2k cos θ-2k sin θ, 即ρ2=2kρcos θ-2kρsin θ,所以圆C 的直角坐标方程为x 2+y 2-2kx +2ky =0, 即⎝⎛⎭⎫x -22k 2+⎝⎛⎭⎫y +22k 2=k 2, 所以圆心C 的直角坐标为⎝⎛⎭⎫22k ,-22k .直线l 的极坐标方程可化为ρsin θ·22-ρcos θ·22=4,所以直线l 的直角坐标方程为x -y +42=0,所以⎪⎪⎪⎪22k +22k +422-|k |=2.即|k +4|=2+|k |, 两边平方,得|k |=2k +3,所以⎩⎪⎨⎪⎧ k >0,k =2k +3或⎩⎪⎨⎪⎧k <0,-k =2k +3,解得k =-1,故圆心C 的直角坐标为⎝⎛⎭⎫-22,22. 6.已知圆C :x 2+y 2=4,直线l :x +y =2.以O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系.(1)将圆C 和直线l 方程化为极坐标方程;(2)P 是l 上的点,射线OP 交圆C 于点R ,又点Q 在OP 上,且满足|OQ |·|OP |=|OR |2,当点P 在l 上移动时,求点Q 轨迹的极坐标方程.解:(1)将x =ρcos θ,y =ρsin θ分别代入圆C 和直线l 的直角坐标方程得其极坐标方程为C :ρ=2,l :ρ(cos θ+sin θ)=2.(2)设P ,Q ,R 的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),则由|OQ |·|OP |=|OR |2,得ρρ1=ρ22. 又ρ2=2,ρ1=2cos θ+sin θ,所以2ρcos θ+sin θ=4,故点Q 轨迹的极坐标方程为ρ=2(cos θ+sin θ)(ρ≠0).7.(2021·贵州联考)已知在一个极坐标系中点C 的极坐标为⎝⎛⎭⎫2,π3. (1)求出以C 为圆心,半径长为2的圆的极坐标方程(写出解题过程);(2)在直角坐标系中,以圆C 所在极坐标系的极点为原点,极轴为x 轴的正半轴建立直角坐标系,点P 是圆C 上任意一点,Q (5,-3),M 是线段PQ 的中点,当点P 在圆C 上运动时,求点M 的轨迹的一般方程.解:(1)如图,设圆C 上任意一点A (ρ,θ),则∠AOC =θ-π3或π3-θ.由余弦定理得,4+ρ2-4ρcos θ-π3=4,所以圆C 的极坐标方程为ρ=4cos ⎝⎛⎭⎫θ-π3. (2)在直角坐标系中,点C 的坐标为(1,3),可设圆C 上任意一点P (1+2cos α,3+2sin α), 又令M (x ,y ),由Q (5,-3),M 是线段PQ 的中点, 得点M 的轨迹的参数方程为⎩⎪⎨⎪⎧x =6+2cos α2,y =2sin α2(α为参数),即⎩⎪⎨⎪⎧x =3+cos α,y =sin α(α为参数), ∴点M 的轨迹的一般方程为(x -3)2+y 2=1.8.在平面直角坐标系中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =2cos φ,y =sin φ(φ为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2是圆心在极轴上且经过极点的圆,射线θ=π3与曲线C 2交于点D ⎝⎛⎭⎫2,π3. (1)求曲线C 1的一般方程和曲线C 2的直角坐标方程;(2)已知极坐标系中两点A (ρ1,θ0),B ⎝⎛⎭⎫ρ2,θ0+π2,若A ,B 都在曲线C 1上,求1ρ21+1ρ22的值. 解:(1)∵C 1的参数方程为⎩⎪⎨⎪⎧x =2cos φ,y =sin φ,∴C 1的一般方程为x 24+y 2=1.由题意知曲线C 2的极坐标方程为ρ=2a cos θ(a 为半径), 将D ⎝⎛⎭⎫2,π3 代入,得2=2a ×12, ∴a =2,∴圆C 2的圆心的直角坐标为(2,0),半径为2, ∴C 2的直角坐标方程为(x -2)2+y 2=4.(2)曲线C 1的极坐标方程为ρ2cos 2θ4+ρ2sin 2θ=1,即ρ2=44sin 2θ+cos 2θ. ∴ρ21=44sin 2θ0+cos 2θ0,ρ22=44sin 2⎝⎛⎭⎫θ0+π2+cos 2⎝⎛⎭⎫θ0+π2=4sin 2θ0+4cos 2θ0.∴1ρ21+1ρ22=4sin 2θ0+cos 2θ04+4cos 2θ0+sin 2θ04=54. 其次节 参数方程突破点(一) 参数方程基础联通 抓主干学问的“源”与“流”1.参数方程一般地,在平面直角坐标系中,假如曲线上任意一点的坐标x ,y 都是某个变数t 的函数:⎩⎪⎨⎪⎧x =f (t ),y =g (t ),并且对于t 的每一个允许值,由方程组⎩⎪⎨⎪⎧x =f (t ),y =g (t )所确定的点M (x ,y )都在这条曲线上,那么方程⎩⎪⎨⎪⎧x =f (t ),y =g (t )就本节主要包括2个学问点: 1.参数方程;2.参数方程与极坐标方程的综合问题.叫做这条曲线的参数方程,变数t 叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方程叫做一般方程.2.直线、圆、椭圆的参数方程(1)过点M (x 0,y 0),倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数).(2)圆心在点M 0(x 0,y 0),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =x 0+r cos θ,y =y 0+r sin θ(θ为参数).(3)椭圆x 2a 2+y 2b 2=1(a >b >0)的参数方程为⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ(φ为参数).考点贯穿 抓高考命题的“形”与“神”参数方程与一般方程的互化1.参数方程化为一般方程基本思路是消去参数,常用的消参方法有:①代入消元法;②加减消元法;③恒等式(三角的或代数的)消元法;④平方后再加减消元法等.其中代入消元法、加减消元法一般是利用解方程的技巧,三角恒等式消元法常利用公式sin 2θ+cos 2θ=1等.2.一般方程化为参数方程 (1)选择参数的一般原则曲线上任意一点的坐标与参数的关系比较明显且关系相对简洁;当参数取某一值时,可以唯一确定x ,y 的值;(2)具体步骤第一步,引入参数,但要选定合适的参数t ;其次步,确定参数t 与变量x 或y 的一个关系式x =f (t )(或y =φ(t ));第三步,把确定的参数与一个变量的关系式代入一般方程F (x ,y )=0,求得另一关系y =g (t )(或x =ψ(t )),问题得解.例1] 将下列参数方程化为一般方程.(1)⎩⎨⎧x =1t,y =1tt 2-1(t 为参数);(2)⎩⎪⎨⎪⎧x =2+sin 2θ,y =-1+cos 2θ(θ为参数). 解] (1)∵⎝⎛⎭⎫1t 2+⎝⎛⎭⎫1t t 2-12=1, ∴x 2+y 2=1.∵t 2-1≥0,∴t ≥1或t ≤-1.又x =1t ,∴x ≠0. 当t ≥1时,0<x ≤1, 当t ≤-1时,-1≤x <0,∴所求一般方程为x 2+y 2=1,其中⎩⎨⎧0<x ≤1,0≤y <1或⎩⎪⎨⎪⎧-1≤x <0,-1<y ≤0.(2)∵y =-1+cos 2θ=-1+1-2sin 2θ=-2sin 2θ,sin 2θ=x -2, ∴y =-2x +4,∴2x +y -4=0. ∵0≤sin 2θ≤1,∴0≤x -2≤1,∴2≤x ≤3,∴所求的一般方程为2x +y -4=0(2≤x ≤3). 易错提示](1)将曲线的参数方程化为一般方程时务必要留意x ,y 的取值范围,保证消参前后的方程的全都性. (2)将参数方程化为一般方程时,要留意参数的取值范围对一般方程中x ,y 的取值范围的影响.直线与圆锥曲线的参数方程及应用1第一步,把直线和圆锥曲线的参数方程都化为一般方程; 其次步,依据直线与圆锥曲线的位置关系解决问题.2.当直线经过点P (x 0,y 0),且直线的倾斜角为α,求直线与圆锥曲线的交点、弦长问题时,可以把直线的参数方程设成⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数),交点A ,B 对应的参数分别为t 1,t 2,计算时把直线的参数方程代入圆锥曲线的直角坐标方程,求出t 1+t 2,t 1·t 2,得到|AB |=|t 1-t 2|=(t 1+t 2)2-4t 1·t 2.例2] (2021·豫南九校联考)在直角坐标系xOy 中,设倾斜角为α的直线l :⎩⎨⎧x =2+t cos α,y =3+t sin α(t 为参数)与曲线C :⎩⎪⎨⎪⎧x =2cos θ,y =sin θ(θ为参数)相交于不同的两点A ,B .(1)若α=π3,求线段AB 的中点M 的坐标;(2)若|PA |·|PB |=|OP |2,其中P (2,3),求直线l 的斜率. 解] (1)将曲线C 的参数方程化为一般方程是x 24+y 2=1.当α=π3时,设点M 对应的参数为t 0.直线l 的方程为⎩⎨⎧x =2+12t ,y =3+32t(t 为参数),代入曲线C 的一般方程x 24+y 2=1,得13t 2+56t +48=0,设直线l 上的点A ,B 对应参数分别为t 1,t 2. 则t 0=t 1+t 22=-2813,所以点M 的坐标为⎝⎛⎭⎫1213,-313.(2)将⎩⎪⎨⎪⎧x =2+t cos α,y =3+t sin α代入曲线C 的一般方程x 24+y 2=1,得(cos 2α+4sin 2α)t 2+(83sin α+4cos α)t +12=0, 由于|PA |·|PB |=|t 1t 2|=12cos 2α+4sin 2α,|OP |2=7, 所以12cos 2α+4sin 2α=7,得tan 2α=516.由于Δ=32cos α(23sin α-cos α)>0, 故tan α=54.所以直线l 的斜率为54.方法技巧]1.解决直线与圆的参数方程的应用问题时一般是先化为一般方程再依据直线与圆的位置关系来解决问题.2.对于形如⎩⎪⎨⎪⎧x=x 0+at ,y =y 0+bt(t 为参数)的直线的参数方程,当a 2+b 2≠1时,应先化为标准形式后才能利用t 的几何意义解题.1.考点一]将下列参数方程化为一般方程.(1)⎩⎨⎧x =3k1+k 2,y =6k21+k2(k 为参数);(2)⎩⎪⎨⎪⎧x =1-sin 2θ,y =sin θ+cos θ(θ为参数). 解:(1)两式相除,得k =y 2x ,将其代入x =3k1+k 2得x =3·y2x 1+⎝⎛⎭⎫y 2x 2,化简得4x 2+y 2-6y =0,由于y =6k 21+k 2=6-11+k 2,所以0<y <6,所以所求的一般方程是4x 2+y 2-6y =0(0<y <6). (2)由(sin θ+cos θ)2=1+sin 2θ=2-(1-sin 2θ) 得y 2=2-x .又x =1-sin 2θ∈0,2], 得所求的一般方程为y 2=2-x ,x ∈0,2].2.考点二](2021·唐山模拟)已知曲线C 的参数方程为⎩⎪⎨⎪⎧x =6cos θ,y =4sin θ(θ为参数),在同一平面直角坐标系中,将曲线C 上的点按坐标变换⎩⎨⎧x ′=13x ,y ′=14y得到曲线C ′.(1)求曲线C ′的一般方程;(2)若点A 在曲线C ′上,点D (1,3).当点A 在曲线C ′上运动时,求AD 中点P 的轨迹方程.解:(1)将⎩⎪⎨⎪⎧x =6cos θ,y =4sin θ代入⎩⎨⎧x ′=13x ,y ′=14y ,得曲线C ′的参数方程为⎩⎪⎨⎪⎧x ′=2cos θ,y ′=sin θ,∴曲线C ′的一般方程为x 24+y 2=1.(2)设点P (x ,y ),A (x 0,y 0),又D (1,3)且AD 的中点为P ,∴⎩⎪⎨⎪⎧x 0=2x -1,y 0=2y -3.又点A 在曲线C ′上,∴将A 点坐标代入C ′的一般方程x 24+y 2=1,得(2x -1)2+4(2y -3)2=4,∴动点P的轨迹方程为(2x -1)2+4(2y -3)2=4.3.考点二](2021·郑州模拟)将曲线C 1:x 2+y 2=1上全部点的横坐标伸长到原来的2倍(纵坐标不变)得到曲线C 2,A 为C 1与x 轴正半轴的交点,直线l 经过点A 且倾斜角为30°,记l 与曲线C 1的另一个交点为B ,与曲线C 2在第一、三象限的交点分别为C ,D .(1)写出曲线C 2的一般方程及直线l 的参数方程; (2)求|AC |-|BD |.解:(1)由题意可得C 2:x 22+y 2=1,对曲线C 1,令y =0,得x =1,所以l :⎩⎨⎧x =1+32t ,y =12t(t 为参数).(2)将⎩⎨⎧x =1+3t 2,y =12t代入x 22+y 2=1,整理得5t 2+43t -4=0.设点C ,D 对应的参数分别为t 1,t 2,则t 1+t 2=-435,且|AC |=t 1,|AD |=-t 2.又|AB |=2|OA |cos 30°=3,故|AC |-|BD |=|AC |-(|AD |-|AB |)=|AC |-|AD |+|AB |=t 1+t 2+3=35. 4.考点二]设直线l 的参数方程为⎩⎪⎨⎪⎧x =3+t cos α,y =4+t sin α(t 为参数,α为倾斜角),圆C 的参数方程为⎩⎪⎨⎪⎧x =1+2cos θ,y =-1+2sin θ(θ为参数). (1)若直线l 经过圆C 的圆心,求直线l 的斜率;(2)若直线l 与圆C 交于两个不同的点,求直线l 的斜率的取值范围.解:(1)由已知得直线l 经过的定点是P (3,4),而圆C 的圆心是C (1,-1),所以,当直线l 经过圆C 的圆心时,直线l 的斜率为k =52.(2)将圆C 的参数方程⎩⎪⎨⎪⎧x =1+2cos θ,y =-1+2sin θ,化成一般方程为(x -1)2+(y +1)2=4,① 将直线l 的参数方程代入①式,得 t 2+2(2cos α+5sin α)t +25=0.②当直线l 与圆C 交于两个不同的点时,方程②有两个不相等的实根,即Δ=4(2cos α+5sin α)2-100>0, 即20sin αcos α>21cos 2α,两边同除以cos 2α, 由此解得tan α>2120,即直线l 的斜率的取值范围为⎝⎛⎭⎫2120,+∞.突破点(二) 参数方程与极坐标方程的综合问题将极坐标方程与参数方程、一般方程交织在一起,考查极坐标方程与参数方程的综合应用.将各类方程相互转化是求解该类问题的前提.,解决问题时要留意:(1)解题时,易将直线与圆的极坐标方程混淆.要娴熟把握特殊直线、圆的极坐标方程的形式.(2)应用解析法解决实际问题时,要留意选取直角坐标系还是极坐标系,建立极坐标系要留意极点、极轴位置的选择,留意点和极坐标之间的“一对多”关系.(3)求曲线方程,常设曲线上任意一点P (ρ,θ),利用解三角形的学问,列出等量关系式,特殊是正弦、余弦定理的应用.圆的参数方程常和三角恒等变换结合在一起,解决取值范围或最值问题.(4)参数方程和一般方程表示同一个曲线时,要留意其中x ,y 的取值范围,即留意两者的等价性.考点贯穿 抓高考命题的“形”与“神”参数方程与极坐标方程的综合问题典例] (2021·长沙模拟)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =-1+cos α,y =sin α(α为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,直线l 的极坐标方程为ρ(cos θ+k sin θ)=-2(k 为实数).(1)推断曲线C 1与直线l 的位置关系,并说明理由;(2)若曲线C 1和直线l 相交于A ,B 两点,且|AB |=2,求直线l 的斜率.解] (1)由曲线C 1的参数方程⎩⎪⎨⎪⎧x =-1+cos α,y =sin α可得其一般方程为(x +1)2+y 2=1.由ρ(cos θ+k sin θ)=-2可得直线l 的直角坐标方程为x +ky +2=0. 由于圆心(-1,0)到直线l 的距离d =11+k 2≤1,所以直线与圆相交或相切,当k =0时,d =1,直线l 与曲线C 1相切; 当k ≠0时,d <1,直线l 与曲线C 1相交. (2)由于曲线C 1和直线l 相交于A ,B 两点, 且|AB |=2,故圆心到直线l 的距离d =11+k 2=1-⎝⎛⎭⎫222=22, 解得k =±1,所以直线l 的斜率为±1. 方法技巧]处理极坐标、参数方程综合问题的方法(1)涉及参数方程和极坐标方程的综合题,求解的一般方法是分别化为一般方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.(2)数形结合的应用,即充分利用参数方程中参数的几何意义,或者利用ρ和θ的几何意义,直接求解,能达到化繁为简的解题目的.1.已知曲线C 的参数方程为⎩⎨⎧x =3+10cos α,y =1+10sin α(α为参数),以直角坐标系原点为极点,x 轴正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程,并说明其表示什么轨迹;(2)若直线的极坐标方程为sin θ-cos θ=1ρ,求直线被曲线C 截得的弦长.解:(1)∵曲线C 的参数方程为⎩⎪⎨⎪⎧x =3+10cos α,y =1+10sin α(α为参数),∴曲线C 的一般方程为(x -3)2+(y -1)2=10,①曲线C 表示以(3,1)为圆心,10为半径的圆.将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ代入①并化简,得ρ=6cos θ+2sin θ, 即曲线C 的极坐标方程为ρ=6cos θ+2sin θ. (2)∵直线的直角坐标方程为y -x =1, ∴圆心C 到直线的距离为d =322, ∴弦长为210-92=22.2.在极坐标系中,圆C 的方程为ρ=2a cos θ(a ≠0),以极点为坐标原点,极轴为x 轴正半轴建立平面直角坐标系,设直线l 的参数方程为⎩⎪⎨⎪⎧x =3t +1,y =4t +3(t 为参数).(1)求圆C 的标准方程和直线l 的一般方程;(2)若直线l 与圆C 恒有公共点,求实数a 的取值范围.解:(1)由ρ=2a cos θ,ρ2=2aρcos θ,又ρ2=x 2+y 2,ρcos θ=x ,所以圆C 的标准方程为(x -a )2+y 2=a 2.由⎩⎪⎨⎪⎧x =3t +1,y =4t +3,得⎩⎪⎨⎪⎧x -13=t ,y -34=t ,因此x -13=y -34,所以直线l 的一般方程为4x -3y +5=0.(2)由于直线l 与圆C 恒有公共点,所以|4a +5|42+(-3)2≤|a |,两边平方得9a 2-40a -25≥0,所以(9a +5)(a-5)≥0,解得a ≤-59或a ≥5,所以a 的取值范围是⎝⎛⎦⎤-∞,-59∪[)5,+∞.全国卷5年真题集中演练——明规律] 1.(2022·全国甲卷)在直角坐标系xOy 中,圆C 的方程为(x +6)2+y 2=25. (1)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程;(2)直线l 的参数方程是⎩⎪⎨⎪⎧x =t cos α,y =t sin α(t 为参数),l 与C 交于A ,B 两点,|AB |=10,求l 的斜率.解:(1)由x =ρcos θ,y =ρsin θ可得圆C 的极坐标方程为ρ2+12ρcos θ+11=0. (2)在(1)中建立的极坐标系中,直线l 的极坐标方程为θ=α(ρ∈R).设A ,B 所对应的极径分别为ρ1,ρ2,将l 的极坐标方程代入C 的极坐标方程得ρ2+12ρcos α+11=0.于是ρ1+ρ2=-12cos α,ρ1ρ2=11. |AB |=|ρ1-ρ2|=(ρ1+ρ2)2-4ρ1ρ2=144cos 2α-44.由|AB |=10得cos 2α=38,tan α=±153.所以直线l 的斜率为153或-153. 2.(2022·全国丙卷)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧x =3cos α,y =sin α(α为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 2的极坐标方程为ρsin ⎝⎛⎭⎫θ+π4=2 2. (1)写出C 1的一般方程和C 2的直角坐标方程;(2)设点P 在C 1上,点Q 在C 2上,求|PQ |的最小值及此时P 的直角坐标. 解:(1)C 1的一般方程为x 23+y 2=1,C 2的直角坐标方程为x +y -4=0.(2)由题意,可设点P 的直角坐标为(3cos α,sin α).由于C 2是直线,所以|PQ |的最小值即为P 到C 2的距离d (α)的最小值, d (α)=|3cos α+sin α-4|2=2⎪⎪⎪⎪sin ⎝⎛⎭⎫α+π3-2, 当且仅当α=2k π+π6(k ∈Z)时,d (α)取得最小值,最小值为2,此时P 的直角坐标为⎝⎛⎭⎫32,12. 3.(2021·新课标全国卷Ⅱ)在直角坐标系xOy 中,曲线C 1:⎩⎪⎨⎪⎧x =t cos α,y =t sin α(t 为参数,t ≠0),其中0≤α<π.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sin θ,C 3:ρ=23cos θ.(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB |的最大值. 解:(1)曲线C 2的直角坐标方程为x 2+y 2-2y =0, 曲线C 3的直角坐标方程为x 2+y 2-23x =0.联立⎩⎪⎨⎪⎧ x 2+y 2-2y =0,x 2+y 2-23x =0,解得⎩⎪⎨⎪⎧x =0,y =0或⎩⎨⎧x =32,y =32.所以C 2与C 3交点的直角坐标为(0,0)和⎝⎛⎭⎫32,32.(2)曲线C 1的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中0≤α<π. 因此A 的极坐标为(2sin α,α),B 的极坐标为(23cos α,α).所以|AB |=|2sin α-23cos α|=4⎪⎪⎪⎪sin ⎝⎛⎭⎫α-π3. 当α=5π6时,|AB |取得最大值,最大值为4.4.(2022·新课标全国卷Ⅰ)已知曲线C :x 24+y 29=1,直线l :⎩⎪⎨⎪⎧x =2+t ,y =2-2t (t 为参数).(1)写出曲线C 的参数方程,直线l 的一般方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.解:(1)曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ,y =3sin θ(θ为参数).直线l 的一般方程为2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|.则|PA |=d sin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43.当sin(θ+α)=-1时,|PA |取得最大值,最大值为2255.当sin(θ+α)=1时,|PA |取得最小值,最小值为255.5.(2022·新课标全国卷Ⅱ)在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为ρ=2cos θ,θ∈⎣⎡⎦⎤0,π2. (1)求C 的参数方程;(2)设点D 在C 上,C 在D 处的切线与直线l :y =3x +2垂直,依据(1)中你得到的参数方程,确定D 的坐标.解:(1)C 的一般方程为(x -1)2+y 2=1(0≤y ≤1).可得C 的参数方程为⎩⎪⎨⎪⎧x =1+cos t ,y =sin t (t 为参数,0≤t ≤π).(2)设D (1+cos t ,sin t ).由(1)知C 是以G (1,0)为圆心,1为半径的上半圆.由于C 在点D 处的切线与l垂直,所以直线GD 与l 的斜率相同,tan t =3,t =π3.故D 的直角坐标为⎝⎛⎭⎫1+cos π3,sin π3,即⎝⎛⎭⎫32,32.6.(2021·新课标全国卷Ⅰ)已知曲线C 1的参数方程为⎩⎪⎨⎪⎧x =4+5cos t ,y =5+5sin t , (t 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ .(1)把C 1的参数方程化为极坐标方程; (2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).解:(1)将⎩⎪⎨⎪⎧x =4+5cos t ,y =5+5sin t消去参数t ,化为一般方程(x -4)2+(y -5)2=25,即C 1:x 2+y 2-8x -10y +16=0.将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ代入x 2+y 2-8x -10y +16=0 得ρ2-8ρcos θ-10ρsin θ+16=0.所以C 1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0. (2)C 2的一般方程为x 2+y 2-2y =0.由⎩⎪⎨⎪⎧ x 2+y 2-8x -10y +16=0,x 2+y 2-2y =0,解得⎩⎪⎨⎪⎧ x =1,y =1,或⎩⎪⎨⎪⎧x =0,y =2.所以C 1与C 2交点的极坐标分别为⎝⎛⎭⎫2,π4,⎝⎛⎭⎫2,π2. 课时达标检测] 基础送分题——高考就考那几点,练通就能把分捡1.(2021·郑州模拟)已知曲线C 1的参数方程为⎩⎨⎧x =-2-32t ,y =12t ,曲线C 2的极坐标方程为ρ=22cos θ-π4,以极点为坐标原点,极轴为x 轴正半轴建立平面直角坐标系. (1)求曲线C 2的直角坐标方程;(2)求曲线C 2上的动点M 到曲线C 1的距离的最大值. 解:(1)ρ=22cos ⎝⎛⎭⎫θ-π4=2(cos θ+sin θ), 即ρ2=2(ρcos θ+ρsin θ),可得x 2+y 2-2x -2y =0, 故C 2的直角坐标方程为(x -1)2+(y -1)2=2.(2)C 1的一般方程为x +3y +2=0,由(1)知曲线C 2是以(1,1)为圆心,以2为半径的圆,且圆心到直线C 1的距离d =|1+3+2|12+(3)2=3+32,所以动点M 到曲线C 1的距离的最大值为3+3+222.2.在极坐标系中,已知三点O (0,0),A ⎝⎛⎭⎫2,π2,B ⎝⎛⎭⎫22,π4. (1)求经过点O ,A ,B 的圆C 1的极坐标方程;(2)以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,圆C 2的参数方程为⎩⎪⎨⎪⎧x =-1+a cos θ,y =-1+a sin θ(θ是参数),若圆C 1与圆C 2外切,求实数a 的值.解:(1)O (0,0),A ⎝⎛⎭⎫2,π2,B ⎝⎛⎭⎫22,π4对应的直角坐标分别为O (0,0),A (0,2),B (2,2),则过点O ,A ,B 的圆的一般方程为x 2+y 2-2x -2y =0,将⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ代入可求得经过点O ,A ,B 的圆C 1的极坐标方程为ρ=22cos ⎝⎛⎭⎫θ-π4. (2)圆C 2:⎩⎪⎨⎪⎧x =-1+a cos θ,y =-1+a sin θ(θ是参数)对应的一般方程为(x +1)2+(y +1)2=a 2,圆心为(-1,-1),半径为|a |,而圆C 1的圆心为(1,1),半径为2,所以当圆C 1与圆C 2外切时,有2+|a |=(-1-1)2+(-1-1)2,解得a =±2.3.(2021·太原模拟)在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立的极坐标系中,直线l 的极坐标方程为θ=π4(ρ∈R),曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =sin θ.(1)写出直线l 的直角坐标方程及曲线C 的一般方程;(2)过点M 且平行于直线l 的直线与曲线C 交于A ,B 两点,若|MA |·|MB |=83,求点M 轨迹的直角坐标方程.解:(1)直线l 的直角坐标方程为y =x ,曲线C 的一般方程为x 22+y 2=1.(2)设点M (x 0,y 0),过点M 的直线为l 1:⎩⎨⎧x =x 0+22t ,y =y 0+22t (t 为参数),由直线l 1与曲线C 相交可得:3t 22+2tx 0+22ty 0+x 20+2y 20-2=0,由|MA |·|MB |=83,得t 1t 2=⎪⎪⎪⎪⎪⎪⎪⎪x 20+2y 20-232=83,即x 20+2y 20=6,x 2。
高考数学二轮复习-专题30 极坐标与参数方程的应用(解析版)
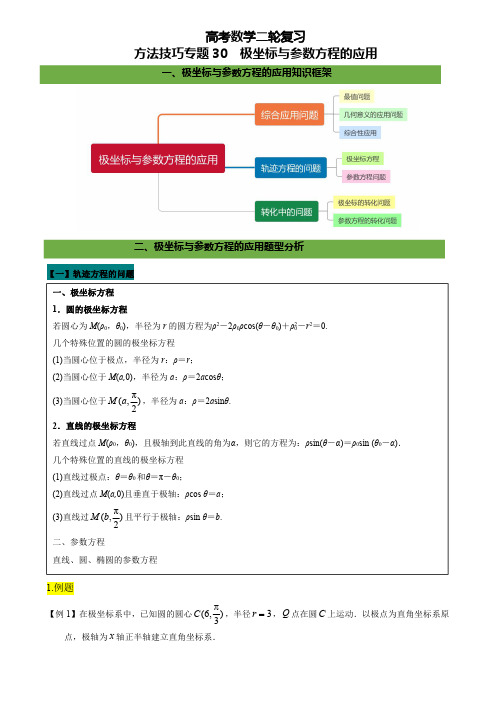
又因为 O是圆 C 上的点,所以 POQ PCQ π 。
26
【三】最值、几何意义的综合问题
1.距离最值(点到点、曲线点到线、) 距离的最值: ---用“参数法” (1)曲线上的点到直线距离的最值问题 (2)点与点的最值问题 “参数法”:设点---套公式--三角辅助角 ①设点: 设点的坐标,点的坐标用该点在所在曲线的的参数方程来设 ②套公式:利用点到线的距离公式 ③辅助角:利用三角函数辅助角公式进行化一 2.面积的最值问题 面积最值问题一般转化成弦长问题+点到线的最值问题 3.几何意义及其综合应用:
P(2,
)
在曲线
cos(
)
2
上.
3
3
所以,l的极坐标方程为
cos(
)
2
.
3
(2)设 P(, ) ,在 Rt△OAP 中, | OP || OA | cos 4 cos , 即 4 cos .
因为P在线段OM上,且
AP
OM
,故
的取值范围是 [
,
]
.
42
所以P点轨迹的极坐标方程为
4 cos ,
(1)分别写出 M1 , M 2 , M 3 的极坐标方程;
(2)曲线 M 由 M1 , M 2 , M 3 构成,若点 P 在 M 上,且 | OP | 3 ,求 P 的极坐标.
【解析】(1)由题设可得,弧 AB, BC,CD 所在圆的极坐标方程分别为
2 cos , 2sin , 2 cos .
[ ,
] .[来源:学*科*网]
42
【练习 2】在极坐标系中,已知圆 C 经过点 P (2 2, ) ,圆心为直线ρsin(θ-π)=- 3与极轴的交点,求
专题 坐标系与参数方程(解析版)

专题 坐标系与参数方程1.【2019年高考北京卷理数】已知直线l 的参数方程为13,24x t y t =+=+⎧⎨⎩(t 为参数),则点(1,0)到直线l的距离是 A .15B .25C .45D .652.【2019年高考全国Ⅰ卷理数】在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为.(1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩,2cos sin 110ρθθ++=3.【2019年高考全国Ⅱ卷理数】在极坐标系中,O 为极点,点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上,直线l 过点(4,0)A 且与OM 垂直,垂足为P . (1)当0=3θπ时,求0ρ及l 的极坐标方程; (2)当M 在C 上运动且P 在线段OM 上时,求P 点轨迹的极坐标方程.4.【2019年高考全国Ⅲ卷理数】如图,在极坐标系Ox 中,(2,0)A ,)4B π,)4C 3π,(2,)D π,弧AB ,BC ,CD 所在圆的圆心分别是(1,0),(1,)2π,(1,)π,曲线1M 是弧AB ,曲线2M 是弧BC ,曲线3M 是弧CD .(1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.5.【2019年高考江苏卷数学】在极坐标系中,已知两点3,,42A B ππ⎛⎫⎫ ⎪⎪⎝⎭⎭,直线l 的方程为sin 34ρθπ⎛⎫+= ⎪⎝⎭.(1)求A ,B 两点间的距离;(2)求点B 到直线l 的距离.6.【重庆西南大学附属中学校2019届高三第十次月考数学】在平面直角坐标系xOy 中,已知曲线1C 的参数方程为5()x y ϕϕϕ⎧=⎪⎨=⎪⎩为参数,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos ρθ=.(1)求曲线1C 与曲线2C 两交点所在直线的极坐标方程;(2)若直线l的极坐标方程为sin()4ρθπ+=,直线l 与y 轴的交点为M ,与曲线1C 相交于,A B 两点,求MA MB +的值.7.【山东省郓城一中等学校2019届高三第三次模拟考试数学】在平面直角坐标系xOy 中,曲线C 的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数),在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,点M 的极坐标为34π⎛⎫ ⎪⎝⎭,直线l 的极坐标方程为sin 04ρθπ⎛⎫-+= ⎪⎝⎭.(1)求直线l 的直角坐标方程与曲线C 的普通方程;(2)若N 是曲线C 上的动点,P 为线段MN 的中点,求点P 到直线l 的距离的最大值.8.【河南省周口市2018–2019学年度高三年级(上)期末调研考试数学】在直角坐标系xOy 中,直线l 的参数方程为4,232x y ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为223sin 12ρθ+=(). (1)求直线l 的普通方程与曲线C 的直角坐标方程; (2)若直线l 与曲线C 交于A B ,两点,且设定点21P (,),求PB PA PAPB+的值.9.【河南省郑州市第一中学2019届高三上学期入学摸底测试数学】以直角坐标系的原点O 为极点,x 轴的正半轴为极轴.已知点P 的直角坐标为15 (,),点M 的极坐标为π42(,).若直线l 过点P ,且倾斜角为π3,圆C 以M 为圆心、4为半径. (1)求直线l 的参数方程和圆C 的极坐标方程; (2)试判定直线l 和圆C 的位置关系.10.【全国I 卷2019届高三五省优创名校联考数学】在直角坐标系xOy 中,直线l的参数方程为22x m t y t ⎧⎪=+⎨=⎪⎪⎪⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,椭圆C 的极坐标方程为2222cos 3sin 48ρθρθ+=,其左焦点F 在直线l 上. (1)若直线l 与椭圆C 交于A B ,两点,求FA FB +的值; (2)求椭圆C 的内接矩形面积的最大值.11.【河北衡水金卷2019届高三12月第三次联合质量测评数学】在直角坐标系中,直线l 的参数方程为1cos ,1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,0πα<<),以坐标原点为极点,x 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C 的极坐标方程为2241sin ρθ=+. (1)当π6a =时,写出直线l 的普通方程及曲线C 的直角坐标方程; (2)已知点()11P -,,设直线l 与曲线C 交于A ,B 两点,试确定PA PB ⋅的取值范围.12.【河南省信阳高级中学2018–2019学年高二上学期期中考试数学】在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为2sin 2cos 0a a ρθθ=+>();直线l的参数方程为22x t y ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).直线l 与曲线C 分别交于M N ,两点.(1)写出曲线C 的直角坐标方程和直线l 的普通方程;(2)若点P 的极坐标为()2πPM PN +=,,a 的值.13.【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学】己知直线l 的参数方程为132x ty t=+⎧⎨=+⎩(t 为参数),曲线C 的极坐标方程为2sin 16cos 0ρθθ-=,直线l 与曲线C 交于A 、B 两点,点13P (,). (1)求直线l 的普通方程和曲线C 的直角坐标方程; (2)求11PA PB+的值.14.【河南省开封市2019届高三上学期第一次模拟考试数学】在直角坐标系xOy 中,直线l 的参数方程是1x t y t ==+⎧⎨⎩(t 为参数),曲线C 的参数方程是22cos 2sin x y ϕϕ=+⎧⎨=⎩(ϕ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系. (1)求直线l 和曲线C 的极坐标方程; (2)已知射线1OP θα=:(其中π02α<<)与曲线C 交于O P ,两点,射线2π2OQ θα=+:与直线l 交于Q 点,若OPQ ∆的面积为1,求α的值和弦长OP .15.【四川省成都市第七中学2019届高三一诊模拟考试数学】在平面直角坐标系xOy中,曲线C的参数标方程为e ee et tt txy--⎧=+⎪⎨=-⎪⎩(其中t为参数),在以O为极点、x轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,直线l的极坐标方程为πsin3ρθ⎛⎫-=⎪⎝⎭(1)求曲线C的极坐标方程;(2)求直线l与曲线C的公共点P的极坐标.16.【黑龙江省大庆市第一中学2019届高三下学期第四次模拟(最后一卷)数学】在平面直角坐标系xOy中,以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系,已知直线l 的参数方程为22x ty t =⎧⎨=+⎩(t为参数),曲线C 的极坐标方程为2cos 8sin ρθθ=. (1)求曲线C 的直角坐标方程,并指出该曲线是什么曲线; (2)若直线l 与曲线C 的交点分别为M ,N ,求MN .17.【河北省石家庄市2018届高中毕业班模拟考试(二)数学】在平面直角坐标系xOy 中,曲线1C 的方程为224x y +=,直线l的参数方程2x ty =--⎧⎪⎨=+⎪⎩(t 为参数),若将曲线1C 上的点的横坐标不变,纵坐标变为原来的32倍,得曲线2C . (1)写出曲线2C 的参数方程;(2)设点2P -(,直线l 与曲线2C 的两个交点分别为A B ,,求11PA PB+的值.答 案1.【2019年高考北京卷理数】已知直线l 的参数方程为13,24x t y t =+=+⎧⎨⎩(t 为参数),则点(1,0)到直线l的距离是 A .15B .25C .45D .65【答案】D【解析】由题意,可将直线l 化为普通方程:1234x y --=,即()()41320x y ---=,即4320x y -+=,所以点(1,0)到直线l的距离65d ==,故选D . 【名师点睛】本题考查直线参数方程与普通方程的转化,点到直线的距离,属于容易题,注重基础知识、基本运算能力的考查.2.【2019年高考全国Ⅰ卷理数】在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为.2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩,2cos sin 110ρθθ++=(1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.【答案】(1)221(1)4y x x +=≠-;l的直角坐标方程为2110x +=;(2.【解析】(1)因为221111t t --<≤+,且()22222222141211y t t x t t ⎛⎫-⎛⎫+=+= ⎪ ⎪+⎝⎭⎝⎭+,所以C 的直角坐标方程为221(1)4y x x +=≠-.l的直角坐标方程为2110x ++=.(2)由(1)可设C 的参数方程为cos ,2sin x y αα=⎧⎨=⎩(α为参数,ππα-<<).C 上的点到lπ4cos 11α⎛⎫-+ ⎪=当2π3α=-时,π4cos 113α⎛⎫-+ ⎪⎝⎭取得最小值7,故C 上的点到l.【名师点睛】本题考查参数方程、极坐标方程与直角坐标方程的互化、求解椭圆上的点到直线距离的最值问题.求解本题中的最值问题通常采用参数方程来表示椭圆上的点,将问题转化为三角函数的最值求解问题.3.【2019年高考全国Ⅱ卷理数】在极坐标系中,O 为极点,点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上,直线l 过点(4,0)A 且与OM 垂直,垂足为P . (1)当0=3θπ时,求0ρ及l 的极坐标方程; (2)当M 在C 上运动且P 在线段OM 上时,求P 点轨迹的极坐标方程. 【答案】(1)0ρ=l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭; (2)4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.【解析】(1)因为()00,M ρθ在C 上,当03θπ=时,04sin 3ρπ==由已知得||||cos23OP OA π==. 设(,)Q ρθ为l 上除P 的任意一点.在Rt OPQ △中,cos ||23OP ρθπ⎛⎫-== ⎪⎝⎭, 经检验,点(2,)3P π在曲线cos 23ρθπ⎛⎫-= ⎪⎝⎭上. 所以,l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭. (2)设(,)P ρθ,在Rt OAP △中,||||cos 4cos ,OP OA θθ== 即 4cos ρθ=. 因为P 在线段OM 上,且AP OM ⊥,故θ的取值范围是,42ππ⎡⎤⎢⎥⎣⎦.所以,P 点轨迹的极坐标方程为4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.【名师点睛】本题主要考查极坐标方程与直角坐标方程的互化,熟记公式即可,属于常考题型.4.【2019年高考全国Ⅲ卷理数】如图,在极坐标系Ox 中,(2,0)A ,)4B π,)4C 3π,(2,)D π,弧AB ,BC ,CD 所在圆的圆心分别是(1,0),(1,)2π,(1,)π,曲线1M 是弧AB ,曲线2M 是弧BC ,曲线3M 是弧CD .(1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.【答案】(1)1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭.(2)π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.【解析】(1)由题设可得,弧,,AB BC CD 所在圆的极坐标方程分别为2cos ρθ=,2sin ρθ=,2cos ρθ=-.所以1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤ ⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭. (2)设(,)P ρθ,由题设及(1)知若π04θ≤≤,则2cos θ=,解得π6θ=;若π3π44θ≤≤,则2sin θ=π3θ=或2π3θ=;若3ππ4θ≤≤,则2cos θ-=5π6θ=.综上,P 的极坐标为π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.【名师点睛】此题考查了极坐标中过极点的圆的方程,思考量不高,运算量不大,属于中档题.5.【2019年高考江苏卷数学】在极坐标系中,已知两点3,,42A B ππ⎛⎫⎫ ⎪⎪⎝⎭⎭,直线l 的方程为sin 34ρθπ⎛⎫+= ⎪⎝⎭.(1)求A ,B 两点间的距离;(2)求点B 到直线l 的距离.【答案】(12)2.【解析】(1)设极点为O .在△OAB 中,A (3,4π),B ,2π),由余弦定理,得AB =. (2)因为直线l 的方程为sin()34ρθπ+=,则直线l 过点)2π,倾斜角为34π.又)2B π,所以点B 到直线l的距离为3sin()242ππ⨯-=. 【名师点睛】本题主要考查曲线的极坐标方程等基础知识,考查运算求解能力.6.【重庆西南大学附属中学校2019届高三第十次月考数学】在平面直角坐标系xOy 中,已知曲线1C 的参数方程为5()x y ϕϕϕ⎧=+⎪⎨=⎪⎩为参数,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos ρθ=.(1)求曲线1C 与曲线2C 两交点所在直线的极坐标方程;(2)若直线l的极坐标方程为sin()4ρθπ+=,直线l 与y 轴的交点为M ,与曲线1C 相交于,A B 两点,求MA MB +的值. 【答案】(1)5cos 2ρθ=;(2) 【解析】(1)曲线1C 的普通方程为:22(5)10x y -+=,曲线2C 的普通方程为:224x y x +=,即22(2)4x y -+=,由两圆心的距离32)d =∈,所以两圆相交, 所以两方程相减可得交线为6215x -+=,即52x =. 所以直线的极坐标方程为5cos 2ρθ=. (2)直线l 的直角坐标方程:4x y +=,则与y 轴的交点为(0,4)M ,直线l的参数方程为24x y ⎧=-⎪⎪⎨⎪=⎪⎩,带入曲线1C 22(5)10x y -+=得2310t ++=.设,A B 两点的参数为1t ,2t ,所以12t t +=-1231t t =,所以1t ,2t 同号.所以1212MA MB t t t t +=+=+=【名师点睛】本题考查了极坐标,参数方程和普通方程的互化和用参数方程计算长度,是常见考题.7.【山东省郓城一中等学校2019届高三第三次模拟考试数学】在平面直角坐标系xOy 中,曲线C 的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数),在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,点M的极坐标为34π⎛⎫ ⎪⎝⎭,直线l 的极坐标方程为sin 04ρθπ⎛⎫-+= ⎪⎝⎭.(1)求直线l 的直角坐标方程与曲线C 的普通方程;(2)若N 是曲线C 上的动点,P 为线段MN 的中点,求点P 到直线l 的距离的最大值.【答案】(1)40x y --=,2213x y +=;(2.【解析】(1)因为直线l 的极坐标方程为πsin 04ρθ⎛⎫-+= ⎪⎝⎭, 即ρsin θ-ρcos θ+4=0.由x =ρcos θ,y =ρsin θ, 可得直线l 的直角坐标方程为x -y -4=0.将曲线C 的参数方程sin x y αα⎧=⎪⎨=⎪⎩,消去参数a ,得曲线C 的普通方程为2213x y +=.(2)设N α,sin α),α∈[0,2π).点M 的极坐标(,3π4),化为直角坐标为(-2,2).则11,sin 12P αα⎫-+⎪⎪⎝⎭.所以点P 到直线l 的距离2d ==≤,所以当5π6α=时,点M 到直线l 的距离的最大值为2. 【名师点睛】本题主要考查参数方程、极坐标方程和普通方程的互化,考查三角函数的图像和性质,考查点到直线的距离的最值的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力. 8.【河南省周口市2018–2019学年度高三年级(上)期末调研考试数学】在直角坐标系xOy 中,直线l 的参数方程为4,32x y ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为223sin 12ρθ+=(). (1)求直线l 的普通方程与曲线C 的直角坐标方程; (2)若直线l 与曲线C 交于A B ,两点,且设定点21P (,),求PB PA PAPB+的值.【答案】(1)l 普通方程为10x y --=,C 直角坐标方程为22143x y +=;(2)867. 【解析】(1)由直线l 的参数方程消去t ,得普通方程为10x y --=.223sin 12ρθ+=()等价于2223sin 12ρρθ+=,将222sin x y y ρρθ=+=,代入上式,得曲线C 的直角坐标方程为222312x y y ++=(), 即22143x y +=. (2)点21P (,)在直线10x y --=上,所以直线l的参数方程可以写为2 1x t y ⎧=+⎪⎪⎨⎪=+⎪⎩,(为参数), 将上式代入22143x y +=,得2780t ++=. 设A B ,对应的参数分别为12t t ,,则1212877t t t t +=-=, 所以22||PA PB PB PAPA PB PA PB ++=22PA PB PA PB PA PB+-=()21212122t t t t t t +-=()2121212||2t t t t t t +-⋅==⋅2828677877--⨯=(. 【名师点睛】本题考查了直线的参数方程,考查了简单曲线的极坐标方程,解答此题的关键是熟练掌握直线参数方程中参数的几何意义.9.【河南省郑州市第一中学2019届高三上学期入学摸底测试数学】以直角坐标系的原点O 为极点,x 轴的正半轴为极轴.已知点P 的直角坐标为15-(,),点M 的极坐标为π42(,).若直线l 过点P ,且倾斜角为π3,圆C 以M 为圆心、4为半径. (1)求直线l 的参数方程和圆C 的极坐标方程; (2)试判定直线l 和圆C 的位置关系.【答案】(1)11252x t y t ⎧=+⎪⎪⎨⎪=-+⎪⎩(t 为参数),8sin ρθ=;(2)直线l 与圆C 相离.【解析】(1)直线l的参数方程1π11cos 23 π5sin 53x t x t y t y ⎧⎧=+=+⋅⎪⎪⎪⎪⇒⎨⎨⎪⎪=-+⋅=-⎪⎪⎩⎩(t 为参数), M 点的直角坐标为(0,4),圆C 的半径为4,∴圆C 的方程为22416x y +-=(),将cos sin x y ρθρθ=⎧⎨=⎩代入,得圆C 的极坐标方程为222cos (sin 4)16ρθρθ+-=,即8sin ρθ=; (2)直线l50y ---=,圆心M 到l的距离为942d ==>, ∴直线l 与圆C 相离.【名师点睛】主要是考查了极坐标与直角坐标的互化,以及运用,属于基础题.10.【全国I 卷2019届高三五省优创名校联考数学】在直角坐标系xOy 中,直线l的参数方程为22x m t y t ⎧⎪=+⎨=⎪⎪⎪⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,椭圆C 的极坐标方程为2222cos 3sin 48ρθρθ+=,其左焦点F 在直线l 上.(1)若直线l 与椭圆C 交于A B ,两点,求FA FB +的值;(2)求椭圆C 的内接矩形面积的最大值. 【答案】(1)2) 【解析】(1)将cos sin x y ρθρθ=⎧⎨=⎩代入ρ2cos 2θ+3ρ2sin 2θ=48,得x 2+3y 2=48,即2214816x y +=, 因为c 2=48-16=32,所以F的坐标为(-,0), 又因为F 在直线l上,所以m =-把直线l的参数方程22x t y =-=⎧⎪⎪⎨⎪⎪⎩代入x 2+3y 2=48,化简得t 2-4t -8=0,所以t 1+t 2=4,t 1t 2=-8,所以12FA FB t t +=-===(2)由椭圆C 的方程2214816x y +=,可设椭圆C 上在第一象限内的任意一点M 的坐标为(θ,4sin θ)(π02θ<<),所以内接矩形的面积8sin 2S θθθ=⋅=, 当π4θ=时,面积S取得最大值 【名师点睛】直角坐标方程转为极坐标方程的关键是利用公式cos sin x y ρθρθ=⎧⎨=⎩,而极坐标方程转化为直角坐标方程的关键是利用公式222tan x y yx ρθ⎧=+⎪⎨=⎪⎩,后者也可以把极坐标方程变形,尽量产生2cos ρρθ,,sin ρθ以便转化.另一方面,当动点在圆锥曲线运动变化时,我们可以用一个参数θ来表示动点坐标,从而利用一元函数求与动点有关的最值问题.11.【河北衡水金卷2019届高三12月第三次联合质量测评数学】在直角坐标系中,直线l 的参数方程为1cos ,1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,0πα<<),以坐标原点为极点,x 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C 的极坐标方程为2241sin ρθ=+.(1)当π6a =时,写出直线l 的普通方程及曲线C 的直角坐标方程; (2)已知点()11P -,,设直线l 与曲线C 交于A ,B 两点,试确定PA PB ⋅的取值范围.【答案】(1)2210142x y x ++=+=,;(2)112⎡⎫⎪⎢⎣⎭,【解析】(1)当π6a =时,直线l的参数方程为π1cos ,162π11sin 162x t x y t y t ⎧⎧=-+=-+⎪⎪⎪⎪⇒⎨⎨⎪⎪=+=+⎪⎪⎩⎩,. 消去参数t得10x ++=. 由曲线C 的极坐标方程为2241sin ρθ=+,得()22sin 4ρρθ+=, 将222x y ρ+=,及sin y ρθ=代入得2224x y +=,即22142x y +=; (2)由直线l 的参数方程为1cos ,1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,0πα<<),可知直线l 是过点P (–1,1)且倾斜角为α的直线,又由(1)知曲线C 为椭圆22142x y +=,所以易知点P (–1,1)在椭圆C 内, 将1cos , 1sin x t y t αα=-+⎧⎨=+⎩代入22142x y +=中,整理得 ()()221sin 22sin c s 10to t ααα++--=,设A ,B 两点对应的参数分别为12t t ,, 则12211sin t t α⋅=-+, 所以12211sin PA PB t t α⋅==+,因为0πα<<,所以(]2sin 01α∈,,所以1221111sin 2PA PB t t α⎡⎫⋅==∈⎪⎢+⎣⎭,,所以PA PB ⋅的取值范围为112⎡⎫⎪⎢⎣⎭,.【名师点睛】利用直线参数方程中参数的几何意义求解问题.经过点P (x 0,y 0),倾斜角为α的直线l 的参数方程为00cos sin x x t y y t θθ=+⎧⎨=+⎩(t 为参数).若A ,B 为直线l 上两点,其对应的参数分别为12t t ,,线段AB 的中点为M ,点M 所对应的参数为0t ,则以下结论在解题中经常用到:(1)1202t t t +=;(2)1202t t PM t +==;(3)21AB t t =-;(4)12··PA PB t t =. 12.【河南省信阳高级中学2018–2019学年高二上学期期中考试数学】在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为2sin 2cos 0a a ρθθ=+>();直线l的参数方程为22x t y ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).直线l 与曲线C 分别交于M N ,两点.(1)写出曲线C 的直角坐标方程和直线l 的普通方程;(2)若点P 的极坐标为()2πPM PN +=,,a 的值.【答案】(1)曲线C 的直角坐标方程为:()()22211x a y a -+-=+,直线l 的普通方程为2y x =+. (2)2a =.【解析】(1)由()2sin 2cos 0a a ρθθ=+>,得()22sin 2cos 0a a ρρθρθ=+>,所以曲线C 的直角坐标方程为2222x y y ax +=+,即()()22211x a y a -+-=+,直线l 的普通方程为2y x =+.(2)将直线l的参数方程2,22x y t ⎧=-+⎪⎪⎨⎪=⎪⎩代入2222x y y ax +=+并化简、整理,得()2440t t a -++=.因为直线l 与曲线C 交于M N ,两点.所以()()2Δ4440a =-+>,解得1a ≠.由根与系数的关系,得121244t t t t a +==+,.因为点P 的直角坐标为()20-,,在直线l上.所以12PM PN t t +=+== 解得2a =,此时满足0a >.且1a ≠,故2a =.【名师点睛】参数方程主要通过代入法或者已知恒等式(如22cos sin 1αα+=等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式222tan cos ,sin x y x y xy ρρθρθθ=⎧+==⎧⎪⎨⎨=⎩⎪⎩等可以把极坐标方程与直角坐标方程互化,这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.13.【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学】己知直线l 的参数方程为132x ty t=+⎧⎨=+⎩(t 为参数),曲线C 的极坐标方程为2sin 16cos 0ρθθ-=,直线l 与曲线C 交于A 、B 两点,点13P (,). (1)求直线l 的普通方程和曲线C 的直角坐标方程; (2)求11PA PB+的值. 【答案】(1)21y x =+,216y x =;(2. 【解析】(1)直线l 的参数方程为132x ty t=+⎧⎨=+⎩(t 为参数),消去参数,可得直线l 的普通方程21y x =+,曲线C 的极坐标方程为2sin 16cos 0ρθθ-=,即22sin 16cos 0ρθρθ-=, 曲线C 的直角坐标方程为216y x =,(2)直线的参数方程改写为135x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),代入221212435167054y x t t t t t =-=+==-,,,121211t t PA PB t t -+==. 【名师点睛】由直角坐标与极坐标互换公式222cos sin x y x y ρθρθρ⎧=⎪=⎨⎪+=⎩,利用这个公式可以实现直角坐标与极坐标的相互转化.14.【河南省开封市2019届高三上学期第一次模拟考试数学】在直角坐标系xOy 中,直线l 的参数方程是1x t y t ==+⎧⎨⎩(t 为参数),曲线C 的参数方程是22cos 2sin x y ϕϕ=+⎧⎨=⎩(ϕ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(1)求直线l 和曲线C 的极坐标方程; (2)已知射线1OP θα=:(其中π02α<<)与曲线C 交于O P ,两点,射线2π2OQ θα=+:与直线l 交于Q 点,若OPQ ∆的面积为1,求α的值和弦长OP . 【答案】(1)cos sin 10ρθρθ-+=,4cos ρθ=;(2)π4OP α==, 【解析】(1)直线l 的普通方程为10x y -+=,极坐标方程为cos sin 10ρθρθ-+=,曲线C 的普通方程为2224x y -+=(),极坐标方程为4cos ρθ=. (2)依题意,∵π02α∈(,),∴4cos OP α=, 1ππsin cos 22OQ αα=+-+()()1sin cos αα=+,12cos 12cos sin OPQ S OP OQ ααα===+△, ∴πtan 102αα=∈,(,),∴π4OP α==,【名师点睛】本题考查的知识要点:三角函数关系式的恒等变变换,参数方程直角坐标方程和极坐标方程之间的转换,三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型. 15.【四川省成都市第七中学2019届高三一诊模拟考试数学】在平面直角坐标系xOy 中,曲线C 的参数标方程为e e e et tt tx y --⎧=+⎪⎨=-⎪⎩(其中t 为参数),在以O 为极点、x 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,直线l的极坐标方程为πsin 3ρθ⎛⎫-= ⎪⎝⎭(1)求曲线C 的极坐标方程;(2)求直线l 与曲线C 的公共点P 的极坐标. 【答案】(1)2ππcos2444ρθθ⎛⎫=-<< ⎪⎝⎭(2)π6⎛⎫ ⎪⎝⎭,【解析】(1)消去参数t ,得曲线C 的直角坐标方程()2242x y x -=≥. 将cos sin x y ρθρθ==,代入224x y -=,得()222cos sin 4ρθθ-=. 所以曲线C 的极坐标方程为2ππcos2444ρθθ⎛⎫=-<< ⎪⎝⎭.(2)将l 与C 的极坐标方程联立,消去ρ得2π4sin 2cos23θθ⎛⎫-=⎪⎝⎭.展开得()22223cos cos sin 2cos sin θθθθθθ-+=-. 因为cos 0θ≠,所以23tan 10θθ-+=.于是方程的解为tan θ=,即π6θ=.代入πsin 3ρθ⎛⎫-=⎪⎝⎭ρ=P 的极坐标为π6⎛⎫ ⎪⎝⎭,.【名师点睛】本题考查曲线的极坐标方程与普通方程的互化,直线的极坐标方程与曲线极坐标方程联立求交点的问题,考查计算能力.16.【黑龙江省大庆市第一中学2019届高三下学期第四次模拟(最后一卷)数学】在平面直角坐标系xOy中,以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系,已知直线l 的参数方程为22x ty t =⎧⎨=+⎩(t为参数),曲线C 的极坐标方程为2cos 8sin ρθθ=.(1)求曲线C 的直角坐标方程,并指出该曲线是什么曲线;(2)若直线l 与曲线C 的交点分别为M ,N ,求MN .【答案】(1)曲线C 方程为28x y =,表示焦点坐标为()0,2,对称轴为y 轴的抛物线;(2)10. 【解析】(1)因为2cos 8sin ρθθ=,所以22cos 8sin ρθρθ=,即28x y =,所以曲线C 表示焦点坐标为()0,2,对称轴为y 轴的抛物线. (2)设点()11,M x y ,点()22,N x y直线l 过抛物线的焦点()0,2,则直线参数方程为22x t y t =⎧⎨=+⎩化为一般方程为122y x =+,代入曲线C 的直角坐标方程,得24160x x --=, 所以12124,16x x x x +==- 所以MN ===10==.【名师点睛】本题考查极坐标方程化直角坐标方程,直线的参数方程化一般方程,弦长公式等,属于简单题.17.【河北省石家庄市2018届高中毕业班模拟考试(二)数学】在平面直角坐标系xOy 中,曲线1C 的方程为224x y +=,直线l的参数方程2x ty =--⎧⎪⎨=⎪⎩(t 为参数),若将曲线1C 上的点的横坐标不变,纵坐标变为原来的32倍,得曲线2C . (1)写出曲线2C的参数方程;(2)设点2P -(,直线l 与曲线2C 的两个交点分别为A B ,,求11PA PB+的值. 【答案】(1)2cos 3sin x y θθ=⎧⎨=⎩(θ为参数);(2)12【解析】(1)若将曲线1C 上的点的纵坐标变为原来的32,31则曲线2C 的直角坐标方程为22243x y +=(),整理得22149x y +=, ∴曲线2C 的参数方程2cos 3sin x y θθ=⎧⎨=⎩(θ为参数). (2)将直线的参数方程化为标准形式为1223332x t y t ''⎧=--⎪⎪⎨⎪=+⎪⎩(t '为参数),将参数方程带入22149x y +=得221(2))22149t --'+=' 整理得27183604t t ''++=(). 12127214477PA PB t t PA PB t t ''''+=+===,, 72111714427PA PB PA PB PA PB++===. 【名师点睛】本题考查了参数方程与普通方程的互化,及直线的参数方程的应用,重点考查了转化与化归能力.遇到求曲线交点、距离、线段长等几何问题时,求解的一般方法是分别化为普通方程和直角坐标方程后求解,或者直接利用直线参数的几何意义求解.要结合题目本身特点,确定选择何种方程.。
完整版坐标系与参数方程知识点

完整版坐标系与参数方程知识点一、坐标系的概念坐标系是为了方便描述平面或空间中点的位置而引入的一种系统。
常见的坐标系包括直角坐标系、极坐标系和参数方程坐标系。
二、直角坐标系直角坐标系是最常见的一种坐标系。
在二维空间中,直角坐标系由两个相互垂直的坐标轴构成,分别是x轴和y轴。
点在直角坐标系中的位置可以用有序数对(x,y)表示,分别代表点在x轴和y轴上的距离。
三、极坐标系极坐标系是一种以原点为中心,以角度和半径表示点的位置的坐标系。
在极坐标系中,点的位置由有序数对(r,θ)表示,其中r代表点到原点的距离,θ代表与正x轴的夹角。
四、参数方程与轨迹参数方程是一种用参数来表示曲线上的点的坐标的方法。
一般形式的参数方程为x=f(t),y=g(t),其中t是参数,f(t)和g(t)是定义在参数域上的函数。
通过改变参数t的取值范围,可以获得曲线上的一系列点,从而绘制出整条曲线。
五、参数方程与直角坐标系的转换将直角坐标系的点(x,y)转换为参数方程的形式,可以使用以下步骤:1.将x和y分别表示为t的函数:x=f(t),y=g(t)。
2.给定t的取值范围,求出对应的x和y的取值。
将参数方程的点(x,y)转换为直角坐标系的形式,可以使用以下步骤:1.通过解参数方程的两个方程,消去t,得到一个方程只包含x和y。
2.求解得到与x和y的关系式。
六、参数方程的性质参数方程可以表示各种各样的曲线,具有以下性质:1.参数方程可以用来表示直线、圆、椭圆、双曲线等曲线。
2.参数方程可以描述曲线的形状、方向、起点和终点等信息。
3.参数方程可以通过调整参数的取值范围来绘制出曲线的其中一部分或整条曲线。
七、应用场景参数方程在数学和物理学中有广泛的应用,例如:1.研究物体的运动轨迹,包括抛体运动、行星运动等。
2.描述动态系统的变化过程,如混沌系统、非线性振动等。
3.研究曲线的特殊性质,如曲率、曲线的长度等。
八、参数方程的解析与图像通过解析参数方程,可以得到曲线的方程,从而进一步研究曲线的性质。
选修4-4数学坐标系与参数方程

选修4-4数学坐标系与参数方程一、基础知识与考点梳理坐标系是解决几何问题的工具之一,包括平面直角坐标系和极坐标系。
参数方程是通过参数的变化来描述图形的方程,常用于描述曲线的运动或变化。
考点:1. 平面直角坐标系:了解坐标系的定义、坐标轴的性质、平面点的坐标表示方法以及表示直线和曲线的方程的求解方法。
2. 极坐标系:了解极坐标系的定义、坐标轴的性质、平面点的极坐标表示方法以及表示曲线的方程的求解方法。
3. 参数方程:了解参数方程的定义和解题步骤,熟练掌握参数方程求交点和极值点的方法。
二、典型例题解析例1、已知函数y=x²-2x+3,求其图像与x轴、y轴、直线x=1、y=3所围成的面积。
【解析】:1. 求该函数的根,即当y=0时x满足的条件:x=1±√2。
2. 绘制函数图像。
由于该函数为二次函数,故开口向上,图像开口向上,存在顶点,而顶点的横坐标为x=-b/2a,即x=1。
当x=0时,y=3,即函数在y轴上截距为3,因此y轴上的一点为(0,3)。
3. 按要求计算所求面积=△x=1△x=-∫1√2(y-3)dx+∫√2^3(y-x²+2x)dx=2-2√2/3例2、考虑曲线x=2cost+cos2t,y=2sint-sin2t的形状和特征,求其极坐标方程,指出极点和极轴,找出曲线上各点的对称点。
【解析】:1. 观察曲线方程,发现x的系数为2,y的系数为-1。
而2cos2t+1=2cos²t-2sin²t+1,故有x=4cos²t-1-y。
2. 代入x²+y²=r²,消去t,即得其极坐标方程r=4cos2θ-3。
3. 极点为(θ=r=0),为对称中心,且曲线轨迹在极轴之上。
4. 若要求曲线上一点的对称点,可先求该点的极坐标系(r,θ),则其对称点的极坐标系为(r,-θ),再用x=rcosθ,y=rsinθ回代直角坐标系。
极坐标与参数方程知识点解析

极坐标知识要点:1. 极坐标系的建立:在平面内取一个定点O ,叫做极点;引一条射线Ox ,叫做极轴;选定一个长度单位和角度单位(通常取弧度)及它的正方向(通常取逆时针方向)。
2. 极坐标系内一点的极坐标的规定:对于平面上任意一点M ,用ρ表示线段OM 的长度,用θ表示以射线Ox 为始边,射线OM 为终边所成的角,ρ叫做点M 的极径,θ叫做点M 的极角,有序实数对(),ρθ叫做M 的极坐标。
①要素:极点、极轴、长度单位、角度单位和正方向;②平面内点的极坐标用(),ρθ表示,极点的极坐标为()0,θ,θ可为任意值。
3.极坐标系下点与它的极坐标的对应情况:① 给定(),ρθ,就可以在极坐标平面内确定唯一的一点M 。
② 给定平面上一点M ,但却有无数个极坐标与之对应。
原因在于:极角有无数个,其坐标为(),2()k k Z ρθπ+∈。
如果限定0,02ρθπ≥≤<,那么除极点外,平面内的点就可以和极坐标一一对应了。
4. 曲线的极坐标方程与极坐标方程的曲线:一般地,如果一条曲线上任意一点都有一个极坐标适合方程(),0fρθ=的点在曲线上,那么这个方程成为这条曲线的极坐标方程,这条曲线成为这个极坐标方程的曲线。
5. 极坐标与直角坐标的互化:设点M 的直角坐标是(),x y ,极坐标是(),ρθ,则()222,tan 0cos ,sin yx y x x y xρθρθρθ=+=≠⇔==。
互化公式的三个前提条件:限定0,02ρθπ≥≤<① 极点与直角坐标系的原点重合;② 极轴与直角坐标系的x 轴的正半轴重合; ③ 两种坐标系的单位长度相同。
6. 圆的极坐标方程的表示方法:(1) 圆心在极点、半径为r 的圆的极坐标方程:r ρ=(r 为常数)(2) 圆心在极轴上且过极点的半径为a 的圆的极坐标方程:2cos a ρθ=。
(3) 圆心在点0,2π⎛⎫⎪⎝⎭处且过极点的圆的方程:[)()2sin ,0,a ρθθπ=∈7. 直线极坐标方程的表示方法:(1) 过极点且极角为α的一条射线方程:θα=;(2) 过点A (),0(0)a a >且垂直于极轴的直线l 的极坐标方程:cos a ρθ=;(3) 设点P 的极坐标为(),0a ,则过点P 且与极轴所成角为α的直线l 的极坐标方程:()sin sin a ραθα-=;(4) 设点P 的极坐标为()11,ρθ,则过点P 且与极轴所成角为α的直线l 的极坐标方程:()()11sin sin ραθραθ-=-8. 曲线极坐标方程的求法:可先写出曲线在直角坐标系中的方程,再通过cos ,sin x y ρθρθ==将直角坐标系中的方程化为极坐标方程。
2020年高考理科数学通用版3维专题复习专题检测:(19)选修4-4坐标系与参数方程版含解析

本资源的初衷 ,是希望通过网络分享 ,能够为广阔读者提供更好的效劳 ,为您水平的提高提供坚强的动力和保证 .内容由一线名师原创 ,立意新 ,图片精 ,是非常强的一手资料 .专题检测 (十九 ) 选修4 -4 坐标系与参数方程1.(2021·合肥一检)直线l 的参数方程为⎩⎪⎨⎪⎧x =1+12ty =3+3t (t 为参数).在以坐标原点为极点 ,x 轴非负半轴为极轴的极坐标系中 ,曲线C 的方程为sin θ-3ρcos 2θ=0.(1)求曲线C 的直角坐标方程;(2)写出直线l 与曲线C 交点的一个极坐标.解:(1)∵sin θ-3ρcos 2θ=0 ,∴ρsin θ-3ρ2cos 2θ=0 , 即y -3x 2=0.故曲线C 的直角坐标方程为y -3x 2=0.(2)将⎩⎨⎧x =1+12ty =3+3t代入y -3x 2=0得 ,3+3t -3⎝⎛⎭⎫1+12t 2=0 , 解得t =0 ,从而交点坐标为(1 ,3) ,∴交点的一个极坐标为⎝ ⎛⎭⎪⎪⎫2 π3.2.在直角坐标系xOy 中 ,以坐标原点为极点 ,x 轴正半轴为极轴建立极坐标系 ,半圆C的极坐标方程为ρ=4cos θ ,θ∈⎣⎢⎢⎡⎦⎥⎥⎤0 π2.(1)求半圆C 的参数方程;(2)假设半圆C 与圆D :(x -5)2+(y -3)2=m (m 是常数 ,m >0)相切 ,试求切点的直角坐标.解:(1)半圆C 的普通方程为(x -2)2+y 2=4(0≤y ≤2) ,那么半圆C 的参数方程为⎩⎨⎧x =2+2cos ty =2sin t (t 为参数 ,0≤t ≤π).(2)C ,D 的圆心坐标分别为(2,0) ,(5 ,3) , 于是直线CD 的斜率k =3-05-2=33. 由于切点必在两个圆心的连线上 , 故切点对应的参数t 满足tan t =33 ,t =π6 , 所以切点的直角坐标为⎝ ⎛⎭⎪⎫2+2cos π6 2sin π6 , 即(2+ 3 ,1).3.(2021·宝鸡质检)在直角坐标系xOy 中 ,以坐标原点为极点 ,x 轴正半轴为极轴建立极坐标系 ,曲线C 的极坐标方程为ρ=2(cos θ+sin θ).(1)求C 的直角坐标方程;(2)直线l :⎩⎪⎨⎪⎧x =12t y =1+32t (t 为参数)与曲线C 交于A ,B 两点 ,与y 轴交于点E ,求|EA |+|EB |.解:(1)由ρ=2(cos θ+sin θ)得ρ2=2ρ(cos θ+sin θ) , 得曲线C 的直角坐标方程为x 2+y 2=2x +2y , 即(x -1)2+(y -1)2=2.(2)将l 的参数方程代入曲线C 的直角坐标方程 , 化简得t 2-t -1=0 , 点E 对应的参数t =0 ,设点A ,B 对应的参数分别为t 1 ,t 2 , 那么t 1+t 2=1 ,t 1t 2=-1 , 所以|EA |+|EB |=|t 1|+|t 2|=|t 1-t 2| =(t 1+t 2)2-4t 1t 2= 5.4.(2021·张掖一诊)在直角坐标系xOy 中 ,曲线C 1:⎩⎨⎧x =cos αy =sin 2α(α为参数) ,在以坐标原点O 为极点 ,x 轴正半轴为极轴的极坐标系中 ,曲线C 2:ρcos ⎝⎛⎭⎫θ-π4=-22 ,曲线C 3:ρ=2sin θ.(1)求曲线C 1与C 2的交点M 的直角坐标;(2)设点A ,B 分别为曲线C 2 ,C 3上的动点 ,求|AB |的最||小值.解:(1)曲线C 1:⎩⎨⎧x =cos αy =sin 2α消去参数α ,得y +x 2=1 ,x ∈[-1,1].①曲线C 2:ρcos ⎝⎛⎭⎫θ-π4=-22⇒x +y +1=0 ,②联立①② ,消去y 可得:x 2-x -2=0 , 解得x =-1或x =2(舍去) ,所以M (-1,0).(2)曲线C 3:ρ=2sin θ的直角坐标方程为x 2+(y -1)2=1 ,是以(0,1)为圆心 ,半径r =1的圆.设圆心为C ,那么点C 到直线x +y +1=0的距离d =|0+1+1|2= 2 ,所以|AB |的最||小值为2-1.5.(2021·成都一诊)在平面直角坐标系xOy 中 ,倾斜角为α⎝⎛⎭⎫α≠π2的直线l 的参数方程为⎩⎨⎧x =1+t cos α y =t sin α(t 为参数).以坐标原点为极点 ,x 轴的正半轴为极轴 ,建立极坐标系 ,曲线C 的极坐标方程是ρcos 2θ-4sin θ=0.(1)写出直线l 的普通方程和曲线C 的直角坐标方程;(2)点P (1,0).假设点M 的极坐标为⎝ ⎛⎭⎪⎪⎫1 π2 ,直线l 经过点M 且与曲线C 相交于A ,B 两点 ,设线段AB 的中点为Q ,求|PQ |的值.解:(1)∵直线l 的参数方程为⎩⎨⎧x =1+t cos αy =t sin α(t 为参数) ,∴直线l 的普通方程为y =tanα·(x -1).由ρcos 2θ-4sin θ=0 ,得ρ2cos 2θ-4ρsin θ=0 , 即x 2-4y =0.∴曲线C 的直角坐标方程为x 2=4y .(2)∵点M 的极坐标为⎝ ⎛⎭⎪⎪⎫1 π2 ,∴点M 的直角坐标为(0,1). ∴tan α=-1 ,直线l 的倾斜角α=3π4. ∴直线l 的参数方程为⎩⎪⎨⎪⎧x =1-22t y =22t (t 为参数).代入x 2=4y ,得t 2-62t +2=0.设A ,B 两点对应的参数分别为t 1 ,t 2. ∵Q 为线段AB 的中点 ,∴点Q 对应的参数值为t 1+t 22=622=3 2.又点P (1,0) ,那么|PQ |=⎪⎪⎪⎪t 1+t 22=3 2.6.(2021·全国卷Ⅱ)在直角坐标系xOy 中 ,以坐标原点为极点 ,x 轴正半轴为极轴建立极坐标系 ,曲线C 1的极坐标方程为ρcos θ=4.(1)M 为曲线C 1上的动点 ,点P 在线段OM 上 ,且满足|OM |·|OP |=16 ,求点P 的轨迹C 2的直角坐标方程;(2)设点A 的极坐标为⎝ ⎛⎭⎪⎪⎫2 π3 ,点B 在曲线C 2上 ,求△OAB 面积的最||大值.解:(1)设P 的极坐标为(ρ ,θ)(ρ>0) ,M 的极坐标为(ρ1 ,θ)(ρ1>0). 由题设知|OP |=ρ ,|OM |=ρ1=4cos θ. 由|OM |·|OP |=16 ,得C 2的极坐标方程ρ=4cos θ(ρ>0). 因此C 2的直角坐标方程为(x -2)2+y 2=4(x ≠0). (2)设点B 的极坐标为(ρB ,α)(ρB >0) ,由题设知|OA |=2 ,ρB =4cos α ,于是△OAB 的面积 S =12|OA |·ρB ·sin ∠AOB =4cos α·⎪⎪⎪⎪sin ⎝⎛⎭⎫α-π3 =2⎪⎪⎪⎪sin ⎝⎛⎭⎫2α-π3-32≤2+ 3.当α=-π12时 ,S 取得最||大值2+ 3.所以△OAB 面积的最||大值为2+ 3.7.(2021·成都二诊)在直角坐标系xOy 中 ,曲线C 的参数方程为⎩⎨⎧x =2cos αy =2+2sin α(α为参数) ,直线l 的参数方程为⎩⎪⎨⎪⎧x =3-32t y =3+12t (t 为参数).在以坐标原点O 为极点 ,x 轴的正半轴为极轴的极坐标系中 ,过极点O 的射线与曲线C 相交于不同于极点的点A ,且点A 的极坐标为(2 3 ,θ) ,其中θ∈⎝ ⎛⎭⎪⎪⎫π2 π.(1)求θ的值;(2)假设射线OA 与直线l 相交于点B ,求|AB |的值. 解:(1)由题意知 ,曲线C 的普通方程为x 2+(y -2)2=4 , ∵x =ρcos θ ,y =ρsin θ ,∴曲线C 的极坐标方程为(ρcos θ)2+(ρsin θ-2)2=4 , 即ρ=4sin θ. 由ρ=2 3 ,得sin θ=32, ∵θ∈⎝ ⎛⎭⎪⎪⎫π2 π ,∴θ=2π3.(2)由题易知直线l 的普通方程为x +3y -43=0 , ∴直线l 的极坐标方程为ρcos θ+3ρsin θ-43=0. 又射线OA 的极坐标方程为θ=2π3(ρ≥0) , 联立⎩⎨⎧θ=2π3(ρ≥0)ρcos θ+3ρsin θ-43=0解得ρ=4 3.∴点B 的极坐标为⎝ ⎛⎭⎪⎪⎫4 3 2π3 ,∴|AB |=|ρB -ρA |=43-23=2 3.8.在极坐标系中 ,曲线C 1:ρ=2cos θ和曲线C 2:ρcos θ=3 ,以极点O 为坐标原点 ,极轴为x 轴非负半轴建立平面直角坐标系.(1)求曲线C 1和曲线C 2的直角坐标方程;(2)假设点P 是曲线C 1上一动点 ,过点P 作线段OP 的垂线交曲线C 2于点Q ,求线段PQ 长度的最||小值.解:(1)C 1的直角坐标方程为(x -1)2+y 2=1 ,C 2的直角坐标方程为x =3.(2)设曲线C 1与x 轴异于原点的交点为A , ∵PQ ⊥OP , ∴PQ 过点A (2,0). 设直线PQ 的参数方程为⎩⎨⎧x =2+t cos θ y =t sin θ(t 为参数) , 代入C 1可得t 2+2t cos θ=0 , 解得t 1=0 ,t 2=-2cos θ , 可知|AP |=|t 2|=|2cos θ|. 代入C 2可得2+t cos θ=3 , 解得t ′=1cos θ, 可知|AQ |=|t ′|=⎪⎪⎪⎪1cos θ ,∴|PQ |=|AP |+|AQ |=|2cos θ|+⎪⎪⎪⎪1cos θ≥2 2 ,当且仅当|2cos θ|=⎪⎪⎪⎪1cos θ时取等号 , ∴线段PQ 长度的最||小值为2 2.。
备战2023年高考数学母题题源解密(全国通用):坐标系与参数方程(解析版)

专题18坐标系与参数方程-备战2023年高考数学母题题源解密(全国通用)考向一极坐标与参数方程【母题来源】2022年高考浙江卷【母题题文】在直角坐标系xOy 中,曲线1C的参数方程为26t x y(t 为参数),曲线2C的参数方程为26s x y(s 为参数).(1)写出1C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线3C 的极坐标方程为2cos sin 0 ,求3C 与1C 交点的直角坐标,及3C 与2C交点的直角坐标.【试题解析】【小问1详解】因为26t x,y ,所以226y x ,即1C 的普通方程为 2620y x y .【小问2详解】因为2,6sx y,所以262x y ,即2C 的普通方程为 2620y x y ,由2cos sin 02cos sin 0 ,即3C 的普通方程为20x y .联立 262020y x y x y ,解得:121x y或12x y,即交点坐标为1,12 , 1,2;联立 262020y x y x y ,解得:121x y或12x y,即交点坐标为1,12 , 1,2 .【命题意图】本题考查极坐标、参数方程与直角坐标的互化,属于较为简单题目.【命题方向】这类试题在考查题型上以解答题的形式出现.试题难度不大,多为低档题,是历年高考的热点,考查学生的基本运算能力.常见的命题角度有:(1)极坐标与直角坐标互化;(2)参数方程与直角坐标互化;(3)直线参数方程中参数的几何意义.【得分要点】(1)运用极坐标,借助极径的几何意义;(2)参数方程与直角方程的互化,借助直线的参数的几何意义;1.(2022·四川成都·模拟预测(理))在平面直角坐标系xOy 中,已知直线l 的参数方程为1cos 1sin x t y t(t 为参数, 为常数且2),在以原点O 为极点,x 轴的非负半轴为极轴的极坐标系中,曲线C 的极坐标方程为:22sin 40 .(1)求直线l 的直角坐标方程和曲线C 的普通方程;(2)点(1,1)P ,直线l 与曲线C 交于两点,若2PA PB ,求直线l 的斜率.【答案】(1)tan (1)1y x ;22240x y y (2)±1【解析】【分析】(1)消参可以把参数方程转化为普通方程,根据极坐标和直角坐标的转化,可将极坐标方程化成直角坐标方程.(2)根据直线的标准参数方程的几何意义以及韦达定理即可求解cos 2,进而可求tan .(1)1cos 1sin x t y ttan 11y x ,2222sin 40240x y y ;(2)将1cos 1sin x t y t代入22240x y y 得22cos 40t t ,12122cos 4t t t t ,因为点P 在圆内,故,A B 在点P 两侧,由题意知,122t t ,因此122152t t t t ,即21212()12t t t t ,故2(2cos )142 ,解得2cos 2,进而tan 1k 因此斜率为±1.2.(2022·河南安阳·模拟预测(文))在直角坐标系xOy 中,1C 的圆心为 11,1C为极点,x 轴正半轴为极轴建立极坐标系,2C的极坐标方程为 .(1)求1C 的极坐标方程,判断1C ,2C 的位置关系;(2)求经过曲线1C ,2C 交点的直线的斜率.【答案】(1)2cos 2sin r q q ,1C ,2C 相交1【解析】【分析】(1)先求解1C 的标准方程,再根据直角坐标与极坐标的转换求解1C 的极坐标方程,再根据2C 的直角坐标方程,分析1C ,2C 圆心之间的距离与半径之和差的关系判断即可;(2)根据1C ,2C 均过极点,联立极坐标方程,求解tan 即可(1)由题意,1C 的标准方程为 22112x y ,即22220x y x y ,故1C 的极坐标方程为22cos 2sin ,即2cos 2sin r q q ,又,2C的极坐标方程为2cos,即22x y,222x y .因为12C C1C ,2C 半径相等,半径和为122C C 1C ,2C 相交.故1C 的极坐标方程2cos 2sin r q q ,1C ,2C 相交.(2)由(1)1C :2cos 2sin r q q,2C :均经过极点且相交,联立2cos 2sin有2cos 2sin ,显然cos0 ,故22tan,即tan 1 ,即经过曲线1C ,2C 交点13.(2023·四川·成都七中模拟预测(理))在直角坐标系xOy 中,倾斜角为的直线l 的参数方程为:2cos sin x t y t,(t 为参数),在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的极坐标方程为22cos 8 .(1)求直线l 的普通方程与曲线C 的直角坐标方程;(2)若直线l 与曲线C 交于A B ,两点,且AB l 的倾斜角.【答案】(1)当π2时,直线l 的普通方程为2x ;当π2 时,直线l 的普通方程为 tan 2y x ;22280x y x (2)π6或π2【解析】【分析】(1)因为直线l 的参数方程为2cossin x t y t(t 为参数),讨论π2 和π2 时,消去参数t ,即可求出直线l 的普通方程,因为222x y ,cos x 即可求出曲线C 的直角坐标方程.(2)将直线l 的参数方程代入曲线C 的方程整理,22cos 50t t .因为0 ,可设该方程的两个根为2,l t t ,所以12AB t t l 的倾斜角.(1)因为直线l 的参数方程为2cossin x t y t(t 为参数),当π2时,直线l 的普通方程为2x .当π2时,直线l 的普通方程为 tan 2y x .因为222x y ,cos x ,因为22cos 8 ,所以2228x y x .所以C 的直角坐标方程为22280x y x .(2)曲线C 的直角坐标方程为22280x y x ,将直线l 的参数方程代入曲线C 的方程整理,得22cos 50t t .因为22cos 200 ,可设该方程的两个根为2,l t t ,则22cos l t t ,25l t t .所以12AB t t整理得2cos 3,故π2sin 6因为0π ,所以ππ63 或π2π63,解得或π6或π2,综上所述,直线l 的倾斜角为π6或π2.4.(2022·青海·海东市第一中学模拟预测(理))在直角坐标系xOy 中,已知曲线1C 的参数方程为x y t (t 为参数).曲线2C 的参数方程为4cos 4sin x y(θ为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.(1)求曲线1C ,2C 的极坐标方程;(2)若曲线1C ,2C 的交点为A ,B ,已知1P,求PA PB .【答案】(1)1:C πsin 06(或5π6 ,R ),2:C ρ=4.(2)12【解析】【分析】(1)利用消参法进行化简曲线方程,然后通过公式将曲线的普通方程转化成极坐标方程;(2)利用直线的极坐标方程,结合参数的几何意义,联立曲线普通方程进行计算即可.(1)由曲线1:x C y t(t 为参数),消去参数t 得0x,化成极坐标方程得cos sin 0 .化简极坐标方程为πsin 06(或5π6 ,R ).曲线24cos :4sin x C y(θ为参数)消去参数θ得2216x y .化简极坐标方程为ρ=4.(2)由已知得P 在曲线1C 上,将曲线1C化为标准参数方程112x y(t 为参数)代入2C 的直角坐标方程2216x y,得2211162t,即24120t t ,即A ,B 所对应的参数分别为1t ,2t ,所以121212PA PB t t t t .5.(2022·内蒙古·海拉尔第二中学模拟预测(文))在平面直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t(其中 为直线的倾斜角,t 为参数),在以为O 极点,x 轴的非负半轴为极轴的极坐标系中,曲线C 的极坐标方程为2sin 4cos 0.(1)当直线l 的斜率k =2时,求曲线C 上的点A 与直线l 上的点B 间的最小距离;(2)如果直线l 与曲线C 有两个不同交点,求直线l 的斜率k 的取值范围.【答案】(2) 【解析】【分析】(1)利用极坐标与平面直角坐标互化公式得到曲线C 的平面直角坐标方程为24y x ,设出曲线上点2,A s s ,求出直线方程230x y ,利用点到直线距离公式,得到曲线C 上的点A 与直线l 上的点B 间的最小距离;(2)直线l 的普通方程为: 11y k x ,与曲线C :24y x 联立消去x 后用根的判别式得到不等式,求出斜率k .(1)2sin 4cos 0 两边同乘以 得:22sin 4cos 0 ,所以曲线C 的平面直角坐标方程为24y x ,设曲线上的一点坐标为 2,2A s s ,当直线l 的斜率k =2时,直线方程为 121y x ,即230x y ,则A点到直线距离为d 当12s 时,d,故曲线C 上的点A 与直线l 上的点B;(2)直线l 的普通方程为: 110y k x k ,与曲线C :24y x 联立得:24440y y k k,由0得:112k或112k ,解得:11(,0))22k 6.(2022·全国·模拟预测(文))在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为2cos 36,圆C 的极坐标方程为2sin .(1)求C 的参数方程;(2)判断l 与C 的位置关系.【答案】(1)cos 1sin x y( 为参数)(2)直线l 与圆C 相切.【解析】【分析】(1)先将圆C 的极坐标方程转化为直角坐标方程,求出圆心及半径,再转化为参数方程即可;(2)将直线l 的极坐标方程转化为直角坐标方程,利用圆心到直线的距离判断直线l 与圆C 的位置关系即可.(1)解:因为圆C 的极坐标方程为2sin ,则22sin ,则其直角坐标方程为222x y y ,即22(1)1y x ,圆心为(0,1),半径为1,则圆C 的参数方程为cos 1sin x y( 为参数).(2)解:因为直线l 的极坐标方程为2cos 36,则2cos cos sin sin 3066cos sin 30 ,所以直线l30y ,由(1)得圆C 的直角坐标方程为22(1)1y x ,圆心为(0,1),半径为1,则圆心(0,1)到直线l1 ,故直线l 与圆C 相切.7.(2022·河南·开封市东信学校模拟预测(理))在平面直角坐标系xOy 中,曲线C 的参数方程为2,2x t y t(t为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos sin 20 .(1)求曲线C 的普通方程和直线l 的直角坐标方程;(2)若直线l 与曲线C 交于P ,Q 两点,且点(0,2)M ,求11||||MP MQ 的值.【答案】(1)曲线2:2C y x ;直线:20 l x y(2)4【解析】【分析】(1)消去参数t 即可得C 的普通方程,并用极坐标与直角坐标互化即可得直线的普通方程;(2)写出直线l 参数方程的标准形式,再与C 的普通方程联立,借助参数的几何意义得解.(1)曲线C 的参数方程为2,2x t y t(t 为参数),转化为直角坐标方程为22yx,可得22y x ;直线l 的极坐标方程为cos sin 20 ,转化为直角坐标方程为20x y ;(2)把直线l的方程换成参数方程,得,22x t y(t 为参数),代入22y x .得2202t t,∴1212,22t t t t ,显然12,t t 异号.由12||,||MP t MQ t ,∴12121212121111||||4t t t t MP MQ t t t t t t.8.(2022·四川·成都市锦江区嘉祥外国语高级中学模拟预测(理))在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系(取相同的单位长度),曲线1C 的极坐标方程为4cos,曲线2C的参数方程为2222x y(t 为参数),曲线1C ,2C 相交于A 、B 两点,曲线3C 经过伸缩变换22x x y y 后得到曲线1C .(1)求曲线1C 的普通方程和线段AB 的长度;(2)设点P 是曲线3C 上的一个动点,求PAB △的面积的最小值.【答案】(1)22(2)4x y,AB(2)4【解析】【分析】(1)利用极坐标与直角坐标的互化公式可求出1C 的普通方程,求出2C 的普通方程,然后求出圆心到直线的距离,再由圆心距,弦和半径的关系可求出AB 的长度,(2)由伸缩变换可求出曲线3C 的方程为2214x y ,设点 2cos ,sin P ,求出点P 到直线AB 的距离,化简后利用三角函数的性质可求出其最小值,从而可求出PAB △的面积的最小值(1)由4cos ,得24cos ,又222x y ,cos x ,所以22(2)4x y .由2222x y(t 为参数),消去参数得4x y ,1C 的圆心为(2,0),半径为2,则圆心到直线4x y的距离为d ,所以AB (2)曲线3C 经过伸缩变换22x x y y后得到曲线1C ,则 222224 x y ,即曲线3C 的方程为2214x y ,设点 2cos ,sin P ,则点P 到直线AB的距离为dsincos ,故当 sin 1 时,d取得最小值,且min d,因此,当点P 到直线AB 的距离最小时,PAB △的面积也最小,所以PAB△的面积的最小值为min 11422AB d .9.(2022·全国·模拟预测(理))在直角坐标系xOy 中,曲线1C 的参数方程是11cos 221sin 2x y( 为参数).以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为1() R .(1)求曲线1C 和曲线2C 除极点外的交点的极坐标(02π) ;(2)若A ,B 分别为曲线1C 和2C 上的异于极点O 的两点,且OA OB ,求OAB 面积的最大值.【答案】(1) 1,0,14π,231【解析】【分析】(1)求出曲线1C 的普通方程,进而求出极坐标方程,与2C 的极坐标方程联立,求出曲线1C 和曲线2C 除极点外的交点的极坐标;(2)设出,A B 两点的极坐标方程,表达出OAB 的面积,利用三角函数的有界性求出最大值.(1)曲线1C 的普通方程为221124x y,化为极坐标方程为: 2211cos sin 24,化简得到:cos ,与1() R 联立,得:cos 1sin ,即π1cos 32,因为02π ,所以ππ7π333,所以π5π33 ,或ππ33 ,解得:14π3或20 ,当4π3时,此时4π1cos 32 ,当0 时,此时cos 01所以曲线1C 和曲线2C 除极点外的交点的极坐标为 1,0与14π,23;(2)因为OA OB ,①设 ππcos ,,1,22A B,则2πcos 1sin cos 1cos cos cos 2OAB S2cos因为 cos 1,1 ,所以当cos 1 时,OAB 31 ;②设ππcos ,,1,22A B,则2πcos 1cos 1cos 2OAB S2cos 612 ,因为 cos 1,1,所以当cosOAB1 OAB1.10.(2022·吉林市教育学院模拟预测(理))以等边三角形的每个顶点为圆心,以其边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形被称为勒洛三角形,如图,在极坐标系Ox 中,曲边三角形OPQ 为勒洛三角形,且π2,6P,π2,6Q,以极点O 为直角坐标原点,极轴Ox 为x 轴正半轴建立平面直角坐标系xOy ,曲线1C的参数方程为112x y t(t 为参数).(1)求 PQ的极坐标方程和 OQ 所在圆2C 的直角坐标方程;(2)已知点M 的直角坐标为 0,1 ,曲线1C 和圆2C 相交于A ,B 两点,求11||||MA MB .【答案】(1)ππ2,,66;222:((1)4 C x y (2)3【解析】【分析】(1)由已知,可根据题意直接写出 PQ的极坐标方程,并标注范围,然后求解出点P 的直角坐标,写出 OQ 所在圆的直角坐标方程即可;(2)由已知,设A ,B 对应的参数分别为12,t t ,将曲线1C 的参数方程带入圆2C ,并根据根与系数关系,求解11||||MA MB 即可.(1)因为π2,6P ,π2,6Q,所以 PQ 的极坐标方程:ππ2,,66 ,因为点P的直角坐标是1) ,所以 OQ所在圆的直角坐标方程为222:((1)4 C x y .(注: PQ的极坐标方程不标明 的取值范围或写错扣1分)(2)设A ,B 对应的参数分别为12,t t ,将112x y t代入22((1)4x y 得:2310,0 t t 所以12123,1t t t t 因为120t t ,由t 的几何意义得:121212*********|||| t t MA MB t t t t t t。
2019年高考数学考纲解读与热点难点突破专题21坐标系与参数方程教学案(文科)含解析

坐标系与参数方程【2019年高考考纲解读】高考主要考查平面直角坐标系中的伸缩变换、直线和圆的极坐标方程、参数方程与普通方程的互化、常见曲线的参数方程及参数方程的简单应用.以极坐标、参数方程与普通方程的互化为主要考查形式,同时考查直线与曲线的位置关系等解析几何知识. 【重点、难点剖析】 1.直角坐标与极坐标的互化把直角坐标系的原点作为极点,x 轴正半轴作为极轴,且在两坐标系中取相同的长度单位.设M 是平面内的任意一点,它的直角坐标、极坐标分别为(x ,y )和(ρ,θ),则⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,⎩⎪⎨⎪⎧ρ2=x 2+y 2,tan θ=y x x2.直线的极坐标方程若直线过点M (ρ0,θ0),且极轴到此直线的角为α,则它的方程为:ρsin(θ-α)=ρ0sin(θ0-α). 几个特殊位置的直线的极坐标方程 (1)直线过极点:θ=α;(2)直线过点M (a,0)(a >0)且垂直于极轴:ρcos θ=a ;(3)直线过M ⎝⎛⎭⎪⎫b ,π2且平行于极轴:ρsin θ=b .3.圆的极坐标方程若圆心为M (ρ0,θ0),半径为r 的圆方程为: ρ2-2ρ0ρcos(θ-θ0)+ρ20-r 2=0. 几个特殊位置的圆的极坐标方程 (1)当圆心位于极点,半径为r :ρ=r ;(2)当圆心位于M (r,0),半径为r :ρ=2r cos θ;(3)当圆心位于M ⎝⎛⎭⎪⎫r ,π2,半径为r :ρ=2r sin θ.(4)圆心在点M (x 0,y 0),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =x 0+r cos θ,y =y 0+r sin θ(θ为参数,0≤θ≤2π).圆心在点A (ρ0,θ0),半径为r 的圆的方程为r 2=ρ2+ρ20-2ρρ0cos(θ-θ0). 4.直线的参数方程经过点P 0(x 0,y 0),倾斜角为α的直线的参数方程为⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数).设P 是直线上的任一点,则t 表示有向线段P 0P →的数量. 5.圆的参数方程圆心在点M (x 0,y 0),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =x 0+r cos θ,y =y 0+r sin θ(θ为参数,0≤θ≤2π).6.圆锥曲线的参数方程(1)椭圆x 2a 2+y 2b 2=1的参数方程为⎩⎪⎨⎪⎧x =a cos θ,y =b sin θ(θ为参数).(2)双曲线x 2a 2-y 2b 2=1的参数方程为⎩⎪⎨⎪⎧ x =a sec θ,y =b tan θ(θ为参数).(3)抛物线y2=2px (p >0)的参数方程为⎩⎪⎨⎪⎧x =2pt 2,y =2pt (t 为参数).【题型示例】题型一 极坐标方程和参数方程【例1】(2018·全国Ⅰ)在直角坐标系xOy 中,曲线C 1的方程为y =k |x |+2.以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ2+2ρcos θ-3=0. (1)求C 2的直角坐标方程;【思路方法】(1)先列方程,再进一步转化为参数方程. (2)解出交点,再求得直线方程,最后转化为极坐标方程.【解析】(1)设(x 1,y 1)为圆上的点,在已知变换下变为曲线C 上的点(x ,y ),依题意,得⎩⎪⎨⎪⎧x =x 1,y =2y 1.由x 21+y 21=1,得x 2+⎝ ⎛⎭⎪⎫y 22=1,即曲线C 的方程为x 2+y 24=1.故C 的参数方程为⎩⎪⎨⎪⎧x =cos t ,y =2sin t(t 为参数).【感悟提升】若极坐标系的极点与直角坐标系的原点重合,极轴与x 轴正半轴重合,两坐标系的长度单位相同,则极坐标方程与直角坐标方程可以互化.求解与极坐标方程有关的问题时,可以转化为熟悉的直角坐标方程求解.若最终结果要求用极坐标表示,则需将直角坐标转化为极坐标. 题型二 参数方程与普通方程的互化【例2】(2018·全国Ⅲ)在平面直角坐标系xOy 中,⊙O 的参数方程为⎩⎪⎨⎪⎧x =cos θ,y =sin θ(θ为参数),过点(0,-2)且倾斜角为α的直线l 与⊙O 交于A ,B 两点. (1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.【解析】 (1)⊙O 的直角坐标方程为x 2+y 2=1. 当α=π2时,l 与⊙O 交于两点.当α≠π2时,记tan α=k ,则l 的方程为y =kx - 2.l 与⊙O 交于两点当且仅当|2|1+k 2<1,解得k <-1或k >1,即α∈⎝⎛⎭⎪⎫π2,3π4或α∈⎝ ⎛⎭⎪⎫π4,π2.综上,α的取值范围是⎝ ⎛⎭⎪⎫π4,3π4.(2)l 的参数方程为⎩⎨⎧x =t cos α,y =-2+t sin α⎝ ⎛⎭⎪⎫t 为参数,π4<α<3π4. 设A ,B ,P 对应的参数分别为t A ,t B ,t P ,则t P =t A +t B2,且t A ,t B 满足t 2-22t sin α+1=0.于是t A +t B =22sin α,t P =2sin α.又点P 的坐标(x ,y )满足⎩⎨⎧x =t P cos α,y =-2+t P sin α,所以点P 的轨迹的参数方程是⎩⎪⎨⎪⎧x =22sin 2α,y =-22-22cos 2α⎝⎛⎭⎪⎫α为参数,π4<α<3π4.【感悟提升】(1)将参数方程化为普通方程,需要根据参数方程的结构特征,选取适当的消参方法.常见的消参方法有代入消参法、加减消参法、平方消参法等.(2)将参数方程化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若x ,y 有范围限制,要标出x ,y 的取值范围.【变式探究】 【2017·江苏】[选修4-4:坐标系与参数方程]在平面坐标系中xOy 中,已知直线l 的参考方程为x 82t ty =-+⎧⎪⎨=⎪⎩(t 为参数),曲线C的参数方程为22,x s y ⎧=⎪⎨=⎪⎩(s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.【答案】5【解析】直线l 的普通方程为. 因为点P 在曲线C 上,设,从而点P 到直线l 的的距离,当s =min d =. 因此当点P 的坐标为()4,4时,曲线C 上点P 到直线l. 【考点】参数方程化普通方程【变式探究】在直角坐标系x O y 中,曲线C 1的参数方程为(t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ. (I )说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(II )直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a . 【答案】(I )圆,(II )1【解析】解:(Ⅰ)消去参数t 得到1C 的普通方程.1C 是以)1,0(为圆心,a 为半径的圆.将代入1C 的普通方程中,得到1C 的极坐标方程为.(Ⅱ)曲线21,C C 的公共点的极坐标满足方程组若0≠ρ,由方程组得,由已知2tan =θ,可得,从而012=-a ,解得1-=a (舍去),1=a .1=a 时,极点也为21,C C 的公共点,在3C 上.所以1=a .【变式探究】在直角坐标系xOy 中,直线C 1:x =-2,圆C 2:(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求C 1,C 2的极坐标方程;(2)若直线C 3的极坐标方程为θ=π4(ρ∈R ),设C 2与C 3的交点为M ,N ,求△C 2MN 的面积.【变式探究】在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =2cos α,y =2+2sin α(α为参数),M 是C 1上的动点,P 点满足OP →=2OM →,点P 的轨迹为曲线C 2.(1)求C 2的方程;(2)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线θ=π3与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B ,求AB .【解析】(1)设P (x ,y ),则由条件知M ⎝ ⎛⎭⎪⎫x 2,y2,由于M 点在C 1上,所以⎩⎪⎨⎪⎧x 2=2cos α,y2=2+2sin α,即⎩⎪⎨⎪⎧x =4cos α,y =4+4sin α.从而C 2的参数方程为⎩⎪⎨⎪⎧x =4cos α,y =4+4sin α(α为参数).(2)曲线C 1的极坐标方程为ρ=4sin θ,曲线C 2的极坐标方程为ρ=8sin θ.射线θ=π3与C 1的交点A的极径为ρ1=4sin π3,射线θ=π3与C 2的交点B 的极径为ρ2=8sin π3.所以AB =|ρ2-ρ1|=2 3.【规律方法】解决这类问题一般有两种思路,一是将极坐标方程化为直角坐标方程,求出交点的直角坐标,再将其化为极坐标;二是将曲线的极坐标方程联立,根据限制条件求出极坐标.要注意题目所给的限制条件及隐含条件.【变式探究】将圆x 2+y 2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C . (1)写出C 的参数方程;(2)设直线l :2x +y -2=0与C 的交点为P 1,P 2,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程.解 (1)设(x 1,y 1)为圆上的点,在已知变换下变为C 上点(x ,y ),依题意,得1,2,x x y y =⎧⎨=⎩由x 21+y 21=1得x 2+⎝ ⎛⎭⎪⎫y 22=1,即曲线C 的方程为x 2+y 24=1.故C 的参数方程为cos 2sin x t y t =⎧⎨=⎩(t 为参数).(2)由解得:1,0x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩不妨设P 1(1,0),P 2(0,2),则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12,1,所求直线斜率为k =12,于是所求直线方程为y -1=12⎝⎛⎭⎪⎫x -12,化为极坐标方程,并整理得 2ρcos θ-4ρsin θ=-3, 即ρ=34sin θ-2cos θ.题型三 极坐标 参数方程及其应用【例3】在直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =1+cos α,y =sin α(α为参数),直线l 的参数方程为⎩⎪⎨⎪⎧x =1-t ,y =3+t(t 为参数),在以坐标原点为极点,x 轴的正半轴为极轴的极坐标系中,射线m :θ=β(ρ>0).(1)求C 和l 的极坐标方程;(2)设点A 是m 与C 的一个交点(异于原点),点B 是m 与l 的交点,求|OA ||OB |的最大值.解 (1)曲线C 的普通方程为(x -1)2+y 2=1,由⎩⎪⎨⎪⎧ρcos θ=x ,ρsin θ=y ,得()ρcos θ-12+ρ2sin 2θ=1,化简得C 的极坐标方程为ρ=2cos θ. 因为l 的普通方程为x +y -4=0,所以极坐标方程为ρcos θ+ρsin θ-4=0, 所以l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ+π4=2 2. (2)设A (ρ1,β),B (ρ2,β), 则|OA ||OB |=ρ1ρ2=2cos β·sin β+cos β4=12(sin βcos β+cos 2β)=24sin ⎝⎛⎭⎪⎫2β+π4+14,由射线m 与C ,直线l 相交,则不妨设β∈⎝ ⎛⎭⎪⎫-π4,π4, 则2β+π4∈⎝ ⎛⎭⎪⎫-π4,3π4,所以当2β+π4=π2,即β=π8时,|OA ||OB |取得最大值,即⎝⎛⎭⎪⎫|OA ||OB |max=2+14. 【感悟提升】 (1)利用参数方程解决问题,要理解参数的几何意义.(2)在解决直线、圆和圆锥曲线的有关问题时,常常将极坐标方程化为直角坐标方程或将参数方程化为普通方程,有助于认识方程所表示的曲线,从而达到化陌生为熟悉的目的,这是转化与化归思想的应用. 【变式探究】在平面直角坐标系中,以原点为极点,以x 轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C 1的极坐标方程为ρ=2cos θ.(1)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(α为参数),求曲线C 1的直角坐标方程和曲线C 2的普通方程;(2)若曲线C 2的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(t 为参数),A (0,1),且曲线C 1与曲线C 2的交点分别为P ,Q ,求1|AP |+1|AQ |的取值范围. 【解析】 (1)∵ρ=2cos θ,∴ρ2=2ρcos θ, 又∵ρ2=x 2+y 2,ρcos θ=x ,∴曲线C 1的直角坐标方程为x 2+y 2-2x =0, 曲线C 2的普通方程为x 2+(y -1)2=t 2.(2)将C 2的参数方程⎩⎪⎨⎪⎧x =t cos α,y =1+t sin α(t 为参数)代入C 1的方程x 2+y 2-2x =0,得t 2+(2sin α-2cos α)t+1=0.∵Δ=(2sin α-2cos α)2-4=8sin 2⎝ ⎛⎭⎪⎫α-π4-4>0,∴⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α-π4∈⎝ ⎛⎦⎥⎤22,1,∴sin ⎝ ⎛⎭⎪⎫α-π4∈⎣⎢⎡⎭⎪⎫-1,-22∪⎝ ⎛⎦⎥⎤22,1. t 1+t 2=-(2sin α-2cos α)=-22sin ⎝⎛⎭⎪⎫α-π4,t 1t 2=1>0,∵t 1t 2=1>0,∴t 1,t 2同号,∴|t 1|+|t 2|=|t 1+t 2|. 由点A 在曲线C 2上,根据t 的几何意义,可得 1|PA |+1|AQ |=1|t 1|+1|t 2|=|t 1|+|t 2||t 1||t 2| =|t 1|+|t 2||t 1t 2|=|t 1+t 2|1=22⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α-π4∈(2,22].∴1|PA |+1|AQ |∈(2,22]. 【变式探究】在直角坐标系xOy 中,曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩(θ为参数),直线l 的参数方程为.(1)若a =−1,求C 与l 的交点坐标;(2)若C 上的点到la. 【答案】(1)C 与l 的交点坐标为()3,0, 2124,2525⎛⎫-⎪⎝⎭;(2)8a =或16a =-. 【解析】(1)曲线C 的普通方程为2219x y +=. 当1a =-时,直线l 的普通方程为.由解得3{ 0x y ==或2125{ 2425x y =-=. 从而C 与l 的交点坐标为()3,0, 2124,2525⎛⎫-⎪⎝⎭. (2)直线l 的普通方程为,故C 上的点到l 的距离为.当4a ≥-时, d=8a =; 当4a <-时, d由题设得,所以16a =-.综上, 8a =或16a =-.【变式探究】在直角坐标系xOy 中,圆C 的方程为.(Ⅰ)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求C 的极坐标方程; (Ⅱ)直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩(t 为参数), l 与C 交于,A B两点,||AB =,求l 的斜率.【答案】(Ⅰ);(Ⅱ)3±. 【解析】(I )由可得C 的极坐标方程(II )在(I )中建立的极坐标系中,直线l 的极坐标方程为由,A B 所对应的极径分别为12,,ρρ将l 的极坐标方程代入C 的极坐标方程得于是由||AB =得,所以l的斜率为3或3-. 【变式探究】已知直线l 的参数方程为1,1x t y t =-+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2cos 2θ=4⎝ ⎛⎭⎪⎫ρ>0,3π4<θ<5π4,则直线l 与曲线C 的交点的极坐标为________.解析 直线l 的直角坐标方程为y =x +2,由ρ2cos 2θ=4得ρ2(cos 2θ-sin 2θ)=4,直角坐标方程为x 2-y 2=4,把y =x +2代入双曲线方程解得x =-2,因此交点为(-2,0),其极坐标为(2,π). 答案 (2,π)【变式探究】已知直线l 的参数方程为⎩⎪⎨⎪⎧ x =a -2t ,y =-4t (t 为参数),圆C 的参数方程为⎩⎪⎨⎪⎧ x =4cos θ,y =4sin θ(θ为参数).(1)求直线l 和圆C 的普通方程;(2)若直线l 与圆C 有公共点,求实数a 的取值范围.【命题意图】本小题主要考查直线与圆的参数方程等基础知识,意在考查考生的运算求解能力及化归与转化思想.【解题思路】(1)消去参数,即可求出直线l 与圆C 的普通方程.(2)求出圆心的坐标,利用圆心到直线l 的距离不大于半径,得到关于参数a 的不等式,即可求出参数a 的取值范围.【解析】(1)直线l 的普通方程为2x -y -2a =0,圆C 的普通方程为x 2+y 2=16.(2)因为直线l 与圆C 有公共点,故圆C 的圆心到直线l 的距离d =|-2a |5≤4, 解得-25≤a ≤2 5. 【感悟提升】1.将参数方程化为普通方程的过程就是消去参数的过程,常用的消参方法有代入消参、加减消参和三角恒等式消参等,往往需要对参数方程进行变形,为消去参数创造条件.2.在与直线、圆、椭圆有关的题目中,参数方程的使用会使问题的解决事半功倍,尤其是求取值范围和最值问题,可将参数方程代入相关曲线的普通方程中,根据参数的取值条件求解. 【变式探究】在平面直角坐标系xOy 中,圆C 的参数方程为(t 为参数).在极坐标系(与平面直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴非负半轴为极轴)中,直线l 的方程为2ρsin ⎝ ⎛⎭⎪⎫θ-π4=m (m ∈R ). ①求圆C 的普通方程及直线l 的直角坐标方程;②设圆心C 到直线l 的距离等于2,求m 的值.。
极坐标与参数方程知识讲解

极坐标与参数方程知识讲解参数方程和极坐标系(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系 x 、y 之间关系的变 数叫做参变数,简称参数.(二)常见曲线的参数方程如下:1. 过定点(X o ,y o ),倾角为a 的直线:其中参数t 是以定点P (x o ,y o )为起点,对 应于t 点M (x, y )为终点的有向线段PM 的数量, 又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.①.设A 、B 是直线上任意两点,它们对应的 参数分别为 t A 和 t B ,则 |AB = |t^t A= J (tBYA )' -4t A t B .2. 中心在(x o , y o ),半径等于r 的圆:知识要点X=X 0tcos :y = y 0(t 为参数)(2 .线段AB 的中点所对应的参数值等于t A t Bx =X Q r COST y = y 0 rsin3 •中心在原点,焦点在x 轴(或y 轴)上的 椭圆: 沃 •为参数)(或 )1y 二 bs iny = asi nr 丿中心在点(x0,y0)焦点在平行于x 轴的直线上 的椭圆的参数方程x]xo:cos[ X-为参数)y = y 0 +bsi na.焦点在x 轴(或y 轴)上的2、极坐标有四个要素:①极点;②极轴;③ 长度单位;④角度单位及它的方向.极坐标与直角 坐标都是一对有序实数确定平面上一个点,在极坐 标系下,一对有序实数 —对应惟一点P (,), 但平面内任一个点P 的极坐标不惟一.一个点可以 有无数个坐标,这些坐标又有规律可循的,PC',) (极点除外)的全部坐标为C',r + 2k :J 或((2k l ):),(k Z ).极点的极径为0,而极角任意取.若5. 线:顶点在原点, 焦点在X 轴正半轴上的抛物x =2pt 2y = 2pt (t 为参数, 4. 双曲线:(A 为参数) (或(二为参数) 中心在原点,P> 0)直线的参数方程和参数的几何意义过定点P (X o, y°),倾斜角为a的直线的参数方程是其阳瞌;(t为参数).J3.2极坐标系1、定义:在平面内取一个定点0,叫做极点,引一条射线Ox,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
专题31 参数与极坐标方程(解析版)

1 10专题31 参数与极坐标方程(解析版)易错点1:混淆圆和直线的参数方程;易错点2:忽视直线参数方程是否具有几何意义; 易错点3:因忽视极坐标系下点的极坐标不唯一性致误; 易错点4:用极坐标求交点时,忽视极径为零的情况;易错点5:混淆参数方程中的角与极坐标中的角的不同几何意义; 易错点6:参数方程与极坐标方程互化时,忽视参数的范围. 题组一:点到直线的距离1.(2019全国I 理22)在直角坐标系xOy 中,曲线C 的参数方程为2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩,(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2cos sin 110ρθθ+=.(1)求C 和l 的直角坐标方程;(2)求C 上的点到l 距离的最小值.【解析】(1)因为221111t t --<≤+,且()22222222141211y t t x t t ⎛⎫-⎛⎫+=+= ⎪ ⎪+⎝⎭⎝⎭+,所以C 的直角坐标方程为221(1)4y x x +=≠-. l的直角坐标方程为2110x ++=.(2)由(1)可设C 的参数方程为cos ,2sin x y αα=⎧⎨=⎩(α为参数,ππα-<<).C 上的点到lπ4cos 11α⎛⎫-+ ⎪=.当2π3α=-时,π4cos 113α⎛⎫-+ ⎪⎝⎭取得最小值7,故C 上的点到l.2.(2017新课标Ⅰ)在直角坐标系xOy 中,曲线C 的参数方程为3cos sin x y θθ=⎧⎨=⎩,(θ为参数),直线l 的参数方程为41x a ty t=+⎧⎨=-⎩(t 为参数).(1)若1a =-,求C 与l 的交点坐标;(2)若C 上的点到l,求a .【解析】(1)曲线C 的普通方程为2219x y +=. 当1a =-时,直线l 的普通方程为430x y +-=.2 10由2243019x y x y +-=⎧⎪⎨+=⎪⎩解得30x y =⎧⎨=⎩或21252425x y ⎧=-⎪⎪⎨⎪=⎪⎩.从而C 与l 的交点坐标为(3,0),2124(,)2525-. (2)直线l 的普通方程为440x y a +--=,故C 上的点(3cos ,sin )θθ到l 的距离为d =当4a -≥时,d=8a =; 当4a <-时,d=16a =-. 综上,8a =或16a =-.3.(2014新课标Ⅰ)已知曲线C :22149x y +=,直线l :222x t y t=+⎧⎨=-⎩(t 为参数). (Ⅰ) 写出曲线C 的参数方程,直线l 的普通方程;(Ⅱ)过曲线C 上任一点P 作与l 夹角为o30的直线,交l 于点A ,求||PA 的最大值与最小值.【解析】2cos .().3sin .x y θθθ=⎧⎨=⎩(I )曲线C 的参数方程为为参数60.l x y +-=直线的普通方程为2 ……5分(Ⅱ)cos sin l θθ曲线C 上任意一点P(2.3)到的距离为3sin 6.d θθ=+-4)6,tan .sin 303d PA θααα==+-=︒则其中为锐角,且sin 5PA θα当(+)=-1时,取得最大值,最大值为sin()15PA θα+=当时,取得最小值,最小值为4.(2017新课标Ⅱ)在直角坐标系xOy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为cos 4ρθ=.(1)M 为曲线1C 上的动点,点P 在线段OM 上,且满足||||16OM OP ⋅=,求点P 的轨迹2C 的直角坐标方程; (2)设点A 的极坐标为(2,)3π,点B 在曲线2C 上,求OAB ∆面积的最大值.【解析】(1)设P 的极坐标为(,)ρθ(0)ρ>,M 的极坐标为1(,)ρθ1(0)ρ>.由椭圆知||OP ρ=,14||cos OM ρθ==.由||||16OM OP ⋅=得2C 的极坐标方程4cos ρθ=(0)ρ>.3 10因此2C 的直角坐标方程为22(2)4(0)x y x -+=≠.(2)设点B 的极坐标为(,)B ρα(0)B ρ>.由题设知||2OA =,4cos B ρα=,于是OAB ∆面积1||sin 2B S OA AOB ρ=⋅⋅∠4cos |sin()|3παα=-2|sin(2)|3πα=-2+≤当12πα=-时,S取得最大值2.所以OAB ∆面积的最大值为2.5.(2016年全国III )在直角坐标系xOy 中,曲线1C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数),以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为sin()4ρθπ+=(Ⅰ)写出1C 的普通方程和2C 的直角坐标方程;(Ⅱ)设点P 在1C 上,点Q 在2C 上,求||PQ 的最小值及此时P 的直角坐标.【解析】(Ⅰ)1C 的普通方程为2213x y +=,2C 的直角坐标方程为40x y +-=. (Ⅱ)由题意,可设点P的直角坐标为,sin )αα,因为2C 是直线, 所以||PQ 的最小值,即为P 到2C 的距离()d α的最小值,()sin()2|3d παα==+-.当且仅当2()6k k Z απ=+∈时,()d α,此时P 的直角坐标为31(,)22.题组二:直线与曲线相切 6.(2014新课标Ⅱ)在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ρθ=,0,2πθ⎡⎤∈⎢⎥⎣⎦.(Ⅰ)求C 的参数方程;(Ⅱ)设点D 在C 上,C 在D处的切线与直线:2l y =+垂直,根据(Ⅰ)中你得到的参数方程,确定D 的坐标. 【解析】(I )C 的普通方程为22(1)1(01)x y y -+=≤≤.可得C 的参数方程为1cos ,sin ,x t y t =+⎧⎨=⎩(t 为参数,0t x ≤≤) (Ⅱ)设D (1cos ,sin )t t +.由(I )知C 是以G (1,0)为圆心,1为半径的上半圆。
5年高考3年模拟【理科数学】考点教法讲解PPT专题十五 坐标系与参数方程(2024课标版)

x y
2
6 t
t
,
(t为参数)消去参数t,可得x=
2
y 6
2
,即y2=6x-2(y≥0).
∴曲线C1的普通方程为y2=6x-2(y≥0).
(2)由
x y
2
6 s
s
,
(s为参数)消去参数s,可得x=-
2
y2 6
,即y2=-6x-2(y≤0),
∴曲线C2的普通方程为y2=-6x-2(y≤0).
数方程,如直线l的参数方程为
x y
a b
t t
cos θ , sin θ
(t为参数).
2.运用参数的几何意义解题前,应先确认参数方程是不是标准参数方程,
如:
x y
x0 y0
at, bt
(t为参数),当a2+b2≠1时,应先化为标准形式,才能利用t的几
何意义解题.
例2 (2022全国甲,22,10分)在直角坐标系xOy中,曲线C1的参数方程为
高考 理数
专题十五 坐标系与参数方程
基础篇
考点一 坐标系与极坐标 1.极坐标与直角坐标的互化 把平面直角坐标系的原点作为极点,x轴的正半轴作为极轴,且在两坐标系 中取相同的单位长度.如图,设M是平面内的任意一点,它的直角坐标、极
坐标分别为(x,y)和(ρ,θ),则
x y
ρ cosθ, ρsin θ,
例1 (2022云南重点中学第一次质检,22)在直角坐标系xOy中,圆C的参数
方程为
x y
1 cos sin φ
φ,
(φ为参数),以O为极点,x轴正半轴为极轴建立极坐标
系.直线l的极坐标方程是2ρsin
θ
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题14 坐标系与参数方程1.【2019年高考北京卷理数】已知直线l 的参数方程为13,24x t y t =+=+⎧⎨⎩(t 为参数),则点(1,0)到直线l的距离是 A .15B .25C .45D .65【答案】D【解析】由题意,可将直线l 化为普通方程:1234x y --=,即()()41320x y ---=,即4320x y -+=,所以点(1,0)到直线l的距离65d ==,故选D . 【名师点睛】本题考查直线参数方程与普通方程的转化,点到直线的距离,属于容易题,注重基础知识、基本运算能力的考查.2.【2019年高考全国Ⅰ卷理数】在直角坐标系xOy 中,曲线C 的参数方程为(t 为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为. (1)求C 和l 的直角坐标方程; (2)求C 上的点到l 距离的最小值.【答案】(1)221(1)4y x x +=≠-;l的直角坐标方程为2110x +=;(2.【解析】(1)因为221111t t --<≤+,且()22222222141211y t t x t t ⎛⎫-⎛⎫+=+= ⎪ ⎪+⎝⎭⎝⎭+,所以C 的直角坐标方程为221(1)4y x x +=≠-.l的直角坐标方程为2110x ++=.(2)由(1)可设C 的参数方程为cos ,2sin x y αα=⎧⎨=⎩(α为参数,ππα-<<).C 上的点到lπ4cos 11α⎛⎫-+ ⎪=当2π3α=-时,π4cos 113α⎛⎫-+ ⎪⎝⎭取得最小值7,故C 上的点到l.【名师点睛】本题考查参数方程、极坐标方程与直角坐标方程的互化、求解椭圆上的点到直线距离的最值问题.求解本题中的最值问题通常采用参数方程来表示椭圆上的点,将问题转化为三角函数的最值求解问题.3.【2019年高考全国Ⅱ卷理数】在极坐标系中,O 为极点,点000(,)(0)M ρθρ>在曲线:4sin C ρθ=上,直线l 过点(4,0)A 且与OM 垂直,垂足为P . (1)当0=3θπ时,求0ρ及l 的极坐标方程; (2)当M 在C 上运动且P 在线段OM 上时,求P 点轨迹的极坐标方程.【答案】(1)0ρ=l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭; (2)4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.【解析】(1)因为()00,M ρθ在C 上,当03θπ=时,04sin 3ρπ== 由已知得||||cos23OP OA π==. 设(,)Q ρθ为l 上除P 的任意一点.在Rt OPQ △中,cos ||23OP ρθπ⎛⎫-== ⎪⎝⎭, 经检验,点(2,)3P π在曲线cos 23ρθπ⎛⎫-= ⎪⎝⎭上. 所以,l 的极坐标方程为cos 23ρθπ⎛⎫-= ⎪⎝⎭. (2)设(,)P ρθ,在Rt OAP △中,||||cos 4cos ,OP OA θθ== 即 4cos ρθ=. 因为P 在线段OM 上,且AP OM ⊥,故θ的取值范围是,42ππ⎡⎤⎢⎥⎣⎦.所以,P 点轨迹的极坐标方程为4cos ,,42ρθθπ⎡⎤=∈⎢⎥⎣⎦π.【名师点睛】本题主要考查极坐标方程与直角坐标方程的互化,熟记公式即可,属于常考题型.4.【2019年高考全国Ⅲ卷理数】如图,在极坐标系Ox 中,(2,0)A ,)4B π,)4C 3π,(2,)D π,弧»AB ,»BC ,»CD 所在圆的圆心分别是(1,0),(1,)2π,(1,)π,曲线1M 是弧»AB ,曲线2M 是弧»BC,曲线3M 是弧»CD. (1)分别写出1M ,2M ,3M 的极坐标方程;(2)曲线M 由1M ,2M ,3M 构成,若点P 在M 上,且||OP =P 的极坐标.【答案】(1)1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤ ⎪⎝⎭.(2)π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.【解析】(1)由题设可得,弧»»»,,AB BCCD 所在圆的极坐标方程分别为2cos ρθ=,2sin ρθ=,2cos ρθ=-.所以1M 的极坐标方程为π2cos 04ρθθ⎛⎫=≤≤⎪⎝⎭,2M 的极坐标方程为π3π2sin 44ρθθ⎛⎫=≤≤ ⎪⎝⎭,3M 的极坐标方程为3π2cos π4ρθθ⎛⎫=-≤≤⎪⎝⎭. (2)设(,)P ρθ,由题设及(1)知若π04θ≤≤,则2cos θ=,解得π6θ=;若π3π44θ≤≤,则2sin θ=π3θ=或2π3θ=;若3ππ4θ≤≤,则2cos θ-=5π6θ=.综上,P 的极坐标为π6⎫⎪⎭或π3⎫⎪⎭或2π3⎫⎪⎭或5π6⎫⎪⎭.【名师点睛】此题考查了极坐标中过极点的圆的方程,思考量不高,运算量不大,属于中档题.5.【2019年高考江苏卷数学】在极坐标系中,已知两点3,,42A B ππ⎛⎫⎫ ⎪⎪⎝⎭⎭,直线l 的方程为sin 34ρθπ⎛⎫+= ⎪⎝⎭.(1)求A ,B 两点间的距离;(2)求点B 到直线l 的距离. 【答案】(12)2.【解析】(1)设极点为O .在△OAB 中,A (3,4π),B,2π), 由余弦定理,得AB=. (2)因为直线l 的方程为sin()34ρθπ+=,则直线l过点)2π,倾斜角为34π.又)2B π,所以点B 到直线l的距离为3sin()242ππ⨯-=. 【名师点睛】本题主要考查曲线的极坐标方程等基础知识,考查运算求解能力.6.【重庆西南大学附属中学校2019届高三第十次月考数学】在平面直角坐标系xOy 中,已知曲线1C 的参数方程为5()x y ϕϕϕ⎧=+⎪⎨=⎪⎩为参数,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为4cos ρθ=.(1)求曲线1C 与曲线2C 两交点所在直线的极坐标方程;(2)若直线l的极坐标方程为sin()4ρθπ+=,直线l 与y 轴的交点为M ,与曲线1C 相交于,A B 两点,求MA MB +的值. 【答案】(1)5cos 2ρθ=;(2) 【解析】(1)曲线1C 的普通方程为:22(5)10x y -+=,曲线2C 的普通方程为:224x y x +=,即22(2)4x y -+=,由两圆心的距离32)d =∈,所以两圆相交, 所以两方程相减可得交线为6215x -+=,即52x =.所以直线的极坐标方程为5cos 2ρθ=. (2)直线l 的直角坐标方程:4x y +=,则与y 轴的交点为(0,4)M ,直线l的参数方程为242x y ⎧=-⎪⎪⎨⎪=+⎪⎩,带入曲线1C 22(5)10x y -+=得2310t ++=.设,A B 两点的参数为1t ,2t ,所以12t t +=-1231t t =,所以1t ,2t 同号.所以1212MA MB t t t t +=+=+=【名师点睛】本题考查了极坐标,参数方程和普通方程的互化和用参数方程计算长度,是常见考题. 7.【山东省郓城一中等学校2019届高三第三次模拟考试数学】在平面直角坐标系xOy 中,曲线C 的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数),在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,点M的极坐标为34π⎛⎫ ⎪⎝⎭,直线l的极坐标方程为sin 04ρθπ⎛⎫-+= ⎪⎝⎭.(1)求直线l 的直角坐标方程与曲线C 的普通方程;(2)若N 是曲线C 上的动点,P 为线段MN 的中点,求点P 到直线l 的距离的最大值.【答案】(1)40x y --=,2213x y +=;(2)2. 【解析】(1)因为直线l的极坐标方程为πsin 04ρθ⎛⎫-+= ⎪⎝⎭, 即ρsin θ-ρcos θ+4=0.由x =ρcos θ,y =ρsin θ, 可得直线l 的直角坐标方程为x -y -4=0.将曲线C的参数方程sin x y αα⎧=⎪⎨=⎪⎩,消去参数a ,得曲线C 的普通方程为2213x y +=.(2)设Nα,sin α),α∈[0,2π).点M的极坐标(,3π4),化为直角坐标为(-2,2).则1cos 1,sin 122P αα⎛⎫-+ ⎪ ⎪⎝⎭.所以点P 到直线l的距离d ==≤, 所以当5π6α=时,点M 到直线l. 【名师点睛】本题主要考查参数方程、极坐标方程和普通方程的互化,考查三角函数的图像和性质,考查点到直线的距离的最值的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力. 8.【河南省周口市2018–2019学年度高三年级(上)期末调研考试数学】在直角坐标系xOy 中,直线l 的参数方程为4,232x y ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为223sin 12ρθ+=(). (1)求直线l 的普通方程与曲线C 的直角坐标方程; (2)若直线l 与曲线C 交于A B ,两点,且设定点21P (,),求PB PA PAPB+的值.【答案】(1)l 普通方程为10x y --=,C 直角坐标方程为22143x y +=;(2)867. 【解析】(1)由直线l 的参数方程消去t ,得普通方程为10x y --=.223sin 12ρθ+=()等价于2223sin 12ρρθ+=,将222sin x y y ρρθ=+=,代入上式,得曲线C 的直角坐标方程为222312x y y ++=(), 即22143x y +=.(2)点21P (,)在直线10x y --=上,所以直线l的参数方程可以写为22 12x t y ⎧=+⎪⎪⎨⎪=+⎪⎩,(为参数), 将上式代入22143x y +=,得2780t ++=. 设A B ,对应的参数分别为12t t ,,则1212877t t t t +=-=, 所以22||PA PB PB PAPA PB PA PB ++=22PA PB PA PB PA PB+-=()21212122t t t t t t +-=()2121212||2t t t t t t +-⋅==⋅2828677877--⨯=(. 【名师点睛】本题考查了直线的参数方程,考查了简单曲线的极坐标方程,解答此题的关键是熟练掌握直线参数方程中参数的几何意义.9.【河南省郑州市第一中学2019届高三上学期入学摸底测试数学】以直角坐标系的原点O 为极点,x 轴的正半轴为极轴.已知点P 的直角坐标为15-(,),点M 的极坐标为π42(,).若直线l 过点P ,且倾斜角为π3,圆C 以M 为圆心、4为半径. (1)求直线l 的参数方程和圆C 的极坐标方程; (2)试判定直线l 和圆C 的位置关系.【答案】(1)11252x t y t ⎧=+⎪⎪⎨⎪=-+⎪⎩(t 为参数),8sin ρθ=;(2)直线l 与圆C 相离.【解析】(1)直线l的参数方程1π11cos 23 π5sin 532x t x t y t y ⎧⎧=+=+⋅⎪⎪⎪⎪⇒⎨⎨⎪⎪=-+⋅=-+⎪⎪⎩⎩(t 为参数), M 点的直角坐标为(0,4),圆C 的半径为4,∴圆C 的方程为22416x y +-=(),将cos sin x y ρθρθ=⎧⎨=⎩代入,得圆C 的极坐标方程为222cos (sin 4)16ρθρθ+-=,即8sin ρθ=; (2)直线l50y ---=,圆心M 到l的距离为942d ==>, ∴直线l 与圆C 相离.【名师点睛】主要是考查了极坐标与直角坐标的互化,以及运用,属于基础题.10.【全国I 卷2019届高三五省优创名校联考数学】在直角坐标系xOy 中,直线l的参数方程为2x m y t ⎧⎪=+⎨=⎪⎪⎪⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,椭圆C 的极坐标方程为2222cos 3sin 48ρθρθ+=,其左焦点F 在直线l 上.(1)若直线l 与椭圆C 交于A B ,两点,求FA FB +的值; (2)求椭圆C 的内接矩形面积的最大值. 【答案】(1)2)【解析】(1)将cos sin x y ρθρθ=⎧⎨=⎩代入ρ2cos 2θ+3ρ2sin 2θ=48,得x 2+3y 2=48,即2214816x y +=, 因为c 2=48-16=32,所以F的坐标为(-,0), 又因为F 在直线l上,所以m =-把直线l的参数方程2x t y =-=⎧⎪⎪⎨⎪⎪⎩代入x 2+3y 2=48,化简得t 2-4t -8=0,所以t 1+t 2=4,t 1t 2=-8,所以12FA FB t t +=-===(2)由椭圆C 的方程2214816x y +=,可设椭圆C 上在第一象限内的任意一点M 的坐标为(θ,4sin θ)(π02θ<<),所以内接矩形的面积8sin 2S θθθ=⋅=, 当π4θ=时,面积S取得最大值 【名师点睛】直角坐标方程转为极坐标方程的关键是利用公式cos sin x y ρθρθ=⎧⎨=⎩,而极坐标方程转化为直角坐标方程的关键是利用公式222tan x y y x ρθ⎧=+⎪⎨=⎪⎩,后者也可以把极坐标方程变形,尽量产生2cos ρρθ,,sin ρθ以便转化.另一方面,当动点在圆锥曲线运动变化时,我们可以用一个参数θ来表示动点坐标,从而利用一元函数求与动点有关的最值问题.11.【河北衡水金卷2019届高三12月第三次联合质量测评数学】在直角坐标系中,直线l 的参数方程为1cos ,1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,0πα<<),以坐标原点为极点,x 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C 的极坐标方程为2241sin ρθ=+.(1)当π6a =时,写出直线l 的普通方程及曲线C 的直角坐标方程; (2)已知点()11P -,,设直线l 与曲线C 交于A ,B 两点,试确定PA PB ⋅的取值范围.【答案】(1)2210142x y x ++=+=,;(2)112⎡⎫⎪⎢⎣⎭, 【解析】(1)当π6a =时,直线l的参数方程为π1cos ,16π11sin 162x t x y t y t ⎧⎧=-+=-⎪⎪⎪⎪⇒⎨⎨⎪⎪=+=+⎪⎪⎩⎩,. 消去参数t得10x ++=. 由曲线C 的极坐标方程为2241sin ρθ=+,得()22sin 4ρρθ+=,将222x y ρ+=,及sin y ρθ=代入得2224x y +=,即22142x y +=; (2)由直线l 的参数方程为1cos ,1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,0πα<<),可知直线l 是过点P (–1,1)且倾斜角为α的直线,又由(1)知曲线C 为椭圆22142x y +=,所以易知点P (–1,1)在椭圆C 内, 将1cos , 1sin x t y t αα=-+⎧⎨=+⎩代入22142x y +=中,整理得 ()()221sin 22sin c s 10to t ααα++--=,设A ,B 两点对应的参数分别为12t t ,, 则12211sin t t α⋅=-+,所以12211sin PA PB t t α⋅==+, 因为0πα<<,所以(]2sin 01α∈,,所以1221111sin 2PA PB t t α⎡⎫⋅==∈⎪⎢+⎣⎭,, 所以PA PB ⋅的取值范围为112⎡⎫⎪⎢⎣⎭,. 【名师点睛】利用直线参数方程中参数的几何意义求解问题.经过点P (x 0,y 0),倾斜角为α的直线l 的参数方程为00cos sin x x t y y t θθ=+⎧⎨=+⎩(t 为参数).若A ,B 为直线l 上两点,其对应的参数分别为12t t ,,线段AB 的中点为M ,点M 所对应的参数为0t ,则以下结论在解题中经常用到:(1)1202t t t +=;(2)1202t t PM t +==;(3)21AB t t =-;(4)12··PA PB t t =. 12.【河南省信阳高级中学2018–2019学年高二上学期期中考试数学】在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为2sin 2cos 0a a ρθθ=+>();直线l的参数方程为22x y ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).直线l 与曲线C 分别交于M N ,两点.(1)写出曲线C 的直角坐标方程和直线l 的普通方程;(2)若点P 的极坐标为()2πPM PN +=,,a 的值.【答案】(1)曲线C 的直角坐标方程为:()()22211x a y a -+-=+,直线l 的普通方程为2y x =+.(2)2a =.【解析】(1)由()2sin 2cos 0a a ρθθ=+>,得()22sin 2cos 0a a ρρθρθ=+>, 所以曲线C 的直角坐标方程为2222x y y ax +=+,即()()22211x a y a -+-=+,直线l 的普通方程为2y x =+. (2)将直线l的参数方程2,2x y t ⎧=-⎪⎪⎨⎪=⎪⎩代入2222x y y ax +=+并化简、整理,得()2440t t a -++=.因为直线l 与曲线C 交于M N ,两点.所以()()2Δ4440a =-+>,解得1a ≠.由根与系数的关系,得121244t t t t a +==+,.因为点P 的直角坐标为()20-,,在直线l上.所以12PM PN t t +=+== 解得2a =,此时满足0a >.且1a ≠,故2a =.【名师点睛】参数方程主要通过代入法或者已知恒等式(如22cos sin 1αα+=等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式222tan cos ,sin x y x y xy ρρθρθθ=⎧+==⎧⎪⎨⎨=⎩⎪⎩等可以把极坐标方程与直角坐标方程互化,这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.13.【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学】己知直线l 的参数方程为132x ty t=+⎧⎨=+⎩(t 为参数),曲线C 的极坐标方程为2sin 16cos 0ρθθ-=,直线l 与曲线C 交于A 、B 两点,点13P (,). (1)求直线l 的普通方程和曲线C 的直角坐标方程;(2)求11PA PB+的值. 【答案】(1)21y x =+,216y x =;(2. 【解析】(1)直线l 的参数方程为132x t y t =+⎧⎨=+⎩(t 为参数), 消去参数,可得直线l 的普通方程21y x =+,曲线C 的极坐标方程为2sin 16cos 0ρθθ-=,即22sin 16cos 0ρθρθ-=,曲线C 的直角坐标方程为216y x =, (2)直线的参数方程改写为1535x t y ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),代入2212124351670554y x t t t t t =--=+==-,,,121211t t PA PB t t -+==. 【名师点睛】由直角坐标与极坐标互换公式222cos sin x y x y ρθρθρ⎧=⎪=⎨⎪+=⎩,利用这个公式可以实现直角坐标与极坐标的相互转化.14.【河南省开封市2019届高三上学期第一次模拟考试数学】在直角坐标系xOy 中,直线l 的参数方程是1x t y t ==+⎧⎨⎩(t 为参数),曲线C 的参数方程是22cos 2sin x y ϕϕ=+⎧⎨=⎩(ϕ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(1)求直线l 和曲线C 的极坐标方程;(2)已知射线1OP θα=:(其中π02α<<)与曲线C 交于O P ,两点,射线2π2OQ θα=+:与直线l 交于Q 点,若OPQ ∆的面积为1,求α的值和弦长OP .【答案】(1)cos sin 10ρθρθ-+=,4cos ρθ=;(2)π4OP α==, 【解析】(1)直线l 的普通方程为10x y -+=,极坐标方程为cos sin 10ρθρθ-+=,曲线C 的普通方程为2224x y -+=(),极坐标方程为4cos ρθ=. (2)依题意,∵π02α∈(,),∴4cos OP α=, 1ππsin cos 22OQ αα=+-+()()1sin cos αα=+, 12cos 12cos sin OPQ S OP OQ ααα===+△, ∴πtan 102αα=∈,(,),∴π4OP α==, 【名师点睛】本题考查的知识要点:三角函数关系式的恒等变变换,参数方程直角坐标方程和极坐标方程之间的转换,三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.15.【四川省成都市第七中学2019届高三一诊模拟考试数学】在平面直角坐标系xOy 中,曲线C 的参数标方程为e e e et t t t x y --⎧=+⎪⎨=-⎪⎩(其中t 为参数),在以O 为极点、x 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,直线l的极坐标方程为πsin 3ρθ⎛⎫-=⎪⎝⎭ (1)求曲线C 的极坐标方程;(2)求直线l 与曲线C 的公共点P 的极坐标.【答案】(1)2ππcos2444ρθθ⎛⎫=-<< ⎪⎝⎭(2)π6⎛⎫ ⎪⎝⎭, 【解析】(1)消去参数t ,得曲线C 的直角坐标方程()2242x y x -=≥.将cos sin x y ρθρθ==,代入224x y -=,得()222cos sin 4ρθθ-=.所以曲线C 的极坐标方程为2ππcos2444ρθθ⎛⎫=-<< ⎪⎝⎭.(2)将l 与C 的极坐标方程联立,消去ρ得2π4sin 2cos23θθ⎛⎫-= ⎪⎝⎭.展开得()22223cos cos sin 2cos sin θθθθθθ-+=-.因为cos 0θ≠,所以23tan 10θθ-+=.于是方程的解为tan 3θ=,即π6θ=.代入πsin 3ρθ⎛⎫-= ⎪⎝⎭ρ=P 的极坐标为π6⎛⎫ ⎪⎝⎭,. 【名师点睛】本题考查曲线的极坐标方程与普通方程的互化,直线的极坐标方程与曲线极坐标方程联立求交点的问题,考查计算能力.16.【黑龙江省大庆市第一中学2019届高三下学期第四次模拟(最后一卷)数学】在平面直角坐标系xOy中,以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系,已知直线l 的参数方程为22x t y t=⎧⎨=+⎩(t 为参数),曲线C 的极坐标方程为2cos 8sin ρθθ=.(1)求曲线C 的直角坐标方程,并指出该曲线是什么曲线;(2)若直线l 与曲线C 的交点分别为M ,N ,求MN .【答案】(1)曲线C 方程为28x y =,表示焦点坐标为()0,2,对称轴为y 轴的抛物线;(2)10.【解析】(1)因为2cos 8sin ρθθ=,所以22cos 8sin ρθρθ=,即28x y =,所以曲线C 表示焦点坐标为()0,2,对称轴为y 轴的抛物线.(2)设点()11,M x y ,点()22,N x y直线l 过抛物线的焦点()0,2,则直线参数方程为22x t y t =⎧⎨=+⎩化为一般方程为122y x =+,代入曲线C 的直角坐标方程,得24160x x --=,所以12124,16x x x x +==-所以MN ===10==.【名师点睛】本题考查极坐标方程化直角坐标方程,直线的参数方程化一般方程,弦长公式等,属于简单题.17.【河北省石家庄市2018届高中毕业班模拟考试(二)数学】在平面直角坐标系xOy 中,曲线1C 的方程为224x y +=,直线l的参数方程2x t y =--⎧⎪⎨=⎪⎩(t 为参数),若将曲线1C 上的点的横坐标不变,纵坐标变为原来的32倍,得曲线2C . (1)写出曲线2C 的参数方程;(2)设点2P -(,直线l 与曲线2C 的两个交点分别为A B ,,求11PA PB+的值. 【答案】(1)2cos 3sin x y θθ=⎧⎨=⎩(θ为参数);(2)12 【解析】(1)若将曲线1C 上的点的纵坐标变为原来的32, 则曲线2C 的直角坐标方程为22243x y +=(),整理得22149x y +=, ∴曲线2C 的参数方程2cos 3sin x y θθ=⎧⎨=⎩(θ为参数).(2)将直线的参数方程化为标准形式为122x t y ''⎧=--⎪⎪⎨⎪=⎪⎩(t '为参数),将参数方程带入22149x y +=得221(2))22149t --'+=' 整理得27183604t t ''++=(). 12127214477PA PB t t PA PB t t ''''+=+===,,72111714427PA PB PA PB PA PB++===. 【名师点睛】本题考查了参数方程与普通方程的互化,及直线的参数方程的应用,重点考查了转化与化归能力.遇到求曲线交点、距离、线段长等几何问题时,求解的一般方法是分别化为普通方程和直角坐标方程后求解,或者直接利用直线参数的几何意义求解.要结合题目本身特点,确定选择何种方程.。
