圆的全章练习题大全非常全
圆测试题及答案解析

圆测试题及答案解析一、选择题1. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是什么?A. 直线与圆相离B. 直线与圆相切C. 直线与圆相交D. 直线在圆内答案:C解析:根据圆心到直线的距离小于圆的半径,可以判断直线与圆相交。
2. 圆的周长公式是什么?A. C = 2πrB. C = πr²C. C = 2rD. C = rπ答案:A解析:圆的周长公式是C = 2πr,其中C表示周长,r表示半径。
二、填空题1. 半径为7的圆的面积是 __________。
答案:153.94解析:圆的面积公式是A = πr²,将半径7代入公式得A = π ×7² ≈ 153.94。
2. 如果一个扇形的半径为10,圆心角为30°,那么它的弧长是__________。
答案:5π解析:弧长公式是L = θ × r,其中θ为圆心角(以弧度为单位),r为半径。
将圆心角30°转换为弧度是π/6,代入公式得L = π/6× 10 = 5π/3 ≈ 5。
三、简答题1. 描述圆的切线的性质。
答案:圆的切线在圆上某一点处与圆相切,且与过该点的半径垂直。
解析:圆的切线是一条直线,它恰好在一个点上与圆接触,并且这个接触点处的切线与从圆心到接触点的半径形成90°的角。
四、计算题1. 已知圆的半径为8,求圆的面积。
答案:圆的面积为200π。
解析:根据圆的面积公式A = πr²,将半径8代入公式得A = π × 8² = 64π ≈ 200π。
2. 已知圆的直径为20,求圆的周长。
答案:圆的周长为20π。
解析:圆的周长公式是C = πd,其中d为直径。
将直径20代入公式得C = π × 20 = 20π。
圆单元测试题及答案解析

圆单元测试题及答案解析一、选择题1. 下列哪个选项不是圆的性质?A. 圆周角等于它所对的弧的一半B. 圆的直径是圆的最长弦C. 圆的半径是圆心到圆周上任意一点的距离D. 圆的周长与直径的比值是一个常数答案:A2. 圆的周长公式是:A. C = πrB. C = 2πrC. C = 2rD. C = πd答案:B3. 如果圆的半径为3,那么它的直径是:A. 6B. 9C. 12D. 15答案:A二、填空题4. 圆的面积公式是 _______。
答案:A = πr²5. 一个圆的半径是4厘米,那么它的周长是 _______ 厘米。
答案:25.12三、简答题6. 圆的切线有哪些特点?答案:圆的切线在圆上只有一个接触点,且在该点的切线与半径垂直。
7. 圆的内接四边形有哪些性质?答案:圆的内接四边形的对角互补,即一个内角等于其对角的补角。
四、计算题8. 已知圆的半径为5厘米,求圆的周长和面积。
答案:周长 C = 2πr = 2 × 3.14 × 5 = 31.4 厘米;面积 A = πr² = 3.14 × 5² = 78.5 平方厘米。
9. 一个圆的周长是44厘米,求这个圆的半径。
答案:半径r = C / (2π) = 44 / (2 × 3.14) ≈ 7 厘米。
五、证明题10. 证明:圆的内接四边形的对角线互相平分。
答案:设圆内接四边形ABCD,连接对角线AC和BD。
由于ABCD是圆内接四边形,所以∠A + ∠C = 180°,同理∠B + ∠D = 180°。
根据圆周角定理,∠BAC和∠BDC是圆心角的一半,所以它们相等。
同理∠CAD和∠ABD也相等。
因此,△ABC和△ADC是全等的,所以AC平分BD。
同理,BD平分AC。
所以圆的内接四边形的对角线互相平分。
六、应用题11. 一个圆形花坛的直径是20米,求花坛的周长和面积。
圆的练习题(含答案)

圆的练习题一.选择题1.⊙O是△ABC的外接圆,直线EF切⊙O于点A,若∠BAF=40°,则∠C等于()A、20°B、40°C、50°D、80°2.如图,BC是⊙O的直径,P是CB延长线上一点,P A切⊙O于点A,如果P A=, PB=1,那么∠APC等于()3.某工件形状如图所示,圆弧BC的度数为,AB=6厘米,点B到点C的距离等于AB,∠BAC=,则工件的面积等于()(A)4π(B)6π(C)8π(D)10π4.下列语句中正确的是()(1)相等的圆心角所对的弧相等;(2)平分弦的直径垂直于弦;(3)长度相等的两条弧是等弧;(4)经过圆心的每一条直线都是圆的对称轴.(A)1个(B)2个(C)3个(D)4个5.如图,两个等圆⊙O和⊙的两条切线OA、OB,A、B是切点,则∠AOB等于() (A)(B)(C)(D)6.如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是()(A)π(B)1。
5π(C)2π(D)2。
5π7。
在Rt△ABC中,已知AB=6,AC=8,∠A=.如果把Rt△ABC绕直线AC旋转一周得到一个圆锥,其表面积为S;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其表面积为S,那么S∶S()(A)2∶3(B)3∶4(C)4∶9(D)5∶128.圆锥的母线长为13cm,底面半径为5cm,则此圆锥的高线长为() A.6 cm B.8 cm C.10 cm D.12 cm9.已知⊙O1和⊙O2相外切,它们的半径分别是1厘米和3厘米.那么半径是4厘米,且和⊙O1、⊙O2都相切的圆共有()(A)1个(B)2个(C)5个(D)6个10.已知圆的半径为6。
5厘米,如果一条直线和圆心距离为6。
5厘米,那么这条直线和这个圆的位置关系是()(A)相交(B)相切(C)相离(D)相交或相离二.填空题1.已知:如图,AB是⊙O的直径,弦CD⊥AB于P,CD=10cm,AP︰PB=1︰5.则:⊙O的半径为。
部编版高中物理必修二第六章圆周运动基础知识题库

(名师选题)部编版高中物理必修二第六章圆周运动基础知识题库单选题1、如图所示,长为L的悬线固定在O点,在O点正下方L2处有一钉子C。
把悬线另一端的小球m拉到跟悬点在同一水平面上无初速度释放,小球运动到悬点正下方时悬线碰到钉子,则小球的()A.线速度突然增大为原来的2倍B.线速度突然减小为原来的一半C.向心加速度突然增大为原来的2倍D.悬线拉力突然增大为原来的2倍答案:CAB.碰到钉子的瞬间,根据惯性可知,小球的速度不能发生突变,即线速度不变,AB错误;C.由a n=v2r知,运动半径变小了一半,向心加速度突然增大为原来的2倍,C正确;D.在最低点,根据牛顿第二定律,满足F−mg=m v2 r故碰到钉子后合力变为原来的2倍,悬线拉力变大,但不是原来的2倍,D错误。
故选C。
2、如图所示为一链条传动装置的示意图。
已知主动轮是逆时针转动的,转速为n,主动轮和从动轮的齿数之比为k,以下说法中正确的是()A.从动轮是顺时针转动的B.主动轮和从动轮边缘的线速度大小相等C.主动轮和从动轮的角速度大小相等D.从动轮的转速为nk答案:BAB.主动轮逆时针转动,带动从动轮也逆时针转动,用链条传动,两轮边缘线速度大小相等,选项A错误,B 正确;C.因为两轮的半径不一样,根据v=rω可知角速度不一样,选项C错误;D.主动轮和从动轮的齿数之比为k,则有r 主:r从=k又2πn⋅r主=2πn从⋅r从可得n从=nk选项D错误。
故选B。
3、2018年11月珠海航展,国产全向矢量发动机公开亮相。
图为安装了中国国产全向矢量技术发动机的歼-10B战机飞出“眼镜蛇”“落叶飘”等超级机动动作。
图为某矢量发动机的模型,O点为发动机转轴,A、B为发动机叶片上的两点,v表示线速度,ω表示角速度,T表示周期,a表示向心加速度,下列说法正确的是()A.v A>v B,T A>T B B.v A<v B,ωA=ωBC.ωA<ωB,a A=a B D.a A>a B,T A=T B答案:B同轴转动,角速度相等,故ωA=ωB 而根据线速度和角速度关系可知v=ωr 因为r B>r A,所以v B>v A 圆周运动周期为T=2πω因为角速度相同,所以周期也相同。
确定圆的条件、外接圆 知识点+例题+练习(非常好 分类全面)

知识点3 三角形外接圆的作法★作图实质:确定圆心和半径例2 如图1,已知Rt∆ABC,求作Rt∆ABC的外接圆.★三角形的外心与∆ABC的位置关系参照下图:请你完成下题.(1)锐角三角形的外心在________________________;(2)直角三角形的外心在________________________;(3)钝角三角形的外心在________________________.二、典型例题例3 如图,在∆ABC中,O点在边AB上,且O点为∆ABC的外心,你能求出∠ACB的度数吗?二、经典题型题型1 利用确定圆的条件解决实际问题例1 如图所示是一块残缺的圆铁片,利用所学知识指出找出它所在圆的圆心.题型2 根据已知条件确定圆例2 已知线段AB和直线l,过A,B两点作圆,并使其圆心在直线l上,问:(1)当l∥AB时,可以作几个这样的圆?(2)当l与AB斜交时,可以作几个这样的圆?(3)当l垂直于AB且不过AB的中点时,可以作几个这样的圆?(4)当l是AB的垂直平分线时,可以作几个这样的圆?题型3 分类讨论思想的应用例3 一个平面内有4个点A,B,C,D,那么这四个点可以确定多少个圆?例4 直角三角形的两边长分别为16和12,则此三角形的外接圆半径是__________.典例精讲:一、选择题1.下列命题中,正确的是()A.平面上三个点确定一个圆B.同圆或等圆中,等弧所对的圆心角相等C.平分弦的直径垂直于这条弦D.弧是半圆2.下列说法错误的是()A.直径是弦B.最长的弦是直径C.垂直弦的直径平分弦D.经过三点可以确定一个圆3.下列命题中的假命题是()A.三点确定一个圆B.三角形的内心到三角形各边的距离都相等C.同圆中,同弧或等弧所对的圆心角相等D.同圆中,相等的弧所对的弦相等4.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4)、(5,4)、(1,-2),则△ABC外接圆的圆心坐标是()A.(2,3) B.(3,2) C.(1,3) D.(3,1)5.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是()A.第①块 B.第②块 C.第③块 D.第④块8.下列说法中错误的是()A.三角形的外心不一定在三角形的外部B.圆的两条非直径的弦不可能互相平分C.两个三角形可能有公共的外心D.任何梯形都没有外接圆9.三角形的外心是三角形中()A.三边垂直平分线的交点 B.三条中线的交点C.三条角平分线的交 D.三条高的交点10、有下列四个命题,其中正确的有()①圆的对称轴是直径;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.A.4个 B.3个 C.2个 D.1个11、若一个三角形的外心在它的一条边上,那么这个三角形一定是()A.等腰三角形 B.直角三角形 C.等边三角形 D.钝角三角形二、填空题1.当点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件 .2.平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3)确定一个圆(填“能”或“不能”).3.如图△ABC中外接圆的圆心坐标是 .三、证明题1.如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.3.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.(1)求证:AC=AE;(2)若AC=6,CB=8,求△ACD外接圆的直径.。
圆练习题及答案

圆练习题及答案【练习题一】题目:已知圆的半径为5厘米,求圆的周长和面积。
【答案】圆的周长公式为:C = 2πr将半径r = 5厘米代入公式,得:C = 2π * 5 = 10π ≈ 31.42厘米圆的面积公式为:A = πr²将半径r = 5厘米代入公式,得:A = π * 5² = 25π ≈ 78.54平方厘米【练习题二】题目:一个圆的直径是10厘米,求这个圆的半径和周长。
【答案】已知圆的直径d = 10厘米,半径r是直径的一半,所以:r = d / 2 = 10 / 2 = 5厘米圆的周长公式为:C = πd将直径d = 10厘米代入公式,得:C = π * 10 ≈ 31.42厘米【练习题三】题目:在一个圆中,弦AB的长度为8厘米,弦AB的圆心距为3厘米,求圆的半径。
【答案】设圆的半径为r厘米,弦AB的圆心距为3厘米,根据勾股定理,我们有:r² = (r - 3)² + 4²解这个方程,得:r² = r² - 6r + 9 + 166r = 25r = 25 / 6 ≈ 4.17厘米【练习题四】题目:一个圆的面积是78.54平方厘米,求圆的半径。
【答案】根据圆的面积公式:A = πr²已知面积A = 78.54平方厘米,我们可以求出半径r:78.54 = πr²r² = 78.54 / π ≈ 25r = √25 = 5厘米【练习题五】题目:已知圆的周长是31.42厘米,求圆的半径。
【答案】根据圆的周长公式:C = 2πr已知周长C = 31.42厘米,我们可以求出半径r:31.42 = 2πrr = 31.42 / (2π) ≈ 5厘米【练习题六】题目:在一个圆中,有一条弧长为5π厘米,圆心角为60度,求圆的半径。
【答案】已知弧长L = 5π厘米,圆心角θ = 60度,根据弧长公式:L = rθ / 180 * π将已知数值代入公式,得:5π = r * 60 / 180 * π5 = r * 60 / 180r = 5 * 180 / 60r = 15厘米以上是六道关于圆的练习题及其答案,希望对你有所帮助。
(完整版)有关圆的经典练习题及答案

圆的经典练习题及答案一、填空题1. (2011浙江省舟山,15 , 4分)如图,AB 是半圆直径,半径0C丄AB于点O, AD平分/ CAB交弧BC于点D,连结CD、0D,给出以下四个结论:① AC// 0D :②CE 0E ;③厶0DE ADO :④2CD2CE AB •其中正确结论的序号是___________________ .【答案】①④2. (2011安徽,13, 5分)如图,O 0的两条弦AB、CD互相垂直,垂足为E,且AB=CD , 已知CE=1 , ED=3,则O 0的半径是 ______________________ •4. (2011山东日照,14, 4分)如图,在以AB为直径的半圆中,有一个边长为1的内接正5. (2011山东泰安,23 , 3分)如图,FA与O 0相切,切点为A, P0交O 0于点C,点B是优弧CBA上一点,若/ ABC==32°,则/ F的度数为 ____________________________ 。
方形CDEF,则以AC和BC的长为两根的元二次方程是(第16题)【答,贝ACD=x+1=0【答案】26°6.(2011山东威海,15,3分)如图,O O的直径A B与弦C D相交于点E,若【答案】(—2,—1)8. (2011浙江杭州,14 , 4 )女口图,点A , B , C , D都在O O上,的度数等于84° CA是/ OCD的平分线,则/ ABD 十/ CAO= ________ °【答案】53°9. (2011浙江温州,14, 5分)如图,AB是O O的直径,点C, D都在O O上,连结CA,D=30 ° BC= 3,贝U AB 的长是.10. (2011浙江省嘉兴,16, 5分)如图,AB是半圆直径,半径OC丄AB于点O, AD平分 /CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下四个结论:① S^2 AEC=2S^DEO ;②AC=2CD ;③线段OD是DE与DA的比例中项;④2CD CE AB .其的度数等于84° CA是/ OCD的平分中正确结论的序号是_________ .2【答案】①④ 11. (2011福建泉州,16, 4分)已知三角形的三边长分别为 3, 4, 5,则它的边与半径为1的圆的公共点个数所有可能的情况是 ______________________ .(写出符合的一种情况即 可)【答案】2 (符合答案即可)12. (2011甘肃兰州,16,4分)如图,0B 是O O 的半径,点C 、D 在O O 上,/ DCB=27 贝OBD=_________ 度。
圆的对称性、垂径定理 知识点+例题+练习(非常好 分类全面)

知识点2:圆的对称性圆是中心对称图形,对称中心是圆心;圆也是轴对称图形,对称轴是经过圆心的任意一条直线。
注意:(1)圆的对称轴有无数条。
(2)圆还具有旋转不变性,即圆绕圆心旋转任何角度后,仍与自身重合。
知识点 3:圆心角、弧、弦之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么他们所对应的其余各组量都分别相等例1如图,⊙O 的半径O A、OB 分别交弦C D 于点E、F,且C E=DF.试问:(1) OE 等于O F 吗?(2) AC 与 B D 有怎样的数量关系?例2如图,AB 是⊙O 的直径.(1)若 OD//AC, C D 与 B D 的大小有什么关系?为什么?(2) 把(1)中的条件和结论交换一下,还能成立吗?说明理由.知识点4:圆心角的度数与它所对的弧的度数的关系1.10的弧:将顶点在圆心的周角等分成360 份时,每一份的圆心角是10的角。
因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360 份,我们把10的圆心角所对的弧叫做10的弧。
2.圆心角的度数与它所对的弧的度数的关系:圆心角的度数与它所对的弧的度数相等。
注意:(1)圆心角的度数与它所对的弧的度数相等,不是指角与弧相等(角与弧是两个不同的图形)(2)度数相等的角为等角,但度数相等的弧不一定是等弧。
例1如图,在☉O 中,弦A D∥BC,DA=DC,∠AOC=1600,则∠BCO 的度数() A.200B.600 C. 400D.500例 2 如图,在△ABC 中,∠A=700,☉O 截△ABC 的三边所得的弦长相等,则∠BOC的度数为例3如图,AB,CD 是⊙O 的两条直径,过点A作A E//CD 交⊙O 于点E,连接B D,DE.求证:BD=DE.例4如图,点O在∠MPN 的平分线上,☉O 分别交P N、PM 于点A、B 和点C、D.求证:∠PCO=∠NAO.知识点5:垂径定理及垂径定理的推论1.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
圆的基础习题(附答案)
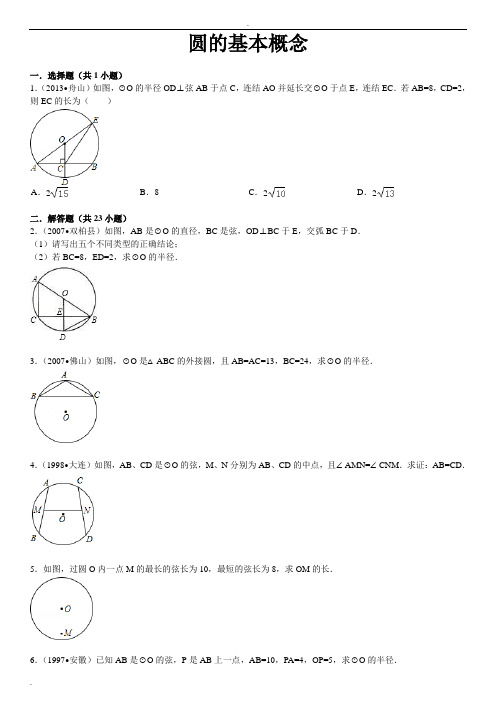
.圆的基本概念一.选择题(共1小题)1.(2013•舟山)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()2二.解答题(共23小题)2.(2007•双柏县)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.(1)请写出五个不同类型的正确结论;(2)若BC=8,ED=2,求⊙O的半径.3.(2007•佛山)如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,求⊙O的半径.4.(1998•大连)如图,AB、CD是⊙O的弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM.求证:AB=CD.5.如图,过圆O内一点M的最长的弦长为10,最短的弦长为8,求OM的长.7.(2010•黔东南州)如图,水平放置的圈柱形水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(结果保留π)8.安定广场南侧地上有两个大理石球,喜爱数学的小明想测量球的半径,于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,请你算出这个大理石球的半径.9.(1999•武汉)已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC.10.已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.11.(2013•温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.12.(2013•长宁区二模)如图,已知等腰直角△ABC中,∠BAC=90°,圆心O在△ABC内部,且⊙O经过B、C 两点,若BC=8,AO=1,求⊙O的半径.13.(2011•潘集区模拟)如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C,若AB是⊙O的直径,D是BC的中点.试判断AB、AC之间的大小关系,并给出证明.14.(2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.(1)若∠AOD=52°,求∠DEB的度数;(2)若OC=3,AB=8,求⊙O直径的长.15.(2006•佛山)已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:(1)四边形EFDC是平行四边形;(2).16.(1999•青岛)如图,⊙O1和⊙O2都经过A,B两点,经过点A的直线CD交⊙O1于C,交⊙O2于D,经过点B的直线EF交⊙O1于E,交⊙O2于F.求证:CE∥DF.17.如图①,点A、B、C在⊙O上,连接OC、OB.(1)求证:∠A=∠B+∠C.(2)若点A在如图②所示的位置,以上结论仍成立吗?说明理由.18.(2013•闸北区二模)已知:如图,在⊙O中,M是弧AB的中点,过点M的弦MN交弦AB于点C,设⊙O半径为4cm,MN=cm,OH⊥MN,垂足是点H.(1)求OH的长度;(2)求∠ACM的度数.19.(2013•张家界)如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.20.(2013•武汉)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.21.(2013•钦州)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.22.(2013•南宁)如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).(1)请画出△ABC关于y轴对称的△A1B1C1;(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.23.(2013•黑龙江)如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC向上平移3个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1的坐标.(2)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A2B2C2,并求点B所经过的路径长(结果保留x)24.(2011•德宏州)如图,在平面直角坐标系中,每个小正方形的边长都为1个单位长度.(1)画出△ABC关于点O的中心对称图形△A1B1C1;(2)画出将△A1B1C1向右平移5个单位长度得到的△A2B2C2;(3)画出△A1B1C1关于x轴对称的图形△A3B3C3.2013年10月dous的初中数学组卷参考答案与试题解析一.选择题(共1小题)1.(2013•舟山)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()2AB=4BE==CE===2二.解答题(共23小题)2.(2007•双柏县)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.(1)请写出五个不同类型的正确结论;(2)若BC=8,ED=2,求⊙O的半径.BE=CE=BE=CE=3.(2007•佛山)如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,求⊙O的半径.=CD=4.(1998•大连)如图,AB、CD是⊙O的弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM.求证:AB=CD.AB CN=AM=5.如图,过圆O内一点M的最长的弦长为10,最短的弦长为8,求OM的长.(;OM=6.(1997•安徽)已知AB是⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径.AB=5==2,OA==7.(2010•黔东南州)如图,水平放置的圈柱形水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(结果保留π)AOE==,×﹣×0.3=8.安定广场南侧地上有两个大理石球,喜爱数学的小明想测量球的半径,于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,请你算出这个大理石球的半径.AD=BD=AB=30cm9.(1999•武汉)已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC.10.已知:如图,∠PAC=30°,在射线AC上顺次截取AD=2cm,DB=6cm,以DB为直径作⊙O交射线AP于E、F两点,又OM⊥AP于M.求OM及EF的长.OM=AO=×cm=EF=11.(2013•温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.=1+(舍去).12.(2013•长宁区二模)如图,已知等腰直角△ABC中,∠BAC=90°,圆心O在△ABC内部,且⊙O经过B、C 两点,若BC=8,AO=1,求⊙O的半径.BCAD=BD=BC==513.(2011•潘集区模拟)如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C,若AB是⊙O的直径,D是BC的中点.试判断AB、AC之间的大小关系,并给出证明.14.(2008•沈阳)如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.(1)若∠AOD=52°,求∠DEB的度数;(2)若OC=3,AB=8,求⊙O直径的长.DEB=AB=×==515.(2006•佛山)已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:(1)四边形EFDC是平行四边形;(2).是两个等圆,因此16.(1999•青岛)如图,⊙O1和⊙O2都经过A,B两点,经过点A的直线CD交⊙O1于C,交⊙O2于D,经过点B的直线EF交⊙O1于E,交⊙O2于F.求证:CE∥DF.17.如图①,点A、B、C在⊙O上,连接OC、OB.(1)求证:∠A=∠B+∠C.(2)若点A在如图②所示的位置,以上结论仍成立吗?说明理由.18.(2013•闸北区二模)已知:如图,在⊙O中,M是弧AB的中点,过点M的弦MN交弦AB于点C,设⊙O半径为4cm,MN=cm,OH⊥MN,垂足是点H.(1)求OH的长度;(2)求∠ACM的度数.MH=MN=4MH=2=MO19.(2013•张家界)如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴反射得到△A2B2C2.20.(2013•武汉)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.,﹣,=21.(2013•钦州)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.22.(2013•南宁)如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).(1)请画出△ABC关于y轴对称的△A1B1C1;(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.,(=23.(2013•黑龙江)如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC向上平移3个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1的坐标.(2)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A2B2C2,并求点B所经过的路径长(结果保留x)=,=24.(2011•德宏州)如图,在平面直角坐标系中,每个小正方形的边长都为1个单位长度.(1)画出△ABC关于点O的中心对称图形△A1B1C1;(2)画出将△A1B1C1向右平移5个单位长度得到的△A2B2C2;(3)画出△A1B1C1关于x轴对称的图形△A3B3C3.成功就是先制定一个有价值的目标,然后逐步把它转化成现实的过程。
圆的练习题及答案

圆的练习题及答案圆是几何学中的重要概念,它在我们的生活中随处可见。
无论是在建筑设计中的圆形窗户,还是在日常生活中的圆形饼干,圆形都扮演着重要的角色。
为了更好地理解和应用圆,我们需要进行一些练习题。
在本文中,我将为大家提供一些圆的练习题及其答案,希望能够帮助大家更好地掌握这一知识点。
练习题一:计算圆的面积和周长1. 已知圆的半径为5cm,求其面积和周长。
答案:圆的面积公式为πr²,其中π取3.14,半径r为5cm。
所以面积为3.14 * 5² = 78.5cm²。
圆的周长公式为2πr,所以周长为2 * 3.14 * 5 = 31.4cm。
2. 已知圆的直径为12cm,求其面积和周长。
答案:圆的直径是半径的两倍,所以半径r为12cm的一半,即6cm。
根据上述公式,可以计算出面积为3.14 * 6² = 113.04cm²,周长为2 * 3.14 * 6 =37.68cm。
练习题二:判断圆的位置关系1. 判断以下两个圆的位置关系:圆A的半径为10cm,圆心坐标为(0, 0);圆B 的半径为5cm,圆心坐标为(8, 0)。
答案:首先,我们可以通过计算两个圆心之间的距离来判断它们的位置关系。
两个圆心的坐标分别为(0, 0)和(8, 0),所以它们的横坐标之差为8-0=8,纵坐标之差为0-0=0。
根据勾股定理,两个圆心之间的距离为√(8²+0²)=8。
由于两个圆的半径之和为10+5=15,大于圆心之间的距离8,所以这两个圆相交。
2. 判断以下两个圆的位置关系:圆A的半径为6cm,圆心坐标为(0, 0);圆B的半径为3cm,圆心坐标为(10, 0)。
答案:同样地,我们计算两个圆心之间的距离。
两个圆心的坐标分别为(0, 0)和(10, 0),横坐标之差为10-0=10,纵坐标之差为0-0=0。
根据勾股定理,两个圆心之间的距离为√(10²+0²)=10。
圆单元测试题及答案

圆单元测试题及答案一、选择题1. 圆的周长公式是()。
A. C = πdB. C = 2πrC. C = 2πdD. C = πr2. 圆的面积公式是()。
A. A = πr²B. A = πd²C. A = 2πrD. A = πd3. 一个圆的半径为3厘米,那么它的直径是()厘米。
A. 6B. 9C. 12D. 184. 如果一个圆的周长是18.84厘米,那么它的半径是()厘米。
A. 3B. 6C. 9D. 125. 圆心角的度数与它所对的弧长成正比,这个比例是()。
A. 半径B. 直径C. 周长D. 面积二、填空题6. 一个圆的半径是4厘米,那么它的周长是________厘米。
7. 一个圆的直径是10厘米,那么它的面积是________平方厘米。
8. 如果一个圆的周长是25.12厘米,它的半径是________厘米。
9. 一个圆的半径增加2厘米,那么它的面积增加了________平方厘米。
三、简答题10. 解释什么是圆的切线,并给出切线的性质。
四、计算题11. 一个圆的半径为5厘米,求它的周长和面积。
12. 如果一个圆的周长是44厘米,求它的半径。
五、解答题13. 一个圆的直径是14厘米,求这个圆的面积。
答案:一、选择题1. B2. A3. A4. A5. A二、填空题6. 25.127. 78.58. 49. 12π三、简答题10. 圆的切线是指在圆上某一点处与圆相切的直线。
切线的性质包括:切线与圆在切点处的夹角为90度,且切线与圆只有一个交点。
四、计算题11. 周长= 2π × 5 = 31.4厘米,面积= π × 5² = 78.5平方厘米。
12. 半径 = 周长÷ 2π = 44 ÷ 2π ≈ 7厘米。
五、解答题13. 面积= π × (14 ÷ 2)² = 153.94平方厘米。
结束语:本单元测试题涵盖了圆的基本性质和公式,通过这些题目的练习,可以帮助学生更好地理解和掌握圆的相关概念和计算方法。
圆练习题及答案

一、选择题(每小题3分,共36分)1.(2021于都期末)如图所示,AB是☉O的直径,C为圆内一点,则下列说法中正确的是( B )第1题图A.AC是☉O的弦B.∠BOC是圆心角C.∠C是圆周角D.AC+OC<AB2.下列图形中,∠1一定小于∠2的是( B )A B C D3.(2021金山一模)已知在矩形ABCD中,AB=5,对角线AC=13,☉C的半径长为12,下列说法正确的是( D )A.☉C与直线AB相交B.☉C与直线AD相切C.点A在☉C上D.点D在☉C内4.(2021金坛模拟)如图所示,AB是☉O的直径,C,D是☉O上两点,若∠ABC=40°,则∠BDC的度数是( C )第4题图A.60°B.55°C.50°D.48°5.(2020湘西)如图所示,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是( B )第5题图A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线6.(2021滨江一模)如图所示,已知线段AB是☉O的直径,弦CD⊥AB于点E.若AE=2,CD=6,则OB的长度为( B )第6题图A.√13B.134C.13D.527.如图所示,AB是圆锥的母线,BC为底面直径,已知BC=6 cm,圆锥的侧面积为15π cm2,则sin∠ABC的值为( C )第7题图A.34 B .35 C .45 D .53 8.如图所示,AB 是半圆O 的直径,C,D 是AB ⏜上的两点,AC ⏜=14BD ⏜,点E 为CD ⏜上一点,且∠CED=52∠COD,则∠DOB 的度数为( B ) A.92° B.96° C.100° D.120°第8题图9.如图所示,点A,B,C,D 都在☉O 上,圆的半径为2,且CB=CD=2,AB=AD,则S 四边形ABCD 等于( A )第9题图A.4√3B.2√3C.3√3D.610.如图所示,AB 为半圆O 的直径,半径OC ⊥AB.以OC 为直径的☉D 交AC 于点E,交BC 于点F,若AB=4,则图中阴影部分的面积为( A )第10题图A.2π-2B.4π-2C.4π-4D.π-211.(2021高青一模)如图所示,圆心为M 的量角器的直径的两个端点A,B 分别在x 轴正半轴、y 轴正半轴上(包括原点O),AB=4.点P,Q 分别在量角器60°,120°刻度线外端,连接MP.量角器从点A 与点O 重合滑动至点Q 与点O 重合的过程中,线段MP 扫过的面积为( D )第11题图A.23π+√3B.43π C.3√3 D.23π+2√3 12.如图所示,AB 是☉O 的直径,弦CD ⊥AB 于点G,点F 是CD 上一点,且满足CF FD =13,连接AF 并延长交☉O 于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF ∽△AED;②FG=3;③tan E=√52;④S △DAF =6√5.其中正确的有( A )第12题图A.1个B.2个C.3个D.4个二、填空题(每小题3分,共18分)13.(2021诸暨期末)如图所示,已知☉O 上三点A,B,C,切线PA 交OC 延长线于点P,若OP=2OC,则 ∠ABC= 30° .第13题图14.(2020益阳)小明家有一个如图所示的闹钟,他观察发现圆心角∠AOB=90°,测得ACB⏜的长为36 cm,则ADB ⏜的长为 12 cm.第14题图15.如图所示,八边形ABCDEFGH 是正八边形,其外接圆的半径为√2,则正八边形的面积为 4√2 .第15题图16.如图所示,☉O 内切于正方形ABCD,O 为圆心,作∠MON=90°,其两边分别交BC,CD 于点N,M,若CM+CN=4,则☉O 的面积为 4π .第16题图17.(2020鸡西)在半径为√5的☉O 中,弦AB 垂直于弦CD,垂足为P,AB=CD=4,则S △ACP = 12或32或92 . 18.如图所示,已知AB=AC=BE=CD,AD=AE,点F 为△ADE 的外心,若 ∠DAE=40°,则∠BFC= 140 °.第18题图三、解答题(共46分)19.(6分)(2021武汉模拟)如图所示,在☉O 中,弦AB 与弦CD 相交于点E,且AB=CD.求证:CE=BE.证明:∵AB=CD,∴AB⏜=CD ⏜. ∴AB⏜-CB ⏜=CD ⏜-CB ⏜,即AC ⏜=BD ⏜. ∴∠C=∠B.∴CE=BE.20.(6分)如图所示,已知等边三角形ABC 内接于☉O,AD 是☉O 的内接正十二边形的一条边,连接CD,若CD=6√2 cm,求☉O 的半径.解:如图所示,连接OA,OD,OC.∵等边三角形ABC 内接于☉O,AD 为内接正十二边形的一边,∴∠AOC=13×360°=120°,∠AOD=112×360°=30°, ∴∠COD=∠AOC-∠AOD=90°.∵OC=OD,∴△OCD 是等腰直角三角形, ∴OC=OD=√22CD=√22×6√2=6,即☉O 的半径为6 cm.21.(10分)如图所示,已知AB 是☉O 的直径,CD 与☉O 相切于点C,过点B 作BE ⊥DC,交DC 延长线于点E.(1)求证:BC 是∠ABE 的平分线;(2)若DC=8,☉O 的半径OA=6,求CE 的长.(1)证明:∵CD 与☉O 相切于点C,∴OC ⊥DC.∵BE ⊥DC,∴BE ∥OC,∴∠EBC=∠OCB.∵OC=OB,∴∠OCB=∠OBC,∴∠EBC=∠OBC,即BC 是∠ABE 的平分线.(2)解:如图所示,过点C 作CM ⊥BD 于点M,∵BC 是∠ABE 的平分线, BE ⊥CE,∴CE=CM.∵OC ⊥DC,∴∠OCD=90°.∵DC=8,OC=OA=6,∴OD=√DC 2+OC 2=√82+62=10.∵S △DCO =12×CD ×OC=12×OD ×CM, ∴8×6=10×CM,解得CM=4.8,即CE=CM=4.8.22.(12分)如图所示,在△ABC 中,AB=AC,以AB 为直径的☉O 分别与BC,AC 交于点D,E,过点D 作DF ⊥AC,垂足为点F.(1)求证:直线DF 是☉O 的切线;(2)求证:BC 2=4CF ·AC;(3)若☉O 的半径为4,∠CDF=15°,求阴影部分的面积.(1)证明:如图所示,连接OD,∵AB=AC,∴∠ABC=∠C.而OB=OD,∴∠ODB=∠ABC=∠C.∵DF ⊥AC,∴∠CDF+∠C=90°.∴∠CDF+∠ODB=90°.∴∠ODF=90°.∵OD 为☉O 的半径,∴直线DF 是☉O 的切线.(2)证明:如图所示,连接AD,则AD ⊥BC.∵AB=AC,∴DB=DC=12BC. ∵∠CDF+∠C=90°,∠C+∠DAC=90°,∴∠CDF=∠DAC.而∠DFC=∠ADC=90°,∴△CFD ∽△CDA.∴CD 2=CF ·AC.即BC 2=4CF ·AC.(3)解:如图所示,连接OE,∵∠CDF=15°,∴∠C=75°.∴∠DAC=15°.∴∠OAE=30°=∠OEA.∴∠AOE=120°.∴S △OAE =12AE ·OE ·sin ∠OEA=12×2×OE ·cos ∠OEA ·OE ·sin ∠OEA= 4√3,∴S 阴影部分=S 扇形OAE -S △OAE =120π×42360-4√3=16π3-4√3.23.(12分)如图所示,在Rt △ABC 中,∠ABC=90°,AC 的垂直平分线与AC,BC 及AB 的延长线分别相交于点D,E,F,☉O 是△BEF 的外接圆, ∠EBF 的平分线交EF 于点G,交☉O 于点H,连接BD,若BC=BF.(1)求证:△ABC ≌△EBF.(2)试判断DB 与☉O 的位置关系,并说明理由.(3)若AB=1,求线段BF 和HG 的长度.(1)证明:∵∠ABC=90°,∴∠EBF=90°.∵DF ⊥AC,∴∠ADF=90°,∴∠C+∠A=∠A+∠AFD=90°,∴∠C=∠BFE.在△ABC 和△EBF 中,∵∠C=∠AFE,BC=BF,∠ABC=∠EBF,∴△ABC ≌ △EBF.(2)解:BD 与☉O 相切.理由如下:如图所示,连接OB.∵OB=OF,∴∠OBF=∠OFB.∵∠ABC=90°,AD=CD,∴BD=CD,∴∠C=∠DBC.∵∠C=∠BFE,∴∠DBC=∠OBF.∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,即∠DBO=90°.∵OB 为☉O 的半径,∴BD 与☉O 相切.(3)解:如图所示,连接AE,FH,EH.由(1)知,△ABC ≌△EBF,∴AB=BE,BF=BC.∵DF 垂直平分AC,∴AE=CE=√2AB=√2,∴BF=BC=BE+EC=AB+CE=1+√2. ∵BH 平分∠EBF,∴∠FBG=12∠EBF=12×90°=45°, ∴∠EGB=∠BFG+∠FBG=∠BFG+45°=∠C+45°=∠CAE+45°=∠CAE+ ∠EAB=∠CAB=∠BEG,∴∠EGB=∠BEG,∴BG=BE=1.∵BH 平分∠FBE,∴HF=HE.∵∠FHE=180°-∠FBE=90°,∴∠HFE=45°,∴∠HFB=45°+∠EFB=∠EGB=∠GEB=∠FHB,∴∠HFB=∠FHB,即HB=BF=1+√2,∴HG=HB-GB=1+√2-1=√2.。
圆的练习题及答案

圆的练习题及答案练习题一:1. 设圆O的半径为5cm,求其直径、周长和面积。
解答:直径:直径是通过圆心的一条线段,等于半径的两倍,所以直径=2 ×半径 = 2 × 5cm = 10cm。
周长:周长等于圆的周长,即2 × π × 半径= 2 × 3.14 × 5cm ≈31.4cm。
面积:面积等于圆的面积,即π × 半径² = 3.14 × 5cm × 5cm ≈78.5cm²。
2. 已知圆O的直径为16cm,求其半径、周长和面积。
解答:半径:半径等于直径的一半,所以半径=直径 ÷ 2 = 16cm ÷ 2 = 8cm。
周长:周长等于圆的周长,即2 × π × 半径= 2 × 3.14 × 8cm ≈50.24cm。
面积:面积等于圆的面积,即π × 半径² = 3.14 × 8cm × 8cm ≈201.06cm²。
3. 若一圆的周长为15πcm,求其半径和面积。
解答:已知周长=2 × π × 半径所以半径=周长÷ (2 × π) = 15πcm ÷ (2 × π) = 7.5cm。
面积等于圆的面积,即π × 半径² = 3.14 × 7.5cm × 7.5cm ≈ 176.625cm²。
练习题二:1. 设圆O的半径为r,若圆周长等于其面积的2倍,求r的值。
解答:已知周长=2 × π × 半径,面积=π × 半径²根据题意,2 ×周长 = 面积,可以得到2 × 2 × π × r = π × r²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.圆的面积公式:。
圆的周长公式:O在一次上时间管理的课上,教授在桌子上放了一个装水的罐子。
然後又从桌子下面拿 出一些正好可以从罐口放进罐子里的鹅卵石。
当教授把石块放完后问他的学生道:“你们 说这罐子是不是满的?”“是。
”所有的学生异口同声地回答说。
“真的吗?”教授笑着问。
然后再从桌底下 拿出一袋碎石子,把碎石子从罐口倒下去,摇一摇,再加一些,再问学生:“你们说,这 罐子现在是不是满的?”这回他的学生不敢回答得太快。
最后班上有位学生怯生生地细声 回答道:“也许没满。
”“很好! ”教授说完后,又从桌下拿出一袋沙子,慢慢的倒进罐子里。
倒完后,于是再问班上的学生:“现在你们再告诉我,这个罐子是满的呢?还是没满?”“没有满。
”全班同学这下学乖了,大家很有信心地回答说。
“好极了! ”教授再一次称赞这些“孺子可教也”的学生们。
称赞完了后,教授从桌底下拿出一大瓶水,把水倒 在看起来已经被鹅卵石、小碎石、沙子填满了的罐子。
当这些事都做完之后,教授正色问 他班上的同学:“我们从上面这些事情得到什麽重要的功课?”班上一阵沈默,然後一位自以为聪明的学生回答说:“无论我们的工作多忙,行程排 得多满,如果要逼一下的话,还是可以多做些事的。
”这位学生回答完後心中很得意地 想:“这门课到底讲的是时间管理啊!”教授听到这样的回答後,点了点头,微笑道:“答案不错,但并不是我要告诉你们的 重要信息。
”说到这里,这位教授故意顿住,用眼睛向全班同学扫了一遍说:“我想告诉 各位最重要的信息是,如果你不先将大的鹅卵石放进罐子里去,你也许以後永远没机会把 它们再放进去了。
”感悟:第一节圆的概念1. 圆的定义:半径:姓名圆的基础学习教案一分数家长评价圆心:3. 圆的记号:以点0为圆心的圆,记作”4. 点与圆的位置关系1点在圆内 ——¥ 点C 在圆内; 2、点在圆上— —点B 在圆上; 3、点在圆外 ——点A 在圆外的三点确定一个圆。
7. 圆的内接多边形概念,多边形的外接圆概念。
同步练习1.在RUABC 中,/ C = 90° AC = 3, BC = 4,以A 为圆心、R 为半径画O A ,使点O A 的内部、点B 在O A 的外部,那么半径 R 应满足的条件是2.在矩形 ABCD 中,AB=3 , BC=4,以A 为圆心画圆,若圆内,且至少有一个在圆外,则OA 的半径r 的取值范围是个圆。
5. 下列命题正确的是(C.三角形的外心是三角形三个角的平分线的交点D.三角形的外心是三角形任意两边的垂直平分线的交点6. 下列命题中,错误的个数为(1平行四边形必有外接圆2等腰三角形的外心一定在底边上的中线上;3等边三角形的外心也是三角形的三条中线、高、角平分线的交点; 4直角三角形的外心是斜边的中点。
A. 0个 B. 1个C. 2个D. 3个7. 在四边形 ABCD 中,/ A = / C = 90°那么四边形 ABCD 不一定”)8. 如图,两个正方形彼此相邻且内接于半圆,若小正方形的面积 为16cm2则该半圆的半径为",读作"II5.在平面上, 经过给定两点的圆有个。
这些 的圆心一定在连接这两点的线段的 上。
6.定理:3.经过一点作圆可以作个圆;经过两点作圆可以作 个圆,这些圆的圆心在这两点的上;经过不在同一直线上的三点可以作个圆,并且只能B ,C ,D 三点中至少有一个在4.已知AB=7cm,则过点A , B ,且半径为3cm 的圆有(A. 0个B. 1个C. 2个D.无数个A.三点确定一个圆B.圆有且只有一个内接三角形9.如图,甲顺着大半圆从A地到B地,A地到乙顺着两个小半圆从地,设甲乙走过的路径分别为a、b,则(A. a=b B . a v b C . a>b D .不能确定10.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(A .第①块B. 第②块C.第③块D. 第④块11.已知:如图,AC=BD求证:△ OCD为等腰三角在O0 中,A、B是线段CD于圆的两个交点,且12.已知△ ABC / C=9C° , AC=3 , BC=4,以点C为圆心作O C,半径为1)当r取什么值时,点A,B在OC 外;2)当r取什么值时,点A在OC内,点B在OC 外;第二节圆心角,弧,弦心距之间的关系1.弦: 。
如图直径是经过的弦,是圆中的弦。
如图2.弧: ,简称弧.半圆弧: ;优弧:劣弧: ;圆心角:如图:优弧ABC记作,半圆弧BC记作半圆BC,劣弧AC记作3.弦心距::4.同心圆:圆心相同,半径的两圆。
5.等圆:能够重合的两个圆。
等圆的半径6.等弧:7.旋转对称图形: BCO9. 四等定理:同步练习3.下列说法中,正确的是(如果圆心角相等,那么圆心角所对的弧和弦也相等6.过O0内一点M 最长的弦为10 cm ,最短的弦长为 8cm ,贝U 0M=7. 已知点P 到O 0最大距离是8,最小距离是2,那么O 0的半径长为 8.在O 0中,P 为其内一点,过点 P 的最长的弦为 8cm ,最短的弦长为4cm ,9.在O 0中,弦AB 、CD 相交于点 P , 0M 丄CD , ON 丄AB , M 、N 是垂足,联结果AD 弧等于BC 弧,求证:△ PMN 是等腰三角形8. 扇形的面积公式:。
弧长的计算公式:1.下列说法正确的是 ______①直径不是弦,弦不是直径 ②半径是弦③过圆心的线段是直径 ④长度相等的两条弧是等弧 ⑤半圆是弧,但弧不一定是半圆⑥周长相等的圆是等圆⑦经过点P 的半径为 3cm 的圆只有一个2.下列说法错误的有(1) 半径相等的两个半圆是等弧O(2)面积相等的圆是等圆 (3)经过P 点的圆有无数(4)优弧一定比劣弧长(5)圆的任意一条弦将圆分成优弧和劣弧两部分过圆心的直线是直径(7)半圆是最长的弧(8)弧AB 的长度大于弦 AB 的长(B) 如果两条弧的长度相等,那么这两条弧是等弧(C ) 如果两条弧所对的圆心角相等,那么这两条弧是等弧(D ) 在同圆或等圆中,弦相等所对的弧也相等4. 在两个圆中,如果有两条弦相等,那么这两条弦的弦心距的关系是((A ) —定相等(B ) —定不相等 (C )不一定相等 5.在O 0,如果AB = 2CD ,那么弦AB 与弦CD 之间的长度关系是( (D ) —定互相平行(A) 弦AB 等于弦CD 的2倍 (B) 弦AB 大于弦CD 的2倍(C) 弦AB 小于弦CD 的2倍(D )弦AB 和弦CD 的关系不定MN.如BO i 和O O 2是等圆,P 是0i 02的中点,过点 P 作直线AD 交O O i 于A 、B ,交11. 如图,AB 是O 0的直径,弦 CD 丄AB 与点E ,点P 在O 0 上,/ 1 = / C , (1)求证:CB // PD ;3(2 )若 BC=3, sin / P=-,求O 0 的直径.5注:对称轴是直线2、垂径定理(垂直于弦的直径平行这条弦,并且平分弦所对的弧)总结:垂径定理及其推论是指一条弦①在“过圆心”②“垂直于另一条弦”③“平分另 一条弦”④“平分另一条弦所对的劣弧”⑤“ 平分这另一条弦所对的优弧”的五个条 件中任意具有两个条件,则必具有另外三个结论 注:当①③为条件时要对另一条弦增加它不是直径的限制同步练习(D )0 0的直径AB 平分弦CD 所对的弧"CD ,贝U AB 丄CD10.如图,OO O 2 于 C 、求证: AB =CD第三节 垂径定理1、圆的对称性 (1圆是轴对称图形,直径所在的直线是圆的对称轴; 2圆既是是旋转对称图形又是中心图形)1.下列判断中,正确的是()(A )垂直于弦的直线必平分这条弦(C ) 一个圆的圆心必在一条弦的垂直平分线上径2. 下列说法中,错误的是((A )(B )(B )平分弦的直径必垂直于这条弦(D )垂直平分一条弦的线段必是直) 圆的半径垂直于弦,必平分这条弦所对的弧 O 0的半径0A , CD 是过0A 的中点的弦,O 0的半径0C 平分圆心角/ A0B ,贝U 0C 丄AB CD 丄 0A DA3.如图,O O的直径AB=12 , CD是O O的弦,CD丄AB,垂足为P,且BP: AP=1:5,则).B.872CD的长为(A. 4 J2 C.275 D. 4J54.如图,已知半径OD与弦AB互相垂直,AB=8cm , CD=3cm,则圆A • % B6O的半径为(5cm垂足为点C,若)C. 4cm D cm5.已知圆内接△ ABC中, AB = AC,圆心O至U BC的距离为3cm,半径r= 7cm,则腰长AB为6. O O的半径OA = 1,弦AB、AC的长分别是罷,典,则/ BAC的度数为7.在半径为5cm的圆内有两条互相平行的弦,一条弦长为8cm,另一条弦长为6cm,则这两条弦之间的距离为8.在O O中,CD是直径,AB是弦,AB丄CD于点M ,求弦AB的长9.已知:如图,O O的直径AB和CDDEB=60 °,求CD 的长。
10.已知以O为圆心两个同心圆中,大圆的弦CD = 15cm , OM : OC = 3: 5,11. 一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:⑴桥拱半径⑵若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?B12.如图,O O 的直径AB 与弦CD 垂直,且/ BAC=40°,则/BOD=第四节直线与圆的位置关系知识梳理1、 直线和圆的位置关系有 ____________ 、 ________2、 圆心O 到直线I 的距离d 与半径r 的大小和直线I 与圆O 的位置关系: (1) 直线和(2)直线和圆 (3) 直线和圆d=3、 ___________________ 直线和圆有 做圆的切线。
这个 ______4、 圆的切线常用判定方法(1 )圆心到直线的距离等于 _________________ ,这条直线是圆的切线。
(2) _____________________________ 经过直径的 _________ ,并且 的直线是圆的切线。
(3) _______________________ 和三角形各边 的圆叫做三角形的内切圆,内切圆的____ (即直线和圆 叫做切点。
圆的切线)时。
这条直线叫过切点的直径同步练习1.已知OO 的半径为10cm ,如果一条直线和圆心 O 的距离为10cm 那么这条直 线和这个圆的位置关系为(A.相离B.相切C. ) 相交D.相交或相离2.如右图,A B 是O0上的两点,AC 是O0 的切线,/ B=70°,则/ BAC 等于(A. 70 °B. 35 °)C. D. 103.如图,PA 切OO 于A ,PB 切OO 于B , OP 交OO 于C ,下列结论中,错误的是(PO9.如图,△ ABC 中,AB=AC=5cm BC=8cm 以A 为圆心,3cm?长为半径的圆与直线BC 的位置关系是10.点A 、B 、C 、D 在同一圆上,AD BC 延长线相交于点 Q, AB DC 延长线相交于点 P,若/ A=50°,/ P=35,则/ Q=11. 在南部沿海某气象站 A 测得一热带风暴从 A 的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时 20千米,风暴周围50千米范围内将受到影响,?若该风暴不 改变速度与方向,问气象站正南方60千米处的沿海城市 B 是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.A. / 1=/2B. PA=PBC. AB 丄 OPD. P A =PC- PO7.如图,从圆0外一点P 引圆0的两条切线PA PB ,切点分别为A,NAPB A. 4=60 , B . PA = 8,那么弦 AB 的长是()8C.必D. 8罷8.O0AC=的直径 AB=10cm C 是OO 上的一点,点 D 平分,DE=2cm 则PA/D Q那么切线长是B .如果外离(图1) —无交点—d > R +r ; 外切(图2) —有一个交点—d = R + r ; 相交(图3) —有两个交点—R-r <d c R + r ; 内切(图4) —有一个交点—d = R — r ; 内含(图5) —无交点—d c R-r ;第五节圆与圆的位置关系如果两圆线外切,,如果两圆相交,连心线同步练习12厘米、13厘米,1 .三角形三边长分别为5厘米、两外切,则此三个圆的半径分别为2.以平面直角坐标系中的两点O (0,3)和C2 (4,的位置关系是()A.内切B.外切图以三角形三个顶点为圆心的三个圆两0)为圆心,以8和3为半径的两圆C . 相离 D.相交3.已知O0 1、O02的半径分别为6和3, O、O的坐标分别是(5, 0)和(0, 6),则两圆的位置关系是()A.相交B.外切C.内切4. R、r是两圆的半径(R> r) , d是两圆的圆心距,若方程根,则以R、r为半径的两圆的位置关系是()B.内切C.外离A.外切5. 已知半径分别为r和2r的两圆相交,则这两圆的圆心距A. 0 < d < 3rB. r < d< 3r6. 是D.2 2x —2Rx + r=d外离(2r —d)有等D. 相交d的取值范围是(C. r < d <2rD. r w d<3r半径分别为1cm和2cm的两圆外切,那么与这两个圆都相切且半径为()A. 5个3cm的圆的个数B. 4个C. 3个D. 2个7.已知圆O i、圆O2的半径不相等,圆O i的半径长为3,右圆O2上的点A满足AO 1 = 3,圆O i 与圆02的位置关系是(8.如果两个圆的一条外公切线长等于5,另一条外公切线长等于 2a +3,那么a =x 2- 12x + 27=0的两个根,圆心距为 9,则两圆的位置关系一定3: 5,当两圆内切时,圆心距为 4cm,那么当此两圆外切时,圆11. 平面上两圆的位置关系可以归纳为三类,即12. 已知两圆直径为 3 + r , 3- r ,若它们圆心距为 r ,则两圆的位置关系是 13.矩形ABCD 中,AB= 5,BC = 12。
