U型渠道水力计算(校核公式)
u型渠体积计算公式

u型渠体积计算公式【最新版】目录1.U 型渠的概述2.U 型渠体积计算公式的推导过程3.U 型渠体积计算公式的应用实例4.结论正文一、U 型渠的概述U 型渠,又称 U 型槽,是一种广泛应用于农田灌溉、排水以及城市排污系统的渠道。
其特点是横断面呈 U 型,因此得名。
U 型渠在设计、施工和使用过程中,需要对其体积进行计算,以便确保其满足流量、水位等要求。
本文将介绍 U 型渠体积计算公式。
二、U 型渠体积计算公式的推导过程U 型渠的体积计算公式推导过程如下:假设 U 型渠的顶部宽度为 B,底部宽度为 b,深度为 D。
首先,我们需要计算 U 型渠的平均宽度 W,公式为:W = (B + b) / 2。
然后,根据 U 型渠的横断面面积 S 和长度 L,我们可以得到 U 型渠的体积 V:V = S * L。
由于 U 型渠的横断面呈梯形,所以横断面面积 S 可以通过底部面积和顶部面积的平均值来计算,公式为:S = (b * D + B * D) / 2。
综上所述,我们可以得到 U 型渠体积计算公式:V = (B + b) * D * L / 4。
三、U 型渠体积计算公式的应用实例假设某 U 型渠的顶部宽度 B 为 2 米,底部宽度 b 为 1 米,深度D 为 1.5 米,长度 L 为 100 米。
我们可以通过公式计算出 U 型渠的体积:V = (2 + 1) * 1.5 * 100 / 4 = 3.75 立方米。
通过这个公式,我们可以方便地计算出 U 型渠的体积,从而为设计和施工提供依据。
四、结论U 型渠体积计算公式为:V = (B + b) * D * L / 4。
U型渠水力计算公式

U型渠水力计算公式U型渠是一种常见的渠道形式,主要应用于农田排灌、水利工程以及城市雨水排水系统等领域。
在U型渠设计和水力计算中,有一些常用的公式可以用来计算流量、水深等参数。
以下是一些常用的U型渠水力计算公式。
1.流量计算公式:U型渠的流量计算公式主要有曼宁公式和查克森公式两种。
其中,曼宁公式是最常用和普遍适用的公式。
曼宁公式:Q=(1.486/n)*A*R^(2/3)*S^(1/2)其中,Q为流量(m³/s),n为曼宁粗糙系数,A为截面面积(m²),R为湿周(m),S为水流坡度(m/m)。
查克森公式:Q=(1.075/n)*A*R*S^(1/2)其中,Q为流量(m³/s),n为查克森系数,A为截面面积(m²),R为湿周(m),S为水流坡度(m/m)。
2.水深计算公式:U型渠的水深可以通过曼宁公式中的截面面积A计算得到。
水深(深度)h=A/B其中,h为水深(m),A为截面面积(m²),B为底宽(m)。
3.临界水深计算公式:临界水深是指水流速度和压力所能达到的最大值,超过该水深后,水流动能转变为压力能,发生跌水现象。
临界水深h_c=(Q^2/(g*A^2))^0.2其中,h_c为临界水深(m),Q为流量(m³/s),g为重力加速度(9.81m/s²),A为截面面积(m²)。
4.断面形状系数计算公式:断面形状系数用于表示U型渠的截面形状,一般取决于渠底与渠壁的比例。
断面形状系数K=B/(h+2h_x)其中,K为断面形状系数,B为底宽(m),h为水深(m),h_x为距渠底1/4处的高度(m)。
5.波速计算公式:波速是指水波在渠道中的传播速度,可以用来计算冲击力和激浪的压力。
波速c=(g*h)^(1/2)其中,c为波速(m/s),g为重力加速度(9.81m/s²),h为水深(m)。
以上是一些常用的U型渠水力计算公式,它们可以帮助工程师和设计者在U型渠项目中进行流量、水深等参数的计算和设计。
u型渠体积计算公式

u型渠体积计算公式U型渠体积计算公式1. U型渠体积计算公式的定义U型渠体积计算公式是一种用于计算U型渠道或槽道的容积的公式。
U型渠道或槽道通常具有底宽较大的“U”形横截面,由于其特殊的形状,需要使用特定的计算公式来计算其体积。
2. U型渠体积计算公式的推导U型渠体积计算公式的推导基于以下几个重要参数: - 渠道底宽(B) - 渠道侧壁高度(H) - 渠道底宽到侧壁高度的比值(β)根据这些参数,我们可以推导出U型渠体积计算公式。
3. U型渠体积计算公式U型渠体积计算公式可以表示为:V = 2BH + βB^2其中: - V 表示U型渠的体积 - B 表示渠道底宽 - H 表示渠道侧壁高度 - β 表示渠道底宽到侧壁高度的比值4. 示例假设一个U型渠道的底宽B为4米,侧壁高度H为2米,底宽到侧壁高度的比值β为。
根据 U型渠体积计算公式:V = 2 * 4 * 2 + * 4^2 = 16 + * 16 = 16 + 24 = 40因此,这个U型渠道的体积为40立方米。
5. 结论U型渠体积计算公式是一种用于计算U型渠道或槽道容积的公式,通过测量底宽、侧壁高度和底宽与侧壁高度的比值,可以快速准确地计算U型渠的体积。
这种公式的应用可以帮助工程师和设计师有效规划和设计U型渠道的容量。
6. 其他应用U型渠体积计算公式在工程设计和土木工程中有广泛的应用。
以下是一些常见的应用场景:水利工程在水利工程中,U型渠道常用于排水系统、灌溉系统和河道等。
通过使用U型渠体积计算公式,可以确定渠道的容量,以确保水流的顺畅和稳定。
道路设计U型渠道在道路设计中作为排水系统的一部分,用于将雨水从道路表面引导到下水道或其他排水设施中。
使用U型渠体积计算公式,可以确定渠道的容量,从而确保道路在降雨期间能够有效排水。
农田灌溉U型渠道被广泛应用于农田灌溉系统中。
通过计算U型渠的体积,农民可以准确地确定灌溉水的用量,并合理规划农田的排水系统。
u型渠体积计算公式

u型渠体积计算公式
摘要:
一、前言
二、U 型渠体积计算公式介绍
1.U 型渠的定义
2.U 型渠体积计算公式推导
三、U 型渠体积计算公式应用
1.实际工程中U 型渠的运用
2.U 型渠体积计算公式在工程设计中的应用
四、总结
正文:
一、前言
在我国的农业灌溉系统中,U 型渠是一种常见的设施。
对于从事农业工程设计、施工和管理工作的人来说,了解U 型渠体积计算公式是十分必要的。
二、U 型渠体积计算公式介绍
1.U 型渠的定义
U 型渠是一种具有特定形状的渠道,主要用于农业灌溉、排水以及工业和城市供水系统中。
它的横截面呈U 型,通常由混凝土、砖石、塑料等材料制成。
2.U 型渠体积计算公式推导
U 型渠体积计算公式为:V = A * L * H / 2,其中:
- V:U 型渠的体积
- A:U 型渠横截面的面积
- L:U 型渠的长度
- H:U 型渠的高度(两侧水面之间的距离)
三、U 型渠体积计算公式应用
1.实际工程中U 型渠的运用
在农业灌溉系统中,U 型渠可用于收集和分配水资源。
了解U 型渠体积计算公式有助于合理设计和选择U 型渠的尺寸,以满足不同场景的需求。
2.U 型渠体积计算公式在工程设计中的应用
在U 型渠的设计过程中,工程师需要根据所需输送的水量、地形和土壤条件来确定渠道的尺寸。
利用U 型渠体积计算公式,可以快速、准确地计算出合适的U 型渠尺寸,从而提高工程设计的效率和质量。
四、总结
U 型渠体积计算公式是农业灌溉和排水系统设计中一个重要的计算工具。
u型渠道过水断面面积的近似计算

u型渠道过水断面面积的近似计算我们需要了解u型渠道的基本形状。
u型渠道是一种常见的渠道形式,其横截面形状类似于字母“U”。
在实际应用中,u型渠道通常用于排水系统、灌溉渠道和河道等场景。
为了估计u型渠道过水断面的面积,我们可以使用简化公式。
其中,渠道的底宽和侧壁坡度是两个关键参数。
底宽是指u型渠道底部的宽度,侧壁坡度是指u型渠道侧壁的斜率。
根据经验公式,可以使用以下近似计算方法来估计u型渠道过水断面的面积:1. 首先,计算渠道的底面积。
底面积可以通过渠道的底宽和底部水深来计算。
底宽通常是已知的,而底部水深可以通过现场测量或其他方法获取。
将底宽乘以底部水深,即可得到底面积。
2. 然后,计算渠道两侧的侧面积。
侧面积可以通过两侧侧壁的长度和坡度来计算。
侧壁长度可以通过现场测量或其他方法获取,而坡度通常是已知的。
将侧壁长度乘以坡度,即可得到侧面积。
由于u 型渠道有两侧侧壁,所以侧面积需要乘以2。
3. 最后,将底面积和侧面积相加,即可得到u型渠道过水断面的近似面积。
需要注意的是,这种近似计算方法适用于u型渠道的简化情况,即底宽和侧壁坡度相对较小且渠道底部比较平坦的情况。
如果底宽和侧壁坡度较大,或者渠道底部不规则,则需要使用更精确的计算方法。
还需要注意单位的一致性。
在进行面积计算时,底宽、底部水深、侧壁长度和坡度的单位应保持一致,通常可以选择米或者其他合适的单位。
通过简化的近似计算方法,我们可以估计u型渠道过水断面的面积。
这种方法简单易用,适用于底宽和侧壁坡度相对较小的u型渠道。
在实际应用中,我们可以根据具体情况选择合适的计算方法,并结合现场实测数据进行验证,以确保计算结果的准确性和可靠性。
U形渠道

H
b
U 形渠道的K r 值 m(a) θ Kr 0(0° ) 180° 0.65-0.72 2) 0.1(5.7° ) 168.6° 0.62-0.68 0.2(11.3° ) 157.4° 0.56-0.63 0.3(16.7° ) 146.6° 0.49-0.56 0.4(21.8° ) 136.4° 0.39-0.47
U 形、弧形底梯形断面设计 1. 流量计算 Q = C × A × Ri 式中: A = K A × H2 X = KX × H KA = (
θ 2
+ 2m − 2m′) × K 2 r + 2×
θ 2
m′ − m × K r + m
K X = 2 × (m + H 为水深,m;
θ 2
− m′) × K r + 2m′
2 θ
(4) 过水断面面积 A: 已知:r、m(a) 、H2 , A=
r2 2
π × 1−
a 90°
− sin 2a + H2 × 2r × cos a + H2 tan a
(5) 湿周 X: 已知:B、r、m(a) 、H2 , X=π r× 1−
a 90°
+
2H 2 cos a
或:X = (6) 水力半径 R: 已知:A、X, R=
A X
B m
× 1 + m2 -
2r m× 1 −m cot −1 m
(7) 弧段水深H1 : 已知:H、H2 , H1 = H − H2 湿周中 2 cot −1 m为弧度值,弧度为 57.32484° 5. U 形渠道计算实例 已知:K r =0.8,m=0.3,H=0.6m,i=0.008 求:U 形渠道过流量 解:1.计算半径 r: r = K r × H = 0.8 × 0.6 = 0.48m 2.计算圆心角θ : θ = 2 × cot −1 m = 2 × cot −1 0.3 = 2 × 90° − 16.7° = 146.6° 3.计算K A KA =
U形渠道的水力特性及水力计算
过程为振荡收敛, 可取相邻二次迭代结果的算术平均值代入迭代公式, 则可减少迭代计算次数。迭代计算时,
可取初值 Β= Π 2。
3. 3 临界水深的迭代公式
当通过渠道的实际流量 Q ≥Q kc时, hk ≥T , hk =
∃hk+
r
1-
co s
Η 2
。 将式 (1) 代入临界流方程可导出求
∃hk 的迭代公式。 迭代计算时, 可取初值 ∃hk= 0。
∃h+
r
1-
co s
Η 2
, 迭代计算出 ∃h 后, 可求得正常水深。将式 (1)、(3) 代入均匀流公式 (10) 可导出求 ∃h 的迭
51 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
水深范围的界限流量及水深的迭代计算公式。
3. 1 界限流量
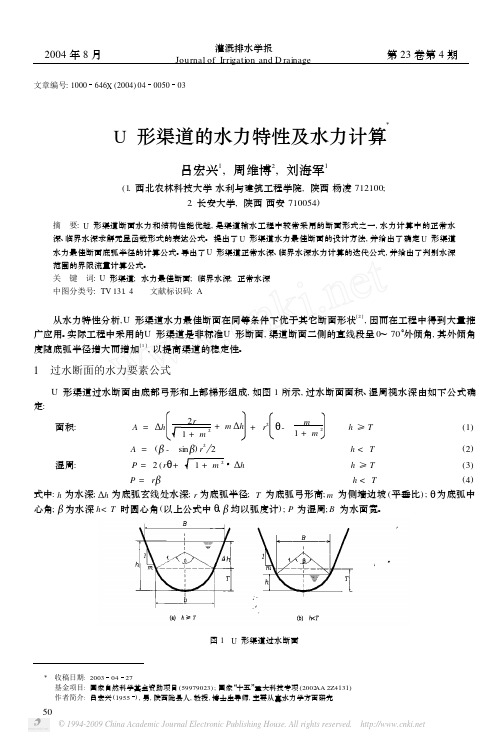
如图 1 所示, U 渠道过水断面由底部弓形和上部梯形二部分组成, 渠道运行中水深存在大于弓形高 T
和小于弓形高 T 二种情况, 因此, 正常水深与临界水深的计算均需首先判定实际水深大于 T 还是小于 T 。若
以通过U 形渠道过水断面中弓形面积的流量为判别水深的界限流量, 将水深等于弓形高对应的过水断面水
Hydraul ic Character istics and Hydraul ic Ca lcula tion of U- shaped Channel
LU Hong2x ing1, ZHOU W ei2bo2, L IU H ai2jun1
(1. Co llege of W ater Con servancy and A rch itecture Engineering of N o rthw est Scienceand T echno logy U n iversity of A griculture & Fo restry, Yangling 712100, Ch ina; 2. Chang’an U n iversity, X ian 710054, Ch ina)
u形渠道的水力最佳断面及正常水深的计算

u形渠道的水力最佳断面及正常水
深的计算
U型渠道的水力最佳断面是指在一定条件下,给定一定的渠底断面形状,能够使得渠道具有最小水力损失的断面积。
U型渠道的水力最佳断面及正常水深的计算,包括断面形状、断面面积、正常水深和水力损失四个方面。
一、断面形状 U型渠道水力最佳断面形状是由水力学原理决定的,经过大量实验研究表明,渠道断面形状最佳的是一种中央凹部,周围凸部的形式,即U型渠道的断面形状。
二、断面面积 U型渠道的断面面积可以根据渠道流量进行计算,在保证水力最佳断面形状的前提下,根据渠道流量不同,可以计算出渠道的断面面积。
三、正常水深正常水深是指渠道在正常情况下的水深,在计算U型渠道的正常水深时,需要考虑到渠底护坡、渠堤高度和渠道水力损失等因素,根据其中的每个因素,依次进行计算,并综合考虑,最后得出U型渠道的正常水深。
四、水力损失水力损失是指在渠道中所发生的损失,在计算U型渠道的水力损失时,需要考虑到渠底护坡、渠
堤高度、渠道断面形状和断面面积等因素,根据其中的每个因素,依次进行计算,并综合考虑,最后得出U型渠道的水力损失。
总之,U型渠道的水力最佳断面及正常水深的计算,需要考虑断面形状、断面面积、正常水深和水力损失四个方面,根据各个因素的影响,综合考虑,最终得出U型渠道的最佳断面形状和正常水深。
u型渠道设计与施工技术浅析

u型渠道设计与施工技术浅析作者:王金奇来源:《农业开发与装备》 2016年第9期摘要:随着现代农业的快速发展和社会生产的不断进步,U型渠道越来被人们所重视,U型渠道的设计与施工是保证农田灌溉,提高渠系水的利用率,提高农作物田间产量的重要环节之一,U型渠道的设计与施工是否合理,对提升农田水利灌溉渠道功能来讲是非常重要的。
为此,针对U型渠道设计与施工进行了全面的浅析,希望对高台县U型渠道的施工和持续发展做出贡献。
关键词:U型渠道;设计;施工1 U型渠道的设计1.1 U型渠道的横断面设计U型渠道采用均匀流原理计算渠道横断面的底宽、口宽、水深和堤顶尺寸,即设计流量。
公式为:Q=AV=A*C√Ri其中:Q为流量;V为流速;A为过水断面面积;i为渠道比降;R为水力半径;c为谢才系数。
设计时首先选择渠道最优设计方案,即工程量最小,投资最少的原则来设计最佳水利断面。
其次选择渠道比降。
渠道比降的选择是否合理直接影响U型渠的工程造价、控制面积的大小,再次也与渠道糙率、边坡系数、稳定渠床宽深及不冲不淤流速有关。
因此渠道比降的选择是很重要的。
为保证U型渠床稳定,设计流速应满足不冲、不淤的要求。
1.2 U型渠纵断面设计U型渠道纵断面设计应根据设计区域的地形图,优先选用等高线平行线以确定其走向,再根据等高线走向、土质情况、田间灌溉要求、水的流量综合确定水力纵坡。
1.3 U型渠水位高程的确定按纵断面中心线确定的纵坡,计算出各里程桩点的渠底、渠顶及设计水位高程数据,结合灌溉面积、流速确定水位高程。
其中:渠底高程为水位高程与设计水深之差,渠顶高程为水位高程与渠道水位超高之和。
1.4 U型渠断面尺寸的确定U型渠水位高程确定后,根据设计区域的灌溉面积、渠道长度与实际情况计算渠道设计损耗流量与净流量之和,再计算U型渠坡降与槽内过水流量,进而确定U型槽断面结构尺寸。
常用的U型槽断面结构尺寸有(宽*深)110*90cm、100*80cm、90*70cm、85*70cm、80*60cm、70*50cm、60*45cm等多种。
U型渡槽结构计算书

一、基本资料1.1工程等别根据《水利水电工程等级划分及洪水标准》(SL252-2000)、《灌溉与排水工程设计规范》(GB50288-99)和《村镇供水工程技术规范》(SL687—2014)的规定,工程设计引水流量为3.9m³/s,供水对象为一般,确定本项目为Ⅳ等小(1)型工程。
主要建筑物等级为4等,次要建筑物等级为5等,临时建筑物等级为5等。
渡槽过水流量≤5m³/s,故渡槽等级均为5级。
1.2设计流量及上下游渠道水力要素正常设计流量1.83m³/s,加大流量2.29 m³/s。
1.3渡槽长度槽身长725m,进出口总水头损失0.5m。
1.4地震烈度工程区位于安陆市北部的洑水镇、接官乡和赵鹏镇三个乡镇,属构造剥蚀丘岗地貌。
根据国家标准1:400万《中国地震动参数区划图》(GB18306-2001),工程区地震动峰值加速度为0.05g,地震动反应谱特征周期为0.35s,相应的地震基本烈度小于Ⅵ度,建筑物不设防。
1.5水文气象资料安陆市属亚热带季风气候区,春秋短,冬夏长,四季分明,兼有南北气候特点。
年最高气温40.5℃,最低气温-15.3℃,多年平均气温15.9℃。
年日照时数1920—2440h,日照率49%,居邻近各县(市)之冠。
太阳总辐射年平均112千卡/cm2,年际变化不大,4-10月辐射量占全年的71.43%。
10℃以上积温为4486—4908℃。
多年平均无霜期246d。
境内多年平均降雨量1117mm,年降雨量很不稳定,最多年份可达1772.6mm (1954年),最少年份只有652.9 mm(1978年),降水量年内分配很不均匀,4-10月份平均降雨量占全年降雨量的85%以上,多年平均蒸发量1587.3mm,由于降水量年际和年内间变化大,导致洪涝旱灾发生频繁。
二、水力计算2.1槽身水力计算槽身水力计算采用明渠均匀流公式:Q=AR2/3i1/2/n式中:Q——设计流量,m3/s;A——槽身过水断面面积,m2;R——水力半径,m;i——槽身纵坡;n——糙率系数,混凝土槽身一般采用n=0.013~0.014。
U型渠道水力计算

U型渠道水力计算U型渠道是一种常用的渠道形式,其横截面呈U形,常用于河流和水渠等地表水体的工程设计中。
U型渠道的水力计算是测算其水流的流速、水位等参数,以确保渠道的正常运行和设计要求的满足。
在进行U型渠道的水力计算时,需要应用一系列的校核公式来进行。
首先,对于U型渠道的水流速度的计算,可以应用曼宁公式来进行校核。
曼宁公式是目前应用较广泛的用于河流和渠道水流速度计算的公式之一,其表达式为:V=(1/n)*R^2/3*S^1/2其中,V表示水流速度,n为曼宁粗糙系数,R为横截面湿周与横截面面积之比,S为单位沟槽降。
这个公式根据实际情况来计算水流速度,并可以结合各种参数进行调整和修正。
其次,对于U型渠道水位的计算,可以应用直线法来进行校核。
直线法是一种常用的渠道水位计算方法,其基本原理是通过一系列的水力计算公式,计算出水的流向、流速等参数,再根据这些参数来计算水位的变化。
直线法主要用于渠道的设计和工程计算,可以结合水力学理论来进行校核计算。
此外,还需要进行U型渠道的水力坡度计算。
水力坡度是指水流下降的高度差与水流的水平距离之比,也可以理解为单位长度内的水流下降量。
水力坡度的计算可以使用差分法和斯特里克勒公式来进行。
差分法是一种常用的计算水力坡度的方法,其基本原理是将渠道分段,分别计算每段的水位、流量等参数,再根据这些参数来计算出水力坡度。
斯特里克勒公式是一种经验公式,主要用于计算水流在渠道中的分布,以及渠道中一些截面的水位、流量等参数。
最后,还需要进行U型渠道的水力半径计算。
水力半径是指渠道横截面的湿周与湿面积之比,可以理解为水流在渠道中的有效面积。
计算水力半径可以使用反曼宁公式来进行,其表达式为:R=A/P其中,R表示水力半径,A为渠道的横截面湿面积,P为横截面湿周。
水力半径的计算可以根据横截面的形状和尺寸来进行,可以结合具体的工程设计要求进行调整和优化。
总之,U型渠道水力计算是一个复杂的过程,需要应用一系列的校核公式来进行。
渠道水力计算
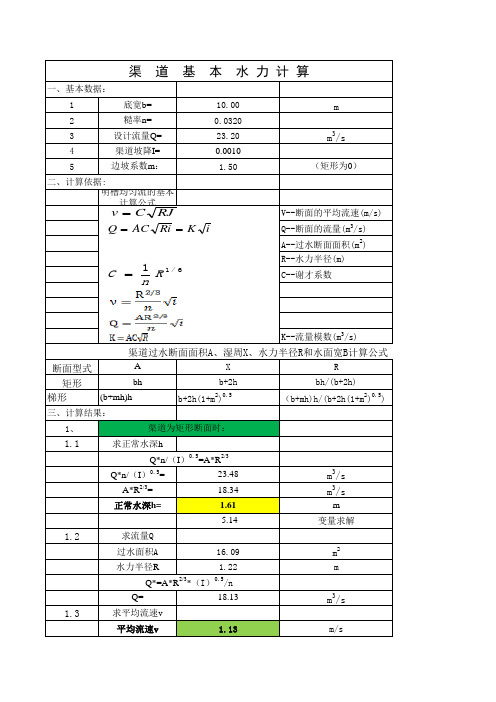
过水面积A
22.73
m2
水力半径R
1.05
Q*=A*R2/3*(I)0.5/n
Q=
23.20
m m3/s
2.3
求平均流速v
平均流速v
1.02
m/s
2.4
渠道超高值
依据灌排设计规范
Fb=h/4+0.2
Fb=
0.65
m
先根据水力计算求出渠道的设计流量下的水面线,再加上相应的渠顶超高
B计算公式
B b b+2mh
Fb=h/4+0.2
Fb=
0.60
m
先根据水力计算求出渠道的设计流量下的水面线,再加上相应的渠顶超高
2、
渠道为梯形断面时:
2.1
求正常水深h
Q*n/(I)0.5=A*R2/3
Q*n/(I)0.5=
23.48
A*R2/3=
23.48
正常水深h=
1.79
m3/s m3/s
m
0.00
变量求解
2.2
求流量Q
渠 道 基 本 水力计算
一、基本数据:
1
底宽b=
10.00
2
糙率n=
0.0320
3
设计流量Q=
23.20
4
渠道坡降I=
0.0010
5
边坡系数m:
1.50
二、计算依据: 明槽均匀流的基本
计算公式
v C RJ
Q AC Ri K i
C
1 R 1/6 n
m
m3/s
(矩形为0)
V--断面的平均流速(m/s) Q--断面的流量(m3/s) A--过水断面面积(m2) R--水力半径(m) C--谢才系数
U形渠道正常水深的直接水力计算公式

U形渠道正常水深的直接水力计算公式张新燕;吕宏兴※;朱德兰【期刊名称】《农业工程学报》【年(卷),期】2013(000)014【摘要】针对水力性能优良的U形渠道,依据明渠均匀流基本原理,以过水断面水深恰好等于U形底弧弓高时断面过流量作为分界流量Qb,引入断面特征参数和无量纲相对正常水深,采用麦考特优化法,以离差平方和最小为目标,利用SAS 软件编程,通过最优化拟合建立了U形渠道正常水深直接水力计算公式。
通过误差分析表明,所建公式在渠道过流量Q小于分界流量Qb时,计算相对误差绝对值均小于0.44%;渠道过流量Q大于分界流量Qb时,计算相对误差绝对值均不超过1%,可见公式具有较高的精度,且物理概念清晰、计算方便快捷;该公式不仅可用于解决宽浅式渠道正常水深水力计算,也适用于窄深式渠道正常水深的水力计算,具有较强的通用性,可为渠道工程设计和运行管理提供理论依据和有益参考。
% The normal depth is an important hydraulic element for channel design, operation and management. U-shaped channel has excellent hydraulic performance and strong ability of anti-frost heave, while the normal depth in the governing equations of the current common methods is implicit and have no analytical solutions. We introduced cross section characteristic parameter and dimensionless relative normal depth and took the actual flow rate in channel as the transitional flow rate when the flow depth is exactly equal to the bottom arc height. The direct calculation formula for the normal depth in U-shaped channel was presented byMarquardt method based on the NLIN procedure using SAS software. Marquardt method was used to assess whether the fitting formula reaches the best fitting result by using the iterative program to calculate the residual sum of squares. Fitting formula is the best one when the minimum residual sum of squares exists, having the characteristics of well adaptable to formula, low requirement to iterative initial value and easy to convergence, etc. This method is an effective one to solve the question of fitting non-linear equation and one of the most popular method in the field of solving non-linear equation at present. The error analysis showed the absolute value of the relative error for the proposed formula was smaller than 0.44%when the actual flow rate in channel was smaller than the transitional flow rate. Though the relative error increases when the actual flow rate in channel was larger than the transitional flow rate, the absolute value of relative error was less than 1%in which the relative error less than 0.08%when the slope coefficient was zero, and the error increased when the slope coefficient was not equal zero, but the absolute error was below 1%. It was thus indicated that the proposed formula had high precise and satisfied the need of Engineering practice. In addition, the proposed formula, with the simple form and the clear physical concept, exhibit both simplicity, easy-to-use and strong generality because it can be used to solve the normal depth of wide-shallow channel and the narrow-deep channel. Therefore, the efficient computational tools presented in this paper will be useful in the design and management of channel.【总页数】5页(P115-119)【作者】张新燕;吕宏兴※;朱德兰【作者单位】西北农林科技大学水利与建筑工程学院,杨凌 712100;西北农林科技大学水利与建筑工程学院,杨凌 712100;西北农林科技大学水利与建筑工程学院,杨凌 712100【正文语种】中文【中图分类】TV131.4【相关文献】1.蛋形断面的正常水深和临界水深的直接计算公式 [J], 卞晓卫;郑新桥;代述兵;简跃;马玉蕾2.窄深式U形渠道正常水深的近似计算公式 [J], 李风玲;文辉;黄寿生3.宽浅式U形渠道正常水深的近似计算公式 [J], 李风玲;文辉;欧军利;黄寿生;彭波4.标准马蹄形断面正常水深的直接近似计算公式 [J], 李风玲;文辉5.悬链线形断面正常水深的直接计算公式 [J], 许晓阳;张根广;陈学彪;刘余;张子钰因版权原因,仅展示原文概要,查看原文内容请购买。
水力计算基本公式

水力计算基本公式水力计算是涉及水流和流体力学的计算过程。
其基本公式包括渠道流量公式、摩擦阻力公式和水力损失公式等。
下面将详细介绍这些基本公式及其应用。
1.渠道流量公式渠道流量公式是用来计算水流通过给定横截面的流量的公式。
根据不同的渠道形状和流量条件,可以使用相应的公式。
以下是几种常见的渠道流量公式:1.1矩形渠道流量公式:Q=b*h*v式中,Q为流量,b为矩形渠道的宽度,h为水深,v为流速。
1.2圆形渠道流量公式:Q=π*r^2*v式中,Q为流量,r为圆形渠道的半径,v为流速。
1.3梯形渠道流量公式:Q=(a+b)*h*v/2式中,Q为流量,a和b为梯形渠道上下底的长度,h为水深,v为流速。
2.摩擦阻力公式摩擦阻力公式用于计算水流通过渠道时所受到的阻力。
常用的摩擦阻力公式有曼宁公式和切比雪夫公式。
2.1曼宁公式:h=(1/n)*(Q/A)^2*l/(2*g)式中,h为渠道水深(摩擦阻力损失),n为曼宁摩擦系数,Q为流量,A为横截面面积,l为渠道长度,g为重力加速度。
2.2切比雪夫公式:h=α*(Q^2/A^2)*l/(2*g)式中,h为渠道水深(摩擦阻力损失),α为切比雪夫系数,Q为流量,A为横截面面积,l为渠道长度,g为重力加速度。
3.水力损失公式水力损失公式用于计算水流通过管道或渠道时所产生的能量损失。
常见的水力损失公式有弗朗西斯公式和达西-魏本巴赫公式。
3.1弗朗西斯公式:h=(f*l*v^2)/(2*g*d)式中,h为水力损失,f为摩擦阻力系数,l为管道或渠道长度,v为流速,g为重力加速度,d为管道或渠道的直径或水深。
3.2达西-魏本巴赫公式:h=(f*l*v^2)/(2*g*d)式中,h为水力损失,f为达西-魏本巴赫摩擦系数,l为管道或渠道长度,v为流速,g为重力加速度,d为管道或渠道的直径或水深。
这些基本公式在水力学相关领域中都有广泛的应用,通过对水流的流速、渠道形状和摩擦阻力等因素的计算,可以帮助工程师设计和优化水利工程。
u型渠道水力计算

U型渠的水力计算U型断面接近水力最优断面,具有较大的输水输沙能力,占地较少,省工省料,而且由于整体性好,抵抗基土冻胀破坏的能力较强。
因此,U型断面受到普遍欢迎,在我国已广泛使用,多用混凝土现场浇筑。
图4-31为U型断面示意图,下部为半圆形,上部为稍向外倾斜的直线段。
直线段下切于半圆,外倾角a=5°~20°,随渠槽加深而增大。
较大的U型渠道采用较宽浅的断面,深宽比H/B=0.65~0.75,较小的U型渠道则宜窄深一点,深宽比可增大到H/B=1.0。
U型渠道的衬砌超高a1和渠堤超高a(堤顶或岸边到加大水位的垂直距离)可参考表4-19确定。
表4-19 U型渠道衬砌超高a1和渠堤超高a值表加大流量(m3/s) <0.5 0.5~1.0 1.0~10 10~30a1(m) 0.1~0.15 0.15~0.2 0.2~0.35 0.35~0.5a(m) 0.2~0.3 0.3~0.4 0.4~0.6 0.6~0.8注:衬砌体顶端以上土堤高一般用0.2~0.3m。
U型断面有关参数的计算公式见表4-20。
表4-20 U型断面有关参数计算公式名称符号已知条件计算式过水断面 A r、α、h2湿周X r、α、h2水力半径R A、X上口宽 B r、α、H直线段外倾角αr、B、H圆心角θr、B、H圆弧段高度h1 r、α圆弧段以上水深 h2 r、α、h水深h r、α、h2衬砌渠槽高度H h、a1U型断面水力计算的任务是根据已知的渠道设计流量Q、渠床糙率系数n和渠道比降i求圆弧半径r和水深h。
由于断面各部分尺寸间的关系复杂,U型断面的设计,需要借助某些尺寸间的经验关系,如公式(4-57)和表4-21给出的经验关系。
设计步骤如下:(1)确定圆弧以上的水深h2,圆弧以上水深h2和圆弧半径r有以下经验关系:(4-57)式中: Na——直线段外倾角为a时的系数。
a=0时的系数用N0表示。
直线段的外倾角a和N0值都随圆弧半径而变化,见表4-21。
U形渠道水力计算的显式计算式

U形渠道水力计算的显式计算式李风玲;文辉;陈雄【摘要】通过选择适当的变量及曲线拟合得到U形断面的正常水深和临界水深的显式公式,代替了目前采用的图解、试算等方法.该公式形式简洁、准确.在工程常用范围内临界水深的最大相对误差小于0.618%, 正常水深的最大相对误差小于1.074%,它将给设计人员带来极大的方便.【期刊名称】《水利水电科技进展》【年(卷),期】2010(030)001【总页数】3页(P65-67)【关键词】U形渠道;近似算法;显式计算式【作者】李风玲;文辉;陈雄【作者单位】惠州学院建筑与土木工程系,广东,惠州,516007;惠州学院建筑与土木工程系,广东,惠州,516007;茂名学院建筑工程学院,广东,茂名,525000【正文语种】中文【中图分类】TV133梯形断面是一种非常传统的输水渠道的断面形式,已有不少国内外学者在其最优断面方面进行了大量研究[1-3]。
与梯形断面相比,U形断面具有以下特点:①渠口宽度小、节省耕地;②水力半径大,从而使沿程水头损失小,水力条件优越;③冻胀分布均匀,冻胀变形很小且易复位。
U形断面渠道在中小型输水渠道中有取代传统梯形渠道的发展趋势。
但在U形断面的设计及水力计算中,其正常水深和临界水深方程为含参数的高次方程,理论上无解析解,传统求解方法是用试算法、图解法及迭代法进行求解,计算过程相当繁琐且误差较大。
U形断面临界水深、正常水深的直接计算尚未见报道。
目前只有张志昌等[4]在U形渠道水力最优断面计算方面得到了一些重要结论。
为此,从U形断面渠道临界流方程、明渠均匀流基本方程出发,对其进行恰当的恒等变形,应用优化拟合的方法,根据文献[5]可知:U形断面渠道圆心半角的取值范围θ0∈[70°,90°],本文重点研究这种U形断面无量纲水深β∈(0,2]范围内的正常水深和临界水深的直接计算公式。
1 U形渠道的水力计算公式U形渠道断面见图1(图中r为底弧半径)。
u型渠体积计算公式

u型渠体积计算公式
摘要:
1.引言
2.U 型渠体积计算公式
3.计算实例
4.总结
正文:
U 型渠体积计算公式是工程师和科学家在进行水文学研究、水力学设计以及相关领域工作时经常需要用到的工具。
通过这个公式,我们可以准确地计算出U 型渠的体积,从而更好地理解和利用水资源。
U 型渠体积计算公式如下:
V = A * L * √(R1 * R2)
其中:
V:U 型渠的体积
A:U 型渠横截面的面积
L:U 型渠的长度
R1:U 型渠上游半径
R2:U 型渠下游半径
为了更好地理解这个公式,我们通过一个具体的实例来进行计算。
假设有一个U 型渠,其横截面的面积为0.5 平方米,长度为10 米,上游半径为2 米,下游半径为1 米。
我们可以将这些数据代入公式进行计算:
V = 0.5 * 10 * √(2 * 1)
V = 5 * √2
V ≈ 7.07(立方米)
因此,这个U 型渠的体积约为7.07 立方米。
通过这个实例,我们可以看到U 型渠体积计算公式在实际应用中的作用。
需要注意的是,在计算过程中,要确保数据的准确性,以便得到更精确的结果。
总之,U 型渠体积计算公式是水文学和水利工程领域中一个重要的工具,掌握这个公式有助于我们更好地了解和利用水资源。
