(完整版)导数及其应用测试题(有详细答案)(文科、整理)
导数应用测试题及参考答案

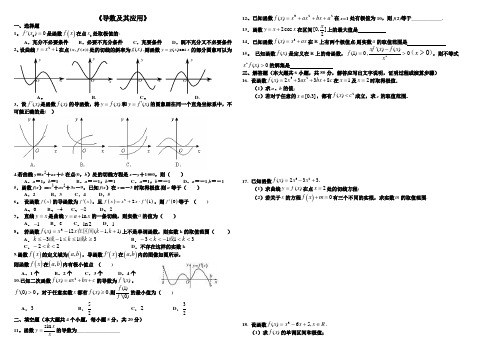
导数应用测试题一、选择题:(本大题共12小题,每小题5分, 共60分) 1.设函数f(x)在0x 处可导,则xx f x x f x ∆-∆-→∆)()(lim000等于 ( )A .)('0x fB .)('0x f -C .)('0x f --D .)(0x f -- 2.若13)()2(lim000=∆-∆+→∆xx f x x f x ,则)('0x f 等于 ( ) A .32 B .23C .3D .2 3.曲线x x y 33-=上切线平行于x轴的点的坐标是( )A .(-1,2)B .(1,-2)C .(1,2)D .(-1,2)或(1,-2) 4.若函数f(x)的导数为f ′(x)=-sinx ,则函数图像在点(4,f (4))处的切 线的倾斜角为( )A .90°B .0°C .锐角D .钝角5.函数5123223+--=x x x y 在[0,3]上的最大值、最小值分别是 ( )A .5,-15B .5,-4C .-4,-1D .5,-166.一直线运动的物体,从时间t 到t+△t 时,物体的位移为△s ,那么ts t ∆∆→∆0lim 为( )A .从时间t 到t+△t 时,物体的平均速度B .时间t 时该物体的瞬时速度C .当时间为△t 时该物体的速度D .从时间t 到t+△t 时位移的平均变化率7.关于函数762)(23+-=x x x f ,下列说法不正确的是( )A .在区间(∞-,0)内,)(x f 为增函数B .在区间(0,2)内,)(x f 为减函数C .在区间(2,∞+)内,)(x f 为增函数D .在区间(∞-,0)),2(+∞⋃内,)(x f 为增函数8.对任意x ,有34)('x x f =,f(1)=-1,则此函数为 ( ) A .4)(x x f = B .2)(4-=x x f C .1)(4+=x x f D .2)(4+=x x f9.函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是 ( )A.5 , -15B.5 , 4C.-4 , -15D.5 , -1610.抛物线y=x 2到直线x-y-2=0的最短距离为 ( )A .2B 。
导数及其应用测试题(有详细答案)

12.已知函数f{x)=x3+ax2+bx+a2在ul处有极值为10,则犬2)等于.JT13.函数y=尤+2cosx在区间[0,—]±的最大值是14.已知函数fM=x3+ax在R上有两个极值点,则实数。
的取值范围是15.已知函数八尤)是定义在R上的奇函数,/(1)=0,二⑴;'3)>0危>0),则不等式%x2f(x)>0的解集是三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)16.设函数/(x)=2x3+3破2+3笊+8c在x=1刚好工=2取得极值.(1)求。
、b的值;(2)若对于随意的xg[0,3],都有/(x)<c2成立,求c的取值范围.17.已知函数f(x)=2x3-3x2+3.(1)求曲线y=f(x)在点工=2处的切线方程;(2)若关于工的方程/(x)+m=0有三个不同的实根,求实数m的取值范围.18.设函S/W=x3-6x+5,x e R.(1)求f(x)的单调区间和极值;《导数及其应用》一、选择题1.r(x0)=o是函数y(尤)在点气处取极值的:A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件2、设曲线y=x2+l在点(x,/(x))处的切线的斜率为g(x),WI函数>=g(x)cosx的部分图象可以4.若曲线y=x2+ax+b在点(0,方)处的切线方程是x-j+l=0,贝!|()A.q=L b=lB.a=—1,b=lC.g=L b=—1D.a=—1,b=—15.函数/(x)=x3+ttx2+3x—9,已知处)在x=—3时取得极值,则0等于()A.2B.3C.4D.56.设函数f⑴的导函数为扩(x),且/(x)=x2+2x-r(l),则广(0)等于()A、0B>-4C、-2D、27.直线y=x是曲线y=a+lnx的一条切线,则实数。
的值为()A.-1B.eC.In2D.18.若函数f(x)=x3-12x^区间以-盘+1)上不是单调函数,则实数k的取值范围()A.kJ—3^4—1■ k<23B.—3<上<—l^(il<k<3C.-2<k<2D.不存在这样的实数k9.函数f(x)的定义域为(m),导函数/(%)在(。
导数及其应用测试题(有详细答案)
《导数及其应用》一、选择题1。
0()0f x '=是函数()f x 在点0x 处取极值的:A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件 2、设曲线21y x =+在点))(,(x f x 处的切线的斜率为()g x ,则函数()cos y g x x =的部分图象可以为A 。
B. C 。
D.3.设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )4.若曲线y =x 2+ax +b在点(0,b )处的切线方程是x -y +1=0,则( )A .a =1,b =1B .a =-1,b =1C .a =1,b =-1D .a =-1,b =-1 5.函数f (x )=x 3+ax 2+3x -9,已知f (x )在x =-3时取得极值,则a 等于( )A .2B .3C .4D .56。
设函数()f x 的导函数为()f x ',且()()221f x x x f '=+⋅,则()0f '等于 ( )A 、0B 、4-C 、2-D 、27。
直线y x =是曲线ln y a x =+的一条切线,则实数a 的值为( )A .1-B .eC .ln 2D .18。
若函数)1,1(12)(3+--=k k x x x f 在区间上不是单调函数,则实数k 的取值范围( ) A .3113≥≤≤--≤k k k 或或 B .3113<<-<<-k k 或C .22<<-kD .不存在这样的实数k9.函数()f x 的定义域为(),a b ,导函数()f x '在(),a b 内的图像如图所示, 则函数()f x 在(),a b 内有极小值点 ( )A .1个B .2个C .3个D .4个 10.已知二次函数2()f x ax bx c =++的导数为'()f x ,'(0)0f >,对于任意实数x 都有()0f x ≥,则(1)'(0)f f 的最小值为( ) A .3 B .52 C .2 D .32二、填空题(本大题共4个小题,每小题5分,共20分) 11。
专题导数及其应用(解答题)(原卷版)(文科专用)-五年(18-22)高考数学真题分项汇编(全国通用)

专题04 导数及其应用(解答题)(文科专用) 1.【2022年全国甲卷】已知函数f(x)=x 3−x,g(x)=x 2+a ,曲线y =f(x)在点(x 1,f (x 1))处的切线也是曲线y =g(x)的切线.(1)若x 1=−1,求a ;(2)求a 的取值范围.2.【2022年全国乙卷】已知函数f(x)=ax −1x −(a +1)lnx . (1)当a =0时,求f(x)的最大值;(2)若f(x)恰有一个零点,求a 的取值范围.3.【2021年甲卷文科】设函数22()3ln 1f x a x ax x =+-+,其中0a >. (1)讨论()f x 的单调性;(2)若()y f x =的图象与x 轴没有公共点,求a 的取值范围. 4.【2021年乙卷文科】已知函数32()1f x x x ax =-++.(1)讨论()f x 的单调性;(2)求曲线()y f x =过坐标原点的切线与曲线()y f x =的公共点的坐标. 5.【2020年新课标1卷文科】已知函数()(2)x f x e a x =-+. (1)当1a =时,讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围.6.【2020年新课标2卷文科】已知函数f (x )=2ln x +1.(1)若f (x )≤2x +c ,求c 的取值范围;(2)设a >0时,讨论函数g (x )=()()f x f a x a--的单调性. 7.【2020年新课标3卷文科】已知函数32()f x x kx k =-+. (1)讨论()f x 的单调性;(2)若()f x 有三个零点,求k 的取值范围.8.【2019年新课标2卷文科】已知函数()(1)ln 1f x x x x =---.证明: (1)()f x 存在唯一的极值点;(2)()=0f x 有且仅有两个实根,且两个实根互为倒数.9.【2019年新课标3卷文科】已知函数32()22f x x ax =-+. (1)讨论()f x 的单调性;(2)当0<<3a 时,记()f x 在区间[]0,1的最大值为M ,最小值为m ,求M m -的取值范围.10.【2018年新课标1卷文科】【2018年新课标I 卷文】已知函数()e 1x f x a lnx =--.(1)设2x =是()f x 的极值点.求a ,并求()f x 的单调区间;(2)证明:当1ea ≥时,()0f x ≥. 11.【2018年新课标2卷文科】已知函数()()32113f x x a x x =-++. (1)若3a =,求()f x 的单调区间;(2)证明:()f x 只有一个零点.12.【2018年新课标3卷文科】已知函数()21x ax x f x e +-=. (1)求曲线()y f x =在点()0,1-处的切线方程; (2)证明:当1a ≥时,()0f x e +≥.。
导数文科大题含详细标准答案

导数文科大题含详细答案————————————————————————————————作者:————————————————————————————————日期:导数文科大题1.知函数,. (1)求函数的单调区间;(2)若关于的方程有实数根,求实数的取值范围. 答案解析2.已知, (1)若,求函数在点处的切线方程; (2)若函数在上是增函数,求实数a 的取值范围; (3)令, 是自然对数的底数);求当实数a等于多少时,可以使函数取得最小值为3.解:(1)时,,′(x),′(1)=3,,数在点处的切线方程为,(2)函数在上是增函数,′(x),在上恒成立,即,在上恒成立,令,当且仅当时,取等号, ,的取值范围为(3),′(x),①当时,在上单调递减,,计算得出(舍去);②当且时,即,在上单调递减,在上单调递增,,计算得出,满足条件;③当,且时,即,在上单调递减,,计算得出(舍去);综上,存在实数,使得当时,有最小值3.解析(1)根据导数的几何意义即可求出切线方程.(2)函数在上是增函数,得到f′(x),在上恒成立,分离参数,根据基本不等式求出答案,(3),求出函数的导数,讨论,,的情况,从而得出答案3.已知函数,(1)分别求函数与在区间上的极值;(2)求证:对任意,解:(1),令,计算得出:,,计算得出:或,故在和上单调递减,在上递增,在上有极小值,无极大值;,,则,故在上递增,在上递减,在上有极大值,,无极小值;(2)由(1)知,当时,,,故;当时,,令,则,故在上递增,在上递减,,;综上,对任意,解析(1)求导,利用导数与函数的单调性及极值关系,即可求得及单调区间及极值;4.已知函数,其中,为自然数的底数.(1)当时,讨论函数的单调性;(2)当时,求证:对任意的,.解:(1)当时,,则,,故则在R上单调递减.(2)当时,,要证明对任意的,.则只需要证明对任意的,.设,看作以a为变量的一次函数,要使,则,即,恒成立,①恒成立,对于②,令,则,设时,,即.,,在上,,单调递增,在上,,单调递减,则当时,函数取得最大值,故④式成立,综上对任意的,.解析:(1)求函数的导数,利用函数单调性和导数之间的关系进行讨论即可.(2)对任意的,转化为证明对任意的,,即可,构造函数,求函数的导数,利用导数进行研究即可.5.已知函数(1)当时,求函数在处的切线方程;(2)求在区间上的最小值.解:(1)设切线的斜率为k.因为,所以,所以,所以所求的切线方程为,即(2)根据题意得, 令,可得①若,则,当时,,则在上单调递增.所以②若,则, 当时,,则在上单调递减. 所以③若,则,所以,随x的变化情况如下表:x 1 20 - 0 + 0-e Φ极小值Γ0所以的单调递减区间为,单调递增区间为所以在上的最小值为综上所述:当时,;当时,;当时,解析(1)设切线的斜率为k.利用导数求出斜率,切点坐标,然后求出切线方程.(2)通过,可得.通过①,②,③,判断函数的单调性求出函数的最值.6.已知函数。
完整版)导数测试题(含答案)

完整版)导数测试题(含答案)1.已知函数y=f(x)=x^2+1,则在x=2,Δx=0.1时,Δy的值为0.41.2.函数f(x)=2x^2-1在区间(1,1+Δx)上的平均变化率为4+4Δx。
3.设f′(x)存在,则曲线y=f(x)在点(x,f(x))处的切线与x 轴相交但不垂直。
4.曲线y=-1/x在点(1,-1)处的切线方程为y=x-2.5.在曲线y=x^2上,且在该点处的切线倾斜角为π/4的点为(2,4)。
6.已知函数f(x)=1/x,则f′(-3)=-1/9.7.函数f(x)=(x-3)ex的单调递增区间是(2,∞)。
8.“函数y=f(x)在一点的导数值为0”是“函数y=f(x)在这点取极值”的充要条件。
9.函数f(x)在开区间(a,b)内的极小值点有2个。
10.函数f(x)=-x^2+4x+7,在x∈[3,5]上的最大值和最小值分别是f(3)和f(5)。
11.函数f(x)=x^3-3x^2-9x+k在区间[-4,4]上的最小值为-71.12.速度为零的时刻是0,1,4秒末。
13.已知函数 $y=f(x)=ax^2+2x$,且 $f'(1)=4$,则 $a=3$。
14.已知函数 $y=ax^2+b$ 在点 $(1,3)$ 处的切线斜率为 $2$,则 $b=a+1$。
15.函数 $y=x e^x$ 的最小值为 $-1/e$。
16.有一长为 $16$ m 的篱笆,要围成一个矩形场地,则矩形场地的最大面积是 $64$ $m^2$。
17.(1) $y'=6x+\cos x$;(2) $y'=\dfrac{1}{(1+x)^2}$;(3)$y'=\dfrac{1}{x}-e^x$。
18.(1) 解方程 $x^2+4=x+10$ 得 $x=3$ 或 $x=-2$,故交点为 $(3,13)$ 或 $(-2,0)$;(2) 在交点 $(3,13)$ 处,抛物线的斜率为 $6$,故该点处的切线方程为 $y=6x-5$。
导数文科测试题及答案

导数文科测试题及答案一、单项选择题(每题3分,共30分)1. 函数y=x^2的导数是()A. 2xB. x^2C. 2D. x答案:A2. 函数y=3x的导数是()A. 3B. 3xC. 1D. 0答案:A3. 函数y=x^3的导数是()A. 3x^2B. x^3C. 3D. x^2答案:A4. 函数y=sin(x)的导数是()A. cos(x)B. sin(x)C. -sin(x)D. -cos(x)答案:A5. 函数y=e^x的导数是()A. e^xB. e^(-x)C. 1D. 0答案:A6. 函数y=ln(x)的导数是()A. 1/xB. xC. ln(x)D. 1答案:A7. 函数y=1/x的导数是()A. -1/x^2B. 1/x^2C. -1/xD. 1/x答案:A8. 函数y=x^(1/2)的导数是()A. 1/2x^(-1/2)B. 1/2x^(1/2)C. 1/2D. 2x^(-1/2)答案:A9. 函数y=tan(x)的导数是()A. sec^2(x)B. tan(x)C. 1D. sec(x)答案:A10. 函数y=arcsin(x)的导数是()A. 1/sqrt(1-x^2)B. 1/xC. xD. sqrt(1-x^2)答案:A二、填空题(每题4分,共20分)11. 函数y=x^4的导数是________。
答案:4x^312. 函数y=cos(x)的导数是________。
答案:-sin(x)13. 函数y=ln(1+x)的导数是________。
答案:1/(1+x)14. 函数y=x^(-2)的导数是________。
答案:-2x^(-3)15. 函数y=arccos(x)的导数是________。
答案:-1/sqrt(1-x^2)三、解答题(每题10分,共50分)16. 求函数y=x^2-2x+1的导数。
答案:y'=2x-217. 求函数y=e^(2x)的导数。
完整版)导数最新文科高考数学真题

完整版)导数最新文科高考数学真题1.曲线y=xex-1在点(1,1)处的切线斜率为2e。
(选项C)2.曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,因此a=3.(选项D)3.根据导函数y'=f'(x)的图象,确定函数y=f(x)的图象为B。
4.函数f(x)=2/x+lnx,其导数为f'(x)=-2/x^2+1/x。
解方程f'(x)=0,得到x=2为f(x)的极小值点。
(选项D)5.如果p:f(x)=q:x是f(x)的极值点,则p是q的必要条件,但不是充分条件。
(选项C)6.曲线y=x^3-x+3在点(1,3)处的切线方程为2x-y+1=0.7.曲线y=kx+lnx在点(1,k)处的切线平行于x轴,因此k=-1.8.曲线y=ax-lnx在点(1,a)处的切线平行于x轴,因此a=1/2.(选项1/2)9.曲线y=-5ex+3在点(0,-2)处的切线方程为5x+y+2=0.10.曲线y=x+1(α∈R)在点(1,2)处的切线经过坐标原点,因此α=2.11.曲线y=x(3lnx+1)在点(1,1)处的切线方程为4x-y-3=0.12.曲线y=e^x上点P处的切线平行于直线2x+y+1=0,因此P的坐标为(-ln2,2)。
13.曲线y=xlnx上点P处的切线平行于直线2x-y+1=0,因此P的坐标为(e,e)。
14.函数y=-x^2没有明显的问题,但是缺少了后面的部分,因此无法确定答案。
15.若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是[1,+∞)。
16.函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为下凸的W 形,拐点为x=0.17.已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax+(a+2)x+1相切,则2a=8.18.函数y=xe在其极值点处的切线方程为y=-x/e。
19.已知函数f(x)=axlnx,其中a为实数,且f'(x)为f(x)的导函数,若f'(1)=3,则a的值为3.20.曲线y=x^2的在点(1,2)处的切线方程为x-y+1=0.21.函数y=f(x)的导函数y=f'(x)的图象为下凸的W形,则函数y=f(x)的图象可能是D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学(文)期末复习题《导数及其应用》一、选择题1.是函数在点处取极值的: ( )()0f x'=()f xxA.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件2、设曲线在点处的切线的斜率为,则函数的部分图象可以为( )21y x=+))(,(xfx()g x()cosy g x x=A. B. C. D.3.在曲线y=x2上切线的倾斜角为的点是( )π4A.(0,0) B.(2,4) C. D.(14,116)(12,14)4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )A.a=1,b=1 B.a=-1,b=1 C.a=1,b=-1 D.a=-1,b=-15.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )A.2 B.3 C.4 D.56. 已知三次函数f(x)=x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )13A.m<2或m>4 B.-4<m<-2 C.2<m<4 D.以上皆不正确7. 直线是曲线的一条切线,则实数的值为( )y x=lny a x=+aA. B. C. D.1-e ln218. 若函数上不是单调函数,则实数k的取值范围())1,1(12)(3+--=kkxxxf在区间A.B.3113≥≤≤--≤kkk或或3113<<-<<-kk或C. D.不存在这样的实数k22<<-k9. 10.函数的定义域为,导函数在内的图像如图所示,()fx(),a b()f x'(),a b则函数在内有极小值点()()f x(),a bA.1个 B.2个 C.3个 D.4个10.已知二次函数的导数为,,对于任意实数都有,则的2()f x ax bx c=++'()f x'(0)0f>x()0f x≥(1)'(0)ff最小值为() A. B. C. D.352232二、填空题(本大题共4个小题,每小题5分,共20分)11.函数的导数为_________________sin xyx=12、已知函数在x=1处有极值为10,则f(2)等于____________.223)(a bx ax x x f +++=13.函数在区间上的最大值是2cos y x x =+[0,]2π14.已知函数在R 上有两个极值点,则实数的取值范围是3()f x x ax =+a 15. 已知函数)(x f 是定义在R 上的奇函数,0)1(=f ,0)()(2>-'xx f x f x )(0>x ,则不等式0)(2>x f x 的解集是三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)16. 设函数f(x)=sinx -cosx +x +1,0<x<2π,求函数f(x)的单调区间与极值.17. 已知函数.(Ⅰ)求的值;(Ⅱ)求函数的单调区间.3()3f x x x =-)2(f '()f x 18. 设函数.(1)求的单调区间和极值;R x x x x f ∈+-=,56)(3)(x f (2)若关于的方程有3个不同实根,求实数的取值范围.x a x f =)(a (3)已知当恒成立,求实数的取值范围.)1()(,),1(-≥+∞∈x k x f x 时k19. 已知是函数的一个极值点,其中(1)求与的关系式; 1x =32()3(1)1f x mx m x nx =-+++,,0m n R m ∈<m n (2)求的单调区间; (3)当,函数的图象上任意一点的切线斜率恒大于,求的取值范()f x [1,1]x ∈-()y f x =3m m 围。
20. 已知函数(I )当时,若函数在其定义域内是增函数,求b 的取值范围;2()ln .f x x ax bx =--1a =-()f x (II )若的图象与x 轴交于两点,且AB 的中点为,求证:()f x 1212(,0),(,0)()A x B x x x <0(,0)C x 0'()0.f x <21. 已知函数2(),()2ln (x f x g x a x e e==为自然对数的底数) (1)求()()()F x f x g x =-的单调区间,若()F x 有最值,请求出最值;(2)是否存在正常数a ,使()()f x g x 与的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出a 的值,以及公共点坐标和公切线方程;若不存在,请说明理由。
高二数学(文)期末复习《导数及其应用》参考答案一、选择题: 题号12345678910答案B ADADDDBAC二、填空题:11.;12. 18 13.; 14.; 15.2cos sin 'x x x y x -=36+π}0|{<a a ),1()0,1(+∞- 三、解答题16. [解析] f′(x)=cosx +sinx +1=sin(x +)+1 (0<x<2π)2π4令f′(x)=0,即sin(x +)=-,解之得x =π或x =π.π42232x ,f′(x)以及f(x)变化情况如下表:x (0,π)π(π,π)32π32(π,2π)32f′(x)+0-0+f(x)递增π+2递减3π2递增∴f(x)的单调增区间为(0,π)和(π,2π)单调减区间为(π,π).f 极大(x)=f(π)=π+2,f 极小(x)=f(π)=.3232323π217. 解:(Ⅰ),所以.33(2-='x x f )9)2(='f (Ⅱ),解,得或.解,得.2()33f x x '=-()0f x '>1x >1x <-()0f x '<11x -<<所以,为函数的单调增区间,为函数的单调减区间.(,1)-∞-(1,)+∞()f x (1,1)-()f x 18. 解:(1) …………………1分2,2,0)(),2(3)(212=-=='-='x x x f x x f 得令∴当,…………………2分()0;,()0x x f x x f x ''<>><<<当时∴的单调递增区间是,单调递减区间是……3分)(x f (,)-∞+∞和)2,2(-当;当.…………4分245)(,2+-=有极大值x f x 245)(,2-=有极小值x f x (2)由(1)可知图象的大致形状及走向(图略))(x f y =∴当的图象有3个不同交点,……6分)(,245245x f y a y a ==+<<-与直线时即当时方程有三解. …………………………………7分55a -<<+α=)(x f (3)∵上恒成立.)1()5)(1()1()(2-≥-+--≥x k x x x x k x f 即),1(5,12+∞-+≤∴>在x x k x 令,由二次函数的性质,上是增函数,5)(2-+=x x x g ),1()(+∞在x g ∴∴所求的取值范围是……………………………………12分,3)1()(-=>g x g k 3-≤k 19. 解:(1)因为是函数的一个极值点.所以2'()36(1).f x mx m x n =-++1x =()f x '(1)0f =即所以36(1)0,m m n -++=36n m =+ (2)由(1)知,22'()36(1)363(1)[(1)]f x mx m x m m x x m=-+++=--+当时,有,当为化时,与的变化如下表:0m <211m>+x ()f x '()f xx2(,1)m-∞+21m+2(1,1)m+1(1,)+∞'()f x -0+0-()f x 单调递减极小值单调递增极大值单调递减故由上表知,当时,在单调递减,在单调递增,在上单调递减.0m <()f x 2(,1)m -∞+2(1,1)m+(1,)+∞(3)由已知得,即又,所以,即'()3f x m >22(1)20mx m x -++>0m <222(1)0x m x m m-++< 设,其函数图象开口向上,由题意知①式恒成立,所以222(1)0,[1,1]x m x x m m -++<∈-212()2(1g x x x m m=-++ 解之得所以即的取值范围为22(1)0120(1)010g m m g ⎧-<+++<⎧⎪⇒⎨⎨<⎩⎪-<⎩403m m -<<又403m -<<m 4(,0)3-20.(1)由题意:,在上递增,对bx x x x f -+=2ln )( )(x f ),0(+∞∴021)(≥-+='b x xx f 恒成立,即对恒成立,只需,),0(+∞∈x x x b 21+≤),0(+∞∈x ∴min )21(x xb +≤,,当且仅当时取“=”,,的取值范围为0>x ∴2221≥+x x22=x ∴22≤b ∴b )22,(-∞(2)由已知得,,两式相减,得:⎩⎨⎧=--==--=0ln )(0ln )(2222212111bx ax x x f bx ax x x f ⇒⎩⎨⎧-=-=22221211ln ln bx ax x bx ax x ,由)())((ln21212121x x b x x x x a x x -+-+=⇒])()[(ln 212121b x x a x x x x++-=及,得:b ax x x f -+='21)(2102x x x +=])([221)(2211000b x x a x x b ax x x f ++-+=--='2111ln 1222x x x x x x +-+=,令,]ln )(2[121111222x x x x x x x x -+--=ln )1()1(2[121212112x x x x x x x x -+--=)1,0(21∈=x x t 且,,在上为减函数,t t t t ln 122)(-+-=ϕ)10(<<t 0)1()1()(22<+--='t t t t ϕ∴)(t ϕ)1,0(,又,∴0)1()(=>ϕϕt 21x x <∴0)(0<'x f 21. 解:(1)3222()()()()(0)x a x ea F x f x g x x e x ex-'''=-=-=>①当0,()0a F x '≤>时恒成立()(0,)F x +∞在上是增函数,()F x F 只有一个单调递增区间(0,-∞),没有最值……3分②当0a>时,()0)F x x =>,若0x<<()0,()F x F x'<在上单调递减;若x>()0,())F x F x'>+∞在上单调递增,x∴=当()F x有极小值,也是最小值,即min()2ln lnF x F a a a a==-=-所以当0a>时,()F x的单调递减区间为,单调递增区间为)+∞,最小值为lna a-,无最大值(2)方法一,若()f x与()g x的图象有且只有一个公共点,则方程()()0f xg x-=有且只有一解,所以函数()F x有且只有一个零点由(1)的结论可知min()ln01F x a a a=-==得此时,2()()()2ln0xF x f x g x xe=-=-≥min()0F x F==1,()()f g f x g x∴==∴与的图象的唯一公共点坐标为又f g''==()()f xg x∴与的图象在点处有共同的切线,其方程为1y x-=-,即1y x=-综上所述,存在a1=,使()()f xg x与的图象有且只有一个公共点,且在该点处的公切线方程为1.y x=-方法二:设()f x与g(x)图象的公共点坐标为00(,)x y,根据题意得即22ln22xa xex ae x⎧=⎪⎪⎨⎪=⎪⎩由②⎩⎨⎧==)()()()(''xfxfxgxf得2xae=,代入①得021ln,2x x=∴=从而1a=此时由(1)可知min()0F x F==0x x∴>≠当且()0,()()F x f x g x>>即因此除x=外,再没有其它x,使00()()f xg x=故存在1a=,使()()f xg x与的图象有且只有一个公共点,且在该公共点处有共同的切线,易求得公共点坐标为,公切线方程为1y x=-。
