(苏教版)八年级下册数学期中试卷【含答案】
苏科版(完整版)八年级数学下册期中试卷及答案
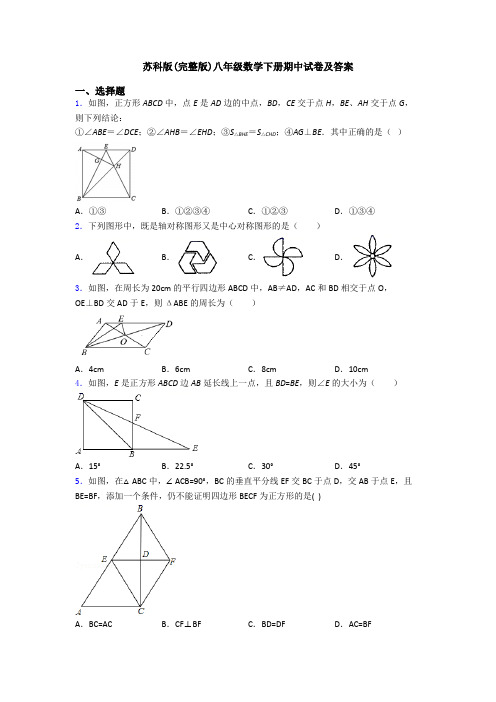
苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE.其中正确的是()A.①③B.①②③④C.①②③D.①③④2.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3.如图,在周长为20cm的平行四边形ABCD中,AB≠AD,AC和BD相交于点O,OE⊥BD交AD于E,则ΔABE的周长为()A.4cm B.6cm C.8cm D.10cm4.如图,E是正方形ABCD边AB延长线上一点,且BD=BE,则∠E的大小为()A.15°B.22.5°C.30°D.45°5.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF6.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.7.下面图形中,既是中心对称图形又是轴对称图形的是()A.B.C.D.8.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:抛掷次数100200300400500正面朝上的频数5398156202244若抛掷硬币的次数为1000,则“正面朝上”的频数最接近()A.20 B.300 C.500 D.8009.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为()A.8 B.7 C.6 D.510.如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG,下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=12AD.其中正确的有( )A.①②B.①②④C.①③④D.①②③④二、填空题11.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是AO 、AD 的中点,若AB =6cm ,BC =8cm ,则EF =_____cm .12.如图,在ABCD 中,对角线AC 、BD 相交于点O .如果AC =6,BD =8,AB =x ,那么x的取值范围是__________.13.为了了解我市八年级男生的体重分布情况,市教育局从各学校共随机抽取了500名八年级男生进行了测量.在这个问题中,样本是指_____.14.如图,在Rt △ABC 中,∠ACB =90°,AC =5,BC =12,D 是AB 上一动点,过点D 作DE ⊥AC 于点E ,DF ⊥BC 于点F ,连接EF ,则线段EF 的最小值是___.15.在一次数学测试中 ,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频率是0.2 ,则第六组的频数是_______. 16.48与最简二次根式23a -是同类二次根式,则a =_____.17.如图,在菱形ABCD 中,8AB =,60B ∠=︒,点G 是边CD 的中点,点E 、F 分别是AG 、AD 上的两个动点,则EF ED +的最小值是_________.18.任意掷一枚质地均匀的骰子,下列事件:①面朝上的点数小于2;②面朝上的点数大于2;③面朝上的点数是奇数,这些事件发生的可能性大小,按从小到大的顺序排列为_____.19.x 千克橘子糖、y 千克椰子糖、z 千克榴莲糖混合成“什锦糖”.已知这三种糖的单价分别为30元/千克、32元/千克、40元/千克,则这种“什锦糖”的单价为_____元.(用含x、y、z的代数式表示)20.如图,在□ABCD中,AB=7,AD=11,DE平分∠ADC,则BE=__.三、解答题21.某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.请根据图中提供的信息,解答下面的问题:(1)此次共调查了名学生,扇型统计图中“艺术鉴赏”部分的圆心角是度.(2)请把这个条形统计图补充完整.(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.22.如图,在ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.(1)求证:四边形BFDE为平行四边形;(2)当∠DOE= °时,四边形BFDE为菱形?23.如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.(1)求证:四边形ABEC是平行四边形;(2)若∠AFC=2∠ADC,求证:四边形ABEC是矩形.24.自2009年以来,“中国•兴化千垛菜花旅游节”享誉全国.“河有万湾多碧水,田无一垛不黄花”所描绘的就是我市发达的油菜种植业.为了解某品种油菜籽的发芽情况,农业部门从该品种油菜籽中抽取了6批,在相同条件下进行发芽试验,有关数据如表: 批次 1 2 3 4 5 6 油菜籽粒数 100400800100020005000发芽油菜籽粒数 a 318 652 793 1604 4005 发芽频率0.8500.7950.8150.793b0.801(1)分别求a 和b 的值;(2)请根据以上数据,直接写出该品种油菜籽发芽概率的估计值(精确到0.1); (3)农业部门抽取的第7批油菜籽共有6000粒.请你根据问题(2)的结果,通过计算来估计第7批油菜籽在相同条件下进行发芽试验时的发芽粒数. 25.如图,平行四边形ABCD 中,已知BC =10,CD =5.(1)试用无刻度的直尺和圆规在AD 边上找一点E ,使点E 到B 、D 两点的距离相等(不要求写作法,但要保留清晰的作图痕迹); (2)求△ABE 的周长.26.为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:调查结果统计表 组别A BCD E分组(元) 030x ≤< 3060x ≤<频数调查结果频数分布直方图 调查结果扇形统计图请根据以上图表,解答下列问题:(1)填空:这次调查的样本容量是 ,a = ,m = ; (2)补全频数分布直方图;(3)求扇形统计图中扇形B 的圆心角度数; (4)该校共有1000人,请估计每月零花钱的数额x 在3090x ≤<范围的人数. 27.为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.(1)本次调查共随机抽取了 名学生; (2)补全条形统计图;(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ︒; (4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.28.如图,点P 是正方形ABCD 对角线AC 上一动点,点E 在射线BC 上,且PB PE =,连接PD ,O 为AC 中点.(1)如图1,当点P 在线段AO 上时,试猜想PE 与PD 的数量关系和位置关系,并说明理由;(2)如图2,当点P 在线段OC 上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P 在AC 的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】根据正方形的性质证得BAE CDE ∆≅∆,推出ABE DCE ∠=∠,可知①正确;证明ABH CBH ∆≅∆,再根据对顶角相等即可得到AHB EHD ∠=∠,可知②正确;根据//AD BC ,求出BDE CDE S S ∆∆=,推出BDE DEH CDE DEH S S S S ∆∆∆∆-=-,即BHE CHD S S ∆∆=,故③正确;利用正方形性质证ADH CDH ∆≅∆,求得HAD HCD ∠=∠,推出ABE HAD ∠=∠;求出90ABE BAG ∠+∠=︒,求得90AGE ∠=︒故④正确.【详解】解:四边形ABCD 是正方形,E 是AD 边上的中点,AE DE ∴=,AB CD =,90BAD CDA ∠=∠=︒,()BAE CDE SAS ∴∆≅∆, ABE DCE ∴∠=∠,故①正确;∵四边形ABCD 是正方形, ∴AB=BC , ∠ABD=∠CBD , ∵BH=BH , ∴ABH CBH ∆≅∆,AHB CHB ∴∠=∠,BHC DHE ∠=∠,AHB EHD ∴∠=∠,故②正确;//AD BC ,BDE CDE S S ∆∆∴=,BDE DEH CDE DEH S S S S ∆∆∆∆∴-=-,即BHE CHD S S ∆∆=, 故③正确;四边形ABCD 是正方形,AD DC ∴=,45ADB CDB ∠=∠=︒,DH DH =,()ADH CDH SAS ∴∆≅∆, HAD HCD ∴∠=∠, ABE DCE ∠=∠ABE HAD ∴∠=∠,90BAD BAH DAH ∠=∠+∠=︒, 90ABE BAH ∴∠+∠=︒, 1809090AGB ∴∠=︒-︒=︒,AG BE ∴⊥, 故④正确;故选:B . 【点睛】本题主要考查了正方形的性质及全等三角形的判定与性质,三角形的面积公式,解答本题关键要充分利用正方形的性质:①四边相等; ②四个内角相等,都是90度; ③对角线相等,相互垂直,且每条对角线平分一组对角.2.D解析:D【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【详解】解:A、是轴对称图形,不是中心对称的图形,故本选项不符合题意;B、不是轴对称图形,也不是中心对称的图形,故本选项不符合题意;C、不是轴对称图形,是中心对称的图形,故本选项不符合题意;D、是轴对称图形,也是中心对称的图形,故本选项符合题意.故选:D.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.3.D解析:D【解析】分析:利用平行四边形、等腰三角形的性质,将△ABE的周长转化为平行四边形的边长之间的和差关系.详解:∵四边形ABCD是平行四边形,∴AC、BD互相平分,∴O是BD的中点.又∵OE⊥BD,∴OE为线段BD的中垂线,∴BE=DE.又∵△ABE的周长=AB+AE+BE,∴△ABE的周长=AB+AE+DE=AB+AD.又∵□ABCD的周长为20cm,∴AB+AD=10cm∴△ABE的周长=10cm.故选D.点睛:本题考查了平行四边形的性质.平行四边形的对角线互相平分.请在此填写本题解析!4.B解析:B【分析】由四边形ABCD是正方形,推出∠ABD=45°,由∠ABD=∠E+∠BDE,BD=BE,推出∠BDE=∠E,即可求解.【详解】∵四边形ABCD是正方形,∴∠ABD=45°,∵∠ABD=∠E+∠BDE,∵BD=BE,∴∠BDE=∠E.∴∠E=12×45°=22.5°,故选:B.【点睛】本题考查了正方形的性质、等腰三角形的判定和性质等知识,解题的关键是熟练掌握正方形的性质.5.D解析:D【详解】解:∵EF垂直平分BC,∴BE=EC,BF=CF;∵CF=BE,∴BE=EC=CF=BF;∴四边形BECF是菱形.当BC=AC时,∠ACB=90°,∠A=45°,∴∠EBC=45°;∴∠EBF=2∠EBC=2×45°=90°.∴菱形BECF是正方形.故选项A不符合题意.当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意.当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项C不符合题意.当AC=BD时,无法得出菱形BECF是正方形,故选项D符合题意.故选D.6.B解析:B【分析】根据轴对称图形和中心对称图形的概念求解即可.【详解】解:A、是轴对称图形,不是中心对称图形,故此选项错误;B、是轴对称图形,又是中心对称图形,故此选项正确;C、不是轴对称图形,是中心对称图形,故此选项错误;D、不是轴对称图形,不是中心对称图形,故此选项错误.故答案为B.【点睛】本题考查了轴对称图形和中心对称图形的识别,掌握轴对称图形和中心对称图形的概念是解答本题的关键.7.D解析:D【分析】根据轴对称图形的定义和中心对称图形的定义对每个选项进行判断即可.【详解】A项是轴对称图形,不是中心对称图形;B项是中心对称图形,不是轴对称图形;C项是中心对称图形,不是轴对称图形;D项是中心对称图形,也是轴对称图形;故选:D.【点睛】本题考查了轴对称图形的定义和中心对称图形的定义,掌握知识点是解题关键.8.C解析:C【分析】随着实验次数的增加,正面向上的频率逐渐稳定到某个常数附近,据此求解即可.【详解】观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,所以抛掷硬币的次数为1000,则“正面朝上”的频数最接近10000.5500⨯=次,故选C.【点睛】本题考查利用频率估计概率的知识,解题的关键是了解在大量重复试验中,可以用频率估计概率.9.D解析:D【分析】连接DN,根据三角形中位线定理得到EF=12DN,根据题意得到当点N与点B重合时,DN最大,根据勾股定理计算,得到答案.【详解】连接DN,∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,∴EF=12 DN,∵点M,N分别为线段BC,AB上的动点,∴当点N与点B重合时,DN最大,此时DN10,∴EF长度的最大值为:12×10=5,故选:D.【点睛】本题考查的是三角形中位线定理、勾股定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.10.D解析:D【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=90°,∵点E、F、H分别是AB、BC、CD的中点,∴△BCE≌△CDF,∴∠ECB=∠CDF,∵∠BCE+∠ECD=90°,∴∠ECD+∠CDF=90°,∴∠CGD=90°,∴CE⊥DF,故①正确;在Rt△CGD中,H是CD边的中点,∴HG=12CD=12AD,故④正确;连接AH,同理可得:AH⊥DF,∵HG=HD=12CD,∴DK=GK,∴AH垂直平分DG,∴AG=AD,故②正确;∴∠DAG=2∠DAH,同理:△ADH≌△DCF,∴∠DAH=∠CDF,∵GH=DH,∴∠HDG=∠HGD,∴∠GHC=∠HDG+∠HGD=2∠CDF,∴∠CHG=∠DAG.故③正确.故选D.【点睛】运用了正方形的性质,全等三角形的判定与性质,等腰三角形的性质以及垂直平分线的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.二、填空题11.5【分析】根据勾股定理求出AC,根据矩形性质得出∠ABC=90°,BD=AC,BO=OD,求出BD、OD,根据三角形中位线求出即可.【详解】∵四边形ABCD是矩形,∴∠ABC=90°,BD解析:5【分析】根据勾股定理求出AC,根据矩形性质得出∠ABC=90°,BD=AC,BO=OD,求出BD、OD,根据三角形中位线求出即可.【详解】∵四边形ABCD是矩形,∴∠ABC=90°,BD=AC,BO=OD,∵AB=6cm,BC=8cm,∴由勾股定理得:(cm),∴DO=5cm,∵点E、F分别是AO、AD的中点,∴EF=12OD=2.5cm,故答案为2.5.【点评】本题考查了勾股定理,矩形性质,三角形中位线的应用,熟练掌握相关性质及定理是解题的关键.12.1<x<7【解析】因为平行四边形的对角线互相平分,所以OA=OC=3,OB=OD=4,所以4-3<x<4+3,即1<x<7,故答案为1<x<7.解析:1<x<7【解析】因为平行四边形的对角线互相平分,所以OA=OC=3,OB=OD=4,所以4-3<x<4+3,即1<x<7,故答案为1<x<7.13.从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解:在解析:从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解:在这个问题中,样本是指从各学校共随机抽取的500名八年级男生体重,故答案为:从各学校共随机抽取的500名八年级男生体重.【点睛】本题考查统计中的总体与样本,属于基本题型.14..【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解解析:60.13【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解即可.【详解】解:如图,连接CD.∵∠ACB=90°,AC=5,BC=12,∴AB22512+=13,A BCC+22∵DE⊥AC,DF⊥BC,∠C=90°,∴四边形CFDE是矩形,∴EF=CD,由垂线段最短可得CD⊥AB时,线段EF的值最小,此时,S△ABC=12BC•AC=12AB•CD,即12×12×5=12×13•CD,解得:CD=60 13,∴EF=60 13.故答案为:60 13.【点睛】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.15.5【详解】解:一个容量为50的样本,把它分成6组,第一组到第四组的频数分别为6,8,9,12,根据第五组的频率是0.2,求出第五组的频数,用样本容量减去前五组的频数,得到第六组的频数是50-6-解析:5【详解】解:一个容量为50的样本,把它分成6组,第一组到第四组的频数分别为6,8,9,12,根据第五组的频率是0.2,求出第五组的频数,用样本容量减去前五组的频数,得到第六组的频数是50-6-8-9-10-12=5.考点:频数与频率16.3【分析】首先化简二次根式,再根据同类二次根式定义可得2a﹣3=3,再解即可.【详解】,∵与最简二次根式是同类二次根式,∴2a﹣3=3,解得:a=3,故答案为:3.【点睛】此题主解析:3【分析】首先化简二次根式48=43,再根据同类二次根式定义可得2a ﹣3=3,再解即可.【详解】4816343=⨯=,∵48与最简二次根式23a -是同类二次根式,∴2a ﹣3=3,解得:a =3,故答案为:3.【点睛】此题主要考查了同类二次根式,关键是掌握把二次根式化为最简二次根式后被开方数相同的二次根式称为同类二次根式.17.【分析】由题意,点D 与点C 关于AG 对称,连接EC ,FC ,再利用垂线段最短求值即可【详解】解:连接,,如图在菱形中,,∴是边长为8的等边三角形∵是的中点∴∴是的垂直平分线∴∵,解析:43【分析】由题意,点D 与点C 关于AG 对称,连接EC ,FC ,再利用垂线段最短求值即可【详解】解:连接EC ,FC ,如图在菱形ABCD 中,60B ∠=︒,8AB =∴ACD ∆是边长为8的等边三角形∵G 是CD 的中点∴AG CD ⊥∴AG 是CD 的垂直平分线∴EC ED =∵EF EC FC +≥,CF AD ⊥时,CF 最小∴EF ED +的最小值是等边ACD ∆的高:82=故答案为:【点睛】本题考查菱形的性质、垂线段最短、等边三角形的判定、勾股定理等知识,解决问题的关键是利用垂线段最短解决最小值问题,属于中考常考题型. 18.①③②【分析】根据概率公式分别求出每种情况发生的概率,然后比较出它们的大小即可.【详解】解:任意掷一枚质地均匀的骰子,共有6种等可能结果,其中①面朝上的点数小于2的有1种结果,其概率为;解析:①③②【分析】根据概率公式分别求出每种情况发生的概率,然后比较出它们的大小即可.【详解】解:任意掷一枚质地均匀的骰子,共有6种等可能结果,其中①面朝上的点数小于2的有1种结果,其概率为16; ②面朝上的点数大于2的有4种结果,其概率为4263=; ③面朝上的点数是奇数的有3种结果,其概率为3162=; ∵112623<<, ∴按从小到大的顺序排列为:①③②;故答案为:①③②.【点睛】考查了基本概率的计算及比较可能性大小,用到的知识点为:可能性等于所求情况数与总情况数之比.19.【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:;故答案为:.【点睛】本题考查列代数式,解题的关键是读懂题意.解析:303240 x y zx y z++++【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:303240x y zx y z++++;故答案为:303240x y zx y z++++.【点睛】本题考查列代数式,解题的关键是读懂题意.20.4【解析】解:∵DE平分∠ADC,∴∠ADE=∠CDE,∵▱ABCD中AD∥BC,∴∠ADE=∠CED,∴∠CDE=∠CED,∴CE=CD,∵在▱ABCD中,AB=7,AD=11,解析:4【解析】解:∵DE平分∠ADC,∴∠ADE=∠CDE,∵▱ABCD中AD∥BC,∴∠ADE=∠CED,∴∠CDE=∠CED,∴CE=CD,∵在▱ABCD中,AB=7,AD=11,∴CD=AB=7,BC=AD=11,∴BE=BC-CE=11-7=4.三、解答题21.解:(1)200,144.(2)见解析;(3)120名【分析】(1)根据阅读写作的人数和所占的百分比,即可求出学生总数,再用艺术鉴赏的人数除以总人数乘以360°,即可得出“艺术鉴赏”部分的圆心角.(2)用总学生数减去“艺术鉴赏”,“科技制作”,“阅读写作”,得出“数学思维”的人数,从而补全统计图.(3)用“科技制作”所占的百分比乘以总人数8000,即可得出答案.【详解】解:(1)学生总数:50÷25%=200(名)“艺术鉴赏”部分的圆心角:80200×360°=144°故答案为:200,144.(2)数学思维的人数是:200-80-30-50=40(名),补图如下:(3)根据题意得:800×30200=120(名),答:其中有120名学生选修“科技制作”项目.22.(1)详见解析;(2)90【分析】(1)证△DOE≌△BOF(ASA),得DE=BF,即可得出结论;(2)由∠DOE=90°,得EF⊥BD,即可得出结论.【详解】(1)∵四边形ABCD是平行四边形,O为对角线BD的中点,∴BO=DO,AD∥BC,∴∠EDO=∠FBO,在△EOD和△FOB中,EDO FBO DO BOEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE≌△BOF(ASA),∴DE=BF,又∵DE∥BF,∴四边形BFDE为平行四边形;(2)∠DOE=90°时,四边形BFDE为菱形;理由如下:由(1)得:四边形BFDE是平行四边形,若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形;故答案为:90.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及菱形的判定等知识,证出△DOE≌△BOF是解题的关键.23.(1)证明见解析;(2)证明见解析.【分析】(1)根据平行四边形的性质得到AB//CD,AB=CD,然后根据CE=DC,得到AB=EC,AB//EC,利用“一组对边平行且相等的四边形是平行四边形”判断即可;(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.【详解】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形;(2)∵由(1)知,四边形ABEC是平行四边形,∴FA=FE,FB=FC.∵四边形ABCD是平行四边形,∴∠ABC=∠D.又∵∠AFC=2∠ADC,∴∠AFC=2∠ABC.∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,∴FA =FE =FB =FC ,∴AE =BC ,∴四边形ABEC 是矩形.【点睛】此题考查的知识点是平行四边形的判定与性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.24.(1)85a,0.802b =;(2)0.8;(3)4800 【分析】(1)用油菜籽粒数乘以发芽频率求得a 的值,用发芽油菜籽粒数除以油菜籽总数即可求得b 的值.(2)观察大量重复试验发芽的频率稳定到哪个常数附近即可用哪个数表示发芽概率. (3)用油菜籽总数乘以发芽概率即可求得发芽粒数.【详解】(1)1000.85085a =⨯=,16040.8022000b ==; (2)∵观察表格发现发芽频率逐渐稳定到0.8附近,∴该品种油菜籽发芽概率的估计值为0.8;(3)60000.8=4800⨯,故估计第7批油菜籽在相同条件下进行发芽试验时的发芽粒数为4800.【点睛】本题考查统计与概率,解题关键在于信息筛选能力,对频率计算公式的理解,其次注意计算仔细即可.25.(1)见解析;(2)15;见解析.【分析】 (1)连接BD 作线段BD 的垂直平分线MN 交AD 于点E ,点E 即为所求.(2)证明△ABE 的周长=AB +AD 即可.【详解】解:(1)如图,点E 即为所求.(2)解:连接BE∵四边形ABCD 是平行四边形∴AD =BC =10,AB =CD =5又由(1)知BE =DE∴15ABE AB AE BE AB AE ED AB C AD +++++====.【点睛】本题主要考查垂直平分线的作法及性质,熟练掌握知识点是解题的关键.26.(1)50,16,8;(2)补全图形见解析;(3)扇形统计图中扇形B的圆心角度数为115.2°;(4)每月零花钱的数额x在30≤x<90范围的人数大约为720人.【解析】分析:(1)根据C组的频数是20,对应的百分比是40%,据此求得调查的总人数,然后求得a的值,m的值;(2)根据a的值补全频数分布直方图;(3)利用360°乘以对应的比例即可求解;(4)利用总人数1000乘以对应的比例即可求解.详解:(1)调查的总人数是20÷40%=50(人),则a=50﹣4﹣20﹣8﹣2=16,A组所占的百分比是450=8%,则m=8.故答案为50,16,8;(2)补全频数分布直方图如图:(3)扇形统计图中扇形B的圆心角度数是360°×1650=115.2°;(4)每月零花钱的数额x在30≤x<90范围的人数是1000×162050=720(人).答:每月零花钱的数额x在30≤x<90范围的人数大约为720人.点睛:本题考查了扇形统计图,观察统计表、扇形统计图获得有效信息是解题的关键,扇形统计图直接反映部分占总体的百分比大小.27.(1)200;(2)图见解析;(3)144;(4)6 500人【分析】(1)用阅读时长在“6小时及以上”的人数除以对应百分比即可计算;(2)先根据统计图中的数据求出课外阅读时长在“2~4小时”和“4~6小时”的人数,然后补全条形统计图即可;(3)用360°乘以课外阅读时长“4~6小时”对应的百分比即可求出;(4)用初中生总数乘以一周课外阅读时长不少于4小时的百分比即可.【详解】(1)本次调查共随机抽取了:50÷25%=200(名);(2)课外阅读时长“2~4小时”的有:200×20%=40(人),课外阅读时长“4~6小时”的有:200-30-40-50=80(人),故条形统计图如下:;(3)阅读时长在“2小时以内”的人数所占的百分比为:30÷200×100%=15%,课外阅读时长“4~6小时”对应的圆心角度数为:360°×(1-20%-25%-15%)=144°; (4)10000×(1-20%-15%)=6500(人).【点睛】本题考查了扇形统计图和条形统计图的结合,由图表获取数据是解题关键.28.(1)PE PD =且PE PD ⊥,详见解析;(2)猜想成立,详见解析;(3)猜想成立【分析】(1)根据点P 在线段AO 上时,利用三角形的全等判定和性质以及四边形内角和定理可以得出PE ⊥PD ,PE=PD ;(2)利用三角形全等得出,BP=PD ,由PB=PE ,得出PE=PD ,要证PE ⊥PD ;从三方面分析,当点E 在线段BC 上(E 与B 、C 不重合)时,当点E 与点C 重合时,点P 恰好在AC 中点处,当点E 在BC 的延长线上时,分别分析即可得出;(3)根据题意作出图形,利用(2)中证明思路即可得出答案.【详解】(1)当点P 在线段AO 上时,PE PD =且PE PD ⊥,理由如下:∵四边形ABCD 是正方形,AC 为对角线,∴BA DA =,45BAP DAP ∠=∠=︒,在△ABP 和△ADP 中,45AB AD BAP DAP AP AP =⎧⎪∠∠︒⎨⎪⎩===,∴△ABP ≌△ADP ,∴PB PD =,ABP ADP ∠=∠,CDP CBP ∠=∠,又∵PB PE =,∴CBP BEP ∠=∠,PE PD =,∴BEP CDP ∠=∠,∵180BEP CEP ∠+∠=︒,∴180CDP CEP ∠+∠=︒,∵正方形ABCD 中,90BCD ∠=︒,∴36090DPE CEP CDP BCD ∠=︒-∠-∠-∠=︒,∴PE PD ⊥;(2)当点P 在线段OC 上时,PE PD =且PE PD ⊥,理由如下:∵四边形ABCD 是正方形,AC 为对角线,∴BA DA =,45BAP DAP ∠=∠=︒,又PA PA =,∴BAP DAP ∆≅∆(SAS),∴PB PD =,又∵PB PE =,∴PE PD =,①当点E 与点C 重合时,PE PD ⊥;②当点E 在BC 的延长线上时,如图所示,∵BAP DAP ∆≅∆,∴ABP ADP ∠=∠,∴CDP CBP ∠=∠,PB PE =,∴CBP PEC ∠=∠,∴PEC PDC ∠=∠,∵12∠=∠,∴90DPE DCE ∠=∠=︒,∴PE PD ⊥,综上所述:PE PD ⊥.∴当点P 在线段OC 上时,(1)中的猜想成立;(3)当点P 在线段OC 的延长线上时,如图所示,(1)中的猜想成立.∵四边形ABCD 是正方形,点P 在AC 的延长线上,∴BA DA =,45BAP DAP ∠=∠=︒,又PA PA =,∴BAP DAP ∆≅∆(SAS),∴PB PD =,又∵PB PE =,∴PE PD =,∵BAP DAP ∆≅∆,∴ABP ADP ∠=∠,∴CDP CBP ∠=∠,PB PE =,∴CBP PEC ∠=∠,∴PEC PDC ∠=∠,∵DGC EGP ∠=∠,∴90DPE DCE ∠=∠=︒,∴PE PD ⊥.【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质以及垂线的证明方法,解题的关键是正确寻找全等三角形解决问题,学会添加常用辅助线,构造特殊三角形解决问题,属于中考压轴题..。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,5AB =,6AC =,过D 作AC 的平行线交BC 的延长线于点E ,则BDE ∆的面积为( )A .22B .24C .48D .442.四边形ABCD 中,对角线AC 、BD 相交于点O ,给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB=CD ,AD=BC ;③AO=CO ,BO=DO ;④AB ∥CD ,AD=BC .其中一定能判断这个四边形是平行四边形的条件共有A .1组B .2组C .3组D .4组 3.满足下列条件的四边形,不一定是平行四边形的是( ) A .两组对边分别平行B .两组对边分别相等C .一组对边平行且相等D .一组对边平行,另一组对边相等 4.如图,将△ABC 沿着它的中位线DE 折叠后,点A 落到点A ’,若∠C =120°,∠A =26°,则∠A ′DB 的度数是( )A .120°B .112°C .110°D .100° 5.下列成语故事中所描述的事件为必然发生事件的是( ) A .水中捞月B .瓮中捉鳖C .拔苗助长D .守株待兔 6.如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD ,则四边形ABCD面积的最大值是( )A .15B .16C .19D .207.如图,在△ABC 中,∠ACB=90°,BC 的垂直平分线EF 交BC 于点D ,交AB 于点E ,且BE=BF ,添加一个条件,仍不能证明四边形BECF 为正方形的是( )A .BC=ACB .CF ⊥BFC .BD=DFD .AC=BF8.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .9.已知反比例函3y x =-,下列结论中不正确的是( ) A .图像经过点(1,3)- B .图像在第二、四象限C .当1x >时,30y <<D .当0x <,y 随着x 的增大而减小 10.小明和同学做“抛掷质地均匀的硬币试验”,获得的数据如表:若抛掷硬币的次数为3000,则“正面朝上”的频数最接近( )A .1000B .1500C .2000D .2500 二、填空题11.不透明的袋子里装有6只红球,1只白球,这些球除颜色外都相同.搅匀后从中任意摸出1只球.摸出的是红球的可能性_____摸出的是白球的可能性(填“大于”、“小于”或“等于”).12.如图,小正方形方格的边长都是1,点A 、B 、C 、D 、O 都是小正方形的顶点.若COD 是由AOB 绕点O 按顺时针方向旋转一次得到的,则至少需要旋转______°.13.若分式x 3x 3--的值为零,则x=______.14.一个样本的50个数据分别落在5个小组内,第1、2、3、4组的数据的个数分别为2、8、15、5,则第5组的频率为______ 。
苏科版(完整版)八年级数学下册期中试卷及答案doc

苏科版(完整版)八年级数学下册期中试卷及答案doc一、选择题1.如图,点E,F,G,H分别为四边形ABCD四条边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的是()A.不是平行四边形B.不是中心对称图形C.一定是中心对称图形D.当AC=BD时,它为矩形2.下列调查中,最适合采用普查的是()A.长江中现有鱼的种类B.八年级(1)班36名学生的身高C.某品牌灯泡的使用寿命D.某品牌饮料的质量3.下列图案中,是中心对称图形的是()A.B.C.D.4.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.5.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.6.为了解我市八年级10000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是()A.每个学生的身高是个体B.本次调查采用的是普查C.样本容量是500名学生D.10000名学生是总体7.如图,函数k y x =-与1y kx =+(0k ≠)在同一平面直角坐标系中的图像大致( ) A . B .C .D .8.已知关于x 的方程23x m x -=+的解是负数,则m 的取值范围为( ) A .6m >-且3m ≠- B .6m >- C .6m <-且3m ≠- D .6m <-9.下列条件中,不能..判定平行四边形ABCD 为矩形的是( ) A .∠A =∠CB .∠A =∠BC .AC =BD D .AB ⊥BC 10.下列事件为必然事件的是( ) A .射击一次,中靶B .12人中至少有2人的生日在同一个月C .画一个三角形,其内角和是180°D .掷一枚质地均匀的硬币,正面朝上 11.关于x 的一元二次方程x 2+(a 2﹣2a )x+a ﹣1=0的两个实数根互为相反数,则a 的值为( )A .2B .0C .1D .2或012.如图,正方形ABCD 中,点E 、F 、H 分别是AB 、BC 、CD 的中点,CE 、DF 交于G ,连接AG 、HG ,下列结论:①CE ⊥DF ;②AG=AD ;③∠CHG=∠DAG ;④HG=12AD .其中正确的有( )A .① ②B .① ② ④C .① ③ ④D .① ② ③ ④二、填空题13.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为_____.14.若菱形的两条对角线分别为2和3,则此菱形的面积是 .15.为了了解我市八年级男生的体重分布情况,市教育局从各学校共随机抽取了500名八年级男生进行了测量.在这个问题中,样本是指_____.16.如图,在Rt △ABC 中,∠ACB =90°,AC =5,BC =12,D 是AB 上一动点,过点D 作DE ⊥AC 于点E ,DF ⊥BC 于点F ,连接EF ,则线段EF 的最小值是___.17.若关于x 的一元二次方程x 2+(2k +4)x +k 2=0没有实数根,则k 的取值范围是_____.18.在函数y =1x x 中,自变量x 的取值范围是_____. 19.x 千克橘子糖、y 千克椰子糖、z 千克榴莲糖混合成“什锦糖”.已知这三种糖的单价分别为30元/千克、32元/千克、40元/千克,则这种“什锦糖”的单价为_____元.(用含x 、y 、z 的代数式表示) 20.如图,△ABC 中,∠BAC =20°,△ABC 绕点A 逆时针旋转至△AED ,连接对应点C 、D ,AE 垂直平分CD 于点F ,则旋转角度是_____°.21.如图所示,直线a 经过正方形ABCD 的顶点A ,分别过顶点D 、B 作DE ⊥a 于点E 、BF ⊥a 于点F ,若DE =4,BF =3,则EF 的长为_______.22.方程x 2=0的解是_______.23.如图,在平面直角坐标系中,四边形OBCD 是菱形,OB =OD =2,∠BOD =60°,将菱形OBCD 绕点O 旋转任意角度,得到菱形OB 1C 1D 1,则点C 1的纵坐标的最小值为_____.24.如图,在矩形ABCD 中,AB =5,AD =3,动点P 满足S △PAB =13S 矩形ABCD ,则点P 到A 、B 两点距离之和PA +PB 的最小值为_____.三、解答题25.如图,将▱ABCD 的边DC 延长到点E ,使CE =DC ,连接AE ,交BC 于点F ,连接AC 、BE .(1)求证:四边形ABEC 是平行四边形;(2)若∠AFC =2∠ADC ,求证:四边形ABEC 是矩形.26.解下列方程:(1)9633x x=+- ; (2)241111x x x -+=-+ . 27.先化简:22241a a a a a+--÷-,再从﹣1、0、1、2中选一个你喜欢的数作为a 的值代入求值.28.如图,在▱ABCD 中,E 为BC 边上一点,且AB =AE(1)求证:△ABC ≌△EAD ;(2)若∠B =65°,∠EAC =25°,求∠AED 的度数.29.如图,矩形ABCD 中,AB =8,AD =6,点O 是对角线BD 的中点,过点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形DEBF是平行四边形;(2)当DE=DF时,求EF的长.30.在矩形ABCD中,AB=3,BC=4,点E为BC延长线上一点,且BD=BE,连接DE,Q 为DE的中点,有一动点P从B点出发,沿BC以每秒1个单位的速度向E点运动,运动时间为t秒.(1)如图1,连接DP、PQ,则S△DPQ=(用含t的式子表示);(2)如图2,M、N分别为AD、AB的中点,当t为何值时,四边形MNPQ为平行四边形?请说明理由;(3)如图3,连接CQ,AQ,试判断AQ、CQ的位置关系并加以证明.31.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是16cm,AC的长为8cm,求线段AB的长度.32.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,﹣1)、B(﹣1,0)、C(0,﹣3)(1)点A关于坐标原点O对称的点的坐标为.(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C,A1A的长为.的顶点33.正方形网格中(每个小正方形边长是1,小正方形的顶点叫做格点),ABC均在格点上,请在所给的平面直角坐标系中解答下列问题:(1)作出ABC ∆绕点A 逆时针旋转90°后的111A B C ∆;(2)作出111A B C ∆关于原点O 成中心对称的222A B C ∆.34.如图,在平行四边形ABCD 中,AE BD CF BD ⊥⊥,,垂足分别为E F 、.(1)求证:AE CF =;(2)求证:四边形AECF 是平行四边形35.如图,点P 是正方形ABCD 对角线AC 上一动点,点E 在射线BC 上,且PB PE =,连接PD ,O 为AC 中点.(1)如图1,当点P 在线段AO 上时,试猜想PE 与PD 的数量关系和位置关系,并说明理由;(2)如图2,当点P 在线段OC 上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P 在AC 的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.36.如图,已知()()1,0,0,3,90,30A B BAC ABC ︒︒∠=∠=.(1)求ABC ∆的面积; (2)在y 轴上是否存在点Q 使得QAB ∆为等腰三角形,若存在,请直接写出点Q 所有可能的坐标,若不存在,请说明理由;(3)如果在第二象限内有一点3,2P m ⎛⎫ ⎪ ⎪⎝⎭,且过点P 作PH x ⊥轴于H ,请用含m 的代数式 表示梯形PHOB 的面积,并求当ABP ∆与ABC ∆面积相等时m 的值?【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】先连接AC,BD,根据EF=HG=12AC,EH=FG=12BD,可得四边形EFGH是平行四边形,当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形;当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,据此进行判断即可.【详解】连接AC,BD,如图:∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,∴EF=HG=12AC,EH=FG=12BD,∴四边形EFGH是平行四边形,故选项A错误;∴四边形EFGH一定是中心对称图形,故选项B错误;当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形,当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,故选项D错误;∴四边形EFGH可能是轴对称图形,∴四边形EFGH是平行四边形,四边形EFGH一定是中心对称图形.故选:C.【点睛】本题主要考查了中点四边形的运用,解题时注意:平行四边形是中心对称图形.解决问题的关键是掌握三角形中位线定理.2.B解析:B【分析】在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【详解】解:A.调查长江中现有鱼的种类,调查的难度大,范围广,适合抽样调查;B.调查八年级(1)班36名学生的身高,难度不大,适合普查;C.调查某品牌灯泡的使用寿命,调查带有破坏性,适合抽样调查;D.调查某品牌饮料的质量,调查带有破坏性,适合抽样调查;故选:B.【点睛】本题考查的是普查与抽样调查的含义与运用,掌握以上知识是解题的关键.3.A【分析】本题根据中心对称图形的概念求解.【详解】A选项是中心对称图形,故本选项符合题意;B选项是轴对称图形,故本选项不合题意;C选项是轴对称图形,故本选项不合题意;D选项是轴对称图形,故本选项不合题意.故选:A.【点睛】本题考查中心对称图形的识别,按照其定义求解即可,注意与轴对称图形的区别.4.D解析:D【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【详解】解:A、是轴对称图形,不是中心对称的图形,故本选项不符合题意;B、不是轴对称图形,也不是中心对称的图形,故本选项不符合题意;C、不是轴对称图形,是中心对称的图形,故本选项不符合题意;D、是轴对称图形,也是中心对称的图形,故本选项符合题意.故选:D.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.5.B解析:B【分析】根据轴对称图形和中心对称图形的概念求解即可.【详解】解:A、是轴对称图形,不是中心对称图形,故此选项错误;B、是轴对称图形,又是中心对称图形,故此选项正确;C、不是轴对称图形,是中心对称图形,故此选项错误;D、不是轴对称图形,不是中心对称图形,故此选项错误.故答案为B.【点睛】本题考查了轴对称图形和中心对称图形的识别,掌握轴对称图形和中心对称图形的概念是解答本题的关键.6.A解析:A由总体、个体、样本、样本容量的概念,结合题意进行分析,即可得到答案.【详解】解:A 、每个学生的身高是个体,故A 正确;B 、本次调查是抽样调查,故B 错误;C 、样本容量是500,故C 错误;D 、八年级10000名学生的身高是总体,故D 错误;故选:A .【点睛】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.7.B解析:B【分析】分k >0和k <0两种情况分类讨论即可确定正确的选项.【详解】解:当k >0时,函数1y kx =+的图象经过一、二、三象限,反比例函数k y x =-的图象分布在二、四象限,没有选项符合题意;当k 0<时,函数1y kx =+的图象经过一、二、四象限,反比例函数k y x=-的图象分布在一、三象限,B 选项正确,故选:B .【点睛】考查了反比例函数和一次函数的性质,解题的关键是能够分类讨论,难度不大. 8.A解析:A【分析】解分式方程,得到含有m 得方程的解,根据“方程的解是负数”,结合分式方程的分母不等于零,得到两个关于m 得不等式,解之即可.【详解】解:方程两边同时乘以1x +得:3(1)x m x -=+,解得:6=--x m ,又∵方程的解是负数,∴60--<m ,解不等式得:6m >-,综上可知:6m >-且3m ≠-,故本题答案为:A.【点睛】本题考查了分式方程的解;解一元一次不等式.解决本题的关键是熟练掌握分式方程的解法过程,注意分式方程分母不为0这一要求.9.A解析:A【分析】根据矩形的判定定理再结合平行四边形的性质对选项逐一进行推理即可.【详解】A、∠A=∠C不能判定这个平行四边形为矩形,故此项错误;B、∵∠A=∠B,∠A+∠B=180°,∴∠A=∠B=90°,可以判定这个平行四边形为矩形,故此项正确;C、AC=BD,对角线相等,可推出平行四边形ABCD是矩形,故此项正确;D、AB⊥BC,即∠B=90°,可以判定这个平行四边形为矩形,故此项正确;故选:A.【点睛】本题考查了平行四边形的性质和矩形的判定,掌握知识点是解题关键.10.C解析:C【分析】必然事件就是一定会发生的事件,依据定义即可判断.【详解】解:A.射击一次,中靶是随机事件;B.12人中至少有2人的生日在同一个月是随机事件;C.画一个三角形,其内角和是180°是必然事件;D.掷一枚质地均匀的硬币,正面朝上是随机事件;故选:C.【点睛】考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.11.B解析:B【解析】设方程的两根为x1,x2,根据题意得x1+x2=0,所以a2-2a=0,解得a=0或a=2,当a=2时,方程化为x2+1=0,△=-4<0,故a=2舍去,所以a的值为0.故选B.12.D解析:D【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=90°,∵点E、F、H分别是AB、BC、CD的中点,∴△BCE≌△CDF,∴∠ECB=∠CDF,∵∠BCE+∠ECD=90°,∴∠ECD+∠CDF=90°,∴∠CGD=90°,∴CE⊥DF,故①正确;在Rt△CGD中,H是CD边的中点,∴HG=12CD=12AD,故④正确;连接AH,同理可得:AH⊥DF,∵HG=HD=12CD,∴DK=GK,∴AH垂直平分DG,∴AG=AD,故②正确;∴∠DAG=2∠DAH,同理:△ADH≌△DCF,∴∠DAH=∠CDF,∵GH=DH,∴∠HDG=∠HGD,∴∠GHC=∠HDG+∠HGD=2∠CDF,∴∠CHG=∠DAG.故③正确.故选D.【点睛】运用了正方形的性质,全等三角形的判定与性质,等腰三角形的性质以及垂直平分线的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.二、填空题13.20【分析】利用频率估计概率,设原来红球个数为x个,根据摸取30次,有10次摸到白色小球结合概率公式可得关于x的方程,解方程即可得.设原来红球个数为x个,则有=,解得,x=20,解析:20【分析】利用频率估计概率,设原来红球个数为x个,根据摸取30次,有10次摸到白色小球结合概率公式可得关于x的方程,解方程即可得.【详解】设原来红球个数为x个,则有1010x=1030,解得,x=20,经检验x=20是原方程的根.故答案为20.【点睛】本题考查了利用频率估计概率和概率公式的应用,熟练掌握概率的求解方法以及分式方程的求解方法是解题的关键.14.3【分析】菱形的面积是对角线乘积的一半,由此可得出结果即可.【详解】解:由题意,知:S菱形=×2×3=3,故答案为3.考点:菱形的性质.解析:3【分析】菱形的面积是对角线乘积的一半,由此可得出结果即可.【详解】解:由题意,知:S菱形=12×2×3=3,故答案为3.考点:菱形的性质.15.从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解析:从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解:在这个问题中,样本是指从各学校共随机抽取的500名八年级男生体重,故答案为:从各学校共随机抽取的500名八年级男生体重.【点睛】本题考查统计中的总体与样本,属于基本题型.16..【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解解析:6013.【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解即可.【详解】解:如图,连接CD.∵∠ACB=90°,AC=5,BC=12,∴AB22A BCC+22512+=13,∵DE⊥AC,DF⊥BC,∠C=90°,∴四边形CFDE是矩形,∴EF=CD,由垂线段最短可得CD⊥AB时,线段EF的值最小,此时,S△ABC=12BC•AC=12AB•CD,即12×12×5=12×13•CD,解得:CD=60 13,∴EF=60 13.故答案为:60 13.【点睛】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.17.k<﹣1【分析】根据判别式的意义得到△=(2k+4)2﹣4k2<0,然后解不等式即可.【详解】∵关于x的一元二次方程x2+(2k+4)x+k2=0没有实数根,∴△=(2k+4)2﹣4k2<解析:k<﹣1【分析】根据判别式的意义得到△=(2k+4)2﹣4k2<0,然后解不等式即可.【详解】∵关于x的一元二次方程x2+(2k+4)x+k2=0没有实数根,∴△=(2k+4)2﹣4k2<0,解得k<﹣1.故答案为:k<﹣1.【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.18.x≠﹣1【分析】根据分母不能为零,可得答案.【详解】解:由题意,得x+1≠0,解得x≠﹣1,故答案为:x≠﹣1.【点睛】本题考查了函数自变量取值范围的求法.要使得本题式子有意义,必解析:x≠﹣1【分析】根据分母不能为零,可得答案.【详解】解:由题意,得x+1≠0,解得x≠﹣1,故答案为:x≠﹣1.【点睛】本题考查了函数自变量取值范围的求法.要使得本题式子有意义,必须满足分母不等于0.19.【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:;故答案为:.【点睛】本题考查列代数式,解题的关键是读懂题意.解析:303240 x y zx y z++++【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:303240x y zx y z++++;故答案为:303240x y zx y z++++.【点睛】本题考查列代数式,解题的关键是读懂题意.20.40【分析】根据旋转的性质得出AD=AC,∠DAE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC的度数即可.【详解】解:∵△ABC绕点A逆时针旋转至△AED,∠BAC解析:40【分析】根据旋转的性质得出AD =AC ,∠DAE =∠BAC =20°,求出∠DAE =∠CAE =20°,再求出∠DAC 的度数即可.【详解】解:∵△ABC 绕点A 逆时针旋转至△AED ,∠BAC =20°,∴AD =AC ,∠DAE =∠BAC =20°,∵AE 垂直平分CD 于点F ,∴∠DAE =∠CAE =20°,∴∠DAC =20°+20°=40°,即旋转角度数是40°,故答案为:40.【点睛】本题主要考查了图像旋转的性质以及垂直平分线的性质,从而得到边相等与角相等的条件.21.7【解析】【详解】因为ABCD 是正方形,所以AB=AD ,∠BFA=∠BAD=90°,则有∠ABF=∠DAE,又因为DE⊥a、BF⊥a,根据AAS 易证△AFB≌△DEA,所以AF=DE=4,BF 解析:7【解析】【详解】因为ABCD 是正方形,所以AB=AD ,∠BFA=∠BAD=90°,则有∠ABF=∠DAE ,又因为DE ⊥a 、BF ⊥a ,根据AAS 易证△AFB ≌△DEA ,所以AF=DE=4,BF=AE=3,则EF=AF+AE=4+3=7.22.【分析】直接开平方,求出方程的解即可.【详解】∵x2=0,开方得,,故答案为:.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.解析:120x x ==【分析】直接开平方,求出方程的解即可.【详解】∵x 2=0,开方得,120x x ==,故答案为:120x x ==.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.23.【分析】连接OC ,过点C 作CE⊥x 轴于E ,由直角三角形的性质可求BE =BC =1,CE =,由勾股定理可求OC 的长,据此进一步分析即可求解.【详解】如图,连接OC ,过点C 作CE⊥x 轴于点E , 解析:23-【分析】连接OC ,过点C 作CE ⊥x 轴于E ,由直角三角形的性质可求BE =12BC =1,CE =3,由勾股定理可求OC 的长,据此进一步分析即可求解.【详解】如图,连接OC ,过点C 作CE ⊥x 轴于点E ,∵四边形OBCD 是菱形,∴OD ∥BC ,∴∠BOD =∠CBE =60°,∵CE ⊥OE ,∴BE =12BC =1,CE 3 ∴2223OC OE CE =+=∴当点C 1在y 轴上时,点C 1的纵坐标有最小值为3-,故答案为:23-【点睛】本题主要考查了菱形的性质与勾股定理的综合运用,熟练掌握相关概念是解题关键.24.【分析】已知S△PAB=S矩形ABCD ,则可以求出△ABP的高,此题为“将军饮马”模型,过P点作直线l∥AB,作点A关于l的对称点E,连接AE,连接BE,则BE 的长就是所求的最短距离.【详解解析:41【分析】已知S△PAB=13S矩形ABCD,则可以求出△ABP的高,此题为“将军饮马”模型,过P点作直线l∥AB,作点A关于l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.【详解】解:设△ABP中AB边上的高是h.∵S△PAB=13S矩形ABCD,∴12AB•h=13AB•AD,∴h=23AD=2,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.在Rt△ABE中,∵AB=5,AE=2+2=4,∴BE=22225441+=+=AB AE,即PA+PB的最小值为41.故答案为:41.【点睛】本题主要考查的是勾股定理以及“将军饮马”的模型,“将军饮马”模型主要是用来解决最小值问题,掌握这模型是解题的关键.三、解答题25.(1)证明见解析;(2)证明见解析.【分析】(1)根据平行四边形的性质得到AB//CD,AB=CD,然后根据CE=DC,得到AB=EC,AB//EC,利用“一组对边平行且相等的四边形是平行四边形”判断即可;(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.【详解】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形;(2)∵由(1)知,四边形ABEC是平行四边形,∴FA=FE,FB=FC.∵四边形ABCD是平行四边形,∴∠ABC=∠D.又∵∠AFC=2∠ADC,∴∠AFC=2∠ABC.∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,∴四边形ABEC是矩形.【点睛】此题考查的知识点是平行四边形的判定与性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.26.(1)35x ;(2)原方程无解【分析】(1)分式方程两边同乘以(3+x)(3﹣x)去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;(2)分式方程两边同乘以(x+1)(x﹣1)去分母转化为整式方程,求出整式方程的解得到x的值,经检验即得结果.【详解】解:(1)方程两边同乘(3+x)(3﹣x),得9(3﹣x)=6(3+x),解这个方程,得x=35,检验:当x =35时,(3+x )(3﹣x )≠0, ∴x =35是原方程的解; (2)方程两边同乘(x +1)(x ﹣1),得4+x 2﹣1=(x ﹣1)2,解这个方程,得x =﹣1,检验:当x =﹣1时,(x +1)(x ﹣1)=0,∴x =﹣1是增根,原方程无解.【点睛】本题考查了分式方程的解法,属于基本题型,熟练掌握解分式方程的方法是解题的关键.27.1a 2--,当1a =-时,原式1=3【分析】 本题根据分式的除法和减法运算法则,结合平方差以及提公因式法将题目化简,然后从1-、0、1、2中选一个使得原分式有意义的值代入化简后的式子即可解答本题.【详解】 原式2(1)1111(2)(2)22a a a a a a a a a +--=-⨯=-=-+---, 由已知得:若使原分式有意义,需满足0a ≠,20a a -≠,240a -≠,即当0a =、1、2、2-时原分式无意义,故当1a =-时,原式11123=-=--. 【点睛】本题考查分式的化简求值,解题关键在于对平方差、完全平方公式等运算法则的运用,其次注意计算仔细即可.28.(1)见解析;(2)∠AED =75°.【分析】(1)先证明∠B =∠EAD ,然后利用SAS 可进行全等的证明;(2)先根据等腰三角形的性质可得∠BAE =50°,求出∠BAC 的度数,即可得∠AED 的度数.【详解】(1)证明:∵在平行四边形ABCD 中,AD ∥BC ,BC =AD ,∴∠EAD =∠AEB ,又∵AB =AE ,∴∠B =∠AEB ,∴∠B =∠EAD ,在△ABC 和△EAD 中,AB AE ABC EAD BC AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△EAD (SAS ).(2)解:∵AB =AE ,∴∠B =∠AEB ,∴∠BAE =50°,∴∠BAC =∠BAE+∠EAC =50°+25°=75°,∵△ABC ≌△EAD ,∴∠AED =∠BAC =75°.【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,注意掌握平行四边形的对边平行且相等的性质.29.(1)见解析;(2)152【分析】(1)由矩形的性质得到AB ∥CD ,再根据平行线的性质得到∠DFO=∠BEO 再证明△DOF ≌△BOE ,根据全等三角形的性质得到DF=BE ,从而得到四边形BEDF 是平行四边形;(2)先证明四边形BEDF 是菱形,再得到DE=BE ,EF ⊥BD ,OE=OF ,设AE=x ,则DE=BE=8-x 根据勾股定理求解即可.【详解】(1)证明:∵四边形ABCD 是矩形,∴AB ∥CD ,∴∠DFO =∠BEO .在△DOF 和△BOE 中 DFO BEO DOF BOE OD OB ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△DOF ≌△BOE(AAS ).∴DF =BE .又∵DF ∥BE ,∴四边形BEDF 是平行四边形.(2)解:∵DE =DF ,四边形BEDF 是平行四边形,∴四边形BEDF 是菱形.∴DE =BE ,EF ⊥BD ,OE =OF .设AE =x ,则DE =BE =8-x ,在Rt △ADE 中,根据勾股定理,有AE 2+AD 2=DE 2,∴x2+62=(8-x)2.解得x=74.∴DE=8-74=254.在Rt△ABD中,根据勾股定理,有AB2+AD2=BD2,∴BD=10.∴OD=12BD=5.在Rt△DOE中,根据勾股定理,有DE2-OD2=OE2,∴OE=154.∴EF=2OE=152.【点睛】考查了菱形的判定和性质、矩形的性质、平行四边形的判定和性质、全等三角形的判定和性质和勾股定理,解题关键是熟练掌握矩形的性质.30.(1)15344t-;(2)当t=52时,四边形MNQP为平行四边形,证明见解析;(3)AQ⊥CQ,证明见解析.【分析】(1)由勾股定理可求BD=5,由三角形的面积公式和S△DPQ=12(S△BED﹣S△BDP)可求解;(2)当t=52时,可得BP=52=12BE,由中位线定理可得MN∥BD,MN=12BD=5,PQ∥BD,PQ=12BD=5,可得MN∥PQ,MN=PQ,可得结论.(3)连接BQ,由等腰三角形的性质可得∠AQD+∠BQA=90°,由直角三角形的性质可得DQ=CQ,∠DCQ=∠CDQ,由“SAS”可证△ADQ≌△BCQ,可得∠AQD=∠BQC,即可得结论.【详解】解:(1)∵四边形ABCD是矩形,AB=3,BC=4,∴BC=4,CD=3,∴BD5,∴BD=BE=5,∵Q为DE的中点,∴S△DPQ=12S△DPE,∴S△DPQ=12(S△BED﹣S△BDP)=11135t3222⎛⎫⨯⨯-⨯⨯⎪⎝⎭=15344t-.故答案为:15344t.(2)当t=52时,四边形MNQP为平行四边形,理由如下:∵M、N分别为AB、AD的中点,∴MN∥BD,MN=12BD=52,∵t=52时,∴BP=52=12BE,且点Q是DE的中点,∴PQ∥BD,PQ=12BD=52,∴MN∥PQ,MN=PQ,∴四边形MNQP是平行四边形.(3)AQ⊥CQ.理由如下:如图,连接BQ,∵BD=BE,点Q是DE中点,∴BQ⊥DE,∴∠AQD+∠BQA=90°,∵在Rt△DCE中,点Q是DE中点,∴DQ=CQ,∴∠DCQ=∠CDQ,且∠ADC=∠BCD=90°,∴∠ADQ=∠BCQ,且BC=AD,DQ=CQ,∴△ADQ≌△BCQ(SAS),∴∠AQD=∠BQC,且∠AQD+∠BQA=90°,∴∠BQC+∠BQA=90°,∴∠AQC=90°,∴AQ⊥CQ.【点睛】本题考查平行四边形中的动点问题,关键在于熟练掌握矩形的性质,全等三角形的性质和判定.31.(1)详见解析;(2)10cm【分析】(1)由三角形中位线定理推知BD∥FC,2DE=BC,然后结合已知条件“EF∥DC”,利用两组对边相互平行得到四边形DCFE为平行四边形;(2)根据在直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC,即可得出四边形DCFE的周长=AB+BC,故BC=16﹣AB,然后根据勾股定理即可求得.【详解】(1)证明:∵D、E分别是AB、AC的中点,∴ED是Rt△ABC的中位线,∴ED∥BC.BC=2DE,又EF∥DC,∴四边形CDEF是平行四边形;(2)解:∵四边形CDEF是平行四边形;∴DC=EF,∵DC是Rt△ABC斜边AB上的中线,∴AB=2DC,∴四边形DCFE的周长=AB+BC,∵四边形DCFE的周长为16cm,AC的长8cm,∴BC=16﹣AB,∵在Rt△ABC中,∠ACB=90°,∴AB2=BC2+AC2,即AB2=(16﹣AB)2+82,解得:AB=10cm,【点睛】本题考查了平行四边形的判定和性质,三角形的中位线定理,直角三角形斜边中线的性质,勾股定理的应用等,熟练掌握性质定理是解题的关键.32.(1)(3,1);(2)作图见解析;26.【分析】(1)根据对称性即可得点A关于坐标原点O对称的点的坐标;(2)根据旋转的性质即可将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C,进而可得A1A的长.【详解】(1)∵A(﹣3,﹣1),∴点A关于坐标原点O对称的点的坐标为(3,1).故答案为:(3,1);(2)如图,△A1B1C即为所求,。
(完整版)苏科版八年级数学下册期中试卷及答案

(完整版)苏科版八年级数学下册期中试卷及答案一、选择题1.下面的图形中,是中心对称图形的是( ) A .B .C .D .2.下列调查中,适宜采用普查方式的是( ) A .对全国中学生使用手机情况的调查B .对五一节期间来花果山游览的游客的满意度调查C .环保部门对长江水域水质情况的调查D .对本校某班学生阅读课外书籍情况的调查3.平行四边形的一条边长为8,则它的两条对角线可以是( ) A .6和12B .6和10C .6和8D .6和64.已知12x <≤ ,则23(2)x x -+-的值为( ) A .2 x - 5B .—2C .5 - 2 xD .25.如图,已知正方形ABCD ,对角线的交点M (2,2).规定“把正方形ABCD 先沿x 轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD 的对角线交点M 的坐标变为( )A .(﹣2012,2)B .(﹣2012,﹣2)C .(﹣2013,﹣2)D .(﹣2013,2)6.用配方法解一元二次方程2620x x --=,以下正确的是( )A .2(3)2x -=B .2(3)11x -=C .2(3)11x +=D .2(3)2x +=7.两个反比例函数3y x =,6y x=在第一象限内的图像如图所示,点1P 、2P 、3P ……2020P 反比例函数6y x=图像上,它们的横坐标分别是1x 、2x 、3x ……2020x ,纵坐标分别是1,3,5,…,共2020个连续奇数,过点1P 、2P 、3P ……2020P 分别作y 轴的平行线,与反比例函数3y x=的图像交点依次是()11,Q x y 、()22,Q x y 、()33,Q x y ……()20202020,Q x y ,则2020y 等于( )A.2019.5 B.2020.5 C.2019 D.40398.我们把顺次连接四边形各边中点所得的四边形叫做中点四边形.若一个任意..四边形的面积为a,则它的中点四边形面积为()A.12a B.23a C.34a D.45a9.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:抛掷次数100200300400500正面朝上的频数5398156202244若抛掷硬币的次数为1000,则“正面朝上”的频数最接近()A.20 B.300 C.500 D.80010.如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG,下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=12AD.其中正确的有( )A.①②B.①②④C.①③④D.①②③④二、填空题11.在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为_____.12.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm2,则阴影部分的面积为_____cm2.13.如图,菱形ABCD的对角线AC、BD相交于点O,∠OBC=30°,则∠OCD=_____°.14.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是___.15.如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为_____.16.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=.17.如图,△ABC中,∠A=60°,∠ABC=80°,将△ABC绕点B逆时针旋转,得到△DBE,若DE∥BC,则旋转的最小度数为_____.18.如图,在菱形ABCD中,若AC=24 cm,BD=10 cm,则菱形ABCD的高为________cm.19.若点()23,在反比例函数ky x=的图象上,则k 的值为________. 20.在△ABC 中,点D ,E 分别为BC ,AC 的中点,若DE =2,则AB 的长为_____.三、解答题21.如图,在Rt △ABC 中,∠BAC =90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于点F .(1)求证:四边形ADCF 是菱形;(3)若AC =6,AB =8,求菱形ADCF 的面积. 22.如图,在▱ABCD 中,E 为BC 边上一点,且AB =AE (1)求证:△ABC ≌△EAD ;(2)若∠B =65°,∠EAC =25°,求∠AED 的度数.23.如图,在正方形网格中,△ABC 的顶点均在格点上,请在所给的直角坐标系中解答下列问题:(1)作出△ABC 关于原点O 成中心对称的△A 1B 1C 1;(2)直接写出:以A 、B 、C 为顶点的平形四边形的第四个顶点D 的坐标 .24.如图,在△ABC 中,点O 是AC 边上(端点除外)的一个动点,过点O 作直线MN∥BC.设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F ,连接AE 、AF .那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.25.已知关于x的方程x2﹣(k+3)x+3k=0.(1)若该方程的一个根为1,求k的值;(2)求证:不论k取何实数,该方程总有两个实数根.26.计算:242933 x x xx x-----27.定义:有一组对角是直角的四边形叫做“准矩形”;有两组邻边(不重复)相等的四边形叫做“准菱形”.如图①,在四边形ABCD中,若∠A=∠C=90°,则四边形ABCD是“准矩形”;如图②,在四边形ABCD中,若AB=AD,BC=DC,则四边形ABCD是“准菱形”.(1)如图,在边长为1的正方形网格中,A、B、C在格点(小正方形的顶点)上,请分别在图③、图④中画出“准矩形”ABCD和“准菱形”ABCD′.(要求:D、D′在格点上);(2)下列说法正确的有;(填写所有正确结论的序号)①一组对边平行的“准矩形”是矩形;②一组对边相等的“准矩形”是矩形;③一组对边相等的“准菱形”是菱形;④一组对边平行的“准菱形”是菱形.(3)如图⑤,在△ABC中,∠ABC=90°,以AC为一边向外作“准菱形”ACEF,且AC=EC,AF=EF,AE、CF交于点D.①若∠ACE=∠AFE,求证:“准菱形”ACEF是菱形;②在①的条件下,连接BD,若BD=,∠ACB=15°,∠ACD=30°,请直接写出四边形ACEF的面积.28.某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大?遇到哪一种灯的可能性最小?根据什么?【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据中心对称图形与轴对称图形的概念依次分析即可.【详解】解:A、B、C只是轴对称图形,D既是轴对称图形又是中心对称图形,故选D.【点睛】本题考查的是中心对称图形与轴对称图形,解答本题的关键是熟练掌握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫对称轴;在同一平面内,如果把一个图形绕某一点旋转180°,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.2.D解析:D【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【详解】解:A.对全国中学生使用手机情况的调查适合抽样调查;B.对五一节期间来花果山游览的游客的满意度调查适合抽样调查;C.环保部门对长江水域水质情况的调查适合抽样调查;D.对本校某班学生阅读课外书籍情况的调查适合普查;故选:D.【点睛】本题考查判别普查的方式,关键在于熟记抽样调查和普查的定义.3.A解析:A 【分析】由四边形ABCD 是平行四边形,根据平行四边形的对角线互相平分,即可求得OB 与OC 的长,然后根据三角形的三边关系,即可求得答案. 【详解】 解:如图:∵四边形ABCD 是平行四边形, ∴OA=OC=12AC ,OB=OD=12BD , 若BC=8,根据三角形三边关系可得:|OB-OC|<8<OB+OC .A 、6和12,则OB+OC=3+6=9>8,OB-OC=6-3=3<8,能组成三角形,故本选项符合题意;B 、6和10,则OB+OC=3+5=8,不能组成三角形,故本选项不符合题意;C 、6和8,则OB+OC=3+4=7<8,不能组成三角形,故本选项不符合题意;D 、6和6,则OB+OC=3+3=6<8,不能组成三角形,故本选项不符合题意; 故选:A . 【点睛】此题考查了平行线的性质与三角形三边关系,解题的关键是注意掌握平行四边形的对角线互相平分,注意三角形三边关系知识的应用.4.C解析:C 【分析】结合1 < x ≤ 2 ,根据绝对值和二次根式的进行计算,即可得到答案. 【详解】因为1 < x ≤ 2 ,所以23(2)x x -+-32x x -+-= 5 - 2 x.故选择C . 【点睛】本题考查不等式、绝对值和二次根式,解题的关键是掌握不等式、绝对值和二次根式.5.A解析:A 【分析】根据题意求得第1次、2次、3次变换后的对角线交点M 的对应点的坐标,即可得规律:第n 次变换后的点M 的对应点的为:当n 为奇数时为(2﹣n ,﹣2),当n 为偶数时为(2﹣n ,2),继而求得结果. 【详解】解:∵对角线交点M 的坐标为(2,2),根据题意得:第1次变换后的点M 的对应点的坐标为(2﹣1,﹣2),即(1,﹣2), 第2次变换后的点M 的对应点的坐标为:(2﹣2,2),即(0,2), 第3次变换后的点M 的对应点的坐标为(2﹣3,﹣2),即(﹣1,﹣2),第n 次变换后的点M 的对应点的为:当n 为奇数时为(2﹣n ,﹣2),当n 为偶数时为(2﹣n ,2),∴连续经过2014次变换后,正方形ABCD 的对角线交点M 的坐标变为(﹣2012,2). 故选:A . 【点睛】此题考查了点的坐标变化,对称与平移的性质.得到规律:第n 次变换后的对角线交点M 的对应点的坐标为:当n 为奇数时为(2﹣n ,﹣2),当n 为偶数时为(2﹣n ,2)是解此题的关键.6.B解析:B 【分析】利用完全平方公式的特征在方程的两边同时加上11即可. 【详解】解:2621111x x --+=,即26911x x -+=,所以2(3)11x -=. 故选:B. 【点睛】本题考查了配方法解一元二次方程,灵活利用完全平方公式是应用配方法解题的关键.7.A解析:A 【分析】主要是找规律,找出规律即可求出本题答案,先根据已知条件求出y 分别为1、3、5时x 的值,即可求出当2020y =时x 的值,再将其代入3y x=中即可求出2020y . 【详解】解:当1,3,52020y =⋅⋅⋅时,1x 、2x 、3x ...2020x 分别为6、2、65 (62020)将1x 、2x 、3x …2020x 代入3y x=, 得:1y 、2y 、3y …2020y202040392019.52y ==, 故选:A . 【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=kx(k ≠0)的图象是双曲线;图象上的点(x ,y )的横纵坐标的积是定值k ,即xy=k .8.A解析:A 【分析】由E 为AB 中点,且EF 平行于AC ,EH 平行于BD ,得到△BEK 与△ABM 相似,△AEN 与△ABM 相似,利用面积之比等于相似比的平方,得到△EBK 面积与△ABM 面积之比为1:4,且△AEN 与△EBK 面积相等,进而确定出四边形EKMN 面积为△ABM 的一半,同理得到四边形KFPM 面积为△BCM 面积的一半,四边形QGPM 面积为△DCM 面积的一半,四边形HQMN 面积为△DAM 面积的一半,四个四边形面积之和即为四个三角形面积之和的一半,即为四边形ABCD 面积的一半,即可得出答案. 【详解】解:如图,画任意四边形ABCD ,设AC 与EH ,FG 分别交于点N ,P ,BD 与EF ,HG 分别交于点K ,Q ,则四边形EFGH 即为它的中点四边形,∵E 是AB 的中点,EF//AC ,EH//BD , ∴△EBK ∽△ABM ,△AEN ∽△ABM , ∴EBK ABM S S ∆∆=14,S △AEN =S △EBK , ∴EKMN ABMS S ∆四边形=12, 同理可得:KFPM BCMS S ∆四边形=12,QGPM DCM S S ∆四边形=12,HQMN DAM S S ∆四边形=12,∴EFGH ABCDS S 四边形四边形=12, ∵四边形ABCD 的面积为a , ∴四边形EFGH 的面积为12a , 故选:A . 【点睛】本题考查了三角形中位线的性质,相似三角形的判定和性质,掌握知识点是解题关键.9.C解析:C【分析】随着实验次数的增加,正面向上的频率逐渐稳定到某个常数附近,据此求解即可.【详解】观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,所以抛掷硬币的次数为1000,则“正面朝上”的频数最接近10000.5500⨯=次,故选C.【点睛】本题考查利用频率估计概率的知识,解题的关键是了解在大量重复试验中,可以用频率估计概率.10.D解析:D【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=90°,∵点E、F、H分别是AB、BC、CD的中点,∴△BCE≌△CDF,∴∠ECB=∠CDF,∵∠BCE+∠ECD=90°,∴∠ECD+∠CDF=90°,∴∠CGD=90°,∴CE⊥DF,故①正确;在Rt△CGD中,H是CD边的中点,∴HG=12CD=12AD,故④正确;连接AH,同理可得:AH⊥DF,∵HG=HD=12CD,∴DK=GK,∴AH垂直平分DG,∴AG=AD,故②正确;∴∠DAG=2∠DAH,同理:△ADH≌△DCF,∴∠DAH=∠CDF,∵GH=DH,∴∠HDG=∠HGD,∴∠GHC=∠HDG+∠HGD=2∠CDF,∴∠CHG=∠DAG.故③正确.故选D.【点睛】运用了正方形的性质,全等三角形的判定与性质,等腰三角形的性质以及垂直平分线的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.二、填空题11.20【分析】利用频率估计概率,设原来红球个数为x个,根据摸取30次,有10次摸到白色小球结合概率公式可得关于x的方程,解方程即可得.【详解】设原来红球个数为x个,则有=,解得,x=20,解析:20【分析】利用频率估计概率,设原来红球个数为x个,根据摸取30次,有10次摸到白色小球结合概率公式可得关于x的方程,解方程即可得.【详解】设原来红球个数为x个,则有1010x=1030,解得,x=20,经检验x=20是原方程的根.故答案为20.【点睛】本题考查了利用频率估计概率和概率公式的应用,熟练掌握概率的求解方法以及分式方程的求解方法是解题的关键.12.10【分析】根据中心对称的性质判断出阴影部分的面积等于菱形的面积的一半,即可得出结果.【详解】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴△OEG≌△OFH,四边形OMAH解析:10【分析】根据中心对称的性质判断出阴影部分的面积等于菱形的面积的一半,即可得出结果.【详解】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,∴阴影部分的面积=12S菱形ABCD=12×20=10(cm2).故答案为:10.【点睛】本题考查了中心对称,菱形的性质,全等三角形的判定与性质等知识;熟记性质并判断出阴影部分的面积等于菱形的面积的一半是解题的关键.13.60【分析】根据菱形的性质:对角线互相垂直以及平分每一组对角解答即可.【详解】解:∵菱形ABCD的对角线AC、BD相交于点O,∴AC⊥BD,∠DBC=∠BDC=30°,∴∠DOC=90°解析:60【分析】根据菱形的性质:对角线互相垂直以及平分每一组对角解答即可.【详解】解:∵菱形ABCD的对角线AC、BD相交于点O,∴AC⊥BD,∠DBC=∠BDC=30°,∴∠DOC=90°,∴∠OCD=90°﹣30°=60°,故答案为:60.【点睛】本题主要考查菱形的性质,熟练掌握菱形的性质是解题的关键.14..【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解解析:6013.【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出求解即可.【详解】解:如图,连接CD.∵∠ACB=90°,AC=5,BC=12,∴AB22A BCC+22512+=13,∵DE⊥AC,DF⊥BC,∠C=90°,∴四边形CFDE是矩形,∴EF=CD,由垂线段最短可得CD⊥AB时,线段EF的值最小,此时,S△ABC=12BC•AC=12AB•CD,即12×12×5=12×13•CD,解得:CD=60 13,∴EF=60 13.故答案为:60 13.【点睛】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.15.18【分析】根据直角三角形的性质得到DF=8,根据EF=1,得到DE=9,根据三角形中位线定理解答即可.【详解】解:∵∠AFB=90°,点D是AB的中点,∴DF=AB=8,∵EF=1,解析:18【分析】根据直角三角形的性质得到DF=8,根据EF=1,得到DE=9,根据三角形中位线定理解答即可.【详解】解:∵∠AFB=90°,点D是AB的中点,∴DF=12AB=8,∵EF=1,∴DE=9,∵D、E分别是AB,AC的中点,∴BC=2DE=18,故答案为:18【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.16..【解析】试题分析:根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠解析:020.【解析】试题分析:根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.解:如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案为20°.17.40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点解析:40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点B逆时针旋转,得到△DBE,∴∠E=∠C=40°,∵DE∥BC,∴∠CBE=∠E=40°,∴旋转的最小度数为40°,故答案为:40°.【点睛】本题主要考查了旋转的性质以及平行线的性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.18.【分析】先根据菱形的面积=两条对角线积的一半得出面积,再求出菱形的边长,由面积即可得出菱形的高.【详解】解:作DE⊥AB于E,如图所示:∵四边形ABCD是菱形,对角线AC=24,BD=1解析:120 13【分析】先根据菱形的面积=两条对角线积的一半得出面积,再求出菱形的边长,由面积即可得出菱形的高.【详解】解:作DE⊥AB于E,如图所示:∵四边形ABCD是菱形,对角线AC=24,BD=10,∴AC⊥BD,OA=12AC=12,OB=12BD=5,菱形ABCD的面积=12AC·BD=12×24×10=120,2212+5,又∵菱形ABCD的面积=AB·DE=120,∴DE=120 13,故答案为:120 13.【点睛】本题考查了菱形的性质、勾股定理、菱形面积的计算;根据菱形的性质由勾股定理求出边长是解题的关键.19.6【详解】解:由题意知:k=3×2=6故答案为:6解析:6【详解】解:由题意知:k=3×2=6故答案为:620.4【分析】根据三角形中位线定理即可得到结论.【详解】解:∵在△ABC中,点D,E分别为BC,AC的中点,∴DE是△ABC的中位线,∵DE=2,∴AB=4,故答案为:解析:4【分析】根据三角形中位线定理即可得到结论.【详解】解:∵在△ABC中,点D,E分别为BC,AC的中点,∴DE是△ABC的中位线,∴AB=2DE,∵DE=2,∴AB=4,故答案为:4.【点睛】本题主要考查中位线的定义和性质,解决本题的关键是要熟练掌握中位线的定义和性质.三、解答题21.(1)详见解析;(2)24【分析】(1)可先证得△AEF≌△DEB,可求得AF=DB,可证得四边形ADCF为平行四边形,再利用直角三角形的性质可求得AD=CD,可证得结论;(2)将菱形ADCF的面积转换成△ABC的面积,再用S△ABC的面积=12AB•A C,结合条件可求得答案.【详解】(1)证明:∵E是AD的中点∴AE=DE∵AF∥BC∴∠AFE=∠DBE在△AEF和△DEB中AFE DBEDEB AEF AE DE∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AEF≌△DEB(AAS)∴AF=DB∵D是BC的中点∴BD=CD=AF∴四边形ADCF是平行四边形∴AD =CD =12BC ∴四边形ADCF 是菱形;(2)解:设AF 到CD 的距离为h ,∵AF ∥BC ,AF =BD =CD ,∠BAC =90°,AC =6,AB =8∴S 菱形ADCF =CD•h =12BC•h =S △ABC =12AB•AC =168242⨯⨯=. 【点睛】本题主要考查菱形的判定和性质,全等三角形的判定与性质及直角三角形的性质,掌握菱形的判定方法是解题的关键.22.(1)见解析;(2)∠AED =75°.【分析】(1)先证明∠B =∠EAD ,然后利用SAS 可进行全等的证明;(2)先根据等腰三角形的性质可得∠BAE =50°,求出∠BAC 的度数,即可得∠AED 的度数.【详解】(1)证明:∵在平行四边形ABCD 中,AD ∥BC ,BC =AD ,∴∠EAD =∠AEB ,又∵AB =AE ,∴∠B =∠AEB ,∴∠B =∠EAD ,在△ABC 和△EAD 中, AB AE ABC EAD BC AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△EAD (SAS ).(2)解:∵AB =AE ,∴∠B =∠AEB ,∴∠BAE =50°,∴∠BAC =∠BAE+∠EAC =50°+25°=75°,∵△ABC ≌△EAD ,∴∠AED =∠BAC =75°.【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,注意掌握平行四边形的对边平行且相等的性质.23.(1)作图见解析;(2)D(1,1),(-5,3),(-3,-1)【分析】(1)根据关于原点对称的点的坐标特征分别写出点A 、B 、C 的对应点A 1、B 1、C 1的坐标,然后描点即可得到△A1B1C1;(2)分类讨论:分别以AB、AC、BC为对角线画平行四边形,根据网格的特点,确定对角线后找对边平行,即可写出D点的坐标.【详解】---,根据关于原点对称的点解:(1)如图,点A、B、C的坐标分别为(1,0),(4,1),(2,2)--,描点连线,的坐标特征,则点A、B、C关于原点对称的点分别为(1,0),(4,1),(2,2)△A1B1C1即为所作:(2)分别以AB、AC、BC为对角线画平行四边形,如下图所示:---,则由图可知D点的坐标分别为:(3,1),(1,1),(5,3)---.故答案为:(1,1),(5,3),(3,1)【点睛】本题考查了中心对称作图即平行四边形存在问题,在直角坐标系中,已知平行四边形的三个点的坐标,确定第四个点的坐标,以对角线作为分类讨论,不容易漏掉平行四边形的各种情况.24.当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.证明见解析.【分析】当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF,而OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.【详解】当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.证明:如图,∵CE平分∠BCA,∴∠1=∠2,又∵MN∥BC,∴∠1=∠3,∴∠3=∠2,∴EO=CO,同理,FO=CO,∴EO=FO,又∵OA=OC,∴四边形AECF是平行四边形,∵CF是∠BCA的外角平分线,∴∠4=∠5,又∵∠1=∠2,∴∠1+∠5=∠2+∠4,又∵∠1+∠5+∠2+∠4=180°,∴∠2+∠4=90°,∴平行四边形AECF是矩形.【点睛】本题考查了角平分线的性质、平行线的性质、平行四边形的判定、矩形的判定.解题的关键是利用对角线互相平分的四边形是平行四边形开证明四边形AECF是平行四边形,并证明∠ECF是90°.25.(1)k=1;(2)证明见解析.【分析】(1)把x=1代入方程,即可求得k的值;(2)求出根的判别式是非负数即可.【详解】(1)把x=1代入方程x2﹣(k+3)x+3k=0得1﹣(k﹣3)+3k=0,1﹣k﹣3+3k=0解得k=1;(2)证明:1,(3),3a b k c k==-+=24b ac∆=-∴△=(k+3)2﹣4•3k =(k﹣3)2≥0,所以不论k取何实数,该方程总有两个实数根.【点睛】本题考查了一元二次方程的解以及根的判别式,熟练掌握相关知识点是解题关键. 26.3x-【分析】先把分式进行合并,再进行因式分解,然后约分,即可得到答案.【详解】解:原式22242969(3)3333x x x x x xxx x x--+-+-====----;【点睛】本题考查了分式的混合运算,分式的化简求值,解题的关键是熟练掌握运算法则进行解题.27.(1)见解析;(2)①②③④;(3)①证明见解析;②23【分析】(1)根据准矩形和准菱形的特点画图即可;(2)根据矩形的判定定理和菱形的判定定理结合准矩形和准菱形的性质对每一个选项进行推断即可;(3)①先根据已知得出△ACF≌△ECF,再结合∠ACE=∠AFE可推出AC∥EF,AF∥CE,则证明了准菱形ACEF是平行四边形,又因为AC=EC即可得出准菱形ACEF是菱形;②取AC的中点M,连接BM、DM,根据四边形ACEF是菱形可得A、B、C、D四点共圆,点M是圆心,根据圆周角定理可推出∠BMD=90°,即可求出AC,再根据∠ACD=30°即可求出AD,CD的长,则可求出菱形的面积.【详解】(1);(2)①因为∠A=∠C=90°,结合一组对边平行可以判断四边形为矩形,故①正确;②因为∠A=∠C=90°,结合一组对边相等可以判断四边形为矩形,故②正确;③因为AB=AD,BC=DC,结合一组对边相等可以判断四边形为菱形,故③正确;④因为AB=AD,BC=DC,结合一组对边平行可以判断四边形为菱形,故④正确;故答案为:①②③④;(3)①证明:∵AC=EC,AF=EF,CF=CF,∴△ACF≌△ECF(SSS).∴∠ACF=∠ECF,∠AFC=∠EFC,∵∠ACE=∠AFE,∴∠ACF=∠EFC,∠ECF=∠AFC,∴AC∥EF,AF∥CE,∴准菱形ACEF是平行四边形,∵AC=EC,∴准菱形ACEF是菱形;②如图:取AC的中点M,连接BM、DM,∵四边形ACEF是菱形,∴AE⊥CF,∠ADC=90°,又∵∠ABC=90°,∴A、B、C、D四点共圆,点M是圆心,∵∠ACB=15°,∴∠AMB=30°,∵∠ACD=30°,∴∠AMD=60°,∴∠BMD=90°,∴△BMD是等腰直角三角形,∴BM=DM=22BD=222=1,∴AC=2(直角三角形斜边上的中线等于斜边的一半),∴AD=AC×sin30°=1,CD=AC×cos30°3∴菱形ACEF的面积=12×13×4=3【点睛】本题考查了矩形的判定和性质,菱形的判定和性质,圆周角定理,全等三角形的判定和性质,掌握知识点是解题关键.28.人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.【分析】根据在这几种灯中,每种灯时间的长短,即可得出答案.【详解】因为绿灯持续的时间最长,黄灯持续的时间最短,所以人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.【点睛】本题考查了事件发生的可能性的大小,根据时间长短确定可能性的大小是解答的关键.。
【苏教版】八年级下学期数学《期中考试试卷》及答案解析

2020-2021学年第二学期期中测试苏教版八年级试题一.选择题(共6小题,满分12分,每小题2分)1.(2分)要使代数式√2x −3有意义,则x 的取值范围是( ) A .x >32 B .x <32C .x ≥32D .x ≤322.(2分)若分式x−22x+1的值为零,则x 的值等于( ) A .﹣3B .0C .2D .33.(2分)反比例函数y =−1x,下列说法不正确的是( ) A .图象经过点(1,﹣1) B .图象位于第二、四象限C .图象关于直线y =﹣x 对称D .y 随x 的增大而增大4.(2分)下列计算正确的是( ) A .√9=±3B .√−83=2C .(√5)2=√5D .√22=25.(2分)暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x 套,由题意列方程正确的是( ) A .600x =800x−40B .600x−40=800xC .600x=800x+40D .600x+40=800x6.(2分)函数y =kx +k 与y =kx (k ≠0)在同一平面直角坐标系的图象可能是( )A .B .C .D .二.填空题(共10小题,满分30分,每小题3分) 7.(3分)计算:√3−2√27= .8.(3分)如图是一个可以自由转动的转盘,转盘分成四个扇形,标号分别为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个数字.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形区域).指针指向扇形Ⅰ的概率是 .9.(3分)在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为 人.10.(3分)已知反比例函数y =k−1x 的图象经过点(2,﹣4),则k 的值为 .11.(3分)若关于x 的分式方程x x−3+2a 3−x=2a 无解,则a 的值为 .12.(3分)如果方程kx+2+x 2x+4=0不会产生增根,那么k 的取值范围是 .13.(3分)如果最简二次根式√3a −8与√17−2a 可以合并,那么使√4a −2x 有意义的x 的取值范围是 .14.(3分)观察下列等式: ①√3+1=√3−1(√3+1)(√3−1)=√3−12;②√5+√3=√5−√3(√5+√3)(√5−√3)=√5−√32③√7+√5=√7−√5(√7+√5)(√7−√5)=√7−√52…参照上面等式计算方法计算:1+√3+√3+√5+√5+√7+⋯+3√11+√101= .15.(3分)如图是三个反比例函数y =k1x ,y =k2x ,y =k3x 在x 轴上方的图象,由此观察得到k 1,k 2,k 3的大小关系为 .16.(3分)如图,在Rt △ABC 中,∠C =90°,AC =BC ,BC ∥x 轴,点A 、B 都在反比例函数y =10x 上,点C在反比例函数y=4x 上,则AB = .三.解答题(共10小题,满分78分)17.(8分)计算题:(1)(√6−√2)×3√2−6√13;(2)(√5+1)(√5−1)﹣(√3−√2)2.18.(8分)解方程:(1)1x−2=4x2−4;(2)xx+1=2x3x+3+1.19.(7分)先化简,再求值:(5m−3+13−m)÷4mm2−6m+9,其中m=9.20.(6分)我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:(1)本次调查共抽取了多少名学生? 并补全条形统计图;(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?21.(8分)体育文化公司为某学校捐赠甲、乙两种品牌的体育器材,甲品牌有A、B两种型号,乙品牌有C、D、E三种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)下列事件是不可能事件的是.A.选购乙品牌的D型号B.既选购甲品牌也选购乙品牌C.选购甲品牌的A型号和乙品牌的D型号D.只选购甲品牌的A型号(2)写出所有的选购方案(用列表法或树状图);(3)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少? 22.(8分)如图,一次函数y1=ax+b与反比例函数y2=kx的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.(1)求一次函数y1的表达式与反比例函数y2的表达式;(2)当y1<y2,时,直接写出自变量x的取值范围为;(3)点P是x轴上一点,当S△P AC=45S△AOB时,请直接写出点P的坐标为.23.(8分)为防控新冠肺炎,某药店用1000元购进若干医用防护口罩,很快售完,接着又用2500元购进第二批口罩,已知第二批所购口罩的数量是第一批所购口罩数的2倍,且每只口罩的进价比第一批的进价多0.5元.求第一批口罩每只的进价是多少元?24.(8分)我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用符号表示为S =√14[a 2b 2−(a 2+b 2−c 22)2](其中a ,b ,c 为三角形的三边长,S 为三角形的面积).请利用这个公式求出当a =√5,b =3,c =2√5时的三角形的面积.25.(8分)我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式, 如:x+1x−1=x−1+2x−1=x−1x−1+2x−1=1+2x−1; 2x−3x+1=2x+2−5x+1=2x+2x+1+−5x+1=2+(−5x+1). (1)下列分式中,属于真分式的是: (填序号) ①a−2a+1;②x 2x+1;③2bb +3;④a 2+3a −1.(2)将假分式4a+32a−1化成整式与真分式的和的形式为:4a+32a−1= + ;(3)将假分式a 2+3a−1化成整式与真分式的和的形式:a 2+3a−1= + .26.(9分)已知一次函数y =kx +b 与反比例函数y =mx的图象交于A (﹣3,2)、B (1,n )两点. (1)求一次函数和反比例函数的表达式; (2)求△AOB 的面积;(3)点P 在x 轴上,当△P AO 为等腰三角形时,直接写出点P 的坐标.答案与解析一.选择题(共6小题,满分12分,每小题2分)1.(2分)要使代数式√2x−3有意义,则x的取值范围是()A.x>32B.x<32C.x≥32D.x≤32【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.【解答】解:根据题意知2x﹣3≥0,解得x≥3 2,故选:C.【点评】本题考查的是二次根式有意义的条件,熟知二次根式中的被开方数是非负数是解答此题的关键.2.(2分)若分式x−22x+1的值为零,则x的值等于()A.﹣3B.0C.2D.3【分析】根据分式值为零的条件列出x﹣2=0,2x+1≠0,解方程和不等式得到答案.【解答】解:要使分式x−22x+1的值为零,必须x﹣2=0,2x+1≠0,解得,x=2,故选:C.【点评】本题考查的是分式的值为零的条件,掌握分式值为零的条件是分子等于零且分母不等于零是解题的关键.3.(2分)反比例函数y=−1x,下列说法不正确的是()A.图象经过点(1,﹣1)B.图象位于第二、四象限C.图象关于直线y=﹣x对称D.y随x的增大而增大【分析】反比例函数y=kx(k≠0)的图象k>0时位于第一、三象限,在每个象限内,y随x的增大而减小;k<0时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.【解答】解:A、图象经过点(1,﹣1),正确;B、图象位于第二、四象限,故正确;C、双曲线关于直线y=﹣x成轴对称,正确;D、在每个象限内,y随x的增大而增大,故错误,【点评】本题考查了反比例函数图象的性质:①、当k >0时,图象分别位于第一、三象限;当k <0时,图象分别位于第二、四象限.②、当k >0时,在同一个象限内,y 随x 的增大而减小;当k <0时,在同一个象限,y 随x 的增大而增大.注意反比例函数的图象应分在同一象限和不在同一象限两种情况分析. 4.(2分)下列计算正确的是( ) A .√9=±3B .√−83=2C .(√5)2=√5D .√22=2【分析】根据算术平方根、立方根以及实数的平方的计算方法,逐项判断即可. 【解答】解:∵√9=3, ∴选项A 不符合题意;∵√−83=−2, ∴选项B 不符合题意;∵(√5)2=5∴选项C 不符合题意;∵√22=2,∴选项D 符合题意. 故选:D .【点评】此题主要考查了实数的运算,算术平方根、立方根的含义和求法,要熟练掌握.5.(2分)暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x 套,由题意列方程正确的是( ) A .600x =800x−40 B .600x−40=800xC .600x=800x+40D .600x+40=800x【分析】根据第一次进书的总钱数÷第一次购进套数=第二次进书的总钱数÷第二次购进套数列方程可得.【解答】解:若设书店第一次购进该科幻小说x 套, 由题意列方程正确的是600x=800x+40,【点评】本题考查由实际问题抽象出分式方程,解题的关键是理解题意找到题目蕴含的相等关系.6.(2分)函数y=kx+k与y=kx(k≠0)在同一平面直角坐标系的图象可能是()A.B.C.D.【分析】分两种情况讨论,当k>0时,分析出一次函数和反比例函数所过象限;再分析出k<0时,一次函数和反比例函数所过象限,符合题意者即为正确答案.【解答】解:①当k>0时,y=kx+k过一、二、三象限;y=kx(k≠0)过一、三象限;②当k<0时,y=kx+k过二、三、四象象限;y=k x(k≠0)过二、四象限.观察图形可知,只有B选项符合题意.故选:B.【点评】本题主要考查了反比例函数的图象和一次函数的图象,熟悉两函数中k的符号对函数图象的影响是解题的关键.二.填空题(共10小题,满分30分,每小题3分)7.(3分)计算:√3−2√27=﹣5√3.【分析】先分母有理化,再把√27化简,然后合并即可.【解答】解:原式=√3−6√3=﹣5√3.故答案为﹣5√3.【点评】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.8.(3分)如图是一个可以自由转动的转盘,转盘分成四个扇形,标号分别为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个数字.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形区域).指针指向扇形Ⅰ的概率是38.【分析】首先计算出扇形Ⅰ的圆心角,再求扇形I 的面积与圆的面积比即可. 【解答】解:扇形Ⅰ的圆心角:360°﹣60°﹣120°﹣45°=135°, 设圆的半径为r ,则指针指向扇形Ⅰ的概率是:135π⋅r 2360⋅π⋅r 2=38,故答案为:38.【点评】此题主要考查了概率,关键是掌握概率公式.9.(3分)在一个有15万人的小镇,随机调查了1000人,其中200人会在日常生活中进行垃圾分类,那么该镇在日常生活中会进行垃圾分类的人数大约为 30000 人.【分析】先求出样本中会进行垃圾分类的人数所占的百分比,再乘以小镇的总人数即可. 【解答】解:由题意可得,该镇在日常生活中会进行垃圾分类的人数大约为: 150000×2001000=30000(人). 故答案为:30000.【点评】本题考查了用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确. 10.(3分)已知反比例函数y =k−1x的图象经过点(2,﹣4),则k 的值为 ﹣7 . 【分析】将已知点的坐标代入解析式,构造方程进而求解. 【解答】解:∵反比例函数y =k−1x 的图象经过点(2,﹣4), ∴k ﹣1=2×(﹣4)=﹣8, 解得k =﹣7. 故答案为﹣7.【点评】题主要考查了反比例函数图象上点的坐标特征,反比例函数图象上的点(x ,y )的横纵坐标的积是定值k,即xy=k.11.(3分)若关于x的分式方程xx−3+2a3−x=2a无解,则a的值为0.5或1.5.【分析】直接解分式方程,再分类讨论当1﹣2a=0时,当1﹣2a≠0时,分别得出答案.【解答】解:xx−3+2a3−x=2a,去分母得:x﹣2a=2a(x﹣3),整理得:(1﹣2a)x=﹣4a,当1﹣2a=0时,方程无解,故a=0.5;当1﹣2a≠0时,x=4a2a−1=3时,分式方程无解,则a=1.5,则a的值为0.5或1.5.故答案为:0.5或1.5.【点评】此题主要考查了分式方程的解,正确分类讨论是解题关键.12.(3分)如果方程kx+2+x2x+4=0不会产生增根,那么k的取值范围是k≠1.【分析】先解方程,再根据不会产生增根,即可得出k的取值范围.【解答】解:kx+2+x2x+4=0,去分母得,2k+x=0,当x=﹣2时,会产生增根,把x=﹣2代入整式方程得,2k﹣2=0,解得k=1,∴解方程kx+2+x2x+4=0时,不会产生增根,实数k的取值范围为k≠1.故答案是:k≠1.【点评】本题考查了分式方程的解,解题关键是要掌握方程的解的定义,使方程成立的未知数的值叫做方程的解.13.(3分)如果最简二次根式√3a−8与√17−2a可以合并,那么使√4a−2x有意义的x的取值范围是x ≤10.【分析】根据二次根式可合并,可得同类二次根式,根据同类二次根式,可得a的值,根据被开方数是非负数,可得答案.【解答】解:由最简二次根式√3a−8与√17−2a可以合并,得3a﹣8=17﹣2a.解得a =5.由√4a −2x 有意义,得 20﹣2x ≥0,解得x ≤10, 故答案为:x ≤10.【点评】本题考查了同类二次根式,利用同类二次根式得出关于a 的方程是解题关键. 14.(3分)观察下列等式:①√3+1=√3−1(√3+1)(√3−1)=√3−12;②√5+√3=√5−√3(√5+√3)(√5−√3)=√5−√32③√7+√5=√7−√5(√7+√5)(√7−√5)=√7−√52…参照上面等式计算方法计算:1+√3+√3+√5+√5+√7+⋯+3√11+√101= √101−12.【分析】先分母有理化,然后合并即可. 【解答】解:原式=√3−12+√5−√32+√7−√52+⋯+√101−√992=√101−12.故答案为√101−12. 【点评】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.15.(3分)如图是三个反比例函数y =k 1x ,y =k 2x ,y =k3x 在x 轴上方的图象,由此观察得到k 1,k 2,k 3的大小关系为 k 1<k 2<k 3 .【分析】本题考查反比例函数与的图象特点.【解答】解:读图可知:三个反比例函数y =k 1x 的图象在第二象限;故k 1<0;y =k 2x ,y =k3x 在第一象限;且y =k3x 的图象距原点较远,故有:k 1<k 2<k 3;综合可得:k 1<k 2<k 3.故填k 1<k 2<k 3.【点评】反比例函数y =kx的图象是双曲线,当k >0时,它的两个分支分别位于第一、三象限;当k <0时,它的两个分支分别位于第二、四象限.且图象距原点越远,k 的绝对值越大.16.(3分)如图,在Rt △ABC 中,∠C =90°,AC =BC ,BC ∥x 轴,点A 、B 都在反比例函数y =10x 上,点C 在反比例函数y =4x 上,则AB = 3√2 .【分析】设C (a ,4a),AC =BC =m ,则A (a ,4a+m ),B (a +m ,4a),根据反比例函数系数k 的几何意义得到a (4a+m )=(a +m )•4a=10,解得m =3,利用勾股定理求得AB =3√2.【解答】解:设C (a ,4a),AC =BC =m ,∴A (a ,4a+m ),B (a +m ,4a),∵点A 、B 都在反比例函数y =10x上, ∴a (4a+m )=(a +m )•4a=10,解得m =3, ∴AC =BC =3,在Rt △ABC 中,AB =√AC 2+BC 2=3√2, 故答案为3√2.【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数k 的几何意义,等腰直角三角形的性质,表示出点的坐标是关键. 三.解答题(共10小题,满分78分) 17.(8分)计算题:(1)(√6−√2)×3√2−6√13;(2)(√5+1)(√5−1)﹣(√3−√2)2.【分析】(1)直接利用二次根式的混合运算法则进而计算得出答案;(2)直接利用乘法公式计算得出答案.【解答】解:(1)(√6−√2)×3√2−6√1 3=√6×3√2−√2×3√2−√363=6√3−6−2√3=4√3−6;(2)(√5+1)(√5−1)−(√3−√2)2=(√5)2−12−[(√3)2−2×√3×√2+(√2)2]=5−1−(3−2√6+2)=2√6−1.【点评】此题主要考查了二次根式的混合运算,正确掌握相关运算法则是解题关键.18.(8分)解方程:(1)1x−2=4x2−4;(2)xx+1=2x3x+3+1.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:x+2=4,解得:x=2,经检验x=2是增根,分式方程无解;(2)去分母得:3x=2x+3x+3,解得:x=−3 2,经检验x=−32是分式方程的解.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.19.(7分)先化简,再求值:(5m−3+13−m)÷4mm2−6m+9,其中m=9.【分析】根据分式的混合运算顺序进行化简,再代入值即可.【解答】解:原式=5−1m−3×(m−3)24m=m−3m, 当m =9时, 原式=9−39=23.【点评】本题考查了分式的化简求值,解决本题的关键是分式的混合运算.20.(6分)我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:(1)本次调查共抽取了多少名学生? 并补全条形统计图; (2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名? 【分析】(1)根据统计图中的数据可以求得本次抽取的学生数;补全条形统计图即可; (2)根据统计图中的数据可以求得“理解”所占扇形的圆心角为120400×360°=108°;(3)由8000×(40%+120400)=5600(名)即可. 【解答】解:(1)本次调查共抽取学生为:205%=400(名),∴不太了解的学生为:400﹣120﹣160﹣20=100(名), 补全条形统计图如下:(2)“理解”所占扇形的圆心角是:120400×360°=108°;(3)8000×(40%+120400)=5600(名), 所以“理解”和“了解”的共有学生5600名.【点评】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.(8分)体育文化公司为某学校捐赠甲、乙两种品牌的体育器材,甲品牌有A 、B 两种型号,乙品牌有C 、D 、E 三种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠. (1)下列事件是不可能事件的是 D . A .选购乙品牌的D 型号 B .既选购甲品牌也选购乙品牌C .选购甲品牌的A 型号和乙品牌的D 型号 D .只选购甲品牌的A 型号(2)写出所有的选购方案(用列表法或树状图);(3)如果在上述选购方案中,每种方案被选中的可能性相同,那么A 型器材被选中的概率是多少? 【分析】(1)根据不可能事件和随机随机的定义进行判断; (2)根据题意画出树状图得出所有等可能的情况数即可; (3)找出A 型器材被选中的结果数,然后根据概率公式求解. 【解答】解:(1)只选购甲品牌的A 型号为不可能事件. 故答案为D ;(2)画树状图为:共有6种等可能的结果数,分别是AC,AD,AE,BC,BD,BE;(3)A型器材被选中的结果数为3,所以A型器材被选中的概率=36=12.【点评】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.22.(8分)如图,一次函数y1=ax+b与反比例函数y2=kx的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.(1)求一次函数y1的表达式与反比例函数y2的表达式;(2)当y1<y2,时,直接写出自变量x的取值范围为x>8或0<x<2;(3)点P是x轴上一点,当S△P AC=45S△AOB时,请直接写出点P的坐标为P(3,0)或P(﹣3,0).【分析】(1)由待定系数法即可得到结论;(2)根据图象中的信息即可得到结论;(3)先求得D的坐标,然后根据S△AOB=S△AOD﹣S△BOD求得△AOB的面积,即可求得S△P AC=45S△AOB=24,根据中心对称的性质得出OA=OC,即可得到S△APC=2S△AOP,从而得到2×12OP×8=24,求得OP,即可求得P的坐标.【解答】解:(1)将A (2,8),B (8,2)代入y =ax +b 得{2a +b =88a +b =2,解得{a =−1b =10,∴一次函数为y =﹣x +10,将A (2,8)代入y 2=kx 得8=k2,解得k =16, ∴反比例函数的解析式为y =16x ;(2)由图象可知,当y 1<y 2时,自变量x 的取值范围为:x >8或0<x <2, 故答案为x >8或0<x <2;(3)由题意可知OA =OC , ∴S △APC =2S △AOP ,把y =0代入y 1=﹣x +10得,0=﹣x +10,解得x =10, ∴D (10,0),∴S △AOB =S △AOD ﹣S △BOD =12×10×8−12×10×2=30, ∵S △P AC =45S △AOB =45×30=24, ∴2S △AOP =24,∴2×12OP ×y A =24,即2×12OP ×8=24, ∴OP =3,∴P (3,0)或P (﹣3,0), 故答案为P (3,0)或P (﹣3,0).【点评】本题考查了一次函数与反比例函数的交点问题,三角形的面积的计算,待定系数法求函数的解析式,数形结合是解题的关键.23.(8分)为防控新冠肺炎,某药店用1000元购进若干医用防护口罩,很快售完,接着又用2500元购进第二批口罩,已知第二批所购口罩的数量是第一批所购口罩数的2倍,且每只口罩的进价比第一批的进价多0.5元.求第一批口罩每只的进价是多少元?【分析】设第一批口罩每只的进价是x 元,则第二批口罩每只的进价是(x +0.5)元,根据数量=总价÷单价结合第二批所购口罩的数量是第一批所购口罩数的2倍,即可得出关于x 的分式方程,解之经检验后即可得出结论.【解答】解:设第一批口罩每只的进价是x 元,则第二批口罩每只的进价是(x +0.5)元, 依题意,得:2500x+0.5=2×1000x, 解得:x =2,经检验,x =2是原方程的解,且符合题意. 答:第一批口罩每只的进价是2元.【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.24.(8分)我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用符号表示为S =√14[a 2b 2−(a 2+b 2−c 22)2](其中a ,b ,c 为三角形的三边长,S 为三角形的面积).请利用这个公式求出当a =√5,b =3,c =2√5时的三角形的面积. 【分析】根据二次根式的混合计算解答即可. 【解答】解:∵a =√5,b =3,c =2√5, ∴a 2=5,b 2=9,c 2=20,∴三角形的面积S =√14[a 2b 2−(a 2+b 2−c 22)2]=√14[45−(5+9−202)2]=√14(45−9)=3. 【点评】此题考查二次根式的应用,关键是根据二次根式的混合计算解答.25.(8分)我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式, 如:x+1x−1=x−1+2x−1=x−1x−1+2x−1=1+2x−1;2x−3x+1=2x+2−5x+1=2x+2x+1+−5x+1=2+(−5x+1).(1)下列分式中,属于真分式的是: ③ (填序号) ①a−2a+1;②x 2x+1;③2bb 2+3;④a 2+3a 2−1.(2)将假分式4a+32a−1化成整式与真分式的和的形式为:4a+32a−1= 2 +52a−1 ;(3)将假分式a 2+3a−1化成整式与真分式的和的形式:a 2+3a−1= a +1 + 4a−1.【分析】(1)利用题中的新定义判断即可; (2)将原式分子变形后,化简即可得到真分式; (3)将原式分子变形后,化简即可得到真分式. 【解答】解:(1)根据题意得:2b b +3属于真分式;(2)4a+32a−1=2(2a−1)+52a−1=2+52a−1;(3)a 2+3a−1=a 2−1+4a−1=a +1+4a−1.故答案为:(1)③;(2)2,52a−1;(3)a +1,4a−1.【点评】此题考查了分式的混合运算,整式,以及分式的定义,熟练掌握运算法则是解本题的关键. 26.(9分)已知一次函数y =kx +b 与反比例函数y =mx 的图象交于A (﹣3,2)、B (1,n )两点. (1)求一次函数和反比例函数的表达式; (2)求△AOB 的面积;(3)点P 在x 轴上,当△P AO 为等腰三角形时,直接写出点P 的坐标.【分析】(1)利用待定系数法求解即可.(2)如图设直线AB 交y 轴于C ,则C (0,﹣4),根据S △AOB =S △OCA +S △OCB 求解即可. (3)分三种情形:①AO =AP ,②OA =OP ,③P A =PO 分别求解即可.【解答】解:(1)∵反比例函数y =mx经过点A (﹣3,2), ∴m =﹣6,∵点B (1,n )在反比例函数图象上, ∴n =﹣6. ∴B (1,﹣6),把A ,B 的坐标代入y =kx +b , 则有{−3k +b =2k +b =−6,解得{k =−2b =−4,∴一次函数的解析式为y =﹣2x ﹣4,反比例函数的解析式为y =−6x.(2)如图设直线AB 交y 轴于C ,则C (0,﹣4), ∴S △AOB =S △OCA +S △OCB =12×4×3+12×4×1=8.(3)由题意OA =√22+32=√13, 当AO =AP 时,可得P 1(﹣6,0),当OA =OP 时,可得P 2(−√13,0),P 4(√13,0), 当P A =PO 时,过点A 作AJ ⊥x 轴于J .设OP 3=P 3A =x , 在Rt △AJP 3中,则有x 2=22+(3﹣x )2, 解得x =136, ∴P 3(−136,0), 综上所述,满足条件的点P 的坐标为(﹣6,0)或(−√13,0)或(√13,0)或(−136,0).【点评】本题属于反比例函数综合题,考查了反比例函数的性质,一次函数的性质,等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.为了解2019年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是()A.2016年泰兴市八年级学生是总体B.每一名八年级学生是个体C.500名八年级学生是总体的一个样本D.样本容量是5002.某市决定从桂花、菊花、月季花中随机选取一种作为市花,选到月季花的概率是( )A.13B.12C.1 D.03.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AB=4,BC=3,则四边形CODE的周长是()A.5 B.8 C.10 D.124.以下问题,不适合用全面调查的是()A.了解全班同学每周体育锻炼的时间B.旅客上飞机前的安检C.学校招聘教师,对应聘人员面试D.了解全市中小学生每天的零花钱5.下列式子为最简二次根式的是()A.22a b+B.2a C.12a D.1 26.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.7.若顺次连接四边形ABCD各边的中点得到一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形8.若分式5xx-的值为0,则()A.x=0 B.x=5 C.x≠0 D.x≠5 9.“抛一枚均匀硬币,落地后正面朝上”这一事件是()A.必然事件B.随机事件C.确定事件D.不可能事件10.如图,将ABC ∆绕点C 顺时针旋转得到DEC ∆,使点A 的对应点D 恰好落在边AB 上,点B 的对应点为E ,连接BE .下列结论一定正确的是( )A .AC AD =B .AB EB ⊥C .BC DE =D .A EBC ∠=∠二、填空题11.如图,点D 、E 分别是△ABC 的边AB 、AC 的中点,若BC=6,则DE= .12.计算326⨯的结果是_____.13.一个不透明的袋中装有3个红球,2个黑球,每个球除颜色外都相同.从中任意摸出3球,则“摸出的球至少有1个红球”是__事件.(填“必然”、“不可能”或“随机”) 14.如图是某市连续5天的天气情况,最大的日温差是________℃.15.如图,在矩形ABCD 中,AC 、BD 交于点O ,DE ⊥AC 于点E ,若∠AOD =110°,则∠CDE =________°.16.在△ABC 中,点D ,E 分别为BC ,AC 的中点,若DE =2,则AB 的长为_____.17.如图,反比例函数y =xk(x >0)的图象经过矩形OABC 的边AB 的中点D ,若矩形OABC 的面积为8,则k =_____.18.如图,菱形ABCD 的边长为6,∠ABC=60°,则对角线AC 的长是 .19.如图,△ABC 中,∠BAC =20°,△ABC 绕点A 逆时针旋转至△AED ,连接对应点C 、D ,AE 垂直平分CD 于点F ,则旋转角度是_____°.20.如图,E 、F 是正方形ABCD 的对角线AC 上的两点,AC =8,AE =CF =1,则四边形BEDF 的周长是_____.三、解答题21.如图,在ABCD 中,点O 为对角线BD 的中点,过点O 的直线EP 分别交AD ,BC 于E ,F 两点,连接BE ,DF .(1)求证:四边形BFDE 为平行四边形; (2)当∠DOE = °时,四边形BFDE 为菱形?22.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?23.已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF求证:四边形BECF是平行四边形.24.一粒木质中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平滑的.将它从定高度下掷,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下.由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如表:试验次数20406080100120140160“帅”字面朝上频数a18384752667888相应频率0.70.450.630.590.520.550.56b=;=;(2)画出“帅”字面朝上的频率分布折线图;(3)如图实验数据,实验继续进行下去,根据上表的这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?的顶点25.正方形网格中(每个小正方形边长是1,小正方形的顶点叫做格点),ABC均在格点上,请在所给的平面直角坐标系中解答下列问题:(1)作出ABC ∆绕点A 逆时针旋转90°后的111A B C ∆; (2)作出111A B C ∆关于原点O 成中心对称的222A B C ∆.26.如图,在平行四边形ABCD 中,AE BD CF BD ⊥⊥,,垂足分别为E F 、.(1)求证:AE CF =;(2)求证:四边形AECF 是平行四边形27.如图,点P 为ABC ∆的BC 边的中点,分别以AB 、AC 为斜边作Rt ABD ∆和Rt ACE ∆,且BAD CAE α∠=∠=,DPE β∠=.(1)求证:PD PE =.(2)探究:α与β的数量关系,并证明你的结论.28.(数学实验)小明在学习轴对称一章角平分线一节后,做了一个实验: 第一步:如图1在一张纸上画了一个平角∠AOB ;第二步:如图2在平角∠AOB 内画一条射线,沿着射线将平角∠AOB 裁开;第三步:如图3将∠AO'C'放在∠COB 内部,使两边分别与OB 、OC 相交,且O'A =O'C'; 第四步:连接OO', 测量∠COB 度数和∠COO'度数.(数学发现与证明)通过以上实验,小明发现OO'平分∠COB.你能根据小明的实验给出的条件:(1)∠AO'C'与∠COB的关系是;(2)线段O'A与O'C'的关系是.请您结合图3将小明的实验条件和发现结论完成下面“已知”“求证”,并给出证明.已知:求证:证明:【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.【详解】A. 2019年泰兴市八年级学生的视力情况是总体,故A错误;B. 每一名八年级学生的视力情况是个体,故B错误;C. 从中随机调查了500名学生的视力情况是一个样本,故C错误;D. 样本容量是500,故D正确;故选:D.【点睛】此题考查总体、个体、样本、样本容量,解题关键在于掌握它们的定义及区别. 2.A解析:A【分析】共有3种花,选到月季花占其中的一种,利用概率公式进行求解即可.【详解】所有机会均等的可能共有3种,而选到月季花的机会有1种,因此选到月季花的概率是13,故选A.【点睛】本题考查了简单的概率计算,用到的知识点为:概率=所求情况数与总情况数之比.3.C解析:C【分析】由矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,易证得四边形CODE是菱形,又由AB=4,BC=3,可求得AC的长,继而求得OC的长,则可求得答案.【详解】解:∵CE∥BD,DE∥AC,∴四边形CODE是平行四边形,∵四边形ABCD是矩形,∴AC=BD,OB=OD,OC=OA,∠ABC=90°∴OC=OD,∴四边形CODE是菱形∵AB=4,BC=35AC∴=∴OC=5 2∴四边形CODE的周长=4×52=10故选:C.【点睛】本题考查菱形的判定,运用勾股定理解三角形,掌握特殊平行四边形的判定与性质是解题的关键.4.D解析:D【解析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,因此,A、了解全班同学每周体育锻炼的时间,数量不大,宜用全面调查,故本选项错误;B、旅客上飞机前的安检,意义重大,宜用全面调查,故本选项错误;C、学校招聘教师,对应聘人员面试必须全面调查,故本选项错误;D、了解全市中小学生每天的零花钱,工作量大,且普查的意义不大,不适合全面调查,故本选项正确.故选D.5.A解析:A【分析】判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行,或直观地观察被开方数的每一个因数(或因式)的指数都小于根指数2,且被开方数中不含有分母,被开方数是多项式时要先因式分解后再观察.【详解】AB|a|,可以化简,故不是最简二次根式;C=D=,可以化简,故不是最简二次根式;故选:A.【点睛】本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.6.B解析:B【分析】根据轴对称图形和中心对称图形的概念求解即可.【详解】解:A、是轴对称图形,不是中心对称图形,故此选项错误;B、是轴对称图形,又是中心对称图形,故此选项正确;C、不是轴对称图形,是中心对称图形,故此选项错误;D、不是轴对称图形,不是中心对称图形,故此选项错误.故答案为B.【点睛】本题考查了轴对称图形和中心对称图形的识别,掌握轴对称图形和中心对称图形的概念是解答本题的关键.7.D解析:D 【分析】先画出图形,再根据中位线定理、矩形的定义、平行线的性质即可得. 【详解】如图,点,,,E F G H 分别为,,,AB BC CD AD 的中点,四边形EFGH 是矩形 连接AC 、BD由中位线定理得://,//AC GH BD EH 四边形EFGH 是矩形 90EHG ∴∠=︒,即EH GH ⊥EH AC ∴⊥BD AC ∴⊥即四边形ABCD 一定是对角线互相垂直的四边形 故选:D .【点睛】本题考查了中位线定理、矩形的定义、平行线的性质,依据题意,正确画出图形,并掌握中位线定理是解题关键.8.B解析:B 【分析】直接利用分式的值为零则分子为零,分母不等于0,进而得出答案. 【详解】解:∵分式5x x-的值为0, ∴x ﹣5=0且x ≠0, 解得:x =5. 故选:B . 【点睛】本题考查了分式,掌握“分式值为0”时的做题方法及分式有意义的条件是解题关键.9.B解析:B 【详解】 随机事件.根据随机事件的定义,随机事件就是可能发生,也可能不发生的事件,即可判断: 抛1枚均匀硬币,落地后可能正面朝上,也可能反面朝上,故抛1枚均匀硬币,落地后正面朝上是随机事件.故选B.10.D解析:D 【分析】利用旋转的性质得AC=CD ,BC=EC ,∠ACD=∠BCE ,所以选项A 、C 不一定正确 再根据等腰三角形的性质即可得出A EBC ∠=∠,所以选项D 正确;再根据∠EBC =∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB 判断选项B 不一定正确即可. 【详解】解:∵ABC ∆绕点C 顺时针旋转得到DEC ∆, ∴AC=CD ,BC=EC ,∠ACD=∠BCE ,∴∠A=∠CDA=180ACD 2∠︒-;∠EBC=∠BEC=180BCE2∠︒-, ∴选项A 、C 不一定正确 ∴∠A =∠EBC∴选项D 正确.∵∠EBC=∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB 不一定等于090, ∴选项B 不一定正确; 故选D . 【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.二、填空题 11.3 【分析】先判断DE 是△ABC 的中位线,从而得解. 【详解】因为点D 、E 分别是△ABC 的边AB 、AC 的中点, 所以DE 是△ABC 的中位线, 所以DE=BC=3. 故答案为3. 考点:三角形的中解析:3 【分析】先判断DE 是△ABC 的中位线,从而得解.因为点D、E分别是△ABC的边AB、AC的中点,所以DE是△ABC的中位线,所以DE=12BC=3.故答案为3.考点:三角形的中位线定理.12.【分析】直接利用二次根式的乘法运算法则计算得出答案.【详解】=2=2×3=6.故答案为:6.【点睛】此题主要考查了二次根式的乘法运算,正确化简二次根式是解题关键.解析:【分析】直接利用二次根式的乘法运算法则计算得出答案.【详解】===.故答案为:.【点睛】此题主要考查了二次根式的乘法运算,正确化简二次根式是解题关键.13.必然【分析】根据事件发生的可能性大小判断相应事件的类型即可.【详解】∵红球和黑球除颜色外其余都相同且黑球只有2个,∴从中任意摸出3球,至少有一个为红球,即事件“摸出的球至少有1个红球”是解析:必然根据事件发生的可能性大小判断相应事件的类型即可.【详解】∵红球和黑球除颜色外其余都相同且黑球只有2个,∴从中任意摸出3球,至少有一个为红球,即事件“摸出的球至少有1个红球”是必然事件,故答案为:必然.【点睛】本题考查了必然事件的定义,正确理解必然事件,不可能事件,随机事件的概念是解题关键.14.10【分析】根据图象找出气温差距最大的一天,然后计算温差即可.【详解】由图可得气温差距最大的一天为5月28日,温差为:25-15=10,故答案为:10.【点睛】本题考查了有理数减法的解析:10【分析】根据图象找出气温差距最大的一天,然后计算温差即可.【详解】由图可得气温差距最大的一天为5月28日,温差为:25-15=10,故答案为:10.【点睛】本题考查了有理数减法的实际应用,根据图象找出温差最大的一天是解题关键.15.35【分析】先根据三角形外角的性质和矩形的性质得到∠OCD的度数,再根据DE⊥AC即可得到∠CDE的度数.【详解】∵∠AOD=110°,∴∠ODC+∠OCD=110°,∵四边形ABCD是解析:35先根据三角形外角的性质和矩形的性质得到∠OCD的度数,再根据DE⊥AC即可得到∠CDE 的度数.【详解】∵∠AOD=110°,∴∠ODC+∠OCD=110°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=∠OCD=55°,又∵DE⊥AC,∴∠CDE=180°-∠OCD-∠DEC=180°-55°-90°=35°,故答案为:35.【点睛】本题考查了矩形的性质,三角形内角和,三角形外角的性质,掌握知识点是解题关键.16.4【分析】根据三角形中位线定理即可得到结论.【详解】解:∵在△ABC中,点D,E分别为BC,AC的中点,∴DE是△ABC的中位线,∴AB=2DE,∵DE=2,∴AB=4,故答案为:解析:4【分析】根据三角形中位线定理即可得到结论.【详解】解:∵在△ABC中,点D,E分别为BC,AC的中点,∴DE是△ABC的中位线,∴AB=2DE,∵DE=2,∴AB=4,故答案为:4.【点睛】本题主要考查中位线的定义和性质,解决本题的关键是要熟练掌握中位线的定义和性质.17.4【分析】设D 的坐标是,则B 的坐标是,根据D 在反比例函数图象上,即可求得ab 的值,从而求得k 的值.【详解】设D 的坐标是,则B 的坐标是,∵∴,∵D 在上,∴.故答案是:4.【点睛】解析:4【分析】设D 的坐标是()a b ,,则B 的坐标是()2a b ,,根据D 在反比例函数图象上,即可求得ab 的值,从而求得k 的值.【详解】设D 的坐标是()a b ,,则B 的坐标是()2a b ,, ∵OABC 8S =矩形∴28ab =,∵D 在k y x=上, ∴1842k ab ==⨯=. 故答案是:4.【点睛】本题主要考查的是反比例函数k 的几何意义,掌握反比例函数系数k 的几何意义是解题的关键.18.6【分析】由菱形的性质可得AB=BC ,再由∠ABC=60°得△ABC 为等边三角形即可求得答案.【详解】根据菱形的性质可得AB=BC=6,∵∠ABC=60°,则△ABC为等边三角形,解析:6【分析】由菱形的性质可得AB=BC,再由∠ABC=60°得△ABC为等边三角形即可求得答案.【详解】根据菱形的性质可得AB=BC=6,∵∠ABC=60°,则△ABC为等边三角形,则AC=AB=6,故答案为:6.【点睛】本题考查了菱形的性质,等边三角形的判定与性质,熟练掌握和灵活运用相关知识是解题的关键.19.40【分析】根据旋转的性质得出AD=AC,∠DAE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC的度数即可.【详解】解:∵△ABC绕点A逆时针旋转至△AED,∠BAC解析:40【分析】根据旋转的性质得出AD=AC,∠DAE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC的度数即可.【详解】解:∵△ABC绕点A逆时针旋转至△AED,∠BAC=20°,∴AD=AC,∠DAE=∠BAC=20°,∵AE垂直平分CD于点F,∴∠DAE=∠CAE=20°,∴∠DAC=20°+20°=40°,即旋转角度数是40°,故答案为:40.【点睛】本题主要考查了图像旋转的性质以及垂直平分线的性质,从而得到边相等与角相等的条件.20.20【分析】连接BD 交AC 于点O ,则可证得OE =OF ,OD =OB ,可证四边形BEDF 为平行四边形,且BD⊥EF,可证得四边形BEDF 为菱形;根据勾股定理计算DE 的长,可得结论.【详解】解:如解析:20【分析】连接BD 交AC 于点O ,则可证得OE =OF ,OD =OB ,可证四边形BEDF 为平行四边形,且BD ⊥EF ,可证得四边形BEDF 为菱形;根据勾股定理计算DE 的长,可得结论.【详解】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 为正方形,∴BD ⊥AC ,OD =OB =OA =OC ,∵AE =CF =2,∴OA ﹣AE =OC ﹣CF ,即OE =OF ,∴四边形BEDF 为平行四边形,且BD ⊥EF ,∴四边形BEDF 为菱形,∴DE =DF =BE =BF ,∵AC =BD =8,OE =OF =8232-=, 由勾股定理得:DE =2222435OD OE +=+=,∴四边形BEDF 的周长=4DE =4×5=20,故答案为:20.【点睛】本题主要考查正方形的性质、菱形的判定和性质及勾股定理,掌握对角线互相垂直平分的四边形为菱形是解题的关键.三、解答题21.(1)详见解析;(2)90【分析】(1)证△DOE ≌△BOF (ASA ),得DE=BF ,即可得出结论;(2)由∠DOE=90°,得EF ⊥BD ,即可得出结论.【详解】(1)∵四边形ABCD 是平行四边形,O 为对角线BD 的中点,∴BO =DO ,AD ∥BC ,∴∠EDO =∠FBO ,在△EOD 和△FOB 中,EDO FBO DO BO EOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE ≌△BOF (ASA ),∴DE =BF ,又∵DE ∥BF ,∴四边形BFDE 为平行四边形;(2)∠DOE =90°时,四边形BFDE 为菱形;理由如下:由(1)得:四边形BFDE 是平行四边形,若∠DOE =90°,则EF ⊥BD ,∴四边形BFDE 为菱形;故答案为:90.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及菱形的判定等知识,证出△DOE ≌△BOF 是解题的关键.22.(1)见解析(2)成立【解析】试题分析:(1)由DF=BE ,四边形ABCD 为正方形可证△CEB ≌△CFD ,从而证出CE=CF . (2)由(1)得,CE=CF ,∠BCE+∠ECD=∠DCF+∠ECD 即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF ,故可证得△ECG ≌△FCG ,即EG=FG=GD+DF .又因为DF=BE ,所以可证出GE=BE+GD 成立.试题解析:(1)在正方形ABCD 中,{BC CDB CDF BE DF∠∠===∴△CBE ≌△CDF (SAS ).∴CE=CF .(2)GE=BE+GD 成立.理由是:∵由(1)得:△CBE ≌△CDF ,∴∠BCE=∠DCF ,∴∠BCE+∠ECD=∠DCF+∠ECD ,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°. CE =CF∵∠GCE=∠GCF, GC=GC∴△ECG≌△FCG(SAS).∴GE=GF.∴GE=DF+GD=BE+GD.考点:1.正方形的性质;2.全等三角形的判定与性质.23.证明见解析.【分析】根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.【详解】如答图,连接BC,设对角线交于点O.∵四边形ABCD是平行四边形,∴OA=OD,OB=OC.∵AE=DF,OA﹣AE=OD﹣DF,∴OE=OF.∴四边形BEDF是平行四边形.24.(1)14,0.55;(2)图见解析;(3)0.55.【分析】(1)根据图中给出的数据和频数、频率与总数之间的关系分别求出a、b的值;(2)将频率作为纵坐标,试验次数作为横坐标,描点连线,可得折线图.(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,即可估计概率的大小.【详解】(1)a=20×0.7=14;b=88160=0.55;故答案为:14,0.55;(2)根据图表给出的数据画折线统计图如下:(3)随着试验次数的增加“帅”字面朝上的频率逐渐稳定在0.55左右,利用这个频率来估计概率,得P (“帅”字朝上)=0.55.【点睛】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.作图时应先描点,再连线.用到的知识点为:部分的具体数目=总体数目×相应频率.频率=所求情况数与总情况数之比.25.(1)见解析 (2)见解析【分析】(1)本题考查图形的旋转变换以及作图,根据网格结构找出点A 、B 、C 绕点A 逆时针旋转90°后的点1A 、1B 、1C 的位置,然后顺次连接即可.(2)本题考查中心对称图形的作图,找出点1A 、1B 、1C 关于原点O 成中心对称的点2A 、2B 、2C 的位置,然后顺次连接即可.【详解】【点睛】解答此类型题目首先要清楚旋转图形和中心对称图形的性质,按照图形定义进行作图,作图时先找点,继而由点连成线.26.(1)见解析;(2)见解析【解析】【分析】(1)证出△ABE ≌△CDF 即可求解;(2)证出AE 平行CF ,AE CF =即可/【详解】(1)∵AE BD CF BD ⊥⊥,∴∠AEB=∠CFD∵平行四边形ABCD∴∠ABE=∠CDF,AB=CD∴△ABE ≌△CDF∴AE=CF(2)∵AE BD CF BD ⊥⊥,∴AE ∥CF∵AE=CF∴四边形AECF 是平行四边形【点睛】本题考查的是平行四边形的综合运用,熟练掌握全等三角形的性质是解题的关键.27.(1)详见解析;(2)2180αβ+=︒,证明见解析.【分析】(1)如图,分别取AB 、AC 的中点M 、N ,连接DM 、PM 、PN 、NE ,根据三角形的中位线定理和直角三角形的性质可得PM NE =,DM PN =,根据等腰三角形的性质、三角形的外角性质和已知条件可得BMD CNE ∠=∠,根据平行线的性质可得BMP BAC ∠=∠=CNP ∠,进而可得DMP PNE ∠=∠,于是可根据SAS 证明MDP NPE ∆≅∆,从而可得结论;(2)根据平行线的性质可得BMP MPN ∠=∠,根据全等三角形的性质可得EPN MDP ∠=∠,然后在DMP ∆中利用三角形的内角和定理和等量代换即可得出结论.【详解】(1)证明:如图,分别取AB 、AC 的中点M 、N ,连接DM 、PM 、PN 、NE . 点P 为ABC ∆的边BC 的中点, ∴12PM AC =, NE 为Rt AEC ∆斜边上的中线, ∴12NE AN AC ==, PM NE ∴=,同理可得:DM PN =, 12DM AM AB ==, ADM BAD ∴∠=∠,2BMD BAD ∴∠=∠,同理,2CNE CAE ∠=∠,又BAD CAE α∠=∠=,BMD CNE ∴∠=∠,又PM 、PN 都是ABC ∆的中位线,//PM AC ∴,//PN AB ,BMP BAC ∴∠=∠,CNP BAC ∠=∠,BMP CNP ∴∠=∠,∴DMP PNE ∠=∠,MDP NPE ∴∆≅∆(SAS),PD PE ∴=;(2)解:α与β的数量关系是:2180αβ+=︒;证明://PN AB ,BMP MPN ∴∠=∠,∵MDP NPE ∆≅∆,EPN MDP ∴∠=∠,在DMP ∆中,∵180MDP DPM DMP ∠+∠+∠=︒,∴180MDP DPM DMB PMB ∠+∠+∠+∠=︒,而22DMB BAD α∠=∠=,2180EPN DPM MPN α∴∠+∠++∠=︒,DPE DPM MPN EPN β∠=∠+∠+∠=, 2180αβ∴+=︒.【点睛】本题考查了三角形的中位线定理、全等三角形的判定和性质、直角三角形的性质、等腰三角形的性质、平行线的性质、三角形的外角性质和三角形的内角和定理等知识,具有一定的综合性,正确添加辅助线、熟练掌握上述知识是解题的关键.28.(1)互补;(2)相等;证明见解析【分析】根据题意写出已知、求证,过O '作O D '⊥OC 于D ,O E '⊥OB 于E ,证明Rt △Rt AO D '≅△C O E '',推出O D O E '=',利用角平分线的判定定理即可证明'OO 平分∠COB .【详解】(1)∠AO'C'与∠COB 的关系是互补;(2)线段O'A 与O'C'的关系是相等.已知:AO C ∠''+∠COB=180︒,O'A=O'C',求证:'OO 平分∠COB .证明:过O '作O D '⊥OC 于D ,O E '⊥OB 于E ,∵O C B O OB C O O ∠=∠+∠''''',∠AO C ''+∠COB=180︒,∴AO O ∠'+'AOO ∠ =180︒-(O OB C O O ∠+∠'''),即O C B O OB C O O ∠=∠+∠'''''=180︒-(AO O ∠'+'AOO ∠),又OAO ∠'=180︒-(AO O ∠'+'AOO ∠),∴O C B OAO ∠=∠''',∵O'A=O'C',∴Rt △Rt AO D '≅△C O E '',∴O D O E '=',∵O D '⊥OC ,O E '⊥OB ,∴'OO 平分∠COB .【点睛】本题考查了全等三角形的判定和性质,角平分线的判定,三角形内角和定理,三角形的外角性质,作出合适的辅助线构造全等三角形是解题的关键.。
苏教版八年级数学下册期中试卷及答案【完整版】

苏教版八年级数学下册期中试卷及答案【完整版】 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.多项式2mx m -与多项式221x x -+的公因式是( )A .1x -B .1x +C .21x -D .()21x - 2.如图,若x 为正整数,则表示()2221441x x x x +-+++的值的点落在( )A .段①B .段②C .段③D .段④3.下列命题中,真命题是( )A .对角线相等的四边形是矩形B .对角线互相垂直的四边形是菱形C .对角线互相平分的四边形是平行四边形D .对角线互相垂直平分的四边形是正方形4.下列各数:-2,0,13,0.020020002…,π,9,其中无理数的个数是( )A .4B .3C .2D .15.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .6.如图,正方形ABCD 和正方形CEFG 边长分别为a 和b ,正方形CEFG 绕点C 旋转,给出下列结论:①BE=DG ;②BE ⊥DG ;③DE 2+BG 2=2a 2+2b 2,其中正确结论有( )A .0个B .1个C .2个D .3个7.下面四个手机应用图标中是轴对称图形的是( )A .B .C .D .8.如图,已知点E 在正方形ABCD 内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )A .48B .60C .76D .809.如图将直尺与含30°角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .30B .40︒C .50︒D .60︒10.如图,已知∠ABC=∠DCB ,下列所给条件不能证明△ABC ≌△DCB 的是( )A .∠A=∠DB .AB=DC C .∠ACB=∠DBCD .AC=BD二、填空题(本大题共6小题,每小题3分,共18分)1.已知关于x 的不等式组5310x a x -≥-⎧⎨-<⎩无解,则a 的取值范围是________.2.已知x ,y 满足方程组x 2y 5x 2y 3-=⎧+=-⎨⎩,则22x 4y -的值为__________. 3.在△ABC 中,AB=15,AC=13,高AD=12,则ABC ∆的周长为____________.4.如图,已知△ABC 的周长是21,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =4,△ABC 的面积是________.5.如图,在▱ABCD 中,∠D=100°,∠DAB 的平分线AE 交DC 于点E ,连接BE.若AE=AB ,则∠EBC 的度数为__________.6.如图,在平面直角坐标系中,将矩形AOCD 沿直线AE 折叠(点E 在边DC 上),折叠后顶点D 恰好落在边OC 上的点F 处.若点D 的坐标为(10,8),则点E 的坐标为 .三、解答题(本大题共6小题,共72分)1.解不等式(1)7252x x -+≥ (2)11132x x -+-<2.先化简,再求值:(1﹣11x -)÷22441x x x -+-,其中x 5 23.已知关于x 的一元二次方程2(4)240x m x m -+++=.(1)求证:该一元二次方程总有两个实数根;(2)若12,x x 为方程的两个根,且22124n x x =+-,判断动点(,)P m n 所形成的数A-,并说明理由.图象是否经过点(5,9)4.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.5.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH 的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)6.某经销商从市场得知如下信息:A品牌手表B品牌手表进价(元/块)700 100售价(元/块)900 160他计划用4万元资金一次性购进这两种品牌手表共100块,设该经销商购进A 品牌手表x块,这两种品牌手表全部销售完后获得利润为y元.(1)试写出y与x之间的函数关系式;(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案;(3)选择哪种进货方案,该经销商可获利最大;最大利润是多少元.参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、B3、C4、C5、B6、D7、D8、C9、C10、D二、填空题(本大题共6小题,每小题3分,共18分)1、a ≥22、-153、32或424、425、30°.6、(10,3)三、解答题(本大题共6小题,共72分)1、(1)2x ≥;(2)11x >-2、12x x +-,55+3、(1)见解析;(2)经过,理由见解析4、(1)见解析(2)成立(3)△DEF 为等边三角形5、(1)略;(2)四边形EFGH 是菱形,略;(3)四边形EFGH 是正方形.6、(1)y=140x+6000;(2)三种,答案见解析;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元.。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,5AB =,6AC =,过D 作AC 的平行线交BC 的延长线于点E ,则BDE ∆的面积为( )A .22B .24C .48D .442.下列调查中,适合采用普查的是( )A .了解一批电视机的使用寿命B .了解全省学生的家庭1周内丢弃塑料袋的数量C .为保证某种新研发的战斗机试飞成功,对其零部件进行检查D .了解扬州市中学生的近视率3.某一超市在“五•一”期间开展有奖促销活动,每买100元商品可参加抽奖一次,中奖的概率为13.小张这期间在该超市买商品获得了三次抽奖机会,则小张( ) A .能中奖一次 B .能中奖两次C .至少能中奖一次D .中奖次数不能确定 4.一个事件的概率不可能是( )A .32B .1C .23D .05.如图,在矩形ABCD 中,E 是BC 边的中点,将△ABE 沿AE 所在的直线折叠得到△AFE ,延长AF 交CD 于点G ,已知CG =2,DG =1,则BC 的长是( )A .2B .6C .5D .36.下列方程中,关于x 的一元二次方程是( ) A .x 2﹣x (x +3)=0B .ax 2+bx +c =0C .x 2﹣2x ﹣3=0D .x 2﹣2y ﹣1=0 7.若分式42x x -+的值为0,则x 的值为( ) A .0 B .-2 C .4 D .4或-28.已知反比例函3y x =-,下列结论中不正确的是( ) A .图像经过点(1,3)- B .图像在第二、四象限C .当1x >时,30y <<D .当0x <,y 随着x 的增大而减小 9.两个反比例函数3y x =,6y x=在第一象限内的图像如图所示,点1P 、2P 、3P ……2020P 反比例函数6y x =图像上,它们的横坐标分别是1x 、2x 、3x ……2020x ,纵坐标分别是1,3,5,…,共2020个连续奇数,过点1P 、2P 、3P ……2020P 分别作y 轴的平行线,与反比例函数3y x=的图像交点依次是()11,Q x y 、()22,Q x y 、()33,Q x y ……()20202020,Q x y ,则2020y 等于( )A .2019.5B .2020.5C .2019D .403910.下列调查中,适宜采用普查方式的是( )A .一批电池的使用寿命B .全班同学的身高情况C .一批食品中防腐剂的含量D .全市中小学生最喜爱的数学家 11.反比例函数3y x =-,下列说法不正确的是( ) A .图象经过点(1,-3)B .图象位于第二、四象限C .图象关于直线y=x 对称D .y 随x 的增大而增大12.甲、乙、丙、丁四位同学在这一学期4次数学测试中平均成绩都是95分,方差分别是2.2S =甲, 1.8S =乙, 3.3S =丙,S a =丁,a 是整数,且使得关于x 的方程2(2)410a x x -+-=有两个不相等的实数根,若丁同学的成绩最稳定,则a 的取值可以是( )A .3B .2C .1D .1-二、填空题13.如图,把△ABC 绕点C 按顺时针方向旋转35°,得到△A’B’C ,A’B’交AC 于点D ,若∠A’DC=90°,则∠A= °.14.不透明的袋子里装有6只红球,1只白球,这些球除颜色外都相同.搅匀后从中任意摸出1只球.摸出的是红球的可能性_____摸出的是白球的可能性(填“大于”、“小于”或“等于”).15.在一次数学测试中 ,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频率是0.2 ,则第六组的频数是_______.16.如图,将正方形ABCD 沿BE 对折,使点A 落在对角线BD 上的A′处,连接A′C ,则∠BA′C=________度.17.若()14,A y -、()22,B y -都在反比例函数6y x=的图像上,则1y 、2y 的大小关系为1y _________2y (填“>”、“<”、“=”)18.根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为________万元.19.若点A (﹣4,y 1),B (﹣2,y 2)都在反比例函数1y x=-的图象上,则y 1,y 2的大小关系是y 1_____y 2. 20.x 千克橘子糖、y 千克椰子糖、z 千克榴莲糖混合成“什锦糖”.已知这三种糖的单价分别为30元/千克、32元/千克、40元/千克,则这种“什锦糖”的单价为_____元.(用含x 、y 、z 的代数式表示)21.空气是混合物,为直观介绍空气各成分的百分比,宜选用_____统计图.22.一个不透明袋子中装有3个红球,2个白球,1个蓝球,从中任意摸一球,则摸到_____(颜色)球的可能性最大.23.方程x2=0的解是_______.24.已知关于x的方程ax2+bx+1=0的两根为x1=1,x2=2,则方程a(x+1)2+b(x+1)+1=0的两根之和为__________.三、解答题25.如图,在ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.(1)求证:四边形BFDE为平行四边形;(2)当∠DOE= °时,四边形BFDE为菱形?26.已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF求证:四边形BECF是平行四边形.27.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.(1)当∠BEA=55°时,求∠HAD的度数;(2)设∠BEA=α,试用含α的代数式表示∠DFA的大小;(3)点E运动的过程中,试探究∠BEA与∠FEA有怎样的数量关系,并说明理由.28.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.(1)求证:四边形DEBF 是平行四边形;(2)当DE =DF 时,求EF 的长.29.计算:(1)2354535⨯; (2)()22360,0x yxy x y ≥≥; (3)()48274153-+÷. 30.如图,在平面直角坐标系中,四边形ABCD 为正方形,已知点A(-6,0),D(-7,3),点B 、C 在第二象限内.(1)点B 的坐标 ;(2)将正方形ABCD 以每秒1个单位的速度沿x 轴向右平移t 秒,若存在某一时刻t,使在第一象限内点B 、D 两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t 的值以及这个反比例函数的解析式;(3)在(2)的情况下,问是否存在x 轴上的点P 和反比例函数图象上的点Q,使得以P 、Q 、B′、D′四个点为顶点的四边形是平行四边形?若存在,请求出符合题意的点P 、Q 的坐标;若不存在,请说明理由.31.2020年4月23日,是第25个世界读书日.为了解学生每周阅读时间,某校随机抽取了部分学生进行调查,根据调查结果,将阅读时间x(单位:小时)分成了4组,A:0≤x <2;B:2≤x<4;C:4≤x<6;D:6≤x<8,试结合图中所给信息解答下列问题:(1)这次随机抽取了名学生进行调查;扇形统计图中,扇形B的圆心角的度数为.(2)补全频数分布直方图;(3)若该校共有2000名学生,试估计每周阅读时间不少于4小时的学生共有多少名?32.如图,四边形ABCD的对角线AC、BD相交于点O,BO=DO,点E、F分别在AO,CO 上,且BE∥DF,AE=CF.求证:四边形ABCD为平行四边形.33.为更有效地开展“线上教学”工作,某市就学生参与线上学习的工具进行了电子问卷调查,并将调查结果绘制成图1和图2所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次调查的总人数是人;(2)请将条形统计图补充完整;(3)在扇形统计图中表示观点B的扇形的圆心角度数为度;(4)在扇形统计图中表示观点E的百分比是.34.如图,在△ABC中,DE∥BC,EF∥AB,BE平分∠ABC,试判断四边形DBFE的形状,并说明理由.35.如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O ,AC ⊥BC ,AC =2,BC =3.点E 是BC 延长线上一点,且CE =3,连结DE .(1)求证:四边形ACED 为矩形.(2)连结OE ,求OE 的长.36.已知:ABC ∆中以CB 为边在ABC ∆外侧作等边CBP ∆.(1)连接AP ,以AP 为边作等边APQ ∆,求证:AC BQ =;(2)当30CAB ∠=︒,4AB =,3AC =时,求AP 的值;(3)若4AB =,3AC =,改变CAB ∠的度数,发现CAB ∠在变化到某一角度时,AP 有最大值.画出CAB ∠为这个特殊角度时的示意图,并直接写出CAB ∠的角度和AP 的最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】先判断出四边形ACED 是平行四边形,从而得出DE 的长度,根据菱形的性质求出BD 的长度,利用勾股定理的逆定理可得出△BDE 是直角三角形,计算出面积即可.【详解】解:∵AD∥BE,AC∥DE,∴四边形ACED是平行四边形,∴AC=DE=6,在RT△BCO中,4=,即可得BD=8,又∵BE=BC+CE=BC+AD=10,∴△BDE是直角三角形,∴S△BDE=124 2DE BD⋅=.故答案为B.【点睛】此题考查了菱形的性质、勾股定理的逆定理及三角形的面积,属于基础题,求出BD的长度,判断△BDE是直角三角形,是解答本题的关键.2.C解析:C【分析】根据调查的实际情况逐项判断即可.【详解】解:A. 了解一批电视机的使用寿命,调查具有破坏性,适合抽样调查,不合题意;B. 了解全省学生的家庭1周内丢弃塑料袋的数量,调查费时费力,适合抽样调查,不合题意;C. 为保证某种新研发的战斗机试飞成功,对其零部件进行检查,考虑安全性,适合全面调查,符合题意;D. 了解扬州市中学生的近视率,调查费时费力,适合抽样调查,不合题意.故选:C【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,事关重大的调查往往选用普查.3.D解析:D【分析】由于中奖概率为13,说明此事件为随机事件,即可能发生,也可能不发生.【详解】解:根据随机事件的定义判定,中奖次数不能确定.故选D.【点睛】解答此题要明确概率和事件的关系:()P A0=①,为不可能事件;()P A1=②为必然事件;()0P A1<<③为随机事件.4.A解析:A【分析】根据概率的意义知,一件事件的发生概率最大是1,所以只有A项是错误的,即找到正确选项.【详解】∵必然事件的概率是1,不可能事件的概率为0,∴B、C、D选项的概率都有可能,∵32>1,∴A不成立.故选:A.【点睛】本题主要考查了概率的定义,正确把握各事件的概率是解题的关键.5.B解析:B【分析】连接EG,由折叠的性质可得BE=EF又由E是BC边的中点,可得EF=EC,然后证得Rt△EGF≌Rt△EGC(HL),得出FG=CG=2,继而求得线段AG的长,再利用勾股定理求解,即可求得答案.【详解】解:连接EG,∵E是BC的中点,∴BE=EC,∵△ABE沿AE折叠后得到△AFE,∴BE=EF,∴EF=EC,∵在矩形ABCD 中,∴∠C =90°,∴∠EFG =∠B =90°,∵在Rt △EGF 和Rt △EGC 中,EF EC EG EG =⎧⎨=⎩, ∴Rt △EGF ≌Rt △EGC (HL ),∴FG =CG =2,∵在矩形ABCD 中,AB =CD =CG +DG =2+1=3,∴AF =AB =3,∴AG =AF +FG =3+2=5,∴BC =AD=.故选:B .【点睛】此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键. 6.C解析:C【分析】一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.【详解】解:A 、x 2﹣x (x +3)=0,化简后为﹣3x =0,不是关于x 的一元二次方程,故此选项不合题意;B 、ax 2+bx +c =0,当a =0时,不是关于x 的一元二次方程,故此选项不合题意;C 、x 2﹣2x ﹣3=0是关于x 的一元二次方程,故此选项符合题意;D 、x 2﹣2y ﹣1=0含有2个未知数,不是关于x 的一元二次方程,故此选项不合题意; 故选:C .【点睛】此题主要考查了一元二次方程的定义,判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.7.C解析:C【分析】根据分式的值为零的条件可以得到4020x x -=⎧⎨+≠⎩,从而求出x 的值.解:由分式的值为零的条件得4020x x -=⎧⎨+≠⎩, 由40x -=,得:4x =,由20x +≠,得:2x ≠-.综上,得4x =,即x 的值为4.故选:C .【点睛】本题考查了分式的值为零的条件,以及分式有意义的条件,解题的关键是熟练掌握分式的值为零的条件进行解题. 8.D解析:D【分析】根据反比例函数的性质对各选项进行逐一分析即可.【详解】解:A 、∵()133-⨯=-,∴图象必经过点(1,3)-,故本选项正确;B 、∵30k =-<,∴函数图象的两个分支分布在第二、四象限,故本选项正确;C 、∵1x =时,3y =-且y 随x 的增大而而增大,∴1x >时,30y -<<,故本选项正确;D 、函数图象的两个分支分布在第二、四象限,在每一象限内,y 随x 的增大而增大,故本选项错误.故选:D .【点睛】本题考查了反比例函数的性质,解题的关键是熟练掌握反比例函数的性质进行解题.9.A解析:A【分析】主要是找规律,找出规律即可求出本题答案,先根据已知条件求出y 分别为1、3、5时x 的值,即可求出当2020y =时x 的值,再将其代入3y x =中即可求出2020y . 【详解】解:当1,3,52020y =⋅⋅⋅时,1x 、2x 、3x …2020x 分别为6、2、65 (62020)将1x 、2x 、3x …2020x 代入3y x =, 得:1y 、2y 、3y …2020y 202040392019.52y ==,【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=k x(k ≠0)的图象是双曲线;图象上的点(x ,y )的横纵坐标的积是定值k ,即xy=k . 10.B解析:B【分析】根据抽样调查和普查的特点分析即可.【详解】解:A .调查一批电池的使用寿命适合抽样调查;B .调查全班同学的身高情况适合普查;C .调查一批食品中防腐剂的含量适合抽样调查;D .调查全市中小学生最喜爱的数学家适合抽样调查;故选:B .【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.11.D解析:D【解析】【分析】通过反比例图象上的点的坐标特征,可对A 选项做出判断;通过反比例函数图象和性质、增减性、对称性可对其它选项做出判断,得出答案.【详解】解:由点()1,3-的坐标满足反比例函数3y x=-,故A 是正确的; 由30k =-<,双曲线位于二、四象限,故B 也是正确的; 由反比例函数的对称性,可知反比例函数3y x =-关于y x =对称是正确的,故C 也是正确的,由反比例函数的性质,0k <,在每个象限内,y 随x 的增大而增大,不在同一象限,不具有此性质,故D 是不正确的,故选:D .【点睛】考查反比例函数的性质,当0k <时,在每个象限内y 随x 的增大而增大的性质、反比例函数的图象是轴对称图象,y x =和y x =-是它的对称轴,同时也是中心对称图形;熟练掌握反比例函数图象上点的坐标特征和反比例函数图象和性质是解答此题的关键.解析:C【分析】根据方程的根的情况得出a 的取值范围,结合乙同学的成绩最稳定且a 为整数即可得a 得取值.【详解】∵关于于x 的方程2(2)410a x x -+-=有两个不相等的实数根, ∴()=16+42>0,a ∆-且20.a -≠ 解得:>-2a 且 2.a ≠∵丁同学的成绩最稳定,∴<1.8a 且0a >.则a=1.故答案选:C.【点睛】本题主要考查了方差的意义理解,结合一元二次方程的根的判别式进行求解.二、填空题13.【详解】试题分析:∵把△ABC 绕点C 按顺时针方向旋转35°,得到△A’B’C∴∠ACA’=35°,∠A =∠A’,.∵∠A’DC=90°,∴∠A’ =55°.∴∠A=55°.考点:1解析:【详解】试题分析:∵把△ABC 绕点C 按顺时针方向旋转35°,得到△A’B’C∴∠ACA’=35°,∠A =∠A’,.∵∠A’DC=90°,∴∠A’ =55°.∴∠A=55°.考点:1.旋转的性质;2.直角三角形两锐角的关系.14.大于【分析】分别计算出摸出的是红球和白球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸出1只球.摸出的是红球的概率=,摸出的是白球的概率=,所以摸出的是红球的可能性大于摸出的解析:大于【分析】分别计算出摸出的是红球和白球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸出1只球.摸出的是红球的概率=67,摸出的是白球的概率=17,所以摸出的是红球的可能性大于摸出的是白球的可能性.故答案为:大于.【点睛】本题考查的是概率的意义,以及求简单随机事件的概率,掌握以上知识是解题的关键.15.5【详解】解:一个容量为50的样本,把它分成6组,第一组到第四组的频数分别为6,8,9,12,根据第五组的频率是0.2,求出第五组的频数,用样本容量减去前五组的频数,得到第六组的频数是50-6-解析:5【详解】解:一个容量为50的样本,把它分成6组,第一组到第四组的频数分别为6,8,9,12,根据第五组的频率是0.2,求出第五组的频数,用样本容量减去前五组的频数,得到第六组的频数是50-6-8-9-10-12=5.考点:频数与频率16.5.【分析】由四边形ABCD是正方形,可得AB=BC,∠CBD=45°,又由折叠的性质可得:A′B=AB,根据等边对等角与三角形内角和定理,即可求得∠BA′C的度数.【详解】解:因为四边形A解析:5.【分析】由四边形ABCD是正方形,可得AB=BC,∠CBD=45°,又由折叠的性质可得:A′B=AB,根据等边对等角与三角形内角和定理,即可求得∠BA′C的度数.【详解】解:因为四边形ABCD是正方形,所以AB=BC,∠CBD=45°,根据折叠的性质可得:A′B=AB,所以A′B=BC ,所以∠BA′C=∠BCA′=1801804522CBD -∠-==67.5°. 故答案为:67.5.【点睛】此题考查了折叠的性质与正方形的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用. 17.>【分析】根据反比例函数的图象与性质即可解答.【详解】解:的图象当时,y 随x 的增大而减小,∵,故,故答案为:>.【点睛】本题考查反比例函数的图象与性质,解题的关键是熟练掌握反比例函数 解析:>【分析】根据反比例函数的图象与性质即可解答.【详解】 解:6y x =的图象当0x <时,y 随x 的增大而减小, ∵4-<-2,故12y y >,故答案为:>.【点睛】本题考查反比例函数的图象与性质,解题的关键是熟练掌握反比例函数的图象与性质. 18.000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-解析:000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-20%=20%,∴该商场全年的营业额为:800÷20%=4000(万元),故答案为:4000.【点睛】本题考查了扇形统计图,由统计图得到二季度所占的百分比是解题关键.19.<【分析】直接利用反比例函数的增减性分析得出答案.【详解】∵反比例函数中,k=﹣1<0,∴在每个象限内,y随x的增大而增大,∵点A(﹣4,y1),B(﹣2,y2)都在反比例函数的图象上,解析:<【分析】直接利用反比例函数的增减性分析得出答案.【详解】∵反比例函数1yx=-中,k=﹣1<0,∴在每个象限内,y随x的增大而增大,∵点A(﹣4,y1),B(﹣2,y2)都在反比例函数1yx=-的图象上,且﹣2>﹣4,∴y1<y2,故答案为:<.【点睛】此题主要考查了反比例函数图象上点的坐标特征,正确把握反比例函数的性质是解题关键.20.【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:;故答案为:.【点睛】本题考查列代数式,解题的关键是读懂题意.解析:303240 x y zx y z++++【分析】根据混合什锦糖单价=三种糖果的总价钱÷混合糖果的重量列式可得答案.【详解】解:根据题意知,这种什锦糖的单价为:303240x y zx y z++++;故答案为:303240x y zx y z++++.【点睛】本题考查列代数式,解题的关键是读懂题意.21.扇形【分析】反映各个部分占整体的百分比,因此选择扇形统计图比较合适.【详解】解:要反映空气中各成分所占的百分比,因此用扇形统计图比较合适,故答案为:扇形.【点睛】本题考查统计图的选择,解析:扇形【分析】反映各个部分占整体的百分比,因此选择扇形统计图比较合适.【详解】解:要反映空气中各成分所占的百分比,因此用扇形统计图比较合适,故答案为:扇形.【点睛】本题考查统计图的选择,扇形统计图可以反映各个部分占整体的百分比.22.红【分析】分别计算出各球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸一球,摸到红球的概率==,摸到白球的概率==,摸到蓝球的概率=,所以从中任意摸一球,则摸到红球的可能性最大解析:红【分析】分别计算出各球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸一球,摸到红球的概率=3321++=12,摸到白球的概率=26=13,摸到蓝球的概率=16, 所以从中任意摸一球,则摸到红球的可能性最大.故答案为:红.【点睛】本题考查了可能性的大小:某事件的可能性等于所求情况数与总情况数之比.23.【分析】直接开平方,求出方程的解即可.【详解】∵x2=0,开方得,,故答案为:.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.解析:120x x ==【分析】直接开平方,求出方程的解即可.【详解】∵x 2=0,开方得,120x x ==,故答案为:120x x ==.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.24.1【解析】分析:利用整体的思想以及根与系数的关系即可求出答案.详解:设x+1=t ,方程a (x+1)2+b (x+1)+1=0的两根分别是x3,x4, ∴at2+bt+1=0,由题意可知:t1=解析:1【解析】分析:利用整体的思想以及根与系数的关系即可求出答案.详解:设x+1=t ,方程a (x+1)2+b (x+1)+1=0的两根分别是x 3,x 4,∴at 2+bt+1=0,由题意可知:t 1=1,t 2=2,∴t 1+t 2=3,∴x3+x4+2=3故答案为:1点睛:本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系,本题属于基础题型.三、解答题25.(1)详见解析;(2)90【分析】(1)证△DOE≌△BOF(ASA),得DE=BF,即可得出结论;(2)由∠DOE=90°,得EF⊥BD,即可得出结论.【详解】(1)∵四边形ABCD是平行四边形,O为对角线BD的中点,∴BO=DO,AD∥BC,∴∠EDO=∠FBO,在△EOD和△FOB中,EDO FBO DO BOEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE≌△BOF(ASA),∴DE=BF,又∵DE∥BF,∴四边形BFDE为平行四边形;(2)∠DOE=90°时,四边形BFDE为菱形;理由如下:由(1)得:四边形BFDE是平行四边形,若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形;故答案为:90.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及菱形的判定等知识,证出△DOE≌△BOF是解题的关键.26.证明见解析.【分析】根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.【详解】如答图,连接BC,设对角线交于点O.∵四边形ABCD是平行四边形,∴OA=OD,OB=OC.∵AE=DF,OA﹣AE=OD﹣DF,∴OE=OF.∴四边形BEDF 是平行四边形.27.(1)10°;(2)135DFA α∠=︒-;(3)∠BEA =∠FEA ,理由见解析【分析】(1)根据正方形的性质和三角形的内角和解答即可;(2)根据正方形的性质和三角形内角和解答即可;(3)延长CB 至I ,使BI =DF ,根据全等三角形的判定和性质解答即可.【详解】解:(1)∵四边形ABCD 是正方形,∴∠EBA =∠BAD =90°,∴∠EAB =90°﹣∠BAE =90°﹣55°=35°,∴∠HAD =∠BAD ﹣∠EAF ﹣∠EAB =90°﹣45°﹣35°=10°;(2)∵四边形ABCD 是正方形,∴∠EBA =∠BAD =∠ADF =90°,∴∠EAB =90°﹣∠BAE =90°﹣α,∴∠DAF =∠BAD ﹣∠EAF ﹣∠EAB =()90459045αα︒-︒-︒--︒=, ∴∠DFA =90°﹣∠DAF =()9045α︒--︒=135°﹣α;(3)∠BEA =∠FEA ,理由如下:延长CB 至I ,使BI =DF ,连接AI .∵四边形ABCD 是正方形,∴AD =AB ,∠ADF =∠ABC =90°,∴∠ABI =90°,又∵BI =DF ,∴△DAF ≌△BAI (SAS ),∴AF =AI ,∠DAF =∠BAI ,∴∠EAI =∠BAI +∠BAE =∠DAF +∠BAE =45°=∠EAF ,又∵AE 是△EAI 与△EAF 的公共边,∴△EAI ≌△EAF (SAS ),∴∠BEA =∠FEA .【点睛】本题主要考查正方形的性质、三角形外角性质及全等三角形,关键是根据正方形的性质及外角和性质得到角之间的关系,然后求解.28.(1)见解析;(2)152【分析】(1)由矩形的性质得到AB ∥CD ,再根据平行线的性质得到∠DFO=∠BEO 再证明△DOF ≌△BOE ,根据全等三角形的性质得到DF=BE ,从而得到四边形BEDF 是平行四边形;(2)先证明四边形BEDF 是菱形,再得到DE=BE ,EF ⊥BD ,OE=OF ,设AE=x ,则DE=BE=8-x 根据勾股定理求解即可.【详解】(1)证明:∵四边形ABCD 是矩形,∴AB ∥CD ,∴∠DFO =∠BEO .在△DOF 和△BOE 中 DFO BEO DOF BOE OD OB ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△DOF ≌△BOE(AAS ).∴DF =BE .又∵DF ∥BE ,∴四边形BEDF 是平行四边形.(2)解:∵DE =DF ,四边形BEDF 是平行四边形,∴四边形BEDF 是菱形.∴DE =BE ,EF ⊥BD ,OE =OF .设AE =x ,则DE =BE =8-x ,在Rt △ADE 中,根据勾股定理,有AE 2+AD 2=DE 2,∴x 2+62=(8-x)2.解得x =74. ∴DE =8-74=254. 在Rt △ABD 中,根据勾股定理,有AB 2+AD 2=BD 2,∴BD=10.∴OD =12BD =5. 在Rt △DOE 中,根据勾股定理,有DE 2-OD 2=OE 2,∴OE =154. ∴EF =2OE =152. 【点睛】 考查了菱形的判定和性质、矩形的性质、平行四边形的判定和性质、全等三角形的判定和性质和勾股定理,解题关键是熟练掌握矩形的性质.29.(1)6;(2)3;(3)【分析】(1)利用二次根式的乘法法则运算;(2)利用二次根式的乘法法则运算;(3)利用二次根式的除法法则运算.【详解】(1=23×35=6;(2()260,0y xy x y ≥≥=3(3)=4﹣=【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并同类二次根式即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.30.(1)(31-,);(2)t=9,6y x =;(3)点P 、Q 的坐标为:P (132,0)、Q (32,4)或P (7,0)、Q (3,2)或P (-7,0)、Q (-3,-2). 【分析】(1)过点D 作DE ⊥x 轴于点E ,过点B 作BF ⊥x 轴于点F ,由正方形的性质结合同角的余角相等即可证出△ADE ≌△BAF ,从而得出DE=AF ,AE=BF ,再结合点A 、D 的坐标即可求出点B 的坐标;(2)设反比例函数为ky x=,根据平行的性质找出点B ′、D ′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k 、t 的二元一次方程组,解方程组解得出结论;(3)假设存在,设点P 的坐标为(m ,0),点Q 的坐标为(n ,6n ).分B ′D ′为对角线或为边考虑,根据平行四边形的性质找出关于m 、n 的方程组,解方程组即可得出结论.【详解】解:(1)过点D 作DE ⊥x 轴于点E ,过点B 作BF ⊥x 轴于点F ,如图1所示.∵四边形ABCD 为正方形,∴AD=AB ,∠BAD=90°,∵∠EAD+∠ADE=90°,∠EAD+∠BAF=90°,∴∠ADE=∠BAF .在△ADE 和△BAF 中,有90AED BFA ADE BAF AD BA ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△BAF (AAS ),∴DE=AF ,AE=BF .∵点A (-6,0),D (-7,3),∴DE=3,AE=1,∴点B 的坐标为(-6+3,0+1),即(-3,1).故答案为:(-3,1).(2)设反比例函数为k y x=, 由题意得:点B ′坐标为(-3+t ,1),点D ′坐标为(-7+t ,3),∵点B ′和D ′在该比例函数图象上,∴33(7)k t k t =-+⎧⎨=⨯-+⎩, 解得:t=9,k=6,∴反比例函数解析式为6yx =.(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,6n).以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:①B′D′为对角线时,∵四边形B′PD′Q为平行四边形,∴63162nm n⎧-=⎪⎨⎪-=-⎩,解得:13232mn⎧=⎪⎪⎨⎪=⎪⎩,∴P(132,0),Q(32,4);②当B′D′为边时.∵四边形PQB′D′为平行四边形,∴626031m nn-=-⎧⎪⎨-=-⎪⎩,解得:73mn=⎧⎨=⎩,∴P(7,0),Q(3,2);∵四边形B′QPD′为平行四边形,∴626031n mn-=-⎧⎪⎨-=-⎪⎩,解得:73mn=-⎧⎨=-⎩.综上可知:存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形,符合题意的点P、Q的坐标为:P(132,0)、Q(32,4)或P(7,0)、Q(3,2)或P(-7,0)、Q(-3,-2).【点睛】。
【苏教版】数学八年级下学期《期中考试卷》含答案
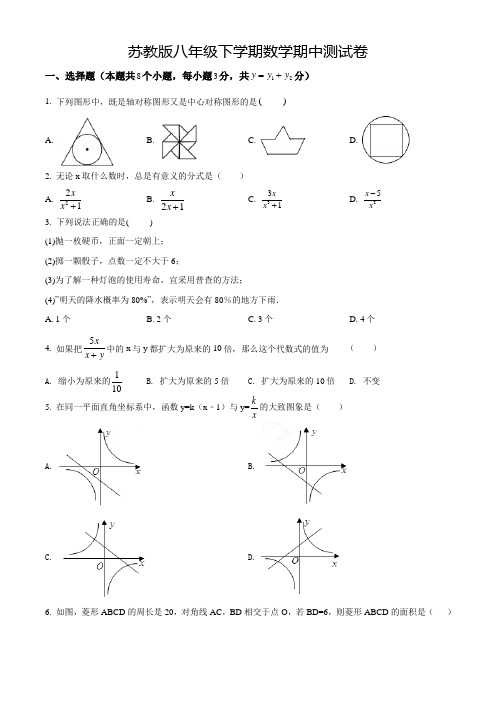
苏教版八年级下学期数学期中测试卷一、选择题(本题共8个小题,每小题3分,共12y y y =+分)1. 下列图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D.2. 无论x 取什么数时,总是有意义的分式是( ) A. 221x x + B. 21x x + C. 331xx + D. 25x x -3. 下列说法正确的是( )(1)抛一枚硬币,正面一定朝上;(2)掷一颗骰子,点数一定不大于6;(3)为了解一种灯泡的使用寿命,宜采用普查的方法;(4)”明天的降水概率为80%”,表示明天会有80%的地方下雨.A. 1个B. 2个C. 3个D. 4个 4. 如果把5xx y +中的x 与y 都扩大为原来的10倍,那么这个代数式的值为 ( )A. 缩小为原来的110 B. 扩大为原来的5倍 C. 扩大为原来的10倍 D. 不变5. 在同一平面直角坐标系中,函数y=k (x ﹣1)与y=kx 的大致图象是( )A. B.C. D.6. 如图,菱形ABCD 的周长是20,对角线AC ,BD 相交于点O ,若BD=6,则菱形ABCD 的面积是( )A. 6B. 12C. 24D. 48 7. 某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时”…”,设实际每天铺设管道x 米,则可得方程 3000300010x x --=15,根据此情景,题中用”…”表示的缺失的条件应补为( )A. 每天比原计划多铺设10米,结果延期15天才完成B. 每天比原计划少铺设10米,结果延期15天才完成C. 每天比原计划多铺设10米,结果提前15天才完成D . 每天比原计划少铺设10米,结果提前15天才完成8. 如图,在□ABCD 中,AD=2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上(E 不与A 、B 重合),连接EF 、CF ,则下列结论中一定成立的是 ( )①∠DCF=12∠BCD ;②EF=CF ;③2BEC CEF S S ∆∆<;④∠DFE=4∠AEF A. ①②③④B. ①②③C. ①②D. ①②④ 二、填空题(每题3分,共30分)9. 在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知口袋中只有3个红球,且一次摸出一个球是红球的概率为13,那么袋中的球共有________个. 10. 在式子2312351094678xy a b c x y x a x yπ+++、、、、、中,分式有________个. 11. 若分式11x x --的值为0,则x 的值是________ 12. 反比例函数-1k y x =图像经过11(,)A x y ,22(,)B x y 两点,其中120x x <<,且12y y >,则k 的范围是_________.13. 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=_____.14. 已知11a b-=4,求2227a ab ba b ab---+的值.15. 若分式方程21111x mx x--=--有增根,则m的值是____.16. 如图,过反比例函数y=kx(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为___________17. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF=_______ .18. 如图,A,B是反比例函数kyx=图象上的两点,过点A作AC y⊥轴,垂足为C,AC交OB于点D.若D为OB的中点,AOD的面积为6,则k的值为______三.计算题(共28分)19化简;(1) 2422a a a +-- (2).22214()244x x x x x x x x +---÷--+ 20. 解方程(1)2323x x =+- (2) 11222x x x -=--- 21. 先化简22321(1)24a a a a -+-÷+-,再从33a -<<中选取一个你喜欢的整数a 的值代入求值. 四、解答题(共68分)22. 某校为了了解学生孝敬父母的情况(选项: A 为父母洗一次脚;B 帮父母做一次家务;C 给父母买一件礼物;D 其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出): 根据以上信息解答下列问题:(1)这次被调查的学生有多少人?(2)求表中m ,n ,p 的值,并补全条形统计图.(3)该校有1600名学生,估计该校全体学生中选择B 选项的有多少人?23. 已知12y y y =+,1y 与x 成正比例,2y 与2x +成反比例,且当1x =-时, 3y =;当3x =时,7y =.求3x =-时,y 的值.24. 当a 为何值时, 12221(2)(1)x x x a x x x x --+-=-+-+的解是负数? 25. 准备一张矩形纸片,按如图操作: 将△ABE 沿BE 翻折,使点A 落在对角线BD 上的M 点,将△CDF 沿DF 翻折,使点C 落在对角线BD 上的N 点.(1)求证: 四边形BFDE 是平行四边形;(2)若四边形BFDE 是菱形,AB=2,求菱形BFDE 的面积.26. 某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:(1)甲队单独完成这项工程刚好如期完成;(2)乙队单独完成这项工程要比规定日期多用6天;(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.试问: (1)规定日期是多少天?(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.27. 如图,已知:直线12y x =与双曲线(0)k y k x=>交于A.B 两点,且点A 的横坐标为4, 若双曲线(0)k y k x=>上一点C 的纵坐标为8,连接AC. (1)填空: k 的值为_______; 点B 的坐标为___________;点C 的坐标为___________. (2)直接写出关于的不等式102k x x -≥的解集. (3)求三角形AOC 的面积(4) 若在x 轴上有点M ,y 轴上有点N ,且点M.N.A.C 四点恰好构成平行四边形,直接写出点M.N 的坐标.28. 已知: 在△AOB 与△COD 中,OA=OB ,OC=OD ,∠AOB=∠COD=90°.(1)如图1,点C 、D 分别在边OA 、OB 上,连结AD 、BC ,点M 为线段BC 的中点,连结OM ,则请你判断线段AD 与OM 之间的数量关系,并加以证明.(2)如图2,将图1中△COD 绕点O 逆时针旋转,旋转角为α(0°<α<90°).连结AD 、BC ,点M 为线段BC 的中点,连结OM .请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.答案与解析一、选择题(本题共8个小题,每小题3分,共12y y y =+分)1. 下列图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D.【答案】D【解析】【分析】根据轴对称图形和中心对称图形的定义逐项识别即可,在平面内,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.【详解】解: A. 是轴对称图形,但不是中心对称图形,故不符合题意;B. 不是轴对称图形,是中心对称图形,故不符合题意;C. 是轴对称图形,但不是中心对称图形,故不符合题意;D. 既是轴对称图形又是中心对称图形,故符合题意.故选D.【点睛】本题考查了轴对称图形和中心对称图形的识别,熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键.2. 无论x 取什么数时,总是有意义的分式是( ) A. 221x x + B. 21x x + C. 331x x + D. 25x x - 【答案】A【解析】试题分析: 分式总是有意义,即分母恒不为0.A 、∵21x +≠0,∴分式恒有意义.B 、当2x+1=0,即x=﹣0.5时,分式无意义.C 、当31x +=0,即x=﹣1时,分式无意义.D 、当2x =0,即x=0时,分式无意义. 故选A .考点: 分式有意义的条件.3. 下列说法正确的是( )(1)抛一枚硬币,正面一定朝上;(2)掷一颗骰子,点数一定不大于6;(3)为了解一种灯泡的使用寿命,宜采用普查的方法;(4)”明天的降水概率为80%”,表示明天会有80%的地方下雨.A. 1个B. 2个C. 3个D. 4个【答案】A【解析】分析: 直接利用概率的意义以及全面调查与抽样调查的意义分析得出答案.详解: (1)抛一枚硬币,正面一定朝上,是随机事件,故此选错误;(2)掷一颗骰子,点数一定不大于6,正确;(3)为了解一种灯泡的使用寿命,宜采用普查的方法,错误,应抽样调查;(4)”明天的降水概率为80%”,表示明天会有80%的地方下雨,错误.故选A.点睛: 本题主要考查了概率的意义以及全面调查与抽样调查的意义,正确理解相关事件的意义是解题的关键.4. 如果把5xx y+中的x与y都扩大为原来的10倍,那么这个代数式的值为()A. 缩小为原来的110B. 扩大为原来的5倍C. 扩大为原来的10倍D. 不变【答案】D【解析】分析: 依题意分别用10x和10y去代换原分式中的x和y,利用分式的基本性质化简即可.详解: ∵5101010xx y⨯+=10510xx y⨯+()=5xx y+,∴把5xx y+中的x与y都扩大为原来的10倍,分式的值不变.故选D.点睛: 本题考查了分式的基本性质,解题的关键是抓住分子、分母变化的倍数,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.5. 在同一平面直角坐标系中,函数y=k(x﹣1)与y=kx的大致图象是()A. B. C. D.【答案】C【解析】分析: 由函数y =k (x ﹣1)知直线必过(1,0)这一点,据此可得.详解: 由函数y =k (x ﹣1)知直线必过(1,0)这一点.故选C .点睛: 本题主要考查一次函数与反比例函数的图象,根据y =k (x ﹣1)知直线必过(1,0)这一点是解题的关键.6. 如图,菱形ABCD 的周长是20,对角线AC ,BD 相交于点O ,若BD=6,则菱形ABCD 的面积是( )A. 6B. 12C. 24D. 48【答案】C【解析】试题分析: 根据菱形的对角线可以求得菱形ABCD 的面积:菱形的对角线为6、8, 则菱形的面积为12×6×8=24. 故选C .考点: 菱形性质.7. 某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时”…”,设实际每天铺设管道x米,则可得方程3000300010x x--=15,根据此情景,题中用”…”表示的缺失的条件应补为()A. 每天比原计划多铺设10米,结果延期15天才完成B. 每天比原计划少铺设10米,结果延期15天才完成C. 每天比原计划多铺设10米,结果提前15天才完成D. 每天比原计划少铺设10米,结果提前15天才完成【答案】C【解析】题中方程表示原计划每天铺设管道(10)x-米,即实际每天比原计划多铺设10米,结果提前15天完成,选C.8. 如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是( )①∠DCF=12∠BCD;②EF=CF;③2BEC CEFS S∆∆<;④∠DFE=4∠AEFA. ①②③④B. ①②③C. ①②D. ①②④【答案】B【解析】【分析】分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.【详解】解: ①∵F是AD的中点,∴AF=FD.∵在▱ABCD中,AD=2AB,∴AF=FD=CD,∴∠DFC=∠DCF.∵AD∥BC,∴∠DFC=∠FCB,∴∠DCF=∠BCF,∴∠DCF=12∠BCD,故①正确;延长EF,交CD延长线于M.∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF.∵F为AD中点,∴AF=FD.在△AEF和△DFM中,A FDMAF DFAFE DFM∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEF≌△DMF(ASA),∴FE=MF,∠AEF=∠M.∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°.∵FM=EF,∴EF=CF,故②正确;③∵EF=FM,∴S△EFC=S△CFM.∵MC>BE,∴S△BEC<2S△EFC故③正确;④设∠FEC=x,则∠FCE=x,∴∠DCF=∠DFC=90°﹣x,∴∠EFC=180°﹣2x,∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x.∵∠AEF=90°﹣x,∴∠DFE=3∠AEF,故④错误.故答案为B.点睛: 本题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DMF是解题的关键.二、填空题(每题3分,共30分)9. 在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知口袋中只有3个红球,且一次摸出一个球是红球的概率为13,那么袋中的球共有________个.【答案】9【解析】试题分析: ∵在一个不透明的口袋中装有若干个质地相同而颜色可能不全相同的球,口袋中只装有3个黄球,且摸出黄球的概率为13,∴袋中共有球的个数为: 3÷13=9.故答案为9.考点: 概率公式.10. 在式子2312351094678xy a b c x yxa x yπ+++、、、、、中,分式有________个.【答案】3【解析】151096x a x y、、++是分式; 2323478xy a b c x y π+、、是整式; 故答案为3.11. 若分式11x x --的值为0,则x 的值是________ 【答案】x=-1【解析】【分析】 根据题意可得10,10x x -=-≠,然后进行求解即可.【详解】解: 由题意可得:10,10x x -=-≠,解得: 1x =-;故答案为1x =-.【点睛】本题主要考查分式为零的条件,熟练掌握分式为零的条件是解题的关键.12. 反比例函数-1k y x =的图像经过11(,)A x y ,22(,)B x y 两点,其中120x x <<,且12y y >,则k 的范围是_________.【答案】k <1;【解析】 ∵反比例函数-1k y x =的图像经过()11,A x y ,()22,B x y 两点,其中120x x <<,且12y y >, ∴k -1<0,∴k <1;故答案是: k<1.点睛: 反比例函数y=k x,它的图象与k 的关系: 反比例函数的图象是两支双曲线.当k>0时,双曲线两个分支在第一、三象限内,如图1.当k<0时,双曲线两个分支在第二、四象限内,如图2.函数的增减性: 当k>0时,在每个象限内y 随x 增大减小;当k<0时,在每个象限内,y 随x 增大而增大.13. 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=_____.【答案】020.【解析】试题分析: 根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.解: 如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案20°.14. 已知11a b-=4,求2227a ab ba b ab---+的值.【答案】6 【解析】由114a b-=可得: 4b a ab-=.原式426247ab abab ab--==-⨯+.15. 若分式方程21111x mx x--=--有增根,则m的值是____.【答案】3【解析】【分析】根据方程有增根,可得出x=1,再代入整式方程即可得出m的值.【详解】解: ∵分式方程21111x mx x--=--有增根,∴x﹣1=0,∴x=1,2x﹣(m﹣1)=x﹣1,把x=1代入得:2﹣(m﹣1)=0,∴m=3.故答案为3.【点睛】本题考查了分式方程的增根,掌握把分式方程化为整式方程以及使分母为0的根是增根是解题的关键.16. 如图,过反比例函数y=kx(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为___________【答案】4.【解析】【分析】【详解】解: ∵AB⊥x轴于点B,且S△AOB=2,∴S△AOB=12|k|=2,∴k=±4.∵函数在第一象限有图象,∴k=4.故答案为4.【点睛】本题考查反比例函数系数k的几何意义.17. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF=_______.【答案】25【解析】分析: 取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.详解: 如图,取BC的中点G,连接EG、FG.∵E、F分别是边AB、CD的中点,∴EG∥AC且EG=12AC=12×4=2,FG∥BD且FG=12BD=12×8=4.∵AC⊥BD,∴EG⊥FG,∴EF=22EG FG+=2224+=25.故答案为25.点睛: 本题考查了三角形的中位线定理,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.18. 如图,A,B是反比例函数kyx=图象上的两点,过点A作AC y⊥轴,垂足为C,AC交OB于点D.若D为OB的中点,AOD的面积为6,则k的值为______【答案】16【解析】【分析】先设点D 坐标为()a b ,,得出点B 的坐标为()2a 2b ,,A 的坐标为()4a b ,,再根据AOD 的面积为6,列出关系式求得k 的值即可.【详解】设点D 坐标为()a b ,,点D 为OB 的中点,∴点B 的坐标为()2a 2b ,,k 4ab∴=, 又AC y ⊥轴,A 在反比例函数图象上,A ∴的坐标为()4a b ,,AD 4a a 3a ∴=-=, AOD 的面积为6,13a b 62∴⨯⨯=, ab 4∴=,k 4ab 4416∴==⨯=,故答案为16.【点睛】本题考查了反比例函数系数k 的几何意义,以及运用待定系数法求反比例函数解析式,根据AOD 的面积为6列出关系式是解题的关键.三.计算题(共28分)19. 化简; (1)2422a a a+-- (2).22214()244x x x x x x x x +---÷--+【答案】(1)2;(2)212)x (- 【解析】分析: (1)先变形为同分母分式加减,再根据法则计算,最后约分即可得;(2)根据分式混合运算顺序和运算法则计算可得.详解: (1)原式=22a a -﹣42a - =242a a -- =222a a --() =2;(2)原式=[22x x x ()+-﹣212x x --()]•4x x - =[2242x x x --()﹣222x x x x --()]•4x x - =242x x x --()•4x x - =212x -(). 点睛: 本题主要考查分式的混合运算,运算时要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.20. 解方程 (1)2323x x =+- (2) 11222x x x-=--- 【答案】(1)-12;(2)无解【解析】分析: 两分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解. 详解: (1)去分母得: 2x ﹣6=3x +6,解得: x =﹣12,经检验x =﹣12是分式方程的解;(2)去分母得: 1﹣x =﹣1﹣2x +4,解得: x =2,经检验x =2增根,分式方程无解.点睛: 本题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.21. 先化简22321(1)24a a a a -+-÷+-,再从33a -<<中选取一个你喜欢的整数a 的值代入求值. 【答案】见解析【解析】分析: 根据分式的运算法则先化简,然后取一个使分式有意义的值,代入计算即可求出答案.详解: 原式=232a a +-+×2221a a a ()()()+-- =21a a -- ∵a ≠﹣2,2,1, ∴a =0.当a =0时,原式=2.点睛: 本题考查了分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.四、解答题(共68分)22. 某校为了了解学生孝敬父母的情况(选项: A 为父母洗一次脚;B 帮父母做一次家务;C 给父母买一件礼物;D 其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出): 根据以上信息解答下列问题:(1)这次被调查的学生有多少人?(2)求表中m ,n ,p 的值,并补全条形统计图.(3)该校有1600名学生,估计该校全体学生中选择B 选项的有多少人?【答案】(1)240;(2)36,96,0.25;(3)400.【解析】试题分析: (1)由选项D 的频数48,频率0.2,根据频数、频率和总量的关系即可求得这次被调查的学生人数.(2)由(1)求得的这次被调查的学生人数,根据频数、频率和总量的关系即可求得表中m ,n ,p 的值,补全条形统计图.(3)应用用样本估计总体计算即可.试题解析: (1)∵480.2240÷=,∴这次被调查的学生有240人.(2)2400.1536,?2400.496,?602400.25m n p =⨯==⨯==÷=.补全条形统计图如图:(3)∵16000.25400⨯=,∴估计该校全体学生中选择B 选项的有400人.考点: 1.频数、频率统计表;2.条形统计图;3.频数、频率和总量的关系;4.用样本估计总体.23. 已知12y y y =+,1y 与x 成正比例,2y 与2x +成反比例,且当1x =-时, 3y =;当3x =时,7y =.求3x =-时,y 的值.【答案】-11【解析】分析: 首先根据正比例和反比例的定义可得y =kx +2m x +,再把x =﹣1,y =3;x =3,y =7代入得到关于k 、m 的方程组,再解可得k 、m 的值,进而可得y 与x 的解析式,再把x =﹣3代入计算出y 的值即可.详解: ∵y 1与x 成正比例,∴设y 1=kx .∵y 2与x +2成反比例,∴设y 2=2m x +. ∵y =y 1+y 2,∴y =kx +2m x +. ∵当x =﹣1时,y =3;当x =3时,y =7, ∴3735k m m k =-+⎧⎪⎨=+⎪⎩,解得: 25k m =⎧⎨=⎩, ∴y =2x +52x +, 当x =﹣3时,y =2×(﹣3)﹣5=﹣11.点睛: 本题主要考查了待定系数法求反比例函数解析式,关键是正确表示出y 与x 的关系式.24. 当a 为何值时, 12221(2)(1)x x x a x x x x --+-=-+-+的解是负数?【答案】57a a <-≠-且 【解析】分析: 首先解分式方程求得方程的解,然后根据方程的解是负数,即可得到一个关于a 的不等式,从而求得a 的范围.详解: 方程两边同时乘以(x ﹣2)(x +1)得:(x ﹣1)(x +1)﹣(x ﹣2)2=2x +a ,即: x 2﹣1﹣(x 2﹣4x +4)=2x +a ,则x 2﹣1﹣x 2+4x ﹣4=2x +a ,移项、合并同类项得: 2x =5+a ,则x =52a +, 根据题意得: 52a +<0,且52a +≠﹣1, 解得: a <﹣5且a ≠﹣7.点睛: 本题考查了分式方程的解法以及一元一次不等式的解法,正确解得方程的解是解题的关键. 25. 准备一张矩形纸片,按如图操作: 将△ABE 沿BE 翻折,使点A 落在对角线BD 上的M 点,将△CDF 沿DF 翻折,使点C 落在对角线BD 上的N 点. (1)求证: 四边形BFDE 是平行四边形;(2)若四边形BFDE 是菱形,AB=2,求菱形BFDE 的面积.【答案】(1)证明见解析;(283 【解析】【分析】 【详解】试题分析:(1)、根据矩形的性质可得∠ABD=∠CDB ,根据折叠可得∠EBD=∠FDB ,则BE ∥DF ,根据两组对边分别平行的四边形为平行四边形进行证明;(2)、根据菱形可得BE=DE ,有折叠可得BM=AB=2,则DM=BM=2,BD=4,根据勾股定理可得3DE=x ,则3-x ,BE=x ,根据Rt △ABE 的勾股定理得出x 的值,然后计算菱形的面积.试题解析: (1)、∵四边形ABCD 是矩形 ∴ AB ∥CD AD ∥BC ∴∠ABD=∠CDB由折叠知: ∠EBD=∠ABD ,∠FDB=∠CDB ∴∠EBD=∠FDB ∴BE//DF∴四边形BFDE 是平行四边形(2)、∵四边形BFDE是菱形 ∴ BE=DE 由折叠知: ∠EMB=∠A=90°BM=AB=2∴DM=BM=2 ∴BD=4 由勾股定理解得DE=x ,则,BE=x在Rt △ABE 中,AE 2+AB 2=BE 2 2+22=x 2 解得: x=3∴菱形BFDE 的面积为3×2=3 考点: (1)、平行四边形的判定;(2)、勾股定理;(3)、菱形的面积计算.26. 某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:(1)甲队单独完成这项工程刚好如期完成;(2)乙队单独完成这项工程要比规定日期多用6天; (3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.试问: (1)规定日期是多少天? (2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.【答案】(1)6天;(2)方案(3)最节省工程款,理由见解析【解析】分析:(1)根据关键描述语为: “甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成”;说明甲队实际工作了3天,乙队工作了x 天完成任务,工作量=工作时间×工作效率等量关系为: 甲3天的工作量+乙规定日期的工作量=1列方程.(2)再看费用情况: 方案(1)、(3)不耽误工期,符合要求,可以求费用,方案(2)显然不符合要求详解: (1)设规定日期为x 天.由题意得:3 x +6x x =1 解得: x =6.经检验: x =6是原方程的根.答: 规定日期为6天;(2)显然,方案(2)不符合要求;方案(1): 1.2×6=7.2(万元);方案(3): 1.2×3+0.5×6=6.6(万元).因为7.2>6.6,所以在不耽误工期的前提下,选方案(3)最节省工程款.点睛: 本题主要考查了分式方程的应用,找到合适的等量关系是解决问题的关键.在既有工程任务,又有工程费用的情况下.先考虑完成工程任务,再考虑工程费用.27. 如图,已知:直线12y x =与双曲线(0)k y k x=>交于A.B 两点,且点A 的横坐标为4, 若双曲线(0)k y k x=>上一点C 的纵坐标为8,连接AC. (1)填空: k 的值为_______; 点B 的坐标为___________;点C 的坐标为___________. (2)直接写出关于的不等式102k x x -≥的解集. (3)求三角形AOC 的面积(4) 若在x 轴上有点M ,y 轴上有点N ,且点M.N.A.C 四点恰好构成平行四边形,直接写出点M.N 的坐标.【答案】(1)k=8 ,B(-4,-2),C(1,8) ;(2)404x x -≤<≥或 ;(3) 15;(4)M(3,0)、N(0,6)或M(-3,0)、N(0,-6)【解析】分析: (1)由直线12y x =与双曲线0k y k x=(>)交于A 、B 两点,A 点横坐标为4,代入正比例函数,可求得点A 的坐标,继而求得k 值,把C 的纵坐标代入反比例函数,即可得到C 的坐标;根据对称性,可求得点B 的坐标.(2)结合图象,即可求得关于x 的不等式102k x x-≥的解集; (3)首先过点C 作CD ⊥x 轴于点D ,过点A 作AE ⊥轴于点E ,可得S △AOC =S △OCD +S 梯形AEDC ﹣S △AOE =S 梯形AEDC ,又由双曲线0ky k x=(>)上有一点C 的纵坐标为8,可求得点C 的坐标,继而求得答案;(4)由当MN ∥AC ,且MN =AC 时,点M 、N 、A 、C 四点恰好构成平行四边形,根据平移的性质,即可求得答案.详解: (1)∵直线12y x =与双曲线0k y k x =(>)交于A 、B 两点,A 点横坐标为4,∴点A 的纵坐标为: y =12×4=2,∴点A (4,2),∴2=4k ,∴k =8,∴8y x =;把y =8代入8y x =,解得: x =1,∴C (1,8).∵直线12y x =与双曲线0k y k x=(>)交于A 、B 两点,∴B (﹣4,﹣2); (2)由图象可知: 关于x 的不等式102k x x -≥的解集为: ﹣4≤x <0或x ≥4; (3)过点C 作CD ⊥x 轴于点D ,过点A 作AE ⊥x 轴于点E .∵双曲线0k y k x =(>)上有一点C 的纵坐标为8,∴把y =8代入y =8x ,得: x =1,∴点C (1,8),∴S △AOC =S △OCD +S 梯形AEDC ﹣S △AOE =S 梯形AEDC =12×(2+8)×(4﹣1)=15; (4)如图,当MN ∥AC ,且MN =AC 时,点M 、N 、A 、C 四点恰好构成平行四边形.∵点A (4,2),点C (1,8),∴根据平移的性质可得: M (3,0),N (0,6)或M ′(﹣3,0),N ′(0,﹣6).点睛: 本题考查了反比例函数的性质、待定系数法求函数的解析式以及一次函数的性质等知识.此题难度较大,综合性很强,注意掌握数形结合思想、分类讨论思想与方程思想的应用.28. 已知: 在△AOB 与△COD 中,OA=OB ,OC=OD ,∠AOB=∠COD=90°.(1)如图1,点C 、D 分别在边OA 、OB 上,连结AD 、BC ,点M 为线段BC 的中点,连结OM ,则请你判断线段AD 与OM 之间的数量关系,并加以证明.(2)如图2,将图1中的△COD 绕点O 逆时针旋转,旋转角为α(0°<α<90°).连结AD 、BC ,点M 为线段BC 的中点,连结OM .请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;(3)如图3,将图1中的△COD 绕点O 逆时针旋转到使△COD 的一边OD 恰好与△AOB 的边OA 在同一条直线上时,点C 落在OB 上,点M 为线段BC 的中点.请你判断(1)中线段AD 与OM 之间的数量关系是否发生变化,写出你的猜想,并加以证明.【答案】(1)OM=12AD,理由见解析;(2)成立,理由见解析;(3)不变化,理由见解析【解析】分析: (1)AD与OM之间的数量关系为AD=2OM;(2)(1)中的结论仍然成立,理由为: 如图2所示,延长BO到F,使FO=BO,连接CF,由M、O分别为BC、BF的中点,得到OM为三角形BCF的中位线,利用中位线定理得到FC=2OM,利用SAS得到三角形AOD与三角形FOC全等,利用全等三角形的对应边相等得到FC=AD,等量代换得到AD=2OM;(3)(1)中线段AD与OM之间的数量关系没有发生变化,理由为: 如图3所示,延长DC交AB于E,连结ME,过点E作EN⊥AD于N,由三角形COD与三角形AOB都为等腰直角三角形,利用等腰直角三角形的性质得到四个角为45度,进而得到三角形MCE与三角形AED为等腰直角三角形,根据EN为直角三角形ADE斜边上的中线得到AD=2EN,再利用三个角为直角的四边形为矩形得到四边形OMEN为矩形,可得出EN=OM,等量代换得到AD=2OM.详解: (1)线段AD与OM之间的数量关系是AD=2OM;(2)(1)的结论仍然成立,理由为:证明: 如图2,延长BO到F,使FO=BO,连结CF.∵M为BC中点,O为BF中点,∴MO为△BCF的中位线,∴FC=2OM.∵∠AOB=∠AOF=∠COD=90°,∴∠AOB+∠BOD=∠AOF+∠AOC,即∠AOD=∠FOC.在△AOD和△FOC中,OA OFAOD FOCOC OD=⎧⎪∠=∠⎨⎪=⎩,∴△AOD≌△FOC(SAS),∴FC=AD,∴AD=2OM.(3)(1)中线段AD与OM之间的数量关系没有发生变化,理由为:证明: 如图3,延长DC交AB于E,连结ME,过点E作EN⊥AD于N.∵OA=OB,OC=OD,∠AOB=∠COD=90°,∴∠A=∠D=∠B=∠BCE=∠DCO=45°,∴AE=DE,BE= CE,∠AED=90°,∴DN=AN,∴AD=2NE.∵M为BC的中点,∴EM⊥BC,∴四边形ONEM是矩形,∴NE=OM,∴AD=2OM.故答案为AD=2OM.点睛: 本题考查了几何变换综合题,涉及的知识有: 全等三角形的判定与性质,等腰直角三角形的判定与性质,三角形的中位线定理,是一道多知识点探究性试题.。
【苏教版】数学八年级下学期《期中考试试卷》含答案

苏教版八年级下学期数学期中测试卷一、选择题: (本大题共10小题,每题3分,共30分.)1. 下列图形中,不是中心对称图形是( ) A. B. C. D.2. 下列四种说法中不正确的是( )A. 为了解一种灯泡的使用寿命,宜采用普查的方法;B. “在同一年出生的367名学生中,至少有两人的生日是同一天”是必然事件;C. “打开电视机,正在播放少儿节目”是随机事件;D. 如果一件事发生的概率只有十万分之一,那么它仍是可能发生的事件.3. 一只不透明的口袋中原来装有1个白球、2个红球,每个球除颜色外完全相同.则下列将袋中球增减的办法中,使得将球摇匀,从中任意摸出一个球,摸到白球与摸到红球的概率不相等为( )A. 在袋中放入1个白球B. 在袋中放入1个白球、2个红球C. 在袋中取出1个红球D. 在袋中放入2个白球、1个红球 4. 下列分式是最简分式的是( ) A. 22a a ab+ B. 63xy a C. 211x x -+ D. 211x x ++ 5. 若222x x y +中的x 和y 的值都缩小2倍,则分式的值( ) A. 缩小2倍B. 缩小4倍C. 扩大2倍D. 扩大4倍6. 下列命题中是真命题的是( )A. 两条对角线相等的四边形是矩形;B. 有一条对角线平分一个内角的平行四边形为菱形;C. 对角线互相垂直且相等的四边形是正方形;D. 依次连结四边形各边的中点,所得四边形是菱形. 7. 如图,将矩形 ABCD 绕点 A 顺时针旋转到矩形 AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( )A. 68°B. 20°C. 28°D. 22°8. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是()A. ①,②B. ①,④C. ③,④D. ②,③9. 如图,四边形ABCD是正方形,直线a,b,c分别通过A,B,C三点,且////a b c,若a与b的距离为5,b与c的距离为7,则正方形ABCD的面积等于( )A. 148B. 70C. 144D. 7410. 如图,在矩形ABCD中,AB=10,BC=5 .若点M、N分别是线段ACAB上的两个动点,则BM+MN 的最小值为()A. 10B. 8C. 5D. 6二、填空题: (本大题共8小题,每题2分,共16分.)11. 若分式242aa-+的值为0,则a的值为____.12. 有5张看上去无差别的卡片,上面分别写着02,227,1.333,随机抽取1张,则取出的数是无理数的概率是_______.13. 已知平行四边形ABCD中,∠C=2∠B,则∠A=___________度.14. 若关于x 的方程2111x mx x++=--产生增根,则m的值为___________15. 菱形的周长为40,两条对角线之比为3: 4,则菱形的面积为_________________.16. 若112a b-=,则422a ab ba ab b+---的值是________ 17. 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是_____________.18. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是___.三、解答题: (本大题共8小题,共54分. 解答需写出必要的文字说明或演算步骤)19.计算或解方程: (1)23232y y x x⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭(2) 214111x x x+-=--20. 先化简228(2)242m m m m m m+÷-+--,若22m-≤≤,请你选择一个你喜欢的整数,代入求值.21. 如图是规格为8×8的正方形网格,请在所给网格中......按下列要求操作:(1)在第二象限内的格点上..........画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是____________,△ABC的面积是_____________________.(2)画出△ABC,以点C为旋转中心、旋转180°后的△A′B′C,连结AB′和A′B,则四边形AB A′B′的形状是何特殊四边形?___________________.(3)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等?若存在,请直接写出点P的坐标(写出一种情况即可)___________________.22. 某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位: kg)分成五组(A: 39.5~46.5;B: 46.5~53.5;C: 53.5~60.5;D: 60.5~67.5;E: 67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.解答下列问题:(1)这次抽样调查的样本容量是,并补全频数分布直方图;(2)C组学生的频率为,在扇形统计图中D组的圆心角是度;(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?23. 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证: 四边形BCED是平行四边形;(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.24. 今年某中学到鹅鼻嘴公园植树,已知该中学离公园约15km,部分学生骑自行车出发40分钟后,其余学生乘汽车出发,汽车速度是自行车速度的3倍,全体学生同时到达,设自行车的速度为v km/h.(1) 求v的值;(2) 植树活动完成后,由于学生比较劳累,骑自行车的学生的速度变为原来的23,汽车速度不变,为了使两批学生同时到达学校,那么骑自行的学生应该提前多少时间出发.25. 如图1,将ABC ∆纸片沿中位线EH 折叠,使点A 的对称点D 落在BC 边上,再将纸片分别沿等腰BED ∆和等腰DHC ∆的底边上的高线EF 、HG 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.(1)将ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ,则操作形成的折痕分别是线段______和______;:ABCD AEFG S S =矩形______.(2)ABCD 纸片还可以按图3的方式折叠成一个叠合矩形EFGH ,若5EF =,12EH =,求AD 的长;(3)如图4,梯形ABCD 纸片满足//AD BC ,AD BC <,AB BC ⊥,8AB =,10CD =.小明把该纸片折叠,得到叠合正方形....请你帮助画出叠合正方形的示意图,并求出AD 、BC 的长.答案与解析一、选择题: (本大题共10小题,每题3分,共30分.)1. 下列图形中,不是中心对称图形是( ) A. B. C. D.【答案】B【解析】分析: 根据中心对称图形的定义判断即可,在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做叫做中心对称图形.详解: A 、C 、D 符合中心对称图形的定义,是中心对称图形;B 不符合中心对称图形的定义,不是中心对称图形,是轴对称图形.故选B.点睛: 本题考查了中心对称图形的识别,准确掌握中心对称图形的定义是解答本题的关键. 2. 下列四种说法中不正确的是( )A. 为了解一种灯泡的使用寿命,宜采用普查的方法;B. “在同一年出生的367名学生中,至少有两人的生日是同一天”是必然事件;C. “打开电视机,正在播放少儿节目”是随机事件;D. 如果一件事发生的概率只有十万分之一,那么它仍是可能发生的事件.【答案】A【解析】分析: 由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据随机事件、必然事件、不可能事件,可得答案.详解: A.为了解一种灯泡的使用寿命,调查具有破坏性,宜采用抽样调查的方法,A 错误;B.”在同一年出生的367名学生中,至少有两人的生日是同一天”是必然事件,故B 正确;C.”打开电视机,正在播放少儿节目”是随机事件,故C 正确;D.如果一件事发生的概率只有十万分之一,那么它仍是可能发生的事件,故D 正确;故选A . 点睛: 本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查;随机事件是可能发生也可能不发生的事件,必然事件是一定发生的事件,不可能事件是一定不发生的事件.3. 一只不透明的口袋中原来装有1个白球、2个红球,每个球除颜色外完全相同.则下列将袋中球增减的办法中,使得将球摇匀,从中任意摸出一个球,摸到白球与摸到红球的概率不相等为( )A. 在袋中放入1个白球B. 在袋中放入1个白球、2个红球C. 在袋中取出1个红球D. 在袋中放入2个白球、1个红球 【答案】B【解析】分析: 根据概率公式,分别求出各选项中摸到白球与摸到红球的概率即可求解.详解:A 、在袋中放入1个白球,则摸到白球的概率为: 1111212+=++,摸到红球的概率为: 211212=++,故本选项不符合题意;B 、在袋中放入1个白球、2个红球,则摸到白球的概率为: 11112123+=+++,摸到红球的概率为: 22212123+=+++,故本选项符合题意; C 、在袋中取出1个红球,则摸到白球的概率为:111212=+-,摸到红球的概率为: 2111212-=+-,故本选项不符合题意;D 、在袋中放入2个白球、1个红球,则摸到白球的概率为: 12112212+=+++,摸到红球的概率为: 21112212+=+++,故本选项不符合题意; 故选B .点睛: 本题考查了概率公式: 概率=所求情况数与总情况数之比,熟练掌握概率的计算公式是解答本题的关键.4. 下列分式是最简分式的是( ) A. 22a a ab+ B. 63xy a C. 211x x -+ D. 211x x ++ 【答案】D【解析】 A 选项中,分式分子、分母中含有公因式a ,因此它不是最简分式.故本选项错误;B 选项中,分式的分子、分母中含有公因数3,因此它不是最简分式.故本选项错误;C 选项中,分子可化为(x +1)(x -1),所以该分式的分子、分母中含有公因式(x +1),因此它不是最简分式.故本选项错误;D 选项中,分式符合最简分式的定义.故本选项正确.故选D .点睛: 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,看分子和分母中有无公因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.5. 若222x x y+中的x 和y 的值都缩小2倍,则分式的值( ) A. 缩小2倍B. 缩小4倍C. 扩大2倍D. 扩大4倍【答案】C【解析】 分析: 依题意分别用12x 和12y 去代换原分式中的x 和y ,利用分式的基本性质化简即可. 详解: 分别用12x 和12y 去代换原分式中的x 和y 得, 222222124211114422x x x x y x y x y ⨯==+⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,∴分式的值变为原来的2倍.故选C.点睛: 本题主要考查分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.解题的关键是抓住分子、分母变化的倍数,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.6. 下列命题中是真命题的是( )A. 两条对角线相等的四边形是矩形;B. 有一条对角线平分一个内角的平行四边形为菱形;C. 对角线互相垂直且相等的四边形是正方形;D. 依次连结四边形各边的中点,所得四边形是菱形.【答案】B【解析】分析: 根据菱形、矩形和正方形的判定来逐一分析各个选项,从而选出正确的答案.详解: A. ∵两条对角线相等的四边形可能是等腰梯形,故A 不正确;B. 有一条对角线平分一个内角的平行四边形为菱形,正确;如图,四边形ABCD 是平行四边形,BD 平分∠ABC .求证: 四边形ABCD是菱形.证明: ∵四边形ABCD是平行四边形,∴AD∥BC,∴∠2=∠3.∵BD平分∠ABC,∴∠1=∠2,∴∠1=∠3,∴AB=AD,∴四边形ABCD是菱形.C. ∵对角线互相垂直且相等的四边形可能是筝形,故C不正确;D. ∵依次连结四边形各边的中点,所得四边形是平行四边形,故D不正确.点睛: 本题主要考查命题的概念、平行四边形的判定定理、菱形的判定定理、矩形的判定定理以及正方形的判定定理.用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.7. 如图,将矩形ABCD 绕点A 顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( )A. 68°B. 20°C. 28°D. 22°【答案】D【解析】试题解析: ∵四边形ABCD为矩形,∴∠BAD=∠ABC=∠ADC=90°,∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α,∴∠BAB′=α,∠B′AD′=∠BAD=90°,∠D′=∠D=90°,∵∠2=∠1=112°,而∠ABD=∠D′=90°,∴∠3=180°-∠2=68°,∴∠BAB′=90°-68°=22°,即∠α=22°.故选D.8. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是()A. ①,②B. ①,④C. ③,④D. ②,③【答案】D【解析】【分析】确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.【详解】只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,∴带②③两块碎玻璃,就可以确定平行四边形的大小.故选D.【点睛】本题考查平行四边形定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.a b c,若a与b的距离9. 如图,四边形ABCD是正方形,直线a,b,c分别通过A,B,C三点,且////为5,b与c的距离为7,则正方形ABCD的面积等于( )A. 148B. 70C. 144D. 74【答案】D【解析】分析: 过A作AM⊥直线b于M,过D作DN⊥直线c于N,求出∠AMD=∠DNC=90°,AD=DC,∠1=∠3,根据AAS推出△AMD≌△CND,根据全等得出AM=CN,求出AM=CN=5,DN=7,在Rt△DNC中,由勾股定理求出DC2即可.详解: 如图:过A作AM⊥直线b于M,过D作DN⊥直线c于N,则∠AMD=∠DNC=90°,∵直线b∥直线c,DN⊥直线c,∴∠2+∠3=90°,∵四边形ABCD是正方形,∴AD=DC,∠1+∠2=90°,∴∠1=∠3,在△AMD和△CND中,∵∠1=∠3,∠AMD=∠CND,AD=DC,∴△AMD≌△CND,∴AM=CN,∵a与b之间的距离是5,b与c之间的距离是7,∴AM=CN=5,DN=7,在Rt△DNC中,由勾股定理得: DC2=DN2+CN2=72+52=74,即正方形ABCD的面积为74,故选B.点睛: 本题考查了全等三角形的性质和判定,正方形的性质的应用,解此题的关键是能正确作出辅助线,并进一步求出△AMD≌△CND,难度适中.10. 如图,在矩形ABCD中,AB=10,BC=5 .若点M、N分别是线段ACAB上的两个动点,则BM+MN 的最小值为()A. 10B. 8C. 5D. 6【答案】B【解析】【分析】过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,EF就是所求的线段.【详解】解: 过B点作AC的垂线,使AC两边的线段相等,到E点,过E作EF垂直AB交AB于F点,5AC边上的高为55∵△ABC∽△EFB,∴AB ACEF BE=,即1055EF45=EF=8.故选B.考点: 轴对称-最短路线问题.二、填空题: (本大题共8小题,每题2分,共16分.)11. 若分式242aa-+的值为0,则a的值为____.【答案】2【解析】【分析】先进行因式分解和约分,然后求值确定a【详解】原式=(2)(2)22a aaa=-++-∵值为0∴a-2=0,解得: a=2故答案为: 2【点睛】本题考查解分式方程,需要注意,此题a不能为-2,-2为分式方程的增根,不成立12. 有5张看上去无差别的卡片,上面分别写着02,227,1.333,随机抽取1张,则取出的数是无理数的概率是_______.【答案】0.4【解析】解: 一共有5个数,无理数有π2共2个,∴抽到写有无理数的卡片的概率是2÷5=0.4.故答案为0.4.点睛: 考查概率公式的应用;判断出无理数的个数是解决本题的易错点.13已知平行四边形ABCD中,∠C=2∠B,则∠A=___________度.【答案】120°【解析】试题分析: 根据题意得: ∠B+∠C=180°,则∠B=60°,∠C=120°,则∠A=∠C=120°.考点: 平行四边形的性质.14. 若关于x的方程2111x mx x++=--产生增根,则m的值为___________【答案】2【解析】【分析】分式方程去分母转化为整式方程,由分式方程有增根,得到x-1=0,求出x的值,代入整式方程即可求出m 的值.【详解】去分母得: x+2=m+1,由分式方程有增根,得到x−1=0,即x=1,把x=1代入整式方程得: m=2,故答案为2.【点睛】此题考查分式方程的增根,解题关键在于掌握运算法则.15. 菱形的周长为40,两条对角线之比为3: 4,则菱形的面积为_________________.【答案】96【解析】【分析】根据已知可分别求得两条对角线的长,再根据菱形的面积等于两对角线乘积的一半即可得到其面积.【详解】设两条对角线长分别为3x,4x,根据勾股定理可得(32x)2+(42x)2=102,解之得,x=4,则两条对角线长分别为12、16,∴菱形的面积=12×16÷2=96.故答案为96.【点睛】此题主要考查菱形的面积公式: 两条对角线的积的一半,综合利用了菱形的性质和勾股定理16. 若112a b-=,则422a ab ba ab b+---的值是________【答案】2 -5.【解析】解: ∵1a﹣1b=2,∴a﹣b=﹣2ab,∴原式=42a b aba b ab-+--()()=244ab abab ab-+--=25abab-=﹣25.故答案为﹣25.17. 如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是_____________.【答案】3【解析】分析: 连接CE,设DE=x,则AE=8-x,判断出OE是AC的垂直平分线,即可推得CE=AE=8-x,然后在Rt△CDE 中,根据勾股定理,求出DE的长是多少即可.详解: 如图,连接CE,,设DE=x,则AE=8-x,∵OE⊥AC,且点O是AC的中点,∴OE是AC的垂直平分线,∴CE=AE=8-x,在Rt△CDE中,x2+42=(8-x)2,解得x=3,∴DE的长是3.故答案为3.点睛: 此题主要考查了矩形的性质、中垂线的性质和勾股定理,熟练掌握矩形的对角线互相平分和中垂线的性质是解题的关键.18. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是___.【答案】()n13-【解析】【分析】【详解】试题分析: 连接DB,BD与AC相交于点M,∵四边形ABCD是菱形,∴AD=AB.AC⊥DB.∵∠DAB=60°,∴△ADB是等边三角形.∴DB=AD=1,∴BM=1 2∴3∴3同理可得332,333,…按此规律所作的第n3)n-1三、解答题: (本大题共8小题,共54分. 解答需写出必要的文字说明或演算步骤)19. 计算或解方程: (1)23232y yx x⎛⎫⎛⎫-÷-⎪ ⎪⎝⎭⎝⎭(2)214111xx x+-=--【答案】(1)489x y -;(2)x=1 【解析】分析: (1)先算乘方,然后把除法转化为乘法约分化简;(2)两边都乘以最简公分母(x +1)(x -1),把分式方程转化为整式方程求解,解分式方程要验根;详解: (1)原式=232698y y x x ⎛⎫÷- ⎪⎝⎭=-262389y x x y ⨯=-489x y; (2)两边都乘以最简公分母(x+1)(x-1),得()22141x x +-=-,∴x 2+2x +1-4=x 2-1, ∴2x =2,∴1x =.点睛: 本题考查了分式的混合运算和分式方程的解法,熟练掌握分式运算的相关法则和解分式方程的步骤是解答本题的关键.20. 先化简228(2)242m m m m m m +÷-+--,若22m -≤≤,请你选择一个你喜欢的整数,代入求值. 【答案】16【解析】分析: 先把括号里通分,再把除法转化为乘法,并把分子、分母分解因式约分化简,然后从22m -≤≤中选一个使分式有意义的数代入计算.详解: 原式= ()()2282222m m m m m m -++÷-- =()()222222m m m m m +-⨯-+ =()122m m + , 当1m =时,原式()()11222112m m ==+⨯⨯+=16(或当1m =-时,原式=12-).点睛: 本题考查了分式的化简求值,明确分式混合运算的顺序是解答本题的关键,不考虑分式有无意义,随便选数是本题的易错点.21. 如图是规格为8×8的正方形网格,请在所给网格中......按下列要求操作: (1)在第二象限内的格点上..........画一点C , 使点C 与线段AB 组成一个以AB 为底的等腰三角形, 且腰长是无理数, 则C 点坐标是____________,△ABC 的面积是_____________________.(2)画出△ABC ,以点C 为旋转中心、旋转180°后的△A′B′C ,连结AB′和A′B , 则四边形AB A′B′的形状是何特殊四边形?___________________.(3)在坐标轴上是否存在P 点,使得△PAB 与△CAB 的面积相等?若存在,请直接写出点P 的坐标(写出一种情况即可)___________________.【答案】 (1). C (-1,1) (2). 4 (3). 矩形 (4). P (0,2)或(-2,0)【解析】分析: (1)根据网格特征选择即可(答案不唯一),利用勾股定理可验证腰长为无理数,用割补法求出△ABC 的面积;(2)由于旋转180°后与原图形成中心对称,所以延长AC 、BD ,使'CA AC =,'CB BC =,即可画出图形,然后根据矩形的判定方法说明即可;(3)根据网格特征选择,然后求出面积验证.详解: (1)如图,取点C (-1,1),则221310+=△ABC 的面积=4×4-111332213134222⨯-⨯⨯-⨯⨯-⨯⨯=. (2)延长AC 、BD ,使'CA AC =,'CB BC =,连接AB′,A′B ,B′′B ,由题意可知,BC=CB′,AC=C A′,∴四边形ABA′B′是平行四边形,又∵AA′=BB′,∴四边形ABA′B′是矩形;(3)如图,当P 1(0,2)时,S △ABP1=11188422AB AP ⋅=⨯⨯=,符合题意; 当P 2(-2,0)时, S △ABP1=21188422AB BP ⋅=⨯⨯=,符合题意; ∴P 点坐标是(0,2)或(-2,0).点睛: 本题考查了旋转作图,矩形的判定,勾股定理的应用,坐标平面内求图形的面积,明确旋转180°后与原图形成中心对称,熟练运用勾股定理求线段的长是解答本题的关键.22. 某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位: kg )分成五组(A: 39.5~46.5;B: 46.5~53.5;C: 53.5~60.5;D: 60.5~67.5;E: 67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.解答下列问题:(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;(2)C 组学生的频率为 ,在扇形统计图中D 组的圆心角是 度;(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?【答案】(1)50;(2)0.32;72(3)360【解析】【分析】(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可;(2)由图表得出C组学生的频率,并计算出D组的圆心角即可;(3)根据样本估计总体即可.【详解】(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12,补全频数分布直方图,如图:(2)C组学生的频率是0.32;D组的圆心角=1050×360°=72°;(3)样本中体重超过60kg的学生是10+8=18人,该校初三年级体重超过60kg的学生=1850×100%×1000=360(人).考点: 频数分布直方图.23. 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证: 四边形BCED是平行四边形;(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.【答案】(1)证明见解析(2)2【解析】(1)根据平行线的性质以及判定定理求得//DF AC 和//EC DB ,从而得证四边形BCED 是平行四边形;(2)根据角平分线的性质得DBN CBN =∠∠,再根据平行线的性质得CNB DBN =∠∠,从而得证BNC NBC =∠∠,根据等腰三角形的性质即可求出CN 的长.【详解】(1)∵∠A=∠F∴//DF AC∵1DMF =∠∠,12∠=∠∴DMF =∠∠2∴//EC DB∴四边形BCED 是平行四边形(2)∵BN 平分∠DBC∴DBN CBN =∠∠∵//EC DB∴CNB DBN =∠∠∴BNC NBC =∠∠∴2CN BC DE ===.【点睛】本题考查了平行线相关的问题,掌握平行线的性质以及判定定理、平行四边形的性质以及判定定理、角平分线的性质、等腰三角形的性质是解题的关键.24. 今年某中学到鹅鼻嘴公园植树,已知该中学离公园约15km ,部分学生骑自行车出发40分钟后,其余学生乘汽车出发,汽车速度是自行车速度的3倍,全体学生同时到达,设自行车的速度为v km/h .(1) 求v 的值;(2) 植树活动完成后,由于学生比较劳累,骑自行车的学生的速度变为原来的23,汽车速度不变,为了使两批学生同时到达学校,那么骑自行的学生应该提前多少时间出发.【答案】(1) 15v =;(2)骑自行车的学生应提前76h 出发. 【解析】分析: (1)根据题意列出方程,求出方程的解即可得到v 的值;(2)根据题意求出骑自行车的速度,即可得到骑自行的学生应该提前的时间.详解: (1)由题意得:1515233v v =+ , 解之得,经检验: 15v =是方程的解;(2)自行车的速度变为210/3v km h =, 应该提前时间1515710456h -= , 则骑自行车的学生应提前76h 出发. 点睛: 本题考查了分式方程的实际应用,根据同时到达找出等量关系: 自行车行完全程所用时间=汽车行完全程所用时间+23是解答本题的关键. 25. 如图1,将ABC ∆纸片沿中位线EH 折叠,使点A 的对称点D 落在BC 边上,再将纸片分别沿等腰BED ∆和等腰DHC ∆的底边上的高线EF 、HG 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.(1)将ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ,则操作形成的折痕分别是线段______和______;:ABCD AEFG S S =矩形______.(2)ABCD 纸片还可以按图3的方式折叠成一个叠合矩形EFGH ,若5EF =,12EH =,求AD 的长;(3)如图4,梯形ABCD 纸片满足//AD BC ,AD BC <,AB BC ⊥,8AB =,10CD =.小明把该纸片折叠,得到叠合正方形....请你帮助画出叠合正方形的示意图,并求出AD 、BC 的长. 【答案】 (1). AE (2). GF (3). 1: 2【解析】分析:(1)由图可直接得到第一、二空答案,根据折叠的性质可得△AEH 与△ABE 面积相等、梯形HFGA 与梯形FCDG 面积相等,据此不难得到第三空答案;(2)对图形进行点标注,如图所示: 首先根据勾股定理求得FH 的长,再根据折叠的性质以及请到的知识可得AH =FN ,HD =HN ,然后根据线段和差关系即可得到AD 的长;(3)根据题目信息,动手这一下,然后将结合画出来,再结合折叠的性质以及勾股定理的知识分析解答即可.详解: (1)根据题意得: 操作形成的折痕分别是线段AE、GF;由折叠的性质得: △ABE≌△AHE,四边形AHFG≌四边形DCFG,∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,∴S矩形AEFG=12S平行四边形ABCD,∴S矩形AEFG: S平行四边形ABCD=1: 2;故答案为AE,GF,1: 2;(2)∵四边形EFGH是矩形,∴∠HEF=90°,∴FH=22512=13,由折叠的性质得: AD=FH=13;由折叠的对称性可知: DH=NH,AH=HM,CF=FN. 易得△AEH≌CGF,所以CF=AH,所以AD=DH+AH=HN+FN=FH=13.(3)有3种折法,如图4、图5、图6所示:①折法1中,如图4所示:由折叠的性质得: AD=BG,AE=BE=12AB=4,CF=DF=12CD=5,GM=CM,∠FMC=90°,∵四边形EFMB是叠合正方形,∴BM=FM=4,∴GM=CM=222254CF FM-=-=3,∴AD=BG=BM-GM=1,BC=BM+CM=7;②折法2中,如图5所示:由折叠的性质得: 四边形EMHG的面积=12梯形ABCD的面积,AE=BE=12AB=4,DG=NG,NH=CH,BM=FM,MN=MC,∴GH=12CD=5,∵四边形EMHG是叠合正方形,∴EM=GH=5,正方形EMHG的面积=52=25,∵∠B=90°,∴2254-,设AD=x,则MN=FM+FN=3+x,∵梯形ABCD的面积=12(AD+BC)×8=2×25,∴AD+BC=252,∴BC=252-x,∴MC=BC-BM=252-x-3,∵MN=MC,∴3+x=252-x-3,解得: x=134,∴AD=134,BC=252-134=374;③折法3中,如图6所示,作GM⊥BC于M,则E、G分别为AB、CD的中点,则AH=AE=BE=BF=4,CG=12CD=5,正方形的边长2,GM=FM=4,2254,∴BC=BF+FM+CM=11,FN=CF=7,DH=NH=8-7=1,∴AD=5.点睛: 本题是四边形综合题,考查了折叠的性质,正方形的性质、勾股定理、梯形面积的计算、解方程等知识,本题综合性强,有一定难度.。
最新苏教版数学八年级下册《期中测试卷》含答案解析

苏教版八年级下学期期中考试数学试题一、单项选择题(本大题共有8小题,每题3分,共24分)1. 若分式11a 有意义,则a 的取值范围是( ) A. a≠1 B. a≠0 C. a≠1且a ≠0 D. 一切实数2. 下列图形中既是轴对称图形,又是中心对称图形的是( )A. B.C. D.3. 今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是( )A. 每位考生的数学成绩B. 3500名考生的数学成绩C. 被抽取的800名考生的数学成绩D. 被抽取的800名学生4. 菱形具有而矩形没有的性质是( )A. 对角线互相平分B. 对边相等C. 对角线相等D. 对角线互相垂直 5. 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )A. 15B.25 C. 35 D. 456. 如图,点P 是边长为2的菱形ABCD 的对角线AC 上一个动点,点M 、N 分别是AB 、BC 边上的中点,MP+NP 的最小值是( )A. 1B. 2C. 3D. 4 7. 已知1112a b -=,则ab a b -的值是 A. 12 B. -12 C. 2 D. -28. 如图,已知□AOBC 的顶点O(0,0),()A 34-,,点B (12,0),按以下步骤作图:①以点O 为圆心、适当长度为半径作弧,分别交OA 、OB 于点D ,E ;②分别以点D ,E 为圆心、大于12DE 的长为半径作弧,两弧∠AOB 在内交于点F ;③作射线OF ,交边AC 于点G ,则CG 的长为( )A. 6B. 7C. 8D. 9二、不定项选择题(本大题共有4小题,每题3分,共12分)9. 在下列各式中①11a -;②243x y ;③h π-;④23x +中,是分式的是( ) 10. 在平行四边形ABCD 中,在对角线BD 上取不同的两点E F ,(点B 、E 、F 、D 依次排列),下列条件中,能得出四边形AECF 一定为平行四边形的是_____________.(A. BE=DF ;B. AE=CF C. AE ∥CF ;D. ∠BAE=∠DCF )11. 数学家针对古希腊数学提出“几何代数”一词,指的是“用几何方法解决代数问题”.《几何原本》第2卷中有着丰富的几何代数内容,在斐波那契的《计算之书》中频繁运用了这种方法.如图,AB=x ,BC=2,矩形ABDE 和ACGH 的面积均是60,下面的代数式可以表示边DF 的是_________A. 60xB. 602x +C. 60(2)x x +D. 60602x x -+12. 如图,E ,F ,M 分别是正方形ABCD 三边的中点,CE 与DF 交于N ,连接AM ,AN ,MN 对于下列四个结论:①AM ∥CE ;②DF ⊥CE ;③AN=BC ;④∠AND=∠CMN . 其中错误的是( )A. ①B. ②C. ③D. ④三、填空题(本大题共有6小题,每题2分,共12分)13. 当x= ____________时,分式123x x -+的值为零. 14. 新冠肺炎疫情爆发后,学生上学检测体温采用的调查方式是_____________ .(填“普查”或“抽样调查”)15. 如图,在周长为10 cm 的□ABCD 中,AB≠AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于点E ,连接BE ,则△ABE 的周长为 .16. 如图,在△ABC 中,∠CAB =70°,将△ABC 在平面内绕点A 旋转到△AB ′C ′的位置,使CC ′∥AB ,则旋转角的度数为_____.17. 菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=22,则点B 的坐标为_________.18. 已知x 为整数,且分式2221x x +-的值为整数,则x = ______ . 四、解答题(本大题共有8小题,共72分)19. 计算(1)2223211a aa a---++(2)21424xx x---20. 小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.(1)在实验中他们共做了50次试验,试验结果如下:朝上的点数 1 2 3 4 5 6出现的次数10 9 6 9 8 8填空:此次实验中,“1点朝上”的频率是;②小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表: 试验总次数100 200 500 1000 2000 5000 100001点朝上的次数18 34 82 168 330 835 16601点朝上的频率0.180 0.170 0.164 0.168 0.165 0.167 0.166“1点朝上”的概率的估计值是.21. 化简:2212211x x xx x x+---÷--,并在-1≤x≤3中选取一个合适的整数x代入求值.22. 已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF求证:四边形BECF是平行四边形.23. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.(1)下列选取样本的方法最合理的一种是__ __.(只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:①m=__ __;n=__ __;②补全条形统计图;③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是__ __;④家庭过期药品的正确处理方式是送回收站点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站点. 24. 如图,在△ABC 中,∠BAC =90°,AD 是中线,E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于F ,连接CF . (1)求证:AD =AF ; (2)如果AB =AC ,试判断四边形ADCF 的形状,并证明你的结论.25. 已知,如图,菱形ABCD 的对角线相交于点O ,DE//AC ,CE//DB ,CE 、DE 相交于E 点. (1)求证:四边形DOCE 是矩形;(2)若四边形DOCE 的面积是3,AC+BD=10,则求AB 的长.26. 观察下列式子,111122=-⨯,1112323=-⨯,1113434=-⨯,…… (1)用正整数n 表示这个规律,并加以证明; (2)设111()1223(1)F n n n ,解决下列问题: ①(10)F __ __.②求证:222(2)(3)()(1)()23F F F n F F n n . 27. 如图1,分别沿矩形纸片ABCD 和正方形EFGH 纸片的对角线AC ,EG 剪开,拼成如图2所示的平行四边形KLMN ,若中间空白部分恰好是正方形OPQR .(1)若AB=m ,BC=n ,用含m 、n 的代数式表示正方形EFGH 的边长;(2)若正方形EFGH 的面积为25,求平行四边形KLMN 的面积;(3)平行四边形KLMN 是否能为菱形?请说明理由.答案与解析一、单项选择题(本大题共有8小题,每题3分,共24分)1. 若分式11a-有意义,则a的取值范围是()A. a≠1B. a≠0C. a≠1且a≠0D. 一切实数【答案】A【解析】分析:根据分母不为零,可得答案详解:由题意,得10a-≠,解得 1.a≠故选A.点睛:本题考查了分式有意义的条件,利用分母不为零得出不等式是解题关键.2. 下列图形中既是轴对称图形,又是中心对称图形的是()A. B.C. D.【答案】D【解析】【分析】根据轴对称与中心对称的定义分别判断即可,轴对称图形是:一定要沿某直线折叠后直线两旁的部分互相重合;中心对称图形是:图形绕某一点旋转180°后与原来的图形重合.【详解】解:A.是中心对称图形,不是轴对称图形,故此选项错误;B.不是中心对称图形,是轴对称图形,故此选项错误;C.不是中心对称图形,不是轴对称图形,故此选项错误;D. 是中心对称图形,是轴对称图形,故此选项正确;故答案为:D.【点睛】本题考查的知识点主要是区分轴对称图形与中心对称图形,熟记二者的定义可以快速的对图形做出判断,轴对称图形要像折纸一样折叠能重合的是轴对称图形;中心对称图形只需把图形倒置,观察有无变化,没变的是中心对称图形.3. 今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是()A. 每位考生的数学成绩B. 3500名考生的数学成绩C. 被抽取的800名考生的数学成绩D. 被抽取的800名学生【答案】C【解析】【分析】根据样本的定义求解.【详解】解:A是个体,B是总体,C是样本,今年我市有近3500名考生参加中考,为了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析,这个问题中样本是抽取的800名考生的数学成绩为样本.故选C.【点睛】本题考查了总体、个体、样本和样本容量:我们把所要考察的对象的全体叫做总体;把组成总体的每一个考察对象叫做个体;从总体中取出的一部分个体叫做这个总体的一个样本;一个样本包括的个体数量叫做样本容量.4. 菱形具有而矩形没有的性质是()A. 对角线互相平分B. 对边相等C. 对角线相等D. 对角线互相垂直【答案】D【解析】【分析】由菱形的对角线互相平分且垂直,矩形的对角线相等且互相平分,即可求得答案.【详解】解:∵菱形具有的性质:对角线互相垂直,对角线互相平分;矩形具有的性质:对角线相等,四个角都是直角,对角线互相平分;∴菱形具有而矩形不具有的性质是:对角线互相垂直.故选:D.【点睛】此题考查了矩形的性质与菱形的性质.注意熟记菱形与矩形的性质区别是关键.5. 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )A. 15B.25C.35D.45【答案】C 【解析】【分析】【详解】解:根据题意,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有5种等可能的结果,使与图中阴影部分构成轴对称图形的有②④⑤,3种情况,因此可知使与图中阴影部分构成轴对称图形的概率为3355÷=故选C6. 如图,点P是边长为2的菱形ABCD的对角线AC上一个动点,点M、N分别是AB、BC边上的中点,MP+NP的最小值是()A. 1B. 2C. 3D. 4【答案】B【解析】【分析】如图,作点M关于AC的对称点M′,连接M′N交AC于P,根据菱形的性质及轴对称性质可得PM=PM′,此时MP+NP有最小值NM′.然后证明四边形AM′NB是平行四边形,即可求出NM′=AB=2.【详解】作点M关于AC的对称点M′,连接M′N交AC于P,∵菱形ABCD关于AC对称,M是AB边上的中点,∴M′是AD的中点,PM=PM′,∴MP+PN=NM′,此时MP+NP有最小值,∵N 是BC 边上的中点,∴AM′∥BN ,AM′=BN ,∴四边形AM′NB 是平行四边形,∴NM′=AB=2.故选:B .【点睛】本题考查菱形的性质、轴对称的性质及平行四边形的判定等知识的综合应用.根据轴对称性质得出NM ′为MP+PN 最小值是解题关键.7. 已知1112a b -=,则ab a b -的值是 A. 12 B. -12 C. 2 D. -2【答案】D【解析】分析:观察已知和所求的关系,容易发现把已知通分后,再求倒数即可.解答:解:∵, ∴a ab -=, ∴=, ∴=-2.故选D .8. 如图,已知□AOBC 的顶点O(0,0),()A 34-,,点B (12,0),按以下步骤作图:①以点O 为圆心、适当长度为半径作弧,分别交OA 、OB 于点D ,E ;②分别以点D ,E 为圆心、大于12DE 的长为半径作弧,两弧∠AOB 在内交于点F ;③作射线OF ,交边AC 于点G ,则CG 的长为( )A. 6B. 7C. 8D. 9【答案】B【解析】【分析】如图,先利用勾股定理计算出OA=5,再利用基本作图和平行线的性质得到∠AOG=∠AGO,则AG=AO=5,从而得到G点坐标,即可得出CG的长.【详解】如图,∵▱AOBC的顶点A的坐标为(-3,4),∴AC∥OB,2234=5,AM=3,OM=4,由作法得OG平分∠AOB,∴∠AOG=∠BOG,而AC∥OB,∴∠AGO=∠BOG,∴∠AOG=∠AGO,∴AG=AO=5,∴MG=5-3=2,∴G点坐标为(2,4).∵点B(12,0),A点坐标为(-3,4).∴C的坐标为(9,4)∴CG的长为9-2=7,故选:B.【点睛】此题考查作图-基本作图,平行四边形的性质,解题关键在于熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).二、不定项选择题(本大题共有4小题,每题3分,共12分)9. 在下列各式中①11a -;②243x y ;③h π-;④23x +中,是分式的是( ) 【答案】①④【解析】【分析】 根据分式的定义对四个选项依次判断即可; 【详解】①11a -,分母含有字母,是分式; ②243x y ,分母中不含字母,不是分式; ③h π-,分母中不含字母,不是分式; ④23x +,分母含有字母,是分式; 故答案是:①④【点睛】本题主要考查分式的基本定义,熟练掌握分式的定义是求解本题的关键.10. 在平行四边形ABCD 中,在对角线BD 上取不同的两点E F ,(点B 、E 、F 、D 依次排列),下列条件中,能得出四边形AECF 一定为平行四边形的是_____________.(A. BE=DF ;B. AE=CF C. AE ∥CF ;D. ∠BAE=∠DCF )【答案】ACD【解析】【分析】连接AC 与BD 相交于O ,根据平行四边形的对角线互相平分可得OA=OC ,OB=OD ,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF 即可,然后根据各选项的条件分析判断即可得解.【详解】解:如图,连接AC 与BD 相交于O ,在▱ABCD 中,OA=OC ,OB=OD ,要使四边形AECF 平行四边形,只需证明得到OE=OF 即可;A 、若BE=DF ,则OB-BE=OD-DF ,即OE=OF ,故本选项不符合题意;B 、若AE=CF ,则无法判断OE=OE ,故本选项符合题意;C 、AE ∥CF 能够利用“角角边”证明△AOE 和△COF 全等,从而得到OE=OF ,故本选项不符合题意;D 、∠BAE=∠DCF 能够利用“角角边”证明△ABE 和△CDF 全等,从而得到DF=BE ,然后同A ,故本选项不符合题意;故答案为:ACD .【点睛】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定方法是解题的关键.11. 数学家针对古希腊数学提出“几何代数”一词,指的是“用几何方法解决代数问题”.《几何原本》第2卷中有着丰富的几何代数内容,在斐波那契的《计算之书》中频繁运用了这种方法.如图,AB=x,BC=2,矩形ABDE和ACGH的面积均是60,下面的代数式可以表示边DF的是_________A. 60 xB.602x+C.60(2)x x+D.60602x x-+【答案】D【解析】【分析】根据图形和两个矩形的面积均为60可得:(x+2)y=60,x(y+DF)=60,再通过运算表示出DF即可.【详解】解:设AH=y,∵矩形ABDE和ACGH的面积均是60,则有:(x+2)y=60,x(y+DF)=60,∴y=602x+,代入x(y+DF)=60中,()26060612002DF x y x x x x=-=-=++,故答案为:D. 【点睛】本题考查了二元一次方程(组)的应用,解题的关键是根据条件表示出矩形的面积.12. 如图,E,F,M分别是正方形ABCD三边的中点,CE与DF交于N,连接AM,AN,MN对于下列四个结论:①AM∥CE;②DF⊥CE;③AN=BC;④∠AND=∠CMN.其中错误的是()A. ①B. ②C. ③D. ④【答案】D【解析】【分析】 证四边形AECM 为平行四边形得①正确,证DCF ∆≌CBE ∆(SAS)易得②正确,证AM 垂直平分DN 得到③正确,而推导不出∠AND=∠CMN ,故④错误【详解】解:∵正方形ABCD ,M,E 分别为DC ,AB 的中点,∴CM ∥AE ,CM=AE,∴四边形AECM 为平行四边形,∴AM//CE ,①正确;∵CD=BC,∠DCB=∠CBE=90°,CF=BE ,∴DCF ∆≌CBE ∆(SAS),∴∠1=∠2,∵∠2+∠3=90°,∴∠1+∠3=90°,∴DF ⊥CE ,∴②正确;∵Rt DCN ∆,M 为斜边DC 的中点,∴DM=CM=MN ,∵AM//CE ,DF ⊥CE ,∴AM ⊥DF ,∴AM 垂直平分DN ,∴AD=AN=BC ,∴③正确,∴∠AND=∠ADN ,∵∠1+∠AND=90°,∠1+∠3=90°,∴∠AND=∠3=∠MNC≠∠CMN ,故④错误.故答案为D.【点睛】本题主要考查了正方形的性质的综合运用,还考查了平行四边形的判定与性质,全等三角形,直角三角形斜边上的中线等于斜边的一半,等腰三角形的三线合一,垂直平分线的判定性质,综合性较强,但难度适中,是中考常考的能力题.三、填空题(本大题共有6小题,每题2分,共12分)13. 当x= ____________时,分式123x x -+的值为零. 【答案】1【解析】【分析】根据分式的值为0即分子为0以及分式有意义的条件,列方程求解即可得到答案;【详解】解:要使分式123xx-+的值为零,即:10 230 xx-=⎧⎨+≠⎩,解得:1x=,故答案为:1;【点睛】本题主要考查了分式为0的条件,即分子为0,在求解时,还注意解得的结果要使分式有意义,即分母不为0;14. 新冠肺炎疫情爆发后,学生上学检测体温采用的调查方式是_____________.(填“普查”或“抽样调查”)【答案】普查【解析】【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行解答即可.【详解】解:因为新冠肺炎疫情事关重大,学生上学必须进行体温检测,所以采用的调查方式是普查,故答案为:普查.【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.15. 如图,在周长为10 cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为.【答案】5cm.【解析】试题分析:先判断出EO是BD的中垂线,得出BE=ED,从而可得出△ABE的周长=AB+AD,再由平行四边形的周长为10cm,即可得出答案.∵点O是BD中点,EO⊥BD,∴EO是线段BD的中垂线,∴BE=ED,故可得△ABE的周长=AB+AD,又∵平行四边形的周长为10cm,∴AB+AD=5cm.考点:1.平行四边形的性质;2.线段垂直平分线的性质.16. 如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为_____.【答案】40°【解析】【分析】先根据平行线的性质得∠ACC′=∠CAB=70°,再根据旋转的性质得AC=AC′,∠CAC′等于旋转角,然后利用等腰三角形的性质和三角形内角和定理计算出∠CAC′的度数即可.【详解】解:∵CC′∥AB,∴∠ACC′=∠CAB=70°,∵将△ABC在平面内绕点A旋转到△AB′C′的位置,∴AC=AC′,∠CAC′等于旋转角,∴∠AC′C=∠ACC′=70°,∴∠CAC′=180°﹣70°﹣70°=40°,∴旋转角的度数为40°.故答案为40°.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形两底角相等的性质,平行线的性质以及三角形内角和定理,熟记性质并准确识图是解题的关键.17. 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,2,则点B的坐标为_________.【答案】(22+2,2)【解析】 【分析】根据菱形的性质,作CD ⊥x 轴,先利用三角函数求出OD 、CD 的长度,从而得出C 点坐标,然后利用菱形的性质求得点B 的坐标.【详解】解:由题意可得OA=OC=2AOC=45°,∴CD=OCsin45°=2,OD=OCcos45°=2, 点C 的坐标为(2,2),则点B 的坐标为(22,2).故答案为(2,2).【点睛】本题综合考查了菱形的性质和坐标的确定,解答本题的关键有两点,①掌握菱形的四边相等,②理解三角函数的定义,及各三角函数在直角三角形中的表示形式.18. 已知x 为整数,且分式2221x x +-的值为整数,则x = ______ . 【答案】0或2或3【解析】【分析】【详解】分式()()()2212221111x x x x x x ++==-+--, ∵分式2221x x +-的值为整数, ∴x -1=﹣2或﹣1或1或2,∴x =﹣1或0或2或3,又∵x 2-1≠0,即x ≠±1,∴x =0或2或3.故答案为0或2或3.【点睛】解此题关键在于将原式化简,然后写出x 可能的值即可,但是需要注意的是分式的分母的值不能为零.四、解答题(本大题共有8小题,共72分)19. 计算(1)2223211a a a a ---++ (2)21424x x x --- 【答案】(1)1a -;(2)124x +. 【解析】【分析】(1)先将分子进行合并,然后因式分解,约分求解即可;(2)先将分母进行因式分解,然后通分计算即可; 【详解】(1)原式=211a a -+ =1a -(2)原式=222(2)(2)2(2)(2)x x x x x x +-+-+- =22(2)(2)x x x -+- =124x + 【点睛】本题主要考查分式的化简,熟练掌握分式的化简过程是求解本题的关键.20. 小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.(1)在实验中他们共做了50次试验,试验结果如下: 朝上的点数1 2 3 4 5 6 出现的次数10 9 6 9 8 8填空:此次实验中,“1点朝上”的频率是;②小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表: .“1点朝上”的概率的估计值是.【答案】(1)①0.2;②不正确;(2)0.166.【解析】【分析】(1)①利用频数除以总数=频率进而得出答案;②利用频率与概率的区别进而得出答案;(2)利用频率估计概率的方法得出概率的估计值.【详解】(1)①此次实验中,“1点朝上”的频率是:100.2 50=,故答案为0.2;②不正确,因为在一次实验中频率并不等于概率,只有当实验中试验次数很大时,频率才趋近于概率.(2)根据图表中数据可得出:“1点朝上”的概率的估计值是0.166.故答案为0.166.【点睛】考查利用频率估计概率,正确理解频率与概率的区别与联系是解题的关键.21. 化简:2212211x x xx x x+---÷--,并在-1≤x≤3中选取一个合适的整数x代入求值.【答案】11x-+;x=3时,原式=14-.【解析】【分析】首先将除法转化为乘法,约分,再通分,最后根据分式有意义的条件,选择适合的数代入计算即可得答案.【详解】原式=2212•112x x x x x x +----- =22111x x x x +--- =2222111x x x x x ++--- =211x x -- =11x -+, ∵2212211x x x x x x+---÷--有意义, ∴x≠±1,x≠0,x≠2,∵-1≤x≤3,x 为整数∴x=3,当x=3时,原式=14-. 【点睛】本题考查分式的化简求值.熟练掌握分式的运算法则是解题关键.22. 已知:如图,在平行四边形ABCD 中,点E 、F 在AD 上,且AE=DF求证:四边形BECF 是平行四边形.【答案】证明见解析.【解析】【分析】根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形式平行四边形,可得证明结论.【详解】如答图,连接BC ,设对角线交于点O .∵四边形ABCD 是平行四边形,∴OA=OD ,OB=OC .∵AE=DF ,OA ﹣AE=OD ﹣DF ,∴OE=OF .∴四边形BEDF 是平行四边形.23. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.(1)下列选取样本的方法最合理的一种是__ __.(只需填上正确答案的序号)①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:①m=__ __;n=__ __;②补全条形统计图;③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是__ __;④家庭过期药品的正确处理方式是送回收站点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站点.【答案】(1)③;(2)①20%,6%;②见解析;③B;④估计为18万户.【解析】【分析】(1)根据抽样调查时选取的样本需具有代表性即可求解;(2)①首先根据A类有80户,占8%,求出抽样调查的家庭总户数,再用D类户数除以总户数求出m,用E类户数除以总户数求出n;②用总户数分别减去A、B、D、E、F类户数,得到C类户数,即可补全条形统计图;③根据调查数据,即可知道该市市民家庭处理过期药品最常见的方式是B类;④用180万户乘以样本中送回收点的户数所占百分比即可.【详解】解:(1)根据抽样调查时选取的样本需具有代表性,可知下列选取样本的方法最合理的一种是③. ①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.(2)①抽样调查的家庭总户数为:80÷8%=1000(户),200%20%201000m m ===,, 60%6%61000n n ===,.故答案为:20%,6%;②C 类户数为:1000-(80+510+200+60+50)=100, 条形统计图补充如下:③根据调查数据,即可知道该市市民家庭处理过期药品最常见的方式是B 类; ④180×10%=18(万户).若该市有180万户家庭,估计大约有18万户家庭处理过期药品的方式是送回收点.【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.24. 如图,在△ABC 中,∠BAC =90°,AD 是中线,E 是AD 的中点,过点A 作AF ∥BC 交BE 的延长线于F ,连接CF . (1)求证:AD =AF ;(2)如果AB =AC ,试判断四边形ADCF 的形状,并证明你的结论.【答案】(1)详见解析;(2)四边形ADCF 是正方形,证明详见解析. 【解析】 【分析】(1)由E 是AD 的中点,AF ∥BC ,易证得△AEF ≌△DEB ,即可得AF =BD ,又由在△ABC 中,∠BAC =90°,AD 是中线,根据直角三角形斜边的中线等于斜边的一半,即可证得AD =BD =CD =12BC ,即可证得:AD =AF ;(2)由AF =BD =DC ,AF ∥BC ,可证得:四边形ADCF 是平行四边形,又由AB =AC ,根据三线合一的性质,可得AD ⊥BC ,AD =DC ,继而可得四边形ADCF 是正方形. 【详解】解:(1)证明:∵AF ∥BC , ∴∠EAF =∠EDB , ∵E 是AD 的中点, ∴AE =DE ,在△AEF 和△DEB 中,EAF EDB AE DEAEF DEB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AEF ≌△DEB (ASA ), ∴AF =BD ,∵在△ABC 中,∠BAC =90°,AD 是中线, ∴AD =BD =DC =12BC , ∴AD =AF ;(2)解:四边形ADCF 是正方形. ∵AF =BD =DC ,AF ∥BC , ∴四边形ADCF 是平行四边形, ∵AB =AC ,AD 是中线, ∴AD ⊥BC , ∵AD =AF ,∴四边形ADCF 是正方形.【点睛】此题考查了正方形的判定、平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中.25. 已知,如图,菱形ABCD 的对角线相交于点O ,DE//AC ,CE//DB ,CE 、DE 相交于E 点. (1)求证:四边形DOCE 是矩形;(2)若四边形DOCE 的面积是3,AC+BD=10,则求AB 的长.【答案】(1)见解析;(219 【解析】 【分析】(1)根据//DE AC ,//CE BD ,得到四边形 OCED 是平行四边形,在根据菱形ABCD 的对角线相交于点O ,得到OC BD ⊥,可证四边形 DOCE 是矩形;(2)设OD x =,OC y =,根据题意可得 5x y +=,3xy =,根据22222AB x y xyxy ,可以求出 AB . 【详解】证明:(1)//DE AC ,//CE BD ,∴四边形OCED 是平行四边形,菱形ABCD 的对角线相交于点O , ∴OC BD ⊥,∴四边形DOCE 是矩形; (2)设OD x =,OC y =, 3DOCES 矩形, 10ACBD ,即有:5x y +=,3xy =, ∴2222219AB x y xyxy ,∴19AB =【点睛】本题既考查了菱形的性质,矩形的判定与性质,熟悉相关性质是解题的关键. 26. 观察下列式子,111122=-⨯,1112323=-⨯,1113434=-⨯,…… (1)用正整数n 表示这个规律,并加以证明;(2)设111()1223(1)F n n n ,解决下列问题:①(10)F __ __.②求证:222(2)(3)()(1)()23F F F n F F n n .【答案】(1)111(1)1n n n n =-++,证明见解析;(2)①1011;②见解析.【解析】 【分析】(1)由已知等式知连续整数乘积的倒数等于各自倒数的差,据此可得; (2)利用()1n F n n 化简2()F n n 得到2()11F n nn n ,则可知222(2)(3)()(1)...23F F F n F n 1n n =+,即可求证.【详解】(1)规律为:111(1)1n n n n =-++证明:∵左边=11111(1)(1)(1)(1)1n n n n n n n n n n n n nn =右边,∴等式成立; (3)∵111()1223(1)F n n n ,∴11111111()1122334111n F n nn n n∴①(10)1011F . ②∵()1n F n n ,∴22()111n F n n nn n n ∴222(2)(3)()(1)...23F F F n F n 1111223(1)n n11111111223341nn111n =-+ 1n n =+ 即:222(2)(3)()(1)...()23F F F n F F n n .【点睛】本题主要考查数字的变化类及解分式方程,解题的关键是根据题意得出连续整数乘积的倒数等于各自倒数的差.27. 如图1,分别沿矩形纸片ABCD 和正方形EFGH 纸片的对角线AC ,EG 剪开,拼成如图2所示的平行四边形KLMN ,若中间空白部分恰好是正方形OPQR .(1)若AB=m ,BC=n ,用含m 、n 的代数式表示正方形EFGH 的边长; (2)若正方形EFGH 的面积为25,求平行四边形KLMN 的面积; (3)平行四边形KLMN 是否能为菱形?请说明理由.【答案】(1)2m n+;(2)50;(3)不能,理由见解析. 【解析】 【分析】(1)设正方形ORQP 的边长为a ,则:EF PMm a ,FG PL n a ,根据四边形EFGH 是正方形,得到EF FG =,即有mana ,2nm a,利用EF m a =+可以得到结果;(2)设正方形ORQP 的边长为a ,根据正方形EFGH 面积为25,可得5AB a ,5BCa ,据此可得平行四边形KLMN 的面积. (3)利用反证法,假设是菱形,则NKLK ,正方形EFGH 的边长为x ,可求出m=n ,则小正方形ROPQ边长为0,与题目描述相矛盾,所以假设不成立,不是菱形. 【详解】(1)设正方形ORQP 的边长为a , 则:EFPMm a ,FGPLn a ,、∵四边形EFGH 是正方形, ∴EF FG =,即有m ana∴2n ma ,∴22n mFanmm E m。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.下列调查中,适合采用普查的是( ) A .了解一批电视机的使用寿命 B .了解全省学生的家庭1周内丢弃塑料袋的数量C .为保证某种新研发的战斗机试飞成功,对其零部件进行检查D .了解扬州市中学生的近视率2.江苏移动掌上营业厅,推出“每日签到——抽奖活动”:每个手机号码每日只能签到1次,且只能抽奖1次,抽奖结果有流量红包、话费充值卷、惊喜大礼包、谢谢参与.小明的爸爸已经连续3天签到,且都抽到了流量红包,则“他第4天签到后,抽奖结果是流量红包”是() A .必然事件 B .不可能事件C .随机事件D .必然事件或不可能事件3.如图,在矩形ABCD 中,AB =4cm ,AD =12cm ,点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动,点Q 在BC 边上,以每秒4cm 的速度从点C 出发,在CB 间往返运动,两个点同时出发,当点P 到达点D 时停止(同时点Q 也停止),在这段时间内,线段PQ 平行于AB 的次数是( )A .2B .3C .4D .54.下列方程中,关于x 的一元二次方程是( )A .x 2﹣x (x +3)=0B .ax 2+bx +c =0C .x 2﹣2x ﹣3=0D .x 2﹣2y ﹣1=05.用配方法解一元二次方程2620x x --=,以下正确的是( )A .2(3)2x -=B .2(3)11x -=C .2(3)11x +=D .2(3)2x +=6.如图,在平面直角坐标系中,菱形OABC 的顶点A 的坐标为(4,3),点D 是边OC 上的一点,点E 在直线OB 上,连接DE 、CE ,则DE+CE 的最小值为( )A.5B.7+1C.25D.24 57.为了解我市八年级10000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是()A.每个学生的身高是个体B.本次调查采用的是普查C.样本容量是500名学生D.10000名学生是总体8.下列调查中,适合普查方式的是()A.调查某市初中生的睡眠情况B.调查某班级学生的身高情况C.调查南京秦淮河的水质情况D.调查某品牌钢笔的使用寿命9.三角形两边长分别为3和6,第三边的长是方程x2﹣13x+36=0的两根,则该三角形的周长为()A.13 B.15 C.18 D.13或1810.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA 并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是()A.9m B.12m C.8m D.10m二、填空题11.“一只不透明的袋子共装有3个小球,它们的标号分别为1,2,3,从中摸出1个小球,标号为“4”,这个事件是______.(填“必然事件”、“不可能事件”或“随机事件”)12.在英文单词tomato中,字母o出现的频数是_____.13.若分式x3x3--的值为零,则x=______.14.为了了解我市八年级男生的体重分布情况,市教育局从各学校共随机抽取了500名八年级男生进行了测量.在这个问题中,样本是指_____.15.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是_____.16.在英语句子“Wish you success”(祝你成功)中任选一个字母,这个字母为“s”的概率是 .17.如图,△ABC 中,∠A =60°,∠ABC =80°,将△ABC 绕点B 逆时针旋转,得到△DBE ,若DE ∥BC ,则旋转的最小度数为_____.18.根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为________万元.19.如图,反比例函数y =xk(x >0)的图象经过矩形OABC 的边AB 的中点D ,若矩形OABC 的面积为8,则k =_____.20.如图,边长为2的正方形ABCD 的对角线相交于点O ,过点O 的直线分别交AD 、BC 于E 、F ,则阴影部分的面积是_____.三、解答题21.把一张矩形ABCD 纸片按如图方式折叠,使点A 与点E 重合,点C 与点F 重合(E 、F 两点均在BD 上),折痕分别为BH 、DG .(1)求证:△BHE≌△DGF;(2)若AB=6cm,BC=8cm,求线段FG的长.22.某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:最喜爱的节目人数歌曲15舞蹈a小品12相声10其它b(1)在此次调查中,该校一共调查了名学生;(2)a=;b=;(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.23.如图,在正方形网格中,△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:(1)作出△ABC关于原点O成中心对称的△A1B1C1;(2)直接写出:以A、B、C为顶点的平形四边形的第四个顶点D的坐标.24.如图,反比例函数ky x=的图像经过第二象限内的点(1,)A m -,AB x ⊥轴于点B ,AOB ∆的面积为2.若直线y ax b =+经过点A ,并且经过反比例函数ky x=的图像上另一点(,2)C n -.(1)求反比例函数ky x=与直线y ax b =+的解析式; (2)连接OC ,求AOC ∆的面积;(3)不等式0kax b x +-≥的解集为_________(4)若()11,D x y 在ky x=(0)k ≠图像上,且满足13y ≥-,则1x 的取值范围是_________.25.如图,在矩形ABCD 中,AB =1,BC =3.(1)在图①中,P 是BC 上一点,EF 垂直平分AP ,分别交AD 、BC 边于点E 、F ,求证:四边形AFPE 是菱形;(2)在图②中利用直尺和圆规作出面积最大的菱形,使得菱形的四个顶点都在矩形ABCD 的边上,并直接..标出菱形的边长.(保留作图痕迹,不写作法)26.为更有效地开展“线上教学”工作,某市就学生参与线上学习的工具进行了电子问卷调查,并将调查结果绘制成图1和图2所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次调查的总人数是 人; (2)请将条形统计图补充完整;(3)在扇形统计图中表示观点B 的扇形的圆心角度数为 度; (4)在扇形统计图中表示观点E 的百分比是 .27.如图,点P 为ABC ∆的BC 边的中点,分别以AB 、AC 为斜边作Rt ABD ∆和Rt ACE ∆,且BAD CAE α∠=∠=,DPE β∠=.(1)求证:PD PE =.(2)探究:α与β的数量关系,并证明你的结论.28.已知四边形ABCD 中,AB ⊥AD ,BC ⊥CD ,AB=BC ,∠ABC =120゜,∠MBN=60゜,∠MBN 绕B 点旋转,它的两边分别交AD ,DC (或它们的延长线)于E ,F .(1)当∠MBN 绕B 点旋转到AE =CF 时(如图1),试猜想线段AE 、CF 、EF 之间存在的数量关系为 .(不需要证明);(2)当∠MBN 绕B 点旋转到AE ≠CF 时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE 、CF 、EF 又有怎样的数量关系?请写出你的猜想,不需证明.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据调查的实际情况逐项判断即可.【详解】解:A. 了解一批电视机的使用寿命,调查具有破坏性,适合抽样调查,不合题意;B. 了解全省学生的家庭1周内丢弃塑料袋的数量,调查费时费力,适合抽样调查,不合题意;C. 为保证某种新研发的战斗机试飞成功,对其零部件进行检查,考虑安全性,适合全面调查,符合题意;D. 了解扬州市中学生的近视率,调查费时费力,适合抽样调查,不合题意.故选:C【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,事关重大的调查往往选用普查.2.C解析:C【解析】分析:直接利用随机事件的定义进而得出答案.详解:∵有流量红包、话费充值卷、惊喜大礼包、谢谢参与四种等可能情况,∴他第4天签到后,抽奖结果是流量红包为随机事件.故选C.点睛:本题主要考查了随机事件,正确把握相关定义是解题的关键.解析:C【分析】当QP∥AB时,由AP∥BQ可得到ABQP为平行四边形,然后依据矩形的性质可得到AP=BQ,然后求得AP=BQ的次数即可.【详解】解:当QP∥AB时,∵在在矩形ABCD,AD∥BC,∴四边形ABQP为平行四边形,∴AP=BQ,∵点P运动的时间=12÷1=12秒,∴点Q运动的路程=4×12=48cm.∴点Q可在BC间往返4次.∴在这段时间内PQ与AB有4次平行.故选:C.【点睛】本题考查了平行四边形的判定.注意能求出符合条件的所有情况是解此题的关键,注意掌握分类讨论思想的应用.4.C解析:C【分析】一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.【详解】解:A、x2﹣x(x+3)=0,化简后为﹣3x=0,不是关于x的一元二次方程,故此选项不合题意;B、ax2+bx+c=0,当a=0时,不是关于x的一元二次方程,故此选项不合题意;C、x2﹣2x﹣3=0是关于x的一元二次方程,故此选项符合题意;D、x2﹣2y﹣1=0含有2个未知数,不是关于x的一元二次方程,故此选项不合题意;故选:C.【点睛】此题主要考查了一元二次方程的定义,判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.5.B解析:B【分析】利用完全平方公式的特征在方程的两边同时加上11即可.解:2621111x x --+=,即26911x x -+=,所以2(3)11x -=. 故选:B. 【点睛】本题考查了配方法解一元二次方程,灵活利用完全平方公式是应用配方法解题的关键.6.D解析:D 【解析】 【分析】首先根据菱形的对角线性质得到DE+CE 的最小值=CF,再利用菱形的面积列出等量关系即可解题. 【详解】解:如下图,过点C 作CF ⊥OA 与F,交OB 于点E,过点E 作ED ⊥OC 与D, ∵四边形OABC 是菱形,由菱形对角线互相垂直平分可知EF=ED, ∴DE+CE 的最小值=CF, ∵A 的坐标为(4,3), ∴对角线分别是8和6,OA=5,∴菱形的面积=24,(二分之一对角线的乘积), 即24=CF×5, 解得:CF=245, 即DE+CE 的最小值=245, 故选D.【点睛】本题考查了菱形的性质,图形中的最值问题,中等难度,利用菱形的对称性找到点E 的位置并熟悉菱形面积的求法是解题关键.7.A解析:A 【分析】由总体、个体、样本、样本容量的概念,结合题意进行分析,即可得到答案. 【详解】解:A 、每个学生的身高是个体,故A 正确;B、本次调查是抽样调查,故B错误;C、样本容量是500,故C错误;D、八年级10000名学生的身高是总体,故D错误;故选:A.【点睛】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.8.B解析:B【分析】根据抽样调查和普查的特点作出判断即可.【详解】A、调查某市初中生的睡眠情况,调查的对象很多,普查的意义或价值不大,应选择抽样调查,故本项错误;B、调查某班级学生的身高情况,调查对象较少,适宜采取普查,故本项正确;C、调查南京秦淮河的水质,调查范围较广,不适宜采取普查,故本项错误;D、调查某品牌圆珠笔芯的使用寿命,普查,破坏性较强,应采用抽样调查,此选项错误;故选:B.【点睛】本题考查了普查和抽样调查的判断,掌握普查和抽样调查的特点是解题关键.9.A解析:A【解析】试题解析:解方程x2-13x+36=0得,x=9或4,即第三边长为9或4.边长为9,3,6不能构成三角形;而4,3,6能构成三角形,所以三角形的周长为3+4+6=13,故选A.考点:1.解一元二次方程-因式分解法;2.三角形三边关系.10.A解析:A【分析】根据三角形的中位线定理解答即可.【详解】解:∵A、B分别是CD、CE的中点,DE=18m,∴AB=12DE=9m,故选:A.【点睛】本题考查了三角形的中位线定理:三角形的中位线平行于第三边并且等于第三边的一半.二、填空题11.不可能事件.【解析】根据题意,可知这个袋子中有3个数字,抽取一个球时不可能抽到数字4,所以是不可能事件.故答案为不可能事件.解析:不可能事件.【解析】根据题意,可知这个袋子中有3个数字,抽取一个球时不可能抽到数字4,所以是不可能事件.故答案为不可能事件.12.2【分析】根据频数定义可得答案.【详解】解:字母o出现的频数是2,故答案为:2.【点睛】本题考查的是频数的含义,掌握频数的含义是解题的关键.解析:2【分析】根据频数定义可得答案.【详解】解:字母o出现的频数是2,故答案为:2.【点睛】本题考查的是频数的含义,掌握频数的含义是解题的关键.13.-3【分析】分式的值为零:分子等于零,且分母不等于零.【详解】依题意,得|x|-3=0且x-3≠0,解得,x=-3.故答案是:-3.【点睛】考查了分式的值为零的条件.若分式的值为零解析:-3【分析】分式的值为零:分子等于零,且分母不等于零.【详解】依题意,得|x|-3=0且x-3≠0,解得,x=-3.故答案是:-3.【点睛】考查了分式的值为零的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.14.从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解:在解析:从各学校共随机抽取的500名八年级男生体重.【分析】所有考查对象的全体就是总体,而组成总体的每一个考查对象称为个体.研究中实际观测或调查的一部分个体称为样本,依据定义即可解答.【详解】解:在这个问题中,样本是指从各学校共随机抽取的500名八年级男生体重,故答案为:从各学校共随机抽取的500名八年级男生体重.【点睛】本题考查统计中的总体与样本,属于基本题型.15.【解析】【分析】根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度【详解】∵四边形ABCD 是菱形,∴CO=A 解析:245 【解析】 【分析】 根据菱形的性质得出BO 、CO 的长,在RT △BOC 中求出BC ,利用菱形面积等于对角线乘积的一半,也等于BC×AE ,可得出AE 的长度【详解】∵四边形ABCD 是菱形,∴CO =12AC =3cm ,BO =12BD =4cm ,AO ⊥BO , ∴BC =22AO BO +=5cm ,∴S 菱形ABCD =2BD AC ⋅==12×6×8=24cm 2, ∵S 菱形ABCD =BC ×AE ,∴BC ×AE =24, ∴AE =24245BC =cm . 故答案为:245 cm . 【点睛】此题考查了菱形的性质,也涉及了勾股定理,要求我们掌握菱形的面积的两种表示方法,及菱形的对角线互相垂直且平分.16.【解析】试题解析:在英语句子“Wishyousuccess!”中共14个字母,其中有字母“s”4个.故其概率为.考点:概率公式.解析:【解析】试题解析:在英语句子“Wishyousuccess!”中共14个字母,其中有字母“s”4个.故其概率为42=147. 考点:概率公式.17.40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点解析:40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点B逆时针旋转,得到△DBE,∴∠E=∠C=40°,∵DE∥BC,∴∠CBE=∠E=40°,∴旋转的最小度数为40°,故答案为:40°.【点睛】本题主要考查了旋转的性质以及平行线的性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.18.000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-解析:000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-20%=20%,∴该商场全年的营业额为:800÷20%=4000(万元),故答案为:4000.【点睛】本题考查了扇形统计图,由统计图得到二季度所占的百分比是解题关键.19.4【分析】设D 的坐标是,则B 的坐标是,根据D 在反比例函数图象上,即可求得ab 的值,从而求得k 的值.【详解】设D 的坐标是,则B 的坐标是,∵∴,∵D 在上,∴.故答案是:4.【点睛】解析:4【分析】设D 的坐标是()a b ,,则B 的坐标是()2a b ,,根据D 在反比例函数图象上,即可求得ab 的值,从而求得k 的值.【详解】设D 的坐标是()a b ,,则B 的坐标是()2a b ,, ∵OABC 8S =矩形∴28ab =,∵D 在k y x=上, ∴1842k ab ==⨯=. 故答案是:4.【点睛】本题主要考查的是反比例函数k 的几何意义,掌握反比例函数系数k 的几何意义是解题的关键.20.1【分析】由题可知△DEO≌△BFO,阴影面积就等于△BOC 面积,根据三角形面积公式求得△BOC 面积即可.【详解】解:由题意可知△DEO≌△BFO,∴S△DEO=S△BFO,阴影面积=解析:1【分析】由题可知△DEO ≌△BFO ,阴影面积就等于△BOC 面积,根据三角形面积公式求得△BOC 面积即可.【详解】解:由题意可知△DEO ≌△BFO ,∴S △DEO =S △BFO ,阴影面积=△BOC 面积=12×2×1=1. 故答案为:1.【点睛】本题考查正方形的性质以及全等三角形的判定,根据全等三角形的性质将阴影部分的面积转化为△BOC 面积是解题的关键. 三、解答题21.(1)见解析 (2)3cm【分析】1)先根据矩形的性质得出∠ABD=∠BDC ,再由图形折叠的性质得出∠1=∠2,∠3=∠4,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH ≌△DFG ;(2)先根据勾股定理得出BD 的长,进而得出BF 的长,由图形翻折变换的性质得出CG=FG ,设FG=x ,则BG=8﹣x ,再利用勾股定理即可求出x 的值.【详解】(1)如图,ABCD 四边形是矩形,AB CD ∴=,90A C ∠=∠=︒,ABD BDC ∠=∠.BEH ∆是BAH ∆翻折而成的,1=2∴∠∠,==90A HEB ∠∠︒,AB BE =.DGF DGC ∆∆是翻折而成的,3=4∴∠∠,90C DFG ∠=∠=︒,CD DF =,∴在BEH ∆和DFG ∆中,HEB DFG ∠=∠,BE DF =,2=3∠∠,BHE DGF ∴∆∆≌.(2)四边形ABCD 是矩形,6AB =,8BC =,6AB CD ∴==,8AD BC ==,10BD ∴=,又由(1)知,DF CD =,CG FG =,=1064BF ∴-=. 设FG x =,则8BG x =-,在Rt BGF ∆中,222BG BF FG =+,即()22284x x -=+,3x ∴=,即3FG =.【点睛】本题主要考查矩形的折叠问题,涉及知识点有全等三角形的证明与性质,勾股定理,折叠性质等知识点,解题关键在于能够灵活运用勾股定理22.(1)50;(2)8,5;(3)108°;(4)240人.【分析】(1)从表格和统计图中可以得到喜欢“小品”的人数为12人,占调查人数的24%,可求出调查人数,(2)舞蹈占50人的16%可以求出a的值,进而从总人数中减去其他组的人数得到b的值,(3)先计算“歌曲”所占的百分比,用360°去乘即可,(4)样本估计总体,用样本喜欢“相声”的百分比估计总体的百分比,进而求出人数.【详解】(1)12÷24%=50人故答案为50.(2)a=50×16%=8人,b=50﹣15﹣8﹣12﹣10=5人,故答案为:8,5.(3)360°×1550=108°答:“歌曲”所在扇形的圆心角的度数为108°;(4)1200×1050=240人答:该校1200名学生中最喜爱“相声”的学生大约有240人.【点睛】考查扇形统计图、频数统计表的制作方法,明确统计图表中的各个数据之间的关系是解决问题的关键.23.(1)作图见解析;(2)D(1,1),(-5,3),(-3,-1)【分析】(1)根据关于原点对称的点的坐标特征分别写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)分类讨论:分别以AB、AC、BC为对角线画平行四边形,根据网格的特点,确定对角线后找对边平行,即可写出D点的坐标.【详解】解:(1)如图,点A、B、C的坐标分别为(1,0),(4,1),(2,2)---,根据关于原点对称的点的坐标特征,则点A、B、C关于原点对称的点分别为(1,0),(4,1),(2,2)--,描点连线,△A1B1C1即为所作:(2)分别以AB、AC、BC为对角线画平行四边形,如下图所示:则由图可知D点的坐标分别为:(3,1),(1,1),(5,3)---,故答案为:(1,1),(5,3),(3,1)---.【点睛】本题考查了中心对称作图即平行四边形存在问题,在直角坐标系中,已知平行四边形的三个点的坐标,确定第四个点的坐标,以对角线作为分类讨论,不容易漏掉平行四边形的各种情况.24.(1)4yx-=;22y x=-+(2)3 (3)1x≤-或02x<≤(4)43x≥或x<0【分析】(1)根据k的几何意义即可求出k;求出k后利用交点C即可求出一次函数(2)利用割补法即可求出面积(3)根据A,C的坐标,结合图象即可求解;(4)先求出3y =-时,43x =,再观察图像即可求解. 【详解】 (1)∵点(1,)A m -在第二象限内,∴AB m =,1OB =, ∴122ABO S AB BO ∆=⋅=即:1122m ⨯=,解得4m =, ∴(1,4)A -,∵点(1,4)A -,在反比例函数k y x =的图像上, ∴41k =-,解得4k =-, ∵反比例函数为4y x-=, 又∵反比例函数4y x -=的图像经过(,2)C n -, ∴42n--=,解得2n =, ∴(2,2)C -,∵直线y ax b =+过点(1,4)A -,(2,2)C -,∴422a b a b=-+⎧⎨-=+⎩解方程组得22a b =-⎧⎨=⎩, ∴直线y ax b =+的解析式为;22y x =-+;(2)24y x =-+当0y =时,220x -+=,1x =,∴22y x =-+与x 轴的交点坐标为(1,0)设直线22y x =-+与x 轴的交点为E ,则1OE =∴AOC AOE COE S S S =+11141222=⨯⨯+⨯⨯ 3=(3)由题:k ax b x+≥ 由图像可知:当1x ≤-或02x <≤时,符合条件;故答案为:1x ≤-或02x <≤;(4)3y =-时,43x =,结合图像可知:当13y ≥-,则1x 的取值范围是43x ≥或x <0.故答案为:43x 或x<0.【点睛】本题主要考查了反比例函数,待定系数法求函数解析式,综合性较强,但只要细心分析题目难度不大.25.(1)见解析;(2)见解析【分析】(1)根据矩形的性质和EF垂直平分AP推出AF=PF=AE=PE即可判断;(2)以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,此时的菱形即为矩形ABCD内面积最大的菱形.【详解】(1)证明:如图①∵四边形ABCD是矩形,∴AD∥BC,∴∠1=∠2,∵EF垂直平分AP,∴AF=PF,AE=PE,∴∠2=∠3,∴∠1=∠3,∴AE=AF,∴AF=PF=AE=PE,∴四边形AFPE是菱形;(2)如图②,以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线,连接各个点,所得的菱形即为矩形ABCD内面积最大的菱形;此时设菱形边长为x,则可得12+(3-x)2=x2,解得x=53,所以菱形的边长为53.【点睛】本题考查了矩形的性质,菱形的性质和判定,掌握知识点是解题关键.26.(1)5000;(2)条形统计图见解析;(3)18;(4)4%.【分析】(1)根据选A 的人数和所占的百分比,可以求得本次调查的总人数;(2)根据(1)中的结果,可以求得选C 的人数,从而可以将条形统计图补充完整; (3)根据选B 的人数为250,调查的总人数为5000,即可计算出在扇形统计图中表示观点B 的扇形的圆心角度数;(4)根据统计图中的数据,可以计算出在扇形统计图中表示观点E 的百分比.【详解】解:(1)本次调查的总人数是:2300÷46%=5000(人),故答案为:5000;(2)选用C 的学生有:5000×30%=1500(人),补充完整的条形统计图如图所示;(3)在扇形统计图中表示观点B 的扇形的圆心角度数为:360°×2505000=18°, 故答案为:18;(4)在扇形统计图中表示观点E 的百分比是:2005000×100%=4%, 故答案为:4%.【点睛】 本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.27.(1)详见解析;(2)2180αβ+=︒,证明见解析.【分析】(1)如图,分别取AB 、AC 的中点M 、N ,连接DM 、PM 、PN 、NE ,根据三角形的中位线定理和直角三角形的性质可得PM NE =,DM PN =,根据等腰三角形的性质、三角形的外角性质和已知条件可得BMD CNE ∠=∠,根据平行线的性质可得BMP BAC ∠=∠=CNP ∠,进而可得DMP PNE ∠=∠,于是可根据SAS 证明MDP NPE ∆≅∆,从而可得结论;(2)根据平行线的性质可得BMP MPN ∠=∠,根据全等三角形的性质可得EPN MDP ∠=∠,然后在DMP ∆中利用三角形的内角和定理和等量代换即可得出结论.【详解】(1)证明:如图,分别取AB 、AC 的中点M 、N ,连接DM 、PM 、PN 、NE . 点P 为ABC ∆的边BC 的中点, ∴12PM AC =, NE 为Rt AEC ∆斜边上的中线, ∴12NE AN AC ==, PM NE ∴=,同理可得:DM PN =,12DM AM AB ==, ADM BAD ∴∠=∠,2BMD BAD ∴∠=∠,同理,2CNE CAE ∠=∠,又BAD CAE α∠=∠=,BMD CNE ∴∠=∠,又PM 、PN 都是ABC ∆的中位线,//PM AC ∴,//PN AB ,BMP BAC ∴∠=∠,CNP BAC ∠=∠,BMP CNP ∴∠=∠,∴DMP PNE ∠=∠,MDP NPE ∴∆≅∆(SAS),PD PE ∴=;(2)解:α与β的数量关系是:2180αβ+=︒;证明://PN AB ,BMP MPN ∴∠=∠,∵MDP NPE ∆≅∆,EPN MDP ∴∠=∠,在DMP ∆中,∵180MDP DPM DMP ∠+∠+∠=︒,∴180MDP DPM DMB PMB ∠+∠+∠+∠=︒,而22DMB BAD α∠=∠=,2180EPN DPM MPN α∴∠+∠++∠=︒,DPE DPM MPN EPN β∠=∠+∠+∠=,2180αβ∴+=︒.【点睛】本题考查了三角形的中位线定理、全等三角形的判定和性质、直角三角形的性质、等腰三角形的性质、平行线的性质、三角形的外角性质和三角形的内角和定理等知识,具有一定的综合性,正确添加辅助线、熟练掌握上述知识是解题的关键.28.(1)AE+CF=EF ;(2)如图2,(1)中结论成立,即AE+CF=EF ;如图3,(1)中结论不成立,AE=EF+CF .【分析】(1)根据题意易得△ABE ≌△CBF ,然后根据全等三角形的性质可得∠ABE=∠CBF=30°,进而根据30°角的直角三角形及等边三角形的性质可求解;(2)如图2,延长FC 到H ,使CH=AE ,连接BH ,根据题意可得△BCH ≌△BAE ,则有BH=BE ,∠CBH=∠ABE ,进而可证△HBF ≌△EBF ,推出HF=EF ,最后根据线段的等量关系可求解;如图3,在AE 上截取AQ=CF ,连接BQ ,根据题意易得△BCF ≌△BAQ ,推出BF=BQ ,∠CBF=∠ABQ ,进而可证△FBE ≌△QBE ,推出EF=QE 即可.【详解】解:(1)如图1,AE+CF=EF ,理由如下:∵AB ⊥AD ,BC ⊥CD ,∴∠A=∠C=90°,∵AB=BC ,AE=CF ,∴△ABE ≌△CBF (SAS ),∴∠ABE=∠CBF ,BE=BF ,∵∠ABC=120°,∠MBN=60°,∴∠ABE=∠CBF=30°, ∴11,22AE BE CF BF ==, ∵∠MBN=60°,BE=BF ,∴△BEF 是等边三角形, ∴1122AE CF BE BF BE EF +=+==, 故答案为AE+CF=EF ; (2)如图2,(1)中结论成立;理由如下:延长FC 到H ,使CH=AE ,连接BH ,∵AB ⊥AD ,BC ⊥CD ,∴∠A=∠BCH=90°,∴△BCH≌△BAE(SAS),∴BH=BE,∠CBH=∠ABE,∵∠ABC=120°,∠MBN=60°,∴∠ABE+∠CBF=120°-60°=60°,∴∠HBC+∠CBF=60°,∴∠HBF=∠MBN=60°,∴∠HBF=∠EBF,∴△HBF≌△EBF(SAS),∴HF=EF,∵HF=HC+CF=AE+CF,∴EF=AE+CF,如图3,(1)中的结论不成立,为AE=EF+CF,理由如下:在在AE上截取AQ=CF,连接BQ,∵AB⊥AD,BC⊥CD,∴∠A=∠BCF=90°,∵AB=BC,∴△BCF≌△BAQ(SAS),∴BF=BQ,∠CBF=∠ABQ,∵∠MBN=60°=∠CBF+∠CBE,∴∠CBE+∠ABQ=60°,∵∠ABC=120°,∴∠QBE=120°-60°=60°=∠MBN,∴∠FBE=∠QBE,∴△FBE≌△QBE(SAS),∴EF=QE,∵AE=QE+AQ=EF+CE,∴AE=EF+CF.【点睛】本题主要考查全等三角形的性质与判定、含30°角的直角三角形的性质及等边三角形的性质,熟练掌握全等三角形的性质与判定、含30°角的直角三角形的性质及等边三角形的性质是解题的关键.。
(一共4套)苏教版八年级下册-期中数学-考试题+详细答案系列(第3套)

(一共4套)苏教版八年级下册-期中数学-考试题+详细答案系列(第3套)(一共4套)苏教版八年级下册期中数学考试题+详细答案系列(第3套)一.选择题(共有6小题,每小题2分,共12分)1.随着人们生活水平的提高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是()A.B.C.D.2.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等3.若反比例函数y=的图象位于第二、四象限,则k的取值可能是()A.﹣1 B.2 C.3 D.44.“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是()转动转盘的次数n 100 150 200 500 800 1000落在“铅笔”区域的次数m 68 108 140 355 560 690落在“铅笔”区域的频率0.68 0.72 0.70 0.71 0.70 0.69A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70B.假如你去转动转盘一次,获得铅笔的概率大约是0.70C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次D.转动转盘10次,一定有3次获得文具盒6.某市举行“一日捐”活动,甲、乙两单位各捐款30000元,已知“…”,设乙单位有x人,则可得方程﹣=20,根据此情景,题中用“…”表示的缺失的条件应补()A.甲单位比乙单位人均多捐20元,且乙单位的人数比甲单位的人数多20%15.已知关于x的方程=3无解,则m的值为______.16.如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为______.三、计算:(8分)17.计算:(1)+(2)﹣x﹣1.四、解方程:(8分)18.解方程(1)﹣=1(2)=﹣1.五、先化简,再求值:(共1小题,满分6分)19.先化简,再求值:(﹣)÷,其中x2﹣4x﹣1=0.六、解答题(共5小题,满分46分)21.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(kPa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16kPa.(1)当V=1.2m3时,求p的值;(2)当气球内的气压大于40kP时,气球将爆炸,为了确保气球不爆炸,气球的体积应满足条件.22.(10分)(2017春•六合区期中)某项工程如果由乙单独完成比甲单独完成多用6天;如果甲、乙先合做4天后,再由乙单独完成,那么乙一共所用的天数刚好和甲单独完成工程所用的天数相等.(1)求甲单独完成全部工程所用的时间;(2)该工程规定须在20天内完成,若甲队每天的工程费用是4.5万元,乙队每天的工程费用是2.5万元,请你选择上述一种施工方案,既能按时完工,又能使工程费用最少,并说明理由?23.如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.(1)求证:OE=CB;(2)如果OC:OB=1:2,OE=,求菱形ABCD的面积.24.(12分)(2014春•江都市校级期末)如图,已知直线与双曲线交于A、B两点,A点横坐标为4.(1)求k值;(2)直接写出关于x的不等式的解集;(3)若双曲线上有一点C的纵坐标为8,求△AOC的面积;(4)若在x轴上有点M,y轴上有点N,且点M、N、A、C四点恰好构成平行四边形,直接写出点M、N的坐标.参考答案与试题解析一.选择题(共有6小题,每小题2分,共12分)1.随着人们生活水平的提高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是()A.B.C.D.【考点】中心对称图形.【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.【解答】解:A、是中心对称图形,故本选项正确;B、不是中心对称图形,故本选项错误;C、不是中心对称图形,故本选项错误;D、不是中心对称图形,故本选项错误;故选A.【点评】本题考查了中心对称图形的知识,判断中心对称图形是要寻找对称中心,图形旋转180度后与原图形重合.2.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等【考点】矩形的性质;菱形的性质.【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.3.若反比例函数y=的图象位于第二、四象限,则k的取值可能是()A.﹣1 B.2 C.3 D.4【考点】反比例函数的性质.【分析】根据反比例函数的性质可知“当k<0时,函数图象位于第二、四象限”,结合四个选项即可得出结论.【解答】解:∵反比例函数y=的图象位于第二、四象限,∴k<0.结合4个选项可知k=﹣1.故选A.【点评】本题考查了反比例函数的性质,解题的关键是找出k<0.本题属于基础题,难度不大,解决该题型题目时,结合函数图象所在的象限找出k值的取值范围是关键.4.“六•一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是()转动转盘的次数n 100 150 200 500 800 1000落在“铅笔”区域的次数m 68 108 140 355 560 690落在“铅笔”区域的频率0.68 0.72 0.70 0.71 0.70 0.69A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70B.假如你去转动转盘一次,获得铅笔的概率大约是0.70C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次D.转动转盘10次,一定有3次获得文具盒【考点】利用频率估计概率.【分析】根据图表可求得指针落在铅笔区域的概率,另外概率是多次实验的结果,因此不能说转动转盘10次,一定有3次获得文具盒.【解答】解:A、频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70,故A选项正确;由A可知B、转动转盘一次,获得铅笔的概率大约是0.70,故B选项正确;C、指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有2000×0.3=600次,故C选项正确;D、随机事件,结果不确定,故D选项正确.故选:D.【点评】本题要理解用面积法求概率的方法.注意概率是多次实验得到的一个相对稳定的值.5.已知矩形的面积为8,则它的长y与宽x之间的函数关系用图象大致可以表示为()A.B.C.D.【考点】反比例函数的应用;反比例函数的图象.【分析】首先由矩形的面积公式,得出它的长y与宽x之间的函数关系式,然后根据函数的图象性质作答.注意本题中自变量x的取值范围.【解答】解:由矩形的面积8=xy,可知它的长y与宽x之间的函数关系式为y=(x>0),是反比例函数图象,且其图象在第一象限.故选B.【点评】本题考查了反比例函数的应用及反比例函数的图象,反比例函数的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.6.某市举行“一日捐”活动,甲、乙两单位各捐款30000元,已知“…”,设乙单位有x人,则可得方程﹣=20,根据此情景,题中用“…”表示的缺失的条件应补()A.甲单位比乙单位人均多捐20元,且乙单位的人数比甲单位的人数多20%B.甲单位比乙单位人均多捐20元,且甲单位的人数比乙单位的人数多20%C.乙单位比甲单位人均多捐20元,且甲单位的人数比乙单位的人数多20%D.乙单位比甲单位人均多捐20元,且乙单位的人数比甲单位的人数多20%【考点】由实际问题抽象出分式方程.【分析】方程﹣=20中,表示乙单位人均捐款额,(1+20%)x表示甲单位的人数比乙单位的人数多20%,则表示甲单位人均捐款额,所以方程表示的等量关系为:乙单位比甲单位人均多捐20元,由此得出题中用“…”表示的缺失的条件.【解答】解:设乙单位有x人,那么当甲单位的人数比乙单位的人数多20%时,甲单位有(1+20%)x人.如果乙单位比甲单位人均多捐20元,那么可列出﹣=20.故选C.【点评】本题考查了由实际问题抽象出分式方程的逆应用,根据所设未知数以及方程逆推缺少的条件.本题难度适中.二.填空题(共有10小题,每小题2分,共20分)7.计算=2.【考点】二次根式的性质与化简.【分析】先求﹣2的平方,再求它的算术平方根,进而得出答案.【解答】解:==2,故答案为:2.【点评】本题考查了二次根式的性质与化简,注意算术平方根的求法,是解此题的关键.8.分式,的最简公分母是6x3(x﹣y).【考点】最简公分母.【分析】确定最简公分母的方法是:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.【解答】解:分式,的分母分别是2x3、6x2(x﹣y),故最简公分母是6x3(x﹣y);故答案为6x3(x﹣y).【点评】本题考查了最简公分母的定义及求法.通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.一般方法:①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.9.袋子里有5只红球,3只白球,每只球除颜色以外都相同,从中任意摸出1只球,是红球的可能性大于(选填“大于”“小于”或“等于”)是白球的可能性.【考点】可能性的大小.【分析】根据“哪种球的数量大哪种球的可能性就打”直接确定答案即可.【解答】解:∵袋子里有5只红球,3只白球,∴红球的数量大于白球的数量,∴从中任意摸出1只球,是红球的可能性大于白球的可能性.故答案为:大于.【点评】本题考查了可能性的大小,可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等.10.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是30°.【考点】旋转的性质.【分析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可.【解答】解:∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,∴∠A′OA=45°,∠AOB=∠A′OB′=15°,∴∠AOB′=∠A′OA﹣∠A′OB=45°﹣15°=30°,故答案是:30°.【点评】此题主要考查了旋转的性质,根据旋转的性质得出∠A′OA=45°,∠AOB=∠A′OB′=15°是解题关键.11.如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB 的中点M,N,测得MN=32m,则A,B两点间的距离是64m.【考点】三角形中位线定理.【分析】根据M、N是OA、OB的中点,即MN是△OAB的中位线,根据三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即可求解.【解答】解:∵M、N是OA、OB的中点,即MN是△OAB的中位线,∴MN=AB,∴AB=2MN=2×32=64(m).故答案为:64.【点评】本题考查了三角形的中位线定理应用,正确理解定理是解题的关键.12.若点P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,则m<n (填“>”“<”或“=”号).【考点】反比例函数图象上点的坐标特征.【分析】根据反比例函数图象上点的坐标特征得到﹣1•m=k,﹣2•n=k,解得m=﹣k,n=﹣,然后利用k>0比较m、n的大小.【解答】解:∵P1(﹣1,m),P2(﹣2,n)在反比例函数y=(k>0)的图象上,∴﹣1•m=k,﹣2•n=k,∴m=﹣k,n=﹣,而k>0,∴m<n.故答案为:<.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.13.某工厂原计划a天生产b件产品,现要提前2天完成,则现在每天要比原来多生产产品件.【考点】列代数式(分式).【分析】根据题意知原来每天生产件,现在每天生产件,继而列式即可表示现在每天要比原来多生产产品件数.【解答】解:根据题意,原来每天生产件,现在每天生产件,则现在每天要比原来多生产产品﹣=件,故答案为:.【点评】本题主要考查根据实际问题列代数式,根据题意表示出原来和现在每天生产的件数是关键.14.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是22.5°.【考点】正方形的性质.【分析】由四边形ABCD是正方形,即可求得∠BAC=∠ACB=45°,又由AE=AC,根据等边对等角与三角形内角和等于180°,即可求得∠ACE的度数,又由∠BCE=∠ACE﹣∠ACB,即可求得答案.【解答】解:∵四边形ABCD是正方形,∴∠BAC=∠ACB=45°,∵AE=AC,∴∠ACE=∠E==67.5°,∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.故答案为:22.5°.【点评】此题考查了正方形的性质与等腰三角形的性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意特殊图形的性质.15.已知关于x的方程=3无解,则m的值为﹣4.【考点】分式方程的解.【分析】分式方程去分母转化为整式方程,根据分式方程无解得到x﹣2=0,求出x=2,代入整式方程即可求出m的值.【解答】解:分式方程去分母得:2x+m=3x﹣6,由分式方程无解得到x﹣2=0,即x=2,代入整式方程得:4+m=0,即m=﹣4.故答案为:﹣4【点评】此题考查了分式方程的解,注意在任何时候都要考虑分母不为0.16.如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为3.【考点】反比例函数系数k的几何意义.【分析】本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、矩形OABC的面积与|k|的关系,列出等式求出k值.【解答】解:由题意得:E、M、D位于反比例函数图象上,则S△OCE =,S△OAD=,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,∴S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则++9=4k,解得:k=3.故答案是:3.【点评】本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,本知识点是中考的重要考点,同学们应高度关注.三、计算:(8分)17.计算:(1)+(2)﹣x﹣1.【考点】分式的加减法.【分析】(1)原式变形后,利用同分母分式的减法法则计算即可得到结果;(2)原式通分并利用同分母分式的减法法则计算即可得到结果.【解答】解:(1)原式=﹣==a+b;(2)原式=﹣=.【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.四、解方程:(8分)18.解方程(1)﹣=1(2)=﹣1.【考点】解分式方程.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得,(x+1)2﹣4=x2﹣1,解得:x=1,经检验x=1是增根,分式方程无解;(2)去分母得,6(x+3)=x(x﹣2)﹣(x﹣2)(x+3),解得,x=﹣,经检验x=﹣是分式方程的解.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程时注意要检验.五、先化简,再求值:(共1小题,满分6分)19.先化简,再求值:(﹣)÷,其中x2﹣4x﹣1=0.【考点】分式的化简求值.【分析】先算括号里面的,再算除法,根据x2﹣4x﹣1=0得出x2﹣4x=1,代入原式进行计算即可.【解答】解:原式=[﹣]•=•=•==,∵x2﹣4x﹣1=0,∴x2﹣4x=1∴原式==.【点评】本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.六、解答题(共5小题,满分46分)20.(10分)(2014•兴化市二模)4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:初中生课外阅读情况调查统计表种类频数频率卡通画 a 0.45时文杂志 b 0.16武侠小说50 c文学名著 d e(1)这次随机调查了200名学生,统计表中d=28;(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是90°;(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?【考点】频数(率)分布表;用样本估计总体;扇形统计图;条形统计图.【分析】(1)由条形统计图可知喜欢武侠小说的人数为30人,由统计表可知喜欢武侠小说的人数所占的频率为0.15,根据频率=频数÷总数,即可求出调查的学生数,进而求出d的值;(2)算出喜欢武侠小说的频率,乘以360°即可;(3)由(1)可知喜欢文学名著类书籍人数所占的频率,即可求出该校1500名学生中有多少名同学最喜欢文学名著类书籍.【解答】解:(1)由条形统计图可知喜欢武侠小说的人数为30人,由统计表可知喜欢武侠小说的人数所占的频率为0.15,所以这次随机调查的学生人数为:=200名学生,所以a=200×0.45=90,b=200×0.16=32,∴d=200﹣90﹣32﹣50=28;(2)武侠小说对应的圆心角是360°×=90°;(3)该校1500名学生中最喜欢文学名著类书籍的同学有1500×=210名;【点评】此题主要考查了条形图的应用以及用样本估计总体和频数分布直方图,根据图表得出正确信息是解决问题的关键.21.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(kPa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16kPa.(1)当V=1.2m3时,求p的值;(2)当气球内的气压大于40kP时,气球将爆炸,为了确保气球不爆炸,气球的体积应满足条件.【考点】反比例函数的应用.【分析】(1)设函数解析式为P=,把V=1.5m3时,p=16kPa代入函数解析式求出k值,即可求出函数关系式;(2)p=40代入求得v值后利用反比例函数的性质确定正确的答案即可.【解答】(1)解:设p与V的函数表达式为p=(k为常数).把p=16、V=1.5代入,得k=24即p与V的函数表达式为;(2)把p=40代入,得V=0.6根据反比例函数的性质,p随V的增加而减少,因此为确保气球不爆炸,气球的体积应不小于0.6m3.【点评】本题考查了反比例函数的实际应用,关键是建立函数关系式,并会运用函数关系式解答题目的问题.22.(10分)(2016春•六合区期中)某项工程如果由乙单独完成比甲单独完成多用6天;如果甲、乙先合做4天后,再由乙单独完成,那么乙一共所用的天数刚好和甲单独完成工程所用的天数相等.(1)求甲单独完成全部工程所用的时间;(2)该工程规定须在20天内完成,若甲队每天的工程费用是4.5万元,乙队每天的工程费用是2.5万元,请你选择上述一种施工方案,既能按时完工,又能使工程费用最少,并说明理由?【考点】分式方程的应用.【分析】(1)利用总工作量为1,分别表示出甲、乙完成的工作量进而得出等式求出答案;(2)分别求出甲、乙单独完成的费用以及求出甲、乙合作的费用,进而求出符合题意的答案.【解答】解:(1)设甲单独完成全部工程所用的时间为x天,则乙单独完成全部工程所用的时间为(x+6)天,根据题意得,+=1,解得,x=12,经检验,x=12是原方程的解,答:甲单独完成全部工程所用的时间为12天;(2)根据题意得上述3个方案都在20天内.甲单独完成的费用:12×4.5=54万元,乙单独完成的费用:18×2.5=45万元,甲乙合做完成的费用:12×2.5+4×4.5=48万元,即乙单独完成既能按时完工,又能使工程费用最少.【点评】此题主要考查了分式方程的应用,根据题意利用总工作量为1得出等式是解题关键.23.如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.(1)求证:OE=CB;(2)如果OC:OB=1:2,OE=,求菱形ABCD的面积.【考点】菱形的性质;勾股定理.【分析】(1)通过证明四边形OCEB是矩形来推知OE=CB;(2)利用(1)中的AC⊥BD、OE=CB,结合已知条件,在Rt△BOC中,由勾股定理求得CO=1,OB=2.然后由菱形的对角线互相平分和菱形的面积公式进行解答.【解答】(1)证明:∵四边形ABCD是菱形,∴AC⊥BD.∵CE∥BD,EB∥AC,∴四边形OCEB是平行四边形,∴四边形OCEB是矩形,∴OE=CB;(2)解:∵由(1)知,AC⊥BD,OC:OB=1:2,∴BC=OE=.∴在Rt△BOC中,由勾股定理得BC2=OC2+OB2,∴CO=1,OB=2.∵四边形ABCD是菱形,∴AC=2,BD=4,∴菱形ABCD的面积是:BD•AC=4.【点评】本题考查了菱形的性质和勾股定理.解题时充分利用了菱形的对角线互相垂直平分、矩形的对角线相等的性质.24.(12分)(2014春•江都市校级期末)如图,已知直线与双曲线交于A、B两点,A点横坐标为4.(1)求k值;(2)直接写出关于x的不等式的解集;(3)若双曲线上有一点C的纵坐标为8,求△AOC的面积;(4)若在x轴上有点M,y轴上有点N,且点M、N、A、C四点恰好构成平行四边形,直接写出点M、N的坐标.【考点】反比例函数综合题.【分析】(1)由直线与双曲线交于A、B两点,A点横坐标为4,代入正比例函数,可求得点A的坐标,继而求得k值;(2)首先根据对称性,可求得点B的坐标,结合图象,即可求得关于x的不等式的解集;(3)首先过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC =S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC,又由双曲线上有一点C的纵坐标为8,可求得点C 的坐标,继而求得答案;(4)由当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,根据平移的性质,即可求得答案.【解答】解:(1)∵直线与双曲线交于A、B两点,A点横坐标为4,∴点A的纵坐标为:y=×4=2,∴点A(4,2),∴2=,∴k=8;(2)∵直线与双曲线交于A、B两点,∴B(﹣4,﹣2),∴关于x的不等式的解集为:﹣4≤x<0或x≥4;(3)过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,∵双曲线上有一点C的纵坐标为8,∴把y=8代入y=得:x=1,∴点C(1,8),∴S△AOC =S△OCD+S梯形AEDC﹣S△AOE=S梯形AEDC=×(2+8)×(4﹣1)=15;(4)如图,当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,∵点A(4,2),点C(1,8),∴根据平移的性质可得:M(3,0),N(0,6)或M′(﹣3,0),N′(0,﹣6).【点评】此题考查了反比例函数的性质、待定系数法求函数的解析式以及一次函数的性质等知识.此题难度较大,综合性很强,注意掌握数形结合思想、分类讨论思想与方程思想的应用.。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,5AB =,6AC =,过D 作AC 的平行线交BC 的延长线于点E ,则BDE ∆的面积为( )A .22B .24C .48D .442.下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )A .1个B .2个C .3个D .4个3.某一超市在“五•一”期间开展有奖促销活动,每买100元商品可参加抽奖一次,中奖的概率为13.小张这期间在该超市买商品获得了三次抽奖机会,则小张( ) A .能中奖一次 B .能中奖两次 C .至少能中奖一次 D .中奖次数不能确定4.下列成语故事中所描述的事件为必然发生事件的是( ) A .水中捞月B .瓮中捉鳖C .拔苗助长D .守株待兔5.已知12x <≤ ,则23(2)x x -- ) A .2 x - 5 B .—2C .5 - 2 xD .26.如果a 32+,b 32,那么a 与b 的关系是( ) A .a +b =0 B .a =bC .a =1bD .a >b7.若分式42x x -+的值为0,则x 的值为( ) A .0 B .-2 C .4 D .4或-2 8.下列条件中,不能..判定平行四边形ABCD 为矩形的是( ) A .∠A =∠C B .∠A =∠BC .AC =BDD .AB ⊥BC9.若分式5x x-的值为0,则( ) A .x =0 B .x =5 C .x ≠0 D .x ≠5 10.在□ ABCD 中,∠A =4∠D ,则∠C 的大小是( )A .36°B .45°C .120°D .144°11.下列调查中,最适宜采用全面调查方式的是( ) A .调查某市成年人的学历水平 B .调查某批次日光灯的使用寿命 C .调查市场上矿泉水的质量情况 D .了解某个班级学生的视力情况12.下列判断正确的是( ) A .对角线互相垂直的平行四边形是菱形 B .两组邻边相等的四边形是平行四边形 C .对角线相等的四边形是矩形D .有一个角是直角的平行四边形是正方形 二、填空题13.“一只不透明的袋子共装有3个小球,它们的标号分别为1,2,3,从中摸出1个小球,标号为“4”,这个事件是______.(填“必然事件”、“不可能事件”或“随机事件”) 14.如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2m 的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是__m 2.15.如图,四边形ABCD 是菱形,O 是两条对角线的交点,过O 点的三条直线将菱形分成阴影和空白部分,若菱形的面积为20cm 2,则阴影部分的面积为_____cm 2.16.如图,点D 、E 分别是△ABC 的边AB 、AC 的中点,若BC=6,则DE= .17.已知a ,b 是一元二次方程x 2﹣2x ﹣2020=0的两个根,则a 2+2b ﹣3的值等于_____. 18.若()14,A y -、()22,B y -都在反比例函数6y x=的图像上,则1y 、2y 的大小关系为1y _________2y (填“>”、“<”、“=”)19.如图,点A 是一次函数13y x =(0)x ≥图像上一点,过点A 作x 轴的垂线l ,点B 是l上一点(B 在A 上方),在AB 的右侧以AB 为斜边作等腰直角三角形ABC ,反比例函数k yx=(0)x>的图像过点B、C,若OAB∆的面积为8,则ABC∆的面积是_________.20.一个不透明的袋中装有3个红球,2个黑球,每个球除颜色外都相同.从中任意摸出3球,则“摸出的球至少有1个红球”是__事件.(填“必然”、“不可能”或“随机”)21.如图,△ABC中,∠BAC=20°,△ABC绕点A逆时针旋转至△AED,连接对应点C、D,AE垂直平分CD于点F,则旋转角度是_____°.22.如图,点E在▱ABCD内部,AF∥BE,DF∥CE,设▱ABCD的面积为S1,四边形AEDF的面积为S2,则12SS的值是_____.23.已知1x,2x,…,10x的平均数是a;11x,12x,…,30x的平均数是b,则1x,2x,…,30x的平均数是_________.24.如图,已知22AB=,C为线段AB上的一个动点,分别以AC,CB为边在AB 的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,120D∠=︒,P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,线段PQ的最小值为________.三、解答题25.某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.请根据图中提供的信息,解答下面的问题:(1)此次共调查了名学生,扇型统计图中“艺术鉴赏”部分的圆心角是度.(2)请把这个条形统计图补充完整.(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.26.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F 两点均在BD上),折痕分别为BH、DG.(1)求证:△BHE≌△DGF;(2)若AB=6cm,BC=8cm,求线段FG的长.27.已知:如图,在 ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.求证:四边形BFDE是平行四边形.28.某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:最喜爱的节目 人数 歌曲 15 舞蹈 a 小品 12 相声 10 其它b(1)在此次调查中,该校一共调查了 名学生; (2)a = ;b = ;(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数; (4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.29.如图,在△ABC 中,AB =AC ,点D 是边AB 的点,DE ∥BC 交AC 于点E ,连接BE ,点F 、G 、H 分别为BE 、DE 、BC 的中点. (1)求证:FG =FH ;(2)当∠A 为多少度时,FG ⊥FH ?并说明理由.30.如图,在平行四边形ABCD 中,AE BD CF BD ⊥⊥,,垂足分别为E F 、.(1)求证:AE CF =;(2)求证:四边形AECF 是平行四边形31.某种油菜籽在相同条件下的发芽实验结果如表:(1)a = ,b = ;(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?32.如图,已知一次函数y =x +2的图象与x 轴、y 轴分别交于点A ,B 两点,且与反比例函数y =mx的图象在第一象限交于点C ,CD ⊥x 轴于点D ,且OA =OD . (1)求点A 的坐标和m 的值;(2)点P 是反比例函数y =mx在第一象限的图象上的动点,若S △CDP =2,求点P 的坐标.33.为更有效地开展“线上教学”工作,某市就学生参与线上学习的工具进行了电子问卷调查,并将调查结果绘制成图1和图2所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次调查的总人数是 人; (2)请将条形统计图补充完整;(3)在扇形统计图中表示观点B 的扇形的圆心角度数为 度; (4)在扇形统计图中表示观点E 的百分比是 .34.如图,在ABC ∆中,90ABC ∠=︒,BD 为AC 的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG 、DF .(1)求证:BD DF =; (2)求证:四边形BDFG 为菱形;(3)若13AG =,6CF =,求四边形BDFG 的周长.35.如图,已知()()1,0,0,3,90,30A B BAC ABC ︒︒∠=∠=.(1)求ABC ∆的面积;(2)在y 轴上是否存在点Q 使得QAB ∆为等腰三角形,若存在,请直接写出点Q 所有可能的坐标,若不存在,请说明理由;(3)如果在第二象限内有一点3,P m ⎛⎫ ⎪ ⎪⎝⎭,且过点P 作PH x ⊥轴于H ,请用含m 的代数式 表示梯形PHOB 的面积,并求当ABP ∆与ABC ∆面积相等时m 的值?36.已知:ABC ∆中以CB 为边在ABC ∆外侧作等边CBP ∆.(1)连接AP ,以AP 为边作等边APQ ∆,求证:AC BQ =; (2)当30CAB ∠=︒,4AB =,3AC =时,求AP 的值;(3)若4AB =,3AC =,改变CAB ∠的度数,发现CAB ∠在变化到某一角度时,AP 有最大值.画出CAB ∠为这个特殊角度时的示意图,并直接写出CAB ∠的角度和AP 的最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】先判断出四边形ACED是平行四边形,从而得出DE的长度,根据菱形的性质求出BD的长度,利用勾股定理的逆定理可得出△BDE是直角三角形,计算出面积即可.【详解】解:∵AD∥BE,AC∥DE,∴四边形ACED是平行四边形,∴AC=DE=6,在RT△BCO中,4=,即可得BD=8,又∵BE=BC+CE=BC+AD=10,∴△BDE是直角三角形,∴S△BDE=124 2DE BD⋅=.故答案为B.【点睛】此题考查了菱形的性质、勾股定理的逆定理及三角形的面积,属于基础题,求出BD的长度,判断△BDE是直角三角形,是解答本题的关键.2.C解析:C【分析】根据轴对称图形与中心对称图形的概念对各选项分析判断即可.【详解】第1个,即不是轴对称图形,也不是中心对称图形,故本选项错误;第2个,既是轴对称图形,也是中心对称图形,故本选项正确;第3个,既是轴对称图形,也是中心对称图形,故本选项正确;第4个,既是轴对称图形,也是中心对称图形,故本选项正确.故选:C.【点睛】本题考查了轴对称图形与中心对称图形,掌握中心对称图形与轴对称图形的概念是解题关键.3.D解析:D【分析】由于中奖概率为13,说明此事件为随机事件,即可能发生,也可能不发生. 【详解】解:根据随机事件的定义判定,中奖次数不能确定. 故选D . 【点睛】解答此题要明确概率和事件的关系:()P A 0=①,为不可能事件; ()P A 1=②为必然事件; ()0P A 1<<③为随机事件. 4.B解析:B 【解析】试题分析:根据必然事件、不可能事件、随机事件的概念可区别各类事件. 解:A 、水中捞月是不可能事件,故A 错误; B 、瓮中捉鳖是必然事件,故B 正确; C 、拔苗助长是不可能事件,故C 错误; D 、守株待兔是随机事件,故D 错误; 故选B . 考点:随机事件.5.C解析:C 【分析】结合1 < x ≤ 2 ,根据绝对值和二次根式的进行计算,即可得到答案. 【详解】因为1 < x ≤ 2 ,所以3x -+32x x -+-= 5 - 2 x.故选择C . 【点睛】本题考查不等式、绝对值和二次根式,解题的关键是掌握不等式、绝对值和二次根式.6.A解析:A 【分析】先利用分母有理化得到a 2),从而得到a 与b 的关系. 【详解】∵a2),而b 2,∴a =﹣b ,即a+b=0. 故选:A . 【点睛】﹣2是解答本题的关键.7.C解析:C 【分析】根据分式的值为零的条件可以得到4020x x -=⎧⎨+≠⎩,从而求出x 的值.【详解】解:由分式的值为零的条件得4020x x -=⎧⎨+≠⎩,由40x -=,得:4x =, 由20x +≠,得:2x ≠-. 综上,得4x =,即x 的值为4. 故选:C . 【点睛】本题考查了分式的值为零的条件,以及分式有意义的条件,解题的关键是熟练掌握分式的值为零的条件进行解题.8.A解析:A 【分析】根据矩形的判定定理再结合平行四边形的性质对选项逐一进行推理即可. 【详解】A 、∠A=∠C 不能判定这个平行四边形为矩形,故此项错误;B 、∵∠A=∠B ,∠A+∠B=180°,∴∠A=∠B=90°,可以判定这个平行四边形为矩形,故此项正确; C 、AC=BD ,对角线相等,可推出平行四边形ABCD 是矩形,故此项正确; D 、AB ⊥BC ,即∠B=90°,可以判定这个平行四边形为矩形,故此项正确; 故选:A . 【点睛】本题考查了平行四边形的性质和矩形的判定,掌握知识点是解题关键.9.B解析:B 【分析】直接利用分式的值为零则分子为零,分母不等于0,进而得出答案. 【详解】解:∵分式5xx的值为0,∴x﹣5=0且x≠0,解得:x=5.故选:B.【点睛】本题考查了分式,掌握“分式值为0”时的做题方法及分式有意义的条件是解题关键.10.D解析:D【解析】【分析】由四边形ABCD是平行四边形可知∠A+∠D=180°,结合∠A=4∠D,可求出∠D的值,从而可求出∠C的大小.【详解】∵四边形ABCD是平行四边形,∴∠A+∠D=180°,∵∠A=4∠D,∴4∠D +∠D=180°,∴∠D=36°,∴∠C=180°-36°=144°.故选D.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边行的性质是解答本题的关键.平行四边形的性质有:平行四边形对边平行且相等;平行四边形对角相等,邻角互补;平行四边形对角线互相平分.11.D解析:D【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,但所费人力、物力和时间较少分析解答即可.【详解】A. 调查某市成年人的学历水平工作量比较大,宜采用抽样调查;B. 调查某批次日光灯的使用寿命具有破坏性,宜采用抽样调查;C. 调查市场上矿泉水的质量情况具有破坏性,宜采用抽样调查;D. 了解某个班级学生的视力情况工作量比较小,宜采用全面调查.故选D.【点睛】本题考查了抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.12.A解析:A【分析】利用特殊四边形的判定定理逐项判断即可.【详解】A、对角线互相垂直的平行四边形是菱形,此项正确B、两组对边分别相等的四边形是平行四边形,此项错误C、对角线相等的平行四边形是矩形,此项错误D、有一个角是直角的平行四边形是矩形,此项错误故选:A.【点睛】本题考查了特殊四边形(平行四边形、菱形、矩形、正方形)的判定定理,掌握理解各判定定理是解题关键.二、填空题13.不可能事件.【解析】根据题意,可知这个袋子中有3个数字,抽取一个球时不可能抽到数字4,所以是不可能事件.故答案为不可能事件.解析:不可能事件.【解析】根据题意,可知这个袋子中有3个数字,抽取一个球时不可能抽到数字4,所以是不可能事件.故答案为不可能事件.14.1【详解】解:由题意可知,正方形的面积为4平方米,因为小石子落在不规则区域的频率稳定在常数0.25附近,所以不规则区域的面积约是4×0.25=1平方米.故答案为:1解析:1【详解】解:由题意可知,正方形的面积为4平方米,因为小石子落在不规则区域的频率稳定在常数0.25附近,所以不规则区域的面积约是4×0.25=1平方米.故答案为:115.10【分析】根据中心对称的性质判断出阴影部分的面积等于菱形的面积的一半,即可得出结果.【详解】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴△OEG≌△OFH,四边形OMAH解析:10【分析】根据中心对称的性质判断出阴影部分的面积等于菱形的面积的一半,即可得出结果.【详解】∵O是菱形两条对角线的交点,菱形ABCD是中心对称图形,∴△OEG≌△OFH,四边形OMAH≌四边形ONCG,四边形OEDM≌四边形OFBN,∴阴影部分的面积=12S菱形ABCD=12×20=10(cm2).故答案为:10.【点睛】本题考查了中心对称,菱形的性质,全等三角形的判定与性质等知识;熟记性质并判断出阴影部分的面积等于菱形的面积的一半是解题的关键.16.3【分析】先判断DE是△ABC的中位线,从而得解.【详解】因为点D、E分别是△ABC的边AB、AC的中点,所以DE是△ABC的中位线,所以DE=BC=3.故答案为3.考点:三角形的中解析:3【分析】先判断DE是△ABC的中位线,从而得解.【详解】因为点D 、E 分别是△ABC 的边AB 、AC 的中点,所以DE 是△ABC 的中位线,所以DE=12BC=3. 故答案为3.考点:三角形的中位线定理.17.2021【分析】根据一元二次方程的根与系数的关系得出,再结合原方程可知,由此进一步求解即可.【详解】∵a 是一元二次方程的一个根,∴,再由根与系数的关系可知:,∴a2+2b −3=a2−解析:2021【分析】根据一元二次方程的根与系数的关系得出2a b +=,再结合原方程可知222020a a -=,由此进一步求解即可.【详解】∵a 是一元二次方程的一个根,∴222020a a -=,再由根与系数的关系可知:2a b +=,∴a 2+2b −3=a 2−2a +2a +2b −3,=2020+2(a +b )−3=2020+2×2−3=2021,故答案为:2021.【点睛】本题主要考查了一元二次方程的性质与根与系数的关系的运用,熟练掌握相关概念是解题关键.18.>【分析】根据反比例函数的图象与性质即可解答.【详解】解:的图象当时,y 随x 的增大而减小,∵,故,故答案为:>.【点睛】本题考查反比例函数的图象与性质,解题的关键是熟练掌握反比例函数 解析:>【分析】根据反比例函数的图象与性质即可解答.【详解】 解:6y x =的图象当0x <时,y 随x 的增大而减小, ∵4-<-2,故12y y >,故答案为:>.【点睛】本题考查反比例函数的图象与性质,解题的关键是熟练掌握反比例函数的图象与性质.19.【分析】过作轴于,交于,设,根据直角三角形斜边中线是斜边一半得:,设,则,,因为.都在反比例函数的图象上,列方程可得结论.【详解】如图,过作轴于,交于.∵轴∴,∵是等腰直角三角形, 解析:163【分析】过C 作CD y ⊥轴于D ,交AB 于E ,设2AB a =,根据直角三角形斜边中线是斜边一半得:BE AE CE a ===,设1,3A x x ⎛⎫ ⎪⎝⎭,则1,23B x x a ⎛⎫+ ⎪⎝⎭,1,3C x a x a ⎛⎫++ ⎪⎝⎭,因为B .C 都在反比例函数的图象上,列方程可得结论.【详解】如图,过C 作CD y ⊥轴于D ,交AB 于E .∵AB x ⊥轴∴CD AB ⊥,∵ABC ∆是等腰直角三角形,∴BE AE CE ==,设2AB a =,则BE AE CE a ===, 设1,3A x x ⎛⎫ ⎪⎝⎭,则1,23B x x a ⎛⎫+ ⎪⎝⎭,1,3C x a x a ⎛⎫++ ⎪⎝⎭, ∵B ,C 在反比例函数的图象上, ∴112()33x x a x a x a ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭, 解得32x a =, ∵112822OAB S AB DE a x ∆=⋅=⋅⋅=, ∴8ax =, ∴2382a =, ∴2163a =, ∵211222ABC S AB CE a a a ∆=⋅=⋅⋅= 163= 故答案为:163. 【点睛】 本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积,熟练掌握反比例函数上的点符合反比例函数的关系式是关键.20.必然【分析】根据事件发生的可能性大小判断相应事件的类型即可.【详解】∵红球和黑球除颜色外其余都相同且黑球只有2个,∴从中任意摸出3球,至少有一个为红球,即事件“摸出的球至少有1个红球”是解析:必然【分析】根据事件发生的可能性大小判断相应事件的类型即可.【详解】∵红球和黑球除颜色外其余都相同且黑球只有2个,∴从中任意摸出3球,至少有一个为红球,即事件“摸出的球至少有1个红球”是必然事件,故答案为:必然.【点睛】本题考查了必然事件的定义,正确理解必然事件,不可能事件,随机事件的概念是解题关键.21.40【分析】根据旋转的性质得出AD=AC,∠D AE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC的度数即可.【详解】解:∵△ABC绕点A逆时针旋转至△AED,∠BAC解析:40【分析】根据旋转的性质得出AD=AC,∠DAE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC的度数即可.【详解】解:∵△ABC绕点A逆时针旋转至△AED,∠BAC=20°,∴AD=AC,∠DAE=∠BAC=20°,∵AE垂直平分CD于点F,∴∠DAE=∠CAE=20°,∴∠DAC=20°+20°=40°,即旋转角度数是40°,故答案为:40.【点睛】本题主要考查了图像旋转的性质以及垂直平分线的性质,从而得到边相等与角相等的条件.22.2【分析】首先由ASA 可证明:△BCE≌△ADF;由平行四边形的性质可知:S△BEC+S△AED =S ▱ABCD ,进而可求出的值.【详解】∵四边形ABCD 是平行四边形,∴AD=BC ,AD∥B解析:2【分析】首先由ASA 可证明:△BCE ≌△ADF ;由平行四边形的性质可知:S △BEC +S △AED =12S ▱ABCD ,进而可求出12S S 的值. 【详解】∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∴∠ABC +∠BAD =180°,∵AF ∥BE ,∴∠EBA +∠BAF =180°,∴∠CBE =∠DAF ,同理得∠BCE =∠ADF ,在△BCE 和△ADF 中, CBE DAF BC ADBCE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△BCE ≌△ADF (ASA ),∴S △BCE =S △ADF ,∵点E 在▱ABCD 内部,∴S △BEC +S △AED =12S ▱ABCD , ∴S 四边形AEDF =S △ADF +S △AED =S △BEC +S △AED =12S ▱ABCD , ∵▱ABCD 的面积为S 1,四边形AEDF 的面积为S 2, ∴12S S =2, 故答案为:2.【点睛】此题主要考查了平行四边形的性质以及全等三角形的判定与性质,熟练利用三角形和平行四边形边的关系得出面积关系是解题关键.23.【分析】利用平均数的定义,利用数据x1,x2,…,x10的平均数为a ,x11,x12,…,x30的平均数为b ,可求出x1+x2+…+x10=10a,x11+x12+…+x30=20b,进而即可求 解析:1(1020)30a b + 【分析】利用平均数的定义,利用数据x 1,x 2,…,x 10的平均数为a ,x 11,x 12,…,x 30的平均数为b ,可求出x 1+x 2+…+x 10=10a ,x 11+x 12+…+x 30=20b ,进而即可求出答案.【详解】解:因为数据x 1,x 2,…,x 10的平均数为a ,则有x 1+x 2+…+x 10=10a ,因为x 11,x 12,…,x 30的平均数为b ,则有x 11+x 12+…+x 30=20b ,∴x 1,x 2,…,x 30的平均数=()1102030a b + 故答案为:1(1020)30a b +. 【点睛】本题考查的是样本加权平均数的求法.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数. 24.【分析】连接QC 、PC ,先证明∠PCQ=90°,设AC=,则BC=,PC=,CQ=(),构建二次函数,利用二次函数的性质即可解决问题.【详解】连接PC 、CQ .∵四边形ACED ,四边形CB【分析】连接QC 、PC ,先证明∠PCQ=90°,设AC=2a ,则BC=2a ,PC=a ,a -),构建二次函数,利用二次函数的性质即可解决问题.【详解】连接PC 、CQ .∵四边形ACED ,四边形CBGF 是菱形,∠D=120°,∴∠ACE=120°,∠FCB=60°,∵P ,Q 分别是对角线AE ,BF 的中点,∴∠ECP=∠ACP=12∠ACE=60°,∠FCQ=∠BCQ=12∠BCF=30°, ∴∠PCQ=90°,设AC=2a ,则BC=222a ,PC=12AC=a ,CQ=BC cos30⋅︒32a ), ∴()2222232332442PQ PC QC a a a ⎛⎫⎡⎤=+=+-=-+ ⎪ ⎪⎣⎦⎝⎭ ∴当324a =PQ 362=. 故答案为:62. 【点睛】 本题考查了菱形的性质、勾股定理、二次函数的性质等知识,解题的关键是学会添加常用辅助线,构建二次函数解决最值问题.三、解答题25.解:(1)200,144.(2)见解析;(3)120名【分析】(1)根据阅读写作的人数和所占的百分比,即可求出学生总数,再用艺术鉴赏的人数除以总人数乘以360°,即可得出 “艺术鉴赏”部分的圆心角.(2)用总学生数减去“艺术鉴赏”,“科技制作”,“阅读写作”,得出“数学思维”的人数,从而补全统计图.(3)用“科技制作”所占的百分比乘以总人数8000,即可得出答案.【详解】解:(1)学生总数:50÷25%=200(名)“艺术鉴赏”部分的圆心角:80200×360°=144° 故答案为:200,144.(2)数学思维的人数是:200-80-30-50=40(名),补图如下:(3)根据题意得:800×30200=120(名), 答:其中有120名学生选修“科技制作”项目.26.(1)见解析 (2)3cm【分析】1)先根据矩形的性质得出∠ABD=∠BDC ,再由图形折叠的性质得出∠1=∠2,∠3=∠4,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH ≌△DFG ;(2)先根据勾股定理得出BD 的长,进而得出BF 的长,由图形翻折变换的性质得出CG=FG ,设FG=x ,则BG=8﹣x ,再利用勾股定理即可求出x 的值.【详解】(1)如图,ABCD 四边形是矩形,AB CD ∴=,90A C ∠=∠=︒,ABD BDC ∠=∠.BEH ∆是BAH ∆翻折而成的,1=2∴∠∠,==90A HEB ∠∠︒,AB BE =.DGF DGC ∆∆是翻折而成的,3=4∴∠∠,90C DFG ∠=∠=︒,CD DF =,∴在BEH ∆和DFG ∆中,HEB DFG ∠=∠,BE DF =,2=3∠∠,BHE DGF ∴∆∆≌.(2)四边形ABCD 是矩形,6AB =,8BC =,6AB CD ∴==,8AD BC ==, 22=10BD BC CD ∴+=,又由(1)知,DF CD =,CG FG =,=1064BF ∴-=. 设FG x =,则8BG x =-,在Rt BGF ∆中,222BG BF FG =+,即()22284x x -=+,3x ∴=,即3FG =.【点睛】本题主要考查矩形的折叠问题,涉及知识点有全等三角形的证明与性质,勾股定理,折叠性质等知识点,解题关键在于能够灵活运用勾股定理27.见解析【分析】先根据平行四边形的性质,得出ED∥BF,再结合已知条件∠ABE=∠CDF推断出EB∥DF,即可证明.【详解】证明:∵四边形ABCD为平行四边形,∴AD∥BC,∠ABC=∠ADC,∴∠ADF=∠DFC,ED∥BF,∵∠ABE=∠CDF,∴∠ABC-∠ABE=∠ADC-∠CDF,即∠EBC=∠ADF,∴∠EBC=∠DFC,∴EB∥DF,∴四边形BFDE是平行四边形.【点睛】本题考查了平行四边形的性质和平行四边形的判定定理,掌握知识点是解题关键.28.(1)50;(2)8,5;(3)108°;(4)240人.【分析】(1)从表格和统计图中可以得到喜欢“小品”的人数为12人,占调查人数的24%,可求出调查人数,(2)舞蹈占50人的16%可以求出a的值,进而从总人数中减去其他组的人数得到b的值,(3)先计算“歌曲”所占的百分比,用360°去乘即可,(4)样本估计总体,用样本喜欢“相声”的百分比估计总体的百分比,进而求出人数.【详解】(1)12÷24%=50人故答案为50.(2)a=50×16%=8人,b=50﹣15﹣8﹣12﹣10=5人,故答案为:8,5.(3)360°×1550=108°答:“歌曲”所在扇形的圆心角的度数为108°;(4)1200×1050=240人答:该校1200名学生中最喜爱“相声”的学生大约有240人.【点睛】考查扇形统计图、频数统计表的制作方法,明确统计图表中的各个数据之间的关系是解决问题的关键.29.(1)见解析;(2)当∠A=90°时,FG⊥FH.【分析】(1)根据等腰三角形的性质得到∠ABC=∠ACB,根据平行线的性质、等腰三角形的判定定理得到AD=AE,得到DB=EC,根据三角形中位线定理证明结论;(2)延长FG交AC于N,根据三角形中位线定理得到FH∥AC,FN∥AB,根据平行线的性质解答即可.【详解】(1)证明:∵AB=AC.∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,∵点F、G、H分别为BE、DE、BC的中点,∴FG是△EDB的中位线,FH是△BCE的中位线,∴FG=12BD,FH=12CE,∴FG=FH;(2)解:延长FG交AC于N,∵FG是△EDB的中位线,FH是△BCE的中位线,∴FH∥AC,FN∥AB,∵FG⊥FH,∴∠A=90°,∴当∠A=90°时,FG⊥FH.【点睛】本题考查的是三角形中位线定理的应用、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.30.(1)见解析;(2)见解析【解析】【分析】(1)证出△ABE ≌△CDF 即可求解;(2)证出AE 平行CF ,AE CF =即可/【详解】(1)∵AE BD CF BD ⊥⊥,∴∠AEB=∠CFD∵平行四边形ABCD∴∠ABE=∠CDF,AB=CD∴△ABE ≌△CDF∴AE=CF(2)∵AE BD CF BD ⊥⊥,∴AE ∥CF∵AE=CF∴四边形AECF 是平行四边形【点睛】本题考查的是平行四边形的综合运用,熟练掌握全等三角形的性质是解题的关键.31.(1)0.70,0.70;(2)0.70,理由见解析;(3)6300棵.【分析】(1)用发芽的粒数m ÷每批粒数n 即可得到发芽的频率m n; (2)6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于0.70,所以估计当n 很大时,频率将接近0.70,由此即可得出答案;(3)首先计算发芽的种子数,然后乘以90%即可得.【详解】(1)5600.70800a ==,7000.701000b == 故答案为:0.70,0.70;(2)这种油菜籽发芽的概率估计值是0.70理由:由表可知,这6批次种子粒数从100粒逐渐增加到1000粒时,种子发芽的频率趋近于0.70,则种子发芽的频率为0.70由频率估计概率可得:这种油菜籽发芽的概率估计值是0.70;(3)这种油菜籽发芽的种子数为100000.707000⨯=(粒)则700090%6300⨯=(棵)答:在相同条件下用10000粒该种油菜籽可得到油菜秧苗6300棵.【点睛】本题考查了频率的计算、利用频率估计概率等知识点,掌握频率的相关知识是解题关键.32.(1)(-2,0);8 (2)(1,8)或(3,83) 【分析】(1)根据待定系数法就可以求出函数的解析式;(2)1||2CDP P C S CD x x =⨯⨯-△,即可求解. 【详解】解:(1)对于一次函数2y x =+,令0x =,则2y =,令0y =,则2x =-, 故点A 、B 的坐标分别为(2,0)-、(0,2), OA OD =,故点(2,0)D ,则点C 的横坐标为2,当2x =时,24y x =+=,故点(2,4)C ,将点C 的坐标代入反比例函数表达式得:42m =, 解得:8m =,故点A 的坐标为(2,0)-,8m =;(2)1142222CDP P C P S CD x x x =⨯⨯-=⨯⨯-=, 解得:3P x =或1,故点P 的坐标为(1,8)或8(3,)3.【点睛】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.33.(1)5000;(2)条形统计图见解析;(3)18;(4)4%.【分析】(1)根据选A 的人数和所占的百分比,可以求得本次调查的总人数;(2)根据(1)中的结果,可以求得选C 的人数,从而可以将条形统计图补充完整; (3)根据选B 的人数为250,调查的总人数为5000,即可计算出在扇形统计图中表示观点B 的扇形的圆心角度数;(4)根据统计图中的数据,可以计算出在扇形统计图中表示观点E 的百分比.【详解】解:(1)本次调查的总人数是:2300÷46%=5000(人),。
【苏教版】数学八年级下册《期中考试卷》带答案解析

八年级下学期数学期中测试卷一、单项选择题:(本题共6小题,每小题2分,共12分.在每小题给出的四个选项中,只有一项是符合题意要求的.)1.下列图形中,是中心对称图形的是( )A .B .C .D .2.相关部门对某厂生产的学生营养午餐重量是否达标进行检查,该厂准备运送午餐有20辆车,每辆车装100箱,每箱有50盒营养午餐,随机选取20箱,每箱抽取3盒进行称重检测,以下说法正确的是( ) A .本次抽查的总体是100营养午餐 B .本次抽查的样本是20箱营养午餐重量 C .本次抽查的个体是1盒营养午餐 D .本次抽查的样本容量是603.将分式方程5231(1)1x x x x --=++去分母,整理后得( )A .830x -=B .2410x x --=C .2720x x -+=D .2720x x --=4.下列各点在反比例函数4y x=-图像上的是( ) A .()1,4B .()2,2-C .()2,2--D .()4,1--5.平面直角坐标系中,以原点O 为旋转中心,将点(9,5)P --顺时针旋转90︒,得到点Q ,则点Q 的坐标为( ). A .(5,9)-B .(5,9)-C .(9,5)D .(9,5)-6.已知平行四边形ABCD 中,8AC =,E 是AD 上一点,DCE 的周长是平行四边形ABCD 周长的一半,且5EC =,连结EO ,则EO 的长为( )A .2B .3C .4D .5二、填空题:(本题共10小题,每小题2分,共20分)7.经过有交通信号灯的路口,遇到红灯,这是一个______事件(从“随机、不可能、必然”中选一个填入). 8.如果函数()21k y k x-=+是反比例函数,那么k 的值为________.9.若0ab ≠,且23b a =,则2a bb+的值是________. 10.如图,风车图案围绕着旋转中心至少旋转_________度,会与原图案重合.11.化简:11123x x x++= __________. 12.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________.13.对于实数a 、b ,定义一种新运算“⊗”为:21a b a b⊗=-,这里等式右边是实数运算.例如:21113138⊗==--,则方程2(2)14x x ⊗-=--的解是__________. 14.如图,菱形ABCD 中,若BD =8,AC =6,则该菱形的面积为___.15.若关于x 的方程211333x kx x x x +-=--有增根,k 的值是_____;若关于x 的方程211333x kx x x x +-=--无解,k 的值是_____.16.如图,矩形ABCD 中,AD =5,AB =7,正方形MBND ′的顶点M ,N 分别在矩形的边AB ,BC 上,点E 为DC 上一个动点,当点D 与点D ′关于AE 对称时,DE 的长为_____.三、解答题:(本题共11小题,共88分.解答应写出文字说明、证明过程或演算步骤.)17.解方程 (1)1214x x =+- (2)()()71112x x x x =+--+18.对某厂生产的直径为4cm 的乒乓球进行产品质量检查,结果如下: (1)计算各次检查中“优等品”的频率,填入表中;(2)该厂生产乒乓球优等品的概率约为多少?19.先化简,再求值:22214244x x x x x x x x +--⎛⎫-÷⎪--+⎝⎭,其中201(2021)2x π-⎫⎛=-+ ⎪⎝⎭.20.如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图.(1)以A 点为旋转中心,将△ABC 绕点A 顺时针旋转90°得△AB 1C 1,画出△AB 1C 1;(2)作出△ABC 关于坐标原点O 成中心对称的△A 2B 2C 2.21.我校为了丰富学生课余生活,计划开设以下课外活动项目:A-篮球,B-乒乓球,C-羽毛球,D-足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅统计图,请回答下列问题:(1)这次被调查的学生共有______人,扇形统计图中,“D-足球”所占圆心角的度数是______︒;(2)请你将条形统计图补充完整;(3)若该校学生总数为1000人,试估计该校学生中最喜欢“乒乓球”项目的人数.=,连接AF.求22.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF CE=.证:AD EF23.列方程解应用题开展“光盘行动”,拒绝“舌尖上的浪费”,已成为一种时尚.某学校食堂为了激励同学们做到光盘不浪费,提出如果学生每餐做到光盘不浪费,那么餐后奖励香蕉或橘子一份.近日,学校食堂花了2800元和2500元分别采购了香蕉和橘子,采购的香蕉比橘子多150千克,香蕉每千克的价格比橘子每千克的价格低30%,求橘子每千克的价格.24.阅读:对于两个不等的非零实数,a b ,若分式x a x b x(-)(-)的值为零,则x a =或x b =.又因为2()()()()x a x b x a b x ab abx a b x x x---++==+-+,所以关于x 的方程abx a b x+=+有两个解,分别为12,x a x b ==. 应用上面的结论解答下列问题: (1)方程86x x+=有两个解,分别为1x =_____,2x =______. (2)关于x 的方程42m n m mn nx mnx mn-+-+=的两个解分别为()1212,x x x x <,若1x 与2x 互为倒数,则1x =_____,2x =______;(3)关于x 的方程22221n nx n x -+=-的两个解分别为()1212,x x x x <,求12212x x -的值.25.已知:如图,在△ABC 中,△ABC =90°, AB =BC ,D 是AC 的中点,DE △DF ,DE 交AB 于点E ,DF 交BC 于点F . (1)求证:AE =BF ;(2)连接EF ,求△DEF 的度数;(3)若AC=EF 的取值范围.26.对于两个不等的非零实数a b 、,若分式()()x a x b x--的值为0,则x a =或x b =,又因为()()()()2x a x b x a b x ab abx a b xxx---++==+-+,所以关于x 的方程abx a b x+=+有两个解,分别为1x a =,2x b =,应用上面的结论解答下列问题: (1)方程8x 6x+=的两个解中较大的一个为_______.(2)关于x 的方程m n m 4mn nx mnx 2mn -+-+=的两个解分别为12x x ,(12x x <),若1x 与2x 互为倒数,则1x =______,2x =_______.(3)关于x 的方程2n 2n 32x 2n 32x 1+-+=+-的两个解分别为12x x ,(12x x <),求21x 22x -的值.27.在直角三角形ABC 中,△B =90°,BC =6 cm ,AB =8 cm ,有一动点P 以3cm/s 的速度从点C 出发向终点B 运动,同时还有一动点Q 以5 cm/s 的速度也从点C 出发,向终点A 运动,连结PQ ,并且PQ △BC ,以CP 、CQ 为邻边作平行四边形CQMP ,设动点P 的运动时间为t (s )(0<t <2).(1)BP = (用含t 的代数式表示); (2)当点M 在△B 的平分线上时,求此时的t 值; (3)当四边形BPQM 是平行四边形时,求CM 的值; (4)连结AM ,直接写出当△AMQ 是等腰三角形时t的值.答案与解析一、单项选择题:(本题共6小题,每小题2分,共12分.在每小题给出的四个选项中,只有一项是符合题意要求的.)1.下列图形中,是中心对称图形的是()A.B.C.D.【答案】A【分析】根据中心对称图形的概念对各选项分析判断即可得解.【详解】解:A、是中心对称图形,故本选项符合题意;B、不是中心对称图形,故本选项不符合题意;C、不是中心对称图形,故本选项不符合题意;D、不是中心对称图形,故本选项不符合题意.故选:A.【点睛】本题考查了中心对称图形的判断,掌握中心对称图形的概念并能准确运用概念对图形进行判断是解题的关键.2.相关部门对某厂生产的学生营养午餐重量是否达标进行检查,该厂准备运送午餐有20辆车,每辆车装100箱,每箱有50盒营养午餐,随机选取20箱,每箱抽取3盒进行称重检测,以下说法正确的是()A.本次抽查的总体是100营养午餐B.本次抽查的样本是20箱营养午餐重量C.本次抽查的个体是1盒营养午餐D.本次抽查的样本容量是60【答案】D【分析】根据总体、个体、样本、样本容量的定义即可判断.【详解】解:A、本次抽查的总体是100000盒营养午餐的重量的全体,故选项错误;B、本次抽查的样本是60盒营养午餐的重量,故选项错误;C 、本次抽查的个体是1盒营养午餐的重量,故选项错误;D 、样本容量是60,故选项正确. 故选:D . 【点睛】此题考查的是总体、个体、样本、样本容量.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”正确理解总体、个体、样本的概念是解决本题的关键.3.将分式方程5231(1)1x x x x --=++去分母,整理后得( )A .830x -=B .2410x x --=C .2720x x -+=D .2720x x --=【答案】C 【分析】方程两边都乘最简公分母,可把分式方程转换为整式方程. 【详解】解:方程两边都乘x (x+1), 得()(1)523x x x x +--=, 化简得:2720x x -+=. 故选:C . 【点睛】本题考查了解分式方程,解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解. 4.下列各点在反比例函数4y x=-图像上的是( ) A .()1,4 B .()2,2-C .()2,2--D .()4,1--【答案】B 【分析】 根据4y x=-得k =xy =﹣4,所以只要点的横坐标与纵坐标的积等于−4,就在函数图象上.【详解】A 、1×4=4≠﹣4,故点()1,4不在反比例函数4y x=-图像上,A 选项不符合题意; B 、﹣2×2=﹣4,故点()2,2-在反比例函数4y x=-图像上,B 选项符合题意; C 、﹣2×﹣2=4≠﹣4,故点()2,2--不在反比例函数4y x=-图像上,C 选项不符合题意; D 、﹣4×﹣1=4≠﹣4,故点()4,1--不在反比例函数4y x =-图像上,D 选项不符合题意; 故选:B【点睛】本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.5.平面直角坐标系中,以原点O 为旋转中心,将点(9,5)P --顺时针旋转90︒,得到点Q ,则点Q 的坐标为( ).A .(5,9)-B .(5,9)-C .(9,5)D .(9,5)- 【答案】A【分析】如图,连接OP ,将OP 顺时针旋转90︒可得到OQ ,过P 点作PM y ⊥轴,过Q 点作QN y ⊥轴,根据旋转的性质可得OP=OQ ,根据角的和差关系可得NOQ MPO ∠=∠,利用AAS 可证明△OPM △△QON ,根据全等三角形的性质可得ON 、QN 的长,即可得答案.【详解】如图,连接OP ,将OP 顺时针旋转90︒可得到OQ ,且90POQ ∠=︒,OP=OQ ,过P 点作PM y ⊥轴,过Q 点作QN y ⊥轴,90QOP ∠=︒,90NOQ POM ∴∠+∠=︒,90OMP ∠=︒,90MPQ POM ∴∠+∠=︒NOQ MPO ∴∠=∠,在OPM 和QON 中,NOQ MPO QNO OMP OQ OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,△(AAS)OPM QON ≅,△5QN OM ==,9ON PM ==, Q 在第二象限,△Q 的坐标为(-5,9).故选:A .【点睛】本题考查坐标与图形变化——旋转,正确添加辅助线构造全等三角形是解题关键. 6.已知平行四边形ABCD 中,8AC =,E 是AD 上一点,DCE 的周长是平行四边形ABCD 周长的一半,且5EC =,连结EO ,则EO 的长为( )A .2B .3C .4D .5【答案】B【分析】 利用DCE 的周长是平行四边形ABCD 周长的一半,可得出AE=EC .再根据点O 为AC 中点,可知EO 垂直平分AC ,再利用勾股定理即可求出EO .【详解】△DCE 的周长是平行四边形ABCD 周长的一半,即AD+CD=CD+DE+EC ,△AE=EC=5,即ACE △为等腰三角形.△点O 是平行四边形ABCD 对角线交点,△点O 为AC 中点.△EO 垂直平分AC .△AO=4.在Rt AOE 中,3EO ===.故选:B .【点睛】本题考查等腰三角形的判定和性质、平行四边形的性质以及勾股定理.根据题意得出AE=EC 是解答本题的关键.二、填空题:(本题共10小题,每小题2分,共20分)7.经过有交通信号灯的路口,遇到红灯,这是一个______事件(从“随机、不可能、必然”中选一个填入).【答案】随机【分析】根据事件发生的可能性的大小,从而可得:经过有交通信号灯的路口,遇到红灯是随机事件,从而可得答案.【详解】解:经过有交通信号灯的路口,遇到红灯,这是一个随机事件,故答案:随机.【点睛】本题考查的是确定事件与随机事件的概念,掌握确定事件分为必然事件,不可能事件,及随机事件的概念是解题的关键.8.如果函数()21k y k x-=+是反比例函数,那么k 的值为________.【答案】1【解析】【分析】根据反比例函数的定义.即y =k x (k≠0),只需令k −2=−1、k +1≠0即可. 【详解】因为()21k y k x-=+是反比例函数,所以2110k k ⎧-=-⎨+≠⎩,所以1k =故答案为:1.【点睛】 本题考查了反比例函数的定义,重点是将一般式y =k x (k≠0)转化为y =kx −1(k≠0)的形式.9.若0ab ≠,且23b a =,则2a b b +的值是________. 【答案】73 【分析】已知等式变形后,代入原式计算即可得到结果.【详解】解:由2b=3a ,得到a=23b , 则原式=4733b b b +=, 故答案为:73. 【点睛】此题考查了分式的求值,熟练掌握运算法则是解本题的关键.10.如图,风车图案围绕着旋转中心至少旋转_________度,会与原图案重合.【答案】60【分析】根据旋转角及旋转对称图形的定义结合图形特点解答即可.【详解】因为该图形被平分为6份,则每一份中心的角度为360660︒÷=︒,即至少旋转60度可与原图形重合,故答案为:60.【点睛】本题考查旋转角的定义及求法,熟记定义是解题关键.11.化简:11123x x x++= __________. 【答案】116x【分析】 先通分,然后再计算即可.【详解】 解:11163223661616x x x x x x x++=++=. 故答案为116x . 【点睛】本题考查了异分母分式加法,正确的通分是解答本题的关键.12.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________.【答案】9cm 12cm 34cm 36cm【分析】(1)根据平行四边形对角线互相平分,对边相等可得结果;(2)根据△AOB 的周长和AB 的长度,得到AO+BO ,从而得到AC+BD .【详解】解:(1)在平行四边形ABCD 中,△AC=18cm ,BD=24cm , △AO=12AC=9cm=CO ,BO=12BD=12cm=DO , △AB=13cm ,△CD=13cm ,△COD △的周长为CO+DO+CD=9+12+13=34cm ,故答案为:9cm ,12cm ,34cm ;(2)△△AOB 的周长为30cm ,△AB+AO+BO=30cm ,△AB=12cm ,△AO+BO=30-12=18cm ,△AC+BD=2AO+2BO=36cm .【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分,平行四边形的对边相等.13.对于实数a 、b ,定义一种新运算“⊗”为:21 a b a b ⊗=-,这里等式右边是实数运算.例如:21113138⊗==--,则方程2(2)14x x ⊗-=--的解是__________. 【答案】5x =【分析】根据题中的新运算法则列出分式方程,再根据分式方程的解法解答即可.【详解】 解:211(2)(2)4x x x ⊗-==--- △方程为:12144x x =--- 去分母得124x =-+,解得:5x =,经检验,5x =是原方程的解,故答案为:x=5.【点睛】本题考查了新定义的运算法则的计算、分式方程的解法,解题的关键是理解题中给出的新运算法则及分式方程的解法.14.如图,菱形ABCD 中,若BD =8,AC =6,则该菱形的面积为___.【答案】24【分析】根据菱形的面积等于对角线乘积的一半列式计算即可得解.【详解】△菱形ABCD 的对角线AC =6,BD =8,△菱形的面积=1·2AC BD =1682⨯⨯=24, 故答案为:24.【点睛】本题考查了菱形的性质,熟练掌握菱形的面积等于对角线乘积的一半是解题的关键. 15.若关于x 的方程211333x k x x x x +-=--有增根,k 的值是_____;若关于x 的方程211333x k x x x x +-=--无解,k 的值是_____. 【答案】6 6或2【分析】△增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母3(1)0x x -=,得到0x =或3,然后代入化为整式方程的方程算出k 的值; △分式方程去分母转化为整式方程,由分式方程无解,得到最简公分母为0求出x 的值,代入整式方程即可求出k 的值.【详解】解:△方程两边都乘3(1)x x -,得3(1)1x x kx +-+=△原方程有增根,△最简公分母3(1)0x x -=,解得0x =或1,当0x =时,方程不成立.当1x =时,6k =,故k 的值是6.△分式方程去分母得:331x x kx +-+=,移项合并得:(2)4k x -=,当20k -=,即2k =时,方程无解;当6k =时,分式方程有增根,故k 的值是6或2,故答案为6;6或2.【点睛】本题考查对分式方程的增根和无解的理解,分式方程有增根即对应化简后的整式方程有解,并且解为使得最简公分母为0的值,而分式方程无解包含有增根或对应整式方程无解两种情况.16.如图,矩形ABCD 中,AD =5,AB =7,正方形MBND ′的顶点M ,N 分别在矩形的边AB ,BC 上,点E 为DC 上一个动点,当点D 与点D ′关于AE 对称时,DE 的长为_____.【答案】52或53【分析】 连接ED ′,AD ′,延长MD ′交DC 于点P .根据题意设MD ′=ND ′=BM =x ,则AM =AB -BM =7-x , AD =AD ′=5,在Rt AMD '△中,利用勾股定理可求出x=3或4,即MD ′的长,分类讨论△当MD ′=3时,设ED ′=a ,则AM =7-3=4,D ′P =5-3=2,EP =4-a ,在Rt△EPD ′中利用勾股定理可求出a 的值,即DE 的长;△当MD ′=4时,同理即可求出DE 的长.【详解】解:如图,连接ED ′,AD ′,延长MD ′交DC 于点P ,△正方形MBND ′的顶点M ,N 分别在矩形的边AB ,BC 上,点E 为DC 上一个动点,点D 与点D ′关于AE 对称,△设MD ′=ND ′=BM =x ,△AM =AB ﹣BM =7﹣x ,△AE 为对称轴,△AD =AD ′=5,在Rt AMD '△中,222AM MD AD ''+=,即22725x x +-()=,解得1234x x ==,,即MD ′=3或4.在Rt△EPD ′中,设ED ′=a ,△当MD ′=3时,AM =7﹣3=4,D ′P =5﹣3=2,EP =4﹣a ,△222PE PD ED ''+=,即22224a a +-=(), 解得a =52,即DE =52. △当MD ′=4时,AM =7﹣4=3,D ′P =5﹣4=1,EP =3﹣a ,同理,22213a a +=(﹣), 解得a =53,即DE =53. 综上所述:DE 的长为:52或53. 故答案为:52或53. 【点睛】本题考查图形对称的性质,矩形的性质以及勾股定理.根据对称并利用勾股定理求出MD ′的长度是解答本题的关键.三、解答题:(本题共11小题,共88分.解答应写出文字说明、证明过程或演算步骤.)17.解方程(1)1214x x =+- (2)()()71112x x x x =+--+ 【答案】(1)x =-6;(2) x =5【分析】(1)由去分母、去括号、移项合并,系数化为1,即可得到答案;(2)由去分母、去括号、移项合并,系数化为1,即可得到答案;【详解】解:()12114x x =+- 方程两边同乘以(x +1)(x -4),得x -4=2(x +1),去括号,得422x x -=+,移项合并,得6x -=,系数化为1,得 x =-6,经检验, x =-6是原分式方程的解;()()()721112x x x x =+--+ 方程两边同乘以(x -1)(x +2),得x (x +2)=(x -1)(x +2)+7去括号,得22227x x x x +=+-+,移项合并,得5x =,经检验, x =5是原分式方程的解;【点睛】本题考查了解分式方程,解题的关键是熟练掌握解饿分式方程的方法,注意解分式方程需要检验.18.对某厂生产的直径为4cm的乒乓球进行产品质量检查,结果如下:(1)计算各次检查中“优等品”的频率,填入表中;(2)该厂生产乒乓球优等品的概率约为多少?【答案】(1)见解析;(2)0.9【分析】(1)根据表格中所给的样本容量和频数,由频率=频数:样本容量,得出“优等品”的频率,然后填入表中即可;(2)用频率来估计概率,频率一般都在0.9左右摆动,所以估计概率为0.9,这是概率与频率之间的关系,即用频率值来估计概率值.【详解】解:(1)“优等品”的频率分别为45÷50=0.9,92÷100=0.92,455÷500=0.91,890÷1000=0.89,4500÷5000=0.9.填表如下:(2)由于“优等品”的频率都在0.9左右摆动,故该厂生产的羽毛球“优等品”的概率约是0.9.【点睛】本题是一个统计问题,考查样本容量,频率和频数之间的关系,这三者可以做到知二求一,本题是一个基础题,可以作为选择题和填空题出现.19.先化简,再求值:22214244x x x x x x x x +--⎛⎫-÷⎪--+⎝⎭,其中201(2021)2x π-⎫⎛=-+ ⎪⎝⎭. 【答案】()212x -,1.9【分析】先通分,计算括号内的分式的减法运算,同步把除法转化为乘法运算,约分后得到化简的结果,再按照零次幂与负整数指数幂的含义化简,x 再代入化简后的代数式求值即可. 【详解】 解:22214244x x x x x x x x +--⎛⎫-÷⎪--+⎝⎭()()221242x x xx x x x ⎡⎤+-=-⎢⎥---⎢⎥⎣⎦ ()()22224422x x x x x x x x x ⎡⎤--=-⎢⎥---⎢⎥⎣⎦()2442x xx x x -=-- ()212x =-当20141(2021)52x π-⎛=⎫=-+⎝⎭+ =⎪时, 原式()211.952==- 【点睛】本题考查的是分式的化简求值,零次幂与负整数指数幂的含义,掌握以上知识是解题的关键. 20.如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图.(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.【答案】(1)△AB1C1如图所示;见解析;(2)△A2B2C2如图所示;见解析.【分析】(1)依据△ABC绕点A顺时针旋转90°,即可得到△AB1C1;(2)依据中心对称的性质进行作图,即可得到△ABC关于坐标原点O成中心对称的△A2B2C2.【详解】(1)△AB1C1如图所示;(2)△A2B2C2如图所示.【点睛】本题主要考查了利用旋转变换进行作图,解题时注意:旋转作图有自己独特的特点,决定图形位置的因素有旋转角度、旋转方向、旋转中心,任意不同,位置就不同,但得到的图形全等.21.我校为了丰富学生课余生活,计划开设以下课外活动项目:A-篮球,B-乒乓球,C-羽毛球,D-足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅统计图,请回答下列问题:(1)这次被调查的学生共有______人,扇形统计图中,“D-足球”所占圆心角的度数是______︒;(2)请你将条形统计图补充完整;(3)若该校学生总数为1000人,试估计该校学生中最喜欢“乒乓球”项目的人数.【答案】(1)200,72°;(2)见详解;(3)400人【分析】(1)根据统计图可得喜欢篮球的人数所占的百分比为10%,进而可得总数,然后问题可求解;(2)由(1)及统计图可直接求解;(3)先求出喜欢乒乓球的百分比,然后问题可求解.【详解】解:(1)由统计图可得:喜欢篮球的百分比为3610010 360︒⨯=︒%%,△被调查的学生共有20÷10%=200人,△喜欢足球的百分比为40÷200×100%=20%,△“D-足球”所占圆心角的度数为360°×20%=72°;故答案为200,72°;(2)由(1)及统计图可得:喜欢“C-羽毛球”的人数为200-20-80-40=60人,△补全条形统计图如图所示:(3)由(2)得:喜欢“B -乒乓球”的人数为80人, △“B -乒乓球”所占百分比为80÷200×100%=40%,△该校学生中最喜欢“乒乓球”项目的人数1000×40%=400人, 答:该校学生中最喜欢“乒乓球”项目的人数1000×40%=400人. 【点睛】本题主要考查条形统计图及扇形统计图,关键是根据统计图得到基本信息,然后进行求解即可.22.如图,点E 在矩形ABCD 的边BC 上,延长EB 到点F ,使BF CE =,连接AF .求证:AD EF =.【答案】见解析 【分析】根据矩形性质可得AD BC =,然后结合等式的性质求得BF CE =,从而使问题得证. 【详解】证明:四边形ABCD 是矩形,AD BC ∴=EF BF BE =+,=+BC CE BE ,BF CE =△EF=BCAD EF ∴=.【点睛】本题考查矩形的性质及等式的性质,题目比较简单,掌握相关性质正确推理论证是解题关键.23.列方程解应用题开展“光盘行动”,拒绝“舌尖上的浪费”,已成为一种时尚.某学校食堂为了激励同学们做到光盘不浪费,提出如果学生每餐做到光盘不浪费,那么餐后奖励香蕉或橘子一份.近日,学校食堂花了2800元和2500元分别采购了香蕉和橘子,采购的香蕉比橘子多150千克,香蕉每千克的价格比橘子每千克的价格低30%,求橘子每千克的价格.【答案】橘子每千克的价格为10元 【分析】设橘子每千克的价格为x 元,则香蕉每千克的价格为70%x 元,根据题意可得等量关系:2800元所购买的香蕉的重量-2500元所购买的橘子的重量=150,再列出方程,解出x 的值即可. 【详解】解:设橘子每千克的价格为x 元,则香蕉每千克的价格为70%x 元. 根据题意,得2800250015070%x x-=, 解得10x =,检验:当10x =时,70%0x ≠.所以原分式方程的解为10x =且符合题意. 答:橘子每千克的价格为10元. 【点睛】本题考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.24.阅读:对于两个不等的非零实数,a b ,若分式x a x b x(-)(-)的值为零,则x a =或x b =.又因为2()()()()x a x b x a b x ab abx a b x x x---++==+-+,所以关于x 的方程abx a b x+=+有两个解,分别为12,x a x b ==.应用上面的结论解答下列问题: (1)方程86x x+=有两个解,分别为1x =_____,2x =______. (2)关于x 的方程42m n m mn nx mnx mn-+-+=的两个解分别为()1212,x x x x <,若1x 与2x 互为倒数,则1x =_____,2x =______;(3)关于x 的方程22221n nx n x -+=-的两个解分别为()1212,x x x x <,求12212x x -的值. 【答案】(1)2,4;(2)12;2;(3)11n n -+. 【分析】(1)方程变形后,利用题中的结论确定出方程的解即可;(2)方程变形后,根据利用题中的结论,以及1x 与2x 互为倒数,确定出1x 与2x 的值即可; (3)方程变形后,根据利用题中的结论表示出为12x x 、,代入原式计算即可得到结果. 【详解】 解:(1)248,246⨯=+=,△方程86x x+=的两个解分别为122,4x x ==. 故答案为:122,4x x ==.(2)方程变形得:2222m nm n mn x x mn-⨯-+=+,由题中的结论得:方程有一根为2,另一根为12, 则121,22x x ==; 故答案为:12;2 (3)方程整理得:(1)21121n n x n n x --+=+--,得211x n -=-或21x n -=, 可得121,22n n x x +==,则原式11 nn-=+.【点睛】本题考查解分式方程、分式方程的解,整体代入法解方程,难度较大,解题时先搞清楚规律,把握已知的结论是解本题的关键.25.已知:如图,在△ABC中,△ABC=90°,AB=BC,D是AC的中点,DE△DF,DE 交AB于点E,DF交BC于点F.(1)求证:AE=BF;(2)连接EF,求△DEF的度数;(3)若AC=EF的取值范围.【答案】(1)见解析;(2)△DEF=45°;(3)≤EF≤4【分析】(1)连结BD,由等腰直角三角形,结合D为AC中点可得AD=BD=CD,BD△AC,可求△A=△DBF=45º,由DE△DF,可得△ADE=△BDF,再证△ADE△△BDF(ASA)即可;(2)由△ADE△△BDF得DE=DF,由DE△DF,可证△DEF是等腰直角三角形即可;(3)由AC=AB=BC=4,当点E与点A重合时EF最大=4,当DE△AB时,由△DEB=△B=△EDF=90º,DE=DF,可证四边形EBFD正方形,可得EF最小=BD=即可求出EF的取值范围为.【详解】解:(1)证明:连结BD,△在△ABC中,△ABC=90°,AB=BC,△△A=△C=45º,△D是AC的中点,△AD=BD=CD,BD△AC,△△DBC=△DBA=45º,△△A=△DBF=45º,△DE△DF,△△ADE+△EDB=90°,△EDB+△BDF=90°,△△ADE=△BDF,△△ADE△△BDF(ASA),△AE=BF,(2)△△ADE△△BDF,△DE=DF,△DE△DF,△△DEF是等腰直角三角形,△△DEF=△DFE=45°;(3)若AC=,在Rt△ABC中,由勾股定理AB=BC=AC=,22当点E与点A重合时EF最大=4,当DE△AB时,△△DEB=△B=△EDF=90º,DE=DF,四边形EBFD正方形,EF 最小=BD=EF的取值范围为. 【点睛】本题考查等腰直角三角形的性质与判定,三角形全等判定与性质,正方形的判定与性质,勾股定理,掌握等腰直角三角形的性质与判定方法,三角形全等判定的方法与性质,正方形的判定方法与性质,勾股定理的应用是解题关键. 26.对于两个不等的非零实数a b 、,若分式()()x a x b x--的值为0,则x a =或x b =,又因为()()()()2x a x b x a b x ab abx a b xxx---++==+-+,所以关于x 的方程abx a b x+=+有两个解,分别为1x a =,2x b =,应用上面的结论解答下列问题: (1)方程8x 6x+=的两个解中较大的一个为_______.(2)关于x 的方程m n m 4mn nx mnx 2mn -+-+=的两个解分别为12x x ,(12x x <),若1x 与2x 互为倒数,则1x =______,2x =_______.(3)关于x 的方程2n 2n 32x 2n 32x 1+-+=+-的两个解分别为12x x ,(12x x <),求21x 22x -的值.【答案】(1)4;(2)12;2;(3)12【分析】(1)方程变形后,利用题中的结论确定出较大的解即可;(2)方程变形后,根据利用题中的结论,以及1x 与2x 互为倒数,确定出1x 与2x 的值即可; (3)方程变形后,根据利用题中的结论表示出为1x 、2x ,代入原式计算即可得到结果. 【详解】 解:(1)方程86x x+=变形得:2424x x ⨯+=+, 根据题意得:12x =,24x =,则方程较大的一个解为4,故答案为:4;(2)方程变形得:2222m n m n mn x x mn-⨯-+=+,由题中的结论得:方程有一根为2,另一根为12, 则112x =,22x =; 故答案为:12;2; (3)方程整理得:(1)(3)211321n n x n n x -+-+=-++-, 得211x n -=-或213x n -=+, 可得12n x =,242n x +=, 则原式4212222n n +-==. 【点睛】此题考查了分式方程的解,弄清题中的规律是解本题的关键.27.在直角三角形ABC 中,△B =90°,BC =6 cm ,AB =8 cm ,有一动点P 以3cm/s 的速度从点C 出发向终点B 运动,同时还有一动点Q 以5 cm/s 的速度也从点C 出发,向终点A 运动,连结PQ ,并且PQ △BC ,以CP 、CQ 为邻边作平行四边形CQMP ,设动点P 的运动时间为t (s )(0<t <2).(1)BP = (用含t 的代数式表示);(2)当点M 在△B 的平分线上时,求此时的t 值;(3)当四边形BPQM 是平行四边形时,求CM 的值;(4)连结AM ,直接写出当△AMQ 是等腰三角形时t 的值.【答案】(1)BF=6-3t ;(2)35t =;(3)(4)t=54或43或5043 【分析】(1)运用线段和差直接用t 表示出BP 即可;(2)如图1,连接BM ,过EM 、DM 作ME△AB ,MD△BC,先说明EM=MD,然后再用t 表示出EM 和MD,最后列方程求出t 即可;(3)先说明四边形BPQM 是平行四边形是矩形,即M 在AB 上,然后求出BM 的长,最后运用勾股定理解答即可;(4)先用t 分别表示出AM 、QM 、AQ,分AM=QM 、AM=AQ 、AQ=QM 三种情况分别解答即可.【详解】解:(1)△PC=3t ,BP=BC -PC△BP=6-3t ;(2)如图1,连接BM ,过EM 、DM 作ME△AB ,MD△BC,△当点M 在△B 的平分线上时△EM=MD△PQ △BC△四边形EBPQ 为矩形, 四边形MDPQ 为矩形△BE=MD=PQ ,MQ=DP△平行四边形CQMP△MQ=PC=3t,即DP=PC=3t△BD=6-6t ,即EM=6-6t△CQ=5t4t = ,即MD=4t △EM=MD△6-6t=4t ,解得35t =;(3)如图2,连接CM△四边形BPQM是平行四边形,PQ△BC△四边形BPQM是矩形,△BM=QP,MQ=BP△△B=90°△M在AB上△平行四边形CQMP,△MQ=PC=3t△BP=PC=3t△BC= BP+PC=6t,即t=1△PC=3t=3,CQ=5t=5==,即BM=44△△B=90°==(4)延长QM交AB于E,过M作MD△BC△BC=6 cm,AB=8 cm,10=,△CQ=5t,△AQ=10-5t,△PC=3t4t=△△B=90°,PQ△BC,∠EQP=90°, MD△BC△四边形BEQP是矩形,四边形MQPD是矩形△BE=QP=4t,MQ=DP=3t,ME=MD△AE=8-4t,EM=6-6t==△AQ=10-5t,MQ=3t,△AMQ是等腰三角形△△AM=QM,即=3t,解得t=5043或t=2(舍);△AM=AQ,即=10-5t,解得t=43或t=0(舍);△MQ=AQ,即3t=10-5t,解得t=5 4 .综上,当△AMQ是等腰三角形时,t=54或43或5043.。
【苏教版】数学八年级下学期《期中考试题》及答案解析

苏教版八年级下学期数学期中测试卷一、选择题: 本大题共10小题,每小题2分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B 铅笔涂在答题卡相对应的位置上............ 1. 下列图案中既是中心对称图形,又是轴对称图形的是( ) A. B. C.D. 2. 下列特征中,平行四边形不一定具有的是( )A. 邻角互补B. 对角互补C. 对角相等D. 内角和为360° 3. 将分式2m mn -中的m 、n 都扩大为原来的3倍,则分式的值( ) A. 不变 B. 扩大3倍 C. 扩大6倍D. 扩大9倍 4. 矩形两条对角线的夹角为60°,一条较短边长为5cm ,则其对角线的长为( )cm .A. 5B. 10C. 15D. 7.55. 平行四边形ABCD 的对角线AC 、BD 相交于点O ,给下条件不能判定它为菱形的是( )A. AB =ADB. AC ⊥BDC. ∠A =∠DD. CA 平分∠BCD6. 对于反比例函数y =﹣2x,下列说法不正确的是( ) A. 图象分布在第二、四象限B. y 随x 的增大而增大C. 图象经过点(1,﹣2)D. 若x >1,则﹣2<y <0 7. 如图,在平面直角坐标系中,平行四边形ABCD 的顶点B 、C 在x 轴上,A 、D 两点分别在反比例函数k y x =(k <0,x <0)与1y x =(x >0)的图像上,若平行四边形ABCD 的面积为4,则k 的值为( ) A. -1 B. -2 C. -3D. -5 8. 如图,将△ABC 绕点A 逆时针旋转一定角度,得到△ADE ,此时点C 恰好在线段DE 上,若∠B=40°,∠CAE=60°,则∠DAC 度数为( )A. 15°B. 20°C. 25°D. 30°9. 如图,已知正方形ABCD边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE长为()A. 22-2B. 3-1C. 2-1D. 2-210. 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= kx(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,23),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )A. (0,- 73) B. (0,-83)C. (0,-3)D. (0,- 103)二、填空题: 本大题共8小题,每小题2分,共16分,把答案直接填在答题卡相对应的位置.........上...11. 若分式x3x2+-有意义,则x≠___.12. 菱形两邻角的度数之比为1:3,边长为52__________.13. 已知点(-1,y1)、(2,y2)、(5y3)在反比例函数21kyx+=-的图像上,则y1、y2、y3的大小关系是__________ (用”>“连接)14. 一个平行四边形的一条边长为3,两条对角线的长分别为4和25,则它的面积为______. 15. 设函数3y x =-与2y x =+的图像的交点为(m ,n ),则11m n-的值为________. 16. 已知关于x 的分式方程111x k k x x +-=+-的解为负数,则k 的取值范围是_______. 17. 如图,在△ABC 中,点D 在BC 上,BD =AB ,BM ⊥AD 于点M ,N 是AC 的中点,连接MN .若AB =5,BC =8,则MN =_______.18. 如图,在Rt ABC ∆中, 90,3,4BAC AB AC ∠=︒==,点P 为BC 上任意一点,连接PA ,以,PA PC 为邻边作平行四边形PAQC ,连接PQ ,则PQ 的最小值为__________.三、解答题: 本大题共8大题,共64分,把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔. 19. 计算:(1)22555x x x+-- (2)22242369x x x x x x --÷+++ (3)211x x x --- 20. 先化简222(1)24p p p p -+÷--, 再求值.(其中 p 是满足-3<p <3 的整数). 21. 解分式方程: 214111x x x ++=--. 22. 某商场进货员预测某商品能畅销市场,就用8万元购进该商品,上市后果然供不应求.商场又用17.6万购进了第二批这种商品,所购数量是第一批购进量的2倍,但进货的单价贵了4元,商场销售该商品时每件定价都是58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商场共盈利多少元? 23. 如图,一次函数4y x =+的图像与反比例函数k y x=(k 为常数,且0k ≠)的图像交于 (1,),(,1)A a B b -两点.(1)求反比例函数的表达式;(2)在x 轴上找一点P ,使PA PB+的值最小,求满足条件的点P 的坐标; (3)在(2)的条件下求PAB ∆的面积.24. 如图,已知菱形ABCD 的对角线AC 、BD 相交于点O ,延长AB 至点E ,使BE =AB ,连接CE .(1)求证: 四边形BECD 是平行四边形;(2)若∠E =60°,AC =43,求菱形ABCD 的面积.25. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y (℃)随时间x (小时)变化的函数图象,其中BC 段是双曲线y=k x的一部分.请根据图中信息解答下列问题: (1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k 的值;(3)当棚内温度不低于16℃时,该蔬菜能够快速生长,请问这天该蔬菜能够快速生长多长时间?26. 如图1,正方形ABCD顶点A、B在函数y =kx(k﹥0)的图像上,点C、D分别在x轴、y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)若点A的横坐标为5,求点D的纵坐标;(2)如图2,当k=8时,分别求出正方形A'B'C'D'的顶点A'、B'两点的坐标;(3)当变化的正方形ABCD与(2)中的正方形A'B'C'D'有重叠部分时,求k的取值范围.答案与解析一、选择题: 本大题共10小题,每小题2分,共20分,在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相对应的位置上............1. 下列图案中既是中心对称图形,又是轴对称图形的是()A. B. C. D.【答案】C【解析】【分析】根据轴对称图形与中心对称图形的概念判断.【详解】A、是轴对称图形,不是中心对称图形;B、是轴对称图形,不是中心对称图形;C、是轴对称图形,也是中心对称图形;D、是轴对称图形,不是中心对称图形.故选: C.【点睛】本题主要考查中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2. 下列特征中,平行四边形不一定具有的是()A. 邻角互补B. 对角互补C. 对角相等D. 内角和为360°【答案】B【解析】【分析】根据平行四边形的性质得到,平行四边形邻角互补,对角相等,内角和360°,而对角却不一定互补.【详解】解: 根据平行四边形性质可知: A、C、D均是平行四边形的性质,只有B不是.故选B.【点睛】本题考查平行四边形的性质: ①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.3. 将分式2mm n中的m、n都扩大为原来的3倍,则分式的值( )A. 不变B. 扩大3倍C. 扩大6倍D. 扩大9倍【答案】A【解析】m 、n 都扩大为原来的3倍得到()662333m m m m n m n m n==--- ,∴分式的值不变. 故选A.4. 矩形两条对角线的夹角为60°,一条较短边长为5cm ,则其对角线的长为( )cm .A. 5B. 10C. 15D. 7.5 【答案】B【解析】【分析】由夹角60°可得△AOB 为等边三角形,进而可得对角线的长.【详解】如图,矩形两条对角线的夹角为60°,可得△AOB 为等边三角形,又AB=5,所以OA=OB=5,所以对角线AC=BD=10故选: B .【点睛】本题考查了等边三角形的判定及性质、矩形的性质,熟练掌握矩形两条对角线相等的性质及等边三角形的性质.5. 平行四边形ABCD 的对角线AC 、BD 相交于点O ,给下条件不能判定它为菱形的是( )A. AB =ADB. AC ⊥BDC. ∠A =∠DD. CA 平分∠BCD 【答案】C【解析】【分析】根据: ①定义: 一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.进行判断即可.【详解】A 、为一组邻边相等平行四边形是菱形,不符合题意;B 、为对角线互相垂直平分的平行四边形是菱形,不符合题意;C 、可判定为矩形,不能判定为菱形,符合题意;D 、为一条对角线平分一角,可得出一组邻边相等,也能判定为菱形,不符合题意;故选C .【点睛】本题考查菱形的判定方法有三种: ①定义: 一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.6. 对于反比例函数y =﹣2x ,下列说法不正确的是( ) A. 图象分布在第二、四象限 B. y 随x 的增大而增大C. 图象经过点(1,﹣2)D. 若x >1,则﹣2<y <0 【答案】B【解析】【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.【详解】解: A .k =﹣2<0,∴它的图象在第二、四象限,故本选项正确;B .k =﹣2<0,函数图象在二、四象限,且在每个象限内y 随x 的增大而增大,故本选项错误;C .∵﹣21=﹣2,∴点(1,﹣2)在它的图象上,故本选项正确; D .若x >1,则﹣2<y <0,故本选项正确.故选: B .【点睛】本题考查反比例函数的性质,对于反比例函数y=k x(k≠0),当k >0时,反比例函数图象在一、三象限,在每一个象限内,y 随x 的增大而减小;当k <0时,反比例函数图象在第二、四象限内,在每一个象限内,y 随x 的增大而增大.7. 如图,在平面直角坐标系中,平行四边形ABCD 的顶点B 、C 在x 轴上,A 、D 两点分别在反比例函数k y x=(k <0,x <0)与1y x =(x >0)的图像上,若平行四边形ABCD 的面积为4,则k 的值为( )A. -1B. -2C. -3D. -5【答案】C【解析】连接OA、OD,如图,∵四边形ABCD为平行四边形,∴AD垂直y轴,∴122OAEkS k=⨯=,11122ODES=⨯=,∴122OADkS=+,∵▱ABCD的面积=2OADS=4.∴|k|+1=4,解得k=−3或3,∵k<0.∴k=−3故C.8. 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为()A. 15°B. 20°C. 25°D. 30°【答案】B【解析】【分析】由旋转的性质得出△ADE≌△ABC,得出∠D=∠B=40°,AE=AC,证出△ACE是等边三角形,得出∠ACE=∠E=60°,由三角形内角和定理求出∠DAE的度数,即可得出结果.【详解】由旋转的性质得: △ADE≌△ABC,∴∠D =∠B =40°,AE =AC ,∵∠CAE =60°,∴△ACE 是等边三角形,∴∠ACE =∠E =60°,∴∠DAE =180°−∠E −∠D =80°∴806020DAC DAE CAE ∠=∠-∠=-=;故选B.【点睛】考查旋转的性质,等腰三角形的性质,三角形的内角和定理,熟练掌握旋转的性质是解题的关键. 9. 如图,已知正方形ABCD 边长为1,连接AC 、BD ,CE 平分∠ACD 交BD 于点E ,则DE 长为( )2-2 B. 3 1 C. 2-1 D. 22【答案】C【解析】【分析】 【详解】解: ∵正方形ABCD 边长为1,2AC BD ∴==22OC OD ∴==.设DE x =. 作EF CD ⊥ 于点F∵CE 平分∠ACD ,22EF OE x ∴==-,22CF OC ==,212DF =- ∵DF 2+EF 2=DE 2, 22222122x x ⎛⎛⎫∴-+-= ⎪ ⎪⎝⎭⎝⎭解之得21x =故选C10. 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反个比例函数y= kx(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,23),过点E作直线l∥BD交y轴于点F,则点F的坐标是( )A. (0,- 73) B. (0,-83)C. (0,-3)D. (0,- 103)【答案】A 【解析】【分析】由A(m,2)得到正方形的边长为2,则BC=2,所以n=2+m,根据反比例函数图象上点的坐标特征得到k=2•m=2 3(2+m),解得m=1,则A(1,2),B(1,0),D(3,2),E(3,),然后利用待定系数法确定直线BD的解析式,再根据平行线的性质和E的坐标求得直线l的解析式,求x=0时对应函数的值,从而得到点F的坐标.【详解】∵正方形的顶点A(m,2),∴正方形的边长为2,∴BC=2,而点E(n,23 ),∴n=2+m,即E点坐标为(2+m,23 ),∴k=2⋅m=23(2+m),解得m=1,∴A(1,2),E(3,23 ),∴B(1,0),D(3,2),设直线BD的解析式为y=ax+b,把B(1,0),D(3,2)代入得32 a ba b+=⎧⎨+=⎩,解得11 ab=⎧⎨=-⎩,∵过点E作直线l∥BD交y轴于点F,∴设直线l的解析式为y=x+q,把E(3,23)代入得3+q=23,解得q=−73,∴直线l的解析式为y=x−7 3当x=0时,y=−73,∴点F的坐标为(0,−73 ),故选A.【点睛】本题考查反比例函数.求出b的值是解题关键.二、填空题: 本大题共8小题,每小题2分,共16分,把答案直接填在答题卡相对应的位置.........上...11. 若分式x3x2+-有意义,则x≠___.【答案】2 【解析】试题分析: 根据分式分母不为0的条件,要使x3x2+-在实数范围内有意义,必须x20x2-≠⇒≠.12. 菱形的两邻角的度数之比为1:3,边长为__________.【答案】5【解析】试题分析: 如图,菱形ABCD 的边长52,BC =CE 为高,:1:3,B A ∠∠=//,+180,AD BC A B ∴∠∠= 45.B ∴∠=BCE ∴为等腰直角三角形,2,BC CE =2252 5.CE BC ∴==⨯=考点: 1、菱形的性质;2、等腰直角三角形的性质.13. 已知点(-1,y 1)、(2,y 2)、(5y 3)在反比例函数21k y x+=-的图像上,则y 1、y 2、y 3的大小关系是__________ (用”>“连接)【答案】y 1>y 3>y 2【解析】【分析】【详解】20k ≥ 211k ∴+≥2110k ∴--≤-<∴反比例函数21k y x+=-的图像在二,四象限,在每一象限内y 随x 的增大而增大 点()11,y -在第二象限10y ∴>()()232,,5,y y 都在第四象限,且25<230y y ∴<<132y y y ∴>>14. 一个平行四边形的一条边长为3,两条对角线的长分别为4和25______.【答案】5【解析】【分析】【详解】如图所示: 3,4,25,AB AC BD ===∵四边形ABCD 是平行四边形112,5,22OA AC OB BD ∴==== ∵22225)3+=,90.AOB ∴∠= 即两条对角线互相垂直,∴这个四边形是菱形, ∴14254 5.2S =⨯⨯= 故答案为4 5.15. 设函数3y x =-与2y x =+的图像的交点为(m ,n ),则11m n -的值为________. 【答案】−23 【解析】【分析】由两函数的交点坐标为(m ,n ),将x=m ,y=n 代入反比例解析式,求出mn 的值,代入一次函数解析式,得出n-m 的值,将所求式子通分并利用同分母分式的加法法则计算后,把mn 及n-m 的值代入即可求出值.【详解】∵函数3y x=-与y=x+2的图象的交点坐标是(m,n), ∴将x=m ,y=n 代入反比例解析式得: mn=−3, 代入一次函数解析式得: n=m+2,即n−m=2,则1122=33n m m n mn --==--. 故答案为−23 . 【点睛】此题考查反比例函数与一次函数的交点问题,解题关键在于求出求出mn 的值.16. 已知关于x 的分式方程111x k k x x +-=+-的解为负数,则k 的取值范围是_______.【答案】12k >且1k ≠. 【解析】 试题分析: 分式方程去分母得: ()()()()211121211x k x k x x x k k +--+=-⇒=-+-+≠±. ∵分式方程解为负数,∴12102k k-+⇒. 由211k -+≠±得0k ≠和1k ≠∴k 的取值范围是12k >且1k ≠. 考点: 1.分式方程的解;2.分式有意义的条件;3.解不等式;4.分类思想的应用.17. 如图,在△ABC 中,点D 在BC 上,BD =AB ,BM ⊥AD 于点M ,N 是AC 的中点,连接MN .若AB =5,BC =8,则MN =_______.【答案】1.5【解析】【分析】根据题目的已知条件易求DC 的长为3,易证MN 是三角形ADC 的中位线,由三角形中位线定理即可求出MN 的长.【详解】∵BD=AB ,BM ⊥AD 于点M ,∴AM=DM ,∵N 是AC 的中点,∴AN=CN ,∴MN 是三角形ADC 的中位线,∴MN=12DC , ∵AB=5,BC=8,∴DC=3,∴MN=1.5,故答案是: 1.5.【点睛】此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半. 18. 如图,在Rt ABC ∆中, 90,3,4BAC AB AC ∠=︒==,点P 为BC 上任意一点,连接PA ,以,PA PC 为邻边作平行四边形PAQC ,连接PQ ,则PQ 的最小值为__________.【答案】125【解析】【分析】【详解】解: 90,3,4,BAC AB AC ︒∠===225BC AC AB ∴=+=四边形APCQ 是平行四边形,,PO QO CO AO ∴==.∵PQ 最短也就是PO 最短,过O 作BC 的垂线OP′.,'90'ACB P CO CP O CAB ︒∠=∠∠=∠=,~',CAB CP O ∴',CO OP BC AB∴= 2',53OP ∴=65OP '∴=. 则PQ 的最小值为122'5OP =. 故答案为: 125. 三、解答题: 本大题共8大题,共64分,把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔. 19. 计算:(1)22555x x x +-- (2)22242369x x x x x x --÷+++ (3)211x x x --- 【答案】(1)x+5;(2)26x x+;(3)11x - 【解析】【分析】(1)原式变形后,利用同分母分式的减法法则计算,约分即可得到结果;(2)原式利用除法法则变形,约分即可得到结果;(3)原式通分并利用同分母分式的减法法则计算,即可得到结果. 【详解】(1)22555x x x+-- =22555x x x --- =2255x x -- =(5)(5)5x x x +-- =5x +(2)22242369x x x x x x --÷+++ =22(2)(3)(3)2x x x x x -++-=2(3)x x+; (3)211x x x --- =2(1)(1)11x x x x x -+--- =2(1)(1)1x x x x --+- =11x -. 【点睛】此题主要考查了分式的加、减、乘、除运算,熟练掌握运算法则是解本题的关键.20. 先化简222(1)24p p p p -+÷--, 再求值.(其中 p 是满足-3<p <3 的整数). 【答案】21p p +-,-12. 【解析】【分析】本题的关键是正确进行分式的通分、约分,并准确代值计算.在-3<p<3中的整数p 是-2,-1,0,1,2;为满足原式有意义,只能取-1. 【详解】222(1)24p p p p -+÷--=()()()22221=221p p p p p p p p +--⨯-++-- . 在−3<p<3中的整数p 是−2,−1,0,1,2;根据题意,这里p 仅能取−1,此时原式=-12. 故答案为-12. 【点睛】此题考查分式的化简求值,解题关键在于掌握运算法则进行化简.21. 解分式方程:214111x x x ++=--. 【答案】3x =-【解析】【分析】首先方程两边乘以最简公分母,把分式方程化成整式方程,求出整式方程的解,再代入最简公分母检验即可.【详解】解: 方程两边乘以(1)(1)x x +-得: 2(1)4(1)(1)x x x ++=+-,解这个方程得: 3x =-,检验: 当3x =-时,(1)(1)0x x +-≠,3x =-是原方程的解;∴原方程的解是: 3x =-.【点睛】本题考查了分式方程的解法、一元一次方程方程的解法;熟练掌握分式方程的解法,方程两边乘以最简公分母,把分式方程化成整式方程是解决问题的关键.22. 某商场进货员预测某商品能畅销市场,就用8万元购进该商品,上市后果然供不应求.商场又用17.6万购进了第二批这种商品,所购数量是第一批购进量的2倍,但进货的单价贵了4元,商场销售该商品时每件定价都是58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商场共盈利多少元?【答案】90260【解析】【分析】盈利=总售价-总进价,应求出衬衫的数量.总价明显,一定是根据单价来列等量关系.本题的关键描述语是: “单价贵了4元”;等量关系为: 第一次的单价=第二次的单价-4.【详解】设商场第一次购进x 件衬衫,则第二次购进2x 件,根据题意得: 8000017600042x x-=. 160000=176000-8x解这个方程得: x=2000.经检验: x=2000是原方程的根.∴2x=4000商场利润: (2000+4000-150)×58+58×0.8×150-80000-176000=90260(元).答: 在这两笔生意中,商场共盈利90260元.【点睛】应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.23. 如图,一次函数4y x =+的图像与反比例函数k y x=(k 为常数,且0k ≠)的图像交于 (1,),(,1)A a B b -两点.(1)求反比例函数的表达式;(2)在x 轴上找一点P ,使PA PB +的值最小,求满足条件的点P 的坐标;(3)在(2)的条件下求PAB ∆的面积.【答案】(1)反比例函数的表达式: 3y x =-; (2) 5(,0)2-; (3) PAB ∆的面积为32. 【解析】【试题分析】 (1)根据()()1,,,1A a B b -两点在一次函数4y x =+的图像上,求出A 、B 两点坐标即可;代入反比例函数求出答案;(2)根据”小马饮水”的思路解决即可,关键是先画出图形,再解答;(3)用割补法求三角形的面积.【试题解析】(1)根据()()1,,,1A a B b -两点在一次函数4y x =+的图像上,得A(-1,3)和B(-3,1),因为点A(-1,3)在k y x =,则31(3)3,k y x=⨯-=-=-即 ; (2)如图,作点B 关于x 轴的对称点D(-3,-1),连接DA ,则直线DA 的解析式为25y x =+ ,当y=0时,x=5-2 ,故点P (5,02-); (3)用割补法求三角形的面积,PAB ∆的面积为提醒ABGH 的面积减去三角形BGH 的面积减去三角形APH 的面积,即(13)21131313222222+⨯-⨯⨯-⨯⨯= .24. 如图,已知菱形ABCD 的对角线AC 、BD 相交于点O ,延长AB 至点E ,使BE =AB ,连接CE .(1)求证: 四边形BECD 是平行四边形;(2)若∠E=60°,AC=43,求菱形ABCD的面积.【答案】(1)证明见解析;(2)菱形ABCD的面积为83【解析】试题分析: (1)根据菱形的对边平行且相等可得AB=AD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形;(2)根据(1)的结论,以及菱形的性质可求出两对角线,然后根据菱形的面积=对角线之积的一半可求解. 试题解析: (1)∵四边形ABCD是菱形,∴AB=CD,AB∥CD.;又∵BE=AB,∴BE=CD.∵BE∥CD,∴四边形BECD是平行四边形.(2)∵四边形BECD是平行四边形,∴BD∥CE.∴∠ABO=∠E=60°.又∵四边形ABCD是菱形,∴AC丄BD,OA=OC.∴∠BOA=90°,∴∠BAO=30°.∵AC=43∴OA=OC=3∴OB=OD=2.∴BD=4.∴菱形ABCD的面积=1143483 22AC BD⨯⨯=⨯=25. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=kx的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?(2)求k的值;(3)当棚内温度不低于16℃时,该蔬菜能够快速生长,请问这天该蔬菜能够快速生长多长时间?【答案】(1)10 ;(2)216;(3)12.5【解析】【分析】【详解】(1)12-2=10(小时)故恒温系统在这天保持大棚内温度18℃的时间有10个小时.(2)把()12,18B代入y=k x得k=12×18=216. (3)设开始部分的函数解析式为y kx b=+,则有21814k b b+=⎧⎨=⎩解得214k b=⎧⎨=⎩214y x∴=+当16y=时,1x=对于216,16y y x==时,13.5x=13.5112.5-=答: 这天该蔬菜能够快速生长12.5h.26. 如图1,正方形ABCD顶点A、B在函数y=k x(k﹥0)的图像上,点C、D分别在x轴、y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)若点A的横坐标为5,求点D的纵坐标;(2)如图2,当k=8时,分别求出正方形A'B'C'D'的顶点A'、B'两点的坐标;(3)当变化的正方形ABCD与(2)中的正方形A'B'C'D'有重叠部分时,求k的取值范围.【答案】(1)5;(2)A'(2,4),B'(4,2);(3)872 9k≤≤【解析】【分析】(1)过点A作AE⊥y轴于点E,如图1,则∠AED=90°.利用正方形的性质得AD=DC,∠ADC=90°,再根据等角的余角相等得到∠EDA=∠OCD,则利用”AAS”可判断△AED≌△DOC,从而得到OD=EA=5,于是确定点D的纵坐标为5;(2)作A′M⊥y轴于M,B′N⊥x轴于点N,如图2,设OD′=a,OC′=b,同理可得△B′C′N≌△C′D′O≌△A′D′E,利用全等的性质得C′N=OD′=A′M=a,B′N=C′O=D′M=b,则A′(a,a+b),B′(a+b,b),再根据反比例函数图象上点的坐标特征得到a(a+b)=8,b(a+b)=8,解方程组求出a、b,从而得到A′、B′两点的坐标;(3)先利用待定系数法求出直线A′B′解析式为y=-x+6,直线C′D′解析式为y=-x+2,设点A的坐标为(m,2m),则点D坐标为(0,m),若当A点在直线C′D′上时,则2m=-m+2,解得m=23,可确定此时点A的坐标,从而得到此时k的值;当点D在直线A′B′上时,则m=6,同样可确定此时点A的坐标和k的值,所以可确定当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时k的取值范围.【详解】(1)过点A作AE⊥y轴于点E,如图1,则∠AED=90°.∵四边形ABCD为正方形,∴AD=DC ,∠ADC=90°,∴∠ODC+∠EDA=90°.∵∠ODC+∠OCD=90°,∴∠EDA=∠OCD ,在△AED 和△DOC 中AED DOC EDA OCD AD DC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△AED ≌△DOC (AAS ),∴OD=EA=5,∴点D 的纵坐标为5;(2)作A′M ⊥y 轴于M ,B′N ⊥x 轴于点N ,如图2,设OD′=a ,OC′=b ,同理可得△B′C′N ≌△C′D′O ≌△A′D′E ,∴C′N=OD′=A′M=a ,B′N=C′O=D′M=b ,∴A′(a ,a+b ),B′(a+b ,b ),∵点A′、B′在反比例函数y=8x 的图象上,∴a (a+b )=8,b (a+b )=8,解得a=b=2或a=b=-2(舍去).∴A′、B′两点的坐标分别为(2,4),(4,2);(3)设直线A′B′的解析式为y=mx+n ,把A′(2,4),B′(4,2)代入得2442m n m n +⎧⎨+⎩==,解得16m n -⎧⎨⎩==, ∴直线A′B′解析式为y=-x+6, 同样可求得直线C′D′解析式为y=-x+2,由(2)可知△OCD 是等腰直角三角形,设点A 坐标为(m ,2m ),点D 坐标为(0,m ).当A 点在直线C′D′上时,则2m=-m+2,解得m=23, 此时点A 的坐标为(23,43),k=23×43=89; 当点D 在直线A′B′上时,有m=6,此时点A 的坐标为(6,12),k=6×12=72; 综上可知: 当变化的正方形ABCD 与(2)中的正方形A′B′C′D′有重叠部分时,k 的取值范围为89≤x≤72. 【点睛】本题考查了反比例函数的图象与性质: 熟练掌握反比例函数图象上点的坐标特征和正方形的性质;灵活运用全等三角形的性质解决线段相等的问题;会运用待定系数法求一次函数解析式;理解坐标与图形性质.。
苏科版(完整版)八年级数学下册期中试卷及答案

苏科版(完整版)八年级数学下册期中试卷及答案一、选择题1.“明天会下雨”这是一个( )A .必然事件B .不可能事件C .随机事件D .以上说法都不对 2.下列成语故事中所描述的事件为必然发生事件的是( ) A .水中捞月B .瓮中捉鳖C .拔苗助长D .守株待兔 3.如果把分式a a b -中的a 、b 都扩大2倍,那么分式的值一定( ) A .是原来的2倍 B .是原来的4倍C .是原来的12D .不变4.已知12x <≤ ,则23(2)x x -+-的值为( )A .2 x - 5B .—2C .5 - 2 xD .25.已知关于x 的分式方程22x m x +-=3的解是5,则m 的值为( ) A .3 B .﹣2C .﹣1D .8 6.下列图形中是轴对称图形但不是中心对称图形的是( )A .B .C .D .7.如图,在平面直角坐标系中,菱形OABC 的顶点A 的坐标为(4,3),点D 是边OC 上的一点,点E 在直线OB 上,连接DE 、CE ,则DE+CE 的最小值为( )A .5B 7+1C .5D .2458.已知反比例函3y x =-,下列结论中不正确的是( ) A .图像经过点(1,3)- B .图像在第二、四象限C .当1x >时,30y <<D .当0x <,y 随着x 的增大而减小 9.已知关于x 的方程23x m x -=+的解是负数,则m 的取值范围为( )A .6m >-且3m ≠-B .6m >-C .6m <-且3m ≠-D .6m <- 10.反比例函数3y x =-,下列说法不正确的是( ) A .图象经过点(1,-3)B .图象位于第二、四象限C .图象关于直线y=x 对称D .y 随x 的增大而增大11.下面调查方式中,合适的是( ) A .试航前对我国第一艘国产航母各系统的检查,选择抽样调查方式B .了解一批袋装食品是否含有防腐剂,选择普查方式C .为有效控制“新冠疫情”的传播,对国外入境人员的健康状况,采用普查方式D .调查某新型防火材料的防火性能,采用普查的方式 12.如图,将ABC ∆绕点C 顺时针旋转得到DEC ∆,使点A 的对应点D 恰好落在边AB 上,点B 的对应点为E ,连接BE .下列结论一定正确的是( )A .AC AD =B .AB EB ⊥C .BC DE =D .A EBC ∠=∠二、填空题13.如图所示,将△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ,添加一个条件_____,使四边形ABCD 为矩形.14.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,∠OBC =30°,则∠OCD =_____°.15.在平行四边形ABCD 中,对角线AC 与BD 相交于点O .要使四边形ABCD 是正方形,还需添加一组条件.下面给出了五组条件:①AB =AD ,且AC =BD ;②AB ⊥AD ,且AC ⊥BD ;③AB ⊥AD ,且AB =AD ;④AB =BD ,且AB ⊥BD ;⑤OB =OC ,且OB ⊥OC .其中正确的是_____(填写序号).16.已知矩形ABCD ,AB =6,AD =8,将矩形ABCD 绕点A 顺时针旋转θ(0°<θ<360°)得到矩形AEFG ,当θ=_____°时,GC =GB .17.如图,在正方形ABCD中,△ABE为等边三角形,连接DE,CE,延长AE交CD于F 点,则∠DEF的度数为_____.18.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体V的反比例函数,其图像如图所示.则其函数解析式为_________.体积()3m19.在整数20200520中,数字“0”出现的频率是_________.20.根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为________万元.21.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=________°.22.已知1x ,2x ,…,10x 的平均数是a ;11x ,12x ,…,30x 的平均数是b ,则1x ,2x ,…,30x 的平均数是_________.23.如图,在矩形ABCD 中,AB =5,AD =3,动点P 满足S △PAB =13S 矩形ABCD ,则点P 到A 、B 两点距离之和PA +PB 的最小值为_____.24.若关于x 的分式方程233x a x x+--=2a 无解,则a 的值为_____. 三、解答题25.如图,四边形ABCD 是正方形,点E 是BC 边上的动点(不与点B 、C 重合),将射线AE 绕点A 按逆时针方向旋转45°后交CD 边于点F ,AE 、AF 分别交BD 于G 、H 两点. (1)当∠BEA =55°时,求∠HAD 的度数;(2)设∠BEA =α,试用含α的代数式表示∠DFA 的大小;(3)点E 运动的过程中,试探究∠BEA 与∠FEA 有怎样的数量关系,并说明理由.26.如图,在正方形ABCD 内有一点P 满足AP AB =,PB PC =.连接AC 、PD .(1)求证:APB DPC ∆∆≌;(2)求PAC ∠的度数.27.已知:如图,在▱ABCD 中,点E 、F 分别在BC 、AD 上,且BE =DF求证:AC 、EF 互相平分.28.如图,在△ABC 中,AB =AC ,点D 是边AB 的点,DE ∥BC 交AC 于点E ,连接BE ,点F 、G 、H 分别为BE 、DE 、BC 的中点.(1)求证:FG =FH ;(2)当∠A 为多少度时,FG ⊥FH ?并说明理由.29.在Rt △AEB 中,∠AEB =90°,以斜边AB 为边向Rt △AEB 形外作正方形ABCD ,若正方形ABCD 的对角线交于点O (如图1).(1)求证:EO 平分∠AEB ;(2)猜想线段OE 与EB 、EA 之间的数量关系为 (直接写出结果,不要写出证明过程);(3)过点C 作CF ⊥EB 于F ,过点D 作DH ⊥EA 于H ,CF 和DH 的反向延长线交于点G (如图2),求证:四边形EFGH 为正方形.30.解方程:224124x x x +-=-- 31.正方形网格中(每个小正方形边长是1,小正方形的顶点叫做格点),ABC ∆的顶点均在格点上,请在所给的平面直角坐标系中解答下列问题:(1)作出ABC ∆绕点A 逆时针旋转90°后的111A B C ∆;(2)作出111A B C ∆关于原点O 成中心对称的222A B C ∆.32.我校对本校的八年级学生对待学习的态度进行了一次抽样调查,结果分成“非常感兴趣”、“比较感兴趣”、“一般般”、“不感兴趣”四种类型,分别记为A 、B 、C 、D .根据调查结果绘制了如下尚不完整的统计图.根据所给数据,解答下列问题:(1)本次问卷共随机调查了_________名学生,扇形统计图中m _________,扇形D 所对应的圆心角为_________°;(2)请根据数据信息补全条形统计图;(3)若该校有2000名学生,估计选择“非常感兴趣”、“比较感兴趣”共约有多少人?33.如图,矩形EFGH 的顶点E ,G 分别在菱形ABCD 的边AD ,BC 上,顶点F ,H 在菱形ABCD 的对角线BD 上.(1)求证:BG =DE ;(2)若E 为AD 中点,FH =2,求菱形ABCD 的周长.34.如图1,在正方形ABCD 中,点E 是边AB 上的一个动点(点E 与点A ,B 不重合)连接CE ,过点B 作BF ⊥CE 于点G ,交AD 于点F .(1)求证:△ABF ≌△BCE ;(2)如图2,连接EF 、CF ,若CE =8,求四边形BEFC 的面积;(3)如图3,当点E 运动到AB 中点时,连接DG ,求证:DC =DG .35.如图,在ABC ∆中,90ABC ∠=︒,BD 为AC 的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG 、DF .(1)求证:BD DF =;(2)求证:四边形BDFG 为菱形;(3)若13AG =,6CF =,求四边形BDFG 的周长.36.如图,点P 是正方形ABCD 对角线AC 上一动点,点E 在射线BC 上,且PB PE =,连接PD ,O 为AC 中点.(1)如图1,当点P 在线段AO 上时,试猜想PE 与PD 的数量关系和位置关系,并说明理由;(2)如图2,当点P 在线段OC 上时,(1)中的猜想还成立吗?请说明理由;(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】在一定条件下,可能发生也可能不发生的事件,称为随机事件.据此可得.【详解】解:“明天会下雨”这是一个随机事件,故选:C.【点晴】本题主要考查随机事件,解题的关键是掌握随机事件的概念:在一定条件下,可能发生也可能不发生的事件,称为随机事件.2.B解析:B【解析】试题分析:根据必然事件、不可能事件、随机事件的概念可区别各类事件.解:A、水中捞月是不可能事件,故A错误;B、瓮中捉鳖是必然事件,故B正确;C、拔苗助长是不可能事件,故C错误;D 、守株待兔是随机事件,故D 错误;故选B .考点:随机事件.3.D解析:D【分析】把2a 、2b 代入分式,然后进行分式的化简计算,从而与原式进行比较得出结论.【详解】解:把2a 、2b 代入分式可得22222()a a a a b a b a b==---, 由此可知分式的值没有改变,故选:D .【点睛】本题主要考查了分式的性质,分式的分子和分母同时扩大或者缩小相同的倍数,分式的值不变.4.C解析:C【分析】结合1 < x ≤ 2 ,根据绝对值和二次根式的进行计算,即可得到答案.【详解】因为1 < x ≤ 2 ,所以3x -+32x x -+-= 5 - 2 x.故选择C .【点睛】本题考查不等式、绝对值和二次根式,解题的关键是掌握不等式、绝对值和二次根式.5.C解析:C【分析】将x =5代入分式方程中进行求解即可.【详解】把x =5代入关于x 的分式方程22x m x +-=3得:25352m ⨯+=-, 解得:m =﹣1,故选:C .【点睛】本题考查分式方程的解,一般直接将解代入分式方程进行求解. 6.B解析:B【分析】根据轴对称图形与中心对称图形的概念对各图形分析判断后利用排除法求解.【详解】A、图形不是中心对称轴图形,也不是轴对称图形,此选项错误;B、图形不是中心对称轴图形,是轴对称图形,此选项正确;C、图形是中心对称轴图形,也是轴对称图形,此选项错误;D、图形是中心对称轴图形,不是轴对称图形,此选项错误;故选:B.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.7.D解析:D【解析】【分析】首先根据菱形的对角线性质得到DE+CE的最小值=CF,再利用菱形的面积列出等量关系即可解题.【详解】解:如下图,过点C作CF⊥OA与F,交OB于点E,过点E作ED⊥OC与D,∵四边形OABC是菱形,由菱形对角线互相垂直平分可知EF=ED,∴DE+CE的最小值=CF,∵A的坐标为(4,3),∴对角线分别是8和6,OA=5,∴菱形的面积=24,(二分之一对角线的乘积),即24=CF×5,解得:CF= 24 5,即DE+CE的最小值=24 5,故选D.【点睛】本题考查了菱形的性质,图形中的最值问题,中等难度,利用菱形的对称性找到点E的位置并熟悉菱形面积的求法是解题关键.8.D解析:D【分析】根据反比例函数的性质对各选项进行逐一分析即可.【详解】解:A 、∵()133-⨯=-,∴图象必经过点(1,3)-,故本选项正确;B 、∵30k =-<,∴函数图象的两个分支分布在第二、四象限,故本选项正确;C 、∵1x =时,3y =-且y 随x 的增大而而增大,∴1x >时,30y -<<,故本选项正确;D 、函数图象的两个分支分布在第二、四象限,在每一象限内,y 随x 的增大而增大,故本选项错误.故选:D .【点睛】本题考查了反比例函数的性质,解题的关键是熟练掌握反比例函数的性质进行解题.9.A解析:A【分析】解分式方程,得到含有m 得方程的解,根据“方程的解是负数”,结合分式方程的分母不等于零,得到两个关于m 得不等式,解之即可.【详解】解:方程两边同时乘以1x +得:3(1)x m x -=+,解得:6=--x m ,又∵方程的解是负数,∴60--<m ,解不等式得:6m >-,综上可知:6m >-且3m ≠-,故本题答案为:A.【点睛】本题考查了分式方程的解;解一元一次不等式.解决本题的关键是熟练掌握分式方程的解法过程,注意分式方程分母不为0这一要求.10.D解析:D【解析】【分析】通过反比例图象上的点的坐标特征,可对A 选项做出判断;通过反比例函数图象和性质、增减性、对称性可对其它选项做出判断,得出答案.【详解】解:由点()1,3-的坐标满足反比例函数3y x=-,故A 是正确的; 由30k =-<,双曲线位于二、四象限,故B 也是正确的; 由反比例函数的对称性,可知反比例函数3y x=-关于y x =对称是正确的,故C 也是正确的,由反比例函数的性质,0k <,在每个象限内,y 随x 的增大而增大,不在同一象限,不具有此性质,故D 是不正确的,故选:D .【点睛】考查反比例函数的性质,当0k <时,在每个象限内y 随x 的增大而增大的性质、反比例函数的图象是轴对称图象,y x =和y x =-是它的对称轴,同时也是中心对称图形;熟练掌握反比例函数图象上点的坐标特征和反比例函数图象和性质是解答此题的关键. 11.C解析:C【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【详解】A 、试航前对我国第一艘国产航母各系统的检查,零部件很重要,应全面检查;B 、了解一批袋装食品是否含有防腐剂,适合抽样调查;C 、为有效控制“新冠疫情”的传播,对国外入境人员的健康状况,适合采用普查方式;D 、调査某新型防火材料的防火性能,适合抽样调查.故选:C .【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.12.D解析:D【分析】利用旋转的性质得AC=CD ,BC=EC ,∠ACD=∠BCE ,所以选项A 、C 不一定正确 再根据等腰三角形的性质即可得出A EBC ∠=∠,所以选项D 正确;再根据∠EBC =∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB 判断选项B 不一定正确即可.【详解】解:∵ABC ∆绕点C 顺时针旋转得到DEC ∆,∴AC=CD ,BC=EC ,∠ACD=∠BCE ,∴∠A=∠CDA=180ACD 2∠︒-;∠EBC=∠BEC=180BCE 2∠︒-,∴选项A 、C 不一定正确∴∠A =∠EBC∴选项D 正确.∵∠EBC=∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB 不一定等于090,∴选项B 不一定正确;故选D .【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.二、填空题13.∠B=90°.【分析】根据旋转的性质得AB=CD ,∠BAC=∠DCA,则AB∥CD,得到四边形ABCD 为平行四边形,根据有一个直角的平行四边形为矩形可添加的条件为∠B=90°.【详解】∵△A解析:∠B=90°.【分析】根据旋转的性质得AB=CD ,∠BAC=∠DCA ,则AB ∥CD ,得到四边形ABCD 为平行四边形,根据有一个直角的平行四边形为矩形可添加的条件为∠B=90°.【详解】∵△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ,∴AB=CD ,∠BAC=∠DCA ,∴AB ∥CD ,∴四边形ABCD 为平行四边形,当∠B=90°时,平行四边形ABCD 为矩形,∴添加的条件为∠B=90°.故答案为∠B=90°.【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的判定.14.60【分析】根据菱形的性质:对角线互相垂直以及平分每一组对角解答即可.【详解】解:∵菱形ABCD 的对角线AC 、BD 相交于点O ,∴AC⊥BD,∠DBC=∠B DC=30°,∴∠DOC=90°解析:60【分析】根据菱形的性质:对角线互相垂直以及平分每一组对角解答即可.【详解】解:∵菱形ABCD的对角线AC、BD相交于点O,∴AC⊥BD,∠DBC=∠BDC=30°,∴∠DOC=90°,∴∠OCD=90°﹣30°=60°,故答案为:60.【点睛】本题主要考查菱形的性质,熟练掌握菱形的性质是解题的关键.15.①②③⑤【分析】】由矩形、菱形、正方形的判定方法对各个选项进行判断即可.【详解】∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AC=BD,∴四边形ABCD是正方解析:①②③⑤【分析】】由矩形、菱形、正方形的判定方法对各个选项进行判断即可.【详解】∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AC=BD,∴四边形ABCD是正方形,①正确;∵四边形ABCD是平行四边形,AB⊥AD,∴四边形ABCD是矩形,又∵AC⊥BD,∴四边形ABCD是正方形,②正确;∵四边形ABCD是平行四边形,AB⊥AD,∴四边形ABCD是矩形,又∵AB=AD,∴四边形ABCD是正方形,③正确;④AB=BD,且AB⊥BD,无法得出四边形ABCD是正方形,故④错误;∵四边形ABCD是平行四边形,OB=OC,∴四边形ABCD是矩形,又∵OB⊥OC,∴四边形ABCD是正方形,⑤正确;故答案为:①②③⑤.【点睛】本题考查了矩形、菱形、正方形的判定,熟记特殊四边形的判定是解答的关键.16.60或300【分析】当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角θ的度数.【详解】解:当GB=GC时,点G在BC的垂直平分线上,分两种情况解析:60或300【分析】当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角θ的度数.【详解】解:当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,∵GC=GB,∴GH⊥BC,∴四边形ABHM是矩形,∴AM=BH=12AD=12AG,∴GM垂直平分AD,∴GD=GA=DA,∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角θ=60°;②当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角θ=360°﹣60°=300°.故答案为60或300【点睛】本题考查了旋转的性质,矩形的性质,利用分类讨论思想解决问题是本题的关键.17.105°【分析】根据四边形ABCD是正方形,可得AB=AD,∠BAD=90°,△ABC为等边三角形,可得AE=BE=AB,∠EAB=60°,从而AE=AD,∠EAD=30°,进而求得∠AED的度解析:105°【分析】根据四边形ABCD是正方形,可得AB=AD,∠BAD=90°,△ABC为等边三角形,可得AE=BE=AB,∠EAB=60°,从而AE=AD,∠EAD=30°,进而求得∠AED的度数,再根据平角定义即可求得∠DEF的度数.【详解】∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵△ABE为等边三角形,∴AE=BE=AB,∠EAB=60°,∴AE=AD,∠EAD=∠BAD﹣∠BAE=30°,∴∠AED=∠ADE=12(180°﹣30°)=75°,∴∠DEF=180°﹣∠AED=180°﹣75°=105°.故答案为105°.【点睛】本题考查了正方形的性质、等边三角形的性质,解决本题的关键是综合运用正方形的性质和等边三角形的性质.18.【分析】根据“气压×体积=常数”可知:先求得常数的值,再表示出气体体积V和气压p的函数解析式.【详解】设,那么点(1.6,60)在此函数解析式上,则k=1.6×60=96,∴.故答案为:解析:96 PV =【分析】根据“气压×体积=常数”可知:先求得常数的值,再表示出气体体积V和气压p的函数解析式.【详解】设kPV=,那么点(1.6,60)在此函数解析式上,则k=1.6×60=96,∴96PV =.故答案为:96PV =.【点睛】解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.19.5【分析】直接利用频率的定义分析得出答案.【详解】解:∵在整数20200520中,一共有8个数字,数字“0”有4个,故数字“0”出现的频率是.故答案为:.【点睛】此题主要考查了频率的求解析:5【分析】直接利用频率的定义分析得出答案.【详解】解:∵在整数20200520中,一共有8个数字,数字“0”有4个,故数字“0”出现的频率是12.故答案为:12.【点睛】此题主要考查了频率的求法,正确把握定义是解题关键.20.000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-解析:000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-20%=20%,∴该商场全年的营业额为:800÷20%=4000(万元),故答案为:4000.【点睛】本题考查了扇形统计图,由统计图得到二季度所占的百分比是解题关键.21.35【分析】先根据三角形外角的性质和矩形的性质得到∠OCD的度数,再根据DE⊥AC即可得到∠CDE的度数.【详解】∵∠AOD=110°,∴∠ODC+∠OCD=110°,∵四边形ABCD是解析:35先根据三角形外角的性质和矩形的性质得到∠OCD 的度数,再根据DE ⊥AC 即可得到∠CDE 的度数.【详解】∵∠AOD =110°,∴∠ODC+∠OCD=110°,∵四边形ABCD 是矩形,∴OC=OD ,∴∠ODC=∠OCD=55°,又∵DE ⊥AC ,∴∠CDE=180°-∠OCD-∠DEC=180°-55°-90°=35°,故答案为:35.【点睛】本题考查了矩形的性质,三角形内角和,三角形外角的性质,掌握知识点是解题关键.22.【分析】利用平均数的定义,利用数据x1,x2,…,x10的平均数为a ,x11,x12,…,x30的平均数为b ,可求出x1+x2+…+x10=10a,x11+x12+…+x30=20b,进而即可求 解析:1(1020)30a b + 【分析】利用平均数的定义,利用数据x 1,x 2,…,x 10的平均数为a ,x 11,x 12,…,x 30的平均数为b ,可求出x 1+x 2+…+x 10=10a ,x 11+x 12+…+x 30=20b ,进而即可求出答案.【详解】解:因为数据x 1,x 2,…,x 10的平均数为a ,则有x 1+x 2+…+x 10=10a ,因为x 11,x 12,…,x 30的平均数为b ,则有x 11+x 12+…+x 30=20b ,∴x 1,x 2,…,x 30的平均数=()1102030a b + 故答案为:1(1020)30a b +. 【点睛】本题考查的是样本加权平均数的求法.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数. 23.【分析】已知S△PAB=S 矩形ABCD ,则可以求出△ABP 的高,此题为“将军饮马”模型,过P 点作直线l∥AB,作点A 关于l 的对称点E ,连接AE ,连接BE ,则BE 的长就是所求的最短距离.解析:41【分析】已知S△PAB=13S矩形ABCD,则可以求出△ABP的高,此题为“将军饮马”模型,过P点作直线l∥AB,作点A关于l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.【详解】解:设△ABP中AB边上的高是h.∵S△PAB=13S矩形ABCD,∴12AB•h=13AB•AD,∴h=23AD=2,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.在Rt△ABE中,∵AB=5,AE=2+2=4,∴BE=22225441+=+=AB AE,即PA+PB的最小值为41.故答案为:41.【点睛】本题主要考查的是勾股定理以及“将军饮马”的模型,“将军饮马”模型主要是用来解决最小值问题,掌握这模型是解题的关键.24.5或1.5【分析】先直接解分式方程,整理得:(1﹣2a)x=﹣4a,再分类讨论①当1﹣2a=0时,方程无解,故a=0.5;②当1﹣2a≠0时,x==3时,分式方程无解,则a =1.5 .【详解】解析:5或1.5【分析】先直接解分式方程,整理得:(1﹣2a)x=﹣4a,再分类讨论①当1﹣2a=0时,方程无解,故a =0.5;②当1﹣2a≠0时,x =421a a -=3时,分式方程无解,则a =1.5 . 【详解】 解:2233x a a x x+=--, 去分母得:x ﹣2a =2a (x ﹣3),整理得:(1﹣2a )x =﹣4a ,当1﹣2a =0时,方程无解,故a =0.5;当1﹣2a≠0时,x =421a a -=3时,分式方程无解,则a =1.5, 则a 的值为0.5或1.5.故答案为:0.5或1.5.【点睛】 本题主要考查了当分式方程无意义时,求字母的值.值得引起注意的是,当分式方程化为整式方程(1﹣2a )x =﹣4a 时,一定要分1-2a=0和1-2a ≠0两种情况,来分别求m 的值.三、解答题25.(1)10°;(2)135DFA α∠=︒-;(3)∠BEA =∠FEA ,理由见解析【分析】(1)根据正方形的性质和三角形的内角和解答即可;(2)根据正方形的性质和三角形内角和解答即可;(3)延长CB 至I ,使BI =DF ,根据全等三角形的判定和性质解答即可.【详解】解:(1)∵四边形ABCD 是正方形,∴∠EBA =∠BAD =90°,∴∠EAB =90°﹣∠BAE =90°﹣55°=35°,∴∠HAD =∠BAD ﹣∠EAF ﹣∠EAB =90°﹣45°﹣35°=10°;(2)∵四边形ABCD 是正方形,∴∠EBA =∠BAD =∠ADF =90°,∴∠EAB =90°﹣∠BAE =90°﹣α,∴∠DAF =∠BAD ﹣∠EAF ﹣∠EAB =()90459045αα︒-︒-︒--︒=,∴∠DFA =90°﹣∠DAF =()9045α︒--︒=135°﹣α;(3)∠BEA =∠FEA ,理由如下:延长CB 至I ,使BI =DF ,连接AI .∵四边形ABCD 是正方形,∴AD =AB ,∠ADF =∠ABC =90°,∴∠ABI =90°,又∵BI =DF ,∴△DAF ≌△BAI (SAS ),∴AF =AI ,∠DAF =∠BAI ,∴∠EAI =∠BAI +∠BAE =∠DAF +∠BAE =45°=∠EAF ,又∵AE 是△EAI 与△EAF 的公共边,∴△EAI ≌△EAF (SAS ),∴∠BEA =∠FEA .【点睛】本题主要考查正方形的性质、三角形外角性质及全等三角形,关键是根据正方形的性质及外角和性质得到角之间的关系,然后求解.26.(1)见解析;(2)15°【分析】(1)根据PB=PC 得∠PBC=∠PCB ,从而可得∠ABP=∠DCP ,再利用SAS 证明即可;(2)由(1)得△PAD 为等边三角形,可求得∠PAB=30°,∠PAC=∠PAD-∠CAD ,因此可得结果.【详解】解:(1)∵四边形ABCD 为正方形,∴∠ABC=∠DCB=90°,AB=CD ,∵BP=PC ,∴∠PBC=∠PCB ,∴∠ABP=∠DCP ,又∵AB=CD ,BP=CP ,在△APB 和△DPC 中,AB CD ABP DCP BP CP =⎧⎪∠=∠⎨⎪=⎩,∴△APB ≌△DPC (SAS );(2)由(1)得AP=DP=AB=AD ,∴△PAD为等边三角形,∴∠PAD=60°,∠PAB=30°,在正方形ABCD中,∠BAC=∠DAC=45°,∴∠PAC=∠PAD-∠CAD=60°-45°=15°.【点睛】本题考查了全等三角形的判定定理,正方形的性质,以及等腰三角形的性质,熟练掌握全等三角形的几种判定方法是解答的关键.27.证明见解析【分析】连接AE、CF,证明四边形AECF为平行四边形即可得到AC、EF互相平分.【详解】解:连接AE、CF,∵四边形ABCD为平行四边形,∴AD∥BC,AD﹦BC,又∵DF﹦BE,∴AF﹦CE,又∵AF∥CE,∴四边形AECF为平行四边形,∴AC、EF互相平分.【点睛】本题考查平行四边形的判定与性质,正确添加辅助线是解题关键.28.(1)见解析;(2)当∠A=90°时,FG⊥FH.【分析】(1)根据等腰三角形的性质得到∠ABC=∠ACB,根据平行线的性质、等腰三角形的判定定理得到AD=AE,得到DB=EC,根据三角形中位线定理证明结论;(2)延长FG交AC于N,根据三角形中位线定理得到FH∥AC,FN∥AB,根据平行线的性质解答即可.【详解】(1)证明:∵AB=AC.∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,∵点F、G、H分别为BE、DE、BC的中点,∴FG是△EDB的中位线,FH是△BCE的中位线,∴FG=12BD,FH=12CE,∴FG=FH;(2)解:延长FG交AC于N,∵FG是△EDB的中位线,FH是△BCE的中位线,∴FH∥AC,FN∥AB,∵FG⊥FH,∴∠A=90°,∴当∠A=90°时,FG⊥FH.【点睛】本题考查的是三角形中位线定理的应用、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.29.(1)求证见解析;(2)2OE=EB+EA;(3)见解析.【分析】(1)延长EA至点F,使AF=BE,连接OF,由SAS证得△OBE≌△OAF,得出OE=OF,∠BEO=∠AFO,由等腰三角形的性质与等量代换即可得出结论;(2)判断出△EOF是等腰直角三角形,根据勾股定理即可得出结论;(3)先根据ASA证得△ABE≌△ADH,△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,得出FG=EF=EH=HG,再由∠F=∠H=∠AEB=90°,由此可得出结论.【详解】(1)证明:延长EA至点F,使AF=BE,连接OF,如图所示:∵四边形ABCD是正方形,∴∠BOA=90°,OB=OA,∵∠AEB=90°,∴∠OBE+∠OAE=360°﹣90°﹣90°=180°,∵∠OAE+∠OAF=180°,∴∠OBE =∠OAE ,在△OBE 与△OAF 中,0OB A OBE OAF BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△OBE ≌△OAF (SAS ),∴OE =OF ,∠BEO =∠AFO ,∴∠AEO =∠AFO ,∴∠BEO =∠AEO ,∴EO 平分∠AEB ;(2OE =EB +EA ,理由如下:由(1)得:△OBE ≌△OAF ,∴OE =OF ,∠BOE =∠AOF ,∵∠BOE +∠AOE =90°,∴∠AOF +∠AOE =90°,∴∠EOF =90°,∴△EOF 是等腰直角三角形,∴2OE 2=EF 2,∵EF =EA +AF =EA +EB ,∴2OE 2=(EB +EA )2,OE =EB +EA ,OE =EB +EA ;(3)证明:∵CF ⊥EB ,DH ⊥EA ,∴∠F =∠H =∠AEB =90°,∵四边形ABCD 是正方形,∴AB =AD ,∠BAD =90°,∴∠EAB +∠DAH =90°,∠EAB +∠ABE =90°,∠ADH +∠DAH =90°,∴∠EAB =∠HDA ,∠ABE =∠DAH .在△ABE 与△ADH 中,EAB HDA AB ADABE DAH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABE ≌△ADH (ASA ),∴BE =AH ,AE =DH ,同理可得:△ABE ≌△BCF ,△ADH ≌△DCG ,△DCG ≌△CBF ,∴BE =CF ,AE =BF ,AH =DG ,DH =CG ,DG =CF ,CG =BF ,∴CG +FC =BF +BE =AE +AH =DH +DG ,∴FG =EF =EH =HG ,∵∠F =∠H =∠AEB =90°,∴四边形EFGH 为正方形.【点睛】本题是四边形综合题,主要考查了正方形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、等腰直角三角形的判定与性质、角平分线定义等知识;熟练掌握正方形的判定和性质,作辅助线构建全等三角形是解题的关键.30.-1【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】去分母得:(x+2)2-4=x 2-4,解得:x=-1,经检验x=-1是分式方程的解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.31.(1)见解析 (2)见解析【分析】(1)本题考查图形的旋转变换以及作图,根据网格结构找出点A 、B 、C 绕点A 逆时针旋转90°后的点1A 、1B 、1C 的位置,然后顺次连接即可.(2)本题考查中心对称图形的作图,找出点1A 、1B 、1C 关于原点O 成中心对称的点2A 、2B 、2C 的位置,然后顺次连接即可.【详解】【点睛】解答此类型题目首先要清楚旋转图形和中心对称图形的性质,按照图形定义进行作图,作图时先找点,继而由点连成线.32.(1)50;32;43.2 (2)见解析 (3)1120人。
(完整版)苏科版八年级数学下册期中试卷及答案

(完整版)苏科版八年级数学下册期中试卷及答案一、选择题1.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC的度数为()A.35°B.40°C.45°D.60°2.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE.其中正确的是()A.①③B.①②③④C.①②③D.①③④3.江苏移动掌上营业厅,推出“每日签到——抽奖活动”:每个手机号码每日只能签到1次,且只能抽奖1次,抽奖结果有流量红包、话费充值卷、惊喜大礼包、谢谢参与.小明的爸爸已经连续3天签到,且都抽到了流量红包,则“他第4天签到后,抽奖结果是流量红包”是()A.必然事件B.不可能事件C.随机事件D.必然事件或不可能事件4.已知关于x的分式方程22x mx+-=3的解是5,则m的值为()A.3 B.﹣2 C.﹣1 D.85.如图,▱ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为()A.8cm B.9cm C.10cm D.11cm6.小明和同学做“抛掷质地均匀的硬币试验”,获得的数据如表:若抛掷硬币的次数为3000,则“正面朝上”的频数最接近()A.1000 B.1500 C.2000 D.25007.下列说法正确的是()A .矩形的对角线相等垂直B .菱形的对角线相等C .正方形的对角线相等D .菱形的四个角都是直角8.某种商品原价200元,连续两次降价a%后,售价为148元.下列所列方程正确的是( )A .200(1+ a%)2=148B .200(1- a%)2=148C .200(1- 2a%)=148D .200(1-a 2%)=1489.在四边形中,能判定这个四边形是正方形的条件是()A .对角线相等,对边平行且相等B .一组对边平行,一组对角相等C .对角线互相平分且相等,对角线互相垂直D .一组邻边相等,对角线互相平分 10.如图所示,在矩形ABCD 中,E 为AD 上一点,EF CE ⊥交AB 于点F ,若2DE =,矩形ABCD 的周长为16,且CE EF =,求AE 的长( )A .2B .3C .4D .611.如图,正方形ABCD 中,点E 、F 、H 分别是AB 、BC 、CD 的中点,CE 、DF 交于G ,连接AG 、HG ,下列结论:①CE ⊥DF ;②AG=AD ;③∠CHG=∠DAG ;④HG=12AD .其中正确的有( )A .① ②B .① ② ④C .① ③ ④D .① ② ③ ④12.如图,是一组由菱形和矩形组成的图案,第1个图中菱形的面积为S (S 为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,依此类推…,则第2020个图中阴影部分的面积可以用含S 的代数式表示为( )(S ≥2且S 是正整数)A .20184S B .20194S C .20204S D .20214S二、填空题13.如图所示,将△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ,添加一个条件_____,使四边形ABCD 为矩形.14.不透明的袋子里装有3只相同的小球,给它们分别标上序号1、2、3后搅匀.事件“从中任意摸出1只小球,序号为4”是_____事件(填“必然”、“不可能”或“随机”). 15.在英文单词tomato 中,字母o 出现的频数是_____.16.如图,点D 、E 分别是△ABC 的边AB 、AC 的中点,若BC=6,则DE= .17.如图,小正方形方格的边长都是1,点A 、B 、C 、D 、O 都是小正方形的顶点.若COD 是由AOB 绕点O 按顺时针方向旋转一次得到的,则至少需要旋转______°.18.已知()22221140ab a b a b +=≠+,则代数式20192020b a a b ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭的值为_____.19.在矩形ABCD 中,对角线AC 、BD 交于点O ,若100AOB ∠=,则OAB ∠=_________.20.如图,在正方形ABCD 中,△ABE 为等边三角形,连接DE ,CE ,延长AE 交CD 于F 点,则∠DEF 的度数为_____.21.当a<0时,化简|2a﹣2a|结果是_____.22.如图,△ABC中,∠A=60°,∠ABC=80°,将△ABC绕点B逆时针旋转,得到△DBE,若DE∥BC,则旋转的最小度数为_____.23.如图,△ABC中,∠BAC=20°,△ABC绕点A逆时针旋转至△AED,连接对应点C、D,AE垂直平分CD于点F,则旋转角度是_____°.24.方程x2=0的解是_______.三、解答题25.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.26.如图,在ABCD中,点O为对角线BD的中点,过点O的直线EP分别交AD,BC于E,F两点,连接BE,DF.(1)求证:四边形BFDE为平行四边形;(2)当∠DOE= °时,四边形BFDE为菱形?27.某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:最喜爱的节目人数歌曲15舞蹈a小品12相声10其它b(1)在此次调查中,该校一共调查了名学生;(2)a=;b=;(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.28.如图,在平面直角坐标系中,点O为坐标原点,AB// OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.(1)在t=3时,M点坐标,N点坐标;(2)当t为何值时,四边形OAMN是矩形?(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.29.已知关于x 的方程x 2﹣(k +3)x +3k =0. (1)若该方程的一个根为1,求k 的值;(2)求证:不论k 取何实数,该方程总有两个实数根. 30.解方程:224124x x x +-=-- 31.某中学八年级共有10个班,每班40名学生,学校对该年级学生数学学科某次学情调研测试成绩进行了抽样分析,请按要求回答下列问题:(1)若要从全年级学生中抽取40人进行调查,你认为以下抽样方法中最合理的是 . ①随机抽取一个班级的40名学生的成绩; ②在八年级学生中随机抽取40名女学生的成绩; ③在八年级10个班中每班各随机抽取4名学生的成绩.(2)将抽取的40名学生的成绩进行分组,绘制如下成绩频数分布表: ①m = ,n = ;②根据表格中的数据,请用扇形统计图表示学生成绩分布情况.32.为了解某区初中生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示不完整的统计图.(1)本次调查共随机抽取了 名学生; (2)补全条形统计图;(3)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 ︒; (4)若该区共有10 000名初中生,估计该地区中学生一周课外阅读时长不少于4小时的人数.33.如图,在平面直角坐标系中,△ABC 和△A 'B 'C '的顶点都在格点上. (1)将△ABC 绕点B 顺时针旋转90°后得到△A 1BC 1;(2)若△A 'B 'C '是由△ABC 绕某一点旋转某一角度得到,则旋转中心的坐标是 .34.某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到哪一种灯的可能性最大?遇到哪一种灯的可能性最小?根据什么? 35.如图,点P 为ABC ∆的BC 边的中点,分别以AB 、AC 为斜边作Rt ABD ∆和Rt ACE ∆,且BAD CAE α∠=∠=,DPE β∠=.(1)求证:PD PE =.(2)探究:α与β的数量关系,并证明你的结论.36.已知ABC ∆是边长为8cm 的等边三角形,动点,P Q 同时出发,分别在三角形的边或延长线上运动,他们的运动时间为()t s .()1如图1,若P 点由A 向B 运动,Q 点由C 向A 运动,他们的速度都是1/cm s ,连接PQ .则AP =__,AQ = ,(用含t 式子表示);()2在(1)的条件下,是否存在某一时刻,使得APQ ∆为直角三角形?若存在,请求出t 的值,若不存在,请说明理由;()3如图2,若P 点由A 出发,沿射线AB 方向运动,Q 点由C 出发,沿射线AC 方向运动,P 的速度为3/,cm s Q 的速度为./acm s 是否存在某个a 的值,使得在运动过程中BPO ∆恒为以BP 为底的等腰三角形?如果存在,请求出这个值,如果不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE ,然后求出△ABE 是等腰直角三角形,根据等腰直角三角形的性质求出∠BAE=∠ABE=45°,再根据等腰三角形两底角相等求出∠ABC ,然后求出∠CBE ,根据等腰三角形三线合一的性质可得BF=CF ,根据直角三角形斜边上的中线等于斜边的一半可得BF=EF ,根据等边对等角求出∠BEF=∠CBE ,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解. 【详解】∵DE 垂直平分AB ,∴AE=BE , ∵BE ⊥AC ,∴△ABE 是等腰直角三角形, ∴∠BAE=∠ABE=45°, 又∵AB=AC ,∴∠ABC=12(180°-∠BAC )=12(180°-45°)=67.5°, ∴∠CBE=∠ABC-∠ABE=67.5°-45°=22.5°, ∵AB=AC ,AF ⊥BC , ∴BF=CF ,∵EF=12BC (直角三角形斜边中线等于斜边的一半), ∴BF=EF=CF ,∴∠BEF=∠CBE=22.5°,∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°. 故选:C . 【点睛】此题考查等腰三角形三线合一的性质,等腰三角形两底角相等的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质并求出△ABE 是等腰直角三角形是解题的关键.2.B解析:B 【分析】根据正方形的性质证得BAE CDE ∆≅∆,推出ABE DCE ∠=∠,可知①正确;证明ABH CBH ∆≅∆,再根据对顶角相等即可得到AHB EHD ∠=∠,可知②正确;根据//AD BC ,求出BDE CDE S S ∆∆=,推出BDE DEH CDE DEH S S S S ∆∆∆∆-=-,即BHE CHD S S ∆∆=,故③正确;利用正方形性质证ADH CDH ∆≅∆,求得HAD HCD ∠=∠,推出ABE HAD ∠=∠;求出90ABE BAG ∠+∠=︒,求得90AGE ∠=︒故④正确.【详解】 解:四边形ABCD 是正方形,E 是AD 边上的中点,AE DE ∴=,AB CD =,90BAD CDA ∠=∠=︒,()BAE CDE SAS ∴∆≅∆, ABE DCE ∴∠=∠,故①正确;∵四边形ABCD 是正方形, ∴AB=BC , ∠ABD=∠CBD , ∵BH=BH , ∴ABH CBH ∆≅∆,AHB CHB ∴∠=∠,BHC DHE ∠=∠,AHB EHD ∴∠=∠,故②正确;//AD BC ,BDE CDE S S ∆∆∴=,BDE DEH CDE DEH S S S S ∆∆∆∆∴-=-,即BHE CHD S S ∆∆=, 故③正确;四边形ABCD 是正方形,AD DC ∴=,45ADB CDB ∠=∠=︒,DH DH =,()ADH CDH SAS ∴∆≅∆, HAD HCD ∴∠=∠, ABE DCE ∠=∠ABE HAD ∴∠=∠,90BAD BAH DAH ∠=∠+∠=︒, 90ABE BAH ∴∠+∠=︒, 1809090AGB ∴∠=︒-︒=︒,AG BE ∴⊥, 故④正确;故选:B . 【点睛】本题主要考查了正方形的性质及全等三角形的判定与性质,三角形的面积公式,解答本题关键要充分利用正方形的性质:①四边相等;②四个内角相等,都是90度;③对角线相等,相互垂直,且每条对角线平分一组对角.3.C解析:C【解析】分析:直接利用随机事件的定义进而得出答案.详解:∵有流量红包、话费充值卷、惊喜大礼包、谢谢参与四种等可能情况,∴他第4天签到后,抽奖结果是流量红包为随机事件.故选C.点睛:本题主要考查了随机事件,正确把握相关定义是解题的关键.4.C解析:C【分析】将x=5代入分式方程中进行求解即可.【详解】把x=5代入关于x的分式方程22x mx+-=3得:25352m⨯+=-,解得:m=﹣1,故选:C.【点睛】本题考查分式方程的解,一般直接将解代入分式方程进行求解.5.D解析:D【解析】【分析】由平行四边形的性质可得AB=CD,AD=BC,AO=CO,可得AD+CD=11cm,由线段垂直平分线的性质可得AE=CE,即可求△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm.【详解】解:∵四边形ABCD是平行四边形∴AB=CD,AD=BC,AO=CO,又∵EO⊥AC,∴AE=CE,∵▱ABCD的周长为22cm,∴2(AD+CD)=22cm∴AD+CD=11cm∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm故选:D.【点睛】本题考查了平行四边形的性质,线段垂直平分线的性质,熟练运用平行四边形的性质是本题的关键.6.B解析:B【分析】随着实验次数的增加,正面向上的频率逐渐稳定到某个常数附近,据此求解即可.【详解】解:观察表格发现:随着实验次数的增加,正面朝上的频率逐渐稳定到0.5附近,所以抛掷硬币的次数为3000,则“正面朝上”的频数最接近3000×0.5=1500次,故选:B.【点睛】本题考查利用频率估算概率,解题的关键是掌握利用频率估算概率的方法.7.C解析:C【分析】根据矩形、菱形的性质和正方形的性质判断即可.【详解】解:A、矩形的对角线相等且平分,选项错误,不符合题意;B、菱形的对角线垂直且平分,选项错误,不符合题意;C、正方形的对角线相等,选项正确,符合题意;D、矩形的四个角都是直角,而菱形的四个角不是直角,选项错误,不符合题意;故选:C.【点睛】本题考查矩形、菱形和正方形的性质,正确区分矩形、菱形和正方形的性质是解题的关键.8.B解析:B【分析】根据题意可得出两次降价后的售价为200(1- a%)2,列方程即可.【详解】解:根据题意可得出两次降价后的售价为200(1- a%)2,∴200(1- a%)2=148故选:B.【点睛】本题主要考查增长率问题,找准题目中的等量关系是解此题的关键.9.C解析:C【分析】根据所给条件逐一进行判断即可得.【详解】A 选项中,根据“对边平行且相等和对角线相等”只能判定该四边形是矩形;B 选项中,根据“一组对边平行,一组对角相等”只能判定该四边形是平行四边形;C 选项中,根据“对角线互相平分且相等,对角线互相垂直”可判定该四边形是正方形;D 选项中,根据“一组邻边相等,对角线互相平分”只能判定该四边形是菱形; 故选C .10.B解析:B【分析】易证△AEF ≌△ECD ,可得AE=CD ,由矩形的周长为16,可得2(AE+DE+CD)=16,可求AE 的长度.【详解】∵四边形ABCD 为矩形,∴∠A=∠D=90°,∵EF ⊥CE ,∴∠CEF=90°,∴∠CED+∠AEF=90°,∵∠CED+∠DCE=90°,∴∠DCE=∠AEF ,在△AEF 和△DCE 中,A D AEF DCE EF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△DCE(AAS),∴AE=DC ,由题意可知:2(AE+DE+CD)=16,DE=2,∴2AE=6,∴AE=3;故选:B .【点睛】本题考查了矩形的性质,全等三角形的性质和判定以及直角三角形的性质等知识,熟练掌握矩形的性质,证明三角形全等是解题的关键.11.D解析:D【详解】∵四边形ABCD 是正方形,∴AB=BC=CD=AD ,∠B=∠BCD=90°,∵点E 、F 、H 分别是AB 、BC 、CD 的中点,∴△BCE ≌△CDF ,∴∠ECB=∠CDF ,∵∠BCE+∠ECD=90°,∴∠ECD+∠CDF=90°,∴∠CGD=90°,∴CE ⊥DF ,故①正确;在Rt △CGD 中,H 是CD 边的中点,∴HG=12CD=12AD ,故④正确; 连接AH ,同理可得:AH ⊥DF ,∵HG=HD=12CD , ∴DK=GK ,∴AH 垂直平分DG ,∴AG=AD ,故②正确;∴∠DAG=2∠DAH ,同理:△ADH ≌△DCF ,∴∠DAH=∠CDF ,∵GH=DH ,∴∠HDG=∠HGD ,∴∠GHC=∠HDG+∠HGD=2∠CDF ,∴∠CHG=∠DAG .故③正确.故选D .【点睛】运用了正方形的性质,全等三角形的判定与性质,等腰三角形的性质以及垂直平分线的性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.12.B解析:B【分析】观察图形发现第2个图形中的阴影部分的面积为S 4,第3个阴影部分的面积为16S ,依此类推,得到第n 个图形的阴影部分的面积即可.【详解】解:观察图形发现:第2个图形中的阴影部分的面积为S 4, 第3个图形中的阴影部分的面积为16S , …第n 个图形中的阴影部分的面积为14n S,故第2020个图中阴影部分的面积可以用含S 的代数式表示为20194S .故选:B .【点睛】 本题考查了图形的变化类问题,解题的关键是仔细的观察图形,找到规律用通项公式表示出来.二、填空题13.∠B=90°.【分析】根据旋转的性质得AB=CD ,∠BAC=∠DCA ,则AB ∥CD ,得到四边形ABCD 为平行四边形,根据有一个直角的平行四边形为矩形可添加的条件为∠B=90°.【详解】∵△A解析:∠B=90°.【分析】根据旋转的性质得AB=CD ,∠BAC=∠DCA ,则AB ∥CD ,得到四边形ABCD 为平行四边形,根据有一个直角的平行四边形为矩形可添加的条件为∠B=90°.【详解】∵△ABC 绕AC 的中点O 顺时针旋转180°得到△CDA ,∴AB=CD ,∠BAC=∠DCA ,∴AB ∥CD ,∴四边形ABCD 为平行四边形,当∠B=90°时,平行四边形ABCD 为矩形,∴添加的条件为∠B=90°.故答案为∠B=90°.【点睛】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的判定.14.不可能【分析】根据三只小球中没有序号为4的小球进行判断即可求解.【详解】解:∵三只小球中没有序号为4的小球,∴事件“从中任意摸出1只小球,序号为4”是不可能事件,故答案为:不可能.【点解析:不可能【分析】根据三只小球中没有序号为4的小球进行判断即可求解.【详解】解:∵三只小球中没有序号为4的小球,∴事件“从中任意摸出1只小球,序号为4”是不可能事件,故答案为:不可能.【点睛】本题考查了事件发生的可能性.一定不可能发生的事件是不可能事件;一定会发生的事件是必然事件;有可能发生,也有可能不发生的事件是随机事件.15.2【分析】根据频数定义可得答案.【详解】解:字母o出现的频数是2,故答案为:2.【点睛】本题考查的是频数的含义,掌握频数的含义是解题的关键.解析:2【分析】根据频数定义可得答案.【详解】解:字母o出现的频数是2,故答案为:2.【点睛】本题考查的是频数的含义,掌握频数的含义是解题的关键.16.3【分析】先判断DE是△ABC的中位线,从而得解.【详解】因为点D、E分别是△ABC的边AB、AC的中点,所以DE是△ABC的中位线,所以DE=BC=3.故答案为3.考点:三角形的中解析:3【分析】先判断DE是△ABC的中位线,从而得解.【详解】因为点D、E分别是△ABC的边AB、AC的中点,所以DE是△ABC的中位线,所以DE=12BC=3.故答案为3.考点:三角形的中位线定理.17.90【分析】由△COD是由△AOB绕点O按顺时针方向旋转而得到,再结合已知图形可知旋转的角度是∠BOD的大小,然后由图形即可求得答案【详解】解:∵△COD是由△AOB绕点O按顺时针方向旋转而解析:90【分析】由△COD是由△AOB绕点O按顺时针方向旋转而得到,再结合已知图形可知旋转的角度是∠BOD的大小,然后由图形即可求得答案【详解】解:∵△COD是由△AOB绕点O按顺时针方向旋转而得,∴OB=OD,∴旋转的角度是∠BOD的大小,∵∠BOD=90°,∴旋转的角度为90°,故答案为: 90.【点睛】本题考查了旋转的性质.解题的关键是理解△COD是由△AOB绕点O按顺时针方向旋转而得的含义,找到旋转角.18.0或-2【分析】根据(ab≠0),可以得到a和b的关系,从而可以求得所求式子的值.【详解】解:∵(ab≠0),∴,∴(a2+b2)2=4a2b2,∴(a2﹣b2)2=0,∴a2=b2解析:0或-2【分析】 根据2222114a b a b +=+(ab ≠0),可以得到a 和b 的关系,从而可以求得所求式子的值.【详解】 解:∵2222114a b a b+=+(ab ≠0), ∴2222224b a a b a b+=+, ∴(a 2+b 2)2=4a 2b 2,∴(a 2﹣b 2)2=0,∴a 2=b 2,∴a =±b ,经检验:a b =±符合题意,当a =b 时,2019202020192020110,b a a b ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭当a =﹣b 时,()()2019202020192020112,b a a b ⎛⎫⎛⎫-=---=- ⎪ ⎪⎝⎭⎝⎭ 故答案为:0或﹣2.【点睛】 本题考查的是代数式的值,同时考查了因式分解的应用,类解分式方程的方法,掌握以上知识是解题是关键.19.40°【详解】因为OA=OB,所以.故答案为:解析:40°【详解】因为OA=OB , 所以180402AOB OAB ︒-∠∠==︒. 故答案为:40︒20.105°【分析】根据四边形ABCD是正方形,可得AB=AD,∠BAD=90°,△ABC为等边三角形,可得AE=BE=AB,∠EAB=60°,从而AE=AD,∠EAD=30°,进而求得∠AED的度解析:105°【分析】根据四边形ABCD是正方形,可得AB=AD,∠BAD=90°,△ABC为等边三角形,可得AE=BE=AB,∠EAB=60°,从而AE=AD,∠EAD=30°,进而求得∠AED的度数,再根据平角定义即可求得∠DEF的度数.【详解】∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵△ABE为等边三角形,∴AE=BE=AB,∠EAB=60°,∴AE=AD,∠EAD=∠BAD﹣∠BAE=30°,∴∠AED=∠ADE=12(180°﹣30°)=75°,∴∠DEF=180°﹣∠AED=180°﹣75°=105°.故答案为105°.【点睛】本题考查了正方形的性质、等边三角形的性质,解决本题的关键是综合运用正方形的性质和等边三角形的性质.21.﹣3a【分析】首先利用a的取值范围化简,进而去绝对值求出答案.【详解】∵a<0,∴|﹣2a|=|﹣a﹣2a|=|﹣3a|=﹣3a.故答案为:﹣3a.【点睛】此题主要考查了二次根解析:﹣3a【分析】首先利用a的取值范围化简,进而去绝对值求出答案.【详解】∵a<0,∴2a|=|﹣a﹣2a|=|﹣3a|=﹣3a.故答案为:﹣3a.【点睛】此题主要考查了二次根式的化简,正确化简二次根式是解题关键.22.40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点解析:40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点B逆时针旋转,得到△DBE,∴∠E=∠C=40°,∵DE∥BC,∴∠CBE=∠E=40°,∴旋转的最小度数为40°,故答案为:40°.【点睛】本题主要考查了旋转的性质以及平行线的性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.23.40【分析】根据旋转的性质得出AD =AC ,∠DAE=∠BAC=20°,求出∠DAE=∠CAE=20°,再求出∠DAC 的度数即可.【详解】解:∵△ABC 绕点A 逆时针旋转至△AED,∠BAC解析:40【分析】根据旋转的性质得出AD =AC ,∠DAE =∠BAC =20°,求出∠DAE =∠CAE =20°,再求出∠DAC 的度数即可.【详解】解:∵△ABC 绕点A 逆时针旋转至△AED ,∠BAC =20°,∴AD =AC ,∠DAE =∠BAC =20°,∵AE 垂直平分CD 于点F ,∴∠DAE =∠CAE =20°,∴∠DAC =20°+20°=40°,即旋转角度数是40°,故答案为:40.【点睛】本题主要考查了图像旋转的性质以及垂直平分线的性质,从而得到边相等与角相等的条件.24.【分析】直接开平方,求出方程的解即可.【详解】∵x2=0,开方得,,故答案为:.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.解析:120x x ==【分析】直接开平方,求出方程的解即可.【详解】∵x 2=0,开方得,120x x ==,故答案为:120x x ==.【点睛】此题考查了解一元二次方程-直接开平方法,比较简单.三、解答题25.解:(1)如图所示:点A 1的坐标(2,﹣4).(2)如图所示,点A 2的坐标(﹣2,4).【解析】试题分析:(1)分别找出A 、B 、C 三点关于x 轴的对称点,再顺次连接,然后根据图形写出A 点坐标.(2)将△A 1B 1C 1中的各点A 1、B 1、C 1绕原点O 旋转180°后,得到相应的对应点A 2、B 2、C 2,连接各对应点即得△A 2B 2C 2.26.(1)详见解析;(2)90【分析】(1)证△DOE ≌△BOF (ASA ),得DE=BF ,即可得出结论;(2)由∠DOE=90°,得EF ⊥BD ,即可得出结论.【详解】(1)∵四边形ABCD 是平行四边形,O 为对角线BD 的中点,∴BO =DO ,AD ∥BC ,∴∠EDO =∠FBO ,在△EOD 和△FOB 中,EDO FBO DO BO EOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DOE ≌△BOF (ASA ),∴DE =BF ,又∵DE ∥BF ,∴四边形BFDE 为平行四边形;(2)∠DOE =90°时,四边形BFDE 为菱形;理由如下:由(1)得:四边形BFDE是平行四边形,若∠DOE=90°,则EF⊥BD,∴四边形BFDE为菱形;故答案为:90.【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质以及菱形的判定等知识,证出△DOE≌△BOF是解题的关键.27.(1)50;(2)8,5;(3)108°;(4)240人.【分析】(1)从表格和统计图中可以得到喜欢“小品”的人数为12人,占调查人数的24%,可求出调查人数,(2)舞蹈占50人的16%可以求出a的值,进而从总人数中减去其他组的人数得到b的值,(3)先计算“歌曲”所占的百分比,用360°去乘即可,(4)样本估计总体,用样本喜欢“相声”的百分比估计总体的百分比,进而求出人数.【详解】(1)12÷24%=50人故答案为50.(2)a=50×16%=8人,b=50﹣15﹣8﹣12﹣10=5人,故答案为:8,5.(3)360°×1550=108°答:“歌曲”所在扇形的圆心角的度数为108°;(4)1200×1050=240人答:该校1200名学生中最喜爱“相声”的学生大约有240人.【点睛】考查扇形统计图、频数统计表的制作方法,明确统计图表中的各个数据之间的关系是解决问题的关键.28.(1)(3,8);(15,0);(2)t=7;(3)能,t=5.【分析】(1)根据点B、C的坐标求出AB、OA、OC,然后根据路程=速度×时间求出AM、CN,再求出ON,然后写出点M、N的坐标即可;(2)根据有一个角是直角的平行四边形是矩形,当AM=ON时,四边形OAMN是矩形,然后列出方程求解即可;(3)先求出四边形MNCB是平行四边形的t值,并求出CN的长度,然后过点B作BC⊥OC于D,得到四边形OABD是矩形,根据矩形的对边相等可得OD=AB,BD=OA,然后求出CD,再利用勾股定理列式求出BC,然后根据邻边相等的平行四边形是菱形进行验证.【详解】解:(1)∵B(15,8),C(21,0),∴AB=15,OA=8,OC=21,当t=3时,AM=1×3=3,CN=2×3=6,∴ON=OC-CN=21﹣6=15,∴点M(3,8),N(15,0);故答案为:(3,8);(15,0);(2)当四边形OAMN是矩形时,AM=ON,∴t=21-2t,解得t=7秒,故t=7秒时,四边形OAMN是矩形;(3)存在t=5秒时,四边形MNCB能否为菱形.理由如下:四边形MNCB是平行四边形时,BM=CN,∴15-t=2t,解得:t=5秒,此时CN=5×2=10,过点B作BD⊥OC于D,则四边形OABD是矩形,∴OD=AB=15,BD=OA=8,CD=OC-OD=21-15=6,在Rt△BCD中,BC=22=10,BD CD∴BC=CN,∴平行四边形MNCB是菱形,故,存在t=5秒时,四边形MNCB为菱形.【点睛】本题主要考查了四边形综合以及矩形的性质,平行四边形与菱形的关系,梯形的问题、勾股定理等知识,根据矩形、菱形与平行四边形的联系列出方程是解题的关键.29.(1)k=1;(2)证明见解析.【分析】(1)把x=1代入方程,即可求得k的值;(2)求出根的判别式是非负数即可.【详解】(1)把x =1代入方程x 2﹣(k +3)x +3k =0得1﹣(k ﹣3)+3k =0,1﹣k ﹣3+3k =0解得k =1;(2)证明:1,(3),3a b k c k ==-+=24b ac ∆=-∴ △=(k +3)2﹣4•3k =(k ﹣3)2≥0,所以不论k 取何实数,该方程总有两个实数根.【点睛】本题考查了一元二次方程的解以及根的判别式,熟练掌握相关知识点是解题关键.30.-1【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】去分母得:(x+2)2-4=x 2-4,解得:x=-1,经检验x=-1是分式方程的解.【点睛】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.31.(1)③;(2)①16,0.2;②见解析【分析】(1)若要从全年级学生中抽取一个40人的样本,在全年级10个班中各随机抽取4名学生比较合理,所以可得出答案;(2)①用40减去A 类,C 类和D 类的频数,即可得到m 值,用C 类的频数除以40即可得到n 值;②根据频数分布表画出扇形统计图即可.【详解】(1)若要从全年级学生中抽取一个40人的样本,在全年级10个班中各随机抽取4名学生比较合理,故答案为:③;(2)①m=40-12-8-4=16, n=840=0.2; ②扇形统计图如下:.【点睛】本题考查了数据的整理和应用,由图表获取数据是解题关键.32.(1)200;(2)图见解析;(3)144;(4)6 500人【分析】(1)用阅读时长在“6小时及以上”的人数除以对应百分比即可计算;(2)先根据统计图中的数据求出课外阅读时长在“2~4小时”和“4~6小时”的人数,然后补全条形统计图即可;(3)用360°乘以课外阅读时长“4~6小时”对应的百分比即可求出;(4)用初中生总数乘以一周课外阅读时长不少于4小时的百分比即可.【详解】(1)本次调查共随机抽取了:50÷25%=200(名);(2)课外阅读时长“2~4小时”的有:200×20%=40(人),课外阅读时长“4~6小时”的有:200-30-40-50=80(人),故条形统计图如下:;(3)阅读时长在“2小时以内”的人数所占的百分比为:30÷200×100%=15%,课外阅读时长“4~6小时”对应的圆心角度数为:360°×(1-20%-25%-15%)=144°;(4)10000×(1-20%-15%)=6500(人).【点睛】本题考查了扇形统计图和条形统计图的结合,由图表获取数据是解题关键.33.(1)见解析 (2)(3,4)【分析】(1)根据网格结构找出点A 、C 绕点B 顺时针旋转90°后的对应点A 1、C 1的位置,然后顺次连接即可;(2)根据旋转的性质,确定出旋转中心即可.【详解】解:(1)三角形的旋转可以分开看作每条边的旋转,分别找到对应的点,连接即可,故△A 1BC 1如图所示;(2)连接'AA 并作其垂直平分线,连接'CC 并作其垂直平分线,交点即为旋转中心.如图所示,旋转中心为(3,4),故答案为(3,4).【点睛】本题考查了利用旋转变换作图,熟练掌握网格结构以及旋转的性质,准确找出对应点的位置是解题的关键.34.人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.【分析】根据在这几种灯中,每种灯时间的长短,即可得出答案.【详解】因为绿灯持续的时间最长,黄灯持续的时间最短,所以人或车随意经过该路口时,遇到绿灯的可能性最大,遇到黄灯的可能性最小.【点睛】本题考查了事件发生的可能性的大小,根据时间长短确定可能性的大小是解答的关键.35.(1)详见解析;(2)2180αβ+=︒,证明见解析.【分析】(1)如图,分别取AB 、AC 的中点M 、N ,连接DM 、PM 、PN 、NE ,根据三角形的中位线定理和直角三角形的性质可得PM NE =,DM PN =,根据等腰三角形的性质、三角形的外角性质和已知条件可得BMD CNE ∠=∠,根据平行线的性质可得BMP BAC ∠=∠=CNP ∠,进而可得DMP PNE ∠=∠,于是可根据SAS 证明MDP NPE ∆≅∆,从而可得结论;(2)根据平行线的性质可得BMP MPN ∠=∠,根据全等三角形的性质可得。
(完整版)苏科版八年级数学下册期中试卷及答案doc

(完整版)苏科版八年级数学下册期中试卷及答案doc一、选择题1.如图,点E ,F ,G ,H 分别为四边形ABCD 四条边AB 、BC 、CD 、DA 的中点,则关于四边形EFGH ,下列说法正确的是( )A .不是平行四边形B .不是中心对称图形C .一定是中心对称图形D .当AC =BD 时,它为矩形2.为了解2019年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是( ) A .2016年泰兴市八年级学生是总体 B .每一名八年级学生是个体 C .500名八年级学生是总体的一个样本 D .样本容量是5003.如图,在四边形ABCD 中,//AB CD ,要使四边形ABCD 是平行四边形,下列可添加的条件不正确的是( )A .AB CD =B .//AD BCC .A C ∠∠=D .AD BC =4.下列调查中,适合采用普查的是( ) A .了解一批电视机的使用寿命 B .了解全省学生的家庭1周内丢弃塑料袋的数量C .为保证某种新研发的战斗机试飞成功,对其零部件进行检查D .了解扬州市中学生的近视率5.下面图形中,既是中心对称图形又是轴对称图形的是( ) A .B .C .D .6.把下列英文字母看成图形,既是轴对称图形又是中心对称图形的是( ) A .B .C .D .7.在□ ABCD 中,∠A =4∠D ,则∠C 的大小是( ) A .36°B .45°C .120°D .144°8.甲、乙、丙、丁四位同学在这一学期4次数学测试中平均成绩都是95分,方差分别是2.2 S=甲, 1.8S=乙, 3.3S=丙,S a=丁,a是整数,且使得关于x的方程2(2)410a x x-+-=有两个不相等的实数根,若丁同学的成绩最稳定,则a的取值可以是()A.3B.2C.1D.1-9.要反应一周气温的变化情况,宜采用()A.统计表B.条形统计图C.扇形统计图D.折线统计图10.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA 并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是()A.9m B.12m C.8m D.10m二、填空题11.不透明的袋子里装有6只红球,1只白球,这些球除颜色外都相同.搅匀后从中任意摸出1只球.摸出的是红球的可能性_____摸出的是白球的可能性(填“大于”、“小于”或“等于”).12.小明用a元钱去购买某种练习本.这种练习本原价每本b元(b>1),现在每本降价1元,则他现在可以购买到这种练习本的本数为_____.13.若分式x3x3--的值为零,则x=______.14.计算326⨯的结果是_____.15.如图,△ABC中,∠A=60°,∠ABC=80°,将△ABC绕点B逆时针旋转,得到△DBE,若DE∥BC,则旋转的最小度数为_____.16.若关于x的一元二次方程x2+(2k+4)x+k2=0没有实数根,则k的取值范围是_____.17.如图,点A是一次函数13y x=(0)x≥图像上一点,过点A作x轴的垂线l,点B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数kyx=(0)x>的图像过点B、C,若OAB∆的面积为8,则ABC∆的面积是_________.18.根据某商场2019年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为800万元,则该商场全年的营业额为________万元.19.一个不透明袋子中装有3个红球,2个白球,1个蓝球,从中任意摸一球,则摸到_____(颜色)球的可能性最大.20.若关于x的一元二次方程2410kx x++=有实数根,则k的取值范围是_______.三、解答题21.一粒木质中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平滑的.将它从定高度下掷,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下.由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如表:试验次数20406080100120140160“帅”字面朝上频数a18384752667888相应频率0.70.450.630.590.520.550.56b=;=;(2)画出“帅”字面朝上的频率分布折线图;(3)如图实验数据,实验继续进行下去,根据上表的这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?22.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.(1)求证:四边形DEBF是平行四边形;(2)当DE=DF时,求EF的长.23.正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.24.已知关于x的方程x2﹣(k+3)x+3k=0.(1)若该方程的一个根为1,求k 的值;(2)求证:不论k 取何实数,该方程总有两个实数根.25.先化简,再求代数式(1﹣32x +)÷212x x -+的值,其中x =4.26.如图,已知一次函数y =x +2的图象与x 轴、y 轴分别交于点A ,B 两点,且与反比例函数y =mx的图象在第一象限交于点C ,CD ⊥x 轴于点D ,且OA =OD . (1)求点A 的坐标和m 的值;(2)点P 是反比例函数y =mx在第一象限的图象上的动点,若S △CDP =2,求点P 的坐标.27.阅读下列材料:已知:实数x 、y 满足22320.25x xy x x +=++(0.75)x ≠-,求y 的最大值. 解:将原等式转化成x 的方程,得21(3)(2)04y x y x y -+-+=①. 若3y =,代入①得0.75x =-,0.75x ≠-,3y ∴≠,因此①必为一元二次方程.21(2)4(3)404y y y y ∴∆=---⨯=-+≥,解得4y ≤,即y 的最大值为4. 根据材料给你的启示,解决下面问题:已知实数x 、y 满足223221x x y x x ++=++15x ⎛⎫≠- ⎪⎝⎭,求y 的最小值.28.已知ABC ∆是边长为8cm 的等边三角形,动点,P Q 同时出发,分别在三角形的边或延长线上运动,他们的运动时间为()t s .()1如图1,若P 点由A 向B 运动,Q 点由C 向A 运动,他们的速度都是1/cm s ,连接PQ .则AP =__,AQ = ,(用含t 式子表示);()2在(1)的条件下,是否存在某一时刻,使得APQ ∆为直角三角形?若存在,请求出t 的值,若不存在,请说明理由;()3如图2,若P 点由A 出发,沿射线AB 方向运动,Q 点由C 出发,沿射线AC 方向运动,P 的速度为3/,cm s Q 的速度为./acm s 是否存在某个a 的值,使得在运动过程中BPO 恒为以BP 为底的等腰三角形?如果存在,请求出这个值,如果不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先连接AC ,BD ,根据EF =HG =12AC ,EH =FG =12BD ,可得四边形EFGH 是平行四边形,当AC ⊥BD 时,∠EFG=90°,此时四边形EFGH 是矩形;当AC=BD 时,EF=FG=GH=HE ,此时四边形EFGH 是菱形,据此进行判断即可. 【详解】连接AC ,BD ,如图:∵点E 、F 、G 、H 分别为四边形ABCD 的四边AB 、BC 、CD 、DA 的中点,∴EF =HG =12AC ,EH =FG =12BD , ∴四边形EFGH 是平行四边形,故选项A 错误; ∴四边形EFGH 一定是中心对称图形,故选项B 错误; 当AC ⊥BD 时,∠EFG =90°,此时四边形EFGH 是矩形,当AC =BD 时,EF =FG =GH =HE ,此时四边形EFGH 是菱形,故选项D 错误; ∴四边形EFGH 可能是轴对称图形,∴四边形EFGH 是平行四边形,四边形EFGH 一定是中心对称图形. 故选:C . 【点睛】本题主要考查了中点四边形的运用,解题时注意:平行四边形是中心对称图形.解决问题的关键是掌握三角形中位线定理.2.D解析:D 【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量. 【详解】A. 2019年泰兴市八年级学生的视力情况是总体,故A 错误;B. 每一名八年级学生的视力情况是个体,故B 错误;C. 从中随机调查了500名学生的视力情况是一个样本,故C 错误;D. 样本容量是500,故D 正确; 故选:D. 【点睛】此题考查总体、个体、样本、样本容量,解题关键在于掌握它们的定义及区别.3.D解析:D 【分析】平行四边形的五种判定方法分别是:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.根据平行四边形的判定,逐个验证即可. 【详解】解:A.∵//AB CD , AB CD∴四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形),故本选项不符合题意;B.∵//AB CD , //AD BC∴四边形ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形),故本选项不符合题意; C.∵//AB CD ∴180C D ∠+∠=︒ ∵A C ∠=∠ ∴180A D +=︒∠∠ ∴//AD BC∴四边形ABCD 是平行四边形(两组对边分别平行的四边形是平行四边形),故本选项不符合题意;D.若添加AD BC =不一定是平行四边形,如图:四边形ABCD 为等腰梯形,故本选项符合题意. 故选:D 【点睛】本题考查了平行四边形的判定,是开放题,可以针对平行四边形的各种判定方法,结合给出相应的条件进行判定.4.C解析:C 【分析】根据调查的实际情况逐项判断即可. 【详解】解:A. 了解一批电视机的使用寿命,调查具有破坏性,适合抽样调查,不合题意; B. 了解全省学生的家庭1周内丢弃塑料袋的数量,调查费时费力,适合抽样调查,不合题意;C. 为保证某种新研发的战斗机试飞成功,对其零部件进行检查,考虑安全性,适合全面调查,符合题意;D. 了解扬州市中学生的近视率,调查费时费力,适合抽样调查,不合题意. 故选:C 【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,事关重大的调查往往选用普查.5.D解析:D根据轴对称图形的定义和中心对称图形的定义对每个选项进行判断即可.【详解】A项是轴对称图形,不是中心对称图形;B项是中心对称图形,不是轴对称图形;C项是中心对称图形,不是轴对称图形;D项是中心对称图形,也是轴对称图形;故选:D.【点睛】本题考查了轴对称图形的定义和中心对称图形的定义,掌握知识点是解题关键.6.C解析:C【解析】解:A.是轴对称图形,不是中心对称图形,故本选项错误;B.既不是轴对称图形,又不是中心对称图形,故本选项错误;C.既是轴对称图形又是中心对称图形,故本选项正确;D.不是轴对称图形,是中心对称图形,故本选项错误.故选C.点睛:本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.D解析:D【解析】【分析】由四边形ABCD是平行四边形可知∠A+∠D=180°,结合∠A=4∠D,可求出∠D的值,从而可求出∠C的大小.【详解】∵四边形ABCD是平行四边形,∴∠A+∠D=180°,∵∠A=4∠D,∴4∠D +∠D=180°,∴∠D=36°,∴∠C=180°-36°=144°.故选D.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边行的性质是解答本题的关键.平行四边形的性质有:平行四边形对边平行且相等;平行四边形对角相等,邻角互补;平行四边形对角线互相平分.8.C【分析】根据方程的根的情况得出a 的取值范围,结合乙同学的成绩最稳定且a 为整数即可得a 得取值. 【详解】∵关于于x 的方程2(2)410a x x -+-=有两个不相等的实数根,∴()=16+42>0,a ∆-且20.a -≠ 解得:>-2a 且 2.a ≠∵丁同学的成绩最稳定, ∴<1.8a 且0a >. 则a=1. 故答案选:C. 【点睛】本题主要考查了方差的意义理解,结合一元二次方程的根的判别式进行求解.9.D解析:D 【分析】反应一周气温的变化情况,即反应一周气温的升高、降低的变化情况,因此采取折线统计图较好. 【详解】解:折线统计图能够直观反应出一组数据的增减变化情况,因此要反应一周的气温变化情况,采用折线统计图较好, 故选:D . 【点晴】本题考查了各种统计图表的特征及应用,掌握统计图表的特征是解题的关键.10.A解析:A 【分析】根据三角形的中位线定理解答即可. 【详解】解:∵A 、B 分别是CD 、CE 的中点,DE =18m , ∴AB =12DE =9m , 故选:A . 【点睛】本题考查了三角形的中位线定理:三角形的中位线平行于第三边并且等于第三边的一半.二、填空题11.大于【分析】分别计算出摸出的是红球和白球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸出1只球.摸出的是红球的概率=,摸出的是白球的概率=,所以摸出的是红球的可能性大于摸出的解析:大于【分析】分别计算出摸出的是红球和白球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸出1只球.摸出的是红球的概率=67, 摸出的是白球的概率=17, 所以摸出的是红球的可能性大于摸出的是白球的可能性.故答案为:大于.【点睛】本题考查的是概率的意义,以及求简单随机事件的概率,掌握以上知识是解题的关键.12.【分析】先由已知条件求出现在每本练习本的单价,再根据“金额÷单价=数量”列出代数式便可.【详解】解:根据题意得,现在每本单价为(b ﹣1)元,则购买到这种练习本的本数为(本),故答案为. 解析:1a b - 【分析】先由已知条件求出现在每本练习本的单价,再根据“金额÷单价=数量”列出代数式便可.【详解】解:根据题意得,现在每本单价为(b ﹣1)元, 则购买到这种练习本的本数为1a b -(本), 故答案为1a b -. 【点睛】本题考查的是列代数式,掌握列代数式的方法是解题的关键.13.-3【分析】分式的值为零:分子等于零,且分母不等于零.【详解】依题意,得|x|-3=0且x-3≠0,解得,x=-3.故答案是:-3.【点睛】考查了分式的值为零的条件.若分式的值为零解析:-3【分析】分式的值为零:分子等于零,且分母不等于零.【详解】依题意,得|x|-3=0且x-3≠0,解得,x=-3.故答案是:-3.【点睛】考查了分式的值为零的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.14.【分析】直接利用二次根式的乘法运算法则计算得出答案.【详解】=2=2×3=6.故答案为:6.【点睛】此题主要考查了二次根式的乘法运算,正确化简二次根式是解题关键.解析:【分析】直接利用二次根式的乘法运算法则计算得出答案.【详解】===.故答案为:.【点睛】此题主要考查了二次根式的乘法运算,正确化简二次根式是解题关键.15.40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点解析:40【分析】根据三角形的内角和和旋转的性质以及平行线的性质即可得到结论.【详解】∵在△ABC中,∠A=60°,∠ABC=80°,∴∠C=180°﹣60°﹣80°=40°,∵将△ABC绕点B逆时针旋转,得到△DBE,∴∠E=∠C=40°,∵DE∥BC,∴∠CBE=∠E=40°,∴旋转的最小度数为40°,故答案为:40°.【点睛】本题主要考查了旋转的性质以及平行线的性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角.16.k<﹣1【分析】根据判别式的意义得到△=(2k+4)2﹣4k2<0,然后解不等式即可.【详解】∵关于x的一元二次方程x2+(2k+4)x+k2=0没有实数根,∴△=(2k+4)2﹣4k2<解析:k<﹣1【分析】根据判别式的意义得到△=(2k +4)2﹣4k 2<0,然后解不等式即可.【详解】∵关于x 的一元二次方程x 2+(2k +4)x +k 2=0没有实数根,∴△=(2k +4)2﹣4k 2<0,解得k <﹣1.故答案为:k <﹣1.【点睛】本题考查了根的判别式:一元二次方程ax 2+bx+c=0(a ≠0)的根与△=b 2-4ac 有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.17.【分析】过作轴于,交于,设,根据直角三角形斜边中线是斜边一半得:,设,则,,因为.都在反比例函数的图象上,列方程可得结论.【详解】如图,过作轴于,交于.∵轴∴,∵是等腰直角三角形, 解析:163 【分析】过C 作CD y ⊥轴于D ,交AB 于E ,设2AB a =,根据直角三角形斜边中线是斜边一半得:BE AE CE a ===,设1,3A x x ⎛⎫ ⎪⎝⎭,则1,23B x x a ⎛⎫+ ⎪⎝⎭,1,3C x a x a ⎛⎫++ ⎪⎝⎭,因为B .C 都在反比例函数的图象上,列方程可得结论.【详解】如图,过C 作CD y ⊥轴于D ,交AB 于E .∵AB x ⊥轴∴CD AB ⊥,∵ABC ∆是等腰直角三角形,∴BE AE CE ==,设2AB a =,则BE AE CE a ===, 设1,3A x x ⎛⎫ ⎪⎝⎭,则1,23B x x a ⎛⎫+ ⎪⎝⎭,1,3C x a x a ⎛⎫++ ⎪⎝⎭, ∵B ,C 在反比例函数的图象上, ∴112()33x x a x a x a ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭, 解得32x a =, ∵112822OAB S AB DE a x ∆=⋅=⋅⋅=, ∴8ax =, ∴2382a =, ∴2163a =, ∵211222ABC S AB CE a a a ∆=⋅=⋅⋅= 163= 故答案为:163. 【点睛】本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积,熟练掌握反比例函数上的点符合反比例函数的关系式是关键.18.000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-解析:000【分析】用1减去其他季度所占的百分比即可得到二季度所占的百分比,再用800除以它所占的百分比,即可求得商场全年的营业额.【详解】解:扇形统计图中二季度所占的百分比=1-35%-25%-20%=20%,∴该商场全年的营业额为:800÷20%=4000(万元),故答案为:4000.【点睛】本题考查了扇形统计图,由统计图得到二季度所占的百分比是解题关键.19.红【分析】分别计算出各球的概率,然后根据概率的大小进行判断.【详解】解:从中任意摸一球,摸到红球的概率==,摸到白球的概率==,摸到蓝球的概率=,所以从中任意摸一球,则摸到红球的可能性最大解析:红【分析】分别计算出各球的概率,然后根据概率的大小进行判断.【详解】 解:从中任意摸一球,摸到红球的概率=3321++=12,摸到白球的概率=26=13,摸到蓝球的概率=16, 所以从中任意摸一球,则摸到红球的可能性最大.故答案为:红.【点睛】本题考查了可能性的大小:某事件的可能性等于所求情况数与总情况数之比.20.且【分析】根据二次项系数非零结合根的判别式△,即可得出关于的一元一次不等式,解之即可得出结论.【详解】解:关于的一元二次方程有实数根,且△,解得:且,故答案为:且.【点睛】本题考查解析:4k ≤且0k ≠【分析】根据二次项系数非零结合根的判别式△0,即可得出关于k 的一元一次不等式,解之即可得出结论.【详解】 解:关于x 的一元二次方程2410kx x ++=有实数根,0k ∴≠且△2440k =-≥,解得:4k ≤且0k ≠,故答案为:4k ≤且0k ≠.【点睛】本题考查了根的判别式以及一元二次方程的定义,牢记“当△0时,方程有实数根”是解题的关键. 三、解答题21.(1)14,0.55;(2)图见解析;(3)0.55.【分析】(1)根据图中给出的数据和频数、频率与总数之间的关系分别求出a 、b 的值; (2)将频率作为纵坐标,试验次数作为横坐标,描点连线,可得折线图.(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,即可估计概率的大小.【详解】(1)a =20×0.7=14;b =88160=0.55; 故答案为:14,0.55;(2)根据图表给出的数据画折线统计图如下:(3)随着试验次数的增加“帅”字面朝上的频率逐渐稳定在0.55左右,利用这个频率来估计概率,得P (“帅”字朝上)=0.55.【点睛】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.作图时应先描点,再连线.用到的知识点为:部分的具体数目=总体数目×相应频率.频率=所求情况数与总情况数之比.22.(1)见解析;(2)152【分析】 (1)由矩形的性质得到AB ∥CD ,再根据平行线的性质得到∠DFO=∠BEO 再证明△DOF ≌△BOE ,根据全等三角形的性质得到DF=BE ,从而得到四边形BEDF 是平行四边形;(2)先证明四边形BEDF 是菱形,再得到DE=BE ,EF ⊥BD ,OE=OF ,设AE=x ,则DE=BE=8-x 根据勾股定理求解即可.【详解】(1)证明:∵四边形ABCD 是矩形,∴AB ∥CD ,∴∠DFO =∠BEO .在△DOF 和△BOE 中DFO BEO DOF BOE OD OB ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△DOF ≌△BOE(AAS ).∴DF =BE .又∵DF ∥BE ,∴四边形BEDF 是平行四边形.(2)解:∵DE =DF ,四边形BEDF 是平行四边形,∴四边形BEDF 是菱形.∴DE =BE ,EF ⊥BD ,OE =OF .设AE =x ,则DE =BE =8-x ,在Rt △ADE 中,根据勾股定理,有AE 2+AD 2=DE 2,∴x 2+62=(8-x)2.解得x =74. ∴DE =8-74=254. 在Rt △ABD 中,根据勾股定理,有AB 2+AD 2=BD 2,∴BD=10.∴OD =12BD =5. 在Rt △DOE 中,根据勾股定理,有DE 2-OD 2=OE 2,∴OE=154. ∴EF =2OE =152. 【点睛】考查了菱形的判定和性质、矩形的性质、平行四边形的判定和性质、全等三角形的判定和性质和勾股定理,解题关键是熟练掌握矩形的性质.23.(1)AP=EF,AP⊥EF,理由见解析;(2)仍成立,理由见解析;(3)仍成立,理由见解析;【解析】【分析】(1)正方形中容易证明∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,利用AAS证明△AMO≌△FOE.(2) (3)按照(1)中的证明方法证明△AMP≌△FPE(SAS),结论依然成立.【详解】解:(1)AP=EF,AP⊥EF,理由如下:连接AC,则AC必过点O,延长FO交AB于M;∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,∴四边形OECF是正方形,∴OM=OF=OE=AM,∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,∴△AMO≌△FOE(AAS),∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,故AP=EF,且AP⊥EF.(2)题(1)的结论仍然成立,理由如下:延长AP交BC于N,延长FP交AB于M;∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,∴四边形MBEP是正方形,∴MP=PE,∠AMP=∠FPE=90°;又∵AB﹣BM=AM,BC﹣BE=EC=PF,且AB=BC,BM=BE,∴AM=PF,∴△AMP≌△FPE(SAS),∴AP=EF,∠APM=∠FPN=∠PEF,∵∠PEF+∠PFE=90°,∠FPN=∠PEF,∴∠FPN+∠PFE=90°,即AP⊥EF,故AP=EF,且AP⊥EF.(3)题(1)(2)的结论仍然成立;如右图,延长AB交PF于H,证法与(2)完全相同.【点睛】利用正方形,等腰三角形,菱形等含等边的特殊图形,不管其他条件如何变化,等边作为证明等边三角形的隐含条件,证明三角形的全等,是证明此类问题的关键.24.(1)k=1;(2)证明见解析.【分析】(1)把x=1代入方程,即可求得k的值;(2)求出根的判别式是非负数即可.【详解】(1)把x =1代入方程x 2﹣(k +3)x +3k =0得1﹣(k ﹣3)+3k =0,1﹣k ﹣3+3k =0解得k =1;(2)证明:1,(3),3a b k c k ==-+=24b ac ∆=-∴ △=(k +3)2﹣4•3k =(k ﹣3)2≥0,所以不论k 取何实数,该方程总有两个实数根.【点睛】本题考查了一元二次方程的解以及根的判别式,熟练掌握相关知识点是解题关键.25.11x +;15【分析】首先把括号内的分式进行通分、相减,把除法转化为乘法,即可化简,最后代入数值计算即可.【详解】 解:原式=()()232211x x x x x +-+⋅++- ()()12211x x x x x -+=⋅++- 11x =+ 当x =4时,原式=15. 【点睛】本题主要考查分式的化简求值,解题的关键是熟练掌握分式混合运算顺序和运算法则.26.(1)(-2,0);8 (2)(1,8)或(3,83)【分析】(1)根据待定系数法就可以求出函数的解析式;(2)1||2CDP P C S CD x x =⨯⨯-△,即可求解. 【详解】解:(1)对于一次函数2y x =+,令0x =,则2y =,令0y =,则2x =-, 故点A 、B 的坐标分别为(2,0)-、(0,2), OA OD =,故点(2,0)D ,则点C 的横坐标为2,当2x =时,24y x =+=,故点(2,4)C ,将点C 的坐标代入反比例函数表达式得:42m =, 解得:8m =,故点A 的坐标为(2,0)-,8m =;(2)1142222CDP P C P S CD x x x =⨯⨯-=⨯⨯-=, 解得:3P x =或1,故点P 的坐标为(1,8)或8(3,)3.【点睛】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强. 27.2316【分析】 类比阅读材料给出的方法,分类探讨得出函数的最小值即可.【详解】解:将原等式转化成关于x 的方程,得:2(3)(21)(2)0y x y x y -+-+-=①,若3y =,代入①得15x =-, ∵15x ≠-, ∴3y ≠,因此①必为一元二次方程.∵3a y =-,21b y =-,2c y =+,∴224(21)4(3)(2)0b ac y y y ∆=-=----≥, 解得:2316y ≥且3y ≠. ∴y 的最小值为2316. 【点睛】 本题考查了根的判别式的运用,把函数转化为关于x 的方程,根据系数的取值范围,结合根的判别式,分类探讨得出答案即可.28.(1)(),6AP tcm AQ t cm ==-;(2)存在,8163t s s=或;(3)存在, 3/a cm s =.【分析】(1)根据路程=时间×速度,即可表示出来(2)要讨论PA AB ⊥,PQ AC ⊥两种情况,即可求出对应的时间(3)根据BPQ ∆以BP 为底的等腰三角形,作QM BP ⊥于M ,用a ,t 的代数式表示出AP ,CQ ,AQ ,BP 等边长,再根据ABC ∆是等边三角形,求出30AQM ︒∠=,从而得出2AQ AM =,讨论P 在线段AB 内运动和P 在AB 外运动两种情况,即可求出结果.【详解】解:()1由题意可知:(),,6AP tcm CQ tcm AQ t cm ===-()2存在8163t s s =或时,使得APQ ∆为直角三角形,理由是 ①当PA AB ⊥时,由题意有28t t =-,解得83t s = ②当PQ AC ⊥时,由题意有()8,2t t =-解得163t s = ∴综上所述,存在8163t s s=或时,使得APQ ∆为直角三角形 ()3存在3/a cm s =时,BPQ ∆恒为以BP 为底的等腰三角形,理由是:作QM BP ⊥于M ,如图2所示由题意得:3,AP t CQ at ==,则8,83AQ at BP t =+=-,PQ BQ QM BP =⊥12PM BM BP ∴==ABC∆是等边三角形,60A︒∴∠=30AQM︒∴∠=2AQ AM∴=,①当83t≤时,由题意有832382tt at-⎛⎫+=+⎪⎝⎭,解得3/a cm s=,②当83t≥时,由题意有382382tt at-⎛⎫-=+⎪⎝⎭,解得3/a cm s=,∴综上所述,存在3/a cm s=时,BPQ∆恒为以BP为底的等腰三角形.【点睛】本题主要考察了直角三角形,等腰三角形,动点等知识点,记住它们的常用性质和把动点问题转换成代数式求解问题是解题关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 填空题(
1. 用科学记数法表示0.000043为 。
2.计算:()=⎪⎭⎫ ⎝⎛+--10311 ; 232()3y x
=__________; 3.当x 时,分式
51-x 有意义; 当x 时,分式1
1x 2+-x 的值为零。
4.反比例函数x
m y 1-=
的图象在第一、三象限,则m 的取值范围是 ;在每一象限内y 随x 的增大而 。
5. 如果反比例函数x m y =过A (2,-3),则m= 。
6.若平行四边形ABCD 的周长为48cm,AB=8cm, 则BC= cm 。
点A (x 1,y 1)和B (x 2,y 2),且当x 1<0<x 2时,有y 1<y 2,则7. 设反比例函数y=3m x
-的图象上有两m 的取值范围是 . 8.如图由于台风的影响,一棵树在离地面
m 6处折断,树顶落在离树干底部m 8处,则这棵树在折断前(不
包括树根)长度是 .
9. 三角形的两边长分别为3和5,要使这个三角形是直角三角
形,则第三条边长是 .
10.
如图若正方形ABCD 的边长是4,BE=1,在AC
上找一使PE+PB 的值最小,则最小值为 。
二.单项选择题
11.在式子1a 、2xy π、2334
a b c 、56x +、78x y +、109x y +中,分式的个数有( ) A 、2个 B 、3个 C 、4个 D 、5个
12.下面正确的命题中,其逆命题不成立的是( )
A.同旁内角互补,两直线平行
B.全等三角形的对应边相等
12
-3-210-13A C.角平分线上的点到这个角的两边的距离相等 D.对顶角相等
13.下列各组数中,以a 、b 、c 为边的三角形不是直角三角形的是( )
A . 1.5,2,3a b c ===
B . 7,24,25a b c ===
C . 6,8,10a b c === D. 3,4,5a b c ===
14.在同一直角坐标系中,函数y=kx+k 与(0)k
y k x =≠的图像大致是( )
15.如图所示:数轴上点A 所表示的数为a ,则a 的值是( ) A 5 B .5 C 5 D 5
16.如图,已知矩形ABCD 沿着直线BD 折叠,使点C 落在C /处,BC /交AD 于E ,AD =8,AB =4,则DE 的长为(
).
A .3
B .4
C .5
D .6
三、解答题:
17.(8分)计算: (1)x y y x y x ---2
2
(2)221
11a a a
a a ++---
18.(6分)先化简代数式112111
2-÷⎪⎭⎫ ⎝⎛+-+-+a a
a a a a ,然后选取一个使原式有意义的a 的值代入求值.
/ 2mm
19.(8分)解方程:
\ (1)
1233x x x =+-- (2)482222-=-+-+x x x x x
20.(6分)已知:如图,四边形ABCD ,AB=8,BC=6,CD=26,AD=24,且AB ⊥BC 。
求:四边形ABCD 的面积。
21. (6分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度)(m y 是面条的粗细(横截面积))(2mm x 的反比例函数,其图像如图所示. (1)写出y 与x 的函数关系式;
(2)当面条的总长度为50m 时,面条的粗细为多少?
(3)若当面条的粗细应不小于26.1mm ,面条的总长度最长是多少?
D
22. (8分) 列方程解应用题:(本小题8分)
某一工程进行招标时,接到了甲、乙两个工程队的投标书,施工1天需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
方案(1):甲工程队单独完成这项工程,刚好如期完成;
方案(2):乙工程队单独完成这项工程,要比规定日期多5天;
方案(3):若甲、乙两队合作4天,余下的工程由乙工程队单独做,也正好如期完成;
在不耽误工期的情况下,你觉得哪种方案最省钱?请说明理由。
23.(10分)已知反比例函数x k y =图象过第二象限内的点A (-2,m )AB ⊥x 轴于B ,Rt △AOB 面积为3, 若直线y=ax+b 经过点A ,并且经过反比例函数x k y =的图象上另一点C (n ,—23), (1) 反比例函数的解析式为 ,m= ,n= ;
(2) 求直线y=ax+b 的解析式;
(3) 在y 轴上是否存在一点P ,使△PAO 为等腰三角形,若存在,请直接写出P 点坐标,若不存在,说明理由。
(4) 求△AOC 的面积。
参考答案
一.1.4.3×10-5 2.4; 36278x y ; 1; 21
y 3.≠5 ; =1 4.m>1;减小 5.-6 6. m<3
7.16 8. 4或34
9.5 10. 320
二.11.B 12.D 13.A 14.C 15.C 16.C
三.17. (1)解:原式=x y y x --2
2 …1分 (2) 解:原式=)1)(1()
1(11
-++--+a a a a a a …..1分 =x y y x y x -+-)
)((……2分 =111
---+a a
a a ……………….2分
=)())((y x y x y x --+-…....3分 =1
1--+a a a ……………………3分 =-x-y …………………4分 =
11-a ………………………4分 18.(6分)解:原式=a a a a a 1.)1(1112-⎪⎪⎭
⎫ ⎝⎛-+-+…………………1分 =a a a a a a 1.)1(1)1()1)(1(22-⎪⎪⎭⎫ ⎝
⎛-+--+…2分 =a a a a 1.)1(1122--+-…3分=1-a a …4分 选一个数代入计算…………………….………6分
19.(8分)解方程:
(1)解:3
231--=-x x x …1分(2)解:)2)(2(8222-+=-+-+x x x x x x …1分 两边同时乘以(x-3)得 两边同时乘以(x+2)(x-2)得
1=2(x-3)-x ………..2分 x(x-2)-2)2(+x =8……..2分
解得x=7 ………...…..3分 解得x=-2.....3分
经检验x=7是原方程的解…..4分 经检验 x=-2不是原方程的解,所以原方程无解…..4分
20.解:连接AC ,∵AB ⊥BC ,∴∠B=90°………………1分
∴AC=
22BC AB +=2268+=10………………….…2分 ∵222222266762410CD AD AC ===+=+………3分
∴⊿ACD 为直角三角形……………………………..………4分
∴四边形ABCD 的面积=ACD ABC S S +=10242
18621⨯⨯+⨯⨯=144………6分 21. (6分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度)(m y 是面条的粗细(横截面积))(2
mm x 的反比例函数,其图像如图所示. (1)x
y 128=
….…2分 (2)当y=50时,x
12850= x=2.56∴面条的粗细为2.562mm ………….…4分 (3)当x=1.6时, 806.1128==y ∴当面条的粗细不小于26.1mm ,面条的总长度最长是80m …6分 22.解:在不耽误工期的情况下,我觉得方案(3)最省钱。
…………1分
理由:设规定日期为x 天,则甲工程队单独完成这项工程需x 天,乙工程队单独完成这项工程需(x+5)天,依题意列方程得:
15
4=++x x x …………4分 解得x=20…………5分
经检验x=20是原方程的解…………6分 x+5=20+5=25
方案(1)所需工程款为:1.5×20=30万元
方案(2)所需工程款为:1.1×25=27.5万元
方案(3)所需工程款为:1.5×4+1.1×20=28万元
∴在不耽误工期的情况下,我觉得方案(3)最省钱…………8分
23.(1)x y 6-=;m=3; n=4….……3分(2)2
343+-=x y …………6分 (3)答:存在点P 使△PAO 为等腰三角形;
点P 坐标分别为:
P 1; P 2(0,6); P 3(0,; P 4(0,6
13) ……10分。
