第11章主成分和因子分析

合集下载

管理统计SPASS第11章主成分分析与因子分析资料

主成分的计算流程
步骤三：
按如下方法得到主成分 Yi ：
Y1 b1T X ,Y2 b2T X ,,Yk bkT X
பைடு நூலகம்
式中，X ( X1, X 2 ,, X k )T 。
Yi (i 1,, k) 是相互正交的综合变量。将k个主成分放到一
起可得矩阵表达式： Y BT X
Y1 b11 b1k X1
简记为
Y AX
向量 Y 满足如下条件：
指标 Yi 之间不相关。
方差尽可能大，即对 n 个对象的分辨率尽可能强，信息损
失尽可能的少。
主成分分析小结：
(1)从相关的多个指标 X1, X 2 ,, X k 中，求出相互独立的多个指标 Y1,Y2 ,,Yk 。
(2) Y (Y1,Y2 ,,Yk )T 的方差信息不损失，尽可能等同于 X ( X1, X 2 ,, X k )T 的方差。
Yk bk1 bkk X k
主成分的计算流程
主成分更为明晰的表达式：
Y1 b11X1 b21 X 2 bk1 X k Y2 b12 X1 b22 X 2 bk 2 X k
Yk bk1 X 1 bk 2 X 2 bkk X k
主成分的计算流程
结语：
X 与 Y 的转换关系为：
Y1 a11 a1k X 1
Yk ak1 akk X k
几何解释
在下图 X1 O X 2 的坐标中，散点大致为椭圆状。经过线性变换可以得到新的坐标 Y1 O Y2 。Y1 在椭圆的长轴上，反映出了散点在这个方向的最大方差。 Y2 在椭圆的短轴上，反映出了散点在这个方向的方差。
X2
Y2
X1
Y1
主成分的计算流程

多元分析：主成分分析与因子分析

第十一章多元分析：主成分分析与因子分析引言主成分分析和因子分析在多元分析框架内是数据结构分析技术，与第六章的多元回归、第七章的多变量协整一起是多变量分析中广泛使用的技术。

它们不同于多元回归。

回归的目标是识别外生变量与内生变量的关系，而在主成分分析和因子分析情形下，仅确定内生变量间的结构关系。

它们也不像协整，变量间不需要平稳性。

在金融、社会科学或其它领域，通常需要识别多变量结构的特征，其有两个特征是被子广泛关心的：1．多变量结构中的波动性。

2．变量间的相关或共线性。

在结构的整体变化中，通常是一些变量起产生主要的影响，而其它变量仅有次要的或不显著的影响。

困难的是要了解哪些变量能被确定在这个结构中和它在结构中应怎样度量。

例如，如果两个变量是完全相关的，则不需要第二个变量，它不会带来进一步的信息。

这类似多元回归的共线问题。

在一般情况下，包含哪个变量，剔除哪个变量并不是很清楚的，我们需要有能够程序化的有效方法来识别带有最可用信息的变量或变量组合。

主成分分析（PCA ）是分析多变量结构波动时有用的技术。

因子分析（F A ）在分析多变量结构变量的相关时很有用。

两者都依赖于方差/协方差矩阵，因为这个矩阵在一定范围内包含了变量间有用的全部信息。

因此在一定范围内，两者是重复的或相互补充的。

在这章，我们将方差/协方差矩阵记为C 。

尽管PCA 和F A 都利用方差/协方差矩阵，但它们不同于第四章和第九章中的均值—方差分析。

均值—方差分析度量了一组变量的总体变异性，而没有特别指明一部分变量对总变异性的贡献。

PCA 识别和排序了部分变量在总变异性中的贡献,每个部分变量称为“主成分”。

它识别了部分变量间组成的协方差的强度，每个主成分对总的变异性的贡献，并根据部分变量组的方差进行排序。

使用PCA ，数据内的总体变异性由特征值之和（它等于C矩阵主对角线上元素之和，也称为迹）度量，成分（变量的线性组合）的选择是依次序减少特征值，直到满足总变异性的一个足够大的比例。

因子分析、主成分分析

通过主成分分析，可以研究多个变量之间的相关性，揭示变量
之间的内在联系。
多元回归分析
03
在多元回归分析中，主成分分析可以用来消除变量间的多重共
线性，提高回归分析的准确性和稳定性。
金融数据分析
风险评估
在金融数据分析中，主成分分析可以用来评估投资组合的风险，通过提取主要因子来反映市场的整体波动。
市场趋势分析
主成分分析案例：金融数据分析
总结词
主成分分析用于金融数据分析中，能够降低数据维度并揭示主要经济趋势。
VS
详细描述
在金融领域，主成分分析被广泛应用于股票、债券等资产组合的风险评估和优化。通过对大量金融数据进行主成分分析，可以提取出几个关键主成分，这些主成分代表了市场的主要经济趋势。投资者可以利用这些信息进行资产配置和风险管理。
特征提取
主成分分析能够提取出数据中的主要特征，突出数据中的主要变化方向，有助于揭示数据的内在规律。
数据可视化
降低数据维度后，数据的可视化变得更加容易，有助于直观地理解和分析数据。
多元统计
多元数据描述
01
主成分分析可以用来描述多元数据的总体特征，提供对多元数
据分布的整体理解。
多元相关分析
02
目的
通过找出影响观测变量的潜在结构，更好地理解数据的意义，简化复杂数据的分析，并解决诸如多重共线性等问题。
因子分析的原理
1 2 3
基于相关性
因子分析基于观测变量之间的相关性，通过找出这些相关性背后的公因子来解释变量之间的依赖关系。
降维
通过提取公因子，将多个观测变量的复杂关系简化为少数几个潜在因子的线性组合，实现数据的降维。

卫生统计学：主成分分析与因子分析

〔factor loading〕矩阵
通常先对x作标准化处理，使其均值为零，方差为１．这样就有
x i a i1 f1 a i2 f2 a im fm e i
假定〔１〕fi的均数为 i22 ０，方差为１；〔２〕ei的均数为０，方差为δi；〔３〕 fi与ei相互独立．
那么称x为具有m个公共因子的因子模型
〔２〕δi称为特殊方差〔specific variance〕，是不能由公共因子解释的局部
▪ 因子载荷〔负荷〕aij是随机变量xi与公共因子fj的相关系数。
▪设
p
g
2 j
a
2 ij
i1
j 1, 2 ,..., m
▪ 称gj2为公共因子fj对x的“奉献〞，是衡量公共因子fj重要性的一个指标。
根本思想：使公共因子的相对负荷〔lij/hi2〕的方差之和最大，且保持原公共因子的正交性和公共方差总和不变。
可使每个因子上的具有最大载荷的变量数最小，因此可以简化对因子的解释。
〔2〕斜交旋转〔oblique rotation〕
因子斜交旋转后，各因子负荷发生了较大变化，出现了两极分化。各因子间不再相互独立，而彼此相关。各因子对各变量的奉献的总和也发生了改变。
ai2j
g
2 j
i1
▪ 极大似然法〔maximum likelihood factor〕
▪ 假定原变量服从正态分布，公共因子和特殊因子也服从正态分布，构造因子负荷和特殊方差的似然函数，求其极大，得 factor〕
▪ 设原变量的相关矩阵为 R=(rij)，其逆矩阵为R-1=(rij)。各变量特征方差的初始值取为逆相关矩阵对角线元素的倒数， δi’=1/rii。那么共同度的初始值为(hi’) 。

主成分分析和因子分析(朱艳科)

主成分分析和因子分析法一、主成分分析概论主成分分析的工作对象是样本点×定量变量类型的数据表。

它的工作目标，就是要对这种多变量的平面数据表进行最佳综合简化。

也就是说，要在力保数据信息丢失最少的原则下，对高维变量空间进行降维处理。

很显然，识辨系统在一个低维空间要比一个高维空间容易得多。

英国统计学家斯格特（M.Scott ）在1961年对157个英国城镇发展水平进行调查时，原始测量的变量有57个。

而通过主成分分析发现，只需5个新的综合变量（它们是原变量的线性组合），就可以95%的精度表示原数据的变异情况，这样，对问题的研究一下子从57维降到5维。

可以想象，在5维空间中对系统进行任何分析，都比在57维中更加快捷、有效。

另一项十分著名的工作是美国的统计学家斯通(Stone)在1947年关于国民经济的研究。

他曾利用美国1929～1938年各年的数据，得到了17个反映国民收入与支出的变量要素，例如雇主补贴、消费资料和生产资料、纯公共支出、净增库存、股息、利息和外贸平衡等等。

在进行主成分分析后，竟以97.4%的精度，用三个新变量就取代了原17个变量。

根据经济学知识，斯通给这三个新变量要别命名为总收入1F 、总收入变化率2F 和经济发展或衰退的趋势3F （是时间t 的线性项）。

更有意思的是，这三个变量其实都是可以直接测量的。

二、主成分分析的基本思想与理论1、主成分分析的基本思想在对某一事物进行实证研究中，为了更全面、准确地反映出事物的特征及其发展规律，人们往往要考虑与其有关系的多个指标，这些指标在多元统计中也称为变量。

这样就产生了如下问题：一方面人们为了避免遗漏重要的信息而考虑尽可能多的指标，而另一方面随着考虑指标的增多增加了问题的复杂性，同时也由于各指标均是对同一事物的反映，不可避免地造成信息的大量重叠，这种信息有时甚至会抹杀事物的真正特征与内在规律。

基于上述问题，人们就希望在定量研究中涉及的变量较少，而得到的信息量又较多。

主成分分析和因子分析的区别

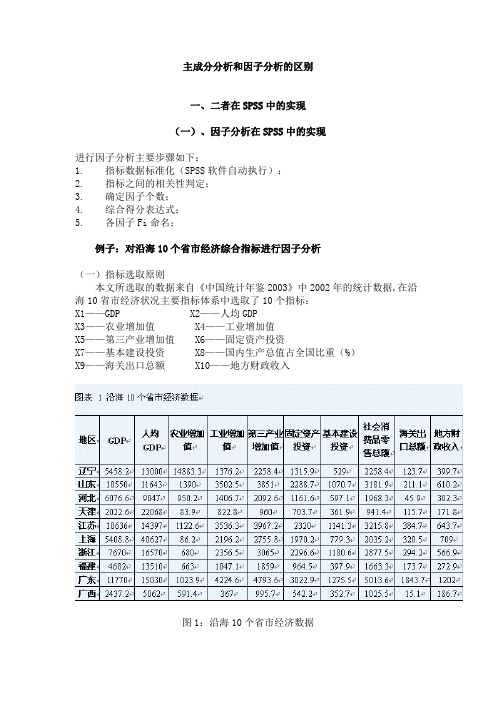
主成分分析和因子分析的区别一、二者在SPSS中的实现（一）、因子分析在SPSS中的实现进行因子分析主要步骤如下：1. 指标数据标准化（SPSS软件自动执行）；2. 指标之间的相关性判定；3. 确定因子个数；4. 综合得分表达式；5. 各因子Fi命名；例子：对沿海10个省市经济综合指标进行因子分析（一）指标选取原则本文所选取的数据来自《中国统计年鉴2003》中2002年的统计数据,在沿海10省市经济状况主要指标体系中选取了10个指标：X1——GDP X2——人均GDPX3——农业增加值X4——工业增加值X5——第三产业增加值X6——固定资产投资X7——基本建设投资X8——国内生产总值占全国比重（%）X9——海关出口总额X10——地方财政收入图1：沿海10个省市经济数据（二）因子分析在SPSS中的具体操作步骤运用SPSS统计分析软件Factor过程[2]对沿海10个省市经济综合指标进行因子分析。

具体操作步骤如下：1. Analyzeà Data Reductionà Factor Analysis，弹出Factor Analysis对话框2. 把X1～X10选入Variables框3. Descriptives: Correlation Matrix框组中选中Coefficients等选项，然后点击Continue，返回Factor Analysis对话框4. 点击“OK”图2：Factor Analyze对话框与Descriptives子对话框SPSS在调用Factor Analyze过程进行分析时，SPSS会自动对原始数据进行标准化处理，所以在得到计算结果后指的变量都是指经过标准化处理后的变量，但SPSS不会直接给出标准化后的数据，如需要得到标准化数据，则需调用Descriptives过程进行计算。

我们可以通过Analyze-Descriptive Statistics- Descriptives对话框来实现：弹出Descriptives对话框后，把X1～X10选入Variables框，在Save standardized values as variables前的方框打上钩，点击“OK”，经标准化的数据会自动填入数据窗口中，并以Z开头命名。

主成分分析与因子分析法

主成分分析与因子分析法主成分分析是一种减少数据维度的统计学方法，通过将多变量数据投影到一个较低维度的空间中，实现数据的降维。

主成分分析的基本思想是将原始数据转换为一组新的变量，这些新的变量称为主成分，通过主成分的降序排列，能够使原始数据中较大方差的信息更好地保留下来。

1.数据标准化：根据数据的特点，将数据进行标准化处理，使得各个变量具有相同的尺度。

2.计算协方差矩阵：通过计算数据的协方差矩阵，了解各个变量之间的相关性。

3.求解特征向量和特征值：通过对协方差矩阵进行特征值分解，得到特征向量和特征值。

4.选择主成分：选取前k个特征向量对应的主成分，使得它们能够解释绝大部分的方差。

通常选择的标准是特征值大于1，或者解释方差的累积比例达到一定的阈值。

5.主成分系数：计算原始变量和主成分之间的线性关系，这个关系可以用主成分的特征向量作为系数矩阵进行表示。

1.降低维度：主成分分析能够将高维数据降维，提取出最能代表原始数据的主成分。

2.去除冗余信息：通过选择主成分，可以去除原始数据中的冗余信息，提取出最有用的信息。

3.可视化：降维后的数据可以更容易地可视化和解释。

二、因子分析法（Factor Analysis）因子分析法是一种用于确定多个观测变量之间的潜在结构的统计学方法。

它假设观测变量是由一组潜在因子决定的，通过观测变量和因子之间的相关性，可以推断出潜在因子之间的关系。

因子分析法的基本步骤如下：1.确定因子数：根据研究的目的和背景，确定潜在因子的个数。

2.求解因子载荷矩阵：通过最大似然估计或主因子方法，求解因子载荷矩阵，得到每个观测变量与潜在因子之间的相关关系。

3.提取因子：根据因子载荷矩阵，提取出与观测变量相关性最高的因子，将原始数据映射到潜在因子空间中。

4.旋转因子：通过旋转因子载荷矩阵，使得因子之间更易解释和解读，常用的旋转方法有正交旋转和斜交旋转。

5.因子得分：根据观测变量的信息和因子载荷矩阵，计算每个样本在每个因子上的得分。

第章主成分分析和因子分析习题答案

-.192
.707
X8
-.066
.575
.090
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
a Rotation converged in 5 iterations.
28
61
65
81
98
94
95
29
79
95
83
89
89
79
30
81
90
79
73
85
80
31
85
77
75
52
73
59
32
68
85
70
84
89
86
33
85
91
95
63
76
66
34
91
85
100
70
65
76
35
74
74
84
61
80
69
36
88
100
85
49
71
66
37
63
82
66
89
78
80
38
87
84
100
55.043
43.677
中国石油
33.441
19.900
0.735
0.923
28.068
1.043
42.682
45.593
广聚能源
6.790
15.650
0.441

主成分分析与因子分析

在实际工作中，为了全面的分析问题，往往会收集很多变量，这些变量之间通常都会存在大量重复信息，如果直接用来分析，不但计算繁琐，模型复杂，而且还有一个更严重的问题就是共线性问题，前面提到过共线性问题会导致模型误差增大，失去意义。

当面对变量过多时，通常的处理方法是降维，即设法将原来众多具有一定相关性的变量，重新组合成一组新的互相无关的综合变量，这些综合变量要尽可能多的反映原有变量的信息。

降维的方法有很多，其中最常用的就是主成分分析和因子分析一、主成分分析(Principal Component Analysis，PCA)1.基本思路设有n个原始变量，如果将它们都用散点图表示，会发现一些变量是存在某种线性关系的，这就是共线性，我们可以利用这个特点，创建一个变量Yi，使它成为某些原始变量的线性组合结果Yi =β+β1x1+...βnxn，这样处理之后，n个原始变量就转化为i个新变量，这i个新变量不同程度的反映了原始变量的信息，并且互不相关，这就解决了共线性问题。

那么接下来的问题是，n个变量的线性组合有很多种，我们取哪种结果作为新变量呢？经典的方法就是根据方差来判断，方差越大，变异越大，而我们的目的并不是消除变异，而是用尽可能少的新变量表示大部分原始变量，因此变异信息也必须尽量完整的反映。

我们将新变量按照方差大小排序，最大者也就是包含变异最多的为第一主成分，以此类推，通常只取前面几个最大的主成分，这样虽然损失部分信息，但是抓住了主要变异，如果全都取的话是没有意义的，因为原则上有多少个原始变量，就可以提取多少个主成分，但是这样做违背了降维的目的，多数情况下，取钱2-3个主成分就可以代表90%以上的变异信息，其余的可以忽略不计。

2.计算过程前面讲了PCA的基本思路，现在用具体数学算法来加以实现<1>数据标准化由于每个变量都有自己的数量级和量纲，首先要对变量进行标准化处理以消除这方面的差异<2>计算协方差矩阵或相关系数矩阵对于一维数据，也就是一个变量的数据，我们可以用均值、方差、标准差来描述，而协方差用于衡量两个变量的总体误差，如果多于两个变量，那就要用协方差矩阵来表示。

主成分分析与因子分析

主成分分析与因⼦分析主成分分析，主成份是原始变量的线性组合，在考虑所有主成份的情况下主成份和原始变量间是可以逆转的。

即“简化变量”，将变量以不同的系数合起来，得到好⼏个复合变量，然后在从中挑⼏个能表⽰整体的复合变量就是主成份，然后计算得分。

因⼦分析，公共因⼦和原始变量的关系是不可逆转的，但是可以通过回归得到。

是将变量拆开，分成公共因⼦和特殊因⼦。

过程是：因⼦载荷计算，因⼦旋转，因⼦得分。

主成份分析主成份分析需要知道两变量之间的相关性，⽣成协⽅差举证和相关新矩阵，对应的⽣成的新向量矩阵Y还有特征值λi，对应是第I个新向量对总体信息的贡献率为λi/(λ1+λ2+...+λn),对应的还有⼀个累积贡献率。

确定主成份的个数的⽅法有：特征值⼤于1（要求原始数据的每⼀个变量⾄少能贡献1各单位的变异）、陡坡检验法（陡坡图中开始平坦的点之前的点的个数）、累积解释变异⽐例法（即（λ1+...+λi）/(λ1+λ2+...+λn)>70%）。

同时也可以知道主成分分析对应的⼏个难点①是使⽤协⽅差矩阵还是相关系数矩阵②如何确定主成份的个数。

当数据中不同变量的度量单位不同并且数值相差较⼤就⽤标准化后的相关系数矩阵，当数值相差不⼤并且指标的权重不⼀样时，考虑⽤协⽅差矩阵。

对于个数的确定就是我们⼀些边界问题是否1左右的也可以囊括进主成份中，是否难以确定开始变平坦的是那个点，是否70%不够。

等⼏个问题。

主成分分析可以⽤两个过程步完成PROC FACTORS 、PROC PRINCOMP。

后者能处理的数据量⼤⼀些，效率⾼⼀些，，前者输出的内容丰富些，还可以做旋转因⼦。

以下是主成分分析过程；proc princomp data=sashelp.cars out=car_component;var mpg_city mpg_highway weight wheelbase length;run;输出结果：先是输出统计结果，再是输出相关性矩阵，这⾥princomp步默认使⽤的是相关系数矩阵，实际应⽤过程中，可以通过cov选项来指定使⽤的矩阵。

因子分析与主成分分析的区别与应用

因子分析与主成分分析的区别与应用因子分析与主成分分析是统计学中常用的多变量分析方法，用于降维和提取数据中的主要信息。

虽然它们都可以用于数据分析，但在方法和应用上存在一些区别。

本文将介绍因子分析与主成分分析的区别，并讨论它们各自的应用。

一、因子分析与主成分分析的定义因子分析是一种用于研究多个观测变量之间的内在相关性结构的统计技术。

它通过将多个变量组合为少数几个“因子”来解释数据的方差。

每个因子代表一组相关性高的变量，可以帮助我们理解数据背后的潜在结构。

主成分分析是一种通过将原始变量转换为线性组合（即主成分）来降低多维数据维度的技术。

它通过找到数据中的最大方差方向来确定主成分，并逐步提取主成分，以解释数据的最大方差。

主成分分析可以帮助我们发现数据中的主要特征。

二、因子分析与主成分分析的区别1. 目的不同：因子分析的目的是确定一组能够最好地描述观测数据之间关系的因子，并解释数据中的方差。

因子分析更加关注变量之间的共同性和相关性，希望通过较少的因子来解释数据。

主成分分析的目的是通过寻找数据中的主要结构和主要特征来降低数据的维度。

主成分分析着重于方差的解释，通过线性组合来减少变量数量，提取出主要成分。

2. 基本假设不同：因子分析基于观察变量之间的共同性，假设观测变量是由一组潜在因子决定的。

它假设每个观测变量都与每个因子有一个固定的因子载荷。

主成分分析假设原始变量之间是线性相关的，并且通过线性变换，可以找到解释大部分数据方差的新变量。

3. 输出结果不同：因子分析输出因子载荷矩阵，该矩阵显示每个因子与每个观测变量之间的关系。

因子载荷表示每个因子对每个变量的贡献程度，可用于解释观测变量之间的共同性。

主成分分析输出的是主成分，每个主成分是原始变量的线性组合。

主成分按照解释的方差大小排序，因此前几个主成分更能代表原始数据的方差。

三、因子分析与主成分分析的应用因子分析的应用广泛，可以用于心理学、社会科学、市场调研等领域。

主成分分析与因子分析法ppt课件

9
事实上，以上问题在平时的研究中，也会经常遇到。它所涉及的问题可以推广到对企业、对学校、对区域进行分析、评价、排序和分类等。
比如对n个样本进行综合评价，可选的描述样本特征的指标很多，而这些指标往往存在一定的相关性（既不完全独立，又不完全相关），这就给研究带来很大不便。若选指标太多，会增加分析问题的难度与复杂性，选指标太少，有可能会漏掉对样本影响较大的指标，影响结果的可靠性。
在各种线性组合中方差达到最大者。
满足上述约束得到的合成变量Y1, Y2, …, Yp分别称为原始变量的第一主成分、第二主成分、…、第 p 主成分，
而且各成分方差在总方差中占的比重依次递减。在实际研究
工作中，仅挑选前几个方差较大的主成分，以达到简化系统
结构的目的。
24
24
三、主成分分析的计算步骤
25
21
(二) 主成分分析的基本思想
假如对某一问题的研究涉及 p 个指标，记为X1，X2, …,
Xp，由这 p 个随机变量构成的随机向量为X=(X1, X2, …,
Xp)，设 X 的均值向量为，协方差矩阵为。设Y=(Y1, Y2 ,
… , Yp)为对 X 进行线性变换得到的合成随机向量，即
Y1 11
主成分分析法与因子分析法
1
主要内容
➢ 主成分分析法 ➢ 因子分析法 ➢ 附：主成分分析法与因子分析法的区别
2
主成分分析法
（Principal Components Analysis,PCA） ➢ 主成分分析法概述 ➢ 主成分分析的基本原理 ➢ 主成分分析的计算步骤
3
一、主成分分析概述
4
引子
假定你是一个公司的财务经理，掌握了公司的所有数据，这包括众多的变量，比如固定资产、流动资金、每一笔借贷的数额和期限、各种税费、工资支出、原料消耗、产值、利润、折旧、职工人数、职工的分工和教育程度等等。

主成分分析和因子分析

3
成绩数据（student.sav）
• 100个学生的数学、物理、化学、语文、历史、英语的成绩如下表（部分）。
4
从本例可能提出的问题
• 目前的问题是，能不能把这个数据的6个变量用一两个综合变量来表示呢？
• 这一两个综合变量包含有多少原来的信息呢？ • 能不能利用找到的综合变量来对学生排序呢？
.435
.002
.079 -.342 -.083
ENGLIS H .836
.425
.000
.074
.276 -.197
Extrac tion Method : Principal Component Analysis.
• 这a里.6每c一om列po代ne表nt一s 个ex主tr成ac分t作ed为. 原来变量线性组合的系数（比
21
• 对于我们的数据，SPSS因子分析输出为
R ot at ed C om po ne nt M at ri xa
Co mpon ent
MA TH
1 -. 387
2 .7 90
PH YS
-. 172
.8 41
CH EM
-. 184
.8 27
LI TERA T
.8 79
-. 343
HI STOR Y
• 这些系数称为主成分载荷（loading），它表示主成分和相应的原先变量的相关系数。
• 比变量如的y1表相示关式系中数x为1的-0系.80数6。为-0.806，这就是说第一主成分和数学 • 相关系数(绝对值）越大，主成分对该变量的代表性也越大。可
以看得出，第一主成分对各个变量解释得都很充分。而最后的几个主成分和原先的变量就不那么相关了。
10

主成分分析和因子分析

主成分分析和因子分析1.对原始数据进行标准化，使得每个特征的均值为0，标准差为12.计算数据集的协方差矩阵。

3.对协方差矩阵进行特征值分解，得到特征值和特征向量。

4.对特征值进行降序排列，并选择最大的k个特征值对应的特征向量作为主成分。

5.计算每个样本在选定的主成分上的投影值，得到降维后的数据集。

主成分分析的应用非常广泛。

它可以用于数据可视化、降维和特征选择。

主成分分析可以帮助我们发现数据中的模式和结构，找到最相关和最有信息的特征，并减少不必要的特征数量。

主成分分析还可以用于数据预处理，减少数据噪声和冗余，从而提高后续分析的效果。

相比之下，因子分析（Factor Analysis）是一种非线性降维技术，它假设原始数据中的观测值是由一组潜在因子造成的，并且通过这些潜在因子来解释观测值的协方差结构。

因子分析的目标是找到最小的因子数量，能够最好地解释观测值的变异性。

因子分析的步骤如下：1.对原始数据进行标准化。

2.构建因子模型，包括确定因子数量和定义因子之间的关系。

3.通过最大似然估计或最小二乘法等方法，估计因子载荷矩阵，描述观测变量和潜在因子之间的线性关系。

4.通过因子旋转，调整因子载荷矩阵的结构，使得因子之间更容易解释，并且使得观测变量和因子之间的关系更简洁。

5.根据因子载荷矩阵，计算每个因子的得分，得到降维后的数据集。

因子分析在社会科学研究和心理学研究中得到了广泛的应用。

它可以用于构建潜在变量模型，检验假设和推断因果关系。

因子分析可以帮助我们理解观测数据中的潜在结构，提取出隐藏的特征，发现变量之间的关系，并用较少的因子代表观测变量。

主成分分析和因子分析之间存在一些差异。

首先，主成分分析是一种无监督学习方法，不需要预先定义因子的数量和含义，而因子分析需要根据实际问题确定因子的数量和解释，需要一定的先验知识。

其次，主成分分析假设原始数据的变量之间是线性相关的，而因子分析假设原始数据是由潜在因子引起的，可以属于非线性关系。