高中立体几何中线面平行的常见方法

空间中的平行与垂直例题和知识点总结

空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。

理解和掌握这些关系，对于解决相关的几何问题具有关键作用。

下面我们通过一些例题来深入探讨，并对相关知识点进行总结。

一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。

2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。

证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。

又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。

（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。

2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。

证明：连接 AC 交 BD 于 O，连接 MO。

因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。

又因为 M 是 PC 的中点，所以MO∥PA。

因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。

（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。

2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。

证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。

二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。

(完整版)线面平行证明的常用方法

线面平行证明的常用方法张磊立体几何在高考解答题中每年是必考内容，必有一个证明题；重点考察：平行与垂直（线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直等），我们现在对线面平行这一方面作如下探讨：方法一：中位线型：找平行线。

例1、如图⑴，在底面为平行四边形的四棱锥P ABCD -中，点E 是PD 的中点.求证：//PB 平面AEC 分析：如图⑴ 如图⑵ 如图⑶ 方法二：构造平行四边形，找平行线例2、如图⑵, 平行四边形ABCD 和梯形BEFC 所在平面相交，BE//CF ，求证：AE//平面DCF.分析：过点E 作EG//AD 交FC 于G ， DG 就是平面AEGD与平面DCF 的交线，那么只要证明AE//DG 即可。

方法三：作辅助面使两个平面是平行, 即：作平行平面，使得过所证直线作与已知平面平行的平面例3、如图⑷，在四棱锥O ABCD -中，底面ABCD 为菱形， M 为OA 的中点，N 为BC 的中点，证明：直线MN OCD 平面‖ 分析：：取OB 中点E ，连接ME ，NE ，只需证平面MEN 平面OCD 。

方法四：利用平行线分线段成比例定理的逆定理证线线平行。

例4、已知正方形ABCD 和正方形ABEF AC 和BF 上，且AM=FN. 求证：MN ‖平面BCE.如图⑷ 如图⑸ 如图⑹E B A D C GF F y C B E D A Sz_ M _ D_ A B _ O E P E D C B O A B CD E F N M例5．如图⑸，已知三棱锥Ｐ—ＡＢＣ，Ａ′，B ′，C ′是△PBC,△PCA,△PAB 的重心.(1)求证：Ａ′Ｂ′∥面ＡＢＣ；(2)求S △A ′B ′C ′：S △ABC .方法五：（向量法）所证直线与已知平面的法向量垂直，关键：建立空间坐标系（或找空间一组基底）及平面的法向量。

例6、如图⑹，在四棱锥S ABCD -中，底面ABCD 为正方形，侧棱SD ⊥底面ABCD E F ，，分别为AB SC ，的中点．证明EF ∥平面SAD ；分析：因为侧棱SD ⊥底面ABCD ，底面ABCD 是正方形，所以很容易建立空间直角坐标系及相应的点的坐标。

立体几何常考定理的总结(八大定理)

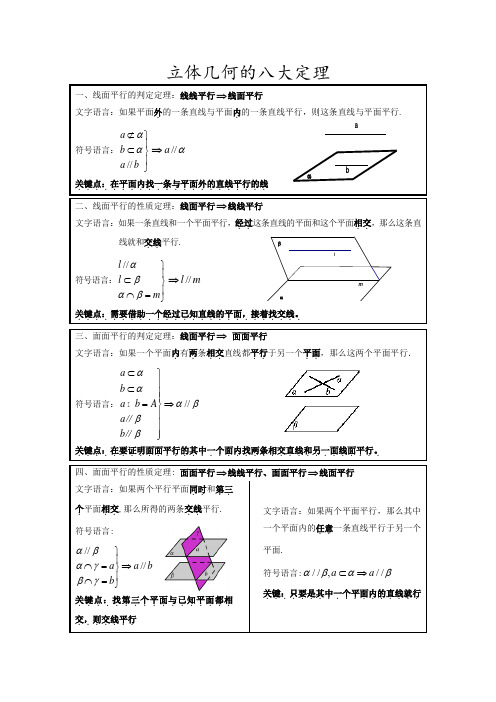
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．．二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。

．．．．．．．．．．．．．．．．．．．．．．．．．．三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行．符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．．六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．．七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：．．．．在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。

立体几何线面平行垂直,线面角二面角的证明方法

APBCED一：线面平行的证明方法：1、用“近似平行法”先找到面上与已知直线平行的直线（一般为表示面的三角形的边界直线，或三角形某边上的中线）看找到的这条线与已知线的长度关系，1）若相等应该构造平行四边形；2）若不相等一般利用三角形中位线的性质（将这两个不相等的线段的端点连结并延长即会出现关键三角形）。

2、若既不能构造平行四边形也不能性用中位线性质，则应再构造一个此直线所在的平面，证明此平面与已知平面平行（先证面面平行，推出线面平行）例一：如图，已知菱形ABCD ，其边长为2，60BAD ∠= ，ABD ∆绕着BD 顺时针旋转120得到PBD ∆，M 是PC 的中点．（1）求证：//PA 平面MBD ；（2）求直线AD 与平面PBD 所成角的正弦值．例二：已知四棱锥P-ABCD ，底面ABCD 是60=∠A 、边长为a 的菱形，又ABCD PD 底⊥，且PD=CD ，点M 、N 分别是棱AD 、PC 的中点．（1）证明：DN//平面PMB ；（2）证明：平面PMB ⊥平面PAD ；（3）求点A 到平面PMB 的距离．例三：如图，已知点P 是平行四边形ABCD 所在平面外的一点，上的点且PE EA BF FD =∶∶，求证：EF //平面PBC ．二：线面垂直的证明方法：通过线线垂直，证明线面垂直1）利用勾股定理逆定理及三角形中两个角和为90°； 2）利用等边、等腰三角形（中线即高线），正方形、矩形邻边垂直，正方形菱形对角线垂直等；3）通过线面垂直，反推线线垂直；4）利用面面垂直的性质，证明垂直于交线即垂直于另一个平面。

例四：如图,四边形ABCD 为矩形，CF ⊥平面ABCD ，DE ⊥平面ABCD ， AB=4a ，BC= CF=2a,P 为AB 的中点.(1)求证：平面PCF ⊥平面PDE ； (2)求四面体PCEF 的体积.C例五：如图，在四棱锥ABCD P -中，ABCD 是矩形，ABCD PA 平面⊥， 3,1===AB AD PA ，点F 是PD 的中点，点E 在CD 上移动。

立体几何常见证明方法

立体几何方法归纳小结一、线线平行的证明方法1、根据公理4，证明两直线都与第三条直线平行。

2、根据线面平行的性质定理，若直线a平行于平面A ，过a的平面B与平面A相交于b ，则a//b。

3、根据线面垂直的性质定理，若直线a与直线b都与平面A垂直，则a//b 。

4、根据面面平行的性质定理，若平面A//平面B，平面C与平面A和平面B的交线分别为直线a与直线b，则a//b 。

二、线面平行的证明方法1、根据线面平行的定义，证直线与平面没有公共点。

2、根据线面平行的判定定理，若平面A内存在一条直线b与平面外的直线a平行，则a//A 。

(用相似三角形或平行四边形)3、根据平面与平面平行的性质定理，若两平面平行，则一个平面内的任一直线与另一个平面平行。

三、面面平行的证明方法1、根据定义，若两平面没有公共点，则两平面平行。

2、根据两平面平行的判定定理，一个平面内有两相交直线与另一平面平行，则两平面平行。

或根据两平面平行的判定定理的推论，一平面内有两相交直线与另一平面内两相交直线平行，则两平面平行。

3、垂直同一直线的两平面平行。

4、平行同一平面的两平面平行。

四、两直线垂直的证明方法1、根据定义,证明两直线所成的角为90°2、一直线垂直于两平行直线中的一条,也垂直于另一条.3、一直线垂直于一个平面,则它垂直于平面内的所有直线.4、根据三垂线定理及逆定理,若平面内的直线垂直于平面的一条斜线(或斜线在平面内的射影),则它垂直于斜线在平面内的射影(或平面的斜线).五、线面垂直的证明方法1、根据定义,证明一直线与平面内的任一(所有)直线垂直,则直线垂直于平面.2、根据判定定理,一直线垂直于平面内的两相交直线,则直线垂直于平面.3、一直线垂直于两平行平面中的一个,也垂直于另一个.4、两平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.5、根据两平面垂直的性质定理,两平面垂直,则一个平面内垂直于它们交线的直线垂直于另一个平面.六、面面垂直的证明方法1、根据面面垂直的定义，两平面相交所成的二面角为直二面角，则两平面垂直。

完整版)立体几何中平行与垂直证明方法归纳

完整版)立体几何中平行与垂直证明方法归纳本文系统总结了立体几何中平行与垂直证明方法，适合高三总复时学生构建知识网络、探求解题思路、归纳梳理解题方法。

以下是常见证明方法：一、“平行关系”常见证明方法一）直线与直线平行的证明1.利用平行四边形的对边互相平行的特性；2.利用三角形中位线性质；3.利用空间平行线的传递性（即公理4）；4.利用直线与平面平行的性质定理；5.利用平面与平面平行的性质定理；6.利用直线与平面垂直的性质定理；7.利用平面内直线与直线垂直的性质；8.利用定义：在同一个平面内且两条直线没有公共点。

二）直线与平面平行的证明1.利用直线与平面平行的判定定理；2.利用平面与平面平行的性质推论；3.利用定义：直线在平面外，且直线与平面没有公共点。

三）平面与平面平行的证明1.利用平面与平面平行的判定定理；2.利用某些空间几何体的特性；3.利用定义：两个平面没有公共点。

二、“垂直关系”常见证明方法一）直线与直线垂直的证明1.利用直角三角形的两条直角边互相垂直的特性；2.看夹角：两条共（异）面直线的夹角为90°，则两直线互相垂直；3.利用直线与平面垂直的性质：如果一条直线与一个平面垂直，则这条直线垂直于此平面内的所有直线。

1.利用空间几何体的特性：例如长方体侧棱垂直于底面。

2.观察直线与平面所成角度：若直线与平面所成角为90度，则该直线垂直于平面。

3.利用直线与平面垂直的判定定理：若一条直线与一个平面内的两条相交直线垂直，则该直线垂直于此平面。

4.利用平面与平面垂直的性质定理：若两个平面互相垂直，则在这两个平面内分别作垂直于交线的直线，则这两条直线互相垂直。

5.利用常用结论：例如若一条直线平行于一个平面的垂线，则该直线也垂直于此平面。

高中立体几何证明线面平行的常见方法

高中立体几何证明线面平行的常见方法1.通过“平移”再利用平行四边形的性质题目1：四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。

证明AF∥平面PCE。

证明：将四棱锥P-ABCD平移，使其底面平移到平面PCE上，得到四棱锥P'-A'B'C'D'，其中A'B'C'D'与ABCD平行，且P'、E'、F'分别为A'B'、C'D'、A'D'的中点。

因为AF∥PD，所以AF'=PD'=C'F'，又因为AD'=C'D'/2=AB'/2=AF'/2，所以AD'∥B'C'。

因此，根据平行四边形的性质，AF'∥B'C'，即AF∥CE。

题目3：四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点，证明EB∥平面PAD。

证明：连接PE，因为E为PC的中点，所以PE∥AD。

又因为CD⊥AD，所以CD∥PE。

又因为CD=2AB，所以AB∥PE。

因此，根据平行四边形的性质，EB∥PA，即EB∥平面PAD。

2.利用三角形中位线的性质题目4：四面体ABCD中，E、F、G、M分别是棱AD、CD、BD、BC的中点，证明AM∥平面EFG。

证明：连接EF、EG、FG，因为E、F、G分别为三角形BCD、ACD、ABD的中点，所以EF、EG、FG分别是这三个三角形的中位线。

因此，EF∥AD，EG∥BD，FG∥AC。

又因为M为BC的中点，所以AM∥FG。

因此，AM∥平面EFG。

3.利用平行四边形的性质题目7：正方体ABCD-A' B' C' D'中O为正方形ABCD的中心，M为B'B的中点，求证D'O∥平面A'BC'。

立体几何线线平行的判定

立体几何线线平行的判定
线线平行是立体几何中的一个基本概念，它可以用来描述两条直线在空间中始终保持相同的距离的关系。

在很多几何问题中，我们需要判定两条直线是否平行，因此，本文将介绍立体几何中线线平行的判定方法。

一、两线斜率相等且不相交
两条直线若在平面内不相交，则可以通过比较它们的斜率是否相等来判断它们是否平行。

但在立体几何中，两条直线可以在空间中相交，因此我们需要另一种方法来判断它们是否平行。

在立体几何中，两条直线的斜率可以用其在平面内的投影来计算。

设直线L1与L2在平面P上的投影分别为l1、l2，且l1与l2的斜率相等，则L1与L2平行。

二、两线所在平面平行或重合
当两条直线分别位于两个平面内，且这两个平面平行或重合时，这两条直线也平行。

这个方法的证明比较复杂，需要用到一些向量知识。

我们可以将两条直线所在的两个平面各取一个法向量，若这两个法向量平行，则两个平面平行。

在这种情况下，两条直线在各自所在的平面内的投影也是平行的，因此它们在空间中也是平行的。

这种方法比起前两种方法，更加简单直观，因为两个平行的平面可以看作是两个相似的平面铺在一起。

同时，这种方法可以直接代入向量公式进行计算，非常方便。

最后，需要注意的是，在实际问题中，我们往往需要综合运用这几种判断方法来判断两条直线是否平行。

同时，我们也需要注意区分线线平行和线面平行的概念，因为这两者有着本质的差别。

立体几何平行与垂直定理总结

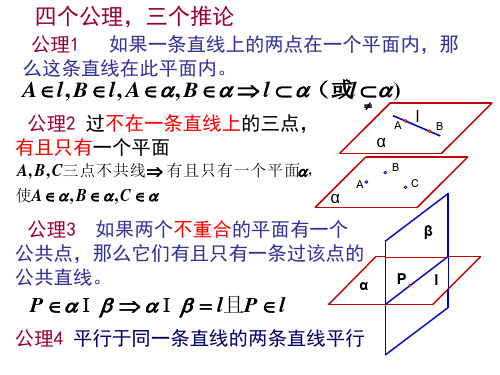
P
A
O
步骤 2：计算线段 PO 的长度。(直接解三角形；等体积法和等面积法；换
点法)方法二：坐标法。 d AP cos n AP n AP n
n α A θ
m
P O
2．线面距、面面距均可转化为点面距。 3．异面直线之间的距离方法一：转化为线面距离。
如图，m 和 n 为两条异面直线， n 且
cos θ1 BO AB cos θ BC AB cos θ2 BC OB
∴ cos cos 1 cos 2
斜线和平面所成的角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角。
一．距离问题。 1．点面距。方法一：几何法。步骤 1：过点 P 作 PO 于 O，线段 PO 即为所求。
(一) 二面角及其平面角 (1)定义：在棱 l 上取一点 P，两个半平面内分别作 l 的垂线（射线）m、n，则射线 m 和 n 的夹角为二面角 —l— 的平面角。 (2)范围： [0,180] (3)求法：方法一：定义法。步骤 1：作出二面角的平面角(三垂线定理)，并证明。步骤 2：解三角形，求出二面角的平面角。方法二：截面法。步骤 1：如图，若平面 POA 同时垂直于平面和，则交线(射线)AP 和 AO 的夹角就是二面角。步骤 2：解三角形，求出二面角。
l l
α
β
l
方法二：计算所成二面角为直角。
(二)夹角问题。 (一) 异面直线所成的角：(1) 范围： (0,90] (2)求法：方法一：定义法。步骤 1：平移，使它们相交，找到夹角。步骤 2：解三角形求出角。(常用到余弦定理)
a θ b c
a2 b2 c2 cos 余弦定理： (计算结果可能是其补角) 2ab

高中立体几何最佳解题方法及考题详细解答

高中立体几何最佳解题方法总结一、线线平行的证明方法1、利用平行四边形；2、利用三角形或梯形的中位线；3、如果一条直线和一个平面平行，经过这条直线的平面与这个相交，那么这条直线和交线平行。

（线面平行的性质定理）4、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（面面平行的性质定理）5、如果两条直线垂直于同一个平面，那么这两条直线平行。

（线面垂直的性质定理）6、平行于同一条直线的两个直线平行。

7、夹在两个平行平面之间的平行线段相等。

二、线面平行的证明方法1、定义法：直线和平面没有公共点。

2、如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线就和这个平面平行。

（线面平行的判定定理）3、两个平面平行，其中一个平面内的任意一条直线必平行于另一个平面。

4、反证法。

三、面面平行的证明方法1、定义法：两个平面没有公共点。

2、如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

（面面平行的判定定理）3、平行于同一个平面的两个平面平行。

4、经过平面外一点，有且只有一个平面与已知平面平行。

5、垂直于同一条直线的两个平面平行。

四、线线垂直的证明方法1、勾股定理；2、等腰三角形；3、菱形对角线;4、圆所对的圆周角是直角；5、点在线上的射影；6、如果一条直线和这个平面垂直，那么这条直线和这个平面内的任意直线都垂直。

7、在平面内的一条直线，如果和这个平面一条斜线垂直，那么它也和这条斜线的射影垂直。

（三垂线定理）8、在平面内的一条直线，如果和这个平面一条斜线的射影垂直，那么它也和这条斜线垂直。

9、如果两条平行线中的一条垂直于一条直线，那么另一条也垂直于这条直线。

五、线面垂直的证明方法：1、定义法：直线与平面内的任意直线都垂直；2、点在面内的射影；3、如果一条直线和一个平面内的两条相交直线垂直，那么这条直线就和这个平面垂直。

（线面垂直的判定定理）4、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线必垂直于另一个平面。

总结证明线面平行的常用方法

BC DA 1B 1C 1D 1图２AFE GαabA图1总结证明线面平行的常用方法空间直线与平面平行问题是立体几何的一个重要内容，也是高考考查的重点，下面就常见的线面平行的判定方法介绍如下：方法一、反证法【例1】求证：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．（直线与平面平行的判定定理）已知：,,a b a αα⊄⊂∥b ，如图1．求证：a ∥α．【分析】要证明直线与平面平行，可以从直线与平面平行的定义入手，但从定义来看，必须说明直线与平面无公共点，这一点直接说明是困难的，但我们可以借助反正法来证明．【证明】假设直线a 与平面α不平行，又∵a α⊄，∴a A α=．下面只要说明aA α=不可能即可．∵a ∥b ，∴a ，b 可确定一平面，设为β．又aA α=， ∴,A a A β∈∈．又b ,A αα⊂∈，∴平面α与平面β中含有相同的元素直线b ，以及不在直线b 上的点Ａ，由公理２的推论知，平面α与平面β重合． ∴a α⊂，这与已知a α⊄相矛盾． ∴a A α=不可能．故a ∥α．方法二、判定定理法【例2】正方体1AC 中，Ｅ、G 分别为BC 、11C D 的中点，求证：EG ∥平面11BDD B 【分析】要证明EG ∥平面11BDD B ，根据线面平行的判定定理，需在平面11BDD B 内找到一条与EG 平行的直线，充分借助Ｅ、G 为中点的条件．【证明】如图２，取BD 的中点为Ｆ，连结EF ，1D F ． ∵Ｅ为BC 的中点， ∴ EF ∥CD 且12EF CD =又∵G 为11C D 的中点， ∴ 1D G ∥CD 且112D G CD =∴ EF ∥1D G ，且1EF D G =B C DA 1B 1C 1D 1AＮＭE Ｆ图３故四边形1EFD G 为平行四边形．∴ 1D F ∥EG又1D F ⊂平面11BDD B ，且EG ⊄平面11BDD B ， ∴ EG ∥平面11BDD B 【评注】根据直线与平面平行的判定定理证明直线和平面平行的关键是在平面内找到一条直线和已知直线平行，常用到中位线定理、平行四边形的性质、成比例线段、平行转移法、投影法等.具体应用时,应根据题目条件而定.方法三、运用面面平行的性质定理【例3】在正方体1111ABCD A B C D -中，点N 在BD 上，点M 在1B C 上，且CM DN =，求证：MN ∥平面11AA BB ．【分析】若过MN 能作一个平面与平面11AA BB 平行，则由面面平行的性质定理，可得MN 与平面11AA BB 平行．【证明】如图3，作MP ∥1BB ，交BC 与点Ｐ，联结NP ． ∵ MP ∥1BB ，∴1CM CPMB PB=． ∵1BD B C =，DN CM =，∴1B M BN =， ∵1CM DN MB NB =，∴DN CPNB PB= ∴NP ∥CD ∥AB ， ∴面MNP ∥面11AA BB ． ∴MN ∥平面11AA BB【评注】本题借助于成比例线段，证明一个平面内的两条相交直线与另一个平面内的两条相交直线分别平行，得到这两个平面平行，进而得到线面平行，很好地体现了线面、线线、面面平行关系之间的转化思想．。

高考理科数学必考——几何证明与利用空间向量求线面角、面面角

高考理科数学必考——几何证明与利用空间向量求线面角、面
面角
时间过的飞快，距离高考的时间就只剩76天了，同学和老师也越来越紧张了，有些地方欠缺的同学开始寝食难安，老师也赶快奉献点干货来帮助几何证明欠缺的学生。

立体几何其实难度不大，只要你会空间向量，会建系，一切就自然而然水到渠成了。

在这先分析这些立体几何的解题思路。

在立体几何中，第一问一般会让你证明线面平行、线面垂直、面面平行、面面垂直
1、证明线面平行的方法1、平移的方法，找到直线与平面内一条直线平行
2、利用面面平行、证明线面平行
2、证明线面垂直的方法1、证明直线与平面内相交的两直线垂直
3、证明面面平行的方法1、证明一个平面内两相交的直线与另一个平面内两相交的直线互相平行
2、证明平面内两相交的直线分别平行另一个平面
4、证明面面垂直的方法1、先证明一条直线垂直于一个平面，这条直线还在另一个平面内
利用这些方法第一问就可以轻松解决了。

在立体几何第二中，会求线面角、面面角，在第二步中，利用空间向量解决就可以
利用空间向量解决第二问的步骤1、找三垂，建立空间直角坐标系
2、写出各个点的坐标
3、求出直线向量、面的法向量
4、利用夹角公式算出余弦值
下面通过两个例题说明一下这个空间几何。

立体几何中有关平行、垂直常用的判定方法

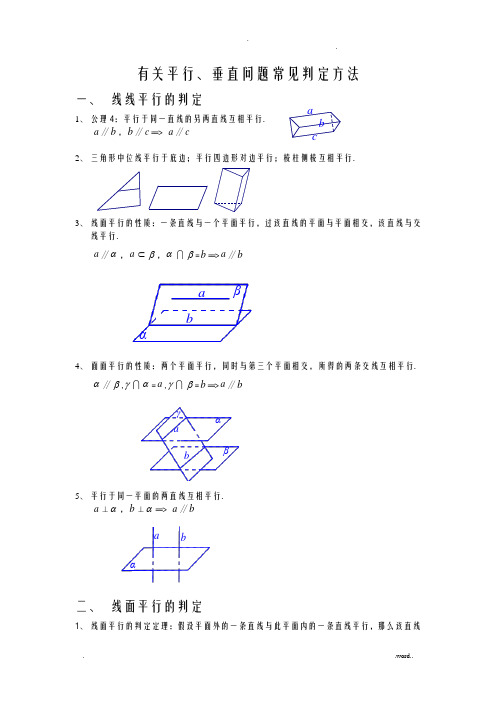
有关平行、垂直问题常见判定方法一、线线平行的判定1、公理4：平行于同一直线的另两直线互相平行. a ∥b ，b ∥c ==> a ∥c2、三角形中位线平行于底边；平行四边形对边平行；棱柱侧棱互相平行．3、线面平行的性质：一条直线与一个平面平行，过该直线的平面与平面相交，该直线与交线平行．a ∥α，a ⊂β，αβ=b ==>a ∥bβαba4、面面平行的性质：两个平面平行，同时与第三个平面相交，所得的两条交线互相平行．α∥β,γα=a ,γβ=b ==>a ∥bγβαb a5、平行于同一平面的两直线互相平行．a ⊥α，b ⊥α==> a ∥bαba二、线面平行的判定1、线面平行的判定定理：假设平面外的一条直线与此平面内的一条直线平行，那么该直线c b a与此平面平行．a ⊄α，b ⊂α，a ∥b ==> a ∥ααba2、假设两平面平行，那么一个平面内的任一直线与另一平面平行．α∥β，a ⊂α==> a ∥βαβa3、 α⊥β，a ⊥β，a ⊄α==> a ∥αβαa4、 a ⊥b ，b ⊥α，a ⊄α==> a ∥ααab三、面面平行的判定1、面面平行的判定定理：假设一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．a ⊂α，b ⊂α，a b =O ,a ∥β,b ∥β==> α∥βO αβa b αβa2、垂直于同一直线的两个平面互相平行．a ⊥α，a ⊥β==> α∥β (见上图)3、平行于同一平面的两个平面互相平行．α∥γ，β∥γ==> α∥βαγβ4、柱体的上下底面互相平行四、线线垂直1、线线垂直的定义：a 与b 所成的角为直角．2、线面垂直的定义：假设一条直线与一个平面垂直，那么该直线与平面内的任一直线都垂直．a ⊥α，b ⊂α==> a ⊥bαab3、a ⊥α，b ∥α==> a ⊥bαab4、三垂直定理及其逆定理l ⊥α( H 为垂足)，a ⊂α，HM 是斜线PM 在平面α内的射影三垂线定理〔垂影那么垂斜〕：a ⊥HM ==> a ⊥PM三垂线定理的逆定理〔垂斜那么垂影〕：a ⊥PM ==> a ⊥HMlM H Pαa5、a ⊥α，b ⊥β，α⊥β==> a ⊥bβαab五、线面垂直的判定1、线面垂直的判定定理：假设一直线和平面内的两相交直线都垂直，那么该直线与此平面垂直．a ⊂α，b ⊂α,ab =O , l ⊥a ,l ⊥b ==> l ⊥αlO αa b2、a∥b，a⊥α==> b⊥ααb a3、直棱柱的侧棱与底面垂直4、一条直线垂直于两平行平面中的一个平面，也垂直于另一个平面α∥β，a⊥α==> a⊥βαβa5、面面垂直性质：两平面垂直，一个平面内垂直于它们交线的直线垂直于另一个平面．α⊥β，αβ=l，a⊂α，a⊥l==> a⊥βlβαa5、两相交平面同时垂直于第三个平面，那么它们的交线也与第三个平面垂直．αβ=l ，α⊥γ,β⊥γ==> l ⊥γl γβα六、面面垂直的判定1、定义:两平面相交所成二面角为直二面角.2、判定定理:假设一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.a ⊥β，a ⊂α ==> α⊥βl βαa2、a ∥α，a ⊥β==> α⊥ββαa。

立体几何证明方法——证面面平行

立体几何证明方法——证面面平行立体几何中，证明面面平行是一个常见的问题，可以通过多种方法进行证明。

下面将介绍几种常用的证明方法。

1.使用直线面法相交性质证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条相交直线AE和BF，然后分别在这两条直线上选择两个点C和D。

根据直线面法相交性质，直线AE与平面ABCD相交于点E，直线AE与平面CDH相交于点C，同理，直线BF与平面ABCD相交于点F，直线BF与平面CDH相交于点D。

连接线段AD和BC，可以得到四边形ABCD。

然后，考察四边形ABCD，如果四边形ABCD是平行四边形，则线段AD与线段BC互相平行。

由直线平行与面平行的性质可知，平面ABCD与平面EFHG平行。

因此，我们只需要证明四边形ABCD为平行四边形即可。

接下来，通过证明线段AD与线段BC互相平行来证明四边形ABCD为平行四边形。

可采用向量法、等距向量法等方法进行证明，具体方法根据题目要求来选择。

2.使用距离法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，在平面ABCD上选择一点P，在平面EFGH上选择一点Q。

然后，构造线段PQ，并将其延长，过点P和Q分别作平行于平面ABCD和EFGH的直线。

两条直线与平面ABCD和EFGH的交点分别为A、B和E、F。

由于点P、Q到平面ABCD的距离相等，点A、B到平面EFGH的距离相等，利用距离的定义可以推出直线AE与直线BF互相平行。

同理可以证明直线BE与直线AF互相平行。

因此，根据平行四边形的性质可知线段AD与线段BC平行。

由于线段AD与线段BC平行，所以平面ABCD与平面EFGH平行。

3.使用垂线法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条垂线，可以是两个相交直线的垂线或两个平行直线的垂线。

然后，在平面EFGH中分别找到与这两条垂线相交的直线段，并将其延长。

立体几何中平行与垂直证明方法归纳

a ∥
a∥
α
a a
β
3) 利用定义：直线在平面外，且直线与平面没有公共点
（三）平面与平面平行的证明
常见证明方法：
1) 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。
3
a ⊂ b ⊂
a ∩b P
a // b //
⇒ /性：如正方体的上下底面互相平行等
一条直线与一个平面内的两条相交直线都垂直，则该直线垂直于此平面。
a
b
ab
A
l
l a l b
l
b
Aa
4) 利用平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
5
l
a
a
a l
l
5) 利用常用结论：
① 一条直线平行于一个平面的一条垂线，则该直线也垂直于此平面。
在同一个平面内，垂直于同一条直线的两条直线互相平行。
8) 利用定义：在同一个平面内且两条直线没有公共点
（二）直线与平面平行的证明
1) 利用直线与平面平行的判定定理：
平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。
a
a
b a∥
a∥b
b
2) 利用平面与平面平行的性质推论：
两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。
a b ba
b a
α
4) 利用平面与平面垂直的性质推论：
如果两个平面互相垂直，在这两个平面内分别作垂直于交线的直线，则这
两条直线互相垂直。
4
l a b al
bl
ab
β b

立体几何中的平行性的证明.

立体几何中的平行性的证明
一、证明两直线平行的方法：
1、定义法：同一平面内无公共点的两条直线（用反证法证明）。

2、判定定理：如果一条直线与一个平面平行，则经过这条直线的平面与这个平
面相交，直线与交线平行。

3、平行与同一直线的两条直线平行。

4、面面平行的性质定理：如果两个平行平面同时和第三个平面相交，则交线平
行。

5、向量法：如果两个直线的方向向量共线，则两直线平行。

6、垂直于同一平面的两直线平行。

二、证明直线和平面平行的方法：
1、定义法：证明直线与平面无公共点（反证法）。

2、判定定理：如果平面外的一条直线和平面内的一条直线平行，则直线和平面
平行。

3、面面平行的性质：如果两个平面平行，那么一个平面内的任何一条直线都平
行于另一个平面。

4、如果平面外的一条直线和平面的一条垂线垂直，那么这条直线和这个平面平
行。

5、如果平面外的一条直线和这个平面都垂直于同一个平面，那么这条直线和这
个平面平行。

三、证明平面与平面平行的方法：
1、定义法：证明两个平面没有公共点（反证法）。

2、判定定理：如果一个平面内的两条相交直线分别和另一个平面平行，那么这
两个平面相互平行。

3、推论：如果一个平面内的两条相交直线分别和另一个平面内的两条直线（相
交）平行，那么这两个平面相互平行。

4、垂直于同一直线的两个平面相互平行。

5、如果两个平面的法向量平行，那么这两个平面平行。

6、。

高中立体几何中线面平行的常见方法

高中立体几何证明平行的专题训练立体几何中证明线面平行或面面平行都可转化为线线平行，而证明线线平行一般有以下的一些方法：（1）通过“平移”。

（2）利用三角形中位线的性质。

（3）利用平行四边形的性质。

（4）利用对应线段成比例。

（5）利用面面平行，等等。

(1) 通过“平移”再利用平行四边形的性质1．如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；分析：取PC 的中点G ，连EG .，FG ，则易证AEGF 是平行四边形2、如图，已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3，过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使得DE ⊥EC.（Ⅰ）求证：BC ⊥面CDE ；（Ⅱ）求证：FG ∥面BCD ；分析：取DB 的中点H ，连GH,HC 则易证FGHC是平行四边形（第1题图）DE B 1A 1C 1CABF M3、已知直三棱柱ABC －A 1B 1C 1中，D, E, F 分别为AA 1, CC 1, AB 的中点， M 为BE 的中点, AC ⊥BE. 求证：（Ⅰ）C 1D ⊥BC ；（Ⅱ）C 1D ∥平面B 1FM. 分析：连EA ，易证C 1EAD 是平行四边形，于是MF//EA4、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面;分析:：取PD 的中点F ，连EF,AF 则易证ABEF 是平行四边形(2) 利用三角形中位线的性质5、如图，已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点，求证：AM ∥平面EFG 。

分析：连MD 交GF 于H ，易证EH 是△AMD 的中位线6、如图，ABCD 是正方形，O 是正方形的中心，E 是PC 的中点。

高中数学知识点总结及公式大全立体几何中的平行与垂直问题

高中数学知识点总结及公式大全立体几何中的平行与垂直问题高中数学知识点总结及公式大全：立体几何中的平行与垂直问题在高中数学中，几何是一个重要的分支，而立体几何更是其中的重要内容之一。

在立体几何中，平行和垂直是我们经常遇到的问题。

本文将对高中数学中的立体几何知识点进行总结，并提供一些常用的公式。

一、平行与垂直的概念在几何中，平行和垂直是两个基本的关系。

平行指的是两条直线永远不会相交的情况，可以想象成两条铁轨永远平行。

垂直则指的是两条直线相互成直角，可以想象成两根彼此垂直的木棍。

二、平行与垂直的判定方法1. 平行关系的判定方法：(1) 同位角相等定理：如果两条直线被一组相交线段所切割，且这些相交线段的对应角相等，则这两条直线是平行的。

(2) 平行线的性质定理：如果一条直线上的两个点分别与另一条直线上的两个点相连，且相连的线段互相平行，则这两条直线是平行的。

(3) 平行线的判定定理：如果两条直线的斜率相等且不相交，则这两条直线是平行的。

2. 垂直关系的判定方法：(1) 两条直线相交且相交角为90度，则这两条直线是垂直的。

(2) 垂直线的性质定理：如果一条直线与另一条直线相互垂直，且这两条直线各自还与第三条直线相交，则第三条直线与这两条直线也是垂直的。

(3) 垂直线的判定定理：如果两条直线的斜率互为负倒数，则这两条直线是垂直的。

三、常用公式在立体几何中，我们经常使用一些公式来求解问题。

下面是一些常用的公式：1. 立方体的表面积公式：立方体的表面积等于6倍的边长平方。

2. 立方体的体积公式：立方体的体积等于边长的立方。

3. 正方体的表面积公式：正方体的表面积等于6倍的边长平方。

4. 正方体的体积公式：正方体的体积等于边长的立方。

5. 圆柱体的表面积公式：圆柱体的表面积等于2πr² + 2πrh，其中r为底面半径，h为高。

6. 圆柱体的体积公式：圆柱体的体积等于πr²h，其中r为底面半径，h为高。