最新数学中考计算专题复习题

合集下载

中考数学计算题100道(58页)

中考数学计算题100道(58页)一、选择题1. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定2. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 03. 下列哪个数不是素数？A. 2B. 3C. 44. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定5. 下列哪个数是质数？A. 4B. 6C. 76. 如果一个数的平方是正数，那么这个数是什么？B. 负数C. 07. 下列哪个数是合数？A. 2B. 3C. 58. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 09. 下列哪个数是素数？A. 4B. 6C. 710. 如果一个数的平方是负数，那么这个数是什么？A. 正数B. 负数C. 011. 下列哪个数不是素数？A. 2B. 3C. 412. 如果一个数是偶数，那么它的平方根也是偶数吗？B. 不是C. 不一定13. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 014. 下列哪个数是质数？A. 4B. 6C. 715. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定16. 下列哪个数是合数？A. 2B. 3C. 517. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 018. 下列哪个数是素数？A. 4B. 6C. 719. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 020. 下列哪个数不是素数？A. 2B. 3C. 421. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定22. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 023. 下列哪个数是质数？A. 4B. 6C. 724. 如果一个数是奇数，那么它的平方是奇数吗？B. 不是C. 不一定25. 下列哪个数是合数？A. 2B. 3C. 526. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 027. 下列哪个数是素数？A. 4B. 6C. 728. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 029. 下列哪个数不是素数？A. 2B. 3C. 430. 如果一个数是偶数，那么它的平方根也是偶数吗？B. 不是C. 不一定31. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 032. 下列哪个数是质数？A. 4B. 6C. 733. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定34. 下列哪个数是合数？A. 2B. 3C. 535. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 036. 下列哪个数是素数？A. 4B. 6C. 737. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 038. 下列哪个数不是素数？A. 2B. 3C. 439. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定40. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 041. 下列哪个数是质数？A. 4B. 6C. 742. 如果一个数是奇数，那么它的平方是奇数吗？B. 不是C. 不一定43. 下列哪个数是合数？A. 2B. 3C. 544. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 045. 下列哪个数是素数？A. 4B. 6C. 746. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 047. 下列哪个数不是素数？A. 2B. 3C. 448. 如果一个数是偶数，那么它的平方根也是偶数吗？B. 不是C. 不一定49. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 050. 下列哪个数是质数？A. 4B. 6C. 751. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定52. 下列哪个数是合数？A. 2B. 3C. 553. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 054. 下列哪个数是素数？A. 4B. 6C. 755. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 056. 下列哪个数不是素数？A. 2B. 3C. 457. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定58. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 059. 下列哪个数是质数？A. 4B. 6C. 760. 如果一个数是奇数，那么它的平方是奇数吗？B. 不是C. 不一定61. 下列哪个数是合数？A. 2B. 3C. 562. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 063. 下列哪个数是素数？A. 4B. 6C. 764. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 065. 下列哪个数不是素数？A. 2B. 3C. 466. 如果一个数是偶数，那么它的平方根也是偶数吗？B. 不是C. 不一定67. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 068. 下列哪个数是质数？A. 4B. 6C. 769. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定70. 下列哪个数是合数？A. 2B. 3C. 571. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 072. 下列哪个数是素数？A. 4B. 6C. 773. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 074. 下列哪个数不是素数？A. 2B. 3C. 475. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定76. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 077. 下列哪个数是质数？A. 4B. 6C. 778. 如果一个数是奇数，那么它的平方是奇数吗？B. 不是C. 不一定79. 下列哪个数是合数？A. 2B. 3C. 580. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 081. 下列哪个数是素数？A. 4B. 6C. 782. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 083. 下列哪个数不是素数？A. 2B. 3C. 484. 如果一个数是偶数，那么它的平方根也是偶数吗？B. 不是C. 不一定85. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 0. 下列哪个数是质数？A. 4B. 6C. 787. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定88. 下列哪个数是合数？A. 2B. 3C. 589. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 090. 下列哪个数是素数？A. 4B. 6C. 791. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 092. 下列哪个数不是素数？A. 2B. 3C. 493. 如果一个数是偶数，那么它的平方根也是偶数吗？A. 是的B. 不是C. 不一定94. 如果一个数的立方是负数，那么这个数是什么？A. 正数B. 负数C. 095. 下列哪个数是质数？A. 4B. 6C. 796. 如果一个数是奇数，那么它的平方是奇数吗？A. 是的B. 不是C. 不一定97. 下列哪个数是合数？A. 2B. 3C. 598. 如果一个数的平方是正数，那么这个数是什么？A. 正数B. 负数C. 099. 下列哪个数是素数？A. 4B. 6C. 7100. 如果一个数的立方是正数，那么这个数是什么？A. 正数B. 负数C. 0中考数学计算题100道(58页)二、填空题1. 一个正方形的边长是5厘米，那么它的面积是多少平方厘米？2. 一个长方形的长是8厘米，宽是4厘米，那么它的面积是多少平方厘米？3. 一个圆的半径是3厘米，那么它的面积是多少平方厘米？4. 一个三角形的底是6厘米，高是4厘米，那么它的面积是多少平方厘米？5. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？6. 一个正方体的边长是4厘米，那么它的体积是多少立方厘米？7. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？8. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？9. 一个球的半径是4厘米，那么它的体积是多少立方厘米？10. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？11. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？12. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？13. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？14. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？15. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？16. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？17. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？18. 一个球的半径是4厘米，那么它的体积是多少立方厘米？19. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？20. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？21. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？22. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？23. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？24. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？25. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？26. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？27. 一个球的半径是4厘米，那么它的体积是多少立方厘米？28. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？29. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？30. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？31. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？32. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？33. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？34. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？35. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？36. 一个球的半径是4厘米，那么它的体积是多少立方厘米？37. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？38. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？39. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？40. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？41. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？42. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？43. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？44. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？45. 一个球的半径是4厘米，那么它的体积是多少立方厘米？46. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？47. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？48. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？49. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？50. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？51. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？52. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？53. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？54. 一个球的半径是4厘米，那么它的体积是多少立方厘米？55. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？56. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？57. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？58. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？59. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？60. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？61. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？62. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？63. 一个球的半径是4厘米，那么它的体积是多少立方厘米？64. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？65. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？66. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？67. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？68. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？69. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？70. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？71. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？72. 一个球的半径是4厘米，那么它的体积是多少立方厘米？73. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？74. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？75. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？76. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？77. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？78. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？79. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？80. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？81. 一个球的半径是4厘米，那么它的体积是多少立方厘米？82. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？83. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？84. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？85. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？87. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？88. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？89. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？90. 一个球的半径是4厘米，那么它的体积是多少立方厘米？91. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？92. 一个等腰三角形的底是6厘米，腰是5厘米，那么它的面积是多少平方厘米？93. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的面积是多少平方厘米？94. 一个菱形的对角线分别是8厘米和6厘米，那么它的面积是多少平方厘米？95. 一个梯形的上底是5厘米，下底是8厘米，高是3厘米，那么它的面积是多少平方厘米？96. 一个正方体的对角线长是10厘米，那么它的体积是多少立方厘米？97. 一个长方体的长是8厘米，宽是4厘米，高是2厘米，那么它的体积是多少立方厘米？98. 一个圆柱的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？99. 一个球的半径是4厘米，那么它的体积是多少立方厘米？100. 一个圆锥的底面半径是3厘米，高是5厘米，那么它的体积是多少立方厘米？。

中考数学计算题训练

中考数学计算题训练中考数学计算题专项训练一、训练一1.计算：1) sin45° - 1/2 + 3/8；2) 2×(-5) + 23 - 3÷4 + 2^2 + (-1)^4 + (5-2) - |-3|；3) -1-16+(-2)^2/(2×1) + 1001+12-33×tan30°；6) -2+(-2)+2sin30°；8) (-1)-16+(-2)^2/[(2×1)+(1×1)]。

2.计算：[-1/2 + 1/3×(-tan45°)] + 3/2.3.计算：1/3 - 2^-1 - (2010-2012+(-1)^-1)/(1001+12-33×tan30°)。

4.计算：18-[cos60°/(2-1-4sin30°)]+[(2-2)/(2-1)]。

5.计算：[cos60°/(-1)]-1^20+|2-8|-2^-1×(tan30°-1)。

二、训练二（分式化简）1.化简：2x/(x^2-4x-2) - 1/(x-2)。

2.化简：(1+1/(x-2))/(x^2-4)。

3.化简：(1-a)/(2a-1) ÷ [(a^2+2a+1)/(3-a^5)]。

4.化简：[(a-1)/(a^2-1)] ÷ [(a-1)/(2a-1)]，其中a≠-1.5.化简：[2x/(x+1)(x-1)] + [1/2(x-1)]。

6.化简：[1/(x-2)^2] ÷ [1/(x^2-4x+1)]，其中x≠1.7.化简：[1-(a-1)/(2a)] ÷ [(a^2+2a)/(a-1)]，其中a≠a。

8.化简：[2/(a+2)-(a-2)/(a-1)] ÷ [2/(a+1)-2/(a-2)]，其中a为整数且-3<a<2.9.化简：[(11/2)x+2]/(x-y) + [9/(x^2+2xy+y^2)]，其中x=1，y=-2.10.化简：[(1/2)-(1/12)x]/[2/(x-4)-x/(x^2-4)]，其中x=2(tan45°-cos30°)-1.三、训练三（求解方程）1.解方程x-4x+1=0.2.解分式方程(3x-2)/(x+1) + (2x+1)/(x-2) =3.3.解方程：x^3-2x^2+5x-6=0.4.解方程：(x-1)/(x+1) + (x+1)/(x-1) = 4.5.解方程：(x-2)/(x+1) + (x+1)/(x-2) = 2.四、解不等式1.解不等式 $x+2>1$，得 $x>-1$，整数解为 $x\in(-1,+\infty)$。

初三中考数学试卷计算题全

一、选择题（每题3分，共15分）1. 若方程x^2 - 5x + 6 = 0的解为x1和x2，则x1 + x2的值为（）A. 2B. 3C. 5D. 62. 在直角坐标系中，点A（2，3）关于y轴的对称点坐标为（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）3. 若a、b是方程x^2 - 4x + 3 = 0的两个根，则a^2 + b^2的值为（）A. 7B. 8C. 9D. 104. 在等腰三角形ABC中，底边BC的长度为8，腰AC的长度为6，则三角形ABC的面积为（）A. 24B. 18C. 14D. 125. 若x + y = 5，x - y = 1，则x^2 - y^2的值为（）A. 24B. 16C. 12D. 8二、填空题（每题3分，共15分）6. 若方程2x - 3 = 5的解为x = 4，则方程3x - 6 = y的解为y = _______。

7. 在等边三角形ABC中，若AB = AC = BC = 5，则三角形ABC的周长为 _______。

8. 若函数f(x) = 2x - 1的图象经过点P(3，f(3))，则点P的坐标为 _______。

9. 若平行四边形ABCD的对角线AC和BD相交于点O，且AC = 10，BD = 8，则三角形AOD的面积为 _______。

10. 若x，y是方程x^2 - 2x - 3 = 0的两个根，则x^2 + y^2的值为 _______。

三、解答题（每题10分，共30分）11. （1）若方程x^2 - 2x - 3 = 0的两个根为a和b，求a + b和ab的值。

（2）若方程x^2 - mx + n = 0有两个相等的实数根，求m和n的值。

12. （1）在直角坐标系中，点A（-2，3）关于原点的对称点坐标为B，求点B的坐标。

（2）若直线y = 2x + 1与y轴的交点为C，求点C的坐标。

13. （1）已知等腰三角形ABC的底边BC的长度为8，腰AC的长度为6，求三角形ABC的面积。

初中中考数学专题03 分式与二次根式(原卷版)

2024年中考数学真题专题分类精选汇编（2025年中考复习全国通用）专题03 分式与二次根式一、选择题1.（2024甘肃威武）计算：4222a b a b a b -=--（） A. 2B. 2a b -C. 22a b -D. 2a b a b -- 2. （2024天津市）计算3311x x x ---的结果等于（） A. 3 B. x C. 1x x - D. 231x - 3. （2024河北省）已知A 为整式，若计算22A y xy y x xy -++的结果为x y xy -，则A =（） A. x B. y C. x y + D. x y -4. （2024黑龙江绥化）m 的取值范围是（） A. 23m ≤ B. 32m ≥- C. 32m ≥ D. 23m ≤-5. （2024四川乐山）已知12x <<2x -的结果为（） A. 1- B. 1 C. 23x - D. 32x -6. （2024湖南省））A. B. C. 14 D.7. （2024江苏盐城），设其面积为2cm S ，则S 在哪两个连续整数之间（）A. 1和2B. 2和3C. 3和4D. 4和58. （2024重庆市B ）的值应在（） A. 8和9之间 B. 9和10之间C. 10和11之间D. 11和12之间9. （2024重庆市A ）已知m =m 的范围是（） A. 23m <<B. 34m <<C. 45m <<D. 56m << 二、填空题1. （2024吉林省）当分式11x +的值为正数时，写出一个满足条件的x 的值为______．2. （2024北京市）x 的取值范围是_________．3. （2024黑龙江齐齐哈尔）在函数12y x =++中，自变量x 的取值范围是______． 4. （2024湖北省）计算：111m m m +=++______．5. （2024四川德阳）__________．6. （2024贵州省）________．7. （2024山东威海）=________．8. （2024天津市）计算)11的结果为___．9. （2024上海市）1=，则x =___________．10. （2024山东威海）计算：2422x x x+=--________． 11. （2024黑龙江绥化）计算：22x y xy y x x x ⎛⎫--÷-= ⎪⎝⎭_________．三、解答题1. （2024江苏连云港）下面是某同学计算21211m m ---的解题过程：解：2121211(1)(1)(1)(1)m m m m m m m +-=---+-+-① (1)2m =+-②1m =-③上述解题过程从第几步开始出现错误？请写出完整的正确解题过程．2. （2024甘肃威武）．3. （2024北京市）已知10a b --=，求代数式()223232a b ba ab b -+-+值. 4. （2024甘肃临夏）化简：21111a a a a a +⎛⎫++÷ ⎪--⎝⎭． 5. （2024江苏苏州）先化简，再求值：2212124x x x x x +-⎛⎫+÷ ⎪--⎝⎭．其中3x =-． 6. （2024四川达州）先化简：22224x x x x x x x +⎛⎫-÷ ⎪-+-⎝⎭，再从2-，1-，0，1，2之中选择一个合适的数作为x 的值代入求值．7. （2024湖南省）先化简，再求值：22432x x x x x -⋅++，其中3x =． 8. （2024深圳）先化简，再求值： 2221111a a a a -+⎛⎫-÷ ⎪++⎝⎭，其中 21a =+ 9. （2024山东烟台）利用课本上的计算器进行计算，按键顺序如下：，若m 是其显示结果的平方根，先化简：27442393m m m m m m --⎛⎫+÷ ⎪--+⎝⎭，再求值．。

(完整版)初中数学中考计算题复习含答案

1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71　220130　3|1|012013567　8　10　111213+|3|+1　151612120130+||222+412　17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一．解答题（共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简，第二项利用负数的绝对值等于它的相反数计算法则计算，第四项利用负指数幂法则计算，第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4　17112013|7|+01211211115218原式第一项利用立方根的定义化简，第二项利用二次根式的化简公式化简，第三项利用零指数幂法则计算，1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021）原式第一项利用负数的绝对值等于它的相反数计算，第二项先计算乘方运算，再计算除法运算，第2131234622212121121313122312+11）原式第一项利用负数的绝对值等于它的相反数计算，第二项利用特殊角的三212172+1+324121）原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算，第三项利用负指数幂法则21+13+3213212512+112112+126121）原式第一项利用特殊角的三角函数值化简，第二项利用零指数幂法则计算，212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113．解方程（本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析：原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用特殊角的三角函数值计算，最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。

中考数学计算题专练

1、某班有40名学生，其中男生占60%，女生占多少？
A. 40%（答案）
B. 50%
C. 60%
D. 70%
2、一个正方形的边长是5cm，它的周长是多少cm？
A. 10cm
B. 15cm
C. 20cm（答案）
D. 25cm
3、如果小明每天步行上学需要30分钟，那么他一周步行上学总共需要多少分钟？
A. 150分钟
B. 210分钟
C. 300分钟
D. 2100分钟（答案）
4、一个三角形的内角和是多少度？
A. 90度
B. 180度（答案）
C. 270度
D. 360度
5、如果一个数的2倍等于6，那么这个数是多少？
A. 1
B. 2（答案）
C. 3
D. 4
6、一个圆的半径是4cm，它的面积大约是多少平方厘米？
A. 16
B. 25
C. 36
D. 50（答案）
7、如果5个苹果的重量是1千克，那么1个苹果的重量大约是多少克？
A. 100克（答案）
B. 200克
C. 300克
D. 400克
8、一个长方形的长是8cm，宽是4cm，它的面积是多少平方厘米？
A. 12
B. 16
C. 32（答案）
D. 64。

中考复习专题——计算题50道专练(含答案)精编版

1．计算：（﹣1）2015+﹣（）﹣2+sin45°．【答案】-7．【解析】试题分析：本题涉及零指数幂、乘方、特殊角的三角函数值、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：原式=-1+2-9+1=-7．考点：实数的混合运算．2．计算：0114cos 452(5)()84π-︒--+-+-．【答案】3【解析】试题分析：根据实数的运算性质计算，要注意2cos 452?，22-=，0(5)1π-=，11()44-=，822=．试题解析：解：原式=22412224-++-⨯=3．考点：实数混合运算 3．（本题6分）9＋(21)－1－2sin45°＋|－2013|【答案】2017【解析】试题分析：原式=3+2-1+2013 =2017考点: 实数的运算4．计算：()101122tan60201413-⎛⎫-︒+-- ⎪⎝⎭．【答案】2-．【解析】试题分析：针对二次根式化简，特殊角的三角函数值，零指数幂，负整数指数幂4个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：解：原式=2323132-+-=-．考点：1．实数的运算；2．二次根式化简；3．特殊角的三角函数值；4．零指数幂；5．负整数指数幂．5．计算：020116sin30223275-⎛⎫⎛⎫--++- ⎪ ⎪-⎝⎭⎝⎭【答案】3．【解析】试题分析：针对负整数指数幂，特殊角的三角函数值，零指数幂，绝对值4个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：解：原式=146123243123232-⨯-++-=--++-=．考点：1．实数的运算；2．负整数指数幂；3．特殊角的三角函数值；4．零指数幂；5．绝对值．6．计算：()20012014sin 60323π-⎛⎫+-++- ⎪⎝⎭．【答案】3122-．【解析】试题分析：针对负整数指数幂，零指数幂，特殊角的三角函数值，绝对值4个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：解：原式=3391231222+++-=-．考点：1．实数的运算；2．负整数指数幂；3．零指数幂；4．特殊角的三角函数值；5．绝对值．7．计算：100120142sin 3082-⎛⎫--+ ⎪⎝⎭．【答案】22.【解析】试题分析：针对负整数指数幂，零指数幂，特殊角的三角函数值，二次根式化简4个考点分别进行计算，然后根据实数的运算法则求得计算结果.试题解析：解：原式=12122221122222--⨯+=--+=. 考点：1.实数的运算；2.负整数指数幂；3.零指数幂；4.特殊角的三角函数值；5.二次根式化简.8．计算：()()020141321sin452-+-+-︒；【答案】2.【解析】试题分析：针对零指数幂，有理数的乘方，二次根式化简，特殊角的三角函数值4个考点分别进行计算，然后根据实数的运算法则求得计算结果. 试题解析：解：原式=2211222++-=. 考点：1.实数的运算；2.零指数幂；3.有理数的乘方；4.二次根式化简；5.特殊角的三角函数值. 9．计算：()20142sin45421--+︒+-【答案】3.【解析】试题分析：针对二次根式化简，有理数的乘方，特殊角的三角函数值，绝对值4个考点分别进行计算，然后根据实数的运算法则求得计算结果.试题解析：解：原式=22122212232+-⨯+=+-+=. 考点：1.实数的运算；2.二次根式化简；3.有理数的乘方；4.特殊角的三角函数值；5.绝对值. 10．计算：12-2sin60°+（-2014）0-（13）-1．【答案】3-2．【解析】试题分析：根据零指数幂、负指数幂、特殊角的三角函数值、二次根式化简四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：原式=23-2×32+1-3 =23-3+1-3 =3-2．考点：1.实数的运算；2.零指数幂；3.负整数指数幂；4.特殊角的三角函数值．11．计算：4 cos45°-8+(π-3) +(-1)3；【答案】0【解析】解：原式=4×22-22+1-1=012．计算：﹣25+（12）﹣1﹣|16﹣8|+2cos60°．【答案】﹣33．【解析】试题分析：第一项利用乘方的意义化简，第二项利用负指数幂法则计算，第三项利用绝对值的代数意义化简，最后一项利用特殊角的三角函数值计算即可．试题解析：原式=﹣32+2﹣4+1=﹣33．考点：1.实数的运算2.负整数指数幂3.特殊角的三角函数值．13．计算：（π﹣3.14）0+（﹣1）2015+|1﹣|﹣3tan30°．【答案】-1【解析】试题分析：按顺序依次利用零指数幂法则、乘方的意义、绝对值的代数意义、特殊角的三角函数值计算即可得到结果试题解析：原式=1﹣1+3﹣1﹣3×33=1﹣1+3﹣1﹣3=﹣1．考点：1、实数的运算；2、零指数幂；3、绝对值；4、特殊角的三角函数值．.14．计算：()10011820082cos 454π-⎛⎫---+ ⎪⎝⎭ 【答案】223+．°【解析】试题分析：原式第一项利用二次根式的化简公式计算，第二项利用零指数幂法则计算，第三项利用特殊角的三角函数计算，最后一项利用负指数幂法则，计算即可得到结果．试题解析：原式=232124=2232--⨯++．考点：1.二次根式的化简2.零指数幂法则3.特殊角的三角函数4.负指数幂法则．15．计算：011(32)4cos30123||--++--（）° 【答案】4．【解析】试题分析：分别用零指数次幂，负指数幂法则，特殊角的三角函数，绝对值的意义，进行化简，最后用实数的运算法则计算即可．试题解析：原式3134122=++-⨯ 42323=+-4= ．考点：1.零指数次幂2.负指数幂法则3.特殊角的三角函数4.绝对值的意义． 16．计算： ()()202012312sin 302813π-︒⎛⎫---+--+- ⎪⎝⎭【答案】10-．【解析】试题分析：分别求出特殊角的三角函数，负指数次幂，零指数次幂，立方根，负数的偶次幂，再依据实数的运算法则计算即可．试题解析：原式=12912119121102-⨯-+-+=--+-+=-．考点：1.特殊角的三角函数2.负指数次幂3.零指数次幂4.立方根．17．计算：|345tan |32)31()21(10-︒+⨯+-- 【答案】33.【解析】试题分析：原式第一项利用零指数幂法则计算，第二项利用负整数指数幂法则计算，第三项化为最简二次根式，最后一项利用绝对值的代数意义化简，计算即可得到结果．试题解析：原式=1+3×233+｜1-3｜ =1+23+31- =33考点：1.实数的混合运算；2.零指数幂；3.负整数指数幂；4.特殊角的三角函数值．18．计算：|1﹣2|+（π﹣2014）0﹣2sin45°+（12）﹣2．【答案】4．【解析】试题分析：先求出绝对值、零指数幂、负整指数幂、特殊角的三角函数值，然后根据实数的运算法则求得计算结果．试题解析：原式=2﹣1+1﹣2+4=4．考点：1.绝对值2.零指数幂3.负整指数幂4.特殊角的三角函数．19．计算：()21-︒-45sin 4+3-+8【答案】4【解析】试题分析：按照运算顺序计算，先算平方、特殊角的三角函数值、绝对值、二次根式的化简，然后按从左到右的顺序依次计算就可以试题解析：原式＝1－4×22+3+22= 4 考点：1、平方；2、绝对值；3、实数的混合运算20．计算：．【答案】3-7【解析】试题分析：先进行二次根式的化简、特殊角的三角函数值、零指数幂、负整数指数幂等运算，然后按照运算顺序进行计算即可．试题解析：原式=23﹣2×23+1﹣8=3-7 考点：1、二次根式的化简；2、零指数幂；3、负整数指数幂；4、特殊角的三角函数值．21．计算：20113015(1)()(cos68)338sin 602π---+++-. 【答案】-8+3【解析】原式31813382=--++-⨯ 83=-+22．计算:【答案】4.【解析】试题分析：根据特殊角的三角函数值进行计算.试题解析：考点:（1）二次根式的运算；（2）特殊角的三角函数.23．计算：01201314cos 452(5)()8(1)4π-︒--+-+---【答案】4.【解析】试题分析：先计算特殊角三角函数值、绝对值、零次幂、负整数指数幂、二次根式、有理数的乘方，再进行加减运算.试题解析：原式=242142212⨯-++-+ 224224=+-=考点：实数的混合运算.24．计算：0(3π)-++︒60tan 211()273--．【答案】43-.【解析】试题分析：针对零指数幂，特殊角的三角函数值，负整数指数幂，二次根式化简4个考点分别进行计算，然后根据实数的运算法则求得计算结果. 试题解析：原式12333343=++-=-.考点：1.零指数幂；2.特殊角的三角函数值；3.负整数指数幂；4．二次根式化简. 25．计算：10012014122sin 605-⎛⎫-+- ⎪⎝⎭．【答案】43+.【解析】试题分析：针对负整数指数幂，零指数幂，二次根式化简，特殊角的三角函数值 4个考点分别进行计算，然后根据实数的运算法则求得计算结果.试题解析：原式=351232432-+-⋅=+. 考点：1. 负整数指数幂；2.零指数幂；3.二次根式化简；4.特殊角的三角函数值.26．计算：1021182sin 45(32)32-⎛⎫-︒+- ⎪⎝⎭．【答案】21-.【解析】试题分析：针对二次根式化简，特殊角的三角函数值，幂零指数幂，负整数指数4个考点分别进行计算，然后根据实数的运算法则求得计算结果. 试题解析：原式223221222212132=⨯-⨯+-=--=-. 考点：1. 二次根式化简；2.特殊角的三角函数值；3. 零指数幂.；4. 负整数指数幂27．计算：()101129tan 3042π-⎛⎫-︒+-- ⎪⎝⎭．【答案】31--．【解析】试题分析：针对二次根式化简，特殊角的三角函数值，零指数幂，负整数指数幂4个考点分别进行计算，然后根据实数的运算法则求得计算结果．试题解析：原式=323912313=-⨯+-=--．考点：1．二次根式化简；2．特殊角的三角函数值；3．零指数幂；4．负整数指数幂．28．计算： 10184sin 4520142-⎛⎫-︒-+ ⎪⎝⎭．【答案】1-.【解析】试题分析：针对二次根式化简，特殊角的三角函数值，负整数指数幂，零指数幂4个考点分别进行计算，然后根据实数的运算法则求得计算结果试题解析：原式=22242+112-⨯-=-. 考点：1.二次根式化简；2.特殊角的三角函数值；3.负整数指数幂；4.零指数幂.29．计算：()1020140113tan 452-⎛⎫-+-π-+ ⎪⎝⎭ 【答案】-1【解析】原式= -1+1-2+1=-130．201(3)323tan 30π-+++-+︒【答案】2【解析】试题分析：先算乘方和去掉绝对值及三角函数的运算，再进行有理数的加减运算.试题解析：原式=-1+1+2-3+3×33=2-3+3=2 考点：有理数的混合运算.31．计算：101()3(3)3tan304-+--π-+︒ 【答案】323+.【解析】试题分析：针对负整数指数幂，绝对值，零指数幂，特殊角的三角函数值4个考点分别进行计算，然后根据实数的运算法则求得计算结果. 试题解析：101()3(3)3tan 343304133233-++--+⨯=-+︒=+-π.考点：1．负整数指数幂；2.绝对值；3.零指数幂；4.特殊角的三角函数值.32．计算：103130tan 3)23()12014(-⎪⎭⎫ ⎝⎛++--- 【答案】6【解析】试题分析：先进行零指数幂；负整数指数幂、三角函数值的运算和去括号，再进行加减运算. 试题解析：原式=103130tan 3)23()12014(-⎪⎭⎫ ⎝⎛++--- =1-32++333⨯ +113=1-32++3+3=6考点：1、零指数幂；2、负整数指数幂、3、三角函数值.33．计算：011|3|π12cos302---+--（）（）【答案】1.【解析】试题分析：针对绝对值，零指数幂，负整数指数幂，特殊角的三角函数值4个考点分别进行计算，然后根据实数的运算法则求得计算结果. 试题解析：0113|3|π12cos303122=122---++-=-+-⨯（）（）. 考点：1.绝对值；2.零指数幂；3.负整数指数幂；4.特殊角的三角函数值.34．计算：︒+--+-⨯-+--60tan )31(64)2()1(42302013π 【答案】23-+.【解析】试题分析：根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案. 原式41493=-+-+ 23=-+.考点：实数的混合运算.35．计算：tan 245°-2sin 30°+（2﹣1）0 -21()2-= 【答案】-3．【解析】试题分析：根据零指数幂、负整指数幂、特殊角的三角函数值，可化简式子，根据实数的运算法则求得计算结果．原式=1-2×12+1−211()2=1-1+1-4=-3．考点：1.实数的运算；2.零指数幂；3.负整数指数幂；4.特殊角的三角函数值．36．计算：432328230232364cos -⨯+︒+-+-（）（）．【答案】-6【解析】试题分析：先计算乘方和开方运算，再根据特殊角的三角函数值和平方差公式得到原式=1888316 2(23)(23)(23)42⨯⨯⨯+⨯+-+-- ，然后进行乘除运算后合并即可．原式=1888316 2(23)(23)(23)42⨯⨯⨯+⨯+-+-- 834323=-++--（）（）8323=-++-=-6．考点：二次根式的混合运算；特殊角的三角函数值．37．3-－(－4)－1+032π⎛⎫ ⎪-⎝⎭－2cos30° 【答案】54. 【解析】试题分析：先计算绝对值、负整数指数幂、零次幂、特殊角的三角函数值，再进行加减运算即可. 原式=1531344++-=. 考点：1.绝对值；2.零次幂；3.负整数指数幂；4.特殊角的三角函数值. 38．计算：︒+--+-⨯-+--60tan )31(64)2()1(42302013π 【答案】23-+.【解析】试题分析：根据绝对值、有理数的乘方、立方根、特殊角三角函数值的意义分别进行计算即可求出答案. 原式41493=-+-+23=-+.考点：实数的混合运算.39．计算：()02822sin 45π+-+--︒ 【答案】122+.【解析】试题分析：针对零指数幂，二次根式化简，绝对值，特殊角的三角函数值4个考点分别进行计算，然后根据实数的运算法则求得计算结果 ()02822sin 4512222122π+-+--︒=++-=+.考点：1.零指数幂；2.二次根式化简；3.绝对值；4.特殊角的三角函数值.40．计算：()10013tan 30132π-⎛⎫--+-+- ⎪⎝⎭ 【答案】1-.【解析】试题分析：针对负整数指数幂，特殊角的三角函数值，零指数幂，绝对值4个考点分别进行计算，然后根据实数的运算法则求得计算结果.原式=3231313--⨯++=-. 考点：1.负整数指数幂；2.特殊角的三角函数值；3.零指数幂；4.绝对值.41．计算： 10182cos 45()(2014)2--︒+-．【答案】21+．【解析】试题分析：针对二次根式化简，特殊角的三角函数值，负整数指数幂，零指数幂4个考点分别进行计算，然后根据实数的运算法则求得计算结果．原式=222221212-⨯+-=+．考点：1．二次根式化简；2．特殊角的三角函数值；3．负整数指数幂；1．零指数幂． 42．计算：-12003+()-2-|3-|+3tan60°。

中考数学计算练习题带答案

中考数学计算练习题带答案1. 有理数的加减法：- 计算：$ 3 - 5 + 2 - 7 $- 答案：$ -7 $2. 有理数的乘除法：- 计算：$ (-2) \times 3 \div (-1) $- 答案：$ 6 $3. 绝对值的计算：- 计算：$ |-8| + |-3| $- 答案：$ 11 $4. 幂的运算：- 计算：$ 2^3 \div 2^2 $- 答案：$ 2 $5. 多项式乘法：- 计算：$ (x + 3)(x - 2) $- 答案：$ x^2 + x - 6 $6. 分数的加减法：- 计算：$ \frac{3}{4} - \frac{1}{2} $- 答案：$ \frac{1}{4} $7. 分数的乘除法：- 计算：$ \frac{2}{3} \times \frac{3}{4} $ - 答案：$ \frac{1}{2} $8. 解一元一次方程：- 解方程：$ 2x + 5 = 11 $- 答案：$ x = 3 $9. 解一元二次方程：- 解方程：$ x^2 - 4x + 4 = 0 $- 答案：$ x = 2 $（重根）10. 代数式的求值：- 计算：$ 3a + 2b - 5a - b $ 当 $ a = 2, b = 3 $- 答案：$ -2a + b = -2 \times 2 + 3 = -1 $练习题答案解析：1. 先进行加法运算，再进行减法运算。

2. 先进行乘法运算，再进行除法运算。

3. 计算绝对值，然后进行加法运算。

4. 根据幂的除法法则，同底数幂相除，指数相减。

5. 根据多项式乘法法则，先进行乘法，再合并同类项。

6. 先通分，再进行分数的加减运算。

7. 根据分数的乘法法则，分子乘分子，分母乘分母。

8. 移项，合并同类项，然后求解。

9. 利用完全平方公式分解因式，然后求解。

10. 先化简代数式，然后代入给定的值求解。

初中数学中考计算题复习(最全)-含答案

by by
4, 2
的解为
x
y
2, 1,
，则
2a-3b
的值为多少？
参考答案与试题解析
一．解答题（共 30 小题）
第 11 题图
米的扇花台，那
a2 b2
．
2x y 5
3、已知 x 2 y 6 那么 x-y 的值是（
）
A. 1
B. ―1
C. 0
D. 2
4、若不等式组
x b
a2 2x 0
的解集是
1
x
1
，求
a
b
2010
的值
（1）23((xy12))5xy18
（5）
y 1 4
x
3
2
2x 3y 1
÷
+ ，其中 x=2 +1．
26．（1）计算：
；
（2）解方程：
．
27．计算：
．
28．计算：
．
29．计算：（1+ ）2013﹣2（1+ ）2012﹣4（1+ ）2011．
30．计算：
．
1．化简求值：
，选择一个你喜欢且有意义的数代入求值．
2．先化简，再求值
，然后选取一个使原式有意义的 x 值代入求值．
一．解答题（共 30 小题）
1．计算题：
①
；
②解方程：
．
2．计算：
+（π﹣2013）0．
3．计算：|1﹣ |﹣2cos30°+（﹣ ）0×（﹣1）2013．
4．计算：﹣
．
5．计算：
．
6．
．
7．计算：
．
8．计算： 9．计算：

中考数学计算题100道(58页)

《中考数学计算题100道（58页）》一、有理数计算1. 计算：(3) + 7 × (2)2. 计算：(4 5) × (6) ÷ 33. 计算：3 × (4) + 5 × 2 84. 计算：(2/3) × (9/4) ÷ (3/8)5. 计算：(5/8) + (3/4) (1/2)二、整式计算6. 计算：2x 3x + 47. 计算：5a^2 3a^2 + 2a8. 计算：4xy 2xy + 6x^29. 计算：(3m + 2n) (2m n)10. 计算：(4ab 3a^2b) ÷ ab三、分式计算11. 计算：(1/2) ÷ (1/3)12. 计算：(3/4) + (2/5) (1/2)13. 计算：(2/3) × (5/6) ÷ (4/9)14. 计算：(a/b) + (b/a)15. 计算：(x/y) (y/x) + 1《中考数学计算题100道（58页）》四、一元一次方程计算16. 解方程：5x 3 = 2x + 417. 解方程：4 3y = 7y 218. 解方程：2/3 z + 1 = 5/619. 解方程：3(2m 1) = 4m + 220. 解方程：5k 15 = 3 2k五、二元一次方程组计算21. 解方程组：\[\begin{cases}2x + 3y = 8 \\x y = 1\end{cases}\]22. 解方程组：\[\begin{cases}4a 3b = 7 \\2a + b = 5\end{cases}\]23. 解方程组：\[\begin{cases}5m + n = 14 \\3m 2n = 1\end{cases}\]24. 解方程组：\[\begin{cases}6p 2q = 16 \\3p + q = 7\end{cases}\]25. 解方程组：\[\begin{cases}x + 4y = 9 \\2x 3y = 1\end{cases}\]六、不等式与不等式组计算26. 解不等式：3x 5 > 2x + 127. 解不等式：4 2y ≤ 3y 128. 解不等式：1/2 a 3 > 1/4 a + 229. 解不等式组：\[\begin{cases}2x 3 > 1 \\x + 4 < 7\end{cases}\]30. 解不等式组：\[\begin{cases}3y + 2 ≥ 5 \\y 1 < 2\end{cases}\]七、乘法公式计算31. 计算：(a + b)^232. 计算：(x y)^233. 计算：(2m + 3n)(m n)34. 计算：(3x 4y)(4x + 3y)35. 计算：(a + b + c)(a b + c)八、因式分解36. 因式分解：x^2 937. 因式分解：a^2 4b^238. 因式分解：2x^2 + 5x + 339. 因式分解：3y^2 6y + 340. 因式分解：4m^2 12mn + 9n^2《中考数学计算题100道（58页）》九、分式化简与计算41. 化简分式：(x^2 y^2) / (x + y)42. 化简分式：(a^3 + b^3) / (a + b)43. 计算分式：1/2 + 1/3 1/644. 计算分式：(2/5) / (1/2) + (3/4)45. 计算分式：(x/y) (y/x) + 2/(x + y)十、根式计算46. 计算根式：√(49) √(16)47. 计算根式：√(64) + √(121)48. 计算根式：√(2/3) × √(3/2)49. 计算根式：√(27) ÷ √(3)50. 计算根式：√(a^2 + b^2)（假设a和b为正数）十一、一元二次方程计算51. 解方程：x^2 5x + 6 = 052. 解方程：2y^2 4y 6 = 053. 解方程：3z^2 + 12z + 9 = 054. 解方程：4m^2 12m + 9 = 055. 解方程：5n^2 + 10n = 0十二、函数计算56. 计算函数值：f(x) = 2x + 3，当x = 1时，求f(x)的值。

中考数学专题复习题：二次根式的乘除法

中考数学专题复习题：二次根式的乘除法一、单项选择题（共6小题）1．下列各式①√8；②√0.3；③√12；④√3；⑤√a2+1；其中一定是最简二次根式的有（）A．4 个B．3 个C．2个D．1个2．已知x是整数，√3⋅√6x是整数，则x的最小值（）A．2B．3C．4D．183．计算(5√2−2√5)×√15的结果是（）A．√10−√2B．√2−2C．√10−2D．√2−√104．计算(1+√2)2024(1−√2)2023的结果是（）A．√2−1B．−1C．1D．−1−√25．通过“由特殊到一般”的方法探究下面二次根式的运算规律：特例1：√1+13=√3+13=√4×13=2√13；特例2：√2+14=√8+14=√9×14=3√14；特例3：√3+15=√15+15=√16×15=4√15……应用发现的规律求√2024+12026×√4052的值（）A．2024B．2025√2C．2023D．2023√2 6．下列各式中，化简正确的是（）A．√(−16)×(−25)=√−16×√−25=20B．√12×27=√4×√81=18C．√16+94=√16+√94=4+32=112D．√4925=√4×√925=2×35=65二、填空题（共4小题）7．计算√3÷√2×2√5÷√110的结果为________．8．计算(√7+√2)(√7−√2)的结果是________．9．长方形的面积为18cm2，一边长为2√3cm，则另一边长为________cm．10．设6−√10的整数部分为a ，小数部分为b ，那么(2a +√10)b =________．三、解答题（共5小题）11．计算：（1）√8×√18；（2）√1.2×102×√3×105；（3）√2×√5×√10；（4）14√12×3√3． 12．计算下列各题．（1）√(−5)2×(−3)2；（2）√(−4)×259×(−169)；（3）√−a ⋅√−ab 3；（4）2b √ab 3⋅(−32√a 3b ⋅3√a b ) (a >0，b >0)．13．计算：（1）√48÷√3−√13×√18+√24；（2）(√5+1)(√5−1)+(−2)0−√273．14．请观察式子：9√127=√9227=√3，−2√12=−√222=−√2，仿照上面的方法解决下列问题：（1）化简：①5√25；②−7√37；③a√−1a (a <0)．（2）把(1−a )√1a−1中根号外的因式移到根号内，化简的结果是________．15．填空（可用计算器计算）：√4×9=__________，√4×√9=__________；√4×5=__________，√4×√5=__________；√916=__________，√9√16=__________； √32=__________，√3√2=__________．比较左右两边的等式，你发现了什么？你能用字母表示发现的规律吗？。

中考数学计算题专项训练(全)

中考专项训练——计算题集训一（计算）1. 计算：3082145+-Sin2.计算：3.计算：2×(－5)＋23－3÷12 ．4.计算：22＋(－1)4＋(5－2)0－|－3|；5.计算：22+|﹣1|﹣．6.计算：︒+-+-30sin 2)2(20．7.计算，8.计算：（1）()()022161-+--（2）a(a-3)+(2-a)(2+a)9. 计算：(3)0- (12)-2 +tan45°10. 计算：()()0332011422---+÷-集训二（分式化简）1. （2011.南京）计算．2. （2011.常州）化简：21422---x x x3.（2011.淮安）化简：（a+b ）2+b （a ﹣b ）．4. （2011.南通）先化简，再求值：(4ab 3－8a 2b 2)÷4ab ＋(2a ＋b )(2a －b )，其中a ＝2，b ＝1．5. （2011.苏州）先化简，再求值：（a ﹣1+）÷（a 2+1），其中a=﹣1．6.（2011.宿迁）已知实数a 、b 满足ab ＝1，a ＋b ＝2，求代数式a 2b ＋ab 2的值．7. （2011.泰州）化简．8.（2011.无锡）a(a-3)+(2-a)(2+a)9.（2011.徐州）化简：11()a a a a--÷；10.（2011.扬州）化简2111x x x -⎛⎫+÷ ⎪⎝⎭集训三（解方程）1. （2011•南京）解方程x 2﹣4x+1=0．2. （2011.常州）解分式方程2322-=+x x3．（2011.连云港）解方程：3x ＝ 2x －1 ．4. （2011.苏州）已知|a ﹣1|+=0，求方裎+bx=1的解．5. (2011.无锡)解方程：x 2+4x －2=06.（2011.盐城）解方程：x x -1 - 31-x= 2．7.（2011.泰州）解方程组，并求的值．集训四（解不等式）1.（2011．南京）解不等式组，并写出不等式组的整数解．2.（2011.常州）解不等式组()()()⎩⎨⎧+≥--+-14615362x x x x3.（2011.连云港）解不等式组：⎩⎨⎧2x ＋3＜9－x ，2x －5＞3x ．4.（2011.南通）求不等式组⎩⎨⎧3x －6≥x －42x ＋1＞3(x －1)的解集，并写出它的整数解．5.（2011.苏州）解不等式：3﹣2（x ﹣1）＜1．6. （2011.宿迁）解不等式组⎪⎩⎪⎨⎧<+>+.221,12x x8.解不等式组：102(2)3x x x -≥⎧⎨+>⎩9. 解不等式组⎩⎪⎨⎪⎧x +23 ＜1，2(1-x )≤5，并把解集在数轴上表示出来。

中考数学专题复习《整式的运算》测试卷-附带答案

中考数学专题复习《整式的运算》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1．计算(−x2)3的结果是（）A．−x6B．x6C．−x5D．−x82．下列计算正确的是（）A．x7÷x＝x7B．(−3x2)2=−9x4C．x3•x3＝2x6D．（x3）2＝x63．下列计算正确的是（）A．3x+3y=6xy B．a2•a3=a6C．b6÷b3=b2D．（m2）3=m6 4．下列计算正确的是（）A．3a3⋅2a3=6a3B．(−4a3b)2=8a6b2C．(a+b)2=a2+b2D．−2a2+3a2=a25．下列运算正确的是（）A．(x−1)(x+1)=x2−x−1B．x2−2x+3=(x−1)2+4C．(x−1)2=x2−2x−1D．(x−1)(−1−x)=1−x26．观察一列单项式：x−3x37x5−15x731x9⋯．则第n个单项式是（）A．(−1)n+1(2n−1)x2n−1B．(−1)n(2n−1)x2n+1C．(−1)n+1(2n−1)x2n−1D．(−1)n(2n+1)x2n−17．若k为任意整数则(2k+3)2−4k2的值总能（）A．被2整除B．被3整除C．被5整除D．被7整除8．已知10a=25,100b=40则a+2b的值是（）A．1B．2C．3D．49．对于任意自然数n关于代数式（n+7）2﹣（n﹣5）2的值说法错误的是（）A．总能被3整除B．总能被4整除C．总能被6整除D．总能被7整除10．若2a-3b=-1 则代数式4a2−12ab+9b2的值为（）A．-1B．1C．2D．311．已知关于x的两个多项式A=x2−ax−2B=x2−2x−3．其中a为常数下列说法：①若A−B的值始终与x无关则a=−2②关于x的方程A+B=0始终有两个不相等的实数根③若A ⋅B 的结果不含x 2的项则a =52④当a =1时若A B 的值为整数则x 的整数值只有2个．以上结论正确的个数有（） A ．4B ．3C ．2D ．112．对于若干个单项式我们先将任意两个单项式作差再将这些差的绝对值进行求和并化简这样的运算称为对这若干个单项式作“差绝对值运算”．例如：对2，3，4作“差绝对值运算” 得到|2−3|+|2−4|+|3−4|=4 则①对1，3，4，7作“差绝对值运算”的结果是19 ②对x 2，x ，−3(x 2>x >−3)进行“差绝对值运算”的结果是38 则x =±4 ③对a ，b ，c （互不相等）进行“差绝对值运算”的结果一共有7种．以上说法中正确的个数为（） A ．0B ．1C ．2D ．3二填空题13．已知3x+y=-3 xy=-6 则 xy 3+9x 3y = .14．若实数m 满足(m −2023)2+(2024−m)2=2025 则(m −2023)(2024−m)= ．15．已知 m +n +2m+n =4，则 (m +n )2+(2m+n )2的值为 . 16．小明在化简：(4x 2−6x +7)−(4x 2−□x +2)时发现系数“□”印刷不清楚老师提示他：“此题的化简结果是常数” 则多项式中的“□”表示的数是 .17．如果一个三位自然数m =abc ̅̅̅̅̅的各数位上的数字互不相等且均不为0 满足a +c =b 那么称这个三位数为“中庸数”．将“中庸数”m =abc ̅̅̅̅̅的百位个位数字交换位置得到另一个“中庸数”m ′=cba ̅̅̅̅̅ 记F(m)=m−m ′99，T(m)=m+m ′121．例如：m =792，m ′=297．F(m)=792−29799=5 T(m)=792+297121=9．计算F(583)= 若“中庸数”m 满足2F(m)=s 2，2T(m)=t 2 其中s ，t 为自然数1 2 3…… 则该“中庸数”m 是．18．一个四位自然数M 若它的千位数字与十位数字的差为3 百位数字与个位数字的差为2 则称M 为“接二连三数” 则最大的“接二连三数”为已知“接二连三数”M 能被9整除将其千位数字与百位数字之和记为P 十位数字与个位数字之差记为Q 当PQ 为整数时满足条件的M 的最小值为．三计算题19．计算：（1）x(1−x)（2）(a−1)(2a+3)−2a(a−4)（3）x 2x−1−x−1．20．计算：（1）(−2xy2)2⋅3x2y．（2）(−2a2)(3ab2−5ab3)．（3）(3m2n)2⋅(−2m2)3÷(−m2n)2．（4）(a−2b−3c)(a−2b+3c)．21．（x+2）2+（2x+1）（2x﹣1）﹣4x（x+1）其中x＝−12 .．22．−12(xy−x2)+3(y2−12x2)+2(14xy−12y2)其中x=−2y=12．23．先化简再求值：[(x+2y)2−(x+2y)(x−2y)]÷4y其中x=1y=−1．四解答题24．观察下面的等式：32−12=8×1，52−32=8×2，72−52=8×3，92−72=8×4，⋯（1）写出192−172的结果．（2）按上面的规律归纳出一个一般的结论（用含n的等式表示n为正整数）（3）请运用有关知识推理说明这个结论是正确的．25．尝试：①152=225=1×2×100+25.②252=625=2×3×100+25.③352=1225=_▲_...运用：小滨给出了猜想和证明请判断是否正确若有错误请给出正确解答.猜想：(10a+5)2=100a(a+1)+25.证明：(10a+5)2=100a(a+1)+25所以10a2+100a+5=100a2+100a+25.所以10a2=100a2.因为a≠0所以10a2≠100a2.所以等式不成立结论错误.26．已知实数a b满足（2a2+b2+1）（2a2+b2-1）＝80 试求2a2+b2的值．解：设2a2+b2＝m则原方程可化为（m+1）（m-1）＝80 即m2＝81 解得：m＝±9 ∵2a2+b2≥0 ∴2a2+b2＝9 上面的这种方法称为“换元法” 换元法是数学学习中最常用的一种思想方法在结构较复杂的数和式的运算中若把其中某些部分看成一个整体并用新字母代替（即换元）则能使复杂问题简单化．根据以上阅读材料解决下列问题：（1）已知实数x y满足（2x2+2y2-1）（x2+y2）＝3 求3x2+3y2-2的值（2）若四个连续正整数的积为120 求这四个正整数．27．阅读下列材料：我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方公式如果一个多项式不是完全平方公式我们常做如下变形：先添加一个适当的项使式子中出现完全平方式再减去这个项使整个式子的值不变这种方法叫做配方法．配方法是一种重要的解决问题的数学方法可以求代数式的最大值或最小值．例如：求代数式x2+2x-3的最小值．解：x2+2x-3＝x2+2x+12-12-3＝（x2+2x+12）-4＝（x+1）2-4．∵（x+1）2≥0 ∴（x+1）2-4≥-4∴当x＝-1时x2+2x-3的最小值为-4．再例如：求代数式-x2+4x-1的最大值．解：-x2+4x-1＝-（x2-4x+1）＝-（x2-4x+22-22+1）＝-[（x2-4x+22）-3]＝-（x-2）2+3∵（x-2）2≥0 ∴-（x-2）2≤0 ∴-（x-2）2+3≤3．∴当x＝2时-x2+4x-1的最大值为3．（1）【直接应用】代数式x2+4x+3的最小值为（2）【类比应用】若M＝a2+b2-2a+4b+2023 试求M的最小值（3）【知识迁移】如图学校打算用长20m的篱笆围一个长方形菜地菜地的一面靠墙（墙足够长）求围成的菜地的最大面积．28．在学习《完全平方公式》时某数学学习小组发现：已知a+b＝5 ab＝3 可以在不求a b的值的情况下求出a2+b2的值．具体做法如下：a2+b2＝a2+b2+2ab-2ab＝（a+b）2-2ab＝52-2×3＝19．（1）若a+b＝7 ab＝6 则a2+b2＝（2）若m满足（8-m）（m-3）＝3 求（8-m）2+（m-3）2的值同样可以应用上述方法解决问题．具体操作如下：解：设8-m＝a 8-m＝a m-3＝b则a+b＝（8-m）+（m-3）＝5 a+b＝（8-m）+（m-3）＝5 ab＝（8-m）（m-3）＝3所以（8-m）2+（m-3）2＝a2+b2＝（a+b）2-2ab＝52-2×3＝19．请参照上述方法解决下列问题：若（3x-2）（10-3x）＝6 求（3x-2）2+（10-3x）2的值29．利用完全平方公式a2+2ab+b2=(a+b)2和a2−2ab+b=2(a−b)2的特点可以解决很多数学问题.下面给出两个例子：例1分解因式：x2+2x−3x2+2x−3=x2+2x+1−4=(x+1)2−4=(x+1+2)(x+1−2)=(x+3)(x−1)例2求代数式2x2−4x−6的最小值：2x2−4x−6=2(x2−2x)−6=2(x2−2x+1−1)−6=2[(x−1)2−1]−6=2(x−1)2−8又∵2(x−1)2≥0∴当x=1时代数式2x2−4x−6有最小值最小值是−8．仔细阅读上面例题模仿解决下列问题：（1）分解因式：m2−8m+12（2）代数式−x2+4x−2有最(大小)值当x=时最值是（3）当x y为何值时多项式2x2+y2−8x+6y+25有最小值？并求出这个最小值．30．发现：一个两位数的平方与其个位数字的平方的差一定是20的倍数．如：132−32=160160是20的8倍262−62=640640是20的32倍．（1）请你仿照上面的例子再举出一个例子：(⋅⋅⋅⋅)2−(⋅⋅⋅⋅⋅)2=(⋅⋅⋅⋅⋅)（2）十位数字为1 个位数字为a的两位数可表示为若该两位数的平方与a的平方的差是20的5倍则a=（3）设一个两位数的十位数字为m个位数字为n（0<m<100≤n<10且m n为正整数）请用含m n的式子论证“发现”的结论是否符合题意．31．灵活运用完全平方公式(a±b)2=a2±2ab+b2可以解决许多数学问题．例如：已知a−b=3，ab=1求a2+b2的值．解：∵a−b=3，ab=1∴(a−b)2=9，2ab=2，∴a2−2ab+b2=9∴a2−2+b2=9，∴a2+b2=9+2=11．请根据以上材料解答下列问题．（1）若a2+b2与2ab−4互为相反数求a+b的值．（2）如图矩形的长为a 宽为b 周长为14 面积为8 求a2+b2的值．32．定义：对于一个三位正整数如果十位数字恰好等于百位数字与个位数字之和的一半我们称这个三位正整数为“半和数”．例如三位正整数234 因为3=12×(2+4)所以234是“半和数”．（1）判断147是否为“半和数” 并说明理由（2）小林列举了几个“半和数”：111 123 234 840… 并且她发现：111÷3=37123÷3=41 234÷3=78840÷3=280… 所以她猜测任意一个“半和数”都能被3整除．小林的猜想正确吗？若正确请你帮小林说明该猜想的正确性若错误说明理由．答案解析部分1．【答案】A2．【答案】D3．【答案】D4．【答案】D5．【答案】D6．【答案】C7．【答案】B8．【答案】C9．【答案】D10．【答案】B11．【答案】B12．【答案】B13．【答案】-27014．【答案】−101215．【答案】1216．【答案】617．【答案】2 121或484或58318．【答案】9967 885619．【答案】（1）解：x(1−x)=x−x2（2）解：(a−1)(2a+3)−2a(a−4)=2a2+3a−2a−3−2a2+8a=9a−3（3）解：x 2x−1−x−1=x2x−1−(x+1)=x2−(x+1)(x−1)x−1=x2−x2+1x−1=1x−1．20．【答案】（1）解：(−2xy2)2⋅3x2y=4x2y4⋅3x2y=12x4y5（2）解：(−2a2)(3ab2−5ab3)=−6a3b2+10a3b3（3）解：(3m2n)2⋅(−2m2)3÷(−m2n)2=9m4n2⋅(−8m6)÷m4n2=−72m10n2÷m4n2=−72m6（4）解：(a−2b−3c)(a−2b+3c)=[(a−2b)−3c][(a−2b)+3c]=(a−2b)2−9c2=a2−4ab+4b2−9c2．21．【答案】解：原式＝x2+4x+4+4x2﹣1﹣4x2﹣4x＝x2+3当x=−1 2时∴原式＝（−12）2+3＝31 4．22．【答案】解：−12(xy−x2)+3(y2−12x2)+2(14xy−12y2)=−12xy+12x2+3y2−32x2+12xy−y2=−x2+2y2当x=−2y=1 2时原式=−(−2)2+2×(12)2=−4+2×1 4=−4+1 2=−72．23．【答案】解：化简方法一：[(x+2y)2−(x+2y)(x−2y)]÷4y=[(x+2y)(x+2y−x+2y)]÷4y=[(x+2y)·4y]÷4y=x+2y化简方法二：[(x+2y)2−(x+2y)(x−2y)]÷4y=[(x2+4xy+4y2)−(x2−4y2)]÷4y=(x2+4xy+4y2−x2+4y2)÷4y=(4xy+8y2)÷4y=4xy÷4y+8y2÷4y=x+2y当x=1y=−1时原式=1+2×(−1)=−1．24．【答案】（1）8×9（2）(2n+1)2−(2n−1)2=8n（3）(2n+1)2−(2n−1)2=(2n+1+2n−1)(2n+1−2n+1)=4n×2=8n。

初中数学中考计算题复习最全)-含答案

一．解答题（共30小题）1．计算题：①；②解方程：．2．计算：+（π﹣2013）0．3．计算：|1﹣|﹣2cos30°+（﹣）0×（﹣1）2013．4．计算：﹣．5．计算：．6．．7．计算：．8．计算：．9．计算：．10．计算：．11．计算：．12．．13．计算：．14．计算：﹣（π﹣3.14）0+|﹣3|+（﹣1）2013+tan45°．15．计算：．16．计算或化简：（1）计算2﹣1﹣tan60°+（π﹣2013）0+|﹣|．（2）（a﹣2）2+4（a﹣1）﹣（a+2）（a﹣2）17．计算：（1）（﹣1）2013﹣|﹣7|+×0+（）﹣1；（2）．18．计算：．（1）19．（2）解方程：．20．计算：（1）tan45°+sin230°﹣cos30°•tan60°+cos245°；（2）．21．（1）|﹣3|+16÷（﹣2）3+（2013﹣）0﹣tan60°（1）计算：.22．（2）求不等式组的整数解．（1）计算：23．（2）先化简，再求值：（﹣）÷，其中x=+1．24．（1）计算：tan30°25．计算：（1）（2）先化简，再求值：÷+，其中x=2+1．26．（1）计算：；（2）解方程：．27．计算：．28．计算：．29．计算：（1+）2013﹣2（1+）2012﹣4（1+）2011．30．计算：．1．化简求值：，选择一个你喜欢且有意义的数代入求值．2．先化简，再求值，然后选取一个使原式有意义的x值代入求值．3．先化简再求值：选一个使原代数式有意义的数代入中求值．4．先化简，再求值：，请选择一个你喜欢的数代入求值．5．（2010•红河州）先化简再求值：．选一个使原代数式有意义的数代入求值．6．先化简，再求值：（1﹣）÷，选择一个你喜欢的数代入求值．7．先化简，再求值：（﹣1）÷，选择自己喜欢的一个x求值．8．先化简再求值：化简，然后在0，1，2，3中选一个你认为合适的值，代入求值．9．化简求值（1）先化简，再求值，选择你喜欢的一个数代入求值．10．化简求值题：（1）先化简，再求值：，其中x=3．（2）先化简，再求值：，请选一个你喜欢且使式子有意义的数字代入求值．（3）先化简，再求值：，其中x=2．（4）先化简，再求值：，其中x=﹣1．11．（2006•巴中）化简求值：，其中a=．12．（2010•临沂）先化简，再求值：（）÷，其中a=2．13．先化简：，再选一个恰当的x值代入求值．14．化简求值：（﹣1）÷，其中x=2．15．（2010•綦江县）先化简，再求值，，其中x=+1．16．（2009•随州）先化简，再求值：，其中x=+1．17．先化简，再求值：÷，其中x=tan45°．18．（2002•曲靖）化简，求值：（x+2）÷（x﹣），其中x=﹣1．19．先化简，再求值：（1+）÷，其中x=﹣3．20．先化简，再求值：，其中a=2．21．先化简，再求值÷（x﹣），其中x=2．22．先化简，再求值：，其中．23．先化简，再求值：（﹣1）÷，其中x—．25．（2011•新疆）先化简，再求值：（+1）÷，其中x=2．26．先化简，再求值：，其中x=2．27．（2011•南充）先化简，再求值：（﹣2），其中x=2．28．先化简，再求值：，其中a=﹣2．29．（2011•武汉）先化简，再求值：÷（x ﹣），其中x=3． 30．化简并求值：•，其中x=21.． 2。

最新数学中考计算专题复习题

中考数学计算题100道(58页)

中考数学计算题训练

初三中考数学试卷计算题全

初中中考数学专题03 分式与二次根式(原卷版)

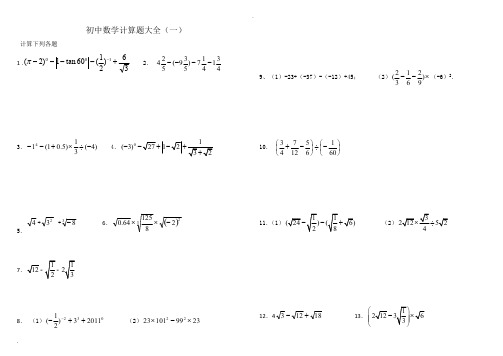
(完整版)初中数学中考计算题复习含答案

中考数学计算题专练

中考复习专题——计算题50道专练(含答案)精编版

中考数学计算练习题带答案

初中数学中考计算题复习(最全)-含答案

中考数学计算题100道(58页)

中考数学专题复习题：二次根式的乘除法

中考数学计算题专项训练(全)

中考数学专题复习《整式的运算》测试卷-附带答案

最新中考数学专题复习-代数式求值(含解析)

初中数学中考计算题复习最全)-含答案