材料力学(金忠谋)第六版答案第06章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第06章.doc

弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
材料力学习题第六章应力状态分析答案详解

第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ=; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的; (C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版答案第08章
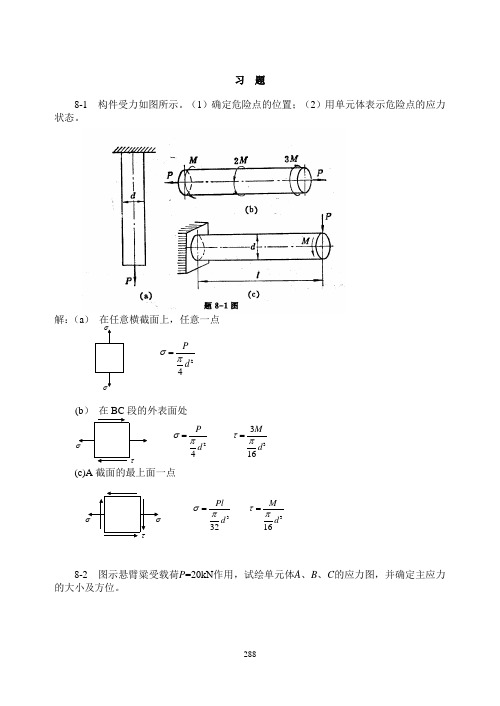
288习 题8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a ) 在任意横截面上,任意一点σσ24Pdσπ=(b ) 在BC 段的外表面处24Pdσπ=3316Mdτπ=τσ(c)A 截面的最上面一点στσ332Pldσπ=316Mdτπ=8-2 图示悬臂粱受载荷P =20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
289解:σσ2620100060520106A M MPa W σ--⨯===-⨯⨯BσB σBτ2386282200005103052010620000557.5102250 2.25520105106B B B M y MPaJKPa MPa στ-----⨯⨯===-⨯⨯⨯⨯⨯⨯===⨯⨯⨯⨯Cτ4020000 1.51.5320510C C Q MPa A στ-=⨯===⨯⨯3σ1σστA <>点1306090σσα=== 1σ3σστB <>点130.16830.16885.7σσα==-=στ1σ3σC<>点133345σσα==-=-8—3 主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa)。
解:(a)()()1212205205cos2cos6013.752222MPa ασσσσσα+---+-=+=+=290291()12205sin 2sin 6010.82522MPa ασστα---=== ()max 20512.52MPa τ--==45α= (与120σ=方向夹角)(b)()()()121220102010cos 2cos 135 5.6062222MPa ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=-()max 2010152MPa τ--== 45α= (与1σ方向夹角)或135(与水平方向交角)(c )()121240104010cos 2cos 12017.52222MPaασσσσσα+-+-=+=+-= ()124010sin 2sin 12013.022MPa ασστα--==-=- max 4010152MPa τ-== 45α= (与140σ=方向夹角)(d) ()121220202020cos 2cos 45202222MPa ασσσσσα+-+-=+=+= 0ατ=max 0τ=8—4 单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学第六版答案第07章

材料力学(金忠谋)第六版答案第07章(总23页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除244习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角,梁的抗弯刚度EI 为常量。
7-1(a ) 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ;'0y =代入上面方程可求得:C=D=0201M 2EJ y x ∴= '01=M EJy x θ= 01=M EJ B l θ 201=M 2EJB y l (b )222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+- 3'2211EJ 226qx y ql x qlx C =-+-+ 422311EJ 4624qx y ql x qlx Cx D =-+-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=02454223111()EJ 4624qx y ql x qlx ∴=-+- '2231111=(-)EJ 226y ql x qlx qx θ=+- 3-1=6EJ B ql θ 4-1=8EJB y ql (c )()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l x q x q lq l x M x q x l x l x l q y l x lq y l x C lq y l x Cx D l-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++ 边界条件:0x = 时 0y = ;'0y = 代入上面方程可求得:4024q l C l -= 50120q l D l= ()455000232230120EJ 24EJ 120EJ (10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =- (d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D =-=-=-+=-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=024623'232321112611253262B C C B y Pax Px EJ y Pax Px EJ Pa Pa Pa y y a a EJ EJ EJ Pa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==- ⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qax a y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=0()()()22118492024EJ 12EJqax qax y a x a x x a ∴=--=--≤≤ ''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++ 边界条件:x a = 时 12y y = ;12θθ=代入上面方程可求得:2296a C = 4224qa D =- ()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤247 43412476B B qa y EJ qa EJθ=-=- (f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件:x a = 时 12y y = ; ''''12y y =3296a C =- 4224a D =- 437124136B B qa y EJ qa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程,端截面转角θA 和θB ,跨度中点的挠度和最大挠度,梁的抗弯刚度EI 为常量。
材料力学金忠谋第六版答案第章

(a) (b)
(c )(d)
(e)
8-6已知矩形截面梁某截面上的弯矩和剪力分别为M=10kN·m,FS=120kN,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:
8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上(与纸平面平行的面),均无应力作用。在AC面和BC面上的正应力均为-15MPa,试求AC和BC面上的剪应力与此单元体主应力的大小和方向。
解:(a)
(b)
(c)
(d)
8-12直径d=2cm的受扭圆轴,今测得与轴线成 方向的线应变 。已知E=200GPa, =,试求扭转力矩 。
解:
8-13一个No28a工字钢梁,受力如图所示,今测得在梁的中性层上K点、与轴线成 方向上的线应变 。已知E=200GPa, =。试求此时梁承受的载荷P。
解: :
解:
8-22图示半径为 ,厚度为t的圆板,在周边受径向均有载荷q作用,试求圆板厚度变化量 及体积应变 。
解:
(1)
(2)
解:
所以三个主应力:
8-10在一块厚钢块上挖了一条贯穿的槽,槽的宽度和深度都是1cm。在此槽内紧密无隙地嵌入了一铝质立方块,其尺寸是111cm,并受P=6kN压缩力如图示,试求铝立方块的三个主应力。假定厚钢块是不变形的,铝的E=71GPa, =。
解
8-11已知单元体的应力圆如图所示(应力单位:MPa)。试作出主单元体的受力图,并指出与应力圆上A点相对应的截面位置(在主单元体图上标出)。
解:(a)
(与 方向夹角)
(b)
(与 方向夹角)或 (与水平方向交角)
(c)
(与 方向夹角)
(d)
8-4单元体各面的应力如图示(应力单位为MPa),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
材料力学课后习题答案6章
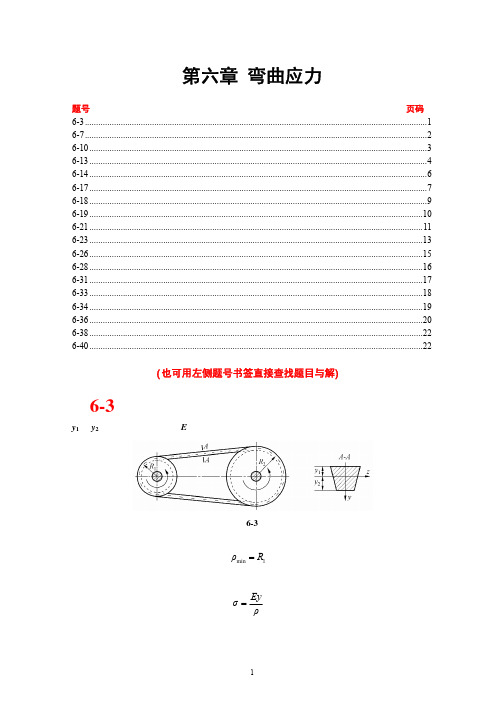
由切应力互等定理可知,纵截面上的切应力 τ x 与 τ 2max 一样大。 左、右端面上弯曲正应力构成的轴向合力分别为
Fx1 =
bh Fa 1 σ1max ( ) = 2 2 2h bh Fa 1 Fx 2 = σ 2max ( ) = h 2 2
左、右端面上弯曲切应力构成的竖向合力大小相等,其值为
(也可用左侧题号书签直接查找题目与解)
6-3
图示带传动装置,胶带的横截面为梯形,截面形心至上、下边缘的距离分别为
y1 与 y2,材料的弹性模量为 E。试求胶带内的最大弯曲拉应力与最大弯曲压应力。
题 6-3 图 解:由题图可见,胶带中性层的最小曲率半径为
ρmin = R1
依据
σ=
Ey ρ
可得胶带内的最大弯曲拉应力和最大弯曲压应力分别为
Fy 1 = F y 2 =
1ห้องสมุดไป่ตู้F 6
Fa 2h
顺便指出,纵截面上弯曲切应力构成的轴向合力为
FSx = τ x ( ab) =
3.检查单元体的平衡方程是否满足
∑F ∑F
x
= 0,Fx 2 − Fx1 − FSx = = 0,Fy1 − Fy 2
y
Fa Fa Fa − − =0 h 2 h 2h F F = − =0 6 6
题 6-10 图 解:1.查№18 工字钢的有关数据 工字钢截面大致形状及尺寸符号示如图 6-10。
图 6-10 由附录 F 表 4 查得
h = 180mm,b = 94mm t = 10.7mm,I z = 1660cm 4,Wz = 185cm 3
2.计算顶边 AB 的长度改变量 顶边处有
3
σ max =
计算中用到 h1 = h / 2 − t = 79.3mm。
材料力学第六版答案第06章

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
4解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
材料力学第六章重点解析

本章基本要求:• 1. 熟练掌握梁的变形计算。
• 2. 熟练掌握弯曲刚度的计算。
•3. 熟练掌握简单超静定梁的计算。
•本章研究:• 1. 二重积分法求弯曲变形。
• 2. 叠加法求弯曲变形。
• 3. 弯曲刚度条件。
•4. 变形比较法求超静定梁。
第六章弯曲变形§6-1 工程中的弯曲变形问题一. 挠曲线、挠度与转角1 . 挠曲线:变形后梁的轴线成为一个光滑、连续的在xy 平面内的曲线称之。
挠曲线方程:w = f (x )—亦称弹性曲线方程。
§6-2 挠曲线的微分方程xy③式为挠曲线的近似┄┄③微分方程。
Arrayx••AθBθmaxw()p ΛΛΛΛ)M ’F s ’F sM w c2•••aLaF a L F a F 12231+-M ’F sM w c22BFθaBF 2θBM θaBMθ•••⎫⎛223l qb xqdxdx x qdx•••mm m 0432.010432.4-=⨯-CδBw EN BθBθ确定超静定次数:一次超静定。
(+)(-)qF RBw B =0等效系统w F w q F sql 8535二. 解题步骤1. 确定超静定次数:以确定补充方程数。
2. 取静定基:解除多余约束,以静定系统代替超静定系统。
3. 建立力的等效系统:在静定基上加上多余约束未知力以及原有的外力,使之与原受力系统等效。
4. 建立变形的等效系统:即找变形协调条件。
为了使变形等效,在多余约束未知力作用点上的挠度或转角一般为:w (或θ)= 0 ;或w (或θ)= 常数。
5. 用叠加法求多余约束未知力作用点上的位移w (或θ)。
此方法称为变形比较法。
6. 作弯矩图;求最大正应力。
MA=+=AM Aq A θθθ;F F F F 808.0167135≈=∴F RC F ’RC•••(+)F RC= w c MlF RCEIFl EI Fl w 33max0208.048≈=EIFl EI ql w 34max 013.03845≈=4.缩小跨度,增加或加固支座:l ↓、M ↓3.采用卸载装置:想法将载荷传递给大地或大件物体。
材料力学金忠谋第六版答案第章
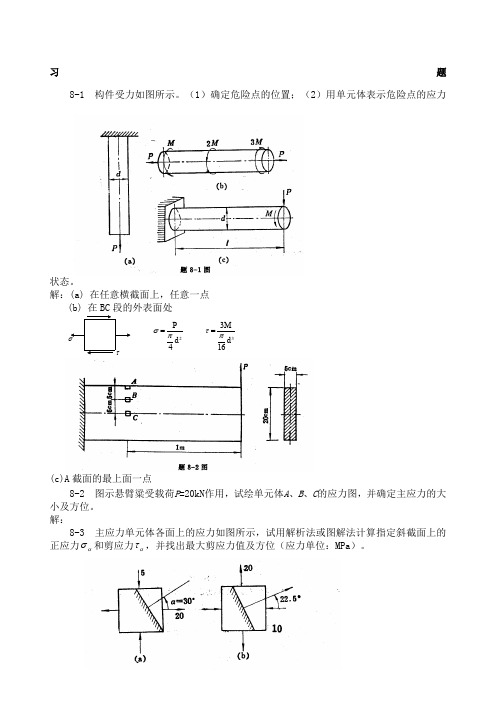
习 题8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a) 在任意横截面上,任意一点(b) 在BC 段的外表面处 24P d σπ=3316M dτπ=(c)A 截面的最上面一点8-2 图示悬臂粱受载荷P =20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
解:8-3 主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa )。
解:(a) ()()1212205205cos 2cos 6013.752222MPa ασσσσσα+---+-=+=+= 45α= (与120σ=方向夹角) (b)()()()121220102010cos 2cos 135 5.6062222MPa ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= (与1σ方向夹角)或135(与水平方向交角) (c)45α= (与140σ=方向夹角)(d)8-4 单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)(b)(c)(d)8-5 作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:(a) (b)(c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M =10kN ·m ,F S =120kN ,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:8-7 在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。
材料力学(金忠谋)第六版答案第08章

8-22图示半径为 ,厚度为t的圆板,在周边受径向均有载荷q作用,试求圆板厚度变化量 及体积应变 。
解:
(1)
(2)
解:
所以三个主应力:
8-10在一块厚钢块上挖了一条贯穿的槽,槽的宽度和深度都是1cm。在此槽内紧密无隙地嵌入了一铝质立方块,其尺寸是111cm,并受P=6kN压缩力如图示,试求铝立方块的三个主应力。假定厚钢块是不变形的,铝的E=71GPa, =0.33。
解
8-11已知单元体的应力圆如图所示(应力单位:MPa)。试作出主单元体的受力图,并指出与应力圆上A点相对应的截面位置(在主单元体图上标出)。
解:(a)
(b)
(c)
(d)
8-12直径d=2cm的受扭圆轴,今测得与轴线成 方向的线应变 。已知E=200GPa, =0.3,试求扭转力矩 。
解:
8-13一个No28a工字钢梁,受力如图所示,今测得在梁的中性层上K点、与轴线成 方向上的线应变 。已知E=200GPa, =0.3。试求此时梁承受的载荷P。
解:(a)
(与 方向夹角)
(b)
(与 方向夹角)或 (与水平方向交角)
(c)
(与 方向夹角)
(d)
8-4单元体各面的应力如图示(应力单位为MPa),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)
(b)
(c)
(d)
8-5作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:
8-19在钢结构的表面某点处,利用直角应变花分别测得应变值为 , , ,试确定该点的主应变大小、方向和最大剪应变值。
8-20若已测得等角应变花三个方向的应变分别为 , , 。试求主应变及其方向,若材料为碳钢,E=200GPa, =0.25。试求主应力及其方向。
材料力学(金忠谋)第六版答案第08章
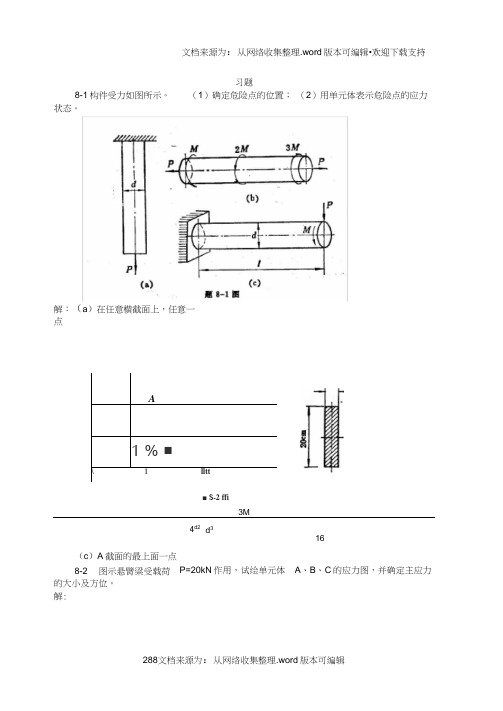
习题8-1构件受力如图所示。
(1)确定危险点的位置; (2)用单元体表示危险点的应力状态。
3M d 3 16(c )A 截面的最上面一点的大小及方位。
解:A1 % ■\ 1 lltt4d2 8-2 图示悬臂粱受载荷 P=20kN 作用,试绘单元体 A 、B 、C 的应力图,并确定主应力 解:(a )在任意横截面上,任意一点■ S -2 ffi解:(a)(b)(c)(d)8-4cos60 13.75MPa -cos 220 10 20 10pcos 1355.606MPa20 10 sin 2—2si n2245;(与1方向夹角)或135「45 (与140方向夹角)单元体各面的应力如图示(应力单位为力的大小及所在截面的方位,并在单元体内注明。
解: (a)(b)(c)(d)8-5135;10.606MPa(与水平方向交角)MPa),试用解析法和图解法计算主应8-3主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力和剪应力,并找出最大剪应力值及方位(应力单位:MPa)。
20方向夹角)145 (与作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
3U解:(a) (b)(c ) (d)(e)8-6出截面上解:已知矩形截面梁某截面上的弯矩和剪力分别为M —10kN • m, F s—120kN,试绘1、2、3、4各点单兀体的应力状态,并求其主应力。
8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC面和BC面上的正应力均为-15MPa,试求AC和BC面上的剪应力与此单元体主应力的大小和方向。
解: X 015MPa1 2 0; 3 30MPa (方向平行于AB)8-8某点的应力状态如图所示,已知、与y,试参考如何根据已知数据直接作出应力图。
8-9 每边均为1cm的钢质立方体,放在边长均为 1.0001cm的刚性方槽内,立方体顶上承受总压力P = 15kN,材料的E= 200GPa, = 0.30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=,h 2=。
解:A 截面:Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ (拉)Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ(压) E 截面Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ (拉)Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ (压) 6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。
(1) 求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2) 若 d =lmm ,材料的屈服极限s σ=700MPa ,弹性模量E =210GPa ,求不使钢丝产生残余变形的轴径D 。
解:EJM =ρ1Dd E EJ M 324πρ== D d E d M W M ⋅===3max 32πσ cm m dE D s 303.01070010110210639==⨯⨯⨯⨯=⋅≥-σ6-5 矩形悬臂梁如图示.已知l = 4 m ,32=h b ,q =10kN/m ,许用应力[σ]=10Mpa 。
试确定此梁横截面尺寸。
解:m KN ql M ⋅=⨯⨯==80410212122max 963266322h h h h W =⨯== 910101080263h M W W M =⨯⨯==⇒=σσ cm m h 6.41416.0==cm b 7.27=6-6 20a 工字钢梁的支承和受力情况如图所示。
若[σ]=160MPa ,试求许用载荷P 。
解:3237cm W = P 32 m KN P M ⋅=32max[][]P W M 32102371016066=⨯⨯⨯=⋅=-σ (M 图) P 32 []KN P 880.5623716023=⨯⨯=6-7 压板的尺寸和载荷情况如图所示。
材料为 45钢,s σ=380 MPa ,取安全系数5.1=n 。
试校核压板强度。
解:2331568)121230122030(101mm W =⨯-⨯⨯= m N M ⋅=⨯⨯⨯=-3601020101833[]σσ<=⨯==-MPa W M 6.22910156836096-8 由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ]=150 MPa ,试选择槽钢号码。
解:m KN M ⋅=60max[]33363m ax 400104.0101501060cm m M W x =⨯=⨯⨯==-σ 查表:(22a , 332006.217cm cm W x >=)m KN ⋅60( M 图)6-9 割刀在切割工件时,受到P =1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解:m N p M ⋅=⨯⨯=-I 81083m N p M ⋅=⨯⨯=-∏30103033242.706135.2mm W =⨯=I 321506154mm W =⨯=∏()MPa W M 114104.7089m ax =⨯==-I I I σ ()MPa W M 20010150309m ax =⨯==-∏∏∏σ 6-10 图示圆木,直径为D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分别为何值(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分别为何值解:6)(6222b D b bh W -==0=db dW∴ 06322=-b D∴ 322D b =2222323D D D h =-=∴从强度讲:D b 57735.0=∴ D h 8165.0=12)(123222b D b bhJ -== 0=dbdJ 0)2()(23)(21222322=-⨯-⨯⨯+-b b D b b D ∴从刚度讲 D b 50.0=D h 866.0=6-11 T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h = 12cm ,t =3cm ,试确定其翼板宽度b 之值。
解:3max max =下上拉压y y =σσ 下上=y y 312=h y y =+下上cm y 3412==下 05.4)39()233)(3(=⨯⨯--⨯=b S cm b 275.135.439=⨯⨯⨯=6-12 图示简支梁,由工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε,试计算梁的最大弯曲正应力σmax 。
已知钢的弹性模量E =200GPa, a =1m 。
解:MPa E A 60100.31020049=⨯⨯⨯==-εσ 28/34/3max max ===A A M M σσ MPa A 1206022max =⨯==σσ243qa 283qa24qa (M 图)6-13 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。
解:1-1截面KN Q 6364.3=m KN M ⋅=6364.3433375.210912155.712cm bh J =⨯==283105.310375.2109106364.3--⨯⨯⨯⨯==y J M a σ MPa 03.6=82310375.2109105.7106364.3--⨯⨯⨯⨯=b σ MPa 93.12=2863105.710375.2109105.5)5.74(106364.3---⨯⨯⨯⨯⨯⨯⨯⨯==Jb QS a τ MPa 379.0=6-14 计算在均布载荷 q =10 kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解:232max 110108181⨯⨯⨯==ql M m N ⋅⨯=31025.11101021213max ⨯⨯⨯==ql Q N 3105⨯=633m ax 105321025.1-⨯⨯⨯==πσW MMPa 86.101= 在跨中点上、下边缘34105410534423max⨯⨯⨯⨯=⨯=-πτA Q MPa 46.25= 在梁端,中性轴上6-15 试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。
解: MPa Wqa 60832= qa 41 3185cm W =KN q 6.29123810185106066=⨯⨯⨯⨯⨯=- qa 43 KN qa Q 2.2216.294343max =⨯⨯==(Q 图) MPa Jt QS 12.22105.6104.15102.22323max =⨯⨯⨯⨯==--τ6-16 矩形截面木梁所受载荷如图示,材料的许用应力[σ]=10Mpa 。
试选择该梁的截面尺寸,设1:2:=b hKN 19 KN 8KNKN 1(Q 图) ( M 图)解:KN R A 19= KN R B 29=126132h bh W == []σσ≤⨯==12101433m ax hW M cm m h 6.25256.01010121014363==⨯⨯⨯= cm b 8.12=[]ττ<=⨯⨯⨯⨯==-MPa A Q 961.0106.258.1210215.15.143max 6-17 试为图示外伸梁选择一工字形截面,材料的许用应力[σ]= 160MPa ,[τ]=80Mpa 。
解:[]3612510160100020cm MW =⨯⨯==σ 取16I , 3141cm W =)(8.13:cm S J =[]ττ<=⨯⨯⨯==-MPa Jt QS 181.01068.13101533故 取No16工字钢)(x Q KN 15 )(x M m KN ⋅20KN 5 m KN ⋅10KN 10(Q 图) (M 图)6-18 图示起重机安装在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采用工字型钢的号码。
已知 l =10 m ,a =4 m ,d =2 m 。
起重机的重量 W =50 kN ,起重机的吊重P =10 kN ,钢梁材料的许用应力[σ]=160 MPa ,[τ]= 100Mpa 。
解:轻压:KN 10 ,KN 50[]x x x R 658)8(10)10(50101-=-+-= x x Rx x M ⋅-==)658()(0=dxdM 01258=-x m x 833.4= m KN M ⋅=⨯⨯-=17.140833.4)833.4658(max[]63m ax 101601017.140⨯⨯==σM W 33387610876.0cm m =⨯=-取 两个 a I 28 33438215.508cm W cm W z =>=KN 10 KN 50dm 106-19 等腰梯形截面梁,其截面高度为h 。
用应变仪测得其上边的纵向线应变611042-⨯-=ε,下边的纵向线应变621014-⨯=ε。
