BP神经网络在生存中应用

合集下载

BP神经网络步骤及应用实例

1、数据归一化‎2、数据分类，主要包括打‎乱数据顺序‎，抽取正常训‎练用数据、变量数据、测试数据3、建立神经网‎络，包括设置多‎少层网络（一般3层以‎内既可以，每层的节点‎数（具体节点数‎，尚无科学的‎模型和公式‎方法确定，可采用试凑‎法，但输出层的‎节点数应和‎需要输出的‎量个数相等‎），设置隐含层‎的传输函数‎等。

关于网络具‎体建立使用‎方法，在后几节的‎例子中将会‎说到。

4、指定训练参‎数进行训练‎，这步非常重‎要，在例子中，将详细进行‎说明5、完成训练后‎，就可以调用‎训练结果，输入测试数‎据，进行测试6、数据进行反‎归一化7、误差分析、结果预测或‎分类，作图等数据归一化‎问题归一化的意‎义：首先说一下‎，在工程应用‎领域中，应用BP网‎络的好坏最‎关键的仍然‎是输入特征‎选择和训练‎样本集的准‎备，若样本集代‎表性差、矛盾样本多‎、数据归一化‎存在问题，那么，使用多复杂‎的综合算法‎、多精致的网‎络结构，建立起来的‎模型预测效‎果不会多好‎。

若想取得实‎际有价值的‎应用效果，从最基础的‎数据整理工‎作做起吧，会少走弯路‎的。

归一化是为‎了加快训练‎网络的收敛‎性，具体做法是‎：1 把数变为（0，1）之间的小数‎主要是为了‎数据处理方‎便提出来的‎，把数据映射‎到0～1范围之内‎处理，更加便捷快‎速，应该归到数‎字信号处理‎范畴之内。

2 把有量纲表‎达式变为无‎量纲表达式‎归一化是一‎种简化计算‎的方式，即将有量纲‎的表达式，经过变换，化为无量纲‎的表达式，成为纯量比如，复数阻抗可‎以归一化书‎写：Z = R + jωL = R(1 + jωL/R) ，复数部分变‎成了纯数量‎了，没有量纲。

另外，微波之中也‎就是电路分‎析、信号系统、电磁波传输‎等，有很多运算‎都可以如此‎处理，既保证了运‎算的便捷，又能凸现出‎物理量的本‎质含义。

神经网络归‎一化方法：由于采集的‎各数据单位‎不一致，因而须对数‎据进行[-1,1]归一化处理‎，归一化方法‎主要有如下‎几种，供大家参考‎：1、线性函数转‎换，表达式如下‎：复制内容到‎剪贴板代码‎:y=(x-MinVa‎l ue)/(MaxVa‎l ue-MinVa‎l ue)说明：x、y分别为转‎换前、后的值，MaxVa‎l ue、MinVa‎l ue分别‎为样本的最‎大值和最小‎值。

bp神经网络的应用综述

bp神经网络的应用综述近年来，人工神经网络（ANN）作为一种神经网络形式在不断发展，因其计算能力强，对现实世界较好地识别和适应能力，已得到越来越广泛的应用，其中，BP神经网络是最典型的人工神经网络之一。

BP神经网络是指以马尔可夫随机过程为基础的反向传播算法，具有自组织学习、泛化、模糊推理的特点，具有非常广泛的应用场景。

它可以用来解决实际问题。

首先，BP神经网络可以用来解决分类问题。

它可以根据给定的输入向量和输出向量，训练模型以分类相关的输入特征。

这种模型可以用来解决工业控制问题、专家系统任务等。

例如，BP神经网络可以用来识别照片中的面孔，帮助改进自动门的判断等。

此外，BP神经网络还可以用于计算机视觉，即以计算机图像识别的形式进行图像处理。

通常，计算机视觉技术需要两个步骤，即识别和分析。

在识别步骤中，BP神经网络可以被用来识别图片中的特征，例如物体的形状、大小、颜色等；在分析步骤中，BP神经网络可以用来分析和判断图片中的特征是否满足要求。

此外，BP神经网络还可以用于机器人技术。

它可以用来识别机器人环境中的物体，从而帮助机器人做出正确的动作。

例如，利用BP神经网络，机器人可以识别障碍物并做出正确的行动。

最后，BP神经网络还可以用于未来的驾驶辅助系统中。

这种系统可以利用各种传感器和摄像机，搜集周围环境的信息，经过BP神经网络分析，判断当前环境的安全程度，及时采取措施，以达到更好的安全驾驶作用。

综上所述，BP神经网络具有自组织学习、泛化、模糊推理的特点，拥有非常广泛的应用场景，可以用于分类问题、计算机视觉、机器人技术和驾驶辅助系统等。

然而，BP神经网络也存在一些问题，例如训练时间长，需要大量的训练数据，容易受到噪声攻击等。

因此，研究人员正在积极改进BP神经网络，使其能够更好地解决各种问题。

BP神经网络模型应用实例

BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起，不仅仅是因为神经科学本身取得了巨大的进展．更主要的原因在于发展新型计算机和人工智能新途径的迫切需要．迄今为止在需要人工智能解决的许多问题中，人脑远比计算机聪明的多，要开创具有智能的新一代计算机，就必须了解人脑，研究人脑神经网络系统信息处理的机制．另一方面，基于神经科学研究成果基础上发展出来的人工神经网络模型，反映了人脑功能的若干基本特性，开拓了神经网络用于计算机的新途径．它对传统的计算机结构和人工智能是一个有力的挑战，引起了各方面专家的极大关注．目前，已发展了几十种神经网络，例如Hopficld模型，Feldmann等的连接型网络模型，Hinton等的玻尔茨曼机模型，以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。

在这众多神经网络模型中，应用最广泛的是多层感知机神经网络。

多层感知机神经网络的研究始于50年代，但一直进展不大。

直到1985年，Rumelhart等人提出了误差反向传递学习算法（即BP算），实现了Minsky的多层网络设想，如图34-1所示。

BP 算法不仅有输入层节点、输出层节点，还可有1个或多个隐含层节点。

对于输入信号，要先向前传播到隐含层节点，经作用函数后，再把隐节点的输出信号传播到输出节点，最后给出输出结果。

节点的作用的激励函数通常选取S 型函数，如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。

该算法的学习过程由正向传播和反向传播组成。

在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。

每一层神经元的状态只影响下一层神经输入层中间层输出层图34-1 BP 神经网络模型元的状态。

如果输出层得不到期望的输出，则转入反向传播，将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使得误差信号最小。

社含有n 个节点的任意网络，各节点之特性为Sigmoid 型。

基于BP神经网络的应用及实现

１ＢＰ神经网络的简介基于误差反向传播（Ｂａｃｋｐｒｏｐａｇａｔｉｏｎ）￣法的多层前馈网络（Ｍｕｌｉｔｐｌｅ — ｌａｙｅｒｆｅｅｄｆｏｒｗａｒｄｎｅｔ－ｗｏｒｋ，简记为ＢＰ网络）【１］，是目前应用最多也是最成功的网络之一，构造一个ＢＰ网络需要确定其处理单元——神经元的特性和网络的拓扑结构。ＢＰ网络可以简单地看作是一个多层的感知器，其输人输出关系与单层感知器完全相同，前一层的输出是下一层的输入。神经网络学习算法要求神经元模型的传递函数为有界连续可微函数如ｓｉｇ — ｍｏｉｄ函数，通过学习可以用一个连续的超曲面（而不仅仅是一个超平面）来完成划分输入样本空间的功能。神经网络的拓扑结构是指神经元之间的互连结构。图１是个ＢＰ网络结构。ＢＰ网络由输入层、输出层以及一个或多个隐含层互连而成的一种多层网，这种结构使多层前馈网络可在
２ＢＰ网络的应用实例
下面采用ＢＰ算法，在Ｍａｔｌａｂ中编程，建立ＢＰ神经网络模型，对其进行训练，最后用于对癌细胞的检测。图１检测的基本原理［６，７１：由于气体分子或固体、液体的蒸气受到一定能量的电子流轰击或强电场作用，丢失价电子生成分子离子；同时，化学键也发生某些有规律裂解，生成各种碎片离子。这些带正电荷的离子在电场和磁场作用下，按质荷比（即质量和电荷比值Ｍ／Ｚ）的大小分开，排列成谱，记录下来即为质谱（ｍａｓｓｓｐｅｃｔｒｕｍ）。因此，可以根据质谱中离子的强度判断其血清蛋白质样本有无癌症细胞。实例中的数据是采用ＦＤＡ — ＮＣＩ诊所蛋白质项目中的数据库中的数据。程序主要完成三部分功能：一是通过ｒａｎｋｆｅａ — 图２ｔｕｒｅｓ０函数，从１５０００个的特征中选取１００个影响较大的特征；二是通过神经网络的专用函数ｎｅｗｆ０建立ＢＰ网络，并对其进Ｔｒａｉｎｂｒ函数对网络进行训练。训练效果如图２所示。行训练和建模；三是给出测试的结果。表１列出了上述实验的关键数据。分析可知：基本梯度下降算２．１特征的提取法（Ｔｒａｉｎｇｄ），迭代次数多，耗时长，收敛速度慢；共轭梯度算法在数据集中共有２１６个病人，其中有１２１个卵巢癌患者和９５Ｔｒａｉｎｃｇｐ）和变梯度法与拟牛顿法的折中算法（Ｔｒａｉｎｏｓｓ）迭代次数个正常的病人。每个病人的输入是其具体特征（Ｍ／Ｚ）下的离子浓度，（耗时少，收敛速度较快；改进型ＬＭ算法（Ｔｒｉａｎｂｒ）虽然迭代次数由于数据中共有１５０００个特征用于判断，计算量过于庞大，而且在少，这些特征当中也没有哪一种特征可以决定正确的分类，。因此，需要较少，但是每个训练周期很长，网络输出与实际输出的均方差ＭＳＥ）偏大。个分类器— — Ｔａｎｋｆｅａｔｕｒｅｓ０ｉ￣数，用来从１５０００个特征中选取１００（２－３神经网络的性能测试个重要的特征用于分类；每个病人的输出则是一个二值矩阵， “ ０ ” 表将１００个测试结果样本分别输入到经过训练的ＢＰ神经网络，示正常病人， “ １ ” 表示患有癌症的病人。其测试结果如表２所示。２．２ＢＰ神经网络的构建及训练３结论文中用于癌症检测的神经网络含有一个输入层，节点数为本文用ＢＰ神经网络对病人样本进行检测，在用大量的真实数１００；一个输出层，节点数为２１６；一个隐含层，节点数为ｌ０。由于其据进行训练后，得到满足误差指标的ＢＰ神经网络；根据不同的算法输出函数在０到１之间，所以隐含层和输出层得激励函数为ｓｉｇ — 训练网络，得到的训练模型的效果也不尽相同。结果表明使用ｍｏｉｄ对数函数和线性函数。ｔｒａｉｎ根据在ｎｅｗｆ函数中确定的训练函

BP神经网络实验报告

BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型，其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用，输出结果达到预测或分类的目标。

本实验旨在探究BP神经网络的基本原理和应用，以及对其进行实验验证。

二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集，每个样本有12个特征。

将数据集进行标准化处理，以提高神经网络的收敛速度和精度。

2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化，常用的初始化方法有随机初始化和Xavier初始化。

本实验采用Xavier初始化方法。

4.前向传播将标准化后的数据输入到神经网络中，在神经网络的每一层进行加权计算和激活函数的作用，传递给下一层进行计算。

5.反向传播根据预测结果与实际结果的差异，通过计算损失函数对神经网络的权重和偏置进行调整。

使用梯度下降算法对参数进行优化，减小损失函数的值。

6.模型评估与验证将训练好的模型应用于测试集，计算准确率、精确率、召回率和F1-score等指标进行模型评估。

三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集，分别进行模型训练和验证。

经过10次训练迭代后，模型在测试集上的准确率稳定在90%以上，证明了BP神经网络在本实验中的有效性和鲁棒性。

通过调整隐藏层结点个数和迭代次数进行模型性能优化实验，可以发现隐藏层结点个数对模型性能的影响较大。

随着隐藏层结点个数的增加，模型在训练集上的拟合效果逐渐提升，但过多的结点数会导致模型的复杂度过高，容易出现过拟合现象。

因此，选择合适的隐藏层结点个数是模型性能优化的关键。

此外，迭代次数对模型性能也有影响。

随着迭代次数的增加，模型在训练集上的拟合效果逐渐提高，但过多的迭代次数也会导致模型过度拟合。

因此，需要选择合适的迭代次数，使模型在训练集上有好的拟合效果的同时，避免过度拟合。

四、实验总结本实验通过搭建BP神经网络模型，对分类数据集进行预测和分类。

BP神经网络详解与实例

人工神经网络
(Artificial Neural Netwroks -----ANN)
-----HZAU 数模基地
引言
❖ 利用机器模仿人类的智能是长期以来人们认识自然、改造自然和认识自身的理想。
❖ 研究ANN目的： ❖ （1）探索和模拟人的感觉、思维和行为的规律，
设计具有人类智能的计算机系统。 ❖ （2）探讨人脑的智能活动，用物化了的智能来
二、神经元与神经网络
❖ 大脑可视作为1000多亿神经元组成的神经网络
• 图3 神经元的解剖图
❖ 神经元的信息传递和处理是一种电化学活动．树突由于电化学作用接受外界的刺激；通过胞体内的活动体现为轴突电位，当轴突电位达到一定的值则形成神经脉冲或动作电位；再通过轴突末梢传递给其它的神经元．从控制论的观点来看；这一过程可以看作一个多输入单输出非线性系统的动态过程
输出层LC
W11 Wi1
Wij
Wiq Wpq W
… b1 Vn1
Vh1 V11
V1i bi Vhi
… Vni
V1p bp Vhp Vnp
隐含层LB V
… a1
… ah
an 输入层LA
a1k
a
k h
a
k n
基本BP网络的拓扑结构
ANN类型与功能
一般而言, ANN与经典计算方法相比并非优越, 只有当常规方法解决不了或效果不佳时ANN方法才能显示出其优越性。尤其对问题的机理不甚了解或不能用数学模型表示的系统,如故障诊断、特征提取和预测等问题,ANN往往是最有利的工具。另一方面, ANN对处理大量原始数据而不能用规则或公式描述的问题, 表现出极大的灵活性和自适应性。
i 1
（p=1,…,P）

BP神经网络模型及其应用

一一
收稿日期：０２７—００５—１６
作者简介：邢进良（９０）男，１６一，河南省淅川县人，沙洋师范高等专科学校副教授，从事数学应用及数学教主要育教学研究。
４６
维普资讯
邢进良
Ｂ神经网络模型及其应用Ｐ ● 步５更新权重刹阈值：ｔ）＝∞ 、 ∞ （＋ｉ＋
ｎ
神经网络的基本处理单元是神经元，它是一个多输入、单输出的非线性元件，输入输出关系其可描述为：
＝
；
结构。＇牵经网络隐层和输出层ｔ的某神经元靠ｆ）的输出出下式确定：
：
（０＝＝（胁）
＋）
Ｄｆ（＋甜（）一∞ （一１）ｔ）ｏ（＋１＝８叼，（，￡ｊｔ），＋（）一８（一１），ｔ）
其中研为学习速率，为动量系数； ● 步６判断误差函数Ｅ否收敛到所给学习、是精度（Ｅ≤占？，）若满足学习精度要求则结束学习，否则转步２继续进行。（参见图２—２）
局部的。］ｍ［（胛；
图１—２ＰＰ模型下的人工神经网络模型Ｄ２Ｐ神经网络的结构和算法、ＢＰ神经网络是一种具有一个输入层，一个或多个隐层和一个输出层的多层网络。隐层和输出 ∑ ＋ ‘ ０＝ｒ０ｊｊ（）层上的每个神经元都对应一个激发函数和一个阈其中（＝１２ …… ），，表示对该神经元的输入，值。每一层上的神经元都通过权重与其相邻层上为神经元的阈值， ∞ 表示从神经元到神经元的的神经元互枢连接。对于输入层上的神经元其阈连接投值，ｎ为输入信号数目，０为神经元输出，值为零，其输出等于输入。２—１图给出了一个带ｊ。ｒ）称为传递函数。（单隐层的二履（含输入层）Ｐ卒经网络的一般不Ｂ申

BP神经网络原理与应用实习论文

学年论文（本科）学院数学与信息科学学院专业信息与计算科学专业年级10级4班姓名徐玉琳于正平马孝慧李运凤郭双双任培培论文题目BP神经网络原理与应用指导教师冯志敏成绩2013年 9月 24日BP神经网络的原理与应用1.BP神经网络的原理1.1 BP神经网络的结构BP神经网络模型是一个三层网络,它的拓扑结构可被划分为:输入层(InputLayer )、输出层(Outp ut Layer ) ,隐含层(Hide Layer )．其中,输入层与输出层具有更重要的意义,因此也可以为两层网络结构(把隐含层划入输入层,或者把隐含层去掉)每层都有许多简单的能够执行并行运算的神经元组成,这些神经元与生物系统中的那些神经元非常类似,但其并行性并没有生物神经元的并行性高．BP神经网络的特点：1）网络由多层构成,层与层之间全连接,同一层之间的神经元无连接．2）BP网络的传递函数必须可微．因此,感知器的传递函数-——二值函数在这里没有用武之地．BP网络一般使用Sigmoid函数或线性函数作为传递函数．3）采用误差反向传播算法(Back-Propagation Algorithm)进行学习．在BP 网络中,数据从输入层隐含层逐层向后传播,训练网络权值时,则沿着减少误差的方向,从输出层经过中间各层逐层向前修正网络的连接权值．随着学习的不断进行,最终的误差越来越来小．BP神经网络的学习过程BP神经网络的学习算法实际上就是对误差函数求极小值的算法,它采用的算法是最速下降法,使它对多个样本进行反复的学习训练并通过误差的反向传播来修改连接权系数,它是沿着输出误差函数的负梯度方向对其进行改变的,并且到最后使误差函数收敛于该函数的最小点．1.3 BP网络的学习算法BP网络的学习属于有监督学习,需要一组已知目标输出的学习样本集．训练时先使用随机值作为权值,修改权值有不同的规则．标准的BP神经网络沿着误差性能函数梯度的反向修改权值,原理与LMS算法比较类似,属于最速下降法．拟牛顿算法牛顿法是一种基于二阶泰勒级数的快速优化算法．其基本方法是1(1)()()()x k x k A k g k -+=-式中 ()A k ----误差性能函数在当前权值和阀值下的Hessian 矩阵（二阶导数）,即2()()()x x k A k F x ==∇牛顿法通常比较梯度法的收敛速度快,但对于前向型神经网络计算Hessian 矩阵是很复杂的,付出的代价也很大．有一类基于牛顿法的算法不需要二阶导数,此类方法称为拟牛顿法（或正切法）,在算法中的Hessian 矩阵用其近似值进行修正,修正值被看成梯度的函数． 1）BFGS 算法在公开发表的研究成果中,你牛顿法应用最为成功得有Boryden,Fletcher,Goldfard 和Shanno 修正算法,合称为BFG 算法．该算法虽然收敛所需的步长通常较少,但在每次迭代过程所需要的计算量和存储空间比变梯度算法都要大,对近似Hessian 矩阵必须进行存储,其大小为n n ⨯,这里n 网络的链接权和阀值的数量．所以对于规模很大的网络用RPROP 算法或任何一种梯度算法可能好些；而对于规模较小的网络则用BFGS 算法可能更有效． 2）OSS 算法由于BFGS 算法在每次迭代时比变梯度算法需要更多的存储空间和计算量,所以对于正切近似法减少其存储量和计算量是必要的．OSS 算法试图解决变梯度法和拟牛顿（正切）法之间的矛盾,该算法不必存储全部Hessian 矩阵,它假设每一次迭代时与前一次迭代的Hessian 矩阵具有一致性,这样做的一个有点是,在新的搜索方向进行计算时不必计算矩阵的逆．该算法每次迭代所需要的存储量和计算量介于梯度算法和完全拟牛顿算法之间．最速下降BP 法最速下降BP 算法的BP 神经网络,设k 为迭代次数,则每一层权值和阀值的修正按下式进行(1)()()x k x k g k α+=-式中()x k —第k 次迭代各层之间的连接权向量或阀值向量；()g k =()()E k x k ∂∂—第k 次迭代的神经网络输出误差对各权值或阀值的梯度向量．负号表示梯度的反方向,即梯度的最速下降方向；α—学习效率,在训练时是一常数．在MATLAB 神经网络工具箱中,,可以通过改变训练参数进行设置；()E K —第k 次迭代的网络输出的总误差性能函数,在MATLAB 神经网络工具箱中BP 网络误差性能函数默认值为均方误差MSE,以二层BP 网络为例,只有一个输入样本时,有2()()E K E e k ⎡⎤=⎣⎦21S≈22221()S i i i t a k =⎡⎤-⎣⎦∑ 222212,1()()()()s ii j i i j a k f w k a k b k =⎧⎫⎪⎪⎡⎤=-⎨⎬⎣⎦⎪⎪⎩⎭∑21221112,,11()(()())()s s i j i j i i i j j f w k f iw k p ib k b k ==⎧⎫⎡⎤⎛⎫⎪⎪=++⎢⎥ ⎪⎨⎬⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭∑∑若有n 个输入样本2()()E K E e k ⎡⎤=⎣⎦21nS ≈22221()S ii i ta k =⎡⎤-⎣⎦∑根据公式和各层的传输函数,可以求出第k 次迭代总误差曲面的梯度()g k =()()E k x k ∂∂,分别代入式子便可以逐次修正其权值和阀值,并是总的误差向减小的方向变化,直到达到所需要的误差性能为止． 1.4 BP 算法的改进BP 算法理论具有依据可靠、推导过程严谨、精度较高、通用性较好等优点,但标准BP 算法存在以下缺点：收敛速度缓慢；容易陷入局部极小值；难以确定隐层数和隐层节点个数．在实际应用中,BP 算法很难胜任,因此出现了很多改进算．利用动量法改进BP 算法标准BP 算法实质上是一种简单的最速下降静态寻优方法,在修正W(K)时,只按照第K 步的负梯度方向进行修正,而没有考虑到以前积累的经验,即以前时刻的梯度方向,从而常常使学习过程发生振荡,收敛缓慢．动量法权值调整算法的具体做法是：将上一次权值调整量的一部分迭加到按本次误差计算所得的权值调整量上,作为本次的实际权值调整量,即：其中：α为动量系数,通常0＜α＜0．9；η—学习率,范围在0．001～10之间．这种方法所加的动量因子实际上相当于阻尼项,它减小了学习过程中的振荡趋势,从而改善了收敛性．动量法降低了网络对于误差曲面局部细节的敏感性,有效的抑制了网络陷入局部极小．自适应调整学习速率标准BP算法收敛速度缓慢的一个重要原因是学习率选择不当,学习率选得太小,收敛太慢；学习率选得太大,则有可能修正过头,导致振荡甚至发散．可采用图所示的自适应方法调整学习率．调整的基本指导思想是：在学习收敛的情况下,增大η,以缩短学习时间；当η偏大致使不能收敛时,要及时减小η,直到收敛为止．动量-自适应学习速率调整算法采用动量法时,BP算法可以找到更优的解；采用自适应学习速率法时,BP算法可以缩短训练时间．将以上两种方法结合起来,就得到动量-自适应学习速率调整算法．1. L-M学习规则L-M（Levenberg-Marquardt）算法比前述几种使用梯度下降法的BP算法要快得多,但对于复杂问题,这种方法需要相当大的存储空间L-M(Levenberg-Marquardt)优化方法的权值调整率选为:其中：e —误差向量；J —网络误差对权值导数的雅可比（Jacobian ）矩阵；μ—标量,当μ很大时上式接近于梯度法,当μ很小时上式变成了Gauss-Newton 法,在这种方法中,μ也是自适应调整的． 1.5 BP 神经网络的设计网络的层数输入层节点数取决于输入向量的维数．应用神经网络解决实际问题时,首先应从问题中提炼出一个抽象模型,形成输入空间和输出空间．因此,数据的表达方式会影响输入向量的维数大小.例如,如果输入的是64*64的图像,则输入的向量应为图像中所有的像素形成的4096维向量．如果待解决的问题是二元函数拟合,则输入向量应为二维向量．理论上已证明：具有偏差和至少一个S 型隐含层加上一个线性输出层的网络,能够逼近任何有理数．增加层数可以更进一步的降低误差,提高精度,但同时也使网络复杂化,从而增加了网络权值的训练时间．而误差精度的提高实际上也可以通过增加神经元数目来获得,其训练效果也比增加层数更容易观察和调整.所以一般情况下,应优先考虑增加隐含层中的神经元数. 隐含层的神经元数网络训练精度的提高,可以通过采用一个隐含层,而增加神经元数了的方法来获得．这在结构实现上,要比增加隐含层数要简单得多．那么究竟选取多少隐含层节点才合适？这在理论上并没有一个明确的规定．在具体设计时,比较实际的做法是通过对不同神经元数进行训练对比,然后适当地加上一点余量．1）0niMi C k =>∑,k 为样本数,M 为隐含层神经元个数,n 为输入层神经元个数．如i>M,规定C i M =0．2）和n 分别是输出层和输入层的神经元数,a 是[0.10]之间的常量．3）M=2log n ,n 为输入层神经元个数．初始权值的选取由于系统是非线性的,初始值对于学习是否达到局部最小、是否能够收敛及训练时间的长短关系很大．如果初始值太大,使得加权后的输入和n落在了S型激活函数的饱和区,从而导致其导数f (n)非常小,从而使得调节过程几乎停顿下来．所以一般总是希望经过初始加权后的每个神经元的输出值都接近于零,这样可以保证每个神经元的权值都能够在它们的S型激活函数变化最大之处进行调节．所以,一般取初始权值在（-1,1）之间的随机数．学习速率学习速率决定每一次循环训练中所产生的权值变化量．大的学习速率可能导致系统的不稳定；但小的学习速率导致较长的训练时间,可能收敛很慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值．所以在一般情况下,倾向于选取较小的学习速率以保证系统的稳定性．学习速率的选取范围在0．01-0．8之间．1.6BP神经网络局限性需要参数多且参数选择没有有效的方法对于一些复杂问题 ,BP 算法可能要进行几小时甚至更长的时间训练,这主要是由于学习速率太小所造成的．标准BP 网络学习过程缓慢,易出现平台,这与学习参数率l r的选取有很大关系．当l r较时,权值修改量大,学习速率也快,但可能产生振荡;当l r较小时,虽然学习比较平稳,但速度十分缓慢．容易陷入局部最优BP网络易陷入局部最小, 使 BP网络不能以高精度逼近实际系统．目前对于这一问题的解决有加入动量项以及其它一些方法．BP 算法本质上是以误差平方和为目标函数 , 用梯度法求其最小值的算法．于是除非误差平方和函数是正定的, 否则必然产生局部极小点, 当局部极小点产生时 , BP算法所求的就不是解．1.6.3 样本依赖性这主要表现在网络出现的麻痹现象上．在网络的训练过程中,如其权值调的过大,可能使得所有的或大部分神经元的加权值偏大,这使得激活函数的输入工作在S型转移函数的饱和区,从而导致其导函数非常小,使得对网络权值的调节过程几乎停顿下来．通常为避免这种现象的发生,一是选取较小的初始权值,二是采用较小的学习速率,但又要增加时间训练．初始权敏感对于一些复杂的问题,BP算法可能要进行几个小时甚至更长时间的训练．这主要是由于学习速率太小造成的．可采用变化的学习速率或自适应的学习速率来加以改进．2．BP神经网络应用2.1 手算实现二值逻辑—异或这个例子中,采用手算实现基于BP网络的异或逻辑．训练时采用批量训练的方法,训练算法使用带动量因子的最速下降法．在MATLAB中新建脚本文件main_xor.m,输入代码如下：%脚本%批量训练方式．BP网络实现异或逻辑%%清理clear allclcrand('seed',2)eb = 0.01; %误差容限eta = 0.6; %学习率mc = 0.8; %动量因子maxiter = 1000; %最大迭代次数%% 初始化网络nSampNum = 4;nSampDim = 2;nHidden = 3;nOut = 1;w = 2*(rand(nHidden,nSampDim)-1/2);b = 2*(rand(nHidden,1)-1/2);wex = [w,b];W = 2*(rand(nOut,nHidden)-1/2);B = 2*(rand(nOut,1)-1/2);WEX = [W,B];%%数据SampIn=[0,0,1,1;...0,1,0,1;…1,1,1,1];expected = [0,1,1,0];%%训练iteration = 0;errRec = [];outRec =[];for i = 1:maxiter% 工作信号正向传播hp = wex*SampIn;tau = logsig(hp);tauex = [tau',1*ones(nSampNum,1)]';HM = WEX*tauex;out = logsig(HM);outRec = [outRec,out'];err = expected - out;sse = sumsqr(err);errRec = [errRec,sse];fprintf('第%d 次迭代,误差：%f \n',i,sse);% 判断是否收敛iteration = iteration + 1;if sse <= ebbreak;end% 误差信号反向传播% DELTA 和delta 为局部梯度DELTA = err.*dlogsig(HM,out);delta = W' * DELTA.*dlogsig(hp,tau);dWEX = DELTA*tauex';dwex = delta*SampIn';% 更新权值if i == 1WEX = WEX + eta*dWEX;wex = wex + eta*dwex;elseWEX = WEX + (1-mc)*eta*dWEX + mc*dWEXold;wex = wex + (1-mc)*eta*dwex+mc*dwexold;enddWEXold = dWEX;dwexold = dwex;W = WEX(:,1:nHidden);end%%显示figure(1)grid[nRow,nCol]=size(errRec);semilogy(1:nCol,errRec,'LineWidth',1.5);title('误差曲线');xlabel('迭代次数');x=-0.2:.05:1.2;[xx,yy] = meshgrid(x);for i=1:length(xx)for j=1:length(yy)xi=[xx(i,j),yy(i,j),1];hp = wex*xi';tau = logsig(hp);tauex = [tau',1]';HM = WEX*tauex;out = logsig(HM);z (i,j) =out;endendfigure(2)mesh(x,x,z);figure(3)plot([0,1],[0,1],'*','LineWidth',2);hold onplot([0,1],[1,0],'O','LineWidth',2);[c,h]=contour(x,x,z,0.5,'b');clabel(c,h);legend('0','1','分类面');title('分类面')2.2 误差下降曲线如下图所示：Finger 1010*******400500600700800900100010-210-110误差曲线迭代次数网格上的点在BP 网络映射下的输出如下图：Finger 2异或本质上是一个分类问题,,分类面如图：Finger 3分类面-0.200.20.40.60.81 1.2本文介绍了神经网络的研究背景和现状,分析了目前神经网络研究中存在的问题．然后描述了BP神经网络算法的实现以及BP神经网络的工作原理,给出了BP网络的局限性．本文虽然总结分析了BP神经网络算法的实现,给出了实例分析,但是还有很多的不足．所总结的BP神经网络和目前研究的现状都还不够全面,经过程序调试的图形有可能都还存在很多细节上的问题,而图形曲线所实现效果都还不够好,以及结果分析不够全面、正确、缺乏科学性等,这些都还是需加强提高的．近几年的不断发展,神经网络更是取得了非常广泛的应用,和令人瞩目的发展．在很多方面都发挥了其独特的作用,特别是在人工智能、自动控制、计算机科学、信息处理、机器人、模式识别等众多方面的应用实例,给人们带来了很多应用上到思考,和解决方法的研究．但是神经网络的研究最近几年还没有达到非常热门的阶段,这还需有很多热爱神经网络和研究神经网络人员的不断研究和创新,在科技高度发达的现在,我们有理由期待,也有理由相信．我想在不久的将来神经网络会应用到更多更广的方面,人们的生活会更加便捷．学年论文成绩评定表。

BP神经网络在医疗诊断中的应用研究

BP神经网络在医疗诊断中的应用研究随着科技的发展和人民生活水平的提高，人们对医疗服务的要求也越来越高。

在这个过程中，好的医疗诊断技术不仅可以提高医疗效率，还可以提高医疗水平和医生的专业素养，这对于医疗领域的整个发展具有重要意义。

在这样的背景下，BP神经网络作为一种较为先进的人工神经网络，在医疗领域也得到了广泛的应用和研究。

本文将结合我国医疗诊断现状，探讨BP神经网络在医疗诊断中的应用研究。

一、BP神经网络介绍BP神经网络是一种基于反向传播算法的前馈型人工神经网络，它具有学习能力和适应性等特点，是一种常用的人工神经网络之一。

BP神经网络的训练过程是通过在高维空间中不断调整权值和阈值，从而实现对样本特征的提取和矫正，从而实现对样本分类的识别。

BP神经网络具有处理能力强、学习速度快、精度高等优点，被广泛应用于计算机视觉、语音识别、医疗诊断、金融分析、飞行控制等领域。

二、BP神经网络在医疗诊断中的应用1、医疗图像识别医疗图像识别是BP神经网络在医疗领域中的重要应用之一。

目前，很多医疗机构利用医学影像技术进行疾病的诊断、治疗和监测，如CT、MRI等医学影像技术，这些技术可以为医生提供详细的病灶信息，但是对于普通人来说，很难正确地解读这些医疗图像。

因此，使用BP神经网络可以对医疗图像进行识别和分析，准确地判断患者的病情和病变程度，帮助医生制定更加科学合理的治疗方案。

2、慢病诊断慢性疾病是指患者长期存在的疾病，由于患病的隐蔽性和病情的反复，很难进行准确的诊断和治疗。

针对这一问题，利用BP神经网络可以对患者的身体状况和病史等信息进行学习和分析，帮助医生更好地评估患者的病情，提供更加精准的慢病诊断结果，对于治疗和管理患者的病情也更加方便。

3、药物研发药物研发是医疗诊断领域中的一个比较困难的领域，传统的药物研发方法需要耗费大量的时间和金钱，而且成果也不一定会有预期效果。

而利用BP神经网络进行药物研发，可以快速筛选出具有潜力的化合物，并进行有效评价。

BP神经网络的简要介绍及应用

BP神经网络的简要介绍及应用BP神经网络（Backpropagation Neural Network，简称BP网络）是一种基于误差反向传播算法进行训练的多层前馈神经网络模型。

它由输入层、隐藏层和输出层组成，每层都由多个神经元（节点）组成，并且每个神经元都与下一层的神经元相连。

BP网络的训练过程可以分为两个阶段：前向传播和反向传播。

前向传播时，输入数据从输入层向隐藏层和输出层依次传递，每个神经元计算其输入信号的加权和，再通过一个激活函数得到输出值。

反向传播时，根据输出结果与期望结果的误差，通过链式法则将误差逐层反向传播至隐藏层和输入层，并通过调整权值和偏置来减小误差，以提高网络的性能。

BP网络的应用非常广泛，以下是一些典型的应用领域：1.模式识别：BP网络可以用于手写字符识别、人脸识别、语音识别等模式识别任务。

通过训练网络，将输入样本与正确的输出进行匹配，从而实现对未知样本的识别。

2.数据挖掘：BP网络可以用于分类、聚类和回归分析等数据挖掘任务。

例如，可以用于对大量的文本数据进行情感分类、对客户数据进行聚类分析等。

3.金融领域：BP网络可以用于预测股票价格、外汇汇率等金融市场的变动趋势。

通过训练网络，提取出对市场变动有影响的因素，从而预测未来的市场走势。

4.医学诊断：BP网络可以用于医学图像分析、疾病预测和诊断等医学领域的任务。

例如，可以通过训练网络，从医学图像中提取特征，帮助医生进行疾病的诊断。

5.机器人控制：BP网络可以用于机器人的自主导航、路径规划等控制任务。

通过训练网络，机器人可以通过感知环境的数据，进行决策和规划，从而实现特定任务的执行。

总之，BP神经网络是一种强大的人工神经网络模型，具有较强的非线性建模能力和适应能力。

它在模式识别、数据挖掘、金融预测、医学诊断和机器人控制等领域有广泛的应用，为解决复杂问题提供了一种有效的方法。

然而，BP网络也存在一些问题，如容易陷入局部最优解、训练时间较长等，因此在实际应用中需要结合具体问题选择适当的神经网络模型和训练算法。

BP神经网络原理及应用

BP神经网络原理及应用BP神经网络，即反向传播神经网络（Backpropagation Neural Network），是一种基于梯度下降算法的多层前馈神经网络，常用于分类与回归等问题的解决。

BP神经网络通过反向传播算法，将误差从输出层往回传播，更新网络权值，直至达到误差最小化的目标，从而实现对输入模式的分类和预测。

BP神经网络的结构包括输入层、隐藏层和输出层。

输入层接收外部输入的特征向量，隐藏层负责将输入特征映射到合适的高维空间，输出层负责输出网络的预测结果。

每个神经元与其前后的神经元相连，每个连接都有一个权值，用于调整输入信号的重要性。

BP神经网络利用激活函数（如sigmoid函数）对神经元的输出进行非线性变换，增加网络的非线性表达能力。

1.前向传播：将输入信号传递给网络，逐层计算每个神经元的输出，直至得到网络的输出结果。

2.计算误差：将网络输出与期望输出比较，计算误差。

常用的误差函数包括平方误差和交叉熵误差等。

3.反向传播：根据误差，逆向计算每个神经元的误差贡献，从输出层往回传播到隐藏层和输入层。

根据误差贡献，调整网络的权值和阈值。

4.更新权值和阈值：根据调整规则（如梯度下降法），根据误差贡献的梯度方向，更新网络的权值和阈值。

1.模式识别与分类：BP神经网络可以通过训练学习不同模式的特征，从而实现模式的自动分类与识别。

例如，人脸识别、文本分类等。

2.预测与回归：BP神经网络可以通过历史数据的训练，学习到输入与输出之间的映射关系，从而实现对未知数据的预测与回归分析。

例如，股票价格预测、天气预测等。

3.控制系统：BP神经网络可以用于建模和控制非线性系统，实现自适应、自学习的控制策略。

例如，机器人控制、工业过程优化等。

4.信号处理与图像处理：BP神经网络可以通过学习复杂的非线性映射关系，实现信号的去噪、压缩和图像的识别、处理等。

例如，语音识别、图像分割等。

5.数据挖掘与决策支持：BP神经网络可以根据历史数据学习到数据之间的相关关系，从而帮助决策者进行数据挖掘和决策支持。

BP神经网络基本原理与应用PPT

BP神经网络的学习
• 网络结构 – 输入层有n个神经元，隐含层有q个神经元, 输出层有m个神经元
BP神经网络的学习
– 输入层与中间层的连接权值: wih
– 隐含层与输出层的连接权值: – 隐含层各神经元的阈值: bh
who
– 输出层各神经元的阈值: bo
– 样本数据个数: k 1,2, m
– 激活函数:
(二)误差梯度下降法
求函数J(a)极小值的问题，可以选择任意初始点a0,从a0出发沿着负梯度方向走，可使得J(a)下降最快。 s(0)：点a0的搜索方向。
BP神经网络的学习
(三) BP算法调整，输出层的权值调整
直观解释
当误差对权值的偏导数大于零时，权值调整量为负，实际输出大于期望输出，权值向减少方向调整，使得实际输出与期望输出的差减少。当误差对权值的偏导数小于零时，权值调整量为正，实际输出少于期望输出，权值向增大方向调整，使得实际输出与期望输出的差减少。
❖ 众多神经元之间组合形成神经网络，例如下图的含有中间层（隐层）的网络
人工神经网络（ANN）
c
k l
c
k j
cqk
… … c1 Wp1
W1j cj Wpj
W1q cq
输出层LC
W11 Wi1
Wij
Wiq Wpq W
… b1 Vn1
Vh1 V11
V1i bi Vhi
… Vni
V1p bp Vhp Vnp
BP神经网络的学习
(三) BP算法调整，输出层的权值调整
式中： —学习率最终形式为：
BP神经网络的学习
(三) BP算法调整，隐藏层的权值调整
隐层各神经元的权值调整公式为：

BP神经网络的优缺点

BP神经网络的优缺点BP神经网络，也称为“反向传播神经网络”，是一种常见的人工神经网络模型。

它是基于误差反向传播算法的一种机器学习方法，广泛应用于分类、回归、预测等场景中。

优点1. 非线性逼近能力强BP神经网络的非线性逼近能力优秀，可以逼近任何非线性的函数。

它的输入层、隐层和输出层之间的结构可以实现对高维非线性数据的拟合。

2. 适用 range 广泛BP神经网络可以应用于许多不同领域，如医药、自然语言处理、图像识别等。

它可以对各种形式的数据进行分类、回归、预测等。

3. 学习能力强BP神经网络可以通过大量的样本数据进行训练，并能够自动学习和自我适应。

可以对训练数据进行高效的学习和泛化，从而适应未知数据。

4. 适应动态环境BP神经网络可以适应不断变化的环境。

当模型和所需输出之间的关系发生变化时，网络可以自适应，自动调整权重和阈值，以适应新的情况。

缺点1. 学习速度慢BP神经网络的学习速度相对较慢。

它需要大量的时间和数据来调整权重和阈值，以达到稳定的状态。

2. 容易陷入局部极小值BP神经网络很容易陷入局部极小值，而无法达到全局最优解。

这可能会导致网络的准确度降低，并影响到后续的预测、分类和回归任务。

3. 需要大量的数据BP神经网络需要大量的数据进行训练，以使网络达到优秀的效果。

如果训练数据不充分，可能会导致网络过度拟合或欠拟合。

4. 对初始参数敏感BP神经网络对初始参数非常敏感。

如果初始参数不好，那么网络可能会无法进行训练，或者陷入局部最小值。

综合来看，BP神经网络具有良好的非线性逼近能力和学习能力，但也存在一些缺点，比如学习速度慢、容易陷入局部极小值等。

因此，在具体应用场景中，我们需要权衡BP神经网络的优点和缺点，选择合适的机器学习模型进行训练和预测。

机器学习-BP(back propagation)神经网络介绍

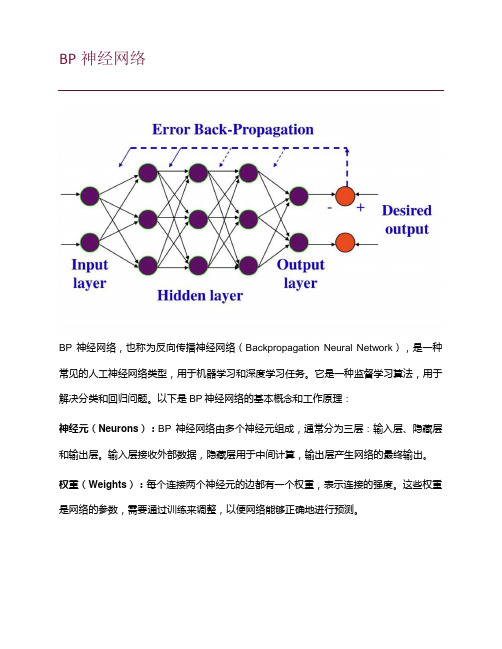
BP神经网络BP神经网络，也称为反向传播神经网络（Backpropagation Neural Network），是一种常见的人工神经网络类型，用于机器学习和深度学习任务。

它是一种监督学习算法，用于解决分类和回归问题。

以下是BP神经网络的基本概念和工作原理：神经元（Neurons）：BP神经网络由多个神经元组成，通常分为三层：输入层、隐藏层和输出层。

输入层接收外部数据，隐藏层用于中间计算，输出层产生网络的最终输出。

权重（Weights）：每个连接两个神经元的边都有一个权重，表示连接的强度。

这些权重是网络的参数，需要通过训练来调整，以便网络能够正确地进行预测。

激活函数（Activation Function）：每个神经元都有一个激活函数，用于计算神经元的输出。

常见的激活函数包括Sigmoid、ReLU（Rectified Linear Unit）和tanh（双曲正切）等。

前向传播（Forward Propagation）：在训练过程中，输入数据从输入层传递到输出层的过程称为前向传播。

数据经过一系列线性和非线性变换，最终产生网络的预测输出。

反向传播（Backpropagation）：反向传播是BP神经网络的核心。

它用于计算网络预测的误差，并根据误差调整网络中的权重。

这个过程分为以下几个步骤：1.计算预测输出与实际标签之间的误差。

2.将误差反向传播回隐藏层和输入层，计算它们的误差贡献。

3.根据误差贡献来更新权重，通常使用梯度下降法或其变种来进行权重更新。

训练（Training）：训练是通过多次迭代前向传播和反向传播来完成的过程。

目标是通过调整权重来减小网络的误差，使其能够正确地进行预测。

超参数（Hyperparameters）：BP神经网络中有一些需要人工设置的参数，如学习率、隐藏层的数量和神经元数量等。

这些参数的选择对网络的性能和训练速度具有重要影响。

BP神经网络在各种应用中都得到了广泛的使用，包括图像分类、语音识别、自然语言处理等领域。

BP神经网络组合预测在城市生活垃圾产量预测中应用

BP神经网络组合预测在城市生活垃圾产量预测中应用
路玉龙;韩靖;余思婧;张鸿雁
【期刊名称】《环境科学与技术》
【年(卷),期】2010(33)5
【摘要】文章分析了组合预测理论,在建立由二次指数平滑预测模型、灰色预测模型、BP神经网络预测模型组成的组合预测模型库的基础上,利用以上三种单一预测模型的组合构成BP神经网络组合预测模型。

分别应用单一预测模型和组合预测模型对湖南省城市生活垃圾产生量进行预测,通过分析和比较预测结果,验证了该组合预测方法的有效性。

【总页数】5页(P186-190)
【关键词】城市生活垃圾产量;组合预测;BP神经网络;Levenberg-Marquardt算法
【作者】路玉龙;韩靖;余思婧;张鸿雁
【作者单位】中南大学数学科学与计算技术学院
【正文语种】中文
【中图分类】X820.3
【相关文献】
1.变权重组合预测模型在生活垃圾产量预测计算中的应用 [J], 李志涛;张宇峰;姚藩照;施向荣
2.Verhulst模型在城市生活垃圾产量预测中的应用 [J], 周文
3.组合模型在城市生活垃圾产生量预测中的应用 [J], 王林昌
4.主成分和BP神经网络在粮食产量预测中的组合应用 [J], 郑建安
5.组合预测模型在城市垃圾产量预测中的研究与应用 [J], 杨晗熠;吴育华
因版权原因，仅展示原文概要，查看原文内容请购买。

BP神经网络原理应用

BP神经网络原理及应用1 人工神经网络简介1.1生物神经元模型神经系统的基本构造是神经元（神经细胞），它是处理人体内各部分之间相互信息传递的基本单元。

据神经生物学家研究的结果表明，人的大脑一般有1011个神经元。

每个神经元都由一个细胞体，一个连接其他神经元的轴突1010和一些向外伸出的其它较短分支——树突组成。

轴突的功能是将本神经元的输出信号（兴奋）传递给别的神经元。

其末端的许多神经末梢使得兴奋可以同时送给多个神经元。

树突的功能是接受来自其它神经元的兴奋。

神经元细胞体将接受到的所有信号进行简单地处理后由轴突输出。

神经元的树突与另外的神经元的神经末梢相连的部分称为突触。

1.2人工神经元模型神经网络是由许多相互连接的处理单元组成。

这些处理单元通常线性排列成组，称为层。

每一个处理单元有许多输入量，而对每一个输入量都相应有一个相关联的权重。

处理单元将输入量经过加权求和，并通过传递函数的作用得到输出量，再传给下一层的神经元。

目前人们提出的神经元模型已有很多，其中提出最早且影响最大的是1943年心理学家McCulloch和数学家Pitts在分析总结神经元基本特性的基础上首先提出的M-P 模型，它是大多数神经网络模型的基础。

)()(1∑=-=ni j i ji j x w f t Y θ （1.1）式(1.1)中,j 为神经元单元的偏置（阈值），ji w 为连接权系数（对于激发状态，ji w 取正值，对于抑制状态，ji w 取负值），n 为输入信号数目，j Y 为神经元输出，t 为时间，f()为输出变换函数，有时叫做激发或激励函数，往往采用0和1二值函数或Ｓ形函数。

1.3人工神经网络的基本特性人工神经网络由神经元模型构成；这种由许多神经元组成的信息处理网络具有并行分布结构。

每个神经元具有单一输出，并且能够与其它神经元连接；存在许多（多重）输出连接方法，每种连接方法对应一个连接权系数。

严格地说，人工神经网络是一种具有下列特性的有向图：（１）对于每个节点存在一个状态变量xi ；（２）从节点i 至节点j ，存在一个连接权系数wji ；（３）对于每个节点，存在一个阈值j ；（４）对于每个节点，定义一个变换函数(,,),j i ji j f x w i j θ≠,对于最一般的情况，此函数取()j ji i j if w x θ-∑形式。

bp神经网络的应用综述

bp神经网络的应用综述近年来，随着人工智能（AI）发展的飞速发展，神经网络技术也在迅速发展。

BP神经网络是一种能够将输入大量信息并有效学习并做出正确决策的广泛应用的深度学习算法。

它的强大的学习能力令人印象深刻，从很多方面来看都是一种具有潜在潜力的技术。

在科学和工程方面，BP神经网络的应用非常广泛。

它可以用于模式识别，数据挖掘，图像处理，语音识别，机器翻译，自然语言处理和知识发现等等。

当可用的数据量很大时，BP神经网络可以有效地自动分析和提取有用的信息，从而有效地解决问题。

例如，在图像处理领域，BP神经网络可以用于图像分类、目标检测和图像语义分析。

它能够以准确的速度检测目标图像，包括人脸、行人、汽车等等，这在过去难以实现。

在机器翻译等技术中，BP神经网络可以用于语义分析，以确定机器翻译的正确语义。

此外，BP神经网络还可以用于人工智能的自动控制，例如机器人与机器人感知、模式识别、语音识别和控制系统。

除此之外，BP神经网络还可以用作在计算机游戏和科学研究中的决策支持系统，以便帮助决策者做出正确的决策。

总而言之，BP神经网络是一种具有广泛应用的深度学习算法，它能够自动处理大量复杂的信息，并能够做出正确的决策。

它可以用于各种科学和工程任务，如模式识别、机器翻译、图像处理、语音识别、机器人感知及自动控制等领域。

此外，它还可以用于决策支持系统，以便帮助决策者做出正确的决策。

BP神经网络在许多领域都具有巨大的潜力，希望以后能得到更多的研究和应用。

因为随着计算机技术的发展，BP神经网络在未来有望发挥更大的作用，帮助人们实现和科学研究的突破。

BP神经网络的潜力巨大，尽管它的应用前景十分广阔，但许多研究仍然存在挑战。

因此，有必要开展更多的研究，并利用其强大的特性，尽可能多地发掘它的潜力，以便最大限度地利用它的优势。

我们期待着BP神经网络会给人类的发展带来更多的惊喜。

BP神经网络在农业发展中的应用

络
农在
播” 过程；二是网络的希望输出与实际输出之差的误差信号由输出层经隐含层向输入层逐层修正连接权的“ 误差逆传播” 过程；三是由“ 模式顺传播” 误差和“
的比重；３Ｘ农村消费品零售额占全社会消费品零售额的比重；４ｘ代表农业各税占财政收入的比重；５Ｘ代表用于农业支出占财政支出的比重；
关键词：神经网络；Ｐ算法；Ｂ农业增加值；测评
中图分类号：Ｐ１Ｔ８文献标识码：Ａ文章编号：６１４９．Ｏ１３００．３１７．７２（ｌ）．１６０２
Ａｂｔｃ：ｈｓｐｐｒｎｒｄｃｓｔｅｂｓｃｐｎｉｌｆｅｒｌｅｗｏｋｉｐｏｏｅ，ａｅｎｔｅＢＰｎｕａｓｒｔｔｉａｅｔｏｕｅａｉｒｃｐｅｏｎｕａｔｒｒｐｓｄｂｓｄｏｅｒｌａｉｈｉＢＰｎｓｈ
售额，农业税，农产品进出口额等方面进行。具体的
评价指标有８，分别为Ｘ１Ｘ，３Ｘ，５Ｘ，个，２Ｘ，４Ｘ，６Ｘ，８７Ｘ。
其中ｘ１代表农业从业人员占社会从业人员的比重；２Ｘ代表农村非农产业劳动力占社会从业人员
四神＿ｏ
经网
（ｃｏｌｆｔｅｔｓｎｏｐｔ；ｒｗｅｔｎｖｒｔｒａｉｎｌｉｓＧａｓａｚｏ３００ＳｈｏｏＭａｍａｉｄＣｍｕｅＮｏｔｓＵｉｓｙｆｔａｉｅ；ｎｕＬｎｈｕ７０３）ｈｃａｒｈｅｉｏＮｏｔ摘要：文简述了Ｂ本Ｐ神经网络的基本原理，出了一种基于Ｂ提Ｐ神经网络对农业增加值占国内生产总值的比重的测评模型。实验表明，该模型的辨识精度高，能正确实现。

基于BP神经网络的数据融合技术在分布式养老系统中的应用

文献标志码：Ａ中图分类号：ＴＰ３９１
在我国随着老龄化社会的逐步趋近，老年人的养老问题显得越来越重要．欧美发达国家，由于更早进入老龄化社会，在智能养老领域有更多的
戴ＲＦＩＤ腕带，实时采集老年人的体征信息．同
速度下降．针对此问题，对传统的基于神经网络的融合算法进行改进，利用粗糙集对输入数据进行约简，使神经网络输人数据降维．同时，将约简后的信息进行训练．算法在训练时间和融合结果的准确性上都有提高．
关键词：粗糙集；ＢＰ神经网络；数据融合；分布式养老系统
系统，用来监视老年人家中情况并记录他们的行为．英国构建出一种全智能化老年公寓，在地板和家电中植入电子芯片，使老人的日常生活处于远
程监控状态．我国的智能养老课题研究虽然起步
国内外针对数据融合的算法多集中在贝叶斯估计
时，养老院的视频监控体系实时采集老年人的图像信息．由于单一的信息不能很好地体现老年人的实时身体状态，而且两类信息的属性不同，所以
在分布式系统中需要将两者进行数据融合处理．
经验．例如，美国的基于ＲＦＩＤ传感器的全新监测
ＢＰ神经网络算法，取得一定的效果．
源信息的协同处理和综合利用．分布式智能养老