六年级小升初组合图形题集
苏教版小升初数学总复习试题---组合图形

苏教版小升初数学总复习试题---组合图形
2020小升初数学专题组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
六年级小升初组合图形题集

六年级小升初组合图形
题集
work Information Technology Company.2020YEAR
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
小升初数学组合图形总复习题
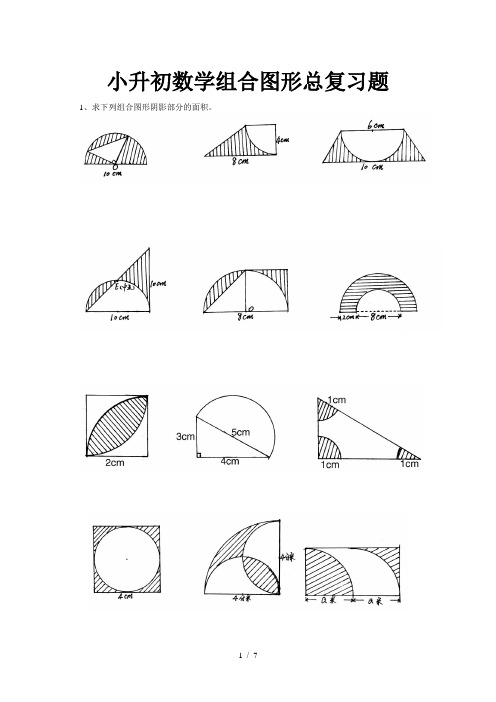
小升初数学组合图形总复习题1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,
求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
小升初数学组合图形总复习题

1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
六年级下册数学-小升初平面图形组合专项试题-s13-人教版
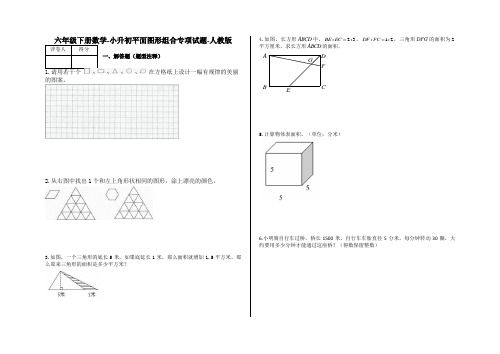
-小升初平面图形组合专项试题-人教版一、解答题(题型注释)1.请用若干个在方格纸上设计一幅有规律的美丽的图案。
2.从右图中找出1个和左上角形状相同的图形,涂上漂亮的颜色。
3.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加1.5平方米。
那么原来三角形的面积是多少平方米?4.如图,长方形中,,,三角形的面积为平方厘米,求长方形的面积.5.计算物体表面积。
(单位:分米)6.小明骑自行车过桥,桥长1500米,自行车车胎直径5分米,每分钟转动30圈,大约要用多少分钟才能通过这座桥?(得数保留整数)ABCD:2:3BE EC=:1:2DF FC=DFG2ABCDAB CDEFG7.三条边长分别是6厘米、8厘米、10厘米的直角三角形.将它的最短边对折到斜边相重合(如图),那么,图中阴影部分面积是多少平方厘米?8.求下图直角梯形中阴影部分的面积。
(单位:厘米)9.下面的一块是从上面哪一块中剪下来的,用线连一连。
10.数一数。
(1)个三角形个正方形(2)按要求涂颜色。
参数答案1.解:【解析】1. 2.解:【解析】2.3.7.5平方米【解析】3.用大三角形的面积减去小三角形的面积即可求出阴影部分的面积。
由图可以看出,大三角形的底为(1+5)米,小三角形的底为5米,高相同。
列出算式:大三角形的面积=(5+1)×高,小三角形的面积=5×高,所以(5+1)×高-5×高=1.5,解这个方程得:高=5,所以原来三角形的面积=5×1.5=7.5(平方米)。
1.5×(5÷1)=7.5(平方米) 4.72【解析】4.连接,.因为,,所以.因为,,所以平方厘米,所以平方厘米.因为,所以长方形的面积是平方厘米. 5.52×6=150平方分米【解析】5.根据正方体的表面积计算公式可得。
6.大约要用32分钟才能通过这座桥【解析】6.试题分析:先利用圆的周长公式求出车轮的周长,再求出每分钟行驶的路程,于是可以利用“路程÷速度=时间”求出通过1500米的路需要的时间. 解答:解:5分米=0.5米, 1500÷(3.14×0.5×30), =1500÷47.1, ≈32(分钟);答:大约要用32分钟才能通过这座桥. 7.6平方厘米【解析】7.试题分析:此题很明显,原直角三角形被分成了三部分,因它们都是直角三角形,依据题目条件可以先找出它们的面积比,总面积已知,则轻松求解. 解:如图所示由题意可以知道:S△ADE=S△ABE, 则S△CDE:S△ADE=2:3;所以S△CDE:S△ABC=2:8=1:4, S△ABC=8×6÷2=24(平方厘米), S△CDE=24×=6(平方厘米);答:图中阴影部分面积是6平方厘米. 8.1.86平方厘米AE FE ABCD EF G:2:3BE EC =:1:2DF FC =3111()53210DEF ABCD ABCD S S S =⨯⨯=V 长方形长方形12AEDABCD S S =V 长方形11::5:1210AG GF ==510AGD GDF S S ==V V 12AFD S =V 16AFD ABCD S S =V 长方形ABCD72【解析】8.本题考查组合图形的面积,其中涉及三角形的周长和面积,梯形的面积,圆的面积等相关知识。
2024年小升初数学精讲专题专题16 组合图形的周长与面积(基础卷)
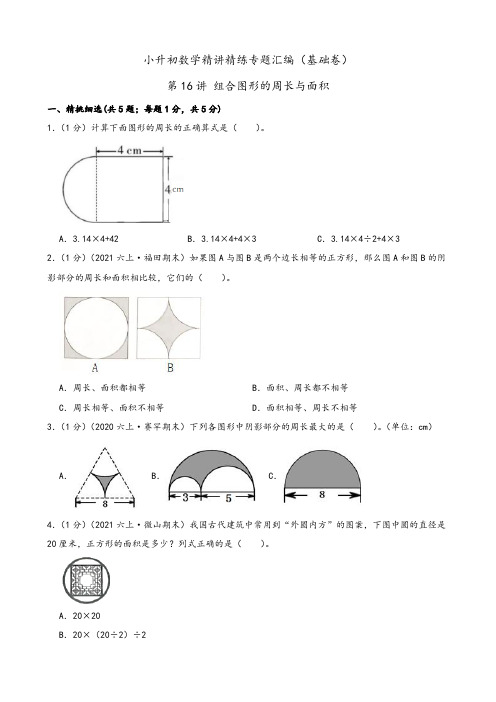
小升初数学精讲精练专题汇编(基础卷)第16讲组合图形的周长与面积一、精挑细选(共5题;每题1分,共5分)1.(1分)计算下面图形的周长的正确算式是()。
A.3.14×4+42 B.3.14×4+4×3 C.3.14×4÷2+4×32.(1分)(2021六上·福田期末)如果图A与图B是两个边长相等的正方形,那么图A和图B的阴影部分的周长和面积相比较,它们的()。
A.周长、面积都相等B.面积、周长都不相等C.周长相等、面积不相等D.面积相等、周长不相等3.(1分)(2020六上·赛罕期末)下列各图形中阴影部分的周长最大的是()。
(单位:cm)A. B. C.4.(1分)(2021六上·微山期末)我国古代建筑中常用到“外圆内方”的图案,下图中圆的直径是20厘米,正方形的面积是多少?列式正确的是()。
A.20×20B.20×(20÷2)÷2C.20×(20÷2)÷2×25.(1分)(2021六上·温江期末)如图,大圆内有3个大小不等的小圆,这四个圆的圆心都在同一直线上,若大圆的直径是5厘米,则三个小圆的周长之和是()厘米.A.7.85 B.15.7 C.31.4 D.78.5二、仔细想,认真填(共8题;每空1分,共9分)6.(1分)(2022六下·巧家期中)请算出下面面图形的面积是cm2。
7.(2分)(2020六上·合山期末)一个半圆,它的半径是r,它的直径是,周长是。
8.(1分)(2020六上·赛罕期末)如图所示,圆的直径20cm,阴影部分的面积是cm2。
9.(1分)(2020六上·福田月考)如图,半圆的半径是2分米,则封闭图形的周长为分米。
10.(1分)(2020·海安模拟)如图,在一大一小两个正方形拼成的图形中,阴影部分的面积是50平方厘米,则小正方形的面积是平方厘米。
六年级组合图形练习题

六年级组合图形练习题在六年级数学学习中,组合图形是一个重要的概念。
通过组合图形的练习,学生们可以锻炼自己的观察力、想象力和逻辑思维能力。
本文将提供一些六年级组合图形练习题,帮助学生们巩固相关知识,并提升解题能力。
以下是一些题目及其解答。
题目一:请根据下图中的组合图形,回答问题。
(插入图像)1. 这个图形由几个单元图形组成?2. 单元图形的种类以及数量是什么?3. 这些图形的面积之和是多少?解答一:1. 这个图形由六个单元图形组成。
2. 单元图形的种类为正方形和长方形,正方形数量为三个,长方形数量为三个。
3. 这些图形的面积之和为...(根据图形具体计算得出结果)。
题目二:请根据下图中的组合图形,回答问题。
(插入图像)1. 这个图形由几个单元图形组成?2. 单元图形的种类以及数量是什么?3. 这些图形的周长之和是多少?解答二:1. 这个图形由五个单元图形组成。
2. 单元图形的种类为正方形和三角形,正方形数量为三个,三角形数量为两个。
3. 这些图形的周长之和为...(根据图形具体计算得出结果)。
题目三:请根据下图中的组合图形,回答问题。
(插入图像)1. 这个图形由几个单元图形组成?2. 单元图形的种类以及数量是什么?3. 这些图形的总体积是多少?解答三:1. 这个图形由八个单元图形组成。
2. 单元图形的种类为正方体和长方体,正方体数量为三个,长方体数量为五个。
3. 这些图形的总体积为...(根据图形具体计算得出结果)。
通过以上的组合图形练习题,学生们可以提高对组合图形的理解和解题能力。
希望同学们能够认真思考每个问题,并尝试自己独立解答。
如果遇到困难,可以向老师或同学寻求帮助,共同进步。
祝大家在六年级的数学学习中取得好成绩!。
2024年人教版六年级下册数学小升初分班考专题:图形的拼组(含答案)

2024年人教版六年级下册数学小升初分班考专题:图形的拼组一、单选题1.下图是一个长3厘米、宽与高都是2厘米的长方体。
将它挖掉一个棱长1厘米的小正方体,它的表面积( )。
A.比原来大B.比原来小C.不变D.无法确定2.在一个长、宽、高分别是30厘米、25厘米、60厘米的长方体箱子里,最多能装进棱长1分米的立方体( )个。
A.45B.30C.36D.723.城市义工协会开展垃圾分类宣传进社区活动。
他们计划在下面右边这张直角梯形卡纸上剪出如左边那样大小的三角形制作宣传标志(如下图),最多可以剪出( )个这样的三角形。
A.3B.4C.5D.64.如图,把一个底面半径4分米、高8分米的圆柱切开并拼成一个近似的长方体。
下面说法中错误的是( )A.长方体的体积与圆柱的体积相等B.长方体的底面积等于圆柱的底面积C.长方体的高等于圆柱的高D.长方体的表面积等于圆柱的表面积5.一个长9厘米、宽6厘米、高3厘米的长方体,切割成3个体积相等的长方体,表面积最大可增加( )A.36平方厘米B.72平方厘米C.108平方厘米D.216平方厘米6.在一个棱长为1dm的正方体的8个角上,各锯下一个棱长为1cm的正方体,现在它的表面积和原来比( )。
A.不变B.减少C.增加D.无法确定二、填空题7.在一块边长是20cm的正方形纸上画一个最大的圆,这个圆的面积是 cm2。
8.用三个完全一样的正方体,拼成一个长方体,长方体的表面积是70平方分米,原来一个正方体的表面积是 平方分米。
9.用3个棱长2分米的正方体拼成一个长方体。
这个长方体的体积是 立方分米,表面积是 平方分米。
10.如图,这个圆的直径是6厘米,把这个圆剪拼成一个近似的长方形,那么这个长方形的宽约 厘米,长方形的长约是 厘米。
11.一个正方体的棱长总和是24厘米,这个正方体的体积是 立方厘米,用两个这样的正方体拼成一个长方体,这个长方体的表面积是 平方厘米.12.如图形体是由棱长为1厘米的小正方体搭拼成的,它的表面积是 平方厘米,至少还需要 个这样的小正方体,才能搭拼成棱长为3厘米的一个正方体.13.一个高5厘米的圆柱体,沿底面直径将圆柱体锯成两块,其表面积增加40平方厘米,原来这个圆柱体的体积是 立方厘米。
【小升初专项训练】01 组合图形的计数

第1讲组合图形的计数第一关【知识点】1.组合图形的概念:圆,三角形,正多边形,梯形,平行四边形为基本图形其余的为组合图形,可以用辅助线分解为基本图.2.组合图形的计数实质上就是分类数图形,解决方法是:(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.【例1】图中有多少个三角形?【答案】3【例2】数一数,图中一共有多少个三角形?【答案】13【例3】数一数,图中一共有多少个三角形?【答案】27【例4】数一数,图中一共有多少个三角形?【答案】48【例5】数一数,图中一共有多少个三角形?【答案】9【例6】数一数,图中一共有多少个三角形?【答案】8【例7】数一数,图中一共有多少个三角形?【答案】8【例8】数一数,图中一共有多少个三角形?【答案】20;24;24【例9】数一数,图中一共有多少个三角形?【答案】35【例10】数一数,图中一共有多少个三角形?【答案】67【例11】数一数,图中一共有多少个三角形?【答案】11【例12】数一数,图中一共有多少个三角形?【答案】40【例13】图中,有多少个三角形?【答案】16【例14】数一数,图中一共有多少个三角形?【答案】8【例15】数一数,图中一共有多少个三角形?【答案】13【例16】数一数,图中一共有多少个三角形?【答案】12【例17】数一数,图中一共有多少个三角形?【答案】11【例18】数一数,图中一共有多少个三角形?【答案】20【例19】数一数,图中一共有多少个三角形?【答案】12【例20】如图中有多少个三角形?【答案】27【例21】如图中有多少个三角形?【答案】17【例22】如图中有多少个三角形?【答案】10【例23】数一数,图中有多少个三角形?【答案】27【例24】图中有多少个三角形?【答案】14【例25】图中有多少个三角形?【答案】11【例26】数一数,图中共有多少个三角形?【答案】15【例27】如图是一些等腰直角三角形组成的图形,图中一共有多少个三角形?【答案】23【例28】如图中,一共有多少个三角板?【答案】12【例29】如图中共能数出多少个三角形?【答案】24【例30】如图中共能数出多少个三角形?【答案】24【例31】在△ABC中,D1、D2、D3为AB边的内分点,E1、E2、E3为AC边的内分点,那么图中有 多少个三角形?【答案】64【例32】如图中共能数出多少个三角形?【答案】11【例33】如图中,共有多少个三角形?【答案】10【例34】数一数,图中共有多少个三角形?【答案】10【例35】数一数,图中共有多少个三角形?【答案】12【例36】数一数,图中共有多少个三角形?【答案】16【例37】数一数,图中共有多少个三角形?【答案】18【例38】数一数,图中共有多少个三角形?【答案】30【例39】数一数,图中共有多少个三角形?【答案】28【例40】如图中,一共有多少个三角形?【答案】32【例41】如图中,一共有多少个三角形?【答案】72【例42】如图中,一共有多少个三角形?【答案】22【例43】图中共有多少个三角形?【答案】60【例44】下图中共有多少个三角形?【答案】8【例45】下图中共有多少个三角形?【答案】24【例46】下图中共有多少个三角形?【答案】34【例47】下图中共有多少个三角形?【答案】35【例48】下图中共有多少个三角形?【答案】16【例49】下图中共有多少个三角形?【答案】30【例50】下图中共有多少个三角形?【答案】22【例51】下图中共有多少个三角形?【答案】62【例52】下图中共有多少个三角形?【答案】10【例53】下图中共有多少个三角形?【答案】35【例54】下图中共有多少个三角形?【答案】32【例55】下图“七角星”中共有多少个三角形?【答案】35【例56】下图中共有多少个三角形?【答案】20【例57】下图中共有多少个三角形?【答案】40【例58】如图,图中3个大三角形都是等边三角形,则图中共有多少个三角形?【答案】30【例59】如图中有多少个三角形?【答案】76【例60】如图中有多少个三角形?【答案】76【例61】如图中,包含“”的三角形有多少个?【答案】4【例62】如图,数一数其中共有多少个包含“☆”的三角形?【答案】8【例63】如图是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形若干个.那么,图中包含“*”号的大、小正三角形一共有多少个?【答案】6【例64】如图,图中包含“★”的大、小三角形共有多少个?【答案】12【例65】数一数如图中共有多少个包含“﹡”号的三角形?【答案】6【例66】图中,共有多少个直角三角形?【答案】16【例67】图中,共有多少个等边三角形?【答案】14【例68】数一数,图中一共有多少个正三角形?【答案】44【例69】如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G在一条直线上,则图中有多少个等腰直角三角形?【答案】22【例70】如图,连接一个正六边形的各顶点,问图中共有多少个等腰三角形(包括等边三角形)?【答案】38【例71】圆周上有8个点,把它们两两相连,若任意三条线都不交于一点,那么图中顶点全在圆内的三角形共有多少个?【答案】56【例72】如图,有这样的两条线,请问从这5个点中任选三个点可以构成多少个不同的三角形?【答案】8【例73】木板上钉有五颗钉子(如图所示,排成两行),用橡皮筋可以套出多少个三角形?【答案】9【例74】如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出多少个正三角形?【答案】13【例75】以平面上4个点为端点连接线段,形成的图形中最多可以有多少个三角形?【答案】8【例76】平面上有四个点,任意三个点都不在﹣条直线上.以这四个点为端点连接六条线段,在所组成的图形中用它们作顶点可以组成多少个三角形?【答案】4【例77】以平面上任意4个点为顶点的三角形中,钝角三角形最多有多少个?【答案】4【例78】从图中两个正方形的7个顶点中选出3个点作为顶点构成三角形,一共可以构成多少个不同的三角形?【答案】32【例79】如图由5个大小相同的正方形构成.以图中12个点为顶点的三角形共有多少个?【答案】200【例80】长方形内有2017个点,连同长方形的4个顶点在内,共有2021个点,任意3个点都不在同一条直线上,以这2021个点中的某三点为顶点,可作出多少个互不重叠的三角形?【答案】4036【例81】如图,是由9个点组成的点阵,那么以图中3个点为顶点的直角三角形有多少个?【答案】44【例82】如图有12个点,相邻两个点之间的距离是1厘米,这些点为顶点可以连成多少个面积为3平方厘米的三角形?【答案】26【例83】如图是由四个边长为1的小正方形组织的图形,图中共有9个格点(格点即为小正方形的顶点).如果以这些格点为顶点,那么一共可组成多少个等腰三角形?【答案】36【例84】如图是由32个面积为1的等边三角形组成的一个大的平行四边形,这个大的平行四边形内部及边上共有25个交叉点.以这些交叉点为顶点,可以连成多少个等边三角形?【答案】28【例85】在一个圆周上均匀分布10个点,以这些点为顶点,可以画出多少个不同的钝角三角形?(补充知识:由直径和圆周上的一点构成的三角形一定是直角三角形,其中直径的边所对的角是直角,所以如果圆周上三点在同一段半圆周上,则这三点构成钝角三角形)【答案】60【例86】用9个钉子钉成相互间隔为l厘米的正方阵(如图).如果用一根橡皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形有多少个?【答案】32【例87】如图由4个正六边形组成,每个面积是6,以这4个正六边形的顶点为顶点,可以连接面积为4的等边三角形有多少个?【答案】8【例88】如图,大三角形由9个形状、大小相同的等边三角形组成,共有10个顶点,以这些顶点为顶点构成的三角形中,面积与阴影部分面积相等的三角形共有多少个?【答案】36【例89】如图,一小正方形的边为边向小正方形外作四个正方形,再依次连接几个定点,若图中阴影三角形的面积是S,则面积为2S的三角形有_______个,面积为8S的正方形有_______个【答案】20;1【例90】如图由九个边长为1厘米的正方形组成,在如图中面积为0.5平方厘米的三角形有_______个.面积为1平方厘米的三角形有_______个,面积为1.5平方厘米的三角形有_______个,面积最大的三角形的面积是_______平方厘米.【答案】5;11;2;2.5【例91】在图中填上2条直线,最多能数出多少个三角形?【答案】10【例92】今有甲、乙两个大小相同的正三角形,各画出了一条两边中点的连线,如图,甲、乙位置左右对称,但甲、乙内部所画线段的位置不对称,从图中所示的位置开始,甲向右水平移动,直至两个三角形重叠后在离开.在移动过程中的每个位置,甲与乙所组成的图形中都有若干个三角形,那么三角形个数最多的位置,图形中有多少个三角形?【答案】11【例93】如图,在正方形的内部放入1个点,就可以把原来的正方形分成了4个小三角形;在正方形的内部放入2个点,就可以把原来的正方形分成了6个小三角形.那么如果在正方形的内部放入10个点,最多能把原来的正方形分成了多少个小三角形?【答案】22【例94】在一张三角形纸内任作2009个互不重合的点(所有的点都不在三角形的任意一条边上),以这2009个点和三角形纸的3个顶点为顶点的三角形,最多能剪出多少个?【答案】4019【例95】在三角形ABC中,D是BC的中点,图中面积相等的三角形共有多少对?【答案】6第二关【知识点】【例96】图中一共能数出多少正方形?【答案】26【例97】图中一共能数出多少正方形?【答案】55【例98】图中一共能数出多少正方形?【答案】26【例99】图中一共能数出多少正方形?【答案】23【例100】图中一共能数出多少正方形?【答案】14【例101】.将4×4的大正方形切割为16个1×1的小正方形,擦去其中的两条线段,得到如图所示图形.则图中一共有多少个正方形?【答案】22【例102】图中一共能数出多少正方形?【答案】20【例103】图中一共能数出多少正方形?【答案】13【例104】图中一共能数出多少正方形?【答案】17【例105】图中一共能数出多少正方形?【答案】35【例106】图中一共能数出多少正方形?【答案】46【例107】图中一共能数出多少正方形?【答案】10【例108】图中一共能数出多少正方形?【答案】14【例109】图中共有多少个正方形?【答案】17【例110】数一数,图中共有多少个正方形?【答案】23【例111】数一数,图中共有多少个正方形?【答案】18【例112】数一数,图中共有多少个正方形?【答案】11【例113】数一数,图中共有多少个正方形?【答案】20【例114】数一数,图中共有多少个正方形?【答案】15【例115】数一数,图中共有多少个正方形?【答案】28【例116】如图由相同的正方形和相同的等腰直角三角形构成,求正方形的个数。
六年级下册数学-小升初平面图形组合专项试题-s-人教版

-小升初平面图形组合专项试题-人教版一、解答题(题型注释)其中最小的地砖边长是1,求这个房间的地面面积.2.用一个长8厘米,宽4厘米的长方形形纸改一个正方形。
最大的正方形的周长是多少厘米?3.如图是一个长方形,请你画一条直线把它分成两部分,沿画的线剪开后,这两部分既能拼成一个三角形,也能拼成一个平行四边形,或梯形.请你用虚线画出分线和拼的示意图.4.用若干块面积都是18平方厘米的长方形拼成一个大正方形(如图),那么阴影部分的面积是多少?5.请你用下图中的任意三角形创作一个密铺平面.6.如图,长方形中,,,三角形的面积为平方厘米,求长方形的面积.ABCD:2:3BE EC=:1:2DF FC=DFG2ABCDAB CDEFG7.两个完全相同的长方体,每个长方体长5分米,宽4分米,高6分米,把它们拼成一个表面积最小的长方体后,表面积比原来两个长方体表面积之和减少了多少平方分米?8.在一个长是12厘米,宽10厘米的长方形中画一个最大的圆,这个圆的面积是()平方厘米。
9.动手操作:画一个半径是2厘米的圆,并求出它的周长和面积.10.一块长方形花圃的宽7米,面积248平方米,扩建后长不变,宽增加到21米,求扩建后的面积是多少平方米?参数答案1.解:如下图所示,黑色部分正方形边长为1,其他正方形边长未知.所以我们可以设AB的长度为x,那么1号正方形边长为x+1,2号正方形边长为x+2,3号正方形边长为x+3,4号正方形边长为x+4,5号正方形边长为4号正方形边长与AB的差,也就是x+4﹣x=4,6号正方形边长为x+8,7号正方形边长为2x+3,8号正方形边长为x+12.根据长方形的宽相等可以列方程(x+3)+(x+2)+(2x+3)=(x+8)+(x+12)解得x=6所以长方形的长为(2x+3)+(x+12)=33宽为(x+8)+(x+12)=32面积为33×32=1056.答:这个房间的地面面积是1056【解析】1.黑色部分正方形边长为1,其他正方形边长未知.所以我们可以设AB的长度为x,那么1号正方形边长为x+1,2号正方形边长为x+2,3号正方形边长为x+3,4号正方形边长为x+4,5号正方形边长为4号正方形边长与AB的差,也就是x+4﹣x=4,6号正方形边长为x+8,7号正方形边长为2x+3,8号正方形边长为x+12.根据长方形的宽相等可以列方程求解即可.2.解:4×4=16﹙厘米﹚答:最大的正方形的周长是16厘米。
新课标人教版六年级数学下册 小升初数学组合图形总复习试题
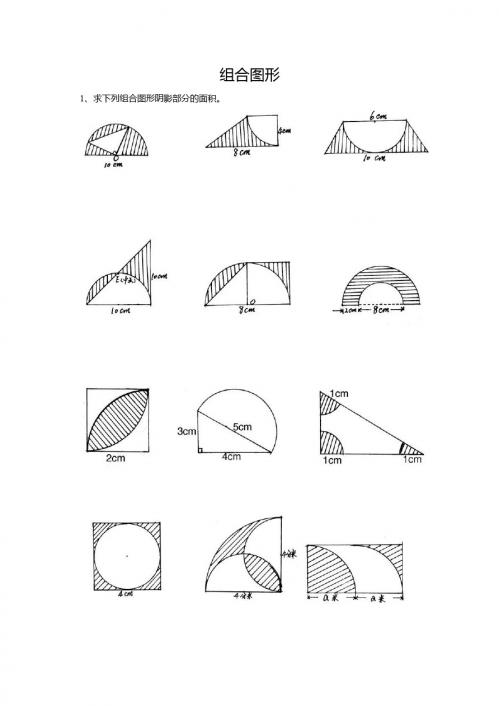
⑩梯形上底 8cm,下底 16cm,阴影 部分面积 64cm2,求梯形面积。
⑾求阴影部分面积。(单位:cm)
厘米, ①比阴影②面积少 3cm2,求 EC 的长。
⑥图中阴影①比阴影②面积小 48 平方 AB=40cm,求 BC 的长。
⑦平行四边形的面积是 30cm2, 积。
求阴影部分的面积。
⑧一个圆的半径是 4cm,求阴影部分面
⑨已知 AB=8cm,AD=12cm,三角形 ABE 和三角形 ADF 的面积,各占长方形 ABCD 的 1/3,求三角形 AEF 的面积。
组合图形
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。(单位:厘米) 积。
②圆的周长是 18.84cm,求阴影部分面
③长方形的面积和圆的面积相等,已知圆
④求直角三角形中阴影部分的面积。
的半径是 3cm,求阴影部分的周长和面积。
cm,已知阴影
小学六年级组合图形试题训练(求面积)

小学六年级(组合图形)试题训练
求阴影部分面积
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求
三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
小学六年级数学总复习题库(组合图形)
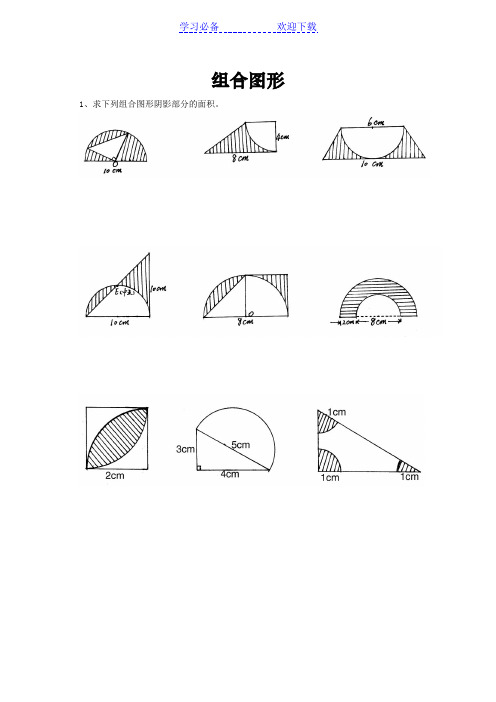
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求
三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
新人教版小升初数学组合图形总复习题
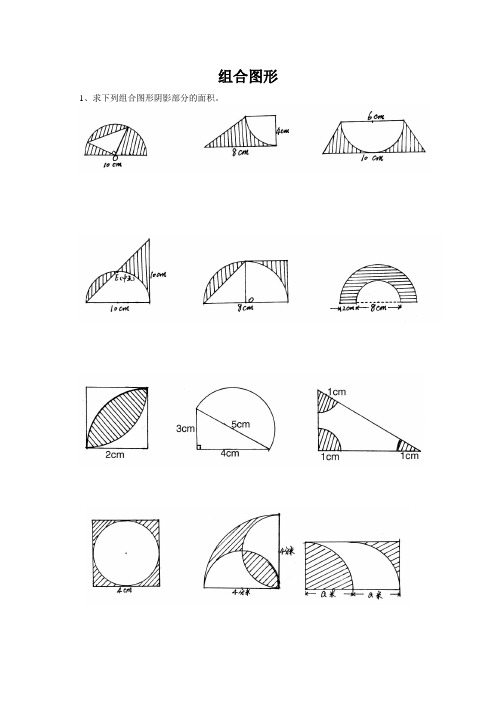
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米) ②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm) 部分面积64cm2,求梯形面积。
2022小升初专题练 第16讲 组合图形的周长与面积(通用版,含详解) (1)
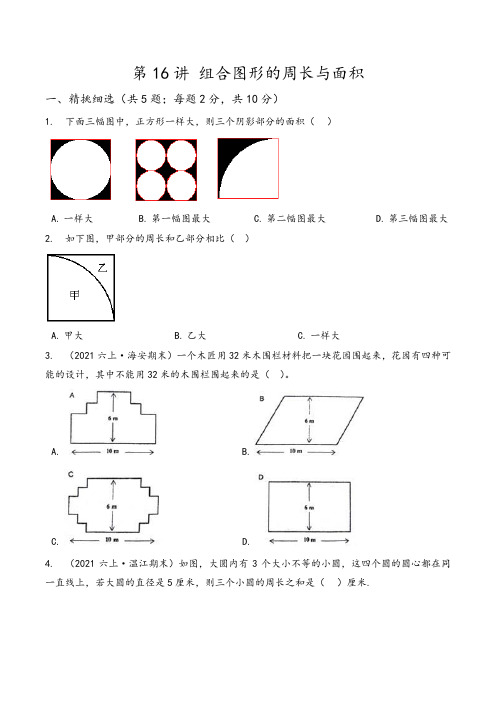
第16讲组合图形的周长与面积一、精挑细选(共5题;每题2分,共10分)1. 下面三幅图中,正方形一样大,则三个阴影部分的面积()A.一样大B.第一幅图最大C.第二幅图最大D.第三幅图最大2. 如下图,甲部分的周长和乙部分相比()A.甲大B.乙大C.一样大3. (2021六上·海安期末)一个木匠用32米木围栏材料把一块花园围起来,花园有四种可能的设计,其中不能用32米的木围栏围起来的是()。
A. B.C. D.4. (2021六上·温江期末)如图,大圆内有3个大小不等的小圆,这四个圆的圆心都在同一直线上,若大圆的直径是5厘米,则三个小圆的周长之和是()厘米.A.7.85B.15.7C.31.4D.78.55. (2020六上·福田月考)如图:这两个图形中涂色的部分周长和面积的大小关系是()A.周长相等,面积不相等B.周长和面积都相等C.周长不相等,面积相等二、判断正误(共3题;每题2分,共6分)6. 用8个1立方厘米的小方块拼成一个正方体.如果拿去一个小方块,它的表面积不变.()7. (2012·广州)右图中的阴影部分面积占长方形的。
()8. 右图的阴影部分的周长是圆的周长+长方形的周长。
()三、填空题(共10题;每空1,共12分)9. 求下面图中阴影部分的面积.面积是________ .10. 一张长方形纸片,长10厘米,宽8厘米.在这张纸片上剪去一个最大的圆后,剩下部分的面积是________平方厘米?(保留两位小数)11. 一座隧道的入口上部是半圆,下部是个长方形(如下图).已知长方形的长是10米,宽是5米.这个隧道横截面的周长是________米?面积是________平方米?(保留一位小数)12. 用一张长8厘米、宽6厘米的长方形纸,剪一个尽可能大的圆后,剩下部分的面积是________平方厘米?(用一张纸剪一剪,再算一算)13. 小玲要在一个长6厘米、宽4厘米的长方形纸片上剪下一个最大的圆.(1)圆的面积是________平方厘米?(结果用小数表示)(2)剩下部分的面积是________平方厘米?(结果用小数表示)14. (2020六上·福田月考)如图,半圆的半径是2分米,则封闭图形的周长为________分米。
(成都市)小升初数学组合图形试题训练

组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,①比阴影②面积少3cm2,求EC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白 ⒀阴影部分比空白部分大6cm 2,求S 阴。
部分少12平方厘米,求阴影部分面积。
一、求出阴影部分面积:(6分)。
4、下图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积(10分)8 4m 48m2020ABO16、下图中阴影部分的面积是( )平方厘米。
25、如图(3),有两个边长是2厘米的正方形,其中一个正方形的一个顶点在另一个的中心上,并且两个涂色的三角形的面积相等。
问两个正方形不重合的部分面积的和是多少?2、右图中阴影部分的面积为 (单位:厘米)。
6 666图(3)5 5 44如图,等腰直角三角形ABC 的面积是8平方厘米。
求阴影部分的面积。
(8分)22. 求阴影部分的面积。
(单位:厘米)1、求右图中阴影部分面积(单位:厘米)。
DAC450 631.下图是由正方形和半圆形组成的图形,其中P点为半圆周的中点,Q点为正方形一边的中点,求阴影部分面积。
(单位:厘米)1、下图中三角形的面积等于梯形的面积,求五边形的面积。
(单位:厘米)16、下图中阴影部分的面积是()平方厘米。
6611、如图:阴影三角形的面积是 。
小升初真题专练组合图形的面积小学数学六年级下册人教版(含答案)

小升初真题特训:组合图形的面积-小学数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________1A.(1)号面积最大B.(2)号面积最大二、填空题7.(2020·江苏南通·统考小升初真题)如图,大正方形被分成了4个相同的三角形和一个小正方形。
大正a b ,则小正方形的面积是()平方厘米。
方形的周长为24厘米,已知:2:18.(2021·全国·小升初真题)(汉阳区)如图,将两个正三角形重叠作出一个星形,在重叠的图形中再作出一个小星形,即阴影部分,已知大星形的面积是40cm2,那么小星形的面积是_____.9.(2020·北京海淀·小升初真题)如图,已知大正方形的面积是a,则小正方形的面积是___________。
10.(2020·北京海淀的面积的面积=的面积=,由此发现,,15.(2020·全国·小升初真题)5平方分米.三、图形计算20.(2022·湖北十堰·统考小升初真题)如图,两个正方形的边长分别是10cm和4cm,求阴影部分的面积。
21.(2022·山东临沂·统考小升初真题)求如图阴影部分的面积。
四、解答题22.(2022·湖南长沙·长沙市开福区青竹湖湘一外国语学校校考小升初真题)如图,大小正方形的边长分别是5厘米、3厘米,求三角形DBF的面积。
23.(2020·江苏常州·校考小升初真题)如下图所示,把三角形DBE沿线段AC折叠,得到一个多边形27.(2021·浙江宁波·小升初真题)28.(2020春·辽宁·六年级统考小升初模拟)如下图,一张边长为4cm的正方形纸,从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩余部分面积是多少?29.(2021春·江苏·六年级统考小升初模拟)如图,一块长方形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪.草坪的面积是多少平方米?(单位:米)30.(2020·河北·小升初真题)李大爷家承包了如图所示的一块地,请你帮他计算一下这块地的面积(单位,米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
