六年级奥数题及答案:容斥原理问题(高等难度)_题型归纳
六年级上册奥数试题-第5讲 容斥原理 全国通用(含答案)

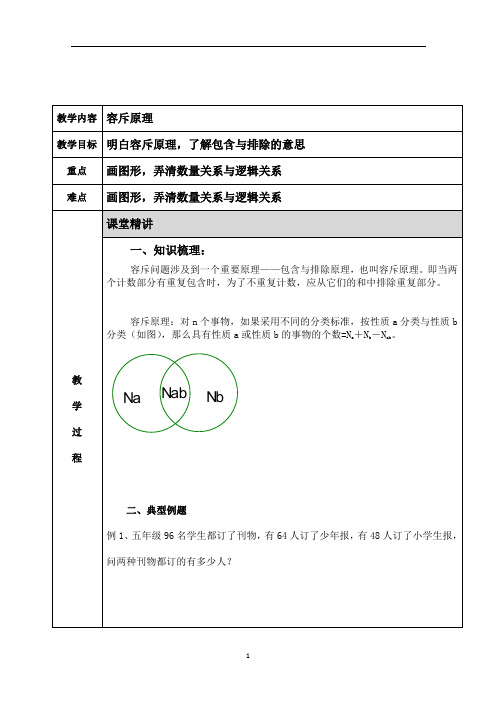
第5讲容斥原理知识网络我们经常会遇到这样一类问题,题目中涉及到包含与排除,也就是说有重叠部分。
解答此类问题的主要依据是容斥原理。
容斥原理一:设A、B是两类有重叠部分的量(如图1所示),若A对应的量为a,B对应的量为b,A与B重叠部分对应的量为ab,那么这两类量的总量可以用下面的公式进行计算:总量=a+b-ab容斥原理二:设A、B、C是三类有重叠部分的量(如图2所示),若A对应的量为a,B 对应的量为b,C以应的量为c,A与B重叠部分以应的量为ab,B与C重叠部分对应的量为bc,C与A重叠部分对应的量为ca,A、B、C三部分重叠部分对应的量为abc,则这三类量的总量可以用下面的公式进行计算:总量=a+b+c-ab-bc-ca+abc重点·难点容斥原理的表述虽然简单,但涉及容斥原理的题型很多,范围很广。
我们往往会遇到一些看似与容斥原理无关的问题,然而通过恰当的转化,便可利用容斥原理顺利求解。
如何分析题目,准确找到重叠部分,将问题转化成可用容斥原理解决的问题是本节的难点。
学法指导解决本节问题的最基本方法是示意图法,即通过示意图来表示题目中的数量关系,使分析、推理与计算结合起来,达到使题目的内容形象化,数量之间关系直观化的目的。
因此,这就要求我们在解题过程中,仔细分析,找出所需量并用示意图表示出来,进而通过观察示意图,确定几类量的重叠部分,然后运用容斥原理解决问题。
经典例题[例1]分母是1001的最简真分数,共有多少个?思路剖析分母是1001的真分数有共1000个,为了方便计算,增加一个分数在1001个分数中考虑问题。
由于1001=7×11×13,所心1~1001的分子里只要含有7、11、13的倍数的就一定能同分母约分,即不是最简真分数,应排除掉。
因此,首先应考虑1~1001中,有多少个7、11或13的倍数。
解答因为1001=7×11×13,所以在1~1001的自然数中,7的倍数共有(11×13)个,11的倍数共有(7×13)个,13的倍数共有(7×11)个;7、11年公倍数有13个,7、13的公倍数有11个,11、13的公倍数有7个;7、11、13的公倍数有1个(即1001)。
小学奥数之容斥原理(二)

容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的没有,例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?分析与解:“每人至少参加两项比赛”说明没有不参加的,也没有参加一项比赛的,我们可以在下图中参加一项的区域用0表示。
人参加,3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参加的只。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?整理后:全班人数=39+x39+x 表示全班人数,当x 取最大值时,全班人数就最多,当x 取最小值时,全班人数就最少。
x 是数学、语文、英语三科都得满分的同学,因而x 中的人数一定不超过两科得满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
(完整版)容斥原理习题加答案

1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有( )A、27人B、25人C、19人D、10人【答案】B【解析】直接代入公式为:50=31+40+4-A∩B得A∩B=25,所以答案为B。
2.某服装厂生产出来的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?()A、15B、25C、35D、40【答案】C【解析】这是一种新题型,该种题型直接从求解出发,将所求答案设为A∩B,本题设小号和蓝色分别为两个事件A和B,小号占50%,蓝色占75%,直接代入公式为:100=50+75+10-A∩B,得:A∩B=35。
3.某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。
问接受调查的学生共有多少人?()A.120B.144C.177D.192【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字24,再推其他部分数字:根据每个区域含义应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47-{(x+24)+(z+24)+(y+24)}+24+15=199-{(x+z+y)+24+24+24}+24+15根据上述含义分析得到:x+z+y只属于两集合数之和,也就是该题所讲的只选择两种考试都参加的人数,所以x+z+y的值为46人;得本题答案为120.4.对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人()A.22人B.28人C.30人D.36人【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字12,再推其他部分数字:根据各区域含义及应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数100=58+38+52-{18+16+(12+ x)}+12+0,因为该题中,没有三种都不喜欢的人,所以三集合之外数为0,解方程得到:x=14。
奥数 容斥原理(例题+详解)

容斥原埋在很多计数问题中常用到数学上的一个包含与排除原理,也称为容斥原理.为了说明这个原理,我们先介绍一些集合的初步知识。
例1、桌上有两张圆纸片A、B.假设圆纸片A的面积为30平方厘米,圆纸片B的面积为20平方厘米.这两张圆纸片重叠部分的面积为10平方厘米.则这两张圆纸片覆盖桌面的面积由容斥原理的公式(1)可以算出为:|A∪B|=30+20-10=40(平方厘米)。
例2、求在1至100的自然数中能被3或7整除的数的个数。
分析解这类问题时首先要知道在一串连续自然数中能被给定整数整除的数的个数规律是:在n个连续自然数中有且仅有一个数能被n整除.根据这个规律我们可以很容易地求出在1至100中能被3整除的数的个数为33个,被7整除的数的个数为14个,而其中被3和7都能整除的数有4个,因而得到解:设A={在1~100的自然数中能被3整除的数},B={在1~100的自然数中能被7整除的数},则A∩B={在1~100的自然数中能被21整除的数}。
∵100÷3=33…1,∴|A|=33。
∵100÷7=14…2,∴|B|=14。
∵100÷21=4…16,∴|A∩B|=4。
由容斥原理的公式(1):|A∪B|=33+14-4=43。
答:在1~100的自然数中能被3或7整除的数有43个。
例3、求在1~100的自然数中不是5的倍数也不是6的倍数的数有多少个?分析如果在1~100的自然数中去掉5的倍数、6的倍数,剩下的数就既不是5的倍数也不是6的倍数,即问题要求的结果。
解:设A={在1~100的自然数中5的倍数的数},B={在1~100的自然数中6的倍数的数},数.为此先求|A∪B|。
∵100÷50=20,∴|A|=20又∵100÷6=16…4,∴|B|=16∵100÷30=3…10,∴|A∩B|=3,|A∪B|=|A|+|B|-|A∩B|=20+16-3=33。
小学奥数趣味学习《容斥问题》典型例题及解答

小学奥数趣味学习《容斥问题》典型例题及解答容斥原理是解决计数问题的重要方法,在汁数时要求注意无一重复无一遗漏,为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数U先计算出来,然后再把计数时重复计算的数LI排斥出去,使得计算的结果既无遗漏乂无重复,这种计数的方法称为容斥原理。
常见的容斥问题有两者容斥、三者容斥两种。
数量关系:AUB = A+B - AABAUBUC = A+B+C - AAB - BAC - CAA + AABAC解题思路和方法:先不考虑重叠的情况,把包含于某内容中的所有对象的数U先计算出来,然后再把计数时重复计算的数L1排斥出去,使得计算的结果既无遗漏乂无重复。
可画文氏(韦恩)图来解题。
例题1:有两块木板各长50厘米,把两块木板钉成一块长木板,中间钉在一起的重叠部分长8厘米。
钉成的木板长 ____ 厘米。
解:1、本题考查了学生的运算能力、应用能力。
解决重叠问题时,要注意重叠的部分不能重复计算。
2、两块木板一共长50+50二100 (厘米),如果钉在一起,说明原来的两个8厘米变成了一个8厘米,这样钉成的木板比100厘米少了8厘米,所以钉成的木板长100-8=92 (厘米)。
例题2:有两张各长20厘米的纸条,粘贴在一起后的总长是36厘米,那么重叠部分长()厘米。
A、2B、4C、8D、16解:1、此题考查孩子的应用能力、运算能力。
孩子没有进行画图理解,只是凭自己的主观想象进行思考,没有找到总长度与重复部分长度之间的关系,在后面计算时出现错误。
2、两张纸条如果没有重叠,那么一共长20 + 20=40 (厘米),而重叠后的长度是36 厘米,短了40 —36=4 (厘米),说明重叠部分的长度是4厘米。
选择B。
例题3:某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,这个班共有多少人?解:根据题意画图2、我们可以先算出19+20+21二60 (人),但是这里有被重复算的和漏算的,我们要注意减去重复的部分,加上漏算的部分。
奥数训练专题容斥原理

容斥原理1、某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?2、某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?3、四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.(6级)4、五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.(6级)5、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?(6级)6、新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有多少人?小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的倍,又是三项活动都参加人数的7倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗诵小组的人数.8、六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?9、在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:三种都带了的有几人?只带了一种的有几个?9、盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.10、全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动项目没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.若全班有6个人数学不及格,那么,数学成绩优秀的有几个学生?有几个人既会游泳,又会滑冰?11、在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓;11个人摘了山莓和李子但没有摘草莓;总共有60人摘了李子.如果参与采摘水果的总人数是100,你能回答下列问题吗?①有人摘了山莓;②有人同时摘了三种水果;③有人只摘了山莓;④有人摘了李子和草莓,而没有摘山莓;⑤有人只摘了草莓.12、五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,若参最少,只有4人.那么,参加B 组的有多少人?13、五一班有28位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是3个小组全参加的人数的5倍,并且知道3个小组全参加的人数是一个不为0的偶数,那么仅参加数学和语文小组的人有多少人?14、某学校派出若干名学生参加体育竞技比赛,比赛一共只有三个项目,已知参加长跑、跳高、标枪三个项目的人数分别为10、15、20人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛项目,求这所学校一共派出多少人参加比赛?图形中的重叠问题1、 把长38厘米和53厘米的两根铁条焊接成一根铁条.已知焊接部分长4厘米,焊接后这根铁条有多长?2、把长23厘米和37厘米的两根铁条焊接成一根铁条.已知焊接部分长3厘米,焊接后这根铁条有多长?3、两张长4厘米,宽2厘米的长方形纸摆放成如图所示形状.把它放在桌面上,覆盖面积有多少平方厘米?4、 如图,一张长8厘米,宽6厘米,另一个正方形边长为6厘米,它们中间重叠的部分是一个边长为4厘米的正方形,求这个组合图形的面积.5、一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积.图32厘米4厘米图36、三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?7、如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?8、如图所示,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38.若A 与B 、B 与C 的公共部分的面积分别为8、7,A 、B 、C 这三张纸片的公共部分为3.求A 与C 公共部分的面积是多少?容斥原理在数论问题中的应用1、 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?2、 在自然数1100~中,能被3或5中任一个整除的数有多少个?3、 在前100个自然数中,能被2或3整除的数有多少个?4、 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?5、求在1至100的自然数中能被3或7整除的数的个数.CB A105、以105为分母的最简真分数共有多少个?它们的和为多少?7、分母是385的最简真分数有多少个?并求这些真分数的和.8、在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有个.9、在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?10、50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?11、有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3, (2000)然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?12、写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?13、在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规则如下:(1)标签号为2的倍数,奖2支铅笔;(2)标签号为3的倍数,奖3支铅笔;(3)标签号既是2的倍数,又是3的倍数可重复领奖;(4)其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支?14、在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,则木棍总共被锯成________段.15、一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.16、一根1.8米长的木棍,从左端开始每隔2厘米画一个刻度,涂完后再从左端开始每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?容斥原理中的最值问题1、将1~13这13个数字分别填入如图所示的由四个大小相同的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?2、如图,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个?3、某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?4、某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.5、60人中有23的人会打乒乓球,34的人会打羽毛球,45的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?6、图书室有100本书,借阅图书者需在图书上签名.已知这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?7、甲、乙、丙都在读同-一本故事书,书中有100个故事.每个人都从某一个故事开始,按顺序往后读.已知甲读了75个故事,乙读了60个故事,丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个?8、在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,已知甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?恰好被1个人浇过的花最多有多少盆?9、甲、乙、丙同时给100盆花浇水.已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?。
小学数学题型归纳:容斥原理练习题(附答案)_

小学数学题型归纳:容斥原理练习题(附答案)_
学习方法网小编为各位同学整理了小学数学题型归纳,是我们平时学习中的一大难点,希望能对各位同学有所帮助。
更多学习材料尽在学习方法网。
小学数学题型归纳:容斥原理练习题(附答案)
【题目】
某大学的一间学生宿舍里居住着8名大学生,已知其中有6人会游泳,有5人会滑冰,有4人会打乒乓球.该宿舍内这两种运动都会的最多能有人。
【答案】
6+5+4=15,152=71,所以最多能有7人会两种。
今天就和大家就分享到这,祝各位同学学习愉快!。
6年级 奥数 容斥原理

姓名
居室
门厅
厨房
厕所
总面积
小明家
14
12
8
4
38
小龙家
20
12
8
4
44
他们住的这套房子共有多少平方米?
课后作业
1.100个小朋友做游戏,每人至少拿一面旗,其中56人拿小红旗,52人拿小黄旗。几人既拿小红旗又拿小黄旗?
容斥原理
专题解读:
在数学中,我们经常会碰到重复包含的现象。为了不重复计数,应从它们的和中减去重复部分,这一原理,我们称之为容斥原理,也称包含排除原理。正确运用这一原理,可以帮助我们解答血多抽象的数学问题。
例1.六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑自行车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?
5.某班学生进行短跑、游泳、篮球三个项目的测试。有4名学生在这三个项目上都没有达到优秀,其余每人至少有一个项目达到优秀,这部分学生达到优秀的人数如下表。求这个班的学生数?
短跑
游泳
篮球
短跑、游泳
游泳、篮球
短跑、篮球
短跑、游泳、篮球
17
18
15
6
6
5
2
课堂检测
1六一班有学生55人,每人至少参加赛跑和跳绳比赛中的一种,已知参加赛跑的有36人,参加跳绳的有38人。问两项比赛都参加的有几人?
例5.某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,请你算出全班人数。
短跑
投掷
跳远
短跑、跳远
短跑、投掷
六年级奥数题及答案:容斥原理问题(高等难度)题型归纳

六年级奥数题及答案:容斥原理问题(高等难度)题型归纳容斥原理问题:(高等难度)
在多元智能大赛的决赛中只有三道题.已知:(1)某校25名学生参加竞赛,每个
学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是
解出第三题的人数的2倍:(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题,那么只解出第二题的学生人数是
容斥原理问题答案:
根据每个人至少答出三题中的一道题可知答题情况分为7类:只答第1题,只答第2题,只答第3题,只答第1、2题,只答第1、3题,只答2、3题,答1、2、3题。
分别设各类的人数为a1、a2、a3、a12、a13、a23、a123
由(1)知:a1+a2+a3+a12+a13+a23+a123=25①
由(2)知:a2+a23=(a3+ a23)2②
由(3)知:a12+a13+a123=a1-1③
由(4)知:a1=a2+a3④
再由②得a23=a2-a32⑤
再由③④得a12+a13+a123=a2+a3-1⑥
然后将④⑤⑥代入①中,整理得到
a24+a3=26
由于a2、a3均表示人数,可以求出它们的整数解:
当a2=6、5、4、3、2、1时,a3=2、6、10、14、18、22
又根据a23=a2-a32⑤可知:a2a3
因此,符合条件的只有a2=6,a3=2。
然后可以推出a1=8,a12+a13+a123=7,a23=2,总人数=8+6+2+7+2=25,检验所有条件均符。
故只解出第二题的学生人数a2=6人。
小学奥数之容斥原理

容斥原理(一)【例题分析】例1. 有长8厘米,宽6厘米的长方形与边长5厘米的正方形。
如图放在桌面上,求这两个图形盖住桌面的面积?分析与解:阴影部分是直角三角形,是两个图形的重叠部分,它的面积是:(平方厘米)方法一:(平方厘米)方法二:(平方厘米)方法三:(平方厘米)答:盖住桌面的面积是67平方厘米。
例2. 六一班参加无线电小组和航模小组的共26人,其中参加无线电小组的有17人,参加航模小组的有14人,两组都参加的有多少人?分析与解:把17人和14人相加,是把两组都参加的人算了两次,所以减去总人数,就是两组都参加的人数(人)。
也可以这样解:(人)或(人)答:两组都参加的有5人。
例3。
六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?分析与解:先求出46人中会骑车或会游泳的有多少人,从中减去会骑车或会游泳的人数,剩下的就是既不会骑车也不会游泳的人数。
(人)(人)答:既不会骑车又不会游泳的有9人。
例4. 某年级的课外小组分为美术、音乐、手工三个小组,参加美术小组有20人,参加音乐小组有24人,参加手工小组有31人,同时参加美术和音乐两个小组有5人,同时参加音乐和手工两个小组有6人,同时参加美术和手工两个小组的有7人,三个小组都参加的有3人,这个年级参加课外小组的同学共有多少人?分析与解:图中的5、6、7人都是两两重叠的部分,图中的3人是三个重叠的部分,要从三个组的总人数中减去重复多余的部分.(人)答:这个年级参加课外小组的有60人。
例5。
某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,请你算出全班人数.短跑投掷跳远跑跳跑投跳投三项19 21 20 9 10 6 3分析与解:根据题意画出如下图要求全班有多少人,先要求出跑、跳、投至少有一项达到优秀的人数,加上三项都未达到优秀的,就是全班人数。
容斥原理奥数原题

容斥原理在计数时,为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
容斥原理(1)如果被计数的事物有A、B两类,那么,A类或B类元素个数= A类元素个数+B类元素个数—既是A类又是B类的元素个数。
例1一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类或B类元素个数”的总和。
试一试:某班学生每人家里至少有空调和电脑两种电器中的一种,已知家中有空调的有41人,有电脑的有34人,二者都有的有27人,这个班有学生多少人?(并说一说你的想法。
)容斥原理(2)如果被计数的事物有A、B、C三类,那么,A类或B类或C类元素个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数1、某艺术团的小演奏家们每人都至少会演奏小提琴和钢琴中的一种。
他们中有32人会拉小提琴,27人会弹钢琴,小提琴和钢琴都能演奏的有11人。
这个团共有多少个小演奏家?2、一个班有学生42人,参加体育队的有30人,参加文艺队的有25人,并且全班每人至少参加一个队。
问:这个班两队都参加的有多少人?3、京华小学五年级学生采集标本。
采集昆虫标本的有25人,采集植物标本的有19人,两种标本都采集的有8人。
全班学生共有40人,没有采集标本的有多少人?4、有100位旅客,其中有10人既不懂英语又不懂日语,有75人懂英语,83人懂日语。
小学奥数 容斥原理 知识点+例题+练习 (分类全面)
5、在1到130的全部自然数中,既不是6的倍数又不是5的倍数的数有多少个?不是6的倍数或不是5的倍数的数有几个?
6、某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。问两科都在90分以上的有多少人?
巩固:刘老师、夏老师和胡老师共有书90本,其中刘老师和夏老师一共有70本,夏老师和胡老师共有50本,三位老师各有书多少本?
例5、在1至10000中不能被5或7整除的数共有多少个?既不能被5整除又不能被7整除的有多少个?
巩固:在1到200的全部自然数中,既不是5的倍数又不是8的倍数的数有多少个?不是5的倍数或不是8的倍数的数有几个?
巩固:某校的每个学生至少爱好体育和文娱中的一种活动,已知有900人爱好体育活动,有850人爱好文娱活动,其中260人两种活动都爱好。这个学校共有学生多少人?
例3、学校开展课外活动,共有250人参加。其中参加象棋组和乒乓球组的同学不同时活动,参加象棋组的有83人,参加乒乓球组的有86人,这两个小组都参加的有25人。问这250名同学中,象棋组、乒乓球组都不参加的有多少人?
课后作业
1、五年级有112人参加语文、数学考试,每人至少有一门功课得优,其中,语文得优的有65人,数学得优的有87人,问语文、数学都得优的有多少人?
2、某班在一次测验中有26人语文获优,有30人数学获优,其中语、数双优的有12人,另外还有8人语、数均未获优,这个班共有多少个学生?
3、五(1)班有学生50人,在一次测试中,语文90分以上的有30人,数学90分以上的35人,语文和数学都在90分以上的有20人,90分以下的有多少人?
奥数训练专题——容斥原理

容斥原理1、某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?2、某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?3、四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.(6级)4、五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.(6级)5、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?(6级)6、新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有多少人?7、五年级三班有46名学生参加三项课外活动,其中24人参加了绘画小组,20人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍,又是三项活动都参加人数的7倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗诵小组的人数.8、六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?9、在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:三种都带了的有几人?只带了一种的有几个?9、盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.10、全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动项目没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.若全班有6个人数学不及格,那么,数学成绩优秀的有几个学生?有几个人既会游泳,又会滑冰?11、在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓;11个人摘了山莓和李子但没有摘草莓;总共有60人摘了李子.如果参与采摘水果的总人数是100,你能回答下列问题吗?①有人摘了山莓;②有人同时摘了三种水果;③有人只摘了山莓;④有人摘了李子和草莓,而没有摘山莓;⑤有人只摘了草莓.12、五年级一班共有36人,每人参加一个兴趣小组,共有A 、B 、C 、D 、E 五个小组,若参加A 组的有15人,参加B 组的人数仅次于A 组,参加C 组、D 组的人数相同,参加E 组的人数最少,只有4人.那么,参加B 组的有多少人?13、五一班有28位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是3个小组全参加的人数的5倍,并且知道3个小组全参加的人数是一个不为0的偶数,那么仅参加数学和语文小组的人有多少人?14、某学校派出若干名学生参加体育竞技比赛,比赛一共只有三个项目,已知参加长跑、跳高、标枪三个项目的人数分别为10、15、20人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛项目,求这所学校一共派出多少人参加比赛?图形中的重叠问题1、 把长38厘米和53厘米的两根铁条焊接成一根铁条.已知焊接部分长4厘米,焊接后这根铁条有多长?2、把长23厘米和37厘米的两根铁条焊接成一根铁条.已知焊接部分长3厘米,焊接后这根铁条有多长?3、两张长4厘米,宽2厘米的长方形纸摆放成如图所示形状.把它放在桌面上,覆盖面积有多少平方厘米?4、 如图,一张长8厘米,宽6厘米,另一个正方形边长为6厘米,它们中间重叠的部分是一个边长为4厘米的正方形,求这个组合图形的面积.图32厘米4厘米图35、一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积.6、三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?7、如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?8、如图所示,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38.若A 与B 、B 与C 的公共部分的面积分别为8、7,A 、B 、C 这三张纸片的公共部分为3.求A 与C 公共部分的面积是多少?容斥原理在数论问题中的应用1、 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?2、 在自然数1100~中,能被3或5中任一个整除的数有多少个?3、 在前100个自然数中,能被2或3整除的数有多少个?4、 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?CB A105、求在1至100的自然数中能被3或7整除的数的个数.5、以105为分母的最简真分数共有多少个?它们的和为多少?7、分母是385的最简真分数有多少个?并求这些真分数的和.8、在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有个.9、在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?10、50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?11、有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3, (2000)然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?12、写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?13、在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规则如下:(1)标签号为2的倍数,奖2支铅笔;(2)标签号为3的倍数,奖3支铅笔;(3)标签号既是2的倍数,又是3的倍数可重复领奖;(4)其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支?14、在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,则木棍总共被锯成________段.15、一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.16、一根1.8米长的木棍,从左端开始每隔2厘米画一个刻度,涂完后再从左端开始每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?容斥原理中的最值问题1、将1~13这13个数字分别填入如图所示的由四个大小相同的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?2、如图,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个?3、某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?4、某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.5、60人中有23的人会打乒乓球,34的人会打羽毛球,45的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?6、图书室有100本书,借阅图书者需在图书上签名.已知这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?7、甲、乙、丙都在读同-一本故事书,书中有100个故事.每个人都从某一个故事开始,按顺序往后读.已知甲读了75个故事,乙读了60个故事,丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个?8、在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,已知甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?恰好被1个人浇过的花最多有多少盆?9、甲、乙、丙同时给100盆花浇水.已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?。
奥数训练专题——容斥原理

容斥原理1、某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?2、某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9 人既爱打篮球又爱踢足球, 4 人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?3、四年级一班有46名学生参加3 项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3 项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍,既参加数学小组又参加语文小组的有10 人.求参加文艺小组的人数.( 6 级)4、五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25 人参加自然兴趣小组,35 人参加美术兴趣小组,27 人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12 人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9 人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.( 6 级)5、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42 人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?( 6 级)6、新年联欢会上,共有90 人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7 人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多 4 人;50 人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40 人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有多少人?7、五年级三班有46名学生参加三项课外活动,其中24 人参加了绘画小组,20 人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的倍,又是三项活动都参加人数的7倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗诵小组的人数.8、六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?9、在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡, 6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:三种都带了的有几人?只带了一种的有几个?9、盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.10、全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动项目没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.若全班有6个人数学不及格,那么,数学成绩优秀的有几个学生?有几个人既会游泳,又会滑冰?11、在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓; 11个人摘了山莓和李子但没有摘草莓;总共有60人摘了李子.如果参与采摘水果的总人数是100,你能回答下列问题吗?①有 _____ 人摘了山莓;②有______ 人同时摘了三种水果;③ 有 ____ 人只摘了山莓;④ 有_____ 人摘了李子和草莓,而没有摘山莓;⑤有 _____ 人只摘了草莓• 12、五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,若参加A组的有15人,参加B组的人数仅次于A组,参加C组、D组的人数相同,参加E组的人数最少,只有4人.那么,参加 B 组的有多少人?13、五一班有28 位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6 个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是 3 个小组全参加的人数的 5 倍,并且知道 3 个小组全参加的人数是一个不为0 的偶数,那么仅参加数学和语文小组的人有多少人?14、某学校派出若干名学生参加体育竞技比赛,比赛一共只有三个项目,已知参加长跑、跳高、标枪三个项目的人数分别为10、15、20 人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛项目,求这所学校一共派出多少人参加比赛?图形中的重叠问题1、把长38厘米和53厘米的两根铁条焊接成一根铁条.已知焊接部分长4厘米,焊接后这根铁条有多长?2、把长23厘米和37厘米的两根铁条焊接成一根铁条.已知焊接部分长 3 厘米,焊接后这根铁条有多长?3、两张长 4 厘米,宽 2 厘米的长方形纸摆放成如图所示形状.把它放在桌面上,覆盖面积有多少平方厘米?4、如图,一张长8厘米,宽6厘米,另一个正方形边长为 6 厘米,它们中间重叠的部分是一个边长为 4 厘米的正方形,求这个组合图形的面积.5、一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长 4 厘米的正方形,求这个组合图形的面积.6、三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?7、如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60 平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?8、如图所示,A、B、C分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38 •若A与B、B与C的公共部分的面积分别为8、7 , A、B、C这三张纸片的公共部分为3 •求A与C公共部分的面积是多少?容斥原理在数论问题中的应用1、在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?2、在自然数1~100中,能被3或5中任一个整除的数有多少个?3、在前100个自然数中,能被2或3整除的数有多少个?4、在从1 至1000的自然数中,既不能被 5 除尽,又不能被7除尽的数有多少个?5、求在1至100的自然数中能被3或7整除的数的个数.5、以105 为分母的最简真分数共有多少个?它们的和为多少?7、分母是385的最简真分数有多少个?并求这些真分数的和8、在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有 ___________ 个.9、在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?10、50名同学面向老师站成一行.老师先让大家从左至右按1, 2, 3,…,49, 50依次报数; 再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?11、有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1, 2, 3,…,2000, 然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?12、写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关, 第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?13、在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规则如下:(1)标签号为2的倍数,奖2支铅笔;(2)标签号为3的倍数,奖3支铅笔;(3)标签号既是2的倍数,又是3的倍数可重复领奖;(4)其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支?14、在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,则木棍总共被锯成_______ .15、一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.16、一根1.8米长的木棍,从左端开始每隔2厘米画一个刻度,涂完后再从左端开始每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?容斥原理中的最值问题1、将1〜13这13个数字分别填入如图所示的由四个大小相同的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?2、如图,5条同样长的线段拼成了一个五角星•如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个?3、某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球•那么,这个班至少有多少学生这三项运动都会?4、某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20 人,每人最多参加两科,那么参加两科的最多有_____________ 人.2 3 45、60人中有3的人会打乒乓球,4的人会打羽毛球,5的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?6、图书室有100 本书,借阅图书者需在图书上签名.已知这100 本书中有甲、乙、丙签名的分别有33,44 和55本,其中同时有甲、乙签名的图书为29 本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36 本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?7、甲、乙、丙都在读同-一本故事书,书中有100 个故事.每个人都从某一个故事开始,按顺序往后读.已知甲读了75个故事,乙读了60 个故事,丙读了52个故事.那么甲、乙、丙 3 人共同读过的故事最少有多少个?8、在阳光明媚的一天下午,甲、乙、丙、丁四人给100 盆花浇水,已知甲浇了30 盆,乙浇了75 盆,丙浇了80 盆,丁浇了90 盆,请问恰好被 3 个人浇过的花最少有多少盆?恰好被 1 个人浇过的花最多有多少盆?9、甲、乙、丙同时给100盆花浇水.已知甲浇了78盆,乙浇了68 盆,丙浇了58盆,那么 3 人都浇过的花最少有多少盆?。
六年级奥数容斥原理

六年级奥数——容斥原理六年级奥数——容斥原理姓名得分1、一个班有45个小学生,统计借课外书的情况:全班学生都借有语文活数学课外书,借语文课外书的有39人,借数学课外书的有32人,语文、数学课外书都借的有多少人?2、六一班有46人,其中会骑自行车的有17人,会游泳的有14人,既会骑自行车又会游泳的4人,问两样都不会的有多少人?3、某区100个外语教师懂英语或俄语,其中懂英语的有75人,既懂英语又懂俄语的20人,那么懂俄语的教师有多少人?4、有长8厘米,宽6厘米的长方形与边长为5厘米的正方形,如图,放在桌面上(阴影是图形的重叠部分),那么这两个图形盖住桌面的面积是多少平方厘米?5、在1~100的自然数中,是5的倍数或是7的倍数的数有几个?6、在1至10000中不能被5或7整除的数有多少个?7、在1至10000之间既不是完全平方数,也不是完全立方数的整数有多少个?8、某班共有30名男生,其中20人参加足球队,已知没有一个人同时参加3个队,且每人至少参加一个队,有6人既参加足球队又参加篮球队,有2人既参加篮球队又参加排球队,那么既参加足球队又参加排球队的有几人?9、分母是385的最简真分数有多少个,并求这些真分数的和?10、在100个学生中,音乐爱好者56,体育爱好者75人,那么既爱好音乐,又爱好体育得最少有几人,最多有几人?11、某校有学生960人,其中有510人订阅“作文报”,有330人订阅“数学报”,有120人订阅“科学爱好者”,全校学生中有270人订阅两种报刊,有58人三种都订,那么学校中没有订阅任何报刊的有几人?12、某门诊部统计某一天挂号的病人,内科150人,外科92人,其中内外两科都求诊的18人,这一天共来了多少个病人?13、在一次运动会中,甲班参加田赛的有15人,参加径赛的有12人,既参加田赛又参加径赛的有7人,没有参加比赛的有21人,那么甲班共有多少人?14、不超过30的正整数中,是3的倍数或4的倍数由多少个?。
六年下册奥数试题-容斥原理一 全国通用含答案

第9讲容斥原理(一)森林中住着很多动物,据说狮子大王派仙鹤去统计鸟类的种数,蝙蝠跑过去对仙鹤说;“我有翅膀,我应该是属于鸟类的。
”于是仙鹤就把蝙蝠统计到鸟类的种类里去了,结果得出森林中一共有80种鸟类。
狮子大王又派大象去统计野兽的种类数,蝙蝠听说又来统计兽类了,急忙跑过去对大象说;“我没有羽毛,我应该是属于兽类的。
”于是大象就把蝙蝠统计到兽类的种类里去了,结果统计出森林中一共有60种兽类。
最后狮子大王问:“森林中共有鸟类和兽类多少种?”狡猾的狐狸听见了仙鹤和大象的统计结果,高兴地向狮子大王汇报:“这还不简单!森林中共有鸟类和兽类140种。
”这个统计正确吗?同学们肯定会说:“不对!蝙蝠被算了两次,应该再减去一,是139种。
”这个故事说明了一个数学问题,那就是被称为“容斥原理”的包含与排除问题。
当需要计数的两类事物互相包含(有部分重复交叉)时,应把重复计数的部分排除掉。
由此我们得到逐步排除法(容斥原理):当两个计数部分有重复时,为了不重复计数,应从它们的和中减去重复部分。
例如:请看下图,在长为30厘米,宽为20厘米的长方形铁板上钻了一个半径为5厘米的圆孔,请问:阴影部分的面积是多少平方厘米?这个图形是一个不规则图形,如果我们直接计算很难,由上图容易看出阴影面积加圆面积恰好等于长方形面积,而长方形面积与圆的面积都很好计算,因而有:阴影面积=20×30-5×5×π=600-25π(平方厘米)。
由此我们得到排除法:两个分量之和等于总量,当计算一个分量时,可用总量减去另一个分量。
即若A+B=C,则A=C-B。
请看下面的例题。
例1 一个班有学生48人,每人至少参加跑步、跳高两项比赛中的一项。
已知参加跑步的有37人,参加跳高的有40人,请问:这两项比赛都参加的学生有多少人?分析:两项比赛都参加的学生人数,就是参加跑步人数、参加跳高人数重复的部分,排除掉重复部分,所得的就是全体参赛人数,也就是全班学生人数。
(完整版)容斥原理习题加答案

1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有( )A、27人B、25人C、19人D、10人【答案】B【解析】直接代入公式为:50=31+40+4-A∩B得A∩B=25,所以答案为B。
2.某服装厂生产出来的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?()A、15B、25C、35D、40【答案】C【解析】这是一种新题型,该种题型直接从求解出发,将所求答案设为A∩B,本题设小号和蓝色分别为两个事件A和B,小号占50%,蓝色占75%,直接代入公式为:100=50+75+10-A∩B,得:A∩B=35。
3.某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。
问接受调查的学生共有多少人?()A.120B.144C.177D.192【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字24,再推其他部分数字:根据每个区域含义应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47-{(x+24)+(z+24)+(y+24)}+24+15=199-{(x+z+y)+24+24+24}+24+15根据上述含义分析得到:x+z+y只属于两集合数之和,也就是该题所讲的只选择两种考试都参加的人数,所以x+z+y的值为46人;得本题答案为120.4.对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人()A.22人B.28人C.30人D.36人【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字12,再推其他部分数字:根据各区域含义及应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数100=58+38+52-{18+16+(12+ x)}+12+0,因为该题中,没有三种都不喜欢的人,所以三集合之外数为0,解方程得到:x=14。
(奥数典型题)容斥原理--2024年六年级下册小升初数学思维拓展含答案

(奥数典型题)容斥原理--2024年六年级下册小升初数学思维拓展容斥原理【知识点归纳】在日常生活中,人们常常需要统计一些数量,在统计的过程中,往往会发现有些数量重复出现,为了使重复出现的部分不致被重复计算,人们研究出一种新的计数方法,既先不考虑重复的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排除出去,使计算的结果既无遗漏又无重复.这种计数方法称为包含排除法,也叫做容斥原理或重叠问题.一般方法:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.容斥原理1:两量重叠问题A类与B类元素个数的总和=A类元素的个数+B类元素个数﹣既是A类又是B类的元素个数用符号可表示成:A∪B=A+B﹣A∩B(其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思,符号“∩”读作“交”,相当于中文“且”的意思).容斥原理2:三量重叠问题A类、B类与C类元素个数的总和=A类元素的个数+B类元素个数+C类元素个数﹣既是A类又是B类的元素个数﹣既是B类又是C类的元素个数﹣既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数.用符号表示为:A∪B∪C=A+B+C﹣A∩B﹣B∩C﹣A∩C+A∩B∩C1.三年级共有80名同学参加书法兴趣小组和美术兴趣小组,其中参加书法组的有52人,参加美术组的有48人.那么,既参加书法组又参加美术组的有多少人?2.我们班参入调查了饭后吃水果情况:30人喜欢吃苹果,27人喜欢吃梨,10人两种都喜欢,问我们班有多少人?3.同学们收集图片.张明、李红、蔡正明、王丹、熊威、高伟、梅芳7个人收集了名山图片,吴凤、李红、王丹、戴月红、高伟这5人收集了河流图片,吴心怡、张冬、李可这3人收集了奥运图片.(1)收集名山图片和奥运图片的共有多少人?(2)收集名山图片和河流图片的共有多少人?4.在校运动会上,共有30人参加跳远和跳高。
参加跳远的有18人,参加跳高的有22人,既参加跳远又参加跳高的有多少人?5.三(1)班有48人,其中订《少年报》的有32人,订《数学报》的有38人,有25人两份报都订。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数题及答案:容斥原理问题(高等难度)_题型归纳
容斥原理问题:(高等难度)
在多元智能大赛的决赛中只有三道题.已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍:(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题,那么只解出第二题的学生人数是
容斥原理问题答案:
根据每个人至少答出三题中的一道题可知答题情况分为7类:只答第1题,只答第2题,只答第3题,只答第1、2题,只答第1、3题,只答2、3题,答1、2、3题。
分别设各类的人数为a1、a2、a3、a12、a13、a23、a123
由(1)知:a1+a2+a3+a12+a13+a23+a123=25①
由(2)知:a2+a23=(a3+ a23)2②
由(3)知:a12+a13+a123=a1-1③
由(4)知:a1=a2+a3④
再由②得a23=a2-a32⑤
再由③④得a12+a13+a123=a2+a3-1⑥
然后将④⑤⑥代入①中,整理得到
a24+a3=26
由于a2、a3均表示人数,可以求出它们的整数解:
当a2=6、5、4、3、2、1时,a3=2、6、10、14、18、22
又根据a23=a2-a32⑤可知:a2a3
因此,符合条件的只有a2=6,a3=2。
然后可以推出a1=8,a12+a13+a123=7,a23=2,总人数=8+6+2+7+2=25,检验所有条件均符。
故只解出第二题的学生人数a2=6人。
