有限元分析报告
有限元分析报告

有限元分析报告
有限元分析是一种工程结构分析的方法,它可以通过数学模型和计算机仿真来
研究结构在受力情况下的应力、应变、位移等物理特性。
本报告将对某桥梁结构进行有限元分析,并对分析结果进行详细的阐述和讨论。
首先,我们对桥梁结构进行了几何建模,包括梁柱节点的建立以及材料属性的
定义。
在建模过程中,我们考虑了桥梁结构的实际工程情况,包括材料的弹性模量、泊松比、密度等参数的输入。
通过有限元软件对桥梁结构进行离散化处理,最终得到了数学模型。
接着,我们对桥梁结构施加了实际工况下的荷载,包括静载、动载等。
通过有
限元分析软件的计算,我们得到了桥梁结构在受力情况下的应力、应变分布,以及节点位移等重要参数。
通过对这些参数的分析,我们可以评估桥梁结构在实际工程情况下的安全性和稳定性。
在分析结果中,我们发现桥梁结构的主要受力部位集中在梁柱节点处,这些地
方的应力、应变值较大。
同时,桥梁结构在受力情况下产生了较大的位移,需要进一步考虑结构的刚度和稳定性。
基于这些分析结果,我们提出了一些改进和加固的建议,以提高桥梁结构的安全性和可靠性。
综合分析来看,有限元分析是一种非常有效的工程结构分析方法,它可以帮助
工程师们更加深入地了解结构在受力情况下的物理特性,为工程设计和施工提供重要的参考依据。
通过本次桥梁结构的有限元分析,我们不仅可以评估结构的安全性,还可以为结构的改进和优化提供重要的参考意见。
总之,有限元分析报告的编制不仅需要对结构进行准确的建模和分析,还需要
对分析结果进行科学的解读和合理的讨论。
只有这样,我们才能为工程结构的设计和施工提供更加可靠的技术支持。
有限元分析实验报告

有限元分析实验报告有限元分析实验报告引言有限元分析是一种广泛应用于工程领域的数值计算方法,它可以通过将复杂的结构划分为许多小的有限元单元,通过计算每个单元的力学特性,来模拟和预测结构的行为。
本实验旨在通过有限元分析方法,对某一结构进行力学性能的分析和评估。
实验目的本实验的目的是通过有限元分析,对某一结构进行应力和变形的分析,了解该结构的强度和稳定性,为结构设计和优化提供参考。
实验原理有限元分析是一种基于弹性力学原理的数值计算方法。
它将结构划分为许多小的有限元单元,每个单元都有自己的力学特性和节点,通过计算每个单元的应力和变形,再将其组合起来得到整个结构的力学行为。
实验步骤1. 建立有限元模型:根据实际结构的几何形状和材料特性,使用有限元软件建立结构的有限元模型。
2. 网格划分:将结构划分为许多小的有限元单元,每个单元都有自己的节点和单元材料特性。
3. 材料参数设置:根据实际材料的力学特性,设置每个单元的材料参数,如弹性模量、泊松比等。
4. 载荷和边界条件设置:根据实际工况,设置结构的载荷和边界条件,如受力方向、大小等。
5. 求解有限元方程:根据有限元方法,求解结构的位移和应力。
6. 结果分析:根据求解结果,分析结构的应力分布、变形情况等。
实验结果与分析通过有限元分析,我们得到了结构的应力和变形情况。
根据分析结果,可以得出以下结论:1. 结构的应力分布:通过色彩图和云图等方式,我们可以清楚地看到结构中各个部位的应力分布情况。
通过对应力分布的分析,我们可以了解结构的强度分布情况,判断结构是否存在应力集中的问题。
2. 结构的变形情况:通过对结构的位移分析,我们可以了解结构在受力下的变形情况。
通过对变形情况的分析,可以判断结构的刚度和稳定性,并为结构的设计和优化提供参考。
实验结论通过有限元分析,我们对某一结构的应力和变形进行了分析和评估。
通过对应力分布和变形情况的分析,我们可以判断结构的强度和稳定性,并为结构的设计和优化提供参考。
有限元分析大作业报告

有限元分析大作业报告一、引言有限元分析是工程领域中常用的数值模拟方法,通过将连续的物理问题离散为有限个子区域,然后利用数学方法求解,最终得到数值解。
有限元分析的快速发展和广泛应用,为工程领域提供了一种强大的工具。
本报告将介绍在大作业中所进行的有限元分析工作及结果。
二、有限元模型建立本次大作业的研究对象是工程结构的应力分析。
首先,通过对结构进行几何建模,确定了结构的尺寸和形状。
然后,将结构离散为有限个单元,每个单元又可以看作一个小的子区域。
接下来,为了求解结构的应力分布,需要为每个单元确定适当的单元类型和单元属性。
最后,根据结构的边界条件,建立整个有限元模型。
三、材料属性和加载条件在建立有限元模型的过程中,需要为材料和加载条件确定适当的参数。
本次大作业中,通过实验获得了结构材料的弹性模量、泊松比等参数,并将其输入到有限元模型中。
对于加载条件,我们选取了其中一种常见的加载方式,并将其施加到有限元模型中。
四、数值计算和结果分析为了求解结构的应力分布,需要进行数值计算。
在本次大作业中,我们选用了一种常见的有限元求解器进行计算。
通过输入模型的几何形状、材料属性和加载条件,求解器可以根据有限元方法进行计算,并得到结构的应力分布。
最后,我们通过对计算结果进行分析,得出了结论。
五、结果讨论和改进方法根据计算结果,我们可以对结构的应力分布进行分析和讨论。
根据分析结果,我们可以得出结论是否满足设计要求以及结构的强度情况。
同时,根据分析结果,我们还可以提出改进方法,针对结构的特点和问题进行相应的优化设计。
六、结论通过对工程结构进行有限元分析,我们得到了结构的应力分布,并根据分析结果进行了讨论和改进方法的提出。
有限元分析为工程领域提供了一种有效的数值模拟方法,可以帮助工程师进行结构设计和分析工作,提高设计效率和设计质量。
【1】XXX,XXXX。
【2】XXX,XXXX。
以上是本次大作业的有限元分析报告,总结了在建立有限元模型、确定材料属性和加载条件、数值计算和结果分析等方面的工作,并对计算结果进行讨论和改进方法的提出。
有限元分析试验报告

有限元分析试验报告
一、试验目的
本次试验的目的是采用有限元分析方法对某零部件进行应力分析,为零部件的优化和设计提供参考。
二、试验原理
有限元分析是采用数学方法对工程结构进行分析,以预测其在外载作用下的变形和应力,从而确定结构的强度和刚度。
分析时将结构划分为有限数量的小单元,利用元件所具有的基本物理特性和相应的数学方程式,计算出每个单元或整个结构的位移、变形、应力等基本的力学量。
三、试验步骤
1.了解零部件的结构和使用环境,建立有限元模型。
2.导入有限元软件,对建立的有限元模型进行网格划分。
3.分配材料性质和加载条件。
4.运行分析,得出计算结果。
5.对计算结果进行分析和评估,对零部件的设计进行改进。
四、试验结果
通过有限元分析,我们得出了零部件在不同工况下的应力云图和变形云图,可以清晰地看到零部件的应力集中区域和变形程度。
同时,我们对零部件的设计进行了改进,使其在承受外力时具有更好的强度和刚度。
五、结论
通过这次试验,我们了解了有限元分析在工程设计中的应用,掌握了分析流程和技术方法。
在实际工程设计中,有限元分析是一种非常重要的工具,有助于提高设计质量和降低成本,值得工程师们广泛运用。
有限元分析报告

有限元分析报告简介:有限元分析是一种应用数学方法,用于工程设计和计算机模拟中的结构力学问题。
它将一个复杂的结构分割成许多小单元,通过数学计算方法求解每个小单元中的力学问题,最终得出整个结构的应力、变形等力学特性。
本报告将针对一座建筑结构进行有限元分析,以提供对该结构的性能和稳定性的评估。
1. 建筑结构的几何模型我们首先根据给定的建筑结构图纸,利用计算机辅助设计软件建立了该建筑结构的几何模型。
模型中包括建筑的各个构件、连接方式以及相关的材料参数。
通过这个模型,我们可以直观地了解到该建筑的整体结构和外形。
2. 材料特性和边界条件接下来,我们对建筑结构中所使用的材料进行了详细调查和测试,获得了相关的材料参数。
这些参数包括了材料的弹性模量、泊松比等力学特性。
同时,我们还确定了建筑结构的边界条件,即建筑结构与外界的固定连接方式。
3. 网格划分和单元选择为了进行有限元分析,我们将建筑结构模型划分成了许多小单元。
在划分时,我们考虑了结构的复杂性、力学特性的分布以及计算资源的限制。
同时,我们还选取了合适的单元类型,包括线单元、面单元和体单元,以确保对结构的各个方向都进行了准确的力学计算。
4. 边界条件和加载在有限元分析中,我们需要给定结构的边界条件和加载情况。
边界条件包括固定支撑和约束,加载则体现了外界对结构的作用力。
这些边界条件和加载方式都是根据实际情况进行的设定,并参考了相关的设计标准和规范。
5. 结果分析通过对建筑结构进行有限元分析,我们得到了结构中各个单元的应力、变形以及稳定性等力学特性。
这些结果可以用来评估结构的性能和安全性。
我们进行了详细的结果分析,并对结果进行了图表化和可视化展示,以方便用户理解和判断。
6. 结论和建议根据有限元分析的结果,我们对建筑结构的性能和稳定性进行了综合评估。
我们发现该结构在设计要求的荷载条件下能够满足安全性要求,具有较好的稳定性和刚度。
然而,我们也发现了一些潜在的问题和改进空间,例如某些结构部位的应力集中以及某些节点处的变形过大。
某法兰盘有限元分析报告

法兰盘有限元分析报告姓名:学号:学院:机械学院法兰盘有限元分析报告一,总述本报告依托于。
,针对一个法兰盘,运用Hypermesh9.0进行有限元分析前处理,并用软件自带的RADIOSS求解器进行求解分析确定法兰盘的设计尺寸。
二,研究背景某自卸车转向节设计:转向节的结构形式如下图所示:本报告针对的是上图标号为10转向节的法兰盘进行设计。
充分考虑到自卸车的工况,进行力学分析,得出此法兰盘的应力分布情况,进而确定此法兰盘的结构及尺寸(主要是法兰的厚度设计)。
具体做法是:首先通过UG建模,然后导入Hypermesh9.0进行画网格,并用RADIOSS 进行求解应力分布,获取完全满足材料的屈服极限及疲劳强度的结构。
最终结构及设计尺寸如下模型所示,分析证明这种结构完全满足了自卸车转向节的力学性能且材料经济性。
三,模型的建立1,UG建模法兰盘的厚度是本报告最主要的设计尺寸。
根据经验和同型号其他车型的设计尺寸,初取法兰盘厚度为30mm,在UG中建模如下图所示。
2,画网格将上述UG模型导入到Hypermesh9.0中进行有限元分析前处理,选用五面体和六面体实体网格,画网格后如下图所示3,设置材料参数定义材料属性:弹性模量E=2.1×105 Mpa,泊松比μ=0.3,设置对话框如下图所示4,施加载荷与约束根据法兰盘的受力情况:受到周向力矩,将其装化成沿周向的切向力,故在8个安装孔中心处施加8个大小相等的周向力153KN;在安装面φ400mm上被压紧,没有位移,故在φ400mm上添加约束。
加载后如下图所示:三,计算结果使用RADIOSS求解器求解法兰盘的应力与应变云图如下图所示:应变云图应力云图附,计算结果运行时间四,计算结果分析根据计算结果对比厚度为30mm ,25mm ,20mm 三种情况的应力与应变分布情况,综合考虑力学性能和经济性,选择厚度尺寸为25mm 。
根据上表可知,厚度为25mm 时,最大变形量为0.05mm ,最大应力为98.47MPa 。
有限元研究报告

有限元研究报告有限元研究报告有限元分析是一种通过数值方法求解工程问题的方法,广泛应用于结构力学、热力学、流体力学等领域。
本文将介绍有限元分析在结构力学领域的研究成果。
首先,我们介绍了有限元分析的基本原理。
有限元分析将结构分割成有限个小单元,利用数值计算方法,求解每个小单元的位移场和应力场,将所有小单元的位移场和应力场组合起来,得到整个结构的位移场和应力场。
有限元分析可以用于解决复杂结构的应力、应变、位移等问题,并可以预测结构在外部荷载作用下的变形和破坏情况。
然后,我们介绍了有限元分析在结构优化设计中的应用。
通过有限元分析,可以评估和优化结构的性能。
我们可以改变结构的几何形状、材料性质和边界条件等参数,通过有限元分析计算不同参数下的结构响应,然后根据设计需求进行优化。
有限元分析在结构优化设计中可以提供较为准确的结果,并能够快速地评估不同设计方案的性能。
接着,我们介绍了有限元分析在结构异常行为分析中的应用。
通过有限元分析,可以模拟和预测结构在不同异常工况下的行为。
例如,我们可以模拟结构在地震、爆炸等异常荷载下的响应,分析结构的稳定性和安全性。
有限元分析在结构异常行为分析中可以提供关键的技术支持,帮助工程师预测和避免结构的异常破坏。
最后,我们介绍了有限元分析在结构动力响应分析中的应用。
通过有限元分析,可以模拟和预测结构在不同动力荷载下的响应。
例如,我们可以模拟桥梁在车辆行驶时的振动响应,分析结构的动力特性和振动响应。
有限元分析在结构动力响应分析中可以提供重要的技术支持,帮助工程师优化结构设计,提高结构的动力性能。
综上所述,有限元分析在结构力学领域有着广泛的应用。
通过有限元分析,我们可以解决复杂结构的应力、应变、位移等问题,评估和优化结构的性能,模拟和预测结构在不同异常工况和动力荷载下的响应。
有限元分析不仅提供了有效的工具,也为工程师提供了重要的技术支持,帮助工程师更好地设计和分析结构。
有限元分析报告

有限元分析报告是一项重要的工程技术和科学技术的应用。
它通过有限元方法的数学原理和实验的技术手段,对材料的物理特性和工程的技术问题进行了系统和科学的分析和研究,为工程设计和技术改进提供了有效的方法和手段。
本文通过对的基本概念、研究方法和应用实例的分析和探讨,帮助读者更好的理解和其在工程技术和科学技术中的应用。
一. 的基本概念是指通过数值模拟和实验技术手段,对材料的物理特性和工程的技术问题进行分析和研究,形成的综合性数据和报告。
它的基本原理就是通过将大的物理系统分解成为小的有限元结构,再通过计算机仿真技术对每个小的结构进行精确计算,综合分析得到整体物理特性和工程问题的实验数据和报告。
的主要作用是提供工程设计和技术改进的决策依据和参考,对工程质量和性能提升具有重要意义。
二. 的研究方法是一项基于数学和实验技术的前沿研究。
它的研究方法主要包括以下几个方面:1. 问题定义和模拟:通过对工程问题的定义和分析,建立适当的数学模型和参考数据,制定模拟方案和计算条件。
2. 离散化和剖分:将大的物理系统离散化成为小的有限元结构,通过精确的剖分和计算,获得每个小结构的物理特性和性能数据。
3. 计算仿真和验证:将累积的数据和模型进行计算仿真和验证,提取重要特征和关联特性,并结合实验数据和模型检验结果。
4. 报告撰写和解读:将仿真数据和实验数据进行综合分析和整理,撰写完整的,并解读和解释其中的重要数据和结论。
三. 的应用实例在工程技术和科学技术中有着广泛的应用。
以下是几个实际案例:1. 材料模拟和分析:通过,对材料的强度和硬度等物理特性进行模拟和分析,提高材料性能和品质。
2. 工程设计和优化:通过,对工程问题进行模拟和分析,提供有关工程设计和改进的决策依据和参考。
3. 故障分析和预测:通过,对工程设备和材料的故障进行分析和预测,提高设备性能和使用寿命。
4. 新技术和新产品的研究和开发:通过,对新技术和新产品进行模拟和研究,提高产品质量和竞争力。
有限元分析实验报告

有限元分析实验报告引言有限元分析是一种工程设计和分析的常用方法。
它通过将结构或物体分割为有限数量的单元,利用数值方法计算每个单元的行为,最终得出整体结构的行为。
本实验使用有限元分析方法来研究一个特定的结构或物体。
实验目的本实验的目的是使用有限元分析方法研究一个给定的结构或物体。
通过实验,我们将探索结构的强度、刚度和变形等性能,评估其设计的合理性,并提出改进的建议。
实验步骤实验的步骤如下:1.准备工作:收集和整理所需的材料和数据,包括结构的几何形状、材料特性和加载条件等。
确保所收集的数据准确无误。
2.建立有限元模型:将结构的几何形状转化为有限元模型。
根据结构的复杂程度和要求,选择合适的单元类型和网格密度。
使用有限元软件,如ANSYS、ABAQUS等,建立有限元模型。
3.定义边界条件:根据实际应用场景,定义结构的边界条件。
这些条件包括约束边界条件和加载边界条件。
约束边界条件用于限制结构的自由度,加载边界条件用于施加外部载荷。
4.分析结构的行为:使用有限元软件进行结构的强度、刚度和变形等分析。
根据加载和边界条件,计算结构在不同工况下的应力、位移和应变等结果。
5.结果分析和讨论:评估结构的性能,比较不同工况下的结果,分析结构的弱点和改进的空间。
提出改进的建议,并讨论其可能的影响和成本。
6.撰写实验报告:根据实验结果和讨论,撰写实验报告。
报告应包括实验目的、方法、结果和讨论等部分。
确保报告的结构清晰,表达准确。
结果与讨论根据实验的结果和讨论,我们得出以下结论:1.结构的强度:分析结果显示,结构在给定的加载条件下具有足够的强度,能够承受预期的载荷。
然而,在某些关键部位,应力集中现象可能会导致局部的应力超过材料的极限强度。
2.结构的刚度:结构的刚度是指结构在受力下的变形情况。
分析结果显示,结构在加载后会发生一定的变形,但变形量较小,不会对结构的正常功能产生明显的影响。
3.结构的优化:根据分析结果和讨论,我们提出了改进结构的建议。
有限元分析报告

有限元分析报告1. 引言有限元分析(Finite Element Analysis)是一种数值计算方法,用于求解工程和科学领域中的复杂问题。
它利用离散化技术将连续问题转化为离散问题,并应用数值算法进行求解。
本报告将主要介绍有限元分析的基本原理、应用和分析结果。
2. 有限元分析基本原理有限元分析的基本原理是将求解区域划分为互不重叠的有限个小单元,并将问题转化为在每个小单元内求解。
这些小单元通常为简单的几何形状,如三角形或四边形。
然后,在每个小单元内应用适当的数学模型和力学方程,得到相应的微分方程。
接着,通过对每个小单元的微分方程进行积分,并利用边界条件和连续性条件,得到整个求解区域的离散形式。
最后,通过求解离散形式的方程组,得到整个系统的解。
3. 有限元分析应用有限元分析在工程领域有着广泛的应用。
以下是几个典型的应用案例:3.1 结构分析有限元分析在结构分析中的应用非常广泛,可以用于确定结构的强度和刚度,评估结构的安全性,并进行结构优化设计。
通过对结构施加正确的边界条件和加载条件,可以得到结构的应力、应变和变形等重要信息。
3.2 流体力学分析有限元分析在流体力学分析中的应用可以用于模拟流体的流动和传热过程,例如气体和液体的流动、传热设备的设计优化等。
通过分析流体系统的流速、压力和温度等参数,可以对流体系统的性能和行为进行合理评估。
3.3 热力学分析有限元分析在热力学分析中的应用可以用于分析和优化热传导、热辐射和热对流等热问题。
通过模拟物体的温度分布和热流动,可以评估物体的热性能和热耗散效果。
4. 有限元分析结果有限元分析的计算结果可以提供丰富的信息,帮助工程师和科学家理解和优化系统的行为和性能。
以下是一些常见的有限元分析结果:4.1 应力分布通过有限元分析,可以得到结构或部件内的应力分布情况。
这对于评估结构的强度和安全性非常重要,并可以指导优化设计。
4.2 变形分析有限元分析可以给出结构或部件的变形情况。
北科大研究生有限元作业 分析报告
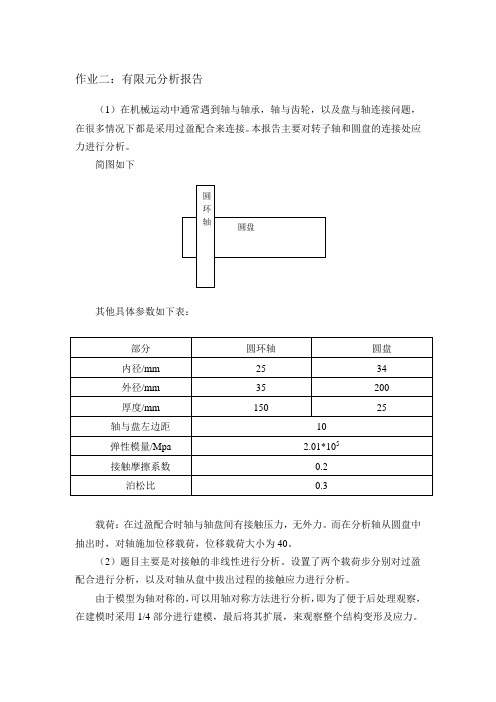
作业二:有限元分析报告(1)在机械运动中通常遇到轴与轴承,轴与齿轮,以及盘与轴连接问题,在很多情况下都是采用过盈配合来连接。
本报告主要对转子轴和圆盘的连接处应力进行分析。
简图如下其他具体参数如下表:部分 圆环轴 圆盘 内径/mm 25 34 外径/mm 35 200 厚度/mm 15025轴与盘左边距 10 弹性模量/Mpa 2.01*105 接触摩擦系数 0.2 泊松比0.3载荷:在过盈配合时轴与轴盘间有接触压力,无外力。
而在分析轴从圆盘中抽出时,对轴施加位移载荷,位移载荷大小为40。
(2)题目主要是对接触的非线性进行分析。
设置了两个载荷步分别对过盈配合进行分析,以及对轴从盘中拔出过程的接触应力进行分析。
由于模型为轴对称的,可以用轴对称方法进行分析,即为了便于后处理观察,在建模时采用1/4部分进行建模,最后将其扩展,来观察整个结构变形及应力。
圆盘圆环轴本题主要分析接触处应力,在建模时不考虑倒角与圆角,这样便于计算与划分网格。
(3)几何模型的建立。
考虑到模型为轴对称问题,在建模时不需要把整个模型都建立出来,只需要建立模型的1/4,在分析完后再映射为整个模型。
报告中模型数据已给出。
在ANSYS中通过前处理模块建模功能创建圆环实体。
利用Create-V olumes-Cylinder-Partial-Cylinder命令赋予圆盘与圆环轴的参数,先后创建圆盘与圆环轴。
进行等轴测显示Pan Zoom Rotate 中Iso,并将圆环轴移动,使其有正确位置(和圆盘Z方向有位移10)。
最终得到模型图如下。
(4)本题目选用的8节点单元,具体为Structural Solid-Brick 8 node185单元。
因为分析内容属于实体范畴,模型形状规则,简单,可以比较方便的划分为六面体单元,计算量小。
故优先选用8 node185。
(5)两接触固体均为规则的几何平面,进行网格划分时采用的线控方式。
对圆环轴以及圆盘分别对各边线进行等分,具体在size controls下Lines中Set 中进行设置。
有限元分析报告模板

有限元分析报告模板1. 引言本文档旨在提供一份有限元分析报告模板,用于记录和展示有限元分析的结果。
有限元分析是一种常用的数值分析方法,用于解决结构力学和热力学问题。
通过将结构划分为有限个小单元,有限元分析能够近似求解结构的应力、应变和变形等参数。
2. 问题描述在本节中,我们将描述待分析的问题。
详细描述问题的几何形状、边界条件和加载情况等。
例如,我们将以一个简单的悬臂梁为例进行说明。
悬臂梁的几何形状为矩形截面,长度为L,宽度为W,高度为H。
其中,梁的一侧通过固定边界条件固定不动,另一侧施加集中力F。
3. 网格划分在本节中,我们将进行网格划分,将问题的几何形状划分为有限个小单元。
我们可以使用一些专业的有限元分析软件,如ANSYS或Abaqus等,来进行网格划分操作。
针对我们的悬臂梁问题,我们可以将其划分为若干个矩形或三角形单元。
4. 材料性质和边界条件在本节中,我们将描述材料性质和边界条件。
材料性质包括弹性模量、泊松比等,而边界条件包括位移约束、力加载等。
对于悬臂梁问题,我们可以假设材料为均匀的弹性材料,边界条件为一侧固定不动,另一侧施加集中力。
5. 有限元模型的建立在本节中,我们将建立有限元模型,将问题转化为一组代数方程。
有限元模型的建立涉及到单元类型选择、单元数目确定等。
我们可以选择合适的单元类型,如梁单元或壳单元等,根据具体情况确定单元数目。
6. 有限元分析在本节中,我们将进行有限元分析,求解代数方程组,得到结构的应力、应变和变形等结果。
有限元分析可以通过数值方法,如有限差分法或有限差分法等,进行求解。
通过有限元分析,我们可以得到悬臂梁在加载条件下的应力分布、应变分布和位移分布等。
7. 结果讨论在本节中,我们将讨论有限元分析的结果。
我们可以对悬臂梁的应力、应变和位移等结果进行分析和评估。
我们可以考虑不同加载条件下的结果差异,或者与理论计算结果进行比较。
通过结果讨论,我们可以评估结构的安全性和合理性。
ansys有限元分析报告

ANSYS有限元分析报告1. 引言有限元分析(Finite Element Analysis, FEA)是一种常用的工程分析方法,可以用于预测材料和结构在各种工况下的行为和性能。
本报告旨在通过使用ANSYS软件进行有限元分析,对某一具体的工程问题进行模拟和分析,并得出相应的结论和建议。
2. 问题描述本次有限元分析的问题是研究某结构在受载情况下的应力分布和变形情况。
具体而言,我们关注的结构是一个柱形零件,其材料为XXX,尺寸为XXX。
该结构在受到垂直向下的均布载荷时,会发生弯曲变形和应力集中现象。
我们的目标是通过有限元方法对该结构进行分析,预测其应力分布情况,并评估其承载能力。
3. 模型建立我们使用ANSYS软件来建立和分析该结构的有限元模型。
首先,我们将导入该零件的几何数据,然后通过ANSYS的建模工具创建相应的有限元模型。
在建立模型的过程中,我们需要注意几何尺寸、材料特性、约束条件和加载方式等参数的设定,以确保模型的准确性和可靠性。
4. 材料属性和加载条件在进行有限元分析之前,我们需要确定材料的特性和加载条件。
根据提供的信息,我们将采用XXX材料的力学特性进行模拟。
同时,我们假设该结构受到均布载荷的作用,其大小为XXX。
这些参数将在后续的分析中使用。
5. 模型网格划分在进行有限元分析之前,我们需要对模型进行网格划分。
网格的密度和质量将直接影响分析结果的准确性和计算效率。
在本次分析中,我们将采用适当的网格划分策略,以满足准确性和计算效率的要求。
6. 模型分析和结果通过ANSYS软件进行有限元分析后,我们得到了该结构在受载情况下的应力分布和变形情况。
根据分析结果,我们可以观察到应力集中区域和变形程度,并根据材料的特性进行评估。
同时,我们可以通过对加载条件的变化进行分析,预测该结构的承载能力和安全系数。
7. 结论和建议根据有限元分析的结果,我们得出以下结论和建议:•该结构在受均布载荷作用下发生应力集中现象,需要对其进行加强和优化设计。
有限元分析实验报告

有限元分析实验报告1. 引言有限元分析是一种常用的工程分析方法,广泛应用于结构力学、流体力学、热传导等领域。
本报告将介绍一个有限元分析实验的结果和分析。
2. 实验目的本实验的目的是通过有限元分析方法,对某个结构进行应力和位移的计算和分析。
通过实验,我们可以了解有限元分析的基本原理和步骤,并掌握有限元分析软件的使用技巧。
3. 实验方法3.1 建模首先,我们需要将实际结构建模成有限元模型。
在本实验中,我们使用了一种常见的有限元建模软件。
根据实际结构的几何形状和材料性质,我们将结构划分为若干个小单元,并在每个小单元内进行网格划分。
3.2 材料参数在建模过程中,我们需要为每个小单元指定材料参数,如弹性模量、泊松比等。
这些参数将影响最终分析结果。
3.3 加载条件为了模拟实际工况,我们需要为模型施加适当的加载条件。
根据实际情况,可以施加静力加载、动力加载等不同的加载方式。
3.4 分析设置在进行有限元分析之前,我们需要设置一些分析参数,如计算步长、收敛准则等。
这些参数将影响计算结果的准确性和计算速度。
3.5 分析求解完成以上步骤后,我们可以进行有限元分析的求解。
通过求解有限元方程组,我们可以得到结构在加载条件下的应力和位移分布。
4. 实验结果与分析在本实验中,我们得到了结构在加载条件下的应力和位移分布。
通过分析这些结果,我们可以得到以下结论:4.1 应力分布根据实验结果,我们可以观察到结构上不同部位的应力分布情况。
通过比较不同材料参数和加载条件下的应力分布,我们可以评估结构的强度和稳定性。
4.2 位移分布位移是另一个重要的分析指标。
通过观察结构上的位移分布情况,我们可以了解结构在加载条件下的变形情况。
这有助于评估结构的刚度和变形限制。
4.3 敏感性分析在实际工程中,材料参数、加载条件等往往存在一定的不确定性。
通过敏感性分析,我们可以评估结构对这些参数变化的敏感程度,从而为工程设计提供参考。
5. 结论通过本次有限元分析实验,我们了解了有限元分析的基本原理和步骤,掌握了有限元分析软件的使用技巧。
有限元分析报告

有限元分析报告有限元分析(Finite Element Analysis, FEA)是一种工程分析方法,通过对结构进行离散建模,然后对每个离散单元进行力学分析,最终得出整个结构的应力、位移等结果。
本报告将对某桥梁结构进行有限元分析,并对分析结果进行详细说明。
1. 结构建模。
首先,我们对桥梁结构进行了建模。
在建模过程中,我们考虑了桥梁的几何形状、材料属性、边界条件等因素。
通过有限元软件,我们将桥梁结构离散为多个单元,并建立了相应的数学模型。
在建模过程中,我们尽可能地考虑了结构的复杂性,以保证分析结果的准确性。
2. 荷载分析。
在建立了结构模型之后,我们对桥梁施加了不同的荷载,包括静载、动载等。
通过有限元分析,我们得出了桥梁在不同荷载下的应力、位移等结果。
同时,我们还对结构的疲劳寿命进行了评估,以确保结构在使用过程中的安全性。
3. 结果分析。
根据有限元分析的结果,我们对桥梁结构的性能进行了分析。
我们发现,在某些局部区域,结构存在应力集中现象;同时,在某些荷载作用下,结构的位移超出了设计要求。
基于这些分析结果,我们对结构的设计提出了一些改进建议,以提高结构的安全性和稳定性。
4. 结论。
通过有限元分析,我们得出了对桥梁结构设计的一些结论。
我们发现,在当前设计下,结构存在一些潜在的安全隐患,需要进行一定的改进。
同时,我们还对结构的使用寿命进行了评估,提出了一些建议。
通过本次有限元分析,我们对桥梁结构的性能有了更深入的了解,为后续的设计和改进提供了重要参考。
综上所述,本报告通过有限元分析,对某桥梁结构的性能进行了评估,并提出了一些改进建议。
有限元分析作为一种重要的工程分析方法,为工程结构的设计和改进提供了重要的技术支持。
希望本报告能对相关工程技术人员提供一定的参考价值。
【精品】有限元分析报告

【精品】有限元分析报告
1、项目简介
本次做的项目是使用有限元方法,对煤矿采空区瓦斯发生器模型进行分析,分析采空
区内瓦斯分布状况,及煤矿采空区内瓦斯渗透速率变化情况。
2、理论基础
本项目使用的是有限元分析方法,它是一种分析空间中受约束的结构模型状态时采用
的数值分析方法,采用有限元分析技术,可以准确预测煤矿采空区瓦斯发生器模型的状态,包括:内部温度分布及瓦斯渗透速率分布情况。
3、模型建立
模型设计分为三部分:一是基础设计,即钻孔煤矿采空区瓦斯生产器模型分析问题,
同时考虑瓦斯灶及直接流出系统;二是热力学模拟,通过有限元分析模型建立温度场,考
虑不同尺度的热力学效应;三是空气液相交互模拟,使用空气和液相控制理论,对瓦斯在
采空区内渗透特征研究,追踪瓦斯的流动路径和渗透效果。
4、结果分析
本次分析的结果表明采空区内瓦斯渗透既受内部温度的影响,也受水平面位置的影响,受控路径瓦斯渗透有明显变化,最低渗透速率为3.3kg/㎥·h,最高渗透速率为18.1kg/㎥·h,平均渗透速率为8.6kg/㎥·h,结果表明,瓦斯的流动路径具有明显的变化趋势,
但其渗透性能较差。
5、结论
本次利用有限元分析技术,对煤矿采空区内瓦斯分布状况及其渗透性进行了分析,结论:采空区内瓦斯渗透状况受内部温度和水平面位置的影响,受控路径瓦斯渗透性能普遍
较差。
有限元分析报告样本【范本模板】

《有限元分析》报告基本要求:1. 以个人为单位完成有限元分析计算,并将计算结果上交;(不允许出现相同的分析模型,如相同两人均为不及格)2. 以个人为单位撰写计算分析报告;3. 按下列模板格式完成分析报告;4. 计算结果要求提交电子版,报告要求提交电子版和纸质版.(以上文字在报告中可删除)《有限元分析》报告一、问题描述(要求:应结合图对问题进行详细描述,同时应清楚阐述所研究问题的受力状况和约束情况。
图应清楚、明晰,且有必要的尺寸数据。
)一个平面刚架右端固定,在左端施加一个y 方向的-3000N 的力P1,中间施加一个Y 方向的—1000N 的力P2,试以静力来分析,求解各接点的位移.已知组成刚架的各梁除梁长外,其余的几何特性相同。
横截面积:A=0.0072 m² 横截高度:H=0.42m 惯性矩:I=0.0021028m4x 弹性模量:E=2.06x10n/ m²/泊松比:u=0。
3二、数学模型(要求:针对问题描述给出相应的数学模型,应包含示意图,示意图中应有必要的尺寸数据;如进行了简化等处理,此处还应给出文字说明。
)(此图仅为例题)三、有限元建模(具体步骤以自己实际分析过程为主,需截图操作过程)用ANSYS 分析平面刚架1.设定分析模块选择菜单路径:MainMenu—preference 弹出“PRreferences for GUI Filtering”对话框,如图示,在对话框中选取:Structural”,单击[OK]按钮,完成选择。
2.选择单元类型并定义单元的实常数(1)新建单元类型并定(2)定义单元的实常数在"Real Constants for BEAM3”对话框的AREA中输入“0。
0072”在IZZ 中输入“0。
0002108”,在HEIGHT中输入“0。
42”。
其他的3个常数不定义。
单击[OK]按钮,完成选择3.定义材料属性在"Define Material Model Behavier”对话框的”Material Models Available”中,依次双击“Structural→Linear→Elastic→Isotropic”如图在如下图的对话框EX中输入“2.06e11",在PRXY框中输入“0.3",完成材料模型的定义.4建立平面刚架节点和单元(1)生成节点选择菜单路,生成节点于目前坐标系统命令,单击以后弹出如图对话框,在对话框的Node number 中输入“1“接着依序输入第一点XYZ的坐标值”2,0,0,然后单击[APPLY]按钮继续生成第二点,如图接着在对话框的Node number 中输入“2“接着依序输入第一点XYZ的坐标值"6,0,0,然后单击[APPLY]按钮继续生成第三点,如图接着在对话框的Node number 中输入“3“接着依序输入第一点XYZ的坐标值”0,2,0,然后单击[APPLY]按钮继续生成第四点,如图接着在对话框的Node number 中输入“4“接着依序输入第一点XYZ的坐标值”4,2,0,然后单击[APPLY]按钮继续生成第五点,如图接着在对话框的Node number 中输入“5“接着依序输入第一点XYZ的坐标值"8,2,0,然后单击[OK]按钮,完成第五点的生成,系统显示生成的五个点的位置,如图校验所输入的节点坐标的正确与否,可以选择菜单路径:弹出如图所示一个文本窗口,如图,列出了所有的节点及其坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安市新城区某公司科研办公楼结构设计有限元分析报告撰写人:王平班级:工程力学1203学号:*************:***2016年6月15日目录1 工程概况 (2)2 分析依据 (3)3 荷载与计算工况 (4)3.1荷载简化及荷载组合 (4)3.2 边界条件 (4)3.3 工况 (5)4 有限元模型 (5)4.1 基本假定 (5)4.2 力学模型 (6)4.3 主要物理参数取值 (6)4.4单元选取 (7)4.5分网与有限元模型 (8)5 静力分析 (9)5.1模态结果 (9)5.2静力分析结果 (12)5.3 强度校核 (15)6基于ANSYS、PKPM、手算的误差分析 (17)6.1计算原理的不同 (17)6.2 研究对象的复杂性 (18)1 工程概况工程名称:西安市新城区某公司科研办公楼;建筑所在地:西安市;建设规模:总建筑面积约4700m2,主体结构6层,无地下室。
结构总高度22.5m,底层结构高度4.5m,其余层结构高度为3.6m,几何模型图如图1所示;抗震设防烈度:抗震设防烈度为8度,设计基本地震加速度值0.2g,第一组。
场地类别为Ⅱ类,特征周期为0.35s。
周期折减系数为0.75。
建筑设计使用年限:50年。
结构重要性等级:二级。
图1 框架几何模型图2 分析依据框架结构是由梁、板、柱以刚接相连接而成,构成承重体系的结构,即由梁、板、柱组成框架共同抵抗使用过程中出现的水平荷载和竖直荷载。
本设计报告采用ANSYS有限元软件分析。
根据框架结构体系特点,本结构分析主要依据以下国家规范:[1]国家标准:《建筑结构荷载规范》(GB50009-2012).北京:中国建筑工业出版社.2012;[2]国家标准:《建筑抗震设计规范》(GB50011-2010).北京:中国建筑工业出版社.2010;[3]国家标准:《混凝土结构设计规范》(GB50010-2010).北京:中国建筑工业出版社.2010;[4]建筑、勘察等技术文件。
3 荷载与计算工况3.1荷载简化及荷载组合1)恒载:含柱、梁、板自重;2)梁间活载以换算线荷载施加(含墙、门、窗等),如图2所示;33.2 边界条件1)柱底固结;2)板四周与梁固结,如图3所示。
XYZ-9800-7866.67-5933.33-4000-2066.67-133.33318003733.335666.677600JUN 14 201618:35:44 PRES-NORM图3 框架结构板边界示意图3.3 工况工况一:模态分析;工况一:分析结构可变荷载组合Qk Gk S S 4.12.1 下的刚度与强度;(注:由于永久荷载组合与可变荷载组合相比较小,故在此不进行校核)工况二:对结构在水平地震力和恒载组合作用下进行分析。
3.3.1模态分析给模型加约束之后,进行前6阶模态分析。
3.3.2 静力分析在可变荷载效应控制的荷载作用下,对框架进行刚度、强度校核。
4 有限元模型4.1 基本假定1)假设混凝土为线弹性材料;2)钢筋混凝土取整体分析,计钢筋贡献;3)节点假定为刚接,底层柱与基础刚接,楼板与梁四边刚接。
4.2 力学模型1)主要受力构件为柱、梁、板;2)抗侧力构件为柱;3)水平联系构件为框架梁(考虑板的贡献);4)柱为压弯构件,框架梁含弯曲、轴向变形、扭转变形。
4.3 主要物理参数取值表1 主要物理参数楼层混凝土等级弹性模量(N/m2)泊松比板厚(mm)柱(b×h)(mm)横梁(b×h)纵梁(b×h)(mm)次梁(b×h)(mm)边跨梁(b×h)(mm)中跨梁(b×h)(mm)1C303×10100.2 100600×600300×600 300×400 300×600 250×5002~5500×5006 120查阅相关资料得:钢筋混凝土有限元模型根据钢筋的处理方式主要分为三种,即分离式、组合式、整体式。
分离式模型把钢筋和混凝土作为不同的单元处理,即混凝土和钢筋各自被划分为足够小的单元。
考虑到钢筋是一细长材料,通常可以忽略其抗剪,一般钢筋可作为线单元来处理。
混凝土则作为实体单元来处理。
分离式模型中在钢筋和混凝土之间可以插入连接单元来模拟钢筋与混凝土的粘结和滑移。
当钢筋和混凝土粘结较好,可以认为两者无滑移时,采用组合式模型。
组合式模型中最常用两种方式第一种是分层式,即在横截面上分成许多混凝土层和若干钢筋层,并对截面的应变做出某些假定,主要适用于杆件系统的分层组合式;另一种组合方式是采用等参数单元,使用带钢筋膜的单元来进行模拟,主要适用于二维或三维结构的带膜组合式或带钢筋的组合式。
整体式模型也是在考虑钢筋与混凝土之间无滑移的情况下使用的。
假定钢筋弥散于整个单元中,并把单元视为连续均匀材料,由此求出的是综合了混凝土与钢筋两种材料的单元刚度矩阵。
在ANSYS中可以考虑的钢筋混凝土模型一般是两种,即分离式模型和整体式模型。
分离式模型虽然在理论上可行,但在进行复杂结构的分析时,对计算机的性能要求较高,计算效率较低。
因此本文空间结构计算模型采用的是整体式有限单元模型来处理钢筋混凝土结构。
4.4单元选取4.4.1 梁、柱单元的选取梁、柱采用空间Timoshenko单元,拟合其弯曲、拉压及扭转受力状态。
Beam 188是一个二节点的三维线性梁, 适用于分析细长的梁, 其元素是基于Timoshenko 梁理论的,具有扭切变形效果。
Beam 188 在每个节点上有6或7个自由度,(自由度)数目的变化是由KEYOPT(1)来控制的。
当KEYOPT(1) = 0时(默认), 每节点有6个自由度。
分别是沿x,y,z的位移及绕其的转动。
当KEYOPT(1) = 1时,会添加第七个自由度(翘曲量) ,Beam 188单元示意图如图4所示。
图4 Timoshenko梁单元示意图4.4.2 板单元的选取板采用弹性壳单元。
Shell 181适用于薄到中等厚度的壳结构。
该单元有四个节点,单元每个节点有六个自由度,分别为沿节点X,Y,Z方向的平动及绕节点X,Y,Z轴的转动。
退化的三角形选项用于网格生成的过渡单元。
Shell 181单元具有应力刚化及大变形功能。
该单元有强大的非线性功能,并有截面数据定义,分析,可视化等功能,还能定义复合材料多层壳;Shell 181单元示意图如图5所示。
图5 弹性壳单元示意图4.5分网与有限元模型4.5.1 建模思路经查阅ANSYS相关书籍得知Beam188 单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木新科梁结构理论,并考虑了剪切变形的影响。
有大量研究也表明该单元可以很好的模拟型钢梁与柱,计算结果与实际比较接近,那是因为钢材的材质比较均匀。
但框架混凝土梁与柱材质并不均匀,混凝土内部含各种钢筋,故采用整体式模型,并把单元视为连续均匀材料,那么Beam188便可以很好的模拟框架混凝土梁与柱了。
Shell 181适用于薄到中等厚度的壳结构.该单元有四个节点,单元每个节点有六个自由度,分别为沿节点X,Y,Z方向的平动及绕节点X,Y,Z轴的转动。
在此处刚好可以模拟板结构。
综上所述,得出以下建模思路:用Beam188、Shell181单元建立空间框架结构模型,与PKPM计算结果进行比较;4.5.2 分网对梁和柱均设置为按份数进行划分,份数取为20;对板进行划分时,考虑到板的边界与梁重合,故分网大小与梁相同,有限元模型图如图4所示。
图6 有限元模型图5 静力分析5.1模态结果对框架结构进行模态分析,提取前六阶振型图,并统计前六阶的频率,周期和振型特点。
表2 ANSYS分析结构动力参数阶数周期(s) 频率(Hz)振幅特点1 0.812 1.2309 平动,横向2 0.756 1.3219 平动,纵向3 0.712 1.4046 扭转4 0.260 3.8421 平动,横向5 0.244 4.0930 平动,纵向6 0.229 4.3756 扭转表3 PKPM计算结构动力参数阶数周期(s) 频率(Hz)振幅特点1 0.905 1.1045 平动,横向2 0.851 1.1758 扭转3 0.842 1.1884 平动,纵向4 0.295 3.3944 平动,横向5 0.277 3.6088 平动,扭转6 0.276 3.6271 平动,扭转对表2及表3的数据进行分析可知,对于PKPM计算结果,结构在二阶模态时发生扭转变形;对于ANSYS计算结果,结构在三阶模态时出现扭转变形。
ANSYS计算各阶模态位移图如图8~13所示。
图7 第一阶振形图8 第二阶振形MNMXXYZ.131E-03.261E-03.392E-03.522E-03 .653E-03 .783E-03 .914E-03 .001045.001175NODAL SOLUTIONSTEP=1 SUB =1FREQ=1.2309USUM (AVG)RSYS=0DMX =.001175 SMX =.001175MNMXXYZ.928E-04.186E-03.278E-03.371E-03.464E-03.557E-03.649E-03.742E-03.835E-03NODAL SOLUTIONSTEP=1 SUB =2FREQ=1.32186USUM (AVG) RSYS=0DMX =.835E-03 SMX =.835E-03图9 第三阶振形图10 第四阶振形MNMXXYZ.162E-03.324E-03.486E-03.648E-03.811E-03.973E-03.001135.001297.001459NODAL SOLUTIONSTEP=1 SUB =3FREQ=1.40461 USUM (AVG)RSYS=0DMX =.001459 SMX =.001459MNMXXYZ.124E-03.248E-03.372E-03.496E-03.620E-03.744E-03.868E-03.992E-03.001116NODAL SOLUTIONSTEP=1 SUB =4FREQ=3.84214 USUM (AVG)RSYS=0DMX =.001116 SMX =.001116图11 第五阶振形图12 第六阶振形5.2静力分析结果 5.2.1 工况二MNMXXYZ.910E-04.182E-03.273E-03.364E-03.455E-03.546E-03.637E-03.728E-03.819E-03NODAL SOLUTIONSTEP=1 SUB =5FREQ=4.09304USUM (AVG) RSYS=0DMX =.819E-03 SMX =.819E-03MNMXXYZ.156E-03.312E-03.467E-03.623E-03.779E-03.935E-03.00109.001246.001402NODAL SOLUTIONSTEP=1 SUB =6FREQ=4.37558 USUM (AVG)RSYS=0DMX =.001402 SMX =.001402图13 可变荷载组合下框架结构变形图由图13可得,在可变荷载组合作用下框架结构最大变形发生在屋面楼板,最大挠度为11.5mm 。
