结构动力学 期末复习重点
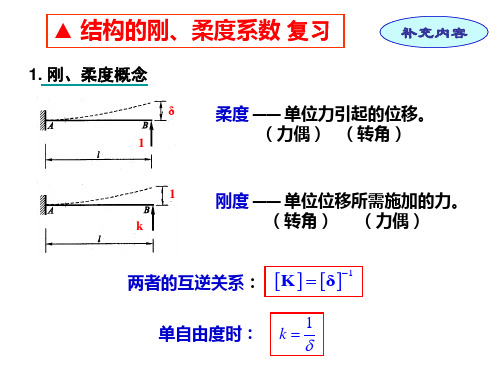
结构动力学的刚度系数柔度系数

(2)柔度法 —— 研究结构上质点的位移,建立位移协调方程, 需要用到柔度系数。
超静定结构,查表(形常数)
取决于结构的
刚度系数 柔度系数
3 E I k 3 l
i
1 k
两端固支梁侧移刚度: 12E I 12i k 3 2 l l
i
1
一固一铰支梁的侧移刚度:(同悬臂梁) 1 3EI 3i k 3 2 l l k 简支梁中点柔度、刚度:
l3 4 8 E I 4 8 E I k 3 l
δ
2. 柱的并联、串联刚度 (1)并联 总侧移刚度:
l/2
解:
l/2
1 ,先求δ m
3 l/ 16
l/2
l/2
P=1
l/2
l/2
l3 1 48EI
l/
2
7 l53l/32 2 7 6 8P=1 EI
l3 3 192 EI
1
48EI ml3
3 l 768 EI 192 EI 1 l 3 l l 5 l 7 l 2 2 ( 2 ) 3 2 3 m l 623 E I6 7 21 2 7 6 8 E I m l3
h1
k1
k1
、k2 — 楼层刚度
1 2 i2 k 2 2 h 2
总刚度:
k
P 1 1 1
k1 k 2
1 2 i 1 k 1 2 h 1
串联一般公式:
1 1 1 1 n1 k k k k j 1k 1 2 n j
结构动力学复习资料微型44

1.什么是坐标耦联,正则坐标,广义坐标,物理坐标?坐标耦联:由于坐标的选择,使得必须由联立的方程组才能求解,这就称为坐标耦联;它取决于表示运动坐标的选择方法,与体系本身的特性无关。
正则坐标:既无动力耦联,又无静力耦联的坐标,叫正则坐标。
广义坐标:能决定质点系的几何位置的彼此独立的量,称为该体系广义坐标;广义坐标可以取长度量纲的量,也可以用角度甚至面积和体积来表示。
物理坐标:即几何坐标,直接建立在体系中坐标系。
2.集中质量法:是结构分析中最常用的处理方法,把连续分布的质量集中到质点,采用真实的物理量,具有直接直观的优点。
广义坐标法:广义坐标是形函数的幅值,有时没有明确的物理意义,但是比较方便快捷。
有限元法:综合了集中质量法与广义坐标法的特点(1)与广义坐标法相似,有限元法采用了形函数的概念,但不同于广义坐标法在全部体系结构上插值,而是采用分片插值,因此形函数表达式形状可相对简单;(2)与集中质量法相比,有限元法中的广义坐标也采用了真实的物理量,具有直接直观的优点。
3.动力问题与静力问题的重要区别?结构动力特性一般指什么?(1)动力反应要计算全部时间上的一系列解,而静力问题是某一时间点上的解,主要原因是动力问题荷载是随时间变化的,但此外因并不足以产生重大不同,那样可将动力问题看成一系列静力问题;(2)考虑惯性力的影响是结构动力学和静力学的一个本质的重要区别。
结构的动力特性:自振频率、振型、阻尼4.动荷载的分类及其特点?根据荷载是否已预先确定,动荷载可以分为两类:确定性(非随机)荷载和非确定性(随机)荷载。
确定性荷载是荷载随时间的变化规律已预先确定,是完全已知的时间过程;非确定性荷载是荷载随时间变化的规律预先不可以确定,是一种随机过程。
5.什么叫静力凝聚?为简化计算,忽略惯性效应不大的方向上的动力效应,而使质量、刚度矩阵保证正定、对称,这种减少体系自由度的方法称为静力凝聚法。
6.动力自由度与静力自由度的概念及二者区别?动力自由度是指动力分析中,为确定体系任一时刻全部质量的几何位置所需要的独立参数的数目;静力自由度是使结构体系静定所需要的独立约束数目。
结构动力学 期末复习重点

一1、结构动力学计算的特点?(对比静力问题)○1动力反应要计算全部时间点上的一系列的解,比静力问题复杂要消耗更多的计算时间。
○2与静力问题相比,由于动力反应中结构的位置随时间迅速变化,从而产生惯性力,惯性力对结构的反应又产生重要的影响。
2、结构动力学是研究什么的?包含什么内容?结构动力学:是研究结构体系的动力特性及其在动力荷载作用下的动力反应分析原理和 方法的一门理论和技术学科。
目的:在于为改善工程结构体系在动力环境中的安全性和可靠性提供坚实的理论基础。
二、1、动力系数(有阻尼、无阻尼。
简谐、半功率点法、位移计……)2、动力系数和哪些因素有关动力放大系数受阻尼比控制,Rd 曲线形状可以反映出阻尼比的影响。
主要有两点:其一是峰值大小;其二是曲线的胖瘦。
3、动力系数在工程(隔震、调频减震)的应用4、如何用动力系数测阻尼比三、1、阻尼 阻尼也称阻尼力,是引起结构能量的耗散,使结构振幅逐渐变小的作用。
阻尼的来源:1固体材料变形时的内摩擦,或材料快速反应引起的热耗散;2结构连接部位的摩擦;3结构周围外部介质引起的阻尼。
2.阻尼比常用的测量方法及其优缺点:(1)对数衰减率法:相邻振动峰值比的自然对数值称为对数衰减率。
采用自由振动试验,测一阶振型的阻尼比较容易。
测量高阶振型阻尼比的关键是能激发出按相应振型的自由振动。
(2) 共振放大法:采用强迫振动试验,通过共振得到(Rd )max 由于静荷载下的位移较难确定,应用上存在一定的技术困难,但通过一定数学上的处理还是可以用的。
(Ust 是零频时的静位移,不容易测得。
)(3) 半功率点(带宽)法:采用强迫振动试验,测出Rd-w/wn 图上振幅值等于倍最大振幅的点,对应的长度的1/2即为阻尼比。
不但能用于单自由度体系,也可以用于多自由度体系,对多自由度体系要求共振频率稀疏,即多个自振频率应相隔较远,保证在确定相应于某一自振频率的半功率点时不受相邻自振频率的影响。
3、等效粘滞阻尼比○1、粘性阻尼是一种理想化的阻尼,具有简单和便于分析计算的优点。
结构动力学的刚度系数柔度系数汇总.
三、自由振动微分方程的解
y(t ) Asin( t )
四、结构的自振周期和频率
k 1 m m
T
2
五、例题
m
l /2 1 EI l /2
[例1] 计算图示结构的频率和周期。 (柔度法) 解:
1 m
l 48EI
ml 3 T 2 48EI
3
48 EI ml 3
1
k22 k2
k12 k2
k2
EI∞
k11 k1 k2
1
k1
k1 、k2 —— 楼层刚度(本楼层单位侧移所需的侧向力) k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij
—— 第j 个结点位移发生单位位移(其它结点位移均锁固)时, 在第i 个结点位移处产生的反力。
h EI EI
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度:
h2
h1
i1
i2
k k左柱 k右柱
3 i1 3 i2 2 2 h1 h2
∞ h
总侧移刚度:
i1
i2
12 i1 12 i2 k k左柱 k右柱 2 2 h h
(刚度并联,两者叠加)
k
k11 k
EI
1
l
3EI l3
k11 m
3 EI
l3
k m
[例7]计算图示刚架的频率和周期。
1
m EI1= I I h
k
解: (刚度法)
由柱刚度并联 得:
12 EI 24 EI k 2 3 3 h h
k 24 EI m mh3
结构动力学复习资料

目录
第二章 单自由度系统的振动......................................................................................................... 1 2.1 单自由度系统的自由振动( F (t ) = 0 )........................................................................ 1 1)无阻尼自由振动......................................................................................................... 1 2)有阻尼自由振动......................................................................................................... 2 2.2 单自由度系统的强迫振动................................................................................................ 4 1)系统对于简谐激励的响应......................................................................................... 4 2)系统对周期激励的响应............................................................................................. 7 3)非周期激励的响应..................................................................................................... 8 第三章 二自由度系统的振动....................................................................................................... 10 3.1 无阻尼自由振动.............................................................................................................. 10 3.2 二自由度系统的强迫振动(简谐激励)...................................................................... 12 第四章 分析动力学基础............................................................................................................... 13 4.1 虚位移原理...................................................................................................................... 13 4.2 拉格朗日方程.................................................................................................................. 13 4.3 汉密尔顿原理.................................................................................................................. 14 第五章 多自由度系统的振动....................................................................................................... 14 5.1 运动方程的建立.............................................................................................................. 14 5.2 无阻尼自由振动.............................................................................................................. 15 5.3 主振型的正交性.............................................................................................................. 17 5.4 正规化与正规坐标.......................................................................................................... 18 5.5 半正定系统...................................................................................................................... 19 5.6 系统对初始条件的响应................................................................................................... 20 5.7 瑞雷—李兹法.................................................................................................................. 20 第六章 连续弹性体系统的振动................................................................................................... 22 6.1 弦的振动.......................................................................................................................... 22 6.2 杆的纵向振动.................................................................................................................. 23 6.3 轴的扭转转动.................................................................................................................. 25 6.4 梁的弯曲振动.................................................................................................................. 26 6.5 振型函数的正交性.......................................................................................................... 29 6.6 主振型叠加法.................................................................................................................. 29
结构动力学复习 新

结构动力学与稳定复习1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度(质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结构动力学复习 新汇总

结构动力学与稳定复习1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度(质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结构动力学复习新资料

结构动力学与稳定复习1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度(质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结力(下)复习(结构动力学)解析

k11
k12
12m1
1 7.5661
8.欲使图示体系的自振频率增大,在下述办法中可采用:
A.增大质量m; C.减小梁的EI;
m EI
B.将质量m 移至梁的跨中位置 ; D.将铰支座改为固定支座 。
k 1
m m
(D )
9.图 示 体 系 的 自 振 频 率 3EI1 / (mh3) 。 ( )
m
EI=oo
EI1
EI1
h
k 6EI1 , k 6EI1
h3
m mh3
10.图示体系 EI 2105 kN m2, 20s-1, k 3105 N/m, P 5103 N, W 10kN。 求质点处最大动位移和最大动弯矩 。
Psin t
k W
2m
2m
解:
1 (1 21 2 1 2) 1 1
Psin t
A
W
l /2
l /2
3l 16 5l 32 M1
解:自振频率
B
1 ( 1 l l 3l 1 l l 2 l 2)
EI 2 4 32 2 4 2 3 4
l3 ( 1 3 ) EI 48 256
要点:
结构动力学
1. 单自由度体系的自由振动,自振频率 (刚度法和柔度法) 2. 单自由度体系的强迫振动,动力系数,动内力和动位
移幅值(振幅) 3. 多自由度体系的自由振动的频率及主振型的计算 (刚度
法和柔度法) 4. 多自由度体系受同步简谐动荷作用下的动内力和动位
移幅值的计算
掌握所涉及到的所有公式。
2 1 [( k11 k22 ) ( k11 k22 )2 4(k11k22 k12k21) ]
2 m1 m2
结构动力学复习题全解

*本章讨论结构在动力荷载作用下的反应。 **学习本章注重动力学的特征------惯性力。 *结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化 的规律,从而找出其最大值作为设计的依据。 *动力学研究的问题:动态作用下结构或构件的强度、刚度及稳定性分析。 一、 本章重点 1.振动方程的建立 2.振动频率和振型的计算 3.振型分解法求解多自由度体系 4.最大动位移及最大动应力 二、 基础知识 1.高等数学 2.线性代数 3.结构力学 三、 动力荷载的特征 1.大小和方向是时间 t 的函数 例如:地震作用,波浪对船体的作用,风荷载,机械振动等 2.具有加速度,因而产生惯性力 四、 动力荷载的分类 1.周期性动力荷载 例如:①机械运转产生的动力荷载,②打桩时的锤击荷载。 P(t) P(t)
Δt 时间内,干扰力的作用近似的看作是初速度为 v (t ) = 的自由振动。 由(3)式可知:
p∆t p ( ∆t ) 2 ,初位移为 y(t ) = =0 m 2m
y(t ) = y 0 cosωt +
v0 p∆t sinωt sinωt = ω mω
---------------------(9)
& (t ) FD= - C y
,称为粘滞阻尼力,阻尼力 与运动方向相反。
一切引起振动衰减的因素均称为阻尼,包括 EI ①材料的内摩擦引起的机械能转化为热能消失 ②周围介质对结构的阻尼(如,空气的紫力) ③节点,构件与支座连接之间的摩擦阻力 ④通过基础散失的能量 2.弹性恢复力 FE= - K y(t) ,K 为侧移刚度系数,弹性恢复力 与运动方向相反。 3.惯性力
,阻尼系数为 C ,横梁具有分布质量 m =
m L
。
结构动力学复习

(5)连续系统的虚位移原理——假定振型法:虚位移在一定程度上近似于连续系统的挠曲特征,这种方法成为假定振型法。
第三章SDOF系统自由振动
(1)线性SDOF系统的运动方程:
无阻尼固有圆频率;粘滞阻尼因数;临界阻尼系数
边界条件:外力-自由端
固定端
(2)线弹性梁横向振动的伯努利-欧拉理论假定:梁上有一根沿x轴的中性轴,表现即没有拉伸也没有压缩;在未变形的梁中,横截面垂直于中性轴,并保持平面,在变形的中性轴上亦保持垂直,忽略横向剪切变形;材料为线弹性,任何截面性质相同;y、z向应力相对x向来说可忽略不计;x-y为柱主平面。可以忽略转动惯量。
(3)无阻尼DPF系统短时作用脉冲响应为:
无阻尼SDOF系统单位脉冲响应函数,即I=1时:
=1的粘滞阻尼SDOF系统单位脉冲函数:
第六章SDOF系统一般动力激励
(1)三种方法得到一般动力荷载系统响应的解析表达式:杜哈梅积分法(时域解),拉普拉斯变换法(拉域解)和傅立叶变换法(频域解)。
(2)杜哈梅积分法:叠加原理为依据,仅对线性系统有效。
总响应的特点:稳态响应与激励频率相同,相位据r而定;
强迫振动和固有运动出现拍的现象,即时而相互增强,时而相互抵消;
最大总响应比最大稳态响应大:总动力放大因数为
共振:r=1时,用假定解求解
(2)粘滞阻尼SDOF系统简谐激励运动方程:
稳态响应与激励不同相位,稳态响应的解可写成:
则稳态响应方程可以写成:
其中:
边界条件:固定端
简支端
自由端
(3)连续系统固有频率瑞利近似表示法:即假定振型法,用来估算无阻尼连续系统基频。
结构动力学学习要点

2
I 0
K M 0
2
两个主振型为:
柔度法:
1 A 1 A
(1) 2 (1) 1
刚度法:
2 1
11m1
12m2
2 2
1 A 2 A
( 2) 2 ( 2) 1
11m1
12m2
(1) A2 12 m1 k11 1 (1) A1 k12 ( 2) 2 A2 2 m1 k11 2 ( 2) A1 k12
i mi y sin t F sin t FIi mi y
0 Ii
Байду номын сангаас
FIi0 mi 2 yi0
—惯性力的最大值
位移、惯性力、干扰力同时达到最大值,将FI、F(t)最大 值作为静力荷载作用于结构,计算最大动力位移和内力。
4. 了解阻尼对自由振动的振幅及强迫振 动动力系数的影响。 5. 掌握两个自由度体系在简谐荷载作用 下的动位移和动内力的计算。
§12-3 单自由度结构的自由振动
单自由度结构 自由振动微分方程
y a sin( t )
则有 a
11 y FI11 m y k11 y 0 m y
yd 2 yst
t0 π t t0 , yd 2 yst sin 2 2 动力系数为 2 sin t0 与荷载作用时间长短有关 2
当t0>T/2时,最大位移发生在前一阶段。
2
短期荷载的最大动力效应与突加荷载相同。
§12-6 多自由度结构的自由振动
0 柔度法: Y M Y
A F 2 2 m( ) 1 1 F 2 m 2
▲ 结构动力计算期末复习

—— 振动微分方程
2.位移方程法(柔度法)
FP=1
静平衡位置为原点 方程与重力无关 单位力引起的位移
δ
δ=1/k
m
(1)确定柔度系数 δ
I (t ) my
y
(2)规定位移的正向(定坐标)
(3)标出惯性力(沿正向)
(4)写出位移方程(考虑结构的位移协调)
y(t ) I (t ) my(t ) —— 惯性力引起的位移
1 192 EI 134.16s 1 m 5ml 3
1 1
2 2
1.552
3)求yDmax , MDmax
yD max 5l 3 1.552 20 103 5 43 P P 5.75 103 m 192 EI 192 90 105
4.弄懂共振原理,以及阻尼对共振区的重大影响。
三.两个(多个)自由度体系的自由振动 1.会列振动方程,并用矩阵式表示,刚、柔度法均掌握;
m1 0 0 1 k11 y k m2 y2 21 k12 y1 0 y 0 k22 2
62.8 2
2
0.33
2)动力荷载幅值所引起的静位移 P P y st P k m 2 4.9 9.8 1000 0.1 mm 2 123 62.6
Psinθt
m 1m
3)最大动力位移 [ y( t )]Dmax yst 0.033mm 4)振幅
——
(3)方法选择
柔度法
取决于结构的 刚度系数 柔度系数
谁较容易求得。
静定结构,图乘法求δ
顺利求解刚(柔)度系数是自由振动分析的关键!
结构动力学公式归纳总结

−
������)������������
h.杜哈梅数值积分(当������(������)不可积时):
无阻尼体系:
������������������������(������ − ������) = sin(������������ − ������������) = ������������������������������������������������������������ − ������������������������������������������������������������
0
−
������)������������
其中ℎ(������ − ������) = 1 ������������������������(������ − ������)
������������
有阻尼稳态解:
������(������)
=
1 ������������������
������
∫ ������(������)������−������������(������−������)������������������������������(������
随机动荷载。所谓非随机动荷载,即荷载的变化规律我们是已经完全掌握的,可以绘制出
荷载随时间变化曲线的荷载,这类荷载一般进行所谓的数定分析以获得荷载-位移曲线。而
随机荷载是指荷载随时间的变化规律我们是无法事先知道的,比如我们需要研究的风荷
载,对这类荷载一般需要采用随机振动理论去进行求解。
下面简单概括结构动力学的理论公式:
b.有阻尼自由振动:
������������̈ (������) + ������������̇ (������) + ������������(������) = 0
结构动力学的刚度系数柔度系数

P
1 k1
P
1 k2
P
1 k1
1 k2
k1 、k2 — 楼层刚度
k1
12i1 h12
k2
12i2 h22
总刚度: k P 1
1 k1
1 k2
串联一般公式:
1 1 1 1 n 1
k k1 k2
kn k j1 j
▲ 楼层刚度与位移法刚度系数的关系
EI∞
k2
EI∞
1 k1
k
my
(惯性力和弹力)
解:(刚度法)
由∑MA=0 得:
2m(2 y) l my 5l k(4 y) l 0
52
45
化简得:
33my 16ky 0
16k
33m
[例9]建立图示结构的振动方程,并计算自振频率。
A
m E1I1=∞ m
EA=∞
A
m E1I1=∞ m
k
(等效图)
EI
l /2
l /2
l
解:(刚度法)
(2l)3 l3
48EI 6EI
k
1
6EI l3
由∑MA=0
得: m( y )
l
my l
ky l
0
22
化简得: 5my 4ky 0
4k 5m
24EI 5ml 3
1y 2
y
(位移几何关系)
ky
A
m(1 y) 2
my
(惯性力和弹力)
k12=k21=-k2
k22=k2
3. 应用举例
求图示三层刚架的顶端侧移。
P
解: 1)计算各楼层(侧移)刚度
i3
i2
i1
结构动力学复习

8.建立运动方程的方法特点?(1)D’ Alembert原理:矢量方法,直观,建立了动平衡概念(2)虚位移原理:半矢量法,可以处理复杂分布质量和弹性问题(3)哈密顿原理:标量方法,表达简洁(4)Lagrange方程:标量方法,运用面广
5.广义力的概念及性质?广义力为广义坐标对应的力,是虚位移对广义坐标的偏导数。广义力是标量而非矢量,广义力与广义坐标的乘积具有功的量纲。
6.阻尼力的概念,产生阻尼力的物理机制有哪些?引起结构能量的耗散,使结构的振幅逐渐变小的这种作用称为阻尼,也称为阻尼力.物理机制:(1)固体材料变形时引起的内摩擦或材料快速应变引起的热耗散(2)结构连接部位的摩擦,混凝土微裂缝的张开闭合结构部件与非结构构件之间的摩擦(3)结构周围外部介质引起的阻尼
3.结构动力计算的特点(与静力学的区别):1、动力反应要计算全部时间点上的一系列解,比静力问题复杂且要消耗更多的计算时间。2、与静力问题相比,由于动力反应中结构的位置随时间迅速变化,从而产生惯性力,惯性力对结构的反应又产生重要影响。
4.结构离散化方法的种类、实质?离散化方法有:集中质量法、广义坐标法、有限元法。离散化方法的实质就是把无限自由度问题转化为有限自由度的过程。
确定荷载根据时间变化规律可分为:周期荷载、非周期性荷载。周期性荷载分为:简谐荷载(荷载随时间周期性变化,并可以用简谐函数表示;正弦、余弦荷载)、非简谐荷载(荷载随时间作周期变化,是时间t的周期函数,但不能简单的用简谐函数表示;平稳情况下波浪对堤坝的动水压力、轮船螺旋桨产生的推力)。非周期荷载可分为:冲击荷载(荷载的幅值在很短时间内急剧增大或急剧减小;爆炸引起的冲击波、突加重量)、一般任意荷载(荷载的幅值变化复杂,难以用解析函数表示的荷载;由环境振动引起的地震动、地震引起的地震动、脉动风的风压)
结构动力学期末复习题_2014

结构动力学期末复习题_2014结构动力学期末复习题1. 试用哈密顿原理推证第二类拉格朗日方程。
2. 在允许大变形的情况下,请采用拉格朗日方程求出图示系统在指定的广义坐标下的运动微分方程。
若仅考虑小变形振动,写出其运动微分方程。
图中弹簧1未变形时的原长为1l ,弹簧2未变形时的原长为a 。
5. 试讨论对于多自由度体系如何形成一致质量矩阵、一致刚度(包括几何刚度)矩阵、一致荷载列阵并分析与集中质量矩阵的区别。
6. 一栋多层楼房,在地震地面运动作用下运动,若结构在运动中保持为弹性,弹簧1(a +q )P(t)ym 3q 弹簧22k 22q 1k 1m 1x试述求解该结构弹性动力反应的振型叠加法的原理以及求解步骤。
7. 一栋多层楼房,在地震地面运动作用下运动,结构产生非线性变形,试讨论如果将结构简化为集中质量的串模型,如何采用逐步积分法分析该结构在地震地面运动作用下结构的非线性反应时程,写出线性加速度法、Wilson-θ法、Newmark-β法、中央差分法等几种方法中的一种方法分析求解非线性多自由度体系的动力反应的步骤,并就你所知,讨论用于结构非线性时程反应分析的这些逐步积分方法在稳定性和求解精度方面的优缺点,提出你的改进意见和方法。
8.9. (ρ1()(EI x EI o +=试采用10. 满载时为m 1=为kg m 5002=度为k 350=呈正弦波形,可表示为lza x s π2sin =,其中,m l 5=。
求拖车在满载和空载时的振幅比。
11. 试推导粘性阻尼力在一周内消耗的能量的表达式。
12. 试求振动系统02=++kx x x m nζω在图示方波激励下的稳态受迫振动。
13. 图示结构,受到如图所示周期性荷载,可表示如下的正弦级数:t b t p n n n ωsin )(1∑∞==,其中,n n n p b )1(20--=π,不考虑阻尼,且荷载频率与结构自振频率之比为:431=ωω,试求出结构在此荷载作用下的稳态反应。
结构动力学-总复习

3) T和ω是结构动力性能的一个重要数量标志。
广西科技大学《结构动力学》 课件. Copyright (c) 2012 by professor Pan. All rights reserved.2020年3月23日
自振周期和自振频率计算举例——例1
m
求δ,作单位荷载作 用下弯矩图,如图示
1 EI
y(0) y0 0产生的静C位2 移0;C1 yst
y&(0) v0 0
y(t)
yst
1
1
2 2
sin
t
稳态反应
sin
t
瞬态反应
1
2 2
稳态反应:按荷载频率振动的部分,起主要作用
瞬态反应:按自振频率振动的部分,在实际振动中,由于 阻尼存在,这部分将会逐渐消失。
广西科技大学《结构动力学》 课件. Copyright (c) 2012 by professor Pan. All rights reserved.2020年3月23日
广西科技大学《结构动力学》 课件. Copyright (c) 2012 by professor Pan. All rights reserved.2020年3月23日
§10.2 单自由度体系的自由振动
h EI
m
EI1 y
EI
y
m k
y km
c y
实际模型
简化模型
弹簧-质点模型
自由振动:结构受到干扰离开平衡位置以后,不再受到任何
m
解:(1)求自振频率
EI
为E1I避 12免 单14 位2l 弄 错23 ,4l 建 议2 都采用l/2国际单1 位l/2!
l3 48EI
l/4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一
1、结构动力学计算的特点?
(对比静力问题)○
1动力反应要计算全部时间点上的一系列的解,比静力问题复杂要消耗更多的计算时间。
○
2与静力问题相比,由于动力反应中结构的位置随时间迅速变化,从而产生惯性力,惯性力对结构的反应又产生重要的影响。
2、结构动力学是研究什么的?包含什么内容?
结构动力学:是研究结构体系的动力特性及其在动力荷载作用下的动力反应分析原理和 方法的一门理论和技术学科。
目的:在于为改善工程结构体系在动力环境中的安全性和可靠性提供坚实的理论基础。
二、
1、动力系数(有阻尼、无阻尼。
简谐、半功率点法、位移计……)
2、动力系数和哪些因素有关
动力放大系数受阻尼比控制,Rd 曲线形状可以反映出阻尼比的影响。
主要有两点:其一是峰值大小;其二是曲线的胖瘦。
3、动力系数在工程(隔震、调频减震)的应用
4、如何用动力系数测阻尼比
三、
1、阻尼 阻尼也称阻尼力,是引起结构能量的耗散,使结构振幅逐渐变小的作用。
阻尼的来源:1固体材料变形时的内摩擦,或材料快速反应引起的热耗散;2结构连接部位的摩擦;3结构周围外部介质引起的阻尼。
2.阻尼比常用的测量方法及其优缺点:
(1)对数衰减率法:相邻振动峰值比的自然对数值称为对数衰减率。
采用自由振动试验,测一阶振型的阻尼比较容易。
测量高阶振型阻尼比的关键是能激发出按相应振型的自由振动。
(2) 共振放大法:采用强迫振动试验,通过共振得到(Rd )max 由于静荷载下的位移较难确定,应用上存在一定的技术困难,但通过一定数学上的处理还是可以用的。
(Ust 是零频
时的静位移,不容易测得。
)
(3) 半功率点(带宽)法:采用强迫振动试验,测出Rd-w/wn 图上振
幅值等于倍最大振幅的点,对应的长度的1/2即为阻尼比。
不但能用于单自由度体系,也可以用于多自由度体系,对多自由度体系要求共振频率稀疏,即多个自振频率应相隔较远,保证在确定相应于某一自振频率的半功率点时不受相邻自振频率的影响。
3、等效粘滞阻尼比
○1、粘性阻尼是一种理想化的阻尼,具有简单和便于分析计算的优点。
○
2工程中结构的阻尼源于多方面,其特点和数学描述更为复杂,这时可以将复杂的阻尼在一定的意义上等效
成粘性阻尼。
○3一般采用基于能量等效的原则。
○4阻尼耗散能量的大小可以用阻尼力的滞回曲线反映。
m st d u u R 0max 2)(21=≈ζn k k ln 21+≈y y n πξn a
b
f f f 2-=ζ
4.Rayleigh 阻尼理论:(阻尼C 推导到阻尼比。
用阻尼比来考虑) 假设结构的阻尼矩阵是质量矩阵和刚度矩阵的组合。
[C]=a0[M]+a1[K] 其中a0和a1是两个比例系数,分别具有s-1和s 的量纲。
可以用实际测量得到的结构阻尼比来确定,或通过给定的两个振型阻尼比的值来确定,为此要把Rayleigh 阻尼公式化成由阻尼比表示的形式。
原则:选择的两个用于确定常数a0和a1的频率点wi 、wj 覆盖结构分析中感兴趣的频段。
在频段内,阻尼比略小于给定的阻尼比ζ。
这样,在该频段内由于计算的阻尼略小于实际阻尼,结构的反应将略大于实际的反应,这样的计算结果对工程设计而言是安全的。
如果ωi 和ωj 选择得好,则可以保证这种增大程度很小。
在频段[ωi ωj]以外,其阻尼比将迅速增大,这样频率成份的振动反应会被抑制,其计算值将远远小于实际值。
四、
1、列运动方程
二自由度体系,求频率、振型 (101页)
2、振型叠加法(有阻尼稳态求解步骤,公式,如何用振型叠加法。
不写推导过程)
3、振型叠加法的优缺点
虽然振型叠加法有计算速度快、节省时间这些突出的优点,但存在局限性。
主要局限是由于采用了叠加原理,因而原则上仅适用于分析线弹性问题,限制了使用范围;第二个局限是由于要求阻尼正交,对实际工程中存在的大量不满足阻尼正交条件的问题,迫使必须采用额外的处理方法,近似处理方法包括采用正交阻尼代替非正交阻尼,或采用复模态方法,但复模态分析将使问题维数扩大一倍。
虽然通过选择合适的振型数目,可保证足够的计算精度,但也会产生一定的误差。
为进一步减小由忽略高阶振型影响而引起的误差,可以采用静力修正法。
所谓静力修正法是指在采用振型叠加法进行求解时,考虑所有高阶振型的影响,但高阶振型相应的振型坐标反应的求解并不通过直接求解动力方程而获得,而是采用简化的静力分析方法。
4、位移按振型展开有限项如何展开,这两种方法的关系、特点。
静力修正法。
P127
∑=--+=Nd n n
n n n n K t P t q t P K t U 11
])()([}{)}({][)}({φ 振型加速度法。
∑=∙
∙∙-+-=Nd n n n n n n n n t q t q t P K t U 121
)](2)([}{)}({][)}({ωςωφ 这两种方法均考虑了高阶振型的影响,且求解并不是直接求解动力方程而获得。
避免了由于采用数值时域逐步积分方法求解高阶振型反应而可以显著节省计算时间。
具有更快的收敛性且误差少。
静力修正法比振型加速度法更合理地解释加快收敛的原因。
比较而言,静力修正法更方便而言,因为它在计算中仅涉及到相对简单的振型位移计算,而振型加速度法中则要涉及振型加速度和速度,但对于计算机而言,这种差异导致的工作量又是可以忽略的。
5、时域积分算法
共性:只假设结构本构关系在一个微小的时间步距内是线性的,相当于用分段直线来逼近实际的曲线;此外,它是研究离散点上的值,体系运动微分方程不一定要求在全部时间上满足,仅要求在离散点上满足。
在每个时间间隔的起点和终点建立动力平衡条件,并以一个假设的反应机理为根据,近似地计算在时间增量范围内体系的运动。
判断方法:1收敛性;当离散时间步长△t—>0时,数值解是否收敛于精确解;2计算精度;截断误差与时间步长△t的关系,若误差ε∝0(△t的N次方),则称具有N阶精度;3稳定性;随计算时间步数i的增大,数值解是否远离精确解;4计算效率;所花费计算时间的多少。
逐步积分法按是否需要联立求解耦联方程组,可分为两大类:隐式方法、显式方法。
算法:
分段解析法,如果结构是线性的,并采用等时间步长,则A—D′均为常数,其计算效率非常高,在p(t)离散采样的定义下是精确解,但如果是非线性问题,则A—D′均为变量,计算效率会大为降低。
分段解析法的误差仅来自对外荷载的假设,而在连续时间轴上严格满足运动微分方程。
中心差分法,中心差分方法用位移的有限差分来近似表示速度和加速度。
中心差分方法存在计算中的起步问题,即仅能给出i=0时刻的反应,而不能给出i=0-1时刻的反应。
因此需要从t=0时刻的位移函数的泰勒展开式中解出i=0-1时刻的位移。
虽然稳定性略差,但因其所具有的简单、高效的特点也得到一系列的应用。
线性加速度法,线性加速度法基本假设:在每个时间增量内,加速度线性变化,且体系的阻尼、刚度特性在这个时间间隔内保持为常量。
Newmark—β法,同样将时间离散化,运动方程仅要求在离散的时间点上满足。
假设在ti时刻的运动均已求得, 然后计算 ti+1时刻的运动。
而是以ti时刻的运动量为初始值,通过积分方法得到计算i+1时刻的运动公式。
当δ= 1/2,β=1/4时,Δt≤∞,即成为无条件稳定的。
(求解步骤)
Wilson—θ法,Wilson—θ法是基于线性加速度法基础之上发展的。
当参数θ>1.37时,方法是无条件稳定的。
而且对于一些强冲击问题,Wilson—θ法无法完成计算。
