电路分析第十章习题解析

《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

《电路第五版课后习题答案

答案及解析115答案第一章电路模型和电路定律【题1】：由U A B 5 V 可得：IA C 2.5 A：U DB 0 ：U S 125. V。

【题2】：D。

【题3】：300；-100。

【题4】：D。

【题5】： a i i 1 i 2 ； b u u1 u2 ； c u u S i i S R S ； d i iS1RSu u S 。

【题6】：3；-5；-8。

【题7】：D。

【题8】：PU S 1 50 W ；P U S 2 6 W ；P U S3 0 ；P I S 1 15 W ；P I S2 14 W ；P I S 3 15 W 。

【题9】：C。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

1【题14】：3 I 1 2 3 ；IA 。

3【题15】：I 4 3 A；I 2 3 A；I 3 1A；I 5 4 A。

【题16】：I 7 A；U 35 V；X 元件吸收的功率为P U I 245 W。

【题17】：由图可得U E B 4 V；流过 2 电阻的电流I E B 2 A；由回路ADEBCA 列KVL 得U A C 2 3I ；又由节点 D 列KCL 得I C D 4 I ；由回路CDEC 列KVL 解得；I 3 ；代入上式，得U A C 7 V。

【题18】：P1 P2 2 II212222 ；故I I122；I 1 I 2 ；⑴KCL：43I I ；I 11 12858A；U I 1 I 1 V 或 1.6 V；或I 1 I2 。

S 2 15⑵KCL：43I I ；I1 121 8 A；U S 24V。

第二章电阻电路的等效变换【题1】：[解答]I9 47 3ab 9 4 8.5 V；A =0 .5 A ；U II 1 U 6ab . A ；P 6 1.2 5 W = 7 .5 W ；吸1 252收功率7.5W。

【题2】：[解答]【题3】：[解答] C。

电路第五版邱关源第10章部分习题及答案

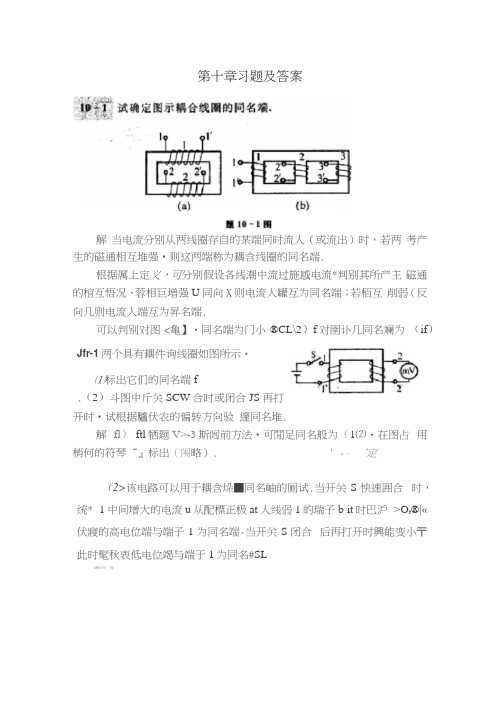
第十章习题及答案解当电流分别从两线圈存自的某端同时流人（或流出）时，若两考产生的磁通相互堆强•则这两端称为耦含线圈的同名端.根据厲上定义，可分别假设各线潮中流过施感电流*判别其所产主磁通的棺互悟况、蓉相巨増强U同向X则电流人罐互为同名端；若栢互削弱（反向几则电流人端互为昇名端.可以判别对图<亀】・同名端为门小®CL\2）f对圉讣几同名斓为（if）Jfr-1两个具有耦件询线圈如图所示・⑴标出它们的同名端f,（2）斗图中斤关SCW合时或闭合JS 再打开时•试根据驢伏农的偏转方向验邃同名堆.解fl）ftl牺题V>-3斯闿前方法•可閒足同名般为（1⑵・在图占用梢何的符琴“』标出（闱略）. ' -- ‘定（2>该电路可以用于耦含垛■同名岫的厕试.当开关S怏速囲合时，统* 1中间增大的电流u从配標正极at人线弱1的瑞子b it时巴沪>O t®|«伏寢的高电位端与端子1为同名端-当开关S闭合后再打开时興能变小〒此时髦秋衷低电位竭与端于1为同名#SLMWTn"「僅若有电流“ =2 + 500.(10/ + 30。

)“2 =血予A・各从图10-13所示线岡的1端和2端流人•并设线耳壬] 圈」的电感。

= 6H,线團2的电感“ =3乩|/,」/yT7T互感为M = 4 H.试求：〈1＞各线圈的磁逋链' (『,；(2＞端电压祝山和班如〈3＞網合因数&・弋、雪#汙解依題慰，作题解10・3图，则」山比(1) p = W LI - W12 严LM1-M" ・ «M 10-Jffl=6 X [? + $＜x^a0£ + 30")] — 4 X 10e_s,=(12 + 30cos( 10Z + 30°) — 40e-b,) Wb®2 = W22 — W21 =匸2 i2 — Mi 1=(-S- 20cos( 1 Or 4- 30") 4- 30e-5f) Wh(-300tjin( 10c + 30)+ 200e-s,) V“22・= 乎二 #「一8—20cos(10i+30j +50亡7叮=C200sin( 10/ + 30°) — 150 严)V(3) k =—厂I = —«二八■ 0943y 2 /6X3解能.隅合舆数A的大小与线圈的结构、两线圈之间的相互位置以及线圏周宙的瞪介质有关.如果让两线圈距离裡远•或者轴线星垂直放置•则因为耦合磁通任这种情况下近似为零，从而使耦合因数& = 0, 即没有輯合.图示电路中I】=6H，S = 3H,M=4H・试求从靖子1-1’看进去的等敕电感・(a) (b)J110-S s(1)去耦等效电路如题解10-5图(計所示■则从端子丨-L'看进去的等效电感为 •Leq =(L1 4 ⑷ +[(丄2+妙 //(-M)]=(6 亠 4) +[(3 + 4) 〃，一 4)] = 10 十[7 〃 1一4)] =10 +佯厂呎=0. G67 H/十\— 4丿 <2>去耦等效电路如题解10-5图(U 斯示•则从瑞子】-1/看进去的等效电感为Lq — (Li — M> + [(S —⑷ /[ Ml=(6 — 4> + [(3—4) 〃们=2+[(- 1) // 4]厶解捉示.含有轄合电感的赴路的分析要注意恰当地便用去剧等效的方法. --=2+曲务O.667 H（3）去耦等效电路如题解10-5图（0所示•则从端子】看进去的等效电恳为（Li -M） 4[M〃CS -M>]h 2 + 口〃（- 1）] = O.667 H（4）去稱等效电路如题解10-5图（小所示，则从端子1・1‘看进去的等效电址为L判=（£-i + M） + [（—M）// （L^十A4） J=10 + [C- 4）〃7] = 0. 667 H1«-4求图乐电路的输入阴抗ZW= 1弼d/$）・•.丄:r T上« 提示1般片况下对于空芯芟圧異电路宜采用原边（或副边）等■妓电略法以利千分析计鼻・对題10-6图（"采用原边等效电路法•对（b）・（c）两电路分別采用去耦等效，得題解io>6图a）・（b）・（c）,则，(1) Z-jeuLj + (0・2 + j0.6)nZgj [十 JZ (2) Z= — jl 十[j2 /!(j5-i 吉刀=—jl a(3) Leq = L] -P Z-2 - Z J M = 2 + 3 - 2 X z = 1 H •而田于电络此时发生并联谐振•则辆入电流为哮•输人阻抗Z 为无穷大•图示电路中 Ri =只2 = 1 0 3 n^t2 = 2 n.sVf =2a,ih = ioo v.求：仃)开关str 开和闭合时的电合时各部分的复功率. '解依腿息作出去耦聊效电路如題解10-7图所示"并设口 =100/0： V,则(1〉开关打开时•为两线圈顺申，则= _____________ _____________ ~ + & + R<L1 + Q + 2M)__________ _____________ A (l + l )+ j(3 + 2 + 2x2>10. 85 /一77, 47^ A开关闭合时[Rz 十辺(「2 十 // (―jai/Vf)十 Ri 十jw( b + M)100/0；(1 + j4)〃 (-)2) + 1+J5 =43. «5 7- 37.88° A丿1 X 1(2)开关S闭合肘，由于线圈2被短路，其电压弧=0•则线圏2 上不吸收友功举•且线FS1上的电压Du二。

电路分析第十章习题解答

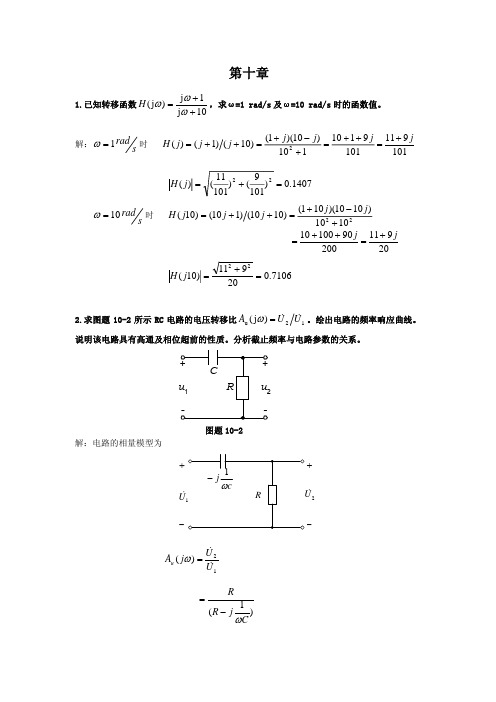
1 + 0.6282
ϕ = − arctan 4000 × 2π ×10−5 0.16 + 1 + 0.6282
= −0.16o
10.求图题 10-10 所示电路的转移电压比 Au ( jω) = U& 2 U&1 。当 R1C1=R2C2 时，此网络函数有何
特性。
R1
+
U&1
-
1 jωC1
1 jωC2
200
20
H ( j10) = 112 + 92 = 0.7106 20
2.求图题 10-2 所示 RC 电路的电压转移比 Au ( jω) = U& 2 U&1 。绘出电路的频率响应曲线。
说明该电路具有高通及相位超前的性质。分析截止频率与电路参数的关系。
+
C
+
u1
R
u2
-
-
解：电路的相量模型为
图题 10-2
当 R1C1 = R2C2 时
U& 2 U& 1
=1 1 + R1
R2
该网络函数为实数，相移为 0，不随频率变化。
11.当ω=5000 rad/s 时，R、L、C 串联电路发生谐振。已知：R=5Ω，L=400 mH，端电压 U=1V。
求电容 C 及电路中电流和各元件电压的瞬时表达式。
解：
R ， L ， C 串联电路谐振时
解：
Q ω0 =
1 LC
∴
L
=
1
ω
2 0
C
=
(2π
1 ×106 )2 × 200 ×10−12
= 127μH
Q

电路分析教程学习指导与题解

内容包括以下各章的学习指导和习题解析：导论、基本概念、电阻电路的分析方法、电路定理与应用、动态电路的瞬态分析、正弦交流电路稳态分析、选频电路与谐振、双口网络分析、磁耦合电路分析、双口网络分析、非线性电路分析。

书中对教材各章的主要内容给出了归纳与学习指导，对典型例题进行分析，并对教材各章的习题进行详细解答。

本书对于教师备课、学生学习和考研都具有重要的参考价值。

目录第1章导论1.1 电气和电子科学与技术的发展1.2 学习电路课程的基本线索1.3 求解电路问题的五步法第2章基本概念2.1 重点学习指导2.1.1 电路的基本变量2.1.2 基本元件R、L、C的特性2.1.3 KCL、KVL和欧姆定律2.1.4 独立源和受控源2.1.5 等效电路的概念2.2 第2章习题解析第3章电阻电路的分析方法3.1 重点学习指导3.1.1 网孔分析法3.1.2 节点分析法3.2 第3章习题解析第4章电路定理与应用4.1 重点学习指导4.1.1 叠加定理的应用4.1.2 戴维宁定理的应用4.2 第4章习题解析第5章动态电路的瞬态分析5.1 重点学习指导5.2 第5章习题解析第6章正弦交流电路稳态分析6.1重点学习指导．6.2 第6章习题解析第7章磁耦合电路分析7.1 重点学习指导7.2 第7章习题解析第8章选频电路与谐振8.1 重点学习指导8.2 第8章习题解析第9章双口网络分析9.1 重点学习指导9.2 第9章习题解析第10章非线性电路分析10.1 重点学习指导10.2 第10章习题解析第1章导论1.1 电气和电子科学与技术的发展诵诗能使人心旷神怡，变得灵秀；读史能使人贯通古今，变得聪慧。

在电的领域中，远的不说，近200多年的发展历史，特别是近100年所取得的成果令人惊叹不已。

电路第五版邱关源第10章部分习题及答案

第十章习题及答案解当电流分别从两线圈存自的某端同时流人（或流出）时，若两考产生的磁通相互堆强•则这两端称为耦含线圈的同名端.根据厲上定义，可分别假设各线潮中流过施感电流*判别其所产主磁通的棺互悟况、蓉相巨増强U同向X则电流人罐互为同名端；若栢互削弱（反向几则电流人端互为昇名端.可以判别对图<亀】・同名端为门小®CL\2）f对圉讣几同名斓为（if）Jfr-1两个具有耦件询线圈如图所示・⑴标出它们的同名端f,（2）斗图中斤关SCW合时或闭合JS 再打开时•试根据驢伏农的偏转方向验邃同名堆.解fl）ftl牺题V>-3斯闿前方法•可閒足同名般为（1⑵・在图占用梢何的符琴“』标出（闱略）. ' -- ‘定（2>该电路可以用于耦含垛■同名岫的厕试.当开关S怏速囲合时，统* 1中间增大的电流u从配標正极at人线弱1的瑞子b it时巴沪>O t®|«伏寢的高电位端与端子1为同名端-当开关S闭合后再打开时興能变小〒此时髦秋衷低电位竭与端于1为同名#SLMWTn"「僅若有电流“ =2 + 500.(10/ + 30。

)“2 =血予A・各从图10-13所示线岡的1端和2端流人•并设线耳壬] 圈」的电感。

= 6H,线團2的电感“ =3乩|/,」/yT7T互感为M = 4 H.试求：〈1＞各线圈的磁逋链' (『,；(2＞端电压祝山和班如〈3＞網合因数&・弋、雪#汙解依題慰，作题解10・3图，则」山比(1) p = W LI - W12 严LM1-M" ・ «M 10-Jffl=6 X [? + $＜x^a0£ + 30")] — 4 X 10e_s,=(12 + 30cos( 10Z + 30°) — 40e-b,) Wb®2 = W22 — W21 =匸2 i2 — Mi 1=(-S- 20cos( 1 Or 4- 30") 4- 30e-5f) Wh(-300tjin( 10c + 30)+ 200e-s,) V“22・= 乎二 #「一8—20cos(10i+30j +50亡7叮=C200sin( 10/ + 30°) — 150 严)V(3) k =—厂I = —«二八■ 0943y 2 /6X3解能.隅合舆数A的大小与线圈的结构、两线圈之间的相互位置以及线圏周宙的瞪介质有关.如果让两线圈距离裡远•或者轴线星垂直放置•则因为耦合磁通任这种情况下近似为零，从而使耦合因数& = 0, 即没有輯合.图示电路中I】=6H，S = 3H,M=4H・试求从靖子1-1’看进去的等敕电感・(a) (b)J110-S s(1)去耦等效电路如题解10-5图(計所示■则从端子丨-L'看进去的等效电感为 •Leq =(L1 4 ⑷ +[(丄2+妙 //(-M)]=(6 亠 4) +[(3 + 4) 〃，一 4)] = 10 十[7 〃 1一4)] =10 +佯厂呎=0. G67 H/十\— 4丿 <2>去耦等效电路如题解10-5图(U 斯示•则从瑞子】-1/看进去的等效电感为Lq — (Li — M> + [(S —⑷ /[ Ml=(6 — 4> + [(3—4) 〃们=2+[(- 1) // 4]厶解捉示.含有轄合电感的赴路的分析要注意恰当地便用去剧等效的方法. --=2+曲务O.667 H（3）去耦等效电路如题解10-5图（0所示•则从端子】看进去的等效电恳为（Li -M） 4[M〃CS -M>]h 2 + 口〃（- 1）] = O.667 H（4）去稱等效电路如题解10-5图（小所示，则从端子1・1‘看进去的等效电址为L判=（£-i + M） + [（—M）// （L^十A4） J=10 + [C- 4）〃7] = 0. 667 H1«-4求图乐电路的输入阴抗ZW= 1弼d/$）・•.丄:r T上« 提示1般片况下对于空芯芟圧異电路宜采用原边（或副边）等■妓电略法以利千分析计鼻・对題10-6图（"采用原边等效电路法•对（b）・（c）两电路分別采用去耦等效，得題解io>6图a）・（b）・（c）,则，(1) Z-jeuLj + (0・2 + j0.6)nZgj [十 JZ (2) Z= — jl 十[j2 /!(j5-i 吉刀=—jl a(3) Leq = L] -P Z-2 - Z J M = 2 + 3 - 2 X z = 1 H •而田于电络此时发生并联谐振•则辆入电流为哮•输人阻抗Z 为无穷大•图示电路中 Ri =只2 = 1 0 3 n^t2 = 2 n.sVf =2a,ih = ioo v.求：仃)开关str 开和闭合时的电合时各部分的复功率. '解依腿息作出去耦聊效电路如題解10-7图所示"并设口 =100/0： V,则(1〉开关打开时•为两线圈顺申，则= _____________ _____________ ~ + & + R<L1 + Q + 2M)__________ _____________ A (l + l )+ j(3 + 2 + 2x2>10. 85 /一77, 47^ A开关闭合时[Rz 十辺(「2 十 // (―jai/Vf)十 Ri 十jw( b + M)100/0；(1 + j4)〃 (-)2) + 1+J5 =43. «5 7- 37.88° A丿1 X 1(2)开关S闭合肘，由于线圈2被短路，其电压弧=0•则线圏2 上不吸收友功举•且线FS1上的电压Du二。

电路分析练习题含答案和经典例题

答案第一章电路模型和电路定律【题1】。

【题2】：D。

【题3】：300；-100。

【题4】：D。

【题5】【题6】：3；-5；-8。

【题7】：D。

【题8【题9】：C。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

【题14】【题15】。

；X。

【题16】【题17】；由回路ADEBCA列KVL得D列KCL CDEC列KVL式，得UAC=-7V。

【题18】：PPII12122222==；故I I1222=；I I12=；⑴KCL：43211-=I I；I185=A；U I IS=-⨯=218511V或16.V；或I I12=-。

⑵KCL：43211-=-I I；I18=-A；U S=-24V。

第二章电阻电路的等效变换【题1】：[解答]I=-+9473A=0.5 A；U Iab.=+=9485V；IU162125=-=ab.A；P=⨯6125. W=7.5 W；吸收功率7.5W。

【题2】：[解答]【题3】：[解答] C。

【题4】：[解答] 等效电路如图所示，I05=.A。

【题5】：[解答] 等效电路如图所示，I L=0.5A。

【题6】：[解答]【题7】：[解答]I=0.6A；U1=-2A=-12V；U2=2I+2=32V【题8】：[解答]由图可得U=4I-4。

【题9】：[解答]⑴U=-3 V 4⑵1 V电压源的功率为P=2 W （吸收功率）7⑶1 A 电流源的功率为P =-5 W （供出功率） 10【题10】：[解答]A第三章电阻电路的一般分析方法【题1】：【题2】：I I 1330+-=；I I 1220++=；I I 2430--=；331301243I I I I -+--+=；解得：I 1=-1.5 A, I 2=-0.5 A, I 3=1.5 A, I 4=-3.5 A 。

【题3】：[解答]()()()11233241233418611218241231213+++--=+-++=+-+++=--⎧⎨⎪⎩⎪I I I I I I I ；I 1655=.A 【题4】：[解答]()()22224122321261212++-+=-++++=-⎧⎨⎩I I I I ；I 21=- A ；P =1 W 【题5】：[解答]答案不唯一，有多解。

10.4 电容器的电容(练习题)(解析版)

第十章静电场中的能量10.4 电容器的电容一、单选题：1.一个电容器带电荷量为Q时，两极板间电压为U，若使其带电荷量增加4.0×10－7 C 时，它两极板间的电势差增加20 V，则它的电容为( )A．1.0×10－8 F B．2.0×10－8 FC．4.0×10－8 F D．8.0×10－8 F答案 B解析C＝ΔQΔU＝4.0×10－720F＝2.0×10－8 F，故选B.2.传感器是自动控制设备中不可缺少的元件，已经渗透到宇宙开发、环境保护、交通运输以及家庭生活等各种领域．下列为几种电容式传感器，其中通过改变电容器两板间距离而引起电容变化的是( )【解析】A选项改变的是介质，B、D选项改变的是正对面积，C选项改变的是两板间距离，故C正确．【答案】 C3.对于两个电容不同的电容器，下列说法正确的是( )A．电容大的电容器带电荷量一定比较多B．电容大的电容器两板间的电势差一定比较大C．由C＝QU知，电容器所带电荷量Q只要不断增大，U可无限增大D ．在相同电压作用下，带电荷量多的电容器的电容比较大答案 D解析电容的大小与电容器两端的电压及电容器所带的电荷量无关，故A 错误；根据公式C ＝Q U 得，电势差U ＝QC ，因此电容大的电容器两板间的电势差不一定比较大，故B 错误；超过击穿电压，电容器将被损坏，故C 错误；根据公式C ＝QU ，在相同电压作用下，带电荷量多的电容器的电容比较大，故D 正确．4.如图所示，先接通S 使电容器充电，然后断开S 。

当增大两极板间距离时，电容器所带电荷量Q 、电容C 、两极板间电势差U 、两极板间场强E 的变化情况是( )A.Q 变小，C 不变，U 不变，E 变小B.Q 变小，C 变小，U 不变，E 不变C.Q 不变，C 变小，U 变大，E 不变D.Q 不变，C 变小，U 变小，E 变小解析电容器充电后再断开S ，其所带电荷量Q 不变，由C ∝εr Sd可知，d 增大时，C 变小，又U ＝Q C ，所以U 变大；由于E ＝U d ，U ＝Q C ＝4πkdQ εr S ，所以E ＝4πkQεr S，故d 增大时，E不变。