西方经济学微观部分第七章课后答案
西方经济学第七章答案
西方经济学第七章答案(总30页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、单项选择题题目1正确获得分中的分标记题目题干构成国民经济简单循环的是（? ? ）选择一项：A. 出口与进口B. 厂商与居民?C. 投资与储蓄D. 政府与居民反馈你的回答正确正确答案是：厂商与居民题目2正确获得分中的分标记题目题干在一个国家或地区的领土上，在一定时期内所生产的最终产品和劳务按市场价格计算的产值是指（? ?）选择一项：A. 国民收入B. 国民生产总值C. 国内生产净值?D. 国内生产总值反馈你的回答正确正确答案是：国内生产净值题目3正确获得分中的分标记题目题干一个国家一定时期内用于生产的各种生产要素所得到的实际收入，即工资、利息、地租和利润的总和扣除间接税净额和对企业转移支付后的余额是指（? ）选择一项：A. 国民生产总值B. 国民收入?C. 国内生产总值D. 国内生产净值反馈你的回答正确正确答案是：国民收入题目4正确获得分中的分标记题目题干国内生产净值等于（? ?）选择一项：A. 国民生产总值-国外要素净收入B. 国民收入-公司所得税-公司未分配利润-社会保险税+政府转移支付和利息支出C. 国内生产总值+本国公民在国外的资本和劳务所创造的价值或收入-外国公民在本国的资本和劳务所创造的价值或收入D. 国内生产总值-折旧?反馈你的回答正确正确答案是：国内生产总值-折旧题目5正确获得分中的分标记题目题干国民收入等于（? ）选择一项：A. 国内生产总值-折旧B. 国内生产净值-（间接税-政府对企业的补贴）-企业转移支付?C. 国民生产总值-国外要素净收入D. 国民收入-公司所得税-公司未分配利润-社会保险税+政府转移支付和利息支出反馈你的回答正确正确答案是：国内生产净值-（间接税-政府对企业的补贴）-企业转移支付题目6正确获得分中的分标记题目题干国内生产总值等于（? ?）选择一项：A. 国内生产净值-（间接税-政府对企业的补贴）-企业转移支付B. 国民生产总值-国外要素净收入?C. 国内生产总值-折旧D. 国民收入-公司所得税-公司未分配利润-社会保险税+政府转移支付和利息支出反馈你的回答正确正确答案是：国民生产总值-国外要素净收入题目7正确获得分中的分标记题目题干国民生产总值等于（? ?）选择一项：A. 国内生产总值+折旧B. 国内生产总值+本国公民在国外的资本和劳务所创造的价值或收入-外国公民在本国的资本和劳务所创造的价值或收入C. 国民收入+公司所得税+公司未分配利润+社会保险税+政府转移支付和利息支出D. 国民生产总值+国外要素净收入反馈你的回答正确正确答案是：国内生产总值+本国公民在国外的资本和劳务所创造的价值或收入-外国公民在本国的资本和劳务所创造的价值或收入题目8正确获得分中的分标记题目题干居民提供的资本与劳动所得到的报酬一部分用于储蓄，这说明（? ）选择一项：A. 企业生产基金存量增加的扩大B. 企业的产品能全部卖掉C. 企业的投资增加D. 企业生产出来的商品和服务积存相应增加?反馈你的回答正确正确答案是：企业生产出来的商品和服务积存相应增加题目9正确获得分中的分标记题目题干两部门的均衡条件是（? ? ）选择一项：A. I+G+X=S+T+MB. AD=ASC. I+G=S+TD. I=S?反馈你的回答正确正确答案是：I=S题目10正确获得分中的分标记题目题干三部门的均衡条件是（? ? ）选择一项：A. I+G=S+TB. AD=ASC. I+G+X=S+T+MD. I=S反馈你的回答正确正确答案是：I+G=S+T题目11正确获得分中的分标记题目题干开放经济的均衡条件是（? ? ）选择一项：A. I+G+X=S+T+MB. I=SC. AD=ASD. I+G=S+T反馈你的回答正确正确答案是：I+G+X=S+T+M题目12正确获得分中的分标记题目题干一个国家在本国（或地区）领土上，在一定时期内生产的全部产品和劳务的市场价值的总和是指（? ?）选择一项：A. 国民生产总值B. 国民收入C. 国内生产总值?D. 国内生产净值反馈你的回答正确正确答案是：国内生产总值题目13正确获得分中的分标记题目题干从使用的角度考察，国民生产总值是指在一个国家或地区的领土上，在一定时期内居民、厂商、政府和国外部门购买最终产品和劳务的支出总额，这种计算方法是（? ?）选择一项：A. 支出法?B. 生产法C. 收入法D. 无法确定反馈你的回答正确正确答案是：支出法题目14正确获得分中的分标记题目题干从分配的角度考察，国民生产总值是指在一个国家或地区的领土上，在一定时期内生产要素所有者得到的报酬总和，这种计算方法是（? ?）选择一项：A. 无法确定B. 收入法?C. 支出法D. 生产法反馈你的回答正确正确答案是：收入法题目15正确获得分中的分标记题目题干从生产的角度考察，国民生产总值是指在一个国家或地区的领土上，在一定时期内各部门的增殖的总和，这种计算方法是（? ?）选择一项：A. 支出法B. 收入法C. 无法确定D. 生产法?反馈你的回答正确正确答案是：生产法标记题目信息文本二、多项选择题题目16正确获得分中的分标记题目题干保证两部门经济正常循环的条件有（? ?）选择一项或多项：A. 国际收支均衡B. 要素市场均衡?C. 金融市场均衡?D. 商品市场均衡?E. 政府收入与支出均衡反馈你的回答正确The correct answers are: 商品市场均衡, 要素市场均衡, 金融市场均衡题目17正确获得分中的分标记题目题干保证三部门经济正常循环的条件有（? ? ?）选择一项或多项：A. 国际收支均衡B. 金融市场均衡?C. 政府收入与支出均衡?D. 要素市场均衡?E. 商品市场均衡?反馈你的回答正确The correct answers are: 商品市场均衡, 要素市场均衡, 金融市场均衡, 政府收入与支出均衡题目18正确获得分中的分标记题目题干保证四部门经济正常循环的条件有（? ?）选择一项或多项：A. 商品市场均衡?B. 政府收入与支出均衡?C. 金融市场均衡?D. 国际收支均衡?E. 要素市场均衡?反馈你的回答正确The correct answers are: 商品市场均衡, 国际收支均衡, 要素市场均衡, 金融市场均衡, 政府收入与支出均衡题目19正确获得分中的分标记题目题干理解国内生产总值应注意以下问题（? ? ）选择一项或多项：A. 只包括中间产品价值B. 最终产品和劳务是当期所生产的?C. 只包括最终产品价值?D. 包括物质产品也包括劳务?E. 包括折旧?反馈你的回答正确The correct answers are: 只包括最终产品价值, 包括物质产品也包括劳务, 包括折旧, 最终产品和劳务是当期所生产的题目20正确获得分中的分标记题目题干按支出法计算GDP的主要项目有（? ? ）选择一项或多项：A. 政府购买?B. 净出口?C. 政府转移支付D. 投资支出?E. 消费支出?反馈你的回答正确The correct answers are: 消费支出, 投资支出, 政府购买, 净出口题目21正确获得分中的分标记题目题干按收入法计算GDP的主要项目有（? ? ）选择一项或多项：A. 家庭与政府支付的利息B. 雇员报酬?C. 租金收入?D. 业主收入?E. 折旧费?反馈你的回答正确The correct answers are: 雇员报酬, 业主收入, 租金收入, 折旧费题目22正确获得分中的分标记题目题干按生产法计算GDP的主要项目有（? ?）选择一项或多项：A. 第二产业?B. 第五产业C. 第一产业?D. 第四产业E. 第三产业?反馈你的回答正确The correct answers are: 第一产业, 第二产业, 第三产业题目23正确获得分中的分标记题目题干国民收入核算中的总量指标包括（? ?）选择一项或多项：A. 国内生产总值?B. 国民生产总值C. 国内生产净值?D. 个人收入?E. 国民收入?反馈你的回答正确The correct answers are: 国内生产总值, 国内生产净值, 国民收入, 个人收入题目24正确获得分中的分标记题目题干国内生产总值的缺陷（? ?）选择一项或多项：A. 不能全面反映一国经济发展的速度B. 不能准确的反映人们的福利状况?C. 不能全面反映整体经济活动?D. 不能反映经济增长效率或社会成本?E. 不能反映社会收入和财富分配状况?反馈你的回答正确The correct answers are: 不能全面反映整体经济活动, 不能反映社会收入和财富分配状况, 不能准确的反映人们的福利状况, 不能反映经济增长效率或社会成本标记题目信息文本三、判断题题目25正确获得分中的分标记题目题干个人储蓄向企业投资的转化是通过金融市场进行的。
微观经济学第七章 习题答案
MR，试求：图7—1(1)A点所对应的MR值；(2)B点所对应的MR值。
解答：(1)根据需求的价格点弹性的几何意义，可得A点的需求的价格弹性为e d ＝eq \f(15－5,5)＝2或者e d ＝eq \f(2,3－2)＝2再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d )))，则A点的MR值为MR＝2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,2)))＝1(2)与(1)类似，根据需求的价格点弹性的几何意义，可得B点的需求的价格弹性为e d ＝eq \f(15－10,10)＝eq \f(1,2)或者e d ＝eq \f(1,3－1)＝eq \f(1,2)再根据公式MR＝P eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,e d )))，则B点的MR值为MR＝1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1－\f(1,1/2)))＝－12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出：(1)长期均衡点及相应的均衡价格和均衡产量；(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线；(3)长期均衡时的利润量。
图7—2图7—3(1)长期均衡点为E点，因为在E点有MR＝LMC。
由E点出发，均衡价格为P0，均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上，SAC曲线和LAC曲线相切；SMC曲线和LMC曲线相交，且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示，即π＝[AR(Q0)－SAC(Q0)]·Q 0。
3. 已知某垄断厂商的短期总成本函数为STC＝0.1Q3－6Q2＋140Q＋3 000，反需求函数为P＝150－3.25Q。
西方经济学微观部分不完全竞争市场习题附答案
第七章不完全竞争市场一、名词解释完全垄断市场部分：完全垄断价格歧视生产者剩余一级价格歧视二级价格歧视三级价格歧视垄断利润垄断竞争市场部分：垄断竞争产品差别主观需求曲线客观需求曲线寡头垄断市场部分：寡头市场纯粹寡头差别寡头折弯的需求曲线串谋卡特尔价格领导二、选择题(一) 完全垄断市场部分知识点：完全垄断市场的条件（或称“完全垄断市场的特征”）1．下列不能成为进入一个垄断行业壁垒的是( A )。
A．垄断利润B．立法C．专利权D．资源控制2．以下最不可能成为垄断者的是( B )。
A．一个小镇上惟一的一名医生B．可口可乐公司C．某地区的电力公司D．某地区的自来水公司3．下列对垄断企业和完全竞争企业的描述中，不正确的是( C)。
A．都试图最大化利润B．都把产量确定在边际收益等于边际成本那一点C．都面对着一条完全有弹性的需求曲线D．如果边际成本超过边际收益，都将减少生产4．对一个垄断企业而言，销售额外一单位产品的边际收益等于( C )。
A．这额外一单位产品的售价B．因所有其他产品以新的更低的价格而造成的收益损失C．这额外一单位产品的售价减去因所有其他单位商品以新的更低的价格出售而造成的收益损失D．这额外一单位产品的售价减去支付给生产这一单位产品的工人的工资5．对一个垄断企业而言，边际收益小于价格，是因为( A)。
A．为了销售更多的数量，企业必须降低所有单位的价格B．它不能控制价格C．在市场价格下，企业可以销售它希望销售的任意数量D．它的产量只占市场总产量的一个很小的份额6．当发生以下哪种情况时，厂商将会倾向于进入一个行业？（ D ）A．该行业存在超额利润B．规模经济不构成一个主要的进入壁垒C．该行业的主要资源不被现存的厂商所控制D．以上全对知识点：完全垄断厂商的供给曲线和需求曲线、三条收益曲线7．垄断厂商拥有控制市场的权力，这意味着( D)。
A．垄断厂商面对一条向下倾斜的需求曲线B．如果他的产品增加一个单位，则全部产品的销售价格必须降低C．垄断厂商的边际收益曲线低于其需求曲线D．以上都正确8．一个垄断企业面对的需求曲线是( A )。
西方经济学课后习题答案-第7章
第七章1．试比较局部均衡分析和一般均衡分析。
局部均衡又被称作“孤立市场”的分析方法。
马歇尔认为，在市场经济中各种经济现象非常复杂，影响市场运作的因素很多，为使分析简化，应该采取“其他情况不变”的假设，孤立分析某种产品的市场价格和供求关系的变动，待到所有的商品价格和供求问题分析完之后，再进行综合分析，便能够得出关于市场均衡的正确结论。
在局部均衡分析中，某一市场上商品的需求和供给仅仅被看做是它本身价格的函数，其他商品的价格则假定不变，这些不变的价格仅仅影响所研究商品的供求曲线的位置。
其结论是，该市场的供求曲线的交点决定均衡价格与均衡数量。
但是，局部均衡分析虽然可以揭示商品均衡价格和数量决定的一般关系，却也显得过于简单化，它不能说明市场经济体系中均衡价格和数量决定的较为复杂的情形。
在市场体系中，各种商品的供给、需求及价格是相互影响的。
一种商品的均衡价格和均衡数量的决定，不仅取决于它本身的供求状况，而且也要受到其他与之有关的其他商品的供求状况及价格的影响。
所以，根据局部均衡分析不能解决市场经济体系中各种市场同时实现均衡的均衡价格和数量的决定问题。
于是，在西方经济学中又出现了一般均衡分析方法。
2．应用埃奇沃斯盒式图解释某一点如何表示两个消费者购买的市场产品组合。
在埃奇沃斯盒式图中，每一点都代表两个消费者的市场产品的组合。
从原点O1沿底部横轴向右和沿左面纵轴向上（如箭头所示）为甲所持有的产品；从原点O2沿上面横轴向左和沿右面纵轴向下（如箭头所示）为乙所持有的产品。
例如，A点表示食品和布的初始分配。
沿底部横轴从左向右，可以看到甲有7单位食品，沿左面纵轴向上看，又看到他有1单位布。
这样，对于甲来说，A点代表他持有的7单位食品（7F）和1单位布（1C），其余的3单位食品（3F）和5单位布（5C）则为乙所持有。
从图上查看乙持有产品的情况，则是沿上面的横轴向左看和沿右面的纵轴向下看，同样可以发现在A点乙持有3单位食品和5单位布。
西方经济学微观部分课后习题答案(高鸿业第六版)
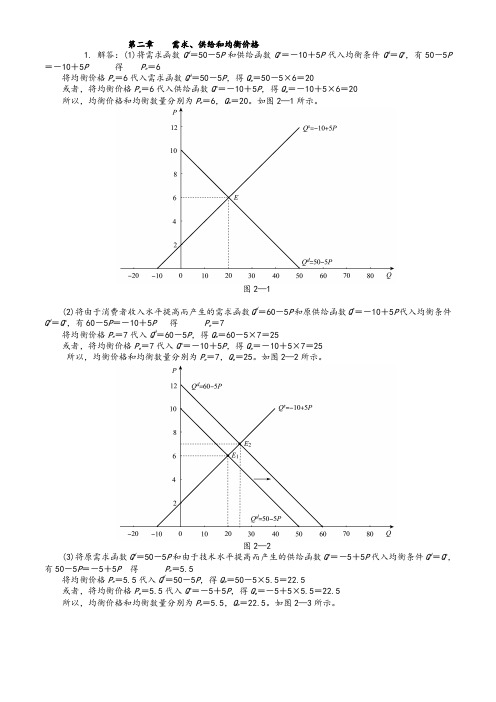
第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d＝50－5P和供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有50－5P＝－10＋5P得P e＝6将均衡价格P e＝6代入需求函数Q d＝50－5P，得Q e＝50－5×6＝20或者，将均衡价格P e＝6代入供给函数Q s＝－10＋5P，得Q e＝－10＋5×6＝20所以，均衡价格和均衡数量分别为P e＝6，Q e＝20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d＝60－5P和原供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有60－5P＝－10＋5P得P e＝7将均衡价格P e＝7代入Q d＝60－5P，得Q e＝60－5×7＝25或者，将均衡价格P e＝7代入Q s＝－10＋5P，得Q e＝－10＋5×7＝25所以,均衡价格和均衡数量分别为P e＝7，Q e＝25。
如图2—2所示。
图2—2（3)将原需求函数Q d＝50－5P和由于技术水平提高而产生的供给函数Q s＝－5＋5P代入均衡条件Q d＝Q s,有50－5P＝－5＋5P得P e＝5。
5将均衡价格P e＝5。
5代入Q d＝50－5P，得Q e＝50－5×5。
5＝22。
5或者,将均衡价格P e＝5.5代入Q s＝－5＋5P,得Q e＝－5＋5×5。
5＝22.5所以,均衡价格和均衡数量分别为P e＝5。
5，Q e＝22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说，静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例，在图2—1中,均衡点E 就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此，给定的供求力量分别用给定的供给函数Q s ＝－10＋5P 和需求函数Q d ＝50－5P 表示，均衡点E 具有的特征是：均衡价格P e ＝6，且当P e ＝6时，有Q d ＝Q s ＝Q e ＝20；同时，均衡数量Q e ＝20，且当Q e ＝20时，有P d ＝P s ＝P e ＝6。
微观经济学第第七章课后答案资料
微观经济学第第七章课后答案第7章 课后练习答案一、基本概念 1、一般均衡：经济中所有经济单位及其市场同时处于均衡的一种状态。
2、帕累托最优条件：1）交换的帕累托最化条件：A B XY XY MRS MRS = ；2）生产的帕累托最优条件：C D LK LK MRTS MRTS = ；3）交换和生产的帕累托最优条件：XY XY MRS MRT = 3、帕累托改进：在资源既定的情况下，如果经济社会通过资源重新配置可以在不使得他人境况受到损害的条件下使得某些人的境况得到改善，则社会福利得到增进。
二、分析简答1、什么是局部均衡和一般均衡，两者的区别和联系是什么？答：局部均衡是指：仅仅是某一种产品实现了均衡或某一种市场(例如，产品市场或要素市场)实现了均衡。
一般均衡是指经济中所有经济单位及其市场同时处于均衡的一种状态。
局部均衡把市场上其他商品和生产要素的数量与价格对这种商品或生产要素价格的影响忽略不计或视为不变，即假定这一商品或生产要素的价格只取决于它本身的供求状况，而不受其他商品的价格和供求状况的影响。
而在一般均衡分析中，不仅要分析影响该商品价格变动的供求关系，还要分析影响该商品生产的生产要素市场、消费者收入等多种因素的影响，即把经济中的所有经济单位和所有市场联系起来加以考虑和分析。
2、为什么完全竞争可以实现帕累托最优所需具备的三个条件？完全竞争经济在一定的假设条件下存在着一般均衡，即存在一组价格，在该组价格下市场中的供求平衡。
假设该组价格为Px ，P Y ，…，P L ，P K ，…。
其中P X ，P Y ，…表示商品X ，Y ，…的均衡价格；P L ，P K ，…表示要素L ，K ，…的均衡价格。
在完全竞争条件下，每个消费者和生产者都是价格的接受者，消费者在既定价格下追求自身效用的最大化，生产者在既定价格下追求自身利润的最大化。
对于消费者而言，任意一个消费者在完全竞争经济中效用最大化的条件是任意两种商品的边际替代率等于两种商品的价格比率，对于消费者C ，有：/A XY X Y MRS P P = ；对于消费者B ，有： /B XY X Y MRS P P =；将以上两式整理可得：A B XY XY MRS MRS =；此公式就是交换的帕累托最优条件。
曼昆《经济学原理》第6版 微观经济学分册 第7章 课后习题答案p157p159
第三篇市场和福利第七章消费者、生产者与市场效率问题与应用1．Melissa用120美元购买了一个iPod，并得到了80美元的消费者剩余。
A．她的支付意愿是多少？答：消费者剩余等于支付意愿减去付出的价格。
因此，梅莉莎须支付200 美元($120 + $80)。
B．如果她在降价销售时买了售价为90美元的iPod，她的消费者剩余会是多少？答：此时，她的消费者剩余为：200-90 =110 美元。
C．如果iPod的价格是250美元，她的消费者剩余会是多少？答：如果iPod 的价格是250 美元，其价格大于梅莉莎的支付愿意，因此她不会再买，这时的消费者剩余就为零。
2．加利福尼亚早来的寒流使柠檬变酸。
柠檬市场上消费者剩余会有什么变动？柠檬水市场上消费者剩余会有什么变动？用图形说明你的答案。
答：柠檬变酸，消费者对柠檬的评价下降，需求曲线向左下方移动。
在其他条件不变的情况下，消费者剩余减少。
如图7－2(a)所示，柠檬质量下降，使需求曲线从D1下降到D 2，△APE是原先的消费者剩余，△A′P′E′是变动后的消费者剩余，△APE>△A′P′E′。
由于柠檬价格的下降，柠檬水的投入成本减少，柠檬水的价格也下降。
在其他条件不变的情况下，柠檬水市场上消费者剩余增加，如图7－2(b)所示。
图7－2 寒流的影响3．假设对法国面包的需求增加。
在法国面包市场上，生产者剩余会发生什么变动？在面粉市场上，生产者剩余会发生什么变动？用图形说明你的答案。
答：由于需求增加，在其他条件不变的情况下，法国面包的价格会上升，市场上的生产者剩余增加。
如图7 －3(a)，价格从P1 上升到P2 ，销量从Q 1上升到Q 2，生产者剩余从面积P1BE1增加到面积P2BE2 。
由于面包产量上升，它的生产要素面粉的需求量也会上升。
在其他条件不变的情况下，面粉价格上升，市场上的生产者剩余增加。
如图7－3(b)所示，生产者剩余从面积P1BE1增加到面积P2BE2 。
西方经济学微观部分课后习题答案(高鸿业第六版)
第二章需求、供给和均衡价格1. 解答：(1)将需求函数Q d＝50－5P和供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有50－5P ＝－10＋5P得P e＝6将均衡价格P e＝6代入需求函数Q d＝50－5P，得Q e＝50－5×6＝20或者，将均衡价格P e＝6代入供给函数Q s＝－10＋5P，得Q e＝－10＋5×6＝20所以，均衡价格和均衡数量分别为P e＝6，Q e＝20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d＝60－5P和原供给函数Q s＝－10＋5P代入均衡条件Q d＝Q s，有60－5P＝－10＋5P得P e＝7将均衡价格P e＝7代入Q d＝60－5P，得Q e＝60－5×7＝25或者，将均衡价格P e＝7代入Q s＝－10＋5P，得Q e＝－10＋5×7＝25所以，均衡价格和均衡数量分别为P e＝7，Q e＝25。
如图2—2所示。
图2—2(3)将原需求函数Q d＝50－5P和由于技术水平提高而产生的供给函数Q s＝－5＋5P代入均衡条件Q d＝Q s，有50－5P＝－5＋5P得P e＝5.5将均衡价格P e＝5.5代入Q d＝50－5P，得Q e＝50－5×5.5＝22.5或者，将均衡价格P e＝5.5代入Q s＝－5＋5P，得Q e＝－5＋5×5.5＝22.5所以，均衡价格和均衡数量分别为P e＝5.5，Q e＝22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说，静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例，在图2—1中，均衡点E 就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此，给定的供求力量分别用给定的供给函数Q s ＝－10＋5P 和需求函数Q d＝50－5P 表示，均衡点E 具有的特征是：均衡价格P e ＝6，且当P e ＝6时，有Q d ＝Q s＝Q e ＝20；同时，均衡数量Q e ＝20，且当Q e ＝20时，有P d ＝P s ＝P e ＝6。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七章 不完全竞争的市场1、根据图1-31（即教材第257页图7-22）中线性需求曲线d 和相应的边际收益曲线MR ，试求：（1）A 点所对应的MR 值； （2）B 点所对应的MR 值.解答：（1）根据需求的价格点弹性的几何意义，可得A 点的需求的价格弹性为：25)515(=-=d e 或者 2)23(2=-=d e 再根据公式MR=P （d e 11-），则A 点的MR 值为：MR=2×（2×1/2）=1（2）与（1）类似，根据需求的价格点弹性的几何意义，可得B 点的需求的价格弹性为：21101015=-=d e 或者 21131=-=d e再根据公式MR=(d e 11-)，则B 点的MR 值为：)2/111(1-⨯=MR =-12、图1-39（即教材第257页图7-23）是某垄断厂商的长期成本曲线、需求曲线和收益曲线.试在图中标出：(1)长期均衡点及相应的均衡价格和均衡产量；（2）长期均衡时代表最优生产规模的SAC曲线和SMC曲线；（3）长期均衡时的利润量.解答：本题的作图结果如图1-40所示：（1）长期均衡点为E点，因为，在E点有MR=LMC.由E点出发，均衡价格为P0，均衡数量为Q0 .(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图所示.在Q0 的产量上，SAC曲线和SMC曲线相切；SMC曲线和LMC曲线相交，且同时与MR曲线相交.(3)长期均衡时的利润量有图中阴影部分的面积表示，即л=(AR(Q0)-SAC(Q0)Q03、已知某垄断厂商的短期成本函数为STC=0.1Q3-6Q2+14Q+3000，反需求函数为P=150-3.25Q求：该垄断厂商的短期均衡产量与均衡价格.解答：因为SMC=dSTC/dQ=0.3Q2-12Q+140且由TR=P(Q)Q=(150-3.25Q)Q=150Q-3.25Q2得出MR=150-6.5Q根据利润最大化的原则MR=SMC0.3Q2-12Q+140=150-6.5Q解得Q=20（负值舍去）以Q=20代人反需求函数，得P=150-3.25Q=85所以均衡产量为20 均衡价格为854、已知某垄断厂商的成本函数为TC=0.6Q2+3Q+2，反需求函数为P=8-0.4Q.求：（1）该厂商实现利润最大化时的产量、价格、收益和利润.（2）该厂商实现收益最大化的产量、价格、收益和利润.（3）比较（1）和（2）的结果.dTC解答：（1）由题意可得：MC=32.1+=QdQ且MR=8-0.8Q于是，根据利润最大化原则MR=MC有：8-0.8Q=1.2Q+3解得 Q=2.5以Q=2.5代入反需求函数P=8-0.4Q，得：P=8-0.4×2.5=7以Q=2.5和P=7代入利润等式，有：л=TR-TC=PQ-TC=（7×0.25）-（0.6×2.52+2）=17.5-13.25=4.25所以，当该垄断厂商实现利润最大化时，其产量Q=2.5，价格P=7，收益TR=17.5，利润л=4.25（2）由已知条件可得总收益函数为： TR=P （Q ）Q=（8-0.4Q ）Q=8Q-0.4Q2令08.08:,0=-==Q dQdTRdQ dTR即有 解得Q=10 且8.0-=dQdTR＜0 所以，当Q=10时，TR 值达最大值. 以Q=10代入反需求函数P=8-0.4Q ，得： P=8-0.4×10=4以Q=10，P=4代入利润等式，有》 л=TR-TC=PQ-TC=（4×10）-（0.6×102+3×10+2） =40-92=-52所以，当该垄断厂商实现收益最大化时，其产量Q=10，价格P=4，收益TR=40，利润л=-52，即该厂商的亏损量为52.（3）通过比较（1）和（2）可知：将该垄断厂商实现最大化的结果与实现收益最大化的结果相比较，该厂商实现利润最大化时的产量较低（因为2.25<10），价格较高（因为7>4），收益较少（因为17.5<40），利润较大（因为4.25>-52）.显然，理性的垄断厂商总是以利润最大化作为生产目标，而不是将收益最大化作为生产目标.追求利润最大化的垄断厂商总是以较高的垄断价格和较低的产量，来获得最大的利润.5．已知某垄断厂商的反需求函数为P=100-2Q+2A ，成本函数为TC=3Q 2+20Q+A ，其中，A 表示厂商的广告支出. 求：该厂商实现利润最大化时Q 、P 和A 的值. 解答：由题意可得以下的利润等式： л=P.Q-TC=（100-2Q+2A ）Q-（3Q 2+20Q+A ） =100Q-2Q 2+2A Q-3Q 2-20Q-A =80Q-5Q 2+2A Q-A将以上利润函数л（Q ，A ）分别对Q 、A 求偏倒数，构成利润最大化的一阶条件如下：+-=∂Q dQ1080π2A =0 0121=-=∂∂Q A Aπ求以上方程组的解：由（2）得A =Q ，代入（1）得： 80-10Q+20Q=0 Q=10 A=100在此略去对利润在最大化的二阶条件的讨论. 以Q=10，A=100代入反需求函数，得： P=100-2Q+2A =100-2×10+2×10=100所以，该垄断厂商实现利润最大化的时的产量Q=10，价格P=100，广告支出为A=100.6.已知某垄断厂商利用一个工厂生产一种产品，其产品在两个分割的市场上出售，他的成本函数为TC=Q2+40Q，两个市场的需求函数分别为Q1=12-0.1P1，Q2=20-0.4P2.求：(1)当该厂商实行三级价格歧视时，他追求利润最大化前提下的两市场各自的销售量、价格以及厂商的总利润.(2)当该厂商在两个市场实行统一的价格时，他追求利润最大化前提下的销售量、价格以及厂商的总利润.(3)比较（1）和（2）的结果.解答：（1）由第一个市场的需求函数Q1=12-0.1P1可知，该市场的反需求函数为P1=120-10Q1，边际收益函数为MR1=120-20Q1.同理，由第二个市场的需求函数Q2=20-0.4P2可知，该市场的反需求函数为P2=50-2.5Q2，边际收益函数为MR2=50-5Q2.而且，市场需求函数Q=Q1+Q2=（12-0.1P）+（20-0.4P）=32-0.5P，且市场反需求函数为P=64-2Q，市场的边际收益函数为MR=64-4Q.dTC.此外，厂商生产的边际成本函数MC=402+=QdQ该厂商实行三级价格歧视时利润最大化的原则可以写为MR1=MR2=MC. 于是：关于第一个市场：根据MR1=MC，有：120-20Q1=2Q+40 即 22Q1+2Q2=80关于第二个市场：根据MR2=MC，有：50-5Q2=2Q+40 即 2Q1+7Q2=10由以上关于Q1、Q2的两个方程可得，厂商在两个市场上的销售量分别为：Q1=3.6 Q2=0.4P1=84，P2=49.在实行三级价格歧视的时候，厂商的总利润为：л=（TR1+TR2）-TC=P1Q1+P2Q2-（Q1+Q2）2-40（Q1+Q2）=84×3.6+49×0.4-42-40×4=146（2）当该厂商在两个上实行统一的价格时，根据利润最大化的原则即该统一市场的MR=MC有：64-4Q=2Q+40解得 Q=4以Q=4代入市场反需求函数P=64-2Q，得：P=56于是，厂商的利润为：л=P.Q-TC=(56×4)-(42+40×4)=48所以，当该垄断厂商在两个市场上实行统一的价格时，他追求利润最大化的销售量为Q=4，价格为P=56，总的利润为л=48.（3）比较以上（1）和（2）的结果，可以清楚地看到，将该垄断厂商实行三级价格歧视和在两个市场实行统一作价的两种做法相比较，他在两个市场制定不同的价格实行实行三级价格歧视时所获得的利润大于在两个市场实行统一定价时所获得的利润（因为146>48）.这一结果表明进行三级价格歧视要比不这样做更为有利可图.7、已知某垄断竞争厂商的长期成本函数为LTC=0.001Q3-0.51Q2+200Q；如果该产品的生产集团内所有的厂商都按照相同的比例调整价格，那么，每个厂商的份额需求曲线（或实际需求曲线）为Ｐ＝238-0.5Ｑ.求：（1）该厂商长期均衡时的产量与价格.（2）该厂商长期均衡时主观需求曲线上的需求的价格点弹性值（保持整数部分）.（3）如果该厂商的主观需求曲线是线性的，推导该厂商长期均衡时的主观需求的函数.解答：（1）由题意可得：ＬＡＣ＝ＬTＣ／Ｑ＝0.001Ｑ2－0.51Ｑ+200ＬＭＣ＝dLTC/dQ=0.003Q2-1.02Q+200且已知与份额需求Ｄ曲线相对应的反需求函数为Ｐ＝238-0.5Ｑ.由于在垄断竞争厂商利润最大化的长期均衡时，Ｄ曲线与ＬＡＣ曲线相交（因为л＝0），即有ＬＡＣ＝Ｐ，于是有：001Ｑ2-0.51Ｑ+200＝238-0.5Ｑ解得Ｑ＝200（负值舍去了）以Ｑ＝200代入份额需求函数，得：Ｐ＝238-0.5×200＝138所以，该垄断竞争厂商实现利润最大化长期均衡时的产量Ｑ＝200，价格Ｐ＝138.（2）由Ｑ＝200代入长期边际成本ＬＭＣ函数，得：ＬＭＣ＝0.003×2002－1.02×200+200＝116因为厂商实现长期利润最大化时必有ＭＲ＝ＬＭＣ，所以，亦有ＭＲ＝116.再根据公式MR=P （de 11-），得： 116=138（d e 11-） 解得d e ≈6所以，厂商长期均衡时主观需求曲线d 上的需求的价格点弹性d e ≈6.（3）令该厂商的线性的主观需求d 曲线上的需求的函数形式 P=A-BQ ，其中，A 表示该线性需求d 曲线的纵截距，-B 表示斜率.下面，分别求A 值和B 值. 根据线性需求曲线的点弹性的几何意义，可以有P A P e d -= ，其中，P 表示线性需求d 曲线上某一点所对应的价格水平.于是，在该厂商实现长期均衡时，由PA P e d -=，得： 6=138138-A 解得 A=161此外，根据几何意义，在该厂商实现长期均衡时，线性主观需求d 曲线的斜率的绝对值可以表示为： B=Q P A -=115.0200138161=- 于是，该垄断竞争厂商实现长期均衡时的线性主观需求函数为：P=A-BQ=161-0.115Q或者 Q=115.0161P - 8.某家灯商的广告对其需求的影响为 P=88-2Q+2A对其成本的影响为C=3Q 2+8Q+A其中 A 为广告费用。
（1）求无广告情况下，利润最大化时的产量、价格与利润（2）求有广告情况下，利润最大化时的产量、价格、广告费与利润（3）比较（1）和（2）的结果解答：（1）若无广告，即A=0，则厂商的利润函数为π(Q)=P(Q)*Q-C(Q)=(88-2Q)Q-(3Q 2+8Q)=88Q-2Q 2-3Q 2-8Q=80Q-5Q 2d π(Q)/d(Q)=80-10Q=0解得Q *=8所以利润最大化时的产量Q *=8P *=88-2Q=88-2*8=72π*=80Q-5Q2=320（2）若有广告，即A>0，即厂商的利润函数为π(Q，A)=P(Q,A)*Q-C(Q,A)=(88-2Q+2A)*Q-(3Q2+8Q+A)=80Q-5Q2+2Q A-A分别对Q,A微分等于0得80-10Q+2A=0Q/A-1=0得出Q=A解得：Q*=10,A*=100代人需求函数和利润函数，有P*=88-2Q+2A=88π*=80Q-5Q2+2Q A-A=400(3)比较以上（1）与（2）的结果可知，此厂商在有广告的情况下，由于支出100的广告费，相应的价格水平由原先无广告时的72上升为88，相应的产量水平由无广告时的8上升为10，相应的利润也由原来无广告时的320增加为4009、用图说明垄断厂商短期和长期均衡的形成及其条件.解答：要点如下：（1）关于垄断厂商的短期均衡.垄断厂商在短期内是在给定的生产规模下，通过产量和价格的调整来实现MR=SMC的利润最大化原则.如图1-41所示（书P83），垄断厂商根据MR=SMC的原则，将产量和价格分别调整到P0和Q0，在均衡产量Q0上，垄断厂商可以赢利即л>0，如分图(a)所示，此时AR>SAC，其最大的利润相当与图中的阴影部分面积；垄断厂商也可以亏损即л＜0，如分图(b)所示，此时，AR＜SAC，其最大的亏待量相当与图中的阴影部分.在亏损的场合，垄断厂商需要根据AR与AVC的比较，来决定是否继续生产：当AR>AVC时，垄断厂商则继续生产；当AR＜AVC时，垄断厂商必须停产；而当AR=AVC 时，则垄断厂商处于生产与不生产的临界点.在分图(b)中，由于AR ＜AVC，故该垄断厂商是停产的.由此，可得垄断厂商短期均衡的条件是： MR=SMC，其利润可以大于零，或小于零，或等于零.(2)关于垄断厂商的长期均衡.在长期，垄断厂商是根据MR=LMC的利润最大化原则来确定产量和价格的，而且，垄断厂商还通过选择最优的生产规模来生产长期均衡产量.所以，垄断厂商在长期可以获得比短期更大的利润.在图1-42中，在市场需求状况和厂商需求技术状况给定的条件下，先假定垄断厂商处于短期生产，尤其要注意的是，其生产规模是给定的，以SAC0曲线和SMC0所代表，于是，根据MR=SMC的短期利润最大化原则，垄断厂商将短期均衡产量和价格分别调整为Q0和P0，并由此获得短期润相当于图中较小的那块阴影部分的面积P0ABC.下面，再假定垄断厂商处于长期生产状态，则垄断厂商首先根据MR=LMC的长期利润最大化的原则确定长期的均衡产量和价格分别为Q*和P*，然后，垄断厂商调整全部生产要素的数量，选择最优的生产规模(以SAC*曲线和SMC*曲线所表示)，来生产长期均衡产量Q*.由此，垄断厂商获得的长期利润相当于图中较大的阴影部分的面积P*DE0F.显然，由于垄断厂商在长期可以选择最优的生产规模，而在短期只能在给定的生产规模下生产，所以，垄断厂商的长期利润总是大于短期利润.此外，在垄断市场上，即使是长期，也总是假定不可能有新厂商加入，因而垄断厂商可以保持其高额的垄断利润.由此可得，垄断厂商长期均衡的条件是：MR=LMC=SMC，且л>0.10、试述古诺模型的主要内容和结论.解答：要点如下：（1）在分析寡头市场的厂商行为的模型时，必须首先要掌握每一个模型的假设条件.古诺模型假设是：第一，两个寡头厂商都是对方行为的消极的追随者，也就是说，每一个厂商都是在对方确定了利润最大化的产量的前提下，再根据留给自己的的市场需求份额来决定自己的利润最大化的产量；第二，市场的需求曲线是线性的，而且两个厂商都准确地知道市场的需求状况；第三，两个厂商生产和销售相同的产品，且生产成本为零，于是，它们所追求的利润最大化目标也就成了追求收益最大化的目标.（2）在（1）中的假设条件下，古诺模型的分析所得的结论为：令市场容量或机会产量为Q O ，则每个寡头厂商的均衡产量为31Q O ，行业的均衡产量为32Q O ，.如果将以上的结论推广到m 个寡头厂商的场合，则每个寡头厂商的均衡产量为11+m Q O ，行业的均衡总产量为1+m m Q O . （3）关于古诺模型的计算题中，关键要求很好西理解并运用每一个寡头厂商的反应函数：首先，从每个寡头厂商的各自追求自己利润最大化的行为模型中求出每个厂商的反映函数.所谓反应函数就是每一个厂商的的最优产量都是其他厂商的产量函数，即Q i=f(Q j )，i 、j=1、2，i j ≠.然后，将所有厂商的反应函数联立成立一个方程组，并求解多个厂商的产量.最后所求出的多个厂商的产量就是古诺模型的均衡解，它一定满足（2）中关于古诺模型一般解的要求.在整个古诺模型的求解过程中，始终体现了该模型对于单个厂商的行为假设：每一个厂商都是以积极地以自己的产量去适应对方已确定的利润最大化的产量.11、弯折的需求曲线是如何解释寡头市场上的价格刚性现象的？ 解答：要点如下：（1）弯折的需求曲线模型主要是用来寡头市场上价格的刚性的.该模型的基本假设条件是：若行业中的一个寡头厂商提高价格，则其他的厂商都不会跟着提价，这便使得单独提价的厂商的销售量大幅度地减少；相反，若行业中的一个寡头厂商降低价格，则其他的厂商会将价格降到同一水平，这便使得首先单独降价的厂商的销售量的增加幅度是有限的.（2）由以上（1）的假设条件，便可以推导出单个寡头厂商弯折的需求曲线：在这条弯折的需求曲线上，对应于单个厂商的单独提价部分，是该厂商的主观的d需求曲线的一部分；对应于单个厂商首先降价而后其他厂商都降价的不分，则是该厂商的实际需求份额D曲线.于是，在d需求曲线和D需求曲线的交接处存在一个折点，这便形成了一条弯折的需求曲线.在折点以上的部分是d需求曲线，其较平坦即弹性较大；在折点以下的部分是D需求曲线，其较陡峭即弹性较小. （3）与（2）中的弯折的需求曲线相适应，便得到间断的边际收益MR曲线.换言之，在需求曲线的折点所对应的产量上，边际收益MR 曲线是间断的，MR值存在一个在上限与下限之间的波动范围.（4）正是由于（3），所以，在需求曲线的折点所对应的产量上，只要边际成本MC曲线的位置移动的范围在边际收益MR曲线的间断范围内，厂商始终可以实现MR=MC的利润最大化的目标.这也就是说，如果厂商在是生产过程中因技术、成本等因素导致边际成本MC发生变化，但只要这种变化使得MC曲线的波动不超出间断的边际收益MR曲线的上限与下限，那就始终可以在相同的产量和相同的价格水平上实现MR=MC的利润最大化原则.至此，弯折的需求曲线便解释了寡头市场上的价格刚性现象.。