盘式制动器制动计算
(完整版)盘式制动器制动计算

前特定车轴可能的最大制动力计算公式如下:
F
这里:FA=^桥可能的总制动力 (N);Mwdyn动态车桥质量(kg);g=重力加速度(s/m2); 卩f=轮胎与地面间摩擦系数;
制动力矩
决定了哪个车轮需要制动来产生足够的制动力,每个车轮扭矩的要求需要确定。对于某些
静态车桥负载分配
丸=屮
M
这里:Mf=静态后车桥负载(kg);M车辆总质量(kg);¥=静态车桥负载分配系数 注:对于满载和空载的车辆的变化往往是不同的。
相对重心高度
h
这里:h=重心到地面的垂直距离(m);wb=l由距;X=相对重心高度
动态车桥负载(仅适用于两轴车辆)
制动过程中车桥负载的变化与哪个车桥制动无关。匕们只依赖于静态负载条件和减速度
注:所不同的是,由于全盘式制动器是全表面接触的,但制动片通常不并是一个扇形体, 而两侧是方形的(由于摩擦力的变化,实际上此不同并不是很重要)。
夹紧力
C
.Uf n
这里:C=制动夹紧力(N);T=制动力矩(Nm;re=有效半径(m);卩f=制动片内衬材料与 制动盘材料的摩擦系数;n=摩擦面数目;
夹紧负荷被假设等效地作用在所有的摩擦表面。对于干盘式制动器,是否是滑动式或对置
n
Time (sees)
比圧=¥
((v/a)
这里:aave=停止过程平均的减速度(g);v=测试速度(m/s);a=减速度(MFDD(g);g=重力加速度(s/m2);
5
这里:s=停止距离(m;v=测试速度(m/s);aave=停止过程平均的减速度(g);g=重力
加速度(s/m2);
下图显示71/320/EEC和ECE R13的测试要求。
制动器设计-计算说明书

制动器设计-计算说明书三、课程设计过程(一)设计制动器的要求:1、具有良好的制动效能—其评价指标有:制动距离、制动减速度、制动力和制动时间。
2、操纵轻便—即操纵制动系统所需的力不应过大。
对于人力液压制动系最大踏板力不大于(500N )(轿车)和700N (货车),踏板行程货车不大于150mm ,轿车不大于120mm 。
3、制动稳定性好—即制动时,前后车轮制动力分配合理,左右车轮上的制动力矩基本相等,汽车不跑偏、不甩尾;磨损后间隙应能调整!4、制动平顺性好—制动力矩能迅速而平稳的增加,也能迅速而彻底的解除。
5、散热性好—即连续制动好,摩擦片的抗“热衰退”能力要高(指摩擦片抵抗因高温分解变质引起的摩擦系数降低);水湿后恢复能力快。
6、对挂车的制动系,还要求挂车的制动作用略早于主车;挂车自行脱钩时能自动进行应急制动。
(二)制动器设计的计算过程:设计条件:车重2t ,重量分配60%、40%,轮胎型175/75R14,时速70km/h ,最大刹车距离11m 。
1. 汽车所需制动力矩的计算根据已知条件,汽车所需制动力矩:M=G/g ·j ·r k (N ·m ) 206.321j )(v S ?=(m/s 2)式中:r k —轮胎最大半径 (m);S —实际制动距离 (m);v 0 —制动初速度 (km/h)。
217018211 3.6j ??=?=(m/s 2) m=G/g=2000kg查表可知,r k 取0.300m 。
M=G/g ·j ·r k =2000·18·0.300=10800(N ·m )前轮子上的制动器所需提供的制动力矩:M ’=M/2?60%=3240(N ·m )为确保安全起见,取安全系数为 1.20,则M ’’=1.20M ’=3888(N ·m )2. 制动器主要参数的确定(1)制动盘的直径D制动盘直径D 希望尽量大些,这时制动盘的有效半径得以增大,就可以降低制动钳的夹紧力,降低摩擦衬块的单位压力和工作温度。
制动器的设计与计算.

第四节 制动器的设计与计算一、鼓式制动器的设计计算1.压力沿衬片长度方向的分布规律除摩擦衬片因有弹性容易变形外,制动鼓、蹄片和支承也有变形,所以计算法向压力在摩擦衬片上的分布规律比较困难。
通常只考虑衬片径向变形的影响,其它零件变形的影响较小而忽略不计。
制动蹄有一个自由度和两个自由度之分。
首先计算有两个自由度的紧蹄摩擦衬片的径向变形规律。
如图8-8a 所示,将坐标原点取在制动鼓中心O 点。
1y 坐标轴线通过蹄片的瞬时转动中心1A 点。
制动时,由于摩擦衬片变形,蹄片一面绕瞬时转动中心转动,同时还顺着摩擦力作用的方向沿支承面移动。
结果蹄片中心位于1O 点,因而未变形的摩擦衬片的表面轮廓(11E E 线),就沿1OO 方向移动进入制动鼓内。
显然,表面上所有点在这个方向上的变形是一样的。
位于半径1OB 上的任意点1B 的变形就是11B B '线段,所以同样一些点的径向变形1δ为 111C B =δ≈111cos ψB B '考虑到︒-+=90)(111αϕψ和max 1111δ=='OO B B ,所以对于紧蹄的径向变形1δ和压图8—8 计算摩擦衬片径向变形简图a)有两个自由度的紧蹄 b)有一个自由度的紧蹄力1p 为:⎭⎬⎫+=+=)sin()sin(11max 1111max 11ϕαϕαδδp p (8-1)式中,1α为任意半径1OB 和1y 轴之间的夹角;1ψ为半径1OB 和最大压力线1OO 之间的夹角;1ϕ为1x 轴和最大压力线1OO 之间的夹角。
其次计算有一个自由度的紧蹄摩擦衬片的径向变形规律。
如图8-8b 所示,此时蹄片在张开力和摩擦力作用下,绕支承销1A 转动γd 角。
摩擦衬片表面任意点1B 沿蹄片转动的切线方向的变形就是线段11B B ',其径向变形分量是这个线段在半径1OB 延长线上的投影,即为11C B 线段。
由于γd 很小,可认为︒='∠90111B B A ,故所求摩擦衬片的变形应为 γγγδd B A B B C B 111111111sin sin ='==考虑到1OA ≈R OB =1,那么分析等腰三角形11OB A ,则有γαsin sin 11RB A =,所以表面的径向变形和压力为⎭⎬⎫==αγαδsin sin max 11p p d R (8-2)综上所述可知,新蹄片压力沿摩擦衬片长度的分布符合正弦曲线规律,可用式(8-1)和式(8-2)计算。
盘式制动器制动计算

盘式制动器制动计算
1.制动力矩计算
制动力矩是盘式制动器产生制动力的重要指标,是制动器设计的基础
参数。
制动力矩的计算可以通过以下公式进行:
T=Fr*r
其中,T为制动力矩,Fr为制动力,r为制动器半径。
制动力的计算
涉及到车辆的质量、速度和制动时间等因素,常用的计算公式为:Fr=m*a/n
其中,m为车辆的质量,a为减速度,n为制动数(通常取2)。
2.摩擦力计算
Ff=μ*N
其中,Ff为摩擦力,μ为摩擦系数,N为垂直于制动盘方向的力。
摩擦系数是制动材料的重要参数,需要通过试验或参考相关文献进行确定。
3.温升计算
ΔT=Q/(m*Cp)
其中,ΔT为温升,Q为制动器吸收的热量,m为制动器的质量,Cp
为制动器的比热容。
制动器吸收的热量可以通过以下公式计算:Q=Ff*v*t
其中,v为车辆的速度,t为制动时间。
4.设计参数计算
A=T/(μ*p)
其中,A为制动器的有效面积,p为盘式制动器的接触压力。
以上为盘式制动器制动计算的主要内容,通过这些计算,可以得到盘
式制动器的设计参数和性能参数,实现对盘式制动器进行合理设计和选型。
同时,根据实际情况和需求,还需要考虑制动器的热稳定性、耐磨性、抗
褪色性等因素,在设计和选用制动器时综合考虑,以确保制动器的安全可
靠性和使用寿命。
最新鼓改盘制动力计算

制动力计算制动器最大制动力计算制动系统的主要参数见表2。
表2 制动系统的主要参数设在制动踏板上施加的力为F 0时前、后制动器产生的制动力分别为F μ1和F μ2,则前、后制动器制动力与施加在踏板上的力之比为(按F 0=500N 时的助力比计算): 1)前制动器1)VS (R r1aC1HzRZ1n μhydr μmech l l F F K i A A21011+⋅⋅⋅⋅⋅⋅⋅==ημ=)13.3(38811176.00.4453.2854285.085.00.806.323+⨯⨯⨯⨯⨯⨯⨯ =352)后制动器1)VS (R r2aC2HzRZ2n μhydr μmech l l F F K i A A21022+⋅⋅⋅⋅⋅⋅⋅==ημ=)13.3(38813676.00.4455.1133285.085.00.806.323+⨯⨯⨯⨯⨯⨯⨯ =17由于国家法规规定F 0≤500N ,所以前、后制动器的最大制动力F μ1max 和F μ2max 分别为 F μ1max =500N ·K 1=500N ×35=17500N (1) F μ2max =500N ·K 2=500N ×17=8500N (2)表3 整车参数由汽车理论知识可知,汽车在附着系数为ϕ的道路制动时,当前、后车轮即将抱死时有最大的制动力,这时前、后车轮的制动力等于前、后轴的附着力。
前、后轴的附着力F ϕ1和F ϕ2分别为F ϕ1=F z1ϕ=()ϕϕg h b LG+ (3) F ϕ2=F z2ϕ=()ϕϕg h a LG- (4) 式(3)和式(4)中,F z1—前轴地面法向反力; F z2—后轴地面法向反力;G —汽车重量;a —质心与前轴距离;b —质心与后轴距离; ϕ—路面附着系数; h g —质心高度。
式(3)为一元二次函数,在0<ϕ<1时,F ϕ1随ϕ的增大而增大。
因道路(沥青或混凝土)的峰值附着系数一般为0.8~0.9,取ϕ=0.9,作为F ϕ1的最大值。
制动器的设计计算部分

制动器的设计计算部分制动器是用来控制或减速机械设备运动的装置。
它通常由摩擦垫、压力单元、驱动装置和控制装置组成。
制动器的设计计算部分包括静态设计与动态设计两个方面。
静态设计主要涉及计算所需的制动力和摩擦垫的尺寸,而动态设计则涉及制动器在运行期间的热量分布和冷却。
在进行静态设计计算之前,首先需要确定制动器所需的制动力。
制动器的制动力通常由下述式子计算:制动力=需要减速度×机械设备的质量其中,需要减速度是由系统要求或运行条件决定的。
机械设备的质量可以通过实际测量或通过计算机辅助设计软件进行估算。
此外,制动器还需要考虑一些额外的因素,如摩擦系数和安全系数,以确保制动器的可靠性和安全性。
在确定制动力后,需要计算摩擦垫的尺寸。
摩擦垫的尺寸取决于制动器的类型和具体应用。
常见的制动器类型包括盘式制动器和鼓式制动器。
对于盘式制动器,摩擦垫通常由摩擦面的直径和宽度来确定。
对于鼓式制动器,摩擦垫的尺寸通常由鼓面的直径和摩擦面的长度来决定。
与摩擦垫尺寸相关的参数还包括摩擦垫的摩擦系数和最大摩擦温度。
摩擦系数表示摩擦垫在制动时的摩擦性能,其数值通常由摩擦材料的选择决定。
最大摩擦温度是指制动器在运行期间可能达到的最高温度,该温度主要取决于摩擦材料和运行工况。
在动态设计方面,制动器的热量分布和冷却是设计中的重要考虑因素。
当制动器运行一段时间后,摩擦垫会产生大量热量,如果不能及时散热,可能会导致制动性能下降、摩擦垫老化或甚至引发火灾。
因此,制动器的设计需要考虑散热系统,以保持摩擦垫的正常工作温度。
散热系统通常包括散热片或散热鳍片,以增加散热面积,帮助热量的有效传递。
此外,制动器还可以采用风冷式冷却系统,通过引入外部冷气来加速热量的散发。
冷却系统的设计需要考虑风量、风速和冷却材料的选择等因素。
综上所述,制动器的设计计算部分涉及静态设计和动态设计两个方面。
静态设计主要包括计算制动力和摩擦垫尺寸,而动态设计则涉及制动器的热量分布和冷却。
盘式制动器制动计算

盘式制动器制动计算盘式制动器是一种常见的机械制动装置,广泛应用于各种车辆和机器中。
它的基本原理是通过摩擦产生的力矩将转动的机械设备停下来。
在进行盘式制动器的制动计算时,需要考虑一些关键参数,包括制动力,制动压力,摩擦片的摩擦系数以及制动盘的参数等。
首先,需要计算出所需的制动力。
制动力是指制动器通过摩擦力对制动盘产生的制动力矩。
制动力的大小取决于需要制动的负载以及要求的制动时间。
一般而言,制动力的大小可以根据公式F=M*a来计算,其中F是制动力,M是转动质量,a是制动加速度。
制动压力是制动器产生摩擦力所需的压力。
一般而言,制动器的设计压力可以根据制动力和摩擦片的面积来计算。
制动压力的大小可以使用公式P=F/A来计算,其中P是制动压力,F是制动力,A是摩擦片的效用面积。
摩擦片的摩擦系数是制动器的核心参数之一、不同材料的摩擦片具有不同的摩擦系数,摩擦系数大小决定了制动效果的好坏。
在制动计算时,需要根据具体材料的摩擦系数来进行计算。
此外,还需要考虑制动盘的参数。
制动盘的尺寸、材料和表面状态等都会对制动效果产生影响。
制动盘的尺寸可以根据所需的制动力和制动盘的材料来计算。
制动盘的材料一般选择具有良好热传导性和抗磨损性能的金属材料。
制动盘表面的状态可以通过摩擦片和制动盘之间的接触面积以及表面的光滑度来表征。
在实际应用中,还需要考虑一些额外的因素,例如制动盘和摩擦片的磨损情况、制动器的热能散失等。
这些因素会影响制动器的实际制动效果,需要根据具体情况进行相应的修正。
总之,盘式制动器的制动计算是一个复杂的过程,需要考虑多个参数和因素。
正确的制动计算可以有效保障机械设备的安全运行和制动效果的稳定性。
(完整版)盘式制动器制动计算

re
这里:卩1=在制动器抱死时制动片内衬材料与对面材料的摩擦系数;S=球坡道倾角;rBT=
球轨道半径(m);re=有效半径(m);
制动灵敏度
高因素的制动对于制造公差和内衬摩擦的变化非常敏感。
衡量敏感性是随着内衬摩擦的变
化,制动系数变化量。它可以计算:
=
(1-
这里:Sb=$U动灵敏度;3=球坡道倾角;卩f=制动片内衬材料与对面材料的摩擦系数;
踏板力
踏板的比例计算到脚垫的中心。踏板回位弹簧对于整体的踏板力显著的作用。
特别是在整
个行程中。
实际的减速度和停止距离
在计算中使用的减速度是一个被称为MFDD(指完全展开的减速)的稳定状态。假设车辆 处于不是制动就是不制动的状态。 在实践中,系统压力的上升与摩擦的产生需要一定的时间。 这并不是司机的反应时间,而是系统的反应时间。凡计算需要停止的距离或平均停止减速度, 那么这个延时必须考虑。对于建立超过0.6秒线性计算,就有0.3秒的延迟。
注:所不同的是,由于全盘式制动器是全表面接触的,但制动片通常不并是一个扇形体, 而两侧是方形的(由于摩擦力的变化,实际上此不同并不是很重要)。
夹紧力
C
.Uf n
这里:C=制动夹紧力(N);T=制动力矩(Nm;re=有效半径(m);卩f=制动片内衬材料与 制动盘材料的摩擦系数;n=摩擦面数目;
夹紧负荷被假设等效地作用在所有的摩擦表面。对于干盘式制动器,是否是滑动式或对置
制动盘的有效半径
夹紧力
制动系数
制动产生
系统压力
伺服助力
踏板力
实际的减速度和停止距离
制动热]
制动耗能
动能
转动能量
势能
制动功率
盘式制动力矩的计算公式

盘式制动力矩的计算公式在汽车制动系统中,制动力矩是一个非常重要的参数,它直接影响着汽车的制动性能。
盘式制动力矩的计算公式是制动系统设计和性能分析的重要依据。
本文将介绍盘式制动力矩的计算公式及其相关知识。
盘式制动力矩的计算公式如下:\[ M = F \times r \]其中,M表示制动力矩,单位为牛·米(Nm);F表示制动力,单位为牛顿(N);r表示制动器半径,单位为米(m)。
制动力矩是制动器产生的力矩,它是制动器在制动过程中对车轮产生的制动力的力矩。
制动力矩的大小取决于制动器的制动力和制动器半径。
制动力是制动器对车轮施加的制动力,它是制动器在制动过程中产生的制动力。
制动力的大小取决于制动器的制动压力和摩擦系数。
制动器半径是制动器摩擦面的半径,它是制动器在制动过程中对车轮产生制动力的作用半径。
盘式制动器是一种常见的汽车制动器,它由制动盘、制动钳和制动片组成。
制动盘固定在车轮上,制动钳固定在车轮悬挂系统上,制动片安装在制动钳内。
当司机踩下制动踏板时,制动器卡钳会夹住制动盘,产生制动力,从而使车轮减速或停止。
盘式制动力矩的计算公式可以帮助工程师和设计师在设计和分析制动系统时进行制动力矩的计算。
在实际应用中,制动力矩的大小需要满足车辆制动的要求,包括制动距离、制动稳定性、制动温升等方面的要求。
制动力矩的大小与制动器的设计参数密切相关。
在设计制动器时,需要考虑制动器的制动力和制动器半径。
制动力的大小取决于制动器的制动压力和摩擦系数。
制动器半径的大小取决于车辆的制动要求和制动器的安装空间。
在实际应用中,制动力矩的计算需要考虑制动器的摩擦系数、制动压力、制动盘直径等因素。
制动力矩的大小直接影响着车辆的制动性能,因此在设计和分析制动系统时,需要对制动力矩进行合理的计算和分析。
在制动系统的设计和分析中,制动力矩的计算是一个重要的工作。
盘式制动力矩的计算公式可以帮助工程师和设计师在设计和分析制动系统时进行制动力矩的计算。
盘式制动器设计计算

盘式制动器的设计计算4.1相关主要技术参数整备质量 1570 kg载客人数 5 人最大总质量 2470 kg轴距 2737 mm载荷分配:空载:前 800 Kg 后 770 Kg满载:前 990 Kg 后 1310 Kg重心位置: Hg(满)=725Hg(空)=776轮胎型号 245/45 R184.2盘式制动器主要参数的确定4.2.1制动前盘直径D制动盘直径D应尽可能取大些,这使制动盘的有效半径得到增加,可以降低制动钳的夹紧力,减少衬块的单位压力和工作温度。
受轮辋直径的限制,制动盘的直径通常选择为轮辋直径的70%~79%。
根据在给出的汽车轮胎半径为18in,即轮辋直径为18×25.4=457.2≈457mm,同时参照一些车型的制动盘直径后选定该轻型较车盘式制动器的制动盘直径为356mm(制动盘的直径取轮辋直径的77.9%)。
4.2.2制动前盘厚度h制动盘在工作时不仅承受着制动块作用的法向力和切向力,而且承受着热负荷。
为了改善冷却效果,钳盘式制动器的制动盘有的铸成中间有径向通风槽的双层盘这样可大大地增加散热面积,降低温升约20%一30%,但盘的整体厚度较厚。
而一般不带通风槽的客车制动盘,其厚度约在l0mm—13mm之间。
为了使质量小些,制动盘厚度不宜取得很大。
这里取厚度为12mm。
4.2.3前盘摩擦衬块外半径2R与内半径1R摩擦衬块的外半径R2与内半径R1的比值不大于1.5。
若此比值偏大,工作时摩擦衬块外缘与内缘的圆周速度相差较大,则其磨损就会不均匀,接触面积将减小,最终会导致制动力矩变化大。
根据前面制动盘直径的确定:R初取168mm。
由于制动盘的半径为178mm,而摩擦衬块的外半径要比制动盘的半径小,2R为124mm。
则1R,对于常见的具有扇行摩擦表面的衬块,若其径向宽度不很大,取R等于平均半径m同时也等于有效半径e R ,而平均半径mm R R R m 146221=+= 而式中1R 、2R 也就是摩擦衬块的内外半径,即mm R R 29221=+ 擦衬块的有效半径文献[3]R e =()()mm R R R R 14712848*32835008*2*3*221223132==-- (4—1)与平均半径R m =146mm 的值相差不大,且满足m=738.016812421==R R <1,()()4124.0738.1738.0122<==+m m 的要求, 所以取R=146mm 。
盘式制动器_毕业设计说明书参考

1.课题研究的目的及意义汽车的设计与生产涉及到许多领域,其独有的安全性、经济性、舒适性等众多指标,也对设计提出了更高的要求。
汽车制动系统是汽车行驶的一个重要主动安全系统,其性能的好坏对汽车的行驶安全有着重要影响。
随着汽车的形式速度和路面情况复杂程度的提高,更加需要高性能、长寿命的制动系统。
其性能的好坏对汽车的行驶安全有着重要影响,如果此系统不能正常工作,车上的驾驶员和乘客将会受到车祸的伤害。
汽车是现代交通工具中用得最多、最普遍、也是运用得最方便的交通工具。
汽车制动系统是汽车底盘上的一个重要系统,它是制约汽车运动的装置,而制动器又是制动系中直接作用制约汽车运动的一个关键装置,是汽车上最重要的安全件。
汽车的制动性能直接影响汽车的行驶安全性。
随着公路业的迅速发展和车流密度的日益增大,人们对安全性、可靠性的要求越来越高,为保证人身和车辆安全,必须为汽车配备十分可靠的制动系统。
车辆在形式过程中要频繁进行制动操作,由于制动性能的好坏直接关系到交通和人身安全,因此制动性能是车辆非常重要的性能之一,改善汽车的制动性能始终是汽车设计制造和使用部门的重要任务。
现代汽车普遍采用的摩擦式制动器的实际工作性能是整个制动系中最复杂、最不稳定的因素,因此改进制动器机构、解决制约其性能的突出问题具有非常重要的意义。
2.汽车制动器的国内外现状及发展趋势对制动器的早期研究侧重于试验研究其摩擦特性,随着用户对其制动性能和使用寿命要求的不断提高,有关其基础理论与应用方面的研究也在深入进行。
目前,汽车所用的制动器几乎都是摩擦式的,可分为鼓式和盘式两大类。
盘式制动器被普遍使用。
但由于为了提高其制动效能而必须加制动增力系统,使其造价较高,故低端车一般还是使用前盘后鼓式。
汽车制动过程实际上是一个能量转换过程,它把汽车行驶时产生的动能转换为热能。
高速行驶的汽车如果频繁使用制动器,制动器因摩擦会产生大量的热量,使制动器温度急剧升高,如果不能及时的为制动器散热,它的效率就会大大降低,影响制动性能,出现所谓的制动效能热衰退现象。
汽车制动力计算

FU1,FU2——分别为前、后轮的制动力,N; p1,p2——分别为前、后轮缸的液压,pa; D1,D2——分别为前、后轮缸直径,m; n1,n2——分别为前、后制动器单侧油缸数目(仅对于盘式制动器而言); C1,C2——分别为前、后制动器的效能因数; R1,R2——分别为前、后制动器的工作半径,m; rd——轮胎动负荷半径;
鼓式刹车的效能因数:(参见“汽车工程手册基础篇 191 页”) 盘式刹车的效能因数:(参见“汽车工程手册基础篇 195 页”)
同步附着系数φ0=(Lβ-b)/ hg
β——制动力分配系数;既前轴制动器制动力与前、后轴制动器总制动力的比值表示。一般 取 0.6
UJ1-390 重心的位置(X,Y,Z):1155,306,-82 L——汽车轴距;=1803mm a——重心到前轴中心线的距离;=1155mm b——重心到后轴中心线的距离;=1803-1155=648mm hg——汽车重心高度;306+280=586mm φb——地面附着系数;取 0.7(干沥青路面) β=(b+φhg)/L=(648+0.7*586)/1803=0.59 制动距离S= (τ1+τ2/2)*V0/3.6+V02/(25.92*amax) 制动器作用时间:τ= τ2‘+ τ2‘‘=0.3+0.6=0.9s (0.2s《τ《0.9s)
汽车制动力计算
G4——
6 个电池组 总重量
6X28=168KG; 530KG;
车辆中心位置(x,y,z):-8,261,1559 (原点在前轮轴中间) 车轮轴距离地面的距离为 230;
轴间距 L=2370
地面对前轮的法向反作用力为:F1=(mg/L)[b+(hg/g)(du/dt)] 地面对后轮的法向反作用力为:F2=(mg/L)[a-(hg/g)(du/dt)]
(完整版)盘式制动器制动计算

制动计算制动系统方面的书籍很多,但如果您由于某事需要找到一个特定的公式,你可能很难找到。
本文面将他们聚在一起并作一些的解释。
他们适用于为任何两轴的车辆,但你的责任就是验证它们。
并带着风险使用.....车辆动力学静态车桥负载分配相对重心高度动态车桥负载(两轴车辆)车辆停止制动力车轮抱死制动力矩制动基本原理制动盘的有效半径夹紧力制动系数制动产生系统压力伺服助力踏板力实际的减速度和停止距离制动热制动耗能动能转动能量势能制动功率干式制动盘温升单一停止式温升逐渐停止式温升斜面驻车车桥负荷牵引力电缆操纵制动的损失液压制动器制动液量要求制动基本要求制动片压缩性胶管膨胀钢管膨胀主缸损失制动液压缩性测功机惯性车辆动力学静态车桥负载分配这里: Mf=静态后车桥负载(kg);M=车辆总质量(kg);Ψ=静态车桥负载分配系数注:对于满载和空载的车辆的变化往往是不同的。
相对重心高度这里: h=重心到地面的垂直距离(m);wb=轴距;X=相对重心高度;动态车桥负载(仅适用于两轴车辆)制动过程中车桥负载的变化与哪个车桥制动无关。
它们只依赖于静态负载条件和减速度大小。
这里:a=减速度(g);M=车辆总质量(kg);Mfdyn=前桥动态负载(kg);注:前桥负荷不能大于车辆总质量。
后桥负荷是车辆质量和前桥负荷之间的差值,并不能为负数。
它可能脱离地面。
(摩托车要注意)!车辆停止制动力总制动力可以简单地用牛顿第二定律计算。
这里:BF=总制动力(N);M=车辆总质量(kg);a=减速度(g);g=重力加速度(s/m2);车轮抱死如果车轮不抱死只能产生制动力,因为轮子滑动摩擦力比滚动摩擦力低得多。
在车轮抱死前特定车轴可能的最大制动力计算公式如下:这里:FA=车桥可能的总制动力(N);Mwdyn=动态车桥质量(kg);g=重力加速度(s/m2);μf=轮胎与地面间摩擦系数;制动力矩决定了哪个车轮需要制动来产生足够的制动力,每个车轮扭矩的要求需要确定。
盘式制动器的制动热计算与仿真

2盘式制动器工作原理及分析模型的建立
在 盘式制动器 主要 由制 动器和与之相配 的液压 系统组成 , 如 的对称关 系,只选其一侧 的工作面进行研究 。经过这些 简化 , D I N A中建立 了只有闸盘和 闸瓦的制动器简化模型。 图1 所示 。 制动器部分包括 : 箱体 、 闸盘 、 闸瓦 、 碟形弹簧和液压缸 A 等部件 。其工作原理如图 , 当油箱 A中通人高压油 时 , 活塞带 动
Ke y Wo r d s : Di s c Br a k e s ; Br a k e Th e r ma l ; ADI NA
1 引言
带式输送机是现代散状 物料 的重要运输方 式 。在各个领 域 都有广泛的应用 。目前 , 带式输送机正朝着大倾角 、 长运距 、 大运 量的方向发展 , 输送机能否安全 、 高效地运行 , 事关煤矿的开采效 率和产量 , 而解决输送机启动 、 运行 和可控制动及停 车的关键 问 题之一 , 就是要有性能优 良的制动装置。盘式制动器以其质量体 积小 , 制动力矩大 , 散热条件好等诸多优点 , 在带式输送机 中应用 较为普遍 。论述了盘式制动器的工作特点和原理 , 分 析探讨 了制
Ca l c u l a t i o n a n d Si mu l a t i o n f o r t h e Th e r ma l o f Di s c Br a k e Br a k i n g
S ONG We i - x i n,GUO Yo n g - c u n
b r ke a . Mo el d i n g a n d s i m u l t a i n g f 船 b r ki a n g p r o c e s s i n A D I N A e n v i r o n en m t .r e v e a l e d t h e d s i t r i b u t o i n a n d v ri a a t i o n f o t h e
关于气压盘式制动器参数计算和分析探讨
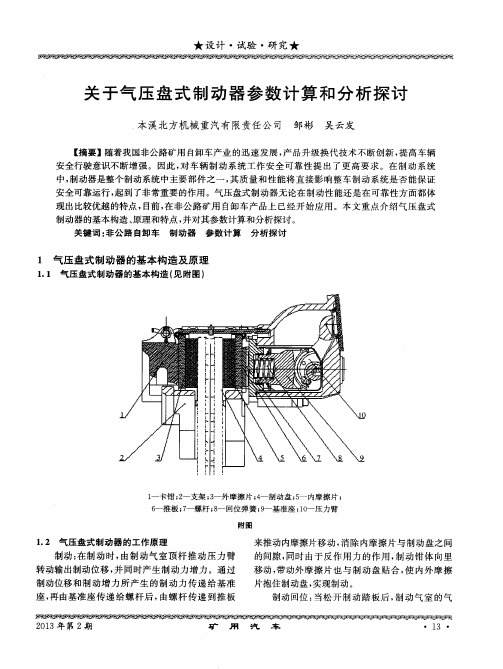
1 气压盘式制动器 的基本构 造及原理
1 . 1 气压 盘 式制 动器 的基本 构 造 ( 见 附图 )
1 一卡钳 ; 2 一支架 ; 3 一外摩擦 片 ; 4 一 制动盘 ; 5 一 内摩擦片 ; 6 一推板 ; 7 一 螺杆 ; 8 一 回位弹簧 ; 9 一基准座 ; 1 O 一 压力臂
★ 设计 ・ 试验 ・ 研 究★
压 释放 , 在 回位 弹 簧 的 作 用 下 , 基 准 座 带 动 螺 杆 回
( 8 ) 制 动盘 的热 膨 胀 不会 像 制 动 鼓 热 膨 胀那 样 引起制 动 踏板行 程 损 失 , 这 也使 得 间隙 自动 调 整装
置 的设 计 可 以简化 。 ( 9 ) 易 于 构 成 多 回路 制 动 驱 动 系统 , 使 系 统 有
2 . 2 气压 盘式 制动 器 结构上 的特 点
气 压 盘式 制 动 器 的 出现 既保 留 了传 统 的液 压
盘式 制动 器 的各 种 优 点 , 又 克 服 了其 原 有 的缺 点 ,
其性 能和 可 靠 性 相 对 于鼓 式 制 动 器 来 说 具 有 无 可
比拟 的优 势 。
2 气压盘式 制动器 的特点
★ 设计 ・试验 ・ 研 究 ★
关 于气 压 盘 式 制 动 器 参 数 计 算 和 分 析探 讨
本溪北方机械 重汽有限责任公 司 邹彬 吴云发
【 摘 要】随 着我 国非 公路 矿用 自卸 车 产业 的迅 速 发展 , 产 品升 级 换代 技 术 不 断创 新 , 提 高 车辆
安 全行驶 意 识不 断 增 强 。 因此 , 对 车辆 制 动 系 统 工作 安 全 可靠 性 提 出 了 更 高 要 求 。在 制 动 系统 中, 制动 器是 整个 制 动系统 中主要 部 件 之 一 , 其 质 量 和 性 能将 直 接 影 响 整 车制 动 系统 是 否 能保 证 安全可靠运行 , 起到了非常重要 的作用 。气压盘式制动器无论在制动性能还是在可靠性方面都体 现 出 比较 优越 的特 点 , 目前 , 在 非 公 路 矿 用 自卸 车 产 品上 已经 开始 应 用 。本 文 重 点 介 绍气 压 盘式 制 动器 的基本 构造 、 原 理 和特点 , 并对 其 参数 计算 和分 析探 讨 。
盘式制动器制动力矩计算

盘式制动器制动力矩计
算
The manuscript was revised on the evening of 2021
盘式制动器制动力矩计算
假定衬块的摩擦表面全部与制动盘接触,且各处单位压力分布均匀,则制动器的制动力矩
PR M μμ2=
其中μ—摩擦系数,一般取μ=。
在假设的理想条件下取μ=可使计算结果接近实
际;
P —单侧制动块对制动盘的压紧力;
R —作用半径。
对于常见的具有扇形摩擦表面的衬块,若其径向宽度不很大,取R 等于Rm 或有效半径Re ,在实际上已经足够精确。
平均半径
2
21R R R m += 式中R 1和R 2分别为摩擦衬块扇形表面的内半径和外半径。
有效半径 )()(32221223132R R R R P M R e --•==μμ
有效半径Re 为扇形摩擦表面的面积中心至制动盘中心的距离。
上式也可写成 ()()m e R m m R R R R R R R ⎥⎦⎤⎢⎣⎡+-=⎪⎭⎫ ⎝⎛+⎥⎦⎤⎢⎣⎡+-
=2212212111342134 其中m=R 1/R 2。
盘式制动器设计计算

盘式制动器设计计算盘式制动器是一种常见的制动装置,广泛应用于汽车、摩托车和一些机械设备中。
它通过将制动力转化为摩擦力来实现制动效果,具有制动力大、制动平稳、制动距离短等优点。
在设计盘式制动器时,需要考虑多个因素,包括制动力的计算、制动器的尺寸选择和材料选用等。
首先,制动力的计算是盘式制动器设计的重要一步。
计算制动力需要考虑车辆质量、速度和刹车时加速度等因素。
根据物理学原理,制动力的大小与车辆的动能和刹车时加速度成正比。
通常,制动力的计算可以使用以下公式:制动力=车辆质量×刹车时加速度其次,盘式制动器的尺寸选择是另一个关键因素。
制动器的尺寸主要包括盘径、盘厚和刹车片面积等。
盘径的选择需要考虑车辆的重量和速度,较大的盘径可以提供更大的制动力。
盘厚的选择通常是根据制动器的散热性能来决定,较薄的盘厚有助于散热,但也容易导致盘片的变形。
刹车片面积的大小影响着制动器的摩擦力,一般情况下,较大的刹车片面积可以提供更大的制动力。
此外,盘式制动器的材料选用也需要仔细考虑。
盘片和刹车片是制动器的核心部件,其材料的选择直接影响着制动器的性能。
常见的盘片材料包括铸铁、钢和复合材料等,而刹车片材料通常是由摩擦材料制成。
铸铁盘片具有较好的散热性能,但容易产生裂纹;钢盘片的散热性能较差,但较为耐用;复合材料盘片则具有较好的散热性能和耐用性。
刹车片材料的选择主要考虑其摩擦性能和耐磨性,常见的刹车片材料有有机材料、半金属材料和陶瓷材料等。
最后,盘式制动器的设计还需要考虑安装的方式和制动系统的调节等。
盘式制动器通常有两种安装方式,一种是固定式,即制动器直接固定在车轮上;另一种是浮动式,即制动器和轮轴连接的部分可以浮动,以减小由于温度变化而引起的失真。
制动系统的调节主要包括两个方面,一是制动压力的调节,通过调节制动液压缸的工作压力来达到合适的制动力;二是制动器的磨损调节,通过调节制动踏板的行程来保证刹车片的磨损均匀。
综上所述,盘式制动器的设计计算需要考虑多个因素,包括制动力的计算、制动器的尺寸选择和材料选用等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
制动计算制动系统方面的书籍很多,但如果您由于某事需要找到一个特定的公式,你可能很难找到。
本文面将他们聚在一起并作一些的解释。
他们适用于为任何两轴的车辆,但你的责任就是验证它们。
并带着风险使用.....车辆动力学静态车桥负载分配相对重心高度动态车桥负载(两轴车辆)车辆停止制动力车轮抱死制动力矩制动基本原理制动盘的有效半径夹紧力制动系数制动产生系统压力伺服助力踏板力实际的减速度和停止距离制动热制动耗能动能转动能量势能制动功率干式制动盘温升单一停止式温升逐渐停止式温升斜面驻车车桥负荷牵引力电缆操纵制动的损失液压制动器制动液量要求制动基本要求制动片压缩性胶管膨胀钢管膨胀主缸损失制动液压缩性测功机惯性车辆动力学静态车桥负载分配这里: Mf=静态后车桥负载(kg);M=车辆总质量(kg);Ψ=静态车桥负载分配系数注:对于满载和空载的车辆的变化往往是不同的。
相对重心高度这里: h=重心到地面的垂直距离(m);wb=轴距;X=相对重心高度;动态车桥负载(仅适用于两轴车辆)制动过程中车桥负载的变化与哪个车桥制动无关。
它们只依赖于静态负载条件和减速度大小。
这里:a=减速度(g);M=车辆总质量(kg);Mfdyn=前桥动态负载(kg);注:前桥负荷不能大于车辆总质量。
后桥负荷是车辆质量和前桥负荷之间的差值,并不能为负数。
它可能脱离地面。
(摩托车要注意)!车辆停止制动力总制动力可以简单地用牛顿第二定律计算。
这里:BF=总制动力(N);M=车辆总质量(kg);a=减速度(g);g=重力加速度(s/m2);车轮抱死如果车轮不抱死只能产生制动力,因为轮子滑动摩擦力比滚动摩擦力低得多。
在车轮抱死前特定车轴可能的最大制动力计算公式如下:这里:FA=车桥可能的总制动力(N);Mwdyn=动态车桥质量(kg);g=重力加速度(s/m2);μf=轮胎与地面间摩擦系数;制动力矩决定了哪个车轮需要制动来产生足够的制动力,每个车轮扭矩的要求需要确定。
对于某些规则,前部和后部制动器之间的分配是确定的。
这可能是通过不同的刹车片大小或更容易使用的阀门以减少执行压力。
这里:T=制动力矩(Nm);BFw=作用于车轮的制动力(N);R=静态负载下的车轮半径(m);r=车轮与制动器间的速比;制动基本原理制动盘的有效半径一个制动盘(扭矩半径)的有效半径是制动片面积中心。
干式制动盘,假设为:这里:re=有效半径(m);D=制动盘可用的外径(m);d=制动盘可用的内径(m);对于全盘式制动器,它是:这里:re=有效半径(m);D=制动盘可用的外径(m);d=制动盘可用的内径(m);注:所不同的是,由于全盘式制动器是全表面接触的,但制动片通常不并是一个扇形体,而两侧是方形的(由于摩擦力的变化,实际上此不同并不是很重要)。
夹紧力这里:C=制动夹紧力(N);T=制动力矩(Nm);re=有效半径(m);μf=制动片内衬材料与制动盘材料的摩擦系数;n=摩擦面数目;夹紧负荷被假设等效地作用在所有的摩擦表面。
对于干盘式制动器,是否是滑动式或对置活塞式制动并不重要。
牛顿第三定律表示,每一个力存在一个大小相等,方向相反的反作用力,作用在滑动卡钳的反作用力与对置活塞上的力相同。
制动系数球坡道制动器拥有自我伺服的作用,正如一个鼓式制动器。
制动系数乘以输出扭矩。
这里:Cb=制动系数;n=摩擦面数目;μf=制动片内衬材料与对面材料的摩擦系数;μL=在制动器抱死时制动片内衬材料与对面材料的摩擦系数;N=伺服摩擦面数目(通常为1或3);这里:μL=在制动器抱死时制动片内衬材料与对面材料的摩擦系数;δ=球坡道倾角;rBT=球轨道半径(m);re=有效半径(m);制动灵敏度高因素的制动对于制造公差和内衬摩擦的变化非常敏感。
衡量敏感性是随着内衬摩擦的变化,制动系数变化量。
它可以计算:这里:Sb=制动灵敏度;δ=球坡道倾角;μf=制动片内衬材料与对面材料的摩擦系数;μL=在制动器抱死时制动片内衬材料与对面材料的摩擦系数;制动产生系统压力压力是所需的夹紧力与活塞面积的作用。
记住对于对置活塞盘式制动器,它的面积只是制动盘一侧。
这里:p=系统压力(MPa);C=制动夹紧力(N);A=总的活塞面积(mm2);伺服助力伺服特点是图形化的定义。
输出将至少有两个斜坡,但也将在底部有一个的死区。
踏板力踏板的比例计算到脚垫的中心。
踏板回位弹簧对于整体的踏板力显著的作用。
特别是在整个行程中。
实际的减速度和停止距离在计算中使用的减速度是一个被称为MFDD(指完全展开的减速)的稳定状态。
假设车辆处于不是制动就是不制动的状态。
在实践中,系统压力的上升与摩擦的产生需要一定的时间。
这并不是司机的反应时间,而是系统的反应时间。
凡计算需要停止的距离或平均停止减速度,那么这个延时必须考虑。
对于建立超过0.6秒线性计算,就有0.3秒的延迟。
这里:aave=停止过程平均的减速度(g);v=测试速度(m/s);a=减速度(MFDD)(g);g=重力加速度(s/m2);这里:s=停止距离(m);v=测试速度(m/s);aave=停止过程平均的减速度(g);g=重力加速度(s/m2);下图显示71/320/EEC和ECE R13的测试要求。
制动热制动耗能在制动过程中,消耗的能量有三个来源,动能,转动能量和势能。
动能假设停止过程测试速度下降到零,动能为:这里:KE=动能(J);M=车辆总质量(kg);v=测试速度(m/s);转动能量转动能量是指缓慢转动部件所需的能量。
它随着所选的不同类型的车辆和齿轮变化而变化,但是定为动能的3%,是一个合理的假设。
势能势能是在山上停止获得或失去的能量。
这里:PE=势能(J);M=车辆总质量(kg);g=重力加速度(s/m2);S=坡度(%)(tanθ);制动功率只有当车轴制动(但依然旋转)时,制动系统中能量消散。
在车轮打滑时,有些制动能量消耗在轮胎上。
ABS发展的最终目标是处理理想的车轮打滑,但这里假设8%。
每次的制动能量取决于制动器的数量和每个车轴上的制动比例。
为了计算的功率,我们需要知道的制动时间:这里:t=制动时间(s);v=测试速度(m/s);a=减速度(MFDD)(g);g=重力加速度(s/m2);功率为:这里:P=平均功率(W);E=能量(J);t=制动时间(s);这是平均功率,制动开始时的峰值功率为其两倍。
干式制动盘温升这些计算是基于以下参考:Ruldolf Limpert的制动设计与安全第2版单一停止式温升为了近似制动盘的温升,需要作出能量去处的假设。
最初绝大多数的热出现在制动盘上,然而,但是它可以迅速被周围元件和气流冷却。
计算假定80%的热流到制动盘上。
流到一侧制动盘的热通量为:这里:q=热通量(W/m2);P=平均功率(W);D=制动盘可用的外径(m);d=制动盘可用的内径(m);单一停止式温升为:这里:制动盘最高温度(℃);q=热通量(W/m2);t=制动时间(s);ρ=制动盘材料密度(kg/m3);c=制动盘特定热容率(J/kg/K);k=制动盘热导率(W/m/K);Tamb=周围温度(℃);典型的铸铁数据:ρ=7250kg/m3; c=500J/kg/K; k=58W/m/K逐渐停止式温升经过反复制动后的温度上升也可以近似,虽然存在这么多的变数,但只是使用在基本的优化工作也是被建议的。
这里:ΔT=每次停止的平均温升(℃);P=平均功率(W);t=制动时间(s);ρ=制动盘材料密度(kg/m3);c=制动盘特定热容率(J/kg/K);V=制动器体积(m3);经过数停止后:这里:Tfoa=最后的停止后相比于周围温度的温升;N=停止次数;h=传热系数(W/℃/m2);A=制动盘表面积(m2);ΔT=每次停止的平均温升(℃);t=制动时间(s);ρ=制动盘材料密度(kg/m3);c=制动盘特定热容率(J/kg/K);V=制动器体积(m3);斜面驻车车桥负荷当斜面上停车时,较低处的车桥比其处于水平状态时承受更高的负载。
这里:Rf=前车桥负荷(kg);M=车辆总质量(kg);xf=水平时重心到后桥的水平距离(m);h=水平时重心到后桥的垂直距离(m);S=坡度(%)(tanθ);wb=轴距(m);后桥负荷是车辆质量和前桥负荷之间的差值。
牵引力如果在斜面上制动轮很轻,那么制动前轮胎有可能会打滑。
面临上下山时,通常需要车辆坡路控制,停车时牵引力是:这里:Tfr=需要的牵引力(N);M=车辆总质量(kg);g=重力加速度(s/m2);S=坡度(%)(tanθ);只有两轴中的一个轴制动,限制坡度为:这里:S=坡度(%)(tanθ);μf=道路与轮胎间的摩擦系数;xf=水平时重心到后桥的水平距离(m);wb=轴距(m);h=水平时重心到后桥的垂直距离(m);电缆操纵制动的损失电缆损耗是不可小视的,根据数量和弯曲的角度不同损失也不同。
一个典型的电缆供应商使用以下的计算,计算电缆效率:这里:η=电缆效率;Ba=弯曲的角度(°);液压制动器制动液量要求当提供液压制动时,制动液需要通过管道流动。
如果制动液来源主缸,它只有有限容量。
制动液需要以下组件:制动基本要求制动液需要占用运转间隙。
这里:Vfl=占用运行间隙所需的的液量(cc);A=总的活塞面积(mm2);Rc=运行间隙(mm2);这也是需要弥补制动室刚度的缺乏。
对于盘式制动器可用于下列近似:这里:Vf2=保持制动室刚度所需的的液量(cc);p=制动系动压力(MPa);dp=制动活塞直径(mm);制动片压缩性制动片的可压缩性在热和冷条件下变化。
在16MPa的压力下最坏情况的数字是冷压缩2%和热压缩5%。
所需的流体计算公式如下:这里:Vf3=由于制动片压缩所需的液量(cc);C3=制动片压缩性(%);t=制动片厚度总和(mm);p=制动系动压力(MPa);dp=制动活塞直径(mm);胶管膨胀胶软膨胀系数通常是:这里:Vf4=由于胶管膨胀所需的液量(cc);Ch=管体膨胀常数对于SAE J1401 3 / 16”橡胶制动软管使用47.58e-6 cc/(MPa.mm)对于SAE J1401 3 / 16”不锈钢编织软管使用0.04e-6 cc/(MPa.mm)对于SAE100R7软管使用2.2e-6Xb2+63.7e-6 cc/(MPa.mm)lh=管长(mm);p=系统压力(MPa);b=软管内径(mm);钢管膨胀钢管膨胀是非常小的,可能没什么兴趣,但是应该指出,它与直径的立方成正比,因此,系统中对于固定的流体体积使用大于必要的管会导致较长的行程,原因有两个,管道的刚度,更重要的是额外的流体压缩损失。
这里:Vf5=由于钢管膨胀所需的液量(cc);Dp=钢管的外径(mm);ls=钢管的长度(mm);p=系统压力(MPa);t=钢管壁厚(mm);E=杨氏模量(206e3MPa);主缸损失主缸液体损失随着孔的大小和压力增加而增加。
