最新小学奥数几何专地题目
小学奥数四五年级几何专项
10 17
5
A D
E B F
O C
1
学而思培优
【例四】如图,正方形 ABCD 的面积等于 625 平方厘米,DE 与 CF 相交于点 G 。已知 S△ADE S△CDG 等 于 125 平方厘米,求: △BFG 的面积。
D C
G F
A
E
B
【例五】如图,四边形 ABCD 中, AD∥BC , AD : BC 1: 2 , S△AOF : S△DOE 1: 3 , S△BEF 24 平方厘 米,求: △AOF 的面积。
A D
F
O
E
B
C
【例六】如图,直角三角形 ABC 中,三角形 ADF ,三角形 BED 和三角形 CFE 分别是以 A 、 B 、C 为 顶点的等腰三角形, AC 17 厘米, BC 15 厘米,那么三角形 DEF 的面积是______平方厘米。
A
F
D
B
E
C
2
学而思培优
【例七】如图,四边形 ABCD 的面积为 6 ,点 M 、 N 、 P 、 Q 分别为各边的中点,点 O 为 ABCD 内 一点。联结 OM 并延长至 E 点,使得 2OM ME 。同样的方式可得点 F 、G 、 H ,求:四边形 EFGH 的面积。
E G H D
A
B
F
C
【例二】如图,△ABC 和 △CDE 均为等腰直角三角形, AB 21 厘米,CD 35 厘米, AE 与 BD 相交 于 O 点,那么图中阴影部分的面积为多少平方厘米?
D A
O
B
C
E
【例三】如图,长方形 ABCD 中,点 E 为 AB 边上靠近点 B 的四等分点,点 F 为 BC 边上靠近点 C 的 四等分点,对角线 AC 交线段 DF 于 O 点,已知三角形 COD 的面积比四边形 AOFE 的面积少 2016 , 则长方形 ABCD 的面积为______。
最新小学奥数几何专题训练附答案

学习奥数的重要性1. 学习奥数是一种很好的思维训练。
奥数包含了发散思维、收敛思维、换元思维、反向思维、逆向思维、逻辑思维、空间思维、立体思维等二十几种思维方式。
通过学习奥数,可以帮助孩子开拓思路,提高思维能力,进而有效提高分析问题和解决问题的能力,与此同时,智商水平也会得以相应的提高。
2. 学习奥数能提高逻辑思维能力。
奥数是不同于且高于普通数学的数学内容,求解奥数题,大多没有现成的公式可套,但有规律可循,讲究的是个“巧”字;不经过分析判断、逻辑推理乃至“抽丝剥茧”,是完成不了奥数题的。
所以,学习奥数对提高孩子的逻辑推理和抽象思维能力大有帮助3. 为中学学好数理化打下基础。
等到孩子上了中学,课程难度加大,特别是数理化是三门很重要的课程。
如果孩子在小学阶段通过学习奥数让他的思维能力得以提高,那么对他学好数理化帮助很大。
小学奥数学得好的孩子对中学阶段那点数理化大都能轻松对付。
4. 学习奥数对孩子的意志品质是一种锻炼。
大部分孩子刚学奥数时都是兴趣盎然、信心百倍,但随着课程的深入,难度也相应加大,这个时候是最能考验人的:少部分孩子凭着天分,凭着在困难面前的百折不挠和愈挫愈坚的毅力,坚持了下来、学了进去、收到了成效;一部分孩子在家长的“威逼利诱”之下,硬着头皮熬了下来;不少孩子更是或因天资不足、或惧怕困难、或受不了这份苦、再或是其它原因而在中途打了退堂鼓。
我以为,只要能坚持学下来,不论最后取得什么样的结果,都会有所收获的,特别是对孩子的意志力是一次很好的锻炼,这对他今后的学习和生活都大有益处。
六年级几何专题复习如图,已知AB =40cm,图中的曲线是由半径不同的三种半圆弧平滑连接而成,那么阴影部分的面积是_____cm2。
(π取3.14)(几何)有7根直径都是5分米的圆柱形木头,现用绳子分别在两处把它们捆在一起,则至少需要绳子_____分米。
(结头处绳长不计,π取 3.14)图中的阴影部分的面积是________平方厘米。
小学奥数几何专题--巧求周长(六年级)竞赛测试.doc

小学奥数几何专题--巧求周长(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】求图中所有线段的总长(单位:厘米)【答案】48【解析】要注意到,题目所求的是图中所有线段的总长,而图中的线段,并不仅仅是、、、四段,还包括、等等,因此不能简单地将图中标示的线段长度进行求和.同时应该注意到,;,等等.因此,为了计算图中所有线段的总长,需要先计算AB、BC、CD 、DE这四条线段分别被累加了几次.这里,可以按照每条线段分别是由几部分组成的加以讨论:由1段组成的线段共有4条,即AB、BC、CD、DE,而求和过程中AB、BC、CD、DE这四条线段各被累加了1次.类似地考虑到,由2段组成的线段共有3条,求和过程中AB、DE各被累加了1次,BC、CD各被累加了2次.由3段组成的线段共有2条,求和过程中AB、DE各被累加了1次,BC、CD各被累加了2次.由4段组成的线段只有AE,其中AB、BC、CD、DE各被计算了1次.综上所述,AB、DE各被计算了4次,BC、CD各被计算了6次.因而图中所有线段的总长度为:{{9}l先考虑大长方形的长上各边:应用上一道题目的结论,每条边上长为4、3、1、2的线段分别被计算了4、6、6、4次.然后再考虑大长方形的宽:因为共有个长方形,所以长度为2的宽被计算了次.故总周长可以用下式计算得到:.【题文】如图,正方形的边长为,被分割成如下个小长方形,求这个小长方形的所有周长之和.评卷人得分【答案】56【解析】.【题文】如右图,正方形的边长是厘米,过正方形内的任意两点画直线,可把正方形分成个小长方形。
这个小长方形的周长之和是多少厘米?【答案】72【解析】从总体考虑,在求这个小长方形的周长之和时,、、、这四条边被用了次,其余四条虚线被用了次,所以个小长方形的周长之和是:(厘米)。
小学奥数几何题100道及答案(完整版)

小学奥数几何题100道及答案(完整版)题目1:一个正方形的边长是5 厘米,它的面积是多少平方厘米?解题方法:正方形面积= 边长×边长,即5×5 = 25(平方厘米)答案:25 平方厘米题目2:一个长方形的长是8 分米,宽是6 分米,它的周长是多少分米?解题方法:长方形周长= (长+ 宽)×2,即(8 + 6)×2 = 28(分米)答案:28 分米题目3:一个三角形的底是10 厘米,高是6 厘米,它的面积是多少平方厘米?解题方法:三角形面积= 底×高÷2,即10×6÷2 = 30(平方厘米)答案:30 平方厘米题目4:一个平行四边形的底是12 米,高是8 米,它的面积是多少平方米?解题方法:平行四边形面积= 底×高,即12×8 = 96(平方米)答案:96 平方米题目5:一个梯形的上底是 4 厘米,下底是6 厘米,高是5 厘米,它的面积是多少平方厘米?解题方法:梯形面积= (上底+ 下底)×高÷2,即(4 + 6)×5÷2 = 25(平方厘米)答案:25 平方厘米题目6:一个圆的半径是3 厘米,它的面积是多少平方厘米?解题方法:圆的面积= π×半径²,即3.14×3²= 28.26(平方厘米)答案:28.26 平方厘米题目7:一个半圆的半径是 4 分米,它的周长是多少分米?解题方法:半圆的周长= 圆周长的一半+ 直径,即3.14×4×2÷2 + 4×2 = 20.56(分米)答案:20.56 分米题目8:一个长方体的长、宽、高分别是5 厘米、4 厘米、3 厘米,它的表面积是多少平方厘米?解题方法:长方体表面积= (长×宽+ 长×高+ 宽×高)×2,即(5×4 + 5×3 + 4×3)×2 = 94(平方厘米)答案:94 平方厘米题目9:一个正方体的棱长是6 分米,它的体积是多少立方分米?解题方法:正方体体积= 棱长³,即6³= 216(立方分米)答案:216 立方分米题目10:一个圆柱的底面半径是2 厘米,高是5 厘米,它的侧面积是多少平方厘米?解题方法:圆柱侧面积= 底面周长×高,底面周长= 2×3.14×2,即2×3.14×2×5 = 62.8(平方厘米)答案:62.8 平方厘米题目11:一个圆锥的底面半径是3 厘米,高是4 厘米,它的体积是多少立方厘米?解题方法:圆锥体积= 1/3×底面积×高,底面积= 3.14×3²,即1/3×3.14×3²×4 = 37.68(立方厘米)答案:37.68 立方厘米题目12:两个边长为4 厘米的正方形拼成一个长方形,长方形的长和宽分别是多少?面积是多少?解题方法:长方形的长为8 厘米,宽为4 厘米,面积= 8×4 = 32(平方厘米)答案:长8 厘米,宽4 厘米,面积32 平方厘米题目13:一个三角形的面积是18 平方厘米,底是6 厘米,高是多少厘米?解题方法:高= 面积×2÷底,即18×2÷6 = 6(厘米)答案:6 厘米题目14:一个平行四边形的面积是24 平方米,底是 4 米,高是多少米?解题方法:高= 面积÷底,即24÷4 = 6(米)答案:6 米题目15:一个梯形的面积是30 平方分米,上底是5 分米,下底是7 分米,高是多少分米?解题方法:高= 面积×2÷(上底+ 下底),即30×2÷(5 + 7)= 5(分米)答案:5 分米题目16:一个圆环,外圆半径是5 厘米,内圆半径是 3 厘米,圆环的面积是多少平方厘米?解题方法:圆环面积= 外圆面积-内圆面积,即 3.14×(5²- 3²)= 50.24(平方厘米)答案:50.24 平方厘米题目17:一个长方体的棱长总和是48 厘米,长、宽、高的比是3:2:1,长方体的体积是多少立方厘米?解题方法:一条长、宽、高的和为48÷4 = 12 厘米,长为6 厘米,宽为4 厘米,高为2 厘米,体积= 6×4×2 = 48(立方厘米)答案:48 立方厘米题目18:一个正方体的表面积是54 平方分米,它的一个面的面积是多少平方分米?解题方法:一个面的面积= 表面积÷6,即54÷6 = 9(平方分米)答案:9 平方分米题目19:一个圆柱的底面直径是4 分米,高是3 分米,它的表面积是多少平方分米?解题方法:底面积= 3.14×(4÷2)²= 12.56 平方分米,侧面积= 3.14×4×3 = 37.68 平方分米,表面积= 2×12.56 + 37.68 = 62.8(平方分米)答案:62.8 平方分米题目20:一个圆锥的底面周长是18.84 分米,高是5 分米,它的体积是多少立方分米?解题方法:底面半径= 18.84÷3.14÷2 = 3 分米,体积= 1/3×3.14×3²×5 = 47.1(立方分米)答案:47.1 立方分米题目21:一个长方体的水箱,长 5 分米,宽4 分米,高 3 分米,里面装满水,把水倒入一个棱长为5 分米的正方体水箱,水深多少分米?解题方法:水的体积= 5×4×3 = 60 立方分米,正方体水箱底面积= 5×5 = 25 平方分米,水深= 60÷25 = 2.4 分米答案:2.4 分米题目22:一块长方形的铁皮,长8 分米,宽6 分米,从四个角各切掉一个边长为1 分米的正方形,然后做成一个无盖的盒子,这个盒子的容积是多少立方分米?解题方法:盒子长6 分米,宽4 分米,高1 分米,容积= 6×4×1 = 24(立方分米)答案:24 立方分米题目23:一个圆柱的体积是60 立方厘米,底面积是12 平方厘米,高是多少厘米?解题方法:高= 体积÷底面积,即60÷12 = 5(厘米)答案:5 厘米题目24:一个圆锥和一个圆柱等底等高,圆柱的体积是27 立方分米,圆锥的体积是多少立方分米?解题方法:等底等高的圆锥体积是圆柱体积的1/3,即27×1/3 = 9(立方分米)答案:9 立方分米题目25:把一个棱长为 6 厘米的正方体铁块熔铸成一个底面积为36 平方厘米的圆柱体,这个圆柱体的高是多少厘米?解题方法:正方体体积= 6³= 216 立方厘米,圆柱体的高= 体积÷底面积,即216÷36 = 6(厘米)答案:6 厘米题目26:一个直角三角形的两条直角边分别是3 厘米和4 厘米,斜边是5 厘米,这个三角形的面积是多少平方厘米?解题方法:直角三角形面积= 两条直角边乘积的一半,即3×4÷2 = 6(平方厘米)答案:6 平方厘米题目27:一个等腰三角形的周长是20 厘米,其中一条腰长8 厘米,底边长多少厘米?解题方法:等腰三角形两腰相等,所以底边长= 周长-腰长×2,即20 - 8×2 = 4(厘米)答案:4 厘米题目28:一个扇形的圆心角是90°,半径是6 厘米,这个扇形的面积是多少平方厘米?解题方法:扇形面积= 圆心角÷360°×圆的面积,即90÷360×3.14×6²= 28.26(平方厘米)答案:28.26 平方厘米题目29:一个长方体的底面是边长为5 厘米的正方形,高是8 厘米,这个长方体的体积是多少立方厘米?解题方法:长方体体积= 底面积×高,底面积= 5×5 = 25 平方厘米,体积= 25×8 = 200(立方厘米)答案:200 立方厘米题目30:一个圆柱的底面周长是18.84 厘米,高是10 厘米,它的体积是多少立方厘米?解题方法:底面半径= 18.84÷3.14÷2 = 3 厘米,体积= 3.14×3²×10 = 282.6(立方厘米)答案:282.6 立方厘米题目31:一个圆锥的底面直径是8 厘米,高是6 厘米,它的体积是多少立方厘米?解题方法:底面半径= 8÷2 = 4 厘米,体积= 1/3×3.14×4²×6 = 100.48(立方厘米)答案:100.48 立方厘米题目32:把一个棱长为8 厘米的正方体木块削成一个最大的圆柱,这个圆柱的体积是多少立方厘米?解题方法:圆柱的底面直径和高都是8 厘米,体积= 3.14×(8÷2)²×8 = 401.92(立方厘米)答案:401.92 立方厘米题目33:一个长方体玻璃缸,从里面量长4 分米,宽 3 分米,高5 分米,缸内水深2.5 分米。
小学数学竞赛《几何图形》专题训练30道题含答案

小学数学竞赛《几何图形》专题训练30题含答一、单选题1.如图,一串黑白相间的珠子,被盒子遮住了一部分.如果这串珠子中白珠子有20个,那么黑珠子共有()A.19B.20C.212.一个三角形三个内角度数的比是2:1:1,这个三角形是()A.钝角三角形B.锐角三角形C.等腰三角形D.等边三角形3.下图中的∠1和∠2相比,()。
A.∠1大B.一样大C.∠2大D.无法确定4.一条直线和它上面的两点组成的图形中含有()条射线。
A.2B.3C.45.用()这几根小棒可以围成一个长方形。
A.6cm、2cm、6cm、2cm B.5cm、3cm、5cm、2cm C.5cm、2cm、6cm、6cm二、填空题6.看一看,写一写,填一填。
(1)(2)个十个一7.(如图)把底面半径3厘米、高10厘米的圆柱切成若干等份,拼成一个近似的长方体。
这个长方体的表面积是平方厘米,体积是立方厘米。
8.一些相同的小方块放在桌面上,小明从正面、上面、左面三个方向观察,图形都是一样的(如图)。
这些小方块最多有个,最少有个。
9.求角的度数.∠2=°10.观察下列各数组成的三角形,根据各数阵的排列规律,写出第五行的数(从左到右填写)11.求下面花园的面积与周长.周长m面积m212.数一数,填一填。
个,个,个,个。
13.把一个棱长为4dm的正方体木块外面涂上红色,然后切割成棱长是1dm的小正方体,一面涂红色的小正方体有块,两面涂红色的小正方体有块。
14.在下图中,一共有个小正方体,从面看到的形状是。
三、作图题15.下面是一个正方形,共16个方格。
其中有4个方格中分别画了一只小兔,请你把这个正方形分成大小、形状完全相同的4块,使每一块中都有1只小兔应怎样分割?(画粗线)16.根据要求在下列图形中分别画一条线段.(1)将图1分成两个钝角三角形.(2)将图2分成一个平行四边形和一个三角形.四、解答题17.填一填,想一想18.找规律填数.19.观察下面数的排列规律。
小学奥数几何专地题目

小学几何面积问题一 姓名引理:如图1中;P 是AD 上一点,连接PB,PC 则S △PBC =S △ABP +S △pcD =21S ABCD 1,是PC △ABP =4,求:平行四边形ABCD 的面积 4..四边形ABCD 中,BF=EF=ED,如图1 若S 四边形ABCD 则S 阴 =2若S △AEF + S △BFC =15 则S 四边形ABCD =3若S △AEF= 3 S △BFC =2 则S 四边形ABCD =5. 四边形ABCD 的对角线BD 被E,F,G 三点四等份,如图若四边形AECG=15 则S 四边形ABCD =6.四边形ABCD 的对角线BD 被E,F,G 三点四等份, 则S 四边形ABCD =7.若ABCD 为正方形,F 是DC 的中点,已知:S △BFC = 11则S 四边形ADFB =2 S △DFE =3 S △AEB =8.直角梯形ABCD 中.AE=ED,BC=18,AD=8,CD=6,且=小学几何面积问题二姓名 1.如图S △AEF= 2, AB=3AE CF=3EF 则S △ABC=2. 如图S △BDE=30 ,AB=2AE, DC=4AC图1 适应长方形、正方形BB ABE AB第1题 第2题B C则S△ABC=3.正方形ABCD中,E,F,G为BC边上四等份点,M,N,P为对角线AC上的四等份点如图若S正方形ABCD=32 则S△NGP=4.已知:S△ABC=30 D是BC的中点AE=2ED 则S△BDE=5. 已知:AD=DB DE=3EC AF=3FE若S△ABC=160求S△EFC=6.已知:在△ABC中,FC=3AF EC=2BE BD=DF 若S△DFE=3则S△ABC=为平行四边形,AG=GC,BE=EF=FC,若S△GEF=2,则 S ABCD =是梯形,AD ABCD 是梯形,AD如图若△DFE的面积等于1 则△ABC的面积为第11题小学几何面积问题三姓名CBCFC1.在梯形ABCD中,AD 在梯形ABCD中,AD梯形ABCD中,ADA若直线L1图二△ACM的AC边上的高H1是△NCB的CB边上的高H2的一半,且AC=CB,若S△NBC =100 则S△ACM=3.把下面的三角形分成三个小三角形,4.△ABC是等边三角形,AD是BC边上的高,若S△ABC =2,则S△=5. △ABC是等边三角形,D是AB的中点,且DH垂直于BC,H为垂足.若S△BDH =2,则S△ABC=CEA FC D Bj F小学几何面积问题四 姓名1.在△ABC 中,AE=BE,BD=2DC,FC=3AF 若△ABC 的面积为1,则S △EFD =2.△ABC 中,三边BC,CA,AB 上分别有点D,E,F,且BC=3CD AB=2BE AC=4AF若△ABC 的面积为240平方厘米,则S △DEF 平方厘米.3.. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC4.两个正方形拼成如图,则阴影部分的面积为5.两个正方形拼成如图,则阴影部分的面积为6.三个正方形拼成如图,求阴影部分的面积为7.如图ABCD 是矩形,EF ∥AB 如果S 矩形ABCD =24 则S 阴= 8.在平行四边形ABCD 中,EF ∥AC,若 △AED 是平行四边形.直线CF 与AB 交于E,与DA 于4cm 2,那么三角形EDA 阴影部分的面积是 cm 小学几何面积问题五 姓名1.有两种自然放法,将正方形内接于等腰直角三角形.如果按左图的放法,那么可求得这个正方形面积为441. 如果按右图的放法,那么可求得这个正方形面积应为2.下图是一块长方形的草地,长方形的长是18米.宽是10米.中间有两条宽2米的路,一条是长方形,另一条是平行四边形,那么草地的面积是 平方米.第2题图3.如图大正方形的边长是20厘米.E,F,G,H 分别是各边中点,问:中间小正方形的面积是 平方厘米.4.“十字架”由五个边长相等的正方形拼成,若AB=20厘米. 求:这个“十字架”的面积是 平方厘米.5.一个边长为21厘米的正方形,被分成了四个长方形如图它们的面积分别是这个正方形面积的101,51,103,52在占52的这一4 5D1厘米块长方形里有一个小正方形是阴影部分.求这个阴影部分的面积为 平方厘米. 6.一个面积小于100的整数的长方形中,它的内部有三个小正方形,边长都是整数.已知正方形二的边长是长方形长的2/5,正方形一的边长是长方形宽的1/8;那么图中阴影部分的面积为 平方单位7. 如图所示ABCD 为正方形,且AB 、8.在长方形ABCD 中,长是宽的4倍,对角线BD=17厘米,求该长方形的面积是 .小学几何面积问题六姓名 1.一个长方形ABCD,向它的形外分别作正方形如图若所作的四边形的周长之和为264厘米,面积之和是1378求原来的长方形的面积是 平方厘米.2. 两个长方形叠放如图,小长方形宽是2厘米,A 是大长方形一边的中点,△ABC 是等腰直角三角形,图中阴影部分的面积和为 平方厘米.3.在边长为10的正方形的四边上分别取E,F,G,H.已知E 与G 的水平距离是5厘米,H 与F 的水平距离是4厘米,求四边形EFGH 的面积为 平方厘米.4.长方形ABCD 的长DC 是8厘米,宽方形,5.如图在直角梯形中,AB=10厘米,梯形面积的一半.6.已知:ABCD 是平行四边形,P 在AD 米,CP=6厘米;米.7. 梯形ABCD 与梯形A /B /C /D /大小相同若EC=4厘米,D /C /=24厘米,高EF=5求阴影部分的面积是 8.在一个梯形内,别是6平方厘米和8平方厘米,阴影部分的面积和是7厘米EBA小学几何面积问题七 姓名1.求图中阴影部分的面积2. 求图中阴影部分的面积3.已知:EF 是梯形ABCD 的中位线,4.求梯形的面积5.求下图四边形的面积6.在下图中,长方形内有一个钝角三形,按照图示的数,求这个三角形的面.7.三个边长为10厘米、12厘米、8厘米的正方形拼放在一起,直线BC 将整个图形面积平分,求线段AB 的长. 8. 如图有两个边长都是10厘米的正方形ABCD 和A /B /C /D /,且正方形A /B /C /D /的顶点A /恰好是正方形ABCD 的中心,那么:阴影部分的面积是 平方厘米.小学几何面积问题八 姓名1. 平行四边形ABCD 的面积是32厘米,AD=8B=45○,求阴影部分的面积是平方厘米.2.如图所示平行四边形ABCD 中阴影部分的面积为7平方厘米,那么,面积是 平方厘米.3.平行四边形ABCD 已知:三角形AHB 米,三角形DFC 的面积是6平方厘米.求阴的面积是 平方厘米. 4. 平行四边形ABCD 中有一点E,已知,三角形ABE 的面积是73平方厘米,三角形BEC 的面积是10平方厘米;求阴影部分三角形BED 的面积是 平方厘米.5.一个45度的直角三角板.最长边为12厘米,那么,它的面积为 平方厘米.6.如图长方形内画了一些直线,已知边上有三块面积分别为13平方厘米,35平方厘米,49平方厘米,那么图中的阴影部分面积是 平方厘米.7.在长方形ABCD 中,DE,DF 份,即三角形ADE 的面积等于三角形DFC BEDF 的面积.如果这个长方形的面积是54平方厘米,那么三角形BEF 的面积是 平方厘米.8.如图三角形ABC 是等腰直角三角形.它与一个正方形叠放在一起;已知AE,EF,FB,三条线段相等.三角形EFD 阴影部分面积是15平方厘米,求:S △ABC = 小学几何面积问题九姓名1..已知平行四边形ABCD 的面积是18平方厘米形DEF 的面积阴影部分是 平方厘米.2.在直角梯形ABCD 中AD=8厘米,DC=6厘米,BC=10厘米,且S △ADE =S △AFB =S 四AFCE 求三角形EFC 的面积为 平方厘米.DCCEC3.已知P 是长方形ABCD 的对角线上一点,M 为线段PC 的中点,如果三角形APB 的面积是2平方厘米,那么三角形BMC 的面积是 平方厘米. 4.长方形ABCD 的面积是48平方厘米; S △ABE =8cm 2 S △AFD =6cm 2求三角形EFC 的 面积是 平方厘米.5. 如图长方形ABCD 中,宽AD=6厘米,长DC=8厘米;E 在DC 的延长线上,AE 交BC 于F 点,如果三角形BFE 的面积是8平方厘米;求:阴影部分的面积是 平方厘米.6.把四边形ABCD 的各边延长一倍,得到一个大四边形A /B /C /D /,如果四边形ABCD 的面积是3平方厘米,那么大四边形A /B /C /D /的面积是 平方厘米.7.四边形ABCD 两条对角线交于E,延长CA 到F,使AF=AE;延长DB 到E,使BE=DE.如果四边形ABCD 的面积是3平方厘米. 求三角形EFG 的面积为 平方厘米.8.如图△ABC 中BD=2DC,AE=2ED,如果FC=12厘米. 那么:AF= 厘米.9.如图△ABC 中,△AEF,△ABE,△EBD 的面积分别是5cm 2,10cm 2,8cm 2 求四边形EDCF 的面积是 平方厘米.小学几何面积问题十 姓名1.如图长方形ABCD 中,AB=15厘米,BC=8厘米,三角形AFD 的面积比三角形FEC 的面积大30平方厘米,求CE 的长是 厘米.2. 如图正方形ABCD 中,边长为6厘米,三角形AFD FEC 的面积小6平方厘米,求CE 的长是 厘米.3.如图ABCD 是长方形,AD=4厘米,AB=9厘米,阴影部分△DEF 的面积是6平方厘米,求梯形ABED 的面积是平方厘米.4.如图,已知阴影部分的面积是120平方厘米,E,F 分别是AB,BC 的中点,长方形宽AB 为16厘米,那么,长方形的长AD 为 厘米.5.如图,ABCD 是梯形,BECE,AD=9厘米, BE ⊥EC,BE=8米,EC=6厘米.求这个梯形的面积是 平方厘米. 6.长方形ABCD 中,E 为BC 的中点, 阴影部分△AFD 的面积是4平方厘米.是 平方厘米.7.正方形ABCD 中,E 为BC 的中点,F 为DC 的中点 已知正方形边长是5厘米.则阴影部分△AGD 积是 平方厘米.8. 正方形ABCD 中,E 为BC 上的四等份点,F 为DC 的中点已知正方形边长是4厘米.则阴影部分△AGB 的面积是 平方厘米.。
最新小学奥数之立体几何问题

立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改.又是多少?【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一次增加两个面)练习.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.表面积最小:互相重合的面最多时表面积最小【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1. 如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2. 某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1. 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2. 如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
小学奥数专题之几何专题

小学奥数几何专题1、(★★)如图,已知四边形ABCD 中,AB=13,BC=3,CD=4,DA=12,并且BD 与AD 垂直,则四边形的面积等于多少?[思 路]:显然四边形ABCD 的面积将由三角形ABD 与三角形BCD 的面积求和得到.三角形ABD 是直角三角形,底AD 已知,高BD 是未知的,但可以通过勾股定理求出,进而可以判定三角形BCD 的形状,然后求其面积.这样看来,BD 的长度是求解本题的关键.解:由于BD 垂直于AD ,所以三角形ABD 是直角三角形.而AB=13,DA=12,由勾股定理,BD 2=AB 2-AD 2=132—122=25=52,所以BD=5.三角形BCD 中BD=5,BC=3,CD=4,又32十42=52,故三角形BCD 是以BD 为斜边的直角三角形,BC 与CD 垂直.那么:ABCD S 四边形=ABD S ∆+BCD S∆=12×5÷2+4×3÷2=36.. 即四边形ABCD 的面积是36. 2、(★★)如图四边形土地的总面积是48平方米,三条线把它分成了4个小三角形,其中2个小三角形的面积分别是7平方米和9平方米.那么最大的一个三角形的面积是________平方米;[分析]:剩下两个三角形的面积和是 48-7-9=32 ,是右侧两个三角形面积和的2 倍,故左侧三角形面积是右侧对应三角形面积的2倍,最大三角形面积是 9×2=18。
3.(★★)将下图中的三角形纸片沿虚线折叠得到右图,其中的粗实线图形面积与原三角形面积之比为2:3。
已知右图中3个阴影的三角形面积之和为1,那么重叠部分的面积为多少?[思 路]:小升初中常把分数,百分数,比例问题处理成份数问题,这个思想一定要养成。
解:粗线面积:黄面积=2:3绿色面积是折叠后的重叠部分,减少的部分就是因为重叠才变少的,这样可以设总共3份,后来粗线变2份,减少的绿色部分为1份,所以阴影部分为2-1=1份,7 94、(★★)求下图中阴影部分的面积:【解】如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
小学奥数题库《几何》几何图形角0星题(含详解)全国通用版

几何-几何图形-角-0星题课程目标知识提要角•定义具有公共端点的两条射线组成的图形叫作角,这个公共端点叫作角的顶点,这两条射线叫作角的两条边。
•角的分类锐角、直角、钝角、平角、周角•互余和互补如果两个角之和为90∘,那么我们就说这两个角互为余角,简称互余;如果两个角之和为180∘,那么我们就说这两个角互为补角,简称互补。
精选例题角1. 如图是3×3的正方形方格,∠1与∠2相比,较大的是.【答案】∠1【分析】从图中我们发现,∠2中上半部分和∠1的下半部分角度相等,但∠1的上半部分是45∘,∠2的下半部分小于45∘,所以∠1>∠2.2. ⑴如图1,四边形内角和,角A+角B+角C+角D=.⑵如图2,五边形内角和,角A+角B+角C+角D+角E=.⑶如图3,六边形内角和,角A+角B+角C+角D+角E+角F=.⑷有没有发现什么规律,试着总结你的规律?⑸如图4,CDGHI是正五边形,ABCDEF是正六边形,试求角BCI=.【答案】⑴360度;⑵540度;⑶720度;⑷N边形内角和为(N−2)×180度;⑸12度【分析】⑴⑵⑶⑷的解析过程略,⑸正五边形的内角和为(5−2)×180度=540度,所以正五边形的内角是540度÷5=108度,即角DCI=108度,正六边形的内角和为(6−2)×180度=720度,所以正六边形的内角是720度÷6=120度,即角DCB=120度,于是角BCI=角DCB−角DCI=120度−108度=12度.3. 如图是2×2的正方形方格,∠1与∠2相比,较大的是.【答案】∠1【分析】从图中我们发现,∠1是45∘,∠2小于45∘,所以∠1>∠2.4. 九个同样的直角三角形卡片,拼成了如图所示的平面图形.这种三角形卡片中的两个锐角较大的一个是度.【答案】54【分析】直角三角形中的两个锐角和是90∘,周角360∘,90∘−180∘÷5=54∘.5. 下图中,∠A+∠B+∠C+∠D+∠F+∠G等于度.【答案】360【分析】连接CD,有∠G+∠F=∠EDC+∠ECD,这样就转化成四边形的内角和了,四边形的内角和是360度.6. 如图,∠1=∠2=∠3=∠4=∠5=∠6=30∘,则图中所有锐角度数的和是.【答案】480∘【分析】共有30∘锐角6个,锐角5个,则共有30∘×6+60∘×5=480∘.7. 如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K= ∘【答案】900【分析】如图所示,顺时针标上∠1,∠2,∠3,∠4,⋯⋯,∠17,∠18,根据三角形内角和可以得到∠A=180∘−(∠1+∠2)那么这九个角的和为180∘×9−(∠1+∠2+∠3+∠4+⋯+∠17+∠18)而∠1+∠2+∠3+∠4+⋯+∠17+∠18=720∘题目所求的九个角的和为180∘×9−720∘=900∘.8. 如图,直角的顶点在直线l上,则图中所有小于平角的角之和是.【答案】450∘【分析】由一部分组成的角之和是180度,由两部分组成的角之和是180∘+90∘,一共180∘+180∘+90∘=450∘.9. 如图,∠1=∘,∠2=∘,∠3=∘.【答案】30;150;60【分析】因为∠2和30∘角组成一个平角,所以∠2=180∘−30∘=150∘;因为∠2和∠1组成一个平角,所以∠1=180∘−∠2=180∘−150∘=30∘;因为∠1、∠3和图中直角组成一个平角,所以∠3=180∘−∠1−90∘=180∘−30∘−90∘= 60∘,故答案为:30∘,150∘,60∘.10. 下图中,∠1、∠2、∠3、∠4的和是.【答案】360∘【分析】图中的四边形是由两个三角形组成的,所以内角和是180∘×2=360∘,而四边形的4个内角分别与∠1、∠2、∠3、∠4构成平角,所以∠1、∠2、∠3、∠4的和是180∘×4−180∘×2=360∘.11. 角可以用它的两边上的大写字母和顶点的字母表示,如下图的∠AOB(符号“∠”表示角),也可以用∠O表示(顶点处只有一个角时).下图的三角形ABC中,∠BAO=∠CAO,∠CBO=∠ABO,∠ACO=∠BCO,∠AOC=110∘,则∠CBO=.【答案】20∘【分析】由题意得,{2(∠CAO +∠ACO +∠CBO)=180∘∠CAO +∠ACO +∠AOC =180∘∠AOC =110∘,解得 ∠CBO =20∘.12. 用 180∘ 与四边形的每一个内角作差,所得到的值叫做这个内角的角亏,四边形所有内角角亏之和为 度.【答案】 360【分析】 180∘×4−四边形内角和=720∘−360∘=360∘13. 如图,已知 ∠1=2∠2,试求 ∠1= 度和 ∠2= 度.【答案】 50;100【分析】 多边形外角和是 360 度,所以 ∠1+∠2=360∘−60∘−70∘−80∘=150∘,因为 ∠1=2∠2,所以 ∠1=100 度,∠2=50 度.14. 若一正 n 边形,其内角度数是其外角度数的 4 倍,则 n = .【答案】 10【分析】 多边形外角和是 360 度,所以这个正多边形的内角和是 360×4=1440 度,根据正多边形的内角和公式 (n −2)×180=1440,n =10.15. 如图,直角的顶点在直线 e 上,则图中所有小于平角的角之和是 度.【答案】540【分析】180∘×2+90∘×2=540∘16. 如下图所示BD,CE,分别是∠ABC,∠ACB的角平分线,如果∠BAC=62∘,那么∠BFC=∘.【答案】121【分析】有三角形内角和得∠ABC+∠ACB=180∘−62∘=118∘,因为BD,CE,分别是∠ABC,∠ACB的角平分线,所以∠DBC+∠ECB=118∘÷2=59∘,所以∠BFC=180∘−59∘=121∘.17. 如图,将四边形ABCD的四条边分别延长一段,得∠CBE,∠BAH,∠ADG,∠DCF,那么,这四个角的和等于∘.【答案】360【分析】凸多边形的外角和和360∘,本题的四个角是四边形形的外角,所以它们的和是360∘.18. 相同的3个直角梯形的位置如图所示,则∠1=.【答案】10∘【分析】90∘−50∘−30∘=10∘.19. 直线AB、CD相交,若∠1、∠2和∠3的关系如图所示,则∠3−∠1=∘.【答案】90【分析】原题图中的∠3等于下图的∠4+∠5,∠1=∠4,所以∠3−∠1=90∘.20. 如图:角A+角B+角C+角D+角E+角F+角G+角H+角J=度.【答案】540【分析】角A+角B+角C+角D+角E+角F+角G+角H+角J=(5−2)×180度=540度.连接AD,JF,如图所示,角B+角C=角BAD+角CDA,角G+角H=角HJF+角GFJ,所以角A+角B+角C+角D+角E+角F+角G+角H+角J=角DAJ+角ADE+角DEF+角EFJ+角FJA=(5−2)×180度=540度.21. 如图,则图中所有小于直角的角之和是∘.【答案】180【分析】小于直角的角一共有4个,一共90∘+90∘=180∘.22. 判断对错(1)角越大,角的两边就越长.(2)大于90∘的角叫作钝角.(3)一个直角减去一个锐角,得到的角一定是锐角.(4)20∘的角用5倍的放大镜看还是20∘.【答案】(1)错;(2)错;(3)对;(4)对.23. 将长方形的纸片ABCD按下图的方式折叠后压平,使三角形DCF落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1=20∘,那么∠2是度.【答案】40【分析】(1)因为三角形DEF是三角形DCF,折叠过来的,所以两个三角形全等.(2)∠CDF=∠1=20∘,根据三角形内角和180∘,∠CFD=∠EFD=70∘.(3)∠2=180∘−70∘−70∘=40∘.24. 如图,∠1=∠2,∠3=∠4,∠A=60∘,那么∠5=∘.【答案】120【分析】因为∠1+∠2+∠3+∠4=180∘−∠A=120∘,又∠1=∠2,∠3=∠4,故∠5= 180∘−60∘=120∘.25. (1)如图,在直角∠AOB内有两条射线OC,OD.已知∠1比∠2小10∘,∠3比∠2大10∘,则∠3=度.(2)直线AB、CD相交,若∠1、∠2和∠3的关系如图所示.则∠3−∠1=度.【答案】(1)40∘(2)90∘【分析】(1)(90∘+10∘+10∘×2)÷3=40∘(2)∠3−∠1=∠AOD−∠1=∠DOL=90∘26. 强强晚上6点多外出锻炼身体,此时时针与分针的夹角是110度;回家时还未到7点,此时时针与分针的夹角仍是110度,则强强外出锻炼身体用了分钟.【答案】40【分析】开始分针落后时针110度,回家后分钟超过时针110度,即分针比时针多走110+110=220度,因每分钟分针比时针多走6−0.5=5.5度,故用了220÷5.5=40分钟.27. 判读对错(1)一个钝角减去一个直角,得到的角一定是锐角.(2)一个钝角减去一个锐角,得到的角不可能还是钝角.(3)25∘的角用10倍的放大镜看就变成了250∘.【答案】(1)对;(2)错;(3)错.28. 有下列说法:(1)一个钝角减去一个直角,得到的角一定是锐角.(2)一个钝角减去一个锐角,得到的角不可能还是钝角.(3)三角形的三个内角中至多有一个钝角.(4)三角形的三个内角中至少有两个锐角.(5)三角形的三个内角可以都是锐角.(6)直角三角形中可能有钝角.(7)25∘的角用10倍的放大镜看就变成了250∘.其中,正确说法的个数是个.【答案】4【分析】(1)、(3)、(4)、(5)是正确的说法.29. 如下图所示,∠1=∠2,∠3=∠4,如果∠A=68∘,那么∠E=∘【答案】34【分析】由图可知:∠3=∠1+∠E,∠AFC=∠ABC+∠A.而,∠ACF=∠3+∠4,∠3=∠4,所以,∠ABC=2∠1,所以2∠3=2∠1+68∘,2∠3=2∠1+2∠E,故有2∠1+68∘=2∠1+2∠E,所以,∠E=34∘.30. 已知α是锐角,β是钝角,4位同学在计算0.25(α+β)时,得到的结果依次是15.2∘、45.3∘、112∘,其中有可能正确的是.【答案】45.3∘【分析】90∘<α+β<270∘,则22.5∘<0.25(α+β)<67.5∘,所以只可能为45.3∘.31. 三个正方形叠放在一起.如下图所示,∠1=.【答案】15∘【分析】∠1+∠2=45∘,∠1+∠3=60∘,∠1+∠2+∠3=90∘,所以∠1=45∘+60∘−90∘=15∘.32. 如图,ABCDEF为正六边形,∠G=100∘,那么∠NBC=.【答案】40【分析】正六边形内角和为720度,每个内角和为120度,∠FAB=∠ABC=120∘,∠BAG=60∘,∠ABG=180∘−100∘−60∘=20∘,所以,∠NBC=180∘−∠ABG−∠ABC= 180∘−120∘−20∘=40∘33. 如图,将长方形纸片ABCD的两边AD与BC对折,得到折痕EF,再将点B折到EF上,得到折痕AM与点M,如果AM=3,那么,MN=.【答案】32【分析】一个内角为30∘或60∘的直角三角形中,较短的直角边长度为斜边的一半,反之亦然,E是AB的中点,所以有AE=12AB=12AN,所以∠EAN=60∘,进而有∠BAM=∠NAM=30∘,所以MN=12AM=12×3=3234. 一个等腰三角形中,有一个角为80∘,则其余两角的度数是.【答案】50∘、50∘或80∘、20∘【分析】如果已知角是顶角.那么剩下的两个底角均为(180∘−80∘)÷2=50∘;如果已知角是底角,那么另一个底角也是80∘,顶角为180∘−80∘×2=20∘.35. 如图,∠3=∘【答案】60【分析】因为∠2和30∘角组成一个平角,所以∠2=180∘−30∘=150∘;因为∠2和∠1组成一个平角,所以∠1=180∘−∠2=180∘−150∘=30∘;因为∠1、∠3和图中直角组成一个平角,所以∠3=180∘−∠1−90∘=180∘−30∘−90∘= 60∘.36. 如图,∠1=∘【答案】30【分析】因为∠2和30∘角组成一个平角,所以∠2=180∘−30∘=150∘;因为∠2和∠1组成一个平角,所以∠1=180∘−∠2=180∘−150∘=30∘.37. 如图所示,角D=75度,那么角B+角G=.【答案】75度.【分析】角B+角G=90度−角BCA+90度−角GEF=180度−角DCE−角CED=角D=75度.38. 某人从某点向前走16米,原地向右转18∘,再向前走16米,再向右转18∘⋯⋯这样走下去,他第一次回到出发点时,一共走了米.【答案】320【分析】这个人每次走相同的长度之后右转18∘,那么如果他要回到出发点,至少需要转360∘,也就是转360∘÷18∘=20(次),期间一共走了20×16=320(米).实际上,由于多边形外角和是360∘,这个人走的轨迹构成一个正二十边形.39. 将一个周角平均分成6000份,其中的一份作为角的度量单位,则可以得到一种新的度量角的单位:密位.显然,360∘=6000密位,那么45∘=密位,1050密位= ∘.【答案】750;63【分析】由于360∘=6000密位,那么1∘=6000÷360=503密位,1密位=360÷6000=3 50 ,所以,45∘=45×503=750密位,1050密位=1050×350=63∘.40. 如图,∠1=2∠2,∠3=2∠4,∠5+∠A=180∘,那么∠A=∘.【答案】45【分析】因为∠5+∠A=180∘,又∠2+∠4+∠5=180∘,∠1=2∠2,∠3=2∠4,故∠A=∠2+∠4,∠A+∠2+∠4+∠1+∠3=180∘,故∠A=45∘.41. ⑴如图1,角A+角B+角C=度.⑵如图2,三角形是等腰直角三角形,那么,角A=度,角C=度,角A+角C=度.⑶如图3,三角形是等边三角形,那么角A=度,角B=度,角C=度.⑷如图4,普通三角形角A=35度、角C=85度,那么角B=度.【答案】⑴180;⑵45,45,90;⑶60,60,60;⑷60【分析】三角形内角和等于180度.42. 如图所示,求角A+角B+角C+角D+角E+角F=.【答案】360度【分析】角A+角B+角C+角D+角E+角F=180度×3−180度=360度.43. 如图,把一张长方形纸片ABCD折叠,使点C与点A重合,折痕为EF,如果∠DEF= 123∘,那么∠BAF=∘【答案】24【分析】四边形EDCF内角和为360度,∠C=∠D=90∘,∠DEF=123∘,所以∠EFC= 57∘因为折叠使A与C重合,所以∠AFE=∠EFC=57∘,平角的度数为180度,所以∠BFA+∠AFE+∠EFC=180∘,所以∠BFA=66∘,∠BAF=90∘−∠BFA=90∘−66∘=24∘44. 如图,若△ABC中,AB=AC,∠BAC=40∘,以AB为边,在△ABC的外部作等边△ABD,∠ADC是度.【答案】40【分析】△ABD是等边三角形,那么AB=AD,又AC=AB,得到△ACD是等腰三角形,∠DAC=∠DAB+∠BAC=60∘+40∘=100∘,所以∠ADC=(180∘−100∘)÷2=40∘.45. 如图,将正方形纸片ABCD折叠,使点A,B重合于O,则角EFO=度.【答案】30【分析】由图可知:OD=OC=CD,故三角形OCD为等边三角形,△OCD=60∘,则∠BCF=∠FCO=(90∘−60∘)÷2=15∘,故∠CFB=∠CFO=180∘−90∘−15∘=75∘,故∠EFO=180∘−75∘−75∘=30∘. 46. 如图,∠1=∠2,∠3=∠4,∠5=130∘,那么∠A=.【答案】80∘【分析】∠2+∠4=180∘−130∘=50∘,因为∠1=∠2,∠3=∠4,所以∠1+∠2+∠3+∠4=100∘,故∠A=180∘−100∘=80∘.47. 如图所示,已知OE与OF垂直,过O点作直线AB,若∠EOA=2∠AOF,则∠BOF=.【答案】150∘【分析】∠EOA=2∠AOF,由和倍问题,∠AOF=90∘÷(1+2)=30∘,所以,∠BOF= 180∘−30∘=150∘.48. 等腰三角形ABC中,两个内角的度数比是1:2,则三角形ABC的内角中,角度最大可以是度.【答案】90【分析】要度数最大,则此三角形三个内角比为1:1:2,所以最大度数为:180÷(1+1+2)×2=90∘.49. 试求下列各图中∠A的度数.【答案】(1)130;(2)100【分析】(1)ABCDE是一个五边形,∠A=(5−2)×180−90−90−90−140=130度;(2)ABCDE是一个五边形,∠A=(5−2)×180−90−90−130−(180−90)−40=100;50. 如图所示,五条线段依次首尾相连组成了一个五角星.问:∠1+∠2+∠3+∠4+∠5等于多少度?【答案】180【分析】连接最下班两个顶点,由于∠8=∠9,则∠6+∠7=∠2+∠5,所以∠1+∠2+∠3+∠4+∠5=∠1+∠3+∠4+∠6+∠7=180∘51. 如图,四边形ABCD中,AB=BC=CD,∠B=168∘,∠C=108∘,求∠D的度数.【答案】54度【分析】将图形沿AD向下翻折,并设B、C关于AD的对称点分别是Bʹ和Cʹ,连结BBʹ可以推出三角形ABBʹ是正三角形,五边形BCDCʹBʹ是正五边形,那么∠D=54∘.52. 如图所示,已知∠1的度数是∠2度数的2倍,求∠1,∠2,∠3,∠4分别是多少度?【答案】∠1=180,∠2=60∠3=120,∠4=60【分析】由和倍问题,∠1是∠2的2倍,而且∠1+∠2=180∘,所以∠2=180∘÷(1+2)=60∘,则∠1=180∘−60∘=120∘,同理,∠3=180∘−∠2=180∘−60∘=120∘,∠4=180∘−∠1=60∘53. 如图所示,在三角形ABC中,∠1=∠2,∠3=∠4,∠5=130∘,那么∠A等于多少度?【答案】80【分析】由于∠2+∠4=180∘−130∘=50∘,所以∠ABC+∠ACB=50∘×2=100∘,所以∠A=180∘−100∘=80∘.54. 在三角形ABC中,∠A−∠C=∠B.那么这个三角形是不是直角三角形?【答案】是.【分析】由∠A−∠C=∠B可知,∠A=∠B+∠C.根据三角形内角和是180∘,于是可知∠A=90∘.55. 三角形的两个内角和为92∘,这个三角形一定是锐角三角形吗?【答案】不一定【分析】92∘=91∘+1∘,91∘为钝角.56. 如图,四边形ABCD中,∠C=90∘,∠D=150∘,AD=DC=BC,求∠A和∠B的度数.【答案】∠A=45,∠B=75【分析】如图,因为BC=CD,∠C=90∘,所以根据这两条边做正方形BCDE,连接AE.因为∠ADC=150∘,∠EDC=90∘,所以∠ADE=60∘,因为AD=BC=ED,所以三角形ADE是正三角形.所以∠AEB=60∘+90∘=150∘,AE=EB,所以∠EAB=∠EBA= (180∘−150∘)÷2=15∘.则∠BAD=60∘−15∘=45∘,∠ABC=360∘−90∘−45∘=75∘.57. 如图所示,角B=70度,角C=90度,角D=60度,求图中角A的度数是多少?【答案】140度【分析】四边形的内角和为360度,角A=360度−角B−角C−角D=140度.58. 如图所示,∠1等于140度,∠2等于80度,∠3等于110度,请问:∠4等于多少度?【答案】30度.【分析】由外角和为360度可得:360−140−80−110=30度.59. 如图所示,∠1+∠3=180∘,∠2=60∘,∠4等于多少度?【答案】120∘【分析】由于任意四边形的外角和均为360∘,所以∠4=360∘−∠1−∠2−∠3=120∘.60. 如图所示:∠1等于100度,∠2等于60度,∠3等于90度,那么∠4等于多少度?【答案】110度.【分析】这些角都是四边形的外角,它们的和是四边形的外角和.因此∠4=360−100−60−90=110度.61. 如图,ABCDJ为正五边形,DEFGHJ为正六边形,试求∠AJH的度数.【答案】132【分析】正六边形的每个内角是120度,正五边形的每个内角是108度,∠AJH=360−120−108=132度.62. 如图,已知角1=2角2,试求角1和角2.【答案】角1=100度,角2=50度.【分析】多边形外角和为360度,即角1+角2+60度+70度+80度=360度,因为已知角1=2角2,解得角1=100度,角2=50度.63. 两条直线相交所成的锐角或直角称为两条直线的“夹角”.现平面上有若干条直线,它们两两相交,并且“夹角”只能是30∘,60∘或90∘.问:至多有多少条直线?【答案】6【分析】如图:64. 如图,ABCDE是正五边形,CDF是正三角形,∠BFE等于多少度(小于180∘的)?【答案】168∘【分析】∠BCF=108∘−60∘=48∘=∠EDF,因为BC=CF,DF=DE,所以∠BFC=∠EFD=(180∘−48∘)÷2=66∘,因此∠BFE=360∘−66∘×2−60∘=168∘.65. 如图1所示,在长方形ABCD中,∠ACB等于34度.现在将其沿对角线AC折起,形成如图2所示的图形.那么∠OCD的度数是多少?【答案】见解析【分析】由于∠ACB=34∘从而∠ACD=56∘,所以∠OCD=22∘.66. 如图:将一个正五边形和一个正六边形放置在同一条直线上,请问角ABH为多少度?【答案】48【分析】角BAF=120度,角BHK=108度,所以角BAH=60度,角BHA=72度,因为三角形内角和为180度,所以角ABH=180度−角BAH−角BHA=48度.67. 如图中∠3=2∠1=2∠2,如果图中所有角的和等于195∘,那么∠AOB是多少度?【答案】60∘【分析】图中所有角的和等于3∠1+4∠2+3∠3=13∠1=195∘.所以∠1=15∘,所以∠AOB=60∘.68. 一个多边形的内角和是1800度,请问它是几边形?【答案】12边形.【分析】1800÷180=10,由多边形内角和公式可知,这是一个10+2=12边形.69. 将图中所有的角表示出来.(只考虑小于平角的角)【答案】枚举:∠AOB,∠BOC,∠AOC.70. 如图所示,角1等于100度,角2等于60度,角3等于90度.角4等于多少度?【答案】110【分析】由于任意四边形的外角和均为360∘,所以角4=360度−角1−角2−角3= 110度.71. 如图所示,从点O引出6条射线OA,OB,OC,OD,OE,OF,且∠AOB=100∘,OF平分∠BOC,OE平分∠AOD,∠EOF=140∘,求∠COD的度数.【答案】20∘【分析】因为∠AOB=100∘,∠EOF=140∘,所以∠AOE+∠BOF=360∘−100∘−140∘=120∘,又因为OF平分∠BOC,OE平分∠AOD,所以∠BOC+∠AOD=2×(∠AOE+∠BOF)=2×120∘=240∘.所以,∠COD=360∘−∠AOB−∠BOC−∠AOD=360∘−240∘−100∘=20∘.72. 若一正n边形,(内角−外角)和外角相等,则求n的值.【答案】n=6【分析】(内角−外角)和外角相等,说明内角是外角的两倍,则外角的度数是180度÷3=60度,因为是正n边形,所以外角相同,外角共有360度÷60度=6(个).即n=6.73. 已知如图的三角形ABC是个等边三角形,试用一个等腰直角三角板,画一个以A为顶点的105∘的角,并写出画图步骤.【答案】见解析.【分析】①延长BA到E,得∠EAC=120∘.②作AD垂直于BC,得∠DAC=30∘;∠DAE=150∘.③以AD为一条边,画一45∘的角DAF,则∠EAF是105∘.74. 如图,将一个正五边形和一个正六边形放置在同一条直线上,请问角CBG为多少度?【答案】角CBG=84【分析】六边形每个内角(6−2)×180度÷6=120度,正五边形每个内角(5−2)×180度÷5=108度,角BAH=180度−120度=60度,角AHB=180度−108度=72度,角ABH=180度−60度−72度=48度,角CBG=360度−120度−108度−48度=84度.75. 如图所示,已知∠4的度数是∠1度数的3倍,求∠1,∠2,∠3,∠4分别是多少度?【答案】∠1=45∘,∠2=135∘,∠3=45∘,∠4=135∘.【分析】由和倍问题,∠4是∠1的3倍,而且∠1+∠4=180∘,所以∠1=180∘÷(1+ 3)=45∘,则∠4=180∘−45∘=135∘,同理,∠3=180∘−∠4=180∘−135∘=45∘,∠2= 180∘−∠1=135∘.76. 如图所示,五条线段依次首尾相连组成了一个五角星.问:角1+角2+角3+角4+角5等于多少度?【答案】180∘【分析】连接最下边两个顶点,由于角8=角9,则角6+角7=角2+角5,所以角1+角2+角3+角4+角5=角1+角3+角4+角6+角7=180度.77. 如图中∠1=∠2,如果图中所有角的和等于80∘,那么∠AOB是多少度?【答案】40∘【分析】图中所有角的和等于2∠1+2∠2=4∠1=80∘.所以∠1=20∘,所以∠AOB=40∘.78. 如图,∠1是多少度?【答案】143【分析】48+95=143度79. 正12边形的内角和是多少度?【答案】1800度.【分析】由多边形内角和公式可得:(12−2)×180=1800度.80. 如图所示,三角形ABC中,AD=CD,∠B=51∘,∠DCB=73∘,求∠CDB和∠A.【答案】∠CDB=56∘,∠A=28∘.【分析】因为∠B+∠DCB+∠CDB+∠ADC+∠A+∠ACD=360∘,又∠CDB+∠ADC= 180∘,∠A=∠ACD,所以51∘+73∘+180∘+2∠A=360∘,解得∠A=28∘,那么∠CDB=∠A+∠ACD=56∘.81. 如图所示,ABCDE是正五边形,CDF是正三角形,那么∠BFE等于多少度?【答案】168∘【分析】正五边形的内角和是(5−2)×180∘=3×180∘=540∘,每个内角是540∘÷5=108∘.而△CDF是正三角形,每个内角是60∘,因此∠CFD=∠FCD=60∘.而∠BCF=108∘−60∘=48∘,是等腰△BCF的顶角,因此∠BFC=(180∘−48∘)÷2=66∘,同理∠DFE也等于66∘.于是∠BFE=360∘−∠BFC−∠CFD−∠DFE=360∘−66∘−60∘−66∘=168∘.82. 如图所示,已知∠BOC,∠AOB,∠AOC分别相差50∘,求∠BOC的度数.【答案】70【分析】由和差问题(见下图)∠BOC=(360∘−50∘−50∘−50∘)÷3=70∘.83. 图中是一个正八边形,试求它的内角和.【答案】1080度.【分析】方法一,正八角形可以看成是正方形去掉四个等腰直角三角形,因此每个内角是180∘−45∘=135∘,总和是135∘×8=1080∘.方法二,八角形可以分成6个三角形,因此内角和是180∘×6=1080∘.84. 若一n边形其2内角分别为100度、80度,剩下的内角均为135度,试求n的值.【答案】6【分析】因为外角和是360度,100度和80度的外角分别为80度和100度,除了这两个外角,其他外角全是45度,剩下的外角个数是(360度−100度−80度)÷45度=4(个),所以n=4+2=6.85. 如图所示,∠1等于130度,∠2等于110度,那么∠3等于多少度?【答案】60【分析】由于∠2=110∘,则与角2互补的那个角为70∘,所以∠3=60∘.86. 如图,CDGHI为正五边形,ABCDEF为正六边形,试求∠BCI的度数.【答案】12∘【分析】正五边形的内角和为(5−2)×180∘=540∘,所以正五边形的内角是540∘÷5=108∘,即∠DCI=108∘.正六边形的内角和为(6−2)×180∘=720∘,所以正六边形的内角是720∘÷6=120∘,∠DCB=120∘.于是∠BCI=∠DCB−∠DCI=120∘−108∘=12∘.87. 三角形内角和是180度,试用不同的方法说明一下?【答案】见解析【分析】方法一:用一张三角形的纸片,将三角形的三个角剪下来,然后拼在一起,从而得到一个平角.说明三角形的内角和为180度.方案二:如下图,延长边BC到D,并过顶点C作CE∥BA;因为CE∥BA(作图),所以角1=角A(两直线平行,内错角相等),角2=角B(两直线平行,同位角相等).又因为角1 +角2 +角ACB=180度(平角的定义),所以角A +角B +角ACB=180度.88. 如图,边长为12厘米的正五边形,分别以正五边形的5个顶点为圆心,12厘米为半径作圆弧,请问:中间阴影部分的周长是多少?(π=3.14)【答案】12.56cm【分析】如图,点C是在以B为中心的扇形上,所以AB=CB,同理CB=AC,则△ABC 是正三角形,同理,有△CDE是正三角形.有∠ACB=∠ECD=60∘,正五边形的一个内角是180∘−360∘÷5=108∘,因此∠ECA=60∘×2−108∘=12∘,也就是说圆弧AE的长度是半径为12厘米的圆周的一部分,这样相同的圆弧有5个,所以中间阴影部分的周长是2××5=12.56(cm).3.14×12×12∘360∘89. 找出图中所有的角(只考虑小于平角的角),并将它们表示出来.【答案】枚举:∠AOB,∠BOC,∠COD,∠AOC,∠BOD,∠AOD.90. 如图所示,两个正方形重叠放在一起,已知∠1=70∘,求:∠3的度数.【答案】70【分析】∠2=90∘−∠1=20∘,∠3=90∘−∠2=70∘.91. 如图所示,三个正方形叠放在一起,有一个公共点,并且已知其中两个角的度数分别为45∘和30∘,求∠1的度数.【答案】15∘【分析】令∠1与45∘角之间的角为∠2,∠1和30∘角之间的角为∠3,在左边的正方形中,∠1+∠2+45∘=90∘,所以,∠1+∠2=45∘.在中间的正方形中,∠3=90∘−∠1−∠2=45∘.在右边的的正方形中,∠1=90∘−30∘−∠3=90∘−30∘−45∘=15∘.92. 如下左图所示,在长方形ABCD中,∠ACB等于34∘,现在将其沿对角线AC折起,形成如下右图所示的图形,那么∠OCD的度数是多少?【答案】22∘【分析】根据折叠对应情况可得:∠ACB=∠ACO=34∘,因为在长方形ABCD中,∠ACB+∠ACD=90∘,所以∠ACD=90∘−34∘=56∘,所以∠OCD=∠ACD−∠ACO=56∘−34∘=22∘.93. 如图中∠1=∠2=∠3,如果图中所有角的和等于180∘,那么∠AOB是多少度?【答案】54∘【分析】图中所有角的和等于3∠1+4∠2+3∠3=10∠1=180∘.所以∠1=18∘,所以∠AOB=54∘.94. 下图是个正五角星,则∠A等于多少度?【答案】36∘【分析】180∘−(180∘−108∘)×2=36∘.95. 如图所示,∠1= ∘,∠2= ∘,∠3= ∘.【答案】∠1=30,∠2=150,∠3=60【分析】因为∠2和30∘角组成一个平角,所以∠2−180∘−30∘=150∘;因为∠2和∠1组成一个平角,所以∠1=180∘−∠2=180∘−150∘=30∘;因为∠1、∠3和图中直角组成一个平角,所以∠3=180∘−∠1−90∘=180∘−30∘−90∘=60∘.96. 如图所示,角1等于130度,角2等于110度,那么角3等于多少度?【答案】60【分析】由于角1等于130度,所以与角1互补的那个角为50度,由于角2为110度,与角2互补的那个角为70度,根据三角形内角和,所以角3等于60度.97. 如图所示,∠1等于40度,∠2等于70度,那么∠3等于多少度?。
小学五年级奥数几何题

小学五年级奥数几何题1.小学五年级奥数几何题1.一个长方体的无盖水族箱, 长是6m, 宽是60cm, 高是1.5m。
这个水族箱占地面积有多大?需要多少平方米的玻璃?它的体积是多少?2.要砌一道长15m, 厚24cm, 高3m的砖墙。
如果每立方米用砖525块, 一共用砖多少块?3.花园小区为居民新安装了50个休息的凳子, 凳面的长、宽、高分别是100cm, 45cm,4.5cm。
凳腿的长、宽、高分别是45cm, 5cm, 35cm, 做这些凳子至少用了混凝土多少方?4、“六一”儿童节前, 全市的小学生代表用棱长3cm的正方体塑料拼插积木在广场中央搭起了一面长6m, 高2.7m, 厚6cm的奥运心愿墙。
这面墙一共用了多少块积木?5、学校运来7.6立方米的沙子, 铺在一个长5米、宽38米的沙坑里, 可以铺多厚?2.小学五年级奥数几何题1.一个长、宽、高分别为40cm、30cm、20cm的小纸箱, 在所有棱上粘上一圈胶带, 至少需要多长的胶带?2.为迎接“五一”劳动节, 要在俱乐部的四周装上彩灯(地面的四边不装)。
已知俱乐部的长90米, 宽55米, 高20米, 工人叔叔至少需要多长的彩灯线?3.小卖部要做一个长2.2m, 宽40cm, 高80cm的玻璃柜台, 现要在柜台各边都安上角铁, 这个柜台需要多少米角铁?4、一个长方体的饼干盒, 长10cm宽6cm, 高12cm。
如果围着它贴一圈商标纸(上、下面不贴), 这张商标纸的面积至少要多少平方厘米?5、光华街口装了一个新的铁皮邮箱, 长50cm, 宽40cm, 高78cm。
做这个邮箱至少需要多少平方厘米的铁皮?3.小学五年级奥数几何题(1)有一个棱长是4厘米的正方体, 从它的一个顶点处挖去一个棱长是1厘米的正方体后, 剩下的物体的体积和表面积各是多少?(2)一个正方体和一个长方体拼成一个新的长方体, 拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。
小学奥数:几何图形的认识.专项练习及答案解析

本讲知识点属于几何模块的第一讲,属于起步内容,难度并不大.要求学生认识各种基本平面图形和立体图形;了解简单的几何图形简拼和立体图形展开;看懂立体图形的示意图,锻炼一定的空间想象能力.几何图形的定义:1、几何图形主要分为点、线、面、体等,他们是构成中最基本的要素.(1)点:用笔在纸上画一个点,可以画大些,也可以画小些.点在纸上占一个位置.(2)线段:沿着直尺把两点用笔连起来,就能画出一条线段.线段有两个端点.(3)射线:从一点出发,沿着直尺画出去,就能画出一条射线.射线有一个端点,另一端延伸的很远很远,没有尽头.(4)直线:沿着直尺用笔可以画出直线.直线没有端点,可以向两边无限延伸(5)两条直线相交: 两条直线相交,只有一个交点.(6)两条直线平行:两条直线平行,没有交点,无论延伸多远都不相交.(7)角:角是由从一点引出的两条射线构成的.这点叫角的顶点,射线叫点的边.(8)角分为锐角、直角和钝角三种:直角的两边互相垂直,三角板有一个角就是这样的直角.教室里天花板上的角都是直角. 锐角比直角小,钝角比直角大.(9)三角形:三角形有三条边,三个角,三个顶点.边边顶点直角锐角钝角知识点拨(10)直角三角形:直角三角形是一种特殊的三角形,它有一个角是直角.它的三条边中有两条叫直角边,一条叫斜边.(11)等腰三角形:等腰三角形也是一种特殊的三角形,它有两条边一样长(相等),相等的两条边叫”腰”,另外的一条边叫”底”.(12)等腰直角三角形:等腰直角三角形既是直角三角形,又是等腰三角形.(13)等边三角形:等边三角形的三条边一样长(相等),三个角也一样大(相等).(14)四边形:四边形有四条边,内部有四个角.(15)长方形:长方形的两组对边分别平行且相等,四个角也都是直角.(16)正方形:正方形的四条边都相等,四个角都是直角.(17)平行四边形:平行四边形的两组对边分别平行而且相等,两组对角分别相等.顶角顶角边边角角角顶角边直角边斜边直角边腰腰底直角边直角边斜边腰腰底边边边角角角(18)等腰梯形:等腰梯形是一种特殊的四边形,它的上下两边平行,左右两边相等.平行的两边分别叫上底和下底,相等的两边叫腰.(19)菱形:菱形的四条边都相等,对角分别相等.(20)圆:圆是个很美的图形.圆中心的一点叫圆心,圆心到圆上一点的连线叫圆的半径,过圆心连接圆上两点的连线叫圆的直径.直径把圆分成相等的两部分,每一部分都叫半圆.(21)扇形:(22)长方体:长方体有六个面,十二条棱,八个顶点.长方体的面一般是长方形,也可能有两个面是正方形.互相垂直的三条棱分别叫做长方体的长、宽、高.(23)正方体:正方体有六个面,十二条棱,八个顶点.正方体的每个面都是同样大的正方形,所以它的十二条棱长都相等.(24)圆柱:圆柱的两个底面是完全相同的圆.(25)圆锥:圆锥的底面是圆.(26)棱柱:这个棱柱的上下底面是三角形.它有三条互相平行的棱,叫三棱柱. 腰腰下底上底半径直径半圆直径弧半径半径高宽长底面底面(27)棱锥:这个棱锥的底面是四边形.它有四条棱斜着立起来,所以叫四棱锥.底面(28)三棱锥:因为三棱锥有四个面,所以通常又叫”四面体”.三棱锥的每一个面都是三角形.(29)球体,简称球:球有球心,球心到球面上一点的连线叫球的半径.例题精讲模块一、几何图形的认识【例 1】请看下图,共有个圆圈。
最新小学奥数几何专题训练附答案

最新小学奥数几何专题训练附答案奥数,即奥林匹克数学竞赛,是培养学生逻辑思维和解决问题能力的重要途径。
而几何作为奥数竞赛中的一个重要领域,对学生的几何直观和推理能力提出了较高的要求。
为此,我们特别准备了最新的小学奥数几何专题训练,并附上了详细的答案。
通过这个专题训练,相信学生们在几何方面的能力将得到有效提升。
1. 三角形的性质三角形是几何学中最基础的图形之一,具有诸多性质。
在本专题中,我们将针对三角形的内角和、外角和以及角平分线等性质进行训练。
在题目中,我们通过图形的给定或条件的陈述,要求学生运用已知的性质推导出未知的结果。
例如:题目:如图1所示,三角形ABC中,∠ABC=80°,∠ACB=50°。
求∠BAC的度数。
解答:由于三角形的内角和为180°,设∠BAC=x,则∠ACB=80°-x,∠ABC=50°。
将三角形的内角和代入等式中,得到:x + (80°-x) + 50° = 180°130° = 180°-xx = 180°-130°x = 50°因此,∠BAC的度数为50°。
2. 直线与平行线直线和平行线是几何学中的重要概念。
在这个专题中,我们将训练学生在应用直线与平行线性质解决问题时的能力。
例如:题目:如图2所示,AB、CD和EF是三条平行线。
若∠AGE=40°,求∠EDF的度数。
解答:由于AB和EF是平行线,所以∠AGE=∠EDF。
因此,∠EDF的度数为40°。
3. 三角形的相似性质相似三角形是指具有对应角相等且对应边成比例的三角形。
相似三角形在数学和实际生活中具有重要应用。
在这个专题中,我们将训练学生识别和应用相似三角形的能力。
例如:题目:如图3所示,△ABC与△DEF相似,且比例尺为1:2。
已知AC=4,求EF的长度。
解答:由于△ABC与△DEF相似,所以AB/DE = BC/EF = AC/DF。
小学奥数:几何计数(一).专项练习及答案解析

1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n条直线最多将平面分成21223(2)2n n n++++=++……个部分;n个圆最多分平面的部分数为n(n-1)+2;n个三角形将平面最多分成3n(n-1)+2部分;n个四边形将平面最多分成4n(n-1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n+1个点(包括两个端点)(或含有n个“基本线段”),那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE上有15条线段,每条线段的两端点与点A相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n条线段,纵边上共有m条线段,则图中共有长方形(平行四边形)mn个.模块一、简单的几何计数【例 1】七个同样的圆如右图放置,它有_______条对称轴.教学目标例题精讲知识要点7-8-1几何计数(一)【考点】简单的几何计数【难度】1星【题型】填空【关键词】迎春杯,六年级,初赛,试题【解析】如图:6条.【答案】6条【例 2】下面的表情图片中:,没有对称轴的个数为()(A) 3 (B) 4 (C) 5 (D) 6【考点】简单的几何计数【难度】2星【题型】选择【关键词】华杯赛,初赛,第1题【解析】通过观察可知,第1,2,5这三张图片是有对称轴的,其他的5张图片都没有对称轴,所以没有对称轴的个数为5,正确答案是C。
几何六年级奥数题

几何六年级奥数题
下面是一道六年级奥数几何题:
题目:在正方形ABCD 中,点 E 是AD 的中点,连接BE 交AC 的延长线于点F,如果AF = 6 cm,BD = 12 cm,则求DF 的长度。
解题思路:
1. 由题意可知,AF = 6 cm,BD = 12 cm,我们需要求得DF 的长度。
2. 由于E 是AD 的中点,所以AE = ED = 1/2 * AD。
根据正方形的特性,可得AE = ED = 1/2 * BC。
3. 由于AF 是BE 的延长线,所以AF = BE。
4. 由正方形的性质可知,BE = BC + CE。
代入前面得到的关系式,可得AF = BC + CE。
5. 根据正方形的对角线相互垂直且相等的特性,可知AFC 和DEB 是直角三角形。
6. 利用勾股定理,可得AFC 的斜边AC 的平方等于AF 的平方加上FC 的平方。
7. 利用勾股定理,可得DEB 的斜边DB 的平方等于DE 的平方加上EB 的平方。
8. 由于AFC 和DEB 相似,可得到相似比:AC:DB = AF:DE = 6:BC。
9. 将AC 和DB 的长度代入相似比,即可得到BC 的长度。
10. 利用BC 的长度和BE 的关系,可得到CE 的长度。
11. 利用BE 和CE 的长度,可得到DF 的长度。
答案和解析:
根据上述步骤计算,DF 的长度为:DF = 3 cm。
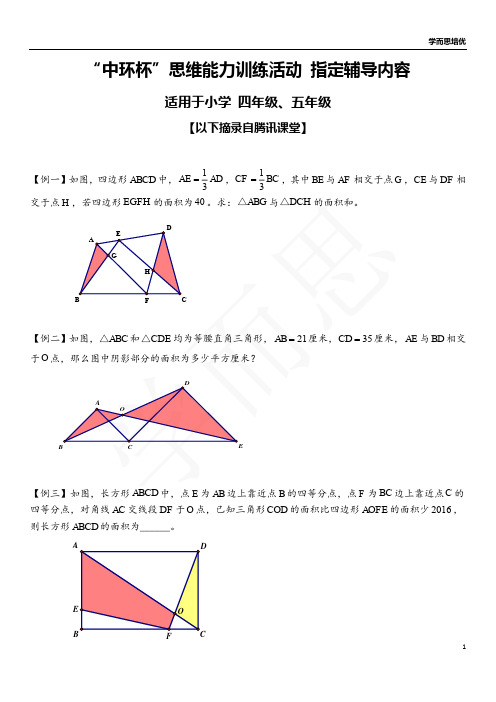
小升初几何专题测试题 数奥 (含标准标准答案)
小升初几何专题测试题数奥(含答案)1、如图,已知每个小正方形格地面积是1平方厘米,则不规则图形地面积是______.2、(西城实验考题)四个完全一样地直角三角形和一个小正方形拼成一个大正方形(如图),如果小正方形面积是1平方米,大正方形面积是5平方米,那么直角三角形中,最短直角边地长度是______米.b5E2R。
3、求出图中梯形ABCD地面积,其中BC=56厘米.(单位:厘米)4、(第十三届“华罗庚金杯”少年组数学邀请赛决赛试卷(小学组))图中,ABCD和CGEF是两个正方形,AG和CF相交与H,已知CH等于CF地三分之一,三角形CHG地面积等于6平方厘米,求五边形ABGEF地面积.p1Ean。
5、(清华附中考题)如图,在三角形ABC中,D为BC地中点,EGHFEDCBA为AB 上地一点,且BE=13AB ,已知四边形EDCA 地面积是35,求三角形ABC 地面积DXDiT 。
6、(101中学考题)一块三角形草坪前,工人王师傅正在用剪草机剪草坪,一看到小灵通,王师傅热情地打招呼:“小灵通,听说你很会动脑筋,我也想问问你,这块草坪我把它分成东、西、南、北四部分(如图).修剪西部、东部、南部个需要10分钟、16分钟、20分钟,请你想一想修剪北部需要多少分钟?”RTCrp 。
7、(101中学考题)求图中阴影部分面积:8、(第十三届“华罗庚金杯”少年组数学邀请赛决赛试卷(小学组))图1是小明用一些半径为1厘米,2厘米,4厘米,和8厘米地圆,半圆,圆弧和一个正方形组成地一个鼠头图案,图中阴影部分地总面积为_______平方厘米.5PCzV。
9、(三帆中学考试题)有一个棱长为1米地立方体,沿长、宽、高分别切二刀、三刀、四刀后,成为60个小长方体,这60个小长方体地表面积总和为_____平方米.jLBHr。
10、(清华附中考题)从一个长为8厘米,宽为7厘米,高为6厘米地长方体中截下一个最大地正方体,剩下地几何体地表面积是______平方厘米.xHAQX。
3 小学奥数——几何图形 试题及解析

3 小学奥数——几何图形试题及解析小学奥数——几何图形试题及解析一、选择题1. 下列各图形中,几何图形的个数最多的是:A. 正方形B. 矩形C. 三角形D. 长方形解析:该题考察学生对几何图形的辨识和计数能力。
正方形有4条边,矩形也有4条边,三角形有3条边,而长方形同样也有4条边。
因此,答案为D,长方形。
2. 以下哪个几何图形不是多边形?A. 正方形B. 圆形C. 五边形D. 六边形解析:多边形是一个有多个直线边的封闭图形。
正方形有4个边,五边形有5个边,六边形有6个边。
但圆形是一个由无限多个点组成的,边是由连续曲线组成的,因此圆形不是多边形。
答案为B,圆形。
二、填空题1. 三角形的内角和是____度。
解析:三角形的内角和是180度。
2. 矩形的对角线互相垂直且长度相等。
解析:矩形的对角线互相垂直且长度相等。
三、解答题1. 已知一个四边形的两个相邻内角分别是50度和100度,另外两个内角分别是多少度?解析:由四边形的内角和为360度可知两个未知角分别为360度 -50度 - 100度 = 210度。
因此,另外两个内角分别是210度。
2. 一个凸多边形的内角和是1620度,它有几个内角?解析:设凸多边形有n个内角。
由凸多边形的内角和为 (n-2) × 180度,可以得到 n × 180度 = 1620度。
解得 n = 9。
因此,该凸多边形有9个内角。
3. 如图所示,在正方形ABCD中,连接AC和BD两条对角线,交于点O。
若AD的长度为12cm,求AC的长度。
解析:由于正方形的对角线相等且互相垂直,可知AO和OC互相垂直,且AO = OC。
根据勾股定理,可以得到 AD^2 = AO^2 + OD^2,解得AO = OD = (12/√2)cm,而AC = AO + OC = 2AO = 2 × (12/√2)cm = 12√2 cm。
因此,AC的长度为12√2cm。
总结:通过以上的几何图形试题和解析,我们可以看到几何图形的基本概念和性质在小学奥数中起着重要的作用。
3 小学奥数——几何图形 试题及解析

小学奥数——几何图形一.选择题(共50小题)1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度,才可以计算出这个八边形的周长.A.4B.3C.5D.102.如图中阴影部分是正方形,最大长方形的周长是()厘米.A.22B.26C.36D.无法确定3.如图,由6个边长为3厘米的小正方形拼成的图形,它的周长是()厘米.A.36B.39C.42D.454.把一个直径是4厘米的圆分成两个完全相等的半圆,这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米5.如图,有8条线段,至少要分别测量编号为()的三条线段的长度,才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦6.如图,是一个台阶的侧面(线段AC,BC,AB的长依次为5米、12米、13米)要在台阶上面铺上红地毯,且上下各多铺出两米,需要地毯的长度是()米.A.17B.18C.20D.217.如图,正方形被一条曲线分成了A、B两部分,下面第()种说法不正确?A.如果a b>,那么A的周长大于B的周长B.如果a b<,那么A的周长小于B的周长C.如果a b=,那么A的周长等于B的周长D.不管a、b哪个大,A、B的周长总是相等8.如图是用3个长8厘米、宽3厘米的长方形拼成的,这个图形的周长是()A.66厘米B.48厘米C.45厘米9.图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道()边长.A.6B.5C.4D.310.一个长方形花园长是30米,宽是10米,沿着花园走两圈,共走了()A.45米B.90米C.160米D.200米11.把如图的长方形用一条曲线分成甲、乙两个图形,甲图与乙图的周长相比,()A.甲图的长B.乙图的长C.甲图与乙图同样长12.如图,在由11⨯的正方形组成的网格中写有2015四个数字(阴影部分),其边线要么是水平或竖直的直线段,要么是连接11⨯的正方形相邻两边中点的线段,或者是11⨯的正方形的对角线,则图中2015四个数字(阴影部分)的面积是()A.47B.1472C.48D.148213.如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()A.12B.23C.35D.5814.如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是( )A.25B.40C.49D.5015.大、中、小三个正方形,边长都是整数厘米,小正方形的周长比中正方形的边长小,把这两个正方形放在大正方形上(如图),大正方形露出的部分的面积是10平方厘米(图中阴影部分).那么,大正方形的面积是( )平方厘米.A.25B.36C.49D.6416.如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是( )平方厘米.A.240B.270C.300D.36017.如图所示,在58 的方格中,阴影部分的面积为237cm .则非阴影部分的面积为( 2)cm .A.43B.74C.80D.11118.图中,将两个正方形放在一起,大、小正方形的边长分别为0l,6,则图中阴影部分面积为()A.42B.40C.38D.3619.下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB、BC、CD、DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,m n的值等于()A.5B.7C.8D.1220.有5个长方形,它们的长和宽都是整数,且5个长和5个宽恰好是1~10这10个整数;现在用这5个长方形拼成1个大正方形,那么,大正方形面积的最小值为()A.169B.144C.121D.10021.一个梯形的上底增加2厘米,下底减少2厘米,高不变,它的面积与原面积相比()A.变大了B.变小了C.不变D.高不知道,所以无法比较22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点,小等腰直角三角形与正方形中的圆面积相等,请问正方形中的阴影面积与大等腰直角三角形面积的比值A.13B.12C.1D.3223.如图,梯形ABCD 中,//AB DC ,90ADC BCD ∠+∠=︒,且2DC AB =,分别以DA 、AB 、BC 为边向梯形外作正方形,其面积分别为1S ,2S ,3S ,则1S ,2S ,3S 之间的关系是下列选项中的( )A.123S S S +>;B.132S S S +=;C.132S S S +<;D.无法确定.24.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;⋯摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片( )张.A.571B.572C.573D.57425.在88⨯网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个88⨯网格中共有( )枚黑色棋子.A.42B.32C.22D.1226.在66⨯网格的所有方格中放入围棋子,每个方格放1枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个66⨯网格中共有( )枚黑A.18B.14C.12D.1027.一块木板上有13枚钉子(如图1所示).用橡皮筋套住其中的几枚钉子,可以构成三角形,正方形,梯形等等(如图2).请回答:可以构成()个正方形.A.9B.10C.11D.1228.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.1429.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.1530.以平面上任意4个点为顶点的三角形中,钝角三角形最多有()个.A.5B.2C.4D.331.图中,有()个三角形.A.13B.15C.14D.1632.图中共有()个三角形.A.10B.9C.19D.1833.两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形34.将长方形ABCD对角线平均分成12段,连接成如图,长方形ABCD内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是()平方厘米.A.14B.16C.18D.2035.在桌面上,将一个边长为1 的正六边形纸片与一个边长为1的正三角形纸片拼接,要求无重叠,且拼接的边完全重合,则得到的新图形的边数为()A.8B.7C.6D.536.用210个大小相同的正方形拼成一个长方形,不同的拼法有()种.A.2B.4C.6D.837.一个长方形由15个小正方形拼成,如图所示,若这个长方形的周长是64cm,则它的面)cm.积为(2A.960B.256C.240D.12838.如图,每条边都相等,每个角都是直角,则根据信息,求下图的面积为()平方厘米.A.16B.20C.24D.3239.如图,四边形ABCD为长方形,四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时,甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的,与丙、丁两部分面积的大小无关40.如图,正方形ABCD的边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.8041.如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小80l 平方厘米,那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米42.如图,一个33的正方形网格,如果小正方形边长是1,那么阴影部分的面积是()A.5B.4C.3D.243.如图所示,四边形BCDE 为平行四边形,AOE ∆的面积为6,求BOC ∆的面积.( )A.3B.4C.5D.644.如图,M 为平行四边形ABCD 的边BC 上的一点,且:2:3BM MC =,已知三角形CMN的面积为245cm ,则平行四边形ABCD 的面积为( 2)cm .A.30B.45C.90D.10045.如图,长方形ABCD 中的AE 、AF 、AG 、AH 四条线段把此长方形面积五等分,又长方形长20厘米、宽12厘米,那么三角形AFG 的面积AFG S ∆等于( )平方厘米.A.41.2B.43.2C.43.1D.42.346.在等腰梯形ABCD 中,AB 平行于CD ,6AB =,14CD =,AEC ∠是直角,CE CB =,则2AE 等于( )A.84B.80C.75D.6447.下面的四个图形中,第()幅图只有2条对称轴.A. B.C. D.48.下面图形中,恰有2条对称轴()A. B. C. D.49.在如图的阴影三角形中,不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B.C. D.50.在下面的阴影三角形中,不能由图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B. C. D.参考答案与试题解析一.选择题(共50小题)1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度,才可以计算出这个八边形的周长.A.4B.3C.5D.10【解析】如上图,把线段①平移到②的位置可以组成一个大长方形,大长方形的4条边,对边相等,所以只需知道相邻两条边的长度,③=④,所以只需知道1条线段的长度,所以求八边形的周长需要知道:213+=条线段的长度.故选:B.2.如图中阴影部分是正方形,最大长方形的周长是()厘米.A.22B.26C.36D.无法确定【解析】+⨯=(94)226答:最大长方形的周长是26厘米.3.如图,由6个边长为3厘米的小正方形拼成的图形,它的周长是()厘米.A.36B.39C.42D.45【解析】3412⨯=(厘米)326⨯=(厘米)+⨯+(126)26366=+=(厘米)42答:它的周长是42厘米.故选:C.4.把一个直径是4厘米的圆分成两个完全相等的半圆,这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米【解析】(3.14424)2⨯÷+⨯=+⨯(6.284)210.282=⨯=(厘米)20.56答:这两个半圆周长之和是20.56厘米.故选:C.5.如图,有8条线段,至少要分别测量编号为()的三条线段的长度,才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦【解析】由图形可知,④+⑥的线段补给⑧所在的长方形边的虚线部分,⑦-⑤等长线段的补给③所在边的虚线部分,这样就构成了一个完整的长方形,原图形的周长就是答长方形的周长2+个⑤的线段总长,所以图形的周长只要知道①②⑤即可求得.故选:A.6.如图,是一个台阶的侧面(线段AC,BC,AB的长依次为5米、12米、13米)要在台阶上面铺上红地毯,且上下各多铺出两米,需要地毯的长度是()米.A.17B.18C.20D.21【解析】12522++⨯=++1254=(米)21答:需要地毯的长度是21米.故选:D.7.如图,正方形被一条曲线分成了A、B两部分,下面第()种说法不正确?A.如果a b>,那么A的周长大于B的周长B.如果a b<,那么A的周长小于B的周长C.如果a b=,那么A的周长等于B的周长D.不管a、b哪个大,A、B的周长总是相等【解析】A的周长=曲线长+正方形边长2b a⨯+-B的周长=曲线长+正方形边长2a b⨯+-所以A、B、C选项都是正确的,错误的是D.8.如图是用3个长8厘米、宽3厘米的长方形拼成的,这个图形的周长是()A.66厘米B.48厘米C.45厘米【解析】8631⨯-⨯483=-=(厘米)45答:这个图形的周长是45厘米.故选:C.9.图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道()边长.A.6B.5C.4D.3【解析】根据题干分析可得:这个图形的横着的边长之和是:2b;竖着的边长之和是:22+;a c所以这个图形的周长是:2222()++=++,故计算这个图形的周长至少需要知道3a b c a b c条边,故选:D.10.一个长方形花园长是30米,宽是10米,沿着花园走两圈,共走了()A.45米B.90米C.160米D.200米【解析】(3010)22160+⨯⨯=(米)故选:C.11.把如图的长方形用一条曲线分成甲、乙两个图形,甲图与乙图的周长相比,()A.甲图的长B.乙图的长C.甲图与乙图同样长【解析】因为,甲图形的周长是:AB BC AC++,乙图形的周长是:DC AD AC++,而AB CD=,AD BC=,所以,甲、乙两个图形的周长相等;故选:C.12.如图,在由11⨯的正方形组成的网格中写有2015四个数字(阴影部分),其边线要么是水平或竖直的直线段,要么是连接11⨯的正方形相邻两边中点的线段,或者是11⨯的正方形的对角线,则图中2015四个数字(阴影部分)的面积是()A.47B.1472C.48D.1482【解析】据分析可知:将小三角形移到空白处补全完整正方形,共47.5个,所以阴影部分的面积是1 472;故选:B.13.如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()A.12B.23C.35D.58【解析】根据分析,将图中阴影部分进行等积变形,由图不难发现,阴影部分和空白部分的面积刚好相等,正八边形中阴影部分的面积占:1 2故选:A.14.如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25B.40C.49D.50【解析】根据分析,如下图所示,图①逆时针旋转90︒,阴影部分可拼成一等腰直角三角形,214449S=÷=故选:C.15.大、中、小三个正方形,边长都是整数厘米,小正方形的周长比中正方形的边长小,把这两个正方形放在大正方形上(如图),大正方形露出的部分的面积是10平方厘米(图中阴影部分).那么,大正方形的面积是()平方厘米.A.25B.36C.49D.64【解析】根据分析,一条阴影部分的面积为1025÷=平方厘米.因为都是整数,所以只能为15⨯.故,大正方形面积(15)(15)6636=+⨯+=⨯=平方厘米.故选:B.16.如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240B.270C.300D.360【解析】如图所示,将图分割成面积相等的小正三角形,显然,图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成,所以,大正六边形是由9个小正六边形组成的.一个小正六边形的面积为:180630÷=(平方厘米),大正六边形的面积为:309270⨯=(平方厘米),故选:B.17.如图所示,在58⨯的方格中,阴影部分的面积为237cm .则非阴影部分的面积为( 2)cm .A.43B.74C.80D.111【解析】如图,阴影部分占了18.5个格,面积为237cm , 每格的面积是:23718.52()cm ÷=;非阴影就分占21.5格,其面积是:221.5243()cm ⨯=; 答:则非阴影部分的面积为243cm ; 故选:A .18.图中,将两个正方形放在一起,大、小正方形的边长分别为0l ,6,则图中阴影部分面积为( )A.42B.40C.38D.36【解析】1010666(106)210102⨯+⨯-⨯+÷-⨯÷ 100364850=+--38=答:阴影部分的面积是38.故选:C.19.下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB、BC、CD、DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,m n+的值等于()A.5B.7C.8D.12【解析】由以上可知,两个阴影面积比为11:3:2 23=,325+=.故选:A.20.有5个长方形,它们的长和宽都是整数,且5个长和5个宽恰好是1~10这10个整数;现在用这5个长方形拼成1个大正方形,那么,大正方形面积的最小值为()A.169B.144C.121D.100【解析】如图所示,,于是可得:正方形的边长为11,则其面积为1111121⨯=.答:大正方形面积的最小值为121.故选:C.21.一个梯形的上底增加2厘米,下底减少2厘米,高不变,它的面积与原面积相比( ) A.变大了 B.变小了C.不变D.高不知道,所以无法比较【解析】因为梯形的面积=(上底+下底)⨯高2÷,若“上底增加2厘米,下底减少2厘米,高不变”则(上底+下底)的和不变,且高不变, 所以梯形的面积不变. 故选:C .22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点,小等腰直角三角形与正方形中的圆面积相等,请问正方形中的阴影面积与大等腰直角三角形面积的比值是( )A.13B.12C.1D.32【解析】设小等腰三角形的边长是a ,大等腰三角形的边长为b , 2a 2b 则正方形的面积是22222222()(222a b a b a b ++=+=小等腰三角形与大等腰三角形的面积和:2222222a b a b ++=又因小等腰直角三角形与正方形中的圆面积相等,所以正方形中的阴影面积与大等腰直角三角形面积相等. 所以它们的比值是1. 故选:C .23.如图,梯形ABCD 中,//AB DC ,90ADC BCD ∠+∠=︒,且2DC AB =,分别以DA 、AB 、BC 为边向梯形外作正方形,其面积分别为1S ,2S ,3S ,则1S ,2S ,3S 之间的关系是下列选项中的( )A.123S S S +>;B.132S S S +=;C.132S S S +<;D.无法确定.【解析】过点A 作//AE BC 交CD 于点E ,因为//AB DC ,所以四边形AECB 是平行四边形,所以AB CE =,BC AE =,BCD AED ∠=∠, 因为90ADC BCD ∠+∠=︒,2DC AB =, 所以AB DE =,90ADC AED ∠+∠=︒, 所以90DAE ∠=︒那么222AD AE DE +=,因为21S AD =,222S AB DE ==,223S BC AE ==, 所以213S S S =+. 故选:B .24.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;⋯摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片( )张.A.571B.572C.573D.574【解析】根据分析可得,第20次摆放后,该图形共用:++++⋯+⨯-13693(201)=++++⋯+136957=+⨯-÷+(357)(201)21=+5701=(个)571答:第20次摆放后,该图形共用了正三角形纸片571张.故选:A.25.在88⨯网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个88⨯网格中共有( )枚黑色棋子.A.42B.32C.22D.12【解析】由分析得+++++++=(枚)0123567832⨯-=(枚)883232故选:B.26.在66⨯网格的所有方格中放入围棋子,每个方格放1枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个66⨯网格中共有()枚黑色围棋子.A.18B.14C.12D.10【解析】每行的数目可以为0~6个,每列都相等,所以一定是6的倍数,++++++=,012345621如果去掉3,那么剩下的数:21318-=正好是6的倍数,所以,白棋子有18个,则,黑色围棋子有:661818⨯-=(个)故选:A.27.一块木板上有13枚钉子(如图1所示).用橡皮筋套住其中的几枚钉子,可以构成三角形,正方形,梯形等等(如图2).请回答:可以构成()个正方形.A.9B.10C.11D.12【解析】第一种正方形有5个,第二种正方形有4个,第三个正方形有1个,第四种正方形有1个,共11个.故选:C.28.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.14【解析】根据分析可得,共有:6612+=(个);答:图中,一共能数出12个含有“☆”的长方形.故选:C.29.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.15【解析】单个的三角形有9个,4个三角形组成的大三角形3个,最外面的最大的三角形1个,共有:93113++=(个)答:用橡皮筋可套出13个正三角形. 故选:C .30.以平面上任意4个点为顶点的三角形中,钝角三角形最多有( )个. A.5B.2C.4D.3【解析】如图,平面上任意4点构成了4个钝角三角形: ABC ∆、ABD ∆、ACD ∆、BCD ∆,所以以平面上任意4个点为顶点的三角形中,钝角三角形最多有4个. 故选:C .31.图中,有( )个三角形.A.13B.15C.14D.16【解析】由题意,由一个小三角形构成的,有6个; 由两个小三角形构成的,有3个; 由三个小三角形构成的,有6个; 大三角形1个,所以三角形的个数为636116+++=个, 故选:D .32.图中共有( )个三角形.A.10B.9C.19D.18【解析】根据题干分析可得:88218++=(个),答:图中一共有18个三角形.故选:D.33.两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形【解析】因为拼在一起的两个小三角形一定有两条边共线,这时能组成一个平角,A、因为两个锐角的和小于180度,所以,两个锐角三角形不可能拼成一个大三角形;B、因为9090180︒+︒=︒,所以两个直角三角形能拼成一个大三角形;C、因为钝角+锐角有可能等于180︒,所以两个钝角三角形可能拼成一个大三角形;D、因为钝角+锐角有可能等于180︒,所以两个钝角三角形可能拼成一个大三角形;故选:A.34.将长方形ABCD对角线平均分成12段,连接成如图,长方形ABCD内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是()平方厘米.A.14B.16C.18D.20【解析】设把中间最小的空白长方形的面积看作单位1ab=,那么与它相邻的阴影部分的面积就是2233a b ab ab⨯-==,同理,相邻的空白部分的面积就是55ab=,依此规律,面积依次下去为7,9,11,则空白部分的面积总和是15915++=,而实际空白部分面积总和是10平方厘米,可得单位1的实际面积是210153÷=(平方厘米);那么阴影部分面积总和是:371121++=,则实际面积是:221143⨯=(平方厘米);答:阴影部分面积总和是14平方厘米.故选:A.35.在桌面上,将一个边长为1 的正六边形纸片与一个边长为1的正三角形纸片拼接,要求无重叠,且拼接的边完全重合,则得到的新图形的边数为()A.8B.7C.6D.5【解析】180(62)6︒⨯-÷18046=︒⨯÷120=︒180660︒÷=︒12060180︒+︒=︒所以,拼接后的图形是:6345+-=(条)答:得到的新图形的边数为5.故选:D.36.用210个大小相同的正方形拼成一个长方形,不同的拼法有()种.A.2B.4C.6D.8【解析】2102357=⨯⨯⨯因数的总个数:(11)(11)(11)(11)16+⨯+⨯+⨯+=(个)不同的拼法有:1628÷=(种)答:不同的拼法有8种.故选:D.37.一个长方形由15个小正方形拼成,如图所示,若这个长方形的周长是64cm,则它的面积为(2)cm.A.960B.256C.240D.128【解析】64[(53)2]÷+⨯=÷6416=(厘米)4⨯⨯=(平方厘米)4415240答:它的面积为2240cm.故选:C.38.如图,每条边都相等,每个角都是直角,则根据信息,求下图的面积为()平方厘米.A.16B.20C.24D.32【解析】如右图进行分割,把图形分成了8个边长是2厘米的小正方形⨯⨯=(平方厘米)22832答:这个图形的面积是32平方厘米.故选:D.39.如图,四边形ABCD为长方形,四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时,甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的,与丙、丁两部分面积的大小无关【解析】四边形ABCD为长方形,所以BC AD=,AB CD=,因为四边形CDEF为平行四边形,所以CD EF=,=,所以AB EF两边同时加上BE,所以BF AE=;根据等底等高的三角形的面积相等,所以得出三角形CBF的面积=三角形DAE的面积,则:三角形CBF的面积-丁的面积=三角形DAE的面积-丁的面积,所以甲、乙两部分面积总是相等,与与丙、丁两部分面积的大小无关;故选:D.40.如图,正方形ABCD的边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.80【解析】⨯-⨯=(平方厘米)10108560故选:C.41.如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小80l 平方厘米,那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米【解析】设N部分的面积为x,那么M部分的面积为180x-,+-=⨯(180)3020x xx-=2180600x=+2600180x=2780x=;390N部分的面积是390平方厘米.设梯形的上底为y,1y+⨯⨯=(30)203902y+=10300390y=1090y=;9AE=-=(厘米);30921故选:B.42.如图,一个33⨯的正方形网格,如果小正方形边长是1,那么阴影部分的面积是()A.5B.4C.3D.2【解析】通过观察可知,阴影部分的面积=长是3宽是1的长方形的面积-中间边长是1的正方形的面积.⨯-⨯=31112故选:D.43.如图所示,四边形BCDE为平行四边形,AOE∆的面积.()∆的面积为6,求BOCA.3B.4C.5D.6【解析】连接BD,因为,//BE CD ,OB OB =,所以,BOC ∆的面积等于BOD ∆的面积,又因为,//DE AC ,AB AB =,所以,ABE ∆的面积等于ABD ∆的面积,又因为,ABO ∆是ABE ∆和ABD ∆的公共部分,所以,BOD ∆的面积等于AOE ∆的面积,即,BOD ∆的面积AOE =∆的面积6=.答:BOC ∆的面积是6.故选:D .44.如图,M 为平行四边形ABCD 的边BC 上的一点,且:2:3BM MC =,已知三角形CMN的面积为245cm ,则平行四边形ABCD 的面积为( 2)cm .A.30B.45C.90D.100【解析】如图,连接AC .Q 四边形ABCD 是平行四边形,//AD BN ∴,ADM NCM ∴∆∆∽,∴24()9ADM MNC S DM S CM ∆∆==, 45MNC S ∆=Q ,20ADM S ∆∴=,:3:2CM DM =Q ,30ACM S ∆∴=,50ADC S ∆∴=,2100ADC ABCD S S ∆∴==平行四边形,故选:D .45.如图,长方形ABCD 中的AE 、AF 、AG 、AH 四条线段把此长方形面积五等分,又长方形长20厘米、宽12厘米,那么三角形AFG 的面积AFG S ∆等于( )平方厘米.A.41.2B.43.2C.43.1D.42.3【解析】由题意可知2012485ABE AEF AGH ADH AFCG S S S S S ∆∆∆∆⨯======四边形, BE EF ∴=,DH HG =,Q 1482BE AB =g g , 8BE EF ∴==,20164CF =-=,Q 1482DH AD =g g , 4.8DH HG ∴==, 2.4CG =,14 2.4 4.82FGC S ∆∴=⨯⨯=, 48 4.843.2AFG S ∆∴=-=,故选:B .46.在等腰梯形ABCD 中,AB 平行于CD ,6AB =,14CD =,AEC ∠是直角,CE CB =,则2AE 等于( )A.84B.80C.75D.64【解析】如图,连接AC ,过点A 作AF CD ⊥于点F ,过点B 作BG CD ⊥于点G ,则AF BG =,6AB FG ==,4DF CG ==.在直角AFC ∆中,22222210100AC AF FC AF AF =+=+=+,在直角BGC ∆中,222222416BC BG GC AF AF =+=+=+,又CE CB =Q ,90AEC ∠=︒,22222100(16)84AE AC EC AF AF ∴=-=+-+=,即284AE =.故选:A .47.下面的四个图形中,第( )幅图只有2条对称轴. A. B. C. D.【解析】如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴.观察易知,符合题意的是C.故选:C.48.下面图形中,恰有2条对称轴()A. B. C. D.【解析】根据轴对称图形的定义,可得:A有4条对称轴,B没有对称轴,C有2条对称轴,D有1条对称轴.故选:C.49.在如图的阴影三角形中,不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B.C. D.【解析】根据分析,可以逆向思维,可以将题中的阴影三角形经过旋转、平移,长直角边旋转和短直角边旋转后得到的图形,不难看出,只有A选项是不可能出现的.图中图中①、②、③三边应为顺时针关系,A不合要求.故选:A.50.在下面的阴影三角形中,不能由图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B. C. D.【解析】解析:由图可知:A、C、D都可由原三角形经过旋转和平移得到,而B选项必须经过对称才能与原三角形重合,故选:B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学几何面积问题一姓名引理:如图1ABCD 中。
P 是AD 上一点,连接PB,PC 则S △PBC =S △ABP +S △pcD =21S ABCD1.已知:四边形ABCD 为平行四边形,图中的阴影部份面积占平行四边形ABCD 的面积的几分之几?2. 的面积为18,E 是PC 的中点,求图中的阴影部份面积3. 在中,CD 的延长线上的一点E ,DC=2DE,连接BE 交AC 于P 点,(如图)知S △PDE =1, S △ABP =4,求:平行四边形ABCD 的面积4..四边形ABCD 中,BF=EF=ED,(如图)(1) 若S 四边形ABCD =15则S 阴 = (2)若S △AEF + S △BFC =15 则S 四边形ABCD =(第一题图)(3)若S △AEF= 3 S △BFC =2 则S 四边形ABCD =5. 四边形ABCD 的对角线BD 被E,F ,G 三点四等份,(如图)若四边形AECG=15 则S 四边形ABCD =E P 图1ADCB (适应长方形、正方形)BGB F C A E D6.四边形ABCD 的对角线BD 被E,F ,G 三点四等份,(如图)若阴影部份面积为15 则S 四边形ABCD =7.若ABCD 为正方形,F 是DC 的中点,已知:S △BFC = 1 (1)则S 四边形ADFB =(2) S △DFE =(3) S △AEB =8.直角梯形ABCD 中.AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S △GED =S △GFC .求S 阴=小学几何面积问题二姓名 1.如图S △AEF= 2, AB=3AE CF=3EF 则S △ABC=2. 如图S △BDE=30 ,AB=2AE , DC=4AC 则S △ABC=3.正方形ABCD 中,E,F,G 为BC 边上四等份点, M,N,P 为对角线AC 上的四等份点(如图) 若S 正方形ABCD=32 则S △NGP=4.已知:S △ABC=30 D 是BC 的中点 AE=2ED 则S △BDE=ACBD第1题第2题5. 已知:AD=DB DE=3EC AF=3FE 若S △ABC =160 求S △EFC =6.已知:在△ABC 中,FC=3AF EC=2BE BD=DF 若S △DFE=3则S △ABC=7.ABCD 为平行四边形,AG=GC,BE=EF=FC,若S △GEF =2,则S ABCD =8.ABCD 是梯形,AD // BC(如图)则S △AOB= S △AOD= (第8题)9. ABCD 是梯形,AD // BC(如图)则S △DOC= S △BOC= (第9题)10.ABCD 是梯形,AD // BC(如图),且BO=3OD, S △AOB=15则S 梯ABCD=(第10题)BACACC CB CCCCB C L 2L 1N11. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC 的面积为(第11题)小学几何面积问题三姓名1.在梯形ABCD 中,AD//BC,图中阴影部分的面积为4,OC=2AO, 求 S 梯ABCD =2在梯形ABCD 中,AD//BC,S △BOC=14 OC=2AO 求 S 梯ABCD =3. 在梯形ABCD 中,AD//BC,S △AOB=14 OC=3AO 求 S 梯ABCD =4.在梯形ABCD 中,AD//BC,图中阴影部分的面积为30,OC=3AO,S △AOB =6求S 空=5.读一读:A 若直线L 1//L 2 (如图一)一.当高不变,底扩大(或缩小)K 倍。
其面积也同时扩大(或缩小)K 倍例:BC=2 AB=4 AB 是BC 扩大2倍而得所以面积Ⅰ就是面积Ⅱ的2倍 (图一)ABC Ⅱ ⅠACBMHHC.若直线L 1//L 2 (如图二)二.当底不变,高扩大(或缩小)K 倍。
其面积也同时扩大(或缩小)K 倍例:AC=BC H 1=2H 2 (图二) 那么:S △NBC =2S △MAC练一练:1如图(一):L 1//L 2 AB=10 BC=5若S △HAB =2.如图(二)△ACM 的AC 边上的高H 1是△NCB 的CB 边上的高H 2的一半,且AC=CB, 若S △NBC =100 则S △ACM =3.把下面的三角形分成三个小三角形,使它们的面积的比为1:2:34.△ABC 是等边三角形,AD 是BC 边上的高,若S △ABC =2,则S △ADC =5. △ABC 是等边三角形,D 是AB 的中点,且DH 垂直于BC ,H 为垂足. 若S △BDH =2,则S △ABC=_ C__B CEAFCDB小学几何面积问题四姓名1.在△ABC 中,AE=BE,BD=2DC,FC=3AF 若△ABC 的面积为1,则S △EFD =2.△ABC 中,三边BC,CA,AB 上分别有点D,E,F,且BC=3CD AB=2BE AC=4AF 若△ABC 的面积为240平方厘米,则S △DEF 平方厘米.3.. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC 的面积为4.两个正方形拼成如图,则阴影部分的面积为______。
5.两个正方形拼成如图,则阴影部分的面积为______。
6D CFE BA6.三个正方形拼成如图,求阴影部分的面积为______。
7.如图ABCD是矩形,EF∥AB如果S矩形ABCD=24 则S阴=8.在平行四边形ABCD中,EF∥AC,若△AED的面积为72平方厘米,则S△DCF=9.ABCD是平行四边形.直线CF与AB交于E,与DA的延长线交于F,连BF,若三角形BEF的面积等于4cm2,那么三角形EDA(阴影部分)的面积是 cm2小学几何面积问题五姓名1.有两种自然放法,将正方形内接于等腰直角三角形.如果按左图的放法,那么可求得这个正方形面积为441. 如果按右图的放法,那么可求得这个正方形面积应为2.下图是一块长方形的草地,长方形的长是18米.宽是10米.中间有两条宽2米的路,一条是长方形,另一条是平行四边形,那么草地的面积是平方米.44 5jF(第2题图)3.如图大正方形的边长是20厘米.E,F,G,H 分别是各边中点,问:中间小正方形的面积是 平方厘米.4.“十字架”由五个边长相等的正方形拼成,若AB=20厘米.求:这个“十字架”的面积是 平方厘米.5.一个边长为21厘米的正方形,被分成了四个长方形(如图)它们的面积分别是这个正方形面积的101,51,103,52在占52的这一块长方形里有一个小正方形是阴影部分.求这个阴影部分的面积为 平方厘米.6.一个面积小于100的整数的长方形中,它的内部有三个小正方形,边长都是整数.已知正方形(二)的边长是长方形长的2/5,正方形(一)的边长是长方形宽的1/8。
那么图中阴影部分的面积为 (平方单位)cmCBC1厘米CBDA7. 如图所示ABCD 为正方形,且AB//EF ,BF=1厘米 则:阴影部分的面积= 平方厘米.、8.在长方形ABCD 中,长是宽的4倍,对角线BD=17厘米,求该长方形的面积是 .小学几何面积问题六 姓名1.一个长方形ABCD ,向它的形外分别作正方形(如图)若所作的四边形的周长之和为264厘米,面积之和是1378平方厘米,求原来的长方形的面积是 平方厘米.2. 两个长方形叠放如图,小长方形宽是2厘米,A 是大长方形一边的中点,△ABC 是等腰直角三角形,图中阴影部分的面积和为 平方厘米.3.在边长为10的正方形的四边上分别取E,F,G,H.已知E 与G 的水平距离是5厘米,H 与F 的水平距离是4厘米,求四边形EFGH 的面积为 平方厘米.EDCBFABA10厘米FED'C'B'A'DCBA8平方厘米6平方厘米DCBAPDCBA684.长方形ABCD 的长DC 是8厘米,宽AD 是4厘米. EFCA 也是长方形,它的面积是多少平方厘米?答:是 平方厘米.5.如图在直角梯形中,AB=10厘米,阴影部分的面积是这个直角梯形面积的一半.求这个直角梯形面积是 平方厘米6.已知:ABCD 是平行四边形,P 在AD 上, BP ⊥CP,且BP=8厘米,CP=6厘米。
求图中的阴影部分的面积 平方厘米.7. 梯形ABCD 与梯形A /B /C /D /大小相同,如图重合(叠) 若EC=4厘米,D /C /=24厘米,高EF=5厘米. 求阴影部分的面积是 平方厘米.8.在一个梯形内,有两个三角形的面积分别是6平方厘米和8平方厘米,梯形的下底长是上底长的2倍,求:阴影部分的面积和是 平方厘米.8平方厘米12厘米4厘米EDCBA24cm28cm2EDCBAGC7厘米C21厘米小学几何面积问题七姓名1.求图中阴影部分的面积2. 求图中阴影部分的面积3.已知:EF 是梯形ABCD 的中位线,求梯形ABCD 的面积4.求梯形的面积5.求下图四边形的面积B'EDFA6.在下图中,长方形内有一个钝角三角形,按照图示的数,求这个三角形的面积.7.三个边长为10厘米、12厘米、8厘米的正方形拼放在一起,直线BC 将整个图形面积平分,求线段AB 的长.8. 如图有两个边长都是10厘米的正方形ABCD 和A /B /C /D /,且正方形A /B /C /D /的顶点A /恰好是正方形ABCD 的中心,那么:阴影部分的面积是 平方厘米.小学几何面积问题八姓名1. 平行四边形ABCD 的面积是32厘米,AD=8厘米,∠B=45○,求阴影部分的面积是 平方厘米.2.如图所示平行四边形ABCD 中,CH=DE=FB=GC ,如果阴影部分的面积为7平方厘米,那么,这个平行四边形的面积是 平方厘米.D354913FEDCBA3.平行四边形ABCD 已知:三角形AHB 的面积是8平方厘米,三角形DFC 的面积是6平方厘米.求阴影部分的面积是 平方厘米.4. 平行四边形ABCD 中有一点E ,已知,三角形ABE 的面积是73平方厘米,三角形BEC 的面积是10平方厘米。
求阴影部分三角形BED 的面积是 平方厘米.5.一个45度的直角三角板.最长边为12厘米,那么,它的面积为 平方厘米.6.如图长方形内画了一些直线,已知边上有三块面积分别为13平方厘米,35平方厘米,49平方厘米,那么图中的阴影部分面积是 平方厘米.7.在长方形ABCD 中,DE,DF 把这个长方形平均分成了三份,即三角形ADE 的面积等于三角形DFC的面积等于四边形BEDF 的面积.如果这个长方形的面积是54平方厘米,那么三角形BEF 的面积是 平方厘米.FB10厘米E6厘米DCFCB8.如图三角形ABC 是等腰直角三角形.它与一个正方形叠放在一起。
