利用栈实现数制转换(10进制转换8进制)
十进制转换为八进制的方法
十进制转换为八进制的方法以十进制转换为八进制的方法为标题，写一篇文章在日常生活和计算机领域中，我们经常需要将十进制数转换为其他进制数以满足特定的需求。
其中，将十进制数转换为八进制数是一种常见的转换方式。
本文将介绍如何将十进制数转换为八进制数的方法。
我们需要了解十进制和八进制的概念。
十进制是我们常用的计数方式，使用0-9这十个数字来表示。
而八进制则使用0-7这八个数字来表示。
十进制数的一个特点是每一位上的权重都是10的幂次方。
而八进制数的一个特点是每一位上的权重都是8的幂次方。
接下来，我们以一个具体的例子来说明十进制转换为八进制的方法。
假设我们要将十进制数37转换为八进制数。
第一步，我们需要找到最大的8的幂次方，使得该幂次方小于或等于37。
在本例中，最大的8的幂次方为8^1，即8。
因为8^1=8，小于37。
第二步，我们将37除以8，得到商4和余数5。
其中，商代表了8进制数的最高位，而余数则代表了8进制数的最低位。
在本例中，商为4，余数为5。
第三步，我们将商继续除以8，得到商0和余数4。
同样地，商代表了8进制数的次高位，余数代表了次低位。
第四步，我们将上述的余数按照从下往上的顺序排列，得到最终的八进制数。
在本例中，37的八进制表示为54。
通过以上的步骤，我们成功地将十进制数37转换为八进制数54。
除了以上的方法，我们还可以通过不断除以8并记录余数的方式来进行转换。
具体步骤如下：1. 将十进制数不断除以8，直到商为0为止。
2. 每次除法运算得到的余数就是八进制数的一位。
3. 将得到的余数按照从下往上的顺序排列，即可得到最终的八进制数。
这种方法更加直观，可以一步步地得到八进制数的每一位。
除了将十进制数转换为八进制数，我们还可以将八进制数转换为十进制数。
具体方法如下：1. 将八进制数的每一位乘以8的幂次方，并相加。
2. 幂次方的起始值为0，对应八进制数的最低位。
3. 依次递增幂次方的值，直到计算完所有的位。
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
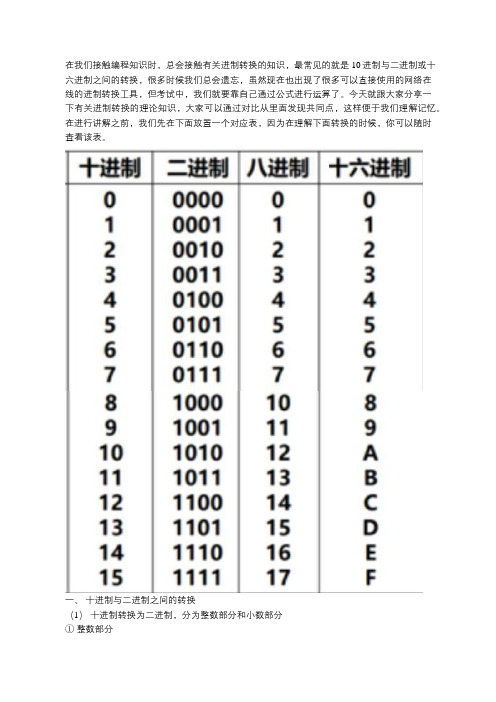
在我们接触编程知识时，总会接触有关进制转换的知识，最常见的就是10进制与二进制或十六进制之间的转换，很多时候我们总会遗忘，虽然现在也出现了很多可以直接使用的网络在线的进制转换工具，但考试中，我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识，大家可以通过对比从里面发现共同点，这样便于我们理解记忆。
在进行讲解之前，我们先在下面放置一个对应表，因为在理解下面转换的时候，你可以随时查看该表。
一、十进制与二进制之间的转换（1）十进制转换为二进制，分为整数部分和小数部分①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。
下面举例：例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2分析:第一步，将168除以2商84余数为0。
第二步，将商84除以2，商42余数为0。
第三步，将商42除以2，商21余数为0。
第四步，将商21除以2，商10余数为1。
第五步，将商10除以2，商5余数为0。
第六步，将商5除以2，商2余数为1。
第七步，将商2除以2，商1余数为0。
第八步，将商1除以2，商0余数为1。
第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000②小数部分方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。
如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数，下面举例：例1：将0.125换算为二进制得出结果：将0.125换算为二进制（0.001）2分析：第一步，将0.125乘以2，得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
(C语言)10进制转换2,8,16进制
（C语言）10进制转换2，8，16进制作者：vinseven#include"stdio.h"#include"conio.h"#include"malloc.h"#include"windows.h"#define ElemType intvoid menu();void TenToTwo();void TenToEight();void TenToSixteen();void InitStack(struct sNode **HS);void Push(struct sNode **HS,ElemType x);ElemType Pop(struct sNode **HS);ElemType Peek(struct sNode **HS);int EmptyStack(struct sNode **HS);void ClearStack(struct sNode **HS);int ten;/*要输入的10进制数*/int x;/*把将要插入到栈中的元素暂时存进 x 中*/struct sNode hs;struct sNode{ElemType data;struct sNode *next;};void main(){menu();getch();}void menu(){char choice;int flag=1;while(1){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 1，10进制转换2进制\n\n\n");printf("\t\t\t 2，10进制转换8进制\n\n\n");printf("\t\t\t 3，10进制转换16进制\n\n\n");printf("\t\t\t 0，退出\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入编号：");while(flag){fflush(stdin);choice=getch();switch(choice){case '1':{system("cls");TenToTwo();flag=0;break;}case '2':{system("cls");TenToEight();flag=0;break;}case '3':{system("cls");TenToSixteen();flag=0;break;}case '0':{printf("\n\t\t\t按任意键退出");getch();exit(0);}default:{printf("\n\t\t\t无此选项可选！请重新输入！\n");flag=1;break;}}}system("cls");flag=1;}}/*10进制转换2进制界面*/void TenToTwo(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换2进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数：");scanf("%d",&ten);while(ten!=0){x=ten%2;Push(&hs,x);ten=ten/2;}printf("\t\t\t二进制数为：");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换8进制界面*/void TenToEight(){printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换8进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数：");scanf("%d",&ten);while(ten!=0){x=ten%8;Push(&hs,x);ten=ten/8;}printf("\t\t\t八进制数为：");while(!EmptyStack(&hs))printf("%d",Pop(&hs));getch();}/*10进制转换16进制界面*/void TenToSixteen(){int temp;printf("\n\t\t\t________________________\n\n\n");printf("\t\t\t 10进制转换16进制界面\n\n\n");printf("\t\t\t________________________\n\n");printf("\t\t\t请输入10进制数：");scanf("%d",&ten);while(ten!=0){x=ten%16;Push(&hs,x);ten=ten/16;}printf("\t\t\t十六进制数为：");while(!EmptyStack(&hs)){temp=Pop(&hs);switch(temp){case 1:case 2:case 3:case 4:case 5:case 6:case 7:case 8:case 9:printf("%d",temp);break;case 10:printf("A");break;case 11:printf("B");break;case 12:printf("C");break;case 13:printf("D");break;case 14:printf("E");break;case 15:printf("F");break;}}getch();}/*关于栈的函数*//*1，初始化链栈为空*/void InitStack(struct sNode **HS) {*HS=NULL;}/*2，向栈中插入一个元素*/void Push(struct sNode **HS,ElemType x){struct sNode *newp;newp=malloc(sizeof(struct sNode));if(newp==NULL){printf("内存动态空间用完，退出运行！");system("pause");exit(0);}newp->data=x;newp->next=*HS;*HS=newp;}/*3，从栈中删除一个函元素并返回它*/ ElemType Pop(struct sNode **HS){struct sNode *p;ElemType temp;if(*HS==NULL){printf("栈空！无法删除！");system("pause");exit(0);}p=*HS;*HS=p->next;temp=p->data;free(p);return temp;}/*4，读取栈顶元素*/ElemType Peek(struct sNode **HS){if(*HS==NULL){printf("栈空！无法读取栈顶结点！");system("pause");exit(1);}return (*HS)->data;}/*5，检查链栈是否为空,空返回1，否则返回0*/ int EmptyStack(struct sNode **HS){if(*HS==NULL)return 1;elsereturn 0;}/*6，清除链栈为空*/void ClearStack(struct sNode **HS){struct sNode *cp,*np;cp=*HS;while(cp!=NULL){np=cp->next;free(cp);cp=np;}*HS=NULL; }。
十进制转八进制c语言
十进制转八进制c语言概述在计算机科学中，数制转换是一个重要的基础知识。
十进制转八进制是其中的一种常见转换方式。
在本文中，我们将学习如何使用C语言编写一个能够实现十进制转八进制的程序。
原理解析要将十进制数转换为八进制数，我们需要了解两个数制之间的转换规则。
在十进制系统中，每一位的权值分别为10的0次方、10的1次方、10的2次方…以此类推。
而在八进制系统中，每一位的权值分别为8的0次方、8的1次方、8的2次方…以此类推。
将十进制数转换为八进制数的步骤如下： 1. 将十进制数不断除以8，直到商为0为止，得到的余数就是八进制数的最低位。
2. 将得到的余数由下往上依次排列，得到的数就是八进制数。
程序设计为了实现十进制转八进制的功能，我们将采用逐步除法法实现。
具体的C代码如下所示：#include <stdio.h>void decimalToOctal(int decimal) {int octalNum[100];int i = 0;while (decimal != 0) {octalNum[i] = decimal % 8;decimal = decimal / 8;i++;}printf("转换为八进制的结果为：");for (int j = i - 1; j >= 0; j--) {printf("%d", octalNum[j]);}}int main() {int decimal;printf("请输入一个十进制数：");scanf("%d", &decimal);decimalToOctal(decimal);return 0;}程序解析让我们一步一步地解析上述代码。
首先，我们定义了一个名为decimalToOctal的函数，该函数用于将十进制数转换为八进制数。
我们使用了一个整型数组octalNum来存储转换后的八进制数，数组的大小设定为100，可根据需要进行调整。
10进制到8进制方法
10进制到8进制方法10进制到8进制方法目录•引言•方法一：递归求解•方法二：位运算•方法三：除法法则•总结引言在计算机科学中，常常需要进行不同进制之间的转换。
本文将讨论如何将10进制数转换为8进制数，同时介绍三种常见的转换方法。
方法一：递归求解递归是一种经典的解决问题的方法，可以用于将10进制数转换为8进制数。
1.首先，将给定的10进制数除以8，得到商和余数。
2.将余数作为最低位的数字，添加到结果中。
3.如果商大于0，则将商作为新的10进制数，重复步骤1。
4.如果商等于0，则递归停止，得到最终的8进制数。
该方法适用于小数位数较少的情况，但对于较大的数值可能会造成递归深度达到系统限制。
方法二：位运算位运算是计算机中常用的高效算法，也可以用于10进制到8进制的转换。
1.将给定的10进制数与7进行按位与运算，得到最低位的数字。
2.将得到的数字添加到结果中。
3.将给定的10进制数右移3位，相当于除以8。
4.重复步骤1-3，直到给定的10进制数等于0。
该方法利用位运算的高效性，可以快速地将10进制数转换为8进制数。
方法三：除法法则除法法则是一种简单的数学方法，可以用于10进制到8进制的转换。
1.将给定的10进制数除以8，得到商和余数。
2.将余数作为最低位的数字，添加到结果中。
3.将商继续除以8，得到新的商和余数。
4.重复步骤2-3，直到商等于0。
该方法不需要使用递归或位运算，而是通过简单的除法计算来完成转换。
总结本文介绍了三种将10进制数转换为8进制数的方法：递归求解、位运算和除法法则。
根据具体情况可以选择相应的方法来实现转换。
递归求解方法适用于小数位数较少的情况，但可能会受到递归深度限制；位运算方法利用位运算的高效性能快速完成转换；除法法则方法则简单直观，不需要使用特殊的算法技巧。
希望本文对读者理解和掌握10进制到8进制的转换方法有所帮助。
十进制转八进制c语言
十进制转八进制c语言十进制转八进制是一种常见的数值转换方法，在C语言中可以非常简单地实现，让我们来看看如何进行这个转换。
首先，需要明确的是十进制和八进制之间的转换规律。
在十进制数转换成八进制数时，我们可以将其每三位一组分离出来，每组数字按权值相加得到对应的八进制数。
例如，十进制数734对应的八进制数为1326，其中：7 x 10^2 + 3 x 10^1 + 4 x 10^0 = 1 x 8^3 + 3 x 8^2 + 2 x 8^1 + 6 x 8^0知道了这个规律之后，我们就可以开始写C语言代码了。
具体而言，可以使用while循环来不断从输入中读取十进制数，然后将其转换成八进制数并输出。
代码如下：```c#include <stdio.h>int main() {int decimal, octal, remainder, place = 1;printf("请输入一个十进制数：");scanf("%d", &decimal);octal = 0;// 将十进制数转换成八进制数while (decimal != 0) {remainder = decimal % 8;octal += remainder * place;place *= 10;decimal /= 8;}printf("该数的八进制表示为：%d\n", octal);return 0;}```在这个代码中，我们首先声明了四个变量：decimal用于存储输入的十进制数，octal用于存储转换后的八进制数，remainder用于临时存储余数，place用于表示当前位数的权值。
接着，我们通过scanf语句从标准输入中读取一个整数，将其赋值给decimal。
然后，在一个while循环中，我们使用类似于上面的转换规律来将decimal转换成八进制数。
具体而言，我们不断地计算decimal除以8的余数，然后将其乘以对应的权值加入到octal中。
栈的应用-数制转换（C语言数据结构）
栈的应⽤-数制转换（C语⾔数据结构）数制转换在计算机中经常⾯对不同数制的转换问题，如将⼀个⼗进制数N转换为d进制B。
数制转换的解决⽅法很多，其中⼀个简单的转换算法是重复下述两步。
直到N等于零为⽌。
x = N mod dN = N div d其中，N为需要转换的⼗进制数，d为转换后的进制，x值为转换后各个数位上的数，div为整除运算，mod为求余运算。
算法的运⾏过程为：第⼀次求出的x值为d进制数的最低位，最后⼀次求出的x值为d进制数的最⾼位，所以上述算法是从低位到⾼位顺序产⽣d进制的各位，然后逆序输出，因为它按“后进先出”的规律进⾏的，所以⽤栈这种结构处理最合适。
根据这个特点，利⽤栈来实现上述数制转换，即将计算过程种⼀次得到的d进制数码按顺序栈进栈。
计算结束后，再返顺序出栈，并按出栈顺序打印输出。
这样即可得到给定的⼗进制数对应的d进制数，由此可以得到数制转换的算法。
实现代码利⽤顺序栈实现数制转换（以⼗进制转换为⼆进制为例）1 #include <stdlib.h>2 #include <stdio.h>3 #define MAXSIZE 102445 /*定义顺序栈*/6 typedef int elemtype;7 typedef struct SequenStack8 {9 elemtype data[MAXSIZE];10 int top;11 }SequenStack;1213 /*判（顺序栈）栈空*/14 SequenStack * Init_SequenStack()15 {16 SequenStack * S;17 S = (SequenStack *)malloc(sizeof(SequenStack));1819 if (S == NULL)20 {21 return S;22 }23 S->top = -1;24 return S;25 }2627 /* 判空栈（顺序栈）*/28 int SequenStack_Empty(SequenStack * S)29 {30 if (S->top == -1)31 {32 return 1;33 }34 else35 {36 return 0;37 }38 }3940 /* ⼊栈（顺序栈） */41 int Push_SequenStack(SequenStack * S, elemtype x)42 {43 if (S->top >= MAXSIZE-1)44 {45 return 0;46 }47 S->top++;48 S->data[S->top] = x;49 return 1;50 }5152 /* 出栈（顺序栈） */53 int Pop_SequenStack(SequenStack * S, elemtype * x)54 {55 if (S->top == -1)56 {57 return 0;58 }59 else60 {61 S->top--;62 *x = S->data[S->top+1];63 return 1;64 }65 }6667 /* 进制转换算法 */68 void SequenStackConversion(int N)69 {70 int x;71 SequenStack * S = Init_SequenStack();72 while (N > 0)73 {74 Push_SequenStack(S, N % 2);75 N = N / 2;76 }77 while (! SequenStack_Empty(S))78 {79 Pop_SequenStack(S, &x);80 printf("%d", x);81 }82 }8384 int main()85 {86 int N;87 printf("Please enter the decimal number you want want to convert:\n");88 scanf("%d", &N);89 printf("The converted binary number is:\n");90 SequenStackConversion(N);91 }实现结果：利⽤链栈栈实现数制转换（以⼗进制转换为⼆进制为例）1 #include <stdio.h>2 #include <stdlib.h>34 /*定义链栈*/5 typedef int elemtype;6 typedef struct LinkedStackNode7 {8 elemtype data;9 struct LinkedStackNode *next;10 }LinkedStackNode, *LinkedStack;11 LinkedStack top;1213 /*链栈的初始化*/14 LinkedStack Init_LinkedStack()15 {16 LinkedStack top = (LinkedStackNode *)malloc(sizeof(LinkedStackNode));1718 if(top != NULL)19 {20 top->next = NULL;21 }22 return top;23 }2425 /*判栈空*/26 int LinkedStack_Empty(LinkedStack top)27 {28 if (top->next == NULL)29 {30 return 1;31 }32 else33 {34 return 0;35 }3637 }3839 /*⼊栈*/40 int Push_LinkedStack(LinkedStack top, elemtype x)41 {42 LinkedStackNode *node;43 node = (LinkedStackNode *)malloc(sizeof(LinkedStackNode));4445 if (node == NULL)46 {47 return 0;48 }49 else50 {51 node->data = x;52 node->next = top->next;53 top->next = node;54 return 1;55 }5657 }5859 /*出栈*/60 int Pop_LinkedStack(LinkedStack top, elemtype * x)61 {62 LinkedStackNode *node;63 if (top->next == NULL)64 {65 return 0;66 }67 else68 {69 node = top->next;70 *x = node->data;71 top->next = node->next;72 free(node);73 return 1;74 }7576 }7778 /*进制转换*/79 void ListStackConversion(int N)80 {81 int x;82 LinkedStack S = Init_LinkedStack();83 while (N > 0)84 {85 Push_LinkedStack(S, N % 2);86 N = N / 2;87 }88 while (! LinkedStack_Empty(S))89 {90 Pop_LinkedStack(S, &x);91 printf("%d", x);92 }9394 }9596 int main()97 {98 int N;99 printf("Please enter the decimal number you want want to convert:\n"); 100 scanf("%d", &N);101 printf("The converted binary number is:\n");102 ListStackConversion(N);103 }实现结果：把顺序栈和链栈两种功能综合在⼀起实现数制转换（以⼗进制转换为⼗六进制为例）1 /* 进制转换 */2 #include <stdlib.h>3 #include <stdio.h>4 #define MAXSIZE 100 /*定义顺序栈的长度*/56 /*定义顺序栈*/7 typedef int elemtype;8 typedef struct SequenStack9 {10 elemtype data[MAXSIZE];11 int top;12 }SequenStack;1314 /*定义链栈*/15 typedef int elemtype;16 typedef struct LinkedStackNode17 {18 elemtype data;19 struct LinkedStackNode *next;20 }LinkedStackNode, *LinkedStack;21 LinkedStack top;2223 /* 顺序栈初始化 */24 SequenStack * Init_SequenStack()25 {26 SequenStack * S;27 S = (SequenStack *)malloc(sizeof(SequenStack));2829 if (S == NULL)30 {31 return S;32 }33 S->top = -1;34 return S;35 }3637 /*链栈的初始化*/38 LinkedStack Init_LinkedStack()39 {40 LinkedStack top = (LinkedStackNode *)malloc(sizeof(LinkedStackNode));4142 if(top != NULL)43 {44 top->next = NULL;45 }46 return top;47 }4849 /*判栈（顺序栈）空*/50 int SequenStack_Empty(SequenStack * S)51 {52 if (S->top == -1)53 {54 return 1;55 }56 else57 {58 return 0;59 }60 }6162 /* 判栈（链栈）空 */63 int LinkedStack_Empty(LinkedStack top)65 if (top->next == NULL)66 {67 return 1;68 }69 else70 {71 return 0;72 }7374 }7576 /* ⼊栈（顺序栈）*/77 int Push_SequenStack(SequenStack * S, elemtype x)78 {79 if (S->top >= MAXSIZE-1)80 {81 return 0;82 }83 S->top++;84 S->data[S->top] = x;85 return 1;86 }8788 /* 出栈（顺序栈） */89 int Pop_SequenStack(SequenStack * S, elemtype * x)90 {91 if (S->top == -1)92 {93 return 0;94 }95 else96 {97 S->top--;98 *x = S->data[S->top+1];99 return 1;100 }101 }102103 /* ⼊栈（链栈） */104 int Push_LinkedStack(LinkedStack top, elemtype x)105 {106 LinkedStackNode *node;107 node = (LinkedStackNode *)malloc(sizeof(LinkedStackNode)); 108109 if (node == NULL)110 {111 return 0;112 }113 else114 {115 node->data = x;116 node->next = top->next;117 top->next = node;118 return 1;119 }120121 }122123 /* 出栈（链栈） */124 int Pop_LinkedStack(LinkedStack top, elemtype * x)125 {126 LinkedStackNode *node;127 if (top->next == NULL)128 {129 return 0;130 }131 else132 {133 node = top->next;134 *x = node->data;135 top->next = node->next;136 free(node);137 return 1;138 }139140 }141142 /* 使⽤顺序⽅式进⾏进制转换的函数 */143 void SequenStackConversion(int N)144 {145 int x;146 SequenStack * S = Init_SequenStack();147 while (N > 0)149 Push_SequenStack(S, N % 16); 150 N = N / 16;151 }152 while (! SequenStack_Empty(S))153 {154 Pop_SequenStack(S, &x);155 switch (x)156 {157 case 10:158 printf("A");159 break;160 case 11:161 printf("B");162 break;163 case 12:164 printf("C");165 break;166 case 13:167 printf("D");168 break;169 case 14:170 printf("E");171 break;172 case 15:173 printf("F");174 break;175 default:176 printf("%d", x);177 break;178 }179 }180 }181182 /* 使⽤链栈⽅式进⾏进制转换的函数 */ 183 void ListStackConversion(int N)184 {185 int x;186 LinkedStack S = Init_LinkedStack(); 187 while (N > 0)188 {189 Push_LinkedStack(S, N % 16);190 N = N / 16;191 }192 while (! LinkedStack_Empty(S))193 {194 Pop_LinkedStack(S, &x);195 switch (x)196 {197 case 10:198 printf("A");199 break;200 case 11:201 printf("B");202 break;203 case 12:204 printf("C");205 break;206 case 13:207 printf("D");208 break;209 case 14:210 printf("E");211 break;212 case 15:213 printf("F");214 break;215 default:216 printf("%d", x);217 break;218 }219220 }221222 }223224 void function()225 {226 printf("-------------------------------------------\n"); 227 }228229 /* 主函数调⽤进制转换函数 */230 int main()231 {232 int N, x;233 printf("Please enter the decimal number you want want to convert:\n");234 scanf("%d", &N);235 function();236 printf("Choose using sequential stack or list stack\n");237 printf("1:Sequential stack 2:list stack:\n");238 function();239 scanf("%d", &x);240 printf("The converted binary number is:\n");241 switch (x)242 {243 case 1:244 SequenStackConversion(N);245 break;246 case 2:247 ListStackConversion(N);248 break;249 default:250 printf("error");251 break;252 }253254 return 0;255 }值得注意的是，当⼗进制转换为⼗六进制的时候，需要考虑输出现实⼤于9的⼗六进制位数，这⾥我们考虑可以使⽤switch开关实现。
[计算机软件及应用]栈的应用和串图
![[计算机软件及应用]栈的应用和串图](https://img.taocdn.com/s3/m/62d61f359ec3d5bbfc0a74c2.png)
A. i-j-1 B. i-j
C. j-i+1 D. 不确定的
5. 若 已 知 一 个 栈 的 入 栈 序 列 是 1,2,3,…,n ， 其 输 出 序 列 为 p1,p2,p3，…，pN,若pN是n，则pi是( D)。
A. i
B. n-i C. n-i+1 D. 不确定
6
2. 在作进栈运算时,应先判别栈是否( ① B),在作退栈运算时应 先判别栈是否( ② A )。当栈中元素为n个,作进栈运算时发生上
if(!In(c,OP)){Push(OPND,c); c=getchar();}//不是运算符则进入 栈
switch(Precede(GetTop(OPTR),c)){ case ‘<’: //栈顶元素的优先级低
Push(OPTR, c); c=getchar(); break;
case ‘=’: //脱括号并接受下一个字符；
例1数制转换
除基取余法
十进制N和其它进制数的转换是计算机实原理:
N=(n div d)*d+n mod d
( 其中:div为整除运算,mod为求余运算)
例如 (1348)10=(2504)8，其运算过程如下：
n n div 8 n mod 8
16. 栈在（ D）中应用。
A. 递归调用 B. 子程序调用 C. 表达式求值 D. A，Ｂ，Ｃ
9
注：上述算法的匹配过程易于理解，且在某些应用场合，如文本 编辑等，效率也较高，但是在有些情况下，该算法的效率却很低。
其主串的指针i在不断的回溯，如i=3,变为i=2,i=7变为i=4… 其时间复杂度可达到O(n*m).
列得不到的出栈排列是( )。
A．XYZ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
//利用栈实现数制转换(10进制转换8进制)
#include <stdio.h>
#include <malloc.h>
#define ERROR 0
#define OK 1
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量
typedef int SElemType;
typedef struct stack
{
SElemType *top;
SElemType *bottom;
int stacksize;
}SqStack;
int InitStack(SqStack *S)
{
//构造一个空栈
S->bottom=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType));
if(!S->bottom) return ERROR; //存储分配失败
S->top=S->bottom;
S->stacksize=STACK_INIT_SIZE;
return OK;
} //InitStack
int Push(SqStack *S,SElemType e)
{
//插入元素e为新的栈顶元素
if(S->top-S->bottom>=S->stacksize-1)
{
S->bottom=(SElemType*)realloc(S->bottom,
(S->stacksize+STACKINCREMENT)*sizeof(SElemType));
if(!S->bottom)
return ERROR; //
S->top=S->bottom+S->stacksize;
}
*S->top++=e;
return OK;
} //Push
int Pop(SqStack *S,SElemType *e)
{
//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK;否则返回ERROR;
if(S->top==S->bottom)
return ERROR;
*e=*--S->top;
return OK;
} //Pop
int StackEmpty(SqStack S)
{
if(S.top==S.bottom)
return 1;
else return 0;
}
void main()
{
SqStack myStack;
int N,e;
InitStack(&myStack);
printf("请输入N：");
scanf("%d",&N);
while(N)
{
Push(&myStack,N%8);
N=N/8;
}
while(!StackEmpty(myStack))
{
Pop(&myStack,&e);
printf("%d",e);
}
printf("\n");
}。