七年级数学认识三角形练习题讲解学习
苏科版七年级数学下册第七章 认识三角形 附答案

1. 看较短的两条线段的和是否大于最长的线段,若是,则
能组成三角形;反之, 则不能组成三角形.
2. 看最长的线段减去最短的线段的差是否小于第三条线段,
若是,则能组成三角形;反之,则不能组成三角形.
感悟新知
知识点 4 三角形的角平分线、中线、高
知4-讲
1. 三角形的角平分线、中线和高是三角形中的三种重要线 段,它们是研究三角形的一些特征的基础,我们需要从 不同的角度进行理解,列表如下:
注意 在三角形的 事项 内部
(1)与角的平分线不同 (2)在三角形的内部
(1)与边的垂线不同 (2)不一定在三角形 的内部
重要 特征
一个三角形有 三条中线,它
●●
们相交于三角 形内一点
●●●●
一个三角形有三条角 ●●
平分线,它们相交于 ●● ●
三角形内一点 ●● ● ●● ●
三角形的三条高所 ●●
在的直线相交于一 ●● ●●● ●
感悟新知
(2)三边长满足(a-b)(b-c)=0. 解:因为(a-b)(b-c)=0, 所以a-b=0 或b-c=0. 所以a=b 或b=c. 所以△ ABC 为等腰三角形.
知2-讲
感悟新知
知2-讲
解题秘方:要判断三角形的形状,可根据“边是否 相等”来判断,所以从条件中分析出三 边长的关系是解决本题的关键.
感悟新知
知2-讲
“a=b 且b=c”与“a=b或b=c”得到的结论是不一样的. 方法点拨:
从边的角度判断三角形的形状,若只能判定两条边 相等,则此三角形是等腰三角形,若能判定三边相等, 则此三角形是等边三角形.
感悟新知
知识点 3 三角形的三边关系
知3-讲
1. 三角形的三边关系 三角形的任意两边之和大于第三边. 我们可以从不同的角度理解,列表如下:
七年级数学下册《认识三角形》学习指导1(含答案)

七年级数学下册《认识三⾓形》学习指导1(含答案)《认识三⾓形》学习指导1 ⼀、学习⽬标导航1、了解三⾓形的有关概念并会表⽰,能证明出“三⾓形内⾓和等于180°”;2、按⾓将三⾓形分成三类,能发现“直⾓三⾓形的两个锐⾓互余”;3、掌握三⾓形的三边关系.重点:三⾓形的内⾓和定理和三⾓形的三边关系.难点:三⾓形内⾓和定理推理和应⽤. ⼆、相关知识链接线段、射线、直线的表⽰⽅法:三、学习引导三⾓形的概念及表⽰(1)你能从中找出四个不同的三⾓形吗?(2)这些三⾓形有什么共同的特点?1、根据⽣活中的三⾓形的特点,总结出三⾓形的定义:叫做三⾓形.2、看图填空:三⾓形有条边、个内⾓和个顶点.三⾓形可以⽤符号表⽰,如右图是顶点为的三⾓形,记作.它的三边有时也⽤来表⽰.如图,顶点A 所对的边BC ⽤表⽰,边AC 、边AB 分别⽤表⽰.三⾓形的内⾓和我们知道,把⼀个三⾓形的三个⾓撕下来,拼在⼀起,可以得到三⾓形的内⾓和为180°.⼩明只撕下三⾓形的⼀个⾓,也得到了上⾯的结论,他是怎样做的呢?⾃⼰剪⼀个三⾓形纸⽚,试⼀试.并与同伴交流你的想法.试⼀试:证明三⾓形的内⾓和为180°独⽴完成例题如图,在△ABC 中,∠B=3∠A ,∠C=5∠A,求∠A ,∠B ,∠C 的度数.三⾓形的分类及其他性质看课本第83页,回答下列问题:1、三⾓形按⾓分,可以分为哪三类?A BCa b c2、直⾓三⾓形两锐⾓之间有什么关系?独⽴完成例题如图,在△ABC中,D为BC上的⼀点,∠ADB=90°,∠1=∠B.若按⾓分类,△ABC是什么形状的三⾓形?为什么?三⾓形的三边关系1、我们已经知道三⾓形按⾓是如何分类的,那么按边有时如何分类的呢?2、(1)元宵节的晚上,房梁上亮起了彩灯,装有黄⾊彩灯的电线与装有红⾊彩灯的电线哪根长呢?说明你的理由.(2)在⼀个三⾓形中,任意两边之和(差)与第三边的长度有怎样的关系?三⾓形任意两边之和第三边三⾓形任意两边之差第三边独⽴完成例题有两根长度分别为5厘⽶和8厘⽶的⽊棒,⽤长度为2厘⽶的⽊棒与它们能摆成三⾓形吗?为什么?长度为13厘⽶的⽊棒呢?预习检测1、已知:如图1,D是BC上⼀点,∠C=62°,∠CAD=32°,则∠ADB=_______度.________三⾓形.3、下列线段不能组成三⾓形的是()A.a=5,b=3,c=3 B.a=6,b=3,c=8C.a=6,b=8,c=10 D.a=9,b=4,c=5参考答案:1、94°2、锐⾓3、D。
专题4.1认识三角形(与三角形有关的线段)(知识讲解)-七年级数学下册基础知识专项讲练(北师大版)

专题4.1 认识三角形(与三角形有关的线段)(知识讲解)【学习目标】1. 理解三角形及与三角形有关的概念,掌握它们的文字、符号语言及图形表述方法;2. 理解并会应用三角形三边间的关系;3. 理解三角形的高、中线、角平分线及重心的概念,学会它们的画法及简单应用;4. 对三角形的稳定性有所认识,知道这个性质有广泛的应用.【要点梳理】要点一、三角形的定义及分类1. 定义: 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.特别说明:(1)三角形的基本元素:①三角形的边:即组成三角形的线段;②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;③三角形的顶点:即相邻两边的公共端点.(2)三角形定义中的三个要求:“不在同一条直线上”、“三条线段”、“首尾顺次相接”.(3)三角形的表示:三角形用符号“△”表示,顶点为A 、B 、C 的三角形记作“△ABC ”,读作“三角形ABC ”,注意单独的△没有意义;△ABC 的三边可以用大写字母AB 、BC 、AC 来表示,也可以用小写字母a 、b 、c 来表示,边BC 用a 表示,边AC 、AB 分别用b 、c 表示.2.三角形的分类(1)按角分类:特别说明:①锐角三角形:三个内角都是锐角的三角形;②钝角三角形:有一个内角为钝角的三角形.(2)按边分类:特别说明:①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;②等边三角形:三边都相等的三角形.要点二、三角形的三边关系定理:三角形任意两边的和大于第三边.推论:三角形任意两边的差小于第三边.特别说明:(1)理论依据:两点之间线段最短.(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形 锐角三角形斜三角形 钝角三角形(3)证明线段之间的不等关系.要点三、三角形的高、中线与角平分线1、三角形的高从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.三角形的高的数学语言:如下图,AD 是ΔABC 的高,或AD 是ΔABC 的BC 边上的高,或AD⊥BC 于D ,或∠ADB=∠ADC=∠90°.注意:AD 是ΔABC 的高∠ADB=∠ADC=90°(或AD⊥BC 于D);特别说明:(1)三角形的高是线段;(2)三角形有三条高,且相交于一点,这一点叫做三角形的垂心;(3)三角形的三条高:(ⅰ)锐角三角形的三条高在三角形内部,三条高的交点也在三角形内部;(ⅱ)钝角三角形有两条高在三角形的外部,且三条高的交点在三角形的外部;(ⅲ)直角三角形三条高的交点是直角的顶点.2、三角形的中线三角形的一个顶点与它的对边中点的连线叫三角形的中线.三角形的中线的数学语言:如下图,AD 是ΔABC 的中线或AD 是ΔABC 的BC 边上的中线或BD =CD =BC. 特别说明:(1)三角形的中线是线段;(2)三角形三条中线全在三角形内部; (3)三角形三条中线交于三角形内部一点,这一点叫三角形的重心; (4)中线把三角形分成面积相等的两个三角形.3、三角形的角平分线三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线. 三角形的角平分线的数学语言:如下图,AD 是ΔABC 的角平分线,或∠BAD=∠CAD 且点D 在BC 上.注意:AD 是ΔABC 的角平分线∠BAD=∠DAC=∠BAC (或∠BAC=2∠BAD=2∠DAC) . 特别说明:(1)三角形的角平分线是线段; ⇔21⇔21(2)一个三角形有三条角平分线,并且都在三角形的内部;(3)三角形三条角平分线交于三角形内部一点,这一点叫做三角形的内心;(4)可以用量角器或圆规画三角形的角平分线.要点四、三角形的稳定性三角形的三条边确定后,三角形的形状和大小就确定不变了,这个性质叫做三角形的稳定性. 特别说明:(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变.(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形.【典型例题】类型一、与三角形有关线段??三角形的边段??概念??分类1.如图所示,(1)图中有几个三角形?(2)说出CDE ∆的边和角.(3)AD 是哪些三角形的边?C ∠是哪些三角形的角?【答案】(1)图中有:ABD ∆,ADC ∆,ADE ∆,EDC ∆,ACB ∆,共5个;(2)CDE ∆的边:CD ,CE ,DE ,角:C ∠,CDE ∠,DEC ∠;(3)AD 是ADB ∆,ADE ∆,ADC ∆的边;C ∠是ABC ∆,ADC ∆,DEC ∆的角.【分析】(1)分类找三角形,含AB 的,含AD (不含AB )的,含DE (不含AD )的三类即可;(2)根据组成三角形的三条线段一一找出,利用三角形两边的夹角即可找出;(3)观察图形,找出含AD 的三角形,先找AD 左边的,再找AD 右边的即可,根据三角形内角的定义,角的两边是三角形的边,找到第三边,在∠C 的内部在线段看与角的两边是否相交即可解:(1)图中有:以AB 为边的三角形有∠ABD ,∠ABC ,以AD 为边的三角形有∠ADE ,∠ADC ,再以DE 为边三角形有∠DEC ,一共有5个三角形分别为ABD ∆,ABC ∆,ADC ∆,ADE ∆,EDC ∆;(2)CDE ∆的边:CD ,CE ,DE ,角:C ∠,CDE ∠,DEC ∠;(3)AD 是ADB ∆,ADE ∆,ADC ∆的边;C ∠是ABC ∆,ADC ∆,DEC ∆的角.【点拨】本题考查三角形的识别,三角形的基本要素,三角形个数,观察图形找出图中的三角形,三角形的组成,找以固定线段的三角形,和固定角的三角形,掌握利用分类思想找出所有的图形,三角形的边与角,共线段三角形以及共角三角形是解题关键.举一反三:【变式】如图,以BD 为边的三角形有哪些?分别写出来;以∠1为内角的三角形有哪些?分别写出来.【分析】先根据BD 边找三角形,再根据∠1找三角形.解:以BD 为边的三角形有:∠BDC ,∠BDO ,以∠1为内角的三角形有:∠EOC ,∠ACD .【点拨】本题考查了三角形的内角和边的概念,学会分类的方法找三角形是本题的解题关键.2.已知ABC 的三边长分别为a ,b ,c .若a ,b ,c 满足22()()0a b b c -+-=,试判断ABC 的形状.【答案】ABC 的形状是等边三角形.【分析】利用平方数的非负性,求解a ,b ,c 的关系,进而判断ABC .解:∠22()()0a b b c -+-=,∠0a b -=,0b c -=∠a =b =c ,∠ ABC ∆是等边三角形.【点拨】本题主要是考查了三角形的分类,熟练掌握各类三角形的特点,例如三边相等为等边三角形,含90︒的三角形为直角三角形等,这是解决此类题的关键.举一反三:【变式】满足下列条件的三角形是锐角三角形、直角三角形还是钝角三角形.(1)∠ABC 中,∠A =30°,∠C =∠B ;(2)三个内角的度数之比为1:2:3.【答案】(1)锐角三角形;(2)直角三角形.【分析】根据角的分类对三角形进行分类即可.解:(1)∠∠A =30°,∠C =∠B ,∠A +∠C +∠B =180°,∠∠C =∠B =75°,∠满足条件的三角形是锐角三角形.(2) ∠三个内角的度数之比为1∠2∠3,∠可求得每个内角的度数分别为30°,60°,90°,∠满足条件的三角形是直角三角形.【点拨】本题主要考查了三角形的分类问题.类型二、与三角形有关线段??构成三角形条件??确定第三边取值范围3.判断下列长度的三条线段能否拼成三角形?为什么?(1)3cm 、8cm 、4cm ; (2)5cm 、6cm 、11cm ; (3)5cm 、6cm 、10cm ;【答案】(1)不能,因为3cm +4cm <8cm ;(2)不能,因为5cm +6cm =11cm ;(3)能,因为5cm +6cm >10cm【分析】略举一反三:【变式】如图所示三条线段a ,b ,c 能组成三角形吗?你是用什么方法判别的?【答案】三条线段a ,b ,c 能组成三角形,理由见分析【分析】只需要利用作图方法证明b a c b c -<<+即可.解:三条线段a ,b ,c 能组成三角形,理由如下:如图所示,根据线段的和差可知b a c b c -<<+,∠三条线段a ,b ,c 能组成三角形.【点拨】本题主要考查了构成三角形的条件,线段的尺规作图,证明b a c b c -<<+是解题的关键.4.己知三角形的两边长为5和7,第三边的边长a .(1)求a 的取值范围;(2)若a 为整数,当a 为何值时,组成的三角形的周长最大,最大值是多少?【答案】(1) 212a << (2)当11a =时,三角形的周长最大为23【分析】(1)根据三角形三边关系求解即可得到答案;(2)由(1)取最大值即可得到答案.(1)解:由三角形的三边关系可知7575a -<<+,即212a <<,∠a 的取值范围是212a <<;(2)解:由(1)知,a 的取值范围是212a <<,a 是整数,∠当11a =时,三角形的周长最大,此时周长为:571123++=,∠周长的最大值是23.【点拨】本题考查三角形三边关系:任意两边之和大于第三边,任意两边之差小于第三边. 举一反三:【变式】已知:ABC 中,5AB =,21BC a =+,12AC =,求a 的范围.【答案】38a <<【分析】根据三角形的三边关系列不等式求解即可.解:∠AB BC AC 、、是ABC 的三边,∠AC AB BC AC AB -<<+,即:a -<+<+12521125,解得:38a <<,故答案为:38a <<.【点拨】本题考查了三角形的三边关系、解不等式组;熟练掌握三角形的三边关系以及解不等式组的方法是解题的关键.类型三、与三角形有关线段??三角形的高??作图??求值(等面积法)5.在如图所示的方格纸中,每个小正方形的边长均为1,点A ,点B ,点C 均在小正方形的顶点上.(1) 画出ABC 中BC 边上的高AD ;(2) 直接写出ABC 的面积为___.【答案】(1)见分析 (2)8【分析】(1)结合网格图,直接利用三角形高线作法得出答案;(2)结合网格图,直接利用三角形的面积求法得出答案.(1)解:如图所示:AD 即为所求;1【变式】如图:(1) 用三角尺分别作出锐角三角形ABC ,直角三角形DEF 和钝角三角形PQR 的各边上的高线.(2) 观察你所作的图形,比较三个三角形中三条高线的位置,与三角形的类型有什么关系?【分析】(1)根据三角形高的画法画图即可;(2)根据(1)所作图形进行求解即可.(1)解;如图所示,即为所求; (2)解:由(1)可知,锐角三角形的三条高线的交点在三角形内部;直角三角形的三条高线的交点为直角顶点;钝角三角形的三条高线的交点在三角形外部.【点拨】本题主要考查了画三角形的高,三角形高线的交点,正确画出三角形的高是解题的关键.6.如图,,AD AE 分别是ABC 的中线和高,3cm AE =,26cm ABD S =△.求BC 和DC 的长.【答案】8cm BC =,4cm CD =ABD S =是ABC 的中线,得到解:由题意,得:BD AE ⋅4cm ,是ABC 的中线,12BD BC =∠4cm,28cm CD BC BD ===.【点拨】本题考查三角形的高线和中线.熟练掌握三角形的中线是三角形的顶点到对边中点所连线段,是解题的关键.举一反三:【变式】如图,AD BE ,分别是ABC 的高,若465AD BC AC ===,,,求BE 的长.2ABC S =分别是ABC 的高,1122ABC S BC AD AC =⨯=⨯45AD BC AC ===,,,462455BC BE ⨯==24BE =【点拨】本题考查了三角形面积的计算公式,掌握等面积法求解是解题的关键.7.如图,在ABC 中()2AB BC AC BC BC >=,,边上的中线AD 把ABC 的周长分成70和50两部分,求AC 和AB 的长.【答案】5636AC AB ==,【分析】先根据2AC BC =和三角形的中线列出方程求解,分类讨论7050AC CD AC CD +=+=①,②,注意答案是否满足条件,即是否满足题目给出的条件、是否满足三角形三边的关系.解:设BD CD x ==,则24AC BC x ==,BC 边上的中线AD 把ABC 的周长分成70和50两部分,AB BC >,①当7050AC CD AB BD +=+=,时,470x x +=,解得:14x =,441456AC x ∴==⨯=,14BD CD ==,50501436AB BD ∴=-=-=,36AB ∴=,36286456BC AB AC +=+=>=,满足三边关系,5636AC AB ∴==,;②当5070AC CD AB BD +=+=,时,450x x +=,解得:10x =,441040AC x ∴==⨯=,10BD CD ∴==,70701060AB BD =-=-=,60AC BC AB +==,不满足三角形三边关系,所以舍去,5636AC AB ∴==,.【点拨】本题考查了三角形中线的性质和三边的关系,解题的关键是找到等量关系,列出方程. 举一反三:【变式】如图,已知AD 、AE 分别是ABC 的高和中线9cm,12cm AB AC ==,15cm BC =,90BAC ∠=︒.试求:(1) ABE 的面积;(2) AD 的长度;(3) ACE △与ABE 的周长的差.2ACE △的周长-ABE 的周长)解:ABC 是直角三角形,2191254(cm )2ABC =⨯⨯,AE 是BC 上的中线,BE EC ∴=,ABE ACE S S ∆∆∴=,2127cm 2ABE ABC S S ∆∆∴=; )解:BAC ∠=,AD 是BC 1122AD BC ∴⋅=AB AC AD BC ⋅∴=)解:AE 是BC BE CE =,ACE 的周长-ABE 的周长和ABE 的周长差是3cm 【点拨】本题考查了三角形的面积公式,以及三角形的中线将三角形分成面积相等的两部分,熟练掌握相关的性质与公式是解决此题的关键.8.如图,ABC 中,90C ∠=︒,8cm AC ,6cm BC ,10cm AB =.若动点P 从点C 开始,按C →A →B →C 的路径运动,且速度为每秒2cm .设运动的时间为t 秒.(1) 当t =___________时,CP 把ABC 的周长分成相等的两部分?(2) 当t =___________时,CP 把ABC 的面积分成相等的两部分?(3) 当t 为何值时,BCP 的面积为12?【答案】(1)6(2)6.5(3) 2或6.5秒先求出ABC的周长为把ABC的周长分成相等的两部分时,12cmBC+=速度即可求解;)根据中线的性质可知,点把ABC的面积分成相等的两部分,进而求解即)分两种情况:∠P在AC1)ABC中,∠8cmAC,6cmBC,10cmAB,∠ABC的周长861024cm=++=,∠当CP把ABC的周长分成相等的两部分时,点P在AB上,此时212t=,解得6t=.故答案为:6;)当点P在AB中点时,把ABC的面积分成相等的两部分,此时213t=,解得 6.5t=.故答案为:6.5;)分两种情况:∠当P在AC∠BCP的面积16 2CP⨯⨯4CP=,24t=,t∠当P在AB∠BCP的面积=12=ABC面积的一半,∠P为AB中点,213t=, 6.5.故t为2或6.5秒时,BCP的面积为12.【点拨】本题考查了一元一次方程的应用,三角形的周长与面积,三角形的中线,难度适中.利用分【变式】已知ABC的面积为S,根据下列条件完成填空.图1图2图3(1) 1AM 是ABC 的边BC 上的中线,如图1,则1ACM 的面积为 (用含S 的式子表示,下同);2CM 是1ACM 的边1AM 上的中线,如图2,则2ACM △的面积为 ;3AM 是2ACM △的边2CM 上的中线,如图3,则3ACM △的面积为 ;…… )中的求解可得规律,利用规律即可求解.是ABC 的边上的中线,ABC 的面积为11122ACM ABC S S S ==; 2CM 是1ACM 的边AM 2, 12111244ACM ACM ABC S S S S ===;3AM 是2ACM △的边2CM 上的中线,如图3,231128ACM ACM S S S ==, 故答案为:12S ,14S ,1)解:∠112ACM SS =,211124ACM ACM S S S ==2312ACM ACM S S ==,以此类推,可得12n ACM S ⎛⎫= ⎪⎝⎭2022=2022ACM S故答案为:202212⎛⎫ ⎪【点拨】本题考查了三角形中线的性质,熟记三角形的一条中线把三角形的面积分成相等的两部分是9.如图,CE 是ABC 的角平分线,EF BC ∥,交AC 于点F ,已知64AFE ∠=︒,求FEC ∠的度数.【答案】32︒ ACB AFE ==∠是ABC 的角平分线,12BCE ACB =∠FEC BCE =∠本题主要考查了平行线的性质,【变式】如图,点E 为直线AB 上一点,B ACB ∠=∠,BC 平分ACD ∠,求证:AB CD .【分析】根据平行线的判定定理求解即可.解:BC 平分ACD ∠,ACB BCD ∴∠=∠,B ACB ∠=∠,B BCD ∴∠=∠,∠AB CD ∥.【点拨】本题考查了平行线的判定,熟记“内错角相等,两直线平行”是解题的关键.10.如图,ABC 中,按要求画图:(1) BAC ∠的平分线AD ;(2) 画出ABC 中BC 边上的中线AE ;(3) 画出ABC 中AB 边上的高CF .【分析】(1)画出BAC ∠的平分线交BC 于D 即可;(2)取BC 的中点E ,连接AE ,中线AE 即为所求;(3)过点C 作CF BA ⊥交BA 的延长线于F ,CF 即为ABC 中AB 边上的高.(1)解:如图,AD 即为所求;(2)解:如图,中线AE 即为所求;(3)解:如图,高CF 即为所求.【点拨】本题考查了作三角形的角平分线、中线和高线,解决本题的关键是掌握基本作图方法.举一反三:【变式】在边长为1的正方形网格中:''';(1)画出ABC沿CB方向平移2个单位后的A B C'''的重叠部分面积为多少?(2)ABC与A B C重叠部分面积为'''即可;)根据题意画出ABC沿CB个单位后的A B C)正方形的边长为,根据图形进行求解即可.'''如图所示:解:(1)ABC沿CB方向平移2个单位后的A B C(2)∠正方形的边长为1,9.下列图形中哪些具有稳定性?【答案】(1)(4)(6)中的图形具有稳定性.【分析】根据三角形的稳定性可直接进行求解.解:具有三角形稳定性的有(1)(4)(6).【点拨】本题主要考查三角形的稳定性,熟练掌握三角形的稳定性是解题的关键.举一反三:【变式1】(1)下列图形中具有稳定性是;(只填图形序号)(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.【答案】(1)∠∠∠;(2)图见分析【分析】根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.解:(1)具有稳定性的是∠∠∠三个.(2)如图所示:【点拨】本题主要考查了三角形的稳定性,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.【变式2】如图(1)扭动三角形木架,它的形状会改变吗?如图(2)扭动四边形木架,它的形状会改变吗?如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?归纳:∠三角形木架的形状______,说明三角形具有______;∠四边形木架的形状______说明四边形没有______.【答案】图(1)扭动三角形木架,它的形状不会改变,因为三角形具有稳定性;图(2)扭动四边形木架,它的形状会改变,四边形不稳定;图(3)斜钉一根木条的四边形木架的形状形状不会改变,四边形变成两个三角形,三角形具有稳定性;归纳:∠是三角形,稳定性;∠四边形,稳定性.【分析】∠根据三角形的稳定性进行解答即可;∠根据四边形的不稳定性进行解答即可.解:图(1)扭动三角形木架,它的形状不会改变,因为三角形具有稳定性;图(2)扭动四边形木架,它的形状会改变,四边形不稳定;图(3)斜钉一根木条的四边形木架的形状形状不会改变,四边形变成两个三角形,三角形具有稳定性;归纳:∠由三角形具有稳定性知,三角形木架的形状不会改变,这说明三角形具有稳定性.故答案为:是三角形,稳定性;∠四边形木架的形状是四边形,四边形具有不稳定性.故答案为:四边形,稳定性.【点拨】本题考查的是三角形的稳定性,三角形的稳定性和四边形的不稳定性在实际生活中的应用问题,比较简单.。
最新北师大版七年级下册数学第四章三角形第1章节认识三角形知识点+测试试题以及答案

三角形第1章节认识三角形知识点+测试试题1、不在同一条直线上的三条线段首尾顺次相接所组成的图形,称为三角形,可以用符号“Δ”表示。
2、顶点是A、B、C的三角形,记作“ΔABC”,读作“三角形ABC”。
3、组成三角形的三条线段叫做三角形的边,即边AB、BC、AC,有时也用a,b,c来表示,顶点A所对的边BC用a表示,边AC、AB分别用b,c来表示;4、∠A、∠B、∠C为ΔABC的三个内角。
5、三角形内角和定理:三角形的三个内角的和等于1800。
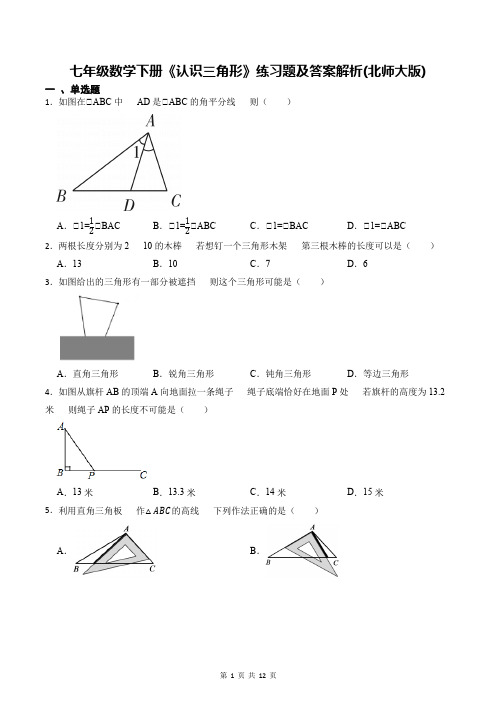
1、如图,在△ABC中,∠B=40°,∠C=60°,则∠A= .(1题)(2题)(6题)2、如图所示,图中三角形的个数共有个。
3、下列叙述不正确的是。
A、三角形内角和是180B、一个三角形不是锐角三角形就是钝角三角形C、三角形中最多有一个钝角D、直角三角形两个锐角的和是90°。
4、在△ABC中,如果∠A-∠B=90°,那么△ABC是()A.直角三角形B.钝角三角形C.锐角三角形D.不能确定5、一个三角形三个内角的度数比是1:2:3,这个三角形最大的角是()度,它是()三角形.6、如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于()7、如图:(1)图中共有______个三角形,它们是__ ____;(2)以AD为边的三角形有____ __;(3)∠C分别为△AEC,△ADC,△ABC中______,______,______边的对角;(4)∠AED是______,______的内角;3倍,第三个角比这两个角的8、三角形的第一个内角是第二个内角的2和大30°,求这三角形的三个内角各是多少度?三角形的内角和以及按角分类(任意一个三角形中,最多有3个锐角,最少有两个锐角,最多一个直角,最多一个钝角)直角三角形(也表示Rt三角形)的两锐角互余1、△ABC中,∠A:∠B:∠C=1:7:4,则最大角是,按角分它是()三角形2、小明测得△ABC中,∠C=3(∠A+∠B),按角分它是三角形。
七年级数学下册第7章7.4 认识三角形 课时练习(含答案解析)

7.4 认识三角形一.选择题1.(2017•河池)三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线2.(2017•台湾)如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为()A.3:5 B.4:5 C.9:10 D.15:163.(2017•金华)下列各组数中,不可能成为一个三角形三边长的是()A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,104.(2017•永州)小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是()A.AB,AC边上的中线的交点B.AB,AC边上的垂直平分线的交点C.AB,AC边上的高所在直线的交点D.∠BAC与∠ABC的角平分线的交点5.(2017•泰州)三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平分线的交点6.(2017•扬州)若一个三角形的两边长分别为2和4,则该三角形的周长可能是()A.6 B.7 C.11 D.127.(2017•舟山)长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是()A.4 B.5 C.6 D.98.(2017•白银)已知a,b,c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为()A.2a+2b﹣2c B.2a+2b C.2c D.09.用12根等长的火柴棒拼三角形(全部用上,不可折断、重叠),不可以拼成的是()A.等腰三角形B.等边三角形C.直角三角形D.以上都有可能10.△ABC周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是()A.12 B.16 C.24 D.3011.如图所示,BE=2EC,D是线段AC的中点,BD和AE交于点F,已知△ABC 的面积是3,求四边形DCEF的面积()A.B.C.D.12.如图,在△ABC中,点D在BC上,点O在AD上,如果S△AOB=3,S△BOD=2,S△ACO=1,那么S△COD等于()A.B.C.D.13.四边形ABCD的对角线AC和BD相交于点E,如果△CDE的面积为3,△BCE的面积为4,△AED 的面积为6,那么△ABE 的面积为( )A .7B .8C .9D .10二、填空题14.已知△ABC 的两条边长分别为2和5,则第三边c 的取值范围是 . 15.如图,点G 是△ABC 的重心,GE ∥AB 交BC 于点E ,GF ∥AC 交BC 于点F ,若△GEF 的周长是2,则△ABC 的周长为 .16.(2017•巴中)如图,在△ABC 中,AD ,BE 是两条中线,则S △EDC :S △ABC = . 17.在Rt △ABC 中,AD 是斜边BC 边上的中线,G 是△ABC 重心,如果BC=6,那么线段AG 的长为 .18.(2017•铁岭)如图,△ABC 的面积为S .点P 1,P 2,P 3,…,P n ﹣1是边BC 的n 等分点(n ≥3,且n 为整数),点M ,N 分别在边AB ,AC 上,且==,连接MP 1,MP 2,MP 3,…,MP n ﹣1,连接NB ,NP 1,NP 2,…,NP n ﹣1,线段MP 1与NB 相交于点D 1,线段MP 2与NP 1相交于点D 2,线段MP 3与NP 2相交于点D 3,…,线段MP n ﹣1与NP n ﹣2相交于点D n ﹣1,则△ND 1P 1,△ND 2P 2,△ND 3P 3,…,△ND n﹣1P n ﹣1的面积和是 .(用含有S 与n 的式子表示)三、解答题19.如图,在△BCD中,BC=4,BD=5,(1)求CD的取值范围;(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.20.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.21.如图,△ABC中,A1,A2,A3,…,A n为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…(1)完成下表:连接个数出现三角形个数(2)若出现了45个三角形,则共连接了多少个点?(3)若一直连接到A n,则图中共有个三角形.22.(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC 的面积为16,则△ABD的面积是,△EBD的面积是.(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?23.请阅读材料,并完成相应的任务.已知点D 在△ABC 的边BC 上(点D 不与点B ,C 重合),点P 是AD 上任意一点,连接BP ,CP . 如图1,若=,显然有S △ABP =S △ACP .如图2,若=,那么S △ABP 与S △ACP 之间的数量关系又是怎样的呢?下面是小李同学的部分求解过程: 如图3,作BM ⊥AD 的延长线于点M ,作CN ⊥AD 于点N . ∴∠BMD=∠CND=90°. 在△BMD 和△CND 中,∵∠BMD=∠CND ,∠BDM=∠CDN ,∴△BMD ~△CND . …(1)请把小李同学的求解过程补充完整. (2)猜想:=,则S △ABP 与S △ACP 之间的数量关系是 .24.如图,在△ABC 中,BC 边上依次有B 、D 、E 、C ,AC 边上依次有A 、G 、F ,满足BD=CE=BC ,CF=AG=AC ,BF 交AE 于点J ,交AD 于I ,BG 交AE 于点K ,交AD 于点H ,且S △ABC =1,求S 四边形KHIJ .25.如图:△ABC的边BC的高为AF,AC边上的高为BG,中线为AD,AF=6,BC=12,BG=5,(1)求△ABD的面积.(2)求AC的长.(3)△ABD和△ACD的面积有何关系.26.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:(1)∠BAE的度数;(2)∠DAE的度数;(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.27.(1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO面积相等;(3)如图3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.参考答案与解析一.选择题1.(2017•河池)三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线【分析】根据等底等高的三角形的面积相等解答.【解答】解:∵三角形的中线把三角形分成两个等底同高的三角形,∴三角形的中线将三角形的面积分成相等两部分.故选A.【点评】本题考查了三角形的面积,主要利用了“三角形的中线把三角形分成两个等底同高的三角形”的知识,本知识点是中学阶段解三角形的面积经常使用,一定要熟练掌握并灵活应用.2.(2017•台湾)如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为()A.3:5 B.4:5 C.9:10 D.15:16【分析】根据三角形面积求法进而得出S△BDC :S△ADC=3:2,S△BDE:S△DCE=3:2,即可得出答案.【解答】解:∵AD:DB=CE:EB=2:3,∴S△BDC :S△ADC=3:2,S△BDE:S△DCE=3:2,∴设S△BDC =3x,则S△ADC=2x,S△BED=1.8x,S△DCE=1.2x,故△DBE与△ADC的面积比为:1.8x:2x=9:10.故选:C.【点评】此题主要考查了三角形面积求法,正确利用三角形边长关系得出面积比是解题关键.3.(2017•金华)下列各组数中,不可能成为一个三角形三边长的是()A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10【分析】根据三角形三边关系定理判断即可.【解答】解:∵5+6<12,∴三角形三边长为5,6,12不可能成为一个三角形,故选:C.【点评】本题考查的是三角形的三边关系,掌握三角形三边关系定理:三角形两边之和大于第三边是解题的关键.4.(2017•永州)小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是()A.AB,AC边上的中线的交点B.AB,AC边上的垂直平分线的交点C.AB,AC边上的高所在直线的交点D.∠BAC与∠ABC的角平分线的交点【分析】根据题意可知所求的圆形玻璃是△ABC的外接圆,从而可以解答本题.【解答】解:由题意可得,所求的圆形玻璃是△ABC的外接圆,∴这块玻璃镜的圆心是△ABC三边垂直平分线的交点,故选B.【点评】本题考查垂径定理的应用,解答本题的关键是明确三角形外接圆的圆心是三边垂直平分线的交点.5.(2017•泰州)三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平分线的交点【分析】根据三角形的重心是三条中线的交点解答.【解答】解:三角形的重心是三条中线的交点,故选:A.【点评】本题考查了三角形重心的定义.掌握三角形的重心是三条中线的交点是解题的关键.6.(2017•扬州)若一个三角形的两边长分别为2和4,则该三角形的周长可能是()A.6 B.7 C.11 D.12【分析】首先求出三角形第三边的取值范围,进而求出三角形的周长取值范围,据此求出答案.【解答】解:设第三边的长为x,∵三角形两边的长分别是2和4,∴4﹣2<x<2+4,即2<x<6.则三角形的周长:8<C<12,C选项11符合题意,故选C.【点评】本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.7.(2017•舟山)长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是()A.4 B.5 C.6 D.9【分析】已知三角形的两边长分别为2和7,根据在三角形中任意两边之和>第三边,任意两边之差<第三边;即可求第三边长的范围,再结合选项选择符合条件的.【解答】解:由三角形三边关系定理得7﹣2<x<7+2,即5<x<9.因此,本题的第三边应满足5<x<9,把各项代入不等式符合的即为答案.4,5,9都不符合不等式5<x<9,只有6符合不等式,故选:C.【点评】考查了三角形三边关系,此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.8.(2017•白银)已知a,b,c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为()A.2a+2b﹣2c B.2a+2b C.2c D.0【分析】先根据三角形的三边关系判断出a﹣b﹣c与c﹣b+a的符号,再去绝对值符号,合并同类项即可.【解答】解:∵a、b、c为△ABC的三条边长,∴a+b﹣c>0,c﹣a﹣b<0,∴原式=a+b﹣c+(c﹣a﹣b)=a+b﹣c+c﹣a﹣b=0.故选D.【点评】本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.9.用12根等长的火柴棒拼三角形(全部用上,不可折断、重叠),不可以拼成的是()A.等腰三角形B.等边三角形C.直角三角形D.以上都有可能【分析】找到符合条件的三边,看符合哪类三角形即可.【解答】解:能组成三角形的三边有:3,4,5,为直角三角形;4,4,4,为等边三角形;5,5,2,为等腰三角形.故选D.【点评】只有较小的两条线段的和大于最大的一条线段才能组成三角形.10.△ABC周长是24,M是AB的中点,MC=MA=5,则△ABC的面积是()A.12 B.16 C.24 D.30【分析】由M是AB的中点,MC=MA=5可知MA=MB=MC,依此可判定∠ACB=90°.斜边为10,两直角边和可求出,再求直角三角形ABC的面积.【解答】解:∵MA=MB=MC=5,∴∠ACB=90°∵周长是24,AB=10∴AC+BC=14,AC2+BC2=102,∴2AC•BC=(AC+BC)2﹣(AC2+BC2)=142﹣102=4×24∴.故选C.【点评】解决本题的关键是根据所给条件判定三角形ABC是直角三角形.11.如图所示,BE=2EC,D是线段AC的中点,BD和AE交于点F,已知△ABC 的面积是3,求四边形DCEF的面积()A.B.C.D.【分析】作DG∥AE交BC于G,根据平行线段成比例求出DF和BF之间的关系,然后求出S△ADF的面积,又知BE=2EC,△ABC的面积是3平方单位,即可求出S△AEC ,最后根据四边形DCEF的面积=S△AEC﹣S△ADF即可得到答案.【解答】解:作DG ∥AE 交BC 于G ,则,∵BE=2EC , ∴, ∴,∴,∵BE=2EC , ∴,∴四边形DCEF 的面积=,故选B【点评】本题主要考查面积及等积变换的知识,解答本题的关键是作DG ∥AE 交BC 于G ,根据平行线段成比例的知识求出EG=BE ,本题难度较大.12.如图,在△ABC 中,点D 在BC 上,点O 在AD 上,如果S △AOB =3,S △BOD =2,S △ACO =1,那么S △COD 等于( )A .B .C .D .【分析】根据题意,利用△AOB 和△AOC 都有公共边OA 可以求得点B 和点C 到直线AO 的距离,进而求得S △COD 的值. 【解答】解:∵S △AOB =3,S △BOD =2,S △ACO =1,∴,设点B到OA所在直线的距离为b,点C到AO所在的直线的距离为c,∴,∴,∴,∴,∴,故选D.【点评】本题考查三角形的面积,解答本题的关键是明确题意,利用三角形的面积和数形结合的思想解答.13.四边形ABCD的对角线AC和BD相交于点E,如果△CDE的面积为3,△BCE 的面积为4,△AED的面积为6,那么△ABE的面积为()A.7 B.8 C.9 D.10【分析】根据三角形的高相等,面积比等于底的比,可得CE:AE=,进而可求出答案.【解答】解:∵S△CDE =3,S△ADE=6,∴CE:AE=3:6=(高相等,面积比等于底的比)∴S△BCE :S△ABE=CE:AE=∵S=4,△BCE=8.∴S△ABE故应选:B.【点评】本题考查了三角形的面积,注意弄清题中各个三角形之间面积的关系.二、填空题14.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是3<c<7.【分析】根据三角形三边关系定理可得5﹣2<c<5+2,进而求解即可.【解答】解:由题意,得5﹣2<c<5+2,即3<c<7.故答案为:3<c<7.【点评】此题主要考查了三角形的三边关系,关键是掌握三角形三边关系定理:三角形两边之和大于第三边.15.如图,点G是△ABC的重心,GE∥AB交BC于点E,GF∥AC交BC于点F,若△GEF的周长是2,则△ABC的周长为6.【分析】由GE∥AB,推出△DGE∽△DAB,推出===,可得AB=3GE,DB=3ED,同理可得AC=3GF,DC=3DF,即可推出△ABC的周长=AB+AC+BC=3GE+3GF+3EF=3(GE+GF+EF);【解答】解:如图,∵G是△ABC的重心,∴=2,∴=,∵GE∥AB,∴△DGE∽△DAB,∴===,∴AB=3GE,DB=3ED,同理可得AC=3GF,DC=3DF,∴△ABC的周长=AB+AC+BC=3GE+3GF+3EF=3(GE+GF+EF)=3×2=6.故答案为6.【点评】本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了相似三角形的判定与性质.16.(2017•巴中)如图,在△ABC中,AD,BE是两条中线,则S△EDC:S△ABC=1:4.【分析】利用三角中位线的性质得出DE AB,进而求出即可.【解答】解:∵在△ABC中,AD,BE是两条中线,∴DE AB,∴=,故答案为:1:4.【点评】此题主要考查了三角形中位线的性质以及相似三角形的性质,得出DE AB是解题关键.17.在Rt△ABC中,AD是斜边BC边上的中线,G是△ABC重心,如果BC=6,那么线段AG 的长为 2 .【分析】根据直角三角形斜边上的中线性质得到AD=BC=3,然后根据重心的性质得=2,所以AG=AD=2.【解答】解:∵AD 是斜边BC 边上的中线, ∴AD=BC=×6=3, ∵G 是△ABC 重心, ∴=2,∴AG=AD=×3=2. 故答案为2.【点评】本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了直角三角形斜边上的中线性质.18.(2017•铁岭)如图,△ABC 的面积为S .点P 1,P 2,P 3,…,P n ﹣1是边BC 的n 等分点(n ≥3,且n 为整数),点M ,N 分别在边AB ,AC 上,且==,连接MP 1,MP 2,MP 3,…,MP n ﹣1,连接NB ,NP 1,NP 2,…,NP n ﹣1,线段MP 1与NB 相交于点D 1,线段MP 2与NP 1相交于点D 2,线段MP 3与NP 2相交于点D 3,…,线段MP n ﹣1与NP n ﹣2相交于点D n ﹣1,则△ND 1P 1,△ND 2P 2,△ND 3P 3,…,△ND n﹣1P n ﹣1的面积和是 •S .(用含有S 与n 的式子表示)【分析】连接MN ,设BN 交MP 1于O 1,MP 2交NP 1于O 2,MP 3交NP 2于O 3.由==,推出MN ∥BC ,推出==,由点P 1,P 2,P 3,…,P n ﹣1是边BC的n 等分点,推出MN=BP 1=P 1P 2=P 2P 3,推出四边形MNP 1B ,四边形MNP 2P 1,四边形MNP 3P 2都是平行四边形,易知S △ABN =•S ,S △BCN =•S ,S △MNB =•S ,推出===•S ,根据S 阴=S △NBC ﹣(n ﹣1)•﹣计算即可;【解答】解:连接MN ,设BN 交MP 1于O 1,MP 2交NP 1于O 2,MP 3交NP 2于O 3. ∵==,∴MN ∥BC , ∴==,∵点P 1,P 2,P 3,…,P n ﹣1是边BC 的n 等分点, ∴MN=BP 1=P 1P 2=P 2P 3,∴四边形MNP 1B ,四边形MNP 2P 1,四边形MNP 3P 2都是平行四边形, 易知S △ABN =•S ,S △BCN =•S ,S △MNB =•S , ∴===•S ,∴S阴=S △NBC ﹣(n ﹣1)•﹣=•S ﹣(n ﹣1)••S ﹣S=•S ,故答案为•S .【点评】本题考查三角形的面积,平行线的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.三、解答题19.如图,在△BCD中,BC=4,BD=5,(1)求CD的取值范围;(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.【分析】(1)利用三角形三边关系得出DC的取值范围即可;(2)利用平行线的性质得出∠AEC的度数,再利用三角形内角和定理得出答案.【解答】解:(1)∵在△BCD中,BC=4,BD=5,∴1<DC<9;(2)∵AE∥BD,∠BDE=125°,∴∠AEC=55°,又∵∠A=55°,∴∠C=70°.【点评】此题主要考查了三角形三边关系以及平行线的性质,得出∠AEC的度数是解题关键.20.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.【解答】解:∵AD是BC边上的高,∠EAD=5°,∴∠AED=85°,∵∠B=50°,∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=70°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.【点评】本题考查了三角形的角平分线、中线和高,主要利用了直角三角形两锐角互余,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记各性质并准确识图是解题的关键.21.如图,△ABC中,A1,A2,A3,…,A n为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…(1)完成下表:连接个数出现三角形个数(2)若出现了45个三角形,则共连接了多少个点?(3)若一直连接到A n,则图中共有(n+1)(n+2).个三角形.【分析】(1)根据图形,可以分析:数三角形的个数,其实就是数AC上线段的个数.所以当上面有3个分点时,有6+4=10;4个分点时,有10+5=15;5个分点时,有15+6=21;6个分点时,有21+7=28;7个分点时,有28+8=36;(2)若出现45个三角形,根据上述规律,则有8个分点;(3)若有n个分点,则有1+2+3+…+n+1=(n+1)(n+2).【解答】解:(1)连接个数123456出现三角形个数3610152128(2)8个点;(3)1+2+3+…+(n+1)=[1+2+3+…+(n+1)+1+2+3+…+(n+1)]=(n+1)(n+2).故答案为(n+1)(n+2).【点评】此题注意数三角形的个数实际上就是数线段的条数.能够正确计算1+2+…+n+(n+1)=(n+1)(n+2).22.(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC 的面积为16,则△ABD的面积是8,△EBD的面积是4.(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?【分析】(1)由点D,E,F分别是BC,AB,AC的中点,三角形中线等分三角形的面积;(2)由三角形中线等分三角形的面积即可结果;【解答】解:(1)∵点D,E,F分别是BC,AB,AC的中点,三角形中线等分三角形的面积,∴S △ABD =S △ABC ==8, S △EBD =S △ABD ==4, 故答案为:8,4;(2)∵在△ABC 中,D 是BC 边的中点,∴S △ABD =S △ABC =8,∵E 是AD 的中点,∴S △BED =S △ABD =4,同理得,S △CDE =4;∴S △BCE =8,∵F 是CE 的中点,∴S △BEF =S △BCE =4.【点评】本题是面积及等积变换综合题目,考查了三角形的面积及等积变换,本题有一定难度,运用三角形中线等分三角形的面积才能得出结果.23.请阅读材料,并完成相应的任务.已知点D 在△ABC 的边BC 上(点D 不与点B ,C 重合),点P 是AD 上任意一点,连接BP ,CP .如图1,若=,显然有S △ABP =S △ACP .如图2,若=,那么S △ABP 与S △ACP 之间的数量关系又是怎样的呢?下面是小李同学的部分求解过程:如图3,作BM ⊥AD 的延长线于点M ,作CN ⊥AD 于点N .∴∠BMD=∠CND=90°.在△BMD 和△CND 中,∵∠BMD=∠CND ,∠BDM=∠CDN ,∴△BMD ~△CND .…(1)请把小李同学的求解过程补充完整.(2)猜想:=,则S △ABP 与S △ACP 之间的数量关系是 S △ABP =S △APC .【分析】(1)由△BMD ~△CND ,可得=,由=,可得=,由S △ABP =•BM•AP ,S △APC =•CN•AP ,可得S △ABP =S △APC .(2)结论:S △ABP =S △APC .证明方法类似.【解答】解:(1)∴=, ∵=, ∴=,∵S △ABP =•BM•AP ,S △APC =•CN•AP ,∴S △ABP =S △APC .(2)同法可得=,∵S △ABP =•BM•AP ,S △APC =•CN•AP ,∴S △ABP =S △APC .故答案为S △ABP =S △APC . 【点评】本题考查三角形的面积、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.24.如图,在△ABC 中,BC 边上依次有B 、D 、E 、C ,AC 边上依次有A 、G 、F ,满足BD=CE=BC ,CF=AG=AC ,BF 交AE 于点J ,交AD 于I ,BG 交AE 于点K ,交AD 于点H ,且S △ABC =1,求S 四边形KHIJ .【分析】作平行线GP和FM,根据平行线分线段成比例定理列比例式得:,=,从而得:BH:HK:KG=52:32:7,BI:IJ:JF=20:32:13,由同高三角形面积的比等于对应底边的比,可以得出S△ABF =,S△ABG=,S△AIJ=S△ABF=×=,S△AHK=S△ABG=×=,作差可得S四边形KHIJ.【解答】解:过G作GP∥BC,交AD于P,AE于Q,则=,∵BD=BC,∴=,∴,∵,∴,同理可得:=,即=,∴,∴=,∴BH:HK:KG=52:32:7,过F作FM∥BC,交AD于M,AE于N,同理得:BI:IJ:JF=20:32:13,∵S△ABC=1,∴S △ABF =,S △ABG =,∴S △AIJ =S △ABF =×=, S △AHK =S △ABG =×=,∴S 四边形KHIJ =S △AIJ ﹣S △AHK , =﹣, =.【点评】本题计算三角形和多边形面积,考查了平行线分线段成比例定理、同高三角形面积的关系,作好本题要从以下几点入手:①作平行线,②根据平行线分线段成比例定理得线段的比,③根据边的比得出面积的比.25.如图:△ABC 的边BC 的高为AF ,AC 边上的高为BG ,中线为AD ,AF=6,BC=12,BG=5,(1)求△ABD 的面积.(2)求AC 的长.(3)△ABD 和△ACD 的面积有何关系.【分析】(1)直接利用三角形的面积计算方法计算得出答案即可;(2)利用三角形的面积计算公式建立方程求得答案即可;(3)利用三角形的面积计算公式以及两个三角形底和高的关系得出答案即可.【解答】解:(1)∵△ABC 的边BC 上的高为AF ,AF=6,BC=12,∴△ABC 的面积=BC•AF=×12×6=36;(2)∵AC 边上的高为BG ,BG=5,∴△ABC 的面积=AC•BG=36,∴AC=;(3)△ABD 和△ACD 的面积相等.∵△ABC 的中线为AD ,∴BD=CD ,∵△ABD 以BD 为底,△ACD 以CD 为底,而且等高,∴S △ABD =S △ACD .【点评】此题考查三角形的面积计算公式,掌握三角形的面积=×底×高是解决问题的关键.26.如图,在△ABC 中,AD ⊥BC ,AE 平分∠BAC ,∠B=70°,∠C=30°.求:(1)∠BAE 的度数;(2)∠DAE 的度数;(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B ﹣∠C=40°,也能得出∠DAE 的度数?若能,请你写出求解过程;若不能,请说明理由.【分析】(1)根据三角形内角和定理得∠BAC=180°﹣∠B ﹣∠C=80°,然后根据角平分线定义得∠BAE=∠BAC=40°;(2)由于AD ⊥BC ,则∠ADE=90°,根据三角形外角性质得∠ADE=∠B +∠BAD ,所以∠BAD=90°﹣∠B=20°,然后利用∠DAE=∠BAE ﹣∠BAD 进行计算;(3)根据三角形内角和定理得∠BAC=180°﹣∠B ﹣∠C ,再根据角平分线定义得∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),加上∠ADE=∠B+∠BAD=90°,则∠BAD=90°﹣∠B,然后利用角的和差得∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),即∠DAE的度数等于∠B与∠C差的一半.【解答】解:(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,∵AE平分∠BAC,∴∠BAE=∠BAC=40°;(2)∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B=90°﹣70°=20°,∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;(3)能.∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C,∵AE平分∠BAC,∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B,∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),∵∠B﹣∠C=40°,∴∠DAE=×40°=20°.【点评】本题考查了三角形内角和定理,关键是根据三角形内角和是180°和三角形外角性质解答.27.(1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO面积相等;(3)如图3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.【分析】(1)根据三角形的面积公式,只需过点A和BC的中点画直线即可;(2)结合平行线间的距离相等和三角形的面积公式即可证明;(3)结合(1)和(2)的结论进行求作.【解答】(1)解:取BC的中点D,过A、D画直线,则直线AD为所求;(2)证明:∵l1∥l2,∴点E,F到l2之间的距离都相等,设为h.∴S△EGH =GH•h,S△FGH=GH•h,∴S△EGH =S△FGH,∴S△EGH ﹣S△GOH=S△FGH﹣S△GOH,∴△EGO的面积等于△FHO的面积;(3)解:取BC的中点D,连接MD,过点A作AN∥MD交BC于点N,过M、N画直线,则直线MN为所求.【点评】此题主要是根据三角形的面积公式,知:三角形的中线把三角形的面积等分成了相等的两部分;同底等高的两个三角形的面积相等.。
初一数学三角形试题答案及解析

初一数学三角形试题答案及解析1.如图,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C =70°,则∠EAD=【答案】20【解析】∵∠B=30°,∠C=70°,∴在△ABC中,∠BAC=180°﹣∠B﹣∠C=80°,∵AE是△ABC的角平分线,∴∠BAE=∠BAC=40°,又∵AD⊥BC,∴∠BAD=90°﹣∠B=60°,∴∠EAD=∠BAD﹣∠BAE=60°﹣40°=20°.故答案为:20.【考点】三角形内角和定理;三角形的外角性质2.腰三角形的底角是顶角的两倍,则此等腰三角形的顶角为【答案】36°.【解析】设等腰三角形的顶角度数为x,则底角度数为2x,根据三角形内角和定理:x+2x+2x=180°,解得x的度数.试题解析:设等腰三角形的顶角度数为x,∵等腰三角形的底角是顶角的两倍,则底角度数为2x,根据三角形内角和定理:x+2x+2x=180°,解得x=36°.【考点】等腰三角形的性质.3.如图,AD是△ABC的角平分线,∠C=90°,BC=9cm,BD=5cm,则点D到AB的距离是()A.4cm B.5cm C.6cm D.9 cm【答案】A.【解析】如图,过点D作DE⊥AB于E,∵BC=9cm,BD=5cm,∴CD=BC-BD=9-5=4cm,∵AD是△ABC的角平分线,∠C=90°,∴DE=CD=4cm,即点D到AB的距离是4cm.故选A.【考点】角平分线的性质.4.在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA,若-3a m-1b2与a n b2n-2是同类项且OA=m,OB=n.(1)m= ;n= .(2)点C的坐标是.(3)若坐标平面内存在一点D,满足△BCD全等△ABO,试求点D的坐标.【答案】(1)3,2;(2)(5,0)或(1,0);(3)(5,2)或(5,-2)或(2,2)或(2,-2),(1,2)或(1,-2)或(-2,2)或(-2,-2).【解析】(1)根据同类项的概念即可求得;(2)根据已知条件即可求得B(2,0)或(-2,0),根据点B在点C的左侧,BC=OA,即可确定C的坐标;(3)根据三角形全等的性质即可确定D的坐标;试题解析:(1)∵-3a m-1b2与a n b2n-2是同类项,∴,解得.(2)∵OA=m,OB=n,∴B(2,0)或(-2,0),∵点B在点C的左侧,BC=OA,∴C(5,0)或(1,0);(3)当C(5,0)时,∵△BCD全等△ABO,BC=OA=3,∴CD=2或BD=2,∴D的坐标为(5,2)或(5,-2)或(2,2)或(2,-2);当C(1,0)时,∵△BCD全等△ABO,BC=OA=3,∴CD=2或BD=2,∴D的坐标为(1,2)或(1,-2)或(-2,2)或(-2,-2).所以D点的坐标为(5,2)或(5,-2)或(2,2)或(2,-2),(1,2)或(1,-2)或(-2,2)或(-2,-2).【考点】1.全等三角形的判定与性质;2.同类项;3.坐标与图形性质.5.如图,在△ABC中,∠B=400,∠C=1100.(1)画出下列图形:①BC边上的高AD;②∠A的角平分线AE.(2)试求∠DAE的度数.【答案】(1)图形见解析;(2)∠DAE=35°.【解析】(1)按照三角形高线和角平分线定义进行画图即可;(2)利用角平分线把一个角平分的性质和高线得到90°的性质可得∠DAE的度数.(1)如图:(2)∵∠DAB=180°﹣∠ABC﹣∠ADB=180°﹣90°﹣40°=50°,∠BAC=180°﹣∠ABC﹣∠C=180°﹣40°﹣110°=30°,又∵AE平分∠BAC,∴∠BAE=∠BAC=150°,(角平分线的定义)∴∠DAE=∠DAB﹣∠BAE=50°﹣15°=35°.【考点】三角形高线和角平分线.6.作图题:(可以不写作法)如图已知三角形ABC内一点P.(1)过P点作线段EF∥AB,分别交AC,BC于点E,F(2)过P点作线段PD使PD⊥BC垂足为D点.【答案】作图见解析.【解析】(1)根据过直线外一点作已知直线平行线的方法作图即可;(2)利用直角三角板,一条直角边与BC重合,沿BC平移,使另一条直角边过点P画垂线即可.(1)如图,EF即为所求.(2) 如图,PD即为所求.【考点】作图—基本作图.7.如图,AD为△ABC的中线,(1)作△ABD的中线BE;(2)作△BED的BD边上的高EF;(3)若△ABC的面积为60,BD=10,则点E到BC边的距离为多少?【解析】(1)找到边AD的中点E,连接BE,线段BE是△ABD的中线;(2)△BED是钝角三角形,所以BD边上的高在BD的延长线上;(3)先根据三角形的中线把三角形分成面积相等的两个小三角形,结合题意可求得△BED 的面积,再直接求点E 到BC 边的距离即可.试题解析:(1)如图所示,BE 是△ABD 的中线;(2)如图所示,EF 即是△BED 中BD 边上的高.(3)∵AD 为△ABC 的中线,BE 为三角形ABD 中线,∴S △BED =S △ABC =×60=15;∵BD=10,∴EF=2S △BED ÷BD=2×15÷10=3,即点E 到BC 边的距离为3.【考点】1.三角形的角平分线、中线和高;2.三角形的面积;8. 在△ABC 中,已知∠A:∠B:∠C=2:3:4,则这个三角形是( )A .钝角三角形B .直角三角形C .锐角三角形D .等腰三角形【答案】C .【解析】根据题意,设∠A 、∠B 、∠C 分别为2k 、3k 、4k ,则∠A+∠B+∠C=2k+3k+4k=180°,解得k=20°,∴4k=4×20°=80°<90°,所以这个三角形是锐角三角形.故选C .考点: 三角形内角和定理.9. 已知等腰三角形的两边长分别为4和9,则第三边为_________.【答案】9【解析】等腰三角形的两边长分别为4和9时,当4为腰时,则可知两腰和=4+4=8<9不符合三角形任意两边和大于第三边。
七年级数学下册《认识三角形》练习题及答案(北师大版)

七年级数学下册《认识三角形》练习题及答案(北师大版)一、单选题 1.如图,ABC 的边BC 上的高是( )A .线段AFB .线段DBC .线段CFD .线段BE2.如图直线1l 2l ∥,线段AB 交1l ,2l 于D ,B 两点,过点A 作AC AB ⊥,交直线1l 于点C ,若120∠=︒则2∠=( )A .70°B .100°C .110°D .160°3.如图,将一副直角三角板,按如图所示叠放在一起,则图中COB ∠的度数是( )A .75︒B .105︒C .115︒D .100︒4.以下列各组线段为边,能组成三角形的是( )A .2cm ,3cm ,5cmB .4cm ,4cm ,10cmC .3cm ,1cm ,3cmD .3cm ,4cm ,9cm 5.如图,,72,32AB CD B D ∠=︒∠=︒∥则F ∠的度数( )A .32︒B .36︒C .40︒D .76︒6.如图所示,一副三角板叠放在一起,则图中α∠的度数为( )A .45︒B .50︒C .75︒D .80︒7.把两块三角板按如图所示那样拼在一起,DEC ∠的大小为( )A .60︒B .75︒C .80︒D .105︒8.某城市几条道路的位置如图所示,道路CD 与道路EF 平行,道路AB 与道路CD 的夹角()CDB ∠为50︒,城市规划部门想修一条新道路BF ,要求F B ∠=∠,则F ∠的大小为( )A .40︒B .35︒C .30︒D .25︒9.如图,AD 是中ABC 边上的中线,CE 是AB 边上的高,4AB = 6ADC S =△ CE =( )A .3B .4C .5D .610.如图,AD 是ABC 的中线,点E 在AD 上,2AE DE =若ABE 的面积是4,则ABC 的面积是( )A .16B .12C .10D .8二、填空题11.将一副直角三角板如图放置,已知0,,345F B ∠=∠=EF BC ∥,则AGD ∠的度数是________.12.将一把直尺与一块三角板如图放置,若1130∠=︒,则2∠的度数为 ________.13.如图,AB//CD 24A ∠=︒ 55C ∠=︒ 则E ∠=_______︒.14.如图,BD EF ∥,AE 与BD 交于点C ,25B ∠=︒ 75A ∠=︒则E ∠的度数为_____.15.将一副直角三角板()90A FDE ∠=∠=︒按如图所示位置摆放,点D 在边AB 上,两条斜边为EF 、BC 且EF BC ∥,则ADF ∠=______︒.三、解答题16.如图,在ABC 中B C ∠=∠,D ,E 分别是BC ,AC 上的点,连接DE ,12∠=∠ 40BAD ∠=︒求EDC ∠的度数.17.如图,网格中的每个小正方形的边长都是1,线段的交点称作格点,请按下列要求作图并填空(1)画出ABC 中,AC 边上的高BE ;(2)画出ABC 中,BC 边上的高AD ;(3)直接写出ABC 的面积是______.18.在ABC 中,BD 平分ABC ∠交AC 于点D ,点E 是线段AC 上的动点(不与点A 、D 、C 重合),过点E 作EF AB ∥交直线BD 于点F ,CEF ∠的角平分线所在直线....与射线BD 交于点G .(1)如图1,点E 在线段AD 上运动.①若40ABC ∠=︒,60A ∠=︒则DGE ∠=______°①若40C ∠=︒,则DGE ∠=______°①试探究DGE ∠与C ∠之间的数量关系,并说明理由;(2)若点E 在线段DC 上运动,请在图2中补全图形,并直接写出DGE ∠与C ∠之间的数量关系(不必说明理由).19.如图,ABC 的中线AD BE 、相交于点F(1)图中与ABE 面积相等是三角形有____个(不含ABE );(2)若ABF △的面积是24cm ,求四边形FDCE 的面积.20.已知,在平面直角坐标系中,AB x ⊥轴于点B ,点(),A a b 满足630a b -+-=,平移线段AB 使点A 与原点重合,点B 的对应点为点C .(1)=a _______,b =_______,点C 坐标为________;(2)如图1,点(),D m n 是线段CB 上一个动点.连接OD ,利用OBC △ OBD OCD 的面积关系,可以得到m 、n 满足一个固定的关系式,请求出这个关系式.(3)如图2,以OB 为边作BOG AOB ∠=∠,交线段BC 于点G ,E 是线段OB 上一动点,连接CE 交OG 于点F ,当点E 在线段OB 上运动过程中,OFC FCG OEC∠+∠∠的值是否发生变化?若变化请说明理由,若不变,求出其值.。
北师大版七年级数学下册4.1《认识三角形(1)》习题含答案

4.1《认识三角形(1)》习题含答案1. 几位同学用三根木棒拼成的图形如图所示,则其中符合三角形定义的是( )A. AB. BC. CD. D2. 如图,过A,B,C,D,E 五个点中任意三点画三角形. (1)其中以AB 为一边可以画出____________个三角形; (2)其中以C 为顶点可以画出____________个三角形.3. 如图,以CD 为公共边的三角形是____________;∠EFB 是____________的内角;在△BCE 中,BE 所对的角是____________,∠CBE 所对的边是____________;以∠A 为公共角的三角形是____________.4. 在△ABC 中,若∠A =95°,∠B =40°,则∠C 的度数为( ) A. 35° B. 40° C. 45° D. 50°5. 在△ABC 中,∠A ∶∠B ∶∠C =3∶4∶5, 则∠C 等于( ) A. 45° B. 60° C. 75° D. 90°6. 如图,在△ABC 中,点D ,E ,F 分别是三条边上的点,EF ∥AC ,DF ∥AB ,∠B =45°,∠C =60°,则∠EFD 等于( ) A. 80° B. 75° C. 70° D. 65°7. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( ) A. 120° B. 90° C. 60° D. 30°8. 如图,直线a ∥b ,直线l 与a ,b 分别相交于A ,B 两点,过点A 作直线l的垂线第2题图第3题图第6题图交直线b于点C,若∠1=58°,则∠2的度数为() A. 58° B. 42° C. 32° D. 28°9. 如图,将一块含有45°角的直角三角板的两个顶点放在长方形直尺的一组对边上,则∠1+∠2=()A. 25°B.45°C. 30°D. 50°10. 在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A. 锐角三角形B. 钝角三角形C. 直角三角形D. 锐角三角形或钝角三角形11. 如图所示的三角形被木板遮住了一部分,这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 以上都有可能12. 根据下列条件,判断△ABC的形状.(1)∠A=40°,∠B=80°;(2)∠A∶∠B∶∠C=2∶3∶7.13. 如图,在△ABC中,D,E是BC,AC上的点,连接BE,AD,交于点F,问:(1)图中有多少个三角形?并把它们表示出来;(2)△BDF的三个顶点是什么?三条边是什么?(3)以AB为边的三角形有哪些?(4)以F为顶点的三角形有哪些?14. 如图,请猜想∠A+∠B+∠C+∠D+∠E+∠F的度数,并说明你的理由.15. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.16. (1)如图①,CD是直角三角形ABC斜边AB上的高,图中有与∠A相等的角吗?为什么?(2)如图②,把图①中的CD平移到ED处,图中还有与∠A相等的角吗?为什么? 第8题图第9题图第11题图第13题图第14题图第15题图(3)如图③,把图①中的CD平移到ED处,交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?4.1《认识三角形(1)》习题答案1. D解析:因为三角形是由不在同一条直线上的三条线段首位顺次相接所成的图形.2. (1) 3 (2)6解析:(1)以AB为一边可以画出3个三角形为:△ABE,△ABD,△ABC;(2)以C为顶点可以画出6个三角形为:△ABC,△BCD,△BCE,△ADC,△DEC,△ACE.3. (1)△CDF与△BCD(2)△BEF(3) ∠BCE(4) CE(5) △ABD,△ACE和△ABC解析:以CD为公共边的三角形是△CDF与△BCD;∠EFB是△BEF的内角;在△BCE中,BE所对的角是∠BCE,∠CBE所对的边是CE;以∠A为公共角的三角形是△ABD,△ACE和△ACB.4. C解析:根据三角形的内角和是180°可知:∠A+∠B+∠C=180°,∴∠C=180°-∠A-∠B=180°-95°-40°=45°.5. C解析:设∠A=3x°,则∠B=4x°,∠C=5x°,根据三角形内角和定理可得:3x+4x+5x=180°,则x=15,则∠C=5x=75°.6. B解析:根据EF∥AC,求出∠EFB=∠C=60°,再根据DF∥AB,求出∠DFC=∠B=45°,从而求出∠EFD=180°﹣60°﹣45°=75°.7. D解析:根据直角三角形两锐角互余列式计算即可得解:∵直角三角形中,一个锐角等于60°,∴另一个锐角的度数=90°﹣60°=30°.8. C解析:∵直线a∥b,∴∠ACB=∠2,∵AC⊥BA,∴∠BAC=90°,∴∠2=ACB=180°﹣∠1﹣∠BAC=180°﹣90°﹣58°=32°.9. B解析:由等腰直角三角形的性质得出∠ABC =45°,由平行线的性质得出∠1=∠ABE ,即可得出答案. 解:如图所示:∵△ABC 是等腰直角三角形, ∴∠ABC =45°, ∵AD ∥BE , ∴∠1=∠ABE ,∴∠1+∠2=∠ABE +∠2=∠ABC =45°. 10. B解析:由三角形内角和定理可得:∠C =180°-∠A -∠B =180°-20°-60°=100°, 所以△ABC 是钝角三角形. 11. D解析:从图中,只能看到一个角是锐角,其他的两个角中,可以都是锐角,或有一个是钝角或有一个直角. 12. 解:(1)∠C =180°-∠A -∠B =60°,因为40°<60°<80°<90°,所以△ABC 是锐角三角形. (2)设∠A =2x ,∠B =3x ,∠C =7x ,则2x +3x +7x =180°,解得x =15°. 所以∠C =7×15°=105°.所以△ABC 是钝角三角形. 13.解:利用三角形的定义以及三角形有关的角和边概念分别得出即可.(1)8个:△ABC ,△ABF ,△ABE ,△ABD ,△BDF ,△AEF ,△ACD ,△BCE ; (2)三个顶点:B ,D ,F ;三条边:BD ,BF ,DF ; (3)△ABC ,△ABF ,△ABD ,△ABE ; (4)△ABF ,△BDF ,△AEF .14. 解:猜想:∠A +∠B +∠C +∠D +∠E +∠F =360°. 理由:因为∠BMP 是△ABM 的外角,所以∠BMP =∠A +∠B . 同理得∠ENM =∠E +∠F ,∠DPN =∠C +∠D .又因为∠BMP +∠ENM +∠DPN =360°,所以∠A +∠B +∠C +∠D +∠E +∠F =360°. 15.解:因为AB ∥CD ,所以∠BEF +∠DFE =180°. 又因为EP 平分∠BEF ,FP 平分∠DFE , 所以∠PEF =12∠BEF ,∠PFE =12∠DFE .所以∠PEF +∠PFE =12(∠BEF +∠DFE )=90°.又因为∠PEF+∠PFE+∠P=180°,所以∠P=90°.所以△PEF是直角三角形.16.解:(1)有.理由:因为CD⊥AB,所以∠B+∠BCD=90°.因为∠ACB=90°,所以∠B+∠A=90°.所以∠BCD=∠A.(2)有与∠A相等的角.理由:因为ED⊥AB,所以∠B+∠BED=90°.因为∠ACB=90°,所以∠B+∠A=90°.所以∠BED=∠A.(3)有与∠A相等的角.理由:因为ED⊥AB,所以∠B+∠E=90°.因为∠ACB=90°,所以∠B+∠A=90°.所以∠E=∠A.。
人教版七年级下数学三角形知识点归纳、典型例题及考点分析

BC三角形知识点归纳、典型练习题及考点分析一、三角形相关概念 1.三角形的概念由不在同一直线上的三条线段首尾顺次连结所组成的图形叫做三角形 要点:①三条线段;②不在同一直线上;③首尾顺次相接.2.三角形的表示通常用三个大写字母表示三角形的顶点,如用A 、B 、C 表示三角形的三个顶点时,此三角形可记作△ABC ,其中线段AB 、BC 、AC 是三角形的三条边,∠A 、∠B 、∠C 分别表示三角形的三个内角.3.三角形中的三种重要线段三角形的角平分线、中线、高线是三角形中的三种重要线段.(1)三角形的角平分线:三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.注意:①三角形的角平分线是一条线段,可以度量,而角的平分线是经过角的顶点且平分此角的一条射线.②三角形有三条角平分线且相交于一点,这一点一定在三角形的内部.③三角形的角平分线画法与角平分线的画法相同,可以用量角器画,也可通过尺规作图来画.(2)三角形的中线:在一个三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线. 注意:①三角形有三条中线,且它们相交三角形内部一点.②画三角形中线时只需连结顶点及对边的中点即可.(3)三角形的高线:从三角形一个顶点向它的对边作垂线,顶点和垂足间的限度叫做三角形的高线,简称三角形的高.注意:①三角形的三条高是线段②画三角形的高时,只需要向对边或对边的延长线作垂线,连结顶点与垂足的线段就是该边上的高.练习题:1、图中共有( A :5 B :6 C :7 D :82、如图,AE ⊥BC ,BF ⊥AC ,CD ⊥AB ,则△ABC 中AC 边上的高是( ) A :AE B :CD C :BF D :AF 3、三角形一边上的高( )。
A :必在三角形内部B :必在三角形的边上C :必在三角形外部D :以上三种情况都有可能 4、能将三角形的面积分成相等的两部分的是( )。
七年级数学下册《认识三角形》练习题及答案解析(北师大版)
七年级数学下册《认识三角形》练习题及答案解析(北师大版) 一、单选题1.如图在△ABC中AD是△ABC的角平分线则()A.△1=12△BAC B.△1=12△ABC C.△1=△BAC D.△1=△ABC2.两根长度分别为2 10的木棒若想钉一个三角形木架第三根木棒的长度可以是()A.13B.10C.7D.63.如图给出的三角形有一部分被遮挡则这个三角形可能是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形4.如图从旗杆AB的顶端A向地面拉一条绳子绳子底端恰好在地面P处若旗杆的高度为13.2米则绳子AP的长度不可能是()A.13米B.13.3米C.14米D.15米5.利用直角三角板作△ABC的高线下列作法正确的是()A.B.C.D.6.若一个直角三角形其中一个锐角为40° 则该直角三角形的另一个锐角是()A.60°B.50°C.40°D.30°7.如图AD BE CF是△ABC的三条中线则下列结论正确的是()A.BC=2AD B.AB=2AF C.AD=CD D.BE=CF8.如图用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限)不计螺丝大小其中相邻两螺丝的距离依次为3 4 5 7 且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框则任意两个螺丝间的距离的最大值为()A.9B.8C.7D.69.将一个三角形纸片剪开分成两个三角形这两个三角形不可能()A.都是直角三角形B.都是钝角三角形C.都是锐角三角形D.是一个直角三角形和一个钝角三角形10.如图若△ABC的三条内角平分线相交于点I 过I作DE△AI分别交AB AC于点D E 则图中与△ICE一定相等的角(不包括它本身)有()个.A.1B.2C.3D.4二、填空题11.如图AD AE分别是△ABC的角平分线和高∠B=50°∠C=70°则∠BAD=度∠EAD=度.12.已知三角形三边长分别为2 x 13 若x为正整数则这样的三角形有个.13.已知△ABC中△A=12△B=13△C 则△ABC是三角形.14.同一平面内有A B C三点A B两点之间的距离为5cm点C到直线AB 的距离为2cm且△ABC为直角三角形则满足上述条件的点C有个.三、作图题15.用圆规和直尺作图:已知△AOB(如图)求作:△AOB的平分线OC.(要求保留作图痕迹不写作法和证明过程).四解答题16.如图AD是△BAC的平分线CE是△ADC边AD上的高若△BAC=80° △ECD=25° 求△ACB的度数.17.已知a b c是△ABC的三边长若b=2a−1c=a+5且△ABC的周长不超过20cm 求a范围.18.如图在△ABC中AD△BC 垂直为D △1=△B △C=67° 求△BAC的度数19.如图所示图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.20.如图在△ABC中CE BF是两条高若△A=70° △BCE=30° 求△EBF与△FBC的度数.21.如图求△A+△B+△C+△D+△E的大小.22.如图1 AB与CD相交于点O 若△D=38° △B=28° △DAB和△BCD的平分线AP和CP 相交于点P 并且与CD AB分别相交于M N.试求:(1)△P 的度数;(2)设△D=α △B=β △DAP= 13 △DAB △DCP= 13 △DCB 其他条件不变 如图2 试问△P 与△D △B 之间存在着怎样的数量关系(用α β表示△P ) 直接写出结论.参考答案1.【答案】A【解析】【解答】解:∵AD 是△ABC 的角平分线 ∴△1=12△BAC故答案为:A.【分析】根据角平分线的定义求解即可.2.【答案】B【解析】【解答】解:设第三边的长度为x则10−2<x <10+2 即8<x <12 则x =10符合题意 故答案为:B.【分析】设第三边的长度为x 根据三角形中任意两边之和大于第三边 任意两边之差小于第三边 列出不等式组 求解可得x 的取值范围 从而一一判断即可得出答案.3.【答案】B【解析】【解答】解:由图形可得:该三角形为锐角三角形.故答案为:B.【分析】观察图形可知:图中的三角形有两个锐角 且第三个角也小于90° 据此可判断出三角形的形状.4.【答案】A【解析】【解答】解:∵旗杆的高度为AB =13.2米又∵AP >AB∴绳子AP 的长度不可能是:13米. 故答案为:A.【分析】直角三角形的性质:斜边大于直角边 据此解答即可.5.【答案】C【解析】【解答】解:由三角形的高线的定义可知:A 作法不符合题意 不符合题意;B 作法不符合题意 不符合题意;C 作法符合题意 符合题意;D 作法不符合题意 不符合题意; 故答案为:C .【分析】根据高线的定义逐项判断即可。
初一数学_几何_三角形基础知识和基本练习题讲解
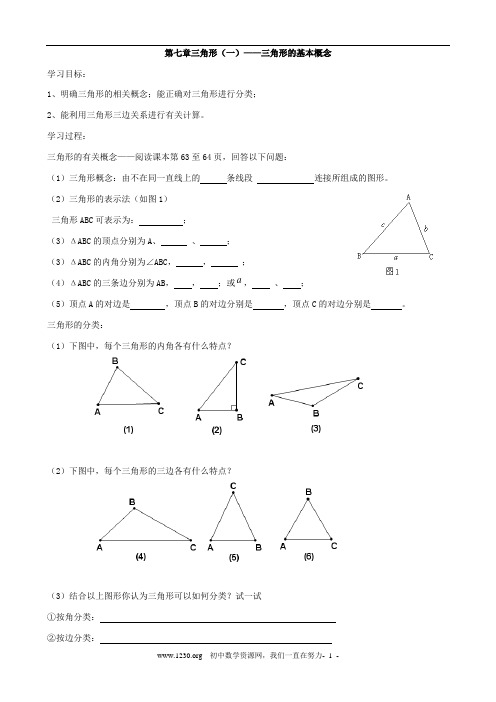
第七章三角形(一)——三角形的基本概念学习目标:1、明确三角形的相关概念;能正确对三角形进行分类;2、能利用三角形三边关系进行有关计算。
学习过程:三角形的有关概念——阅读课本第63至64页,回答以下问题:(1)三角形概念:由不在同一直线上的条线段连接所组成的图形。
(2)三角形的表示法(如图1)三角形ABC可表示为:;(3)ΔABC的顶点分别为A、、;(3)ΔABC的内角分别为∠ABC,,;(4)ΔABC的三条边分别为AB,,;或a,、;(5)顶点A的对边是,顶点B的对边分别是,顶点C的对边分别是。
三角形的分类:(1)下图中,每个三角形的内角各有什么特点?(2)下图中,每个三角形的三边各有什么特点?(3)结合以上图形你认为三角形可以如何分类?试一试①按角分类:②按边分类:第1题3、三角形的三边关系问题1:如图,现有三块地,问从A 地到B 地有几种走法,哪一种走法的距离最近?请将你的设计方案填写在下表中:(3)阅读课本第64页,填写:三角形两边的和 (4)用式子表示:BC + AC AB (填上“> ”或“ < ” ) ① BC + AB AC (填上“> ”或“ < ” ) ②AB + AC BC (填上“> ”或“ < ” ) ③4、三角形的稳定性问题2:盖房子时,在窗框未安装好前,木工师傅常先在窗框上斜钉一根木条,为什么?5、例题:用一条长为18cm 的细绳围成一个等腰三角形,如果腰长是底边的2倍,那么各边的长是多少? 解:设底边长为xcm ,则腰长是 cm 因为三角形的周长为 cm所以: 所以x= cm答:三角形的三边分别是 、 、课堂练习: A 组A 地(6)(5)(4)(3)(2)(1)1.①图中有 个三角形,分别为 ②△ABC 的三个顶点是 、 、 ; 三个内角是 、 、 ; 三条边是 、 、 ;2、如图中有 个三角形,用符号表示 3.判断下列线段能否组成三角形:①4,5,6 ( )②1,2,3 ( ) ③2,2,6 ( )④8,8,2 ( ) 4、下列的图形中具有稳定性的是 (写编号)5、等腰三角形一腰长为6,底边长为7,则另一腰为 ,周长为 。
初中数学鲁教版(五四制)七年级上册第一章 三角形1 认识三角形-章节测试习题(10)

章节测试题1.【题文】如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.【答案】不是,理由见解析.【分析】考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.【解答】解:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD 满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分线.2.【题文】如图,AD为△ABC的中线,BE为△ABD的中线.若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?【答案】4【分析】首先根据三角形的中线把三角形的面积分成相等的两部分可得△EBD的面积是10,再利用三角形的面积公式进而得到BD边上的高.【解答】解:∵AD为△ABC的中线,BE为△ABD的中线,∴S△ABD=S△ABC,S△BDE=S△ABD,∴S△BDE=×S△ABC=S△ABC,∵△ABC的面积为40,∴S△BDE=×40=10,设△BDE中BD边上的高为x,∵BD=5,∴×5•x=10,解得x=4,故△BDE中BD边上的高为4.3.【题文】已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.【答案】8厘米,8厘米,11厘米或10厘米,10厘米,7厘米【分析】本题D点把三角形ABC的周长分成两部分(AB+AD)和(BC+CD),题中未说明12cm和15cm分别是哪一部分,因此要分类讨论.【解答】解:∵AB=AC,BD是AC边上的中线,∴AB=2AD=2CD,∴AB+AD=3AD.①当AB与AD的和是12厘米时,AD=12÷3=4(厘米),所以AB=AC=2×4=8(厘米),BC=12+15-8×2=12+15-16=11(厘米);②当AB与AD的和是15厘米时,AD=15÷3=5(厘米),所以AB=AC=2×5=10(厘米),BC=12+15-10×2=12+15-20=7(厘米).所以三角形的三边可能是8厘米,8厘米,11厘米或10厘米,10厘米,7厘米.4.【题文】如图:(1)画出△ABC的BC边上的高线AD;(2)画出△ABC的角平分线CE.【答案】(1)作图见解析;(2)作图见解析.【分析】(1)利用钝角三角形高线作法延长BC进而作出高线即可;(2)利用角平分线作法得出CE即可.解:(1)如图所示:AD即为所求;(2)如图所示:CE即为所求.5.【题文】已知AD为△ABC的中线,AB=5 cm,且△ACD的周长比△ABD的周长少2 cm,求AC的长度.【答案】3cm【分析】由AD是△ABC的中线可得CD=BD,从而可得C△ABD-C△ACD=(AB+AD+BD)-(AC+AD+CD)=AB-AC=2,由AB=5,可解得AC=3(cm).【解答】解:∵AD为△ABC的中线,∴BD=CD.∵△ACD的周长比△ABD的周长少2 cm,∴(AB+BD+AD)-(AC+AD+CD)=AB-AC=2 cm,∴AC=AB-2=5-2=3(cm).6.【题文】如图,在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,BE的长为多少?【答案】9【分析】由已知易得:S △ABC=AC BE=BC AD,代入BC=12,AC=8,AD=6即可解得BE的长.【解答】解:∵在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,∴S △ABC=BC AD ==36,又∵S△ABC=AC·BE,∴×8×BE=36,解得:BE=9.7.【题文】如图,D是△ABC中BC边上的一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线.【答案】见解析【分析】由DE∥AC交AB于点E可得∠CAD=∠EDA,结合∠EDA=∠EAD,可得∠CAD=∠EAD,即可得到结论.【解答】解:∵DE∥AC,∴∠EDA=∠CAD.∵∠EDA=∠EAD,∴∠CAD=∠EAD.∴AD是△ABC的角平分线.8.【题文】如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8,求PF+PE的值.【答案】8【分析】连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解;【解答】解:连结P A,由图形可知:S△ABC=S△ABP+S△ACP,即AC·BD=AB·PF+AC·PE,∵AB=AC,∴BD=PF+PE,∴PF+PE=8.9.【题文】如图,在△ABC中,∠B = 50º,∠C = 70º,AD是∠BAC的角平分线,AE是高,求∠EAD的度数。
华师大版初中数学七年级下册《9.1.1 认识三角形》同步练习卷(含答案解析
华师大新版七年级下学期《9.1.1 认识三角形》同步练习卷一.填空题(共50小题)1.如果一个三角形的三边长度之比是2:3:4,周长为36cm,则最大的边长为.2.一棵小树被风刮歪了,小明用两根木棒撑住这棵小树,他运的数学知识是.3.下列图形中具有稳定性有(填序号)4.如图,在△ABC中,点D、E分别是BC、AD边的中点,且S△ABC=8cm2,则S =cm2.△ABE5.线段的重心是;三角形的重心是.6.如图,在△ABC中,BC边上的高是;在△AEC中,AE边上的高是,EC边上的高是.AC边上的高是.7.如图,在△ABC中,已知AB=8cm,AC=5cm,AD是△ABC的中线,则△ABD 的周长比△ACD的周长多cm.8.如图,AD为△ABC的中线,点E为AD的中点,若△AEC面积为12cm2,则△ABC的面积为cm2.9.在△ABC,AD、BE分别是BC、AC边上的中线,交于点O,则OD:OA=.10.在△ABC中,AC=3cm,AD是△ABC中线,若△ABD周长比△ADC的周长大2cm,则BA=cm.11.如图,△ABC中,AD为中线,DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE=.12.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则△ABC中BC边上的高是.13.如图,△ABC中,点D、E、F分别在三边上,E是AB的中点,AD、BE、CF 交于点O,DC=3BD,S=12,S△AOE=3,则AF与CF之间的等量关系为.△DOC14.如图,AD⊥BC于D,那么图中△ABC的高是线段.15.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,CD是△ABC的中线,则△ACD 的面积是.16.平面上有四个点A、B、C、D,其中任意三个点都不在一条直线上,用它们作顶点可以组成三角形的个数是个.17.如图,E,F,G分别是AB,BC,AC边上的中点,则S△ABC=S△BEF=S .△FGC18.如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是.19.如图是阳光广告公司为某件商品设计的商标图案,图中阴影部分为斜线,若每个小长方形的面积都是1,则阴影部分的面积是.20.图中可数出的三角形个数为个.21.建筑工地上,我们经常会见到木工师傅在木门框上斜钉上一根木条,这是因为的缘故.22.观察下面两图形的形成过程,若AD=3,DB=4,则△ADE和△BDF面积的和为.23.已知,锐角三角形ABC的三边AB=6cm,BC=7cm,AC=8cm,∠A=α,则△ABC的面积等于cm2(用含α的式子表示).24.如图,AD、BE、CF是△ABC的三条中线,若△ABC的周长是a cm.则AE+CD+BF= cm.25.一个三角形的面积为25cm2,一边为5cm,则这条边上的高为.26.如图,在四边形ABCD中,AC与BD相交于点O,S△ABD:S△CBD=3:2,则OA:OC的值为.27.△ABC中,D、E分别在AB、AC上,并且AD:DB=2:1,AE:EC=1:2,则S△ADE:S△ABC=.28.已知在△ABC中,AD是中线,G是重心,如果GD=2cm,那么AG=cm.29.如图,G是△ABC的重心,S△DGC=4,S△ABC=.30.一个三角形的三边之比为3:4:5,其中最长边比最短边长4cm,则这个三角形的周长为cm.31.如图,图中阴影部分是黄鹤楼公司某产品的商品图案,若每个小长方形的面积都是1,则阴影部分的面积为.32.AD为△ABC中BC边上的中线,则以下面积的关系:S△ADB S△ADC (填“>”、“<”或“=”).33.为了使做好的木门窗在运输、安装过程中不变形,木工师傅在木门窗上斜着加钉了一根木条.其原理是.34.如图中△ABC的面积为.35.如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2cm,则△BCD 和△ACD的周长的差是cm.36.如图所示,在△ABC中,BC边上的高是,AB边上的高是;在△BCE中,BE边上的高是;EC边上的高是;在△ACD中,AC边上的高是;CD边上的高是.37.三角形按角分类,可以把三角形分为.38.三角形的高线、中线、角平分线中,一定能把三角形分为面积相等的两个部分的是.39.已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=cm2.40.已知BD是△ABC的一条中线,△ABD与△BCD的周长分别为21,12,则AB﹣BC的长是.41.如图△ABC中,F是BC上的一点,且CF=BF,那么△ABF与△ACF的面积比是.42.如图,在Rt△ABC中,∠ABC=90°,AB=12cm,BC=5cm,AC=13cm,若BD 是AC边上的高,则BD的长为cm.43.如图,在Rt△ABC中,∠ABC=90°,AB=12cm,BC=5cm,AC=13cm,若BD 是AC边上的高,则BD的长为cm.44.如图,AE是△ABC的中线,BF是△ABE的中线,若△ABC的面积是20cm2,=cm2.则S△ABF45.工人师傅在门框的背面钉一根木条,运用了.46.屋顶钢架常常做成三角形形状,这是利用.47.如图,为了使木门不变形,木工师傅在木门上加钉了一根木条,这样是利用三角形的.48.如图,已知BE⊥AD,CF⊥AD,且BE=CF.那么AD是△ABC的.(填“中线”或“角平分线”)49.如图,已知AD,AE分别是△ABC的中线和高,且AB=5cm,AC=3cm,则△ABD与△ACD的周长的差为cm.△ABD的面积与△ACD的面积的关系为.50.如图,长方形ABCD的长为8,宽为5,E是AB的中点,点F在BC上,若△DEF的面积为16,则△DCF的面积为.华师大新版七年级下学期《9.1.1 认识三角形》同步练习卷参考答案与试题解析一.填空题(共50小题)1.如果一个三角形的三边长度之比是2:3:4,周长为36cm,则最大的边长为16cm.【分析】根据比例设三角形的三边分别为2k、3k、4k,然后根据周长为36列出方程求解即可.【解答】解:设三角形的三边分别为2k、3k、4k,根据题意得,2k+3k+4k=36,解得k=4,所以,最大的边长为4×4=16cm.故答案为:16cm.【点评】本题考查了三角形,利用“设k法”表示出三边求解更简便.2.一棵小树被风刮歪了,小明用两根木棒撑住这棵小树,他运的数学知识是三角形的稳定性.【分析】当一棵小树被风刮歪了,用两根木棒撑住这棵小树,即是组成三角形,故可用三角形的稳定性解释.【解答】解:一棵小树被风刮歪了,小明用两根木棒撑住这棵小树,他运的数学知识是三角形的稳定性.故答案为:三角形的稳定性.【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.3.下列图形中具有稳定性有(2),(4)(填序号)【分析】根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.【解答】解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.显然(2)、(4)2个.故答案为:(2),(4).【点评】此题考查了三角形的稳定性和四边形的不稳定性,注意根据三角形的稳定性进行判断.4.如图,在△ABC中,点D、E分别是BC、AD边的中点,且S△ABC=8cm2,则S =2cm2.△ABE【分析】根据三角形的中线平分三角形面积进而得出答案.【解答】解:∵点D、E分别是BC、AD边的中点,=S△ABC,S△ABE=S△ABD,∴S△ABD=S△ABC,∴S△ABE∵S=8cm2,∴S△ABE=8×=2(cm2),△ABC故答案为:2.【点评】此题主要考查了三角形面积求法以及三角形中线的性质,利用三角形中=S△ABC是解题关键.线的性质得出S△ABE5.线段的重心是线段的中点;三角形的重心是中线的交点.【分析】根据线段,三角形的重心的定义填空.【解答】解:线段的重心是线段的中点;三角形的重心是中线的交点.故答案为:线段的中点;中线的交点.【点评】本题考查了三角形与线段的重心的定义,是基础题,熟记概念是解题的关键.6.如图,在△ABC中,BC边上的高是AB;在△AEC中,AE边上的高是CD,EC边上的高是AB.AC边上的高是EF.【分析】三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段,依此即可求解.【解答】解:如图,在△ABC中,BC边上的高是AB;在△AEC中,AE边上的高是CD,EC边上的高是AB.AC边上的高是EF.故答案为:AB;CD;AB;EF.【点评】本题考查了三角形高线的概念,是基础题型.7.如图,在△ABC中,已知AB=8cm,AC=5cm,AD是△ABC的中线,则△ABD 的周长比△ACD的周长多3cm.【分析】根据中线的定义可得BD=CD,然后求出△ABD的周长与△ACD的周长的差为AB﹣AC,从而得解.【解答】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD的周长﹣△ACD的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB+AD+BD﹣AC﹣AD﹣CD=AB﹣AC,∵AB=8cm,AC=5cm,∴△ABD的周长﹣△ACD的周长=8﹣5=3cm,故△ABD的周长比△ACD的周长多3cm.故答案为:3.【点评】本题考查了三角形的中线,求出两个三角形的周长的差等于AB﹣AC是解题的关键.8.如图,AD为△ABC的中线,点E为AD的中点,若△AEC面积为12cm2,则△ABC的面积为48cm2.【分析】根据△ACE的面积=△DCE的面积,△ABD的面积=△ACD的面积计算出各部分三角形的面积,最后再计算△ABC的面积.【解答】解:∵AD是BC边上的中线,E为AD的中点,根据等底同高可知,△ACE的面积=△DCE的面积=12cm2,△ABD的面积=△ACD的面积=2△AEC的面积=24cm2,△ABC的面积=2△ABD的面积=48cm2.故答案为:48.【点评】考查了三角形的面积,关键是利用三角形的中线平分三角形面积进行计算.9.在△ABC,AD、BE分别是BC、AC边上的中线,交于点O,则OD:OA=.【分析】根据三角形的重心是三角形三边中线的交点,得出O为△ABC重心,利用重心到顶点的距离与重心到对边中点的距离之比为2:1,即可得出答案.【解答】解:∵AD、BE分别是BC、AC边上的中线,交于点O,∴O为△ABC重心,∴OD:OA=,故答案为:.【点评】此题主要考查了重心的定义与性质,根据已知得出O为△ABC重心是解题关键.10.在△ABC中,AC=3cm,AD是△ABC中线,若△ABD周长比△ADC的周长大2cm,则BA=5cm.【分析】先根据中线的性质得出BD=CD,再根据若△ABD周长比△ADC的周长大2cm得出AB﹣AC=2cm,即可求出结果.【解答】解:∵AD是△ABC中线,∴BD=CD,∵△ABD周长比△ADC的周长大2cm,∴(AB+BD+AD)﹣(AC+CD+AD)=2cm,∴AB+BD+AD﹣AC﹣CD﹣AD=AB﹣AC=2cm.∵AC=3cm,∴BA=5cm.故答案为:5.【点评】本题主要考查了三角形中线的性质,解题时要注意三角形的中线和周长的综合应用.11.如图,△ABC中,AD为中线,DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE=2.【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.【解答】解:∵△ABC中,AD为中线,=S△ADC,∴BD=DC,∴S△ABD∵DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,∴•AB•ED=•AC•DF,∴×3×ED=×4×1.5,∴ED=2.【点评】三角形的中线,把三角形的面积分成相等的两部分.本题的解答充分利用了面积相等这个知识点.12.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则△ABC中BC边上的高是AD.【分析】根据过三角形的一个顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:∵AD⊥BC,∴△ABC中BC边上的高是AD.故答案为:AD.【点评】本题考查了三角形的角平分线、中线和高,是基础题,熟记概念是解题的关键.13.如图,△ABC中,点D、E、F分别在三边上,E是AB的中点,AD、BE、CF=12,S△AOE=3,则AF与CF之间的等量关系为AF=交于点O,DC=3BD,S△DOCCF.,等底等高的三【分析】根据等高的三角形的面积的比等于底边的比求出S△BOD,再根据等高的三角形的面积的比等于底边的比列角形的面积相等求出S△BOE式求解即可.=12,【解答】解:∵DC=3BD,S△DOC=×12=4,∴S△BOD∵E是AB的中点,∴S=S△AOE=3,△BOE=x,S△COF=y,设S△AOF=3+3+x=6+x,则S△ABFS△BCF=4+12+y=16+y,∴==,∴x(16+y)=y(6+x),整理得,16x=6y,=,∴AF=CF.故答案为:AF=CF.【点评】本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,等高的三角形的面积的比等于底边的比,熟记并灵活运用是解题的关键.14.如图,AD⊥BC于D,那么图中△ABC的高是线段AD.【分析】根据过三角形的顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:△ABC的高是线段AD.故答案为:AD.【点评】本题考查了三角形的高线,熟记概念并准确识图是解题的关键.15.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,CD是△ABC的中线,则△ACD 的面积是12.【分析】根据直角三角形的面积公式求出△ABC的面积,再根据中线的性质,求得△ACD的面积.【解答】解:∵在△ABC中,∠ACB=90°,AC=6,BC=8,∴△ABC的面积:6×8÷2=24,∵CD是△ABC的中线,∴△ACD的面积:24÷2=12.答:△ACD的面积是12.故答案为:12.【点评】考查了直角三角形的面积,中线的性质等知识点,关键是熟悉三角形的中线将三角形的面积分成面积相等的两部分.16.平面上有四个点A、B、C、D,其中任意三个点都不在一条直线上,用它们作顶点可以组成三角形的个数是4个.【分析】根据三角形的定义(由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形)填空.【解答】解:∵平面上有四个点A、B、C、D,其中任意三个点都不在一条直线上,∴用它们作顶点可以组成三角形有:△ABC、△ABD、△ACD和△BCD,共4个.故填:4.【点评】本题考查了三角形的定义.注意,是不在同一直线上的三个点才可以连接成为三角形.17.如图,E,F,G分别是AB,BC,AC边上的中点,则S△ABC=4S△BEF=4 S△FGC.【分析】根据三角形的中位线定理得出EF∥AC,GF∥AB,EF=AC,GF=AB,再根据相似三角形的性质得出S△BEF :S△FGC:S△ABC=1:1:4,即可求出答案.【解答】证明:∵E,F,G分别是AB,BC,AC边上的中点,∴EF∥AC,GF∥AB,EF=AC,GF=AB,∴S△BEF :S△FGC:S△ABC=1:1:4,∴S△ABC=4S△BEF=4S△FGC,故答案为:4,4.【点评】本题主要考查了三角形的面积;关键是根据三角形的中位线的性质和相似三角形的性质求出答案.18.如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是12.【分析】求出正方形的面积和四个三角形的面积,再相减即可求出四边形ABCD 的面积.【解答】解:四边形ABCD的面积S=5×5﹣×2×3﹣×2×3﹣×3×4﹣×1×2=12.故答案为:12.【点评】本题考查了三角形面积的应用,解此题的关键是把不规则图形的面积转化成规则图形的面积.19.如图是阳光广告公司为某件商品设计的商标图案,图中阴影部分为斜线,若每个小长方形的面积都是1,则阴影部分的面积是 3.5.【分析】由图可得,图中阴影部分的面积等于大正方形的面积减去三个三角形的面积,三角形的底、高可根据小正方形的边长为1得到,解答出即可.【解答】解:由题意可得,阴影部分的面积=4×4﹣×1×4﹣×3×3﹣×3×4=16﹣2﹣﹣6=3.5.故答案为3.5.【点评】本题主要考查了三角形的面积,注意不规则图形面积的求法,体现了转化思想.20.图中可数出的三角形个数为48个.【分析】因为图中线段DE上的每条线段都对着两个三角形,故数出线段条数即可求出三角形的个数,以及以AC为轴,左右还有6个,即可得出总数.【解答】解:如图,共有6+5+4+3+2+1=21条线段,则有三角形21×2=42个.以AC为轴,左右还有6个,∴三角形个数一共有48个,故答案为:48.【点评】此题考查了线段的条数的数法,解题过程中利用了转化思想,将三角形个数问题转化为线段条数问题是解题的关键.21.建筑工地上,我们经常会见到木工师傅在木门框上斜钉上一根木条,这是因为三角形具有稳定性的缘故.【分析】根据三角形的三边一旦确定,则形状大小完全确定,即三角形的稳定性.【解答】解:木工师傅在木门框上斜钉上一根木条,是为了构成三角形,因为三角形具有稳定性.【点评】本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.22.观察下面两图形的形成过程,若AD=3,DB=4,则△ADE和△BDF面积的和为6.【分析】由图形的旋转可知,图形顺时针旋转了90°,即∠EDF=∠ADA′=90°,可得∠ADB=90°,△ADE和△BDF面积的和即为△A′DB的面积.【解答】解:观察图形的旋转可知:旋转角∠EDF=∠ADA′=90°,AD=A′D=3,∴∠A′DB=180°﹣∠ADA′=90°,∴S△ADE +S△BDF=S△A′BD=×A′D×BD=6.故答案为:6.【点评】本题考查了旋转的性质,通过旋转将两个图形“移”到同一个图形中去,便于计算面积.23.已知,锐角三角形ABC的三边AB=6cm,BC=7cm,AC=8cm,∠A=α,则△ABC的面积等于24sinαcm2(用含α的式子表示).【分析】过B点作BD⊥AC垂足为D,在三角形ABD中,根据三角函数的定义求出BD的长,然后根据三角形面积公式进行解答.【解答】解:过B点作BD⊥AC垂足为D,在Rt△ABD中,∵sinα=,∴BD=6sinα,=AC•BD=24sinα,∴S△ABC故答案为24sinα.【点评】本题主要考查三角形面积的知识点,熟记三角形的面积公式是解答本题的关键.24.如图,AD、BE、CF是△ABC的三条中线,若△ABC的周长是a cm.则AE+CD+BF= cm.【分析】由于AD、BE、CF是△ABC的三条中线,根据中线的性质可以得到AE+CD+BF=(AC+BC+AB),利用这个结论即可求解.【解答】解:∵AD、BE、CF是△ABC的三条中线,∴AF=AB,CD=CB,BF=AB,∴AE+CD+BF=(AC+BC+AB),而△ABC的周长是a cm,∴AE+CD+BF=cm.故答案为:.【点评】此题主要考查了三角形中线的性质,也利用了三角形的周长计算公式,比较简单.25.一个三角形的面积为25cm 2,一边为5cm ,则这条边上的高为 10cm .【分析】根据三角形面积的计算公式S=ah ,解答出即可;【解答】解:设这条边上的高为h ,∵三角形的面积为25cm 2,一边为5cm ,∴,解得,h=10cm ;故答案为:10cm .【点评】本题主要考查了三角形面积的计算公式,熟记三角形面积计算公式,是解答本题的基础.26.如图,在四边形ABCD 中,AC 与BD 相交于点O ,S △ABD :S △CBD =3:2,则OA :OC 的值为 .【分析】首先根据同底不同高的两个三角形的面积比S △ABD :S △CBD =3:2推知两个三角形的同底上的高线比=;然后利用相似三角形的判定定理AA 推知Rt △AOE ∽Rt △COF ;最后根据相似三角形的对应边成比例求得==. 【解答】解:过点A 作AE ⊥BD 于点E ,过C 点作CF ⊥BD 于点F .∵S △ABD :S △CBD =3:2,∴BD•AE :BD•CF=3:2,∴=;在Rt △AOE 和Rt △COF 中,,∴Rt △AOE ∽Rt △COF (AA ),∴==(相似三角形的对应边成比例).故答案是:.【点评】本题考查了三角形的面积比.解答该题时,借用了相似三角形的判定定理AA 和相似三角形的对应边成比例的性质.27.△ABC 中,D 、E 分别在AB 、AC 上,并且AD :DB=2:1,AE :EC=1:2,则S △ADE :S △ABC = 2:9 .【分析】连接CD ,根据同高三角形的面积等于底边长为比可得△ADE 和△EDC 的面积是1:2,△BCD 的面积是S △ADC =S △ADE ;从而可得△ABC 面积是S △ADC .【解答】解:连接CD ,△ADE 和△EDC 同高,底边长为AE :EC=1:2,所以面积也是1:2,所以△ADC 面积就是△ADE 的3倍;又因为△BCD 和△ADC 也是同高,底边是AD :DB=2:1,所以△BCD 的面积是S △ADC =S △ADE ;所以△ABC 面积是S △ADC ,即S △ADE :S △ABC =2:9.故答案为:2:9.【点评】考查了三角形的面积,本题的关键是熟练掌握等高的三角形面积比等于底边比的运用及辅助线的添加.28.已知在△ABC 中,AD 是中线,G 是重心,如果GD=2cm ,那么AG= 4 cm .【分析】根据三角形重心的性质即可求出AG 的长.【解答】解:∵G 是△ABC 的重心,且AD 是中线,∴AG=2GD=4cm.故答案为:4.【点评】此题考查了三角形重心性质:三角形的重心到顶点的距离是它到对边中点的距离的2倍.29.如图,G是△ABC的重心,S△DGC=4,S△ABC=24.【分析】由于G是△ABC的重心,可得AG=2GD,BD=CD,根据等高三角形的面=12;同理D是BC中点,可得出△ABD和△ABC 积比等于底之比,可求出S△ABD的面积比,由此得解.【解答】解:如图,连接BG.∵G是△ABC的重心,∴AG=2GD,BD=CD,=2S△BGD=2S△CGD=8,∴S△AGB=3S△BGD=12.∴S△ABD∵BD=CD,=2S△ABD=24.∴S△ABC故答案为:24.【点评】此题主要考查了重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.30.一个三角形的三边之比为3:4:5,其中最长边比最短边长4cm,则这个三角形的周长为24cm.【分析】设三角形的三边长分别为:3xcm,4xcm,5xcm,根据关键语句“最短的边比最长的边短4m,”可得5x﹣3x=4,解可得到x的值,进而可以算出三边长,再计算出周长即可.【解答】解:设三角形的三边长分别为:3xcm,4xcm,5xcm,由题意得:5x﹣3x=4,解得:x=2,则三角形的三边长分别为:6cm,8cm,10cm,周长为:6+8+10=24(cm),故答案为:24.【点评】此题主要考查了一元一次方程的应用,解决问题的关键是根据三边的比值表示出三边长,再根据关键语句列出方程即可.31.如图,图中阴影部分是黄鹤楼公司某产品的商品图案,若每个小长方形的面积都是1,则阴影部分的面积为 2.5.【分析】把阴影部分分成两个三角形和一个平行四边形:左边的三角形,中间的平行四边形,右边的三角形.然后根据面积公式分别计算各部分的面积.【解答】解:阴影部分的面积为=2.5.【点评】考查了根据三角形面积公式进行计算的能力.32.AD为△ABC中BC边上的中线,则以下面积的关系:S△ADB=S△ADC=(填“>”、“<”或“=”).【分析】本题从等底(DB=CD),同高而解得.【解答】解:∵AD为△ABC中BC边上的中线∴BD=CD,S△ADB和S△ADC的高是相等的,∴S△ADB=S△ADC=故填:=,=.【点评】本题考查了三角形的面积,从底边和高考虑,从而解决了问题.33.为了使做好的木门窗在运输、安装过程中不变形,木工师傅在木门窗上斜着加钉了一根木条.其原理是三角形的稳定性.【分析】根据安装过程中不变形,木工师傅在木门窗上斜着加钉了一根木条,是利用了三角形的稳定性.【解答】解:其原理是:三角形的稳定性.【点评】考查了三角形的稳定性的性质.34.如图中△ABC的面积为9.5.【分析】分别过点A、B、C作x轴,y轴的垂线,围成矩形CDEF,S△ABC=S矩形CDEF﹣S△ABE ﹣S△ACD﹣S△BCF.【解答】解:过点A、B、C作x轴,y轴的垂线,围成矩形CDEF,∴S△ABC=S矩形CDEF﹣S△ABE﹣S△ACD﹣S△BCF=4×5﹣3×4÷2﹣1×5÷2﹣1×4÷2=20﹣6﹣2.5﹣2=9.5.【点评】本题考查了三角形面积的计算,并且用了割补法.35.如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2cm,则△BCD和△ACD的周长的差是2cm.【分析】由题意易得△ACD和△BCD的周长的差就是线段AC与BC的差,据此求解.【解答】解:∵CD是AB边上的中线,∴AD=BD,又∵△ACD的周长=AC+AD+CD,△BCD的周长=BC+BD+CD,∴△BCD的周长﹣△ACD的周长=BC﹣AC=2cm.【点评】此题主要考查三角形的周长和中线的应用.36.如图所示,在△ABC中,BC边上的高是AF,AB边上的高是CE;在△BCE中,BE边上的高是CE;EC边上的高是BE;在△ACD中,AC 边上的高是CD;CD边上的高是AC.【分析】根据三角形的高的定义即可求出答案.【解答】解:根据三角形的高的定义:三角形的一个顶点向它的对边所在的直线作垂线,这点和垂足之间的线段是三角形的这边上的高,得出:在△ABC中,BC边上的高是AF,AB边上的高是CE;在△BCE中,BE边上的高是CE;EC边上的高是BE;在△ACD中,AC边上的高是CD;CD边上的高是AC.故答案为:AF,CE,CE,BE,CD,AC.【点评】本题主要考查对三角形的高的定义的理解和掌握,能区分一条线段是否是三角形的高是解此题的关键.37.三角形按角分类,可以把三角形分为锐角三角形,直角三角形和钝角三角形.【分析】角有锐角、直角和钝角,三角形按角分类分为锐角三角形,直角三角形和钝角三角形.【解答】解:锐角三角形,直角三角形和钝角三角形,故答案为:锐角三角形,直角三角形和钝角三角形.【点评】此题考查的知识点是三角形,关键明确:有一个角是直角的三角形是直角三角形.三个角都为锐角的三角形是锐角三角形.有一个角是钝角的三角形是钝角三角形.38.三角形的高线、中线、角平分线中,一定能把三角形分为面积相等的两个部分的是中线.【分析】根据等底等高的两个三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分.【解答】解:把三角形的面积分为相等的两部分的是三角形的中线.故答案为:中线.【点评】本题考查了三角形的角平分线、中线、高线,以及等底等高的三角形的面积相等的性质,三角形的中线是三角形的一个顶点与对边中点连接的线段,它把三角形的面积分为相等的两部分.39.已知如图,△ABC的中线AD的中点为E,S△BDE=2cm2,那么S△ABC=8cm2.=S△ABD,S△ABD=S△ABC,所以【分析】△ABC的中线AD的中点为E,所以S△BDES△ABC=4S△BDE.【解答】解:∵△ABC的中线AD的中点为E,=S△ABD,S△ABD=S△ABC,∴S△BDE=4S△BDE,∴S△ABC=2cm2,又∵S△BDE∴S=8cm2.△ABC【点评】解答这类题目时,只要找准了图形的底边和底边之间的关系,高和高之间的关系,再根据面积公式来计算就不难理解其中的规律了.40.已知BD是△ABC的一条中线,△ABD与△BCD的周长分别为21,12,则AB﹣BC的长是9.【分析】由于BD是△ABC的一条中线,由此可以得到AD=CD,而△ABD与△BCD 的周长分别为21,12,并且BD公共,利用三角形的周长公式即可求出AB﹣BC的长.【解答】解:∵BD是△ABC的一条中线,∴AD=CD,而△ABD与△BCD的周长分别为21,12,并且BD公共,∴AB﹣BC的长=21﹣12=9.【点评】此题主要考查了三角形的中线的性质,也考查了三角形的周长公式,比较简单.41.如图△ABC中,F是BC上的一点,且CF=BF,那么△ABF与△ACF的面积比是2:1.【分析】根据三角形的面积公式可得,因为CF=BF,则S=BC×高×,S△ABF=BC×高×,即可求得比值.△ACF【解答】解:∵CF=BF,=BC×高×,S△ACF=BC×高×,∴S△ABF∴△ABF与△ACF的面积比是2:1.【点评】不同底同高的两个三角形面积比等于底边的比.42.如图,在Rt△ABC中,∠ABC=90°,AB=12cm,BC=5cm,AC=13cm,若BD 是AC边上的高,则BD的长为cm.【分析】根据三角形的面积公式,即可得出关于BD的一元一次方程,解之即可得出结论.=AB•BC=AC•BD,【解答】解:∵S△ABC∴12×5=13•BD,∴BD=cm.故答案为:.【点评】本题考查了三角形的面积以及解一元一次方程,利用面积法找出关于BD的一元一次方程是解题的关键.43.如图,在Rt△ABC中,∠ABC=90°,AB=12cm,BC=5cm,AC=13cm,若BD 是AC边上的高,则BD的长为4cm.【分析】根据三角形的面积等于底边长与高线乘积的一半,以及直角三角形的特征,可得:AB•BC=AC•BD,据此求出BD的长为多少即可.【解答】解:∵△ABC是直角三角形,∴AB•BC=AC•BD,∴BD===4(cm).故答案为:4.【点评】此题主要考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:三角形的面积等于底边长与高线乘积的一半.44.如图,AE是△ABC的中线,BF是△ABE的中线,若△ABC的面积是20cm2,=5cm2.则S△ABF【分析】利用三角形的中线把三角形分成面积相等的两个三角形进行解答.【解答】解:∵AE是△ABC的中线,BF是△ABE的中线,=S△ABC=×20=5cm2.∴S△ABF故答案为:5【点评】本题考查了三角形的面积,能够利用三角形的中线把三角形分成面积相等的两个三角形的性质求解是解题的关键.45.工人师傅在门框的背面钉一根木条,运用了三角形的稳定性.【分析】用木条固定门框,即是组成三角形,故可用三角形的稳定性解释.【解答】解:工人师傅在门框的背面钉一根木条,运用了三角形的稳定性,故答案为:三角形的稳定性.【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.46.屋顶钢架常常做成三角形形状,这是利用三角形的稳定性.【分析】屋顶钢架常常做成三角形形状,即是组成三角形,故可用三角形的稳定性解释.【解答】解:屋顶钢架常常做成三角形形状,这是利用三角形的稳定性,故答案为:三角形的稳定性【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.。
七年级数学思维探究(24)认识三角形(含答案)

24.认识三角形 解读课标从房屋的顶梁到自行车的三脚架,从起重机的三角形吊臂再到爱因妥芬(心电图的发明者)三角形,生活中处处可看到三角形,三角形是最简单、最基本的几何图形,它不仅是研究其他图形的基础,在解决实际问题中也有着广泛的应用.认识三角形,就是认识三角形的概念及基本要素——边与角,与边与角相关的知识有:三角形三边关系定理、三角形内角和定理及推论,它们在线段、角度的计算,图形的计数等方面有广泛的应用. 代数化及分类讨论法是解与三角形基本要素相关问题的重要方法.代数化即用方程、不等式解边与角的计算及简单推理题,分类讨论即按边或角对三角形进行分类. 问题解决例1 在ABC △中,高BD 和CE 所在直线想交于O 点,若ABC △不是直角三角形,且60A ∠=︒,则BOC ∠=_________度.试一试 因三角形的高不一定在三角形内部,这样ABC △形状应分两种情况讨论. 例2 如图,将纸片ABC △沿着DE 折叠压平,则( ).A .12A ∠=∠+∠B .()122A ∠=∠1+∠C .()113A ∠=∠+∠2D .()1124A ∠=∠+∠试一试 在折叠动态变化中,不变关系是B C AED ADE ∠+∠=∠+∠,这是解本例的关键.例3 (1)如图①,AD BC ⊥于D ,AE 平分BAC ∠,试探寻DAE ∠与C ∠、B ∠的关系.(2)如图②,若将点A 在AE 上移动到F ,FD BC ⊥于D ,其他条件不变,那么EFD ∠与C ∠、D ∠是否还有(1)中的关系?说明理由. (3)请你提出一个类似的问题.试一试 对于(2),通过作辅助线,将问题转化为(1).例4 如图①,已知A 为x 轴负半轴上一点,B 为x 轴正半轴上一点,()0,2C -,()3,2D --. (1)求BCD △的面积;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交CO 于P ,交CA 于Q ,判断CPQ ∠与CQP ∠的大小关系,并证明你的结论;(3)如图③,若ADC DAC ∠=∠,点B 在x 轴正半轴上运动,ACB ∠的平分线CE 交DA 的延长线于21DAB ED ABCE 图①DABCF 图②点E ,在B 点的运动过程中,EABC∠∠的值是否变化?若不变,求出其值;若变化,请说明理由.试一试 对于(3),ABC ∠能否用E ∠的式子表示?由数到形,分解出基本图形是解题的关键. 例5 在三角形纸片内有2008个点,连同三角形纸片的3个顶点,共有2011个点,在这些点中,没有三点在一条直线上.问:以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形?解法一 我们不妨先退一步,考察三角形内有一个点、两个点、三个点…的简单情形,有下表所示的3个小三角形,以后每增加一个点,这个点必落在已连好的某一个小三角形内,它与该三角形的三个顶点可得到三个小三角形,从而增加了两个小三角形,于是可以推出,当三角形内有2008个点时,连接可得到小三角形的个数为:()32200814017+⨯-=(个).解法二 整体核算法.设连线后把原三角形分割成n 个小三角形,则它们的内角和为180n ︒⋅,又因为原三角形内每一个点为小三角形顶点时,能为小三角形提供360︒的内角,2008个点共提供内角2008360⨯︒,于是得方程1803602008180n =⨯+,解得4017n =,即这2008个点能将原三角形纸片分割成4017个小三角形. 角平分线角平分线是联系角与角之间关系的纽带,当角平分线与三角形相遇可生成内涵上有关联性、解法上有共通性的组图.例6 (1)如图①,已知ABC △中的两内角平分线交于P 点,两外角平分线交于M 点,一内角平分线与一外角平分线交于N 点.试分别探究BPC ∠、M ∠、N ∠与A ∠关系;(2)如图②,在凹四边形ABCD 中,已知ABD ∠与ACD ∠的平分线交于点E ,求证:2ADE ∠+∠∠=.分析与解 (1)1902BPC A ∠=︒+∠,1902M A ∠=︒-∠,12N A ∠=∠.(2)凹四边形ABCD 形似“规形”,易证BDC A B C ∠=∠+∠+∠.图①图②图③NPABC图①x y yxD A BCE 图②图②可分解为两个“规形”,BE ∵、CE 分别平分ABD ∠、ACD ∠,∴可设ABE DBE x ∠=∠=,ACE DCE y ∠=∠=. 由(1)得E A x y ∠=∠++,① D E x y ∠=∠++,②②-①得D E E A ∠-∠=∠-∠,2A DE ∠+∠∠=∴.数学冲浪 知识技能广场1.一副三角板叠在一起如图放置,最小锐角的顶点D 恰好放在等腰直角三角板的斜边AB 上,BC 与DE 交于点M .若100ADF ∠=︒,则BM D ∠=_________度.2.一副三角板,如图所示叠放在一起,则图中1∠的度数为_______.3.如图,ABC △中,80A ∠=︒,剪去A ∠后,得到四边形BCED ,则12∠+∠=_______.4.如图,在ABC △中,A α∠=,ABC ∠的平分线与ACD ∠的平分线交于点1A ,得1A ∠;1A BC ∠的平分线与1ACD ∠的平分线相交于点2A ,得2A ∠;…,2008A BC ∠的平分线与2008A CD ∠的平分线相交于点2009A ,得2009A ∠,则2009A ∠=________.5.如图,ABC △中,A ∠、B ∠、C ∠的外角分别记为α、β、γ.若::3:4:5αβγ=,则::A B C ∠∠∠=( ).A .3:2:1B .1:2:3C .3:4:5D .5:4:3MABCEF 1ECBA DABA 1A 26.如图,BP 是ABC △中ABC ∠的平分线,CP 是ACB ∠的邻补角的平分线.若20ABP ∠=︒,50ACP ∠=︒,则A P ∠+∠=( ).A .70︒B .80︒C .90︒D .100︒7.在等腰ABC △中,AB AC =,一边上的中线BD 将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( ).A .7B .11C .7或11D .7或108.如图,ABC △中,ABD DBE EBC ∠=∠=∠,ACD DCE ECB ∠=∠=∠,若145BEC ∠=︒,则B D C ∠等于( ).A .100︒B .105︒C .110︒D .115︒9.如图,已知射线OM 与射线ON 互相垂直,B 、A 分别为OM 、ON 上一动点,ABM ∠、BAN ∠的平分线交于C .问:B 、A 在OM 、ON 上运动过程中,C ∠的度数是否改变?若不改变,求出其值;若改变,说明理由.10.如图①,已知ABC △中,ABC ACB ∠=∠,D 为BC 边上一点,E 为直线AC 上一点,且ADE AED ∠=∠.(1)求证:2BAD CDE ∠=∠,(2)如图②,若D 在BC 的反向延长线上,其他条件不变,(1)中的结论是否仍成立?证明你的结论.CBA γαβMPABCECBA D OMNA C思维方法天地11.在ABC △中,50A ∠=︒,高BE 、CF 交于O ,且O 不与B 、C 重合,则BOC ∠的度数为_______. 12.如图,已知C ∠=45︒,452B α∠=︒+,453BAC α∠=︒+,AE 平分BAD ∠,则CAE ∠=_______.13.如图,BP 平分ABC ∠交CD 于F ,DP 平分ADC ∠交AB 于E ,AB 与CD 相交于G ,如果42A ∠=︒,38C ∠=︒,那么P ∠的度数为________.14.如图,已知ABC △中,A ACB ∠=∠,CP 平分ACB ∠,BD 、CD 分别为ABC △的两外角的平分线,给出下列结论:①CP CD ⊥;②1902D A ∠=︒-∠;③P D A C ∥.其中正确结论的个数是( ).A .0B .1C .2D .315.如图,31ABC ∠=︒,又BAC ∠的平分线AE 与FCB ∠的平分线CE 相交于E 点,则AEC ∠为( ). A .14.5︒ B .15.5︒ C .16.5︒ D .20︒图①A BCE 图②EC BADDABCEDGPABCEF DPAB C EFDABCEF16.如图,ABC △中,90BAC ∠=︒,AD BC ⊥,ABC ∠的平分线BE 交AD 于点F ,AG 平分DAC ∠.给出下列结论:①BAD C ∠=∠;②A E F A F E ∠=∠;③E B C C ∠=∠;④A G E F ∠⊥.其中正确的结论是( ).A .②③④B .①③④C .①②④D .①②③17.平面内的四条线段AB 、BC 、CD 、DA 首尾顺次连接,已知24ABC ∠=︒,42ADC ∠=︒. (1)如图①,若BAD ∠与BCD ∠的平分线交于点M ,求AMC ∠的值;(2)如图②,点E 在BA 的延长线上,DAE ∠的平分线和BCD ∠的平分线交于点N ,求ANC ∠的值.18.如图,在BCD △中,BE 平分DBC ∠交CD 于F ,延长BC 至G ,CE 平分DCG ∠,且EC 、DB的延长线交于A 点,若30A ∠=︒,75DFE ∠=︒. (1)求证:DFE A D E ∠=∠+∠+∠; (2)求E ∠的度数;(3)若在图中作CBE ∠与GCE ∠的平分线交于1E ,作1C B E ∠与1GCE ∠的平分线交于2E ,作2CB E ∠与2GCE ∠的平分线交于3E ,依此类推,n CBE ∠与n GCE ∠的平分线交于1n E +,请用含有n 的式子表示1n E +∠的度数.应用探究乐园19.把一副学生用三角板(30︒、60︒、90︒和45︒、45︒、90︒)如图①放置在平面直角坐标系中,点A 在y 轴正半轴上,直角边AC 与y 轴重合,斜边AD 与y 轴重合,直角边AE 交x 轴于F ,斜边AB 交x 轴于G ,O 是AC 中点,8AC =.(1)把图①中的Rt AED △绕A 点顺时针旋转α度得图②,此时AGH △的面积是10,AHF △的面积是8,分别求F 、H 、B 三点的坐标;(2)如图③,设AHF ∠的平分线和AGH ∠的平分线交于点M ,EFH ∠的平分线和FOC ∠的平分线交于点N ,当AED △绕A 点转动时,N M ∠+∠的值是否会改变,若改变,请说明理由,若不改变,请求出其值.GABCEFCBAD图①DNABCE图②DGABC F20.问题提出 以n 边形的他个顶点和它内部的m 个点,共()m n +个点作为顶点,可把原n 边形分割成多少个互不重叠的小三角形?问题探究 为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:探究一:以ABC △的三个顶点和它内部的1个点P ,共4个点为顶点,可把ABC △分割成多少个互不重叠的小三角形?如图①,显然,此时可把ABC △分割成3个互不重叠的小三角形.探究二:以ABC △的三个顶点和它内部的2个点P ,Q ,共5个点为顶点,可把ABC △分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①ABC △的内部,再添加1个点Q ,那么点Q 的位置会有两种情况:一种情况,点Q 在图①分割成的某个小三角形内部,不妨假设点Q 在PAC △内部,如图②; 另一种情况,点Q 在图①分割成的小三角形的某条公共边上,不妨假设点Q 在PA 上,如图③. 显然,不管哪种情况,都可把ABC △分割成5个互不重叠的小三角形. 探究三:以ABC △的三个顶点和它内部的3个点P ,Q ,R 共6个点为顶点,可把ABC △分割成______个互不重叠的小三角形,并在图④中画出一种分割示意图.探究四:以ABC △的三个顶点和它内部的m 个点,共()3m +个顶点,可把ABC △分割成______个互不重叠的小三角形.探究拓展:以四边形的4个顶点和它内部的m 个点,共()4m +个顶点,可把四边形分割成_____个互不重叠的小三角形,问题解决 以n 边形的挖个顶点和它内部的m 个点,共()m n +个顶点,可把ABC △分割成____个互不重叠的小三角形.实际应用 以八边形的8个顶点和它内部的2012个点,共2020个顶点,可把八边形分割成多少个互不重叠的小三角形?(要求列式计算)图①图②图③图①图②图③ABC图④24.认识三角形 问题解决例l 当ABC △为锐角三角形时,120BOC ∠=︒;当ABC △为钝角三角形时,60BOC ∠=︒.例2 B 180B C AED ADE A ∠+∠=∠+∠=︒-∠,又12360B C A E D A D E ∠+∠+∠+∠+∠+∠=︒,得()218012360A ︒-∠+∠+∠=︒,化简得()1122A ∠=∠+∠.例3 (1)()12DAE C B ∠=∠-∠;(2)过A 作AG BC ⊥于G ,则()12EFD EAG C B ∠=∠=∠-∠;(3)略例4 (1)3BCD S =△(2)可证明CPQ CQP ∠=∠.(3)CD AB ∥,可证明1122ABCE ABC ABC ∠∠==∠∠为定值.数学冲浪1.85 2.75︒ 3.260︒ 4.20092α5.A 6.C 7.C 8.C9.190452C AOB ∠=︒-∠=︒,为一定值.10.(1)证明略;(2)(1)中的结论仍然成立 11.50︒或130︒ 12.126︒13.40︒ 如图,由对顶三角形性质得122122A P A C ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩,解得40P ∠=︒.14. D 15. B 16.C17.(1)可证明()1332AMC ABC ADC ∠=∠+∠=︒.(2)可证明()11801232ANC B D ∠=︒+∠+∠=︒.18.(1)略;(2)2D E ∠=∠,代入(1)得15E ∠=︒;(3)122113022n n n E D +++∠=∠=⋅︒.19.(1)()5,0F -,()1,0H -,()8,4B -. (2)22.52M α∠=︒+,752N α∠=︒-,97.5M N ∠+∠=︒,故M N ∠+∠的值不会改变.20.探究三:7分割示意图:(答案不唯一). 探究四:()321m +-或21m + 探究拓展:()421m +-或22m +21PGFEDCBA问题解决:()21n m +-或22m n +-实际应用:把8n =,2012m =代入上述代数式,得2222012824024824030m n +-=⨯+-=+-=.CBA。
数学七年级上册第一章第1节--《认识三角形》专题训练及答案解析
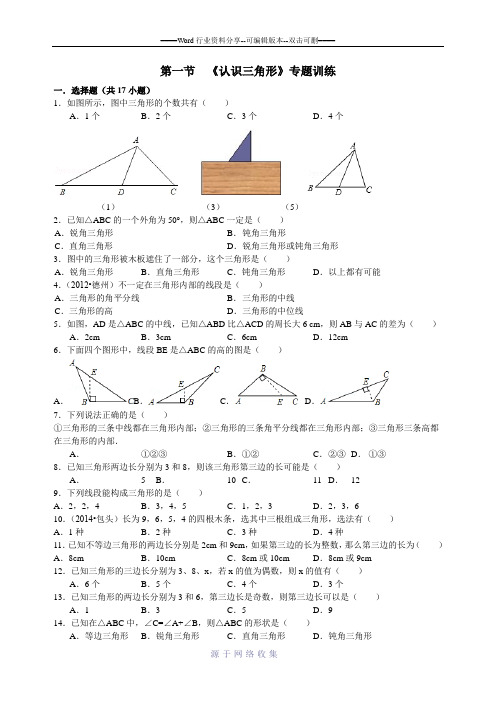
第一节《认识三角形》专题训练一.选择题(共17小题)1.如图所示,图中三角形的个数共有()A.1个B.2个C.3个D.4个(1)(3)(5)2.已知△ABC的一个外角为50°,则△ABC一定是()A.锐角三角形B.钝角三角形C.直角三角形D.锐角三角形或钝角三角形3.图中的三角形被木板遮住了一部分,这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.以上都有可能4.(2012•德州)不一定在三角形内部的线段是()A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线5.如图,AD是△ABC的中线,已知△ABD比△ACD的周长大6 cm,则AB与AC的差为()A.2cm B.3cm C.6cm D.12cm6.下面四个图形中,线段BE是△ABC的高的图是()A.B.C.D.7.下列说法正确的是()①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.A.①②③B.①②C.②③D.①③8.已知三角形两边长分别为3和8,则该三角形第三边的长可能是()A. 5 B.10 C.11 D.129.下列线段能构成三角形的是()A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,610.(2014•包头)长为9,6,5,4的四根木条,选其中三根组成三角形,选法有()A.1种B.2种C.3种D.4种11.已知不等边三角形的两边长分别是2cm和9cm,如果第三边的长为整数,那么第三边的长为()A.8cm B.10cm C.8cm或10cm D.8cm或9cm12.已知三角形的三边长分别为3、8、x,若x的值为偶数,则x的值有()A.6个B.5个C.4个D.3个13.已知三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是()A.1 B.3C.5D.914.已知在△ABC中,∠C=∠A+∠B,则△ABC的形状是()A.等边三角形B.锐角三角形C.直角三角形D.钝角三角形15.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°(15)(16)(17)(19)16.如图,在△ABC中,∠A=70°,∠C=60°,D、E分别是AB、AC上的点,且DE∥BC,则∠ADE 的度数为()A.60°B.70°C.50°D.80°17.如图,DE∥BC,∠A=60°,∠ADE=40°,则∠C为()A.60°B.7O°C.80°D.100°二.填空题(共5小题)18.(2014•淮安)若一个三角形三边长分别为2,3,x,则x的值可以为_________(只需填一个整数)19.如图所示,CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD的周长差是_________ cm.(20)(21)(22)20.(2014•威海)直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=85°,则∠2=_________.21.(2014•随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_________度.2·1·c·n·j·y22.(2013•大连一模)如图,AB∥CD,CE与AB交于点A,BE⊥CE,垂足为E.若∠C=37°,则∠B= _________°.三.解答题(共3小题)23.如图:(1)在△ABC中,BC边上的高是_________.(2)在△AEC中,AE边上的高是_________.(3)在△FEC中,EC边上的高是_________.(4)若AB=CD=2cm,AE=3cm,则S△AEC=_________cm2,CE=_________cm.24.已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于F点,∠A=60°,∠CEF=55°,求∠EFB的度数.25.如图,在△ABC中,∠A=80°,∠C=75°,求∠B的度数.第一节《认识三角形》专题训练参考答案一.选择题(共17小题)1.C.2.B.3.D.4.C.5.C.6.D.7.B.8.B.9.B.10.C.11.C.12.D.13.C.14.C.15.C.16.C.17.C.二.填空题(共5小题)18.419.620.40°21.7522.53°三.解答题(共3小题)23.如图:(1)在△ABC中,BC边上的高是AB.(2)在△AEC中,AE边上的高是CD.(3)在△FEC中,EC边上的高是FE.(4)若AB=CD=2cm,AE=3cm,则S△AEC=3cm2,CE=3cm.24.解:∵EF∥BC,∠CEF=55°,∴∠ECD=∠CEF=55°,∵CE是△ABC的一个外角平分线,∴∠ACD=2∠ECD=2×55°=110°,∵∠A=60°,∴∠B=∠ACD﹣∠A=110°﹣60°=50°,∵EF∥BC,∴∠EFB=180°﹣∠B=180°﹣50°=130°.25.解:∵∠A=80°,∠C=75°,∴∠B=180°﹣∠A﹣∠C=180°﹣80°﹣75°=25°.。
七年级数学下册《认识三角形》例题解析(含答案)

《认识三角形》例题解析例1(1)已知:如图1,D是BC上一点,∠C=62°,∠CAD=32°,则∠ADB=_______度.(2)(黑龙江)一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是()A.14B.15C.16D.17(3)用7根火柴首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为________.解:(1)∠ADB=∠CAD+∠C=32°+62°=94°.故应填94°.(2)∵这个三角形第三边应满足4<x<10,∴最小边为5.则周长最小值为3+5+7=15.故应选B.(3)7根火柴可分为:1,1,5;1,2,4;1,3,3;2,2,3四种,其中能摆成三角形的是:1,3,3;2,2,3两种.故应填2.评析:第(3)小题要分类讨论,并要用三角形三边关系来检验每种情况能否构成三角形.例2如图2,在△ABC中,AD平分∠BAC,BE是高,∠BAC=60°,∠EBC=20°,试求∠ADC的度数.解:因为∠BAC=60°,AD平分∠BAC,所以∠BAD=30°.又因为BE是高,所以∠ABE=30°.而∠EBC=20°,所以∠ABD=50°.所以∠ADC=∠ABD+∠BAD=50°+30°=80°.评析:解这类题目要明确所求的角属于哪一个三角形的内角或外角,抓住题目中存在的等量关系列式计算即可.有时运用列方程解会更简捷.例3如图3,已知:在直角三角形ABC中,∠A=90°,BP平分∠ABC,若CP平分∠ACB且交BP于P,求∠BPC的度数.解:因为BP、CP分别平分∠ABC、∠ACB,所以∠PBC=12∠ABC,∠PCB=12∠ACB.因为∠BPC=180°-(∠PBC+∠PCB),又∠ABC+∠ACB=180°-∠A,所以∠BPC=180°-12(∠ABC+∠ACB)=90°+12∠A.即∠BPC=90°+12×90°=135°.跟踪练习:1.如图4所示,∠1和∠2是A、B两木板与地面的夹角,∠3是两木板间的夹角.若∠3=110°,则∠2-∠1=________.2.如图5,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为______.3.如图7,已知DE分别交△ABC的边AB、AC于D、E,交BC的延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.4.如图8,BP、CP分别平分△ABC的内角∠ABC和外角∠ACD,BP、CP交于P点,若∠A=80°,试求∠P的度数.参考答案:1.702.603.874.40。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的认识练习题
一、填空(每空3分,共60分)
1.三角形的三边关系:①三角形任意两边之和 第三边;②三角形任意两边之
差 第三边.
2.下列每组分别是三根小木棒的长度,用它们能摆成三角形吗?(填“能”或“不能”):
(1)3㎝,4㎝,5㎝( ) (2)8㎝,7㎝,15㎝ ( ) (3)13㎝,12
㎝,20㎝( )
(4)5㎝,5㎝,11㎝ ( ) (5)6cm, 8cm, 10cm ( ) (6)7cm, 7cm,
14cm ( )
3.在△ABC 中,∠A =10°,∠B =30°,则∠C =_________.
(2)一个等腰三角形的一边是5cm ,另一边是7cm ,则这个三角形的周长是 _____________cm.
4.如果∠B +∠C =∠A ,那么△ABC 是 三角形.
5.在△ABC 中,AB =6 cm ,AC =8 cm 那么BC 长的取值范围是 .
6.ABC ∆中,AD 是ABC ∆的中线,且cm BC 10=,则BD= cm.
7.在ABC ∆中,︒=∠80A ,AD 为A ∠的平分线,则BAD ∠=
8.如果一个三角形两边上的高的交点,恰好是三角形的一个顶点,则此三角形是 _____________三角形.
9.判断具备下面条件的三角形是直角三角形、锐角三角形还是钝角三角形:
(1)如果4:3:1::=∠∠∠C B A ,那么ABC ∆是 三角形;(2)如果B A ∠=∠,
︒=∠30C ,那么ABC ∆是 三角形;(3)如果C B A ∠=∠=∠5
1,那么ABC ∆是 三角形.
二、选择(每题3分,共27 分)
1.在△ABC 中,∠A 是锐角,那么△ABC 是( )
A 、锐角三角形
B 、直角三角形
C 、钝角三角形
D 、不能确定
2.△ABC 中,若∠A ∶∠B ∶∠C =1∶2∶3,则△ABC 的形状是( )
A 、锐角三角形
B 、直角三角形
C 、钝角三角形
D 、不确定
3.以下是由四位同学描述三角形的三种不同的说法,正确的是( )
A 、由三个角组成的图形叫三角形
B 、由三条线段组成的图形叫三角形
C 、由三条直线组成的图形叫三角形
D 、由不在同一直线上的三条线段首尾顺次相接
所组成的图形叫三角形
4.△AB C 中,已知a =8, b =5,则c 为( )
A 、c =3
B 、c =13
C 、c 可以是任意正整数
D 、c 可以是大于3小于13
的任意数值
5. 下面说法中正确的是:( )
A 、三角形的角平分线,中线,高都在三角形内
B 、直角三角形的高只有一条
C 、钝角三角形的三条高都在三角形外
D 、三角形至少有一条高在三角形内
6. 如果一个三角形的三条高线的交点恰好是三角形的一个顶点,那么这个三角形是
( )
A 、直角三角形
B 、锐角三角形
C 、钝角三角形
D 、不能确定
7.在一个三角形,若︒=∠=∠40B A ,则ABC ∆是( )
A 、直角三角形
B 、锐角三角形
C 、钝角三角形
D 、以上都不对
8.三角形的高线是 ( ) A 、线段 B 、垂线 C 、射线 D 、直
线
9.在Rt △中,两个锐角关系是( )A 、互余 B 、互补 C 、相等 D 、以上都不对
三、解答题
1.如图,在△ABC 中,∠BAC=60°,∠B=45°,AD 是△ABC 的一条角平分线求∠ADB
的度数. (7分)
2.在下列图中,分别画出三角形的三条高。
(6分)
提高题
1.已知三角形的两边分别为4和9,则此△的周长L 的取值范围是( )
A 、5<L <13
B 、4<L <9
C 、18<L <26
D 、14<L <22
2.三角形的三边长为3,a ,7,则a 的取值范围是 ;
如果这个三角形中有两条边相等,那么它的周长是 .
3.如图,△ABC 中,∠ABC 和∠ACB 的平分线交于点O ,若∠BOC=120°,则∠
A=________°
如图,在△ABC 中,∠A=50°,∠B 与∠C 的角平分线相交于点E ,则∠BEC=
度.
A
B C
O
4、小林已经画出了一个三角形的两条角平分线,他说:“我不用再将第三个角平分,
就能画出第三条角平分线.”他说的有道理吗?.他会怎样
作?,他这样做的理由是.
13.如图:(1)在△ABC中,BC边上的高是;(2)在△AEC中,CE边
上的高是;(3)在△BCF中,BC边上的高是.
14.(3分)如图,∠ACB=90°,CD⊥AB于D,则BC边上的高是,AC
边上的高是,AB边上的高是,三条高的交点
是.
15.如图,AD,BE,CF是△ABC的三条中线,则AB=2,BD=
AE=.
16.(3分)如图,△ABC的周长是21cm,AB=AC,中线BD分△ABC为两个三角
形,且△ABD的周长比△BCD的周长大6cm,则AB=,BC=,
△ABD的面积与△CBD的面积的比为.>
(16题)
二、选择题:
36.如图,D是△ABC中BC边延长线上一点,DF⊥AB于F,交AC于E,∠A=40°,∠D=30°,求∠ACB 的度数.
43.如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为多少?
精品文档
44.如图,在△ABC中,AD⊥BC,BE⊥AC,BC=12,AC=8,AD=6,BE的长为多少?。
