一般位置直线段实长及倾角讲解方法的探讨
画法几何求直线实长与倾角教法的探讨

画法几何求直线实长与倾角教法的探讨作者:杨莉来源:《亚太教育》2016年第07期摘要:针对空间解析几何求一般位置直线实长的方法,论述了直角三角形法和换面法两种方法,对比一般的教学方法,探讨出新的教学方法,结合典型实例进行分析求解,通过应用于教学实际,效果较好。
关键词:直角三角形法;换面法;直线实长中图分类号:TU204文献标志码:A文章编号:2095-9214(2016)03-0133-01引言当空间直线或平面对投影面处于一般位置时,它们的投影都不反映其真实长度、大小和形状,也不反映实际距离和夹角,如何求一般位置的实际长度以及与投影面的夹角,也是工程实际需要解决的问题,如同一个管道处于无法测量的位置,要求出它的实际长度,类似的工程问题的应用,需要从画法几何的角度进行求解。
一般的教学法里有利用空间直线具有长、宽、高三个尺度,即实长的平方等于长的平方加宽的平方加高的平方[1],为了解决此问题,探讨了两种求解方法,即直角三角形法和换面法。
1.直角三角形法(1)直角三角形法的新教法。
为了更加直观的理解一般位置直线在三个投影面的投影特性,将三个投影面理解成教室中由地面(H 面)、侧墙面(W 面)和黑板面(V 面)组成。
[2]一般位置直线就相当于在这三个投影面中的投影。
将三个投影面组成的立体空间中的一般位置直线转换成平面求解空间直线的实长及对各投影面倾角的求法。
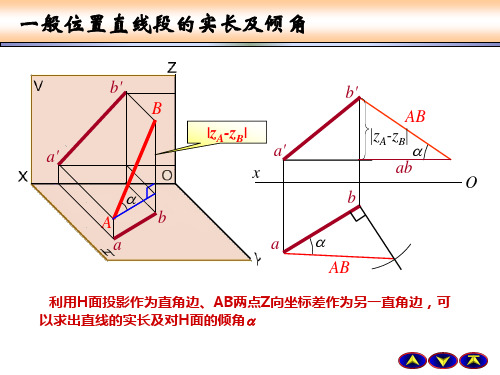
如图1(a)所示,若已知H面上直线AB的投影a’b’,要求出直线AB的实长以及与H面的倾角,需要过a’(b’)做一条直线,且该直线垂直于a’b’,量取△Z(直线两端A和B点的Z坐标值之差),过b’(a’)点首尾连接成斜边,此斜边就是空间直线AB的实长,直角三角形中△Z边对着的夹角即为直线AB与H面的夹角α。
如图1(b)所示,若已知V面上直线AB的投影ab,要求出直线AB的实长以及与V面的倾角,需要过a(b)做一条直线,且该直线垂直于ab,量取△Y(直线两端A和B点的Y 坐标值之差),过b(a)点首尾连接成斜边,此斜边为实长,△Y所对夹角即为β。
求一般位置直线段实长及倾角方法的比较分析

求一般位置直线段实长及倾角方法的比较分析作者:刘英平来源:《现代企业文化·理论版》2008年第01期【摘要】直角三角形法与换面法是求解一般位置直线段的实长及其对投影面倾角的两种常用方法,文章分析了两种方法的联系与区别,指出直角三角形法是换面法的简化形式,换面法是直角三角形法的推广及一般形式。
通过比较分析,有助于学生深入理解这两种方法。
【关键词】直角三角形法;换面法;一般位置直线;实长;倾角【中图分类号】 O221 【文献标识码】A【文章编号】1674-1145(2008)02-0177-02机械制图中,有时需要由投影求出直线段的实长及其对投影面的倾角。
投影面平行线和投影面垂直线属于特殊位置直线,其投影能直接反映出线段的实长及其对投影面的倾角;一般位置直线的三个投影均呈类似性,既不能反映该线段的實长,也不能反映该线段对投影面的倾角。
对于一般位置直线,可以采用直角三角形法或换面法求其实长及对投影面的倾角[1~2]。
在求解时,采用这两种方法的任意一种都可以求出一般位置直线的实长及其对投影面的倾角,即直角三角形法和换面法是独立使用的。
通常,机械制图教材[3~4]都对这两种方法进行了介绍,并指出两种方法都可以用来求解一般位置直线段的实长及其对投影面的倾角,但并没有对其进行深入分析。
通过比较分析,发现在求解一般位置直线段的实长及其对投影面的倾角时,直角三角形法和换面法并不是孤立的,而是存在一定的关系,即:直角三角形法可以看作是换面法的简化形式,换面法可以看作是直角三角形法的推广及一般形式,这为学生深入理解这两种方法提供了一种新的模式。
一、直角三角形法二、换面法保持空间几何元素的位置不动,建立新的直角投影面体系,使几何元素在新投影面体系中处于有利于解题的位置,然后用正投影法得到几何元素的新投影,这种方法叫做变换投影面法,简称换面法。
三、直角三角形法与换面法的比较直角三角形法和换面法是求一般位置直线的实长及其对投影面的倾角的两种常用方法。
深入浅出,由浅入深,循序渐进的直线位置关系教学教案篇

深入浅出,由浅入深,循序渐进的直线位置关系教学教案篇。
本文将会从以下几个方面来阐述如何进行直线位置关系的教学:一、学习直线位置关系前的必要准备直线位置关系的学习有一些前置知识必须掌握。
学生需要了解基本的坐标系知识,包括笛卡儿坐标系和直角坐标系等。
学生需了解基本的代数概念,包括函数、方程等。
这些前置知识不仅对于直线位置关系的学习有帮助,而且这些知识也是数学学习的基础。
因此,在进行直线位置关系的教学前,我们应该对学生进行必要的前置知识讲解,以确保学生能够在之后的直线位置关系的学习中能够理解和应用其中的知识。
二、深入浅出教学:基本概念的讲解在直线位置关系的教学中,我们需要从基本概念入手,进行深入浅出的教学。
我们需要讲解直线这一基本概念,并引入直线的方程。
然后我们可以引入直线的斜率概念,进一步加深学生们对直线的理解。
接下来,我们将学习如何将两条直线的位置关系表示出来。
这里有四种基本的位置关系:平行、相交、重合和异向平行。
针对不同的位置关系,我们需要给出不同的表达式进行表示。
例如对于两条平行的直线,其斜率相同。
这种深入浅出的教学方法可以帮助学生逐渐掌握直线位置关系。
三、由浅入深教学:附加概念的学习在掌握了直线位置关系的基本概念后,我们还需要学习一些重要的附加概念,例如夹角、垂直、水平等。
学生需要了解这些概念,以便更好地应用直线位置关系。
同样,我们也可以采用由浅入深的教学策略,逐渐引入这些概念并加深对它们的理解。
例如对于直线的垂直,我们可以从垂直线段的概念开始引入,然后再引入垂直直线的定义和性质。
四、循序渐进教学:练习题的慢慢加难度练习题是学习中非常重要的环节。
学生需要通过练习题来巩固并深化自己对于直线位置关系的掌握。
因此,我们需要按照从简单到难的顺序来出题。
在开始时,我们可以出一些基础练习题,例如直线方程的求解、斜率的计算等。
然后逐渐加入涉及到位置关系的题目,例如求两条直线是否平行、是否相交等。
我们可以出一些更加复杂的练习题,例如在三维坐标系中的直线位置关系等。
一般位置直线段实长及倾角讲解方法的探讨

三、结论
以学生为中心,发挥学生的想象空 间,从日常生活中所见到的一些事物开 始,探讨求一般位置直线实长及其对投影 面倾角求解的必要性,总结实长、倾角和 夹角的求解规律。即在投影图上求线段的 实长和倾角的方法是:以线段在某个投影 面上的投影为一条直角边,以线段的两端 点到该投影面的距离差为另一条直角边作 直角三角形,该直角三角形的斜边就是所 求线段的实长,而此斜边与投影的夹角, 就是该线段对该投影面的倾角。
画法几何与工程制图2-1-复习
边,半径为33mm作 弧,可截得正面投影
长③;以投影b'为圆心, 以ea0长为半径作弧, 得到a',连接a'b'及
完成正面投影
一般位置直线段的实长及倾角
[补充题] 如图所示,已知ab、a 且知 =30 º 试求直线AB的正面
投影ab。
b
a
x
a
O a'b' 30 º 60 º
b
垂直两直线
平面立体截交线
s'
s"
2'
2"
例 求出立体被截切
后的三面投影。
1'
3'
4'
4"
1" 3"
S
a'
好镜b'cc' c"
a"
b"
4
1
a
2
s
注意:
3 b
截平面之
间的交线
A
B
〔例〕完成圆柱体左边被切凹槽,右边被切凸台后的水平投影
a'
b'
a"( b" )
a
b
AB
平面与圆锥相交
截交线的形状有几种?
圆
三角形
椭圆
φ18
54
φ10
27
★
Φ30
10 24 Φ54
适
当
105
调
12
70
整
812 30
,
标
注
全
100
部
尺
寸
65
47
R18 2-Φ18 64
电中在线-工程图学基础试题及答案

工程图学基础1.用()水泥石灰砂浆、纸筋石灰膏浆、水泥十字浆等糊状料抹饰于墙体表面,再经加工处理即成。
A.石灰砂浆B.石灰水泥错误正确答案:A学生答案:B2.办公类建筑包含()A.居住类建筑B.行政和企业办公房屋C.科研类建筑D.体育类建筑正确正确答案:B学生答案:B3.建筑工程图是表达建筑工程设计的重要技术资料,是施工的依据。
A.错误B.正确正确正确答案:B学生答案:B4.办公类建筑包含科研建筑。
A.错误B.正确错误正确答案:A学生答案:B5.如果物体的长度为1000mm,绘图比例是1:20,则在绘图时其长度应取()。
A.1000B.20C.100D.50正确正确答案:D学生答案:D6.图上标注的尺寸数字,表示物体的真实大小,尺寸的单位如果在图中附注没有声明,则为()。
A.米B.厘米C.根据绘图比例确定D.毫米错误正确答案:D学生答案:B7.图样的比例,应为图形与实物相对应的线性尺寸之比。
1:100是表示()在图形中按比例缩小只画成()。
A.100m,1mB.100m,0.1mmC.100mm,10mm错误正确答案:A学生答案:B8.若用一个平行于某一投影面的平面切割某一立体,移去立体的一部分,对剩余部分所作的投影称为()。
A.移出断面图B.断面图C.剖面图D.全剖图正确正确答案:C学生答案:C9.在正投影图的展开图中,A点的水平投影a和正a’的连线必定()于相应的投影轴。
A.倾斜B.垂直C.投影D.平行正确正确答案:B学生答案:B10.在生活中我们可以看到光线照射物体在墙面或地面上产生影子,当光线照射角度或广元位置改变时,影子的()也会随之变化。
A.位置B.颜色C.状态正确正确答案:A学生答案:A11.已知A点的三面投影a、a’、a’’,其中a反映A到()投影面的距离。
A.H面和V面B.H面和W面C.V面和W面D.所有面错误正确答案:C学生答案:B12.已知点M坐标(10,20,10),点N坐标(10,20,0),则以下描述M、N两点相对位置关系的说法哪一种是正确的?()A.点M位于点N正左方B.点M位于点N正后方C.点M位于点N正上方D.点M位于点N正下方错误正确答案:C学生答案:D13.组合体的尺寸包含:()A.总宽尺寸B.定形尺寸正确正确答案:B学生答案:B14.用圆弧连接直线或圆弧,关键是确定()A.连接点B.直线的长度C.连接圆圆心和连接点D.连接圆的半径错误正确答案:C学生答案:A15.轴测投影能将一个形体的()()()三个尺寸同时反映在一个图上,图形比较直观。
画法几何与工程制图2-1-复习

S
4
a
1
2
s
3
注意:
截平面之 间的交线
b
A
B
〔例〕完成圆柱体左边被切凹槽,右边被切凸台后的水平投影
a'
b'
a"( b" )
A
B
a
b
平面与圆锥相交
截交线的形状有几种?
圆
三角形
椭圆
双曲线
抛物线
平面与圆锥相交
5' 7' (8')
(4') (6')
3'
4'' 6'' 8''
3'' 5'' 7''
8
6
4
2、判断截平面的数量及各截面位置。
3、作截面与立体各棱线交点的投影。
4、连接立体同一表面上交点的投影。 5、分析并作出各截平面之间的交线。 6、判断交线可见性,补全棱线投影。
平面立体截交线
s'
s"
例 求出立体被截切
后的三面投影。
2'
3'
2"
1'
a'
4'
b' c' c" 好镜 c
4"
1"
a"
3"
b"
平面立体截交线
1.平面与棱锥相交
s'
p' q'
1'
2'(3') 4'(5') 5"
S”
例题:求三棱锥正面
基于AutoCAD探究一般位置直线求实长的方法

基于AutoCAD探究一般位置直线求实长的方法作者:贺健琪来源:《陕西教育·高教版》2008年第10期[摘要]在机械制图画法几何部分,当空间直线处于一般位置直线时,其投影就无法反映该直线的实际长度,特别在求平面图形的实际形状时都会经常面对这样的问题,而现在好多教材都因为《机械制图》教学课时的不断压缩而删减甚至取消了相关内容,使学生在该知识点上形成了缺憾,本文将求一般位置直线实长的不同图解方法集锦在一起,从原理、要领和CAD作图技巧方面加以探究。
[关键词]AutoCAD 直角三角形法换面法旋转法实长前言:在机械制图的画法几何部分,当对直线进行投影时,由于一般位置直线与投影面都是倾斜的,所以在正常的三面投影体系中,一般位置直线的投影都无法反映其真实长度。
通过计算固然可以求得实长,但《机械制图》更讲究用图解的方法来解决问题,本文力图说明几种解决此类问题方法的精华所在,并结合现代绘图软件AutoCAD克服以往手工绘图解决此类问题时容易出现的弊端,诸如视觉误差、测量误差和作图误差使得求解不够精准。
为了简化问题,这里多以两面投影体系进行阐述。
直角三角形法1.原理:如图1所示,在将一般位置直线AB向水平投影面做正投影时,我们会发现由直线AB的实长、水平投影ab以及A、B两点的Z轴坐标之差组成了一个直角三角形,且直线实长与水平投影之间的夹角就是空间直线与水平投影面的真实夹角角。
而直线的水平投影ab和其端点的△Z在两面投影中都是已知的,所以借助ab作为直角边,以△Z做另一个直角边,就能完成直角三角形,斜边就是直线AB的真实长度,斜边与水平投影之间的夹角就是空间直线AB与H面的夹角角。
同理,在将直线AB向V面和W面作投影时,也会出现各自的直角三角形。
原理相同。
2.要领:必须分清直角三角形几何要素的“黄金搭档”:一定是直线的某个投影(如H面投影)+与该投影所在投影面垂直轴线的直线两端点之坐标差(Z轴坐标差)+直线的实长+空间直线与该投影所在的投影面的夹角(角)。
画法几何及机械制图-求一般位置线段的实长

二、换面法
例1 求AB 线段的实长及α。 都与不变投影面有关
作图要点: X1 ∥ab
X1 轴平行不变a' 投影,求得
a’1
实长
A a’
αXα
b’1
Ba
b X1
线段对不变投影面的倾角。
b'
X
V H
a
b’
b
O
a'1
α
实长
b'1
解题完毕
§3-3 求一般位置线段的实长
二、换面法
H 投影面的倾 角α。
§3-3 求一般位置线段的实长
一、直角三角形法
1.原理分析2
△A A0B 为直角三角形
结论:
A0B=a’b’ V
a'
X
A0
AA0=ya-yb
b'
β
A a
Z
已知线段的
两个投影,可
B实 长
O
利用直角三角 形法,求出线 段的实长及对
V 投影面的倾
b
角。
Y
ya-yb
§3-3 求一般位置线段的实长
a’1
实长
A a’
α
Xα
b’1
Ba
b X1
建立新投影系:
增设新投影面V1,使 V1⊥H ,且∥直线AB ;
在V1 / H 新投影体系中, b’ AB 为投影面平行线直线。
AB 在新投影面上的投影 O 反映实长及对H 面的倾角。
§3-3 求一般位置线段的实长
二、换面法
新投影面的设立条件
1. 新投影面必须垂直原V/H 投影体系中的某一投影面;
二、换面法
第2章 投影理论1(点线、一般直线的实长与倾角)

轴测图(3D Pictorials )与三视图(Three-View Drawing):
第5章 轴测投影图 3D Pictorials 5.1 轴测图的概念
P159~168
轴测投影图,简称轴测图,它是将物体连同其参考直角 坐标体系,沿不平行于任一坐标平面的方向,用平行投影法 将其投射在单一投影面上所得到的图形。 正轴测图:投射方向垂直于轴测投影面(正等测); 斜轴测图:投射方向倾斜于轴测投影面(斜二测)。
b) 轴测投影图 a) 正投影图 图5.1 正投影图与轴测投影图
相交:若空间两直线相交,则其同面投影必相交,且交点的 投影必符合空间一点的投影规律。反之亦然。
交叉:若两直线既不平行又不相交,则它们是交叉直线。
两种特殊情况: 1)当两直线有两个投影均互相平行,且又同 时平行于第三个投影面时,一般应观察该两 直线所平行的那个投影面上的投影来判断两 直线是否平行。
a) 斜投影法
图3.3 平行投影法
b) 正投影法
2.1.2 (正)投影的特性
P29 表2-1
平行
垂直
倾斜
黑板、练习本、投影屏幕就是投影面
实形性(真实性)
积 聚 性
类 似 性 ( 收 缩 性 )
投影法的应用
1. 2. 中心投影法的应用—透视图 斜投影法的应用---斜轴测图
王成刚制作
透视图(two view points)
P38
图2-11 直线的投影及直线与投影图倾角
直角三角形法求实长、倾角:ab+Δz(求α), a'b'+Δy(求β) 讨论:a"b" +Δ?(求γ) 记住:搭配关系!!!
机械制图习题集(第6版)答案

《机械制图》(第六版)习题集答案第3页图线、比例、制图工具的用法、尺寸注法、斜度和锥度●要掌握和理解比例、斜度、锥度的定义;各种图线的画法要规范。
第4页椭圆画法、曲线板用法、平面图形的尺寸注法、圆弧连接1、已知正六边形和正五边形的外接圆,试用几何作图方法作出正六边形,用试分法作出正五边形,它们的底边都是水平线。
●注意多边形的底边都是水平线;要规范画对称轴线。
●正五边形的画法:①求作水平半径ON的中点M;②以M为圆心,MA为半径作弧,交水平中心线于H。
③AH为五边形的边长,等分圆周得顶点B、C、D、E④连接五个顶点即为所求正五边形。
2、用四心圆法画椭圆(已知椭圆长、短轴分别为70mm、45mm)。
●参教P23四心圆法画椭圆的方法做题。
注意椭圆的对称轴线要规范画。
3~4、在平面图形上按1:1度量后,标注尺寸(取整数)。
5、参照左下方所示图形的尺寸,按1:1在指定位置处画全图形。
第6页点的投影1、按立体图作诸点的两面投影。
●根据点的两面投影的投影规律做题。
2、已知点A在V面之前36,点B在H面之上,点D在H面上,点E在投影轴上,补全诸的两面投影。
●根据点的两面投影的投影规律、空间点的直角坐标与其三个投影的关系及两点的相对位置做题。
3、按立体图作诸点的两面投影。
●根据点的三面投影的投影规律做题。
4、作出诸点的三面投影:点A(25,15,20);点B距离投影面W、V、H分别为20、10、15;点C在A之左,A之前15,A之上12;点D在A之下8,与投影面V、H等距离,与投影面W的距离是与H面距离的3.5倍。
●根据点的投影规律、空间点的直角坐标与其三个投影的关系及两点的相对位置做题。
各点坐标为:A(25,15,20)B(20,10,15)C(35,30,32)D(42,12,12)5、按照立体图作诸点的三面投影,并表明可见性。
●根据点的三面投影的投影规律做题,利用坐标差进行可见性的判断。
(由不为0的坐标差决定,坐标值大者为可见;小者为不可见。
求一般位置直线段实长及倾角方法的比较分析

角三 角形法的推 广及一般 形式。通过 比较分析 。 有助 于学生深入 直角三角形。由于 () b 的作图本质是一样的 , a 和( ) 因此 作出的直
即直角边 A C等于线段 A B的水平投影 , 直角边 B C等于线段 A B
两端点的 Z坐标差 , 斜边 A B等于空间直线段 A B的实长 , B C ZA 等于线段 A B对 面 H的倾角 。
Z
用换 面法求直线段实长和倾 角的空间几何关系如 图 3所示 。 在投影 面体系 f/ H中, 直线 A B为一般位置直线 , 正面投影a ’ 其 ' b 和水平 投影 a 均不反映实长。为求直线段 的实长及其对投影面 b H的倾 角 , 建立一个新投影 面 , 使 面平行 于直线 A , B 同时
理 解 这 两种 方 法 。
角三角形是相同的。
【 关键词 】 直角三角形 法; 面法; 换 一般位置直 线; 实长; 倾角 【 中图分 类号 】 2 02 1 【 文献标识码 】 A 【 文章编号 】6 4 14 (0 8 0— 17 0 17 — 52 0 )2 0 7 — 2 1
‘
与 H面垂直。显然 , 在新的投影面体系 / 中, H 直线 A B成为投 影面 的平行线 ,其在 面上的投影 口 6反映直线段 A B的实
0
.
f
长, 角 为该直线对 H面的倾角。 在 投影图 中, 新投影 轴 OX. 作 i 平行 于 a , b 按点 的换面规 律 ,
二 、 面法 换
保持空问几何元素 的位置不 动 ,建立新 的直角投影 面体 系, 有对其进行深入 分析 。通过 比较分析 , 发现在求解一般位置直线 使几何元素在新投影 面体系 中处于有 利于解题 的位置 , 然后用 正 段 的实长及其对投影 面的倾角时 , 角三角形法和换面法并不是 投影法得到几何元 素的新投影 ,这种方法 叫做变换 投影 面法 , 直 简 孤立 的, 而是存在一定的关系 , 直 角三角形法可 以看作是换面 称 换 面 法 。 即: 法的简化形式 , 换面法可 以看作是直 角三角形法的推广及一般形 式。 这为学生深入理解这两种方 法提供 了一种新的模式。
§34 直线的实长和倾角

(a)立体图
(b) 二直相交线垂直 (c) 二直相交线垂直
(d) 二直相交线垂直
定理一 垂直的两直线,其中有一条直线平行于投影面时,则两直线在该投 影面上的投影仍反映直角。
定理二 两直线在同一投影面上的投影反映直角,且有一条直线平行于该投 影面,则空间两直线的夹角必是直角。
2. 例题
[例题12] 求一点到水平线的距离 [例题13] 过一点作两线段的公垂线
c
b
|yA-yB|
3. 求直线的实长及对侧面投影面的夹角 角
|xA-xB|
§3-5 两直线的相对位置
一、两相交直线 二、两平行直线 三、两交叉直线 四、两相互垂直直线
一、两相交直线
1. 相交直线的投影 2. 例题
1. 相交直线的投影
[例题8] 给出平面四边形ABCD的V投影及其两条边的H投影, 试完成四边形的H投影。
[例题14] 作三角形ABC,ABC为直角,使BC在MN上, 且BCAB=23
[例题12] 求一点A到水平线BC的距离
AD
2
d'
y
d
[例题13] 过点E 作线段AB、CD 的公垂线EF。
f
f
[例题14] 作三角形ABC,ABC为直角,使BC在MN上,且
BCAB =23。
bc=BC
ab
b'
c'
AB
§3.4 直线的实长和倾角 求解一般位置线段的实长及倾角是求解画法几何综合题时经常遇到的基 本问题之一,也是工程上经常遇到的问题。而用直角三角形法求解实长、 倾角又最为方便.简捷。
一、直角三角形法的作图要领 用线段在某一投影面上的投影长作为一 条直角边,再以线段的两端点相对于该投影面的坐标差作为另一条直角边 ,所作直角三角形的斜边即为线段的实长,斜边与投影长间的夹角即为线 段与该投影面的夹角。
直线段的实长和对投影面的倾角

计算方法
通过测量直线段在投影面上的投影长 度和实际长度,利用三角函数计算得 出倾角。
不同投影面对倾角影响
水平投影面对倾角的影响
当直线段与水平投影面平行时,倾角为0度;当直线段与水平投影面垂直时,倾角为90度 ;其他情况下,倾角介于0度和90度之间。
正立投影面对倾角的影响
投影性质
投影保持了直线段的某些性质,如直线性、连续性等。
投影长度
直线段在投影面上的投影长度一般小于或等于原直线段的 长度,当且仅当直线段与投影面垂直时,投影长度等于原 长度。
倾角定义
直线段与投影面之间的夹角称为倾角,其取值范围为[0°, 90°]。当倾角为0°时,表示直线段与投影面平行;当倾角为 90°时,表示直线段与投影面垂直。
多学科交叉融合研究的加强
直线段实长和投影面倾角的研究涉及数学、计算机图形学、机械工程等多个学科领域,未来有望通过多学科交叉融合 研究,推动相关领域的创新和发展。
拓展应用领域的探索
除了在计算机图形学、机械工程等领域的应用外,未来还可以探索直线段实长和投影面倾角在建筑设计、 地理信息系统等领域的应用潜力,拓展其应用范围。
THANKS FOR WATCHING
感谢您的观看
由于观测者的感官鉴别能力、 技术水平或工作态度等因素引 起的误差。
环境误差
由于测量时的温度、湿度、气 压等环境因素变化引起的误差 。
方法误差
由于测量方法本身不完善或采 用近似公式等引起的误差。
误差传播规律ቤተ መጻሕፍቲ ባይዱ
误差传播定律
阐述了测量误差在数据处理过程中的传播规律,即误差会随着测 量数据的处理而逐级传递。
解析几何法
建立坐标系
《机械制图教案》第二章(2)

第九讲§2—4 直线的投影课题:1、直线的投影图2、直线对于一个投影面的投影特性3、各种位置直线的投影特性4、一般位置直线的实长和对投影面的倾角课堂类型:讲授教学目的:1、讲解三种投影面平行线和三种投影面垂直线的投影特性2、讲解用直角三角形法求一般位置直线的实长和倾角教学要求:1、理解并掌握各种位置直线的投影特性,并能根据投影特性判别直线对投影面的相对位置2、熟练掌握求一般位置直线的实长及其对各投影面倾角的直角三角形法教学重点:1、各种位置直线的投影特性2、直角三角形法教学难点:直角三角形法教具:自制的三投影面体系模型;挂图:“投影面平行线的投影特性”、“投影面垂直线的投影特性”教学方法:直线投影的实质,就是线段两个端点的同面投影的连线;尤其是投影面垂直线,实质就是重影点。
为了进一步加强空间思维的训练,要用一定量的例题作演示性讲解,并布置适当的练习加以巩固。
教学过程:一、复习旧课1、讲评上次作业。
2、复习点的投影与与其直角坐标的关系3、复习点的三面投影规律4、复习特殊位置点的投影5、复习两点的相对位置和重影点二、引入新课题空间两点确定一条空间直线段,空间直线的投影一般也是直线。
直线段投影的实质,就是线段两个端点的同面投影的连线;所以学习直线的投影,必须于点的投影联系起来。
三、教学内容(一)直线的投影图空间一直线的投影可由直线上的两点(通常取线段两个端点)的同面投影来确定。
如图2-19所示的直线AB,求作它的三面投影图时,可分别作出A、B两端点的投影(a、a′、a″)、(b、b′、b″),然后将其同面投影连接起来即得直线AB的三面投影图(a b、a′b′、a″b″)。
(a)(b)(c)图2-19 直线的投影(二)直线对于一个投影面的投影特性空间直线相对于一个投影面的位置有平行、垂直、倾斜三种,三种位置有不同的投影特性。
1、真实性当直线与投影面平行时,则直线的投影为实长。
如图2-20(a)所示。
画法几何第3讲09

a
θH
∆z 实长 B1
的作图方法。 同理可推得求θV和θW的作图方法。
解题要点:倾角是关键,选准三角,对好边,倾角夹在“ ”“影 解题要点:倾角是关键,选准三角,对好边,倾角夹在“斜”“影” 依据倾角,选准空间直角三角形 两直角边与投影、 空间直角三角形, 间。(依据倾角,选准空间直角三角形,两直角边与投影、标差 对应好,标对倾角。) 对应好,标对倾角。)
l b k a l′ b′ k′ 实长 p′
a′ p
作 业
习题集: 习题集: P12 、P13、 、 P14(直角投影定理) 直角投影定理) 预习教材: 预习教材:P132~P142 ~
主讲教师: 主讲教师:耿春明
H
1. 投影作图
已知AB两投影, 已知 两投影,求AB实长及倾角θH。 两投影 实长及倾角
b´ ´ a´ ´ ∆z 实长
作图思路: 作图思路:倾角θH ⇒ ∆ACB ⇒
A1
θH
b0´ ab b
直角边1=ab ,直角边 ∆z 。 直角边2=∆ 直角边 作图步骤: 在 内求解 内求解) 作图步骤:(在H内求解) 1)作出∆z ; )作出∆ 2)基于ab作直角边 ∆z ; )基于 作直角边 作直角边2=∆ 3)连出斜边; )连出斜边 4)标出实长及倾角。 )标出实长及倾角。
1.6 直角投影定理
• 成直角 直角的两条直线相互位置关系? • 相交 相交垂直 交叉垂直 交叉
1.6.1 直角投影定理
成直角的两直线的投影会是怎样? 直角的两直线的投影会是怎样? 的两直线的投影会是怎样
直角投影定理——当空间角的一边平行于投影 当空间角的一边平行 一边平行于投影 面时, 空间角为直角, 面时,若空间角为直角,则空间角在该投影面上的 投影也为直角。 投影也为直角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们知道,直线由两点确定,要作直线 的投影,实质就是作出线上两点的投影,也就 是说,它的投影由直线上两点的同面投影的连 线来确定。由此得到直线 AB 的 V 投影 a ' b ' 和 H 面的投影 ab,其中 ab 垂直 Bb。过 A 点 作 A A 1 平行于 a b ,则 A A 1 垂直于 B b ,由此 得一直角三角形 B A A 1 。
综上所述,借助于直角三角形,就可以 用图解法求出线段AB的实长和与投影面的倾 角 。 这 种 方 法 称 之 为 “ 直 角 三 角 形 法 ”。
用直角三角形法求线段实长及倾角时, 特别要注意倾角与两直角边一定是与同一投影 面发生关系。直角三角形的构成图将这种关 系表达得十分清晰。用直角三角形法求实长
三、结论
以学生为中心,发挥学生的想象空 间,从日常生活中所见到的一些事物开 始,探讨求一般位置直线实长及其对投影 面倾角求解的必要性,总结实长、倾角和 夹角的求解规律。即在投影图上求线段的 实长和倾角的方法是:以线段在某个投影 面上的投影为一条直角边,以线段的两端 点到该投影面的距离差为另一条直角边作 直角三角形,该直角三角形的斜边就是所 求线段的实长,而此斜边与投影的夹角, 就是该线段对该投影面的倾角。
A novel instruction way for solving general line’s length and its obliquity angle between projection planes HU Shaoxing1 ZHANG Aiwu2 LIU Jinghua1 WANG Yunqiao1
习题 1 已知直线 A B 的两投影,见图 4,求直线 A B 对 V 面的倾角和线段的实长。
解:有两种解法,求解过程见图 4 。
如图 5 。
图 5 习题 2 的求解过程 作图步骤: (1 )以 c d 为一直角边,过 c 点作一直 线 cm 垂直于 cd ; (2 )以 d 点为圆心,以 4 5 为半径,作 一圆弧与直线 c m 相交于 n 点,得直角三角 形,cn 的长度即为空间直线 CD 的 Z 坐标差; (3 )根据投影关系,得到直线 C D 正面 投影,即 c ' d '。 习题 3 已知直线 A B 的投影 a ' b ',与 V 面的倾角β = 3 0 °,求其水平投影。 分析:由直角三角形的构成图可知, 若倾角为β,则该直角三角形的两条直角 边一定是线段在 V 面的投影和两端点对 V 面的距离之差。a ' b '已知,倾角已知,该 直角三角形可以得到。另一直角边即为两 端点对 V 面的距离之差△ Y ,从而可以求 出 H 面投影,求解过程见图 6 。
摘 要 从观察日常生活中诸多部件或零件开始, 引出一般位置直线实长及其对投影面倾角 求解的必要性,给出由投影求出一般位置 直线的实长及其对投影面倾角及直线与投 影轴夹角的方法,总结实长、倾角和夹角 的求解规律。而后通过几个典型习题的作 图过程分析,加深学生对定理的理解。几 轮讲述表明:采用该种形式学生不仅能够 快速掌握直角三角形法,而且也能激发学 生学习工程制图的兴趣。 关键词 一般位置直线;直角三角形法;实长;倾 角;夹角 中图分类号:O221 文献标志码:A
图 4 习题 1 的求解过程
方法一:在 H 投影面上作图,这里直 线 A B 的水平投影已知,可以直接得到 Y 坐 标差。过 b 点作 OX 轴的平行线,与 a ' a 相 交与 m ,则 m a 的长度为 Y 坐标差,延长使 m n =a ' b ',连接 n a ,得直角三角形 n m a 、。 这里 n a 为 A B 的实长,直角边 m a 所对的夹 角为空间直线 A B 与 V 面所成的倾角β。
例 2:求空间直线 AB 的实长及对 V 面的 夹角β。
解:求解过程见图 2 。
图 3 倾角γ的求法示意图
从图中看出:对应的直角三角形为 B 2 B A 。在该三角形中,∠ B 2 B A 即空间直 线 AB 与 W 面所成的倾角,定义为γ;该角所 对的边为空间直线 AB 的 X 坐标差,另一条直 角边为直线 A B 的 W 投影 a ’ b ’ 的长度。斜 边是直线 AB 的实长,该角的余角为空间直线 与X轴的夹角。可见求实长及夹角最主要的问 题也是找到对应的直角三角形。
例 1:求空间直线 AB 的实长及对 H 面的 夹角α。
解:求解过程见图 1 。
图 2 倾角β的求法示意图
从图中看出:对应的直角三角形为 B 1 B A 。在该三角形中,∠ B 1 B A 即空间直 线 AB 与 V 面所成的夹角,定义为β;该角所 对的边为空间直线 AB 的 Y 坐标差,另一条直 角边为直线 AB 的 V 投影 a ' b '的长度。斜边 是直线 AB 的实长,该角的余角为空间直线与 Y 轴的夹角。可见求实长、倾角及夹角最主要 的问题仍是找到对应的直角三角形。
Abstract Basing on numerous observation of many mechanical parts and components, the importance of solving general line’s length and its obliquity angle between projection planes is discussed. A novel method for solving general line’s length and its angles between projection planes and projection axle is proposed. A generalized method for solving space line’s length and its angles between projection planes and axles is also given. Author’s teaching experiments indicate that this method can not only make students understand and master right triangle method but also can stimulate students’ interests of engineering drawing. Key words General location line; Right triangle method; Length; Obliquity; Angle
方法二:在 V 投影面上作图,过 a '做 直线 a ' k 垂直于 a ' b ',并使 a ' k = a m ,连 接 k b ',同样可得直角三角形,三角形的 各边及角度含义同法一。
习题 2 已知线段 C D = 4 5 m m 及水平投 影,求其正面投影。
分析:由已知条件,由于直角三角形的 斜边已知、一直角边已知,可得直角三角 形。另一直角边即为两端点对 H 面的距离之 差△ Z ,从而可以求出 V 面投影,求解过程
DOI:10.3969/j.issn.1001-8972.2011.16.123
一般位置直线段实长及倾角讲解方法的探讨
胡少兴 1 张爱武 2 刘静华 1 王运巧 1 1 北京航空航天大学机械工程及自动化学院,北京 100191 2 首都师范大学三维信息获取与应用教育部重点实验室,北京 100037
图 6 习题 3 的求解过程
作图步骤: (1 )首先,过 b '作一直线 b ' n 垂直于 a ' b '; (2 )过 a '点作与 a ' b '成 3 0 0 的直线, 与直线 b ' n 交于 m 点,则 b ' m 即为△ Y ; (3 )根据投影关系,得到直线 A B 水平 投影,即 a b 。
二、典型习题
由直角三角形的构成可知,该部分内 容涉及四个基本作图问题:
已知直线的两投影,求直线与投影面的 夹角和线段的实长;
已知直线的一投影及其与投影面的夹 角,求直线的投影;
已知线段的一投影及其实长,求线段的 投影;
已知线段的实长及其与投影面的夹角, 求直线的投影。
其中第 3 和 4 可以合成一种情况,下面 我们以习题方式进行讲述,以加深学生对 该方法的理解。
(2)求直线的实长及对 V 面的夹角。首 先找出空间直线的 Y 坐标差和直线的正面 投影,由这两条边组成直角三角形,Y 坐 标差这条直角边所对的角度为空间直线与 正立投影面所成的倾角,另一条直角边所对 的角度为空间直线与 Y 轴所成的角,斜边为 实际长度。
(3)求直线的实长及对 W 面的夹角。首 先找出空间直线的 X 坐标差和直线的侧立投 影,由这两条边组成直角三角形,X 坐标差 这条直角边所对的角度为空间直线与侧立投影 面所成的倾角,另一条直角边所对的角度为 空间直线与 X 轴所成的角,斜边为实际长 度。
1.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191,China; 2. Ministry of Education Key Laboratory of 3D Information Acquisitionand Application,Capital Normal University, Beijing 100037,China
例 3:求空间直线 AB 的实长及对 W 面的 夹角γ。
解:求解过程见图 3。
图 1 倾角α的求法示意图
在日常生活中,同学们看到的联通信 号塔、体育馆的屋顶、电视塔等等都是根 据我们讲述的制图基本知识绘制的工程图 纸加工出来的。这些物体无论选择哪个方 向投影,在其工程图上,都会出现许多在 三个投影面上的投影均呈类似性,既不能 反映该线段的实长,也不能反映该线段对 投影面倾角的一般位置直线。因此在施工 过程中,必须求出实长,才能进行加工。这 样不仅节省材料,而且可以加快施工速 度。类似的一般位置直线的例子在机电产 品的设计过程中出现的频率更是数不胜 数,所以对于一般位置直线,我们必须求 出实长。
