java面向对象程序设计报告

合集下载

Java实验报告模板

实验报告课程名称Java 面向对象程序设计实验名称检查危险品姓名吴超益学号201424134114专业年级14 物联网一、实验目的：本实验的目的是让学生掌握try-catch 语句二、实验内容：车站检查危险品的设施，假如发现危险品就会发出警示。

编写 Exception 的子类 DangeException，编写 Machine 类办理异样主类 main 方法中的 try-catch 办理 machine 类的实例调用三、实验步骤实验源代码：import java.io.*;import .*;import java.util.*;public class Client {public static void main(String agrs[]){Scanner scanner= new Scanner (System.in);Socket mysocket=null;ObjectInputStream inObject=null;ObjectOutputStream outObject=null;Thread thread;ReadWindow readWindow =null;try {mysocket =new Socket();readWindow =new ReadWindow();thread =new Thread(readWindow);System.out.println("输入服务器的 IP");String IP=scanner.nextLine();System.out.println("输入端口号： ");int port =scanner.nextInt();if(mysocket.isConnected()){}else{InetAddress address =InetAddress.getByName(IP);InetSocketAddress socketAddress=newInetSocketAddress(address,port);mysocket.connect(socketAddress);InputStream in=mysocket.getInputStream();OutputStream out=mysocket.getOutputStream();inObject=new ObjectInputStream(in);outObject=new ObjectOutputStream(out);readWindow.setObjectInputStream(inObject);thread.start();}}catch(Exception e){System.out.println("服务器已经断开 "+e);}}}class ReadWindow implements Runnable{ObjectInputStream in;public void setObjectInputStream( ObjectInputStream in){this .in=in;}public void run(){double result =0;while (true){try{javax.swing.JFrame window=(javax.swing.JFrame)in.readObject();window.setTitle("这是从服务器上读入的窗口");window.setVisible(true);window.requestFocusInWindow();window.setSize(600, 800);}catch (Exception e){System.out.println("服务器已经断开 "+e);break;}}}}///**异样类继承 Exception*当你要抛出的自定义的异样类，一定继承 Exception，不然错误*catch 捕获抛出的异样*/public class DangerException extends Exception {String message;public DangerException() {message = 危"险品！ ";}public void toShow() {System.out.print(message + " ");}}public class Goods {public boolean isDanger;String name;public void setIsDanger(boolean boo) {isDanger = boo;}public boolean isDanger() {return isDanger;}public void setName(String s) {name = s;}public String getName() {return name;}}/**异样的办理和抛出*throws，申明异样的实例*格式为： throws 异样类名*exp：throws DangerExeption*申明异样后应当在调用者里面对捕获的异样办理*throw ，抛出异样*格式为： throw 异样实例*exp：throw new DangerException*假如捕获到申明的异样。

JAVAJDK实验报告模板

JAVAJDK实验报告模板学院实验报告课程名称Java面向对象程序设计项目名称:Java环境配置和命令姓名_专业：_班级：学号：_同组成员一无_一、实验准备：实验目的：1、掌握Java开发环境的安装与配置；2、了解环境变量的设置；3、掌握Java应用程序的编写、编译、运行过程。

相关知识点：Java 的源程序代码放在某个文件夹要记得相应位置，编译时不要忘了.java 后缀；“publcclassHelloWorld”用来声明HelloWorld类，class是关键字定义一个类；publc是访问控制修饰符，表示一个公有类；mport关键字引进来的JDK提供XXX包、XXX,以便类Grapcs和Applet的使用；实验过程记录:(1)并安装JDK根据需要的选择的JDK安装包，根据自己电脑情况选择32位或者64位JavaSEDevelopmentKt8u144YoumustaccepttheOracleBrryCodeLcenseAgr eementforJavaSEtodownloadthsThankyouforacceptngtheOracleBnaryCo deLcenseAgreementforJavaSE;youmayno?/downloadthssoftwareProduct FleDescrptonFleSzeDov/XXXXXXXXX.6LB,dkTacos_8u144sparcbt99.18MB, XXX.99MBjdk_6u144solar3wndows8u144_&XXX,双击文件执行安装WndowsnstallerPreparngton&XXXcel安装目录可以默认也可以自定义安装成功后配置环境变量，右击【我的电脑】【高级】j,LzraempC/.rocramLleGngjukl且(_1441Cefnpe_OCESWR40$WndowsNTpcdavacjaacarL5此电脈新加巻（D:）JavaCStrngargs）”“System,outJavajavaHelloYarldHellolarldP：JavApplet小应用程序此电脑新加卷(D:)ava人名称HelloWorldAppletjava此电庭新加卷(D:)JavaHelloWorldAppletchss:XXX.applet._,XXX.+.publcclassHel1口VorldApplete_tendsAppletpublcvodpant(Graphcsg)gdrawStrngCHelloVorl d!10,50);XXX(c)于McrosoftCorporaton保留所有权利。

实验报告

计算机工程系实验报告课程名称：Java面向对象程序设计班级：网络二班姓名：尚晶晶学号：一、实验目的:1、掌握char类型数据和int类型数据之间的互相转换，了解Unicode字符表；2、掌握从键盘输入基本类型的数据。

二、实验要求:1、有一函数：-1+2x x<0Y= -1 x=0-1+3x x>0 编写一个Java应用程序，从键盘输入一个x值，程序输出y的值。

2、编写一个Java应用程序，使用while循环语句计算1-1000之间能被3和7同时整除的整数之和。

3、编写一个Java应用程序，使用for循环计算8+88+888+8888+88888+...的前10项之和。

4、编写一个Java应用程序，计算1-1/3+1/5-1/7+1/9-1/11+...的前10000项之和。

5、编写一个Java应用程序，计算1+2！+3！+4！+...从第100项到第200项之和。

三、程序代码:1．import java.util.*;public class Example3_1{public static void main(String args[]){Scanner reader=new Scanner(System.in);int x=0,y=0;System.out.println("输入x: ");x=reader.nextInt();if(x<0){y=-1+2*x;}else if(x>0){y=-1+3*x;}else{y=-1;}System.out.printf("%d",y);}}2.public class Example3_2{public static void main(String args[]){int sum=0;int i=1;while(i<=1000){if(i%3==0&&i%7==0){sum=sum+i;}i++;}System.out.println("1000以内能同时被3和7整除的整数之和为："+sum);}}3.public class Example3_3{public static void main(String srgs[]){long sum=0,a=8,b=a,i=1;for(i=1;i<=10;i++){sum=sum+b;b=b*10+a;}System.out.println("e="+sum);}}4.public class Example3_4{public static void main(String args[]){double sum=0;double a=0;int i=0;for(i=0;i<10000;i++){a=(i%2==0?1:-1)/(2*i+1);sum=sum+a;}System.out.println("前10000项之和为："+sum);}5.public class Example3_5{public static void main(String args[]){int i=1,a=1;int sum=0;while(i<=200){if(i>=100){a=a*i;sum=sum+a;}i++;}System.out.println("从100项到第200项的和为："+sum); }}四、运行结果:1.2.3.5.。

南京邮电大学java实验报告面向对象

实验报告班级：姓名：学号：课程名称Java程序设计实验项目Java的面向对象编程实验项目类型验证演示综合设计指导教师吴伟敏成绩√一、实验目的1、掌握Java程序面向对象编程的基本架构；2、掌握有关面向对象的基本概念，如：类、对象、接口继承和多态等；3、掌握包程序设计的方法，了解大型软件的构造方式二、实验步骤1、录入并测试以下程序，说出此程序的作用，体会类和对象的关系。

程序如下：class CCircle{double pi;double radius;double getRadius(){return radius;}void setCircle(double r, double p){pi=p;radius=r;}}public class Ex2_1{public static void main(String args[]) {CCircle cir1=new CCircle();cir1.setCircle(2.0,3.1416);System.out.println("radius="+cir1.getRadius());}}[基本要求]运行程序并观察运行结果。

[思考问题]试述程序中每条语句的作用。

2、录入并测试和完善以下程序，体会接口的用法。

interface Sittable{void sit();}interface Lie{void sleep();}interface HealthCare{void massage();}class Chair implements Sittable{public void sit(){System.out.println("It is sittable!");};}class Sofa extends Chair implements Lie,HealthCare{ public void sleep(){System.out.println("It is sleep!");};public void massage(){System.out.println("give a message!");};public static void main(String[] args) {Sofa cottonSofa=new Sofa();System.out.println(" Sofa is ok!");}}[基本要求]运行程序并观察运行结果。

JAVA实验报告心得

北京联合大学信息学院“面向对象程序设计”课程上机实验报告题目： java上机实验心得体会姓名（学号）：专业：计算机科学与技术编制时间： 2012年12月19日版本： 1.0.0指导教师：北京联合大学-信息学院编制实验1 熟悉java运行环境实验目的：熟悉jdk环境和操作，编写简单的java应用程序。

心得体会：在该实验中，我碰到的问题是jdk环境变量的设置。

解决方法是通过查阅资料书和网上搜索相关解决方法及同学的有力帮助。

实验2 选择语句练习实验目的：正确理解并能够熟练操作和使用java的if和switch语句。

心得体会：我个人感觉有了c的编程基础，if和switch这些简单的流程控制语句运用起来比较轻松，实现简单的逻辑运算也跟c非常相近，所以上手比较快。

但是在这次程序中，首次涉及到了java程序的数据输入，与c区别很大。

但经过老师的讲解和查阅相关资料，基本明白相关的使用规则和注意事项。

在第二个小题中还涉及到了charat（）方法，经查阅jdk 文档，知道charat()方法返回一个位于提供给它的参数索引处的字符，如: str.chatat(0)检索str中的第一个字符,str.charat(str.length()-1)检索最后一个字符。

我运用此方法解决了比较字符串间首字母异同的问题。

实验3 迭代练习实验4 方法的实现练习实验目的：声明、定义和调用方法，理解实参和形参的含义。

心得体会：在该实验中，我掌握如何写方法、调用方法，并掌握如何向方法中传递信息和从方法中返回信息。

方法声明为非void（构造方法除外）则需要用return语句返回一个相应类型的返回值。

实验5 简单类型数组练习实验目的：学习创建简单类型的数组，并能用循环语句处理数组。

心得体会：通过该实验，我学会了如何让建立简单类型的数组，并掌握了将数组作为方法的传入参数和返回值。

在该实验中，遇到的问题主要是如何将一个连续的多位数在存入数组时，每个数组元素只对应改多位数的一个组成数。

20155313实验三《Java面向对象程序设计》实验报告

20155313实验三《Java⾯向对象程序设计》实验报告⼀、实验内容XP基础XP核⼼实践相关⼯具⼆、实验要求1.没有Linux基础的同学建议先学习《Linux基础⼊门（新版）》《Vim编辑器》课程2.完成实验、撰写实验报告，实验报告以博客⽅式发表在博客园，注意实验报告重点是运⾏结果，遇到的问题(⼯具查找，安装，使⽤，程序的编辑，调试，运⾏等)、解决办法（空洞的⽅法如“查⽹络”、“问同学”、“看书”等⼀律得0分）以及分析（从中可以得到什么启⽰，有什么收获，教训等）。

报告可以参考范飞龙⽼师的指导3.严禁抄袭，有该⾏为者实验成绩归零，并附加其他惩罚措施。

三、实验步骤1. 在IDEA中使⽤⼯具（Code->Reformate Code）把下⾯代码重新格式化，再研究⼀下Code菜单，找出⼀项让⾃⼰感觉最好⽤的功能。

提交截图，加上⾃⼰学号⽔印。

public class CodeStandard {public static void main(String [] args){StringBuffer buffer = new StringBuffer();buffer.append('S');buffer.append("tringBuffer");System.out.println(buffer.charAt(1));System.out.println(buffer.capacity());System.out.println(buffer.indexOf("tring"));System.out.println("buffer = " + buffer.toString());if(buffer.capacity()<20)buffer.append("1234567");for(int i=0; i<buffer.length();i++)System.out.println(buffer.charAt(i));}}2. 在码云上把⾃⼰的学习搭档加⼊⾃⼰的项⽬中，确认搭档的项⽬加⼊⾃⼰后，下载搭档实验⼆的Complex代码，加⼊不少于三个JUnit单元测试⽤例，测试成功后git add .; git commit -m "⾃⼰学号添加内容"；git push;提交搭档项⽬git log的截图，包含上⾯git commit的信息，并加上⾃⼰的学号⽔印信息。

Java程序设计实训报告

Java程序设计实训报告Java程序设计实训报告一、实训目标本次Java程序设计实训旨在让学生掌握Java语言的基础知识和编程技能，能够独立完成Java程序的设计和开发，提高学生的实际编程能力和解决问题能力。

二、实训内容本次Java程序设计实训包括以下内容：1. Java基础语法和面向对象编程的基本概念。

2. Java程序的运行和调试方法。

3. Java标准库的使用和常用数据结构的实现。

4. 常用算法的实现和优化。

5. Java GUI编程和多线程编程的基本概念。

三、实训流程1. 熟悉Java基础语法和面向对象编程的基本概念，在Eclipse 或IntelliJ IDEA等集成开发环境中编写HelloWorld程序，理解程序结构和运行方式。

2. 学习Java标准库的使用和常用数据结构的实现，实现常用算法，如排序、查找等。

掌握调试和优化技巧，以提高程序性能。

3. 学习Java GUI编程和多线程编程的基本概念，实现基本的窗体应用程序和多线程程序，例如计算器、文本编辑器等。

4. 综合应用所学知识，开发一个较为复杂的Java程序，如网络聊天室、小游戏等。

5. 学习Java框架，例如Spring、Hibernate等，实现web应用的设计和开发。

四、实训总结通过这次Java程序设计实训，我加深了对Java语言的理解和认识，学会了使用Java标准库进行编程，掌握了常用算法的实现和优化技巧，学会了Java GUI编程和多线程编程的基本概念，能够独立开发基本的窗体应用程序和多线程程序。

同时，我还学习了Java框架，并能够应用框架进行web应用的设计和开发。

在实训过程中，我遇到了很多困难和问题，但通过查阅资料、询问老师和同学等方式，最终解决了这些问题，加深了对Java程序设计的了解和认识，也提高了我的解决问题的能力。

总的来说，这次实训让我受益匪浅，我会继续学习和探索Java程序设计领域，提高自己的编程水平。

Java实验报告面向对象

实验报告学年第学期任课老师：m=max[i];}}System.out.println("5个人中java成绩最大值是："+m);}}实验结果分析与总结1、程序运行结果（请提供所完成的各道题运行结果界面截图）：2、在实验过程中遇到的问题与解决方法：实验中并未有太多技术上的问题，除了对软件运用的不够熟练造成最初的一些错误，比如，用Jcreator时未编译便运行，一直出错，检查多次后才发现此处与eclipse的不同（上机时没问题，写实验报告用的Jcreator出错了，所以是软件用的不熟记错的缘故。

）而且要先编译Student类才可编译Main。

3、实验过程中的发现与收获，未解决或需进一步解决的问题：实验中的发现便是java其实较C/C++简单许多，很多东西都不要自己多加考虑，但试验还是太少所以会在一些小的细节方面浪费很多时间。

指导老师评阅意见指导老师：年月日填写内容时，可把表格扩大。

附：实验源程序代码//Mainpackage Test;public class Main {public static void main(String[] args) {Main ma=new Main();Student stu1=new Student();stu1.setAge(18);stu1.setJava(86);stu1.setName("aaa");stu1.setNo("001");stu1.setSex("M");int a=stu1.getJava();System.out.println("第一个学生的信息为：\r\n"+"姓名是:"+stu1.getName()+"\r\n"+"年龄是："+stu1.getAge()+"\r\n"+"性别是:"+stu1.getSex()+"\r\n"+"学号是："+stu1.getNo()+"\r\n"+"成绩是："+stu1.getJava()+"\r\n");Student stu2=new Student();stu2.setAge(18);stu2.setJava(90);stu2.setName("bbb");stu2.setNo("011");stu2.setSex("M");int b=stu2.getJava();System.out.println("第二个学生的信息为：\r\n"+"姓名是:"+stu2.getName()+"\r\n"+"年龄是："+stu2.getAge()+"\r\n"+"性别是:"+stu2.getSex()+"\r\n"+"学号是："+stu2.getNo()+"\r\n"+"成绩是："+stu2.getJava()+"\r\n");System.out.println("两个人的java平均成绩为:"+(stu1.getJava()+stu2.getJava())/2);Student stu3=new Student();stu3.setAge(20);stu3.setJava(76);stu3.setName("ccc");stu3.setNo("067");stu3.setSex("F");int c=stu3.getJava();System.out.println("第三个学生的信息为：\r\n"+"姓名是:"+stu3.getName()+"\r\n"+"年龄是："+stu3.getAge()+"\r\n"+"性别是:"+stu3.getSex()+"\r\n"+"学号是："+stu3.getNo()+"\r\n"+"成绩是："+stu3.getJava()+"\r\n");Student stu4=new Student();stu4.setAge(19);stu4.setJava(100);stu4.setName("ddd");stu4.setNo("09091219");stu4.setSex("M");int d=stu4.getJava();System.out.println("第四个学生的信息为：\r\n"+"姓名是:"+stu4.getName()+"\r\n"+"年龄是："+stu4.getAge()+"\r\n"+"性别是:"+stu4.getSex()+"\r\n"+"学号是："+stu4.getNo()+"\r\n"+"成绩是："+stu4.getJava()+"\r\n");Student stu5=new Student();stu5.setAge(22);stu5.setJava(89);stu5.setName("eee");stu5.setNo("097");stu5.setSex("F");int e=stu2.getJava();System.out.println("第五个学生的信息为：\r\n"+"姓名是:"+stu5.getName()+"\r\n"+"年龄是："+stu5.getAge()+"\r\n"+"性别是:"+stu5.getSex()+"\r\n"+"学号是："+stu5.getNo()+"\r\n"+"成绩是："+stu5.getJava()+"\r\n");int max[]={a,b,c,d,e};int m=max[0];for(int i=0;i<5;i++){if(m<max[i]){m=max[i];}}System.out.println("5个人中java成绩最大值是："+m);}}//Student类package Test;public class Student {private String sNo;private String sName;private String sSex;private int sJava;private int sAge;//set方法public void setJava(int java){sJava=java;;}public void setAge(int age){sAge=age;}public void setNo(String no){sNo=no;}public void setName(String name){ sName=name;}public void setSex(String sex){sSex=sex;}//get方法public int getJava(){return sJava;}public int getAge(){return sAge;}public String getNo(){return sNo;}public String getName(){return sName;}public String getSex(){return sSex;}}。

JAVA-面向对象程序设计-学生个人信息管理系统

JAVA-面向对象程序设计-学生个人信息管理系统软件学院课程设计报告书课程名称面向对象程序设计设计题目学生个人信息管理系统专业班级嵌入式软件09-2学号**********姓名王翀指导教师2011 年6 月目录1 设计时间 (5)2 设计目的 (5)3设计任务 (5)4 设计内容 (5)4.1需求分析 (5)4.1.1问题描述 (5)4.1.2基本要求 (5)4.2总体设计 (6)4.2.1包的描述 (9)4.2.2类的描述 (10)4.2.3类之间的关系 (10)类MainTest继承JFrame。

(10)类jenter实现接口ActionListener。

(10)4.3 详细设计 (10)4.3.1类图 (14)4.3.2页面设计 (14)4.4 测试与分析 (15)4.5 程序代码 (17)5 总结与展望 (32)参考文献 (32)课程设计成绩评定 (34)1 设计时间2012年6月13日——6月19日2 设计目的《面向对象程序设计》是一门实践性很强的计算机专业基础课程，课程设计是学习完该课程后进行的一次较全面的综合练习。

其目的在于通过实践加深学生对面向对象程序设计的理论、方法和基础知识的理解，掌握使用Java语言进行面向对象设计的基本方法，提高运用面向对象知识分析实际问题、解决实际问题的能力，提高学生的应用能力3设计任务设计一个简单学生个人信息管理系统，该系统具有录入，查询，修改三项基本功能。

要求如下：(1)具有简单的录入，查询和修改功能。

(2)修改学生信息必须输入学号，然后对姓名、性别和专业等进行修改；(3)使用文件存储数据。

（也可用数据库）(4)学生个人信息必须包括：学号、姓名、性别、出生日期、身份证号、专业、班级自我简介，其余可自行丰富。

4 设计内容4.1需求分析学生管理系统需要对学生的基本信息进行简单的录入，查询，修改三项基本功能。

具体实现使用Access2003数据库实现基本操作，前台窗口使用GUI编程创建图形界面，对图形界面的窗口和按钮进行事件监听，执行相应的SQL语句。

面向对象程序设计java

面向对象程序设计Java是一种面向对象的编程语言，它提供了一种灵活的方式来构建可重用的软件组件。

它的主要特点是：
1. 面向对象：Java是一种面向对象的编程语言，它支持封装、继承和多态等面向对象的特性，可以更好地抽象和组织代码，提高代码的可重用性。

2. 平台无关性：Java是一种跨平台的编程语言，它可以在多种操作系统上运行，而不需要重新编译代码。

3. 安全性：Java提供了一种安全的运行环境，可以防止恶意代码的执行，保护系统免受病毒和恶意软件的攻击。

4. 强大的类库：Java提供了一个强大的类库，可以让开发者更快捷地开发应用程序。

5. 自动垃圾回收：Java拥有一个自动垃圾回收机制，可以自动回收不再使用的内存，减少内存泄漏的可能性。

面向对象程序设计实验报告

《面向对象程序设计实验》实验一、Java实验环境的建立（2学时）1、目的要求（1）掌握Java编程环境的搭建过程；（2）掌握Jcreator pro软件的使用方法；（3）能使用Java doc文档。

2、实验内容（1）下载并安装JDK1.6，配置JDK环境变量；（2）下载Javadoc压缩包并解压在JDK安装路径下；（3）下载Jcreator pro 4.0并安装和配置使用环境；（4）使用实验环境运行书中实例代码，在屏幕上输出“Hello Java”字符串。

①Java application程序代码如下：public class HelloJava{public static void main(String args[]){ System.out.println("Hello Java!"); }}②Java applet程序代码如下：import java.awt.*;public class Hello extends java.applet.Applet{public void paint(Graphics g){ g.drawString("Hello!",30,30); }}3、仪器与材料：计算机实验二、Java语言程序设计训练（2学时）1、目的要求（1）输入、输出操作实现原理和方法；（2）掌握程序流程控制的实现方法；（3）掌握数组的定义和操作方法。

2、实验内容（1）计算Result=1!+2!+3!+...+10!。

public class Test3 {public static void main(String[] args) {int sum = 0, fact, n, i;for (n = 1; n <= 10; n++) {fact = 1;for (i = 1; i <= n; i++)fact *= i;sum += fact;}System.out.println("sum=" + sum);}}（2）计算1---50之间所有素数的和。

JAVA语言程序设计实验报告

实验一、安装JDK并熟悉java的运行环境实验二、基本语法练习实验三、面向对象编程实验(4)实验四、异常处理实验实验五、小应用程序实验实验六、图形图像实验实验七、GUI（图形用户接口）实验(4)实验八、多线程实验实验九、输入输出流实验(4)实验十、数据库应用实验(4)实验一、安装JDK并熟悉java的运行环境一、实验目的熟悉JA V A的运行环境及学习简单的编程。

二、预习内容安装工具软件的基本方法。

三、实验设备与环境装有JA V A语言工具软件(Eclipse )的微机若干四、实验内容安装Eclipse及JA V A的核心编译程序J2SDK。

1、打开Eclipse的安装盘安装Eclipse。

2、在相同目录下安装J2SDK。

3、打开Eclipse软件对J2SDK文件进行配置。

4、编写一应用程序，在屏幕上显示“HELLO WORLD”和爱心标志。

Pulic class Hello{public static void main(String args[]){//在屏幕上显示“HELLO WORLD”和爱心标志}}5、编写一小程序实现上述功能：在屏幕上显示“HELLO WORLD”和爱心标志。

实验结果五、注意事项⒈认真填写实验报告⒉遵守实验室各项制度，服从实验指导教师的安排⒊按规定的时间完成实验六、说明本次实验建议学时数2学时七、实验总结与体会实验二、基本语法练习一、实验目的⒈熟悉Java的基本语法⒉编写应用程序接收命令行参数⒊编写应用程序接收用户从键盘的输入⒋掌握字符串与数组的基本方法二、预习内容java编程的基本结构三、实验设备与环境装有JA V A语言工具软件(Eclipse )的微机若干四、实验内容⒈编写一个应用程序求若干个数的平均数，原始数字要求从命令行输入。

应用程序中main方法的参数String类型的数组args能接受用户从命令行键入的参数。

(1)编辑A verage.java。

class A verage{public static void main(String args[ ]){double n,sun=0;for (int l=0;l<args.legth;l++){sum=sum+Double.valueOf(arg[l].doubleV alue();)}n=sum/args.length;System.out.println(“average=”+n);}}命令行参数：12.34 34.45 21212121注意：1）参数的个数可以利用args.length来取得。

面向对象程序设计实验报告2

面向对象程序设计实验报告一．实验目的进一步熟悉Java程序的结构,掌握Java的运算符、表达式、数组及流程控制语句的应用。

二. 实验内容(1)编写Application。

实现：将上学期所学的各门课程的名称及考试成绩的信息用数组存放，并在for（或while）循环中利用排序算法，将成绩进行升（或降）序排列，最后输出排序后的课程成绩。

(2)编写Applet程序，实现：将上学期所学的各门课程的名称及考试成绩的信息用数组存放，并在for（或while）循环中利用排序算法，将成绩进行升（或降）序排列，最后输出排序后的课程成绩。

三. 实验步骤（1）进行模板设计，设计出自己想要的模板。

（2）根据自己设计的模板编写出代码，并进行Java Application程序调试。

（3）编写并调试Java Applet程序。

四．实验结果1．编写一个application程序。

截图如下代码如下：import javax.swing.*;import java.awt.*;import java.awt.event.*;public class applicationInOut{public static void main(String args[]){new FrameInOut();}}class FrameInOut extends Frame implements ActionListener{JPanel p1,p2,p3,p4;JButton btn1,btn2,btn3;JTextArea t1;TextField text1,text2,text3,text4,text5,text6,text7,text8;Label lab1,lab2,lab3,lab4,lab5,lab6,lab7,lab8;String information1[]={"姓名","性别：","学号","班级"};String information2[]={"","","",""};String course[]={"数据结构","线性代数","大学英语","电子电路"}; int score[]={0,0,0,0};FrameInOut(){super("学生成绩信息排名");btn1=new JButton("信息显示");btn2=new JButton("按成绩排名");btn3=new JButton("退出");lab1=new Label("姓名");lab2=new Label("性别");lab3=new Label("学号");lab4=new Label("班级");lab5=new Label("数据结构");lab6=new Label("线性代数");lab7=new Label("大学英语");lab8=new Label("电子电路");text1=new TextField(10);text2=new TextField(10);text3=new TextField(10);text4=new TextField(10);text5=new TextField(10);text6=new TextField(10);text7=new TextField(10);text8=new TextField(10);t1=new JTextArea(10,20);p1=new JPanel();p2=new JPanel();p3=new JPanel();p4=new JPanel();p1.add(btn1);p1.add(btn2);p1.add(btn3);p2.add(lab1);p2.add(text1);p2.add(lab2);p2.add(text2);p2.add(lab3);p2.add(text3);p2.add(lab4);p2.add(text4);p3.add(lab5);p3.add(text5);p3.add(lab6);p3.add(text6);p3.add(lab7);p3.add(text7);p3.add(lab8);p3.add(text8);p4.add(t1);add(p1);add(p2);add(p3);add(p4);setLayout(new FlowLayout());p1.setBackground(Color.red);p2.setBackground(Color.orange);p3.setBackground(Color.orange);p4.setBackground(Color.blue);t1.setForeground(Color.blue);btn1.addActionListener(this);btn2.addActionListener(this);btn3.addActionListener(this);setSize(700,400);setVisible(true);}public void actionPerformed(ActionEvent e){if(e.getSource()==btn1){t1.setText("");information2[0]=text1.getText();information2[1]=text2.getText();information2[2]=text3.getText();information2[3]=text4.getText();score[0]=Integer.parseInt( text5.getText());score[1]=Integer.parseInt( text6.getText());score[2]=Integer.parseInt( text7.getText());score[3]=Integer.parseInt( text8.getText());for(int i=0;i<information1.length;i++){t1.setFont(new Font("黑体",Font.BOLD,15));t1.append(information1[i]+":"+information2[i]+"\n");}for(int i=0;i<course.length;i++){t1.setFont(new Font("黑体",Font.BOLD,15));t1.append(course[i]+":"+score[i]+"\n");}}else if(e.getSource()==btn2){information2[0]=text1.getText();information2[1]=text2.getText();information2[2]=text3.getText();information2[3]=text4.getText();score[0]=Integer.parseInt( text5.getText());score[1]=Integer.parseInt( text6.getText());score[2]=Integer.parseInt( text7.getText());score[3]=Integer.parseInt( text8.getText());int i,j,m;String coursename;for(i=0;i<score.length;i++){for(j=i+1;j<course.length;j++){if(score[i]>score[j]){m=score[j];score[j]=score[i];score[i]=m;coursename=course[i];course[i]=course[j];course[j]=coursename;}}}t1.setText("");for(i=0;i<information1.length;i++){t1.setFont(new Font("黑体",Font.BOLD,15));t1.append(information1[i]+":"+information2[i]+"\n");}for(i=0;i<course.length;i++){t1.setFont(new Font("黑体",Font.BOLD,15));t1.append(course[i]+" 成绩为："+score[i]+"\n");}}if(e.getSource()==btn3){dispose();System.exit(0);}}}2．编写一个applet程序。

java程序设计实验报告

java程序设计实验报告
实验一：实现个人信息管理系统
实验目的：学习如何使用Java语言来完成一个简单的面向对象程序设计。

实验内容：
本次实验的任务是开发一个个人信息管理系统，可以完成一些基本的信息管理功能，如增加、删除、查询和修改个人信息等。

实验步骤：
1. 定义Person类并实现其属性和方法。

2. 在主类中实现简单的用户交互界面。

3. 实现文件持久化，将程序中的信息储存在文件中。

4. 实现增加、删除、查询和修改个人信息的功能。

实验结论：
通过本次实验，我学会了如何使用Java语言来实现一个简单的面向对象程序设计。

在开发过程中，我学会了如何定义类、实现属性和方法，如何进行用户交互界面的设计，以及如何将程序中的信息储存在文件中。

《Java程序设计》上机实验报告实验三面向对象程序设计的继承、多态等特性的练习

信息科学与工程学院《Java程序设计》上机实验报告专业班级姓名学号实验时间指导教师成绩主要实验记录及个人小结（包括部分实验源程序、调试结果及实验结果分析等）Student(String name,String sex,int age,String sno,String classno) {super(name,sex,age);this.sno=sno;this.classno=classno;}public String toString(){ return("姓名:"+name+" 性别:"+sex +" 年龄:"+age+ " 学号:"+sno+" 班号:"+classno+" ");}}public class TestStudentPerson {public static void main(String[] args){int i;Student stu[]=new Student[3];stu[1]=new Student("小明","男",20,"200912135138","2班");stu[2]=new Student("小木","女",23,"200912135136","5班");stu [1].updateAge(25);stu [2].updateAge(26);for(i=1;i<3;i++){System.out.println(stu[i]);}}}2)调试结果:主要实验记录及个人小结（包括部分实验源程序、调试结果及实验结果分析等）调试结果:2)将Shape类定义为abstact class Shape{……}public class TestVirtualInvoke {static void doStuff(Shape s){s.draw();}public static void main(String[] args) {Circle c=new Circle();Triangle t=new Triangle();Line l=new Line();doStuff(c); //作为实参,调用对象是3个类对象,上溯造型使其隐藏.doStuff(t);doStuff(l);}}abstract class Shape{abstract void draw();}class Circle extends Shape{void draw(){System.out.println("Draw Circle");}} //定义Shape抽象类的派生类Circleclass Triangle extends Shape{void draw(){System.out.println("Draw Three Triangle");}}//定义Shape抽象类的派生类Triangleclass Line extends Shape{void draw(){System.out.println("Draw Line");}}//定义Shape抽象类的派生类Line主要实验记录及个人小结（包括部分实验源程序、调试结果及实验结果分析等）调试结果:3)将Shape定义为interface Shape{……}public class TestVirtualInvoke {static void doStuff(Shape s){s.draw();}public static void main(String[] args) {Circle c=new Circle();Triangle t=new Triangle();Line l=new Line();doStuff(c); //作为实参,调用对象是3个类对象,上溯造型使其隐藏.doStuff(t);doStuff(l);}}interface Shape{public void draw();} //定义一个Shape接口class Circle implements Shape{public void draw(){System.out.println("Draw Circle");}} //基于Shape接口利用implements实现类Circleclass Triangle implements Shape{public void draw(){System.out.println("Draw Three Triangle");}}class Line implements Shape{public void draw(){System.out.println("Draw Line");}}调试结果:3.思考题:某小型公司，主要有三类人员：经理、兼职技术人员和兼职推销员。

实验二面向对象编程实验报告

实验二面向对象编程实验报告一、实验目的本次实验旨在深入理解和掌握面向对象编程的基本概念和方法，通过实际编程操作，提高运用面向对象思想解决问题的能力，熟悉面向对象编程的开发流程和技巧，培养良好的编程习惯和代码规范。

二、实验环境本次实验使用的编程环境为具体编程环境名称及版本，操作系统为操作系统名称及版本。

三、实验内容（一）问题描述设计一个简单的学生管理系统，能够实现对学生信息（包括姓名、学号、年龄、成绩等）的录入、查询、修改和删除操作。

（二）类的设计1、设计一个｀Student` 类，用于表示学生对象。

该类包含以下属性：｀name`（姓名）、｀student_id`（学号）、｀age`（年龄）、｀score`（成绩）。

2、为｀Student` 类添加构造函数，用于初始化学生对象的属性。

3、为｀Student` 类添加｀get` 和｀set` 方法，用于获取和设置学生对象的属性值。

（三）功能实现1、录入功能：实现用户输入学生信息，并创建｀Student` 对象进行存储。

2、查询功能：根据学号或姓名查询学生信息，并输出查询结果。

3、修改功能：根据学号或姓名找到对应的学生对象，修改其属性值。

4、删除功能：根据学号或姓名删除对应的学生对象。

四、实验步骤（一）类的实现｀｀｀javapublic class Student ｛private String name;private String studentId;private int age;private double score;public Student(String name, String studentId, int age, double score) ｛thisname ＝ name;thisstudentId ＝ studentId;thisage ＝ age;thisscore ＝ score;｝public String getName(）｛return name;｝public void setName(String name) ｛thisname ＝ name;｝public String getStudentId(）｛return studentId;｝public void setStudentId(String studentId) ｛thisstudentId ＝ studentId;｝public int getAge(）｛return age;｝public void setAge(int age) ｛thisage ＝ age;｝public double getScore(）｛return score;｝public void setScore(double score) ｛thisscore ＝ score;｝｝｀｀｀（二）主函数实现｀｀｀javaimport javautilArrayList;import javautilScanner;public class StudentManagementSystem ｛private ArrayList<Student> students;public StudentManagementSystem(）｛students ＝ new ArrayList<＞（）；｝public static void main(String args) ｛StudentManagementSystem system ＝ new StudentManagementSystem(）；Scanner scanner ＝ new Scanner(Systemin)；while （true) ｛Systemoutprintln(＂1、录入学生信息"）；Systemoutprintln(＂2、查询学生信息"）；Systemoutprintln(＂3、修改学生信息"）；Systemoutprintln(＂4、删除学生信息"）；Systemoutprintln(＂5、退出系统"）；int choice ＝ scannernextInt(）；switch （choice) ｛case 1:systemaddStudent(scanner)；break;case 2:systemqueryStudent(scanner)；break;case 3:systemmodifyStudent(scanner)；break;case 4:systemdeleteStudent(scanner)；break;case 5:Systemoutprintln(＂感谢使用，再见！＂）；Systemexit(0)；default:Systemoutprintln(＂输入有误，请重新输入！＂）；｝｝｝／／录入学生信息public void addStudent(Scanner scanner) ｛Systemoutprintln(＂请输入学生姓名：＂）；String name ＝ scannernext(）；Systemoutprintln(＂请输入学生学号：＂）；String studentId ＝ scannernext(）；Systemoutprintln(＂请输入学生年龄：＂）；int age ＝ scannernextInt(）；Systemoutprintln(＂请输入学生成绩：＂）；double score ＝ scannernextDouble(）；Student student ＝ new Student(name, studentId, age, score)；studentsadd(student)；Systemoutprintln(＂学生信息录入成功！＂）；｝／／查询学生信息public void queryStudent(Scanner scanner) ｛Systemoutprintln(＂请输入查询方式（1、按学号查询 2、按姓名查询）：＂）；int queryType ＝ scannernextInt(）；if （queryType ＝＝ 1) ｛Systemoutprintln(＂请输入学号：＂）；String studentId ＝ scannernext(）；for （Student student ： students) ｛if （studentgetStudentId(）equals(studentId)）｛Systemoutprintln(＂姓名：＂＋ studentgetName(））；Systemoutprintln(＂学号：＂＋ studentgetStudentId(））；Systemoutprintln(＂年龄：＂＋ studentgetAge(））；Systemoutprintln(＂成绩：＂＋ studentgetScore(））；return;｝｝Systemoutprintln(＂未找到该学号对应的学生信息！＂）；｝ else if （queryType ＝＝ 2) ｛Systemoutprintln(＂请输入姓名：＂）；String name ＝ scannernext(）；for （Student student ： students) ｛if （studentgetName(）equals(name)）｛Systemoutprintln(＂姓名：＂＋ studentgetName(））；Systemoutprintln(＂学号：＂＋ studentgetStudentId(））；Systemoutprintln(＂年龄：＂＋ studentgetAge(））；Systemoutprintln(＂成绩：＂＋ studentgetScore(））；return;｝｝Systemoutprintln(＂未找到该姓名对应的学生信息！＂）；｝ else ｛Systemoutprintln(＂输入有误，请重新输入！＂）；｝｝／／修改学生信息public void modifyStudent(Scanner scanner) ｛Systemoutprintln(＂请输入修改方式（1、按学号修改 2、按姓名修改）：＂）；int modifyType ＝ scannernextInt(）；if （modifyType ＝＝ 1) ｛Systemoutprintln(＂请输入学号：＂）；String studentId ＝ scannernext(）；for （Student student ： students) ｛if （studentgetStudentId(）equals(studentId)）｛Systemoutprintln(＂请输入新姓名：＂）；String newName ＝ scannernext(）；Systemoutprintln(＂请输入新年龄：＂）；int newAge ＝ scannernextInt(）；Systemoutprintln(＂请输入新成绩：＂）；double newScore ＝ scannernextDouble(）；studentsetName(newName)；studentsetAge(newAge)；studentsetScore(newScore)；Systemoutprintln(＂学生信息修改成功！＂）；return;｝｝Systemoutprintln(＂未找到该学号对应的学生信息！＂）；｝ else if （modifyType ＝＝ 2) ｛Systemoutprintln(＂请输入姓名：＂）；String name ＝ scannernext(）；for （Student student ： students) ｛if （studentgetName(）equals(name)）｛Systemoutprintln(＂请输入新学号：＂）；String newStudentId ＝ scannernext(）；Systemoutprintln(＂请输入新年龄：＂）；int newAge ＝ scannernextInt(）；Systemoutprintln(＂请输入新成绩：＂）；double newScore ＝ scannernextDouble(）；studentsetStudentId(newStudentId)；studentsetAge(newAge)；studentsetScore(newScore)；Systemoutprintln(＂学生信息修改成功！＂）；return;｝｝Systemoutprintln(＂未找到该姓名对应的学生信息！＂）；｝ else ｛Systemoutprintln(＂输入有误，请重新输入！＂）；｝｝／／删除学生信息public void deleteStudent(Scanner scanner) ｛Systemoutprintln(＂请输入删除方式（1、按学号删除 2、按姓名删除）：＂）；int deleteType ＝ scannernextInt(）；if （deleteType ＝＝ 1) ｛Systemoutprintln(＂请输入学号：＂）；String studentId ＝ scannernext(）；for （Student student ： students) ｛if （studentgetStudentId(）equals(studentId)）｛studentsremove(student)；Systemoutprintln(＂学生信息删除成功！＂）；return;｝｝Systemoutprintln(＂未找到该学号对应的学生信息！＂）；｝ else if （deleteType ＝＝ 2) ｛Systemoutprintln(＂请输入姓名：＂）；String name ＝ scannernext(）；for （Student student ： students) ｛if （studentgetName(）equals(name)）｛studentsremove(student)；Systemoutprintln(＂学生信息删除成功！＂）；return;｝｝Systemoutprintln(＂未找到该姓名对应的学生信息！＂）；｝ else ｛Systemoutprintln(＂输入有误，请重新输入！＂）；｝｝｝｀｀｀五、实验结果通过对程序的运行和测试，能够成功实现学生信息的录入、查询、修改和删除功能。

Java实验报

实验报告课程名称Java面向对象程序设计实验名称一个简单的应用程序姓名***学号***专业年级14 物联网一、实验目的：本实验的目的是让学生掌握开发Java 应用程序的三个步骤：编写源文件、编译源文件和运转应用程序。

二、实验内容：编写一个简单的 Java 应用程序，该程序在命令行窗口输出两行文字：“你好，很快乐学习 Java”和“ Wearestudents ”。

三、实验步骤实验源代码：publicclassHello{publicstaticvoidmain(Stringargs[]){你好，很快乐学习Java");Aa=newA();();}}classA{voidfA(){arestudents");}}四、实验结果五、总结此次实验让我首次认识了Java 编程软件的环境，为今后编程打下基础实验报告课程名称Java 面向对象程序设计实验名称教室、老师和学生姓名***学号***专业年级14 物联网一、实验目的：熟习 Java 应用程序的基本结构，并能联合编译应用程序所需要的类。

二、实验内容：编写 3 个源文件：、和，每个源文件只有一个类。

含有应用程序的主类（含有 main 方法），并使用了 Teacher 和 Student 类。

将 3 个源文件保存到同一目录中，比方 C:\1000 ，尔后编译。

三、实验步骤实验源代码：publicclassClassRoom{publicstaticvoidmain(String[]args){Teacherzhang=newTeacher();Studentjiang=newStudent();();();}}publicclassStudent{voidintroduceSelf(){}}publicclassTeacher{voidintroduceSelf(){}}四、实验结果五、总结此次实验熟习了 Java 应用程序的基本结构，并将不一样类保存运转在同个目录中。

java面向对象编程实验报告

java面向对象编程实验报告篇一：java面向对象编程实验报告信息工程学院Java程序设计实验/实习报告学院:信息工程学院班级:信息112 姓名:吴连梅学号:XX013305 成绩:A实验二面向对象编程1．实验目的（1）掌握类与对象基本知识；（2）Java中的继承机制及包（package）、接口（interface）等的设计方法；（3）掌握static、this、super等关键字的使用；（4）掌握Java中两种比较器的用法。

2．实验内容实验题 1 定义一个类Book，包含两个属性：一个是private的String类型的属性title、一个是private的float类型的属性listPrice，封装这两个属性的四个方法setTitle（）和getTitle（）、setListPrice( )和geListPrice （）。

基本要求：（1）设计类Book及类BookManagement，在类BookManagement中输出Book类的对象的两个private属性；（2）重写父类的toString（）方法，实现Book类实例的两个属性的输出。

实验过程：新建工程后，在工程下面建立一个包Book，在包下再建立一个Book类，类中包含两个属性，一个是private的String类型的属性title、一个是private的float类型的属性listPrice，之后是封装这两个属性的四个方法，用快捷键Alt+Shift+S选择gennerate Getters and Setters,再实验报告的内容与格式按任课教师的要求书写。

然后就是重写父类的toString（）方法，用快捷键Alt+Shift+S选择gennerate toString，快捷重写。

这段程序写完是这样的：接下来便是BookManagement类，在包book下新建一个类BookManagement，写完的程序是这样的：BookManagement类中创建了书的对象，在主方法中调用output函数，赋值，输出。

Java综合实验报告_3

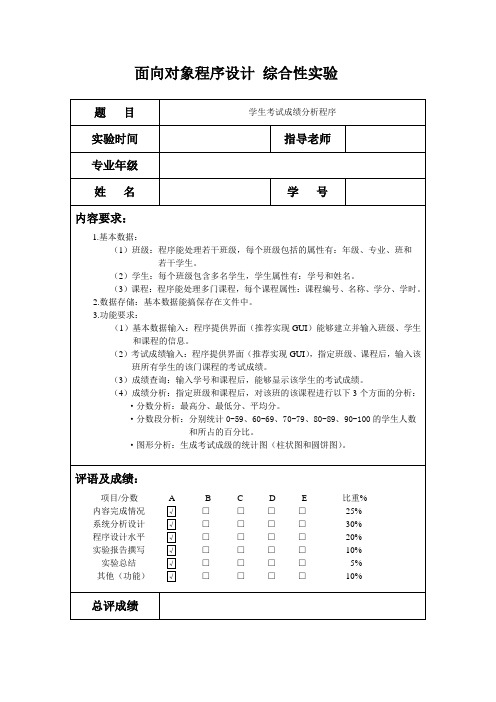
面向对象程序设计综合性实验（一）系统分析：本系统为学生考试成绩分析系统，系统要求可以让用户输入若干学生的基本信息、课程信息，还有对应的课程成绩。

而主要功能则是可以实现按条件进行相应学生的成绩查询和按条件进行成绩的分析，并且能够通过绘制柱状图与圆饼图来显示相应结果。

因此，我设计了3个保存数据的类，分别是年级班级类、学生类以及课程类，其中学生类继承了课程类，而年级班级类则继承学生类。

每当新建一条信息（一个学生的信息），则新建一个年级班级类，在内部会自动新建一个学生类以及课程类，用于记录一个学生的信息。

本系统采用了窗口GUI来实现，因此大量采用了按钮、文本框、单选按钮、滚动窗口等等，所以必不可少的当然是不少的监听器与对应的实现方法。

（二）系统设计：1.基本数据：Class—Grade : String—major : String—classname : String—Student : Student+getGrade() : String+getStudent() : Student+getClassname() : String+getMajor() : String+setGrade(Grade : String) : void+setClassname(classname : String) : void +setMajor(major : String) : voidStudent—StudentID : String—StudentName : String—Course : Course—couseMark : double+getCourse() : Course+getCouseMark () : double+getStudentID () : String+getStudentName () : String+setCouseMark (couseMark : double) : void+setStudentID (StudentID : String) : void+setStudentName (StudentName : String) : voidCourse—coureNumber : String—courseName : String—coureScore : double—courseHour : double+getCoureNumber () : String+getCoureScore () : double+getCourseHour () : double+getCourseName () : String+setCoureNumber (coureNumber : String) : void +setCoureScore (coureScore: double) : void+setCourseHour (courseHour: double) : void+setCourseName(courseName : String) : voidjava.io.Serializable2.主要方法实现及其他类(总共有20个，简单罗列5个)：（三）系统实现：1.显示全部信息：利用窗口进行显示，而该窗口由菜单栏、滚动窗口、单选按钮和复选按钮组成。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《面向对象程序设计—Java》课程设计报告题目图的最短路径学院（部）信息工程学院专业计算机科学与技术专业班级组长：组员:12 月17 日至12 月28 日共两周指导教师目录1.背景 -------------------------------------------------------------------------22.总体设计------------------------------------------------------------------23. Dijkstra算法实现部分-------------------------------------------------44.图形用户界面--------------------------------------------------------------65.总结-------------------------------------------------------------------------166.相关代码-------------------------------------------------------------------171.背景乘汽车旅行的人总希望找出到目地的尽可能短的行程。

如果有一张地图并在图上标出没对十字路楼之间的距离，可是如何让找出这以最短路径？计算机网络中的路由就是通过互联网把信息从源地址输到目的地址的活动。

为了高效引导数据的传输，如何找出源和目的地址之间的最优路径？这些问题中的网络（交通网，计算机通信网）可以适用一个带权图来建筑，寻找最有路径的需求可转化为带权图的最短径问题。

最短路径问题是图论研究中的一个经典算法问题，问题具体的形式包括：●确定起点的最短路径问题，即已知起始起点，求最短路径问题。

适合使用Dijkstra算法。

●确定终点的最短路径问题，与确定起点的问题相反，该问题是已知终结节点，求最短路径的问题，在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向翻转确定起点的问题。

确定的起点终点的最短路径问题，记忆之起点和终点，求两节点之间的问题。

2.总体设计思路：1.Dijkstra算法实现部分。

2.图形用户界面的设计。

效果图：3.Dijkstra算法功能：根据用户所给出的节点关系矩阵，利用Dijkstra算法计算出某个节点到其余所有节点的最短路径，返回路径的一个数组。

实现：1、通过文件读入用户的矩阵。

2、将矩阵传入Dijkstra算法中，计算出最短路径并返回。

代码：class CaclDijkstra{private static final int Bound=12;private double[][] p=new double[Bound][Bound];private final int INF = 200;private final int Maxsize = 18;FileReader F;BufferedReader B;public static double[][] dp=new double[Bound][Bound];public CaclDijkstra(){try{F=new FileReader("E:\\Text.txt");B=new BufferedReader(F);}catch(IOException Ie){System.out.println("文件不存在!");Ie.printStackTrace();}}public double[][] GetP(){return p;}public void ReaderPrint(){try{String Read=B.readLine();while(Read!=null){String[] a=Read.split(" ");p[Integer.parseInt(a[0])][Integer.parseInt(a[1])]= Double.parseDouble(a[2]);p[Integer.parseInt(a[1])][Integer.parseInt(a[0])]=p[Integer.parseInt(a[0])][ Integer.parseInt(a[1])];Read=B.readLine();}B.close();F.close();for(int m=0;m<Bound;m++){for(int n=0;n<Bound;n++){if(p[m][n]==0.0){p[m][n]=200.0;}}}}catch(IOException Ie){System.out.println("文件读取失败!");Ie.printStackTrace();}}String[] dijkstra(int v) {int i=0;double[] dist;//结点的权String[] s1=new String[Bound];s1[0]="";dist=new double[Maxsize];String[] path;//路径path=new String[Maxsize];char vertex[]={'a','b','c','d','e','f','g','h','i','j','k','l'} ;for(i=0;i< Bound;i++) //初始化数组dist[], path[]{ dist[i]=p[v][i]; path[i]="";if(dist[i]!=INF){ path[i]+=vertex[v]; path[i]+=vertex[i]; }}int[] s =new int[Maxsize];s[0]=v;//初始化集合sdist[v]=0; //标记顶点v为源点int num = 1;while(num<Bound) //当顶点数num小于图的顶点数{double max = INF;//max=INF;int k;for(k=1,i=0;i<Bound;i++){ //在dist中查找最小元素if((dist[i]!=0) && (dist[i]<max)){ k=i; max=dist[k];}}s[num++]=k; //将新生的终点加入集合sfor(i=0;i<Bound;i++){ //修改数组dist和pathif(dist[i]>dist[k]+p[k][i]){ dist[i]=dist[k]+p[k][i];path[i]=path[k]+vertex[i];}}for(i=1;i< Bound;i++){ //输出结果s1[i]=path[i];}dist[k]=0;//置顶点k为已生成终点标记*/}return s1;}}4.图形用户界面的设计功能：首先展现用户的图形关系。

在点击“求最短路径”按钮时，将最短路径在图中画出，并且将最短路径打印出来，将最短距离输出。

实现：1)创建Frame窗体，添加两个Jpanel，在第一个Jpanel中展现图形，第二个添加按钮和相应的JTextFiled用于展示结果。

2)图形展示需要根据节点的个数均分画布区域，然后在每个区域内将节点的位置坐标计算出来。

为了防止节点位于一条直线上从而发生连线重叠现象，需要将节点位置在相应区域内随机。

3)点击“计算最短路径”按钮后，要在原图上使用不同颜色的线连接最短路径，但是为了清楚，应该保持节点坐标不变，将图重绘一遍。

同时将最短路径和距离以文字的形式输出。

代码：import java.io.*;import java.awt.*;import javax.swing.*;import java.io.*;import java.awt.event.*;import java.awt.geom.*;public class Dijkstra extends JFrame {public Dijkstra() {initComponents();}@SuppressWarnings("unchecked")private void initComponents() {int CW=1000;int CH=500;double point[][]=null,dis=0;double c[][];int xb=9;String s[],sdjk="";CaclDijkstra R=new CaclDijkstra();R.ReaderPrint();s=R.dijkstra(0);c=R.GetP();sdj=s[xb];for(int nn=0;nn<sdj.length();nn++){sdjk=sdjk+"A"+(sdj.charAt(nn)-96)+"->";}sdj=sdjk;int dp[][]=new int[12][12];//System.out.println(s[2].length());for(int a=0;a<s[xb].length();a++){for(int b=0;b<s[xb].length();b++){dp[a][b]=dp[b][a]=0;}int dpx,dpy;for(int l=0;l<s[xb].length()-1;l++){dpx=((char)s[xb].charAt(l)-97);dpy=((char)s[xb].charAt(l+1)-97);dp[dpx][dpy]=dp[dpy][dpx]=1;dis=dis+c[dpx][dpy];}sdj=sdj+Double.toString(dis);/*System.out.println();for(int k=0;k<dp.length;k++){for(int f=0;f<dp.length;f++){System.out.print( dp[k][f]+" ");}System.out.println();}*///int Dp[][]={{0},{0,2},{32,4,0},{1,4,0,5}};jPanel1 = new JPanel();canvas1 = new drawPic(null,null,null,3f,12,c,dp,CW,CH);jLabel2 = new JLabel();jPanel2 = new JPanel();jLabel1 = new JLabel();jButton1 = new JButton();jTextField1 = new JTextField();setDefaultCloseOperation(javax.swing.WindowConstants.EXIT_ON_CLOSE);setTitle("Dijkstra");jPanel1.setBackground(new java.awt.Color(153, 255, 255));jPanel1.setBorder(javax.swing.BorderFactory.createTitledBorder(null, "图形", javax.swing.border.TitledBorder.DEFAULT_JUSTIFICATION, javax.swing.border.TitledBorder.DEFAULT_POSITION, null, new java.awt.Color(255, 0, 51)));javax.swing.GroupLayout jPanel1Layout = new javax.swing.GroupLayout(jPanel1);jPanel1.setLayout(jPanel1Layout);jPanel1Layout.setHorizontalGroup(jPanel1Layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADI NG).addGroup(javax.swing.GroupLayout.Alignment.TRAILING, jPanel1Layout.createSequentialGroup().addContainerGap().addComponent(canvas1, CH, CW, javax.swing.GroupLayout.PREFERRED_SIZE).addContainerGap()));jPanel1Layout.setVerticalGroup(jPanel1Layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADI NG).addGroup(jPanel1Layout.createSequentialGroup().addContainerGap().addComponent(canvas1,javax.swing.GroupLayout.PREFERRED_SIZE, 500, javax.swing.GroupLayout.PREFERRED_SIZE).addContainerGap(javax.swing.GroupLayout.DEFAULT_SIZ E, Short.MAX_V ALUE)));jPanel2.setBackground(new java.awt.Color(0, 153, 255));jPanel2.setBorder(javax.swing.BorderFactory.createBevelBorder(javax.swing.bor der.BevelBorder.RAISED));jLabel1.setText("最短路径为：");jTextField1.setEditable(false);jButton1.setText("点击计算最短路径");jButton1.addActionListener(new java.awt.event.ActionListener() { public void actionPerformed(java.awt.event.ActionEvent evt) {jButton1ActionPerformed(evt);}});javax.swing.GroupLayout jPanel2Layout = new javax.swing.GroupLayout(jPanel2);jPanel2.setLayout(jPanel2Layout);jPanel2Layout.setHorizontalGroup(jPanel2Layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADING).addGroup(jPanel2Layout.createSequentialGroup().addContainerGap().addGroup(jPanel2Layout.createParallelGroup(javax.swing.Gr oupLayout.Alignment.LEADING).addGroup(jPanel2Layout.createSequentialGroup().addComponent(jLabel1).addPreferredGap(pon entPlacement.RELATED).addComponent(jTextField1)).addGroup(jPanel2Layout.createSequentialGroup().addComponent(jButton1).addGap(0, 0, Short.MAX_V ALUE))).addContainerGap()));jPanel2Layout.setVerticalGroup(jPanel2Layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADI NG).addGroup(javax.swing.GroupLayout.Alignment.TRAILING, jPanel2Layout.createSequentialGroup().addGap(24, 24, 24).addComponent(jButton1).addPreferredGap(ponentPlace ment.RELATED, 23, Short.MAX_V ALUE).addGroup(jPanel2Layout.createParallelGroup(javax.swing.Gr oupLayout.Alignment.BASELINE).addComponent(jLabel1).addComponent(jTextField1,javax.swing.GroupLayout.PREFERRED_SIZE,javax.swing.GroupLayout.DEFAULT_SIZE,javax.swing.GroupLayout.PREFERRED_SIZE)).addContainerGap()));javax.swing.GroupLayout layout = new javax.swing.GroupLayout(getContentPane());getContentPane().setLayout(layout);layout.setHorizontalGroup(layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADING) .addGroup(layout.createSequentialGroup().addContainerGap().addGroup(layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADING).addComponent(jPanel2,javax.swing.GroupLayout.DEFAULT_SIZE,javax.swing.GroupLayout.DEFAULT_SIZE, Short.MAX_V ALUE).addComponent(jPanel1,javax.swing.GroupLayout.DEFAULT_SIZE,javax.swing.GroupLayout.DEFAULT_SIZE, Short.MAX_V ALUE)).addContainerGap()));layout.setVerticalGroup(layout.createParallelGroup(javax.swing.GroupLayout.Alignment.LEADING) .addGroup(layout.createSequentialGroup().addContainerGap().addComponent(jPanel1,javax.swing.GroupLayout.PREFERRED_SIZE,javax.swing.GroupLayout.DEFAULT_SIZE,javax.swing.GroupLayout.PREFERRED_SIZE).addGap(18, 18, 18).addComponent(jPanel2,javax.swing.GroupLayout.PREFERRED_SIZE,javax.swing.GroupLayout.DEFAULT_SIZE,javax.swing.GroupLayout.PREFERRED_SIZE).addContainerGap(javax.swing.GroupLayout.DEFAULT_SIZ E, Short.MAX_V ALUE)));pack();}private void jTextField1ActionPerformed(java.awt.event.ActionEvent evt) { }private void jButton1ActionPerformed(ActionEvent e){ //按钮动作*******jTextField1.setText(sdj);drawPic.repaint=REPAINT;canvas1.repaint();}public static void main(String args[]) {try {for (UIManager.LookAndFeelInfo info : UIManager.getInstalledLookAndFeels()) {if ("Nimbus".equals(info.getName())) {UIManager.setLookAndFeel(info.getClassName());break;}}} catch (ClassNotFoundException ex) {java.util.logging.Logger.getLogger(Dijkstra.class.getName()).log(java.util.logging .Level.SEVERE, null, ex);} catch (InstantiationException ex) {java.util.logging.Logger.getLogger(Dijkstra.class.getName()).log(java.util.logging .Level.SEVERE, null, ex);} catch (IllegalAccessException ex) {java.util.logging.Logger.getLogger(Dijkstra.class.getName()).log(java.util.logging .Level.SEVERE, null, ex);} catch (UnsupportedLookAndFeelException ex) {java.util.logging.Logger.getLogger(Dijkstra.class.getName()).log(java.util.logging .Level.SEVERE, null, ex);}java.awt.EventQueue.invokeLater(new Runnable() {@Overridepublic void run() {new Dijkstra().setVisible(true);}});/* test=new ();Node start=test.init();putePath(start);s=test.printPathInfo(); */}private drawPic canvas1;private JButton jButton1;private JLabel jLabel1;private JLabel jLabel2;private JPanel jPanel1;private JPanel jPanel2;private JTextField jTextField1;private final String REPAINT="YES";private static String sdj;}class drawPic extends Canvas{private Graphics2D Pic=null;private Color BgColor=new Color(100,180,100);private Color UsualColor=new Color(0,0,0);private Color PColor=new Color(100,100,100);private Color SpeColor=new Color(0,0,255);private float PenWidth=3f;private int pNum=1;private double Width;private double Height;private double p[][];//private double p[][]={{50.0,200.0},{50.0,400.0},{200.0,200.0},{200.0,400.0}};private double conn[][]=null;private int Dp[][]=null;public static String repaint;//构造函数drawPic(Color BgColor,Color UsualColor,Color SpeColor,float PenWidth,int pNum,double args[][],int dp[][],double Width,double Height){if(BgColor!=null){this.BgColor=BgColor;}if(UsualColor!=null){ualColor=UsualColor;}if(SpeColor!=null){this.SpeColor=SpeColor;}this.pNum=pNum;this.conn=args;this.Width=Width;this.Height=Height;this.Dp=dp;}@Overridepublic void paint(Graphics g){Pic=(Graphics2D)g;//setBackground(new Color(255,255,255));setBackground(new Color(250,250,250));Pic.setColor(UsualColor);if(repaint!="YES"){//调用CalcDis函数计算节点坐标CalcDis();//写文字//drawWord();//调用drawPoint方法画节点drawPoint();//调用connect方法链接节点connect();}else{drawPoint();connect();}}//写数字protected void drawWord(double s,int xd,int yd){Pic.setColor(new Color(255,0,200));Pic.drawString(Double.toString(s), xd, yd);}//画节点——描绘一个圆形直径为40protected void drawPoint(){for(int i=0;i<p.length;i++){Pic.setColor(new Color(0,255,51));Pic.setStroke(new BasicStroke(PenWidth));Ellipse2D.Double circle;circle = new Ellipse2D.Double(p[i][0],p[i][1],30,30);Pic.draw(circle);Pic.setColor(new Color(0,0,0));Pic.setStroke(new BasicStroke(50));Pic.drawString("A"+Integer.toString(i+1),(float)p[i][0]+8, (float)p[i][1]);}}//连线protected void connect(){for(int i=0;i<p.length;i++){for(int j=0;j<i;j++){if(conn[i][j]!=200){Line2D.Double line=new Line2D.Double(p[i][0]+15,p[i][1]+15,p[j][0]+15,p[j][1]+15);Pic.setColor(new Color(150,150,200));Pic.setStroke(new BasicStroke(2));Pic.draw(line);//打印节点名称//写上节点间距离,调用drawWord函数double xd=(p[i][0]+p[j][0])/2;double yd=(p[i][1]+p[j][1])/2+20;drawWord(conn[i][j],(int)xd,(int)yd);}}}if(repaint=="YES"){for(int i=0;i<Dp.length;i++){for(int j=0;j<i;j++){if(Dp[i][j]!=0){Line2D.Double line=new Line2D.Double(p[i][0]+15,p[i][1]+15,p[j][0]+15,p[j][1]+15);Pic.setColor(new Color(255,0,0));Pic.setStroke(new BasicStroke(2));Pic.draw(line);}}}}}//计算节点的坐标/*** W、H 分别是圆心坐标可随机的宽度和高度* xL、yL分别是圆心的横纵坐标* Wr、Hr分别是从基本位置增加的X和Y坐标的量* xW 、yH分别是计算出来的基本坐标*/protected void CalcDis(){int i=0,j=0;double W=0,H=0,z=0,xL=0,yL=0,xW=0,yH=0,Wr=0,Hr=0;double p1[][]=new double[pNum][2];boolean flag=true;for(i=1;flag;i++){for(j=1;flag&&j<=i;j++){if(i*j>=pNum){flag=false;//System.out.println("j*i= "+j*i);W=Width/i-40;H=Height/j-40;//System.out.println("W= "+W + " H= " +H);//把每个节点的坐标计算出来for(int h=0;h<pNum;h++){z=(h)%i;System.out.println("i= "+i +" j= "+ j);xW=(20+(z)*(40+W));System.out.println("xW= "+xW+" z= "+z);yH=(20+(Math.floor(h/i))*(H+40));System.out.println("Math.floor((h+1)/i)= "+Math.floor((h+1)/i));System.out.println("yH= "+yH);Wr=Math.random()*W;Hr=Math.random()*H;xL=xW+Wr;yL=yH+Hr;p1[h][0]=xL;System.out.println();p1[h][1]=yL;System.out.println("横坐标："+p1[h][0]+" 纵坐标："+ p1[h][1]);}}}}p=p1;}//类结束标记}5.总结经验：在此次课程设计中，按照功能模块的不同进行了分组。