期末复习题三(材料题部分)
【解析版】初中数学八年级下期末经典复习题(课后培优)(3)

一、选择题1.(0分)[ID :10227]若63n 是整数,则正整数n 的最小值是( )A .4B .5C .6D .72.(0分)[ID :10223]下列各命题的逆命题成立的是( )A .全等三角形的对应角相等B .如果两个数相等,那么它们的绝对值相等C .两直线平行,同位角相等D .如果两个角都是45°,那么这两个角相等3.(0分)[ID :10222]一次函数y kx b =+的图象如图所示,点()3,4P 在函数的图象上.则关于x 的不等式4kx b +≤的解集是( )A .3x ≤B .3x ≥C .4x ≤D .4x ≥ 4.(0分)[ID :10220]顺次连接对角线互相垂直且相等的四边形各边中点所围成的四边形是( )A .矩形B .菱形C .正方形D .平行四边形5.(0分)[ID :10218]某体育用品商店一天中卖出某种品牌的运动鞋15双,其中各种尺码的鞋的销售量如表所示: 鞋的尺码/cm 2323.5 24 24.5 25 销售量/双 1 3 3 6 2 则这15双鞋的尺码组成的一组数据中,众数和中位数分别为( )A .24.5,24.5B .24.5,24C .24,24D .23.5,246.(0分)[ID :10217]已知M 、N 是线段AB 上的两点,AM =MN =2,NB =1,以点A 为圆心,AN 长为半径画弧;再以点B 为圆心,BM 长为半径画弧,两弧交于点C ,连接AC ,BC ,则△ABC 一定是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形7.(0分)[ID :10208]下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有()个.A.4B.3C.2D.18.(0分)[ID:10202]如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是()A.30B.36C.54D.729.(0分)[ID:10193]如图,以 Rt△ABC的斜边 BC为一边在△ABC的同侧作正方形 BCEF,设正方形的中心为 O,连接 AO,如果 AB=4,AO=62,那么 AC 的长等于()A.12B.16C.43D.8210.(0分)[ID:10180]如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是()A.B.C.D.的自变量取值范围是( )11.(0分)[ID:10175]函数y=√x+3A.x≠0B.x>﹣3C.x≥﹣3且x≠0D.x>﹣3且x≠0 12.(0分)[ID:10171]()23-)A.﹣3B.3或﹣3C.9D.313.(0分)[ID:10167]如图,在▱ABCD中,AB=6,BC=8,∠BCD的平分线交AD于点E,交BA的延长线于点F,则AE+AF的值等于()A .2B .3C .4D .614.(0分)[ID :10157]如图,一个工人拿一个2.5米长的梯子,底端A 放在距离墙根C 点0.7米处,另一头B 点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑( )米A .0.4B .0.6C .0.7D .0.815.(0分)[ID :10152]正比例函数()0y kx k =≠的函数值y 随x 的增大而增大,则y kx k =-的图象大致是( )A .B .C .D .二、填空题16.(0分)[ID :10325]将一次函数y=3x ﹣1的图象沿y 轴向上平移3个单位后,得到的图象对应的函数关系式为__.17.(0分)[ID :10319]在平面直角坐标系xOy 中,一次函数y =kx 和y =﹣x +3的图象如图所示,则关于x 的一元一次不等式kx <﹣x +3的解集是_____.18.(0分)[ID :10309]若ab <0,则代数式2a b 可化简为_____.19.(0分)[ID :10301]如图所示,将四根木条组成的矩形木框变成▱ABCD 的形状,并使其面积变为原来的一半,则这个平行四边形的一个最小的内角的度数是_____.20.(0分)[ID :10295]一艘轮船在小岛A 的北偏东60°方向距小岛80海里的B 处,沿正西方向航行3小时后到达小岛的北偏西45°的C 处,则该船行驶的速度为____________海里/时.21.(0分)[ID :10281]如图,在平行四边形ABCD 中,AB =3,BC =5,∠B 的平分线BE 交AD 于点E ,则DE 的长为____________.22.(0分)[ID :10260]在ABC ∆中,13AC BC ==, 10AB =,则ABC ∆面积为_______. 23.(0分)[ID :10259]甲、乙、丙三人进行飞镖比赛,已知他们每人五次投得的成绩如图6-Z -2所示,那么三人中成绩最稳定的是________.24.(0分)[ID :10251]A 、B 、C 三地在同一直线上,甲、乙两车分别从A ,B 两地相向匀速行驶,甲车先出发2小时,甲车到达B 地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A 地后,继续保持原速向远离B 的方向行驶,经过一段时间后两车同时到达C 地,设两车之间的距离为y (千米),甲行驶的时间x (小时).y 与x 的关系如图所示,则B 、C 两地相距_____千米.25.(0分)[ID :10246]一组数据:1、2、5、3、3、4、2、4,它们的平均数为_______,中位数为_______,方差是_______.三、解答题26.(0分)[ID :10421]如图,菱形ABCD 中,对角线AC 、BD 交于O 点,DE ∥AC ,CE ∥BD .(1)求证:四边形OCED为矩形;(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.27.(0分)[ID:10412]如图,在Rt△ABC中,∠A=90°,∠B=30°,D、E分别是AB、BC 的中点,若DE=3,求B C的长.28.(0分)[ID:10365]如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC 上的点,AE=CF,并且∠AED=∠CF D.求证:(1)△AED≌△CFD;(2)四边形ABCD是菱形.29.(0分)[ID:10359]已知:如图,E,F是正方形ABCD的对角线BD上的两点,且BE DF=.求证:四边形AECF是菱形.30.(0分)[ID:10337]将函数y=x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|x+b|(b为常数)的图象(1)当b=0时,在同一直角坐标系中分别画出函数112y x=+与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,112x+比|x|大?(2)若函数y=|x+b|(b为常数)的图象在直线y=1下方的点的横坐标x满足0<x<3,直接写出b的取值范围【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.D2.C3.A4.C5.A6.B7.C8.D9.B10.C11.B12.D13.C14.D15.B二、填空题16.y=3x+2【解析】【详解】将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后可得y=3x﹣1+3=3x+2故答案为y=3x+217.x<1【解析】观察图象即可得不等式kx<-x+3的解集是x<1点睛:本题主要考查了一次函数的交点问题及一次函数与一元一次不等式之间的关系会利用数形结合思想是解决本题的关键18.【解析】【分析】二次根式有意义就隐含条件b>0由ab<0先判断出ab的符号再进行化简即可【详解】若ab<0且代数式有意义;故有b>0a<0;则代数式=|a|=-a故答案为:-a【点睛】本题主要考查二19.30°【解析】【分析】过A作AE⊥BC于点E由四根木条组成的矩形木框变成▱ABCD的形状面积变为原来的一半可得AE=AB由此即可求得∠ABE=30°即平行四边形中最小的内角为30°【详解】解:过A作20.【解析】【分析】设该船行驶的速度为x海里/时由已知可得BC=3xAQ⊥BC∠BAQ=60°∠CAQ=45°AB=80海里在直角三角形ABQ中求出AQBQ再在直角三角形AQC中求出CQ得出BC=40+21.2【解析】【分析】根据平行四边形的性质可得出AD∥BC则∠AEB=∠CBE再由∠ABE =∠CBE则∠AEB=∠ABE则AE=AB从而求出DE【详解】解:∵四边形ABCD是平行四边形∴AD∥BC∴∠A22.60【解析】【分析】根据题意可以判断为等腰三角形利用勾股定理求出AB边的高即可得到答案【详解】如图作出AB边上的高CD∵AC=BC=13AB=10∴△ABC是等腰三角形∴AD=BD=5根据勾股定理C23.乙【解析】【分析】通过图示波动的幅度即可推出【详解】通过图示可看出一至三次甲乙丙中乙最稳定波动最小四至五次三人基本一样故选乙【点睛】考查数据统计的知识点24.【解析】【分析】根据题意和函数图象中的数据可以求得甲乙两车的速度再根据路程=速度×时间即可解答本题【详解】解:设甲车的速度为a千米/小时乙车的速度为b千米/小时解得∴AB两地的距离为:80×9=7225.33【解析】【分析】根据平均数的公式即可求出答案将数据按照由小到大的顺序重新排列中间两个数的平均数即是中位数根据方差的公式计算即可得到这组数据的方差【详解】平均数=将数据重新排列是:12233445三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.D解析:D【解析】【分析】7n是完全平方数,满足条件的最小正整数n为7.【详解】∴7n是完全平方数;∴n的最小正整数值为7.故选:D.【点睛】主要考查了乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.二次根式的运算法则:乘法法则a b ab ⋅=,除法法则b b a a=.解题关键是分解成一个完全平方数和一个代数式的积的形式. 2.C解析:C【解析】试题分析:首先写出各个命题的逆命题,再进一步判断真假.解:A 、逆命题是三个角对应相等的两个三角形全等,错误;B 、绝对值相等的两个数相等,错误;C 、同位角相等,两条直线平行,正确;D 、相等的两个角都是45°,错误.故选C .3.A解析:A【解析】【分析】观察函数图象结合点P 的坐标,即可得出不等式的解集.【详解】解:观察函数图象,可知:当3x ≤时,4kx b +≤.故选:A .【点睛】考查了一次函数与一元一次不等式以及一次函数的图象,观察函数图象,找出不等式4kx b +≤的解集是解题的关键.4.C解析:C【解析】【分析】根据三角形中位线定理得到所得四边形的对边都平行且相等,那么其为平行四边形,再根据邻边互相垂直且相等,可得四边形是正方形.【详解】解:∵E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点,∴EH//FG//BD ,EF//AC//HG ,EH =FG =12BD ,EF =HG =12AC , ∴四边形EFGH 是平行四边形,∵AC ⊥BD ,AC =BD ,∴EF ⊥FG ,FE =FG ,∴四边形EFGH 是正方形,故选:C .【点睛】本题考查的是三角形中位线定理以及正方形的判定,解题的关键是构造三角形利用三角形的中位线定理解答.5.A解析:A【解析】【分析】根据众数和中位数的定义进行求解即可得.【详解】这组数据中,24.5出现了6次,出现的次数最多,所以众数为24.5,这组数据一共有15个数,按从小到大排序后第8个数是24.5,所以中位数为24.5, 故选A .【点睛】本题考查了众数、中位数,熟练掌握中位数、众数的定义以及求解方法是解题的关键.6.B解析:B【解析】【分析】依据作图即可得到AC =AN =4,BC =BM =3,AB =2+2+1=5,进而得到AC 2+BC 2=AB 2,即可得出△ABC 是直角三角形.【详解】如图所示,AC =AN =4,BC =BM =3,AB =2+2+1=5,∴AC 2+BC 2=AB 2,∴△ABC 是直角三角形,且∠ACB =90°,故选B .【点睛】本题主要考查了勾股定理的逆定理,如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2,那么这个三角形就是直角三角形.7.C解析:C【解析】【分析】【详解】∵四边相等的四边形一定是菱形,∴①正确;∵顺次连接矩形各边中点形成的四边形一定是菱形,∴②错误;∵对角线相等的平行四边形才是矩形,∴③错误;∵经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分,∴④正确;其中正确的有2个,故选C.考点:中点四边形;平行四边形的性质;菱形的判定;矩形的判定与性质;正方形的判定.8.D解析:D【解析】【分析】求▱ABCD的面积,就需求出BC边上的高,可过D作DE∥AM,交BC的延长线于E,那么四边形ADEM也是平行四边形,则AM=DE;在△BDE中,三角形的三边长正好符合勾股定理的逆定理,因此△BDE是直角三角形;可过D作DF⊥BC于F,根据三角形面积的不同表示方法,可求出DF的长,也就求出了BC边上的高,由此可求出四边形ABCD的面积.【详解】作DE∥AM,交BC的延长线于E,则ADEM是平行四边形,∴DE=AM=9,ME=AD=10,又由题意可得,BM=12BC=12AD=5,则BE=15,在△BDE中,∵BD2+DE2=144+81=225=BE2,∴△BDE是直角三角形,且∠BDE=90°,过D作DF⊥BE于F,则DF=365 BD DEBE⋅=,∴S▱ABCD=BC•FD=10×365=72.【点睛】此题主要考查平行四边形的性质和勾股定理的逆定理,正确地作出辅助线,构造直角三角形是解题的关键.9.B解析:B【解析】【分析】首选在AC 上截取4CG AB ==,连接OG ,利用SAS 可证△ABO ≌△GCO ,根据全等三角形的性质可以得到:62OA OG ==,AOB COG ∠=∠,则可证△AOG 是等腰直角三角形,利用勾股定理求出12AG =,从而可得AC 的长度.【详解】解:如下图所示,在AC 上截取4CG AB ==,连接OG ,∵四边形BCEF 是正方形,90BAC ∠=︒,∴OB OC =,90BAC BOC ∠=∠=︒,∴点B 、A 、O 、C 四点共圆,∴ABO ACO ∠=∠,在△ABO 和△GCO 中,{BA CGABO ACO OB OC=∠=∠=,∴△ABO ≌△GCO ,∴62OA OG ==,AOB COG ∠=∠,∵90BOC COG BOG ∠=∠+∠=︒,∴90AOG AOB BOG ∠=∠+∠=︒,∴△AOG 是等腰直角三角形,∴()()22626212AG =+=,∴12416AC =+=.故选:B .本题考查正方形的性质;全等三角形的判定与性质;勾股定理;直角三角形的性质.10.C解析:C【解析】【分析】根据m、n同正,同负,一正一负时利用一次函数的性质进行判断.【详解】解:①当mn>0时,m、n同号,y=mnx过一三象限;同正时,y=mx+n经过一、二、三象限,同负时,y=mx+n过二、三、四象限;②当mn<0时,m、n异号,y=mnx过二四象限,m>0,n<0时,y=mx+n经过一、三、四象限;m<0,n>0时,y=mx+n过一、二、四象限;故选:C.【点睛】本题考查了一次函数的性质,熟练掌握一次函数的性质是解题的关键.11.B解析:B【解析】【分析】【详解】由题意得:x+3>0,解得:x>-3.故选B.12.D解析:D【解析】【分析】本题考查二次根式的化简,(0)(0)a aa a⎧=⎨-<⎩.【详解】|3|3=-=.故选D.【点睛】本题考查了根据二次根式的意义化简.a≥0a;当a≤0a.13.C解析:C【解析】【详解】解:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC=8,CD=AB=6,∴∠F=∠DCF,∵∠C平分线为CF,∴∠FCB=∠DCF,∴∠F=∠FCB,∴BF=BC=8,同理:DE=CD=6,∴AF=BF−AB=2,AE=AD−DE=2∴AE+AF=4故选C14.D解析:D【解析】【分析】【详解】解:∵AB=2.5米,AC=0.7米,∴BC(米).∵梯子的顶部下滑0.4米,∴BE=0.4米,∴EC=BC﹣0.4=2(米),∴DC(米),∴梯子的底部向外滑出AD=1.5﹣0.7=0.8(米).故选D.【点睛】此题主要考查了勾股定理在实际生活中的应用,关键是掌握直角三角形中,两直角边的平方和等于斜边的平方.15.B解析:B【解析】【分析】由于正比例函数y=kx(k≠0)函数值随x的增大而增大,可得k>0,-k<0,然后判断一次函数y=kx-k的图象经过的象限即可.【详解】解:∵正比例函数y=kx(k≠0)函数值随x的增大而增大,∴k>0,∴-k<0,∴一次函数y=kx-k的图象经过一、三、四象限;故选:B.本题主要考查了一次函数的图象,一次函数y=kx+b(k≠0)中k,b的符号与图象所经过的象限如下:当k>0,b>0时,图象过一、二、三象限;当k>0,b<0时,图象过一、三、四象限;k<0,b>0时,图象过一、二、四象限;k<0,b<0时,图象过二、三、四象限.二、填空题16.y=3x+2【解析】【详解】将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后可得y=3x﹣1+3=3x+2故答案为y=3x+2解析:y=3x+2.【解析】【详解】将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,可得y=3x﹣1+3=3x+2.故答案为y=3x+2.17.x<1【解析】观察图象即可得不等式kx<-x+3的解集是x<1点睛:本题主要考查了一次函数的交点问题及一次函数与一元一次不等式之间的关系会利用数形结合思想是解决本题的关键解析:x<1【解析】观察图象即可得不等式kx<-x+3的解集是x<1.点睛:本题主要考查了一次函数的交点问题及一次函数与一元一次不等式之间的关系,会利用数形结合思想是解决本题的关键.18.【解析】【分析】二次根式有意义就隐含条件b>0由ab<0先判断出ab的符号再进行化简即可【详解】若ab<0且代数式有意义;故有b>0a<0;则代数式=|a|=-a故答案为:-a【点睛】本题主要考查二解析:【解析】【分析】二次根式有意义,就隐含条件b>0,由ab<0,先判断出a、b的符号,再进行化简即可.【详解】若ab<0故有b>0,a<0;.故答案为:.【点睛】本题主要考查二次根式的化简方法与运用:当a>0;当a<0;当a=0.19.30°【解析】【分析】过A作AE⊥BC于点E由四根木条组成的矩形木框变成▱ABCD的形状面积变为原来的一半可得AE=AB由此即可求得∠ABE=30°即平行四边形中最小的内角为30°【详解】解:过A作解析:30°【解析】【分析】过A作AE⊥BC于点E,由四根木条组成的矩形木框变成▱ABCD的形状,面积变为原来的一半,可得AE=12AB,由此即可求得∠ABE=30°,即平行四边形中最小的内角为30°.【详解】解:过A作AE⊥BC于点E,如图所示:由四根木条组成的矩形木框变成▱ABCD的形状,面积变为原来的一半,得到AE=12AB,又△ABE为直角三角形,∴∠ABE=30°,则平行四边形中最小的内角为30°.故答案为:30°【点睛】本题考查了平行四边形的面积公式及性质,根据题意求得AE=12AB是解决问题的关键.20.【解析】【分析】设该船行驶的速度为x海里/时由已知可得BC=3xAQ⊥BC∠BAQ=60°∠CAQ=45°AB=80海里在直角三角形ABQ中求出AQBQ 再在直角三角形AQC中求出CQ得出BC=40+404033【解析】【分析】设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+3=3x,解方程即可.【详解】如图所示:该船行驶的速度为x海里/时,3小时后到达小岛的北偏西45°的C处,由题意得:AB=80海里,BC=3x海里,在直角三角形ABQ中,∠BAQ=60°,∴∠B=90°−60°=30°,∴AQ=12AB=40,BQ3AQ=3在直角三角形AQC中,∠CAQ=45°,∴CQ=AQ=40,∴BC=40+33x,解得:x=4033+.40403+/时;40403+【点睛】本题考查的是解直角三角形,熟练掌握方向角是解题的关键.21.2【解析】【分析】根据平行四边形的性质可得出AD∥BC则∠AEB=∠CBE 再由∠ABE=∠CBE则∠AEB=∠ABE则AE=AB从而求出DE【详解】解:∵四边形ABCD是平行四边形∴AD∥BC∴∠A解析:2【解析】【分析】根据平行四边形的性质,可得出AD∥BC,则∠AEB=∠CBE,再由∠ABE=∠CBE,则∠AEB=∠ABE,则AE=AB,从而求出DE.【详解】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE,∵∠B的平分线BE交AD于点E,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AE =AB ,∵AB =3,BC =5,∴DE =AD -AE =BC -AB =5-3=2.故答案为2.【点睛】本题考查了平行四边形的性质、角平分线的定义,解题的关键是掌握平行四边形的性质:对边相等.22.60【解析】【分析】根据题意可以判断为等腰三角形利用勾股定理求出AB 边的高即可得到答案【详解】如图作出AB 边上的高CD∵AC=BC=13AB=10∴△ABC 是等腰三角形∴AD=BD=5根据勾股定理C 解析:60【解析】【分析】根据题意可以判断ABC ∆为等腰三角形,利用勾股定理求出AB 边的高,即可得到答案.【详解】如图作出AB 边上的高CD∵AC=BC=13, AB=10,∴△ABC 是等腰三角形,∴AD=BD=5,根据勾股定理 CD 2=AC 2-AD 2, 22135-,12ABC SCD AB =⋅=112102⨯⨯=60, 故答案为:60.【点睛】 此题主要考查了等腰三角形的判定及勾股定理,关键是判断三角形的形状,利用勾股定理求出三角形的高.23.乙【解析】【分析】通过图示波动的幅度即可推出【详解】通过图示可看出一至三次甲乙丙中乙最稳定波动最小四至五次三人基本一样故选乙【点睛】考查数据统计的知识点解析:乙【解析】【分析】通过图示波动的幅度即可推出.【详解】通过图示可看出,一至三次甲乙丙中,乙最稳定,波动最小,四至五次三人基本一样,故选乙【点睛】考查数据统计的知识点24.【解析】【分析】根据题意和函数图象中的数据可以求得甲乙两车的速度再根据路程=速度×时间即可解答本题【详解】解:设甲车的速度为a 千米/小时乙车的速度为b 千米/小时解得∴AB 两地的距离为:80×9=72解析:【解析】【分析】根据题意和函数图象中的数据,可以求得甲乙两车的速度,再根据“路程=速度×时间”,即可解答本题.【详解】解:设甲车的速度为a 千米/小时,乙车的速度为b 千米/小时,(62)()560(62)(96)a b b a -⨯+=⎧⎨-=-⎩,解得8060a b =⎧⎨=⎩, ∴A 、B 两地的距离为:80×9=720千米, 设乙车从B 地到C 地用的时间为x 小时,60x =80(1+10%)(x+2﹣9),解得,x =22,则B 、C 两地相距:60×22=1320(千米) 故答案为:1320.【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.25.33【解析】【分析】根据平均数的公式即可求出答案将数据按照由小到大的顺序重新排列中间两个数的平均数即是中位数根据方差的公式计算即可得到这组数据的方差【详解】平均数=将数据重新排列是:12233445解析:3, 3,32. 【解析】【分析】根据平均数的公式即可求出答案,将数据按照由小到大的顺序重新排列,中间两个数的平均数即是中位数,根据方差的公式计算即可得到这组数据的方差.【详解】平均数=1(12533424)38⨯+++++++=,将数据重新排列是:1、2、2、3、3、4、4、5,∴中位数是3332+=, 方差=222221(13)2(23)2(33)2(43)(53)8⎡⎤⨯-+⨯-+⨯-+⨯-+-⎣⎦=32, 故答案为:3,3,32. 【点睛】此题考查计算能力,计算平均数,中位数,方差,正确掌握各计算的公式是解题的关键.三、解答题26.(1)证明见解析;(2)2165. 【解析】【分析】(1)由DE ∥AC ,CE ∥BD 可得四边形OCED 为平行四边形,又AC ⊥BD 从而得四边形OCED 为矩形;(2)过点O 作OH ⊥BC ,垂足为H ,由已知可得三角形OBC 、OCD 的面积,BC 的长,由面积法可得OH 的长,从而可得三角形OCF 的面积,三角形OCD 与三角形OCF 的和即为所求.【详解】(1)∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形.又∵四边形ABCD 是菱形,∴AC ⊥BD .∴∠DOC=90°.∴四边形OCED 为矩形.(2)∵菱形ABCD ,∴AC 与BD 互相垂直平分于点O ,∴OD =OB =12BD =6,OA =OC =12AC =8,∴CF=CO=8,S △BOC =S △DOC =12OD OC ⋅=24,在Rt △OBC 中,BC =10,.作OH ⊥BC 于点H ,则有12BC·OH=24,∴OH=245,∴S △COF =12CF·OH=965.∴S 四边形OFCD =S △DOC +S △OCF =2165.【点睛】本题考查菱形的性质,矩形的判定与性质,勾股定理,三角形面积的计算方法等知识点,熟练掌握基础知识点,计算出OH 的长度是解题关键.27.【解析】【分析】根据三角形中位线定理得AC=2DE=6,再根据30°的角所对的直角边等于斜边的一半求出BC 的长即可.【详解】∵ D 、E 是AB 、BC 的中点,DE=3∴AC=2DE=6∵∠A=90°,∠B=30°∴BC=2AC=12.【点睛】此题主要考查了三角形中位线定理以及30°的角所对的直角边等于斜边的一半,熟练掌握定理是解题的关键.28.(1)证明见解析;(2)证明见解析.【解析】分析:(1)由全等三角形的判定定理ASA 证得结论;(2)由“邻边相等的平行四边形为菱形”证得结论.详解:(1)证明:∵四边形ABCD 是平行四边形,∴∠A=∠C .在△AED 与△CFD 中,A C AE CFAED CFD ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AED ≌△CFD (ASA );(2)由(1)知,△AED ≌△CFD ,则AD=CD .又∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形.点睛:考查了菱形的判定,全等三角形的判定与性质以及平行四边形的性质,解题的关键是掌握相关的性质与定理.29.见解析【解析】【分析】连接AC,交BD于O,由正方形的性质可得OA=OC,OB=OD,AC⊥BD根据BE=DF可得OE=OF,由对角线互相垂直平分的四边形是菱形即可判定,【详解】∵四边形ABCD是正方形,∴OD=OB,OA=OC,BD⊥AC,∵BE=DF,∴DE=BF,∴OE=OF,∵OA=OC,AC⊥EF,OE=OF,∴四边形AECF为菱形.【点睛】本题考查了正方形对角线互相垂直平分的性质,考查了菱形的判定,对角线互相垂直且互相平分的四边形是菱形,熟练掌握菱形的判定方法是解题关键.30.(1)见解析,223x-<<;(2)21b--【解析】【分析】(1)画出函数图象,求出两个函数图象的交点坐标,利用图象法即可解决问题;(2)利用图象法即可解决问题.【详解】解:(1)当b=0时,y=|x+b|=|x|列表如下:x-101112y x =+ 121 12 y =|x|1 0 1 描点并连线;∴如图所示:该函数图像为所求∵1y x 12||y x ⎧=+⎪⎨⎪⎩= ∴2x=-32=-y 3⎧⎪⎪⎨⎪⎪⎩或y=x=22⎧⎨⎩ ∴两个函数的交点坐标为A 2233⎛⎫- ⎪⎝⎭,,B(2,2), ∴观察图象可知:223x -<<时,112x +比||x 大; (2)如图,观察图象可知满足条件的b 的值为21b --,【点睛】本题主要考查了一次函数的图象,一次函数的性质,一次函数图象与几何变换,掌握一次函数的图象,一次函数的性质,一次函数图象与几何变换是解题的关键.。
四川省成都市2023-2024学年高二上学期期末复习数学试题(三)含解析

成都高2025届高二期末考试数学复习试题(三)(答案在最后)一、单选题(共8个小题,每个小题5分,共40分)1.设直线l sin 20y θ++=,则直线l 的倾斜角的取值范围是()A.[)0,πB.πππ2π,,3223⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦C.π2π,33⎡⎤⎢⎥⎣⎦D.π2π0,,π33⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭U 【答案】D 【解析】【分析】根据直线斜率的范围求倾斜角的取值范围.sin 20y θ++=的倾斜角为[)0πa a Î,,,则由直线可得tan a q =Î,所以π2π0,,π33a 轾轹÷Î犏÷犏臌滕,故选:D2.能够使得圆x 2+y 2-2x +4y +1=0上恰有两个点到直线2x +y +c =0距离等于1的c 的一个值为()A.2B.C.3D.【答案】C 【解析】【分析】利用圆心到直线的距离大于1且小于3,列不等式求解即可.【详解】由圆的标准方程()()22124x y -++=,可得圆心为()1,2-,半径为2,根据圆的性质可知,当圆心到直线的距离大于1且小于3时,圆上有两点到直线20x y c ++=的距离为1,由()1,3d =可得(c ∈-⋃,经验证,3c =∈,符合题意,故选C.【点睛】本题主要考查圆的标准方程,点到直线距离公式的距离公式以及圆的几何性质,意在考查数形结合思想的应用,属于中档题.3.若椭圆的中心为原点,对称轴为坐标轴,短轴的一个端点与两焦点构成个正三角形,焦点到椭圆上点的)A.221129x y +=B.221129x y +=或221912x y +=C.2213612x y += D.以上都不对【答案】B 【解析】【分析】由短轴的一个端点与两焦点构成个正三角形可得b =,由焦点到椭圆上点的最短距离为a c -,结合222a b c =+可得.【详解】由题意,当椭圆焦点在x 轴上,设椭圆方程为:22221x ya b+=,由题意b =,a c -=所以2a c ===,c =a =,3b =,所以椭圆方程为:221129x y +=,当椭圆焦点在y 轴上时,同理可得:221912x y+=,故选:B4.某市经济开发区的经济发展取得阶段性成效,为深入了解该区的发展情况,现对该区两企业进行连续11个月的调研,得到两企业这11个月利润增长指数折线图(如下图所示),下列说法正确的是()A.这11个月甲企业月利润增长指数的平均数没超过82%B.这11个月的乙企业月利润增长指数的第70百分位数小于82%C.这11个月的甲企业月利润增长指数较乙企业更稳定D.在这11个月中任选2个月,则这2个月乙企业月利润增长指数都小于82%的概率为411【答案】C 【解析】【分析】根据折线图估算AC ,对于B 项把月利润增长指数从小到大排列,计算1170⨯%=7.7可求,对于D 项用古典概型的概率解决.【详解】显然甲企业大部分月份位于82%以上,故利润增长均数大于82%,A 不正确;乙企业润增长指数按从小到大排列分别是第2,1,3,4,8,5,6,7,9,11,10又因为1170⨯%=7.7,所以从小到大排列的第8个月份,即7月份是第70百分位,从折线图可知,7月份利润增长均数大于82%,故B 错误;观察折现图发现甲企业的数据更集中,所以甲企业月利润增长指数较乙企业更稳定,故C 正确;P (2个月乙企业月利润增长指数都小于82%)26211C 3C 11==,故D 错误.故选:C.5.已知空间三点(4,1,9),(10,1,6),(2,4,3)A B C -,则下列结论不正确的是()A.||||AB AC =B.点(8,2,0)P 在平面ABC 内C.AB AC ⊥D.若2AB CD =,则D 的坐标为31,5,2⎛⎫-- ⎪⎝⎭【答案】D 【解析】【分析】根据空间两点距离公式判断A ,根据数量积的坐标运算判断B ,根据共面向量基本定理判断C ,根据向量的坐标运算判断D.【详解】因为||7AB ==,||7AC ==,故A 正确;因为(6,2,3)(2,3,6)126180AB AC →→⋅=--⋅--=--+=,所以AB AC ⊥,故C 正确;因为(6,2,3),(2,3,6)AB AC →→=--=--,(4,1,9)AP →=-,所以(4,1,9)AP AB AC →→→=+=-,所以点(8,2,0)P 在平面ABC 内,故B 正确;因为92(1,9,))(62(22,31,8,,),92AB CD ==------=-- ,显然不成立,故D 错误.故选:D6.已知某人收集一个样本容量为50的一组数据,并求得其平均数为70,方差为75,现发现在收集这些数据时,其中得两个数据记录有误,一个错将80记录为60,另一个错将70记录为90,在对错误得数据进行更正后,重新求得样本的平均数为X ,方差为2s ,则()A.270,75X sB.270,75X s ><C.270,75X s =>D.270,75X s =<【答案】D 【解析】【分析】根据平均数与方差的定义判断.【详解】因为80706090+=+,因此平均数不变,即70X =,设其他48个数据依次为1248,,,a a a ,因此()()()()()222221248707070607090705075a a a -+-++-+-+-=⨯ ,()()()()()22222212487070708070707050a a a s -+-++-+-+-=⨯ ,()250751004001004000s -=--=-<,∴275s <,故选:D .7.如图所示,在直三棱柱111ABC A B C -中,ACBC ⊥,且3BC =,4AC =,13CC =,点P 在棱1AA 上,且三棱锥A PBC -的体积为4,则直线1BC 与平面PBC 所成角的正弦值等于()A.4B.4C.5D.5【答案】C 【解析】【分析】利用锥体的体积公式可求得2PA =,然后以点C 为坐标原点,CB 、CA 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可求得直线1BC 与平面PBC 所成角的正弦值.【详解】由已知得1AA ⊥底面ABC ,且AC BC ⊥,所以111344332A PBC P ABC ABC V V S PA PA --==⨯⨯=⨯⨯⨯⨯=△,解得2PA =.如图所示,以点C 为坐标原点,CB 、CA 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则()0,0,0C 、()0,4,2P 、()3,0,0B 、()10,0,3C ,则()3,0,0CB = ,()0,4,2CP = ,()13,0,3BC =-.设平面BCP 的法向量为(),,n x y z =,则由00n CB n CP ⎧⋅=⎨⋅=⎩可得30420x y z =⎧⎨+=⎩,即020x y z =⎧⎨+=⎩,得0x =,令1y =,得2z =-,所以()0,1,2n =-为平面BCP 的一个法向量.设直线1BC 与平面PBC 所成的角为θ,则11110sin cos ,5n BC n BC n BC θ⋅=<>==⋅.故选:C.【点睛】方法点睛:求直线与平面所成角的方法:(1)定义法,①作,在直线上选取恰当的点向平面引垂线,确定垂足的位置是关键;②证,证明所作的角为直线与平面所成的角,证明的主要依据是直线与平面所成角的概念;③求,利用解三角形的知识求角;(2)向量法,sin cos ,AB n AB n AB nθ⋅=<>=⋅ (其中AB 为平面α的斜线,n为平面α的法向量,θ为斜线AB 与平面α所成的角).8.已知F 1,F 2分别为双曲线C :221412x y -=的左、右焦点,E 为双曲线C 的右顶点.过F 2的直线与双曲线C的右支交于A ,B 两点(其中点A 在第一象限),设M ,N 分别为△AF 1F 2,△BF 1F 2的内心,则ME NE -的取值范围是()A.44,33⎛⎫-⎪⎝⎭B.,33⎛⎫- ⎪ ⎪⎝⎭C.3333,55⎛⎫- ⎪⎪⎝⎭ D.,33⎛⎫- ⎪ ⎪⎝⎭【答案】B 【解析】【分析】利用平面几何和内心的性质,可知M ,N 的横坐标都是a ,得到MN ⊥x 轴,设直线AB 的倾斜角为θ,有22,22-∠=∠=EF M EF N πθθ,根据θ∈(60∘,90∘],将ME NE -表示为θ的三角函数可求得范围.【详解】解:设1212,,AF AF F F 上的切点分别为H 、I 、J ,则1122||||,,===AH AI F H F J F J F I .由122AF AF a -=,得()()12||||2+-+=AH HF AI IF a ,∴122-=HF IF a ,即122-=JF JF a.设内心M 的横坐标为0x ,由JM x ⊥轴得点J 的横坐标也为0x ,则()()002c x c x a +--=,得0x a =,则E 为直线JM 与x 轴的交点,即J 与E 重合.同理可得12BF F △的内心在直线JM 上,设直线AB 的领斜角为θ,则22,22-∠=∠=EF M EF N πθθ,||||()tan()tan 22--=---ME NE c a c a πθθcos sin 2cos 222()()()sin tan sin cos 22⎛⎫ ⎪=-⋅-=-=-⎪ ⎪⎝⎭c a c a c a θθθθθθθ,当2πθ=时,||||0ME NE -=;当2πθ≠时,由题知,2,4,===b a c a,因为A ,B 两点在双曲线的右支上,∴233ππθ<<,且2πθ≠,所以tan θ<tan θ>,∴3133tan 3θ-<<且10tan θ≠,∴44343||||,00,tan 33⎛⎫⎛⎫-=∈- ⎪ ⎪⎝⎭⎝⎭ME NE θ,综上所述,44343||||,tan 33⎛⎫-=∈- ⎪⎝⎭ME NE θ.故选:B.二、多选题(共4个小题,每个小题5分,共20分)9.已知甲罐中有五个相同的小球,标号为1,2,3,4,5,乙罐中有四个相同的小球,标号为1,4,5,6,现从甲罐、乙罐中分别随机抽取1个小球,记事件A =“抽取的两个小球标号之和大于6”,事件B =“抽取的两个小球标号之积小于6”,则()A.事件A 与事件B 是互斥事件B.事件A 与事件B 不是对立事件C.事件A B ⋃发生的概率为1920D.事件A 与事件B 是相互独立事件【答案】ABC 【解析】【分析】由两球编号写出事件,A B 所含有的基本事件,同时得出所有的基本事件,然后根据互斥事件、对立事件的定义判断AB ,求出A B ⋃的概率判断C ,由公式()()()P AB P A P B =判断D .【详解】甲罐中小球编号在前,乙罐中小球编号在后,表示一个基本事件,事件A 含有的基本事件有:16,25,26,34,35,36,44,45,46,54,55,56,共12个,事件B 含有的基本事件有:11,14,15,21,31,41,51,共7个,两者不可能同时发生,它们互斥,A 正确;基本事件15发生时,事件,A B 均不发生,不对立,B 正确;事件A B ⋃中含有19个基本事件,由以上分析知共有基本事件20个,因此19()20P A B =,C 正确;123()205P A ==,7()20P B =,()0P AB =()()P A P B ≠,,A B 不相互独立,D 错.故选:ABC .10.在如图所示试验装置中,两个长方形框架ABCD 与ABEF 全等,1AB =,2BC BE ==,且它们所在的平面互相垂直,活动弹子,M N 分别在长方形对角线AC 与BF 上移动,且(0CM BN a a ==<<,则下列说法正确的是()A.AB MN⊥ B.MN 2C.当MN 的长最小时,平面MNA 与平面MNB 所成夹角的余弦值为13D .()25215M ABN a V-=【答案】ABC 【解析】【分析】建立空间直角坐标系,写出相应点的坐标,利用空间向量数量积的运算即可判断选项A ;利用空间两点间距离公式即可判断选项B ;根据二面角的余弦值推导即可判断选项C ;根据棱锥的体积计算公式即可判断选项D .【详解】由题意可知:,,BA BC BE 两两互相垂直,以点B 为坐标原点,,,BA BE BC为,,x y z 轴正方向,建立空间直角坐标系,建系可得525525,0,2,,,05555a a a a M N ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭()25250,,2,1,0,055a a MN BA ⎛⎫∴=-= ⎪ ⎪⎝⎭,0,AB MN AB MN ∴⋅=∴⊥,故选项A 正确;又MN===∴当2a=时,min||MN=,故选项B正确;当MN最小时,,,2a M N=分别是,AC BF的中点,取MN中点K,连接AK和BK,,AM AN BM BN==,,AK MN BK MN∴⊥⊥,AKB∠∴是二面角A MN B--的平面角.BMN中,,2BM BN MN===,可得2BK==,同理可得2AK=,由余弦定理可得331144cos322AKB∠+-==,故选项C 正确;2125252522365515M ABN ABNa aV S h-⎛⎫-=⨯⨯=⨯-=⎪⎪⎝⎭,故选项D错误.故选:ABC.11.抛物线有如下光学性质:由其焦点射出的光线经拋物线反射后,沿平行于拋物线对称轴的方向射出.反之,平行于拋物线对称轴的入射光线经拋物线反射后必过抛物线的焦点.已知抛物线2:,C y x O=为坐标原点,一束平行于x轴的光线1l从点41,116P⎛⎫⎪⎝⎭射入,经过C上的点()11,A x y反射后,再经C上另一点()22,B x y 反射后,沿直线2l 射出,经过点Q ,则()A.PB 平分ABQ ∠B.121y y =-C.延长AO 交直线14x =-于点D ,则,,D B Q 三点共线D.2516AB =【答案】ACD 【解析】【分析】对于A ,根据题意求得()1,1A ,11,164B ⎛⎫- ⎪⎝⎭,从而证得PA AB =,结合平面几何的知识易得PB 平分ABQ ∠;对于B ,直接代入12,y y 即可得到1214y y =-;对于C ,结合题意求得11,44D ⎛⎫-- ⎪⎝⎭,由,,D B Q 的纵坐标相同得,,D B Q 三点共线;对于D ,由选项A 可知2516AB =.【详解】根据题意,由2:C y x =得1,04F ⎛⎫⎪⎝⎭,又由//PA x 轴,得()1,1A x ,代入2:C y x =得11x =(负值舍去),则()1,1A ,所以141314AF k ==-,故直线AF 为4134y x ⎛⎫=- ⎪⎝⎭,即4310x y --=,依题意知AB 经过抛物线焦点F ,故联立24310x y y x --=⎧⎨=⎩,解得11614x y ⎧=⎪⎪⎨⎪=-⎪⎩,即11,164B ⎛⎫- ⎪⎝⎭,对于A ,412511616PA =-=,2516AB =,故PA AB =,所以APB ABP ∠=∠,又因为//PA x 轴,//BQ x 轴,所以//PA BQ ,故APB PBQ =∠∠,所以ABP PBQ ∠=∠,则PB 平分ABQ ∠,故A 正确;对于B ,因为12141,y y =-=,故1214y y =-,故B 错误;对于C ,易得AO 的方程为y x =,联立14y x x =⎧⎪⎨=-⎪⎩,故11,44D ⎛⎫-- ⎪⎝⎭,又//BQ x 轴,所以,,D B Q 三点的纵坐标都相同,则,,D B Q 三点共线,故C 正确;对于D ,由选项A 知2516AB =,故D 正确.故选:ACD..12.己知椭圆222:1(02)4x y C b b+=<<的左,右焦点分别为1F ,2F ,圆22:(2)1M x y +-=,点P 在椭圆C 上,点Q 在圆M 上,则下列说法正确的有()A.若椭圆C 和圆M 没有交点,则椭圆C的离心率的取值范围是2,1⎛⎫⎪ ⎪⎝⎭B.若1b =,则||PQ 的最大值为4C.若存在点P 使得213PF PF =,则0b <≤D.若存在点Q使得12QF =,则1b =【答案】ACD 【解析】【分析】A 根据已知,数形结合得01b <<时椭圆C 和圆M 没有交点,进而求离心率范围;B 令(,)P x y ,求得||MP =,结合椭圆有界性得max ||MP =即可判断;C 由题设123,1PF PF ==,令(,)P x y,进而得到((222291x y x y⎧++=⎪⎨⎪-+=⎩,结合点在椭圆上得到公共解(0,2]x =求范围;D将问题化为圆心为的圆与圆22:(2)1M x y +-=有交点.【详解】由椭圆C 中2a =,圆M 中圆心(0,2)M ,半径为1,如下图示,A :由于02b <<,由图知:当01b <<时椭圆C 和圆M 没有交点,此时离心率,12e ⎛⎫⎪ ⎪⎝==⎭,对;B :当1b =时,令(,)P x y,则||MP =,而224(1)x y =-,所以||MP =,又11y -≤≤,故max ||MP =所以||PQ1+,错;C :由1224PF PF a +==,若213PF PF =,则123,1PF PF ==,由12(F F ,令(,)P x y ,且2221)(4x y b =-,则((222291x y x y⎧++=⎪⎨⎪+=⎩,即2222(4)200(4)120b x b x ⎧-+-=⎪⎨--+=⎪⎩,所以(0,2]x =,则23b ≤,且02b <<,故0b <≤D :令(,)Q x y,若12QF =,所以2222(3[(]x y x y +=-+,则222(4)0x b y -+-+=,所以222(3(4)x y b -+=-,Q轨迹是圆心为的圆,而(0,2)M与的距离为,要使点Q 存在,则1|1-≤≤,可得22(1)0b -≤,且02b <<,即1b =,对;故选:ACD【点睛】关键点点睛:对于C ,根据已知得到123,1PF PF ==,设(,)P x y ,利用两点距离公式得到方程组,求出公共解(0,2]x =为关键;对于D ,问题化为圆心为的圆与圆22:(2)1M x y +-=有交点为关键.三、填空题(共4个小题,每个小题5分,共20分)13.若直线1x y +=与直线2(1)40m x my ++-=平行,则这两条平行线之间的距离是__.【答案】322【解析】【分析】由题意结合直线平行的性质可得2m =-,再由平行线间的距离公式即可得解.【详解】 直线1x y +=与直线2(1)40m x my ++-=平行,∴2(1)4111m m +-=≠-,解得2m =-,故直线1x y +=与直线2(1)40m x my ++-=即为直线10x y +-=与直线20x y ++=,2=,故答案为:2.【点睛】本题考查了直线平行性质的应用,考查了平行线间距离公式的应用,属于基础题.14.曲线1y =+与直线l :y =k (x -2)+4有两个交点,则实数k 的取值范围是________.【答案】53124,纟çúçú棼【解析】【分析】首先画出曲线表示的半圆,再判断直线l 是过定点()24,的直线,利用数形结合判断k 的取值范围.【详解】直线l 过点A (2,4),又曲线1y =+0,1)为圆心,2为半径的半圆,如图,当直线l 与半圆相切,C 为切点时,圆心到直线l 的距离d =r,2=,解得512k =.当直线l 过点B (-2,1)时,直线l 的斜率为()413224-=--,则直线l 与半圆有两个不同的交点时,实数k 的取值范围为53124,纟çúçú棼.故答案为:53124,纟çúçú棼15.数学兴趣小组的四名同学各自抛掷骰子5次,分别记录每次骰子出现的点数,四名同学的部分统计结果如下:甲同学:中位数为3,方差为2.8;乙同学:平均数为3.4,方差为1.04;丙同学:中位数为3,众数为3;丁同学:平均数为3,中位数为2.根据统计结果,数据中肯定没有出现点数6的是______同学.【答案】乙【解析】【分析】假设出现6点,利用特例法,结合平均数和方差的计算公式,即可求解.【详解】对于甲同学,当投掷骰子出现结果为1,2,3,3,6时,满足中位数为3,平均数为:()11233635x =++++=,方差为()()()()()22222211323333363 2.85S ⎡⎤-+-+-+-+-⎣⎦==,可以出现点数6;对于乙同学,若平均数为3.4,且出现点数6,则方差221(6 3.4) 1.352 1.045S >-=>,所以当平均数为3.4,方差为1.04时,一定不会出现点数6;对于丙同学,当掷骰子出现的结果为1,2,3,3,6时,满足中位数为3,众数为3,可以出现点数6;对于丁同学,当投掷骰子出现的结果为2,2,2,3,6时,满足平均数为3,中位数为2,可以出现点数6.综上,根据统计结果,数据中肯定没有出现点数6的是乙同学.故答案为:乙16.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,离心率为e ,点P 在椭圆上,连接1PF 并延长交C 于点Q ,连接2QF ,若存在点P 使2PQ QF =成立,则2e 的取值范围为___________.【答案】)11,1⎡-⎣【解析】【分析】设11,QF m PF n ==,所以存在点P 使2PQ QF =等价于()2min0,PQ QF -≤由2112am n b +=可求222PQ QF m n a -=+-的最小值,求得22b a的范围,从而得到2e 的取值范围.【详解】设11,QF m PF n ==,则22QF a m =-.显然当P 靠近右顶点时,2PQ QF >,所以存在点P 使2PQ QF =等价于()22min0,22PQ QF PQ QF m n a -≤-=+-,在12PF F △中由余弦定理得22221121122cos PF PF F F PF F F θ=+-⋅⋅,即()2222422cos a n n c n c θ-=+-⋅⋅,解得2cos b n a c θ=-,同理可得2cos b m a c θ=+,所以2112a m n b +=,所以()(2223112223222b b b n m m n m n a m n a m n a +⎛⎫⎛⎫+=++=++≥ ⎪ ⎝⎭⎝⎭,所以22min1)(22)22b m n a a a++-=-,当且仅当n =时等号成立.由221)202b a a+-≤得2212b a ≤-,所以2111e -≤<.故答案为:)11,1⎡-⎣【点睛】关键点点睛:求离心率范围关键是建立,,a b c 的不等式,此时将问题转化为()2min0PQ QF -≤,从而只需求222PQ QF m n a -=+-的最小值,求最小值的方法是结合焦半径性质211112aPF QF b+=使用基本不等式求解.四、解答题(共7个题,17题10分,18题—22题每题12分,共70分)17.在平面直角坐标系xOy 中,存在四点()0,1A ,()7,0B ,()4,9C ,()1,3D .(1)求过A ,B ,C 三点的圆M 的方程,并判断D 点与圆M 的位置关系;(2)若过D 点的直线l 被圆M 截得的弦长为8,求直线l 的方程.【答案】(1)228870x y x y +--+=,D 在圆M 内;(2)43130x y +-=或1x =.【解析】【分析】(1)设出圆的一般方程,利用待定系数法计算可得圆的方程,把D 坐标代入圆的方程判定位置关系即可;(2)对直线分类讨论,设出直线方程,利用直线与圆相交,已知弦长求直线方程.【小问1详解】设圆M 方程为220x y Dx Ey F ++++=,把A ,B ,C 三点坐标代入可得:10,4970,1681490,E F D F D E F ++=⎧⎪++=⎨⎪++++=⎩解得8D =-,8E =-,7F =,所以圆M 方程是228870x y x y +--+=,把D 点坐标代入可得:1982470+--+<,故D 在圆M 内;【小问2详解】由(1)可知圆M :()()224425x y -+-=,则圆心()4,4M ,半径=5r ,由题意可知圆心到直线l 的距离是3,当直线l 斜率存在时,设直线l 方程为:()1330y k x kx y k =-+⇒-+-=,3=,解得43k =-,故直线l 的方程为43130x y +-=;当直线l 斜率不存在时,则直线l 方程为:1x =,此时圆心到直线l 的距离是3,符合题意.综上所述,直线l 的方程为43130x y +-=或1x =.18.我校举行的“青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:频率分布表组别分组频数频率第1组[50,60)80.16第2组[60,70)a ▓第3组[70,80)200.40第4组[80,90)▓0.08第5组[90,100]2b 合计▓▓(1)求出a ,b ,x ,y 的值;(2)在选取的样本中,从成绩是80分以上的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差(同一组的数据用该组区间的中点值作代表).【答案】(1)a =16,b =0.04,x =0.032,y =0.004(2)35(3)中位数为70.5,平均数为70.2,方差为96.96【解析】【分析】(1)利用频率=100%⨯频数样本容量,及频率组距表示频率分布直方图的纵坐标即可求出a ,b ,x ,y ;(2)由(2)可知第四组的人数,已知第五组的人数是2,利用组合的计算公式即可求出从这6人中任选2人的种数,再分两类分别求出所选的两人来自同一组的情况,利用互斥事件的概率和古典概型的概率计算公式即可得出.(3)根据频率分布直方图,估计这50名学生成绩的中位数、平均数和方差.【小问1详解】由题意可知,样本容量n =8500.16=,∴b =250=0.04,第四组的频数=50×0.08=4,∴508202416a =----=.y =0.0410=0.004,x =1650×110=0.032.∴a =16,b =0.04,x =0.032,y =0.004.【小问2详解】由题意可知,第4组共有4人,记为A ,B ,C ,D ,第5组共有2人,记为X ,Y .从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学,有AB ,AC ,AD ,BC ,BD ,CD ,AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY ,共15种情况.设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E ,有AX ,AY ,BX ,BY ,CX ,CY ,DX ,DY ,XY 共9种情况.所以随机抽取的2名同学中至少有1名同学来自第5组的概率是P (E )=93155=.∴随机抽取的2名同学中至少有1名同学来自第5组的概率35.【小问3详解】∵[50,70)的频率为:0.160.320.48+=,[70,80)的频率为0.4,∴中位数为:0.50.48701070.50.4-+⨯=,平均数为:550.16650.32750.4850.08950.0470.2⨯+⨯+⨯+⨯+⨯=.方差为:()()()()()222225570.20.166570.20.327570.20.48570.20.089570.20.0496.96⨯+⨯+⨯+⨯+⨯﹣﹣﹣﹣﹣=.19.已知抛物线()2:20C y px p =>的焦点为F ,点0(,4)M x 在C 上,且52pMF =.(1)求点M 的坐标及C 的方程;(2)设动直线l 与C 相交于,A B 两点,且直线MA 与MB 的斜率互为倒数,试问直线l 是否恒过定点?若过,求出该点坐标;若不过,请说明理由.【答案】(1)M 的坐标为()4,4,C 的方程为24y x =;(2)直线l 过定点()0,4-.【解析】【分析】(1)利用抛物线定义求出0x ,进而求出p 值即可得解.(2)设出直线l 的方程x my n =+,再联立直线l 与抛物线C 的方程,借助韦达定理探求出m 与n 的关系即可作答.【小问1详解】抛物线2:2C y px =的准线:2px =-,于是得0522p p MF x =+=,解得02x p =,而点M 在C 上,即2164p =,解得2p =±,又0p >,则2p =,所以M 的坐标为()4,4,C 的方程为24y x =.【小问2详解】设()()1122,,,A x y B x y ,直线l 的方程为x my n =+,由24x my n y x =+⎧⎨=⎩消去x 并整理得:2440y my n --=,则()2160m n ∆=+>,124y y m +=,124y y n =-,因此,121222121212444444144444444MA MB y y y y k k y y x x y y ----⋅=⋅==⋅=--++--,化简得()121240y y y y ++=,即4n m =,代入l 方程得4x my m =+,即()40x m y -+=,则直线l 过定点()0,4-,所以直线l 过定点()0,4-.【点睛】思路点睛:直线与圆锥曲线相交,直线过定点问题,设出直线的斜截式方程,与圆锥曲线方程联立,借助韦达定理求出直线斜率与纵截距的关系即可解决问题.20.如图,在四棱锥P ABCD -中,底面ABCD 是直角梯形,AD AB ⊥,//AB DC ,PA ⊥底面ABCD ,点E 为棱PC 的中点.22AD DC AP AB ====.()1证明://BE 平面PAD .()2若F 为棱PC 上一点,满足BF AC ⊥,求二面角F AD C --的余弦值.【答案】()1证明见解析;()210.【解析】【分析】()1在PD 上找中点G ,连接AG ,EG ,利用三角形中位线性质得出12EG CD =,因为底面ABCD 是直角梯形,2CD AB =,所以能得出EG 平行且等于AB ,得出四边形ABEG 为平行四边形,再利用线面平行的判定,即可证出//BE 平面PAD ;()2根据BF AC ⊥,求出向量BF的坐标,进而求出平面FAD 和平面ADC 的法向量,代入向量夹角公式,可得二面角F AD C --的余弦值.【详解】解:()1证明:在PD 上找中点G ,连接AG ,EG ,图象如下:G 和E 分别为PD 和PC 的中点,∴EG //CD ,且12EG CD =,又 底面ABCD 是直角梯形,2CD AB =∴AB //CD ,且12AB CD =,∴AB GE //且AB GE =.即四边形ABEG 为平行四边形.∴AG E //B .AG ⊂平面PAD ,BE ⊄平面PAD ,∴//BE 平面PAD.()2以A 为原点,以AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴,建立如图所示的空间直角坐标系,可得()1,0,0B ,()2,2,0C ,()0,2,0D ,()002P ,,,()1,1,1E ,()1,2,0BC = ,()2,2,2CP =-- ,()2,2,0AC = .由F 为棱PC 上一点,设()2,2,2CF CP λλλλ==-- ()01λ≤≤,所以()12,22,2BF BC CF λλλ=+=-- ()01λ≤≤,由BF AC ⊥,得()()2122220BF AC λλ⋅=-+-= ,解得34λ=,即113,,222BF ⎛⎫=- ⎪⎝⎭ ,()1131131,0,0,,,,222222AF AB BF ⎛⎫⎛⎫=+=+-= ⎪ ⎪⎝⎭⎝⎭,设平面FAD 的法向量为(),,n a b c = ,由00n AF n AD ⎧⋅=⎨⋅=⎩ 可得113022220a b c b ⎧++=⎪⎨⎪=⎩所以030b a c =⎧⎨+=⎩,令1c =,则3a =-,则()3,0,1n =- ,取平面ADC 的法向量为()0,0,1m = ,则二面角F AD C --的平面角α满足:cos 10m n m nα⋅===⋅ ,故二面角F AD C --的余弦值为10.【点睛】本题考查线面平行的判定,空间二面角的平面角,建立空间直角坐标系,将二面角问题转化为向量夹角问题,属于难题.21.已知O 为坐标原点,()120F -,,()220F ,,点P 满足122PF PF -=,记点P 的轨迹为曲线.E (1)求曲线E 的方程;(2)过点()220F ,的直线l 与曲线E 交于A B ,两点,求+ OA OB 的取值范围.【答案】(1)()2211.3y x x -=≥(2)[)4∞+,【解析】【分析】(1)根据双曲线的定义,易判断点P 的轨迹是双曲线的右支,求出,a b 的值,即得;(2)设出直线方程与双曲线方程联立消元得到一元二次方程,推出韦达定理,依题得出参数m 的范围,将所求式等价转化为关于m 的函数式,通过整体换元即可求出其取值范围.【小问1详解】因()120F -,,()220F ,,且动点P 满足12122PF PF F F -=<,由双曲线的定义知:曲线E 是以12F F ,为焦点的双曲线的右支,且2c =,1a =,则2223b c a =-=,故曲线E 的方程为()2211.3y x x -=≥【小问2详解】当直线l 的斜率为0时,直线l 与双曲线的右支只有一个交点,故不符题意.如图,不妨设直线l 方程为:2x my =+,设()11A x y ,,()22B x y ,,联立22213x my y x =+⎧⎪⎨-=⎪⎩,得()22311290m y my -++=,由韦达定理得1221221231931m y y m y y m -⎧+=⎪⎪-⎨⎪⋅=⎪-⎩,2121222124()443131m x x m y y m m -+=++=+=---,2212121212234(2)(2)2()431m x x my my m y y m y y m +⋅=++=+++=--.由题意:()()22212221223101243190403134031m m m x x m m x x m ⎧-≠⎪-⨯-⨯>⎪⎪⎪⎨+=->⎪-⎪+⎪⋅=->⎪-⎩,解得:210.3m ≤<OA OB +=====,令2131t m =-,因210,3m ≤<故1t ≤-,而OA OB +== ,在(],1t ∞∈--为减函数,故4OA OB +≥ ,即OA OB + 的取值范围为[)4∞+,.22.如图,已知椭圆22122:1(0)x y C a b a b+=>>与等轴双曲线2C 共顶点(±,过椭圆1C 上一点P (2,-1)作两直线与椭圆1C 相交于相异的两点A ,B ,直线PA 、PB 的倾斜角互补,直线AB 与x ,y 轴正半轴相交,分别记交点为M ,N .(1)求直线AB 的斜率;(2)若直线AB 与双曲线2C 的左,右两支分别交于Q ,R ,求NQ NR 的取值范围.【答案】(1)12-(2)11(1,9+【解析】【分析】(1)先求出椭圆方程,联立直线与椭圆方程,利用韦达定理求解A ,B 坐标,直接计算直线AB 斜率即可.(2)联立直线与双曲线的方程,利用求根公式表示出Q ,R 的坐标,化简NQ NR 的表达式,整理求出NQ NR的取值范围即可得出结果.【小问1详解】由题椭圆22122:1(0)x y C a b a b+=>>,顶点(±,可得a =(2,1)P -在椭圆1C 上,即24118b +=,得22b =,所以椭圆方程为22182x y +=,设等轴双曲线2C :222x y m -=,0m >,由题意等轴双曲线2C 的顶点为(±,可得2=8m ,所以双曲线2C 的方程为:228x y -=,因为直线PA 、PB 的倾斜角互补,且A ,B 是不同的点,所以直线PA 、PB 都必须有斜率,设直线PA 方程为(2)1y k x =--,联立22(2)1182y k x x y =--⎧⎪⎨+=⎪⎩,整理得2222(14)(168)161640k x k k x k k +-+++-=,A 和P 点横坐标即为方程两个根,可得221681+4A P k k x x k ++=,因为=2P x ,所以22882=14A k k x k +-+,代入直线PA 可得2244114A k k y k--=+,即2222882441(,)1414k k k k A k k+---++,又因为直线PA 、PB 的倾斜角互补,将k 换成k -,可得2222882441(,)1414k k k k B k k --+-++,两点求斜率可得出12AB k =-所以直线AB 的斜率为12-【小问2详解】由(1)可设直线AB 的方程:12y x n =-+,又因为直线AB 与x ,y 轴正半轴相交,则0n >,联立方程组2212182y x n x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,整理得2224480x nx n -+-=,22Δ168(48)0n n =-->,解得02n <<.联立直线AB 和双曲线方程221(02)28y x n n x y ⎧=-+<<⎪⎨⎪-=⎩,消去y 得22344320x nx n +--=,利用求根公式可得23n x -±=,所以1Q R x NQ NR x ====,又因为204n <<,所以2632n >,则11>,即29<,所以1121019NQNR+<<,所以NQNR 的取值范围为11210(1,9+【点睛】方法点睛:(1)解答直线与圆锥曲线题目时,时常把两个曲线的方程联立,消去一个未知数建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率不存在的特殊情况.。
2023年小学六年级下册科学期末综合复习题(三)【含答案】

【详解】为了便于观察,人们把星空中相互之间 距离保持不变的星星分成一群,划分成不同区域,根据其形态想象成人、动物或者其他物体的形状,并且给它们命名。天空中这些被人们分成的许多区域叫做星座。夏季是观察星座的好季节,天空中有许多亮星。其中有三颗亮星构成了一个巨大的三角形,人们称之为夏季大三角。夏季大三角是由天琴座的织女星、天鹅座的天津四和天鹰座的牛郎星。
7.物质的化学变化过程往往伴随产生种种现象,常见诸如_____、_____、_____、_____ 等。
8.米饭遇到碘酒颜色会发生_______变化,产生了一种_______的新物质。利用这一特性可以检验食物中是否含有____________。
9.月球是一个________、________的球体,我们看到的月光是它反射太阳的光。由于观察角度的不同,所以看到的月相亮面的_________、__________也不同。
24.草蛉和它 幼虫都是蚜虫的天敌。( )
25.两个凸透镜组合起来能把物体的图象放得更大。( )
26.沙和豆子混合过程中发生了化学变化。( )
27.我们能直接或间接观察到的实际存在的东西都是物质。( )
28.建立自然保护区是保护生物多样性的有效方法。________
三、选择:请把正确的答案蕃号填入括号内。
13.二氧化碳气体能使燃着的火焰熄灭。( )
14.利用淀粉和碘酒反应时会发生颜色变化这一特性,我们可以用来检验食物中是否含有淀粉。( )
15.宇宙中每时每刻都有许多恒星诞生,同时也有许多恒星消亡。________
16.月球不明亮的部分总是向着太阳。( )
17.废电池是一种需要谨慎处理的垃圾。 ( )
A. 嫦娥B. 阿姆斯特朗C. 杨利伟
44.太阳是太阳系里唯一发光的( )。
材料力学期末复习题及答案
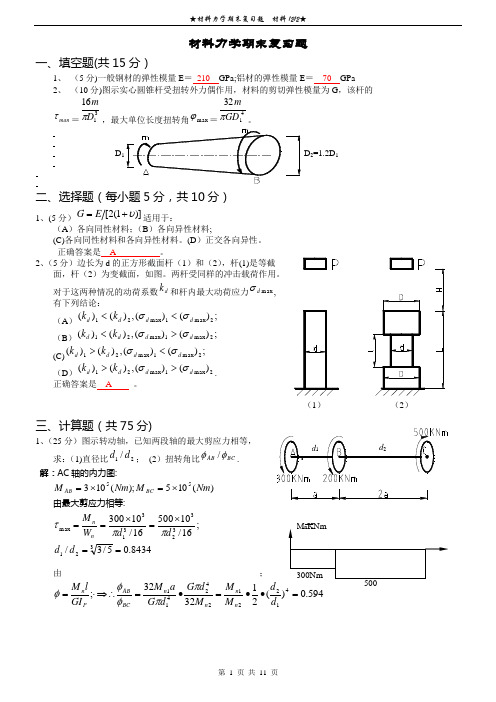
材料力学期末复习题一、填空题(共15分)1、 (5分)一般钢材的弹性模量E = 210 GPa;铝材的弹性模量E = 70 GPa2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的τ1、(5(A )各向同性材料;(B )各向异性材料;(C)各向同性材料和各向异性材料。
(D 正确答案是 A 。
2、(5分)边长为d 的正方形截面杆(1)和(2)面,杆(2对于这两种情况的动荷系数d k 有下列结论:(A );)()(,)()(2max 1max 21d d d d k k σσ<< (B );)()(,)()(2max 1max 21d d d d k k σσ>< (C);)()(,)()(2max 1max 21d d d d k k σσ<> (D )2max 1max 21)()(,)()(d d d d k k σσ>>. 正确答案是 A 。
三、计算题(共75分)1、(25求:(1)直径比21/d d ; (2)扭转角比BC AB φφ/. 解:AC 轴的内力图:)(105);(10355Nm M Nm M BC AB ⨯=⨯=由最大剪应力相等: 8434.05/3/;16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ由;594.0)(213232;41221242411=••=•=⇒∴⋅=d d M M M d G d G a M GI l M n n n n BC AB P n ππφφφKNm2、(解:3、(15分)有一厚度为6mm 的钢板在板面的两个垂直方向受拉,拉应力分别为150Mpa 和55Mpa ,材料的E=2.1×105Mpa ,υ =0.25。
求钢板厚度的减小值。
解:钢板厚度的减小值应为横向应变所产生,该板受力后的应力状态为二向应力状态,由广义胡克定律知,其Z向应变为:0244.010)55150(101.225.0)(69-=⨯+⨯-=+-=y x z E σσνε则 mm t Z Z 146.0-=⨯=∆ε材料力学各章重点一、绪论1.各向同性假设认为,材料沿各个方向具有相同的 A 。
《中国现代文学专题》期末复习题 及答案 -3

《中国现代文学专题》期末复习题及答案第三部分三、填空题1.十九世纪末戊戌变法的失败,促进了维新运动的领导者梁启超的反思,他从政治斗争的需要出发,倡导“新小说”,于1902年创办《新小说》杂志。
2.1915年,陈独秀创办《青年杂志》,从第二卷起改名为《新青年》。
3.1918年5月,鲁迅的《狂人日记》发表于《新青年》。
此后,他的《药》、《孔乙己》、《阿Q正传》、《祝福》等接连发表,引起巨大反响。
4.在受到老师们主办《新青年》影响而创办的北京大学学生刊物《新潮》上,出现了一个活跃的作家群,创作出新文学早期的一批诗歌、小说、散文和戏剧。
5.五四时期表现青年男女情感纠葛的小说主要有鲁迅的《伤逝》、庐隐的《海滨故人》、郁达夫的《沉沦》、郭沫若的《喀尔美罗姑娘》、张资平的《她怅望着祖国的天野》等。
6.阿Q式的流氓无产者,对于革命和社会的危害,到四十年代赵树理的《李有才板话》、《邪不压正》,和八十年代古华的《芙蓉镇》、张炜的《古船》中,才得到了充分的展现。
7.创造社初创时期,有两座高峰,一是以《女神》闻名的郭沫若,一是以《沉沦》闻名的郁达夫,他们共同建构了创造社重主观抒情和浪漫主义的特色。
8.1921年6月,郁达夫与郭沫若、成仿吾、张资平、田汉、郑伯奇等人在东京酝酿成立了新文学团体创造社。
9.1921年7月,郁达夫的第一部短篇小说集《沉沦》问世,产生很大影响。
10.郁达夫的小说,开创了现代小说中的“零余者”形象系列。
11.30年代前期的叶灵凤,和张资平一样,创作了《时代的姑娘》、《永久的女性》等一批现代言情小说,将新文学与商业化结合在一起,成为海派文学的重要作家。
12.叶绍钧是中国现代童话创作的拓荒者,出版有童话集《稻草人》和《古代英雄的石像》。
13.13.文学研究会成立于1921年,是新文学史上成立最早、存在时间最长、成员数量最多、地域分布最广的文学社团。
14.乡土小说,最初得名于鲁迅的命名。
15.同样着力于乡土文学,却走着诗意化道路的废名(原名冯文炳)是“浅草社”成员。
材料科学与工程期末考核复习试题

材料科学与工程期末考试复习试题篇一:材料科学与工程基础期末试题《材料科学基础》试卷Ⅴ一、填空题(20分,每空格1分)1. 相律是在完全平衡状态下,系统的相数、组元数和温度压力之间的关系,是系统的平衡条件的数学表达式: f=C-P+22.二元系相图是表示合金系中合金的间关系的图解。
3.晶体的空间点阵分属于大晶系,其中正方晶系点阵常数的特点为,请列举除立方和正方晶系外其他任意三种晶系的名称交(任选三种)。
4.合金铸锭的宏观组织包括三部分。
5.在常温和低温下,金属的塑性变形主要是通过的方式进行的。
此外还有和折等方式。
6.成分过冷区从小到大,其固溶体的生长形态分别为。
1.原子扩散的驱动力是:组元的化学势梯度2.凝固的热力学条件为:过冷度3. 某金属凝固时的形核功为△G*,其临界晶核界面能为△G,则△G*和△G的关系为△G* =1/3 △G5.金属液体在凝固时产生临界晶核半径的大小主要取决于过冷度。
6.菲克第一定律表述了稳态扩散的特征,即浓度不随变化。
7. 冷变形金属加热过程中发生回复的驱动力是:冷变形过程中的存储能9.合金铸锭的缺陷可分为缩孔和偏析两种。
二、判断题(正确的打“√”错误的打“×”,每题1分,共12分)1. 体心立方结构是原子的次密排结构,其致密度为0.74。
(× )2. 同一种空间点阵可以有无限种晶体结构,而不同的晶体结构可以归属于同一种空间点阵。
(√ )3. 结晶时凡能提高形核率、降低生长率的因素,都能使晶粒细化。
(√ )4. 合金液体在凝固形核时需要能量起伏、结构起伏和成分起伏。
(√ )5. 小角度晶界的晶界能比大角度晶界的晶界能高。
(× )6. 非均匀形核时晶核与基底之间的接触角越大,其促进非均匀形核的作用越大。
(× )7. 固溶体合金液体在完全混合条件下凝固后产生的宏观偏析较小。
(× )8. 冷形变金属在再结晶时可以亚晶合并、亚晶长大和原晶界弓出三种方式形核。
高一数学期末复习题三(试题和答案)

高一数学期末复习题(三)一、选择题(本大题共12小题,每小题4分,共48分)1.设集合M={x|-1≤x<2},N={x|x-k ≤0},若M ∩N ≠∅,则k 的取值范围是( ) A.k ≤2 B.k ≥-1 C.k>-1 D.-1≤k ≤2 解析:由图形可知k ≥-1.答案:B2.设f 是从集合A 到集合B 的映射,下列四个说法,其中正确的是( )①集合A 中的每一个元素在集合B 中都有元素与之对应 ②集合B 中的每一个元素在集合A 中也都有元素与之对应 ③集合A 中不同的元素在集合B 中的对应元素也不同 ④集合B 中不同的元素在集合A 中的对应元素也不同A.①和②B.②和③C.③和④D.①和④思路解析:根据映射的定义,从集合A 到集合B 的映射f ,只要求集合A 的每一个元素在集合B 中都有“唯一”“确定”的元素与之对应即可.即集合A 中不同的元素在集合B 中的对应元素可以相同,也没有要求集合B 中的元素在集合A 中都要有对应元素.解:①符合映射的定义,∴正确;映射的定义不要求集合B 中的元素在集合A 中都要有对应元素,∴②不正确;集合A 中不同的元素在集合B 中的对应元素可以相同,∴③不正确;④正确.∵如果集合B 中不同的元素在集合A 中的对应元素相同,那么就违背了映射定义的“唯一”性原则.综上,①和④正确,因此,选D. 答案:D3.函数y=(21)x -(21)-x是( ) A.奇函数,在(0,+∞)上是减函数 B.偶函数,在(0,+∞)上是减函数C.奇函数,在(0,+∞)上是增函数D.偶函数,在(0,+∞)上是增函数解析:利用奇偶性定义可知为奇函数,再取特殊点验证知在(0,+∞)上单调递减. 答案:A4.若函数f(x)=3sin(2x+5θ)的图象关于y 轴对称,则( )A.1052πθθ+=k ,k ∈Z B.552ππθ+=k ,k ∈Z C.552πθθ+=k ,k ∈Z D.55ππθ+=k ,k ∈Z 思路分析:∵函数f(x)=3sin(2x+5θ)的图象关于y 轴对称,∴当x=0时,有5θ=kπ+2π,k ∈Z ,∴θ=105ππ+k ,k ∈Z .故B 正确. 答案:B5.下列各等式中,正确的是( )A.44a =|a|B.3622)2(-=-C.a 0=1 D.21105)12()12(-=-思路解析:要想判断等式是否正确,首先要使等式两边都有意义,然后计算两边的值,如果相等则正确,如果不相等,则不正确,在计算时要充分应用幂的运算法则.解:44a =|a|,由于不知道a 的符号,因此A 不正确;∵62)2(->0,32-<0,∴62)2(-≠32-.因此B 不正确;如果 a=0,则a 0没有意义,因此C 也不正确;∵2>1,∴105)12(-=21105)12()12(-=-.∴D 正确.因此,选D. 答案:D6.已知0<α<2π<β<π,又sinα=53,cos(α+β)=54-,则sinβ等于( )A.0B.0或2524C.2524D.±2524思路分析:∵0<α<2π<β<π,∴2π<α+β<23π.∵sinα=53.∴cosα=54.由cos(α+β)=-54<0,得sin(α+β)=±53.∴sinβ=sin [(α+β)-α]=sin(α+β)·cosα-cos(α+β)·sinα053)54(5453=∙--∙±=或2524. 又∵2π<β<π,∴sinβ=2524.答案:C7.函数y=122+x x的值域是( )A.{x|0<x<1}B.{x|0<x ≤1}C.{x|x>0}D.{x|x ≥0} 思路解析:求值域要在定义域中求,本题中函数的定义域为R ,∴要求值域就要对函数解析式进行变形,由于分子和分母的“次数”相同,因此想到部分分式法.或者根据指数函数y= 2x 的值域为正,即2x >0来求解. 解法一:因此y=122+x x=1-121+x. 又∵2x +1>1,∴0<121+x <1,∴0<y <1. 因此,选A. 解法二:由2x =yy-1>0, 得0<y <1.因此,选A. 答案:A8.对于函数f(x)=2sin(2x+3π),给出下列结论: ①图象关于原点成中心对称;②图象关于直线x=12π成轴对称;③图象可由函数y=2sin2x 的图象向左平移3π个单位得到;④图象向左平移12π个单位,即得到函数y=2cos2x 的图象.其中正确结论的个数为( )A.0B.1C.2D.3解析:∵f(x)是非奇非偶函数,∴①错误. ∵f(x)是由y=2sin2x 向左平移6π得到的, ∴③错误. 把x=12π代入f(x)中使函数取到最值, ∴②正确.f(x)=2sin(2x+3π)−−−−→−个单位左移12πf(x)=2sin [2(x+12π)+3π]=2cos2x, ∴④正确.答案:C9.偶函数y=f(x)(x ∈R)在x<0时是增函数,若x 1<0,x 2>0且|x 1|<|x 2|,下列结论中正确的是( ) A.f(-x 1)<f(-x 2) B.f(-x 1)>f(-x 2)C.f(-x 1)=f(-x 2)D.f(-x 1)和f(-x 2)的大小关系不能确定 解析:由条件知-x 2<x 1,∴f(-x 2)<f(x 1),又f(x)是偶函数, ∴f(-x 1)=f(x 1),∴f(-x 2)<f(-x 1). 答案:B10.设函数f(x)=sin3x+|sin3x|,则f(x)为( )A.周期函数,最小正周期为3πB.周期函数,最小正周期为32πC.周期函数,最小正周期为2πD.非周期函数 解析:f(x)=sin3x+|sin3x|=⎪⎪⎩⎪⎪⎨⎧+<<++≤≤.3232332,0,33232,3sin 2πππππππk x k k x k x∴B 正确. 答案:B11.某种电热水器的水箱盛满水是200升,加热到一定温度,即可用来洗浴.洗浴时,已知每分钟放水34升,在放水的同时按4升/分钟2的匀加速度自动注水.当水箱内的水量达到最小值时,放水程序自动停止,现假定每人洗浴用水量为65升,则该热水器一次至多可供( ) A. 3人洗浴 B. 4人洗浴 C. 5人洗浴 D. 6人洗浴思路解析:设经过时间t 时水箱中的水量为y,可知y=2t 2-34t+200,当t=434=217时,y 取得最小值,此时放水为172,易求出至多可供四人洗浴.12.已知函数f(x)=asin(x-φ)(a≠0,x ∈R )在x=4π处取得最小值,则函数y=f(43π-x)是( )A.偶函数且它的图象关于点(π,0)对称B.偶函数且它的图象关于点(23π,0)对称C.奇函数且它的图象关于点(23π,0)对称 D.奇函数且它的图象关于点(π,0)对称思路解析:f(x)=asin(x-φ)的周期为2π,函数在x=4π处取得最小值,不妨设f(x)=sin(x-43π),则函数y=f(43π-x)=sin(43π-x-43π)=sinx , 所以y=f(43π-x)是奇函数且它的图象关于点(π,0)对称.答案:D二、填空题(本大题共4小题,每小题4分,共16分.答案需填在题中横线上)13.如果函数y=x 2+2x+m+3至多有一个零点,则m 的取值范围是_________________. 解析:Δ=4-4(m+3)≤0,解得m ≥-2. 答案:[-2,+∞) .14.在△ABC 中,若sinB·sinC=2cos 2A,则此三角形为_______.思路分析:∵A+B+C=π,∴A=π-(B+C).又∵sinB·sinC=cos 22A ,∴21[cos(B-C)-cos(B+C)]=21 (1+cosA),即cos(B-C)-cos(B+C)=1+cosA.又∵cos(B+C)=-cosA ,∴cos(B-C)=1. 又∵-π<B-C <π,∴B-C=0,即B=C. ∴△ABC 是等腰三角形. 答案:等腰三角形 .15.①已知函数y=21log (x 2-2x+a)定义域为R ,则a 的取值范围是_____________,②已知函数y=21log (x 2-2x+a)值域为R ,则a 的取值范围是________________.思路解析:两题乍一看似乎一样,但若仔细分析,其设问角度不同,解题方法也有区别.①对x ∈R ,x 2-2x+a >0恒成立,②由于当t ∈(0,+∞)时,21log t ∈R 故要求x 2-2x+a 取遍每一个正实数,换言之,若x 2-2x+a 的取值范围为D,则(0,+∞)∈D.①x 2-2x+a=(x-1)2+a-1≥a-1,故只要a-1>0则x ∈R 时,x 2-2x+a >0恒成立.因此,填a >1;②x 2-2x+a=(x-1)2+a-1≥a-1,故x 2-2x+a 的取值范围为[a-1, +∞],要求(0,+∞) ⊆[a-1, +∞)只要a-1≤0.因此,填a ≤1.答案:a >1 a ≤116.函数y=1gsinx+216x -的定义域是________________.思路解析:要使函数有意义,x 应满足下列不等式组⎩⎨⎧≥->.016.0sin 2x x 解得⎩⎨⎧≤≤-∈+<<.44),(22x Z k k x k πππ当k=0时,不等式组的解为0<x <π; 当k=-1时,不等式组的解为-4≤x <-π; 当k 取其他整数时,无解.所以定义域为{x|-4≤x <-π或0<x <π}. 答案:{x|-4≤x <-π或0<x <π}三、解答题(本大题共5小题,共56分.解答应写出必要的文字说明、解题步骤或证明过程)17.已知集合A={x|(x-2)[x-(3a+1)]<0},B={x|)1(22+--a x ax <0}. (1)当a=2时,求A ∩B;(2)求使B ⊆A 的实数a 的取值范围.解:(1)当a=2时,A=(2,7),B=(4,5),∴A ∩B=(4,5).(2)∵B=(2a,a 2+1) 当a<13时,A=(3a+1,2) , 要使B ⊆A ,必须⎩⎨⎧≤++≥212132a a a ,此时a=-1;当a=31时,A =∅,使B ⊆A 的a 不存在; 当a>31时,A =(2,3a +1),要使B ⊆A ,必须⎩⎨⎧+≤+≥131222a a a ,此时1≤a ≤3.综上,可知使B ⊆A 的实数a 的取值范围为[1,3]∪{-1}.18.(1).求函数y=sinx·cosx+sinx+cosx 的最大值.思路分析:sinx+cosx 与sinxcosx 有相互转化的关系,若将sinx+cosx 看成整体,设为新的元,函数式可转化为新元的函数式,注意新元的取值范围.解:设sinx+cosx=t ,t ∈[2,2-],则(sinx+cosx)2=t 2,即1+2sinxcosx=t 2,sinxcosx=212-t .1)1(2121)2(2121222-+=-+=-+=t t t t t y ,当t=2时,y max =212+(2).已知tanα-4sinβ=3,3tanα+4sinβ=1,且α是第三象限角,β是第四象限角,求α、β.思路分析:由已知利用方程组求出tanα和sinβ,再依据α和β所在的象限,确定其具体值,注意要写出所有的角.解:由⎩⎨⎧=+=-,1sin 4tan 3,3sin 4tan βαβα得⎪⎩⎪⎨⎧-==.21sin ,1tan βα由tanα=1,α是第三象限角,∴α=2kπ+45π,k ∈Z . 由sinβ=21-且β是第四象限角,∴β=2kπ-6π,k ∈Z .19.已知函数2221()(xx a f x a+=-为常数). (1)证明:函数f(x)在()-∞,+∞上是减函数; (2)若f(x)为奇函数,求a 的值.解:(1)在()-∞,+∞上任取两个值12x x ,且12x x <,12122212222121()()()()xxx x a a f x f x ++-=--- 2121211222222121(21)(21)x x x xx x x x -++++=-=, ∵2>1且12x x <,∴21220x x->.又12(21)(21)0x x++>,∴12()()0f x f x ->,即12()()f x f x >. ∴函数f(x)在()-∞,+∞上是减函数. (2)∵f(x)为奇函数且在x=0处有意义,∴f(0)=0,即0022210a +-=.∴a=1.20.已知某海滨浴场的海浪高度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下表是某日各时的浪高数据: t(h) 0 3 6 9 12 15 18 21 24 y(m) 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5 经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b 的图象.(1)根据以上数据,求出函数y=Aco sωt+b 的最小正周期T 、振幅A 及函数表达式;(2)依据规定,当海浪高度高于1 m 时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多少时间可供冲浪爱好者进行运动? 解析:由表中数据,知周期T=12.∴ω=1222ππ=T =6π.① 由t=0,y=1.5,得A+b=1.5.② 由t=3,y=1.0,得b=1.0.由①②得A=0.5,b=1.0,∴振幅为21. ∴y=21cos 6πt+1. (2)由题知,当y >1时才可对冲浪者开放.∴21cos 6πt+1>1,∴cos 6πt >0. ∴2kπ-2π<6πt <2kπ+2π,即12k-3<t <12k+3.③故可令③中k 分别为0,1,2,得0≤t <3或9<t <15或21<t≤24.∴在规定的时间上午8:00至晚上20:00之间,有6个小时时间可供冲浪者运动,即上午9:00至下午15:00. 21.已知函数f(x)=log 11(xa x +-其中a>0且1)a ≠.(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性并给出证明;(3)若12[0]x ∈,时,函数f(x)的值域是[0,1],求实数a 的值.解:(1)由条件知110x x +->,解得-1<x<1.∴函数f(x)的定义域为(-1,1). (2)函数f(x)为奇函数.证明:由(1)知函数f(x)的定义域关于原点对称.f(-x)=log 11x a x -+=-log 11()xa x f x +-=-.因此f(x)是奇函数.(3)f(x)=log 11x a x +-=log 121x a x -+- =log 1211()x a x x ---+=log 21(1)a x ---,记21()1x g x -=--,则21()1x g x -=--在12[0],上单调递增,因此当a>1时,f(x)在12[0],上单调递增, 由12()1f =,得a=3;当0<a<1时,f(x)在12[0],上单调递减, 由f(0)=1得出矛盾a ,∈;综上可知a=3。
材料科学基础期末复习考试题

综合题一:材料的结构1 谈谈你对材料学科和材料科学的认识。
2按照能级写出N、O、Si、Fe、Cu、Br原子的电子排布。
N 1S2 2S2 2P3O 1S2 2S2 2P4 Si 1S2 2S2 2P6 3S2 3P2 Fe 1S2 2S2 2P6 3S2 3P2 3D6 4S2 Cu 1S2 2S2 2P6 3S2 3P2 3D10 4S1 Br 1S2 2S2 2P6 3S2 3P6 3D10 4S2 4P53原子的结合键有哪几种?各有什么特点?金属键与其它结合键有何不同,如何解释金属的某些特性?离子键:正负离子相互吸引;键合很强,无方向性;熔点、硬度高,固态不导电,导热性差。
共价键:相邻原子通过共用电子对结合;键合强,有方向性;熔点、硬度高,不导电,导热性有好有差。
金属键:金属正离子于自由电子相互吸引;键合较强,无方向性;熔点、硬度有高有低,导热导电性好。
分子键:分子或分子团显弱电性,相互吸引;键合很弱,无方向性;熔点、硬度低,不导电,导热性差。
氢键:类似分子键,但氢原子起关键作用XH-Y;键合弱,有方向性;熔点、硬度低,不导电,导热性好。
金属键是由自由电子和属离子之间的静电吸引力组合而成,没有饱和性和方向性,因此使金属具有导电的性质。
4 理解空间点阵、晶体结构、晶胞概念,理解三者之间的关系(区别联系)。
组成晶体的粒子(原子、离子或分子)在三维空间中形成有规律的某种对称排列,如果我们用点来代表组成晶体的粒子,这些点的空间排列就称为空间点阵.晶体以其内部原子、离子、分子在空间作三维周期性的规则排列为其最基本的结构特征。
能够保持晶体结构的对称性而体积又最小称晶胞。
点阵+基元=晶体结构5 晶向指数和晶面指数的标定有何不同?其中有何须注意的问题?(说明这个是基础,可能不会直接让你标定六方指数,但是要掌握其他综合题目会考)晶面指数与晶向指数垂直6 画出Fcc(面心立方)晶体结构晶胞结构示意图,其表示符号、原子数、配位数、致密度各是什么?密排面、密排方向,相应关系式。
《马克思主义基本原理概论》期末考试复习题材料分析题题及参考答案

《马克思主义基本原理概论》期末考试复习题材料分析题题及参考答案1、材料一:鲁迅说过:“描神画鬼,毫无对证,本可以专靠神思,所谓‘天马行空’地挥写了。
然而他们写出来的却是三只限、长颈于,也就是在正常的人体身上增加了眼睛一只,拉长了颈子二三尺而已。
”材料二:《传习录》记载:先生(指哲学家王阳明)游南镇,一友指岩中花树问曰:“天下无心外之物,如此花树在深山中自开自落,于我心亦何相关?”先生曰:“你未看此花时,此花与汝心同归于寂;你来看此花时,此花颜色一时明白起来,便知此花不在你的心外。
”运用哲学基本问题原理分别评述鲁迅和王阳明的观点。
2、春秋时期,宋国有一个农夫,他总是嫌田里的庄稼长得太慢,今天去瞧瞧,明天去看看,觉得禾苗好像总没有长高。
他心想:有什么办法能使它们长得高些快些呢?有一天,他来到田里,把禾苗一棵一棵地往上拔。
一大片禾苗,一棵一棵地拔真费了不少的力气,等他拔完了禾苗,已经累得筋疲力尽了,可是他心里却很高兴。
回到家里还夸口说:“今天可把我累坏了,我帮助禾苗长高了好几寸!”他儿子听了,赶忙跑到田里去看,发现田里的禾苗全都已经枯死了。
运用客观规律性与主观能动性辩证关系原理分析说明拔苗助长故事对我们有什么样的启示?主观能动性和客观规律性辩证关系的原理:规律是客观的,不可抗拒的,我们要尊重客观规律,而不能违背规律;人在规律面前也不是完全被动的,人具有主观能动性,能在承认规律客观性、尊重客观规律的前提下,发挥主观能动性去认识规律,把握规律,从而利用规律,改造客观事物的具体联系,创造条件促进事物的发展,从而改造客观世界,让客观世界更好地为人类服务的目的。
主观能动性和客观规律性辩证关系原理的启示:它要求我们在社会主义现代化建设中要尊重规律,坚持一切从实际出发,实事求是。
要发挥主观能动性,努力创造条件,促进社会主义现代化建设的发展。
3、一个身患成骨不全症的女孩,从出生起全身骨头脆如玻璃,稍受力就会频繁断裂。
《西方经济学》期末复习题(3)

《西方经济学》期末复习题(3)《西方经济学》期末复习题一、单选题1.经济学上所说的稀缺性是指(资源的相对有限性)2.稀缺性问题(存在于所有经济中)3.稀缺性的存在意味着(必须作出选择)4.当资源不足以满足所有人的需求时(必须做出选择)5.当资源有限,欲望无限时,人们必须(做出选择)6.选择具有重要性,基本上是因为(相对于人类社会的无穷欲望而言,生产物品所需要的资源总是不足的)7.生产可能性曲线是指(在资源既定的条件下所能达到的各种最大产量的组合)8.生产可能性曲线上的任何一个组合都表明(没有闲置资源)9.位于生产可能线以内的任何一点表示(资源没有得到充分利用)10.生产可能性曲线内的任何一点都表明(一些资源可能被闲置)11.生产可能性曲线中的任何一点都表明(一些资源闲置,这是低效的生产)12.生产可能性曲线之所以凹向原点,是因为(要增加一种物品的生产就必须减少对另一种物品的生产)13.由政府来回答生产什么、如何生产和为谁生产这三个经济学基本问题的经济制度属于(计划经济)14.作为经济学的一个分支,微观经济学主要研究(家庭和企业的行为)15.作为经济学的一个分支,微观经济学主要研究(单个经济单位的经济行为)16.微观经济学要解决的问题是(资源配置)17.微观经济学的中心理论是(价格理论)18.以下哪项是微观经济学研究的问题(某一品牌彩电降价对全国彩电市场价格的影响)19.以下哪项不是微观经济学的研究对象(整体经济形势,如失业和通货膨胀)20作为经济学的一个分支,宏观经济学主要研究经济的全局,例如失业和通货膨胀宏观经济学要解决的问题是(资源利用)22宏观经济学的核心理论是(国民收入决定理论)23研究单个经济单位的经济行为的经济学称为(微观经济学)24经济学可分为(微观经济学和宏观经济学)25作为经济学的两个组成部分,微观经济学和宏观经济学是(互补的)26经济研究方法中的实证方法(主要研究“什么”的问题)27以下陈述是实证陈述(低利率将刺激投资)28以下陈述是实证陈述(医生比工人赚更多的钱)29经济研究方法(研究“应该是什么”的问题)30在以下陈述中,规范的是(控制通货膨胀比增加就业更重要)31在以下陈述中,规范的是(应降低利率以刺激投资)32以下陈述是规范的(收入分配中存在太多不平等)33由经济学建立的理论(源自一系列假设)34.经济理论或模型是(基于若干假设以及由这些假设推导出来的结论)35.假说就是(未经证明的理论)36.对企业所得税税率提高的部分均衡分析将得出结论(企业部门的投资者受到影响)37部分均衡分析指对以下哪一项的分析(仅考虑一个市场的变化而忽略其他市场)38企业所得税税率的提高将得出一个结论(所有行业的投资回报率都将受到影响)。
六年级上册语文期末复习题语言运用、综合实践题专项练习(含答案)

2021-2022学年第一学期六年级语文期末复习题(三)(语言运用、综合实践)班级:________ 姓名:________一、日积月累。
1.迎着和煦的春风,看着眼前繁花盛开、万紫千红的景象,我想起了代诗人写的春日中的诗句:“,。
”2.从曹植的“”中,我们感受到他的爱国热情。
3.我知道古代的“五音”指的是。
4.“其实,地上本没有路,,。
”这句话告诉我们要勇于实践,勇于开拓创新,只有努力奋斗,才能实现自己的理想。
5.什么人是中国的吉良?鲁迅先生这样回答:“我们从古以来,就有的人,有有的人,有的人,有的人……这就是中国的脊梁。
二、给下列句子加标点,使其表达不同的意思。
1.弟弟找不到奶奶心里很着急弟弟找不到奶奶心里很着急2.今年好倒霉少不得打官司今年好倒霉少不得打官司3.这份报告我写不好这份报告我写不好三、这句话有两种意思,请你把它写出来。
1.小明在理发。
(1)(2)2.饭不热了。
(1)(2)3.张红一个早上就写了三封信。
(1)(2)四、请根据下面提供的材料完成练习。
1.从上面的公交站牌可以得知,本站是。
2.王鲁一打算去南河小区,他应该乘坐路公交车。
3.王鲁一发现站牌上的地名拼写错误,可以改为。
A.HAODEGUANGCHANGB.HaoDe GuangChangC.Hao De Guang ChangD.HAODE GUANGCHANG五、语言运用。
互联网时代,一些互助类App应运而生。
有不少人认为应该通过互助类App捐献爱心,给那些真正需要帮助的人“雪中送炭”;也有一些人认为那些求助的人与“我”素不相识,无需捐赠。
为此,班里举行了一个小小的辩论会,就“面对科利用网络互助类APP求助的陌生人,捐还是不捐”这个问题展开了辩论,你赞同以上哪种观点?写出来,并有条理地说明理由(至少写三点)。
我赞同六、请简要概括漫画的内容,揭示其中寓意。
漫画的内容:漫画的寓意:漫画的内容:漫画的寓意:2021-2022学年第一学期六年级语文期末复习题(三)(语言运用、综合实践)(答案)二、日积月累。
电大《中国现代文学专题》期末复习题及答案(三)

电大《中国现代文学专题》期末复习题及答案(三)四、简答题31.巴金通过汪文宣一家的遭遇,控诉了那个使善良人受苦的罪恶社会。
除了控诉,作者还挖掘了哪些更深层的内容?A.写出了对新式生活的反省。
汪文宣和曾树生都接受过高等教育,有勇气追求爱情,也有过自己的抱负,但是,现实的日常生活,消磨了他们的锐气,更压迫着他们的身心,让他们或谨小慎微地看上司的脸色行事,或以身体换取某些现实利益。
(5分)B.写出了爱的悲哀。
曾树生和汪母,作为妻子或母亲,都爱着汪文宣,但是,这两个女性之间,却形成很大的对立,无法妥协,给汪文宣造成新的伤害,造成家庭的破裂。
(5分)32.请简要说明《金锁记》的前一部分主要通过哪些对话写出了曹七巧的婚姻及生存现状。
A.从丫头的对话中,可以了解到七巧身为麻油店女儿,只是因为姜家二爷身患骨痨,才得以“攀附”高门。
(3分)B.从七巧与姜家人的谈话中,可以了解到她在这大家庭中受排挤、遭嘲讽的地位。
(3分)C.从七巧与姜家三爷季泽的调笑中,可以了解到七巧压抑的情欲。
(2分)D.从七巧与哥嫂的对话及怄气中,则展示出金钱关系支配下的亲情。
(2分)33.请简要说明“苏张”小说的异同。
A.苏青与张爱玲的小说同样摹写上海市民,尤其是职业女性的生活。
(4分)B.苏青的笔墨比张爱玲更显质直激切一些,张爱玲是“苍凉”,苏青则是“哀恸”。
(3分)C.苏青的创作则差不多是她的“自叙传”,而张爱玲的小说故事及人物原型则多从她的远近亲友而来。
(3分)34.现代通俗文学的发展大致上可分“晚清文学时期”、“鸳鸯蝴蝶派时期”、“市场化时期”和“新生代时期”四个阶段。
请简要说明这四个阶段的大致时间和主要特点。
A.“晚清文学时期”大致在1902年到1911年左右。
以开启民智、批评社会为主要的创作取向,涉及到社会的各个方面,出现了著名的“四大谴责小说”等。
(2分)B.“鸳鸯蝴蝶派时期” 大致在1911年中华民国成立前后至1921年。
“谴责”逐步地被“揭黑”所取代,“社会”逐步地被“言情”所取代,“批判意识”逐步地被“传奇煽情”所取代,大致上可分为“黑幕文学”和“言情文学”两类。
材料力学期末考试复习题及答案
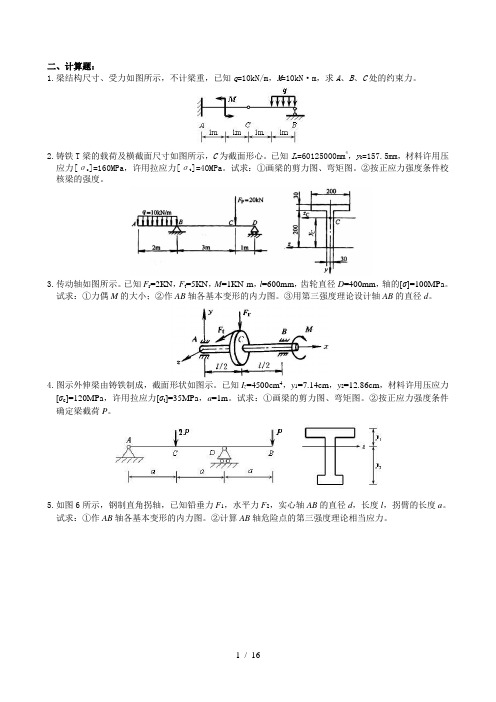
二、计算题:1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
已知I z=60125000mm4,y C=157.5mm,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
3.传动轴如图所示。
已知F r=2KN,F t=5KN,M=1KN·m,l=600mm,齿轮直径D=400mm,轴的[σ]=100MPa。
试求:①力偶M的大小;②作AB轴各基本变形的内力图。
③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成,截面形状如图示。
已知I z=4500cm4,y1=7.14cm,y2=12.86cm,材料许用压应力[σc]=120MPa,许用拉应力[σt]=35MPa,a=1m。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5.如图6所示,钢制直角拐轴,已知铅垂力F1,水平力F2,实心轴AB的直径d,长度l,拐臂的长度a。
试求:①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力。
6.图所示结构,载荷P=50KkN,AB杆的直径d=40mm,长度l=1000mm,两端铰支。
已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=1.12MPa,稳定安全系数n st=2.0,[σ]=140MPa。
试校核AB杆是否安全。
7.铸铁梁如图5,单位为mm,已知I z=10180cm4,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa,试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。
已知M=200GPa,μ=0.3,[σ]=140MPa。
发酵工程原理及技术期末复习试题3套含答案(大学期末复习资料)

样卷1一、填空(每空1分,共30分)1,工业上的发酵产品分为菌体、代谢产物、微生物酶和生物转化产品四个类别。
2,从本质上来说,微生物代谢是通过酶量调节和酶活性调节两种方式来进行调节的。
3,根据对氧需求的不同可将发酵分为通风发酵和厌氧发酵两种类型。
4,根据产物合成途径,我们可将次级代谢分为与糖代谢有关的类型、与脂肪酸代谢有关的类型、与萜烯和甾体化合物有关的类型、与TCA环有关的类型和与氨基酸代谢有关的类型五种类型。
5,卡尔文循环由羧化、还原和再生三个阶段(部分)组成。
6,发酵厂用于原料除杂的方法有筛选、风选和磁力除铁。
7,种子的制备可分为实验室种子制备和车间种子制备两个阶段。
8,空气除菌的方法有加热、静电、射线和介质过滤。
10,常用的连续灭菌工艺有喷射加热、薄板换热器和喷淋冷却。
11,氢化酶是氢细菌进行无机化能营养方式生长的关键酶,在多数氢细菌中有两种氢化酶,它们是颗粒状氢化酶和可溶性氢化酶。
二、名词解释(每题4分,共20分)1,发酵工程应用微生物学等相关的自然科学以及工程学原理,利用微生物等生物细胞进行酶促转化,将原料转化成产品或提供社会性服务的一门科学。
2,无菌空气发酵工业应用的“无菌空气”是指通过除菌处理使空气中含菌量降低在一个极低的百分数,从而能控制发酵污染至极小机会。
此种空气称为“无菌空气”。
3,种子的扩大培养是指将保存在砂土管、冷冻干燥管中处于休眠状态的生产菌种接入试管斜面活化后,在经过扁瓶或摇瓶及种子罐逐级放大培养而获得一定数量和质量的纯种过程。
这些纯种培养物称为种子。
4,酶合成的阻遏某些酶在微生物生长时可正常地产生,但当生化途径的终产物浓度增加时或向生长培养基加入这种终产物时,酶的合成就被阻遏。
这种低分子量的终产物(辅阻遏物)被认为是同胞内由调节基因编码的蛋白质(阻遏蛋白)结合,产生一种阻遏物,该阻遏物“关闭”对酶编码的结构基因。
这样的酶称为可受阻遏的酶。
阻遏酶合成的物质称为阻遏物。
复合材料期末复习题库

复合材料期末复习题库一、选择题1. 复合材料是由两种或两种以上不同性质的材料,通过物理或化学方法复合而成的新材料,其主要特点不包括以下哪项?A. 高强度B. 轻质C. 易加工D. 导电性2. 纤维增强复合材料中,纤维主要作用是提供:A. 韧性B. 耐腐蚀性C. 强度D. 绝缘性3. 以下哪种不是常用的树脂基体材料?A. 环氧树脂B. 聚酯树脂C. 聚乙烯D. 酚醛树脂4. 复合材料的层合板结构中,每层材料的铺设角度对材料的性能有重要影响,其中0°铺设主要提供:A. 抗拉强度B. 抗弯强度C. 抗剪强度D. 抗冲击强度5. 复合材料的界面结合力是影响复合材料性能的关键因素之一,以下哪种方法可以增强界面结合力?A. 增加基体材料的粘度B. 提高纤维的表面粗糙度C. 降低纤维与基体的相容性D. 减少纤维的表面处理二、填空题6. 复合材料通常由______和______两部分组成。
7. 复合材料的命名通常遵循“______+基体材料”的规则。
8. 复合材料的力学性能主要取决于______和______的性能以及它们之间的______。
9. 复合材料的制备工艺包括______、______、______等。
10. 复合材料在______、______、______等领域有广泛的应用。
三、简答题11. 简述复合材料的优势和局限性。
12. 解释什么是复合材料的界面相容性和界面结合力,并说明它们对复合材料性能的影响。
13. 描述复合材料的常见制备工艺,并简述每种工艺的特点。
14. 举例说明复合材料在航空航天领域的应用。
15. 讨论复合材料在环境友好和可持续发展方面的优势。
四、计算题16. 假设有一块碳纤维增强环氧树脂基复合材料,其体积分数为60%碳纤维和40%环氧树脂。
已知碳纤维的密度为1.75 g/cm³,环氧树脂的密度为1.15 g/cm³,试计算该复合材料的密度。
五、论述题17. 论述复合材料在现代汽车工业中的应用及其对汽车性能的影响。
新材料科学导论期末复习题(有答案版)

新材料科学导论期末复习题(有答案版)一、填空题:1.材料性质的表述包括力学性能、物理性质和化学性质。
2.化学分析、物理分析和谱学分析是材料成分分析的三种基本方法。
3.材料的结构包括键合结构、晶体结构和组织结构。
4.材料科学与工程有四个基本要素,它们分别是:使用性能、材料的性质、制备/加工和结构/成分。
5.按组成和结构分,材料分为金属材料,无机非金属材料,高分子材料和复合材料。
6.高分子材料分子量很大,是由许多相同的结构单元组成,并以共价键的形式重复连接而成。
7.复合材料可分为结构复合材料和功能复合材料两大类。
8.聚合物分子运动具有多重性和明显的松弛特性。
9.功能复合材料是指除力学性能以外,具有良好的其他物理性能并包括部分化学和生物性能的复合材料。
如有光,电,热,磁,阻尼,声,摩擦等功能。
10.材料的物理性质表述为光学性质、磁学性质、电学性质和热学性质。
11.由于高分子是链状结构,所以把简单重复(结构)单元称为链节,简单重复(结构)单元的个数称为聚合度。
12.对于脆性的高强度纤维增强体与韧性基体复合时,两相间若能得到适宜的结合而形成的复合材料,其性能显示为增强体与基体的互补。
(ppt-复合材料,15页)13.影响储氢材料吸氢能力的因素有:(1)活化处理;(2)耐久性(抗中毒性能);(3)抗粉末化性能;(4)导热性能;(5)滞后现象。
14.典型热处理工艺有淬火、退火、回火和正火。
15.功能复合效应是组元材料之间的协同作用与交互作用表现出的复合效应。
复合效应表现线性效应和非线性效应,其中线性效应包括加和效应、平均效应、相补效应和相抵效应。
16.新材料发展的重点已经从结构材料转向功能材料。
17.功能高分子材料的制备一般是指通过物理的或化学的方法将功能基团与聚合物骨架相结合的过程。
功能高分子材料的制备主要有以下三种基本类型:①功能小分子固定在骨架材料上;②大分子材料的功能化;③已有功能高分子材料的功能扩展;18.材料的化学性质主要表现为催化性能和抗腐蚀性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一历史期末复习题(非选择题)1.(26分)阅读下列材料:材料一汉哀帝曾经说:‚丞相者,朕之股肱,所与共承庙宇,统理海内,辅朕之不逮以治天下也。
‛——《汉书·孔光传》材料二唐太宗曾说:‚以天下之广,四海之众,千端万绪,须合变通,皆委百司商量、宰相筹划,于事稳便,方可奏行。
岂得以一日万机,独断一人之虑也。
‛——《贞观政要》材料三明太祖曾说:‚自秦以下,人君天下者,皆不鉴秦设相之患,相从而命之,往往病及于国君者,其故在擅专威福。
‛——黄佐《南雍志》材料四清高宗(乾隆帝)曾说:‚昔程子云:‘天下之治乱系宰相’,此只可就彼时朝政闒冗者而言。
若以国家治乱专倚宰相,则为之君者不几如木偶旒缀乎?且用宰相者,非人君其谁为乎?使为人君者,深居高处,以天下之治乱,付之宰相,大不可也。
使为宰相者,居然以天下之治乱为己任,目无其君,此尤大不可也。
‛——《十二朝东华录》请回答:(1)材料一、材料二中统治者对宰相的态度是怎样的?(8分)(2)材料三、材料四中统治者对宰相的态度怎样?其态度与材料一、材料二的统治者有无本质的区别?为什么?(说明有无本质区别的原因,11分)(3)统治者对宰相态度的变化,对中国社会造成了怎样的影响?(7分)2.(26分)阅读下列材料:材料一……秦创建御史大夫为中央监察机构,在地方设臵监郡御史。
汉承秦制,在中央设御史府的同时,地方设立十三州部刺史,监察地方长吏。
……唐在御史台下设台院、殿院、察院,分工明确,互相配合,地方则分十道(后增至十五道)监察区,形成比较严密的监察网。
宋代,中央沿袭唐制,御史台仍设三院。
地方设监司和通判,直属皇帝。
元朝,地方设行御史台,统辖二十二道监察区,还制定了一整套监察法规。
明朝改御史台为都察院,地方设十三道巡按御史和各省提刑按察司。
清朝,地方监察沿用明制。
材料二宋代明确规定,未经两任县令者不得任御史之职。
按规定,御史有‚闻风弹人‛之权,每月必须向上奏事一次,称‚月课‛;上任后百日必须弹人,否则就要罢黜为外官或受罚俸处分,名为‚辱台钱‛。
材料三元世祖时明确规定:‚凡有官守不勤于职者,勿问汉人回回,皆以论诛之,且没其家。
‛——《元史》卷十材料四凡御史犯罪加三等,有赃从重论。
——《明史〃职官志》材料五清皇太极下诏:‚凡有正事背谬,及贝勒大臣骄肆慢上、贪酷不法、无礼妄行者,许都察院直言无讳。
‛‚倘知情蒙蔽,以误国论。
‛——《大清会典》卷九百九十八请回答:(1)依据材料一概括中国古代监察制度发展过程中的主要特点。
(9分)(2)材料二中,宋代对担任监察官员的资格有何要求?根据你的理解,“月课”“辱台钱”可能会产生什么不良后果?(6分)(3)根据材料三、材料四、材料五,分析元明清时期在吏治方面的特点。
(5分)(4)综合上述材料及所学知识,简析中国古代监察制度在政治方面的重要影响。
(6分)3.(28分)2010年是中国人民抗日战争胜利65周年纪念,为了弘扬爱国主义和振奋民族精神,我省XX中学举办一期“纪念抗日战争胜利65周年图片展”。
请你参加这次活动,并帮助完成下列问题:(1)下面是该校同学设计的三个专题,请你仿照第一专题的表达,写出后面专题应选择的图片名称。
(注意:只写图片名称,无须画图,每一专题至少写2个,8分)专题名称图片名称一日军全面侵华卢沟桥事变、八一三事变二国共合作,全民抗战三抗日战争的胜利(2)小红同学找到下面两幅图片,请你为这两幅图片确定一个新的专题名称。
就本专题内容,你认为在东北地区还可以找到哪些方面的典型图片资料?(6分)(3)在这次图片展上,还有一幅书法作品,写的是清末诗人丘逢甲的《春愁》:“春愁难遣强看山,往事惊心泪欲潸。
四百万人同一哭,去年今日割台湾。
”请简要说明在近代史上,日本帝国主义强占台湾和台湾回归祖国的过程。
(8分)(4)现今日本右翼势力千方百计否认战争事实,竭力掩盖侵华战争罪行,结合这次图片展,请谈谈你的感想(最少写二点)。
(6分)4.(24分)近代以来,面对西方列强的野蛮侵略,中国人民进行了前赴后继,不屈不挠的抗争。
观察下列图片,结合所学知识回答下列问题:请回答:(1)上述四幅图片,分别反映了近代中国民主革命中的重大历史事件,请根据图中信息,完成下表。
图号重大事件性质历史意义图一太平天国运动__________________(2分)沉重地打击了清朝封建统治,提出了中国第一个具有资本主义性质的社会改革方案。
图二义和团运动__________________(2分)体现了中国人民反侵略的斗争精神,打击了帝国主义,一定程度上推动了清王朝的改革运动图三辛亥革命__________________(2分)________________________________________________________________________(4分)图四_________________________________(2分)反帝反封建的爱国运动__________________________________________________________(4分)(2)你从上述大事中能得到什么认识?(8分)5.(28分)阅读下面材料:材料1949年9月30日,中国人民政治协商会议第一次会议的代表们在天安门广场,挥铲为“人民英雄纪念碑”奠基,毛泽东当场宣读碑文:“三年以来,在人民解放战争和人民革命中牺牲的人民英雄永垂不朽!三十年以来,在人民解放战争和人民革命中牺牲的人民英雄们永垂不朽!由此上溯到一千八百四十年,从那时起,为了反对内外敌人,争取民族独立和人民自由幸福,在历次斗争中牺牲的人民英雄永垂不朽!”请回答:(1)“三年以来,在人民解放战争和人民革命中”拉开解放战争中战略决战序幕的是什么?(4分)(2)“三十年以来”,是中国共产党探索中国特色革命道路并取得了胜利的时期。
试概说这“三十年”期间,中国共产党探索具有中国特色革命道路、并取得成功的事例两个。
(10分)(3)从“一千八百四十年”起,“为了反对内外敌人,争取民族独立和人民自由幸福”,中国人民开始学习西方,探索现代化之路。
请仿照下例,另举两例。
(10分) 例:洋务运动,学习西方科学技术,自强求富。
(4)中华民族100多年来浴血奋斗,写成了一部可歌可泣的历史,留下了许许多多的宝贵经验和惨痛的教训。
这一切对于我们走现代化道路有什么启迪?(4分)6.(26分)2012年10月1日是中华人民共和国成立63周年。
63年来,新中国的民主政治建设上不断创新发展,而且在实践中不断开创新局面。
阅读下列材料:材料一1949年10月,诗人胡风以一句“时间开始了”表达自己对新中国诞生的称颂,这句话也以其高超的艺术手法被誉为“开国的绝唱”。
材料二“新中国的建立,使中国实现了从两千多年的封建专制政治、近代以来照搬西方民主政治模式的失败到尝试向新型人民民主政治的伟大跨越。
”——《中国的民主政治建设》白皮书材料三2007年3月16日,温家宝总理在回答记者提问时指出:“……民主、法制、自由、人权、平等、博爱,这不是资本主义所特有的,这是整个世界在漫长的历史过程中共同形成的文明成果,也是人类共同追求的价值观。
我同时强调,世界上有2 000多个民族,200多个国家和地区,他们的社会历史发展不同,他们的发展水平不同,民主的形式和途径也是不相同的……民主制度同任何真理一样,都要接受实践的考验。
”材料四请回答:(1)为迎接这一伟大“时间”的到来,1949年中国共产党在政治、军事和组织方面各做了哪些准备?(9分)(2)简述1949~1956年新中国民主政治建设的主要成果。
概括新中国政治制度的突出特点。
(10分)(3)据材料四概括指出我国新时期民主政治建设的主要成就。
(7分)7.(26分)阅读下列材料:材料一尼克松在回顾1972年访华时说:‚我知道,1954年在日内瓦会议时福斯特〃杜勒斯(当时的美国国务卿)拒绝同周(周恩来)握手,使他深受侮辱。
因此我走完梯级时决心伸出我的手,一边向他走去。
当我们的手相握的时候,一个时代结束了,另一个时代开始了。
”材料二历届联大恢复中国在联合国合法权利时支持中国票数增长示意图到1970年,支持恢复中华人民共和国在联合国合法席位的提案,第一次超过支持美国反对恢复中国在联合国合法席位提案的票数。
中国恢复在联合国合法席位的步伐不可阻挡。
材料三20世纪80年代,美售台武器虽然数量较大,但是主要是一些陈旧落后、退役淘汰的‚滞销品‛。
20世纪90年代,美国强化对华遏制政策,对台军售规模较大、性能较好。
1992年,布什政府卖给台湾150架F16战斗机。
1999年3月24日,美国为首的北约发动了对南联盟的空中打击,科索沃战争爆发。
5月8日,美国B2轰炸机悍然袭击了中国驻南联盟大使馆,导致3人死亡、多人受伤和馆舍的毁坏。
材料四左图:2008年11月,APEC第16次领导人非正式会议召开前夕,中国国家主席胡锦涛在利马会见美国总统布什。
右图:2008年11月,赢得美国总统选举的奥巴马在庆祝大会上发表演说。
请回答:(1)据材料一,1954年美国国务卿杜勒斯拒绝同周恩来总理握手的原因有哪些?(10分)(2)据材料一、材料二与所学知识,促成尼克松与周恩来这次“握手”的主要因素有哪些?尼克松说这次历史性的握手使“一个时代结束了,另一个时代开始了”,如何理解这句话?(13分)(3)据材料三,20世纪八九十年代中美关系出现不和谐音的根本原因是什么?(3分) 8.(26分)民主政治的发展,推动了人类社会的不断进步。
阅读下列材料:材料一古代希腊的民主与今天西方的民主不能完全相提并论。
在雅典,城邦的所有公民都有可能亲自参加选举和表决……材料二在现代社会中,无论是哪一个统治阶级,只要实行民主政治,都普遍采取代议制的形式,只是具体方式有所不同。
在代议机构的设臵上,有的资本主义国家实行两院制,有的实行一院制。
材料三发展社会主义民主政治是我们党始终不渝的奋斗目标。
要坚持中国特色社会主义政治发展道路,坚持党的领导、人民当家做主、依法治国有机统一……不断推进社会主义政治制度自我完善和发展。
——中共十七大报告请回答:(1)依据材料一、材料二指出,与西方现代民主相比,古代希腊民主的特点是什么?结合所学知识分析其成因。
(10分)(2)依据材料二并结合所学知识概括指出西方代议制民主是怎样确立的?代议制民主政治的“具体方式”又有哪些不同?试举例说明。
(10分)(3)结合所学知识概括指出,改革开放后我国是如何“不断推进社会主义政治制度自我完善和发展”的?(6分)9.(26分)阅读下列材料:材料一康熙帝说:‚今天下大小事务,皆朕一人亲理,无可旁贷。
若将要务分任于他人,则断不可行。
所以无论巨细,朕必躬自断制。
