奇偶校验_校验和实验
奇偶校验名词解释(一)

奇偶校验名词解释(一)奇偶校验1. 奇偶校验的定义和作用•奇偶校验是一种数据传输中常用的差错检测方法,通过给数据添加一个奇偶位来检测数据传输过程中产生的错误。
•奇偶校验的作用是检测传输中的数据是否出现错误,并进行纠错操作。
2. 相关名词解释奇偶位•奇偶位是指在进行奇偶校验时所需要添加到数据末尾的一位二进制数。
•根据数据中1的个数是奇数还是偶数,确定奇偶位的取值:奇数个1时奇偶位为0,偶数个1时奇偶位为1。
校验位•校验位是指用于奇偶校验的二进制数,用于检测数据传输过程中是否发生错误。
•校验位的取值由奇偶校验算法决定,通过计算数据中1的个数来确定。
校验和•校验和是一种用于奇偶校验的简化模型,通过对数据中所有位进行求和运算得到一个二进制数作为校验结果。
3. 示例解释奇偶位示例假设需要传输的数据为8位二进制数:。
通过奇偶校验方法,计算数据中1的个数为4个,为偶数个,因此奇偶位的取值为1。
添加奇偶位后的数据为。
校验位示例假设需要传输的数据为8位二进制数:。
通过奇偶校验算法,计算数据中1的个数为4个,为偶数个,因此校验位的取值为1。
添加校验位后的数据为。
校验和示例假设需要传输的数据为8位二进制数:。
计算数据中所有位(包括奇偶位)的和为8,转换为二进制数为1000。
校验和为1000。
总结奇偶校验是一种常用的差错检测方法,通过添加奇偶位来检测数据传输过程中的错误。
相关名词包括奇偶位、校验位和校验和。
奇偶位是计算数据中1的个数并确定取值的位,校验位是用于检测错误的二进制数,校验和是对所有位进行求和得到的结果。
通过奇偶校验方法,可以提高数据传输的可靠性和纠错能力。
奇偶校验电路设计

奇偶校验电路设计一、实验目的1.熟悉QuartusII的使用;2. 学习在QuartusII中;3. 学习原理图方式自定义元件的输入,封装,调用;4. 掌握奇偶校验原理;5. 学会使用现成的芯片搭建目标电路。
二、实验内容和原理实验内容:(1)在QuartusII环境下以原理图方式建立顶层文件工程。
利用多个74386芯片搭建一个奇偶校验电路。
74386提供四个2输入异或门(2)建立仿真文件,观察输出结果。
实验原理:奇偶校验码是最简单的数据校验码,其码距为2,可以检测出一位错误,但无法指出错误的位置。
具体校验实现方法为将有效信息位和校验位读入,判断其1的个数是奇数个还是偶数个,在奇校验的情况下正常情况下个数应该为奇数个,偶校验正常情况下应该是偶数个。
校验码的生成:对于奇校验,判断有效信息位1的个数,若为偶数则校验位为1,奇数则校验位为0;偶校验反之。
具体实现的逻辑表达式如下:三、 实验设计原理图以及综合结果记录逻辑单元<Le>的消耗情况等。
原理图如下: 76543210校奇形成偶校验出错奇校验出错偶形成A B =1=1=1=1=1=1=1=111经过设计后用74386实现的原理图如下:综合结果如下图所示:四、仿真波形图画出波形图以及波形图中仿真信号的说明。
并分析结果(实验现象结论)。
仿真波形图如下所示:其中,D0-7为信息位,Djiao为校验位。
实验结果如下:说明:波形信息位为奇数个1,校验位为0时,输出的奇校验位为0,偶校验位为1,奇校验错误为0,偶校验错误为1(即有错)。
同理其他测试分别测试了信息位为奇数个1,校验位为1、信息位为偶数个1,校验位为1、信息位为偶数个1,校验位为0的情况,图中波形的测试完全符合预期要求。
五、实验中遇到的问题和解决方法。
在实验中遇到的主要问题:(1)操作不熟悉导找不到部分功能元件(2)由于连线有误,在仿真时结果出现错误。
解决方法:(1)寻找芯片时双击面板在搜索的框内打入全名(打入部分名字不显示)(2)仿真结果与预期不一致时,可以分析错误波形,从而准确找到出错的地方。
奇偶校验

概述奇偶校验法常用于识别数据是否发生传输错误,并且可以启动校正措施,或者舍弃传输发生错误的数据,要求重新传输有错误的数据块。
编辑本段奇偶校验法奇偶校验法是一种很简朴并且广泛使用的校验方法。
这种方法是在每一字节中加上一个奇偶校验位,并被传输,即每个字节发送九位数据。
数据传输以前通常会确定是奇校验还是偶校验,以保证发送端和接收端采用相同的校验方法进行数据校验。
假如校验位不符,则认为传输出错。
奇校验是在每个字节后增加一个附加位,使得“1”的总数为奇数。
奇校验时,校验位按如下规则设定:假如每字节的数据位中“1”的个数为奇数,则校验位为“0”若为偶数,则校验位为“1”。
奇校验通常用于同步传输。
而偶校验是在每个字节后增加一个附加位,使得“1”的总数为偶数。
偶校验时,校验位按如下规则设定:假如每字节的数据位中“1”的个数为奇数,则校验位为“1”;若为偶数,则校验位为“0”。
偶校验常用于异步传输或低速传输。
校验的原理是:假如采用奇校验,发送端发送的一个字符编码(含校验位)中,“1”的个数一定为奇数个,在接收端对接收字符二进制位中的“1”的个数进行统计,若统计出“1”的个数为偶数个,则意味着传输过程中有1位(或奇数位)发生差错。
事实上,在传输中偶尔—位出错的机会最多,故奇偶校验法常常采用。
然而,奇偶校验法并不是一种安全的检错方法,其识别错误的能力较低。
假如发生错误的位数为奇数,那么错误可以被识别,而当发生错误的位数为偶数时,错误就无法被识别了,这是因为错误互相抵消了。
数位的错误,以及大多数涉及偶数个位的错误都有可能检测不出来。
它的缺点在于:当某一数据分段中的一个或者多位被破坏时,并且在下一个数据分段中具有相反值的对应位也被破坏,那么这些列的和将不变,因此接收方不可能检测到错误。
常用的奇偶校验法为垂直奇偶校验、水平奇偶校验和水平垂直奇偶校验。
编辑本段垂直奇偶校验垂直奇偶校验是在垂直方向上以列的形式附加上校验位。
假设数据格式及其发送顺序如图1所示,则垂直奇偶校验的编码规则如图2所示。
数字校验算法

数字校验算法数字校验算法是一种用于验证数据完整性和准确性的数学算法。
它通过对数据进行计算和比较,确定数据是否被篡改或损坏。
数字校验算法广泛应用于计算机网络、数据传输以及存储系统等领域,保证数据的可靠性和安全性。
本文将介绍几种常见的数字校验算法及其原理。
一、奇偶校验算法奇偶校验算法是最简单的数字校验算法之一。
它通过在数据位中添加一个奇偶位来确保数据的正确性。
具体操作是在数据中添加一个位,使得数据位和奇偶位的总位数为奇数或偶数。
接收端通过计算数据位和奇偶位的总位数是否为奇数或偶数来判断数据是否正确。
如果总位数不匹配,则说明数据传输中发生了错误。
二、循环冗余校验算法循环冗余校验算法(CRC)是一种常用的数字校验算法。
它通过对数据进行多项式的除法运算来生成校验码。
发送端首先将数据和生成多项式进行除法运算,得到余数作为校验码,然后将数据和校验码一起发送。
接收端将接收到的数据和生成多项式进行除法运算,如果余数为0,则说明数据传输正确;如果余数不为0,则说明数据传输错误。
三、哈希校验算法哈希校验算法是一种基于哈希函数的数字校验算法。
它通过对数据进行哈希运算,得到一个固定长度的校验值。
发送端将数据和校验值一起发送,接收端对接收到的数据进行相同的哈希运算,并将得到的校验值与接收到的校验值进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
四、消息认证码算法消息认证码算法(MAC)是一种常用的数字校验算法。
它通过对数据进行加密和认证来确保数据的完整性和真实性。
发送端使用密钥对数据进行加密和认证,并将加密后的数据和认证标签一起发送。
接收端使用相同的密钥对接收到的数据进行解密和认证,并将得到的认证标签与接收到的认证标签进行比较。
如果两者相同,则说明数据传输正确;如果不同,则说明数据传输错误。
五、数字签名算法数字签名算法是一种常用的数字校验算法。
它通过使用私钥对数据进行加密和签名,确保数据的完整性、真实性和不可抵赖性。
奇偶校验与和校验

在数据传输前附加一位奇校验位,用来表示传输的数据中"1"的个数是奇数还是偶数,为奇数时,校验位置为"0",否则置为"1",用以保持数据的奇偶性不变。
例如,需要传输"11001110",数据中含5个"1",所以其奇校验位为"0",同时把"110011100"传输给接收方,接收方收到数据后再一次计算奇偶性,"110011100"中仍然含有5个"1",所以接收方计算出的奇校验位还是"0",与发送方一致,表示在此次传输过程中未发生错误。
2、对数据长度没限制的实现
unsigned short cksum (struct ip *ip, int len){
long sum = 0;
while ( len >1 ){
sum += *((unsigned short *) ip)++;
if (sum & 8x00000000)
count -= 2;
}
if( count > 0 )
sum += * (unsigned char *) addr;
while (sum>>16)
sum = (sum & 0xffff) + (sum >> 16);
return ~sum;
}
第一个while循环是做普通加法(2进制补码加法),因为IP包头和TCP整个报文段比较短(没达到2^17数量级),所以不可能导致4字节的sum溢出(unsigned long 一般至少为4字节)).
奇偶校验实验报告

一、实验目的1. 理解奇偶校验的基本原理及作用。
2. 掌握奇偶校验的实现方法。
3. 学会使用Verilog语言设计奇偶校验电路。
4. 通过仿真验证奇偶校验电路的正确性。
二、实验原理奇偶校验是一种简单的错误检测码,用于检测数据在传输过程中是否发生错误。
其基本原理是在数据末尾添加一个校验位,使得数据位和校验位中1的个数为奇数或偶数。
如果接收方收到的数据位和校验位中1的个数不是奇偶性相同,则说明传输的数据出现了错误。
奇偶校验分为奇校验和偶校验两种:1. 奇校验:数据位和校验位中1的个数为奇数。
2. 偶校验:数据位和校验位中1的个数为偶数。
三、实验环境1. FPGA开发板:如Xilinx、Altera等。
2. Verilog开发工具:如Vivado、Quartus等。
3. 仿真工具:如ModelSim等。
四、实验步骤1. 设计奇偶校验电路(1)根据实验要求,设计一个同步时序电路,对串行二进制输入进行奇偶校验,每检测5位输入,输出一个结果。
(2)定义输入信号和输出信号:- 输入信号:serial_in(串行输入)- 输出信号:parity_out(奇偶校验输出)(3)编写Verilog代码实现奇偶校验电路:```verilogmodule parity_checker(input wire [4:0] serial_in,output reg parity_out);always @(posedge serial_in[0]) beginif (serial_in == 5'b11111) beginparity_out = 1'b1; // 5位输入中1的数目为奇数,输出1end else beginparity_out = 1'b0; // 5位输入中1的数目为偶数,输出0endendendmodule```2. 仿真验证(1)使用ModelSim进行仿真,验证奇偶校验电路的正确性。
奇偶校验_校验和实验

实验5-1纠错与检错1.实验内容读程序,在所有红色的“#”后面添加解释,说明程序的作用2.实验题目(1)奇偶校验码在原始模式上增加一个附加比特位,即奇偶校验位,使最后整个模式中1的个数为奇数(奇校验)或偶数(偶校验)。
本程序用到列表、字符串合并、取模等概念。
code=input("Please input a 7-bit-binary code:")a=0# for 循环作用是什么for i in range(0,6,1):if code[i]=='1':a=a+1print("After odd parity checking the code is:")if a%2==0:print(code+'1') # 这句做了什么else:print(code) # 这句做了什么print("After even parity checking the code is:")# 下面 if .. else …作用是什么if a%2==0:print(code)else:print(code+'1')(2)垂直水平奇偶校验如下图所示,14个字符纵向排列形成一个数据块,每个字符占据一列,低位比特在上,高位比特在下,用b8(第8位)作为垂直奇偶校验位,各字符的同一比特位形成一行,每一行的最右边一位作为水平奇偶校验位,这里在垂直和水平方向均采用偶校验。
#下面的函数做了什么 def oddeven(l): a=0for i in range(0,len(l),1): if l[i]=='1': a=a+1 if a%2==0: return '0' else:return '1'block=[['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['0']*15]for i in range(0,14,1):vcode=input("Please input a 7-bit-binary code:") for j in range(0,7,1): block[j][i]=vcode[j]block[7][i]=oddeven(vcode)# 这句做了什么 hcode=['0']*14for j in range(0,8,1):for i in range(0,14,1): hcode[i]=block[j][i]block[j][14]=oddeven(hcode)# 这句做了什么 print(block)(3)循环冗余校验任何一个二进制位串都可以用一个多项式来表示,多项式的系数只有0和1,n 位长度的码C 可以用下述n -1次多项式表示:()n 1n 210C x C x C x C x C --=++++ n-1n-21例如位串1010001可以表示为x 6+x 4+1。
校验之:海明码校验、奇偶校验

校验之:海明码校验、奇偶校验1、奇偶校验码奇偶校验通过在编码中增加⼀个校验位来使编码中的1的个数为奇数(奇校验)或者偶数(偶校验),从⽽使码距变为2.对于奇校验,它可以检测代码中奇数位出错的编码,但不能发现偶数位出错的情况。
既当合法编码中奇数位出现错误。
也就是1变成0或者0变成1,其编码的奇偶性就发⽣了变化,从⽽发现错误。
但是这种校验只能发现出现了错误但是不知道具体是哪⼀位发⽣了错误。
8421码的奇偶校验码⼗进制数 8421 BCD码带奇校验位的8421码带偶校验位的8421码000000000 10000 0100010001 00001 1200100010 00010 1300110011 00011 0401000100 10100 1501010101 00101 0601100110 10110 0701110111 00111 1810001000 01000 1910011001 11001 0常⽤的奇偶校验有三种:⽔平奇偶校验,垂直奇偶校验校验和⽔平垂直奇偶校验。
⽔平奇偶校验:对每⼀种数据的编码添加校验位,使信息位与校验位处于同⼀⾏垂直奇偶校验:这种校验将数据分为若⼲组,⼀组⼀⾏,整齐排列,再加上⼀⾏校验位,针对每⼀列采样奇校验或偶校验。
对32位数据:10100101 00110110 11001100 10101011 进⾏校验:编码分类垂直奇校验垂直偶校验数据1010010100110110110011001010101110100101001101101100110010101011校验位0000101111110100就是这个意思:--------------------------------------------------------------------------------------------------------------⽔平校验与垂直⽔平校验都类似。
各种校验码校验算法分析

各种校验码校验算法分析校验码校验算法是一种用于数据传输或存储中验证数据完整性和准确性的技术,它能够检测出数据在传输或存储过程中是否发生了错误或损坏,从而确保数据的可靠性。
在实际应用中,校验码校验算法广泛应用于通信、网络传输、存储和数据处理等领域,其设计和选择对数据可靠性和安全性至关重要。
常见的校验码校验算法包括奇偶校验码、循环冗余校验码(CRC)、校验和、哈希校验码等。
下面将对这几种常见的校验码校验算法进行详细分析:1.奇偶校验码:奇偶校验码是最简单的一种校验码校验算法,它通过检测数据中的奇偶位来判断数据是否正确。
在奇偶校验中,通常规定数据中的位数为偶数个或奇数个,如果数据中出现奇数个1,则在校验位中加上1,使总的1的数量为偶数;如果数据中出现偶数个1,则在校验位中加上0,使总的1的数量仍为偶数。
在数据传输或存储中,接收方会通过比较校验位和数据位的和是否为偶数来判断数据的正确性。
奇偶校验码虽然简单易实现,但只能检测出奇数个错误位(例如一个错误的位),并不能检测出多个错误位或连续错误的情况。
因此,奇偶校验码一般用于对数据传输的基本错误进行检测。
2.循环冗余校验码(CRC):CRC是一种基于多项式除法的校验码校验算法,它通过对数据进行特定的多项式运算来计算出校验码。
接收方在收到数据后,也会对数据进行相同的多项式运算,然后比较计算出的校验码与发送方发送的校验码是否一致,从而判断数据是否正确。
CRC校验码具有较高的检错能力和容错率,能够有效地检测出多个位错误和定位错误的位置,因此广泛应用于计算机网络传输、磁盘存储、通信协议等领域。
3.校验和:校验和是一种简单的校验码校验算法,它通过对数据中所有位进行求和操作来计算出校验码。
接收方在接收到数据后,也会对数据进行相同的求和操作,然后比较计算出的校验和与发送方发送的校验和是否一致,从而判断数据是否正确。
校验和算法比较简单,计算速度较快,但只能检测出简单的错误情况,对于复杂的错误或多位错误检测能力有限。
实验五 奇偶校验器的设计
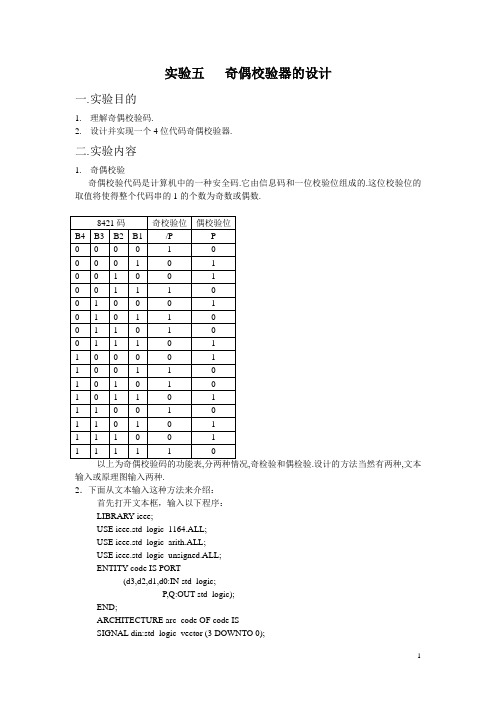
实验五奇偶校验器的设计一.实验目的1.理解奇偶校验码.2.设计并实现一个4位代码奇偶校验器.二.实验内容1.奇偶校验奇偶校验代码是计算机中的一种安全码.它由信息码和一位校验位组成的.这位校验位的取值将使得整个代码串的1的个数为奇数或偶数.以上为奇偶校验码的功能表,分两种情况,奇检验和偶检验.设计的方法当然有两种,文本输入或原理图输入两种.2.下面从文本输入这种方法来介绍:首先打开文本框,输入以下程序:LIBRARY ieee;USE ieee.std_logic_1164.ALL;USE ieee.std_logic_arith.ALL;USE ieee.std_logic_unsigned.ALL;ENTITY code IS PORT(d3,d2,d1,d0:IN std_logic;P,Q:OUT std_logic);END;ARCHITECTURE arc_code OF code ISSIGNAL din:std_logic_vector (3 DOWNTO 0);SIGNAL dout:std_logic_vector (1 DOWNTO 0);BEGINdin<=d3&d2&d1&d0;PROCESS (din)BEGINCASE din ISWHEN"0000"=>dout<="10";WHEN"0001"=>dout<="01";WHEN"0010"=>dout<="01";WHEN"0011"=>dout<="10";WHEN"0100"=>dout<="01";WHEN"0101"=>dout<="10";WHEN"0110"=>dout<="10";WHEN"0111"=>dout<="01";WHEN"1000"=>dout<="01";WHEN"1001"=>dout<="10";WHEN"1010"=>dout<="10";WHEN"1011"=>dout<="01";WHEN"1100"=>dout<="10";WHEN"1101"=>dout<="01";WHEN"1110"=>dout<="01";WHEN others=>dout<="10";END CASE;END PROCESS;P<=dout(1);Q<=dout(0);END arc_code;3.打开波形图输入,并导入图形三、心得体会:经过此次实验,体会到文本输入方式在某种程序上比原理输入方法会简单易操作,进一步熟悉MAXPLUS的操作。
奇偶校验、无校验、SPACE校验、MARK校验五种方式互发实验

奇偶校验、无校验、SPACE校验、MARK校验五种方式互发实验------分隔线----------------------------最近在研究串口的五各校验方式,在网上找到一篇文章是用这五种不同校验方式互发数据的结果比较,可以方便地理解这五种校验方式的作用。
首先再来复习一下这几中校验的原理及定义,其中奇校验、偶校验、无校验这三种在《VC串口编程基础-奇偶校验》一文中有详细的解释,这里再解释一下SPACE校验和MARK校验。
MARK校验是把校验位固定设为1,而SPACE校验是把校验位固定设为0,我个人认为这两种校验方式没有奇偶校验方式“保险”。
理解了各种校验方式的含义,再通过下面的实验来可以加深这一理解。
作者使用的是MsComm控件,试验中发现,发生校验错的那些数据在后面能校验通过的数据被收到时才被输出,而且输出值一律为5BH,也许用其它串口控件或串口类不是输出5BH,还有待进一步的实验。
下面是试验过程中的截图:第一组试验:发送方发送的1个数据桢有10位组成:1位起始位,8位数据位,1位停止位试验(1.1)发方:9600,N,8,1(发出的数据位数为8)收方:9600,N,8,1解读:协议完全匹配,所有数据均能被正确收到。
试验(1.2)发方:9600,N,8,1(发出的数据位数为8)收方:9600,O,8,1解读:此时发送方的停止位被接收方当作校验位,由于是奇校验,而此时的校验位为1,所以只有含有偶数个1的那些数据才能被PC正确收到,比如00H,03H,05H,06H,09H,0AH,0CH,0FH等。
(发生校验错的那些数据在后面能校验通过的数据被收到时才被输出,输出为5BH)试验(1.3)发方:9600,N,8,1(发出的数据位数为8)收方:9600,E,8,1解读:此时发送方的停止位被接收方当作校验位,由于是偶校验,而此时的校验位为1,所以只有含有奇数个1的那些数据才能被PC正确收到,比如01H,02H,04H,07H,08H,0BH,0DH,0EH等。
偶校验的方法

偶校验的方法偶校验是一种常见的错误检测方法,通常用于数据传输和存储中。
下面是关于偶校验的50条方法,并对每种方法进行详细描述:1. 奇偶校验法:将数据中的二进制1的个数进行奇偶性校验,使得总位数包括校验位为偶数(偶校验)或奇数(奇校验)。
2. 横向奇偶校验:将数据按行进行奇偶校验,生成校验位,用于检测每行数据中的错误。
3. 纵向奇偶校验:将数据按列进行奇偶校验,生成校验位,用于检测每列数据中的错误。
4. 二维奇偶校验:利用行和列的奇偶校验位,构成二维奇偶校验检测机制,有效地检测数据中的错误。
5. 纠错码奇偶校验法:结合奇偶校验位和纠错码,实现对数据传输和存储中的错误进行检测和纠正。
6. 补位奇偶校验:在数据长度不满足整数倍的情况下,通过补足位数进行奇偶校验,保证数据的完整性。
7. 循环冗余校验(CRC):通过生成多项式进行奇偶校验的一种方法,对数据进行检测和纠正,常用于通信协议中。
8. 奇偶校验位重计算:当数据发生变化时,重新计算奇偶校验位,用于动态地进行数据检测。
9. 单个校验位检测:为每个数据字节添加一个奇偶校验位,用于检测单个数据字节是否出错。
10. 校验和奇偶校验:将数据中的各个位相加,并进行奇偶性校验,用于检测数据传输中的错误。
11. 奇偶校验算法优化:对奇偶校验算法进行优化,减少计算量,提高效率和准确性。
12. 奇偶校验信道编码:在数据传输中引入奇偶校验信道编码,增强对信道传输中错误的检测和纠正能力。
13. 带偶校验的差错检测码:结合偶校验和差错检测码,提高数据传输中错误的检测和纠正能力。
14. 奇偶校验的完整性校验:对数据进行奇偶校验以及完整性校验,确保数据的正确性和完整性。
15. 动态奇偶校验:根据数据变化情况,动态地进行奇偶校验,保证检测结果的准确性。
奇偶校验、无校验、SPACE校验、MARK校验五种方式互发实验

奇偶校验、无校验、SPACE校验、MARK校验五种方式互发实验------分隔线----------------------------最近在研究串口的五各校验方式,在网上找到一篇文章是用这五种不同校验方式互发数据的结果比较,可以方便地理解这五种校验方式的作用。
首先再来复习一下这几中校验的原理及定义,其中奇校验、偶校验、无校验这三种在《VC串口编程基础-奇偶校验》一文中有详细的解释,这里再解释一下SPACE校验和MARK校验。
MARK校验是把校验位固定设为1,而SPACE校验是把校验位固定设为0,我个人认为这两种校验方式没有奇偶校验方式“保险”。
理解了各种校验方式的含义,再通过下面的实验来可以加深这一理解。
作者使用的是MsComm控件,试验中发现,发生校验错的那些数据在后面能校验通过的数据被收到时才被输出,而且输出值一律为5BH,也许用其它串口控件或串口类不是输出5BH,还有待进一步的实验。
下面是试验过程中的截图:第一组试验:发送方发送的1个数据桢有10位组成:1位起始位,8位数据位,1位停止位试验(1.1)发方:9600,N,8,1(发出的数据位数为8)收方:9600,N,8,1解读:协议完全匹配,所有数据均能被正确收到。
试验(1.2)发方:9600,N,8,1(发出的数据位数为8)收方:9600,O,8,1解读:此时发送方的停止位被接收方当作校验位,由于是奇校验,而此时的校验位为1,所以只有含有偶数个1的那些数据才能被PC正确收到,比如00H,03H,05H,06H,09H,0AH,0CH,0FH等。
(发生校验错的那些数据在后面能校验通过的数据被收到时才被输出,输出为5BH)试验(1.3)发方:9600,N,8,1(发出的数据位数为8)收方:9600,E,8,1解读:此时发送方的停止位被接收方当作校验位,由于是偶校验,而此时的校验位为1,所以只有含有奇数个1的那些数据才能被PC正确收到,比如01H,02H,04H,07H,08H,0BH,0DH,0EH等。
计算机组成原理数据校验实验

计算机组成原理数据校验实验
计算机组成原理中的数据校验是指通过一定的算法和技术来确保数据在传输或存储过程中的完整性和准确性。
常见的数据校验方法包括奇偶校验、循环冗余校验(CRC)、校验和等。
在实验中,可以选择其中一种数据校验方法,比如奇偶校验,进行实际操作。
首先,需要准备一些数据,可以是一段文本或者一组数字。
然后,通过编程或者计算器等工具,对这些数据进行奇偶校验的计算,得到校验位。
接着,将包含校验位的数据传输或存储到另一个地方,然后再对接收到的数据进行校验,验证数据的完整性。
在实验过程中,需要注意以下几点:
1. 确保对所选数据校验方法的原理和算法有充分的理解,包括如何计算校验位以及如何验证数据的完整性。
2. 确保选择的数据能够清晰地展示数据校验的过程和结果,便于实验的进行和观察。
3. 实验过程中要注意记录每一步的操作和结果,包括原始数据、计算得到的校验位、传输或存储后的数据以及验证结果,以便后续
分析和总结。
通过这样的实验,可以加深对计算机组成原理中数据校验方法
的理解,同时也能够锻炼实际操作和数据处理的能力。
同时,也可
以思考不同数据校验方法的适用场景和特点,为今后的实际应用打
下基础。
奇偶校验实验报告

奇偶校验实验报告奇偶校验实验报告引言:在计算机科学领域,数据传输的准确性是至关重要的。
为了确保数据的完整性和正确性,奇偶校验是一种常用的方法。
本实验旨在通过实际操作,深入了解奇偶校验的原理和应用。
一、实验目的本实验的目的是通过实际操作,掌握奇偶校验的原理和应用。
具体包括以下几个方面:1.了解奇偶校验的基本原理;2.掌握奇偶校验的实际应用;3.通过实验验证奇偶校验的有效性。
二、实验器材本实验所需的器材和软件如下:1.计算机;2.串口通信线;3.终端仿真软件。
三、实验步骤1.连接计算机和终端仿真软件。
2.打开终端仿真软件,并设置串口参数。
3.在终端仿真软件中输入一段文本数据。
4.计算文本数据的奇偶校验位。
5.将带有奇偶校验位的数据发送给计算机。
6.计算机接收到数据后,验证奇偶校验位的正确性。
四、实验结果与分析在本实验中,我们选择了一段文本数据进行奇偶校验实验。
首先,在终端仿真软件中输入了以下文本数据:“Hello, World!”。
接下来,我们计算了这段文本数据的奇偶校验位,结果为奇校验。
然后,我们将带有奇偶校验位的数据发送给计算机。
计算机接收到数据后,验证奇偶校验位的正确性。
经过验证,奇偶校验位与原始数据的奇偶性一致,校验通过。
通过本实验,我们深入了解了奇偶校验的原理和应用。
奇偶校验是一种简单而有效的数据传输校验方法,可以检测并纠正单个位的错误。
在实际应用中,奇偶校验常用于串口通信、网络传输等场景,能够提高数据传输的可靠性。
五、实验总结通过本次实验,我们掌握了奇偶校验的基本原理和应用。
奇偶校验是一种常用的数据传输校验方法,能够有效检测和纠正错误。
在实际应用中,我们应该根据具体情况选择适当的奇偶校验方式,并在数据传输过程中进行校验,以确保数据的准确性和完整性。
在今后的学习和工作中,我们应该进一步深入了解其他校验方法,并灵活运用于实际场景中。
只有不断学习和实践,我们才能不断提高自己的技能和能力。
六、参考文献[1] 《计算机网络技术与应用》[2] 《数据通信与网络》以上是本次奇偶校验实验的报告,通过实际操作和验证,我们对奇偶校验有了更深入的了解。
奇偶校验

奇/偶校验(ECC)是数据传送时采用的一种校正数据错误的一种方式,分为奇校验和偶校验两种。
如果是采用奇校验,在传送每一个字节的时候另外附加一位作为校验位,当实际数据中“1”的个数为偶数的时候,这个校验位就是“1”,否则这个校验位就是“0”,这样就可以保证传送数据满足奇校验的要求。
在接收方收到数据时,将按照奇校验的要求检测数据中“1”的个数,如果是奇数,表示传送正确,否则表示传送错误。
同理偶校验的过程和奇校验的过程一样,只是检测数据中“1”的个数为偶数。
如0100101偶校验码就是10100101推理偶校验: 当实际数据中“1”的个数为偶数的时候,这个校验位就是“0”,否则这个校验位就是“1”,这样就可以保证传送数据满足偶校验的要求。
在接收方收到数据时,将按照偶校验的要求检测数据中“1”的个数,如果是偶数个“1”,表示传送正确,否则表示传送错误。
血压标准值:高压(收缩压)120mmHg.低压(舒张压)80mmHg.一般:高压90-140.低压90-60都属于正常的.血压高压低于90mmHg.低压低于60mmHg都属于低血压.从安全角度划分,0-36V算低压,36V以上算高压实际用的更多的一种划法是1kV(1000伏,交流)以下算低压,以上算高压.主设备一:LINEAR MOTION SHALE SHAKER 直线运动振动筛相应配件:1、VIBRATOR 振荡器2、VIBRATOR BEARING FOR MOTOR 振荡器电机轴承3、MOTOR MOUNT BOLT ASSEMBLY 电机装配螺栓部件4COMPLETE EXPF STARTER5、CROWN RUBBER 钻头橡胶?6、DECK SPRING 平台弹簧7、WEDGE BAR 楔形条?8、WEDGE 桩腿楔块9、PRETENSION SCREEN ACCORDING TO API 13C AS BELOW 根据如下所示的API 13C 预拉筛网9-1、MESH 80 OR EQUAL 80目或同值9-2、MESH 115 OR EQUAL9-3、MESH 145 OR EQUAL9-4、MESH 180 OR EQUAL9-5、MESH 215 OR EQUAL9-6、MESH 255 OR EQUAL9-7、MESH 330 OR EQUAL主设备二:LINEAR MOTION MUD CLEANER(MUD CONDITIONER) 线性运动泥浆清洁器配件1、4"DESILER CONE COMPLETE ?2、CONE INSERT 锥形垫圈/锥形插入物3、12"DESANDER CONE COMPLETE ?12"除砂器锥形主体4、DESANDER CONE APEX 除砂器锥形顶点5、DESANDER CONE NUT 除砂器螺母主设备三、COMPLETE MACHANICAL SEAL TYPE CENTRIFUGAL PUMP 机械密封式离心泵主体配件1、8"X6"X14"CASING 8"X6"X14"密封外壳2、14"IMPELLER 14"叶轮3、WEAR PLATE 防磨板4、MECHANICAL SEAL KIT COMPLETE 机械密封成套工具包5、SHAFT SLEEVE(CERAMIC) 轴套(陶瓷)主设备四;COMPLETE HORIZONTAL MUD AGITATORS 卧式泥浆搅拌机主体配件1、INPUT OIL SEAL 输入油封配件2、OUTPUT OIL SEAL 输出油封配件3、GEAR AND WORM GEAR 齿轮与蜗轮传动装置。
奇偶校验

计算机术语
01 基本介绍
03 单向校验 05 范例
目录
02 监督码 04 双向校验
奇偶校验(Parity Check)是一种校验代码传输正确性的方法。根据被传输的一组奇数的称为奇校验,反之,称为偶校验。采用何种校验是事先规定好的。 通常专门设置一个奇偶校验位,用它使这组代码中“1”的个数为奇数或偶数。若用奇校验,则当接收端收到这组 代码时,校验“1”的个数是否为奇数,从而确定传输代码的正确性。
双向校验
为了提高奇偶校验的检错能力,可采用双向奇偶校验(Row and Column Parity),也可称为双向冗余校验 (Vertical and Longitudinal Redundancy Checks)。
双向奇偶校验,又称“方块校验”或“垂直水平”校验。 例: × × × × × × ×××××××
范例
串行数据在传输过程中,由于干扰可能引起信息的出错,例如,传输字符‘E’,其各位为: 0100,0101=45H D7 D0 由于干扰,可能使位变为1,(为什么不变0?)这种情况,我们称为出现了“误码”。我们把如何发现传输 中的错误,叫“检错”。发现错误后,如何消除错误,叫“纠错”。最简单的检错方法是“奇偶校验”,即在传 送字符的各位之外,再传送1位奇/偶校验位。 奇校验:所有传送的数位(含字符的各数位和校验位)中,“1”的个数为奇数,如: 1 0110,0101 0 0110,0101 偶校验:所有传送的数位(含字符的各数位和校验位)中,“1”的个数为偶数,如: 1 0100,0101 0 0100,0101
监督码
奇偶监督码是一种增加二进制传输系统最小距离的简单和广泛采用的方法。例如,单个的奇偶监督将使码的 最小距离由一增加到二。
数据校验方法

数据校验方法数据校验方法是指在数据传输、存储或处理过程中,对数据进行验证和检查的一种技术手段。
通过数据校验,可以确保数据的准确性、完整性和一致性,避免数据错误对系统和业务产生的负面影响。
本文将介绍几种常用的数据校验方法。
一、校验和方法校验和是一种简单而有效的数据校验方法。
它通过对数据进行求和运算,并将结果附加到数据中,以便接收方进行校验。
校验和方法适用于数据传输过程中,可以检测出一些简单的传输错误,如位错误和传输丢失。
但是,这种方法无法检测到复杂的错误类型,且对数据的校验能力有限。
二、循环冗余校验(CRC)循环冗余校验(CRC)是一种常见的数据校验方法,广泛应用于网络通信和存储系统中。
通过将数据视为多项式,使用特定的生成多项式进行计算,得到校验码。
接收方根据接收到的数据和校验码进行计算,若计算结果为0,则数据传输无误。
CRC方法可以高效地检测到多种错误类型,具有较高的校验能力和安全性。
三、奇偶校验奇偶校验是一种简单的数据校验方法,用于检测单个字节的错误。
通过检查二进制数据中1的个数,确定数据的奇偶性,并将奇偶位添加到数据中作为校验位。
接收方根据接收到的数据和奇偶位进行校验,若奇偶性一致,则数据无误。
奇偶校验方法适用于对数据进行简单的校验,但对于多字节数据的校验不够有效。
四、哈希校验哈希校验是一种基于哈希算法的数据校验方法。
通过对数据进行哈希运算,生成固定长度的哈希值,作为数据的校验码。
接收方根据接收到的数据和校验码进行计算,若计算结果一致,则数据传输正确。
哈希校验方法能够高效地检测数据的完整性和一致性,适用于大规模数据的校验。
五、差错检测码差错检测码是一种纠正和检测数据传输中的错误的数据校验方法。
它通过对数据进行编码,生成冗余的检测码,并将其附加到数据中。
接收方根据接收到的数据和检测码进行解码和校验,若发现错误,则根据检测码进行错误的纠正或报告。
差错检测码方法具有较高的校验能力和纠错能力,常用于对数据传输的可靠性要求较高的场景。
高等数学1 奇偶校验

高等数学1 奇偶校验
奇偶校验是一种常用于数据传输中的错误检测方法。
它通过对数据中的位进行统计,来确定传输过程中是否发生了奇数个位的错误。
在高等数学1中,奇偶校验通常是指对二进制数中的每一位进行检查。
在奇偶校验中,假设有一个长度为n的二进制数据,其中有k 个位被置为1。
进行奇偶校验时,在数据的最后一位添加一个校验位。
如果k是偶数,则校验位为0;如果k是奇数,则校验位为1。
这样,传输的数据就有(n+1)位,其中1的个数一定是偶数,方便在接收端进行错误检测。
例如,对于数据1011101,其中有4个1。
根据奇偶校验规则,在最后一位添加一个校验位,得到10111010。
这样,传输的数据就有8位,其中1的个数是偶数,可以通过检查校验位得知传输中是否存在错误。
在接收端,会对接收到的数据进行奇偶校验。
如果传输中没有发生错误,则校验位与数据中的1的个数应该一致。
否则,就可以判断传输中发生了错误,并进行相应的错误纠正或重传操作。
奇偶校验是一种简单有效的错误检测方法,广泛应用于串行通信和存储器等领域。
奇偶校验实验报告

竭诚为您提供优质文档/双击可除奇偶校验实验报告篇一:奇偶校验实验项目四:数据的校验(2学时)一、实验目的:1.了解数据的校验机制。
*2.掌握海明码校验实施过程(选做)。
*3.掌握循环冗余码校验实施过程(选做)。
二、实验要求:1.设计一个程序模拟奇偶校验实施过程(提示:主函数、发送函数、传输函数、校验函数)。
首先奇偶校验过程的基本过程:奇偶校验位有两种类型:偶校验位与奇校验位。
如果一组给定数据位中1的个数是奇数,那么偶校验位就置为1,从而使得总的1的个数是偶数。
如果给定一组数据位中1的个数是偶数,那么奇校验位就置为1,使得总的1的个数是奇数。
偶校验实际上是循环冗余校验的一个特例,通过多项式x+1得到1位cRc。
*2.设计一个程序模拟海明码校验实施过程(提示:主函数、发送函数、传输函数、校验函数、纠错函数)。
*3.设计一个程序模拟循环冗余码校验实施过程(提示:主函数、发送函数、传输函数、校验函数、纠错函数)。
三、实验报告:1.给出源程序和执行结果。
#include#include#includevoidproduct();voidtrans();voidpop();intp1,p2;inta[8]={0};intmain(){product();//产生一个随机的八位二进制的数trans();//设置传输出错一位或者没有出错的情况pop();//判断有无出错的情况return0;}voidproduct(){inti,data;intcount1=0;srand((unsigned)time(0));data =0+rand()%128;//产生0-127的随机数printf("随机的产生一个128以内的十进制数为%d\n",data);for(i=0;iif(count1%2==0)//奇校验奇数个1校验位为0,偶数个1为1a[7]=1;}for(i=0;i elsea[7]=0;p1=a[7];printf("初始二进制校验位放在最高位它为:%d\n",p1);printf("产生随机二进制数为");/*while(i>=0)printf("%d",a[--i]);*/for(i=7;i>=0;--i){printf("%d",a[i]);}printf("\n");}voidtrans(){inti;srand((unsigned)time(0));i=0+rand()%9;//产生0-8的随机数if(i==0)printf("机器内部设置传输过程中没有出错\n");else{a[i-1]=(a[i-1]==0)?1:0;printf("传输过程将机器内部的数据进行了一位改动,改动位为%d\n",i);}voidpop(){printf("接收数据计算出的校验位为:%d\n",p2);if(p2!=a[7])printf("通过校验位p1与p2的比较得出传输过程中数据出错了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验5-1纠错与检错
1.实验内容
读程序,在所有红色的“#”后面添加解释,说明程序的作用
2.实验题目
(1)奇偶校验码
在原始模式上增加一个附加比特位,即奇偶校验位,使最后整个模式中1的个数为奇数(奇校验)或偶数(偶校验)。
本程序用到列表、字符串合并、取模等概念。
code=input("Please input a 7-bit-binary code:")
a=0
# for 循环作用是什么
for i in range(0,6,1):
if code[i]=='1':
a=a+1
print("After odd parity checking the code is:")
if a%2==0:
print(code+'1') # 这句做了什么
else:
print(code) # 这句做了什么
print("After even parity checking the code is:")
# 下面 if .. else …作用是什么
if a%2==0:
print(code)
else:
print(code+'1')
(2) 垂直水平奇偶校验
如下图所示,14个字符纵向排列形成一个数据块,每个字符占据一列,低位比特在上,高位比特在下,用b8(第8位)作为垂直奇偶校验位,各字符的同一比特位形成一行,每一行的最右边一位作为水平奇偶校验位,这里在垂直和水平方向均采用偶校验。
# 下面的函数做了什么 def oddeven(l): a=0
for i in range(0,len(l),1): if l[i]=='1': a=a+1 if a%2==0: return '0' else:
return '1'
block=[['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['0']*15,['
0']*15]
for i in range(0,14,1):
vcode=input("Please input a 7-bit-binary code:") for j in range(0,7,1): block[j][i]=vcode[j]
block[7][i]=oddeven(vcode) # 这句做了什么 hcode=['0']*14
for j in range(0,8,1):
for i in range(0,14,1): hcode[i]=block[j][i]
block[j][14]=oddeven(hcode) # 这句做了什么 print(block)
(3)循环冗余校验
任何一个二进制位串都可以用一个多项式来表示,多项式的系数只有0和1,n 位长度的码C 可以用下述n -1次多项式表示:
()n 1n 210C x C x C x C x C --=++
++n-1n-21
例如位串1010001可以表示为x 6
+x 4
+1。
数据后面附加上冗余码的操作可以用多项式的算术运算来表示。
例如,一个k 位的信息码后面附加上r 位的冗余码,组成长度为n=k+r 的码,它对应一个(n -1)次的多项式C(x),信息码对应一个(k -1)次的多项式K(x),冗余码对应一个(r -1)次的多项式R(x),C(x)与K(x)和R(x)之间的关系满足:
()()()r C x x K x R x =+ 由信息码生成冗余码的过程,即由已知的K(x)求R(x)的过程,也是用多项式的算术运
算来实现。
其方法是:通过用一个特定的r 次多项式G(x)去除x r
K(x),即:
()
()
r x K x G x 得到的r 位余数作为冗余码R(x)。
其中G(x)称为生成多项式(generator polynomial ),是由通信的双方预先约定的。
除法中使用模2减法(无借位减,相当于作异或运算)。
要进行的多项式除法,只要用其相对应的系数进行除法运算即可。
本例中,10位二进制信息位串对应K(x)=x 9+x 8+ x 6+x 4+ x 3
+ x+1;CRC_4对应的G(x)=
x 4+ x +1,r=4,则生成位串为10011B=19。
则x r K(x)= x 13+x 12+ x 10+x 8+x 7+x 5+x 4 ,对应位串
11010110110000,R(x)的计算如错误!未找到引用源。
所示,得出的4位余数1110作为冗余码,于是实际传输的位串为11010110111110。
参考程序:(本程序用到函数,列表、字符串合并、取整、取模等概念。
) # 这个函数做了什么
def c2n(l): a=0
for i in range(0,len(l),1):
a=a+int(l[i])*(2**(len(l)-1-i)) return a
# 下面这个函数做了什么 def n2c(d): b = ''
while d!=0:
b = str(d%2)+b d = d//2 return b
informationcode=input("Please input a 10-bit-binary code:") code=informationcode+'0000' producecode=19 p=0 j=0
xorcode='' while p<14:
j=5-len(xorcode) # 下面语句做了什么
xorcode=n2c(c2n(xorcode+code[p:p+j-1])^producecode) p=p+j
print(informationcode+xorcode)
(4)校验和
校验和的算法流程如下: 发送方算法:
将待发送的数据划分成若干长度为16位的位串,每个位串看成是一个二进制数。
对这些16位的二进制数进行1的补码和累加运算,累加的结果再取反作为校验和,附
1 1 0 0 0 0 1 0 1 0
1 1 0 1 0 1 1 0 1 1 0 0 0 01 0 0 1 1
1 0 0 1 1 1 0 0 1 1 1 0 0 1 1
0 0 0 0 0 1 0 1 1 0
1 0 0 1 1
1 0 1 0 0 1 0 0 1 1
1 1 1 0
余数
加到数据后面,一起发送到接收方。
上述计算中,1的补码和就是指带循环进位(end round carry)的加法,最高位有进位应循环进到最低位。
接收方算法:
将接收的数据(包括校验和)进行1的补码和累加运算,累加的结果再取反。
若结果为0,表明传输正确;否则,表明传输有差错。
如图所示,在该例中,(a)是发送方的计算,①、②、③是3个数据。
④是它们的1的补码和,⑤是④的反码,即校验和。
发送方将⑤和数据一同发送,(b)是接收方的运算,如果没有传输差错,最后的结果应该为0。
(a)发送方的运算
(b)接收方的运算
由于输入的信息串是字符,要用到异或运算,而该运算只能针对数值,因此需要有将字符转换成数值,已经将数值转换成字符的相关运算,这里分别写了两个类型转换函数。
实现1的补码和的关键就是要判断最高位是否有进位,对于16进制无符号数来说,就是判断是否大于65535。
本程序只给出了发送方计算校验和的过程,用到函数、列表、字符串合并、取整、取模等概念。
def c2n(l):
a=0
for i in range(0,len(l),1):
a=a+int(l[i])*(2**(len(l)-1-i))
return a
def n2c(d):
b = ''
while d!=0:
b = str(d%2)+b
d = d//2
return b
s=0
for i in range(0,3,1):
code=input("please input a 16-bit-binary code:")
s=s+c2n(code) # 这个语句做了什么
if s>65535:
# 下面语句做了什么
s=s-65536+1
s=s^65535 # 这个语句做了什么print(n2c(s))。
