高斯列主元消去法解线性方程组VC课程设计报告

合集下载

Gauss列主元消去法实验

<数值计算方法>实验报告1.实验名称实验2 Gauss 列主元消去法2.实验题目用Gauss 列主元消去法求解线性方程组。

0.0011 2.0002 3.0003 1.0001.0001 3.7122 4.6233 2.0002.0001 1.0722 5.6433 3.000x x x x x x x x x ++=⎧⎪-++=⎨⎪-++=⎩3.实验目的加深自己对Gauss 列主元消去法的理解和认识，并且通过做实验或做练习来加强自己Gauss 列主元消去法的掌握，学会并灵活运用Gauss 列主元消去法来求解方程组。

4.基础理论-------Gauss 列主元消去法1.Gauss 列主元消去法的基本思想是：在进行第k （k=1,2，...，n-1)步消元时，从第k 列的kk a 及以下的各元素中选取绝对值最大的元素，然后通过行变换将它交换到主元素kk a 的位置上，再进行消元。

2.Gauss 列主元消去法的优点：当kk a （k=1,2，...，n-1)的绝对值很小时，用Gauss 列主元消去法来求解方程组时，可以避免所的数值结果产生较大误差或失真。

5.实验环境实验系统：Win 7实验平台：VisualC++语言6.实验过程写出算法→编写程序→计算结果Gauss 列元消去法的算法Input:方程组未知量的个数n;增广矩阵()()1,2,...,T ij A a A A An ==，其中i=1,2,…,n; j=1,2,…,n+1Output:方程组的解x1,x2,…,xn,或失败信息。

1. for i ←1ton-1 do;2. temp ←|ii a |;3. p ←I;4. for j ←i+1 to n do5. if ||ji a >temp then6. p ←j;8. end9. end10. if temp=0 then11. |return False;12. end13. if p ≠I then14. p A ⇔i A ;//i,p 两行交换15. end//列选主元16. for j ←i+1 to n do17.*j ji i A m A -ji m ←/ji ii a a ;18. j A ←*j ji i A m A -;//消元19. end7.实验结果原方程组的解为：X1=-0.490396 , x2=-0.051035 ,x3=0.3675208.附录程序清单#include<iostream.h> #include"stdio.h"#include"math.h"void main ( ){ int n=3,i,j,k,p;doubleA[10][10]={{0.001,2.000,3.000,1.000},{-1.000,3.712,4.623,2.000},{-2.0 00,1.072,5.643,3.000}},temp,m,x[100];for(i=0;i<n;i++){ //选主元temp=fabs(A[i][i]); p=i;for(k=i+1;k<n;k++)if(fabs(A[k][i])>temp){temp=fabs(A[k][i]); p=k;}if(temp==0){ printf("\n无法求解：");return;}if(p!=i)for(j=0;j<n+1;j++){ temp=A[i][j];A[i][j]=A[p][j];A[p][j]=temp;}//消元for(k=i+1;k<n;k++){ m=A[k][i]/A[i][i];for(j=i+1;j<=n;j++)A[k][j]=A[k][j]-m*A[i][j];}}//回代for(i=n-1;i>=0;i--){x[i]=A[i][n];for(j=i+1;j<n;j++)x[i]=x[i]-A[i][j]*x[j];x[i]=x[i]/A[i][i];}printf("\nx=\n");for(i=0;i<n;i++)printf("%f \n",x[i]);}。

高斯列主元消去法实验报告

《数值计算方法》实验报告专业：年级：学号：姓名：成绩：1.实验名称实验2高斯列主元消去法2. ：用Gauss列主消去法求解线性方程组0.001*X1+2.000*X2+3.000*X3=1.000-1.000*X1+3.217*X2+4.623*X3=2.000-2.000*X1+1.072*X2+5.643*X3=3.0003.实验目的a.熟悉运用已学的数值运算方法求解线性方程—Gauss列主消去法；b.加深对计算方法技巧的认识，正确使用计算方法来求解方程；c.培养用计算机来实现科学计算和解决问题的能力。

4.基础理论列主元消去法：a.构造增广矩阵b.找到每列绝对值的最大数；c.行变换；d.消去；e.回代5.实验环境Visual C++语言6.实验过程实现算法的流程图：7.结果分析a.实验结果与理论一致；b.由于数值设置成双精度浮点型，所以初值对计算结果影响不大；c.运用程序能更好的实现计算机与科学计算的统一和协调。

8. 附录程序清单#include<stdio.h>#include<math.h>int main(){int n=3,i,j,k,p;double a[4][4];double b[4];double x[4];double m[4][4];double temp;a[1][1]=0.001; a[1][2]=2.000; a[1][3]=3.000; b[1]=1.000;a[2][1]=-1.000; a[2][2]=3.1712; a[2][3]=2.000; b[2]=2.000;a[3][1]=-2.000; a[3][2]=1.072; a[3][3]=5.643; b[3]=3.000;for(i=1;i<=n-1;i++){temp=a[i][i];p=i;for(j=i+1;j<=n;j++)if(fabs(a[j][i])>temp){temp=a[j][i];p=j;}if(temp==0)return 0;if(p!=i) //换行{for(j=1;j<=n;j++)a[0][j]=a[i][j];for(j=1;j<=n;j++)a[i][j]=a[p][j];for(j=1;j<=n;j++)a[p][j]=a[0][j];b[0]=b[i];b[i]=b[p];b[p]=b[0];}for(j=i+1;j<=n;j++){m[j][i]=a[j][i]/a[i][i];for(k=i;k<=n;k++)a[j][k]=a[j][k]-m[j][i]*a[i][k];}}if(a[n][n]==0)return 0;x[n]=b[n]/a[n][n];for(i=n-1;i>=1;i--)//回代{temp=0;for(j=i+1;j<=n;j++)temp=temp+a[i][j]*x[j];temp=b[i]-temp;x[i]=temp/a[i][i];}for(i=1;i<=n;i++)//输出结果{printf("输出结果为：x[%d]=%lf ",i,x[i]);}printf("\n");return 0;}。

高斯消去法和列主元高斯消去法解线性方程组的程序(C语言)精品资料

高斯消去法和列主元高斯消去法解线性方程组的程序(C语言)
//Gauss消去法解线性方程组
//参考教材《计算方法教程》第二版，西安交通大学出版社
#include<stdio.h>
int main(void)
{
float A[7][7]={{3,-5,6,4,-2,-3,8},
{1,1,-9,15,1,-9 ,2},
for(k=0;k<size-1;k++)
{
max=fabs(A[k][k]);
col=k;
//查找最大元素所在的行
for(i=k;i<size;i++)
{
if(max<fabs(A[i][k]))
{
max=fabs(A[i][k]);
col=i;
}
}
printf("col:%d\n",col);
for(j=k;j<size;j++)
printf("\n\n");
//消去过程
for(k=0;k<size-1;k++)
{
if(!A[k][k])
return -1;
for(i=k+1;i<size;i++)
{
Aik=A[i][k]/A[k][k];
for(j=k;j<size;j++)
{
A[i][j]=A[i][j]-Aik*A[k][j];
{
A[i][j]=A[i][j]-Aik*A[k][j];
}
b[i]=b[i]-Aik*b[k];
}

高斯列主元消去法解线性方程组VC++课程设计报告

课程设计报告一．课程设计目的：采用高斯列主元消去法解线性方程组。

用C 语言或C ＋＋设计一个程序来通过高斯列主元消去法解线性方程组AX=b 的解。

二．课程设计的内容1. 课程设计的题目及简介题目：高斯列主元消去法解线性方程组。

简介：对线性方程组AX ＝b 等价于⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n n nn n n n n b b b x x x a a a a a a a a a 2121212222111211方法说明（以4阶为例）：（1）第1步消元——在增广矩阵（A ，b ）第一列中找到绝对值最大的元素，将其所在行与第一行交换，再对（A ，b ）做初等行变换使原方程组的第一列元素除了第一行的全变为0；（2）第2步消元——在增广矩阵（A ，b ）中的第二列中（从第二行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A ，b ）做初等行变换使原方程组转化为： ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡******00**00***0****4321x x x x 注：*代表非零的数。

（3）第3步消元——在增广矩阵（A ，b ）中的第三列中（从第三行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A ，b ）做初等行变换使原方程组转化为： ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡*****000**00***0****4321x x x x（4）按x4 → x3→ x2→ x1 的顺序回代求解出方程组的解。

此方法即高斯列主元消去法，若在变换的过程中没有选出绝对值最大的数放在最前面进行消元而求出未知数的方法就叫高斯消去法。

高斯消去法有一很明显的缺点，即在消元的过程中可能出现小主元，这种小主元可能导致解的不稳定，为了避免小主元的出现正是高斯列主元消去法的主要目的。

而通过每次消元之前的调换方程的次序也正是计算机实现高斯列主元消去法的关键。

高斯列主元消去法解线性方程组--课程设计报告

北京化工大学北方学院课程设计报告课程名称课程设计设计题目线性方程组求解专业、班级计科0701 学号 070202021 姓名张海艳指导教师刘佩贤设计时间 2010.9.1——2010.9.30 2010年 9 月 30 日一、引言1.1编写目的测试分析报告是把测试的结果写成文档，并对测试结果进行分析，为纠正软件的缺陷提供依据，也为软件验收和交付打下基础。

是软件开发的另一里程碑。

及时记录测试阶段的工作过程和工作成果，如实反映测试过程中所解决的各种问题，把集成测试和确认测试的结果以文件形式加以记载，使开发者能在第一时间对遇到的问题做迅速反应。

1.2 背景软件名称：线性方程组求解具体要求：输入是N（N<256）元线性方程组Ax=B，输出是方程组的解，也可能无解或有多组解。

1.3算法说明首先将线性方程组做成增广矩阵，对增广矩阵进行行变换。

对元素aii，在第i列中，第i行及以下的元素选取绝对值最大的元素，将该元素最大的行与第i行交换，然后采用高斯消元法将新得到的aii消去第i行以下的元素。

一次进行直到ann。

从而得到上三角矩阵。

再对得到的上三角矩阵进行回代操作，即可以得到方程组的解。

二、正文(1)设计部分该软件用于求解线性方程组的解。

执行过程：（1）首先执行main()（主函数），输入待求解方程组的增广矩阵的行数，接着输入增广矩阵。

i. 调用uptrbk(double *A,int N)（上三角变换函数），在此函数中又调用了两个函数：FindMax(int p,int N,double *A)和ExchangeRow(int p,int j,double *A,int N)。

ii. FindMax（）函数用于找出列向量中绝对值最大项的标号，ExchangeRow（）用于交换两行。

iii. uptrbk（）函数将矩阵行数N、增广矩阵指针A、行号p传给FindMax（）函数，找出绝对值最大项的标号；iiii. 接着将绝对值最大项的标号传给ExchangeRow（）函数，最终将绝对值最大的那行换到第一行。

c高斯消元法解方程-课程设计报告

《高级语言程序设计》课程设计报告题目：高斯消元法解方程专业：网络工程(对口)班级： 16网工（3）姓名：代应豪指导教师：成绩：计算机学院2017 年 4月 25 日2016-2017学年第2学期计算机学院《高斯消元法解方程》课程设计报告目录一设计内容及要求 ............................................... 错误！未定义书签。

1.设计内容......................................................... 错误！未定义书签。

2.设计要求 (3)二概要设计 (3)三设计过程或程序代码 (8)四设计结果与分析 (12)五参考文献.......................................................... 错误！未定义书签。

41设计内容及要求1.1 设计内容：高斯消去法的解题思路：反代来求得所要的答案.矩阵的基本列运算规则为：（1）任一列均可乘以一非零的常数；（2）将任一列乘以一常数后加到其他列；（3）可任意对调任两列。

第1步消元——在增广矩阵（A，b）第一列中找到绝对值最大的元素，将其所在行与第一行交换，再对（A，b）做初等行变换使原方程组转化为如下形式：第 1 页共16 页第2步消元——在增广矩阵（A，b）中的第二列中（从第二行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A，b）做初等行变换使原方程组转化为：第3步消元——在增广矩阵（A，b）中的第三列中（从第三行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A，b）做初等行变换使原方程组转化为：按x4 x3 x2 x1 的顺序回代求解出方程组的解按照解题的思路，整个程序大概由以下几个部分组成：输入方程组；判断用户输入的维数是否大于自定义10的维数；输入各行未知项的系数；开始反代；开始计算；退出程序。

试验四 Gauuss列主元消去法解线性方程组实验报告

for(j=0;j<m+1;j++) scanf("%lf",&ab[i][j]); printf("您输入的系数增广矩阵为:\n"); for(i=0;i<m;i++) { for(j=0;j<=m;j++) printf(" %10.9f",ab[i][j]); printf("\n"); } for(i=0;i<m-1;i++)//i 是行 { Change(ab,m,i); for(k=i+1;k<m;k++) { f=ab[i][i]; g=ab[k][i]; e=-(g/f); for(t=0;t<m+1;t++) { ab[k][t]+=ab[i][t]*e; } } } printf("经行处理后原矩阵变为:\n"); for(k=0;k<m;k++) { for(t=0;t<=m;t++) printf(" %10.9f",ab[k][t]); printf("\n"); } printf("方程组的解为:\n"); ab[2][2]=ab[2][3]/ab[2][2]; ab[1][1]=(ab[1][3]-ab[1][2]*ab[2][2])/ab[1][1]; ab[0][0]=(ab[0][3]-ab[0][2]*ab[2][2]-ab[0][1]*ab[1][1])/ab[0][0]; for(i=0;i<m;i++) printf("x%d=%10.9f\n",i+1,ab[i][i]); }

列主元高斯消去法和列主元三角分解法解线性方程

计算方法实验报告1课题名称用列主元高斯消去法和列主元三角分解法解线性方程目的和意义高斯消去法是一个古老的求解线性方程组的方法,但由它改进得到的选主元的高斯消去法则是目前计算机上常用的解低阶稠密矩阵方程组的有效方法;用高斯消去法解线性方程组的基本思想时用矩阵行的初等变换将系数矩阵A 约化为具有简单形式的矩阵上三角矩阵、单位矩阵等,而三角形方程组则可以直接回带求解用高斯消去法解线性方程组b Ax =其中A ∈Rn ×n 的计算量为：乘除法运算步骤为32(1)(1)(21)(1)(1)262233n n n n n n n n n n nMD n ----+=+++=+-,加减运算步骤为(1)(21)(1)(1)(1)(25)6226n n n n n n n n n n AS -----+=++=;相比之下,传统的克莱姆法则则较为繁琐,如求解20阶线性方程组,克莱姆法则大约要19510⨯次乘法,而用高斯消去法只需要3060次乘除法;在高斯消去法运算的过程中,如果出现absAi,i 等于零或过小的情况,则会导致矩阵元素数量级严重增长和舍入误差的扩散,使得最后的计算结果不可靠,所以目前计算机上常用的解低阶稠密矩阵方程的快速有效的方法时列主元高斯消去法,从而使计算结果更加精确; 2、列主元三角分解法高斯消去法的消去过程,实质上是将A 分解为两个三角矩阵的乘积A=LU,并求解Ly=b 的过程;回带过程就是求解上三角方程组Ux=y;所以在实际的运算中,矩阵L 和U 可以直接计算出,而不需要任何中间步骤,从而在计算过程中将高斯消去法的步骤进行了进一步的简略,大大提高了运算速度,这就是三角分解法采用选主元的方式与列主元高斯消去法一样,也是为了避免除数过小,从而保证了计算的精确度计算公式1、列主元高斯消去法设有线性方程组Ax=b,其中设A 为非奇异矩阵;方程组的增广矩阵为第1步k=1：首先在A 的第一列中选取绝对值最大的元素1l a ,作为第一步的主元素:111211212222112[,]n n n l n nn n a a a a b a a a b a a a b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦a b然后交换A,b 的第1行与第l 行元素,再进行消元计算;设列主元素消去法已经完成第1步到第k -1步的按列选主元,交换两行,消元计算得到与原方程组等价的方程组 Akx=bk第k 步计算如下：对于k=1,2,…,n -11按列选主元：即确定t 使 2如果t ≠k,则交换A,b 第t 行与第k 行元素; 3消元计算消元乘数mik 满足:4回代求解2、列主元三角分解法对方程组的增广矩阵经过k -1步分解后,可变成如下形式：111max 0l i i n a a ≤≤=≠(1)(1)(1)(1)(1)1112111(2)(2)(2)(2)22222()(()1)()()()()()1,1()(,)()[,][,] k k k k nk k nk n k k k k k kk kn k k k k n k k k n nn a a a a b a a a b a a b a b b a a a +++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥→=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A b A b ()()max 0k k tk ik k i na a ≤≤=≠,(1,,)ik ik ik kka a m i k n a ←=-=+, (,1,,), (1,,)ij ij ik kji i ik k a a m a i j k n b b m b i k n ←+=+⎧⎨←+=+⎩⎪⎪⎩⎪⎪⎨⎧--=-←←∑+=)1,,2,1(,)(1n n i a x a b x a b x ii n i j j ij i i nnn n [,]A A b =11121,11111222,122221,11,1,1,211,11,2121,112,112,1k k k k k k k j n k k j n k k k i i i k n n kk kj kn k ik ij in i nknjk k k j k n n nnk k n a a a b A a u u u u u u y l l l l l l ll l l l u u u u u y u u u u y a a b a a b l a -------------⎡→⎣⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦第k 步分解,为了避免用绝对值很小的数kku 作除数,引进量1111 (,1,,;1,2,,) ()/ (1,2,,;1,2,,)k kj kj km mj m k ik ik im mk kkm u a l u j k k n k n l a l u u i k k n k n -=-=⎧=-=+=⎪⎪⎨⎪=-=++=⎪⎩∑∑11(,1,,)k i ik im mk m s a l u i k k n -==-=+∑,于是有kk u =ks ;如果 ,则将矩阵的第t 行与第k 行元素互换,将i,j 位置的新元素仍记为jjl 或jja ,然后再做第k 步分解,这时列主元高斯消去法程序流程图max t ik i n s s ≤≤= ()/ 1,2,,)1 (1,2,,),kk k k t iki k ik u s s s l s s i k k n l i k k n ===++≤=++即交换前的，（且列主元高斯消去法Matlab主程序function x=gauss1A,b,c %列主元法高斯消去法解线性方程Ax=bif lengthA~=lengthb %判断输入的方程组是否有误disp'输入方程有误'return;enddisp'原方程为AX=b：' %显示方程组Abdisp'------------------------'n=lengthA;for k=1:n-1 %找列主元p,q=maxabsAk:n,k; %找出第k列中的最大值,其下标为p,qq=q+k-1; %q在Ak:n,k中的行号转换为在A中的行号if absp<cdisp'列元素太小,detA≈0';break;elseif q>ktemp1=Ak,:; %列主元所在行不是当前行,将当前行与列主Ak,:=Aq,:; 元所在行交换包括bAq,:=temp1;temp2=bk,:;bk,:=bq,:;bq,:=temp2;end%消元for i=k+1:nmi,k=Ai,k/Ak,k; %Ak,k将Ai,k消为0所乘系数Ai,k:n=Ai,k:n-mi,kAk,k:n; %第i行消元处理bi=bi-mi,kbk; %b消元处理endenddisp'消元后所得到的上三角阵是'A %显示消元后的系数矩阵bn=bn/An,n; %回代求解for i=n-1:-1:1bi=bi-sumAi,i+1:nbi+1:n/Ai,i;endclear x;disp'AX=b的解x是' x=b;调用函数解题列主元三角分解法程序流程图列主元三角分解法Matlab主程序①自己编的程序：function x=PLUA,b,eps %定义函数列主元三角分解法函数if lengthA~=lengthb %判断输入的方程组是否有误disp'输入方程有误'return;enddisp'原方程为AX=b：' %显示方程组Abdisp'------------------------'n=lengthA;A=A b; %将A与b合并,得到增广矩阵for r=1:nif r==1for i=1:nc d=maxabsA:,1; %选取最大列向量,并做行交换if c<=eps %最大值小于e,主元太小,程序结束break;elseendd=d+1-1;p=A1,:;A1,:=Ad,:;Ad,:=p;A1,i=A1,i;endA1,2:n=A1,2:n;A2:n,1=A2:n,1/A1,1; %求u1,ielseur,r=Ar,r-Ar,1:r-1A1:r-1,r; %按照方程求取ur,iif absur,r<=eps %如果ur,r小于e,则交换行p=Ar,:;Ar,:=Ar+1,:;Ar+1,:=p;elseendfor i=r:nAr,i=Ar,i-Ar,1:r-1A1:r-1,i; %根据公式求解,并把结果存在矩阵A中endfor i=r+1:nAi,r=Ai,r-Ai,1:r-1A1:r-1,r/Ar,r; %根据公式求解,并把结果存在矩阵A中endendendy1=A1,n+1;for i=2:nh=0;for k=1:i-1h=h+Ai,kyk;endyi=Ai,n+1-h; %根据公式求解yiendxn=yn/An,n;for i=n-1:-1:1h=0;for k=i+1:nh=h+Ai,kxk;endxi=yi-h/Ai,i; %根据公式求解xiendAdisp'AX=b的解x是'x=x'; %输出方程的解②可直接得到P,L,U并解出方程解的的程序查阅资料得子函数PLU1,其作用是将矩阵A分解成L乘以U的形式;PLU2为调用PLU1解题的程序,是自己编的Ⅰ.function l,u,p=PLU1A %定义子函数,其功能为列主元三角分解系数矩阵A m,n=sizeA; %判断系数矩阵是否为方阵if m~=nerror'矩阵不是方阵'returnendif detA==0 %判断系数矩阵能否被三角分解error'矩阵不能被三角分解'endu=A;p=eyem;l=eyem; %将系数矩阵三角分解,分别求出P,L,Ufor i=1:mfor j=i:mtj=uj,i;for k=1:i-1tj=tj-uj,kuk,i;endenda=i;b=absti;for j=i+1:mif b<abstjb=abstj;a=j;endendif a~=ifor j=1:mc=ui,j;ui,j=ua,j;ua,j=c;endfor j=1:mc=pi,j;pi,j=pa,j;pa,j=c;endc=ta;ta=ti;ti=c;endui,i=ti;for j=i+1:muj,i=tj/ti;endfor j=i+1:mfor k=1:i-1ui,j=ui,j-ui,kuk,j;endendendl=trilu,-1+eyem;u=triuu,0Ⅱ.function x=PLU2A,b %定义列主元三角分解法的函数l,u,p=PLU1A %调用PLU分解系数矩阵A m=lengthA; %由于A左乘p,故b也要左乘p v=b;for q=1:mbq=sumpq,1:mv1:m,1;endb1=b1 %求解方程Ly=b for i=2:1:mbi=bi-sumli,1:i-1b1:i-1;endbm=bm/um,m; %求解方程Ux=y for i=m-1:-1:1bi=bi-sumui,i+1:mbi+1:m/ui,i;endclear x;disp'AX=b的解x是' x=b;调用函数解题①②编程疑难这是第一次用matlab编程,对matlab的语句还不是非常熟悉,因此在编程过程中,出现了许多错误提示;并且此次编程的两种方法对矩阵的运算也比较复杂;问题主要集中在循环控制中,循环次数多了一次或者缺少了一次,导致数据错误,一些基本的编程语句在语法上也会由于生疏而产生许多问题,但是语句的错误由于系统会提示,比较容易进行修改,数据计算过程中的一些逻辑错误,比如循环变量的控制,这些系统不会提示错误,需要我们细心去发现错误,不断修正,调试;。

c课程设计(高斯消元

c 课程设计(高斯消元一、教学目标本节课的学习目标主要包括以下三个方面：1.知识目标：学生需要掌握高斯消元法的基本原理和步骤，了解其在我国数学发展史上的地位和应用。

2.技能目标：学生能够运用高斯消元法解决二元一次方程组和三元一次方程组的问题，提高解题能力。

3.情感态度价值观目标：通过学习高斯消元法，培养学生对数学的兴趣和热爱，增强民族自豪感，激发学生积极探索数学奥秘的热情。

二、教学内容本节课的教学内容主要包括以下三个方面：1.高斯消元法的原理与步骤：介绍高斯消元法的起源、发展及其基本原理，讲解消元法的具体步骤。

2.高斯消元法的应用：通过例题讲解，让学生掌握高斯消元法在解决二元一次方程组和三元一次方程组中的应用。

3.高斯消元法在我国数学发展史上的地位：介绍高斯消元法在我国数学研究中的应用和地位，激发学生的民族自豪感。

三、教学方法为了提高教学效果，本节课将采用以下几种教学方法：1.讲授法：讲解高斯消元法的原理、步骤及其应用，让学生掌握基本知识。

2.案例分析法：通过分析典型例题，让学生学会如何运用高斯消元法解决问题。

3.讨论法：学生分组讨论，培养学生的合作精神和解决问题的能力。

4.实验法：让学生动手实践，体会高斯消元法的实际应用，提高学生的操作能力。

四、教学资源为了支持教学内容和教学方法的实施，本节课将准备以下教学资源：1.教材：选用国内权威的数学教材，为学生提供系统的学习资料。

2.参考书：推荐学生阅读相关数学参考书，丰富学生的知识体系。

3.多媒体资料：制作课件、动画等多媒体资料，直观展示高斯消元法的原理和应用。

4.实验设备：准备足够的计算机和数学软件，让学生进行实践操作。

五、教学评估为了全面、客观地评估学生的学习成果，本节课将采用以下几种评估方式：1.平时表现：通过观察学生在课堂上的参与程度、提问回答等方式，了解学生的学习态度和掌握程度。

2.作业：布置与高斯消元法相关的练习题，要求学生在规定时间内完成，以此评估学生的理解程度和应用能力。

用高斯列主元消元法解线性方程分析解析

沈阳航空工业学院课程设计学号2008040201105班级84020103姓名李荣飞指导教师尹航2009年9月11日沈阳航空工业学院课程设计任务书电子信息工程学院电子信息工程专业84020103班学号2008040201105一、课程设计题目：用高斯列主元消元法解线性方程二、课程设计工作自2009年9月6日起至2009年9月11日止三、课程设计内容：运用所学的C语言知识,编制和调试程序,拥有以下功能：请用高斯列主元消元法解以下方程组：2x12x25x3 53x14x27x3 6x13x23x3 5四、课程设计要求：程序质量：贯彻构造化程序设计思想。

用户界面友善，功能明确，操作方便；能够加以其余功能或修饰。

用户界面中的菜单起码应包含“输入数据”、“开始计算”、“退出”3项。

代码应适合缩进，并给出必需的说明，以加强程序的可读性。

课程设计说明书：课程结束后，上交课程设计说明书（打印稿和电子稿），其内容以下：封面课程设计任务书目录需求剖析（剖析题目的要求）程序流程图（整体流程图和主要功能模块流程图）中心技术的实现说明及相应程序段个人总结参照资料源程序及适合的说明指导教师：________学生署名：________目录一、需求剖析1二、程序流程图2三、中心技术的实现说明及相应程序段8四、个人总结11五、参照文件11六、源程序 (11)沈阳航院设计用纸一、需求剖析经过对程序设计题目的剖析可知，整个程序的设计实现大概分为三个模块，分别是：输入方程组，计算方程组，持续运算/退出。

计算方程组模块对应三个函数，其函数名和功能以下：一、互换行的距函数（huanhang）：主要实现线性代数高斯列主元消元法求解线性方程组中的初等行变换。

二、比较系数大小的函数（bijiao）：实现比较系数大小的算法。

三、实现菜单项选择择的函数（caidan）：使用户界面友善，操作方便。

除上边介绍的功能以外，程序还拥有“持续运算/退出”功能，能够在程序的一次运转中间循环履行全部的功能，并依据需要，停止程序的履行。

高斯列主元消去法解线性方程组的实现

高斯列主元消去法解线性方程组的实现班级学号姓名榴莲一、实验任务采用高斯列主元消去法求解线性方程组，以下消解方程为例。

1 2 1 x1 02 2 2 x2 = 3-1 -3 0 x3 2二、编程环境Windows7，Codeblock.三、算法步骤Gauss 消去法的基本思想是，通过将一个方程乘或除某个数以及两个方程相加减这两种运算手续，逐步减少方程组中变元的数目，最终使某个方程只含有一个变元，从而得出所求的解。

对于，G auss消去法的求解思路为：（1）若，先让第一个方程组保持不变，利用它消去其余方程组中的,使之变成一个关于变元的n-1阶方程组。

（2）按照（1）中的思路继续运算得到更为低阶的方程组。

（3）经过n-1步的消元后，得到一个三角方程。

（4）利用求解公式回代得到线性方程组的解。

四、程序流程图数据结构：i，j 变量double a[10][10] a 矩阵double b[10] b 矩阵double x[10] 求解的x矩阵n 矩阵的维度五、程序#include<stdio.h>#include<math.h>void guess(double a[][10],double b[],double x[],int n) { int k,i,j;for(k=0; k<n-1; k++){ double ma =a[k][k]; int tab = k;for(i=k+1; i<n; i++) {if(fabs(ma)<fabs(a[i][k])){ ma = a[i][k];tab = i;}}double mid; mid= b[k]; b[k] =b[tab]; b[tab] =mid; for(i=k; i<n;i++) {mid = a[k][i];a[k][i] = a[tab][i];a[tab][i] = mid;}for(i=k+1; i<n; i++) { b[i]=b[i]-a[i][k]/a[k][k]* b[k];for(j=k+1; j<n; j++) {a[i][j]=a[i][j]-a[i][k]/a[k][k]*a[k][j];}a[i][k]=0;}}for(k=n-1; k>=0; k--){ double s =0;for(j=k+1; j<n; j++) s += a[k][j]*x[j];x[k]=(b[k]-s)/a[k][k];}}int main(){ int i,j;double a[10][10] = {{1,2,1},{2,2,3},{-1,-3,0}};double b[10] = {0,3,2};double x[10];int k,n=3;guess(a,b,x,n);printf("三角化矩阵A:\n");for(i=0; i<n; i++) {for(j=0; j<n; j++){ printf("%7.2lf",a[i][j]);}printf("\n");}printf("\n 方程数值 b:\n");for(i=0; i<n; i++) printf("%7.2lf",b[i]);printf("\n");printf("\n 求得的函数值 x:\n");for(i=0; i<n; i++) printf("%7.2lf",x[i]);printf("\n");}六、实验结果及分析高斯消去法由消元和回代两个过程组成。

高斯消元法与列主元消去法实验报告

实验报告：Gauss消元法小组成员：李岚岚、邱粉珊、缪晓浓、杨水清学号：0917020040、0917010078、0917010073、0917010112一、实验问题编写两个程序，分别利用Gauss消元法和列主元消去法求解方程组二、分析及其计算过程Gauss顺序消元法：源程序：function [x]=gaussl(A,b)[n1,n2]=size(A);n3=size(b);if n1~=n2|n2~=n3|n1~=n3disp('A的行和列的维数不同!');return;endif det(A)==0disp('系数矩阵A奇异');return;end%消元过程L=eye(n1);for j=2:n1for i=j:n1L(i,j-1)=A(i,j-1)/A(j-1,j-1);A(i,:)=A(i,:)-L(i,j-1)*A(j-1,:);b(i)=b(i)-L(i,j-1)*b(j-1);endend%回代过程x(n1)=b(n1)/A(n1,n1);for t=n1-1:-1:1for k=n1:-1:t+1b(t)=b(t)-A(t,k)*x(k);endx(t)=b(t)/A(t,t);end程序的运行以及结果：>>A=[1 2/3 1/3;9/20 1 11/20;2/3 1/3 1];>>b=[2 2 2];>> [x]=gaussl(A,b)x =1 1 1Gauss列主元消去法：源程序：function [x]=gaussll(A,b) [n1,n2]=size(A);n3=size(b);if n1~=n2|n1~=n3|n2~=n3disp('输入的方程错误！');return;endif det(A)==0disp('系数矩阵A奇异');return;endmax=zeros(n1);for m=1:n1%找主元for i=m:n1if abs(A(i,m))>maxmax=A(i,:);A(i,:)=A(m,:);A(m,:)=max;maxb=b(i);b(i)=b(m);b(m)=maxb;endend%消元过程L=eye(n1);for j=2:n1for i=j:n1L(i,j-1)=A(i,j-1)/A(j-1,j-1);A(i,:)=A(i,:)-L(i,j-1)*A(j-1,:);b(i)=b(i)-L(i,j-1)*b(j-1);endendend%回代过程x(n1)=b(n1)/A(n1,n1);for t=n1-1:-1:1for k=n1:-1:t+1b(t)=b(t)-A(t,k)*x(k);endx(t)=b(t)/A(t,t);end程序的运行以及结果：>>A=[-0.002 2 2;1 0.78125 0;3.996 5.5625 4]; >>b=[0.4 1.3816 7.4178];>>[x]= gaussll(A,b)x =1.9273 -0.6985 0.9004。

列主元消去法解方程组实验报告

实验名称：列主元消去法解方程组 1 引言我们知道，高斯消去法是一个古老的解线性方程组的方法。

而在用高斯消去法解Ax=b时，其中设A 为非奇异矩阵，可能出现()0k kka =的情况，这时必须进行带行交换的高斯消去法。

但在实际计算中即使()0k kk a ≠但其绝对值很小时，用()k kka 作除数，会导致中间结果矩阵()k A 元素数量级严重增长和舍入误差的扩散，使得最后的结果不可靠。

因此，小主元可能导致计算的失败，我们应该避免采用绝对值很小的主元素。

为此，我们在高斯消去法的每一步应该在系数矩阵或消元后的低阶矩阵中选取绝对值最大的元素作为主元素，保持乘数1ik m ≤，以便减少计算过程中舍入误差对计算解的影响。

一种方式是完全主元消去法，这种消去法是在每次选主元时，选择()()max 0k kk k i j ij k i nk j na a ≤≤≤≤=≠为主元素。

这种方法是解低阶稠密矩阵方程组的有效方法，但这种方法在选取主元时要花费一定的计算机时间。

实际计算中我们常采用部分选主元的的消去法。

列主元消去法即在每次选主元时，仅依次按列选取绝对值最大的元素作为主元素，且仅交换两行，再进行消元计算。

2 实验目的和要求运用matlab 编写一个.m 文件，要求用列主元消去法求解方程组（实现PA=LU ）：12345671111111721111118321111110432111113543211117654321122765432128x x x x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦要求输出以下内容：（1）计算解x ；（2） L,U ；（3）整形数组IP （i ）（i=1,2，…，n-1）（记录主行信息）3 算法原理与流程图（1）算法原理设有线性方程组A x =b ，其中设A 为非奇异矩阵。

高斯消去法和列主元高斯消去法解线性方程组的程序(C语言)精品资料

for(i=0;i<size;i++)
{
for(j=0;j<size;j++)
printf("%f ",A[i][j]);
printf("\n");
}
printf("b[]\n");
for(i=0;i<size;i++)
printf("%f ",b[i]);
printf("\n\n");
//-------消去过程---------
{7,2,-1, 2,7,-1,9}};
float b[7]={11,2,29,9,5,8,25};
float x[7]={0};
float Aik,S,temp;
int i,j,k;
float max;//列主元的绝对值
int col;//列主元所在的行
int size=7;
printf("A[][]\n");
int i,j,k;
int size=7;
printf("A[][]\n");
for(i=0;i<size;i++)
{
for(j=0;j<size;j++)
printf("%f ",A[i][j]);
printf("\n");
}
printf("b[]\n");
for(i=0;i<size;i++)
printf("%f ",b[i]);
printprintprintprintprintprint消去的结果printprintprintprintprintprintprintprint列主元gauss消去法解线性方程组参考教材计算方法教程第二版西安交通大学出版社includestdioincludemathh1611b7112299ze7

C++课程设计高斯消元法求线性代数方程组的解

C++课程设计高斯消元法求线性代数方程组的解第一篇：C++课程设计高斯消元法求线性代数方程组的解河北工业大学计算机软件技术基础（VC）课程设计报告学院管理班级管理104班姓名杨立宝 __ 学号 101707____ 成绩 __ ____一、题目：求线性代数方程组的解（高斯消去法）（C13）二、设计思路1、总体设计1）分析程序的功能第一：编写输入程序，通过键盘先输入对应的已知量及函数的大小n和系数a[i]和得数b[i]。

第二：编写中间程序，通过函数的调用先定义线性代数方程，然后通过程序求出方程的梯形矩阵系数，并最终得出结果。

第三编写输出程序，输出最终结果。

2）系统总体结构：设计程序的组成模块，简述各模块功能。

模块一：各函数的具体内容A：三个输入函数，分别输入n，一维数组，二维数组。

即输入已知量。

B：中间运算函数，计算是使得方程系数所成的矩阵成梯形矩阵，未知数的结果。

即计算中间变量及结果。

C：最后输出函数，输出最后计算结果。

模块二：各函数原型的声明 a写头文件。

b变量声明:存放输入数据的数组的声明，存放中间变量的数组的声明，存放运算结果的数组的声明。

分别存放对应数据。

c输入有关操作的文字d函数调用，在运算中自动调用对应的函数解决对应问题。

模块三:主函数2、各功能模块的设计：说明各功能模块的实现方法模块一：各个函数的声明，直接声明。

模块二：各函数都通过for循环来实现各个数组之间的基本运算。

3、设计中的主要困难及解决方案在这部分论述设计中遇到的主要困难及解决方案。

1）困难1 函数调用是怎么用？解决方案：仔细阅读课本，以及同学之间的讨论，和老师的帮助。

4、你所设计的程序最终完成的功能1）说明你编制的程序能完成的功能输入线性代数的系数后，运行程序即可得到梯形矩阵和结果。

2）准备的测试数据及运行结果三、程序清单如果是使用一个文件完成的程序，只需列出程序代码。

如果是使用多文件完成的程序，首先说明程序中的代码存放在哪些文件中，说明文件名（例如：本程序包含first.cpp、second.cpp、third.cpp和all.h四个文件）；然后依次给出每个文件名及该文件清单，例如：#include const N= 10;//设定矩阵大小范围 /* * 使用已经求出的x，向前计算x（供getx()调用）* double a[][] 系数矩阵 * double x[] 方程组解 * int i 解的序号 * int n 矩阵大小 * return 公式中需要的和 */ double getm(double a[N][N], double x[N], int i, int n){ double m = 0;int r;for(r=i+1;rresult = double(b[n-1]/a[n-1][n-1]);else //计算其他x值（对于公式中的求和部分，需要调用getm()函数）result = double((b[i]-getm(a,x,i,n))/a[i][i]);return result;} void main(){ //double a[N][N] = {{2},{1,3,2},{1,2,2}};//double b[N] = {4,6,5};double a[N][N];//系数矩阵 double b[N];//右端项 double x[N];//方程组解 int i,j,k;int n=N;//矩阵大小/*用户手工输入矩阵*/ cout<>n;cout<>a[i][j];} cout<>b[i];} /*显示原始矩阵*/ cout</*进行高斯消去*/ for(j=0;j/*显示处理后矩阵*/ cout</*回代方式解方程组*/ for(i=n-1;i>=0;i--){ x[i] = getx(a,b,x,i,n);} /*显示方程组解*/ cout<四、对该设计题目有何更完善的方案1、对自己完成程序进行自我评价。

列主元高斯消去法实验报告

a[i][j]=a[i][j]-l*a[k][j];
}
}
printf("高斯消去:\n");
for(i=0;i<n;i++)
{
for(j=0;j<n+1;j++)
printf("%f",a[i][j]);
printf("\n");
}
if(fabs(a[n-1][n-1])<DETLA)
{
printf("A奇异，break \n");
int i,j,n,k,m;
printf("确定一个初元数:n=");
scanf("%d",&n);
printf("输入数组:a[%d][%d]\n",n,n+1);
for(i=0;i<n;i++)
{
for(j=0;j<n+1;j++)
scanf("%f",&a[i][j]);
}
printf("得到数组:\n");
若m≠k，交换第k行与第m行对应的元素（换行）：
消元：
对i=k+1,…,n-1，计算l=lik=aik/akk;
对j=k+1,…,n-1,n，计算aij=aij-lik*akj=aij-l*akj
回代：
若|ann|<DELTA，则A奇异，结束程序，否则继续
xn-1=an-1,n/ an-1, n-1
对i=n-2 ,…, 1, 0，计算：
编程要求：
1）方程组的矩阵系数用二维数组表示，不用指针，且其值要求用输入语句输入。（数组形式的完成，经检查后，有能力的可以改用指针方式）

课程设计报告-高斯列主元消元法解线性方程组

《计算机数值方法》课程设计报告题目高斯列主元消元法解线性方程组学生姓名班级学号成绩指导教师学号：姓名：题目：用高斯列主元消元法解线性方程组内容用C 语言编写软件完成以下任务：用高斯列主元消元法解下列线性方程组：⎪⎩⎪⎨⎧=++=++=++53367435522321321321x x x x x x x x x指导教师和学生签字指导教师：____ ____ 学生签名：_____ ___成绩：教师评语：目录一、程序设计题目 (1)二、需求分析（高斯列主元消元法） (1)三、程序流程图 (3)四、核心技术的实现方法及程序段 (7)五、个人总结 (9)六、参考文献 (9)七、源程序 (10)一、程序设计题目用C 语言编写软件完成以下任务：用高斯列主元消元法解下列线性方程组：⎪⎩⎪⎨⎧=++=++=++53367435522321321321x x x x x x x x x二、需求分析（高斯列主元消元法）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n n nn n n n n b b b x x x a a a a a a a a a 2121212222111211方法说明（以4阶为例）：第1步消元——在增广矩阵（A ，b ）第一列中找到绝对值最大的元素，将其所在行与第一行交换，再对（A ，b ）做初等行变换使原方程组转化为如下形式：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡*******0***0***0****4321x x x x第2步消元——在增广矩阵（A ，b ）中的第二列中（从第二行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A ，b ）做初等行变换使原方程组转化为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡******00**00***0****4321x x x x第3步消元——在增广矩阵（A ，b ）中的第三列中（从第三行开始）找到绝对值最大的元素，将其所在行与第二行交换，再对（A ，b ）做初等行变换使原方程组转化为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡*****000**00***0****4321x x x x按x 4 → x 3→ x 2→ x 1 的顺序回代求解出方程组的解附：下面三种变换称为初等行变换： ① 对调两行；② 以数k ≠0乘某一行中的所有元素；③ 把某一行所有元素的k 倍加到另一行对应的元素上去。

计算方法实验报告_列主元高斯消去法

double row_first; //行首元素 //主对角元素单位化 for(int i=0;i<n;i++) {
row_first=A[i][i]; for(int j=0;j<n+1;j++)
计算方法实验报告
{ A[i][j]=A[i][j]/row_first;
} }
for(int k=n-1;k>0;k--) {
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
A_B[i][j]=A[i][j]; } A_B[i][N]=B[i][0]; } return A_B; }
3
//输出矩阵 A 的 row x col 个元素 void Show_Matrix(double **A,int row,int col) {
for(int i=0;i<N;i++)
{
int row=Choose_Colum_Main_Element(N,A_B,i);
if(Main_Element<=e) goto A_0;
Exchange(A_B,N+1,row,i);
Elimination(N,A_B,i);
cout<<"选取列主元后第"<<i+1<<"次消元:"<<endl;
double factor; for(int i=start+1;i<n;i++) {
factor=A[i][start]/A[start][start]; for(int j=start;j<n+1;j++) {

高斯列主消元法求解方程 c语言程序报告

HUNAN UNIVERSITY 程序设计训练报告专业班级材料科学与工程四班指导老师院长 (系主任)2012 年6 月30 日目录1 软件开发平台 (1)2 软件功能说明 (1)2.1 功能分析说明 (1)2.2 功能说明图 (4)3 软件设计详细内容 (5)3.1 采用的主要数据结构类型 (5)3.2 流程图 (5)4 软件测试 (11)4.1 软件测试用例 (11)4.2 软件测试报告 (16)5 总结和致谢 (16)6 附录 (17)6.1 源码 (17)6.2 二人分工说明 (22)6.3 参考文献 (22)1软件开发平台Visul C++ 6.02软件功能说明用高斯列主消元法求解方程个数不超过15个的线性方程组2.1 功能分析说明线性方程组可以表示为以下形式：通解于：方程等价于AX=b对其增广矩阵进行初等行换不改变方程组的解，从而将其化为简单形式来求解方程组。

|A|= (-1)21(j j t)3jn j a11j a22j…a njn&calculate(intn,int m)功能：quanpailie_A()功能：计算一个全排列(-1)21(j j t )3jn j a 11j a 22j …a njn 的值gauss_row_xiaoqu()功能：将增广矩阵通过交换两行的方法使得第一列中a 11绝对值最大第二行各元素分别减去第一行对应元素的a 21/a 11倍，使得a 21化为零；第三行各元素分别减去第一行对应元素的a 31/a 11倍，使得a 31化为零；同理将a 31,a 41…a 1n 都化为零；通过交换两行的方法使得第一列中a 22绝对值最大第三行各元素分别减去第二行对应元素的a 32/a 22倍，使得a 32化为零；第四行各元素分别减去第二行对应元素的a 42/a 22倍，使得a 42化为零；同理将a 32,a 42…a 2n 都化为零；以此类推，可将主对角线下的元素全化为零，变为上三角矩阵。

c++课程设计报告书-高斯消元

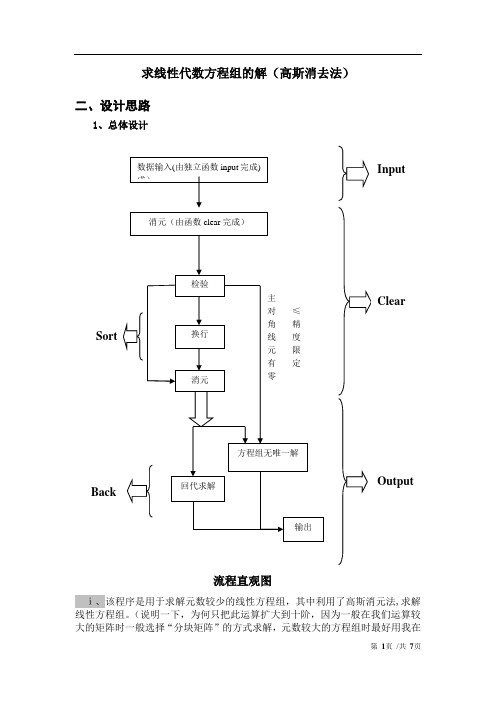
求线性代数方程组的解（高斯消去法）二、设计思路1、总体设计ⅰ、该程序是用于求解元数较少的线性方程组，其中利用了高斯消元法,求解线性方程组。

（说明一下，为何只把此运算扩大到十阶，因为一般在我们运算较大的矩阵时一般选择“分块矩阵”的方式求解，元数较大的方程组时最好用我在流程直观图InputOutput“对程序提出完善方案”中提到的拉默克求解法再配合分块矩阵求解的方法，进行求解，既可以简化运算过程，又节约计算资源。

）ⅱ、系统总体结构：程序总体分为三个大部分、五个小部分：①输入部分，由input构成，其中a[][]负责系数矩阵的数据输入及保存,b[]负责方程值的数据输入及保存。

②消元部分，由clear构成，并有调用sort函数进行换行，其中运算公式是核心，换行是保障运算顺利进行的必要条件。

③输出部分，由output构成，并有调用back函数进行回代运算求方程的解，其中回代部分是求解的核心，最终方程有没有唯一解或者唯一解是什么，都要从这里输出才能被运行程序者识别，直观辨别出方程组的解，计算结果存放在x[]当中。

④换行部分，由sort构成，负责运算过程中出现主对角线元比同列数据小时换行。

⑤回代部分，由back构成，负责运算最后求得满足条件的方程组的解，核心是运算公式。

2、各功能模块的设计：说明各功能模块的实现方法①输入函数（input）：利用循环的嵌套，将二维数组数据输入计算机，并保存在a[][]当中，而方程组中各个方程的值则由一个循环记录在一维数组b[]当中。

②消去（clear）：此部分是程序的难点之一，首先我们要考虑在消去过程中会出现由于找不到非零主元素而造成的计算中断（详见“3、设计中的主要困难及解决方案 3）计算中断”。

），又要考虑如何进行循环将系数矩阵化为上三角矩阵。

利用循环嵌套，对消去公式进行相应次数的循环即可达到目标（详见“3、设计中的主要困难及解决方案 1)简化矩阵”）。

③换行（sort）：在判断满足换行的条件后，利用中间变量t即可完成相应数据的交换。