控制工程-典型环节的对数坐标图(Bode图)
合集下载
自动控制原理3第三节典型环节的频率特性
左图是不同阻尼系数情况下的 对数幅频特性和对数相频特性 图。上图是不同阻尼系数情况 下的对数幅频特性实际曲线与 渐近线之间的误差曲线。
1 2T 1 T 2 T 5 T 10 T
1 5T
Saturday, November 05, 2016
15
微分环节的频率特性
⒌ 微分环节的频率特性： 微分环节有三种：纯微分、一阶微分和二阶微分。传递函 数分别为： G( s) s
05, 2016
12
振荡环节的波德图
2 T ( ) tg 相频特性： 1 T 2 2
1
几个特征点： 0, ( ) 0;
1 , ( ) ; , ( ) 。 T 2
由图可见：
K 10, T 1, 0.3 10 G ( j ) 2 s 0.6s 1 1 o T
1
幅频特性为： 相频特性为：
A( )
(1 T 2 2 )2 (2T )2 2 T ( ) tg 1 1 T 2 2
L( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2 对数幅频特性为：
低频段渐近线： T 1时，L( ) 0 高频段渐近线： T 1时， L( ) 20 log (T 2 2 ) 2 40 log T 1 两渐进线的交点 o 称为转折频率。斜率为-40dB/Dec。 T Saturday, November
1 2
T
时，无谐振峰值。当
M p A( p )
1 2
1 0.707时， p 0 。 2
时，有谐振峰值。
1 2 1 2
1 当 0 ， A(0 ) ， 。 L ( ) 20 lg 2 0 2
自动控制原理之伯德图
2020 12:43:14 AM00:43:142020/12/12
• 11、自己要先看得起自己，别人才会看得起你。12/12/
谢 谢 大 家 2020 12:43 AM12/12/2020 12:43 AM20.12.1220.12.12
• 12、这一秒不放弃，下一秒就会有希望。12-Dec-2012 December 202020.12.12
• 13、无论才能知识多么卓著，如果缺乏热情，则无异 纸上画饼充饥，无补于事。Saturday, December 12, 2020
12-Dec-2020.12.12
• 14、我只是自己不放过自己而已，现在我不会再逼自 己眷恋了。20.12.1200:43:1412 December 202000:43
斜率增加-40dB/十倍频。
5.4 系统开环频率特性的绘制
⑤ 绘出用渐近线表示的对数幅频特性以后，如果需要，可以进
行修正。通常只需修正交接频率处以及交接频率的二倍频和 1/2倍频处的幅值就可以了。
对于一阶项，在交接频率处的修正值为±3dB；
在交接频率的二倍频和1/2倍频处的修正值为±1dB。
对于二阶项，在交接频率处的修正值可由公式 20lg 1
•
8、业余生活要有意义，不要越轨。20 20年12 月12日 星期六 12时43 分14秒 00:43:1 412 December 2020
•
9、一个人即使已登上顶峰，也仍要自 强不息 。上午 12时43 分14秒 上午12 时43分 00:43:1 420.12. 12
• 10、你要做多大的事情，就该承受多大的压力。12/12/
5.4 系统开环频率特性的绘制
二、绘制系统开环频率特性伯德图的步骤
对数坐标图
112 2T T T
-90°
5 10 20
111
T T T 20T 10T 5T
112 2T T T
5 10 20 TTT
一阶微分环节的波德图
惯性环节的波德图
32
③ 二阶微分环节：
G (s)T2s22T s1
幅频和相频特性为：
A ()( 1 T 22 ) 2 ( 2T ) 2 ， () t 1 g 1 2 T 2 T 2
更详细的刻度如下图所示
1
2
3 4 5 6 7 8 910
20
一倍频程 一倍频程 一倍频程
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω １ 2 3 4 5 6 7 8 9 10 lgω 0.000 0.301 0.477 0.602 0.699 0.778 0.845 0.903 0.954 1.000
29
① 纯微分：
L( )(dB)
A()
20
L() 20logA() 20log
0 0.1
1
()
20
2
20dB / dec
微分环节 (rad / s)
10 20dB / dec
积分环节
( )(deg)
微分环节
90
0 0.1
90
1
10
积分环节
(rad / s)
30
② 一阶微分：
A ()1T2 2 ， ()tg 1 T
。
p
1 2 2 p T
该频率称为谐振峰值频率。可见，谐振峰值频率与阻尼系数有关，当
《典型环节伯德图》课件
Maya：一汇报人：
稳定性分析
稳定性定义：系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类：稳定、 不稳定、临界稳定
稳定性分析方法： 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析：通过绘制 伯德图，观察系统在不 同频率下的增益和相位 变化，判断系统的稳定 性。
动态性能分析
伯德图：描述系统动态性能的图形工具 频率响应：系统对不同频率信号的响应 相位裕度：系统稳定性的指标 增益裕度：系统放大能力的指标 动态性能分析方法：如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库，可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称： Simulink
开发商： MathWorks
公司
软件功能：用 于建模、仿真 和分析动态系
统
应用领域：广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点：图 形化界面，易 于操作，支持 多种编程语言
软件版本：最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD：一款专业的CAD软件，可以绘制 各种类型的伯德图
SolidWorks：一款三维设计软件，可以绘制 伯德图
Inventor：一款三维设计软件，可以绘制伯 德图
SketchUp：一款三维设计软件，可以绘制伯 德图
Blender：一款三维设计软件，可以绘制伯德 图
幅频特性的分析
幅频特性的定义：描述信号在频率域上的分布特性 幅频特性的表示方法：通常采用伯德图或奈奎斯特图 幅频特性的应用：用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法：通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义：描述信号频率与相位之间的关系 相频特性的表示方法：通常用相频特性曲线表示 相频特性的应用：在信号处理、通信等领域有广泛应用 相频特性的测量方法：通过实验或仿真进行测量
稳定性分析
稳定性定义：系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类：稳定、 不稳定、临界稳定
稳定性分析方法： 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析：通过绘制 伯德图，观察系统在不 同频率下的增益和相位 变化，判断系统的稳定 性。
动态性能分析
伯德图：描述系统动态性能的图形工具 频率响应：系统对不同频率信号的响应 相位裕度：系统稳定性的指标 增益裕度：系统放大能力的指标 动态性能分析方法：如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库，可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称： Simulink
开发商： MathWorks
公司
软件功能：用 于建模、仿真 和分析动态系
统
应用领域：广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点：图 形化界面，易 于操作，支持 多种编程语言
软件版本：最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD：一款专业的CAD软件，可以绘制 各种类型的伯德图
SolidWorks：一款三维设计软件，可以绘制 伯德图
Inventor：一款三维设计软件，可以绘制伯 德图
SketchUp：一款三维设计软件，可以绘制伯 德图
Blender：一款三维设计软件，可以绘制伯德 图
幅频特性的分析
幅频特性的定义：描述信号在频率域上的分布特性 幅频特性的表示方法：通常采用伯德图或奈奎斯特图 幅频特性的应用：用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法：通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义：描述信号频率与相位之间的关系 相频特性的表示方法：通常用相频特性曲线表示 相频特性的应用：在信号处理、通信等领域有广泛应用 相频特性的测量方法：通过实验或仿真进行测量
考研复习题典型环节伯德图
二阶微分环节的频率特性是： 其对数幅频特性是：
相频特性是：
二阶微分环节与振荡节 的Bode图关于ω轴对称 ，如图5-21。渐近线的 转折频率为，相角变化 范围是00至+1800。 二阶微分环节的Bode图
七不稳定环节
不稳定环节的频率特性是:
其对数幅频特性和相频特性分别为:
不稳定惯性环节的Bode图
二积分环节
积分环节的频率特性是: 其幅频特性为: 对数幅频特性是:
设
，则有: (5-68)
可见，其对数幅频特性是一条 在ω=1（弧度/秒）处穿过零分贝 线（ω轴），且以每增加十倍频率 降低20分贝的速度（-20dB/dec） 变化的直线。 积分环节的相频特性是:
(5-69)
是一条与ω无关，值为-900 且平行于ω轴的直线。积分环 节的对数幅频特性和相频特性 如图5-12所示。
振荡环节的相频特性是:
除上面三种特殊情况外，振荡环节相频特性还是 阻尼比ξ的函数，随阻尼比ξ变化，相频特性在转折 频率 附近的变化速率也发生变化，阻尼比ξ越小， 变化速率越大，反之愈小。但这种变化不影响整个相 频特性的大致形状。不同阻尼比ξ的相频特性如图520 所示。
振荡环节对数相频特性图
六二阶微分环节
一放大环节（比例环节）
放大环节的频率特性为:
其幅频特性是:
对数幅频特性为:
放大环节的对数幅频特性如图5-11所示，它是一条与角 频率ω无关且平行于横轴的直线，其纵坐标为20lgK。 当有n个放大环节串联时，即:
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示，它是一条与角频率ω无 关且与ω轴重合的直线。
相频特性是：
二阶微分环节与振荡节 的Bode图关于ω轴对称 ，如图5-21。渐近线的 转折频率为，相角变化 范围是00至+1800。 二阶微分环节的Bode图
七不稳定环节
不稳定环节的频率特性是:
其对数幅频特性和相频特性分别为:
不稳定惯性环节的Bode图
二积分环节
积分环节的频率特性是: 其幅频特性为: 对数幅频特性是:
设
，则有: (5-68)
可见，其对数幅频特性是一条 在ω=1（弧度/秒）处穿过零分贝 线（ω轴），且以每增加十倍频率 降低20分贝的速度（-20dB/dec） 变化的直线。 积分环节的相频特性是:
(5-69)
是一条与ω无关，值为-900 且平行于ω轴的直线。积分环 节的对数幅频特性和相频特性 如图5-12所示。
振荡环节的相频特性是:
除上面三种特殊情况外，振荡环节相频特性还是 阻尼比ξ的函数，随阻尼比ξ变化，相频特性在转折 频率 附近的变化速率也发生变化，阻尼比ξ越小， 变化速率越大，反之愈小。但这种变化不影响整个相 频特性的大致形状。不同阻尼比ξ的相频特性如图520 所示。
振荡环节对数相频特性图
六二阶微分环节
一放大环节（比例环节）
放大环节的频率特性为:
其幅频特性是:
对数幅频特性为:
放大环节的对数幅频特性如图5-11所示，它是一条与角 频率ω无关且平行于横轴的直线，其纵坐标为20lgK。 当有n个放大环节串联时，即:
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示，它是一条与角频率ω无 关且与ω轴重合的直线。
北航机电控制工程基础(自动控制原理)第五章2-典型环节频率特性
北京航空航天大学
二、积分环节 Integral links 1、伯德图
机电控制工程基础
K G (s) s
Fundamentals of Mechatronic Control Engineering
K G ( j ) j
K A( )
K ( ) 0 arctan j 0 2
幅值
机电控制工程基础
袁松梅教授 Tel：82339630
下半个圆对应于正频率部分，而上 半个圆对应于负频率部分。
Email：yuansm@
北京航空航天大学
四、振荡环节Oscillation link 2、伯德图 讨论 0
机电控制工程基础
1 时的情况。当K=1时，频率特性为：
K Kn G( s ) 2 2 2 T s 2Ts 1 s 2 n s n 2
G( s) K , G( j ) K
相频特性： ( )
1、伯德图
幅频特性：A( ) K ；
0
；
L( ) / dB
20log K 20log K 20log K
K 1
对数幅频特性：
K 1 lg
0 K 1
( )
180
0 L( ) 20 lg K 0 0
1.0 -45 100 -89.4
1 1 当 0时， (0) 0;当 时， ( ) ;当 时， () 。 T T 4 2
当时间常数T 变化时，对数幅频特性和对数相频特性的形状都不变，仅仅是根据转折 频率1/T 的大小整条曲线向左或向右平移即可。而当增益改变时，相频特性不变，幅 频特性上下平移。
K P ( ) 1 T 2 2 KT Q ( ) 1 T 2 2 Q ( ) T P( )
典型环节的频率特性
G( j)
1
2
1
j2
2 n
n
n
1 Tn
1 L() 20lg1 0
n
1 L() 20 lg( )2 40 lg
n
n
n
两条渐近线相交于=n，称n为二阶振荡环节的转折频率。
精确幅频特性曲线的形状及其渐近线的误差均与值有关。当值在 某范围时，幅频特性曲线存在峰值，且值越小，对数幅频曲线的 峰值就越大，它与渐近线之间的误差也就越大。
2
1
1 2
0 0.707 系统存在峰值。
0.707 系统不存在峰值
20 18 16 14 12 10
8 6 4 2 0
0 0.2 0.4 0.6 0.8 1
5．时滞环节
0
-100
G( j) ej 1
-200
-300
()
-400
-500
-600
-1
0
1
10
10
10
二 典型环节的奈氏图（极坐标图）
与一阶惯性环节频率特性
30
相反。
0
10-1
100
101
3. 积分、微分环节
L() 20 lg () 90
20
0
-20
-1
0
1
10
10
10
0
-90
-180
-1
0
1
10
10
10
L() 20 lg () 90
20
0
-20
-1
0
1
10
10
10
180
90
0
-1
0
1
10
自控理论 4-3对数坐标图
(2) 将各环节的L(w),j(w)曲线画于对数坐标纸上 1) L1(w) = 20lg4 ≈12(dB)是幅值为12dB的水平线。 2) L2(w)是过ω=1, L(w)0dB,斜率为 -20dB/dec的直线。 3) L3(w)是转角频率为ω=0.5的惯性环节对数幅频曲线。 4) L4(w)是转角频率为ω=2的微分环节对数幅频曲线。 5) L5(w)是转角频率为ω=8的振荡环节对数幅频曲线。
惯性环节L(w) 1 ① G(s)= 0.5s+1
L(w)dB 40 26dB 20
100 ② G(s)= s+5
[-20]
0dB 0o -20 - 30o - 45o o -40 - 60 - 90o 0.1 0.2
ω
1
2
10 20
[-20]
100
5. 一阶微分环节 (Ts 1) L(w ) 20lg 1 (wT) 2 j (w ) tg -1wT 1 Ts 1与 两环节的 Bode 图关于 Ts 1 横轴成镜像对称 关系。
斜率 40 20 20
40
30
-20
20
17.5
10
-60 -80
0
-10
-60
-20
-30
-40 -1 10
10
0
10
1
图4-19 例4-6的幅频特性
1 7.5( s 1) 3 G( s) 1 s 2 1 s( s 1)[( ) s 1] 2 2 2
图4-19 例4-6的相频特性
j
290o w r w n 1 2
2
wn
0dB
L(w r ) 20 lg 2
典型系统波特图
1800
900
1
10 1
00
图4-26 二阶微分环节的Bode图
24
8.延滞环节
频率特性为 G( j) e j
对数幅频特性
20lg G( j) 20lg1 0(dB)
对数相频特性
() （弧度） 57.3（度）
(4-28a) (4-28b)
25
L() (dB)
T
1 T
,
20lg
G(
j)
20lg
1T 2 2 20lg T(dB)
14
L() (dB)
0
20
1
10 1 20 1
T
TT
20dB / dec
()(度)
00
450
900
图4-23（a) 惯性环节的Bode图
16 17
15
当
1
T
2 101
(4-23a) (4-23b)
12
L() dB 40 20
20dB / dec
0 0.01
0.1
ห้องสมุดไป่ตู้
20
1
10
100
40
()
900 450
00 0.01
0.1
450
1
10
100
900
图4-22 微分环节的Bode图
13
4.惯性环节
频率特性为
G( j) 1 jT 1
对数幅频特性
27
G( j) G1( j)G2 ( j) Gn ( j)
A1()e j1() A2 ()e j2 () An ()e jn ()
900
1
10 1
00
图4-26 二阶微分环节的Bode图
24
8.延滞环节
频率特性为 G( j) e j
对数幅频特性
20lg G( j) 20lg1 0(dB)
对数相频特性
() （弧度） 57.3（度）
(4-28a) (4-28b)
25
L() (dB)
T
1 T
,
20lg
G(
j)
20lg
1T 2 2 20lg T(dB)
14
L() (dB)
0
20
1
10 1 20 1
T
TT
20dB / dec
()(度)
00
450
900
图4-23（a) 惯性环节的Bode图
16 17
15
当
1
T
2 101
(4-23a) (4-23b)
12
L() dB 40 20
20dB / dec
0 0.01
0.1
ห้องสมุดไป่ตู้
20
1
10
100
40
()
900 450
00 0.01
0.1
450
1
10
100
900
图4-22 微分环节的Bode图
13
4.惯性环节
频率特性为
G( j) 1 jT 1
对数幅频特性
27
G( j) G1( j)G2 ( j) Gn ( j)
A1()e j1() A2 ()e j2 () An ()e jn ()
机械工程控制基础 第四章第三节_典型环节频率特性的绘制
0
-0.5
-1
-1.5
-2
-2.5
-3 -1 10
10
0
10
1
一阶系统的频率响应曲线以渐近线表示时 引起的对数幅值误差 23
Bode Diagram of G(jw )=jw T+1) T=0.1 25 20
Magnitude (dB)
15 10 5 0 90
0(dB)
20lg T (dB)
Phase (deg)
1 为转角(转折、交接)频率 T
20
L( ) 20 lg [1 (T ) 2 ]( dB) ( ) arctan(T )
低频时，即
1 , T 1 T
L( ) 20 lg [1 (T ) 2 ] 20 lg1 0( dB)
1 n 为转折频率。 T
25
L( ) 20 log (1 2T 2 ) 2 (2T ) 2
( ) arctan
1 低频时， ,即T 1时 T
2T 1 2T 2
L() 20lg1 0
() 00
1 高频时， ,即T 1时 T 2 L() 20lg(T ) 40lg T
0
Re
4
3. 积分环节
传递函数：G ( s )
1 s
频率特性： G( j ) [G(s)]s j
1 A( ) 0 ( ) 90
1 1 1 900 0 j e j
由于() = - 90°是常数。A()随 增大而减小。因此，积分环节是 极坐标图一条与虚轴负段相重合的
18
Bode Diagram of )=jw Bode Diagram ofG(jw G(j )=j 40 30
经典控制理论
典型信号（单位）阶跃函数（Step function ） 0,)(1≥t t室温调节系统和水位调节系统（单位）斜坡函数（Ramp function ） 速度 0,≥t t （单位）加速度函数（Acceleration function ）抛物线0,212≥t t （单位）脉冲函数（Impulse function ） 0,)(=t t δ正弦函数（Simusoidal function ）Asinut ，当输入作用具有周期性变化时。
============================================================================设线性定常系统由下述n 阶线性常微分方程描述：)()()()()()()()(1111011110t r b t r dt db t r dt d b t r dt d b tc a t c dt da t c dtd a t c dt d a m m m m m m n n n n n n ++⋅⋅⋅++=++⋅⋅⋅++------系统传递函数为：)()()()()(11101110s N s M a s a s a s a b s b s b s b s R s C s G n n n n m m m m =++⋅⋅⋅++++⋅⋅⋅++==----传递函数与微分方程之间有关系)()()(s R s C s G =如果将dtdS ⇔置换 微分方程传递函数⇔ ============================================================================传递函数的极点和零点对输出的影响)()()()()(11*jnj imi P S Z S K s N s M s G --==∏∏== i Z ),,2,1(m i ⋅⋅⋅= 为传递函数的零点j P ),,2,1(n j ⋅⋅⋅= 为传递函数的极点 极点是微分方程的特征跟，因此，决定了所描述系统自由运动的模态。
4-3 第三节 对数坐标图
第三节 对数坐标图（伯德图）对数幅频特性曲线：前面提到过伯德图中对数幅频特性曲线的纵坐标采用()()20lg dB L w G j =w ，这是因为传递函数总可以分解为因子相乘、除的形式，从而其频率传递函数的模必然由相应各因子的模相乘、除得之，取其对数可将乘、除变为加、减而便于计算，至于前面的系数“20”则是沿用电信技术的增益表达式而来的，这样就使得()L w 的单位成为分贝“”。
dB 横坐标按自变量的常用对数进行刻度。
原因一方面可使变动范围得到扩展，在有限的图面上比起均匀刻度来能表现出更大的变动范围；另一方面，w w ()L w 中往往都含有lg 因子，采用自变量的常用对数刻度，可使自变w w量的对数曲线成为直线，便于绘制。
对数相频特性曲线：纵坐标()(w G j )w φ=∠均匀刻度；横坐标也按自变量的常用对数进行刻度。
w 若在横轴上取两点满足2110w w =，则距离为()2121lg lg lg lg101w w w w −===。
即横坐标每变化一个单位，相当于频率变化10倍，叫做一个“十倍频程”，用“”表示。
dec在标注横轴时，往往只标出w 的值，并不标出值。
lg w 这种计量坐标系称为半对数坐标系。
若212w w =，则距离为：()2121lg lg lg lg 20.301w w w w −=== 这表示横坐标每变化一个单位，相当于频率变化一倍，叫做一个“倍频程”，用“”表示。
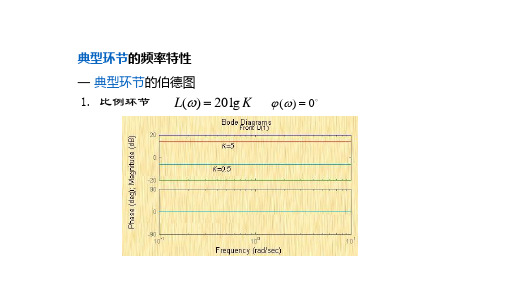
oct一、典型环节的对数坐标图1、比例环节（K ）()G jw K =（K 为常数） ()()20lg 20lg L w G jw K==（） dB ()()()011010Lw K K L w K L w ⎫==⎧⎪⎪>>⎨⎬⎪⎪<<⎩⎭()()0w G jw φ=∠=jw w()()()===−（dB）20lg20lg120lgL w G jw w w()20lg L w w =−()()011020L w w w L w ⎫==⎧⎪⎨⎬==−⎩⎪⎭()()90w G jw φ=∠=− ()L w 曲线为过（1，0）点，斜率为每十倍频程下降的一条直线，记为“20dB 20dB dec −”。
5.3 对数频率特性(Bode图)
（5-58）
式中， Li (ω) 和ϕi (ω ) 分别表示各典型环节的对数幅频特性和对数相频特性。 式（5-58）表明，只要能作出 G( jω ) 所包含的各典型环节的对数幅频和对数相频曲线，
将它们进行代数相加，就可以求得开环系统的 Bode 图。实际上，在熟悉了对数幅频特性的
性质后，可以采用更为简捷的办法直接画出开环系统的 Bode 图。具体步骤如下：
5.3 对数频率特性（Bode 图）
5.3.1 典型环节的 Bode 图
1．比例环节
比例环节 G( jω ) = K 的频率特性与频率无关，其对数幅
频特性和对数相频特性分别为
⎧L(ω) = 20 lg K ⎨⎩ϕ(ω) = 0o
（5-50）
相应 Bode 图如图 5-23 所示。
2．微分环节
微分环节 G( jω) = s 的对数幅频特性与对数相频特性
显然，当ω ωn = 1，即ω = ωn 时，是两条渐近线的相交点，所以，振荡环节的自然
频率ωn 就是其转折频率。
振荡环节的对数幅频特性不仅与ω ωn 有关，而且与阻尼比ξ 有关，因此在转折频率附
近一般不能简单地用渐近线近似代替，否则可能引起较大的误差。图 5-27 给出当ξ 取不同 值时对数幅频特性的准确曲线和渐近线，由图可见，当ξ < 0.707 时，曲线出现谐振峰值， ξ 值越小，谐振峰值越大，它与渐近线之间的误差越大。必要时，可以用图 5-28 所示的误
差修正曲线进行修正。
由式（5-55）可知，相角ϕ (ω ) 也是ω ωn 和ξ 的函数，当ω = 0 时，ϕ (ω ) = 0 ；当ω → ∞ 时，ϕ (ω ) = −180o ；当ω = ωn 时，不管ξ 值的大小，ωn 总是等于 − 90o ，而且相频特性 曲线关于 (ωn , − 90°) 点对称，如图 5-27 所示。
自动控制原理5第二节对数频率特性
19
② 一阶微分： A(w) 1 T 2w2，(w) tg1Tw
一阶微分环节的波德图
L(w) 20lg 1 T 2w2 对数幅频特性（用渐近线近似）：
低频段渐近线：当Tw 1时，A(w) 1， 20 log A(w) 0 高频段渐近线：当Tw 1时，A(w) Tw，L(w) 20 log Tw
第二节 对数频率特性
1
一、对数频率特性曲线（波德图，Bode图）
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率，纵坐标是幅值和相角)的分度：
横坐标(称为频率轴)分度：它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值，因此对w 而言是 非线性刻度。w 每变化十倍，横坐标变化一个单位长度，称为 十倍频程(或十倍频)，用dec表示。类似地，频率w 的数值变化
来计算只能求出±90°之间的值(tg-1函数的主值范围)，也就是
说当 w ( 1 , ) 时，用计算器计算的结果要经过转换才能得到 。 即当 w (T1 , ) 时，用计算器计算的结果要减180°才能得到 。
T
或用下式计算
(w) tg1 Tw 1 2 tg1 Tw 1 2
17
微分环节的频率特性
(w) K
0 180
K 0 K 0
180
7
K 0
⒉ 积分环节的频率特性：G(s) K
s
频率特性：
G( jw )
K
j
K
K
e2
jw w w
积分环节的Bode图
L(w) / dB
40 20w ) tg1( K 0)
w
2
L(w) 20log A(w) 20log K
完整版bode图习题解析
作出以分段直线表示的渐近线后，如果需要， 再按典型因子的误差曲线对相应的分段直线进 行修正
作相频特性曲线。根据表达式，在低频中频 和高频区域中各选择若干个频率进行计算， 然后连成曲线
Example
G ?s ??
10
s ?1
?1 ?
?1
2ss??,
H ?s ?? 1
Description
10 1 s 1? s
0.01 start plot
0
-20 0
Frequency(rad/s)
1 start 1 ? s
2 start 1 ? 1
20
20
1? 1 2s
0
Total slope
-20
(db/decade )
0
-20
0
-20
40
M db
20
0
-20
-40 10 -2
Example
40
G(s) ?
K?T2s ? 1?2 s?T1s ? 1?
when ? ? 1 rad s
30
???dBL
20 10
? 20
? 40
that is f ? 1 ?2? ?Hz 0
-10
20 lg K ? 30dB
So
K ? 31.6
-20 10-1
1
2?
0.54 100
4.4 101
102
The break frequencies are 0.54Hz and 4.4Hz respectively，then
10
20
1? s
0
1
1?1 2s
1
-20
s
-40
作相频特性曲线。根据表达式，在低频中频 和高频区域中各选择若干个频率进行计算， 然后连成曲线
Example
G ?s ??
10
s ?1
?1 ?
?1
2ss??,
H ?s ?? 1
Description
10 1 s 1? s
0.01 start plot
0
-20 0
Frequency(rad/s)
1 start 1 ? s
2 start 1 ? 1
20
20
1? 1 2s
0
Total slope
-20
(db/decade )
0
-20
0
-20
40
M db
20
0
-20
-40 10 -2
Example
40
G(s) ?
K?T2s ? 1?2 s?T1s ? 1?
when ? ? 1 rad s
30
???dBL
20 10
? 20
? 40
that is f ? 1 ?2? ?Hz 0
-10
20 lg K ? 30dB
So
K ? 31.6
-20 10-1
1
2?
0.54 100
4.4 101
102
The break frequencies are 0.54Hz and 4.4Hz respectively，then
10
20
1? s
0
1
1?1 2s
1
-20
s
-40
频率特性分析(2)
G ( j ) ( ) i ( )
i 1
n n
n
i 1 n
开环相频特性 开环对数幅频特性
20 lg G ( j ) 20 lg A( ) 20 lg Ai ( ) 20 lg Ai ( )
i 1 i 1
1.将系统的开环传递函数写成典型环节乘积（即串联）的形 式；
L( ) dB
40
20
40dB / dec
0.01
0
20 40
0.1
1
10
100
( )
900
450
45
0 0 0.01
0
0.1
1
10
100
900
1800
3.微分环节 频率特性为
G( j ) j
对数幅频特性 20lg G( j ) 20lg
对数相频特性
( ) 90
0
L( ) dB
40
20dB / dec
20
0
20 40
( )
900
0.01
0.1
1
10
100
450
45
0 0 0.01
0
0.1
1
10
100
900
微分环节的Bode图
4.惯性环节
频率特性为
对数幅频特性
G ( j )
1 jT 1
20lg G( j) 20lg T 2 2 1 10lg(T 2 2 1)
2 2
L( )
(dB )
1 T
10
0
20
1 1 20 T T
i 1
n n
n
i 1 n
开环相频特性 开环对数幅频特性
20 lg G ( j ) 20 lg A( ) 20 lg Ai ( ) 20 lg Ai ( )
i 1 i 1
1.将系统的开环传递函数写成典型环节乘积（即串联）的形 式；
L( ) dB
40
20
40dB / dec
0.01
0
20 40
0.1
1
10
100
( )
900
450
45
0 0 0.01
0
0.1
1
10
100
900
1800
3.微分环节 频率特性为
G( j ) j
对数幅频特性 20lg G( j ) 20lg
对数相频特性
( ) 90
0
L( ) dB
40
20dB / dec
20
0
20 40
( )
900
0.01
0.1
1
10
100
450
45
0 0 0.01
0
0.1
1
10
100
900
微分环节的Bode图
4.惯性环节
频率特性为
对数幅频特性
G ( j )
1 jT 1
20lg G( j) 20lg T 2 2 1 10lg(T 2 2 1)
2 2
L( )
(dB )
1 T
10
0
20
1 1 20 T T
典型环节的频率特性
1 1 G ( j ) j
Im
G
Re
900
0
积分环节的频率响应
频率特性如图所示。由图可知，积分环节的相频特性等于 -900 ， 与角频率ω 无关，表明积分环节对正弦输入信号有900的滞后作用；其幅 频特性等于 1 ，是ω 的函数， 当ω 由零变到无穷大时，输出幅值则由 无穷大衰减至零。
（3） 用渐近线表示幅频特性，使作图简单方便；
（4） 横轴（ω 轴）用对数分度，扩展了低频段，同时兼顾 了中、高频段，有利于系统的分析与综合。
（一）放大环节（比例环节） 放大环节的频率特性为 G ( j ) K ( K 0)
其幅频特性是
G( j ) K
对数幅频特性为
20 lg G( j ) 20 lg K
-20
-40
( )
两个图形上下放置（幅
频特性在上，相频特性
在下），且将纵轴对齐， 便于求出同一频率的幅
90o
值和相角的大小，同时
为求取系统相角裕度带
45o
0 -45o -90o 0.01 0.1 1 10 100
来方便。
用伯德图分析系统有如下优点： （1） 将幅频特性和相频特性分别作图，使系统（或环节）
2 2 2
2
1 是一个标准圆方程，其圆心坐标是 ,0 ，半径为 1 。且
当ω 由 0 时， G ( j ) 由 0 90 ，说明惯性环节的频率特 性在G( j ) 平面上是实轴下方半个圆周，如图所示。
2
2
Im
G
0
0.5
0
450
幅频特性和相频特性分别为
Im
G
Re
900
0
积分环节的频率响应
频率特性如图所示。由图可知，积分环节的相频特性等于 -900 ， 与角频率ω 无关，表明积分环节对正弦输入信号有900的滞后作用；其幅 频特性等于 1 ，是ω 的函数， 当ω 由零变到无穷大时，输出幅值则由 无穷大衰减至零。
（3） 用渐近线表示幅频特性，使作图简单方便；
（4） 横轴（ω 轴）用对数分度，扩展了低频段，同时兼顾 了中、高频段，有利于系统的分析与综合。
（一）放大环节（比例环节） 放大环节的频率特性为 G ( j ) K ( K 0)
其幅频特性是
G( j ) K
对数幅频特性为
20 lg G( j ) 20 lg K
-20
-40
( )
两个图形上下放置（幅
频特性在上，相频特性
在下），且将纵轴对齐， 便于求出同一频率的幅
90o
值和相角的大小，同时
为求取系统相角裕度带
45o
0 -45o -90o 0.01 0.1 1 10 100
来方便。
用伯德图分析系统有如下优点： （1） 将幅频特性和相频特性分别作图，使系统（或环节）
2 2 2
2
1 是一个标准圆方程，其圆心坐标是 ,0 ，半径为 1 。且
当ω 由 0 时， G ( j ) 由 0 90 ，说明惯性环节的频率特 性在G( j ) 平面上是实轴下方半个圆周，如图所示。
2
2
Im
G
0
0.5
0
450
幅频特性和相频特性分别为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(
j
)
arctan
1
2T T 2
2
南华大学
第四章 系统的频率响应分析
特点：
转折频率：
TT
=1，T
=1
T
=
n
。
低频段T<<1,→ 0dB线；
高频段T>>1,→-40dB/dec 线。
L() 20 0 -20 -40 () 0
-90
-180
-40dB/dec
T
T
100 ω(rad/s)
南华大学
典型环节的对数坐标图
(1) 比例环节
对数幅频特性为：
G( j) K
L() 20lg G( j) 20lg K
L(ω)为常数是平行于横轴的一条直线。
对数相频特性为(ω)=0 ，与横轴重合。
L(ω )
20lgK
0 ω
(ω)
0 ω
第四章 系统的频率响应分析
南华大学
第四章 系统的频率响应分析
(3) 积分环节
对数幅频特性：
G( j ) 1 j
dB 20lg G( j)
40
L( ) 20 lg G( j ) 20 lg 1 20 lg 20
-20dB/dec
对数相频特性：
0.1 1 10
( ) 90
180 G
南华大学
(2) 惯性环节
对数幅频特性为：
G( j) 1 jT 1
L( ) 20lg G( j ) 20lg
1
20lg 1 T 2 2
1 T 2 2
对数相频特性： ( ) G( j ) arctan T
L(ω)
0
L( ) 0 ( ) 0 -20
南华大学
第四章 系统的频率响应分析
4.4 典型环节的对数坐标图（Bode图）
南华大学
第四章 系统的频率响应分析
对数坐标图：
对数幅频特性曲线：
20lgG(jω) dB
40 20
0
20dB/dec 1 10 20 ω(rad/s)
说明：
-20dB/dec
1. 横坐标表示ω，但按对数均匀分度；
2. 纵坐标为20lgG(jω) ，均匀分度；
斜率为+20dB/dec的直线。
90
20lg G( j)
+20dB/dec
0.1
1 10
G
- 90
南华大学
第四章 系统的频率响应分析
(5) 一阶微分环节 G( j) 1 j
对数幅频特性： L() 20lg G( j) 20lg 1 ()2
对数相频特性： ( ) arctan
对数相频特性：
+40dB/dec
(
)
G(
j
)
arctan
1
2T T 2
2
180
南华大学
第四章 系统的频率响应分析
(8) 延时环节
G( j) e j 1
对数幅频特性：
dB
20lg G
L( ) 20lg G( j ) 0dB
0
ω
对数相频特性：
特点： 转折频率ω=1/T; 低频段ω<<1/T: 0dB线，0～45°; 高频段ω>>1/T: +20dB/dec,45°~ 90°;
dB 20lg G( j)
40 20
T G 90
45
0
+20 dB dec ( s -1 )
10T
( s -1 )南华大学来自第四章 系统的频率响应分析
G
() G( j)
0°
ω
南华大学
第四章 系统的频率响应分析
各典型环节Bode图特点总结：
比例环节 积分环节 微分环节 惯性环节 一阶微分环节 二阶振荡环节 二阶微分环节 延时环节
详见教材
南华大学
第四章 系统的频率响应分析
两个环节串联的Bode图
比例环节 惯性环节
G1(s) K 1
90
积分环节的对数幅频特性曲线为过(1，0)点，斜率
为-20dB/dec的直线
- 90 - 180
南华大学
第四章 系统的频率响应分析
(4) 微分环节
G( j ) j
对数幅频特性：
dB
L( ) 20lg A( ) 20lg
20
对数相频特性：
( ) 90
- 20
对数幅频特性曲线为过(1，0)点， 180
1/T
ω
-90 °
南华大学
第四章 系统的频率响应分析
三个环节串联的Bode图
比例环节 G(s) K
南华大学
第四章 系统的频率响应分析
(7)
二阶微分环节
G( j )
( j )2 n2
j2 n
1
(0 1)
对数幅频特性：
令T 1 ，则G( j ) 1 T 2 2 j2T n
L( ) 20lg G( j ) 20lg (1 T 2 2 )2 (2T )2
G2(s) Ts 1
G(
s)
G1(
s)
G2
(
s)
K Ts
1
G( j) K
jT 1
L() 20lg G( j) 20lg K (20lg 1 (T)2 )
L( ω ) 20lgK
0 (ω )
0 -45°
-20dB/dec
1/T
ω -20dB/dec
φ(ω)
转折频率
低频段ω<<1/T 1
-20dB/dec 1/T 10
折线处 理
L( ) 20lgT 20lg
高频段ω>>1/T ω
100
0
ω
-45°
-90 °
( ) 90
南华大学
第四章 系统的频率响应分析
近似折线段法:
转折频率ω=1/T 低频段ω<<1/T : 0dB线，0～-45 高频段ω>>1/T : -20dB/dec线，-45～-90
3. dec：十倍频，即频率增加10倍；
4. ±20dB/dec：频率每增加10倍，分贝值增加或下降20；
5. 坐标原点0只是纵坐标的0，横坐标没有0。
南华大学
第四章 系统的频率响应分析
对数相频特性曲线：
∠G(jω)
90° 45°
0
1
10
说明： 1. 横坐标仍然表示ω，仍然按对数均匀分度； 2. 纵坐标为(ω)=∠G(jω)，均匀分度； 3.坐标原点0只是纵坐标的0，横坐标没有0。
(6) 二阶振荡环节
对数幅频特性：
G(
j)
(
j)2
n2 j2n
n2
(0 1)
令T
1 n
，则G(
j)
1 1 T 2 2
j2T
L() 20lg G( j) 20lg (1T 22)2 4 2T 22
对数相频特性：
(
)
G