计量经济学 张晓峒 第二章习题
计量经济学 张晓峒 第三版 南开大学出版社

数量经济学复习试题一.对于模型:n i X Y ii i ,,1 =++=εβα从10个观测值中计算出;20,200,26,40,822=====∑∑∑∑∑i i i i i iY X X Y X Y,请回答以下问题:(1)求出模型中α和β的OLS 估计量; (2)当10=x 时,计算y 的预测值。
(3) 求出模型的2R ,并作出解释;(4)对模型总体作出检验;(5)对模型系数进行显著性检验;二.根据我国1978——2000年的财政收入Y 和国内生产总值X 的统计资料,可建立如下的计量经济模型:ˆ516.64770.0898t tY X =+ (1) (2.5199) (0.005272)2R =0.9609,E S .=731.2086,F =516.3338,W D .=0.2174 1、 模型(1)斜率项是显著的吗?它有什么经济意义已知(048.2)28(025.0=t ) 2、检验该模型的误差项是否存在自相关。
(已知在23,1%,5===n k α条件下,489.1,352.1==U L d d )3、如果存在自相关,请您用广义差分法来消除自相关问题。
4、根据下面的信息,检验回归方程(1)的误差项是否存在异方差。
如果存在异方差的话,请写出异方差的形式。
表1:此表为Eviews 输出结果。
RE 为模型(1)中残差的平方5、我们通常用什么方法解决异方差问题,在这里,你建议使用什么方法修正模型?如何修正(要求写出修正后的模型)?三、设货币需求方程式的总体模型为t t t ttRGDP r P M εβββ+++=)ln()ln()ln(210 其中M 为广义货币需求量,P 为物价水平,r 为利率,RGDP 为实际国内生产总值。
假定根据容量为n =19的样本,用最小二乘法估计出如下样本回归模型;1.09.0)3()13()ln(54.0)ln(26.003.0)ln(2==++-=DW R e RGDP r P M t t t tt其中括号内的数值为系数估计的t 统计值,t e 为残差。
最新计量经济学答案-南开大学---张晓峒
1244.567
为此,装潢美观,亮丽,富有个性化的店面环境,能引起消费者的注意,从而刺激顾客的消费欲望。这些问题在今后经营中我们将慎重考虑的。10.12101
大学生的消费是多种多样,丰富多彩的。除食品外,很大一部分开支都用于。服饰,娱乐,小饰品等。女生都比较偏爱小饰品之类的消费。女生天性爱美,对小饰品爱不释手,因为饰品所展现的魅力,女人因饰品而妩媚动人,亮丽。据美国商务部调查资料显示女人占据消费市场最大分额,随社会越发展,物质越丰富,女性的时尚美丽消费也越来越激烈。因此也为饰品业创造了无限的商机。据调查统计,有50%的同学曾经购买过DIY饰品,有90%的同学表示若在学校附近开设一家DIY手工艺制品,会去光顾。我们认为:我校区的女生就占了80%。相信开饰品店也是个不错的创业方针。0.0000
-123.0126
F-statistic
42.79505
Durbin-Watson stat
0.859998
Prob(F-statistic)
0.000028
obs
Y
GDP
1985
18249
161.69
1986
18525
171.07
1987
18400
184.07
1988
16693
194.75
1989
计量经济学答案
第二单元课后第六题答案
Dependent Variable: Y
Method: Least Squares
Date: 04/05/13 Time: 00:07
(2)文化优势Sample: 1985 1998
在上海,随着轨道交通的发展,地铁商铺应运而生,并且在重要的商业圈已经形成一定的气候,投资经营地铁商铺逐渐成为一大热门。在人民广场地下“的美”购物中心,有一家DIY自制饰品店---“碧芝自制饰品店”。Included observations: 14
计量经济学第二章练习题及参考解答
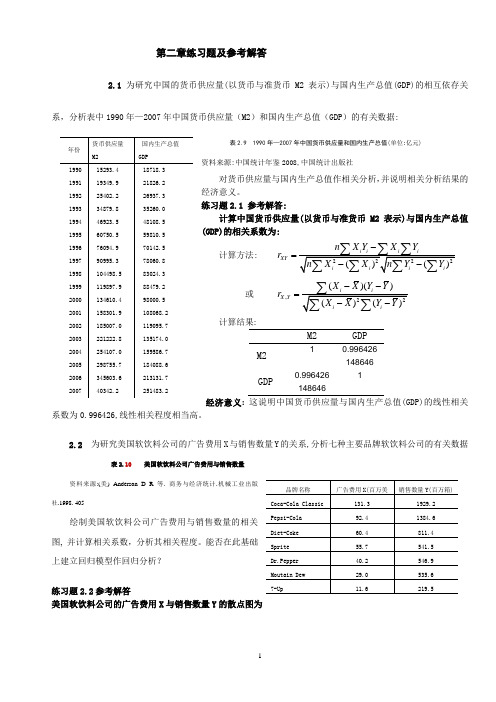
第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: 2222()()i i i iXY i i i i n X Y X Y r n X X n Y Y -=--∑∑∑∑∑∑∑或 ,22()()()()ii X Y iiX X Y Y r X X Y Y --=--∑∑∑计算结果:M2GDPM2 1 0.996426148646 GDP0.9964261486461经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X 与销售数量Y 的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量 资料来源:(美) Anderson D R 等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X 与销售数量Y 的散点图为年份货币供应量M2国内生产总值GDP1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 200715293.4 19349.9 25402.2 34879.8 46923.5 60750.5 76094.9 90995.3 104498.5 119897.9 134610.4 158301.9 185007.0 221222.8 254107.0 298755.7 345603.6 40342.218718.3 21826.2 26937.3 35260.0 48108.5 59810.5 70142.5 78060.8 83024.3 88479.2 98000.5 108068.2 119095.7 135174.0 159586.7 184088.6 213131.7 251483.2品牌名称广告费用X(百万美销售数量Y(百万箱)Coca-Cola Classic 131.3 1929.2 Pepsi-Cola 92.4 1384.6 Diet-Coke60.4 811.4 Sprite 55.7 541.5 Dr.Pepper 40.2 546.9 Moutain Dew 29.0 535.6 7-Up11.6219.5说明美国软饮料公司的广告费用X 与销售数量Y 正线性相关。
计量经济学 张晓峒 第二章习题

计量经济学张晓峒第二章习题1.最小二乘法对随机误差项u作了哪些假定?说明这些假定条件的意义。
答:假定条件:(1)均值假设:E(u i)=0,i=1,2,…;(2)同方差假设:Var(u i)=E[u i-E(u i)]2=E(u i2)=σu2 ,i=1,2,…;(3)序列不相关假设:Cov(u i,u j)=E[u i-E(u i)][u j-E(u j)]=E(u i u j)=0,i≠j,i,j=1,2,…;(4)Cov(u i,X i)=E[u i-E(u i)][X i-E(X i)]=E(u i X i)=0;(5)u i服从正态分布, u i~N(0,σu2)。
意义:有了这些假定条件,就可以用普通最小二乘法估计回归模型的参数。
2.阐述对样本回归模型拟合优度的检验及回归系数估计值显著性检验的步骤。
答:样本回归模型拟合优度的检验:可通过总离差平方和的分解、样本可决系数、样本相关系数来检验。
回归系数估计值显著性检验的步骤:(1)提出原假设H0 :β1=0;(2)备择假设H1 :β1≠0;(3)计算t=β1/Sβ1;(4)给出显著性水平α,查自由度v=n-2的t分布表,得临界值tα/2(n-2);(5)作出判断。
如果|t|<tα/2(n-2),接受H0 :β1=0,表明X对Y无显著影响,一元线性回归模型无意义;如果|t|>tα/2(n-2),拒绝H0 ,接受H1:β1≠0,表明X对Y有显著影响。
4.试说明为什么∑e i2的自由度等于n-2。
答:在模型中,自由度指样本中可以自由变动的独立不相关的变量个数。
当有约束条件时,自由度减少,其计算公式:自由度=样本个数-受约束条件的个数,即df=n-k。
一元线性回归中SSE残差的平方和,其自由度为n-2,因为计算残差时用到回归方程,回归方程中有两个未知参数β0和β1,而这两个参数需要两个约束条件予以确定,由此减去2,也即其自由度为n-2。
计量经济学 张晓峒 第三版 南开大学出版社

第四章一、练习题 (一)简答题1、多元线性回归模型的基本假设是什么?试说明在证明最小二乘估计量的无偏性和有效性的过程中,哪些基本假设起了作用?2、多元线性回归模型与一元线性回归模型有哪些区别?3、某地区通过一个样本容量为722的调查数据得到劳动力受教育的一个回归方程为fedu medu sibs edu 210.0131.0094.036.10++-=R 2=0.214式中,edu 为劳动力受教育年数,sibs 为该劳动力家庭中兄弟姐妹的个数,medu 与fedu 分别为母亲与父亲受到教育的年数。
问(1)若medu 与fedu 保持不变,为了使预测的受教育水平减少一年,需要sibs 增加多少?(2)请对medu 的系数给予适当的解释。
(3)如果两个劳动力都没有兄弟姐妹,但其中一个的父母受教育的年数为12年,另一个的父母受教育的年数为16年,则两人受教育的年数预期相差多少? 4、以企业研发支出(R&D )占销售额的比重为被解释变量(Y ),以企业销售额(X1)与利润占销售额的比重(X2)为解释变量,一个有32容量的样本企业的估计结果如下:099.0)046.0()22.0()37.1(05.0)log(32.0472.0221=++=R X X Y其中括号中为系数估计值的标准差。
(1)解释log(X1)的系数。
如果X1增加10%,估计Y 会变化多少个百分点?这在经济上是一个很大的影响吗?(2)针对R&D 强度随销售额的增加而提高这一备择假设,检验它不虽X1而变化的假设。
分别在5%和10%的显著性水平上进行这个检验。
(3)利润占销售额的比重X2对R&D 强度Y 是否在统计上有显著的影响? 5、什么是正规方程组?分别用非矩阵形式和矩阵形式写出模型:i ki k i i i u x x x y +++++=ββββ 22110,n i ,,2,1 =的正规方程组,及其推导过程。
6、假设要求你建立一个计量经济模型来说明在学校跑道上慢跑一英里或一英里以上的人数,以便决定是否修建第二条跑道以满足所有的锻炼者。
计量经济学第2章习题参考答案

量 y 是随机变量, 解释变量 x 是非随机变量, 相关分析对资料的要求是两个变量都是随机变 量。 2. 答: 相关关系是指两个以上的变量的样本观测值序列之间表现出来的随机数学关系, 用相关 系数来衡量。 因果关系是指两个或两个以上变量在行为机制上的依赖性, 作为结果的变量是由作为原因的 变量所决定的, 原因变量的变化引起结果变量的变化。 因果关系有单向因果关系和互为因果 关系之分。 具有因果关系的变量之间一定具有数学上的相关关系。 而具有相关关系的变量之间并不一定 具有因果关系。 3. 答:主要区别:①描述的对象不同。总体回归模型描述总体中变量 y 与 x 的相互关系,而样 本回归模型描述所观测的样本中变量 y 与 x 的相互关系。 ②建立模型的不同。 总体回归模型 是依据总体全部观测资料建立的, 样本回归模型是依据样本观测资料建立的。 ③模型性质不 同。总体回归模型不是随机模型,样本回归模型是随机模型,它随着样本的改变而改变。 主要联系:样本回归模型是总体回归模型的一个估计式,之所以建立样本回归模型,目的是 用来估计总体回归模型。
1 n ∑ ui = 0 ,因为 n i =1
前者是条件期望,即针对给定的 X i 的随机干扰的期望,而后者是无条件的平均值,即针对 所有 X i 的随机干扰取平均值。
二、单项选择题 1. A 2. D 3. A 4. B 5. C 6. B 7. D 8. B 9. D 10. C 11. D 12. D 13. C
14. D 15. D 16. A 17. B
三、多项选择题 1. ACD 2. ABE 3. AC 4. BE 5. BEFH 6. DG, ABCG, G, EF 7. ABDE 8. ADE 9. ACDE
计量经济学答案 南开大学 张晓峒
1989
15543
197.86
1990
15929
208.55
1991
18308
221.06
1992
17522
246.92
1993
21640
276.8
1994
23783
316.38
1995
24040
363.52
1996
24133
415.51
1997
25090
465.78
1998
24505
509.1
0.00366225249927
R-squared
0.979630987789
Mean dependent var
755.65
Adjusted R-squared
0.976915119495
S.D.dependent var
258.174979992
S.E. of regression
39.22635618
第一单元微小世界Variable
Coefficient
Std. Error
8、晶体的形状多种多样,但都很有规则。有的是立方体,有的像金字塔,有的像一簇簇的针……有的晶体较大,肉眼可见,有的较小,要在放大镜或显微镜下才能看见。t-Statistic
Prob.
C
2、如果我们想要设计一个合理、清洁的垃圾填埋场,我们首先应考虑要解决的问题有哪些呢?12596.27
0.106295
0.9162
X1
0.919472
0.235789
3.899556
0.0006
X2
2.933351
1.655564
计量经济学第二章作业答案

计量经济学第二章作业答案标准化文件发布号:(9312-EUATWW-MWUB-WUNN-INNUL-DQQTY-
习题为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2012年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:
表 1990年—2012年中国货币供应量和国内生产总值(单位:亿元)
解答:中国货币供应量(M2)X与国内生产总值(GDP)Y的相关系数为:
利用EViews估计其参数结果为:
Yi=+
t=
R2= F=
经济意义:根据估计的参数,说明货币供应量每增加1亿元平均可导致国内生产总值增加亿元,线性相关程度很高。
为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下数据:
表深圳市地方预算内财政收入与国内生产总值
(1)建立深圳地方预算内财政收入对本市生产总值GDP的回归模型;
(2)估计所建立模型的参数,解释斜率系数的经济意义;
(3)对回归结果进行检验。
解答:
(1)建立深圳地方预算内财政收入对本市GDP(X)的回归模型,建立EViews 文件,利用地方预算内财政收入(Y)和本市GDP(X)的数据表,作散点图:
可看图得出地方预算内财政收入(Y )和GDP 的关系近似直线关系,可建立线性回归模型:
i i i u X Y ++=21ββ (2)利用EViews 估计其参数结果为:
即 Yi=+ () t= R 2= F=
(3)经检验说明,深圳市的GDP 对地方财政收入有显著影响。
R 2=,说明GDP 解释了地方财政收入变动的近98%,模型拟合程度较好。
模型说明当GDP 每增长1亿元时,平均说来地方财政收入将增长亿元。
计量经济学 课后题答案

第二章练习题参考解答练习题2.1 为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下数据:资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建立深圳地方预算内财政收入对GDP 的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验;(4)若是2005 年年的国内生产总值为3600 亿元,确定2005 年财政收入的预测值和预测区间(α= 0.05)。
2.2 某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费10 10 8 8 8 12 12 12 11 11利润额100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3 为研究中国的货币供应量(以货币与准货币M2 表示)与国内生产总值(GDP)的相互依存关系,分析表中1990 年—2001 年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:货币供应量(亿元) 年份M2 国内生产总值(亿元)GDP1990 1529.3 18598.4 1991 19349.9 21662.5199225402.226651.9199334879.834560.5199446923.546670.0199560750.557494.9199676094.966850.5199790995.373142.71998104498.576967.21999119897.980579.42000134610.388228.12001158301.994346.4资料来源:《中国统计年鉴2002》,第51 页、第662 页,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明分析结果的经济意义。
2.4 表中是16 支公益股票某年的每股帐面价值和当年红利:根据上表资料:(1)建立每股帐面价值和当年红利的回归方程;(2)解释回归系数的经济意义;(3)若序号为6 的公司的股票每股帐面价值增加1 元,估计当年红利可能为多少?2.5 美国各航空公司业绩的统计数据公布在《华尔街日报1999 年年鉴》(The Wall Street1。
计量经济学 第2章练习题参考解答

第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验;(4)若是2005年年的国内生产总值为3600亿元,确定2005年财政收入的预测值和预测区间(0.05α=)。
2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2001年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.2 26651.91993 34879.8 34560.51994 46923.5 46670.01995 60750.5 57494.91996 76094.9 66850.51997 90995.3 73142.71998 104498.5 76967.21999 119897.9 80579.42000 134610.3 88228.12001158301.994346.4资料来源:《中国统计年鉴2002》,第51页、第662页,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明分析结果的经济意义。
2.4表中是16支公益股票某年的每股帐面价值和当年红利:根据上表资料:(1)建立每股帐面价值和当年红利的回归方程; (2)解释回归系数的经济意义;(3)若序号为6的公司的股票每股帐面价值增加1元,估计当年红利可能为多少?2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street Journal 1。
计量经济学第二章习题集

第一题:一、研究的目的和要求亚洲各国人均寿民对国民生活具有重要的参考价值,也是人民日常生活中密切关注的问题。
为此,在生活中一些因素比如人均GDP则反映了生活条件对寿命的影响,成人识字率也就是受教育的程度是否对寿命也有相应的影响,从这方面看,受教育的程度反应在生活环境的各个方面。
而一岁儿童疫苗接种可能反映的是早期因素对未来身体等方面的影响。
那么这些因素是否对寿命有影响呢?对此,可以进行研究,以便发现因素的影响,这样就能有效地采取相应的措施,对这些影响因子进行调整,这些对如何`提高人均寿命是具有指导意义的。
二、模型设定为了分析亚洲各国人均寿民分别与按购买力平价计算的人均GDP、成人识字率、一岁儿童疫苗接种率的关系,选择“亚洲各国人均寿命”(单位:/年)为被解释变量;分别选择按购买力平价计算的人均GDP(单位:100美元)(用X1表示),成人识字率(单位:%)(用X2表示)、一岁儿童疫苗率(单位:%)(用X3表示)为解释变量。
为了分析亚洲各国人均寿命(Y)分别与按购买力平价计算的GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数量关系,可以运用eviews 去做计量分析。
利用eviews做简单线性回归分析的基本步骤如下:1.建立工作文件首先,双击Eviews图标,进入Eviews主页。
依次点击File/New/Workfile,在出现对话框的菜单中选择文件数据的类型,本利分析的是亚洲各国的人均寿命的横截面数据,则选择“integer date”。
在“Start date”中输入开始顺序号“1”,在“end data”中输入最后顺序号“22”。
点击“ok”出现未命名的“Workfile UNTITLED”工作框。
其中已有对象:“c”为截距项,“resid”为剩余项。
若要将工作文件存盘,点击窗口上方的“Save”,在“Save as”对话框中选择存盘路径,并输入工作文件名,再点击“OK”,文件即被保存,并确定了文件名。
计量经济学 第二章课后答案与分析

练习题2.1(1)如上图:从散点图我们可以看出亚洲各国人均寿命(Y)与人均GDP(X1) 近似于线性关系,故建立以下模型:β+μβY0X=11+(2)根据回归结果图分析:我们可将参数估计和检验的结果写成如下:1Y+=56X1284.06479.(1.9608) (0.0272)t=(28.8899)(4.7118)R^2=0.5261 n=22a、根据所估计参数β0=56.6479,β1=0.1284,说明亚洲人均GDP 每增加100美元,人均寿命(Y)将增加0.1284年。
与预期的经济意义相符。
b、R^2=0.5261,说明数据拟合程度较好。
C、取α=0.05,查t表自由度为n-2=22-2=20的临界值t (20)=2.086.因为 4.7118>2.086,28.8899>2.086,故拒绝原假设H :β0=0,β1=0.对斜率系数的显著性检验表明,亚洲各国人均寿命(Y)与人均GDP(X1)有显著影响。
(1)如上图:从散点图我们可以看出亚洲各国人均寿命(Y)与成人识字率(X2)近似于线性关系,故建立以下模型: μββ++=210X Y(2)根据回归结果图分析:我们可将参数估计和检验的结果写成如下: 23320.07942.38X Y += (3.5321) (0.0467) t=(10.9834)(7.1153) R^2=0.7168 n=22a 、根据所估计参数β0=38.7942,β1=0.3320,说明亚洲各国成人识字率每增加1个百分比,人均寿命将增加0.3320年,与预期的经济意义相符。
b 、R^2=0.7168,说明数据拟合程度较好。
C 、取α=0.05,查t 表自由度为n-2=22-2=20的临界值t (20)=2.086.因为10.9834>2.086,7.1153>2.086,故拒绝原假设H :β0=0,β1=0.对斜率系数的显著性检验表明,亚洲各国人均寿命(Y)与成人识字率(X2)有显著影响。
计量经济学第二章作业答案
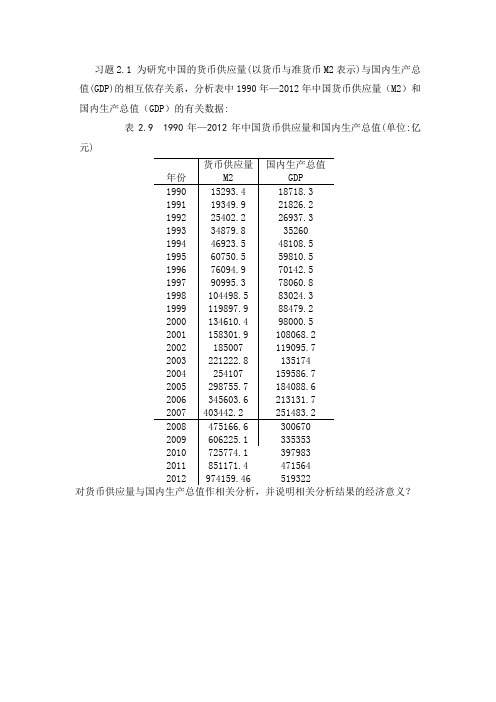
习题2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2012年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:表2.9 1990年—2012年中国货币供应量和国内生产总值(单位:亿元)解答:中国货币供应量(M2)X与国内生产总值(GDP)Y的相关系数为: 利用EViews估计其参数结果为:Yi=24351.34+0.524085Xit=(8.381061) (69.38808)R2=0.995657 F=4814.705经济意义:根据估计的参数,说明货币供应量每增加1亿元平均可导致国内生产总值增加0.995657亿元,线性相关程度很高。
2.3 为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下数据:表2.11 深圳市地方预算内财政收入与国内生产总值(1)建立深圳地方预算内财政收入对本市生产总值GDP的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验。
解答:(1)建立深圳地方预算内财政收入对本市GDP(X)的回归模型,建立EViews 文件,利用地方预算内财政收入(Y)和本市GDP(X)的数据表,作散点图:可看图得出地方预算内财政收入(Y )和GDP 的关系近似直线关系,可建立线性回归模型:i i i u X Y ++=21ββ (2)利用EViews 估计其参数结果为:即 Yi=-23.23698+0.108689Xi (19.43977) (0.004013) t=(-1.195332) (27.08762) R 2=0.973466 F=733.7392(3)经检验说明,深圳市的GDP 对地方财政收入有显著影响。
R 2=0.973466,说明GDP 解释了地方财政收入变动的近98%,模型拟合程度较好。
模型说明当GDP 每增长1亿元时,平均说来地方财政收入将增长0.004013亿元。
计量经济学第二版第二章练习题
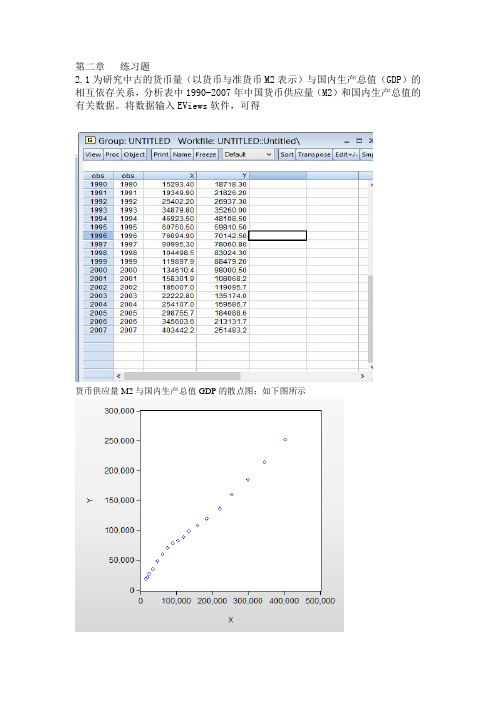
第二章练习题2.1为研究中古的货币量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990-2007年中国货币供应量(M2)和国内生产总值的有关数据。
将数据输入EViews软件,可得货币供应量M2与国内生产总值GDP的散点图:如下图所示由上图可以看出,两者关系近似一条直线,故对货币供应量和国民生产总值的数量关系进行回归分析。
回归分析结果如下图:解释变量X 为货币供应量,被解释变量Y 是国内生产总值。
结果分析:由回归结果可以得到参数估计的结果为X Y 522321.050.30413ˆ+=,此处用P 值法进行检验,由于P 值远远小于给定的显著性水平α,故应当拒绝原假设,则1β和2β显著不为0。
又因为R-squared(可决系数)为0.866782接近1,调整后的可决系数仍接近1,故可知XY 之间存在较强的正相关关系,即拟合程度较高,线性关系较为显著。
2.2为研究美国软饮料公司的广告费用X 与销售数量Y 之间的关系,分析七种主要品牌软饮料公司的有关数据,将数据输入EViews 软件中,可得折线图输入命令Cor X Y可得相关系数如下图:对解释变量X和被解释变量Y进行回归分析,可得图如上表中,x、y之间的相关系数为0.978148非常接近于1,故可知,其正线性相关关系较为显著,故可拟合为一条直线。
回归方程如下:12+=77853﹣.XY40359.14经t检验表明,广告费用X对美国软饮料公司的销售数量Y确有显著影响。
回归结果表明,广告费用X每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
2.3 为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下数据。
将数据录入到EViews软件中。
散点图如下:运用软件,得到回归结果如下图所示:结果分析:2.4为研究中国改革开放以来国民总收入和最终消费的关系,搜集到以下数据,输入软件eviews可得根据数据画出折线图为:由折线图可知,x 与y 近似于线性关系,故对xy 进行回归分析,可得结果分析:(1) 以最终消费为被解释变量Y ,以国民总收入为解释变量X ,建立线性回归模型,结果如下:X Y 530112.0345.3044+=(859.4073)(0.009670) T=(3.399956)(54.82057) 990439.02=R (调整后的可决系数)N=302.5美国各航空公司业绩的统计数据公布在年鉴上,航班正点到达的比率和每10万名乘客投诉的次数的数据如下表所示:航班正点率为解释变量x ,投诉率为被解释变量y用软件画出散点图可得到下图:如上图所示,xy 之间存在负相关关系,故用软件对其进行回归分析,可得分析结果如下图:分析结果:因为可决系数为0.746303接近1,其调整后的可决系数也接近于1,故拟合程度较高线性相关关系显著。
计量经济学张晓峒第三版课后作业
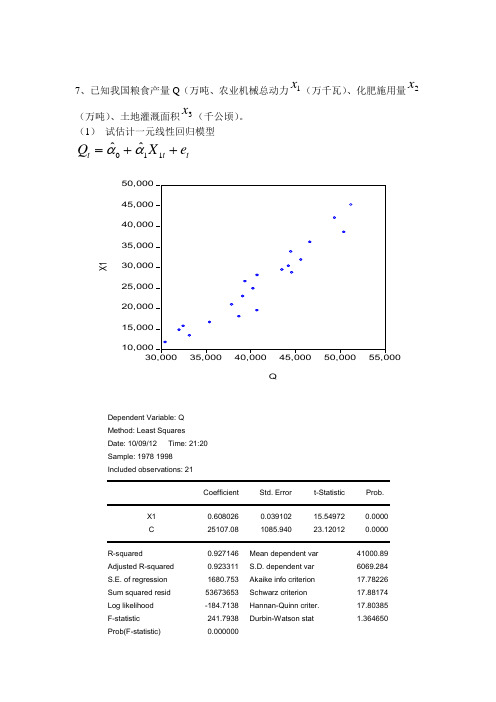
7、已知我国粮食产量Q (万吨、农业机械总动力1x (万千瓦)、化肥施用量2x (万吨)、土地灌溉面积3x (千公顷)。
(1) 试估计一元线性回归模型011ˆˆ t t t Q X e αα=++Dependent Variable: Q Method: Least Squares Date: 10/09/12 Time: 21:20 Sample: 1978 1998 Included observations: 21Coefficient Std. Error t-Statistic Prob.X1 0.608026 0.039102 15.54972 0.0000 C25107.081085.94023.120120.0000R-squared0.927146 Mean dependent var 41000.89 Adjusted R-squared 0.923311 S.D. dependent var 6069.284 S.E. of regression 1680.753 Akaike info criterion 17.78226 Sum squared resid 53673653 Schwarz criterion 17.88174 Log likelihood -184.7138 Hannan-Quinn criter. 17.80385 F-statistic 241.7938 Durbin-Watson stat 1.364650Prob(F-statistic)0.000000025107.08α= 10.61α= 0t 23.12= 1t 15.55=则样本回归方程为1Q 25107.080.61X t t =+(23.12) (15.55) r 2=0.93括号内的数字为回归系数对应的t 统计量的值,以下同。
0121ˆˆt t Q X e ββ=++Dependent Variable: Q Method: Least Squares Date: 10/09/12 Time: 21:21 Sample: 1978 1998 Included observations: 21Coefficient Std. Error t-Statistic Prob.X2 5.909473 0.356747 16.56488 0.0000 C26937.69916.697229.385590.0000R-squared0.935241 Mean dependent var 41000.89 Adjusted R-squared 0.931833 S.D. dependent var 6069.284 S.E. of regression 1584.623 Akaike info criterion 17.66447 Sum squared resid 47709547 Schwarz criterion 17.76395 Log likelihood -183.4770 Hannan-Quinn criter. 17.68606 F-statistic 274.3953 Durbin-Watson stat 1.247710Prob(F-statistic)0.000000026937.69β= 1 5.91β= 0t 29.39= 1t 16.56=则样本回归方程为2Q 26937.69 5.91X t t =+(29.39) (16.56) r 2=0.94013ˆˆt t t Q X e γγ=++Dependent Variable: Q Method: Least Squares Date: 10/09/12 Time: 21:23 Sample: 1978 1998 Included observations: 21Coefficient Std. Error t-Statistic Prob.X3 1.946877 0.270895 7.186827 0.0000 C-49775.6212650.60-3.9346450.0009R-squared0.731070 Mean dependent var 41000.89 Adjusted R-squared 0.716916 S.D. dependent var 6069.284 S.E. of regression 3229.199 Akaike info criterion 19.08825 Sum squared resid 1.98E+08 Schwarz criterion 19.18773 Log likelihood -198.4266 Hannan-Quinn criter. 19.10984 F-statistic 51.65048 Durbin-Watson stat 0.300947Prob(F-statistic)0.000001049774.62γ= 1 1.95γ= 0t 3.93=- 1t 7.19=3Q 49775.62 1.95X t t =-+(-3.93) (7.19) r 2=0.73(2) 对以上三个模型的估计结果进行结构分析和统计检验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.最小二乘法对随机误差项u作了哪些假定?说明这些假定条件的意义。
答:假定条件:(1)均值假设:E(u i)=0,i=1,2,…;(2)同方差假设:Var(u i)=E[u i-E(u i)]2=E(u i2)=σu2 ,i=1,2,…;(3)序列不相关假设:Cov(u i,u j)=E[u i-E(u i)][u j-E(u j)]=E(u i u j)=0,i≠j,i,j=1,2,…;(4)Cov(u i,X i)=E[u i-E(u i)][X i-E(X i)]=E(u i X i)=0;(5)u i服从正态分布, u i~N(0,σu2)。
意义:有了这些假定条件,就可以用普通最小二乘法估计回归模型的参数。
2.阐述对样本回归模型拟合优度的检验及回归系数估计值显著性检验的步骤。
答:样本回归模型拟合优度的检验:可通过总离差平方和的分解、样本可决系数、样本相关系数来检验。
回归系数估计值显著性检验的步骤:(1)提出原假设H0 :β1=0;(2)备择假设H1 :β1≠0;(3)计算t=β1/Sβ1;(4)给出显著性水平α,查自由度v=n-2的t分布表,得临界值tα/2(n-2);(5)作出判断。
如果|t|<tα/2(n-2),接受H0 :β1=0,表明X对Y无显著影响,一元线性回归模型无意义;如果|t|>tα/2(n-2),拒绝H0 ,接受H1:β1≠0,表明X对Y有显著影响。
4.试说明为什么∑e i2的自由度等于n-2。
答:在模型中,自由度指样本中可以自由变动的独立不相关的变量个数。
当有约束条件时,自由度减少,其计算公式:自由度=样本个数-受约束条件的个数,即df=n-k。
一元线性回归中SSE残差的平方和,其自由度为n-2,因为计算残差时用到回归方程,回归方程中有两个未知参数β0和β1,而这两个参数需要两个约束条件予以确定,由此减去2,也即其自由度为n-2。
5.试说明样本可决系数与样本相关系数的关系及区别,以及样本相关系数与β^1的关系。
答:样本相关系数r的数值等于样本可决系数的平方根,符号与β1相同。
但样本相关系数与样本可决系数在概念上有明显的区别,r建立在相关分析的理论基础之上,研究两个随机变量X与Y之间的线性相关关系;样本可决系数r²建立在回归分析的理论基础之上,研究非随机变量X对随机变量Y的解释程度。
6.已知某市的货物运输量Y(万吨),国内生产总值GDP(亿元,1980年不变价)1985~1998年的样本观测值见下表(略)。
Dependent Variable: Y Method: Least Squares Date: 10/07/16 Time: 00:47 Sample: 1985 1998 Included observations: 14Variable Coefficient Std. Error t-Statistic Prob. C 12596.27 1244.567 10.12101 0.0000 GDP26.954154.1203006.5417920.0000R-squared 0.781002 Mean dependent var 20168.57 Adjusted R-squared 0.762752 S.D. dependent var 3512.487 S.E. of regression 1710.865 Akaike info criterion 17.85895 Sum squared resid 35124719 Schwarz criterion 17.95024 Log likelihood -123.0126 Hannan-Quinn criter. 17.85050 F-statistic 42.79505 Durbin-Watson stat 0.859998Prob(F-statistic)0.000028(1) 一元线性回归方程 Y t =12596.27+26.95415GDP (2) 对回归方程的结构分析126.95β∧=是样本回归方程的斜率,它表示某市的边际货运运输倾向,说明年GDP 每增加一亿元就增加26.95万吨的货物运输量;012596.27β∧=是样本回归方程的截距,它表示不受GDP 影响的货物运输量;01ββ∧∧的符号和大小均符合经济理论和目前某市的实际情况。
(3)统计检验2r 检验:20.78r =,说明总离差平方和的78%被样本回归直线解释了,有22%未被解释,样本回归直线对样本点到拟合优度比较好。
显著性水平 0.05α=,查自由度v=14-2=12的t 分布表,得临界值t 0.025(12)=2.18 t 0=10.1>t 0.025(12),t 1=6.5>t 0.025(12),回归系数显著不为零,回归模型中应包含常数项,GDP 对Y 有显著影响。
(4)预测区间1980~2000当2000年的时候GDP 为620亿元时,运输量预测值为OY =29307.84万吨计算得到:280.93X =21277340ix=∑213262.66e s =则:()222211e i X X s n x σ∧⎡⎤-⎢⎥=++⎢⎥⎣⎦∑=15403.69 0022,O Y Y t Y t αασσ∧∧∧∧⎡⎤⎢⎥∈-+⎢⎥⎣⎦即[]29037.28,29578.40O Y ∈7. 我国粮食产量Q (万吨)、农业机械总动力X1(万瓦时)、化肥施用量X2(万吨)、土地灌溉面积X3(千公顷)1978~1998年样本观测值见下表。
(略) (1)我国粮食产量Q (万吨)和农业机械总动力X1(万瓦时)1) 估计模型Dependent Variable: Q Method: Least Squares Date: 10/07/16 Time: 01:42 Sample: 1978 1998 Included observations: 21Variable Coefficient Std. Error t-Statistic Prob. C 40772.47 1389.795 29.33704 0.0000 X10.0012200.0019090.6391940.5303R-squared 0.021051 Mean dependent var 40996.12 Adjusted R-squared -0.030473 S.D. dependent var 6071.868 S.E. of regression 6163.687 Akaike info criterion 20.38113 Sum squared resid 7.22E+08 Schwarz criterion 20.48061 Log likelihood -212.0019 Hannan-Quinn criter. 20.40272 F-statistic 0.408568 Durbin-Watson stat 0.206201Prob(F-statistic)0.530328估计一元回归模型:011t t t Q X e αα∧∧=++即样本回归模型为:140774.470.00122t tQ X ∧=+2)对估计结果作结构分析10.00122α∧=是样本回归方程的斜率,说明农业机械总动力每增加1万瓦时我国粮食产量就增加0.00122万吨;040772.47α∧=是样本回归方程的截距,它表示不受农业机械总动力影响的粮食总量;01αα∧∧的符号和大小均符合经济理论和我国的实际情况。
3)对估计结果进行统计检验2r 检验:20.02r =,说明总离差平方和的2%被样本回归直线解释了,有98%未被解释,样本回归直线对样本点到拟合优度很差。
T 检验:给出显著水平0.05α=,查自由度v=19的t 分布表,得()0.02519 2.09t =,023.34 2.09t =>,故回归系数均显著为零,回归模型中应包含常数项,X1对Q 无显著影响.(2) 我国粮食产量Q (万吨)和化肥施用量X2(万吨) 1)作散点图并估计模型估计一元回归模型:012tt t Q X e ββ∧∧=++Dependent Variable: Q Method: Least Squares Date: 10/07/16 Time: 01:51Sample: 1978 1998 Included observations: 21Variable Coefficient Std. Error t-Statistic Prob. C 26925.65 915.8657 29.39912 0.0000 X25.9125340.35642316.588510.0000R-squared 0.935413 Mean dependent var 40996.12 Adjusted R-squared 0.932014 S.D. dependent var 6071.868 S.E. of regression 1583.185 Akaike info criterion 17.66266 Sum squared resid 47623035 Schwarz criterion 17.76214 Log likelihood -183.4579 Hannan-Quinn criter. 17.68425 F-statistic 275.1787 Durbin-Watson stat 1.264400 Prob(F-statistic) 0.000000即样本回归模型为:226925.65 5.91t tQ X ∧=+2)对估计结果作结构分析1 5.91β∧=是样本回归方程的斜率,说明化肥施用量每增加1万吨我国粮食产量就增加5.91万吨;026925.65β∧=是样本回归方程的截距,它表示不受化肥施用量影响的粮食总量;01ββ∧∧的符号和大小均符合经济理论和我国的实际情况。
3)对估计结果进行统计检验2r 检验:20.94r =,说明总离差平方和的94%被样本回归直线解释了,有6%未被解释,样本回归直线对样本点到拟合优度很高。
T 检验:给出显著水平0.05α=,查自由度v=19的t 分布表,得()0.02519 2.09t =,029.40 2.09t =>,1 5.91 2.09t =>,故回归系数均显著不为零,回归模型中应包含常数项,X2对Q 有显著影响.(3) 我国粮食产量Q (万吨)和土地灌溉面积X3(千公顷) 1)作散点图并估计模型 估计一元回归模型:013tt t Q X e γγ∧∧=++Dependent Variable: Q Method: Least Squares Date: 10/07/16 Time: 01:55 Sample: 1978 1998 Included observations: 21Variable Coefficient Std. Error t-Statistic Prob. C -49865.39 12638.40 -3.945545 0.0009 X31.9487000.2706347.2004980.0000R-squared 0.731817 Mean dependent var 40996.12 Adjusted R-squared 0.717702 S.D. dependent var 6071.868 S.E. of regression 3226.087 Akaike info criterion 19.08632 Sum squared resid 1.98E+08 Schwarz criterion 19.18580 Log likelihood -198.4064 Hannan-Quinn criter. 19.10791 F-statistic 51.84718 Durbin-Watson stat 0.304603 Prob(F-statistic) 0.000001即样本回归模型为:349865.39 1.9487t t Q X ∧=-+ 2)对估计结果作结构分析1 1.95γ∧=是样本回归方程的斜率,说明土地灌溉面积每增加1千公顷我国粮食产量就增加1.95万吨;049865.39γ∧=-是样本回归方程的截距,它表示不受化肥施用量影响的粮食总量;3)对估计结果进行统计检验2r 检验:20.73r =,说明总离差平方和的73%被样本回归直线解释了,有27%未被解释,样本回归直线对样本点到拟合优度较好。
