框架结构设计竖向荷载
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
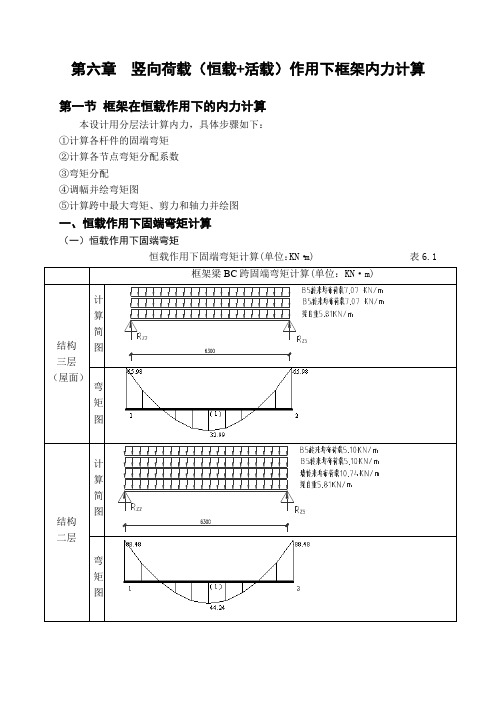
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
12.4多层框架结构在竖向荷载下的内力计算方法

12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
2.计算模型的确定 在计算简图中,框架节点多为刚接,柱子下端在基础顶面,也按刚接 考虑。杆件用轴线表示,梁柱的连接区用节点表示。等截面轴线取截面形 心位置,当上下柱截面尺寸不同时,则取上层柱形心线作为柱轴线。跨度 取柱轴线间的距离。计算简图中的柱高,对楼层取层高;对底层柱,现浇 楼板取基础顶面与二层楼板顶面之间的高度。 当各跨跨度不等但相差不超过10%时,可当作具有平静跨度的等跨框架。
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
4.荷载计算
作用在多、高层建筑结构上的荷载有竖向荷载和水平荷载。竖向 荷载包括恒载和楼(屋)面活荷载、雪荷载,水平荷载包括风荷载和 水平地震作用。 活荷载大小见《建筑结构荷载规范》GB50009-2012第5.1.1条。
12.4竖向荷载作用下的内力近似计算
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
由于计算时假定柱的远端为固定端,实际上除底层柱在基础处为固定 端外,其余各住的远端均有转角而非固定端。为减少由此引起的误差,除 底层柱外,其他各层柱的线刚度均乘以折减系数0.9,并取传递系数为1/3; 底层柱及梁的传递系数仍为1/2。 例12-2 用分层法计算例12-1框架的弯矩,并绘制弯矩图。
1转动刚度第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算2分配系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算3传递系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算4杆端弯矩第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算例121三跨二层钢筋混凝土框架各层框架梁所承受的竖向荷载设计值如图所示图中括号内数值为各杆件的相对线刚度
第四章 框架结构内力计算

4、计算和确定梁、柱弯矩分配系数。 按修正后的刚度计算各结点周围杆件的杆 端分配系数。 5、按力矩分配法计算单层梁、柱弯矩。 6、将每个单层框架的计算结果按相应部分迭 加起来便得到原框架的计算结果,即柱的弯矩 取相邻两个单元中同一柱对应弯矩之和,而梁 的弯矩直接采用。
四、计算例题
作业2
3.2 水平荷载下内力的近似计算—反弯点法
d
i 1
m
V pj
ij
4、柱端弯矩的确定 M j V jY j 柱下端弯矩 柱上端弯矩 M j V j (h j Yj )
5、梁端弯矩的确定 M ml (M mt M m1b ) 对于边柱 ibl 对于中柱
M ml ( M mt M m1b ) M mr ibl ibr ibr ( M mt M m1b ) ibl ibr
第3章 框架结构的内力和位移计算
3.1 竖向荷载下内力的近似计算—分层法 3.2 水平荷载下内力的近似计算—反弯点法 3.3 水平荷载下内力的近似计算—D值法 3.4 水平荷载作用下侧移的近似计算
3.1 竖向荷载下内力近似计算—分层法
一、竖向荷载 自重、活荷、雪荷载及施工检修荷载等。 二、分层法的基本假设 1、忽略侧移的影响; 2、忽略每层梁的竖向荷载对其它各层梁 的影响。 三、分层法计算要点 1、将N层框架划分成N个单层框架,柱 端假定为固端, 用力矩分配法计算。
三、柱的侧移刚度D 12ic D 2 h
—为柱侧移刚度修正系数,表示梁柱刚 度比对柱侧移刚度的影响。
四、剪力计算 有了D值后,与反弯点法类似,计算各柱分 配的剪力 Dij Vij V pj Dij 五、确定柱反弯点高度比 影响柱反弯点高度的主要因素是柱上下端的 约束条件。
框架结构竖向荷载作用下的内力计算
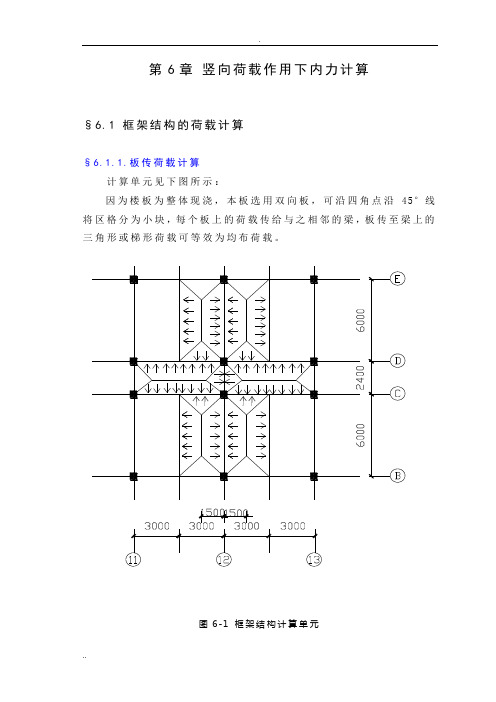
第6章竖向荷载作用下内力计算§6.1 框架结构的荷载计算§6.1.1.板传荷载计算计算单元见下图所示:因为楼板为整体现浇,本板选用双向板,可沿四角点沿45°线将区格分为小块,每个板上的荷载传给与之相邻的梁,板传至梁上的三角形或梯形荷载可等效为均布荷载。
图6-1 框架结构计算单元图6-2 框架结构计算单元等效荷载一.B ~C, (D ~E)轴间框架梁:屋面板传荷载:恒载:2226.09KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=17.128KN/m ⨯⨯+⨯活载:2222.0KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=5.625KN/m ⨯⨯⨯+⨯楼面板传荷载:恒载:2223.83KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=10.772KN/m ⨯⨯⨯+⨯活载:2222.0KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=5.625KN/m ⨯⨯⨯+⨯梁自重:3.95KN/mB ~C, (D ~E)轴间框架梁均布荷载为:屋 面 梁:恒载=梁自重+板传荷载=17.128 KN/m+3.95 KN/m=21.103 KN/m活载=板传荷载=5.625 KN/m楼面板传荷载:恒载=梁自重+板传荷载=3.95 KN/m+10.772 KN/m=14.747 KN/m活载=板传荷载=5.625 KN/m二. C ~D 轴间框架梁:屋面板传荷载:恒载:26.09KN/m 1.2m 5/82=9.135KN/m ⨯⨯⨯活载:22.0KN/m 1.5m 5/82=3KN/m ⨯⨯⨯楼面板传荷载:恒载:23.83KN/m 1.25/82=5.745KN/m ⨯⨯⨯活载:22.0KN/m 1.2m 5/82=3.75KN/m ⨯⨯⨯梁自重:3.95KN/mC ~D 轴间框架梁均布荷载为:屋 面 梁:恒载=梁自重+板传荷载=2.349 KN/m+9.135 KN/m=11.484 KN/m活载=板传荷载=3 KN/m楼面板传荷载:恒载=梁自重+板传荷载=2.349 KN/m+5.745KN/m=8.09KN/m活载=板传荷载=3.75 KN/m三.B 轴柱纵向集中荷载计算:顶层柱:女儿墙自重:(做法:墙高900㎜,100㎜的混凝土压顶)330.240.918/25/0.10.24m m kn m KN m m m ⨯⨯+⨯⨯+()1.220.240.5 5.806/m m m KN m ⨯+⨯=顶层柱恒载=女儿墙+梁自重+板传荷载=5.806/6 3.975/(60.6)KN m KN m m m ⨯+⨯-⨯()()2212 1.5/6 1.5/66/42 6.09/ 1.55/832123.247KN m m KN ⎡⎤-⨯+⨯⨯+⨯⨯⨯⨯=⎣⎦顶层柱活载=板传荷载=()()222.0/ 1.512 1.5/6 1.5/66/42KN m m ⎡⎤⨯⨯-⨯+⨯⨯+⎣⎦2.0/ 1.55/83219.688KN m m KN ⨯⨯⨯⨯=标准层柱恒载=墙自重+梁自重+板荷载=7.794/(60.6) 3.975/(60.6) 3.83/ 1.55/832KN m KN m KN m m ⨯-+⨯-+⨯⨯⨯⨯(2.332311.52)61/42 2.3325/61/42KN m ++⨯⨯⨯+⨯⨯⨯+()()223.83 1.512 1.5/6 1.5/66/42124.172m m KN ⎡⎤⨯⨯-⨯+⨯⨯=⎣⎦标准层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63 2.0 1.55/83219.688m m m m KN ⎡⎤⨯⨯-⨯+⨯+⨯⨯⨯⨯=⎣⎦基础顶面荷载=底层外纵墙自重+基础自重=9.738/(60.6) 2.5/(60.6)16.085KN m m m KN m m m KN ⨯-+⨯-=四.C 柱纵向集中力计算:顶层柱荷载=梁自重+板传梁荷载=3.975/(90.9) 2.349/(1.20.3) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯ 6.09/ 1.25/8 1.22(2.3323/11.52/)61/42KN m m KN m KN m m +⨯⨯⨯⨯++⨯⨯⨯154.318KN =顶层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63m m ⎡⎤⨯⨯-⨯+⨯+⎣⎦()()222.0 1.212 1.2/6 1.2/63 2.0 1.2m m m m ⎡⎤⨯⨯-⨯+⨯+⨯⎣⎦5/8 1.22 2.0 1.55/83239.272m m KN ⨯⨯⨯+⨯⨯⨯⨯=标准柱恒载=墙+梁自重+板传荷载=11.52/(30.6)15.12/(30.6)15.12/(30.6)KN m m KN m m KN m m ⨯-+⨯-+⨯-+2.349/(1.20.3)3.975/(60.6) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯+26.09/61/21/2 2.67/ 2.4/26 3.83/36200.173KN m m KN m m KN m m m KN ⨯⨯⨯+⨯⨯+⨯⨯=标准层活载=板传荷载=222.0/36 2.5/ 1.2654KN m m m KN m m m KN ⨯⨯+⨯⨯=基础顶面恒载=底层外纵墙自重+基础自重9.738/(60.6) 2.5/(60.6)66.085KN m m m KN m m m KN ⨯-+⨯-=(3).框架柱自重:柱自重: 底层:1.2×0.6m ×0.6m ×253/KN m ×4.55m=49.14KN其余柱:1.2×0.6m ×0.6m ×253/KN m ×3.6m=38.88KN§6.2恒荷载作用下框架的内力§6.2.1.恒荷载作用下框架的弯矩计算一.恒荷载作用下框架可按下面公式求得:21/12ab M ql =- (61)-21/12ba M ql = (62)-故:2771/1221.03663.09.B C M KN m =-⨯⨯=-7763.09.C B M KN m =2771/1211.4846 5.512.C D M KN m =-⨯⨯=-77 5.512.C D M KN m =2661/1214.747644.241.B C M KN m =-⨯⨯=-6644.241.C B M KN m =2661/128.096 3.883.C D M KN m =-⨯⨯=-66 3.883.D C M KN m =恒荷载作用下框架的受荷简图如图6-3所示:图6-3竖向受荷总图:注:1.图中各值的单位为KN2.图中数值均为标准值3.图中括号数值为活荷载图6-4:恒载作用下的受荷简图(2).根据梁,柱相对线刚度,算出各节点的弯矩分配系数ij μ:/()ij c b i i i μ=∑+∑ (63)-分配系数如图6-5 , 图6-6所示:图6-5 B 柱弯矩各层分配系数简图B 柱:底层:0.801/(0.8010.609 1.0)0.332i ++=下柱=1.0/(0.8010.609 1.0)0.415i ++=上柱=0.609/(0.8010.609 1.0)0.253i ++=左梁=标准层: 1.0/(0.609 1.0 1.0)0.383i ++=上柱=1.0/(0.609 1.0 1.0)0.383i ++=下柱=0.609/(0.609 1.0 1.0)0.234i ++=左梁=顶层: 1.0/(0.609 1.0)0.622i +=下柱=0.609/(0.609 1.0)0.622i +=左梁=图6-6 C 柱弯矩各层分配系数简图C 柱: 0.609/(0.609 1.00.2110.801)0.232i +++=右梁=1.0/(0.609 1.00.2110.801)0.382i +++=上柱= 0.801/(0.609 1.00.2110.801)0.306i +++=下柱=0.211/(0.609 1.00.2110.801)0.081i +++=左梁=标准层: 1.0/(0.609 1.00.2110.801)0.355i +++=下柱=1.0/(0.609 1.00.2110.801)0.355i +++=上柱=0.609/(0.609 1.00.2110.801)0.216i +++=右梁=0.211/(0.609 1.00.2110.801)0.074i +++=左梁=顶层: 1.0/(0.609 1.00.211)0.549i ++=下柱=0.211/(0.609 1.00.211)0.116i ++=左梁=0.609/(0.609 1.00.211)0.335i ++=右梁=三.恒荷载作用下的弯矩剪力计算,根据简图(6-4)梁:A M 0∑= 21/2.0A B B M M ql Q l ---=/1/2B A B Q M M l ql =--B M 0∑= 21/2.0A B A M M ql Q l -+-=/1/2A A B Q M M l ql =-+ (6-4)柱:C M 0∑= .0C D D M M Q h ---=()/D C D Q M M h =-+D M 0∑= .0C D C M M Q h ---=()/C C D Q M M h =-+ (6-5)四.恒荷载作用下的边跨框架的轴力计算,包括连梁传来的荷载及柱自重.7123.24721.1036/2186.556N KN =+⨯=67124.17214.7476/238.88393.849N N KN =++⨯+=56124.17214.7476/238.88601.142N N KN =++⨯+=45124.17214.7476/238.88808.435N N KN =++⨯+=34124.17214.7476/238.881015.728N N KN =++⨯+=23124.17214.7476/238.881223.021N N KN =++⨯+=12124.17214.7476/238.881382.487N N KN =++⨯+=恒荷载作用下的中跨框架的轴力计算:7154.31811.484 2.4/2168.099N KN =+⨯=67200.1738.09 2.4/238.88416.88N N KN =++⨯+=56200.1738.09 2.4/238.88665.621N N KN =++⨯+=45200.1738.09 2.4/238.88808.435N N KN =++⨯+=34200.1738.09 2.4/238.881015.728N N KN =++⨯+=23200.1738.09 2.4/238.881223.021N N KN =++⨯+=12200.1738.09 2.4/238.881382.487N N KN=++⨯+=图6-5 恒荷载作用下的计算简图五.弯矩分配及传递弯矩二次分配法比分层法作了更进一步的简化。
框架结构竖向荷载作用下的内力计算

框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的,在受到竖向荷载作用下,会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先,通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱,节点是构件之间的连接点,连接关系表示构件之间的刚性约束。
在竖向荷载作用下,框架结构的内力主要有两种情况:梁内力和柱内力。
1.梁内力计算:在竖向荷载作用下,梁会产生弯矩和剪力。
根据梁的基本理论,可以得出计算弯矩和剪力的公式。
-弯矩计算:弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义,弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时,弯矩的计算公式为M=w*l^2/8,其中w为荷载大小,l为梁的跨度。
-剪力计算:剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义,剪力V等于施加在梁上的力。
当梁需要承受重力荷载时,剪力的计算公式为V=w*l/2,其中w为荷载大小,l为梁的跨度。
2.柱内力计算:在竖向荷载作用下,柱会产生压力和拉力。
根据柱的基本理论,可以得出计算压力和拉力的公式。
-压力计算:压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理,压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时,压力的计算公式为P=∑w,其中w为荷载大小。
-拉力计算:拉力是由竖向荷载作用在柱上引起的。
和压力类似,拉力T等于施加在柱上的荷载之和。
在实际计算过程中,需要考虑梁和柱的截面形状和材料性质,以及节点和连接部位的刚性约束等因素。
同时,还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中,可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理,可以建立结构方程组,并通过求解方程组得到内力的值。
总结起来,框架结构竖向荷载作用下的内力计算是一个复杂的过程,需要考虑多个因素和使用多种方法。
竖向荷载计算(弯矩二次分配法)实例

05
结论
竖向荷载计算的重要性
确保结构安全
竖向荷载计算是结构设计中的重要环节,准确计 算竖向荷载对于保证结构安全至关重要。
提高结构性能
合理的竖向荷载计算有助于优化结构设计,提高 结构的承载能力、稳定性和抗震性能。
降低成本
竖向荷载计算的误差可能导致结构加固或重建, 准确计算可降低不必要的成本。
弯矩二次分配法的限制条件
01
假定楼板为刚性,不考虑楼板的变形和位移。
ቤተ መጻሕፍቲ ባይዱ02
仅适用于规则的结构,对于不规则的结构需要进行 特殊处理。
03
对于节点平衡条件,仅考虑节点左右两侧的平衡, 不考虑上下平衡。
弯矩二次分配法的优化建议
01 考虑楼板的变形和位移,采用有限元法或其他数 值方法进行计算。
02 对于不规则的结构,采用特殊处理方法,如引入 弹性支座或采用有限元模型进行模拟。
弯矩二次分配法的优势与局限性
优势
局限性
弯矩二次分配法计算过程较为复杂,需要耗费较多 时间和计算资源,对于大型复杂结构可能不适用。
弯矩二次分配法能够考虑各杆件之间的相互 作用和影响,计算结果相对准确,适用于多 种结构形式。
适用范围
弯矩二次分配法适用于梁、柱等杆系结构, 但对于板、壳等连续介质,需要采用其他方 法进行计算。
03
竖向荷载计算实例
实例一:简单框架结构
总结词
简单框架结构适用于跨度较小、层数较少的建筑,其竖向荷载计算相对简单。
详细描述
简单框架结构通常由梁和柱组成,竖向荷载通过梁传递至柱,再由柱传递至基 础。弯矩二次分配法在此类结构中应用广泛,能够快速准确地计算出各构件的 弯矩值。
第七章 竖向荷载作用下框架内力计算
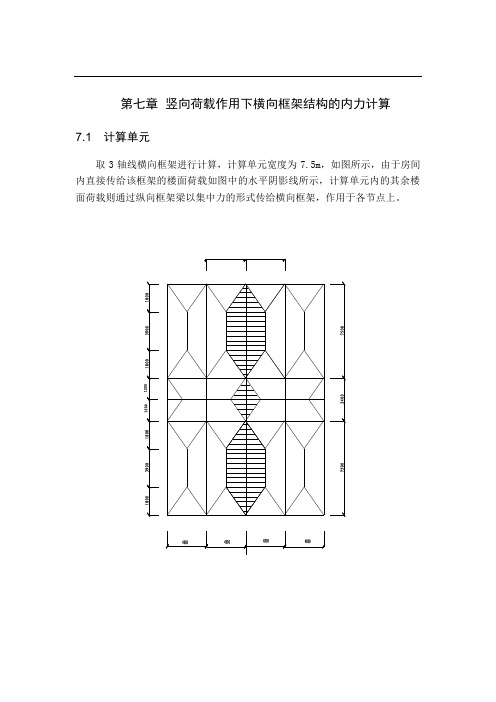
第七章 竖向荷载作用下横向框架结构的内力计算7.1 计算单元取3轴线横向框架进行计算,计算单元宽度为7.5m ,如图所示,由于房间内直接传给该框架的楼面荷载如图中的水平阴影线所示,计算单元内的其余楼面荷载则通过纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
7.2 荷载计算节点集中荷载1P : 边纵梁传来:(a)屋面自重(三角形部分):N k 78.56298.423.3.26.3=⨯⨯⨯(b)边纵梁自重: 5.709⨯6.0=43.73kN 女儿墙自重: kN 87.330.6312.3=⨯合计: 1P = 154.32kN节点集中荷载2P :纵梁传来(a )屋面自重(三角形部分):KN 12.27298.40.326.3=⨯⨯⨯(b )走道屋面板自重0.5⨯(6.0+6.0-3)⨯1.5⨯4.98=58.79KN纵梁自重: 5.709⨯6.0=43.73kN合计: 2P = 170.55kN对于1~4层,计算的方法基本与第五层相同,计算过程如下: 1 5.709/q kN m =1q '=3.46/kN/mm KN q /99.103.333.32=⨯= m KN q /99.74.233.32=⨯=节点集中荷载1P :纵梁自重: 5.709⨯6.0=43.73kN外墙自重:()88.76KN 68.37.03.3225.00.6=⨯-⨯⨯-)( 来纵梁传楼面自重(三角形部分): (0.5 3.60.5 3.6 3.33)221.58kN ⨯⨯⨯⨯⨯= 扣窗面积墙重加窗重: 2 2.4 2.0 3.682 2.1631.01kN -⨯⨯⨯+⨯=-合计: 174.24kN节点集中荷载2P :纵梁自重: 5.709⨯7.2=41.10kN 内墙自重: 71.50kN 纵梁传来(a)楼面自重(三角形部分):()KN5.0=⨯0.3⨯⨯5.0⨯⨯66.233.3780.3(b)走道楼面板自重(梯形部分)()KN⨯5.0=⨯5.7⨯+-48.9333.30.38.15.7扣窗面积墙重加窗重: 2.412 3.6820.4816.10kN-⨯⨯⨯+⨯=-合计: 152.58kN 7.2.2活荷载计算:活荷载作用下各层框架梁上的荷载分布如图:合计: 7.99KNP:节点集中荷载2屋面活载(三角形部分):2⨯(0.5⨯3.0⨯0.5⨯3.0⨯0.5)=2.72KN走道传来屋面荷载(梯形部分): ()KN 05.45.05.14.20.60.621=⨯⨯-+合计: 12.04KN 对于1~4层,m KN /6.60.30.2q 2=⨯= m KN q /64.25.2'2=⨯= 节点集中荷载1P : 楼面活载(三角形部分):2⨯(0.5⨯3.30.5⨯3.3⨯2)=10.89KN合计: 31.97KN中节点集中荷载2P : 楼面活载(三角形部分):2⨯(0.5⨯3.30.5⨯3.3⨯2)=10.89KN走道传来屋面荷载(梯形部分):()KN 25.205.25.14.20.60.621=⨯⨯-+ 纵梁传来的屋面活载(梯形部分):()KN 08.2128.10.35.75.75.0=⨯⨯-+⨯ 合计: 52.22KN7.2.3.屋面雪荷载标准值:同理,在屋面雪荷载作用下KN/m 16.10.335.0q 2=⨯= m KN q /84.04.235.0'2=⨯=节点集中荷载1P : 屋面雪载(三角形部分):2⨯(0.5⨯3.3⨯0.5⨯3.3⨯0.35)=2.08KN纵梁传来的屋面雪载(梯形部分)()KN 69.335.08.16.35.75.75.0=⨯⨯-+⨯ 合计: 5.77KN中节点集中荷载2P : 屋面雪载(三角形部分):2⨯(0.5⨯3.3⨯0.5⨯3.3⨯0.35)=2.08KN走道传来屋面雪载(梯形部分): ()KN 835.235.05.14.25.75.721=⨯⨯-+纵梁传来的屋面雪载(梯形部分): 3.97KN 合计: 8.72KN 1~4层,雪荷载作用下的节点集中力同屋面活荷载作用下的。
毕业设计指导书(框架结构设计)-内力计算及组合

计算杆件固端弯矩时应带符号,杆端弯矩一律以顺时针方向为正,如图3-6。
图 3-6 杆端及节点弯矩正方向
1)横梁固端弯矩:
(1)顶层横梁
自重作用:
板传来的恒载作用:
(2)二~四层横梁
自重作用:
板传来的恒载作用:
2)纵梁引起柱端附加弯矩:(本例中边框架纵梁偏向外侧,中框架纵梁偏向内侧)
顶层外纵梁
相交于同一点的多个杆件中的某一杆件,其在该节点的弯矩分配系数的计算过程为:
(1)确定各杆件在该节点的转动刚度
杆件的转动刚度与杆件远端的约束形式有关,如图3-1:
(a)杆件在节点A处的转动刚度
(b)某节点各杆件弯矩分配系数
图 3-1 A节点弯矩分配系数(图中 )
(2)计算弯矩分配系数μ
(3)相交于一点杆件间的弯矩分配
(3)求某柱柱顶左侧及柱底右侧受拉最大弯矩——该柱右侧跨的上、下邻层横梁布置活荷载,然后隔跨布置,其它层按同跨隔层布置(图3-4c);
当活荷载作用相对较小时,常先按满布活荷载计算内力,然后对计算内力进行调整的近似简化法,调整系数:跨中弯矩1.1~1.2,支座弯矩1.0。
(a)(b) (c)
图 3-4 竖向活荷载最不利布置
∑Mik/l
V1/A=gl/2+u-∑Mik/l
M=gl/2*l/4+u*1.05-MAB-V1/A*l/2
4
21.9
4.08
2.25
6
12.24
41.06
-30.54
2.55
50.75
-60.24
3
16.61
4.08
2.25
6
12.24
31.14
结构设计:框架结构设计中竖向荷载有哪些最不利布置?[工程类精品文档]
![结构设计:框架结构设计中竖向荷载有哪些最不利布置?[工程类精品文档]](https://img.taocdn.com/s3/m/2e0cc27525c52cc58bd6be8b.png)
结构设计:框架结构设计中竖向荷载有哪些最不利布置?[工程类精品文档]本文内容极具参考价值,如若有用,请打赏支持,谢谢!大于大于大于(1)分跨计算组合法将活荷载逐层逐跨单独地作用在结构上,分别计算出整个结构的内力,根据不同的构件、不同的截面、不同的内力种类,组合出最不利内力。
共有(跨数X层数)种不同的活荷载布置方式。
为减少计算工作量,可不考虑屋面活荷载的最不利分布而按满布考虑。
(2)最不利荷载位置法为求某一指定截面的最不利内力,可以根据影响线方法,直接确定产生此最不利内力的活荷载布置。
梁端最大负弯矩或柱端最大弯矩的活荷载最不利布置,亦可用上述方法得到。
柱最大轴向力的活荷载最不利布置,是在该柱以上的各层中,与该柱相邻的梁跨内都布满活荷载。
(3)分层组合法(1)对于梁,只考虑本层活荷载的不利布置,而不考虑其他层活荷载的影响。
因此,其布置方法和连续梁的活荷载最不利布置方法相同。
(2)对于柱端弯矩,只考虑柱相邻上下层的活荷载的影响,而不考虑其他层活荷载的影响。
(3)对于柱最大轴力,则考虑在该层以上所有层中与该柱相邻的梁上满布活荷载的情况,但对于与柱不相邻的上层活荷载,仅考虑其轴向力的传递而不考虑其弯矩的作用。
(4)满布荷载法当活荷载产生的内力远小于恒荷载及水平力所产生的内力时,可不考虑活荷载的最不利布置,而把活荷载同时作用于所有的框架梁上,这样求得的内力在支座处与按最不利荷载位置法求得的内力极为相近,可直接进行内力组合。
但求得的梁的跨中弯矩却比最不利荷载位置法的计算结果要小,因此对梁跨中弯矩应乘以1.1~1.2的系数予以增大。
结语:借用拿破仑的一句名言:播下一个行动,你将收获一种习惯;播下一种习惯,你将收获一种性格;播下一种性格,你将收获一种命运。
事实表明,习惯左右了成败,习惯改变人的一生。
在现实生活中,大多数的人,对学习很难做到学而不厌,学习不是一朝一夕的事,需要坚持。
希望大家坚持到底,现在需要沉淀下来,相信将来会有更多更大的发展前景。
混凝土板框架结构设计标准

混凝土板框架结构设计标准一、前言混凝土板框架结构是一种常见的建筑结构形式,其具有承载能力强、耐久性好、施工方便等优点,被广泛应用于居住建筑、商业建筑、公共建筑等领域。
为保障混凝土板框架结构的安全可靠性,制定一套全面的具体的详细的标准是必要的。
本文将从结构设计的角度出发,对混凝土板框架结构的设计标准进行详细阐述,旨在为建筑设计师和施工人员提供指导。
二、设计载荷混凝土板框架结构的设计应根据其承受的外部荷载和内部荷载确定结构的尺寸、形式和材料。
外部荷载包括自重、活荷载和风荷载等,内部荷载包括水平荷载、竖向荷载和温度荷载等。
1、自重混凝土板框架结构的自重应按国家规定的密度计算,一般取24kN/m³。
混凝土板框架结构的活荷载应根据建筑用途和规模确定,一般参考国家规范《建筑荷载规范》。
3、风荷载混凝土板框架结构的风荷载应根据国家规范《建筑结构荷载标准》计算,考虑风速、地形、建筑高度等因素。
对于超高层建筑,应进行风洞试验,确定设计风速和风荷载。
4、水平荷载混凝土板框架结构在地震等自然灾害中承受的水平荷载应根据国家规范《建筑抗震设计规范》计算确定。
对于地震烈度较高的地区,应根据当地烈度等级确定设计抗震烈度。
5、竖向荷载混凝土板框架结构的竖向荷载包括建筑本身的重量、设备荷载和人员荷载等。
建筑本身的重量应按照规范计算,设备荷载和人员荷载应根据实际情况确定。
混凝土板框架结构在温度变化时会发生热胀冷缩,产生一定的荷载。
设计时应根据规范计算。
三、结构设计混凝土板框架结构的设计应满足以下要求:1、满足强度和稳定性要求混凝土板框架结构应满足强度和稳定性要求,确保在荷载作用下不发生破坏和失稳。
设计时应采用合理的截面尺寸和钢筋配筋,确保结构的承载能力和变形能力。
2、满足刚度和振动要求混凝土板框架结构应满足刚度和振动要求,确保在使用过程中不产生过大的变形和振动。
设计时应合理选择刚度系数和振动频率,采用减震措施,如阻尼器、减震器等。
第六章-框架在竖向荷载作用下的内力分析
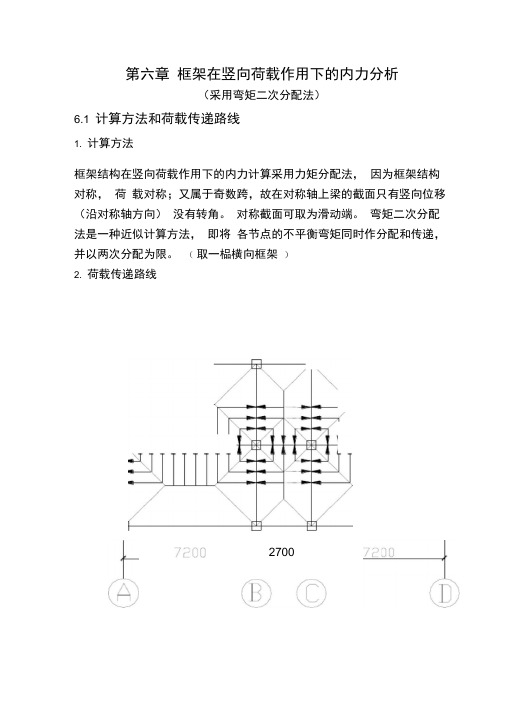
第六章框架在竖向荷载作用下的内力分析(采用弯矩二次分配法)6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法,因为框架结构对称,荷载对称;又属于奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向)没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法,即将各节点的不平衡弯矩同时作分配和传递,并以两次分配为限。
(取一榀横向框架)2. 荷载传递路线2700对于边跨板,为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板,为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载: 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载:0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载: 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载: 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重: 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁:恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载: 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载:0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载: 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载: 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重: 3.9kN/mB-C 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁:恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正,反之为负。
框架结构设计计算步骤(参考)

框架结构毕业设计内力计算步骤(仅供参考,配筋计算不在内)一.进行结构方案比较,选定结构方案,进行结构布置1. 结构选型:在建筑设计的基础上,从抗震要求方面、房屋总高度、层数、柱最大间距等,说明为何选用框架结构,而不采用框剪结构、内框架结构、剪力墙结构以及砖混结构。
2. 楼盖结构方案比较:确定承重方案,进行结构布置,比较选用现浇板及预制板的不同点,画出三种以上结构平面布置草图,比较后全组共同确定一种方案,画出结构平面布置图,进行编号对框架负载面积基本相同的编同一个号:“KJ-X ”;连续梁用“L-X ”表示;现浇板用“B-X ”表示;构造柱用“GZ-X ”表示;预制板放在选板后再补画,其他见结构参考图。
二.初步选择梁柱截面尺寸及材料强度等级1. 确定梁柱剪力墙截面尺寸 (1)梁1)框架梁:b b b h b l h )31~21()121~81(==按抗震要求:42120041≥≥≥≥bnc b b b b h l b b mmb h b 荷载大(一般指活荷大或负荷面积大),取大值。
2)连续梁:b b b h b l h )31~21()181~121(==另外,确定梁宽时,尽量与填充墙厚度相同,可使室内不见梁棱角,纵向框架梁还要考虑下皮最好与窗上口标高相同,以免再设过梁。
(2)现浇板及预制板现浇板厚:工业建筑:;80mm h ≥ 连续单向板:40l h ≥;双向板:50l h ≥; (3)柱截面尺寸:;300mm b c ≥柱净高与截面高度之比4≥cnh H ; 截面积cc f NA )55.0~45.0(≥;式中N 为首层柱根估算轴力设计值,计算方法如下:对于中柱与边柱,分别找出负荷面积最大的柱,算出一层楼面的面荷载,假设屋面荷载同楼面荷载,用此荷载乘以层数再乘以负荷面积,即为所求N 。
柱自重略去不计,各层Ac 宜相同。
2. 确定材料强度等级钢筋:按抗震要求,确定纵筋与箍筋级别;混凝土:按抗震要求,并考虑现浇板砼质量,经济确定砼强度等级,考虑首层较高,变形较大,可适当提高砼强度等级。
竖向荷载作用下框架结构的内力计算
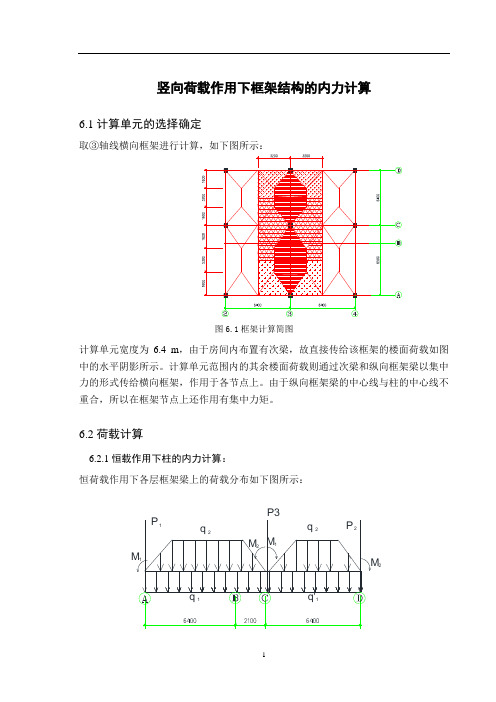
竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算,如下图所示:图6.1框架计算简图计算单元宽度为6.4 m,由于房间内布置有次梁,故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,所以在框架节点上还作用有集中力矩。
6.2荷载计算6.2.1恒载作用下柱的内力计算:恒荷载作用下各层框架梁上的荷载分布如下图所示:2图6.2恒荷载作用下各层框架梁上的荷载分布图(1)、对于顶层屋面,q1、q1'代表横梁自重,为均布荷载形式。
q1=0.3×0.75×25=5.625kN/mq1'=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。
q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载,它包括主梁自重、次梁自重、楼板重等重力荷载,计算如下:P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×(0.6 -0.3)/2=16.23kN·mM2=P2e2=147.23×(0.6 -0.3)/2=14.31kN·m(2)、对于3层,包括梁自重和其上横墙自重,为均布荷载,其它荷载的计算方法同第顶层。
竖向荷载作用下框架荷载计算方法

竖向荷载作用下框架荷载计算方法
框架结构是一种常见的建筑结构形式,其承受荷载的能力是建筑物安全稳定的重要保障。
在框架结构中,竖向荷载是一种常见的荷载形式,因此,正确计算竖向荷载对框架结构的影响是非常重要的。
竖向荷载是指垂直于地面方向的荷载,包括自重、人员活动荷载、家具设备荷载、风荷载、雪荷载等。
在框架结构中,竖向荷载主要通过柱子传递到地基,因此,柱子的承载能力是决定框架结构承受竖向荷载能力的关键因素。
框架结构的竖向荷载计算方法主要包括以下几个步骤:
1. 确定荷载类型和荷载大小:根据建筑物的用途和设计要求,确定竖向荷载的类型和大小。
不同类型的荷载对框架结构的影响不同,因此需要根据实际情况进行合理的选择。
2. 确定荷载作用位置:竖向荷载的作用位置对框架结构的影响也非常重要。
在计算荷载大小时,需要考虑荷载作用位置对柱子的影响,以确定柱子的承载能力。
3. 计算柱子的承载能力:柱子的承载能力是框架结构承受竖向荷载的关键因素。
在计算柱子的承载能力时,需要考虑柱子的截面形状、材料强度、长度等因素。
4. 计算框架结构的稳定性:在承受竖向荷载时,框架结构的稳定性
也非常重要。
需要通过计算框架结构的稳定性来确定其承受竖向荷载的能力。
正确计算竖向荷载对框架结构的影响是保障建筑物安全稳定的重要保障。
在实际工程中,需要根据实际情况进行合理的选择和计算,以确保框架结构的安全可靠。
计算竖向荷载作用下的框架结构的方法

计算竖向荷载作用下的框架结构的方法框架结构是一种常见的建筑结构,它由柱子和梁组成。
竖向荷载是作用在结构的垂直方向上的力,包括自重、楼层荷载、雨水荷载、雪荷载等。
为了确保框架结构的安全性和承载能力,需要进行竖向荷载的计算和分析。
在计算竖向荷载作用下的框架结构时,一般采用结构分析的方法,包括静力分析和动力分析。
静力分析是指在结构不考虑振动和位移的情况下进行的力学分析。
它主要采用受力平衡方程来计算结构的内力和变形。
对框架结构来说,可以采用刚度法、位移法和力法等方法进行分析。
1. 刚度法:刚度法是一种常用的静力分析方法。
它基于结构刚度和受力平衡原理,将结构划分为单元,通过计算单元的刚度矩阵和节点位移来求解结构的内力和变形。
刚度法适用于简单框架结构的分析,通过构建刚度方程组,可以求解出结构的内力和位移。
2. 位移法:位移法是一种将结构的位移作为主要未知量的静力分析方法。
它基于受力平衡原理和位移相容条件,将结构划分为单元,在每个单元内根据位移的连续性和力的平衡关系建立方程。
通过求解位移方程组,可以得到结构的内力和位移。
3. 力法:力法是一种以力作为主要未知量的静力分析方法。
它基于受力平衡原理和材料力学性质,通过构建力的平衡方程组和力的变形关系式,求解出结构的内力和位移。
力法适用于结构相对复杂,难以直接建立刚度方程的情况。
动力分析是指考虑结构的振动和变形对受力和稳定性的影响进行分析。
在竖向荷载作用下的框架结构中,垂直地震荷载是最常见且重要的动力荷载。
动力分析一般分为静态分析和动态分析。
1. 静态分析:静态分析是指在地震作用下无需考虑结构的动力响应,主要考虑的是结构的受力和变形。
通过采用静态等效荷载法,将地震荷载转化为与之等效的静态荷载进行分析。
静态分析适用于低层次、简单结构,不涉及结构的动力特性。
2. 动态分析:动态分析是指考虑结构的动力响应,对地震荷载进行全面分析。
动态分析可以细分为线性动力分析和非线性动力分析。
竖向荷载作用下框架结构的内力计算计算书3:正文6-11章

第6章竖向荷载作用下框架结构的内力计算6.1计算单元的确定取7轴线横向框架进行计算,计算单元宽度为2.75m,如图6.1所示。
传给该框架的楼面荷载如图中的水平阴影线所示,计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架的中心线与柱的中心线不重合,因此在框架节点上还作用有集中力矩。
图6.1 计算单元6.2 竖向荷载计算6.2.1恒荷计算1.1-5层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1kN/m梁DE=2.1kN/m挑梁=0.525kN/m板传递给梁的梯形及三角形荷载:板AB(左)=3.742kN/m×1.35m=5.05kN/m板AB(右)=3.742kN/m×1.5m=5.61kN/m板BD(左)=3.742kN/m×1.95m=7.29kN/m板BD(右)=3.742kN/m×2.1m=7.85kN/m板DE(左)=3.742kN/m×1.35m=5.05kN/m板DE(右)=3.742kN/m×1.4m=5.24kN/m悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零墙自重:墙AB =2.12×2.4=5.09kN/m墙BD =2.12×2.4=5.09kN/m墙DE =2.12×2.4=5.09kN/m墙悬挑=2.12×2.6=5.51kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重+墙自重柱的集中力:A 3.740.50.5 2.71.350.531.5 2.850.525 2.375 2.6 2.8526.78kNP=⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++B 3.740.50.5 2.7 1.350.53 1.5 2.850.5250.5 3.743.150.750.50.5 1.95 1.950.5 2.1 3.9 2.12 2.6 2.8538.31k NP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.743.150.750.50.5 1.951.950.5 2.1 3.5 2.12 2.6 2.7536.31kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.52.375 2.6 2.8532.8kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++E 0.5 3.740.65 5.5 2.750.525 2.375110.5kN P -=⨯⨯⨯⨯+⨯=+柱所受集中力产生的弯矩:A 26.78(0.450.2)/2 3.35kN m M =⨯-=⋅B 0kN m M =⋅D 36.31(0.450.2)/2 4.45kN m M =⨯-=⋅E 32.8(0.450.2)/2 4.1kN m M =⨯-=⋅ 2.6层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1 kN/m 梁DE=2.1kN/m挑梁=0.525 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=3.742kN/m ×1.35m=5.05kN/m 板AB (右)=3.742kN/m ×1.5m=5.61kN/m 板BD (左)=3.742kN/m ×1.95m=7.29kN/m 板BD (右)=3.742kN/m ×2.1m=7.85kN/m 板DE (左)=3.742kN/m ×1.35m=5.05kN/m 板DE (右)=3.742kN/m ×1.4m=5.24kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零 墙自重: 墙AB =2.12×1.925=4.081kN/m墙BD =2.12×3.36=7.12kN/m 墙DE =2.12×1.725=3.657kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重 柱的集中力 A 3.740.50.5 2.71.350.531.5 2.850.525 2.3750.6 2.8513.17kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++ B 3.740.50.5 2.71.350.531.5 2.850.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.922.6kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.521.15kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.5 2.375 0.6 2.8519.26 kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++-E 0.5 3.740.65 5.5 2.750.5258.13kN P =⨯⨯⨯⨯=+柱所受集中力产生的弯矩:A 13.17(0.450.2)/2 1.65kN m M =⨯-=⋅B 0kN m M =⋅D 21.15(0.450.2)/2 2.64kN m M =⨯-=⋅E 19.26(0.450.2)/2 2.41kN m M =⨯-=⋅ 3.顶层荷载计算:梁自重:梁AB=2.35 kN/m 梁BD=2.35 kN/m 梁DE=2.35 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=5.192kN/m ×1.35m=7.01kN/m 板AB (右)=5.192kN/m ×1.5m=7.79kN/m 板BD (左)= 5.192kN/m ×1.95m=7.29kN/m 板BD (右)= 5.192kN/m ×2.1m=10.9kN/m 板DE (左)= 5.192kN/m ×1.35m=7.01kN/m 板DE (右)= 5.192kN/m ×1.4m=7.27kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零柱的集中力: A 5.190.50.5 2.71.350.531.5 2.850.5251.1212.24kN P =⨯⨯⨯⨯+⨯⨯⨯⨯=()+ B 5.190.50.5 2.7 1.350.53 1.5 2.850.525 1.120.55.19 3.15 0.750.50.51.951.950.5 2.1 3.915.83kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 5.190.50.5 2.71.350.5 2.81.4 2.750.5251.120.5 5.19 3.150.750.50.51.951.950.5 2.1 3.528.97kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 5.190.50.5 2.7 1.350.5 2.8 1.49.82k NP =⨯⨯⨯⨯+⨯⨯=()柱所受集中力产生的弯矩:A 12.24(0.450.2)/2 1.53kN m M =⨯-=⋅B 0kN m M =⋅ D 28.97(0.450.2)/2 3.62kN m M =⨯-=⋅ E 9.82(0.450.2)/2 1.23kN m M =⨯-=⋅6.2.2 活荷载计算活荷载作用下各层框架梁上活载为板传递给梁的荷载。
承受竖向荷载的框架结构模型设计

并 进行 相关 计算 。
1 结 构 选 型 及 设 计
结构 模型选 择 框架 支撑体 系。 框 架结 构是 一种 最
常见 的结 构形 式 。 其设计 简单 、 施 工方便 。 在 多层 建 筑
及 机械 中运用 较 多 。框 架 结 构 既能 承 受竖 向荷 载作 用, 又 能 承受 水平 载 荷 作用 , 可有 效 减 少地 震 造 成 的 人员 伤亡 和经 济损 失 。从 结 构体 系来说 。 大 多数 中小 学教 学楼 都使用 框 架结构 。在对结 构平 面选 型 时 . 结 构在 两个 方 向的 刚度应 尽量 相等 , 不 能相差 过 大 。现
承受竖 向荷载 的框 架结构模型设计
孙长青 , 张 凯, 肖 楠, 刘 劲 涛
( 沈 阳 工程 学院 机 械 工程 系 , 沈阳 1 1 0 0 3 6 )
摘要 : 充 分 利 用 纸 张 的抗 拉 强 度 , 采 用 框 架 和 中心 支 撑 体 系 , 进 行 承 受 竖 向荷 载 的 框 架 结 构 模 型 结 构 设 计 和 有 限 元 计 算 , 锻 炼 学 生 的动 手 能 力 和 创 新 能 力 , 为高校的教学改革( 教学体系 、 教 学 内容 、 教 学方 法 和教 学 手 段 等 ) 提 供参 考 。
基金项 目: 沈 阳 工程 学 院教 育教 学 研 究 项 目( Y1 2 0 9 )
作者 简介 : 孙长青( 1 9 7 7 一) , 男, 博士 , 讲师 , 从 事断裂力 学、 机
械 强 度 和 高温 合 金 材料 的科 研 及 教 学工 作 。
试验 数 据表 明 :白乳胶 粘 接 面 的抗 剪 强度 远 远
张 的抗 拉 强度优 势 。结构 采用 框架 支撑 结构 , 主要构 件 包括 框架 柱 和柔性 支撑 。框 架柱 与地 基相 连 , 承受 结构 的重 力荷 载 ( 见图 1 ) 。 柔 性支 撑体 系可 保证 结构 的整体 性 , 并适 当施 加预应 力 以增 强结构 刚度 。根据
多层和高层框架结构设计-竖向荷载作用

2/5/2020
6
3.竖向荷载作用下的内力计算方法
(1)分层法 ①基本假定
忽略竖向荷载作用下框架结构的侧移; 每层梁上的荷载只在本层梁及与其相连的上、
下层柱产生内力,不在其他层梁和其他层柱 上产生内力。 应当指出,上述假定中所指的内力不包 括柱轴力,因为某层梁上的荷载对下部 各层柱的轴力均有较大影响,不能忽略。
8.89
kN m
M
F FE
3.4 5.62 12
kN m
8.89
kN m
A
2/5/2020
H
I
3.8 kN/m
3.4 kN/m
E
F
B 7500
C 5600
顶计 层算
各 节 点 弯 矩 :
下柱 右梁 0.332 0.668
G -13.13
4.36 8.77
-1.25 0.41 0.84 4.77 -4.77
3.竖向荷载作用下的内力计算方法 • 弯矩二次分配法
基本假定 (1) 不考虑框架结构的侧移对其内力的影响; (2) 每层梁上的荷载仅对本层梁及其上、下柱的 内力产生影响,对其它各层梁、柱内力的影 响可忽略不计。 上述假定中所指的内力同样不包括柱轴力。
2/5/2020
3.竖向荷载作用下的内力计算方法 • 弯矩二次分配法
-1.66
1.43 0.23 0.77 -0.77
E -0.48
F -0.26
29
1.20 G
底计 层算
各 节 点 弯 矩 :
上柱 下柱 右梁
0.186 0.348 0.466
D
-17.81
3.31 6.20 8.30 -1.53
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
框架结构设计
④ 内力分析
E. 内力计算
a. 竖向荷载作用下 f) 弯矩迭代法
节点固端弯矩之和 远端弯矩
M jk
jk
M
F j
Mkj
( j)
✓ 计算步骤
近端弯矩
(4) 计算各杆件近端弯矩,记在相应的杆端处;
(5) 循环若干轮直至达到要求的精度为止;
(6) 计算得到每一杆件的最终弯矩值。
M jk
-7.32 7.32 7.32 -2.33 -2.12 -0.075 -1.77 -2.18 -0.37
循
2.35
-0.72
-0.38
环 迭
1.70 1.64
-0.101
-0.62 -0.33
-0.067
-0.37 -0.42
-0.049
-0.152 -0.204 -0.351
-0.229
代 计 算
-17.81 -0.170 2.76
-17.81
3.72 3.86
17.81 8.92
-0.76 -1.41
-0.077
-0.38
-8.89 8.89
-1.02 -2.99 -1.90 -2.63
8.89 -0.100
-0.85
2.87
-0.72
-0.75
M jk
jk
M
F j
Mkj
( j)
11
-2.33 -2.12 -0.075 -1.77 -2.18 -0.37 -1.65 -2.25 -0.38 -0.32 -1.62 -2.29 -0.40 -0.32
环 迭
1.70 2.25 1.64
-0.101
-0.66 -0.62 -0.33
-0.067
-0.40 -0.37 -0.42
-0.049
4400
3600
2.8 kN/m
G
(7.63) H
(4.21) (4.21)
3.8 kN/m
I (10.21)
(1.79)
3.4 kN/m
D
(9.53) E (12.77) F
(7.11) (4.84)
(3.64)
A
B
C
7500
5600 4
框架结构设计
计算节点弯矩分配系数
节点 G:
GH
0.5 7.63 7.63 4.21
5
3.2 框架结构设计
节点 H:
HG
0.5 7.63 7.63 4.2110.21
0.173
G
(7.63) H
(4.21) (4.21)
I (10.21)
(1.79)
HE
0.5 4.21 7.63 4.2110.21
0.095
D
(9.53) E
HI
0.510.21 7.63 4.2110.21
B
C
8
框架结构设计
节点 F:
G
(7.63) H
FE
0.5 12.77 1.79 12.77 3.64
0.351
(4.21)
(4.21)
I (10.21)
(1.79)
FI
0.51.79 1.79 12.77 3.64
0.049
D
(9.53) E
(7.11)
FC
0.5 3.64 1.79 12.77 3.64
-0.152 -0.204 -0.351
-0.229
代 计 算
-17.81 -0.170 2.76
-17.81
3.72 3.86 3.90
17.81 8.92
-0.76 -1.41
-0.077
-1.49 -0.38
-8.89 8.89
-1.02 -2.99 -1.90 -2.63 -2.00 -2.31
框架结构设计
-0.173 -0.232 -0.425
-0.322
循
-13.13
-13.13 4.23
-0.178 4.26
2.34 4.10
1.72 2.35 4.07
1.72 2.27
13.13 5.81 -7.32 7.32 7.32
-1.74 -1.32
-1.23 -1.20
-0.095
-0.95 -0.72 -0.66 -0.68 -0.66
0.100
A
(4.84) B
(12.77) F梁固端弯矩(同前例)
10
框架结构设计
-0.173 -0.232 -0.425
-0.322
-13.13
-13.13 4.23
-0.178 2.34
4.26
13.13 5.81
-1.74 -1.32
-0.095 -0.95
框架结构设计
④ 内力分析
E. 内力计算
a. 竖向荷载作用下 f) 弯矩迭代法
✓ 计算步骤
' jk
1 2
i jk i jk
( j)
( j)
' jk
1 2
(1) 绘出结构计算简图,在各节点上绘两方框;
(2) 计算节点各杆件的弯矩分配系数,沿杆件方 向记在外框的内边缘;
(3) 计算固端弯矩,将各节点固端弯矩之和写在 内框中;
(1.79)
EH
9.53
0.5 4.21 4.2112.77
4.84
0.067
D
(9.53) E
EF
9.53
0.512.77 4.2112.77
4.84
0.204
(7.11)
(4.84)
(12.77) F (3.64)
A
EB
9.53
0.5 4.84 4.21 12.77
4.84
0.077
DA
0.5 7.11 4.21 9.53 7.11
0.170
D
(9.53) E
(7.11) (4.84)
A
B
(12.77) F (3.64) C
7
框架结构设计
节点 E:
G
ED
9.53
0.5 9.53 4.2112.77
4.84
0.152
(7.63) H (4.21) (4.21)
I (10.21)
0.322
G
(7.63) H
(4.21) (4.21)
I (10.21)
(1.79)
GD
0.5 4.21 7.63 4.21
0.178
节点 I:
IH
0.510.21 10.211.79
0.425
IF
0.51.79 10.211.79
0.075
D
(9.53) E
(7.11) (4.84)
A
B
(12.77) F (3.64) C
0.232
(7.11) A
(4.84) B
(12.77) F (3.64) C
6
框架结构设计
节点 D:
DG
0.5 4.21 4.21 9.53 7.11
0.101
G
(7.63) H
(4.21) (4.21)
I (10.21)
(1.79)
DE
0.5 9.53 4.21 9.53 7.11
0.229
8.89 -0.100
M
F jk
2Mjk
Mkj
2
框架结构设计
远端弯矩
k
l
j
n
m
M jk
jk
M
F j
Mkj
( j)
近端弯矩
对节点 j 而言,j 端为其近端, k, l, m, n 端为 其远端。
3
框架结构设计
④ 内力分析
E. 内力计算
a. 竖向荷载作用下 g) 弯矩迭代法 ✓ 计算例题
右图括号中为梁、
柱线刚度的相对值
