《电路分析基础》_第4章
《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出,P2=6W吸收,P3=16W吸收,P4=-lOW发出,PS=-7W发出,PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开:UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合:12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。
电路分析基础第四章(李瀚荪)

一、陈述 对任意含源单口网络N,都可以用一个电压源 与一个电阻相串联来等效。 R0 i i + + 即 + 等效 u N u u oc _ _ _
电压源的电压等于该网络的开路电压uoc, 这个电阻等于从此单口网络两端看进去,当网 络内部所有独立源均置零(No)时的等效电阻R0 i =0
+
4.6 戴维南定理
7Ω
10Ω
例(2) a 44 b
20 60 60
20
20 60
22
结论 只含电阻单口网络 等效为一个电阻
只含 电阻
R
2.含独立源电路 1V 例(1)
+
_
2
3
0.5A
0.2A 5
0.5A
5
5 0.3A
+ 1.5V _
结论 含独立源单口网络 等效为实际电压源 或实际电流源 含独立 源和电 阻电路
试用电压源与电流源等效变换的方 法计算2电阻中的电流。
1 2A
解:
I
1 3 2A 2A 6
1
3 + 6V –
6 + – 12V (a)
1 2
(b)
– 2V 2
I + +
由图(d)可得
82 I A 1A 2 2 2
2 2 +
2 2 4A
–
8V (d)
(c)
+
– 2V 2
第四章
分解方法及单口网络
——用等效化简的方法分析电路
本章的主要内容: 1、分解、等效的概念; 2、二端网络的等效化简,实际电源 的等效变换 ; 3、置换、戴维南、诺顿定理, 最大功率传递定理; 4、三端网络T形和形的等效变换。
电路分析基础第四、第五章测验测试题

第四章测试一、填空题(共6 题,75.0分)1.只要求出__________、__________和__________这三个量,就能立即写出换路后的电压或电流________________的表达式。
2.具有一个独立初始条件的动态电路叫( )电路。
3.换路后的一瞬间,电容的端_________和电感中的___________都保持换路前一瞬间的数值,这叫做___________。
4.R、C串联电路过渡过程的时间常数τ=( ),而R、L串联电路过渡过程的时间常数τ=( )5.线性动态电路的全响应,根据叠加定理可表示为( )响应与( )响应之和。
6.换路后的一瞬间,电容的端________和电感的_________都保持前一瞬间的数值,这叫_________。
二.判断题(共2 题,25.0分)1.一阶动态电路三要素法的通式为f(t)=f(∞)+[f(0+)-f(∞)]·e-t/τ答案:对2.RC一阶电路中,电容电压UC的零输入响应是按指数规律增长。
答案:对第五章测试一、单选题(共8 题,20.0分)1.标有额定值220V 60W的灯泡,将它接在电源上,它消耗的功率()。
A.小于60WB.等于60WC.大于60WD.无法确定答案:B2.在电阻和电容串联电路中,阻抗1Z1=( )A.A+XCB.sqrt(R*R±Xc*Xc)C.uc/icD.Ucm/Ic答案:B3.启辉器中装有一只电容器,其作用是( )A.启辉器中装有一只电容器,其作用是B.保护启辉器的动静触片C.通交流隔直流答案:A4.在纯电容电路中,电压有效值不变,频率增大时,电路中的电流将( )A.增大B.减小C.不变D.无法确定答案:A5.若频率为f时电路的感抗等于容抗,当频率为2f时,该感抗为容抗的( )。
A.2倍B.0.25倍C.相等D.4倍答案:D6.两个同频率正弦交流电流i1、i2的有效值各为40A和30A, 当i1+i2的有效值为70A时,i1与i2的相位差是( )。
电路分析基础第4章 相量法(2h)

Im
U 2
U
U 1
41.9
60 30
Re
U
Im
U 2
首
U 1
60 尾
41.9
相 接
30
Re
/38 章目录 上一页 下一页 返回 退出
第4章 正弦稳态电路分析
4.3 基尔霍夫定律的相量形式和基本
元件伏安关系的相量形式
一. 电阻 i(t)
+
uR(t) R -
•
I
+
•
UR
R
-
相量模型
已知 i(t) 2I cos(wt y i )
设 i(t)=Imcos(w t+ )
I
1 T
T 0
I
2 m
cos2
(
wt
Ψ
) dt
def
I
1 T i 2 (t )dt
T0
cos2 ( wt Ψ ) 1 cos2(wt Ψ )
2
I 0.707Im Im 2I
i(t) Im cos(wt Ψ ) 2I cos(wt Ψ )
10/38 章目录 上一页 下一页 返回 退出
u2 (t) 4 2cos(314t 60o ) V
U1 630o V U 2 460o V
U U1 U 2 630 460 5.19 j3 2 j3.46
7.19 j6.46 9.6441.9o V
u(t) u1(t) u2 (t) 9.64 2cos(314 t 41.9o ) V
dt
C 相量形式:
•
U Uy u
•
IC
wCUy u
π 2
1 相量关系:
电路分析基础第5版第4章 分解方法及单、双口网络

9V
4Ω 3
I1
应用举例
例1:求图示电路中各支路电流。
解: 将3Ω电阻用电流源置换
I3 = 2.7
I1
9 4
1 2
0.9
2.7
A
I2
9 4
1 2
0.9
1.8
A
I4
I5
1 2
I3
0.45
A
I1
2
+
9V
I3 3
2
2
I2
I4
4- 3
2 I5
I1
0.9A I3
2
+
9V
2
I2
2 2
I4
I5
结论:置换后对其他支路没有任何影响。
电压u =α和端口电流i =β,则N2 (或N1)可用一个电压为 α 的电
压源或用一个电流为 β 的电流源置换 ,置换后对 N1 (或N2 ) 内各支路电压、电流没有影响。
i=β
N1
+
u=α
N2
i=β
+
N1
α
N1
+ u=α
β
置换定理适用于线性和非线性电路。
二. 置换的实质
置换:如果一个网络N由两个单口网络组成,且已
联立(1)、(2),解得 u=12V, i=-1A
用12V电压源置换N1,可求得 i1
用-1A电流源置换N2,可求得 u2=12V
[例]求上一例题中N1和N2的等效电路
0.5i1
6Ω
i
5Ω i1
+
+ 10Ω 1A
12V u
- -2
+
电路分析基础第4章 动态电路的时域分析

第4章 动态电路的时域分析 解 (1) 先计算电容电压uC(0-)和电感电流iL(0-)。开关
开启前电路已处于直流稳定状态,这时电容相当于开路,电 感相当于短路,t=0-时的等效电路如图4.2-5(a)所示。由图(a) 可得
图4.2-5 例4.2-2用图(二)
第4章 动态电路的时域分析
第4章 动态电路的时域分析
(2) 根据换路定律,有
iL(0+)=iL(0-)=1 A (3) 画出换路后瞬间t=0+时的等效电路,计算其他支路 电压、电流的初始值。根据置换定理,用一个电流值等于
iL(0+)=1 A的理想电流源代替电感元件,画出t=0+时的等效电 路如图(b)所示。对图(b)中右边一个回路应用KVL,得
第4章 动态电路的时域分析 图4.2-1 动态电路过渡过程说明用图
第4章 动态电路的时域分析
4.2.2 换路定律 如果电容电流iC和电感电压uL在无穷小区间[t0-,t0+]
为有限值,则上面两式中等号右边第二项积分为零,于是有
uC (t0 iL (t0
) uC (t0 ) iL (t0 )
4.2.1 动态电路的过渡过程 当动态电路的结构或元件参数发生变化时,电路将从一
个稳定状态变化到另一个稳定状态,这种变化一般需要经历 一个过程,这个过程称为过渡过程。通常把电路中电源的接 入或断开,以及元件参数或电路结构的突然改变,统称为 “换路”。下面以图4.2-1(a)所示的动态电路为例来说明过 渡过程的概念。
第4章 动态电路的时域分析
4.1 电容元件和电感元件
4.1.1 电容元件 1. 电容元件的定义 电容元件是从实际电容器中抽象出来的理想化模型。实
电路分析基础 网络的VAR和电路的等效

解: 设端口电压u,支路电路i1和i2
有
KCL I i1 3 0
I a
i1 10
+
i2
2A
u
10
i1 2 i2 0 可得 i1 I 3, i2 I 1
-
3A
b
u/V
2A
u 10i1 10i2 20I 40
i/A
-40V
返节目录
电路分析基础
测试题2 求单口网络的VAR,并画出其伏安特性曲线。
uS= uSk 注意参考方向 2、理想电压源并联
+
º
uS1_
+
-
uS _
uS2+
º
uS= uS1- u S2
实电际压电值压相源同可的电压源 才能以并并联联吗?
+
+
uS_ uS _
+ uS_
这种情况下每个电源的电流不确定。
返节目录
电路分析基础
3、理想电流源并联
iS1
iS2
iS
iS= iSk
iS3
注意参考方向
返节目录
电路分析基础
如何找到电路的最简等效电路呢?
+i
首先求出电路外端口的VAR。
u
-
①若VAR为 u K i 则电路等效为R=K的电阻
②若VAR为 u K i A
则电路等效为R=K的电阻 串联一个电压为A的电压源
或者 i K u A 则电路等效为R=1/K'的电阻
并联一个电流为A'的电流源
(1)分压电路:
uk
Rk
n
u
两个电阻串联:
Rk
k 1
u1
电路分析基础第四版课后习题第四章第五章第六章答案
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
电路分析基础 第4章 一阶电路的时域分析

时域模型:
电路模型中,元件用R、L、C等参数表征,激励 用电压源电压、电流源电流的时间t的函数表征。
成都信息工程学院-控制工程学院
《电路分析基础》
第四章 一阶电路的时域分析
第4章 一阶电路的时域分析
知识
能力
建立并深刻理解电路的暂态和稳态、 根据给定电路问题合理选择分析方
电路的换路、电路的零输入响应、
线性时不变电容:库伏特性曲线为q-u平面上一条过
原点的直线,且不随时间而变的电容元件。 q(t)=Cu(t)
(2) 符号: q(t) C
i(t) + u(t)
关联参考方向 系数C :电容;
单位:法[拉], F; μF 10-6F ; pF 10-12F;
成都信息工程学院-控制工程学院
《电路分析基础》
《电路分析基础》
第四章 一阶电路的时域分析
动态电路的时域分析
集总电路分:电阻电路和动态电路。 动态电路:至少含有一个动态元件的电路。 动态元件:元件的VCR关系均要用微分或积分来表示的元件。
时域分析: 在时域模型中,以时间为主变量列写电路的 微分方程并确定初始条件,通过求解微分方 程获得电压、电流的时间函数(变化规律)。
即:仅以电场方式存储能量,并可将此能量释放出去,电容本身并不消耗 能量;电容电压反映了电容的储能状态,称电容电压为状态变量。
成都信息工程学院-控制工程学院
《电路分析基础》 5、电容电路的分析 第四章 一阶电路的时域分析
例1 设0.2F电容流过的电流波形如图a所示,
i
5A
已知 u(0) 3。0V试计算电容电压的
C uc(t0)=U0
uc(t) U0
uc1(t) u1(t0)=0
电路分析基础第4章分解方法及单口网络

is
is is1 is2 isK
5.电流源的串联 电流值相等的电流源可作方向相同的串联,电 流值不相等的电流源不允许串联。
a is1 is2 b
a
is b
is is1 is2
17
6.电流源与二端网络的串联 N1的等效网络不是理想电流源支路。
a
is N1 b
a is b
3
4-2 单口网络的电压电流关系
单口网络的描述方式:
• 详尽的电路图; • VCR(表现为特性曲线或数学公式); • 等效电路。
VCR只取决于单口本身的性质,与外接电路无关。
因而:
• 可以孤立出单口,而用外施电源法求它的VCR; • 求解单口(例如N2)内各电压、电流时,其外部 (例如N1)可 用适当的电路代替。
a
10
10
-
4
2 24V
I +-
+
b 12V
Isc
-
2 24V
+-
+
12V 图(a)
解:把原电路除4电阻以外的部分化简为诺顿等效电 路。为此先把拟化简的单口网络短路,如图(a)所示:
根据叠加原理求短路电流Isc,可得:
Isc
24 10
12 10 // 2
2.4
7.2
9.6 A
35
N a iK
N' uK NK
b
已知:
uk ,或 ik
a
a
N' isk
N'
usk
b
b
isk
usk
11
例:已知电路中U=1.5V,试用置换定理求U1
《电路分析基础》第2版-习题参考答案

《电路分析基础》各章习题参考答案《电路分析基础》各章习题参考答案第 1 章 习题参考答案习题参考答案1- 1 (1) 50W ; (2) 300 V 、25V, 200V 、75 V ; (3)2=12.5 QR a =100 Q, R 4=37.5 Q 1- 2 V A =8.5V =8.5V,, V m =6.5V =6.5V,, V B =0.5V =0.5V,, V C =- 12V , V D =-19V =-19V,, V p =-21.5V =-21.5V,, U A B AB =8V =8V,, U B C BC =12.5=12.5,,U DA =-27.5V1-3 电源电源((产生功率产生功率)): A 、 B 元件;负载元件;负载元件;负载((吸收功率吸收功率)): C 、 D 元件;电路满足功率平衡元件;电路满足功率平衡元件;电路满足功率平衡 条件。
1-4 (1) V A =1 00V , V B =99V, V C =97V, V D =7V, V E =5V, V F =1V, U A F AF =99V, U C E CE =92V,U BE =94V, U BF =98V, U CA =- 3 V ; (2) V C =90V, V B =92V , V A =93V, V E =-2V, V F =-6V, V G =- 7V, U AF =99V, U CE =92V, U B E BE =94V, U B F BF =98V, U C A CA =- 3 V1-5 I 〜0.18A ,6 度,度,2.7 2.7 元 1- 6 I=4A , I 1=11A =11A,,I 2=19A 1-7 (a) U=6V , , (b) U=24 V , (c) R=5Q , Q, (d) I=23.5A 1- 8 (1) i 6=-1A ; (2) u 4=10V, u 6=3 V ; (3) P 1=-2W 发出发出, P , P 2 2 =6W 吸收吸收, P , P 3 3 =16W 吸收吸收, ,P 4 =-10W 发出发出, P , P 5 5 =-7W 发出发出, P , P 6 6 =-3W 发出发出1- 9 I=1A, , U s =134V , R ~ 7.8Q 1- 10 S断开:断开:断开:U U AB =- 4.8V , U AO =- 12V , U BO =-7.2V ;S 闭合:闭合:闭合:U U AB = -12V, U A O AO = - 12V , U BO =0V 1- 11支路支路 3 3,节点,节点,节点 2 2,网孔,网孔,网孔 2 2 ,回路,回路,回路 3 3 1- 12节点电流方程:节点电流方程: (A) I (A) I 1 +I 3- I 6=0=0,,(B)I 6- I 5- I 7=0=0,,(C)I 5 +I 4-I 3=0 回路电压方程:① I6 R 6+ U S 5 S5 +I 5 R 5- U S 3 +1 3 3 R 3=0 ,②-15 R 5- U S 5+ I 7R 7- U S 4 =0 ,③-丨3 R 3+ U S3 + U S 4 S4 + I 1 1 R 2+ I 1 1 R 1=01- 13 UA B AB =11V , I 2=0.5A , l 3=4.5A , R 3~ 2.4 Q 1-14 VA =60V V C =140V V D =90V U A C AC =- 80V U AD =- 30V U CD =50V 1- 15 I 1=- 2A I 2=3A I 3=- 5A I 4=7A I 5=2A第 2 章 习题参考答案习题参考答案2- 1 1 2.42.4 Q 5 A 2- 2 (1) 4 V 2 V 1 V; (2) 40 mA 20 mA 10 mA 2-3 1.5 Q 2 A 1/3 A 2-4 6 Q 36 Q 2-5 2 2 A 1 A A 1 A 2-6 1 1 A A2-7 2 2 A A 2- 8 1 1 A A2- 9 I1 1 = -1.4 A I2 = 1.6 A I3 = 0.2 A 2- 10 I1 1 = 0 A I2 = -3 A P 1 = 0 W P 2 = -18 W 2-11 I i = -1 mA , I 2 = - 2 mA , E 3 = 10 V 2- 12 I 1 = 6 A , I 2 = -3 A ,I 3 = 3 A 2- 13 I1 1 =2 A , , I 2 = 1A , , I3 = 1 A , I4 =2 A , , I5 = 1 A 2-14 2-14 V V a = 12 V , I 1 = - 1 A ,I 2 = 2 A 2-15 2-15 V V a = 6 V , I 1= 1.5 A , I 2 = - 1 A ,I 3= 0.5 A 2-16 2-16 V V a = 15 V , , I 1 = - 1 A , , I 2 =2 A , , I 3= 3 A 2-17 2-17 I I 1 = -1 A ,, I 2 = 2 A 2-18 2-18 I I 1 =1.5 A , , I 2 = - 1 A , , I 3= 0.5 A 2-19 2-19 I I 1 =0.8 A , , I 2 = - 0.75 A , , I 3 = 2 A , I 4 = - 2.75 A , I 5 = 1.55 A 2-20 2-20 I I 3= 0.5 A 2-21 U o o = 2 V , R o = 4 Q ,Q, I 00 = 0.1 A 2-22 I 55 = -1 A 2-23 2-23 (1) I (1) I5 5 = 0 A , U ab = 0 V ; (2) I 5 5 = 1 A , U ab = 11 V 2-24 I L = 2 A2-25 I s s =11 A , , R 0 = 2 QQ 2-26 2-26 18 18 Q, - 2 Q ,Q, 12 Q 2-27 U == 5 V 2-28 I =1 A2-29 U == 5 V 2-30 I =1 A2-31 2-31 10 V 10 V ,, 180 Q 2-32 U 0 = 9 V , R 0 = 6 Q ,Q, U=15 V 第3章习题参考答案章习题参考答案3- 1 50Hz, 314rad/s, 0.02s, 141V, 100V, 120° 3-2 200V, 141.4V 3-3 u=14.1si n (314t-60 °V3- 4 (1) ®u1-贏2= 120° (2) ®1 = -90-90° °%= - 210°210°, , %1-屁=120=120° (不变° (不变) 3-5 (1) U^50 .^_90V , U 2 =50 .2.2 - 0 V ; ; (2) U 3=100 2 sin (3t+ 45 °)V , U, U 4=100 ■■ 2 sin ( ®t + 135 °)V 3- 6 (1) i 1=14.1 sin ( 72 °)A ;; (2) U 2=300 sin ( 3—60 °)V3- 7错误:(1),1),⑶,⑶,⑶,(4), (5) (4), (5) 3-8 (1) R ; (2) L ; (3) C; (4) R 3-9 i=2.82 sin (10t-30 °)A , Q~ 40 var , Q~ 40 var 3-10 u =44.9sin (3141-135 °V, Q=3.18 var 3- 11 (1) I=20A ; (2) P=4.4kW3- 12 (1)I ~ 1.4A , I 1.4 - 30 A; (3)Q~ 308 var, P=0W ; (4) i~ 0.98 sin (628t-30 °)A 3- 13 (1)I=9.67A , I =9.67450 A ,i=13.7 sin (314t+150 °) A ; (3)Q=2127.4 var, P=0W; (4) I C =0A3- 14 (1)C=20.3 尸;(2) I L = 0.25A ,l c = 16A第4章习题参考答案章习题参考答案4-1 (a) Z =5. 36.87 J, Y =0.2 / 36.87 S ; (b) ; (b) ZZ =2.5 - 2/ 45 门,Y =0.2.2/45 S 4- 2 Y=(0.06-j0.08) S , , R ~ 16.67 Q, X L =12.5 Q, L ~0.04 H 4-3 U R =6 0^0 V U L =8080//90 V , , U S =100100^^53.13 V 4-4 卩=2 0 £ 3 6.874-5 Z =100 =100 22^45 ;:;: ■,卩=1^0 A , , U R =100100^^0 V , U L =125125//90 V , , U C =2525/ /90 V 4-6 Y =0.25 2^45 S , U =4 “2/0 V ,卩R = .2. 0 A , , I L =0.^ 2 / 90 A , , I C =1.21.2..2/90 A4-7 ll =1 0.=1 0.「2 4 5,A U S =100 乙 90 V 4-8 (a) 30 V ; (b) 2.24 A 4-9 (a) 10 V ; (b) 10 A (b) 10 A 4-10 10 (a) (a) 10 V ; (b) 10 V (b) 10 V 4- 11 U=14.1 V4- 12 UL 1 =15 V , U C 2 =8 V , U S =15.65 V 4-13 4-13 U U X 1 =100 V , U 2 =600 V , , X 1=10Q, X 2=20 Q, X 3=30 Q 4-14 Z =20 .2 45 门,l =2. -45 A , h , h = 2 0 = 2 0 A , .2/-90 A , U ab ab==0V 4- 15 (1)1 =£2 2 A A , Z RC =5、2「,「, Z =5 10 门;门;(2) R (2) R =10 门,门,X X ^1010'J 'J4-16 P = 774.4 W , Q = 580.8 var, S = 968 V A- 4-17 l 1 = 5 A , l 2 = 4 A 4-18 4-18 I I 1 = 1 A , I 2 =2 A , l =.5. 26.565 A , S =44.72. -26.565 V V V A A 4-19 Z=10", I =190A I=190A ,U R2 =5 2 135 V , P =10 W 64-20 a =5X10 rad/s , p = 1000 = 1000 Q ,Q, Q = 100 , l = 2 mA , U R =20 mV , U L = U C = 2 V 4-21 30 =104 rad/s , p = 100 = 100 Q ,Q, Q = 100 , U = 10 V , I R = 1 mA , I L = I C = 100 mA 4-22 L 1 1 = 1 H , L 2 ~ 0.33 H 第5章习题参考答案章习题参考答案5- 3 M = 35.5 mH5- 4 301 =1000 rad/s ,3,302=2236 rad/s5-5 Z 1 = j31.4 Q , Q , Z 2 = j6.28 Q Q 5-6 Z r = 3+7.5 Q Q 5-7 M = 130 mH 5- 8 “2 二-2/45 A5- 9 U1 = 44.8 V 5- 10 M12 12 = 20 mH , 11 = 4 A 5- 11 U 2 = 220 V , I 1 = 4 A5- 12 n = 1.95- 13 N2 = 254 匝,匝,匝,N N3 = 72 匝 5- 14 n = 10 , P 2 = 31.25 mW章习题参考答案章习题参考答案(1) A 相灯泡电压为零,相灯泡电压为零,B B 、C 相各位为220V I L = I p = 4.4 A ,U p = 220 V ,U L = 380 V ,P = 2.3 kW (2) I p = 7.62 A ,I L = 13.2 A A 、C 相各为2.2A 2.2A,,B 相为3.8A U L = 404 VU A N =202202/ -/ -47 47 Vcos $ = 0.961 , Q = 5.75 kvar Z =334 28.4 门(1) I p p = 11.26 A , Z = 19.53 / 42.3 °Q; (2) I p p = I l l = 11.26 A , P = 5.5 kW U l = 391 Vi A =22 2sin(・t —53.13 ) Ai B =22 .2sin(・t —173.13 ) Ai C =22 2 sin(,t 66.87 ) AU V = 160 V(1) 负载以三角形方式接入三相电源负载以三角形方式接入三相电源(2) I — =3.8 T 2 -15 A , 1仁 =3.3.^-2/ ^-2/ 135 A , , 仁 =3.8、「2也105 AI A =3.8、. 6/「45 A , I B =3.8I Q 165 A , , I c =3.8.6. 75 AL = 110 mH , C = 91.9 mF 章习题参考答案章习题参考答案P = 240 W, Q = 360 var P = 10.84 W(1) i(t) 4.7sin( t 100 ) - 3sin3 t A(2) I ~ 3.94 A , U ~ 58.84 V , P ~ 93.02 W 0MU m n o L 1 r~2 ------------- 2u 2(t) msin(,t —-arctan 1)V , R 2 (丄J 2z 2 R '直流电源中有交流,交流电源中无直流直流电源中有交流,交流电源中无直流U 1=54.3 V , , R = 1 Q, L = 11.4 mH ;约为约为 8% 8% , , ( L'= 12.33 mH ) 使总阻抗或总导纳为实数使总阻抗或总导纳为实数((虚部为虚部为 0)0)的条件为的条件为的条件为 尺二尺二& = & = R x = Rx = ■ L/C ■ L/C G =9.39 折,C 2 =75.13 M F L 1 = 1 H , L 2 = 66.7 mHC 1 = 10 M F, C 2 2 = 1.25 M F章习题参考答案章习题参考答案第6 6-1 6-3 6-4 6-5 6-6 6-7 6-8 6-9 6-10 6-11 6-12 6-13 6-14 6- 15 第7 7- 1 7-2 7-3 7-4 7-5 7-6 7-7 7-87-9 7- 10 第88- 6 8-78-8i L (0+) = 1.5mA , U L (0+) = - 15V- 15V h (0+) = 4A , i 2(0+) = 1A , U L (0+) = 2V 2V ,i 1(s )= 3A , i 2(^)= 0, U L ()= 0 i 1 1 (0+) = 75mA , i 2(0+) = 75mA , i 3(0+) = 0, U L 1 (0+) = = 0, U L 2(0+) = 2.25V 2.25V6i c (t)二 2訂 A 4t U L (t) =6e _V u C (t) =10(1 _eg )V , i C (t) =56说*人 500t 貝 u C (t) =115e~ sin(866 亠60 ) V10t 10t 山⑴=12e - V , L(t) =2(1 —e — )A 1 1 t t U R (t) =~U s e 下2C V , U R (3 J - -U S e-V (1) T = 0.1s, (2) u c (t) =10e -V , (3) t = 0.1s u C (t) =10 _9e 」° V 10t _ i L (t) =5e 一 A (a)f(t) =1(t —t 。
电路分析基础(英文版)课后答案第四章

DE 4.4 [a]
vn vn ¡ vo + = 0; 4500 63;000 Thus vo = 15vp ;
therefore vo = 15vn ; vp = 0:4Rx 15;000 + Rx vp = 0:32 V; 123
So when Rx = 60 k−;
vo = 4:8 V
124
0 0 ¡ va 0 ¡ vo + + in = 0; Ra Rb
in = 0
Therefore 0 vo va =¡ ; Rb Ra
0 vo =
Rb va Ra
Assume vb is acting alone. Replace va with a short circuit. Now vp = vn = vb Rd Rc + Rd in = 0
Rd Ra =
Rb Ra + Rb vb ¡ va Rc + Rd Ra therefore Rd (Ra + Rb ) = Rb (Rc + Rd ) Ra Rc = Rb Rd
Rd [b] Ra
µ
Ra + Rb Rc + Rd
¶
Rb ; Ra
Rd Ra = Rb Rc ; Rd When Ra
µ
vb = 0 V; vb = 0 V; vb = 2 V; vb = 2 V; vb = 8 V;
vo = 18 V (sat)
vo = 40:5 ¡ 8va = §18
:¢: 2:8125 · va · 7:3125 V P 4.4 [a] ia = 120 £ 10¡6 = 20 ¹A 6
[b]
250 250 va ¡ vb = ¡50(0:1) ¡ 10(0:25) = ¡5 ¡ 2:5 = ¡7:5 V 5 25 [b] vo = ¡50va ¡ 2:5 = ¡10 V; therefore 50va = 7:5; va = 0:15 V [d] vo = ¡50va + 10vb = ¡5 + 2:5 = ¡2:5 V vo = ¡50va + 2:5 = ¡10 V; 50va = 12:5; va = 0:25 V 10vb = 20; vb = 2:0 V vn = vp vo = ¡5 + 10vb = 15 V; [c] vo = ¡5 ¡ 10vb = ¡10 V; 10vb = 5; vb = 0:5 V
《电路分析基础》第2版-习题参考答案

《电路分析基础》各章习题参考答案第 1 章习题参考答案1- 1 (1) 50W ; (2) 300 V、25V, 200V、75 V ; (3) 2=12.5 Q R a=100 Q, R4=37.5 Q1- 2 V A=8.5V, V m=6.5V, V B=0.5V, V C=- 12V, V D=-19V, V p=-21.5V, U AB=8V, U BC=12.5,U DA=-27.5V1- 3 电源(产生功率): A 、 B 元件;负载(吸收功率): C、 D 元件;电路满足功率平衡条件。
1- 4 (1) V A=1 00V , V B=99V, V C=97V, V D=7V, V E=5V, V F=1V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V;(2) V C=90V, V B=92V , V A=93V, V E=-2V, V F=-6V, V G=- 7V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V1- 5 I 〜0.18A , 6 度,2.7 元1- 6 I=4A, I1=11A,I2=19A1- 7 (a) U=6V, (b) U=24 V, (c) R=5Q, (d) I=23.5A1- 8 (1) i6=-1A ; (2) u4=10V, u6=3 V; (3) P1=-2W 发出, P2 =6W 吸收, P3 =16W 吸收, P4 =-10W 发出, P5 =-7W 发出, P6 =-3W 发出1- 9 I=1A , U s=134V , R~ 7.8Q1- 10 S 断开:U AB=- 4.8V , U AO=- 12V , U BO=-7.2V ;S 闭合:U AB =-12V, U AO =- 12V , U BO=0V1- 11 支路 3,节点 2,网孔 2 ,回路 31- 12 节点电流方程: (A) I1 +I3- I6=0,(B)I6- I5- I7=0,(C)I5 +I 4-I3=0回路电压方程:① I6 R6+ U S5 +I 5 R5- U S3 +1 3 R3=0 ,②-15 R5- U S5+ I 7R7- U S4 =0 ,③-丨3 R3+ U S3 + U S4 + I 1 R2+ I 1 R1=01- 13 U AB=11V , I2=0.5A , l3=4.5A , R3~ 2.4 Q1-14 V A=60V V C=140V V D=90V U AC=- 80V U AD=- 30V U CD=50V1- 15 I1=- 2A I2=3A I3=- 5A I4=7A I5=2A第 2 章习题参考答案2- 1 2.4 Q 5 A2- 2 (1) 4 V 2 V 1 V; (2) 40 mA 20 mA 10 mA2- 3 1.5 Q 2 A 1/3 A2- 4 6 Q 36 Q2- 5 2 A 1 A2- 6 1 A2- 7 2 A2- 8 1 A2- 9 I1 = -1.4 A I2 = 1.6 A I3 = 0.2 A2- 10 I1 = 0 A I2 = -3 A P1 = 0 W P2 = -18 W2- 11 I i = -1 mA , I2 = - 2 mA , E3 = 10 V2- 12 I1 = 6 A , I2 = -3 A , I3 = 3 A2- 13 I1 =2 A , I2 = 1A , I3 = 1 A , I4 =2 A , I5 = 1 A2-14 V a = 12 V , I1 = - 1 A, I2 = 2 A2-15 V a = 6 V , I1= 1.5 A , I2 = - 1 A ,I3 = 0.5 A2-16 V a = 15 V , I1 = - 1 A , I2 =2 A , I3 = 3 A2-17 I1 = -1 A , I2 = 2 A2-18 I1 =1.5 A , I2 = - 1 A , I3 = 0.5 A2-19 I1 =0.8 A , I2 = - 0.75 A , I3 = 2 A , I4 = - 2.75 A , I5 = 1.55 A2-20 I3 = 0.5 A2-21 U o = 2 V , R o = 4 Q, I0 = 0.1 A2-22 I5 = -1 A2-23 (1) I5 = 0 A , U ab = 0 V ; (2) I5 = 1 A , U ab = 11 V2-24 I L = 2 A2-25 I s =11 A , R0 = 2 Q2-26 18 Q, - 2 Q, 12 Q2-27 U = 5 V2-28 I =1 A2-29 U = 5 V2-30 I =1 A2-31 10 V , 180 Q2-32 U0 = 9 V , R0 = 6 Q, U=15 V第3章习题参考答案3- 1 50Hz, 314rad/s, 0.02s, 141V, 100V, 120 °3- 2 200V, 141.4V3- 3 u=14.1si n (314t-60 °V3- 4 (1) ®u1-贏2= 120°(2) ®1 = -90° %= - 210°, %1-屁=120° (不变)3-5 (1) U^50 .^_90 V , U2 =50 .2 -0 V ;(2) U3=100 2 sin (3t+ 45 °)V , U4=100 ■■ 2 sin ( ®t+ 135 °)V3- 6 (1) i 1=14.1 sin ( 72 °)A ; (2) U2=300 sin ( 3—60 °)V3- 7 错误:(1),⑶,(4), (5)3- 8 (1) R; (2) L ; (3) C; (4) R3- 9 i=2.82 sin (10t-30 °)A , Q~ 40 var3- 10 u=44.9sin (3141-135 °V, Q=3.18 var3- 11 (1) I=20A ; (2) P=4.4kW3- 12 (1)I ~ 1.4A , I 1.4 - 30 A ; (3)Q~ 308 var, P=0W ; (4) i~ 0.98 sin (628t-30 °)A3- 13 (1)I=9.67A , I =9.67450 A , i=13.7 sin (314t+150 °) A ; (3)Q=2127.4 var, P=0W;(4) I C=0A3- 14 (1)C=20.3 尸;(2) I L = 0.25A ,l c = 16A第4章习题参考答案4-1 (a) Z =5. 36.87 J, Y =0.2 /36.87 S; (b) Z =2.5 - 2/45 门,Y =0.2.2/45 S4- 2 Y=(0.06-j0.08) S , R~ 16.67 Q, X L=12.5 Q, L~0.04 H4- 3 U R=6 0^0 V U L=80/90 V , U S=100^53.13 V4- 4 卩=2 0 £ 3 6.874-5 Z =100 2^45 ;:■,卩=1^0 A , U R=100^0 V , U L=125/90 V , U C=25/ 90 V4-6 Y =0.25 2^45 S , U =4 “2/0 V ,卩R = .2. 0 A , I L =0.^ 2 / 90 A , I C=1.2.2/90 A4- 7 ll =1 0.「2 4 5,A U S=100 乙90 V4- 8 (a) 30 V ; (b) 2.24 A4- 9 (a) 10 V ; (b) 10 A4- 10 (a) 10 V ; (b) 10 V4- 11 U=14.1 V4- 12 U L1 =15 V , U C2 =8 V , U S=15.65 V4-13 U X1 =100 V, U2 =600 V, X1=10 Q, X2=20 Q, X3=30 Q4- 14 Z =20 .2 45 门,l =2. -45 A , h = 2 0 A , .2/-90 A , U ab=0V 4- 15 (1)1 =£2 A, Z RC=5、2「,Z =5 10 门;(2) R =10 门,X^10'J4- 16 P = 774.4 W , Q = 580.8 var, S = 968 V A-4- 17 l1 = 5 A , l2 = 4 A4-18 I1 = 1 A , I2 =2 A , l =.5. 26.565 A , S =44.72. -26.565 V A4-19 Z=10", I=190A, U R2 =5 2 135 V , P =10 W64-20 a =5X10 rad/s , p= 1000 Q, Q = 100 , l = 2 mA , U R =20 mV , U L = U C = 2 V4-21 30 =104rad/s , p= 100 Q, Q = 100 , U = 10 V, I R = 1 mA , I L = I C = 100 mA4-22 L1 = 1 H , L2 ~ 0.33 H第5章习题参考答案5- 3 M = 35.5 mH5- 4 301 =1000 rad/s ,302 =2236 rad/s5- 5 Z1 = j31.4 Q , Z2 = j6.28 Q 5- 6 Z r = 3+7.5 Q5- 7 M = 130 mH5- 8 “2 二-2/45 A5- 9 U1 = 44.8 V5- 10 M12 = 20 mH , 11 = 4 A5- 11 U2 = 220 V , I1 = 4 A5- 12 n = 1.95- 13 N2 = 254 匝,N3 = 72 匝5- 14 n = 10 , P2 = 31.25 mW章习题参考答案 (1) A 相灯泡电压为零,B 、C 相各位为220V I L = I p = 4.4 A ,U p = 220 V ,U L = 380 V ,P = 2.3 kW (2) I p = 7.62 A ,I L = 13.2 A A 、C 相各为2.2A ,B 相为3.8A U L = 404 V U A N =202/ -47 V cos $ = 0.961 , Q = 5.75 kvar Z =334 28.4 门 (1) I p = 11.26 A , Z = 19.53 / 42.3 °Q; (2) I p = I l = 11.26 A , P = 5.5 kW U l = 391 V i A =22 2sin(・t —53.13 ) A i B =22 .2sin(・t —173.13 ) A i C =22 2 sin(,t 66.87 ) A U V = 160 V (1) 负载以三角形方式接入三相电源 (2) I — =3.8 T 2 -15 A , 1仁 =3.^-2/ 135 A , 仁 =3.8、「2也105 A I A =3.8、. 6/「45 A , I B =3.8I Q 「165 A , I c =3.8.6. 75 A L = 110 mH , C = 91.9 mF 章习题参考答案 P = 240 W, Q = 360 var P = 10.84 W (1) i(t) 4.7sin( t 100 ) - 3sin3 t A (2)I ~ 3.94 A , U ~ 58.84 V , P ~ 93.02 W 0MU m n o L 1 r~2 ------------- 2 u 2(t) m sin(,t —-arctan 1)V , R 2 (丄J 2 z 2 R ' 直流电源中有交流,交流电源中无直流 U 1=54.3 V , R = 1 Q, L = 11.4 mH ;约为 8% , ( L'= 12.33 mH ) 使总阻抗或总导纳为实数(虚部为 0)的条件为 尺二& = Rx = ■ L/C G =9.39 折,C 2 =75.13 M F L 1 = 1 H , L 2 = 66.7 mH C 1 = 10 M F, C 2 = 1.25 M F 章习题参考答案 第66-16-36-46-56-66-76-86-96-106-116-126-136-146- 15第77- 17-27-37-47-57-67-77-87-97- 10第88- 68-78-8i L(0+) = 1.5mA , U L(0+) = - 15Vh(0+) = 4A, i2(0+) = 1A , U L(0+) = 2V, i1(s)= 3A , i2(^)= 0, U L()= 0 i1 (0+) = 75mA , i2(0+) = 75mA , i3(0+) = 0, U L1 (0+) = 0, U L2(0+) = 2.25V6i c (t)二 2訂 A 4tU L (t) =6e _V u C (t) =10(1 _eg 0t )V , i C (t) =56说*人 500t 貝 u C (t) =115e~ sin(866 亠60 ) V10t 10t 山⑴=12e - V , L(t) =2(1 —e — )A 1 t U R (t) =~U s e 下2C V , U R (3 J - -U S e-V (1) T = 0.1s, (2) u c (t) =10e -0t V , (3) t = 0.1s u C (t) =10 _9e 」°t V 10t _ i L (t) =5e 一 A (a)f(t) =1(t —t 。
《电路分析基础》课程练习题及答案

《电路分析基础》课程练习题及答案电路分析基础第⼀章⼀、1、电路如图所⽰,其中电流为答( A )A 0.6 A B. 0.4 A C. 3.6 A D. 2.4 A2、电路如图⽰, 应为答( C )A. 0 VB. -16 VC. 0 VD. 4 V3、电路如图所⽰, 若、、均⼤于零,, 则电路的功率情况为答( B )A. 电阻吸收功率, 电压源与电流源供出功率B. 电阻与电流源吸收功率, 电压源供出功率C. 电阻与电压源吸收功率, 电流源供出功率D. 电阻吸收功率,供出功率⽆法确定UI S⼆、 1、图⽰电路中, 欲使⽀路电压之⽐,试确定电流源之值。
I SU解:由KCL 定律得:22328222U U U ++=V由KCL 定律得:0422=++U I U S1160-=S I A 或-5.46 A 2、⽤叠加定理求解图⽰电路中⽀路电流,可得:2 A 电流源单独作⽤时,2/3A;4 A 电流源单独作⽤时,-2A, 则两电源共同作⽤时-4/3A 。
3、图⽰电路ab端的戴维南等效电阻 4 ;开路电压22 V。
解:U=2*1=2 I=U+3U=8A Uab=U+2*I+4=22V Ro=4第⼆章⼀、1、图⽰电路中,7 V电压源吸收功率为答( C )A. 14 WB. -7 WC. -14 WD. 7 W2、图⽰电路在时开关闭合,时为答(D )精品⽂档A. B.C. D.3、图⽰桥式电路中,已知,欲使图中u=0,应满⾜的条件为答( A )A. B.C. D.⼆、1、试⽤叠加定理求图⽰电路中的电压。
4Ω解:4Ω电路可分为图1和图2单独作⽤图1U 1=-3v图2U 2=- 249+ ×(4×4)=-3V U=U 1+U 2=-6v 2、图⽰电路在换路前已达稳态。
当时开关断开,求的。
100u C解:Uc(0)=100vUc(∞)=40150×20=75v 10RC ==τUc (t )=75+25e-0.1t3、求:⽰⽹络ab ⼆端间的戴维南等效电路。
电路分析基础第四版 课后习题答案
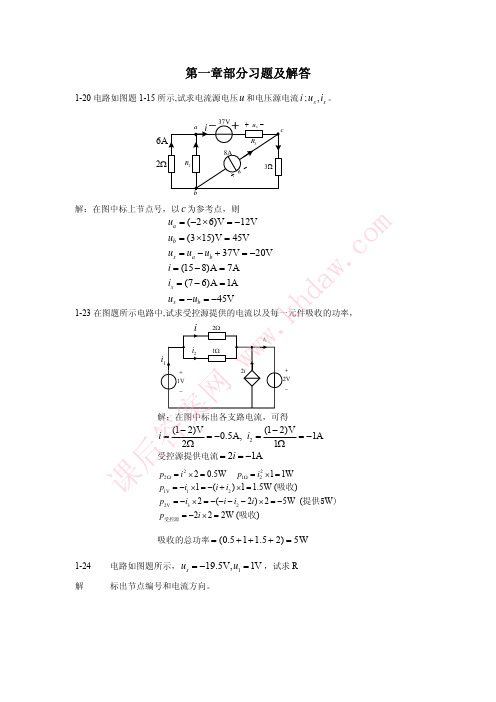
+
−
120V
Ro
a
+
U OC −
20kΩ
b
w. Ra = 60k // 30k = 20kΩ
khd 故
i3
=
udc 4
= −2.5A, i4
= is
− i3
= (−3.5 + 2.5)A =
− 1A
. 由此判定
R = 0Ω
www 试用支路电流法求解图题所示电路中的支路电流 i1,i2,i3 。
a
1Ω
网 i1
i2 3Ω
案 2Ω
答5A
d+ 8V
c
i3
+ 6V
−
−
后
b
解
课 求解三个未知量需要三个独立方程。由 KCL 可得其中之一,即
(2)当 N 内含电源 iS = 1A 能产生 ux 为 c ,则根据叠加定理列出方程,
⎧⎪⎨8−a8a++124bb++iiSScc==800 ⎪⎩iSc = −40
⇒
⎧8a +12b = 120 ⎩⎨−8a + 4b = 40
⇒
⎧a ⎨⎩b
= =
0 10
⇒ ux = (20× 0 + 20×10 − 40)V = 160V
i1 + i2 + i3 = 5
对不含电流源的两个网孔,列写 KVL 方程,得
网孔badb 2i1 − 3i2 + 8 = 0 网孔bdacb − 8 + 3i2 − i3 + 6 = 0
整理得:
⎧⎪⎨i−1 2+i1i2++3ii32
李瀚荪《电路分析基础》(第4版)课后习题详解-第4章 分解方法及单口网络【圣才出品】

第4章 分解方法及单口网络§4-2 单口网络的电压电流关系4-1 求图4-1所示单口网络的VCR。
图4-1解:标出端口u和i,电压u可认为是外施电压源电压,i流出网络,指向外施电源正极。
用网孔法列出电路方程。
设网孔电流和i均为顺时针方向。
找出i和u的关系得u=-12.5i+11.25 (1)如i指向网络内部,则u=12.5i+11.25 (2)u、i的单位分别为V、A。
列网孔方程就是如此规定的。
4-2 试用外施电源法求图4-2所示含源单口网络的VCR,并绘出伏安特性曲线。
图4-2解:图中u可认为是外施电压源的电压。
根据图中所示i的参考方向,可列出u=(3 Ω)i+(6 Ω)(i+5 A)+20 V=(3 Ω+6 Ω)i+(6 Ω)(5 A)+20 V=(9 Ω)i+50 V伏安特性曲线是条直线。
i=0时u=50 V,即u轴截距为50;u=0时,即i轴截距为4-3 试求图4-3所示电路的VCR。
图4-3解:施加电压源u于a、b两端,由KVL和KCL,可得§4-3 单口网络的置换——置换定理4-4 在图4-4所示电路中已知N的VCR为5u=4i+5,试求电路中各支路电流。
图4-4解:分割出图4-4所示虚线框内电路,设外施电压为u,为求其VCR,可列出节点方程整理得VCRu=2-1.2i以之与N的VCR联立可解出i,即5(2-1.2i)=4i+5解得i=0.5 A,u=1.4 V以1.4 V电压源置换N,可简便地估计到N存在的影响,由此可得4-5 试设法利用置换定理求解图4-5所示电路中的电压何处划分为好?置换时用电压源还是电流源为好?图4-5图4-6解:试从图4-6的虚线处将电路划分成两部分,对网络有整理得15u=117-14i(1)对网络有 联立(1)、(2)两式解得i=3 A。
用3 A电流源置换较为方便,置换后利用分流关系,可得4-6 电路如图4-7(a)所示,网络N的VCR如图4-7(b)所示,求u和i,并求流过两线性电阻的电流。
(大学物理电路分析基础)第4章网络定理

目录
• 基尔霍夫定律 • 叠加定理 • 戴维南定理 • 诺顿定理
01
CATALOGUE
基尔霍夫定律
定义
基尔霍夫定律是电路分析中的基本定律之一,它包括基尔霍夫电流定律(KCL)和 基尔霍夫电压定律(KVL)。
基尔霍夫电流定律指出,对于电路中的任一节点,流入该节点的电流之和等于流出 该节点的电流之和。
流和电压、计算功率等。
在解决复杂电路问题时,通常需要结合 其他电路定理和定律,如欧姆定律、电
源定理等,以简化问题的解决过程。
基尔霍夫定律是电路分析中的基础理论 之一,对于理解电路的工作原理、设计 电路以及解决实际问题具有重要的意义
。
02
CATALOGUE
叠加定理
定义
• 叠加定理:线性电路中,多个独立源共同作用产生的响应 ,等于各个独立源单独作用于电路所产生的响应之和。
内容
线性电路
01
叠加定理适用于线性电路,即电路元件的电压和电流成正比关
系。
独立源
02
叠加定理只适用于独立源,即源之间没有相互影响。
响应之和
03
各个独立源单独作用于电路所产生的响应是相互独立的,它们
的响应之和即为多个独立源共同作用产生的响应。
应用
简化计算
在复杂电路中,通过应用叠加定理, 可以将多个独立源的共同作用分解为 各个独立源单独作用于电路所产生的 响应,从而简化计算过程。
诺顿定理还可以用于验证电路分析的正确性和解决复杂电路问题,提高电 路分析的效率和准确性。
THANKS
感谢观看
基尔霍夫电压定律指出,对于电路中的任一闭合路径,沿该路径的电压降之和等于 零。
电路分析基础第四章

开路电压
等效电阻
二、戴维南定理证明:
置换
叠加
线性含源
线性或非线性
u ' = uoc
N中所有独立源产生的电压 电流源开路
' ''
u '' = − Rabi
电流源产生的电压 N0中所有独立源为零值
u = u + u = uoc − Rabi
u = uoc − Rabi
含源线性单口网络N可等效为 电压源串联电阻支路
Rab = 6 + 15 //(5 + 5) = 6 + 6 = 12Ω
Rcd = 5 //(15 + 5) = 4Ω
例3:试求图示电阻网络的Rab和Rcd。
Rab = 8 + {4 //[2 + 1 + ( 2 // 2)]} = 8 + {4 // 4} = 10Ω
Rcd = ( 2 // 2) + {1 //[4 + 2 + ( 2 // 2)]} = 1 + (1 // 7) = 1.875Ω
例5:求图中所示单口网络的等效电阻。
u R i = = ( μ + 1) R i
例6:求图所示单口网络的等效电阻。
u R Ri = = i 1+α
例7:求图示电路输入电阻Ri,已知α =0.99。
1. 外施电源法 2. 电源变换法
Ri = 35Ω
三、含独立源单口网络的等效电路:
1. 只含独立源、电阻,不含受控源 只含独立源、电阻不含受控源的网络,端口 VCR为u=A+Bi,u和i关联时,B为正。 2. 含受控源的有源单口网络 含受控源、独立源、线性电阻的网络,端口 VCR为u=A+Bi,B可正可负。 等效为电压源串联电阻组合或电流源并联电阻组合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RO
+
– B
40 RO 8 // 10 4.44 9
A
10 280 uoc 10 ( 20 10) 15.6V 10 8 18
此例从一个侧面证明了戴维南定 理的正确性。也反映了其简便性。
RO
4.44
15.6V B
uoc
+
–
戴维南定理也可以在单口外加电流源i ,用叠加定理计算端 口电压表达式的方法证明。
—
i NS
+ –
a
+
RO
u
b 含源单口网络的VCR表达式:
uoc
–
b
u =K1+K2i = uoc+ Roi
其中:
uoc等于该网络NS的端口开路电压;
a + u
—
i RO
+ –
i
NS
a
+
端口开路时: i =0 u = uoc
u
uoc
–
b
b
RO等于该网络中所有独立源置零时所得网络NR 的等效电阻Rab。 独立源置零
I
+ +
I
º +
5V _
5V _
º
5V _
与电压源并联的元件称为多余元件,多余元件的存在与否并 不影响端口电压的大小,端口电压总等于电压源电压。
us
is
提示:多余元件的存在会使电压源的电流有所改变,但电压源 的电流可为任意值。
总结:一个理想电压源与任何一条支路并联后,对外 等效为理想电压源。 i
(3)外加电压源,求入端电流:
网孔法列方程
( R1+R2 )I + R1IS = - US - U
U = - ( R1+R2 )I - R1IS - US
§4 -2 单口网络的伏安关系
注意:
1)单口网络的伏安关系是由其本身性质决定的,与外接 电路无关。 2)含有独立电源单口网络的伏安关系,可表示为u=A+Bi 的形式。 3)外加电流源求电压法和外加电压源求电流法是常用 的方法,也是用实验方法确定VCR的依据。这是求单口 网络VCR的基本方法。
1.5k
I
º + U _ º
课堂练习 1. 化成最简电路
20 4A
+ 30V 3 6
10
6
2.
求等效电路中R和US的参数 3I1 I
2A
I1
2
+
-
+ U _
º US
R
I
+
_
º + U _ º
º
§4-6 戴维南定理 (Thevenin Theorem)
线性含源单口网络NS ,就其端口VCR而言,可以等效 为一个电压源串联电阻的支路。 i a + u
解:引入中间变量i1 、i2 u = 2 ·i2 +4+1 ·i1 i2= i +4 i1= i + 4 –1 u = 2(i +4) +4+(i + 4 –1) = 3i +15 = uOC+ROi 得: uOC = 15V RO = 3 RO 3 uOC +
– 15V
i2
。
i
4V
+
–
2 4A 1
电路分析课的本质: 在 KCL 和 KVL 的前提下,找到求解电路变 量(电压和电流)的简便方法。 结构简单电路 分解 结构复杂电路 等效 分解?核心思想? 分析过程或步骤?
第4章 分解方法及单口网络
几个名词: (1) 端口( port ): 电路引出的一对端钮,其中从一个端钮(如a) 流入的电流一定等于从另一端钮(如b)流出的 i a 电流。
+ U _
2A
6A
+ U 5∥ 5 _
U=20V
含受控源单口网络的等效电路
可用加压求流法或加流求 压法,求得VCR
10V
1k 1k 0.5I I º + U _ º
U 1500 I 10
含受控源、电阻及独立源的单口网 10V 络与含电阻及独立源的单口网络一 样,可以等效为电压源-串联电阻组 合或电流源-并联电阻组合。
Req=( R1+ R2 +…+Rn) = Rk 结论: 串联电路的等效电阻等于各分电阻之和。
+
_
2.并联等效电阻Req
i
+ u _ R1 i1 R2 i2 Rk ik Rn in 等效 + u _
i
Req
由KCL:
i = i1+ i2+ …+ ik+ …+in= u / Req
故有 u/R = i = u/R +u/R + …+u/R =u(1/R +1/R +…+1/R ) eq 1 2 n 1 2 n
+
+
任意 元件
i
uS _
u _
uS
+ _
+ u _
对外等效 等效理想电压源中的电流不等于替代前的理想 电压源的电流,而等于外部电流。
理想电流源的串并联 并联:
is is1 is 2 isk isn
º iS2 iSk º
( 注意参考方向)
º iS º
iS1
串联:
只有电流相等且方向一致的电流源才允许串联,否则违背 KCL,此时等效电路为其中任一电流源。 i S1 i i S2 iS
u=k1i+A1
u=k2i+A2
4. 分别求单口网络N1,N2内部各支路的电压,电流。
§4 -2 单口网络的伏安关系
单口网络的伏安关系的求法
1. 根据电路模型直接列写u与i的关系 ; 2. 外接电流源求电压法; + IS + US R2 + R1 I1 I + U -
3. 外接电压源求电流法 。
例 求图示电路的VCR。 解:(1)列电路方程: U= -R2I - US + (-I-IS)R1 = -(R1+R2)I - R1IS-US
§4 -2 单口网络的伏安关系
(2)外加电流源,求入端电压: 4 节点法列方程
U1 U S IS I R1 R1
IS
US R2 2 . + + R1 I1 1
.
+ -
I
3 + U
I
-
U1 R2 I U 0
U= - ( R1+R2 )I - R1IS - US
§4 -2 单口网络的伏安关系
A
1A
i1
+ u –
B A
B
例3, 用戴维南定理求 i 。 解: 把 i 支路以外的电路 作戴维宁等效; (1) 求uOC uOC = uA – uB uA=2A·10 +10V=30V uB=2A·10 +35V= 55V
uS
_
+
u _Leabharlann iSRu=uS – Ri
u=R’iS –R’i
通过比较,得等效的条件: R=R’
us=R’iS 或 iS=us /R’
等效是指对外等效(等效互换前后对外伏安特性一致)
对内不等效 a RS I a I'
Is + - US
Uab RL
RS'
Uab' b RL
b
具有串联电阻的电压源称为有伴电压源,
2 1
(b) 伏安特性曲线相交 法求解图(a)电路
u = US i =US / R
§4 -l 分解的基本步骤
上例启示
如果在端钮1 1'处相连接的 是两个内部结构复杂或是内部 情况不明的单口网络,也可按 此思路求得这两个网络的端口 电压u和端口电流i,所不同的 是,需要的是这两个 单口网络 的VCR而不是元件的VCR。
第四章 分解方法与单口网络
§4-l 分解的基本步骤 §4-2单口网络的电压、电流关系 §4-3单口网络的置换——置换定理 §4-4单口网络的等效电路 §4-5一些简单的等效规律和公式 §4-6 戴维南定理√ §4-7 诺顿定理 √ §4-8 最大功率传递定理 §4-9 T形网络和Π形网络的等效变换
第4章 分解方法及单口网络
在第一章我们学过,一个元件的伏安关系 是由这个元件本身所决定的,这一关系不会因外接 电路不同而有所不同。同样,一个单口网络的伏安 关系也是由这个单口网络本身所确定的,与外接电 路无关,只要这个单口网络除了通过它的两个端钮 与外界相连接外,别无其他联系。
§4 -l 分解的基本步骤
i 1 + US N1 + u 1' N2 (a) 电压源及电阻的串联电路看 成两个单口N1和N2相连的电路 u = US u = Ri 0 US / R R u US Q
具有并联电阻的电流源称为有伴电流源。
有伴电压源和有伴电流源才能进行等效互换。
恒压源和恒流源不能等效互换
+
a I
I'
a
Uab'
US -
b
Is
b
应用:利用电源转换可以简化电路计算。 例1.
5A 2A 3 7 4 I
7 + 15v _ _ 8v + I 7
I=0.5A
例2.
5 10V 10V 5 6A
独立电压源短路; 独立电流源开路。
一、验证
例1 , 化简电路, 应用电源变换。
8 + 20V – 10V A 10 2.5A 8 10 A
