Koch分形曲线200812219
Koch类方波曲线的解析表达式的开题报告
Koch类方波曲线的解析表达式的开题报告开题报告：题目：Koch类方波曲线的解析表达式研究背景：Koch曲线是由瑞典数学家Helge von Koch于1904年首次提出的。
Koch曲线是一种分形曲线，它可以通过每次迭代将直线的每个线段替换为一系列更小的线段来生成。
Koch曲线的变形还有Koch雪花，是一种结构简单但却充满美感的曲线，很受数学爱好者的喜爱。
Koch类方波曲线是一类特殊的Koch曲线，它是由一条直线分别向左和向右延伸形成的折线，并且其每一段线段的长度都相等。
与其他Koch曲线不同，Koch类方波曲线的曲线形状更加接近方波，具有更加显著的周期性和对称性，因此在信号处理、图像处理以及计算机图形学等领域都有很广泛的应用。
研究目的：本文旨在研究Koch类方波曲线的解析表达式，通过推导该曲线的解析表达式，可以更加直观地描述其特征和性质，并且为进一步的应用研究提供理论上的基础。
研究方法：本文将采用数学分析、计算机模拟等方法来研究Koch类方波曲线的解析表达式。
具体地，通过对Koch类方波曲线进行多次迭代，得到其逐渐逼近方波的形状，并且通过数学分析和计算机模拟的方法，得到该曲线的解析表达式。
研究意义：研究Koch类方波曲线的解析表达式，不仅可以帮助我们了解这种特殊类型的Koch曲线的特点和性质，还可以为信号处理、图像处理以及计算机图形学等领域的应用提供理论上的支持和参考。
此外，在数学教学中，Koch类方波曲线也是一种非常好的教学资源，可以帮助学生更加深入地理解分形几何的概念和原理，提高学生的数学素养和创新思维能力。
预期成果：本文预期能够推导出Koch类方波曲线的解析表达式，并且通过计算机模拟和图像处理的方法来验证其正确性和可靠性。
同时，本文还将探讨Koch类方波曲线的一些特征和性质，并且对其应用研究进行简要介绍，为相关领域的研究提供理论支持和参考。
研究计划：第一步：收集和整理Koch类方波曲线的相关研究资料，包括历史沿革、数学原理、应用研究等方面的内容。
分形曲线与面积计算-精品
sinx1 cos x2
cos sin
Asin
cos
(1, 0)
1
0
cos sin
(0, 1)
0 sin
1
cos
5/11
MATLAB代码
function koch0(P,N)
end
plot(P(:,1),P(:,2)),axis off axis image
6/11
Kn的边数: Kn的周长:
Sn 4n
Ln
1 3n
4n
L0
Kn的维数: Dnln4/ln31.2618
Dn
lnN
/
ln
1
相邻两次的边数比和边长比
参考资料: 分形论——奇异 性探索,作者:林鸿溢
第 k 条边: x y((tt)) ((1 1 tt))x yk k ttyx kk 11,t(0,1)
1
L kyd 0 x [1 ( t)yk tk y 1](x k 1x k)dt
1 2(xk1xk)(ykyk1)
x L k
9/11
面积计算的数学实验报告(三选一,或题材自选)
一、 Koch分形雪花 1.算法描述Koch分形雪花
2.证明Koch分形雪花图 Kn 的边数为
Ln 34n1
3.求Koch分形雪花图 Kn 的面积
ln im Are(aKn)
10/11
二、竞赛题的实验设 (第一届全国大学生数学夏令营第6题 )
课外作业:完成面积计算的 数学实验报告(电子文档)
科赫曲线python代码
科赫曲线python代码科赫曲线是一种分形图形，它由一条线段不断地被三等分并替换成一个等边三角形的两个边构成。
在这个过程中，每个边都会被替换成另外两条边，形成越来越复杂的图形。
在Python中，我们可以使用递归函数来绘制科赫曲线。
下面是一个实现科赫曲线的Python代码：## 导入绘图库import turtle## 定义一个递归函数，绘制科赫曲线def koch(t, order, size):if order == 0:t.forward(size)else:for angle in [60, -120, 60, 0]:koch(t, order-1, size/3)t.left(angle)## 设置画布大小和背景颜色turtle.setup(width=800,height=600) turtle.bgcolor("white")## 创建海龟对象t = turtle.Turtle()## 设置海龟初始位置和朝向t.penup()t.goto(-300,-100)t.pendown()t.left(60)## 绘制第一层科赫曲线koch(t, 4, 600)## 隐藏海龟对象t.hideturtle()## 等待用户关闭窗口turtle.done()代码解析：1. 导入绘图库：使用import语句导入turtle库。
2. 定义递归函数：使用def语句定义一个名为koch的函数，该函数接受三个参数：海龟对象t、曲线阶数order和线段长度size。
3. 绘制基本线段：如果曲线阶数为0，直接向前画一条长度为size的直线段；否则，执行下一步。
4. 递归绘制科赫曲线：对于每个角度（60度、-120度、60度、0度），递归地绘制下一层科赫曲线。
其中，左转60度和右转-120度分别对应着等边三角形的两条边，左转0度用于连接两个三角形。
5. 设置画布和海龟对象：使用turtle.setup()函数设置画布大小和背景颜色，并创建一个海龟对象t。
koch分形维数
koch分形维数
Koch分形是一种经典的几何分形，它的构造过程是一种递归的过程。
在Koch 分形的构造中，我们可以看到随着递归层次的增加，分形的形状会变得越来越复杂，但同时它的面积却没有增加太多。
这是因为Koch分形是一种自相似结构，它的每一个小部分都与整体相似，但规模更小。
要计算Koch分形的维数，我们可以使用盒计数法。
盒计数法是一种通过将分形填充到一系列的盒子中，然后计算所需的最少盒子数来估计分形维数的方法。
对于Koch分形，随着递归层次的增加，每个盒子中的“点”数量会增加，因此所需的最少盒子数也会增加。
具体来说，我们可以将Koch分形划分为一系列边长为1的正方形，然后计算每个正方形中的“点”数量。
随着递归层次的增加，每个正方形中的“点”数量会增加，因此所需的最少盒子数也会增加。
当递归层次趋于无穷时，所需的最少盒子数会趋于一个常数，这个常数就是Koch分形的盒维数。
通过计算我们可以得到，当递归层次趋于无穷时，所需的最少盒子数为4/3^n，其中n是递归层次。
因此，Koch分形的盒维数为log(4)/log(3)约等于1.26185。
除了盒维数之外，Koch分形还有其他的维数，如填充维数和Hausdorff维数等。
其中Hausdorff维数是描述分形结构精细程度的重要参数，也是描述分形复杂性的重要指标之一。
总之，Koch分形是一种具有自相似结构的经典几何分形，其维数的计算方法有多种，其中盒计数法是一种常用的方法。
通过计算我们可以得到Koch分形的盒维数约为1.26185，这也是Koch分形的一个重要特征。
Koch分形雪花图的面积计算
Koch 分形雪花图的面积计算一、问题叙述分形几何图形最基本的特征是自相似性，这种自相似性是指局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似。
在具有自相似性的图形中，图形局部只是整体的缩影，而整体图形则是局部的放大。
而本文我们要分析的是Koch 分形雪花图，包含以下三个问题：1.描述Koch 分形雪花2.证明Koch 分形雪花图K n 的边数为n 1L 34n -=⨯3.求Koch 分形雪花图的面积（数据），求n n lim Area(K )→∞二、问题分析在分析Koch 分形雪花图之前，我们首先介绍Koch 分形曲线。
Koch 分形曲线的绘制原理是：从一条直线段开始，将线段中间的三分之一部分用一个等边三角形的两边代替，形成四条线段的折线，如图2.1所示：图2.1 对一条线段进行第一次Koch 分形然后，对形成的四条直线段的每一条的中间的三分之一部分用等边三角形的两边代替，形成十六条线段的折线。
这种迭代继续进行下去可以形成Koch 分形曲线。
在迭代过程中，图形中的点数将越来越多，而曲线的最终显示细节的多少将取决于迭代次数和显示系统的分辨率。
设P1和P2分别是原始的两个端点，现在需要在直线段的中间依次插入点Q1，Q2,Q3以产生第一次迭代图形。
显然，Q1位于P1右端直线段的三分之一处，Q3位于P1点右端直线段的三分之二处，而Q2点的位置可以看作由Q3绕Q1逆时针旋转60度而得到的，故可以处理Q Q 13经过正交变换而得到Q Q 12。
算法如下：（1）Q1P1+P P Q P1+P P /3;←←（2-1）/3;32（2-1）（2）T Q2Q1+Q3-Q A ←⨯（1）; （3）P5P2P2Q1P3Q P Q3←←←←；；2；4。
在算法中，用正交矩阵A 构造正交变换，其功能作用是对向量作旋转，使之成为长度不变的另一向量。
在绘制Koch 曲线的过程中，取旋转的角度为3π，则正交矩阵A 应取为：cos()sin()33A=sin()cos()33ππππ⎛⎫- ⎪⎪ ⎪ ⎪⎝⎭ 1.Koch 分形雪花的描述Koch 分形雪花的原始图形是等边三角形，它是由三条相等的线段围成的三角形。
koch曲线 迭代函数
Koch曲线是一种经典的分形图形，由瑞典数学家Helge von Koch于1904年提出。
科赫曲线的生成过程是一个递归的过程，可以由以下步骤描述：首先取一条长度为1的线段，然后将其等分为三段，中间那段用等边三角形替换，之后对每个小线段进行同样的操作。
具体来说，迭代步骤如下：
1. 取一条长度为1的线段；
2. 将线段等分为三等分，中间的那一段不变，其余两段分别替换为两个等边三角形；
3. 对新得到的每一段（包括两个等边三角形和中间的线段）进行相同的操作。
这个过程会一直重复进行，直到线段的长度变为0为止。
这样，我们就可以得到一条科赫曲线。
初始线的起点和终点可以是任意的，例如[0,0]和[1,0]。
此外，我们也可以通过编程来绘制科赫曲线。
例如在Python中，我们可以使用turtle库来实现；在MATLAB中，也有专门的函数用于绘制科赫曲线。
分形几何中一些经典图形的Matlab画法+[文档在线提供]
![分形几何中一些经典图形的Matlab画法+[文档在线提供]](https://img.taocdn.com/s3/m/da97d930c5da50e2524d7ff5.png)
分形几何中一些经典图形的Matlab画法（1）Koch曲线程序koch.mfunction koch(a1,b1,a2,b2,n)%koch(0,0,9,0,3)%a1,b1,a2,b2为初始线段两端点坐标,n为迭代次数a1=0;b1=0;a2=9;b2=0;n=3;%第i-1次迭代时由各条线段产生的新四条线段的五点横、纵坐标存储在数组A、B中[A,B]=sub_koch1(a1,b1,a2,b2);for i=1:nfor j=1:length(A)/5;w=sub_koch2(A(1+5*(j-1):5*j),B(1+5*(j-1):5*j));for k=1:4[AA(5*4*(j-1)+5*(k-1)+1:5*4*(j-1)+5*(k-1)+5),BB(5*4*(j-1)+5*(k-1)+1:5*4*(j-1)+5*(k-1)+5)] =sub_koch1(w(k,1),w(k,2),w(k,3),w(k,4));endendA=AA;B=BB;endplot(A,B)hold onaxis equal%由以(ax,ay),(bx,by)为端点的线段生成新的中间三点坐标并把这五点横、纵坐标依次分别存%储在数组A,B中function [A,B]=sub_koch1(ax,ay,bx,by)cx=ax+(bx-ax)/3;cy=ay+(by-ay)/3;ex=bx-(bx-ax)/3;ey=by-(by-ay)/3;L=sqrt((ex-cx).^2+(ey-cy).^2);alpha=atan((ey-cy)./(ex-cx));if (ex-cx)<0alpha=alpha+pi;enddx=cx+cos(alpha+pi/3)*L;dy=cy+sin(alpha+pi/3)*L;A=[ax,cx,dx,ex,bx];B=[ay,cy,dy,ey,by];%把由函数sub_koch1生成的五点横、纵坐标A,B顺次划分为四组,分别对应四条折线段中%每条线段两端点的坐标,并依次分别存储在4*4阶矩阵k中,k中第i(i=1,2,3,4)行数字代表第%i条线段两端点的坐标function w=sub_koch2(A,B)a11=A(1);b11=B(1);a12=A(2);b12=B(2);a21=A(2);b21=B(2);a22=A(3);b22=B(3);a31=A(3);b31=B(3);a32=A(4);b32=B(4);a41=A(4);b41=B(4);a42=A(5);b42=B(5);w=[a11,b11,a12,b12;a21,b21,a22,b22;a31,b31,a32,b32;a41,b41,a42,b42];图1 V on Koch曲线（2）Levy 曲线程序levy.mfunction levy(n)% levy(16),n为levy曲线迭代次数%x1,y1,x2,y2为初始线段两端点坐标,nn为迭代次数n=16;x1=0;y1=0;x2=1;y2=0;%第i-1次迭代时由各条线段产生的新两条线段的三端点横、纵坐标存储在数组X、Y中[X,Y]=levy1(x1,y1,x2,y2);for i=1:nfor j=1:length(X)/3w=levy2(X(1+3*(j-1):3*j),Y(1+3*(j-1):3*j));[XX(3*2*(j-1)+1:3*2*(j-1)+3),YY(3*2*(j-1)+1:3*2*(j-1)+3)]=levy1(w(1,1),w(1,2),w(1,3),w(1,4) );[XX(3*2*(j-1)+3+1:3*2*(j-1)+3+3),YY(3*2*(j-1)+3+1:3*2*(j-1)+3+3)]=levy1(w(2,1),w(2,2),w( 2,3),w(2,4));endX=XX;Y=YY;endplot(X,Y)hold onaxis equal%由以(x1,y1),(x2,y2)为端点的线段生成新的中间点坐标并把(x1,y1),(x2,y2)连同新点横、纵坐%标依次分别存储在数组X,Y中function [X,Y]=levy1(x1,y1,x2,y2)x3=1/2*(x1+x2+y1-y2);y3=1/2*(-x1+x2+y1+y2);X=[x1,x3,x2];Y=[y1,y3,y2];%把由函数levy1生成的三点横、纵坐标X,Y顺次划分为两组,分别对应两条折线段中每条线%段两端点的坐标,并依次分别存储在2*4阶矩阵w中,w中第i(i=1,2)行数字代表第i条线段%两端点的坐标function w=levy2(X,Y)a11=X(1);b11=Y(1);a12=X(2);b12=Y(2);a21=X(2);b21=Y(2);a22=X(3);b22=Y(3);w=[a11,b11,a12,b12;a21,b21,a22,b22];图2 Levy 曲线（3）分形树程序tree.hfunction tree(n,a,b)% tree(8,pi/8,pi/8),n为分形树迭代次数%a,b为分枝与竖直方向夹角%x1,y1,x2,y2为初始线段两端点坐标,nn为迭代次数n=8;a=pi/8;b=pi/8;x1=0;y1=0;x2=0;y2=1;plot([x1,x2],[y1,y2])hold on[X,Y]=tree1(x1,y1,x2,y2,a,b);hold onW=tree2(X,Y);w1=W(:,1:4);w2=W(:,5:8);% w为2^k*4维矩阵,存储第k次迭代产生的分枝两端点的坐标, % w的第i(i=1,2,…,2^k)行数字对应第i个分枝两端点的坐标w=[w1;w2];for k=1:nfor i=1:2^k[X,Y]=tree1(w(i,1),w(i,2),w(i,3),w(i,4),a,b);W(i,:)=tree2(X,Y);endw1=W(:,1:4);w2=W(:,5:8);w=[w1;w2];end%由每个分枝两端点坐标(x1,y1),(x2,y2)产生两新点的坐标(x3,y3),(x4,y4),画两分枝图形,并把%(x2,y2)连同新点横、纵坐标分别存储在数组X,Y中function [X,Y]=tree1(x1,y1,x2,y2,a,b)L=sqrt((x2-x1)^2+(y2-y1)^2);if (x2-x1)==0a=pi/2;else if (x2-x1)<0a=pi+atan((y2-y1)/(x2-x1));elsea=atan((y2-y1)/(x2-x1));endendx3=x2+L*2/3*cos(a+b);y3=y2+L*2/3*sin(a+b);x4=x2+L*2/3*cos(a-b);y4=y2+L*2/3*sin(a-b);a=[x3,x2,x4];b=[y3,y2,y4];plot(a,b)axis equalhold onX=[x2,x3,x4];Y=[y2,y3,y4];%把由函数tree1生成的X,Y顺次划分为两组,分别对应两分枝两个端点的坐标,并存储在一维%数组w中function w=tree2(X,Y)a1=X(1);b1=Y(1);a2=X(2);b2=Y(2);a3=X(1);b3=Y(1);a4=X(3);b4=Y(3);w=[a1,b1,a2,b2,a3,b3,a4,b4];图3 分形树（4）IFS算法画Sierpinski三角形程序sierpinski_ifs.hfunction sierpinski_ifs(n,w1,w2,w3)%sierpinski_ifs(10000,1/3,1/3,1/3)%w1,w2,w3出现频率n=10000;w1=1/3;w2=1/3;w3=1/3;M1=[0.5 0 0 0 0.5 0];M2=[0.5 0 0.5 0 0.5 0];M3=[0.5 0 0.25 0 0.5 0.5];x=0;y=0;% r为[0,1]区间内产生的n维随机数组r=rand(1,n);B=zeros(2,n);k=1;% 当0<r(i)<1/3时,进行M1对应的压缩映射;% 当1/3=<r(i)<2/3时,进行M2对应的压缩映射;% 当2/3=<r(i)<1时,进行M3对应的压缩映射;for i=1:nif r(i)<w1a=M1(1);b=M1(2);e=M1(3);c=M1(4);d=M1(5);f=M1(6);else if r(i)<w1+w2a=M2(1);b=M2(2);e=M2(3);c=M2(4);d=M2(5);f=M2(6);else if r(i)<w1+w2+w3a=M3(1);b=M3(2);e=M3(3);c=M3(4);d=M3(5);f=M3(6);endendendx=a*x+b*y+e;y=c*x+d*y+f;B(1,k)=x;B(2,k)=y;k=k+1;endplot(B(1,:),B(2,:),'.','markersize',0.1)图4 Sierpinski三角形（5）IFS算法画Julia集程序julia_ifs.hfunction julia_ifs(n,cx,cy)% julia_ifs(100000,-0.77,0.08)% f(z)=z^2+c,cx=real(c);cy=image(c);n=10000;cx=-0.77;cy=0.08;% z^2+c=z0,x=real(z0);y=image(z0);x=1;y=1;B=zeros(2,n);k=1;% A为产生的服从标准正态分布的n维随机数组A=randn(1,n);for i=1:nwx=x-cx;wy=y-cy;if wx>0alpha=atan(wy/wx);endif wx<0alpha=pi+atan(wy/wx);endif wx==0alpha=pi/2;endalpha=alpha/2;r=sqrt(wx^2+wy^2);if A(i)<0r=-sqrt(r);elser=sqrt(r);endx=r*cos(alpha);y=r*sin(alpha);B(1,k)=x;B(2,k)=y;k=k+1;endplot(B(1,:),B(2,:),'.','markersize',0.1)图5 Julia 集(6)逃逸时间算法画Sierpinski垫片程序sierpinski.hfunction sierpinski(a,b,c,d,n,m,r)%sierpinski(0,0,1,1,12,200,200)%(a,b),(c,d)收敛区域左上角和右下角坐标,m为分辨率% n为逃逸时间,需要反复试探,r逃逸半径a=0;b=0;c=1;d=1;n=12;m=200;r=200;B=zeros(2,m*m);w=1;for i=1:mx0=a+(c-a)*(i-1)/m;for j=1:my0=b+(d-b)*(j-1)/m;x=x0;y=y0;for k=1:nif y>0.5x=2*x;y=2*y-1;else if x>=0.5x=2*x-1;y=2*y;elsex=2*x;y=2*y;endif x^2+y^2>rbreak;endendif k==nB(1,w)=i;B(2,w)=j;w=w+1;endendendplot(B(1,:),B(2,:),'.','markersize',0.1)图6 Sierpinski三角形垫片(7)元胞自动机算法画Sierpinski三角形程序一维元胞自动机sierpinski_ca1.hfunction sierpinski_ca1(m,n)%sierpinski_ca1(1000,3000)m=1000;n=3000;x=1;y=1;t=1;w=zeros(2,m*n);s=zeros(m,n);s(1,fix(n/3))=1;for i=1:m-1for j=2:n-1if (s(i,j-1)==1&s(i,j)==0&s(i,j+1)==0)|(s(i,j-1)==0&s(i,j)==0&s(i,j+1)==1) s(i+1,j)=1;w(1,t)=x+3+3*j;w(2,t)=y+5*i;t=t+1;endendendplot(w(1,:),w(2,:),'.','markersize',1)图7.1 一维元胞自动机画Sierpinski三角形二维元胞自动机sierpinski_ca2.hfunction sierpinski_ca2(m,n)%sierpinski_ca2(400,400)m=400;n=400;t=1;w=zeros(2,m*n);s=zeros(m,n);s(m/2,n/2)=1;for i=[m/2:-1:2,m/2:m-1]for j=[n/2:-1:2,n/2:n-1]ifmod(s(i-1,j-1)+s(i,j-1)+s(i+1,j-1)+s(i-1,j)+s(i+1,j)+s(i-1,j+1)+s(i,j+1)+s(i+1,j+1),2)==1 s(i,j)=1;w(1,t)=i;w(2,t)=j;t=t+1;endendendplot(w(1,:),w(2,:),'.','markersize',0.1)图7.2 二维元胞自动机画Sierpinski三角形(8)IFS算法画Helix曲线程序helix_ifs.hfunction helix_ifs(n,w1,w2,w3)%helix_ifs(20000,0.9,0.05,0.05)%w1,w2,w3为出现频率n=20000;w1=0.9;w2=0.05;w3=0.05;M1=[0.787879 -0.424242 1.758647 0.242424 0.859848 1.408065];M2=[-0.121212 0.257576 -6.721654 0.05303 0.05303 1.377236];M3=[0.181818 -0.136364 6.086107 0.090909 0.181818 1.568035];x=0;y=0;% r为[0,1]区间内产生的n维随机数组r=rand(1,n);B=zeros(2,n);k=1;% 当0<r(i)<1/3时,进行M1对应的压缩映射;% 当1/3=<r(i)<2/3时,进行M2对应的压缩映射;% 当2/3=<r(i)<1时,进行M3对应的压缩映射;for i=1:nif r(i)<w1a=M1(1);b=M1(2);e=M1(3);c=M1(4);d=M1(5);f=M1(6);else if r(i)<w1+w2a=M2(1);b=M2(2);e=M2(3);c=M2(4);d=M2(5);f=M2(6);else if r(i)<w1+w2+w3a=M3(1);b=M3(2);e=M3(3);c=M3(4);d=M3(5);f=M3(6);endendendx=a*x+b*y+e;y=c*x+d*y+f;B(1,k)=x;B(2,k)=y;k=k+1;endplot(B(1,:),B(2,:),'.','markersize',0.1)图8 Helix曲线。
Koch曲线
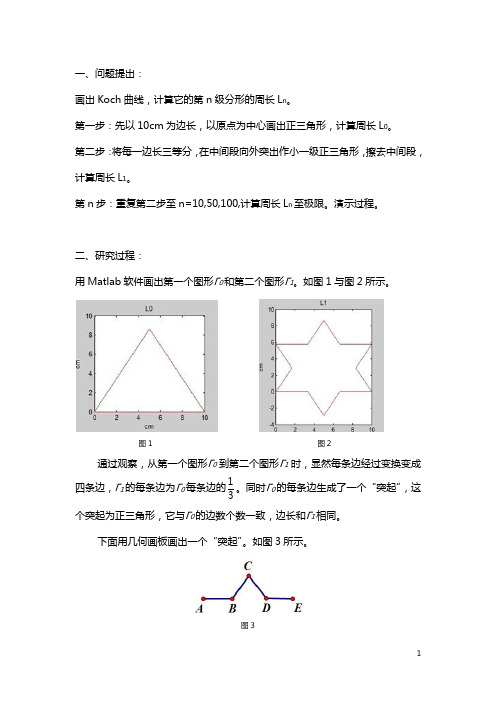
一、问题提出：画出Koch 曲线，计算它的第n 级分形的周长L n 。
第一步：先以10cm 为边长，以原点为中心画出正三角形，计算周长L 0。
第二步：将每一边长三等分，在中间段向外突出作小一级正三角形，擦去中间段，计算周长L 1。
第n 步：重复第二步至n=10,50,100,计算周长L n 至极限。
演示过程。
二、研究过程：用Matlab 软件画出第一个图形Γ0和第二个图形Γ1。
如图1与图2所示。
图1 图2通过观察，从第一个图形Γ0到第二个图形Γ1时，显然每条边经过变换变成四条边，Γ1的每条边为Γ0每条边的31。
同时Γ0的每条边生成了一个“突起”，这个突起为正三角形，它与Γ0的边数个数一致，边长和Γ1相同。
下面用几何画板画出一个“突起”。
如图3所示。
图3由图3可以看出：AE 为原来的边，取它的三分点B 、D ，在由BD 为边做出△BCD 。
C 点可以看成D 绕B 点逆时针旋转60°得到，此时B 、C 、D 确定。
设A （x 1，y ）, E （x 2，y ），则B ⎪⎭⎫ ⎝⎛-+,y x x x 3121；D ⎪⎭⎫ ⎝⎛--,y x x x 3122；设()00,y x BC =→，而⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡032123232103cos sin sin cos 121200x x x x θθθθy x ， 得到()⎪⎪⎩⎪⎪⎨⎧-=-=636120120x x y x x x ，即()⎪⎪⎭⎫ ⎝⎛--=→63,61212x x x x BC 。
故用Matlab 演示过程时，在正三角形三边均取两个三分点，然后通过转轴变换移动D 至C 点，最后连接BC 、CD 即可得到图像。
同理可得，从Γn-1到Γn 的过程中，每条边经过变换变成四条边，Γn 的每条边为Γn-1每条边的31。
同时Γn-1的每条边生成了一个正三角形，它与Γn-1的边数个数一致，边长和Γn 相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n=m; end plot(p(:,1),p(:,2),'k') axis equal axis off 矩形生成元第二种曲线 p=[0 0;10 0];n=2; A=[0 -1;1 0]; for k=1:4 d=diff(p/3);m=5*n-4; q=p(1:n-1,:); p(6:5:m,:)=p(2:n,:); p(2:5:m,:)=q+d; p(3:5:m,:)=q+d+.7*d*A'; p(4:5:m,:)=q+2*d+.7*d*A'; p(5:5:m,:)=q+2*d; n=m; end plot(p(:,1),p(:,2),'k') axis equal axis off
A=
cos 3 sin 3
π π
− sin 3 cos 3
π
π
算法根据初始数据(和点的坐标)，产生图1中5个结点的坐标。结点的坐标数组 形成一个5× 2矩阵，矩阵的第一行为P1的坐标，第二行为P2的坐标，⋯⋯，第五行为P5 的坐标。矩阵的第一列元素分别为5个结点的X坐标，第二列元素分别为5个结点的Y 坐标。 进一步考虑Koch曲线形成过程中结点数目的变化规律。设第 k次迭代产生结点 数 为 nk ， 第 k+1 次 迭 代 产 生 结 点 数 为 nk+1 ， 则 nk 和 nk+1 之 间 的 递 推 关 系 式 为
7
6
i=1; for j=1:2:n p1=p(j,:); p2=p(j+1,:); d=(p2-p1)/3; new(i,:)=p1;i=i+1; q1=p1+d; new(i,:)=q1;i=i+1; new(i,:)=q1;i=i+1; new(i,:)=p1+d+e*d*a';i=i+1; new(i,:)=q1;i=i+1; new(i,:)=p1+d+e*d*a;i=i+1; new(i,:)=p1+d;i=i+1; q2=p1+2*d; new(i,:)=q2;i=i+1; new(i,:)=q2;i=i+1; new(i,:)=p1+2*d+d*a;i=i+1; new(i,:)=q2;i=i+1; new(i,:)=p1+2*d+d*a';i=i+1; new(i,:)=p1+2*d;i=i+1; new(i,:)=p2;i=i+1; end n=n*7;p=new; end for m=1:2:n line([p(m,1) p(m+1,1)],[p(m,2) p(m+1,2)],'Color','k'); end axis equal axis off 矩形生成元第一种曲线 p=[0 0;10 0];n=2; A=[0 -1;1 0]; for k=1:4 d=diff(p/3);m=5*n-4; q=p(1:n-1,:); p(6:5:m,:)=p(2:n,:); p(2:5:m,:)=q+d; p(3:5:m,:)=q+d+1*d*A'; p(4:5:m,:)=q+2*d+1*d*A'; p(5:5:m,:)=q+2*d;
3
程序运行后，可得如下分形曲线图形：
图1所示的简单图形被称为是koch曲线的生成元。 下面给出其它几种生成元及对 应曲线：
4
5
1.4 附源程序
第一种树形源程序： p=[0 0;10 10];n=2; line(p(:,1),p(:,2),'Color','k'); A=[cos(pi/6) -sin(pi/6);sin(pi/6) cos(pi/6)]; for k=1:4 i=1; for j=1:2:n p1=p(j,:);p2=p(j+1,:); d=(p2-p1)/3; r(i,:)=p1;i=i+1; q1=p1+d; r(i,:)=q1;i=i+1; r(i,:)=q1;i=i+1; q2=q1+d*A'; r(i,:)=q2;i=i+1; r(i,:)=q1;i=i+1; q3=p1+2*d; r(i,:)=q3;i=i+1; r(i,:)=q3;i=i+1; q4=q3+d*A; r(i,:)=q4;i=i+1; r(i,:)=q3;i=i+1; r(i,:)=p2;i=i+1; xy=[q1;q2]; line(xy(:,1),xy(:,2),'Color','k'); xy=[q3;q4]; line(xy(:,1),xy(:,2),'Color','k'); end p=r; n=5*n; end axis equal axis off 第二种树形源程序 clear p=[0 0;0 15]; b=pi/8;e=1.5; a=[cos(b) -sin(b);sin(b) cos(b)]; n=2; for k=1:4
nk+1=4nk-3。
2
1.3 MATLAB实现
p=[0 0;10 0];n=2; A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; for k=1:5 d=diff(p)/3;m=4*n-3; q=p(1:n-1,:);p(5:4:m,:)=p(2:n,:); p(2:4:m,:)=q+d; p(3:4:m,:)=q+d+d*A'; p(4:4:m,:)=q+2*d; n=m; end plot(p(:,1),p(:,2),'k') axis equal axis off 。
这种迭代继续进行下去可以形成 Koch 分形曲线。在迭代过程中，图形中的点 将越来越多，而曲线最终显示细节的多少将取决于迭代次数和显示系统的分辩率。
1.2 算法分析
算法分析：考虑由直线段(2 个点)产生第一个图形(5 个点)的过程。设P1和P5分 别为原始直线段的两个端点。现在需要在直线段的中间依次插入P2、P3、P4三个点产 生第一次迭代的图形(图1)。显然，P2 位于P1点右端直线段的三分之一处，P4 位于P1 点右端直线段的三分之二处；而P3点的位置可以看成是P4由点绕P2旋转60 度(逆时针 方向)而得到的，故可以处理为向量P2P4经正交变换而得到向量P2P3。算法如下: P2=P1+(P5-P1)/3; P4=P1+2*(P5-P1)/3; P3=P2+(P4-P2)*AT; 在(3)中， A为正交矩阵:
Koch 分形曲线
姓名：赵仓仓 学号：200812219 专业：统计学
注：
摘 要：分形理论是当今世界十分风靡和活跃的新理论、新学科。分形的概念是美籍
数学家曼德布罗特(B.B.Mandelbort)首先提出的。
关键词：分形原理
算法分析
MATLAB实现
源程序
1
Koch 分形曲线
1.1 分ቤተ መጻሕፍቲ ባይዱ原理
这是一类复杂的平面曲线，可用算法描述。从一条直线段开始，将线段中间三 分之一部分用等边三角形的两条边代替，形成具有5 个结点的图形(图1)；在新的图 形中，又将图中每一直线段中间的三分之一部分都用一等边三角形的两条边代替， 再次形成新的图形(图2)，这时，图形中共有17 个结点。