各种有趣的分形
魏尔斯特拉斯曲线

魏尔斯特拉斯曲线
魏尔斯特拉斯曲线是一条著名的分形曲线,由德国数学家魏尔斯特拉斯于19世纪提出。
这条曲线的特点是在任何局部都有类似于整个曲线的形态,因此被称为自相似曲线。
魏尔斯特拉斯曲线的构造方法非常简单,从一条线段开始,每次将其分成三等份,然后将中间一段替换成两条形状相同的线段,这样就得到了新的曲线。
重复这个过程无限次,就可以得到越来越复杂的魏尔斯特拉斯曲线。
尽管魏尔斯特拉斯曲线看起来非常复杂,但它却有许多有趣的性质和应用。
例如,它可以用于描述自然界中的许多曲线形态,如树枝、河流、山脉等。
此外,魏尔斯特拉斯曲线还可以用于解决一些数学问题,如分形几何、复杂度理论等。
- 1 -。
自然界中的数学

自然界中的数学你是否曾经停下来环顾四周,注意到我们周围世界中的神奇的形状和图案?数学构成了自然世界的基石,并以惊人的方式展现出来。
下面是一些自然界数学的例子。
斐波那契序列(The Fibonacci Sequence)斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
它是一个简单而深奥的数列。
序列从数字1和1开始,然后每个后续的数字通过将前面的两个数字相加来找到。
因此,在1和1之后,下一个数字是2(1 + 1)。
下一个数字是3(1+ 2) ,然后是5(2 + 3) ,如此类推。
值得注意的是,序列中的数字在自然界中经常可以看到。
一些例子包括松果的螺旋数,菠萝或向日葵的种子数,或一朵花的花瓣数。
上图:向日葵的两条螺旋线符合斐波那契数列的数字规律上图:松果的螺旋数斐波那契数列中的数字还形成了一个独特的形状,被称为斐波那契螺旋,我们在自然界中看到它的形式是贝壳和飓风的形状。
上图:贝壳的形状自然界的分形(Fractals in Nature):分形是我们在自然界中看到的另一种有趣的数学形状。
分形是一种相似的、重复的形状,这意味着同样的基本形状在形状本身中反复出现。
换句话说,如果你要放大或缩小,整个形状都是一样的。
上图:蕨类植物的叶子分形构成了我们世界的许多方面,包括蕨类植物的叶子、树枝、我们大脑中的神经元分支和海岸线。
上图:神经元分支自然界的六边形(Hexagons in Nature):自然界的另一个几何奇观是六边形。
牛顿迭代分形

牛顿迭代分形牛顿迭代分形,也被称为牛顿分形或牛顿法则,是一种基于数学原理的图像生成算法。
它利用牛顿迭代的思想和复数运算,通过不断迭代计算,可以生成一幅幅美丽而神奇的分形图形。
牛顿迭代分形的生成过程可以简单描述如下:首先,选择一个复数作为初始值,然后通过不断迭代计算来寻找该复数的根。
根据牛顿迭代法的原理,我们可以得到下一个近似根的值,然后再将该值作为新的初始值进行迭代计算,直到达到预设的迭代次数或者满足停止条件。
最终,我们可以将迭代过程中的所有值映射到一个二维平面上,从而生成一张牛顿迭代分形图。
牛顿迭代分形的生成过程中,不同的初始值会产生不同的分形图形。
在分形图中,我们可以看到许多迭代过程中的轨迹,这些轨迹形成了分形的结构。
分形通常具有自相似性,即无论观察整个图像还是它的一部分,都会发现相似的形态或图案。
牛顿迭代分形在数学研究、计算机图形学、艺术创作等领域都有广泛的应用。
它不仅可以帮助我们理解复数和迭代的概念,还可以产生出许多美丽而复杂的图像。
这些图像不仅能够为我们提供视觉上的享受,还可以激发我们对数学和艺术的兴趣。
通过牛顿迭代分形的创作过程,我们可以感受到数学的魅力和无穷的可能性。
每一次的迭代计算,都是在数学的世界中进行探索和发现。
而每一张生成的分形图像,都是对数学美的一次呈现和诠释。
当我们深入探索牛顿迭代分形时,我们会发现其中隐藏着无限的奥秘和惊喜。
这些分形图像不仅令人惊叹,还能够启发我们对数学和艺术的思考。
通过创作和欣赏牛顿迭代分形,我们可以感受到数学的美妙和艺术的魅力,同时也能够培养我们的创造力和思维能力。
牛顿迭代分形是一种令人着迷的图像生成算法。
它不仅展示了数学的美丽和复杂性,还激发了我们对数学和艺术的兴趣。
通过创作和欣赏牛顿迭代分形,我们可以感受到数学的魅力和艺术的魔力,同时也能够培养我们的创造力和思维能力。
让我们一起沉浸在牛顿迭代分形的世界中,探索数学与艺术的交汇之处!。
乌龟壳数学

乌龟壳数学乌龟壳是一种独特的天然结构,也是数学中的一个有趣的研究对象。
在数学领域中,乌龟壳有着许多有趣的应用和性质。
本文将介绍乌龟壳在数学中的应用和相关概念,并探讨一些和乌龟壳相关的数学问题。
一、乌龟壳的结构特点乌龟壳是由一系列分层的骨质板块组成的,这些板块呈现出环形的形状。
乌龟壳的外观呈现出一种美丽的几何图形,其中既有规则的对称性,也有不规则的变化。
乌龟壳的基本结构特点包括以下几个方面:1. 螺旋结构:乌龟壳呈现出螺旋形的结构,这种结构使得乌龟壳能够提供良好的保护和支撑功能。
螺旋结构在数学中有着广泛的应用,例如斐波那契数列中的螺旋形式就与乌龟壳的形状相似。
2. 分层结构:乌龟壳由一系列分层的骨质板块组成,每一层都呈现出环形的形状。
这种分层结构使得乌龟壳能够具备一定的韧性和可承受压力的能力。
在数学中,分层结构也是一个重要的研究对象,例如分层图形和分层算法等就与乌龟壳的结构特点有关。
3. 几何形状:乌龟壳的外观呈现出一种美丽而复杂的几何图形。
乌龟壳的形状包括了曲线、直线、圆形等多种几何形状,同时还包括了一些不规则的变化。
几何形状在数学中是一个广泛研究的领域,乌龟壳为数学家们提供了一个有趣的几何模型。
二、乌龟壳在数学中的应用乌龟壳作为一种特殊的几何结构,在数学中有着广泛的应用。
以下是部分乌龟壳在数学中的应用:1. 曲线绘制:乌龟壳的曲线形状能够通过数学模型进行准确绘制。
乌龟壳曲线的绘制方法可以通过数学建模和计算机程序实现,这不仅有助于数学研究,还可以应用于艺术设计和计算机图形学等领域。
2. 分形结构:乌龟壳的分层结构具有分形的特性。
分形是一种具有自相似性的几何结构,这种特性在计算机图形学、优化算法和信息压缩等领域有着广泛的应用。
乌龟壳的分形结构为数学家们提供了一个有趣的分形模型。
3. 压力分析:乌龟壳的分层结构使得它能够承受来自外部的压力。
数学家可以通过分析乌龟壳的结构和力学特性,研究乌龟壳在不同压力下的形变和破坏过程。
数学故事数学中的趣味事件

数学故事数学中的趣味事件数学故事:数学中的趣味事件在平淡的数学世界中,也有一些趣味十足的事件发生。
它们或让人眼前一亮,或令人大跌眼镜,但无论如何,都为数学增添了一抹有趣的色彩。
让我们一起来聆听这些数学中的趣味故事。
1. 神奇的费马大定理有关费马大定理的故事可谓数学界的传奇。
费马大定理初次被提出于17世纪,由法国数学家费马提出,并在其藏书中注明了“此处证明过程太长,无法在此一页内展示”的字样。
这个问题经历了数百年的研究,直到1994年,英国数学家安德鲁·怀尔斯才终于找到了证明该定理的方法,不过其证明也十分复杂,需要大量高深的数学知识。
费马大定理因其数学深奥且引人入胜的历程而成为数学界的经典之作。
2. 无限的神秘数字ππ这个神秘的数字早已为人所熟知,它代表着圆周率的近似值。
然而,尽管π是一个无理数,并且无限不循环,但人们却发现了一些有趣有趣的与其相关的现象。
例如,将π前1000位的数字进行排列,可以发现出现“0123456789”等连续数字的次数近乎相等。
此外,π还具有自表达的能力,人们已经发现无穷多个可以表示π的公式,这给数学家们带来了无尽的探索空间。
3. 引人入胜的拓扑学拓扑学是数学中的一个分支,研究的是空间的性质和形状。
在拓扑学中,有一种有趣的结构叫做莫比乌斯带。
莫比乌斯带是一个由一个带形纸条做成的结构,其特点是只有一边和一个面。
当你沿着莫比乌斯带的一侧画一笔时,你会发现,最终画满整个带的两侧,这种独特的性质让人颇感神奇。
拓扑学中还有许多类似的有趣结构和问题,令人着迷。
4. 可视化的分形世界分形是一种自相似的结构,即在不同的尺度上仍然保持着相似性。
分形的美妙之处在于,无论我们放大还是缩小一个分形结构,我们总能够看到这个结构中不断重复出现的相似图案。
著名的科赫雪花和曼德勃罗集合就是分形的代表作。
通过数学的计算和图形的可视化,我们能够进一步探索分形世界的奥秘。
5. 数学与艺术的完美结合数学与艺术之间的关系一直以来都备受争议。
各种有趣的分形

各种有趣的分形我们看到正方形,圆,球等物体时,不仅头脑里会迅速反映出它是什么,同时,只要我们有足够的数学知识,我们头脑中也反映出它的数学概念,如正方形是每边长度相等的四边形,圆是平面上与某一点距离相等的点的集合,等等。
但是,当我们看到一个山的形状时,我们会想到什么"这是山",没错,山是如此的不同于其他景象,以至于你如果绘画水平不高,根本画不出象山的东西。
可是,山到底是什么"它既不是三角形,也不是球,我们甚至不能说明山具有怎样的几何轮廓,但为什么我们却有如此直观而又强烈的山的印象"分形的创始人是曼德布洛特思考了这个问题。
让我们先来熟悉几个典型的分形。
图中的风景图片又是说明分形的另一很好的例子。
这美丽的图片是利用分形技术生成的。
在生成自然真实的景物中,分形具有独特的优势,因为分形可以很好地构建自然景物的模型。
这是一棵厥类植物,仔细观察,你会发现,它的每个枝杈都在外形上和整体一样,仅仅在尺寸上小了一些。
而枝杈的枝杈也和整体一样,只是变得更加小了。
Sierpinski三角形具有严格的自相似特性Kohn雪花具有严格的自相似特性分维及分形的定义分维概念的提出对于欧几里得几何所描述的整形来说,可以由长度、面积、体积来测度。
但用这种方法对分形的层层细节做出测定是不可能的。
曼德尔布罗特放弃了这些测定而转向了维数概念。
分形的主要几何特征是关于它的构造的不规那么性和复杂性,主要特征量应该是关于它的不规那么性和复杂性程度的度量,这可用"维数〞来表征。
维数是几何形体的一种重要性质,有其丰富的涵。
整形几何学描述的都是有整数维的对象:点是零维的,线是一维的,面是二维的,体是三维的。
这种几何对象即使做拉伸、压缩、折叠、扭曲等变换,它们的维数也是不变的;这种维数称为"拓扑维〞,记为d。
例如当把一地图卷成筒,它仍然是一个二维信息载体;一根绳子团成团,仍然是一维构造。
但曼德尔布罗特认为,在分形世界里,维数却不一定是整数的。
立体几何中的数学文化——“四面体”与“阳蛇”

立体几何中的数学文化——“四面体”与“阳蛇”引言立体几何是数学中的一个重要分支,它研究的是三维空间中的几何形体和其性质。
在立体几何中,有两个非常有趣的几何形体,即“四面体”和“阳蛇”。
本文将重点探讨这两个几何形体在数学文化中的作用和意义。
“四面体”的数学文化四面体是一个由四个面组成的多面体,在立体几何中具有独特的性质和形状。
它在数学文化中扮演了重要角色。
首先,四面体是许多数学问题和定理的基础,如欧拉公式和拓扑学中的一些理论。
其次,四面体也被广泛应用于建筑、工程和科学研究等领域,它的几何性质和稳定性使其成为一种理想的结构形体。
“阳蛇”的数学文化阳蛇是一个立体几何中的特殊形体,它具有蛇状的结构特征。
阳蛇在数学文化中也有着重要的地位。
一方面,阳蛇是一个很好的几何分形模型,它可以用来研究分形几何和混沌理论等方面的问题。
另一方面,阳蛇还被应用于艺术和设计等领域,其独特的形状和美学价值使其成为一种受欢迎的艺术元素。
结论立体几何中的数学文化以“四面体”和“阳蛇”为代表,它们在数学研究、工程应用和艺术设计等领域都发挥着重要作用。
通过深入研究和理解这些几何形体,我们能够更好地欣赏数学的美妙和应用于实际生活中。
参考文献:- Smith, J. (2010). The Mathematics of Geometry: An Introduction to Non-Euclidean Geometry. Cambridge University Press.- Johnson, R. (2015). Fractals Everywhere. Elsevier.。
分形布朗运动原理-概述说明以及解释

分形布朗运动原理-概述说明以及解释1.引言1.1 概述概述分形布朗运动是一种具有分形特征的随机运动模型,它结合了分形几何学和布朗运动理论。
分形几何学是一门研究自相似性和自统一性的几何学,而布朗运动则是描述粒子在液体或气体中的随机运动。
分形布朗运动的研究源于对自然界中许多复杂现象的观察和模拟。
自然界中的很多系统表现出分形的特征,如树枝的分支、云朵的形状、山脉的轮廓等。
而布朗运动则是对微观粒子在液体和气体中的扩散运动进行建模,是统计物理学的重要研究内容之一。
本文旨在介绍分形布朗运动的基本原理和特征,并探讨其在不同领域的应用。
首先,我们将介绍分形的概念与特征,包括分形维度、自相似性和分形集合的构造方式。
接着,我们会详细讲解布朗运动的基本原理,包括随机性、随机步长和随机时间。
最后,我们将针对分形布朗运动给出其定义和特性,并探讨其在金融、医学、图像处理等领域的应用前景。
通过深入了解分形布朗运动的原理和特性,我们可以更好地理解和解释自然界中的复杂现象,并为相关领域的研究和应用提供理论基础。
同时,对于金融市场的预测、医学图像的处理和模拟等问题,分形布朗运动也有着重要的应用价值。
在未来的研究中,我们相信分形布朗运动将继续发挥其重要作用,并推动相关领域的进一步发展。
1.2 文章结构文章结构部分的内容可以包括以下内容:本文主要分为三个部分,分别是引言、正文和结论。
在引言部分,我们首先对分形布朗运动的概念进行了概述,介绍了其在自然界和科学领域中的广泛应用。
接着,我们对本文的结构进行了简要的介绍,概括了各个章节的内容和目的。
最后,我们明确了本文的目的,旨在深入探讨分形布朗运动的原理及其应用前景。
正文部分分为两个章节,分别是分形的概念与特征以及布朗运动的基本原理。
在分形的概念与特征章节中,我们先对分形的基本概念进行了阐述,介绍了分形几何学的起源和发展。
然后,我们详细讨论了分形的主要特征,如自相似性、分形维度等,并且给出了一些实例进行说明。
大班数学:树叶里的秘密

大班数学:树叶里的秘密介绍在许多季节中,我们围绕着一组树木生活,但有时候我们会注意到树叶的形状和大小不同。
这些树叶的差异可能是由不同的遗传基因、气候、水分等因素造成的,但也有可能是由数学规律决定的。
在这篇文章中,我们将探讨树叶中隐藏的数学之美。
斐波那契数列斐波那契数列是一个递增的数字序列,其中每个数字是前两个数字的和。
在自然界中,许多植物都遵循斐波那契数列,特别是在它们的果实、花瓣和树叶中。
树叶的排列方式让我们把树叶摘下来并排列起来。
如果我们将树叶从左到右编号,并将空着的位置表示为0,则前十个斐波那契数列序列是:1, 1, 2, 3, 5, 8, 13, 21, 34, 55现在,我们把这些数字相邻的两个数视为一个旋转角度,从而重新排列树叶。
每个角度都对应相邻的两片叶子。
第一个角度是1/1,第二个角度是2/1,依此类推。
这样排列起来的树叶,其排列方式与数列中的数字是一致的。
这是因为树叶的排列是由树的生长方式以及其依次排列的角度决定的,而这些角度与斐波那契数列是一致的。
树干和树枝的分形结构树叶的排列方式不是唯一与斐波那契数列相关的事物。
树的树干和树枝也有类似的结构。
树干和树枝的分形结构被称为“树形分形”或“树形几何”。
树形分形有一个有趣的特点,即每个分支的长度和角度与主干的长度和角度成比例。
这与斐波那契数列有相似之处,因为斐波那契数列中的每个数字都与前面两个数字成比例。
黄金比例黄金比例是一个神奇的数字,它是斐波那契数列的极限比例。
它可以用一个无限小数来描述,即1.6180339887…。
许多自然界中的事物都符合黄金比例,如两片黄金叶子之间的距离,哥特式教堂的高度比,以及周长与长轴比例为黄金比例的椭圆。
在树叶中,黄金比例的应用也非常明显。
树叶姿态角度中的黄金角度约为137.5度。
这个角度非常接近于360度与黄金比例之比的旋转角度。
具体来说,这个角度等于360度的黄金比例平方。
结论在这篇文章中,我们探讨了树叶中隐藏的数学之美。
生活中的数学——有趣的分形

有趣的分形
让我们动手来画图。
(1)先画一个正三角形,每一边的长度是1;
(2)在每个边的三等份的中间一等份处再凸出造一个正三角形,小三角形在三个边上出现,使原三角形变成六角形;
(3)再在六角形的12条边上重复进行三等份的中间一等份处凸出造一个正三角形的过程,得到4×12=48边形;
……
每边三等分的中间一等分处凸出一个小正三角形,如此至于无穷。
其外缘曲线的构造越
来越精细,它好象是一片理想的雪花。
整体地
看,它仍具有对称性;部分地看,它们每一个
自身内部结构间具有相似性(叫自相似性),我科克雪片的前三个阶段的构造们把这样的曲线叫做科克曲线(雪花曲线),它是1904年瑞典科学家科克所描述的。
雪花曲线的产生过程充分展现了它具有自相似的特点。
数学家芒德勃罗创造了一个词“fractal”,中文译为“分形”,来描述这样的图形特点。
留意观察,我们会发现大自然中充满着这种“分形”现象,如,天空中云彩、天体的分布、闪电、雪花……地球的表面、绵延不断的山脉、河流的分布、蜿蜒曲折的海岸线、崎岖的道路、人体肺气管和血管的分布、正常人的脑电脑图……
人们认识分形,在于探索事物的自相似结构,自相似是跨越不同尺度的对称性。
通过认识分形,人们能更好地认识事物的结构,还可以指导我们创造出令人赏心悦目的艺术品……。
有意思的闭合曲线

有意思的闭合曲线
1. 莫比乌斯带:这是一种单侧、无间断的闭合曲面,由德国数学家莫比乌斯发现。
它只有一面,但可以通过扭曲一个纸条来制作。
2. 克莱因瓶:这是一种无定向的二维图形,看起来像一个瓶子。
在三维空间中,克莱因瓶是一个无底的、自身相交的曲面。
3. 曼德布罗集:这是一组无穷的复杂分形集合,其形状像一个树状的分形。
它可以产生一些美丽的图案和形状。
4. 康托尔集:这是另一种无穷的复杂分形集合,由德国数学家康托尔发现。
它可以产生一些有趣的视觉效果。
5. 玫瑰线:这是一种几何图形,表示平面上的某些点按照一定的规律连接所形成的曲线。
因为这些曲线在极坐标下呈现出玫瑰花般的形状,所以被称为玫瑰线。
有趣的形变换 hadroncfy's notebook

有趣的形变换 hadroncfy'snotebook简单的例子我们下面来看一些简单的变换例子,看一下图片在各种基本函数变换下的形态。
这个变换叫做复反演变换,影片里面也介绍过了。
我们知道,复数的除法就是它的模长相除,幅角相减,所以对于靠近原点的复数变换后模就会变得很大,原点本身被映射到了复无穷上,远离原点的点被压缩到了原点附近。
我们看到最终原点以外的点都被图片充满了,只有原点附近的点是空的,这就是那些远离原点的点的像。
这也是影片里面出现过的变换,正是因为它是平方映射,所以直线会被变换成抛物线:不过,注意照片的左下角,它和原点是重合的,与它相邻的两条边是相互垂直的,而在变换之后这个直角却成了平角!这似乎违背了共形变换的保角性。
但看其他地方又是正常的,比如那些变换前后的坐标网格,似乎例外只发生在原点处。
其实,我们知道复数的乘法就是模长相乘,幅角相加,那么顶点位于原点处的角在变换后就会变为以前的两倍;而除了原点以外的其他点仍然有保角性。
像平方变换这样的保角性不是在全平面成立的变换称为亚纯变换。
其实,数学上保角性只是共形变换的一个必要条件,共形变换的这是一个很有意思的变换,称为指数映射。
影片中数学家的照片在变换后成了一个圆,而且被压得很小,还说“用显微镜就能看到我的头”。
为什么这个变换会有这种性质呢?我们设平面上的一点z为,代入变换公式,我们得到像点也就是说,像的模长为,幅角为b。
由于照片是矩形的,边界上a或b为常数,所以变换后它就会变成同心扇形,如果照片的左右边界的实部(横坐标)分别为和,上下边界的虚部(纵坐标)分别为和,那么大半径和小半径就分别为和,扇形的角度范围是到。
如果照片的宽度超过了那么它变换之后就会是一个同心圆,这就是影片里面的情形。
仔细看它的变换动画我们发现照片的右边界是固定的,左边界迅速被压小成一个“点”,也就是说,变换前右边界和y轴是重合的,左边界的横坐标是负的,这样变换后得到的小半径就会被指数映射压得很小。
有趣的图形(数学)

有趣的图形(数学)数学中有很多有趣的图形,它们不仅具有美学价值,还能帮助我们理解数学概念和现象。
以下我将介绍几个有趣的图形及其背后的数学原理。
1. 波浪线波浪线是一种连续的曲线,它的形状像波浪一样起伏。
数学上,波浪线可以通过正弦函数或余弦函数来描述。
我们可以通过改变正弦函数或余弦函数的参数,如振幅和频率,来调整波浪线的形状和大小。
波浪线在自然界中很常见,比如海浪、声波等都具有波浪线的形态。
在艺术和设计中,波浪线也被广泛应用,它能够给人一种舒适、柔和的感觉。
2. 分形图形分形图形是一种特殊的几何图形,它具有自相似性。
简单来说,分形图形的一部分或一小段可以看作整体的缩小版。
例如,分形树是一种常见的分形图形,它的树枝可以看作整个树的缩小版。
分形图形具有无限的细节,无论我们放大还是缩小它,都能够发现新的图案。
这使得分形图形在艺术、科学和计算机图形学等领域中有广泛的应用。
3. 曲线拟合曲线拟合是一种数学方法,用于找出最适合一组数据点的曲线。
在实际应用中,我们经常会遇到一组散点数据,而需要找到一个函数曲线来描述这些数据的趋势。
常见的曲线拟合方法包括线性拟合和多项式拟合。
线性拟合使用一条直线来逼近数据,而多项式拟合则使用多项式函数来逼近。
通过曲线拟合,我们可以更好地理解数据的分布规律,并进行预测和分析。
4. 网格图形网格图形由平行的水平线和垂直线组成,形成了一个方格状的结构。
网格图形在计算机图形学和几何学中具有重要的作用。
例如,网格图形可以用于定义三维空间中的网格模型,进而用于建模和渲染复杂的物体。
网格图形还可以用于离散化数学模型,将连续的数学问题转化为离散的问题。
这种离散化的处理方法在数值方法和计算数学中得到广泛应用。
5. 几何图形的运动几何图形的运动是一种令人着迷的数学现象。
通过对几何图形进行平移、旋转、缩放等操作,我们可以观察到图形的形态和位置的变化。
几何图形的运动在几何学、动画和计算机图形学中有广泛应用。
有趣的分形图教学设计

教学设计山东省潍坊市高新区北海学校戴璐璐无止境知识拓展如果你是个有心人,你一定会发现在自然界中,有许多景物在某种程度上存在着这种自相似特性。
下图是一棵蕨类植物,仔细观察,你会发现,它的每个枝杈都在外形上和整体相同,仅仅在尺寸上小了一些.而枝杈的枝杈也和整体相同,只是变得更加小了。
那么枝杈的枝杈的枝杈呢?自不必赘言.二、闪电奇观据英国《每日邮报》2009年12月3日报道,美国伊利诺伊州雕刻家波特·赫克曼,用500万伏的粒子加速器对着玻璃板轰出完美分形图案,如同将闪电冻结在冰块中似的。
赫克曼用500万伏的粒子加速器轰击玻璃板,在玻璃中创造出如同冰雕一样的闪电奇观。
这些玻璃上的图案,就好像闪电被突然冻结一样,赫克曼称这一过程为“捕捉闪电”。
三、其它图形除了闪电外形外,赫克曼还可以制造出星星、蝴蝶、橡树以及太极八卦的阴阳图制造太极闪电图时,首先要将电流注入玻璃板内部,然后按照赫克曼先前雕刻好的路径突然爆发。
案。
三、月球表面图片除了自相似以外,分形具有的另一个普遍特征是具有无限的细致性.不管你信不信,上面的这张月球表面的照片是用分形技术生成的.如果你把图片放大观看,也可以看到更加细致的东西.因为,分形能够保持自然物体无限细致的特性,所以,无论你怎么放大,最终,还是可以看见清晰的细节.3.学生跟同伴交流体会数学的神奇美学生感到有趣感到震撼让学生去看去欣赏学生换个角度去欣赏去思考借助网络:展示生活中的分形,体会数学的美、神奇的数学世界,小小组学生完成小结,并请两名学生到讲台上展示总结的过程。
可以利用老师的课件。
教学反思开始设计这节课的时候,学生的活动只有作品展示,而涉及到课本58页“席尔宾斯基三角形”有关的四个问题的探究时采用教师讲解法。
后来,我认为在学生的潜力应该是无限的,你把他估计成什么水平,他就是什么水平。
鉴于此,我把探究活动改为学生代替教师,让学生讲给学生听的方式。
结果收到了很理想的效果。
我在不断的思考中,干脆将反馈训练这个题目也放手给学生,在课堂上,让他们先独立思考,再小组讨论,然后推出代表展示小组成果。
分形公式大全

分形公式大全在数学中,分形是一种具有自相似性的几何图形或数学对象。
它们通常通过递归或迭代的方式构建,并且无论观察其任何一部分,都能看到整体的特征。
分形在自然界中广泛存在,例如树枝、云朵、山脉等都展现出分形的特征。
为了描述和生成分形,数学家们创造了许多分形公式和算法。
以下是一些常见的分形公式和它们的特点:1. 曼德勃罗集(Mandelbrot Set):由法国数学家Mandelbrot于1975年引入的分形集合。
曼德勃罗集是复平面上一组复数的集合,满足迭代公式:Z_(n+1) = Z_n^2 + C,其中C是一个常数,Z是复数。
通过迭代计算,可以将复平面上的点分为属于集合内或集合外,形成具有分形特征的图像。
2. 朱利亚集(Julia Set):与曼德勃罗集相对应,朱利亚集也是由C 值所确定的复平面上的一组复数。
朱利亚集的迭代公式为:Z_(n+1) = Z_n^2 + C,其中Z是复数。
朱利亚集的形状和曼德勃罗集不同,但同样展现出分形的特征。
3. 希尔伯特曲线(Hilbert Curve):希尔伯特曲线是一种填充空间的曲线,它具有自相似性和紧凑性。
希尔伯特曲线是通过递归地将二维空间划分为四个子空间,并将曲线从每个子空间的一个角落延伸到另一个角落而生成的。
4. 科赫曲线(Koch Curve):科赫曲线是一种无限细分的曲线,它由自相似的三角形构成。
科赫曲线的构造方法是在每条线段的中间插入一个等边三角形,然后重复该过程。
除了以上几种常见的分形公式外,还有许多其他有趣的分形公式和算法,如分形树、分形花朵等。
这些分形公式不仅在数学研究中有着重要的应用,还被广泛应用于计算机图形学、自然科学、艺术创作等领域。
总之,分形公式是描述和生成分形图形的重要工具。
通过这些公式,我们可以深入研究分形的特性和美妙之处,并将其应用于各个领域,探索自然界和数学世界中的无限奇妙。
课题学习有趣的分形图_黄正祥

请你借助网络学习类植物等等
蓝天白云,高山流水,红花绿草, 大自然的美丽和神奇是难以描绘 的可是伽利略却说:
“自然界这本伟大的书是用数学 语言写成的。”热爱数学吧!数 学里趣味横生,其乐无穷!
第1次 2
新树枝的条数
新树枝的长度
假设第一条线段的长是单 位1 3 4 ……
n
2
1
4
8
16
2n 1\2n
0.5
0.2 0.125 5
用类似的画法设计一棵与它形状不同 的分形树
• 请你用手中的笔和
纸画自己喜欢的图 形吧! • 先独立思考,再小 组合作! • 5分钟后请每个小组 推XNTE1Njc3MDE2.html
(1) (3)
(2)
图1 • ①在图1(2)中有没有全等三角形?有没有不全 等的相似三角形?图1(3)呢? • ②如果把图1(1)中的三角形的面积作为1,那 么图1(2)中的中点三角形的面积等于多少? • ③图1(2)中的中点三角形的周长与图1(1)中 的周长面积之比等于多少? • ④图1(3)中所有涂色三角形的面积之和是多少? 涂色三角形的周长与图1(1)中三角形的周长之 比等于多少?
用以上方法画出的图形叫分形图【百科】/view/2072306.htm338。 2、再画两条线段,都为基础线条的一半,与 第一条的 夹角都是120度。 3、依次再画。
《课题学习 有趣的分形图》 教学软件设计
课件制作默是赵本山这个 “医生 ”与“病人”范伟一样都得了相似 的“心病”。对于身外之物的“钱”的“心 病”上,“医生”治好了“病人”的“心 病”,他自己却是同样的“心病”大发,而 且更为甚之。这就是我们现实中的相似。
• • (1)根据图①②③的规律,图④的三角形 的个数为 . • (2)图②中,四个三角形是 三 角形(填全等或相似);图③中的所有不 涂色三角形是 三角形.所有涂色三 角形是 三角形.
趣味数学图形

趣味数学图形趣味数学图形数学图形是数学研究中必不可少的一部分,而其中许多图形不仅具有美丽的外观,还有趣味性。
下面就让我们一起来探究一些趣味数学图形吧!1、菱形菱形是一种非常简单的几何图形,它由四条相等的线段组成。
菱形由于具有四个对称面,因此非常适合用来进行平移对称。
我们常用带有菱形的图形来设计华丽的地毯、壁纸以及服装等。
2、斐波那契螺线在斐波那契数列中,第一个数是0,第二个数是1,之后的每个数都是前面两个数的和。
这个数列是由一位公元数学家得出的。
斐波那契螺线就是在矩形中不断画斐波那契数列的单位矩形,并将这些矩形逆时针旋转90度。
最终,我们得到的图形就是斐波那契螺线。
3、三角形三角形也是一种基本图形,它是由三条线段组成的。
三角形不仅可以通过平移变换来生成新的图形,还可以通过其内角度数的不同而具有不同的性质。
例如,等边三角形的内角都是60度,而直角三角形一边的内角是90度。
4、梅比乌斯环梅比乌斯环是一种非常有趣的图形,它的特点是仅有一个面,并且它的面积是无限长的。
梅比乌斯环是由一条长带子围成的,将这条带子折叠成一个圆圈,并将其中一侧反转。
当然,这需要大量的数学技巧来进行证明和构造,但是这个图形确实非常神奇。
5、Klein瓶Klein瓶也是一种只有一个面的图形,但它与梅比乌斯环的不同之处在于它是一个立体图形而不是平面图形。
Klein瓶由一条带子折叠而成,但是与梅比乌斯环不同的是,它的一条边不是反转的,而是穿过了带子的中心。
6、Mandelbrot集合Mandelbrot集合是一种非常有趣的复数图形,它的形状类似于分形。
Mandelbrot集合由一系列的点组成,这些点将复平面分为两部分:属于Mandelbrot集合的点和不属于Mandelbrot集合的点。
Mandelbrot集合的形状非常复杂,但是它的构造却非常简单。
7、双曲线双曲线是一种非常有趣的曲线,它具有两个渐进线和两个顶点。
双曲线通常用于建模椭圆体表面的形状,比如在相对论中。
数学真美妙中有趣的数学现象

数学真美妙中有趣的数学现象1. 金字塔数学:这是一个涉及数字金字塔的现象,其中最顶端的数字是通过底层数字经过加减乘除等运算得出的。
这种数学现象展示了数字之间的复杂关系和运算的巧妙。
2. Fibonacci序列:这是一个由自然数组成的无限序列,其中每个数字都是前两个数字的和。
这种序列在自然界中经常出现,例如在植物生长、动物繁殖和自然界的其他方面。
Fibonacci序列的神奇之处在于它的数学性质和实际应用。
3. 谢尔宾斯基三角形:这是一种具有特殊数学性质的三角形,它的每一行数字都比上一行多一个,而且可以通过它计算出许多有趣的数学表达式。
谢尔宾斯基三角形展示了数学中的递归和自相似性。
4. 乌拉姆现象:这是一个关于质数分布的现象,由美国数学家乌拉姆发现。
他在一张纸上画出方格,将自然数按逆时针方向螺旋分布,并将质数圈出来。
他发现这些质数有秩序地集中在一些斜线上,显示出令人惊讶的规则性。
这个现象展示了质数分布的神秘和规律性。
5. 幻方:这是一种由数字组成的正方形阵列,其每一行、每一列以及对角线上的数字之和都相等。
最著名的幻方是3x3的洛伊斯幻方,它展示了数学中的对称性和平衡性。
6. 柯西-施瓦茨不等式:这是一个在向量空间中描述向量长度和向量之间夹角关系的不等式。
尽管它看起来可能很复杂,但它的应用却非常广泛,从几何到统计学,再到信号处理等多个领域都可以找到它的影子。
7. 分形:这是一种在数学和自然世界中都非常常见的结构,它们的特点是自相似性,也就是说,无论你放大多少倍,都可以看到相同的形状和结构。
最著名的分形之一就是曼德勃罗特集,它是由法国数学家曼德勃罗特提出的,展示了数学的复杂性和美感。
8. 四色定理:这是一个关于地图着色的定理,它说任何一张地图都可以只用四种颜色进行着色,使得没有两个相邻的区域颜色相同。
这个定理虽然看起来简单,但它的证明却非常复杂,涉及到了图论和组合数学的许多概念。
9. 欧拉公式:欧拉公式是复变函数论的基础,它将三角函数与复数指数函数相关联。
谢尔宾斯三角形

谢尔宾斯三角形
谢尔宾斯三角形(Sierpinski triangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出。
它是一个自相似集的例子,其豪斯多夫维为log(3)/log(2)≈1.585。
在构造谢尔宾斯三角形时,通常从一个实心的等边三角形开始。
然后,沿着三角形的三边中点的连线,将这个三角形分成四个小的等边三角形。
接着,去掉中间的那个小三角形,剩下的三个小三角形会构成一个新的更大的三角形。
对这个新的三角形重复同样的步骤,就可以得到下一级的谢尔宾斯三角形。
这个过程可以无限重复,从而形成谢尔宾斯三角形的无限嵌套结构。
此外,也可以用正方形或其他形状来构造谢尔宾斯三角形。
例如,如果从一个正方形开始,沿着对角线的连线将它分成四个小的正方形,然后去掉中间的那个小正方形,剩下的三个小正方形会构成一个新的更大的正方形。
对这个新的正方形重复同样的步骤,就可以得到下一级的谢尔宾斯三角形。
谢尔宾斯三角形的有趣之处在于它的自相似性和无限嵌套结构。
从某种意义上来说,它在数学和艺术之间架起了一座桥梁,表现了数学的美感。
“懂数学”的宝塔花菜
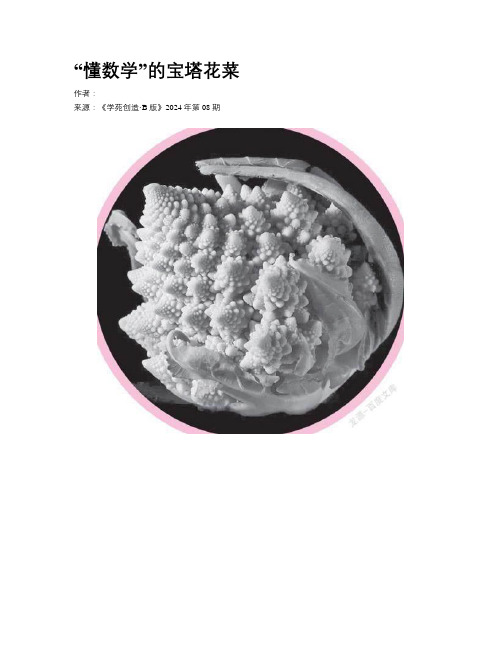
“懂数学”的宝塔花菜作者:来源:《学苑创造·B版》2024年第08期宝塔花菜的外形十分奇特,每一棵宝塔花菜都是由许多簇形状相同的塔形小侧芽组成的,而每一簇小侧芽又是由更小些的塔形小小侧芽组成的,而且这些侧芽沿着螺旋结构堆积排列,组成了特殊的塔形结构。
这种独特的外形是怎么出现的?一起走进宝塔花菜背后的数学世界吧!背后的数学原理宝塔花菜这种外形的背后蕴含了数学中的分形和斐波那契数列的知识。
宝塔花菜是著名的分形蔬菜。
分形是描述复杂几何形体结构的一种数学概念,指的是简单的相似图案在不同维度上不断重复,构成复杂的图形或形状。
宝塔花菜的食用部分的结構具有自相似性,即每个宝塔状的小侧芽,看起来都像是大侧芽的缩小版。
所以可以说宝塔花菜是分形蔬菜。
而且,宝塔花菜上的每一簇小侧芽的生长位置都是按照斐波那契螺旋线进行排列的。
而斐波那契螺旋线是根据一个数学数列——斐波那契数列绘制出来的。
斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始,每一项都等于前两项之和。
“不会开花”的花菜宝塔花菜的这种特殊结构从何而来?2021年,法国科学研究中心的一个团队给出了宝塔花菜为何会长成这样的原因——它“不会开花”。
研究者发现,主要参与宝塔花菜生长发育的有四个基因,其中一个基因在生长过程中会缺失,这导致它们在开花的过程中会不断失败,开不出花,只能转而发育茎。
而且这一过程会反复进行,在茎上又不断发育出茎,却不长叶子和花。
最终使宝塔花菜长成了“茎上加茎”的标志性结构。
生活中的数学知识树木的外形也是分形。
仔细观察,你会发现整棵树的外形可以看作“Y”形的重复。
对植物来说,这样可以让它们的枝叶最大限度地暴露在阳光下,从而更好地进行光合作用。
除了宝塔花菜,还有很多植物的花瓣、萼片、果实的数目等都与斐波那契数列中的数字吻合。
比如向日葵的花盘里就藏着斐波那契数列的蛛丝马迹,在有300朵小花的向日葵花盘上,可以找到34条左旋的螺旋线和21条右旋的螺旋线,越大的花盘能找到的螺旋线越多,且螺旋线的数目总是斐波那契数列中的数字。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各种有趣的分形我们看到正方形,圆,球等物体时,不仅头脑里会迅速反映出它是什么,同时,只要我们有足够的数学知识,我们头脑中也反映出它的数学概念,如正方形是每边长度相等的四边形,圆是平面上与某一点距离相等的点的集合,等等。
但是,当我们看到一个山的形状时,我们会想到什么?"这是山",没错,山是如此的不同于其他景象,以至于你如果绘画水平不高,根本画不出象山的东西。
可是,山到底是什么?它既不是三角形,也不是球,我们甚至不能说明山具有怎样的几何轮廓,但为什么我们却有如此直观而又强烈的山的印象?分形的创始人是曼德布洛特思考了这个问题。
让图中的风景图片又是说明分形的另一很好的例子。
这张美丽的图片是利用分形技术生成的。
在生成自然真实的景物中,分形具有独特的优势,因为分形可以很好地构建自然景物的模型。
这是一棵厥类植物,仔细观察,你会发现,它的每个枝杈都在外形上和整体相同,仅仅在尺寸上小了一些。
而枝杈的枝杈也和整体相同,只是变得更加小了。
Sierpinski三角形具有严格的自相似特性Kohn雪花具有严格的自相似特性分维及分形的定义分维概念的提出对于欧几里得几何所描述的整形来说,可以由长度、面积、体积来测度。
但用这种办法对分形的层层细节做出测定是不可能的。
曼德尔布罗特放弃了这些测定而转向了维数概念。
分形的主要几何特征是关于它的结构的不规则性和复杂性,主要特征量应该是关于它的不规则性和复杂性程度的度量,这可用“维数”来表征。
维数是几何形体的一种重要性质,有其丰富的内涵。
整形几何学描述的都是有整数维的对象:点是零维的,线是一维的,面是二维的,体是三维的。
这种几何对象即使做拉伸、压缩、折叠、扭曲等变换,它们的维数也是不变的;这种维数称为“拓扑维”,记为d。
例如当把一张地图卷成筒,它仍然是一个二维信息载体;一根绳子团成团,仍然是一维结构。
但曼德尔布罗特认为,在分形世界里,维数却不一定是整数的。
特别是由于分形几何对象更为不规则,更为粗糙,更为破碎,所以它的分数维(简称“分维”,记为D)不小于它的拓扑维,即D≥d。
维数和测量有密切关系。
如为了测一平面图形的面积,就要用一个边长为l、面积为l2的标准面元去覆盖它,所得的数目就是所测的面积。
如果用长度l去测面积,就会得到无穷大;而如果用l3去测这块面积,结果就是零。
这就表明,用n维的标准体l n去测量一个几何对象,只当n与拓扑维数d一致时,才能得出有限的数值。
如果n<d,就会得到无穷大;如果n>d,则结果为零。
分数维也是按照这个要求来定义的。
由于分形的复杂性有多种不同类型,所以可以提出不同定义的分维概念,从不同的角度表示分形的不规则性。
通常用的是“容量维”。
简单地说,分维所表示的不规整程度,相当于一个物体占领空间的本领。
一条光滑的一维直线,完全不能占领空间;但是“科赫曲线”却有无穷的长度,比光滑的直线有更多的折皱,拥挤在一个有限的面积里,的确占领了空间,它已不同于一条直线,但又小于一个平面。
所以它大于一维,又小于二维,它的容量维为1.2618,这看来是理所当然的。
海岸线的分维数通常在1.15到1.25之间。
曼德尔布罗特指出,对于各种分形来说,即使在不同的尺度上,用分维表示的不规整程度却是一个常量。
这真是一个令人惊奇的性质,也表明“分维”概念的客观现实特性。
分维所表征的正是大自然的规则的不规则性。
一个分形的曲线意味着一种有组织的结构,这个结构隐藏在奇特怪异的形状之中。
分数维概念我们知道0维是点,一维是线,二维是面,三维是空间。
那么,谁能告诉我1.5维是什么? 一条直线段是一维的,由四条这样的直线段组成的正方形是二维的。
六个这样的正方形组成的正方体是三维的。
直线的长度数值,正方形的面积数值和立方体的体积数值都和我们测量的单位有关。
测量的单位也往往是我们所能分辨的最小单位。
假设我们的分辨能力增加了一倍,因此我们把直线段长度单位减小到原单位的一半,直线段长度的计量值就变为原来的两倍,正方形面积就变为原来的四倍,体积则变为原来的八倍。
我们有下式:log4/log2=2 log8/log2=3这里的二和三不是巧合,这是另一种维数的定义:测度维的概念。
为了定量地描述客观事物的“非规则”程度,1919年,数学家从测度的角度引入了维数概念,将维数从整数扩大到分数,从而突破了一般拓扑集维数为整数的界限。
如果某图形是由把原图缩小为1/λ的相似的b个图形所组成,有:λ^D=kD即维数D=logk/logλ其中的λ为线度的放大倍数,K为“体积”的放大倍数。
回到海岸线长度的问题。
当用直线段来近似曲线时,长度单位减为原来的一半往往意味着我们可以用长度为原来的二分之一的直线段来近似曲线。
这时,海岸线长度增加程度近似于一个固定的倍数。
对于英国海岸线来说,其值约为 2.7,而log2.7/log2=1.41,1.41就是英国海岸线的维数。
1.41由于是一个分式所得出的比值,因此人们称之为分数维。
还有其他一些分数维的定义方法,但得出的结果都比较近似。
分数维是衡量分形的基本参数之一。
自然界的山,其分形维数在2.2维左右,但从2.1维到2.5维画出来的都有一定的山的效果.下面详细介绍分维及计算1)新的维数(全维数:整数维+分维)a.由欧氏几何的"整数维"引出的非欧几何----分维:a).欧氏几何的"整数维"欧氏几何学是一门具有2000多年历史的数学分支,他是以规整几何图形为其研究对象的.有线性和曲线两大类.这些规整几何图形的点,直线,平面图形(曲线),空间图形的维数(欧氏维数)都是整数维,分别为0,1,2,3.对规整几何图形的几何测量是指长度,面积和体积的测量.则上述两类几何图形的测量结果,可以归纳简化表述为如下两点:i. 长度=l,面积=l2 ,体积=l3ii.长度(半径)=r1,面积=πr2,(球)体积=(4/3)πr3上述各种关系的量纲分别是长度单位l的1,2,3次方,即这些方次恰与该几何图形的欧氏维数相等,并且是整数.归结上述两点,各类几何图形的测量都是以长度l为基础的.所以,欧氏几何中对规整几何图形的测量,可以概括表述为长度=l 面积A=al2体积V=bl3式中a和b为常数,称为几何因子,他与具体的几何图形的形状有关.如圆a=π;球b=4π/3. 以上都是欧几里得几何规则图形的整数维.而对于不规则的非欧几何图形,其维数关系也就不那末规整了,即欧几里得测度----长度,宽度,厚度----不能抓住不规则形状的本质,于是曼德勃罗特转向新的想法,即关于维数的新想法.b).非欧几何的"分维"欧氏几何中的空间是3维的,平面是2维的,直线是1维的,而点是0维的.那末,一个线团的维数如何呢?这与观察方法有关.远看,他是一个点,是0维;近些看,象球,有空间3维感;再近看,就看到了绳子,又成为1维的了.引发人们注意到几何中也具有"相对关系",以及维数的多样性.曼德勃罗特"越过"了0,1,2,3,......的"传统整数维"(同时也超越了传统观念),进入了看起来象是不可能的"分数维数",分维出现了.从概念上说,这是一场走钢丝表演,是冒险.对于非数学家,"外行",(年轻的)新手,生手,即开拓创新者(或所谓的"半瓶子醋"),他要求先自愿地暂停疑虑(思考),再另寻它路.而对数学家或该行业保守的专家,可能会不懈一顾,不予考虑,不许生疑,被传统所限制束缚住,以至难有大突破.而事实证明前者的方法和策略是极为强劲有力的成就大功者.分维与古典的欧几里得维数是有联系的.将欧氏维数统一扩展成M=l d则由对数定义可知,指数d可以表示为以l为底的,M的对数,即d=log l M经用换底公式换底,就可以得到关于维数的解析通式,分维中广泛使用的关系式d=lnM/lnl他可以被看成是各种维数的综合表达式,即广义维数(欧氏维数及各种分维)的由来或基准式.分维是一种测度,是用其它方法不能明确定义的一些性质----一个对象粗糙,破碎或不规则程度----的手段.即对某种特征性的粗糙度的量度.是有规则的不规则性的反映.此法的关键要点就是使在不同的尺度上(放大或缩小)不规则(图形,功能等)的程度保持恒定.2).拓扑维和豪斯道夫维——维数的定义连续空间的概念,空间维数是连续的,不是间断离散的.对数,换底,拓扑维数是比分形维数更基本的量,以Dt表示,它取整数值,在不作位相变换的基础上是不变的,即通过把空间适当地放大或缩小,甚至扭转,可转换成孤立点那样的集合的拓扑维数是0,而可转换成直线那样的集合的拓扑维数是1.所以,拓扑维数就是几何对象的经典维数Dt=d.拓扑维数是不随几何对象形状的变化而变化的整数维数.对于任何一个有确定维数的几何体,若用与它相同维数的"尺r"去度量,则可得到一确定的数值N;若用低于它维数的"尺"去量它,结果为无穷大;若用高于它维数的"尺"去量它,结果为零.其数学表达式为:N(r)~r-Dh.上式两边取自然对数,整理后可得Dh=lnN(r)/ln(1/r) 或Dh=lim[lnN(σ)/ln(1/σ)] σ→0式中的Dh就称为豪斯道夫维数,它可以是整数,也可以是分数.欧氏几何体,它们光滑平整,其D值是整数.人们常把豪斯道夫维数是分数的物体称为分形,把此时的Dh值称为该分形的分形维数,简称分维.也有人把该维数称为分数维数.当然还必须看其是否具有自相似性和标度不变性.维数的其它定义(1) 信息维数Di = lim (∑PilnPi/lnσ) σ→0(2) 关联维数Dg = lim (lnC(σ)/ln(1/σ)) σ→0(3) 相似维数Ds = lnN/ln(1/r)(4) 容量维数Dc = lim (lnN(ε)/ln(1/ε)) σ→0Dc≥Dh(5) 谱维数 D (分形子维数)——是研究具有自相似分布的随机过程,如随机行走的粒子的统计性质,可用渗流模型来描述的多孔介质,高聚物凝胶(经络的通道及传质)等一类"蚂蚁在迷宫中"的问题.(6) 填充维数Dp——由半径不同的互不相交的小球尽可能稠密的填充定义的维数称之为填充维数(Packing Dimension).(7) 分配维数Dd——可以看成是利用两脚间隔距离为σ的两脚规测量曲线C所得的"长度".即定义为Dd = lim (lnMσ(C)/(-lnσ)) σ→0曲线的分配维数至少等于盒维数.(8) 李雅普诺夫(Lyapunov)维数Dl——是作为混沌的吸引子维数,他是利用Lyapunov指数来定义的.奇怪吸引子的断面图总是呈分形构造的(经络的断面切片),因此就可以测定其分形维数.分形维数的测量1.基本方法分形维数的定义有很多,但适合所有事物的定义还没出现.每个维数的测定对象常是不同的,所以要区别对待,物适其用.实际的测定分形维数的方法,大致可以分成如下五类:(1)改变观察尺度求维数:是用圆和球,线段和正方形,立方体等具有特征长度的基本图形去近似分形图形.(2)根据测度关系求维数:这个方法是利用分形具有非整数维数的测度来定义维数的.(3)根据相关函数求维数;C(r)∝r-a,a=d-D(4)根据分布函数求维数;p(r)∝p(λr) p(r) ∝r-D(5)根据频谱求维数.2.盒维数(计盒维数,Kolmogorov熵,熵维数,度量维数,对崐数密度等)3.函数图的维数4.码尺与分形维数的关系----分形维数的不确定性对实际分形体而言,测量的分形维数值随码尺而变化,•也就是说,对同一分形体由于选取的码尺不同,会得到不同的分维值.原因是,结构层次不同,自相似的程度不同.测量时要注意.分形定义分形难下确切的定义。
