清华大学《高等水文学》L8_Calibration_103805499

合集下载

清华大学《高等水文学》地貌瞬时单位线理论_41702857

河流级别
Ni
Li（km） Ai(km2)
RB
1
16
4.8
16.03
2
4
13.4 89.03
4
3
1
7
402
RL 1.58
RA 4.83
5. 实例计算
若忽略不计坡面汇流时间，且采用式（27）作为各级河流状态的持留时间的概率密度函数，则3级流域的地貌瞬时单位线公式为：
u(t=)
π
r1
[
k1k2 (k2 (k2 − k1
另一方面，在流域汇流阶段，其水量平衡为：
dW (t) = −Q(t) + I (t) dt
（4）
特别地，对于仅在0时刻有净雨量瞬时注入流域时，
dW (t) = −Q(t),t > 0 dt
将式（3）代入式（5），可得：
（5）
−I0
dFB (t) dt
= −Q(t ), t
>
0
Q(t) = I0 fB (t)
π r2
= RB − RB3 + 2RB2 − 2RB
RA
RA (2RB −1)
= 0.289
π r3
=1 −
RB RA
−
RB3 − 3RB2 + 2RB RA2 (2RB −1)
=0.025
= k1 1= .56, k2 0.5= 59, k3 1.07
将以上各参数代入u(t)，得
u(t) =0.525e−1.56t +1.322e−1.559t + 0.979e−1.07t
= Ki
LΩ∆= τi , i vΩ∆τ Ω
1, 2,, Ω
（29）

清华大学《高等水文学》L06-新安江模型_95380393

以此时段为基础，降雨P，蒸散发E，径流量R，满足如下水量平衡关系（超蓄产流方程）：
R = (P − E) − (W2 − W1)
(3)
大量资料表明，WWM～f/F有如下关系：
1 − f = (1 − WWM )B
F
WWMM
或 f =1 − (1 − WWM )B
F
WWMM
∫ = WM
1
= WWMd(f / F)
WM = WUM + WLM + WDM
W = WU + WL + WD
(12)
WUM,WLM,WDM----上层,下层,深层土壤蓄水容量
WU, WL, WD----上层,下层深, 层土壤蓄水量
当则WU > EM,
EU = EM
EL = 0
(13)
当则WU < EM,
EU = WU
EL = (EM-EU) WL WLM
二层模型：WU>EM EU=EM WU<=EM EU=WU EL=(EM-EU)WL/ WLM
二层模型在久旱之后，WL已很小，如仍不下雨，计算出的蒸发EL会很小，这与实际不符。因为由于植物根系的作用，深层的水分会通过植物腾发到大气。故宜采用三层模型。
16
三层模型：
模型中流域蓄水容量和WM流域蓄水量都是W上层下层和,深层之和即 , :
n+1 j +1
=
C1Q
n j
+
C2Q
n+1 j
+
C3Q
n j
+1
C1
=
kx + 0.5∆t k(1− x) + 0.5∆t

实验图书资源

实验图书资源
（1）
图书名：《水文学》
作者：黄锡荃主编
ISBN：978-7-04-004173-6
出版单位：高等教育出版社
出版时间：1993.6
简介：本书以水循环为纲，阐明了水循环各要素和各种水体水文现象的物理机制、时空分布及其相互关系。

主要内容有：水文学基础知识；水循环及水量平衡的基本理论与计算方法；陆地表面水、海洋水和地下水诸水体水循环具体过程的分析；人类活动对水环境的影响。

全书力图体现地理水文学的方向，反映水文科学的新观点和新成就，体系新颖，内容丰富，既适合师范院校地理系作教材，也可作为综合大学地理系、工科院校有关专业师生及水文工作者的参考用书。

（2）
图书名：《水文测验学》
作者：赵志贡等编著
ISBN：7-80621-956-0
出版单位：黄河水利出版社
出版时间：2005.8
简介：本书根据中华人民共和国水利部近期颁布的一系列水文测验规范，结合目前比较先进的测验手段和方法，对江河的水文测验与水文资料整编的基本概念、原理和操作方法等进行了系统介绍。

全书共份8章，主要内容包括：水文测站布设，水位、流量、泥沙等水文要素采集与资料整编，水文要素测验误差分析等。

本书内容丰富，条理清晰，通俗易懂，是一本系统研究水文测验的理想教材和工具书，可作为高等学校教材，适合水文水资源专业使用，亦可供水利工程技术人员和水文测站职工参考。

田间土壤含水率测量的几种主要方法

- 1 -田间土壤含水率测量的几种主要方法1林剑辉孙宇瑞※ 马道坤中国农业大学精细农业研究中心，北京，100083摘要：土壤含水率是农业生产中一重要参数，本文对土壤水分的各种测量方法进行了全面的综合介绍。

首先讨论了称重法，张力计法，电阻法，中子法，r-射线法，驻波比法，时域反射击法及光学法等的基本原理。

其次由于土壤含水率受土壤质地，容重，含盐量，温度等影响，因此各种测量方法在实地测量时均会产生误差，本文紧接着详细分析了各种方法使用过程中产生误差的主要原因，并提出了相应的补偿措施。

最后，通过对这些方法的对比分析，得出了一些结论，并提出了土壤水分测量方法进一步研究的重点。

关键词：土壤含水率、传感器、测量1. 引言水乃生命之源，对于农作物而言，土壤水更是其发育、生长的重要条件。

在古中国农业中，将湿润的土壤称为“墒”，并有丰富的关于保墒、散墒等调节土壤水分状况（墒情）的技术和作业。

在现代农业中，能否对土壤水分进行有效测量与控制，是实现“精细农业”与“精细灌溉”的关键所在。

同时在水文科学、气象科学和生态科学中，土壤水分的测量也具有相当重要的意义。

土壤中水分含量称之为土壤含水率（Soil Moisture Content），是由土壤三相体（固相骨架、水或水溶液、空气）中水分所占的相对比例表示的，通常采用重量含水率（g θ）和体积含水率（v θ）两种表示方法[1]。

重量含水率是指土壤中水分的重量与相应固相物质重量的比值，体积含水率是指土壤中水分占有的体积和土壤总体积的比值。

体积含水率与重量含水率两都之间可以换算：c g v γθθ=，其中c γ为土壤干容重。

而Reynolds（1970）指出，采用体积含水率是克服土壤变异性对土壤含水率测量的影响的一种有效方法[2]。

由于作为水载体的土壤是一种多孔介质，物理化学特性复杂，空间变异性大，这些给土壤含水率的测量提出了很高的技术要求。

半个多世纪以来，科研人员针对这种状况，采用了不同的方法进行土壤水分测量的研究，各种测量技术也层出不穷。

清华大学《高等水文学》壤中流_56503930

况下，水及溶质的施加速率越大，其运移速度就越快，相对大孔隙流也越多
1.5 大孔隙——测定
1. 水的吸附-解吸附、N的吸附和汞压法 2. 田间土壤开挖法 3. 室内土柱浸泡法 4. 染色法 5. CT扫描法 6. 地透雷达法 7. 土壤水穿透曲线法 8. 张力渗透仪法
1.6 壤中流触发
壤中流触发：地下水位的快速响应，机理：垂向优先流
preferential flow，优先流不适用于Darcy-Richards方程计算流动受重力主导连通的大孔隙：虫洞、节理、侵蚀
1.4 优先流
preferential flow，优先流不适用于Darcy-Richards方程计算流动只受重力影响连通的大孔隙：虫洞、节理、侵蚀
Preferential flow (Zehe & Sivapalan, 2009)
需要更有组织的研究框架：不同研究地点如何对比？利用什么工具定义首要控制因素？
产流过程的进一步把握
2. 物理因素：干湿交替；冻融交替
3. 化学因素：化学风化形成的溶液管道 4. 人类活动：间歇灌造成的干湿交替，会形成大量裂隙 5. 土壤结构：结构性土壤中最大穿透深度明显大于非结构性土
壤 6. 土壤质地：质地好的土壤大孔隙流较多 7. 土壤初始含水量：初始含水量越高，土壤有效大孔隙越多 8. 水和溶质的施加速度、施加量和方式：在其他条件相同的情
Engler(1919)，第一个概念性模型
Hursh and Brater (1941)，量化其作用
1960’s，产流过程分析 1990’s，引入同位素方
法
研究意义：水文、污染、滑坡
Reprint from McGlynn et al., 2002

The numerical computation of turbulent flows

K p
&
V
4 P 0, Oti
‘h
7
of turbulence energy von Karman’s constant appearing in (2.1 - 11) Molecular viscosity Turbulent viscosity Kinematic viscosity A generalized dependent variable Density Effective turbulent Prandtl number Effective turbulent Prandtl number for transport Molecular Prandtl number Shear stress
Nomen constant Curte t number defined by (3.1 - 1) Coefficients in approximated turbulent transport equations Specific heat at constant pressure Diffusion coefficient for quantity (p Rate of diffusive transport of Reynolds stress Constant in near-wall description of velocity profile (- 9) Functional defined by (2.2 - 6) Turbulence kinetic energy uiuj/2 Length of energy containing eddies Fluctuating component of static pressure Heat flux Radius Reynolds number in pipe flow based on bulk velocity and pipe diameter Rate of redistribution of Reynolds stress through pressure fluctuations Turbulent Reynolds number k2/ve Temperature Fluctuating component of velocity in direction xi Mean component of velocity in direction Xi Streamwise velocity nondimen~onalized by T,JP Mean streamwise velocity on axis Change in mean velocity across shear flow ‘Vorticity’ fluctuations squared Cartesian space coordinate

清华大学《高等水文学》L09_Diagnostic_618204110

has become a common jargon…
纳什效率系数本质上是比较所研究的水文模型和简单的平均值模型的模拟效果
① An NSE value=1.0 indicates perfect model
performance ② An NSE value<0 indicates an altogether
Data Base
Context A
Analysis
Context B
Information A Information B
Prior Information Prior Knowledge
25
DATA INFORMATION DIAGNOSTICS
Information is obtained by viewing data in a certain context
Models that can ‘learn’ from their mistakes and ‘heal’
much as living organisms do !
The Model Building & Evaluation Process
CLOSENESS
Qualitative Evaluation of Form & Function Consistency
均值模型不能。
Summary
① Every modeling study should explain and justify the choice of benchmark.
② The appropriate benchmark model will necessarily be different for different types of case studies.

清华大学任玉新---高等计算流体力学

主要内容任玉新1.Basics2.Methods for compressible flows1) The mathematical properties of Euler equations2) Shock wave and entropy conditions3) Riemann problem and the Godunov scheme4) Approximate Riemann solvers: HLL solver and Roe solver5) TVD scheme6) ENO/WENO scheme7) The compact scheme3.Methods for incompressible flows1) The staggered and the colocated grids2) The MAC method3) The SIMPLE method4) The projection method5) Other methods6) Solution of N-S equations on the nonstaggered gridReferences[1] E. F. Toro, Riemann solvers and numerical methods for fluid dynamics, Springer, 1997 (First edition)[2] J.D. Anderson, Computational fluid dynamics: basics with applications, Springer (清华大学出版社影印版)[3] Barth and Deconinck (eds.) High order method for computational physics, Lecture Notes in Computational Science and Engineering, 9. Springer, 1999[4] Ferziger and Peric, Computational method for fluid dynamics, Springer, 1996[5] T. J. Chung, Computational fluid dynamics, Cambridge University Press, 2002[6] J. W. Thomas, Numerical partial differential equations: conservation laws and elliptic equations. Texts in applied mathematics 33, Springer, 1999[7] 吴子牛，计算流体力学基本原理，科学出版社， 2002.[8] Sherrie L. Krist, Robert T. Biedron, Christopher L. Rumsey，CFL3D User＇s Manual, The NASA Langley Research Center,Hampton, VA[9] S. K. Lele, J. Comput. Phys. 103, 16 (1992)[10] S. Pirozzoli, J. Comput. Phys. 178 (2002)[11]Yu-Xin Ren, Miao＇er Liu, Hanxin Zhang, J. Comput. Phys. 192 (2003)3FTP: 166.111.37.201Usr:cfdPasswd:cfd2005Email：****************.cn高等计算流体力学讲义(1)第一章计算流体力学基本原理第1节流体力学基本方程一、非定常可压缩Navier－Stokes方程5不计品质力的情况下，在直角坐标系中，守恒型N －S 方程可以写为下列向量形式：()()()0v v v t x y z∂∂-∂-∂-+++=∂∂∂∂U F F G G H H ， (1) 其中u v w E ρρρρρ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭U 2()u u p uv uw E p u ρρρρρ⎛⎫ ⎪+ ⎪ ⎪= ⎪ ⎪ ⎪+⎝⎭F 2()v vu v p vw E p v ρρρρρ⎛⎫ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪+⎝⎭G 2()w uw vw w p E p w ρρρρρ⎛⎫ ⎪ ⎪⎪= ⎪+ ⎪ ⎪+⎝⎭H ，0xx xyv xzxx xy xz T u v w kx ττττττ⎛⎫⎪ ⎪⎪=⎪ ⎪⎪∂+++ ⎪∂⎝⎭F 0xy yy v yzxy yy yz T u v w k y ττττττ⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪∂+++ ⎪∂⎝⎭G ，0xz zyv zzxz zy zz T u v w k z ττττττ⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪∂+++ ⎪∂⎝⎭H 。

高等水文学-1

(四)按模型的基本性质和建模技术分类 2．类比模型类比模型是以另一现象的物理性质类比水文现象的物理性质，借此以便于观测或形象化。这种类比模型在水文学的研究中运用很少。 3.模拟模型模拟模型详细仿制(模拟)水文现象的重要特性，但并不仿造水文现象的本身。目前，水文学上的模拟模型都是指用数学方法进行模拟的模型，所以模拟模型习惯上又称数学模型。这种模型是以数学上的定量方式来表达水文原型，并用计算机进行模拟计算。
本课程的内容主要包括三大部分：水文过程的物理基础、流域水文过程的确定性模拟方法和水文过程的随机模拟。第一部分主要讲述流域水循环过程中水文过程的形成机制，第二部分主要介绍流域水文过程的确定性模拟方法，第三部分主要介绍水文过程非确定性模拟中的随机模拟方法。
《高等水文学》
第二部分流域水文过程的确定性模拟方法
四、模型率定和参数优选
3.目标最优拟合法的最优化技术
虽然为达到目标最佳拟合的最优化技术是很多的，重要的是，在选用某种技术时，必须使该种技术能与模型的结构相适应。 1.常用的几种最优化技术模拟径流形成过程的概念性模型，具有比较明确的物理概念，但模型中参数多，其中有很多是需要通过优选才能确定的参数。优选参数时首先要选定一种目标函数，当目标函数选定以后，常用的优选方法有试凑法、自动化优选法以及人与计算机联合优选三种。 (1)用试凑法优选参数用试凑法优选参数，也叫人工优选法。不论模型的结构如何复杂，用试凑法(是一种逐步逼近法)率定模型并优选参数总是一种可行的方法。试凑法的基本原则是：设定一组参数，在计算机上运算，比较模拟值与实测值，分析对比，调整参数。或计算其目标函数，直至达到最优，参数即为所求。
(3)确定性系数准则我国《水文情报预报规范》规定：以流域水文模型等制定的水文预报方案的有效性的评定采用确定性系数dQ进行。

水文学原理

3) Q(t), I(t) and u(0,t)三者矩之间的关系
原点矩：M1(Q) = M1(u) + M1(I ) 式中下“1”表示原点矩的阶数中心矩：N (Q = N (u) + N (I) 式中下“2”表示中心矩的阶数 )
2 2 2
⎧ τ = M 1 (Q ) − M 1 ( I ) ⎪ ⇒ τ = M 1 (u ) ⎨ ⎪ M 1 (u ) = M 1 (Q ) − M 1 ( I ) ⎩
L ：拉普拉斯变换
令：A( p) = am D m +1 + am −1 D m + ⋅⋅⋅ + a0 D − 1 B( p) = bn D n +1 + bn −1 D n + ⋅⋅⋅ + b0 D + 1
A( p) L[u (0, t )] = − L[δ (t )] Q L 则有 B( p)
再取上式的逆拉普拉斯变换，得
• 状态路径 (State paths)：由各状态按流域汇流的物理顺序组成的集合。
状态：水滴在流域上所处的空间位置，指某级坡面或某级河流。对一个Ω=3级的流域，水滴可能取的路径为：
S1 : r1 → C1 → C2 → C3 → C4 S 2 : r1 → C1 → C3 → C4 S3 : r2 → C2 → C3 → C4 S 4 : r3 → C3 → C4
18
2-3 流域瞬时单位线和卷积公式
(Watershed instantaneous unit hydrograph and Convolution formula)
2)卷积公式(Convolution formula)
当I (t ) = δ (t ), Q(t ) = u (0, t )

电解质溶液自扩散系数的布朗动力学模拟

电解质溶液自扩散系数的布朗动力学模拟史红兵,于养信,高光华(清华大学化学工程系,北京100084)摘要　采用布朗动力学方法对电解质溶液进行了模拟,在传统布朗动力学的基础上综合考虑了流体力学的影响,并且引入S m art M onte Carl o 方法的接受概率,避免了离子不现实的移动和位型重叠,这样不仅可以将模拟过程中的时间步长大幅度提高,而且还可使溶质在相空间的演化过程更接近实际.模拟过程以电解质溶液的原始模型为基础,将溶剂看作连续介质,溶质分子之间的相互作用采用软核加静电的势能函数模型,长程静电力采用Ew ald 加和的处理方法.模拟得到KC l 和N aC l 溶液的径向分布函数g +-(r ),g ++(r )和g --(r ),并与文献中HN C 计算以及模拟的结果进行比较,使用推广的Green 2Kubo 公式模拟计算溶液中各种离子的自扩散性质,计算结果与实验数据吻合良好.关键词　布朗动力学模拟;电解质溶液;径向分布函数;自扩散系数中图分类号　O 646 文献标识码　A 文章编号　025120790(2004)1222317205收稿日期:2003210210基金项目:国家自然科学基金(批准号:20176020)资助.联系人简介:高光华(1974年出生),男,博士,教授,博士生导师,从事分子热力学研究.E 2m ail :gaogh @m ail .tsinghua .edu .cn 在化学化工、湿法冶金、环境化学、生物化学、地球化学以及盐湖卤水等资源的开发利用领域涉及很多电解质溶液,但是长程静电力和溶剂化效应的同时存在使得电解质溶液的热力学处理比非电解质溶液的处理复杂得多.因此有关电解质水溶液体系的研究已经成为一个非常活跃的领域[1～3].分子模拟不仅是分子水平上研究流体性质的一种重要手段,而且也为分子热力学模型的检验和完善提供了新的方法.分子模拟通常有蒙特卡罗方法、分子动力学方法和布朗动力学方法[4～6].其中布朗动力学方法是以布朗粒子为研究对象,在布朗运动理论的基础上,随着随机微分方程的发展而发展起来的.连续溶剂模型的B row n 动力学模拟最早由E r m ark 和M cCa mmon [7,8]等提出并加以完善,但他们都忽略了流体动力学作用.本文在传统布朗动力学模拟的基础上,考虑了流体力学对体系的影响,引入Sm art M on te Carl o (S M C )方法中接受概率的判据,拒绝了不现实的移动,从而使溶质在相空间的演化过程更接近实际,并且大幅度提高了模拟的时间步长,使得对电解质溶液的模拟快速、准确.通过模拟KC l 和N aC l 电解质水溶液得到了一系列状态下阴阳离子的径向分布函数和扩散系数,讨论了浓度和温度对电解质溶液径向分布函数和自扩散系数的影响.1　理论、方法及模拟1.1　布朗动力学理论在布朗动力学方法中,某些自由度是通过对其它自由度的随机影响表现出来的.假设粒子系与某一粘性媒质相互作用,但不详细说明每个粒子与粘性媒质相互作用的细节,而是用作用在粒子上的一个随机力来代表这一媒质,这种随机力的引入减少了动力学的维数,有助于问题的简化.流体分子对布朗粒子的作用包括外力场的力和周围分子的作用力,如浮力、粘滞阻力和涨落不定的无规则力等.具有N 个布朗粒子的系统,其L angevin 方程为[8]m a i =-6j Νij v j +F i +6j Αij f j (1)V ol .25高等学校化学学报　N o .12　2004年12月 CH E M I CAL JOU RNAL O F CH I N ESE UN I V ERS IT IES 2317～2321　式中,Νij是摩擦系数,v j是j粒子的速度,F i代表布朗粒子之间的相互作用和外部力的和,m是粒子的质量,a i是粒子的加速度,Αij是与流体力学有关的系数,f i符合Gaussian分布.如果假定离子动量的弛豫远比系统位型的弛豫快,并且相空间的空间梯度分布是相对光滑的,那么描述粒子布朗运动的L angevin方程可以近似地由Smo luchow sk i方程来描述,即∃r=ΒD F+55r D∃t+R c(2)式中,Β=1 k B T,∃t是时间步长,r=(r T1,r T2,…,r T N)T是3N维的无因次位型矢量.F= (F T1,F T2,…,F T N)T是作用在离子上的力,R c是随机位移,符合均值为零的Gaussian分布.离子之间的流体力学作用通过3N×3N的Ro tne2P rager张量D来表示.考虑流体力学的作用后,需要对传统的S M C方法的接受概率进行改进,参照Ro ssky和Jardat等[9]的结果,从t时刻的位型Λ到t+∃t时刻的位型Μ的接收概率为P=m in1,det DΛdet DΜ1 2exp(-ΒΘ), ∃rΛdrift=ΒDΛ・FΛ+55r DΛ∃t(3)Θ=U N(v)-U N(Λ)+14∃t(-∃r-∃r driftΜ)・D-1Μ(-∃r-∃r driftΜ)-　14∃t(-∃r-∃r driftΛ)・D-1Λ(-∃r-∃r driftΛ)(4)式中的U N是系统的势能,角标Λ和Μ分别代表t时刻和t+∃t时刻的位型.1.2　势能函数在模拟过程中,阴阳离子均被看作球型离子,离子之间的距离从质心算起,对N aC l和KC l溶液来说,2个离子之间的相互作用的溶剂平均势能可以通过离子对相互排斥的软核作用和静电作用模型表示,即势能V ij的表达式是V ij(r)=14ΠΕ0B ij e2n(a i+a j)a i+a jrn+q i q j4ΠΕ0Εr r(5)式中,a i是i离子的半径,Ε0是真空介电常数,Εr是纯溶剂的相对介电常数,e是基本电荷,q i和q j是离子的电量,B ij是一个可调参数.对于长程作用的静电力,通常采用Ew ald加和方法和反应场方法[10]处理,我们采用了Ew ald加和的方法.模拟中势能函数的参数见表1.Table1　Param eters of the solven t-averaged poten ti a l3E lectrolyte B ij r+ nm r- nm n N aC l01289801200011859 KC l01013011740117412 3r+and r-rep resent radii of cati on and ani on res pectively.1.3　Rot ne-Prager张量离子之间的流体力学作用可以用只与位型相关的3N×3N的Rotne2P rager张量D来表示[11].各元素的表示式如下:D ij=D0i I∆ij+(1-∆ij)k B T8ΠΓr3ijI r2ij+r ij r T ij+Ρ2i+Ρ2jr2ij13I r2ij-r ij r T ij(6)式中,Ρi是i离子的Stokes半径,Ρi+Ρj<r ij,∆ij是K ronecker函数,r ij是离子i,j之间的距离,Γ是溶剂的粘度,k B是Bo ltz m ann常数,T是溶液的温度,I是单位矩阵,D0i是i离子无限稀释自扩散系数.1.4　模拟对于电解质溶液的理论研究通常采用2种模型,一种是原始模型,即把溶剂分子看作连续介质,只考虑离子之间的相互作用;另一种是非原始模型,它在真空介电常数下同时考虑溶剂分子和溶质离子之间的各种相互作用.由于布朗动力学的特点,我们选择原始模型.将溶剂看作是具有一定介电常数和粘度的连续介质,该介质作为一种粘滞流体,对于溶质的扩散施加摩擦力,使其扩散变慢;此外,与溶质分子碰撞,给其一个随机的运动.在模拟过程中,假定溶剂分子对离子的作用包括随机位移和具有确定的介电常数2个部分.溶剂分子的介电常数Εr取为78136,采用正则系综,体系处在周期性8132 高等学校化学学报V ol.25边界条件的立方体盒子内,其中离子的总数为216,有108个金属阳离子(N a +或者K +)和108个阴离子(C l -),初始位型按立方体结构排列.盒子边长L 由盒子内的离子数和体系的密度确定,位能和离子受力的计算采用最小影像约束,非静电力计算的截断半径为0149L ,系统演化过程中时间步长因密度的大小不同而不同,范围在011×10-13～011×10-12s 之间,系统演化30万步,前10万步用以达到平衡,后20万步用以统计计算系统的热力学性质.每个体系计算5次,取平均值.2　结果与讨论2.1　径向分布函数径向分布函数是反映流体微观结构特征的物理量.为了检验程序的正确性,我们先将015mo l LF i g .1　The radi a l distr i buti on functi on of 015m ol LKCl soluti on a t 298K KC l 溶液的模拟结果与Jardat 等[9]用超网链方程(HN C )计算以及布朗动力学模拟的结果进行了比较.如图1所示,g +-(r ),g ++(r )和g --(r )都能很好地吻合,证明了我们的程序的可靠性.在此基础上,我们模拟了不同浓度的KC l 水溶液在298K,结果如图2所示.不同温度下的0.5mo l L KC l 溶液的径向分布函数如图3所示.由图2可知,在一定温度下,异号离子径向分布函数g +-(r )出峰的位置未发生变化,但是,峰值随着浓度的降低而增大;同号离子的径向分布函数g ++(r )和g --(r )随着浓度的变化而略有变化,浓度降低,远程的作用增强.由图3可知,在浓度相同的情况下,异号离子径向分布函数g +-(r )出峰的位置未发生变化,但是,峰值随着温度的增大而降低;同号离子的径向分布函数g ++(r )和g --(r )随温度的变化不大.2.2　自扩散系数流体扩散系数是化工传质过程中最重要的物性参数之一,用分子模拟获得扩散系数的方法主要是Enstein 方法和Green 2Kubo 方法[10].在布朗动力学中,采用的时间步长较大,粒子的速度被看作是快速变量,几乎所有的速度信息在相空间的演化过程中都被丢失,所以,在模拟的过程中舍去了速度变量,系统的演化只在位型空间中进行描述.因此,包括速度变量的标准Green 2Kubo 方法不能用来计算扩散系数.但是,可以在Smoluchow sk i 级别的线性相关理论基础上推导出类似的Green 2Kubo 表达式[12]:D i =13tr 〈D ii 〉-∫∞0dt 〈U i (0)U i (t )〉(7)式中,D ii 是D 的3×3的次级矩阵,U i 是第i 个离子的流体力学速度,tr 是矩阵的迹,〈〉表示系综平均,在数值上与时间平均等价.U i =∑N j =1ΒD ij F j +55r j D ij (8)9132N o .12史红兵等:电解质溶液自扩散系数的布朗动力学模拟 K +和C l -在不同浓度KC l 溶液中的自扩散系数分别如图4(A )和(B )所示.图4中实验数据是由T urq 等[13]测定的,文献数据是Jardat 等[9]在没有考虑流体力学影响时布朗动力学模拟的结果.由图4可以看出,我们的模拟结果与实验值和文献值吻合较好,随着电解质溶液浓度的升高,离子的自扩散系数明显减小,但是这种减小的趋势随着浓度的继续增大而减弱.此外,流体力学对离子扩散的影响非常明显,说明考虑了流体力学作用的布朗动力学更接近实际体系.F i g .4　Self -di ffusi on coeff i c i en ts of Cl -(A )and K +(B )i n KCl soluti on a t 298KN a +和C l -在不同浓度N aC l 溶液中的自扩散系数分别见图5(A )和(B ).图5中,C l -的自扩散系数是由R eginald [14]用磁力搅拌隔膜池法实验测定的数据,N a +的自扩散系数是由Bernd 等[15]用自旋回波核磁共振法实验测定的数据.由图5可看出,布朗动力学模拟的结果和实验数据吻合良好.浓度对于N a +自扩散系数的影响非常明显,随着浓度的增大,溶液中N a +自扩散系数降低,而且趋势增强,C l -的自扩散系数随着浓度的增大也呈现减小的趋势,但是没有N a +明显.F i g .5　Self -di ffusi on coeff i c i en ts of Cl -(A )and Na +(B )i n NaCl soluti on a t 298K综合比较图4和图5可发现,溶液浓度的变化对阴阳离子扩散系数有一定的影响,N aC l 溶液比KC l 溶液更加敏感.3　结论在传统布朗动力学模拟的基础上,考虑流体力学对体系的影响,引入Sm art M onte Carl o (S M C )方法中接受概率的判据,拒绝了不现实的移动,不仅使溶质在相空间的演化过程中更接近实际,而且大幅度提高了模拟的时间步长,使得对电解质溶液的模拟快速、准确.对KC l 和N aC l 电解质水溶液模拟的结果表明,异号离子径向分布函数g +-(r )出峰的位置随溶液浓度和温度的变化不发生明显的变化,但是,峰值的大小随着温度和浓度各自的增大而降低;同号离子的径向分布函数g ++(r )和g --(r )随温度的改变变化不大,随浓的变化而略有变化,浓度降低,远程作用更加明显.离子的自扩散系数随着浓度的增大均呈现下降趋势,但是,浓度对于N aC l 溶液自扩散系数的影响更显著.同时,流体力学对离子自扩散的影响非常明显,考虑了流体力学影响作用的布朗动力学更接近实际体系,通过模拟获得的电解质溶液自扩散系数可以与实验数据较好地吻合.参　考　文　献[1]　Bernard O .,Cartailler T .,Turq P .et al ..Journal of M olecular L iquids [J ],1997,73—74:403—411232 高等学校化学学报V ol.25N o.12史红兵等:电解质溶液自扩散系数的布朗动力学模拟 [2]　Lobaskin V.,L inse P..J.Che m.Phys.[J],1998,109(9):3530—3541[3]　L I Chun2X i(李春喜),T I AN Ru(田　茹),LU Gui2W u(卢贵武)et al..A cta Chi m ica Sinica(化学学报)[J],2003,61(2):175—180[4]　A llen M.P.,T ildesley puter Si m ulati on of L iquids[M],O xford:C larendon P ress,1987:257—264[5]　GU Chong(顾　冲),GAO Guang2H ua(高光华),YU Yang2X in(于养信)et al..Che m.J.Chinese U niversities(高等学校化学学报)[J],2001,22(6):958—961[6]　YU Kun2Q ian(于坤千),L I Ze2Sheng(李泽生),L I Zhi2Ru(李志儒)et al..Che m.J.Chinese U niversities(高等学校化学学报)[J],2002,23(7):1327—1330[7]　E r m ak D.L..J.Che m.Phys.[J],1975,62(10):4189—4196[8]　E r m ak D.L.,M cCa mmon J.A..J.Che m.Phys.[J],1978,69(4):1352—1360[9]　Jardat M.,D urand2V idal S.,Turq P.et al..Journal of M olecular L iquids[J],2000,85:45—55[10]　F renkel D.,S m it B..U nderstandingM olecular Si m ulati on from A lgorithm s to A pp licati ons[M],N e w York:A cade m ic P ress,1996:347—357[11]　Rotne J.,P rager S..J.Che m.Phys.[J],1969,50(11):4831—4837[12]　Felderhof B.U.,Jones R.B..Physica A[J],1983,119:591—608[13]　Turq P.L antel m e F.,Roum egous Y.et al..J.Chi m.Phys.[J],1971,68:527—532[14]　M ills R..J.Phys.Che m.[J],1957,61:1631—1634[15]　Bernd M.,B raun H er m ann W eingartner.J.Phys.Che m.[J],1988,92:1342—1346Brown i a n D ynam i cs Si m ula ti on of Self-di ffusi on Coeff i c i en tsof Electrolyte Soluti on sSH I Hong2B ing,YU Yang2X in,GAO Guang2H ua3(D ep art m ent of Che m ical E ng ineering,T sing hua U niversity,B eij ing100084,China)Abstract　B row n ian dyna m ics si m ulati on is carried out to study the electrolyte s o luti on.W e take into account the effect of hydrodyna m ic interacti ons and com bine an accep tance criteri on know n from the Sm art M on te Carl o m ethod w ith the traditi onal m ethod.A s a result,unrealistic move m en ts are avoided and overlapp ing configurati ons are p revented,further more,bigger ti m e step can be app lied.T he s olvent2 averaged in teracti on po ten tial betw een the i on s is modeled by pair w ise repulsive s oft2co re interacti ons and Coul om b fo rces w h ich is handled by Ew ald Summ ati on T echnique.T he radial distributi on functi on g+-(r),g++(r)and g--(r)are obtained and compared w ith that from HN C integral equati on and si m ulati ons available in literature.Self2diffusi on coefficien ts of i ons are obtained w ith the equivalent Green2 Kubo exp ressi on s derived from the linear res ponse theory on the Smo luchow sk i L evel.T he results are in good agree m ent w ith those from experi m en ts.Keywords　B row n ian dyna m ics si m ulati on;E lectro lyte s o luti on;R adial distributi on functi on;Self2 diffusi on coefficien t(Ed.:S,X)1232。

高级水生生物学复习资料

一、概念与术语1、河流连续体（river continuum concept）：1980年，Vannote等以水生昆虫为基础对河流生物群落结构和上下游逆变提出了一个新理论，即河流连续统概念。

他们根据外源性物质进入河流后的变化，即上游为粗有机质颗粒（CPOM，>1mm），至下游降解为细小或超微颗粒（FROM，50um-1mm；UPOM，0.5-50um）这一事实，认为群落中的优势类群因利用相应颗粒亦自上而下依次为利用CPOM的撒食者，利用着生生物的刮食者和利用FROM-UPOM 的收集者，收集者又可分利用悬浮颗粒的过滤收集者和利用沉积颗粒的直接收集者。

2、洪水（河流）脉动概念FPC：洪水脉冲理论是继河流连续统理论之后的第4个河流生态理论,主要阐述洪水脉冲驱动下,河流与其洪泛区之间的横向水力联系对河流洪泛区系统进程的重要性,强调洪水脉冲的重要性及河流洪泛区系统的整体性.本文论述洪水脉冲理论的概念模型、主要观点及其在河流洪泛区系统的应用进展.洪水脉冲理论的应用主要体现在三方面:在洪水塑造河流洪泛区系统地貌进程方面,侧重于河流形态的"主导径流"研究,成果不断提升;在生物地球化学循环上,以对氮的研究为主,提出洪水脉冲是河流洪泛区新陈代谢及生物地球化学循环的重要驱动力;在生物进程上,集中在对大型植物和以水鸟和鱼类为代表的动物研究上.文中提出要提高河滨生物量,并重建全局的生物多样性,应提倡人为的洪水脉冲.对于干旱半干旱区湿地水鸟的保护核心是洪水发生频率和淹没范围对水鸟繁殖及避难的作用,以及水在湿地景观中的分配,这一点对于中国松嫩平原西部干旱半干旱区湿地水鸟的保护具有重要意义.洪水脉冲理论的提出是基于对热带亚马逊河的观察实验,随着其在其它类型区域的推广应用,除洪水脉冲以外的其它因素的作用突现出来,人类干扰洪水脉冲的生态效应亦愈来愈显现.因此,有必要加强洪水脉冲与其它环境因子的耦合作用,及这种作用在人类干扰活动下,导致的河流洪泛区系统进程变化的研究,提出更具有普适性的洪水脉冲理论.3、r-K连续谱r-K continuum：r选择和k选择是进化生态学中的一个重要问题。

生态水文学ppt

山柳菊鸡冠草凤仙花羊狐茅
老鹳草沙伯早熟禾总状花直立委陵菜
9
植物水分关系
• 多数植物体内的水流是由水压差驱动的。根据汁液上升的内聚力－张力理论，水分移动是由叶的蒸腾表面张力驱动的。表面张力降低了蒸腾生境的水压，导致水分从根里向上流动。 • 在溶质被渗透障碍物所阻的时候，水分移动比溶质移动容易，水流通过膜进出细胞的运动是由细胞内外之间的水势差所驱动的。 • 植物体内水势差主要是由压力差和溶质势差所决定的。通过根的水流通常是由土壤水分和植物基部压力差所驱动的。 10
32
湿地的水化学成分
• 关于湿地的水化学问题已经做过大量研究工作，研究的重点在于：了解水化学条件；确定供水化学过程及其量化问题；探讨化学与湿地植被的关系。 • 与植物种分布和湿地植被有直接关水文条件对水化学有很大影系的水化学问题包括：响；植物种的生长和分布更
水力传导率
11
凋萎和渍水
• 凋萎是指植物在干旱时的软柔、松弛和下垂状态。 • 凋萎在叶上表现的最明显。叶靠细胞膨压维持其形状，当膨压降到零时，叶就出现凋萎现象。 • 植物接近凋萎点时，气孔传导度逐渐丧失，蒸腾量和光合作用随之降低。 • 渍水指土壤水分饱和或积水的一种环境条件，可能持续几小时或数月之久。 • 渍水往往影响根的形态和生理活动。当根的水分通量受阻日趋严重时，可引起对水淹敏感的植物凋萎和落叶，耐水淹植物由于根的 12 适应性反应不容易受渍水影响。
25
斑块状植被的生态水文效应
26
干旱区生态水文模型
• 描述生态水文模型动态的数值模型，从大气环流模型的回格到个体植物这一系列尺度上应用；就时间尺度而言，以几小时用以模拟过程和事件，以几百年用于模拟气候变化。 • 针对干旱区开发的模型很多，包括水文模型、生态模型和生态水文耦合模型。 • 模型需要采用可变时段进行模拟：用高分辨率时段模拟短暂和突发性事件，用低分辨率时段模拟上述活动以外时间的通量； • 应采用适用于干旱区稀疏作物的蒸散方程； • 需要采用足够小的空间尺度描述干旱区土壤、地面和植被性质的空间变异性。

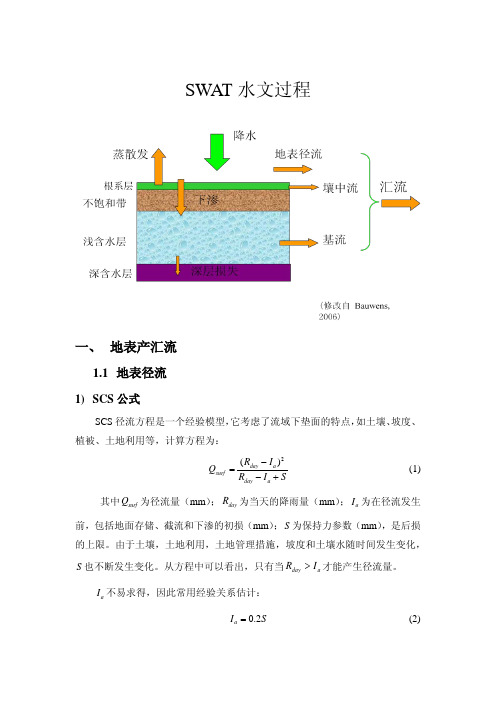
清华大学《高等水文学》SWAT水文过程_62101469

∆t
2
(24)
式中： qin,ave 时段内的平均入流速率：
qin,ave
=
qin,1
+ qin,2 2
(25)
传播时间通过将水流量除以水流速度求得：
= TT V= stored V = stored ,1 Vstored ,2
qout
qout ,1
qout ,2
(26)
式中：TT 为传播时间(s)，Vstored 为存储量 (m3 H2O)，qout 为出流速率 (m3/s).
qch
=
qc*h
⋅ Area 3.6
(18)
qc∗=h q0∗ ⋅ (100 * Area)−0.5
(19)
q0∗ 是单元产流面积流速（mm hr-1），Area 为子流域面积（km2），100 为单位转换
系数。建议单位产流面积流速为 6.35mm/hr，将方程(18)和(19)带入方程(17)，得
面的含水量，不包括萎蔫系数下土壤剖面的含水量，w1和 w2 为形状系数。Smax 是
把 CN1 带入方程
S
=
25.4 ⋅ 1000 CN
−10 计算求得。
3) CN 值计算
CN 值是反映土壤透水性、土地利用和土壤前期含水状况的综合参数。SCS
模型的 CN 值，与土壤的渗透性，土地利用与前期土壤湿度有关，
径流； surlag 是地表径流滞后系数， tconc 是子流域的汇流时间（hrs）。汇流时间 tconc 为降雨时间开始到整个子流域面积内汇流均到达出口，从子流
域最远的一点到出口的时间，包括坡面汇流时间( tov )和河道汇流时间( tch ):
tcon=c tov + tch

高等水文学-3

第二节洪水实时预报校正模型
洪水预报的可靠性与精度不仅依赖于洪水预报模型，而且还取决佑实时水文信息资料的及时收集与传递，特别还取决于洪水预见期流域上的降雨过程变化。流域上降雨过程的预报，其难度远远超过洪水预报本身。采用不确切的降雨进行洪水预报必然引起较大的预报误差，因此，利用预报校正方法与技术将明显地改进洪水预报精度。洪水实时预报涉及到两方面的内容；一是建立实时预报校正模型，二是实时校正技术。实时预报校正模型在很大程度上取决于水文模型的结构 1）“显式”结构水文模型当水文模型为“显式”结构时，一种处理方法是将水文模型视为 “时变”的水文系统，利用新的观测信息实时校正水文模型的动态参数，使模型预报值快速地跟踪洪水的变化过程。这种方法实际上是将水文模型处理成具有实时预报校正功能的水文模型，模型的动态参数“在线”识别和实时预报是关键。另一种处理方法是将水文预报模型改造成系统状态方程和系统观测方程，利用滤波的方法进行实时校正。
《高等水文学》
武汉大学水利水电学院宋星原
第九章水文实时预报校正模型与方法第一节概述汉阳屯降雨
流域产流模型
高丽城降雨
流域产流模型流域汇流模型实时校正模型高丽城洪水预报过程
问题的提出洪水预报总是有误差的，预报误差可表现为系统误差，也可表现为随机误差。因此，在发布实时洪水预报之前，对预报值进行误差实时校正是十分必要的。实时洪水预报是一种在联机水情测报系统中使用实时雨水情及其它有关水文气象信息作为洪水预报模型输入，并不断根据新信息校正或改善原有模型参数，力争预报结果逐步逼近真值的洪水预报。
1、状态方程对于离散的线性系统，系统状态方程可表示为：
X(t ) = Φ ( t)X(t - 1) + B(t)U(t) + Γ ( t ) W(t)

第三章水循环要素

Beijing Forestry University 高甲荣水文与水资源学 19
降水过程线与降水累积曲线
Beijing Forestry University
高甲荣水文与水资源学
20
降水的基本表示方法

ቤተ መጻሕፍቲ ባይዱ

等降水线，在一个较大的区域内，常用等降水量线表现区域内降水的分布情况。所谓等降水量线是区域内降水量相等地各点连成的曲线，它反映区域内降水的分布变化规律，在等降水量线图上可以查出各地的降水量和降水面积，但无法确定降水历时和降水强度降水特性综合曲线是反映降水特性的一些曲线，常用的有降水强度历时曲线、平均雨深面积曲线、雨深面积历时曲线三种
Beijing Forestry University 高甲荣水文与水资源学 24
降雨综合特征曲线
Beijing Forestry University
高甲荣水文与水资源学
25
降水综合特征曲线
Beijing Forestry University 高甲荣水文与水资源学 26
降水综合特征曲线
Beijing Forestry University
Diese Schichten verhalten sich wie Kugellager
11
高甲荣水文与水资源学
雪覆盖层结构
Typischer Scheedeckenaufbau mit verschieden festen Schneeschichten (McCLUND & SCHAERER, 1993, S.59)
Beijing Forestry University 高甲荣水文与水资源学 27