15题压轴题练习--图形折叠及动点问题的相关计算
2023-2024年人教版七年级上册数学期末动点问题压轴题专题训练(含答案)

2023-2024年人教版七年级上册数学期末动点问题压轴题专题训练(1) ______, ______(1)若点P 到A 、B 两点的距离都相等,请直接写出点P 对应的数(2)数轴上是否存在点P ,使点P 到点A ,点B 的距离之和为10=a b =(1)___________,___________.(2)若在数轴上有两动点、分别从同时出发向右运动,点的速度为2个单位长度/秒,点的速度为1个单位长度秒,当点在点追上了点,求点对应的数为多少?=a c =P Q A B ,P Q P D Q D(1)写出数轴上点B 表示的数 ;(2)表示5与3之差的绝对值,实际上也可理解为(1)求出线段的长度;(1)点表示的数为________,点|53|-AB A(1)请直接写出a 、b 、c 的值. ______,设点P 运动时间为t 秒.(1)若M ,N ,P 三点同时出发,=a(1)数轴上点B 表示的数是 ;当点P 运动到(1)则______,______. A =a b =(1)A 点所表示的数是___________,C 点所表示的数是___________;(2)若动点P 从点C 出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一动点Q 恰好从点A 出发,以每秒2个单位长度的速度沿数轴向右移动,设点P 和点Q 在数轴上的点M 相遇,求点M所表示的数是多少?(3)若动点P 从C 点出发,以每秒3个单位长度的速度沿数轴向左运动,另一动点Q 恰好从A 点出发,以每秒2个单位长度的速度沿数轴也向左运动,是否存在时间t ,使得P ,Q 到原点的距离相等,并求出此时点P 和点Q 所表示的数.13.如图,点在线段上,,,动点从点出发,沿线段以每秒个单位长度的速度向终点匀速运动;同时,动点从点出发,沿线段以每秒个单位长度的速度向终点匀速运动.当点到达终点时,点也随之停止运动.设点的运动时间为秒.(1)线段的长为______.(2)当点与点相遇时,求的值.(3)当点与点之间的距离为个单位长度时,求的值.(4)当时,直接写出的值.14.如图,在数轴上点A 、C 、B 表示的数分别是、1、12.动点P 从点A 出发,沿数轴以每秒3个单位长度的速度向终点B 匀速运动;同时,点Q 从点B 出发,沿数轴以每秒2个单位长度的速度向终点A 匀速运动,设点Q 的运动时间为t 秒.C AB 3AC =11BC =P A AB 3B Q B BA 2A P Q P t AB P Q t P Q 9t 2.5PC QB +=t 8-(1)的长为________;AB(2)当点P与点Q相遇时,求t的值;(1)点A表示的数为___________,点B表示的数为(1)OA=__________cm,OB=__________cm参考答案:。
高中数学立体几何动点和折叠问题-含答案

高中数学立体几何动点和折叠问题-含答案1.在正方体ABCD-A1B1C1D1中,BC的中点为M,点P在正方体的表面DCC1D1上移动,且满足∠APD=∠MPC。
求三棱锥P-BCD的体积的最大值。
2.△ABC是边长为23的等边三角形,E、F分别为AB、AC的中点,沿EF把四面体OAEF折起,使点A翻折到点P的位置,连接PB、PC。
当四棱锥P-BCFE的外接球的表面积最小时,求四棱锥P-BCFE的体积。
3.△ABC是边长为23的等边三角形,E、F分别在线段AB、AC上滑动,且EF//BC,沿EF把△AEF折起,使点A翻折到点P的位置,连接PB、PC。
求四棱锥P-BCFE的体积的最大值。
4.已知三棱锥P-ABC满足PA⊥底面ABC,在△ABC中,AB=6,AC=8,且AB⊥AC,D是线段AC上一点,且AD=3DC,球O为三棱锥P-ABC的外接球,过点D作球O的截面。
若所得截面圆的面积的最小值与最大值之和为44π,则求球O的表面积。
5.已知A、B、C、D四点均在半径为R(R为常数)的球O的球面上运动,且AB=AC,AB⊥AC,AD⊥BC。
若四面体ABCD的体积的最大值为V,求V的值。
6.已知A、B、C是球O的球面上的三点,AB=2,AC=23,∠ABC=60°,且三棱锥O-ABC的体积为V。
求V的值。
7.已知三棱柱ABC-A1B1C1内接于一个半径为3的球,四边形A1ACC1与B1BCC1为两个全等的矩形,M是A1B1的中点,且C1M=√3.求三棱锥C1-ABC的体积。
8.在四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是菱形,∠ADC=120°,连接AC,BD交于点O,A1O⊥平面ABCD,AO=BD=4,点C'与点C关于平面BC1D对称。
求三棱锥C'-ABD的体积。
1.删除该题,因为这明显是一道数学计算题,没有文章可言。
2.球O的表面积为4π,则球O的体积为(4/3)π。
中考数学压轴题:几何图形的折叠与动点问题

几何图形的折叠与动点问题1. 如图,在矩形ABCD 中,AB =4,AD =9,点E 在BC 上,CE =4,点F 是AD 上的一个动点,若把△BEF 沿EF 折叠,点B 落在点B ′处,当点B ′恰好落在矩形ABCD 的一边上,则AF 的长为________.第1题图3或 113 【解析】如解图①,当点B ′落在边AD 上时,则易证四边形BEB ′F 为菱形,∴BF =BE =9-4=5,由勾股定理易求AF =3;如解图②,当点B ′落在边CD 上时,BE =B ′E =9-4=5.由勾股定理易求B ′C =3,∴B ′D =4-3=1.设AF =x ,则FD =9-x .根据折叠的性质得BF =B ′F ,∴x 2+42=(9-x )2+12,解得x =113,∴AF =3或 113.第1题解图2.如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC 上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是________.第2题图6-25≤BP≤4【解析】①如解图①,当F、D重合时,BP的值最小,根据折叠的性质可知:AF=PF=6,在Rt△PFC中,PF=6,FC=4,则PC=25,∴BP min=6-25;②如解图②,当E、B重合时,BP的值最大,根据折叠的性质即可得到AB=BP=4,即BP的最大值为4;故BP的取值范围是6-25≤BP≤4.第2题解图3.如图,在矩形ABCD中,AB=2,AD=6,E,F分别是线段AD、BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C 落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为__________.第3题图4或4-22【解析】当C落在BE的延长线上时,对应点为P1,如解图①,连接FP1,AP1,过P1点作P1H⊥FC,垂足为点H,交AD于点N,设FH=x,∵∠P1BH=45°,∴P1H =BH=x+2,由折叠性质可得P1F=FC=6-2=4,在Rt△P1HF中,x2+(x+2)2=42,解得x=7-1或x=-7-1(舍去),∴P1H=2+7-1=7+1,P1N=7+1-2=7-1,在Rt△P1NA中,AP1=AN2+P1N2=(7+1)2+(7-1)2=4;当点C落在F A的延长线上时,对应点为P2,如解图②,易知P2F=CF=4,AF=22+22=22,∴AP2=P2F-AF=4-2 2 .第3题解图4.如图,在四边形ABCD中,AD∥BC(AD<BC),AB与CD 不平行,AB=CD=5,BC=12,点E是BC上的动点,将∠B沿着AE折叠,使点B落在直线AD上的点B′处,DB′=1,直线BB′与直线DC交于点H,则DH=________.第4题图511或513 【解析】如解图①所示,∵AD ∥BC ,∴△HB ′D∽△HBC ,∴HD HC =DB ′CB ,∵AB =CD =5,BC =12,DB ′=1,∴HD 5+HD=112,解得:HD =511;如解图②所示,∵AD ∥BC ,∴△HB ′D ∽△HBC ,∴HD HC =DB ′BC ,∵AB =CD =5,BC =12,DB ′=1,∴HD 5-HD=112,解得:DH =513.故DH 的长度为511或513.5.如图,已知AD ∥BC ,AB ⊥BC ,AB =8,点E 为射线BC 上一个动点,连接AE ,将△ABE 沿AE 折叠,点B 落在点B ′处,过点B ′作AD 的垂线,分别交AD ,BC 于点M ,N .当点B ′分线段MN 为3∶5的两部分时,EN 的长为________.第5题图 35511或53913【解析】由翻折的性质,得AB =AB ′,BE =B ′E .①当MB ′=3,B ′N =5时,设EN =x ,得B ′E =x 2+25.由题意得△B ′EN ∽△AB ′M ,∴EN B ′M =B ′E AB ′,即x 3=x 2+258,解得x 2=4511,∴EN =x =35511;②当MB ′=5,B ′N =3时,设EN =x ,得B ′E =x 2+9,由题意得△B ′EN ∽△AB ′M ,∴EN B ′M =B ′E AB ′,即x 5=x 2+98,解得x 2=7513,∴EN =x =53913,故EN 的长为35511或53913.6.如图,在矩形纸片ABCD 中,AB =6,BC =8,点P 是对角线BD 上一动点,将纸片折叠,使点C 与点P 重合,折痕为EF ,折痕EF 的两端分别在BC 、DC 边上(含端点),当△PDF 为直角三角形时,FC 的长为________.第6题图247或 83 【解析】在矩形ABCD 中,AB =CD =6,BC =AD =8,在Rt △BCD 中,由勾股定理得BD =10.由折叠得PE =EC ,PF =CF ,∠EPF =∠FCE =90°.∵∠PDF <90°,∴△PDF 为直角三角形有以下两种情况:(Ⅰ)如解图1,当∠PFD =90°时,∵∠FCE =∠FPE =∠PFC =90°,∴四边形PECF 是矩形.∵PF =FC ,∴四边形PECF 是正方形,∴PF ∥BC ,∴△DPF ∽△DBC ,∴PF BC =DF DC .设FC =PF =x ,则DF =6-x ,∴x 8=6-x 6,解得:x =247,即FC =247;(Ⅱ)如解图2,当∠DPF=90°时,∵∠FPE=∠FCB=90°,∴此时点E与点B 重合,∴BP=BC=8,∴PD=10-8=2.∵∠PDF公用,∠DPF=∠DCB=90°,∴△DPF∽△DCB,∴PFBC=PDDC,即:PF8=26,解得:PF=83,∴FC=83.综上所述,FC的长为247或83.第6题解图7.如图,正方形的边长为4,E是BC的中点,点P是射线AD 上一动点,过P作PF⊥AE于F.若以P、F、E为顶点的三角形与△ABE相似,则P A=________.第7题图2或5【解析】分两种情况:如解图①,当△EFP∽△ABE 时,则有∠PEF=∠EAB,∴PE∥AB,∴四边形ABEP为矩形,∴P A=EB=2;如解图②,当△PFE∽△ABE时,则有∠PEF=∠AEB,又∵∠P AF=∠AEB,∴∠PEF=∠P AF,∴PE=P A,∵PF⊥AE,∴点F为AE的中点,∵AE=42+22=25,PEAE=EFEB,即PE25=52,得PE=5,∴P A=5,∴当P A=2或P A=5时,以P、F、E为顶点的三角形与△ABE相似.第7题解图8.如图,矩形ABCD中,AB=1,AD=2,E是AD中点,点P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于____________.第8题图2或53或655 【解析】∵在矩形ABCD 中,AB =1,AD =2,E 是AD 的中点,∴∠BAD =90°,AE =DE =1,∴△ABE 是等腰直角三角形,∴BE =2AB = 2.若△BEP 为等腰三角形,则分三种情况:①当BP =BE 时,显然BP =2;②当PB =PE 时,如解图①,连接AP .∵PB =PE ,AB =AE ,∴AP 垂直平分BE ,∵△ABE 是等腰直角三角形,∴∠BAP =∠EAP =45°,作PM ⊥AB 于点M ,设PM =x ,∵S △ABD =S △ABP +S △APD ,∴12×1×2=12×1×x +12×2×x ,解得x =23,∴PM =23,∴BP =PM sin ∠ABD=2325=53;③当EB =EP 时,如解图②,过点A 作AF ⊥BD 于点F ,过点E 作EG ⊥BD 于点G ,在Rt △ABF 中,AF =AB ·sin ∠ABF =1×25=255,∵AE =ED ,EG ∥AF ,∴EG =12AF =55,在Rt △BEG 中,∵BE =2,EG =55,∴BG =BE 2-EG 2=355,∵EB =EP ,EG ⊥BP ,∴BP =2BG =655.综上所述,线段BP 的长度等于2或53或655.第8题解图① 第8题解图②9.如图,在▱ABCD 中,∠B =30°,AB =AC ,O 是两条对角线的交点,过点O 作AC 的垂线分别交边AD 、BC 于点E 、F ;点M 是边AB 的一个三等分点.则△AOE 与△BMF 的面积比为__________.第9题图3∶4或3∶8 【解析】如解图,连接AF 、MF ,∵AB =AC ,∠B =30°,∴∠ACB =∠B =30°, ∵点O 是对角线的交点,EF ⊥AC ,∴AF =FC ,∴∠ACB =∠F AC =30°,∴∠F AB =90°,∴BF =2AF =2FC ,∵点M 为AB 的三等分点,如解图①,当BM =13AB 时,设S △BMF =a ,则S △AMF =2a ,S △ABF =3a ,∴S △AFC =3a 2,∴S △AOE =3a 4,∴S △AOE ∶S △BMF =3a 4∶a =3∶4.则△AOE 与△BMF 的面积比为3∶4;如解图②,当BM =23AB时,S △AOE ∶S △BMF =3a 4∶2a =3∶8.综上所述:△AOE 与△BMF的面积比为3∶4或3∶8.第9题解图① 第9题解图②10.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AC =2,E 为斜边AB 的中点,点P 是射线BC 上的一个动点,连接AP 、PE ,将△AEP 沿着边PE 折叠,折叠后得到△EP A ′,若△EP A ′与△ABC 的另一个交点为F ,当EF =14AB 时,则BP的长为________.第10题图 2或23 【解析】∵∠ACB =90°,∠B =30°,AC =2,E为斜边AB 的中点,∴AB =4,AE =12AB =2,BC =2 3.①若P A ′与AB 交于点F ,连接A ′B ,如解图①,由折叠可得S △A ′EP =S △AEP ,A ′E =AE =2,∵点E 是AB 的中点,∴S △BEP =S △AEP =12S △ABP .∵EF =14AB ,∴S △EFP =12S △BEP =12S △AEP =12S △A ′EP ,∴EF =12BE =BF ,PF =12A ′P =A ′F .∴四边形A ′EPB 是平行四边形,∴BP =A ′E =2;②若EA ′与BC 交于点F ,连接AA ′,交EP 于H ,如解图②.同理可得FP =12BP =BF ,EF=12×2=1.∵BE =AE ,∴EF =12EA ′=12AP =1,∴AP =2=AC ,∴点P 与点C 重合,∴BP =BC =2 3.故BP 的长为2或2 3.第10题解图① 第10题解图②。
2024年中考数学压轴突破【几何中的折叠】题型汇编(解析版)

几何中的折叠问题一、单选题1如图,在菱形ABCD中,AD=5,tan B=2,E是AB上一点,将菱形ABCD沿DE折叠,使B、C的对应点分别是B 、C ,当∠BEB =90°时,则点C 到BC的距离是()A.5+5B.25+2C.6D.35【答案】D【分析】过C作CH⊥AD于H,C 作C F⊥AD于F,HD=5,HC=25,再由折叠证明∠BED=∠B ED=135°,∠EDC=∠EDC =45°,△CHD≌△DFC ,C F= HD=5,【C作CH⊥AD于H,C 作C F⊥AD于F,由已知AD=5,tan B=2,=2,∴CD=5,tan∠CDH=HCHD∴设HD=x,HC=2x,∴在Rt△HDC中HC2+HD2=CD2,2x2+x2=52,解得x=5,∴HD=5,HC=25,由折叠可知∠BED=∠B ED,∠EDC=∠EDC ,CD=C D∵∠BEB =90°,∴∠BED=∠B ED=135°,∵AB∥DC,∴∠EDC=180°-∠BED=45°,∴∠EDC=∠EDC =45°∴∠CDC =90°∵∠CHD =∠C AD =90°,∴∠CDH +C DF =90°,∵∠CDH +∠HCD =90°,∴∠C DF =∠HCD ,∴△CHD ≌△DFC ,∴C F =HD =5,∴点C 到BC 的距离是C F +CH =5+25=35.故选:D .【点睛】本题考查了全等三角形的性质和判定、菱形的性质、图形的折叠以及正切定义的应用,解答关键是根据折叠的条件推出∠BED =∠B ED =135°.2如图,将△ABC 折叠,使AC 边落在AB 边上,展开后得到折痕l 与BC 交于点P ,且点P 到AB 的距离为3cm ,点Q 为AC 上任意一点,则PQ 的最小值为()A.2cmB.2.5cmC.3cmD.3.5cm【答案】C【分析】由折叠可得:PA 为∠BAC 的角平分线,根据垂线段最短即可解答.【详解】解:∵将△ABC 折叠,使AC 边落在AB 边上,∴PA 为∠BAC 的角平分线,∵点Q 为AC 上任意一点,∴PQ 的最小值等于点P 到AB 的距离3cm .故选C .【点睛】本题主要考查了折叠的性质、角平分线的性质定理等知识点,掌握角平分线上的点到两边距离相等是解答本题的关键.3如图,在▱ABCD 中,BC =8,AB =AC =45,点E 为BC 边上一点,BE =6,点F 是AB 边上的动点,将△BEF 沿直线EF 折叠得到△GEF ,点B 的对应点为点G ,连接DE ,有下列4个结论:①tan B =2;②DE =10;③当GE ⊥BC 时,EF =32;④若点G 恰好落在线段DE 上时,则AF BF=13.其中正确的是()A.①②③B.②③④C.①③④D.①②④【答案】D【分析】过点A 作AH ⊥BC 于点H ,利用三线和一以及正切的定义,求出tan B ,即可判断①;过点D 作DK ⊥BC 于点K ,利用勾股定理求出DE ,判断②;过点F 作FM ⊥BC 于点M ,证明△EMF 为等腰直角三角形,设EM =FM =x ,三角函数求出BM 的长,利用BE =BM +EM ,求出x 的值,进而求出EF 的长,判断③;证明△AND ∽△CNE ,推出∠ENC =∠ECN ,根据折叠的性质,推出EF ∥CA ,利用平行线分线段成比例,即可得出结论,判断④.【详解】解:①过点A 作AH ⊥BC 于点H ,∵BC =8,AB =AC =45,∴BH =12BC =4,∴AH =AB 2-BH 2=8,∴tan B =AHBH=2;故①正确;②过点D 作DK ⊥BC 于点K ,则:四边形AHKD 为矩形,∴DK =AH =8,HK =AD =BC =8,∵BE =6,∴CE =2,∵CH =12BC =4,∴CK =4,∴EK =CE +CK =6,∴DE =EK 2+DK 2=10;故②正确;③过点F 作FM ⊥BC 于点M ,∵GE ⊥BC ,∴∠BEG =90°,∵翻折,∴∠BEF =∠GEF =45°,∴∠EFM =∠BEF =45°,∴EM =FM ,设EM =FM =x ,∵tan B =FMBM =2,∴BM =12FM =12x ,∴BE =BM +EM =12x +x =6,∴x =4,∴EM =FM =4,∴EF =2EM =42;故③错误;④当点G 恰好落在线段DE 上时,如图:设AC 与DE 交于点N ,∵▱ABCD ,∴AD ∥BC ,∴△AND ∽△CNE ,∴EN DN =CE AD=28=14,∴EN DE =15,∴EN =15DE =2=CE ,∴∠ENC =∠ECN ,∴∠BEN =∠ENC +∠ECN =2∠ECN ,∵翻折,∴∠BEN =2∠BEF ,∴∠BEF =∠ECN ,∴EF ∥AC ,∴AF BF =CE BE=26=13;故④正确,综上:正确的是①②④;故选D .【点睛】本题考查平行四边形的折叠问题,同时考查了解直角三角形,相似三角形的判定和性质,等腰三角形的判定和性质,勾股定理.本题的综合性强,难度较大,是中考常见的压轴题,熟练掌握相关性质,添加合适的辅助线,构造特殊三角形,是解题的关键.4如图,AB 是⊙O 的直径,点C 是⊙O 上一点,将劣弧BC 沿弦BC 折叠交直径AB 于点D ,连接CD ,若∠ABC =α0°<α<45° ,则下列式子正确的是()A.sin α=BCABB.sin α=CD ABC.cos α=AD BDD.cos α=CD BC【答案】B【分析】连AC ,由AB 是⊙O 的直径,可知∠ACB =90°,由折叠,AC和CD所在的圆为等圆,可推得AC =CD ,再利用正弦定义求解即可.【详解】解:连AC ,∵AB 是⊙O 的直径,∴∠ACB =90°,由折叠,AC 和CD所在的圆为等圆,又∵∠CBD =∠ABC ,∴AC和CD所对的圆周角相等,∴AC=CD,∴AC =CD ,在Rt △ACB 中,sin α=AC AB =CDAB,故选:B .【点睛】本题考查圆周角定理和圆心角、弦、弧之间的关系以及正弦、余弦定义,解答关键是通过折叠找到公共的圆周角推出等弦.5如图,在平面直角坐标系中,OA 在x 轴正半轴上,OC 在y 轴正半轴上,以OA ,OC 为边构造矩形OABC ,点B 的坐标为8,6 ,D ,E 分别为OA ,BC 的中点,将△ABE 沿AE 折叠,点B 的对应点F 恰好落在CD 上,则点F 的坐标为()A.3213,3013B.3013,3213C.3013,2013D.2013,3013【答案】A【分析】先求得直线CD 的解析式,过点F 作FM ⊥CE 于点M ,过点F 作FN ⊥OC 于点N ,设点F m ,-32m +6 ,在Rt △EMF 中,再利用勾股定理得到关于m 的方程,解方程即可.【详解】解:∵点B 的坐标为8,6 ,四边形OABC 是矩形,D ,E 分别为OA ,BC 的中点,∴C 0,6 ,D 4,0 ,E 4,6 ,由折叠的性质可得:EF =BE =4,设直线CD 的解析式为y =kx +b ,则6=b 4k +b =0 ,解得:k =-32b =6,∴直线CD 的解析式为y =-32x +6,过点F 作FM ⊥CE 于点M ,过点F 作FN ⊥OC 于点N ,设点F m,-32m+6,则MF=CN=6--32m+6=32m,EM=4-m,在Rt△EMF中,EM2+MF2=EF2,∴4-m2+32m2=42,解得:m=3213或m=0(不合题意,舍去),当m=3213时,y=-32×3213+6=3013,∴点F的坐标为3213,30 13,故选:A.【点睛】本题是一次函数与几何综合题,考查了求一次函数解析式,勾股定理,翻折的性质,矩形的性质,中点的性质,熟练掌握知识点并灵活运用是解题的关键.6综合与实践课上,李老师让同学们以矩形纸片的折叠为主题开展数学活动.如图,将矩形纸片ABCD对折,折痕为EF,再把点A折叠在折痕EF上,其对应点为A ,折痕为DP,连接A B,若AB=2,BC =3,则tan∠A BF的值为()A.33B.3 C.32D.12【答案】A【分析】先证明EF=AB=CD=2,CF=BF=DE=32,∠DEA=90°,∠A FB=90°,AD=A D=3,可得A E=A D2-DE2=32,AF=2-32=12,再利用正切的定义求解即可.【详解】解:∵矩形纸片ABCD对折,折痕为EF,AB=2,BC=3,∴EF=AB=CD=2,CF=BF=DE=32,∠DEA=90°,∠A FB=90°,由折叠可得:AD=A D=3,∴A E=A D2-DE2=32,∴A F=2-32=12,∴tan ∠A BF =1232=33.故选A【点睛】本题考查的是轴对称的性质,矩形的性质,勾股定理的应用,求解锐角的正切,熟记轴对称的性质是解本题的关键.7如图,矩形ABCD 中,AB =2,BC =3,P 是边BC 中点,将顶点D 折叠至线段AP 上一点D ,折痕为EF ,此时,点C 折叠至点C .下列说法中错误的是()A.cos ∠BAP =45B.当AE =53时,D E ⊥AP C.当AE =18-65时,△AD E 是等腰三角形 D.sin ∠DAP =45【答案】C【分析】根据矩形的性质,直角三角形的性质,三角函数,勾股定理,折叠的性质计算判断即可.【详解】∵矩形ABCD 中,AB =2,BC =3,P 是边BC 中点,∴BP =12BC =32,∠B =90°,∴AP =AB 2+BP 2=22+32 2=52,∴cos ∠BAP =AB AP=252=45,故A 正确;∵矩形ABCD ,∴AD ∥BC ,∴∠DAP =∠APB ,∴sin ∠DAP =sin ∠APB =cos ∠BAP =45,故D 正确;设DE =D E =x ,根据题意,得AE =AD -DE =3-x ,sin ∠DAP =45,∵D E ⊥AP ,∴sin ∠DAP =D E AE=x 3-x =45,解得x =43,∴AE =AD -DE =3-x =53,故B 正确;当D E =AE 时,∴x =3-x ,解得x =32;此时D ,A 重合,三角形不存在,不符合题意;当D E =AD 时,过点D 作D N ⊥AD 于点N ,则AN =NE ;∵矩形ABCD ,∴AD ∥BC ,∴∠DAP =∠APB ,∴cos ∠DAP =cos ∠APB =3252=35,设DE =D E =x ,根据题意,得AE =AD -DE =3-x ,D E =AD =x ,∴AN AD=AN x =35,解得AN =35x ;∴AE =AD -DE =3-x =2AN =65x ,解得x =1511;∴AE =65×1511=1811;当AE =AD 时,过点D 作D H ⊥AD 于点H ,设DE =D E =x ,根据题意,得AE =AD =AD -DE =3-x ,∴D H =AD sin ∠DAP =453-x ,AH =AD cos ∠DAP =353-x ,∴HE =AE -AH =3-x -353-x =253-x ,根据勾股定理,得HE 2+D H 2=D E 2,∴253-x 2+453-x2=x 2解得x =65-12;∴AE =3-x =15-65;综上所述,AE =15-65或AE =1811,故C 错误,故选C .【点睛】本题考查了矩形的性质,直角三角形的性质,三角函数,勾股定理,折叠的性质,熟练掌握三角函数,勾股定理,矩形的性质,折叠的性质是解题的关键.8如图,AB 为半圆O 的直径,点O 为圆心,点C 是弧上的一点,沿CB 为折痕折叠BC交AB 于点M ,连接CM ,若点M 为AB 的黄金分割点(BM >AM ),则sin ∠BCM 的值为()A.5-12B.5+12C.5-14D.12【答案】A【分析】过点M作MD⊥CB,垂足为D,延长MD交半⊙O于点M′,连接CM ,BM′,根据折叠的性质可得:∠CMB=∠CM′B,BC⊥MM′,从而可得∠BDM=90°,再根据黄金分割的定义可得BMAB =5-12,然后利用直径所对的圆周角是直角可得∠ACB=90°,从而证明A字模型相似三角形△DBM∽△CBA,进而利用相似三角形的性质可得DMAC=BMAB=5-12,最后根据圆内接四边形对角互补以及平角定义定义可得:∠A=∠AMC,从而可得CA=CM,再在Rt△CDM中,利用锐角三角函数的定义进行计算,即可解答.【详解】解:过点M作MD⊥CB,垂足为D,延长MD交半⊙O于点M′,连接CM ,BM′,由折叠得:∠CMB=∠CM′B,BC⊥MM′,∴∠BDM=90°,∵点M为AB的黄金分割点(BM>AM),∴BMAB =5-12,∵AB为半圆O的直径,∴∠ACB=90°,∴∠ACB=∠MDB,∵∠DBM=∠CBA,∴△DBM∽△CBA,∴DMAC =BMAB=5-12,∵四边形ACM′B是半⊙O的内接四边形,∴∠A+∠CM′B=180°,∵∠AMC+∠CMB=180°,∠CMB=∠CM′B,∴∠A=∠AMC,∴CA=CM,在Rt△CDM中,sin∠BCM=DMCM=DMAC=5-12.故选:A.【点睛】本题考查了相似三角形的判定与性质,黄金分割,解直角三角形,翻折变换(折叠问题),圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.二、填空题9如图,将一张矩形纸片ABCD折叠,折痕为EF,折叠后,EC的对应边EH经过点A,CD的对应边HG交BA的延长线于点P.若PA=PG,AH=BE,CD=3,则BC的长为.【答案】43【分析】本题考查了矩形与折叠问题,全等三角形的判定和性质,勾股定理.连接PF ,设BC =2x ,AH =BE=a ,证明Rt △PAF ≌Rt △PGF HL ,求得FA =FG =FD =x ,由折叠的性质求得BE =12x ,在Rt △ABE中,利用勾股定理列式计算,即可求解.【详解】解:连接PF ,设BC =2x ,AH =BE =a ,由矩形的性质和折叠的性质知FG =FD ,∠G =∠FAP =90°,AB =CD =3,AD =BC ,∵PA =PG ,PF =PF ,∴Rt △PAF ≌Rt △PGF HL ,∴FA =FG =FD =12AD =12BC =x ,由矩形的性质知:AD ∥BC ∴∠AFE =∠FEC ,折叠的性质知:∠FEA =∠FEC ,∴∠FEA =∠AFE ,∴AE =FA =x ,由折叠的性质知EC =EH =AE +AH =x +a ,∴BC =BE +EC =a +x +a =2x ,∴a =12x ,即BE =12x ,在Rt △ABE 中,AB 2+BE 2=AE 2,即32+12x 2=x 2,解得x =23,∴BC =2x =43,故答案为:4310如图,在矩形ABCD 中,AB =3,AD =6,M 为AD 的中点,N 为BC 边上一动点,把矩形沿MN 折叠,点A ,B 的对应点分别为A ,B ,连接AA '并延长交射线CD 于点P ,交MN 于点O ,当N 恰好运动到BC 的三等分点处时,CP 的长为.【答案】1或5【分析】分两种情况:①当CN =2BN 时.过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形;②当BN =2CN 时,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,根据矩形的性质得GM =AM -AG =1.再由折叠的性质可得∠AOM =90°,然后根据相似三角形的判定与性质可得答案.【详解】解:①当CN =2BN 时.如图1,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,∴NG =AB =3,AG =BN =2.∵M 为AD 的中点,∴AM =3,∴GM =AM -AG =1.由折叠A 与A 对应,∴∠AOM =90°,∵∠MAO +∠APD =90°,∠MAO +∠AMO =90°,∴∠AMO =∠APD ,即∠GMN =∠APD .又∵∠NGM =∠ADP =90°,∴△ADP ∽△NGM ,∴NG AD=GM DP =12,解得DP =2,∴CP =CD -DP =1.②当BN =2CN 时,如图2,过点N 作NG ⊥AD 于点G ,则四边形ABNG 为矩形,∴NG =AB =3,AG =BN =4.∵M 为AD 的中点,∴AM =3,∴GM =AG -AM =1.由折叠A 与A 对应,∴∠AOM =90°∠MAO +∠AMO =90°,∠MAO +∠APD =90°,∴∠AMO =∠APD ,即∠GMN =∠APD .又∠ADP =∠NGM =90°,∴△ADP ∽△NGM ,∴NG AD=GM DP =12,解得DP =2,∴CP =CD +DP =5.综上,CP 的长为1或5.故答案为:1或5.【点睛】此题考查的是翻折变换-折叠问题、矩形的性质,正确作出辅助线是解决此题的关键.11如图,DE 平分等边△ABC 的面积,折叠△BDE 得到△FDE ,AC 分别与DF ,EF 相交于G ,H 两点.若DG =m ,EH =n ,用含m ,n 的式子表示GH 的长是.【答案】m 2+n 2【分析】先根据折叠的性质可得S △BDE =S △FDE ,∠F =∠B =60°,从而可得S △FHG =S △ADG +S △CHE ,再根据相似三角形的判定可证△ADG ∽△FHG ,△CHE ∽△FHG ,根据相似三角形的性质可得S △ADG S △FHG =DG GH2=m 2GH 2,S △CHE S △FHG =EH GH 2=n 2GH 2,然后将两个等式相加即可得.【详解】解:∵△ABC 是等边三角形,∴∠A =∠B =∠C =60°,∵折叠△BDE 得到△FDE ,∴△BDE ≌△FDE ,∴S △BDE =S △FDE ,∠F =∠B =60°=∠A =∠C ,∵DE 平分等边△ABC 的面积,∴S 梯形ACED =S △BDE =S △FDE ,∴S △FHG =S △ADG +S △CHE ,又∵∠AGD =∠FGH ,∠CHE =∠FHG ,∴△ADG ∽△FHG ,△CHE ∽△FHG ,∴S △ADG S △FHG =DG GH 2=m 2GH 2,S △CHE S △FHG =EH GH 2=n 2GH 2,∴S △ADG S △FHG +S △CHE S △FHG =m 2+n 2GH 2=S △ADG +S △CHE S △FHG =1,∴GH 2=m 2+n 2,解得GH =m 2+n 2或GH =-m 2+n 2(不符合题意,舍去),故答案为:m 2+n 2.【点睛】本题考查了等边三角形的性质、折叠的性质、相似三角形的判定与性质等知识点,熟练掌握相似三角形的判定与性质是解题关键.12在矩形ABCD 中,点E 为AD 边上一点(不与端点重合),连接BE ,将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,连接并延长EF ,BF 分别交BC ,CD 于G ,H 两点.若BA =6,BC =8,FH =CH ,则AE 的长为.【答案】92【分析】连接GH ,证明Rt △FHG ≅Rt △CHG (HL ),可得FG =CG ,设FG =CG =x ,在Rt △BFG 中,有62+x 2=(8-x )2,可解得CG =FG =74,知BG =254,由矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,得∠AEB =∠FEB ,可得∠FEB =∠EBG ,EG =BG =254,故EF =EG -FG =92,从而得到AE =92.【详解】连接GH ,如图:∵四边形ABCD 是矩形,∴∠A =∠C =90°,∵将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,∴BF =AB =6,AE =EF ,∠BFE =∠A =90°,∴∠GFH =90°=∠C ,∵GH =GH ,FH =CH ,∴Rt △FHG ≅Rt △CHG (HL ),∴FG =CG ,设FG =CG =x ,则BG =BC -CG =8-x在Rt △BFG 中,BF 2+FG 2=BG 2∴62+x 2=(8-x )2,解得:x =74,∴CG =FG =74,∴BG =8-x =25x,∵将矩形ABCD 沿BE 折叠,折叠后点A 与点F 重合,∴∠AEB =∠FEB ,∵AD ⎳BC ,∴∠AEB =∠EBG ,∴∠FEB =∠EBG ,∴EG =BG =254,∴AE =92,故答案为:92.【点睛】本题考查矩形中的翻折变换,涉及三角形全等的判定与性质,勾股定理及应用,掌握相关知识是解题的关键.13如图,在矩形ABCD 中,AD =23,CD =6,E 是AB 的中点,F 是线段BC 上的一点,连接EF ,把△BEF 沿EF 折叠,使点B 落在点G 处,连接DG ,BG 的延长线交线段CD 于点H .给出下列判断:①∠BAC =30°;②△EBF ∽△BCH ;③当∠EGD =90°时,DG 的长度是23 ④线段DG 长度的最小值是21-3;⑤当点G 落在矩形ABCD 的对角线上,BG 的长度是3或33;其中正确的是.(写出所有正确判断的序号)【答案】①②③【分析】利用正切函数的定义即可判断①正确;利用同角的余角相等推出∠HBC =∠BEF ,可判断②正确;推出点D 、G 、F 三点共线,证明Rt △EAD ≌Rt △EGD HL ,可判断③正确;当点D 、G 、E 三点共线,线段DG 长度的最小值是21-3,由于F 是线段BC 上的一点,不存在D 、G 、E 三点共线,可判断④不正确;证明△BGE 是等边三角形,可判断⑤.【详解】解:连接AC ,∵矩形ABCD 中,AD =23,CD =6,∴tan ∠ACD =AD CD=236=33,∴∠ACD =30°,∴∠BAC =30°,故①正确;由折叠的性质知EF 是BG 的垂直平分线,∴∠HBC +∠BFE =90°=∠BEF +∠BFE ,∴∠HBC =∠BEF ,∴△EBF ∽△BCH ,故②正确;由折叠的性质知∠EGF =∠ABC =90°,∵∠EGD =90°,∴点D 、G 、F 三点共线,连接DE ,在Rt △EAD 和Rt △EGD 中,AE =BE =EG ,DE =DE ,∴Rt △EAD ≌Rt △EGD HL ,∴DG =AD =23,故③正确;∵AE =BE =EG ,∴点A 、G 、B 都在以E 为圆心,3为半径的圆上,DE =23 2+32=21,∴当点D 、G 、E 三点共线,线段DG 长度的最小值是21-3,但F 是线段BC 上的一点,∴D 、G 、E 三点不可能共线,故④不正确;当点G 落在矩形ABCD 的对角线AC 上时,由折叠的性质知BE =EG ,∵E 是AB 的中点,由①知∠BAC =30°,∴BE =EG =EA ,∠BAC =∠EGA =30°,∴∠BEG =∠BAC +∠EGA =60°,∴△BGE 是等边三角形,∴BG 的长度是3;由于F 是线段BC 上的一点,则点G 不会落在矩形ABCD 的对角线BD 上,故⑤不正确;综上,①②③说法正确,故答案为:①②③.【点睛】本题考查了矩形与折叠问题,正切函数,相似三角形的判定,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.14如图,将矩形ABCD沿BE折叠,点A与点A 重合,连接EA 并延长分别交BD、BC于点G、F,且BG=BF.(1)若∠AEB=55°,则∠GBF=;(2)若AB=3,BC=4,则ED=.【答案】40°/40度5-10/-10+5【分析】(1)先证明∠DEF=180°-2×55°=70°,∠BFG=∠DEF=70°,利用BG=BF,可得答案;(2)如图,过F作FQ⊥AD于Q,可得CF=DQ,FQ=CD=3,同理可得:∠BGF=∠BFG,∠DEG=∠BFG,而∠DGE=∠BGF,则∠DEG=∠DGE,设DE=DG=x,而BD=32+42=5,则BG=BF=5-x,CF=4-5-x=1,再求解EF=12+32=10,由折叠可得:A E=AE=4 =x-1,EQ=x-x-1-x,AF=10-4+x,利用cos∠BFA=cos∠FEQ,再建立方程求解即可.【详解】解:(1)∵∠AEB=55°,结合折叠可得:∠AEB=∠A EB=55°,∴∠DEF=180°-2×55°=70°,∵矩形ABCD,∴AD∥BC,∴∠BFG=∠DEF=70°,∵BG=BF,∴∠BGF=∠BFG=70°;∴∠GBF=180°-2×70°=40°;故答案为:40°.(2)如图,过F作FQ⊥AD于Q,∴四边形FCDQ是矩形,则CF=DQ,FQ=CD=3,同理可得:∠BGF=∠BFG,∠DEG=∠BFG,而∠DGE=∠BGF,∴∠DEG=∠DGE,∴设DE=DG=x,∵矩形ABCD,AB=3,BC=4,∴BD=32+42=5,∴BG=BF=5-x,∴CF=4-5-x=x-1,∴EQ=x-x-1=1,∴EF=12+32=10,由折叠可得:A E=AE=4-x,∴AF =10-4+x,∵∠QEF=∠BFA ,∴cos∠BFA =cos∠FEQ,∴EQEF=A FBF,∴110=10-4+x5-x,解得:x=5-10,经检验符合题意;∴DE=5-10.故答案为:5-10.【点睛】本题考查的是轴对称的性质,矩形的性质与判定,勾股定理的应用,锐角三角函数的应用,等腰三角形的判定与性质,熟练的利用以上知识解题是关键.三、解答题15综合与实践课上,老师让同学们以“正方形的折叠”为主题开展实践活动.(1)操作判断操作一:如图(1),正方形纸片ABCD,点E是BC边上(点E不与点B,C重合)任意一点,沿AE折叠△ABE到△AFE,如图(2)所示;操作二:将图(2)沿过点F的直线折叠,使点E的对称点G落在AE上,得到折痕MN,点C的对称点记为H,如图(3)所示;操作三:将纸片展平,连接BM,如图(4)所示.根据以上操作,回答下列问题:①B,M,N三点(填“在”或“不在”)一条直线上;②AE和BN的位置关系是,数量关系是;③如图(5),连接AN,改变点E在BC上的位置,(填“存在”或“不存在”)点E,使AN平分∠DAE.(2)迁移探究苏钰同学将正方形纸片换成矩形纸片ABCD,AB=4,BC=6,按照(1)中的方式操作,得到图(6)或图(7).请完成下列探究:①当点N在CD上时,如图(6),BE和CN有何数量关系?并说明理由;②当DN的长为1时,请直接写出BE的长.【答案】(1)①在,②AE⊥BN,相等;③不存在;(2)①BECN =23,理由见解析;②BE=2或165.【分析】(1)①E的对称点为E ,BF⊥EE ,MF⊥EE ,即可判断;②由①AE⊥BN,由同角的余角相等得∠BAE=∠CBN,由AAS可判定△ABE≌△BCN,由全等三角形的性质即可得证;③由AAS可判定△DAN≌△MAN,由全等三角形的性质得AM=AD,等量代换得AB=AM,与AB>AM矛盾,即可得证;(2)①由(1)中的②可判定△ABE∽△BCN,由三角形相似的性质即可求解;②当N在CD上时,△ABE∽△BCN,由三角形相似的性质即可求解;当N在AD上时,同理可判定△ABE∽△NAB,由三角形相似的性质即可求解.【详解】(1)解:①E的对称点为E ,∴BF⊥EE ,MF⊥EE ,∴B、F、M共线,故答案为:在;②由①知:B、F、M共线,N在FM上,∴AE⊥BN,∴∠AMB=90°,∴∠ABM+∠BAE=90°,∵四边形ABCD是正方形,∴∠ABC=∠BCN=90°,AB=BC,∴∠CBN+∠ABM=90°,∴∠BAE=∠CBN,在△ABE和△BCN中,∠BAE=∠CBN ∠ABC=∠BCN AB=BC,∴△ABE≌△BCN(AAS),∴AE=BN,故答案为:相等;③不存在,理由如下:假如存在,∵AN平分∠DAE,∴∠DAN=∠MAN,∵四边形ABCD是正方形,AM⊥BN,∴∠D=∠AMN=90°,在△DAN和△MAN中,∠D=∠AMN∠DAN=∠MAN AN=ANN∴△DAN≌△MAN(AAS),∴AM=AD,∵AD=AB,∴AB=AM,∵AB是Rt△ABM的斜边,∴AB>AM,∴AB =AM 与AB >AM 矛盾,故假设不成立,所以答案为:不存在;(2)解:①BE CN=23,理由如下:由(1)中的②得:∠BAE =∠CBN ,∠ABE =∠C =90°,∴△ABE ∽△BCN ,∴BE CN =AB BC=23;②当N 在CD 上时,CN =CD -DN =3,由①知:△ABE ∽△BCN ,∴BE CN =AB BC =23,∴BE =23CN =2,当N 在AD 上时,AN =AD -DN =5,∵∠BAE =∠CBN =∠ANB ,∠ABE =∠BAN =90°,∴△ABE ∽△NAB ,∴BE AB =AB AN ,∴BE 4=45,∴BE =165,综上所述:BE =2或165.【点睛】本题考查了折叠的性质,矩形的性质,正方形的性质,全等三角形的判定及性质,三角形相似的判定及性质,掌握相关的判定方法及性质,“十字架”典型问题的解法是解题的关键.16在矩形ABCD 中,AD =2AB =8,点P 是边CD 上的一个动点,将△BPC 沿直线BP 折叠得到△BPC .(1)如图1,当点P 与点D 重合时,BC ′与AD 交于点E ,求BE 的长度;(2)当点P 为CD 的三等分点时,直线BC ′与直线AD 相交于点E ,求DE 的长度;(3)如图2,取AB 中点F ,连接DF ,若点C ′恰好落在DF 边上时,试判断四边形BFDP 的形状,并说明理由.【答案】(1)BE 的长度为5;(2)DE 的长度为113或83;(3)四边形BFDP 是平行四边形(理由见解析)【分析】本题利用了折叠的知识(折叠后的两个图形全等)以及矩形的性质(矩形的对边相等,对角相等),以及平行四边形的判定有关知识.(1)利用矩形性质和折叠的性质可推出BE=DE,设BE=x,则DE=x,AE=8-x,利用勾股定理建立方程求解即可得出答案;(2)设DE=m,则AE=m+8,设BE交CD于G,可证得△AEB∽△CBG,得出CGAB =BCAE,即CG4=8m+8,求得CG=32m+8,分两种情况:当PC=13CD=43时,当PC=23CD=83时,分别添加辅助线构造相似三角形,利用相似三角形性质建立方程求解即可得出答案;(3)由中点定义可得AF=BF,过点C 作C M∥AD交AB于点M,过点F作FN⊥BC 于点N,由矩形性质和翻折的性质可得∠C BP=∠CBP=12∠C BC,可证得△FC M∽△FDA,得出FMAF=C MAD,再证得△BFN∽△BC M,进而推出FM=FN,利用角平分线的判定定理可得∠BC F=∠MC F=12∠BC M推出∠BC F=∠C BP,再由平行线的判定定理可得DF∥BP,运用平行四边形的判定定理即可证得四边形BFDP是平行四边形.【点睛】点睛片段【详解】(1)解:∵AD=2AB=8,∴AB=4,∵四边形ABCD是矩形,∴∠A=90°,AD∥BC,∴∠ADB=∠DBC,由折叠得:∠DBC=∠DBC ,∴∠ADB=∠DBC ,即∠EDB=∠EBD,∴BE=DE,设BE=x,则DE=x,AE=8-x,在Rt△ABE中,AE2+AB2=BE2,∴(8-x)2+42=x2,解得:x=5,∴BE的长度为5;(2)设DE=m,则AE=m+8,设BE交CD于G,∵四边形ABCD是矩形,∴BC=AD=8,CD=AB=4,AD∥BC,∠A=∠BCG=90°,∴∠AEB=∠CBG,∴△AEB∽△CBG,∴CG AB =BCAE,即CG4=8m+8,∴CG=32m+8,当PC=13CD=43时,BP=BC2+PC2=82+432=4373,连接CC ,过点C 作C H⊥CD于点H,如图,∵将△BPC沿直线BP折叠得到△BPC ,∴CC ⊥BP,△BPC ≌△BPC,∴S四边形BCPC =2S△BPC,∴1BP⋅CC =2×1BC⋅PC,即12×4373CC =2×12×8×43,∴CC =163737,∵∠C CH +∠BPC =90°,∠PBC +∠BPC =90°,∴∠C CH =∠PBC ,∵∠CHC =∠BCP =90°,∴△CC H ∽△BPC ,∴C H PC =CH BC =CC BP ,即CH 43=CH 8=1637374373,∴C H =1637,CH =9637,∵∠C HG =∠EDG =90°,∴C H ∥AE ,∴∠GC ′H =∠AEB ,∴△C GH ∽△EBA ,∴GH AB =C H AE ,即GH 4=1637m +8,∴GH =6437(m +8),∵CH +GH =CG ,∴9637+6437(m +8)=32m +8,解得:m =113,经检验,m =113是该方程的解,∴DE =113;当PC =23CD =83时,BP =BC 2+PC 2=82+83 2=8103,连接CC ,过点C 作C H ⊥CD 交CD 的延长线于点H ,作C G ⊥AD 于点G ,如图,同理可得:CC =8105,同理△CC H ∽△BPC ,∴C H PC =CH BC =CC BP ,即CH 83=CH 8=81058103,∴C H =85,CH =245,∴DH =CH -CD =245-4=45,∵∠HDG =∠H =∠C GD =90°,∴四边形DGC H 是矩形,∴C G =DH =45,DG =C H =85,∵∠C GE =∠A =90°,∠C EG =∠BEA ,∴△C EG ∽△BEA ,∴EG AE =C G AB =454=15,∴AE =5EG ,∵AE +EG =AG =AD -DG =8-85=325,∴5EG +EG =325,∴EG =1615,∴DE =DG +EG =85+1615=83,综上所述,DE 的长度为113或83;(3)四边形BFDP 是平行四边形,理由如下:∵点F 是AB 的中点,∴AF =BF ,过点C 作C M ∥AD 交AB 于点M ,过点F 作FN ⊥BC 于点N ,如图,则∠FC M =∠ADF ,∵四边形ABCD 是矩形,∴AD ∥BC ,AB ∥CD ,∴C M ∥BC ,∴∠BC M =∠C BC ,由翻折得:∠C BP =∠CBP =12∠C BC ,BC =BC =8,∵C M ∥AD ,∴△FC M ∽△FDA ,∴FM AF =C M AD ,∴FM BF =C MBC ,∵∠BNF =∠BMC =90°,∠FBN =∠C BM ,∴△BFN ∼△BC M∴FN BF =C MBC ,∴FM BF =FN BF ,∴FM =FN ,又∵FM ⊥C M ,FN ⊥C B ,∴∠BC F =∠MC F =12∠BC M ,∴∠BC F =∠C BP ,∴DF ∥BP ,∴四边形BFDP 是平行四边形.17矩形ABCD 中,AB =6,AD =8,点E 为对角线AC 上一点,过点E 作EF ⊥AD 于点F ,EG ⊥AC 交边BC 于点G ,将△AEF 沿AC 折叠得△AEH ,连接HG .(1)如图1,若点H 落在边BC 上,求证:AH =CH ;(2)如图2,若A ,H ,G 三点在同一条直线上,求HG 的长;(3)若△EHG 是以EG 为腰的等腰三角形,求EF 的长.【答案】(1)见解析(2)HG =94(3)EF =103或4【分析】(1)根据矩形的性质和翻折的性质证明∠ACH =∠HAC ,即可解决问题;(2)结合(1)的方法AG =CG ,解Rt △AEG ,Rt △HEG 分别求得EG ,HG ;(3)当△EHG 是以EG 为腰的等腰三角形时,分两种情况:①当EG =EH ,②当EG =HG ,结合(2)的方法,利用全等三角形的判定与性质和相似三角形的判定与性质即可解决问题.【详解】(1)∵四边形ABCD 是矩形,∴AD ∥BC .∴∠DAE =∠ACH .∵△AHE 由△AFE 折叠得到,∴∠HAC =∠DAE ,∴∠HAC =∠ACH ,∴AH =CH ;(2)∵矩形ABCD 中,AB =6,AD =8.∴AC =10.当A ,H ,G 三点在同一条直线上时,∠EHG =90°.同(1)可得AG =CG .又∵EG ⊥AC ,∴AE =12AC =5.∵∠AEH +∠HEG =90°,∠AEH +∠HAE =90°,∴∠HEG =∠HAC =∠CAD .∵在Rt △AEG 中,tan ∠EAG =EG AE =34,∴EG =34AE =154.∵在Rt △HEG 中,sin ∠HEG =HG EG =35,∴HG =35EG =94.(3)①若EH =EG ,如图3①设EF =EH =EG =x ,∵EF ⊥AD ,∴EF ∥CD ,∴△AEF ∽△ACD ,∴AE AC =AF AD =EF CD ∴AE 10=AF 8=x 6∴AE =53x ,AF =43x ,∴AH =AF =43x ,∵∠AHE =∠CEG =90°,∠HAE =∠GCE ,EH =EH ,∴△AHE ≌△CGE AAS ,∴AH =CE ,∴43x =10-53x ,∴x =103∴EF =103.②若HG =GE ,如图3②.(图3②)过点G 作GM ⊥HE ,设EF =a ,∵EC =10-53a ,∵∠AHE =∠CEG =90°,∠HAE =∠GCE ,∴△AHE ∽△CGE ,∴EG =34EC =3410-53a =152-54a ,∵∠GME =∠EHA ,∠MGE =90°-∠MEG =∠HAE ,∴△MGE ∽△HEA ,∴ME AH =EG AE ,∵AH AE =AD AC =45,∴AH =45AE ,∴ME =45EG =45152-54a =6-a ,∴HE =2ME =12-2a =EF ,∴12-2a =a ,∴a =4,∴EF =4,综上,EF =103或4.【点睛】本题考查了矩形的性质,解直角三角形,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰三角形的性质,翻折的性质,解决本题的关键是综合运用以上知识.18综合与实践【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.【初步尝试】把正方形对折,折痕为EF,然后展开,沿过点A与点E所在的直线折叠,点B落在点B 处,连接 B C,如图1,请直接写出∠AEB 与∠ECB 的数量关系.【能力提升】把正方形对折,折痕为EF,然后展开,沿过点A与BE上的点G所在的直线折叠,使点B落在EF上的点P处,连接PD,如图2,猜想∠APD的度数,并说明理由.【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A ,连接PA ,BA ,AC,如图3,求∠PA B的度数.【答案】初步尝试:∠AEB =∠ECB ;能力提升:猜想:∠APD=60°,理由见解析;拓展延伸:∠PA B=15°【分析】初步尝试:连接BB ,由折叠的性质可知,BE=CE,BE=BE ,∠AEB=∠AEB ,BB ⊥AE,根据等边对等角的性质和三角形内角和定理,得出∠BB C=90°,推出AE∥CB ,即可得出答案;能力提升:根据正方形的性质和折叠的性质,易证△AFP≌△DFP SAS,从而证明△APD是等边三角形,即可得到答案;拓展延伸:连接A C、AA ,由(2)得△APD是等边三角形,进而得出∠PDC=30°,再结合等边对等角的性质和三角形内角和定理,求得∠PAC=15°,∠ACP=30°,由对称性质得:AC=A C,∠ACP=∠A CP=30°,证明△AA B≌△CA B SSS,得到∠CA B=30°,再由∠CA P=∠CAP=15°,即可求出∠PA B的度数.【详解】解:初步尝试:∠AEB =∠ECB ,理由如下:如图,连接BB ,由折叠的性质可知,BE=CE,BE=BE ,∠AEB=∠AEB ,BB ⊥AE,∴BE=CE=BE ,∴∠EBB =∠EB B,∠ECB =∠EB C,∵∠EBB +∠EB B+∠EB C+∠ECB =2∠EB B+∠EB C=180°,∴∠BB C=90°,即BB ⊥CB ,∴AE∥CB ,∴∠AEB=∠ECB ,∴∠AEB =∠ECB ;解:能力提升:猜想:∠APD=60°,理由如下:理由:∵四边形ABCD是正方形,∴AB=AD,∠ADC=90°,由折叠性质可得:AF =DF ,EF ⊥AD ,AB =AP ,在△AFP 和△DFP 中,AF =DF∠AFP =∠DFP =90°FP =FP,∴△AFP ≌△DFP SAS ,∴AP =PD ,∴AP =AD =PD ,∴△APD 是等边三角形,∴∠APD =60°;解:拓展延伸:如图,连接A C 、AA ,由(2)得△APD 是等边三角形,∴∠PAD =∠PDA =∠APD =60°,AP =DP =AD ,∵∠ADC =90°,∴∠PDC =30°,又∵PD =AD =DC ,∴∠DPC =∠DCP =12×180°-30° =75°,∠DAC =∠DCA =45°,∴∠PAC =∠PAD -∠DAC =60°-45°=15°,∠ACP =∠DCP -∠DCA =75°-45°=30°,由对称性质得:AC =A C ,∠ACP =∠A CP =30°,∴∠ACA =60°,∴△ACA 是等边三角形,在△AA B 与△CA B 中,A A =A CA B =A B AB =BC,∴△AA B ≌△CA B SSS ,∴∠AA B =∠CA B =12∠AA C =30°,又∵∠CA P =∠CAP =15°,∴∠PA B =∠CA B -∠CA P =15°.【点睛】本题考查了折叠的性质,等腰三角形的判定和性质,三角形内角和定理,正方形的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,作辅助线构造全等三角形是解题关键.19综合与实践数学活动课上,数学老师以“矩形纸片的折叠”为课题开展数学活动:将矩形纸片ABCD 对折,使得点A ,D 重合,点B ,C 重合,折痕为EF ,展开后沿过点B 的直线再次折叠纸片,点A 的对应点为点N ,折痕为BM . (1)如图(1)若AB =BC ,则当点N 落在EF 上时,BF 和BN 的数量关系是,∠NBF 的度数为.思考探究:(2)在AB=BC的条件下进一步进行探究,将△BMN沿BN所在的直线折叠,点M的对应点为点M .当点M 落在CD上时,如图(2),设BN,BM 分别交EF于点J,K.若DM =4,请求出三角形BJK的面积.开放拓展:(3)如图(3),在矩形纸片ABCD中,AB=2,AD=4,将纸片沿过点B的直线折叠,折痕为BM,点A的对应点为点N,展开后再将四边形ABNM沿BN所在的直线折叠,点A的对应点为点P,点M的对应点为点M ,连接CP,DP,若PC=PD,请直接写出AM的长.(温馨提示:12+3=2-3,12+1=2-1)【答案】(1)BF=12BN,60°(2)2+2(3)4-23【分析】(1)根据折叠的性质得:AB=BN,BF=CF=12BC,根据直角三角形的性质可得∠BNF=30°,由直角三角形的两锐角互余可得结论;(2)由折叠得:BM=BM ,证明Rt△ABM≌Rt△CBM (HL),可知AM=CM ,∠ABM=∠CBM ,得△BFJ是等腰直角三角形,再证明四边形ABCD是正方形,分别计算BF=FJ=12BC=2+2,JK=2,由三角形面积公式可得结论;(3)如图(3),过点P作PG⊥BC于G,PH⊥CD于H,根据等腰三角形的三线合一可得DH=CH=12CD=12AB=1,由折叠的性质和矩形的性质可得PG=CH=1,BN=BP=AB=2,∠NBP=∠ABN,设PL=x,则M L=2x,M P=3x,根据NL=233=NM +M L,列方程可解答.【详解】(1)解:由折叠得:AB=BN,BF=CF,∠BFN=90°,∵AB=BC,∴BF=12BN,∴∠BNF=30°,∴∠NBF=90°-30°=60°,故答案为:BF=12BN,60°;(2)由折叠得:BM=BM ,∵四边形ABCD是矩形,∴∠A=∠C=90°,∵AB=BC,∴Rt△ABM≌Rt△CBM (HL),∴AM=CM ,∠ABM=∠CBM ,∴∠ABM=∠MBN=∠NBM =∠CBM ,∴∠FBJ=45°,∴△BFJ是等腰直角三角形,∵四边形ABCD是矩形,AB=BC,∴矩形ABCD是正方形,∴AD=CD,∠D=90°,∴DM=DM =4,∴MM =42,∵AM=MN=M N=CM ,∴CM =22,∴BC =CD =4+22,∴BF =FC =2+2,∵FK ∥CM ,∴BK =KM ,∴FK =12CM =2,∵△BFJ 是等腰直角三角形,∴BF =FJ =12BC =2+2,∴JK =2+2-2=2,∴S △BJK =12⋅JK ⋅BF =12×2×(2+2)=2+2;(3)如图,过点P 作PG ⊥BC 于G ,PH ⊥CD 于H ,∵PC =PD ,∴DH =CH =12CD =12AB =1,∵∠PGC =∠PHC =∠BCH =90°,∵四边形PGCH 是矩形,∴PG =CH =1,由折叠得:BN =BP =AB =2,∠NBP =∠ABN ,Rt △BPG 中,∠PBG =30°,∴∠ABN =∠NBP =90°-30°2=30°,延长NM ,BP 交于L ,Rt △BNL 中,BN =2,∠NBL =30°,∴NL =2×33=233,Rt △M PL 中,∠M LP =90°-30°=60°,∴∠PM L =30°,设PL =x ,则M L =2x ,M P =3x ,∵NL =233=NM +M L ,∴3x +2x =233,∴x =433-2,∴AM =3x =3×433-2 =4-23.【点睛】本题是四边形的综合题,考查了折叠的性质,含30°角的直角三角形的性质,矩形的性质和判定,正方形的判定和性质,三角函数等知识,掌握折叠的性质和正确作辅助线是解题的关键,题目具有一定的综合性,比较新颖.20综合与实践综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.(1)操作判断如图1,先用对折的方式确定矩形ABCD 的边AB 的中点E ,再沿DE 折叠,点A 落在点F 处,把纸片展平,延长DF ,与BC 交点为G .。
15题压轴题练习--图形折叠及动点问题的相关计算

图形折叠及动点问题的相关计算考情总结:图形折叠及动点问题的相关计算是近五年河南中招考试的重点及必考点,均在填空题第15题进行考查,分值为3分,常见的类型有三角形折叠相关计算、四边形结合的相关计算,常见的设问为探究特殊三角形存在时的线段长、探究动点在特殊位置时的线段长.【方法指导】对于河南中招考试中的几何图形折叠与动点问题的计算,常涉及特殊三角形的探究及动点特殊位置的探究.1.掌握折叠的性质是解决问题的关键.(1)折叠前后位置的图形全等,对应边、角相等;(2)折痕两边的图形关于折痕对称;(3)折叠前后对应点的连线被折痕垂直平分;2.特殊三角形:(1)直角或等腰三角形的判定:首先从可能满足直角的顶点或腰入手,通过矩形的性质、折叠的性质或结合直角三角形勾股定理直接计算,或设出某条线段长,根据相似、勾股定理等,列方程进行求解;3.河南中招考试中,此类问题的重点为分类讨论,即该题多为多解题,注意等腰三角形的腰,直角三角形的直角顶点,特殊点的位置等.1.(2017年)如图,在Rt △ABC 中,∠A=90°,AB=AC ,BC=+1,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠∠B ,使点B 的对应点B′始终落在边AC 上,若△MB′C 为直角三角形,则BM 的长为21221 或1.【分析】①如图1,当∠B′MC=90°,B′与A 重合,M 是BC 的中点,于是得到结论;②如图2,当∠MB′C=90°,推出△CMB′是等腰直角三角形,得到CM=MB′,列方程即可得到结论.【解答】解:①如图1,当∠B′MC=90°,B′与A 重合,M 是BC 的中点,∴BM=BC=+;②如图2,当∠MB′C=90°,∵∠A=90°,AB=AC ,∴∠C=45°,∴△CMB′是等腰直角三角形,∴CM=MB′,∵沿MN 所在的直线折叠∠B ,使点B 的对应点B′,∴BM=B′M ,∴CM=BM ,∵BC=+1,∴CM +BM=BM +BM=+1,∴BM=1,综上所述,若△MB′C 为直角三角形,则BM 的长为+或1,故答案为:+或1.【点评】本题考查了翻折变换﹣折叠问题,等腰直角三角形的性质,正确的作出图形是解题的关键.2.(2016年)如图,已知AD ∥BC ,AB ⊥BC ,AB=3.点E 为射线BC 上一个动点,连接AE ,将△ABE 沿AE 折叠,点B 落在点B′处,过点B′作AD 的垂线,分别交AD ,BC 于点M ,N .当点B′为线段MN 的三等分点时,BE 的长为__________223或553________.解:由翻折的性质可得:AB=AB’BE=B’E①当MB’=2,B’N=1时,设EN=x 得B’E=12+x △B’EN ∽△AB’E'''AB EB M B EN =即3122+=x x解得2x =54BE=B’E=154+=553②当MB’=1,B’N=2时,设EN=x 得B’E=222+x △B’EN ∽△AB’E'''AB EB M B EN =即3412+=x x解得2x =21BE=B’E=421+=223故答案为:223或5533.(2015年)如图,正方形ABCD 的边长是16,点E 在边AB 上,AE =3,点F 是边BC 上不与点B ,C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B'处.若△CDB'恰为等腰三角形,则DB'的长为16或45.4.(2014年)如图,矩形ABCD 中,AD=5,AB=7.点E 为DC 上一个动点,把△ADE 沿AE 折叠,当点D 的对应点D /落在∠ABC 的角平分线上时,DE 的长为53或52.5.(2013年)如图,矩形ABCD 中,AB=3,BC=4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B'处,当△CEB'为直角三角形时,BE 的长为___32或3_______.对应练习1.如图,在矩形ABCD 中,AB=3,BC=6,点E 是射线BC 上一动点,将△ABE 沿AE 翻折得到△AEF ,延长AF 交CD 的延长线于点G ,当BE=3EC 时,DG=25或8.如图①,当E 点在边BC 上时,BE=3EC ,BE=4.5,EC=1.5设AH=HE=x ,FH=4.5-x在Rt △AHF 中:222)5.4(3x x =-+解得:x=3.25FH=4.5-3.25=1.25∵△AHF ∽△AGD ,∴DG FHAD AF =DG25.163=解得DG=2.5=25如图②,当E 点在BC 延长线上时,BE=3EC ,BC=6,EC=3设AH=HE=x ,FH=9-x在Rt △AHF 中:222)9(3x x =-+解得:x=5FH=9-5=4∵△AHF ∽△AGD ,∴DG FHAD AF =DG463=解得DG=82.如图,在Rt △ABC 中,∠ABC=90°,AC=10,BC=8,AD 是∠BAC 的平分线,点E 是斜边AC 上的一点,且AE=AB 。
2020中考数学 压轴专题:图形折叠(包含答案)

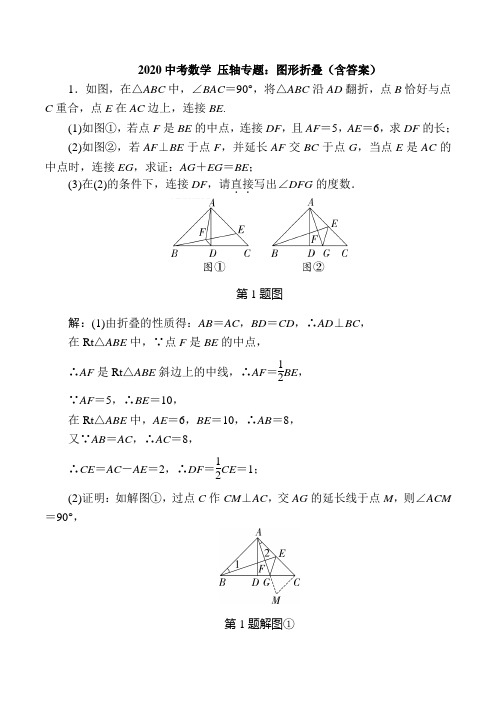
2020中考数学 压轴专题:图形折叠(含答案)1.如图,在△ABC 中,∠BAC =90°,将△ABC 沿AD 翻折,点B 恰好与点C 重合,点E 在AC 边上,连接BE .(1)如图①,若点F 是BE 的中点,连接DF ,且AF =5,AE =6,求DF 的长; (2)如图②,若AF ⊥BE 于点F ,并延长AF 交BC 于点G ,当点E 是AC 的中点时,连接EG ,求证:AG +EG =BE ; (3)在(2)的条件下,连接DF ,请直接..写出∠DFG 的度数.第1题图解:(1)由折叠的性质得:AB =AC ,BD =CD ,∴AD ⊥BC , 在Rt △ABE 中,∵点F 是BE 的中点, ∴AF 是Rt △ABE 斜边上的中线,∴AF =12BE , ∵AF =5,∴BE =10,在Rt △ABE 中,AE =6,BE =10,∴AB =8, 又∵AB =AC ,∴AC =8,∴CE =AC -AE =2,∴DF =12CE =1;(2)证明:如解图①,过点C 作CM ⊥AC ,交AG 的延长线于点M ,则∠ACM =90°,第1题解图①又∵∠BAC =90°,∴∠BAC =∠ACM , ∵AF 是△ABE 的高,∴∠AFB =90°,∴∠1+∠BAF =90°, ∵∠BAC =90°,∴∠2+∠BAF =90°,∴∠1=∠2, 在△ABE 和△CAM 中, ⎩⎪⎨⎪⎧∠BAE =∠ACM AB =CA∠1=∠2, ∴△ABE ≌△CAM (ASA), ∴AE =CM ,BE =AM , 又∵点E 是AC 边的中点, ∴CE =AE =CM , ∵AB =AC ,∠BAC =90°, ∴∠ABC =∠ACB =45°, 又∵∠ACM =90°, ∴∠MCG =∠ACB =45°, 在△CEG 和△CMG 中, ⎩⎪⎨⎪⎧CE =CM ∠ECG =∠MCG CG =CG, ∴△CEG ≌△CMG (SAS),∴EG =GM , 又∵BE =AM ,∴AG +EG =AG +GM =AM =BE ; (3)∠DFG =45°.【解法提示】如解图②,过点D 作DN ⊥DF ,交AG 的延长线于点N ,则∠NDF =90°,第1题解图②∵AD ⊥BC ,∴∠ADB =90°=∠NDF ,∴∠ADB +∠ADF =∠NDF +∠ADF ,即∠BDF =∠ADN ,∵∠ADB =∠AFB =90°,∠5=∠6, ∴∠3=∠4,在Rt △ABC 中,BD =DC , ∴AD =12BC =BD ,在△BDF 和△ADN 中,⎩⎪⎨⎪⎧∠BDF =∠ADN BD =AD ∠3=∠4,∴△BDF ≌△ADN (ASA), ∴DF =DN , 又∵∠NDF =90°,∴∠DFN =∠DNF =45°,即∠DFG =45°.2.如图,在平行四边形ABCD 中,AB =9,AD =13,tan A =125,P 是射线AD 上一点,连接PB ,沿PB 将△APB 折叠,得到△A ′PB .第2题图(1)当∠DP A′=10°时,∠APB=________;(2)当P A′⊥BC时,求线段P A的长度;(3)当点A′落在平行四边形ABCD的边所在的直线上时,求线段P A的长度.解:(1)85°或5°或95°;【解法提示】当点P在线段AD上,且∠APB<90°时,点A′在平行四边形ABCD 的内部,∵∠DP A′=10°,∴∠AP A′=180°-∠DP A′=170°,∴∠APB=12∠AP A′=85°;如解图①,当点P在线段AD上,且∠APB>90°时,点A′在平行四边形ABCD 的外部,∵∠DP A′=10°,∴∠AP A′=180°-∠DP A′=170°,∴∠APB=12(360°-∠AP A′)=95°;如解图②,当点P在AD的延长线上,则∠APB=12∠DP A′=5°;第2题解图(2)∵四边形ABCD是平形四边形,∴AD∥BC,若P A′⊥BC,则P A′⊥AD,∴∠APB=∠A′PB=45°,如解图③,作BH ⊥AD 于点H ,第2题解图③∵tan A =125,∴设AH =5x ,BH =12x ,在Rt △ABH 中,由勾股定理得AB =AH 2+BH 2=13x = 9,解得x =913, ∴AH =4513,BH =10813,∵在Rt △BHP 中,∠BPH =45°, ∴BH =PH =10813, ∴AP =AH +PH =15313;(3)①如解图④,当点A ′在AD 上时,第2题解图④∵AB =A ′B , ∴∠1=∠2,∴BP ⊥AD ,且A ′P =AP ,∵tan A =125, ∴AP =513·AB =4513;②如解图⑤,当点A ′在BC 上时,第2题解图⑤由折叠可知,A ′B =AB ,AP =A ′P ,∠3=∠4, 又∵AD ∥BC , ∴∠5=∠4, ∴∠3=∠5, ∴AB =P A ,∴四边形ABA ′P 为菱形, ∴AP =9;③如解图⑥,当点A ′在AB 的延长线上时,∠ABP = 12∠ABA ′=90°, ∴AP =135×AB =1175.第2题解图⑥综上,线段P A 的长度为4513或9或1175.3.如图,已知一个直角三角形纸片ACB ,其中∠ACB =90°,AC =4,BC =3,E 、F 分别是AC 、AB 边上的点,连接EF .(1)如图①,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在AB 边上的点D 处,且使S 四边形ECBF =3S △EDF ,求AE 的长;(2)如图②,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在BC 边上的点M 处,且使MF ∥CA .①试判断四边形AEMF 的形状,并证明你的结论; ②求EF 的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AF BF 的值.第3题图解:(1)如解图①,第3题解图①∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF . ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF , ∴S 四边形ECBF =3S △AEF . ∵S △ACB =S △AEF +S 四边形ECBF , ∴S △ACB =S △AEF +3S △AEF =4S △AEF . ∴ACBAEFS S △△=14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC . ∴ABC AEF S S △△=(AE AB )2. ∴(AE AB )2=14.在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB 2=AC 2+BC 2.即AB =42+32=5. ∴(AE 5)2=14,∴AE =52; (2)①四边形AEMF 是菱形.证明:∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA , ∴∠CEM =∠EMF . ∴∠CAB =∠CEM . ∴EM ∥AF .∴四边形AEMF 是平形四边形. 又∵AE =ME ,∴四边形AEMF 是菱形.②连接AM 、AM 与EF 交于点O ,如解图②,第3题解图②设AE =x ,则AE =ME =x ,EC =4-x . ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴Rt △ECM ∽Rt △ACB . ∴EC AC =EM AB , ∵AB =5,∴4-x 4=x 5,解得x =209. ∴AE =ME =209,EC =169. 在Rt △ECM 中, ∵∠ECM =90°, ∴CM 2=EM 2-EC 2. 即CM =EM 2-EC 2=(209)2-(169)2=43.∵四边形AEMF 是菱形, ∴OE =OF ,OA =OM ,AM ⊥EF . ∴S 菱形AEMF =4S AOE =2OE ·AO . 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠CAM , ∴OE AO =CM AC . ∵CM =43,AC =4,∴AO =3OE , ∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE ·CM , ∴6OE 2=209×43.∴OE =2109. ∴EF =4109.(3)如解图③,过点F 作FH ⊥CB 于点H ,第3题解图③在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH , ∴EC NC =FH NH , ∵NC =1,EC =47,∴FH NH =47,设FH =x ,则NH =74x , ∴CH =74x -1. ∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x . 在Rt △BHF 和Rt △BCA 中,∵tan∠FBH=tan∠ABC,∴HFBH=ACBC,解得x=85.∴HF=85.∵∠B=∠B,∠BHF=∠BCA=90°,∴△BHF∽△BCA.∴HFCA=BFBA,即HF·BA=CA·BF.∴85×5=4BF.∴BF=2.∵AF=3.∴AFBF=32.4.如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止.△ADP以直线AP为轴翻折,点D落到点D1的位置.设DP=x,△AD1P与原纸片重叠部分的面积为y.(1)当x为何值时,直线AD1过点C?(2)当x为何值时,直线AD1过点BC的中点E?(3)求出y与x的函数表达式.第4题图解:(1)由题意得,△ADP≌△AD1P,∴AD1=AD=2,PD=PD1=x,∠PD1A=∠PDA=90°,∵直线AD1过点C,∴PD1⊥AC,在Rt △ABC 中,∵AB =3,BC =2, ∴AC =22+32=13, CD 1=13-2,在Rt △PCD 1中,PC 2=PD 21+CD 21,即(3-x )2=x 2+(13-2)2, 解得x =213-43, ∴当x =213-43时,直线AD 1过点C ; (2)如解图①,连接PE ,第4题解图①∵E 为BC 中点, ∴BE =CE =1, 在Rt △ABE 中, AE =AB 2+BE 2=10,又∵AD 1=AD =2,PD =PD 1=x , ∴D 1E =10-2,PC =3-x , 在Rt △PD 1E 和Rt △PCE 中, 有x 2+(10-2)2=(3-x )2+12, 解得x =210-23, ∴当x =210-23时,直线AD 1过BC 的中点E ; (3)如解图②,当0<x ≤2时,点D 1在矩形内部,y =x ;图② 图③ 第4题解图如解图③,当2<x ≤3时,点D 1在矩形外部,PD 1与AB 交于点F , ∵AB ∥CD ,∴∠1=∠2,∵∠1=∠3,∴∠2=∠3,∴FP =F A , 作PG ⊥AB ,垂足为点G , 设FP =F A =a ,由题意得,AG =DP =x ,FG =x -a , 在Rt △PFG 中,由勾股定理,得 (x -a )2+22=a 2, 解得a =4+x 22x ,∴y =12×2×4+x 22x =x 2+42x ,综上所述,当0<x ≤2时,y =x ;当2<x ≤3时,y =x 2+42x .5.阅读下列材料:如图①,在Rt △ABC 中,∠C =90°,D 为边AC 上一点,DA =DB ,E 为BD 延长线上一点,∠AEB =120°.(1)猜想AC 、BE 、AE 的数量关系,并证明.小明的思路是:根据等腰△ADB 的轴对称性,将整个图形沿着AB 边的垂直平分线翻折,得到点C 的对称点F ,如图②,过点A 作AF ⊥BE ,交BE 的延长线于F ,请补充完成此问题;(2)参考小明思考问题的方法,解答下列问题:如图③,在等腰△ABC 中,AB =AC ,D 、F 在直线BC 上,DE =BF ,连接AD ,过点E 作EG ∥AC 交FH 的延长线于点G ,∠DFG +∠D =∠BAC .①探究∠BAD 与∠CHG 的数量关系;②请在图中找出一条和线段AD 相等的线段,并证明.第5题图解:猜想:AC =BE +12AE . 理由如下:如题图②, ∵DA =DB , ∴∠DAB =∠DBA , ∵AF ⊥BF , ∴∠F =∠C =90°, 在△ABF 和△BAC 中, ⎩⎪⎨⎪⎧∠F =∠C =90°∠ABF =∠BAC AB =BA, ∴△ABF ≌△BAC (AAS), ∴AC =BF ,∵∠AEB =120°=∠F +∠F AE , ∴∠F AE =30°, ∴EF =12AE ,∴AC =BF =BE +EF =BE +12AE ,∴AC =BE+12AE ; 问题:(1)如题图③中,∵∠ACF =∠D +∠CAD ,∠D +∠DFG =∠BAC ,∴∠CHG =∠CFH +∠FCH =∠CFH +∠D +∠CAD =∠BAC +∠CAD =∠BAD ,∴∠CHG =∠BAD ; (2)结论:AD =FG . 理由如下:如解图③中,反向延长BD 到R ,使得BR =CD ,连接AR ,作AJ ∥CD 交EG 的延长线于点J ,连接FJ ,第5题解图③∵AJ ∥CE ,AC ∥JE ,∴四边形ACEJ 是平行四边形, ∴AJ =CE ,AC =JE , ∵AB =AC ,∴JE =AB ,∠ABC =∠ACB , ∴∠ABR =∠ACD , 在△ABR 和△ACD 中, ⎩⎪⎨⎪⎧AB =AC ∠ABR =∠ACD BR =CD, ∴△ABR ≌△ACD (SAS), ∴AR =AD ,∵BR =CD ,BF =DE , ∴FR =CE =AJ ,EF =BD ,又∵AJ ∥RF ,∴四边形ARFJ 是平行四边形, ∴JF =AR =AD ,在△ABD 和△JEF 中,⎩⎪⎨⎪⎧AB =JE AD =JF BD =EF ,∴△ABD ≌△JEF (SSS), ∴∠EJF =∠BAD , 又∵∠JGH =∠GHC , ∵∠BAD =∠CHG =∠FGJ , ∴∠EJF =∠FGJ , ∴FG =FJ , ∴AD =FG .6.如图,长方形纸片ABCD 中,AB =8,将纸片折叠,使顶点B 落在边AD 上的E 点处,折痕的一端G 点在边BC 上.(1)如图①,当折痕的另一端F 在AB 边上且AE =4时,求AF 的长; (2)如图②,当折痕的另一端F 在AD 边上且BG =10时, ①求证:EF =EG ; ②求AF 的长;(3)如图③,当折痕的另一端F 在AD 边上,B 点的对应点E 在长方形内部,E 到AD 的距离为2,且BG =10时,求AF 的长.第6题图(1)解:∵纸片折叠后顶点B 落在边AD 上的E 点处, ∴BF =EF ,∵AB =8,∴EF =8-AF ,在Rt △AEF 中,AE 2+AF 2=EF 2, 即42+AF 2=(8-AF )2,解得AF =3;(2)①证明:∵纸片折叠后顶点B 落在边AD 上的E 点处,∴∠BGF =∠EGF , ∵长方形纸片ABCD 的边AD ∥BC ,∴∠BGF =∠EFG ,∴∠EGF =∠EFG ,∴EF =EG ; ②解:∵纸片折叠后顶点B 落在边AD 上的E 点处, ∴EG =BG =10,HE =AB =8,FH =AF , ∴EF =EG =10,在Rt △EFH 中,由勾股定理得FH =EF 2-HE 2=102-82=6,∴AF =FH =6;(3)解:如解图,设EH 与AD 相交于点K ,过点E 作MN ∥CD 分别交AD 、BC 于点M 、N ,第6题解图∵E 到AD 的距离为2, ∴EM =2,EN =8-2=6,在Rt △ENG 中,GN =EG 2-EN 2=102-62=8, ∵∠GEN +∠KEM =180°-∠GEH =180°-90°=90°, ∠GEN +∠NGE =180°-90°=90°, ∴∠KEM =∠NGE ,又∵∠ENG =∠KME =90°,∴△GEN ∽△EKM , ∴EK GE =KM EN =EM GN ,即EK 10=KM 6=28, 解得EK =52,KM =32, ∴KH =EH -EK =8-52=112,∵∠FKH=∠EKM,∠H=∠EMK=90°,∴△FKH∽△EKM,∴FHEM=KHKM,即FH2=11232,解得FH=223,∴AF=FH=223.7.在等腰Rt△ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.(1)如图①,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=2时,求AE′的值;(2)如图②,在AC上取一点E,使得CE=13AC,连接DE,将△CDE沿CD 翻折到△CDE′,且AE′交BC于点F,求证:DF=CF.第7题图(1)解:∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴∠ADC=90°,∠ACD=45°,在Rt△ADC中,AC=ADsin 45°=2,∵E是AC的中点,∴CE=12AC=1,∵将△CDE沿CD翻折到△CDE′,∴CE ′=CE =1,∠ACE ′=90°, 由勾股定理得:AE ′=CE ′+AC 2=5;(2)证明:如解图,过B 作AE ′的垂线交AD 于点G ,交AC 于点H ,第7题解图∵∠ABH +∠BAF =90°,∠CAF +∠BAF =90°, ∴∠ABH =∠CAF ,又∵AB =AC ,∠BAH =∠ACE ′=90°, ∴△ABH ≌△CAE ′, ∴AH =CE ′=CE , ∵CE =13AC , ∴AH =HE =CE , ∵D 是BC 中点, ∴DE ∥BH , ∴G 是AD 中点, 在△ABG 和△CAF 中 ⎩⎪⎨⎪⎧∠BAD =∠ACD =45°AB =AC∠ABH =∠CAF, ∴△ABG ≌△CAF (ASA),∴AG =CF , ∵AG =12AD ,∴CF =12AD =12CD ,∴DF =CF . 8.【问题情境】在数学综合与实践课上,老师让同学们以“正方形的折叠为主题开展活动”,如图①,四边形ABCD是正方形,AB=5,点E是CD边上的一动点,连接AE.【操作发现】(1)将△ADE沿AE折叠得△AD′E,如图②,当点D′到BC的距离等于1时,求点E到BC的距离.【继续探究】(2)在(1)的条件下,创新小组在图②中,连接BE,如图③,发现∠AEB=2∠EBC,请你证明这个结论.【深入探究】(3)创新小组将图②沿MN向下折叠,使点A与点E,连接DD′并延长交BC 于点F,如图④,求四边形MNFD的面积.第8题图解:(1)如解图①,过点D′作XY∥BC,与AB、CD分别交于点X、Y,∵四边形ABCD是正方形,第8题解图①∴∠B=∠C=90°,AB∥CD,∴四边形BCYX 是矩形, ∵点D ′到BC 的距离为1, ∴BX =CY =1,∴AX =AB -BX =5-1=4, 由折叠知:AD ′=AD =5,在Rt △AXD ′中,由勾股定理得XD ′=52-42=3, ∴D ′Y =XY -XD ′=5-3=2, 由题易证△AXD ′∽△D ′YE , ∴AXD ′Y=XD ′YE , ∴42=3YE , ∴YE =32,∴CE =YE +YC =32+1=52, ∴点E 到BC 的距离等于52; (2)证明:由(1)知,CE =52, ∴DE =DC -CE =5-52=52, ∴DE =CE ,又∵AD =BC ,∠C =∠ADE , ∴△ADE ≌△BCE , ∴AE =BE ,如解图②,过点E 作EZ ⊥AB 于点Z ,第8题解图②∴EZ 平分∠AEB , ∴∠AEB =2∠BEZ , ∵EZ ⊥AB ,BC ⊥AB , ∴EZ ∥BC . ∴∠BEZ =∠EBC , ∴∠AEB =2∠EBC ;(3)∵点A 、点E 关于MN 对称, ∴MN 垂直平分AE , 同理:AE 垂直平分DD ′, ∴MN ∥DF , 又∵MD ∥NF ,∴四边形MNFD 是平行四边形,如解图③,设AE 与MN ,DD ′分别相交于点G 、H ,第8题解图③在Rt △ADE 中,由勾股定理得 AE =AD 2+DE 2 =52+(52)2=552,∴GE =12AE =12×552=554. 在Rt △ADE 中,DH ·AE =AD ·DE ,∴DH =AD ·DEAE =5×52552=5,在Rt △DEH 中,由勾股定理得 EH =DE 2-DH 2=(52)2-(5)2=52,∴GH =GE -EH =554-52=354,∵△ADE ≌△DCF ,∴AE =DF ,∴DF =552, ∴S 四边形MNFD =DF ·GH =552×354=758. 9.【问题情境】(1)数学课上,老师出了一道题,如图①,Rt △ABC 中,∠C =90°,AC =12AB ,求证:∠B =30°,请你完成证明过程;【继续探究】(2)如图②,四边形ABCD 是一张边长为2的正方形纸片,E 、F 分别为AB 、CD 的中点,沿过点D 的折痕将纸片翻折,使点A 落在EF 上的点A ′处,折痕交AE 于点G ,请运用(1)中的结论求∠ADG 的度数和AG 的长;【拓展应用】(3)若矩形纸片ABCD 按如图③所示的方式折叠,B 、D 两点恰好重合于一点O (如图④),当AB =6时,求EF 的长.第9题图(1)证明:Rt △ABC 中,∠C =90°,AC =12AB , ∵sin B =AC AB =12, ∴∠B =30°;(2)解:∵正方形边长为2,E 、F 分别为AB 、CD 的中点, ∴EA =FD =12×CD =1,∵沿过点D 的折痕将纸片翻折,使点A 落在EF 上的点A ′处, ∴A ′D =AD =2, ∴FD A ′D =12, ∴∠F A ′D =30°,可得∠FDA ′=90°-30°=60°,由折叠性质可得∠ADG =∠A ′DG ,AG =A ′G , ∴∠ADG =∠ADA ′2=90°-60°2=15°, ∵A ′D =2,FD =1,∴A′F=A′D2-FD2=3,∴EA′=EF-A′F=2-3,∵∠EA′G+∠DA′F=180°-∠GA′D=90°,∴∠EA′G=90°-∠DA′F=90°-30°=60°,∴∠EGA′=90°-∠EA′G=90°-60°=30°,则AG=AG′=2EA′=2(2-3);(3)解:∵折叠后B、D两点恰好重合于一点O,∴AO=AD=CB=CO,∴DA=AC 2,∵∠D=90°,∴∠DCA=30°,∵AB=CD=6,在Rt△ACD中,ADDC=tan30°,则AD=DC·tan30°=6×33=23,∵∠DAF=∠F AO=12∠DAO=90°-∠DCA2=30°,∴DFAD=tan30°=33,∴DF=33AD=2,∴DF=FO=2,同理EO=2,∴EF=EO+FO=4.10.如图,在矩形ABCD纸片中,AB=10 cm,BC=12 cm.点P在BC边上,将△P AB沿AP折叠得△P AE,连接CE,DE.(1)当点E落在AD边上时,CE=________;(2)当△CDE分别满足下列条件时,求PB的长.①DE=CD;②DE=CE.第10题图解:(1)226 cm ; 【解法提示】如解图①,∵将△P AB 沿AP 折叠,得△P AE ,E 落在AD 边上, ∴四边形ABPE 是正方形, ∴PB =PE =AB =10 cm , ∴PC =2 cm ,∴CE =PE 2+PC 2=226 cm.第10题解图①(2)①如解图②,过E 作MN ⊥AD 于M ,交BC 于N ,则MN ⊥BC ,第10题解图②∵DE =CD ,AE =AB =CD =DE , ∴AE =10 cm ,∴AM =12AD =BN =6 cm ,∴ME =AE 2-AM 2=8 cm , ∴EN =MN -ME =2 cm , 易知△AME ∽△ENP , ∴AM AE =EN PE , ∴610=2PE , ∴PE =103 cm , ∴PB =PE =103 cm ;②如解图③,过E 作MN ⊥AD 于M ,交BC 于N ,过E 作EQ ⊥CD 于Q ,第10题解图③∵DE =CE ,∴DQ =12CD =5 cm ,∴ME =5 cm , ∴EN =MN -ME =5 cm , ∴AM =AE 2-ME 2=5 3 cm , ∴BN =5 3 cm , 同理得AM AE =EN PE , ∴5310=5PE , ∴PE =1033 cm ,103∴PB=PE=3cm.。
2020中考数学压轴专题:图形折叠(含答案)
2020中考数学 压轴专题:图形折叠(含答案)1.如图,在△ABC 中,∠BAC =90°,将△ABC 沿AD 翻折,点B 恰好与点C 重合,点E 在AC 边上,连接BE .(1)如图①,若点F 是BE 的中点,连接DF ,且AF =5,AE =6,求DF 的长; (2)如图②,若AF ⊥BE 于点F ,并延长AF 交BC 于点G ,当点E 是AC 的中点时,连接EG ,求证:AG +EG =BE ; (3)在(2)的条件下,连接DF ,请直接..写出∠DFG 的度数.第1题图解:(1)由折叠的性质得:AB =AC ,BD =CD ,∴AD ⊥BC , 在Rt △ABE 中,∵点F 是BE 的中点, ∴AF 是Rt △ABE 斜边上的中线,∴AF =12BE , ∵AF =5,∴BE =10,在Rt △ABE 中,AE =6,BE =10,∴AB =8, 又∵AB =AC ,∴AC =8,∴CE =AC -AE =2,∴DF =12CE =1;(2)证明:如解图①,过点C 作CM ⊥AC ,交AG 的延长线于点M ,则∠ACM =90°,第1题解图①又∵∠BAC =90°,∴∠BAC =∠ACM , ∵AF 是△ABE 的高,∴∠AFB =90°,∴∠1+∠BAF =90°, ∵∠BAC =90°,∴∠2+∠BAF =90°,∴∠1=∠2, 在△ABE 和△CAM 中, ⎩⎪⎨⎪⎧∠BAE =∠ACM AB =CA∠1=∠2, ∴△ABE ≌△CAM (ASA), ∴AE =CM ,BE =AM , 又∵点E 是AC 边的中点, ∴CE =AE =CM , ∵AB =AC ,∠BAC =90°, ∴∠ABC =∠ACB =45°, 又∵∠ACM =90°, ∴∠MCG =∠ACB =45°, 在△CEG 和△CMG 中, ⎩⎪⎨⎪⎧CE =CM ∠ECG =∠MCG CG =CG, ∴△CEG ≌△CMG (SAS),∴EG =GM , 又∵BE =AM ,∴AG +EG =AG +GM =AM =BE ; (3)∠DFG =45°.【解法提示】如解图②,过点D 作DN ⊥DF ,交AG 的延长线于点N ,则∠NDF =90°,第1题解图②∵AD ⊥BC ,∴∠ADB =90°=∠NDF ,∴∠ADB +∠ADF =∠NDF +∠ADF ,即∠BDF =∠ADN ,∵∠ADB =∠AFB =90°,∠5=∠6, ∴∠3=∠4,在Rt △ABC 中,BD =DC , ∴AD =12BC =BD ,在△BDF 和△ADN 中,⎩⎪⎨⎪⎧∠BDF =∠ADN BD =AD ∠3=∠4,∴△BDF ≌△ADN (ASA), ∴DF =DN , 又∵∠NDF =90°,∴∠DFN =∠DNF =45°,即∠DFG =45°.2.如图,在平行四边形ABCD 中,AB =9,AD =13,tan A =125,P 是射线AD 上一点,连接PB ,沿PB 将△APB 折叠,得到△A ′PB .第2题图(1)当∠DP A′=10°时,∠APB=________;(2)当P A′⊥BC时,求线段P A的长度;(3)当点A′落在平行四边形ABCD的边所在的直线上时,求线段P A的长度.解:(1)85°或5°或95°;【解法提示】当点P在线段AD上,且∠APB<90°时,点A′在平行四边形ABCD 的内部,∵∠DP A′=10°,∴∠AP A′=180°-∠DP A′=170°,∴∠APB=12∠AP A′=85°;如解图①,当点P在线段AD上,且∠APB>90°时,点A′在平行四边形ABCD 的外部,∵∠DP A′=10°,∴∠AP A′=180°-∠DP A′=170°,∴∠APB=12(360°-∠AP A′)=95°;如解图②,当点P在AD的延长线上,则∠APB=12∠DP A′=5°;第2题解图(2)∵四边形ABCD是平形四边形,∴AD∥BC,若P A′⊥BC,则P A′⊥AD,∴∠APB=∠A′PB=45°,如解图③,作BH ⊥AD 于点H ,第2题解图③∵tan A =125,∴设AH =5x ,BH =12x ,在Rt △ABH 中,由勾股定理得AB =AH 2+BH 2=13x = 9,解得x =913, ∴AH =4513,BH =10813,∵在Rt △BHP 中,∠BPH =45°, ∴BH =PH =10813, ∴AP =AH +PH =15313;(3)①如解图④,当点A ′在AD 上时,第2题解图④∵AB =A ′B , ∴∠1=∠2,∴BP ⊥AD ,且A ′P =AP ,∵tan A =125, ∴AP =513·AB =4513;②如解图⑤,当点A ′在BC 上时,第2题解图⑤由折叠可知,A ′B =AB ,AP =A ′P ,∠3=∠4, 又∵AD ∥BC , ∴∠5=∠4, ∴∠3=∠5, ∴AB =P A ,∴四边形ABA ′P 为菱形, ∴AP =9;③如解图⑥,当点A ′在AB 的延长线上时,∠ABP = 12∠ABA ′=90°, ∴AP =135×AB =1175.第2题解图⑥综上,线段P A 的长度为4513或9或1175.3.如图,已知一个直角三角形纸片ACB ,其中∠ACB =90°,AC =4,BC =3,E 、F 分别是AC 、AB 边上的点,连接EF .(1)如图①,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在AB 边上的点D 处,且使S 四边形ECBF =3S △EDF ,求AE 的长;(2)如图②,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在BC 边上的点M 处,且使MF ∥CA .①试判断四边形AEMF 的形状,并证明你的结论; ②求EF 的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AF BF 的值.第3题图解:(1)如解图①,第3题解图①∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF . ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF , ∴S 四边形ECBF =3S △AEF . ∵S △ACB =S △AEF +S 四边形ECBF , ∴S △ACB =S △AEF +3S △AEF =4S △AEF . ∴ACBAEFS S △△=14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC . ∴ABC AEF S S △△=(AE AB )2. ∴(AE AB )2=14.在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB 2=AC 2+BC 2.即AB =42+32=5. ∴(AE 5)2=14,∴AE =52; (2)①四边形AEMF 是菱形.证明:∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA , ∴∠CEM =∠EMF . ∴∠CAB =∠CEM . ∴EM ∥AF .∴四边形AEMF 是平形四边形. 又∵AE =ME ,∴四边形AEMF 是菱形.②连接AM 、AM 与EF 交于点O ,如解图②,第3题解图②设AE =x ,则AE =ME =x ,EC =4-x . ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴Rt △ECM ∽Rt △ACB . ∴EC AC =EM AB , ∵AB =5,∴4-x 4=x 5,解得x =209. ∴AE =ME =209,EC =169. 在Rt △ECM 中, ∵∠ECM =90°, ∴CM 2=EM 2-EC 2. 即CM =EM 2-EC 2=(209)2-(169)2=43.∵四边形AEMF 是菱形, ∴OE =OF ,OA =OM ,AM ⊥EF . ∴S 菱形AEMF =4S AOE =2OE ·AO . 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠CAM , ∴OE AO =CM AC . ∵CM =43,AC =4,∴AO =3OE , ∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE ·CM , ∴6OE 2=209×43.∴OE =2109. ∴EF =4109.(3)如解图③,过点F 作FH ⊥CB 于点H ,第3题解图③在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH , ∴EC NC =FH NH , ∵NC =1,EC =47,∴FH NH =47,设FH =x ,则NH =74x , ∴CH =74x -1. ∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x . 在Rt △BHF 和Rt △BCA 中,∵tan∠FBH=tan∠ABC,∴HFBH=ACBC,解得x=85.∴HF=85.∵∠B=∠B,∠BHF=∠BCA=90°,∴△BHF∽△BCA.∴HFCA=BFBA,即HF·BA=CA·BF.∴85×5=4BF.∴BF=2.∵AF=3.∴AFBF=32.4.如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止.△ADP以直线AP为轴翻折,点D落到点D1的位置.设DP=x,△AD1P与原纸片重叠部分的面积为y.(1)当x为何值时,直线AD1过点C?(2)当x为何值时,直线AD1过点BC的中点E?(3)求出y与x的函数表达式.第4题图解:(1)由题意得,△ADP≌△AD1P,∴AD1=AD=2,PD=PD1=x,∠PD1A=∠PDA=90°,∵直线AD1过点C,∴PD1⊥AC,在Rt △ABC 中,∵AB =3,BC =2, ∴AC =22+32=13, CD 1=13-2,在Rt △PCD 1中,PC 2=PD 21+CD 21,即(3-x )2=x 2+(13-2)2, 解得x =213-43, ∴当x =213-43时,直线AD 1过点C ; (2)如解图①,连接PE ,第4题解图①∵E 为BC 中点, ∴BE =CE =1, 在Rt △ABE 中, AE =AB 2+BE 2=10,又∵AD 1=AD =2,PD =PD 1=x , ∴D 1E =10-2,PC =3-x , 在Rt △PD 1E 和Rt △PCE 中, 有x 2+(10-2)2=(3-x )2+12, 解得x =210-23, ∴当x =210-23时,直线AD 1过BC 的中点E ; (3)如解图②,当0<x ≤2时,点D 1在矩形内部,y =x ;图② 图③ 第4题解图如解图③,当2<x ≤3时,点D 1在矩形外部,PD 1与AB 交于点F , ∵AB ∥CD ,∴∠1=∠2,∵∠1=∠3,∴∠2=∠3,∴FP =F A , 作PG ⊥AB ,垂足为点G , 设FP =F A =a ,由题意得,AG =DP =x ,FG =x -a , 在Rt △PFG 中,由勾股定理,得 (x -a )2+22=a 2, 解得a =4+x 22x ,∴y =12×2×4+x 22x =x 2+42x ,综上所述,当0<x ≤2时,y =x ;当2<x ≤3时,y =x 2+42x .5.阅读下列材料:如图①,在Rt △ABC 中,∠C =90°,D 为边AC 上一点,DA =DB ,E 为BD 延长线上一点,∠AEB =120°.(1)猜想AC 、BE 、AE 的数量关系,并证明.小明的思路是:根据等腰△ADB 的轴对称性,将整个图形沿着AB 边的垂直平分线翻折,得到点C 的对称点F ,如图②,过点A 作AF ⊥BE ,交BE 的延长线于F ,请补充完成此问题;(2)参考小明思考问题的方法,解答下列问题:如图③,在等腰△ABC 中,AB =AC ,D 、F 在直线BC 上,DE =BF ,连接AD ,过点E 作EG ∥AC 交FH 的延长线于点G ,∠DFG +∠D =∠BAC .①探究∠BAD 与∠CHG 的数量关系;②请在图中找出一条和线段AD 相等的线段,并证明.第5题图解:猜想:AC =BE +12AE . 理由如下:如题图②, ∵DA =DB , ∴∠DAB =∠DBA , ∵AF ⊥BF , ∴∠F =∠C =90°, 在△ABF 和△BAC 中, ⎩⎪⎨⎪⎧∠F =∠C =90°∠ABF =∠BAC AB =BA, ∴△ABF ≌△BAC (AAS), ∴AC =BF ,∵∠AEB =120°=∠F +∠F AE , ∴∠F AE =30°, ∴EF =12AE ,∴AC =BF =BE +EF =BE +12AE ,∴AC =BE+12AE ; 问题:(1)如题图③中,∵∠ACF =∠D +∠CAD ,∠D +∠DFG =∠BAC ,∴∠CHG =∠CFH +∠FCH =∠CFH +∠D +∠CAD =∠BAC +∠CAD =∠BAD ,∴∠CHG =∠BAD ; (2)结论:AD =FG . 理由如下:如解图③中,反向延长BD 到R ,使得BR =CD ,连接AR ,作AJ ∥CD 交EG 的延长线于点J ,连接FJ ,第5题解图③∵AJ ∥CE ,AC ∥JE ,∴四边形ACEJ 是平行四边形, ∴AJ =CE ,AC =JE , ∵AB =AC ,∴JE =AB ,∠ABC =∠ACB , ∴∠ABR =∠ACD , 在△ABR 和△ACD 中, ⎩⎪⎨⎪⎧AB =AC ∠ABR =∠ACD BR =CD, ∴△ABR ≌△ACD (SAS), ∴AR =AD ,∵BR =CD ,BF =DE , ∴FR =CE =AJ ,EF =BD ,又∵AJ ∥RF ,∴四边形ARFJ 是平行四边形, ∴JF =AR =AD ,在△ABD 和△JEF 中,⎩⎪⎨⎪⎧AB =JE AD =JF BD =EF ,∴△ABD ≌△JEF (SSS), ∴∠EJF =∠BAD , 又∵∠JGH =∠GHC , ∵∠BAD =∠CHG =∠FGJ , ∴∠EJF =∠FGJ , ∴FG =FJ , ∴AD =FG .6.如图,长方形纸片ABCD 中,AB =8,将纸片折叠,使顶点B 落在边AD 上的E 点处,折痕的一端G 点在边BC 上.(1)如图①,当折痕的另一端F 在AB 边上且AE =4时,求AF 的长; (2)如图②,当折痕的另一端F 在AD 边上且BG =10时, ①求证:EF =EG ; ②求AF 的长;(3)如图③,当折痕的另一端F 在AD 边上,B 点的对应点E 在长方形内部,E 到AD 的距离为2,且BG =10时,求AF 的长.第6题图(1)解:∵纸片折叠后顶点B 落在边AD 上的E 点处, ∴BF =EF ,∵AB =8,∴EF =8-AF ,在Rt △AEF 中,AE 2+AF 2=EF 2, 即42+AF 2=(8-AF )2,解得AF =3;(2)①证明:∵纸片折叠后顶点B 落在边AD 上的E 点处,∴∠BGF =∠EGF , ∵长方形纸片ABCD 的边AD ∥BC ,∴∠BGF =∠EFG ,∴∠EGF =∠EFG ,∴EF =EG ; ②解:∵纸片折叠后顶点B 落在边AD 上的E 点处, ∴EG =BG =10,HE =AB =8,FH =AF , ∴EF =EG =10,在Rt △EFH 中,由勾股定理得FH =EF 2-HE 2=102-82=6,∴AF =FH =6;(3)解:如解图,设EH 与AD 相交于点K ,过点E 作MN ∥CD 分别交AD 、BC 于点M 、N ,第6题解图∵E 到AD 的距离为2, ∴EM =2,EN =8-2=6,在Rt △ENG 中,GN =EG 2-EN 2=102-62=8, ∵∠GEN +∠KEM =180°-∠GEH =180°-90°=90°, ∠GEN +∠NGE =180°-90°=90°, ∴∠KEM =∠NGE ,又∵∠ENG =∠KME =90°,∴△GEN ∽△EKM , ∴EK GE =KM EN =EM GN ,即EK 10=KM 6=28, 解得EK =52,KM =32, ∴KH =EH -EK =8-52=112,∵∠FKH=∠EKM,∠H=∠EMK=90°,∴△FKH∽△EKM,∴FHEM=KHKM,即FH2=11232,解得FH=223,∴AF=FH=223.7.在等腰Rt△ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.(1)如图①,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=2时,求AE′的值;(2)如图②,在AC上取一点E,使得CE=13AC,连接DE,将△CDE沿CD 翻折到△CDE′,且AE′交BC于点F,求证:DF=CF.第7题图(1)解:∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴∠ADC=90°,∠ACD=45°,在Rt△ADC中,AC=ADsin 45°=2,∵E是AC的中点,∴CE=12AC=1,∵将△CDE沿CD翻折到△CDE′,∴CE ′=CE =1,∠ACE ′=90°, 由勾股定理得:AE ′=CE ′+AC 2=5;(2)证明:如解图,过B 作AE ′的垂线交AD 于点G ,交AC 于点H ,第7题解图∵∠ABH +∠BAF =90°,∠CAF +∠BAF =90°, ∴∠ABH =∠CAF ,又∵AB =AC ,∠BAH =∠ACE ′=90°, ∴△ABH ≌△CAE ′, ∴AH =CE ′=CE , ∵CE =13AC , ∴AH =HE =CE , ∵D 是BC 中点, ∴DE ∥BH , ∴G 是AD 中点, 在△ABG 和△CAF 中 ⎩⎪⎨⎪⎧∠BAD =∠ACD =45°AB =AC∠ABH =∠CAF, ∴△ABG ≌△CAF (ASA),∴AG =CF , ∵AG =12AD ,∴CF =12AD =12CD ,∴DF =CF . 8.【问题情境】在数学综合与实践课上,老师让同学们以“正方形的折叠为主题开展活动”,如图①,四边形ABCD是正方形,AB=5,点E是CD边上的一动点,连接AE.【操作发现】(1)将△ADE沿AE折叠得△AD′E,如图②,当点D′到BC的距离等于1时,求点E到BC的距离.【继续探究】(2)在(1)的条件下,创新小组在图②中,连接BE,如图③,发现∠AEB=2∠EBC,请你证明这个结论.【深入探究】(3)创新小组将图②沿MN向下折叠,使点A与点E,连接DD′并延长交BC 于点F,如图④,求四边形MNFD的面积.第8题图解:(1)如解图①,过点D′作XY∥BC,与AB、CD分别交于点X、Y,∵四边形ABCD是正方形,第8题解图①∴∠B=∠C=90°,AB∥CD,∴四边形BCYX 是矩形, ∵点D ′到BC 的距离为1, ∴BX =CY =1,∴AX =AB -BX =5-1=4, 由折叠知:AD ′=AD =5,在Rt △AXD ′中,由勾股定理得XD ′=52-42=3, ∴D ′Y =XY -XD ′=5-3=2, 由题易证△AXD ′∽△D ′YE , ∴AXD ′Y=XD ′YE , ∴42=3YE , ∴YE =32,∴CE =YE +YC =32+1=52, ∴点E 到BC 的距离等于52; (2)证明:由(1)知,CE =52, ∴DE =DC -CE =5-52=52, ∴DE =CE ,又∵AD =BC ,∠C =∠ADE , ∴△ADE ≌△BCE , ∴AE =BE ,如解图②,过点E 作EZ ⊥AB 于点Z ,第8题解图②∴EZ 平分∠AEB , ∴∠AEB =2∠BEZ , ∵EZ ⊥AB ,BC ⊥AB , ∴EZ ∥BC . ∴∠BEZ =∠EBC , ∴∠AEB =2∠EBC ;(3)∵点A 、点E 关于MN 对称, ∴MN 垂直平分AE , 同理:AE 垂直平分DD ′, ∴MN ∥DF , 又∵MD ∥NF ,∴四边形MNFD 是平行四边形,如解图③,设AE 与MN ,DD ′分别相交于点G 、H ,第8题解图③在Rt △ADE 中,由勾股定理得 AE =AD 2+DE 2 =52+(52)2=552,∴GE =12AE =12×552=554. 在Rt △ADE 中,DH ·AE =AD ·DE ,∴DH =AD ·DEAE =5×52552=5,在Rt △DEH 中,由勾股定理得 EH =DE 2-DH 2=(52)2-(5)2=52,∴GH =GE -EH =554-52=354,∵△ADE ≌△DCF ,∴AE =DF ,∴DF =552, ∴S 四边形MNFD =DF ·GH =552×354=758. 9.【问题情境】(1)数学课上,老师出了一道题,如图①,Rt △ABC 中,∠C =90°,AC =12AB ,求证:∠B =30°,请你完成证明过程;【继续探究】(2)如图②,四边形ABCD 是一张边长为2的正方形纸片,E 、F 分别为AB 、CD 的中点,沿过点D 的折痕将纸片翻折,使点A 落在EF 上的点A ′处,折痕交AE 于点G ,请运用(1)中的结论求∠ADG 的度数和AG 的长;【拓展应用】(3)若矩形纸片ABCD 按如图③所示的方式折叠,B 、D 两点恰好重合于一点O (如图④),当AB =6时,求EF 的长.第9题图(1)证明:Rt △ABC 中,∠C =90°,AC =12AB , ∵sin B =AC AB =12, ∴∠B =30°;(2)解:∵正方形边长为2,E 、F 分别为AB 、CD 的中点, ∴EA =FD =12×CD =1,∵沿过点D 的折痕将纸片翻折,使点A 落在EF 上的点A ′处, ∴A ′D =AD =2, ∴FD A ′D =12, ∴∠F A ′D =30°,可得∠FDA ′=90°-30°=60°,由折叠性质可得∠ADG =∠A ′DG ,AG =A ′G , ∴∠ADG =∠ADA ′2=90°-60°2=15°, ∵A ′D =2,FD =1,∴A′F=A′D2-FD2=3,∴EA′=EF-A′F=2-3,∵∠EA′G+∠DA′F=180°-∠GA′D=90°,∴∠EA′G=90°-∠DA′F=90°-30°=60°,∴∠EGA′=90°-∠EA′G=90°-60°=30°,则AG=AG′=2EA′=2(2-3);(3)解:∵折叠后B、D两点恰好重合于一点O,∴AO=AD=CB=CO,∴DA=AC 2,∵∠D=90°,∴∠DCA=30°,∵AB=CD=6,在Rt△ACD中,ADDC=tan30°,则AD=DC·tan30°=6×33=23,∵∠DAF=∠F AO=12∠DAO=90°-∠DCA2=30°,∴DFAD=tan30°=33,∴DF=33AD=2,∴DF=FO=2,同理EO=2,∴EF=EO+FO=4.10.如图,在矩形ABCD纸片中,AB=10 cm,BC=12 cm.点P在BC边上,将△P AB沿AP折叠得△P AE,连接CE,DE.(1)当点E落在AD边上时,CE=________;(2)当△CDE分别满足下列条件时,求PB的长.①DE=CD;②DE=CE.第10题图解:(1)226 cm ; 【解法提示】如解图①,∵将△P AB 沿AP 折叠,得△P AE ,E 落在AD 边上, ∴四边形ABPE 是正方形, ∴PB =PE =AB =10 cm , ∴PC =2 cm ,∴CE =PE 2+PC 2=226 cm.第10题解图①(2)①如解图②,过E 作MN ⊥AD 于M ,交BC 于N ,则MN ⊥BC ,第10题解图②∵DE =CD ,AE =AB =CD =DE , ∴AE =10 cm ,∴AM =12AD =BN =6 cm ,∴ME =AE 2-AM 2=8 cm , ∴EN =MN -ME =2 cm , 易知△AME ∽△ENP , ∴AM AE =EN PE , ∴610=2PE , ∴PE =103 cm , ∴PB =PE =103 cm ;②如解图③,过E 作MN ⊥AD 于M ,交BC 于N ,过E 作EQ ⊥CD 于Q ,第10题解图③∵DE =CE ,∴DQ =12CD =5 cm ,∴ME =5 cm , ∴EN =MN -ME =5 cm , ∴AM =AE 2-ME 2=5 3 cm , ∴BN =5 3 cm , 同理得AM AE =EN PE , ∴5310=5PE , ∴PE =1033 cm ,103∴PB=PE=3cm.。
中考数学压轴题---《与折叠有关的计算》题型讲解

中考数学压轴题---《与折叠有关的计算》题型讲解1、(2020•青岛)如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为()A.B.C.2D.4【答案】C【解答】解:∵矩形ABCD,∴AD∥BC,AD=BC,AB=CD,∴∠EFC=∠AEF,由折叠得,∠EFC=∠AFE,∴∠AFE=∠AEF,∴AE=AF=5,由折叠得,FC=AF,OA=OC,∴BC=3+5=8,在Rt△ABF中,AB==4,在Rt△ABC中,AC==4,∴OA=OC=2,故选:C.2、如图,在△ABC纸片中,∠B=30°,AB=AC=,点D在AB上运动,将纸片沿CD折叠,得到点B的对应点B′(D在A点时,点D的对应点是本身),则折叠过程对应点B′的路径长是()A.3B.6C.πD.2π【答案】C【解答】解:过点A作AE⊥BC于点E,∵∠B=30°,AB=AC=,∴BE=AB cos∠B=,∴BC=2BE=3,由折叠的性质可得:∠BCB''=2∠ACB=60°,∴B′的路径长==π.故选:C.3、(2022•宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为()A.B.C.D.【答案】C【解答】解:∵四边形ABCD是矩形,∴∠A=90°,AB∥CD,AD=BC=3,AB=CD=5,∴∠BDC=∠DBF,由折叠的性质可得∠BDC=∠BDF,∴∠BDF=∠DBF,∴BF=DF,设BF=x,则DF=x,AF=5﹣x,在Rt△ADF中,32+(5﹣x)2=x2,∴x=,∴cos∠ADF=,故选:C.4、(2022•毕节市)矩形纸片ABCD中,E为BC的中点,连接AE,将△ABE沿AE折叠得到△AFE,连接CF.若AB=4,BC=6,则CF的长是()A.3B.C.D.【答案】D【解答】解:连接BF,交AE于O点,∵将△ABE沿AE折叠得到△AFE,∴BE=EF,∠AEB=∠AEF,AE垂直平分BF,∵点E为BC的中点,∴BE=CE=EF=3,∴∠EFC=∠ECF,∵∠BEF=∠ECF+∠EFC,∴∠AEB=∠ECF,∴AE∥CF,∴∠BFC=∠BOE=90°,在Rt△ABE中,由勾股定理得,AE==,∴BO==,∴BF=2BO=,在Rt△BCF中,由勾股定理得,CF===,故选:D.5、(2022•湖州)如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是()A.BD=10B.HG=2C.EG∥FH D.GF⊥BC 【答案】D【解答】解:∵四边形ABCD是矩形,∴∠A=90°,BC=AD,∵AB=6,BC=8,∴BD===10,故A选项不符合题意;∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,∴AB=BG=6,CD=DH=6,∴GH=BG+DH﹣BD=6+6﹣10=2,故B选项不符合题意;∵四边形ABCD是矩形,∴∠A=∠C=90°,∵将△ABE沿BE翻折,将△DCF沿DF翻折,点A,C分别落在对角线BD上的点G,H处,∴∠A=∠BGE=∠C=∠DHF=90°,∴EG∥FH.故C选项不符合题意;∵GH=2,∴BH=DG=BG﹣GH=6﹣2=4,设FC=HF=x,则BF=8﹣x,∴x2+42=(8﹣x)2,∴x=3,∴CF=3,∴,又∵,∴,若GF⊥BC,则GF∥CD,∴,故D选项符合题意.故选:D.6、(2021•天津)如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是()A.∠ABC=∠ADC B.CB=CD C.DE+DC=BC D.AB∥CD【答案】D【解答】解:由旋转的性质得出CD=CA,∠EDC=∠BAC=120°,∵点A,D,E在同一条直线上,∴∠ADC=60°,∴△ADC为等边三角形,∴∠DAC=60°,∴∠BAD=60°=∠ADC,∴AB∥CD,故选:D.7、(2022•滨州)正方形ABCD的对角线相交于点O(如图1),如果∠BOC绕点O按顺时针方向旋转,其两边分别与边AB、BC相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是()A.线段B.圆弧C.折线D.波浪线【答案】A【解答】解:建立如图平面直角坐标系,设正方形ABCD的边长为1,∵四边形ABCD是正方形,∴∠OAE=∠OBF=45°,OA=OB,∵∠AOB=∠EOF=90°,∴∠AOE=∠BOF,∴△AOE≌△BOF(ASA),∴AE=BF,设AE=BF=a,则F(a,0),E(0,1﹣a),∵EG=FG,∴G(a,﹣a),∴点G在直线y=﹣x+上运动,∴点G的运动轨迹是线段,故选:A.8、(2022•眉山)如图,四边形ABCD为正方形,将△EDC绕点C逆时针旋转90°至△HBC,点D,B,H在同一直线上,HE与AB交于点G,延长HE与CD的延长线交于点F,HB=2,HG=3.以下结论:①∠EDC=135°;②EC2=CD•CF;③HG=EF;④sin∠CED=.其中正确结论的个数为()A.1个B.2个C.3个D.4个【答案】D【解答】解:∵△EDC旋转得到△HBC,∴∠EDC=∠HBC,∵ABCD为正方形,D,B,H在同一直线上,∴∠HBC=180°﹣45°=135°,∴∠EDC=135°,故①正确;∵△EDC旋转得到△HBC,∴EC=HC,∠ECH=90°,∴∠HEC=45°,∴∠FEC=180°﹣45°=135°,∵∠ECD=∠ECF,∴△EFC∽△DEC,∴,∴EC2=CD•CF,故②正确;设正方形边长为a,∵∠GHB+∠BHC=45°,∠GHB+∠HGB=45°,∴∠BHC=∠HGB=∠DEC,∵∠GBH=∠EDC=135°,∴△GBH∽△EDC,∴,即,∵△HEC是等腰直角三角形,∴,∵∠GHB=∠FHD,∠GBH=∠HDF=135°,∴△HBG∽△HDF,∴,即,解得:EF=3,∵HG=3,∴HG=EF,故③正确;过点E作EM⊥FD交FD于点M,∴∠EDM=45°,∵ED=HB=2,∴,∴,∵∠DEC+∠DCE=45°,∠EFC+∠DCE=45°,∴∠DEC=∠EFC,∴,故④正确综上所述:正确结论有4个,故选:D.9、(2022•单县一模)如图,将边长为8cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG 的周长是cm.【答案】16【解答】解:设EF=x,∵EF=DF,∴DF=x,则AF=8﹣x;而AE=4,由勾股定理得:x2=42+(8﹣x)2,解得:x=5;AF=8﹣5=3;∠GEF=∠D=90°,∠A=∠B=90°,∴∠AEF+∠AFE=∠AEF+∠BEG,∴∠AFE=∠BEG;∴△AEF∽△BGE,∴==,∴EG==,BG==,∴△EBG的周长=++4=16.故答案为16.10、如图,在矩形ABCD中,AB=3,BC=5,点P在CD边上,联结AP.如果将△ADP沿直线AP翻折,点D恰好落在线段BC上,那么的值为.【答案】【解答】解:如图:∵将△ADP沿直线AP翻折,点D恰好落在线段BC上的D',∴AD'=AD=5,PD=PD',∠AD'P=∠D=90°,在Rt△ABD'中,BD'===4,∴CD'=BC﹣BD'=5﹣4=1,设CP=x,则PD=PD'=3﹣x,在Rt△CPD'中,CD'2+CP2=PD'2,∴12+x2=(3﹣x)2,解得x=,∴CP=,PD=,∴S△ADP=AD•PD=×5×=,S四边形ABCP=S矩形ABCD﹣S△ADP=3×5﹣=,∴==,故答案为:.11、(2022•铜仁市)如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE 上的动点,过点N作NP∥EM交MC于点P,则MN+NP的最小值为.【答案】【解答】解:作点P关于CE的对称点P′,由折叠的性质知CE是∠DCM的平分线,∴点P′在CD上,过点M作MF⊥CD于F,交CE于点G,∵MN+NP=MN+NP′≥MF,∴MN+NP的最小值为MF的长,连接DG,DM,由折叠的性质知CE为线段DM的垂直平分线,∵AD=CD=2,DE=1,∴CE==,∵CE×DO=CD×DE,∴DO=,∴EO=,∵MF⊥CD,∠EDC=90°,∴DE∥MF,∴∠EDO=∠GMO,∵CE为线段DM的垂直平分线,∴DO=OM,∠DOE=∠MOG=90°,∴△DOE≌△MOG,∴DE=GM,∴四边形DEMG为平行四边形,∵∠MOG=90°,∴四边形DEMG为菱形,∴EG=2OE=,GM=DE=1,∴CG=,∵DE∥MF,即DE∥GF,∴△CFG∽△CDE,∴,即,∴FG=,∴MF=1+=,∴MN+NP的最小值为;方法二:同理方法一得出MN+NP的最小值为MF的长,DO=,∴OC==,DM=2DO=,∵S△CDM=DM•OC=CD•MF,即×=2×MF,∴MF=,∴MN+NP的最小值为;故答案为:。
九年级中考数学动点问题压轴题专题训练(含答案)

九年级中考数学动点问题压轴题专题训练1.如图1, 在平面直角坐标系中, 四边形OABC各顶点的坐标分别为O(0, 0), A(3, 3 ), B(9, 5 ), C(14, 0). 动点P与Q同时从O点出发, 运动时间为t秒, 点P沿OC方向以1单位长度/秒的速度向点C运动, 点Q沿折线OA-AB-BC运动, 在OA, AB, BC上运动的速度分别为3, , (单位长度/秒). 当P, Q中的一点到达C点时, 两点同时停止运动.(1)求AB所在直线的函数表达式.(2)如图2, 当点Q在AB上运动时, 求△CPQ的面积S关于t的函数表达式及S的最大值.(3)在P, Q的运动过程中, 若线段PQ的垂直平分线经过四边形OABC的顶点, 求相应的t值.图1 图22.如图, 抛物线y=-x2+bx+c与x轴交于A, B两点(A在B的左侧), 与y轴交于点N, 过A点的直线l:y=kx+n与y轴交于点C, 与抛物线y=-x2+bx+c的另一个交点为D, 已知A(-1, 0), D(5, -6), P 点为抛物线y=-x2+bx+c上一动点(不与A, D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时, 过P点作PE∥x轴交直线l于点E, 作PF ∥y轴交直线l于点F, 求PE+PF的最大值;(3)设M为直线l上的点, 探究是否存在点M, 使得以点N, C, M, P为顶点的四边形为平行四边形.若存在, 求出点M的坐标;若不存在, 请说明理由.3.如图, 在平面直角坐标系中, 抛物线y=ax2+bx+c经过A(-2, -4 )、O(0, 0)、B(2, 0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点, 求AM+OM的最小值.4.设直线l1: y=k1x+b1与l2: y=k2x+b2, 若l1⊥l2, 垂足为H, 则称直线l1与l2是点H的直角线.(1)已知直线①;②;③;④和点C(0, 2), 则直线_______和_______是点C的直角线(填序号即可);(2)如图, 在平面直角坐标系中, 直角梯形OABC的顶点A(3, 0)、B(2, 7)、C(0, 7), P为线段OC上一点, 设过B、P两点的直线为l1, 过A、P两点的直线为l2, 若l1与l2是点P的直角线, 求直线l1与l2的解析式.5.如图①, 在平面直角坐标系xOy中, 已知抛物线y=ax2-2ax-8a与x轴相交于A, B两点(点A在点B的左侧), 与y轴交于点C(0, -4).(1)点A的坐标为, 点B的坐标为, 线段AC的长为, 抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.如果在x轴上存在点Q, 使得以点B, C, P, Q为顶点的四边形是平行四边形, 求点Q的坐标.①6.如图, 已知抛物线(b是实数且b>2)与x轴的正半轴分别交于点A.B(点A位于点B是左侧), 与y轴的正半轴交于点C.(1)点B的坐标为______, 点C的坐标为__________(用含b的代数式表示);(2)请你探索在第一象限内是否存在点P, 使得四边形PCOB的面积等于2b, 且△PBC是以点P为直角顶点的等腰直角三角形?如果存在, 求出点P的坐标;如果不存在, 请说明理由;(3)请你进一步探索在第一象限内是否存在点Q, 使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在, 求出点Q的坐标;如果不存在, 请说明理由.7.如图, 已知A.B是线段MN上的两点, , , . 以A为中心顺时针旋转点M, 以B为中心逆时针旋转点N, 使M、N两点重合成一点C, 构成△ABC, 设.(1)求x的取值范围;(2)若△ABC为直角三角形, 求x的值;(3)探究: △ABC的最大面积?8.如图, 已知抛物线y=-x2+bx+c经过A(0, 1)、B(4, 3)两点.(1)求抛物线的解析式;(2)求tan∠ABO的值;(3)过点B作BC⊥x轴, 垂足为C, 在对称轴的左侧且平行于y轴的直线交线段AB于点N, 交抛物线于点M, 若四边形MNCB为平行四边形, 求点M的坐标.9.在平面直角坐标系中, 反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).(1)当k=-2时, 求反比例函数的解析式;(2)要使反比例函数与二次函数都是y随x增大而增大, 求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q, 当△ABQ是以AB为斜边的直角三角形时, 求k的值.10.如图, 已知抛物线y=ax2+bx+4(a≠0)的对称轴为直线x=3, 抛物线与x轴相交于A, B两点, 与y轴相交于点C, 已知B点的坐标为(8, 0).(1)求抛物线的解析式;(2)点M为线段BC上方抛物线上的一点, 点N为线段BC上的一点, 若MN∥y 轴, 求MN的最大值;(3)在抛物线的对称轴上是否存在点Q, 使△ACQ为等腰三角形?若存在, 求出符合条件的Q点坐标;若不存在, 请说明理由.11.如图, 直线y=2x+6与反比例函数y=(k>0)的图象交于点A(m, 8), 与x轴交于点B, 平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M, 交AB于点N, 连接BM.(1)求m的值和反比例函数的解析式;(2)观察图象, 直接写出当x>0时不等式2x+6->0的解集;(3)直线y=n沿y轴方向平移, 当n为何值时, △BMN的面积最大?最大值是多少?12.如图, 在平面直角坐标系xOy中, 顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B, AO=BO=2, ∠AOB=120°.(1)求这条抛物线的表达式;(2)连结OM, 求∠AOM的大小;(3)如果点C在x轴上, 且△ABC与△AOM相似, 求点C的坐标.13.在直角梯形OABC中, CB//OA, ∠COA=90°, CB=3, OA=6, BA=. 分别以OA.OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.(1)求点B的坐标;(2)已知D.E分别为线段OC.OB上的点, OD=5, OE=2EB, 直线DE交x轴于点F. 求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点, 在x轴上方的平面内是否存在另一点N, 使以O、D、M、N为顶点的四边形是菱形?若存在, 请求出点N的坐标;若不存在, 请说明理由.14.如图, 已知一次函数y=-x+7与正比例函数的图象交于点A, 且与x轴交于点B. (1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C, 过点B作直线l//y轴. 动点P从点O出发, 以每秒1个单位长的速度, 沿O—C—A的路线向点A运动;同时直线l从点B出发, 以相同速度向左平移, 在平移过程中, 直线l交x轴于点R, 交线段BA或线段AO于点Q. 当点P到达点A时, 点P和直线l都停止运动. 在运动过程中, 设动点P运动的时间为t秒.①当t为何值时, 以A.P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在, 求t的值;若不存在, 请说明理由.15.如图, 二次函数y=a(x2-2mx-3m2)(其中a、m是常数, 且a>0, m>0)的图像与x轴分别交于A.B(点A位于点B的左侧), 与y轴交于点C(0,-3), 点D在二次函数的图像上, CD//AB, 联结AD. 过点A作射线AE交二次函数的图像于点E, AB平分∠DAE.(1)用含m的式子表示a;(2)求证: 为定值;(3)设该二次函数的图像的顶点为F.探索:在x轴的负半轴上是否存在点G, 联结GF, 以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在, 只要找出一个满足要求的点G即可, 并用含m的代数式表示该点的横坐标;如果不存在, 请说明理由.16.如图, 二次函数y=-x2+4x+5的图象的顶点为D, 对称轴是直线l, 一次函数y= x+1的图象与x轴交于点A, 且与直线DA关于l的对称直线交于点B.(1)点D的坐标是.(2)直线l与直线AB交于点C, N是线段DC上一点(不与点D, C重合), 点N的纵坐标为n.过点N作直线与线段DA, DB分别交于点P, Q, 使得△DPQ与△DAB 相似.①当n= 时, 求DP的长;②若对于每一个确定的n的值, 有且只有一个△DPQ与△DAB相似, 请直接写出n的取值范围.17.已知直线y=3x-3分别与x轴、y轴交于点A, B, 抛物线y=ax2+2x+c经过点A, B. (1)求该抛物线的表达式, 并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l, 点B关于直线l的对称点为C, 若点D在y 轴的正半轴上, 且四边形ABCD为梯形.①求点D的坐标;②将此抛物线向右平移, 平移后抛物线的顶点为P, 其对称轴与直线y=3x-3交于点E, 若, 求四边形BDEP的面积.18.如图, 在平面直角坐标系xOy中, 二次函数y=-x2+2x+8的图象与一次函数y=-x+b的图象交于A.B两点, 点A在x轴上, 点B的纵坐标为-7.点P是二次函数图象上A.B两点之间的一个动点(不与点A.B重合), 设点P的横坐标为m, 过点P作x轴的垂线交AB于点C, 作PD ⊥AB于点D.(1)求b及sin∠ACP的值;(2)用含m的代数式表示线段PD的长;(3)连接PB, 线段PC把△PDB分成两个三角形, 是否存在适合的m值, 使这两个三角形的面积之比为1∶2?如果存在, 直接写出m的值;如果不存在, 请说明理由.19.如图, 抛物线与x轴交于A.B两点(点A在点B的左侧), 与y轴交于点C.(1)求点A.B的坐标;(2)设D为已知抛物线的对称轴上的任意一点, 当△ACD的面积等于△ACB 的面积时, 求点D的坐标;(3)若直线l过点E(4, 0), M为直线l上的动点, 当以A、B、M为顶点所作的直角三角形有且只有三个时, 求直线l的解析式.20.已知平面直角坐标系中两定点A(-1, 0)、B(4, 0), 抛物线y=ax2+bx-2(a≠0)过点A.B, 顶点为C, 点P(m, n)(n<0)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时, 求m的取值范围;(3)若m>, 当∠APB为直角时, 将该抛物线向左或向右平移t(0<t<)个单位, 点C、P平移后对应的点分别记为C′、P′, 是否存在t, 使得顺次首尾连接A、B、P′、C′所构成的多边形的周长最短?若存在, 求t的值并说明抛物线平移的方向;若不存在, 请说明理由.2021中考数学压轴专题训练之动点问题-答案一、解答题(本大题共20道小题)1.【答案】【思维教练】(1)设一次函数解析式, 将已知点A、B的坐标值代入求解即可;(2)S △CPQ=·CP·Qy, CP=14-t, 点Q在AB上, Qy即为当x=t时的y值, 代入化简得出S与t的函数关系式, 化为顶点式得出最值;(3)垂直平分线过顶点需以时间为临界点分情况讨论, 当Q在OA上时, 过点C;当Q在AB上时, 过点A;当Q在BC上时, 过点C和点B, 再列方程并求解.解图1解: (1)把A(3, 3 ), B(9, 5 )代入y=kx+b,得, 解得,∴y=33x+23;(3分)(2)在△PQC中, PC=14-t,∵OA==6且Q在OA上速度为3单位长度/s,AB==4 且Q点在AB上的速度为单位长度/s,∴Q在OA上时的横坐标为t, Q在AB上时的横坐标为t,PC边上的高线长为33t+2 3.(6分)所以S=(14-t)( t+2 )=-t2+t+14 (2≤t≤6).当t=5时, S有最大值为.(7分)解图2(3)①当0<t ≤2时, 线段PQ 的中垂线经过点C(如解图1). 可得方程(332t )2+(14-32t )2=(14-t )2.解得t1= , t2=0(舍去), 此时t = .(8分)解图3②当2<t ≤6时, 线段PQ 的中垂线经过点A(如解图2).可得方程(33)2+(t -3)2=[3(t -2)]2.解得t1= , ∵t2= (舍去), 此时t = .③当6<t ≤10时,(1)线段PQ 的中垂线经过点C(如解图3).可得方程14-t =25- t, 解得t = .(10分)解图4(2)线段PQ 的中垂线经过点B(如解图4).可得方程(53)2+(t -9)2=[52(t -6)]2.解得t1= , t2= (舍去).此时t=38+2027.(11分)综上所述, t的值为, , , .(12分)【难点突破】解决本题的关键点在于对PQ的垂直平分线过四边形顶点的情况进行分类讨论, 在不同阶段列方程求解.2.【答案】[分析] (1)将点A, D的坐标分别代入直线表达式、抛物线的表达式, 即可求解;(2)设出P点坐标, 用参数表示PE, PF的长, 利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况, 分别求解即可.解:(1)将点A, D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A, D的坐标代入抛物线表达式,得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1,∴C(0, -1), 则直线l与x轴的夹角为45°, 即∠OAC=45°,∵PE∥x轴, ∴∠PEF=∠OAC=45°.又∵PF∥y轴, ∴∠EPF=90°, ∴∠EFP=45°.则PE=PF.设点P坐标为(x, -x2+3x+4),则点F(x, -x-1),∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18,∵-2<0, ∴当x=2时, PE+PF有最大值, 其最大值为18.(3)由题意知N(0, 4), C(0, -1), ∴NC=5,①当NC是平行四边形的一条边时, 有NC∥PM, NC=PM.设点P坐标为(x, -x2+3x+4), 则点M的坐标为(x, -x-1),∴|yM-yP|=5, 即|-x2+3x+4+x+1|=5,解得x=2±或x=0或x=4(舍去x=0),则点M坐标为(2+ , -3- )或(2- , -3+ )或(4, -5);②当NC是平行四边形的对角线时, 线段NC与PM互相平分.由题意, NC的中点坐标为0, ,设点P坐标为(m, -m2+3m+4),则点M(n', -n'-1),∴0= = ,解得:n'=0或-4(舍去n'=0), 故点M(-4, 3).综上所述, 存在点M, 使得以N, C, M, P为顶点的四边形为平行四边形, 点M的坐标分别为:(2+ , -3- ), (2- , -3+ ), (4, -5), (-4, 3).3.【答案】(1)。
中考数学中考最后压轴题训练---折叠旋转问题

一.折叠类 【1 】1. (13江苏徐州卷)在平面直角坐标系中,已知矩形ABCD 中,边2AB =,边1AD =,且AB .AD 分离在x 轴.y 轴的正半轴上,点A 与坐标原点重合.将矩形折叠,使点A 落在边DC 上,设点A '是点A 落在边DC 上的对应点.(1)当矩形ABCD 沿直线12y x b =-+折叠时(如图1),求点A '的坐标和b 的值;(2)当矩形ABCD 沿直线y kx b =+折叠时,①求点A '的坐标(用k 暗示);求出k 和b 之间的关系式; ② 假如我们把折痕地点的直线与矩形的地位分 为如图2.3.4所示的三种情况,请你分离写出每种情况时k 的取值规模. (将答案直接填在每种情况下的横线上)(——当如图1.2折叠时,求D A '的取值规模?)k 的取值规模是; k 的取值规模是;k 的取值规模是;[解] (1)如图答5,设直线12y x b =-+与OD 交于点E ,与OB 交于点F ,贯穿连接A O ',则OE = b ,OF = 2b ,设点A '的坐标为(a ,1)因为90DOA A OF ''∠+∠=︒,90OFE A OF '∠+∠=︒, 所以DOA OFE '∠=∠,所以△DOA '∽△OFE .所以DA DO OE OF '=,即12a b b =,所以12a =. 所以点A '的坐标为(12,1).贯穿连接A E ',则A E OE b '==.在R t △DEA '中,依据勾股定理有222A E A D DE ''=+ ,即2221()(1)2b b =+-,解得58b =.(2)如图答6,设直线y kx b =+与OD 交于点E ,与OB 交于点F ,贯穿连接A O ',则OE = b ,bOF k =-,设点A '的坐标为(a ,1).因为90DOA A OF ''∠+∠=︒,90OFE A OF '∠+∠=︒. 所以DOA OFE '∠=∠,所以△DOA '∽△OFE . 所以DA DOOE OF'=,即1a b b k=-,所以a k =-. 所以A '点的坐标为(k -,1).贯穿连接A E ',在Rt △DEA '中,DA k '=-,1DE b =-,A E b '=. 因为222A E A D DE ''=+,所以222()(1)b k b =-+-.所以212k b +=.在图答6和图答7中求解参照给分. (3)图13﹣2中:21k -≤≤-; 图13﹣3中:1-≤k≤2-+图13﹣4中:20k -≤[点评]这是一道有关折叠的问题,重要考核一次函数.四边形.类似形等常识,试题中贯串了方程思惟和数形结合的思惟,请留意领会.2. (13广西钦州卷)如图,在平面直角坐标系中,矩形OABC 的极点O 为原点,E 为AB 上一点,把CBE △沿CE 折叠,使点B 正好落在OA 边上的点D 处,点AD ,的坐标分离为(50),和(30),.(1)求点C的坐标;(2)求DE地点直线的解析式;(3)设过点C的抛物线22(0)y x c b=+<与直线BC的另一个交点为M,问在该抛物线上是否消失点G,使得CMG△为等边三角形.若消失,解释来由.[解] (1)依据题意,得53CD CB OA OD====,,90COD=∠,4OC∴=.∴点C的坐标是(04),;(2)4AB OC==,设AE x=,则4DE BE x==-,532AD OA OD=-=-=,在Rt DEA△中,222DE AD AE=+.222(4)2x x∴-=+.解之,得32x=,即点E的坐标是352⎛⎫⎪⎝⎭,.设DE地点直线的解析式为y kx b=+,30352k bk b+=⎧⎪∴⎨+=⎪⎩,,解之,得3494kb⎧=⎪⎪⎨⎪=-⎪⎩,.DE∴地点直线的解析式为3944y x=-;(3)点(04)C ,在抛物线22y x c =++上,4c ∴=.即抛物线为224y x =++.假设在抛物线224y x =++上消失点G ,使得CMG △为等边三角形,依据抛物线的对称性及等边三角形的性质,得点G 必定在该抛物线的极点上. 设点G 的坐标为()m n ,,224m ∴=-=-⨯,22424)323428b n ⨯⨯--==⨯,即点G 的坐标为232348b ⎛⎫-- ⎪ ⎪⎝⎭,.设对称轴x =CB 交于点F ,与x 轴交于点H .则点F 的坐标为4⎛⎫⎪⎪⎝⎭. 00b m <∴>,,点G 在y 轴的右侧,CF m ==2232334488b b FH FG -==-=,.2CM CG CF ===∴在Rt CGF △中,222CG CF FG =+,222238b ⎛⎛⎛⎫=+ ⎪ ⎝⎭⎝⎭⎝⎭.解之,得2(0)b b =-<..42m ∴=-=,2323582b n -==. ∴点G 的坐标为522⎛⎫⎪ ⎪⎝⎭,.∴在抛物线224(0)y x b =++<上消失点G 52⎫⎪⎪⎝⎭,,使得CMG △为等边三角形.[点评]这是一道以折叠为布景的分解型压轴题,分解性较强,这类试题在各地中考题中消失的频率不小,本题中第1.2小题只需依据折叠的基赋性质结合函数常识即可得解,第3小题是探讨型问题,是一道检测学生才能的好题.3(13湖北咸宁卷)如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,53OA OC ==,.(1)在AB 边上取一点D ,将纸片沿OD 翻折,使点A 落在BC 边上的点E 处,求点D ,E 的坐标;(2)若过点D E ,的抛物线与x 轴订交于点(50)F -,,求抛物线的解析式和对称轴方程; (3)若(2)中的抛物线与y 轴交于点H ,在抛物线上是否消失点P ,使PFH △的心坎在坐标轴...上?若消失,求出点P 的坐标,若不消失,请解释来由. (4)若(2)中的抛物线与y 轴订交于点H ,点Q 在线段OD 上移动,作直线HQ ,当点Q 移动到什么地位时,O D ,两点到直线HQ 的距离之和最大?请直接写出此时点Q 的坐标及直线HQ 的解析式.4. .(14台州市)24.如图,四边形OABC坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,折叠,使点B 落在边OA 的点D 处.已知折叠CE =3tan 4EDA ∠=.(1)断定OCD △与ADE △是否类似?请解释来由; (2)求直线CE 与x 轴交点P 的坐标;题)(3)是否消失过点D 的直线l ,使直线l .直线CE 与x 轴所围成的三角形和直线l .直线CE 与y 轴所围成的三角形类似?假如消失,请直接写出其解析式并画出响应的直线;假如不消失,请解释来由.解:(1)OCD △与ADE △类似. 来由如下:由折叠知,90CDE B ∠=∠=°,1290∠+∠=∴°,13902 3.∠+∠=∴∠=∠,又90COD DAE ∠=∠=∵°,OCD ADE ∴△∽△.(2)3tan 4AE EDA AD ∠==∵,∴设3AE t =,则4AD t =.由勾股定理得5DE t =.358OC AB AE EB AE DE t t t ==+=+=+=∴.由(1)OCD ADE △∽△,得OC CDAD DE=, 845t CDt t=∴, 10CD t =∴.在DCE △中,222CD DE CE +=∵,222(10)(5)t t +=∴,解得1t =.83OC AE ==∴,,点C 的坐标为(08),, 点E 的坐标为(103),, 设直线CE 的解析式为y kx b =+,1038k b b +=⎧⎨=⎩,∴,解得128k b ⎧=-⎪⎨⎪=⎩,,(第24题图2)182y x =-+∴,则点P 的坐标为(160),. (3)知足前提的直线l 有2条:212y x =-+,212y x =-.如图2:精确画出两条直线. 5. (14宁德市)26. 已知:矩形纸片ABCD 中,26AB =厘米,18.5BC =厘米,点E 在AD 上,且6AE =厘米,点P 是AB 边上一动点.按如下操纵:步调一,折叠纸片,使点P 与点E 重合,睁开纸片得折痕MN (如图1所示); 步调二,过点P 作PT AB ⊥,交MN 地点的直线于点Q ,衔接QE (如图2所示) (1)无论点P 在AB 边上任何地位,都有PQ QE (填“>”.“=”.“<”号); (2)如图3所示,将纸片ABCD 放在直角坐标系中,按上述步调一.二进行操纵: ①当点P 在A 点时,PT 与MN 交于点11Q Q ,点的坐标是(,); ②当6PA =厘米时,PT 与MN 交于点22Q Q ,点的坐标是(,);③当12PA =厘米时,在图3中画出MN PT ,(不请求写画法),并求出MN 与PT 的交点3Q 的坐标;(3)点P 在活动进程,PT 与MN 形成一系列的交点123Q Q Q ,,,…不雅察.猜测:浩瀚的交点形成的图象是什么?并直接写出该图象的函数表达式.解: (1)PQ QE =.C B图1图3CE图2(2)①(03),;②(66),. ③绘图,如图所示.解:办法一:设MN 与EP 交于点F . 在Rt APE △中,PE ==∵12PF PE ==∴390Q PF EPA ∠+∠=∵°,90AEP EPA ∠+∠=°,3Q PF AEP ∠=∠∴.又390EAP Q FP ∠=∠=∵°, 3Q PF PEA ∴△∽△.3Q P PFPE EA=∴. 315PE PFQ P EA==·∴. 3(1215)Q ∴,.办法二:过点E 作3EG Q P ⊥,垂足为G ,则四边形APGE 是矩形.6GP =∴,12EG =.设3Q G x =,则336Q E Q P x ==+. 在3Rt Q EG △中,22233EQ EG Q G =+∵. 222(6)12x x +=+∴.9x =∴.3125Q P =∴. 3(1215)Q ∴,.(3)这些点形成的图象是一段抛物线. 函数关系式:213(026)12y x x =+≤≤. 6. (14日照市)24. 如图,直线EF 将矩形纸片ABCD 分成面积相等的两部分,E .F 分离与BC 交于点E ,与AD 交于点F (E ,F 不与极点重合),设AB=a,AD=b,BE=x .(Ⅰ)求证:AF=EC ;(Ⅱ)用铰剪将纸片沿直线EF 剪开后,再将纸片ABEF 沿AB 对称翻折,然后平移拼接在梯形ECDF 的下方,使一底边重合,直腰落在边DC 的延伸线上,拼接后,下方的梯形记作EE′B′C .(1)求出直线EE ′分离经由原矩形的极点A 和极点D 时,所对应的 x ︰b 的值;(2)在直线EE ′经由原矩形的一个极点的情况下,衔接B E′,直线BE ′与EF 是否平行?你若认为平行,请赐与证实;你若认为不服行,请你解释当a 与b 知足什么关系时,它们垂直? 解: (Ⅰ)证实:∵AB=a ,AD=b ,BE=x ,S 梯形ABEF =S 梯形CDFE . ∴21a (x +AF )=21a (EC +b -AF ), ∴2AF =EC +(b -x ). 又∵EC =b -x ,∴2AF =2EC ,即AF=EC ;(Ⅱ)(1)当直线EE′经由原矩形的极点D 时,如图(一), ∵EC ∥E ′B ′, ∴B E EC ''=BD DC'. 由EC =b -x ,E ′B ′=EB =x ,DB ′=DC +CB ′=2a , 得aax x b 2=-, ∴x ︰b =32;当直线E′E 经由原矩形的极点A 时,如图(二), 在梯形AE ′B ′D 中,∵EC ∥E ′B ′,点C 是DB ′的中点, ∴CE =21(AD + E ′B ′),即b -x =21(b +x ), ∴x ︰b =31.(2) 如图(一), 当直线EE′ 经由原矩形的极点D 时,BE ′∥EF . 证实:衔接BF . ∵FD ∥BE , FD =BE ,∴四边形FBED 是平行四边形, ∴FB ∥DE , FB =DE ,又∵EC ∥E ′B ′, 点C 是DB ′的中点, ∴DE =EE ′,∴FB ∥EE ′, FB = EE ′,∴四边形BE ′EF 是平行四边形 ∴BE ′∥EF .如图(二), 当直线EE′ 经由原矩形的极点A 时,显然BE ′与EF 不服行,设直线EF 与BE′交于点G .过点E ′作E ′M ⊥BC 于M , 则E ′M =a ..∵x ︰b =31, ∴EM =31BC =31b .若BE′与EF 垂直,则有∠GBE +∠BEG =90°,又∵∠BEG =∠FEC =∠MEE ′, ∠MEE ′+∠ME ′E =90°, ∴∠GBE =∠ME ′E .在R t △BME ′中,tan ∠E ′BM = tan ∠GBE =BM M E '=b a32. 在R t △EME ′中,tan ∠ME ′E =M E EM '=ab31,∴b a 32=a b 31. 又∵a >0,b >0,=ba32, ∴当=ba32时,BE′与EF 垂直. 7. (14荆门市)28. 如图1,在平面直角坐标系中,有一张矩形纸片OABC ,已知O (0,0),A (4,0),C (0,3),点P 是OA 边上的动点(与点O .A 不重合).现将△P AB 沿PB 翻折,得到△PDB ;再在OC 边上拔取恰当的点E ,将△POE 沿PE 翻折,得到△PFE ,并使直线PD .PF 重合.(1)设P (x ,0),E (0,y ),求y 关于x 的函数关系式,并求y 的最大值;(2)如图2,若翻折后点D 落在BC 边上,求过点P .B .E 的抛物线的函数关系式;(3)在(2)的情况下,在该抛物线上是否消失点Q ,使△PEQ 是以PE 为直角边的直角三角形?若不消失,解释来由;若消失,求出点Q 的坐标.解:(1)由已知PB 等分∠APD ,PE 等分∠OPF ,且PD .PF 重合,则∠BPE =90°.∴∠OPE +∠APB =90°.又∠APB +∠ABP =90°,∴∠OPE =∠PBA . ∴Rt △POE ∽Rt △BP A . ∴PO BA OE AP =.即34x y x =-.∴y =2114(4)333x x x x -=-+(0<x <4). 且当x =2时,y 有最大值13.图2图1(2)由已知,△P AB .△POE 均为等腰三角形,可得P (1,0),E (0,1),B (4,3).设过此三点的抛物线为y =ax 2+bx +c ,则1,0,164 3.c a b c a b c =⎧⎪++=⎨⎪++=⎩∴1,23,21.a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩y =213122x x -+. (3)由(2)知∠EPB =90°,即点Q 与点B 重应时知足前提. 直线PB 为y =x -1,与y 轴交于点(0,-1). 将PB 向上平移2个单位则过点E (0,1), ∴该直线为y =x +1.由21,131,22y x y x x =+⎧⎪⎨=-+⎪⎩得5,6.x y =⎧⎨=⎩∴Q(5,6). 故该抛物线上消失两点Q (4,3).(5,6)知足前提.8. (14湖北省孝感市)25.在我们进修过的数学教科书中,有一个数学活动,其具体操纵进程是:第一步:半数矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片睁开(如图1); 第二步:再一次折叠纸片,使点A 落在EF 上,并使折痕经由点B ,得到折痕BM ,同时得到线段BN (如图2).(图1) (图2)请解答以下问题:(1)如图2,若延伸MN 交BC 于P ,△BMP 是什么三角形?请证实你的结论.(2)在图2中,若AB=a ,BC=b,a .b 知足什么关系,才干在矩形纸片ABCD 上剪出相符(1)中结论的三角形纸片BMP ?(3)设矩形ABCD 的边AB =2,BC =4,并树立如图3所示的直角坐标系. 设直线BM '为y kx =,当M BC '∠=60°时,求k 的值.此时,将△ABM ′沿BM ′折叠,点A 是否落在EF 上(E.F 分离为AB.CD 中点)?为什么?(图3)解:(1)△BMP 是等边三角形. 证实:贯穿连接AN ∵EF 垂直等分AB ∴AN = BN由折叠知 AB = BN∴AN = AB = BN ∴△ABN 为等边三角形 ∴∠ABN =60°∴∠PBN =30°又∵∠ABM =∠NBM =30°,∠BNM =∠A =90° ∴∠BPN =60°∠MBP =∠MBN +∠PBN =60° ∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60° ∴△BMP 为等边三角形 .(2)要在矩形纸片ABCD 上剪出等边△BMP ,则BC ≥BP在Rt △BNP 中, BN = BA =a ,∠PBN =30°∴BP =cos30a∴b ≥cos30a ∴a ≤23b .∴当a ≤23b 时,在矩形上能剪出如许的等边△BMP . (3)∵∠M ′BC =60°∴∠ABM ′=90°-60°=30°在Rt △ABM ′中,tan ∠ABM ′=AM AB '∴tan30°=2AM '∴AM ′∴M ′,2).代入y =kx 中 ,得k设△ABM ′沿BM ′折叠后,点A 落在矩形ABCD 内的点为A ' 过A '作A 'H ⊥BC 交BC 于H .∵△A 'BM ′≌△ABM ′∴A BM ''∠=ABM '∠=30°,A 'B = AB =2∴A BH MBH''∠=∠-A BM ''∠=30°. 在Rt △A 'BH 中,A 'H =12A 'B =1 ,BH=3 ∴()3,1A '∴A '落在EF 上.(图2) (图3)9. (14广东省茂名市)25. 如图,已知平面直角坐标系xoy 中,有一矩形纸片OABC ,O 为坐标原点,AB x ∥轴, B (3),现将纸片按如图折叠,AD ,DE 为折痕,30OAD ∠=︒.折叠后,点O 落在点1O ,点C 落在点1C ,并且1DO 与1DC 在统一向线上. (1)求折痕AD 地点直线的解析式; (2)求经由三点O ,1C ,C 的抛物线的解析式;(3)若⊙P 的半径为R ,圆心P 在(2)的抛物线上活动, ⊙P 与两坐标轴都相切时,求⊙P 半径R 的值. 解:(第25题图)C DOA BEO 1C 1 xy30OA OAD =∠=︒.∴tan 3013OD OA =︒==,∴(()010A D ,,. 设直线AD 的解析式为y kx b =+. 把A ,D 坐标代入上式得:b k b ⎧=⎪⎨+=⎪⎩,解得:k b ⎧=⎪⎨=⎪⎩,折痕AD地点的直线的解析式是y = (2)过1C 作1C F OC ⊥于点F ,由已知得160ADO ADO ∠=∠=︒,∴160C DC ∠=︒. 又DC =3-1=2,∴12DC DC ==.∴在1Rt C DF △中,111sin 2sin60C F DC C DF =∠=⨯︒1112DF DC ==,∴(1C ,罢了知()3,0C .法一:设经由三点O ,C 1,C 的抛物线的解析式是()3y ax x =-点(12C 在抛物线上,∴()223a -=∴a =∴()23222y x x x x =--=-+为所求 法二:设经由三点O ,C 1,C 的抛物线的解析式是2,(0)y ax bx c a =++≠. 把O ,C 1,C 的坐标代入上式得:042930c a b c a b c =⎧⎪++=⎨⎪++=⎩解得0a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴2y x x =为所求.(3)设圆心(),P x y ,则当⊙P 与两坐标轴都相切时,有y x =±.由y x =,得2x x x =,解得10x =(舍去),233x =-. 由y x =-,得2x x x +=-解得10x =(舍去),23x =. ∴所求⊙P的半径3R =-或3R =+ 10. (14重庆市) 28.已知,在Rt △OAB 中,∠OAB =900,∠BOA =300,AB =2.若以O 为坐标原点,OA 地点直线为x 轴,树立如图所示的平面直角坐标系,点B 在第一象限内.将Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处.(1)求点C 的坐标;(2)若抛物线bx ax y +=2(a ≠0)经由C.A 两点,求此抛物线的解析式;(3)若抛物线的对称轴与OB 交于点D,点P 为线段DB 上一点,过P 作y 轴的平行线,交抛物线于点M.问:是否消失如许的点P,使得四边形CDPM 为等腰梯形?若消失,请求出此时点P 的坐标;若不消失,请解释来由.注:抛物线c bx ax y ++=2(a ≠0)的极点坐标为⎪⎪⎭⎫⎝⎛--a b ac ,a b 4422,对称轴公式为abx 2-=解: (1)过点C 作CH ⊥x 轴,垂足为H∵在Rt △OAB 中,∠OAB =900,∠BOA =300,AB =2 ∴OB =4,OA =32由折叠知,∠COB =300,OC =OA =32 ∴∠COH =600,OH =3,CH =3 ∴C 点坐标为(3,3)(2)∵抛物线bx ax y +=2(a ≠0)经由C (3,3).A (32,0)两点∴()()⎪⎩⎪⎨⎧+=+=b a b a 3232033322解得:⎩⎨⎧=-=321b a∴此抛物线的解析式为:x x y 322+-=(3)消失.因为x x y 322+-=的极点坐标为(3,3)即为点CMP ⊥x 轴,设垂足为N,PN =t ,因为∠BOA =300,所以ON =3t ∴P (3t ,t )作PQ ⊥CD,垂足为Q,ME ⊥CD,垂足为E把t x ⋅=3代入x x y 322+-=得:t t y 632+-=∴ M (3t ,t t 632+-),E (3,t t 632+-)同理:Q (3,t ),D (3,1)要使四边形CDPM 为等腰梯形,只需CE =QD 即()16332-=+--t t t ,解得:341=t ,12=t (舍) ∴ P 点坐标为(334,34) ∴ 消失知足前提的点P,使得四边形CDPM 为等腰梯形,此时P 点的坐为(334,34)11. (15山东青岛)24.(本小题满分12分)已知:如图①,在Rt ACB △中,90C ∠=,4cm AC =,3cm BC =,点P 由B 动身沿BA 偏向向点A 匀速活动,速度为1cm/s;点Q 由A 动身沿AC 偏向向点C 匀速活动,速度为2cm/s;衔接PQ .若设活动的时光为(s)t (02t <<),解答下列问题: (1)当t 为何值时,PQ BC ∥?(2)设AQP △的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否消失某一时刻t ,使线段PQ 正好把Rt ACB △的周长和面积同时等分?若消失,求出此时t 的值;若不消失,解释来由;(4)如图②,衔接PC ,并把PQC △沿QC 翻折,得到四边形PQP C ',那么是否消失某一时刻t ,使四边形PQP C '为菱形?若消失,求出此时菱形的边长;若不消失,解释来由.12. (15浙江湖州)24.(本小题12分)已知:在矩形AOBC 中,4OB =,3OA =.分离以OB OA ,地点直线为x 轴和y 轴,树立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反图①比例函数(0)ky k x=>的图象与AC 边交于点E . (1)求证:AOE △与BOF △的面积相等;(2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为若干?(3)请摸索:是否消失如许的点F ,使得将CEF △沿EF 半数后,C 点正好落在OB 上?若消失,求出点F 的坐标;若不消失,请解释来由.(15浙江湖州24题解析)24.(本小题12分)(1)证实:设11()E x y ,,22()F x y ,,AOE △与FOB △的面积分离为1S ,2S , 由题意得11k y x =,22k y x =.1111122S x y k ∴==,2221122S x y k ==. 12S S ∴=,即AOE △与FOB △的面积相等.(2)由题意知:E F ,两点坐标分离为33kE ⎛⎫ ⎪⎝⎭,,44k F ⎛⎫ ⎪⎝⎭,, 1111432234ECF S EC CF k k ⎛⎫⎛⎫∴==-- ⎪⎪⎝⎭⎝⎭△, 11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S ∴=---=---=--△△△△△△矩形11112212243234OEF ECF ECF S S S k S k k k ⎛⎫⎛⎫∴=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△2112S k k ∴=-+.当161212k =-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值.131412S -==⎛⎫⨯- ⎪⎝⎭最大值.(3)解:设消失如许的点F ,将CEF △沿EF 半数后,C 点正好落在OB 边上的M 点,过点E 作EN OB ⊥,垂足为N .由题意得:3EN AO ==,143EM EC k ==-,134MF CF k ==-, 90EMN FMB FMB MFB ∠+∠=∠+∠=,EMN MFB ∴∠=∠.又90ENM MBF ∠=∠=,ENM MBF ∴△∽△.EN EM MB MF∴=,11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭∴==⎛⎫-- ⎪⎝⎭, 94MB ∴=. 222MB BF MF +=,222913444k k ⎛⎫⎛⎫⎛⎫∴+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得218k =.21432k BF ∴==. ∴消失相符前提的点F ,它的坐标为21432⎛⎫⎪⎝⎭,.13(15浙江衢州)24.(本题14分)已知直角梯形纸片OABC 在平面直角坐标系中的地位如图所示,四个极点的坐标分离为O(0,0),A(10,0),B(8,32),C(0,32),点T 在线段OA 上(不与线段端点重合),将纸片折叠,使点A 落在射线AB 上(记为点A ′),折痕经由点T,折痕TP 与射线AB 交于点P,设点T 的横坐标为t,折叠后纸片重叠部分(图中的暗影部分)的面积为S; (1)求∠OAB 的度数,并求当点A ′在线段AB 上时,S 关于t 的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t 的取值规模;(3)S 消失最大值吗?若消失,求出这个最大值,并求此时t 的值;若不消失,请解释来由.(15浙江衢州24题解析)24.(本题14分)解:(1)∵A,B 两点的坐标分离是A(10,0)和B(8,32),∴381032OAB tan =-=∠,∴︒=∠60OAB当点A ´在线段AB 上时,∵︒=∠60OAB ,TA=TA ´, ∴△A ´TA 是等边三角形,且A T TP '⊥, ∴)t 10(2360sin )t 10(TP -=︒-=,)t 10(21AT 21AP P A -===', ∴2TPA )t 10(83TP P A 21S S -=⋅'=='∆, 当A ´与B 重应时,A T=AB=460sin 32=︒, 所以此时10t 6<≤.(2)当点A ´在线段AB 的延伸线,且点P 在线段AB(不与B 重合)上时, 纸片重叠部分的图形是四边形(如图(1),个中E 是TA ´与CB 的交点),(3)S 消失最大值○1当10t 6<≤时,2)t 10(83S -=, 在对称轴t=10的左边,S 的值跟着t 的增大而减小,∴当t=6时,S 的值最大是32.○2当6t 2<≤时,由图○1,重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A , ∴23)4t 10(21)t 10(83S 22⨯----=34)2t (83)28t 4t (8322+--=++-=当t=2时,S 的值最大是34;○3当2t 0<<,即当点A ´和点P 都在线段AB 的延伸线是(如图○2,个中E 是TA ´与CB 的交点,F 是TP 与CB 的交点),∵ETF FTP EFT ∠=∠=∠,四边形ETAB 是等腰形,∴EF=ET=AB=4, ∴3432421OC EF 21S =⨯⨯=⋅=综上所述,S 的最大值是34,此时t 的值是2t 0≤<.14 15浙江绍兴)24.将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.动点Q 从点O 动身以每秒1个单位长的速度沿OC 向终点C 活动,活动23秒时,动点P 从点A 动身以相等的速度沿AO 向终点O 活动.当个中一点到达终点时,另一点也停滞活动.设点P 的活动时光为t (秒). (1)用含t 的代数式暗示OP OQ ,;(2)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 正好落在CB 边上的点D 处,求点D 的坐标;AT COF(3)贯穿连接AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PQ 与AC 可否平行?PE 与AC 可否垂直?若能,求出响应的t 值;若不克不及,解释来由.(15浙江绍兴24题解析)24.(本题满分14分) 解:(1)6OP t =-,23OQ t =+.(2)当1t =时,过D 点作1DD OA ⊥,交OA 于1D ,如图1, 则53DQ QO ==,43QC =, 1CD ∴=,(13)D ∴,. (3)①PQ 能与AC 平行. 若PQ AC ∥,如图2,则OP OAOQ OC=, 即66233t t -=+,149t ∴=,而703t ≤≤, 149t ∴=.②PE 不克不及与AC 垂直.图1图1(第24题图)若PE AC ⊥,延伸QE 交OA 于F ,如图3,则23335t QF OQ QFAC OC +==.23QF t ⎫∴=+⎪⎭.EF QF QE QF OQ ∴=-=- 2233t t ⎫⎛⎫=+-+⎪ ⎪⎭⎝⎭21)1)3t =+.又Rt Rt EPF OCA △∽△,PE OCEF OA∴=, 63261)3t t -∴=⎛⎫+ ⎪⎝⎭,3.45t ∴≈,而703t ≤≤,t ∴不消失.15. (15浙江宿迁24题解析)24.如图,在矩形ABCD 中,9AB =,AD =,点P 是边BC 上的动点(点P 不与点B ,点C 重合),过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 半数,点C 的对应点是R 点,设CP 的长度为x ,PQR △与矩形ABCD 重叠部分的面积为y . (1)求CQP ∠的度数;(2)当x 取何值时,点R 落在矩形ABCD 的AB 边上? (3)①求y 与x 之间的函数关系式;②当x 取何值时,重叠部分的面积等于矩形面积的727?二.扭转类1. (15湖南常德26题)如图9,在直线l 上摆放有△ABC 和直角梯形DEFG ,且CD =6㎝;在△ABC 中:∠C =90O ,∠A =300,AB =4㎝;在直角梯形DEFG 中:EF//DG,∠DGF =90O ,DG =6㎝,DE =4㎝,∠EDG =600.解答下列问题:(1)扭转:将△ABC 绕点C 顺时针偏向扭转900,请你在图中作出扭转后的对应图形 △A 1B 1C,并求出AB 1的长度;(2)翻折:将△A 1B 1C 沿过点B 1且与直线l 垂直的直线翻折,得到翻折后的对应图形 △A 2B 1C 1,试剖断四边形A 2B 1DE 的外形?并解释来由;(3)平移:将△A 2B 1C 1沿直线l 向右平移至△A 3B 2C 2,若设平移的距离为x,△A 3B 2C 2与直角梯形重叠部分的面积为y,当y等于△ABC 面积的一半时,x的值是若干?(15湖南常德26题解析)解:(1)在△ABC 中由已知得:BC=2,AC =AB×cos30°=32,∴AB 1=AC+C B 1=AC+CB=322 .……………………………………2分AC DG图9(2)四边形A 2B 1DE 为平行四边形.来由如下:∵∠EDG =60°,∠A 2B 1C 1=∠A 1B 1C =∠ABC =60°,∴A 2B 1∥DE又A 2B 1=A 1B 1=AB =4,DE =4,∴A 2B 1=DE,故结论成立.………………4分 (3)由题意可知: S △ABC =3232221=⨯⨯, ① 当20<≤x 或10≥x 时,y=0此时重叠部分的面积不会等于△ABC 的面积的一半……………5分②当42<≤x 时,直角边B 2C 2与等腰梯形的下底边DG 重叠的长度为DC 2=C 1C 2-DC 1=(x-2)㎝,则y=()()()222323221-=--x x x , 当y=21S △ABC = 3时,即()32232=-x , 解得22-=x (舍)或22+=x .∴当22+=x 时,重叠部分的面积等于△ABC 的面积的一半.③当84<≤x 时,△A 3B 2C 2完整与等腰梯形重叠,即32=y ……………7分 ④当108<≤x 时,B 2G=B 2C 2-GC 2=2-(x -8)=10-x则y=()()()210231031021x x x -=-⋅-, 当y=21S △ABC = 3时,即()310232=-x , 解得210-=x ,或210+=x (舍去).∴当210+=x 时,重叠部分的面积等于△ABC 的面积的一半.………9分由以上评论辩论知,当22+=x 或210+=x 时, 重叠部分的面积等于△ABC 的面积的一半.………10分2. (广西玉林卷)在矩形ABCD 中,4AB =,2BC =,认为A 坐标原点,AB 地点的直线为x 轴,树立直角坐标系.然后将矩形ABCD 绕点A 逆时针扭转,使点B 落在y 轴的E 点上,则C 和D 点依次落在第二象限的F 点上和x 轴的G 点上(如图). (1)求经由B E G ,,三点的二次函数解析式;(2)设直线EF 与(1)的二次函数图象订交于另一点H ,试求四边形EGBH 的周长. (3)设P 为(1)的二次函数图象上的一点,BP EG ∥,求P 点的坐标. [解] (1)解:由题意可知,4AE AB ==,2AG AD BC ===.(40)B ,∴,(04)E ,,(20)G -,.设经由B E G ,,三点的二次函数解析式是(2)(4)y a x x =+-.把(04)E ,代入之,求得12a =-. 3分 ∴所求的二次函数解析式是:211(2)(4)422y x x x x =-+-=-++.(2)解:由题意可知,四边形AEFG 为矩形.FH GB ∴∥,且6GB =.∵直线4y =与二次函数图象的交点H 的坐标为(24)H ,, 2EH =∴.G ∵与B E ,与H 关于抛物线的对称轴对称,BH EG ===∴. ∴四边形EGBH 的周长262=++⨯8=+.BP EG ∵∥,::AB AG AM AE =∴,即4:2:4AM =.8AM =∴,于是(08)M -,. 设直线BM 的解析式为y kx b =+. 把(40)B ,,(08)M -,代入之,得408.k b b +=⎧⎨=-⎩,解得28.k b =⎧⎨=-⎩,28y x =-∴.结合一次,二次函数解析式构成方程组2281 4.2y x y x x =-⎧⎪⎨=-++⎪⎩,解得620x y =-⎧⎨=-⎩,或40.x y =⎧⎨=⎩,(此组数为B 点坐标)∴所求的P 点坐标为(620)P -,. 解法2:过P 作PN x ⊥轴于N .由BP EG ∥,得EGB PBN ∠=∠. 设所求P 点的横坐标为(0)a a <,则纵坐标为214(0)2a a a -++<. tan PN PBN NB ∠=∵,4tan 22AE EGB AG ∠===, 2PN AENB AG==∴. 4NB NA AB a =+=-∴,22114422PN a a a a ⎛⎫=--++=-- ⎪⎝⎭,214224a a a--=-∴. 解之,得6a =-或4a =.经磨练可知,6a =-是原方程的根;4a =是原方程的增根,故应舍去.当6a =-时,22114(6)642022a a -++=-⨯--+=. ∴所求的P 点坐标为(620)P -,. [点评]此题的分解性较强,考核的常识点较多,但是解法较多,使试题的切入点也较多,很轻易入题.3. (14南京市) 27.在平面内,先将一个多边形以点O 为位似中间放大或缩小,使所得多边形与原多边形对应线段的比为k ,并且原多边形上的任一点P ,它的对应点P '在线段OP 或其延伸线上;接着将所得多边形以点O 为扭转中间,逆时针扭转一个角度θ,这种经由和扭转的图形变换叫做扭转类似变换,记为()O k θ,,个中点O 叫做扭转类似中间,k 叫做类似比,θ叫做扭转角.(1)填空:①如图1,将ABC △以点A 为扭转类似中间,放大为本来的2倍,再逆时针扭转60,得到ADE △,这个扭转类似变换记为A (,);②如图2,ABC △是边长为1cm 的等边三角形,将它作扭转类似变换)A ,得到ADE △,则线段BD 的长为cm ;(2)如图3,分离以锐角三角形ABC 的三边AB ,BC ,CA 为边向外作正方形ADEB ,BFGC ,CHIA ,点1O ,2O ,3O 分离是这三个正方形的对角线交点,试分离应用12AO O △与ABI △,CIB △与2CAO △之间的关系,应用扭转类似变换的常识解释线段12O O 与2AO 之间的关系.解:(1)①2,60; ②2;(2)12AO O △经由扭转类似变换)A ,得到ABI △,此时,线段12O O 变成线段BI ; CIB △经由扭转类似变换45C ⎫⎪⎪⎝⎭,得到2CAO △,此时,线段BI 变成线段1AO . 2212⨯=,454590+=, 122O O AO ∴=,122O O AO ⊥.4. (15湖北恩施)六.(本大题满分12分)C ADE图1ABCDE图2EDBFGCHAI3O1O2O图324. 如图11,在统一平面内,将两个全等的等腰直角三角形ABC 和AFG 摆放在一路,A 为公共极点,∠BAC =∠AGF =90°,它们的斜边长为2,若∆ABC 固定不动,∆AFG 绕点A 扭转,AF .AG 与边BC 的交点分离为D .E (点D 不与点B 重合,点E 不与点C 重合),设BE =m,CD =n. (1)请在图中找出两对类似而不全等的三角形,并拔取个中一对进行证实. (2)求m 与n 的函数关系式,直接写出自变量n 的取值规模.(3)以∆ABC 的斜边BC 地点的直线为x 轴,BC 边上的高地点的直线为y 轴,树立平面直角坐标系(如图12).在边BC 上找一点D ,使BD =CE ,求出D 点的坐标,并经由过程盘算验证BD 2+CE 2=DE 2.(4)在扭转进程中,(3)中的等量关系BD 2+CE 2=DE 2是否始终成立,若成立,请证实,若不成立,(15湖北恩施24题解析)六.(本大题满分12分)24. 解:(1)∆ABE ∽∆DAE , ∆ABE ∽∆DCA 1分 ∵∠BAE =∠BAD +45°,∠CDA =∠BAD +45° ∴∠BAE =∠CDA 又∠B =∠C =45° ∴∆ABE ∽∆DCA 3分 (2)∵∆ABE ∽∆DCA ∴CDBACA BE由依题意可知CA =BA =2 ∴nm 22∴m=n25分 自变量n 的取值规模为1<n<2. 6分 (3)由BD =CE 可得BE =CD ,即m=n ∵m=n2 ∴m=n=2 ∵OB =OC =21BC =1 ∴OE =OD =2-1 ∴D (1-2, 0) 7分∴BD =OB -OD =1-(2-1)=2-2=CE , DE =BC -2BD =2-2(2-2)=22-2∵BD 2+CE 2=2 BD 2=2(2-2)2=12-82, DE 2=(22-2)2= 12-82∴BD 2+CE 2=DE 28分 (4)成立 9分证实:如图,将∆ACE 绕点A 顺时针扭转90°至∆ABH 的地位,则CE =HB ,AE =AH , ∠ABH =∠C =45°,扭转角∠EAH =90°.衔接HD ,在∆EAD 和∆HAD 中∵AE =AH , ∠HAD =∠EAH -∠F AG =45°=∠EAD , AD∴∆EAD ≌∆HAD ∴DH =DE又∠HBD =∠ABH +∠ABD =90°∴BD 2+HB 2=DH 2 即BD 2+CE 2=DE 2 12分5.(15湖北武汉)(本题答案暂缺)25.(本题 12分)如图 1,抛物线y=ax2-3ax+b 经由A (-1,0),C (3,2)两点,与y 轴交于点D,与x 轴交于另一点B.(1)求此抛物线的解析式;(2)若直线y=kx-1(k≠0)将 四 边 形ABCD 面积二等分,求k 的值;(3)如图2,过点 E (1,-1)作EF ⊥x 轴于点F,将△AEF 绕平面内某点扭转 180°后得△MNQ (点M,N,Q 分离与 点 A,E,F 对应),使点M,N 在抛物线上,求点M,N 的坐标.(15湖北武汉25题解析)25.⑴213222y x x =-++;⑵43k =;⑶M (3,2),N (1,3) 6. (15江苏淮安)(本题答案暂缺)28.(本小题14分)如图所示,在平面直角坐标系中.二次函数y=a(x-2)2-1图象的极点为P,与x 轴交点为 A.B,与y 轴交点为C .贯穿连接BP 并延伸交y 轴于点D. (1)写出点P 的坐标;(2)贯穿连接AP,假如△APB 为等腰直角三角形,求a 的值及点C.D 的坐标;(3)在(2)的前提下,贯穿连接BC.AC.AD,点E(0,b)在线段CD(端点C.D 除外)上,将△BCD 绕点E 逆时针偏向扭转90°,得到一个新三角形.设该三角形与△ACD 重叠部分的面积为S,依据不合情况,分离用含b 的代数式暗示S .选择个中一种情况给出解答进程,其它情况直接写出成果;断定当b 为何值时,重叠部分的面积最大?写出最大值.7. (15江苏徐州)(本题答案暂缺)28.如图1,一副直角三角板知足AB =BC,AC =DE,∠ABC =∠DEF =90°,∠EDF =30°【操纵】将三角板DEF 的直角极点E 放置于三角板ABC 的斜边AC 上,再将三角板....DEF ...绕.点.E .扭转..,并使边DE 与边AB 交于点P,边EF 与边BC 于点Q 【探讨一】在扭转进程中, (1) 如图2,当CE1EA=时,EP 与EQ 知足如何的数目关系?并给出证实. (2) 如图3,当CE2EA=时EP 与EQ 知足如何的数目关系?,并解释来由. (3) 依据你对(1).(2)的探讨成果,试写出当CEEA=m 时,EP 与EQ 知足的数目关系式为_________,个中m 的取值规模是_______(直接写出结论,不必证实)【探讨二】若,AC =30cm,持续PQ,设△EPQ 的面积为S(cm 2),在扭转进程中: (1) S 是否消失最大值或最小值?若消失,求出最大值或最小值,若不消失,解释来由. (2) 跟着S 取不合的值,对应△EPQ 的个数有哪些变更?不出响应S 值的取值规模.(15山东青岛24题解析)24.(本小题满分12分)FC(E)A(D)Q PDEFCBAQPDEFCBA解:(1)在Rt△ABC 中,522=+=AC BC AB ,由题意知:AP = 5-t ,AQ = 2t , 若PQ ∥BC ,则△APQ ∽△ABC ,∴=AC AQ AB AP, ∴5542t t -=, ∴710=t .3′(2)过点P 作PH ⊥AC 于H . ∵△APH ∽△ABC , ∴=BC PH AB AP, ∴=3PH 55t-,∴t PH 533-=, ∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=.6′ (3)若PQ 把△ABC 周长等分, 则AP+AQ=BP+BC+CQ .∴)24(32)5(t t t t -++=+-, 解得:1=t .若PQ 把△ABC 面积等分,则ABC APQ S S ∆∆=21, 即-253t +3t =3. ∵ t =1代入上面方程不成立,∴不消失这一时刻t ,使线段PQ 把Rt △ACB 的周长和面积同时等分.9′ (4)过点P 作PM ⊥AC 于M,PN ⊥BC 于N ,若四边形PQP ′ C 是菱形,那么PQ =PC . ∵PM ⊥AC 于M , ∴QM=CM .图①B∵PN ⊥BC 于N,易知△PBN ∽△ABC .∴AB BPAC PN =, ∴54t PN =, ∴54tPN =, ∴54t CM QM ==, ∴425454=++t t t , 解得:910=t .∴当910=t 时,四边形PQP ′ C 是菱形.此时37533=-=t PM , 9854==t CM ,在Rt△PMC 中,9505816494922=+=+=CM PM PC , ∴菱形PQP ′ C 边长为9505.12′ 7.(15山东枣庄)25.(本题满分10分)把一副三角板如图甲放置,个中90ACB DEC ==∠∠,45A =∠,30D =∠,斜边6cm AB =,7cm DC =.把三角板DCE 绕点C 顺时针扭转15°得到△D 1CE 1(如图乙).这时AB 与CD 1订交于点O ,与D 1E 1订交于点F . (1)求1OFE ∠的度数; (2)求线段AD 1的长;(3)若把三角形D 1CE 1绕着点C 顺时针再扭转30°得△D 2CE 2,这时点B 在△D 2CE 2的内部.外部.照样边上?解释来由.BN(甲)ACE DBB(乙)AE 1CD 1OF(15山东枣庄25题解析)25.(本题满分10分) 解:(1)如图所示,315∠=,190E ∠=,∴1275∠=∠=. ………………………………1分 又45B ∠=,∴114575120OFE B ∠=∠+∠=+=. ………3分 (2)1120OFE ∠=,∴∠D 1FO =60°.1130CD E ∠=,∴490∠=.4分又AC BC =,6AB =,∴3OA OB ==.90ACB ∠=,∴116322CO AB ==⨯=.5分 又17CD =,∴11734OD CD OC =-=-=.在1Rt AD O △中,15AD ===.6分 (3)点B 在22D CE △内部.7分来由如下:设BC (或延伸线)交22D E 于点P ,则2153045PCE ∠=+=. 在2Rt PCE △中,2CP ==…………9分3CB =<,即CB CP <,∴点B 在22D CE △内部. ……………10分 815浙江金华)(本题答案暂缺)24. (本题12分) 如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,贯穿连接AP,并把ΔAOP 绕着点A 按逆时针偏向扭转.使边AO 与AB 重合.得到ΔABD.(1)求直线AB 的解析式;(2)当点P 活动到点(3,0)时,求此时DP的长及点D 的坐标;(3)是否消失点P,使ΔOPD 的面积等于43,若消失,请求出相符前提的点P 的坐标;若不消失,请解释来由.1EC A 19. (15辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =矩形ABOC绕点O 按顺时针偏向扭转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)断定点E 是否在y 轴上,并解释来由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否消失点P ,点Q ,使以点O B P Q ,,,为极点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若消失,请求出点P ,点Q 的坐标;若不消失,请解释来由.(15辽宁沈阳26题解析)解:(1)点E 在y 轴上1分 来由如下:衔接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上.3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=。
题型四--几何图形的折叠与动点问题

题型四--几何图形的折叠与动点问题题型四几何图形的折叠与动点问题试题演练1. 如图,在矩形 ABCD 中,AB = 3, AD = 1,点P 在线段AB 上运动,设AP = x ,现将纸片 折叠,使点D 与点P 重合,得折痕EF (点E 、 F 为折痕与矩形边的交点),再将纸片还原, 则x 的取值范围是 ___________ .2. 如图,在 Rt △ ABC 中,/ ACB = 90° AC = 4,BC = 6,点D 是边BC 的中点,点E 是边 AB 上的任意一点(点E 不与点B 重合),沿 DE 翻折△ DBE 使点B 落在点F 处,连接 AF ,则线段AF 长的最小值是 __________ .3. ( ' 1洛阳模拟)如图,在边长为 4的正方形ABCD 中,M 为BC 的中点,E 、F 分别为 AB 、CD 边上的动点.在点 E 、F 运动的过 程中始终保持△ EMF 为直角三角形,其中L) FA E p a第]题图 第2题图/ EMF = 90°.则直角三角形的斜边EF的取值范围是 _________CB M C第3题图第4題图4. 如图,在边长为2的菱形ABCD中,/ A = 60°点P为射线AB上一个动点,过点P作PE丄AB交射线AD于点E,将厶AEP沿直线PE折叠,点A的对应点为F,连接FD、FC ,若厶FDC为直角三角形时,AP的长为5. 如图,正方形ABCD的边长为2,Z DAC的平分线AE交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ + PQ的最小值为____________ .6. 如图,在矩形ABCD中,AD = 3, AB = 4,点E为DC上一个动点,把厶ADE沿AE折叠, 当点D的对应点D "落在矩形的对角线上时,DE的长为_________ .7. 如图,矩形纸片ABCD中,AB = 8,将纸片折叠,使顶点B落在AD上,对应点为点E,BG = 10,则折痕FG 长为 __________ .w c第5题图B 第6题图第7题图8. 如图,在Rt△ ABC 中,/ ABC = 90° AC =10, BC = 8, AD是/ BAC的平分线,点E 是斜边AC上的一点,且AE = AB,沿△ DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为_____________ .9. (' 1商丘模拟)如图,在Rt△ ABC中,/ ACB=90° AC = 4, BC = 3,点E 是AB 边上一动点,过点E作DE丄AB交AC边于点D,将/ A沿直线DE翻折,点A落在线段AB 上的点F处,当△ BCF为等腰三角形时,AE的长为_________________ .E\A FB 第10題图10. ( ' 1郑州模拟)如图,在矩形ABCD 中,AD=6, CD = 4, AD 的中点为E ,点F 是AB 边上一点(不与A 、B 重合),连接EF ,把/ A 沿EF 折叠,使点A 落在点G 处,连接CG. 则线段CG 的取值范围是 ______________ .11. ( ' 1 江西)如图,在△ ABC 中,AB = BC = 4,AO = BO ,P 是射线CO 上的一个动点,/ AOC = 60°则当△ PAB 为直角三角形时, AP 的长为 _____________ .12. 如图,在矩形 ABCD 中,AB = 12,BC = 8,点E 是边BC 上一动点,把△ DCE 沿DE 折叠得△ DFE ,射线DF 交直线CB 于点P , 当厶AFD 为等腰三角形时,DP 的长为 ___________【答案】1. K x < 3【解析】通过观察图形,可得当点 E 与点A 重合时AP 最小,则AP = EP = AD = 1; 当点P第11题图 BP E~~C 第12题图与点B 重合时,AP 最大,则AP = 3,・・・・・・FA = 5— 3= 2,即线段AF 长的最小值是2.3. 4W EF < 5 【解析】•••点M 为BC 的中点, 正方形ABCD 的边长为4,・・・BM = CM = 2,v / EMF = 90° ・•・/ BME +Z CMF = 90° vZ 最大时为4,此时BE = 1, BE 最大时为4,此时 CF = I ,/ O W |CF — BE|< 3,过点 E 作 EG 丄 CD 于点 G ,贝V EG = BC = 4,在 Rt △ EFG 中,EF 2• Z B =Z [C = 90° ・•・△ BME CFM ,/ 豐 CFCFM +Z CMF = 90° /.Z BME =Z CFM ,又BE CM ,・•・ BE ・ CF = BM CM = 2X 2= 4, •・• CF K x < 3.=EG2+ FG2= 16+ (CF —BE)2, / 16W EF2< 16 4笫3題解图4 2或2【解析】根据题意可得△ FDC为直角三角形时分三种情况考虑:(1)如解图①,当Z FDC = 90°时,DF 丄AB,在△ AFD 中,Z A1=60° AD = 2,・・・AF = 1, AP =扌;⑵如解图②,当/DCF = 90°时,CF 丄AB ,在△ CFB 中,/3CBF = 60° BC = 2,・・・ BF = 1, AF = 3, AP =2;(3)当/DFC = 90 °不存在•综上可知 AP 的值 点D ;则D 落在对角线AC 上,过点D 作 D'P '丄AD 于点P ;・・・D ‘ P '即为DQ + PQ 的 最小值,T DD '丄 AE ,・•・/ AFD = Z AFD ' v AF = AF ,/ DAF =Z D 'AF ,二△ DAF D AF ,二AD = AD = 2,v 四边形ABCD 是正方形, ・•・/ DAD ' = 45° ・•・ AP ' = P A A ・••在Rt △ AP ' D '中,P ' D ' 2+ AP '2 = AD '2,AD ' 2= 4,・•・ P ' D '= 9,即 DQ + PQ 的最小 1/J 〈/-H 4 P 图①图2 第4題解图为1或号. 5. 2【解析】如解图,作D 关于AE 的对称值为- 2.【解析】分两种情况进行讨论,设DE=x. i )D 落在AC 上,如解图1,在Rt △ ED ' C中,EC = 4— x , D ‘ C = AC — AD = 5— 3= 2, ED '= x ,根据 ED /2+ D C 2= EC 2 可得 x 2 + 22=3(4 — x)2,解得x = 2;ii )D 落在BD 上,如解图 2,设DD 交AE 于F 根据轴对称性质可知 AE 垂直平分 DD '在 Rt △ DFA 中,sin / ADF = AD , ••• sin ZADF = sin / ADB = AB = 4,-爲=5’12 9又•・• AD = 3,・•・ AF =:,・•・ DF =,又T Z DEF 5 5=Z ADF ,二sin Z DEF = sin Z ADF = 5, 595, 即DE = 5," DE = 5X 4 = 4综上 DE 的长为 2/ FEG = 90° ・•・ EH = 6 , AE = 4,/ AEF + / HEG = 90° I/ AEF +/ AFE = 90° /.ZHEG = Z AFE ,又•・•/ A =Z EHG = 90° /・△EF AE.DEDEEAF s\GHE ,•/ EG = G H ,•/ EF = 5,/ FG =102 + 52 = 5 5; (2)如解图②,由图形的折叠 可知四边形 ABGF 也四边形HEGF ,・・・BG = EG , AB = EH , Z BGF = Z EGF , • EF II BG ,/・Z BGF = Z EFG ,/・Z EFG = Z EGF ,•/ EF = EG , / BG = EF ,•/四边形BGEF 为平行四边形,• EF = EG ,/.平行四边形 BGEF 为菱形,连接 BE ,•/ BE 、FG 互相垂直平分.在Rt △ EFH 中, EF = BG = 10,EH = AB = 8,由勾股定理可得 FH = AF = 6,•/ AE = AF + EF = 16,•/ BE =AE 2 + AB 2 = 8 5,・/ BO = 45,・/ OG =BG 2-BO 2= 2 5, ••四边形 BGEF 为菱形,•/ FG = 2OG = 4 5.第7題解图8. 7或丁 【解析】在Rt △ ABC 中,Z ABC=90° AC = 10,BC = 8,/・ AB =A / 102-82= 6,n (:c图① 12 2 .3 5贝V AE = 6, EC = AC —AE = 10 —6 = 4;v AB = AE,/ BAD = Z EAD , AD = AD , :、△ABD 也Z AED = 90° △AED ,・•・BD = DE,/ B =设BD = x,贝V DE = x, CD = 8 —x,二x2+ 42= (8 —x)2,解得:x = 3,.・. CD = 5, DE = 3.(1)如解图①,若沿/ DEC的角平分线EG折叠,使点C 落在ED延长线上F点处,过G分别作GM 丄EC, GN丄EF,垂足分别为M、N.・•・GN = GM,v S1 1 3△DEC = 2 3 X 4= 6,S A DEG = 2 3 • GN = 2GN,S1 3 门= 2X4 ・GM = 2GM,二2GM + ?GN = 6,△CEG即3 12 12 22GN + 2GN = 6,解得:GN =〒,故EG =^^ ; ⑵如解图②,若沿/ EDC的角平分线DG折叠,使点C落在DE延长线上F点处・・•・CG= FG , DC= DF = 5,v DE = 3,・・・EF = 2,设CG = y, 则FG = y, EG = 4—y, A (4 —y)2+ 22= y2,解得:5 5 3y = 2, A EG = 4 —2 = 2,v DE = 3,二DG =9. 1或4或盘【解析】本题考查三角形的折叠,等腰三角形的性质求线段的长.在Rt △ ABC中,AC = 4,BC = 3,由勾股定理得AB = AC2+ BC2 =5.由折叠性质得AE = EF,在△ BCF中,当BF = BC 时,有BF = AB —AF = AB —2AE = 3, 则AE = 1;当BF = CF时,过BC中点作AC的平行线,交AB于点F,此时F点满足题意,且AF = BF = 5」AE = 5;当CF = CB 时,如解图,过C作CN丄AB于点N.由等面积法得CN如解图所示,在Rt△ ADC中,AD = 6, CD = 4, ・•・ AC= AD2+ CD2= 2 13,把/ A 沿EB 折叠,此时CG最小,使点A落在点G处,连接AG, DG,・•・/EAG = Z EGA, AE = EG, v AE = DE , ・•・ EG = ED ,・•・/ ADG = Z EGD ,「・/ AGD = / AGE + Z EGD = Z DAG +Z ADG = 90°•/ AE =3, AB = 4, .•・22=AE AB,二AG =胃,在Rt △ ADG 中,DG = ;AD2-AG2= ,,62—(24)2= ¥,过G 点作・•・/ AMG = Z AGD = 90 ° v/ MAG CN2+ GN2= 2 37.在Rt △ ABC 中,AC =,AB2+ BC2= 2T3,「.线段CG的取值范围是|37 V CG v 2 13.MN 丄AD,=Z ,・•・△ AMG AGD ,.AM MGAG = DG =AG AM MG 24AD,即:24 = 18 = 5 ,5 56 •••AM=黑,MG 7225,v BN = AM 9625, MN = CD = 4,CN = 6-9625=54 25, GN =72= 2825= 25,在Rt △ CNG 中,CG =11. 2或2 3或2 7【解析】由于点P 在射线 CO 上运动,.••当△ PAB 为直角三角形时,有三 种情况:⑴当/ APB = 90°时,①如解图①,当 点 P 在线段 CO 上时,I AB = BC = 4,AO = BO , AO = 2,— PO = AO = 2,v/ AOC = 60° △ APO 是等边三角形,••• AP = AO = 2;②如解 图②所示,当点P 在CO 的延长线上时,••• AB =BC = 4, AO = BO ,Z AOC = 60° • OP = OA =OB = 2,vZ POB =Z AOC = 60°POB 是等边三角形,即PB = OB = 2,• AP = AB 2— PB 2= 42 — 22 = 2 3; (2)当Z ABP = 90° 时,如解图③所示,T AB = BC = 4, AO = BO , ・・・ AO = BO = 2,又•・•/ BOP =Z AOC = 60° Z ABP = 90 ° ・•・ BP = 口,在 Rt △ APB 中,AP = AB 2+ PB 2= 42£( 2 3) 2= 2 7;・・・ AP 的 长度为2或2 3或2 7.c (: c形,・•・ A* BC= 8,AB- DC= 12, —【解析】• •四边形ABCD 是矩 圏②第11題解图\ iAD// BQ / C= 90°. v把厶DCE沿DE 折叠得△ DFE ・•・ DC= DF= 12. v A》DF,二△ AFD为等腰三角形只有两种情况:(1)当A& FA 12时,如解图①,过点F作FM L AD于点M二AM= MD =4,在Rt△ MD中,由勾股定理,得MF= , 122—42=8A/2,V AD// BQ ・•・/ MD RZ DPC v/ DM R o MF FD 8J~2 / C= 90° , /.△ MD Fo^CPD 二QD= pD 即:肯12 —=pD解得PD=凶2;⑵当AD= AF= 8时,如解图②,DF的延长线交CB的延长线于点P,过点A作AN LDF于点N,・•・ FN k ND= 6,在Rt △ AND中,由勾股定理,得AN=82—62= 2 7,v AD// BC /./ ADN=Z DPC v/ AND=Z C=90。
2020中考数学 结合压轴专题:折叠问题与动点问题(含答案)

2020中考数学结合压轴专题:折叠问题与动点问题(含答案)1.如图①,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图②,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=_____ .第1题图132.边长为4的菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在直线上的C′处,得到经过点D的折痕DE,则CE=________.43-43.如图,在矩形ABCD中,点E是AD的中点,连接BE,将∠ABE沿着BE翻折得到∠FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则BH=_______.第2题图第3题图7584.如图,在矩形ABCD中,点E是AD的中点,将∠ABE沿BE折叠后得到∠GBE,延长BG交CD于点F,若CF=1,FD=2,则BC 的长为________.第4题图第4题解图265.如图,在∠ABCD中,AC与BD相交于点O,∠AOB=75°,BD=4,将∠ABC沿AC所在直线翻折,若点B的落点记为E,连接BE 与OA交于点F,则OF的长度为______.第5题图6-226.如图①,已知AD∥BC,AB∥CD,∠B=∠C.(1)求证:四边形ABCD为矩形;(2)如图②,M为AD的中点,在AB上取一点N,使∠BNC=2∠DCM.①若N为AB中点,BN=2,求CN的长;②若CM=3,CN=4,求BC的长.第题图(1)证明:∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∵AB∥CD,∴∠B+∠C=180°,∵∠B=∠C,∴∠B=∠C=90°,∴四边形ABCD是矩形.(2)解:如解图①中,延长CM、BA交于点E.第6题解图①∵AN =BN =2, ∴AB = CD =4, ∵AE ∥DC , ∴∠E =∠MCD , 在△AEM 和△DCM 中, ⎩⎪⎨⎪⎧∠E =∠MCD ∠AME =∠DMC AM =DM, ∴△AME ≌△DMC , ∴AE =CD =4,∵∠BNC =2∠DCM =∠NCD , ∴∠NCE =∠ECD =∠E , ∴CN =EN =AE +AN = 4+2= 6. ②如解图②中,延长CM 、BA 交于点E .第6题解图②由①可知,△EAM ≌△CDM ,EN =CN , ∴EM = CM = 3,EN = CN = 4,设BN = x ,则BC 2= CN 2-BN 2= CE 2-EB 2, ∴42-x 2=62-(x +4)2, ∴x =12,∴BC =CN 2-BN 2=42-(12)2= 372.7. 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B 、C 重合),以AD为边作等边△ADE (顶点A 、D 、E 按逆时针方向排列),连接CE .(1)如图①,当点D 在边BC 上时,求证:①BD =CE ,②AC =CE +CD ;第7题图(2)如图②,当点D 在边BC 的延长线上且其他条件不变时,结论AC =CE +CD 是否成立?若不成立,请写出AC 、CE 、CD 之间存在的数量关系,并说明理由;(3)如图③,当点D 在边BC 的反向延长线上且其他条件不变时,补全图形,并直接写出AC 、CE 、CD 之间存在的数量关系.(1)证明:①∵△ABC 和△ADE 都是等边三角形, ∴AB =AC =BC ,AD =AE , ∠BAC = ∠DAE = 60°,∴∠BAC -∠CAD =∠DAE -∠CAD ,即∠BAD = ∠CAE , 在△ABD 和△ACE 中,⎩⎪⎨⎪⎧AB =AC ∠BAD = ∠CAE AD =AE, ∴△ABD ≌△ACE (SAS), ∴BD =CE ;②∵BC =BD +CD ,AC =BC ,BD =CE , ∴AC =CE +CD ;(2)解:AC =CE +CD 不成立,AC 、CE 、CD 之间存在的数量关系是:AC =CE -CD . 理由:∵△ABC 和△ADE 都是等边三角形, ∴AB =AC =BC ,AD =AE , ∠BAC =∠DAE =60°,∴∠BAC +∠CAD = ∠DAE +∠CAD , 即∠BAD = ∠CAE , 在△ABD 和△ACE 中, ⎩⎪⎨⎪⎧AB =AC ∠BAD =∠CAE AD =AE, ∴△ABD ≌△ACE (SAS), ∴BD =CE , ∵BC =BD -CD , ∴BC =CE -CD , ∵AC =BC , ∴AC =CE -CD ;(3)解:补全图形如解图,第7题解图AC、CE、CD之间存在的数量关系是:AC=CD-CE.8.如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连接CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.(1)求证:△CDE≌△CBF;(2)当DE=12时,求CG的长;(3)连接AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.第8题图(1)证明:如解图,在正方形ABCD中,DC=BC,∠D=∠CBA=∠CBF=∠DCB =90°,第8题解图∴∠1+∠2= 90°, ∵CF ⊥CE , ∴∠2+∠3= 90°, ∴∠1= ∠3, 在△CDE 和△CBF 中, ⎩⎪⎨⎪⎧∠D = ∠CBF DC =BC ∠1= ∠3, ∴△CDE ≌△CBF (ASA);(2)解:在正方形ABCD 中,AD ∥BC , ∴△GBF ∽△EAF , ∴BG AE = BFAF, 由(1)知,△CDE ≌△CBF , ∴BF = DE = 12,∵正方形的边长为1, ∴AF =AB +BF = 32,AE =AD -DE = 12,∴BG 12=1232, ∴BG =16,∴CG =BC -BG = 56;(3)解:不能.理由:若四边形CEAG 是平行四边形,则必须满足AE ∥CG ,AE = CG ,∴AD-AE=BC-CG,∴DE=BG,由(1)知,△CDE≌△CBF,∴DE=BF,CE=CF,∴△GBF和△ECF是等腰直角三角形,∴∠GFB=45°,∠CFE=45°,∴∠CF A=∠GFB+∠CFE=90°,此时点F与点B重合,点D与点E重合,与题目条件不符,∴点E在运动过程中,四边形CEAG不能是平行四边形.9.如图,已知△ABC中,AB=10 cm,AC=8 cm,BC=6 cm.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动,它们的速度均为2 cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).第9题图(1)当t为何值时,PQ∥BC;(2)设△AQP的面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值;(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.解:(1)由题意知BP=2t,AP=10-2t,AQ=2t,∵PQ∥BC,∴△APQ ∽△ABC , ∴AP AB =AQ AC, 即10-2t 10=2t 8,解得t =209, 即当t 为209s 时,PQ ∥BC ;(2)∵AB =10 cm ,AC =8 cm ,BC =6 cm , ∴AB 2=AC 2+BC 2, ∴△ABC 为直角三角形, ∴∠C =90°,如解图,过点P 作PD ⊥AC 于点D ,第9题解图则PD ∥BC , ∴△APD ∽△ABC , ∴AP AB =PD BC, ∴10-2t 10=PD6, ∴PD =35(10-2t ),∴S =12AQ ·PD =12 ·2t ·35(10-2t )=-65t 2+6t =-65(t -52)2+7.5,∵-65<0,抛物线开口向下,有最大值,∴当t =52 秒时,S 有最大值,最大值是7.5 cm 2;(3)不存在.理由如下:假设存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分,则S △AQP =12S △ABC ,即-65t 2+6t =12×12×8×6,整理得t 2-5t +10=0,∵b 2-4ac =(-5)2-4×10=-15<0, ∴此方程无解,即不存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分.10. 已知:如图,在矩形ABCD 中,AB = 6 cm ,BC = 8 cm ,对角线AC ,BD 交于点O .点P 从点A 出发,沿AD 方向匀速运动,速度为 1 cm/s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1 cm/s ;当一个点停止运动时,另一个点也停止运动.连接PO 并延长,交BC 于点E ,过点Q 作QF ∥AC ,交BD 于点F .设运动时间为t (s)(0<t <6),解答下列问题:(1)当t 为何值时,AP = PO ;(2)设五边形OECQF 的面积为S (cm 2),试确定S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使OD 平分∠COP ?若存在,求出t 的值;若不存在,请说明理由.第10题图解:(1)∵在矩形ABCD 中,AB =6 cm ,BC =8 cm ,∠ABC =90°, ∴AC =10 cm ,AO =12AC =5 cm ,如解图①,过点P 作PM ⊥AO ,第10题解图①∵AP =PO =t , ∴AM =12AO =52 cm ,∵∠PMA =∠ADC =90°, ∠P AM =∠CAD , ∴△APM ∽△ACD , ∴AP AC =AM AD ,即t 10=528, 解得t =258,即t =258s 时,AP =PO ;(2)如解图②,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3 cm.由矩形的性质可知∠PDO =∠EBO ,DO =BO , 在△DOP 和△BOE 中, ⎩⎪⎨⎪⎧∠PDO =∠EBOOD =OB∠DOP =∠BOE, ∴△DOP ≌△BOE (ASA), ∴BE =PD =(8-t )cm ,则S △BOE =12BE ·OH =12×(8-t )×3=12-32t .∵FQ ∥AC ,第10题解图②∴△DFQ ∽△DOC ,相似比为DQ DC =t6,∴S △DFQ S △DOC =t 236, ∵S △DOC =14S 矩形ABCD =14×6×8=12 cm 2,∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC -S △BOE -S △DFQ =12×6×8-(12-32t )-t 23=-13t 2+32t +12,∴S 与t 的函数关系式为S =-13t 2+32t +12;(3)存在.如解图③,过点D 作DM ⊥PE 于点M ,作DN ⊥AC 于点N , 易证△ADN ∽△ACD , ∴DN CD =AD AC ,即DN 6=810, ∴DN =245,第10题解图③∵∠POD =∠COD ,∴DM =DN =245,∴ON =OM =OD 2-DN 2=75,∵S △POD =12OP ·DM ,S △POD =12×12PD ·DC ,∴OP ·DM =3PD , ∴OP =5-58t ,∴PM =185-58t ,∵PD 2=PM 2+DM 2, 即(8-t )2=(185-58t )2+(245)2,解得t 1=16(不合题意,舍去),t 2=11239,∴当t =11239s 时,OD 平分∠COP .11. 已知四边形ABCD 是菱形,AB = 4,∠ABC = 60°,∠EAF 的两边分别与射线CB ,DC相交于点E ,F ,且∠EAF = 60°.(1)如图①,当点E 是线段CB 的中点时,直接写出线段AE ,EF ,AF 之间的数量关系; (2)如图②,当点E 是线段CB 上任意一点时(点E 不与点B 、C 重合),求证:BE = CF ; (3)如图③,当点E 在线段CB 的延长线上,且∠EAB = 15°时,直接写出点F 到BC 的距离.第11题图(1)解:AE = EF = AF ;【解法提示】如解图①,连接AC ,第11题解图①∵四边形ABCD 是菱形,∠ABC = 60°, ∴∠BCD = 120°, ∴∠ACE = ∠ACF = 60°,∴AB = BC = AC ,即△ABC 为等边三角形, 又∵∠BAC = ∠1+∠2= 60°, ∠EAF = ∠2+∠3= 60°, ∴∠1= ∠3, 在△ABE 和△ACF 中, ⎩⎪⎨⎪⎧∠1= ∠3AB = AC∠ABE = ∠ACF , ∴△ABE ≌△ACF (ASA), ∴AE = AF , 又∵∠EAF = 60°, ∴△AEF 为等边三角形, ∴AE = EF = AF ;(2)证明:如解图②,连接AC ,由(1)知,AB = AC ,∠ACF = 60°,第11题解图②∵∠BAC = ∠4+∠5= 60°, ∠EAF = ∠5+∠6= 60°, ∴∠4= ∠6, 在△ABE 和△ACF 中, ⎩⎪⎨⎪⎧∠4= ∠6AB = AC∠ABE = ∠ACF , ∴△ABE ≌△ACF (ASA), ∴BE = CF ;(3)解:点F 到BC 的距离为3- 3.【解法提示】由(2)知,BE = CF ,如解图③,过点A 作AG ⊥CE 于点G ,过点F 作FH ⊥CE 于点H ,第11题解图③∵∠EAB = 15°,∠ABC = 60°, ∴∠BAG = 90°-∠ABC = 30°, ∴∠EAG = 15°+30°= 45°, ∴△AEG 为等腰直角三角形, 又∵AB = 4,∴AG = AB ·cos ∠BAG = 4×32= 23, ∴BG =AB 2-AG 2=42-(23)2= 2,∵EG = AG = 23,∴BE = EG -BG = 23-2, ∴CF = 23-2, ∵FH ⊥CE ,∴∠FCH = 180°-∠BCD = 60°,∴FH=CF ·sin∠FCH=(23-2)×32=3-3,∴点F到BC的距离为3- 3.12.在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.第12题图(1)问题猜想:如图①,若点E在线段CD上,试猜想AG与EG的数量关系和位置关系;(2)类比探究:如图②,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在图③中画出图形,并直接写出DE的长度.解:(1)由平移得EF=CD=AD,∵BD是正方形ABCD的对角线,∴∠ADB=∠CDB=45°,∵FG⊥BD,∴∠DGF=90°,∴∠GFD+∠CDB=90°,∴∠DFG=45°,∴GD = GF ,在△AGD 和△EGF 中,⎩⎪⎨⎪⎧AD = EF ∠ADG = ∠EFG DG = FG ,∴△AGD ≌△EGF (SAS), ∴AG = EG ,∠AGD = ∠EGF ,∴∠AGE = ∠AGD +∠DGE = ∠EGF +∠DGE = 90°, ∴AG ⊥EG ;(2)证明:由平移得EF =CD =AD , ∵BD 是正方形ABCD 的对角线, ∴∠ADB =∠CDB = 45°, ∵FG ⊥BD , ∴∠DGF = 90°, ∴∠GFD +∠CDB = 90°, ∴∠DFG =45°, ∴GD =GF ,在△AGD 和△EGF 中,⎩⎪⎨⎪⎧AD = EF ∠ADG = ∠EFG DG = FG ,∴△AGD ≌△EGF (SAS), ∴AG =EG ,∠AGD =∠EGF ,∴∠AGE =∠AGD-∠DGE =∠EGF-∠DGE =90°, ∴AG ⊥EG ;(3)画出图形如解图,DE = 2 3.第12题解图【解法提示】同(1)可得,AG=EG,AG⊥EG,∴∠GEA=45°,∵∠AGF=120°,∴∠AGB=∠EGF=30°,又∵∠GFD=45°,∴由外角性质得∠CEG=∠EFG+∠EGF=75°,∴∠AED=∠CEG-∠GEA=30°,在Rt△ADE中,AD=2,∴DE=2 3.。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
中考数学复习《抛物线压轴题中的动点问题》(五大必考题型汇编)专题练习

中考数学复习高频考点提升《抛物线压轴题中的动点问题》(五大必考题型汇编)专题练习考型一:平移型动点问题1. 如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.2.如图,抛物线y=x2+(m+2)x+4的顶点C在x轴正半轴上,直线y=x+2与抛物线交于A,B两点(点A在点B的左侧).(1)求抛物线的函数表达式;(2)将直线AB上下平移,平移后的直线y=x+t与抛物线交于A′、B′两点(A′在B′的左侧),当以点A′、B′、(2)中第二象限的点P为顶点的三角形是直角三角形时,求t的值.3. 如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1.0),B(4.0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E.垂直于x 轴的动直线l分别交抛物线和线段BC于点P和点F,动直线l在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)连接CP,CD,在移动直线l移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似,如果存在,求出点P的坐标,如果不存在,请说明理由.考型二:动点与面积问题1. 如图,抛物线经过A(-2,0),B,C(0,2)三点.(1)求抛物线的解析式;(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标.CA O EFBPDlxy2.如图,在平面直角坐标系中,直线y=mx+3与抛物线交于点A(9,-6),与y 轴交于点B,抛物线的顶点C的坐标是(4,-11).(1)分别求该直线和抛物线的函数表达式;(2)D是抛物线上位于对称轴左侧的点,若△ABD的面积为812,求点D的坐标;3.如图,抛物线y=x2+(m+2)x+4的顶点C在x轴正半轴上,直线y=x+2与抛物线交于A,B两点(点A在点B的左侧).(1)求抛物线的函数表达式;(2)点P是抛物线上一点,若S△PAB=2S△ABC,求点P的坐标;4. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的表达式.(2)如图1,点P是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点P的坐标.考型三:动点与角度变换问题1. 如图,已知点A(-1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.2. 如图,已知抛物线y=ax2+bx+6经过两点A(﹣1,0),B(3,0),C是抛物线与y轴的点.(1)求抛物线的解析式;(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90°,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.3. 如图,在平面直角坐标系中,直线y=mx+3与抛物线交于点A(9,-6),与y轴交于点B,抛物线的顶点C的坐标是(4,-11).(1)分别求该直线和抛物线的函数表达式;(2)在y轴上是否存在一点P,使∠APC=45°?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.考型四:动点与图形周长问题1. 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的表达式.(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.2. 如图,抛物线y=x2+(m+2)x+4的顶点C在x轴正半轴上,直线y=x+2与抛物线交于A,B两点(点A在点B的左侧).(1)求抛物线的函数表达式;(2)点P是抛物线上一点,若S△PAB=2S△ABC,求点P的坐标;3. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的解析式;(2)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.4. 已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的表达式.(2)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,求出点G的坐标;若不存在,请说明理由.考型五:动点与图形存在问题1. 如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,-2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=-1.(1)求抛物线的函数表达式;(2)若点P在第二象限内,且PE=2OD,求△PBE的面积;(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM 是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.2. 如图1所示,直线y=x+c与x轴交于点A(-4,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A,C.(1)求抛物线的解析式;(2)点E在抛物线的对称轴上,求CE+OE的最小值;(3)如图2所示,M是线段OA上的一个动点,过点M垂直于x轴的直线与直线AC 和抛物线分别交于点P,N.若点P恰好是线段MN的中点,点F是直线AC上的一个动点,在坐标平面内是否存在点D,使以点D,F,P,M为顶点的四边形是菱形?若存在,请直接写出点D的坐标;若不存在,请说明理由.3. 如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.(1)如图1,当AC∥x轴时,①已知点A的坐标是(﹣2,1),求抛物线的解析式;②若四边形AOBD是平行四边形,求证:b2=4c.(2)如图2,若b=﹣2,BCAC =35,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.4. 如图,在平面直角坐标系xOy中,直线y=kx+3分别交x轴、y轴于A,B 两点,经过A,B两点的抛物线y=-x2+bx+c与x轴的正半轴相交于点C (1,0).(1)求抛物线的解析式;(2)若P为线段AB上一点,∠APO=∠ACB,求AP的长;(3)在(2)的条件下,设M是y轴上一点,试问:抛物线上是否存在点N,使得以A,P,M,N为顶点的四边形为平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.。
立体几何动点和折叠问题—热点小题

最新立体几何折叠动点问题1.(2020•湖南模拟)在棱长为6的正方体1111ABCD A B C D -,中,M 是BC 的中点,点P 是正方体的表面11DCC D (包括边界)上的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -体积的最大值是()A .B .36C .24D .2.(2020•德阳模拟)ABC ∆是边长为的等边三角形,E ,F 分别为AB ,AC 的中点,沿EF 把OAEF折起,使点A 翻折到点P 的位置,连接PB 、PC ,当四棱锥P BCFE -的外接球的表面积最小时,四棱锥P BCFE -的体积为()A B C D 3.(2020•德阳模拟)ABC ∆是边长为的等边三角形,E 、F 分别在线段AB 、AC 上滑动,//EF BC ,沿EF 把AEF ∆折起,使点A 翻折到点P 的位置,连接PB 、PC ,则四棱锥P BCFE -的体积的最大值为()A .BC .3D .24.(2020春•江西月考)已知三棱锥P ABC -满足PA ⊥底面ABC ,在ABC ∆中,6AB =,8AC =,AB AC ⊥,D 是线段AC 上一点,且3AD DC =,球O 为三棱锥P ABC -的外接球,过点D 作球O 的截面,若所得截面圆的面积的最小值与最大值之和为44π,则球O 的表面积为()A .72πB .86πC .112πD .128π5.(2020春•沙坪坝区校级期中)已知A ,B ,C ,D 四点均在半径为(R R 为常数)的球O 的球面上运动,且AB AC =,AB AC ⊥,AD BC ⊥,若四面体ABCD 的体积的最大值为16,则球O 的表面积为()A .32πB .2πC .94πD .83π6.(2020春•五华区校级月考)已知A ,B ,C 是球O 的球面上的三点,2AB =,AC =60ABC ∠=︒,且三棱锥O ABC -的体积为3,则球O 的体积为()A .24πB .48πC .D .7.(2020•东莞市模拟)已知三棱柱111ABC A B C -的球,四边形11A ACC 与11B BCC 为两个全等的矩形,M 是11A B 的中点,且11112C M A B =,则三棱柱111ABC A B C -体积的最大值为()A .12B .16C .4D .438.(2020•江西模拟)四棱柱1111ABCD A B C D -中,底面四边形ABCD 是菱形,120ADC ∠=︒,连接AC ,BD 交于点O ,1A O ⊥平面ABCD ,14A O BD ==,点C '与点C 关于平面1BC D 对称,则三棱锥C ABD '-的体积为()A .33B .23C .63D .439.(2020•浙江模拟)在长方体1111ABCD A B C D -中,底面ABCD 是边长为4的正方形,侧棱1(4)AA t t =>,点E 是BC 的中点,点P 是侧面11ABB A 内的动点(包括四条边上的点),且满足tan 4tan APD EPB ∠=∠,则四棱锥P ABED -的体积的最大值是()A .433B .163C .1633D .643910.(2019秋•包河区校级期末)矩形ABCD 中,2BC =,沿对角线AC 将三角形ADC 折起,得到四面体A BCD -,四面体A BCD -外接球表面积为16π,当四面体A BCD -的体积取最大值时,四面体A BCD -的表面积为()A .39432+B .4339+C .39232+D .2339+11.(2020•山东模拟)如图,正方体1111ABCD A B C D -的棱长为1,线段11A C 上有两个动点E ,F ,且12EF =;则下列结论错误的是()A .BD CE⊥B .//EF 平面ABCDC .三棱锥E FBC -的体积为定值D .BEF ∆的面积与CEF ∆的面积相等12.(2020•海淀区校级模拟)在边长为1的正方体中,E ,F ,G ,H 分别为11A B ,11C D ,AB ,CD 的中点,点P 从G 出发,沿折线GBCH 匀速运动,点Q 从H 出发,沿折线HDAG 匀速运动,且点P 与点Q 运动的速度相等,记E ,F ,P ,Q 四点为顶点的三棱锥的体积为V ,点P 运动的路程为x ,在02x时,V 与x 的图象应为()A .B .C .D .13.(2019秋•襄城区校级月考)如图,在四棱锥P ABCD -中,顶点P 在底面的投影O 恰为正方形ABCD 的中心且22AB =,设点M ,N 分别为线段PD ,PO 上的动点,已知当AN MN +取得最小值时,动点M 恰为PD 的中点,则该四棱锥的外接球的表面积为()A .643πB .163πC .253πD .649π14.(2019春•昆明期末)在平行四边形ABCD 中,3BAD π∠=,点E 在AB 边上,112AD AE AB ===,将ADE ∆沿直线DE 折起成△A DE ',F 为A C '的中点,则下列结论正确的是()A .直线A E '与直线BF 共面B .12BF =C .△A EC '可以是直角三角形D .A C DE'⊥15.(2019秋•安顺月考)如图,正方体1111ABCD A B C D -的棱长为2m ,E 为1AA 的中点,动点P 从点D 出发,沿DA AB BC CD ---运动,最后返回D .已知P 的运动速度为1/m s ,那么三棱锥11P EC D -的体积y (单位:3)m 关于时间x (单位:)s 的函数图象大致为()A .B .C .D .16.(2019秋•沙坪坝区校级期中)如图,正方体1111ABCD A B C D -中,E 为AB 中点,F 在线段1DD 上.给出下列判断:①存在点F 使得1A C ⊥平面1B EF ;②在平面1111A B C D 内总存在与平面1B EF 平行的直线;③平面1B EF 与平面ABCD 所成的二面角(锐角)的大小与点F 的位置无关;④三棱锥1B B EF -的体积与点F 的位置无关.其中正确判断的有()A .①②B .③④C .①③D .②④17.(2019秋•镜湖区校级期中)如图,正方体1111ABCD A B C D -的棱长为1,动点E 在线段11A C 上,F 、M 分别是AD 、CD 的中点,则下列结论中错误的是()A .11//FM A C B .BM ⊥平面1CC FC .存在点E ,使得平面//BEF 平面11CCD DD .三棱锥B CEF -的体积为定值18.(2019•越城区校级学业考试)如图,线段AB 是圆的直径,圆内一条动弦CD 与AB 交于点M ,且22MB AM ==.现将半圆ACB 沿直径AB 翻折,则三棱锥C ABD -体积的最大值是()A .23B .13C .3D .1参考答案与试题解析1.(2020•湖南模拟)在棱长为6的正方体1111ABCD A B C D -,中,M 是BC 的中点,点P 是正方体的表面11DCC D (包括边界)上的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -体积的最大值是()A .B .36C .24D .【解答】解: 在棱长为6的正方体1111ABCD A B C D -中,M 是BC 的中点,点P 是面11DCC D 所在的平面内的动点,且满足APD MPC ∠=∠,Rt ADP ∴∆∽△Rt PMC ∆,∴2AD PD MC PC ==,即2PD PC =,设DO x =,PO h =,作PO CD ⊥,∴=,化简得:223348144h x x =-+-,06x ,根据函数单调性判断:6x =时,23h 最大值为36,h =最大值,在正方体中PO ⊥面BCD ,∴三棱锥P BCD -的体积最大值:116632⨯⨯⨯⨯=2.(2020•德阳模拟)ABC ∆是边长为的等边三角形,E ,F 分别为AB ,AC 的中点,沿EF 把OAEF折起,使点A 翻折到点P 的位置,连接PB 、PC ,当四棱锥P BCFE -的外接球的表面积最小时,四棱锥P BCFE -的体积为()A .534B .334C .64D .364【解答】解:如图,由题意,BC 的中点O 为等腰梯形BCFE 的外接圆的圆心,则四棱锥P BCFE -的外接球的球心在过O 且垂直于平面BCFE 的直线上,要使四棱锥P BCFE -的外接球的表面积最小,则半径最小,即需要O 为四棱锥P BCFE -的外接球的球心,此时OP OB ==1322PG OG OA ===,则993344cos 3322POG +-∠==,P ∴到平面BCFE的距离为sin d OP POG =∠=13224BCFE S =+⨯=.∴四棱锥P BCFE -的体积为13V =⨯=.故选:D .3.(2020•德阳模拟)ABC ∆是边长为的等边三角形,E 、F 分别在线段AB 、AC 上滑动,//EF BC ,沿EF 把AEF ∆折起,使点A 翻折到点P 的位置,连接PB 、PC ,则四棱锥P BCFE -的体积的最大值为()A.BC .3D .2【解答】解:要想体积最大,高得最大,底面积也得最大,当平面AEF ⊥平面EFCB 时,体积才最大;设2EF a =;设O 为EF 的中点,如图: 等边ABC ∆中,点E ,F 分别为AB ,AC 上一点,且//EF BC ,AE AF ∴=,O 为EF 的中点,AO EF ∴⊥,平面AEF ⊥平面EFCB ,平面AEF ⋂平面EFCB EF =,AO ∴⊥平面EFCB ,2EF a =,AO ∴=.∴四棱锥A EFCB -的体积311(2(3)()332V a a a a a a =⨯⨯+⨯==-,2330V a ∴'=-=,1a ∴=(负值舍),01a <<,V1a >>,V 单调递减,1a ∴=,四棱锥A EFCB -的体积最大,最大值为:312-=.故选:D.4.(2020春•江西月考)已知三棱锥P ABC -满足PA ⊥底面ABC ,在ABC ∆中,6AB =,8AC =,AB AC ⊥,D 是线段AC 上一点,且3AD DC =,球O 为三棱锥P ABC -的外接球,过点D 作球O 的截面,若所得截面圆的面积的最小值与最大值之和为44π,则球O 的表面积为()A .72πB .86πC .112πD .128π【解答】解:如图.M 是BC 边中点,E 是AC 边中点,AB AC ⊥ ,M ∴是ABC ∆的外心,作//OM PA ,PA ⊥ 平面ABC ,OM ∴⊥平面ABC ,OM AM ∴⊥,OM MD ⊥,取12OM PA =,易得OA OP =,O ∴是三棱锥P ABC -的外接球的球心.E 是AC 中点,则//ME AB ,132ME AB ==,ME AC ∴⊥,3AD DC = ,∴124ED AC ==,∴MD ==,设2PA a =,则OM a =,222213OD OM MD a =+=+,又152AM BC ===,222225OA OM AM a ∴=+=+,过D 且与OD 垂直的截面圆半径为r ,则r ==,这是最小的截面圆半径,最大的截面圆半径等于球半径OA ,222(25)1244OA r a πππππ∴+=++=,22(25)32OA a ππ=+=.∴24128S OA ππ==球.故选:D .5.(2020春•沙坪坝区校级期中)已知A ,B ,C ,D 四点均在半径为(R R 为常数)的球O 的球面上运动,且AB AC =,AB AC ⊥,AD BC ⊥,若四面体ABCD 的体积的最大值为16,则球O 的表面积为()A .32πB .2πC .94πD .83π【解答】解:因为AB AC =,AB AC ⊥,AD BC ⊥,作AN BC ⊥于N ,则N 为BC 的中点,且12AN BC =,若四面体ABCD 的体积的最大值时,则DN ⊥面ABC ,则外接球的球心在DN 上,设为O ,设外接球的半径为R ,连接OA ,则OA OD R ==,211112()()3263D ABC V BC AN DN AN AN R ON AN R ON -==+=+ 2211()()()()()33OA ON R ON R ON R ON R ON =-+=+-+3311()(22)()14()(22)()(()66363R ON R ON R ON R R ON R ON R ON ++-++=+-+= ,当且仅当22R ON R ON -=+,即3R ON =时取等号,因为三棱锥的最大体积为16,所以3141()636R = ,可得34R =,所以外接球的表面积为29944164S R πππ===,6.(2020春•五华区校级月考)已知A ,B ,C 是球O 的球面上的三点,2AB =,AC =60ABC ∠=︒,且三棱锥O ABC -的体积为,则球O 的体积为()A .24πB .48πC.D.【解答】解:O 到截面ABC 的投影为三角形ABC 的外接圆的圆心,设为E ,连接AE ,则AE 为底面外接圆的圆心,OE OB OC ==为球的半径R ,因为2AB =,AC =,60ABC ∠=︒,由余弦定理可得:22221412cos cos602222AB BC AC BC ABC AB BC BC+-+-∠=︒=== ,整理可得:2280BC BC --=,解得4BC =,设三角形ABC 的外接圆半径为r ,则2sin 6032AC r ==︒2r =,111346sin 602432623O ABC V AB BC OE OE -=︒==,所以OE =,在三角形OAE中,R OA ===,所以外接球的体积为3441233V R ππ===.7.(2020•东莞市模拟)已知三棱柱111ABC A B C -的球,四边形11A ACC 与11B BCC 为两个全等的矩形,M 是11A B 的中点,且11112C M A B =,则三棱柱111ABC A B C -体积的最大值为()A .12B .16C .4D .43【解答】解: 四边形11A ACC 与11B BCC 为两个全等的矩形,AC BC ∴=,1CC AC ⊥,1CC BC ⊥,又AC BC C = ,AC ,BC ⊂平面ABC ,1CC ∴⊥平面ABC ;M 是11A B 的中点,且11112C M A B =,∴底面△111A B C 是直角三角形;综上,三棱柱111ABC A B C -是底面为等腰三角形的直棱柱.设AC BC a ==,1CC b =,将三棱柱还原为长方体,=,即22212a b +=;∴三棱柱的体积2231111(12)(12),244ABC V S CC a b b b b b b ∆===-=-+∈ ;记31()(12)4f b b b =-+,则213()(312)(2)(2)44f b b b b '=-+=--+,当f '(b )0>时,02b <<;当f '(b )0<时,2b <<f ∴(b )在(0,2)上单调递增,(2,上单调递减,故f (b )max f =(2)4=.故选:C .8.(2020•江西模拟)四棱柱1111ABCD A B C D -中,底面四边形ABCD 是菱形,120ADC ∠=︒,连接AC ,BD 交于点O ,1A O ⊥平面ABCD ,14A O BD ==,点C '与点C 关于平面1BC D 对称,则三棱锥C ABD '-的体积为()A .B .C .D .【解答】解:连接1OC ,过点C 作1CM OC ⊥,垂足为M ,因为1OA ⊥平面ABCD ,故1OA BD ⊥,因为四边形ABCD 是菱形,故OA BD ⊥,故BD ⊥平面11ACC A ,故BD CM ⊥,又1CM OC ⊥,故CM ⊥平面1BDC ,又ABD ∆是边长为4的等边三角形,可得OC OA ==所以11A C AC ==,在Rt △11A C O 中,可得1160A OC ∠=︒,则30MOC ∠=︒,可知OCC '∆为等边三角形,且所在平面垂直底面,故114432C ABD V '-=⨯⨯⨯=三棱锥,故选:D .9.(2020•浙江模拟)在长方体1111ABCD A B C D -中,底面ABCD 是边长为4的正方形,侧棱1(4)AA t t =>,点E 是BC 的中点,点P 是侧面11ABB A 内的动点(包括四条边上的点),且满足tan 4tan APD EPB ∠=∠,则四棱锥P ABED -的体积的最大值是()A .3B .C .3D .9【解答】解:作PN AB ⊥于N ,在长方体1111ABCD A B C D -中,DA ⊥平面11A ABB ,CB ⊥平面11A ABB ,在Rt PAD ∆和Rt PBC ∆中,tan AD APD AP ∠=,tan BE EPB PB ∠=,tan 4tan APD EPB ∠=∠ ,1122BE BC AD ==,12PA PB ∴=,设PN h =,AN x =,则4BN x =-,[0x ∈,4],由12PA PB =,得2214PA PB =,即22221[(4)]4h x h x +=+-,整理得2281633h x x =--+,[0x ∈,4],开口向下,对称轴为43x =-,∴在[0x ∈,4]单调递减,则0x =时,2h 取到最大值163,即h∴四棱锥P ABED -的体积的最大值是11(24)432⨯+⨯故选:C .10.(2019秋•包河区校级期末)矩形ABCD 中,2BC =,沿对角线AC 将三角形ADC 折起,得到四面体A BCD -,四面体A BCD -外接球表面积为16π,当四面体A BCD -的体积取最大值时,四面体A BCD -的表面积为()A .392+B .C .392D .【解答】解:由题意可知,直角三角形斜边的中线是斜边的一半,所以长宽分别为2和1的长方形ABCD 沿对角线AC 折起二面角,得到四面体A BCD -,则四面体A BCD -的外接球的球心O 为AC 中点,半径12R AC =,所求四面体A BCD -的外接球的表面积为2416R ππ⨯=;2423R AC AB ⇒=⇒=⇒=∴矩形ABCD 中,23AB =,2BC =,沿AC 将三角形ADC 折起,当平面ADC ⊥平面ABC 时,得到的四面体A BCD -的体积最大,如图所示;过点D 作DO ⊥平面ABC ,垂足为O ,则点D 到平面ABC 的距离为22334AD CD d OD AC ⨯⨯====,过点O 作OM AB ⊥,作ON BC ⊥,垂足分别为M 、N ,连接DM ,DN ;则BM AB ⊥,DN BC ⊥;所以1AO =,3OC =,所以12OM =,332ON =;所以22132DM DO OM =+=,22392DN DO ON =+=;又122ADC ABC S S ∆∆==⨯322⨯=3,11222ACD S AB DM ∆==⨯ 1339322⨯=,11393922222BCD S BC DN ∆==⨯⨯= ;所以四面体A BCD -的表面积为:24ABC ACD BCD S S S S ∆∆∆=++=339+;故选:B .11.(2020•山东模拟)如图,正方体1111ABCD A B C D -的棱长为1,线段11A C 上有两个动点E ,F ,且12EF =;则下列结论错误的是()A .BD CE⊥B .//EF 平面ABCDC .三棱锥E FBC -的体积为定值D .BEF ∆的面积与CEF ∆的面积相等【解答】解:对于A ,连接AC ,则BD AC ⊥,1BD AA ⊥,BD ∴⊥平面11AA C C ,又AE ⊂平面11AA C C ,BD AE ∴⊥.故A 正确;对于B ,11//AC A C ,即//EF AC ,又EF ⊂/平面ABCD ,AC ⊂平面ABCD ,//EF ∴平面ABCD ,故B 正确;对于C ,1111112224AEF S EF AA ∆==⨯⨯= ,点B 到平面AEF 的距离为B 到平面11AA C C 的距离1222d BD ==,112234224A BEFB AEF V V --∴==⨯⨯=,故C 正确;对于D ,连接1A B ,1C B ,则△11A BC 是边长为2的等边三角形,B ∴到EF 的距离为16222-=,而A 到EF 的距离为11AA =,AEF ∴∆的面积与BEF ∆的面积不相等.故D 错误.故选:D .12.(2020•海淀区校级模拟)在边长为1的正方体中,E ,F ,G ,H 分别为11A B ,11C D ,AB ,CD 的中点,点P 从G 出发,沿折线GBCH 匀速运动,点Q 从H 出发,沿折线HDAG 匀速运动,且点P 与点Q运动的速度相等,记E ,F ,P ,Q 四点为顶点的三棱锥的体积为V ,点P 运动的路程为x ,在02x时,V 与x 的图象应为()A .B .C.D.【解答】解:(1)当102x 时,点P 与点Q 运动的速度相等根据下图得出:面OEF 把几何体PEFQ 分割为相等的几何体,111122OEF S ∆=⨯⨯= ,P 到面OEF 的距离为x ,112223263PEFQ P OEF x x V V x -==⨯⨯== ,23(2)当1322x < 时,P 在AB 上,Q 在11C D 上,P 到12,111122OEF S ∆=⨯⨯=,1111223226PEFQ P OEF V V -==⨯⨯⨯==定值.(3)当322x < 时,111122OEF S ∆=⨯⨯=,P 到面OEF 的距离为2x -,112122(2)3233PEFQ P OEF V V x x -==⨯⨯⨯-=-,1,032113,622213,2332x x V x x x ⎧<⎪⎪⎪=<⎨⎪⎪-⎪⎩故选:C.13.(2019秋•襄城区校级月考)如图,在四棱锥P ABCD -中,顶点P 在底面的投影O 恰为正方形ABCD 的中心且22AB =,设点M ,N 分别为线段PD ,PO 上的动点,已知当AN MN +取得最小值时,动点M 恰为PD 的中点,则该四棱锥的外接球的表面积为()A .643πB .163πC .253πD .649π【解答】解:将三角形POD 展开到与平面PAO 共面,则AN MN +的最小值时,A 、M 、N 三点共线,记作AM .M 点在线段PD 上,AM 最短时恰为PD 中点,AM PD ∴⊥,AM ∴既为PD 中线,又是PD 边上的高,AP AD ∴=.顶点P 在底面的投影恰为正方形ABCD 的中心,则四棱锥为正四棱锥,AP PD ∴=,∴三角形APD 为等边三角形. 22AB =,2AO ∴=,24AP AD AO ∴===,则1643PO =-=,设球心为Q ,连接QA ,则在Rt QOA ∆中,222QA AO QO =+,∴224(23)R R =+-,解得43R =,∴外接球的表面积216644433S R πππ==⨯=.故选:A .14.(2019春•昆明期末)在平行四边形ABCD 中,3BAD π∠=,点E 在AB 边上,112AD AE AB ===,将ADE ∆沿直线DE 折起成△A DE ',F 为A C '的中点,则下列结论正确的是()A .直线A E '与直线BF 共面B .12BF =C .△A EC '可以是直角三角形D .A C DE '⊥【解答】解:在平行四边形ABCD 中,3BAD π∠=,点E 在AB 边上,112AD AE AB ===,将ADE ∆沿直线DE 折起成△A DE ',F 为A C '的中点,在A 中,取CD 中点G ,连结BG ,FG ,则//BG DE ,//FG A D ',BG FG G = ,∴平面//BGF 平面A DE ',BF ⊂ 平面BFG ,//BF ∴平面A DE ',∴直线A E '与直线BF 平行或异面,故A 错误;在B 中, 将ADE ∆沿直线DE 折起成△A DE ',F 为A C '的中点,A '点位置不确定,BF ∴的长不是常数,故B 错误;在C 中,1A E '=,2211211cos1203CE =+-⨯⨯⨯︒=,∴当2A E '=时,A E CE '⊥,△A EC '是直角三角形,故D 正确;在D 中,DE CE ⊥ ,60DEA ∠'=︒,DE ∴与A C '不垂直,故D 错误.故选:C .15.(2019秋•安顺月考)如图,正方体1111ABCD A B C D -的棱长为2m ,E 为1AA 的中点,动点P 从点D 出发,沿DA AB BC CD ---运动,最后返回D .已知P 的运动速度为1/m s ,那么三棱锥11P EC D -的体积y (单位:3)m 关于时间x (单位:)s 的函数图象大致为()A .B .C .D .【解答】解:(1)当02x时,P 在线段DA 上运动,此时DP x =,112224()22222PED x x x S ⨯-=-++=- ,所以1111112(2(4)323P EC D C PED x V V x --==⨯⨯-=-;(2)当24x时,P 在线段AB 上,因为//AB 平面11EC D ,所以P 到平面11EC D 的距离为定值,所以11P EC D V -为定值,1112(42)33A EC D V -=-=;(3)当46x时,P 在线段BC 上,取1BB 的中点F ,1111P EC D P FC E E PFC V V V ---==,此时6CP x =-,同理可得112PC F x S =- ,所以11(2)3E PFC V x -=-;(4)当68x时,P 在线段CD 上,因为//CD 平面11EC D ,所以P 到平面11EC D 的距离为定值,所以11P EC D V -为定值,1114(62)33D EC D V -=-=.综上,三棱锥11P EC D -的体积y (单位:3)m 关于时间x (单位:)s 的函数大致图象如右图所示.故选:B .16.(2019秋•沙坪坝区校级期中)如图,正方体1111ABCD A B C D -中,E 为AB 中点,F 在线段1DD 上.给出下列判断:①存在点F 使得1A C ⊥平面1B EF ;②在平面1111A B C D 内总存在与平面1B EF 平行的直线;③平面1B EF 与平面ABCD 所成的二面角(锐角)的大小与点F 的位置无关;④三棱锥1B B EF -的体积与点F 的位置无关.其中正确判断的有()A .①②B .③④C .①③D .②④【解答】解:对于①,假设存在F 使得1A C ⊥平面1B EF ,则11A C B E ⊥,又1BC B E ⊥,1BC A C C = ,1B E ∴⊥平面1A BC ,则11B E A B ⊥,这与11A B AB ⊥矛盾,所以①错误;对于②,因为平面1B EF 与平面1111A B C D 相交,设交线为l ,则在平面1111A B C D 内与l 平行的直线平行于平面1B EF ,故②正确;对于③,以D 点为坐标原点,以DA 所在直线为x 轴,DC 所在直线为y 轴,1DD 所在直线为z 轴,建立空间坐标系,则平面ABCD 的法向量为(0m = ,0,1),而平面1B EF 的法向量n ,随着F 位置变化,故平面1B EF 与平面ABCD 所成的二面角(锐角)的大小与点F 的位置有关,故③错误;对于④,三棱锥1B B EF -的体积即为三棱锥1F BB E -,因为1//DD 平面11ABB A ,所以,当F 在线段1DD 上移动时,F 到平面11ABB A 的距离不变,故三棱锥1B B EF -的体积与点F 的位置无关,即④正确.故选:D .17.(2019秋•镜湖区校级期中)如图,正方体1111ABCD A B C D -的棱长为1,动点E 在线段11A C 上,F 、M 分别是AD 、CD 的中点,则下列结论中错误的是()A .11//FM A C B .BM ⊥平面1CC FC .存在点E ,使得平面//BEF 平面11CCD DD .三棱锥B CEF -的体积为定值【解答】解:在A 中,因为F 、M 分别是AD 、CD 的中点,所以11////FM AC A C ,故A 正确;在B 中,由平面几何得BM CF ⊥,又有1BM C C ⊥,所以BM ⊥平面1CC F ,故B 正确;在C 中,BF 与平面11CC D D 有交点,所以不存在点E ,使得平面//BEF 平面11CC D D ,故C 错误.在D 中,三棱锥B CEF -以面BCF 为底,则高是定值,所以三棱锥B CEF -的体积为定值,故D 正确.故选:C .18.(2019•越城区校级学业考试)如图,线段AB 是圆的直径,圆内一条动弦CD 与AB 交于点M ,且22MB AM ==.现将半圆ACB 沿直径AB 翻折,则三棱锥C ABD -体积的最大值是()A .23B .13C .3D .1【解答】解:记翻折后CM 与平面ABD 所成角为α,则三棱锥C ABD -的高为sin h CM α=,∴三棱锥C ABD -体积:11(sin )sin 32C ABD V AB DM DMA CM α-=⨯⨯⨯⨯∠⨯⨯16AB DM CM ⨯⨯⨯ ,3AB = ,2DM CM AM BM ⨯=⨯=,∴三棱锥C ABD -体积的最大值是:1()3216C ABD max V -=⨯⨯= .故选:D .。
中考数学动点问题专题练习(含答案)

动点专题一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥O A,垂足为H,△OPH 的重心为G .(1)当点P在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设P Hx =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围).(3)如果△PG H是等腰三角形,试求出线段PH 的长.二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ABC 中,AB=AC =1,点D,E在直线B C上运动.设BD=,x CE=y . (1)如果∠B AC=30°,∠DA E=105°,试确定y 与x 之间的函数解析式;(2)如果∠B AC的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.AEDCB 图2H M NG PO A B 图1 x yC三、应用求图形面积的方法建立函数关系式例4(2004年·上海)如图,在△A BC中,∠BAC =90°,AB=AC =22,⊙A 的半径为1.若点O在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A相切时, △AO C的面积.一、以动态几何为主线的压轴题 (一)点动问题.1.(09年徐汇区)如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F . (1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; (3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE的长.AB C O 图8HAB CDEOlA ′(二)线动问题2,在矩形A BCD 中,AB =3,点O 在对角线A C上,直线l过点O ,且与AC 垂直交AD于点E .(1)若直线l 过点B,把△ABE 沿直线l 翻折,点A 与矩形A BCD的对称中心A '重合,求BC 的长; (2)若直线l 与AB 相交于点F,且AO=41AC,设AD 的长为x ,五边形BCDEF 的面积为S.①求S 关于x 的函数关系式,并指出x 的取值范围;②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在,请求出x 的值;若不存在,请说明理由.(三)面动问题3.如图,在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点(D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG .(1)试求ABC ∆的面积;(2)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =,ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4)当BDG ∆是等腰三角形时,请直接写出AD 的长.解决动态几何问题的常见方法有:C一、 特殊探路,一般推证例2:(2004年广州市中考题第11题)如图,⊙O 1和⊙O2内切于A,⊙O1的半径为3,⊙O2的半径为2,点P为⊙O1上的任一点(与点A 不重合),直线PA 交⊙O2于点C,PB 切⊙O2于点B ,则PCBP的值为(A)2 (B)3 (C)23(D)26二、 动手实践,操作确认例4(2003年广州市中考试题)在⊙O中,C 为弧AB 的中点,D 为弧A C上任一点(与A 、C 不重合),则(A)A C+CB=AD+DB (B) A C+C B<AD+DB(C) AC+CB >A D+D B (D) AC+C B与AD+DB 的大小关系不确定例5:如图,过两同心圆的小圆上任一点C 分别作小圆的直径CA 和非直径的弦CD ,延长CA 和C D与大圆分别交于点B 、E,则下列结论中正确的是( * ) (A)AB DE = (B )AB DE >(C)AB DE <(D )AB DE ,的大小不确定三、 建立联系,计算说明例6:如图,正方形ABCD 的边长为4,点M在边DC 上,且DM=1,N为对角线A C上任意一点,则DN +MN 的最小值为 .BMND CBA以圆为载体的动点问题中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重例1.在Rt ABC合),Q是BC边上的动点(与点B、C不重合),当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由。
中考数学压轴题(六)折叠问题

折叠问题折叠对象有三角形、矩形、正方形、梯形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;解题时,灵活运用轴对称性质和背景图形性质。
轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。
压轴题是由一道道小题综合而成,常常伴有折叠;解压轴题时,要学会将大题分解成一道道小题;那么多作折叠的选择题填空题,很有必要。
1、(2009年浙江省绍兴市)如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°,则APD ∠等于( )A .42°B .48°C .52°D .58°2、(2009湖北省荆门市)如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则A DB '∠=( )A .40°B .30°C .20°D .10°3、(2009年日照市)将三角形纸片(△ABC )按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′,F ,C 为顶点的三角形与△ABC 相似,那么BF 的长度是 .4、(2009年衢州)在△ABC 中,AB =12,AC =10,BC =9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为A .9.5B .10.5C .11D .15.55、(2009泰安)如图,在Rt △ABC 中,第2题图 A 'B D A C(第18题图)A CB ∠ACB=90°,∠A <∠B ,沿△ABC 的中线CM 将△CMA 折叠,使点A 落在点D 处, 若CD 恰好与MB 垂直,则tanA 的值 为 .6、(2009年上海市)在Rt ABC △中,903BAC AB M ∠==°,,为边BC 上的点,联结AM (如图3所示).如果将ABM △沿直线AM 翻折后,点B 恰好落在边AC 的中点处,那么点M 到AC 的距离是 .7、(2009宁夏) 如图:在Rt ABC △中,90ACB ∠=°,CD 是AB 边上的中线,将ADC △沿AC 边所在的直线折叠,使点D 落在点E 处,得四边形ABCE .求证:EC AB ∥.8、(2009年清远)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,B ∠和C ∠都为锐角,M 为AB 一动点(点M 与点A B 、不重合),过点M 作MN BC ∥,交AC 于点N ,在AMN △中,设MN 的长为x ,MN 上的高为h .(1)请你用含x 的代数式表示h .(2)将AMN △沿MN 折叠,使AMN △落在四边形BCNM 所在平面,设点A 落在平面的点为1A ,1A MN △与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?9、(2009恩施市)如图,在ABC △中,9010A BC ABC ∠==°,,△的面积为25,点D 为AB 边上的任意一点(D 不与A 、B 重合),过点D 作DE BC ∥,交AC 于点E .设DE x =,以DE 为折线将BC NM AA图3 BMC EC B A DADE △翻折(使ADE △落在四边形DBCE 所在的平面内),所得的A DE '△与梯形DBCE 重叠部分的面积记为y .(1)用x 表示ADE △的面积;(2)求出05x <≤时y 与x 的函数关系式;(3)求出510x <<时y 与x 的函数关系式;(4)当x 取何值时,y 的值最大?最大值是多少?提示:相似、二次函数10、(2009年天津市)已知一个直角三角形纸片OAB ,其中9024AOB OA OB ∠===°,,.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D .(Ⅰ)若折叠后使点B 与点A 重合,求点C 的坐标;提示:画出图形,图中性质△ACD ≌△BCD,△BDC ∽△BOA,BC=AC(Ⅱ)若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并确定y 的取值范围;提示:画图,△COB '中由勾股定理得出函数关系式,由x 取值范围确定y 范围。
中考数学压轴题(六)折叠问题

(第18题图)MAC B 折叠问题折叠对象有三角形、矩形、正方形、梯形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;解题时,灵活运用轴对称性质和背景图形性质。
轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。
压轴题是由一道道小题综合而成,常常伴有折叠;解压轴题时,要学会将大题分解成一道道小题;那么多做折叠的选择题填空题,很有必要。
1、(2009年浙江省绍兴市)如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°,则APD ∠等于( ) A .42° B .48° C .52° D .58°2、(2009湖北省荆门市)如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则A DB '∠=( ) A .40° B .30° C .20° D .10°3、(2009年日照市)将三角形纸片(△ABC )按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′,F ,C 为顶点的三角形与△ABC 相似,那么BF 的长度是 .4、(2009年衢州)在△ABC 中,AB =12,AC =10,BC =9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为 A .9.5 B .10.5 C .11 D .15.5第4题图 第5题图 第6题图 5、(2009泰安)如图,在Rt △ABC 中,∠ACB=90°,∠A <∠B ,沿△ABC 的中线CM 将△CMA 折叠,使点A 落在点D 处,若CD 恰好与MB 垂直,则tanA 的值为 .6、(2009年上海市)在Rt ABC △中,903BAC AB M ∠==°,,为边BC 上的点,联结AM (如图3所示).如果将ABM △沿直线AM 翻折后,点B 恰好落在边AC 的中点处,那么点M 到AC 的距离是 .7、(2009宁夏) 如图:在Rt ABC △中,90ACB ∠=°,CD 是AB 边上的中线,将ADC △沿AC 边所在的直线折叠,使点D 落在点E 处,得四边形ABCE .求证:EC AB ∥.第2题图A 'BDAC E C 第3题图A 图3B M C8、(2009年清远)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,B ∠和C ∠都为锐角,M 为AB 一动点(点M 与点A B 、不重合),过点M 作MN BC ∥,交AC 于点N ,在AMN △中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h . (2)将AMN △沿MN 折叠,使AMN △落在四边形BCNM 所在平面,设点A 落在平面的点为1A ,1A MN △与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?9、(2009恩施市)如图,在ABC △中,9010A BC ABC ∠==°,,△的面积为25,点D 为AB 边上的任意一点(D 不与A 、B 重合),过点D 作DE BC ∥,交AC 于点E .设DE x =,以DE 为折线将ADE △翻折(使ADE △落在四边形DBCE 所在的平面内),所得的A DE '△与梯形DBCE 重叠部分的面积记为y .(1)用x 表示ADE △的面积;(2)求出05x <≤时y 与x 的函数关系式;(3)求出510x <<时y 与x 的函数关系式; (4)当x 取何值时,y 的值最大?最大值是多少?提示:相似、二次函数10、(2009天津)已知一个直角三角形纸片OAB ,其中9024AOB OA OB ∠===°,,.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D .(Ⅰ)若折叠后使点B 与点A 重合,求点C 的坐标;提示:画出图形,图中性质△ACD ≌△BCD,△BDC ∽△BOA,BC=ACB C N M AE A 'D BC AB CA(Ⅱ)若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并确定y 的取值范围;提示:画图,△COB '中由勾股定理得出函数关系式,由x 取值范围确定y 范围。
2021年中考数学压轴题型精讲练 题型一 几何图形的折叠与动点问题

类型1 动点或图形的相对位置不定型 ②确定主动点D的位置(根据被动定主动),如图(6);
类型1 动点或图形的相对位置不定型
③确定解法. 如图(7),在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC= , ∴AB=2,∠ABC=30°. ∵∠CBE=15°, ∴∠ABE=15°=∠DBE. 设AD,BE交于点H. ∵点E,B关于直线AD对称,∴AD⊥BE. 易证△ABH≌△DBH,∴BD=AB=2.
类型1 动点或图形的相对位置不定型
过点D作DF⊥AB于点F,则∠ADF=∠DAF=45°,∴AF=DF. 设DF=AF=x,则BF= DF= x,BD=2DF=2x. ∵AB=AF+BF, ∴2=x+ x,解得x= -1, ∴BD=2x=2 -2.
类型1 动点或图形的相对位置不定型
(2)情况2:射线BE在射线BC的上方. ①确定被动点E的位置(根据条件定被动),如图(5);
类型1 动点或图形的相对位置不定型 ②确定主动点D的位置(根据被动定主动),如图(3);
类型1 动点或图形的相对位置不定型
③确定解法. 如图(4),在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC= , ∴AB=2,∠ABC=30°. 由轴对称的性质可得,AE=AB,∠EAD=∠BAD, ∴∠AEB=∠ABE=30°+15°=45°, ∴∠BAE=90°, ∴∠BAD= ∠BAE=45°.
类型1 动点或图形的相对位置不定型
②如图(1),以点A为圆心、AD长为半径作☉A; ③作出矩形ABCD的两条对称轴,☉A与这两条对称轴的交点即为被动点D'(由 图(1)可知有三种情况).
类型1 动点或图形的相对位置不定型
(2)步骤2:根据被动点的位置确定主动点的位置. 根据折叠的性质可知,∠DAE=∠D'AE,所以点E在∠DAD'的平分线上,∠DAD'的 平分线与射线DC的交点即为点E. 2.分情况讨论. (1)情况1:点D'落在对称轴PQ上. ①确定被动点D'的位置(根据条件定被动),如图(2);
最新九年级数学中考复习:动点问题综合压轴题含答案

2023年九年级数学中考复习:动点问题综合压轴题1.如图,已知AB=5,AD=4,AD∥BM,3cos5B=,点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE使得∥DAE=∥BAC,射线EA交射线CD于点F.设,AFBC x yAC==(1)如图1,当x=4时,求AF的长;(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;(3)若AC∥AE,求AF的长.2.如图,正方形ABCD的边长为6,点E为射线AB上的动点,连接DE,作点A关于DE的对称点F,连接DF,EF,BF,CF(1)如图,当点落在BD上时,求AE的长;(2)如图,当2AE=时,探索BF与CF的位置关系,并说明理由;(3)在点E从点A出发后,当BCF△为等腰三角形时,直接写出AE的长.3.如图1,将等腰三角形ABC沿着底边AC对折得到∥ADC,∥ABC是锐角,E是BC(1)求证:四边形ABCD 是菱形;(2)当AE ∥BC ,∥EAF =∥ABC 时,求证:AC 垂直平分EF ;(3)如图2,当∥EAF =∥BAC 时,延长BC 交射线AF 于点M ,延长DC 交射线AE 于点N ,连接BD ,MN ,若AB =4,sin∥ABD 14=,则当CE = 时,∥AMN 是等腰三角形.4.如图1,在矩形ABCD 中,3AB =,5BC =,点E 在AB 边上,1AE =.点F 是直线BC 上的动点.将BEF 沿EF 折叠得到将GEF △.直线GF 与直线BD 的交点为点H .(1)若点G 落在AD 边上(如图2),连结BG ,请判断BGF 的形状并说明理由; (2)若点F 与点C 重合(如图3),求点G 到直线BC 的距离;(3)在点F 的运动过程中,是否存在某一时刻,使得BHF 是以FH 为腰的等腰三角形?若存在,求CF 的长;若不存在,请说明理由.5.已知,在矩形ABCD 中,BCAB=m ,F 、G 分别为AB 、DC 边上的动点,连接GF . (1)如图,当F 为AB 的中点,G 与D 重合时,将∥AFD 沿FD 翻折至∥EFD ,连AE ,BE .∥若C ,E ,F 三点共线,求m 的值.(2)当F ,G 不与端点重合时,将四边形AFGD 沿FG 翻折至四边形FHPG ,点H 恰好落在BC 上,HP 交CD 于点Q ,连AH ,交GF 干占O ,若m =1516,tan∥CGP =247,GF =752,求CP 的长.6.如图,在矩形ABCD 中,3cm AB =,AD .动点P 从点A 出发沿折线AB BC -向终点C 运动,在边AB 上以1cm/s 的速度运动;在边BC 的速度运动,过点P 作线段PQ 与射线DC 相交于点Q ,且60PQD ∠=︒,连接PD ,BD .设点P 的运动时间为()s x,DPQ 与DBC △重合部分图形的面积为()2cm y .(1)当点P 与点A 重合时,直接写出DQ 的长;(2)当点P 在边BC 上运动时,直接写出BP 的长(用含x 的代数式表示); (3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.7.如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为()3,4-,点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H .(1)求直线AC 的解析式;(2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设PMB △的面积为S (0S ≠),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围).(3)在(2)的条件下,当t 为何值时,M PB ∠与BCO ∠互为余角,并求此时直线OP 的解析式.8.如图,菱形ABCD 中,AB =BD ,点P 是线段BC 上一动点(不与点B 重合),AP 与对角线BD 交于点E ,连接EC . (1)求证:△ABE ∥ △CBE ;(2)如图∥,若∥ABC =60°,BPBE 的长;(3)若AB =AC ,如图∥,点P 、N 分别从点B 、C 同时出发,以相同速度沿BC 、CA向终点C 和A 运动,连接AP 和BN 交于点G ,当tan ∥CBN 求BG 与GN 的比值.9.如图,在Rt ABC 中,90ACB ∠=︒,15BC =,25AB =.动点P 从点A 出发,以每秒7个单位长度的速度沿折线AC CB -向终点B 运动,当点P 不与ABC 顶点重合时,作135CPQ ∠=︒,交边AB 于点Q ,以CP 、PQ 为边作CPQD .设点P 的运动时间为t 秒.(1)求AC 的长(2)当点P 在边AC 上时,求点Q 到边AC 的距离(用含t 的代数式表示) (3)当CPQD 的某条对角线与ABC 的直角边垂直时,求CPQD 的面积(4)以点P 为直角顶点作等腰直角三角形EPQ ,使点E 与点C 在PQ 同侧,设EQ 的中点为F ,CPQD 的对称中心为点O ,连结OF .当//OF PQ 时,直接写出t 的值10.如图,矩形ABCD 中,AB=6,AD=8,点P 是对角线BD 上一动点,PQ∥BD 交BC 于点Q ,以PQ 为一边作正方形PQMN ,使得N 点落在射线PD 上,点O 是边CD 上一点, 且OD :BP=3:4.(1)联结DQ ,当DQ 平分∥BDC 时,求PQ 的长; (2)证明:点O 始终在QM 所在直线的左侧;(3)若以O 为圆心,半径长为0.8作∥O,当QM 与∥O 相切时,求BP 的长.11.如图,已知∥ABC 中,∥ABC =45°,CD 是边AB 上的高线,E 是AC 上一点,连接BE ,交CD 于点F .(1)如图1,若∥ABE =15°,BC1,求DF 的长;(2)如图2,若BF =AC ,过点D 作DG ∥BE 于点G ,求证:BE =CE +2DG ; (3)如图3,若R 为射线BA 上的一个动点,以BR 为斜边向外作等腰直角∥BRH ,M 为RH 的中点.在(2)的条件下,将∥CEF 绕点C 旋转,得到∥CE ′F ′,E ,F 的对应点分别为E ′,F ′,直线MF ′与直线AB 交于点P ,tan∥ACD =13,直接写出当MF ′取最小值时'RMPF 的值.12.(1)问题发现如图1,在Rt ABC 和Rt CDE △中,90,45ACB DCE CAB CDE ∠=∠=︒∠=∠=︒,点D 是线段AB 上一动点,连接BE . 填空:∥BEAD的值为___________________,∥DBE ∠的度数为__________; (2)类比探究如图2,在Rt ABC 和Rt CDE 中,90,60ACB DCE CAB CDE ∠=∠=︒∠=∠=︒,点D 是线段AB 上一动点,连接BE .请判断BEAD的值及DBE ∠的度数,并说明理由; (3)拓展延伸如图3,在(2)的条件下,将点D 改为直线AB 上一动点,其余条件不变.取线段DE 的中点M ,连接,BM CM ,若2AC =,以B 、C 、D 、M 为顶点的四边形是菱形时,则菱形的边长是多少?请直接写出答案.13.如图,在Rt ABC 中,90ABC ∠=︒,A α∠=,点D 为射线AC 上一动点,作BDE α∠=,过点B 作BE BD ⊥,交DE 于点E ,(点A ,E 在BD 的两侧)连接CE .(1)如图1,若45α=︒时,请直接写出线段AD ,CE 的数量关系:(2)如图2,若60α=︒时,(1)中的结论是否成立;如果成立,请说明理由,如果不成立,请写出它们的数量关系,并说明理由:(3)若30α=︒,6AC =,且ABD △为等腰三角形时,请直接写出线段CE 的长.14.如图1,在Rt∥ABC 中,点C 为直角顶点,点D 为AB 上的一点,且AB =10. (1)当CD ∥AB 时,求证:BC 2=AB ·BD ;(2)如图2,当点D 为AB 的中点时,AC =8,点E 是边BC 上的动点,连结DE ,作DF ∥DE 交AC 于点F ,连结EF 、CD 交于点G ,当EG ∥FG =1∥2时,求线段CE 的长; (3)当∥CAB =15°时,点P 是AC 上一点,求12P A +PB 的最小值.15.如图1,在△ABC 中,AB =BC =20,cos A =4,点D 为AC 边上的动点(点D 不与点A ,C 重合),以D 为顶点作∥BDF =∥A ,射线DE 交BC 边于点E ,过点B 作BF ∥BD 交射线DE 于点F ,连接CF . (1)求证:△ABD ∥∥CDE ;(2)当DE ∥AB 时(如图2),求AD 的长;(3)点D 在AC 边上运动的过程中,若DF =CF ,则CD = .16.平行四边形ABCD 中,N 为线段CD 上一动点.(1)如图1,已知90ADC ∠<︒.若DR BN =,求证:四边形DRBN 为平行四边形; (2)如图2,已知60ABC ∠=︒.若BN 为ABC ∠的角平分线,T 为线段BN 上一点,DT 的延长线交线段BC 于点M ,满足:1tan 2BTM ∠=且DN BM =.请认真思考(1)中图形,探究MDAD的值. (3)如图3,平行四边形ABCD 中,60ABC ∠=︒,2AB BC ==,P 在线段BD 上,Q 在线段CD 上,满足:2BP CQ =.直接写出()2QA AP +的最小值为________.17.如图,已知在平行四边形ABCD 中,AB =10,BC =16,cos B =45,点P 是边BC上的动点,以CP 为半径的圆C 与边AD 交于点E 、F (点F 在点E 的右侧),射线CE 与射线BA 交于点G .(2)联结AP ,当AP //CG 时,求弦EF 的长 (3)当∥AGE 是等腰三角形时,求圆C 的半径长.18.(1)在一节数学探究课上,学生们发现了一个规律:如图∥,当四边形ABCD 是矩形时,Rt EMF 的直角顶点M 在BC 边上运动,直角边分别与线段BA 、线段CD 交于E 、F 两点,在点M 运动的过程中,始终存在着EBM MCF ∽.于是又有同学提出了问题,如果将四边形换成三角形时,是否仍存在同样的规律呢?如图∥,在ABC 中,A B ∠=∠,点D 为AB 边上的动点,过点D 作EDF A ∠=∠,交AC 于点E ,交BC 于点F ,请问是否存在两个相似的三角形,若存在,请证明;若不存在,请说明理由;(2)结合上述规律,解决下列问题:如图∥,在ABC 中,5AB AC ==,6BC =,点P 为BC 上一点(不与B 、C 重合),过点P 作PE AB ⊥于点E ,PF BC ⊥交AC 于点F ,若PEF 为等腰三角形,求PC 的长.19.在Rt ABC 中,90BCA A ABC D ∠︒∠∠=,<,是AC 边上一点,且DA DB =,O 是AB 的中点,CE 是BCD △的中线.()1如图a ,连接OC ,请直接写出OCE ∠和OAC ∠的数量关系:;()2点M 是射线EC 上的一个动点,将射线OM 绕点O 逆时针旋转得射线ON ,MON ADB ON ∠∠=,与射线CA 交于点N .∥如图b ,猜想并证明线段OM 和线段ON 之间的数量关系;∥若30BAC BC m ∠︒=,=,当15AON ∠︒=时,请直接写出线段ME 的长度(用含m 的代数式表示).20.在平面直角坐标系中,线段AB 的两个端点A (0,2),B (1,0),点C 为线段AB 的中点.将线段BA 绕点B 按顺时针方向旋转90°得到线段BD ,连结CD ,AD .点P 是直线BD 上的一个动点.(1)求点D 的坐标和直线BD 的解析式; (2)当∥PCD =∥ADC 时,求点P 的坐标;(3)若点Q 是经过点B ,点D 的抛物线y =ax 2+bx +2上的一个动点,请你探索:是否存在这样的点Q ,使得以点P 、点Q 、点D 为顶点的三角形与∥ACD 相似.若存在,请求出点P 的坐标;若不存在,请说明理由.参考答案:1.(2)220425y x x =---(0<x <5);2.(1)6(2)CF BF ⊥,(3)12+12-3. (3)43或2或454.(1)BGF 是等边三角形 (2)10029 (3)195或2535.(1)∥∥AEB =90°;∥m(2)CP. 6.(1)1;(2))3PB x -;(3)222)3)(34)x x y x x x x ≤≤⎪⎪⎪=<≤⎨⎪⎪<≤⎪⎪⎩7.(1)1522y x =-+;(2)52524S t =-(552t <≤);(3)1,22t y x ==-或256t =;13y x = 8.(2)125;(3)34 9.(1)20;(2)3MQ t =;(3)36或3600121;(4)2013t =或4t = 10.(1)PQ =3;(3)163BP =. 11.(1(312.(1)1;90︒;(2)90BE DBE AD=∠=︒;(3)2或13.(1)AD CE =;(2)不成立,EC ;(33或14.(2)7541;(3)15.(2)252;(3)14.16.(2(3)17.(1)10;(2)72;(3)18.(1)存在两个相似的三角形,AED BDF ∽;(2)PC 的长为94或10843或2.19.(1)∠∠=ECO OAC (2)∥=OM ON ;∥满足条件的EM 的值为m 或12m . 20.(1)1122y x =-;(2)点P 的坐标为(2,12)或(8,72);(。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形折叠及动点问题的相关计算考情总结:图形折叠及动点问题的相关计算是近五年河南中招考试的重点及必考点,均在填空题第15题进行考查,分值为3分,常见的类型有三角形折叠相关计算、四边形结合的相关计算,常见的设问为探究特殊三角形存在时的线段长、探究动点在特殊位置时的线段长.【方法指导】对于河南中招考试中的几何图形折叠与动点问题的计算,常涉及特殊三角形的探究及动点特 殊位置的探究.1.掌握折叠的性质是解决问题的关键.(1)折叠前后位置的图形全等,对应边、角相等;(2)折痕两边的图形关于折痕对称;(3)折叠前后对应点的连线被折痕垂直平分;2.特殊三角形:(1)直角或等腰三角形的判定:首先从可能满足直角的顶点或腰入手,通过矩形的性质、折叠的性质或结合直角三角形勾股定理直接计算,或设出某条线段长,根据相似、勾股定理等,列方程进行求解;3.河南中招考试中,此类问题的重点为分类讨论,即该题多为多解题,注意等腰三角形的腰,直角三角形的直角顶点,特殊点的位置等.1.(2017年)如图,在Rt △ABC 中,∠A=90°,AB=AC ,BC=+1,点M ,N 分别是边BC ,AB 上的动点,沿MN 所在的直线折叠∠B ,使点B 的对应点B′始终落在边AC 上,若△MB′C 为直角三角形,则BM 的长为 21221 或1 .【分析】①如图1,当∠B′MC=90°,B′与A 重合,M 是BC 的中点,于是得到结论;②如图2,当∠MB′C=90°,推出△CMB′是等腰直角三角形,得到CM=MB′,列方程即可得到结论. 【解答】解:①如图1,当∠B′MC=90°,B′与A 重合,M 是BC 的中点,∴BM=BC=+; ②如图2,当∠MB′C=90°,∵∠A=90°,AB=AC ,∴∠C=45°,∴△CMB′是等腰直角三角形,∴CM=MB′,∵沿MN 所在的直线折叠∠B ,使点B 的对应点B′,∴BM=B′M ,∴CM=BM , ∵BC=+1,∴CM +BM=BM +BM=+1, ∴BM=1,综上所述,若△MB′C 为直角三角形,则BM 的长为+或1, 故答案为: +或1.【点评】本题考查了翻折变换﹣折叠问题,等腰直角三角形的性质,正确的作出图形是解题的关键.2.(2016年)如图,已知AD ∥BC ,AB ⊥BC ,AB=3. 点E 为射线BC 上一个动点,连接AE ,将△ABE 沿AE 折叠,点B 落在点B′处,过点B′作AD 的垂线,分别交AD ,BC 于点M ,N .当点B′为线段MN 的三等分点时,BE 的长为__________223或553________.解:由翻折的性质可得:AB=AB ’ BE=B ’E①当MB ’=2,B ’N=1时,设EN=x 得 B ’E=12+x△B ’EN ∽△AB ’E '''AB E B M B EN = 即3122+=x x 解得2x =54BE=B ’E=154+=553 ②当MB ’=1,B ’N=2时,设EN=x 得 B ’E=222+x△B ’EN ∽△AB ’E '''AB E B M B EN = 即3412+=x x 解得2x =21 BE=B ’E=421+=223 故答案为:223或5533.(2015年)如图,正方形ABCD 的边长是16,点E 在边AB 上,AE =3,点F 是边BC 上不与点B ,C 重合的一个动点,把△EBF 沿EF 折叠,点B 落在B'处.若△CDB'恰为等腰三角形,则DB'的长为 16或45 .4.(2014年)如图,矩形ABCD 中,AD=5,AB=7.点E 为DC 上一个动点,把△ADE 沿AE 折叠,当点D 的对应点D /落在∠ABC 的角平分线上时,DE 的长为 53或52.5.(2013年)如图,矩形ABCD 中,AB=3,BC=4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B'处,当△CEB'为直角三角形时,BE 的长为___32或3_______.对应练习 1.如图,在矩形ABCD 中,AB=3,BC=6,点E 是射线BC 上一动点,将△ABE 沿AE 翻折得到△AEF ,延长AF 交CD 的延长线于点G ,当BE=3EC 时,DG= 25或8 .如图①,当E 点在边BC 上时,BE=3EC ,BE=4.5,EC=1.5设AH=HE=x ,FH=4.5-x在Rt △AHF 中:222)5.4(3x x =-+ 解得:x=3.25FH=4.5-3.25 =1.25 ∵△AHF ∽△AGD ,∴DG FH AD AF = DG 25.163= 解得DG=2.5=25 如图②,当E 点在BC 延长线上时,BE=3EC ,BC=6,EC=3设AH=HE=x ,FH=9-x在Rt △AHF 中:222)9(3x x =-+ 解得:x=5FH=9-5=4 ∵△AHF ∽△AGD ,∴DG FH AD AF = DG463= 解得DG=82.如图,在Rt △ABC 中,∠ABC=90°,AC=10,BC=8,AD 是∠BAC 的平分线,点E 是斜边AC 上的一点,且AE=AB 。
若沿△DEC 的一个内角平分线折叠∠C ,使点C 落在DE 所在的直线上,则折痕的长度为 7212或253由题可知:AED ABD ∆≅∆,则∠AED=∠ABC ,BD=DE如图①,若沿∠DEC 的平分线折叠∠C 时,∠DEC=90°,过点M 做MP 丄DE 于点P∵EM 平分∠DEC ,∴∠PEM=45°∴PE=PM ,EC ’=EC=AC-AE=4,设PE=PM=x ,PC ’=4-x∵43''tan tan ====BC AB PC PM C C ,∴434=-x x ,解得712=x ,∴EM=2PM=7212 如图②,若沿∠EDC 的平分线折叠∠C 时,BCAB CE DE C ==tan ,∴DE=BD=3,∴CD=C ’D=5,∴C ’E=2 ∵43'tan 'tan ====BC AB E C EM C C ,∴EM=23,∴DM=22233⎪⎭⎫ ⎝⎛+=2533.(2017·濮阳模拟)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为__________.【分析】由题意得:DF=DB,得到点F在以D为圆心,BD为半径的圆上,作⊙D;连接AD 交⊙D于点F,此时AF值最小,由点D是边BC的中点,得到CD=BD=3;而AC=4,由勾股定理得到AD=5,求得线段AF长的最小值是2,连接BF,过F作FH⊥BC于H,根据相似三角形的性质即可得到结论.【解答】解:由题意得:DF=DB,∴点F在以D为圆心,BD为半径的圆上,作⊙D;连接AD交⊙D于点F,此时AF值最小,∵点D是边BC的中点,∴CD=BD=3;而AC=4,由勾股定理得:AD2=AC2+CD2∴AD=5,而FD=3,∴FA=5﹣3=2,即线段AF长的最小值是2,连接BF,过F作FH⊥BC于H,∵∠ACB=90°,∴FH∥AC,∴△DFH∽△ADC,∴,∴HF=,DH=,∴BH=,∴BF==,故答案为:.【点评】该题主要考查了翻折变换的性质、勾股定理、最值问题等几何知识点及其应用问题;解题的关键是作辅助线,从整体上把握题意,准确找出图形中数量关系.4.(2017·开封模拟)在矩形ABCD 中,AD =8,AB =6,点E 为射线DC 上一个动点,把△ADE 沿AE 折叠,使点D 落在点F 处,若△CEF 为直角三角形时,DE 的长为__________83或8或32-873__________.【分析】当△CEF 为直角三角形时,有两种情况:①当点F 落在矩形内部时,此时点F 在对角线AC 上,先利用勾股定理计算出矩形对角线,根据折叠的性质得∠AFE =∠D =90°,设DE =x ,则CE =6-x ,然后在Rt △CEF 中运用勾股定理列方程即可计算出x ;②当点F 落在AB 边上时,可证得此时四边形ADEF 为正方形,根据正方形的的性质可得DE =AD 进而求解5.(2017·新乡模拟)如图,在矩形ABCD 中,AB =5,BC =3,点E 为射线BC 上一动点,将△ABE 沿AE折叠,得到△AB′E.若B′恰好落在射线CD 上,则BE 的长为___53或15_____.6.(2016·金华)如图,Rt △ABC 纸片中,∠C =90°,AC =5,BC =12,点D 在边BC 上,以AD 为折痕将△ABD 折叠得到△AB′D ,AB ′与边BC 交于点E .若△DEB′为直角三角形,则BD 的长是__7或326________.图①图② 如图①22213)12()5(=-++x x 解得x=7如图②222)12(8x x -+= 解得x=3267.已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为或.【考点】翻折变换(折叠问题).【分析】设BP=t,AQ=m,首先过点P作PE⊥OA于E,易证△PC′E∽△C′QA,由勾股定理可求得C′Q的长,然后利用相似三角形的对应边成比例得到m=t2﹣t+6,即可求得t的值.【解答】解:过点P作PE⊥OA于E,∴∠PEA=∠QAC′=90°,∴∠PC′E+∠EPC′=90°,∵∠PC′E+∠QC′A=90°,∴∠EPC′=∠QC′A,∴△PC′E∽△C′QA,∴=,设BP=t,AQ=m,∵PC′=PC=11﹣t,PE=OB=6,C′Q=CQ=6﹣m,AC′==,∴=.∵=,∴m=t2﹣t+6,又∵36﹣12m=t2,将m=t2﹣t+6代入36﹣12m=t2,化简得,3t2﹣22t+36=0,解得:t1=,t2=.故答案为:或.。
