NOI国家集训队论文分类(至2008)(摘抄自C博客)
全国青少年信息学奥林匹克联赛范文

全国青少年信息学奥林匹克联赛noip 即全国青少年信息学奥林匹克联赛。
全国青少年信息学奥林匹克联赛(National Olympiad in Informatics in Provinces,简称NOIP)自1995年至今已举办19次。
每年由中国计算机学会统一组织。
NOIP在同一时间、不同地点以各省市为单位由特派员组织。
全国统一大纲、统一试卷。
初、高中或其他中等专业学校的学生可报名参加联赛。
联赛分初赛和复赛两个阶段。
初赛考察通用和实用的计算机科学知识,以笔试为主。
复赛为程序设计,须在计算机上调试完成。
参加初赛者须达到一定分数线后才有资格参加复赛。
联赛分普及组和提高组两个组别,难度不同,分别面向初中和高中阶段的学生。
目录1加分保送2命题宗旨3普及内容4竞赛形式▪比赛形式▪比赛时间▪试题形式5知识范围1加分保送2010年11月19日,教育部宣布取消了各项奥林匹克竞赛全国决赛一等奖以下的高校保送资格,改由所在地招生委员会决定是否给予20分及以下的加分。
调整政策从2011年秋季进入高中阶段一年级的学生开始适用,2010年(含)以前已进入高中阶段学习的学生,仍可适用调整前的相关政策。
根据教育部现行《普通高校招收保送生办法》中关于保送生选拔条件的规定,获得全国青少年信息学奥林匹克联赛(NOIP)一等奖的应届高中毕业生,均具有保送进入高校就读的资格。
部分地区一等奖获奖选手还享有高考加分优惠,具体情况视省招办政策而定。
获奖选手可申请参加高校自主招生和保送生考试,经高校测试通过,可享受高考降分优惠或直接保送录取。
NOIP中成绩优秀的非高三选手,可以作为省代表队成员参加全国决赛(NOI)及夏令营比赛(部分省市代表队人员须经过选拔赛决出)。
NOIP获奖选手同样具有保送资格,并且成绩优秀的选手能够当场获得高校点招,免试进入名牌大学。
夏令营作为全国决赛的扩大赛,本身不具有保送资格,但如果选手之前已获得NOIP一等奖,则同样可以参与现场保送。
NOI国家集训队论文分类(至2008)(摘抄自C博客)

摘抄自C博客组合数学计数与统计2001 - 符文杰:《Pólya原理及其应用》2003 - 许智磊:《浅谈补集转化思想在统计问题中的应用》2007 - 周冬:《生成树的计数及其应用》2008 - 陈瑜希《Pólya计数法的应用》数位问题2009 - 高逸涵《数位计数问题解法研究》2009 - 刘聪《浅谈数位类统计问题》动态统计2004 - 薛矛:《解决动态统计问题的两把利刃》2007 - 余江伟:《如何解决动态统计问题》博弈2002 - 张一飞:《由感性认识到理性认识——透析一类搏弈游戏的解答过程》2007 - 王晓珂:《解析一类组合游戏》2009 - 曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》2009 - 方展鹏《浅谈如何解决不平等博弈问题》2009 - 贾志豪《组合游戏略述——浅谈SG游戏的若干拓展及变形》母函数2009 - 毛杰明《母函数的性质及应用》拟阵2007 - 刘雨辰:《对拟阵的初步研究》线性规划2007 - 李宇骞:《浅谈信息学竞赛中的线性规划——简洁高效的单纯形法实现与应用》置换群2005 - 潘震皓:《置换群快速幂运算研究与探讨》问答交互2003 - 高正宇:《答案只有一个——浅谈问答式交互问题》猜数问题2003 - 张宁:《猜数问题的研究:<聪明的学生>一题的推广》2006 - 龙凡:《一类猜数问题的研究》数据结构数据结构2005 - 何林:《数据关系的简化》2006 - 朱晨光:《基本数据结构在信息学竞赛中的应用》2007 - 何森:《浅谈数据的合理组织》2008 - 曹钦翔《数据结构的提炼与压缩》结构联合2001 - 高寒蕊:《从圆桌问题谈数据结构的综合运用》2005 - 黄刚:《数据结构的联合》块状链表2005 - 蒋炎岩:《数据结构的联合——块状链表》2008 - 苏煜《对块状链表的一点研究》动态树2006 - 陈首元:《维护森林连通性——动态树》2007 - 袁昕颢:《动态树及其应用》左偏树2005 - 黄源河:《左偏树的特点及其应用》跳表2005 - 魏冉:《让算法的效率“跳起来”!——浅谈“跳跃表”的相关操作及其应用》2009 - 李骥扬《线段跳表——跳表的一个拓展》SBT2007 - 陈启峰:《Size Balance Tree》线段树2004 - 林涛:《线段树的应用》单调队列2006 - 汤泽:《浅析队列在一类单调性问题中的应用》哈希表2005 - 李羽修:《Hash函数的设计优化》2007 - 杨弋:《Hash在信息学竞赛中的一类应用》Splay2004 - 杨思雨:《伸展树的基本操作与应用》图论图论2005 - 任恺:《图论的基本思想及方法》模型建立2004 - 黄源河:《浅谈图论模型的建立与应用》2004 - 肖天:《“分层图思想”及其在信息学竞赛中的应用》网络流2001 - 江鹏:《从一道题目的解法试谈网络流的构造与算法》2002 - 金恺:《浅谈网络流算法的应用》2007 - 胡伯涛:《最小割模型在信息学竞赛中的应用》2007 - 王欣上:《浅谈基于分层思想的网络流算法》2008 - 周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》最短路2006 - 余远铭:《最短路算法及其应用》2008 - 吕子鉷《浅谈最短径路问题中的分层思想》2009 - 姜碧野《SPFA算法的优化及应用》欧拉路2007 - 仇荣琦:《欧拉回路性质与应用探究》差分约束系统2006 - 冯威:《数与图的完美结合——浅析差分约束系统》平面图2003 - 刘才良:《平面图在信息学中的应用》2007 - 古楠:《平面嵌入》2-SAT2003 - 伍昱:《由对称性解2-SAT问题》最小生成树2004 - 吴景岳:《最小生成树算法及其应用》2004 - 汪汀:《最小生成树问题的拓展》二分图2005 - 王俊:《浅析二分图匹配在信息学竞赛中的应用》Voronoi图2006 - 王栋:《浅析平面Voronoi图的构造及应用》偶图2002 - 孙方成:《偶图的算法及应用》树树2002 - 周文超:《树结构在程序设计中的运用》2005 - 栗师:《树的乐园——一些与树有关的题目》路径问题2009 - 漆子超《分治算法在树的路径问题中的应用》最近公共祖先2007 - 郭华阳:《RMQ与LCA问题》划分问题2004 - 贝小辉:《浅析树的划分问题》数论欧几里得算法2009 - 金斌《欧几里得算法的应用》同余方程2003 - 姜尚仆:《模线性方程的应用——用数论方法解决整数问题》搜索搜索2001 - 骆骥:《由“汽车问题”浅谈深度搜索的一个方面——搜索对象与策略的重要性》2002 - 王知昆:《搜索顺序的选择》2005 - 汪汀:《参数搜索的应用》启发式2009 - 周而进《浅谈估价函数在信息学竞赛中的应用》优化2003 - 金恺:《探寻深度优先搜索中的优化技巧——从正方形剖分问题谈起》2003 - 刘一鸣:《一类搜索的优化思想——数据有序化》2006 - 黄晓愉:《深度优先搜索问题的优化技巧》背包问题2009 - 徐持衡《浅谈几类背包题》匹配2004 - 楼天城:《匹配算法在搜索问题中的巧用》概率概率2009 - 梅诗珂《信息学竞赛中概率问题求解初探》数学期望2009 - 汤可因《浅析竞赛中一类数学期望问题的解决方法》字符串字符串2003 - 周源:《浅析“最小表示法”思想在字符串循环同构问题中的应用》多串匹配2004 - 朱泽园:《多串匹配算法及其启示》2006 - 王赟:《Trie图的构建、活用与改进》2009 - 董华星《浅析字母树在信息学竞赛中的应用》后缀数组2004 - 许智磊:《后缀数组》2009 - 罗穗骞《后缀数组——处理字符串的有力工具》字符串匹配2003 - 饶向荣:《病毒的DNA———剖析一道字符匹配问题解析过程》2003 - 林希德:《求最大重复子串》动态规划动态规划2001 - 俞玮:《基本动态规划问题的扩展》2006 - 黄劲松:《贪婪的动态规划》2009 - 徐源盛《对一类动态规划问题的研究》状态压缩2008 - 陈丹琦《基于连通性状态压缩的动态规划问题》状态设计2008 - 刘弈《浅谈信息学中状态的合理设计与应用》树形DP2007 - 陈瑜希:《多角度思考创造性思维——运用树型动态规划解题的思路和方法探析》优化2001 - 毛子青:《动态规划算法的优化技巧》2003 - 项荣璟:《充分利用问题性质——例析动态规划的“个性化”优化》2004 - 朱晨光:《优化,再优化!——从《鹰蛋》一题浅析对动态规划算法的优化》2007 - 杨哲:《凸完全单调性的加强与应用》计算几何立体几何2003 - 陆可昱:《长方体体积并》2008 - 高亦陶《从立体几何问题看降低编程复杂度》计算几何思想2004 - 金恺:《极限法——解决几何最优化问题的捷径》2008 - 程芃祺《计算几何中的二分思想》2008 - 顾研《浅谈随机化思想在几何问题中的应用》圆2007 - 高逸涵:《与圆有关的离散化》半平面交2002 - 李澎煦:《半平面交的算法及其应用》2006 - 朱泽园:《半平面交的新算法及其实用价值》矩阵矩阵2008 - 俞华程《矩阵乘法在信息学中的应用》高斯消元2002 - 何江舟:《用高斯消元法解线性方程组》数学方法数学思想2002 - 何林:《猜想及其应用》2003 - 邵烜程:《数学思想助你一臂之力》数学归纳法2009 - 张昆玮《数学归纳法与解题之道》多项式2002 - 张家琳:《多项式乘法》数形结合2004 - 周源:《浅谈数形结合思想在信息学竞赛中的应用》黄金分割2005 - 杨思雨:《美,无处不在——浅谈“黄金分割”和信息学的联系》其他算法遗传算法2002 - 张宁:《遗传算法的特点及其应用》2005 - 钱自强:《关于遗传算法应用的分析与研究》信息论2003 - 侯启明:《信息论在信息学竞赛中的简单应用》染色与构造2002 - 杨旻旻:《构造法——解题的最短路径》2003 - 方奇:《染色法和构造法在棋盘上的应用》一类问题区间2008 - 周小博《浅谈信息学竞赛中的区间问题》序2005 - 龙凡:《序的应用》系2006 - 汪晔:《信息学中的参考系与坐标系》物理问题2008 - 方戈《浅析信息学竞赛中一类与物理有关的问题》编码与译码2008 - 周梦宇《码之道—浅谈信息学竞赛中的编码与译码问题》对策问题2002 - 骆骥:《浅析解“对策问题”的两种思路》优化算法优化2002 - 孙林春:《让我们做得更好——从解法谈程序优化》2004 - 胡伟栋:《减少冗余与算法优化》2005 - 杨弋:《从<小H的小屋>的解法谈算法的优化》2006 - 贾由:《由图论算法浅析算法优化》程序优化2006 - 周以苏:《论反汇编在时间常数优化中的应用》2009 - 骆可强《论程序底层优化的一些方法与技巧》语言C++2004 - 韩文弢:《论C++语言在信息学竞赛中的应用》策略策略2004 - 李锐喆:《细节——不可忽视的要素》2005 - 朱泽园:《回到起点——一种突破性思维》2006 - 陈启峰:《“约制、放宽”方法在解题中的应用》2006 - 李天翼:《从特殊情况考虑》2007 - 陈雪:《问题中的变与不变》2008 - 肖汉骏《例谈信息学竞赛分析中的“深”与“广”》倍增2005 - 朱晨光:《浅析倍增思想在信息学竞赛中的应用》二分2002 - 李睿:《二分法与统计问题》2002 - 许智磊:《二分,再二分!——从Mobiles(IOI2001)一题看多重二分》2005 - 杨俊:《二分策略在信息学竞赛中的应用》调整2006 - 唐文斌:《“调整”思想在信息学中的应用》随机化2007 - 刘家骅:《浅谈随机化在信息学竞赛中的应用》非完美算法2005 - 胡伟栋:《浅析非完美算法在信息学竞赛中的应用》2008 - 任一恒《非完美算法初探》提交答案题2003 - 雷环中:《结果提交类问题》守恒思想2004 - 何林:《信息学中守恒法的应用》极限法2003 - 王知昆:《浅谈用极大化思想解决最大子矩形问题》贪心2008 - 高逸涵《部分贪心思想在信息学竞赛中的应用》压缩法2005 - 周源:《压去冗余缩得精华——浅谈信息学竞赛中的“压缩法”》逆向思维2005 - 唐文斌:《正难则反——浅谈逆向思维在解题中的应用》穷举2004 - 鬲融:《浅谈特殊穷举思想的应用》目标转换2002 - 戴德承:《退一步海阔天空——“目标转化思想”的若干应用》2004 - 栗师:《转化目标在解题中的应用》类比2006 - 周戈林:《浅谈类比思想》分割与合并2006 - 俞鑫:《棋盘中的棋盘——浅谈棋盘的分割思想》2007 - 杨沐:《浅析信息学中的“分”与“合”》平衡思想2008 - 郑暾《平衡规划——浅析一类平衡思想的应用》。
noi2008B试题
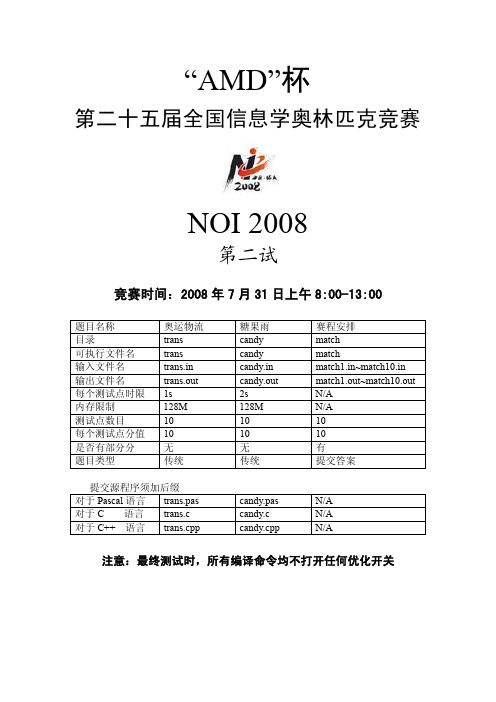
“AMD”杯第二十五届全国信息学奥林匹克竞赛NOI 2008第二试竞赛时间:2008年7月31日上午8:00-13:00题目名称奥运物流糖果雨赛程安排matchcandy目录 trans可执行文件名 trans candy match输入文件名 trans.in candy.in match1.in~match10.in 输出文件名 trans.out candy.out match1.out~match10.out 每个测试点时限1s 2s N/A内存限制128M 128M N/A测试点数目10 10 10每个测试点分值10 10 10是否有部分分无无有题目类型传统传统提交答案提交源程序须加后缀对于Pascal语言 trans.pas candy.pas N/A对于C 语言 trans.c candy.c N/A对于C++ 语言 trans.cpp candy.cpp N/A注意:最终测试时,所有编译命令均不打开任何优化开关“AMD ”杯浙江 绍兴第25届全国信息学奥林匹克竞赛第二试 奥运物流 trans奥运物流【问题描述】2008北京奥运会即将开幕,举国上下都在为这一盛事做好准备。
为了高效率、成功地举办奥运会,对物流系统进行规划是必不可少的。
物流系统由若干物流基站组成,以1…N 进行编号。
每个物流基站i 都有且仅有一个后继基站S i ,而可以有多个前驱基站。
基站i 中需要继续运输的物资都将被运往后继基站S i ,显然一个物流基站的后继基站不能是其本身。
编号为1的物流基站称为控制基站,从任何物流基站都可将物资运往控制基站。
注意控制基站也有后继基站,以便在需要时进行物资的流通。
在物流系统中,高可靠性与低成本是主要设计目。
对于基站i ,我们定义其“可靠性”()R i 如下:设物流基站i 有w 个前驱基站12,,w P P P ",即这些基站以i 为后继基站,则基站i 的可靠性R (i )满足下式:1()()wi j j R i C k R P ==+∑其中C i 和k 都是常实数且恒为正,且有k 小于1。
国家集训队2009论文集信息学竞赛中概率问题

2.1 例一:LastMarble1
题目描述: 有 red 个红球,blue 个蓝球在一个袋子中。两个玩家轮流从袋子中取球,每个人每次 可以取 1,2 或 3 个球,但在他把球拿出袋子之前,他并不知道所取球的颜色。每次球被取 出袋子后,它们的颜色被公布给所有人。取走最后一个红球的人输。现在已知有人在游戏开 始前取走了 removed 个球,并且谁也不知道球的颜色。在两个玩家都采取最优策略时,先手 的胜率是多少? 约束条件: 1≤red,blue≤100 , 0≤removed≤red-1。 分析: 当 removed=0 的时候,这个问题是很普通的动态规划问题。我们只需设 F(r,b)代表现 在剩 r 个红球,b 个蓝球,面对当前局面的玩家所能得到的最大胜率。那么:
D
f ( x1 , x2 ,..., x N )dx1dx2 ...dxN ,其中等式右端表
示 N 重积分,就称 f(x1,x2,…,xN)是 N 为随机向量(X1,X2,…,XN)的联合概率密度函数。如 果有 X1,X2,…,XN 互相独立,并且分别有概率密度函数 f1(x1),f2(x2),…,fN(xN),那么
1
IOI2009 冬令营论文 梅诗珂 3.2 例四:Random Shooting ........................................... 4 总结................................................................. 感谢 ....................................................................... 参考文献.................................................................... 附录 ....................................................................... 附录 1 区域体积的表示 .................................................. 附录 2 例三方法一中区域体积公式的证明 ................................. 附录 3 论文原题 ........................................................ 12 16 16 16 16 16 17 17
历年国家集训队论文题目

1999年陈宏- 数据结构的选择与算法效率——从IOI98试题PICTURE谈起来煜坤- 把握本质,灵活运用——动态规划的深入探讨齐鑫- 搜索方法中的剪枝优化邵铮- 数学模型的建立、比较和应用石润婷- 隐蔽化、多维化、开放化──论当今信息学竞赛中数学建模的灵活性睢》?- 准确性、全面性、美观性——测试数据设计中的三要素周咏基- 论随机化算法的原理与设计2000年陈彧- 信息学竞赛中的思维方法方奇- 动态规划高寒蕊- 递推关系的建立及在信息学竞赛中的应用郭一- 数学模型及其在信息学竞赛中的应用江鹏- 探索构造法解题模式李刚- 动态规划的深入讨论龙翀- 解决空间规模问题的几种常用的存储结构骆骥- 数学模型的建立和选择施遥- 人工智能在围棋程序中的应用肖洲- 数据结构的在程序设计中的应用谢婧- 规模化问题的解题策略徐串- 论程序的调试技巧徐静- 图论模型的建立与转化杨江明- 论数学策略在信息学问题中的应用杨培- 非最优化算法初探张辰- 动态规划的特点及其应用张力- 类比思想在解题中的应用张一飞- 冗繁削尽留清瘦——浅谈信息的充分利用2001年高寒蕊- 从圆桌问题谈数据结构的综合运用符文杰- Pólya原理及其应用高岳- 中等硬度解题报告江鹏- 从一道题目的解法试谈网络流的构造与算法刘汝佳- 搬运工问题的启示李益明- 计算几何的相关问题李源- 树的枚举骆骥- 由“汽车问题”浅谈深度搜索的一个方面——搜索对象与策略的重要性毛子青- 动态规划算法的优化技巧俞玮- 基本动态规划问题的扩展张一飞- 求N!的高精度算法2002年戴德承- 退一步海阔天空——“目标转化思想”的若干应用方奇- 浅谈必要条件的应用符文杰- 排序网络何江舟- 用高斯消元法解线性方程组何林- 猜想及其应用黄芸- POI0110 跳舞蝇金恺- 浅谈网络流算法的应用李澎煦- 半平面交的算法及其应用李睿- 二分法与统计问题骆骥- 浅析解“对策问题” 的两种思路——从《取石子》问题谈起孙方成- 偶图的算法及应用孙林春- 让我们做得更好——从《Parity》的解法谈程序的优化王知昆- 搜索顺序的选择许智磊- 二分,再二分!――从Mobiles(IOI 2001)一题看多重二分顣F旻- 构造法——解题的最短路径张家琳- 多项式乘法张宁- 遗传算法的特点及其应用张一飞- 由感性认识到理性认识——透析一类搏弈游戏的解答过程周文超- 树结构在程序设计中的运用2003年方奇- 染色法和构造法在棋盘上的应用高正宇- 答案只有一个——浅谈问答式交互问题何林- 一类称球问题的解法侯启明- 信息论在信息学竞赛中的简单应用姜尚仆- 模线性方程的应用——用数论方法解决整数问题金恺- 探寻深度优先搜索中的优化技巧——从正方形剖分问题谈起雷环中- 结果提交类问题林希德- 求最大重复子串刘才良- 平面图在信息学中的应用刘一鸣- 一类搜索的优化思想——数据有序化陆可昱- 长方体体积并饶向荣- 病毒的DNA——剖析一道字符匹配问题解析过程邵烜程- 数学思想助你一臂之力王知昆- 浅谈用极大化思想解决最大子矩形问题伍昱- 由对称性解2-SAT问题项荣璟- 充分利用问题性质——例析动态规划的“个性化”优化许智磊- 浅谈补集转化思想在统计问题中的应用张宁- 猜数问题的研究张云亮- 论对算法的选择周源- 浅析“最小表示法”思想在字符串循环同构问题中的应用2004年何林- 信息学中守恒法的应用胡伟栋- 减少冗余与算法优化金恺- 极限法——解决几何最优化问题的捷径李锐喆- 细节——不可忽视的要素鬲融- 浅谈特殊穷举思想的应用周源- 浅谈数形结合思想在信息学竞赛中的应用朱晨光- 优化,再优化!肖天- “分层图思想”及其在信息学竞赛中的应用汪汀- 最小生成树问题的拓展吴景岳- 最小生成树算法及其应用栗师- 转化目标在解题中的应用薛矛- 解决动态统计问题的两把利刃黄源河- 浅谈图论模型的建立与应用楼天城- 匹配算法在搜索问题中的应用贝小辉- 浅析树的划分问题林涛- 线段树的应用杨思雨- 伸展树的基本操作与应用许智磊- 后缀数组朱泽园- 多串匹配算法及其启示韩文弢- 论C++语言在信息学竞赛中的应用2005年龙凡- 序的应用魏冉- 浅谈“跳跃表”的相关操作及其应用任恺- 图论的基本思想及方法杨俊- 二分策略在信息学竞赛中的应用张伟达- 用改进算法的思想解决规模维数增大的问题黄刚- 数据结构的联合杨弋- 从“小H的小屋”的解法谈算法的优化朱晨光- 浅析倍增思想在信息学竞赛中的应用李羽修- Hash函数的设计优化王俊- 浅析二分图匹配在信息学竞赛中的应用唐文斌- 正难则反——浅谈逆向思维在解题中的应用黄源河- 左偏树的特点及其应用钱自强- 遗传算法应用的分析与研究杨思雨- 浅谈“黄金分割”和信息学的联系潘震皓- 置换群快速幂运算研究与探讨胡伟栋- 非完美算法在信息学竞赛中的应用何林- 数据关系的简化汪汀- 参数搜索的应用周源- 浅谈信息学竞赛中的“压缩法”朱泽园- 回到起点---- 一种突破性思维。
国家集训队2004论文集 朱晨光

优化,再优化!——从《鹰蛋》一题浅析对动态规划算法的优化安徽省芜湖市第一中学朱晨光目录Ø关键字 (2)Ø摘要 (2)Ø正文 (2)n引言 (2)n问题 (2)n分析 (3)u算法一 (3)u算法二 (4)u算法三 (4)u算法四 (6)u小结 (7)u算法五 (7)Ø总结 (10)Ø结束语 (11)关键字优化动态规划模型摘要本文就Ural 1223 《鹰蛋》这道题目介绍了五种性能各异的算法,并在此基础上总结了优化动态规划算法的本质思想及其一般方法。
全文可以分为四个部分。
第一部分引言,阐明优化动态规划算法的重要性;第二部分给出本文讨论的题目;第三部分详细讨论这道题目五种不同的动态规划算法,并阐述其中的优化思想;第四部分总结全文,再次说明对于动态规划进行优化的重要性,并分析优化动态规划的本质思想与一般方法。
正文引言在当今的信息学竞赛中,动态规划可以说是一种十分常用的算法。
它以其高效性受到大家的青睐。
然而,动态规划算法有时也会遇到时间复杂度过高的问题。
因此,要想真正用好用活动态规划,对于它的优化方法也是一定要掌握的。
优化动态规划的方法有许多,例如四边形不等式、斜率优化等。
但是这些方法只能对某些特定的动态规划算法进行优化,尚不具有普遍的意义。
本文将就《鹰蛋》这道题目做较为深入的分析,并从中探讨优化动态规划的本质思想与一般方法。
问题有一堆共M个鹰蛋,一位教授想研究这些鹰蛋的坚硬度E。
他是通过不断从一幢N层的楼上向下扔鹰蛋来确定E的。
当鹰蛋从第E层楼及以下楼层落下时是不会碎的,但从第(E+1)层楼及以上楼层向下落时会摔碎。
如果鹰蛋未摔碎,还可以继续使用;但如果鹰蛋全碎了却仍未确定E,这显然是一个失败的实验。
教授希望实验是成功的。
例如:若鹰蛋从第1层楼落下即摔碎,E=0;若鹰蛋从第N层楼落下仍未碎,E=N。
这里假设所有的鹰蛋都具有相同的坚硬度。
给定鹰蛋个数M与楼层数N。
【OI 国家集训队】对一类动态规划问题的研究

12 人
12
f2[1][3]
34
f1[1][3]
34 人
问题一
• 考虑f1[1][3],当前处于位置1。 • 可以由f1[2][3]沿着2->1走来。再
射落1号彩蛋。
12 人 12
人
34 34
问题一
• 考虑f1[1][3],当前处于位置1。 • 可以由f1[2][3]沿着2->1走来。再
射落1号彩蛋。 • 可以由f2[2][3]沿着3->1走来。再
小结
• 当前射击的费用受到之前决策的影响。 • 如果新增状态t表示过去决策的影响,状态数将会无法承受。 • 改变“时间观”,从过去考虑当前,即从当前考虑未来,把当前决
策对未来的影响算作当前决策费用,计算到当前状态。
将费用提前计算
当前决策 对未来“行动”
的费用影响 只与当前决策有关
将未来的费用 的一部分视作 当前决策费用 计算在当前的状态中
j 1
问题二
• 考虑如何计算R(1)。
• R(1)=R2*k+R3*k+C1 • =C1+C2*k+C3*k+R4*k2+R5*k2+R6*k2 • x对1的贡献为Cx*kd(x,1)。
1
×k
2
×k
×k
×k 3 ×k
4
5
6
×k
CX
问题二
• R(1)=
n
cik d (i,1)
j 1
• 每次修改都应该把点的后继直接设置为1。
2
3
4
点2的距离变成3
问题二
• 再加一维状态d,假设在未来的决策导致点i 的距离为d。
从“k倍动态减法游戏”出发探究一类组合游戏问题

这是因为若正整数 m0、n0 使得 NP(m0,n0)=1,则对于任意 n>n0,m=m0 都有 NP(m,n)=1。这是因为,状态(m0,n0)时玩家可以完成的操作,在状态(m,n)也允许 操作(这利用了 n>n0) ,且到达相同的状态(这利用 m=m0)。
NOI2009 冬令营论文
从“k 倍动态减法游戏”出发探究一类组合游戏问题
摘
要
组合游戏是指,信息完全轮流操作的双人游戏。本文将从一个游戏——k 倍 动态减法游戏(k-based dynamic subtraction game)的解答出发,讨论游戏中的一 个重要分支——组合游戏, 并探讨解决这一类的问题的高效方法。探索的过程力 求兼顾游戏论中的普遍真理以及问题的独特性质。 作为一篇信息学的论文, 本文将着重讨论与组合游戏有关的相关算法和这些 算法时间复杂性分析, 而不是游戏论中的一些经典的理论、典型的游戏实例或者 一些存在性的证明。 “k 倍动态减法游戏”在 k 为一般正实数的情况,在 2002 年的国家集训队 论文中已经给出 O(S3)的算法,本文将在第 4.1 节给出一个优化到 O(S)的算法。 “Nim 积”运算是利用 SG 函数解决游戏论问题的必要工具之一。本文将在 第 4.4.5 节给出一个 O(log2x)的计算“Nim 积”的算法。 2008 年的 BOI(Baltic Olympiad in Informatics)中 knight 一题就是游戏论问 题,官方解答给出了 O(n3)的算法,但没有给出算法时间复杂度的证明。本文在 第 5 章提出了对这个 O(n3)的上界的质疑,并举出了质疑的确实依据,举出反例 证明了官方解答时间复杂度估计的错误之处。 同时, 本文经过对算法进一步优化, 得到了一个 O(n2)的算法。 上面这些内容都是原创的独立研究成果。
国家集训队2008论文集浅谈信息学竞赛中的区

浅谈信息学竞赛中的区间问题华东师大二附中周小博【摘要】本文对一些常用的区间问题模型做了简单介绍,包括一些算法及其正确性的证明,并从国际、国内的信息学竞赛与大学生程序设计竞赛中选了近10道相关例题,进行简要分析。
【关键字】区间模型转化贪心动态规划优化在信息学竞赛中,有很多问题最终都能转化为区间问题:例如从若干个区间中选出一些满足一定条件的区间、将各个区间分配到一些资源中、或者将一些区间以某种顺序放置等。
这类问题变化繁多,解法各异,需要用到贪心、动态规划等算法,并可以用一些数据结构优化算法。
本文将从几个方面对区间问题做一个简单的介绍,给出一些算法及其正确性的证明,具体分如下几个方面进行讨论:1.最大区间调度问题2.多个资源的调度问题3.有最终期限的区间调度问题4.最小区间覆盖问题5.带权区间调度、覆盖问题6.区间和点的有关问题我们将对上述每个问题都给出基本模型、算法、证明及其实现,并从ACM-ICPC、CEOI、CTSC等比赛中选出了近10道相关例题,进行简要分析,有的例题还给出了各种不同的算法及其时间效率的分析。
本文中所讨论的问题主要由两个部分组成,一部分为近几年来各类竞赛题的归纳总结,另一部分来自于参考文献。
数轴上有n 个区间,选出最多的区间,使得这些区间不互相重叠。
算法:将所有区间按右端点坐标从小到大排序,顺序处理每个区间。
如果它与当前已选的所有区间都没有重叠,则选择该区间,否则不选。
证明:显然,该算法最后选出的区间不互相重叠,下面证明所选出区间的数量是最多的。
设i f 为该算法所接受的第i 个区间的右端点坐标,i g 为某最优解中的第i 个区间的右端点坐标。
命题1.1 当1≥i 时,该算法所接受的第i 个区间的右端点坐标i f ≤某最优解中的第i 个区间的右端点坐标i g 。
该命题可以运用数学归纳法来证明。
对于1=i ,命题显然为真,因为算法第一个选择的区间拥有最小右端点坐标。
令1>i ,假定论断对1-i 为真,即11--≤i i g f 。
国家集训队2009论文集浅析字母树在信息学竞

浅析字母树在信息学竞赛中的应用浙江省绍兴市第一中学董华星二〇〇八年十二月目录摘要 (3)关键字 (3)前言 (3)正文 (4)1.预备知识 (4)1.1.试题分析 (4)1.2.结构简介 (5)2.字母树在串的快速检索中的应用 (7)3.字母树在“串”排序方面的应用 (9)4.字母树在减少无效转移方面的应用 (11)5.字母树在最长公共前缀问题的应用 (13)5.1.串的最长公共前缀问题 (13)5.2.数字相关的公共前缀问题 (14)6.拓展思考 (16)6.1.字母树应用的扩展 (16)6.2.字母树的局限 (16)7.总结 (17)参考文献 (17)附录 (18)1.单词查找树 (18)2.感谢名单 (20)感谢 (21)字母树(又叫单词查找树、Trie树,Trie Tree),构造简单,并能很好地处理和“串”相关的检索(Retrieval)问题。
本文从此着手,归纳了笔者的学习经验,详细论述了其在快速查找、排序、优化转移等方面的常见应用,并对其扩展做了提示。
关键字字母树快速检索“串”排序无效转移最长公共前缀问题前言当我们走进图书馆的阅览室寻找书时,会不Array由自主地根据书架上的分类标签寻找自己所喜好的书籍;当打开电脑中的资源管理器时,我们会看到一层一层的目录结构。
它们的存在,方便了我们生活中的一个重要的问题——检索。
在信息学竞赛(Olympiad in Informatics,简称OI)的学习过程中,我们也经常会遇到关于“检索”的问题。
而通常采用的不借助任何数据结构(Data Structure)的的枚举方法,虽然简单易写,但往往存在着效率低下的弊端。
那我们如何才能图一资源管理器通过简单的途径提高算法中的检索效率?接下来笔者将浅析并推荐一种数据结构——字母树,借助它我们便能够很好地处理与“串”相关的检索问题。
1.预备知识为了更深入地让读者了解这种数据结构,本文首先将对其进行一番具体介绍并说明其构造。
国家集训队2004论文集 栗师

IOI2004 国家集训队论文 栗师
பைடு நூலகம்
21 41 4 -2 2 -2 输出样例 TAK NIE
2.1 确定算法模型。
看到题目,最 容易想 到的算法是广 搜。从当前已知能 够到达 的格子 出发 , 按照马的走法,扩展出另外一些能到达的格子,一直扩展下去,最后判断是不 是扩展完了所有的棋盘。 很快会 发现这 种做法是不行 的,棋盘上 格子的个数是无限的,不能 判断 能 够到达所有的格子。但这个困难马上就有了解决的办法,显然只要判断超级马 是否能到达开始点的 4 个相邻格。因为如果能够到达这 4 个格子,那么必然能 够到达棋盘上的任意一个位置。 问题解决了没 有?没 有。虽然最终 目标 只需要判断四 个格子 ,但是,它 在 走到这 4 个格子的过程中经过的点可能会有很多个。更糟糕的是,当问题无解 时,无法进行正确的判断,最后实现算法时造成死机。 如果把 无限的 棋盘变 成相当大的有界棋盘,看 它在这个有界 棋盘上能否 到 达这 4 个格子。但这仍然是无用功,这个有界棋盘会有很大,这样时间效率很 低,算法也缺乏证明。 尝试各种图论算法、 动态规划、贪心等 ,最后 都以意 料之中的结果—— 失 败而告终。 要得到高效的算法,似乎只有一条出路:数学思想。 要用数 学思想 解题, 先要建立数学 模型 。以超级马最 开始的 格子为 原点 建 立平面坐标系。然后把马的一种动作用一个平面向量 Pi 来表示,Pi=(xi,yi)。那 么,我们要判断,对于任意的 x,y,是否都存在一组 c1,c2,c3……cn(ci>=0,1≤i≤n), 使得 ∑ ci Pi = ( x, y ) 。
i=2 k k
所 以 存 在 整 数 序 列 d2,d3……dk 使
∑d g
国家集训队论文:浅谈信息学竞赛中的“0”和“1”

01
树状数组中 的每一个元 素的编号变 成了二制
02
编码,再通过 这些二进制编 码末尾的0的 个数来
03
决定存储什 么信息,假 设节点编号 为x,那么这
04
个节点存储 数据的区间 为2k(其中 k为x二进制
05
末尾0 的个 数)个元素 。
06
又由于每个十进制 数转化成二进制位 的话,1的个数最 多只有O(logN)个, 所以,复杂度只有 O(logN)。
2k:X and –X
具体操作:
1 插入或删除: While
2 查询: While x>0
x<=max do
do
Begin
Begin
C[x]:=c[x]+ delta;
Sum:=sum+ c[x];
X:=x+(x and –x);
X:=x-(x and –x);
End;
End;
单击添加标题
Add a title
•模型转化 Add a title
•01二叉树
例题一: Matrix
有一个M*N的矩阵,每一 个格子中的数是1或0,初 始时为0。有两种操作:
修改一个子矩阵, 将子矩阵中的数字 全部01取反。
查询第x行第y列的 格子中的数字。
01
02
如果给定的是一 个长度为N的一 排格子。
从而达到转十为二,事半功倍的效果!
欢迎提问~
Thank You!
每次询问的时候只 需计算出Sumx就可 以 求出第x个格子被修 改过几次。
查询
01 寻根溯源
02
用上面的方法看 看能否解决原来 的问题。
推而广之
怎么办呢???
2009年国家集训队几道试题的另解

2009年国家集训队几道试题的另解
单墫
【期刊名称】《中等数学》
【年(卷),期】2010(000)008
【摘要】@@ 每年华东师范大学出版社都要出一本<走向IMO*数学奥林匹克试题集锦>,其中收集了当年国家集训队的测试题与选拔考试题.虽然这些题较难,但解法值得讨论.
【总页数】5页(P10-14)
【作者】单墫
【作者单位】南京师范大学数学系,210097
【正文语种】中文
【中图分类】G424.79
【相关文献】
1.一道2009年Serbia国家集训队试题的推广 [J], 朱纯刚
2.一道国家集训队测试题的另解及思考 [J], 朱天明
3.另解三道中国国家集训队选拔考试题 [J], 卢梓潼
4.2009年中国国家集训队几道试题另解 [J], 邹明
5.另解一道中国国家集训队选拔考试题 [J], 万喜人
因版权原因,仅展示原文概要,查看原文内容请购买。
国家集训队2004论文集 何林

信息学中的守恒法【摘要】本文提出和总结了“守恒法”,以及它在信息学竞赛中的一些应用。
守恒的本质是寻找变化中的不变量。
守恒法能帮助我们跳过、避开纷繁复杂的细节,直接看透问题的本质。
【关键字】守恒法不变量【正文】一、引言现实生活和实际问题是纷繁复杂的。
问题1两个质量相等的小球,速度分别为5m/s, 4m/s,他们相向运动,完全弹性碰撞之后速度分别变成多少?问题210g C和10g O2在密闭容器中反应一个小时。
最后的总质量是多少?问题1我们大概耳熟能详:动量守恒、动能守恒,两个方程就能解出速度。
实际上小球碰撞的过程是复杂的,究竟两对力如何互相作用、互相影响、如何做功,思考起来是非常的复杂。
如果忽略它们变化的具体过程,我们很容易发现“动量”和“动能”这两个变化中的不变量,抓住不变量,就能跳过繁琐的细节,直达目标。
问题2也是类似的题目。
C和O2的反应同样是复杂的。
在不同的局部,条件不同,可能产生CO,也可能产生CO2;CO2和C还可能重新转化为CO……事实上不可能有人列出三个化学方程去分析——在一个密闭容器中,无论怎么变,总质量必然不变——也就是质量守恒。
抓住这一点,我们在1秒钟内就能说出答案:20g。
以上两个例子生动的说明守恒的作用。
现实生活和实际问题如此纷繁复杂,条件和变化如此之多,以至于我们考虑稍不周密就可能全盘皆错;抑或限于问题本身的复杂性,根本无法分析。
但是如果能找到一两个守恒量——也就是变化中的不变量,那么问题就能大大的简化了。
忽略细节,抓住主要矛盾,这就是守恒法。
二、一个简单的例子例题1有一个数列a1, a2, a3, ……, a n。
每次可以从中任意选3个相邻的数a i-1, a i, a i+1,进行如下操作(此操作称为“对a i进行操作”)(a i-1, a i, a i+1)à(a i-1+a i, -a i, a i+a i+1)给定初始和目标序列。
问:能不能通过以上操作,将初始序列转换到目标序列。
08年数模国赛优秀论文

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话): 20001001 所属学校(请填写完整的全名):国防科学技术大学参赛队员(打印并签名) :1. 许睿2. 杨小柱3. 刘帅指导教师或指导教师组负责人(打印并签名):日期: 2008 年 9 月 21 日 赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):国防科技大学:许睿、杨小柱、刘帅数码相机定位摘要相机系统标定是精密光学测量的基础,为了确定相机的相对位置,我们必须通过拍摄图像并提取图像上的特征点,利用已知靶标的两幅图像的信息确定交会方程,从而求解出两部相机的相对参数。
在解出两部相机的相对参数后就可以进行相关的测量。
本文在不考虑相机镜头畸变的情况下,建立了相机的针孔成像模型。
同时为了方便建模建立了MATLAB像坐标系、像坐标系、第一相机坐标系、第二相机坐标系。
然后我们通过观察图像发现图像清晰度很好,于是选择合适的阈值将图像进行二值化处理。
在二值化图像的基础上我们采取了重心法和切线法两种方法来求解圆心的像坐标,重心法是通过像求取像的灰度重心从而得到圆心的像坐标,而切线法是通过求取圆的外公切线之像的方程,从而确定圆的外切正四边形的顶点,再根据正四边形的对角线为圆心而求得圆心的像坐标,比较这两种方法求解的结果发现其相差基本在1个像素单位以内。
国家集训队2009论文集数学归纳法与解题之道

数学归纳法与解题之道山西省实验中学张昆玮教练:唐文斌胡伟栋2008年12月16日引言我们在学习算法的时候,总会有这样那样的疑惑:如此之多的浑然天成的算法,是怎样想到的?这些算法巧诚巧矣,可它们为什么是正确的呢?其实林林总总的算法背后,无不隐藏着真正的解题之道。
解题之道博大精深,该从何谈起?上面的疑惑又该如何解决?两千五百多年前,著名的哲学家和思想家老子对道之本质参透得可谓淋漓尽致。
引文中他给我们的答案是:参悟解题之道,从数学归纳法开始。
摘要本文简述了数学归纳法的相关理论,并结合作者的解题实践,以一些经典问题与竞赛题目为例,从证明算法正确性、构造性算法、与算法优化的关系等几个方面介绍了数学归纳法在信息学竞赛中的应用,讨论了数学归纳法的实用性与适用范围,以及归纳式算法设计相关的其他一些延伸与拓展。
目录●引言 (1)●摘要 (1)●目录 (2)●关于数学归纳法 (3)简短的回顾 (3)基本的定理、概念与方法 (3)是总结更是探索 (5)●在证明算法正确性上的应用 (6)贪心算法 (6)其他算法 (7)●在构造性算法中的应用 (8)数据结构的恢复性构造 (9)策略与解决方案的构造 (12)●数学归纳法与算法优化 (14)巧妙选择归纳对象 (14)力求完善归纳基础 (16)慎重选择归纳方向 (16)适当加强归纳假设 (17)●启发作用与美学价值 (19)●问题与缺陷 (19)理论上是否欠完备 (20)应用上是否较繁琐 (20)不适用的问题 (20)●后记 (21)●题目来源 (21)关于数学归纳法简短的回顾数学归纳法原理的发现可以追溯到公元1494年意大利数学家Francesco Maurolico 的著作Arithmeticorum libri duo 。
作为皮亚诺公理系统的应用,它自诞生之日就受到广泛关注。
同时,作为应对与正整数相关的问题的一种通用而简洁的处理方法,数学归纳法在许多算术、逻辑问题的解决中都占有核心地位。
NOIP历届习题(2000-2008)

2000年全国青少年信息学(计算机)奥林匹克分区联赛复赛试题(高中组竞赛用时:3小时)题一进制转换问题描述我们可以用这样的方式来表示一个十进制数:将每个阿拉伯数字乘以一个以该数字所处位置的(值减1)为指数,以10为底数的幂之和的形式。
例如:123可表示为1*102+2*101+3*100这样的形式。
与之相似的,对二进制数来说,也可表示成每个二进制数码乘以一个以该数字所处位置的(值-1)为指数,以2为底数的幂之和的形式。
一般说来,任何一个正整数R或一个负整数-R都可以被选来作为一个数制系统的基数。
如果是以R或-R为基数,则需要用到的数码为0,1,....R-1。
例如,当R=7时,所需用到的数码是0,1,2,3,4,5和6,这与其是R或-R无关。
如果作为基数的数绝对值超过10,则为了表示这些数码,通常使用英文字母来表示那些大于9的数码。
例如对16进制数来说,用A表示10,用B表示11,用C表示12,用D表示13,用E表示14,用F表示15。
在负进制数中是用-R作为基数,例如-15(十进制)相当于110001(-2进制),并且它可以被表示为2的幂级数的和数:110001=1*(-2)5+1*(-2)4+0*(-2)3+0*(-2)2+0*(-2)1+1*(-2)0问题求解设计一个程序,读入一个十进制数和一个负进制数的基数, 并将此十进制数转换为此负进制下的数:-R∈{-2,-3,-4,...,-20}输入输入的每行有两个输入数据。
第一个是十进制数N(-32768<=N<=32767);第二个是负进制数的基数-R。
输出结果显示在屏幕上,相对于输入,应输出此负进制数及其基数,若此基数超过10,则参照16进制的方式处理。
样例输入30000-2-20000-228800-16-25000-16输出30000=11011010101110000(base-2)-20000=1111011000100000(base-2)28000=19180(base-16)-25000=7FB8(base-16)题二乘积最大问题描述今年是国际数学联盟确定的“2000——世界数学年”,又恰逢我国著名数学家华罗庚先生诞辰90周年。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOI国家集训队论文分类(至2008)摘抄自C博客组合数学计数与统计2001 - 符文杰:《Polya原理及其应用》2003 -许智磊:《浅谈补集转化思想在统计问题中的应用》2007 -周冬:《生成树的计数及其应用》2008 - 陈瑜希《Polya计数法的应用》数位问题2009 -高逸涵《数位计数问题解法研究》2009 -刘聪《浅谈数位类统计问题》动态统计2004 -薛矛:《解决动态统计问题的两把利刃》2007 -余江伟:《如何解决动态统计问题》博弈2002 -张一飞:《由感性认识到理性认识一一透析一类搏弈游戏的解答过程》2007 -王晓珂:《解析一类组合游戏》2009 -曹钦翔《从“k倍动态减法游戏”出发探究一类组合游戏问题》2009 -方展鹏《浅谈如何解决不平等博弈问题》2009 -贾志豪《组合游戏略述一一浅谈SG游戏的若干拓展及变形》母函数2009 -毛杰明《母函数的性质及应用》拟阵2007 -刘雨辰:《对拟阵的初步研究》线性规划2007 -李宇骞:《浅谈信息学竞赛中的线性规划一一简洁高效的单纯形法实现与应用》置换群2005 -潘震皓:《置换群快速幕运算研究与探讨》问答交互2003 -高正宇:《答案只有一个一一浅谈问答式交互问题》猜数问题2003 -张宁:《猜数问题的研究:< 聪明的学生> 一题的推广》2006 -龙凡:《一类猜数问题的研究》数据结构数据结构2005 -何林:《数据关系的简化》2006 -朱辰光:《基本数据结构在信息学竞赛中的应用》2007 -何森:《浅谈数据的合理组织》2008 -曹钦翔《数据结构的提炼与压缩》结构联合2001 -高寒蕊:《从圆桌问题谈数据结构的综合运用》2005 -黄刚:《数据结构的联合》块状链表2005 -蒋炎岩:《数据结构的联合——块状链表》2008 -苏煜《对块状链表的一点研究》动态树2006 -陈首元:《维护森林连通性——动态树》2007 -袁昕颢:《动态树及其应用》左偏树2005 -黄源河:《左偏树的特点及其应用》跳表2005 -魏冉:《让算法的效率跳起来”——浅谈跳跃表”的相关操作及其应用》2009 -李骥扬《线段跳表——跳表的一个拓展》SBT2007 - 陈启峰:《Size Bala nee Tree 》线段树2004 -林涛:《线段树的应用》单调队列2006 -汤泽:《浅析队列在一类单调性问题中的应用》哈希表2005 - 李羽修:《Hash函数的设计优化》2007 - 杨弋:《Hash在信息学竞赛中的一类应用》Splay2004 -杨思雨:《伸展树的基本操作与应用》图论2005 - 任恺:《图论的基本思想及方法》模型建立2004 -黄源河:《浅谈图论模型的建立与应用》2004 -肖天:《分层图思想”及其在信息学竞赛中的应用》网络流2001 -江鹏:《从一道题目的解法试谈网络流的构造与算法》2002 -金恺:《浅谈网络流算法的应用》2007 -胡伯涛:《最小割模型在信息学竞赛中的应用》2007 -王欣上:《浅谈基于分层思想的网络流算法》2008 -周冬《两极相通一一浅析最大一最小定理在信息学竞赛中的应用》最短路2006 -余远铭:《最短路算法及其应用》2008 -吕子鉷《浅谈最短径路问题中的分层思想》2009 -姜碧野《SPFA算法的优化及应用》欧拉路2007 -仇荣琦:《欧拉回路性质与应用探究》差分约束系统2006 -冯威:《数与图的完美结合一一浅析差分约束系统》平面图2003 -刘才良:《平面图在信息学中的应用》2007 - 古楠:《平面嵌入》2-SAT2003 - 伍昱:《由对称性解2-SAT问题》最小生成树2004 -吴景岳:《最小生成树算法及其应用》2004 -汪汀:《最小生成树问题的拓展》二分图2005 -王俊:《浅析二分图匹配在信息学竞赛中的应用》Voronoi 图2006 - 王栋:《浅析平面Voronoi图的构造及应用》偶图2002 -孙方成:《偶图的算法及应用》树2002 -周文超:《树结构在程序设计中的运用》2005 -栗师:《树的乐园——一些与树有关的题目》路径问题2009 -漆子超《分治算法在树的路径问题中的应用》最近公共祖先2007 - 郭华阳:《RMQ与LCA问题》划分问题2004 -贝小辉:《浅析树的划分问题》数论欧几里得算法2009 -金斌《欧几里得算法的应用》同余方程2003 -姜尚仆:《模线性方程的应用一一用数论方法解决整数问题》搜索搜索2001 -骆骥:《由汽车问题”浅谈深度搜索的一个方面一一搜索对象与策略的重要性》2002 -王知昆:《搜索顺序的选择》2005 -汪汀:《参数搜索的应用》启发式2009 -周而进《浅谈估价函数在信息学竞赛中的应用》优化2003 -金恺:《探寻深度优先搜索中的优化技巧一一从正方形剖分问题谈起》2003 -刘一鸣:《一类搜索的优化思想——数据有序化》2006 -黄晓愉:《深度优先搜索问题的优化技巧》背包问题2009 -徐持衡《浅谈几类背包题》匹配2004 -楼天城:《匹配算法在搜索问题中的巧用》概率概率2009 -梅诗珂《信息学竞赛中概率问题求解初探》2009 -汤可因《浅析竞赛中一类数学期望问题的解决方法》字符串字符串2003 -周源:《浅析最小表示法”思想在字符串循环同构问题中的应用》多串匹配2004 -朱泽园:《多串匹配算法及其启示》2006 - 王赟:《Trie图的构建、活用与改进》2009 -董华星《浅析字母树在信息学竞赛中的应用》后缀数组2004 -许智磊:《后缀数组》2009 -罗穗骞《后缀数组一一处理字符串的有力工具》字符串匹配2003 -饶向荣:《病毒的DNA --------------剖析一道字符匹配问题解析过程》2003 -林希德:《求最大重复子串》动态规划动态规划2001 -俞玮:《基本动态规划问题的扩展》2006 -黄劲松:《贪婪的动态规划》2009 -徐源盛《对一类动态规划问题的研究》状态压缩2008 -陈丹琦《基于连通性状态压缩的动态规划问题》状态设计2008 -刘弈《浅谈信息学中状态的合理设计与应用》树形DP2007 -陈瑜希:《多角度思考创造性思维一一运用树型动态规划解题的思路和方法探析》优化2001 -毛子青:《动态规划算法的优化技巧》2003 -项荣璟:《充分利用问题性质——例析动态规划的个性化”优化》2004 -朱晨光:《优化,再优化!一一从《鹰蛋》一题浅析对动态规划算法的优化》2007 -杨哲:《凸完全单调性的加强与应用》立体几何2003 - 陆可昱:《长方体体积并》2008 -高亦陶《从立体几何问题看降低编程复杂度》计算几何思想2004 -金恺:《极限法一一解决几何最优化问题的捷径》2008 -程芃祺《计算几何中的二分思想》2008 -顾研《浅谈随机化思想在几何问题中的应用》圆2007 -高逸涵:《与圆有关的离散化》半平面交2002 -李澎煦:《半平面交的算法及其应用》2006 -朱泽园:《半平面交的新算法及其实用价值》矩阵矩阵2008 -俞华程《矩阵乘法在信息学中的应用》高斯消元2002 -何江舟:《用高斯消元法解线性方程组》数学方法数学思想2002 -何林:《猜想及其应用》2003 -邵烜程:《数学思想助你一臂之力》数学归纳法2009 -张昆玮《数学归纳法与解题之道》多项式2002 - 张家琳:《多项式乘法》数形结合2004 -周源:《浅谈数形结合思想在信息学竞赛中的应用》黄金分割2005 -杨思雨:《美,无处不在一一浅谈黄金分割”和信息学的联系》其他算法遗传算法2002 -张宁:《遗传算法的特点及其应用》2005 -钱自强:《关于遗传算法应用的分析与研究》信息论2003 -侯启明:《信息论在信息学竞赛中的简单应用》染色与构造2002 -杨旻旻:《构造法——解题的最短路径》2003 -方奇:《染色法和构造法在棋盘上的应用》一类问题区间2008 -周小博《浅谈信息学竞赛中的区间问题》序2005 - 龙凡:《序的应用》系2006 -汪晔:《信息学中的参考系与坐标系》物理问题2008 -方戈《浅析信息学竞赛中一类与物理有关的问题》编码与译码2008 -周梦宇《码之道一浅谈信息学竞赛中的编码与译码问题》对策冋题2002 -骆骥:《浅析解对策问题”的两种思路》优化算法优化2002 -孙林春:《让我们做得更好一一从解法谈程序优化》2004 -胡伟栋:《减少冗余与算法优化》2005 -杨弋:《从< 小H的小屋> 的解法谈算法的优化》2006 -贾由:《由图论算法浅析算法优化》程序优化2006 -周以苏:《论反汇编在时间常数优化中的应用》2009 -骆可强《论程序底层优化的一些方法与技巧》语言C++2004 -韩文弢:《论C++语言在信息学竞赛中的应用》策略策略2004 -李锐詰:《细节——不可忽视的要素》2005 -朱泽园:《回到起点一一一种突破性思维》2006 -陈启峰:《约制、放宽”方法在解题中的应用》2006 - 李天翼:《从特殊情况考虑》2007 - 陈雪:《问题中的变与不变》2008 -肖汉骏《例谈信息学竞赛分析中的深”与广” 倍增2005 -朱晨光:《浅析倍增思想在信息学竞赛中的应用》二分2002 - 李睿:《二分法与统计问题》2002 - 许智磊:《二分,再二分!——从Mobiles(IOI2001) 2005 -杨俊:《二分策略在信息学竞赛中的应用》调整2006 -唐文斌:《调整”思想在信息学中的应用》随机化2007 -刘家骅:《浅谈随机化在信息学竞赛中的应用》非完美算法2005 -胡伟栋:《浅析非完美算法在信息学竞赛中的应用》2008 -任一恒《非完美算法初探》提交答案题2003 -雷环中:《结果提交类问题》守恒思想2004 -何林:《信息学中守恒法的应用》极限法2003 -王知昆:《浅谈用极大化思想解决最大子矩形问题》贪心2008 -高逸涵《部分贪心思想在信息学竞赛中的应用》压缩法2005 -周源:《压去冗余缩得精华一一浅谈信息学竞赛中的逆向思维2005 -唐文斌:《正难则反 ------ 浅谈逆向思维在解题中的应用》穷举2004 -鬲融:《浅谈特殊穷举思想的应用》题看多重二分》压缩法”》目标转换2002 -戴德承:《退一步海阔天空一一目标转化思想”的若干应用》2004 -栗师:《转化目标在解题中的应用》类比2006 -周戈林:《浅谈类比思想》分割与合并2006 -俞鑫:《棋盘中的棋盘 - —浅谈棋盘的分割思想》2007 -杨沐:《浅析信息学中的分”与合”平衡思想2008 -郑暾《平衡规划一一浅析- 一类平衡思想的应用》。
