三角函数诱导公式练习题--答案

合集下载

三角函数诱导公式

三角函数诱导公式1．对于诱导公式中的角α，下列说法正确的是（）A ．α一定是锐角B ．0≤α＜2πC ．α一定是正角D ．α是使公式有意义的任意角2．已知sin()0πθ+<，cos()0θπ->，则下列不等式关系中必定成立的是（）A ．sin θ＜0，cos θ＞0B ．sin θ＞0，cos θ＜0C ．sin θ＞0，cos θ＞0D ．sin θ＜0，cos θ＜03．sin300的值为（）A ．12-B ．12C ．4．若1sin 3A =，则sin(6)A π-的值为（） A ．13B ．13-C ．5．若1sin()2πα+=-，则cos α的值为（） A ．12± B ．12 CD．±6．在直角坐标系，若α与β的终边关于y 轴对称，则下列等式恒成立的是（）A ．sin()sin απβ+=B ．sin()sin απβ-=C ．sin(2)sin παβ-=-D ．sin()sin αβ-= 7．sin34π²cos 625π²tan 45π的值是（） A ．－43 B ．43 C ．－43 D ．43 8．)2cos()2sin(21++-ππ等于（） A ．sin2－cos2 B ．cos2－sin2C ．±（sin2－cos2）D ．sin2+cos2 9．tan2010°的值为．10．已知53sin -=α，且α是第四象限的角，则)2cos(απ-的值是． 11．sin315°―cos135°+2sin570°的值是________。

12．已知cos 2πϕ⎛⎫+=⎪⎝⎭，则||2πϕ<，则tan ϕ=________。

13. 若22tan(4)cos()sin (3)152tan(3)cos 2αππααπππαα-⋅+⋅+=-⎛⎫+⋅+ ⎪⎝⎭，求tan α的值。

三角函数的诱导公式练习题含答案

三角函数的诱导公式练习题（1）1. tan225∘的值为()A.1B.√22C.−√22D.−12. 已知3sin(θ+π2)+sin(θ+π)=0，θ∈(−π,0)，则sinθ=( )A.−3√1010B.−√1010C.3√1010D.√10103. 若sin(π3−α)=−13，则cos(α+π6)=( )A.−13B.13C.−2√23D.2√234. 已知sin(α+π4)=35，则cos(π4−α)=( )A.4 5B.−45C.−35D.355. 已知α是第二象限角，若sin(π2−α)=−13，则sinα＝（）A.−2√23B.−13C.13D.2√236. 已知函数f(x)={1x,x0,log2x−3,x0,则f(−12)⋅f(16)=()A.3B.1C.−1D.−27. （5分）已知x∈R，则下列等式恒成立的是( )A.sin(−x)=sin xB.sin(3π2−x)=cos xC.cos(π2+x)=−sin x D.cos(x−π)=−cos x8. sin 14π3−cos (−25π4)=________．9. 已知sin α=45，则cos (α+π2)=________． 10. cos 85∘+sin 25∘cos 30∘cos 25∘等于________11. 已知cos θ=−35，则sin (θ+π2)=________．12. 已知cos (π−α)=35，α∈(0,π)，则tan α=________．13. 已知f (α)=sin (α−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)，其中α≠12kπ(k ∈Z )．(1)化简f (α)；(2)若f (π2+β)=−√33，且角β为第四象限角，求sin (2β+π6)的值．14. 已知α为第二象限角，且sin α+cos α=−713，分别求tan α，sin 2α−2sin αcos α的值．15. 如图，四边形ABCD 中，△ABC 是等腰直角三角形，其中AC ⊥BC ，AB =√6，又CD//AB ，cos ∠ABD =√63．(1)求BD 的长；(2)求△ACD的面积．参考答案与试题解析三角函数的诱导公式练习题（1）一、选择题（本题共计 6 小题，每题 5 分，共计30分）1.【答案】A【考点】运用诱导公式化简求值【解析】原式中的角度变形后，利用诱导公式及特殊角的三角函数值计算即可得到结果．【解答】解：原式=tan(180∘+45∘)=tan45∘=1，故选A．2.【答案】A【考点】同角三角函数间的基本关系诱导公式【解析】利用诱导公式，同角三角函数基本关系式即可求解．【解答】解：∵sin(θ+π2)=sinθcosπ2+cosθsinπ2=cosθ，sin(θ+π)=sinθcosπ+cosθsinπ=−sinθ，∴ 3cosθ−sinθ=0，∴cosθ=13sinθ，由于sin2θ+cos2θ=1，而θ∈(−π,0)，∴sinθ<0，∴109sin2θ=1．∴sinθ=−3√1010．故选A．3.【答案】A【考点】运用诱导公式化简求值【解析】观察所求角和已知角可得cos(α+π6)=cos[π2−(π3−α)]，再利用诱导公式即可求解．【解答】解：∵ (α+π6)+(π3−a)=π2，∴ cos (α+π6)=cos [π2−(π3−α)]=sin (π3−α)=−13．故选A ．4.【答案】 D【考点】运用诱导公式化简求值【解析】由题意利用利用诱导公式化简三角函数式的值，可得结果．【解答】解：∵ sin (α+π4)=35， ∴ cos (π4−α)=sin [π2−(π4−α)] =sin (π4+α)=35. 故选D . 5. 【答案】 D【考点】同角三角函数间的基本关系运用诱导公式化简求值【解析】直接利用诱导公式以及同角三角函数基本关系式转化求解即可．【解答】α是第二象限角，若sin (π2−α)=−13 可得cos α=−13，所以sin α=√1−cos 2α=2√23． 6.【答案】 D【考点】求函数的值分段函数的应用函数的求值【解析】推导出f(−12)=1−12=−2，f(16)＝log 216−3＝4−3＝1，由此能求出f(−12)⋅f(16)的值．【解答】∵ 函数f(x)={1x,x0,log 2x −3,x0,∴ f(−12)=1−12=−2，f(16)＝log 216−3＝4−3＝1， ∴ f(−12)⋅f(16)=(−2)×1＝−2．二、多选题（本题共计 1 小题，共计5分） 7.【答案】 C,D【考点】运用诱导公式化简求值【解析】此题暂无解析【解答】解：A ，sin (−x )=−sin x ，故 A 不成立； B ，sin (3π2−x)=−cos x ，故B 不成立； C ，cos (π2+x)=−sin x ，故C 成立；D ，cos (x −π)=−cos x ，故D 成立．故选CD ．三、填空题（本题共计 5 小题，每题 5 分，共计25分） 8.【答案】√3−√22【考点】运用诱导公式化简求值【解析】本题考查利用诱导公式求值．【解答】解：sin14π3−cos (−25π4)=sin (4π+2π3)−cos (−6π−π4) =sin 2π3−cos π4=√3−√22．故答案为：√3−√22．−4 5【考点】运用诱导公式化简求值【解析】原式利用诱导公式化简，将sinα的值代入计算即可求出值．【解答】解：∵sinα=45，∴cos(π2+α)=−sinα=−45．故答案为：−45.10.【答案】12【考点】三角函数的恒等变换及化简求值【解析】把cos85∘化为cos(60∘+25∘)，由两角和的余弦公式化简即可．【解答】cos85∘+sin25∘cos30∘cos25∘=cos(60∘+25∘)+sin25∘cos30∘cos25∘=12cos25∘−√32sin25∘+√32sin25∘cos25∘=12．11.【答案】−3 5【考点】三角函数的恒等变换及化简求值【解析】由已知利用诱导公式即可化简求值得解．【解答】∵cosθ=−35，∴sin(θ+π2)=cosθ=−35．−43【考点】同角三角函数间的基本关系运用诱导公式化简求值【解析】由诱导公式可得cos a 的值，及α的范围，利用同角三角函数间的基本关系求出tan α的值即可．【解答】解： ∵ cos (π−α)=−cos α=35，α∈(0,π)， ∴ cos α=−35<0，则α∈(π2,π)，则sin α=√1−cos 2α=45， ∴ tan α=sin αcos α=45−35=−43．故答案为：−43．四、解答题（本题共计 3 小题，每题 5 分，共计15分） 13.【答案】解：（1） f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α．（2）由f (π2+β)=−cos (π2+β)=−√33，得sin β=−√33，又角β为第四象限角，所以cos β−√63， sin 2β=−2√23,cos 2β=13，所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6 =(−2√23)⋅√32+13⋅12=1−2√66．【考点】运用诱导公式化简求值同角三角函数间的基本关系【解析】此题暂无解析【解答】解：（1） f(α)=sin (a−π2)cos (3π2+α)tan (π−α)tan (−α−π)sin (−α−π)=(−cos α)⋅sin α⋅(−tan α)(−tan α)⋅sin α=−cos α．（2）由f (π2+β)=−cos (π2+β)=−√33，得sin β=−√33，又角β为第四象限角，所以cos β−√63， sin 2β=−2√23,cos 2β=13，所以sin (2β+π6)=sin 2βcos π8+cos 2βsin π6=(−2√23)⋅√32+13⋅12=1−2√66． 14. 【答案】解：因为sin α+cos α=−713，所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169，整理得2sin αcos α=−120169，则(sin α−cos α)2=1−2sin αcos α=289169．因为α为第二象限角，所以sin α−cos α=1713，解得sin α=513，cos α=−1213．所以tan =sin αcos α=−512， sin 2α−2sin αcos α=25169−(−120169)=145169．【考点】同角三角函数间的基本关系三角函数的恒等变换及化简求值【解析】【解答】解：因为sin α+cos α=−713，所以(sin α+cos α)2=sin 2α+2sin αcos α+cos 2α=49169，整理得2sin αcos α=−120169，则(sin α−cos α)2=1−2sin αcos α=289169．因为α为第二象限角，所以sin α−cos α=1713，解得sin α=513，cos α=−1213．所以tan =sin αcos α=−512，sin 2α−2sin αcos α=25169−(−120169)=145169．15.【答案】解：(1)因为CD // AB ，AC ⊥BC ，△ABC 是等腰直角三角形，所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘，所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =√1−(√63)2=√33，在△ABC 中，BC =AC =√3，在△BCD 中，由正弦定理得， BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22．(2)在△BCD 中，由正弦定理可得， CD =BC ⋅sin (45∘−∠ABD)sin ∠BDC=√3×√22×(√63−√33)√33=2√3−√62．所以S △ACD =12AC ⋅CD ⋅sin ∠ACD =12×√3×2√3−√62×√22=3(√2−1)4．【考点】正弦定理同角三角函数间的基本关系【解析】(1)由题意可求∠BCD =135∘，在△BCD 中，由正弦定理可得BD 的值．(2)在△BCD 中，由正弦定理可得CD 的值，根据三角形的面积公式即可求解．【解答】解：(1)因为CD // AB ，AC ⊥BC ，△ABC 是等腰直角三角形，所以∠ABC =∠CA =∠ACD =12×(180∘−90∘)=45∘，所以∠BCD =90∘+45∘=135∘.所以sin ∠BDC =sin ∠ABD =(√63)=√33，在△ABC 中，BC =AC =√3，在△BCD 中，由正弦定理得， BD =BC⋅sin ∠BCD sin ∠BDC=√3×√22√33=3√22．(2)在△BCD 中，由正弦定理可得，CD=BC⋅sin(45∘−∠ABD)sin∠BDC=√3×√22×(√63−√33)√33=2√3−√62．所以S△ACD=12AC⋅CD⋅sin∠ACD=12×√3×2√3−√62×√22=3(√2−1)4．试卷第11页，总11页。

02三角函数诱导公式(含经典例题+答案)

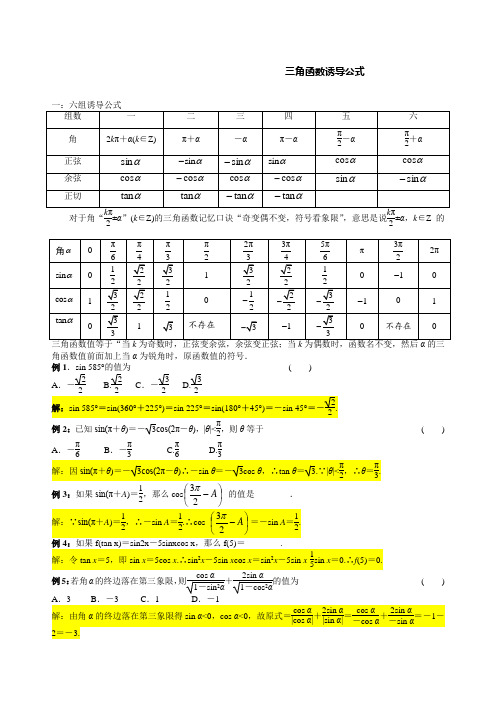
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变，符号看象限”，意思是说k π2±α，k ∈Z 的角函数值前面加上当α为锐角时，原函数值的符号．例1．sin 585°的值为 ( )A ．－2 B.2 C ．－3 D.3例2：已知sin(π＋θ)＝－3cos(2π－θ)，|θ|<π2，则θ等于 ( )A ．－πB ．－π C.π D.π例3：如果sin(π＋A )＝12，那么cos ⎪⎫⎛-A 3 的值是________．例5：若角α的终边落在第三象限，则cos α1－sin 2α＋2sin α1－cos 2α的值为 ( )例6：已知α∈(－π，0)，tan(3π＋α)＝31，则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B ．－1010 C.31010 D ．－31010解：tan α＝13，cos ⎪⎭⎫⎝⎛+απ23＝sin α.∵α∈(－π，0)，∴sin α＝－1010. A ．－32 B.32 C.3－12 D.3＋12解：sin 600°＋tan 240°＝sin(720°－120°)＋tan(180°＋60°)＝－sin 120°＋tan 60°＝－32＋3＝32. ( ) A ．3 B ．5 C ．1 D ．不能确定解：f(2 011)＝asin(2 011π＋α)＋bcos(2 011π＋β)＋4＝asin(π＋α)＋bcos(π＋β)＋4＝－asin α－bcos β＋4 ＝5.∴asin α＋bcos β＝－1.∴f(2 012)＝asin(2 012π＋α)＋bcos(2 012π＋β)＋4＝asin α＋bcos β＋4 ＝－1＋4＝3.1.诱导公式在三角形中经常应用，常用的变形结论有：A ＋B ＝π－C ； 2A ＋2B ＋2C ＝2π；A 2＋B 2＋C 2＝π2.2.求角时，一般先求出该角的某一三角函数值，再确定该角的范围，最后求角．例9：△ABC 中，cos A ＝13，则sin(B ＋C )＝________.解：∵△ABC 中，A ＋B ＋C ＝π，∴sin(B ＋C )＝sin(π－A )＝sin A ＝1－cos 2A ＝223.例10：在△ABC 中，若sin(2π－A )＝－2sin(π－B )，3cos A ＝－2cos(π－B )，求△ABC 的三个内角．解：由已知得⎩⎨⎧sin A ＝2sin B ①3cos A ＝2cos B ②①2＋②2得2cos 2A ＝1，即cos A ＝22或cos A ＝－22.(1)当cos A ＝22时，cos B ＝32，又A 、B 是三角形的内角，∴A ＝π4，B ＝π6，∴C ＝π－(A ＋B )＝712π. A ．B ．C ．D ．2.cos （﹣30°）的值是（） A ．B ．C ．D ．3.下列能与sin20°的值相等的是（） A ．cos20° B ．sin （﹣20°） C ．sin70° D ．sin160°4.已知，则下列各式中值为的是（）A ．B ．sin （π+α）C ．D ．sin （2π﹣α）换元法与诱导公式例11：已知41)3sin(=+απ，则=-)6cos(απ 。

三角函数诱导公式练习题含答案

三角函数诱导公式练习题含答案三角函数定义及诱导公式练习题1．将120o化为弧度为（）A．B．C．D．2．代数式的值为（）A.B.C.D.3．（）A．B．C．D．4．已知角α的终边经过点(3a，－4a)(a<0)，则inα＋coα等于()A.B.C．D．－5．已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为()(A)2cm(B)4cm(C)6cm(D)8cm6．若有一扇形的周长为60cm，那么扇形的最大面积为()A．500cm2B．60cm2C．225cm2D．30cm27．已知，则的值为（）A．B．－C．D．－8．已知，且，则（）A、B、C、D、9．若角的终边过点，则_______.10．已知点P(tanα，coα)在第二象限，则角α的终边在第________象限．11．若角θ同时满足inθ<0且tanθ<0，则角θ的终边一定落在第________象限．12．已知，则的值为．13．已知，，则_____________.14．已知，则_________.15．已知tan=3，则.16．(14分)已知tanα＝，求证：(1)=－；(2)in2α＋inαcoα＝．17．已知（1）求的值；（2）求的值；（3）若是第三象限角，求的值.18．已知in(α－3π)＝2co(α－4π)，求的值．参考答案1．B【解析】试题分析：，故.考点：弧度制与角度的相互转化.2．A.【解析】试题分析：由诱导公式以可得，in120°co210°=in60°某(-co30°)=-某=,选A.考点：诱导公式的应用．3．C【解析】试题分析：本题主要考查三角诱导公式及特殊角的三角函数值.由，选C.考点：诱导公式.4．A【解析】试题分析：,,.故选A.考点：三角函数的定义5．C【解析】设扇形的半径为R,则R2θ=2,∴R2=1R=1,∴扇形的周长为2R+θ·R=2+4=6(cm).6．C【解析】设扇形的圆心角为,弧长为cm,由题意知，∴∴当时，扇形的面积最大；这个最大值为.应选C.7．A【解析】试题分析：，=====.考点：诱导公式.8．【解析】试题分析：.又因为，所以为三象限的角，.选B.考点：三角函数的基本计算.9．【解析】试题分析：点即，该点到原点的距离为，依题意，根据任意角的三角函数的定义可知.考点：任意角的三角函数.10．四【解析】由题意，得tanα＜0且coα＞0，所以角α的终边在第四象限．11．四【解析】由inθ<0，可知θ的终边可能位于第三或第四象限，也可能与y轴的非正半轴重合．由tanθ<0，可知θ的终边可能位于第二象限或第四象限，可知θ的终边只能位于第四象限．12．-3【解析】13．【解析】试题分析：因为α是锐角所以in(π－α)＝inα＝考点：同角三角函数关系，诱导公式.14．【解析】试题分析：，又，则原式=.考点：三角函数的诱导公式.15．45【解析】试题分析：已知条件为正切值，所求分式为弦的齐次式，所以运用弦化切，即将分子分母同除以得.考点：弦化切16．证明：(1)＝－．(2)in2α＋inαcoα＝．【解析】(1)原式可以分子分母同除以co某,达到弦化切的目的.然后将tan某=2代入求值即可.（2）把”1”用替换后，然后分母也除以一个”1”，再分子分母同除以,达到弦化切的目的.证明：由已知tanα＝．(1)＝＝＝－．(2)in2α＋inαcoα＝＝＝＝．17．（1）;（2）;（3）.【解析】试题分析：（1）因为已知分子分母为齐次式，所以可以直接同除以转化为只含的式子即可求得；（2）用诱导公式将已知化简即可求得；（3）有，得，再利用同角关系，又因为是第三象限角，所以；试题解析：⑴2分．3分⑵9分．10分⑶解法1：由，得，又，故，即，12分因为是第三象限角，，所以．14分解法2：，12分因为是第三象限角，，所以．14分考点：1.诱导公式；2.同角三角函数的基本关系.18．【解析】∵in(α－3π)＝2co(α－4π)，∴－in(3π－α)＝2co(4π－α)，∴inα＝－2coα，且coα≠0.∴原式＝三角函数的诱导公式1一、选择题1．如果|co某|=co （某+π），则某的取值集合是（）A．－+2kπ≤某≤+2kπB．－+2kπ≤某≤+2kπC．+2kπ≤某≤+2kπD．（2k+1）π≤某≤2（k+1）π（以上k∈Z）2．in（－）的值是（）A．B．－C．D．－3．下列三角函数：①in（nπ+）；②co（2nπ+）；③in（2nπ+）；④co［（2n+1）π－］；⑤in［（2n+1）π－］（n∈Z）．其中函数值与in的值相同的是（）A．①②B．①③④C．②③⑤D．①③⑤4．若co（π+α）=－，且α∈（－，0），则tan（+α）的值为（）A．－B．C．－D．5．设A、B、C是三角形的三个内角，下列关系恒成立的是（）A．co（A+B）=coCB．in （A+B）=inCC．tan（A+B）=tanCD．in=in6．函数f（某）=co（某∈Z）的值域为（）A．{－1，－，0，，1}B．{－1，－，，1}C．{－1，－，0，，1}D．{－1，－，，1}二、填空题7．若α是第三象限角，则=_________．8．in21°+in22°+in23°+…+in289°=_________．三、解答题9．求值：in（－660°）co420°－tan330°cot（－690°）．10．证明：．11．已知coα=，co（α+β）=1，求证：co（2α+β）=．12．化简：．13、求证：=tanθ．14．求证：（1）in（－α）=－c oα；（2）co（+α）=inα．参考答案1一、选择题1．C2．A3．C4．B5．B6．B二、填空题7．－inα－coα8．三、解答题9．+1．10．证明：左边==－，右边=，左边=右边，∴原等式成立．11．证明：∵co（α+β）=1，∴α+β=2kπ．∴co（2α+β）=co（α+α+β）=co（α+2kπ）=coα=．12．解：=====－1．13．证明：左边==tanθ=右边，∴原等式成立．14证明：（1）in（－α）=in［π+（－α）］=－in（－α）=－coα．（2）co（+α）=co［π+（+α）］=－co（+α）=inα．三角函数的诱导公式2一、选择题：1．已知in(+α)=，则in(-α)值为（）A.B.—C.D.—2．co(+α)=—，6．co(-某)=，某∈（-，），则某的值为．7．tanα=m，则．8．|inα|=in（-+α），则α的取值范围是．三、解答题：9．．10．已知：in（某+）=，求in（+co2（-某）的值．11．求下列三角函数值：（1）in；（2）co；（3）tan（－）；12．求下列三角函数值：（1）in·co·tan；（2）in［（2n+1）π－］.13．设f（θ）=，求f（）的值.参考答案21．C2．A3．C4．C5．A6．±7．8．[(2k-1),2k]9．原式===inα10．11．解：（1）in=in（2π+）=in=.（2）co=co（4π+）=co=.（3）tan（－）=co（－4π+）=co=.（4）in（－765°）=in［360°某（－2）－45°］=in（－45°）=－in45°=－.注：利用公式（1）、公式（2）可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数，从而求值.12．解：（1）in·co·tan=in（π+）·co（4π+）·tan（π+）=（－in）·co·tan=（－）··1=－.（2）in ［（2n+1）π－］=in（π－）=in=.13．解：f（θ）======＝coθ－1，∴f（）=co－1=－1=－.三角函数公式1．同角三角函数基本关系式in2α＋co2α=1=tanαtanαcotα=12．诱导公式(奇变偶不变，符号看象限)（一）in(π－α)＝inαin(π+α)＝-inαco(π－α)＝-coαco(π+α)＝-coαtan(π－α)＝-tanαtan(π+α)＝tanαin(2π－α)＝-inαin(2π+α)＝inαco(2π－α)＝coαco(2π+α)＝coαtan(2π－α)＝-tanαtan(2π+α)＝tanα（二）in(－α)＝coαin(+α)＝coαco(－α)＝inαco(+α)＝-inαtan(－α)＝cotαtan(+α)＝-cotαin(－α)＝-coαin(+α)＝-coαco(－α)＝-inαco(+α)＝inαtan(－α)＝cotαtan(+α)＝-cotαin(－α)＝－inαco(－α)=coαtan(－α)=－tanα3．两角和与差的三角函数co(α+β)=coαcoβ－inαinβco(α－β)=coαcoβ＋inαinβin(α+β)=inαcoβ＋coαinβin(α－β)=inαcoβ－coαinβtan(α+β)=tan(α－β)=4．二倍角公式in2α=2inαcoαco2α=co2α－in2α＝2co2α－1＝1－2in2αtan2α=5．公式的变形（1）升幂公式：1＋co2α＝2co2α1—co2α＝2in2α（2）降幂公式：co2α＝in2α＝（3）正切公式变形：tanα+tanβ＝tan(α+β)（1－tanαtanβ）tanα－tanβ＝tan(α－β)（1＋tanαtanβ)（4）万能公式（用tanα表示其他三角函数值）in2α＝co2α＝tan2α＝6．插入辅助角公式ain某＋bco某=in(某+φ)(tanφ=)特殊地：in某±co某＝in(某±)7．熟悉形式的变形（如何变形）1±in某±co某1±in某1±co某tan某＋cot某若A、B是锐角，A+B＝，则（1＋tanA）(1+tanB)=28．在三角形中的结论若：A＋B＋C=π,=则有tanA＋tanB＋tanC=tanAtanBtanCtantan＋tantan＋tantan＝1很赞的文章！介绍的很全面，对我很有帮助。

三角函数诱导公式练习题-带答案

三角函数的诱导公式(1)一、选择题1．如果|cos x |=cos （x +π），则x 的取值集合是（）A ．－2π+2k π≤x ≤2π+2k π B ．－2π+2k π≤x ≤2π3+2k π C ． 2π+2k π≤x ≤2π3+2k π D ．（2k +1）π≤x ≤2（k +1）π（以上k ∈Z ） 2．sin （－6π19）的值是（） A ． 21 B ．－21 C ．23 D ．－23 3．下列三角函数：①sin （n π+3π4）；②cos （2n π+6π）；③sin （2n π+3π）；④cos ［（2n +1）π－6π］； ⑤sin ［（2n +1）π－3π］（n ∈Z ）．其中函数值与sin3π的值相同的是（） A ．①② B ．①③④ C ．②③⑤ D ．①③⑤4．若cos （π+α）=－510，且α∈（－2π，0），则tan （2π3+α）的值为（） A ．－36 B ．36 C ．－26 D ．26 5．设A 、B 、C 是三角形的三个内角，下列关系恒成立的是（）A ．cos （A +B ）=cosC B ．sin （A +B ）=sin C C ．tan （A +B ）=tan CD ．sin2A B +=sin 2C 6．函数f （x ）=cos3πx （x ∈Z ）的值域为（） A ．{－1，－21，0，21，1} B ．{－1，－21，21，1} C ．{－1，－23，0，23，1} D ．{－1，－23，23，1} 二、填空题7．若α．8．sin 21°+sin 22°+sin 23°+…+sin 289°=_________．三、解答题9．求值：sin （－660°）cos420°－tan330°cot （－690°）．11．．12、求证：tan(2π)sin(2π)cos(6π)cos(π)sin(5π)q q qq q-----+=tanθ．三角函数的诱导公式(2)一、选择题：1．已知sin(4π+α)=23，则sin(43π-α)值为（） A. 21 B. —21 C. 23 D. —23 2．cos(π+α)= —21，23π<α<π2,sin(π2-α) 值为（） A. 23 B. 21 C. 23± D. —23 3．化简：)2cos()2sin(21-•-+ππ得（）A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4．已知α和β的终边关于x 轴对称，则下列各式中正确的是（）A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD. cos(π2-α) =-cosβ5．设tanθ=-2, 2π-<θ<0，那么sin 2θ+cos(θ-π2)的值等于（）， A. 51（4+5） B. 51（4-5） C. 51（4±5） D. 51（5-4）二、填空题：6．cos(π-x)= 23，x ∈（-π，π），则x 的值为． 7．tanα=m ，则=+-+++)cos(-sin()cos(3sin(απα）απ）απ ． 8．|sinα|=sin （-π+α），则α的取值范围是．三、解答题：9．)cos(·3sin()cos()n(s 2sin(απα）παπα）π----+-απi ．10．已知：sin （x+6π）=41，求sin （)67x +π+cos 2（65π-x ）的值．11．求下列三角函数值：（1）sin3π7；（2）cos 4π17；（3）tan （－6π23）；12．求下列三角函数值：（1）sin 3π4·cos 6π25·tan 4π5；（2）sin ［（2n +1）π－3π2］.13．设f （θ）=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+，求f （3π）的值.。

高一数学知识点三角函数诱导公式常考题经典题 50道含答案和解析

高一数学三角函数诱导公式50道常考题经典题一、单选题1.若角的终边上有一点(-4,a)，则a的值是（）A. B. C. D.【答案】A【考点】任意角的三角函数的定义，诱导公式一【解析】【解答】由三角函数的定义知：，所以，因为角的终边在第三象限，所以<0,所以的值是。

【分析】三角函数是用终边上一点的坐标来定义的，和点的位置没有关系。

属于基础题型。

================================================================================2.若,则的值是( )A. B. C. D.【答案】C【解析】【解答】即，所以，，=，故选C。

【分析】简单题，此类题解的思路是：先化简已知条件，再将所求用已知表示。

================================================================================3.若，则（）A. B. C. D.【答案】C【考点】诱导公式一，同角三角函数间的基本关系【解析】【解答】，故选C.================================================================================4.函数图像的一条对称轴方程是（）A. B. C. D.【答案】A【考点】诱导公式一，余弦函数的图象，余弦函数的对称性【解析】【分析】，由y=cosx的对称轴可知，所求函数图像的对称轴满足即，当k=-1时，，故选A.================================================================================5.已知，则（）A. B. C. D.【答案】C【考点】诱导公式一，同角三角函数间的基本关系，弦切互化【解析】【解答】因为，所以，可得，故C符合题意.故答案为：C .【分析】利用诱导公式将已知条件化简可求出tan，将中分子分母同时除以cos.================================================================================6.函数（）A. 是奇函数B. 是偶函数C. 既是奇函数，又是偶函数D. 是非奇非偶函数【答案】A【考点】奇函数，诱导公式一【解析】【解答】∵，∴,∴是奇函数．故答案为：A【分析】首先利用诱导公式整理化简f(x) 的解析式，再根据奇函数的定义即可得证出结果。

高中数学专题6.5三角函数的诱导公式(2个考点六大题型) 试卷及答案

专题6.5三角函数的诱导公式（2个考点六大题型）【题型1 诱导公式一】【题型2 诱导公式二、三、四】【题型3 诱导公式五、六】【题型4 诱导公式-恒等式的证明】【题型5 诱导公式-化简、求值】【题型6 正切函数的诱导公式】【题型1 诱导公式一】cos390=（D．-sin1080=)2820 1．（2023春·北京东城·高一北京市第一六六中学校考阶段练习）sin210=（）1210cos120tan 45+= 根据诱导公式，填适当的式子，使为第二象限角，且sin θcos165=（-24sin(α-是ABC的高一校考开学考试）已知ABC为锐角三角形，则下列不等关系中cos cosA>sin cosA>高一重庆市杨家坪中学校考阶段练习）（多选）已知cos2cos882sin47sin133+=；（cos5cos852sin50sin130+=．根据以上恒等式，请你猜想出一个一般性的结论并证明．秋·高一课时练习）求证：当2=或3时，tan(cos(2k 2π1203=πsin(2α-秋·高一课时练习）)tan2022,sin2022位于(2)若()0,πθ∈,且()25fθ=-,求cos sinθθ-的值．专题6.5三角函数的诱导公式（2个考点六大题型）【题型1 诱导公式一】【题型2 诱导公式二、三、四】【题型3 诱导公式五、六】【题型4 诱导公式-恒等式的证明】【题型5 诱导公式-化简、求值】【题型6 正切函数的诱导公式】【题型1 诱导公式一】cos390=（D．-()3cos390cos36030cos302=+==.辽宁葫芦岛·高一统考期末）17sin4π的值为（sin1080=.()sin1080sin33600sin00=⨯+==；cos高一课时练习）已知12cot5θ=-，且θ为第二象限角，．)2820)()32820sin 836060sin 602=-⨯+==.ππtan 144⎫==⎪⎭. ππ2⎫()1sin210sin 18030sin 302=+=-=-.高一校联考阶段练习）在平面直角坐标系中，若角【详解】(sin πθ+的终边可能在第三或第四象限CD.2023春·吉林长春列结论正确的是（210cos120tan 45+= 【分析】利用诱导公式及特殊角的三角函数值化简求值. ()()11sin 18030cos 18060210cos120sin 30cos 60221tan 45tan 45tan 451--++-+--====-. 故答案为：-12023春·福建福州·高二校考期末）根据诱导公式，填适当的式子，使 cosα=-cos165=（ 24- ()cos165cos 9075sin 75=+=-，则()75sin 3045sin30cos 45cos30sin 45=+=+1222=⨯+26cos165sin 754+︒=-︒=-．故选：A ．是ABC的高一校考开学考试）已知ABC 为锐角三角形，则下列不等关系中cos cos A >sin cos A >【分析】因为ABC 为锐角三角形，所以π【详解】因为ABC 为锐角三角形，,,3πcos A >,4πcos A <π因为ABC 为锐角三角形，,2B π+>∴,02A π<<sin(2A π>cos2cos882sin47sin133+=；（cos5cos852sin50sin130+=．根据以上恒等式，请你猜想出一个一般性的结论并证明． ()()()cos 90cos 2sin 45sin 135αααα-+=+-，证明见详解.【分析】观察结构猜想等式，利用三角恒等变换证明即可)()()cos 90cos 245sin 135αααα-+=+- 证明：由诱导公式可得()()()cos 90sin ,sin 135sin 45αααα-=-=+，)()()()90cos sin cos cos 2sin cos 45cos sin 4545sin 135sin 45ααααααααααα-+++===++-+ 秋·高一课时练习）求证：当2k =或3时，tan(π)tan(π)cos(2π)sin[(21)π]k k k k αααα-+=-++【答案】证明见解析【详解】(tan 3π+C.2023·全国·高三专题练习）已知【答案】B2π1203=πsin(2α-ABD2π1203=πtan 4=cos α，所以【详解】(cos πα-)πsin α-=-AB.2023秋·广东河源3π⎫⎛）π6θ⎛⎫-+ ⎪⎝⎭所以，5π6fθ⎛+⎝故答案为：（1）1．（2022秋·甘肃兰州·高一校考期末）在平面直角坐标系中，点()tan2022,sin2022P 位于第（）象限 A ．一 B ．二 C ．三 D ．四【答案】D【分析】运用诱导公式计算出P 点坐标的符号就可判断出P 点所在的象限.【详解】()tan 2022tan 5360222tan 2220︒︒︒︒=⨯+=> ，()sin 2022sin 5360222sin 2220︒︒︒︒=⨯+=< ， ()tan 2022,sin 2022P ︒︒∴ 在第四象限；故选：D.2．（2022秋·江苏常州·高一常州高级中学校考期末）已知偶函数()f x 在(0,)+∞上单调递减，若tan114a =︒，tan172b =︒，tan 287c =︒，则下列不等关系中正确的是（） A ．()()()f c f b f a >> B ．()()()f c f a f b >> C ．()()()f b f c f a >> D ．()()()f b f a f c >>【答案】D【分析】根据题意，由三角函数的诱导公式可得tan114tan 66a =︒=-︒，tan172tan8b =︒=-︒，tan 287tan107tan 73c =︒=︒=-︒，由正切函数的性质结合函数的奇偶性和单调性分析可得答案．，04π<-，而060<正确；23,cos π⎛⎫= ⎪3013π<<故选：ACD.4．（2023【答案】－【分析】利用诱导公式化简计算即可π25π5ππππcos tan sin πcos 32πtan π346346⎛⎫⎛⎫⎛⎫=+⨯+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ πππ3232cos tan 3462234⎛⎫⎛⎫-=-⨯⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭；故答案为：24. 2021秋·北京通州·高一校考阶段练习）已知cos α是方程2320x x --=三象限角，求3sin α⎛-+ ⎝，2sin cos α+3cos 2sin 2ππα⎫⎛+⎪ ⎭⎝⎫⎛+⎪ ⎭⎝全国·高一专题练习）已知）()f θ=-cos θθ=-sin 0θθ-<sin θθ-=。

(完整版)高中数学-三角函数诱导公式练习题与答案

三角函数定义及诱导公式练习题1．代数式sin120cos210o o 的值为（） A.34-C.32-D.142．tan120︒=（） AB．．3．已知角α的终边经过点(3a ，－4a)(a<0)，则sin α＋cos α等于( ) A.51 B.57 C ．51- D ．－57 4．已知扇形的面积为2cm 2,扇形圆心角θ的弧度数是4,则扇形的周长为( ) (A)2cm (B)4cm (C)6cm (D)8cm5．已知3cos()sin()22()cos()tan()f ππ+α-αα=-π-απ-α，则25()3f -π的值为（）A ．12 B ．－12C．2 D ．－26．已知3tan()4απ-=，且3(,)22ππα∈，则sin()2πα+=（） A 、45 B 、45- C 、35 D 、35-7．若角α的终边过点(sin 30,cos30)︒-︒，则sin α=_______. 8．已知(0,)2πα∈，4cos 5α=，则sin()πα-=_____________.9．已知tan α=3，则224sin 3sin cos 4cos sin cos αααααα+=- .10．(14分)已知tan α＝12，求证： (1)sin cos sin cos a a a a -3+=－53；(2)sin 2α＋sin αcos α＝35．11．已知.2tan =α（1）求ααααcos sin cos 2sin 3-+的值；（2）求)cos()sin()3sin()23sin()2cos()cos(αππααππααπαπ+-+-+-的值；（3）若α是第三象限角，求αcos 的值.12．已知sin (α－3π)＝2cos (α－4π)，求52322sin cos sin sin παπαπαα⎛⎫⎪⎝⎭（－）＋（－）－－（－）的值．参考答案1．B 【解析】试题分析：180o π=，故21203oπ=. 考点：弧度制与角度的相互转化. 2．A. 【解析】试题分析：由诱导公式以可得，sin120°cos210°=sin60°×(-cos30°)=-2×=34-,选A. 考点：诱导公式的应用． 3．C 【解析】试题分析：本题主要考查三角诱导公式及特殊角的三角函数值.由tan120tan(18060)tan 60︒=︒-︒=-︒= C.考点：诱导公式. 4．A 【解析】试题分析：σσ55-==r ,53cos ,54sin -===σσr y ,51cos sin =+∴σσ.故选A. 考点：三角函数的定义5．C 【解析】设扇形的半径为R,则错误!未找到引用源。

(完整版)高中数学-三角函数诱导公式练习题与答案

三角函数定义及诱导公式练习题代数式sin 120o cos21C °的值为（A.6 .已知 tan( ) 4 A 、4B5A. B. C. D.2. tan120 A.、.3.■■ 3贝U sin a+ cos a 等于()7 5a 的终边经过点 B.753. A.154. 已知扇形的面积为2cm,扇形圆心角B 的弧度数是4,则扇形的周长为（已知角 (3a ,— 4a)(a <0), C . -15D .(A)2cm(B)4cm (C)6cm (D)8cm5 .已知f ()cos(— 2 cos(3 )si n()2，则 f( )tan()25§ ）的值为（3“)，则sin( ?)10. (14分)已知tan a =—，求证: /八 sin a cosa ⑴ 二_ _ ；sin a cosa(2)sin 2 a+ sin a COS a = - .11 .已知 tan 2.(1)求 3sin 一2CO 二的值; sin coscos( )cos( )sin()⑵求品盘窗勺的值;(3)若是第三象限角，求cos 的值. 312.已知 sin ( a — 3n ) = 2cos( a — 4n )，求 si (2si n— — si n(—二)+ 5cos (2 —3-的值. )f(25 )=cos 325 325 =cos- 3 = cos 8 1 —=cos —= 3 3 2参考答案1. B【解析】试题分析：180°，故1200 -.3考点：弧度制与角度的相互转化•2. A.【解析】试题分析：由诱导公式以可得，sin 120 ° cos210° =sin60 ° x (-cos30 ° )=- ^ x2十3,选A.考点：诱导公式的应用. 3. C【解析】试题分析：本题主要考查三角诱导公式及特殊角的三角函数值.由tan120 tan(18060 ) tan 603，选 C.考点：诱导公式• 4. A【解析】试题分析：r 55 , sin —-, cos -, sin cos r 55考点：三角函数的定义 5. C【解析】设扇形的半径为R,则错误！未找到引用源。

高一三角函数诱导公式练习题(带详解答案)

三角函数诱导公式1.全国Ⅱ)假设sin α<0且tan α>0，那么α是( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角2.(07·湖北)tan690°的值为( )A ．－33 B.33 C. 3 D ．－ 33.f (sin x )＝cos19x ，那么f (cos x )＝( )A ．sin19xB ．cos19xC ．－sin19xD ．－cos19x4.设f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)，其中a ，b ，α，β∈R ，且ab ≠0，α≠k π(k ∈Z)．假设f (2021)＝5，那么f (2021)等于( )A ．4B ．3C ．－5D ．55.(09·全国Ⅰ文)sin585°的值为( )A ．－22 B.22 C ．－32 D.326.函数y ＝5sin ⎝⎛⎭⎫25x ＋π6的最小正周期是( ) A.25π B.52π C.π3 D ．5π7.(2021·重庆文，6)以下函数中，周期为π，且在[π4，π2]上为减函数的是( ) A ．y ＝sin(2x ＋π2) B ．y ＝cos (2x ＋π2) C ．y ＝sin(x ＋π2) D ．y ＝cos(x ＋π2)8.函数y ＝－2tan ⎝⎛⎭⎫3x ＋π4的单调递减区间是________．三角函数诱导公式〔答案〕1.[答案] C2.[答案] A[ 解析] tan690°＝tan(－30°＋2×360°)＝tan(－30°)＝－tan30°＝－33，选A. 3.[答案] C[解析] f (cos x )＝f (sin(90°－x ))＝cos19(90°－x )＝cos(270°－19x )＝－sin19x .4.[答案] C[解析] ∵f (2021)＝a sin(2021π＋α)＋b cos(2021π＋β)＝－a sin α－b cos β＝5， ∴a sin α＋b cos β＝－5.∴f (2021)＝a sin α＋b cos β＝－5.5.[答案] A[解析] sin585°＝sin(360°＋225°)＝sin225°＝sin(180°＋45°)＝－sin45°＝－22. 6.[答案] D[解析] T ＝2π25＝5π. 7.7.[答案] A[解析] 选项A ：y ＝sin(2x ＋π2)＝cos2x ，周期为π，在[π4，π2]上为减函数；选项B ：y ＝cos(2x ＋π2)＝－sin2x ，周期为π，在[π4，π2]上为增函数；选项C ：y ＝sin(x ＋π2)＝cos x ，周期为2π；选项D ：y ＝cos(x ＋π2)＝－sin x ，周期为2π.应选A. 8. [答案] ⎝⎛⎭⎫k π3－π4，k π3＋π12(k ∈Z)[解析] 求此函数的递减区间，也就是求y ＝2tan ⎝⎛⎭⎫3x ＋π4的递增区间，由k π－π2<3x ＋π4<k π＋π2，k ∈Z 得：k π3－π4<x <k π3＋π12， ∴减区间是⎝⎛⎭⎫k π3－π4，k π3＋π12，k ∈Z.。

(完整版)三角函数诱导公式练习题附答案

三角函数诱导公式练习题一、选择题（共21小题）1、已知函数f（x）=sin，g（x）=tan（π﹣x），则（）A、f（x）与g（x）都是奇函数B、f（x）与g（x）都是偶函数C、f（x）是奇函数，g（x）是偶函数D、f（x）是偶函数，g（x）是奇函数2、点P（cos2009°，sin2009°）落在（）A、第一象限B、第二象限C、第三象限D、第四象限3、已知，则=（）A、B、C、D、4、若tan160°=a，则sin2000°等于（）A、B、C、D、﹣5、已知cos（+α）=﹣，则sin（﹣α）=（）A、﹣B、C、﹣D、6、函数的最小值等于（）A、﹣3B、﹣2C、D、﹣17、本式的值是（）A、1B、﹣1C、D、8、已知且α是第三象限的角，则cos（2π﹣α）的值是（）A、B、C、D、9、已知f（cosx）=cos2x，则f（sin30°）的值等于（）A、B、﹣C、0 D、110、已知sin（a+）=，则cos（2a﹣）的值是（）A、B、C、﹣D、﹣11、若，，则的值为（）A、B、C、D、12、已知，则的值是（）A、B、C、D、13、已知cos（x﹣）=m，则cosx+cos（x﹣）=（）A、2mB、±2mC、D、14、设a=sin（sin20080），b=sin（cos20080），c=cos（sin20080），d=cos（cos20080），则a，b，c，d的大小关系是（）A、a＜b＜c＜dB、b＜a＜d＜cC、c＜d＜b＜aD、d＜c＜a＜b15、在△ABC中，①sin（A+B）+sinC；②cos（B+C）+cosA；③tan tan；④，其中恒为定值的是（）A、②③B、①②C、②④D、③④16、已知tan28°=a，则sin2008°=（）A、B、C、D、17、设，则值是（）A、﹣1B、1C、D、18、已知f（x）=asin（πx+α）+bcos（πx+β）+4（a，b，α，β为非零实数），f（2007）=5，则f（2008）=（）A、3B、5C、1D、不能确定19、给定函数①y=xcos（+x），②y=1+sin2（π+x），③y=cos（cos（+x））中，偶函数的个数是（）A、3B、2C、1D、020、设角的值等于（）A、B、﹣C、D、﹣21、在程序框图中，输入f0（x）=cosx，则输出的是f4（x）=﹣csx（）A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题（共9小题）22、若（﹣4，3）是角终边上一点，则Z的值为．23、△ABC的三个内角为A、B、C，当A为°时，取得最大值，且这个最大值为．24、化简：=25、化简：=．26、已知，则f（1）+f（2）+f（3）+…+f（2009）=．27、已知tanθ=3，则（π﹣θ）=．28、sin（π+）sin（2π+）sin（3π+）…sin（2010π+）的值等于．29、f（x）=，则f（1°）+f（2°）+…+f（58°）+f（59°）= ．30、若，且，则cos（2π﹣α）的值是．答案与评分标准一、选择题（共21小题）1、已知函数f（x）=sin，g（x）=tan（π﹣x），则（）A、f（x）与g（x）都是奇函数B、f（x）与g（x）都是偶函数C、f（x）是奇函数，g（x）是偶函数D、f（x）是偶函数，g（x）是奇函数考点：函数奇偶性的判断；运用诱导公式化简求值。

高中数学三角函数诱导公式(带答案)

习题精炼一、选择题1、下列各式不正确的是（）A ． sin （α＋180°）=－sin αB ．cos （－α＋β）=－cos （α－β）C ． sin （－α－360°）=－sin αD ．cos （－α－β）=cos （α＋β） 2、若sin （π＋α）＋sin （－α）=－m ,则sin （3π＋α）＋2sin （2π－α）等于（） A ．－23 m B ．－32 m C ．23 m D ．32 m3、⎪⎭⎫⎝⎛-π619sin 的值等于（） A ．21B ． 21-C ．23 D ． 23-4、如果).cos(|cos |π+-=x x 则x 的取值范围是（ C ）A ．)(]22,22[Z k k k ∈++-ππππB ．)()223,22(Z k k k ∈++ππππC ．)(]223,22[Z k k k ∈++ππππD ．)()2,2(Z k k k ∈++-ππππ5．已知函数1tan sin )(++=x b x a x f ，满足.7)5(=f 则)5(-f 的值为（）A ．5B ．－5C ．6D ．－66、sin34π·cos 625π·tan 45π的值是A ．－43B ．43C ．－43D ．437．设,1234tan a =︒那么)206cos()206sin(︒-+︒-的值为（）A ．211aa ++ B ．－211aa ++ C ．211aa +-D ．211aa +-8．若)cos()2sin(απαπ-=+，则α的取值集合为（）A ．}42|{Z k k ∈+=ππαα B ．}42|{Z k k ∈-=ππααC ．}|{Z k k ∈=πααD ．}2|{Z k k ∈+=ππαα二、填空题1、求值：sin160°cos160°（tan340°＋cot340°）= ．2、若sin （125°－α）=1213,则sin （α＋55°）=．3、cos π7 ＋cos 2π7 ＋cos 3π7 ＋cos 4π7 ＋cos 5π7 ＋cos 6π7 = ．4、已知,1)sin(=+βα则=+++)32sin()2sin(βαβα .三、解答题1、已知 3)tan(=+απ, 求)2sin()cos(4)sin(3)cos(2a a a a -+-+--πππ的值．2、若cos α＝23，α是第四象限角，求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值．3、设sin ,(0)()(1)1,(0)x x f x f x x π<⎧=⎨-+≥⎩和1cos ,()2()1(1)1,()2x x g x g x x π⎧<⎪⎪=⎨⎪-+≥⎪⎩求)43()65()31()41(f g f g +++的值.4．设)(x f 满足)2|(|cos sin 4)(sin 3)sin (π≤⋅=+-x xx x f x f ,（１）求)(x f 的表达式；（2）求)(x f 的最大值．《诱导公式》参考答案一、选择题ABAC BABC二、填空题1、1．2、1312．3、0．4、0三、解答题1、7．2、25．3、22)41(=g ， 5312()1,()s i n ()1,6233g f π=+=-+ 1)4sin()43(+-=πf ，故原式=3．4、解析：（１）由已知等式(sin )3(sin )4sin cos f x f x x x -+=⋅ ①得x x x f x f cos sin 4)sin (3)(sin -=-+ ② 由３⨯①－②，得8x x x f cos sin 16)(sin ⋅=，故212)(x x x f -=．（２）对01x ≤≤，将函数212)(x x x f -=的解析式变形，得2242()2(1)2f x x x x x =-=-+＝22112()24x --+，当22x =时，max 1.f =。

三角函数诱导公式专项练习(含答案)

三角函数诱导公式专项练习(含答案) 三角函数诱导公式专项练一、单选题1.sin(-600°)的值为（）A。

-√3/2B。

-1C。

1D。

√3/22.cos(11π/3)的值为（）A。

-√3/2B。

-13/2C。

√2D。

23.已知sin(30°+α)=√3/2，则cos(60°-α)的值为A。

1/2B。

-1/2C。

√3/2D。

-√3/24.已知cos(π/3+α)=-5/2，且α∈(2π/5,π)，则XXX(α-π)=（）A。

-34/4B。

-3C。

4D。

35.已知sin(π-α)=-2/√3，且α∈(-2,0)，则tan(2π-α)的值为A。

2√5/5B。

-2√5/2√5C。

±5D。

√5/26.已知cos(π/4-α)=√2/2，则sin(α+π/4)=（）A。

-3B。

1C。

√2D。

√14/47.已知sinα=3/5，2<α<π/2，则sin(2-α)=（）A。

3/5B。

-3/5C。

4/5D。

-4/58.已知tanx=-12/5π，x∈(π/2,π)，则cos(-x+3π/2)=（）A。

5/13B。

-5/12C。

13D。

-12/139.如果cos(π+A)=-1，那么sin(π/2+A)=A。

-1/2B。

2C。

1D。

-110.已知cos(π/2-α)-3cosα/(sinα-cos(π+α))=2，则tanα=（）A。

12/5B。

-3C。

1/2D。

-511.化简cos480°的值是（）A。

1B。

-1C。

√3/2D。

-√3/212.cos(-585°)的值是（）A。

√2/2B。

√3/2C。

-√3/2D。

-√2/213.已知角α的终边经过点P(-5,-12)，则sin(3π/2+α)的值等于()A。

-5B。

-12/13C。

13D。

12/1314.已知cos(π+α)=2/3，则tanα=（）A。

√55/2B。

2√5/52.已知cosα=2/5，-2/5<α<0，则tan(α+α)cos(-α)tanα的值为（）答案：D解析：由cosα=2/5可得sinα=-√(21)/5，代入公式可得tan(α+α)cos(-α)tanα=-1/√3=-√3/3，故选D。

三角函数诱导公式练习题集附答案解析

三角函数诱导公式练习题一、选择题（共21小题）1、已知函数f（x）=sin，g（x）=tan（π﹣x），则（）A、f（x）与g（x）都是奇函数B、f（x）与g（x）都是偶函数C、f（x）是奇函数，g（x）是偶函数D、f（x）是偶函数，g（x）是奇函数2、点P（cos2009°，sin2009°）落在（）A、第一象限B、第二象限C、第三象限D、第四象限3、已知，则=（）A、B、C、D、4、若tan160°=a，则sin2000°等于（）A、B、C、D、﹣5、已知cos（+α）=﹣，则sin（﹣α）=（）A、﹣B、C、﹣D、6、函数的最小值等于（）A、﹣3B、﹣2C、D、﹣17、本式的值是（）A、1B、﹣1C、D、8、已知且α是第三象限的角，则cos（2π﹣α）的值是（）A、B、C、D、9、已知f（cosx）=cos2x，则f（sin30°）的值等于（）A、B、﹣C、0 D、110、已知sin（a+）=，则cos（2a﹣）的值是（）A、B、C、﹣D、﹣11、若，，则的值为（）A、B、C、D、12、已知，则的值是（）A、B、C、D、13、已知cos（x﹣）=m，则cosx+cos（x﹣）=（）A、2mB、±2mC、D、14、设a=sin（sin20080），b=sin（cos20080），c=cos（sin20080），d=cos（cos20080），则a，b，c，d的大小关系是（）A、a＜b＜c＜dB、b＜a＜d＜cC、c＜d＜b＜aD、d＜c＜a＜b15、在△ABC中，①sin（A+B）+sinC；②cos（B+C）+cosA；③tan tan；④，其中恒为定值的是（）A、②③B、①②C、②④D、③④16、已知tan28°=a，则sin2008°=（）A、B、C、D、17、设，则值是（）A、﹣1B、1C、D、18、已知f（x）=asin（πx+α）+bcos（πx+β）+4（a，b，α，β为非零实数），f（2007）=5，则f（2008）=（）A、3B、5C、1D、不能确定19、给定函数①y=xcos（+x），②y=1+sin2（π+x），③y=cos（cos（+x））中，偶函数的个数是（）A、3B、2C、1D、020、设角的值等于（）A、B、﹣C、D、﹣21、在程序框图中，输入f0（x）=cosx，则输出的是f4（x）=﹣csx（）A、﹣sinxB、sinxC、cosxD、﹣cosx二、填空题（共9小题）22、若（﹣4，3）是角终边上一点，则Z的值为．23、△ABC的三个内角为A、B、C，当A为°时，取得最大值，且这个最大值为．24、化简：=25、化简：= ．26、已知，则f（1）+f（2）+f（3）+…+f（2009）= ．27、已知tanθ=3，则（π﹣θ）= ．28、sin（π+）sin（2π+）sin（3π+）…sin（2010π+）的值等于．29、f（x）=，则f（1°）+f（2°）+…+f（58°）+f（59°）= ．30、若，且，则cos（2π﹣α）的值是．答案与评分标准一、选择题（共21小题）1、已知函数f（x）=sin，g（x）=tan（π﹣x），则（）A、f（x）与g（x）都是奇函数B、f（x）与g（x）都是偶函数C、f（x）是奇函数，g（x）是偶函数D、f（x）是偶函数，g（x）是奇函数考点：函数奇偶性的判断；运用诱导公式化简求值。

(完整版)三角函数诱导公式专项练习(含答案)

三角函数诱导公式专项练习学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．sin (−600∘)=（） A ． −√32 B ． −12C ． 12D ．√322．cos 11π3的值为（） A ． −√32B ． −12 C ．√32D ． 123．已知sin(30°+α)=√32，则cos （60°–α）的值为A ． 12 B ． −12 C ．√32 D ． –√324．已知 cos (π2+α)=−35，且 α∈(π2,π)，则tan (α−π)=（） A ． −34 B ． −43 C ． 34 D ． 435．已知sin(π－α)＝－23，且α∈(－π2，0)，则tan(2π－α)的值为( )A ．2√55B ．－2√55C ． ±2√55 D ．√526．已知cos(π4−α)=√24，则sin(α+π4)=( )A ． −34B ． 14C ． √24D ．√1447．已知sinα=35，π2<α<3π2，则sin(7π2−α)=（） A ． 35B ． −35C ． 45D ． −458．已知 tanx =−125, x ∈(π2,π)，则cos⁡(−x +3π2)=（）A ．513B ． -513C ．1213D ． -12139．如果cos(π+A)=−12，那么sin(π2+A)= A ． -12 B ． 12 C ． 1 D ． -1 10．已知cos(π2−α)−3cosαsinα−cos (π+α)=2，则tanα=（） A ． 15 B ． −23 C ． 12 D ． −5 11．化简cos480∘的值是（）A．12B．−12C．√32D．−√3212．cos(−585°)的值是（）A．√22B．√32C．−√32D．−√2213．已知角α的终边经过点P(−5,−12)，则sin(3π2+α)的值等于()A．−513B．−1213C．513D．121314．已知cos(π+α)=23，则tanα=（）A．√52B．2√55C．±√52D．±2√5515．已知cosα=15,−π2<α<0,则cos(π2+α)tan(α+π)cos(−α)tanα的值为（）A．2√6B．−2√6C．−√612D．√61216．已知sinα=13,α∈(π2,π)则cos(−α)=（）A．13B．−13C．2√23D．−2√2317．已知sin(π+α)=45，且α是第四象限角，则cos(α−2π)的值是( )A．−35B．35C．±35D．4518．已知sin＝，则cos＝( ) A．B．C．－D．－19．已知cos α＝k，k∈R，α∈，则sin(π＋α)＝( ) A．－B．C．±D．－k20．＝( )A．sin 2－cos 2B．sin 2＋cos 2C．±(sin 2－cos 2)D．cos 2－sin 221．sin585∘的值为A．√22B．−√22C．√32D．−√3222．sin(−1020°)=（）A．12B．−12C．√32D．−√3223．若α∈(0,π)，sin(π−α)+cosα=√23，则sinα−cosα的值为（）A ．√23B ． −√23C ． 43 D ． −4324．已知α∈(π2,π)且sin (π+α)=−35，则tan α=（） A ． −34B ． 43C ． 34D ． −4325．已知sin (π2+θ)+3cos (π−θ)=sin (−θ)，则sinθcosθ+cos 2θ=( )A ． 15B ． 25C ． 35 D ．√5526．若sinθ−cosθ=43，且θ∈(34π,π)，则sin(π−θ)−cos(π−θ)=（） A ． −√23B ．√23C ． −43D ． 4327．已知sin (π2+θ)+3cos (π−θ)=sin (−θ)，则sinθcosθ+cos 2θ=( ) A ． 15 B ． 25 C ． 35 D ． √5528．已知sin(2015π2+α)=13，则cos(π−2α)的值为（）A ． 13 B ． -13 C ． 79 D ． −79 29．若α∈(0,π)，sin(π−α)+cosα=√23，则sinα−cosα的值为（）A ．√23B ． −√23C ． 43 D ． −4330．已知a =tan (−π6),b =cos (−23π4),c =sin25π3，则a,b,c 的大小关系是( )A ． b >a >cB ． a >b >cC ． c >b >aD ． a >c >b 31．cos7500= A ．√32B ． 12C ． −√32D ． −1232．sin (−236π)的值等于（）A ．√32B ． −12 C ． 12 D ． −√3233．sin300°+tan600°+cos (−210°)的值的（） A ． −√3 B ． 0 C ． −12+√32D ． 12+√3234．已知α∈(π2,3π2)，tan(α−π)=−34，则sinα+cosα等于（）． A ． ±15 B ． −15 C ． 15 D ． −75 35．已知sin1100=a ，则cos200的值为（）A ． aB ． −aC ． √1−a 2D ． −√1−a 2 36．点A (cos2018∘,tan2018∘)在直角坐标平面上位于（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 37．如果sin (π−α)=13，那么sin (π+α)−cos (π2−α)等于（） A ． −23B ． 23C ．2√23 D ． −2√2338．已知角α的终边过点(a,−2)，若tan (π+α)=3，则实数a = A ． 6 B ． −23C ． −6D ． 2339．cos (2π+α)tan (π+α)sin (π−α)cos (π2−α)cos (−α)=A ． 1B ． −1C ． tan αD ． −tan α 40．已知sin (−α)=−√53，则cos (π2+α)的值为（）A ． √53B ． −√53C ． 23 D ． −23参考答案1．D【解析】【分析】直接运用诱导公式，转化为特殊角的三角函数值求解。

三角函数诱导公式练习题--答案