高考数学复习专题比大小全套练习题及答案解析

合集下载

专题04比较大小(解析版)

《比较大小》专项突破高考定位比较大小题型每年必考，而且以多种形式出现，可以囊括高中各部分知识，综合性极强，该题型很好的考察了学生的综合素养。

考点解析（1）特殊值法（2）单调性法（3)基本不等式法（4）放缩法（5）图像法（6）作差法（7）作商法（8）构造法（9）反证法题型解析类型一、特殊值法例1-1．已知111,,,a b a M a N a P b a b <<===，则,,M N P 的大小关系正确的为（） A ．N M P <，即N M >，又幂函数a y x =在()0,∞+上单调递增，a a ab ∴>，即M P >，N M P ∴>>，故选：B.例1-2．设02x π<<，记lnsin a x =，sin b x =，sin x c e =，则比较a ，b ，c 的大小关系为（） A ．a b c <，所以a b c <<，故选：A例1-3．已知()()2221,2,2,2,2x x xx a b c ∈===，则,,a b c 的大小关系为（） A ．a b c >>B ．b c a >>C ．b a c >>D ．c a b >> 【答案】B【分析】根据指数函数的单调性，将问题转化为比较当()1,2x ∈时2,2,2x x x 的大小，利用特值法即可求得结果.【详解】因为()2222x x b ==，函数2x y =是单调增函数，所以比较a ，b ，c 的大小，只需比较当()1,2x ∈时2,2,2x x x 的大小即可.用特殊值法，取 1.5x =，容易知3222.25,23,22x x x ===，再对其均平方得()()()2222232.25 5.0625,29,228x x x =====，显然()()()22232229228 2.25 5.0625x x x =>==>==，所以222x x x >>，所以b c a >>故选：B.【点睛】本题考查利用指数函数的单调性比较指数式的大小关系，属基础题.本题解题的关键在于将问题转化为比较当()1,2x ∈时2,2,2x x x 的大小，再通过特殊值法即可得答案.例1-4．设0x y >>，1x y +=，若1ya x ⎛⎫= ⎪⎝⎭，1log xyb xy ⎛⎫ ⎪⎝⎭=，1log yc x =，则实数a ，b ，c 的大小关系是（）A ．a b c <>，1x y +=可知01y x <<<，结合不等式性质知11x >，01xy <<，1111xy y x >>>，再利用指数函数、对数函数的性质直接求解．【详解】 0x y >>，1x y +=，01y x ∴<<<利用不等式性质可知11x>，01xy <<，1111xy y x >>>， ∴011()()1y a x x=>=，1()log 10xy b xy ==-<，111log 1log log 1y y y c x y =>>=-， ∴实数a ，b ，c 的大小关系为b c a <<．故选：C.【点睛】方法点睛：本题考查指数对数的大小判断，判断方法：解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1，考查学生的转化能力，属于基础题.类型二、单调性法例2-1．设233344443,,332a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则,,a b c 的大小关系是（） A ．a c b >>B ．a b c >>C ．c b a >>D ．b c a >> 【答案】C【分析】根据指数函数43⎛⎫= ⎪⎝⎭x y 与幂函数34y x =的单调性判断,,a b c 的大小关系. 【详解】因为函数43⎛⎫= ⎪⎝⎭x y 在R 上是增函数，所以23344433<⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，即a b <，又因为函数34y x =在(0,)+∞上是增函数，所以33444332⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，所以b c <，故a b c <<.故选：C练．已知 4.10.90.1445,,554a b c -⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则这三个数的大小关系为（） A ．a c b >>B ．b c a >>C ．c a b >>D ．c b a >> 【答案】B【分析】利用指数函数的单调性即可比较大小.【详解】0.90.94554b -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，因为54xy ⎛⎫= ⎪⎝⎭在R 上单调递增﹐则1b c >>，又 4.1044155a ⎛⎫⎛⎫=<= ⎪ ⎪⎝⎭⎝⎭. 故b c a >>.故选：B.练．设3log πa =，32log 2b =，1ln e 4c =，则a ，b ，c 大小关系为（）A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >> 【答案】B【分析】根据指数函数、对数函数的性质判断可得；【详解】解：因为1ln ln10e<=，所以1ln 0e 0441<<=，即01c <<，又2333332log 2log 2log 4log log 31π==>>=，即1b a >>，所以b a c >>；故选：B类型三、简单同构法（同底、同指、同真、同分母、同分子等）例3-1．已知43a =，3log 4b =，0.13c -=，则a 、b 、c 的大小关系为（） A ．a b c >>B ．c b a >>C ．b a c >>D ．a c b >> 【答案】A【分析】首先根据题意得到4333log 3log 4>，从而得到a b >，又根据3log 41b =>，100.313c -<==，从而得到b c >，即可得到答案.【详解】因为4334log 33a ==， 344333=3=81464⎛⎫>= ⎪⎝⎭，所以4333log 3log 4>，即a b >.又因为33log 4log 31b =>=，100.313c -<==，即b c >，所以a b c >>.故选：A练．已知2516log 3,log 9,0.3a a b c -===，则a ，b ，c 的大小关系是（）A ．a >b >cB ．a >c >bC ．c >a >bD ．c >b >a【答案】D【分析】利用对数运算、指数运算化简,b c ，结合对数函数的性质比较三者的大小关系.【详解】22444log 3log 3log 41b ==<=，所以01a b <<<，5555325log log log 5253log 32231010100.30.3110333a c --⎛⎫⎛⎫⎛⎫====>=> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以cb a >>.故选：D例3-2．已知ln 22a =，ln33b =，ln 55c =，则a ，b ，c 的大小关系为（） A ．a b c <，所以a c >，所以c ab <<.故选：D.练．已知12019ln 20202020a =+，12020ln 20212021b =+，12021ln 20222022c =+，则a ，b ，c 的大小关系是（）A ．a b c >>B ．a c b >>C ．c b a >>D ．c a b >>【答案】A【分析】根据三个数的形式，构造函数，利用导数判断函数的单调性，最后根据单调性进行比较大小即可.【详解】构造函数()ln 1f x x x =+-，()111x f x x x -'=-=，当01x <<时，()0f x '>， ()f x 单调递增，所以111202*********f f f ⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，a b c >>. 故选：A练．已知ln 22a =，1b e =，ln 33c =，则a 、b 、c 的大小关系为（） A ．b c a <>，令a c -，结合对数的运算性质可判断出c a >，从而可选出正确答案.【详解】解：设()ln x f x x =，则()21ln x f x x-'=，当0x e <<时，()0f x '>；当x e >时，()0f x '<，则()f x 在()0,e 上单调递增，在(),e +∞上单调递减，则当x e =时，()max ln 1e f x e e ==，即,b a b c >>； ln 2ln 33ln 22ln 3ln8ln 902366a c ---=-==<，则c a >，所以bc a >>，故选：C ．【点睛】思路点睛：比较几个数的大小关系时，常用的思路是：1、求出函数的单调性，结合增减性进行判断；2、利用作差法，判断两数与零的关系；3、利用作商法，判断两数与1的关系.练．已知7log 22a =，7log 33b =，7log 66c =，则a ，b ，c 的大小关系为（） A ．a b c >>B ．b a c >>C ．a c b >>D ．b c a >> 【答案】B【分析】先把a 、b 、c 化为“同构”形式，利用函数的单调性判断大小.【详解】∵log log m a a m b b =， ∵777log lo 6g 23g 2826lo a ===， 777log 3lo 6g 2g 3936lo b ===7log 66c = 因为7log y x =为增函数，所以777log 6log 8log 9<<，所以b a c >>.故选：B【点睛】指、对数比较大小：（1）结构相同的，构造函数，利用函数的单调性比较大小；（2）结构不同的，寻找“中间桥梁”，通常与0、1比较.练．已知e a =，33log e b =，5ln 5c =，则a ，b ，c 的大小关系为（） A ．c a b <<B ．a c b <<C ．b c a <<D ．a b c <<【答案】D【分析】设()ln x f x x =，e x ≥，利用导数判断函数的单调性，利用函数的单调性比较函数值的大小；【详解】解：设()ln x f x x=，e x ≥，则()2ln 10(ln )x f x x -'=≥恒成立，∵函数()f x 在[e )+∞，上单调递增，又(e)a f =，333log e (3)ln 3b f ===，5(5)ln 5c f ==，∵e 35<<，()()()e 35f f f ∴<<，∵a b c <<，故选：D . 例3-3．已知0a b c d <<<<，若c a a c =，则d b 与b d 的大小关系为（）A ．d b b d D ．不确定【分析】由c a a c =得ln ln a c a c =，构造新函数ln x y x =，利用导数讨论ln x y x =的单调性，从而判断出ln ln ln b c d b c d >>，即可得到d bb d >.【详解】因为c a a c =，所以ln ln c a a c =，即ln ln aca c =，设ln x y x =，则21ln x y x -'=，令21ln xy x -'==0，得x e =，当(0,)x e ∈时，0y '>，ln xy x =单调递增，当(,)x e ∈+∞时，0y '<，ln xy x =单调递减；因为ln ln aca c =，0abcd <<<<，所以ae c <<，所以ln ln ln b cdb c d >>，即d b b d >.故选：C.【点睛】指、对数比较大小：（1）结构相同的，构造函数，利用函数的单调性比较大小；（2）结构不同的，寻找“中间桥梁”，通常与0、1比较.练．若e a =π，3e b =，3c π=，则a ，b ，c 的大小关系为（） A ．b a c <，再构造函数，利用导数得到函数的单调性得到a c <，即可得到答案.【详解】因为3x y =在R 上为增函数，所以33e π<，即b c <.因为e y x =在(0,)+∞为增函数，所以3e e π>，即a b >. 设ln ()x f x x=， 21ln ()x f x x -'=，令()0f x '=，x e =. (0,)x e ∈，()0f x '>，()f x 为增函数，(,)x e ∈+∞，()0f x '<，()f x 为减函数.则()(3)f f π<，即ln ln 33ππ<，因此3ln ln3ππ<，即3ln ln 3ππ<，33ππ<.又33e πππ<<，所以a c <.所以b a c <<.故选：A【点睛】本题主要考查指数和幂的比较大小，利用导数得到函数的单调性来比较大小为解决本题的关键，属于中档题.练．已知5ln 4a π=，4ln5b π=，45ln c π=，则a ，b ，c 的大小关系是A ．c b a <∴>∴>，同理可得：44ln ln 4,4ln ln 4,4,5ln 5ln 4,4c a ππππππππ>∴>∴>∴>∴>， ∵b a c <<.故选：C.【点睛】本题考查了利用导数研究函数的单调性、对数函数的单调性，考查了推理能力与计算能力，属于中档题.类型四、中间量例4-1．若0.80.2a =，0.20.8b =，0.31.1c =，lg0.2d =，则a ，b ，c ，d 的大小关系是（） A ．c b a d >>>B ．c a b d >>>C ．b c a d >>>D ．a c b d >>>【答案】A【分析】由指数函数、幂函数以及对数函数的单调性比较大小即可.【详解】由指数函数的单调性知：0.20.80.20.2>，0.301.1 1.11>=由幂函数的单调性知：0.20.20.80.2>，所以0.20.20.810.80.20.20c b a >>=>>=>，又由对数函数的单调性可知：lg 0.2lg10d =<=综上有：c b a d >>>.故选：A例4-2．已知1253a -⎛⎫= ⎪⎝⎭，2log 5b =，3log 7c =，则a ，b ，c 的大小顺序是（） A ．a b c >>B ．c a b >>C ．c b a >>D ．b c a >> 【答案】D【分析】由11225335-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，22log 5log 4>，333log 3log 7log 9<<判断.【详解】因为112253135a -⎛⎫⎛⎫==< ⎪ ⎪⎝⎭⎝⎭，22log 5log 42b =>=，3331log 3log 7log 92c =<=<=，所以b c a >>故选：D练．已知a =b =2log 3c =，则a ，b ，c 的大小关系为（）A ．b a c >>B ．a c b >>C ．a b c >>D ．b c a >>【答案】C【分析】根据指数运算与对数的性质，求得2a >，2b <，12c <<，再结合22log log 3b c ==，利用对数函数的单调性，即可求解.【详解】根据指数运算与对数运算的性质，可得122a =>=，2b =<，2log 3(1,2)c =∈，设22log log 3b c =，因为函数2log y x =为增函数，由于8523>，所以b c >，所以a b c >>.故选：C.练．已知0.352,ln 2,2a b c ===，则,,a b c 的大小关系为（）A ．a b c >>B ．c b a >>C ．b c a >>D ．c a b >> 【答案】B【分析】根据指数式与对数式互化公式，结合指数函数和对数函数的性质进行判断即可.【详解】由51log 2log log 522a a a =⇒==<，由112b >>>，0.312c =>，所以c b a >>，故选：B类型五、放缩法例5-1．若1(,1)x e -∈，ln a x =，ln 1()2x b =，ln 2x c =，则a ，b ，c 的大小关系为（） A ．c b a >>B ．b a c >>C ．a b c >>D ．b c a >>【答案】D【分析】先利用ln y x =的单调性求出a 值范围；再利用2x y =的单调性比较b 和c 的大小而得解.【详解】因1(,1)x e -∈，且函数ln y x =是增函数，于是10a -<<；函数2x y =是增函数，1ln 0ln 1x x -<<<-<，而ln ln 1()22x x -=，则ln 11()22x <<，ln 1212x <<，即1122c b <<<<，综上得：b c a >>故选：D练．设02x π<<，记lnsin a x =，sin b x =，sin x c e =，则比较a ，b ，c 的大小关系为（）A ．a b c <，所以a b c <<，故选：A练．已知sin3a =，3log sin 3b =，sin33c =，则a ，b ，c 的大小关系是（） A ．a b c >> B ．b a c >>C ．c a b >>D ．c b a >>【答案】C【分析】利用指数函数、对数函数以及三角函数值即可得出选项.【详解】因为32ππ<<，所以()sin30,1a =∈，33log sin 3log 10b =<=，sin30331c =>=，所以c a b >>.故选：C练．已知0.32=a ， 1.12.3b =，3log 6c =，则a ，b ，c 的大小关系为（）A ．c a b <，332log 6log 1.5c >=>，所以a ，b ，c 的大小关系为a c b <<.故选：C.类型六、比较法例6-1作差法．设2log 3a =，32log 2b =，32log 2c =-，则a ，b ，c 的大小顺序为（）A ．b c a <=即可得解.【详解】由33333392log 2log 9log 2log log 42log 22c b =-=-=>==，23log 3log 222220a c -=+->>-=，所以a c >，所以a c b >>，故选：A.【点睛】本题考查了对数函数的比较大小，对数函数的比较大小是高考中重点考查对象，考查了利用中间量以及作差法比较大小，考查了变形转化以及对数的运算能力，比较大小有以下几种方法：（1）利用函数单调性比较大小；（2）中间量法比较大小；（3）作差法、作商法比较大小.例6-2作商法．已知0.75a =，52log 2=b ，21log 32=c ，则a 、b 、c 的大小关系是（） A ．a c b <，故85165>，因为5832<，故8532<，所以8555558225222log 24log 2log 16log 511log 3log 3log 3log 22b c ===>=，所以b c >，故a c b <<，故选：A【点睛】关键点点睛：根据对数的运算性质将a 写成对数345log 5，342log 2，利用函数的单调性比较真数大小即可，利用作商及放缩的方法可得,b c 的大小，属于较难题目. 练．已知1ln 23a =，24log 25b =，25log 26c =，则a ，b ，c 的大小关系为 A ．a b c >>B ．a c b >>C ．c b a >>D ．b c a >> 【答案】D【分析】先由题，易知1ln 231a =<，而2425log 251,?log 261b c =>=>，再将b ，c 作商，利用对数的运算以及基本不等式，求得比值与1作比较即可得出答案.【详解】因为1ln 02<，故1ln 231a =< 2425log 251,?log 261b c =>=>2225252525252524log 26log 26log 241log 26log 24()[log (251)(251)]1log 2524c b +==⋅<=+⋅-< 所以c b < ，即b c a >>故选D【点睛】本题考查了对数的运算以及基本不等式的综合，解题的关键是在于运算的技巧以及性质，属于中档偏上题型.类型七、图像法例7-1．若()122211log ,0,222a b c a b b c -⎛⎫⎛⎫==>= ⎪ ⎪⎝⎭⎝⎭，则,,a b c 的大小关系是（） A ．c a b <<B ．c b a <<C ．a c b <<D ．b c a <<【答案】B【分析】分别画出函数1221(),log ,2x y y x y x ===的图象，由图象交点坐标，即可判断得出,,a b c 的大小关系.【详解】分别画出函数1221(),log ,2x y y x y x ===的图象，如图所示，由图象，可得c b a <<.故选：B.练．若44log x x -=，144log y y =，44log 0z z -+=，则实数x ，y ，z 的大小关系为（） A ．x y z <<B ．z y x <<C ．z x y <<D ．y z x <<【答案】D【分析】利用指数与对数函数的单调性，确定各方程根的范围，进而比较它们的大小.【详解】对于44log x x -=，由()4x f x -=与4()log g x x =有交点，()f x 过一、二象限，()g x 过一、四象限，∵()f x 与()g x 的交点必在第一象限且()f x 单调递减、()g x 单调递增，而1(1)(1)04f g =>=，11(2)(2)162f g =<=，可得()1,2x ∈，对于144log y y =，由()4y m y =与14()log n y y =有交点，()m y 过一、二象限，()n y 过一、四象限，∵()m y 与()n y 的交点必在第一象限且()m y 单调递增、()n y 单调递减，而(0)1m =，0lim ()y n y +→→+∞，111()2()222m n =>=，可得10,2y ⎛⎫∈ ⎪⎝⎭，对于44log 0z z -+=，显然有12z =， ∵x ，y ，z 的大小关系为y z x <<，故选：D.例7-2．已知,,(0,)a b c ∈+∞，且ln 1a a =-，ln 1b b =，e 1c c =，则a ，b ，c 的大小关系是（）A ．c b a <<B ．a b c <<C ．c a b <<D ．b a c <<【答案】C【分析】由题意可得ln 1a a =-，1ln b b =，1e c c =.依次作出e x y =，ln y x =，1y x =-，1y x =在(0,)+∞上的图像，然后根据函数图像可求得答案【详解】ln 1a a =-，1ln b b =，1e c c =.依次作出e x y =，ln y x =，1y x =-，1y x =在(0,)+∞上的图像，如图所示.由图像可知01c <<，1a =，1b >，所以c a b <<.故选：C.练．正实数a ，b ，c 满足22a a -+=，33b b +=，4log 4c c +=，则实数a ，b ，c 之间的大小关系为（）A ．b a c <<B ．a b c <<C ．a c b <<D ．b c a <<【答案】A【分析】将22a a -+=，33b b +=，4log 4c c +=，转化为函数13x y =+，122x y =+，4log y x =与4y x =-的图象交点的横坐标，利用数形结合法求解.【详解】4log 4c c +=4log 4c c ⇒=-，即c 为函数4log y x =与4y x =-的图象交点的横坐标，33b b +=134b b ⇒+=-，即b 为函数13x y =+与4y x =-的图象交点的横坐标，22a a -+=1242a a ⇒+=-，即a 为函数122x y =+与4y x =-的图象交点的横坐标，在同一坐标系中画出图象，如图所示：由图象可知：b a c <<.故选：A.练．已知5630x y ==，log x z y =，则x ，y ，z 的大小关系为（）A ．x y z <<B ．z y x <<C ．y x z <<D ．z x y <<【答案】B【分析】首先对5630x y ==取对数，可比较x ，y 的大小关系，利用对数的运算判断,x y 与1的大小关系，即可利用单调性判断z 的范围，进而可得出x ，y ，z 的大小关系.【详解】对5630x y ==两边同时取常用对数可得lg 5lg 6lg 30x y ==, 所以lg 30lg 5x =，lg 30lg 6y =，因为lg y x =在()0,∞+单调递增，所以0lg5lg6<<，所以lg30lg30lg5lg 6>，即x y >，又因为5lg30lg5lg 61log 61lg5lg5x +===+>， 6lg30lg5lg 61log 51lg 6lg 6y +===+>，所以0log log 1x x z y x <=<=，所以z y x <<.故选：B.【点睛】关键点点睛：本题解题的关键点是取对数判断x ，y 的大小关系，判断x 与1的关系利用单调性得出z 的范围.类型八、方程中隐含条件例8-1．已知正数x ，y ，z 满足ln z x y ye zx ==，则x ，y ，z 的大小关系为（） A ．x y z >>B ．y x z >>C ．x z y >>D ．以上均不对【答案】A【分析】将z 看成常数，然后根据题意表示出,x y ，再作差比较出大小即可【详解】解：由ln z x y ye zx ==，得ln x y zx =，则ln z y =，得z y e =，所以z ze e zx ⋅=，所以2ze x z =，令()(0)z f z e z z =->，则()10z f z e -'=>，所以函数()f z 在(0,)+∞上单调递增，所以0()(0)01f z f e >=-=，所以z e z >，即y z > 所以22()0z z z z z z e e ze e e z x y e z z z---=-==>，所以x y >，综上x y z >>，故选：A练．设正实数a ，b ，c ，满足2ln 2a c e b b ce ===，则a ，b ，c 的大小关系为（） A ．a b c <，利用导数判断函数的单调性，并判断c 的范围，通过变形得c b e =，得,b c 的大小关系，再直接解方程求a 的范围，最后三个数比较大小.【详解】设()(0)x f x xe x =>，0x >时，()()10x f x x e '=+>恒成立，()f x 在(0,)+∞单调递增，1,12x ⎛⎫∈ ⎪⎝⎭时，()f x e ⎫∈⎪⎝⎭，2<，所以1,12c ⎛⎫∈ ⎪⎝⎭，ln ln ln b c b b b e ce =⋅=，故ln b c =，即)c b e e =∈，而ln 2122a =<，所以a c b <<．故选：B【点睛】关键点点睛：本题的关键是构造函数()(0)x f x xe x =>，并且根据指对互化ln ln ln b b b b e =⋅，这样根据单调性可得ln b c =.练．设x ，y ，z 为正实数，且235log log log 1x y z ==>，则2x ，3y ，5z 的大小关系是（） A ．532z y x <，可得：22,33,55k k k x y z =>=>=>,然后变形，构造函数，利用幂函数的单调性即可得出．【详解】,,x y z 为正实数，且235log log log 1x y z k ===>，可得22,33,55k k k x y z =>=>=>． ∵11121,31,51235k k k x y z ---=>=>=>，令()1k f x x -=，又()f x 在()0+∞，上单调递增， ∵()()()532f f f >>，即532z y x >>，故选：B ．【点睛】关键点睛：本题的关键是指数式与对数式的互化、构造幂函数并运用其的单调性．例8-2．已知a 、b 、c 均为不等于1的正实数，且ln ln a c b =，ln ln c b a =，则a 、b 、c 的大小关系是（）A ．c a b >>B ．b c a >>C ．a b c >>D ．a c b >>【答案】A【分析】分析可知，ln a 、ln b 、ln c 同号，分a 、b 、()0,1c ∈和a 、b 、()1,c ∈+∞两种情况讨论，结合对数函数的单调性可得出a 、b 、c 的大小关系.【详解】ln ln a c b =，ln ln c b a =，且a 、b 、c 均为不等于1的正实数，则ln a 与ln b 同号，ln c 与ln a 同号，从而ln a 、ln b 、ln c 同号.∵若a 、b 、()0,1c ∈，则ln a 、ln b 、ln c 均为负数，ln ln ln a c b b =>，可得a b >，ln ln ln c b a a =>，可得c a >，此时c a b >>；∵若a 、b 、()1,c ∈+∞，则ln a 、ln b 、ln c 均为正数，ln ln ln a c b b =>，可得a b >，ln ln ln c b a a =>，可得c a >，此时c a b >>.综上所述，c a b >>.故选：A.【点睛】思路点睛：解答比较函数值大小问题，常见的思路有两个：（1）判断各个数值所在的区间；（2）利用函数的单调性直接解答.数值比较多的比较大小问题也也可以利用两种方法的综合应用.练．已知大于1的三个实数,,a b c 满足2(lg )2lg lg lg lg 0a a b b c -+=，则,,a b c 的大小关系不可能是（）A ．a b c ==B ．a b c >>C ．b c a >>D ．b a c >> 【答案】D【分析】令()22lg lg lg f x x x b b c =-+，则lg a 为()f x 的零点，根据判别式可得b c ≥，就b c =和b c >分类讨论后可得,,a b c 的大小关系.【详解】令()22lg lg lg f x x x b b c =-+，则lg a 为()f x 的零点且该函数图象的对称轴为lg x b =，故24lg 4lg lg 0b b c ∆=-≥，因为1,1b c >>，故lg 0,lg 0b c >>，所以lg lg b c ≥即b c ≥.又()()()()22lg lg lg lg lg lg lg ,lg lg lg lg lg lg lg f b b c b b c b f c c b c c c b =-=-=-=-，若b c =，则()()lg lg 0f b f c ==，故lg lg lg a b c ==即b c =.若b c >，则()()lg 0,lg 0f b f c <<，所以lg lg a c <或者lg lg b a <，即a c b <<或a b c >>.故选：D.【点睛】本题考查二次函数的零点，注意先根据方程的形式构建二次函数，再利用零点存在定理来讨论，注意合理分类，本题为中档题.例8-3．已知22,32a b a b +=+=，则lg b a 与lg a b 的大小关系是（）A ．lg lg b a a b D ．不确定【答案】C【分析】令()()2,3x x f x x g x x =+=+，结合题意可知01b a <<<，进而有b b a a b b >>，再利用对数函数的单调性和运算性质即可求解【详解】令()()2,3x x f x x g x x =+=+，则当0x >时，()()g x f x >，当0x <时，()()g x f x <；由22,32a b a b +=+=，得()()2,2f a g b ==考虑到()()2f a g b ==得01b a <<<，b b a a b b ∴>>由b a a b >，得()()lg lg b aab >，即lg lg b a a b >故选：C练．设实数a ，b 满足51118a b a +=，7915a b b +=，则a ，b 的大小关系为（） A ．a b D ．无法比较【答案】A【分析】从选项A 或C 出发，分析其对立面，推理导出矛盾结果或成立的结果即可得解.【详解】假设a b ≥，则1111a b ≥，77a b ≥，由51118a b a +=得51151118()()11818a a a a a +≥⇒+≥，因函数511()()()1818x x f x =+在R 上单调递减，又51116(1)1181818f =+=<，则()1(1)f a f ≥>，所以1a <；由7915a b a +=得797915()()11515b b b b b +≤⇒+≤，因函数79()()()1515x x g x =+在R 上单调递减，又7916(1)1151515g =+=>，则()1(1)g b g ≤<，所以1b >；即有1a b <<与假设a b ≥矛盾，所以a b <，故选：A【点睛】思路点睛：应用反证法解决问题时必须先否定结论，把结论的反面作为条件，且必须根据这一条件进行推理，否则，仅否定结论，不从结论的反面出发进行推理，就不是反证法．巩固训练（精选以一敌百）1．（多选）（2022·全国·高三期中）已知a ，b 为正数，且1a b -=，则（） A ．221a b +C ．222log log 2-<a bD ．211b b a+> 【答案】BD【详解】由于1a b -=，取1,2b a ==，代入四个选项对于A ：221a b +<，左边2251a b +=>故A 错误；对于C ，222log log 2a b -=，故C 错误2．（多选）（2022·江苏·南京市第一中学高三期中）已知实数,,x y z 满足ln 1y z x z e ⋅=⋅=.则下列关系式中可能成立的是（）A ．x y z >>B ．x z y >>C ．z x y >>D ．z y x >> 【答案】ABC 设1ln y x e k z ===，0k >，则k x e =，ln y k =，1z k=，画出函数图象，如图所示：当1k x =时，z x y >>；当2k x =时，x z y >>；当3k x =时，x y z >>；故选：ABC。

指、对、幂数比较大小问题【八大题型】(举一反三)(新高考专用)(解析版)2025年新高考数学一轮复习

指、对、幂数的大小比较问题【八大题型】【题型1 利用函数的性质比较大小】....................................................................................................................2【题型2 中间值法比较大小】................................................................................................................................3【题型3 特殊值法比较大小】................................................................................................................................4【题型4 作差法、作商法比较大小】....................................................................................................................6【题型5 构造函数法比较大小】............................................................................................................................7【题型6 数形结合比较大小】................................................................................................................................9【题型7 含变量问题比较大小】..........................................................................................................................12【题型8 放缩法比较大小】. (14)1、指、对、幂数的大小比较问题指数与对数是高中一个重要的知识点，也是高考必考考点，从近几年的高考情况来看，指、对、幂数的大小比较是高考重点考查的内容之一，是高考的热点问题，主要考查指数、对数的互化、运算性质，以及指数函数、对数函数和幂函数的性质，一般以选择题或填空题的形式考查.这类问题的主要解法是利用函数的性质与图象来求解，解题时要学会灵活的构造函数.【知识点1 指、对、幂数比较大小的一般方法】1.单调性法：当两个数都是指数幂或对数式时，可将其看成某个指数函数、对数函数或幂函数的函数值，然后利用该函数的单调性比较，具体情况如下：①底数相同，指数不同时，如1x a 和2x a ，利用指数函数x y a =的单调性；②指数相同，底数不同时，如1ax 和2ax ，利用幂函数a y x =单调性比较大小；③底数相同，真数不同时，如1log a x 和2log a x ，利用指数函数log a x 单调性比较大小.2.中间值法：当底数、指数、真数都不同时，要比较多个数的大小，就需要寻找中间变量0、1或者其它能判断大小关系的中间量，然后再各部分内再利用函数的性质比较大小，借助中间量进行大小关系的判定．3.作差法、作商法：(1)一般情况下，作差或者作商，可处理底数不一样的对数比大小；(2)作差或作商的难点在于后续变形处理，注意此处的常见技巧与方法.4.估算法：(1)估算要比较大小的两个值所在的大致区间；(2)可以对区间使用二分法(或利用指对转化)寻找合适的中间值，借助中间值比较大小.5.构造函数法：构造函数，观察总结“同构”规律，很多时候三个数比较大小，可能某一个数会被可以的隐藏了“同构”规律，所以可能优先从结构最接近的的两个数来寻找规律，灵活的构造函数来比较大小.6、放缩法：(1)对数，利用单调性，放缩底数，或者放缩真数；(2)指数和幂函数结合来放缩；(3)利用均值不等式的不等关系进行放缩.【题型1 利用函数的性质比较大小】【例1】（2024·湖南衡阳·模拟预测）已知a=30.3，b=0.33，c=log0.33，则a，b，c的大小关系是（）A．a>b>c B．b>a>c C．c>b>a D．c>a>b【解题思路】利用指数函数、对数函数的单调性可得答案.【解答过程】a=30.3>30=1，0<b=0.33<1=0.30，c=log0.33<log0.31=0，∴a>b>c.故选：A.，b=1.20.2，c=0.52.1，则a，b，c的大小关系是【变式1-1】（2024·四川自贡·三模）已知a=log213（）A．a<c1.20=1即b>1；因为y=0.5x为减函数，故0<0.52.1<0.50=1即0<c<1，综上a<c<b.故选：A.【变式1-2】（2024·贵州贵阳·三模）已知a=40.3,b=(log4a)4,c=log4(log4a)，则（）A．a>b>c B．a>c>b C．b>c>a D．c>a>b【解题思路】利用指数函数单调性得到a>1，利用指对运算和指数函数单调性得到0<b<1，利用对数函数单调性得到c<0，则比较出大小.【解答过程】因为a=40.3>40=1,b=(log4a)4=0.34<1，且0.34>0，则0<b<1，c=log4(log4a)=log40.3<0，所以a>b>c，故选：A.【变式1-3】（2024·山东泰安·模拟预测）已知a=log0.20.3，b=ln a，c=2a，则a,b,c的大小关系为（）A．c>b>a B．a>b>c C．b>a>c D．c>a>b【解题思路】利用对数函数的单调性求得a,b的范围，根据指数函数的单调性得c的范围，即可比较大小.【解答过程】因为y=log0.2x在(0,+∞)上单调递减，所以log0.21<log0.20.3<log0.20.2，即0<a<1，因为y=ln x在(0,+∞)上单调递增，所以ln a<ln1，即b<0，因为y=2x在R上单调递增，所以2a>20，即c>1，综上，c>a>b.故选：D.【题型2 中间值法比较大小】【例2】（23-24高三上·天津南开·阶段练习）已知a=e0.1，b=1―2lg2，c=2―log310，则a，b，c的大小关系是（）A．b>c>a B．a>b>c C．a>c>b D．b>a>c【解题思路】根据指、对数函数单调性，结合中间值0，1，分析判断即可.【解答过程】由题意可得：a=e0.1>e0=1，b=1―2lg2=1―lg4，且0=lg1<lg4<lg10=1，则0<b<1，因为log310>log39=2，则c=2―log310<0，故选：B.【变式2-1】（2024·陕西铜川·模拟预测）已知a=―12,b=log65,c=log56，则（）A．a<b<c B．c<b<a C．b<c<a D．a<c<b【解题思路】取两个中间值1和32，由a =>32，b <log 66=1，1=log 55<c <32即可比较三者大小.【解答过程】a =―12=>=32，b =log 65<log 66=1，1=log 55<log 56=c <log =32，因此b <c <a ．故选：C ．【变式2-2】（2024·山东潍坊·二模）已知a =e ―1，b =lg a ，c =e 0，则（）A ．b <a <c B ．b <c <a C ．a <b <cD ．c <b <a【解题思路】根据对数函数和指数函数单调性并结合中间量0和1即可比较大小.【解答过程】a =e ―1∈(0,1)，b =lg a =lge ―1=―lge <0，c =e 0=1，所以b <a <c ，故选：A.【变式2-3】（2024·天津北辰·三模）已知a =0.53.1，b =log 0.90.3，c =log 1312，则a ，b ，c 的大小关系为（）A ．c log 0.90.9=1，即b >1；可得c =log 1312=log 32，且y =log 3x 在(0,+∞)上单调递增，则12=log <log 32<log 33=1，即12<c <1；综上所述：a <c b >aB ．b >a >cC ．b >c >aD ．c >a >b【解题思路】利用幂函数、指数函数、对数函数的单调性，结合特殊值判定即可.【解答过程】因为y =log 0.5x 在(0,+∞)上单调递减，所以log 0.51<log 0.50.6<log 0.50.5，即0<a <1.因为y =x 0.6在(0,+∞)上单调递增，又0.49―0.3=0.7―0.6=，0.6―0.6=，又53>107>1>>10.6，故c >b >1，所以c >b >a .故选：A.【变式3-1】（23-24高二下·云南玉溪·期中）已知实数a,b,c 满足2a +a =2，2b +b =c =log 163，则（）A ．c <a <bB ．a <b <cC ．a <c <bD ．b <c <a【解题思路】由对数函数单调性得c <12，构造函数f(x)=2x +x,x ∈R ，由函数的单调性得12<a f(12)，即a >12，所以c <a b >d >cB ．a >b >c >dC ．b >d >a >cD ．a >d >b >c【解题思路】根据指数函数和对数函数的单调性判断即可.【解答过程】因为a =log 1314=log 34>log 33=1<<⇒13b >d >c .故选：A ．【变式3-3】（2024·天津和平·=2,b =log 123―log 129,c =―13，则有（）A ．a c 3得出b,c 大小.=2可得a =log 132<log 131=0，b =log 123―log 129=log 1213=log 23>1，c =―13=213=>0，下面比较b,c ，因为32>=8，所以3>232，所以b =log 23>log 2232=32，而c 3=3=2<=278，故c <32，所以c c >a .故选：B.【题型4 作差法、作商法比较大小】【例4】（2023·四川成都·一模）若a =3―14，b =―13，c =log 1225，则a ，b ，c 的大小关系为（）A ．a >b >cB ．b >c >aC ．c >a >bD ．c >b >a【解题思路】先根据指对函数的单调性可得0<a <1，01，再作商比较a,b 的大小，从而可求解.【解答过程】因为0<a =3―14<30=1，0log 12510>log 1212=1，所以c >b >a .故选：D.【变式4-1】（2023·贵州六盘水·模拟预测）若a =ln22，b =ln33，c =ln55，则（）A ．a 0，所以b >a ；又因为c ―a =ln55―ln22=2ln5―5ln210=ln25―ln3210<0，所以a >c ；综上所述：c <a <b .故选：C.【变式4-2】（2024·四川成都·二模）若a =ln 26,b =4ln2⋅ln 3,c =(1+ln3)2，则a,b,c 的大小关系是（）A ．c <a <bB ．a <b <cC ．c <b <aD ．b <a <c【解题思路】作差法比较a,b 的大小，利用对数的性质比较a,c 的大小.【解答过程】a =ln 26=(ln2+ln3)2，c =(lne +ln3)2因为ln2+ln3<lne +ln3，所以(ln2+ln3)2<(lne +ln3)2，即a <c ，a =ln 26=(ln2+ln3)2，b =4ln2⋅ln3，则a ―b =(ln2+ln3)2―4ln2⋅ln3=(ln2―ln3)2>0，即b <a ，所以b <a <c .故选：D.【变式4-3】（2024·全国·模拟预测）若a =20.4,b =30.25,c =log 0.70.5，则a,b,c 的大小关系为（）A ．a 1，所以b <a <因为0.52=0.25<0.343，故0.5<=0.732,y =log 0.7x 在(0,+∞)上单调递减，所以log 0.70.5>log 0.70.732=32>a <c ，所以实数a,b,c 的大小关系为b <a <c ，故选：B ．【题型5 构造函数法比较大小】【例5】（2024·全国·模拟预测）已知a =ln 72，b =ln7×ln2，c =ln7ln2，则（）A ．b <c <aB ．b <a <cC ．a ln7，故c 的值最大．下面比较a ，b 的大小．构造函数f (x )=ln x ―ln2―ln x ⋅ln2=(1―ln2)ln x ―ln2，显然f (x )在(0,+∞)上单调递增．因为f (8)=ln8―ln2―ln8⋅ln2=ln2(2―ln8)=ln2(lne 2―ln8)<0，所以a ―b =f (7)<f (8)<0，所以a b >cB ．a >c >bC ．b >a >cD ．b >c >a【解题思路】利用常见函数的单调性比较大小即可.【解答过程】先比较a 和b ，构造函数y =x 4在上(0,+∞)单调递增，∵5=5>625256=，∴514>54，即a >b ；又∵4b =5，4c =4log 45=log 454，且45=4×256>54=625，∴ 4c =log 454<log 445=5=4b ，∴b >c ，∴a >b >c .故选：A.【变式5-2】（2024·天津和平·一模）已知a =log 0.20.3,b =log 0.30.2,c =log 23，则a,b,c 的大小关系为（）A ．b <c <aB ．c 1，c =log 23>1，又b c=log 0.30.2⋅log 32=lg2―1lg3―1⋅lg2lg3=lg 22―lg2lg 23―lg3，因为函数f (x )=x 2―x =x―14，在0,f (0)=0，又因为12>lg3>lg2>0，所以f (lg3)<f (lg2)<0，所以f (lg2)f (lg3)<1，即lg 22―lg2lg 23―lg3<1，所以bc <1，∴b <c ，即a <b <c ．故选：C ．【变式5-3】（2023·河南·校联考模拟预测）已知实数a,b,c 满足a 2+log 2a =0,2023―b =log 2023b,c =log 7）A ．a 0，所以12<a <1；设g(x) =―log 2023x ， g(x)在(0,+∞)上单调递减，又g(1)=12023>0,g(2023)=―1<0，所以1< b <2023，因为c =log <log =12，所以c <12.综上可知，c <a log 3π=b >log 33=1，即a >b >1，∵a =ln π=2, c ==ln2下面比较2与 y =x 2与y =2x ，由指数函数y =2x 与幂函数y =x 2的图像与单调性可知，当x ∈(0,2)时，x 2<2x ；当x ∈(2,4)时，x 2>2x由x =(0,2)，故2 <ln π<a < c ，所以b <a <c ，故选：A.【变式6-1】（2023·江西赣州·二模）若log 3x =log 4y =log 5z <―1，则（）A ．3x <4y <5zB ．4y <3x <5zC ．4y <5z <3xD ．5z <4y <3x【解题思路】设log 3x =log 4y =log 5z =m <―1，得到x =3m ,y =4m ,z =5m ，画出图象，数形结合得到答案.【解答过程】令log 3x =log 4y =log 5z =m <―1，则x =3m ,y =4m ,z =5m ，3x =3m +1,4y =4m +1,5z =5m +1，其中m +1<0，在同一坐标系内画出y =3x ,y =4x ,y =5x ，故5z <4y <3x 故选：D.【变式6-2】（2024·全国·模拟预测）已知a ==log a b,a c =log 12c ，则实数a,b,c 的大小关系为（）A ．a a ，根据单调性得到c =c<=a ，从而得到答案.【解答过程】令f (x )=―x ，其在R 上单调递减，又f (0)=1>0,f (1)=12―1=―12<0，由零点存在性定理得a ∈(0,1)，则y =log a x 在(0,+∞)上单调递减，画出y 1=与y =log a x 的函数图象，可以得到b ∈(0,1)，又y 2=a x 在R 上单调递减，画出y 2=a x 与y 3=log 12x 的函数图象，可以看出c ∈(0,1)，<=1，故log a b <1=log a a ，故b >a ，因为a,c ∈(0,1)，故a c >a 1=a ，由a c=log 12c 得，c =c<=a ．综上，c <a y >zB ．x >z >yC ．z >x >yD ．z >y >x【解题思路】根据题意，将问题转化为函数y =2x ,y =3x ,y =log 5x 与直线y =t >1的交点的横坐标的关系，再作出图像，数形结合求解即可.【解答过程】解：因为x,y,z 均为大于0的实数，所以2x =3y =log 5z =t >1，进而将问题转化为函数y =2x ,y =3x ,y =log 5x 与直线y =t >1的交点的横坐标的关系，故作出函数图像，如图，由图可知z >x >y 故选：C.【题型7 含变量问题比较大小】【例7】（23-24高三上·天津滨海新·阶段练习）设a ､b ､c 都是正数，且4a =6b =9c ，则下列结论错误的是（）A ．c 1，所以a =log 4k =1log k 4，b =log 6k =1log k 6，c =log 9k =1log k 9，A.由对数函数的单调性可知，0<log k 4<log k 6<log k 9，可知c <b <a ，故A 正确；B.b (a +c )==1log k6⋅log k 36logk 4⋅log k 9=1log k6⋅2log k 6logk 4⋅log k 9=2logk 4⋅log k 9=2ac ，故B 错误；C.4a ⋅9c =(6b )2=36b =(4⋅9)b =4b ⋅9b ，故C 正确.D.1a +1c =log k 4+log k 9=log k 36=2log k 6=2b ，则1c =2b ―1a ，故D 正确.故选：B.【变式7-1】（2024·江西·模拟预测）若a e a =b ln b (a >0)，则（）A ．a <bB ．a =bC ．a >bD ．无法确定【解题思路】令a e a =b ln b =k ，k >0，构造函数，作出函数图象，即可比大小.【解答过程】因为a >0，所以a e a >a >0，因为a e a=b ln b，所以b ln b>0，可得b>1，令a e a=b ln b=k，k>0，所以e a=ka ,ln b=kb，设f(x)=e x，g(x)=ln x，ℎ(x)=kx，作出它们的图象如图：由图可知a<b.故选项A正确.故选：A.【变式7-2】（2023·全国·模拟预测）已知a,b,c均为不等于1的正实数，且ln c=a ln b,ln a=b ln c，则a,b,c的大小关系是（）A．c>a>b B．b>c>aC．a>b>c D．a>c>b【解题思路】分析可知，ln a、ln b、ln c同号，分a、b、c∈(0,1)和a、b、c∈(1,+∞)两种情况讨论，结合对数函数的单调性可得出a、b、c的大小关系.【解答过程】∵ln c=a ln b,ln a=b ln c且a、b、c均为不等于1的正实数，则ln c与ln b同号，ln c与ln a同号，从而ln a、ln b、ln c同号.①若a、b、c∈(0,1)，则ln a、ln b、ln c均为负数，ln a=b ln c>ln c，可得a>c，ln c=a ln b>ln b，可得c>b，此时a>c>b；②若a、b、c∈(1,+∞)，则ln a、ln b、ln c均为正数，ln a=b ln c>ln c，可得a>c，ln c=a ln b>ln b，可得c>b，此时a>c>b.综上所述，a>c>b.故选：D.【变式7-3】（2024·全国·模拟预测）已知正实数a，b，c满足e c+e―2a=e a+e―c，b=log23+log86，c+log2c=2，则a，b，c的大小关系为()A．a<b<c B．a<c<b C．c<a<b D．c<b<a【解题思路】根据e c+e―2a=e a+e―c可得e c―e―c=e a―e―2a，由此可构造函数f(x)=e x―e―x，根据f(x)的单调性即可判断a和c的大小；根据对数的计算法则和对数的性质可得b与2的大小关系；c+log2c=2变形为log2c=2―c，利用函数y=log2x与函数y=2―x的图象可判断两个函数的交点的横坐标c的范围，从而判断b与c的大小.由此即可得到答案．【解答过程】e c+e―2a=e a+e―c⇒e c―e―c=e a―e―2a，故令f(x)=e x―e―x，则f(c)=e c―e―c，f(a)=e a―e―a．和y=e x均为(0,+∞)上的增函数，故f(x)在(0,+∞)为增函数．易知y=―e―x=―1e x∵e―2a<e―a，故由题可知，e c―e―c=e a―e―2a>e a―e―a，即f(c)>f(a)，则c>a>0．易知b=log23+log=log2>2，log2c=2―c，作出函数y=log2x与函数y=2―x的图象，如图所示，则两图象交点横坐标在(1,2)内，即1<c<2，∴c<b，∴a<c<b．故选：B．【题型8 放缩法比较大小】【例8】（2024·陕西西安·模拟预测）若a=0.311.5,b=log312,c=log26,d=）A．a>b>c B．b>a>dC．c>a>b D．b>c>a【解题思路】由题意首先得0<a<1,d=<0，进一步b=log312=1+log34>2,c=log26=1+log23>2，从而我们只需要比较log34,log23的大小关系即可求解，两式作商结合基本不等式、换底公式即可比较.【解答过程】a =0.311.5<0.310=1，所以0<a <1,d =<0，b =log 312=1+log 34>2,c =log 26=1+log 23>2，又因为log 34log 23=ln4⋅ln2ln3⋅ln3<=<1，所以b <c ，即d <a b >cB ．c >b >aC ．b >a >cD ．c >a >b【解题思路】根据指数函数、对数函数的性质及基本不等式判断即可.【解答过程】因为a =log 35=12log 325<12log 327=32，34=<=b =>32且b <2，c =3log 72+log 87=log 78+log 87>=2，所以c >b >a .故选：B.【变式8-2】（2023上·安徽·高二校联考阶段练习）已知a ==6―34,c =log 53―29log 35，则（）A ．a =<=13，故b ∈c =log 53―29log 35=13log 527―19log 325>13log 525―19log 327=23―13=13，所以a 0,c >0，利用比商法结合基本不等式证明c 0，c =ln2.1>0，所以c b=ln2.1log 3.1e=ln2.1×ln3.1<==，又e 2≈7.389<e ，所以<lne =1，所以cb <1，故c e 2，所以>1，所以a <ln2，又ln2<ln2.1=c ，所以a <c ，所以a <c <b ，故选：A.一、单选题1．（2024·全国·模拟预测）设a =log 62，b =log 123，c =log 405，则（）A ．a <b <cB ．b <a <cC ．c <a <bD ．a <c <b【解题思路】取到数计算得1b =1+2lg2lg3，1c=1+3lg2lg5，作差法比较1b ,1c的大小，即可得到b,c 大小，利用中间值25即可比较a,c 大小.【解答过程】∵1b =log 312=1+log 34=1+lg4lg3=1+2lg2lg3，1c=log 540=1+log 58=1+lg8lg5=1+3lg2lg5，∴1b ―1c =2lg2lg3―3lg2lg5=2lg2×lg5―3lg2×lg3lg3×lg5=lg2(2lg5―3lg3)lg3×lg5=lg2(lg25―lg27)lg3×lg5<0，∴1b <1c ，又b >0，c >0，∴b >c .∵1c =1+log 58<1+log =1+log 5532=52，∴c >25；∵1a =log 26=1+log 23>1+log =1+log 2232=52，∴a <25，∴a <c .∴a <c 0>bB ．b >0>aC ．a >b >0D ．b >a >0【解题思路】由作差法，结合对数换底公式、对数运算性质、基本不等式比较得log 23>log 34>log 45，即可判断大小.【解答过程】由3m =4⇒m =log 34，log 23―log 34=lg3lg2―lg4lg3=lg 23―lg2⋅lg4lg2⋅lg3>=4lg 23―lg 284lg2⋅lg3=lg 29―lg 284lg2⋅lg3>0，log 34―log 45=lg4lg3―lg5lg4=lg 24―lg3⋅lg5lg3⋅lg4>=4lg 24―lg 2154lg3⋅lg4=lg 216―lg 2154lg3⋅lg4>0，∴log 23>log 34>log 45，∴b =4m ―5>4log 45―5=0，a =2m ―3<2log 23―3=0，∴b >0>a .故选：B.3．（2024·贵州毕节·一模）已知a =3log 83，b =―12log 1316，c =log 43，则a ，b ，c 的大小关系为（）A ．a >b >cB ．c >a >bC ．b >c >aD ．b >a >ca,b,c ，并判断范围，采用作差法结合基本不等式可判断a >b ，即可得答案.【解答过程】由题意可得a =3log 83=3×log 23log 223=log 23>1，b =―12log 1316=―12×log 316log 313=log 34>1，0<c =log 43<1，又log 23―log 34=lg3lg2―lg4lg3=(lg3)2―lg2lg4lg2lg3，由于lg2>0,lg4>0，lg2≠lg4,∴lg2lg4<(lg2+lg42)2=2<(lg3)2，故log 23―log 34>0,∴a >b ，综合可得a >b >c ，故选：A.4．（2023·内蒙古赤峰·模拟预测）设a =，b =，c =log 34(log 34)，则（）A ．c =1；由y =的值域，且在R 上单调递增可知，0log 33=1，由y =log 34x 在(0,+∞)上单调递减，故c =log 34(log 34)<log 341=0.结合上述分析可知：c <0c >bB ．a >b >cC ．b >c >aD ．c >b >a【解题思路】引入中间变量1，再利用作差法比较b,c 的大小，即可得答案；【解答过程】∵ a =e 13>e 0=1，b =ln2<lne =1，c =log 32<log 33=1∴ a 最大，∵ b ―c =ln2―log 32=lg2lge―lg2lg3=lg2⋅>0，∴ b >c ，∴ a >b >c ，故选：B.6．（2024·陕西宝鸡·一模）已知实数a,b,c 满足e 2a 2=e 3b 3=e 5c 5=2，则（）A ．a >b >cB ．a a >cD ．c >a >b【解题思路】先应用指对数转换求出a,b,c ,再转化成整数幂比较即可.【解答过程】因为e 2a2=e 3b 3=e 5c 5=2,所以e 2a =4,e 3b =6,e 5c =10,即得2a =ln 4,3b =ln 6,5c =ln10得a =ln 2,b ==因为y =ln x 是(0,+∞)上的增函数,比较a,b,c ,的大小关系 ,15次幂,因为幂函数y =x 15在(0,+∞)上是单调递增的，比较215,65,103即可,因为215=524288,65=7776,103=1000 所以215>103>65即2>>a >b >c .故选：A.7．（2023·湖南永州·一模）已知a =log 3π,b =1log 3π―1,c =12―log 3π，则（）A ．a 2，c ∈(1,2)，作差法判断出a <c ，从而求出答案.【解答过程】a =log 3π>log 33=1，因为332=>π，所以a =log 3π<log 3332=1.5，所以a ∈(1,1.5)，log 3π―1∈(0,0.5)，故b =1log3π―1>2，2―log 3π∈(0.5,1)，故c =12―log 3π∈(1,2)，令a ―c =log 3π―12―log 3π=2log 3π―(log 3π)2―12―log 3π=―(log 3π―1)22―log 3π<0所以a <c <b .故选：D.8．（2023·陕西西安·一模）已知函数f(x)=―2x ，若2a =log 2b =c ，则（）A ．f(b)<f(c)<f(a)B ．f(a)<f(b)<f(c)C ．f(a)<f(c)<f(b)D ．f(c)<f(b)<f(a)【解题思路】在同一坐标系中作y =c,y =2x ,y =log 2x,y =x 的图像,得到a <c 2―0.001B．log>log2π―1C．log1.85<log1.75D．log33.01>e―0.01【解题思路】利用指数函数的性质判断A；由对数函数的性质判断B，C；由对数函数的性质可得log3 3.01>1，由指数函数的性质可得e―0.01<1，即可判断．【解答过程】解：对于A，因为―0.01<―0.001，所以2―0.01<2―0.001，所以A错误；对于B，因为log>log2π2=log2π―1，所以B正确；对于C，因为log1.85>0,log1.75>0，所以log1.85=ln5ln1.8<ln5ln1.7=log1.75，所以C正确；对于D，因为log33.01>log33=1,e―0.01<e0=1，所以log33.01>e―0.01，所以D正确.故选：BCD．10．（2024·重庆·模拟预测）若b>c>1，0<a<1，则下列结论正确的是（）A．b a<c a B．log b a>log c aC．cb a<bc a D．b log c a>c log b a【解题思路】由已知可得，由幂函数性质可判断A; 由对数函数性质可判断B; 由幂函数性质可判断C;由不等式的性质可判断D.【解答过程】对于A：∵0<a<1，幂函数y=x a在(0,+∞)上单调递增，且b>c>1，∴b a>c a，故选项A错误；对于B：∵0<a<1，∴函数y=log x在(0,+∞)上单调递减，又∵b>c>1，∴log a b<log a c<log a1=0，∴0>1log b c >1log c a，即0>log b a>log c a，故B正确；对于选项C：∵0<a<1，则a―1<0，∵幂函数y=x a―1在(0,+∞)上单调递减，且b>c>1，∴b a―1<c a―1，∴cb a<bc a，故选项C正确；对于选项D：由选项B可知：0>log b a>log c a，∴0<―log b a<―log c a，∵b>c>1，∴c(―log b a)<b(―log c a)，∴b log c a<c log b a，故D错误.故选：BC.11．（2024·重庆·一模）已知3a=5b=15，则下列结论正确的是（）A．lg a>lg b B．a+b=abC>D．a+b>4【解题思路】根据指对互化与运算以及指数函数、对数函数单调性即可判断ABC，利用基本不等式即可判断D.【解答过程】由题意得a=log315>log31>0，b=log515>log51=0，0<1a =log153，0<1b=log155，则0<1a<1b，则a>b>0，对A，根据对数函数y=lg x在(0,+∞)上单调递增，则lg a>lg b，故A正确；对B，因为1a +1b=log153+log155=1，即a+bab=1，则a+b=ab，故B正确；对C，因为a>b>0，根据指数函数y=在R<，故C错误；对D，因为a>b>0，1a +1b=1，a+b=(a+b=2+ba +ab≥2+=4，当且仅当a=b时等号成立，而显然a≠b，则a+b>4，故D正确；故选：ABD.三、填空题12．（2023·北京昌平·二模）3―2,213,log25三个数中最大的数是log25.【解题思路】利用特殊值1和2作为“桥梁”比较大小即可.【解答过程】∵1<213=<23―2==19<1，log25>log24=2，∴log25>213>3―2，即三个数中最大的数是log25.故答案为：log25.13．（2024·北京通州·三模）已知a=2―1.1，b=log1413，c=log23，则三者大小关系为a<b<c（按从小到大顺序）【解题思路】根据指数函数和对数函数的性质确定出a,b,c的范围，即可求解.【解答过程】因为a=2―1.1<2―1=12，b=log1413=log43>log42=12，且b=log1413=log43<1，c=log23>log22=1，故a<b<c，故答案为：a 1，c =―12，从而得到大小关系.【解答过程】因为y =在(0,+∞)上单调递减，1>>故a =<=1且a =>=0，所以a ∈(0,1)，因为y =在R 上单调递减，<0，所以b =>=1，c ==lne―12=―12，故c <a e ，所以lnπ>lne =1，即x =lnπ∈(1,+∞)因为1<2<5，所以0=log 51<log 52<log 55=1，即log 52∈(0,1)，所以x >y ；（2）y =log 52<log =12，且log 52>0，所以log 52∈0,z =e ―12=>=12，所以e ―12∈+∞，所以y <z .16．（23-24高三·全国·对口高考）（1）比较a a b b 与b a a b (a >0,b >0)的大小；（2）已知a >2，比较log (a―1)a 与log a (a +1)大小【解题思路】（1）利用作商法，分类讨论即可；（2）利用做差法、换底公式以及不等式的性质分析即可.【解答过程】（1）因为a>0,b>0，所以a a b bb a a b=，所以①当a=b>0时，a a b bb a a b==1，所以a a b b=b a a b，②当a>b>0时，ab>1,a―b>0，>1，所以a a b b>b a a b，③当b>a>0时，0<ab<1,a―b<0，>1，所以a a b b>b a a b，综上所述：当a>0,b>0，a a b b≥b a a b.（2）log(a―1)a―log a(a+1)=lg alg(a―1)―lg(a+1)lg a=lg2a―lg(a+1)lg(a―1)lg a lg(a―1)，因为a>2，所以lg(a+1)>0,lg(a―1)>0,lg a>0，所以lg a lg(a―1)>0，由lg(a+1)lg(a―1)<=<=lg2a，所以lg2a―lg(a+1)lg(a―1)>0，所以lg2a―lg(a+1)lg(a―1)lg a lg(a―1)>0，即log(a―1)a―log a(a+1)>0，故log(a―1)a>log a(a+1).17．（23-24高一·湖南·课后作业）比较a，b，c的大小：(1)已知1<x<2，a=(log2x)2，b=log2x2，c=log2(log2x)；(2)已知a=log36，b=log510，c=log714．【解题思路】(1)根据1<x<2，求出log2x的范围，由此判断c＜0，0＜a＜b；(2)a=1+log32，b=1+log52，c=1+log72，由换底公式比较log32,log52,log72大小即可.【解答过程】（1）∵1<x<2，∴0=log21<log2x<log22=1，即log2x∈(0,1)，∴c=log2(log2x)<log21=0，a=(log2x)2<(log2x)1=log2x，∴0＜a<log2x，∴b=log2x2=2log2x>log2x>a，∴c＜0＜a＜b，∴c<a<b；（2）∵a=log36=log3(3×2)=1+log32，b=log510=log5(5×2)=1+log52，c=log714=log7(7×2)=1+log72，又∵0<lg3<lg5<lg7，∴lg2lg3>lg2lg5>lg2lg7，∴log32>log52>log72，∴1+log32>1+log52>1+log72，即a＞b＞c﹒18．（23-24高一上·广东江门·阶段练习）已知正实数x，y，z满足3x=4y=6z．（1）求证：1z ―1x=12y；（2）比较3x,4y,6z的大小．【解题思路】（1）令3x=4y=6z=m，利用指数式和对数式的互化求出x,y,z，再利用对数的运算即可的证得结果；（2）因为正实数x，y，z，利用作商法可证明大小关系.【解答过程】（1）证明：令3x=4y=6z=m，利用指数式和对数式的互化知x=log3m，y=log4m，z=log6m则1x =log m3，1y=log m4，1z=log m6∴1z ―1x =log m 6―log m 3=log m 2=12y .（2）3x <4y <6z证明：因为正实数x ，y ，z ，∴3x >0, 4y >0, 6z >0，∴3x 4y =3log 3m 4log 4m =3lg m lg34lg m lg4=34×lg4lg3=34log 34=log<3，∴log <1，∴3x <4y∴4y 6z =4log 4m 6log 6m =4lg m lg46lg m lg6=23×lg6lg4=23log 46=log<2，∴log <1，∴4y <6z ∴3x <4y <6z ．19．（23-24高一上·广东广州·阶段练习）已知函数f(x)=x 2x 2+1(1)判断并证明函数f(x)在区间(0,+∞)上的单调性；(2)已知a =f (20.5),b =f (log 25),c =f (0.25)，试比较三个数a ，b ，c 的大小，并说明理由．【解题思路】（1）根据函数单调性的定义判断和证明即可；（2）先比较20.5,log 25,0.25三个数的大小，再利用函数f (x )的单调性即可比较a ，b ，c 的大小.【解答过程】（1）函数f(x)=x 2x 2+1=1―1x 2+1，任取x 1,x 2∈(0,+∞)，且x 1<x 2则f(x1)―f(x 2)=1―1x 21+1―1―=1x 22+1―1x 21+1 =22=因为x 1,x 2∈(0,+∞)，且x 1<x 2，所以x 22+1>0,x 21+1>0，x 1―x 2<0，x 1+x 2>0所以f(x 1)―f(x 2)<0，即f(x 1)<f(x 2)，所以函数f (x )在区间(0,+∞)上是增函数.（2）因为20.5>20=1，2=log 24<log 25<log 28=3，0<0.25<0.20=1，所以0<0.25<20.5<log 25，由（1）可知函数f (x )在区间(0,+∞)上是增函数，所以f (0.25)<f (20.5)<f (log 25)，即c <a <b .。

高考数学复习专题比大小全套练习题及答案解析

8．【2018届福建省龙岩市4月检查】已知定义在上的偶函数对于上任意两个不相等实数和，都满足，若，则的大小关系为（）
A. B. C. D.
【答案】D
【解析】分析：根据条件判断出函数的单调性，结合函数的奇偶性和单调性的关系进行转化求解即可.
详解：因为定义在上的偶函数对于上任意两个不相等实数和，
详解：，在上为减函数，
且时，时，，
且，，
且，
且，，
在上单调递减，
，
即，故选D.
点睛：本题主要考查对数函数的性质、指数函数的单调性及比较大小问题，属于难题.解答比较大小问题，常见思路有两个：一是判断出各个数值所在区间（一般是看三个区间）；二是利用函数的单调性直接解答；数值比较多的比大小问题也可以两种方法综合应用
B．（log3 ）＞（）＞（）
C．（）＞（）＞（log3 ）
D．（）＞（）＞（l的偶函数，．
，
又在(0，+∞)上单调递减，
∴ ，
即 .
故选C．
例4.【2017天津，文理】已知奇函数在R上是增函数， .若，，，则a，b，c的大小关系为（）
11.【2018届天津市9校联考】定义在上的奇函数满足，当时，，设，，，则（）
A. B.
C. D.
【答案】A
【解析】∵f（x+2）=﹣f（x），
∴f（x+4）=f[（x+2）+2]=﹣f（x+2）=f（x），
∴函数f（x）是周期为4的周期函数，
，
，
，
又，且在上单调递增，
∴ ，即
详解：因为时， , , ,

高考数学复习选填题专项练习22---比较大小(解析版)

高考数学复习选填题专项练习22---比较大小第I 卷（选择题)一、单选题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（2020·福建高三期末）若0,a b c R >>∈，则（）A ．ac bc >B ．32a bC ．2233a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D ．22log log a b >【答案】D 【解析】【分析】取特殊值排除AB 选项，根据指数函数以及对数函数的单调性判断CD 选项. 【详解】当1c =-时，a b ac bc >⇒<，故A 错误；当3,1a b ==时，3212a b=<=，故B 错误；由于函数23xy ⎛⎫= ⎪⎝⎭在R 上单调递减，a b >，则2233ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，故C 错误；由于函数2log yx =在0,上单调递增，0a b >>则22log log a b >，故D 正确；故选：D【点睛】本题主要考查了根据所给条件判断不等式是否成立以及利用函数单调性比较大小，属于基础题.2．（2020·江西省南城一中高三期末）三个数0.20.40.44,3,log 0.5的大小顺序是（）A ．0.40.20.43<4log 0.5，lg ln x x <，:0q x ∃>，2x <则下列命题中真命题是（） A ．p q ∧ B ．()p q ∧⌝C ．p q ∨D ．()p q ∨⌝【答案】C 【解析】【分析】分别判断命题,p q 的真假再利用或且非的关系逐个选项判断即可. 【详解】易得当1x =时, lg ln x x =,故p 为假命题.当14x =时, 2x <.故q 为真命题.故p q ∨为真命题.故选：C【点睛】本题主要考查了命题真假的判断,属于基础题型. 4．（2020·钦州市第三中学高三月考）设sin6a π=，2log 3b =，2314c ⎛⎫= ⎪⎝⎭，则( )A ．a c b <<B ．c a b <<C ．b a c <<D ．c b a <<【答案】B 【解析】【分析】利用相关知识分析各值的范围，即可比较大小.【详解】1sin 62a π==,21log 32b <=<,12343111421202c ⎛⎫=<= ⎛⎫⎛⎫<= ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭,c a b ∴<<,故选：B 【点睛】本题主要考查了指数函数的单调性，对数函数的单调性，属于中档题. 5．（2020·福建高三）已知log e a π=，lneb π=，2e lnc π=，则（）A ．a b c <，最后利用作差法比较a 、c 的大小即可.【详解】因为1b c +=，分别与中间量12做比较，2223111ln ln e ln 022e 2e b ππ⎛⎫-=-=< ⎪⎝⎭，432211e 1e ln ln e ln 0222c ππ⎛⎫-=-=> ⎪⎝⎭，则12b c <<，211log e log e 22a ππ==>，()112ln ln 20ln ln a c ππππ-=--=+->，所以b c a <<，故选：B . 【点睛】本题考查作差法比较大小，对数的运算及对数的性质的应用，属于中档题.6．（2020·天津二十五中高三月考）已知13313711log ,(),log 245a b c ===，则,,a b c 的大小关系为A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >>【答案】D 【解析】【详解】分析：由题意结合对数的性质，对数函数的单调性和指数的性质整理计算即可确定a ,b ,c 的大小关系.详解：由题意可知：3337392log log log <<，即12a <<，13111044⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭=，即01b <<， 133317552log log log =>，即c a >，综上可得：c a b >>.本题选择D 选项. 点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．7．（2020·榆林市第二中学高三月考）已知函数()f x 是定义在R 上的偶函数，当0x ≥，3()3f x x x =+，则32(2)a f =,31(log )27b f =，c f =的大小关系为（） A ．a b c >> B ．a c b >>C ．b a c >>D ．b c a >>【答案】C 【解析】【分析】利用导数判断3()3f x x x =+在[0,)+∞上单调递增，再根据自变量的大小得到函数值的大小.【详解】函数()f x 是定义在R 上的偶函数，31(log )(3)(3)27b f f f ∴==-=，320223<<=，当0x ≥，'2()330f x x =+>恒成立，∴3()3f x x x =+在[0,)+∞上单调递增，3231(log )(2)27f f f ∴>>，即b a c >>.故选：C.【点睛】本题考查利用函数的性质比较数的大小，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意将自变量化到同一个单调区间中.8．（2020·内蒙古高三期末）已知π为圆周率，e 为自然对数的底数，则A ．e π＜3eB ．π23e －＜32e π－C ．log e π＞3log eD ．π3log e ＞3log e π【答案】D 【解析】【分析】利用指数函数与对数函数的单调性、不等式的性质即可得出．【详解】对于A ：函数y=x e 是（0，+∞）上的增函数，A 错；对于B ：π3e ﹣2＜3πe ﹣2⇔3e ﹣3＜πe ﹣3，而函数 y=x e ﹣3是（0，+∞）上的减函数，B 错；对于C ：31133e e e e log e log e log log log log πππ⇔⇔＞＞＜，而函数y=log e x 是（0，+∞）上的增函数，C 错，对于D ：33333333e e e e log e log e log log log log ππππππππ⇔⇔⇔＞＞＞＞，D 正确；故答案为：D ．【点睛】本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题． 9．（2020·天津静海一中高三学业考试）已知()f x 是定义在R 上的偶函数，且在(],0-∞上是增函数.设()8log 0.2a f =，()0.3log 4b f =，()1.12c f =，则a ，b ，c 的大小关系是（）A ．c b a <<B ．a b c <<C ．a c b <<D ．c a b <<【答案】A 【解析】【分析】利用偶函数的对称性分析函数的单调性，利用指数函数、对数函数的单调性比较出 1.180.3log 0.2log 42、、的大小关系从而比较函数值的大小关系.【详解】由题意可知()f x 在(],0-∞上是增函数，在0,上是减函数.因为0.30.30.3100102log log 4log 193-=<<=-，3881log 0.125log 0.2log 10-=<<=， 1.122>，所以 1.180.3log 0.2log 42<<，故c b a <<.故选：A【点睛】本题考查函数的性质，利用函数的奇偶性及对称性判断函数值的大小关系，涉及指数函数、对数函数的单调性，属于基础题.10.（2020·湖南高三期末）已知 3x >，且357log log log ==x y z ，则下列不等式关系中正确的是（）A ．357<<x y zB ．753<<z y xC ．735<<z x yD ．537<<y x z【答案】B 【解析】【分析】令357log log log x y z k ===，求得1313k x -=，1515k y -=，1717k z -=，再根据幂函数的单调性即可得出结论．【详解】令357log log log x y z k ===()1k >，∴3k x =，5ky =，7k z =，∴133133k k x -==，155155k k y -==，177177k k z -==，∵3x >，∴1k >，∴10k ->，∴幂函数1k y x -=在()0,∞+上单调递增，∴1110357k k k ---<<<，∴111111753k k k ---<<，即753<<z y x ，故选：B ．【点睛】本题主要考查指数式与对数式的互化，考查根据幂函数的单调性比较大小，属于中档题．11．（2020·福建高三月考）函数()f x 的定义域为R ，其导函数为()f x '，()01f x x '>+，且(1)=-y f x 为偶函数，则（）A ．(2)(1)f f -D ．|(2)||(1)|f f ->【答案】A 【解析】【分析】根据()01f x x '>+以及(1)=-y f x 为偶函数判断出函数()f x 的单调性和对称性，由此判断出()2f -和()1f 的大小关系.【详解】由于(1)=-y f x 为偶函数，所以函数()f x 关于1x =-对称.由于()01f x x '>+，所以当1,10x x <-+<时()'0f x <，()f x 递减，当1,10x x >-+>时，()'0f x >，()f x 递增.所以(2)(1)f f -<.故选：A【点睛】本小题主要考查利用导数研究函数的单调性，考查函数的奇偶性，考查函数的图像变换，考查函数的对称性，属于中档题.12．（2020·福建高三月考）已知25log 5log 2a =+，25log 5log 2b =⋅，25log 5log 2c =，则（） A ．b a c <=，再比较. 【详解】因为2225552log log 5log 83,0log log 24log 511=<<==<=<，所以252log 5log 24<+<，所以24a <<，又因为25221log 5log 2log 51log 5b =⋅=⋅=，()()222225log 5log 5log 44log 2c ==>=，所以b a c <<.故选：A 【点睛】本题主要考查对数的换底公式和对数比较大小，还考查了运算求解的能力，属于中档题.13．（2020·江西省南城一中高三期末）若23a ⎛= ⎪⎝⎭，log 3b π=，2log ec π=，则a 、b 、c 的大小关系为（）A ．c a b >>B ．b c a >>C ．a b c >>D ．b a c >>【答案】D 【解析】【分析】利用指数函数与对数函数比较a 、b 、c 三个数与0和23的大小关系，进而可得出这三个数的大小关系. 【详解】指数函数23xy ⎛⎫= ⎪⎝⎭为R上的减函数，则22033⎛<<⎪⎝⎭，即023a <<；对数函数log y x π=为()0,∞+上的增函数，()322333ππ⎡⎤=<⎢⎥⎣⎦，233π∴<，所以，232log log 33πππ=<，即23b >；对数函数2log y x =为()0,∞+上的增函数，则22log log 10ec π=<=.因此，b a c >>.故选：D.【点睛】本题考查指数式和对数式的大小比较，一般利用指数函数、对数函数的单调性结合中间值法来得出各数的大小关系，考查推理能力，属于基础题.14．（2020·山西高三月考）若()10,,2nm m n a b e e c >>==+=，则（）A ．b a c >>B ．a c b >>C ．c b a >>D ．b c a >>【答案】A 【解析】【分析】由基本不等式得出2m nm n ++>>，再根据函数的单调性即可比较大小．【详解】当0m n >>时，2m n m n ++>>，且xy e =是定义域R 上的单调增函数，2m n a e+==,所以2m ne+>a c >；又22m n m n e e e++>=，所以21()2m nm ne e e ++>，即b a >；所以b a c >>．故选：A ．【点睛】本题主要考查了根据基本不等式和函数的单调性比较大小的问题，意在考查学生对这些知识的理解掌握水平．15．（2020·广西师大附属外国语学校高三）已知函数()1y f x =+是偶函数，且函数()y f x =在区间[)1,∞+上是增函数，则下列大小关系中正确的是（）A ．()211log 323f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B ．()211log 323f f f ⎛⎫⎛⎫>> ⎪ ⎪⎝⎭⎝⎭ C ．()211log 332f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D ．()211log 332f f f ⎛⎫⎛⎫>> ⎪ ⎪⎝⎭⎝⎭【答案】D 【解析】【分析】根据函数()1y f x =+是偶函数，关于x ＝0对称，则()y f x =的图象关于直线x =1对称，结合单调性比较大小.【详解】函数()1y f x =+是偶函数，关于x ＝0对称，()y f x =的图象关于直线x =1对称，且在区间[)1,∞+上是增函数，则在(0，1)上为减函数，1123>，2211322303327log log --=>， ()22119230228log log --=>，所以()2211112332323log f f log f ⎛⎫⎛⎫>-><< ⎪ ⎪⎝⎭⎝⎭.故选：D 【点睛】此题考查函数奇偶性的辨析，根据对称性和单调性比较函数值的大小关系，关键在于准确识别函数的单调区间.16．（2020·山西高三月考）已知()f x 是定义在(0,)+∞上的可导函数，满足(1)1f =，2()()xf x f x x '-<，则不等式①(2)2f <，②(2)4f <，③1122⎛⎫> ⎪⎝⎭f ，④1124f ⎛⎫< ⎪⎝⎭中一定成立的个数为（） A ．1 B ．2C ．3D ．4【答案】A 【解析】【分析】根据题意构造函数()()f x g x x=-x ，并判断其在（0，+∞）上单调递减，然后分别算出g （1）、g （2）和g （12），并利用单调性比较大小，即可判断每个选项．【详解】令()()f x g x x=-x ，则()()()2''xf x f x g x x -=-1()()22'xf x f x x x --=，∵xf '（x ）﹣f （x ）＜x 2，∴g '（x ）＜0在（0，+∞）上恒成立，即g （x ）在（0，+∞）上单调递减， ∵f （1）＝1，∴()()1111101f g =-=-=，对于()()()222102f g g =-=＜，即f （2）＜4，∴①错误，②正确；对于()1112101222f g g ⎛⎫ ⎪⎛⎫⎝⎭=-= ⎪⎝⎭＞，即1124f ⎛⎫ ⎪⎝⎭＞，∴③和④均错误；因此一定成立的只有②，故选：A ．【点睛】本题主要考查导数的综合应用，构造新函数是解题的关键，考查学生的逻辑推理能力和运算能力，属于中档题．。

高考数学复习---《指、对、幂形数的大小比较问题》专项练习题(含答案解析)

高考数学复习---《指、对、幂形数的大小比较问题》专项练习题（含答案解析）一、单选题1．（2022春·天津和平·高三耀华中学阶段练习）已知0.5x x =，0.5log y y x =，log 0.5zx z =，则（） A ．y x z <，故0.50.51log 0log x >=，∵0.5log y x =在定义域上单调递减， 0.501,0log 1x x ∴<<<<， 0.51x ∴<<，∵0.50z >， ∴1log 0log x x z >=， ∵0.51x <<， ∴01z <<，故()0.50,1z∈，则()log 0,1x z ∈，1x z ∴<<，0.5log y y x =，由定义域可知：0y >，又∵0.51x <<，∴()0,1yx ∈，则()0.5log 0,1y ∈，()0.5,1y ∴∈，故y x x <，∵0.5log x x =，0.5log yy x =，∴0.50.5log log x y <，x y ∴>，y x z ∴<<.故选：A.2．（2022·浙江·模拟预测）已知正数a ，b ，c 满足3e 1.1a =，251030b b +−=，e 1.3c =，则（） A ．a c b <−，显然2()01x f x x −'=<+，故()f x 是减函数，结合(0)0f =，故0x >时，()0f x <，故21ln(1)2x x x +>−，(0)x >，再令2311()ln(1)23g x x x x x =−+−+，(1)x >−，3()1x g x x'=+，当0x >时，()0g x '>，故()g x 在(0,)+∞单调递增，结合(0)0g =，故2311ln(1)23x x x x +<−+，(0)x >，则11ln1.3ln(10.3)0.30.090.0270.26423c ==+<−⨯+⨯=，13ln1.13(0.10.01)0.2852a =>⨯−⨯=，所以22(1)(10.285) 1.651225a +>+=，28(1) 1.65b +==，22(1)(10.264) 1.597696c +=+=，故222(1)(1)(1)a b c +>+>+，由a ，b ，c 都是正数，故a b c >>．故选：D ．3．（2022·天津滨海新·天津市滨海新区塘沽第一中学校考模拟预测）已知正实数x ，y ，z 满足236x y z ==，则不正确的是（）A ．111x y z +=B ．236x y z >>C ．236x y z >> D ．24xy z >【答案】B【解析】设236x y z t ===，1t >，则2log x t =，3log y t =，6log z t =.选项A ，1log 2t x =，1log 3t y =，1log 6t z =，则111log 2log 3log 6t t t x y z +=+==，故A 正确；选项B ，222log x t ==，333log y t ==，666log z t ==，因为68=69=66=，所以666<<，，又1t >，所以=<=<326y x z <<，故B 不正确；选项C ，241log log 22x t t ==，3271log log 33y t t ==，6661log log 66z t t ==，因为64276<<，又1t >，所以642766lg lg lg log log log lg 4lg 27lg 6t t t t t t =>=>=，即236x y z>>，故C 正确；选项D ，()223lg lg lg log log lg 2lg3lg 2lg3t t tt t xy ⨯===⨯⨯，因为()22lg 6lg 2lg3lg 2lg324+⎛⎫⨯<= ⎪⎝⎭，所以()()224lg lg 6t xy >，又()()()2622244lg log lg 64t z t ==，所以24xy z >，故D 正确；故选：B.4．（2023春·山东济南·高三统考期中）设方程e e 0x x ++=和ln e 0x x ++=的根分别为p 和q ，函数()()e xf x p q x =++，则（）A ．()42033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭B ．()24033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C ．()24033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D ．()24033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭【答案】B【解析】方法一：由e e 0x x ++=得e e x x =−−，由ln e 0x x ++=得ln e x x =−−，因为方程e e 0x x ++=的根为p ，所以函数e x y =与e y x =−−的图象交点P 的横坐标为p ，同理：函数ln y x =与e y x =−−的图象交点Q 的横坐标为q ，因为e x y =与ln y x =互为反函数，所以两函数图象关于y x =对称，易知直线y x =与直线e y x =−−互相垂直，所以,P Q 两点关于直线y x =对称，即,P Q 的中点M 一定落在y x =，亦即点M 为y x =与e y x =−−的交点，联立e y x y x =⎧⎨=−−⎩，解得e 2e2x y ⎧=−⎪⎪⎨⎪=−⎪⎩，即e e ,22M ⎛⎫−− ⎪⎝⎭，所以e p q +=−，故()()e e e x x f x p q x x =++=−，则()e e xf x '=−，令()0f x ¢>，得1x >；令()0f x '<，得1x <；所以()f x 在(),1−∞上单调递减，在()1,+∞上单调递增，所以()203f f ⎛⎫< ⎪⎝⎭，而()01f =，2322e e 33f ⎛⎫=− ⎪⎝⎭，4344e e 33f ⎛⎫=− ⎪⎝⎭，则()43440e e 133f f ⎛⎫−=−− ⎪⎝⎭，4242333342422e e e e e e e 33333f f ⎛⎫⎛⎫⎛⎫−=−−−=−− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令()()4341e 3g x x x x =−−≥，则()11133344444e e 1033333g x x ⎛⎫'=−≥−=−> ⎪⎝⎭，所以()g x 在[)e,+∞上单调递增，所以()()()4433e 33503811255g g <=−<=<=，即434e e 1<03−−，故()403f f ⎛⎫< ⎪⎝⎭，令()()4233213h x x x x x =−−≥，则()1133422333h x x x −'=−−，令()0h x '>，得1x >，所以()h x 在[)1,+∞上单调递增，所以()4233423327272722781918e 101010310101010h h ⎛⎫⎛⎫⎛⎫⎛⎫>=−−⨯=−−⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21113333811090101809109101020100100⎡⎤⎛⎫⨯−⨯−==⨯−−⎢⎥⎪⎢⎥⎝⎭⎣⎦()()3992.159 2.1510200.1025010 2.15100100⎡⎤>⨯−−=⨯>>⎣⎦，则42332e e e 03−−>，故4233f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，综上：()24033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭.故选：B.方法二：前面部分同方法一得，()()e e e x x f x p q x x =++=−，则()e e xf x '=−，令()0f x ¢>，得1x >；令()0f x '<，得1x <；所以()f x 在(),1−∞上单调递减，在()1,+∞上单调递增，所以()203f f ⎛⎫< ⎪⎝⎭，而()01f =，2322e e 33f ⎛⎫=− ⎪⎝⎭，4344e e 33f ⎛⎫=− ⎪⎝⎭，因为e 1x x ≥+，当且仅当0x =时取等号，所以e 1x x −≥−+，当()0,1x ∈时，1e 1xx <−，所以413344414e 1e e=e e e 133336213f ⎛⎫⎪⎛⎫⎛⎫=−−<−=< ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪−⎝⎭，即()403f f ⎛⎫< ⎪⎝⎭，下面比较42,33f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭的大小关系，设()()()2g x f x f x =−−，()0,1x ∈，所以()()()222e e e e e e 2e 0x x x x g x f x f x −−'''=+−=−+−=+−=，故()g x 在()0,1x ∈上递增，()()10g x g <=，即有222033f f ⎛⎫⎛⎫−−< ⎪ ⎪⎝⎭⎝⎭，亦即4233f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，综上：()24033f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭.故选：B.5．（2023春·福建宁德·高三校考阶段练习）已知e 1.02, 1.01a cb ===，则（） A ．a bc <，又()()22120x x x −+=−−≥，10x −≥，即()f x '0≥，故()f x 在[]0,1单调递增，()()00f x f ≥=，则当0.01x =时，()2ln 1.0110>，即()2ln 1.011>，c b >；令()()[]ln 11,0,1h x x x =+∈，则()h x '11x ==+ 当[]0,1x ∈0,10x +>，又()22210x x −+=−≤，1x +，即()h x'0≤，故()h x 在[]0,1单调递减，()()00h x h ≤=，故当0.02x =时，ln1.0210<，即ln1.021<，a b <；综上所述，a b c <<. 故选：A.6．（2023·江苏·高三专题练习）已知正实数a ，b ，c 满足2e e e e c a a c −−+=+，28log 3log 6b =+，2log 2c c +=，则a ，b ，c 的大小关系为( )A ．a b c <<B ．a c b <<C ．c a b <<D ．c b a <<【答案】B【解析】22e e e e e e e e c a a c c c a a −−−−⇒+=+−=−，故令()e e x x f x −=−，则()e e c c f c −=−，()e e a af a −=−．易知1eexx y −=−=−和e x y =均为()0,+∞上的增函数，故()f x 在()0,+∞为增函数． ∵2e e a a −−<，故由题可知，2e e e e e e c c a a a a −−−−=−>−，即()()f c f a >，则0c a >>．易知222log 3log log 2b =+>，2log 2c c =−，作出函数2log y x =与函数2y x =−的图象，如图所示，则两图象交点横坐标在()1,2内，即12c <<，c b ∴<，a cb ∴<<．故选：B ．7．（2023·全国·高三专题练习）已知02,1,1b a b a b <<<≠≠，且满足log b a a b =，则下列正确的是（） A ．1ab >B ．1(1)b a ab +<+ C ．11a b a b a a b b ++−>− D ．52+>a b 【答案】B【解析】由log b a a b =，可得1log log log b a b a b a==，所以log 1b a =，或log 1b a =−， ∴b a =(舍去)，或1b a=，即1ab =，故A 错误；又02b a b <<<，故120a a a<<<，∴1a <<(11y x x x=+<<，则2221110x y x x−'=−=>，函数(11y x x x =+<<单调递增，∴1a b a a ⎛+=+∈ ⎝⎭，故D 错误；∵02b a b <<<，11a b<=< ∴1212a b b <<<+<，令()()ln 12x g x x x=<<，则()21ln 0xg x x −'=>，∴函数()()ln 12xg x x x=<<单调递增， ∴()ln 1ln 1b a a b +<+，即()()1ln ln 1b a a b +<+， ∴()1ln ln 1ab a b +<+，即1(1)b a a b +<+，故B 正确；∵011b a b <<<<+，∴函数,x x y a y b ==−单调递增，故函数x xy a b =−单调递增，∴11a a b b a b a b ++−<−，即11a b a b a a b b ++−<−，故C 错误. 故选：B.8．（2023·全国·高三专题练习）已知函数()e 2xf x x =+−的零点为a ，函数()ln 2g x x x =+−的零点为b ，则下列不等式中成立的是（） A ．1a b ⋅> B ．e ln 2a b +<C ．223a b +<D ．2214a b >【答案】C【解析】由()0f x =，()0g x =得e 2x x =−，ln 2x x =−，因为e x y =与ln y x =关于直线y x =对称，在同一坐标系下，画出e x y =，ln y x =，y x =，2y x =−的图象，则()1,12y xC y x=⎧⇒⎨=−⎩，(),e a A a ，(),ln B b b ，,A B 关于()1,1对称. 所以2a b +=，e ln 2a b +=，故B 错误. 因为0a >，0b >，a b ¹，所以()214a b ab +<=，故A 错误.因为()e 2x f x x =+−，()e 10xf x '=+>，()f x 在R 上为增函数，()00e 20f =−<，13022f ⎛⎫=> ⎪⎝⎭，所以102a <<.又因为点(),e aa 在直线2y x =−上，且2ab +=，所以e 2a a b =−=.22221e e 34a a b a +=+<+<，故C 正确. 因为e a b =，所以e aa ab =，设()10e 2x x h x x ⎛⎫=<< ⎪⎝⎭，()10e x x h x −'=>，()h x 在10,2⎛⎫⎪⎝⎭为增函数.所以()12h x h ⎛⎫< ⎪⎝⎭即a b <22114e 4a b <<，故D 错误. 故选：C9．（2023·全国·高三专题练习）在给出的①3log 3ππ<；②56log 6log 7>ln 21<．三个不等式中，正确的个数为（） A ．0个B ．1个C ．2个D ．3个【解析】①令3log ()x f x x=，则3log ()f πππ=，3log 31(3)33f ==，所以21ln ()ln 3xf x x −'=，在(e,)+∞上()0f x '<，即()f x 递减，而3e π>>，所以()(3)f f π<，即3log 13ππ<，故3log 3ππ<，正确；②令ln(1)()log (1)ln xx f x x x+=+=，则2ln (1)ln(1)()(1)(ln )x x x x f x x x x −++'=+，又ln y x x =，在(1,)+∞上ln 10y x '=+>，则y 递增，所以，在(1,)x ∈+∞上ln (1)ln(1)0x x x x −++<，即()0f x '<，则()f x 递减，所以56(5)log 6(6)log 7f f =>=，正确；③2ln 2(e e ==>=>，而e xy =ln 21>，错误.故选：C10．（2023·全国·高三专题练习）设2022ln 2020a =，2021ln 2021b =，2020ln 2022c =，则下列选项正确的是（） A ．a c b >> B ．c b a >> C ．b a c >> D ．a b c >>【答案】D 【解析】令()ln x f x x =，则'()f x 21ln x x−=，令'()f x 0=，解得e x =，故当e x >时，()f x 单调递减，故()()20202022f f >，即ln 2020ln 202220202022>，则2022ln 2020a =>2020ln 2022c =.令()()ln 1h x x x =−+，则'()h x 1111x x x =−=++，故当0x >时，()h x 单调递增，10x −<<时，()h x 单调递减，则()()00h x h ≥=，即()ln 1x x +≤.b a −=2021ln 20212022ln 20202021ln 20212021ln 2020ln 2020−=−−112021ln 1ln 20202021ln 2020020202020⎛⎫=+−≤⨯−< ⎪⎝⎭，故b a <； 2020ln 20222021ln 20212021ln 2022ln 20222021ln 2021c b −=−=−−112021ln 1ln 20222021ln 2022020212021⎛⎫=+−≤⨯−< ⎪⎝⎭，故c b <；综上所述：c b a <<. 故选：D.11．（2023·全国·高三专题练习）已知1ln 2a =，()ln lg 2b =，()lg ln 2c =则a ，b ，c 的大小关系是（） A ．c a b >> B ．c b a >> C ．a b c >> D ．b c a >>【答案】A【解析】先比较,a b ，易知1lg 22<,故1ln(lg 2)ln 2<，即b a < 又10e <，故1x >时ln lg x x >，01x <<时ln lg x x < 故11lgln 22>，而1ln 22>，故11lg(ln 2)lg ln 22>>，有c a > 故选：A12．（2023·全国·高三专题练习）已知实数a ，b 满足28log 3log 6a =+，51213a a b +=，则下列判断正确的是（） A ．2a b >> B ．2b a >> C ．2b a >> D ．2a b >>【答案】D【解析】()28221log 3log 6log 3log 233a =+=+⨯2241414317log 3log 233333233=+>=⨯+=>，所以2a >；由51213a a b +=且2a >，所以51225144169a a +>+=，所以2b >，令()51213x x xf x =+−，2x >，令20t x =−>，则2x t =+，则()51213x x x f x =+−，2x >等价于()2551441216913t t tg t =⨯+⨯−⨯，0t >；又()255144121691316912169130t t t t tg t =⨯+⨯−⨯<⨯−⨯<，所以当2x >时，()512130x x xf x =+−<，故5121313a a b a +=<，所以2a b >>.故选：D.13．（2023·全国·高三专题练习）已知24ln 25a =+， 1.222b =+， 2.12c =，则（）A ．a b c <⎢⎥⎣⎦，所以b c >；令()()1ln 1f x x x x =−−>，1()10'=−>f x x，所以()f x 在()1,+∞上单调递增，因为0.221>，所以0.2(2)(1)f f >，即0.20.221ln 20−−>，所以()1.20.20.20.20.22224ln 22222ln 2221ln 205b a −=+−−=⋅−−=−−>，所以b a >；同理0.121>，所以0.1(2)(1)f f >，即0.10.121ln 20−−>，也即0.10.112ln 20−+<，所以()2.10.120.10.10.124ln 2244ln 22241ln 2205a c −=+−=+−⋅=+−<，所以a c <. 综上，a c b <<，故选：D.14．（2023·全国·高三专题练习）已知a =eb =，c =，则（）A ．a b c <=，1eb =<=所以a b >；又()222c ==+−构造()2222xf x e x x =−++，则a c f−=因为()()()22222222211x xx x e f x e x x x ⎡⎤−+−⎣⎦=−=−+−+，()21110x −+≥> ，由于函数()f x 的分母为正数，此时只需要判断分子()2222xx x e ⎡⎤−+−⎣⎦的符号，设22()(22)2,()0,x xg x x x e g x x e '=−+−=≥则()g x 在R上递增，(0)0g g >=，即当0x > 时，()f x 的分子总是正数，()()()00,f x x ∴>∈+∞ ，0a c f−=>，即a c >，应用排除法，故选：B.15．（2023·全国·高三专题练习）已知ln72a =，ln63b =，ln54c =，则（） A ．b<c<a B ．a b c <<C ．b a c <<D ．a c b <<【答案】B【解析】对a ，b ，c 取对数得：ln ln 2ln 7a =⋅，ln ln3ln 6b =⋅，ln ln 4ln5c =⋅，令()()ln ln 9f x x x =⋅−(24x ≤≤)，()()ln 9x f x x−'=−()()()9ln 9ln ln 99x x x xx x x x −−−=−−，令()ln ,1g x x x x =>，()ln 10g x x '=+>，即()ln g x x x =在(1,)+∞上单调递增，由24x ≤≤得，951x x −≥>>，于是得()()9ln 9ln x x x x −−>，又()90x x −>，因此，()0f x ¢>，即()f x 在[]2,4上单调递增，从而得()()()234f f f <<，即ln 2ln 7ln3ln 6ln 4ln5<<，ln ln ln a b c <<，所以a b c <<. 故选：B16．（2023·全国·高三专题练习）设2ln1.01a =，ln1.02b =，1c =．则（）A ．a b c <=，所以b a <；下面比较c 与,a b 的大小关系.记()()2ln 11f x x =+，则()00f =，()2121x f x x −='=+，由于()()2214122x x x x x x +−+=−=−所以当0<x <2时，()21410x x +−+>()1x >+，()0f x ¢>，所以()f x 在[]0,2上单调递增，所以()()0.0100f f >=，即2ln1.011，即a c >；令()()ln 121g x x =+，则()00g =，()212212x g x x −=+'，由于()2214124x x x +−+=−，在x >0时，()214120x x +−+<，所以()0g x '<，即函数()g x 在[0，+∞)上单调递减，所以()()0.0100g g <=，即ln1.021，即b <c ；综上，b<c<a ，故选：B.[方法二]：令()21ln 1(1)2x f x x x ⎛⎫+=−−> ⎪⎝⎭()()221-01x f x x =+'−<，即函数()f x 在（1，+∞)上单调递减()10,ff b c <=∴<令()232ln 1(13)4x g x x x ⎛⎫+=−+<< ⎪⎝⎭()()()21303x x g x x −−+'=>，即函数()g x 在（1，3)上单调递增()10,gg a c =∴综上，b<c<a ，故选：B.17．（2023·全国·高三专题练习）设4log 3a =，5log 4b =，0.012c −=，则,,a b c 的大小关系为（） A ．b a c <，即84105455>=，4555log 4log 50.8∴>=；81043>，即84105344<=，4544log 3log 40.8∴<=；54log 4log 3∴>，即a b <.设()()210x f x x x =−−<，则()2ln 21xf x '=−，当0x <时，()20,1x ∈，又()ln 20,1∈，()2ln 20,1x∴∈，()0f x '∴<，()f x \在(),0∞−上单调递减，()()00f x f ∴>=，即当0x <时，21x x >+，0.0120.0110.990.9−∴>−+=>，0.015log 42−∴<，即b c <.综上所述：a b c <<. 故选：B . 二、多选题18．（2023·全国·高三专题练习）当121x x <<时，不等式1221e e 0x xx x −<成立．若e e a b >>，则（） A ．e 1e e b b −> B ．e e e aa b b +<C ．e ln b a b a <D ．e ln a ab b >【答案】AD【解析】当121x x <<时，不等式12122112e e e e 0x x x x x x x x −<⇔<，令e (),1xf x x x=>，则()f x 在(1,)+∞上单调递增，因e>1b >，则ee 1e e ()(e)e e eb b f b f b b −>⇔>⇔>，A 正确；因e a b >>1，则e e e e ()(e )e e eaa b aa b a f b f b b +>⇔>⇔>，B 不正确；由e e a>知，1a >，有()()e 1e 1e a a f a f a a>⇔>>⇔>，则ln ln 1a a a a >⇔<，由选项A 知，e 1b b>，即e ln e ln b b aa b a b a >⇔>，C 不正确；由e e ab >>得，ln 1b a >>，则ln e e (ln )()e ln ln b aa fb f a ab b b a>⇔>⇔>，D 正确. 故选：AD19．（2023·全国·高三专题练习）已知01b a <<<，则下列不等式成立的是（） A ．log log a b b a C ．ln ln a b b a <D ．ln ln a a b b >【答案】BC【解析】选项A ：()()22lg lg lg lg lg lg lg lg log log lg lg lg lg lg lg a b b a b a b a b a b a a b a b a b−+−−=−==由01b a <<<，可得lg lg 0b a <<，则lg lg 0b a >，lg lg 0b a −<，lg lg 0b a +< 则()()lg lg lg lg 0lg lg b a b a a b−+>，则log log a b b a >.判断错误；选项B ：由01a <<，可得log a y x =为(0,)+∞上减函数，又0b a <<，则log log 1a a b a >=.判断正确；选项C ：由01a <<，可知xy a =为R 上减函数，又b a <，则a b a a >由0a >，可知a y x =为(0,)+∞上增函数，又b a <，则a a b a <，则b a a b > 又ln y x =为(0,)+∞上增函数，则ln ln b a a b >，则ln ln a b b a <.判断正确；选项D ：令211e e a b ==，，则01b a <<<，e ln l 111e n e a a =−=，222ln ln 112e e eb b =−=则22122e0e ln eln e a a b b −−+==<−，即ln ln a a b b <.判断错误.故选：BC20．（2022·全国·模拟预测）下列不等式关系成立的是（） A ．57log 6log 8C ．0.40.60.40.6<D ．π3sin3>+【答案】BCD【解析】A 选项：当n ∈N 且3n ≥时，有()log 1n n −+()()22log 1log 1log 2n n n n n n +=−<=，进一步可得()()log 1log 11n n n n −⋅+<，（()()2log 1log 1n n n n >−++>）从而得当n ∈N 且3n ≥时，有()()1log 1log n n n n −+<，所以567log 6log 7log 8>>，故A 选项不成立.B 选项：令π()sin ,(0)2f x x x x =−<<，则()cos 10f x x '=−<，所以在π(0,)2上函数()f x 单调递减，所以()(0)0f x f <=，也即在π(0,)2上，()sin 0f x x x =−<，即sin x x <，所以当π02α<<时，0sin 22αα<<，22cos 12sin1222ααα⎛⎫=−>− ⎪⎝⎭，即21cos 12αα>−，在上式中取13α=，得211117cos 132318⎛⎫>−⨯= ⎪⎝⎭，即118cos 173>，故B 选项成立.C 选项：因为()()520.40.40.40.16==，()50.630.60.60.216==，所以0.40.60.40.6<，故C 选项成立.D 选项：当π02α<<时，sin αα<，取π3α=−，得()sin π3π3−<−，即π3sin3>+，故D 选项成立.21．（2022春·广东深圳·高三深圳中学校考阶段练习）下列大小关系正确的是（）． A ．2 1.91.92，()f x 递增，而0 1.92e <<<，所以(1.9)(2)f f <，即ln1.9ln 21.92<，2 1.9ln1.9ln 2<，即2 1.91.92<，A 正确；2.9322288.41 2.9<=<=，B 正确；770log 4log 12<<，所以222777777(log 4log 12)(log 48)(log 49)log 4log 121444+⋅<=<=，所以71271log 4log 7log 12<=，C 正确； 10102264(2)102410==>，76107823543104=<<， 7107710log 4log 417=>，所以77log 40.710>=， 472401=，341217287=<，所以3412124log 7log 713=>，123log 70.754>=，所以712log 4log 70.70.75 1.45+>+=>D 错．故选：ABC ．22．（2022·湖南·模拟预测）已知1x >，1y >，且()()1e 11e yx x y ++=+，则下列结论一定正确的是（） A ．()ln 0x y −> B ．122x y +< C ．226x y +> D ．()ln ln 3x y +<【答案】AC【解析】令()e x f x x =，则()()2e 1e e xx x x x f x x x−−'==，所以当1x >时，()0f x ¢>，所以()f x 在()1,+∞上单调递增；由()()1e 11e yxx y ++=+得1e e 111x y x y y +=+++，即1e e 111x y x y y +−=++，∵1y >，∴11012y <<+， ∴1e e 1012x y x y +<−<+，即()()1012f x f y <−+<， ∴1x y >+，即1−>x y ，∴()ln 0x y −>，A 正确；由1x y >+知12x y +>+，所以12222x y y ++>>，所以选项B 错误；由1x y >+知12222326x y y y y ++>+=⋅>，所以选项C 正确．由1x y >+，1y >知213x y y +>+>，所以()()ln ln 21ln 3x y y +>+>，所以D 错误，故选：AC ．23．（2022·福建泉州·统考模拟预测）若2ln ln b b a a a +=+，则下列式子可能成立的是（） A ．1a b >> B ．1b a >> C ．1b a >> D ．1a b >>【答案】BCD【解析】令()ln f x x x =+，0x > 则()110f x x=+>'恒成立，所以()ln f x x x =+单调递增，其中1110e ef ⎛⎫=−< ⎪⎝⎭，()110f =>，则存在01,1x e ⎛⎫∈ ⎪⎝⎭，使得()00f x =①当a b >时，2ln ln ln a a a b b a a +=+<+ 即()()1ln 0a a a −+<，若1a ≥，则ln 0a a +>，且10a −≥，则()()1ln 0a a a −+≥，不满足()()1ln 0a a a −+<，故1a <，且()0f a >，所以01x a <<又因为a b >，所以1a b >>，D 正确； ②当a b <时，2ln ln ln a a a b b a a +=+>+，即()()1ln 0a a a −+>（1）当1a >时，10a −>，ln 0a a +>，则()()1ln 0a a a −+>成立，故1b a >>，B 正确；（2）当1a <时，10a −<，若()()1ln 0a a a −+>，则ln 0a a +<，因为()00f x =，且()ln f x x x =+在()0,∞+上单调递增，所以当00a x <<时，ln 0a a +<，则2ln 0a a a +<，所以ln 0b b +<，所以1b <，又因为a b <，所以1b a >>，选项C 正确. 故选：BCD24．（2022春·江苏泰州·高三泰州中学校考开学考试）已知0e sin e sin y xx y x y π<<<，＝，则（） A ．sin sin x y − C ．sin cos x y > D ．cos sin x y >【答案】ABC【解析】由题意，0e sin e sin y xx y x y π<<<，＝，得0y x −> ，e sin e sin y xy x=，e 1y x−>，∴sin 1sin y x >，∴sin sin y x >，A 对； e e sin sin y x y x =，令e (),(0,)sin xf x x xπ=∈，即有()()f x f y =，令2e (sin cos )()0,sin 4x x x f x x x π=='−=，()f x 在0,4π⎛⎫⎪⎝⎭上递减，在,4ππ⎛⎫⎪⎝⎭上递增，因为()()f x f y = ，∴04x y ππ<<<<，作出函数e (),(0,)sin xf x x xπ=∈以及sin ,[0,]y x x π=∈ 大致图象如图：则30sin sin 4y y x ππ<−<>，，∴sin()sin y x π−>，结合图象则y x π−>， ∴cos()cos y x π−<，∴cos cos x y >−，B 对；结合以上分析以及图象可得2x y π+>，∴2x y π>−，且,4224y y πππππ<<−<−<，∴sin sin cos 2x y y π⎛⎫>−= ⎪⎝⎭，C 对；由C 的分析可知，224y x πππ−<−<<，在区间[,]24ππ−上，函数cos y x = 不是单调函数，即cos()cos 2y x π−<不成立，即sin cos y x <不成立，故D 错误；故选：ABC ．25．（2022·湖南长沙·雅礼中学校联考二模）下列不等式正确的有（）A ．90911013100125> B ．5645⎛⎛> ⎪⎪⎝⎭⎝⎭C ．23e2>D ．3tan12> 【答案】AD 【解析】由90901223390909090909090101(10.01)1C 0.01C 0.01C 0.01C 0.01100=+=+⨯+⨯+⨯++⨯122339090901C 0.01C 0.01C 0.01>+⨯+⨯+⨯10.90.40050.11748 2.4=+++>，则有909110130.024100125>=，A 正确；假定56(()45<5625656(452545()4⇔<⇔<<，令2(1)()ln ,11x f x x x x −=−>+，求导得，()f x 在(1,)+∞上单调递增，则()(1)0f x f >=，即当1x >时，2(1)ln 1x x x −>+，62ln 511>，62511>，令()ln 1g x x x=>，求导得，()g x 在(1,)+∞上单调递减，则()(1)0g x g <=，即当1x >时，ln x<25ln 24<2524< 260114911⇔−>⇔>因49>256245<成立，所以56((45<成立，B 不正确；假定23e2<，有23333133e 2ln ln ln 2222222<⇔<⇔−<⇔−< 令()ln ,1h x x x x =−>，，则()h x 在(1,)+∞上单调递增，32>，则3()2h h >，所以23e 2<成立，C 不正确；令tan ,02y x x π=<<，求导得，，曲线tan y x =在3x π=处切线方程为4()3y x π=−令()tan 4()33x x x x ππϕ=−−<<，求导得，即()ϕx 在(0,)3π上单调递减，而13π<，则(1)()03πϕϕ>=，即3543 3.153tan14(1)()(2.5 1.74)3223232ππ>−+>++−⨯=，D 正确.故选：AD26．（2022·全国·高三专题练习）已知1201x x <<<，下列不等式恒成立的是（）A ．1221e e x xx x >B ．2112ln ln x x x x <C ．1122ln ln x x x x <D ．1221ln e l e n x xx x +<+【答案】AB 【解析】令()()()()1,0,1,,e e 0x xx xf x x f x f x '−=∈=>在()0,1x ∈内单调递增. 1201x x ∴<<<时，1212e ex x x x<，即2112e e ,x x x x <A 选项正确；令()()()()2ln 1ln ,0,1,0,x x g x x g x g x x x−=∈>'=在()0,1x ∈内单调递增， 121212ln ln 01,x xx x x x ∴<<<<，即2112ln ln x x x x <，B 选项正确；令()()()()ln ,0,1,ln 1,0,1h x x x x h x x x '=∈=+∈，当10,e ⎛⎫∈ ⎪⎝⎭x 时，()()0,h x h x '<单调递减，当1,1e x ⎛⎫∈ ⎪⎝⎭时，()()0,h x h x '>单调递增，()1h x 与()2h x 大小不确定，C 错误；当1201x x <<<时，2112ln ln 00e e x xx x +<+>，D 错误故选：AB。

专题2.18比较大小(解析版)

秒杀题型：比较大小①同底或同指〔或可化简为同底与同指〕比较大小:【解析】：x y ，而y x 3为增函数，所以选A 。

1.〔2021年新课标全国卷118〕设a log 3 6,b log 510,clog 714.那么 ( )A. c b aB. b c aC. a c bD. a b c【解析】：法一：可化简为同底对数型log 3 6 1 log 3 21 1， 1 b log 510=1 log 5 2 1 -log 23log 2 51c log 714 = 1 log 7 21 - ，选D 。

log 2 7秒杀思路：构造指、对数及其它函数，利用增减性比较大小。

1 法二:构造函数为减函数，选 D。

f (x) log x 2x 1 log x 21log 2 X2.〔高考题〕log 2 a 5 g2,b 5Iog 4,clog 3-，那么 5A. a b cB. b a cC. a c bD. C【解析】：a 5log 2,b5log ^'3T6,clog 510 3可,log 2log10 log 2，选C 。

3.(高考题)a log 2 3.6, b C. ba cD. c a选B 。

4 21a 23,b45,c253，那么()C.bc aD .c ab422a 23 4345 ，由幕函数的单调性得2 2 2c 25353 43，选 A 。

( )33A. x yB.sinx sinyC.l n(x 21) ln(y 21)1 1 x2 1 y 2 1log 4 3.2, c log 4,那么( ) A. a b cB. a c b【解析】log 2 3.6 log 42，4. 〔2021年新课标全国卷III6〕 A. b a cB. a b c【解析】：由指数函数的单调性得 5. 〔高考题〕实数x, y 满足a xa y 〔0 a 1〕,那么以下关系式恒成立的是b6.〔高考题〕定义在R 上的函数f x 2|x m1 〔 m 为实数〕为偶函数，记法二:构造函数 —，求导可知单调区间为：当X e 时,单调递减，而 — —x24仿照上题的两种解法，选②不同底或不同指比较大小:秒杀思路：先划分区间，一般划分为〔,0〕,〔0,1〕,〔1,〕三个区间，假设比较不出，再细化区间。

高考数学复习专题：比较大小

考法一特殊值型【例1-1】（2022·河南驻马店·高考数学复习专题：比较大小高三期中（文））已知=a 50.3,=b 0.35,=c log 50.3,则a b c ,,的大小关系是（） A ．>>a b c B ．>>b a c C ．>>c a b D ．>>c b a【答案】A【解析】构造=f x x 5)(可知f x )(单调递增,===>a f f 0150.30.3)()(,∴>a 1,造=g x x 0.3)(可知g x )(单调递减,<=<==g b g 50100.35)()(,∴<>a b c .故选:A【例1-2】（2021·全国·统考高考真题）已知=a log 25，=b log 38，=c 21，则下列判断正确的是（） A ．<<c b a B ．<>a b c B ．>>a c bC ．>>c a bD ．>>c b a【答案】C【解析】因为>>2220511,所以<<a 12,=−=<=b 2log 2log log 101555,即=c 54log log 2112211,即c >2,所以>>c a b ,故选:C.【例1-4】（2022·河南）已知===a b c log 0.5,0.5,50.2，则（） A ．<<a b c B ．b<c<a C ．<<c b a D ．<<a c b【答案】D【解析】=<=a log 0.5log 1055，=<=<=b 20.50.50.51110.20，<==c 201，所以．故选：D.考法二单调型【例2-1】（2023·新疆乌鲁木齐·统考一模）已知函数+=−xf x x 3ln 2)(，=a log 32，=b log 43，=c 23，则（） A ．<<f a f b f c )()()( B ．<<f a f c f b )()()( C ．<<f c f a f b )()()( D ．<<f c f b f a )()()(【答案】B 【解析】因为+>−x x 302，所以定义域为−3,2)(，+==−−+−xf x x x x 3ln ln 2ln 32)()()(；易知=−y x ln 2)(为减函数，=+y x ln 3)(为增函数，所以+=−x f x x 3ln 2)(为减函数.因为=>=a 2log 3log 322，所以>a c ；又=<==b c 2log 4log 33，所以，所以<<f a f c f b )()()(.故选：B.【例2-2】（2022·四川）已知函数=+f x x x ()2cos 2，设=a f 20.5)(，=b f 0.52)(，=c f log 20.5)(，则（）A ．B ．C ．D ．【答案】A【解析】=+f x x x ()2cos 2，定义域为R ， −=−+−=+=f x x x x x f x 2cos 2cos 22)()()()(，所以是偶函数，=−'f x x x 22sin )(，令=−g x x x 22sin )(，则=−≥'g x x 22cos 0)(，所以在R 上'f x )(单调递增，='f 00)(，即在+∞(0,)上0fx ，单调递增，因为==−=c f f f log 2(1)10.5)()(，>>210.50.52，所以>>f f f 210.50.52)()()(，即，故选：A【例2-3】（2022·江西）函数=−−−f x x x xe e 2sin )(.若=a 420，=b log 105，=c b a log ，则有（）A ．>>f a f b f c )()()(B ．>>f a f c f b )()()(C ．>>f b f a f c )()()(D ．>>f b f c f a )()()(【答案】A【解析】因为函数=−−−f x x x x e e 2sin )(，所以=+'−−f x x x xe e 2cos )(，当>x 0时，−≥'>f x x 22cos 0)(，所以在+∞0,)(上递增，因为=>=<=<=<=<=a b c b a a a log 20log 162,1log 10log 252,0log log 14455，所以>>>a b c 0，所以>>f a f b f c ()()()，故选：A考法三导函数型【例3-1】（2023·湖南衡阳·校考模拟预测）设是定义在R 上的函数，其导函数为'f x )(，满足−>'f x xf x 0)()(，若=a f 41)(，=b f 22)(，=c f 4)(，则（）A ．B ．C ．>>b c aD ．【答案】A【解析】因为满足−<'f x xf x 0)()(，令=xg x f x )()(，则=<'−'xg x xf x f x 02)()()(，所以在R 上单调递减，所以>>g g g 124)()()(，即>>f f f 24124)()()(，所以>>f f f 41224)()()(.所以.故选：【例3-2】（2022·四川雅安·三模（理））定义在R 上的偶函数f x ()的导函数为'f x ()，且当>x 0时，+<'xf x f x ()2()0．则（）A ．>f f 4e(e)(2)2 B ．f f >9(3)(1) C ．f f −<−4(2)9(3) D ．>−f f 9e (e)(3)2【答案】D【解析】令=g x x f x 2)()(，因为f x ()是偶函数，所以g x )(为偶函数，当>x 0时，⎣⎦⎡⎤=+=+<'''g x xf x x f x x f x xf x 2202)()()()()(，所以g x )(在+∞0,)(单调递减，在−∞,0)(单调递增，则<g g e 2)()(，即<f f e e 2222)()(，则<f f 4e(e)(2)2，故A 错误； <g g 31)()(，即<f f 931)()(，故B 错误；−>−g g 23)()(，即−>−f f 4(2)9(3)，故C 错误； >=−g g g e 33)()()(，即>−f f e e 932)()(，则>−f f 9e (e)(3)2，故D 正确. 故选：D.【例3-3】（2022·贵州）已知奇函数的导函数为'f x )(，且在⎝⎭⎪⎛⎫20,π上恒有<'xx f x f x sin cos )()(成立，则下列不等式成立的（）A ⎝⎭⎝⎭⎪ ⎪>⎛⎫⎛⎫f 64ππB ．⎝⎭⎝⎭ ⎪ ⎪−<−⎛⎫⎛⎫f 36ππC ⎝⎭⎝⎭ ⎪ ⎪−<−⎛⎫⎛⎫43ππD ⎝⎭⎝⎭⎪ ⎪<⎛⎫⎛⎫f 34ππ 【答案】B【解析】构造函数=x F x f x sin )()(，由在⎝⎭ ⎪⎛⎫20,π上恒有<'x xf x f x sin cos )()(成立，即'=∴'∴>'−>−x f x x f x x F x F x f x x f x x (sin )sin cos 0,0,sin cos 2)()()()()()(在⎝⎭⎪⎛⎫20,π上为增函数，又由()−−−===∴−−x xF x F x F x f x f x sin sin ,)()()()()(为偶函数，ππ,,,2646464<∴<∴<∴<⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎛⎫⎛⎫ππF F f f f f 64sin sin ππ64ππππ，故A 错误.偶函数F x )(在⎝⎭ ⎪⎛⎫20,π上为增函数，∴F x )(在⎝⎭ ⎪−⎛⎫2,0π上为减函数，π363636−<−∴−>−∴>∴−−>−−⎝⎭⎝⎭⎪ ⎪−−⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪−−⎛⎫⎛⎫F F f f f f 36sin sin ππ,,,3,36πππππππ⎝⎭⎝⎭⎪ ⎪∴−<−⎛⎫⎛⎫f 36ππ，故B 正确；⎝⎭⎝⎭⎪ ⎪−−⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪−<−∴<⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪−⎛⎫⎛⎫F F f f 43sin sin 43ππ,43ππππ，⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪ ⎪ ⎪−<−−>−⎛⎫⎛⎫⎛⎫⎛⎫4343,ππππ，故C 错误；ππ>34，⎝⎭⎝⎭⎝⎭⎝⎭ ⎪ ⎪ ⎪ ⎪∴>∴>>⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎛⎫⎛⎫F F f f 34sin sin 3434ππ,,34ππππππ，故D 错误.故选：B考法四构造函数x ln x 或ln xx类型【例4-1】（2022·新疆乌鲁木齐·模拟预测（文））设=a e 22，=b 2ln 2，=c 3ln 3，则（）A ．B ．C ．c<a<bD ．【答案】A 【解析】设=xf x x ln )(，则='−x f x x1ln 2)(，令=='−x f x x 01ln 2)(，则=x e ，所以当∈x 0,e )(时，>'f x 0)(，f x )(单调递增；当∈+∞x e,)(时，<'f x 0)(，f x )(单调递减；又==a f e e 222)(，===f b 24ln 2ln 44)(，==c f 33ln 3)(，又>>f f f 3e 42)()()(，所以.选：A.【例4-2】（2022·山西吕梁）已知===−a b c ln e ,ln 1a ，b ，c 的大小关系为（） A ． B ．>>b c a C ． D ．【答案】B【解析】===a 2022lnln 2022ln 202220221，===−b e e e 1ln e 1，===c 2021lnln 2021ln 202120211，令=x f x x ()ln ，则='−x f x x ()1ln 2，当<<x 0e 时，>'f x ()0，当>x e 时，<'f x ()0，所以f x ()在(0,e)上单调递增，在+∞(e,)上单调递减，由<<e 20212022，所以>>f f f (e)(2021)(2022)，所以>>b c a .故选：B. 【例4-3】（2023·贵州贵阳·统考模拟预测）已知正实数，若>=a b c ca b ln ln ln 11，>b e ，则的大小关系为（）A ．B ．C ．>>b c aD ．【答案】D 【解析】令=x f x x ln )(，则='−x f x x1ln 2)(， ∴当∈x 0,e )(时，0f x；当∈+∞x e,)(时，<'f x 0)(；f x 在0,e )(上单调递增，在+∞e,)(上单调递减，∴==f x f ee 1max )()(，又=f 10)(，当>x 1时，>f x 0)(恒成立，可得图象如下图所示，ln ln a ba b>，>b e ，∴<<a b 1； ln 11ln b c b c c c ==−>ln 0，∴<cc 0ln ，∴<<c 01；综上所述：.故选：D.【例4-4】（2022·内蒙古·赤峰二中模拟预测（理））已知=+a 3ln 21，=+b 4ln31，+=+c e 1e 2，则a 、b 、c 的大小关系为（） A ． B ．>>b c a C ．D ．【答案】B【解析】构造函数+=+x f x x 1ln 1)(，其中>x 0，则()()()+++=−==>'⎝⎭++ ⎪++⎛⎫x x x x x x f x x x x 1110241111322222)(，所以，函数在+∞0,)(上单调递增，因为=+=a f 3ln 221)(，=+=b f 4ln 331)(，+++==+=+=+c f e 1e 1e 11ln e e e 211)(，因为>>>3e 20，所以，.故选：B.【例4-5】（2023·湖南·模拟预测）设=−a e 52ln52)(，=b e 1，=c 4ln4，则a ，b ，c 的大小顺序为（） A ．<<a c b B ．<<c a bC ．D ．<<b a c【答案】A【解析】因为==−a 5e e 55(2ln 5)lne 222，==b e e 1ln e ，=c 4ln 4 故构造函数=xf x x ln )(，则='−x f x x1ln 2)(，令='−x f x x=01ln 2)(，解得x =e ，当，∈x 0e )(时，0f x，在，0e )(上单调递增，当，∈∞x e +)(时，<'f x 0)(，在，∞e +)(上单调递减，又因为⎝⎭ ⎪=⎛⎫a f 5e 2，=b f e )(，=c f 4)(所以<a b ，<c b ．因为====c f f 4242ln 4ln 2)()(，又<<52e e 2，所以⎝⎭ ⎪<⎛⎫f f 52e 2)(，即>c a ，故，故选：A ．【例4-6】（2023·全国·模拟预测）已知实数a b c ∈,,1,e )(，且=a a πln ln π，=b beeln 2，⎭=c c 10ln ，则实数a ，b ，c 的大小关系为（） A ． B ． C ． D ．<x e 时，单调递减，当<<x 0e时，单调递增，当=x e 时，取最大值e1，其图象如图所示：分别取=−x ,e ,10e π221，由于a b c ∈,,1,e )(，且 1.6e<1.7,,<∴<<e 1.7 1.6101010，又，，∈∴>e 2.7 2.8e 72222)(，故<e πe<2，由于>x e 时，单调递减，在<<x 0e 时，单调递增，结合图象得：b c a <<，故选：D【例4-7】（2022·贵州毕节·三模（理））已知=a ln 33，=b e ，=c 2e 2（e为自然对数的底数），则a ，b ，c 的大小关系为（） A ．B ．C ．D ．>>b c a【答案】A 【解析】令=xf x xln )(，>x 0)(，所以()='−x f x x ln ln 12)(，当∈x 0,e )(时，<'f x 0)(，函数单调递减当∈+∞x e,)(时，0fx，函数单调递增；所以==a f ln 333)(，==b lne e e ，===c f lne2e e e 2222)(，所以，故选：A.考法五取对数构造函数【例5-1】（2022·广西·模拟预测（理））已知===a b c 6,7,8876，则的大小关系为（） A ．>>b c a B ．C ．D ．【答案】D【解析】令=−f x x x 14ln )()(,则=−+−'xf x x ln 114)(. 因为=−y x ln 在+∞0,)(上单调递减，=−xy 114在+∞0,)(上单调递减，所以=−+−'xf x x ln 114)(在+∞0,)(上单调递减. 而=−+−>=−+−<''f f 565ln510,6ln610,1414)()( 所以在+∞6,)(上有<'f x 0)(.所以=−f x x x 14ln )()(在+∞6,)(上单调递减. 所以>>f f f 67 8)()()(，即>>8ln67ln76ln8 故>>678876.故.故选：D【例5-2】（2023·全国·高三专题练习）已知=a 2ln7，=b 3ln 6，=c 4ln5，则（） A ．<<b c a B ．C ．D ．【答案】B【分析】对a ，b ，c 取对数，探求它们的结构特征，构造函数=⋅−f x x x ln ln 9)()((≤≤x 24)，借助导数判断单调性即可作答.【详解】对a ，b ，c 取对数得：=⋅a ln ln 2ln 7，=⋅b ln ln3ln 6，=⋅c ln ln 4ln5，令=⋅−f x x x ln ln 9)()((≤≤x 24)，=−'−xf x x ln 9)()(()−−=−−−x x x x x x x x99ln 9ln 9ln )()(，令=>g x x x x ()ln ,1，=+>'g x x ()ln 10，即=g x x x ()ln 在+∞(1,)上单调递增，由≤≤x 24得，−≥>>x x 951，于是得−−>x x x x 9ln 9ln )()(，又−>x x 90)(，因此，>'f x 0)(，即在2,4][上单调递增，从而得<<f f f 234)()()(，即<<ln 2ln 7ln3ln 6ln 4ln5，<<a b c ln ln ln ，所以.故选：B【例5-3】（2022·全国·高三专题练习）已知====a b c d 3.9, 3.9, 3.8, 3.83.9 3.8 3.9 3.8，则,,,a b c d 的大小关系为（）A ．<<<d c b aB ．<<<d b c aC ．<<<b d c aD ．<<<b c d a【答案】B【分析】构造函数=xf x xln )(，利用导数判断函数的单调性，可得<f f 3.9(3.8))(，从而可得<3.9 3.83.8 3.9，再由=y x 3.8在+∞0,)(上单调递增，即可得出选项. 【详解】构造函数=x f x x ln )(，则='−x f x x1ln 2)(，当∈+∞x e ,)(时，<'f x 0)(，故=xf x xln )(在∈+∞x e ,)(上单调递减，所以<f f 3.9(3.8))(，所以<3.9 3.8ln 3.9ln 3.8，<3.8ln3.9 3.9ln3.8所以<ln 3.9ln 3.83.8 3.9，<3.9 3.83.8 3.9，因为=y x 3.8在+∞0,)(上单调递增，所以<3.8 3.93.8 3.8，同理<3.8 3.93.9 3.9，所以<<<3.8 3.9 3.8 3.93.8 3.8 3.9 3.9，故选：B考法六 −+x xe 1)(−−ln x (x 1)构造指对数切线或【例6-1】（2022·江西景德镇）已知=−a e 10.03，=b 1033，=c ln1.03，则a ，b ，c 的大小关系为（） A ． B ． C ．D ．【答案】B【解析】记=−−≥f x x x xe 1,0)()(.因为，所以当>x 0时，，所以f x )(在+∞0,)(上单调递增函数，所以当>x 0时，>=f x f 00)()(，即−>e x x 1，所以−>e 10.030.03.记=+−≥g x x x x ln 1,0)()()(.因为，所以g x )(在+∞0,)(上单调递减函数，所以当>x 0时，<=g x g 00)()(，即+<x x ln 1)(，所以<ln1.030.03.所以>a c . 记+=+−≥xh x x x x1ln 1,0)()()(. 因为，所以当>x 0时，，所以h x )(在+∞0,)(上单调递增函数，所以当>x 0时，>=h x h 00)()(，即++>xx x 1ln 1)(，所以+>=10.03103ln1.030.033.所以>c b . 综上所述：.故选：B【例6-2】（2022·全国·武功县普集高级中学模拟预测（理））设=a 2022ln 2023，=b 20221，=c 2023log 12，则（） A ． B ． C ． D ．c<a<b【答案】D【解析】令=>t 202212023，则==−a t b t ln ,1，设=−−f t t t ()1ln ，则'=−=−t tf t t ()111，当>t 1时，>'f t ()0，所以f t ()在+∞(1,)上单调递增，故>=f t f ()(1)0，即>b a ；又因为=>=<a c 20222023ln0,log 0202312，所以<c a ，综上，c<a>b c a【答案】B【解析】设函数=−−∈f x x x x ()e 1,R ,则=−'f x x ()e 1，当<x 0时，<'f x ()0，f x ()递减；当>x 0时，>'f x ()0，f x ()递增，故≥=f x f ()(0)0，即≥+x x e 1，当=x 0时取等号；∵≥+x xe 1，∴>−=−100100e199110099，∴>b a ，由以上分析可知≥+x x e 1，则>x 0时，有≥−x x e 1成立，当=x 1时取等号，，即x x ≤−ln 1，当=x 1时取等号，∴<−=100100100ln 11011011，∴>a c ，故，故选：B.【例6-4】（2023·湖北·校联考模拟预测）设===−a b c 21,ln1.05,e 110.05，则下列关系正确的是（） A ． B ． C ．D ．【答案】C【解析】记=−−≥f x x x x ()e 1,(0)，因为=−'f x x ()e 1，当>x 0时，>'f x ()0，所以f x ()在+∞(0,)上单调递增，则当>x 0时，=−−>=f x x f x ()e 1(0)0，即−>e x x 1，取=x 0.05，所以−>e 10.050.05，记=+−≥g x x x x ()ln(1),(0)，因为+<'+=−=−x xg x x 11()101，所以g x ()在+∞(0,)上单调递减，则当>x 0时，<=g x g ()(0)0，即+<x x ln(1)，取=x 0.05，所以<ln1.050.05，故<−ln1.05e 110.05，即x 0时，>'h x ()0，所以h x ()在+∞(0,)上单调递增，所以当>x 0时，>=h x h ()(0)0，即++>xx x1ln(1)，取=x 0.05，所以+>==10.0510521ln1.050.0551，即>b a ；所以.故选：C.考法七作差作商构造函数【例7-1】（2023·安徽宿州·统考一模）已知=m 34，=−a m 23，=−b m 45，则（） A ．>>a b 0 B ．>>b a 0 C ．>>a b 0 D ．>>b a 0【答案】B【解析】由=⇒=m m34log 43，22222223lg 2lg 4lg 3lg 3lg 4lg 3lg 2lg 44lg 3lg 8lg 9lg 82log 3log 40lg 2lg 3lg 2lg 3lg 2lg 34lg 2lg 34lg 2lg 32，22222234lg 3lg 5lg 4lg 4lg 5lg 4lg 3lg 54lg 4lg 15lg 16lg 152log 4log 50lg 3lg 4lg 3lg 4lg 3lg 44lg 3lg 44lg 3lg 42，∴>>log 3log 4log 5234，∴=−>−=b m 45450log 54，=−<−=a m 23230log 32， ∴>>b a 0. 故选：B.【例7-2】（2023·四川乐山·统考一模）已知，，，===a b c 29sin0.10.09ln 111则（） A ．c >a >b B ．a >c >b C ．b >c >aD ．a >b >c【答案】A【解析】令=−+∈f x x x x x ()sin ,[0,1]2，则=−+'f x x x ()cos 12，设=−+=−+>'g x x x g x x ()cos 12,()sin 20恒成立，所以=−+g x x x ()cos 12在∈x [0,1]单调递增，所以≥=g x g ()(0)0，即≥'x f ()0在∈x [0,1]时恒成立，所以=−+∈f x x x x x ()sin ,[0,1]2单调递增，则=−+>=f f (0.1)sin 0.10.10.01(0)0，即>sin 0.10.09，故>a b ，令−=−∈+xh x x x x1()ln 2sin ,0,11)(， ='+−−=+−−x x x h x x x 1112cos 2cos 1122)(，因为−>x 1222，<x 2cos 2，所以−=−>'xh x x 1()2cos 022在∈x 0,1)(恒成立，所以h x ()在∈x 0,1)(单调递增，所以>=h x h ()(0)0，所以>=h h (0.1)(0)0，即−>0.9ln2sin 0.101.1，即>29ln sin 0.1111，所以>c a ，所以，故选:A.考法八其他模型【例8-1】（2022·全国·统考高考真题）已知===a b c 3244,cos ,4sin 3111，则（）A ．B ．C ．D ．【答案】A【解析】[方法一]：构造函数因为当⎝⎭⎪∈<⎛⎫x x x 20,,tan π故=>b c 44tan 11，故>b c1，所以>c b ；设=+−∈+∞f x x x x 2()cos 1,(0,)12， =−+>'f x x x ()sin 0，所以f x ()在+∞(0,)单调递增，故⎝⎭ ⎪>⎛⎫f f 4(0)=01，所以−>432cos 0131，所以>b a ，所以，故选A[方法二]：不等式放缩因为当⎝⎭⎪∈<⎛⎫x x x 20,,sin π，取18x得：⎝⎭ ⎪=−>−=⎛⎫48832cos 12sin 121113122，故>b a⎝⎭⎪+=+⎛⎫ϕ4444sin cos 111，其中⎝⎭ ⎪∈⎛⎫ϕπ20,，且==ϕϕsin当+=444sin cos 11+=ϕπ421，及=−ϕπ241此时=ϕ4sin cos 1=ϕ4cos sin 1故=4cos 1<=<44sin 4sin 11，故b a ，所以，故选A[方法三]：泰勒展开设=x 0.25，则==−a 3221310.252，=≈−+b 424!cos 110.250.2524，==≈−+c 443!5!14sin1410.250.25sin124，计算得，故选A.[方法四]：构造函数因为=b c 44tan 1，因为当⎝⎭⎪∈<<⎛⎫x x x x 20,,sin tan π，所以>44tan 11,即>b c 1，所以>c b ；设=+−∈+∞f x x x x 2()cos 1,(0,)12，=−+>'f x x x ()sin 0，所以f x ()在+∞(0,)单调递增，则⎝⎭⎪>⎛⎫f f 4(0)=01,所以−>432cos 0131，所以>b a ,所以，故选：A ．[方法五]：【最优解】不等式放缩因为=b c 44tan 1，因为当⎝⎭⎪∈<<⎛⎫x x x x 20,,sin tan π，所以>44tan 11,即>b c 1，所以>c b ；因为当⎝⎭⎪∈<⎛⎫x x x 20,,sin π，取18x得⎝⎭⎪=−>−=⎛⎫48832cos 12sin 121113122，故>b a ，所以．故选：A ．【例8-2】（2023·新疆·校联考模拟预测）若=a 0.6e 0.4，=−b 2ln 4，=−c e 2，则a ，b ，c 的大小关系为（） A ．B ．C ．>>b c aD ．【答案】B 【解析】由题意，=a 0.6e 0.4，=−b 2ln 4，=−c e 2对于a 和b ， ∵==−a 0.6ee 1ln e 0.40.40.4)(，=−=−b 2ln 421ln 2)(，∴可以构造函数=−f x x x 1ln )()(，则=a f e 0.4)(，=b f (2).对求导，得=−'f x x ln )(，当∈+∞x 1,)(时，<'f x 0)(， ∴在+∞1,)(上单调递减.∵=<<<1e e e 200.40.5，∴>f f e (2)0.4)(，即>a b ；对于b 和c ，∵−=−−=−−b c 4ln 4e 42ln 2e . ∴可以构造函数=−−g x x x x ()2ln e ，则=−'g x x ()1ln ，当∈x 0,e )(时，>'g x 0)(；当∈+∞x e,)(时，<'g x 0)(， ∴在0,e )(上单调递增，在+∞e,)(上单调递减，∴==g x g e 0max )()(， ∴<g 20)(，∴−c b ；对于a 和c ，∵−=−−+a c 10.4e e 20.4)(，∴可以构造函数=−−+h x x x1e e 2)()(，则=−'h x x x ()e ，当∈x 0,1)(时，<'h x 0)(， ∴在0,1)(上单调递减.又∵=−+h 0.50.5e e 20.5)(，且>e 1.60.5，∴>h 0.50)(，∴>>h h 0.40.50)()(， ∴−>a c 0，即>a c . ∴，故选：B.【例8-3】（2023·山西临汾·统考一模）已知===a b c 11ln1.1,,1,则（） A ．B ．C ．D ．【答案】D【解析】解:由题知构造=+f x x ln 1)()(≥x 0)(,所以+==≤'+−x f x x 101112)(,故在+∞0,)[单调递减,所以<=f f 0.100)()(,即<ln 1.10)(,即<ln 1.1)(即<a c 因为⎝⎭⎪==−=−=−−⎛⎫−10111111ln1.1lnln ln ln 111101111, 构造=+−g x x x ln 1)()(,∈−x 1,0](, 所以++=−=≥'−x xg x x11101)(, 即在−1,0](上单调递增,所以⎝⎭⎪−<=⎛⎫g g 11001)(,即⎝⎭ ⎪−+<⎛⎫1111ln 1011,即⎝⎭ ⎪<−−⎛⎫1111ln 111,即=25，∴>b 1， 0.3000.40.41<<=，∴<<c 01，∴<<a c b .故选：D.2．（2023·陕西西安·统考一模）已知函数=−f x x ()2，若==b c a2log 2，则（）A ．<<f b f c f a ()()()B ．<<f a f b f c ()()()C ．<<f a f c f b ()()()D ．<<f c f b f a ()()()【答案】A【解析】=−f x x ()2在R 上单调递减，在同一坐标系中作====y c y x y x y x,,2log ,2的图像，如图：所以，故<<f b f c f a )()()(，故选：A.3．（2023·辽宁·校联考模拟预测）已知函数=f x x3tan π)(的最小正周期为T ，设=a T sin ，=b T cos ，=c T log 8，则（）A ．B ．C ．c<a<bD ．【答案】B【解析】因为函数=f x x 3tan π)(的最小正周期为T ，所以==ωT 3π，因为<<6π3π5，所以⎝⎭⎪=∈⎛⎫a T 2sin 0,1，===c ln 8ln 92log 3log 3ln 3ln 3189，所以.故选：B4．（2023·陕西西安·统考一模）若=a lg 0.2，=b log 23，=c log 46，则关于a 、b 、c 的大小关系，下列说法正确的是（） A ． B ．>>b c a C ．D ．【答案】A【解析】lg 0.2lg10a =<=又24222222log 3log 6log 3log 6log 3log 6log log 10−=−=−=>=6213即>>>log 3log 6log 10244∴<<log 3log 601124 即>>>log 4log 20lg 263所以故选：A5．（2023·黑龙江·黑龙江实验中学校考一模）已知===a b c log log 3340.1，则（） A ．B ．C ．<<c a bD ．【答案】B【解析】00.13311>=∴>c ，>==>=3log log 33443111log log log 33331333，即<<a 311，==<==b lo 4g 4433411log log log 1444144，因此，故选：B6．（2023·陕西宝鸡·校联考模拟预测）已知a =20.3，=b 0.32，=c log 32，则（） A ．B ．C ．D ．【答案】A【解析】因为<<22200.30.5，所以∈a (，因为<<00.30.320，所以∈b 0,1)(，因为<<log log 3log 4222，所以⎝⎭ ⎪∈⎛⎫c 2,23，则．故选：A.7．（2023·福建·统考一模）设===a b c log 8,2,0.75 1.3 1.3，则a ，b ，c 的大小关系为（）A ．B ．C ．D ．c<a<b【答案】D【解析】因为=<<=1log 5log 8log 252555，所以，因为>=2221.31，所以>b 2，又因为<<=00.70.711.30，所以<<c 01，所以c<a'xf x 0)(恒成立，则下列不等式成立的是（） A ．−−<<f f f 5()()34)( B ．<−>−f f f 435)()()( C ．−<−<f f f 534)()()( D ．<−<−f f f 453)()()(【答案】A【解析】∈−∞x ,0)(时，>'xf x 0)(即<'f x 0)(， ∴在−∞,0)(上单调递减，又为偶函数，∴在+∞0,)(上单调递增．∴<<f f f 345)()()(， ∴−<<−f f f 345)()()(. 故选：A ．9．（2023·全国·模拟预测）已知∈+∞a b c ,,1,)(，且−−=−a a ln 1e 1，−−=−b b ln 2e 2，−−=−c c ln 4e 4，其中e 是自然对数的底数，则（）A ．B ．C ．D ．【答案】A【解析】由题意可得−=+−a a ln e 11，−=+−b b ln e 22，−=+−c c ln e 44，令=+−f x x x e )(，则=−+'−f x xe 1)(，因为当>x 0时0f x ，单调递增，所以<<f f f 124)()()(，即−<−<−a a b b c c ln ln ln ，令=−g x x x ln )(，则=−'x g x 11)(，因为当>x 1时，>'g x 0)(，所以在+∞1,)(上单调递增，又因为∈+∞a b c ,,1,)(且<<g a g b g c )()()(，所以，故选：A10．（2023·湖南长沙·统考一模）已知=a log 1.82，=b log 3.64，，则（）A ．B ．C ．D ．>>b c a【答案】C【解析】】==a log 1.8log 1.8242，所以==−=−<a b 3.6log 1.8log 3.6log log 101.8444422，所以<a b .=>==a c 2log 1.8log 122，所以>a c .所以有.故选：C.11．（2023·河南信阳·河南省信阳市第二高级中学校联考一模）已知=a log 0.30.2，=b log 0.20.6，=c 20.2，则a ，b ，c 的大小关系为（） A ． B ． C ． D ．>>b c a【答案】D【解析】因为=<=a log 0.3log 0.210.20.2， ∴<a 1，又=>=b log 0.2log 0.3620.60.6， ∴>b 2，∵<<00.20.5，<=<=c 1220.20.5∴<<c 12， ∴>>b c a ．故选：D ．12．（2022·全国·统考高考真题）已知==−=−a b m m m 910,1011,89，则（） A ．>>a b 0 B ．>>a b 0 C ．>>b a 0 D ．>>b a 0【答案】A【解析】［方法一］：（指对数函数性质）由=m910可得==>m lg9log 101lg109，而⎝⎭⎝⎭⎪ ⎪<=<=⎛⎫⎛⎫+22lg9lg111lg10lg9lg11lg99222)(，所以>lg9lg10lg10lg11，即>m lg11，所以=−>−=a m 101110110lg11.又⎝⎭⎝⎭⎪ ⎪<=<⎛⎫⎛⎫+22lg8lg10lg9lg8lg10lg80222)(，所以>lg8lg9lg9lg10，即>m log 98，所以=−<−=b m 89890log 98.综上，>>a b 0. ［方法二］：【最优解】（构造函数）由=m 910，可得=∈m log 10(1,1.5)9．根据a b ,的形式构造函数=−−>f x x x x m ()1(1) ，则=−'−f x mx m ()11，令='f x ()0，解得=−x m m 011，由=∈m log 10(1,1.5)9 知∈x (0,1)0 .f x () 在 +∞(1,) 上单调递增，所以>f f (10)(8) ，即 >a b ，又因为=−=f (9)9100log 109，所以>>a b 0 .故选：A.13．（2023·陕西西安·统考一模）已知函数满足+−=−f x f x x 22)()(，若==b c a 2log 2，则（）A ．<<f a f b f c )()()(B ．<<f b f c f a )()()(C ．<<f a f c f b )()()(D ．<<f c f b f a )()()(【答案】B【解析】因为+−=−f x f x x 2()()2，所以−+=f x f x x 2()()2，联立⎩−+=⎨⎧+−=−f x f x x f x f x x2()()22()()2，得=−f x x ()2，在R 上单调递减，在同一坐标系中作=y c ，=y x 2，=y x log 2，=y x 的图象，如图，所以，故<<f b f c f a )()()(.故选：B.14．（2023·云南·统考模拟预测）已知实数a 、b 、c 满足==b a c ln(ln )ln ，则a 、b 、c 的大小关系为（） A ． B ． C ．>>b c a D ．>>a c d【答案】C【解析】设=−f x x x ()ln ，则=−'−=x xf x x ()111，当<<x 01时，>'f x ()0，则函数f x ()在(0,1)上单调递增，当>x 1时，<'f x ()0，则函数f x ()在+∞(1,)上单调递减，所以==−<f x f ()(1)10max ，所以<x x ln ，所以=<a c c ln ，又=b c ln(ln )ln ，所以=<c b b ln ，所以>>b c a . 故选：C.15．（2023·贵州毕节·统考一模）已知=a 3log 38，=−b 2log 16131，=c log 34，则a ，b ，c 的大小关系为（） A ．B ．C ．>>b c aD ．【答案】A【解析】由题意可得==⨯=>a log 23log 33log 31log 322328，=−=−⨯=>b 3log 221log 16log 4111log 1633133，<=<c 0log 314，又=−=−−log 3log lg 2lg3lg 2lg34lg3lg 4(lg3)lg 2lg 4232，由于，>>≠∴<=<+2lg 20,lg 40lg 2lg 4,lg 2lg 4()(lg3)lg 2lg 4222，故∴>−>a b og ,3l 0log 423，综合可得，故选：A16．（2023·安徽蚌埠·统考二模）已知=x log 215，+=x x ln 022，=−x x3log 233，则（）A ．<<x x x 123B ．<<x x x 213C ．<<x x x 132D ．<<x x x 231【答案】A【解析】=<=x 2log 2log 1155，设=+f x x x ()ln ，因为函数f x ()在+∞0,)(上递增（增+增=增），⎝⎭ ⎪=+===<⎛⎫f 2222ln ln 01111，=f 11)(，即⎝⎭⎪<⎛⎫f f 2101)(，由零点存在定理可知<<x 2112；设函数⎝⎭⎪=−⎛⎫h x x x3log 12)(，易知在+∞0,)(上递减（减+减=减），=h 311)(，=−<h 92101)(，即<h h 210)()(，由零点存在定理可知<<x 123. 即<<<<x x x 211123. 故选：A ．17．（2023·浙江·永嘉中学校联考模拟预测）已知=ae sin π，=b e 2，=c e 为自然对数的底数），则（） A ．B ．>>b c aC ．D ．【答案】A【解析】因为<<3e 2πππ，所以=>=a e 3sin sin ππ，又>2e 5，=<a b ，设=x f x x ln )(，则='−xf x x1ln 2)(，由0f x，可得<<x 0e ，函数单调递增，由<'f x 0)(，可得>x e ，函数函数单调递减，所以≤=f x fe e 1)()(<e 1<e 2，即>b c ，所以.故选：A.18．（2023·安徽淮南·统考一模）若=a 75，86b ，=+c e 2e 22，则实数a ，b ，c 的大小关系为（） A ．B ．C ．>>b c aD ．【答案】B【解析】由已知可得，==a ln 7log 5ln 57，==b ln8log 6ln 68，由=+ce 2e 22可得，=+c ln e 222)(，所以()()++==c ln e 2ln e 22ln e 222. 设+=>x f x x xln(2),1ln )(，则()++=>'++−x x x f x x x x x x 2ln (2),12ln 2ln 2)()()(，因为>x 1，故+>>+>>x x x x 21,ln 2ln 0)(，所以++−>x x x x 2ln 2ln 0)()(即0f x，所以在+∞1,)(上为增函数，又=a f 5)(，=b f 6)(，=c f e 2)(，又>>e 652，所以.故选：B.19．（2023·陕西咸阳·校考模拟预测）已知===−−a b c 5,e ,ln5ln 4253，则（）A ．B ．C ．D ．>>b c a【答案】C【解析】=−−f x x x ()e 1=−f x x ()e 1'，则∈+∞>∈−∞<x f x x f x 0,,()0,,0,()0'')()(，故函数f x ()在−∞,0)(单调递减，+∞0,)(单调递增，则≥=f x f ()(0)0 则−−≥x x e 10，即≥+x x e 1 由≥+x xe 1，∴>−5e253，故>b a 同理可证+≤x x ln(1) 又+≤x x ln(1)，∴⎝⎭ ⎪−=+<⎛⎫44ln5ln 4ln 111，则故选：C.20．（2023·内蒙古赤峰·统考模拟预测）设⎝⎭ ⎪=⎛⎫a 230.7，⎝⎭ ⎪=⎛⎫b 320.7，=c log log 4433)(，则（） A ． B ． C ．c<a⎝⎭⎪⎪=⎛⎫⎛⎫a 223310.7；由⎝⎭ ⎪=⎛⎫y x32的值域，且在R 上单调递增可知，<=⎝⎭⎝⎭⎪⎪<=⎛⎫⎛⎫b 3302210.7；根据对数函数的单调性，=y x log 3在+∞(0,)上单调递增，故>=log 4log 3133，由=y x log 43在+∞(0,)上单调递减，故=<=c log log 4log 1044333)(.结合上述分析可知：<<<<c b a 01.故选：A21．（2023·浙江·统考一模）若正数a ，b ，c 满足ac a a b b ++=+=+−e 1ln 1） A ．b c a <x 1时，>'f x ()0，f x ()为增函数；当<x 1时，<'f x ()0，f x ()为减函数；所以≥=f x f ()(1)0，即≥−x x e 1；所以+=++>+≥+−−ab c a a a b b b e e 111，即>c a . 设=−+g x x x ()ln 1，则=−'xg x ()11，当>x 1时，<'g x ()0，g x ()为减函数；当<<x 01时，>'g x ()0，g x ()为增函数；所以≤=g x g ()(1)0，即x x ≤−ln 1；所以+=+≤−++=+b c a a c a c ln 11，即≤b a . 若=b a ，则==a c 1，与>c a 矛盾，故x (0)，则='⋅−x f x x x x ()e e 2=−x x x ()e 12，令>'f x ()0，得>x 1，令<'f x ()0，得<<x 01，所以f x ()在(0,1)上为减函数，在+∞(1,)上为增函数，因为<<<20ln 211，所以>f f 2()(ln 2)1，即=>b 21e 21=a ln 2eln 2，因为>8e 2，所以>2e 32，所以>3ln 22，所以>>3ln 414，所以>f f 3(ln 4)()4，即>=f f c 3(ln 4)()4，因为==f ln 42ln 2(ln 4)e 4ln 4=ln 22=a ，所以>a c ，综上所述：.故选：D23．（2023·四川绵阳·绵阳中学校考模拟预测）已知正数a ，b ，c 满足=a 3ln1.1，+=b 1 1.62)(，=c ln1.3，则（）A ．B ．C ．c<a<bD ．【答案】B【解析】==>=a c ln1.1ln1.331ln1.33；b 1构造=+>−f x x x 6()3ln(1)1,1，则='f x ()，令=>'f x ()0>+x 1解得：<<x 04，所以函数f x ()在(0,4]上单调递增，则>=f f (0.1)(0)0，即=>=a b 3ln1.11，所以>a b ，构造=+>−g x x x 2()ln(1)1,1，则='g x ()，令=≤'g x ()0+x (1)，解得：>−x 21，所以函数g x ()在−+∞2(,)1上单调递减，则=>g g 0(0)(0.3)，即<ln1.310，所以<c b ，综上可知：，故选：B .24．（2023·四川广安·统考一模）设=a 0.035，=−b 2.25e 10.01)(，=c 4ln1.01，则a ，b ，c的大小关系是（） A ． B ． C ．=f f 0.0100)()(，即−>8ln1.0100.07， ∴>4ln1.010.035，即>c a ，构建=−−g x x x e e 141)(，则=−'g x x e e 41)(，当<<x 401时，则<'g x 0)(，故在⎝⎭⎪⎛⎫40,1上单调递减， ∵⎝⎭⎪∈⎛⎫40.010,1，则<=g g 0.0100)()(，即−−<e 0.01e 1040.011，∴−<e 10.01e 40.011，又∵⎝⎭⎪=>>⎛⎫965613e 14384164，则<9e 1441，∴−<<9e10.01e 0.1440.011，故−<2.25e 10.0350.01)(，即<b a ，综上所述：.。

高考数学知识点：函数比较大小(解析版)

函数比较大小专项突破一指数式、对数式，幂式比较大小1.已知a=log2e，b=ln2，c=1e，其中e为自然对数的底数，则( )A.a>b>cB.a>c>bC.b>a>cD.b>c>a【解析】∵log2e>log22=1=ln e>ln2>ln2=12>1e，∴a>b>c.故选：A.2.设a=325，b=25 3，c=log325，则( )A.a>b>cB.a>c>bC.b>a>cD.c>b>a【解析】结合指数函数性质和对数函数性质可知a=325>30=1，0<b=253<250=1，c=log325<log31=0，∴a>b>c，故选：A.3.已知a,b,c,d∈R,2a=3b=log12c=log13d=2，则( )A.a<b,c<dB.a<b,c>dC.a>b,c<dD.a>b,c>d【解析】因为a,b,c,d∈R,2a=3b=log12c=log13d=2，所以a=1,b=log32<1，故a>b，c=12 2=14,d=13 2=19，所以c>d.故选：D.4.若a=50.3，b=0.35，c=ln sin22020，则a，b，c的大小关系为( )A.a>b>cB.a>c>bC.b>a>cD.c>a>b【解析】a=50.3>1，b=0.35∈0,1，0<sin22020<1，所以c=ln sin22020<0，所以a>b>c 故选：A5.已知a=12 13，b=53 12，c=log2352，则a,b,c的大小关系为( )A.a<b<cB.c<b<aC.c<a<bD.b<a<c【解析】a=1213<12 0=1，b=53 12>53 0=1，c=log2352<log231=0，∴b>1>a>0>c.故选：C.6.已知a=30.5，b=log32，c=tan56π，则( )A.a>b>cB.b>a>cC.c>a>bD.a>c>b【解析】∵30.5>30=1=log33>log32>log31=0>-33=tan5π6，∴a>b>c.故选：A.7.已知幂函数f x 的图象经过点A3,27与点B t,64，a=log0.1t，b=0.2t，c=t0.1，则( ) A.c<a1，所以a<b<c，故选：B8.已知函数f(x)是定义在R上的偶函数，对任意x1，x2∈(0,+∞)，都有f(x1)-f(x2)x1-x2>0(x1≠x2)，a=f log 1312，b =f log 213 ，c =f 512，则( )A.a >b >c B.c >a >b C.b >a >c D.c >b >a【解析】因为对任意x 1，x 2∈(0,+∞)，都有f (x 1)-f (x 2)x 1-x 2>0(x 1≠x 2)，所以f (x )在(0,+∞)上单调递增，又函数f (x )是定义在R 上的偶函数，所以f (x )=f (-x )因为log 1312=log 32，又0=log 31<log 32<log 33=1所以log 1312∈0,1 ，又1=log 22<log 23<log 24=2，512=5>2所以0<log 1312<log 23<512，所以f log 1312 <f log 23 =f -log 23 =f log 213 <f 512 所以c >b >a .故选：D .9.已知定义在R 上的偶函数f x 满足f x +6 =f x ，且当x ∈0,3 时，f x =xe x ，则下面结论正确的是( )A.f ln3 <f e 3 <f -eB.f -e <f ln3 <f e 3C.f e 3 <f -e <f ln3D.f ln3 <f -e <f e 3【解析】∵x ∈0,3 ，f x =xe x ，∴f x =e x x +1 ，∴x ∈0,3 时，f x 单调递增；∵f x +6 =f x ，∴x ∈18,21 ，f x 单调递增；∵2+3×6<e 3<e +3×6 ，∴f 2+3×6 <f e 3 <f e +3×6 ，∴f 2 <f e 3 <f e ，∵f -x =f x ∴f -e =f e ，∴0<ln3<ln e 2=2，∴f ln3 <f 2 ，综上所述，f ln3 <f e 3 <f -e .故选：A .10.已知定义在R 上的函数y =f (x -1)的图象关于点(1，0)对称，且函数y =f (x )在(0,+∞)上单调递增，a =0.23，b =30.2，c =log 0.20.3，则f (a )，f (b )，f (c )的大小关系为( )A.f (a )>f (b )>f (c )B.f (c )>f (a )>f (b )C.f (b )>f (c )>f (a )D.f (c )>f (b )>f (a )【解析】因为函数y =f (x -1)的图象关于点(1，0)对称，所以y =f (x )的图象关于点(0，0)对称,即函数y =f (x )为奇函数，所以a =0.23=0.008，b =30.2>30=1，c =log 0.20.3=log 0.20.09>log 0.20.2=12，故b >c >a >0，又函数y =f (x )在(0,+∞)上单调递增，所以f (b )>f (c )>f (a )，故选：C .11.已知a =ln12，b =ln lg2 ，c =lg ln2 则a ，b ，c 的大小关系是( )A.c >a >bB.c >b >aC.a >b >cD.b >c >a【解析】先比较a ,b ，易知lg2<12,故ln (lg2)<ln 12，即b <a ，又e <10，故x >1时ln x >lg x ，0<x <1时ln x <lg x ，故lg 12>ln 12，而ln2>12，故lg (ln2)>lg 12>ln 12，有c >a ，故选：A ，12.已知x ∈1,2 ，则下列说法正确的是( )A.ln22x>2ln2x >x 2ln2 B.x 2ln2>ln22x>2ln2x C.2ln2x >x 2ln2>ln22xD.2ln2x >ln22x>x 2ln2【解析】∵x 2ln2=ln2x 2，2ln2x =ln 2x 2，∴比较2x 2，2x 2，22x的大小关系即可．1、当x ∈1,2 时，x 2<2x ，x 2<2x ，故2x 2<22x，2x 2<2x 2，故x 2ln2<ln22x，x 2ln2<2ln2x ．2、令2x =t ∈2,4 ，则2x 2=t 2，22x =2t ．由2t <t 2，即22x <2x 2，则2ln2x >ln22x．综上，2ln2x >ln22x>x 2ln2.故选：D ．13.(多选)已知a ,b ,c ∈R ，且ln a =e b =1-c ，则下列关系式中可能成立的是( )A.a >b >cB.a >c >bC.c >a >bD.c >b >a【解析】设ln a =e b =1-c =t ,t >0，则a =e t ,b =ln t ,c =1-t ，在同一直角坐标系中分别画出函数y =e x ,y =ln x ,y =1-x 的图像，当0<t <1时，a >c >b ，当t =1时，a >c =b ，当t >1时，a >b >c ，故AB 正确.14.(多选)若b >c >32，13<a <12，则( )A.b log c a <c log b aB.bc a <cb aC.b a >c aD.log b a <log c a【解析】对于A 选项，因为b >c >32，13<a <12，则log c a <0，log b a <0，b b >b c >c c >1，b log c a c log b a =b lg a lg c ⋅lg b c lg a =lg b blg c c>1，所以，b log c a <c log b a ，A 对；对于B 选项，bc a cba =bc ⋅b c -a =b c 1-a >b c 0=1，则bc a >cb a ，B 错；对于C 选项，b a >c a ，C 对；对于D 选项，log b a log c a =lg a lg b ⋅lg c lg a =lg clg b<1，所以，log b a >log c a ，D 错.故选：AC .15.已知a =2-13，b =log 213，c =log 1213，则a ，b ，c 的大小关系为___________.【解析】因为y =2x 在R 上为增函数，且-13<0，所以0<2-13<20=1，即0<a <1，c =log 1213=log 23因为y =log 2x 在(0,+∞)上为增函数，且0<13<1<2<3，所以log 213<log 21<log 22<log 23，即log 213<0<1<log 23，即b <0<1<c ，所以b <a <c ，16.若a =log 23，b =log 48，c =log 58，则a ,b ,c 的从大到小顺序为______________.【解析】由于b =log 48=12log 28=log 28<log 29=a ，即a >b .由b =log 48=1log 84>1log 85=c ，即b >c .所以a >b >c .17.已知a =35 25，b =25 35，c =2525，则a ，b ，c 的大小关系为____.(用“<”连接)【解析】由于函数y =25 x 在R 上是减函数，且35>25，∴c =25 25>b =2535，由于函数y =x 25在0,+∞ 上是增函数，且35>25，∴a =35 25>c =2525，故a ，b ，c 的大小关系是b <c <a .18.1.10.9，log 1.10.9，log 0.70.8的大小关系是________.【解析】因为y =1.1x 单调递增，所以1.10.9>1.10=1；因为y =log 1.1x 在0,+∞ 上单调递增，所以log 1.10.9<log 1.11=0；因为y =log 0.7x 在0,+∞ 上单调递减，所以0=log 0.71<log 0.70.8<log 0.70.7=1；所以1.10.9>log 0.70.8>log 1.10.9.19.已知a >b >0，且a +b =1，x =1a b ，y =log ab 1a +1b ，z =log b 1a，则x ，y ，z 从大到小为__________.【解析】∵a >b >0，a +b =1，∴1>a >12>b >0，∴1<1a <1b，∴x =1a b >1a 0=1，y =log (ab )1a +1b =log (ab )1ab =-1，z =log b 1a >log b 1b=-1.∴x >z >y .20.已知55<84，134<85，设a =log 53，b =log 85，c =log 138，则a ，b ，c 的大小关系是______.(用“<”连接)【解析】由题意，知a ,b ,c ∈0,1 .因为a b =log 53log 85=lg3lg5⋅lg8lg5<1lg52⋅lg3+lg82 2=lg3+lg82lg5 2=lg24lg25 2<1，所以a 4，可得c >45，综上所述，a ，b ，c 的大小关系是a <b <c .21.已知x ,y ,z 分别满足下列关系：18x =19,19y =20,log 1918z =2019，则x ,y ,z 的大小关系(从小写到大)_______.【解析】因为18x=19,19y=20,log 1918z =2019，所以x =log 1819,y =log 1920,z =1918 2019，x -y =log 1819-log 1920=ln19ln18-ln20ln19=ln19 2-ln20⋅ln18ln18⋅ln19ln20⋅ln18<ln20+ln182 2=ln3602 2<ln36122=ln19 2，所以x -y >0即x >y ，z =1918 2019>1918，z x >1918log 1819=1918⋅ln18ln19=ln1818÷ln1919>1所以z >x ，故有y <x <z22.设a ,b ,c 均为正数，且2a =log 12a ,12b =log 12b ,12 c=log 2c ，则a ,b ,c 的大小关系为______________．【解析】a ,b ,c 分别是函数y =2x ,y =log 12x 的交点，函数y =12x,y =log 12x 的交点，函数y =12x,y =log 2x 的交点，做出三函数图像，由图像可知a 13，∴25 0.3>130.3；(2)∵y =x -1在-∞，0 上是减函数，又-23<-35，∴-23 -1>-35 -1；(3)∵y =x 0.3在0,+∞ 上为增函数，∴由25>0.3，可得250.3>0.30.3，①又y=0.3x在(-∞,+∞)上为减函数，∴0.30.3>0.325，②由①②知250.3>0.325.24.比较下列几组值的大小：(1)(-2.5)23和(-2.5)45；(2)25 -12和(0.4)-32；(3)13 -12和32 -12；(4)0.4-2.5，2-0.2，2.51.6．【解析】(1)由于(-2.5)23=2.523，(-2.5)45=2.545．∵y=2.5x在R上为增函数，且45>23，∴2.545>2.523，即(-2.5)45>(-2.5)23；(2)由于(0.4)-32=25 -32．∵y=25 x在R上为减函数，且-12>-32，∴25 -12<(0.4)-32；(3)∵y=13 x在R上为减函数，y=32 x在R上为增函数，且-12<0，∴13 -12>1，32 -12<1，∴13 -12>32 -12；(4)∵0.4-2.5=2.52.5，y=2.5x在R上为增函数，且2.5>1.6>0>-0.2∴2.52.5>2.51.6>1>2.5-0.2，∴0.4-2.5>2.51.6>2-0.2．25.已知正实数x，y，z满足3x=4y=6z．(1)求证：1z-1x=12y；(2)比较3x,4y,6z的大小．【解析】(1)证明：令3x=4y=6z=m，利用指数式和对数式的互化知x=log3m，y=log4m，z=log6m则1x=log m3，1y=log m4，1z=log m6∴1z-1x=log m6-log m3=log m2=12y.(2)3x<4y<6z，证明：因为正实数x，y，z，∴3x>0,4y>0,6z>0，∴3x4y=3log3m4log4m=3lg mlg34lg mlg4=34×lg4lg3=34log34=log3464又464<3，∴log3464<1，∴3x<4y∴4y6z=4log4m6log6m=4lg mlg46lg mlg6=23×lg6lg4=23log46=log236又36<2，∴log236<1，∴4y<6z，∴3x<4y<6z．专项突破二构造函数比较大小1.已知f (x)是定义在R上的函数f(x)的导函数，且满足xf (x)+f(x)>0对任意的x∈R都成立，则下列选项中一定正确的是( )A.f(1)>f(2)2 B.f(1)2>f(2) C.f(1)<f(2)2 D.f(1)2<f(2)【解析】令F x =xf x ，则F x =xf (x)+f(x)>0，故F x 为R上的增函数，所以F2 >F1 即2f2 >f1 ，故选：D.2.若a=ln33，b=e-1，c=5ln2010(e为自然对数的底数)，则实数a，b，c的大小关系为( )A.b<a<cB.c<a<bC.c<b<aD.b<c<a【解析】令f(x)=ln xx，则f (x)=1-ln xx2，故当x∈(0,e)时，f(x)>0；当x∈(e,+∞)时，f (x)<0；而a=ln33=ln33=f(3)，b=e-1=ln ee=f(e)，c=5ln2010=ln2525=f25，而e<3<25，故b>a>c，故选：B3.已知a=ln33，b=1e，c=ln55，则以下不等式正确的是( )A.c>b>aB.a>b>cC.b>a>cD.b>c>a【解析】令f x =ln xx,则f x =1-ln xx2,当0<x<e时,f x >0,f x 单调递增,当x>e时,f x <0,f x 单调递减,因为e<3<5,所以f e >f3 >f5 ,所以b>a>c，故选:C 4.设a=3e2ln e23，b=1e，c=ln22，则a，b，c的大小顺序为( )A.a<c<bB.c<a<bC.a<b<cD.b<a<c【解析】令f x =ln xx x>0，则f (x)=1-ln xx2，当x>e时，f (x)<0，函数单调递减，当0<x<e时，f (x)>0，函数单调递增，故当x=e时，函数取得最大值f e =1 e，因为a=3e2ln e23=f e23，c=ln22=f2 ，b=1e=f e ，∵2<e23<e，当0<x<e时，函数f x 单调递增，可得f2 <fe23<f e ，即c<a<b．故选：B．5.已知a=810，b=99，c=108，则a，b，c的大小关系为( )A.b>c>aB.b>a>cC.a>c>bD.a>b>c【解析】构造f x =18-xln x，x≥8，f x =-ln x+18x-1，f x =-ln x+18x-1在8,+∞时为减函数，且f 8 =-ln8+94-1=54-ln8<54-ln e2=54-2<0，所以f x =-ln x+18x-1<0在8,+∞恒成立，故f x =18-xln x在8,+∞上单调递减，所以f8 >f9 >f10，即10ln8>9ln9>8ln10，所以810>99>108，即a>b>c.故选：D6.已知实数a，b满足a=log23+log86，5a+12a=13b，则下列判断正确的是( )A.a>2>bB.b>2>aC.b>a>2D.a>b>2【解析】a=log23+log86=log23+13log22×3=43log23+13>43log222+13=43×32+13=73>2，所以a>2；由5a+12a=13b且a>2，所以5a+12a>25+144=169，所以b>2，令f x =5x+12x-13x，x>2，令t=x-2>0，则x=t+2，则f x =5x+12x-13x，x>2等价于g t =25×5t+144×12t-169×13t，t>0；又g t =25×5t+144×12t-169×13t<169×12t-169×13t<0，所以当x>2时，f x =5x+12x-13x<0，故5a+12a=13b<13a，所以a>b>2.故选：D.7.设a=20202022，b=20212021，c=20222020，则( )A.a >b >cB.b >a >cC.c >a >bD.c >b >a【解析】∵ln a ln b =2022ln20202021ln2021=ln20202021ln20212022，构造函数f x =ln x x +1x ≥e 2，f x =x +1-x ln x x x +1 2，令g x =x +1-x ln x ，则gx =-ln x <0，∴g x 在e 2,+∞ 上单减，∴g x ≤g e 2 =1-e 2<0，故f x <0，∴f x 在e 2,+∞ 上单减，∴f 2020 >f 2021 >0，∴ln aln b =f 2020 f 2021>1∴ln a >ln b .∴a >b ，同理可得ln b >ln c ，b >c ，故a >b >c ，故选：A 8.设a =23e1.5，b =23(4-ln2)，c =e 33，则a ,b ,c 的大小关系是( )A.b <c <aB.c 0得函数f (x )在(2,+∞)单调递增所以f (3)<f 32即c <a ；②再比较b ,c ：由①知f min (x )=f (2)=e 24<f (3)=c ，而b =2232-12ln2 =232+ln 12 12，设h (x )=23(ln x +2)x ，h (x )=-23(ln x +1)x 2当0<x <1e ，h (x )>0，h (x )单调递增，当x >1e，h(x )<0，h (x )单调递减，所以b =h 12 <h max (x )=h 1e =23e ，而23e <e 4.e =e 24<f (3)=c ，所以b <c ，故选：A9.已知a ,b ,c ∈(0,1)，且a 2-2ln a +1=e ，b 2-2ln b +2=e 2，c 2-2ln c +3=e 3，其中e 是自然对数的底数，则( )A.a >b >cB.a >c >bC.c >a >bD.c >b >a【解析】设f x =x 2-2ln x ,g x =e x -x ，则f a =g 1 ,f b =g 2 ,f c =g 3 ，又g x =e x -1>0x >0 ，所以g x 在0,+∞ 上单调递增，所以g 3 >g 2 >g 1 ，即f c >f b >f a ，因为fx =2x -2x =2x 2-1 x<0x ∈0,1 ，所以f x 在0,1 上单调递减，所以a >b >c ，故选：A 10.设a =e 1.3-27,b =4 1.1-4,c =2ln1.1，则( )A.a 33，∴e 1.3<27，∴a <0；b -c =4 1.1-4-2ln1.1=22 1.1-2-ln1.1 ，令f x =2x -2-ln x ，∴f x =1x-1x =x -1x ，∴当0<x <1时，f x <0，f x 单调递减；当x >1时，f x >0，f x 单调递增；∴f (x )min =f 1 =0，∴f 1.1 >0，即2 1.1-2-ln1.1>0，∴c 2ln1=0，∴a <c <b ．故选：B ．11.已知定义在R 上的偶函数f x 满足f x +6 =f x ，且当x ∈0,3 时，f x =xe x ，则下面结论正确的是( )A.f ln3 <f e 3 <f -eB.f -e <f ln3 <f e 3C.f e 3 <f -e <f ln3D.f ln3 <f -e <f e 3【解析】∵x ∈0,3 ，f x =xe x ，∴f x =e x x +1 ，∴x ∈0,3 时，f x 单调递增；∵f x +6 =f x ，∴x ∈18,21 ，f x 单调递增；∵2+3×6<e 3<e +3×6 ，∴f 2+3×6 <f e 3 <f e +3×6 ，∴f 2 <f e 3 <f e ，∵f -x =f x ∴f -e =f e ，∴0<ln3<ln e 2=2，∴f ln3 <f 2 ，综上所述，f ln3 <f e 3 <f -e .故选：A .12.设a =10099，b =e 0.01，c = 1.02，则( )A.a >b >cB.a >c >bC.b >a >cD.c >a >b【解析】令f x =e x -x +1 ，则f x =e x -1，所以当x <0时f x <0，当x >0时f x >0，所以f x 在0,+∞ 上单调递增，在-∞,0 上单调递减，所以f x ≥f 0 =0，即e x -x +1 ≥0恒成立，即e x ≥x +1(当x =0时取等号)，所以e 0.02>1+0.02⇒e 0.01> 1.02，∴b >c ，又e -x ≥1-x (当x =0时取等号)，所以当x <1且x ≠0时，有1e x >1-x ⇒e x <11-x ，∴e 0.01<11-0.01=10099，∴a >b ．故选：A13.已知a =e 0.1-1，b =sin0.1，c =ln1.1，则( )A.a 0时，e x >1，∴e x -cos x >0，∴f x >0，f x 单调递增，∴f 0.1 >f 0 ，即e 0.1-1-sin0.1>0，∴e 0.1-1>sin0.1，即a >b ，令g x =ln x +1 -sin x ，∴g x =1x +1-cos x =1-x +1 cos x x +1=1-x cos x -cos xx +1，令h x =1-x cos x -cos x ，∴h x =x +1 sin x -cos x 令φx =x +1 sin x -cos x ，∴φ x =2sin x +x +1 cos x ，当0<x <π6时，φ x >0，∴h x 单调递增，∴h x <h π6 =π6+1 sin π6-cos π6=π+61-3 12<0∴h x 在x ∈0,0.1 上单调递减，∴h x <h 0 =0，∴g x <0，∴g x 在x ∈0,0.1 上单调递减，∴g 0.1 <g 0 =0，即ln1.1-sin0.1<0，∴c 0时，xf x -f x <0，记a =f 20.2 20.2，b =f 0.22 0.22，c =f log 25log 25，则错误的有( )A.a 0时，xf x -f x <0，得g x <0，g x 在0,+∞ 上单调递减，又log 25>log 24=2，1<20.2<2，0<0.22=0.04<1，可得log 25>20.2>0.22，故g log 25 <g 20.2 <g 0.22 ，故c <a bB.a ≤bC.a <2bD.a ≥2b【解析】设f x =13x+log 13x ，则f x 在0,+∞ 为减函数，因为13 a +log 13a =19 b +2log 19b =19 b +log 13b ,所以f a -f b =13 a +log 13a -13 b+log 13b =19 b +log 13b -13 b +log 13b =19 b -13 b =13 2b -13 b ，因为2b >b >0,所以13 2b <13 b ，所以13 2b -13b<0，即f a <f b ，从而a >b ,所以A 正确，B 错误；而f a -f 2b =13 a +log 13a -13 2b +log 132b =13 2b +log 13b -13 2b +log 132b =log 13b -log 132b >0,所以f a >f 2b ,所以a <2b ，所以C 正确，D 错误.故选：AC .16.(多选)已知定义在0,π2上的函数f (x )的导函数为f (x )，且f (0)=0，f (x )⋅cos x +f (x )sin x <0，则下列选项中正确的是( )A.f π6<62f π4B.f π3>0 C.f π6>3f π3D.f π4>2f π3【解析】令g (x )=f (x )cos x ，x ∈0,π2 ，则g(x )=f(x )cos x +f (x )sin x cos 2x.因为f (x )cos x +f (x )sin x <0，所以g(x )=f (x )cos x +f (x )sin x cos 2x<0在0,π2 上恒成立，所以函数g (x )=f (x )cos x 在0,π2 上单调递减，所以g π6 >g π4 ，即f π6 cos π6>f π4 cos π4，f π6 >62f π4，故A 错误；又f (0)=0，所以g (0)=f (0)cos0=0，所以g (x )=f (x )cos x≤0在0,π2 上恒成立，因为π3∈0,π2，所以f π3 ≤0，故B 错误；又g π6 >g π3 ，所以f π6 cos π6>f π3cosπ3，即f π6 >3f π3 ，故C 正确；又g π4 >g π3 ，所以f π4 cos π4>f π3cosπ3，即f π4 >2f π3 ，故D 正确.故选：CD .17.若a =2ln (ln1.01),b =ln ln3π 2,c =23ln2，则a ，b ，c 的大小关系为____________．【解析】因为b =ln ln 3π 2=2ln ln 3π =2ln ln π3 ，c =23ln2=2ln213，所以构造函数f x =2ln x ，由对数函数的性质知，f x 在0,+∞ 上单调递增，所以只需比较ln1.01，ln π3，213的大小，由于1.01×3=3.03<π，故π3>1.01,所以ln1.01<lnπ3<1<213,所以a=2ln(ln1.01)<b=2ln ln π3<2ln213=23ln2=c,故答案为：a<b<c18.已知f x 是定义在R上的奇函数，对任意两个不相等的正数x1，x2，都有x2f x1-x1f x2x1-x2<0，记a=f4.10.24.10.2，b=f0.42.10.42.1，c=f log0.24.1log0.24.1，则a，b，c的大小关系__________．【解析】设0<x1<x2，因为x2f x1-x1f x2x1-x2<0，则x2f x1-x1f x2>0，即f x1x1>f x2x2，所以函数g x =f xx在0,+∞上单调递减．因为f x 是定义在R上的奇函数，所以g-x=f-x-x=-f x-x=f xx=g x ，所以g x 是定义在-∞,0∪0,+∞上的偶函数，因此a=f4.10.24.10.2=g4.10.2<g1 ，b=f0.42.10.42.1=g0.42.1>g0.42>g0.5，c=f log0.24.1log0.24.1=g log0.24.1=g log54.1∈g1 ,g12，即a<c<b．。

专题07 比较大小(选填题11种考法)(解析版)2024届高三数学二轮复习《考法分类》专题训练

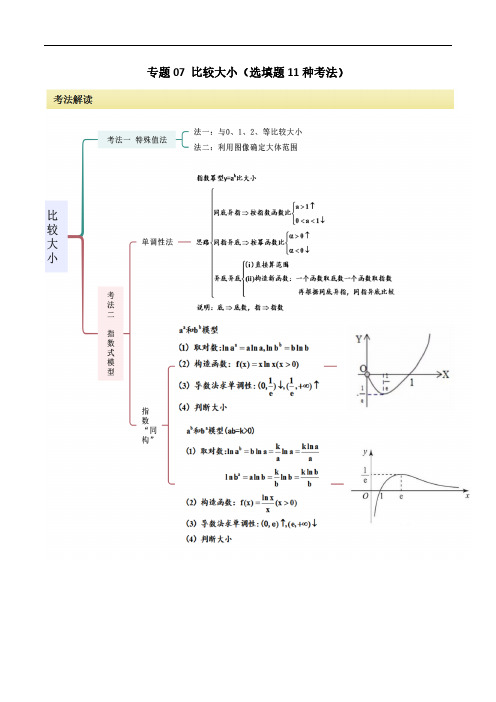
专题07 比较大小（选填题11种考法）考法一与特殊值比较大小【例1-1】（2023·海南海口·农垦中学校考模拟预测）已知0.23a =，30.2b =，3log 0.2c =，则（）A ．a b c>>B ．a c b >>C ．c a b >>D ．b c a>>【答案】A【解析】因为3x y =在R 上单调递增，且0.20>，所以0.20331a =>=；因为0.2x y =在R 上单调递减，且30>，所以3000.20.21b <=<=；因为3log y x =在()0,∞+上单调递增，且0.21<，所以33log 0.2log 10c =<=．综上所述，a b c >>，故选：A ．【例1-2】（2023·西藏林芝·校考模拟预测）若2log 3a =，3log 2b =，41log 3c =，则下列结论正确的是（）A ．a c b<=，可得()1,a ∈+∞；由对数函数3log y x =在()0,x ∈+∞上单调递增可知，3330log log 2log 131b =<<==，可得()0,1b ∈；由对数函数4log y x =在()0,x ∈+∞上单调递增可知，441log log 103c =<=，可得(),0c ∈-∞；所以可得c b a <<.故选：B【变式】1．（2023·陕西安康）设 1.2311,log 2,33a b c ⎛⎫=== ⎪⎝⎭，则（）A ．b a c>>B ．b c a >>C ．c a b >>D ．c b a >>【答案】A【解析】因为3311log 2log 23b =>=>， 1.211133c a ⎛⎫⎛⎫=<= ⎪ ⎪⎝⎭⎝⎭，所以b a c >>.故选：A2．（2022·天津·统考高考真题）已知0.72a =，0.713b ⎛⎫= ⎪⎝⎭，21log 3c =，则（）A ．a c b >>B ．b c a >>C ．a b c >>D ．c a b>>【答案】C 【解析】因为0.70.7221120log 1log 33⎛⎫>>=> ⎪⎝⎭，故a b c >>.故答案为：C.3．（2021·天津·统考高考真题）设0.3212log 0.3,log 0.4,0.4a b c ===，则a ，b ，c 的大小关系为（）A ．a b c <= ，1b ∴>，0.3000.40.41<<= ，01c ∴<<，a cb ∴<<.故选：D.4．（2023·西藏拉萨）设0.23a =，0.2log 0.3b =，3πtan 5c =则（）A ．a b c <=，所以1a >；0.20.20.20log 1log 0.3log 0.21b =<=<=，所以01b <<；3ππ52>，所以3πtan 05c =<，则c b a <<．故选：C.考法二指数式比较大小【例2-1】（2023·天津·统考高考真题）若0.50.60.51.01, 1.01,0.6a b c ===，则,,a b c 的大小关系为（）A ．c a b >>B ．c b a>>C ．a b c >>D ．b a c>>【答案】D【解析】由 1.01x y =在R 上递增，则0.50.61.01 1.01a b =<=，由0.5y x =在[0,)+∞上递增，则0.50.51.010.6a c =>=.所以b a c >>.故选：D【例2-2】（2023·山东聊城·统考三模）设0.50.2a =，0.20.5b =，0.5log 0.2c =则（）A ．a c b>>B ．b c a >>C ．c a b>>D ．c b a >>【答案】D【解析】由0.2x y =单调递减可知：0.50.20.20.2<.由0.2y x =单调递增可知：0.20.20.20.5<，所以0.50.20.20.5<，即a b <，且1b <.由0.5log y x =单调递减可知：0.50.5log 0.2log 0.51c =>=，所以c b a >>.故选：D【例2-3】（2023·安徽淮南·统考一模）若75a =，86b =，22e 2e c =+，则实数a ，b ，c 的大小关系为（）A ．a c b>>B ．c b a >>C ．b c a>>D ．b a c >>【答案】B 【解析】由已知可得，7ln 5log 5ln 7a ==，8ln 6log 6ln 8b ==，由22e 2e c =+可得，()22ln e 2c =+，所以()()2222ln e ln e 2ln e 2c ==++.设()ln ,1ln(2)x f x x x =>+，则()()()()22ln 2ln ,12ln (2)x x x x f x x x x x ++-'=>++，因为1x >，故()21,ln 2ln 0x x x x +>>+>>，所以()()2ln 2ln 0x x x x ++->即()0f x ¢>，所以()f x 在()1,+∞上为增函数，又()5a f =，()6b f =，()2e c f =，又2e 65>>，所以c b a >>.故选：B.【变式】1．（2023秋·湖北荆州·高三沙市中学校考阶段练习）设0.30.232,3,log 2a b c ===，则,,a b c 的大小关系为（）A ．a b c <=，则c a <，所以c<a>B ．b c a >>C ．a c b>>D ．c b a >>【答案】A【解析】0.2y x = 在()0,∞+上单调递增，0.20.20.30.2∴>；又0.2x y =在R 上单调递减，0.20.30.20.2∴>，0.20.30.30.2∴>，即a b >；0.311110.20.2115ln 0.355ln 5ln 3e-<-<-==< ，c b ∴<；综上所述：a b c >>.故选：A.3.（2022·全国·高三专题练习）已知 3.9 3.8 3.9 3.83.9, 3.9, 3.8, 3.8a b c d ====，则a b c d ,,,的大小关系为（）A ．d c b a<<<B ．d b c a <<<C ．b d c a<<<D ．b c d a <<<【答案】B【分析】构造函数()ln x f x x=，利用导数判断函数的单调性，可得()3.9(3.8)f f <，从而可得 3.8 3.93.9 3.8<，再由 3.8y x =在()0,∞+上单调递增，即可得出选项.【详解】构造函数()ln x f x x =，则()21ln x f x x -'=，当(),x e ∈+∞时，()0f x '<，故()ln x f x x =在(),x e ∈+∞上单调递减，所以()3.9(3.8)f f <，所以ln 3.9ln 3.83.9 3.8<，3.8ln 3.9 3.9ln 3.8<所以 3.8 3.9ln 3.9ln 3.8<， 3.8 3.93.9 3.8<，因为 3.8y x =在()0,∞+上单调递增，所以 3.8 3.83.8 3.9<，同理 3.9 3.93.8 3.9<，所以 3.8 3.8 3.9 3.93.8 3.9 3.8 3.9<<<，故选：B考法三函数的性质比较大小【例3-1】（2022·江西）函数()e e 2sin x x f x x -=--.若420a =，5log 10b =，log a c b =，则有（）A ．()()()f a f b f c >>B ．()()()f a f c f b >>C ．()()()f b f a f c >>D ．()()()f b f c f a >>【答案】A 【解析】因为函数()e e 2sin x x f x x -=--，所以()e e 2cos x x f x x --'=+，当0x >时，()22cos 0f x x >'-≥，所以()f x 在()0,∞+上递增，因为4455log 20log 162,1log 10log 252,0log log 1a a a b c b a =>=<=<=<=<=，所以0a b c >>>，所以()()()f a f b f c >>，故选：A【例3-2】（2023·江苏苏州·苏州中学校考模拟预测）已知()2cos f x x x =--，若34e a f -⎛⎫= ⎪⎝⎭，4ln 5b f ⎛⎫= ⎪⎝⎭，14c f ⎛⎫=- ⎪⎝⎭，则a ，b ，c 的大小关系为（）A ．c b a<<B ．c a b <<C ．b c a <<D ．a c b<<【答案】D 【解析】因为2()cos ,R f x x x x =--∈，定义域关于原点对称，()22()()cos()cos f x x x x x f x -=----=--=，所以()f x 为R 上的偶函数，当0x ≥时,()2sin ,f x x x '=-+，设()2sin g x x x =-+，则()2cos g x x '=-+，1cos 1x -≤≤ ，()0g x '∴<，所以()g x 即()f x '在[0,)+∞上单调递减,所以()(0)0f x f ''≤=,所以()f x 在[0,)+∞上单调递减,又因为()f x 为偶函数,所以()f x 在(,0]-∞上单调递增，又因为41ln 0,054<-<,445ln ln ln 554b f f f ⎛⎫⎛⎫⎛⎫==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,1144c f f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭又因为31411e e e 4-->=>,因为141ln e 4=,41445e e, 2.4e 4⎛⎫⎛⎫=≈< ⎪ ⎪⎝⎭⎝⎭，所以145e 4>,所以145ln e ln 4>，即15ln 44>,所以3415e ln 44->>,所以3441e 5ln 4f f f -⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即a c b <<.故选：D.【变式】1（2022·江苏）已知函数()e e x x f x -=-，则0.60.60.4(0.4),(0.6),(0.4)a f b f c f ===的大小关系为（）A ．b a c <<B ．a b c <<C ．c a b <<D ．a c b<<【答案】D【解析】由0.630.20.20.6(0.6)0.216==，0.420.20.20.4(0.4)0.16==，即0.20.20.160.216<，所以0.40.60.40.6<，又0.60.40.40.4<，所以0.60.40.60.40.40.6<<，而()e e x x f x -=-递增，故0.60.40.6(0.4)(0.4)(0.6)a f c f b f =<=<=故选：D2．（2023·全国·统考高考真题）已知函数()2(1)e x f x --=．记,,a f b f c f ===，则（）A ．b c a >>B ．b a c >>C ．c b a >>D ．c a b>>【答案】A【解析】令2()(1)g x x =--，则()g x 开口向下，对称轴为1x =，4112⎛-= ⎝，而22491670+-=+=>，41102⎛-=> ⎝11>由二次函数性质知g g <，4112⎛-= ⎝，而22481682)0-=+==<，11<g g >，综上，g g g <<，又e x y =为增函数，故a c b <<，即b c a >>.故选：A.3．（2023·河北沧州·统考三模）已知()f x 为奇函数，当02x ≤≤时，2()2f x x x =-，当2x >时，()31f x x =--，则（）A ．(()()0.30.323f f f ->>B ．()()(0.30.323f f f >>-C ．(()()0.30.332f f f ->>D ．()()(0.30.332f f f >>-【答案】A【解析】因为当02x ≤≤时，()22f x x x =-，则()f x 在()0,1上单调递增，在[]1,2上单调递减，当2x >时，()31f x x =--，则()f x 在()2,3上单调递减，在[)3,+∞上单调递增.且()20231f ==--，所以()f x 在()0,1上单调递增，在[]1,3上单调递减，在()3,+∞上单调递增.因为(()51(1)f f f f -=>==，0.30.31233<<<，则()()()0.30.3123f f f >>所以(()()0.30.323f f f ->>.故选：A4.（2023春·广西·高三校联考阶段练习）已知函数()f x 在10,2⎡⎤⎢⎥⎣⎦上单调递减，()()1f x f x +=--，()1y f x =-为偶函数，当[]2,1x ∈--时，()1f x x =--，若a f ⎛= ⎝，(ln 2)b f =，()3log 1458c f =，则a ，b ，c 的大小关系是（）A ．b<c<aB ．c b a <<C ．a b c <<D ．a c b<<【答案】A【解析】因为函数(1)=-y f x 为偶函数，得()y f x =的图象关于直线=1x -对称，且(1)(1)f x f x --=-，由()()1f x f x +=--得(2)(1)f x f x +=---，所以(2)(1)f x f x +=--，即(3)()f x f x +=-，则(6)(3)()f x f x f x +=-+=，所以函数()y f x =的一个周期为6，则()()()333log 14586log 2log 2c f f f ==+=，当[]2,1x ∈--时，()1f x x =--，又()y f x =的图象关于直线=1x -对称，所以2(2110a f f ⎛⎛==-=--+-=> ⎝⎝，由()()1f x f x +=--得102f ⎛⎫= ⎪⎝⎭，()y f x =的图象关于点1(,0)2对称，又函数()f x 在10,2⎡⎤⎢⎥⎣⎦上单调递减，所以函数()f x 在[]0,1上单调递减，又331log log 2ln 212=<<<，所以()()33(ln 2)log 2log 14580b f f f c =<==<，所以b<c<a .故选：A考法四导函数模型比较大小【例4-1】（2022·四川遂宁）已知定义在R 上的函数()y f x =满足：函数()y f x =为奇函数，且当0x <时，()()0f x xf x '+>成立（()f x '为()f x 的导函数），若()1a f =--，()()ln 2ln 2b f =，1212log 4c f ⎛⎫= ⎪⎝⎭，则a 、b 、c 的大小关系是（）A ．a c b >>B ．b a c>>C ．c b a>>D ．a b c>>【答案】B【解析】设()(),0g x xf x x =<，则()()()g x f x xf x ''=+，因为当0x <时，()()0f x xf x '+>成立，所以()0g x '>，()g x 为递增函数，又因为函数()y f x =为奇函数，可得()()f x f x -=-，则()()()()g x xf x xf x g x -=--==，所以函数()g x 为偶函数，所以函数()g x 在(0,)+∞为单调递减函数，由()()()111a f g g =--=-=，()()()ln 2ln 2ln 2==b f g ，()1212(log 2(2)24c f f g ===，因为ln 212<<，所以()()()ln 212g g g >>，即b a c >>.故选：B【例4-2】（2023·广西柳州·统考模拟预测）设函数(),R y f x x =∈的导数为()f x '，且()f x 为偶函数，()()f x f x '>，则不等式成立的是（）A ．()()()120e 1e 2f f f -<，可得()g x 在R 上递增，又()f x 为偶函数，则1(1)(1)e (1)e f g f -==，0(0)(0)(0)e f g f ==，22(2)(2)e (2)e f g f ---==，33(3)(3)e (3)ef g f ---==，由3201-<-<<，可得(3)(2)(0)(1)g g g g -<-<<，即有132e (3)e (2)(0)e (1)f f f f -<<<.故选：B.【例4-3】（2022·吉林）（多选）已知函数()y f x =是偶函数，对于任意的π0,2x ⎛⎫∈ ⎪⎝⎭满足()()cos sin 0f x x f x x '+>（其中()f x '是函数()f x 的导函数），则下列不等式成立的是（）Aππ34f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭Bππ46⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭Cππ46⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭D．ππ63f ⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭【答案】ABD【解析】构造函数()()cos f x g x x =，其中ππ,22x ⎛⎫∈- ⎪⎝⎭，则()()()2cos sin cos f x x f x x g x x '+'=，∵对于任意的π0,2x ⎛⎫∈ ⎪⎝⎭满足()()cos sin 0f x x f x x '+>，∴ 当π0,2x ⎛⎫∈ ⎪⎝⎭时，()0g x '>，则函数()()cos f x g x x =在π0,2⎛⎫⎪⎝⎭上单调递增，又函数()y f x =是偶函数，()()f x f x -=，∴()()()()()cos cos f x f x g x g x x x--===-，∴()y g x =在ππ,22⎛⎫- ⎪⎝⎭上为偶函数，∴函数()()cos f x g x x =在π,02⎛⎫- ⎪⎝⎭上单调递减．∵ππ34>，则ππ34g g ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，即ππ34ππcos cos 34f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭>，即π312f ⎛⎫ ⎪⎝⎭>ππ34f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，A 正确；同理可知ππ46g g ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭，即ππ46ππcos cos 46f f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭>⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭>ππ46⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，B 正确；ππ64g g ⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭，且ππ66g g ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭即ππ64ππcos cos 46f f ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭<⎛⎫- ⎪⎝⎭<，化简得ππ46⎛⎫⎛⎫>- ⎪ ⎪⎝⎭⎝⎭，C 错误；ππ63g g ⎫⎫⎛⎛< ⎪ ⎪⎝⎝⎭⎭，且ππ33g g ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭，即ππ63ππcos cos 63f f ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭<⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭π312f ⎛⎫- ⎪⎝⎭<，化简得ππ36f ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭，D 正确．故选：ABD.【变式】1．（2023·安徽黄山·统考三模）已知定义域为的函数，其导函数为，且满足，，则（）A ．B ．C ．D ．【答案】C【解析】，则，R ()f x ()f x '()()20f x f x '-<()01f =()2e 11f -<()21ef >1e2f ⎛⎫< ⎪⎝⎭()11e 2f f ⎛⎫> ⎪⎝⎭()()2e x f x g x =()()()()()()22222e 2e 2e e x x x x f x f x f x f x g x ''⋅-='-=因为在上恒成立，所以在上恒成立，故在上单调递减，所以，，故A 不正确；所以，即，即，故B 不正确；，即，即，故C 正确；，即，即，故D 不正确；故选：C.2．（2021·山东·高三开学考试）（多选）已知定义在π02⎡⎫⎪⎢⎣⎭，上的函数()f x 的导函数为()'f x ，且(0)0f =，()cos ()sin 0f x x f x x '+<，则下列判断中正确的是（）A ．π6f ⎛⎫ ⎪⎝⎭π4f ⎛⎫⎪⎝⎭B ．πln 3f ⎛⎫⎪⎝⎭>0C ．π6f ⎛⎫ ⎪⎝⎭π3⎛⎫ ⎪⎝⎭D ．π4f ⎛⎫⎪⎝⎭π3⎛⎫ ⎪⎝⎭【答案】CD【解析】令()()π,0,cos 2f x g x x x ⎡⎫=∈⎪⎢⎣⎭，则()()()2cos sin cos f x x f x x g x x +''=，因为()()cos sin 0f x x f x x '+<，所以()()()2cos sin 0cos f x x f x x g x x +='<'在π0,2⎡⎫⎪⎢⎣⎭上恒成立，因此函数()()cos f x g x x =在π0,2⎡⎫⎪⎢⎣⎭上单调递减，故ππ64g g ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，即ππ64ππcos cos 64f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭>，即ππ64f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，故A 错；又()00=f ，所以()()000cos0f g ==，所以()()0cos f x g x x=≤在π0,2⎡⎫⎪⎢⎣⎭上恒成立，因为ππ0ln1lnln e 132=<<=<，所以πln 03f ⎛⎫< ⎪⎝⎭，故B 错；又ππ63g g ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，所以ππ63ππcos cos 63f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭>，即ππ63f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，故C 正确；()()20f x f x '-<R ()0g x '<R ()g x R ()()10g g ->()()()22010e 11e e f f f --=->=()()10g g <()()210e e f f <()()221e 0e f f <=()102g g ⎛⎫< ⎪⎝⎭()101021e e f f ⎛⎫ ⎪⎝⎭<=1e 2f ⎛⎫< ⎪⎝⎭()112g g ⎛⎫> ⎪⎝⎭()12112e ef f ⎛⎫ ⎪⎝⎭>()11e 2f f ⎛⎫< ⎪⎝⎭又ππ43g g ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，所以ππ43ππcos cos 43f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>，即ππ43f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，故D 正确.故选：CD3．（2023湖南）设函数()f x '是定义在()0,π上的函数()f x 的导函数，有()()cos sin 0f x x f x x '->，若123a f π⎛⎫=⎪⎝⎭，0b =，56c f π⎛⎫= ⎪⎝⎭，则a ，b ，c 的大小关系是（）A ．a b c <，所以()0g x '>，所以()g x 在()0,π上是增函数，1cos ()23333a f f g ππππ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，cos ()2202f g b πππ⎛⎫= ⎪⎝⎭==，5555cos ()6666c f f g ππππ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，所以a b c <<，故选：A考法五根据图像交点比较大小【例5】（2023秋·广东江门）已知()122xf x x ⎛⎫=-- ⎪⎝⎭，()12log 2g x x x =--，()32h x x x =--的零点分别是a ，b ，c ，则a ，b ，c 的大小顺序是（）A ．a b c >>B ．c b a >>C ．b c a >>D ．b a c>>【答案】B【解析】函数()122xf x x ⎛⎫=-- ⎪⎝⎭，()12log 2g x x x =--，()32h x x x =--的零点，即为函数2y x =+分别与函数12xy ⎛⎫= ⎪⎝⎭、12log y x =、3y x =的图象交点的横坐标，如图所示：由图可得a b c <<.故选：B 【变式】1．（2023·天津和平·统考三模）已知,,a b c 满足3222,log 2,20a a b b c c -=++=---=，则,,a b c 的大小关系为（）A ．b a c <-+，0202<+，易知10a -<<；把b 的值看成函数32log y x =与42y x =--图像的交点的横坐标，2log 112>--，易知01b <<；把c 的值看成函数35y x =与62y x =+图像的交点的横坐标，3112<+，与3222>+，易知12c <<.所以a b c <<.故选：B.2．（2023秋·北京）已知1x ，2x ，3x 满足11121log 2x x ⎛⎫= ⎪⎝⎭，211221log 2x x +⎛⎫= ⎪⎝⎭，31321log 3xx ⎛⎫= ⎪⎝⎭，则1x ，2x ， 3x 的大小关系为（）A ．123x x x <<B ．231x x x <<C ．132x x x <<D ．213x x x <<【答案】C【解析】在同一平面直角坐标系内作出+112111log 232x x x y x y y y ⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、、、的图像12log y x =过点1(,1)(1,0)2、；12xy ⎛⎫= ⎪⎝⎭过点1(0,1)(1,)2、；13xy ⎛⎫= ⎪⎝⎭过点1(0,1)(1,3、；112x y +⎛⎫= ⎪⎝⎭过点11(0,)(1,24、，则+1111232x x x y y y ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、、与12log y x =图像交点横坐标依次增大，又+1111232xxx y y y ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭、、与12log y x =图像交点横坐标分别为132x x x 、、，则132x x x <<.故选：C3．（2023·全国·高三专题练习）设21log 3aa ⎛⎫= ⎪⎝⎭，132log bb =，154c⎛⎫= ⎪⎝⎭，则a 、b 、c 的大小关系是（）A ．b a c <，因为()0f a =，由零点存在定理可知12a <<；构造函数()132log xg x x =-，因为函数2x y =、13log y x =-在()0,∞+上均为增函数，所以，函数()g x 为上的增函数，且，，因为，由零点存在定理可知.因为，则，因此，.故选：B.考法六导数法之同构函数【例6-1】（2023·河南·校联考模拟预测）设ln 44a =，24ln 4e b -=，c =，则（）A ．a b c < ⎪⎝⎭()0g b =1193b <<154c⎛⎫= ⎪⎝⎭1144log 5log 10c =<=c b a <<【解析】由题意可得ln 4ln 242a ==，222e ln4ln 42e e 2b -==，c =设()ln x f x x =，0x >，则()21ln xf x x -'=，故当()0,e x ∈时，()0f x ¢>，()f x 单调递增；当()e,x ∈+∞时，()0f x '<，()f x 单调递减；因为()()42a f f ==，2e 2b f ⎛⎫= ⎪⎝⎭，c f=，且2e 02e 42<<<<<，可得()2a f f c =>=，()2e 42a f f b ⎛⎫=<= ⎪⎝⎭，所以<<c a b .故选：D.【例6-2】（2023·全国·模拟预测）已知(),,1,a b c ∈+∞，且1ln 1e a a ---=，2ln 2e b b ---=，4ln 4e c c ---=，其中e 是自然对数的底数，则（）A ．a b c <时()0f x ¢>，()f x 单调递增，所以()()()124f f f <<，即ln ln ln a a b b c c -<-<-，令()ln g x x x =-，则()11g x x'=-，因为当1x >时，()0g x '>，所以()g x 在()1,+∞上单调递增，又因为(),,1,a b c ∈+∞且()()()g a g b g c <<，所以a b c <<，故选：A 【变式】1.（2022·山西吕梁）已知1ln e ,ln a b c -===a ，b ，c 的大小关系为（）A ．a b c >>B ．b c a>>C ．b a c>>D ．a b c<<【答案】B【解析】12022ln2022ln ln20222022a===，11ln eee eb-===，12021ln2021ln ln20212021c===，令ln()xf xx=，则21ln()xf xx-'=，当0ex<<时，()0f x'>，当ex>时，()0f x'<，所以()f x在(0,e)上单调递增，在(e,)+∞上单调递减，由e20212022<<，所以(e)(2021)(2022)f f f>>，所以b c a>>.故选：B.2.（2022·内蒙古）已知1ln23a=+，1ln34b=+，e2e1c+=+，则a、b、c的大小关系为（）A．a b c>>B．b c a>>C．c b a>>D．b a c>>【答案】B【解析】构造函数()1ln1f x xx=++，其中0x>，则()()()()222221311124111xx xf xx x x x x x⎛⎫++⎪++⎝⎭'=-==>+++，所以，函数()f x在()0,∞+上单调递增，因为()1ln223a f=+=，()1ln334b f=+=，()e2111ln e ee1e1e1c f+==+=+=+++，因为3e20>>>，所以，a c b<<.故选：B.3（2023·广西桂林·统考一模）已知a、b、()1,c∈+∞，2e ln39a a=，3e ln28b b=，22e c c-=，则（）A．a b c>>B．a c b>>C．b c a>>D．c a b>>【答案】A【解析】因为a、b、()1,c∈+∞，由2e ln39a a=可得ln9e9aa=，由3e ln28b b=可得ln8e8bb=，由22e c c-=可得22e ecc=，构造函数()ln xf xx=，其中0x>，则()21ln xf xx-'=，当0ex<<时，()0f x¢>；当ex>时，()0f x'<.所以，函数()f x的增区间为()0,e，减区间为()e,+∞，因为2e e 89<<<，所以，()()()2e 89f f f >>，即e e ec b a c b a>>，即()()()e e e c b af f f >>，因为a 、b 、()1,c ∈+∞，则e a 、e b 、()e e,c∈+∞，所以，e e e a b c >>，因此，a b c >>.故选：A.4.（2022·贵州毕节·三模（理））已知3ln 3a =，e b =，2e 2c =（e为自然对数的底数），则a ，b ，c 的大小关系为（）A ．c a b >>B ．c b a>>C ．a c b>>D ．b c a>>【答案】A【解析】令()ln x f x x =，()0x >，所以()()2ln 1ln x f x x -'=，当()0,e x ∈时，()0f x '<，函数()f x 单调递减当()e,x ∈+∞时，()0f x ¢>，函数()f x 单调递增；所以()33ln 3a f ==，e e lne b ==，()2222e e e lne 2c f ===，所以c a b >>，故选：A.考点七作差作商比较大小【例7-1】（2023·全国·模拟预测）已知8.1log 4a =， 3.1log e b =，ln 2.1c , =，则（）A ．a c b <，ln 2.10c =>，所以(2223.1ln 2.1ln 2.1ln 3.1ln 6.51ln 2.1ln 3.1log e 22c b +⎛⎫⎛⎫==⨯<== ⎪ ⎪⎝⎭⎝⎭，又2e 7.389≈e <，所以ln e=1<，所以1cb<，故c b <，因为8.1ln 42ln 24ln 8.1ln 8.1g lo a ====，又2e 7.389≈，所以28.1e >，所以1>，所以ln 2a <，又ln 2ln 2.1c <=，所以a c <，所以a c b <<，故选：A.【例7-2】（2023·全国·高三专题练习）已知910a =，19e b -=，10=1+ln 11c ，则a ，b ，c 的大小关系为（）A ．a b c <时，()0f x '>，()f x 单调递增，故()(0)0,f x f ≥=即e 10x x --≥，当且仅当0x =时，等号成立，所以1(0)x e x x >+≠，则1911101e 1099b a=>+==>，所以.b a <因为10191=1+ln1ln ,11111010110c a =+==-+，所以11ln ,110110c a -=++令1()lnln(1),1h x x x x x =+=-+++得1()111xh x x x=-+=++'，令()0h x '>得0,x >令()0h x '<得10,x -<<所以()h x 在(0,)+∞上单调递增，在(1,0)-上单调递减，所以()(0)0,h x h ≥=所以1()0,10h >即11ln 0,110110c a -=+>+所以0,c a ->则,c a >所以b a c <<，故选：B.【变式】1.（2023·云南·校联考模拟预测）已知21625log 9,log 16,e a b c -===，则（）A ．b a c >>B ．b c a >>C ．c b a >>D ．c a b>>【答案】A【解析】221644log 9log 3log 30a ===>，222555log 16log 4log 40b ===>，4445log 3log 3log 5log 4a b ==⋅22444log 3log 5log 1522+⎛⎫⎛⎫<= ⎪ ⎪⎝⎭⎝⎭22244log 16log 422⎛⎫⎛⎫<= ⎪ ⎪⎝⎭⎝⎭1=，所以a b <，224421log 3log 2log 2e 2a c -=>==>=，所以b a c >>.故选：A 2．（2023·贵州黔东南·凯里一中校考模拟预测）若ln 3ln 2a =-，ln 2ln 3b =，ln 3ln 2c =⨯，则（）A ．a c b<=∴∈ ⎪⎝⎭，故a b <，2ln 2ln 3ln 2ln 2ln 3ln 2,ln 3ln 3ln l 311n 3b c ⎛⎫⎛⎫-=-⨯=--= ⎪ ⎪⎝⎭⎝⎭由于1ln 20,ln 31>>>，所以21ln 3ln 20ln 3b c ⎛⎫--=< ⎪⎝⎭，故b c <，因此a b c <<，故选：B3．（2023·江西·校联考模拟预测）已知11cos 55a =，425b =，1sin 5c =，则a ，b ，c 的大小关系为（）A ．c a b >>B ．b a c>>C ．c b a>>D ．a c b>>【答案】A【解析】由题意可得：∵1sin155tan 115cos 55c a ==，利用三角函数线可得当0,2x π⎛⎫∈ ⎪⎝⎭时，tan x x >115tan5155⇒>⋅=，∴c a >构造函数()()()cos 1cos 1H x x x x x x x x =--=⋅+-∴()00H =，1114cos 55525H ⎛⎫=- ⎪⎝⎭，即15H a b ⎛⎫=- ⎪⎝⎭，令()()cos 1sin 10G x x x G x x '=+-⇒=-+>∴()cos 1G x x x =+-在R 上单调递增，即()105G G ⎛⎫< ⎪⎝⎭，∴()()1111005555G G H H ⎛⎫⎛⎫<⇒< ⎪ ⎪⎝⎭⎝⎭，∴0a b b a <-⇒<，∴b a c <<．故选：A ．4.（2023·甘肃定西·统考模拟预测）已知0.3e a =，1310b =，()2ln 0.3e c =，则a ，b ，c 的大小关系为（）A ．a c b >>B ．c b a>>C ．a b c >>D ．b a c>>【答案】C【解析】由题意得().20310.3,ln 0.e ,3e 2ln 0.3a b c =+==+=，可得0.310.e 3b a -=+-，设()1e ,0x f x x x =+->，可得()1e 0xf x '=-<，所以()f x 单调递减，则()()0.300f f <=，即0b a -<，所以b a <；又由2ln 0.3(10.3)1ln 0.30.3c b -=+-+=+-，设函数()1ln ,(0,1)g x x x x =+-∈，可得()111x g x x x-'=-=，当(0,1)x ∈时，()0g x '>，()g x 单调递增，所以()()0.310g g <=，即0c b -<，所以c b <，所以c b a <<.故选：C.考点八指对数切线比较大小【例8】（2023·全国·高三专题练习）已知9899198,e ,ln 9999-===a b c ，则,,a b c 的大小关系是（）A ．a b c <，所以()f x 单调递增，则()989898981ln 1ln 109999999999f f ⎛⎫=+-=-<= ⎪⎝⎭，所以981ln9999<，则c a <；()e 1x g x x =--，()e 1x g x '=-，当()0,x ∈+∞时，()0g x '>，所以()g x 在()0,∞+上单调递增，所以()9898999998981e 1e 00999999g g --⎛⎫-=-+=->= ⎪⎝⎭，所以98991e99->，故b a >，故c<a>B ．b a c >>C ．c a b >>D ．b c a>>【答案】B【解析】设函数()e 1,R x f x x x =--∈,则()e 1x f x '=-，当0x <时，()0f x '<，()f x 递减；当0x >时，()0f x '>，()f x 递增，故()(0)0f x f ≥=，即e 1x x ≥+，当0x =时取等号；∵e 1xx ≥+，∴99100991e1100100->-=，∴b a >，由以上分析可知e 1x x ≥+，则0x >时，有1e x x -≥成立，当1x =时取等号，，即ln 1≤-x x ，当1x =时取等号，∴1011011ln 1100100100<-=，∴a c >，故b a c >>，故选：B.2.（2023·河南开封·统考模拟预测）已知13a =，13e 1b =-，4ln 3c =，则（）A ．a b c <，所以()f x 在()0,1上单调递增，所以()()00f x f >=，即()e 101xx x -><<.所以131e 13->，即a b <.设()()()ln 101g x x x x =+-<<，则()11011x g x x x-'=-=<++，所以()g x 在()0,1上单调递减，所以()()00g x g <=，即()()ln 101x x x +<<<.所以11ln 133⎛⎫+< ⎪⎝⎭，即c a <.所以c<a>B ．b a c >>C ．a b c >>D ．c b a>>【答案】B【解析】令()e 1),(0)(x f x x x +-=>，则e ()10x f x '=->，则()f x 在(0,)+∞上单调递增，故()(0)0f x f >=，则e 1,(0)x x x >+>．令()sin ,(0)g x x x x =->，则()1cos 0g x x '=-≥，则()g x 在(0,)+∞上单调递增，故()(0)0g x g >=，则sin ,(0)x x x >>．所以0.1e 10.11sin 0.1>+>+，即b a >；令()5πsin 086h x x x x ⎛⎫=-<< ⎪⎝⎭，则()5cos 8h x x '=-，因为π06x <<cos 1x <<，则5cos 8x >，故()0h x '>，所以()h x 在π0,6⎛⎫⎪⎝⎭上单调递增，则()()00h x h >=，即5sin 8x x >，易知π0.10,6⎛⎫∈ ⎪⎝⎭，所以51sin 0.10.1816>⨯=，则1171sin 0.111616+>+=，即a c >；综上：b a c >>.故选：B.考法九导数法之异构函数【例9】（2023·全国·河南省实验中学校考模拟预测）比较11101011a =-，ln1.2b =，0.115ec =的大小关系为（）A ．a c b >>B ．b c a >>C ．b a c >>D ．a b c>>【答案】D【解析】构造函数()12ln f x x x x =--，其中1x >，则()()22211210x f x x x x-'=+-=>，所以，函数()f x 在()1,+∞上为增函数，所以，()()111011101.12ln1.1ln1.211010111011f f =--=-->=，所以，1110ln1.21ln1.21011a b =->>=，令()()2ln 211xg x x x =+-+，其中0x >，则()()()222220111x g x x x x '=-=>+++对任意的0x >恒成立，所以，函数()g x 在()0,∞+上为增函数，所以，()()0.220.1ln1.2ln1.2001.111g g =-=->=，即2ln1.211b =>，令()e 1x h x x =--，其中0x >，则()e 10xh x '=->对任意的0x >恒成立，所以，函数()h x 在()0,∞+上为增函数，则()()0.10.1e 1.100g g =->=，则0.1e 1.1>，所以，0.11125e 5 1.111c =<=⨯，综上所述，a b c >>.故选：D.【变式】1．（2023·四川·校联考一模）设a =ln 3ln 2b =-，13c =，下列判断正确的是（）A ．a b c <，则构造函数()()12ln 1f t t t t t =-->，有()()22211210t f x t t t-'=+-=>，则()f t 单调递增，且()10f =，所以a b >；再构造函数()()212ln 11g t t t t =-+>，有()23322120t g t t t t-'=-=⨯>，则()g t 单调递增，且()10g =，所以c b <，综上：c b a <<．故选：D2．（2023·辽宁·大连二十四中校联考模拟预测）已知1ln 2ln e 3231ln 2ln 3,,e 23a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，试比较,,a b c 的大小关系（）A ．a b c <⇒=，当e x >时，()0f x '<，()f x 单调递减，所以有()()()4e 3f f f >>，因为1ln e ln 22ln 2ln 4,e e 244===，所以1ln 3ln 4e 34>>，设()()(0)ln ln xg x x x g x x x =>⇒=，设ln ln 1y x x y x '=⇒=+，当10ex <<时，0'<y ，函数ln y x x =单调递减，因为1ln 3ln 40e 34>>>，所以1ln 3ln 4ln ln ln e 34g g g ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦，因为函数ln y x =是正实数集上的增函数，故1ln 3ln 4e 34g g g ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦，即e 1ln3ln 4ln 23421ln 3ln 4ln 2e 342⎛⎫⎛⎫⎛⎫⎛⎫< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭<=，所以a c b <<，故选：C3（2023·山东烟台·校联考三模）已知sin1a =，3πb =，31log πc =，则a ，b ，c 的大小关系为（）A ．a c b >>B ．c b a>>C ．c a b>>D ．b a c>>【答案】B。

专题2-1 比大小(幂指对及三角函数值)(解析版)2023年高考数学二轮专题全套热点题型

例题 2．（2022·江西·高三阶段练习（理））设 a
2 ,b 33
0.80.3,c
log 0.90.8
，则（
）
A． c a b
B． a ห้องสมุดไป่ตู้c b
C． a b c
D． c b a
【答案】A
【详解】因为 3 3 1且 3 3 3 8 2 ，所以1 a 2,b 0.80.3 1, c log0.9 0.8 log0.9 0.81 2 ，所以 c a b .
b
b
b
【变式演练】
1．（2022·全国·高一课时练习）若 a lg3 0.7 ， b lg 0.72 ， c lg 0.7 ，则（）
c 的大小关系为（
）
A． a b c
B． b a c
C． c b a
D． a c b
【答案】A
ln 3
【详解】依题意，
a b
log2 log4
3 5
ln ln
2 5
ln 3 2 ln 2 ln 2 ln 5
2 ln 3 ln 9 1, a ln 5 ln 5
b ，
ln 4
b log4 5 log4 4 1, c 20.1 20 1，
综上， b<c<a .
故选：D.
2．（2022·湖南·长沙市雅礼洋湖实验中学高二开学考试）已知 a log3 2 ， b 70.01 ， c log9 5 log5 3 ，则（）
A． c b a
B． c<a<b
C． b<c<a
D． a c b
【答案】B
【详解】因为
b
70.01
1，
c

(完整版)函数比较大小专题40道-带答案

函数比较大小专题 2 学校: __________ 姓名： ____________ 班级： ____________ 考号： _____________11．设 f x lnx ，则 f sin 与 f cos 的大小关系x 55 、单选题A ． f sin 5 cos 5B ． f sin 5 f cos5C ． f sin 5 cos 5D ．大小不确定2．已知 f (x) |lg x|，则 1 f(14),f , f (2) 的大小关系是 (A. f (2) C. f(13) 11 f( ) f( ) 34 1 f (4) f (2)B. D. 3．已知 log 728， b log 25， lg2 A ．ba C ．ac 4．设1 2，则 ln x (lnx )2 A ． (lnx )2 x ln x ln x 2 2 x C ． (ln x x )2 x ln x 2 2x ln x 5．已知函数 A ． f(2) f(14)lg5 2 ，f(14) f(13)f(13)f (2)则 a,b,c 的大小关系为 (ln 2 x ln x 2x的大小关系是((lnx )2 xln x 22 x ln x 22 x (ln x x )2 x、、则 B．ln x的大小关系(6．设 a log 54 log 5 2 ， b ln 2ln3 ， 3lg5c 102 ，则 a,b,c 的大小关系为 () A ．b ca B ． abc C ． b a c D ． c a b7．设 a log 25 ，b log415 ， c 20.5 ，则 a,b,c 大小关系为( )C ．> > D ．A ． a c bB ． a b cC ． c b aD ． c a bA ．B ．C ．D ． 14．定义新运算：当时，；当，则在上值域为( ) C ．时，. 设函数A ．B ． D ．15．已知定义域为 R 的奇函数的导函数，当，则下列关于的大小关系正确的是时，，若 A ．B ．C ．D ． 16．设函数的导函数为，且，则 A ．0 B ．－4 C ．－ 2 D ．2310．若 f(x) xsinx cosx,则f (1), f( )以及f( )的大小关系是(22A ． f(1) f ( 2) f (32)3 C ． f(3) f( ) f (1) 2211．设函数是偶函数的导函数，，当时，，则使得成立的的取值范围是( )B ． D ．13 ．已知点在幂函数的图象上，设则的大小关系为(8．已知，，则的大小关系是A ． C ． D ．9．已知，，，则，，的大小关系为( A ． B ． C ． D ．3B ． f( ) f(3) f (1) 22 D ． f(1) f(3) f ( ) 22A ．C ． 12．已知函数，则的大小关系为A ．C ．D ．且则不等式的解集是B ．C ．20 ．设函数是定义在上的可导函数，其导函数为，且有的解集为（）21．设定义在上的偶函数满足：，且当时，，，，则，，的大小关系为（）A ． 17 ．若函数是定义在上的奇函数，在上是增函数，且，，则使得的的取值范围是（）A ．B ．C ．D ．已知定义在上的函数满足，且，则的解集是（ 18．A ．B ．C ．D ． 19．设分别是定义在 R 上的奇函数和偶函数，且，当时， A ．，则不等式 A ．B ．C ．D ． B ．D ．22．已知，则不等式的解集为（） A ．B ．C ．D ．23 ．若定义在 R 上的函数满足，且当的的取值范围是时，，则满足 B ． C D ．24．已知函数 f （ x ）（ x ∈ R ）满足 f （x ）= f （2-x ），且对任意的 x 1，x 2∈（-∞，1］（x 1≠x 2）有（ x 1-x 2）（f （x 1）-f （x 2））＜ 0．则（） A ． B ． C DC．大小关系为（）26．已知定义在 R 上的函数满足：函数的图像关于直线对称，且当时，. 若递增，则不等式的解集为（B ．D ． A ． C ．，则 a,b,c 的大小关系是（）A ． a>b>cB ． b>a>cC ．c>a>bD ． a>c>b27．设函数是定义在上的奇函数，且当时，，记，，则的大小关系为（）C ．D ． 28．已知为定义在上的偶函数，，且当时，单调A ．29．已知函数 B ．是定义在上的偶函数，在区间的解集为（） C ．上递减，且 D ．，则不等A ．C ．30．已知函数等式 A ．C ．B ． D ．是定义在上的偶函数，在区间的解集为（）B ． D ．上递减，且，则不时，，若，，，则，，的大小关系正确的是（31．已知定义域为的奇函数的导函数为，当 A ． B ． C ． D ．32．已知函数 f （x ）的导函数为 f'（ x ），若 f （x ）=x 3+f' （1）x 2-2，则 f' （1）的值为A ．A ．B ．C． D ．033 ．已知函数在上单调递减，且是偶函数，则，的大小关系是（）A ．B ．C． D ．34．函数的图象关于点（1,0）对称，当时，成立，若，则的大小关系是（）A ．B．C ．D ．35．函数的导函数，对，都有成立，若，则满足不等式的x 的范围是C．D．36．已知奇函数的导函数为，当时，，若，，则，，的大小关系是B．A．考点：对数函数的图象与性质3．A当对数函数的底数大于 0 小于 1 时，对数函数是单调递减的，当底数大于1 时，对数函数是单调递增的；另外由于对数函数过点（ 1， 0），所以还经常借助特殊值 0,1，2 等比较大小 4．A解析】参考答案 1．A 解析】 lnx 1 ， x 1 1 x 1 f ' x 2 2 ，令 f ' x 0 ，解得： x x x 0 x 1 ，故 f x 在（0，1）递减，而 sin cos 55 1，故 f sin 5 f cos ，故选 5 A. 点睛：本题考查了三角函数的性质，考查函数的单调性问题，是一道基础题；考查函数的单调性，由 f x 0 ，得函数单调递增， f x 0得函数单调递减；求出函数 f x 的单调区间，判断 sin 与 cos 的大小， 5 从而求出 f sin 5 与 f cos 的大小即可 . 5 2．D 解析】试题分析：因为函数 lg x 在 (0, ）单调递增，且当 x (0,1)时y 0 ，当 x (1, ）时， y 0. 所以 f(1) 4 1 |lg 14| 1 lg 14 lg( 14 ) 1 lg4， 4 f(2) |lg2| lg2，由 lg4 lg3 lg 2可知 f (1)4 f(13) f(13) 1 |lg 13| f (2) ， 1 lg 13 故选 11 lg( 13) 1 D.lg3 ，解析】由题 1 a log 728 2， b log 25 2 , c lg2 lg5 2 1,所以 a,b,c 的大小关系为 c a b . 故选 A.点晴：本题考查的是对数式的大小比较。

高中比较大小的练习题及讲解

高中比较大小的练习题及讲解### 高中比较大小的练习题及讲解在数学学习中，比较大小是一个基础而重要的概念。

它不仅涉及到数字的大小比较，还包括函数、不等式等更复杂的数学对象。

下面，我们将通过几个练习题来巩固和提高比较大小的能力。

练习题1：数字大小比较比较下列数字的大小：1. \( 3.14 \) 和 \( \pi \)2. \( \sqrt{2} \) 和 \( 1.4 \)3. \( 0.999... \) 和 \( 1 \)解答：1. \( \pi \) 是一个无理数，其值约为 \( 3.14159... \)，因此\( 3.14 < \pi \)。

2. \( \sqrt{2} \) 约等于 \( 1.414 \)，显然 \( \sqrt{2} > 1.4 \)。

3. \( 0.999... \) 实际上等于 \( 1 \)，这是一个数学上的极限概念，因此 \( 0.999... = 1 \)。

练习题2：函数值比较给定函数 \( f(x) = x^2 \) 和 \( g(x) = 2x \)，比较 \( f(2) \) 和 \( g(2) \) 的大小。

解答：计算 \( f(2) \) 和 \( g(2) \) 的值：\( f(2) = 2^2 = 4 \)\( g(2) = 2 \times 2 = 4 \)因此，\( f(2) = g(2) \)。

练习题3：不等式比较解不等式 \( 3x - 2 < 5x + 3 \) 并比较 \( x \) 的取值范围。

解答：首先，将不等式中的 \( x \) 项移到一边：\( 3x - 5x < 3 + 2 \)\( -2x < 5 \)然后，两边同时除以 \( -2 \)（注意，除以负数时不等号方向要改变）：\( x > -\frac{5}{2} \)所以，\( x \) 的取值范围是 \( x > -2.5 \)。

高考数学小题-比较大小专练解析版

比较大小专练解析版一．选择题（共60小题）1．设a＝log54，则，c＝0.5﹣0.2，则a，b，c的大小关系是（）A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b【分析】利用对数函数的单调性得到b＜a＜1，再利用指数函数的单调性得到c＞1，可得到答案．【解答】解：∵＝log53，a＝log54＜log55＝1，∴b＜a＜1，∵c＝0.5﹣0.2＞0.50＝1，∴b＜a＜c，故选：B．2．设a＝log5，b＝20.1，c＝log32，则（）A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b【分析】利用指数函数，对数函数的单调性，再借助中间量1和0即可求解．【解答】解：∵a＝log5＜log51＝0，b＝20.1＞20＝1，0＜c＝log32＜log33＝1，∴a＜c＜b，故选：A．3．设a＝log32，b＝ln2，，则a，b，c的大小关系为（）A．a＜b＜c B．c＜a＜b C．b＜a＜c D．c＜b＜a【分析】利用对数函数和指数函数的性质求解．【解答】解：∵a＝log32＝，且ln3＞1，∴，即a＜b，又∵c＝＝＝＜log32，即c＜a，∴c＜a＜b，故选：B．4．若a＝ln（ln）2，b＝2ln（ln2），c＝ln2，则a，b，c的大小关系为（）A．b＜a＜c B．c＜a＜b C．b＜c＜a D．a＜b＜c【分析】根据对数的运算性质以及对数函数的单调性即可判断．【解答】解：∵a＝2ln（|ln|）＝2ln（ln），b＝2ln（ln2），c＝2ln，而函数f（x）＝2lnx在定义域（0，+∞）上单调递增，0＜ln＜ln2＜1＜，∴a＜b＜c，故选：D．5．已知3a＝2b＝log2c＝6，则3a，2b，的大小关系为（）A．B．C．D．【分析】由3a＝2b＝log2c＝6可得a＝1+log32，b＝1+log23，c＝26，再根据指数函数和对数函数的性质即可比较出大小．【解答】解：∵3a＝2b＝log2c＝6，∴a＝log36＝1+log32，b＝log26＝1+log23，c＝26，∵3a＝3+3log32＝3+log38，且1＜log38＜2，∴4＜3a＜5，∵2b＝2+2log23＝2+log29，且3＜log29＜4，∴5＜2b＜6，∵＝＝23＝8，∴3a＜2b＜，故选：B．6．设a＝log23，b＝log34，c＝log48，则（）A．b＜c＜a B．c＜b＜a C．a＜c＜b D．a＜b＜c【分析】利用对数函数的性质求解．【解答】解：∵，∴b＜c＜a，故选：A．7．已知a＝21.2，b＝log54，，则a，b，c的大小关系为（）A．c＜a＜b B．c＜b＜a C．b＜a＜c D．b＜c＜a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵21.2＞20.8＝＞20＝1，∴a＞c＞1，∵log54＜log55＝1，∴b＜1，∴b＜c＜a，故选：D．8．设a＝，b＝ln2，c＝，则a，b，c的大小关系为（）A．a＜b＜c B．b＜c＜a C．c＜a＜b D．c＜b＜a 【分析】利用指数函数，对数函数的单调性，再借助中间量1和0求解即可．【解答】解：a＝＜log31＝0，∵ln1＜ln2＜lne，∴0＜b＜1，c＝＞50＝1，∴a＜b＜c，故选：A．9．已知a＝log0.92，b＝log0.90.7，c＝0.70.9，则a，b，c的大小关系是（）A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜a＜b 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log0.92＜log0.91＝0，∴a＜0，∵log0.90.7＞log0.90.9＝1，∴b＞1，∵0＜0.70.9＜0.70＝1，∴0＜c＜1，∴a＜c＜b，故选：C．10．已知a＝log30.3，b＝30.3，c＝0.31.3，则a，b，c的大小关系是（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log30.3＜log31＝0，∴a＜0，∵30.3＞30＝1，∴b＞1，∵0＜0.31.3＜0.30＝1，∴0＜c＜1，∴a＜c＜b，故选：B．11．已知，b＝log32，c＝log2，则a，b，c的大小关系为（）A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜b＜a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴a＞1，∵log31＜log32＜log33＝1，∴0＜b＜1，∵，∴c＜0，∴c＜b＜a，故选：D．12．令a＝60.7，b＝0.76，c＝log0.76，则a，b，c的大小顺序是（）A．b＜c＜a B．c＜b＜a C．b＜a＜c D．c＜a＜b 【分析】利用指数函数和对数函数的性质求解．【解答】解：∵60.7＞60＝1，∴a＞1，∵0＜0.76＜0.70＝1，∴0＜b＜1，∵log0.76＜log0.71＝0，∴c＜0，∴c＜b＜a，故选：B．13．已知a＝log20.3，b＝30.2，c＝0.32，则（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log20.3＜log21＝0，∴a＜0，∵30.2＞30＝1，∴b＞1，∵0＜0.32＜0.30＝1，∴0＜c＜1，∴a＜c＜b，故选：B．14．已知a＝log27，b＝log38，c＝0.30.2，则a，b，c的大小关系为（）A．a＜b＜c B．c＜b＜a C．b＜c＜a D．c＜a＜b【分析】根据对数函数和指数函数的单调性即可比较出a，b，c的大小关系．【解答】解：∵log27＞log24＝2，1＝log33＜log38＜log39＝2，0.30.2＜0.30＝1，∴c＜b＜a．故选：B．15．设a＝logπ3，b＝+log23，c＝（），则（）A．b＜a＜c B．b＜c＜a C．c＜a＜b D．c＜b＜a【分析】根据对数的运算和对数函数的单调性即可得出b＜0，0＜a＜1，根据指数函数的单调性即可得出c＞1，这样即可得出a，b，c的大小关系．【解答】解：，0＝logπ1＜logπ3＜logππ＝1，，∴b＜a＜c．故选：A．16．设a＝log35，b＝log49，c＝log57，则（）A．c＜b＜a B．b＜a＜c C．a＜c＜b D．c＜a＜b【分析】利用对数函数的性质求解．【解答】解：∵a＝log35＝，b＝log49＝，c＝log57＝，∴a﹣c＝＝，∵lg3•lg7＝＜＝（lg5）2，∴a﹣c＞0，∴a＞c，∵b＝log49＝log23＝，a＝＝，∴b＞a，∴c＜a＜b，故选：D．17．若x＝log50.3，y＝30.3，z＝0.32，则x，y，z的大小关系是（）A．y＞z＞x B．z＞y＞x C．z＞x＞y D．y＞x＞z 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log50.3＜log51＝0，∴x＜0，∵30.3＞30＝1，∴y＞1，∵0＜0.32＜0.30＝1，∴0＜z＜1，∴y＞z＞x，故选：A．18．已知a＝0.80.9，b＝ln，c＝1.20.8，则a，b，c的大小关系是（）A．a＞b＞c B．c＞a＞b C．a＞c＞b D．c＞b＞a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵0＜0.80.9＜0.80＝1，∴0＜a＜1，∵，∴b＜0，∵1.20.8＞1.20＝1，∴c＞1，∴c＞a＞b，故选：B．19．设a＝log34，b＝，c＝，则（）A．a＜b＜c B．b＜c＜a C．c＜a＜b D．c＜b＜a 【分析】利用指数函数，对数函数的单调性，再借助中间量1和0求解即可．【解答】解：a＝log34＞log33＝1，∵0＜＜30，∴0＜b＜1，c＝＝﹣1，∴c＜b＜a，故选：D．20．若a＝0.54，b＝30.5，c＝ln0.5，则下列结论正确的是（）A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞a＞b 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵0＜0.54＜0.50＝1，∴0＜a＜1，∵30.5＞30＝1，∴b＞1，∵ln0.5＜ln1＝0，∴c＜0，∴b＞a＞c，故选：B．21．已知，则a，b，c的大小关系为（）A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜b＜a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴a＞1，∵log31＜log32＜log33＝1，∴0＜b＜1，∵，∴c＜0，∴c＜b＜a，故选：D．22．已知a＝ln3，b＝3﹣0.4，c＝3﹣0.5，则（）A．a＞b＞c B．c＞a＞b C．a＞c＞b D．c＞b＞a 【分析】利用指数函数，对数函数的单调性求解即可．【解答】解：a＝ln3＞lne＝1，∵y＝3x在R上为增函数，∴30＞3﹣0.4＞3﹣0.5，即1＞b＞c，∴a＞b＞c，故选：A．23．已知实数a，b，c满足1.5a＝3.1，5b＝0.1，c＝，则（）A．c＞a＞b B．a＞c＞b C．b＞a＞c D．c＞b＞a【分析】先把指数式化为对数式，求出a，b，再利用对数函数的性质进行求解．【解答】解：∵1.5a＝3.1，5b＝0.1，∴a＝log1.53.1，b＝log50.1，∵，∴a＞2，∵log50.1＜log51＝0，∴b＜0，∵c＝＝＝＝ln2，且ln1＜ln2＜lne，∴0＜c＜1，∴a＞c＞b，故选：B．24．已知a＝log35，b＝π，c＝2﹣0.1，则（）A．a＜b＜c B．c＜a＜b C．b＜c＜a D．a＜c＜b 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log33＜log35＜log39＝2，∴1＜a＜2，∵0＜2﹣0.1＜20＝1，∴0＜c＜1，∴c＜a＜b，故选：B．25．已知a＝e﹣0.5，b＝ln5，c＝log0.5e，则（）A．c＜a＜b B．c＜b＜a C．b＜a＜c D．a＜b＜c 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵0＜e﹣0.5＜e0＝1，∴0＜a＜1，∵ln5＞lne＝1，∴b＞1，∵log0.5e＜log0.51＝0，∴c＜0，∴c＜a＜b，故选：A．26．已知a＝log0.20.02，b＝log660，c＝ln6，则（）A．c＜b＜a B．b＜a＜c C．c＜a＜b D．a＜c＜b 【分析】利用对数函数的性质求解．【解答】解：a＝log0.20.02＝＝1﹣log0.210＝1+log510，b＝log660＝1+log610＞1+log66＝2，∵log510＞log610，∴a＞b＞2，∵c＝ln6＜lne2＝2，∴c＜2，∴c＜b＜a，故选：A．27．已知a＝log0.20.05，b＝0.51.002，c＝4cos1，则下列判断正确的是（）A．a＜b＜c B．b＜c＜a C．c＜b＜a D．b＜a＜c【分析】根据对数函数、指数函数和余弦函数的单调性即可得出a，b，c的大小关系．【解答】解：∵，0.51.002＜0.50＝1，，∴b＜a＜c．故选：D．28．下列不等式成立的是（）A．log3＜log23＜log25B．log3＜log25＜log23C．log23＜log3＜log25D．log23＜log25＜log3【分析】根据对数函数的单调性即可得出正确的选项．【解答】解：∵，0＝log21＜log23＜log25，∴．故选：A．29．已知a＝2，b＝log2，c＝π0，则（）A．a＞c＞b B．b＞c＞a C．c＞a＞b D．c＞b＞a【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴a＞1，∵，∴b＜0，又∵c＝π0＝1，∴a＞c＞b，故选：A．30．已知，b＝log32，c＝cos3，则a、b、c的大小关系为（）A．a＞b＞c B．a＞c＞b C．b＞a＞c D．c＞a＞b 【分析】利用对数函数、指数函数和余弦函数的性质求解．【解答】解：∵，∴a＞1，∵log31＜log32＜log33＝1，∴0＜b＜1，∵，∴cos3＜0，即c＜0，∴a＞b＞c，故选：A．31．a＝sin1，b＝lg sin1，c＝10sin1，则（）A．a＜b＜c B．b＜a＜c C．b＜c＜a D．c＜b＜a 【分析】根据对数函数和指数函数的单调性即可得出a，b，c的大小关系．【解答】解：∵0＜sin1＜1，∴lg sin1＜0，10sin1＞1，∴b＜a＜c．故选：B．32．设a＝30.3，，c＝log0.60.8，则a，b，c的大小关系为（）A．a＜b＜c B．b＜a＜c C．c＜b＜a D．c＜a＜b 【分析】利用指数函数，对数函数的单调性，再借助中间量求解即可．【解答】解：∵，∴1，∵，∴b＞2，∵log0.60.8＜log0.60.6＝1，∴c＜1，∴c＜a＜b．故选：D．33．已知，，c＝sin1，则（）A．a＜b＜c B．b＜c＜a C．c＜b＜a D．c＜a＜b【分析】利用对数函数、指数函数和正弦函数的性质求解．【解答】解：∵，∴a＞1，∵，∴0，∵，∴，即，∴b＜c＜a，故选：B．34．已知a＝ln2，，，则（）A．b＜c＜a B．c＜a＜b C．a＜b＜c D．b＜a＜c【分析】根据对数函数和指数函数的单调性即可得出0＜a＜1，b＜0，c＞1，然后即可得出a，b，c的大小关系．【解答】解：∵0＝ln1＜ln2＜lne＝1，，，∴b＜a＜c．故选：D．35．已知a＝log2π，b＝ln，c＝π﹣2，则（）A．b＜c＜a B．b＜a＜c C．c＜a＜b D．a＜c＜b【分析】利用对数函数和指数函数的性质求解．【解答】解：∵log2π＞log22＝1，∴a＞1，∵，∴b＜0，∵0＜π﹣2＜π0＝1，∴0＜c＜1，∴b＜c＜a，故选：A．36．已知a＝log52，b＝log83，c＝2﹣1，则下列判断正确的是（）A．c＜b＜a B．b＜a＜c C．a＜c＜b D．a＜b＜c【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴a＜，∵，∴b＞，又∵c＝，∴a＜c＜b，故选：C．37．若，，，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a 【分析】利用对数函数和指数函数的性质求解．【解答】解：∵＝＝，＝，∴b＞c，∵，即，∴，即，又∵＝log43，∴a＞c，∵28＝256＞243＝35，∴，∴＝，即＞3，∴，即，∴b＞a，∴b＞a＞c，故选：B．38．若，则（）A．a＞c＞b B．a＞b＞c C．c＞a＞b D．b＞c＞a 【分析】利用指数函数和对数函数的性质求解．【解答】解：∵＞20＝1，∴a＞1，∵＜＝0，∴b＜0，∵ln1＜＜lne＝1，∴0＜c＜1，∴a＞c＞b，故选：A．39．已知a＝ln3，b＝sin，c＝3，则a，b，c的大小关系是（）A．a＞b＞c B．a＞c＞b C．c＞b＞a D．c＞a＞b【分析】利用指数函数、对数函数以及正弦函数的性质求解．【解答】解：∵ln3＞lne＝1，∴a＞1，∵＝＝﹣sin＝﹣，即b＝﹣，∵，∴0＜c＜1，∴a＞c＞b，故选：B．40．以下四组数中大小比较正确的是（）A．log3.1π＜logπ3.1B．π﹣0.2＜π﹣0.1C．0.50.3＜0.40.3D．0.40.3＜0.10.7【分析】利用指数函数、对数函数和幂函数的单调性求解．【解答】解：对于选项A：∵log3.1π＞log3.13.1＝1，logπ3.1＜logππ＝1，∴log3.1π＞logπ3.1，故选项A错误，对于选项B：∵函数y＝πx在R上单调递增，且﹣0.2＜﹣0.1，∴π﹣0.2＜π﹣0.1，故选项B 正确，对于选项C：∵函数y＝x0.3在（0，+∞）上单调递增，且0.5＞0.4，∴0.50.3＞0.40.3，故选项C错误，对于选项D：由指数函数y＝0.4x和幂函数y＝x0.7的单调性可知，0.40.3＞0.40.7＞0.10.7，故选项D错误，故选：B．41．设a＝30.2，b＝log0.23，c＝sin（﹣2021°），则（）A．c＜b＜a B．b＜c＜a C．a＜b＜c D．b＜a＜c【分析】可得出c＝sin41°，从而得出0＜c＜1，然后根据指数函数和对数函数的单调性即可得出a，b，c的大小关系．【解答】解：sin（﹣2021°）＝sin（﹣221°）＝﹣sin（﹣41°）＝sin41°，0＜sin41°＜1，30.2＞30＝1，log0.23＜log0.21＝0，∴b＜c＜a．故选：B．42．已知a，b，c均为正实数，且b≠1，若，则下列关系中可能成立的是（）A．a＝b＜c B．a＝c＜b C．a＜c＜b D．b＜c＜a【分析】利用对数函数、指数函数以及幂函数的性质求解．【解答】解：∵a b＜1，c a＜1，且a，b，c均为正实数，∴0＜a＜1，0＜c＜1，又∵0＜log b c＜1，∴0＜b＜1，且c＞b，故排除BC，若a＝b，则a b＝b b，c a＝c b，又∵a b＜c a，∴b b＜c b，∵幂函数y＝x b（b＞0）在（0，+∞）上单调递增，又c b＞b b，∴c＞b，符合题意，故选项A可能成立，若b＜c＜a，则a b＞c b＞c a，∴a b＞c a，与题意不符，故选项D不可能，故选：A．43．三个数的大小关系是（）A．B．C．D．【分析】根据对数函数、正弦函数和指数函数的单调性即可得出这三个数的大小关系．【解答】解：∵logπ0.3＜logπ1＝0，3π＞30＝1，，∴．故选：A．44．已知，b＝log92，，则a，b，c的大小关系为（）A．a＞b＞c B．c＞b＞a C．b＞a＞c D．a＞c＞b【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴a＞1，∵，∴0＜b＜，∵，∴，∴a＞c＞b，故选：D．45．已知a＝log0.30.5，b＝30.5，c＝cos3，则a，b，c的大小关系为（）A．c＜b＜a B．b＜c＜a C．c＜a＜b D．b＜a＜c【分析】利用对数函数和指数函数的性质求解．【解答】解：∵0＝log0.31＜log0.30.5＜log0.30.3＝1，∴0＜a＜1，∵30.5＞30＝1，∴b＞1，∵，∴cos3＜0，即c＜0，∴c＜a＜b，故选：C．46．已知，，b＝（sinα）α，c＝（cosα）α，则（）A．c＞a＞b B．b＞c＞a C．a＞c＞b D．c＞b＞a【分析】由可得0＜sinα＜cosα＜1，再利用对数函数和幂函数的单调性求解．【解答】解：∵，∴0＜sinα＜cosα＜1，∴＞1，∴＜logα1＝0，即a＜0，∵函数y＝xα在（0，+∞）上单调递增，∴0＜（sinα）α＜（cosα）α，∴c＞b＞a，故选：D．47．设a＝log20.3，b＝0.4，c＝0.40.3，则三者大小关系为（）A．a＜b＜c B．c＜a＜b C．b＜c＜a D．a＜c＜b【分析】利用指数函数和对数函数的性质．【解答】解：∵log20.3＜log21＝0，∴a＜0，∵＞log0.5＝1，∴b＞1，∵0＜0.40.3＜0.40＝1，∴0＜c＜1，∴a＜c＜b，故选：D．48．已知a＝log52，b＝log83，c＝，则下列判断正确的是（）A．c＜b＜a B．b＜a＜c C．a＜c＜b D．a＜b＜c【分析】可得出，然后即可得出a，b，c的大小关系．【解答】解：∵，，∴a＜c＜b．故选：C．49．已知a＝log1.10.9，b＝0.91.1，c＝1.10.9，则a，b，c的大小关系为（）A．a＜b＜c B．a＜c＜b C．b＜a＜c D．b＜c＜a【分析】可以得出，然后即可得出a，b，c的大小关系．【解答】解：∵log1.10.9＜log1.11＝0，0＜0.91.1＜0.90＝1，1.10.9＞1.10＝1，∴a＜b＜c．故选：A．50．已知a＝log65，b＝60.1，c＝log56，则a，b，c的大小关系为（）A．b＞a＞c B．c＞a＞b C．b＞c＞a D．c＞b＞a【分析】由题意可知0＜a＜1，b＞1，，由56＞65得a，由62＜53可得c＜，所以b＞a＞c．【解答】解：由题意可知0＜a＝log65＜log66＝1，b＝60.1＞60＝1，，∵56＞65，∴，即，∴a＝log65＝，∵62＜53，∴，∴c＝＜＝，∴a＞c，∴b＞a＞c，故选：A．51．已知a＝log32，b＝ln2，c＝0.5﹣0.2，则a，b，c的大小关系为（）A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b【分析】可得出，从而可得出a＜b＜1，并且可得出c＞1，这样即可得出a，b，c的大小关系．【解答】解：，∵log23＞log2e＞1，∴，且0.5﹣0.2＞0.50＝1，∴a＜b＜c．故选：B．52．已知函数f（x）＝e﹣|x|，，，，则下述关系式正确的是（）A．b＞a＞c B．b＞c＞a C．c＞a＞b D．a＞b＞c【分析】由题意可知函数f（x）是偶函数，且当x≥0时，f（x）单调递减，利用函数f （x）是偶函数结合对数的运算性质，化简a，b，c的值，再利用函数f（x）的单调性即可比较a，b，c的大小关系．【解答】解：∵函数f（x）＝e﹣|x|，∴函数f（x）是偶函数，且当x≥0时，f（x）单调递减，∴＝f（﹣log e3）＝f（log e3），＝f（﹣log3e）＝f（log3e），＝f（log e9）＝f（2log e3），∵1＜log e3＜2，0＜log3e＜1，2log e3＞2，∴f（2log e3）＜f（log e3）＜f（log3e），即c＜a＜b，故选：A．53．设a＝，b＝log0.30.4，c＝3ln2，则a，b，c的大小关系为（）A．b＜a＜c B．a＜c＜b C．b＜c＜a D．a＜b＜c【分析】可得出a＝3，b＜1，1＜c＜3，然后即可得出a，b，c的大小关系．【解答】解：a＝3，b＝log0.30.4＜log0.30.3＝1，c＝ln23＞lne＝1，ln2＜1，∴1＜c＜3，∴b＜c＜a．故选：C．54．已知a＝log0.22，b＝30.3，c＝log32，则（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a【分析】利用指数函数和对数函数的性质求解．【解答】解：∵log0.22＜log0.21＝0，∴a＜0，∵30.3＞30＝1，∴b＞1，∵log31＜log32＜log33＝1，∴0＜c＜1，∴a＜c＜b，故选：B．55．已知函数f（x）＝2|x|，a＝f（（）），b＝f（log3），c＝f（log5），则a、b、c的大小关系为（）A．c＞b＞a B．b＞a＞c C．a＞b＞c D．c＞a＞b【分析】可得出f（﹣x）＝f（x），从而得出c＝f（log35），然后即可得出，并且可看出f（x）在（0，+∞）上是增函数，从而可得出a，b，c的大小关系．【解答】解：∵f（﹣x）＝f（x），∴c＝f（﹣log35）＝f（log35），∵，，∴，且f（x）在（0，+∞）上是增函数，∴，∴c＞b＞a．故选：A．56．已知a＝（）﹣0.8，b＝，c＝40.3，则a，b，c的大小关系是（）A．a＜b＜c B．a＜c＜b C．c＜b＜a D．b＜c＜a【分析】可得出a＝20.8，c＝20.6，然后可得出，然后即可得出a，b，c的大小关系．【解答】解：∵，且20.8＞20.6＞20＝1，，∴b＜c＜a．故选：D．57．已知2020a＝2021，2021b＝2020，c＝ln2，则（）A．log a c＞log b c B．log c a＞log c bC．a c＜b c D．c a＜c b【分析】根据条件可得出a＞1，0＜b＜1，0＜c＜1，然后根据对数函数、指数函数和幂函数的单调性即可判断每个选项的正误．【解答】解：∵a＝log20202021＞log20202020＝1，b＝log20212020，0＜b＜1，c＝ln2，0＜c＜1，∴log a c＜0，log b c＞0，∴log a c＜log b c，即A错误；∵a＞b，0＜c＜1，∴log c a＜log c b，a c＞b c，c a＜c b，即BC都错误，D正确．故选：D．58．已知a＝4ln3π，b＝3ln4π，c＝4lnπ3，则a，b，c的大小关系是（）A．c＜b＜a B．b＜c＜a C．b＜a＜c D．a＜b＜c【分析】可以得出a＝ln34π，b＝ln43π，c＝lnπ12，显然43π＜π12＜34π，从而根据对数函数的单调性即可得出a，b，c的大小关系．【解答】解：a＝ln34π，b＝ln43π，c＝lnπ12，，且2π＜π2，∴，，且27π＞π3，∴，∴43π＜π12＜34π，∴b＜c＜a．故选：B．59．已知a＝，b＝，c＝2ln，则（）A．a＞b＞c B．a＞c＞b C．c＞b＞a D．c＞a＞b【分析】可得出，然后即可得出a，b，c的大小关系．【解答】解：∵，，，∴a＞c＞b．故选：B．60．已知a＝log 3，b＝2cosθ，c＝πe，则a，b，c的大小关系是（）A．a＞b＞c B．a＞c＞b C．c＞b＞a D．c＞a＞b【分析】利用对数函数和指数函数的性质求解．【解答】解：∵，∴0，∵﹣1≤cosθ≤1，∴2﹣1≤2cosθ≤21，即，∵πe＞3，∴c＞3，∴c＞b＞a，故选：C．第21 页共21 页。

压轴题型04 比大小问题(解析版)-2023年高考数学压轴题专项训练

压轴题04比大小问题函数“比大小”是非常经典的题型，难度不以，方法无常，很受命题者的青睐。

高考命题中，常常在选择题或填空题中出现这类型的问题，往往将幂函数、指数函数、对数函数、三角函数等混在一起，进行排序。

这类问题的解法往往可以从代数和几何来那个方面加以探寻，即利用函数的性质与图象解答。

○热○点○题○型1比较大小的常见方法1、单调性法：当两个数都是指数幂或对数式时，可将其看成某个指数函数、对数函数或幂函数的函数值，然后利用该函数的单调性比较；2、作差法、作商法：（1）一般情况下，作差或者作商，可处理底数不一样的对数比大小；（2）作差或作商的难点在于后续变形处理，注意此处的常见技巧与方法；3、中间值法或1/0比较法：比较多个数的大小时，先利用“0”“1”作为分界点，然后再各部分内再利用函数的性质比较大小；4、估值法：（1）估算要比较大小的两个值所在的大致区间；（2）可以对区间使用二分法（或利用指对转化）寻找合适的中间值；5、构造函数，运用函数的单调性比较：构造函数，观察总结“同构”规律，很多时候三个数比较大小，可能某一个数会被可以的隐藏了“同构”规律，所以可能优先从结构最接近的的两个数规律（1）对于抽象函数，可以借助中心对称、轴对称、周期等性质来“去除f()外衣”比较大小；（2）有解析式函数，可以通过函数性质或者求导等，寻找函数的单调性、对称性，比较大小。

6、放缩法：（1）对数，利用单调性，放缩底数，或者放缩真数；（2）指数和幂函数结合来放缩；（3）利用均值不等式的不等关系进行放缩；（4）“数值逼近”是指一些无从下手的数据，如果分析会发现非常接近某些整数（主要是整数多一些），那么可以用该“整数”为变量，构造四舍五入函数关系。

一、单选题1．已知函数()f x 满足()()1ln 0f x x f x x'+<（其中()f x '是()f x 的导数），若12e a f ⎛⎫=⎪⎝⎭，13e bf ⎛⎫= ⎪⎝⎭，14e c f ⎛⎫= ⎪⎝⎭，则下列选项中正确的是（）A ．643a b c <>B ．a b c>>C ．c b a>>D ．b a c>>A ．a b c <<B ．b a c<<C ．c<a<bD ．b<c<a4．已知2()cos f x x x =+，若3441e ,ln ,54a f b f c f -⎛⎫⎛⎫⎛⎫===- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则a ，b ，c 的大小关系为（）A ．b c a <>B ．b c a >>C ．a b c >>D ．b a c>>6．已知函数()31sin 2f x x x =-，若π0,12θ⎛⎫∈ ⎪⎝⎭，()()sin cos a fθθ=，()()sin sin b f θθ=，12c f ⎛⎫=-- ⎪⎝⎭，则a ，b ，c 的大小关系为（）A ．a b c >>B ．b a c>>C ．a c b>>D ．c a b>>R ，当0x >时，，f x 为其导函数，且满足()()f x f x '<恒成立，若01a <<，则()30f ，()f a ，()1af 三者的大小关系为（）A ．()()()130af f a f >>B ．()()()301f f a af >>C ．()()()301f af f a >>D ．()()()301f a f af >>8．已知a ，b ，()1,c ∈+∞，且ln 2a a -=，ln 2ln 22b b -=+，sin1ln tan1c c -=+，其中e 是自然对数的底数，则（）A ．a b c <<B ．b a c<<C ．a c b<<D ．b<c<aA ．b c a <<B ．b a c <<C ．c b a <<D ．a c b<<利用单调性即可判断,,a b c 的大小关系.10．已知 1.4a =，0.41.1e b =，0.5e c =，则,,a b c 的大小关系是（）A ．a b c <，函数()f x 在(),0.5-∞上单调递增，当0.5x >时，()0f x '<，函数()f x 在()0.5,+∞上单调递减，所以()()0.40.5b f f c =<=；设()e 1x g x x =--，则()e 1xg x '=-，当0x <时，()0g x '<，函数()g x 在(),0∞-上单调递减，当0x >时，()0g x '>，函数()g x 在()0,∞+上单调递增，所以()e 100xx g --≥=故e 1x x ≥+，所以0.41.1e 1.11.4 1.4>⨯>，即a b <．综上，a b c <<，故选：A ．【点睛】关键点睛：本题解决的关键在于观察数的结构特征，通过构造函数，利用导数判断函数的单调性函数的单调性比较大小.11．设130121,sin ,e 124330a b c ===-，则a ，b ，c 的大小关系是（）A ．b a c >>B ．a b c >>C ．a c b>>D ．c a b>>12．已知0.1e a =，1110b =，c =，则（）A ．c b a >>B ．b a c >>C ．a b c >>D ．a c b>>A ．c b a <<B ．a c b <<C ．c a b <<D ．a b c<<A．c b a<<B．c<a，且0a >，1c >，构造()e 1xg x x =--并研究其最值得c a ≥，结合e e a b c a =>=，得到1c a b b >>+>，求导得()f x '，然后由函数单调性即可得到其大小关系.【详解】由e ln b a c ==，则,b c 是y a =是e ,ln x y y x ==的交点横坐标，如下图示，由图易知：c b >，且0a >，1c >，构造()e 1xg x x =--，则()e 1x g x '=-，令()00g x x '=⇒=，当0x <时，()0g x '<，则()g x 递减；当0x >时，()0g x '>，则()g x 递增；所以当0x =时，()()min 00g x g ==，所以()()0g x g ≥,即e 1x x ≥+，16．若 1.1ln1.1a =，0.10.1e b =，10c =，则a ，b ，c 的大小关系为（）A ．a b c <>B ．x z y >>C ．z x y >>D ．y x z>>【答案】B19．已知7a =，ln1.4b =，0.2e 1c =-，则（）A ．a b c <,()()222exf x f x --=,则下列判断一定不正确的是()A ．(1)(0)f f C ．33e 0f f >()()D ．()()44e 0f f <22．已知函数，其中a ，b ，0,c ∈+∞，20f =，则下列结论正确的是（）A ．102f ⎛⎫> ⎪⎝⎭B ．()30f <C ．()f x 在R 上单调递减D ．()()11f f -最大值为4-23．若ln1.1a =，111b =，sin 0.1c =，21220d =，则（）．A ．a b B ．0.013ab<C ．b c>D ．0.013ab>【答案】AB【分析】考虑 2.99 2.983.01,3.02类似于()33xx -+的函数形式，因此构造函数()()33xf x x -=+，运用函数的单调性求解.A ．()ππsin *n nn>∈N B ．2log 3>C ．3e ln 3<D ．e ln 9>26．已知当关于x 的不等式2e 0x λλ-≥在()1,+∞上恒成立时，正数λ的取值范围为集合D ，则下列式子的值是集合D 的元素的是（）A ．ln 2ln 3B ．5131log log 53-C ．3π2tan 5e D ．22cos 1sin 1-27．已知定义域为R 的函数在1,0-上单调递增，11f x f x +=-，且图像关于2,0对称，则()f x （）A ．()()02f f =B ．周期2T =C ．在(]1,2单调递减D ．满足()()()202120222023f f f >>【答案】ACD【分析】根据已知条件由对称抽和对称中心得出周期为4判断A,B 选项，周期再结合已知单调性判断C 选项,应用周期性和单调性求函数值的大小判断D.【详解】由()()11f x f x +=-知()f x 的对称轴为1x =，所以()()02,f f =故A 正确;由()()11f x f x +=-知：()()2f x f x +=-，又图像关于()2,0对称，即()()22f x f x +=--，故()()4f x f x +=--，所以()()24f x f x -+=+，即()()2f x f x -=+，所以()()()4,f x f x f x =+的周期为4，故B 错误;因为()f x 在(]1,0-上单调递增，且4T =，所以()f x 在(]3,4上单调递增，又图像关于()2,0对称，所以()f x 在(]0,1上单调递增，因为关于1x =对称，所以()f x 在(]1,2上单调递减，故C 正确；根据周期性，()()()()()()20211,20222,20233f f f f f f ===，因为关于1x =对称，所以()()20f f =，因为周期4T =，所以()()31f f =-；结合()f x 在(1,2]上单调递减，且(]1,0-上单调递增，故()()()()()31021f f f f f =-<=<，即()()()202120222023f f f >>，故D 正确.故选:ACD.三、填空题28．已知sin13a =，b =π9c =，则,,a b c 的大小关系是___________.29．设191e10a=，19b=，32ln2c=，则____>______>______(填a，b，c)．【点睛】关键点睛：本题解决的关键在于根据数据之间的联系，构造函数，利用导数判断函数的单调性，利用单调性比较函数值的大小.四、解答题30．已知函数()y f x =的定义域为D ，区间M D ⊆，若存在非零实数t 使得任意x M ∈都有x t D +∈，且()()f x t f x +>，则称()y f x =为M 上的t -增长函数．(1)已知()f x x =，判断函数()y f x =是否为区间[]1,0-上的32-增长函数，并说明理由；(2)已知0n >，设()2g x x =，且函数()y g x =是区间[]4,2--上的n -增长函数，求实数n 的取值范围；(3)如果函数()y h x =是定义域为R 的奇函数，当0x ≥时，()22h x x a a =--，且函数()y h x =为R 上的4-增长函数，求实数a 的取值范围．④当)22,x a a ⎡∈-⎣时，则22443x a a +≥-+>，注意到()h x 在)22,a a ⎡-⎣上单调递减，在()2,a +∞上单调递增，可得()()()()2234h x h a h a h x ≤-=<+；⑤当)2,x a ⎡∈+∞⎣时，则24x x a +>≥，且()h x 在)2,a ⎡+∞⎣上单调递增，可得()()4h x h x <+；综上所述：当()1,1a ∈-时，对x ∀∈R ，均有()()4h x h x <+.故实数a 的取值范围为()1,1-.【点睛】关键点点睛：根据()h x 的单调性，取特值2x a =-，先求出实数a 的取值范围，再证明其充分性.。

2025年高考数学一轮复习-2.1.1-不等关系与比较大小-专项训练【含解析】

2.1.1-不等关系与比较大小-专项训练【原卷版】时间：45分钟一、选择题1．下面表示“a 与b 的差是非负数”的不等关系的是()A ．a －b>0B ．a －b<0C ．a －b ≥0D ．a －b ≤02．有一家三口的年龄和为65岁，设父亲，母亲和小孩的年龄分别为x ，y ，z ，则下列选项中能反映x ，y ，z 关系的是()A ．x ＋y ＋z ＝65＋y ＋z ＝65，，＋y ＋z ＝65，，＋y ＋z ＝65，，，3．设a ＝3x 2－x ＋1，b ＝2x 2＋x ，x ∈R ，则()A ．a >bB ．a <bC ．a ≥bD ．a ≤b4．某同学拿50元钱买纪念邮票，票面8角的每套5张，票面2元的每套4张，如果每种邮票至少买两套，那么买票面8角的x 套与票面2元的y 套用不等式表示为()≥2，x ∈N ＋，≥2，y ∈N ＋，×5x ＋2×4y ≤50≥2，≥2，×5x＋2×4y≤50≥2，≥2D．0.8×5x＋2×4y≤505．已知a，b，c为不全相等的实数，P＝a2＋b2＋c2＋3，Q＝2(a ＋b＋c)，那么P与Q的大小关系是()A．P>Q B．P≥QC．P<Q D．P≤Q6．不等式：①a2＋2>2a；②a2＋b2≥2(a－b－1)；③a2＋b2≥ab 恒成立的个数是()A．0B．1C．2D．37．若a<0，b<0，则p＝b2a＋a2b与q＝a＋b的大小关系为() A．p<q B．p≤qC．p>q D．p≥q8．若m<n，p<q，且(p－m)(p－n)<0，(q－m)(q－n)<0，则m，n，p，q从小到大的排列顺序是()A．m<p<q<n B．p<m<q<nC．m<p<n<q D．p<m<n<q二、填空题9．某旅游公司年初以98万元购进一辆豪华旅游车，第一年各种费用为12万元，以后每年都增加4万元，该车每年的旅游效益为50万元，设第n年开始获利，列出关于n的不等关系为.10．设实数a，b，c满足b＋c＝6－4a＋3a2，c－b＝4－4a＋a2，则a，b，c的大小关系是.三、解答题11．某球迷协会一行56人从旅馆乘出租车到球场为球队加油，现有A ，B 两个出租车队，A 队比B 队少3辆车．若全部安排乘A 队的车，每辆车坐5人，车不够；每辆车坐6人，有的车未坐满；若全部安排乘B 队的车，每辆车坐4人，车不够，每辆车坐5人，有的车未坐满．试用不等式表示上述不等关系．12．试比较下列各组式子的大小：(1)x ＋1－x 与x －x －1，其中x >1；(2)x 3－2y 3与xy 2－2x 2y ，其中x >y >0.13．(多选题)下列四个选项中能推出1a <1b 的有()A ．b >0>aB ．0>a >bC ．a >0>bD ．a >b >014．有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色，且三个房间颜色各不相同．已知三个房间的粉刷面积(单位：m 2)分别为x ，y ，z ，且x <y <z ，三种颜色涂料的粉刷费用(单位：元/m 2)分别为a ，b ，c ，且a <b <c .在不同的方案中，最低的总费用(单位：元)是()A ．ax ＋by ＋czB ．az ＋by ＋cxC ．ay ＋bz ＋cxD ．ay ＋bx ＋cz15．一辆汽车原来每天行驶x km ，如果这辆汽车每天行驶的路程比原来多19km ，那么在8天内它的行程就超过2200km ，写成不等式为；如果它每天行驶的路程比原来少12km ，那么它原来行驶8天的路程就得花9天多的时间，用不等式表示为.16．已知－12<a <0，A ＝1＋a 2，B ＝1－a 2，C ＝11＋a ，D ＝11－a ，试比较A 、B 、C 、D 的大小关系．2.1.1-不等关系与比较大小-专项训练【解析版】时间：45分钟一、选择题1．下面表示“a 与b 的差是非负数”的不等关系的是(C )A ．a －b>0B ．a －b<0C ．a －b ≥0D ．a －b ≤02．有一家三口的年龄和为65岁，设父亲，母亲和小孩的年龄分别为x ，y ，z ，则下列选项中能反映x ，y ，z 关系的是(C )A ．x ＋y ＋z ＝65＋y ＋z ＝65，，＋y ＋z ＝65，，＋y ＋z ＝65，，，3．设a ＝3x 2－x ＋1，b ＝2x 2＋x ，x ∈R ，则(C )A ．a >b B ．a <b C ．a ≥bD ．a ≤b解析：∵a －b ＝x 2－2x ＋1＝(x －1)2≥0，∴a ≥b .4．某同学拿50元钱买纪念邮票，票面8角的每套5张，票面2元的每套4张，如果每种邮票至少买两套，那么买票面8角的x 套与票面2元的y 套用不等式表示为(A )≥2，x ∈N ＋，≥2，y ∈N ＋，×5x ＋2×4y ≤50≥2，≥2，×5x＋2×4y≤50≥2，≥2D．0.8×5x＋2×4y≤505．已知a，b，c为不全相等的实数，P＝a2＋b2＋c2＋3，Q＝2(a ＋b＋c)，那么P与Q的大小关系是(A)A．P>Q B．P≥QC．P<Q D．P≤Q解析：P－Q＝a2＋b2＋c2＋3－2a－2b－2c＝(a－1)2＋(b－1)2＋(c－1)2≥0.∵a，b，c不全相等，∴P－Q>0，∴P>Q.6．不等式：①a2＋2>2a；②a2＋b2≥2(a－b－1)；③a2＋b2≥ab 恒成立的个数是(D)A．0B．1C．2D．3解析：①a2＋2－2a＝(a－1)2＋1>0，故①正确；②a2＋b2－2(a－b－1)＝a2－2a＋b2＋2b＋2＝(a－1)2＋(b＋1)2≥0，故②正确；③a2＋b2－ab＝a2－ab＋14b2＋34b2－12b＋34b2≥0，故③正确，故选D.7．若a<0，b<0，则p＝b2a＋a2b与q＝a＋b的大小关系为(B) A．p<q B．p≤qC．p>q D．p≥q解析：p－q＝b2a＋a2b－(a＋b)＝b 2－a 2a ＋a 2－b 2b ＝(b 2－a 2)(b －a )ab ＝(b －a )2(b ＋a )ab，∵a <0，b <0，∴ab >0，a ＋b <0，(b －a )2≥0，∴p －q ≤0，∴p ≤q .8．若m <n ，p <q ，且(p －m )(p －n )<0，(q －m )(q －n )<0，则m ，n ，p ，q 从小到大的排列顺序是(A )A ．m <p <q <nB ．p <m <q <nC ．m <p <n <qD ．p <m <n <q解析：∵(p －m )(p －n )<0，∴m ，n 中一个大于p ，一个小于p .∵m <n ，∴m <p <n .∵(q －m )(q －n )<0，∴m ，n 中一个大于q ，一个小于q .∵m <n ，∴m <q <n .∵p <q ，∴m <p <q <n .二、填空题9．某旅游公司年初以98万元购进一辆豪华旅游车，第一年各种费用为12万元，以后每年都增加4万元，该车每年的旅游效益为50万元，设第n 年开始获利，列出关于n 的不等关系为98＋12＋(12＋4)＋(12＋4×2)＋…＋[12＋4×(n －1)]<50n ，n ∈N *.10．设实数a ，b ，c 满足b ＋c ＝6－4a ＋3a 2，c －b ＝4－4a ＋a 2，则a ，b ，c 的大小关系是c ≥b >a .解析：∵c －b ＝4－4a ＋a 2＝(2－a )2≥0，∴c ≥b .＋c ＝6－4a ＋3a 2，－b ＝4－4a ＋a 2，得b ＝a 2＋1.∴b －a ＝a 2＋1－a ＋34，∴b >a .∴c ≥b >a .三、解答题11．某球迷协会一行56人从旅馆乘出租车到球场为球队加油，现有A ，B 两个出租车队，A 队比B 队少3辆车．若全部安排乘A 队的车，每辆车坐5人，车不够；每辆车坐6人，有的车未坐满；若全部安排乘B队的车，每辆车坐4人，车不够，每辆车坐5人，有的车未坐满．试用不等式表示上述不等关系．解：设A队有出租车x辆，则B队有出租车(x＋3)辆．x<56，x>56，(x＋3)<56，(x＋3)>56，∈N*.12．试比较下列各组式子的大小：(1)x＋1－x与x－x－1，其中x>1；(2)x3－2y3与xy2－2x2y，其中x>y>0.解：(1)x＋1－x＝1x＋1＋x，x－x－1＝1x＋x－1，∵x＋1＋x>x＋x－1>0，∴x＋1－x<x－x－1.(2)(x3－2y3)－(xy2－2x2y)＝x3－xy2＋2x2y－2y3＝x(x2－y2)＋2y(x2－y2)＝(x2－y2)(x＋2y)＝(x－y)(x＋y)(x＋2y)．∵x>y>0，∴x－y>0，x ＋y>0，x＋2y>0，∴(x3－2y3)－(xy2－2x2y)>0，即x3－2y3>xy2－2x2y.13．(多选题)下列四个选项中能推出1a<1b的有(ABD) A．b>0>a B．0>a>bC．a>0>b D．a>b>0解析：1a<1b⇔b－aab<0⇔ab(a－b)>0.A．ab<0，a－b<0，ab(a－b)>0成立；B．ab>0，a－b>0，ab(a－b)>0成立；C ．ab <0，a －b >0，ab (a －b )<0，不成立；D ．ab >0，a －b >0，ab (a －b )>0成立．故选ABD.14．有三个房间需要粉刷，粉刷方案要求：每个房间只用一种颜色，且三个房间颜色各不相同．已知三个房间的粉刷面积(单位：m 2)分别为x ，y ，z ，且x <y <z ，三种颜色涂料的粉刷费用(单位：元/m 2)分别为a ，b ，c ，且a 0，∴ax ＋by ＋cz >az ＋by ＋cx ；同理，ay ＋bz ＋cx －(ay ＋bx ＋cz )＝b (z －x )＋c (x －z )＝(z －x )(b －c )<0，∴ay ＋bz ＋cx <ay ＋bx ＋cz ；同理，az ＋by ＋cx －(ay ＋bz ＋cx )＝a (z －y )＋b (y －z )＝(z －y )(a －b )<0，∴az ＋by ＋cx <ay ＋bz ＋cx ，∴最低费用为(az ＋by ＋cx )元．故选B.方法二：特殊值法，取x ＝1，y ＝2，z ＝3，a ＝1，b ＝2，c ＝3，则ax ＋by ＋cz ＝1×1＋2×2＋3×3＝14，az ＋by ＋cx ＝1×3＋2×2＋3×1＝10，ay ＋bz ＋cx ＝1×2＋2×3＋3×1＝11，ay ＋bx ＋cz ＝1×2＋2×1＋3×3＝13，故选B.15．一辆汽车原来每天行驶x km ，如果这辆汽车每天行驶的路程比原来多19km ，那么在8天内它的行程就超过2200km ，写成不等式为8(x ＋19)>2_200；如果它每天行驶的路程比原来少12km ，那么它原来行驶8天的路程就得花9天多的时间，用不等式表示为8xx －12>9.16．已知－12<a <0，A ＝1＋a 2，B ＝1－a 2，C ＝11＋a ，D ＝11－a ，试比较A 、B 、C 、D 的大小关系．解：∵－12<a <0，∴取a ＝－14，则A ＝1716，B ＝1516，C ＝43，D ＝45.由此猜测：C >A >B >D .证明如下：C －A ＝11＋a －(1＋a 2)＝－a (a 2＋a ＋1)1＋a ＝∵1＋a >0，－a >0＋34>0，∴C >A .∵A －B ＝(1＋a 2)－(1－a 2)＝2a 2>0，∴A >B .B －D ＝1－a 2－11－a＝a (a 2－a －1)1－a ＝∵－12<a <0，∴1－a >0.－54<－12－－54<0，∴B >D .综上所述，C >A >B >D .。

考点3-3 导数应用：比大小(练习)(含解析)-高考数学二轮复习

考点3-3 函数与导数应用：比大小1．（2022·江苏南京·模拟预测）设ln5a =，b =c = ） A ．a b c >> B ．a c b >> C ．b a c >> D ．b c a >>【答案】B 【分析】根据中间值及函数单调性进行判断大小. 【详解】因为2ln e ln5ln e <<，所以()ln51,2∈，所以(c =且a c >，又11ln 5,122b ⎛⎫==∈ ⎪⎝⎭，所以a c b >>．故选：B2．（2022·青海·海东市第一中学模拟预测（文））已知 1.5log 0.5a =，0.51.5b =， 1.50.15c =⨯，则（） A ．a b c << B ．a c b << C ．c a b << D ．b c a <<【答案】B 【分析】本题根据对数与指数大小以及对数与指数的运算与性质，进行大小的比较．【详解】解：由题意得：因为 1.5 1.5log 0.5log 10a =<=，0.51.5b ==， 1.50.50.150.55c =⨯=⨯=所以a c b <<．故选：B3．（2022·全国·模拟预测）设7log 4a =，171log 3b =，172c =，则a ，b ，c 的大小关系是（）A ．a b c >>B ．b c a >>C ．c a b >>D ．c b a >>【答案】C 【分析】根据指数函数、对数函数的单调性，分析比较，即可得答案.因为2x y =在R 上为增函数，所以017221>=，即1c >．因为7log y x =在()0,∞+上为增函数，所以177771log log 3log 4log 713=<<=，即1b a <<，所以c a b >>．故选：C ．4．（2022·广东·大埔县虎山中学高三阶段练习）设0.30.50.514,log 0.6,16a b c -⎛⎫=== ⎪⎝⎭，则a ，b ，c 的大小关系为（） A ．a b c < ⎪⎝⎭即可判断【详解】由题意，0.542a ==，()()0.50.50.5log 0.6log 1,log 0.50,1b =∈=，0.30.30.2511616216c a -⎛⎫==>== ⎪⎝⎭，故b a c << 故选：B5．（2022·全国·高三专题练习）已知825,log 3ab ==，则34a b -=（）A ．25B ．5C ．259 D ．53【答案】C 【分析】根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．【详解】因为25a=，821log 3log 33b ==，即323b =，所以()()22323232452544392a a a bb b -====．故选：C.6．（2022·全国·高考真题（理））已知3111,cos ,4sin 3244a b c ===，则（） A ．c b a >> B ．b a c >>C ．a b c >>D ．a c b >>【答案】A由14tan 4c b =结合三角函数的性质可得c b >；构造函数21()cos 1,(0,)2f x x x x =+-∈+∞，利用导数可得b a >，即可得解. 【详解】因为14tan 4c b =,因为当π0,,sin tan 2x x x x ⎛⎫∈<< ⎪⎝⎭所以11tan44>,即1cb >,所以c b >；设21()cos 1,(0,)2f x x x x =+-∈+∞， ()sin 0f x x x '=-+>，所以()f x 在(0,)+∞单调递增，则1(0)=04f f ⎛⎫> ⎪⎝⎭,所以131cos 0432->，所以b a >,所以c b a >>，故选：A7．（2022·河南·开封市东信学校模拟预测（理））已知函数()()()2|| 1.00125()e ,log 3,log 8,2x f x x a f b f c f ===-=-，则a ，b ，c 的大小关系为（）A ．a c b >>B ．a b c >>C ．c b a >>D ．c a b >>【答案】D 【分析】先判断出()f x 为偶函数，再求导确定单调性，借助指数、对数运算比较15 1.002log 3,log 8,2的大小，再由单调性即可求解. 【详解】显然，定义域为R ，由()()f x f x -=可知函数()f x 为偶函数，又当0x >时，2()e x f x x =，有()2()2e 0x f x x x =+>'，可知函数()f x 的减区间为(,0)-∞，增区间为[0,)+∞，又由22222113log 3log 9log 8,log 3log 42222=>=<=，1.0015555333log 83log 2log 4log 5,22222==<=>，由()()1.0015log 8,2b f c f ==，可得c a b >>．故选：D.8．（2023·全国·高三专题练习）已知910,1011,89m m m a b ==-=-，则（） A ．0a b >> B ．0a b >> C ．0b a >> D ．0b a >>【答案】A 【分析】根据指对互化以及对数函数的单调性即可知9log 101m =>，再利用基本不等式，换底公式可得lg11m >，8log 9m >，然后由指数函数的单调性即可解出．【详解】由910m=可得9lg10log 101lg 9m ==>，而()222lg9lg11lg99lg9lg111lg1022+⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，所以lg10lg11lg 9lg10>，即lg11m >，所以lg11101110110m a =->-=．又()222lg8lg10lg80lg8lg10lg922+⎛⎫⎛⎫<=< ⎪ ⎪⎝⎭⎝⎭，所以lg9lg10lg8lg9>，即8log 9m >，所以8log 989890m b =-<-=．综上，0a b >>．故选：A.9．（2023·湖北·高三阶段练习）若3410,log x yx z y ===，则（）A ．x y z >>B ．y x z >>C ．z x y >>D ．x z y >>【答案】A 【分析】利用对数的单调性证明1x y >>，即得解. 【详解】解：因为3410x y ==，则33444log 10log 92;1log 4log 10log 162x y =>==<=<=，则12y <<，所以1x y >>，从而log log 1x x z y x =<=，所以.x y z >> 故选：A ．10．（2022·青海·模拟预测（理））设log a =2020ln 2021b =，120212020c =，则a 、b 、c 的大小关系为（） A ．c a b >> B ．a c b >> C ．a b c >>D ．c b a >>【答案】A 【分析】利用指数函数、对数函数的性质，再借助“媒介”数比较大小作答. 【详解】函数2021log ,ln y x y x ==在(0,)+∞上都是增函数，12021<，即01a <<，2020012021，则0b <，函数2020x y =在R 上单调递增，而102021>，则1202102012c =>，所以c a b >>. 故选：A11．（2022·江西师大附中三模（理））设23,e 2a b c ===．则a ，b ，c 大小关系是（）A ．c b a <、a c >，构造函数()ln (1)h x x x x =->，利用导数研究函数的单调性可得32h h ⎛⎫> ⎪⎝⎭，进而可得b c >，即可得出结果.【详解】由122293e 2.718 2.25e 42a b =≈>==>，，故a b >；132222e e e a c -==>=，故a c >；假设23e2<，有23333133e 2ln ln ln 2222222<⇔<⇔-⇔-< 令()ln (1)h x x x x =->，则1()10h x x'=->，所以()h x 在(1,)+∞上单调递增，32，则32h h ⎛⎫> ⎪⎝⎭，所以23e 2<成立，b c >；故c b a <<．故选：A ．12．（2022·湖北·襄阳四中模拟预测）若ln5a =，43b =，c =则它们的大小关系是（） A ．a c b >> B ．b c a >> C ．c b a >> D ．c a b >>【答案】D 【分析】先判断,b c 大小，再分别判断,a b 和,a c 的大小即可【详解】因为43c b =>=，故c b >.又33ln5ln125a ==，4434ln e ln3ln81ln1253b a ==<=<=，故b a <.再分析,a c 和53的大小，因为21635c =>，2525339⎛⎫=< ⎪⎝⎭，故53c >，又553ln125ln 2.7ln e 5a =<<=，故53a <，故c a >.综上有c a b >> 故选：D13．（2022·全国·高考真题）设0.110.1e ,ln 0.99a b c ===-，，则（）A ．a b c <-，因为1()111x f x x x'=-=-++，当(1,0)x ∈-时，()0f x '>，当,()0x ∈+∞时()0f x '<，所以函数()ln(1)f x x x =+-在(0,)+∞单调递减，在(1,0)-上单调递增，所以1()(0)09f f <=，所以101ln 099-<，故110ln ln 0.999>=-，即b c >，所以1()(0)010f f -<=，所以91ln +01010<，故1109e 10-<，所以11011e 109<，故a b <，设()e ln(1)(01)xg x x x x =+-<<，则()()21e 11()+1e 11x xx g x x x x -+'=+=--, 令2()e (1)+1x h x x =-，2()e (21)x h x x x '=+-，当01x <<时，()0h x '<，函数2()e (1)+1x h x x =-单调递减，11x <<时，()0h x '>，函数2()e (1)+1x h x x =-单调递增，又(0)0h =，所以当01x <<时，()0h x <，所以当01x <<时，()0g x '>，函数()e ln(1)x g x x x =+-单调递增，所以(0.1)(0)0g g >=，即0.10.1e ln 0.9>-，所以a c > 故选：C.14．（2022·全国·高三专题练习（文））实数x ，y ，z 分别满足212022log 21x =，2122y=，2021z =，则x ，y ，z 的大小关系为（） A ．x y z >> B ．x z y >> C ．z x y >> D ．y x z >>【答案】B 【分析】由题意得22212120x ⎛⎫= ⎪⎝⎭，21log 22y =，20log 21z =，然后y 与z 作差结合基本不等式比较大小，构造函数ln ()xf x x=，可判断其在(e,)+∞上单调递减，则(21)(20)f f <，化简可得21202120<，则2021log 2120z >=，则可比较出z 与y 的大小即可【详解】由题意得22212120x ⎛⎫= ⎪⎝⎭，21log 22y =，20log 21z =，则 2021lg 21lg 22log 21log 22lg 20lg 21z y -=-=-2lg 21lg 20lg 22lg 20lg 21-⋅=⋅，因为2211lg 20lg 22(lg 20lg 22)lg 44022⎡⎤⎛⎫⋅<+= ⎪⎢⎥⎣⎦⎝⎭，所以222111lg 21lg 440lg 21lg 440lg 21lg 440lg 21lg 20lg 222220lg 20lg 21lg 20lg 21lg 20lg 21⎛⎫⎛⎫⎛⎫-+- ⎪ ⎪⎪-⋅⎝⎭⎝⎭⎝⎭>=>⋅⋅⋅，所以z y >，设ln ()xf x x=，则21ln ()x f x x -'=，当(e,)x ∈+∞时，()0f x '<，所以()f x 在(e,)+∞上单调递减，所以(21)(20)f f <，即ln 21ln 202120<，所以20ln 2121ln 20<，所以2021ln 21ln 20<，所以20212120<，所以21202120<，所以2021log 2120z >=，因为222121212020x ⎛⎫=>⎪⎝⎭，所以>x z ，所以x z y >>，故选：B 【点睛】关键点点睛：此题考查对数与指数的互化，考查基本不等式的应用，考查导数的应用，解题的关键是构造函数ln ()xf x x=判断出其单调性，可得20212120<，再转化为2021log 2120>，考查数学转化思想和计算能力，属于难题15．（2022·河南·模拟预测（理））若0.2e a =，b =ln3.2c =，则a ，b ，c 的大小关系为（） A ．a b c >> B ．a c b >> C ．b a c >> D ．c b a >>【答案】B 【分析】构造函数()()e 10xf x x x =-->，利用导数可得0.2e 1.2b a >>=，进而可得 1.2e 3.2>，可得a c >，再利用函数()()21ln 1x g x x x -=-+，可得ln3.2 1.1>，即得. 【详解】令()()e 10xf x x x =-->，则()e 10x f x '=->，∴()f x 在()0,∞+上单调递增，∴0.20.21 1.2e a b >+=>=， 0.2 1.21.e ln 2e a >==，ln3.2c =，∴()()()6551.262.7387.4,3.2335.5e e >≈≈=，∴ 1.2e 3.2>，故a c >，设()()21ln 1x g x x x -=-+，则()()()()()22221211011x x x g x x x x x +--=-=≥++'，所以函数在()0,∞+上单调递增，由()10g =，所以1x >时，()0g x >，即()21ln 1x x x ->+， ∴()()22121.6155ln 3.2ln 2ln1.611 1.1211.613950--=+>+=>=++，又1 1.2 1.21,1 1.1b <<<=<， ∴ 1.1c b >>，故a c b >>.【点睛】本题解题关键是构造了两个不等式()e 10xx x >+>与()21ln (1)1x x x x ->>+进行放缩，需要学生对一些重要不等式的积累.16．（2022·全国·高三专题练习（文））已知108a =，99b =，810c =，则a ，b ，c 的大小关系为（） A ．b c a >> B ．b a c >> C ．a c b >> D ．a b c >>【答案】D 【分析】构造函数()()18ln f x x x =-，8x ≥，求其单调性，从而判断a ，b ，c 的大小关系. 【详解】构造()()18ln f x x x =-，8x ≥， ()18ln 1f x x x+'=--， ()18ln 1f x x x+'=--在[)8,+∞时为减函数，且()295558ln81ln8ln e 204444f =-+-=-<-=-<'，所以()18ln 10f x x x=-+-<'在[)8,+∞恒成立，故()()18ln f x x x =-在[)8,+∞上单调递减，所以()()()8910f f f >>，即10ln89ln98ln10>>，所以10988910>>，即a b c >>. 故选：D 【点睛】对于指数式，对数式比较大小问题，通常方法是结合函数单调性及中间值比较大小，稍复杂的可能需要构造函数进行比较大小，要结合题目特征，构造合适的函数，通过导函数研究其单调性，比较出大小.17．（2022·全国·模拟预测（理））设0.02e 1a =-，()0.012e 1b =-，sin0.01tan0.01c =+，则（） A ．a b c >> B ．a c b >> C ．c a b >> D ．b c a >>【答案】A因为()20.020.010.01e 2e 1e 10a b -=-+=->，所以a b >．设()()2e 1sin tan xf x x x =---，则()f x '=212e cos cos xx x--，令()()g x f x '=，则32sin ()2e sin cos xxg x x x'=+-．当π0,6x ⎛⎫∈ ⎪⎝⎭时，2e 2x >，sin 0x >，33π2sin2sin 62πcos cos 6x x <=<，所以()0g x '>，所以当π0,6x ⎛⎫∈ ⎪⎝⎭时，()(0)0f x f ''>=，所以()f x 在π0,6x ⎛⎫∈ ⎪⎝⎭上单调递增，从而()(0)0f x f >=，因此(0.01)0f >，即b c >．综上可得a b c >>．故选：A 【点睛】比较函数值的大小，要结合函数值的特点，选择不同的方法，本题中，,a b 可以作差进行比较大小，而,b c 的大小比较，则需要构造函数，由导函数得到其单调性，从而比较出大小，有难度，属于难题.18．（2022·陕西·西安中学模拟预测（理））已知1,,,e a b c ⎛⎫∈+∞ ⎪⎝⎭，且ln55ln a a =-，ln33ln b b =-，ln 22ln c c=-，则（） A ．b c a < ⎪⎝⎭，此时()f x 单调递增，当10,,()0e x f x ⎛⎫'∈< ⎪⎝⎭，此时()f x 单调递减，由题ln55ln a a =-，ln33ln b b =-，ln 22ln c c =-，得11111111ln ln ,ln ln ,ln ln ln 55332244a a b b c c ====，因为1111543e<<<，所以111111ln ln ln 554433>>，则ln ln ln a a c c b b >>，且1,,,e a b c ⎛⎫∈+∞ ⎪⎝⎭，所以a c b >>. 故选：A.【点睛】解本题的关键是发掘题中三个式子的相似性，并进行等价变形，易于构造函数，本题多次利用函数的单调性，先利用单调性判断函数值大小，再由函数单调性判断自变量大小.。

2023年高考数学专题之比较大小专题练习题

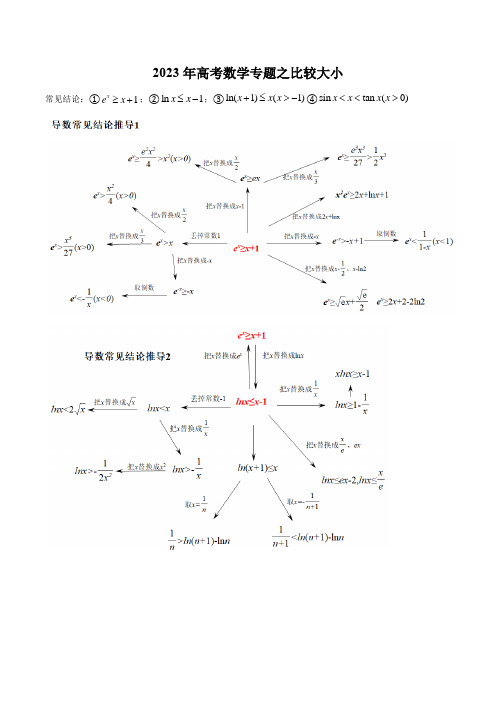
2023年高考数学专题之比较大小常见结论：①1x e x ≥+；②ln 1x x ≤-；③ln(1)(1)x x x +≤>-④sin tan (0)x x x x <<>带有拉格朗日型余项的n 阶麦克劳林公式()2''(0)(0)()(0)'(0).....2!!n n f f f x f f x x x n =++++ 常用展开式：①357sin ()3!5!x x x x o x =-++；①246cos 1()2!4!x x x o x =-++ ①234ln(1)()23x x x x o x +=-++；①23(1)(1)1()2x x x o x αααα-+=+++ ⑤35712tan ()315x x x x o x =+++；⑥231()2x x e x o x =+++ 2022全国I 卷第7题若a =0.1e 0.1，b =19，c =-ln0.9,则( ) A. a b c << B.c b a << C.c a b << D.a c b << 方法一：作差构造函数,,ln(1)1x x a xe b c x x===---,ln ln ln [ln ln(1)]a b x x x x -=+---1ln(1),'1011x y x x y x x -=+-=-=<--,所以0,ln ln 0,y a b ≤-≤故b a > ln(1),(0,0.1]x a c xe x x -=+-∈,1(1)(1)1'11x x xx x e y xe e x x +--=+-=--2()(1)(1)1,'()(12)0x x k x x x e k x x x e =+--=-->,()(0)0k x k >>,a c >故c a b <<方法二：带有拉格朗日型余项的n 阶麦克劳林公式()2''(0)(0)()(0)'(0).....2!!n n f f f x f f x x x n =++++ 231()2!xx e x o x =+++，0.10.10.10.1(10.1)0.11052a e ≈≈++=,231ln(1)()2x x x o x +=-+ 0.01ln(10.1)0.10.09052c =+≈-=,0.1111b ≈,故c a b << 方法三：利用常用结论：①1x e x ≥+，②ln(1)x x ≥+，③11ln ()2x x x<- 令x =-0.1得0.10.11e ->-+得0.110.9e >即有0.11100.99e <=所以0.110.19e <，故a==-<; 令x =109,0.11011091911ln()()0.1(10.1)0.192910180100e <-=<=+<，10ln()ln 0.99c =-= 故a>c ③11ln ()2x x x<-(x >1成立)的证明点评：虽是一道选择题，但难度较大，对同学们的要求较高，三种方法各有特点；对于多数同学构造函数需要耗费较多时间，过程比较繁杂,是一道压轴题.学习建议：掌握并熟悉常见的结论，提升解题效率;学会构造函数，熟练应用导数研究函数的单调性来比较大小.对于学有余力的同学可以记住常见函数的泰勒展开式,这对数据快速估值有较大的帮助.练习题：1. 设0.10.4ln1.1,1,tan 0.1,,a b e c d π==-==则( )A. a<b<c<dB.a<c<b<d C .a<b<d<c D.a<c<d<b2. 设11166,2ln(sin cos ),ln ,5101055a b c ==+=则a,b,c 的大小关系是____________. 3. 0.30.22,3,a b ==若()2log ,a b c +=则a,b,c 的大小关系是___________.4. 已知1ln,2,sin 0.041),32a b c π===-则a,b,c 的大小关系是_________. 5. 0.21,ln1.1,tan 0.2,a e b c =-==则a,b,c 的大小关系是_________.6. 已知a ＝e 0.1﹣1，b ＝sin0.1，c ＝ln 1.1，则（）A ．a ＜b ＜cB ．b ＜c ＜aC ．c ＜a ＜bD ．c ＜b ＜a7. 在给出的•ln 2＜1；②329ln 32e >；③e 0.2＞ln 3．三个不等式中，正确的个数为（） A ．0个 B ．1个 C ．2个 D ．3个8. 若a ＝sin1+tan1，b ＝2，1ln 42c =+，则a ，b ，c 的大小关系为（）A ．c ＜b ＜aB ．c ＜a ＜bC ．a ＜b ＜cD ．b ＜c ＜a 9．若20a ＝21，21b ＝22，c ＝222121()20，则a ，b ，c 的大小关系是（） A ．a ＜b ＜cB ．b ＜a ＜cC ．a ＜c ＜bD ．b ＜c ＜a10．设2354323,,455a e b e c ===，则（） A ．b ＜c ＜aB ．a ＜b ＜cC ．c ＜b ＜aD ．c ＜a ＜b11．已知a ，b 满足a 2e a +lna ＝0，1ln(ln )1b b b b +-=，则（）A ．ab ＜e a ＜bB ．ab ＜e a ＝bC ．b ＜e a ＜abD ．e a ＝b ＜ab12．已知a ＝3132，b ＝cos 14，c ＝4sin 14，则（） A ．c ＞b ＞aB ．b ＞a ＞cC ．a ＞b ＞cD ．a ＞c ＞b 13.已知实数a ，b 满足a ＞b ＞0，且a a ＝b b ，e 为自然对数的底数，则（）A ．1b e >B ．2a b e +>C ．a a ＜e a ﹣1D ．1a ea e < 14．已知a ＝e 0.03﹣1，3103b =，c ＝ln 1.03，则a ，b ，c 的大小关系为（） A ．a ＞b ＞cB ．a ＞c ＞bC ．c ＞a ＞bD ．b ＞a ＞c15．已知a ＝ln π，b c ＝ln a ，b ，c 的大小关系是（） A ．b ＜a ＜cB ．a ＜b ＜cC ．c ＜a ＜bD ．a ＜c ＜b 16．已知2319,sin ,224a b c ππ===，则（） A ．c ＜b ＜aB ．a ＜b ＜cC ．a ＜c ＜bD ．c ＜a ＜b 17．若222122ln(0,0)2a b a e b b e a a a b b +++=++>>，则（） A ．a ＞2bB ．a ＜2bC ．a ＞b 2D ．a ＜b 2 18．设24(2ln 4)1ln 4,,4a b c e e -===，则a ，b ，c 的大小顺序为（） A ．a ＜c ＜b B ．c ＜a ＜b C ．a ＜b ＜c D ．b ＜a ＜c。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五篇不等式专题30 十拿九稳----比较大小【热点聚焦与扩展】高考命题中，常常在选择题或填空题中出现一类比较大小的问题，往往将幂函数、指数函数、对数函数、三角函数等混在一起，进行排序.这类问题的解法往往可以从代数和几何两方面加以探寻，即利用函数的性质及图象解答.本专题以一些典型例题来说明此类问题的方法与技巧. （一）常用技巧和方法1、如何快速判断对数的符号？八字真言“同区间正，异区间负”，容我慢慢道来：判断对数的符号，关键看底数和真数，区间分为()0,1和()1,+∞（1）如果底数和真数均在()0,1中，或者均在()1,+∞中，那么对数的值为正数（2）如果底数和真数一个在()0,1中，一个在()1,+∞中，那么对数的值为负数例如：30.52log 0.50,log 0.30,log 30<>>等2、要善于利用指对数图象观察指对数与特殊常数（如0,1）的大小关系，一作图，自明了3、比较大小的两个理念：（1）求同存异：如果两个指数（或对数）的底数相同，则可通过真数的大小与指对数函数的单调性，判断出指数（或对数）的关系，所以要熟练运用公式，尽量将比较的对象转化为某一部分相同的情况例如：1113423,4,5，比较时可进行转化，尽管底数难以转化为同底，但指数可以变为相同()()()11111143634212121233,44,55===，从而只需比较底数的大小即可（2）利用特殊值作“中间量”：在指对数中通常可优先选择“-1，0,1”对所比较的数进行划分，然后再进行比较，有时可以简化比较的步骤（在兵法上可称为“分割包围，各个击破”，也有一些题目需要选择特殊的常数对所比较的数的值进行估计，例如2log 3，可知2221log 2log 3log 42=<<=，进而可估计2log 3是一个1点几的数，从而便于比较 4、常用的指对数变换公式：（1）nm mn a a ⎛⎫= ⎪⎝⎭（2）log log log a a a M N MN += log log log a a a M M N N-= （3）()log log 0,1,0n a a N n N a a N =>≠> （4）换底公式：log log log c a c bb a=进而有两个推论：1log log a b b a =（令c b =） log log m na a n N N m= （二）利用函数单调性比较大小1、函数单调性的作用：()f x 在[],a b 单调递增，则[]()()121212,,,x x a b x x f x f x ∀∈<⇔<(在单调区间内，单调性是自变量大小关系与函数值大小关系的桥梁）2、导数运算法则：（1）()()()()()()()'''f x g x fx g x f x g x =+（2）()()()()()()()'''2f x f xg x f x g x g x g x ⎛⎫-= ⎪⎝⎭3、常见描述单调性的形式（1）导数形式：()()'0fx f x >⇒单调递增；()()'0f x f x <⇒单调递减（2）定义形式：()()12120f x f x x x ->-或()()()12120x x f x f x -->⎡⎤⎣⎦：表示函数值的差与对应自变量的差同号，则说明函数单调递增，若异号则说明函数单调递减 4、技巧与方法：（1）此类问题往往条件比较零散，不易寻找入手点.所以处理这类问题要将条件与结论结合着分析.在草稿纸上列出条件能够提供什么，也列出要得出结论需要什么.两者对接通常可以确定入手点（2）在构造函数时要根据条件的特点进行猜想，例如出现轮流求导便猜有可能是具备乘除关系的函数.在构造时多进行试验与项的调整（3）在比较大小时，通常可利用函数性质（对称性，周期性）将自变量放入至同一单调区间中进行比较（三）数形结合比较大小1、对称性与单调性：若已知单调性与对称性，则可通过作出草图观察得到诸如“距轴越近，函数值越……”的结论，从而只需比较自变量与坐标轴的距离，即可得到函数值的大小关系（1）若()f x 关于x a =轴对称，且(),a +∞单调增，则图象可能以下三种情况，可发现一个共同点：自变量距离轴越近，其函数值越小（2）若()f x 关于x a =轴对称，且(),a +∞单调减，则图象可能以下三种情况，可发现一个共同点：自变量距离轴越近，其函数值越大2、函数的交点：如果所比较的自变量是一些方程的解，则可将方程的根视为两个函数的交点.抓住共同的函数作为突破口，将其余函数的图象作在同一坐标系下，观察交点的位置即可判断出自变量的大小.【经典例题】例1.【2019年高考全国Ⅰ卷理数】已知0.20.32log 0.220.2a b c ===，，，则（） A ．a b c <=0.3000.20.21,c <=<=即01,c <<则a c b <<．故选B ．【名师点睛】本题考查指数和对数大小的比较，考查了数学运算的素养．采取中间量法，根据指数函数和对数函数的单调性即可比较大小．例2.【2019年高考全国Ⅱ卷理数】若a >b ，则（） A ．ln(a −b )>0 B ．3a <3b C ．a 3−b 3>0 D ．│a │>│b │【答案】C【解析】取2,1a b ==，满足a b >，但ln()0a b -=，则A 错，排除A ；由219333=>=，知B 错，排除B ；取1,2a b ==-，满足a b >，但|1||2|<-，则D 错，排除D ；因为幂函数3y x =是增函数，a b >，所以33a b >，即a 3−b 3>0，C 正确. 故选C ．例3.【2019年高考全国Ⅲ卷理数】设()f x 是定义域为R 的偶函数，且在()0,+∞单调递减，则A ．f （log 314）＞f （322-）＞f （232-）B ．f （log 314）＞f （232-）＞f （322-）C ．f （322-）＞f （232-）＞f （log 314）D ．f （232-）＞f （322-）＞f （log 314）【答案】C 【解析】()f x 是定义域为R 的偶函数，331(log )(log 4)4f f ∴=．223303322333log 4log 31,1222,log 422---->==>>∴>>，又()f x 在(0，+∞)上单调递减，∴23323(log 4)22f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭，即23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选C ．例4.【2017天津，文理】已知奇函数()f x 在R 上是增函数，()()g x xf x =.若2(log 5.1)a g =-，0.8(2)b g =，(3)c g =，则a ，b ，c 的大小关系为（）（A ）a b c << （B ）c b a << （C ）b a c <<（D ）b c a <<【答案】C【解析】因为()f x 是奇函数且在R 上是增函数，所以在0x >时，()0f x >，从而()()g x xf x =是R 上的偶函数，且在[0,)+∞上是增函数，22(log 5.1)(log 5.1)a g g =-=，0.822<，又4 5.18<<，则22log 5.13<<，所以即0.8202log 5.13<<<，0.82(2)(log 5.1)(3)g g g <<，所以b a c <<，故选C ．【名师点睛】比较大小是高考常见题，指数式、对数式的比较大小要结合指数函数、对数函数，借助指数函数和对数函数的图象，利用函数的单调性进行比较大小，特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小，还可以解不等式.例5.【2018届山东、湖北部分重点中学冲刺模拟（三）】已知，,,则的大小关系为（）A. B. C. D.【答案】D【解析】分析：借助于中间值1和0，利用各实数的范围可比较大小.详解：，,，∴，故选D.点睛：比较大小常用的方法有：（1）作差法（作商法）；（2）利用函数单调性比较大小；（3）借助中间变量比较大小.例6.【2018年辽宁省部分重点中学协作体高三模拟】函数，若，，，则有（）A. B. C. D.【答案】D【解析】分析：首先分离常数得出，可判断出在上单调递减，且时，，时，，从而判断出，再根据在上减函数，判断出的大小关系，从而最后得出大小关系.详解：，在上为减函数，且时，时，，且，，且，且，，在上单调递减，，即，故选D.点睛：本题主要考查对数函数的性质、指数函数的单调性及比较大小问题，属于难题.解答比较大小问题，常见思路有两个：一是判断出各个数值所在区间（一般是看三个区间）；二是利用函数的单调性直接解答；数值比较多的比大小问题也可以两种方法综合应用例7.【2018届天津市十二校二模】已知定义在上的函数，则三个数，，，则，，之间的大小关系是（）A. B. C. D.【答案】C【解析】分析：求出的导数，得到函数的在上递增，利用对数函数与指数函数的性质可得，，从而比较函数值的大小即可.详解：时，，,可得在上递增，由对数函数的性质可得所以，由指数函数的性质可得,由可得,所以，根据函数的单调性可得，故选C.例8．【2018届华大新高考联盟4月检测】已知为定义在上的偶函数，且，当时，，记，则的大小关系为（）A. B.C. D.【答案】D【解析】分析：根据的周期性和单调性进行判断．详解：当时，，则在上是增函数，且当]时，，∵，∴的周期为2．故选D ．例9.已知函数()2log 1y x =+，且0a b c >>>，则()()(),,f a f b f c a b c 的大小关系是（） A.()()()f a f b f c ab c >>B.()()()f c f b f a c b a>>C.()()()f b f a f c bac>>D.()()()f a f c f b acb>>【答案】B【解析】思路：本题具备同构特点()()2log 1f x x y xx+==，但导数()()2'2log 11ln 2xx x y x -++=难于分析()f x 单调性，故无法比较()()(),,f a f b f c a b c 的大小.换一个角度，可发现()f x 的图象可作，且()f x x具备几何含义，即()()00f x f x xx -=-，即()(),x f x 与原点连线的斜率.所以作出()f x 的图象，可观察到图象上的点横坐标越大，与原点连线的斜率越小，所以由0a b c >>>可得：()()()f c f b f a cba>>答案：B例10.【2018届安徽省六安市第一中学三模】设是函数的导数，且满足，若、、是锐角三角形的三个内角，则（）A. B. C. D.【答案】D【解析】设则其导数又由满足，则有则函数在上为增函数，若是锐角三角形，则有即即有或对于又由，则有，即可以排除A 、B ，对于又由，则有，即可得D 正确，故选：D ．【点睛】本题考查函数的导数与函数的单调性的关系，解题的关键是构造函数h （x ）并分析其单调性．【精选精练】1.【2019年高考天津理数】已知5log 2a =，0.5og2.l 0b =，0.20.5c =，则,,a b c 的大小关系为（） A ．a c b <=， 10.20.50.50.5c <=<，即112c <<，所以a c b <<. 故选A.2.已知,,a b c 均为正数，且11222112log ,log ,log 22b caa b c ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，则（）A. a b c <<B. c b a <<C. c a b <<D. b a c << 【答案】A【解析】本题要通过左右相等的条件，以某一侧的值作为突破口，去推断,,a b c 的范围.首先观察等式左侧，左侧的数值均大于0，所以可得：11222log ,log ,log a b c 均大于0，由对数的符号特点可得：(),0,1,1a b c ∈>，只需比较,a b 大小即可.观察到1212ba⎛⎫>> ⎪⎝⎭，从而1122log log a b a b >⇒<，所以顺序为a b c <<，选A.【名师点睛】本题也可用数形结合的方式比较大小，观察发现前两个等式右侧为12log y x =的形式，而第三个等式也可变形为2121log log 2cc c ⎛⎫-=-= ⎪⎝⎭，从而可以考虑视,,a b c 分别为两个函数的交点.先作出12log y x =图象，再在这个坐标系中作出112,,22xxx y y y ⎛⎫⎛⎫===- ⎪ ⎪⎝⎭⎝⎭，比较交点的位置即可.3.【天津市北辰区2019届高考模拟考试数学】已知函数是定义在上的偶函数，且在上单调递增，则三个数，，的大小关系为（） A ． B ． C ．D ．【答案】C 【解析】∵，，，∴，为偶函数，，又在上单调递增，，即.故选C.4.【2018届内蒙古鄂伦春自治旗二模（420模拟）】已知函数，设，，，则（）A. B.C.D.【答案】D 【解析】∵∴∴ ∵当时，；当时，∴当时，，；当时；.∴ ∴函数是偶函数 ∴当时，易得为增函数∴，∵，，∴ ∴故选D.5.【2018届北京市海淀区二模】已知，则( ) A.B.C.D.【答案】D 【解析】分析：取，利用排除法，逐一排除即可的结果. 详解：因为时， ,,,所以可排除选项，故选D.点睛：特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率，又能提高准确性，这种方法主要适合下列题型:(1)求值问题（可将选项逐个验证）；（2）求范围问题（可在选项中取特殊值，逐一排除）；（3）图象问题（可以用函数性质及特殊点排除）；（4）解方程、求解析式、求通项、求前项和公式问题等等. 6.【2017年高考山东卷】若a>b>0，且ab=1，则下列不等式成立的是 A. ()21log 2a b a a b b +<<+ B. ()21log 2a b a b a b<+<+C. ()21log 2a b a a b b +<+< D. ()21log 2a b a b a b +<+< 【答案】B【解析】因为0a b >>，且1ab =，所以()221,01,1,log log 21,2a ba b a b ab ><<∴<+>= ()12112log a ba ab a a b b b+>+>+⇒+>+ ，所以选B. 7．【2018届广东省中山市第一中学高三第一次统测】实数()0.220.220.2,log ,2a b c ===的大小关系正确的是( )A. a c b <<B. a b c <<C. b a c <<D. b c a << 【答案】D【解析】根据指数函数和对数函数的性质，知2log 0.20<， 200.21＜＜， 0.221>，即01a <<，0b <， 1c >，∴b a c <<，故选C.8．【2018届福建省龙岩市4月检查】已知定义在上的偶函数对于上任意两个不相等实数和，都满足，若，则的大小关系为（）A. B.C.D.【答案】D【解析】分析：根据条件判断出函数的单调性，结合函数的奇偶性和单调性的关系进行转化求解即可. 详解：因为定义在上的偶函数对于上任意两个不相等实数和，由都满足，所以函数在上为增函数，因为是偶函数，所以，又由，所以，即，故选D.点睛：本题考查了函数值的比较大小，结合函数的奇偶性和函数的单调性进行合理转化是解答的关键，注重考查了学生分析维问题和解答问题的能力，以及推理与运算能力. 9．【2018届福建省闽侯第一中学高三上学期开学】记则A,B,C 的大小关系是（） A. B.C.D.【答案】B【解析】，即A>C ，，即B<C ，综合知A>C>B. 本题选择B 选项.10．【2018届湖北省荆州中学高三第二次月考】已知()sin 0,,sin ,4a απαα⎛⎫∈= ⎪⎝⎭()sin cos ,b αα=()cos sin c αα=，则( )A. a b c <<B. a c b <<C. b a c <<D. c a b << 【答案】D 【解析】令0,4πα⎛⎫∈ ⎪⎝⎭， 20sin α<<， cos sin αα>，令()()sin xf x α=在R 上单调递减，所以()sin sin αα>()cos sin αα,即a>c,又因为()sin g x x α=，在（0,1）上单调递增，所以()()sin sin sin cos αααα<,即a<b,所以c a b <<，选D.11.【2018届天津市9校联考】定义在R 上的奇函数()f x 满足()()2f x f x +=-，当[]0,1x ∈时，()21xf x =-，设1lna π=， 2ln5b e-=， 0.113c -⎛⎫= ⎪⎝⎭，则（）A. ()()()f a f b f c <<B. ()()()f b f c f a <<C. ()()()f b f a f c <<D. ()()()f c f b f a << 【答案】A【解析】∵f （x+2）=﹣f （x ），∴f （x+4）=f[（x+2）+2]=﹣f （x+2）=f （x ）， ∴函数f （x ）是周期为4的周期函数，()()1ln ln π0f a f f π⎛⎫==-< ⎪⎝⎭，()2ln 555130222f b f e f f f-⎛⎫⎛⎫⎛⎫⎛⎫===-=-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， ()()()()0.10.10.10.113322303f c f f f f -⎛⎫⎛⎫===--=-> ⎪ ⎪ ⎪⎝⎭⎝⎭，又1ln π2>=，且()21xf x =-在[]0,1上单调递增， ∴()1ln π2f f ⎛⎫> ⎪⎝⎭，即()()f a f b < 故选：A点睛：利用指数函数对数函数及幂函数的性质比较实数或式子的大小，一方面要比较两个实数或式子形式的异同，底数相同，考虑指数函数增减性，指数相同考虑幂函数的增减性，当都不相同时，考虑分析数或式子的大致范围，来进行比较大小，另一方面注意特殊值0,1的应用，有时候要借助其“桥梁”作用，来比较大小．12.【2018届重庆市巴蜀中学月考七】已知sin(x+ ϕ)cos(x+ ϕ)+2cos (x+ ϕ)-12 (|ϕ|<3π),若f(0)=12,a=f(π),b=f(11-12π），c=f （5324π），则（） A. a<c<b B. a<b<c C. c<a<b D. c<b<a 【答案】B【解析】 ()()()12212222cos x f x sin x ϕϕ++=++- ()()122222x cos x ϕϕ=+++ 226sin x πϕ⎛⎫=++ ⎪⎝⎭．由题意得()10262f sin πϕ⎛⎫=+= ⎪⎝⎭ ∵33ππϕ-<<，∴52266πππϕ-<+<， ∴266ππϕ+=，解得0ϕ=．∴()26f x sin x π⎛⎫=+⎪⎝⎭，∴()111112,262121262a fsin b f sin ππππππ⎡⎤⎛⎫⎛⎫⎛⎫==+==-=⨯-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，5353224246b f sin πππ⎛⎫⎛⎫==⨯+=⎪ ⎪⎝⎭⎝⎭， ∴a b c <<．选B ．。

高考数学复习专题 比大小 全套练习题及答案解析

专题04比较大小(解析版)

指、对、幂数比较大小问题【八大题型】(举一反三)(新高考专用)(解析版)2025年新高考数学一轮复习

高考数学复习专题 比大小 全套练习题及答案解析

高考数学复习选填题专项练习22---比较大小(解析版)

高考数学复习---《指、对、幂形数的大小比较问题》专项练习题(含答案解析)

专题2.18比较大小(解析版)

高考数学复习专题：比较大小

高考数学知识点：函数比较大小(解析版)

专题07 比较大小(选填题11种考法)(解析版)2024届高三数学二轮复习《考法分类》专题训练

专题2-1 比大小(幂指对及三角函数值)(解析版)2023年高考数学二轮专题全套热点题型

(完整版)函数比较大小专题40道-带答案

高中比较大小的练习题及讲解

高考数学小题-比较大小专练解析版

压轴题型04 比大小问题(解析版)-2023年高考数学压轴题专项训练

2025年高考数学一轮复习-2.1.1-不等关系与比较大小-专项训练【含解析】

考点3-3 导数应用：比大小(练习)(含解析)-高考数学二轮复习

2023年高考数学专题之比较大小专题练习题

高考数学复习专题比大小全套练习题及答案解析

高考数学复习专题比大小全套练习题及答案解析