四边形专题复习中点四边形
各种四边形各边中点形成什么图形

《各种四边形各边中点形成什么图形》专项练习中点四边形定义:顺次连接四边形各边中点所得的四边形解决办法:连接对角线,利用三角形中位线定理证明一、顺次连接四边形各边中点所得的四边形是平行四边形已知:四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是平行四边形(提示:连接AC)利用三角形中位线证明,两组对边分别平行的四边形是平行四边形二、顺次连接平行四边形各边中点所得的四边形是平行四边形已知:平行四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是平行四边形(提示:连接AC)利用三角形中位线证明,一组对边培训且相等的四边形是平行四边形三、顺次连接矩形各边中点所得的四边形是菱形已知:矩形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是菱形(提示:连接AC、BD)利用矩形对角线相等、中位线性质可得四边相等的四边形是菱形四、顺次连接菱形各边中点所得的四边形是矩形已知:菱形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是矩形(提示:连接AC、BD)利用菱形对角线垂直、中位线性质可得四个角是直角的四边形是矩形五、顺次连接正方形各边中点所得的四边形是正方形已知:正方形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是正方形利用正方形对角线垂直相等、中位线性质可得四边相等又有一直角的四边形是正方形六、顺次连接等腰梯形各边中点所得的四边形是菱形已知:梯形ABCD中,AD//BC AB=DC, 点E,F,G,H分别是边AB,BC,CD,DA的中点求证:四边形EFGH是菱形(提示:连接AC,BD)利用梯形对角线相等、中位线性质可得四边相等的四边形是菱形。
中点四边形ppt

快速练习:
(1)中点四边形是菱形,原四边形是( D ) A 矩形 B 菱形 C 正方形 D 对角线相等的四边形 (2)中点四边形是矩形,原四边形是( D ) A 矩形 B 菱形 C 正方形 D 对角线互相垂直的四边形 (3)中点四边形是正方形,原四边形是( D ) A 矩形 B 正方形 C 对角线互相垂直且平分的四边形 D 对角线互相垂直且相等的四边形 (4)一个梯形的中点四边形是菱形,这个梯形是 (等腰梯形 )
什么情况是矩形呢? 若四边形EFGH是矩形,则FH⊥BC B 连接AO ∵FH//AO ∴AO⊥BC E G O A F H C
小结1: 从一般到特殊的研究方法
我们从原四边形两条对角线的位置关系 和数量关系探索了中点四边形的形状变化, 从中我们可以体会到当原四边形从一般到特 殊的变化中(也就是对角线关系从一般到特 殊),常常伴随着中点四边形从一般到特殊 的变化。
H A
D G
证明:连接AC、BD.
E
∵AE=EB,BF=FC, B F ∴EF∥ AC EF=1/2AC. 同理GH ∥ AC GH=1/2AC. ∴EF ∥ GH EF=GH=1/2AC, ∴四边形EFGH是平行四边形. 注:同理 HE=FG=1/2BD ∴EF+FG+GH+HE=AC+BD
C
分析:根据上题我们有“任意四边形 的中点四边形都是平行四边形” ,再结 合四边形对角线的关系我们可以得出 结论:(课堂点睛P55第4题)
B
D
F
E
C
中点四边形: 定义:顺次连接一个四边形四边中点所 得四边形称为这个四边形的中点四边形。 思考:依次连接任意四边形各边中点 所成的中点四边形是什么图形呢?
已知:如图,点E、
中点四边形模型(4种题型)-2023年新九年级数学核心知识点与常见题型(北师大版)(解析版)

重难点专项突破:中点四边形模型(4种题型)【知识梳理】【考点剖析】题型一、利用中点求长度例1.如图,某花木场有一块四边形ABCD的空地,其各边的中点为E、F、G、H,测得对角线AC=11米,BD=9米,现想用篱笆围成四边形EFGH场地,则需篱笆总长度是()A.20米B.11米C.10米D.9米【答案】A【解析】∵E 、F 、G 、H 分别为四边形ABCD 各边的中点,∴EF 、FG 、GH 、HE 分别为△ABC 、△BCD 、△CDA 、△ABD 的中位线, ∴EF =12AC =112(米),FG =12BD =92(米),HG =12AC =112(米), HE =12BD =92(米),∴四边形EFGH 总长度=EF +FG +GH +HE =20(米), 故选:A .【变式1】在四边形ABCD 中,8AC BD ==,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则22EG FH +的值为( )A .18B .36C .48D .64【答案】D【解析】连接EF 、FG 、GH 、EH ,∵E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点, ∴11//,//,,22EF AC HG AC EF AC FG BD ==,∴//EF HG ,同理//EH FG , ∴四边形EFGH 为平行四边形,∵AC BD =,∴EF FG =,∴平行四边形 EFGH 为菱形, ∴EG FH ⊥,2EG OG =,2FH OH =,()2222222221(2)(2)4448642EG FH OE OH OE OH EH BD ⎛⎫+=+=+==⨯== ⎪⎝⎭故选:D .【变式2】如图,已知矩形ABCD 的对角线AC 的长为10cm ,连结矩形各边中点E 、F 、G 、H 得四边形EFGH ,则四边形EFGH 的周长为( )cm .A .20B .C .D .25【答案】A 【解析】连接BD ,∵H 、G 是AD 与CD 的中点,∴HG 是△ACD 的中位线, ∴HG=12AC=5cm ,同理EF=5cm , ∵四边形ABCD 是矩形,∴根据矩形的对角线相等,即BD=AC=10cm , ∵H 、E 是AD 与AB 的中点,∴EH 是△ABD 的中位线, ∴EH=12BD=5cm ,同理FG=5cm ,∴四边形EFGH 的周长为20cm . 故选A .【变式3】如图,点O 为四边形ABCD 内任意一点,E ,F ,G ,H 分别为OA ,OB ,OC ,OD 的中点,则四边形EFGH 的周长为( )A .9B .12C .18D .不能确定【答案】C【解析】∵E ,F 分别为OA ,OB 的中点,∴EF 是△AOB 的中位线,∴EF=12AB=3, 同理可得:FG=12BC=5,HG=12DC=6,EH=12AD=4,∴四边形EFGH 的周长为=3+5+6+4=18, 故选C .题型二、利用中点求面积例2.如图,四边形ABCD 中,点E 、F 、G 分别为边AB 、BC 、CD 的中点,若△EFG 的面积为4,则四边形ABCD 的面积为( )A .8B .12C .16D .18【答案】C【解析】记△BEF ,△DGH ,△CFG ,△AEH 的面积分别为1234,,,S S S S ,四边形ABCD 的面积为S .连接AC .∵BF =CF ,BE =AE ,CG =DG ,AH =DH ,∴EF ∥AC ,1,2EF AC =GH ∥AC ,12GH AC =,∴EF ∥GH ,EF =GH ,∴四边形EFGH 是平行四边形,∴S 平行四边形EFGH =2S △EFG =8,∵△BEF ∽△BAC ,∴11,4S S ABC =同理可得214S S ACD ,= ∴1211()44ABC ACD S S S S S +=+=, 同法可得3414S S S +=,∴123412S S S S S ,+++= ∴S 四边形EFGH =12S , ∴S =2S 四边形EFGH =16.故选C.【变式1】定义,我们把对角线互相垂直的四边形叫做和美四边形,对角线交点作为和美四边形的中心.(1)写出一种你学过的和美四边形______;(2)顺次连接和美四边形四边中点所得四边形是( ) A .矩形 B ,菱形 C .正方形 D .无法确定(3)如图1,点O 是和美四边形ABCD 的中心,E F G H 、、、分别是边AB BC CD DA 、、、的中点,连接OE OF OG 、、OH 、,记四边形AEOH BEOF CGOF DHOG 、、、的面积为1234S S S S 、、、,用等式表示1234S S S S 、、、的数量关系(无需说明理由)(4)如图2,四边形ABCD 是和美四边形,若4,2,5AB BC CD ===,求AD 的长.【答案】(1)正方形;(2)A ;(3)S 1+S 3=S 2+S 4;(4 【解析】(1)正方形是学过的和美四边形,故答案为:正方形; (2)顺次连接和美四边形四边中点所得四边形是矩形, 如图,四边形ACBD 中,对角线AB ⊥CD ,即为“和美四边形”, 点E 、F 、G 、H 分别是AC 、AD 、BD 、BC 的中点, ∴EF ∥CD ∥HG ,且EF=HG=12CD ,EH ∥FG ∥AB ,且EH=FG=12AB , ∴四边形EFGH 为平行四边形,∵AB ⊥CD ,∴EF ⊥EH ,∴平行四边形EFGH 是矩形;故选:A .(3)连接AC 和BD ,由和美四边形的定义可知,AC ⊥BD ,则∠AOB=∠BOC=∠COD=∠DOA=90°, 又E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点,∴△AOE 的面积=△BOE 的面积,△BOF 的面积=△COF 的面积,△COG 的面积=△DOG 的面积,△DOH 的面积=△AOH 的面积,∴S 1+S 3=△AOE 的面积+△COF 的面积+△COG 的面积+△AOH 的面积=S 2+S 4;(4)如图,连接AC 、BD 交于点O ,则AC ⊥BD , ∵在Rt △AOB 中,AO 2=AB 2-BO 2,Rt △DOC 中,DO 2=DC 2-CO 2,AB=4,BC=2,CD=5,∴可得AD 2=AO 2+DO 2=AB 2-BO 2+DC 2-CO 2=AB 2+DC 2-BC 2=42+52-22=37,即可得AD =.【变式2】如图,在四边形ABCD 中,对角线AC BD ⊥,且8AC =,6BD =,E ,F ,G ,H 分别是四边的中点,则四边形EFGH 的面积为__________.【答案】12【解析】∵点E 、F 分别为边AB 、BC 的中点,∴EF ∥AC ,EF=12AC , ∵AC=8,∴EF=4,同理,HE ∥BD ,HE=1BD 32=, ∴四边形EFGH 是平行四边形, ∵EH ∥BD ,AC ⊥BD ,∴EH ⊥AC ,∵EF ∥AC ,∴EF ⊥HE ,∴四边形EFGH 是矩形, ∴矩形EFGH 的面积=HE ×EF=12. 故答案为:12.题型三、找规律问题例3.如图,四边形ABCD 中,对角线AC BD ⊥,且8AC =,4BD =,各边中点分别为1A 、1B 、1C 、1D ,顺次连接得到四边形1111D C B A ,再取各边中点2A 、2B 、2C 、2D ,顺次连接得到四边形2222A B C D ,……,依此类推,这样得到四边形n n n n A B C D ,则四边形n n n n A B C D 的面积为( )A .162n−B .182n − C .412n −−D .不确定【答案】B【解析】∵四边形A 1B 1C 1D 1的四个顶点A 1、B 1、C 1、D 1分别为AB 、BC 、CD 、DA 的中点,∴A 1B 1∥AC ,A 1B 112=AC ,∴△BA 1B 1∽△BAC .∴△BA 1B 1和△BAC 的面积比是相似比的平方,即14. 即1114BA B S=S △ABC ,同理可证:1114DD C S =S △ADC , 1114AD A S =S △ABD ,S △CB 1C 114=S △BDC ,∴111112A B C D S =四边形S 四边形ABCD ,同法可证2222111112A B C D A B C D S S =四边形四边形,又四边形ABCD 的对角线AC =8,BD =4,AC ⊥BD ,∴四边形ABCD 的面积是16.∴四边形A n B n ∁n D n 的面积116822n n −==.故选:B .【变式1】如图1,1A ,1B ,1C ,1D 分别是四边形ABCD 各边的中点,且AC BD ⊥,6AC =,10BD =.(1)试判断四边形1111D C B A 的形状,并证明你的结论;(2)如图2,依次取11A B ,11B C ,11C D ,11D A 的中点2A ,2B ,2C ,2D ,再依次取22A B ,22B C ,22C D ,22D A 的中点3A ,3B ,3C,3D ……以此类推,取11n n A B −−,11n n B C −−,11n n C D −−,11n n D A −−的中点n A ,n B ,n C ,n D ,根据信息填空:①四边形1111D C B A 的面积是__________; ②若四边形n n n n A B C D 的面积为1516,则n =________; ③试用n 表示四边形n n n n A B C D 的面积___________. 【答案】(1)矩形,见解析;(2)①15,②5,③1152n − 【解析】(1)四边形1111D C B A 是矩形,证明:∵1A ,1B ,1C ,1D 分别是四边形ABCD 各边的中点, ∴11A B AC ,11C D AC ,∴1111A B C D ,同理可得1111A D B C ∥,∴四边形1111D C B A 是平行四边形,又∵AC BD ⊥,易得1111A B B C ⊥,∴四边形1111D C B A 是矩形; (2)①由题意可知:A 1B 1=12AC=3,A 1D 1=12BD=5,四边形1111D C B A 的面积=3×5=15;②由构图过程可得:A 2D 2=B 2C 2=12B 1D 1=12C 2D 2=B 2A 2=12A 1C 1=12可知四边形2222A B C D 为菱形,∴2222A B C D S =222212A C B D ⨯=111112A B B C ⨯=152;同理可求:3333A B C D S =154,4444A B C D S =158,…,n n n n A B C D S =1152n −,故当四边形n n n n A B C D 的面积为1516时,1152n −=1516,解得:n=5;③由②可知:用n 表示四边形n n n n A B C D 的面积为1152n −.故答案为:(1)矩形,见解析;(2)①15,②5,③1152n −题型四、中点综合问题例4.通过解方程(组)使问题得到解决的思维方式就是方程思想,已学过的《勾股定理》及《一次函数》都与它有密切的联系,最近方程家族的《一元二次方程》我们也学习了它的求解方法和应用。
中点四边形的判定

中点四边形的判定
中点四边形是指由四个顶点和四条边组成的四边形,其中一条对角线的中点是该四边形的中心点。
中点四边形的性质有以下几点:
1. 中点四边形的对角线相等,且互相平分。
2. 中点四边形的对边平行。
3. 中点四边形的对边长度相等。
4. 中点四边形的对角线相交于中心点,且互相垂直。
下面以一个例子来说明如何判断一个四边形是否是中点四边形。
假设有一个四边形ABCD,其中AC为对角线,E是AC的中点。
我们需要判断该四边形是否是中点四边形。
首先,我们需要判断AC是否为对角线。
如果AC不是对角线,那么该四边形肯定不是中点四边形。
其次,我们需要判断AE和EC是否相等。
如果AE和EC的长度不相
等,那么该四边形也不是中点四边形。
最后,我们需要判断BD是否与AC相交,并且交点为O(四边形的中心点)。
如果BD与AC不相交,或者相交但交点不在O上,那么该四边形仍不是中点四边形。
综上所述,只有当一个四边形满足AC为对角线,AE和EC相等,且BD与AC相交于O点时,才可以判定它为中点四边形。
中点四边形在数学、物理、工程等领域都有重要应用。
例如在三角形的内心和外心问题中,中点四边形可以用来推导内心和外心与三角形三个顶点的连线关系。
此外,中点四边形也可以用来设计具有对称性的建筑和艺术品等。
总之,中点四边形是一个有趣且实用的几何概念,掌握其基本性质和判定方法对于提高数学素养和解决实际问题都具有重要意义。
四边形中点知识点

四边形中点知识点四边形是一个拥有四条边的几何图形,它的四个顶点可以用直线相连,形成四个内角和四个外角。
在四边形中,中点是指连接两个非相邻顶点的线段的中点。
本文将通过逐步思考的方式,介绍四边形中点的一些基本知识点。
第一步:了解四边形和中点的定义四边形是一个几何图形,它有四条边和四个顶点。
四边形的中点是指连接两个非相邻顶点的线段的中点。
例如,如果我们有一个四边形ABCD,连接顶点A和C的线段AC的中点就是四边形中点。
第二步:了解四边形中点的性质四边形中点具有一些有趣的性质。
首先,连接四边形的相对边的中点会形成一个平行四边形。
例如,在四边形ABCD中,连接顶点A和C的线段AC的中点和连接顶点B和D的线段BD的中点所形成的线段会平行且等于彼此。
第三步:了解四边形中点的重要性四边形中点在几何学中有着重要的作用。
它可以帮助我们更好地理解四边形的性质和特征。
其中一个重要的应用是在证明四边形平行的问题中。
如果我们能够证明四边形的对角线中点连线平行,那么我们就能得出四边形是平行四边形的结论。
第四步:探索四边形中点的性质在四边形中,连接相对顶点的线段的中点被称为对角线中点。
对角线中点有一些有趣的性质。
首先,四边形的对角线中点相互连接会形成一个平行四边形。
其次,如果四边形的对角线中点互相连接,那么这两条线段的交点将是四边形的中点。
第五步:应用四边形中点的知识应用四边形中点的知识可以帮助我们解决一些几何问题。
例如,如果我们知道一个四边形的两个对角线的中点,我们可以通过连接这两个中点来构造一个平行四边形。
另外,我们还可以利用四边形中点的性质来证明四边形的平行性、相似性等等。
总结:通过逐步思考,我们可以了解到四边形中点的定义、性质和重要性。
四边形中点对于理解四边形的性质、进行证明和解决几何问题非常有帮助。
深入研究四边形中点的知识将为我们探索几何学的更多奥秘提供基础。
注:本文介绍了四边形中点的基本知识点,但未涉及Ai人工智能等字样。
专题15 四边形的综合 题型全覆盖(16题)-2020-2021学年八年级数学下(人教版)(原卷版)

专题15 四边形的综合 题型全覆盖(16题)【思维导图】【考查题型】考查题型一 中点四边形1.(2020·天津河西区·八年级期中)如图,已知四边形ABCD 中,,,,E F G H 分别为,,,AB BC CD DA 上的点(不与端点重合).(1)若,,,E F G H 分别为,,,AB BC CD DA 的中点.求证:四边形EFGH 是平行四边形;(2)在(1)的条件下,根据题意填空:若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是矩形;若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是菱形;若四边形ABCD 的对角线AC 和BD 满足 时,四边形EFGH 是正方形.(3)判断对错:①若已知的四边形ABCD 是任意矩形,则存在无数个四边形EFGH 是菱形;( )②若已知的四边形ABCD 是任意矩形,则至少存在一个四边形EFGH 是正方形.( )2.(2020·山东济宁市·八年级期中)综合与实践问题情境:在数学活动课上,我们给出如下定义:顺次连按任意一个四边形各边中点所得的四边形叫中点四边形.如图(1),在四边形ABCD 中,点E ,F ,G ,H 分别为边AB ,BC ,CD ,DA 的中点.试说明中点四边形EFGH 是平行四边形.探究展示:勤奋小组的解题思路:反思交流:(1)①上述解题思路中的“依据1”、“依据2”分别是什么?依据1:;依据2:;②连接AC,若AC=BD时,则中点四边形EFGH的形状为;创新小组受到勤奋小组的启发,继续探究:(2)如图(2),点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并说明理由;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其它条件不变,则中点四边形EFGH的形状为.3.(2020·静宁县八年级期中)已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是,证明你的结论.(2)当四边形ABCD的对角线满足条件时,四边形EFGH是矩形;(3)你学过的哪种特殊四边形的中点四边形是矩形?.4.(2020·广东深圳市八年级期中)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)考查题型二 特殊四边形的动点问题5.(2020·菏泽市期末)如图,在长方形ABCD 中,6AB cm =,AD 2cm =,动点P 、Q 分别从点A 、C 同时出发,点P 以2厘米/秒的速度向终点B 移动,点Q 以1厘米/秒的速度向D 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为t ,问:(1)当1t =秒时,四边形BCQP 面积是多少?(2)当t 为何值时,点P 和点Q 距离是3cm ?(3)当t =_________时,以点P 、Q 、D 为顶点的三角形是等腰三角形.(直接写出答案)6.(2020·四川成都市七年级期中)如图1,在长方形ABCD 中,12AB cm =,BC 10cm =,点P 从A 出发,沿A B C D →→→的路线运动,到D 停止;点Q 从D 点出发,沿D C B A →→→路线运动,到A 点停止.若P 、Q 两点同时出发,速度分别为每秒1cm 、2cm ,a 秒时P 、Q 两点同时改变速度,分别变为每秒2cm 、54cm (P 、Q 两点速度改变后一直保持此速度,直到停止),如图2是APD ∆的面积2()s cm 和运动时间x (秒)的图象.(1)求出a 值;(2)设点P 已行的路程为1()y cm ,点Q 还剩的路程为2()y cm ,请分别求出改变速度后,12,y y 和运动时间x (秒)的关系式;(3)求P 、Q 两点都在BC 边上,x 为何值时P ,Q 两点相距3cm ?7.(2020·耒阳市八年级期中)如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm、bcm,满足(a﹣3)2+|2a+b﹣9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D.设运动时间为ts.(1)a=cm,b=cm;(2)t为何值时,EP把四边形BCDE的周长平分?(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.8.(2020·石阡县期末)如图,在Rt ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s 的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,DEF为直角三角形?请说明理由.考查题型三四边形中线段最值∆沿CD所在直线折叠,9.(2020·南宁市八年级期中)如图,矩形ABCD的对角线AC,BD相交于点O,将COD∆.得到CED(1)求证:四边形OCED 是菱形;(2)若2AB =,当四边形OCED 是正方形时,OC 等于多少?(3)若3BD =,30ACD ∠=︒,P 是CD 边上的动点,Q 是CE 边上的动点,那么PE PQ +的最小值是多少? 10.(2020·北京市八年级期中)如图,长方形ABCD 中,AB =8,BC =10,在边CD 上取一点E ,将△ADE 折叠后点D 恰好落在BC 边上的点F 处(1)求CE 的长;(2)在(1)的条件下,BC 边上是否存在一点P ,使得PA +PE 值最小?若存在,请求出最小值:若不存在,请说明理由.11.(2020·福建龙岩市·八年级期中)如图,在边长为2cm 的正方形ABCD 中,Q 为BC 边的中点,P 为对角线AC 上的一个动点,连接PB ,PQ ,求△PBQ 周长的最小值.12.(2020·河南周口市期末)如图,在Rt △ABC 中,∠ACB =90°,AC =4,BC =6,点E 是斜边AB 上的一个动点,连接CE ,过点B ,C 分别作BD ∥CE ,CD ∥BE ,BD 与CD 相交于点D .(1)当CE ⊥AB 时,求证:四边形BECD 是矩形;(2)填空:①当BE 的长为______时,四边形BECD 是菱形;②在①的结论下,若点P是BC上一动点,连接AP,EP,则AP+EP的最小值为______.考查题型四四边形其他综合问题13.(2020·黄石市八年级期中)如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.14.(2020·四川广安市九年级期末)给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.①求证:△BCE是等边三角形;②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.15.(2020·山东临沂市·八年级期中)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.16.(2020·山东德州市·八年级期末)以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.。
九年级数学中点四边形练习题

中点四边形练习题1.顺次连接四边形各边中点,所得的图形是;顺次连接平行四边形各边中点,所得的图形是;顺次连结矩形四边中点所得四边形是;顺次连结菱形四边中点所得四边形是;顺次连结等腰梯形四边中点所得四边形是。
由此猜想:顺次连结的四边形四边中点所得四边形是矩形,顺次连结的四边形四边中点所得四边形是菱形。
即新四边形的形状与原四边形的有关。
2.一个四边形ABCD的对角线为AC、DB,顺次连接各边中点M、N、P、Q,得到四边形MNPQ。
①若AC⊥BD,AC=3,BD=4则四边形MNPQ的形状为,周长为,面积为;②若四边形ABCD为矩形,则四边形MNPQ的形状一定为;③当四边形ABCD满足条件时,四边形MNPQ为矩形;④若四边形MNPQ为正方形,则四边形ABCD需满足条件。
3.已知四边形ABCD和对角线AC,BD,顺次连接各边中点得四边形MNPQ,给出以下六个命题:①若所得四边形MNPQ为矩形,则原四边形一定是菱形;②若所得四边形MNPQ为菱形,则原四边形一定是矩形;③若所得四边形MNPQ为矩形,则AC⊥BD;④若所得四边形MNPQ为菱形,则AC=BD;⑤若所得四边形MNPQ为矩形,则∠BAD=90°;⑥若所得四边形MNPQ为菱形,则AB=AD。
以上命题正确的是:() A.①② B.③④ C.③④⑤⑥ D.①②③④4. 如图1,E、F、G、H分别是四边形ABCD四条边的中点,要使EFCH为矩形,四边形ABCD应该具备的条件是()A. 一组对边平行而另一组对边不平行B. 对角线相等C. 对角线相互垂直D. 对角线互相平分5题5.如图,ABCD是面积为a2的任意四边形,顺次连结ABCD各边中点得到四边形A1B1C1D1,再顺次连结各边中点得到四边形A2B2C2D2重复同样的方法直到得到四边形A n B n C n D n,则四边形A n B n C n D n的面积为。
6.如图2,在四边形ABCD中,E、F、G、H分别是边AB、BD、CD、DA的中点,请添加一个条件,使四边形EFGH为菱形,并说明理由。
【初中数学】人教版八年级下册专题训练(二)中点四边形(练习题)

人教版八年级下册专题训练(二)中点四边形(146) 1.如图,在四边形ABCD中,AC=BD=6,E,F,G,H分别是AB,BC,CD,DA的中点,求EG2+FH2的值.2.四边形ABCD为边长等于1的菱形,顺次连接它的各边中点组成四边形EFGH(四边形EFGH称为原四边形的中点四边形),再顺次连接四边形EFGH的各边中点组成第二个中点四边形……则按上述规律组成的第八个中点四边形的边长等于.3.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.(1)当四边形ABCD是矩形时,四边形EFGH是形,并说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH是正方形?并说明理由.4.如图,在四边形ABCD中,E,F,G,H分别是BC,AD,BD,AC的中点.(1)求证:EF与GH互相平分;(2)当四边形ABCD的边满足条件时,EF⊥GH.5.顺次连接对角线相等的四边形的各边中点,所得四边形是()A.矩形B.平行四边形C.菱形D.任意四边形6.顺次连接菱形各边中点所得到的四边形是()A.梯形B.矩形C.菱形D.正方形7.若四边形的对角线互相垂直,则顺次连接这个四边形各边中点所得的四边形是()A.平行四边形B.矩形C.菱形D.正方形8.如图,顺次连接任意四边形ABCD各边中点,所得的四边形EFGH是中点四边形.下列四个叙述:①中点四边形EFGH一定是平行四边形;②当四边形ABCD是矩形时,中点四边形EFGH也是矩形;③当中点四边形EFGH是菱形时,四边形ABCD是矩形;④当四边形ABCD是正方形时,中点四边形EFGH也是正方形.其中正确的是(填序号).9.如图,在四边形ABCD中,AD=CD,AB=CB,E,F,G,H分别是AD,AB,CB,CD的中点.求证:四边形EFGH是矩形.10.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形11.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是()A.矩形B.正方形C.对角线相等的四边形D.对角线互相垂直的四边形12.如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB,CD应满足的条件是.13.如图所示,E,F,G,H为四边形ABCD各边的中点,若对角线AC,BD的长都为20,则四边形EFGH的周长是()A.80B.40C.20D.1014.如图,已知E,F,G,H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60∘,则四边形EFGH的面积为cm2.15.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.16.如图,在四边形ABCD中,AC=8,BD=6,且AC⊥BD,E,F,G,H分别是AB,BC,CD,DA 的中点,则EG2+FH2=.参考答案1.【答案】:如图,连接EF ,FG ,GH ,EH ,∵E ,H 分别是AB ,DA 的中点,∴EH 是△ABD 的中位线,∴EH =12BD =3. 同理可得EF ,FG ,GH 分别是△ABC ,△BCD ,△ACD 的中位线, ∴EF =GH =12AC =3,FG =12BD =3,∴EH =EF =GH =FG =3,∴四边形EFGH 为菱形,∴EG ⊥HF ,且垂足为O ,∴EG =2OE ,FH =2OH .在Rt △OEH 中,根据勾股定理得:OE 2+OH 2=EH 2=9,等式两边同时乘4得4OE 2+4OH 2=9×4=36,∴(2OE)2+(2OH)2=36,即EG 2+FH 2=36.【解析】:连接EH,HG,GF,FE ,根据题目条件提供的四个中点,结合中位线的性质,证明四边形EFGH 为菱形,再根据菱形的性质及勾股定理求出结果.2.【答案】:116【解析】:根据题意,结合图形寻找规律:第二、四、六、八个中点四边形为菱形,第一个菱形边长为12,第二个菱形边长为14,第三个菱形边长为18,第四个菱形边长为116,即为第八个菱形的边长3(1)【答案】当四边形ABCD 是矩形时,四边形EFGH 是菱形.理由:∵四边形ABCD 是矩形,∴AC =BD .∵E ,F ,H 分别是AB ,BC ,AD 的中点,∴EF=12AC,EH=12BD,∴EF=EH.同理可得EF=GH=GF,∴四边形EFGH是菱形【解析】:利用矩形及中位线的性质,结合菱形的判定方法进行推导证明.(2)【答案】当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH是正方形.理由:∵E,F分别是四边形ABCD的边AB,BC的中点,∴EF∥AC,EF=12AC,同理,EH∥BD,EH=12BD,GF=12BD,GH=12AC.∵AC=BD,∴EF=EH=GH=GF,∴四边形EFGH是菱形.∵AC⊥BD,∴EF⊥EH,∴菱形EFGH是正方形【解析】:根据三角形的中位线平行于第三边并等于第三边的一半,先判断出AC=BD,又正方形的四个角都是直角,可以得到正方形的邻边互相垂直,然后证出AC与BD垂直,得到四边形ABCD满足的条件.4(1)【答案】证明:连接GE,GF,HF,EH.∵E,G分别是BC,BD的中点,∴EG=12CD.同理FH=12CD,FG=12AB,EH=12AB,∴EG=FH,GF=EH,∴四边形EHFG是平行四边形.∴EF与GH互相平分【解析】:根据题中提供的四个中点,得到几组中位线,利用中位线的性质,及平行四边形的判定方法,推导出四边形EHFG是平行四边形,进而推导出结论(2)【答案】当四边形ABCD的边满足条件AB=CD时,EF⊥GH.【解析】:理由如下:当EF⊥GH时,四边形EGFH是菱形,此时GF=EG.∵EG=12CD,FG=12AB,∴AB=CD.∴当四边形ABCD的边满足条件AB=CD时,EF⊥GH5.【答案】:C【解析】:顺次连接对角线相等的四边形的各边中点,所得四边形是菱形.如图,∵E,F,G,H分别为四边形ABCD各边的中点,∴EH为△ABD的中位线,FG为△CBD的中位线,∴EH∥BD,EH=12BD,FG∥BD,FG=12BD,∴EH∥FG,EH=FG=12BD,∴四边形EFGH为平行四边形.又∵EF为△ABC的中位线,∴EF=12AC.又∵EH=12BD,且AC=BD,∴EF=EH,∴平行四边形EFGH为菱形.故选C.6.【答案】:B【解析】:利用菱形的性质、矩形的判定方法及中位线的性质推导出结果.7.【答案】:B【解析】:如图,在四边形ABCD中,AC⊥BD,连接各边的中点E,F,G,H,则EH∥AC,FG∥AC,EF∥BD,GH∥BD.又因为对角线AC⊥BD,所以GH⊥EH,EH⊥EF,EF⊥FG,FG⊥HG.故可判定该四边形是矩形.故选B.8.【答案】:①④【解析】:如图四边形ABCD,连接AC,BD.∵E,F,G,H分别是四边形各边的中点,∴EF∥AC,HG∥AC,EH∥BD,GF∥BD,∴EF∥GH,EH∥FG,∴四边形EFGH是平行四边形,故①正确.若四边形ABCD是矩形,则AC=BD.∵EF=12AC,EH=12BD,∴EF=EH,∴平行四边形EFGH是菱形,故②错误.若四边形EFGH是菱形,则AC=BD,但四边形ABCD不一定是矩形,故③错误.若四边形ABCD是正方形,则AC=BD,AC⊥BD,∴四边形EFGH是正方形,故④正确.∴正确的叙述是①④.9.【答案】:连接AC,BD,交于点O,如图.∵E,F,G,H分别是AD,AB,CB,CD的中点,∴EF∥BD∥GH,EH∥AC∥FG,EF=GH=12BD,EH=FG=12AC,∴四边形EFGH是平行四边形.∵AD=CD,AB=CB,∴点D,B都在线段AC的垂直平分线上,∴DB垂直平分AC,∴DB⊥AC,OA=OC.∵EF∥DB,∴EF⊥AC.∵FG∥AC,∴EF⊥FG,∴四边形EFGH是矩形【解析】:利用三角形的中位线解题.10.【答案】:D【解析】:若得到的四边形是矩形,那么邻边互相垂直,根据三角形中位线定理,故原四边形的对角线必互相垂直,由此得解.11.【答案】:C【解析】:若得到的四边形是菱形,那么四条边都相等,根据三角形中位线定理,故原四边形的对角线必相等,由此得解.12.【答案】:AB=CD【解析】:若四边形EFGH是菱形,则GH=EH,又根据题中条件所给的四个中点,利用中位线的性质推导出AB=2GH,CD=2EH,所以AB=CD.13.【答案】:B【解析】:∵E,F,G,H是四边形ABCD各边的中点,∴HG=EF=12AC,GF=HE=12BD,∴四边形EFGH的周长=HG+EF+GF+HE=12(AC+AC+BD+BD)=12×(20+20+20+20)=40 14.【答案】:9√3【解析】:连接AC,BD,相交于点O,如图所示, ∵点E,F,G,H分别是菱形四边的中点,∴EH=12BD=FG,EH∥BD∥FG, EF=12AC=HG,∴四边形EHGF是平行四边形.∵菱形ABCD中,AC⊥BD,∴EF⊥EH,∴平行四边形EFGH是矩形.∵四边形ABCD是菱形,∠ABC=60∘,∴∠ABO=30∘.∵AC⊥BD,∴∠AOB=90∘,∴AO=12AB=3cm,∴AC=6cm.在Rt△AOB中,由勾股定理,得OB=√AB2−OA2=3√3cm, ∴BD=6√3cm.∵EH=12BD,EF=12AC,∴EH=3√3cm,EF=3cm,∴矩形EFGH的面积=EF·EH=9√3cm2. 故答案为9√315.【答案】:12【解析】:∵E,F,G,H分别为边AD,AB,BC,CD的中点,∴HE=12AC=4,HE∥AC,GF∥AC,∴HE∥GF.同理,HG∥EF,HG=12BD=3,∴四边形EFGH是平行四边形.∵AC⊥BD,∴∠EHG=90∘,∴四边形EFGH是矩形,∴四边形EFGH的面积为3×4=1216.【答案】:50【解析】:连接HG,EH,EF,FG,∵E,F,G,H分别是AB,BC,CD,DA的中点,∴HG=EF=12AC=4,EH=FG=12BD=3,∵E,H分别是AB,AD的中点,∴HE∥BD,HE=12BD,同理FG∥BD,FG=12BD,∴四边形HEFG是平行四边形.∵AC⊥BD,∴HG⊥EH,∴四边形HEFG为矩形,∴EG2+FH2=EF2+FG2+EF2+EH2=52+52=50。
专题中点四边形综合问题重难点培优八年级数学下册尖子生同步培优题典原卷版浙教版

八年级数学下册尖子生同步培优题典【浙教版】专题5.9中点四边形综合问题(重难点培优)姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2021秋•兴宁市期末)若正方形ABCD各边的中点依次为E、F、G、H,则四边形EFGH是()A.平行四边形B.矩形C.菱形D.正方形2.(2021秋•成华区期末)顺次连接菱形四边中点形成的四边形是()A.矩形B.菱形C.正方形D.无法判定3.(2021春•霍林郭勒市校级月考)顺次连结对角线相等的四边形各边中点所得到的四边形一定是()A.菱形B.矩形C.平行四边形D.正方形4.(2021秋•和平区期末)顺次连接对角线互相垂直的四边形的各边中点,所形成的新四边形是()A.菱形B.矩形C.正方形D.三角形5.(2019秋•龙岗区期末)如图,四边形ABCD中,AC=BD,顺次连接四边形各边中点得到的图形是()A.菱形B.矩形C.正方形D.以上都不对6.(2021春•宣城期末)下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相垂直的四边形是菱形;③四条边相等的四边形是正方形;④顺次连接菱形各边中点形成的四边形一定是矩形.其中正确的个数是()A.4B.3C.2D.17.(2020秋•岐山县期中)如图,任意四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,连接AC,BD,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若AC=BD,则四边形EFGH为菱形B.若AC⊥BD,则四边形EFGH为矩形C.若AC=BD,且AC⊥BD,则四边形EFGH为正方形D.若AC与BD互相平分,且AC=BD,则四边形EFGH是正方形8.(2021春•武昌区校级期中)如图,顺次连接四边形ABCD各边中点得到中点四边形EFGH,下列说法中正确的是()A.当AC⊥BD时,四边形EFGH为菱形B.当AC=BD时,四边形EFGH为矩形C.当AC⊥BD,AC=BD时,四边形EFGH为正方形D.以上说法都不对9.(2018•临沂)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:①若AC=BD,则四边形EFGH为矩形;②若AC⊥BD,则四边形EFGH为菱形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.410.(2021春•遵化市期末)如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第n个矩形的面积为()A.B.C.D.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上、11.(2021春•宜兴市月考)若顺次连接四边形各边中点所得的四边形是菱形,则原四边形.12.(2021秋•南海区月考)顺次连接矩形ABCD各边中点得到四边形EFGH,它的形状是.13.(2021春•泰兴市月考)四边形ABCD中,对角线AC⊥BD,则顺次连接四边形ABCD各边中点所得的四边形为形.14.(2021秋•南海区月考)已知:在四边形ABCD中,AD=BC,点E,F,G,H分别是AB,CD,AC,BD的中点,四边形EHFG是.15.(2020春•孝义市期末)如图,菱形ABCD的对角线AC,BD相交于点O,依次连接AO,BO,CO,DO的中点E,F,G,H,得到四边形EFGH,点M是EF的中点,连接OM,若AB=10,则OM的长为.16.(2021秋•榆阳区校级月考)点E、F、G、H分别是任意四边形ABCD中AD、AB、BC、CD各边的中点,对角线AC,BD交于点O,当四边形ABCD满足条件时,四边形EFGH是正方形.17.(2021•西城区校级开学)如图,点A,B,C为平面内不在同一直线上的三点,点D为平面内一个动点,线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④中点四边形MNPQ不可能是正方形;所有结论正确的序号是.18.(2021春•昆明期末)如图,某小区要在一块矩形ABCD的空地上建造一个如图所示的四边形花园EFGH,点E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=10m,AD=20m,则四边形EFGH的面积为m².三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020春•海陵区校级期中)如图,O为∠BAC内一点,E、F、G、H分别为AB,AC,OC,OB的中点.(1)求证:四边形EFGH为平行四边形;(2)当AB=AC,AO平分∠BAC时,求证:四边形EFGH为矩形.20.(2020春•工业园区期末)已知:如图,在四边形ABCD中,AB与CD不平行,E,F,G,H分别是AD,BC,BD,AC的中点.(1)求证:四边形EGFH是平行四边形;(2)①当AB与CD满足条件时,四边形EGFH是菱形;②当AB与CD满足条件时,四边形EGFH是矩形.21.(2021春•滦州市期末)已知:如图,四边形ABCD中,M、N、P、Q分别是AD、BC、BD和AC的中点.(1)求证:四边形MPNQ是平行四边形.(2)若满足AB=CD.试判断MN与PQ的位置关系(不用说明理由).22.(2021春•集贤县期末)在四边形ABCD中,AB、BC、CD、DA的中点分别为P、Q、M、N.(1)如图1,试判断四边形PQMN怎样的四边形,并证明你的结论;(2)若在AB上取一点E,连结DE,CE,恰好△ADE和△BCE都是等边三角形(如图2),判断此时四边形PQMN的形状,并证明你的结论.23.(2021春•盐城期末)如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、EH.(1)求证:四边形EFGH是平行四边形;(2)再加上条件后,能使得四边形EFGH是矩形.请从①四边形ABCD是菱形,②四边形ABCD 是矩形.这两个条件中选择1个条件填空(写序号),重新画图并写出证明过程.24.(2021春•泗阳县期末)已知:如图,在四边形ABCD中,AB与CD不平行,E,F,G,H分别是AD,BC,BD,AC的中点.(1)求证:四边形EGFH是平行四边形;(2)当AB=CD,四边形EGFH是怎样的四边形?证明你的结论.。
中考专题复习:中点四边形

3、连接对角线互相垂直的四边形四条边中点 得到的四边形是矩形
试一试
1、如图,四边形ABCD中,E,F,G,H分别是AB,
BC,CD,DA边上的中点,请你添加一个条件使四边
形EFGH是菱形,应添加的条件是
。
使四边形EFGH是矩形,应添加的条件是
四边形EFGH,四边形MNPQ的形状是( A )
A)矩形,菱形
B)菱形,矩形
C)矩形,矩形
D)矩形,正方形
4、如图,四边形ABCD中,AC=12,BD=8,面积 为40,点E、F、G、H分别是边AB、BC、CD、DA 中点,求:四边形 EFGH的周长是多少
D H A E
B
解:∵E、F分别是AB、BC中点
腰梯形中的哪一种,并写出证明过程。
A
DA
DA
D AQ D
F
B
E CB E
F CE B
M P
CE B N F
C F
小结:
本节课你学到了哪些知识?还有需要老师帮 你解决的难题吗?
D
D1
C3
C2
C1
B3 B2
C
A D2 O
D3
A1
A3
A2
B1
B
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE
相交于点G,则可得结论:
①AF=DE ②AF⊥DE(不须证明)
⑴如图②,若点E,F不是正方形ABCD的边BC,CD的中点,但满足
CE=DF则上面的结论①②是否仍然成立?(请直接回答“成立”
。
D
H A
G C
F E
B
四边形中点专题

• 3.如图△ABC,D是△ABC内的一点,延长 BA至点E,延长DC至点F,使得AE=CF,G, H,M分别为BD,AC,EF的中点,如果G, H,M三点共线,求证:AB=CD.
.
• 4.如图,在△ABC中,AD是BC边上的中线, F为AC边上的一点,连接BF交AD于点E,若 ∠BED=∠CAD,求证:AC=BE.
• :5.如图,在△ABC中,∠ABC=2∠C,AD平 分∠A,过BC的中点M作AD的垂线,交AD的 延长线于F,交AB的延长线于E,求证: BE=1/2BD。 •
• .6.如图,在△ABC中,AB=AC,延长AB到D, 使BD=AB,E为AB中点,连接CE、CD,求证: CD=2EC..
• 7.证明:三角形一条中线两侧所对边平方和 等于底边的一半平方与该边中线平方的和 的2倍。
•
中点问题Βιβλιοθήκη 1.在△ABC中,D为AB的中点,分别延 长CA,CB到点E,F,使DE=DF;过E, F分别作CA,CB的垂线,相交于P.求 证:∠PAE=∠PBF.
3
4
2.在三角形ABC中,D.E是BC上的两点,且AD平行 于EG,EG交AC于点F,交BA的延长线于点G,若 EF+EG=2AD,求AD是中线 •
• 8.已知如图,ABC中D是BC边的中点,E是AD边的 中点,连结BE并延长交AC于点F求证:FC=2AF • •
专题01 中点四边形模型(全国通用)(原卷版)

专题01 中点四边形模型中点四边形:依次连接四边形四边中点连线的四边形得到中点四边形O。
结论1: 点M、N、P、Q 是任意四边形的中点,则四边形MNPQ 是平行四边形结论2: 对角线垂直的四边形的中点四边形是矩形结论3:对角线相等的四边形的中点四边形是菱形结论4: 对角线垂直且相等的四边形的中点四边形是正方形【典例1】(2024•长沙模拟)如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是()A.平行四边形B.矩形C.菱形D.正方形【典例2】(2023•阳春市二模)若顺次连接四边形ABCD各边的中点所得的四边形是菱形,则四边形ABCD 的两条对角线AC,BD一定是()A.互相平分B.互相平分且相等C.互相垂直D.相等【典例3】(2023•铜川一模)如图,AC、BD是四边形ABCD的两条对角线,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A.AC⊥BD B.AB=CD C.AB∥CD D.AC=BD1.(2023春•宿豫区期中)顺次连接对角线相等且垂直的四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形2.(2023春•福山区期末)如图,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则下列结论一定正确的是()A.四边形EFGH是矩形B.四边形EFGH的面积等于四边形ABCD面积的C.四边形EFGH的内角和小于四边形ABCD的内角和D.四边形EFGH的周长等于四边形ABCD的对角线长度之和3.(2023春•覃塘区期末)在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=3,AD=4,则中点四边形EFGH的面积为()A.8B.6C.4D.34.(2023春•费县期末)顺次连接四边形ABCD各边中点所得四边形是菱形.则四边形ABCD一定是()A.矩形B.对角线相等的四边形C.菱形D.对角线互相垂直的四边形5.(2023•商丘模拟)一个四边形四边中点的连线所构成的中点四边形是菱形,那么这个原四边形是()A.矩形B.菱形C.正方形D.对角线相等6.(2023春•路北区期末)顺次连接矩形各边中点,所得图形的对角线一定满足()A.互相平分.B.互相平分且相等C.互相垂直.D.互相平分且垂直7.(2023春•达州期末)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长是()A.7B.9C.11D.138.(2023•浦东新区二模)顺次连接四边形ABCD各边中点所得的四边形是矩形,那么四边形ABCD一定是()A.菱形B.对角线相等的四边形C.对角线互相垂直的四边形D.对角线互相垂直且平分的四边形9.(2023•晋中模拟)如图,顺次连接正六边形纸板ABCDEF各边中点得到一个新的正六边形.若将一个飞镖随机投掷到正六边形纸板ABCDEF上,则飞镖落在阴影区域的概率为()A.B.C.D.10.(2023•佛山模拟)如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件是()A.AC⊥BD B.AC=BDC.AC⊥BD且AC=BD D.不确定11.(2023春•南京期中)如图,在四边形ABCD中,E、F、G、H分别是线段AD、BD、BC、AC的中点,要使四边形EFGH是菱形,需添加的条件是()A.AC=BD B.AC⊥BD C.AB=CD D.AB⊥CD12.(2022春•惠城区校级期中)在四边形ABCD中,E,F,G,H分别为各边的中点,顺次连结E,F,G,H,得到中点四边形EFGH.当AC=BD时,则四边形EFGH是()A.平行四边形B.矩形C.菱形D.正方形13.(2022•老河口市模拟)如图,四边形ABCD是矩形,E,F,G,H分别为各边的中点,则四边形EFGH 一定是()A.菱形B.矩形C.正方形D.对角线相等的四边形14.(2022春•青白江区校级月考)如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E、F、G、H分别为边AD、AB、BC、CD的中点.若AC=8,BD=6,则四边形EFGH的面积为()A.48B.24C.32D.1215.(2023春•金湖县期中)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=8,AD=10,则AO的长为.16.(2022春•皇姑区期末)在四边形ABCD中,AC=6cm,BD=9cm,E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH的周长为cm.17.(2023秋•丹东期末)【问题初探】数学活动课上,张老师引导学生探究中点四边形的形状及性质.首先,张老师给出中点四边形的定义:顺次连接任意四边形各边中点所得的四边形叫做中点四边形.接下来张老师提出问题:如图1,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,则中点四边形EFGH是什么形状?中点四边形EFGH的面积与原四边形ABCD的面积有怎样的关系?请各组讨论,并给出证明过程.班级的“希望小组”经讨论发现:中点四边形EFGH是平行四边形,且中点四边形EFGH的面积是原四边形ABCD面积的一半.证明如下:证明:如图2,连接AC,BD∵点H,G分别为AD,CD的中点∴HG是△ADC的中位线,根据三角形中位线定理可得:HG与AC的位置关系为,数量关系为.同理可得:EF∥AC,∴HG∥EF,HG=EF∴四边形EFGH是平行四边形根据线段HG,AC的关系,进而可得△DHG∽△DAC,且=同理∴(1)请你将“希望小组”的证明过程补充完整.【类比探究】(2)在(1)问的讨论过程中,“善思小组”有了新的发现:中点四边形EFGH的形状还可能是菱形、矩形或正方形,中点四边形EFGH的周长与对角线AC,BD长度有一定的数量关系.张老师把这个问题同时给了其它小组进行研究.请你结合(1)的分析过程,解决下面的问题:(其中①,②问直接填空)①当对角线AC,BD满足关系时,中点四边形EFGH为菱形?②当对角线AC,BD满足关系时,中点四边形EFGH为矩形?③中点四边形EFGH的周长与对角线AC,BD长度有怎样的数量关系,并说明理由.【学以致用】(3)如图3,在四边形ABCD内部有一点O,连接OA,OB,OC,OD,点H,G分别是AD,BC的中点,连接HG,若∠AOB=∠COD=90°,∠BOC=150°,OA=OB=2,OC=OD=3,求HG的长.18.(2023春•盐城期中)阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH.(1)这个中点四边形EFGH的形状是;(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明.19.(2022春•仙居县期末)如图,在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.(1)求证:四边形EFGH是平行四边形.(2)若四边形ABCD的对角线互相垂直且它们的乘积为48,求四边形EFGH的面积.。
2023学年北师大版九年级数学上学期专项讲练1-17 中点四边形(巩固篇)
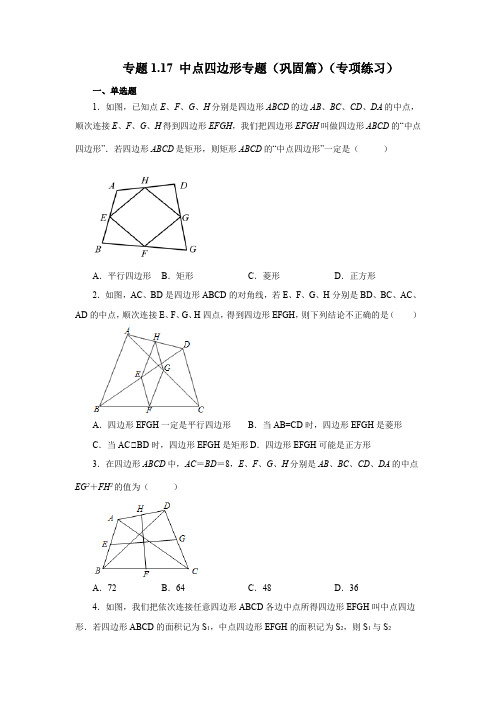
专题1.17 中点四边形专题(巩固篇)(专项练习)一、单选题1.如图,已知点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到四边形EFGH,我们把四边形EFGH叫做四边形ABCD的“中点四边形”.若四边形ABCD是矩形,则矩形ABCD的“中点四边形”一定是()A.平行四边形B.矩形C.菱形D.正方形2.如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是()A.四边形EFGH一定是平行四边形B.当AB=CD时,四边形EFGH是菱形C.当AC⊥BD时,四边形EFGH是矩形D.四边形EFGH可能是正方形3.在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点EG2+FH2的值为()A.72B.64C.48D.364.如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是()A.S1=3S2B.2S1=3S2C.S1=2S2D.3S1=4S25.如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点,则下列说法:=,则四边形EFGH为矩形;⊥若AC BD⊥若AC BD⊥,则四边形EFGH为菱形;⊥若四边形EFGH是平行四边形,则AC与BD互相垂直平分;⊥若四边形EFGH是正方形,则AC与BD互相垂直且相等.其中正确的个数是()A.1B.2C.3D.46.如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是()A.80cm B.40cm C.20cm D.10cm7.如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为()A.一定不是平行四边形B.一定不是中心对称图形C.可能是轴对称图形D.当AC=BD时它是矩形8.顺次连接一个四边形的各边中点得到一个正方形,则这个四边形可能是().A.梯形B.菱形C.矩形D.正方形9.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则对四边形EFGH表述最确切的是()A.四边形EFGH是矩形B.四边形EFGH是菱形C.四边形EFGH是正方形D.四边形EFGH是平行四边形10.如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是()A.当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形B.当M,N,P,Q是各边中点,且90∠=时,四边形MNPQ为正方形ABC=时,四边形MNPQ为菱形C.当M,N、P,Q是各边中点,且AC BD⊥时,四边形MNPQ为矩形D.当M,N、P、Q是各边中点,且AC BD二、填空题11.如图,连接四边形ABCD 各边中点,得到四边形EFGH ,只要添加_____条件,就能保证四边形EFGH 是菱形.12.如图,在四边形ABCD 中,AC =BD =6,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则EG 2+FH 2=______.13.如图,四边形 ABCD 是菱形, E 、F 、G 、H 分别是各边的中点,随机地向菱形ABCD 内掷一粒米,则米粒落到阴影区域内的概率是__________.14.如图,▱ABCD 中,AC =8,BD =6,则顺次连接四边形ABCD 各边中点所得四边形的周长是_____.15.如图,已知矩形ABCD 中,6cm AB =,8cm BC =,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,则四边形EFGH 的周长等于_____cm .16.如图,H 是⊥ABC 内一点,BH ⊥CH ,AH =6,CH =3,BH =4,D 、E 、F 、G 分别是AB 、AC 、CH 、BH 的中点,则四边形DEFG 的周长是______.17.如图,四边形ABCD 为正方形,点E F G H 、、、分别为AB BC CD DA 、、、的中点,其中4BD =,则四边形EFGH 的面积为________________________.18.如图,四边形ABCD 的对角线AC BD ⊥,E ,F ,G ,H 分别是AD ,AB ,BC ,CD 的中点,若在四边形ABCD 内任取一点,则这一点落在图中阴影部分的概率为_____________.19.如图,在菱形ABCD 中,点E 、F 、G 、H 分别是AB 、BC 、CD 、AD 的中点,EF =2EH ,则AB 与EH 的数量关系是AB =_____EH .20.如图,点A ,B ,C 为平面内不在同一直线上的三点.点D 为平面内一个动点.线段AB ,BC ,CD ,DA 的中点分别为M ,N ,P ,Q .在点D 的运动过程中,有下列结论:①存在无数个中点四边形MNPQ 是平行四边形;②存在无数个中点四边形MNPQ 是菱形;③存在无数个中点四边形MNPQ 是矩形;④存在两个中点四边形MNPQ 是正方形.所有正确结论的序号是_____.三、解答题21.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是,证明你的结论;(2)当四边形ABCD的对角线满足条件时,四边形EFGH是菱形;(3)你学过的哪种特殊四边形的中点四边形是菱形?22.我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.(1)任意四边形的中点四边形是什么形状?为什么?(2)任意平行四边形的中点四边形是什么形状?为什么?(3)任意矩形、菱形和正方形的中点四边形分别是什么形状?为什么?23.我们给出如下定义:顺次连接任意一个四边形各边中所得的四边形叫中点四边形.(1)如图1,在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,中点四边形EFGH是.(2)如图2,点P是四边形ABCD内一点,且满足P A=PB,PC=PD,⊥APB=⊥CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点.猜想中点四边形EFGH的形状,并证明你的猜想.(3)若改变(2)中的条件,使⊥APB=⊥CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).24.如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.(1)求证:四边形EGFH是菱形.(2)当⊥ABC与⊥DCB满足什么关系时,四边形EGFH为正方形,并说明理由.(3)猜想:⊥GFH、⊥ABC、⊥DCB三个角之间的关系,并证明你的猜想是成立的.25.我们给出如下定义:顺次连接任意一个四边形各边中所得的四边形叫中点四边形. (1)如图1,在四边形ABCD 中,点E ,F ,G ,H 分别为边AB ,BC ,CD ,DA 的中点,中点四边形EFGH 是_______________.(2)如图2,点P 是四边形ABCD 内一点,且满足PA PB =,PC PD =,APB CPD ∠=∠,点E ,F ,G ,H 分别为边AB ,BC ,CD ,DA 的中点.猜想中点四边形EFGH 的形状,并证明你的猜想.(3)若改变(2)中的条件,使90APB CPD ∠=∠=︒,其他条件不变,直接写出中点四边形EFGH 的形状(不必证明).参考答案1.C 【分析】原四边形ABCD 是矩形时,它的对角线相等,那么中点四边形EFGH 是菱形(平行四边形相邻的两边都相等).解:连接AC 和BDH 、G 分别是AD 、DC 的中点,HG ∴是DAC ∆的中位线, HG AC ∴∥,1=2HG AC同理,//EF AC ,EH FG BD ∥∥,1=2EH BD .∴四边形EFGH 是平行四边形. 四边形ABCD 是矩形时,∴AC BD =,则HG EF =, ∴平行四边形EFGH 是菱形 故选:C.【点拨】本题主要考查了矩形的性质和判定,菱形的性质和判定等知识点. 2.C 【分析】根据三角形中位线定理、平行四边形、矩形、菱形、正方形的判定定理判断即可. 解:⊥E 、F 分别是BD 、BC 的中点,⊥EF⊥CD ,EF=12CD ,⊥H 、G 分别是AD 、AC 的中点, ⊥HG⊥CD ,HG=12CD , ⊥HG⊥EF ,HG=EF ,⊥四边形EFGH 是平行四边形,A 说法正确,不符合题意;⊥F、G分别是BC、AC的中点,⊥FG=12AB,⊥AB=CD,⊥FG=EF,⊥当AB=CD时,四边形EFGH是菱形,B说法正确,不符合题意;当AB⊥BC时,EH⊥EF,⊥四边形EFGH是矩形,C说法错误,符合题意;当AB=CD,AB⊥BC时,四边形EFGH是正方形,说法正确,不符合题意;故选:C.【点拨】此题考查中点四边形、三角形中位线定理,掌握平行四边形、矩形、菱形、正方形的判定定理是解题的关键.3.B【分析】作辅助线,构建四边形EFGH,证明它是菱形,利用对角线互相垂直和勾股定理列等式,再利用中位线性质等量代换可得结论.解:连接EF、FG、GH、EH,⊥E、F、G、H分别是AB、BC、CD、DA的中点,⊥EF⊥AC,HG⊥AC,11,22EF AC FG BD==,⊥EF⊥HG,同理EH⊥FG,⊥四边形EFGH为平行四边形,⊥AC=BD,⊥EF=FG,⊥平行四边形EFGH为菱形,⊥EG⊥FH,EG=2OG,FH=2OH,⊥EG 2+FH 2=(2OE )2+(2OH )2=4(OE 2+OH 2)=4EH 2=2214()8642BD ⨯==,故选:B .【点拨】本题考查了中点四边形,运用了三角形中位线的性质,将三角形和四边形有机结合,把边的关系由三角形转化为四边形中,可以证明四边形为特殊的四边形;对于线段的平方和可以利用勾股定理来证明.4.C 【分析】根据题意由E 为AB 中点,且EF 平行于AC ,EH 平行于BD ,得到△BEK 与△ABM 相似,△AEN 与△ABM 相似,利用面积之比等于相似比的平方,得到△EBK 面积与△ABM 面积之比为1:4,且△AEN 与△EBK 面积相等,进而确定出四边形EKMN 面积为△ABM 的一半,同理得到四边形MKFP 面积为△MBC 面积的一半,四边形QMPG 面积为△DMC 面积的一半,四边形MNHQ 面积为△ADM 面积的一半,四个四边形面积之和即为四个三角形面积之和的一半,即为四边形ABCD 面积的一半.解:设AC 与EH 、FG 分别交于点N 、P ,BD 与EF 、HG 分别交于点K 、Q ,⊥E 是AB 的中点,EF⊥AC ,EH⊥BD , ⊥⊥EBK⊥⊥ABM ,△AEN⊥⊥EBK , ⊥14EBK ABMS S=,S △AEN =S △EBK , ⊥12EKMN ABM S S =四边形,同理可得12KFPM BCM S S 四边形=,12QGPM DCM S S =四边形,12HQMN DAM S S =四边形, ⊥12EFGH ABCDS S 四边形四边形=, ⊥四边形ABCD 的面积为S 1,中点四边形EFGH 的面积记为S 2,则S 1与S 2的数量关系是S 1=2S 2.故选C .【点拨】此题主要考查了中点四边形以及相似三角形的判定与性质等知识,熟练应用三角形中位线的性质是解题关键.5.A【分析】根据三角形中位线定理、平行四边形的判定定理得到四边形EFGH是平行四边形,根据矩形、菱形、正方形的判定定理判断即可.解:⊥E、F分别是边AB、BC的中点,⊥EF⊥AC,EF=12AC,同理可知,HG⊥AC,HG=12AC,⊥EF⊥HG,EF=HG,⊥四边形EFGH是平行四边形,若AC=BD,则四边形EFGH是菱形,故⊥说法错误;若AC⊥BD,则四边形EFGH是矩形,故⊥说法错误;若四边形EFGH是平行四边形,AC与BD不一定互相垂直平分,故⊥说法错误;若四边形EFGH是正方形,AC与BD互相垂直且相等,故⊥说法正确;故选:A.【点拨】本题考查中点四边形、平行四边形、矩形、菱形的判定等知识,掌握三角形中位线定理、平行四边形、矩形、菱形、正方形的判定定理是解题的关键.6.B解:利用三角形中位线定理易得所求四边形的各边长都等于AC,或BD的一半,进而求四边形周长即可.7.C解:连接AC,BD,⊥点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,⊥EF=HG=12AC,EH=FG=12BD,⊥四边形EFGH是平行四边形,⊥四边形EFGH一定是中心对称图形,当AC⊥BD时,⊥EFG=90°,此时四边形EFGH是矩形,当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,⊥四边形EFGH可能是轴对称图形,故选C.【点拨】本题考查中点四边形;平行四边形的判定;矩形的判定;轴对称图形.8.D【分析】利用连接四边形各边中点得到的四边形是正方形,则结合正方形的性质及三角形的中位线的性质进行分析,从而不难求解.解:如图点E,F,G,H分别是四边形ABCD各边的中点,且四边形EFGH是正方形.⊥点E,F,G,H分别是四边形各边的中点,且四边形EFGH是正方形.⊥EF=EH,EF⊥EH,⊥BD=2EF,AC=2EH,EF//BD,EH//AC⊥AC=BD,AC⊥BD,即四边形ABCD满足对角线相等且垂直,选项D满足题意.故选:D.【点拨】本题考查了利用三角形中位线定理得到新四边形各边与相应线段之间的数量关系和位置.熟练掌握特殊四边形的判定是解题的关键.9.B【分析】根据三角形中位线定理得到EH=12BC,EH⊥BC,得到四边形EFGH是平行四边形,根据菱形的判定定理解答即可.解:⊥点E、H分别是AB、AC的中点,⊥EH=12BC ,EH⊥BC ,同理,EF=12AD ,EF⊥AD ,HG=12AD ,HG⊥AD , ⊥EF=HG ,EF⊥HD ,⊥四边形EFGH 是平行四边形, ⊥AD=BC , ⊥EF=EH ,⊥平行四边形EFGH 是菱形, 故选B .【点拨】本题考查的是中点四边形的概念和性质、掌握三角形中位线定理、菱形的判定定理是解题的关键.10.B 【分析】连接AC 、BD ,根据三角形中位线定理得到PQ AC ∥,12PQ AC =,MN AC ∥,12MN AC =,根据平行四边形、矩形、菱形、正方形的判定定理判断即可. 解:连接AC 、BD 交于点O ,M ,N ,P ,Q 是各边中点, ⊥PQ AC ∥,12PQ AC =,MN AC ∥,12MN AC =,⊥PQ MN ∥,PQ MN =,∴四边MNPQ 一定为平行四边形,A 说法正确,不符合题意;90ABC ∠=时,四边形MNPQ 不一定为正方形,B 说法错误,符合题意;AC BD =时,MN MQ =,∴四边形MNPQ 为菱形,C 说法正确,不符合题意;AC BD ⊥时,90MNP ∠=,∴四边形MNPQ 为矩形,D 说法正确,不符合题意. 故选B .【点拨】本题考查的是中点四边形,掌握平行四边形、矩形、菱形、正方形的判定定理、三角形中位线定理是解题的关键.11.AC=BD【分析】根据中位线的性质易得四边形EFGH为平行四边形,那么只需让一组邻边相等即可,而邻边都等于对角线的一半,那么对角线需相等.解:⊥E、F为AD、AB中点,⊥EF为⊥ABD的中位线,⊥EF BD,EF=12BD,同理可得GH BD,GH=12BD,FG AC,FG=12AC,⊥EF GH,EF=GH,⊥四边形EFGH为平行四边形,⊥当EF=FG时,四边形EFGH为菱形,⊥FG=12AC,EF=12BD,EF=FG⊥AC=BD,故答案为:AC=BD.【点拨】本题考查菱形的判定,四边相等的四边形是菱形和中位线定理,解题的关键是了解菱形的判定定理,难度不大.12.36【分析】连接EF,FG,GH,EH,由E、F、G、H分别是AB、BC、CD、DA的中点,得到EH,EF,FG,GH分别是⊥ABD,⊥ABC,⊥BCD,⊥ACD的中位线,根据三角形中位线定理得到EH,FG等于BD的一半,EF,GH等于AC的一半,由AC=BD=6,得到EH=EF=GH=FG=3,根据四边都相等的四边形是菱形,得到EFGH为菱形,然后根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH,在Rt⊥OEH中,根据勾股定理得到OE2+OH2=EH2=9,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH 代入变形后的等式中,即可求出EG2+FH2的值解:如图,连接EF,FG,GH,EH,⊥E、H分别是AB、DA的中点,⊥EH是⊥ABD的中位线,⊥EH=12BD=3,同理可得EF,FG,GH分别是⊥ABC,⊥BCD,⊥ACD的中位线,⊥EF=GH=12AC=3,FG=12BD=3,⊥EH=EF=GH=FG=3,⊥四边形EFGH为菱形,⊥EG⊥HF,且垂足为O,⊥EG=2OE,FH=2OH,在Rt⊥OEH中,根据勾股定理得:OE2+OH2=EH2=9,等式两边同时乘以4得:4OE2+4OH2=9×4=36,⊥(2OE)2+(2OH)2=36,即EG2+FH2=36.故答案为36.【点拨】此题考查了菱形的判定与性质,勾股定理,三角形的中位线定理以及等式的基本性质,本题的关键是连接EF,FG,GH,EH,得到四边形EFGH为菱形,根据菱形的性质得到EG⊥HF,建立直角三角形,利用勾股定理来解决问题.13.12解:则根据菱形的性质可得菱形ABCD的面积=12AC·BD,根据E、F、G、、H为各边中点可得四边形HEFG为矩形,根据中点可得HE=FG=12BD,HG=EF=12AC,则矩形HEFG的面积=12BD·12AC=14AC·BD,即四边形HEFG的面积是菱形ABCD面积的一半,则可得概率为12.故答案为;12.14.14【分析】根据三角形的中位线定理得出EF=GH=1BD2=3,EH=FG=12AC=4,代入四边形的周长式子求出即可.解:⊥E、F、G、H分别是边AD、AB、BC、CD的中点,⊥EF=GH=1BD2=3,EH=FG=12AC=4,⊥EF+FG+GH+EH=3+4+3+4=14,故答案为14【点拨】本题主要考查对三角形的中位线定理的理解和掌握,能熟练运用性质求出EF+GH+EH+FG=AC+BD是解此题的关键.15.20【分析】连接AC、BD,根据三角形的中位线求出HG,GF,EF,EH的长,再求出四边形EFGH 的周长即可.解:如图,连接AC、BD,四边形ABCD是矩形,AC=BD=8cm,E、F、G、H分别是AB、BC、CD、DA的中点,HG=EF=12AC=4cm,EH=FG=12BD=4cm,四边形EFGH的周长等于4+4+4+4=16cm.【点拨】本题考查了矩形的性质,三角形的中位线的应用,能求出四边形的各个边的长是解此题的关键,注意:矩形的对角线相等,三角形的中位线平行于第三边,并且等于第三边的一半.16.11【分析】根据勾股定理求出BC的长,根据三角形的中位线定理得到ED=FG=12BC,EF=DG=12AH,而⊥CHB为直角三角形,可求出BC,再求出EF、HG、EH、FG的长,代入即可求出四边形EFGH的周长.解:⊥BH⊥CH,BH=4,CH=3,由勾股定理得:BC,⊥D、E、F、G分别是AB、AC、CH、BH的中点,⊥ED=FG=12BC,EF=DG=12AH,⊥AH=6,⊥EF=DG=3,ED=FG=52,⊥四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.故答案为11.【点拨】本题主要考查对勾股定理,三角形的中位线定理等知识点的理解和掌握,能根据三角形的中位线定理求出EF、DG、ED、FG的长是解此题的关键.17.4.【分析】先判定四边形EFGH为矩形,再根据中位线的定理分别求出EF、EH的长度,即可求出四边形EFGH的面积.解:⊥四边形ABCD是正方形,点E、F、G、H分别是AB、BC、CD、DA的中点,⊥⊥AEH、⊥BEF、⊥CFG、⊥DGH都为等腰直角三角形,⊥⊥HEF、⊥EFG、⊥FGH、⊥GHE都为直角,⊥四边形EFGH是矩形,边接AC,则AC=BD=4,又⊥EH是⊥ABD的中位线,⊥EH=12BD=2,同理EF=12AC=2,⊥四边形EFGH的面积为2×2=4.故答案为4.【点拨】本题考查了正方形的性质,矩形的判定,三角形中位线定理.18.12##0.5【分析】先由三角形的中位线定理推知四边形EFGH是平行四边形,然后由AC⊥BD可以证得平行四边形EFGH是矩形.解:如图,⊥E、F、G、H分别是线段AD,AB,BC,CD的中点,⊥EH、FG分别是△ACD、△ABC的中位线,EF、HG分别是△ABD、△BCD 的中位线,根据三角形的中位线的性质知,EF⊥BD,GH⊥BD且EF=12BD,GH=12BD,⊥四边形EFGH是平行四边形,又⊥AC⊥BD,⊥EF⊥FG⊥四边形EFGH是矩形,⊥四边形EFGH的面积=EF•FG=14 AC•BD,⊥四边形ABCD的面积=12AC•BD,⊥这一点落在图中阴影部分的概率为:114122AC BDAC BD,故答案为:12.【点拨】本题主要考查了几何概率,中点四边形,解题时,利用三角形中位线定理判定四边形EFGH是平行四边形是解题的关键.19【分析】连接AC、BD交于O,根据菱形的性质得到AC⊥BD,OA=OC,OB=OD,根据三角形中位线定理、矩形的判定定理得到四边形EFGH是矩形,根据勾股定理计算即可.解:连接AC、BD交于O,⊥四边形ABCD是菱形,⊥AC⊥BD,OA=OC,OB=OD,⊥点E、F、G、H分别是边AB、BC、CD和DA的中点,⊥EH=12BD,EH⊥BD,GH=12AC,GH⊥AC,⊥EF=2EH,⊥OA=2OD,⊥AB,⊥AB,【点拨】本题考查的是中点四边形,掌握菱形的性质、三角形中位线定理是解题的关键.20.①②③④.【分析】连接AC、BD,根据三角形中位线定理得到PQ⊥AC,PQ=12AC,MN⊥AC,MN=12AC,根据平行四边形、矩形、菱形、正方形的判定定理判断即可.解:⊥当AC与BD不平行时,中点四边形MNPQ是平行四边形;故存在无数个中点四边形MNPQ是平行四边形;⊥当AC与BD相等且不平行时,中点四边形MNPQ是菱形;故存在无数个中点四边形MNPQ是菱形;⊥当AC与BD互相垂直(B,D不重合)时,中点四边形MNPQ是矩形;故存在无数个中点四边形MNPQ是矩形;⊥如图所示,当AC与BD相等且互相垂直时,中点四边形MNPQ是正方形.故存在两个中点四边形MNPQ是正方形.故答案为:⊥⊥⊥⊥.【点拨】本题考查的是中点四边形,掌握平行四边形、矩形、菱形、正方形的判定定理、三角形中位线定理是解题的关键.21.(1)平行四边形,证明见分析;(2)AC=BD;(3)矩形【分析】(1)连接BD、AC,利用三角形的中位线性质和平行四边形的判定定理即可解答;(2)根据菱形的判定定理即可解答;(3)根据矩形的性质和菱形的判定解答即可.解:(1)四边形EFGH的形状是平行四边形,证明:连接BD、AC,⊥四边形ABCD四条边上的中点分别为E、F、G、H,⊥12EH FG BD==,12EF HG AC==,⊥四边形EFGH是平行四边形,故答案为:平行四边形;(2)当四边形ABCD的对角线满足AC=BD条件时,四边形EFGH是菱形,理由:⊥BD=AC,12EH FG BD==,12EF HG AC==,⊥=EH FG EF HG,⊥四边形EFGH是菱形,故答案为:AC=BD;(3)由于矩形的对角线相等,且由(1)(2)结论知,矩形的中点四边形是菱形.【点拨】本题考查平行四边形的判定、菱形的判定、矩形的性质、三角形的中位线性质,熟练掌握相关知识的联系与运用是解答的关键.22.(1)平行四边形,理由见分析;(2)平行四边形;理由见分析;(3)菱形、矩形、正方形.理由见分析.【分析】(1)连接BD ,根据三角形的中位线定理,可得EH ⊥GF ,EH =FG ,即可求证;(2)连接AC ,DB ,根据三角形的中位线定理,可得EH ⊥GF ,EH =FG ,即可求证; (3)利用(1)的判定方法,再根据三角形的中位线定理和矩形、菱形、正方形的判定方法来判定,即可求证.解:(1)任意四边形的中点四边形是平行四边形,理由如下:已知四边形ABCD ,E ,F ,G ,H 分别是AB ,BC ,CD ,AD 的中点,连接BD ,如图1:⊥E 是AB 的中点,H 是AD 的中点,⊥EH 是⊥ABD 的中位线,⊥//EH BD ,12EH BD = ,⊥G 是CD 的中点,F 是BC 的中点,⊥FG 是⊥BCD 的中位线,⊥//FG BD ,12FG BD = , ⊥EH ⊥GF ,EH =FG ,⊥四边形EFGH 为平行四边形;(2)任意平行四边形的中点四边形是平行四边形,理由如下:已知平行四边形ABCD,E,N,M,F分别是DA,AB,BC,DC的中点,连接AC,DB,如图2:⊥E,F分别是DA,DC的中点,⊥EF是⊥ACD的中位线,⊥EF⊥AC,EF=12AC,⊥M,N分别是BC,AB的中点,⊥MN是⊥ABC的中位线,⊥MN⊥AC,MN=12AC,⊥EF⊥MN,EF=MN,⊥四边形MNEF是平行四边形;(3)如果原四边形为矩形,则形成的中点四边形为菱形,理由如下:已知矩形ABCD,H,E,F,G分别是DA,AB,BC,DC的中点,连接AC,DB,如图:⊥四边形ABCD是矩形,⊥AC=BD,⊥E是AB的中点,H是AD的中点,⊥EH是⊥ABD的中位线,⊥EH=12BD,⊥G是CD的中点,F是BC的中点,⊥GF是⊥BCD的中位线,⊥GF =12BD , ⊥E 是AB 的中点,F 是BC 的中点,⊥EF 是⊥ABC 的中位线,⊥EF =12AC ,⊥G 是CD 的中点,H 是AD 的中点,⊥GH 是⊥ACD 的中位线,⊥GH =12 AC ,又⊥AC =BD ,⊥EF =GF =EH =GH ,四边形EFGH 是菱形;如果原四边形为菱形,则形成的中点四边形为矩形,理由如下;已知菱形ABCD ,E ,F ,G ,H 分别是AB ,,BC ,CD ,AD 的中点,连接BD ,AC ,如图:⊥四边形ABCD 是菱形,⊥AC ⊥BD ,⊥E 是AB 的中点,H 是AD 的中点,⊥EH 是⊥ABD 的中位线,⊥EH ⊥BD ,12EH BD = ,⊥G 是CD 的中点,F 是BC 的中点,⊥GF 是⊥BCD 的中位线,⊥GF ⊥BD ,12GF BD = , ⊥EH ⊥BD ⊥GF ,EH =GF ,⊥四边形EFGH 是平行四边形,又⊥AC ⊥BD ,⊥E是AB的中点,F是BC的中点,⊥EF是⊥ABC的中位线,⊥EF⊥AC,⊥EH⊥EF,⊥四边形EFGH是矩形;如果原四边形为正方形,则形成的中点四边形为正方形,理由如下:已知正方形ABCD,E,F,G,H分别是AB,BC,CD,AD的中点,连接BD,AC,如图:⊥四边形ABCD是正方形,⊥AC⊥BD,AC=BD,⊥E是AB的中点,H是AD的中点,⊥EH是⊥ABD的中位线,BD,⊥EH⊥BD,EH=12⊥G是CD的中点,F是BC的中点,⊥GF是⊥BCD的中位线,⊥GF⊥BD,GF=1BD,2⊥EH⊥BD⊥GF,EH=GF,⊥四边形EFGH是平行四边形,又⊥AC⊥BD,⊥AC⊥EH,⊥E是AB的中点,F是BC的中点,⊥EF是⊥ABC的中位线,AC,⊥EF⊥AC,EF=12⊥四边形EFGH是矩形,⊥AC=BD,⊥EF=EH,⊥四边形EFGH是正方形.【点拨】本题主要考查了平行四边形的判定和性质,矩形的判定和性质,菱形的判定和性质,正方形的性质和判定,熟练掌握相关知识是解题的关键.23.(1)平行四边形;(2)菱形,见分析;(3)正方形【分析】(1)连接BD,根据三角形中位线定理证明EH⊥FG,EH=FG,根据平行四边形的判定定理证明即可;(2)证明⊥APC⊥⊥BPD,根据全等三角形的性质得到AC=BD,再证明EF=FG,根据菱形的判定定理证明结论;(3)证明⊥EHG=90°,利用⊥APC⊥⊥BPD,得到⊥ACP=⊥BDP,即可证明⊥COD=⊥CPD=90°,再根据平行线的性质证明⊥EHG=90°,根据正方形的判定定理证明即可.解:(1)如图1,连接BD,⊥点E,H分别为边AB,DA的中点,⊥EH⊥BD,EH=12 BD,⊥点F,G分别为边BC,CD的中点,⊥FG⊥BD,FG=12 BD,⊥EH⊥FG,EH=GF,⊥中点四边形EFGH是平行四边形,故答案为:平行四边形;(2)结论:四边形EFGH 是菱形,理由:如图2,连接AC ,BD .⊥⊥APB =⊥CPD ,⊥⊥APB +⊥APD =⊥CPD +⊥APD ,即⊥APC =⊥BPD ,在⊥APC 和⊥BPD 中,AP BP APC BPD PC PD =⎧⎪∠=∠⎨⎪=⎩,⊥⊥APC ⊥⊥BPD (SAS ),⊥AC =BD ,⊥点E ,F ,G 分别为边AB ,BC ,CD 的中点,⊥EF =12AC ,FG =12BD , ⊥EF =FG ,由(1)知中点四边形EFGH 是平行四边形,⊥平行四边形EFGH 是菱形;(3)结论:四边形EFGH 是正方形,理由:如图2,设AC 与BD 交于点O .AC 与PD 交于点M ,⊥⊥APC ⊥⊥BPD ,⊥⊥ACP =⊥BDP ,⊥⊥DMO =⊥CMP ,⊥⊥COD =⊥CPD =90°,⊥EH ⊥BD ,AC ⊥HG ,⊥⊥EHG =⊥DOC =90°,由(2)知中点四边形EFGH是菱形,⊥菱形EFGH是正方形.【点拨】本题考查的是平行四边形的判定和性质、全等三角形的判定和性质、菱形的判定和性质、正方形的判定和性质,解题的关键是灵活应用三角形中位线定理,学会添加常用辅助线.24.(1)见分析(2)当⊥ABC+⊥DCB=90°时,四边形EGFH为正方形(3)⊥GFH+⊥ABC+⊥DCB=180°【分析】(1)根据三角形中位线的性质得到EG=12AB,EH=12CD,HF=12AB,EG//AB,HF//AB,根据菱形的判定定理即可得到结论;(2)根据平行线的性质得到⊥ABC=⊥HFC,⊥DCB=⊥GFB,根据平角的定义得到⊥GFH=90°,于是得到结论;(3)由平行线的性质得到⊥ABC=⊥HFC,⊥DCB=⊥GFB,根据平角的定义即可得到结论.解:(1)⊥E、F、G、H分别为AD、BC、BD、AC的中点,⊥EG=12AB,EH=12CD,HF=12AB,EG//AB,HF//AB,⊥四边形EGFH是平行四边形,EG=EH,⊥四边形EGFH是菱形;(2)当⊥ABC+⊥DCB=90°时,四边形EGFH为正方形,理由:⊥GF//CD,HF//AB,⊥⊥ABC=⊥HFC,⊥DCB=⊥GFB,⊥⊥ABC+⊥DCB=90°,⊥⊥GFH=90°,⊥菱形EGFH是正方形;(3)⊥GFH+⊥ABC+⊥DCB=180°,理由:⊥GF//CD,HF//AB,⊥⊥ABC=⊥HFC,⊥DCB=⊥GFB,⊥⊥BFG+⊥GFH+⊥HFC=180°,⊥⊥GFH+⊥ABC+⊥DCB=180°.【点拨】本题考查了中点四边形,菱形的判定和性质,正方形的判定,三角形中位线的性质,熟练掌握三角形中位线的性质是解题的关键.25.(1)平行四边形;(2)四边形EFGH 是菱形,证明见分析;(3)四边形EFGH 是正方形.【分析】(1)如图1中,连接BD ,根据三角形中位线定理可得:EH ⊥FG ,EH FG =,然后利用平行四边形的判定定理即可证明;(2)四边形EFGH 是菱形.先证明APC BPD ≌,得到AC BD =,再利用三角形中位线定理可得EF FG =,根据菱形的判定定理即可证明;(3)四边形EFGH 是正方形,只要证明90EHG ∠=︒,利用APC BPD ≌,得ACP BDP ∠=∠,即可证明90COD CPD ∠=∠=︒,然后根据正方形的判定定理即可得出结论.解:(1)证明:如图1中,连接BD ,⊥点E ,H 分别为边AB ,DA 的中点,⊥EH ⊥BD ,12EH BD =, ⊥点F ,G 分别为边BC ,CD 的中点,⊥FG ⊥BD ,12FG BD =, ⊥EH ⊥FG ,EH GF =,⊥四边形EFGH 是平行四边形;(2)解:如图2中,连接AC ,BD ,⊥APB CPD ∠=∠, ⊥APB APD CPD APD ∠+∠=∠+∠ 即APC BPD ∠=∠, 在APC ∆和BPD ∆中, AP PB APC BPD PC PD =⎧⎪∠=∠⎨⎪=⎩,⊥()APC BPD SAS ∆∆≌, ⊥AC BD =⊥点E ,F ,G 分别为边AB ,BC ,CD 的中点, ⊥12EF AC =,12FG BD =, ⊥EF FG =,⊥四边形EFGH 是平行四边形, ⊥四边形EFGH 是菱形;(3)四边形EFGH 是正方形,证明:如图2中,设AC 与BD 交于点O ,AC 与PD 交于点M ,AC 与EH 交于点N . ⊥APC BPD ≌,⊥ACP BDP ∠=∠,⊥DMO CMP ∠=∠, ⊥90COD CPD ∠=∠=︒, ⊥EH ⊥BD ,AC ⊥HG , ⊥90EHG ENO BOC DOC ∠=∠=∠=∠=︒,⊥四边形EFGH是菱形,⊥四边形EFGH是正方形.【点拨】题目主要考查平行四边形、菱形、正方形的判定定理及三角形的中位线的性质,熟练掌握知识点并作出相应辅助线是解题关键.。
中点四边形复习课

A G
D
P C
N F
E
B
C
E
B
图3
F
图4
• (2010广东) 如图⑴、⑵所示,矩形ABCD的边长AB=6,BC=4, 点F在DC上,DF=2,动点M、N分别从点D、B同时出发,沿射 线DA、线段BA向点A的方向运动(点M可以运动到DA的延长线 上),当点N运动到点A时,M,N两点同时停止运动。连接FM、 MN、FN,当F、N、M不在同一直线上时,可得△FMN,过△ FMN三边的中点作△ PQW。设动点M、N的速度都是1个单位/秒, M、N运动的时间为x秒。试解答下列问题: • ⑴说明△ FMN ∽ △ QWP; • ⑵设 0 x 4(即M从D到A运动的时间段),试问x为何值时, △ PQW为直角三角形?当x在何范围时, △ PQW不为直角三角 形? • ⑶问当x为何值时线段MN最短?求此时MN的值。
2
1
理由如下:①∵MQ=PN= 2 BD 1 ∴PQ=MN= 2 AC ∴四边形MNPQ的周长=PQ+QM+MN+NP =2(MQ+PQ)=BD+AC=a+b
Q
A
D
P
M
N
1 4
②∵ MN∥AC
∴ △BMN∽△BAC ∴SBMN= SBAC
4 1
1
B
C
同理SDQP= SDAC
4
∴S四边形MNPQ=2X S四边形ABCD
1
∴ SBMN+SDQO= (SABC+SADC)= 4 S四边形ABCD
4
1
= S
2
1
同理SAMQ+SCNP= (SABD+SCNP)= 1 S四边形ABCD
中点四边形与判定定理

中点四边形与判定定理中点四边形是指一个四边形的对角线的交点是四条边的中点。
中点四边形有一些特殊的性质和定理。
本文将介绍中点四边形的性质,并讲解与之相关的判定定理。
一、中点四边形的性质1. 中点连线性质:在中点四边形中,连接两个相邻顶点的线段恰好是另一条对边的中点连线。
例如,对于四边形ABCD,若AC的中点为E,BD的中点为F,则AE与BF相交于中点四边形的对角线交点G。
2. 对角线平分性质:在中点四边形中,对角线互相平分。
即对于四边形ABCD,AC和BD作为对角线,则AC平分BD,BD也平分AC。
这是因为中点四边形的定义决定了对角线的交点G是AC和BD的中点,所以AC平分BD,BD也平分AC。
3. 斜边性质:在中点四边形中,连接中点的斜边恰好等于两个对角线的一半。
以四边形ABCD为例,若AC的中点为E,BD的中点为F,则EF = AG = BG = CG = DG = 1/2(AC + BD)。
二、中点四边形判定定理根据中点四边形的性质,我们可以得出两个判定定理:1. 判定定理一:如果一个四边形的对角线交点是该四边形两对相对边中点,那么这个四边形一定是中点四边形。
证明:设四边形ABCD的对角线交点为E,且E是AC和BD的中点。
根据中点连线性质,连接AE和BE,连接CE和DE。
则AE和BE分别平分CD,CE和DE分别平分AB。
根据对角线平分性质,AC 和BD互相平分。
因此,四边形ABCD满足中点四边形的定义,即为中点四边形。
2. 判定定理二:如果一个四边形的两对相对边互相平分,并且对角线交于一点,那么这个四边形一定是中点四边形。
证明:设四边形ABCD的对角线为AC和BD,且AC平分BD,BD平分AC,交于点E。
根据中点连线性质,连接AE和BE,连接CE和DE。
由于AC平分BD,根据转角平分定理,角EAB等于角EDB,角EBA等于角EAD。
同理,角ECD等于角EBC,角EDC等于角ECA。
因此,四边形ABCD满足中点四边形的定义,即为中点四边形。
四边形的中点专题

四边形的中点专题四边形的中点专题1..如图,正方形ABCD中,E为AB边上一点,过点D作DF丄DE与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.(1)若BF=BD=2 ,求BE的长;(2)若M是EF中点,求证:MC垂直平分DB(1)解:•••四边形ABCDE方形,•••/ BCD=90,••• Rt△ BCD中, BC2 CD2 BD2,2 2即BC22 2 • BC=AB=1T DF丄DE, ADE y EDC=90 =Z EDC k CDF•/ ADE y CDFADE CDF在^ ADE?3 CDF中, AD CD ,A DCF 90•△ ADE^A CDF(ASA,-——2•AE=CF=BF-BC=2 1 • BE=AB-AE=1-1 .2 =21(2)证明:如图:连接DM BM T DF丄DE M为EF中点,• DM= EF,2vZ EBF=90,M 为EF 中点,• BM」EF,:BM=DM2• M在BD的垂直平分线上v BC=CD,.C在BD的垂直平分线上• MC垂直平分DB2.如图,在平行四边形ABCD中,对角线丄AC于点E,求证:AD=2OE证明:取CD的中点F,连接EF, OFv四边形ABCD是平行四边形,•AO=COV DE I AC••/ DEC=90•••EF=FCV CD// AB•••/ CAB2 DCA=x.•••/ FEC K DCE= x.•••/ DAC K FOC=2 x.•••/ FEO K EFO= x••• OE=OFAD=2OE3.在平行四边形ABC冲,对角线相交于点O. E、F、P分别OB OC AD的中点, 且AC=2AB 求证:EP=EF证明:连接AE, V四边形ABCD是平行四边形3题••• AD=BC AC=2OA=2OC: AC=2AB•••OA=AB V E 为OB中点,••• AE! BD (三线合一定理),•••K AED=90 , V P 为AD中点,••• AD=2Ep v BC=AD •- BC=2EPV E、F分别是OB OC中点,• BC=2EF • EP=EF4.如图,点E为正方形ABCD外一点,/ BCE K BAE=15 ,AE=T3,O为BD的中点,连接OE,求OE的长。
中点四边形规律总结

中点四边形规律总结
中点四边形是许多图形中的一个,它是由2对对称的对称角组成的一种平行四边形。
两对对称角并列并相等,即边a=边c,边b=边d。
因此,中点四边形也可
以被称为等对角线四边形。
这种形状在生活中经常出现,如板条箱,手机键盘以及一些实用的棋子,如棋盘和四子棋。
它们可以用来装载一些工具或物品,看起来很实用又很美观。
此外,中点四边形也是计算机绘图的常用基本图形。
在计算机绘图中,它有着极为重要的作用,因为它是视觉游戏的一个重要部分。
在几何学中,中点四边形也有一定的规律性。
例如,它的面积可以通过其两个对称角(α,α),(β,β)和对角线(a,b)求得,面积就是锐角α、β中所写的定理应用表达式:
S=1/2(a^2+b^2)sinα
还有,中点四边形的其他要素也有一定的表达式:
内接圆半径:r=1/2√[(a^2+b^2)sinα]
外接圆半径:R=1/2[a/sinα+b/sinβ]
中点四边形的边和有表达式:a+b+c+d=2(α+β)
总之,中点四边形的规律总结是:拥有等对角的平行四边形,其面积的表达式是S=1/2(a2+b2)si nα,还可以从其内接圆半径、外接圆半径和边和的表达式中总结
出中点四边形的其他规律。
中点四边形

中点四边形《平行四边形》一章,主要讲了平行四边形的性质与判定,特殊平行四边形:矩形,菱形,正方形的性质与判定,对于初学的初二学生来说,感觉知识点较多,又很相近,容易混淆,尤其是各种图形有关对角线的知识点,学生们总是分不清,为了让学生更加清楚的掌握有关对角线的性质,引入中点四边形概念,使学生在运用中辨析各种图形的对角线的性质.中点四边形的定义:顺次连接四边形各边中点的四边形叫中点四边形。
中点四边形的形状取决于四边形的对角线的位置关系或数量关系。
研究中点四边形的方法是连接四边形的对角线,构造三角形中位线,根据三角形的中位线性质定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.第一情况:顺次连接任意四边形各边中点所得到的四边形是平行四边形.例1.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点,求证:四边形EFGH是平行四边形.【证明】连接AC,BD在△ABD中,1BD∵E,H分别是AB,AD中点,∴EH∥BD且EH=21BD∵G,F分别是BC,CD中点,∴FG∥BD且FG=2∴EH=FG,且EH∥FG∴四边形EFGH是平行四边形.思考:顺次连接平行四边形各边中点所得到的四边形是平行四边形.第二种情况:顺次连接对角线相等的四边形各边中点所得到的四边形是菱形例3,如图任意四边形ABCD各边中点分别是E,F,G,H,若对角线AC,BD 的长都为20cm,求四边形EFGH的周长.【解】在△ABD中,∵E,H分别是AB,AD中点,1BD=10cm∴EH∥BD且EH=2在△BCD中1BD=10cm∵F,G分别是BC,CD中点,∴FG∥BD且FG=2∴EH=FG,且EH∥FG∴四边形EFGH是平行四边形在△ABC中,1AC=10cm∵E,F分别是AB,BC中点,∴EF=2∵AC=BD=20cm,∴平行四边形EFGH是菱形.∴四边形EFGH的周长为:10×4=40(cm)【小结】四边形ABCD的对角线相等,则它的中点四边形是菱形.例4.如图,C是线段BD上一点,△ABC和△ECD都是等边三角形,R,F,G,H,分别是四边形ABDE各边中点,求证四边形RFGH是菱形【分析】要证四边形RFGH是菱形,只要证明四边形ABDE的对角线相等即可.所以需要连接AD,BE,,然后证明三角形全等,就可证出BE=AD【证明】如图,连接AD,BE∵△ABC和△ECD都是等边三角形,∴AC=BC,DC=EC,∠ACB=∠ECD=60°∴∠BCE=∠ACD∴△BCE≌△ACD,∴AD=BE根据顺次连接对角线相等的四边形各边中点的四边形是菱形,可得四边形RFGH是菱形.思考:顺次连接矩形各边中点所得到的四边形是.第三种情况:顺次连接对角线互相垂直的四边形各边中点所得到的四边形是距形思考:顺次连接菱形各边中点所得到四边形是.第四种情况:顺次连接对角线互相垂直相等的四边形各边中点所得到的四边形是正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考专题复习:中点四边形教学设计
教学目标:
1.激发学生的学习兴趣,培养学生勇于探索、勇于创新的精神。
2.培养学生独立分析问题、解决问题的能力以及研究能力和创新意识。
3.理解中点四边形的概念,掌握中点四边形判定、证明及应用。
教学重点:中点四边形形状判定和证明
教学难点:对确定中点四边形形状的主要因素的分析和概括
如果我们依次连接任意一个四边形各边中点,得到的图形又是什么呢?
今天我们就来研究这个问题。
问题:连结三角形的各边中点的线段叫做 ,他们组成的图形与原三角形 。
B
C
例题:(2012•孝感)我们把依次连接任意一个四边形各边中点得到的四边
形叫做中点四边形.如图,在四边形ABCD 中,E 、F 、G 、H 分别是边A B 、BC 、CD 、DA 的中点,依次连接各边中点得到的中点四边形EFGH.(1)这个中点四边形EFGH 的形状是________;(2)请证明你的结论.
问题1:在 中,四边的中点分别为
E,F,G,H,请猜想四边形EFGH 是什么四边形?并证明你的结论?
B
D
问题2:如果这个四边形是菱形呢,请猜想四边形EFGH 是什么四边形?并证明你的结论?矩形呢?正方形
呢?
B
A D
归纳:
原四边形的对角线
中点四边形形状正方形
菱形
矩形平行四边形
任意四边形
原四边形
探究:1、对于任意的四边形,只要满足什么条件,它所构成的中点四边形图形可能是矩形?或者菱形?2、如何证明?请说明理由。
••••••
⇒⇒
⇒
1、如图,依次连结第一个矩形的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去。
已知第一个矩形的面积是1,则第n 个图形的面积是 。
应用与实践:
2、如图,四边形ABCD 中,AC=a ,CD=b ,且AC ⊥BD ,顺次连结四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1,再顺次连结A 1B 1C 1D 1各边中点,
得到A 2B 2C 2D 2,•••,如此进行下去,得到四边形A n B n C n
(1)证明:证明A 1B 1C 1D 1是矩形;
(2)写出四边形A 1B 1C 1D 1面积和A 2B 2C 2D 2面积;
(3)写出四边形A n B n C n D n 面积和四边形A 5B 5C 5D 5.
B
D。
