氢原子光谱
高中物理氢原子光谱知识点

高中物理氢原子光谱知识点一、氢原子光谱的发现历程。
1. 巴尔末公式。
- 1885年,巴尔末发现氢原子光谱在可见光区的四条谱线的波长可以用一个简单的公式表示。
巴尔末公式为(1)/(λ)=R((1)/(2^2) - (1)/(n^2)),其中λ是谱线的波长,R称为里德伯常量,R = 1.097×10^7m^-1,n = 3,4,5,·s。
- 巴尔末公式的意义在于它反映了氢原子光谱的规律性,表明氢原子光谱的波长不是连续的,而是分立的,这是量子化思想的体现。
2. 里德伯公式。
- 里德伯将巴尔末公式推广到更一般的形式(1)/(λ)=R((1)/(m^2)-(1)/(n^2)),其中m = 1,2,·s,n=m + 1,m + 2,·s。
当m = 1时,对应赖曼系(紫外区);当m = 2时,就是巴尔末系(可见光区);当m = 3时,为帕邢系(红外区)等。
二、氢原子光谱的实验规律与玻尔理论的联系。
1. 玻尔理论对氢原子光谱的解释。
- 玻尔提出了三条假设:定态假设、跃迁假设和轨道量子化假设。
- 根据玻尔理论,氢原子中的电子在不同的定态轨道上运动,当电子从高能级E_n向低能级E_m跃迁时,会发射出频率为ν的光子,满足hν=E_n-E_m。
- 结合氢原子的能级公式E_n=-(13.6)/(n^2)eV(n = 1,2,3,·s),可以推出氢原子光谱的波长公式,从而很好地解释了氢原子光谱的实验规律。
例如,对于巴尔末系,当电子从n(n>2)能级跃迁到n = 2能级时,发射出的光子频率ν满足hν = E_n-E_2,进而可以得到波长与n的关系,与巴尔末公式一致。
2. 氢原子光谱的不连续性与能级量子化。
- 氢原子光谱是分立的线状光谱,这一现象表明氢原子的能量是量子化的。
在经典理论中,电子绕核做圆周运动,由于辐射能量会逐渐靠近原子核,最终坠毁在原子核上,且辐射的能量是连续的,这与实验观察到的氢原子光谱不相符。
18.3 氢原子光谱(45张PPT)

分布。
C 在研究太阳光谱时发现太阳光谱中有许多暗线, 这说明了太阳内部缺少对应的元素。
D 在研究太阳光谱时发现太阳光谱中有许多暗线, 这些暗线与某些元素的特征谱线相对应,这说明 了太阳大气层内存在对应的元素。
随堂练习
1. 对原子光谱,下列说法正确 的是(ACD).
A.原子光谱是不连续的
B.由于原子都是由原子核 和电子组成的,所以各种原 子的原子光谱是相同的
X射线照射激发荧光, 通过分析荧光判断越王 勾践宝剑的成分.
(5)意义:原子光谱的不连续性反映出原子结构的不 连续性,所以光谱分析也可以用于探索原子的结构。
------光谱分析还为深入原子世界打开了道路。近代原 子物理学正式从原子光谱的研究中开始的。
研究原子结构规律有两条途径:
1.利用高能粒子轰击原子—轰出未知粒子来 研究(高能物理);
σ其它谱系
三、经典理论的困难
三、经典理论的困难
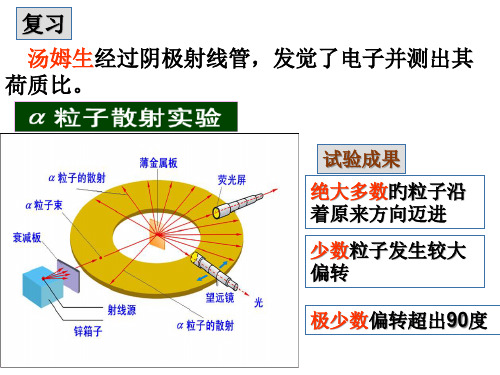
卢瑟福的原子核式模型正确地指出了原子核的存在,很好地解释了α粒子散射实验。
卢瑟福原子核式模型无法解释原子光谱的分立特征
原子核式结构模型与经典电磁理论的矛盾
核外电子绕核运动
辐射电磁波
电子轨道半径连续变小
原子不稳定 辐射电磁波频率连续变化 事实上:原子是稳定的 原子光谱是线状谱,频率不变
《波尔的原子模型》预习问题:
【问题1】什么是轨道量子化?什么是能量量子化? 【问题2】什么是能级?什么是基态?什么是激发态? 【问题3】什么是跃迁?什么是频率条件? 【问题4】画出氢原子n=1、2、3、4的能级图。
谱是线状谱
太阳光谱是吸收光谱,不连续 稀薄的氢气和钠蒸汽产生 的是原子光谱为线状谱
白光通过钠蒸汽产生的光谱是
氢原子光谱优秀课件
令
T
(m)
R m2
,
T
(n)
R n2
1 T (m) T (n)
T (m),T (n) 称为光谱项。
三、经典理论旳困难
卢瑟福原子核式模型正确地指出了原子核旳存 在,很好地解释了α粒子散射试验。但是。经 典物理学既无法解释原子旳稳定性,又无法解 释原子光谱旳分立特征。
按经典物理学电子绕核旋转,作加速运动,电子 将不断向四面辐射电磁波,它旳能量不断减小, 从而将逐渐接近原子核,最终落入原子核中。但 实际上原子是个稳定旳系统。
还 有 三
布喇开系
1
R
1 42
1 n2
n 5,6,7,
个 线 系
普丰特系
1
R
1 52
1 n2
n 6,7,8,
氢原子光谱不是不相关旳,而是有内在联络旳。体现在 其波数可用一普遍公式来表达:1 NhomakorabeaR
1
m
2
1 n2
其 中
m 1,2,3
n m 1, m 2, m 3,
相应一种m构成一种谱线系 每一谱线旳波数都等于两项旳差数
二、光谱分类:
1.发射光谱:物体发光直接产生旳光谱叫做发射光谱。
发射光谱可分为两类:连续谱和线状谱。
2.吸收光谱:
特点:在连续谱上 缺失了某些成份旳光
此光谱图有何特点?
成因:高温物体发出旳白光(其中包括连续分布旳一切 波长旳光)经过物质时,某些波长旳光被物质吸收后产 生旳光谱,叫做吸收光谱。
3.发射光谱与吸收光谱旳相应关系:
轨道及转动频率不断变化,辐射电磁波频率 也是连续旳, 原子光谱应是连续旳光谱。而 实际上看到旳是分立旳线状谱。
这些矛盾阐明尽管经典物理学理论能够很好地 应用宏观物休,但它不能解释原子世界旳现象, 引入新观念是必要旳。
氢原子光谱

1885年巴耳末(Balmer,J.J.182 1885年巴耳末(Balmer,J.J.182 年巴耳末(Balmer,J.J. 1898) 5—1898)根据埃格斯充(Augstrom, 1898 根据埃格斯充(Augstrom, A.J.1814 1874)对光谱线的精确测量,提 A.J.1814—1874)对光谱线的精确测量, 1814 1874 出了氢原子光谱可见光区域光谱线波长的经验公式。 出了氢原子光谱可见光区域光谱线波长的经验公式。19 13年 玻尔(Bohr,N.H.D.1885 19 13年,玻尔(Bohr,N.H.D.1885—19 (Bohr,N.H.D.1885 62)引入量子概念提出的氢原子模型假说, 62)引入量子概念提出的氢原子模型假说,给出了氢光 谱线系规律的理论解释。 谱线系规律的理论解释。
五.数据记录与处理
1.高压汞灯 入射线= 入射线
φ0 右 + φ
2
0左
2、氢灯
特征 谱线
谱线位置
波数Leabharlann 红青蓝若此时仍保持入射角i不变, 若此时仍保持入射角 不变,用未知波长的光线入 不变 射,测出相应的偏向角θ′,便可从定标曲线上找 测出相应的偏向角 , 出它所对应的波长来。 出它所对应的波长来。本实验用汞原子光谱作出 定标曲线,再测出氢原子三条可观察到的光谱线 定标曲线, 的偏向角,在定标曲线上求出它们所对应的波长, 的偏向角,在定标曲线上求出它们所对应的波长, 验算里德伯常数。 验算里德伯常数。
氢原子光谱
引言
每种原子、分子都有其特征光谱。 每种原子、分子都有其特征光谱。因此分析其特征 光谱,对研究不同原子、分子及其结构有着重大的意义。 光谱,对研究不同原子、分子及其结构有着重大的意义。 光谱学已成为光学的一个重要分支, 光谱学已成为光学的一个重要分支,并被广泛用于科研 和生产中。 和生产中。 氢原子是最简单的原子,其光谱线在按波长( 氢原子是最简单的原子,其光谱线在按波长(或波 数)大小的排列次序上显示出简单的规律性。研究原子 大小的排列次序上显示出简单的规律性。 结构,很自然氢原子首先被关注。 结构,很自然氢原子首先被关注。
氢原子光谱实验

将实验结果与理论预测进行 比较,验证量子力学的相关 理论。
根据特征峰的波长和强度, 分析氢原子能级结构及其跃 迁规律。
根据实验结果,进一步探讨 氢原子光谱与其他原子光谱 的共性和差异。
04
结果分析
观察到的光谱类型
发射光谱
氢原子在受激跃迁时释放出的光 子,形成明亮的谱线。
吸收光谱
氢原子吸收特定频率的光子,导 致暗线出现在连续光谱背景上。
特征谱线
氢原子光谱中具有特定波长的谱 线,是氢原子能级跃迁的标志。
能级跃迁的判定
跃迁类型
确定是从高能级向低能级跃迁还是低能级向高能 级跃迁。
跃迁能量
通过测量谱线的波长或频率来确定能级跃迁所需 的能量差。
跃迁选择定则
根据量子力学原理,确定哪些能级间的跃迁是被 允许的。
与理论预期的比较
理论模型
比较实验结果与氢原子波尔模型 的预测,验证理论模型的准确性。
波长与能量
谱线的波长与能量之间存 在反比关系,即波长越短, 能量越高。
03
实验步骤
准备实验器材
氢气
选择纯度较高的氢气, 以减少其他气体对实验
结果的影响。
真空玻璃管
光源
光谱仪
用于装载氢气,保证实 验环境的真空度。
选择稳定、连续高分辨率和
低噪声性能。
参考文献
参考文献
[1] Atkins, P. W., & De Paula, J. (2005). Physical Chemistry for the Biosciences. Academic Press.
[2] Bersohn, R. L., & Guiochon, G. (1975). Experimental methods in physical chemistry. Academic Press.
氢原子光谱课件

氢原子光谱课件引言氢原子光谱是量子力学和原子物理学领域的基础内容,对于理解原子结构、光谱现象以及化学键的形成具有重要意义。
本课件旨在介绍氢原子光谱的基本原理、实验观测和理论解释,帮助读者深入理解氢原子的能级结构和光谱特性。
一、氢原子的基本结构1.1电子轨道和量子数氢原子由一个质子和一个电子组成,电子围绕质子旋转。
根据量子力学的原理,电子在氢原子中只能存在于特定的轨道上,这些轨道被称为能级。
每个能级由主量子数n来描述,n的取值为正整数。
1.2能级和能级跃迁氢原子的能级可以用公式E_n=-13.6eV/n^2来表示,其中E_n 是第n能级的能量,单位为电子伏特(eV)。
当电子从一个能级跃迁到另一个能级时,会吸收或发射一定频率的光子,这个频率与能级之间的能量差有关。
二、氢原子光谱的实验观测2.1光谱仪和光谱图氢原子光谱可以通过光谱仪进行观测。
光谱仪将入射光分解成不同频率的光谱线,并将这些光谱线投射到感光材料上,形成光谱图。
通过观察光谱图,可以得知氢原子的能级结构和光谱特性。
2.2巴尔末公式实验观测到的氢原子光谱线可以通过巴尔末公式来描述,公式为1/λ=R_H(1/n1^21/n2^2),其中λ是光谱线的波长,R_H是里德伯常数,n1和n2是两个能级的主量子数。
巴尔末公式可以准确地预测氢原子光谱线的位置。
三、氢原子光谱的理论解释3.1玻尔模型1913年,尼尔斯·玻尔提出了氢原子的量子理论模型,即玻尔模型。
该模型假设电子在氢原子中只能存在于特定的轨道上,每个轨道对应一个能级。
当电子从一个能级跃迁到另一个能级时,会吸收或发射一定频率的光子。
3.2量子力学解释1925年,海森堡、薛定谔和狄拉克等人发展了量子力学理论,为氢原子光谱提供了更为精确的解释。
量子力学认为,电子在氢原子中的状态可以用波函数来描述,波函数的平方表示电子在空间中的概率分布。
通过解薛定谔方程,可以得到氢原子的能级和波函数。
四、结论氢原子光谱是量子力学和原子物理学的基础内容,对于理解原子结构、光谱现象以及化学键的形成具有重要意义。
氢原子光谱实验结果

氢原子光谱实验结果氢原子光谱实验是研究氢原子光谱线的分布和强度的重要实验之一。
通过该实验,我们可以获得氢原子能级跃迁的详细信息,从而深入了解氢原子的结构和性质。
以下是氢原子光谱实验结果的2000字报告。
一、实验原理氢原子光谱是由氢原子能级跃迁产生的光子分布组成的。
根据波恩定理,氢原子光谱线的波长与能级之间存在一定的关系。
通过测量不同波长的光谱线,我们可以确定氢原子的能级结构,进一步了解氢原子的性质。
二、实验步骤1.准备实验设备:氢原子光谱实验需要使用高精度的光谱仪、激光器、单色仪等设备。
在实验前,需要对这些设备进行仔细的检查和校准,确保实验结果的准确性。
2.制备氢原子:在实验中,需要使用纯度较高的氢气,并通过激光激发制备氢原子。
制备的氢原子需要满足实验所需的光谱条件。
3.测量光谱线:将制备好的氢原子通过单色仪照射到光谱仪上,测量不同波长的光谱线。
在测量时,需要注意控制实验条件,如温度、压力等,以减小误差。
4.数据处理与分析:对测量得到的光谱数据进行处理和分析,提取出不同能级跃迁的光谱线位置和强度信息。
三、实验结果表1展示了实验中测量的部分氢原子光谱线的波长和强度信息。
从表中可以看出,不同能级跃迁产生的光谱线波长和强度都有所不同。
这些数据为我们提供了氢原子能级跃迁的详细信息,有助于我们了解氢原子的结构和性质。
表1:实验中测量的部分氢原子光谱线波长和强度信息图1展示了实验中测量的部分氢原子光谱线的波长与能级之间的关系。
从图中可以看出,不同能级跃迁产生的光谱线波长与能级之间存在明显的规律性。
这进一步验证了波恩定理的正确性,说明我们可以通过测量光谱线的波长来确定氢原子的能级结构。
图1:部分氢原子光谱线的波长与能级之间的关系四、结果分析通过对比实验数据与理论预测,我们发现实验结果与理论预测基本一致。
这表明我们的实验设备和方法是可靠的,能够准确测量氢原子光谱线的波长和强度信息。
同时,实验结果也验证了波恩定理的正确性,进一步证实了氢原子的能级结构。
氢原子光谱

e2
rn
0h
2 2
π me
n r1n (n 1,2,3,)
2 2
n 1 , 玻尔半径 r1
0h
2 2
π me
5.2910 m
11
氢原子能级公式 第 n 轨道电子总能量
1 e2 2 En mvn 2 4π 0 rn
me 1 E1 En 2 2 2 2 8 0 h n n
答案C
2.具有下列哪一能量的光子,能被处在n = 2的能 级的氢原子吸收? (A) 1.51 eV. (B) 1.89 eV.
(C) 2.16 eV.
(D) 2.40 eV.
答案B
例题1. 实验发现基态氢原子可吸收能量为 12.75 eV的 光子. (1) 试问氢原子吸收该光子后将被激发到哪个能级? (2) 受激发的氢原子向低能级跃迁时,可能发出哪几 条谱线?请画出能级图(定性),并将这些跃迁画在能 级图上. (3)巴耳末线系有几条? 莱曼系有几条?
e +
玻尔(1885-1962)丹麦人,是原子 物理学的奠基人。他在研究量子运动 时,提出了一整套新观点,建立了原 子的量子论,首次打开了人类认识原 子结构的大门,为近代物理研究开辟 了道路。近代物理学大厦的基础-量 子力学,是以玻尔为领袖的一代杰出 物理学家集体才华的结晶。1922年诺 贝尔物理学奖获得者。
例题2. 求巴耳末系光谱的最大和最小波长
解:
玻尔频率条件 h Ei E f
ch Ei E2
最大波长 最小波长
ch 658 nm E3 E2
ch 366 nm E E 2
例题3
欲使氢原子能发射巴耳末系中波长为
氢原子光谱ppt课件

03
氢原子光谱实验观测与分析
氢原子光谱实验装置介绍
光源
氢原子灯或放电管,产生氢原子 光谱。
单色仪
将复合光分解为单色光,并可选 择特定波长的光通过。
光探测器
如光电倍增管或CCD,将光信号 转换为电信号进行记录和分析。
数据采集与处理系统
对实验数据进行采集、处理和分 析,得出实验结果。
氢原子光谱观测方法
氢原子光谱研究挑战与机遇
实验技术挑战
01
尽管精密测量技术取得了显著进展,但进一步提高测量精度仍
面临诸多挑战,如如何消除系统误差、提高信噪比等。
理论模型挑战
02
现有理论模型在描述某些复杂现象时仍存在一定局限性,需要
进一步完善和发展。
交叉学科机遇
03
氢原子光谱研究与粒子物理、宇宙学等领域密切相关,这些领
04
氢原子光谱理论解释与应用
薛定谔方程与波函数概念
薛定谔方程
描述了微观粒子状态随时间变化 的规律,是量子力学的基本方程
之一。
波函数
量子力学中用来描述粒子状态的函 数,其模平方表示粒子在特定位置 被发现的概率。
量子数
描述原子或分子中电子运动状态的 参数,如主量子数、角量子数等。
氢原子光谱理论解释
玻尔模型
玻尔提出的氢原子模型,假设电子在 特定轨道上运动,且能量是量子化的。
能量级与光谱线
选择定则
解释了为何只有特定能级间的跃迁才 会产生光谱线,如偶极跃迁选择定则 等。
氢原子光谱由一系列分立的谱线组成, 对应着电子在不同能级间的跃迁。
氢原子光谱在物理、化学等领域应用
01
02
03
04
原子钟
利用氢原子光谱的稳定性和精 确性,制成高精度原子钟,用
原子物理学第二章氢原子光谱

激发态(excited state) 电子轨道
巴耳末系 帕邢系
n 3
பைடு நூலகம்
赖曼系
2
能级(energy level)
1
n
1
2
3
4
En R Tn 2 n hc
hcR En 2 n
根据波尔理论,氢原子的光谱可以作如下的解释: 氢原子在正常状态时,它的能级最小,电子 位于最小的轨道,当原子吸收或放出一定的 能量时,电子就会在不同的能级间跃迁,多 余的能量便以光子的形式向外辐射,从而形 成氢原子光谱。
e Ze
Ze2 F 4π 0 r 2
e2 Ze2
2
n2 Z c rn a1 vn n 1, 2, 3, Z n Z 2 hcR 1 Z 2e2 En 2 2n 4π 0 a1 n2
En2 En1 hc
1 1 1 1 Z R 2 2 R 2 2 n1 Z n2 Z n1 n2
2 2 e 4 RA 2 3 (4 0 ) h c
2 2 me 4 M M R 2 3 (4 0 ) h c M m M m
(3)
我们看到,当原子核质量M→∞时, RA=R∞=109737.31cm-1。在一般情况下,可以 通过(3)式来计算里德伯常数。
里德伯常数随原子核质量变化的情况曾被 用来证实氢的同位素—氘的存在。还可以测 定原子量、电子的核质比、质子的质量和电 子的质量之比等。 起初有人从原子质量的测定问题估计有质量 是2个单位的中氢。 1932年,尤雷在实验中发现,所摄液氢赖 曼系的头四条谱线都是双线,双线之间波长 差的测量值与通过里德伯常数 R 计算出的双 线波长差非常相近,从而确定了氘的存在。
氢原子光谱

氢原子光谱
氢原子的发现和光谱特性
氢原子是最简单的原子之一,在光谱学中具有重要的地位。
氢原子光谱是研究
原子结构和光谱学的基础。
它对研究光谱的性质和发展原子理论有着重要的意义。
氢原子光谱的基本原理
氢原子光谱是指氢原子在特定条件下发射或吸收的光线的谱线。
氢原子光谱是
由氢原子的特有能级结构和跃迁引起的。
氢原子的光谱具有一定的规律性,可以通过一系列的数学模型进行描述和解释。
氢原子光谱的光谱线
氢原子光谱的典型谱线分为巴尔末系列、帕邢系列和莱曼系列。
这些系列分别
对应不同的跃迁过程,反映了氢原子的不同能级结构和性质。
巴尔末系列
巴尔末系列是氢原子光谱中最常见的系列之一,对应着n元素的n=2的跃迁。
巴尔末系列谱线主要在紫外和可见光区域,具有重要的实验和理论价值。
帕邢系列
帕邢系列对应着n元素的n=3的跃迁。
帕邢系列谱线分布在可见光区域,是
研究氢原子光谱的重要线系之一。
莱曼系列
莱曼系列对应着n元素的n=1的跃迁。
莱曼系列包含了氢原子最基本的谱线,是氢原子光谱中的重要部分。
氢原子光谱的应用
氢原子光谱不仅在基础科学研究中具有重要意义,还在实际应用中发挥着重要
作用。
氢原子光谱在天文学、材料科学、化学等领域有着广泛的应用。
结语
氢原子光谱是原子光谱学中的重要内容,研究氢原子光谱有助于深入理解原子
结构和光谱现象。
通过对氢原子光谱的研究,人们可以更好地认识原子的结构和性质,推动光谱学领域的进步与发展。
氢原子光谱

在光谱上表现为谱线的分裂和位移,可通过高分辨率光谱仪 进行观测。
氢原子光谱超精细结构探讨
超精细结构成因
在精细结构的基础上,由于原子核自旋与电子总角动量的耦合,导致能级进一步分裂。
超精细结构特点
在光谱上表现为谱线的更细微分裂和位移,需要更高精度的观测手段进行探测。
总结
氢原子光谱是量子力学和原子物理领域的重要研究对象,其性质和特点包括多个线系、精 细结构和超精细结构等。通过对氢原子光谱的深入研究,可以揭示原子内部结构和能级分 布的奥秘,为现代物理学的发展提供重要支撑。
02
氢原子光谱实验方法
氢原子光谱实验装置
光源
提供足够能量的光源,如钨丝 灯或激光器,以激发氢原子。
分光仪
将光源发出的光分成不同波长 的光谱。
探测器
用于检测分光后各波长光的强 度,如光电倍增管或CCD。
数据采集与处理系统
记录并处理实验数据,如计算 机和专用软件。
氢原子光谱实验步骤
1. 准备实验装置
量子力学对氢原子光谱解释
波函数与概率密度
量子力学用波函数描述电子状态,波函数的模平方表示电子在空间 中出现的概率密度。
能级与跃迁
量子力学中的能级概念与玻尔理论相似,但更为精确。电子在不同 能级间跃迁时,同样会发射或吸收光子。
选择定则
量子力学中的选择定则规定了哪些能级间的跃迁是允许的,从而解释 了氢原子光谱的特定结构。
氢原子光谱研究前景展望
• 高精度测量技术的发展:随着实验技术的不断进步,未来有望实现更高精度的氢原子光谱测量,从而更深入地 揭示原子结构和相互作用的奥秘。
• 新理论模型的探索:尽管现有的理论模型能够很好地解释氢原子光谱,但仍存在一些尚未解决的问题,如高阶 效应的处理、相对论和量子电动力学的结合等。未来有望通过发展新的理论模型,更准确地描述氢原子光谱。
183氢原子光谱

发射与吸收光谱
发射光谱
当氢原子从高能级跃迁到低能级时, 会发射出特定波长的光子,形成发射 光谱。这些谱线对应于不同能级间的 跃迁。
吸收光谱
当连续光谱的光通过氢原子气体时, 某些特定波长的光会被吸收,从而在 连续光谱上形成暗线。这些暗线对应 于氢原子的吸收光谱。
02
氢原子光谱实验方法
氢原子放电实验
氢原子的基态(最低能级)是 n=1,激发态则是n>1的能级 。
光谱线系与命名
氢原子光谱线系主要包括巴尔末 系、莱曼系、帕邢系、布拉开系
和普丰特系等。
巴尔末系是最早被发现的氢原子 光谱线系,位于可见光区,由 Hα、Hβ、Hγ、Hδ等谱线组成 。
其他线系如莱曼系位于紫外区, 帕邢系、布拉开系和普丰特系则
应用领域的拓展
随着氢原子光谱研究的深入,未来有望在更多领域实现应用拓展,如利用氢原子光谱进 行精密测量、探索宇宙中的物质组成等。
THANKS
感谢观看
量子力学描述与薛定谔方程
波函数与概率密度
在量子力学中,氢原子的状态用波函数$psi(r,theta,phi)$ 描述,波函数的模平方$|psi|^2$表示电子在空间中出现 的概率密度。
薛定谔方程
氢原子的波函数满足薛定谔方程$hat{H}psi = Epsi$,其 中$hat{H}$是哈密顿算符,$E$是能量本征值。
荧光观测
将激光照射到荧光物质上 ,观测荧光光谱,分析氢 原子能级结构。
其他实验方法
原子束实验
利用原子束技术,将氢原子束射 入磁场或电场中,观测其偏转或 分裂现象,研究氢原子光谱和能
级结构。
光电子能谱实验
利用光电子能谱技术,研究氢原子 在光照条件下的电子能级跃迁和光 谱特性。
氢(氘)原子光谱

氢(氘)原子光谱姓名:唐方学号:091120119引言光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1883 年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932 年尤里(H .C.Urey)根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氧的同位素——氚的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
WGD-3 型光栅光谱仪用于近代物理实验中的氢(氘)原子光谱实验,一改以往在大型摄谱仪上用感光胶片记录的方法,而使光谱既可在微机屏幕上显示,又可打印成谱图保存,实验结果准确明了。
实验目的1.熟悉光栅光谱仪的性能与用法。
2.用光栅光谱仪测量氢原子光谱巴尔末线系的波长,求里德伯常数。
实验原理1.氢原子光谱氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102 Pa左右),可得到线状氢原子光谱。
瑞士物理学家巴尔未根据实验结果给出氢原子光谱在可见光区域的经验公式=(2.5-1)式中为氢原子谱线在真空中的波长,=364.57 nm 是一经验常数;n取3,4,5等整数。
若用波数表示,则(2.5-1)式变为==() (2.5-2) 式中称为氢的里德伯常数。
根据玻尔理论,对氢和类氢原子的里德伯常数的计算,得=(2.5-3)式中M为原子核质量,m为电子质量,e为电子电荷,c 为光速,h 为普朗克常数,为真空介电常数,Z为原子序数。
当时,由(2.5-3)式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)(2.5-4) 所以(2.5-5)对于氢,有(2.5-6)这里是氢原子核的质量。
由此可知,通过实验测得氢的巴尔末线系的前几条谱线的波长,借助(2.5-6)式可求得氢的里德伯常数。
第三节氢原子光谱
R(
1 22
1 n2
)
n=3,4,5,6……
其中R称为里德伯常量
R 1.097 10 m 对于氢原子
7
-1
注意表达的顺序,因为不同
的原子,该常数也不同.
氢原子光谱的实验规律
H
H H H
H
656.3n m 486.1n m 434.1nm 410.2nm 364.6nm
n=3
n=4
不同的m对应不同的谱系;当m一定时,每 T (n)
式中
T
(m)
R m2
,
T
(n)
R n2
称为光谱项
6、原子光谱
氢原子光谱只是众多原子光谱中最简单的一种,下图列出 了钠、氦和汞等原子的光谱。
科学家观察了大量的 原子光谱,发现每种原子都有 自己特定的原子光谱。不同的原子,其原子光谱均不相同, 因而,原子光谱被称为原子的“指纹”。我们可以通过对 光谱的分析鉴别不同的原子,确定物体的化学组成并发现 新元素。
1 R( 42
1 n2
)
n=5,6,7,8……
普丰德系(红外区)1 R( 1 1 ) n=6,7,8,9……
52
n2
简称为莱巴帕布普. 请标出课本图3-3-4中帕邢系的4.5.6.7;强调n越小,波长越大
3、广义巴尔末公式
1
1 R( m2
1 n2 )
式中 m与n都是正整数,且 n > m.
莱区 用曼发一系现个(了简紫氢单原的外子公区的式)其表他示1线。系,R这(些11线2 系也n和12巴)耳n末=系2,一3样,可4,以5,…
氢原子光谱

根据玻尔的第二个假设,原子系统中 电子从较高能级Wn,跃迁到较低能级Wk时, 发出单色光,其频率为(图2)
两谱系.这些谱系,的确都在氢原子光谱中观 察到,而且有些还是在玻尔理论发表以后先从理 论上计算出来,然后才通过实验找到的.在k=1时 所表示的谱系在光谱的远紫外部分,称为赖曼系. k=3所表示的谱系在红外部分,称为帕邢系.k=4 和k=5所表示的谱系也都在红外范围,分别称为布 喇开系和普芳德系.在某一瞬时,一个氢原子只 能发射一个一定频率的光子,这一频率相应于一 条谱线,不同的受激氢原子才能发射不同的谱线. 实验中观察到的是大量不同受激状态的原子所发 射光的组合,所以能观察到大量的谱线.[1]
按照经典物理学,核外电子受到原子的库仑引力 的作用,不可能是静止的,它一定是以一定的速 度绕核转动.既然电子在运动,它的电磁场就在 变化,而变化的电磁场会激发电磁波.也就是说, 它将把自己绕核转动的能量以电磁波的形式辐射 出去.因此,电子绕核转动这个系统是不稳定的, 电子会失去能量,最后一头栽在原子核上.但是 事实不是这样,原子是个很稳定的系统. ②连续光谱与明线光谱的矛盾
根据经典电磁理论,电子辐射的电磁波的频率, 就是它绕核转动的频率.电子越转能量越小,它 离原子核就越来越近,转的也就越来越快.这个 变化是连续的,也就是说,我们应该看到原子辐 射的各种频率(波长)的光,即原子的光谱应该 总是连续的.而实际上我们看到的是分立的线状 谱. 这些矛盾说明,尽管经典物理学理论可以很 好地应用于宏观物体,但它不能用于解释原子世 界的现象,引入新观念是必要的.
(2)当原子从一个具有较大能量E2的定态 跃迁到另一个能量较低的定态E1时,它辐 射出具有一定频率的光子,光子的能量为 这一假设确定了原子发光的频率—— 它就是频率假设.
近代物理实验-氢原子光谱

近代物理实验——氢原子光谱一、 实验简介光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法.1885年巴尔末总结了人们对氢光谱的测量结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础.1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素——氘的存在.通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原理论可靠性的标准和测量其它基本物理常数的依据.原子光谱的观测,为量子理论的建立提供了坚实的实验基础。
Johannes Rober Rydberg Johann Jakob Balmer 1825 ~1898 1854~1919瑞士数学兼物理学家 瑞典物理学家、数学家,光谱学的奠基人之一二、 实验目的1.测量氢原子光谱中巴尔末线系的几条谱线的波长,并将在空气中的波长修正为真空中的波长。
2.测量计算各谱线的里德伯常数RH ,并求其平均值或用线性拟和的方法求出RH 。
3.学习多功能组合光谱仪的使用。
三、实验原理在量子化的原子体系中,原子能量状态1E ,2E …为一系列分立的值,原子的每一个能量状态称为原子的一个能级。
原子的最低能级称为原子的基态,高于基态的其余各能级称为原子的激发态。
处于高能级的原子,总是会自发跃迁到低能级,并发射出光子。
设光子能量为ε ,频率为ν,高能级为2E ,低能极为1E ,则2121,.E E h E E hενν-==-=由于原子能级是分立的,所以原子由高能级向低能级跃迁时,会发射一些特定频率的光子,在分光仪上表现为一条条分立的光谱线,称为“线状光谱”或“原子光谱”。
波长λ的倒数是波数,它的值由巴耳末公式决定。
对于H 原子有2212111,H HR n n λ⎛⎫=- ⎪ ⎪⎝⎭(2-1-1)式中H R 为H 原子的里德伯常量,H R =1.096776⨯107m-1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
氢(氘)原子光谱侯建强(南京大学匡亚明学院理科强化部2010级,学号:101242015)1.引言光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
2.实验目的(1)熟悉光栅光谱仪的性能和用法;(2)用光栅光谱仪测量氢原子光谱巴尔末系数的波长,求里德伯常数。
3.实验原理1.氢原子光谱氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102Pa 左右),可得到线状氢原子光谱。
瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式4220-=n n H λλ (1)式中λH 为氢原子谱线在真空中的波长。
λ0=364.57nm是一经验常数。
n取3,4,5等整数。
若用波数表示,则上式变为⎪⎭⎫ ⎝⎛-==221211~n R v H H H λ (2)式中RH 称为氢的里德伯常数。
根据玻尔理论,对氢和类氢原子的里德伯常数的计算,得)/1()4(2320242M m ch z me R z +=πεπ (3)式中M为原子核质量,m为电子质量,e 为电子电荷,c 为光速,h 为普朗克常数,ε0为真空介电常数,z 为原子序数。
当M →∞时,由上式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)320242)4(2ch z me R πεπ=∞ (4)所以错误!未找到引用源。
(5) 对于氢,有)/1(H H M m R R +=∞(6)这里MH 是氢原子核的质量。
由此可知,通过实验测得氢的巴尔末线系的前几条谱线的波长,借助(6)式可求得氢的里德伯常数。
里德伯常数R∞是重要的基本物理常数之一,对它的精密测量在科学上有重要意义,目前它的推荐值为R ∞=10973731.568549(83)/m 。
表2.5-1为氢的巴尔末线系的波长表。
谱线符号 波长(nm ) H α 656.280 H β 486.133 H γ 434.047 H δ 410.174 H ε 397.007 H ζ 388.906 H η 383.540 H θ 379.791 H ι 377.063 H κ375.015值得注意的是,计算R H 和R ∞时,应该用氢谱线在真空中的波长,而实验是在空气中进行的,所以应将空气中的波长转换成真空中的波长。
即λ真空=λ空气+Δλ,氢巴尔末线系前6条谱线的修正值如表2.5-2所示。
氢谱线 H α H β H γ H δ H ε H ζ △λ(nm)0.1810.1360.1210.1160.1120.1102.同位素位移同一元素的不同同位素具有不同的核质量和电荷分布,由此引起原子光谱波长的微笑差别称为“同位素位移”。
一般来说,元素光谱线同位素位移的定量关系是很复杂的,只有像氢原子这样的系统,同位素位移才可以用简单的公式计算。
经原子核是一个质子,其质量为,氘核比氢核多一个中子,其质量为。
由可知氘原子的里德伯常数为1/2D DR R m M ∞=+ (7)由(7)式和(6)式可知氘原子核的质量比11DD HH H D H R M R M M Rm R =⎛⎫-- ⎪⎝⎭(8)对于巴尔末系,氢和氘的谱线计算公式分别为221112H H H R n υλ⎛⎫==- ⎪⎝⎭ (9) 221112D D D R n υλ⎛⎫==- ⎪⎝⎭ (10) 对于相同的n ,由上二式可得氢和氘的同位素位移为(1)(1)HD H D H H HM M mm M M λλλλ-=-=+ (11)H λ和D λ是能够直接测量的量,测出H λ和D λ,就可以计算出氢和氘原子核的质量比。
4.实验仪器实验中用的仪器室WGD-3型组合式多功能光栅光谱仪,其主要由光栅单色仪、接收单元、扫描系统、电子放大器、A/D 采集单元、计算机组成。
其光学原理图如图2.5-2所示,入射狭缝、出射狭缝均为直狭缝,宽度范围0~2.5mm 连续可调,光源发出的光束进入入射狭缝,位于反射式准光镜的焦面上,通过入射的光束经反射成平行光束投向平面光栅G 上,衍射后的平行光束经物镜成像在上和上,通过可以观察光的衍射情况,以便调节光栅;光通过后用光电倍增管接收,送入计算机进行分析。
图2.5-2 光栅光谱仪光学原理图 图2.5-3 闪耀光栅示意图 在光栅光谱仪中常使用反射式闪耀光栅。
如图2.5-3所示,锯齿形是光栅刻痕形状。
现考虑相邻刻槽的相应点上反射的光线。
PQ和P′Q′是以I角入射的光线。
QR和Q′R′是以I′角衍射的两条光线。
PQR和P′Q′R′两条光线之间的光程差是b(sinI+sin I′),其中b是相邻刻槽间的距离,称为光栅常数。
当光程差满足光栅方程b(sin I+sin I′)=kλ, k=0,±1,±2,…时,光强有一极大值,或者说将出现一亮的光谱线。
对同一k,根据I、I′可以确定衍射光的波长λ,这就是光栅测量光谱的原理。
闪耀光栅将同一波长的衍射光集中到某一特定的级k上。
为了对光谱扫描,将光栅安装在转盘上,转盘由电机驱动,转动转盘,可以改变入射角I,改变波长范围,实现较大波长范围的扫描,软件中的初始化工作,就是改变I的大小,改变测试波长范围。
5.实验内容1. 实验准备(1) 实验按图2.5-4接线。
接通电源前,认真检查接线是否正确。
并检查转换开关的位置。
如用光电倍增管接收,将扳手置“光电倍增管”档;如目视,将扳手置“观察缝”档。
然后接通电箱电源,并将电压调到500900V。
(2) 狭缝调整。
根据光源等实际情况,调节123,,S S S 狭缝。
顺时针旋转为狭缝宽度加大,反之减小。
每旋转一周狭缝宽度变化0.5nm 。
为保护狭缝,最大不超过。
不要使狭缝刀口相接触。
用力要轻。
(3) 开启计算机。
启动WGD-3型组合式光栅光谱仪控制处理软件。
(4) 初始化。
屏幕上显示工作界面后,弹出对话框,让操作者确认当前的波长位置是否有效,是否重新初始化。
如果选择取消,则初始化,波长位置回到200nm 处。
软件工作界面主要由菜单栏、主工具栏、辅工具栏、工作区、状态栏、参数设置区以及寄存器信息提示区等组成。
菜单栏有文件、信息/视图、工作、读取数据、数据图形处理等项。
与一般的Windows 应用程序类似。
2. 氢原子发射光谱的测量(1) 利用氦原子发射光谱修正仪器的系统误差由于计算机处理软件存在系统误差,即测得的原子光谱有整体偏移,初始值不为零,在仪器上选择氦原子谱的测量,在“读取数据”项下对曲线进行寻峰,读出波长,和定标光源的已知谱线波长相比较,对波长进行修正,调整系统误差。
实验的具体方法如下:选定光谱光源为氦光源,打开放电管电源。
将光源对准光谱仪入射狭缝,通过螺旋测微器调节狭缝宽度。
必要时可在光源前加聚光镜,移动聚光镜,均匀照亮入射狭缝。
将扳手置“观察缝”,由出射狭缝目视入射狭缝是否均匀照明。
选择参数设置区的“参数设置”项,设置工作方式、范围及状态。
工作方式→模式:所采集的数据格式,有能量、透过率、吸光度、基线。
测光谱时选能量。
间隔:两个数据点之间的最小波长间隔,根据需要在0.1nm 1nm 之间选择。
工作范围:在起始、终止波长和最大、最小值4个编辑框中输入相应的值。
工作状态→负高压:提供给光电倍增管的负高压,设18共八档。
增益:设置放大器的放大率,设18共八档。
采集次数:在每个数据点上采集数据取平均的次数。
拖动滑块,在11000次之间选择。
在参数设置区中,选择“数据”项,在“寄存器”下拉列表框中选择某一寄存器,在数值框中显示该寄存器的数据。
参数设置区中,“系统”、“高级”两个选项,一般不要改动。
待初始化完毕,用鼠标点击文件→新建,并点击工具栏中的“单程”扫描,开始显示图像。
如果在扫描过程中发现峰值超出最高标度,可点击“停止”。
然后寻找最高峰对应的波长,进行定波长扫描(在“工作”菜单内)。
同时调节倍增管前面的狭缝宽度,将峰值调到合适位置。
调节完毕,将波长范围设置成200nm 800nm ,重新初始化,再单程扫描。
扫描完毕,保存文件。
测量氦原子的发射光谱,并与标准值对照,用以修正仪器的系统误差。
(2) 氢原子发射光谱的测量将光源换成氢灯,测量氢光谱的谱线。
注意,换光源前,先关闭先前光源,选择待测光源,再开启电源。
进行单程扫描,获得氢光谱的谱线,通过“寻峰”或“读取谱线数据”求出巴尔末线系前条谱线的波长。
注意测得的氢原子巴尔末线系前4条谱线的波长需要经过校正。
可使用软件进行校正,也可手工校正。
这样获得的光谱数据为氢原子巴尔末线系前4条谱线在空气中的值。
6.实验结果和分析(1)测得的氦元素的峰值和谱线相对能量如表2.5-3所示谱线 He δ He γ He β He α He a 谱线相对能量 717.5 205.1 72.8 771.7 444.0 光谱波长/nm 447.7 471.8 501.9 587.1 705.3 标准波长/nm 447.1 468.6 501.6 587.6 706.6 差值/nm0.63.20.3-0.5-1.3表2.5-3 氦原子光谱实测波长考虑到仪器测量的误差以及零点选择的误差,实测波长与标准波长存在一定的误差,对数据进行一次直线拟合,结果如下:所以真实波长λ与实测波长λ的关系为:1.0120 6.9770λλ=-线性相关系数为0.9999.考虑到471.8nm λ=的数据与标准值误差较大,将其去掉重新拟合结果如下:谱线 He δ He γ He β He α He a 标准值标准波长/nm 447.1 468.6 501.6 587.6 706.6 实测光谱波长/nm 447.7 471.8 501.9 587.1 705.3 差值/nm0.63.20.3-0.5-1.3从表中可以看出修正后一次拟合的结果出了舍去点以外的各个值都与标准值误差很小,因此在对氢原子测量数据进行处理时我们采用修正后的定标函数。
(2)对氢原子光谱进行测量,测得的氢元素的峰值和谱线相对能量如表2.5-4所示 考虑到测量氦原子时已将零点调至真空中的值,所以这里不用再将波长修正到真空中的值。
(3)计算氢原子光谱各谱线的里德堡常数H R 将拟合后的波长代入221112H H H R n υλ⎛⎫==- ⎪⎝⎭计算里德堡常数,结果如下: (4)计算普适里德堡常数,并与推荐值比较,求相对误差 利用公式1/H HR R m M ∞=+计算出普适里德伯常数(已知电子质量319.10910m kg -=⨯,氢原子核质量271.67310H M kg -=⨯),得出3171279.10910(1/) 1.097(1) 1.907(10)1.67310H H R R m M m --∞-⨯=+=⨯+≈⨯ 已知R ∞的推荐值为10973731.568549(83)/m ,故相对误差为:1.097 1.097100%01.097η-=⨯=7.思考题(1)氢光谱巴尔末线系的极限波长是多少?答:氢原子光谱在可见光区域的经验公式为2024Hnnλλ=-,式中Hλ为氢原子谱线在真空中的波长,0364.57nmλ=是一经验常数。
