游戏中的数学模型
游戏中的数学模型

Q4= 0
1 0
0
0
0
1
0
0
0
0
1 0 0
0 1 0
0 0 0
Q5=
1
0
1
0
0
Q6=
0 1
Q7=
0 0 0 1 0 0 0 1 可以证明, Dü rer空间(简称D空间)中任何一个元 素都可以用Q1,Q2,…,Q8来线性表示,但它们能 0 0 1 0 否构成D空间的一组基呢? 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1
类似于矩阵的加法和数乘,定义魔方的加法和数乘。
易验证,D 对加法和数乘封闭,且构成一线性空间。 记 M ={所有的4×4数字方} ,则其维数为16。 而D是M的子空间,则D是有限维的线性空间。 根据线性空间的性质,如果能得到D的一组基, 则任一个Durer方均可由这组基线性表示。
Durer魔方的维数和生成集
140 110 50 70 20
160 90 60
120 130 30
a11 a12 a13 a14
b11 b12 b13 b14
A=
a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44
B=
b21 b22 b23 b24 b31 b32 b33 b34 b41 b42 b43 b44
(i)可取状态:根据题意,并非所有状态都是允许的,例如 (0,1,1,0)就是一个不可取的状态。本题中可取状态(即系 统允许的状态)可以用穷举法列出来,它们是: 人在此岸 人在对岸 (1,1,1,1) (0,0,0,0) (1,1,1,0) (0,0,0,1) (1,1,0,1) (0,0,1,0) (1,0,1,1) (0,1,0,0) (1,0,1,0) (0,1,0,1) 总共有十个可取状态,对一般情况,应找出状态为可取的充 要条件。 (ii)可取运算:状态转移需经状态运算来实现。在实际问题 中,摆一次渡即可改变现有状态。为此也引入一个四维向量 (转移向量),用它来反映摆渡情况。例如 (1,1,0,0) 表示人带狗摆渡过河。根据题意,允许使用的转移向量只能 有(1,0,0,0,)、(1,1,0,0)、(1,0,1,0)、 (1,0,0,1)四个。
关于扫雷游戏地雷的合理性设置的数学模型

关于扫雷游戏地雷的合理性设置的数学模型摘要:本文主要利用了最小二乘法和统计学知识,从合理性的角度出发,分析和解决了地雷数量最优化的问题,根据地雷数量对游戏难度进行了分级。
问题一:考虑到地雷分布以及触雷概率的合理性,人为提出了地雷分布的约束条件,即:方阵中至少有一个方块中是小于8的数字,以此为约束,得出方阵中最多可容地雷数sum=331。
然后,针对结果分析,并建立了优化模型,追加提出最高触雷率pm在0.5左右的理念,并以此对方块中数字上限M加以约束,利用统计学知识得到最佳上限M。
然后,根据M的值,利用最小二乘法,得出了最多可容地雷数sum=212。
最后进行模型推广,将模型应用于求19阶以上的方阵最大容雷数。
问题二:衡量游戏难度的重要标准是“在能判断雷分布之前游戏猜测触雷的概率和进行必要的无雷操作次数x”。
根据统计学的基本规律,分析求解出在分隔区域与整体区域猜测触雷的概率和已进行的无触雷操作的个数x之间的关系。
利用这个关系解出前者概率为1时,x的取值临界。
得出x关于地雷数n的函数,并将这个函数代入整体区域猜测触雷的概率与x的关系。
这样就把衡量游戏难度的两个重要标准都化成了关于地雷数n的数学模型。
分析这个模型,绘制出函数图像。
这样就实现了地雷数量对游戏难度的控制和分级。
利用问题1、2的分析结果,模拟出符合要求的游戏程序。
一:问题重述已知,在一个19*19的正方形中有19*19个小方块,每个方块可能是1到8的八个数字也可能是地雷,并且每个数字周围8个位置的地雷数等于这个数字。
在这种条件下,我们设计了一款挖地雷的游戏,并解决了如下问题:在这个19×19的方块中最多能放多少个地雷,并对游戏的难度进行了分级。
根据题目要求,我们要注意以下几点:1、题目要求设计的游戏与传统的挖地雷游戏有一些不同,它要求对于任意的一个小郑方块,它周围的几个小方块不可以全部是地雷,也不可以没有地雷。
2、根据1的要求,可以求出出最多能放多少个地雷,这是一个最优化的问题,其中,优化的对象就是地雷的数目。
游戏中的数学模型50页PPT

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
游戏中的数学模型
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
Байду номын сангаас 1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
数独中的数学模型

数独中的数学模型摘要现如今数独游戏风靡全球,深受人们喜爱。
其难度等级多样,求解数独难度等级较高的常常需要花费大量的时间和精力,因此我们试图用计算机来解决这一问题。
在问题一中,我们主要考虑空格数的多少以及空格自由度与数独难度等级的关系。
由一定的案例分析得出数独题目的难度等级与空格数存在正比关系,接着我们考虑如果只是简单的按照空格的数目多少来划分数独题目的难易程度是不全面的,因此继续分析,得出空格自由度与数独的难度等级存在正比的关系,最后又以空格数和空格自由度综合分析进行验证,得出此数独等级为3级。
[1] 空格自由度法模型如下:在问题二中,我们运用穷举法分析大量可能情况,再用MATLAB编写程序得出此数独游戏的终盘。
在问题三中,我们运用了比较排除法、唯一解法和综合法来求解此数独游戏,最终选用综合法作为较优方法。
[1]在问题四中,我们用循环回溯法进行求解,使用MATLAB编写程序得出结果(见表8)。
[1]关键字:穷举法比较排除法唯一解法循环回溯法数独空格数空格自由度一、问题背景数独是一种数字解谜游戏,英文名叫Sudoku,前身为“九宫格”,当时的算法比现在的更为复杂,要求纵向、横向、斜向上的三数之和等于15,而不只是数字的不能重复,儒家典籍《易经》中的“九宫图”也是来源于此。
关于它的起源一直存有争议,有人认为最早起源于中国,也有人认为起源于瑞士。
1970年由美国一家数学逻辑游戏杂志首先发表,名为Number。
后在日本流行,于1984年把Sudoku取名为数独。
数独全面考验做题者观察能力和逻辑推理能力,它的玩法逻辑简单,除了1到9的阿拉伯数字以外,不必用到任何东西,但数字的排列方式却又千变万化,不少教育者认为,数独是锻炼大脑的绝佳方式。
它不仅具有很强的趣味性,也是一种对智慧和毅力的考验。
二、问题重述芬兰一位数学家号称设计出全球最难的“数独游戏”,并刊登在报纸上,让大家去挑战。
这位数学家说,他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。
游戏数值数学建模——常规篇

数值设定——常规篇——Written by Mervin 本文是数值设定系列的第3篇(第4版),前篇讲述了数学建模的方法和起点;本文主要内容是一些常规内容的构建方法:属性、技能、装备、怪物、任务;Part1.基本属性第一部分——人物基本属性所扮演的角色、常用构建方法和成长模式。
p1.1角色扮演基本属性,特色就全在这个“基础”里面。
顾名思义,基本属性就是人物的一切属性的根本。
好比,攻击力、防御力是操作系统,技能是应用软件,而基本属性是底层汇编;p1.2构建方法作为最底层的计算模块,设计时遵循两个原则:划分到最细;以最简单的方式计算;通常,我们除了基本属性外,还有在中间起作用的属性。
比如闪躲、致命等。
那么,我们需要构建的基本属性模块就是为这一层工作的。
将每一个基本属性划分到足够细、不能再划分,在进行内部联系(计算公式)构建时以简单曲线为主;简单曲线通常指的是以下几种:✓f(x)=ax+b✓f(x)=a(x∈[m,n]); b(x∈[j,k])✓f(x)=ax(x∈[m,n]); =bx(x∈[j,k])举几个简单的例子:✧致命几率=敏捷值/30;1点耐力=10点生命;✧火球术,需要30智力值才能学习;(二段常函数,0:不能学和1:能学);✧60级前,猎人的致命几率=敏捷值/30;60级时,=10%+敏捷值/50;✧p1.3成长模式底层的计算满足的特点就是一目了然、易于控制;这种成长模式可以实现的几种主要功能都是最基本的:开关:0/1;分段、索引:非连续型;递增:连续型;最基本的功能往往是最经的起推敲和反复使用的;一切的关键在于两个基本原则,尤其是划分到最细的原则;最细原则的重要性,在于牵涉到互相之间的联系,足够细致的划分才能整体与局部很好的结合。
我们也有看到一些将属性设定做的很复杂的例子,比如RO;RO在对属性的设定上显得极其复杂,尤其在攻击速度之类的设定上;因为RO的属性点控制的非常紧,所以在一些极限值的做法上,一直是一个非常好的案例,这是我们都应该学习的;而也正是因为这个原因,才使得在原本不多的玩法上,需要强化属性设定这一块;我想开发者在这部分是付出了极大的劳动和付出的。
电子行业电子游戏中的数学

电子行业电子游戏中的数学引言电子游戏已成为当代年轻人生活中不可或缺的一部分。
在这个快节奏和高度竞争的行业中,数学一直被广泛应用于游戏的设计与开发。
本文将探讨电子行业中电子游戏中数学的不同应用领域,并详细介绍这些应用对游戏体验和玩法的影响。
游戏物理学中的数学在电子游戏中,物理引擎起着至关重要的作用。
物理引擎是一套计算机程序,模拟物体之间的交互作用、运动和碰撞。
物理引擎中广泛应用了数学模型,例如牛顿的运动定律和质点系统等。
这些数学模型使得游戏中的物体可以以真实的方式运动、碰撞和交互,增强了游戏的真实感和可玩性。
物理引擎中的数学模型还能够实现游戏角色的动画效果。
通过利用数学曲线和插值算法,开发人员可以将角色的运动和动作流畅地呈现在玩家眼前。
数学模型的运用使得游戏角色的动作更加自然,提升了玩家的沉浸感。
游戏AI中的数学人工智能(AI)在电子游戏中扮演着重要的角色。
游戏中的AI决策根据一系列的算法和数学模型来进行。
例如,路径规划算法使用图论和搜索算法来确定NPC(非玩家角色)移动的最佳路径,使其看起来像是在思考和做出决策。
另外,机器学习算法也被应用于游戏AI中,用于训练NPC学习玩家的行为和策略。
数学模型也用于游戏中的概率模型和随机数生成。
概率模型用于模拟伤害、掉落物品和游戏事件的发生概率。
通过数学计算,开发人员可以精确控制游戏的难度和平衡,确保玩家能够获得具有挑战性和趣味性的游戏体验。
图形学中的数学在电子游戏中,图形学是不可或缺的一部分。
图形学使用数学算法和模型来生成和呈现游戏中的图像和动画。
其中,最常使用的数学技术之一是三维几何学。
通过三维几何学,开发人员可以处理游戏中的维度和空间位置,并在屏幕上生成逼真的三维图像和动画。
在图形学中,线性代数也被广泛应用。
矩阵、向量和变换等概念被用于描述和操作游戏中的物体、光照和相机视角等。
通过线性代数的运算,开发人员可以实现游戏中的旋转、缩放和平移等操作,以及光照效果的模拟。
数独中的数学模型

数独中的数学模型摘要现如今数独游戏风靡全球,深受人们喜爱。
其难度等级多样,求解数独难度等级较高的常常需要花费大量的时间和精力,因此我们试图用计算机来解决这一问题。
在问题一中,我们主要考虑空格数的多少以及空格自由度与数独难度等级的关系。
由一定的案例分析得出数独题目的难度等级与空格数存在正比关系,接着我们考虑如果只是简单的按照空格的数目多少来划分数独题目的难易程度是不全面的,因此继续分析,得出空格自由度与数独的难度等级存在正比的关系,最后又以空格数和空格自由度综合分析进行验证,得出此数独等级为3级。
[1] 空格自由度法模型如下:在问题二中,我们运用穷举法分析大量可能情况,再用MATLAB编写程序得出此数独游戏的终盘。
在问题三中,我们运用了比较排除法、唯一解法和综合法来求解此数独游戏,最终选用综合法作为较优方法。
[1]在问题四中,我们用循环回溯法进行求解,使用MATLAB编写程序得出结果(见表8)。
[1]关键字:穷举法比较排除法唯一解法循环回溯法数独空格数空格自由度一、问题背景数独是一种数字解谜游戏,英文名叫Sudoku,前身为“九宫格”,当时的算法比现在的更为复杂,要求纵向、横向、斜向上的三数之和等于15,而不只是数字的不能重复,儒家典籍《易经》中的“九宫图”也是来源于此。
关于它的起源一直存有争议,有人认为最早起源于中国,也有人认为起源于瑞士。
1970年由美国一家数学逻辑游戏杂志首先发表,名为Number。
后在日本流行,于1984年把Sudoku取名为数独。
数独全面考验做题者观察能力和逻辑推理能力,它的玩法逻辑简单,除了1到9的阿拉伯数字以外,不必用到任何东西,但数字的排列方式却又千变万化,不少教育者认为,数独是锻炼大脑的绝佳方式。
它不仅具有很强的趣味性,也是一种对智慧和毅力的考验。
二、问题重述芬兰一位数学家号称设计出全球最难的“数独游戏”,并刊登在报纸上,让大家去挑战。
这位数学家说,他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。
基本数学模型-关灯游戏

i 1
i 1
( f1, , f25 )AX (g1, , g25 )X ( f1, , f25 )1
AX 1
11
记号约定
• 若不特别说明,加法和数乘均为 F2 中的运 算,加法用 表示,矩阵相乘略去 号
• 对任意矩阵 B ,B B 0,B1 B2 B1 B2 , 但矩阵乘法仍不可交换
9
i5
i 1 i i 1
i5
12 6
分块矩阵
1 1 0 0 0
1
1
1
0
0
1 0 0 0 0
0
1
0
0
0
•
令
H5
0
1
1
1
0
,I5
0
0
1
0
0
0 0 1 1 1
0 0 0 1 0
0 0 0 1 1 H5 I5 0 0
0 0 0 0 0 1
则
Α
I5 0
H5 I5 I5 H5
• 在讨论 55 方格棋盘时,略去表示矩阵阶 数的下标
12
初等变换
H I 0 0 0 1
0 H2 I H 0 0 H1 1
I
H
I
0
0 1
I
H
I 00
1
Α 1 0 I H I 0 1 H (2) (1) 0 I H I 0 1
0
0
I
H
I 1
0 0
IHI
1
0 0 0 I H 1
0 0 0 0 H5 H (H4 H3 H I)1
I
H
I
0
0
1
(H4 H2 I) (5) (1) 0 I H I 0 0 0 I H I
随机演化博弈模型

随机演化博弈模型随机演化博弈模型是指在博弈过程中,参与者之间的策略随机发生变化,从而影响游戏结果的一种数学模型。
在随机演化博弈模型中,每个参与者都可能随机选择一种新的策略,这会改变他们的策略与其他参与者的互动,导致游戏结果的不确定性。
随机演化博弈模型最早由生物学家简·梅耶卢普和马斯坦提出,被广泛应用于生物学、经济学、社会学、政治学等领域。
通过这个模型,人们可以深入研究群体行为现象、政治投票行为、市场竞争、合作与竞争的权衡等重要问题。
在随机演化博弈模型中,参与者在每一轮游戏中都需要选择一种策略,这个策略可以是个人的选择,也可以是一种群体决策的结果。
游戏过程中,每个参与者都会被随机选择,然后会随机选择一种新的策略。
这个新的策略可能来自于其他参与者,也可能是一个随机的选择。
通过随机的选择和演化,参与者的策略逐渐演化,直到游戏结束。
经过数学分析和计算机中的模拟实验,研究者们发现,在随机演化博弈模型中,参与者的策略会随着时间的推移而趋于平均值,从而导致游戏结果趋于合作。
这种结果与实际经验相一致,也得到了很好的验证。
随机演化博弈模型为我们提供了一种新的思路,可以用来解决人类社会中的一些重要问题,如如何保持社会稳定和如何推动社会进步。
总之,随机演化博弈模型是一种非常有价值的数学模型,它能够帮助我们理解博弈过程中参与者之间的竞争和合作关系。
随机演化博弈模型为我们提供了一种新的思考框架,可以应用到生物学、社会学、经济学和政治学等多个领域。
随着技术的不断进步,随机演化博弈模型还将继续为我们解决更多的实际问题。
《游戏中的数学研究》总结报告

《游戏中的数学研究》总结报告课题《游戏中的数学模型教学研究》中期总结报告厦门市逸夫中学数学组2006年4月,我组根据我校实际,申请并承担了思明区“十一、五”教育科研课题《游戏中的数学模型教学研究》的研究任务,随即成立了相应的课题研究小组,并积极组织相应的课题培训和学习,我们对课题的内涵进行了认真的思考和研究,对本课题相关概念和理论依据有了更清晰的认识和定位,确立了研究方案。
启动研究至今,在区、校教科室的指导和校领导的支持、帮助下,我们严格按课题计划开展研究,强化课题的过程管理,在课题组全体教师共同努力下,课题研究有序开展,初步取得了一些研究成果和相应的实践成效,现将该课题的工作情况总结如下:一、问题的提出1、素质教育呼唤课堂教学模式的创新如何改变现有教学模式,提高驾驭课堂的能力,符合新课程标准的教学要求,是我们学校数学组在教学改革中必须面对、必须解决的问题。
在教学实践中我们发现,学生对于游戏中的数学有很浓厚的兴趣,更容易激发学生学习数学的兴趣,而且绝大部分数学学习的困难学生也会变得很专注,能积极思考问题,勇于发表自己的见解。
素质教育要求我们改变传统教学模式,进行课堂教学模式的创新,因此,我们从游戏中的数学模型入手,帮助学生逐步养成用数学的思维和方法思考问题,使他们真正体会到学习数学的乐趣以及如何在生活中应用数学,做到活学活用,提高数学能力,通过课堂教学模式的创新,达到新课程标准的要求。
2、本校实际要求课堂教学模式的创新我校的学生大多是外来员工的子弟,他们很多缺少扎实的数学基础知识,课堂上不能专心学习,缺乏学习的积极性、主动性。
如何通过课堂教学模式的创新,促使学生课堂上能集中注意力,逐渐培养学习数学的兴趣,提高数学学习成绩,是每位数学教师都在认真思考的问题。
这对于我校学生在将来能不能得到持续发展,我校的教学成绩能否得到进一步提高都是非常重要的。
因此,我们决定以游戏中的初中数学模型的研究作为突破口,努力使我校现有数学教学情况有较大转变为目标,积极推进我校数学课堂教学模式的创新。
马尔可夫网络在智能游戏中的应用(六)

马尔可夫网络在智能游戏中的应用马尔可夫链是一种数学模型,描述的是在给定当前状态下,转移到下一个状态的概率。
这种模型在智能游戏中有着广泛的应用,能够帮助游戏开发者提高游戏的智能化程度,增加游戏的趣味性和挑战性。
1. 游戏中的随机事件智能游戏中经常会出现一些随机事件,比如怪物的移动轨迹、玩家的行为选择等。
马尔可夫链可以帮助游戏引擎根据当前状态和转移概率,预测下一个状态的情况。
这样就可以让游戏中的随机事件更加合理和自然,增加游戏的真实感和挑战性。
2. 游戏中的人工智能在智能游戏中,人工智能扮演着重要的角色。
马尔可夫链可以被用来建模游戏中的人工智能的行为模式。
通过分析玩家的行为和游戏环境的变化,游戏引擎可以根据马尔可夫链模型,预测人工智能的下一步行动,从而使人工智能更加智能化和逼真。
3. 游戏场景的生成马尔可夫链还可以被用来生成游戏场景,比如地图、怪物分布等。
通过分析游戏内部的环境特征和玩家的行为,游戏引擎可以根据马尔可夫链,预测下一个场景的生成情况,从而使得游戏的可玩性和趣味性大大增加。
4. 游戏的难度调整在智能游戏中,难度的调整是一项重要的工作。
通过马尔可夫链,游戏引擎可以根据玩家的实时行为和游戏环境的变化,调整游戏的难度。
这样就可以让游戏更加贴近玩家的需求,增加游戏的可玩性和挑战性。
5. 游戏中的自然语言处理在一些角色扮演游戏中,玩家和游戏角色的对话是非常重要的一部分。
通过马尔可夫链和自然语言处理技术,游戏引擎可以根据玩家的对话和游戏角色的个性特点,生成更加智能化和逼真的对话内容,增加游戏的趣味性和交互性。
总结马尔可夫链作为一种重要的数学模型,在智能游戏中有着广泛的应用。
通过马尔可夫链,游戏引擎可以根据当前状态和转移概率,预测游戏中的随机事件、人工智能的行为、游戏场景的生成、难度的调整和对话内容的生成,从而增加游戏的智能化程度,提高游戏的趣味性和挑战性。
未来,随着人工智能技术的不断发展,马尔可夫链在智能游戏中的应用也将会变得更加广泛和深入。
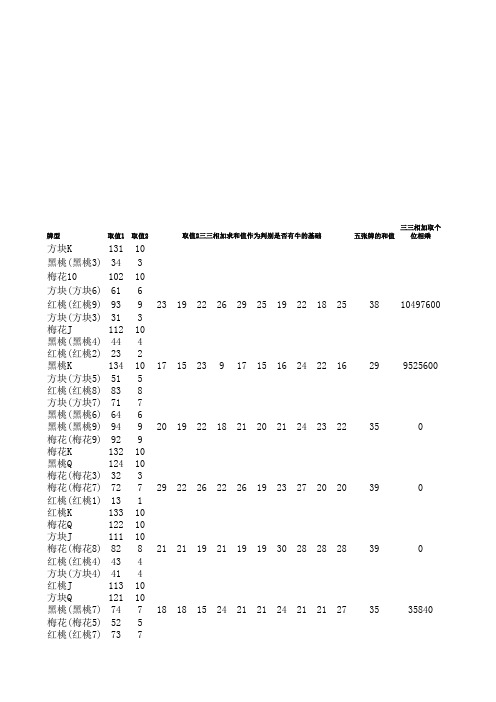
斗牛游戏数学模型及EXCEL公式应用实例1.0版
方块10
101 10
梅花(梅花6) 62 6
方块(方块2) 21 2
红桃(红桃5) 53 5 21 17 20 13 16 12 18 21 17 13 28
0
红桃(红桃6) 63 6
红桃10
103 10
方块(方块9) 91 9
红桃Q
123 10
黑桃(黑桃2) 24 2 25 26 18 25 17 18 29 21 22 21 37 1209600
0
红桃(红桃4) 43 4
方块(方块4) 41 4
红桃J
113 10
方块Q
121 10
黑桃(黑桃7) 74 7 18 18 15 24 21 21 24 21 21 27 35
梅花(梅花5) 52 5
红桃(红桃7) 73 7
35840
13 22 15 16 9 18 18 11 20 14 26
0
黑桃(黑桃1) 14 1
黑桃J
114 10
红桃(红桃3) 33 3 13 22 15 16 9 18 18 11 20 14 26
0
黑桃(黑桃8) 84 8
方块(方块1) 11 1
方块(方块8) 81 8
梅花(梅花2) 22 2
梅花(梅花1) 12 1 17 11 10 18 17 11 11 10 4 11 20
0
黑桃(黑桃5) 54 5
牌型
取值1 取值2
取值2三三相加求和值作为判别是否有牛的基础
三三相加取个 五张牌的和值 位相乘
方块K
131 10
黑桃(黑桃3) 34 3
梅花10
102 10
方块(方块6) 61 6
红桃(红桃9) 93 9 23 19 22 26 29 25 19 22 18 25 38 10497600
数学在游戏设计中的应用

数学在游戏设计中的应用数学是一门与游戏设计息息相关的学科。
从游戏的物理引擎到角色的动画,从世界观的构建到玩家的数值分析,数学的应用无处不在。
本文将探讨数学在游戏设计中的应用,并展示它对游戏体验的重要性。
一、物理引擎物理引擎是游戏设计中最重要的组成部分之一。
它负责模拟游戏中物体的运动和碰撞等物理现象。
这些现象都可以用数学模型来表示和计算。
比如,通过牛顿运动定律和万有引力定律,可以计算出游戏中弹射物体的轨迹和碰撞后的反弹角度。
数学模型的精确性和效率直接影响着游戏的真实感和流畅度。
二、角色动画游戏中的角色动画是通过数学计算来实现的。
通过对角色骨骼的数学建模,可以实现人物的各种动作。
例如,通过线性插值和贝塞尔曲线,可以实现平滑的运动轨迹。
通过对角色的关节角度进行计算,可以实现逼真的姿势和动画效果。
数学的应用使得游戏中的角色动画更加流畅和逼真。
三、世界观构建游戏的世界观构建过程中也少不了数学的应用。
比如,通过三维欧几里得空间的坐标变换和投影技术,可以实现游戏中的三维场景。
使用三角函数和矩阵运算,可以实现光影效果和物体的变形效果。
数学的应用为游戏的世界观构建提供了强大的工具和支持。
四、数值分析游戏中的数值分析是优化游戏体验的关键环节。
通过对游戏中各种数值的计算和分析,可以确定游戏的难度、平衡性和进度等方面。
数学模型可以帮助设计师进行优化和调整,以达到最佳的游戏体验。
同时,数值分析也可以用于评估玩家的游戏成绩和技能水平,进而提供相应的挑战和奖励。
综上所述,数学在游戏设计中的应用是不可或缺的。
物理引擎、角色动画、世界观构建和数值分析等方面都离不开数学模型和计算。
数学的应用使得游戏更加逼真、流畅和有趣。
作为游戏设计师,我们应该充分认识到数学的重要性,并善于运用数学来创造出更好的游戏体验。
智力游戏中的数学模型研究

智力游戏中的数学模型研究作者:李阳门博来源:《科技视界》 2014年第5期李阳门博(沈阳师范大学,辽宁沈阳 110034)【摘要】随着时代的发展,探索新型的教学模式已经受到越来越多的关注。
在教学实践中我们发现,学生对游戏中的数学更有兴趣,更能激发学习数学的热情,素质教育要求教师改变传统教学模式,进行课堂教学模式的创新[1]。
因此,我们从智力游戏中的数学模型入手,帮助学生逐步养成用数学的思维和方法思考问题,针对较为经典的递归与兑换问题,我们利用数学知识进行分析,建立相应的数学模型,并注意与中学数学研究性课题内容的衔接,为学生提供更多的教育模式,让更多的学生参与到数学模型研究性学习中去,达到为学校教育建设提供可借鉴的有效途径的目的。
【关键词】新型教学模式;智力游戏;递归与兑换;数学模型;教育建设1 课题研究的背景及意义随着人们对教育的逐步重视,探索新型的教育模式已经成为教育发展的新要求。
为了能够使学生主动参与到数学探究式学习中去,教育者就必须考虑在原有的教育模式上进行创新,必须明白智力游戏在数学教学中的重要作用。
因此,应用游戏中的数学模型来启发学生的学习显得尤为重要。
数学建模是数学研究的重要方法,它是沟通数学知识与实践的重要桥梁。
通过对游戏中的数学模型教学研究,可以推进学生对数学建模知识的学习,促进探究能力的提高。
游戏中的数学模型研究,能更好的将数学知识与实际联系起来,让学生体会到数学的价值,提高学生应用数学,学习数学的兴趣,诣在为学校教育建设提供宝贵的意见。
2探究过程2.1前期阶段2.1.1查看并整理有关不同种类的智力游戏的网络资料及书籍,统计出所有智力游戏中应用数学建模方法的模型实例。
2.1.2对不同的智力游戏进行整合,分析其在实际教学中的作用。
2.1.3分析典型实例,建立对应的数学模型, 并注意与中学数学研究性课题衔接,为学生提供更多的教育模式,让更多的学生参与到数学模型研究性学习中。
2.2数学模型构建与求解阶段:问题:把一张壹佰元的纸币兑换成伍拾元、拾元、伍元、贰元和壹元的纸币,所有的兑换种数有多少[3]?分析:解此题需要运用数学建模的方法,这个问题的数学模型为:100=50u+10v+5x+2y+z(1.1)其中u,v分别代表伍拾元和拾元的纸币张数,x,y,z代表伍元,贰元和壹元的纸币张数,显然,u只能取0,1,2三种可能。
电子游戏中的数学模型

电子游戏中的数学模型林彩密葛欣雨蒋耀萱摘要针对电子游戏的换牌规则与策略问题,可以通过比较各种策略下玩家所获得的期望奖金金额的多少评价策略优劣。
还可以根据期望值E<1得出结论——玩家吃亏。
对于问题一,首先计算出各事件换牌前出现的概率,再根据玩家的策略利用条件概率计算出换牌后相应事件变化的概率,然后利用Matlab编程求出换牌后各事件的概率,并根据期望知识得出换牌前后玩家获得的期望奖金金额分别为0.3318元和0.8293元。
对于问题二,主要是评价玩家的策略,根据第一问得出的换牌前后玩家获得的期望奖金金额,可说明玩家的策略优点在于换牌后其获得的期望奖金金额变大,同时根据玩家策略中的其它牌型全换可看出其不足之处。
对于问题三,主要从换牌方式入手,可以从同花大顺依次考虑,得出更好的换牌策略。
关键词:策略概率期望Matlab一、问题的提出随着科技的发展,计算机和网络技术日益发达和普及,电子游戏业也随之有了突飞猛进的发展,成为重要的信息技术和文化方面的交叉产业。
而对电子游戏中的一些数学问题的分析和研究,也成为了一个日益热门的话题。
已知在某电子游戏中设有如下的规则:在该游戏中,玩家每次下注一元,由机器随机分配给玩家五张扑克牌,然后允许玩家有一次换牌的机会,即可以放弃其中的某几张牌,放弃的牌留下的空缺由机器在剩下的47张牌中再次随机分配。
1、该游戏的设奖规则如下:玩家的奖金依据其最后所持有的牌型而定。
下面是一份典型的奖金分配表:牌型奖金(元)同花大顺(10到A)800同花顺50四张相同点数的牌25满堂红(三张同点加一对)8同花 5顺子 4三张相同点数的牌 3两对 2一对高分对(J及以上) 1其它0在上表中,玩家的牌型属于某一类型且不属于任何更高的类型,则赢得该牌型相应的奖金。
2、我们需要解决的问题:(1)若某玩家采取以下策略,当原始的牌型构成一个顺子或更高的牌型时,则放弃换牌的机会;否则,除保留对子或三张相同点数的牌外,将手中其余的牌放弃,由机器再次随机分配。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 图解法 状态s=(x,y) ~ 16个格点 允许状态 ~ 10个 点 允许决策 ~ 移动1或2格; k奇,左下移; k偶,右上移. d1, d11给出安全渡河方案
3 2 1 d11 0 1 2
s1
d1
sn+1
3
x
商人们怎样安全过河
智力游戏 多步决策过程(数学模型)
规格化方法 便于求解 (计算机编程等) 易于推广: 商人和随从人数增加或小船容量加大; 考虑4名商人各带一随从的情况.
(i)可取状态:根据题意,并非所有状态都是允许的,例如 (0,1,1,0)就是一个不可取的状态。本题中可取状态(即系 统允许的状态)可以用穷举法列出来,它们是: 人在此岸 人在对岸 (1,1,1,1) (0,0,0,0) (1,1,1,0) (0,0,0,1) (1,1,0,1) (0,0,1,0) (1,0,1,1) (0,1,0,0) (1,0,1,0) (0,1,0,1) 总共有十个可取状态,对一般情况,应找出状态为可取的充 要条件。 (ii)可取运算:状态转移需经状态运算来实现。在实际问题 中,摆一次渡即可改变现有状态。为此也引入一个四维向量 (转移向量),用它来反映摆渡情况。例如 (1,1,0,0) 表示人带狗摆渡过河。根据题意,允许使用的转移向量只能 有(1,0,0,0,)、(1,1,0,0)、(1,0,1,0)、 (1,0,0,1)四个。
140 110 50 70 20
160 90 60
120 130 30
a11 a12 a13 a14
b11 b12 b13 b14
A=
a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44
B=
b21 b22 b23 b24 b31 b32 b33 b34 b41 b42 b43 b44
由 0,1 数字组合,构造所有的R=C=D=S=1的魔方。 共有8 个,记为Qi, i=1,2,…,8。
1 0
0
0
1
0
0
1
0
0
0
0
0
1
Q1=
0
0
0 0
0
1 0 0 0 1
0
0 0 0 1 0
1
0 1 0 0 0
Q2=
0
0
0 0
1
0 0 1 0 0
0
1 0 0 0 1
0
0 1 0 0 0
Q3=
1 0 0
:
(1,1,0,0) (0,0,1,1) (1,0,1,0) (0,1,0,1) (1,1,1,1) (1,0,0,1) (0,1,1,0) (1,0,0,0) (0,1,1,1)
(不可取) (可取) (不可取) (不可取)
(第二次渡河)
Q8=
0 1
0 0
1 0
0 0
1
0
0
0
Q , Q2 , Q8是否线性无关? , 1
容易看出:
Q1 Q4 Q5 Q8 Q2 Q3 Q6 Q7 0
Q1,…,Q8这8个基本方是线性相关的,即至少存在一个Qj,可 以通过其它7个基本方的线性组合得到。这8个基本方的地位是等 同的,故可不妨设j=8。下面验证Q1,Q2,…,Q7是否线性相关。 令:
多步决策模型: 恰当地设置状态和决策, 确定状态 转移律及目标(目标函数).
例2. 人、狗、鸡、米过河问题
这是一个人所共知而又十分简单的智力游戏。某人要带狗、 鸡、米过河,但小船除需要人划外,最多只能载一物过河, 而当人不在场时,狗要咬鸡、鸡要吃米,问此人应如何过河。
在本问题中,可采取如下方法:一物在此岸时相应分量为1, 而在彼岸时则取 为0,例如(1,0,1,0)表示人和鸡在此岸, 而狗和米则在对岸。
规定一个状态向量与转移向量之间的运算。规定状态向量与 转移向量之和为一新的状态向量,其运算为对应分量相加, 且规定0+0=0,1+0=0+1=1,1+1=0。 (解释) 在具体转移时,只考虑由可取状态到可取状态的转移。问题 化为: 由初始状态(1,1,1,1)出发,经奇数次上述运算转化为 (0,0,0,0)的转移过程。 我们可以如下进行分析 (第一次渡河)
同阶魔方的个数
三阶 四阶 五阶 1个 880个 反射和中心旋转生成8个 反射和中心旋转生成7040个
没人知道有多少个!!! 魔方数量随阶数n增长 的速度实在是太惊人了!
仍以4阶方阵为例 定义:如果4×4数字方,它的每一行、每一列、每一对 角线及每个小方块上的数字之和都为一确定的数,则称
这个数字方为 Durer魔方。
数学模型与游戏
2011年2月21日
过河问题
过河问题是世界名题,有很多种说法。最早引进中国的 是中国数学会第一届理事,扬州中学的数学教师陈怀书 先生。后我国数学科普作家、哈军工大教授薛鸿达先生 曾写过一篇专文《渡河难题》,对此进行了全面介绍。 我们将介绍三种不同的形式。
例1 商人们怎样安全过河
问题(智力游戏) 随从们密约, 在河的任 一岸, 一旦随从的人数 比商人多, 就杀人越货. 乘船渡河的方案由商人决定. 商人们怎样才能安全过河? 问题分析 多步决策过程
什么是Dü rer魔方
所谓的魔方是指由1~n2这n2个正整 数按一定规则排列成的一个n行n列 的正方形 。n称为此魔方的阶 。
多么奇妙的 Dü rer魔方:4阶,每一行之和为 魔方! 34,每一列之和为34,对角线 (或反对角线)之和是34,每个 小方块中的数字之和是34,四个 角上的数字加起来也是34 铜币铸造时间:1514年
R=C=D=S=1的方阵构成的线性空间具有什么样的性质? (这是非常必要的,因为我们一般取的是整数。)
类似于构造n维欧氏空间 1在第一行中共有4种取法,为保持上述 的标准基,利用0和1我们 性质的成立,第二行中的1还有两种取法。当 来构造一些R=C=D=S=1 第二行的1也取定后,第三行与第四行的1就完 的最简单的方阵。 全定位了,故一共可作出8个不同的最简方阵, 称之为基本魔方并记之为Q1,… ,Q8
始,到(3)结束。 方案之一:
开始 铁链下去 侍女下去铁链上来 铁链拿到筐外 公主在下面 可把铁链拿到筐里
(9,5,4,3) →(9,5,4) →(9,5,3) → (9,5)→(9,4)→(5,4,3) →(5,4) →(5,3) →(5)→(4)→(3)。
Dü rer魔方(或幻方)问题
德国著名的艺术家Albrecht Dü rer(1471-1521) 于1514年曾铸造了一枚名为“Melencotia I”的铜 币。令人奇怪的是在这枚铜币的画面上充满了数 学符号、数字及几何图形。这里,我们仅研究铜 币右上角的数字问题
构造魔方是一个古老的数学游戏,起初它 还和神灵联系在一起,带有深厚的迷信色彩。 传说三千二百多年前(公元前2200年),因治 水出名皇帝大禹就构造了三阶魔方(被人们称 “洛书”),至今还有人把它当作符咒用于某 些迷信活动,大约在十五世纪时,魔方传到了 西方,著名的科尼利厄斯· 阿格里帕(1486-1535) 先后构造出了3~9阶的魔方 。
r Q
i 1 i
7
i
0 ,即
r6 r4 r7 r2 r5 r1 r3 r5 r7 r1 r6 r3 r2 r4 r3 r4 r2 r1 r7 r5 r6
r1 r2 r r 3 5 r4 r6 r7
=
0 0 0 0
0,0,1,0
1,0,1,0
0,0,0,0
例3:高塔逃生:铁匠海乔90,公主安娜50,侍女40,铁 链30 原则: 人下来时两个筐子必须都有人或铁链,并且重量相差 10公斤。 注意不同于过河 问题,此过程是 两个筐子装的总重量不超过170公斤。
不可逆的。共有 八种不同的方案, 转化:用向量表示状态:如(9,5,4,3)表示四者均在上面, 可试着做一下。 (9,4)表示海乔和侍女在上面,其余在下面。从(9,5,4,3)开
R=C=D=S
其中:R为行和,C为列和,D为对角线和,S为小方块和
设D为所有满足R=C=D=S的Durer魔方的集合。
10 80 100 150 40 0 9 15 1 6 1 18 0 7 1 允许取相同的数字, 18 并且允许数字在某 9 10 7 0 10 6 0 个数域里任意取值。 0 9 1 16 0 9 1 9 9 6 1 9 9 7
类似于矩阵的加法和数乘,定义魔方的加法和数乘。
易验证,D 对加法和数乘封闭,且构成一线性空间。 记 M ={所有的4×4数字方} ,则其维数为16。 而D是M的子空间,则D是有限维的线性空间。 根据线性空间的性质,如果能得到D的一组基, 则任一个Durer方均可由这组基线性表示。
Durer魔方的维数和生成集
0 0 0 0
0 0 0 0
0 0 0 0
等号两边对应元素相比较,得r1=r2=…=r7=0, , 所以 Q1, Q2 , Q7是线性无关
k=1,2,
S ~ 允许状态集合 S={(x , y) x=0, y=0,1,2,3; x=3, y=0,1,2,3; x=y=1,2}
uk~第k次渡船上的商人数
vk~第k次渡船上的随从数 dk=(uk , vk) ~过程的决策 D={(u , v) u+v=1, 2} 状态因决策而改变
uk, vk=0, 1, 2;
如何构造魔方
奇数(不妨n=5)阶的情况 Step1: 在第一行中间写1 Step2: 每次向右上方移一格依次填按由小到大排列的下 一个数,向上移出界时填下一列最后一行的小方格;向 右移出界时填第一列上一行的小方格。若下面想填的格 你想构造Durer魔方吗? 已填过数或已达到魔方的右上角时,改填刚才填的格子 如何构成所有的Durer魔方?Durer魔方有多少? 正下方的小方格,继续Step2直到填完 偶数阶的情况 偶数阶的魔方可以利用奇数 阶魔方拼接而成,拉尔夫· 斯特雷 奇给出了一种拼接的方法 ,这里 不作详细介绍 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 20
