二次函数压轴题专题一 最短路径问题 (1)
中考数学教学指导:二次函数与最短路程问题

二次函数与路径最值问题一、二次函数与方程、不等式综合【例1】 已知P (3,m -)和Q (1,m )是抛物线221y x bx =++上的两点.(1)求b 的值;(2)判断关于x 的一元二次方程221x bx ++=0是否有实数根,若有,求出它的实数根;若没有,请说明理由;(3)将抛物线221y x bx =++的图象向上平移k (k 是正整数)个单位,使平移后的图象与x 轴无交点,求k 的最小值.【例2】 已知抛物线1C :22y x x =-的图象如图所示,把1C 的图象沿y 轴翻折,得到抛物线2C 的图象,抛物线1C 与抛物线2C 的图象合称图象3C .(1)求抛物线1C 的顶点A 坐标,并画出抛物线2C 的图象;(2)若直线y kx b =+与抛物线2(0)y ax bx c a =++≠有且只有一个交点时,称直线与抛物线相切.若直线y x b =+与抛物线C 1相切,求b 的值;(3)结合图象回答,当直线y x b =+与图象3C 有两个交点时,b 的取值范围.【例3】 关于x 的一元二次方程240x x c -+=有实数根,且c 为正整数.(1)求c 的值;(2)若此方程的两根均为整数,在平面直角坐标系xOy 中,抛物线24y x x c =-+与x 轴交于A 、B 两点(A 在B 左侧),与y 轴交于点C . 点P 为对称轴上一点,且四边形OBPC 为直角梯形,求PC的长;(3)将(2)中得到的抛物线沿水平方向平移,设顶点D 的坐标为(),m n ,当抛物线与(2)中的直角梯形OBPC 只有两个交点,且一个交点在PC 边上时,直接写出m 的取值范围.【例4】 关于x 的一元二次方程22(1)2(2)10m x m x ---+=.(1)当m 为何值时,方程有两个不相等的实数根; (2)点()11A --,是抛物线22(1)2(2)1y m x m x =---+上的点,求抛物线的解析式;(3)在(2)的条件下,若点B 与点A 关于抛物线的对称轴对称,是否存在与抛物线只交于点B 的直线,若存在,请求出直线的解析式;若不存在,请说明理由.【例5】 已知关于x 的一元二次方程()2130x m x m --+-=.(1)求证:不论m 取何值时,方程总有两个不相等的实数根.(2)若直线()13y m x =-+与函数2y x m =+的图象1C 的一个交点的横坐标为2,求关于x 的一元二次方程()2130x m x m --+-=的解.(3)在(2)的条件下,将抛物线()213y x m x m =--+-绕原点旋转180︒,得到图象2C ,点P 为x 轴上的一个动点,过点P 作x 轴的垂线,分别与图象1C 、2C 交于M N 、两点,当线段MN 的长度最小时,求点P 的坐标.【例6】 已知关于x 的一元二次方程220ax x ++=(1)求证:当0a <时,方程220ax x ++=一定有两个不等的实数根; (2)若代数式22x x -++的值为正整数,且x 为整数时,求x 的值; (3)当1a a =时,抛物线22y ax x =++与x 轴的正半轴相交于点(,0)M m ;当2a a =时,抛物线22y ax x =++与x 轴的正半轴相交于点)0,(n N ;若点M 在点N 的左边,试比较1a 与2a 的大小.二、二次函数与路径最值问题【例7】 已知抛物线21y ax bx =++经过点()13A ,和点()21B ,.(1)求此抛物线解析式;(2)点C D ,分别是x 轴和y 轴上的动点,求四边形ABCD 周长的最小值; (3)过点B 作x 轴的垂线,垂足为E 点.点P 从抛物线的顶点出发,先沿抛物线的对称轴到达F 点,再沿FE 到达E 点,若P 点在对称轴上的运动速度是它在直线FE定点F 的位置,使得点P 按照上述要求到达E 点所用的时间最短.(要求:简述确定F 点位置的方法,但不要求证明)【例8】 如图:抛物线经过()()()300440A B C -,,,,,三点.(1)求抛物线的解析式.(2)已知AD AB =(D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的条件下,M 为抛物线的对称轴上一动点,当MQ MC +的值最小时,请求出点M 的坐标.【例9】 在平面直角坐标系xOy 中,抛物线2y x bx c =++经过A (2,0)、B (4,0)两点,直线122y x =+交y 轴于点C ,且过点(8,)D m . (1)求抛物线的解析式;(2)在x 轴上找一点P ,使CP DP +的值最小,求出点P 的坐标;(3)将抛物线2y x bx c =++左右平移,记平移后点A 的对应点为'A ,点B 的对应点为'B ,当四边形''A B DC 的周长最小时,求抛物线的解析式及此时四边形''A B DC 周长的最小值.【例10】 如图,在平面直角坐标系xOy 中,点B 的坐标为(0,2),点D 在x 轴的正半轴上,30ODB ∠=︒,OE为△BOD 的中线,过B 、E两点的抛物线2y ax c =++与x 轴相交于A 、F 两点(A 在F 的左侧)(1)求抛物线的解析式;(2)等边△OMN 的顶点M 、N 在线段AE 上,求AE 及AM 的长;(3)点P 为△ABO 内的一个动点,设m PA PB PO =++,请直接写出m 的最小值,以及m 取得最小值时,线段AP 的长.【例11】 如图,在平面直角坐标系中,O 是坐标原点,点A B ,的坐标分别为()03A ,和()50B ,,连结AB .(1)现将AOB △绕点O 按逆时针方向旋转90°,得到COD △,(点A 落到点C 处),请画出COD △,并求经过B 、C 、D 三点的抛物线对应的函数关系式;(2)将(1)中抛物线向右平移两个单位,点B的对应点为点E,平移后的抛物线与原抛物线相交于点F.P为平移后的抛物线对称轴上一个动点,连结PE PF取得最大值时,,,当PE PF求点P的坐标;(3)在(2)的条件下,当点P在抛物线对称轴上运动时,是否存在点P使EPF△为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.。
二次函数典型例题——最短路径

二次函数典型例题——最短路径1、已知抛物线2:(1)1C y x m x =-++的顶点在坐标轴...上. (1)求m 的值;(2)0>m 时,抛物线C 向下平移n (n > 0)个单位后与抛物线C 1:c bx ax y ++=2关于y 轴对称,且1C 过点(n ,3),求C 1的函数关系式; (3)03<<-m 时,抛物线C 的顶点为M ,且过点P (1,y 0)问在直线1-=x 上是否存在一点Q 使得△QPM 的周长最小,如果存在,求出点Q 的坐标, 如果不存在,请说明理由.(1)m 的值=1,-1,-3;(2)C 1的函数关系式:22y x x =+;(3)Q 的坐标4(1,)3-.2、在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B .⑴直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3)已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值. 解:(1)21(2)4A n n +,,()B n n ,. (2) d =AB =A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+∴ 当14n =时,d 取得最小值18.当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB =PM . (如图10)(3) ∵ 对一切实数x 恒有 x ≤y ≤2124x +, ∴ 对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ① 图10xy111APBMO3、已知关于x 的一元二次方程()0312=-+--m x m x .(1)求证:不论m 取何值时,方程总有两个不相等的实数根.(2)若直线()31+-=x m y 与函数m x y +=2的图象1C 的一个交点的横坐标为2,求关于x 的一元二次方程()0312=-+--m x m x 的解.(3)在(2)的条件下,将抛物线()312-+--=m x m x y 绕原点旋转︒180,得到图象2C ,点P 为x 轴上的一个动点,过点P 作x 轴的垂线,分别与图象1C 、2C 交于N M 、两点,当线段MN 的长度最小时,求点P 的坐标.解:(1)证明:()[]()3412----=∆m m124122+-+-=m m m 1362+-=m m()432+-=m∵不论m 取何值时,()032≥-m ∴()0432>+-m ,即0>∆∴不论m 取何值时,方程总有两个不相等的实数根. (2)将2=x 代入方程()0312=-+--m x m x ,得3=m再将3=m 代入,原方程化为022=-x x , 解得2,021==x x . (3)将3=m 代入得抛物线:x x y 22-=,将抛物线x x y 22-=绕原点旋转︒180得到的图象2C 的解析式为:x x y 22--=.设()0,x P则()3,2+x x M ,()x x x N 2,2--()()25212322232222+⎪⎭⎫ ⎝⎛+=++=---+=x x x x x x MN∴当21-=x 时,MN 的长度最小,此时点P 的坐标为⎪⎭⎫⎝⎛-0,21(昌平)27.已知抛物线2y ax bx c =++经过原点O 及点A (-4,0)和点B (-6,3). (1)求抛物线的解析式以及顶点坐标;(2)如图1,将直线2y x =沿y 轴向下平移后与(1)中所求抛物线只有一个交点C ,平移后的直线与y 轴交于点D ,求直线CD 的解析式;(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离.yx图1BACD O yx图2CD O解:(1)∵ 抛物线经过()0,0,()4,0- ,()6,3-三点,∴ 01640,366 3.c a b a b =⎧⎪-=⎨⎪-=⎩ ………………………………………… 1分解得 1410a b c ⎧=⎪⎪=⎨⎪=⎪⎩,,. …………………………… 2分∴ 抛物线的解析式为214y x x =+.∵()()22211144421444y x x x x x =+=++-=+-∴抛物线的顶点坐标为()2,1-- ……………3分 (2)设直线CD 的解析式为2y x m =+,根据题意,得2124x x x m +=+, …………… 4分 化简整理,得2440x x m --=,由16160m ∆=+=,解得1m =-, ……………… 5分∴直线CD 的解析式为21y x =- .(3)点的坐标为()2,7, …………………………… 6分. ……………………… 7分。
次函数之距离最小

二次函数之最短路径问题例1.(广东)已知二次函数y=x 2-2mx+m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC+PD 最短若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.例2.(甘肃兰州)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线y =23x 2+bx +c 经过点B ,且顶点在直线x =52上.(1)求抛物线对应的函数关系式;(2)若把△ABO 沿x 轴向右平移得到△DCE ,点A 、B 、O 的对应点分别是D 、C 、E ,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD ,已知对称轴上存在一点P 使得△PBD 的周长最小,求出P 点的坐标;例3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例4.(湖南郴州)已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小若存在,请求出点G的坐标;若不存在,请说明理由.例5.(辽宁)如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由; (3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.例6.(山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x 2+2x+3与x 轴交于A 、B 两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求直线AC 的解析式及B 、D 两点的坐标;(2)点P 是x 轴上一个动点,过P 作直线l ∥AC 交抛物线于点Q ,试探究:随着P 点的运动,在抛物线上是否存在点Q ,使以点A 、P 、Q 、C 为顶点的四边形是平行四边形若存在,请直接写出符合条件的点Q 的坐标;若不存在,请说明理由.(3)请在直线AC 上找一点M ,使△BDM 的周长最小,求出M 点的坐标.A O xyBFCA O xyBFC例7.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P 是∠AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使∠CPN=90°若存在,请直接写出点P的坐标.例8.(德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.练习:(烟台)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.例10.已知抛物线y=ax2+bx+1经过点A(1,3)和点B(2,1)。
常考二次函数综合题整理(全)

常考二次函数综合题整理 题型一最短路径问题1、如图,抛物线y=﹣12x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,并证明你的结论;(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.【变式】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;题型二最大面积(线段最长)问题2、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?并求出这个最大值.3、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH△x轴于点H,与BC交于点M,连接PC,求线段PM的最大值.【变式】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,过点P作PE△y轴于点E,连接AE.求△PAE面积S的最大值;题型三 存在点构成等腰三角形问题4、如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.5、如图,已知二次函数y=ax 2+bx+3的图象交x 轴于点A (1,0),B (3,0),交y 轴于点C .(1)求这个二次函数的表达式;(2)直线x=m 分别交直线BC 和抛物线于点M ,N ,当△BMN 是等腰三角形时,直接写出m 的值.【变式】已知二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 、DB ,求证:△BCD 是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P ,使得△PDC 为等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由.【变式】如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点()0,2C -,点A 的坐标是()2,0,P 为抛物线上的一个动点,过点P 作PD x ⊥轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线1x =-.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且14PE OD =,求PBE ∆的面积. (3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的下方,是否存在点M ,使BDM ∆是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.题型四 存在点构成直角三角形问题6、如图,抛物线2y ax bx 4=+-经过()A 3,0-,()B 5,4-两点,与y 轴交于点C ,连接AB ,AC ,BC .()1求抛物线的表达式;()2求证:AB 平分CAO ∠;()3抛物线的对称轴上是否存在点M ,使得ABM V 是以AB 为直角边的直角三角形,若存在,求出点M 的坐标;若不存在,请说明理由.【变式】如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求抛物线的解析式和直线AC 的解析式;(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.●题型四存在点构成等腰直角三角形问题7、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)过点P作x轴的垂线,交线段AB于点D,再过点P做PE△x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.●题型四存在点构成平行四边形问题8、如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.()B-,对称轴为直线l,点M是线段AB的中点.0,5(1)求抛物线的表达式;(2)写出点M的坐标并求直线AB的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.9、如图,已知抛物线y=12x2+bx+c与直线AB:y=12x+12相交于点A(1,0)和B(t,52),直线AB交y轴于点C.(1)求抛物线的解析式及其对称轴;(2)设点M是抛物线对称轴上一点,点N在抛物线上,以点A、B、M、N为顶点的四边形是否可能为矩形?若能,请求出点M的坐标,若不能,请说明理由.10、如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.11、如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在x轴下方且在抛物线对称轴上,是否存在一点Q,使△BQC=△BAC?若存在,求出Q点坐标;若不存在,说明理由.12、如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.连接AC,当直线AM与直线BC的夹角等于△ACB 的2倍时,请直接写出点M的坐标【变式】如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C 两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.【变式】如图,抛物线y=ax 2+bx+c 经过A (﹣1,0),B (4,0),C (0,3)三点,D 为直线BC 上方抛物线上一动点,DE△BC 于E .(1)求抛物线的函数表达式;(2)如图1,求线段DE 长度的最大值;(3)如图2,设AB 的中点为F ,连接CD ,CF ,是否存在点D ,使得△CDE 中有一个角与△CFO 相等?若存在,求点D 的横坐标;若不存在,请说明理由.【变式】如图,已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ,B 两点,直线y x m =+过顶点C 和点B .(1)求m 的值;(2)求函数2(0)y ax b a =+≠的解析式;(3)抛物线上是否存在点M ,使得15MCB ∠=︒?若存在,求出点M 的坐标;若不存在,请说明理由.题型七 存在点使三角形相似问题13、如图,以D 为顶点的抛物线y=﹣x 2+bx+c 交x 轴于A 、B 两点,交y 轴于点C ,直线BC 的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在x 轴上是否存在一点Q ,使得以A 、C 、Q 为顶点的三角形与△BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.14、如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣12x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【变式】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(32,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求△ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE△AC,当△DCE 与△AOC相似时,求点D的坐标.【变式】如图,抛物线y=12x2+bx+c与直线y=12x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).(1)求抛物线的解析式;(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ△PA交y轴于点Q,问:是否存在点P 使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.题型七二次函数与圆结合问题15、如图,△E的圆心E(3,0),半径为5,△E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.(1)求抛物线的解析式;(2)判断直线l与△E的位置关系,并说明理由;(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.16、如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣x+与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).(1)求抛物线m的解析式;(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.【变式】在平面直角坐标系中,二次函数y=ax2+53x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣13x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.【变式】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B (点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP△x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.。
二次函数压轴题专题一最短路径问题

二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1 、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折〞转“直〞,近两年出现“三折线〞转“直〞等变式问题考查。
例题导航例1:如图 A 是锐角∠ MON内部任意一点,在∠ MON的两边 OM, ON上各取一点 B,C,组成三角形,使三角形周长最小 .例:如图, A.B 两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从的路径 AMNB最短?〔假设河的两岸是平行的直线,桥要与河垂直〕解: 1. 将点 B 沿垂直与河岸的方向平移一个河宽到E,2. 连接 AE 交河对岸与点M,那么点 M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得BN∥ EM 且 BN=EM, MN=CD, BD∥CE, BD=CE,所以 A.B 两地的距 :AM+MN+BN=AM+MN+EM=AE+MN,假设桥的位置建在 CD处,连接 AC.CD.DB.CE,那么 AB两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ ACE中,∵ AC+CE> AE, ∴AC+CE+MN> AE+MN,即 AC+CD+DB>AM+MN+BN 所以桥的位置建在 CD处, AB两地的路程最短。
例:如图, A、 B 是两个蓄水池,都在河流 a 的同侧,为了方便灌溉作物, ?A ·要在河边建一个抽水站,将河水送到A、B 两地,问该站建在河边什么地方,?可使所修的渠道最短,试在图中确定该点。
作法:作点 B 关于直线 a 的对称点点 C, 连接 AC交直线 a 于点 D,那么点 D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E,连接 AE.CE.BE.BD,A 到 BB·aDEC∵点 B.C 关于直线 a 对称 , 点在直线 a 上,∴ DB=DC,EB=EC,∴AD+DB=AD+DC=AC,AE+EB=AE+EC在△ ACE中, AE+EC> AC,即 AE+EC>AD+DB所以抽水站应建在河边的点 D 处,常见问题归纳“和最小〞问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小〔将军饮马问题〕.如下图,在直线l上找一点P使得+最小.当点P为直线PA PBAB′与直线 l 的交点时, PA+PB最小.A AB BlPlB'【方法归纳】①如下图,在直线 l 上找一点 B 使得线段 AB最小.过点 A 作 AB⊥ l ,垂足为 B,那么线段AB即为所求.A Al lB②如下图,在直线l 上找一点P使得+最小.过点B作关于直线l的对称点′,PA PB BBB′与直线 l 交于点 P,此时 PA+ PB最小,那么点P 即为所求.A AB BlPlB'③如下图,在∠的边,上分别找一点,D 使得++最小.过点P分别AOB AO BO C PC CD PD作关于 AO,BO的对称点 E, F,连接 EF,并与 AO, BO分别交于点C, D,此时 PC+ CD+ PD 最小,那么点 C, D即为所求.A E AP CPO B O D BF④如下图,在∠AOB的边 AO,BO上分别找一点E, F 使得 DE+ EF+ CF最小.分别过点C,D作关于 AO, BO的对称点 D′, C′,连接 D′C′,并与 AO, BO分别交于点E,F,此时 DE++最小,那么点,即为所求.EF CF E FA D'AD E DC CO B O F BC'⑤如下图,长度不变的线段CD在直线 l 上运动,在直线l 上找到使得AC+ BD最小的CD的位置.分别过点A,D作 AA′∥ CD, DA′∥ AC, AA′与 DA′交于点 A′,再作点 B关于直线 l 的对称点 B′,连接 A′B′与直线 l 交于点 D′,此时点 D′即为所求.B BA AA'ClC D D'l DB'12⑥如下图,在平面直角坐标系中,点P 为抛物线〔 y=4x〕上的一点,点A〔0,1〕在 y 轴正半轴.点 P在什么位置时PA+ PB最小?过点 B作直线 l :y=-1的垂线段 BH′, BH′与抛物线交于点P′,此时 PA+ PB最小,那么点 P 即为所求.yy BBPPAAxP'x OOlH H'二次函数中最短路径例题22例 1.〔 13 广东〕二次函数y=x - 2mx+m-1.(1〕当二次函数的图象经过坐标原点 O〔0,0〕时,求二次函数的解析式;(2〕如图,当 m=2 时,该抛物线与 y 轴交于点 C,顶点为 D,求 C、D 两点的坐标;(3〕在〔2〕的条件下, x 轴上是否存在一点 P,使得 PC+PD最短?假设 P 点存在,求出 P 点的坐标;假设 P 点不存在,请说明理由.【解题过程】 O 〔 , 〕,解:〔 1〕∵二次函数的图象经过坐标原点0 02- mx +22∴代入二次函数 y =xm - ,得出:m2 1- 1= 0,解得:1 y =x 2- x 或 y = x 2∴二次函数的解析式为: + 2x ; 222-得:〔 〕∵ m = , ∴二次函数 y =xmx +m -12 22y =x 2- 4x +3=〔 x - 2〕 2-1,∴抛物线的顶点为: D 〔2,- 1〕,当 x =0 时,y = 3,∴C 点坐标为:〔0,3〕,∴ C 〔0,3〕、D 〔2,- 1〕;( 3〕当 P 、C 、D 共线时 PC +y PD 最短,【方法一】∵C 〔0,3〕、 D 〔 2,- 1〕,设直线 CD 的解析式为 y = kx +3,代入得: 2k C+ 3=- 1,∴ k =- 2,∴ y =- 2x + 3,yCxOD3当 y =0 时,- 2x +3=0,解得 x = 2,PxO3 ∴ PC +PD 最短时, P 点的坐标E为: P 〔D ,0〕.2【方法二】过点 D 作 DE ⊥y 轴于点 E ,PO DEPO CO ,∴ PO 3PO 3∵ ∥ ,∴=CE 2 = ,解得:= ,DE 423∴ PC +PD 最短时, P 点的坐标为: P 〔2,0〕.练习 1.〔 11 菏泽〕如图,抛物线y = 1 2+﹣ 2 与 x 轴交于 , B 两点,与 y 轴交于 C 点,2xbx A且 A 〔﹣ 1, 0〕.( 1〕求抛物线的解析式及顶点D 的坐标;( 2〕判断△ ABC 的形状,证明你的结论;〔3〕点 M 〔 m , 0〕是 x 轴上的一个动点,当 MC + MD 的值最小时,求m 的值.练习 2.〔 12 滨州〕如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A〔﹣ 2,﹣ 4〕,O〔0,0〕,B〔2,0〕三点.(1〕求抛物线y=ax2+bx+c的解析式;(2〕假设点M是该抛物线对称轴上的一点,求AM+ OM的最小值.yO B xA例 2.〔14 海南〕如图,对称轴为直线x=2的抛物线经过A〔-1,0〕,C〔0,5〕两点,与x轴另一交点为 B. M〔0,1〕, E〔 a,0〕, F〔 a+1,0〕,点 P 是第一象限内的抛物线上的动点.〔1〕求此抛物线的解析式;〔2〕当a= 1 时,求四边形MEFP的面积的最大值,并求此时点P 的坐标;〔3〕假设△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.y yPC CPMx MxA O E FB A O E F B【思路点拨】〔1〕由对称轴为直线x= 2,可以得出顶点横坐标为 2,设二次函数的解析式为y=a〔x- 2〕2+ k,再把点 A, B 的代入即可求出抛物线的解析式;(2〕求四边形MEFP的面积的最大值,要先表示出四边形MEFP面积.直接求不好求,可以考虑用割补法来求,过点 P作 PN⊥ y 轴于点 N,由 S 四边形MEFP= S梯形OFPN- S△PMN- S△OME即可得出;(3〕四边形PMEF的四条边中,线段PM,EF长度固定,当ME+PF取最小值时,四边形PMEF 的周长取得最小值.将点 M向右平移1个单位长度〔 EF的长度〕,得到点 M1〔1,1〕,作点 M1关于 x 轴的对称点 M2〔1,-1〕,连接 PM2,与 x 轴交于 F 点,此时 ME+ PF= PM2最小.【解题过程】解:〔 1〕∵对称轴为直线x=2,∴设抛物线解析式为y=a〔 x-2〕2+ k.将 A〔-1,0〕, C〔0,5〕代入得:9a+k= 0a=-1 4a+k= 5,解得k=9,∴y=-〔 x-2〕2+9=- x2+4x+5.〔 2〕当a= 1 时,E〔 1,0〕,F〔 2, 0〕,OE= 1,OF=2.设P〔x,-x2+ 4x+ 5〕,如答图 2,过点P 作⊥y轴于点,那么=,=-x2+4 + 5,PN N PN x ON x∴MN= ON-OM=- x211+4x+ 4.S四边形MEFP=S梯形OFPN-S△PMN-S△OME=〔PN+OF〕?ON-PN22 112121299?MN-2OM?OE=2〔x+ 2〕〔-x+ 4x+ 5〕-2x?〔-x+ 4x+4〕-2×1× 1=-x+2x+2=9215391539-〔 x-4〕+16∴当 x=4时,四边形 MEFP的面积有最大值为16,此时点 P 坐标为〔4,153〕.16〔 3〕∵M〔 0,1〕,C〔 0,5〕,△PCM是以点P为顶点的等腰三角形,∴点 P的纵坐标为3.令 y=- x2+4x+5=3,解得 x=2±6.∵点P在第一象限,∴P〔2+6, 3〕.四边形 PMEF的四条边中, PM、EF长度固定,因此只要+最小,那么的周长将取得最小值.ME PF PMEF如答图3,将点M向右平移 1 个单位长度〔EF的长度〕,得M〔 1, 1〕;1作点 1关于 x 轴的对称点2,那么2〔1,- 1〕;MM M连接 PM 2,与 x 轴交于 F 点,此时 ME + PF = PM 2最小.设直线 PM 2的解析式为 y = mx + n ,将 P 〔 2+ 6, 3〕, M 2〔 1,- 1〕代入得: (2 + 6) + = 3 4 6- 4 4 6+ 4 4 6-4 4 6+ 4m n,解得: m = 5 , n = 5 ,∴ y = 5 x - 5.m + n =- 16+ 5 6+ 56+ 56+ 1 当 y = 0 时,解得 x = .∴ F 〔,0〕.∵ a +1=,∴ a =4 .444∴a =6+ 1PMEF 周长最小.4 时,四边形y yN PCCPMM M 1xxAOEFBAOEF M 2图 1图 2练习 3.〔 11 眉山〕如图,在直角坐标系中,点 A 〔 0, 1〕,B 〔﹣ 4,4〕,将点 B 绕点 A 顺时针方向 90°得到点 ;顶点在坐标原点的拋物线经过点 .CC 的坐标;B〔1〕求抛物线的解析式和点〔2〕抛物线上一动点 ,设点 P 到 x 轴的距离为d 1,点 P 到点A 的距离为 2,试说明2=d 1+1;Pdd〔3〕在〔 2〕的条件下,请探究当点P 位于何处时,△ PAC 的周长有最小值,并求出△ PAC的周长的最小值.yCBPAxO例 4.〔 14 福州〕如图,抛物线12A 在点B 的左侧〕,y=( x 3) 1 与x轴交于A,B两点〔点2与y 轴交于点 C,顶点为 D了.〔1〕求点A,B,D的坐标;〔2〕连接CD,过原点O作OE⊥CD,垂足为H,OE与抛物线的对称轴交于点E,连接 AE,AD.求证:∠ AEO=∠ ADC;〔3〕以〔 2〕中的点E为圆心, 1 为半径画圆,在对称轴右侧的抛物线上有一动点P,过点P 作⊙E的切线,切点为,当的长最小时,求点P的坐标,并直接写出点Q的坐标.Q PQyyCCEHxxOABOABDD【思路点拨】〔1〕由顶点式直接得出点D 的坐标, 再令1y =0,得 2( x23)1= 0 解出方程, 即可得出点A ,B 的坐标;( 2〕设 HD 与 AE 相交于点 F ,可以发现△ HEF 与△ ADF 组成一个“ 8 字型〞.对顶角∠ HFE =∠AFD ,只要∠ FHE =∠ FAD 即可.因为∠ EHF = 90°,只需证明∠ EAD = 90°即可.由勾股定理的逆定理即可得出△ ADE 为直角三角形,得∠ FHE =∠ FAD = 90°即可得出结论;( 3〕先画出图形.因为 PQ 为⊙ E 的切线,所以△ PEQ 为直角三角形,半径 EQ 长度不变,当斜边 PE 最小时, PQ 的长度最小.设出点 P 的坐标,然后表示出 PE ,求出 PE 的最小值,得到点P 的坐标,再求出点 Q 的坐标即可.【解题过程】解:〔 1〕顶点 D 的坐标为〔 3, 1〕.令 y = 0,得1( x 3) 2 1= 0,解得 x 1= 3+ 2,x 2= 32.2∵点 A 在点 B 的左侧,∴ A 点坐标 (3 2, 0) , B 点坐标〔 3 2, 0〕.〔 2〕过 D 作 ⊥ 轴,垂足为 .那么 〔0, 1〕, = 3.令 x = 0,那么 y = 7,∴ C 点坐DG y G G GD27 标为〔 0,2〕.∴GC = 79x 轴于点 M .∵ OE ⊥ CD ,∴∠ GCD +∠ COH = 90 . 2 ( 1) = 2.设对称轴交 ∵∠ MOE +∠ COH = 90 ,∴∠ MOE =∠ GCD .又∵∠ CGD =∠ OMN =90 ,∴△ DCG ∽△ EOM .9 CG DG23∴=,即 = .∴ EM = 2,即点 E 坐标为 (3 , 2) , ED = 3.OM EM3 EM由勾股定理,得 2= 6, 2= 3,∴ 2+ 2= 6+ 3= 9= 2.AE ADAE AD ED∴△ AED 是直角三角形,即∠ DAE = 90 .设 AE 交 CD 于点 F .∴∠ ADC +∠ AFD = 90 .又∵∠ AEO +∠ HFE = 90 , ∴∠ AFD =∠ HFE ,∴∠ AEO =∠ ADC .〔 3〕由⊙ E 的半径为 1,根据勾股定理,得 2 2PQ = EP - 1.要使切线长 最小,只需 长最小,即 2 最小.PQ EPEP设 P 坐标为〔 x , y 〕,由勾股定理,得 22 2.EP = ( x - 3) +( y - 2)∵ y = 1( x -3) 2- 1,∴ ( x - 3) 2= 2 + 2.∴ 2= 2 + 2+ y 2 - 4 + 4= ( y - 1) 2 +5.2 y EP y y当 = 1 时, 2 最小值为 5.把 = 1 代入 1 2 1 - 3) 2y EP y y = ( x -3) - 1,得 (x 1=1,解得2 2 x 1=1, x 2= 5.又∵点 P 在对称轴右侧的抛物线上,∴x 1=1 舍去.∴点 P 坐标为 (5 , 1) .19 13此时 Q 点坐标为〔 3,1〕或 ( 5 , 5 ) .yyCCQ 2EEHPQ 1F xxABO AOBGDD例 5.〔 14 遂宁〕:直线l: =﹣ 2,抛物线y =ax 2++ c 的对称轴是y 轴,且经过点ybx( 0,﹣ 1〕,〔 2, 0〕. ( 1〕求该抛物线的解析式;( 2〕如图①,点 P 是抛物线上任意一点,过点P 作直线 l 的垂线,垂足为 Q ,求证: PO =PQ .( 3〕请你参考〔 2〕中结论解决以下问题:( i 〕如图②,过原点作任意直线 AB ,交抛物线 y = ax 2+ bx + c 于点 A 、 B ,分别过 A 、 B 两点作直线 l 的垂线,垂足分别是点 M 、 N ,连结 ON 、 OM ,求证: ON ⊥OM .〔ii 〕:如图③,点D 〔1, 1〕,试探究在该抛物线上是否存在点 F ,使得 FD + FO 取得最小值?假设存在,求出点F 的坐标;假设不存在,请说明理由.yyyPADOEx OxOFxBlQlN Ml【解题过程】二次函数压轴题专题一最短路径问题b1解:〔 1〕由题意,得-2a= 0a=4 1 2- 1;- 1=,解得:= 0,∴抛物线的解析式为: y=4xc b0= 4a+ 2b+c c=-112121〔 2〕如图①,设P〔a,4a﹣ 1〕,就有OE=a,PE=4a﹣ 1,∵PQ⊥l,∴EQ= 2,∴QP=4 a2+1.212212在 Rt △POE中,由勾股定理,得PO= a +(4a -1)=4a +1,∴ PO= PQ;〔 3〕〔i〕如图②,∵BN⊥l,AM⊥l,∴BN=BO,AM=AO,BN∥AM,∴∠ BNO=∠ BON,∠ AOM=∠ AMO,∠ ABN+∠ BAM=180°.∵∠ BNO+∠ BON+∠ NBO=180°,∠ AOM+∠ AMO+∠ OAM=180°,∴∠ BNO+∠ BON+∠ NBO+∠ AOM+∠ AMO+∠ OAM=360°,∴2∠ BON+2∠ AOM=180°,∴∠ BON+∠ AOM=90°,∴∠ MON=90°,∴ ON⊥ OM;〔 ii 〕如图③,作F′ H⊥ l 于 H, DF⊥ l 于 G,交抛物线与F,作 F′ E⊥ DG于 E,yDO EF'x FlG H∴∠ EGH=∠ GHF′=∠ F′ EG=90°, FO=FG, F′ H= F′ O,∴四边形 GHF′E 是矩形, FO+ FD= FG+ FD= DG,F′O+ F′ D=F′ H+ F′ D,∴ EG= F′H,∴ DE< DF′,∴DE+ GE< HF′+ DF′,∴ DG< F′O+ DF′,∴ FO+ FD< F′ O+DF′,∴ F 是所求作的点.5∵ D〔1,1〕,∴ F 的横坐标为1,∴F〔 1,4〕.。
二次函数压轴题专题一 最短路径问题

二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下 两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
例题导航例1:如图A 是锐角∠MON 内部任意一点,在∠MON 的两边OM ,ON 上各取一点B ,C ,组成三角形,使三角形周长最小.例:如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在何处才能使从A 到B 的路径AMNB 最短?(假设河的两岸是平行的直线,桥要与河垂直) 解:1.将点B 沿垂直与河岸的方向平移一个河宽到E , 2.连接AE 交河对岸与点M,则点M 为建桥的位置,MN 为所建的桥。
证明:由平移的性质,得 BN ∥EM 且BN=EM, MN=CD, BD ∥CE, BD=CE, 所以A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在CD 处,连接AC.CD.DB.CE, 则AB 两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE 中,∵AC+CE >AE, ∴AC+CE+MN >AE+MN,即AC+CD+DB >AM+MN+BN 所以桥的位置建在CD 处,AB 两地的路程最短。
例:如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
作法:作点B 关于直线 a 的对称点点C,连接AC 交直线a 于点D ,则点D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E ,连接AE.CE.BE.BD,··CDA BEa∵点B.C 关于直线 a 对称,点D.E 在直线 a 上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE 中,AE+EC >AC, 即 AE+EC >AD+DB所以抽水站应建在河边的点D 处,常见问题归纳“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DElBAllllBAOBOB+EF +CF 最小,则点E ,F 即为所求.⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y轴正半轴.点P 在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.二次函数中最短路径例题例1.(13广东)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BOB Oll练习1.(11菏泽)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.练习2.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.例2.(14海南)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由.【思路点拨】 (1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出; (3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5,∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN•MN -12OM •OE =12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1=-x 2+92x +92 =-(x -94)2+15316 ∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316). (3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1);作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图2练习3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.例4.(14福州)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了. (1)求点A ,B ,D 的坐标; (2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可.【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12 (x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).例5.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【解题过程】解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1; (2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ; (3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°.∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).l。
九年级数学上册复习专题15二次函数中最短路径问题

专题15二次函数中最短路径问题【做题思路】:一般在二次函数中,会求PA+PC的最小值,且点P为动点;对于这类问题,首先将动点所在直线作为“河”,根据“将军饮马问题”的作图步骤,作出图形。
【做题步骤】:①首先找出“河”:动点所在直线就是“河”;②选出其中一个特殊定点,做关于“河”的对称点;③连接对称点与另一个定点;④连线与河的交点即为动点所在位置,连线长度即为最短路径长(可以用两点之间距离公式);【变换类型】求一个三角形的周长最短:周长就是三条线段相加,其中有一条线段是确定的,两条线段长随着动点运动而变化,那么只需要求出与动点相连两定点的线段最小值即可,也就是求两个线段的最小值。
【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】1.直线y =23x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( )A .(-3,0)B .(-6,0)C .(-52,0) D .(-32,0) 2.如图,点P 是边长为1的菱形ABCD 对角线AC 上的一个动点,点M,N 分别是AB,BC 边上的中点,则MP+PN 的最小值是( )A .12B .1C D .23.如图,在平面直角坐标系中,已知点A (2,3),点B (﹣2,1),在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是 .4.如图,A (3,4),B (0,1),C 为x 轴上一动点,当△ABC 的周长最小时,则点C 的坐标为_________.1.如图,已知直线y=12x+1与y 轴交于点A ,与x 轴交于点D ,抛物线y= 12x 2+bx+c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使|AM ﹣MC|的值最大,求出点M 的坐标__________.2.如图,抛物线y=﹣x 2﹣2x+3与x 轴交于A 、B 两点,与y 轴交于C 点,M 点在抛物线的对称轴上,当点M 到点B 的距离与到点C 的距离之和最小时,点M 的坐标为_____.3.如图,已知直线1y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使AM MC -的值最大,求出点M 的坐标___阅读材料:例:说明代数式的几何意义,并求它的最小值.P (x ,0)是x 轴上P 与点A (0,1P 与点B (3,2)的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA +PB 的最小值.设点A 关于x 轴的对称点为A′,则PA =PA′,因此,求PA +PB 的最小值,只需求PA′+PB 的最小值,而点A′、B 间的直线段距离最短,所以PA′+PB 的最小值为线段A′B 的长度.为此,构造直角三角形A′CB,因为A′C=3,CB =3,所以A′B=.根据以上阅读材料,解答下列问题:(1)P (x ,0)与点A (1,1)、点B 的距离之和.(填写点B 的坐标)(2)代数式已知()()1,2,7,4A B ,M ,N 是x 轴上两动点(M 在N 左边),3MN =,请在x 轴上画出当AM MN NB ++的值最小时,M ,N 两点的位置.1.如图1,抛物线2y ax bx =+与x 轴交于点A ,对称轴与抛物线交于点()2,2B -,与x 轴交于点C .(1)求抛物线的解析式.(2)点D 是y 轴上的动点,求DAB ∆的最小周长.(3)如图2,点P 是抛物线上一个动点,,PA PO 分别与BC 交于点,M N .①若动点P 在第一象限,问MC NC -的值是否发生变化.若不变,求出其值;若发生变化,请说明理由. ②若动点P 在第二象限,请给出①中类似的关于MC 与NC 长的结论(不必证明).2.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A 、B 两点,与y 轴交于点C ,其中()30A -,、()0,2C -.(1)求这条抛物线的函数表达式.(2)在对称轴上是否存在一点P ,使得PBC ∆的周长最小.若存在请求出点P 的坐标.若不存在请说明理由.3.如图,已知直线33y x =-分别交x 轴、y 轴于A 、B 两点,抛物线2y x bx c =++经过A 、B 两点,点C 是抛物线与x 轴的另一个交点(与A 点不重合).(1)求抛物线的解析式;(2)在抛物线的对称轴上求一点P ,使ABP ∆的周长最小,并求出最小周长和P 点的坐标;(3)在抛物线的对称轴上,是否存在点M ,使ABM ∆为等腰三角形?若不存在,请说明理由;若存在,求出点M 的坐标.4.如图,一元二次方程x 2+2x,3=0的两根x 1,x 2,x 1,x 2)是抛物线y=ax 2+bx+c 与x 轴的两个交点C,B 的横坐标,且此抛物线过点A,3,6,, ,1)求此二次函数的解析式;,2)设此抛物线的顶点为P ,对称轴与线段AC 相交于点G ,则P 点坐标为 ,G 点坐标为 , ,3)在x 轴上有一动点M ,当MG+MA 取得最小值时,求点M 的坐标.5.如图,以D 为顶点的抛物线2y ax 2x c =++交x 轴于点A ,(6,0)B ,交y 轴于点(0,6)C .(1)求抛物线的解析式;(2)在直线BC 上有一点P ,使PO PA +的值最小,求点P 的坐标;(3)在x 轴上是否存在一点Q ,使得以A ,C ,Q 为顶点的三角形与BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由. 6.如图,抛物线y=12x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A(一1,0). (1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M 是x 轴上的一个动点,当△DCM 的周长最小时,求点M 的坐标.7.如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A,,1,0,B,3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点.,1)求抛物线的解析式和直线AC 的解析式;,2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;,3)试探究:在拋物线上是否存在点P ,使以点A,P,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.8.在平面直角坐标系中,O 为原点,抛物线2(0)y ax x a =≠经过点3)A -,对称轴为直线l ,点O 关于直线l 的对称点为点B .过点A 作直线//AC x 轴,交y 轴于点C . (Ⅰ)求该抛物线的解析式及对称轴;(Ⅱ)点P 在y 轴上,当PA PB +的值最小时,求点P 的坐标; (Ⅲ)抛物线上是否存在点Q ,使得13AOC AOQ S S ∆∆=,若存在,求出点Q 的坐标;若不存在,请说明理由. 9.如图,直线43y x =与抛物线268y x x =-+交于A ,B 两点(其中点A 在点B 的左侧),与抛物线的对称轴交于点C ,抛物线的顶点为D ,点B 的坐标为()6,8,在抛物线的对称轴上找一点F ,使35BF CF +的值最小,求满足条件的点F 的坐标.试卷第11页,总11页。
最短路径专题 含答案

最短路径专题含答案1. 某同学的茶杯是圆柱体,如图是茶杯的立体图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图.解:如图1,将圆柱的侧面展开成一个长方形,如图示,则A,B分别位于如图所示的位置,连接AB,即是这条最短路线图.问题:某正方形盒子,如图左边下方A处有一只蚂蚁,从A处爬行到侧棱GF上的中点M点处,如果蚂蚁爬行路线最短,请画出这条最短路线图.2. 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.3. 如图一只蚂蚁要从正方体的一个顶点A爬一个顶点B,如果正方体棱是2,求最短的路线长.4. 如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.5. 如图,有一半径为2cm,高为10cm的圆柱体,在棱AA1的P点上有一只蜘蛛,PA=3cm,在棱BB1的Q点上有一只苍蝇,QB2=2cm.蜘蛛沿圆柱爬到Q点吃苍蝇,请你算出蜘蛛爬行的最短路线长.(π取3.14;结果精确到0.01cm)6. 一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B处,如图所示,假设蚊子不动,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条?7. 如图,圆柱的高为8cm,底面直径4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(π≈3)8. 如图1,是一个长方体盒子,长AB=4,宽BC=2,高CG=1.(1)一只蚂蚁从盒子下底面的点A沿盒子表面爬到点G,求它所行走的最短路线的长.(2)这个长方体盒子内能容下的最长木棒的长度为多少?9. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45∘,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=√2,求AD的长.10. 如图,平行四边形ABCD中,AB=2,AD=1,∠ADC=60∘,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点Dʹ处,折痕交CD边于点E.(1)求证:四边形BCEDʹ是菱形;(2)若点P时直线l上的一个动点,请计算PDʹ+PB的最小值.11. 已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.(1)求证:AG与⊙O相切;(2)若AC=6,AB=8,BE=3,求线段OE的长.12. 已知抛物线C1的函数解析式为y=ax2−2x−3a,若抛物线C1经过点(0,−3).(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为√(x2−x1)2+(y2−y1)2)(1)求抛物线C1的顶点坐标.(2)已知实数x>0,请证明x+1x ≥2,并说明x为何值时才会有x+1x=2.(3)若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90∘,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.13. 如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.(1)求证:四边形ADCE是菱形;(2)若BC=6,CE=5,求四边形ADCE的面积.14. 如图,一个正方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你在正方体木柜的表面展开图中画出蚂蚁能够最快达到目的地的可能路径;(2)当正方体木柜的棱长为4时,求蚂蚁爬过的最短路径的长.15. 如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.(1)求证:CF与⊙O相切;(2)若AD=2,F为AE的中点,求AB的长.16. 已知圆锥的底面半径为r=20cm,高ℎ=20√15cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.17. 已知,点P是Rt△ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.18. 已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45∘.(1)如图①,判断CD与⊙O的位置关系,并说明理由;(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.19. 图①,图②为同一长方体房间的示意图,图③为该长方体的表面展开图.(1)已知蜘蛛在顶点Aʹ处;①苍蝇在顶点B处时,试在图①中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;②苍蝇在顶点C处时,图②中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线AʹGC和往墙面BBʹCʹC爬行的最近路线AʹHC,试通过计算判断哪条路线更近;(2)在图③中,半径为10dm的⊙M与DʹCʹ相切,圆心M到边CCʹ的距离为15dm,蜘蛛P 在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线.若PQ与⊙M相切,试求PQ的长度的范围.20. 如图所示,长方体的长为15cm,宽为10cm,高为20cm,点B与点C之间相距5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?21. 如图,平行四边形ABCD中,AB=3,BC=5,∠B=60∘,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.(1)求证:四边形CEDF是平行四边形;(2)①当AE=时,四边形CEDF是矩形;②当AE=时,四边形CEDF是菱形.22. 葛藤是一种植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一个绝招,就是它绕树盘升的路线,总是沿最短路线螺旋前进的.(1)如果树的周长为3m,绕一圈升高4m,则它爬行路程是多少?(2)如果树的周长为8m,绕一圈爬行10m,则爬行一圈升高多少m?如果爬行10圈到达树顶,则树干多高?23. 实践操作在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E,F是折痕与矩形的边的交点),再将纸片还原.(1)初步思考若点P落在矩形ABCD的边AB上(如图①).①当点P与点A重合时,∠DEF=∘,当点E与点A重合时,∠DEF=∘;②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时菱形EPFD的边长.(2)深入探究若点P落在矩形ABCD的内部(如图③),且点E,F分别在AD,DC边上,请直接写出AP的最小值.(3)拓展延伸若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一种情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.24. 如图,已知抛物线y=−x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.(1)求点D的坐标;(2)连接CD,BC,求∠DBC的余切值;(3)设点M在线段CA的延长线上,如果△EBM和△ABC相似,求点M的坐标.25. 如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x−2交于B,C两点.(1)求抛物线的解析式及点C的坐标;(2)求证:△ABC是直角三角形;(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.26. 阅读下面材料:小明遇到这样一个问题:如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45∘,连接EF,则EF=BE+DF,试说明理由.小明是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.他先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.他的方法是将△ABE绕着点A逆时针旋转90∘得到△ADG,再利用全等的知识解决了这个问题(如图2).参考小明同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90∘,点E,F分别在边BC,CD上,∠EAF=45∘.若∠B,∠D都不是直角,则当∠B与∠D满足关系时,仍有EF= BE+DF;(2)如图4,在△ABC中,∠BAC=90∘,AB=AC,点D,E均在边BC上,且∠DAE=45∘,若BD=1,EC=2,求DE的长.27. 如图,在△MNQ中,MN=11,NQ=3√5,cosN=√5.在矩形ABCD中,BC=4,CD=3,5点A与点M重合,AD与MN重合,矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与点Q重合时停止运动.(1)MQ的长度是;(2)运动秒,BC与MN重合;(3)设矩形ABCD与△MNQ重叠部分的面积为S,运动时间为t,求出S与t之间的函数关系式,并直接写出t的取值范围.的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为28. 如图1,对称轴为直线x=12A .(1)求抛物线的解析式;(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.29. 如图,矩形ABCD中,AB=2,BC=2√3,将矩形沿对角线AC剪开,请解决以下问题:(1)将△ACD绕点C顺时针旋转90∘得到△AʹCDʹ,请在备用图中画出旋转后的△AʹCDʹ,连接AAʹ,并求线段AAʹ的长度;(2)在(1)的情况下,将△AʹCDʹ沿CB向左平移的长度为t(0<t<2√3),设平移后的图形与△ABC重叠部分的面积为S,求S与t的函数关系式,并直接写出t的取值范围.30. 如图甲,在△ABC中,∠ACB=90∘,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/ s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQPʹC,当四边形PQPʹC为菱形时,求t的值;(3)当t为何值时,△APQ是等腰三角形?31. 如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2−2x−8=0的两个根.(1)求这条抛物线的解析式;(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.32. 如图,在平面直角坐标系xOy中,抛物线y=x2+1与y轴相交于点A,点B与点O关于点A4对称.(1)填空:点B的坐标是;(2)过点B的直线y=kx+b(其中k<0与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;(3)在(2)的条件下,若点C关于直线BP的对称点Cʹ恰好落在该抛物线的对称轴上,求此时点P的坐标.33. 已知:如图①,在Rt△ACB中,∠C=90∘,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:(1)当t为何值时,PQ∥BC ?(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;(3)是否存在某一时刻,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时的值;若不存在,说明理由;(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQPʹC,那么是否存在某一时刻,使四边形PQPʹC为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.34. 如图,四边形ABCD,BEFG均为正方形,(1)如图1,连接AG,CE,试判断AG和CE的数量关系和位置关系并证明;(2)将正方形BEFG绕点B顺时针旋转β角(0∘<β<180∘),如图2,连接AG,CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB 的度数;若发生变化,请说明理由.(3)在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系:.35. 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE.设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为y=ax2+bx+c.(1)求点D的坐标(用含m的式子表示);(2)若点G的坐标为(0,−3),求该抛物线的解析式.(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使EA ?若存在,直接写出P的坐标,若不存在,说明理由.PM=1236. 如图,在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180∘,∠AFE=∠BDE.(1)如图1,当DE=DF时,图1 中是否存在与AB相等的线段?若存在,请找出并加以证明.若不存在说明理由.(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90∘,AF=m,求BD的长(用含k,m的式子表示).37. 如图,顶点为C(−1,1)的抛物线经过点D(−5,−3),且与x轴交于A,B两点(点B在点A的右侧).(1)求抛物线的解析式;,求出点Q的坐标;(2)若抛物线上存在点Q,使得S△OAQ=32(3)点M在抛物线上,点N在x轴上,且∠MNA=∠OCD,是否存在点M,使得△AMN与△OCD相似?若存在,直接写出点M的坐标;若不存在,说明理由.38. 阅读下面材料:小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.小明经探究发现,过点 A 作 AF ⊥BC ,垂足为 F ,得到 ∠AFB =∠BEA ,从而可证 △ABF ≌△BAE (如图 2),使问题得到解决.(1)根据阅读材料回答:△ABF 与 △BAE 全等的条件是 (填" SSS "、 " SAS " 、" ASA" 、 " AAS “或”HL "中的一个)参考小明思考问题的方法,解答下列问题:(2)如图3,△ABC 中,AB =AC ,∠BAC =90∘,D 为 BC 的中点,E 为 DC 的中点,点 F 在AC 的延长线上,且 ∠CDF =∠EAC ,若 CF =2,求 AB 的长;(3)如图 4,△ABC 中,AB =AC ,∠BAC =120∘,点 D ,E 分别在 AB ,AC 边上,且 AD =kDB (其中 0<k <√33),∠AED =∠BCD ,求 AE EC 的值(用含 k 的式子表示).39. 如图,已知二次函数 y =−x 2+bx +c (b ,c 为常数)的图象经过点 A (3,1),点 C (0,4),顶点为点 M ,过点 A 作 AB ∥x 轴,交 y 轴于点 D ,交该二次函数图象于点 B ,连接 BC .(1)求该二次函数的解析式及点 M 的坐标;(2)若将该二次函数图象向下平移 m (m >0) 个单位,使平移后得到的二次函数图象的顶点落在 △ABC 的内部(不包括 △ABC 的边界),求 m 的取值范围;(3)点 P 是直线 AC 上的动点,若点 P ,点 C ,点 M 所构成的三角形与 △BCD 相似,请直接写出所有点 P 的坐标(直接写出结果,不必写解答过程).40. 在平面直角坐标系中,O为原点,四边形OABC是矩形,点A,C的坐标分别为(3,0),(0,1).点D是边BC上的动点(与端点B,C不重合),过点D作直线y=−1x+b交边OA2于点E.(1)如图(1),求点D和点E的坐标(用含b的式子表示);(2)如图(2),若矩形OABC关于直线DE的对称图形为矩形O1A1B1C1,试探究矩形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由;(3)矩形OABC绕着它的对称中心旋转,如果重叠部分的形状是菱形,请直接写出这个菱形的面积的最小值和最大值.41. 如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60∘得到线段AM,连接FM.(1)求AO的长;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=√3AM;(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.(温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.)42. 如图,矩形纸片ABCD中,AB=6,BC=8.折叠纸片使点B落在AD上,落点为Bʹ.点Bʹ从点A开始沿AD移动,折痕所在直线l的位置也随之改变,当直线l经过点A时,点Bʹ停止移动,连接BBʹ.设直线l与AB相交于点E,与CD所在直线相交于点F,点Bʹ的移动距离为x,点F与点C的距离为y.(1)求证:∠BEF=∠ABʹB;(2)求y与x的函数关系式,并直接写出x的取值范围.43. 如图1,△ABC中,∠C=90∘,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图 2 所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)(1)填空:BC的长是;(2)求S关于x的函数关系式,并写出x的取值范围.x2+bx−2与x轴交于A,B两点,与y轴交于C点,且A(−1,0).44. 如图,抛物线y=12(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,证明你的结论;(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.45. 定义:我们把三角形被一边中线分成的两个三角形叫做"友好三角形".性质:如果两个三角形是"友好三角形",那么这两个三角形的面积相等.理解:如图1,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.(1)应用:如图2,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.(i)求证:△AOB和△AOE是“友好三角形”;(ii)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.(2)探究:在△ABC中,∠A=30∘,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△AʹCD,若△AʹCD与△ABC 重合部分的面积等于△ABC面积的1,请直接写出△ABC的面积.446. 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90∘,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.(1)求点A和点C的坐标;(2)当0<t<30时,求m关于t的函数关系式;(3)当m=35时,请直接写出t的值;(4)直线l上有一点M,当∠PMB+∠POC=90∘,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.47. 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.(1)求抛物线的解析式;(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.48. 在四边形ABCD中,对角线AC,BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1,旋转角为θ(0∘<θ<90∘),连接AC1,BD1,AC1与BD1交于点P.(1)如图1,若四边形ABCD是正方形.①求证:△AOC1≌△BOD1.②请直接写出AC1与BD1的位置关系.(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1.判断AC1与BD1的位置关系,说明理由,并求出k的值.(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1,设AC1= kBD1.请直接写出k的值和AC12+(kDD1)2的值.49. 如图,四边形ABCD为一个矩形纸片.AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止.△ADP以直线AP为轴翻折,点D落到点D1的位置.设DP=x,△AD1P与原纸片重叠部分的面积为y.(1)当x为何值时,直线AD1过点C?(2)当x为何值时,直线AD1过BC的中点E?(3)求出y与x的函数表达式.50. 如图,以点P(−1,0)为圆心的圆,交x轴于B,C两点(B在C的左侧),交y轴于A,D两点(A在D的下方),AD=2√3,将△ABC绕点P旋转180∘,得到△MCB.(1)求B,C两点的坐标;(2)请在图中画出线段MB,MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ,QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.51. 定义:当点P在射线OA上时,把OPOA的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA上的射影值均为OPOA =13.(1)在△OAB中,①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形;其中真命题有.A.①②B.②③C.①③D.①②③(2)已知:点C是射线OA上一点,CA=OA=1,以O为圆心,OA长为半径画圆,点B是⊙O上任意一点.①如图2,若点B在射线OA上的射影值为12,求证:直线BC是⊙O的切线.②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x,点D在射线OB上的射影值为y,直接写出y与x之间的函数关系式.x2交于A,B两点,其中点A的横坐标是−2.52. 如图,已知一条直线过点(0,4),且与抛物线y=14(1)求这条直线的函数关系式及点B的坐标;(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由;(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?53. 已知:如图,AB是半圆O的直径,弦CD∥AB,动点P,Q分别在线段OC,CD上,且DQ=OP,AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C,D不重合),AB=20,cos∠AOC=4.设OP=x,△CPF的面积为y.5(1)求证:AP=OQ;(2)求y关于x的函数关系式,并写出它的自变量x的取值范围;(3)当△OPE是直角三角形时,求线段OP的长.x2+bx+c与x轴分别相交于点A(−2,0),B(4,0),与y轴交于点C,顶54. 如图,抛物线y=−12点为点P.(1)求抛物线的解析式;(2)动点M,N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB,OC上向点B,C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.(i)当四边形OMHN为矩形时,求点H的坐标;(ii)是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.55. 如图,在Rt△ABC中,∠ACB=90∘,AC=5cm,∠BAC=60∘,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒√3cm 的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.56. 爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图1,图2,图3中,AM,BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.(1)【特例探究】如图1,当tan∠PAB=1,c=4√2时,a=,b=;如图2,当∠PAB=30∘,c=2时,a=,b=;(2)【归纳证明】请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.(3)【拓展证明】如图4,平行四边形ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC= 3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3√5,AB=3,求AF的长.57. 在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O,B,C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r 的圆形区域.(只考虑在海平面上的探测)(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60∘方向上,同时军舰C测得A位于南偏东30∘方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?(3)若敌舰A沿最短距离的路线以20√2海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15∘的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?58. 如图,在坐标系xOy中,已知D(−5,4),B(−3,0),过D点分别作DA,DC垂直于x轴、y轴,垂足分别为A,C两点.动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.(1)当t为何值时,PC∥DB;(2)当t为何值时,PC⊥BC;(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边(或边所在的直线)相切时,求t的值.x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴59. 如图,抛物线y=−12交x轴于点D,已知A(−1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.60. 如图1,在Rt△ABC中,∠ACB=90∘,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.(1)证明△COF是等腰三角形,并求出CF的长;(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?61. 如图,在每个小正方形的边长为1的网格中,A,B为小正方形边的中点,C,D为格点,E为BA,CD的延长线的交点.(1)CD的长等于;(2)若点N在线段BE上,点M在线段CE上,且满足AN=NM=MC,请在如图所示的网格中,用无刻度的直尺,画出线段MN,并简要说明点M,N的位置是如何找到的(不要求证明).62. 如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(−1,0),B(4,0),与y轴相交于点C.(1)求该函数的表达式;(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.①求线段PQ的最大值;②若以点P,C,Q为顶点的三角形与△ABC相似,求点P的坐标.63. 如图,在平面直角坐标系中,直线y=−2x+10与x轴,y轴相交于A,B两点.点C的坐标是(8,4),连接AC,BC.(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.64. 将矩形纸片OABC放在平面直角坐标系中,O为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠,使点A落在点Q处.(1)如图①,当点Q恰好落在OB上时,求点P的坐标.。
二次函数最短路径问题

(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(2015湖南)如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
例题:已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.(1) 求抛物线的解析式;(2) 抛物线的对称轴上有一动点P,求出PA+PD的最小值;
步骤:1:找对称点。2:连线求直线。3:求线段的长度或交点(利用勾股定理)
例题:已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.(1) 求抛物线的解析式;(2) 抛物线的对称轴上有一动点P,求出PA+PD的最小值;
步骤:1:找对称点。2:连线求直线。3:求线段的长度或交点(利用勾股定理)
二次函数综合题
例题:(2013滨州)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
跟踪练习:
1.(2015•甘肃武威)如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
二次函数有关的线段最短问题

与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点
. (5)若M为抛物线对称轴上任 意一点,是否存在一点M使得
y (0,3) C
D(1,4)
△ACM的周长最小.若有,求 出点M的坐标,若没有,说明 理由.
(-1,0) A
M
0
B(3,0) x
典例分析
例 如图,在平面直角坐标系中,抛物线 y x2 2x 3
数
的图象经过A、C两点.
(1)求该二次函数的表达式; (2)F、G分别为x轴、y轴上的动点,顺次连结D、E、F、G构 成四边形DEFG,求四边形DEFG周长的最小值;
2.如图,抛物线y=-x 2+bx+c与x轴交于A(1,0),B(-3,0) 两点.
(1)求该抛物线的解析式; (2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是 否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标; 若不存在,请说明理由;
Py P
Q C
(1)抛物线解析式为y x2 - 2x 3
Q(1,2)
B
A
O
x
P( 3 , 15) 24
. (1)求A、B、C、D的坐标.
y (0,3) C
D (1,4)
(2)在x轴上是否存在一点P,
使得P到C,D两点的距离之和最 小.若有,求出点P的坐标,若
(-1,0) A 0P
B(3,0) x
没有,说明理由.
典例分析
例 如图,在平面直角坐标系中,抛物线 y x2 2x 3
Hale Waihona Puke 与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点
. (1)求A、B、C、D的坐标.
y (0,3) C
D (1,4)
九年级数学上册复习专题15二次函数中最短路径问题(1)

专题15二次函数中最短路径问题【做题思路】:一般在二次函数中,会求PA+PC的最小值,且点P为动点;对于这类问题,首先将动点所在直线作为“河”,根据“将军饮马问题”的作图步骤,作出图形。
【做题步骤】:①首先找出“河”:动点所在直线就是“河”;②选出其中一个特殊定点,做关于“河”的对称点;③连接对称点与另一个定点;④连线与河的交点即为动点所在位置,连线长度即为最短路径长(可以用两点之间距离公式);【变换类型】求一个三角形的周长最短:周长就是三条线段相加,其中有一条线段是确定的,两条线段长随着动点运动而变化,那么只需要求出与动点相连两定点的线段最小值即可,也就是求两个线段的最小值。
【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】1.直线y=23x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为()A.(-3,0)B.(-6,0)C.(-52,0)D.(-32,0)【答案】C【解析】【分析】【详解】作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.直线y=23x+4与x轴、y轴的交点坐标为A(﹣6,0)和点B(0,4),因点C、D分别为线段AB、OB的中点,可得点C(﹣3,2),点D(0,2).再由点D′和点D关于x轴对称,可知点D′的坐标为(0,﹣2).设直线CD′的解析式为y=kx+b,直线CD′过点C(﹣3,2),D′(0,﹣2),所以2=-3k+b-2=b⎧⎨⎩,解得:4k=-3b=-2⎧⎪⎨⎪⎩,即可得直线CD′的解析式为y=﹣43x﹣2.令y=﹣43x﹣2中y=0,则0=﹣43x﹣2,解得:x=﹣32,所以点P的坐标为(﹣32,0).故答案选C.考点:一次函数图象上点的坐标特征;轴对称-最短路线问题.2.如图,点P 是边长为1的菱形ABCD 对角线AC 上的一个动点,点M,N 分别是AB,BC 边上的中点,则MP+PN 的最小值是( )A .12B .1C D .2【答案】B 【解析】 【分析】先作点M 关于AC 的对称点M′,连接M′N 交AC 于P ,此时MP+NP 有最小值.然后证明四边形ABNM′为平行四边形,即可求出MP+NP=M′N=AB=1. 【详解】 解:如图,作点M 关于AC 的对称点M′,连接M′N 交AC 于P ,此时MP+NP 有最小值,最小值为M′N 的长. ∵菱形ABCD 关于AC 对称,M 是AB 边上的中点, ∴M′是AD 的中点, 又∵N 是BC 边上的中点, ∴AM′∥BN ,AM′=BN , ∴四边形ABNM′是平行四边形, ∴M′N=AB=1,∴MP+NP=M′N=1,即MP+NP 的最小值为1, 故选B .3.如图,在平面直角坐标系中,已知点A (2,3),点B (﹣2,1),在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是 .【答案】(﹣1,0).【解析】试题分析:作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,求出C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出k、b,得出直线BC的解析式,求出直线与x轴的交点坐标即可.试题解析: 作A关于x轴的对称点C,连接BC交x轴于P,则此时AP+BP最小,,A点的坐标为(2,3),B点的坐标为(﹣2,1),,C(2,﹣3),设直线BC的解析式是:y=kx+b,把B、C的坐标代入得:21 {23k bk b-+=+=-解得1 {1 kb=-=-.即直线BC的解析式是y=﹣x﹣1,当y=0时,﹣x﹣﹣1=0,解得:x=﹣1,,P点的坐标是(﹣1,0).考点:1.轴对称-最短路线问题;2.坐标与图形性质.4.如图,A(3,4),B(0,1),C为x轴上一动点,当△ABC的周长最小时,则点C的坐标为_________.【答案】305⎛⎫ ⎪⎝⎭,【解析】 【分析】先作出点B 关于x 轴的对称点'B ,连接'AB 交x 轴于点C,再用待定系数法求出直线'AB 的解析式,进而求出点C 的坐标即可. 【详解】先作出点B 关于x 轴的对称点'B ,连接'AB 交x 轴于点C,则点'B 的坐标为(0,1)-由两点之间线段最短可知,'AB 的长即为AC BC +的长,因为AB 是定值,所以此时△ABC 的周长最小 设直线'AB 的解析式为y kx b =+ 将(3,4),'(0,1)A B -代入解析式得341k b b +=⎧⎨=-⎩ 解得531k b ⎧=⎪⎨⎪=-⎩ ∴直线'AB 的解析式为513y x =- 当0y = 时,5103x -=,解得35x = ∴点3(,0)5C故答案为:305⎛⎫ ⎪⎝⎭,.【点睛】本题主要考查周长的最小值,能够作出点B 的对称点,掌握待定系数法是解题的关键.1.如图,已知直线y=12x+1与y 轴交于点A ,与x 轴交于点D ,抛物线y= 12x 2+bx+c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使|AM ﹣MC|的值最大,求出点M 的坐标__________.【答案】31-22(,) 【解析】分析:易得点A,0,1),那么把A,B 坐标代入y=12x 2+bx+c 即可求得函数解析式,然后求出对称轴,找到C 关于对称轴的对称点B ,连接AB 交对称轴的一点就是M .应让过AB 的直线解析式和对称轴的解析式联立即可求得点M 坐标.详解: ,1)将A,0,1,,B,1,0)坐标代入y=12x 2+bx+c, 得1102c b c =⎧⎪⎨++=⎪⎩, 解得321b c ⎧=-⎪⎨⎪=⎩,∴抛物线的解折式为y=12x 2-32x+1, ∴抛物线的对称轴为x=32, ∵B,C 关于x=32对称, ∴MC=MB,要使|AM -MC|最大,即是使|AM -MB|最大,由三角形两边之差小于第三边得,当A,B,M 在同一直线上时|AM -MB|的值最大. 易知直线AB 的解析式为y=-x+1∴由132y x x =-+⎧⎪⎨=⎪⎩, 得3212x y ⎧=⎪⎪⎨⎪=-⎪⎩, ∴M,32,-12,, 点睛: 本题综合考查了待定系数法求二次函数的解析式,二次函数的性质,直线和抛物线的交点,求两条线段和或差的最值,要考虑做其中一点关于所求的点在的直线的对称点.2.如图,抛物线y=﹣x 2﹣2x+3与x 轴交于A 、B 两点,与y 轴交于C 点,M 点在抛物线的对称轴上,当点M 到点B 的距离与到点C 的距离之和最小时,点M 的坐标为_____.【答案】(﹣1,2). 【解析】 【分析】因为点B 关于对称轴的对称点为点A ,连接AC ,设直线AC 与对称轴x =,1的交点为M ,则此时MB +MC 的值最小,再求得点M 的坐标即可, 【详解】∵抛物线y =,x 2,2x +3与x 轴交于A ,B 两点,令y =0,得,,x 2,2x +3=0,解得,x =,3或x =1,∴点A ,,3,0,,C ,0,3,,设直线AC 的解析式为y =kx +b ,把A ,,3,0,,C ,0,3)分别代入直线y =kx +b ,得,303k b b -+=⎧⎨=⎩,解得,13k b =⎧⎨=⎩,∴直线AC 解析式为y =x +3, 设直线AC 与对称轴x =,1的交点为M ,则此时MB +MC 的值最小, 把x =,1代入直线y =x +3得,y =2,∴M ,,1,2,,即当点M 到点B 的距离与到点C 的距离之和最小时M 的坐标为(﹣1,2,,故答案为,,1,2,,【点睛】本题考查了抛物线与x 轴的交点问题,轴对称﹣最短路线问题,求得直线AC 的解析式是解答本题的关键, 3.如图,已知直线1y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使AM MC -的值最大,求出点M 的坐标___【答案】31,22⎛⎫-⎪⎝⎭【解析】【分析】 找到C 关于对称轴的对称点B ,连接AB 交对称轴的一点就是M .应让过AB 的直线解析式和对称轴的解析式联立即可求得点M 坐标.【详解】解:将A (0,1)、B (1,0)坐标代入212y x bx c =++ 1102c b c =⎧⎪⎨++=⎪⎩ 解得321b c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解折式为213-122y x x =+ ∴抛物线的对称轴为x =32,∵B 、C 关于x=32对称, ∴MC=MB , 要使|AM -MC|最大,即是使|AM -MB|最大,由三角形两边之差小于第三边得,当A 、B 、M 在同一直线上时|AM -MB|的值最大.易知直线AB 的解析式为y=-x+1321x y x ⎧=⎪∴⎨⎪=-+⎩ ∴3212x y ⎧=⎪⎪⎨⎪=-⎪⎩ ∴31,22M ⎛⎫- ⎪⎝⎭ 故答案为:31,22⎛⎫- ⎪⎝⎭【点睛】本题考查了抛物线与直线的问题,求两条线段和或差的最值,都要考虑做其中一点关于所求的点在的直线的对称点.阅读材料:例:说明代数式的几何意义,并求它的最小值.P (x ,0)是x 轴上P 与点A (0,1P 与点B (3,2)的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA +PB 的最小值.设点A 关于x 轴的对称点为A′,则PA =PA′,因此,求PA +PB 的最小值,只需求PA′+PB 的最小值,而点A′、B 间的直线段距离最短,所以PA′+PB 的最小值为线段A′B 的长度.为此,构造直角三角形A′CB,因为A′C=3,CB =3,所以A′B=.根据以上阅读材料,解答下列问题:(1)P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)(2)代数式【答案】(1)B(2,3)或(2,-3);(2)10.【解析】试题分析:(1(2P (x,0)与点A(0,7)、点B(6,1)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.试题解析:(1的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B(2,±3)的距离之和,故答案为:B(2,3)或(2,-3);(2∴所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)的距离之和,如图所示:设点A关于x轴的对称点为A′,则PA=PA′,∴PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,∴PA′+PB的最小值为线段A′B的长度,∵A(0,7),B(6,1),∴A′(0,﹣7),A′C=6,A B'==,故答案为:10.BC=8,∴10考点:1.轴对称-最短路线问题;2.坐标与图形性质;3.探究型.已知()()1,2,7,4A B ,M ,N 是x 轴上两动点(M 在N 左边),3MN =,请在x 轴上画出当AM MN NB ++的值最小时,M ,N 两点的位置.【答案】见解析【解析】【分析】作点A 关于x 轴的对称点()1,2'-A ,再将点B 向左平移3个单位得到点B ',连接A B '',与x 轴的交点即为点M ,将A '向右平移3个单位得到点C ,连接CB ,与x 轴的交点即为N .点M ,N 即为所求.【详解】如图,作点A 关于x 轴的对称点()1,2'-A ,再将点B 向左平移3个单位得到点B ',连接A B '',与x 轴的交点即为点M ,将A '向右平移3个单位得到点C ,连接CB ,与x 轴的交点即为N .点M ,N 即为所求.【点睛】本题主要考查了坐标与图形的性质和最短路线问题,准确计算是解题的关键.1.如图1,抛物线2y ax bx =+与x 轴交于点A ,对称轴与抛物线交于点()2,2B -,与x 轴交于点C .(1)求抛物线的解析式.(2)点D 是y 轴上的动点,求DAB ∆的最小周长.(3)如图2,点P 是抛物线上一个动点,,PA PO 分别与BC 交于点,M N .①若动点P 在第一象限,问MC NC -的值是否发生变化.若不变,求出其值;若发生变化,请说明理由. ②若动点P 在第二象限,请给出①中类似的关于MC 与NC 长的结论(不必证明).【答案】(1)2122y x x =-;(2);(3)①MC NC -的值不发生变化,4MC NC -=,理由见解析;②当点P 在第二象限时,有4NC MC -=.【解析】【分析】(1)将表达式写为顶点式,再利用待定系数法求解即可;(2)取A 关于y 轴的对称点A ',连接BA '与y 轴交于点D ,此时ABD △的周长最小,再利用勾股定理计算即可; (3)①设()21,242P m m m m ⎛⎫-> ⎪⎝⎭,利用待定系数法求出直线PO 、直线PA 的表达式,从而求出MC 、NC 计算即可;②以①为基础求出MC 、NC 计算即可.【详解】解:(1)由题意,点()2,2B -是顶点,解析式可写为()222y a x =--, 又∵抛物线经过原点,∴420a -=, ∴12a =,∴解析式为()21222y x =--,即2122y x x =-; (2)由21202x x -=,得0x =,或4x =, ∴()4,0A ,如图,取()4,0A 关于y 轴的对称点()4,0A '-,连接BA '与y 轴交于点D ,此时CD A D '=,∴CD BD A D BD A B ''+=+=,由“两点之间线段最短”可知,此时ABD △的周长最小,最小周长等于AB A B '+==(3)①MC NC -的值不发生变化,理由如下: 设()21,242P m m m m ⎛⎫-> ⎪⎝⎭,直线PO 为y kx =,直线PA 为y k x n '=+, 将P 点坐标代入直线PO ,得:2122km m m =-, ∴122k m =-, ∴直线PO 为122y m x ⎛⎫=-⎪⎝⎭, 当2x =时,4y m =-,∴4NC m =-,将点,P A 的坐标代入直线PA ,得:212240m m mk n k n ⎧-=+⎪⎨⎪+='⎩',解得:12k m '=,2n m =-, ∴直线PA 为122y mx m =-, 当2x =时,2y m m m =-=-,∴MC m =,∴4MC NC -=,∴MC NC -的值不发生变化,4MC NC -=;②当点P 在第二象限时,有4NC MC -=,理由如下:以①为基础,当点P '在第二象限时,0m <,直线P O '为122y m x ⎛⎫=- ⎪⎝⎭,直线P A '为122y mx m =-, ∴P O '与BC 的交点为()2,4N m -,P A '与BC 的交点为()2,M m -,∴(4)NC m =--,MC m =-,∴4NC MC -=.【点睛】本题考查了二次函数的综合应用,一次函数及轴对称,熟练掌握待定系数法求表达式是解题的关键.2.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A 、B 两点,与y 轴交于点C ,其中()30A -,、()0,2C -.(1)求这条抛物线的函数表达式.(2)在对称轴上是否存在一点P ,使得PBC ∆的周长最小.若存在请求出点P 的坐标.若不存在请说明理由.【答案】(1)224233y x x =+-;(2)存在,P(-1,43-) 【解析】【分析】 (1)将点()30A -,,()0,2C -和对称轴公式代入即可求出a 、b 、c 的值,从而求出结论; (2)点A 、B 关于直线1x =-对称,连接AC 交直线1x =-于点P ,由对称的性质可得此时△PBC 的周长=PB +PC +BC= PA +PC +BC=AC +BC ,根据两点之间线段最短即可求出此时△PBC 的周长最小,利用待定系数法求出直线AC 的解析式,即可求出结论.【详解】解:(1)函数()20y ax bx c a =++≠过点()30A -,,()0,2C -,且对称轴为1x =-, 则:129302b a a b c c ⎧-=-⎪⎪-+=⎨⎪=-⎪⎩解得:23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩224233y x x ∴=+- (2)答:存在点A 、B 关于直线1x =-对称,连接AC 交直线1x =-于点P ,∴PA=PB此时△PBC 的周长=PB +PC +BC= PA +PC +BC=AC +BC根据两点之间线段最短可得此时△PBC 的周长最小设直线AC 为1y kx b =+,代入()30A -,和()0,2C -得:11302k b b -+=⎧⎨=-⎩, 解得:1232k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 为:223y x =-- 将1x =-代入223y x =--中, 24(1)233y =-⨯--=- ∴P (-1,43-)【点睛】此题考查的是求二次函数的解析式和轴对称性质的应用,掌握利用待定系数法求二次函数解析式、一次函数解析式和轴对称的性质是解决此题的关键.3.如图,已知直线33y x =-分别交x 轴、y 轴于A 、B 两点,抛物线2y x bx c =++经过A 、B 两点,点C 是抛物线与x 轴的另一个交点(与A 点不重合).(1)求抛物线的解析式;(2)在抛物线的对称轴上求一点P ,使ABP ∆的周长最小,并求出最小周长和P 点的坐标;(3)在抛物线的对称轴上,是否存在点M ,使ABM ∆为等腰三角形?若不存在,请说明理由;若存在,求出点M 的坐标.【答案】(1)223y x x =+- ;(2) ;(3)存在,1(1M -,2(1,M -,3(1,0)M -,4(1,1)M --.【解析】【分析】(1)由直线解析式可求得A 、B 两点的坐标,根据待定系数法可求得抛物线解析式;(2)连接BC ,直线BC 与对称轴的交点即为点P.求出直线BC 的解析式,求出点P 的坐标,即可求解.(3)分MA=AB ,MB=AB ,MB=MA 三种情况进行讨论.【详解】解:(1)直线y 3x 3x ,y A,B =-分别交轴轴于两点()()1,0,0,3A B 可得∴-,把A ,B 两点的坐标分别代入2y x bx c =++得:10233b c b c c ++==⎧⎧⎨⎨=-=-⎩⎩解得 ∴抛物线的解析式为223y x x =+- (2)连接BC ,直线BC 与对称轴的交点即为点P.易求直线BC 的解析式为3y x =--,抛物线对称轴为直线1x =-,当P(-1,-2)(3)存在,理由如下:抛物线的对称轴为:()1,M 1,m :x =--假设存在满足题意讨论:①当MA=AB 时,∵OA=1,OB=3:AB m ∴==解得((12,1,M M --,②当MB=AB 时, 34:0,6m m ===-解得(不合题意) ()31,0M -,③当MB=MA :1m 解得==- ()41,1M --, 故共存在四个点 ((()()1234,1,,1,0,1,1ΔABM M M M M -----使为等腰三角形.【点睛】考查一次函数图象上点的坐标特征,待定系数法求二次函数解析式,等腰三角形的性质等,注意分类讨论思想在解题中的应用.4.如图,一元二次方程x2+2x,3=0的两根x1,x2,x1,x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A,3,6,,,1)求此二次函数的解析式;,2)设此抛物线的顶点为P,对称轴与线段AC相交于点G,则P点坐标为,G点坐标为,,3)在x轴上有一动点M,当MG+MA取得最小值时,求点M的坐标.【答案】(1)抛物线解析式为y=12x2+x,32,,2,抛物线顶点P的坐标为(﹣1,,2,,G点坐标为(﹣1,2,,,3,M点坐标为(0,0,【解析】【分析】,1)可先根据一元二次方程求出x1,x2的坐标,也就求出了B,C两点的坐标,然后可用交点式的二次函数通式来设二次函数的解析式,根据已知的A点的坐标求出二次函数的解析式.,2)根据(1)二次函数解析式可得出顶点P的坐标和对称轴的解析式,G点就是直线AC与抛物线对称轴的交点,可先根据A,C的坐标,用待定系数法求出AC所在直线的解析式,然后将P点的横坐标代入求得的一次函数的解析式中即可求出G的坐标.,3)本题的关键是先确定M点的位置,可先做A关于x轴的对称点A′然后连接A′C,与x轴的交点就是点M,那么可根据A′,C两点的坐标求出A′C所在直线的解析式,又已知了M在x轴上即可求出M点的坐标.【详解】解:(1)解方程x2+2x,3=0得x1=,3,x2=1,∴抛物线与x轴的两个交点坐标为:C,,3,0,,B,1,0,,设抛物线的解析式为y=a,x+3,,x,1,,∵A,3,6)在抛物线上,∴6=a,3+3,•,3,1,,∴a=1 2,∴抛物线解析式为y=12x2+x,32,,2)由y=12x 2+x,32=12,x+1,2,2, ∴抛物线顶点P 的坐标为(﹣1,,2),对称轴方程为x=,1,设直线AC 的解析式为y=kx+b,∵A,3,6,,C,,3,0)在该直线上,∴3630k b k b +⎧⎨-+⎩== , 解得:k=1,b=3,∴直线AC 的解析式为:y=x+3,将x=,1代入y=x+3得y=2,∴G 点坐标为(﹣1,2,,,3)作A 关于x 轴的对称点A′,3,,6,,连接A′G,A′G 与x 轴交于点M 即为所求的点.设直线A′G 的解析式为y=kx+b,∴362k b k b +-⎧⎨-+⎩== ,解得:02b k ⎧⎨-⎩== , ∴直线A′G 的解析式为y=,2x ,令x=0,则y=0,∴M 点坐标为(0,0,,【点睛】考查了用待定系数法求一次函数与二次函数解析式的方法.确定M 点的位置是解题的关键.5.如图,以D 为顶点的抛物线2y ax 2x c =++交x 轴于点A ,(6,0)B ,交y 轴于点(0,6)C .(1)求抛物线的解析式;(2)在直线BC 上有一点P ,使PO PA +的值最小,求点P 的坐标;(3)在x 轴上是否存在一点Q ,使得以A ,C ,Q 为顶点的三角形与BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.【答案】(1)21262y x x =-++;(2)点P 的坐标为1824,77⎛⎫ ⎪⎝⎭;(3)存在,当Q 的坐标为(0,0)或(18,0)时,以A ,C ,Q 为顶点的三角形与BCD 相似.【解析】【分析】(1)将点B 和点C 的坐标代入二次函数解析式中即可求出结论;(2)先求出点A 的坐标,利用待定系数法求出BC 的解析式,作点O 关于BC 的对称点O ′,连接AO ′交BC 于点P ,连接OP ,O ′B ,根据两点之间线段最短,此时PO PA +最小,求出点O ′的坐标,利用待定系数法求出AO ′的解析式,联立方程即可求出结论;(3)求出顶点D 的坐标,利用平面直角坐标系中任意两点之间的距离公式求出CD 、BC 、CD 和AC ,根据勾股定理的逆定理证出△BCD 是直角三角形,然后根据相似三角形的对应情况分类讨论,根据相似三角形的性质列出比例式即可求出结论.【详解】解:(1)将点B 和点C 的坐标代入2y ax 2x c =++中,得036126a c c =++⎧⎨=⎩解得:126a c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解析式为21262y x x =-++;(2)把y=0代入21262y x x =-++中,得 210262=-++x x 解得:x 1=-2,x 2=6,∴点A 的坐标为(-2,0)设直线BC 的解析式为y=kx +b将点B 和点C 的坐标代入,得066k b b =+⎧⎨=⎩解得:16k b =-⎧⎨=⎩ ∴直线BC 的解析式为6y x =-+作点O 关于BC 的对称点O ′,连接AO ′交BC 于点P ,连接OP ,O ′B根据对称可得PO=PO ′,OB=O ′B此时PO PA +='+PO PA =O A '根据两点之间线段最短,此时PO PA +最小∵OB=OC=6,∠BOC=90°∴∠OBC=45°∴∠OBO ′=90°∵OB= O ′B =6∴点O ′的坐标为(6,6)设直线AO ′的解析式为y=mx +n将点A 和点O ′的坐标代入,得0266m n m n =-+⎧⎨=+⎩解得:3432m n ⎧=⎪⎪⎨⎪=⎪⎩∴直线AO ′的解析式为33y x 42=+ 联立63342y x y x =-+⎧⎪⎨=+⎪⎩解得:187247x y ⎧=⎪⎪⎨⎪=⎪⎩∴点P 的坐标为1824,77⎛⎫ ⎪⎝⎭ (3)∵21262y x x =-++=()21282--+x ∴点D 的坐标为(2,8)∴======CD BCBD =AC∴CD 2+BC 2=80=BD 2∴△BCD 为直角三角形,且∠BCD=90°点Q 在点A 左侧时,△QAC 为钝角三角形,∴△QAC 不可能与△BCD 相似∴点Q 必在点A 右侧,设点Q 的坐标为(q ,0),则AQ=q -(-2)=q +2∵tan ∠CAO=632==CO AO ,tan ∠BDC=3==BC CD ∴∠CAO=∠BDC当△CQA ∽△BCD 时, ∴=AC AQ BD CD= 解得:q=0∴点Q 的坐标为(0,0);当△QCA ∽△BCD 时, ∴=AC AQ CD BD=解得:q=18∴点Q 的坐标为(18,0);综上:点Q 的坐标为(0,0)或(18,0).【点睛】此题考查的是二次函数、一次函数和图形的综合大题,掌握利用待定系数法求出二次函数解析式、一次函数解析式、两点之间线段最短、联立方程求交点坐标、相似三角形的判定及性质和锐角三角函数的性质是解决此题的关键. 6.如图,抛物线y=12x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A(一1,0). (1)求抛物线的解析式及顶点D 的坐标;(2)判断△ABC 的形状,证明你的结论;(3)点M 是x 轴上的一个动点,当△DCM 的周长最小时,求点M 的坐标.【答案】(1)213222y x x =--, D (32, 258-);(2)△ABC 是直角三角形,证明见解析; (3)M (2441,0). 【解析】 试题分析:,1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;,2)根据勾股定理的逆定理,可得答案;,3)根据轴对称的性质,两点之间线段最短,可得M 点是对称轴与BC 的交点,根据自变量与函数值的对应关系,可得答案.试题解析:(1)∵点A (−1,0)在抛物线22y x bx =+-上, ∴()()2111202b ⨯-+⨯--=, 解得 32b =-, ∴抛物线的解析式为213 2.22y x x =-- ∵221313252()22228y x x x =--=--, ∴顶点D 的坐标为325,.28⎛⎫- ⎪⎝⎭ (2)△ABC 是直角三角形,理由如下:当x =0时,y =−2,∴C (0,−2),则OC =2.当y =0时, 21320.22x x --= ∴121,4,x x =-= 则B (4,0),∴OA =1,OB =4,∴AB =5.222222225,5,20AB AC OA OC BC OC OB ==+==+=,∴222AC BC AB +=,∴△ABC 是直角三角形;(3)由题意A. B 两点关于对称轴对称,故直线BC 与对称轴的交点即为点M .由B (4,0),C (0,−2)设直线BC :y =kx −24k −2=0,1.2k = 所以直线1: 2.2BC y x =- 当32x =时,1352.224y =⨯-=- 所以35,.24M ⎛⎫- ⎪⎝⎭7.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A,,1,0,B,3,0)两点,与y轴交于点C,点D 是该抛物线的顶点.,1)求抛物线的解析式和直线AC的解析式;,2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;,3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【答案】,1)抛物线解析式为y=,x2+2x+3;直线AC的解析式为y=3x+3,,2)点M的坐标为(0,3,,,3)符合条件的点P的坐标为(73,209)或(103,,139,,【解析】分析:(1)设交点式y=a,x+1,,x-3),展开得到-2a=2,然后求出a即可得到抛物线解析式;再确定C,0,3),然后利用待定系数法求直线AC的解析式;,2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′,-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;,3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a,x+1,,x,3,,即y=ax2,2ax,3a,∴,2a=2,解得a=,1,∴抛物线解析式为y=,x2+2x+3,当x=0时,y=,x2+2x+3=3,则C,0,3,,设直线AC的解析式为y=px+q,把A,,1,0,,C,0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3,,2,∵y=,x2+2x+3=,,x,1,2+4,∴顶点D的坐标为(1,4,,作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′,,3,0,,∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3,,,3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC的解析式为y=3x+3,∴直线PC的解析式可设为y=,13x+b,把C,0,3)代入得b=3,∴直线PC的解析式为y=,13x+3,解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==,解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩,则此时P点坐标为(73,209,,过点A 作AC 的垂线交抛物线于另一点P ,直线PC 的解析式可设为y=,x+b,把A,,1,0)代入得13+b=0,解得b=,13, ∴直线PC 的解析式为y=,13x,13, 解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩==,解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩,则此时P 点坐标为(103,,139,. 综上所述,符合条件的点P 的坐标为,73,209,或,103,,139,. 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.8.在平面直角坐标系中,O为原点,抛物线2(0)y ax x a =≠经过点3)A -,对称轴为直线l ,点O 关于直线l 的对称点为点B .过点A 作直线//AC x 轴,交y 轴于点C .(Ⅰ)求该抛物线的解析式及对称轴;(Ⅱ)点P 在y 轴上,当PA PB +的值最小时,求点P 的坐标;(Ⅲ)抛物线上是否存在点Q ,使得13AOC AOQ S S ∆∆=,若存在,求出点Q 的坐标;若不存在,请说明理由. 【答案】(Ⅰ)抛物线的解析式为2122y x x =-;抛物线的对称轴为直线x ;P 点坐标为9(0,)4-;(Ⅲ)存在,Q点坐标为或(-,理由见解析【解析】【分析】(Ⅰ)将3)A -点代入二次函数的解析式,即可求出a ,再根据对称轴的公式即可求解.(Ⅱ)先求出B 点胡坐标,要求PA PB +胡最小值,只需找到B 关于轴的对称点1B ,则直线A 1B 与y 轴的交点就是点P ,根据待定系数法求出AB 1的解析式,令y=0,即可求出P 点的坐标.(Ⅲ)设点Q 的坐标,并求出△AOQ 面积,从而得到△AOQ 面积,根据Q 点胡不同位置进行分类,用m 及割补法求出面积方程,即可求解.【详解】(Ⅰ)∵2(0)2y ax x a =-≠经过点3)A -,∴232a-=⨯-12a=,∴抛物线的解析式为212y x x=-,∵212222bxa=-=-=⨯,∴抛物线的对称轴为直线x=.(Ⅱ)∵点(0,0)O,对称轴为x=,∴点O关于对称轴的对称点B点坐标为.作点B关于轴的对称点1B,得1(B-,设直线AB1的解析式为y kx b=+,把点3)A-,点1(B-代入得3bb⎧-=+⎪⎨=-+⎪⎩,解得94kb⎧=⎪⎪⎨⎪=-⎪⎩,∴944y x=--.∴直线94y x=-与y轴的交点即为P点.令0x=得9y4=-,∵P点坐标为9(0,)4-.(Ⅲ)∵3)A-,//AC x轴,∴AC=3OC=,∴11322AOCS OC AC∆=⋅=⋅=又∵13AOC AOQS S∆∆=,∴3AOQ AOCS S∆∆==设Q点坐标为21(,)2m m,如图情况一,作QR CA⊥,交CA延长线于点R,∵2AOQ AOC AQR OCRQ S S S S ∆∆∆=--=梯形,∴(211113332222m m m ⎛⎫⋅++-- ⎪ ⎪⎭⎝2132m ⎛⎫-+= ⎪ ⎪⎝⎭化简整理得2180m -=,解得1m =,2m =-如图情况二,作QN AC ⊥,交AC 延长线于点N ,交x 轴于点M ,∵AOQ AQN QMO OMNA S S S S ∆∆∆=--=梯形∴221111m)3()222222m m m ⎛⎫⎛⎫-+--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3()2m m --+=,化简整理得2180m -=,解得1m =,2m =-∴Q 点坐标为或(-,∴抛物线上存在点Q ,使得13AOC AOQ S S ∆∆=.【点睛】主要考查了二次函数的性质,以及求两边和的最小值,面积等常见的题型,计算量较大,但难度不是很大.9.如图,直线43y x =与抛物线268y x x =-+交于A ,B 两点(其中点A 在点B 的左侧),与抛物线的对称轴交于点C ,抛物线的顶点为D ,点B 的坐标为()6,8,在抛物线的对称轴上找一点F ,使35BF CF +的值最小,求满足条件的点F 的坐标.【答案】233,4⎛⎫ ⎪⎝⎭【解析】【分析】 作B 点关于对称轴的对称点B′,过点B '作B M BC '⊥于点M ,交对称轴于点F ,连接BF ,设抛物线的对称轴与x 轴交于点E .再通过解直角三角形求出NF 的长,进而即可找出点F 的坐标.【详解】解:如图,作点B 关于对称轴的对称点B ',交抛物线对称轴于点N ,过点B '作B M BC '⊥交直线BC 于点M ,交对称轴于点F ,连接BF ,设抛物线的对称轴与x 轴交于点E .易得抛物线268y x x =-+的对称轴为直线3x =.∵直线BC 的解析式为43y x =, ∴点C 的坐标为()3,4.∵FM BC ⊥, ∴3tan tan 4OE FCM OCD CE ∠=∠==. ∴3sin 5FM FCM FC ∠==,即35FM CF =. ∵B 、B '关于对称轴对称,∴BF B F '=. ∴35BF CF B F FM '+=+.当点B '、F 、M 三点共线且B M FM '⊥时,B F FM '+的值最小,∵点B 的坐标为()6,8,抛物线对称轴为直线3x =,∴点B '的坐标为()0,8.又∵B M BC '⊥,∴NB F FCM '∠=∠. ∴3tan 4NF NB F B N '∠=='. ∴9tan 4NF B N NB F ''=⋅∠=. ∴点F 的纵坐标为:923844-=. ∴点F 的纵坐标为233,4⎛⎫ ⎪⎝⎭. 【点睛】本题考查了二次函数的性质、一次函数的性质、解直角三角形、轴对称的性质,以及坐标与图形,解题的关键是熟练掌握所学的知识进行解题,注意寻找F 点的位置是关键,此处在直角三角形中利用了角的三角函数值寻找到点F 的位置.。
二次函数之距离最小(思维)

二次函数之最短路径问题例1.(广东)已知二次函数y=x 2-2mx+m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.例2.(甘肃兰州)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线y =23x 2+bx +c 经过点B ,且顶点在直线x =52上.(1)求抛物线对应的函数关系式;(2)若把△ABO 沿x 轴向右平移得到△DCE ,点A 、B 、O 的对应点分别是D 、C 、E ,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD ,已知对称轴上存在一点P 使得△PBD 的周长最小,求出P 点的坐标;例3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例4.(湖南郴州)已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.例5.(辽宁)如图16,在平面直角坐标系中,直线y=x轴交于点A,与y轴交于点C,抛物线2(0)y ax c a=+≠经过A B C,,三点.(1)求过A B C,,三点抛物线的解析式并求出顶点F的坐标;(2)在抛物线上是否存在点P,使ABP△为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由;(3)试探究在直线AC上是否存在一点M,使得MBF△的周长最小,若存在,求出M点的坐标;若不存在,请说明理由.xx例6.(山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.例7.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使∠CPN=90°?若存在,请直接写出点P的坐标.例8.(德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.练习:(烟台)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B 两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=1.5(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.例10.已知抛物线y=ax2+bx+1经过点A(1,3)和点B(2,1)。
二次函数压轴题最短路径问题

最短路径问题一一和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题)•如图所示,在直线 丨上找一点P 使得P%PB 最小•当点P 为直线AB 与直线丨的交点时,PA + PB 最小.B-r | P ,B'B4 P .B'③如图所示,在/ AOB 勺边AO B0上分别找一点 C D 使得PO C 戻PD 最小•过点P 分别作关于 AO BO 的对称点E ,F ,连接EF,并与AO B0分别交于点C, D,此时PO C 戻PD 最小,则点C D 即为所求.④如图所示,在/ AOB 勺边AO BO 上分别找一点 E F 使得D 可EF + CF 最小•分别过点 C , D 作关于AO BO 的对称点D ; C ;连接DC,并与AO BC 分别交于点E, F ,此时DE^EF + CF 最小,则点E, F 即为所求.⑤如图所示,长度不变的线段 CD 在直线丨上运动,在直线丨上找到使得AO BD 最小的CD 的位置•分别过 点A ,D 作AA// CD DA// AC AA 与 DA 交于点A ;再作点B 关于直线丨的对称点B',连接A'B 与直线丨交于【方法归纳】在直线丨上找一点B 使得线段AB 最小•过点A 作AB1丨,垂足为B,则线段AB 即为所求.在直线 ②如图所示,点P ,此时PA^ PB 最小,则点P 即为所求.丨上找一点P 使得PA^ PB 最小•过点B 作关于直线丨的对称点B',BB'与直线丨交于BFB点D ,此时点D 即为所求.1⑥如图所示,在平面直角坐标系中,点P 为抛物线(y = 4X 1 2)上的一点,点A ( 0, 1)在y 轴正半轴.点P在什么位置时PA+PB 最小?过点B 作直线I : y =— 1的垂线段BH, BH 与抛物线交于点 P ,此时PA+ PB最小,则点P 即为所求.【思路点拨】 (1)由二次函数的图象经过坐标原点 0(0,0),直接代入求出 m 的值即可;1 (13广东)已知二次函数 y = x2 — 2m 灶卅一1. (1)当二次函数的图象经过坐标原点 0(0, 0)时,求二次函数的解析式;(2) 如图,当m= 2时,该抛物线与y 轴交于点C ,顶点为D 求C 、D 两点的坐标;(3) 在(2)的条件下,x 轴上是否存在一点 P ,使得PO PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BBB'(2) 把m= 2代入求出二次函数解析式,令 X = o ,求出y 的值,得出点C 的坐标;利用配方法或顶点坐标 公式求岀顶点坐标即可; (3) 根据当P C 、D 共线时根据"两点之间,线段最短"得出PC +PD 最短,求出CD 的直线解析式,令y=0,求出x 的值,即可得出P 点的坐标. 【解题过程】解:(1)T 二次函数的图象经过坐标原点0(0,0),•••代入二次函数y = X 3 4 5-2m 对m — 1,得出:m — 1 = 0,解得:m=± 1, •••二次函数的解析式为:y =x 2— 2x 或y = X 2 + 2x ;(2) v m= 2, •二次函数 y = x 2 — 2m 灶 m - 1 得:y = x 2— 4x + 3=( x — 2) 2 — 1,•抛物线的顶点为:D (2,— 1),当 x = 0 时,y = 3,• C 点坐标为:(0, 3),• C (0, 3)、D( 2,— 1 ); (3) 当P 、C D 共线时PO PD 最短,【方法一】:C ( 0, 3)、D( 2,— 1),设直线CD 的解析式为y = kx + 3,代入得:2k + 3=— 1 ,• k =— 2, • y = — 2x + 3, 3 3当y = 0时,一2x + 3= 0,解得x = 2,二PO PD 最短时,P 点的坐标为:P ( 2,0). 【方法二】过点D 作DEL y 轴于点E ,3• PO PD 最短时,P 点的坐标为:P (2,0).12. (11菏泽)如图,抛物线 y = 2x 2 + bx - 2与x 轴交于A , B 两点,与y 轴交于C 点,且A (- 1, 0).3 求抛物线的解析式及顶点 D 的坐标;4 判断△ ABC 勺形状,证明你的结论;5 点M(m 0)是x 轴上的一个动点,当 M G MD 的值最小时,求 m 的值.v PO/ DEPO =CODE" CE P0=32 = 4,解得:3 P0=2,【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标;(2) 观察发现A ABC 是直角三角形,可以通过勾股定理的逆定理证明. 由抛物线的解析式,分别求出点B , C 的坐标,再得出AB AC BC 的长度,易得AC + BC = AB ,得出△ ABC 是直角三角形; (3) 作出点C 关于x 轴的对称点C ;连接C D 交x 轴于点M 根据“两点之间,线段最短”可知 MO MD 的值最小•求岀直线 C D 的解析式,即可得岀点 M 的坐标,进而求岀 m 的值. 【解题过程】1 2 1 23解:(1) v 点 A (- 1, 0)在抛物线 y =於 + bx — 2 上, /• 2^ (- 1 ) + b x (- 1) — 2= 0,解得 b =- ,1 2 31 32 25 一3 25二抛物线的解析式为 y =—必—2= 2 (x — 2)— 8,二顶点D 的坐标为 (2,— 8)•(2)当 x = 0 时 y = — 2,「. C (0,— 2),OC= 2•, 亠 1 2 3当 y = 0 时,2X — q x — 2 = 0,二 X 1=— 1, X 2= 4,•: B (4, 0),「• OA= 1, OB= 4, AB= 5.V A B = 25, A C = oA + oC = 5, B C = OC + OB = 20,「. A C + B C = A B • •••△ ABO 直角三角形. (3) 作出点C 关于x 轴的对称点C',则C'(0, 2), OC = 2,连接C'D 交x 轴于点M 根据轴对称性及两点之间线段最短可知, MO MD 勺值最小.【方法一】设直线C'D 的解析式为y = kx +n ,则3丄=_ 25,解得:2k + n = — ~8 41 24 24.当 y = 0 时,一12x + 2 = 0, x = 41 • . n== 41 • 【方法二】设抛物线的对称轴交x 轴于点E.v ED/ y 轴,OCM=/ EDM /C‘OM= / DEM .△ C’Og DEM .OM =OC . = 2 . 24…EM = E D 3 = 25,n 41 •2 — m 百n = 2十4141 .. y = — —x + 2 k =— • y 12x 十 23. (11福州)已知,如图,二次函数 y = ax 2+ 2ax - 3a (a H))图象的顶点为 H,与x 轴交于A B 两点(B 在A 点右侧),点H B 关于直线丨:y=£x +冷3对称.(1 )求A 、B 两点坐标,并证明点 A 在直线丨上; (2) 求二次函数解析式;(3) 过点B 作直线BK// AH 交直线丨于K 点,M N 分别为直线AH 和直线丨上的两个动点,连接 HN NM MK 求HN^ NMF MK 和的最小值.【思路点拨】(1 )二次函数y = ax 2+ 2ax - 3a(a 旳)中只有一个未知参数 a ,令y = 0,解出方程ax 2 + 2ax - 3a = 0(a ^D ), 即可得到点A ,B 的坐标•把点A 的坐标代入直线丨的解析式即可判断 A 是否在直线上;(2) 根据点H B 关于过A 点的直线丨:y = jx + 3对称,得出AH= AB= 4,过顶点H 作HCL AB 交AB 于1C 点,得AC= 2AB= 2,利用勾股定理求出 HC 的长,即可得出点 H 的坐标,代入二次函数解析式,求出 a ,即可得到二次函数解析式;(3) 直线BK// AH 易得直线BK 的解析式,联立直线 丨的解析式方程组,即可求出 K 的坐标•因为点 H B 关于直线AK 对称,所以HN= BN 所以根据“两点之间,线段最短"得出 HN b MN 的最小值是MB 作点K 关 于直线AH 的对称点Q 连接QK 交直线AH 于 E ,所以Ql = KM 易得BW MK 的最小值为BQ 即BQ 的长是 HN F NMF MK 勺最小值,求出 QB 的长即可. 【解题过程】解:(1)依题意,得 ax' + 2ax - 3a = 0 ( a®,解得 X 1=- 3,X 2 = 1,v B 点在A 点右侧,A 点坐标为(-3,0),B 点坐标为(1,0),丁直线丨:y =3,当x =- 3时,y = X - 3) + 3 = 0,点A 在直线丨上.过顶点 H 作 HCLAB 交 AB 于 C 点,贝U AC= 2AB= 2, HC= 2 3, 顶点H ( — 1, 2寸3),代入二次函数解析式,解得 a =—芈 二次函数解析式为y = — 2^x 2 — ^ 3x + ~2^,(2) v 点H 、B 关于过A 点的直线丨:二 AH= AB= 4,(3)直线AH 的解析式为y = »:;3x + 3 3,直线BK 的解析式为y =-J 3x + 3寸3, 由y=老X 十护,解得x- 3即K ( 3, 2、0,则BK= 4,y - 3x - 3 y - 6 7 3T 点H B 关于直线 AK 对称,••• HW M N 勺最小值是 MB KD= KE - 2*3,过点K 作直线AH 的对称点 Q 连接QK 交直线AH 于巳_则QM= MK QE F EK= ^-3, AE 1QK 二B 冊 MK 勺最小值是 BQ 即BQ 的长是HN b NM- MK 勺最小值, v BK// AHBK —/HE(- 90° ° 由勾股定理得 QB= 8 , 二HN - NM- MK 勺最小值为8.当a -1时,求四边形 MEFP 勺面积的最大值,并求此时点 P 的坐标;若厶PCM!以点P 为顶点的等腰三角形,求 a 为何值时,四边形 PMEF 周长最小?请说明理由.(2) (3)4. (14海南) 如图,对称轴为直线x - 2的抛物线经过A (- 1 , 0), C(0 , 5)两点,与x 轴另一交点为 B-已知 M (0, 1),E (a , 0),F (a +1, 0),点P 是第一象限内的抛物线上的动点.(1) 求此抛物线的解析式;【思路点拨】(1 )由对称轴为直线x = 2,可以得出顶点横坐标为 2,设二次函数的解析式为 y = a (x -2) 2+ k ,再把点 A , B 的代入即可求出抛物线的解析式; (2) 求四边形MEF 的面积的最大值,要先表示出四边形MEF 面积•直接求不好求,可以考虑用割补法来求,过点P 作PN4L y 轴于点N,由S 四边形MEFP = S 梯形OFP — S ^PM — S OM 即可得出;(3) 四边形PMEF 勺四条边中,线段 PM EF 长度固定,当M H PF 取最小值时,四边形 PMEF 勺周长取得最 小值•将点M 向右平移1个单位长度(EF 的长度),得到点M (1,1),作点M 关于x 轴的对称点M (1, —1),连接PM ,与x 轴交于F 点,此时MB PF = PM 最小.【解题过程】解:(1 )v 对称轴为直线x = 2,.••设抛物线解析式为 y = a (x — 2) °+ k .2 2.y = —( x — 2) + 9= — x +4x + 5.(2)当 a = 1 时,E (1 , 0) , F ( 2, 0) , OE= 1 , OF= 2•设 P( x , — x 2 + 4x + 5), 如答图2,过点P 作PNL y 轴于点N,则PNhx , O = — x 2+ 4x + 5,.Mf = ONF OM= — x 2 + 4x + 4.1 1 1MEF= S梯形 OFP— S A PM — ® OM =2 ( PI H OF ?O — 2PN?M — 2OMOE1 1 1=2 (x + 2) (— x +4x + 5) — ?x ?( — x + 4x + 4) —1 X 19 153 9 153•••当x = 4时,四边形MEFP 勺面积有最大值为16,此时点P 坐标为(4, 16 .(3)v M( 0, 1), C (0, 5) ,△ PCM!以点P 为顶点的等腰三角形,•点 P 的纵坐标为3 . 令 y =— X 2 + 4X + 5 =3,解得 x = 2± 6.T 点 P 在第一象限,• P (2 + 6, 3). 四边形PMEF 勺四条边中,PM EF 长度固定, 因此只要MH PF 最小,则PMEF 勺周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M (1, 1); 作点M 关于x 轴的对称点M ,则M (1,- 1);连接PM,与x 轴交于 F 点,此时 M 曰PF = PM 最小.设直线PM 的解析式为y = m>H n ,将P(2 + 6, 3) , M ( 1,- 1)代入得:将 A (— 1, 0), C (0, 5 )代入得:9a + k = 04a + k = 5,解得a =— 1 k = 9 S四边形9 =-(X -4)153 16(m +n =6—T n = 3,解得:m =呼6+ 5当y = 0时,解得x = 4,0). 丁 a +1 =•斗咛1时,四边形PME 周长最小.4 6+ 4 n =5 ,顶点为D 了.(1) 求点A B , D 的坐标;(2) 连接CD 过原点O 作O 吐CD 垂足为H, OE 与抛物线的对称轴交于点 E,连接AE AD 求证:/ AEO=Z ADC(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点 切点为Q,当PQ 的长最小时,求点 P 的坐标,并直接写岀点 Q 的坐标.【思路点拨】1(1) 由顶点式直接得出点 D 的坐标,再令y = 0,得2(x 3)2 1 = 0解出方程,即可得出点 A B 的坐标; (2) 设HD 与AE 相交于点F ,可以发现厶ADF 组成一个“ 8字型” •对顶角/ HFE=Z AFD 只要/ FHE=/FAD 即可•因为/ EHF= 90 °,只需证明/ EAD= 90°即可•由勾股定理的逆定理即可得出△ ADE 为 直角三角形,得/FHE=Z FAD= 90°即可得出结论;(3) 先画出图形.因为PQ 为。
二次函数中求线段和差最短

二次函数压轴题专项练习(一) 由运动产生的线段和差问题一、线段的和最短问题例1、如图,已知抛物线的方程C 1:()()1y x 2(x m)m 0m=-+->与x 轴相交于点B 、C ,与y 轴相交 于点E ,且点B 在点C 的左侧.(1)若抛物线C 1过点M(2,2),求实数m 的值.(2)在(1)的条件下,求△BCE的面积.(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使BH+EH 最小,并求出点H 的坐标.对应练习:1、如图,已知抛物线2y ax bx c =++经过A (4,0),B (2,3),C (0,3)三点.(1)求抛物线的解析式及对称轴.(2)在抛物线的对称轴上找一点M ,使得MA+MB 的值最小,并求出点M 的坐标.变一:已知:抛物线的对称轴为与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.1、如图,抛物线2y ax bx c=++的顶点P的坐标为13⎛⎫-⎪⎪⎝⎭,,交x轴于A、B两点,交y轴于点(0C,.、(1)求抛物线的表达式.(2)把△ABC绕AB的中点E旋转180°,得到四边形ADBC.判断四边形ADBC的形状,并说明理由.(3)试问在线段AC上是否存在一点F,使得△FBD的周长最小,若存在,请写出点F的坐标;若不存在,请说明理由.变二:如图,已知抛物线223y x x=-++与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)求A、B、C三点的坐标;(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;(3)在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
中考数学压轴题:二次函数中两线段的和最小问题(及差最大问题)

抛物线中两线段和最小问题(及差最大问题)1. (2012湖北恩施8分)如图,已知抛物线y=﹣x 2+bx+c 与一直线相交于A (﹣1,0),C (2,3)两点,与y 轴交于点N .其顶点为D .(1)抛物线及直线AC 的函数关系式;(2)设点M (3,m ),求使MN+MD 的值最小时m 的值;(3)若抛物线的对称轴与直线AC 相交于点B ,E 为直线AC 上的任意一点,过点E 作EF ∥BD 交抛物线于点F ,以B ,D ,E ,F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由;(4)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值.1,(2012湖北恩施8分)【分析】(1)利用待定系数法求二次函数解析式、一次函数解析式。
(2)根据轴对称的性质和三角形三边关系作N 点关于直线x=3的对称点N′,当M (3,m )在直线DN′上时,MN+MD 的值最小。
(3)分BD 为平行四边形对角线和BD 为平行四边形边两种情况讨论。
(4)如图,过点P 作PQ ⊥x轴交AC 于点Q ;过点C 作CG ⊥x 轴于点G ,设Q (x ,x+1),则P (x ,﹣x 2+2x+3),求得线段PQ=﹣x 2+x+2。
由图示以及三角形的面积公式知APCAPQ CPQ S S +S ∆∆∆=,由二次函数的最值的求法可知△APC 的面积的最大值解:(1)由抛物线y=﹣x 2+bx+c 过点A (﹣1,0)及C (2,3)得,1b+c=04+2b+c=3--⎧⎨-⎩, 解得b=2c=3⎧⎨⎩。
∴抛物线的函数关系式为2y x 2x 3=-++。
设直线AC 的函数关系式为y=kx+n ,∵AC 过点A (﹣1,0)及C (2,3)得k+n=02k+n=3-⎧⎨⎩,解得k=1n=1⎧⎨⎩。
∴直线AC 的函数关系式为y=x+1。
(2)作N 点关于直线x=3的对称点N′, 令x=0,得y=3,即N (0,3)。
中考专题复习:二次函数压轴题分类训练 最大最小问题(含答案)

中考压轴题专练(一)——二次函数综合考点一:距离之和最小问题 1.如图,抛物线y =21x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A (一1,0). ⑴求抛物线的解析式及顶点D 的坐标; ⑵判断△ABC 的形状,证明你的结论;⑶点M (m ,0)是x 轴上的一个动点,当CM +DM 的值最小时,求m 的值. 解:(1)b =23-解析式y =21x 2-23x -2. 顶点D (23, -825).(2)当x = 0时y = -2, ∴C (0,-2),OC = 2。
∴B (4,0) ∴OA = 1, OB = 4, AB = 5. △ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C ′,则C ′(0,2),OC ′=2,连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC + MD 的值最小。
解法一:设抛物线的对称轴交x 轴于点E .∵ED ∥y 轴, ∴∠OC ′M =∠EDM ,∠C ′O M =∠DEM ∴△C ′O M ∽△DEM . ∴EDC O EM OM '=∴825223=-m m ,∴m =4124. 解法二:设直线C ′D 的解析式为y = kx + n ,则⎪⎩⎪⎨⎧-=+=825232n k n ,解得n = 2, 1241-=k .∴21241+-=x y . ∴当y = 0时, 021241=+-x , 4124=x . ∴4124=m .2.(2016河池第26题)在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,顶点为D . (1)请直接写出点A ,C ,D 的坐标;(2)如图(1),在x 轴上找一点E ,使得△CDE 的周长最小,求点E 的坐标;(3)如图(2),F 为直线AC 上的动点,在抛物线上是否存在点P ,使得△AFP 为等腰直角三角形?若存在,求出点P 的坐标,若不存在,请说明理由.解析:(1)当223y x x =--+中y =0时,有2230x x --+=,解得:1x =﹣3,2x =1,∵A 在B 的左侧,∴A (﹣3,0),B (1,0).当223y x x =--+中x =0时,则y =3,∴C (0,3). ∵223y x x =--+=2(1)4x -++,∴顶点D (﹣1,4).(3)设直线AC 的解析式为y =ax +c ,则有:330c a c =⎧⎨-+=⎩,解得:13a c =⎧⎨=⎩,∴直线AC 的解析式为y =x +3.假设存在,设点F (m ,m +3),△AFP 为等腰直角三角形分三种情况(如图2所示):①当∠P AF =90°时,P (m ,﹣m ﹣3),∵点P 在抛物线223y x x =--+上,∴2323m m m --=--+,解得:m 1=﹣3(舍去),m 2=2,此时点P 的坐标为(2,﹣5);②当∠AFP =90°时,P (2m +3,0)∵点P 在抛物线223y x x =--+上,∴20(23)2(23)3m m =-+-++,解得:m 3=﹣3(舍去),m 4=﹣1,此时点P 的坐标为(1,0);③当∠APF =90°时,P (m ,0),∵点P 在抛物线223y x x =--+上,∴2023m m =--+,解得:m 5=﹣3(舍去),m 6=1,此时点P 的坐标为(1,0).综上可知:在抛物线上存在点P ,使得△AFP 为等腰直角三角形,点P 的坐标为(2,﹣5)或(1,0).3.(2016铜仁第25题)如图,抛物线21y ax bx =+-(a ≠0)经过A (-1,0),B (2,0)两点,与y 轴交于点C .(1)求抛物线的解析式及顶点D 的坐标;(2)点P 在抛物线的对称轴上,当△ACP 的周长最小时,求出点P 的坐标;(3) 点N 在抛物线上,点M 在抛物线的对称轴上,是否存在以点N 为直角顶点的Rt △DNM 与Rt △BOC 相似,若存在,请求出所有符合条件的点N 的坐标;若不存在,请说明理由.解析:(1)由于抛物线21y ax bx =+- (a ≠0)经过A (-1,0),B (2,0)两点,因此把A 、B 两点的坐标代入21y ax bx =+- (a ≠0),可得:104210a b a b --=⎧⎨+-=⎩;解方程组可得:1212a b ⎧=⎪⎪⎨⎪=-⎪⎩,故抛物线的解析式为:211122y x x =--,∵211122y x x =--=2119()228x --,所以D 的坐标为(12,98-). (2)如图1,设P (12,k ),∵211122y x x =--,∴C (0,-1),∵A (-1,0),B (2,0),∴A 、B 两点关于对称轴对称,连接CB 交对称轴于点P ,则△ACP 的周长最小.设直线BC 为y =kx +b ,则:201k b b +=⎧⎨=-⎩,解得:121k b ⎧=⎪⎨⎪=-⎩,∴直线BC 为:112y x =-.当x =12时,11122y =⨯-=34-,∴P (12,34-); (3)存在.如图2,过点作NF ⊥DM ,∵B (2,0),C (0,﹣1),∴OB =2,OC =1,∴tan ∠OBC =12OC OB =,tan ∠OCB =OBOA=2,设点N (m ,211122m m --),∴FN =|m ﹣12|,FD =|21191228m m --+|=|2111228m m -+|,∵Rt △DNM 与Rt △BOC 相似,∴∠MDN =∠OBC ,或∠MDN=∠OCB;①当∠MDN=∠OBC时,∴tan∠MDN=FNFD=12,∴21121112228mm m-=-+,∴m=12(舍)或m=92或m=72-,∴N(92,558)或(72-,558);②当∠MDN=∠OCB时,∴tan∠MDN=FNFD=2,∴2122111228mm m-=-+,∴m=12(舍)或m=32或m=12-,∴N(32,58-)或(12-,58-);∴符合条件的点N的坐标(92,558)或(72-,558)或(32,58-)或(12-,58-).考点:二次函数综合题;相似三角形的判定与性质;分类讨论;压轴题.4.(2016湘西州第26题)如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.(1)求抛物线的解析式;(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.(2)如图1所示;∵BD⊥DE,∴∠BDE=90°.∴∠BDC+∠EDO=90°.又∵∠ODE+∠DEO=90°,∴∠BDC=∠DE0.在△BDC和△DOE中,,∴△BDC≌△DEO.。
二次函数线段和最值--最短路径
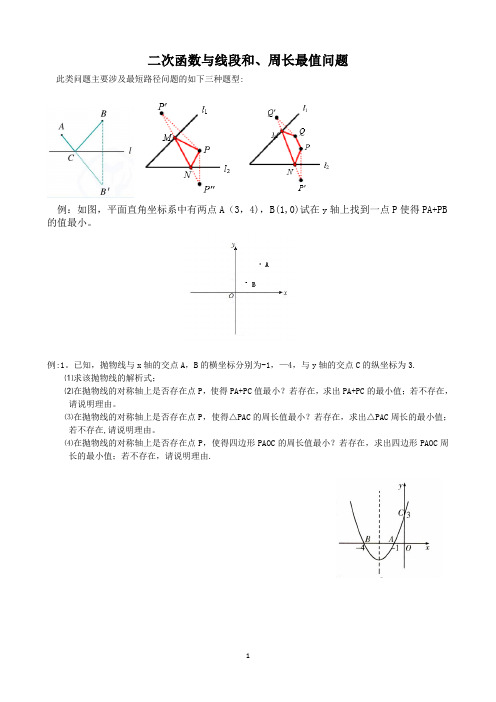
二次函数与线段和、周长最值问题此类问题主要涉及最短路径问题的如下三种题型:例:如图,平面直角坐标系中有两点A(3,4),B(1,0)试在y轴上找到一点P使得PA+PB 的值最小。
例:1。
已知,抛物线与x轴的交点A,B的横坐标分别为-1,—4,与y轴的交点C的纵坐标为3.⑴求该抛物线的解析式;⑵在抛物线的对称轴上是否存在点P,使得PA+PC值最小?若存在,求出PA+PC的最小值;若不存在,请说明理由。
⑶在抛物线的对称轴上是否存在点P,使得△PAC的周长值最小?若存在,求出△PAC周长的最小值;若不存在,请说明理由。
⑷在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长值最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.2。
如图,直线5+-=x y 与x 轴交于点B ,与y 轴交于点C,抛物线c bx x y ++-=2与直线5+-=x y 交于B 、C 两点.已知点D 的坐标为(0,3).⑴求该抛物线的解析式;⑵点M 、N 分别是直线BC 和x 轴上的动点,则当△DMN 的周长最小时,求点M ,N 的坐标,并写出△DMN 周长的最小值.3。
如图,二次函数)0(2>++=a c bx ax y 图像的顶点为D ,与x 轴的交点为A (—1,0),B(3,0),与y 轴负半轴交于点C.⑴若△ABD 为等腰直角三角形,求该抛物线的解析式; ⑵在⑴的条件下,抛物线与直线4-45x y =交于M 、N 两点(点M 在点N 的左侧),动点P 从M 点出发,先到达抛物线对称轴上的某点E ,再到达x 轴上的某点F ,最后运动到点N ,若使点P 运动的总路径最短,求点P 运动的总路径的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
例题导航例1:如图A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.例:如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)解:1.将点B沿垂直与河岸的方向平移一个河宽到E,2.连接AE交河对岸与点M,则点M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,若桥的位置建在CD处,连接AC.CD.DB.CE,则AB两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE中,∵AC+CE>AE, ∴AC+CE+MN>AE+MN,即AC+CD+DB >AM+MN+BN所以桥的位置建在CD处,AB两地的路程最短。
例:如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,•要A B a··在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
作法:作点B 关于直线 a 的对称点点C,连接AC 交直线a 于点D ,则点D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E ,连接AE.CE.BE.BD, ∵点B.C 关于直线 a 对称,点D.E 在直线 a 上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE 中,AE+EC >AC, 即 AE+EC >AD+DB所以抽水站应建在河边的点D 处,常见问题归纳“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.lBAllAllBAl④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DE +EF +CF 最小,则点E ,F 即为所求.⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y轴正半轴.点P 在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.OBOBBOB Oll二次函数中最短路径例题例1.(13广东)已知二次函数y=x2-2mx+m2-1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.练习1.(11菏泽)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.练习2.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.【思路点拨】 (1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出; (3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5,∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN•MN -12OM •OE =12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1=-x 2+92x +92 =-(x -94)2+15316 ∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316). (3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1); 作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF周长最小.图1 图2练习3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.例4.(14福州)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了. (1)求点A ,B ,D 的坐标; (2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可.【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12 (x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).例5.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【解题过程】解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1; (2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ; (3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°.∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).l。
