高一数学基本初等函数

合集下载

高一数学上册讲义基本初等函数

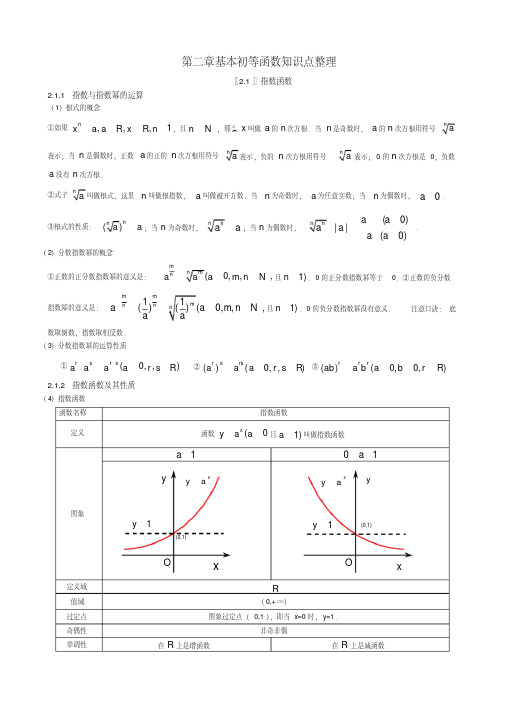
基本初等函数（Ⅰ）内容讲解：指数函数①定义：函数)1,0(≠>=a a a y x 且称指数函数， 1）函数的定义域为R ； 2）函数的值域为),0(+∞； 3）当10<<a 时函数为减函数，当1>a 时函数为增函数。

②函数图像：1）指数函数的图象都经过点（0，1），且图象都在第一、二象限；2）指数函数都以x 轴为渐近线（当10<<a 时，图象向左无限接近x 轴，当1>a 时，图象向右无限接近x 轴）；3）对于相同的)1,0(≠>a a a 且，函数x x a y a y -==与的图象关于y 轴对称 ③函数值的变化特征：对数的概念①定义：如果)1,0(≠>a a a 且的b 次幂等于N ，就是N a b=，那么数b 称以a 为底N 的对数，记作,log b N a =其中a 称对数的底，N 称真数。

10<<a1>a①100<<>y x 时， ②10==y x 时， ③10><y x 时 ①10>>y x 时， ②10==y x 时， ③100<<<y x 时，1）以10为底的对数称常用对数，N 10log 记作N lg ；2）以无理数)71828.2( =e e 为底的对数称自然对数，N e log ，记作N ln ； ②基本性质：1）真数N 为正数（负数和零无对数）； 2）01log =a ； 3）1log =a a ；4）对数恒等式：N aNa =log 。

③运算性质：如果,0,0,0,0>>≠>N M a a 则 1）N M MN a a a log log )(log +=； 2）N M NMa a alog log log -=； 3）∈=n M n M a n a (log log R ） ④换底公式：),0,1,0,0,0(log log log >≠>≠>=N m m a a aNN m m a1）1log log =⋅a b b a ；2）b mnb a na m log log =。

高一数学必修一第二章基本初等函数知识点总结

在 R 上是减函数
函数值的变化情况
a 变化对
图象的影响
y＞1(x ＞ 0), y=1(x=0), 0 ＜ y＜1(x ＜ 0)
y＞ 1(x ＜ 0), y=1(x=0), 0 ＜ y＜ 1(x ＞ 0)
在第一象限内， a 越大图象越高，越靠近 y 轴；在第一象限内， a 越小图象越高，越靠近 y 轴；在第二象限内， a 越大图象越低，越靠近 x 轴．在第二象限内， a 越小图象越低，越靠近 x 轴．
y
f ( x) 中反解出 x
1
f ( y) ；
③将 x f 1( y ) 改写成 y f 1 ( x) ，并注明反函数的定义域．
（ 8）反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称．
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域． ③若 P(a,b) 在原函数 y f (x ) 的图象上，则 P' (b, a) 在反函数 y f 1(x ) 的图象上．
③根式的性质： (n a )n a ；当 n 为奇数时， n an
a ；当 n 为偶数时， n an | a |
a (a 0)
．
a (a 0)
（ 2）分数指数幂的概念
m
①正数的正分数指数幂的意义是： a n n a m (a 0, m, n N , 且 n 1) ． 0 的正分数指数幂等于 0．②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ，且 x1 x2 ．令 f ( x) ax 2 bx c ，从以下四个方
面来分析此类问题：①开口方向： a ②对称轴位置： x

基本初等函数

图乙
一种对应 p q r B
A
图丙
图 2-1-3
图丁
图甲不是映射，因为集合A中的一个元素对应了集合B中的两个元素；图乙是映射，符合映射的定义；图丙是映射，虽然，集合B中有的元素没有A中的元素与之对应，但仍符合映射的定义；图丁不是映射，因为集合A中的每一个元素都要对应集合B中的元素，但是A中的元素-1,-2没有对应B中的元素．
课堂例题
例1.某种笔记本的单价是5元，买 x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x). 解：函数的定义域是数集{1,2,3,4,5}. 用解析法可将函数y=f(x)表示为y=5x，
x∈{1,2,3,4,5}.
用列表法可将函数y=f(x)表示为
笔记本数x
其中x叫做自变量，x的取值范围A叫作函数的定义域（domain）；与x的值对应的y值叫作函数值，函数值的集合 f ( x) x A 叫作函数的值域（range）. 值域是集合B的子集.
2．对概念的理解
（1）定义域、值域和对应关系是决定函数的三要素，这是一个整体.一般来说值域由定义域和对应关系所确定，因为对于定义域中的数x，按照确定的对应关系f，在集合B中都有唯一确定的数f(x)和x对应. （2）记住y=f(x)的内涵.例如对于f(x)=x2，对应关系f就是“取平方”，而对于 f ( x) x ，对应关系f就是“开平方”，f就是函数符号，对于具体的函数它有具体的涵义.函数符号还可以记作 y=g(x),y=u(x)等．
（2）f(x)=1和g(x)=x0.
2.请你再举出函数相等的例子.
课堂小结
1．函数的值域由定义域和对应关系确定. 2．如果两个函数的定义域、对应关系都相同，

高一数学基本初等函数Ⅰ试题答案及解析

高一数学基本初等函数Ⅰ试题答案及解析1.方程的根的情况是（）A．仅有一根B．有两个正根C．有一正根和一个负根D．有两个负根【答案】C【解析】主要考查指数函数、对数函数的图象和性质。

解：采用数形结合的办法，在同一坐标系中，画出的图象可知。

2.已知 .【答案】8【解析】主要考查指数函数、二次函数的性质。

利用换元法。

解：可化为，令，又因为所以，，，故。

3.若下列命题正确的个数为（）A．0B．1C．2D．3【答案】B【解析】主要考查对数运算法则。

解：根据对数的运算性质易知只有④是正确的。

4.已知_____________【答案】【解析】主要考查对数运算。

解：5.已知镭经过100年，剩留原来质量的95．76%，设质量为1的镭经过x年的剩留量为y，则y 与x的函数关系是A．y=（0．9576）B．y=（0．9576）100xC．y=（）x D．y=1－（0．0424）【答案】A【解析】设每年减少q%，因为镭经过100年，剩留原来质量的95．76%，所以=95．76%, q%=1－（0．9576）,所以=（0．9576）。

故选A。

【考点】主要考查函数的概念、解析式，考查应用数学知识解决实际问题的能力。

点评：审清题意，构建函数解析式。

6.一个体户有一种货，如果月初售出可获利100元，再将本利都存入银行，已知银行月息为2．4%，如果月末售出可获利120元，但要付保管费5元，问这种货是月初售出好，还是月末售出好？【答案】当成本大于525元时，月末售出好；成本小于525元时，月初售出好．【解析】解：设这种货的成本费为a元，则若月初售出，到月末共获利润为：y1=100+（a+100）×2．4%若月末售出，可获利y2=120－5=115（元）y 2－y1=0．024a－12．6=0．024（a－525）故当成本大于525元时，月末售出好；成本小于525元时，月初售出好．【考点】主要考查函数模型的广泛应用，考查应用数学知识解决实际问题的能力。

人教版《第二章基本初等函数》PPT完美课件1

例2：求下面对数式中x 的取值范围.
lo2g x1x2
2x 1 0 解： 2 x 1 1
x 2 0
x 1 2
x1
x 2
x
x
1,且x 2
1
人教版《第二章基本初等函数》PPT完美课件1
人教版《第二章基本初等函数》PPT完美课件1
例3：解方程.
lo2lgo4xg 0
解所l：以 to 4 x 2 0g t ,则 1,设即 llo 2 ot4 gx0 g 1注验大意证于0：真，一数底定是数要否是
思考：你发现了什么？
lo a a g 1 a 0 ,且 a 1
人教版《第二章基本初等函数》PPT完美课件1
人教版《第二章基本初等函数》PPT完美课件1
4.求下列各式的值：
12log28
2 3log327
3
1
log
18
2
2
猜想： a lo a N g ? a 0 ,且 a 1
赋予它的含义就是：1.2的多少次幂等于2.
人教版《第二章基本初等函数》PPT完美课件1
人教版《第二章基本初等函数》PPT完美课件1
对数的定义：
若ax N（a0,a1） ,则数 x叫做
以a为底 N的对数，x记 lo作 ga N,
其中 a为底数N为，真.数loga N
指数
对数
幂
真
ax N
数 loga Nx
ax N
xloga N
等函数》PPT完美课件1
人教版《第二章基本初等函数》PPT完美课件1
对数的性质：
1零和负数没有对数
2 lo a 1 0 g a 0 ,且 a 1 3 lo a a 1 g a 0 ,且 a 1

高一数学基本初等函数的导数公式

高一数学基本初等函数的导数公式1、恒定函数恒定函数的导数定义为0，即$f(x)=C$时，$f'(x)=0$，其中C为常数。

2、幂函数幂函数定义为$f(x)=x^n$，其中n为常数，其导数定义为：$f'(x)=nx^{n-1}$。

3、指数函数指数函数定义为$f(x)=a^x$，其中a为常数，其导数定义为：$f'(x)=a^xln(a)$。

4、对数函数对数函数定义为$f(x)=lnx$，其导数定义为：$f'(x)=\frac{1}{x}$。

5、三角函数三角函数的导数的公式是由函数的定义以及欧拉公式来计算，即：$f'(x)=cosx$时，$f(x)=sinx$；$f'(x)=-sinx$时，$f(x)=cosx$；$f'(x)=sec^2x$时，$f(x)=tanx$；$f'(x)=-csc^2x$时，$f(x)=cotx$；$f'(x)=×2sinxcscx$时，$f(x)=−cosxcotx$；$f'(x)=×2cosxsecx$时，$f(x)=sinxsecx$。

6、反三角函数反三角函数的导数的公式也是由函数的定义以及欧拉公式来计算，即：$f'(x)=cosecx$时，$f(x)=arcsinx$；$f'(x)=-cosecxcotx$时，$f(x)=arccosx$；$f'(x)=secxcotx$时，$f(x)=arctanx$；$f'(x)=-secx$时，$f(x)=arccotx$；$f'(x)=×2secxcosx$时，$f(x)=−arcsinxcosecx$；$f'(x)=×2cscxsinz$时，$f(x)=arcsecxsinx$。

7、椭圆型函数椭圆型函数定义为$f(x)=a\sqrt{x^2+c^2}+b$，其中a、b、c为常数，其导数定义为$f'(x)=\frac{ax}{\sqrt{x^2+c^2}}$。

高一数学基本初等函数

基本初等函数一、知识梳理1.指数与对数的概念b a ＝N N b a log =⇔（a ＞0，a ≠1）2.指数与对数的性质指数运算性质①r a a a a sr sr,0(>=⋅+、∈s Q ），②r a aa sr s r ,0()(>=⋅、∈s Q ），③∈>>⋅=⋅r b a b a b a rrr ,0,0()( Q ）（注）上述性质对r 、∈s R 均适用. 对数运算性质①log MN a ＝log N M a a log + ②log N M NMa a alog log -= ③M n M a na log log =（M 、N ＞0, a ＞0, a ≠1）推广：M mnMa na m log log =④换底公式：aNN b b a log log log =（a ，b ＞0，a ≠1，b ≠1）3.指数函数、对数函数的概念形如y ＝x a （a ＞0且a ≠1，x ＞0）叫做指数函数（exponential function ），其中x 是自变量，函数的定义域为R .形如y ＝x a log （a ＞0且a ≠1，x ＞0）的函数，叫做对数函数（logarithmic function ）.（1）指数函数、对数函数的定义是一个形式定义，注意指数函数与幂函数的区别；（2）注意底数的取值范围.4.指数函数、对数函数的图像和性质（略）.5.幂函数（1）幂函数定义：一般地，形如αx y =()R α∈的函数称为幂函数，其中α为常数.（2）幂函数性质：① 所有的幂函数在（0，+∞）都有定义并且图象都过点（1，1）；②0>α时，幂函数的图象通过原点，并且在区间),0[+∞上是增函数.特别地，当1>α时，幂函数的图象下凸；当10<<α时，幂函数的图象上凸；③0<α时，幂函数的图象在区间),0(+∞上是减函数.在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于∞+时，图象在x 轴上方无限地逼近x 轴正半轴.二、方法归纳1.解决与对数函数有关的问题，要特别重视定义域；2.指数函数、对数函数的单调性决定于底数大于1还是小于1，要注意对底数的讨论；3.比较几个数（幂或对数值）的大小的常用方法有：①以0和1为桥梁；②利用函数的单调性；③作差.4.指数函数与对数函数中的绝大部分问题是指数函数与对数函数与其他函数的复合问题，讨论复合函数的单调性是解决问题的重要途径.三、典型例题精讲【例1】比较下列各数的大小：3312122,15lg ,53,25lg ,53,35.0log ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛ 解析：∵35.0log 2＜0 ，其他各数都大于零，故35.0log 2最小；又∵10lg ＝1，100lg ＝2， ∴ 1＜15lg ＜25lg ＜2＜32＝8，对于2153⎪⎭⎫⎝⎛与3153⎪⎭⎫ ⎝⎛ ，首先，它们都属于区间（0,1），且是同底的幂，考虑函数y ＝x⎪⎭⎫ ⎝⎛53 为减函数，∴2153⎪⎭⎫ ⎝⎛＜3153⎪⎭⎫ ⎝⎛.于是有331212225lg 15lg 535335.0log <<<⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛<.又例:比较下列各组数的大小：（1）7.06，67.0，6log 7.0；（2）7.0log 1.1，7.0log 2.1 解析：（1）∵7.06＞1， 0＜67.0＜1，6log 7.0＜0 ，∴6log 7.0＜67.0＜7.06.（2）∵1.1log 17.0log 7.01.1=，2.1log 17.0log 7.02.1=.又函数y ＝x 7.0log 为减函数，∴ 0＞1.1log 7.0＞2.1log 7.0.∴7.0log 1.1＜7.0log 2.1.再例：当０＜a ＜b ＜1，下列不等式正确的有（） A.()()bba a ->-111 B.()()bab a +>+11C.()()211bba a ->- D.()()bab a ->-11解析：∵0＜()b -1＜()a -1＜1，又函数y ＝xb )1(- 为减函数，y ＝a x 在（0,1）上为增函数， ∴()bb -1＜()ab -1＜()aa -1，故选D.技巧提示：利用指数函数、对数函数、幂函数的单调性，同时充分利用0和1为桥梁，能使比较大小的问题得到解决.【例2】已知函数y ＝122-+x x a a （a ＞0，a ≠1）在区间[－1，1]上的最大值为14，求a 的值.解析：∵y ＝2)1(2-+x a ＝2)1(2-+u ，又11≤≤-x ，当a ＞1时，],1[a au ∈，1-≥u ，2)1(2-+u 为u 的增函数. ∴函数的最大值为)(5312142舍或-==⇒-+=a a a a 当0＜a ＜1时，]1,[aa u ∈，1-≥u ，2)1(2-+u 为u 的增函数.∴函数的最大值为舍）或(51311121142-==⇒-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=a a a a综上得，331==a a 或. 技巧提示：指数函数与二次函数的复合函数，讨论复合函数的单调性是解决问题的重要途径又例：已知)(x f ＝)32(log 24x x -+.求（1）)(x f 的单调区间；（2）求函数)(x f 的最大值及对应的x 的值.解析：（1）由0322>-+x x ，得)(x f 的定义域为)3,1(-，记u ＝232x x -+＝－（x －1）2＋4，对称轴为x ＝1.∴)(x f 的增区间为（－1，1】，减为区间【1，3）. （2）∵u ＝－（x －1）2＋4≤4，∴当x ＝1 时有最大值y ＝1.【例3】函数12311-⎪⎭⎫⎝⎛-=x y 的定义域是（）A.),21[+∞B.]21,(-∞ C.),(+∞-∞ D.]1,(-∞解析：由 031112≥⎪⎭⎫⎝⎛--x ，得13112≤⎪⎭⎫⎝⎛-x ，即012)31(31≤⎪⎭⎫⎝⎛-x ，由x)31( 为减函数，∴012≥-x .故所求定义域为21≥x .选A. 技巧提示：这里充分利用指数函数的单调性，通过解简单的指数不等式得到所求定义域.同样，可以充分利用对数函数的单调性，通过解简单的对数不等式得到某些问题的解.又例：若132log <a，则a 的取值范围是 . 解析：由 132log <a，即 a a a log 32log <，当a ＞１时，x a log 是增函数，于是 32>a ，∴a ＞１. 当０＜a ＜１时，x a log 是减函数，于是 32<a ，∴０＜a ＜32. 综上可知a 的取值范围是a ＞１或０＜a ＜32. 再例：解不等式 0)1)(2(log 2221<+--x x xb ab a（a ＞0，b ＞0）.解析：由0)1)(2(log 2221<+--x x xb ab a，得xxxb ab a22)(2--＞0，即0122>-⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛xxb a b a . ∴21+>⎪⎭⎫ ⎝⎛xb a 或21-<⎪⎭⎫⎝⎛xb a （舍去）.当a ＞b 时, )21(log +>ba x ；当a ＜b 时，)21(log +<ba x ；当a ＝b 时，不等式无解.【例4】函数)2(log 221x x y +-=的单调递增区间是 .解析：由022>+-x x ，得20<<x ，而函数22)1(12--=+-=x x x u ，即u 在)1,0(上是增函数，在)2,1(上是减函数.又u y 21log =是减函数，∴)2(log 221x x y +-=单调递增区间是)2,1(.技巧提示：对于复合函数的单调性，一要注意在定义域内研究问题；二是对组成复合函数的每一个函数的单调性作出判断；最后根据复合函数的单调性原则做出结论.又例：求函数93221-+-⎪⎭⎫ ⎝⎛=x x y 的单调递减区间.解析：显然93221-+-⎪⎭⎫ ⎝⎛=x x y 的定义域是R .设932-+-=x x u ，则427)23(2---=x u . ∴932-+-=x x u 的单调递增区间为)23,(-∞有93221-+-⎪⎭⎫ ⎝⎛=x x y ＝u⎪⎭⎫⎝⎛21是u 的减函数， ∴93221-+-⎪⎭⎫ ⎝⎛=x x y 的单调递减区间为)23,(-∞.再例：已知a ＞0且a ≠1,函数x x f a log )(=在定义域[2,3]上的最大值比最小值大1 ,则a 的值为 .解析：由题意，有12log 3log =-a a ，即 123log ±=a，∴a ＝32，23.【例5】当a ＞1时，证明函数)(x f ＝11-+x x a a 是奇函数.解析：由x a －1≠0得x ≠0.故函数定义域｛x ｜x ≠0｝是关于原点对称的点集.又)(x f -＝1111)1()1(11-+-=-+=-+=-+----xx xx x x x x x x a a a a a a a a a a ，=-)(x f －11-+x x a a ， ∴)(x f -＝－)(x f .所以函数)(x f ＝11-+x x a a 是奇函数.技巧提示：对于指数形式的复合函数的奇偶性的证明，在判定)(x f -与)(x f 关系时，也可采用如下等价证法.1)()()()(=-⇔=-x f x f x f x f （)(x f ≠０），1)()()()(-=-⇔-=-x f x f x f x f （)(x f ≠０）. 如本题可另证如下：∵=-)()(x f x f 11111x x x x x x x x a a a a a a a a ----+--⋅==--+-，即)(x f -＝－)(x f ， ∴所以函数)(x f ＝11-+x x a a 是奇函数.又例：设a 是实数，)(x f ＝a －122+x（x ∈R ）（1）试证明对于任意a ，)(x f 为增函数；（2）试确定a 值，使)(x f 为奇函数. 解析：（1）设1x ，2x ∈R ，且1x ＜2x ，则)()(21x f x f -＝（)122()12221+--+-x x a a )12)(12()22(2122122212112++-=+-+=x x x x x x 由于指数函数x y 2=在R 上是增函数，且1x ＜2x ，所以12x ＜22x ，即12x －22x＜0，又由2x ＞0得12x＋1＞0，22x＋1＞0，所以)()(21x f x f -＜0.即)()(21x f x f <. 因为此结论与a 取值无关，所以对于a 取任意实数，)(x f 为增函数. （2）若)(x f 为奇函数，则)(x f -＝－)(x f ，即22()2121x x a a --=--++，变形得：12)12(21222)12(222++=++⋅+⋅=-xx x x x x a ，解得a ＝1.所以当a ＝1时，)(x f 为奇函数.【例6】已知0＜x ＜1，a ＞0，a ≠1，比较)1(log x a -和)1(log x a +的大小.解析：方法一：当a ＞1时，)1(log x a -－)1(log x a +＝－)1(log x a -－)1(log x a +＝－)1(log 2x a -＞0，∴)1(log x a -＞)1(log x a +.当0＜a ＜1时，)1(log x a -－)1(log x a +＝)1(log x a -+)1(log x a +＝)1(log 2x a -＞0，∴)1(log x a -＞)1(log x a +.综上所述，在题设条件下，总有)1(log x a -＞)1(log x a +.方法二：∵)1(log )1(log x x a a +-＝)1(log )1(x x -+＝)1(log )1(x x --+＝xx -+11log )1( ＝2)1(11log xxx -++＞)1(log )1(x x ++＝1. ∴)1(log x a -＞)1(log x a +.技巧提示：比较大小通常采取作差－变形－判定符号.如果比较两个正数的大小时，亦可采取作商－变形－与“1”比较的办法.又例：解不等式)1(log )3(log 238+>++x x x解析：原不等式可化为⎪⎩⎪⎨⎧+>++>+>++333)1(30103x x x x x x ，即等价于⎩⎨⎧<-+>+0223012x x x ，即⎪⎩⎪⎨⎧+-<<--->3713711x x ，解得：3711+-<<-x ，所以原不等式的解集为｛x ︱3711+-<<-x ｝. 【例7】（1）已知a =3log 2，b =7log 3，用a ，b 表示56log 42；（2）已知,6log ,3log ,2log ===c b a x x x 求x abc log 的值.解析：（1）56log 42＝42lg 56lg ＝,3lg 2lg 7lg 2lg 37lg +++ 又 ∵,3lg 2lg ,3lg 7lg 3lg 7lg ,2lg 3lg ab b a ==⇒== ∴56log 42＝131133lg 3lg 3lg 3lg 33lg +++=+++=+++a ab ab ab a b a b a b . （2）∵a ＝2x ，b ＝63,x c x =，∴111log log 11==x x x abc . 技巧提示：掌握对数与指数的运算性质，是本部分的基本要求.尽管近几年高考中很少直接考查对数与指数的运算，但由于指数函数与对数函数几乎是必考内容，不能熟练的进行对数与指数的运算，会影响解题技巧的把握，至少会影响解题速度.又例：判断下列函数的奇偶性（1）)(x f ＝1212+-x x ；（2）)(x g ＝x1－)1ln(2++x x . 解析:（1）)(121221212)12(2)12(1212)(x f x f x x x x x x x x x x -=+--=+-=+-=++=-----，∴)(x f 为奇函数.（2）--=+-x x g x g 1)()()1ln(2++-x x ＋x1－)1ln(2++x x ＝－)]1)(1ln[(22++++-x x x x ＝－1ln ＝0.∴)(x g 为奇函数.四、课后训练1.已知732log [log (log )]0x =，那么12x -等于（）A.132.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于（） A.x 轴对称 B.y 轴对称 C.原点对称 D.直线y x =对称3.函数(21)log x y -= ）A.()2,11,3⎛⎫+∞⎪⎝⎭B.()1,11,2⎛⎫+∞⎪⎝⎭C.2,3⎛⎫+∞⎪⎝⎭ D.1,2⎛⎫+∞ ⎪⎝⎭4.函数212log (617)y x x =-+的值域是（） A.R B.[)8,+∞ C.(],3-∞- D.[)3,+∞5.下列函数中，在()0,2上为增函数的是（）A.12log (1)y x =+ B.2log y =C.21log y x = D.2log (45)y x x =-+ 6.已知|1|log )(+=x x g a )1,0(≠>a a 在()10-，上有()0g x >，则1()x f x a +=是（）A.在(),0-∞上是增加的B.在(),0-∞上是减少的C.在(),1-∞-上是增加的D.在(),1-∞-上是减少的 7.函数xa x f )1()(2-=是减函数，则实数a 的取值范围是 . 8.计算=+⋅+3log 22450lg 2lg 5lg .9.已知11log )(--=x mxx f a 是奇函数（其中)1,0≠>a a ，（1）求m 的值；（2）讨论)(x f 的单调性；（3）求)(x f 的反函数)(1x f-；（4）当)(x f 定义域区间为)2,1(-a 时，)(x f 的值域为),1(+∞，求a 的值. 10.对于函数)32(log )(221+-=ax x x f ，解答下述问题：（1）若函数的定义域为R ，求实数a 的取值范围；（2）若函数的值域为R ，求实数a 的取值范围；（3）若函数在),1[+∞-内有意义，求实数a 的取值范围；（4）若函数的定义域为),3()1,(+∞-∞ ，求实数a 的值；（5）若函数的值域为]1,(--∞，求实数a 的值；（6）若函数在]1,(-∞内为增函数，求实数a 的取值范围.五、参考答案1.C.2.C.3.A.4.C.5.D.6.C.7.)2,1()1,2( --8.109.解析：（1）011log 11log 11log )()(222=--=--+--+=+-x x m x mx x mx x f x f a a a对定义域内的任意x 恒成立，∴10)1(11122222±=⇒=-⇒=--m x m xx m ，当1m =，()f x 无意义，舍去， 1-=∴m ，（2）∵11log )(-+=x x x f a， ∴ 定义域为),1()1,(+∞--∞ ，而)121(log 11log )(-+=-+=x x x x f a a， ①当1>a 时，)(x f 在),1()1,(+∞--∞与上都是减函数； ②当10<<a 时，)(x f 在),1()1,(+∞--∞与上都是增函数；（3）111)1(1111log -+=⇒+=-⇒-+=⇒-+=y y y y y a a a x a x a x x a x x y ， ∵ 001≠≠-y a y，，∴ )10,0(11)(1≠>≠-+=-a a x a a x f xx 且. （4）)2,1()(,3,21->∴-<<a x f a a x 在上为减函数，∴命题等价于1)2(=-a f ，即014131log 2=+-⇒=--a a a a a ，解得32+=a .10.解析：记2223)(32)(a a x ax x x g u -+-=+-==，（1）R x u ∈>对0 恒成立，33032min <<-⇒>-=∴a a u ，∴a 的取值范围是)3,3(-；（2）这是一个较难理解的问题。

高一数学基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析

x x 2 2x 2 x 4 1 4 a a 2 1
.
2
a 3 3a
【法二】 8 x 8 x 2 x
2
3 2
x 3
2 2 2 x 2 x 2 x 2 x 2 x 2 x
1

2 3
3
37 48
5 9 37 100 3 100 . 3 16 48
4
（4）原式 0.4 1 1 2 2 3 0.1

5 1 1 1 143 . 1 2 16 8 10 80
4.函数 f x a 2 7a 7 a x 是指数函数,求实数 a 的值. 【解析】∵函数 f x a 2 7a 7 a x 是指数函数,
1
0 a2 a1 1 a4 a3 . 1 又由题知： 0 10 1 3 10 ,∴ A 项正确. 3
1 x
a1 a2
O
x 1 x
b 7.已知二次函数 y ax 2 bx 与指数函数 y 的图象只能是下列图形中的 a y
1 1
1 2
1 1 , y x 2 的图像,了解它们的变化情况. x
二、重点知识总结
1.指数与指数幂运算（1）①
a
n n n
n
a. a , 当n是奇数时 . a , 当n是偶数时
② a
（2）分数指数幂 ①a ②a
m n
n a m （ a 0 , m, n N * ,且 n 1 ）
x y
2
是非负数，故④对.
7 （3） 2 9

高一数学基本初等函数的导数公式(新编201912)

爸和遇险渔船在灯塔指引下安全返回做了铺垫。 15.①萨拉的爸爸是一个对工作认真负责、恪尽职守的人。他每天准时点亮、守护灯塔，为渔船指引方向；他认真观察天气，冒着生命危险营救遇险渔船。②萨拉的爸爸是一个爱孩子、教导有方的人。他让女儿每天指示自己准时点亮灯塔，有意培
养孩子的责任心；他得知萨拉独自点亮灯塔整夜守护时，能及时肯定孩子的表现和成长。 16.①对待爸爸交代的事情，萨拉能专注地做好，并能持之以恒；②她既能遵守爸爸的叮嘱，又能在关键时刻做出正确决定，勇敢，有主见；③在孤立无援的处境下，她能承担起爸爸的工作，经历了磨难，
• [解析] (1)方法一：y′＝[(x＋1)2]′(x－1)＋ (x＋1)2(x－1)′＝2(x＋1)(x－1)＋(x＋1)2＝ 3x2＋2x－1.
方法二：y＝(x2＋2x＋1)(x－1)＝x3＋x2－x －1，
y′＝(x3＋x2－x－1)′＝3x2＋2x－1.
(2)y′＝(x2sinx)′＝(x2)′sinx＋x2(sinx)′＝2xsinx ＋x2cosx.
20.填入第⑤段括号里的句子，符合语境的一项是（）（3分） A.顶着火辣辣的太阳
B.冒着冷丝丝的寒风 C.踩着金灿灿的落叶
D.迎着雾蒙蒙的细雨 21.小说以“单车”为线索，情节生动。请在括号里填写恰当的内容。（4分) 母亲购买旧车—（）— （） —父子骑车看病 22.第⑨段与第⑦段内容基本相同，简析作者这样写的用意。（5分） 23.细读第段，紧扣加点之处，说说结尾的妙
变得坚强、独立。野蔷薇（2017·衢州市中考）［日］小川未明很久以前有一个大国和一个比较小的王国相邻着，很长一段时间里，两国都没有发生什么事情，和睦相处着。在国界线上，两国都只派了一位士兵来驻守确定国界的石碑。大国派来的是个老人，小国派来的是个青年。两人一左

高一数学第二章基本初等函数知识点整理

高一数学第二章基本初等函数知识点整理高一数学第二章基本初等函数知识点整理高中学习数学重要的是基础的掌握，以下是第二章基本初等函数知识点，请大家仔细阅读。

一、指数函数(一)指数与指数幂的运算1.根式的概念：一般地，如果，那么叫做的次方根(n th root)，其中 1，且 *. 当是奇数时，正数的次方根是一个正数，负数的次方根是一个负数.此时，的次方根用符号表示.式子叫做根式(radical)，这里叫做根指数(radical exponent)，叫做被开方数(radicand).当是偶数时，正数的次方根有两个，这两个数互为相反数.此时，正数的正的次方根用符号表示，负的次方根用符号- 表示.正的次方根与负的次方根可以合并成?( 0).由此可得：负数没有偶次方根;0的任何次方根都是0，记作。

注意：当是奇数时，，当是偶数时， 2.分数指数幂正数的分数指数幂的意义，规定：，0的正分数指数幂等于0，0的负分数指数幂没有意义指出：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂. 3.实数指数幂的运算性质 (1)(2) ; (3) .(二)指数函数及其性质数，记作： ( 底数，真数，对数式)说明：○1 注意底数的限制，且; ○2 ;○3 注意对数的书写格式.两个重要对数：○1 常用对数：以10为底的对数 ;○2 自然对数：以无理数为底的对数的对数 . 对数式与指数式的互化 (二)对数的运算性质如果，且，，，那么：○1 ○2 - ; ○3 .注意：换底公式( ，且 ; ，且 ; ).利用换底公式推导下面的结论(1) ;(2) . (二)对数函数1、对数函数的概念：函数，且叫做对数函数，其中是自变量，函数的定义域是(0，+). 注意：○1 对数函数的定义与指数函数类似，都是形式定义，注意辨别。

如：，都不是对数函数，而只能称其为对数型函数. ○2 对数函数对底数的限制：，且 .2、对数函数的性质： a1 0图象特征函数性质函数图象都在y轴右侧函数的定义域为(0，+) 图象关于原点和y轴不对称非奇非偶函数向y轴正负方向无限延伸函数的值域为R 函数图象都过定点(1，0) 自左向右看，图象逐渐上升自左向右看，图象逐渐下降增函数减函数第一象限的图象纵坐标都大于0 第一象限的图象纵坐标都大于0 第二象限的图象纵坐标都小于0 第二象限的图象纵坐标都小于0 (三)幂函数1、幂函数定义：一般地，形如的函数称为幂函数，其中为常数.2、幂函数性质归纳.(1)所有的幂函数在(0，+)都有定义，并且图象都过点(1，1);(2) 时，幂函数的图象通过原点，并且在区间上是增函数.特别地，当时，幂函数的图象下凸;当时，幂函数的图象上凸;(3) 时，幂函数的图象在区间上是减函数.在第一象限内，当从右边趋向原点时，图象在轴右方无限地逼近轴正半轴，当趋于时，图象在轴上方无限地逼近轴正半轴. 第二章基本初等函数知识点就为大家分享到这里，希望可以帮助大家提高成绩。

高一数学基本初等函数Ⅰ试题答案及解析

高一数学基本初等函数Ⅰ试题答案及解析1.的值域是_______ ；【答案】[0,30]【解析】，因为，结合二次函数的图象可知函数在上单调递减，当时当时，所以函数的值域为[0,30].【考点】本小题主要考查二次函数在闭区间上的值域，考查学生的运算求解能力.点评：对于二次函数要采用配方法求函数的值域，结合函数的图象进行即可.2.如图所示，当时，函数的图象是 ( )【答案】D【解析】因为当时，函数，因为a,b同号，则可知当a>0,b>0,或者a<0,b<0那么分析可知选D3.已知奇函数；（1）求实数m的值，并在给出的直角坐标系中画出的图象；（2）若函数在区间[－1，||－2]上单调递增，试确定的取值范围.【答案】(1)证明：的定义域为,令,则，令,则，即.，故为奇函数. 4分（2）证明：任取且,则又，，，即.故是上的减函数. 8分（3）解:又为奇函数,由(2)知是上的减函数,所以当时，取得最大值，最大值为；当时，取得最小值，最小值为. 11分所以函数在区间上的值域为. 12分【解析】考查奇函数的定义，应用转化的思想求值；作函数的图象，求a的取值范围，体现了作图和用图的能力，属中档题．（1）由奇函数的定义，对应相等求出m的值；画出图象．（2）根据函数的图象知函数的单调递增区间，从而得到|a|-2的一个不等式，解不等式就求得a 的取值范围．(1)证明：的定义域为,令,则，令,则，即.，故为奇函数. 4分（2）证明：任取且,则又，，，即.故是上的减函数. 8分（3）解:又为奇函数,由(2)知是上的减函数,所以当时，取得最大值，最大值为；当时，取得最小值，最小值为. 11分所以函数在区间上的值域为. 12分4.设，则的大小关系为（）A．B．C．D．【答案】D【解析】因为，所以，选D.5.若定义运算，则函数的值域是（）A．B．C．D．【答案】B【解析】因为，那么化简可知则其值域为，选B.6.已知偶函数在区间上单调递增，则满足不等式的的取值范围是（）A．B．C．D．【答案】A【解析】因为解：根据函数在区间[0，+∞）单调递增，得当2x-1≥0，即x≥时，不等式f(2x-1)<f()等价于2x-1<，解之得x<而当2x-1＜0，即x＜时，由于函数是偶函数，所以f(2x-1)＞f()等价于f(1-2x)<f()再根据单调性，得1-2x<，解之得x>综上所述，不等式f(2x-1)<f()的解集为{x|x>}故选A7.求函数的定义域；【答案】【解析】要使原式有意义，则满足，求解不等式得到定义域为。

高一数学基本初等函数的导数公式

y′＝－1/2cosx.
例3.某运动物体自始点起经过t秒后的距离s满足s= -4t3+16t2. (1)此物体什么时刻在始点? (2)什么时刻它的速度为零? 解:(1)令s=0,即1/4t4-4t3+16t2=0,所以t2(t-8)2=0,解得: t1=0,t2=8.故在t=0或t=8秒末的时刻运动物体在始点. (2) s(t ) t 3 12t 2 32t , 令s(t ) 0, 即t3-12t2+32t=0, 解得:t1=0,t2=4,t3=8, 故在t=0,t=4和t=8秒时物体运动的速度为零.
3.2.2
基本初等函数的导数公式及导数的运算法则
基本初等函数的导数公式：
公式1.若f ( x) c, 则f '( x) 0; 公式2.若f ( x) x n , 则f '( x) nx n 1 ; 公式3.若f ( x) sin x, 则f '( x) cos x; 公式4.若f ( x) cos x, 则f '( x) sin x; 公式5.若f ( x) a x , 则f '( x) a x ln a ( a 0); 公式6.若f ( x) e x , 则f '( x) e x ; 1 公式7.若f ( x) log a x, 则f '( x) ( a 0, 且a 1); x ln a 1 公式8.若f ( x) ln x, 则f '( x) ; x
1 4 t 4
例4.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均相切,求l的方程.
解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).

高一数学必修1第一章第二节基本初等函数

第二章：函数及其表示第一讲：函数的概念：知识点一：函数的概念：典型例题：判断下列对应关系是否为集合A到集合B的函数：（1）A=R，B={x |x>0},f:（2）A=z,B=Z,]（3）A=Z,B=Z,（4）A={-1,1},B={0},f:知识点二：函数的三要素：典型例题2：求下列函数的定义域：（1）（2）（3）巩固练习：已知函数(1)求函数定义域；(2)就f(-3),的值(3)当a>0时，求f(a)的值，求f(a-1)的值。

知识点三：函数相等：如果两个函数的定义域相等，并且对应关系完全一致，那么我们称这两个函数一致。

典型例题3：下列函数中，f(x)与g(x)相等的是（）A、B、C、D、巩固练习：下列函数中哪个与函数y=x相等（1）(2)（3）(4)知识点四：区间的表示：典型例题：将下列集合用区间表示出来（1）{x|2x-1≥0}；（2）{x|x<-4或-1<x≤2}第二讲：函数的表示方法：知识点一：函数的三种表示方法解析法：就是用数学表达式表示两个变量之间对应关系图像法：就是用图像表示两个变量之间的对应关系列举法：就是列举出表格来表示两个变量之间的对应关系月份t 1 2 3 4 5 6 7 8 9 10 11 12 零售量y 81 84 45 46 9 5 6 15 94 161 144 123 零售量是否为月份的函数？为什么？知识点二：分段函数：典型例题1：作出下列函数的图像：（1）f(x)=2x,x∈Z，且|x|≤2（2）y=|x|典型例题2：某市“招手即停”公共汽车票价按下列规则制定：（1）5公里以内（含5公里），票价2元（2）5公里以上，每增加5公里，票价增加一元（不足5公里按5公里计算）如果某条线路的总里程为20公里，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图像。

知识点三：映射1、定义：一般地，我们有设A，B是两个非空集合，如果按某一个确定的函数关系f，使对于集合A中的任意一个元素x在集合B中都有唯一确定的元素y与之对应，那么就称对应f:为从集合A到集合B的一个映射。

高一数学基本初等函数

高一数学上册 讲义 基本初等函数

高一数学必修一第二章基本初等函数知识点总结

基本初等函数

高一数学基本初等函数Ⅰ试题答案及解析

人教版《第二章 基本初等函数》PPT完美课件1

高一数学基本初等函数的导数公式

高一数学 基本初等函数

高一数学 基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析

高一数学基本初等函数的导数公式(新编201912)

高一数学第二章基本初等函数知识点整理

高一数学基本初等函数Ⅰ试题答案及解析

高一数学基本初等函数的导数公式

高一数学必修1第一章第二节基本初等函数

高一数学上册讲义基本初等函数

人教版《第二章基本初等函数》PPT完美课件1

高一数学基本初等函数

高一数学基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析